problem
stringlengths 14
10.4k
| solution
stringlengths 1
24.1k
| answer
stringlengths 1
250
⌀ | problem_is_valid
stringclasses 4
values | solution_is_valid
stringclasses 3
values | question_type
stringclasses 4
values | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
10.4k
| solution_raw
stringlengths 1
24.1k
| metadata
dict |
|---|---|---|---|---|---|---|---|---|---|
Call an $2 n$-digit number special if we can split its digits into two sets of size $n$ such that the sum of the numbers in the two sets is the same. Let $p_{n}$ be the probability that a randomly-chosen $2 n$-digit number is special (we will allow leading zeros in the number).
(a) [25] The sequence $p_{n}$ converges to a constant $c$. Find $c$.
|
$\frac{1}{2}$ We first claim that if a $2 n$-digit number $x$ has at least eight 0 's and at least eight 1's and the sum of its digits is even, then $x$ is special.
Let $A$ be a set of eight 0 's and eight 1 's and let $B$ be the set of all the other digits. We split $b$ arbitrily into two sets $Y$ and $Z$ of equal size. If $\left|\sum_{y \in Y} y-\sum_{z \in Z} z\right|>8$, then we swap the biggest element of the set with the bigger sum with the smallest element of the other set. This transposition always decreases the absolute value of the sum: in the worst case, a 9 from the bigger set is swapped for a 0 from the smaller set, which changes the difference by at most 18 . Therefore, after a finite number of steps, we will have $\left|\sum_{y \in Y} y-\sum_{z \in Z} z\right| \leq 8$.
Note that this absolute value is even, since the sum of all the digits is even. Without loss of generality, suppose that $\sum_{y \in Y} y-\sum_{z \in Z} z$ is $2 k$, where $0 \leq k \leq 4$. If we add $k 0$ 's and $8-k$ 's to $Y$, and we add the other elements of $A$ to $Z$, then the two sets will balance, so $x$ is special.
[^1](b) $[\mathbf{3 0}]$ Let $q_{n}=p_{n}-c$. There exists a unique positive constant $r$ such that $\frac{q_{n}}{r^{n}}$ converges to a constant $d$. Find $r$ and $d$.
|
not found
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Call an $2 n$-digit number special if we can split its digits into two sets of size $n$ such that the sum of the numbers in the two sets is the same. Let $p_{n}$ be the probability that a randomly-chosen $2 n$-digit number is special (we will allow leading zeros in the number).
(a) [25] The sequence $p_{n}$ converges to a constant $c$. Find $c$.
|
$\frac{1}{2}$ We first claim that if a $2 n$-digit number $x$ has at least eight 0 's and at least eight 1's and the sum of its digits is even, then $x$ is special.
Let $A$ be a set of eight 0 's and eight 1 's and let $B$ be the set of all the other digits. We split $b$ arbitrily into two sets $Y$ and $Z$ of equal size. If $\left|\sum_{y \in Y} y-\sum_{z \in Z} z\right|>8$, then we swap the biggest element of the set with the bigger sum with the smallest element of the other set. This transposition always decreases the absolute value of the sum: in the worst case, a 9 from the bigger set is swapped for a 0 from the smaller set, which changes the difference by at most 18 . Therefore, after a finite number of steps, we will have $\left|\sum_{y \in Y} y-\sum_{z \in Z} z\right| \leq 8$.
Note that this absolute value is even, since the sum of all the digits is even. Without loss of generality, suppose that $\sum_{y \in Y} y-\sum_{z \in Z} z$ is $2 k$, where $0 \leq k \leq 4$. If we add $k 0$ 's and $8-k$ 's to $Y$, and we add the other elements of $A$ to $Z$, then the two sets will balance, so $x$ is special.
[^1](b) $[\mathbf{3 0}]$ Let $q_{n}=p_{n}-c$. There exists a unique positive constant $r$ such that $\frac{q_{n}}{r^{n}}$ converges to a constant $d$. Find $r$ and $d$.
|
{
"exam": "HMMT",
"problem_label": "10",
"problem_match": "\n10. ",
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-team2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
Call an $2 n$-digit number special if we can split its digits into two sets of size $n$ such that the sum of the numbers in the two sets is the same. Let $p_{n}$ be the probability that a randomly-chosen $2 n$-digit number is special (we will allow leading zeros in the number).
(a) [25] The sequence $p_{n}$ converges to a constant $c$. Find $c$.
|
$\left(\frac{1}{4},-1\right)$ To get the next asymptotic term after the constant term of $\frac{1}{2}$, we need to consider what happens when the digit sum is even; we want to find the probability that such a number isn't balanced. We claim that the configuration that contributes the vast majority of unbalanced numbers is when all numbers are even and the sum is $2 \bmod 4$, or such a configuration with all numbers increased by 1. Clearly this gives $q_{n}$ being asymptotic to $-\frac{1}{2} \cdot 2 \cdot\left(\frac{1}{2}\right)^{2 n}=-\left(\frac{1}{4}\right)^{n}$, so $r=\frac{1}{4}$ and $d=-1$.
To prove the claim, first note that the asymptotic probability that there are at most 4 digits that occur more than 10 times is asymptotically much smaller than $\left(\frac{1}{2}\right)^{n}$, so we can assume that there exist 5 digits that each occur at least 10 times. If any of those digits are consecutive, then the digit sum being even implies that the number is balanced (by an argument similar to part (a)).
So, we can assume that none of the numbers are consecutive. We would like to say that this implies that the numbers are either $0,2,4,6,8$ or $1,3,5,7,9$. However, we can't quite say this yet, as we need to rule out possibilities like $0,2,4,7,9$. In this case, though, we can just pair 0 and 7 up with 2 and 4 ; by using the same argument as in part (a), except using 0 and 7 both (to get a sum of 7 ) and 2 and 4 both (to get a sum of 6 ) to balance out the two sets at the end.
In general, if there is ever a gap of size 3 , consider the number right after it and the 3 numbers before it (so we have $k-4, k-2, k, k+3$ for some $k$ ), and pair them up such that one pair has a sum that's exactly one more than the other (i.e. pair $k-4$ with $k+3$ and $k-2$ with $k$ ). Since we again have pairs of numbers whose sums differ by 1 , we can use the technique from part (a) of balancing out the sets at the end.
So, we can assume there is no gap of size 3 , which together with the condition that no two numbers are adjacent implies that the 5 digits are either $0,2,4,6,8$ or $1,3,5,7,9$. For the remainder of the solution, we will deal with the $0,2,4,6,8$ case, since it is symmetric with the other case under the transformation $x \mapsto 9-x$.
If we can distribute the odd digits into two sets $S_{1}$ and $S_{2}$ such that (i) the differense in sums of $S_{1}$ and $S_{2}$ is small; and (ii) the difference in sums of $S_{1}$ and $S_{2}$, plus the sum of the even digits, is divisible by 4 , then the same argument as in part (a) implies that the number is good.
In fact, if there are any odd digits, then we can use them at the beginning to fix the parity mod 4 (by adding them all in such that the sums of the two sets remain close, and then potentially switching one with an even digit). Therefore, if there are any odd digits then the number is good. Also, even if there are no odd digits, if the sum of the digits is divisible by 4 then the number is good.
So, we have shown that almost all non-good numbers come from having all numbers being even with a digit sum that is $2 \bmod 4$, or the analogous case under the mapping $x \mapsto 9-x$. This formalizes the claim we made in the first paragraph, so $r=\frac{1}{4}$ and $d=-1$, as claimed.
[^0]: ${ }^{1}$ This is the maximum possible number of new regions, but it's not too hard to see that this is always attainable.
${ }^{2}$ While the fact that a curve going through a region splits it into two new regions is intuitively obvious, it is actually very difficult to prove. The proof relies on some deep results from algebraic topology and is known as the Jordan Curve Theorem. If you are interested in learning more about this, see http://en.wikipedia.org/wiki/Jordan_curve_theorem
[^1]: ${ }^{3}$ See http://www.artofproblemsolving.com/Forum/weblog_entry.php?p=1263378
${ }^{4}$ See http://en.wikipedia.org/wiki/Lagrange_polynomial
|
not found
|
Yes
|
Incomplete
|
math-word-problem
|
Combinatorics
|
Call an $2 n$-digit number special if we can split its digits into two sets of size $n$ such that the sum of the numbers in the two sets is the same. Let $p_{n}$ be the probability that a randomly-chosen $2 n$-digit number is special (we will allow leading zeros in the number).
(a) [25] The sequence $p_{n}$ converges to a constant $c$. Find $c$.
|
$\left(\frac{1}{4},-1\right)$ To get the next asymptotic term after the constant term of $\frac{1}{2}$, we need to consider what happens when the digit sum is even; we want to find the probability that such a number isn't balanced. We claim that the configuration that contributes the vast majority of unbalanced numbers is when all numbers are even and the sum is $2 \bmod 4$, or such a configuration with all numbers increased by 1. Clearly this gives $q_{n}$ being asymptotic to $-\frac{1}{2} \cdot 2 \cdot\left(\frac{1}{2}\right)^{2 n}=-\left(\frac{1}{4}\right)^{n}$, so $r=\frac{1}{4}$ and $d=-1$.
To prove the claim, first note that the asymptotic probability that there are at most 4 digits that occur more than 10 times is asymptotically much smaller than $\left(\frac{1}{2}\right)^{n}$, so we can assume that there exist 5 digits that each occur at least 10 times. If any of those digits are consecutive, then the digit sum being even implies that the number is balanced (by an argument similar to part (a)).
So, we can assume that none of the numbers are consecutive. We would like to say that this implies that the numbers are either $0,2,4,6,8$ or $1,3,5,7,9$. However, we can't quite say this yet, as we need to rule out possibilities like $0,2,4,7,9$. In this case, though, we can just pair 0 and 7 up with 2 and 4 ; by using the same argument as in part (a), except using 0 and 7 both (to get a sum of 7 ) and 2 and 4 both (to get a sum of 6 ) to balance out the two sets at the end.
In general, if there is ever a gap of size 3 , consider the number right after it and the 3 numbers before it (so we have $k-4, k-2, k, k+3$ for some $k$ ), and pair them up such that one pair has a sum that's exactly one more than the other (i.e. pair $k-4$ with $k+3$ and $k-2$ with $k$ ). Since we again have pairs of numbers whose sums differ by 1 , we can use the technique from part (a) of balancing out the sets at the end.
So, we can assume there is no gap of size 3 , which together with the condition that no two numbers are adjacent implies that the 5 digits are either $0,2,4,6,8$ or $1,3,5,7,9$. For the remainder of the solution, we will deal with the $0,2,4,6,8$ case, since it is symmetric with the other case under the transformation $x \mapsto 9-x$.
If we can distribute the odd digits into two sets $S_{1}$ and $S_{2}$ such that (i) the differense in sums of $S_{1}$ and $S_{2}$ is small; and (ii) the difference in sums of $S_{1}$ and $S_{2}$, plus the sum of the even digits, is divisible by 4 , then the same argument as in part (a) implies that the number is good.
In fact, if there are any odd digits, then we can use them at the beginning to fix the parity mod 4 (by adding them all in such that the sums of the two sets remain close, and then potentially switching one with an even digit). Therefore, if there are any odd digits then the number is good. Also, even if there are no odd digits, if the sum of the digits is divisible by 4 then the number is good.
So, we have shown that almost all non-good numbers come from having all numbers being even with a digit sum that is $2 \bmod 4$, or the analogous case under the mapping $x \mapsto 9-x$. This formalizes the claim we made in the first paragraph, so $r=\frac{1}{4}$ and $d=-1$, as claimed.
[^0]: ${ }^{1}$ This is the maximum possible number of new regions, but it's not too hard to see that this is always attainable.
${ }^{2}$ While the fact that a curve going through a region splits it into two new regions is intuitively obvious, it is actually very difficult to prove. The proof relies on some deep results from algebraic topology and is known as the Jordan Curve Theorem. If you are interested in learning more about this, see http://en.wikipedia.org/wiki/Jordan_curve_theorem
[^1]: ${ }^{3}$ See http://www.artofproblemsolving.com/Forum/weblog_entry.php?p=1263378
${ }^{4}$ See http://en.wikipedia.org/wiki/Lagrange_polynomial
|
{
"exam": "HMMT",
"problem_label": "10",
"problem_match": "\n10. ",
"resource_path": "HarvardMIT/segmented/en-132-2010-feb-team2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
Jacob flips five coins, exactly three of which land heads. What is the probability that the first two are both heads?
|
$\frac{3}{10}$ We can associate with each sequence of coin flips a unique word where $H$ represents heads, and T represents tails. For example, the word HHTTH would correspond to the coin flip sequence where the first two flips were heads, the next two were tails, and the last was heads. We are given that exactly three of the five coin flips came up heads, so our word must be some rearrangement of HHHTT. To calculate the total number of possibilities, any rearrangement corresponds to a choice of three spots to place the H flips, so there are $\binom{5}{3}=10$ possibilities. If the first two flips are both heads, then we can only rearrange the last three HTT flips, which corresponds to choosing one spot for the remaining $H$. This can be done in $\binom{3}{1}=3$ ways. Finally, the probability is the quotient of these two, so we get the answer of $\frac{3}{10}$. Alternatively, since the total number of possiblities is small, we can write out all rearrangements: HHHTT, HHTHT, HHTTH, HTHHT, HTHTH, HTTHH, THHHT, THHTH, THTHH, TTHHH. Of these ten, only in the first three do we flip heads the first two times, so we get the same answer of $\frac{3}{10}$.
|
\frac{3}{10}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Jacob flips five coins, exactly three of which land heads. What is the probability that the first two are both heads?
|
$\frac{3}{10}$ We can associate with each sequence of coin flips a unique word where $H$ represents heads, and T represents tails. For example, the word HHTTH would correspond to the coin flip sequence where the first two flips were heads, the next two were tails, and the last was heads. We are given that exactly three of the five coin flips came up heads, so our word must be some rearrangement of HHHTT. To calculate the total number of possibilities, any rearrangement corresponds to a choice of three spots to place the H flips, so there are $\binom{5}{3}=10$ possibilities. If the first two flips are both heads, then we can only rearrange the last three HTT flips, which corresponds to choosing one spot for the remaining $H$. This can be done in $\binom{3}{1}=3$ ways. Finally, the probability is the quotient of these two, so we get the answer of $\frac{3}{10}$. Alternatively, since the total number of possiblities is small, we can write out all rearrangements: HHHTT, HHTHT, HHTTH, HTHHT, HTHTH, HTTHH, THHHT, THHTH, THTHH, TTHHH. Of these ten, only in the first three do we flip heads the first two times, so we get the same answer of $\frac{3}{10}$.
|
{
"exam": "HMMT",
"problem_label": "1",
"problem_match": "\n1. [2]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-gen1-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
How many sequences $a_{1}, a_{2}, \ldots, a_{8}$ of zeroes and ones have $a_{1} a_{2}+a_{2} a_{3}+\cdots+a_{7} a_{8}=5$ ?
|
9 First, note that we have seven terms in the left hand side, and each term can be either 0 or 1 , so we must have five terms equal to 1 and two terms equal to 0 . Thus, for $n \in\{1,2, \ldots, 8\}$, at least one of the $a_{n}$ must be equal to 0 . If we can find $i, j \in\{2,3, \ldots, 7\}$ such that $a_{i}=a_{j}=0$ and $i<j$, then the terms $a_{i-1} a_{i}, a_{i} a_{i+1}$, and $a_{j} a_{j+1}$ will all be equal to 0 . We did not count any term twice because $i-1<i<j$, so we would have three terms equal to 0 , which cannot happen because we can have only two. Thus, we can find at most one $n \in\{2,3, \ldots, 7\}$ such that $a_{n}=0$. We will do casework on which $n$ in this range have $a_{n}=0$.
If $n \in\{3,4,5,6\}$, then we know that the terms $a_{n-1} a_{n}=a_{n} a_{n+1}=0$, so all other terms must be 1 , so $a_{1} a_{2}=a_{2} a_{3}=\ldots=a_{n-2} a_{n-1}=1$ and $a_{n+1} a_{n+2}=\ldots=a_{7} a_{8}=1$. Because every $a_{i}$ appears in one of these equations for $i \neq n$, then we must have $a_{i}=1$ for all $i \neq n$, so we have 1 possibility for each choice of $n$ and thus 4 possibilities total for this case.
If $n=2$, then again we have $a_{1} a_{2}=a_{2} a_{3}=0$, so we must have $a_{3} a_{4}=a_{4} a_{5}=\ldots=a_{7} a_{8}=1$, so $a_{3}=a_{4}=\ldots=a_{8}=1$. However, this time $a_{1}$ is not fixed, and we see that regardless of our choice of $a_{1}$ the sum will still be equal to 5 . Thus, since there are 2 choices for $a_{1}$, then there are 2 possibilities total for this case. The case where $n=7$ is analogous, with $a_{8}$ having 2 possibilities, so we have another 2 possibilities.
Finally, if $a_{n}=1$ for $n \in\{2,3, \ldots, 7\}$, then we will have $a_{2} a_{3}=a_{3} a_{4}=\ldots=a_{6} a_{7}=1$. We already have five terms equal to 1 , so the remaining two terms $a_{1} a_{2}$ and $a_{7} a_{8}$ must be 0 . Since $a_{2}=1$, then we must have $a_{1}=0$, and since $a_{7}=1$ then $a_{8}=0$. Thus, there is only 1 possibility for this case.
Summing, we have $4+2+2+1=9$ total sequences.
|
9
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
How many sequences $a_{1}, a_{2}, \ldots, a_{8}$ of zeroes and ones have $a_{1} a_{2}+a_{2} a_{3}+\cdots+a_{7} a_{8}=5$ ?
|
9 First, note that we have seven terms in the left hand side, and each term can be either 0 or 1 , so we must have five terms equal to 1 and two terms equal to 0 . Thus, for $n \in\{1,2, \ldots, 8\}$, at least one of the $a_{n}$ must be equal to 0 . If we can find $i, j \in\{2,3, \ldots, 7\}$ such that $a_{i}=a_{j}=0$ and $i<j$, then the terms $a_{i-1} a_{i}, a_{i} a_{i+1}$, and $a_{j} a_{j+1}$ will all be equal to 0 . We did not count any term twice because $i-1<i<j$, so we would have three terms equal to 0 , which cannot happen because we can have only two. Thus, we can find at most one $n \in\{2,3, \ldots, 7\}$ such that $a_{n}=0$. We will do casework on which $n$ in this range have $a_{n}=0$.
If $n \in\{3,4,5,6\}$, then we know that the terms $a_{n-1} a_{n}=a_{n} a_{n+1}=0$, so all other terms must be 1 , so $a_{1} a_{2}=a_{2} a_{3}=\ldots=a_{n-2} a_{n-1}=1$ and $a_{n+1} a_{n+2}=\ldots=a_{7} a_{8}=1$. Because every $a_{i}$ appears in one of these equations for $i \neq n$, then we must have $a_{i}=1$ for all $i \neq n$, so we have 1 possibility for each choice of $n$ and thus 4 possibilities total for this case.
If $n=2$, then again we have $a_{1} a_{2}=a_{2} a_{3}=0$, so we must have $a_{3} a_{4}=a_{4} a_{5}=\ldots=a_{7} a_{8}=1$, so $a_{3}=a_{4}=\ldots=a_{8}=1$. However, this time $a_{1}$ is not fixed, and we see that regardless of our choice of $a_{1}$ the sum will still be equal to 5 . Thus, since there are 2 choices for $a_{1}$, then there are 2 possibilities total for this case. The case where $n=7$ is analogous, with $a_{8}$ having 2 possibilities, so we have another 2 possibilities.
Finally, if $a_{n}=1$ for $n \in\{2,3, \ldots, 7\}$, then we will have $a_{2} a_{3}=a_{3} a_{4}=\ldots=a_{6} a_{7}=1$. We already have five terms equal to 1 , so the remaining two terms $a_{1} a_{2}$ and $a_{7} a_{8}$ must be 0 . Since $a_{2}=1$, then we must have $a_{1}=0$, and since $a_{7}=1$ then $a_{8}=0$. Thus, there is only 1 possibility for this case.
Summing, we have $4+2+2+1=9$ total sequences.
|
{
"exam": "HMMT",
"problem_label": "2",
"problem_match": "\n2. [3]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-gen1-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
Triangle $A B C$ has $A B=5, B C=7$, and $C A=8$. New lines not containing but parallel to $A B$, $B C$, and $C A$ are drawn tangent to the incircle of $A B C$. What is the area of the hexagon formed by the sides of the original triangle and the newly drawn lines?
|
$\frac{31}{5} \sqrt{3}$
From the law of cosines we compute $\measuredangle A=\cos ^{-1}\left(\frac{5^{2}+8^{2}-7^{2}}{2(5)(8)}\right)=60^{\circ}$. Using brackets to denote the area of a region, we find that
$$
[A B C]=\frac{1}{2} A B \cdot A C \cdot \sin 60^{\circ}=10 \sqrt{3}
$$
The radius of the incircle can be computed by the formula
$$
r=\frac{2[A B C]}{A B+B C+C A}=\frac{20 \sqrt{3}}{20}=\sqrt{3}
$$
Now the height from $A$ to $B C$ is $\frac{2[A B C]}{B C}=\frac{20 \sqrt{3}}{7}$. Then the height from $A$ to $D E$ is $\frac{20 \sqrt{3}}{7}-2 r=\frac{6 \sqrt{3}}{7}$. Then $[A D E]=\left(\frac{6 \sqrt{3} / 7}{20 \sqrt{3} / 7}\right)^{2}[A B C]=\frac{9}{100}[A B C]$. Here, we use the fact that $\triangle A B C$ and $\triangle A D E$ are similar.
Similarly, we compute that the height from $B$ to $C A$ is $\frac{2[A B C]}{C A}=\frac{20 \sqrt{3}}{8}=\frac{5 \sqrt{3}}{2}$. Then the height from $B$ to $H J$ is $\frac{5 \sqrt{3}}{2}-2 r=\frac{\sqrt{3}}{2}$. Then $[B H J]=\left(\frac{\sqrt{3} / 2}{5 \sqrt{3} / 2}\right)^{2}[A B C]=\frac{1}{25}[A B C]$.
Finally, we compute that the height from $C$ to $A B$ is $\frac{2[A B C]}{5}=\frac{20 \sqrt{3}}{5}=4 \sqrt{3}$. Then the height from $C$ to $F G$ is $4 \sqrt{3}-2 r=2 \sqrt{3}$. Then $[C F G]=\left(\frac{2 \sqrt{3}}{4 \sqrt{3}}\right)^{2}[A B C]=\frac{1}{4}[A B C]$.
Finally we can compute the area of hexagon $D E F G H J$. We have
$$
\begin{gathered}
{[D E F G H J]=[A B C]-[A D E]-[B H J]-[C F G]=[A B C]\left(1-\frac{9}{100}-\frac{1}{25}-\frac{1}{4}\right)=[A B C]\left(\frac{31}{50}\right)=} \\
10 \sqrt{3}\left(\frac{31}{50}\right)=\frac{31}{5} \sqrt{3} .
\end{gathered}
$$
|
\frac{31}{5} \sqrt{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Triangle $A B C$ has $A B=5, B C=7$, and $C A=8$. New lines not containing but parallel to $A B$, $B C$, and $C A$ are drawn tangent to the incircle of $A B C$. What is the area of the hexagon formed by the sides of the original triangle and the newly drawn lines?
|
$\frac{31}{5} \sqrt{3}$

From the law of cosines we compute $\measuredangle A=\cos ^{-1}\left(\frac{5^{2}+8^{2}-7^{2}}{2(5)(8)}\right)=60^{\circ}$. Using brackets to denote the area of a region, we find that
$$
[A B C]=\frac{1}{2} A B \cdot A C \cdot \sin 60^{\circ}=10 \sqrt{3}
$$
The radius of the incircle can be computed by the formula
$$
r=\frac{2[A B C]}{A B+B C+C A}=\frac{20 \sqrt{3}}{20}=\sqrt{3}
$$
Now the height from $A$ to $B C$ is $\frac{2[A B C]}{B C}=\frac{20 \sqrt{3}}{7}$. Then the height from $A$ to $D E$ is $\frac{20 \sqrt{3}}{7}-2 r=\frac{6 \sqrt{3}}{7}$. Then $[A D E]=\left(\frac{6 \sqrt{3} / 7}{20 \sqrt{3} / 7}\right)^{2}[A B C]=\frac{9}{100}[A B C]$. Here, we use the fact that $\triangle A B C$ and $\triangle A D E$ are similar.
Similarly, we compute that the height from $B$ to $C A$ is $\frac{2[A B C]}{C A}=\frac{20 \sqrt{3}}{8}=\frac{5 \sqrt{3}}{2}$. Then the height from $B$ to $H J$ is $\frac{5 \sqrt{3}}{2}-2 r=\frac{\sqrt{3}}{2}$. Then $[B H J]=\left(\frac{\sqrt{3} / 2}{5 \sqrt{3} / 2}\right)^{2}[A B C]=\frac{1}{25}[A B C]$.
Finally, we compute that the height from $C$ to $A B$ is $\frac{2[A B C]}{5}=\frac{20 \sqrt{3}}{5}=4 \sqrt{3}$. Then the height from $C$ to $F G$ is $4 \sqrt{3}-2 r=2 \sqrt{3}$. Then $[C F G]=\left(\frac{2 \sqrt{3}}{4 \sqrt{3}}\right)^{2}[A B C]=\frac{1}{4}[A B C]$.
Finally we can compute the area of hexagon $D E F G H J$. We have
$$
\begin{gathered}
{[D E F G H J]=[A B C]-[A D E]-[B H J]-[C F G]=[A B C]\left(1-\frac{9}{100}-\frac{1}{25}-\frac{1}{4}\right)=[A B C]\left(\frac{31}{50}\right)=} \\
10 \sqrt{3}\left(\frac{31}{50}\right)=\frac{31}{5} \sqrt{3} .
\end{gathered}
$$
|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n3. [3]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-gen1-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
An ant starts at the point $(1,0)$. Each minute, it walks from its current position to one of the four adjacent lattice points until it reaches a point $(x, y)$ with $|x|+|y| \geq 2$. What is the probability that the ant ends at the point $(1,1)$ ?
|
$\frac{7}{24}$ From the starting point of $(1,0)$, there is a $\frac{1}{4}$ chance we will go directly to $(1,1)$, a $\frac{1}{2}$ chance we will end at $(2,0)$ or $(1,-1)$, and a $\frac{1}{4}$ chance we will go to $(0,0)$. Thus, if $p$ is the probability that we will reach $(1,1)$ from $(0,0)$, then the desired probability is equal to $\frac{1}{4}+\frac{1}{4} p$, so we need only calculate $p$. Note that we can replace the condition $|x|+|y| \geq 2$ by $|x|+|y|=2$, since in each iteration the quantity $|x|+|y|$ can increase by at most 1 . Thus, we only have to consider the eight points $(2,0),(1,1),(0,2),(-1,1),(-2,0),(-1,-1),(0,-2),(1,-1)$. Let $p_{1}, p_{2}, \ldots, p_{8}$ be the probability of
reaching each of these points from $(0,0)$, respectively. By symmetry, we see that $p_{1}=p_{3}=p_{5}=p_{7}$ and $p_{2}=p_{4}=p_{6}=p_{8}$. We also know that there are two paths from $(0,0)$ to $(1,1)$ and one path from $(0,0)$ to $(2,0)$, thus $p_{2}=2 p_{1}$. Because the sum of all probabilities is 1 , we have $p_{1}+p_{2}+\ldots+p_{8}=1$. Combining these equations, we see that $4 p_{1}+4 p_{2}=12 p_{1}=1$, so $p_{1}=\frac{1}{12}$ and $p_{2}=\frac{1}{6}$. Since $p=p_{2}=\frac{1}{6}$, then the final answer is $\frac{1}{4}+\frac{1}{4} \cdot \frac{1}{6}=\frac{7}{24}$
|
\frac{7}{24}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
An ant starts at the point $(1,0)$. Each minute, it walks from its current position to one of the four adjacent lattice points until it reaches a point $(x, y)$ with $|x|+|y| \geq 2$. What is the probability that the ant ends at the point $(1,1)$ ?
|
$\frac{7}{24}$ From the starting point of $(1,0)$, there is a $\frac{1}{4}$ chance we will go directly to $(1,1)$, a $\frac{1}{2}$ chance we will end at $(2,0)$ or $(1,-1)$, and a $\frac{1}{4}$ chance we will go to $(0,0)$. Thus, if $p$ is the probability that we will reach $(1,1)$ from $(0,0)$, then the desired probability is equal to $\frac{1}{4}+\frac{1}{4} p$, so we need only calculate $p$. Note that we can replace the condition $|x|+|y| \geq 2$ by $|x|+|y|=2$, since in each iteration the quantity $|x|+|y|$ can increase by at most 1 . Thus, we only have to consider the eight points $(2,0),(1,1),(0,2),(-1,1),(-2,0),(-1,-1),(0,-2),(1,-1)$. Let $p_{1}, p_{2}, \ldots, p_{8}$ be the probability of
reaching each of these points from $(0,0)$, respectively. By symmetry, we see that $p_{1}=p_{3}=p_{5}=p_{7}$ and $p_{2}=p_{4}=p_{6}=p_{8}$. We also know that there are two paths from $(0,0)$ to $(1,1)$ and one path from $(0,0)$ to $(2,0)$, thus $p_{2}=2 p_{1}$. Because the sum of all probabilities is 1 , we have $p_{1}+p_{2}+\ldots+p_{8}=1$. Combining these equations, we see that $4 p_{1}+4 p_{2}=12 p_{1}=1$, so $p_{1}=\frac{1}{12}$ and $p_{2}=\frac{1}{6}$. Since $p=p_{2}=\frac{1}{6}$, then the final answer is $\frac{1}{4}+\frac{1}{4} \cdot \frac{1}{6}=\frac{7}{24}$
|
{
"exam": "HMMT",
"problem_label": "4",
"problem_match": "\n4. [4]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-gen1-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
A polynomial $P$ is of the form $\pm x^{6} \pm x^{5} \pm x^{4} \pm x^{3} \pm x^{2} \pm x \pm 1$. Given that $P(2)=27$, what is $P(3)$ ?
|
439 We use the following lemma:
Lemma. The sign of $\pm 2^{n} \pm 2^{n-1} \pm \cdots \pm 2 \pm 1$ is the same as the sign of the $2^{n}$ term.
Proof. Without loss of generality, let $2^{n}$ be positive. (We can flip all signs.) Notice that $2^{n} \pm 2^{n-1} \pm$ $2^{n-2} \pm \cdots 2 \pm 1 \geq 2^{n}-2^{n-1}-2^{n-2}-\cdots-2-1=1$, which is positive.
We can use this lemma to uniquely determine the signs of $P$. Since our desired sum, 27, is positive, the coefficient of $x^{6}$ must be positive. Subtracting 64 , we now have that $\pm 2^{5} \pm 2^{4} \pm \ldots \pm 2 \pm 1=-37$, so the sign of $2^{5}$ must be negative. Continuing in this manner, we find that $P(x)=x^{6}-x^{5}-x^{4}+x^{3}+x^{2}-x+1$, so $P(3)=3^{6}-3^{5}-3^{4}+3^{3}+3^{2}-3+1=439$.
|
439
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
A polynomial $P$ is of the form $\pm x^{6} \pm x^{5} \pm x^{4} \pm x^{3} \pm x^{2} \pm x \pm 1$. Given that $P(2)=27$, what is $P(3)$ ?
|
439 We use the following lemma:
Lemma. The sign of $\pm 2^{n} \pm 2^{n-1} \pm \cdots \pm 2 \pm 1$ is the same as the sign of the $2^{n}$ term.
Proof. Without loss of generality, let $2^{n}$ be positive. (We can flip all signs.) Notice that $2^{n} \pm 2^{n-1} \pm$ $2^{n-2} \pm \cdots 2 \pm 1 \geq 2^{n}-2^{n-1}-2^{n-2}-\cdots-2-1=1$, which is positive.
We can use this lemma to uniquely determine the signs of $P$. Since our desired sum, 27, is positive, the coefficient of $x^{6}$ must be positive. Subtracting 64 , we now have that $\pm 2^{5} \pm 2^{4} \pm \ldots \pm 2 \pm 1=-37$, so the sign of $2^{5}$ must be negative. Continuing in this manner, we find that $P(x)=x^{6}-x^{5}-x^{4}+x^{3}+x^{2}-x+1$, so $P(3)=3^{6}-3^{5}-3^{4}+3^{3}+3^{2}-3+1=439$.
|
{
"exam": "HMMT",
"problem_label": "5",
"problem_match": "\n5. [5]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-gen1-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
What is the sum of the positive solutions to $2 x^{2}-x\lfloor x\rfloor=5$, where $\lfloor x\rfloor$ is the largest integer less than or equal to $x$ ?
|
$\frac{3+\sqrt{41}+2 \sqrt{11}}{4}$ We first note that $\lfloor x\rfloor \leq x$, so $2 x^{2}-x\lfloor x\rfloor \geq 2 x^{2}-x^{2}=x^{2}$. Since this function is increasing on the positive reals, all solutions must be at most $\sqrt{5}$. This gives us 3 possible values of $\lfloor x\rfloor: 0,1$, and 2 .
If $\lfloor x\rfloor=0$, then our equation becomes $2 x^{2}=5$, which has positive solution $x=\sqrt{\frac{5}{2}}$. This number is greater than 1 , so its floor is not 0 ; thus, there are no solutions in this case.
If $\lfloor x\rfloor=1$, then our equation becomes $2 x^{2}-x=5$. Using the quadratic formula, we find the positive solution $x=\frac{1+\sqrt{41}}{4}$. Since $3<\sqrt{41}<7$, this number is between 1 and 2 , so it satisfies the equation.
If $\lfloor x\rfloor=2$, then our equation becomes $2 x^{2}-2 x=5$. We find the positive solution $x=\frac{1+\sqrt{11}}{2}$. Since $3<\sqrt{11}<5$, this number is between 2 and 3 , so it satisfies the equation.
We then find that the sum of positive solutions is $\frac{1+\sqrt{41}}{4}+\frac{1+\sqrt{11}}{2}=\frac{3+\sqrt{41}+2 \sqrt{11}}{4}$.
|
\frac{3+\sqrt{41}+2 \sqrt{11}}{4}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
What is the sum of the positive solutions to $2 x^{2}-x\lfloor x\rfloor=5$, where $\lfloor x\rfloor$ is the largest integer less than or equal to $x$ ?
|
$\frac{3+\sqrt{41}+2 \sqrt{11}}{4}$ We first note that $\lfloor x\rfloor \leq x$, so $2 x^{2}-x\lfloor x\rfloor \geq 2 x^{2}-x^{2}=x^{2}$. Since this function is increasing on the positive reals, all solutions must be at most $\sqrt{5}$. This gives us 3 possible values of $\lfloor x\rfloor: 0,1$, and 2 .
If $\lfloor x\rfloor=0$, then our equation becomes $2 x^{2}=5$, which has positive solution $x=\sqrt{\frac{5}{2}}$. This number is greater than 1 , so its floor is not 0 ; thus, there are no solutions in this case.
If $\lfloor x\rfloor=1$, then our equation becomes $2 x^{2}-x=5$. Using the quadratic formula, we find the positive solution $x=\frac{1+\sqrt{41}}{4}$. Since $3<\sqrt{41}<7$, this number is between 1 and 2 , so it satisfies the equation.
If $\lfloor x\rfloor=2$, then our equation becomes $2 x^{2}-2 x=5$. We find the positive solution $x=\frac{1+\sqrt{11}}{2}$. Since $3<\sqrt{11}<5$, this number is between 2 and 3 , so it satisfies the equation.
We then find that the sum of positive solutions is $\frac{1+\sqrt{41}}{4}+\frac{1+\sqrt{11}}{2}=\frac{3+\sqrt{41}+2 \sqrt{11}}{4}$.
|
{
"exam": "HMMT",
"problem_label": "6",
"problem_match": "\n6. [5]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-gen1-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
What is the remainder when $(1+x)^{2010}$ is divided by $1+x+x^{2}$ ?
|
1 We use polynomial congruence $\bmod 1+x+x^{2}$ to find the desired remainder. Since $x^{2}+x+1 \mid x^{3}-1$, we have that $x^{3} \equiv 1\left(\bmod 1+x+x^{2}\right)$. Now:
$$
\begin{aligned}
(1+x)^{2010} & \equiv\left(-x^{2}\right)^{2010} \quad\left(\bmod 1+x+x^{2}\right) \\
& \equiv x^{4020} \quad\left(\bmod 1+x+x^{2}\right) \\
& \equiv\left(x^{3}\right)^{1340} \quad\left(\bmod 1+x+x^{2}\right) \\
& \equiv 1^{1340} \quad\left(\bmod 1+x+x^{2}\right) \\
& \equiv 1 \quad\left(\bmod 1+x+x^{2}\right)
\end{aligned}
$$
Thus, the answer is 1 .
|
1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
What is the remainder when $(1+x)^{2010}$ is divided by $1+x+x^{2}$ ?
|
1 We use polynomial congruence $\bmod 1+x+x^{2}$ to find the desired remainder. Since $x^{2}+x+1 \mid x^{3}-1$, we have that $x^{3} \equiv 1\left(\bmod 1+x+x^{2}\right)$. Now:
$$
\begin{aligned}
(1+x)^{2010} & \equiv\left(-x^{2}\right)^{2010} \quad\left(\bmod 1+x+x^{2}\right) \\
& \equiv x^{4020} \quad\left(\bmod 1+x+x^{2}\right) \\
& \equiv\left(x^{3}\right)^{1340} \quad\left(\bmod 1+x+x^{2}\right) \\
& \equiv 1^{1340} \quad\left(\bmod 1+x+x^{2}\right) \\
& \equiv 1 \quad\left(\bmod 1+x+x^{2}\right)
\end{aligned}
$$
Thus, the answer is 1 .
|
{
"exam": "HMMT",
"problem_label": "7",
"problem_match": "\n7. [6]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-gen1-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
Two circles with radius one are drawn in the coordinate plane, one with center $(0,1)$ and the other with center $(2, y)$, for some real number $y$ between 0 and 1 . A third circle is drawn so as to be tangent to both of the other two circles as well as the $x$ axis. What is the smallest possible radius for this third circle?
|
$3-2 \sqrt{2}$ Suppose that the smaller circle has radius $r$. Call the three circles (in order from left to right) $O_{1}, O_{2}$, and $O_{3}$. The distance between the centers of $O_{1}$ and $O_{2}$ is $1+r$, and the distance in their $y$-coordinates is $1-r$. Therefore, by the Pythagorean theorem, the difference in $x$-coordinates
is $\sqrt{(1+r)^{2}-(1-r)^{2}}=2 \sqrt{r}$, which means that $O_{2}$ has a center at $(2 \sqrt{r}, r)$. But $O_{2}$ is also tangent to $O_{3}$, which means that the difference in $x$-coordinate from the right-most point of $O_{2}$ to the center of $O_{3}$ is at most 1. Therefore, the center of $O_{3}$ has an $x$-coordinate of at most $2 \sqrt{r}+r+1$, meaning that $2 \sqrt{r}+r+1 \leq 2$. We can use the quadratic formula to see that this implies that $\sqrt{r} \leq \sqrt{2}-1$, so $r \leq 3-2 \sqrt{2}$. We can achieve equality by placing the center of $O_{3}$ at $(2, r)$ (which in this case is $(2,3-2 \sqrt{2}))$.
|
3-2 \sqrt{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Two circles with radius one are drawn in the coordinate plane, one with center $(0,1)$ and the other with center $(2, y)$, for some real number $y$ between 0 and 1 . A third circle is drawn so as to be tangent to both of the other two circles as well as the $x$ axis. What is the smallest possible radius for this third circle?
|
$3-2 \sqrt{2}$ Suppose that the smaller circle has radius $r$. Call the three circles (in order from left to right) $O_{1}, O_{2}$, and $O_{3}$. The distance between the centers of $O_{1}$ and $O_{2}$ is $1+r$, and the distance in their $y$-coordinates is $1-r$. Therefore, by the Pythagorean theorem, the difference in $x$-coordinates
is $\sqrt{(1+r)^{2}-(1-r)^{2}}=2 \sqrt{r}$, which means that $O_{2}$ has a center at $(2 \sqrt{r}, r)$. But $O_{2}$ is also tangent to $O_{3}$, which means that the difference in $x$-coordinate from the right-most point of $O_{2}$ to the center of $O_{3}$ is at most 1. Therefore, the center of $O_{3}$ has an $x$-coordinate of at most $2 \sqrt{r}+r+1$, meaning that $2 \sqrt{r}+r+1 \leq 2$. We can use the quadratic formula to see that this implies that $\sqrt{r} \leq \sqrt{2}-1$, so $r \leq 3-2 \sqrt{2}$. We can achieve equality by placing the center of $O_{3}$ at $(2, r)$ (which in this case is $(2,3-2 \sqrt{2}))$.
|
{
"exam": "HMMT",
"problem_label": "8",
"problem_match": "\n8. [7]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-gen1-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
What is the sum of all numbers between 0 and 511 inclusive that have an even number of 1 s when written in binary?
|
65408 Call a digit in the binary representation of a number a bit. We claim that for any given $i$ between 0 and 8 , there are 128 numbers with an even number of 1 s that have a 1 in the bit representing $2^{i}$. To prove this, we simply make that bit a 1 , then consider all possible configurations of the other bits, excluding the last bit (or the second-last bit if our given bit is already the last bit). The last bit will then be restricted to satisfy the parity condition on the number of 1 s . As there are 128 possible configurations of all the bits but two, we find 128 possible numbers, proving our claim.
Therefore, each bit is present as a 1 in 128 numbers in the sum, so the bit representing $2^{i}$ contributes $128 \cdot 2^{i}$ to our sum. Summing over all $0 \leq i \leq 8$, we find the answer to be $128(1+2+\ldots+128)=$ $128 \cdot 511=65408$.
|
65408
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
What is the sum of all numbers between 0 and 511 inclusive that have an even number of 1 s when written in binary?
|
65408 Call a digit in the binary representation of a number a bit. We claim that for any given $i$ between 0 and 8 , there are 128 numbers with an even number of 1 s that have a 1 in the bit representing $2^{i}$. To prove this, we simply make that bit a 1 , then consider all possible configurations of the other bits, excluding the last bit (or the second-last bit if our given bit is already the last bit). The last bit will then be restricted to satisfy the parity condition on the number of 1 s . As there are 128 possible configurations of all the bits but two, we find 128 possible numbers, proving our claim.
Therefore, each bit is present as a 1 in 128 numbers in the sum, so the bit representing $2^{i}$ contributes $128 \cdot 2^{i}$ to our sum. Summing over all $0 \leq i \leq 8$, we find the answer to be $128(1+2+\ldots+128)=$ $128 \cdot 511=65408$.
|
{
"exam": "HMMT",
"problem_label": "9",
"problem_match": "\n9. [7]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-gen1-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
You are given two diameters $A B$ and $C D$ of circle $\Omega$ with radius 1. A circle is drawn in one of the smaller sectors formed such that it is tangent to $A B$ at $E$, tangent to $C D$ at $F$, and tangent to $\Omega$ at $P$. Lines $P E$ and $P F$ intersect $\Omega$ again at $X$ and $Y$. What is the length of $X Y$, given that $A C=\frac{2}{3}$ ?
|
\( \frac{4\sqrt{2}}{3} \). Let \( O \) denote the center of circle \( \Omega \). We first prove that \( OX \perp AB \) and \( OY \perp CD \). Consider the homothety about $P$ which maps the smaller circle to $\Omega$. This homothety takes $E$ to $X$ and also takes $A B$ to the line tangent to circle $\Omega$ parallel to $A B$. Therefore, $X$ is the midpoint of the arc $A B$, and so $O X \perp A B$. Similarly, $O Y \perp C D$.
Let $\theta=\angle A O C$. By the Law of Sines, we have $A C=2 \sin \frac{\theta}{2}$. Thus, $\sin \frac{\theta}{2}=\frac{1}{3}$, and $\cos \frac{\theta}{2}=\sqrt{1-\left(\frac{1}{3}\right)^{2}}=$ $\frac{2 \sqrt{2}}{3}$. Therefore,
$$
\begin{aligned}
X Y & =2 \sin \frac{\angle X O Y}{2} \\
& =2 \sin \left(90^{\circ}-\frac{\theta}{2}\right) \\
& =2 \cos \frac{\theta}{2} \\
& =\frac{4 \sqrt{2}}{3}
\end{aligned}
$$
|
\frac{4\sqrt{2}}{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
You are given two diameters $A B$ and $C D$ of circle $\Omega$ with radius 1. A circle is drawn in one of the smaller sectors formed such that it is tangent to $A B$ at $E$, tangent to $C D$ at $F$, and tangent to $\Omega$ at $P$. Lines $P E$ and $P F$ intersect $\Omega$ again at $X$ and $Y$. What is the length of $X Y$, given that $A C=\frac{2}{3}$ ?
|
\( \frac{4\sqrt{2}}{3} \). Let \( O \) denote the center of circle \( \Omega \). We first prove that \( OX \perp AB \) and \( OY \perp CD \). Consider the homothety about $P$ which maps the smaller circle to $\Omega$. This homothety takes $E$ to $X$ and also takes $A B$ to the line tangent to circle $\Omega$ parallel to $A B$. Therefore, $X$ is the midpoint of the arc $A B$, and so $O X \perp A B$. Similarly, $O Y \perp C D$.
Let $\theta=\angle A O C$. By the Law of Sines, we have $A C=2 \sin \frac{\theta}{2}$. Thus, $\sin \frac{\theta}{2}=\frac{1}{3}$, and $\cos \frac{\theta}{2}=\sqrt{1-\left(\frac{1}{3}\right)^{2}}=$ $\frac{2 \sqrt{2}}{3}$. Therefore,
$$
\begin{aligned}
X Y & =2 \sin \frac{\angle X O Y}{2} \\
& =2 \sin \left(90^{\circ}-\frac{\theta}{2}\right) \\
& =2 \cos \frac{\theta}{2} \\
& =\frac{4 \sqrt{2}}{3}
\end{aligned}
$$
|
{
"exam": "HMMT",
"problem_label": "10",
"problem_match": "\n10. [8]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-gen1-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
16 progamers are playing in a single elimination tournament. Each player has a different skill level and when two play against each other the one with the higher skill level will always win. Each round, each progamer plays a match against another and the loser is eliminated. This continues until only one remains. How many different progamers can reach the round that has 2 players remaining?
|
9 Each finalist must be better than the person he beat in the semifinals, both of the people they beat in the second round, and all 4 of the people any of those people beat in the first round. So, none of the 7 worst players can possibly make it to the finals. Any of the 9 best players can make it to the finals if the other 8 of the best 9 play each other in all rounds before the finals. So, exactly 9 people are capable of making it to the finals.
|
9
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
16 progamers are playing in a single elimination tournament. Each player has a different skill level and when two play against each other the one with the higher skill level will always win. Each round, each progamer plays a match against another and the loser is eliminated. This continues until only one remains. How many different progamers can reach the round that has 2 players remaining?
|
9 Each finalist must be better than the person he beat in the semifinals, both of the people they beat in the second round, and all 4 of the people any of those people beat in the first round. So, none of the 7 worst players can possibly make it to the finals. Any of the 9 best players can make it to the finals if the other 8 of the best 9 play each other in all rounds before the finals. So, exactly 9 people are capable of making it to the finals.
|
{
"exam": "HMMT",
"problem_label": "1",
"problem_match": "\n1. [3]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
16 progamers are playing in another single elimination tournament. Each round, each of the remaining progamers plays against another and the loser is eliminated. Additionally, each time a progamer wins, he will have a ceremony to celebrate. A player's first ceremony is ten seconds long, and afterward each ceremony is ten seconds longer than the last. What is the total length in seconds of all the ceremonies over the entire tournament?
|
260 At the end of the first round, each of the 8 winners has a 10 second ceremony. After the second round, the 4 winners have a 20 second ceremony. The two remaining players have 30 second ceremonies after the third round, and the winner has a 40 second ceremony after the finals. So, all of the ceremonies combined take $8 \cdot 10+4 \cdot 20+2 \cdot 30+40=260$ seconds.
|
260
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
16 progamers are playing in another single elimination tournament. Each round, each of the remaining progamers plays against another and the loser is eliminated. Additionally, each time a progamer wins, he will have a ceremony to celebrate. A player's first ceremony is ten seconds long, and afterward each ceremony is ten seconds longer than the last. What is the total length in seconds of all the ceremonies over the entire tournament?
|
260 At the end of the first round, each of the 8 winners has a 10 second ceremony. After the second round, the 4 winners have a 20 second ceremony. The two remaining players have 30 second ceremonies after the third round, and the winner has a 40 second ceremony after the finals. So, all of the ceremonies combined take $8 \cdot 10+4 \cdot 20+2 \cdot 30+40=260$ seconds.
|
{
"exam": "HMMT",
"problem_label": "2",
"problem_match": "\n2. [4]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
Dragoons take up $1 \times 1$ squares in the plane with sides parallel to the coordinate axes such that the interiors of the squares do not intersect. A dragoon can fire at another dragoon if the difference in the $x$-coordinates of their centers and the difference in the $y$-coordinates of their centers are both at most 6 , regardless of any dragoons in between. For example, a dragoon centered at $(4,5)$ can fire at a dragoon centered at the origin, but a dragoon centered at $(7,0)$ can not. A dragoon cannot fire at itself. What is the maximum number of dragoons that can fire at a single dragoon simultaneously?
|
168 Assign coordinates in such a way that the dragoon being fired on is centered at $(0,0)$. Any dragoon firing at it must have a center with $x$-coordinates and $y$-coordinates that are no smaller than -6 and no greater than 6 . That means that every dragoon firing at it must lie entirely in the region bounded by the lines $x=-6.5, x=6.5, y=-6.5$, and $y=6.5$. This is a square with sides of length 13 , so there is room for exactly 169 dragoons in it. One of them is the dragoon being fired on, so there are at most 168 dragoons firing at it.
|
168
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Dragoons take up $1 \times 1$ squares in the plane with sides parallel to the coordinate axes such that the interiors of the squares do not intersect. A dragoon can fire at another dragoon if the difference in the $x$-coordinates of their centers and the difference in the $y$-coordinates of their centers are both at most 6 , regardless of any dragoons in between. For example, a dragoon centered at $(4,5)$ can fire at a dragoon centered at the origin, but a dragoon centered at $(7,0)$ can not. A dragoon cannot fire at itself. What is the maximum number of dragoons that can fire at a single dragoon simultaneously?
|
168 Assign coordinates in such a way that the dragoon being fired on is centered at $(0,0)$. Any dragoon firing at it must have a center with $x$-coordinates and $y$-coordinates that are no smaller than -6 and no greater than 6 . That means that every dragoon firing at it must lie entirely in the region bounded by the lines $x=-6.5, x=6.5, y=-6.5$, and $y=6.5$. This is a square with sides of length 13 , so there is room for exactly 169 dragoons in it. One of them is the dragoon being fired on, so there are at most 168 dragoons firing at it.
|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n3. [5]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
A zerg player can produce one zergling every minute and a protoss player can produce one zealot every 2.1 minutes. Both players begin building their respective units immediately from the beginning of the game. In a fight, a zergling army overpowers a zealot army if the ratio of zerglings to zealots is more than 3 . What is the total amount of time (in minutes) during the game such that at that time the zergling army would overpower the zealot army?
|
1.3 At the end of the first minute, the zerg player produces a zergling and has a superior army for the 1.1 minutes before the protoss player produces the first zealot. At this point, the zealot is at least a match for the zerglings until the fourth is produced 4 minutes into the game. Then, the zerg army has the advantage for the .2 minutes before a second zealot is produced. A third zealot will be produced 6.3 minutes into the game, which will be before the zerg player accumulates the 7 zerglings needed to overwhelm the first 2 zealots. After this, the zerglings will never regain the advantage because the zerg player can never produce 3 more zerglings to counter the last zealot before another one is produced. So, the zerg player will have the military advantage for $1.1+.2=1.3$ minutes.
|
1.3
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
A zerg player can produce one zergling every minute and a protoss player can produce one zealot every 2.1 minutes. Both players begin building their respective units immediately from the beginning of the game. In a fight, a zergling army overpowers a zealot army if the ratio of zerglings to zealots is more than 3 . What is the total amount of time (in minutes) during the game such that at that time the zergling army would overpower the zealot army?
|
1.3 At the end of the first minute, the zerg player produces a zergling and has a superior army for the 1.1 minutes before the protoss player produces the first zealot. At this point, the zealot is at least a match for the zerglings until the fourth is produced 4 minutes into the game. Then, the zerg army has the advantage for the .2 minutes before a second zealot is produced. A third zealot will be produced 6.3 minutes into the game, which will be before the zerg player accumulates the 7 zerglings needed to overwhelm the first 2 zealots. After this, the zerglings will never regain the advantage because the zerg player can never produce 3 more zerglings to counter the last zealot before another one is produced. So, the zerg player will have the military advantage for $1.1+.2=1.3$ minutes.
|
{
"exam": "HMMT",
"problem_label": "4",
"problem_match": "\n4. [5]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
There are 111 StarCraft progamers. The StarCraft team SKT starts with a given set of eleven progamers on it, and at the end of each season, it drops a progamer and adds a progamer (possibly the same one). At the start of the second season, SKT has to field a team of five progamers to play the opening match. How many different lineups of five players could be fielded if the order of players on the lineup matters?
|
4015440 We disregard the order of the players, multiplying our answer by $5!=120$ at the end to account for it. Clearly, SKT will be able to field at most 1 player not in the original set of eleven players. If it does not field a new player, then it has $\binom{11}{5}=462$ choices. If it does field a new player, then it has 100 choices for the new player, and $\binom{11}{4}=330$ choices for the 4 other players, giving 33000 possibilities. Thus, SKT can field at most $33000+462=33462$ unordered lineups, and multiplying this by 120 , we find the answer to be 4015440 .
## Unfair Coins
|
4015440
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There are 111 StarCraft progamers. The StarCraft team SKT starts with a given set of eleven progamers on it, and at the end of each season, it drops a progamer and adds a progamer (possibly the same one). At the start of the second season, SKT has to field a team of five progamers to play the opening match. How many different lineups of five players could be fielded if the order of players on the lineup matters?
|
4015440 We disregard the order of the players, multiplying our answer by $5!=120$ at the end to account for it. Clearly, SKT will be able to field at most 1 player not in the original set of eleven players. If it does not field a new player, then it has $\binom{11}{5}=462$ choices. If it does field a new player, then it has 100 choices for the new player, and $\binom{11}{4}=330$ choices for the 4 other players, giving 33000 possibilities. Thus, SKT can field at most $33000+462=33462$ unordered lineups, and multiplying this by 120 , we find the answer to be 4015440 .
## Unfair Coins
|
{
"exam": "HMMT",
"problem_label": "5",
"problem_match": "\n5. [7]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
When flipped, a coin has a probability $p$ of landing heads. When flipped twice, it is twice as likely to land on the same side both times as it is to land on each side once. What is the larger possible value of $p$ ?
|
$\frac{3+\sqrt{3}}{6}$ The probability that the coin will land on the same side twice is $p^{2}+(1-p)^{2}=$ $2 p^{2}-2 p+1$. The probability that the coin will land on each side once is $p(p-1)+(p-1) p=$ $2 p(1-p)=2 p-2 p^{2}$. We are told that it is twice as likely to land on the same side both times, so $2 p^{2}-2 p+1=2\left(2 p-2 p^{2}\right)=4 p-4 p^{2}$. Solving, we get $6 p^{2}-6 p+1=0$, so $p=\frac{3 \pm \sqrt{3}}{6}$. The larger solution is $p=\frac{3+\sqrt{3}}{6}$.
|
\frac{3+\sqrt{3}}{6}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
When flipped, a coin has a probability $p$ of landing heads. When flipped twice, it is twice as likely to land on the same side both times as it is to land on each side once. What is the larger possible value of $p$ ?
|
$\frac{3+\sqrt{3}}{6}$ The probability that the coin will land on the same side twice is $p^{2}+(1-p)^{2}=$ $2 p^{2}-2 p+1$. The probability that the coin will land on each side once is $p(p-1)+(p-1) p=$ $2 p(1-p)=2 p-2 p^{2}$. We are told that it is twice as likely to land on the same side both times, so $2 p^{2}-2 p+1=2\left(2 p-2 p^{2}\right)=4 p-4 p^{2}$. Solving, we get $6 p^{2}-6 p+1=0$, so $p=\frac{3 \pm \sqrt{3}}{6}$. The larger solution is $p=\frac{3+\sqrt{3}}{6}$.
|
{
"exam": "HMMT",
"problem_label": "6",
"problem_match": "\n6. [4]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
George has two coins, one of which is fair and the other of which always comes up heads. Jacob takes one of them at random and flips it twice. Given that it came up heads both times, what is the probability that it is the coin that always comes up heads?
|
\( \frac{4}{5} \). In general, \( P(A|B) = \frac{P(A \cap B)}{P(B)} \), where \( P(A|B) \) is the probability of \( A \) given \( B \) and $P(A \cap B)$ is the probability of $A$ and $B$ (See http://en.wikipedia.org/wiki/Conditional_probability for more information). If $A$ is the event of selecting the "double-headed" coin and $B$ is the event of Jacob flipping two heads, then $P(A \cap B)=\left(\frac{1}{2}\right)(1)$, since there is a $\frac{1}{2}$ chance of picking the doubleheaded coin and Jacob will always flip two heads when he has it. By conditional probability, $P(B)=$ $\left(\frac{1}{2}\right)(1)+\left(\frac{1}{2}\right)\left(\frac{1}{4}\right)=\frac{5}{8}$, so $P(A \mid B)=\frac{1 / 2}{5 / 8}=\frac{4}{5}$.
|
\frac{4}{5}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
George has two coins, one of which is fair and the other of which always comes up heads. Jacob takes one of them at random and flips it twice. Given that it came up heads both times, what is the probability that it is the coin that always comes up heads?
|
\( \frac{4}{5} \). In general, \( P(A|B) = \frac{P(A \cap B)}{P(B)} \), where \( P(A|B) \) is the probability of \( A \) given \( B \) and $P(A \cap B)$ is the probability of $A$ and $B$ (See http://en.wikipedia.org/wiki/Conditional_probability for more information). If $A$ is the event of selecting the "double-headed" coin and $B$ is the event of Jacob flipping two heads, then $P(A \cap B)=\left(\frac{1}{2}\right)(1)$, since there is a $\frac{1}{2}$ chance of picking the doubleheaded coin and Jacob will always flip two heads when he has it. By conditional probability, $P(B)=$ $\left(\frac{1}{2}\right)(1)+\left(\frac{1}{2}\right)\left(\frac{1}{4}\right)=\frac{5}{8}$, so $P(A \mid B)=\frac{1 / 2}{5 / 8}=\frac{4}{5}$.
|
{
"exam": "HMMT",
"problem_label": "7",
"problem_match": "\n7. [4]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
Allison has a coin which comes up heads $\frac{2}{3}$ of the time. She flips it 5 times. What is the probability that she sees more heads than tails?
|
\(\frac{6}{81}\). The probability of flipping more heads than tails is the probability of flipping 3 heads, 4 heads, or 5 heads. Since 5 flips will give $n$ heads with probability $\binom{5}{n}\left(\frac{2}{3}\right)^{n}\left(\frac{1}{3}\right)^{5-n}$, our answer is $\binom{5}{3}\left(\frac{2}{3}\right)^{3}\left(\frac{1}{3}\right)^{2}+\binom{5}{4}\left(\frac{2}{3}\right)^{4}\left(\frac{1}{3}\right)^{1}+\binom{5}{5}\left(\frac{2}{3}\right)^{5}\left(\frac{1}{3}\right)^{0}=\frac{64}{81}$.
|
\frac{64}{81}
|
Yes
|
Incomplete
|
math-word-problem
|
Combinatorics
|
Allison has a coin which comes up heads $\frac{2}{3}$ of the time. She flips it 5 times. What is the probability that she sees more heads than tails?
|
\(\frac{6}{81}\). The probability of flipping more heads than tails is the probability of flipping 3 heads, 4 heads, or 5 heads. Since 5 flips will give $n$ heads with probability $\binom{5}{n}\left(\frac{2}{3}\right)^{n}\left(\frac{1}{3}\right)^{5-n}$, our answer is $\binom{5}{3}\left(\frac{2}{3}\right)^{3}\left(\frac{1}{3}\right)^{2}+\binom{5}{4}\left(\frac{2}{3}\right)^{4}\left(\frac{1}{3}\right)^{1}+\binom{5}{5}\left(\frac{2}{3}\right)^{5}\left(\frac{1}{3}\right)^{0}=\frac{64}{81}$.
|
{
"exam": "HMMT",
"problem_label": "8",
"problem_match": "\n8. [5]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
Newton and Leibniz are playing a game with a coin that comes up heads with probability $p$. They take turns flipping the coin until one of them wins with Newton going first. Newton wins if he flips a heads and Leibniz wins if he flips a tails. Given that Newton and Leibniz each win the game half of the time, what is the probability $p$ ?
|
$\frac{\frac{3-\sqrt{5}}{2}}{}$ The probability that Newton will win on the first flip is $p$. The probability that Newton will win on the third flip is $(1-p) p^{2}$, since the first flip must be tails, the second must be heads, and the third flip must be heads. By the same logic, the probability Newton will win on the $(2 n+1)^{\text {st }}$ flip is $(1-p)^{n}(p)^{n+1}$. Thus, we have an infinite geometric sequence $p+(1-p) p^{2}+(1-p)^{2} p^{3}+\ldots$ which equals $\frac{p}{1-p(1-p)}$. We are given that this sum must equal $\frac{1}{2}$, so $1-p+p^{2}=2 p$, so $p=\frac{3-\sqrt{5}}{2}$ (the other solution is greater than 1).
|
\frac{3-\sqrt{5}}{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Newton and Leibniz are playing a game with a coin that comes up heads with probability $p$. They take turns flipping the coin until one of them wins with Newton going first. Newton wins if he flips a heads and Leibniz wins if he flips a tails. Given that Newton and Leibniz each win the game half of the time, what is the probability $p$ ?
|
$\frac{\frac{3-\sqrt{5}}{2}}{}$ The probability that Newton will win on the first flip is $p$. The probability that Newton will win on the third flip is $(1-p) p^{2}$, since the first flip must be tails, the second must be heads, and the third flip must be heads. By the same logic, the probability Newton will win on the $(2 n+1)^{\text {st }}$ flip is $(1-p)^{n}(p)^{n+1}$. Thus, we have an infinite geometric sequence $p+(1-p) p^{2}+(1-p)^{2} p^{3}+\ldots$ which equals $\frac{p}{1-p(1-p)}$. We are given that this sum must equal $\frac{1}{2}$, so $1-p+p^{2}=2 p$, so $p=\frac{3-\sqrt{5}}{2}$ (the other solution is greater than 1).
|
{
"exam": "HMMT",
"problem_label": "9",
"problem_match": "\n9. [6]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
Justine has a coin which will come up the same as the last flip $\frac{2}{3}$ of the time and the other side $\frac{1}{3}$ of the time. She flips it and it comes up heads. She then flips it 2010 more times. What is the probability that the last flip is heads?
|
| $\frac{3^{2010}+1}{2 \cdot 3^{2010}}$ | Let the "value" of a flip be 1 if the flip is different from the previous flip and let |
| :---: | :---: | it be 0 if the flip is the same as the previous flip. The last flip will be heads if the sum of the values of all 2010 flips is even. The probability that this will happen is $\sum_{i=0}^{1005}\binom{2010}{2 i}\left(\frac{1}{3}\right)^{2 i}\left(\frac{2}{3}\right)^{2010-2 i}$.
We know that
$$
\begin{gathered}
\sum_{i=0}^{1005}\binom{2010}{2 i}\left(\frac{1}{3}\right)^{2 i}\left(\frac{2}{3}\right)^{2010-2 i}+\binom{2010}{2 i+1}\left(\frac{1}{3}\right)^{2 i+1}\left(\frac{2}{3}\right)^{2010-(2 i+1)}= \\
\sum_{k=0}^{2010}\binom{2010}{k}\left(\frac{1}{3}\right)^{k}\left(\frac{2}{3}\right)^{2010-k}=\left(\frac{1}{3}+\frac{2}{3}\right)^{2010}=1
\end{gathered}
$$
and
$$
\begin{gathered}
\sum_{i=0}^{1005}\binom{2010}{2 i}\left(\frac{1}{3}\right)^{2 i}\left(\frac{2}{3}\right)^{2010-2 i}-\binom{2010}{2 i+1}\left(\frac{1}{3}\right)^{2 i+1}\left(\frac{2}{3}\right)^{2010-(2 i+1)}= \\
\sum_{k=0}^{2010}\binom{2010}{k}\left(\frac{-1}{3}\right)^{k}\left(\frac{2}{3}\right)^{2010-k}=\left(\frac{-1}{3}+\frac{2}{3}\right)^{2010}=\left(\frac{1}{3}\right)^{2010}
\end{gathered}
$$
Summing these two values and dividing by 2 gives the answer $\frac{1+\left(\frac{1}{3}\right)^{2010}}{2}=\frac{3^{2010}+1}{2 \cdot 3^{2010}}$.
|
\frac{3^{2010}+1}{2 \cdot 3^{2010}}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Justine has a coin which will come up the same as the last flip $\frac{2}{3}$ of the time and the other side $\frac{1}{3}$ of the time. She flips it and it comes up heads. She then flips it 2010 more times. What is the probability that the last flip is heads?
|
| $\frac{3^{2010}+1}{2 \cdot 3^{2010}}$ | Let the "value" of a flip be 1 if the flip is different from the previous flip and let |
| :---: | :---: | it be 0 if the flip is the same as the previous flip. The last flip will be heads if the sum of the values of all 2010 flips is even. The probability that this will happen is $\sum_{i=0}^{1005}\binom{2010}{2 i}\left(\frac{1}{3}\right)^{2 i}\left(\frac{2}{3}\right)^{2010-2 i}$.
We know that
$$
\begin{gathered}
\sum_{i=0}^{1005}\binom{2010}{2 i}\left(\frac{1}{3}\right)^{2 i}\left(\frac{2}{3}\right)^{2010-2 i}+\binom{2010}{2 i+1}\left(\frac{1}{3}\right)^{2 i+1}\left(\frac{2}{3}\right)^{2010-(2 i+1)}= \\
\sum_{k=0}^{2010}\binom{2010}{k}\left(\frac{1}{3}\right)^{k}\left(\frac{2}{3}\right)^{2010-k}=\left(\frac{1}{3}+\frac{2}{3}\right)^{2010}=1
\end{gathered}
$$
and
$$
\begin{gathered}
\sum_{i=0}^{1005}\binom{2010}{2 i}\left(\frac{1}{3}\right)^{2 i}\left(\frac{2}{3}\right)^{2010-2 i}-\binom{2010}{2 i+1}\left(\frac{1}{3}\right)^{2 i+1}\left(\frac{2}{3}\right)^{2010-(2 i+1)}= \\
\sum_{k=0}^{2010}\binom{2010}{k}\left(\frac{-1}{3}\right)^{k}\left(\frac{2}{3}\right)^{2010-k}=\left(\frac{-1}{3}+\frac{2}{3}\right)^{2010}=\left(\frac{1}{3}\right)^{2010}
\end{gathered}
$$
Summing these two values and dividing by 2 gives the answer $\frac{1+\left(\frac{1}{3}\right)^{2010}}{2}=\frac{3^{2010}+1}{2 \cdot 3^{2010}}$.
|
{
"exam": "HMMT",
"problem_label": "10",
"problem_match": "\n10. [7]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
David, Delong, and Justin each showed up to a problem writing session at a random time during the session. If David arrived before Delong, what is the probability that he also arrived before Justin?
|
$\sqrt[2]{3}$ Let $t_{1}$ be the time that David arrives, let $t_{2}$ be the time that Delong arrives, and let $t_{3}$ be the time that Justin arrives. We can assume that all times are pairwise distinct because the probability of any two being equal is zero. Because the times were originally random and independent before we were given any information, then all orders $t_{1}<t_{2}<t_{3}, t_{1}<t_{3}<t_{2}, t_{3}<t_{1}<t_{2}, t_{2}<t_{1}<t_{3}$, $t_{2}<t_{3}<t_{1}, t_{3}<t_{2}<t_{1}$ must all be equally likely. Since we are given that $t_{1}<t_{2}$, then we only have the first three cases to consider, and $t_{1}<t_{3}$ in two cases of these three. Thus, the desired probability is $\frac{2}{3}$.
|
\frac{2}{3}
|
Yes
|
Incomplete
|
math-word-problem
|
Combinatorics
|
David, Delong, and Justin each showed up to a problem writing session at a random time during the session. If David arrived before Delong, what is the probability that he also arrived before Justin?
|
$\sqrt[2]{3}$ Let $t_{1}$ be the time that David arrives, let $t_{2}$ be the time that Delong arrives, and let $t_{3}$ be the time that Justin arrives. We can assume that all times are pairwise distinct because the probability of any two being equal is zero. Because the times were originally random and independent before we were given any information, then all orders $t_{1}<t_{2}<t_{3}, t_{1}<t_{3}<t_{2}, t_{3}<t_{1}<t_{2}, t_{2}<t_{1}<t_{3}$, $t_{2}<t_{3}<t_{1}, t_{3}<t_{2}<t_{1}$ must all be equally likely. Since we are given that $t_{1}<t_{2}$, then we only have the first three cases to consider, and $t_{1}<t_{3}$ in two cases of these three. Thus, the desired probability is $\frac{2}{3}$.
|
{
"exam": "HMMT",
"problem_label": "1",
"problem_match": "\n1. [5]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
A circle of radius 6 is drawn centered at the origin. How many squares of side length 1 and integer coordinate vertices intersect the interior of this circle?
|
132 By symmetry, the answer is four times the number of squares in the first quadrant. Let's identify each square by its coordinates at the bottom-left corner, $(x, y)$. When $x=0$, we can have $y=0 \ldots 5$, so there are 6 squares. (Letting $y=6$ is not allowed because that square intersects only the boundary of the circle.) When $x=1$, how many squares are there? The equation of the circle is $y=\sqrt{36-x^{2}}=\sqrt{36-1^{2}}$ is between 5 and 6 , so we can again have $y=0 \ldots 5$. Likewise for $x=2$ and $x=3$. When $x=4$ we have $y=\sqrt{20}$ which is between 4 and 5 , so there are 5 squares, and when $x=5$ we have $y=\sqrt{11}$ which is between 3 and 4 , so there are 4 squares. Finally, when $x=6$, we have $y=0$, and no squares intersect the interior of the circle. This gives $6+6+6+6+5+4=33$. Since this is the number in the first quadrant, we multiply by four to get 132 .
|
132
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A circle of radius 6 is drawn centered at the origin. How many squares of side length 1 and integer coordinate vertices intersect the interior of this circle?
|
132 By symmetry, the answer is four times the number of squares in the first quadrant. Let's identify each square by its coordinates at the bottom-left corner, $(x, y)$. When $x=0$, we can have $y=0 \ldots 5$, so there are 6 squares. (Letting $y=6$ is not allowed because that square intersects only the boundary of the circle.) When $x=1$, how many squares are there? The equation of the circle is $y=\sqrt{36-x^{2}}=\sqrt{36-1^{2}}$ is between 5 and 6 , so we can again have $y=0 \ldots 5$. Likewise for $x=2$ and $x=3$. When $x=4$ we have $y=\sqrt{20}$ which is between 4 and 5 , so there are 5 squares, and when $x=5$ we have $y=\sqrt{11}$ which is between 3 and 4 , so there are 4 squares. Finally, when $x=6$, we have $y=0$, and no squares intersect the interior of the circle. This gives $6+6+6+6+5+4=33$. Since this is the number in the first quadrant, we multiply by four to get 132 .
|
{
"exam": "HMMT",
"problem_label": "2",
"problem_match": "\n2. [5]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
Jacob flipped a fair coin five times. In the first three flips, the coin came up heads exactly twice. In the last three flips, the coin also came up heads exactly twice. What is the probability that the third flip was heads?
|
| $\frac{4}{5}$ |
| :---: |
| How many sequences of five flips satisfy the conditions, and have the third flip be heads? | We have __H_- , so exactly one of the first two flips is heads, and exactly one of the last two flips is heads. This gives $2 \times 2=4$ possibilities. How many sequences of five flips satisfy the conditions, and have the third flip be tails? Now we have __T__, so the first two and the last two flips must all be heads. This gives only 1 possibility. So the probability that the third flip was heads is $\frac{4}{(4+1)}=\frac{4}{5}$
|
\frac{4}{5}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Jacob flipped a fair coin five times. In the first three flips, the coin came up heads exactly twice. In the last three flips, the coin also came up heads exactly twice. What is the probability that the third flip was heads?
|
| $\frac{4}{5}$ |
| :---: |
| How many sequences of five flips satisfy the conditions, and have the third flip be heads? | We have __H_- , so exactly one of the first two flips is heads, and exactly one of the last two flips is heads. This gives $2 \times 2=4$ possibilities. How many sequences of five flips satisfy the conditions, and have the third flip be tails? Now we have __T__, so the first two and the last two flips must all be heads. This gives only 1 possibility. So the probability that the third flip was heads is $\frac{4}{(4+1)}=\frac{4}{5}$
|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n3. [5]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
Let $x$ be a real number. Find the maximum value of $2^{x(1-x)}$.
|
$\sqrt[4]{2}$ Consider the function $2^{y}$. This is monotonically increasing, so to maximize $2^{y}$, you simply want to maximize $y$. Here, $y=x(1-x)=-x^{2}+x$ is a parabola opening downwards. The vertex of the parabola occurs at $x=(-1) /(-2)=1 / 2$, so the maximum value of the function is $2^{(1 / 2)(1 / 2)}=\sqrt[4]{2}$.
|
\sqrt[4]{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $x$ be a real number. Find the maximum value of $2^{x(1-x)}$.
|
$\sqrt[4]{2}$ Consider the function $2^{y}$. This is monotonically increasing, so to maximize $2^{y}$, you simply want to maximize $y$. Here, $y=x(1-x)=-x^{2}+x$ is a parabola opening downwards. The vertex of the parabola occurs at $x=(-1) /(-2)=1 / 2$, so the maximum value of the function is $2^{(1 / 2)(1 / 2)}=\sqrt[4]{2}$.
|
{
"exam": "HMMT",
"problem_label": "4",
"problem_match": "\n4. [6]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
An icosahedron is a regular polyhedron with twenty faces, all of which are equilateral triangles. If an icosahedron is rotated by $\theta$ degrees around an axis that passes through two opposite vertices so that it occupies exactly the same region of space as before, what is the smallest possible positive value of $\theta$ ?
|
$72^{\circ}$ Because this polyhedron is regular, all vertices must look the same. Let's consider just one vertex. Each triangle has a vertex angle of $60^{\circ}$, so we must have fewer than 6 triangles; if we had 6 , there would be $360^{\circ}$ at each vertex and you wouldn't be able to "fold" the polyhedron up (that is, it would be a flat plane). It's easy to see that we need at least 3 triangles at each vertex, and this gives a triangular pyramid with only 4 faces. Having 4 triangles meeting at each vertex gives an octahedron (two square pyramids with the squares glued together) with 8 faces. Therefore, an icosahedron has 5 triangles meeting at each vertex, so rotating by $\frac{360^{\circ}}{5}=72^{\circ}$ gives another identical icosahedron.
Alternate solution: Euler's formula tells us that $V-E+F=2$, where an icosahedron has $V$ vertices, $E$ edges, and $F$ faces. We're told that $F=20$. Each triangle has 3 edges, and every edge is common to 2 triangles, so $E=\frac{3(20)}{2}=30$. Additionally, each triangle has 3 vertices, so if every vertex is common to $n$ triangles, then $V=\frac{3(20)}{n}=\frac{60}{n}$. Plugging this into the formula, we have $\frac{60}{n}-30+20=2$, so $\frac{60}{n}=12$ and $n=5$. Again this shows that the rotation is $\frac{360^{\circ}}{5}=72^{\circ}$
|
72^{\circ}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
An icosahedron is a regular polyhedron with twenty faces, all of which are equilateral triangles. If an icosahedron is rotated by $\theta$ degrees around an axis that passes through two opposite vertices so that it occupies exactly the same region of space as before, what is the smallest possible positive value of $\theta$ ?
|
$72^{\circ}$ Because this polyhedron is regular, all vertices must look the same. Let's consider just one vertex. Each triangle has a vertex angle of $60^{\circ}$, so we must have fewer than 6 triangles; if we had 6 , there would be $360^{\circ}$ at each vertex and you wouldn't be able to "fold" the polyhedron up (that is, it would be a flat plane). It's easy to see that we need at least 3 triangles at each vertex, and this gives a triangular pyramid with only 4 faces. Having 4 triangles meeting at each vertex gives an octahedron (two square pyramids with the squares glued together) with 8 faces. Therefore, an icosahedron has 5 triangles meeting at each vertex, so rotating by $\frac{360^{\circ}}{5}=72^{\circ}$ gives another identical icosahedron.
Alternate solution: Euler's formula tells us that $V-E+F=2$, where an icosahedron has $V$ vertices, $E$ edges, and $F$ faces. We're told that $F=20$. Each triangle has 3 edges, and every edge is common to 2 triangles, so $E=\frac{3(20)}{2}=30$. Additionally, each triangle has 3 vertices, so if every vertex is common to $n$ triangles, then $V=\frac{3(20)}{n}=\frac{60}{n}$. Plugging this into the formula, we have $\frac{60}{n}-30+20=2$, so $\frac{60}{n}=12$ and $n=5$. Again this shows that the rotation is $\frac{360^{\circ}}{5}=72^{\circ}$
|
{
"exam": "HMMT",
"problem_label": "5",
"problem_match": "\n5. [6]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
How many ordered pairs $(S, T)$ of subsets of $\{1,2,3,4,5,6,7,8,9,10\}$ are there whose union contains exactly three elements?
|
3240 Let the three elements in the union be $a, b$, and $c$. We know that $a$ can be only in $S$, only in $T$, or both, so there are 3 possibilities for placing it. (Recall that $S=\{a\}, T=\{b, c\}$ is different from $S=\{b, c\}, T=\{a\}$ because $S$ and $T$ are an ordered pair.) Likewise for $b$ and $c$. The other 7 elements are in neither $S$ nor $T$, so there is only 1 possibility for placing them. This gives $3^{3}=27$ ways to pick $S$ and $T$ once you've picked the union. There are $\binom{10}{3}=120$ ways to pick the elements in the union, so we have $120 \times 27=3240$ ways total.
|
3240
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
How many ordered pairs $(S, T)$ of subsets of $\{1,2,3,4,5,6,7,8,9,10\}$ are there whose union contains exactly three elements?
|
3240 Let the three elements in the union be $a, b$, and $c$. We know that $a$ can be only in $S$, only in $T$, or both, so there are 3 possibilities for placing it. (Recall that $S=\{a\}, T=\{b, c\}$ is different from $S=\{b, c\}, T=\{a\}$ because $S$ and $T$ are an ordered pair.) Likewise for $b$ and $c$. The other 7 elements are in neither $S$ nor $T$, so there is only 1 possibility for placing them. This gives $3^{3}=27$ ways to pick $S$ and $T$ once you've picked the union. There are $\binom{10}{3}=120$ ways to pick the elements in the union, so we have $120 \times 27=3240$ ways total.
|
{
"exam": "HMMT",
"problem_label": "6",
"problem_match": "\n6. [6]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
Let $f(x, y)=x^{2}+2 x+y^{2}+4 y$. Let $\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right),\left(x_{3}, y_{3}\right)$, and $\left(x_{4}, y_{4}\right)$ be the vertices of a square with side length one and sides parallel to the coordinate axes. What is the minimum value of $f\left(x_{1}, y_{1}\right)+f\left(x_{2}, y_{2}\right)+f\left(x_{3}, y_{3}\right)+f\left(x_{4}, y_{4}\right) ?$
|
-18 The square's corners must be at $(x, y),(x+1, y),(x+1, y+1)$, and $(x, y+1)$ for some $x$ and $y$. So,
$$
\begin{aligned}
f\left(x_{1}, y_{1}\right) & +f\left(x_{2}, y_{2}\right)+f\left(x_{3}, y_{3}\right)+f\left(x_{4}, y_{4}\right) \\
& =2\left(x^{2}+2 x\right)+2\left((x+1)^{2}+2(x+1)\right)+2\left(y^{2}+4 y\right)+2\left((y+1)^{2}+4(y+1)\right) \\
& =4 x^{2}+12 x+6+4 y^{2}+20 y+10 \\
& =(2 x+3)^{2}-3+(2 y+5)^{2}-15 \\
& \geq-18
\end{aligned}
$$
This attains its minimum value of -18 when $x=-\frac{3}{2}$ and $y=-\frac{5}{2}$.
|
-18
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $f(x, y)=x^{2}+2 x+y^{2}+4 y$. Let $\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right),\left(x_{3}, y_{3}\right)$, and $\left(x_{4}, y_{4}\right)$ be the vertices of a square with side length one and sides parallel to the coordinate axes. What is the minimum value of $f\left(x_{1}, y_{1}\right)+f\left(x_{2}, y_{2}\right)+f\left(x_{3}, y_{3}\right)+f\left(x_{4}, y_{4}\right) ?$
|
-18 The square's corners must be at $(x, y),(x+1, y),(x+1, y+1)$, and $(x, y+1)$ for some $x$ and $y$. So,
$$
\begin{aligned}
f\left(x_{1}, y_{1}\right) & +f\left(x_{2}, y_{2}\right)+f\left(x_{3}, y_{3}\right)+f\left(x_{4}, y_{4}\right) \\
& =2\left(x^{2}+2 x\right)+2\left((x+1)^{2}+2(x+1)\right)+2\left(y^{2}+4 y\right)+2\left((y+1)^{2}+4(y+1)\right) \\
& =4 x^{2}+12 x+6+4 y^{2}+20 y+10 \\
& =(2 x+3)^{2}-3+(2 y+5)^{2}-15 \\
& \geq-18
\end{aligned}
$$
This attains its minimum value of -18 when $x=-\frac{3}{2}$ and $y=-\frac{5}{2}$.
|
{
"exam": "HMMT",
"problem_label": "7",
"problem_match": "\n7. [7]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
What is the sum of all four-digit numbers that are equal to the cube of the sum of their digits (leading zeros are not allowed)?
|
10745 We want to find all integers $x$ between 1000 and 9999 that are the cube of the sum of their digits. Of course, our search is only restricted to perfect cubes. The smallest such cube is $10^{3}=1000$ and the largest such cube is $21^{3}=9261$. This means we only have to check 12 different cubes, which is quite doable, but we can reduce the search even further with a little number theory.
Suppose we write our number as $x=1000 a+100 b+10 c+d$, where $a, b, c$, and $d$ are the decimal digits of $x$. Then we have
$$
(a+b+c+d)^{3} \equiv 1000 a+100 b+10 c+d \equiv a+b+c+d(\bmod 9)
$$
If we let $k=a+b+c+d$, then $k$ must be a solution to the modular equation $k^{3} \equiv k(\bmod 9)$. A quick check of the values 0 through 8 shows that the only solutions are 0,1 , and 8 .
Now, in our search, we only have to check values that are the cube of a number which is either 0 , 1 , or $8 \bmod 9$.
$$
\begin{aligned}
& 10^{3}=1000, \text { but } 1+0+0+0 \neq 10 \\
& 17^{3}=4913, \text { and } 4+9+1+3=17 \\
& 18^{3}=5832, \text { and } 5+8+3+2=18 \\
& 19^{3}=6859, \text { but } 6+8+5+9 \neq 19
\end{aligned}
$$
So the only solutions are 4913 and 5832, which sum to 10745 .
|
10745
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
What is the sum of all four-digit numbers that are equal to the cube of the sum of their digits (leading zeros are not allowed)?
|
10745 We want to find all integers $x$ between 1000 and 9999 that are the cube of the sum of their digits. Of course, our search is only restricted to perfect cubes. The smallest such cube is $10^{3}=1000$ and the largest such cube is $21^{3}=9261$. This means we only have to check 12 different cubes, which is quite doable, but we can reduce the search even further with a little number theory.
Suppose we write our number as $x=1000 a+100 b+10 c+d$, where $a, b, c$, and $d$ are the decimal digits of $x$. Then we have
$$
(a+b+c+d)^{3} \equiv 1000 a+100 b+10 c+d \equiv a+b+c+d(\bmod 9)
$$
If we let $k=a+b+c+d$, then $k$ must be a solution to the modular equation $k^{3} \equiv k(\bmod 9)$. A quick check of the values 0 through 8 shows that the only solutions are 0,1 , and 8 .
Now, in our search, we only have to check values that are the cube of a number which is either 0 , 1 , or $8 \bmod 9$.
$$
\begin{aligned}
& 10^{3}=1000, \text { but } 1+0+0+0 \neq 10 \\
& 17^{3}=4913, \text { and } 4+9+1+3=17 \\
& 18^{3}=5832, \text { and } 5+8+3+2=18 \\
& 19^{3}=6859, \text { but } 6+8+5+9 \neq 19
\end{aligned}
$$
So the only solutions are 4913 and 5832, which sum to 10745 .
|
{
"exam": "HMMT",
"problem_label": "8",
"problem_match": "\n8. [7]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
How many functions $f:\{1,2, \ldots, 10\} \rightarrow\{1,2, \ldots, 10\}$ satisfy the property that $f(i)+f(j)=11$ for all values of $i$ and $j$ such that $i+j=11$.
|
100000 To construct such a function $f$, we just need to choose a value for $f(x)$ from $\{1,2, \ldots, 10\}$ for each $x \in\{1,2, \ldots, 10\}$. But the condition that $f(i)+f(j)=11$ whenever $i+j=11$ means that
$$
\begin{aligned}
f(10) & =11-f(1) \\
f(9) & =11-f(2) \\
\vdots & \\
f(6) & =11-f(5)
\end{aligned}
$$
This means that once we have chosen $f(1), f(2), f(3), f(4)$, and $f(5)$, the five remaining values of $f(6), f(7), f(8), f(9)$, and $f(10)$ are already determined. The answer is therefore just the number of ways to choose these first five values. Since there are 10 possibilities for each one, we get that the answer is $10^{5}=100000$.
|
100000
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
How many functions $f:\{1,2, \ldots, 10\} \rightarrow\{1,2, \ldots, 10\}$ satisfy the property that $f(i)+f(j)=11$ for all values of $i$ and $j$ such that $i+j=11$.
|
100000 To construct such a function $f$, we just need to choose a value for $f(x)$ from $\{1,2, \ldots, 10\}$ for each $x \in\{1,2, \ldots, 10\}$. But the condition that $f(i)+f(j)=11$ whenever $i+j=11$ means that
$$
\begin{aligned}
f(10) & =11-f(1) \\
f(9) & =11-f(2) \\
\vdots & \\
f(6) & =11-f(5)
\end{aligned}
$$
This means that once we have chosen $f(1), f(2), f(3), f(4)$, and $f(5)$, the five remaining values of $f(6), f(7), f(8), f(9)$, and $f(10)$ are already determined. The answer is therefore just the number of ways to choose these first five values. Since there are 10 possibilities for each one, we get that the answer is $10^{5}=100000$.
|
{
"exam": "HMMT",
"problem_label": "9",
"problem_match": "\n9. [7]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
What is the smallest integer greater than 10 such that the sum of the digits in its base 17 representation is equal to the sum of the digits in its base 10 representation?
|
153 We assume that the answer is at most three digits (in base 10). Then our desired number can be expressed in the form $\overline{a b c}_{10}=\overline{d e f}_{17}$, where $a, b, c$ are digits in base 10 , and $d, e, f$ are digits in base 17 . These variables then satisfy the equations
$$
\begin{aligned}
100 a+10 b+c & =289 d+17 e+f \\
a+b+c & =d+e+f
\end{aligned}
$$
Subtracting the second equation from the first, we obtain $99 a+9 b=288 d+16 e$, or $9(11 a+b)=$ $16(18 d+e)$. From this equation, we find that $11 a+b$ must be divisible by 16 , and $18 d+e$ must be divisible by 9 . To minimize $\overline{a b c}$, we find the minimal possible value of $a$ : If $a=0$, then the only way for $11 a+b=b$ to be divisible by 16 is to set $b=0$; however, this is disallowed by the problem condition, which stipulates that the number must be greater than 10 . If we try $a=1$, then we find that the only possible value of $b$ which lets $11 a+b=b+11$ be divisible by 16 is $b=5$. Plugging these in and simplifying, we find that we must have $18 d+e=9$. The only possible solution to this is $d=0, e=9$. Now to satisfy $a+b+c=d+e+f$, we must have $1+5+c=0+9+f$, or $c=f+3$. The minimal possible solution to this is $c=3, f=0$. So our answer is $\overline{a b c}=153$, which is also equal to $090_{17}$.
|
153
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
What is the smallest integer greater than 10 such that the sum of the digits in its base 17 representation is equal to the sum of the digits in its base 10 representation?
|
153 We assume that the answer is at most three digits (in base 10). Then our desired number can be expressed in the form $\overline{a b c}_{10}=\overline{d e f}_{17}$, where $a, b, c$ are digits in base 10 , and $d, e, f$ are digits in base 17 . These variables then satisfy the equations
$$
\begin{aligned}
100 a+10 b+c & =289 d+17 e+f \\
a+b+c & =d+e+f
\end{aligned}
$$
Subtracting the second equation from the first, we obtain $99 a+9 b=288 d+16 e$, or $9(11 a+b)=$ $16(18 d+e)$. From this equation, we find that $11 a+b$ must be divisible by 16 , and $18 d+e$ must be divisible by 9 . To minimize $\overline{a b c}$, we find the minimal possible value of $a$ : If $a=0$, then the only way for $11 a+b=b$ to be divisible by 16 is to set $b=0$; however, this is disallowed by the problem condition, which stipulates that the number must be greater than 10 . If we try $a=1$, then we find that the only possible value of $b$ which lets $11 a+b=b+11$ be divisible by 16 is $b=5$. Plugging these in and simplifying, we find that we must have $18 d+e=9$. The only possible solution to this is $d=0, e=9$. Now to satisfy $a+b+c=d+e+f$, we must have $1+5+c=0+9+f$, or $c=f+3$. The minimal possible solution to this is $c=3, f=0$. So our answer is $\overline{a b c}=153$, which is also equal to $090_{17}$.
|
{
"exam": "HMMT",
"problem_label": "10",
"problem_match": "\n10. [8]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
How many nondecreasing sequences $a_{1}, a_{2}, \ldots, a_{10}$ are composed entirely of at most three distinct numbers from the set $\{1,2, \ldots, 9\}$ (so $1,1,1,2,2,2,3,3,3,3$ and $2,2,2,2,5,5,5,5,5,5$ are both allowed)?
|
3357 From any sequence $a_{1}, a_{2}, \ldots, a_{10}$, construct a sequence $b_{1}, b_{2}, \ldots, b_{9}$, where $b_{i}$ counts the number of times $i$ occurs in the sequence. There is a correspondence from all possible sequences $b_{1}, b_{2}, \ldots, b_{9}$ with at most 3 nonzero terms which add to 10 , since any sequence of $a_{1}, a_{2}, \ldots, a_{10}$ will be converted to this form, and from any sequence $b_{1}, b_{2}, \ldots, b_{9}$, we can construct a unique sequence of $a$-s by listing $i b_{i}$ times (for $1 \leq i \leq 9$ ) in nondecreasing order.
Our goal now is to count the number of possible sequences $b_{1}, b_{2}, \ldots, b_{9}$ meeting our conditions. We casework on the number of nonzero terms in the sequence:
Case 1: The sequence has exactly one nonzero term.
Then exactly one of $b_{1}, b_{2}, \ldots, b_{9}$ is equal to 10 , and all the rest are equal to 0 . This gives us 9 possible sequences in this case.
Case 2: The sequence has exactly two nonzero terms.
There are $\binom{9}{2}=36$ ways to choose the two terms $b_{i}, b_{j}(i<j)$ which are nonzero. From here, we have 9 choices for the value of $b_{i}$, namely 1 through 9 (since both $b_{i}$ and $b_{j}$ must be nonzero), and $b_{j}$ will be fixed, so this case gives us $36 \cdot 9=324$ possible sequences.
Case 3: The sequence has exactly three nonzero terms.
There are $\binom{9}{3}=84$ ways to choose the three terms $b_{i}, b_{j}, b_{k}(i<j<k)$ which are nonzero. Letting
$c_{i}=b_{i}-1, c_{j}=b_{j}-1, c_{k}=b_{k}-1$, we have that $c_{i}, c_{j}, c_{k}$ are nonnegative integers which sum to 7 . There are $\binom{9}{2}=36$ solutions to this equation (consider placing two dividers in the nine spaces between the ten elements), giving $84 \cdot 36=3024$ possbilities in this case.
We then have $9+324+3024=3357$ possible sequences.
|
3357
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
How many nondecreasing sequences $a_{1}, a_{2}, \ldots, a_{10}$ are composed entirely of at most three distinct numbers from the set $\{1,2, \ldots, 9\}$ (so $1,1,1,2,2,2,3,3,3,3$ and $2,2,2,2,5,5,5,5,5,5$ are both allowed)?
|
3357 From any sequence $a_{1}, a_{2}, \ldots, a_{10}$, construct a sequence $b_{1}, b_{2}, \ldots, b_{9}$, where $b_{i}$ counts the number of times $i$ occurs in the sequence. There is a correspondence from all possible sequences $b_{1}, b_{2}, \ldots, b_{9}$ with at most 3 nonzero terms which add to 10 , since any sequence of $a_{1}, a_{2}, \ldots, a_{10}$ will be converted to this form, and from any sequence $b_{1}, b_{2}, \ldots, b_{9}$, we can construct a unique sequence of $a$-s by listing $i b_{i}$ times (for $1 \leq i \leq 9$ ) in nondecreasing order.
Our goal now is to count the number of possible sequences $b_{1}, b_{2}, \ldots, b_{9}$ meeting our conditions. We casework on the number of nonzero terms in the sequence:
Case 1: The sequence has exactly one nonzero term.
Then exactly one of $b_{1}, b_{2}, \ldots, b_{9}$ is equal to 10 , and all the rest are equal to 0 . This gives us 9 possible sequences in this case.
Case 2: The sequence has exactly two nonzero terms.
There are $\binom{9}{2}=36$ ways to choose the two terms $b_{i}, b_{j}(i<j)$ which are nonzero. From here, we have 9 choices for the value of $b_{i}$, namely 1 through 9 (since both $b_{i}$ and $b_{j}$ must be nonzero), and $b_{j}$ will be fixed, so this case gives us $36 \cdot 9=324$ possible sequences.
Case 3: The sequence has exactly three nonzero terms.
There are $\binom{9}{3}=84$ ways to choose the three terms $b_{i}, b_{j}, b_{k}(i<j<k)$ which are nonzero. Letting
$c_{i}=b_{i}-1, c_{j}=b_{j}-1, c_{k}=b_{k}-1$, we have that $c_{i}, c_{j}, c_{k}$ are nonnegative integers which sum to 7 . There are $\binom{9}{2}=36$ solutions to this equation (consider placing two dividers in the nine spaces between the ten elements), giving $84 \cdot 36=3024$ possbilities in this case.
We then have $9+324+3024=3357$ possible sequences.
|
{
"exam": "HMMT",
"problem_label": "11",
"problem_match": "\n11. [8]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
An ant starts at the origin of a coordinate plane. Each minute, it either walks one unit to the right or one unit up, but it will never move in the same direction more than twice in the row. In how many different ways can it get to the point $(5,5)$ ?
|
84 We can change the ant's sequence of moves to a sequence $a_{1}, a_{2}, \ldots, a_{10}$, with $a_{i}=0$ if the $i$-th step is up, and $a_{i}=1$ if the $i$-th step is right. We define a subsequence of moves $a_{i}, a_{i+1}, \ldots, a_{j}$, ( $i \leq j$ ) as an up run if all terms of the subsequence are equal to 0 , and $a_{i-1}$ and $a_{j+1}$ either do not exist or are not equal to 0 , and define a right run similarly. In a sequence of moves, up runs and right runs alternate, so the number of up rights can differ from the number of right runs by at most one.
Now let $f(n)$ denote the number of sequences $a_{1}, a_{2}, \ldots, a_{n}$ where $a_{i} \in\{1,2\}$ for $1 \leq i \leq n$, and $a_{1}+a_{2}+\cdots+a_{n}=5$. (In essence, we are splitting the possible 5 up moves into up runs, and we are doing the same with the right moves). We can easily compute that $f(3)=3, f(4)=4, f(5)=1$, and $f(n)=0$ otherwise.
For each possible pair of numbers of up runs and right runs, we have two choices of which type of run is first. Our answer is then $2\left(f(3)^{2}+f(3) f(4)+f(4)^{2}+f(4) f(5)+f(5)^{2}\right)=2(9+12+16+4+1)=84$.
|
84
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
An ant starts at the origin of a coordinate plane. Each minute, it either walks one unit to the right or one unit up, but it will never move in the same direction more than twice in the row. In how many different ways can it get to the point $(5,5)$ ?
|
84 We can change the ant's sequence of moves to a sequence $a_{1}, a_{2}, \ldots, a_{10}$, with $a_{i}=0$ if the $i$-th step is up, and $a_{i}=1$ if the $i$-th step is right. We define a subsequence of moves $a_{i}, a_{i+1}, \ldots, a_{j}$, ( $i \leq j$ ) as an up run if all terms of the subsequence are equal to 0 , and $a_{i-1}$ and $a_{j+1}$ either do not exist or are not equal to 0 , and define a right run similarly. In a sequence of moves, up runs and right runs alternate, so the number of up rights can differ from the number of right runs by at most one.
Now let $f(n)$ denote the number of sequences $a_{1}, a_{2}, \ldots, a_{n}$ where $a_{i} \in\{1,2\}$ for $1 \leq i \leq n$, and $a_{1}+a_{2}+\cdots+a_{n}=5$. (In essence, we are splitting the possible 5 up moves into up runs, and we are doing the same with the right moves). We can easily compute that $f(3)=3, f(4)=4, f(5)=1$, and $f(n)=0$ otherwise.
For each possible pair of numbers of up runs and right runs, we have two choices of which type of run is first. Our answer is then $2\left(f(3)^{2}+f(3) f(4)+f(4)^{2}+f(4) f(5)+f(5)^{2}\right)=2(9+12+16+4+1)=84$.
|
{
"exam": "HMMT",
"problem_label": "12",
"problem_match": "\n12. $[\\mathbf{8}]$",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
How many sequences of ten binary digits are there in which neither two zeroes nor three ones ever appear in a row?
|
28 Let $a_{n}$ be the number of binary sequences of length $n$ satisfying the conditions and ending in 0 , let $b_{n}$ be the number ending in 01, and let $c_{n}$ be the number ending in 11. From the legal sequences of length $201,11,10$, we find that $a_{2}=b_{2}=c_{2}=1$. We now establish a recursion by building sequences of length $n+1$ from sequences of length $n$. We can add a 0 to a sequence of length $n$ if and only if it ended with a 1 , so $a_{n+1}=b_{n}+c_{n}$. We can have a sequence of length $n+1$ ending with 01 only by adding a 1 to a sequence of length $n$ ending in 0 , so $b_{n+1}=a_{n}$. We can have a sequence of length $n+1$ ending with 11 only by adding a 1 to a sequence of length $n$ ending in 01 , so $c_{n+1}=b_{n}$. We can now run the recursion:
| $n$ | $a_{n}$ | $b_{n}$ | $c_{n}$ |
| :---: | :---: | :---: | :---: |
| 2 | 1 | 1 | 1 |
| 3 | 2 | 1 | 1 |
| 4 | 2 | 2 | 1 |
| 5 | 3 | 2 | 2 |
| 6 | 4 | 3 | 2 |
| 7 | 5 | 4 | 3 |
| 8 | 7 | 5 | 4 |
| 9 | 9 | 7 | 5 |
| 10 | 12 | 9 | 7 |
Our answer is then $12+9+7=28$.
|
28
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
How many sequences of ten binary digits are there in which neither two zeroes nor three ones ever appear in a row?
|
28 Let $a_{n}$ be the number of binary sequences of length $n$ satisfying the conditions and ending in 0 , let $b_{n}$ be the number ending in 01, and let $c_{n}$ be the number ending in 11. From the legal sequences of length $201,11,10$, we find that $a_{2}=b_{2}=c_{2}=1$. We now establish a recursion by building sequences of length $n+1$ from sequences of length $n$. We can add a 0 to a sequence of length $n$ if and only if it ended with a 1 , so $a_{n+1}=b_{n}+c_{n}$. We can have a sequence of length $n+1$ ending with 01 only by adding a 1 to a sequence of length $n$ ending in 0 , so $b_{n+1}=a_{n}$. We can have a sequence of length $n+1$ ending with 11 only by adding a 1 to a sequence of length $n$ ending in 01 , so $c_{n+1}=b_{n}$. We can now run the recursion:
| $n$ | $a_{n}$ | $b_{n}$ | $c_{n}$ |
| :---: | :---: | :---: | :---: |
| 2 | 1 | 1 | 1 |
| 3 | 2 | 1 | 1 |
| 4 | 2 | 2 | 1 |
| 5 | 3 | 2 | 2 |
| 6 | 4 | 3 | 2 |
| 7 | 5 | 4 | 3 |
| 8 | 7 | 5 | 4 |
| 9 | 9 | 7 | 5 |
| 10 | 12 | 9 | 7 |
Our answer is then $12+9+7=28$.
|
{
"exam": "HMMT",
"problem_label": "13",
"problem_match": "\n13. [8]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
The positive integer $i$ is chosen at random such that the probability of a positive integer $k$ being chosen is $\frac{3}{2}$ times the probability of $k+1$ being chosen. What is the probability that the $i^{\text {th }}$ digit after the decimal point of the decimal expansion of $\frac{1}{7}$ is a 2 ?
|
$\frac{108}{665}$ First we note that the probability that $n$ is picked is $\frac{1}{2} \times\left(\frac{2}{3}\right)^{n}$, because this is the sequence whose terms decrease by a factor of $\frac{2}{3}$ each time and whose sum is 1 (recall that probabilities must sum to 1).
Now note that $\frac{1}{7}=.142857142857 \ldots$, meaning that 2 occurs at digits $3,9,15,21$, etc. We can then calculate the probability that we ever pick 2 as
$$
\begin{aligned}
\sum_{k=0}^{\infty} \frac{1}{2} \cdot\left(\frac{2}{3}\right)^{6 k+3} & =\frac{4}{27} \sum_{k=0}^{\infty}\left(\frac{2}{3}\right)^{6 k} \\
& =\frac{4}{27} \cdot \frac{1}{1-\left(\frac{2}{3}\right)^{6}} \\
& =\frac{4}{27} \cdot \frac{729}{729-64} \\
& =\frac{4}{27} \cdot \frac{729}{665} \\
& =\frac{108}{665}
\end{aligned}
$$
|
\frac{108}{665}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
The positive integer $i$ is chosen at random such that the probability of a positive integer $k$ being chosen is $\frac{3}{2}$ times the probability of $k+1$ being chosen. What is the probability that the $i^{\text {th }}$ digit after the decimal point of the decimal expansion of $\frac{1}{7}$ is a 2 ?
|
$\frac{108}{665}$ First we note that the probability that $n$ is picked is $\frac{1}{2} \times\left(\frac{2}{3}\right)^{n}$, because this is the sequence whose terms decrease by a factor of $\frac{2}{3}$ each time and whose sum is 1 (recall that probabilities must sum to 1).
Now note that $\frac{1}{7}=.142857142857 \ldots$, meaning that 2 occurs at digits $3,9,15,21$, etc. We can then calculate the probability that we ever pick 2 as
$$
\begin{aligned}
\sum_{k=0}^{\infty} \frac{1}{2} \cdot\left(\frac{2}{3}\right)^{6 k+3} & =\frac{4}{27} \sum_{k=0}^{\infty}\left(\frac{2}{3}\right)^{6 k} \\
& =\frac{4}{27} \cdot \frac{1}{1-\left(\frac{2}{3}\right)^{6}} \\
& =\frac{4}{27} \cdot \frac{729}{729-64} \\
& =\frac{4}{27} \cdot \frac{729}{665} \\
& =\frac{108}{665}
\end{aligned}
$$
|
{
"exam": "HMMT",
"problem_label": "14",
"problem_match": "\n14. [8]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
Distinct points $A, B, C, D$ are given such that triangles $A B C$ and $A B D$ are equilateral and both are of side length 10 . Point $E$ lies inside triangle $A B C$ such that $E A=8$ and $E B=3$, and point $F$ lies inside triangle $A B D$ such that $F D=8$ and $F B=3$. What is the area of quadrilateral $A E F D$ ?
|
$\frac{\frac{91 \sqrt{3}}{4}}{}$ Since $A E B \cong D F B$, we have $\angle E B A=\angle F B D$. Thus, $\angle E B F=\angle E B A+\angle A B F=$ $\angle F B D+\angle A B F=\angle A B D=60^{\circ}$. Since $E B=B F=3$, this means that $E B F$ is an equilateral triangle of side length 3. Now we have $[A E F D]=[A E B D]-[E B F]-[F B D]=[A E B]+[A B D]-[E B F]-$ $[F B D]=[A B D]-[E B F]=\frac{\sqrt{3}}{4}\left(10^{2}-3^{2}\right)=\frac{91 \sqrt{3}}{4}$.
|
\frac{91 \sqrt{3}}{4}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Distinct points $A, B, C, D$ are given such that triangles $A B C$ and $A B D$ are equilateral and both are of side length 10 . Point $E$ lies inside triangle $A B C$ such that $E A=8$ and $E B=3$, and point $F$ lies inside triangle $A B D$ such that $F D=8$ and $F B=3$. What is the area of quadrilateral $A E F D$ ?
|
$\frac{\frac{91 \sqrt{3}}{4}}{}$ Since $A E B \cong D F B$, we have $\angle E B A=\angle F B D$. Thus, $\angle E B F=\angle E B A+\angle A B F=$ $\angle F B D+\angle A B F=\angle A B D=60^{\circ}$. Since $E B=B F=3$, this means that $E B F$ is an equilateral triangle of side length 3. Now we have $[A E F D]=[A E B D]-[E B F]-[F B D]=[A E B]+[A B D]-[E B F]-$ $[F B D]=[A B D]-[E B F]=\frac{\sqrt{3}}{4}\left(10^{2}-3^{2}\right)=\frac{91 \sqrt{3}}{4}$.
|
{
"exam": "HMMT",
"problem_label": "15",
"problem_match": "\n15. [8]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
Triangle $A B C$ is given in the plane. Let $A D$ be the angle bisector of $\angle B A C$; let $B E$ be the altitude from $B$ to $A D$, and let $F$ be the midpoint of $A B$. Given that $A B=28, B C=33, C A=37$, what is the length of $E F$ ?
|
$14 \triangle A B E$ is a right triangle, and $F$ is the midpoint of the hypotenuse (and therefore the circumcenter), so $E F=B F=A F=14$.
|
14
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Triangle $A B C$ is given in the plane. Let $A D$ be the angle bisector of $\angle B A C$; let $B E$ be the altitude from $B$ to $A D$, and let $F$ be the midpoint of $A B$. Given that $A B=28, B C=33, C A=37$, what is the length of $E F$ ?
|
$14 \triangle A B E$ is a right triangle, and $F$ is the midpoint of the hypotenuse (and therefore the circumcenter), so $E F=B F=A F=14$.
|
{
"exam": "HMMT",
"problem_label": "16",
"problem_match": "\n16. [9]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
A triangle with side lengths $5,7,8$ is inscribed in a circle $C$. The diameters of $C$ parallel to the sides of lengths 5 and 8 divide $C$ into four sectors. What is the area of either of the two smaller ones?
|
$\sqrt{\frac{49}{18} \pi}$ Let $\triangle P Q R$ have sides $p=7, q=5, r=8$. Of the four sectors determined by the diameters of $C$ that are parallel to $P Q$ and $P R$, two have angles equal to $P$ and the other two have angles equal to $\pi-P$. We first find $P$ using the law of cosines: $49=25+64-2(5)(8) \cos P$ implies $\cos P=\frac{1}{2}$ implies $P=\frac{\pi}{3}$. Thus the two smaller sectors will have angle $\frac{\pi}{3}$. Next we find the circumradius of $\triangle P Q R$ using the formula $R=\frac{p q r}{4[P Q R]}$, where $[P Q R]$ is the area of $\triangle P Q R$. By Heron's Formula we have $[P Q R]=\sqrt{10(5)(3)(2)}=10 \sqrt{3}$; thus $R=\frac{5 \cdot 7 \cdot 8}{4(10 \sqrt{3})}=\frac{7}{\sqrt{3}}$. The area of a smaller sector is thus $\frac{\pi / 3}{2 \pi}\left(\pi R^{2}\right)=\frac{\pi}{6}\left(\frac{7}{\sqrt{3}}\right)^{2}=\frac{49}{18} \pi$
|
\frac{49}{18} \pi
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A triangle with side lengths $5,7,8$ is inscribed in a circle $C$. The diameters of $C$ parallel to the sides of lengths 5 and 8 divide $C$ into four sectors. What is the area of either of the two smaller ones?
|
$\sqrt{\frac{49}{18} \pi}$ Let $\triangle P Q R$ have sides $p=7, q=5, r=8$. Of the four sectors determined by the diameters of $C$ that are parallel to $P Q$ and $P R$, two have angles equal to $P$ and the other two have angles equal to $\pi-P$. We first find $P$ using the law of cosines: $49=25+64-2(5)(8) \cos P$ implies $\cos P=\frac{1}{2}$ implies $P=\frac{\pi}{3}$. Thus the two smaller sectors will have angle $\frac{\pi}{3}$. Next we find the circumradius of $\triangle P Q R$ using the formula $R=\frac{p q r}{4[P Q R]}$, where $[P Q R]$ is the area of $\triangle P Q R$. By Heron's Formula we have $[P Q R]=\sqrt{10(5)(3)(2)}=10 \sqrt{3}$; thus $R=\frac{5 \cdot 7 \cdot 8}{4(10 \sqrt{3})}=\frac{7}{\sqrt{3}}$. The area of a smaller sector is thus $\frac{\pi / 3}{2 \pi}\left(\pi R^{2}\right)=\frac{\pi}{6}\left(\frac{7}{\sqrt{3}}\right)^{2}=\frac{49}{18} \pi$
|
{
"exam": "HMMT",
"problem_label": "17",
"problem_match": "\n17. [9]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
Jeff has a 50 point quiz at 11 am . He wakes up at a random time between 10 am and noon, then arrives at class 15 minutes later. If he arrives on time, he will get a perfect score, but if he arrives more than 30 minutes after the quiz starts, he will get a 0 , but otherwise, he loses a point for each minute he's late (he can lose parts of one point if he arrives a nonintegral number of minutes late). What is Jeff's expected score on the quiz?
|
$\sqrt{\frac{55}{2}}$ If Jeff wakes up between 10:00 and 10:45, he gets 50. If he wakes up between 10:45 and 11:15, and he wakes up $k$ minutes after 10:45, then he gets $50-k$ points. Finally, if he wakes up between 11:15 and 12:00 he gets 0 points. So he has a $\frac{3}{8}$ probability of 50 , a $\frac{3}{8}$ probability of 0 , and a $\frac{1}{4}$ probability of a number chosen uniformly between 20 and 50 (for an average of 35). Thus his expected score is $\frac{3}{8} \times 50+\frac{1}{4} \times 35=\frac{75+35}{4}=\frac{110}{4}=\frac{55}{2}$.
|
\frac{55}{2}
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
Jeff has a 50 point quiz at 11 am . He wakes up at a random time between 10 am and noon, then arrives at class 15 minutes later. If he arrives on time, he will get a perfect score, but if he arrives more than 30 minutes after the quiz starts, he will get a 0 , but otherwise, he loses a point for each minute he's late (he can lose parts of one point if he arrives a nonintegral number of minutes late). What is Jeff's expected score on the quiz?
|
$\sqrt{\frac{55}{2}}$ If Jeff wakes up between 10:00 and 10:45, he gets 50. If he wakes up between 10:45 and 11:15, and he wakes up $k$ minutes after 10:45, then he gets $50-k$ points. Finally, if he wakes up between 11:15 and 12:00 he gets 0 points. So he has a $\frac{3}{8}$ probability of 50 , a $\frac{3}{8}$ probability of 0 , and a $\frac{1}{4}$ probability of a number chosen uniformly between 20 and 50 (for an average of 35). Thus his expected score is $\frac{3}{8} \times 50+\frac{1}{4} \times 35=\frac{75+35}{4}=\frac{110}{4}=\frac{55}{2}$.
|
{
"exam": "HMMT",
"problem_label": "18",
"problem_match": "\n18. [9]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
How many 8 -digit numbers begin with 1 , end with 3 , and have the property that each successive digit is either one more or two more than the previous digit, considering 0 to be one more than 9 ?
|
21 Given an 8-digit number $a$ that satifies the conditions in the problem, let $a_{i}$ denote the difference between its $(i+1)$ th and $i$ th digit. Since $i \in\{1,2\}$ for all $1 \leq i \leq 7$, we have $7 \leq$ $a_{1}+a_{2}+\cdots+a_{7} \leq 14$. The difference between the last digit and the first digit of $m$ is $3-1 \equiv 2$ (mod 10), which means $a_{1}+\cdots+a_{7}=12$. Thus, exactly five of the $a_{i}$ s equal to 2 and the remaining two equal to 1 . The number of permutations of five 2 s and two 1 s is $\binom{7}{2}=21$.
|
21
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
How many 8 -digit numbers begin with 1 , end with 3 , and have the property that each successive digit is either one more or two more than the previous digit, considering 0 to be one more than 9 ?
|
21 Given an 8-digit number $a$ that satifies the conditions in the problem, let $a_{i}$ denote the difference between its $(i+1)$ th and $i$ th digit. Since $i \in\{1,2\}$ for all $1 \leq i \leq 7$, we have $7 \leq$ $a_{1}+a_{2}+\cdots+a_{7} \leq 14$. The difference between the last digit and the first digit of $m$ is $3-1 \equiv 2$ (mod 10), which means $a_{1}+\cdots+a_{7}=12$. Thus, exactly five of the $a_{i}$ s equal to 2 and the remaining two equal to 1 . The number of permutations of five 2 s and two 1 s is $\binom{7}{2}=21$.
|
{
"exam": "HMMT",
"problem_label": "19",
"problem_match": "\n19. [11]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
Given a permutation $\pi$ of the set $\{1,2, \ldots, 10\}$, define a rotated cycle as a set of three integers $i, j, k$ such that $i<j<k$ and $\pi(j)<\pi(k)<\pi(i)$. What is the total number of rotated cycles over all permutations $\pi$ of the set $\{1,2, \ldots, 10\}$ ?
|
72576000 Let us consider a triple $(i, j, k)$ with $i<j<k$ and determine how many permutations rotate it. There are $\binom{10}{3}$ choices for the values of $\pi(i), \pi(j), \pi(k)$ and the choice of this set of three determines the values of $\pi(i), \pi(j), \pi(k)$. The other 7 values then have 7 ! ways to be arranged (any permutation of them will work), so exactly $\binom{10}{3} 7$ ! permutations rotate $(i, j, k)$. Therefore, as there are $\binom{10}{3}$ such triples, the total number of rotated triples is $\binom{10}{3}^{2} \cdot 7!=72576000$.
|
72576000
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Given a permutation $\pi$ of the set $\{1,2, \ldots, 10\}$, define a rotated cycle as a set of three integers $i, j, k$ such that $i<j<k$ and $\pi(j)<\pi(k)<\pi(i)$. What is the total number of rotated cycles over all permutations $\pi$ of the set $\{1,2, \ldots, 10\}$ ?
|
72576000 Let us consider a triple $(i, j, k)$ with $i<j<k$ and determine how many permutations rotate it. There are $\binom{10}{3}$ choices for the values of $\pi(i), \pi(j), \pi(k)$ and the choice of this set of three determines the values of $\pi(i), \pi(j), \pi(k)$. The other 7 values then have 7 ! ways to be arranged (any permutation of them will work), so exactly $\binom{10}{3} 7$ ! permutations rotate $(i, j, k)$. Therefore, as there are $\binom{10}{3}$ such triples, the total number of rotated triples is $\binom{10}{3}^{2} \cdot 7!=72576000$.
|
{
"exam": "HMMT",
"problem_label": "20",
"problem_match": "\n20. [11]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
George, Jeff, Brian, and Travis decide to play a game of hot potato. They begin by arranging themselves clockwise in a circle in that order. George and Jeff both start with a hot potato. On his turn, a player gives a hot potato (if he has one) to a randomly chosen player among the other three (if a player has two hot potatoes on his turn, he only passes one). If George goes first, and play proceedes clockwise, what is the probability that Travis has a hot potato after each player takes one turn?
|
| $\frac{5}{27}$ |
| :---: |
| Notice that Travis can only have the hot potato at the end if he has two potatoes | before his turn. A little bit of casework shows that this can only happen when
Case 1: George gives Travis his potato, while Jeff gives Brian his potato, which in then goes to Travis. The probability of this occuring is $\left(\frac{1}{3}\right)^{3}=\frac{1}{27}$
Case 2: George gives Travis his potato, while Jeff gives Travis his potato. The probability of this occuring is $\left(\frac{1}{3}\right)^{2}=\frac{1}{9}$
Case 3: George gives Brian his potato, Jeff gives Travis his potato, and then Brian gives Travis his potato. The probability of this occuring is $\frac{1}{27}$
Because these events are all disjoint, the probability that Travis ends up with the hot potato is $\frac{5}{27}$
|
\frac{5}{27}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
George, Jeff, Brian, and Travis decide to play a game of hot potato. They begin by arranging themselves clockwise in a circle in that order. George and Jeff both start with a hot potato. On his turn, a player gives a hot potato (if he has one) to a randomly chosen player among the other three (if a player has two hot potatoes on his turn, he only passes one). If George goes first, and play proceedes clockwise, what is the probability that Travis has a hot potato after each player takes one turn?
|
| $\frac{5}{27}$ |
| :---: |
| Notice that Travis can only have the hot potato at the end if he has two potatoes | before his turn. A little bit of casework shows that this can only happen when
Case 1: George gives Travis his potato, while Jeff gives Brian his potato, which in then goes to Travis. The probability of this occuring is $\left(\frac{1}{3}\right)^{3}=\frac{1}{27}$
Case 2: George gives Travis his potato, while Jeff gives Travis his potato. The probability of this occuring is $\left(\frac{1}{3}\right)^{2}=\frac{1}{9}$
Case 3: George gives Brian his potato, Jeff gives Travis his potato, and then Brian gives Travis his potato. The probability of this occuring is $\frac{1}{27}$
Because these events are all disjoint, the probability that Travis ends up with the hot potato is $\frac{5}{27}$
|
{
"exam": "HMMT",
"problem_label": "21",
"problem_match": "\n21. [11]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
Let $g_{1}(x)=\frac{1}{3}\left(1+x+x^{2}+\cdots\right)$ for all values of $x$ for which the right hand side converges. Let $g_{n}(x)=g_{1}\left(g_{n-1}(x)\right)$ for all integers $n \geq 2$. What is the largest integer $r$ such that $g_{r}(x)$ is defined for some real number $x$ ?
|
5 Notice that the series is geometric with ratio $x$, so it converges if $-1<x<1$. Also notice that where $g_{1}(x)$ is defined, it is equal to $\frac{1}{3(1-x)}$. The image of $g_{1}(x)$ is then the interval $\left(\frac{1}{6}, \infty\right)$. The image of $g_{2}(x)$ is simply the values of $g_{1}(x)$ for $x$ in $\left(\frac{1}{6}, 1\right)$, which is the interval $\left(\frac{2}{5}, \infty\right)$. Similarly, the image of $g_{3}(x)$ is $\left(\frac{5}{9}, \infty\right)$, the image of $g_{4}(x)$ is $\left(\frac{3}{4}, \infty\right)$, and the image of $g_{5}(x)$ is $\left(\frac{4}{3}, \infty\right)$. As this does not intersect the interval $(-1,1), g_{6}(x)$ is not defined for any $x$, so the answer is 5 .
|
5
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $g_{1}(x)=\frac{1}{3}\left(1+x+x^{2}+\cdots\right)$ for all values of $x$ for which the right hand side converges. Let $g_{n}(x)=g_{1}\left(g_{n-1}(x)\right)$ for all integers $n \geq 2$. What is the largest integer $r$ such that $g_{r}(x)$ is defined for some real number $x$ ?
|
5 Notice that the series is geometric with ratio $x$, so it converges if $-1<x<1$. Also notice that where $g_{1}(x)$ is defined, it is equal to $\frac{1}{3(1-x)}$. The image of $g_{1}(x)$ is then the interval $\left(\frac{1}{6}, \infty\right)$. The image of $g_{2}(x)$ is simply the values of $g_{1}(x)$ for $x$ in $\left(\frac{1}{6}, 1\right)$, which is the interval $\left(\frac{2}{5}, \infty\right)$. Similarly, the image of $g_{3}(x)$ is $\left(\frac{5}{9}, \infty\right)$, the image of $g_{4}(x)$ is $\left(\frac{3}{4}, \infty\right)$, and the image of $g_{5}(x)$ is $\left(\frac{4}{3}, \infty\right)$. As this does not intersect the interval $(-1,1), g_{6}(x)$ is not defined for any $x$, so the answer is 5 .
|
{
"exam": "HMMT",
"problem_label": "22",
"problem_match": "\n22. [12]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
Let $a_{1}, a_{2}, \ldots$ be an infinite sequence of positive integers such that for integers $n>2, a_{n}=$ $3 a_{n-1}-2 a_{n-2}$. How many such sequences $\left\{a_{n}\right\}$ are there such that $a_{2010} \leq 2^{2012}$ ?
|
$36 \cdot 2^{2009}+36$ Consider the characteristic polynomial for the recurrence $a_{n+2}-3 a_{n+1}+$ $2 a_{n}=0$, which is $x^{2}-3 x+2$. The roots are at 2 and 1 , so we know that numbers $a_{i}$ must be of the form $a_{i}=a 2^{i-1}+b$ for integers $a$ and $b$. Therefore $a_{2010}$ must equal to $a 2^{2009}+b$, where $a$ and $b$ are both integers. If the expression is always positive, it is sufficient to say $a_{1}$ is positive and $a$ is nonnegative, or $a+b>0$, and $a \geq 0$.
For a given value of $a, 1-a \leq b \leq 2^{2012}-a 2^{2009}$, so there are $2^{2012}-a 2^{2009}+a$ possible values of $b$ for each $a$ (where the quantity is positive). $a$ can take any value between 0 and $2^{3}$, we sum over all such a in this range, to attain $9 \cdot 2^{2012}-(1+2+3+4+5+6+7+8) 2^{2009}+(1+2+3+4+5+6+7+8)$, or $36\left(2^{2009}\right)+36$, which is our answer.
|
36 \cdot 2^{2009} + 36
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $a_{1}, a_{2}, \ldots$ be an infinite sequence of positive integers such that for integers $n>2, a_{n}=$ $3 a_{n-1}-2 a_{n-2}$. How many such sequences $\left\{a_{n}\right\}$ are there such that $a_{2010} \leq 2^{2012}$ ?
|
$36 \cdot 2^{2009}+36$ Consider the characteristic polynomial for the recurrence $a_{n+2}-3 a_{n+1}+$ $2 a_{n}=0$, which is $x^{2}-3 x+2$. The roots are at 2 and 1 , so we know that numbers $a_{i}$ must be of the form $a_{i}=a 2^{i-1}+b$ for integers $a$ and $b$. Therefore $a_{2010}$ must equal to $a 2^{2009}+b$, where $a$ and $b$ are both integers. If the expression is always positive, it is sufficient to say $a_{1}$ is positive and $a$ is nonnegative, or $a+b>0$, and $a \geq 0$.
For a given value of $a, 1-a \leq b \leq 2^{2012}-a 2^{2009}$, so there are $2^{2012}-a 2^{2009}+a$ possible values of $b$ for each $a$ (where the quantity is positive). $a$ can take any value between 0 and $2^{3}$, we sum over all such a in this range, to attain $9 \cdot 2^{2012}-(1+2+3+4+5+6+7+8) 2^{2009}+(1+2+3+4+5+6+7+8)$, or $36\left(2^{2009}\right)+36$, which is our answer.
|
{
"exam": "HMMT",
"problem_label": "23",
"problem_match": "\n23. [12]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
Let $P(x)$ be a polynomial of degree at most 3 such that $P(x)=\frac{1}{1+x+x^{2}}$ for $x=1,2,3,4$. What is $P(5)$ ?
|
$\frac{-3}{91}$ The forward difference of a polynomial $P$ is $\Delta P(x)=P(x+1)-P(x)$, which is a new polynomial with degree reduced by one. Therefore, if we apply this operation three times we'll get a constant function, and we can work back up to get a value of $P(5)$. Practically, we create the following table of differences:
$$
\begin{array}{ccccccc}
\frac{1}{3} & & \frac{1}{7} & & \frac{1}{13} & & \frac{1}{21} \\
& \frac{-4}{21} & & \frac{-6}{91} & & \frac{-8}{273} & \\
& \frac{34}{273} & & \frac{10}{273} & & \\
& & \frac{-24}{273} & & &
\end{array}
$$
Then extend it to be the following table:
So our answer is $\frac{-9}{273}=\frac{-3}{91}$
|
\frac{-3}{91}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $P(x)$ be a polynomial of degree at most 3 such that $P(x)=\frac{1}{1+x+x^{2}}$ for $x=1,2,3,4$. What is $P(5)$ ?
|
$\frac{-3}{91}$ The forward difference of a polynomial $P$ is $\Delta P(x)=P(x+1)-P(x)$, which is a new polynomial with degree reduced by one. Therefore, if we apply this operation three times we'll get a constant function, and we can work back up to get a value of $P(5)$. Practically, we create the following table of differences:
$$
\begin{array}{ccccccc}
\frac{1}{3} & & \frac{1}{7} & & \frac{1}{13} & & \frac{1}{21} \\
& \frac{-4}{21} & & \frac{-6}{91} & & \frac{-8}{273} & \\
& \frac{34}{273} & & \frac{10}{273} & & \\
& & \frac{-24}{273} & & &
\end{array}
$$
Then extend it to be the following table:
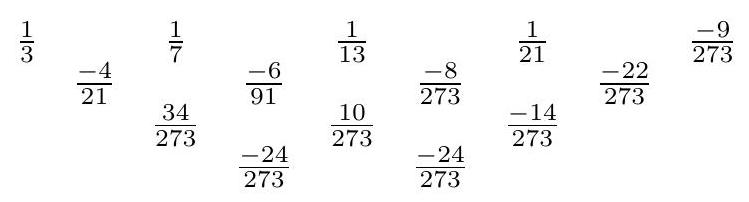
So our answer is $\frac{-9}{273}=\frac{-3}{91}$
|
{
"exam": "HMMT",
"problem_label": "24",
"problem_match": "\n24. [12]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
Triangle $A B C$ is given with $A B=13, B C=14, C A=15$. Let $E$ and $F$ be the feet of the altitudes from $B$ and $C$, respectively. Let $G$ be the foot of the altitude from $A$ in triangle $A F E$. Find $A G$.
|
| $\frac{396}{65}$ |
| :---: | By Heron's formula we have $[A B C]=\sqrt{21(8)(7)(6)}=84$. Let $D$ be the foot of the altitude from $A$ to $B C$; then $A D=2 \cdot \frac{84}{14}=12$. Notice that because $\angle B F C=\angle B E C, B F E C$ is cyclic, so $\angle A F E=90-\angle E F C=90-\angle E B C=\angle C$. Therefore, we have $\triangle A E F \sim \triangle A B C$, so $\frac{A G}{A D}=\frac{A E}{A B} ; \frac{1}{2}(B E)(A C)=84 \Longrightarrow B E=\frac{56}{5} \Longrightarrow A E=\sqrt{13^{2}-\left(\frac{56}{5}\right)^{2}}=\sqrt{\frac{65^{2}-56^{2}}{5^{2}}}=\frac{33}{5}$. Then $A G=A D \cdot \frac{A E}{A B}=12 \cdot \frac{33 / 5}{13}=\frac{396}{65}$.
|
\frac{396}{65}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Triangle $A B C$ is given with $A B=13, B C=14, C A=15$. Let $E$ and $F$ be the feet of the altitudes from $B$ and $C$, respectively. Let $G$ be the foot of the altitude from $A$ in triangle $A F E$. Find $A G$.
|
| $\frac{396}{65}$ |
| :---: | By Heron's formula we have $[A B C]=\sqrt{21(8)(7)(6)}=84$. Let $D$ be the foot of the altitude from $A$ to $B C$; then $A D=2 \cdot \frac{84}{14}=12$. Notice that because $\angle B F C=\angle B E C, B F E C$ is cyclic, so $\angle A F E=90-\angle E F C=90-\angle E B C=\angle C$. Therefore, we have $\triangle A E F \sim \triangle A B C$, so $\frac{A G}{A D}=\frac{A E}{A B} ; \frac{1}{2}(B E)(A C)=84 \Longrightarrow B E=\frac{56}{5} \Longrightarrow A E=\sqrt{13^{2}-\left(\frac{56}{5}\right)^{2}}=\sqrt{\frac{65^{2}-56^{2}}{5^{2}}}=\frac{33}{5}$. Then $A G=A D \cdot \frac{A E}{A B}=12 \cdot \frac{33 / 5}{13}=\frac{396}{65}$.
|
{
"exam": "HMMT",
"problem_label": "25",
"problem_match": "\n25. [14]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
$w, x, y, z$ are real numbers such that
$$
\begin{aligned}
w+x+y+z & =5 \\
2 w+4 x+8 y+16 z & =7 \\
3 w+9 x+27 y+81 z & =11 \\
4 w+16 x+64 y+256 z & =1
\end{aligned}
$$
What is the value of $5 w+25 x+125 y+625 z ?$
|
-60 We note this system of equations is equivalent to evaluating the polynomial (in $a$ ) $P(a)=w a+x a^{2}+y a^{3}+z a^{4}$ at $1,2,3$, and 4 . We know that $P(0)=0, P(1)=5, P(2)=7, P(3)=11$, $P(4)=1$. The finite difference of a polynomial $f$ is $f(n+1)-f(n)$, which is a polynomial with degree one less than the degree of $f$. The second, third, etc finite differences come from applying this operation repeatedly. The fourth finite difference of this polynomial is constant because this is a fourth degree polynomial. Repeatedly applying finite differences, we get

and we see that the fourth finite difference is -21 . We can extend this table, knowing that the fourth finite difference is always -21 , and we find that that $P(5)=-60$. The complete table is
| 0 | | 5 | | 7 | | 11 | | 1 | | -60 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| | 5 | 2 | | 4 | | -10 | | -61 | | |
| | | -3 | | 2 | | -14 | | -51 | | |
| | | 5 | | -16 | | -37 | | | | |
| | | | | -21 | | -21 | | | | |
|
-60
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
$w, x, y, z$ are real numbers such that
$$
\begin{aligned}
w+x+y+z & =5 \\
2 w+4 x+8 y+16 z & =7 \\
3 w+9 x+27 y+81 z & =11 \\
4 w+16 x+64 y+256 z & =1
\end{aligned}
$$
What is the value of $5 w+25 x+125 y+625 z ?$
|
-60 We note this system of equations is equivalent to evaluating the polynomial (in $a$ ) $P(a)=w a+x a^{2}+y a^{3}+z a^{4}$ at $1,2,3$, and 4 . We know that $P(0)=0, P(1)=5, P(2)=7, P(3)=11$, $P(4)=1$. The finite difference of a polynomial $f$ is $f(n+1)-f(n)$, which is a polynomial with degree one less than the degree of $f$. The second, third, etc finite differences come from applying this operation repeatedly. The fourth finite difference of this polynomial is constant because this is a fourth degree polynomial. Repeatedly applying finite differences, we get

and we see that the fourth finite difference is -21 . We can extend this table, knowing that the fourth finite difference is always -21 , and we find that that $P(5)=-60$. The complete table is
| 0 | | 5 | | 7 | | 11 | | 1 | | -60 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| | 5 | 2 | | 4 | | -10 | | -61 | | |
| | | -3 | | 2 | | -14 | | -51 | | |
| | | 5 | | -16 | | -37 | | | | |
| | | | | -21 | | -21 | | | | |
|
{
"exam": "HMMT",
"problem_label": "26",
"problem_match": "\n26. [14]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
Let $f(x)=-x^{2}+10 x-20$. Find the sum of all $2^{2010}$ solutions to $\underbrace{f(f(\ldots(x) \ldots))}_{2010 f \mathrm{~s}}=2$.
|
$5 \cdot 2^{2010}$ Define $g(x)=f(f(\ldots(x) \ldots))$. We calculate:
$f(10-x)=-(10-x)^{2}+10(10-x)-20=-100+20 x-x^{2}+100-10 x-20=-x^{2}+10 x-20=f(x)$.
This implies that $g(10-x)=g(x)$. So if $g(x)=2$, then $g(10-x)=2$. Moreover, we can calculate $f(5)=-25+50-20=5$, so $g(5)=5 \neq 2$. Thus the possible solutions to $g(x)=2$ can be grouped into pairs, $\left(x_{1}, 10-x_{1}\right),\left(x_{2}, 10-x_{2}\right), \ldots$ The sum of the members of each pair is 10 , and there are $2^{2009}$ pairs, so the sum is
$$
10 \cdot 2^{2009}=5 \cdot 2^{2010}
$$
|
5 \cdot 2^{2010}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $f(x)=-x^{2}+10 x-20$. Find the sum of all $2^{2010}$ solutions to $\underbrace{f(f(\ldots(x) \ldots))}_{2010 f \mathrm{~s}}=2$.
|
$5 \cdot 2^{2010}$ Define $g(x)=f(f(\ldots(x) \ldots))$. We calculate:
$f(10-x)=-(10-x)^{2}+10(10-x)-20=-100+20 x-x^{2}+100-10 x-20=-x^{2}+10 x-20=f(x)$.
This implies that $g(10-x)=g(x)$. So if $g(x)=2$, then $g(10-x)=2$. Moreover, we can calculate $f(5)=-25+50-20=5$, so $g(5)=5 \neq 2$. Thus the possible solutions to $g(x)=2$ can be grouped into pairs, $\left(x_{1}, 10-x_{1}\right),\left(x_{2}, 10-x_{2}\right), \ldots$ The sum of the members of each pair is 10 , and there are $2^{2009}$ pairs, so the sum is
$$
10 \cdot 2^{2009}=5 \cdot 2^{2010}
$$
|
{
"exam": "HMMT",
"problem_label": "27",
"problem_match": "\n27. [14]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
In the game of set, each card has four attributes, each of which takes on one of three values. A set deck consists of one card for each of the 81 possible four-tuples of attributes. Given a collection of 3 cards, call an attribute good for that collection if the three cards either all take on the same value of that attribute or take on all three different values of that attribute. Call a collection of 3 cards two-good if exactly two attributes are good for that collection. How many two-good collections of 3 cards are there? The order in which the cards appear does not matter.
|
25272 In counting the number of sets of 3 cards, we first want to choose which of our two attributes will be good and which of our two attributes will not be good. There are $\binom{4}{2}=6$ such choices.
Now consider the two attributes which are not good, attribute X and attribute Y. Since these are not good, some value should appear exactly twice. Suppose the value $a$ appears twice and $b$ appears once for attribute $X$ and that the value $c$ appears twice and $d$ appears once for attribute $Y$. There are three choices for $a$ and then two choices for $b$; similarly, there are three choices for $c$ and then two choices for $d$. This gives $3 \cdot 2 \cdot 3 \cdot 2=36$ choices of $a, b, c$, and $d$.
There are two cases to consider. The first is that there are two cards which both have $a$ and $c$, while the other card has both $b$ and $d$. The second case is that only one card has both $a$ and $c$, while one card has $a$ and $d$ and the other has $b$ and $c$.
Case 1:
| Card $1 \quad$ Card 2 | Card 3 | |
| :---: | :---: | :---: |
| - Good attribute 1 - | | |
| - Good attribute $2-$ | | |
| a | a | b |
| c | c | d |
The three cards need to be distinct. Card 3 is necessarily distinct from Card 1 and Card 2, but we need to ensure that Card 1 and Card 2 are distinct from each other. There are 9 choices for the two good attributes of Card 1, and then 8 choices for the two good attributes of Card 2. But we also want to divide by 2 since we do not care about the order of Card 1 and Card 2. So there are $\frac{9 \cdot 8}{2}=36$ choices for the good attributes on Card 1 and Card 2. Then, the values of the good attributes of Card 1 and Card 2 uniquely determine the values of the good attributes of Card 3.
Case 2:
Card 1 Card 2 Card 3
- Good attribute 1 -
- Good attribute 2 -
| $a$ | $a$ | $b$ |
| :--- | :--- | :--- |
| $c$ | $d$ | $c$ |
Card 1, Card 2, and Card 3 will all be distinct no matter what the values of the good attributes are, because the values of attributes $X$ and $Y$ are unique to each card. So there are 9 possibilities for the the values of the good attributes on card 1, and then there are 9 more possibilities for the values of the good attribute on Card 2. We do not have to divide by 2 this time, since Card 1 and Card 2 have distinct values in $X$ and $Y$. So there are $9^{2}=81$ possibilities here.
So our final answer is $6 \cdot 6^{2} \cdot(36+81)=25272$.
|
25272
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In the game of set, each card has four attributes, each of which takes on one of three values. A set deck consists of one card for each of the 81 possible four-tuples of attributes. Given a collection of 3 cards, call an attribute good for that collection if the three cards either all take on the same value of that attribute or take on all three different values of that attribute. Call a collection of 3 cards two-good if exactly two attributes are good for that collection. How many two-good collections of 3 cards are there? The order in which the cards appear does not matter.
|
25272 In counting the number of sets of 3 cards, we first want to choose which of our two attributes will be good and which of our two attributes will not be good. There are $\binom{4}{2}=6$ such choices.
Now consider the two attributes which are not good, attribute X and attribute Y. Since these are not good, some value should appear exactly twice. Suppose the value $a$ appears twice and $b$ appears once for attribute $X$ and that the value $c$ appears twice and $d$ appears once for attribute $Y$. There are three choices for $a$ and then two choices for $b$; similarly, there are three choices for $c$ and then two choices for $d$. This gives $3 \cdot 2 \cdot 3 \cdot 2=36$ choices of $a, b, c$, and $d$.
There are two cases to consider. The first is that there are two cards which both have $a$ and $c$, while the other card has both $b$ and $d$. The second case is that only one card has both $a$ and $c$, while one card has $a$ and $d$ and the other has $b$ and $c$.
Case 1:
| Card $1 \quad$ Card 2 | Card 3 | |
| :---: | :---: | :---: |
| - Good attribute 1 - | | |
| - Good attribute $2-$ | | |
| a | a | b |
| c | c | d |
The three cards need to be distinct. Card 3 is necessarily distinct from Card 1 and Card 2, but we need to ensure that Card 1 and Card 2 are distinct from each other. There are 9 choices for the two good attributes of Card 1, and then 8 choices for the two good attributes of Card 2. But we also want to divide by 2 since we do not care about the order of Card 1 and Card 2. So there are $\frac{9 \cdot 8}{2}=36$ choices for the good attributes on Card 1 and Card 2. Then, the values of the good attributes of Card 1 and Card 2 uniquely determine the values of the good attributes of Card 3.
Case 2:
Card 1 Card 2 Card 3
- Good attribute 1 -
- Good attribute 2 -
| $a$ | $a$ | $b$ |
| :--- | :--- | :--- |
| $c$ | $d$ | $c$ |
Card 1, Card 2, and Card 3 will all be distinct no matter what the values of the good attributes are, because the values of attributes $X$ and $Y$ are unique to each card. So there are 9 possibilities for the the values of the good attributes on card 1, and then there are 9 more possibilities for the values of the good attribute on Card 2. We do not have to divide by 2 this time, since Card 1 and Card 2 have distinct values in $X$ and $Y$. So there are $9^{2}=81$ possibilities here.
So our final answer is $6 \cdot 6^{2} \cdot(36+81)=25272$.
|
{
"exam": "HMMT",
"problem_label": "28",
"problem_match": "\n28. [17]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
In the game of Galactic Dominion, players compete to amass cards, each of which is worth a certain number of points. Say you are playing a version of this game with only two kinds of cards, planet cards and hegemon cards. Each planet card is worth 2010 points, and each hegemon card is worth four points per planet card held. You start with no planet cards and no hegemon cards, and, on each turn, starting at turn one, you take either a planet card or a hegemon card, whichever is worth more points given the hand you currently hold. Define a sequence $\left\{a_{n}\right\}$ for all positive integers $n$ by setting $a_{n}$ to be 0 if on turn $n$ you take a planet card and 1 if you take a hegemon card. What is the smallest value of $N$ such that the sequence $a_{N}, a_{N+1}, \ldots$ is necessarily periodic (meaning that there is a positive integer $k$ such that $a_{n+k}=a_{n}$ for all $\left.n \geq N\right)$ ?
|
503 If you have $P$ planets and $H$ hegemons, buying a planet gives you $2010+4 H$ points while buying a hegemon gives you $4 P$ points. Thus you buy a hegemon whenever $P-H \geq 502.5$, and you buy a planet whenever $P-H \leq 502.5$. Therefore $a_{i}=1$ for $1 \leq i \leq 503$. Starting at $i=504$ (at which point you have bought 503 planets) you must alternate buying planets and hegemons. The sequence $\left\{a_{i}\right\}_{i \geq 503}$ is periodic with period 2 .
|
503
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In the game of Galactic Dominion, players compete to amass cards, each of which is worth a certain number of points. Say you are playing a version of this game with only two kinds of cards, planet cards and hegemon cards. Each planet card is worth 2010 points, and each hegemon card is worth four points per planet card held. You start with no planet cards and no hegemon cards, and, on each turn, starting at turn one, you take either a planet card or a hegemon card, whichever is worth more points given the hand you currently hold. Define a sequence $\left\{a_{n}\right\}$ for all positive integers $n$ by setting $a_{n}$ to be 0 if on turn $n$ you take a planet card and 1 if you take a hegemon card. What is the smallest value of $N$ such that the sequence $a_{N}, a_{N+1}, \ldots$ is necessarily periodic (meaning that there is a positive integer $k$ such that $a_{n+k}=a_{n}$ for all $\left.n \geq N\right)$ ?
|
503 If you have $P$ planets and $H$ hegemons, buying a planet gives you $2010+4 H$ points while buying a hegemon gives you $4 P$ points. Thus you buy a hegemon whenever $P-H \geq 502.5$, and you buy a planet whenever $P-H \leq 502.5$. Therefore $a_{i}=1$ for $1 \leq i \leq 503$. Starting at $i=504$ (at which point you have bought 503 planets) you must alternate buying planets and hegemons. The sequence $\left\{a_{i}\right\}_{i \geq 503}$ is periodic with period 2 .
|
{
"exam": "HMMT",
"problem_label": "29",
"problem_match": "\n29. [17]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
In the game of projective set, each card contains some nonempty subset of six distinguishable dots. A projective set deck consists of one card for each of the 63 possible nonempty subsets of dots. How many collections of five cards have an even number of each dot? The order in which the cards appear does not matter.
|
109368 We'll first count sets of cards where the order does matter. Suppose we choose the first four cards. Then there is exactly one card that can make each dot appear twice. However, this card could be empty or it could be one of the cards we've already chosen, so we have to subtract for these two cases. First, there are $63 \cdot 62 \cdot 61 \cdot 60$ ways to choose the first four cards. Let's now count how many ways there are that the fifth card could be empty.
The fifth card is empty if and only if the first four cards already have an even number of each dot. Suppose we choose the first two cards. There is a possible fourth card if the third card is not either of the first two or the card that completes a set. If that is the case, then the fourth card is unique. This comes to $63 \cdot 62 \cdot 60$ cases.
Now consider how many ways there are for the fifth card to be a duplicate. This is just the number of ways for three cards to have an even number of each dot, then have two copies of the same card in the other two slots, one of which needs to be the fifth slot. The number of ways for three cards to have an even number of each dot is just the number of ways to choose two cards. Therefore, we'll choose two cards ( $63 \cdot 62$ ways), choose the slot in the first four positions for the duplicate card ( 4 ways), and the duplicate card, which can't be any of the nonduplicated cards, so there are 60 choices. Therefore, there are $63 \cdot 62 \cdot 4 \cdot 60$ ways for the fifth card to be the same as one of the first four.
This means that the number of five card sets where the order does matter is $63 \cdot 62 \cdot 61 \cdot 60-63 \cdot 62 \cdot 60-$ $63 \cdot 62 \cdot 4 \cdot 60$, so our final answer is $\frac{63 \cdot 62 \cdot 61 \cdot 60-63 \cdot 62 \cdot 60-63 \cdot 62 \cdot 4 \cdot 60}{120}=\frac{63 \cdot 62 \cdot(61-1-4)}{2}=63 \cdot 31 \cdot 56=109368$.
|
109368
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In the game of projective set, each card contains some nonempty subset of six distinguishable dots. A projective set deck consists of one card for each of the 63 possible nonempty subsets of dots. How many collections of five cards have an even number of each dot? The order in which the cards appear does not matter.
|
109368 We'll first count sets of cards where the order does matter. Suppose we choose the first four cards. Then there is exactly one card that can make each dot appear twice. However, this card could be empty or it could be one of the cards we've already chosen, so we have to subtract for these two cases. First, there are $63 \cdot 62 \cdot 61 \cdot 60$ ways to choose the first four cards. Let's now count how many ways there are that the fifth card could be empty.
The fifth card is empty if and only if the first four cards already have an even number of each dot. Suppose we choose the first two cards. There is a possible fourth card if the third card is not either of the first two or the card that completes a set. If that is the case, then the fourth card is unique. This comes to $63 \cdot 62 \cdot 60$ cases.
Now consider how many ways there are for the fifth card to be a duplicate. This is just the number of ways for three cards to have an even number of each dot, then have two copies of the same card in the other two slots, one of which needs to be the fifth slot. The number of ways for three cards to have an even number of each dot is just the number of ways to choose two cards. Therefore, we'll choose two cards ( $63 \cdot 62$ ways), choose the slot in the first four positions for the duplicate card ( 4 ways), and the duplicate card, which can't be any of the nonduplicated cards, so there are 60 choices. Therefore, there are $63 \cdot 62 \cdot 4 \cdot 60$ ways for the fifth card to be the same as one of the first four.
This means that the number of five card sets where the order does matter is $63 \cdot 62 \cdot 61 \cdot 60-63 \cdot 62 \cdot 60-$ $63 \cdot 62 \cdot 4 \cdot 60$, so our final answer is $\frac{63 \cdot 62 \cdot 61 \cdot 60-63 \cdot 62 \cdot 60-63 \cdot 62 \cdot 4 \cdot 60}{120}=\frac{63 \cdot 62 \cdot(61-1-4)}{2}=63 \cdot 31 \cdot 56=109368$.
|
{
"exam": "HMMT",
"problem_label": "30",
"problem_match": "\n30. [17]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
What is the perimeter of the triangle formed by the points of tangency of the incircle of a 5-7-8 triangle with its sides?
|
$\frac{9 \sqrt{21}}{7}+3$ Let $\triangle A B C$ be a triangle with sides $a=7, b=5$, and $c=8$. Let the incircle of $\triangle A B C$ be tangent to sides $B C, C A$, and $A B$ at points $D, E$, and $F$. By the law of cosines (using the form $\left.\cos (A)=\frac{b^{2}+c^{2}-a^{2}}{2 b c}\right)$, we have
$$
\begin{aligned}
& \cos (A)=\frac{8^{2}+5^{2}-7^{2}}{2(5)(8)}=\frac{1}{2} \\
& \cos (B)=\frac{8^{2}+7^{2}-5^{2}}{2(7)(8)}=\frac{11}{14} \\
& \cos (C)=\frac{5^{2}+7^{2}-8^{2}}{2(7)(5)}=\frac{1}{7}
\end{aligned}
$$
Now we observe that $A E F, B D F$, and $C D E$ are all isosceles. Let us call the lengths of the legs of these triangles $s, t$, and $u$, respectively. Then we know that $s+t=8, t+u=7$, and $u+s=5$, so $s=3, t=5$, and $u=2$.
Our final observation is that an isosceles angle with legs of length $l$ and whose non-equal angle is $\theta$ has a base of length $l \sqrt{2(1-\cos (\theta))}$. This can be proven using the law of cosines or the Pythagorean theorem.
Using this, we can calculate that
$$
\begin{aligned}
D E & =2 \sqrt{2(1-\cos (C))} \\
& =2 \sqrt{\frac{12}{7}} \\
E F & =3 \sqrt{2(1-\cos (A))} \\
& =3 \\
F D & =5 \sqrt{2(1-\cos (B))} \\
& =5 \sqrt{\frac{3}{7}}
\end{aligned}
$$
and then
$$
\begin{aligned}
D E+E F+F D & =2 \sqrt{\frac{12}{7}}+3+5 \sqrt{\frac{3}{7}} \\
& =3+9 \sqrt{\frac{3}{7}} \\
& =3+9 \frac{\sqrt{21}}{7}
\end{aligned}
$$
|
3+\frac{9\sqrt{21}}{7}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
What is the perimeter of the triangle formed by the points of tangency of the incircle of a 5-7-8 triangle with its sides?
|
$\frac{9 \sqrt{21}}{7}+3$ Let $\triangle A B C$ be a triangle with sides $a=7, b=5$, and $c=8$. Let the incircle of $\triangle A B C$ be tangent to sides $B C, C A$, and $A B$ at points $D, E$, and $F$. By the law of cosines (using the form $\left.\cos (A)=\frac{b^{2}+c^{2}-a^{2}}{2 b c}\right)$, we have
$$
\begin{aligned}
& \cos (A)=\frac{8^{2}+5^{2}-7^{2}}{2(5)(8)}=\frac{1}{2} \\
& \cos (B)=\frac{8^{2}+7^{2}-5^{2}}{2(7)(8)}=\frac{11}{14} \\
& \cos (C)=\frac{5^{2}+7^{2}-8^{2}}{2(7)(5)}=\frac{1}{7}
\end{aligned}
$$
Now we observe that $A E F, B D F$, and $C D E$ are all isosceles. Let us call the lengths of the legs of these triangles $s, t$, and $u$, respectively. Then we know that $s+t=8, t+u=7$, and $u+s=5$, so $s=3, t=5$, and $u=2$.
Our final observation is that an isosceles angle with legs of length $l$ and whose non-equal angle is $\theta$ has a base of length $l \sqrt{2(1-\cos (\theta))}$. This can be proven using the law of cosines or the Pythagorean theorem.
Using this, we can calculate that
$$
\begin{aligned}
D E & =2 \sqrt{2(1-\cos (C))} \\
& =2 \sqrt{\frac{12}{7}} \\
E F & =3 \sqrt{2(1-\cos (A))} \\
& =3 \\
F D & =5 \sqrt{2(1-\cos (B))} \\
& =5 \sqrt{\frac{3}{7}}
\end{aligned}
$$
and then
$$
\begin{aligned}
D E+E F+F D & =2 \sqrt{\frac{12}{7}}+3+5 \sqrt{\frac{3}{7}} \\
& =3+9 \sqrt{\frac{3}{7}} \\
& =3+9 \frac{\sqrt{21}}{7}
\end{aligned}
$$
|
{
"exam": "HMMT",
"problem_label": "31",
"problem_match": "\n31. [20]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
Let $T$ be the set of numbers of the form $2^{a} 3^{b}$ where $a$ and $b$ are integers satisfying $0 \leq a, b \leq 5$. How many subsets $S$ of $T$ have the property that if $n$ is in $S$ then all positive integer divisors of $n$ are in $S$ ?
|
924 Consider the correspondence $(a, b) \leftrightarrow 2^{a} 3^{b}$ for non-negative integers $a$ and $b$. So we can view $T$ as the square of lattice points $(a, b)$ where $0 \leq a, b \leq 5$, and subsets of $T$ as subsets of this square.
Notice then that the integer corresponding to $\left(a_{1}, b_{1}\right)$ is a divisor of the integer corresponding to $\left(a_{2}, b_{2}\right)$ if and only if $0 \leq a_{1} \leq a_{1}$ and $0 \leq b_{1} \leq b_{2}$. This means that subsets $S \subset T$ with the desired property,
correspond to subsets of the square where if a point is in the set, then so are all points to the left and south of it.
Consider any such subset $S$. For each $0 \leq x \leq 5$, let $S_{x}$ be the maximum $y$ value of any point $(x, y) \in S$, or -1 if there is no such point. We claim the values $S_{x}$ uniquely characterize $S$. This is because each $S_{x}$ characterizes the points of the form $(x, y)$ in $S$. In particular, $(x, z)$ will be in $S$ if and only if $z \leq S_{x}$. If $(x, z) \in S$ with $z>S_{x}$, then $S_{x}$ is not the maximum value, and if $(x, z) \notin S$ with $z \leq S_{x}$, then $S$ fails to satisfy the desired property.
We now claim that $S_{x} \geq S_{y}$ for $x<y$, so the sequence $S_{0}, \ldots, S_{1}$ is decreasing. This is because if $\left(y, S_{y}\right)$ is in the set $S$, then so must be $\left(x, S_{y}\right)$. Conversely, it is easy to see that if $S_{0}, \ldots, S_{1}$ is decreasing, then $S$ is a set satisfying the desired property.
We now claim that decreasing sequences $S_{0}, \ldots, S_{5}$ are in bijective correspondence with walks going only right and down from $(-1,5)$ to $(5,-1)$. The sequence $S_{0}, \ldots, S_{5}$ simply corresponds to the walk $(-1,5) \rightarrow\left(-1, S_{0}\right) \rightarrow\left(0, S_{0}\right) \rightarrow\left(0, S_{1}\right) \rightarrow\left(1, S_{1}\right) \rightarrow \cdots \rightarrow\left(4, S_{5}\right) \rightarrow\left(5, S_{5}\right) \rightarrow(5,-1)$. Geometrically, we are tracing out the outline of the set $S$.
The number of such walks is simply $\binom{12}{6}$, since we can view it as choosing the 6 of 12 steps at which to move right. Thus the number of subsets $S$ of $T$ with the desired property is $\binom{12}{6}=924$.
|
924
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $T$ be the set of numbers of the form $2^{a} 3^{b}$ where $a$ and $b$ are integers satisfying $0 \leq a, b \leq 5$. How many subsets $S$ of $T$ have the property that if $n$ is in $S$ then all positive integer divisors of $n$ are in $S$ ?
|
924 Consider the correspondence $(a, b) \leftrightarrow 2^{a} 3^{b}$ for non-negative integers $a$ and $b$. So we can view $T$ as the square of lattice points $(a, b)$ where $0 \leq a, b \leq 5$, and subsets of $T$ as subsets of this square.
Notice then that the integer corresponding to $\left(a_{1}, b_{1}\right)$ is a divisor of the integer corresponding to $\left(a_{2}, b_{2}\right)$ if and only if $0 \leq a_{1} \leq a_{1}$ and $0 \leq b_{1} \leq b_{2}$. This means that subsets $S \subset T$ with the desired property,
correspond to subsets of the square where if a point is in the set, then so are all points to the left and south of it.
Consider any such subset $S$. For each $0 \leq x \leq 5$, let $S_{x}$ be the maximum $y$ value of any point $(x, y) \in S$, or -1 if there is no such point. We claim the values $S_{x}$ uniquely characterize $S$. This is because each $S_{x}$ characterizes the points of the form $(x, y)$ in $S$. In particular, $(x, z)$ will be in $S$ if and only if $z \leq S_{x}$. If $(x, z) \in S$ with $z>S_{x}$, then $S_{x}$ is not the maximum value, and if $(x, z) \notin S$ with $z \leq S_{x}$, then $S$ fails to satisfy the desired property.
We now claim that $S_{x} \geq S_{y}$ for $x<y$, so the sequence $S_{0}, \ldots, S_{1}$ is decreasing. This is because if $\left(y, S_{y}\right)$ is in the set $S$, then so must be $\left(x, S_{y}\right)$. Conversely, it is easy to see that if $S_{0}, \ldots, S_{1}$ is decreasing, then $S$ is a set satisfying the desired property.
We now claim that decreasing sequences $S_{0}, \ldots, S_{5}$ are in bijective correspondence with walks going only right and down from $(-1,5)$ to $(5,-1)$. The sequence $S_{0}, \ldots, S_{5}$ simply corresponds to the walk $(-1,5) \rightarrow\left(-1, S_{0}\right) \rightarrow\left(0, S_{0}\right) \rightarrow\left(0, S_{1}\right) \rightarrow\left(1, S_{1}\right) \rightarrow \cdots \rightarrow\left(4, S_{5}\right) \rightarrow\left(5, S_{5}\right) \rightarrow(5,-1)$. Geometrically, we are tracing out the outline of the set $S$.
The number of such walks is simply $\binom{12}{6}$, since we can view it as choosing the 6 of 12 steps at which to move right. Thus the number of subsets $S$ of $T$ with the desired property is $\binom{12}{6}=924$.
|
{
"exam": "HMMT",
"problem_label": "32",
"problem_match": "\n32. [20]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
Convex quadrilateral $B C D E$ lies in the plane. Lines $E B$ and $D C$ intersect at $A$, with $A B=2$, $A C=5, A D=200, A E=500$, and $\cos \angle B A C=\frac{7}{9}$. What is the largest number of nonoverlapping circles that can lie in quadrilateral $B C D E$ such that all of them are tangent to both lines $B E$ and $C D$ ?
|
5 Let $\theta=\angle B A C$, and $\cos \theta=\frac{7}{9}$ implies $\cos \frac{\theta}{2}=\sqrt{\frac{1+\frac{7}{9}}{2}}=\frac{2 \sqrt{2}}{3} ; \sin \frac{\theta}{2}=\frac{1}{3} ; B C=$ $\sqrt{4+25-2(2)(5) \frac{7}{9}}=\frac{11}{3}$. Let $O_{1}$ be the excircle of $\triangle A B C$ tangent to lines $A B$ and $A C$, and let $r_{1}$ be its radius; let $O_{1}$ be tangent to line $A B$ at point $P_{1}$. Then $A P_{1}=\frac{A B+B C+C A}{2}$ and $\frac{r_{1}}{A P_{1}}=\tan \frac{\theta}{2}=$ $\frac{1}{2 \sqrt{2}} \Longrightarrow r_{1}=\frac{16}{3 \cdot 2 \sqrt{2}}$. Let $O_{n}$ be a circle tangent to $O_{n-1}$ and the lines $A B$ and $A C$, and let $r_{n}$ be its radius; let $O_{n}$ be tangent to line $A B$ at point $P_{n}$. Then $\frac{O_{n} P_{n}}{A O_{n}}=\sin \frac{\theta}{2}=\frac{1}{3}$; since $\triangle A P_{n} O_{n} \sim$ $\triangle A P_{n-1} O_{n-1}$ and $O_{n} O_{n-1}=r_{n}+r_{n-1}$, we have $\frac{1}{3}=\frac{O_{n} P_{n}}{A O_{n}}=\frac{r_{n}}{A O_{n-1}+O_{n-1} O_{n}}=\frac{r_{n}}{3 r_{n-1}+r_{n}+r_{n-1}} \Longrightarrow$ $r_{n}=2 r_{n-1}=2^{n-1} \frac{16}{3 \cdot 2 \sqrt{2}}$. We want the highest $n$ such that $O_{n}$ is contained inside $\triangle A D E$. Let the incircle of $\triangle A D E$ be tangent to $A D$ at $X$; then the inradius of $\triangle A D E$ is $\frac{A X}{\tan \frac{\theta}{2}}=\frac{\frac{500+200-\frac{1100}{2}}{2 \sqrt{2}}}{2}=\frac{500}{3 \cdot 2 \sqrt{2}}$. We want the highest $n$ such that $r_{n} \leq \frac{500}{3 \cdot 2 \sqrt{2}}$; thus $2^{n-1} \cdot 16 \leq 500 \Longrightarrow n=5$.
|
5
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Convex quadrilateral $B C D E$ lies in the plane. Lines $E B$ and $D C$ intersect at $A$, with $A B=2$, $A C=5, A D=200, A E=500$, and $\cos \angle B A C=\frac{7}{9}$. What is the largest number of nonoverlapping circles that can lie in quadrilateral $B C D E$ such that all of them are tangent to both lines $B E$ and $C D$ ?
|
5 Let $\theta=\angle B A C$, and $\cos \theta=\frac{7}{9}$ implies $\cos \frac{\theta}{2}=\sqrt{\frac{1+\frac{7}{9}}{2}}=\frac{2 \sqrt{2}}{3} ; \sin \frac{\theta}{2}=\frac{1}{3} ; B C=$ $\sqrt{4+25-2(2)(5) \frac{7}{9}}=\frac{11}{3}$. Let $O_{1}$ be the excircle of $\triangle A B C$ tangent to lines $A B$ and $A C$, and let $r_{1}$ be its radius; let $O_{1}$ be tangent to line $A B$ at point $P_{1}$. Then $A P_{1}=\frac{A B+B C+C A}{2}$ and $\frac{r_{1}}{A P_{1}}=\tan \frac{\theta}{2}=$ $\frac{1}{2 \sqrt{2}} \Longrightarrow r_{1}=\frac{16}{3 \cdot 2 \sqrt{2}}$. Let $O_{n}$ be a circle tangent to $O_{n-1}$ and the lines $A B$ and $A C$, and let $r_{n}$ be its radius; let $O_{n}$ be tangent to line $A B$ at point $P_{n}$. Then $\frac{O_{n} P_{n}}{A O_{n}}=\sin \frac{\theta}{2}=\frac{1}{3}$; since $\triangle A P_{n} O_{n} \sim$ $\triangle A P_{n-1} O_{n-1}$ and $O_{n} O_{n-1}=r_{n}+r_{n-1}$, we have $\frac{1}{3}=\frac{O_{n} P_{n}}{A O_{n}}=\frac{r_{n}}{A O_{n-1}+O_{n-1} O_{n}}=\frac{r_{n}}{3 r_{n-1}+r_{n}+r_{n-1}} \Longrightarrow$ $r_{n}=2 r_{n-1}=2^{n-1} \frac{16}{3 \cdot 2 \sqrt{2}}$. We want the highest $n$ such that $O_{n}$ is contained inside $\triangle A D E$. Let the incircle of $\triangle A D E$ be tangent to $A D$ at $X$; then the inradius of $\triangle A D E$ is $\frac{A X}{\tan \frac{\theta}{2}}=\frac{\frac{500+200-\frac{1100}{2}}{2 \sqrt{2}}}{2}=\frac{500}{3 \cdot 2 \sqrt{2}}$. We want the highest $n$ such that $r_{n} \leq \frac{500}{3 \cdot 2 \sqrt{2}}$; thus $2^{n-1} \cdot 16 \leq 500 \Longrightarrow n=5$.
|
{
"exam": "HMMT",
"problem_label": "33",
"problem_match": "\n33. [20]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
Estimate the sum of all the prime numbers less than $1,000,000$. If the correct answer is $X$ and you write down $A$, your team will receive $\min \left(\left\lfloor\frac{25 X}{A}\right\rfloor,\left\lfloor\frac{25 A}{X}\right\rfloor\right)$ points, where $\lfloor x\rfloor$ is the largest integer less than or equal to $x$.
|
37550402023 A decent approximation to the sum of all the primes can be obtained with the following two facts. First, there are approximately $\frac{n}{\ln n}$ primes less than $n$ and second, the $n^{\text {th }}$ prime is approximately $n \ln n$. We'll approximate $\ln 1000000$ as 15 (the actual number is 13.8), so there are approximately $\frac{10^{6}}{15}$ primes. Then we want $\sum_{n=1}^{\frac{106}{15}} n \ln n$. If you know calculus, this can be approximated by the integral $\int_{1}^{\frac{10^{6}}{15}} x \ln x d x$, which has the antiderivative $\frac{1}{2} x^{2} \ln x-\frac{1}{4} x^{2}$, giving an answer of around $\frac{1}{2} \cdot \frac{10^{12}}{225} \cdot(15-\ln 15)-\frac{1}{4} \cdot \frac{10^{12}}{225}$. Estimating $\ln 15$ as about 3 , this is approximately $\frac{23 \cdot 10^{12}}{900}=2.5 \cdot 10^{10}=25,000,000,000$. The actual answer is $37,550,402,023$, so an approximation of this accuracy would get 16 points. We can arrive at the same answer without calculus by approximating $\ln n$ as $\sum_{k=1}^{n} \frac{1}{k}$, so that our sum becomes $\sum_{n=1}^{\frac{106}{15}} \sum_{k=1}^{n} \frac{n}{k}=\sum_{k=1}^{\frac{106}{15}} \sum_{n=k}^{\frac{10^{6}}{15}} \frac{n}{k} \approx \sum_{k=1}^{\frac{10^{6}}{15}} \frac{1}{2} \cdot \frac{\frac{10^{12}}{225}-k^{2}}{k}=$ $\frac{1}{2} \cdot \frac{10^{12}}{225} \cdot \ln \left(\frac{10^{6}}{15}\right)-\frac{1}{2} \sum_{k=1}^{\frac{10^{6}}{15}} k \approx \frac{1}{2} \cdot \frac{10^{12}}{225} \cdot \ln \left(\frac{10^{6}}{15}\right)-\frac{1}{4} \frac{10^{12}}{225} \approx 2.5 \cdot 10^{10}$.
|
37550402023
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Estimate the sum of all the prime numbers less than $1,000,000$. If the correct answer is $X$ and you write down $A$, your team will receive $\min \left(\left\lfloor\frac{25 X}{A}\right\rfloor,\left\lfloor\frac{25 A}{X}\right\rfloor\right)$ points, where $\lfloor x\rfloor$ is the largest integer less than or equal to $x$.
|
37550402023 A decent approximation to the sum of all the primes can be obtained with the following two facts. First, there are approximately $\frac{n}{\ln n}$ primes less than $n$ and second, the $n^{\text {th }}$ prime is approximately $n \ln n$. We'll approximate $\ln 1000000$ as 15 (the actual number is 13.8), so there are approximately $\frac{10^{6}}{15}$ primes. Then we want $\sum_{n=1}^{\frac{106}{15}} n \ln n$. If you know calculus, this can be approximated by the integral $\int_{1}^{\frac{10^{6}}{15}} x \ln x d x$, which has the antiderivative $\frac{1}{2} x^{2} \ln x-\frac{1}{4} x^{2}$, giving an answer of around $\frac{1}{2} \cdot \frac{10^{12}}{225} \cdot(15-\ln 15)-\frac{1}{4} \cdot \frac{10^{12}}{225}$. Estimating $\ln 15$ as about 3 , this is approximately $\frac{23 \cdot 10^{12}}{900}=2.5 \cdot 10^{10}=25,000,000,000$. The actual answer is $37,550,402,023$, so an approximation of this accuracy would get 16 points. We can arrive at the same answer without calculus by approximating $\ln n$ as $\sum_{k=1}^{n} \frac{1}{k}$, so that our sum becomes $\sum_{n=1}^{\frac{106}{15}} \sum_{k=1}^{n} \frac{n}{k}=\sum_{k=1}^{\frac{106}{15}} \sum_{n=k}^{\frac{10^{6}}{15}} \frac{n}{k} \approx \sum_{k=1}^{\frac{10^{6}}{15}} \frac{1}{2} \cdot \frac{\frac{10^{12}}{225}-k^{2}}{k}=$ $\frac{1}{2} \cdot \frac{10^{12}}{225} \cdot \ln \left(\frac{10^{6}}{15}\right)-\frac{1}{2} \sum_{k=1}^{\frac{10^{6}}{15}} k \approx \frac{1}{2} \cdot \frac{10^{12}}{225} \cdot \ln \left(\frac{10^{6}}{15}\right)-\frac{1}{4} \frac{10^{12}}{225} \approx 2.5 \cdot 10^{10}$.
|
{
"exam": "HMMT",
"problem_label": "34",
"problem_match": "\n34. [25]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
A mathematician $M^{\prime}$ is called a descendent of mathematician $M$ if there is a sequence of mathematicians $M=M_{1}, M_{2}, \ldots, M_{k}=M^{\prime}$ such that $M_{i}$ was $M_{i+1}$ 's doctoral advisor for all $i$. Estimate
the number of descendents that the mathematician who has had the largest number of descendents has had, according to the Mathematical Genealogy Project. Note that the Mathematical Genealogy Project has records dating back to the 1300s. If the correct answer is $X$ and you write down $A$, your team will receive max $\left(25-\left\lfloor\frac{|X-A|}{100}\right\rfloor, 0\right)$ points, where $\lfloor x\rfloor$ is the largest integer less than or equal to $x$.
|
82310 First let's estimate how many "generations" of mathematicians there have been since 1300. If we suppose that a mathematician gets his PhD around age 30 and becomes a PhD advisor around age 60 , then we'll get a generation length of approximately 30 years. However, not all mathematicians will train more than one PhD . Let's say that only $40 \%$ of mathematicians train at least 2 PhDs. Then effectively we have only $40 \%$ of the generations, or in other words each effective generation takes 75 years. Then we have $\frac{22}{3}$ branching generations. If we assume that all of these only train 2 PhDs , then we get an answer of $2^{\frac{22}{3}} \approx 1625$. But we can ensure that our chain has at least a single person who trained 100 PhDs (this is approximately the largest number of advisees for a single mathematician), allowing us to change one factor of 2 into a factor of 100 . That gives us an answer of $1625 \cdot 50=81250$, which is very close to the actual value of 82310 .
|
82310
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A mathematician $M^{\prime}$ is called a descendent of mathematician $M$ if there is a sequence of mathematicians $M=M_{1}, M_{2}, \ldots, M_{k}=M^{\prime}$ such that $M_{i}$ was $M_{i+1}$ 's doctoral advisor for all $i$. Estimate
the number of descendents that the mathematician who has had the largest number of descendents has had, according to the Mathematical Genealogy Project. Note that the Mathematical Genealogy Project has records dating back to the 1300s. If the correct answer is $X$ and you write down $A$, your team will receive max $\left(25-\left\lfloor\frac{|X-A|}{100}\right\rfloor, 0\right)$ points, where $\lfloor x\rfloor$ is the largest integer less than or equal to $x$.
|
82310 First let's estimate how many "generations" of mathematicians there have been since 1300. If we suppose that a mathematician gets his PhD around age 30 and becomes a PhD advisor around age 60 , then we'll get a generation length of approximately 30 years. However, not all mathematicians will train more than one PhD . Let's say that only $40 \%$ of mathematicians train at least 2 PhDs. Then effectively we have only $40 \%$ of the generations, or in other words each effective generation takes 75 years. Then we have $\frac{22}{3}$ branching generations. If we assume that all of these only train 2 PhDs , then we get an answer of $2^{\frac{22}{3}} \approx 1625$. But we can ensure that our chain has at least a single person who trained 100 PhDs (this is approximately the largest number of advisees for a single mathematician), allowing us to change one factor of 2 into a factor of 100 . That gives us an answer of $1625 \cdot 50=81250$, which is very close to the actual value of 82310 .
|
{
"exam": "HMMT",
"problem_label": "35",
"problem_match": "\n35. [25]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
Paul Erdős was one of the most prolific mathematicians of all time and was renowned for his many collaborations. The Erdős number of a mathematician is defined as follows. Erdős has an Erdős number of 0, a mathematician who has coauthored a paper with Erdős has an Erdős number of 1, a mathematician who has not coauthored a paper with Erdős, but has coauthored a paper with a mathematician with Erdős number 1 has an Erdős number of 2, etc. If no such chain exists between Erdős and another mathematician, that mathematician has an Erdős number of infinity. Of the mathematicians with a finite Erdős number (including those who are no longer alive), what is their average Erdős number according to the Erdős Number Project? If the correct answer is $X$ and you write down $A$, your team will receive $\max (25-\lfloor 100|X-A|\rfloor, 0)$ points where $\lfloor x\rfloor$ is the largest integer less than or equal to $x$.
|
4.65 We'll suppose that each mathematician collaborates with approximately 20 people (except for Erdős himself, of course). Furthermore, if a mathematician has Erdős number $k$, then we'd expect him to be the cause of approximately $\frac{1}{2^{k}}$ of his collaborators' Erdős numbers. This is because as we get to higher Erdős numbers, it is more likely that a collaborator has a lower Erdős number already. Therefore, we'd expect about 10 times as many people to have an Erdős number of 2 than with an Erdős number of 1 , then a ratio of $5,2.5,1.25$, and so on. This tells us that more mathematicians have an Erdős number of 5 than any other number, then 4 , then 6 , and so on. If we use this approximation, we have a ratio of mathematicians with Erdős number 1, 2, and so on of about $1: 10: 50: 125: 156: 97: 30: 4: 0.3$, which gives an average Erdős number of 4.8. This is close to the actual value of 4.65 .
|
4.65
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Paul Erdős was one of the most prolific mathematicians of all time and was renowned for his many collaborations. The Erdős number of a mathematician is defined as follows. Erdős has an Erdős number of 0, a mathematician who has coauthored a paper with Erdős has an Erdős number of 1, a mathematician who has not coauthored a paper with Erdős, but has coauthored a paper with a mathematician with Erdős number 1 has an Erdős number of 2, etc. If no such chain exists between Erdős and another mathematician, that mathematician has an Erdős number of infinity. Of the mathematicians with a finite Erdős number (including those who are no longer alive), what is their average Erdős number according to the Erdős Number Project? If the correct answer is $X$ and you write down $A$, your team will receive $\max (25-\lfloor 100|X-A|\rfloor, 0)$ points where $\lfloor x\rfloor$ is the largest integer less than or equal to $x$.
|
4.65 We'll suppose that each mathematician collaborates with approximately 20 people (except for Erdős himself, of course). Furthermore, if a mathematician has Erdős number $k$, then we'd expect him to be the cause of approximately $\frac{1}{2^{k}}$ of his collaborators' Erdős numbers. This is because as we get to higher Erdős numbers, it is more likely that a collaborator has a lower Erdős number already. Therefore, we'd expect about 10 times as many people to have an Erdős number of 2 than with an Erdős number of 1 , then a ratio of $5,2.5,1.25$, and so on. This tells us that more mathematicians have an Erdős number of 5 than any other number, then 4 , then 6 , and so on. If we use this approximation, we have a ratio of mathematicians with Erdős number 1, 2, and so on of about $1: 10: 50: 125: 156: 97: 30: 4: 0.3$, which gives an average Erdős number of 4.8. This is close to the actual value of 4.65 .
|
{
"exam": "HMMT",
"problem_label": "36",
"problem_match": "\n36. [25]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
Travis is hopping around on the vertices of a cube. Each minute he hops from the vertex he's currently on to the other vertex of an edge that he is next to. After four minutes, what is the probability that he is back where he started?
|
$\boxed{\frac{7}{27}}$ Let the cube have vertices all 0 or 1 in the $x, y, z,$ coordinate system. Travis starts at $(0,0,0)$. If after 3 moves he is at $(1,1,1)$ he cannot get back to $(0,0,0)$. From any other vertex he has a $\frac{1}{3}$ chance of getting back on the final move. There is a $\frac{2}{9}$ chance he ends up at $(1,1,1)$, and thus a $\frac{7}{9}$ chance he does not end up there, and thus a $\frac{7}{27}$ chance he ends up at $(0,0,0)$.
|
\frac{7}{27}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Travis is hopping around on the vertices of a cube. Each minute he hops from the vertex he's currently on to the other vertex of an edge that he is next to. After four minutes, what is the probability that he is back where he started?
|
$\boxed{\frac{7}{27}}$ Let the cube have vertices all 0 or 1 in the $x, y, z,$ coordinate system. Travis starts at $(0,0,0)$. If after 3 moves he is at $(1,1,1)$ he cannot get back to $(0,0,0)$. From any other vertex he has a $\frac{1}{3}$ chance of getting back on the final move. There is a $\frac{2}{9}$ chance he ends up at $(1,1,1)$, and thus a $\frac{7}{9}$ chance he does not end up there, and thus a $\frac{7}{27}$ chance he ends up at $(0,0,0)$.
|
{
"exam": "HMMT",
"problem_label": "1",
"problem_match": "\n1. [3]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-team-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
In terms of $k$, for $k>0$ how likely is he to be back where he started after $2 k$ minutes?
|
$\frac{1}{4}+\frac{3}{4}\left(\frac{1}{9}\right)^{k}$ Again, Travis starts at $(0,0,0)$. At each step, exactly one of the three coordinates will change. The parity of the sum of the three coordinates will change at each step, so after $2 k$ steps, the sum of the coordinates must be even. There are only four possibilites for Travis's position: $(0,0,0),(1,1,0),(1,0,1)$, and $(0,1,1)$. Let $p_{k}$ be the probability that Travis is at $(0,0,0)$ after $2 k$ steps. Then $1-p_{k}$ is the probability that he is on $(1,1,0),(1,0,1)$, or $(0,1,1)$. Suppose we want to compute $p_{k+1}$. There are two possibilities: we were either at $(0,0,0)$ after $2 k$ steps or not. If we were, then there is a $\frac{1}{3}$ probability that we will return (since our $(2 k+1)^{\text {th }}$ step can be arbitary, but there is a $\frac{1}{3}$ chance that we will reverse that as our $(2 k+2)^{\text {th }}$ step). If we were not at $(0,0,0)$ after our $2 k^{\text {th }}$ steps, then two of our coordinates must have been ones. There is a $\frac{2}{3}$ probability that the $(2 k+1)^{\text {th }}$ step will change one of those to a zero, and there is a $\frac{1}{3}$ step that that the $(2 k+2)^{\text {th }}$ step will change the remaining one. Hence, in this case, there is a $\left(\frac{2}{3}\right)\left(\frac{1}{3}\right)=\frac{2}{9}$ probability that Travis ends up $(0,0,0)$ in this case. So we have:
$$
\begin{aligned}
p_{k+1} & =p_{k}\left(\frac{1}{3}\right)+\left(1-p_{k}\right)\left(\frac{2}{9}\right) \\
p_{k+1} & =\frac{1}{9} p_{k}+\frac{2}{9} \\
\left(p_{k+1}-\frac{1}{4}\right) & =\frac{1}{9}\left(p_{k}-\frac{1}{4}\right)
\end{aligned}
$$
(We get the value $\frac{1}{4}$ either by guessing that the sequence $p_{0}, p_{1}, p_{2}, \ldots$ should converge to $\frac{1}{4}$ or simply by solving the equation $-\frac{1}{9} x+x=\frac{2}{9}$.) This shows that $p_{0}-\frac{1}{4}, p_{1}-\frac{1}{4}, \ldots$ is a geometric series with ratio $\frac{1}{9}$. Since $p_{0}-\frac{1}{4}=1-\frac{1}{4}=\frac{3}{4}$, we get that $p_{k}-\frac{1}{4}=\frac{3}{4}\left(\frac{1}{9}\right)^{k}$, or that $p_{k}=\frac{1}{4}+\frac{3}{4}\left(\frac{1}{9}\right)^{k}$.
|
\frac{1}{4}+\frac{3}{4}\left(\frac{1}{9}\right)^{k}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In terms of $k$, for $k>0$ how likely is he to be back where he started after $2 k$ minutes?
|
$\frac{1}{4}+\frac{3}{4}\left(\frac{1}{9}\right)^{k}$ Again, Travis starts at $(0,0,0)$. At each step, exactly one of the three coordinates will change. The parity of the sum of the three coordinates will change at each step, so after $2 k$ steps, the sum of the coordinates must be even. There are only four possibilites for Travis's position: $(0,0,0),(1,1,0),(1,0,1)$, and $(0,1,1)$. Let $p_{k}$ be the probability that Travis is at $(0,0,0)$ after $2 k$ steps. Then $1-p_{k}$ is the probability that he is on $(1,1,0),(1,0,1)$, or $(0,1,1)$. Suppose we want to compute $p_{k+1}$. There are two possibilities: we were either at $(0,0,0)$ after $2 k$ steps or not. If we were, then there is a $\frac{1}{3}$ probability that we will return (since our $(2 k+1)^{\text {th }}$ step can be arbitary, but there is a $\frac{1}{3}$ chance that we will reverse that as our $(2 k+2)^{\text {th }}$ step). If we were not at $(0,0,0)$ after our $2 k^{\text {th }}$ steps, then two of our coordinates must have been ones. There is a $\frac{2}{3}$ probability that the $(2 k+1)^{\text {th }}$ step will change one of those to a zero, and there is a $\frac{1}{3}$ step that that the $(2 k+2)^{\text {th }}$ step will change the remaining one. Hence, in this case, there is a $\left(\frac{2}{3}\right)\left(\frac{1}{3}\right)=\frac{2}{9}$ probability that Travis ends up $(0,0,0)$ in this case. So we have:
$$
\begin{aligned}
p_{k+1} & =p_{k}\left(\frac{1}{3}\right)+\left(1-p_{k}\right)\left(\frac{2}{9}\right) \\
p_{k+1} & =\frac{1}{9} p_{k}+\frac{2}{9} \\
\left(p_{k+1}-\frac{1}{4}\right) & =\frac{1}{9}\left(p_{k}-\frac{1}{4}\right)
\end{aligned}
$$
(We get the value $\frac{1}{4}$ either by guessing that the sequence $p_{0}, p_{1}, p_{2}, \ldots$ should converge to $\frac{1}{4}$ or simply by solving the equation $-\frac{1}{9} x+x=\frac{2}{9}$.) This shows that $p_{0}-\frac{1}{4}, p_{1}-\frac{1}{4}, \ldots$ is a geometric series with ratio $\frac{1}{9}$. Since $p_{0}-\frac{1}{4}=1-\frac{1}{4}=\frac{3}{4}$, we get that $p_{k}-\frac{1}{4}=\frac{3}{4}\left(\frac{1}{9}\right)^{k}$, or that $p_{k}=\frac{1}{4}+\frac{3}{4}\left(\frac{1}{9}\right)^{k}$.
|
{
"exam": "HMMT",
"problem_label": "2",
"problem_match": "\n2. [6]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-team-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
While Travis is having fun on cubes, Sherry is hopping in the same manner on an octahedron. An octahedron has six vertices and eight regular triangular faces. After five minutes, how likely is Sherry to be one edge away from where she started?
|
$\frac{11}{16}$ Let the starting vertex be the 'bottom' one. Then there is a 'top' vertex, and 4 'middle' ones. If $p(n)$ is the probability that Sherry is on a middle vertex after $n$ minutes, $p(0)=0$,
$p(n+1)=(1-p(n))+p(n) \cdot \frac{1}{2}$. This recurrence gives us the following equations.
$$
\begin{aligned}
p(n+1) & =1-\frac{p(n)}{2} \\
p(0) & =0 \\
p(1) & =1 \\
p(2) & =\frac{1}{2} \\
p(3) & =\frac{3}{4} \\
p(4) & =\frac{5}{8} \\
p(5) & =\frac{11}{16}
\end{aligned}
$$
|
\frac{11}{16}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
While Travis is having fun on cubes, Sherry is hopping in the same manner on an octahedron. An octahedron has six vertices and eight regular triangular faces. After five minutes, how likely is Sherry to be one edge away from where she started?
|
$\frac{11}{16}$ Let the starting vertex be the 'bottom' one. Then there is a 'top' vertex, and 4 'middle' ones. If $p(n)$ is the probability that Sherry is on a middle vertex after $n$ minutes, $p(0)=0$,
$p(n+1)=(1-p(n))+p(n) \cdot \frac{1}{2}$. This recurrence gives us the following equations.
$$
\begin{aligned}
p(n+1) & =1-\frac{p(n)}{2} \\
p(0) & =0 \\
p(1) & =1 \\
p(2) & =\frac{1}{2} \\
p(3) & =\frac{3}{4} \\
p(4) & =\frac{5}{8} \\
p(5) & =\frac{11}{16}
\end{aligned}
$$
|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n3. [3]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-team-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
In terms of $k$, for $k>0$, how likely is it that after $k$ minutes Sherry is at the vertex opposite the vertex where she started?
|
| $\frac{1}{6}+\frac{1}{3(-2)^{k}}$ |
| :---: | Take $p(n)$ from the last problem. By examining the last move of Sherry, the probability that she ends up on the original vertex is equal to the probability that she ends up on the top vertex, and both are equal to $\frac{1-p(n)}{2}$ for $n \geq 1$.
From the last problem,
$$
\begin{aligned}
p(n+1) & =1-\frac{p(n)}{2} \\
p(n+1)-\frac{2}{3} & =-\frac{1}{2}\left(p(n)-\frac{2}{3}\right)
\end{aligned}
$$
and so $p(n)-\frac{2}{3}$ is a geometric series with ratio $-\frac{1}{2}$. Since $p(0)=0$, we get $p(n)-\frac{2}{3}=-\frac{2}{3}\left(-\frac{1}{2}\right)^{n}$, or that $p(n)=\frac{2}{3}-\frac{2}{3}\left(-\frac{1}{2}\right)^{n}$.
Now, for $k \geq 1$, we have that the probability of ending up on the vertex opposite Sherry's initial vertex after $k$ minutes is $\frac{1-p(k)}{2}=\frac{1}{2}-\frac{1}{2}\left(\frac{2}{3}-\frac{2}{3}\left(-\frac{1}{2}\right)^{k}\right)=\frac{1}{6}+\frac{1}{3}\left(-\frac{1}{2}\right)^{k}=\frac{1}{6}+\frac{1}{3(-2)^{k}}$.
## Circles in Circles
|
\frac{1}{6}+\frac{1}{3(-2)^{k}}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In terms of $k$, for $k>0$, how likely is it that after $k$ minutes Sherry is at the vertex opposite the vertex where she started?
|
| $\frac{1}{6}+\frac{1}{3(-2)^{k}}$ |
| :---: | Take $p(n)$ from the last problem. By examining the last move of Sherry, the probability that she ends up on the original vertex is equal to the probability that she ends up on the top vertex, and both are equal to $\frac{1-p(n)}{2}$ for $n \geq 1$.
From the last problem,
$$
\begin{aligned}
p(n+1) & =1-\frac{p(n)}{2} \\
p(n+1)-\frac{2}{3} & =-\frac{1}{2}\left(p(n)-\frac{2}{3}\right)
\end{aligned}
$$
and so $p(n)-\frac{2}{3}$ is a geometric series with ratio $-\frac{1}{2}$. Since $p(0)=0$, we get $p(n)-\frac{2}{3}=-\frac{2}{3}\left(-\frac{1}{2}\right)^{n}$, or that $p(n)=\frac{2}{3}-\frac{2}{3}\left(-\frac{1}{2}\right)^{n}$.
Now, for $k \geq 1$, we have that the probability of ending up on the vertex opposite Sherry's initial vertex after $k$ minutes is $\frac{1-p(k)}{2}=\frac{1}{2}-\frac{1}{2}\left(\frac{2}{3}-\frac{2}{3}\left(-\frac{1}{2}\right)^{k}\right)=\frac{1}{6}+\frac{1}{3}\left(-\frac{1}{2}\right)^{k}=\frac{1}{6}+\frac{1}{3(-2)^{k}}$.
## Circles in Circles
|
{
"exam": "HMMT",
"problem_label": "4",
"problem_match": "\n4. [6]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-team-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
Circle $O$ has chord $A B$. A circle is tangent to $O$ at $T$ and tangent to $A B$ at $X$ such that $A X=2 X B$. What is $\frac{A T}{B T}$ ?
|
2 Let $T X$ meet circle $O$ again at $Y$. Since the homethety centered at $T$ takes $X$ to $Y$ also takes $A B$ to the tangent line of circle $O$ passing through $Y$, we have $Y$ is the midpoint of arc $A B$. This means that $\angle A T Y=\angle Y T B$. By the Angle Bisector Theorem, $\frac{A T}{B T}=\frac{A X}{B X}=2$.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Circle $O$ has chord $A B$. A circle is tangent to $O$ at $T$ and tangent to $A B$ at $X$ such that $A X=2 X B$. What is $\frac{A T}{B T}$ ?
|
2 Let $T X$ meet circle $O$ again at $Y$. Since the homethety centered at $T$ takes $X$ to $Y$ also takes $A B$ to the tangent line of circle $O$ passing through $Y$, we have $Y$ is the midpoint of arc $A B$. This means that $\angle A T Y=\angle Y T B$. By the Angle Bisector Theorem, $\frac{A T}{B T}=\frac{A X}{B X}=2$.
|
{
"exam": "HMMT",
"problem_label": "5",
"problem_match": "\n5. [4]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-team-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
$A B$ is a diameter of circle $O . X$ is a point on $A B$ such that $A X=3 B X$. Distinct circles $\omega_{1}$ and $\omega_{2}$ are tangent to $O$ at $T_{1}$ and $T_{2}$ and to $A B$ at $X$. The lines $T_{1} X$ and $T_{2} X$ intersect $O$ again at $S_{1}$ and $S_{2}$. What is the ratio $\frac{T_{1} T_{2}}{S_{1} S_{2}}$ ?
|
| $\frac{3}{5}$ | Since the problem only deals with ratios, we can assume that the radius of $O$ is 1 . As |
| :---: | :---: | we have proven in Problem 5, points $S_{1}$ and $S_{2}$ are midpoints of arc $A B$. Since $A B$ is a diameter, $S_{1} S_{2}$ is also a diameter, and thus $S_{1} S_{2}=2$.
Let $O_{1}, O_{2}$, and $P$ denote the center of circles $\omega_{1}, \omega_{2}$, and $O$. Since $\omega_{1}$ is tangent to $O$, we have $P O_{1}+O_{1} X=1$. But $O_{1} X \perp A B$. So $\triangle P O_{1} X$ is a right triangle, and $O_{1} X^{2}+X P^{2}=O_{1} P^{2}$. Thus, $O_{1} X^{2}+1 / 4=\left(1-O_{1} X\right)^{2}$, which means $O_{1} X=\frac{3}{8}$ and $O_{1} P=\frac{5}{8}$.
Since $T_{1} T_{2} \| O_{1} O_{2}$, we have $T_{1} T_{2}=O_{1} O_{2} \cdot \frac{P T_{1}}{P O_{1}}=2 O_{1} X \cdot \frac{P T_{1}}{P O_{1}}=2\left(\frac{3}{8}\right) \frac{1}{5 / 8}=\frac{6}{5}$. Thus $\frac{T_{1} T_{2}}{S_{1} S_{2}}=\frac{6 / 5}{2}=\frac{3}{5}$.
|
\frac{3}{5}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
$A B$ is a diameter of circle $O . X$ is a point on $A B$ such that $A X=3 B X$. Distinct circles $\omega_{1}$ and $\omega_{2}$ are tangent to $O$ at $T_{1}$ and $T_{2}$ and to $A B$ at $X$. The lines $T_{1} X$ and $T_{2} X$ intersect $O$ again at $S_{1}$ and $S_{2}$. What is the ratio $\frac{T_{1} T_{2}}{S_{1} S_{2}}$ ?
|
| $\frac{3}{5}$ | Since the problem only deals with ratios, we can assume that the radius of $O$ is 1 . As |
| :---: | :---: | we have proven in Problem 5, points $S_{1}$ and $S_{2}$ are midpoints of arc $A B$. Since $A B$ is a diameter, $S_{1} S_{2}$ is also a diameter, and thus $S_{1} S_{2}=2$.
Let $O_{1}, O_{2}$, and $P$ denote the center of circles $\omega_{1}, \omega_{2}$, and $O$. Since $\omega_{1}$ is tangent to $O$, we have $P O_{1}+O_{1} X=1$. But $O_{1} X \perp A B$. So $\triangle P O_{1} X$ is a right triangle, and $O_{1} X^{2}+X P^{2}=O_{1} P^{2}$. Thus, $O_{1} X^{2}+1 / 4=\left(1-O_{1} X\right)^{2}$, which means $O_{1} X=\frac{3}{8}$ and $O_{1} P=\frac{5}{8}$.
Since $T_{1} T_{2} \| O_{1} O_{2}$, we have $T_{1} T_{2}=O_{1} O_{2} \cdot \frac{P T_{1}}{P O_{1}}=2 O_{1} X \cdot \frac{P T_{1}}{P O_{1}}=2\left(\frac{3}{8}\right) \frac{1}{5 / 8}=\frac{6}{5}$. Thus $\frac{T_{1} T_{2}}{S_{1} S_{2}}=\frac{6 / 5}{2}=\frac{3}{5}$.
|
{
"exam": "HMMT",
"problem_label": "6",
"problem_match": "\n6. [6]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-team-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
$A B C$ is a right triangle with $\angle A=30^{\circ}$ and circumcircle $O$. Circles $\omega_{1}, \omega_{2}$, and $\omega_{3}$ lie outside $A B C$ and are tangent to $O$ at $T_{1}, T_{2}$, and $T_{3}$ respectively and to $A B, B C$, and $C A$ at $S_{1}, S_{2}$, and $S_{3}$, respectively. Lines $T_{1} S_{1}, T_{2} S_{2}$, and $T_{3} S_{3}$ intersect $O$ again at $A^{\prime}, B^{\prime}$, and $C^{\prime}$, respectively. What is the ratio of the area of $A^{\prime} B^{\prime} C^{\prime}$ to the area of $A B C$ ?
|
$\frac{\sqrt{3}+1}{2}$ Let $[P Q R]$ denote the area of $\triangle P Q R$. The key to this problem is following fact: $[P Q R]=\frac{1}{2} P Q \cdot P R \sin \angle Q P R$.
Assume that the radius of $O$ is 1 . Since $\angle A=30^{\circ}$, we have $B C=1$ and $A B=\sqrt{3}$. So $[A B C]=\frac{\sqrt{3}}{2}$. Let $K$ denote the center of $O$. Notice that $\angle B^{\prime} K A^{\prime}=90^{\circ}, \angle A K C^{\prime}=90^{\circ}$, and $\angle B^{\prime} K A=\angle K A B=$ $30^{\circ}$. Thus, $\angle B^{\prime} K C^{\prime}=\angle B^{\prime} K A+\angle A K C^{\prime}=120^{\circ}$ and consequently $\angle C^{\prime} K A^{\prime}=150^{\circ}$.
Therefore, $\left[A^{\prime} B^{\prime} C^{\prime}\right]=\left[A^{\prime} K B^{\prime}\right]+\left[B^{\prime} K C^{\prime}\right]+\left[C^{\prime} K A^{\prime}\right]=\frac{1}{2}+\frac{1}{2} \sin 120^{\circ}+\frac{1}{2} \sin 150^{\circ}=\frac{3}{4}+\frac{\sqrt{3}}{4}$. This gives the desired result that $\left[A^{\prime} B^{\prime} C^{\prime}\right]=\frac{\sqrt{3}+1}{2}[A B C]$.
## Linear? What's The Problem?
A function $f\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ is said to be linear in each of its variables if it is a polynomial such that no variable appears with power higher than one in any term. For example, $1+x+x y$ is linear in $x$ and $y$, but $1+x^{2}$ is not. Similarly, $2 x+3 y z$ is linear in $x, y$, and $z$, but $x y z^{2}$ is not.
|
\frac{\sqrt{3}+1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
$A B C$ is a right triangle with $\angle A=30^{\circ}$ and circumcircle $O$. Circles $\omega_{1}, \omega_{2}$, and $\omega_{3}$ lie outside $A B C$ and are tangent to $O$ at $T_{1}, T_{2}$, and $T_{3}$ respectively and to $A B, B C$, and $C A$ at $S_{1}, S_{2}$, and $S_{3}$, respectively. Lines $T_{1} S_{1}, T_{2} S_{2}$, and $T_{3} S_{3}$ intersect $O$ again at $A^{\prime}, B^{\prime}$, and $C^{\prime}$, respectively. What is the ratio of the area of $A^{\prime} B^{\prime} C^{\prime}$ to the area of $A B C$ ?
|
$\frac{\sqrt{3}+1}{2}$ Let $[P Q R]$ denote the area of $\triangle P Q R$. The key to this problem is following fact: $[P Q R]=\frac{1}{2} P Q \cdot P R \sin \angle Q P R$.
Assume that the radius of $O$ is 1 . Since $\angle A=30^{\circ}$, we have $B C=1$ and $A B=\sqrt{3}$. So $[A B C]=\frac{\sqrt{3}}{2}$. Let $K$ denote the center of $O$. Notice that $\angle B^{\prime} K A^{\prime}=90^{\circ}, \angle A K C^{\prime}=90^{\circ}$, and $\angle B^{\prime} K A=\angle K A B=$ $30^{\circ}$. Thus, $\angle B^{\prime} K C^{\prime}=\angle B^{\prime} K A+\angle A K C^{\prime}=120^{\circ}$ and consequently $\angle C^{\prime} K A^{\prime}=150^{\circ}$.
Therefore, $\left[A^{\prime} B^{\prime} C^{\prime}\right]=\left[A^{\prime} K B^{\prime}\right]+\left[B^{\prime} K C^{\prime}\right]+\left[C^{\prime} K A^{\prime}\right]=\frac{1}{2}+\frac{1}{2} \sin 120^{\circ}+\frac{1}{2} \sin 150^{\circ}=\frac{3}{4}+\frac{\sqrt{3}}{4}$. This gives the desired result that $\left[A^{\prime} B^{\prime} C^{\prime}\right]=\frac{\sqrt{3}+1}{2}[A B C]$.
## Linear? What's The Problem?
A function $f\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ is said to be linear in each of its variables if it is a polynomial such that no variable appears with power higher than one in any term. For example, $1+x+x y$ is linear in $x$ and $y$, but $1+x^{2}$ is not. Similarly, $2 x+3 y z$ is linear in $x, y$, and $z$, but $x y z^{2}$ is not.
|
{
"exam": "HMMT",
"problem_label": "7",
"problem_match": "\n7. [7]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-team-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
A function $f(x, y)$ is linear in $x$ and in $y . f(x, y)=\frac{1}{x y}$ for $x, y \in\{3,4\}$. What is $f(5,5)$ ?
|
$\frac{1}{36}$ The main fact that we will use in solving this problem is that $f(x+2, y)-f(x+1, y)=$ $f(x+1, y)-f(x, y)$ whenever $f$ is linear in $x$ and $y$. Suppose that $f(x, y)=a x y+b y+c x+d=$ $x(a y+c)+(b y+d)$ for some constants $a, b, c$, and $d$. Then it is easy to see that
$$
\begin{aligned}
f(x+2, y)-f(x+1, y) & =(x+2)(a y+c)+(b y+d)-(x+1)(a y+c)-(b y+d)=a y+c \\
f(x+1, y)-f(x, y) & =(x+1)(a y+c)+(b y+d)-x(a y+c)-(b y+d)=a y+c
\end{aligned}
$$
which implies that $f(x+2, y)-f(x+1, y)=f(x+1, y)-f(x, y)$. In particular, $f(5, y)-f(4, y)=$ $f(4, y)-f(3, y)$, so $f(5, y)=2 f(4, y)-f(3, y)$. Similarly, $f(x, 5)=2 f(x, 4)-f(x, 3)$. Now we see that:
$$
\begin{aligned}
f(5,5) & =2 f(5,4)-f(5,3) \\
& =2[2 f(4,4)-f(3,4)]-[2 f(4,3)-f(3,3)] \\
& =4 f(4,4)-2 f(3,4)-2 f(4,3)+f(3,3) \\
& =\frac{4}{16}-\frac{4}{12}+\frac{1}{9} \\
& =\frac{1}{4}-\frac{1}{3}+\frac{1}{9} \\
& =\frac{1}{9}-\frac{1}{12} \\
& =\frac{1}{36}
\end{aligned}
$$
so the answer is $\frac{1}{36}$.
|
\frac{1}{36}
|
Incomplete
|
Yes
|
math-word-problem
|
Algebra
|
A function $f(x, y)$ is linear in $x$ and in $y . f(x, y)=\frac{1}{x y}$ for $x, y \in\{3,4\}$. What is $f(5,5)$ ?
|
$\frac{1}{36}$ The main fact that we will use in solving this problem is that $f(x+2, y)-f(x+1, y)=$ $f(x+1, y)-f(x, y)$ whenever $f$ is linear in $x$ and $y$. Suppose that $f(x, y)=a x y+b y+c x+d=$ $x(a y+c)+(b y+d)$ for some constants $a, b, c$, and $d$. Then it is easy to see that
$$
\begin{aligned}
f(x+2, y)-f(x+1, y) & =(x+2)(a y+c)+(b y+d)-(x+1)(a y+c)-(b y+d)=a y+c \\
f(x+1, y)-f(x, y) & =(x+1)(a y+c)+(b y+d)-x(a y+c)-(b y+d)=a y+c
\end{aligned}
$$
which implies that $f(x+2, y)-f(x+1, y)=f(x+1, y)-f(x, y)$. In particular, $f(5, y)-f(4, y)=$ $f(4, y)-f(3, y)$, so $f(5, y)=2 f(4, y)-f(3, y)$. Similarly, $f(x, 5)=2 f(x, 4)-f(x, 3)$. Now we see that:
$$
\begin{aligned}
f(5,5) & =2 f(5,4)-f(5,3) \\
& =2[2 f(4,4)-f(3,4)]-[2 f(4,3)-f(3,3)] \\
& =4 f(4,4)-2 f(3,4)-2 f(4,3)+f(3,3) \\
& =\frac{4}{16}-\frac{4}{12}+\frac{1}{9} \\
& =\frac{1}{4}-\frac{1}{3}+\frac{1}{9} \\
& =\frac{1}{9}-\frac{1}{12} \\
& =\frac{1}{36}
\end{aligned}
$$
so the answer is $\frac{1}{36}$.
|
{
"exam": "HMMT",
"problem_label": "8",
"problem_match": "\n8. [4]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-team-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
A function $f(x, y, z)$ is linear in $x, y$, and $z$ such that $f(x, y, z)=\frac{1}{x y z}$ for $x, y, z \in\{3,4\}$. What is $f(5,5,5)$ ?
|
$\frac{1}{216}$ We use a similar method to the previous problem. Notice that $f(x, y, 5)=2 f(x, y, 4)-$ $f(x, y, 3)$. Let $f_{2}$ denote the function from the previous problem and $f_{3}$ the function from this problem.
Since $3 f_{3}(x, y, 3)$ is linear in $x$ and $y$, and $3 f_{3}(x, y, 3)=\frac{1}{x y}$ for all $x, y \in\{3,4\}$, the previous problem implies that $3 f_{3}(5,5,3)=\frac{1}{36}=f_{2}(5,5)$. Similarly, $4 f_{3}(5,5,4)=f_{2}(5,5)$. Now we have
$$
\begin{aligned}
f_{3}(5,5,5) & =2 f_{3}(5,5,4)-f_{3}(5,5,3) \\
& =\frac{1}{2} f_{2}(5,5)-\frac{1}{3} f_{2}(5,5) \\
& =\frac{1}{6} f_{2}(5,5) \\
& =\frac{1}{6 \cdot 36} \\
& =\frac{1}{216}
\end{aligned}
$$
|
\frac{1}{216}
|
Incomplete
|
Yes
|
math-word-problem
|
Algebra
|
A function $f(x, y, z)$ is linear in $x, y$, and $z$ such that $f(x, y, z)=\frac{1}{x y z}$ for $x, y, z \in\{3,4\}$. What is $f(5,5,5)$ ?
|
$\frac{1}{216}$ We use a similar method to the previous problem. Notice that $f(x, y, 5)=2 f(x, y, 4)-$ $f(x, y, 3)$. Let $f_{2}$ denote the function from the previous problem and $f_{3}$ the function from this problem.
Since $3 f_{3}(x, y, 3)$ is linear in $x$ and $y$, and $3 f_{3}(x, y, 3)=\frac{1}{x y}$ for all $x, y \in\{3,4\}$, the previous problem implies that $3 f_{3}(5,5,3)=\frac{1}{36}=f_{2}(5,5)$. Similarly, $4 f_{3}(5,5,4)=f_{2}(5,5)$. Now we have
$$
\begin{aligned}
f_{3}(5,5,5) & =2 f_{3}(5,5,4)-f_{3}(5,5,3) \\
& =\frac{1}{2} f_{2}(5,5)-\frac{1}{3} f_{2}(5,5) \\
& =\frac{1}{6} f_{2}(5,5) \\
& =\frac{1}{6 \cdot 36} \\
& =\frac{1}{216}
\end{aligned}
$$
|
{
"exam": "HMMT",
"problem_label": "9",
"problem_match": "\n9. [5]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-team-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
A function $f\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ is linear in each of the $x_{i}$ and $f\left(x_{1}, x_{2}, \ldots, x_{n}\right)=\frac{1}{x_{1} x_{2} \cdots x_{n}}$ when $x_{i} \in\{3,4\}$ for all $i$. In terms of $n$, what is $f(5,5, \ldots, 5) ?$
|
$\frac{1}{6^{n}}$ Let $f_{n}\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ denote the $n$-variable version of the function. We will prove that $f_{n}(5, \ldots, 5)=\frac{1}{6^{n}}$ by induction. The base case was done in the two previous problems. Suppose we know that $f_{n-1}(5,5, \ldots, 5)=\frac{1}{.6^{n-1}}$. Let $g\left(x_{1}, \ldots, x_{n-1}\right)=3 f_{n}\left(x_{1}, \ldots, x_{n-1}, 3\right)$. We have that $g$ is linear in $x_{1}, \ldots, x_{n-1}$ and $g\left(x_{1}, \ldots, x_{n-1}\right)=\frac{1}{x_{1} \cdots x_{n-1}}$ for all $x_{1}, \ldots, x_{n-1} \in\{3,4\}$. By the inductive hypothesis, we have $g(5, \ldots, 5)=\frac{1}{6^{n-1}}=f_{n-1}(5, \ldots, 5)$. Therefore, $f_{n}(5, \ldots, 5,3)=\frac{f_{n-1}(5, \ldots, 5)}{3}$. Similarly, $f_{n}(5, \ldots, 5,4)=\frac{f_{n-1}(5, \ldots, 5)}{4}$.
$$
\begin{aligned}
f_{n}(5,5, \ldots, 5,5) & =2 f_{n}(5,5, \ldots, 5,4)-f_{n}(5,5, \ldots, 5,3) \\
& =\frac{1}{2} f_{n-1}(5,5, \ldots, 5)-\frac{1}{3} f_{n-1} \\
& =\frac{1}{6} f_{n-1}(5,5, \ldots, 5) \\
& =\frac{1}{6 \cdot 6^{n-1}} \\
& =\frac{1}{6^{n}}
\end{aligned}
$$
and this proves our conjecture by induction.
|
\frac{1}{6^{n}}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
A function $f\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ is linear in each of the $x_{i}$ and $f\left(x_{1}, x_{2}, \ldots, x_{n}\right)=\frac{1}{x_{1} x_{2} \cdots x_{n}}$ when $x_{i} \in\{3,4\}$ for all $i$. In terms of $n$, what is $f(5,5, \ldots, 5) ?$
|
$\frac{1}{6^{n}}$ Let $f_{n}\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ denote the $n$-variable version of the function. We will prove that $f_{n}(5, \ldots, 5)=\frac{1}{6^{n}}$ by induction. The base case was done in the two previous problems. Suppose we know that $f_{n-1}(5,5, \ldots, 5)=\frac{1}{.6^{n-1}}$. Let $g\left(x_{1}, \ldots, x_{n-1}\right)=3 f_{n}\left(x_{1}, \ldots, x_{n-1}, 3\right)$. We have that $g$ is linear in $x_{1}, \ldots, x_{n-1}$ and $g\left(x_{1}, \ldots, x_{n-1}\right)=\frac{1}{x_{1} \cdots x_{n-1}}$ for all $x_{1}, \ldots, x_{n-1} \in\{3,4\}$. By the inductive hypothesis, we have $g(5, \ldots, 5)=\frac{1}{6^{n-1}}=f_{n-1}(5, \ldots, 5)$. Therefore, $f_{n}(5, \ldots, 5,3)=\frac{f_{n-1}(5, \ldots, 5)}{3}$. Similarly, $f_{n}(5, \ldots, 5,4)=\frac{f_{n-1}(5, \ldots, 5)}{4}$.
$$
\begin{aligned}
f_{n}(5,5, \ldots, 5,5) & =2 f_{n}(5,5, \ldots, 5,4)-f_{n}(5,5, \ldots, 5,3) \\
& =\frac{1}{2} f_{n-1}(5,5, \ldots, 5)-\frac{1}{3} f_{n-1} \\
& =\frac{1}{6} f_{n-1}(5,5, \ldots, 5) \\
& =\frac{1}{6 \cdot 6^{n-1}} \\
& =\frac{1}{6^{n}}
\end{aligned}
$$
and this proves our conjecture by induction.
|
{
"exam": "HMMT",
"problem_label": "10",
"problem_match": "\n10. [6]",
"resource_path": "HarvardMIT/segmented/en-141-2010-nov-team-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2010"
}
|
Let $a, b$, and $c$ be positive real numbers. Determine the largest total number of real roots that the following three polynomials may have among them: $a x^{2}+b x+c, b x^{2}+c x+a$, and $c x^{2}+a x+b$.
|
4 If all the polynomials had real roots, their discriminants would all be nonnegative: $a^{2} \geq$ $4 b c, b^{2} \geq 4 c a$, and $c^{2} \geq 4 a b$. Multiplying these inequalities gives $(a b c)^{2} \geq 64(a b c)^{2}$, a contradiction. Hence one of the quadratics has no real roots. The maximum of 4 real roots is attainable: for example, the values $(a, b, c)=(1,5,6)$ give $-2,-3$ as roots to $x^{2}+5 x+6$ and $-1,-\frac{1}{5}$ as roots to $5 x^{2}+6 x+1$.
|
4
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $a, b$, and $c$ be positive real numbers. Determine the largest total number of real roots that the following three polynomials may have among them: $a x^{2}+b x+c, b x^{2}+c x+a$, and $c x^{2}+a x+b$.
|
4 If all the polynomials had real roots, their discriminants would all be nonnegative: $a^{2} \geq$ $4 b c, b^{2} \geq 4 c a$, and $c^{2} \geq 4 a b$. Multiplying these inequalities gives $(a b c)^{2} \geq 64(a b c)^{2}$, a contradiction. Hence one of the quadratics has no real roots. The maximum of 4 real roots is attainable: for example, the values $(a, b, c)=(1,5,6)$ give $-2,-3$ as roots to $x^{2}+5 x+6$ and $-1,-\frac{1}{5}$ as roots to $5 x^{2}+6 x+1$.
|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n1. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcalc-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
Josh takes a walk on a rectangular grid of $n$ rows and 3 columns, starting from the bottom left corner. At each step, he can either move one square to the right or simultaneously move one square to the left and one square up. In how many ways can he reach the center square of the topmost row?
|
$2^{n-1}$ Note that Josh must pass through the center square of each row. There are 2 ways to get from the center square of row $k$ to the center square of row $k+1$. So there are $2^{n-1}$ ways to get to the center square of row $n$.
|
2^{n-1}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Josh takes a walk on a rectangular grid of $n$ rows and 3 columns, starting from the bottom left corner. At each step, he can either move one square to the right or simultaneously move one square to the left and one square up. In how many ways can he reach the center square of the topmost row?
|
$2^{n-1}$ Note that Josh must pass through the center square of each row. There are 2 ways to get from the center square of row $k$ to the center square of row $k+1$. So there are $2^{n-1}$ ways to get to the center square of row $n$.
|
{
"exam": "HMMT",
"problem_label": "4",
"problem_match": "\n2. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcalc-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a differentiable function such that $f(0)=0, f(1)=1$, and $\left|f^{\prime}(x)\right| \leq 2$ for all real numbers $x$. If $a$ and $b$ are real numbers such that the set of possible values of $\int_{0}^{1} f(x) d x$ is the open interval $(a, b)$, determine $b-a$.
|
$\boxed{\frac{3}{4}}$ Draw lines of slope $\pm 2$ passing through $(0,0)$ and $(1, 1)$. These form a parallelogram with vertices $(0,0),(.75,1.5),(1,1),(.25,-.5)$. By the mean value theorem, no point of $(x, f(x))$ lies outside this parallelogram, but we can construct functions arbitrarily close to the top or the bottom of the parallelogram while satisfying the condition of the problem. So $(b-a)$ is the area of this parallelogram, which is $\frac{3}{4}$.
|
\frac{3}{4}
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a differentiable function such that $f(0)=0, f(1)=1$, and $\left|f^{\prime}(x)\right| \leq 2$ for all real numbers $x$. If $a$ and $b$ are real numbers such that the set of possible values of $\int_{0}^{1} f(x) d x$ is the open interval $(a, b)$, determine $b-a$.
|
$\boxed{\frac{3}{4}}$ Draw lines of slope $\pm 2$ passing through $(0,0)$ and $(1, 1)$. These form a parallelogram with vertices $(0,0),(.75,1.5),(1,1),(.25,-.5)$. By the mean value theorem, no point of $(x, f(x))$ lies outside this parallelogram, but we can construct functions arbitrarily close to the top or the bottom of the parallelogram while satisfying the condition of the problem. So $(b-a)$ is the area of this parallelogram, which is $\frac{3}{4}$.
|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n3. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcalc-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
Let $A B C$ be a triangle such that $A B=7$, and let the angle bisector of $\angle B A C$ intersect line $B C$ at $D$. If there exist points $E$ and $F$ on sides $A C$ and $B C$, respectively, such that lines $A D$ and $E F$ are parallel and divide triangle $A B C$ into three parts of equal area, determine the number of possible integral values for $B C$.
|
13
Algebra \& Calculus Individual Test
Note that such $E, F$ exist if and only if
$$
\frac{[A D C]}{[A D B]}=2
$$
([] denotes area.) Since $A D$ is the angle bisector, and the ratio of areas of triangles with equal height is the ratio of their bases,
$$
\frac{A C}{A B}=\frac{D C}{D B}=\frac{[A D C]}{[A D B]}
$$
Hence (1) is equivalent to $A C=2 A B=14$. Then $B C$ can be any length $d$ such that the triangle inequalities are satisfied:
$$
\begin{aligned}
d+7 & >14 \\
7+14 & >d
\end{aligned}
$$
Hence $7<d<21$ and there are 13 possible integral values for $B C$.
|
13
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle such that $A B=7$, and let the angle bisector of $\angle B A C$ intersect line $B C$ at $D$. If there exist points $E$ and $F$ on sides $A C$ and $B C$, respectively, such that lines $A D$ and $E F$ are parallel and divide triangle $A B C$ into three parts of equal area, determine the number of possible integral values for $B C$.
|
13

Algebra \& Calculus Individual Test
Note that such $E, F$ exist if and only if
$$
\frac{[A D C]}{[A D B]}=2
$$
([] denotes area.) Since $A D$ is the angle bisector, and the ratio of areas of triangles with equal height is the ratio of their bases,
$$
\frac{A C}{A B}=\frac{D C}{D B}=\frac{[A D C]}{[A D B]}
$$
Hence (1) is equivalent to $A C=2 A B=14$. Then $B C$ can be any length $d$ such that the triangle inequalities are satisfied:
$$
\begin{aligned}
d+7 & >14 \\
7+14 & >d
\end{aligned}
$$
Hence $7<d<21$ and there are 13 possible integral values for $B C$.
|
{
"exam": "HMMT",
"problem_label": "2",
"problem_match": "\n4. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcalc-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
Nathaniel and Obediah play a game in which they take turns rolling a fair six-sided die and keep a running tally of the sum of the results of all rolls made. A player wins if, after he rolls, the number on the running tally is a multiple of 7. Play continues until either player wins, or else indefinitely. If Nathaniel goes first, determine the probability that he ends up winning.
|
$\frac{5}{11}$ For $1 \leq k \leq 6$, let $x_{k}$ be the probability that the current player, say $A$, will win when the number on the tally at the beginning of his turn is $k$ modulo 7 . The probability that the total is $l$ modulo 7 after his roll is $\frac{1}{6}$ for each $l \not \equiv k(\bmod 7)$; in particular, there is a $\frac{1}{6}$ chance he wins immediately. The chance that $A$ will win if he leaves $l$ on the board after his turn is $1-x_{l}$. Hence for $1 \leq k \leq 6$,
$$
x_{k}=\frac{1}{6} \sum_{1 \leq l \leq 6, l \neq k}\left(1-x_{l}\right)+\frac{1}{6}
$$
Letting $s=\sum_{l=1}^{6} x_{l}$, this becomes $x_{k}=\frac{x_{k}-s}{6}+1$ or $\frac{5 x_{k}}{6}=-\frac{s}{6}+1$. Hence $x_{1}=\cdots=x_{6}$, and $6 x_{k}=s$ for every $k$. Plugging this in gives $\frac{11 x_{k}}{6}=1$, or $x_{k}=\frac{6}{11}$.
Since Nathaniel cannot win on his first turn, he leaves Obediah with a number not divisible by 7. Hence Obediah's chance of winning is $\frac{6}{11}$ and Nathaniel's chance of winning is $\frac{5}{11}$.
|
\frac{5}{11}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Nathaniel and Obediah play a game in which they take turns rolling a fair six-sided die and keep a running tally of the sum of the results of all rolls made. A player wins if, after he rolls, the number on the running tally is a multiple of 7. Play continues until either player wins, or else indefinitely. If Nathaniel goes first, determine the probability that he ends up winning.
|
$\frac{5}{11}$ For $1 \leq k \leq 6$, let $x_{k}$ be the probability that the current player, say $A$, will win when the number on the tally at the beginning of his turn is $k$ modulo 7 . The probability that the total is $l$ modulo 7 after his roll is $\frac{1}{6}$ for each $l \not \equiv k(\bmod 7)$; in particular, there is a $\frac{1}{6}$ chance he wins immediately. The chance that $A$ will win if he leaves $l$ on the board after his turn is $1-x_{l}$. Hence for $1 \leq k \leq 6$,
$$
x_{k}=\frac{1}{6} \sum_{1 \leq l \leq 6, l \neq k}\left(1-x_{l}\right)+\frac{1}{6}
$$
Letting $s=\sum_{l=1}^{6} x_{l}$, this becomes $x_{k}=\frac{x_{k}-s}{6}+1$ or $\frac{5 x_{k}}{6}=-\frac{s}{6}+1$. Hence $x_{1}=\cdots=x_{6}$, and $6 x_{k}=s$ for every $k$. Plugging this in gives $\frac{11 x_{k}}{6}=1$, or $x_{k}=\frac{6}{11}$.
Since Nathaniel cannot win on his first turn, he leaves Obediah with a number not divisible by 7. Hence Obediah's chance of winning is $\frac{6}{11}$ and Nathaniel's chance of winning is $\frac{5}{11}$.
|
{
"exam": "HMMT",
"problem_label": "6",
"problem_match": "\n5. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcalc-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
Let $a \star b=a b+a+b$ for all integers $a$ and $b$. Evaluate $1 \star(2 \star(3 \star(4 \star \ldots(99 \star 100) \ldots)))$.
|
101!-1 We will first show that $\star$ is both commutative and associative.
- Commutativity: $a \star b=a b+a+b=b \star a$
- Associativity: $a \star(b \star c)=a(b c+b+c)+a+b c+b+c=a b c+a b+a c+b c+a+b+c$ and $(a \star b) \star c=(a b+a+b) c+a b+a+b+c=a b c+a b+a c+b c+a+b+c$. So $a \star(b \star c)=(a \star b) \star c$.
So we need only calculate $((\ldots(1 \star 2) \star 3) \star 4) \ldots \star 100)$. We will prove by induction that
$$
((\ldots(1 \star 2) \star 3) \star 4) \ldots \star n)=(n+1)!-1 .
$$
- Base case $(n=2):(1 \star 2)=2+1+2=5=3!-1$
- Inductive step:
Suppose that
$$
(((\ldots(1 \star 2) \star 3) \star 4) \ldots \star n)=(n+1)!-1
$$
Then,
$$
\begin{aligned}
((((\ldots(1 \star 2) \star 3) \star 4) \ldots \star n) \star(n+1)) & =((n+1)!-1) \star(n+1) \\
& =(n+1)!(n+1)-(n+1)+(n+1)!-1+(n+1) \\
& =(n+2)!-1
\end{aligned}
$$
Hence, $((\ldots(1 \star 2) \star 3) \star 4) \ldots \star n)=(n+1)$ ! - 1 for all $n$. For $n=100$, this results to $101!-1$.
|
101!-1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $a \star b=a b+a+b$ for all integers $a$ and $b$. Evaluate $1 \star(2 \star(3 \star(4 \star \ldots(99 \star 100) \ldots)))$.
|
101!-1 We will first show that $\star$ is both commutative and associative.
- Commutativity: $a \star b=a b+a+b=b \star a$
- Associativity: $a \star(b \star c)=a(b c+b+c)+a+b c+b+c=a b c+a b+a c+b c+a+b+c$ and $(a \star b) \star c=(a b+a+b) c+a b+a+b+c=a b c+a b+a c+b c+a+b+c$. So $a \star(b \star c)=(a \star b) \star c$.
So we need only calculate $((\ldots(1 \star 2) \star 3) \star 4) \ldots \star 100)$. We will prove by induction that
$$
((\ldots(1 \star 2) \star 3) \star 4) \ldots \star n)=(n+1)!-1 .
$$
- Base case $(n=2):(1 \star 2)=2+1+2=5=3!-1$
- Inductive step:
Suppose that
$$
(((\ldots(1 \star 2) \star 3) \star 4) \ldots \star n)=(n+1)!-1
$$
Then,
$$
\begin{aligned}
((((\ldots(1 \star 2) \star 3) \star 4) \ldots \star n) \star(n+1)) & =((n+1)!-1) \star(n+1) \\
& =(n+1)!(n+1)-(n+1)+(n+1)!-1+(n+1) \\
& =(n+2)!-1
\end{aligned}
$$
Hence, $((\ldots(1 \star 2) \star 3) \star 4) \ldots \star n)=(n+1)$ ! - 1 for all $n$. For $n=100$, this results to $101!-1$.
|
{
"exam": "HMMT",
"problem_label": "5",
"problem_match": "\n6. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcalc-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
Let $f:[0,1) \rightarrow \mathbb{R}$ be a function that satisfies the following condition: if
$$
x=\sum_{n=1}^{\infty} \frac{a_{n}}{10^{n}}=. a_{1} a_{2} a_{3} \ldots
$$
is the decimal expansion of $x$ and there does not exist a positive integer $k$ such that $a_{n}=9$ for all $n \geq k$, then
$$
f(x)=\sum_{n=1}^{\infty} \frac{a_{n}}{10^{2 n}} .
$$
Determine $f^{\prime}\left(\frac{1}{3}\right)$.
|
0 Note that $\frac{1}{3}=\sum_{n=1}^{\infty} \frac{3}{10^{n}}$.
Clearly $f$ is an increasing function. Also for any integer $n \geq 1$, we see from decimal expansions that $f\left(\frac{1}{3} \pm \frac{1}{10^{n}}\right)-f\left(\frac{1}{3}\right)= \pm \frac{1}{10^{2 n}}$.
Consider $h$ such that $10^{-n-1} \leq|h|<10^{-n}$. The two properties of $f$ outlined above show that $\left\lvert\, f\left(\frac{1}{3}+\right.\right.$ $h)-f\left(\frac{1}{3}\right) \left\lvert\,<\frac{1}{10^{2 n}}\right.$. And from $\left|\frac{1}{h}\right| \leq 10^{n+1}$, we get $\left|\frac{f\left(\frac{1}{3}+h\right)-f\left(\frac{1}{3}\right)}{h}\right|<\frac{1}{10^{n-1}}$. Taking $n \rightarrow \infty$ gives $h \rightarrow 0$ and $f^{\prime}\left(\frac{1}{3}\right)=\lim _{n \rightarrow \infty} \frac{1}{10^{n-1}}=0$.
|
0
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Let $f:[0,1) \rightarrow \mathbb{R}$ be a function that satisfies the following condition: if
$$
x=\sum_{n=1}^{\infty} \frac{a_{n}}{10^{n}}=. a_{1} a_{2} a_{3} \ldots
$$
is the decimal expansion of $x$ and there does not exist a positive integer $k$ such that $a_{n}=9$ for all $n \geq k$, then
$$
f(x)=\sum_{n=1}^{\infty} \frac{a_{n}}{10^{2 n}} .
$$
Determine $f^{\prime}\left(\frac{1}{3}\right)$.
|
0 Note that $\frac{1}{3}=\sum_{n=1}^{\infty} \frac{3}{10^{n}}$.
Clearly $f$ is an increasing function. Also for any integer $n \geq 1$, we see from decimal expansions that $f\left(\frac{1}{3} \pm \frac{1}{10^{n}}\right)-f\left(\frac{1}{3}\right)= \pm \frac{1}{10^{2 n}}$.
Consider $h$ such that $10^{-n-1} \leq|h|<10^{-n}$. The two properties of $f$ outlined above show that $\left\lvert\, f\left(\frac{1}{3}+\right.\right.$ $h)-f\left(\frac{1}{3}\right) \left\lvert\,<\frac{1}{10^{2 n}}\right.$. And from $\left|\frac{1}{h}\right| \leq 10^{n+1}$, we get $\left|\frac{f\left(\frac{1}{3}+h\right)-f\left(\frac{1}{3}\right)}{h}\right|<\frac{1}{10^{n-1}}$. Taking $n \rightarrow \infty$ gives $h \rightarrow 0$ and $f^{\prime}\left(\frac{1}{3}\right)=\lim _{n \rightarrow \infty} \frac{1}{10^{n-1}}=0$.
|
{
"exam": "HMMT",
"problem_label": "8",
"problem_match": "\n7. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcalc-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
Find all integers $x$ such that $2 x^{2}+x-6$ is a positive integral power of a prime positive integer.
|
$-3,2,5$ Let $f(x)=2 x^{2}+x-6=(2 x-3)(x+2)$. Suppose a positive integer $a$ divides both $2 x-3$ and $x+2$. Then $a$ must also divide $2(x+2)-(2 x-3)=7$. Hence, $a$ can either be 1 or 7. As a result, $2 x-3=7^{n}$ or $-7^{n}$ for some positive integer $n$, or either $x+2$ or $2 x-3$ is $\pm 1$. We consider the following cases:
- $(2 x-3)=1$. Then $x=2$, which yields $f(x)=4$, a prime power.
- $(2 x-3)=-1$. Then $x=1$, which yields $f(x)=-3$, not a prime power.
- $(x+2)=1)$. Then $x=-1$, which yields $f(x)=-5$ not a prime power.
- $(x+2)=-1$. Then $x=-3$, which yields $f(x)=9$, a prime power.
- $(2 x-3)=7$. Then $x=5$, which yields $f(x)=49$, a prime power.
- $(2 x-3)=-7$. Then $x=-2$, which yields $f(x)=0$, not a prime power.
- $(2 x-3)= \pm 7^{n}$, for $n \geq 2$. Then, since $x+2=\frac{(2 x-3)+7}{2}$, we have that $x+2$ is divisible by 7 but not by 49. Hence $x+2= \pm 7$, yielding $x=5,-9$. The former has already been considered, while the latter yields $f(x)=147$.
So $x$ can be either $-3,2$ or 5 .
(Note: In the official solutions packet we did not list the answer - 3 . This oversight was quickly noticed on the day of the test, and only the answer $-3,2,5$ was marked as correct.
|
-3,2,5
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all integers $x$ such that $2 x^{2}+x-6$ is a positive integral power of a prime positive integer.
|
$-3,2,5$ Let $f(x)=2 x^{2}+x-6=(2 x-3)(x+2)$. Suppose a positive integer $a$ divides both $2 x-3$ and $x+2$. Then $a$ must also divide $2(x+2)-(2 x-3)=7$. Hence, $a$ can either be 1 or 7. As a result, $2 x-3=7^{n}$ or $-7^{n}$ for some positive integer $n$, or either $x+2$ or $2 x-3$ is $\pm 1$. We consider the following cases:
- $(2 x-3)=1$. Then $x=2$, which yields $f(x)=4$, a prime power.
- $(2 x-3)=-1$. Then $x=1$, which yields $f(x)=-3$, not a prime power.
- $(x+2)=1)$. Then $x=-1$, which yields $f(x)=-5$ not a prime power.
- $(x+2)=-1$. Then $x=-3$, which yields $f(x)=9$, a prime power.
- $(2 x-3)=7$. Then $x=5$, which yields $f(x)=49$, a prime power.
- $(2 x-3)=-7$. Then $x=-2$, which yields $f(x)=0$, not a prime power.
- $(2 x-3)= \pm 7^{n}$, for $n \geq 2$. Then, since $x+2=\frac{(2 x-3)+7}{2}$, we have that $x+2$ is divisible by 7 but not by 49. Hence $x+2= \pm 7$, yielding $x=5,-9$. The former has already been considered, while the latter yields $f(x)=147$.
So $x$ can be either $-3,2$ or 5 .
(Note: In the official solutions packet we did not list the answer - 3 . This oversight was quickly noticed on the day of the test, and only the answer $-3,2,5$ was marked as correct.
|
{
"exam": "HMMT",
"problem_label": "7",
"problem_match": "\n8. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcalc-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
Let $A B C D E F$ be a regular hexagon of area 1 . Let $M$ be the midpoint of $D E$. Let $X$ be the intersection of $A C$ and $B M$, let $Y$ be the intersection of $B F$ and $A M$, and let $Z$ be the intersection of $A C$ and $B F$. If $[P]$ denotes the area of polygon $P$ for any polygon $P$ in the plane, evaluate $[B X C]+[A Y F]+[A B Z]-[M X Z Y]$.
|
0

Let $O$ be the center of the hexagon. The desired area is $[A B C D E F]-[A C D M]-[B F E M]$. Note that $[A D M]=[A D E] / 2=[O D E]=[A B C]$, where the last equation holds because $\sin 60^{\circ}=\sin 120^{\circ}$. Thus, $[A C D M]=[A C D]+[A D M]=[A C D]+[A B C]=[A B C D]$, but the area of $A B C D$ is half the area of the hexagon. Similarly, the area of $[B F E M]$ is half the area of the hexagon, so the answer is zero.
|
0
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D E F$ be a regular hexagon of area 1 . Let $M$ be the midpoint of $D E$. Let $X$ be the intersection of $A C$ and $B M$, let $Y$ be the intersection of $B F$ and $A M$, and let $Z$ be the intersection of $A C$ and $B F$. If $[P]$ denotes the area of polygon $P$ for any polygon $P$ in the plane, evaluate $[B X C]+[A Y F]+[A B Z]-[M X Z Y]$.
|
0

Let $O$ be the center of the hexagon. The desired area is $[A B C D E F]-[A C D M]-[B F E M]$. Note that $[A D M]=[A D E] / 2=[O D E]=[A B C]$, where the last equation holds because $\sin 60^{\circ}=\sin 120^{\circ}$. Thus, $[A C D M]=[A C D]+[A D M]=[A C D]+[A B C]=[A B C D]$, but the area of $A B C D$ is half the area of the hexagon. Similarly, the area of $[B F E M]$ is half the area of the hexagon, so the answer is zero.
|
{
"exam": "HMMT",
"problem_label": "7",
"problem_match": "\n9. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcalc-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
For all real numbers $x$, let
$$
f(x)=\frac{1}{\sqrt[2011]{1-x^{2011}}}
$$
Evaluate $(f(f(\ldots(f(2011)) \ldots)))^{2011}$, where $f$ is applied 2010 times.
|
$2011^{2011}$ Direct calculation shows that $f(f(x))=\frac{\sqrt[2011]{1-x^{2011}}}{-x}$ and $f(f(f(x)))=x$. Hence $(f(f(\ldots(f(x)) \ldots)))=x$, where $f$ is applied 2010 times. So $(f(f(\ldots(f(2011)) \ldots)))^{2011}=$ $2011^{2011}$.
|
2011^{2011}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
For all real numbers $x$, let
$$
f(x)=\frac{1}{\sqrt[2011]{1-x^{2011}}}
$$
Evaluate $(f(f(\ldots(f(2011)) \ldots)))^{2011}$, where $f$ is applied 2010 times.
|
$2011^{2011}$ Direct calculation shows that $f(f(x))=\frac{\sqrt[2011]{1-x^{2011}}}{-x}$ and $f(f(f(x)))=x$. Hence $(f(f(\ldots(f(x)) \ldots)))=x$, where $f$ is applied 2010 times. So $(f(f(\ldots(f(2011)) \ldots)))^{2011}=$ $2011^{2011}$.
|
{
"exam": "HMMT",
"problem_label": "9",
"problem_match": "\n10. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcalc-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
Evaluate $\int_{1}^{\infty}\left(\frac{\ln x}{x}\right)^{2011} d x$.
|
$\frac{2011!}{2010^{2012}}$ By the chain rule, $\frac{d}{d x}(\ln x)^{n}=\frac{n \ln ^{n-1} x}{x}$.
We calculate the definite integral using integration by parts:
$$
\int_{x=1}^{\infty} \frac{(\ln x)^{n}}{x^{2011}} d x=\left[\frac{(\ln x)^{n}}{-2010 x^{2010}}\right]_{x=1}^{x=\infty}-\int_{x=1}^{\infty} \frac{n(\ln x)^{n-1}}{-2010 x^{2011}} d x
$$
But $\ln (1)=0$, and $\lim _{x \rightarrow \infty} \frac{(\ln x)^{n}}{x^{2010}}=0$ for all $n>0$. So
$$
\int_{x=1}^{\infty} \frac{(\ln x)^{n}}{x^{2011}} d x=\int_{x=1}^{\infty} \frac{n(\ln x)^{n-1}}{2010 x^{2011}} d x
$$
It follows that
$$
\int_{x=1}^{\infty} \frac{(\ln x)^{n}}{x^{2011}} d x=\frac{n!}{2010^{n}} \int_{x=1}^{\infty} \frac{1}{x^{2011}} d x=\frac{n!}{2010^{n+1}}
$$
So the answer is $\frac{2011!}{2010^{2012}}$.
|
\frac{2011!}{2010^{2012}}
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Evaluate $\int_{1}^{\infty}\left(\frac{\ln x}{x}\right)^{2011} d x$.
|
$\frac{2011!}{2010^{2012}}$ By the chain rule, $\frac{d}{d x}(\ln x)^{n}=\frac{n \ln ^{n-1} x}{x}$.
We calculate the definite integral using integration by parts:
$$
\int_{x=1}^{\infty} \frac{(\ln x)^{n}}{x^{2011}} d x=\left[\frac{(\ln x)^{n}}{-2010 x^{2010}}\right]_{x=1}^{x=\infty}-\int_{x=1}^{\infty} \frac{n(\ln x)^{n-1}}{-2010 x^{2011}} d x
$$
But $\ln (1)=0$, and $\lim _{x \rightarrow \infty} \frac{(\ln x)^{n}}{x^{2010}}=0$ for all $n>0$. So
$$
\int_{x=1}^{\infty} \frac{(\ln x)^{n}}{x^{2011}} d x=\int_{x=1}^{\infty} \frac{n(\ln x)^{n-1}}{2010 x^{2011}} d x
$$
It follows that
$$
\int_{x=1}^{\infty} \frac{(\ln x)^{n}}{x^{2011}} d x=\frac{n!}{2010^{n}} \int_{x=1}^{\infty} \frac{1}{x^{2011}} d x=\frac{n!}{2010^{n+1}}
$$
So the answer is $\frac{2011!}{2010^{2012}}$.
|
{
"exam": "HMMT",
"problem_label": "10",
"problem_match": "\n11. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcalc-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
Let $f(x)=x^{2}+6 x+c$ for all real numbers $x$, where $c$ is some real number. For what values of $c$ does $f(f(x))$ have exactly 3 distinct real roots?
|
$\frac{\frac{11-\sqrt{13}}{2}}{}$ Suppose $f$ has only one distinct root $r_{1}$. Then, if $x_{1}$ is a root of $f(f(x))$, it must be the case that $f\left(x_{1}\right)=r_{1}$. As a result, $f(f(x))$ would have at most two roots, thus not satisfying the problem condition. Hence $f$ has two distinct roots. Let them be $r_{1} \neq r_{2}$.
Since $f(f(x))$ has just three distinct roots, either $f(x)=r_{1}$ or $f(x)=r_{2}$ has one distinct root. Assume without loss of generality that $r_{1}$ has one distinct root. Then $f(x)=x^{2}+6 x+c=r_{1}$ has one root, so that $x^{2}+6 x+c-r_{1}$ is a square polynomial. Therefore, $c-r_{1}=9$, so that $r_{1}=c-9$. So $c-9$ is a root of $f$. So $(c-9)^{2}+6(c-9)+c=0$, yielding $c^{2}-11 c+27=0$, or $\left(c-\frac{11}{2}\right)^{2}=\frac{13}{2}$. This results to $c=\frac{11 \pm \sqrt{13}}{2}$.
If $c=\frac{11-\sqrt{13}}{2}, f(x)=x^{2}+6 x+\frac{11-\sqrt{13}}{2}=\left(x+\frac{7+\sqrt{13}}{2}\right)\left(x+\frac{5-\sqrt{13}}{2}\right)$. We know $f(x)=\frac{-7-\sqrt{13}}{2}$ has a double root, -3 . Now $\frac{-5+\sqrt{13}}{2}>\frac{-7-\sqrt{13}}{2}$ so the second root is above the vertex of the parabola, and is hit twice.
If $c=\frac{11+\sqrt{13}}{2}, f(x)=x^{2}+6 x+\frac{11+\sqrt{13}}{2}=\left(x+\frac{7-\sqrt{13}}{2}\right)\left(x+\frac{5+\sqrt{13}}{2}\right)$. We know $f(x)=\frac{-7+\sqrt{13}}{2}$ has a double root, -3 , and this is the value of $f$ at the vertex of the parabola, so it is its minimum value. Since $\frac{-5-\sqrt{13}}{2}<\frac{-7+\sqrt{13}}{2}, f(x)=\frac{-5-\sqrt{13}}{2}$ has no solutions. So in this case, $f$ has only one real root.
So the answer is $c=\frac{11-\sqrt{13}}{2}$.
Note: In the solutions packet we had both roots listed as the correct answer. We noticed this oversight on the day of the test and awarded points only for the correct answer.
|
\frac{11-\sqrt{13}}{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $f(x)=x^{2}+6 x+c$ for all real numbers $x$, where $c$ is some real number. For what values of $c$ does $f(f(x))$ have exactly 3 distinct real roots?
|
$\frac{\frac{11-\sqrt{13}}{2}}{}$ Suppose $f$ has only one distinct root $r_{1}$. Then, if $x_{1}$ is a root of $f(f(x))$, it must be the case that $f\left(x_{1}\right)=r_{1}$. As a result, $f(f(x))$ would have at most two roots, thus not satisfying the problem condition. Hence $f$ has two distinct roots. Let them be $r_{1} \neq r_{2}$.
Since $f(f(x))$ has just three distinct roots, either $f(x)=r_{1}$ or $f(x)=r_{2}$ has one distinct root. Assume without loss of generality that $r_{1}$ has one distinct root. Then $f(x)=x^{2}+6 x+c=r_{1}$ has one root, so that $x^{2}+6 x+c-r_{1}$ is a square polynomial. Therefore, $c-r_{1}=9$, so that $r_{1}=c-9$. So $c-9$ is a root of $f$. So $(c-9)^{2}+6(c-9)+c=0$, yielding $c^{2}-11 c+27=0$, or $\left(c-\frac{11}{2}\right)^{2}=\frac{13}{2}$. This results to $c=\frac{11 \pm \sqrt{13}}{2}$.
If $c=\frac{11-\sqrt{13}}{2}, f(x)=x^{2}+6 x+\frac{11-\sqrt{13}}{2}=\left(x+\frac{7+\sqrt{13}}{2}\right)\left(x+\frac{5-\sqrt{13}}{2}\right)$. We know $f(x)=\frac{-7-\sqrt{13}}{2}$ has a double root, -3 . Now $\frac{-5+\sqrt{13}}{2}>\frac{-7-\sqrt{13}}{2}$ so the second root is above the vertex of the parabola, and is hit twice.
If $c=\frac{11+\sqrt{13}}{2}, f(x)=x^{2}+6 x+\frac{11+\sqrt{13}}{2}=\left(x+\frac{7-\sqrt{13}}{2}\right)\left(x+\frac{5+\sqrt{13}}{2}\right)$. We know $f(x)=\frac{-7+\sqrt{13}}{2}$ has a double root, -3 , and this is the value of $f$ at the vertex of the parabola, so it is its minimum value. Since $\frac{-5-\sqrt{13}}{2}<\frac{-7+\sqrt{13}}{2}, f(x)=\frac{-5-\sqrt{13}}{2}$ has no solutions. So in this case, $f$ has only one real root.
So the answer is $c=\frac{11-\sqrt{13}}{2}$.
Note: In the solutions packet we had both roots listed as the correct answer. We noticed this oversight on the day of the test and awarded points only for the correct answer.
|
{
"exam": "HMMT",
"problem_label": "11",
"problem_match": "\n12. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcalc-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
Sarah and Hagar play a game of darts. Let $O_{0}$ be a circle of radius 1. On the $n$th turn, the player whose turn it is throws a dart and hits a point $p_{n}$ randomly selected from the points of $O_{n-1}$. The player then draws the largest circle that is centered at $p_{n}$ and contained in $O_{n-1}$, and calls this circle $O_{n}$. The player then colors every point that is inside $O_{n-1}$ but not inside $O_{n}$ her color. Sarah goes first, and the two players alternate turns. Play continues indefinitely. If Sarah's color is red, and Hagar's color is blue, what is the expected value of the area of the set of points colored red?
|
$\boxed{\frac{6\pi}{7}}$ Let $f(r)$ be the average area colored red on a dartboard of radius $r$ if Sarah plays first. Then $f(r)$ is proportional to $r^{2}$. Let $f(r)=(\pi x) r^{2}$ for some constant $x$. We want to find $f(1)=\pi x$.
In the first throw, if Sarah's dart hits a point with distance $r$ from the center of $O_{0}$, the radius of $O_{1}$ will be $1-r$. The expected value of the area colored red will be $\left(\pi-\pi(1-r)^{2}\right)+\left(\pi(1-r)^{2}-f(1-r)\right)=$ $\pi-f(1-r)$. The value of $f(1)$ is the average value of $\pi-f(1-r)$ over all points in $O_{0}$. Using polar coordinates, we get
$$
\begin{aligned}
& f(1)=\frac{\int_{0}^{2 \pi} \int_{0}^{1}(\pi-f(1-r)) r d r d \theta}{2 \pi} \int_{0}^{1} \int_{0}^{1} r d r d \theta \\
& \pi x=\frac{\int_{0}^{1}\left(\pi-\pi x(1-r)^{2}\right) r d r}{\int_{0}^{1} r d r} \\
& \frac{\pi x}{2}=\int_{0}^{1} \pi r-\pi x r(1-r)^{2} d r \\
& \frac{\pi x}{2}=\frac{\pi}{2}-\pi x\left(\frac{1}{2}-\frac{2}{3}+\frac{1}{4}\right) \\
& \frac{\pi x}{2}=\frac{\pi}{2}-\frac{\pi x}{12}
\end{aligned}
$$
$$
\pi x=\frac{6 \pi}{7}
$$
|
\frac{6\pi}{7}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Sarah and Hagar play a game of darts. Let $O_{0}$ be a circle of radius 1. On the $n$th turn, the player whose turn it is throws a dart and hits a point $p_{n}$ randomly selected from the points of $O_{n-1}$. The player then draws the largest circle that is centered at $p_{n}$ and contained in $O_{n-1}$, and calls this circle $O_{n}$. The player then colors every point that is inside $O_{n-1}$ but not inside $O_{n}$ her color. Sarah goes first, and the two players alternate turns. Play continues indefinitely. If Sarah's color is red, and Hagar's color is blue, what is the expected value of the area of the set of points colored red?
|
$\boxed{\frac{6\pi}{7}}$ Let $f(r)$ be the average area colored red on a dartboard of radius $r$ if Sarah plays first. Then $f(r)$ is proportional to $r^{2}$. Let $f(r)=(\pi x) r^{2}$ for some constant $x$. We want to find $f(1)=\pi x$.
In the first throw, if Sarah's dart hits a point with distance $r$ from the center of $O_{0}$, the radius of $O_{1}$ will be $1-r$. The expected value of the area colored red will be $\left(\pi-\pi(1-r)^{2}\right)+\left(\pi(1-r)^{2}-f(1-r)\right)=$ $\pi-f(1-r)$. The value of $f(1)$ is the average value of $\pi-f(1-r)$ over all points in $O_{0}$. Using polar coordinates, we get
$$
\begin{aligned}
& f(1)=\frac{\int_{0}^{2 \pi} \int_{0}^{1}(\pi-f(1-r)) r d r d \theta}{2 \pi} \int_{0}^{1} \int_{0}^{1} r d r d \theta \\
& \pi x=\frac{\int_{0}^{1}\left(\pi-\pi x(1-r)^{2}\right) r d r}{\int_{0}^{1} r d r} \\
& \frac{\pi x}{2}=\int_{0}^{1} \pi r-\pi x r(1-r)^{2} d r \\
& \frac{\pi x}{2}=\frac{\pi}{2}-\pi x\left(\frac{1}{2}-\frac{2}{3}+\frac{1}{4}\right) \\
& \frac{\pi x}{2}=\frac{\pi}{2}-\frac{\pi x}{12}
\end{aligned}
$$
$$
\pi x=\frac{6 \pi}{7}
$$
|
{
"exam": "HMMT",
"problem_label": "12",
"problem_match": "\n13. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcalc-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
How many polynomials $P$ with integer coefficients and degree at most 5 satisfy $0 \leq P(x)<120$ for all $x \in\{0,1,2,3,4,5\}$ ?
|
86400000 For each nonnegative integer $i$, let $x^{\underline{i}}=x(x-1) \cdots(x-i+1)$. (Define $x^{0}=1$.)
Lemma: Each polynomial with integer coefficients $f$ can be uniquely written in the form
$$
f(x)=a_{n} x^{\underline{n}}+\ldots+a_{1} x^{\underline{1}}+a_{0} x^{\underline{0}}, a_{n} \neq 0
$$
Proof: Induct on the degree. The base case (degree 0 ) is clear. If $f$ has degree $m$ with leading coefficient $c$, then by matching leading coefficients we must have $m=n$ and $a_{n}=c$. By the induction hypothesis, $f(x)-c x^{\underline{n}}$ can be uniquely written as $a_{n-1} x \frac{n-1}{}(x)+\ldots+a_{1} x^{\underline{1}}+a_{0} x^{\underline{0}}$.
There are 120 possible choices for $a_{0}$, namely any integer in $[0,120)$. Once $a_{0}, \ldots, a_{i-1}$ have been chosen so $0 \leq P(0), \ldots, P(i-1)<120$, for some $0 \leq i \leq 5$, then we have
$$
P(i)=a_{i} i!+a_{i-1} i^{\frac{i-1}{}}+\cdots+a_{0}
$$
so by choosing $a_{i}$ we can make $P(i)$ any number congruent to $a_{i-1} i \frac{i-1}{}+\cdots+a_{0}$ modulo $i$ !. Thus there are $\frac{120}{i!}$ choices for $a_{i}$. Note the choice of $a_{i}$ does not affect the value of $P(0), \ldots, P(i-1)$. Thus all polynomials we obtain in this way are valid. The answer is
$$
\prod_{i=0}^{5} \frac{120}{i!}=86400000
$$
Note: Their is also a solution involving finite differences that is basically equivalent to this solution. One proves that for $i=0,1,2,3,4,5$ there are $\frac{5!}{i!}$ ways to pick the $i$ th finite difference at the point 0 .
|
86400000
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
How many polynomials $P$ with integer coefficients and degree at most 5 satisfy $0 \leq P(x)<120$ for all $x \in\{0,1,2,3,4,5\}$ ?
|
86400000 For each nonnegative integer $i$, let $x^{\underline{i}}=x(x-1) \cdots(x-i+1)$. (Define $x^{0}=1$.)
Lemma: Each polynomial with integer coefficients $f$ can be uniquely written in the form
$$
f(x)=a_{n} x^{\underline{n}}+\ldots+a_{1} x^{\underline{1}}+a_{0} x^{\underline{0}}, a_{n} \neq 0
$$
Proof: Induct on the degree. The base case (degree 0 ) is clear. If $f$ has degree $m$ with leading coefficient $c$, then by matching leading coefficients we must have $m=n$ and $a_{n}=c$. By the induction hypothesis, $f(x)-c x^{\underline{n}}$ can be uniquely written as $a_{n-1} x \frac{n-1}{}(x)+\ldots+a_{1} x^{\underline{1}}+a_{0} x^{\underline{0}}$.
There are 120 possible choices for $a_{0}$, namely any integer in $[0,120)$. Once $a_{0}, \ldots, a_{i-1}$ have been chosen so $0 \leq P(0), \ldots, P(i-1)<120$, for some $0 \leq i \leq 5$, then we have
$$
P(i)=a_{i} i!+a_{i-1} i^{\frac{i-1}{}}+\cdots+a_{0}
$$
so by choosing $a_{i}$ we can make $P(i)$ any number congruent to $a_{i-1} i \frac{i-1}{}+\cdots+a_{0}$ modulo $i$ !. Thus there are $\frac{120}{i!}$ choices for $a_{i}$. Note the choice of $a_{i}$ does not affect the value of $P(0), \ldots, P(i-1)$. Thus all polynomials we obtain in this way are valid. The answer is
$$
\prod_{i=0}^{5} \frac{120}{i!}=86400000
$$
Note: Their is also a solution involving finite differences that is basically equivalent to this solution. One proves that for $i=0,1,2,3,4,5$ there are $\frac{5!}{i!}$ ways to pick the $i$ th finite difference at the point 0 .
|
{
"exam": "HMMT",
"problem_label": "14",
"problem_match": "\n14. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcalc-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
Let $f:[0,1] \rightarrow[0,1]$ be a continuous function such that $f(f(x))=1$ for all $x \in[0,1]$. Determine the set of possible values of $\int_{0}^{1} f(x) d x$.
|
$\left(\frac{3}{4}, 1\right]$ Since the maximum value of $f$ is $1, \int_{0}^{1} f(x) d x \leq 1$.
By our condition $f(f(x))=1, f$ is 1 at any point within the range of $f$. Clearly, 1 is in the range of $f$, so $f(1)=1$. Now $f(x)$ is continuous on a closed interval so it attains a minimum value $c$. Since $c$ is in the range of $f, f(c)=1$.
If $c=1, f(x)=1$ for all $x$ and $\int_{0}^{1} f(x) d x=1$.
Now assume $c<1$. By the intermediate value theorem, since $f$ is continuous it attains all values between $c$ and 1 . So for all $x \geq c, f(x)=1$. Therefore,
$$
\int_{0}^{1} f(x) d x=\int_{0}^{c} f(x) d x+(1-c)
$$
Since $f(x) \geq c, \int_{0}^{c} f(x) d x>c^{2}$, and the equality is strict because $f$ is continuous and thus cannot be $c$ for all $x<c$ and 1 at $c$. So
$$
\int_{0}^{1} f(x) d x>c^{2}+(1-c)=\left(c-\frac{1}{2}\right)^{2}+\frac{3}{4} \geq \frac{3}{4}
$$
Therefore $\frac{3}{4}<\int_{0}^{1} f(x) d x \leq 1$, and it is easy to show that every value in this interval can be reached.
|
\left(\frac{3}{4}, 1\right]
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Let $f:[0,1] \rightarrow[0,1]$ be a continuous function such that $f(f(x))=1$ for all $x \in[0,1]$. Determine the set of possible values of $\int_{0}^{1} f(x) d x$.
|
$\left(\frac{3}{4}, 1\right]$ Since the maximum value of $f$ is $1, \int_{0}^{1} f(x) d x \leq 1$.
By our condition $f(f(x))=1, f$ is 1 at any point within the range of $f$. Clearly, 1 is in the range of $f$, so $f(1)=1$. Now $f(x)$ is continuous on a closed interval so it attains a minimum value $c$. Since $c$ is in the range of $f, f(c)=1$.
If $c=1, f(x)=1$ for all $x$ and $\int_{0}^{1} f(x) d x=1$.
Now assume $c<1$. By the intermediate value theorem, since $f$ is continuous it attains all values between $c$ and 1 . So for all $x \geq c, f(x)=1$. Therefore,
$$
\int_{0}^{1} f(x) d x=\int_{0}^{c} f(x) d x+(1-c)
$$
Since $f(x) \geq c, \int_{0}^{c} f(x) d x>c^{2}$, and the equality is strict because $f$ is continuous and thus cannot be $c$ for all $x<c$ and 1 at $c$. So
$$
\int_{0}^{1} f(x) d x>c^{2}+(1-c)=\left(c-\frac{1}{2}\right)^{2}+\frac{3}{4} \geq \frac{3}{4}
$$
Therefore $\frac{3}{4}<\int_{0}^{1} f(x) d x \leq 1$, and it is easy to show that every value in this interval can be reached.
|
{
"exam": "HMMT",
"problem_label": "14",
"problem_match": "\n15. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcalc-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
Let $f(x)=x^{2}-r_{2} x+r_{3}$ for all real numbers $x$, where $r_{2}$ and $r_{3}$ are some real numbers. Define a sequence $\left\{g_{n}\right\}$ for all nonnegative integers $n$ by $g_{0}=0$ and $g_{n+1}=f\left(g_{n}\right)$. Assume that $\left\{g_{n}\right\}$ satisfies the following three conditions: (i) $g_{2 i}<g_{2 i+1}$ and $g_{2 i+1}>g_{2 i+2}$ for all $0 \leq i \leq 2011$; (ii) there exists a positive integer $j$ such that $g_{i+1}>g_{i}$ for all $i>j$, and (iii) $\left\{g_{n}\right\}$ is unbounded. If $A$ is the greatest number such that $A \leq\left|r_{2}\right|$ for any function $f$ satisfying these properties, find $A$.
|
2 Consider the function $f(x)-x$. By the constraints of the problem, $f(x)-x$ must be negative for some $x$, namely, for $x=g_{2 i+1}, 0 \leq i \leq 2011$. Since $f(x)-x$ is positive for $x$ of large absolute value, the graph of $f(x)-x$ crosses the $x$-axis twice and $f(x)-x$ has two real roots, say $a<b$. Factoring gives $f(x)-x=(x-a)(x-b)$, or $f(x)=(x-a)(x-b)+x$.
Now, for $x<a, f(x)>x>a$, while for $x>b, f(x)>x>b$. Let $c \neq b$ be the number such that $f(c)=f(b)=b$. Note that $b$ is not the vertex as $f(a)=a<b$, so by the symmetry of quadratics, $c$ exists and $\frac{b+c}{2}=\frac{r_{2}}{2}$ as the vertex of the parabola. By the same token, $\frac{b+a}{2}=\frac{r_{2}+1}{2}$ is the vertex of $f(x)-x$. Hence $c=a-1$. If $f(x)>b$ then $x<c$ or $x>b$. Consider the smallest $j$ such that $g_{j}>b$. Then by the above observation, $g_{j-1}<c$. (If $g_{i} \geq b$ then $f\left(g_{i}\right) \geq g_{i} \geq b$ so by induction, $g_{i+1} \geq g_{i}$ for all $i \geq j$. Hence $j>1$; in fact $j \geq 4025$.) Since $g_{j-1}=f\left(g_{j-2}\right)$, the minimum value of $f$ is less than $c$. The minimum value is the value of $f$ evaluated at its vertex, $\frac{b+a-1}{2}$, so
$$
\begin{aligned}
f\left(\frac{b+a-1}{2}\right) & <c \\
\left(\frac{b+a-1}{2}-a\right)\left(\frac{b+a-1}{2}-b\right)+\frac{b+a-1}{2} & <a-1 \\
\frac{1-(b-a)^{2}}{4}+\frac{b-a+1}{2} & <0 \\
\frac{3}{4} & <\frac{(b-a)^{2}}{4}-\frac{b-a}{2} \\
4 & <(b-a-1)^{2}
\end{aligned}
$$
Then either $b-a-1<-2$ or $b-a-1>2$, but $b>a$, so the latter must hold and $(b-a)^{2}>9$. Now, the discriminant of $f(x)-x$ equals $(b-a)^{2}$ (the square of the difference of the two roots) and $\left(r_{2}+1\right)^{2}-4 r_{3}$ (from the coefficients), so $\left(r_{2}+1\right)^{2}>9+4 r_{3}$. But $r_{3}=g_{1}>g_{0}=0$ so $\left|r_{2}\right|>2$.
We claim that we can make $\left|r_{2}\right|$ arbitrarily close to 2 , so that the answer is 2 . First define $G_{i}, i \geq 0$ as follows. Let $N \geq 2012$ be an integer. For $\varepsilon>0$ let $h(x)=x^{2}-2-\varepsilon, g_{\varepsilon}(x)=-\sqrt{x+2+\varepsilon}$ and $G_{2 N+1}=2+\varepsilon$, and define $G_{i}$ recursively by $G_{i}=g_{\varepsilon}\left(G_{i+1}\right), G_{i+1}=h\left(G_{i}\right)$. (These two equations are consistent.) Note the following.
(i) $G_{2 i}<G_{2 i+1}$ and $G_{2 i+1}>G_{2 i+2}$ for $0 \leq i \leq N-1$. First note $G_{2 N}=-\sqrt{4+2 \varepsilon}>-\sqrt{4+2 \varepsilon+\varepsilon^{2}}=$ $-2-\varepsilon$. Let $l$ be the negative solution to $h(x)=x$. Note that $-2-\varepsilon<G_{2 N}<l<0$ since $h\left(G_{2 N}\right)>0>G_{2 N}$. Now $g_{\varepsilon}(x)$ is defined as long as $x \geq-2-\varepsilon$, and it sends $(-2-\varepsilon, l)$ into $(l, 0)$ and $(l, 0)$ into $(-2-\varepsilon, l)$. It follows that the $G_{i}, 0 \leq i \leq 2 N$ are well-defined; moreover, $G_{2 i}<l$ and $G_{2 i+1}>l$ for $0 \leq i \leq N-1$ by backwards induction on $i$, so the desired inequalities follow.
(ii) $G_{i}$ is increasing for $i \geq 2 N+1$. Indeed, if $x \geq 2+\varepsilon$, then $x^{2}-x=x(x-1)>2+\varepsilon$ so $h(x)>x$. Hence $2+\varepsilon=G_{2 N+1}<G_{2 N+2}<\cdots$.
(iii) $G_{i}$ is unbounded. This follows since $h(x)-x=x(x-2)-2-\varepsilon$ is increasing for $x>2+\varepsilon$, so $G_{i}$ increases faster and faster for $i \geq 2 N+1$.
Now define $f(x)=h\left(x+G_{0}\right)-G_{0}=x^{2}+2 G_{0} x+G_{0}^{2}-G_{0}-2-\varepsilon$. Note $G_{i+1}=h\left(G_{i}\right)$ while $g_{i+1}=f\left(g_{i}\right)=h\left(g_{i}+G_{0}\right)-G_{0}$, so by induction $g_{i}=G_{i}-G_{0}$. Since $\left\{G_{i}\right\}_{i=0}^{\infty}$ satisfies (i), (ii), and (iii), so does $g_{i}$.
We claim that we can make $G_{0}$ arbitrarily close to -1 by choosing $N$ large enough and $\varepsilon$ small enough; this will make $r_{2}=-2 G_{0}$ arbitrarily close to 2 . Choosing $N$ large corresponds to taking $G_{0}$ to be a larger iterate of $2+\varepsilon$ under $g_{\varepsilon}(x)$. By continuity of this function with respect to $x$ and $\varepsilon$, it suffices to
take $\varepsilon=0$ and show that (letting $g=g_{0}$ )
$$
g^{(n)}(2)=\underbrace{g(\cdots g}_{n}(2) \cdots) \rightarrow-1 \text { as } n \rightarrow \infty
$$
But note that for $0 \leq \theta \leq \frac{\pi}{2}$,
$$
g(-2 \cos \theta)=-\sqrt{2-2 \cos \theta}=-2 \sin \left(\frac{\theta}{2}\right)=2 \cos \left(\frac{\pi}{2}-\frac{\theta}{2}\right)
$$
Hence by induction, $g^{(n)}(-2 \cos \theta)=-2 \cos \left(\frac{\pi}{2}-\frac{\pi}{4}+\cdots+(-1)^{n}\left(\theta-\frac{\pi}{2^{n}}\right)\right)$. Hence $g^{(n)}(2)=g^{(n-1)}(-2 \cos 0)$ converges to $-2 \cos \left(\frac{\pi}{2}-\frac{\pi}{4}+\cdots\right)=-2 \cos \left(\frac{\pi}{3}\right)=-1$, as needed.
|
2
|
Yes
|
Incomplete
|
math-word-problem
|
Algebra
|
Let $f(x)=x^{2}-r_{2} x+r_{3}$ for all real numbers $x$, where $r_{2}$ and $r_{3}$ are some real numbers. Define a sequence $\left\{g_{n}\right\}$ for all nonnegative integers $n$ by $g_{0}=0$ and $g_{n+1}=f\left(g_{n}\right)$. Assume that $\left\{g_{n}\right\}$ satisfies the following three conditions: (i) $g_{2 i}<g_{2 i+1}$ and $g_{2 i+1}>g_{2 i+2}$ for all $0 \leq i \leq 2011$; (ii) there exists a positive integer $j$ such that $g_{i+1}>g_{i}$ for all $i>j$, and (iii) $\left\{g_{n}\right\}$ is unbounded. If $A$ is the greatest number such that $A \leq\left|r_{2}\right|$ for any function $f$ satisfying these properties, find $A$.
|
2 Consider the function $f(x)-x$. By the constraints of the problem, $f(x)-x$ must be negative for some $x$, namely, for $x=g_{2 i+1}, 0 \leq i \leq 2011$. Since $f(x)-x$ is positive for $x$ of large absolute value, the graph of $f(x)-x$ crosses the $x$-axis twice and $f(x)-x$ has two real roots, say $a<b$. Factoring gives $f(x)-x=(x-a)(x-b)$, or $f(x)=(x-a)(x-b)+x$.
Now, for $x<a, f(x)>x>a$, while for $x>b, f(x)>x>b$. Let $c \neq b$ be the number such that $f(c)=f(b)=b$. Note that $b$ is not the vertex as $f(a)=a<b$, so by the symmetry of quadratics, $c$ exists and $\frac{b+c}{2}=\frac{r_{2}}{2}$ as the vertex of the parabola. By the same token, $\frac{b+a}{2}=\frac{r_{2}+1}{2}$ is the vertex of $f(x)-x$. Hence $c=a-1$. If $f(x)>b$ then $x<c$ or $x>b$. Consider the smallest $j$ such that $g_{j}>b$. Then by the above observation, $g_{j-1}<c$. (If $g_{i} \geq b$ then $f\left(g_{i}\right) \geq g_{i} \geq b$ so by induction, $g_{i+1} \geq g_{i}$ for all $i \geq j$. Hence $j>1$; in fact $j \geq 4025$.) Since $g_{j-1}=f\left(g_{j-2}\right)$, the minimum value of $f$ is less than $c$. The minimum value is the value of $f$ evaluated at its vertex, $\frac{b+a-1}{2}$, so
$$
\begin{aligned}
f\left(\frac{b+a-1}{2}\right) & <c \\
\left(\frac{b+a-1}{2}-a\right)\left(\frac{b+a-1}{2}-b\right)+\frac{b+a-1}{2} & <a-1 \\
\frac{1-(b-a)^{2}}{4}+\frac{b-a+1}{2} & <0 \\
\frac{3}{4} & <\frac{(b-a)^{2}}{4}-\frac{b-a}{2} \\
4 & <(b-a-1)^{2}
\end{aligned}
$$
Then either $b-a-1<-2$ or $b-a-1>2$, but $b>a$, so the latter must hold and $(b-a)^{2}>9$. Now, the discriminant of $f(x)-x$ equals $(b-a)^{2}$ (the square of the difference of the two roots) and $\left(r_{2}+1\right)^{2}-4 r_{3}$ (from the coefficients), so $\left(r_{2}+1\right)^{2}>9+4 r_{3}$. But $r_{3}=g_{1}>g_{0}=0$ so $\left|r_{2}\right|>2$.
We claim that we can make $\left|r_{2}\right|$ arbitrarily close to 2 , so that the answer is 2 . First define $G_{i}, i \geq 0$ as follows. Let $N \geq 2012$ be an integer. For $\varepsilon>0$ let $h(x)=x^{2}-2-\varepsilon, g_{\varepsilon}(x)=-\sqrt{x+2+\varepsilon}$ and $G_{2 N+1}=2+\varepsilon$, and define $G_{i}$ recursively by $G_{i}=g_{\varepsilon}\left(G_{i+1}\right), G_{i+1}=h\left(G_{i}\right)$. (These two equations are consistent.) Note the following.
(i) $G_{2 i}<G_{2 i+1}$ and $G_{2 i+1}>G_{2 i+2}$ for $0 \leq i \leq N-1$. First note $G_{2 N}=-\sqrt{4+2 \varepsilon}>-\sqrt{4+2 \varepsilon+\varepsilon^{2}}=$ $-2-\varepsilon$. Let $l$ be the negative solution to $h(x)=x$. Note that $-2-\varepsilon<G_{2 N}<l<0$ since $h\left(G_{2 N}\right)>0>G_{2 N}$. Now $g_{\varepsilon}(x)$ is defined as long as $x \geq-2-\varepsilon$, and it sends $(-2-\varepsilon, l)$ into $(l, 0)$ and $(l, 0)$ into $(-2-\varepsilon, l)$. It follows that the $G_{i}, 0 \leq i \leq 2 N$ are well-defined; moreover, $G_{2 i}<l$ and $G_{2 i+1}>l$ for $0 \leq i \leq N-1$ by backwards induction on $i$, so the desired inequalities follow.
(ii) $G_{i}$ is increasing for $i \geq 2 N+1$. Indeed, if $x \geq 2+\varepsilon$, then $x^{2}-x=x(x-1)>2+\varepsilon$ so $h(x)>x$. Hence $2+\varepsilon=G_{2 N+1}<G_{2 N+2}<\cdots$.
(iii) $G_{i}$ is unbounded. This follows since $h(x)-x=x(x-2)-2-\varepsilon$ is increasing for $x>2+\varepsilon$, so $G_{i}$ increases faster and faster for $i \geq 2 N+1$.
Now define $f(x)=h\left(x+G_{0}\right)-G_{0}=x^{2}+2 G_{0} x+G_{0}^{2}-G_{0}-2-\varepsilon$. Note $G_{i+1}=h\left(G_{i}\right)$ while $g_{i+1}=f\left(g_{i}\right)=h\left(g_{i}+G_{0}\right)-G_{0}$, so by induction $g_{i}=G_{i}-G_{0}$. Since $\left\{G_{i}\right\}_{i=0}^{\infty}$ satisfies (i), (ii), and (iii), so does $g_{i}$.
We claim that we can make $G_{0}$ arbitrarily close to -1 by choosing $N$ large enough and $\varepsilon$ small enough; this will make $r_{2}=-2 G_{0}$ arbitrarily close to 2 . Choosing $N$ large corresponds to taking $G_{0}$ to be a larger iterate of $2+\varepsilon$ under $g_{\varepsilon}(x)$. By continuity of this function with respect to $x$ and $\varepsilon$, it suffices to
take $\varepsilon=0$ and show that (letting $g=g_{0}$ )
$$
g^{(n)}(2)=\underbrace{g(\cdots g}_{n}(2) \cdots) \rightarrow-1 \text { as } n \rightarrow \infty
$$
But note that for $0 \leq \theta \leq \frac{\pi}{2}$,
$$
g(-2 \cos \theta)=-\sqrt{2-2 \cos \theta}=-2 \sin \left(\frac{\theta}{2}\right)=2 \cos \left(\frac{\pi}{2}-\frac{\theta}{2}\right)
$$
Hence by induction, $g^{(n)}(-2 \cos \theta)=-2 \cos \left(\frac{\pi}{2}-\frac{\pi}{4}+\cdots+(-1)^{n}\left(\theta-\frac{\pi}{2^{n}}\right)\right)$. Hence $g^{(n)}(2)=g^{(n-1)}(-2 \cos 0)$ converges to $-2 \cos \left(\frac{\pi}{2}-\frac{\pi}{4}+\cdots\right)=-2 \cos \left(\frac{\pi}{3}\right)=-1$, as needed.
|
{
"exam": "HMMT",
"problem_label": "15",
"problem_match": "\n16. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcalc-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
Let $f:(0,1) \rightarrow(0,1)$ be a differentiable function with a continuous derivative such that for every positive integer $n$ and odd positive integer $a<2^{n}$, there exists an odd positive integer $b<2^{n}$ such that $f\left(\frac{a}{2^{n}}\right)=\frac{b}{2^{n}}$. Determine the set of possible values of $f^{\prime}\left(\frac{1}{2}\right)$.
|
$\{-1,1\}$ The key step is to notice that for such a function $f, f^{\prime}(x) \neq 0$ for any $x$.
Assume, for sake of contradiction that there exists $0<y<1$ such that $f^{\prime}(y)=0$. Since $f^{\prime}$ is a continuous function, there is some small interval $(c, d)$ containing $y$ such that $\left|f^{\prime}(x)\right| \leq \frac{1}{2}$ for all $x \in(c, d)$. Now there exists some $n, a$ such that $\frac{a}{2^{n}}, \frac{a+1}{2^{n}}$ are both in the interval $(c, d)$. From the definition, $\frac{f\left(\frac{a+1}{2^{n}}\right)-f\left(\frac{a}{2^{n}}\right)}{\frac{a+1}{2^{n}}-\frac{a}{2^{n}}}=2^{n}\left(\frac{b^{\prime}}{2^{n}}-\frac{b}{2^{n}}\right)=b^{\prime}-b$ where $b, b^{\prime}$ are integers; one is odd, and one is even. So $b^{\prime}-b$ is an odd integer. Since $f$ is differentiable, by the mean value theorem there exists a point where $f^{\prime}=b^{\prime}-b$. But this point is in the interval $(c, d)$, and $\left|b^{\prime}-b\right|>\frac{1}{2}$. This contradicts the assumption that $\left|f^{\prime}(x)\right| \leq \frac{1}{2}$ for all $x \in(c, d)$.
Since $f^{\prime}(x) \neq 0$, and $f^{\prime}$ is a continuous function, $f^{\prime}$ is either always positive or always negative. So $f$ is either increasing or decreasing. $f\left(\frac{1}{2}\right)=\frac{1}{2}$ always. If $f$ is increasing, it follows that $f\left(\frac{1}{4}\right)=\frac{1}{4}, f\left(\frac{3}{4}\right)=\frac{3}{4}$, and we can show by induction that indeed $f\left(\frac{a}{2^{n}}\right)=\frac{a}{2^{n}}$ for all integers $a, n$. Since numbers of this form are dense in the interval $(0,1)$, and $f$ is a continuous function, $f(x)=x$ for all $x$.
It can be similarly shown that if $f$ is decreasing $f(x)=1-x$ for all $x$. So the only possible values of $f^{\prime}\left(\frac{1}{2}\right)$ are $-1,1$.
Query: if the condition that the derivative is continuous were omitted, would the same result still hold?
|
\{-1,1\}
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Let $f:(0,1) \rightarrow(0,1)$ be a differentiable function with a continuous derivative such that for every positive integer $n$ and odd positive integer $a<2^{n}$, there exists an odd positive integer $b<2^{n}$ such that $f\left(\frac{a}{2^{n}}\right)=\frac{b}{2^{n}}$. Determine the set of possible values of $f^{\prime}\left(\frac{1}{2}\right)$.
|
$\{-1,1\}$ The key step is to notice that for such a function $f, f^{\prime}(x) \neq 0$ for any $x$.
Assume, for sake of contradiction that there exists $0<y<1$ such that $f^{\prime}(y)=0$. Since $f^{\prime}$ is a continuous function, there is some small interval $(c, d)$ containing $y$ such that $\left|f^{\prime}(x)\right| \leq \frac{1}{2}$ for all $x \in(c, d)$. Now there exists some $n, a$ such that $\frac{a}{2^{n}}, \frac{a+1}{2^{n}}$ are both in the interval $(c, d)$. From the definition, $\frac{f\left(\frac{a+1}{2^{n}}\right)-f\left(\frac{a}{2^{n}}\right)}{\frac{a+1}{2^{n}}-\frac{a}{2^{n}}}=2^{n}\left(\frac{b^{\prime}}{2^{n}}-\frac{b}{2^{n}}\right)=b^{\prime}-b$ where $b, b^{\prime}$ are integers; one is odd, and one is even. So $b^{\prime}-b$ is an odd integer. Since $f$ is differentiable, by the mean value theorem there exists a point where $f^{\prime}=b^{\prime}-b$. But this point is in the interval $(c, d)$, and $\left|b^{\prime}-b\right|>\frac{1}{2}$. This contradicts the assumption that $\left|f^{\prime}(x)\right| \leq \frac{1}{2}$ for all $x \in(c, d)$.
Since $f^{\prime}(x) \neq 0$, and $f^{\prime}$ is a continuous function, $f^{\prime}$ is either always positive or always negative. So $f$ is either increasing or decreasing. $f\left(\frac{1}{2}\right)=\frac{1}{2}$ always. If $f$ is increasing, it follows that $f\left(\frac{1}{4}\right)=\frac{1}{4}, f\left(\frac{3}{4}\right)=\frac{3}{4}$, and we can show by induction that indeed $f\left(\frac{a}{2^{n}}\right)=\frac{a}{2^{n}}$ for all integers $a, n$. Since numbers of this form are dense in the interval $(0,1)$, and $f$ is a continuous function, $f(x)=x$ for all $x$.
It can be similarly shown that if $f$ is decreasing $f(x)=1-x$ for all $x$. So the only possible values of $f^{\prime}\left(\frac{1}{2}\right)$ are $-1,1$.
Query: if the condition that the derivative is continuous were omitted, would the same result still hold?
|
{
"exam": "HMMT",
"problem_label": "17",
"problem_match": "\n17. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcalc-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
Let $z=\cos \frac{2 \pi}{2011}+i \sin \frac{2 \pi}{2011}$, and let
$$
P(x)=x^{2008}+3 x^{2007}+6 x^{2006}+\ldots \frac{2008 \cdot 2009}{2} x+\frac{2009 \cdot 2010}{2}
$$
for all complex numbers $x$. Evaluate $P(z) P\left(z^{2}\right) P\left(z^{3}\right) \ldots P\left(z^{2010}\right)$.
|
$2011^{2009} \cdot\left(1005^{2011}-1004^{2011}\right)$ Multiply $P(x)$ by $x-1$ to get
$$
P(x)(x-1)=x^{2009}+2 x^{2008}+\ldots+2009 x-\frac{2009 \cdot 2010}{2}
$$
or,
$$
P(x)(x-1)+2010 \cdot 1005=x^{2009}+2 x^{2008}+\ldots+2009 x+2010
$$
Multiplying by $x-1$ once again:
$$
\begin{aligned}
(x-1)\left(P(x)(x-1)+\frac{2010 \cdot 2011}{2}\right) & =x^{2010}+x^{2009}+\ldots+x-2010 \\
& =\left(x^{2010}+x^{2009}+\ldots+x+1\right)-2011 .
\end{aligned}
$$
Hence,
$$
P(x)=\frac{\frac{\left(x^{2010}+x^{2009}+\ldots+x+1\right)-2011}{x-1}-2011 \cdot 1005}{x-1}
$$
Note that $x^{2010}+x^{2009}+\ldots+x+1$ has $z, z^{2}, \ldots, z^{2010}$ as roots, so they vanish at those points. Plugging those 2010 powers of $z$ into the last equation, and multiplying them together, we obtain
$$
\prod_{i=1}^{2010} P\left(z^{i}\right)=\frac{(-2011) \cdot 1005 \cdot\left(x-\frac{1004}{1005}\right)}{(x-1)^{2}} .
$$
Note that $(x-z)\left(x-z^{2}\right) \ldots\left(x-z^{2010}\right)=x^{2010}+x^{2009}+\ldots+1$. Using this, the product turns out to be $2011^{2009} \cdot\left(1005^{2011}-1004^{2011}\right)$.
|
2011^{2009} \cdot\left(1005^{2011}-1004^{2011}\right)
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $z=\cos \frac{2 \pi}{2011}+i \sin \frac{2 \pi}{2011}$, and let
$$
P(x)=x^{2008}+3 x^{2007}+6 x^{2006}+\ldots \frac{2008 \cdot 2009}{2} x+\frac{2009 \cdot 2010}{2}
$$
for all complex numbers $x$. Evaluate $P(z) P\left(z^{2}\right) P\left(z^{3}\right) \ldots P\left(z^{2010}\right)$.
|
$2011^{2009} \cdot\left(1005^{2011}-1004^{2011}\right)$ Multiply $P(x)$ by $x-1$ to get
$$
P(x)(x-1)=x^{2009}+2 x^{2008}+\ldots+2009 x-\frac{2009 \cdot 2010}{2}
$$
or,
$$
P(x)(x-1)+2010 \cdot 1005=x^{2009}+2 x^{2008}+\ldots+2009 x+2010
$$
Multiplying by $x-1$ once again:
$$
\begin{aligned}
(x-1)\left(P(x)(x-1)+\frac{2010 \cdot 2011}{2}\right) & =x^{2010}+x^{2009}+\ldots+x-2010 \\
& =\left(x^{2010}+x^{2009}+\ldots+x+1\right)-2011 .
\end{aligned}
$$
Hence,
$$
P(x)=\frac{\frac{\left(x^{2010}+x^{2009}+\ldots+x+1\right)-2011}{x-1}-2011 \cdot 1005}{x-1}
$$
Note that $x^{2010}+x^{2009}+\ldots+x+1$ has $z, z^{2}, \ldots, z^{2010}$ as roots, so they vanish at those points. Plugging those 2010 powers of $z$ into the last equation, and multiplying them together, we obtain
$$
\prod_{i=1}^{2010} P\left(z^{i}\right)=\frac{(-2011) \cdot 1005 \cdot\left(x-\frac{1004}{1005}\right)}{(x-1)^{2}} .
$$
Note that $(x-z)\left(x-z^{2}\right) \ldots\left(x-z^{2010}\right)=x^{2010}+x^{2009}+\ldots+1$. Using this, the product turns out to be $2011^{2009} \cdot\left(1005^{2011}-1004^{2011}\right)$.
|
{
"exam": "HMMT",
"problem_label": "17",
"problem_match": "\n18. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcalc-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
Let
$$
F(x)=\frac{1}{\left(2-x-x^{5}\right)^{2011}},
$$
and note that $F$ may be expanded as a power series so that $F(x)=\sum_{n=0}^{\infty} a_{n} x^{n}$. Find an ordered pair of positive real numbers $(c, d)$ such that $\lim _{n \rightarrow \infty} \frac{a_{n}}{n^{d}}=c$.
|
$\left.\frac{(1}{6^{2011} 2010}, 2010\right)$ First notice that all the roots of $2-x-x^{5}$ that are not 1 lie strictly outside the unit circle. As such, we may write $2-x-x^{5}$ as $2(1-x)\left(1-r_{1} x\right)\left(1-r_{2} x\right)\left(1-r_{3} x\right)\left(1-r_{4} x\right)$ where $\left|r_{i}\right|<1$, and let $\frac{1}{\left(2-x-x^{5}\right)}=\frac{b_{0}}{(1-x)}+\frac{b_{1}}{\left(1-r_{1} x\right)}+\ldots+\frac{b_{4}}{\left(1-r_{4} x\right)}$. We calculate $b_{0}$ as $\lim _{x \rightarrow 1} \frac{(1-x)}{\left(2-x-x^{5}\right)}=$ $\lim _{x \rightarrow 1} \frac{(-1)}{\left(-1-5 x^{4}\right)}=\frac{1}{6}$.
Now raise the equation above to the 2011th power.
$$
\frac{1}{\left(2-x-x^{5}\right)^{2011}}=\left(\frac{1 / 6}{(1-x)}+\frac{b_{1}}{\left(1-r_{1} x\right)}+\ldots+\frac{b_{4}}{\left(1-r_{4} x\right)}\right)^{2011}
$$
Expand the right hand side using multinomial expansion and then apply partial fractions. The result will be a sum of the terms $(1-x)^{-k}$ and $\left(1-r_{i} x\right)^{-k}$, where $k \leq 2011$.
Since $\left|r_{i}\right|<1$, the power series of $\left(1-r_{i} x\right)^{-k}$ will have exponentially decaying coefficients, so we only need to consider the $(1-x)^{-k}$ terms. The coefficient of $x^{n}$ in the power series of $(1-x)^{-k}$ is $\binom{n+k-1}{k-1}$, which is a $(k-1)$ th degree polynomial in variable $n$. So when we sum up all coefficients, only the power series of $(1-x)^{-2011}$ will have impact on the leading term $n^{2010}$.
The coefficient of the $(1-x)^{-2011}$ term in the multinomial expansion is $\left(\frac{1}{6}\right)^{2011}$. The coefficient of the $x^{n}$ term in the power series of $(1-x)^{-2011}$ is $\binom{n+2010}{2010}=\frac{1}{2010!} n^{2010}+\ldots$. Therefore, $(c, d)=$ $\left(\frac{1}{6^{2011} 2010!}, 2010\right)$.
|
\left(\frac{1}{6^{2011} 2010!}, 2010\right)
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let
$$
F(x)=\frac{1}{\left(2-x-x^{5}\right)^{2011}},
$$
and note that $F$ may be expanded as a power series so that $F(x)=\sum_{n=0}^{\infty} a_{n} x^{n}$. Find an ordered pair of positive real numbers $(c, d)$ such that $\lim _{n \rightarrow \infty} \frac{a_{n}}{n^{d}}=c$.
|
$\left.\frac{(1}{6^{2011} 2010}, 2010\right)$ First notice that all the roots of $2-x-x^{5}$ that are not 1 lie strictly outside the unit circle. As such, we may write $2-x-x^{5}$ as $2(1-x)\left(1-r_{1} x\right)\left(1-r_{2} x\right)\left(1-r_{3} x\right)\left(1-r_{4} x\right)$ where $\left|r_{i}\right|<1$, and let $\frac{1}{\left(2-x-x^{5}\right)}=\frac{b_{0}}{(1-x)}+\frac{b_{1}}{\left(1-r_{1} x\right)}+\ldots+\frac{b_{4}}{\left(1-r_{4} x\right)}$. We calculate $b_{0}$ as $\lim _{x \rightarrow 1} \frac{(1-x)}{\left(2-x-x^{5}\right)}=$ $\lim _{x \rightarrow 1} \frac{(-1)}{\left(-1-5 x^{4}\right)}=\frac{1}{6}$.
Now raise the equation above to the 2011th power.
$$
\frac{1}{\left(2-x-x^{5}\right)^{2011}}=\left(\frac{1 / 6}{(1-x)}+\frac{b_{1}}{\left(1-r_{1} x\right)}+\ldots+\frac{b_{4}}{\left(1-r_{4} x\right)}\right)^{2011}
$$
Expand the right hand side using multinomial expansion and then apply partial fractions. The result will be a sum of the terms $(1-x)^{-k}$ and $\left(1-r_{i} x\right)^{-k}$, where $k \leq 2011$.
Since $\left|r_{i}\right|<1$, the power series of $\left(1-r_{i} x\right)^{-k}$ will have exponentially decaying coefficients, so we only need to consider the $(1-x)^{-k}$ terms. The coefficient of $x^{n}$ in the power series of $(1-x)^{-k}$ is $\binom{n+k-1}{k-1}$, which is a $(k-1)$ th degree polynomial in variable $n$. So when we sum up all coefficients, only the power series of $(1-x)^{-2011}$ will have impact on the leading term $n^{2010}$.
The coefficient of the $(1-x)^{-2011}$ term in the multinomial expansion is $\left(\frac{1}{6}\right)^{2011}$. The coefficient of the $x^{n}$ term in the power series of $(1-x)^{-2011}$ is $\binom{n+2010}{2010}=\frac{1}{2010!} n^{2010}+\ldots$. Therefore, $(c, d)=$ $\left(\frac{1}{6^{2011} 2010!}, 2010\right)$.
|
{
"exam": "HMMT",
"problem_label": "19",
"problem_match": "\n19. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcalc-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
Let $\left\{a_{n}\right\}$ and $\left\{b_{n}\right\}$ be sequences defined recursively by $a_{0}=2 ; b_{0}=2$, and $a_{n+1}=a_{n} \sqrt{1+a_{n}^{2}+b_{n}^{2}}-b_{n}$; $b_{n+1}=b_{n} \sqrt{1+a_{n}^{2}+b_{n}^{2}}+a_{n}$. Find the ternary (base 3) representation of $a_{4}$ and $b_{4}$.
|
1000001100111222 and 2211100110000012
Note first that $\sqrt{1+a_{n}^{2}+b_{n}^{2}}=3^{2^{n}}$. The proof is by induction; the base case follows trivially from what is given. For the inductive step, note that $1+a_{n+1}^{2}+b_{n+1}^{2}=1+a_{n}^{2}\left(1+a_{n}^{2}+b_{n}^{2}\right)+b_{n}^{2}-2 a_{n} b_{n} \sqrt{1+a_{n}^{2}+b_{n}^{2}}+$ $b_{n}^{2}\left(1+a_{n}^{2}+b_{n}^{2}\right)+a_{n}^{2}+2 a_{n} b_{n} \sqrt{1+a_{n}^{2}+b_{n}^{2}}=1+\left(a_{n}^{2}+b_{n}^{2}\right)\left(1+a_{n}^{2}+b_{n}^{2}\right)+a_{n}^{2}+b_{n}^{2}=\left(1+a_{n}^{2}+b_{n}^{2}\right)^{2}$. Invoking the inductive hypothesis, we see that $\sqrt{1+a_{n+1}^{2}+b_{n+1}^{2}}=\left(3^{2^{n}}\right)^{2}=3^{2^{n+1}}$, as desired.
The quickest way to finish from here is to consider a sequence of complex numbers $\left\{z_{n}\right\}$ defined by $z_{n}=a_{n}+b_{n} i$ for all nonnegative integers $n$. It should be clear that $z_{0}=2+2 i$ and $z_{n+1}=z_{n}\left(3^{2^{n}}+i\right)$. Therefore, $z_{4}=(2+2 i)\left(3^{2^{0}}+i\right)\left(3^{2^{1}}+i\right)\left(3^{2^{2}}+i\right)\left(3^{2^{3}}+i\right)$. This product is difficult to evaluate in
the decimal number system, but in ternary the calculation is a cinch! To speed things up, we will use balanced ternary ${ }^{1}$, in which the three digits allowed are $-1,0$, and 1 rather than 0,1 , and 2 . Let $x+y i=\left(3^{2^{0}}+i\right)\left(3^{2^{1}}+i\right)\left(3^{2^{2}}+i\right)\left(3^{2^{3}}+i\right)$, and consider the balanced ternary representation of $x$ and $y$. For all $0 \leq j \leq 15$, let $x_{j}$ denote the digit in the $3^{j}$ place of $x$, let $y_{j}$ denote the digit in the $3^{j}$ place of $y$, and let $b(j)$ denote the number of ones in the binary representation of $j$. It should be clear that $x_{j}=-1$ if $b(j) \equiv 2(\bmod 4), x_{j}=0$ if $b(j) \equiv 1(\bmod 2)$, and $x_{j}=1$ if $b(j) \equiv 0(\bmod 4)$. Similarly, $y_{j}=-1$ if $b(j) \equiv 1(\bmod 4), y_{j}=0$ if $b(j) \equiv 0(\bmod 2)$, and $y_{j}=1$ if $b(j) \equiv 3(\bmod 4)$. Converting to ordinary ternary representation, we see that $x=221211221122001_{3}$ and $y=110022202212120_{3}$. It remains to note that $a_{4}=2 x-2 y$ and $b_{4}=2 x+2 y$ and perform the requisite arithmetic to arrive at the answer above.
[^0]
[^0]: ${ }^{1}$ http://en.wikipedia.org/wiki/Balanced_ternary
|
1000001100111222 \text{ and } 2211100110000012
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $\left\{a_{n}\right\}$ and $\left\{b_{n}\right\}$ be sequences defined recursively by $a_{0}=2 ; b_{0}=2$, and $a_{n+1}=a_{n} \sqrt{1+a_{n}^{2}+b_{n}^{2}}-b_{n}$; $b_{n+1}=b_{n} \sqrt{1+a_{n}^{2}+b_{n}^{2}}+a_{n}$. Find the ternary (base 3) representation of $a_{4}$ and $b_{4}$.
|
1000001100111222 and 2211100110000012
Note first that $\sqrt{1+a_{n}^{2}+b_{n}^{2}}=3^{2^{n}}$. The proof is by induction; the base case follows trivially from what is given. For the inductive step, note that $1+a_{n+1}^{2}+b_{n+1}^{2}=1+a_{n}^{2}\left(1+a_{n}^{2}+b_{n}^{2}\right)+b_{n}^{2}-2 a_{n} b_{n} \sqrt{1+a_{n}^{2}+b_{n}^{2}}+$ $b_{n}^{2}\left(1+a_{n}^{2}+b_{n}^{2}\right)+a_{n}^{2}+2 a_{n} b_{n} \sqrt{1+a_{n}^{2}+b_{n}^{2}}=1+\left(a_{n}^{2}+b_{n}^{2}\right)\left(1+a_{n}^{2}+b_{n}^{2}\right)+a_{n}^{2}+b_{n}^{2}=\left(1+a_{n}^{2}+b_{n}^{2}\right)^{2}$. Invoking the inductive hypothesis, we see that $\sqrt{1+a_{n+1}^{2}+b_{n+1}^{2}}=\left(3^{2^{n}}\right)^{2}=3^{2^{n+1}}$, as desired.
The quickest way to finish from here is to consider a sequence of complex numbers $\left\{z_{n}\right\}$ defined by $z_{n}=a_{n}+b_{n} i$ for all nonnegative integers $n$. It should be clear that $z_{0}=2+2 i$ and $z_{n+1}=z_{n}\left(3^{2^{n}}+i\right)$. Therefore, $z_{4}=(2+2 i)\left(3^{2^{0}}+i\right)\left(3^{2^{1}}+i\right)\left(3^{2^{2}}+i\right)\left(3^{2^{3}}+i\right)$. This product is difficult to evaluate in
the decimal number system, but in ternary the calculation is a cinch! To speed things up, we will use balanced ternary ${ }^{1}$, in which the three digits allowed are $-1,0$, and 1 rather than 0,1 , and 2 . Let $x+y i=\left(3^{2^{0}}+i\right)\left(3^{2^{1}}+i\right)\left(3^{2^{2}}+i\right)\left(3^{2^{3}}+i\right)$, and consider the balanced ternary representation of $x$ and $y$. For all $0 \leq j \leq 15$, let $x_{j}$ denote the digit in the $3^{j}$ place of $x$, let $y_{j}$ denote the digit in the $3^{j}$ place of $y$, and let $b(j)$ denote the number of ones in the binary representation of $j$. It should be clear that $x_{j}=-1$ if $b(j) \equiv 2(\bmod 4), x_{j}=0$ if $b(j) \equiv 1(\bmod 2)$, and $x_{j}=1$ if $b(j) \equiv 0(\bmod 4)$. Similarly, $y_{j}=-1$ if $b(j) \equiv 1(\bmod 4), y_{j}=0$ if $b(j) \equiv 0(\bmod 2)$, and $y_{j}=1$ if $b(j) \equiv 3(\bmod 4)$. Converting to ordinary ternary representation, we see that $x=221211221122001_{3}$ and $y=110022202212120_{3}$. It remains to note that $a_{4}=2 x-2 y$ and $b_{4}=2 x+2 y$ and perform the requisite arithmetic to arrive at the answer above.
[^0]
[^0]: ${ }^{1}$ http://en.wikipedia.org/wiki/Balanced_ternary
|
{
"exam": "HMMT",
"problem_label": "19",
"problem_match": "\n20. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcalc-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
Let $a, b$, and $c$ be positive real numbers. Determine the largest total number of real roots that the following three polynomials may have among them: $a x^{2}+b x+c, b x^{2}+c x+a$, and $c x^{2}+a x+b$.
|
4 If all the polynomials had real roots, their discriminants would all be nonnegative: $a^{2} \geq$ $4 b c, b^{2} \geq 4 c a$, and $c^{2} \geq 4 a b$. Multiplying these inequalities gives $(a b c)^{2} \geq 64(a b c)^{2}$, a contradiction. Hence one of the quadratics has no real roots. The maximum of 4 real roots is attainable: for example, the values $(a, b, c)=(1,5,6)$ give $-2,-3$ as roots to $x^{2}+5 x+6$ and $-1,-\frac{1}{5}$ as roots to $5 x^{2}+6 x+1$.
|
4
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $a, b$, and $c$ be positive real numbers. Determine the largest total number of real roots that the following three polynomials may have among them: $a x^{2}+b x+c, b x^{2}+c x+a$, and $c x^{2}+a x+b$.
|
4 If all the polynomials had real roots, their discriminants would all be nonnegative: $a^{2} \geq$ $4 b c, b^{2} \geq 4 c a$, and $c^{2} \geq 4 a b$. Multiplying these inequalities gives $(a b c)^{2} \geq 64(a b c)^{2}$, a contradiction. Hence one of the quadratics has no real roots. The maximum of 4 real roots is attainable: for example, the values $(a, b, c)=(1,5,6)$ give $-2,-3$ as roots to $x^{2}+5 x+6$ and $-1,-\frac{1}{5}$ as roots to $5 x^{2}+6 x+1$.
|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n1. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcomb-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
A classroom has 30 students and 30 desks arranged in 5 rows of 6 . If the class has 15 boys and 15 girls, in how many ways can the students be placed in the chairs such that no boy is sitting in front of, behind, or next to another boy, and no girl is sitting in front of, behind, or next to another girl?
|
$2 \cdot 15!^{2}$ If we color the desks of the class in a checkerboard pattern, we notice that all of one gender must go in the squares colored black, and the other gender must go in the squares colored white. There are 2 ways to pick which gender goes in which color, 15 ! ways to put the boys into desks and 15 ! ways to put the girls into desks. So the number of ways is $2 \cdot 15!^{2}$.
(There is a little ambiguity in the problem statement as to whether the 15 boys and the 15 girls are distinguishable or not. If they are not distinguishable, the answer is clearly 2. Given the number of contestants who submitted the answer 2, the graders judged that there was enough ambiguity to justify accepting 2 as a correct answer. So both 2 and $2 \cdot 15!^{2}$ were accepted as correct answers.)
|
2 \cdot 15!^{2}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A classroom has 30 students and 30 desks arranged in 5 rows of 6 . If the class has 15 boys and 15 girls, in how many ways can the students be placed in the chairs such that no boy is sitting in front of, behind, or next to another boy, and no girl is sitting in front of, behind, or next to another girl?
|
$2 \cdot 15!^{2}$ If we color the desks of the class in a checkerboard pattern, we notice that all of one gender must go in the squares colored black, and the other gender must go in the squares colored white. There are 2 ways to pick which gender goes in which color, 15 ! ways to put the boys into desks and 15 ! ways to put the girls into desks. So the number of ways is $2 \cdot 15!^{2}$.
(There is a little ambiguity in the problem statement as to whether the 15 boys and the 15 girls are distinguishable or not. If they are not distinguishable, the answer is clearly 2. Given the number of contestants who submitted the answer 2, the graders judged that there was enough ambiguity to justify accepting 2 as a correct answer. So both 2 and $2 \cdot 15!^{2}$ were accepted as correct answers.)
|
{
"exam": "HMMT",
"problem_label": "1",
"problem_match": "\n2. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcomb-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
Let $A B C$ be a triangle such that $A B=7$, and let the angle bisector of $\angle B A C$ intersect line $B C$ at $D$. If there exist points $E$ and $F$ on sides $A C$ and $B C$, respectively, such that lines $A D$ and $E F$ are parallel and divide triangle $A B C$ into three parts of equal area, determine the number of possible integral values for $B C$.
|
13
Note that such $E, F$ exist if and only if
$$
\frac{[A D C]}{[A D B]}=2
$$
([] denotes area.) Since $A D$ is the angle bisector, and the ratio of areas of triangles with equal height is the ratio of their bases,
$$
\frac{A C}{A B}=\frac{D C}{D B}=\frac{[A D C]}{[A D B]}
$$
Hence (1) is equivalent to $A C=2 A B=14$. Then $B C$ can be any length $d$ such that the triangle inequalities are satisfied:
$$
\begin{aligned}
d+7 & >14 \\
7+14 & >d
\end{aligned}
$$
Hence $7<d<21$ and there are 13 possible integral values for $B C$.
|
13
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle such that $A B=7$, and let the angle bisector of $\angle B A C$ intersect line $B C$ at $D$. If there exist points $E$ and $F$ on sides $A C$ and $B C$, respectively, such that lines $A D$ and $E F$ are parallel and divide triangle $A B C$ into three parts of equal area, determine the number of possible integral values for $B C$.
|
13

Note that such $E, F$ exist if and only if
$$
\frac{[A D C]}{[A D B]}=2
$$
([] denotes area.) Since $A D$ is the angle bisector, and the ratio of areas of triangles with equal height is the ratio of their bases,
$$
\frac{A C}{A B}=\frac{D C}{D B}=\frac{[A D C]}{[A D B]}
$$
Hence (1) is equivalent to $A C=2 A B=14$. Then $B C$ can be any length $d$ such that the triangle inequalities are satisfied:
$$
\begin{aligned}
d+7 & >14 \\
7+14 & >d
\end{aligned}
$$
Hence $7<d<21$ and there are 13 possible integral values for $B C$.
|
{
"exam": "HMMT",
"problem_label": "2",
"problem_match": "\n3. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcomb-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
Josh takes a walk on a rectangular grid of $n$ rows and 3 columns, starting from the bottom left corner. At each step, he can either move one square to the right or simultaneously move one square to the left and one square up. In how many ways can he reach the center square of the topmost row?
|
$2^{n-1}$ Note that Josh must pass through the center square of each row. There are 2 ways to get from the center square of row $k$ to the center square of row $k+1$. So there are $2^{n-1}$ ways to get to the center square of row $n$.
|
2^{n-1}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Josh takes a walk on a rectangular grid of $n$ rows and 3 columns, starting from the bottom left corner. At each step, he can either move one square to the right or simultaneously move one square to the left and one square up. In how many ways can he reach the center square of the topmost row?
|
$2^{n-1}$ Note that Josh must pass through the center square of each row. There are 2 ways to get from the center square of row $k$ to the center square of row $k+1$. So there are $2^{n-1}$ ways to get to the center square of row $n$.
|
{
"exam": "HMMT",
"problem_label": "4",
"problem_match": "\n4. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcomb-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
Let $a \star b=a b+a+b$ for all integers $a$ and $b$. Evaluate $1 \star(2 \star(3 \star(4 \star \ldots(99 \star 100) \ldots)))$.
|
$101!-1$ We will first show that $\star$ is both commutative and associative.
- Commutativity: $a \star b=a b+a+b=b \star a$
- Associativity: $a \star(b \star c)=a(b c+b+c)+a+b c+b+c=a b c+a b+a c+b c+a+b+c$ and $(a \star b) \star c=(a b+a+b) c+a b+a+b+c=a b c+a b+a c+b c+a+b+c$. So $a \star(b \star c)=(a \star b) \star c$.
So we need only calculate $((\ldots(1 \star 2) \star 3) \star 4) \ldots \star 100)$. We will prove by induction that
$$
((\ldots(1 \star 2) \star 3) \star 4) \ldots \star n)=(n+1)!-1 .
$$
- Base case $(n=2):(1 \star 2)=2+1+2=5=3!-1$
- Inductive step:
Suppose that
$$
(((\ldots(1 \star 2) \star 3) \star 4) \ldots \star n)=(n+1)!-1
$$
Then,
$$
\begin{aligned}
((((\ldots(1 \star 2) \star 3) \star 4) \ldots \star n) \star(n+1)) & =((n+1)!-1) \star(n+1) \\
& =(n+1)!(n+1)-(n+1)+(n+1)!-1+(n+1) \\
& =(n+2)!-1
\end{aligned}
$$
Hence, $((\ldots(1 \star 2) \star 3) \star 4) \ldots \star n)=(n+1)!-1$ for all $n$. For $n=100$, this results to $101!-1$.
|
101!-1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $a \star b=a b+a+b$ for all integers $a$ and $b$. Evaluate $1 \star(2 \star(3 \star(4 \star \ldots(99 \star 100) \ldots)))$.
|
$101!-1$ We will first show that $\star$ is both commutative and associative.
- Commutativity: $a \star b=a b+a+b=b \star a$
- Associativity: $a \star(b \star c)=a(b c+b+c)+a+b c+b+c=a b c+a b+a c+b c+a+b+c$ and $(a \star b) \star c=(a b+a+b) c+a b+a+b+c=a b c+a b+a c+b c+a+b+c$. So $a \star(b \star c)=(a \star b) \star c$.
So we need only calculate $((\ldots(1 \star 2) \star 3) \star 4) \ldots \star 100)$. We will prove by induction that
$$
((\ldots(1 \star 2) \star 3) \star 4) \ldots \star n)=(n+1)!-1 .
$$
- Base case $(n=2):(1 \star 2)=2+1+2=5=3!-1$
- Inductive step:
Suppose that
$$
(((\ldots(1 \star 2) \star 3) \star 4) \ldots \star n)=(n+1)!-1
$$
Then,
$$
\begin{aligned}
((((\ldots(1 \star 2) \star 3) \star 4) \ldots \star n) \star(n+1)) & =((n+1)!-1) \star(n+1) \\
& =(n+1)!(n+1)-(n+1)+(n+1)!-1+(n+1) \\
& =(n+2)!-1
\end{aligned}
$$
Hence, $((\ldots(1 \star 2) \star 3) \star 4) \ldots \star n)=(n+1)!-1$ for all $n$. For $n=100$, this results to $101!-1$.
|
{
"exam": "HMMT",
"problem_label": "5",
"problem_match": "\n5. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcomb-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
Nathaniel and Obediah play a game in which they take turns rolling a fair six-sided die and keep a running tally of the sum of the results of all rolls made. A player wins if, after he rolls, the number on the running tally is a multiple of 7. Play continues until either player wins, or else indefinitely. If Nathaniel goes first, determine the probability that he ends up winning.
|
| $\frac{5}{11}$ |
| :---: |
| For $1 \leq k \leq 6$, let $x_{k}$ be the probability that the current player, say $A$, will win when | the number on the tally at the beginning of his turn is $k$ modulo 7 . The probability that the total is $l$ modulo 7 after his roll is $\frac{1}{6}$ for each $l \not \equiv k(\bmod 7)$; in particular, there is a $\frac{1}{6}$ chance he wins
immediately. The chance that $A$ will win if he leaves $l$ on the board after his turn is $1-x_{l}$. Hence for $1 \leq k \leq 6$,
$$
x_{k}=\frac{1}{6} \sum_{1 \leq l \leq 6, l \neq k}\left(1-x_{l}\right)+\frac{1}{6} .
$$
Letting $s=\sum_{l=1}^{6} x_{l}$, this becomes $x_{k}=\frac{x_{k}-s}{6}+1$ or $\frac{5 x_{k}}{6}=-\frac{s}{6}+1$. Hence $x_{1}=\cdots=x_{6}$, and $6 x_{k}=s$ for every $k$. Plugging this in gives $\frac{11 x_{k}}{6}=1$, or $x_{k}=\frac{6}{11}$.
Since Nathaniel cannot win on his first turn, he leaves Obediah with a number not divisible by 7. Hence Obediah's chance of winning is $\frac{6}{11}$ and Nathaniel's chance of winning is $\frac{5}{11}$.
|
\frac{5}{11}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Nathaniel and Obediah play a game in which they take turns rolling a fair six-sided die and keep a running tally of the sum of the results of all rolls made. A player wins if, after he rolls, the number on the running tally is a multiple of 7. Play continues until either player wins, or else indefinitely. If Nathaniel goes first, determine the probability that he ends up winning.
|
| $\frac{5}{11}$ |
| :---: |
| For $1 \leq k \leq 6$, let $x_{k}$ be the probability that the current player, say $A$, will win when | the number on the tally at the beginning of his turn is $k$ modulo 7 . The probability that the total is $l$ modulo 7 after his roll is $\frac{1}{6}$ for each $l \not \equiv k(\bmod 7)$; in particular, there is a $\frac{1}{6}$ chance he wins
immediately. The chance that $A$ will win if he leaves $l$ on the board after his turn is $1-x_{l}$. Hence for $1 \leq k \leq 6$,
$$
x_{k}=\frac{1}{6} \sum_{1 \leq l \leq 6, l \neq k}\left(1-x_{l}\right)+\frac{1}{6} .
$$
Letting $s=\sum_{l=1}^{6} x_{l}$, this becomes $x_{k}=\frac{x_{k}-s}{6}+1$ or $\frac{5 x_{k}}{6}=-\frac{s}{6}+1$. Hence $x_{1}=\cdots=x_{6}$, and $6 x_{k}=s$ for every $k$. Plugging this in gives $\frac{11 x_{k}}{6}=1$, or $x_{k}=\frac{6}{11}$.
Since Nathaniel cannot win on his first turn, he leaves Obediah with a number not divisible by 7. Hence Obediah's chance of winning is $\frac{6}{11}$ and Nathaniel's chance of winning is $\frac{5}{11}$.
|
{
"exam": "HMMT",
"problem_label": "6",
"problem_match": "\n6. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcomb-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
Find all integers $x$ such that $2 x^{2}+x-6$ is a positive integral power of a prime positive integer.
|
$-3,2,5$ Let $f(x)=2 x^{2}+x-6=(2 x-3)(x+2)$. Suppose a positive integer $a$ divides both $2 x-3$ and $x+2$. Then $a$ must also divide $2(x+2)-(2 x-3)=7$. Hence, $a$ can either be 1 or 7. As a result, $2 x-3=7^{n}$ or $-7^{n}$ for some positive integer $n$, or either $x+2$ or $2 x-3$ is $\pm 1$. We consider the following cases:
- $(2 x-3)=1$. Then $x=2$, which yields $f(x)=4$, a prime power.
- $(2 x-3)=-1$. Then $x=1$, which yields $f(x)=-3$, not a prime power.
- $(x+2)=1)$. Then $x=-1$, which yields $f(x)=-5$ not a prime power.
- $(x+2)=-1$. Then $x=-3$, which yields $f(x)=9$, a prime power.
- $(2 x-3)=7$. Then $x=5$, which yields $f(x)=49$, a prime power.
- $(2 x-3)=-7$. Then $x=-2$, which yields $f(x)=0$, not a prime power.
- $(2 x-3)= \pm 7^{n}$, for $n \geq 2$. Then, since $x+2=\frac{(2 x-3)+7}{2}$, we have that $x+2$ is divisible by 7 but not by 49 . Hence $x+2= \pm 7$, yielding $x=5,-9$. The former has already been considered, while the latter yields $f(x)=147$.
So $x$ can be either $-3,2$ or 5 .
(Note: In the official solutions packet we did not list the answer - 3 . This oversight was quickly noticed on the day of the test, and only the answer $-3,2,5$ was marked as correct.
|
-3,2,5
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all integers $x$ such that $2 x^{2}+x-6$ is a positive integral power of a prime positive integer.
|
$-3,2,5$ Let $f(x)=2 x^{2}+x-6=(2 x-3)(x+2)$. Suppose a positive integer $a$ divides both $2 x-3$ and $x+2$. Then $a$ must also divide $2(x+2)-(2 x-3)=7$. Hence, $a$ can either be 1 or 7. As a result, $2 x-3=7^{n}$ or $-7^{n}$ for some positive integer $n$, or either $x+2$ or $2 x-3$ is $\pm 1$. We consider the following cases:
- $(2 x-3)=1$. Then $x=2$, which yields $f(x)=4$, a prime power.
- $(2 x-3)=-1$. Then $x=1$, which yields $f(x)=-3$, not a prime power.
- $(x+2)=1)$. Then $x=-1$, which yields $f(x)=-5$ not a prime power.
- $(x+2)=-1$. Then $x=-3$, which yields $f(x)=9$, a prime power.
- $(2 x-3)=7$. Then $x=5$, which yields $f(x)=49$, a prime power.
- $(2 x-3)=-7$. Then $x=-2$, which yields $f(x)=0$, not a prime power.
- $(2 x-3)= \pm 7^{n}$, for $n \geq 2$. Then, since $x+2=\frac{(2 x-3)+7}{2}$, we have that $x+2$ is divisible by 7 but not by 49 . Hence $x+2= \pm 7$, yielding $x=5,-9$. The former has already been considered, while the latter yields $f(x)=147$.
So $x$ can be either $-3,2$ or 5 .
(Note: In the official solutions packet we did not list the answer - 3 . This oversight was quickly noticed on the day of the test, and only the answer $-3,2,5$ was marked as correct.
|
{
"exam": "HMMT",
"problem_label": "7",
"problem_match": "\n7. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcomb-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
Let $A B C D E F$ be a regular hexagon of area 1 . Let $M$ be the midpoint of $D E$. Let $X$ be the intersection of $A C$ and $B M$, let $Y$ be the intersection of $B F$ and $A M$, and let $Z$ be the intersection of $A C$ and $B F$. If $[P]$ denotes the area of polygon $P$ for any polygon $P$ in the plane, evaluate $[B X C]+[A Y F]+[A B Z]-[M X Z Y]$.
|
0
Algebra \& Combinatorics Individual Test
Let $O$ be the center of the hexagon. The desired area is $[A B C D E F]-[A C D M]-[B F E M]$. Note that $[A D M]=[A D E] / 2=[O D E]=[A B C]$, where the last equation holds because $\sin 60^{\circ}=\sin 120^{\circ}$. Thus, $[A C D M]=[A C D]+[A D M]=[A C D]+[A B C]=[A B C D]$, but the area of $A B C D$ is half the area of the hexagon. Similarly, the area of $[B F E M]$ is half the area of the hexagon, so the answer is zero.
|
0
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D E F$ be a regular hexagon of area 1 . Let $M$ be the midpoint of $D E$. Let $X$ be the intersection of $A C$ and $B M$, let $Y$ be the intersection of $B F$ and $A M$, and let $Z$ be the intersection of $A C$ and $B F$. If $[P]$ denotes the area of polygon $P$ for any polygon $P$ in the plane, evaluate $[B X C]+[A Y F]+[A B Z]-[M X Z Y]$.
|
0

Algebra \& Combinatorics Individual Test
Let $O$ be the center of the hexagon. The desired area is $[A B C D E F]-[A C D M]-[B F E M]$. Note that $[A D M]=[A D E] / 2=[O D E]=[A B C]$, where the last equation holds because $\sin 60^{\circ}=\sin 120^{\circ}$. Thus, $[A C D M]=[A C D]+[A D M]=[A C D]+[A B C]=[A B C D]$, but the area of $A B C D$ is half the area of the hexagon. Similarly, the area of $[B F E M]$ is half the area of the hexagon, so the answer is zero.
|
{
"exam": "HMMT",
"problem_label": "7",
"problem_match": "\n8. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcomb-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
For all real numbers $x$, let
$$
f(x)=\frac{1}{\sqrt[2011]{1-x^{2011}}}
$$
Evaluate $(f(f(\ldots(f(2011)) \ldots)))^{2011}$, where $f$ is applied 2010 times.
|
$2011^{2011}$ Direct calculation shows that $f(f(x))=\frac{\sqrt[2011]{1-x^{2011}}}{-x}$ and $f(f(f(x)))=x$. Hence $(f(f(\ldots(f(x)) \ldots)))=x$, where $f$ is applied 2010 times. So $(f(f(\ldots(f(2011)) \ldots)))^{2011}=$ $2011^{2011}$.
|
2011^{2011}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
For all real numbers $x$, let
$$
f(x)=\frac{1}{\sqrt[2011]{1-x^{2011}}}
$$
Evaluate $(f(f(\ldots(f(2011)) \ldots)))^{2011}$, where $f$ is applied 2010 times.
|
$2011^{2011}$ Direct calculation shows that $f(f(x))=\frac{\sqrt[2011]{1-x^{2011}}}{-x}$ and $f(f(f(x)))=x$. Hence $(f(f(\ldots(f(x)) \ldots)))=x$, where $f$ is applied 2010 times. So $(f(f(\ldots(f(2011)) \ldots)))^{2011}=$ $2011^{2011}$.
|
{
"exam": "HMMT",
"problem_label": "9",
"problem_match": "\n9. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcomb-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
The integers from 1 to $n$ are written in increasing order from left to right on a blackboard. David and Goliath play the following game: starting with David, the two players alternate erasing any two consecutive numbers and replacing them with their sum or product. Play continues until only one number on the board remains. If it is odd, David wins, but if it is even, Goliath wins. Find the 2011th smallest positive integer greater than 1 for which David can guarantee victory.
|
4022 If $n$ is odd and greater than 1 , then Goliath makes the last move. No matter what two numbers are on the board, Goliath can combine them to make an even number. Hence Goliath has a winning strategy in this case.
Now suppose $n$ is even. We can replace all numbers on the board by their residues modulo 2. Initially the board reads $1,0,1,0, \ldots, 1,0$. David combines the rightmost 1 and 0 by addition to make 1 , so now the board reads $1,0,1,0, \ldots, 0,1$. We call a board of this form a "good" board. When it is Goliath's turn, and there is a good board, no matter where he moves, David can make a move to restore a good board. Indeed, Goliath must combine a neighboring 0 and 1 ; David can then combine that number with a neighboring 1 to make 1 and create a good board with two fewer numbers.
David can ensure a good board after his last turn. But a good board with one number is simply 1 , so David wins. So David has a winning strategy if $n$ is even. Therefore, the 2011th smallest positive integer greater than 1 for which David can guarantee victory is the 2011th even positive integer, which is 4022 .
|
4022
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
The integers from 1 to $n$ are written in increasing order from left to right on a blackboard. David and Goliath play the following game: starting with David, the two players alternate erasing any two consecutive numbers and replacing them with their sum or product. Play continues until only one number on the board remains. If it is odd, David wins, but if it is even, Goliath wins. Find the 2011th smallest positive integer greater than 1 for which David can guarantee victory.
|
4022 If $n$ is odd and greater than 1 , then Goliath makes the last move. No matter what two numbers are on the board, Goliath can combine them to make an even number. Hence Goliath has a winning strategy in this case.
Now suppose $n$ is even. We can replace all numbers on the board by their residues modulo 2. Initially the board reads $1,0,1,0, \ldots, 1,0$. David combines the rightmost 1 and 0 by addition to make 1 , so now the board reads $1,0,1,0, \ldots, 0,1$. We call a board of this form a "good" board. When it is Goliath's turn, and there is a good board, no matter where he moves, David can make a move to restore a good board. Indeed, Goliath must combine a neighboring 0 and 1 ; David can then combine that number with a neighboring 1 to make 1 and create a good board with two fewer numbers.
David can ensure a good board after his last turn. But a good board with one number is simply 1 , so David wins. So David has a winning strategy if $n$ is even. Therefore, the 2011th smallest positive integer greater than 1 for which David can guarantee victory is the 2011th even positive integer, which is 4022 .
|
{
"exam": "HMMT",
"problem_label": "8",
"problem_match": "\n10. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcomb-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
Let $f(x)=x^{2}+6 x+c$ for all real numbers $x$, where $c$ is some real number. For what values of $c$ does $f(f(x))$ have exactly 3 distinct real roots?
|
$\frac{11-\sqrt{13}}{2}$ Suppose $f$ has only one distinct root $r_{1}$. Then, if $x_{1}$ is a root of $f(f(x))$, it must be the case that $f\left(x_{1}\right)=r_{1}$. As a result, $f(f(x))$ would have at most two roots, thus not satisfying the problem condition. Hence $f$ has two distinct roots. Let them be $r_{1} \neq r_{2}$.
Since $f(f(x))$ has just three distinct roots, either $f(x)=r_{1}$ or $f(x)=r_{2}$ has one distinct root. Assume without loss of generality that $r_{1}$ has one distinct root. Then $f(x)=x^{2}+6 x+c=r_{1}$ has one root, so that $x^{2}+6 x+c-r_{1}$ is a square polynomial. Therefore, $c-r_{1}=9$, so that $r_{1}=c-9$. So $c-9$ is a root of $f$. So $(c-9)^{2}+6(c-9)+c=0$, yielding $c^{2}-11 c+27=0$, or $\left(c-\frac{11}{2}\right)^{2}=\frac{13}{2}$. This results to $c=\frac{11 \pm \sqrt{13}}{2}$.
If $c=\frac{11-\sqrt{13}}{2}, f(x)=x^{2}+6 x+\frac{11-\sqrt{13}}{2}=\left(x+\frac{7+\sqrt{13}}{2}\right)\left(x+\frac{5-\sqrt{13}}{2}\right)$. We know $f(x)=\frac{-7-\sqrt{13}}{2}$ has a double root, -3 . Now $\frac{-5+\sqrt{13}}{2}>\frac{-7-\sqrt{13}}{2}$ so the second root is above the vertex of the parabola, and is hit twice.
If $c=\frac{11+\sqrt{13}}{2}, f(x)=x^{2}+6 x+\frac{11+\sqrt{13}}{2}=\left(x+\frac{7-\sqrt{13}}{2}\right)\left(x+\frac{5+\sqrt{13}}{2}\right)$. We know $f(x)=\frac{-7+\sqrt{13}}{2}$ has a double root, -3 , and this is the value of $f$ at the vertex of the parabola, so it is its minimum value. Since $\frac{-5-\sqrt{13}}{2}<\frac{-7+\sqrt{13}}{2}, f(x)=\frac{-5-\sqrt{13}}{2}$ has no solutions. So in this case, $f$ has only one real root.
So the answer is $c=\frac{11-\sqrt{13}}{2}$.
Note: In the solutions packet we had both roots listed as the correct answer. We noticed this oversight on the day of the test and awarded points only for the correct answer.
|
\frac{11-\sqrt{13}}{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $f(x)=x^{2}+6 x+c$ for all real numbers $x$, where $c$ is some real number. For what values of $c$ does $f(f(x))$ have exactly 3 distinct real roots?
|
$\frac{11-\sqrt{13}}{2}$ Suppose $f$ has only one distinct root $r_{1}$. Then, if $x_{1}$ is a root of $f(f(x))$, it must be the case that $f\left(x_{1}\right)=r_{1}$. As a result, $f(f(x))$ would have at most two roots, thus not satisfying the problem condition. Hence $f$ has two distinct roots. Let them be $r_{1} \neq r_{2}$.
Since $f(f(x))$ has just three distinct roots, either $f(x)=r_{1}$ or $f(x)=r_{2}$ has one distinct root. Assume without loss of generality that $r_{1}$ has one distinct root. Then $f(x)=x^{2}+6 x+c=r_{1}$ has one root, so that $x^{2}+6 x+c-r_{1}$ is a square polynomial. Therefore, $c-r_{1}=9$, so that $r_{1}=c-9$. So $c-9$ is a root of $f$. So $(c-9)^{2}+6(c-9)+c=0$, yielding $c^{2}-11 c+27=0$, or $\left(c-\frac{11}{2}\right)^{2}=\frac{13}{2}$. This results to $c=\frac{11 \pm \sqrt{13}}{2}$.
If $c=\frac{11-\sqrt{13}}{2}, f(x)=x^{2}+6 x+\frac{11-\sqrt{13}}{2}=\left(x+\frac{7+\sqrt{13}}{2}\right)\left(x+\frac{5-\sqrt{13}}{2}\right)$. We know $f(x)=\frac{-7-\sqrt{13}}{2}$ has a double root, -3 . Now $\frac{-5+\sqrt{13}}{2}>\frac{-7-\sqrt{13}}{2}$ so the second root is above the vertex of the parabola, and is hit twice.
If $c=\frac{11+\sqrt{13}}{2}, f(x)=x^{2}+6 x+\frac{11+\sqrt{13}}{2}=\left(x+\frac{7-\sqrt{13}}{2}\right)\left(x+\frac{5+\sqrt{13}}{2}\right)$. We know $f(x)=\frac{-7+\sqrt{13}}{2}$ has a double root, -3 , and this is the value of $f$ at the vertex of the parabola, so it is its minimum value. Since $\frac{-5-\sqrt{13}}{2}<\frac{-7+\sqrt{13}}{2}, f(x)=\frac{-5-\sqrt{13}}{2}$ has no solutions. So in this case, $f$ has only one real root.
So the answer is $c=\frac{11-\sqrt{13}}{2}$.
Note: In the solutions packet we had both roots listed as the correct answer. We noticed this oversight on the day of the test and awarded points only for the correct answer.
|
{
"exam": "HMMT",
"problem_label": "11",
"problem_match": "\n11. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcomb-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
Mike and Harry play a game on an $8 \times 8$ board. For some positive integer $k$, Mike chooses $k$ squares and writes an $M$ in each of them. Harry then chooses $k+1$ squares and writes an $H$ in each of them. After Harry is done, Mike wins if there is a sequence of letters forming " $H M M$ " or " $M M H$," when read either horizontally or vertically, and Harry wins otherwise. Determine the smallest value of $k$ for which Mike has a winning strategy.
|
16 Suppose Mike writes $k M$ 's. Let $a$ be the number of squares which, if Harry writes an $H$ in, will yield either $H M M$ or $M M H$ horizontally, and let $b$ be the number of squares which, if Harry writes an $H$ in, will yield either $H M M$ or $M M H$ vertically. We will show that $a \leq k$ and $b \leq k$. Then, it will follow that there are at most $a+b \leq 2 k$ squares which Harry cannot write an $H$ in. There will be at least $64-k-2 k=64-3 k$ squares which Harry can write in. If $64-3 k \geq k+1$, or $k \leq 15$, then Harry wins.
We will show that $a \leq k$ (that $b \leq k$ will follow by symmetry). Suppose there are $a_{i} M$ 's in row $i$. In each group of 2 or more consective $M$ 's, Harry cannot write $H$ to the left or right of that group, giving at most 2 forbidden squares. Hence $a_{i}$ is at most the number of $M$ 's in row $i$. Summing over the rows gives the desired result.
Mike can win by writing 16 M's according to the following diagram:

|
16
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Mike and Harry play a game on an $8 \times 8$ board. For some positive integer $k$, Mike chooses $k$ squares and writes an $M$ in each of them. Harry then chooses $k+1$ squares and writes an $H$ in each of them. After Harry is done, Mike wins if there is a sequence of letters forming " $H M M$ " or " $M M H$," when read either horizontally or vertically, and Harry wins otherwise. Determine the smallest value of $k$ for which Mike has a winning strategy.
|
16 Suppose Mike writes $k M$ 's. Let $a$ be the number of squares which, if Harry writes an $H$ in, will yield either $H M M$ or $M M H$ horizontally, and let $b$ be the number of squares which, if Harry writes an $H$ in, will yield either $H M M$ or $M M H$ vertically. We will show that $a \leq k$ and $b \leq k$. Then, it will follow that there are at most $a+b \leq 2 k$ squares which Harry cannot write an $H$ in. There will be at least $64-k-2 k=64-3 k$ squares which Harry can write in. If $64-3 k \geq k+1$, or $k \leq 15$, then Harry wins.
We will show that $a \leq k$ (that $b \leq k$ will follow by symmetry). Suppose there are $a_{i} M$ 's in row $i$. In each group of 2 or more consective $M$ 's, Harry cannot write $H$ to the left or right of that group, giving at most 2 forbidden squares. Hence $a_{i}$ is at most the number of $M$ 's in row $i$. Summing over the rows gives the desired result.
Mike can win by writing 16 M's according to the following diagram:

|
{
"exam": "HMMT",
"problem_label": "10",
"problem_match": "\n12. ",
"resource_path": "HarvardMIT/segmented/en-142-2011-feb-algcomb-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2011"
}
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.