problem
stringlengths 14
10.4k
| solution
stringlengths 1
24.1k
| answer
stringlengths 1
250
⌀ | problem_is_valid
stringclasses 4
values | solution_is_valid
stringclasses 3
values | question_type
stringclasses 4
values | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
10.4k
| solution_raw
stringlengths 1
24.1k
| metadata
dict |
|---|---|---|---|---|---|---|---|---|---|
Prove that any real solution of
$$
x^{3}+p x+q=0
$$
satisfies the inequality $4 q x \leq p^{2}$.
|
Let $x_{0}$ be a root of the qubic, then $x^{3}+p x+q=\left(x-x_{0}\right)\left(x^{2}+a x+b\right)=$ $x^{3}+\left(a-x_{0}\right) x^{2}+\left(b-a x_{0}\right) x-b x_{0}$. So $a=x_{0}, p=b-a x_{0}=b-x_{0}^{2},-q=b x_{0}$. Hence $p^{2}=b^{2}-2 b x_{0}^{2}+x_{0}^{4}$. Also $4 x_{0} q=-4 x_{0}^{2} b$. So $p^{2}-4 x_{0} q=b^{2}+2 b x_{0}^{2}+x_{0}^{4}=\left(b+x_{0}^{2}\right)^{2} \geq 0$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Prove that any real solution of
$$
x^{3}+p x+q=0
$$
satisfies the inequality $4 q x \leq p^{2}$.
|
Let $x_{0}$ be a root of the qubic, then $x^{3}+p x+q=\left(x-x_{0}\right)\left(x^{2}+a x+b\right)=$ $x^{3}+\left(a-x_{0}\right) x^{2}+\left(b-a x_{0}\right) x-b x_{0}$. So $a=x_{0}, p=b-a x_{0}=b-x_{0}^{2},-q=b x_{0}$. Hence $p^{2}=b^{2}-2 b x_{0}^{2}+x_{0}^{4}$. Also $4 x_{0} q=-4 x_{0}^{2} b$. So $p^{2}-4 x_{0} q=b^{2}+2 b x_{0}^{2}+x_{0}^{4}=\left(b+x_{0}^{2}\right)^{2} \geq 0$.
|
{
"exam": "BalticWay",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2003"
}
|
Prove that any real solution of
$$
x^{3}+p x+q=0
$$
satisfies the inequality $4 q x \leq p^{2}$.
|
As the equation $x_{0} x^{2}+p x+q=0$ has a root $\left(x=x_{0}\right)$, we must have $D \geq 0 \Leftrightarrow p^{2}-4 q x_{0} \geq 0$. (Also the equation $x^{2}+p x+q x_{0}=0$ having the root $x=x_{0}^{2}$ can be considered.)
|
proof
|
Yes
|
Incomplete
|
proof
|
Algebra
|
Prove that any real solution of
$$
x^{3}+p x+q=0
$$
satisfies the inequality $4 q x \leq p^{2}$.
|
As the equation $x_{0} x^{2}+p x+q=0$ has a root $\left(x=x_{0}\right)$, we must have $D \geq 0 \Leftrightarrow p^{2}-4 q x_{0} \geq 0$. (Also the equation $x^{2}+p x+q x_{0}=0$ having the root $x=x_{0}^{2}$ can be considered.)
|
{
"exam": "BalticWay",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"solution_match": "\nSolution 2:",
"tier": "T3",
"year": "2003"
}
|
Let $x, y$ and $z$ be positive real numbers such that $x y z=1$. Prove that
$$
(1+x)(1+y)(1+z) \geq 2\left(1+\sqrt[3]{\frac{y}{x}}+\sqrt[3]{\frac{z}{y}}+\sqrt[3]{\frac{x}{z}}\right)
$$
|
Put $a=b x, b=c y$ and $c=a z$. The given inequality then takes the form
$$
\begin{aligned}
\left(1+\frac{a}{b}\right)\left(1+\frac{b}{c}\right)\left(1+\frac{c}{a}\right) & \geq 2\left(1+\sqrt[3]{\frac{b^{2}}{a c}}+\sqrt[3]{\frac{c^{2}}{a b}}+\sqrt[3]{\frac{a^{2}}{b c}}\right) \\
& =2\left(1+\frac{a+b+c}{3 \sqrt[3]{a b c}}\right) .
\end{aligned}
$$
By the AM-GM inequality we have
$$
\begin{aligned}
\left(1+\frac{a}{b}\right)\left(1+\frac{b}{c}\right)\left(1+\frac{c}{a}\right) & =\frac{a+b+c}{a}+\frac{a+b+c}{b}+\frac{a+b+c}{c}-1 \\
& \geq 3\left(\frac{a+b+c}{\sqrt[3]{a b c}}\right)-1 \geq 2 \frac{a+b+c}{\sqrt[3]{a b c}}+3-1=2\left(1+\frac{a+b+c}{\sqrt[3]{a b c}}\right) .
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x, y$ and $z$ be positive real numbers such that $x y z=1$. Prove that
$$
(1+x)(1+y)(1+z) \geq 2\left(1+\sqrt[3]{\frac{y}{x}}+\sqrt[3]{\frac{z}{y}}+\sqrt[3]{\frac{x}{z}}\right)
$$
|
Put $a=b x, b=c y$ and $c=a z$. The given inequality then takes the form
$$
\begin{aligned}
\left(1+\frac{a}{b}\right)\left(1+\frac{b}{c}\right)\left(1+\frac{c}{a}\right) & \geq 2\left(1+\sqrt[3]{\frac{b^{2}}{a c}}+\sqrt[3]{\frac{c^{2}}{a b}}+\sqrt[3]{\frac{a^{2}}{b c}}\right) \\
& =2\left(1+\frac{a+b+c}{3 \sqrt[3]{a b c}}\right) .
\end{aligned}
$$
By the AM-GM inequality we have
$$
\begin{aligned}
\left(1+\frac{a}{b}\right)\left(1+\frac{b}{c}\right)\left(1+\frac{c}{a}\right) & =\frac{a+b+c}{a}+\frac{a+b+c}{b}+\frac{a+b+c}{c}-1 \\
& \geq 3\left(\frac{a+b+c}{\sqrt[3]{a b c}}\right)-1 \geq 2 \frac{a+b+c}{\sqrt[3]{a b c}}+3-1=2\left(1+\frac{a+b+c}{\sqrt[3]{a b c}}\right) .
\end{aligned}
$$
|
{
"exam": "BalticWay",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2003"
}
|
Let $x, y$ and $z$ be positive real numbers such that $x y z=1$. Prove that
$$
(1+x)(1+y)(1+z) \geq 2\left(1+\sqrt[3]{\frac{y}{x}}+\sqrt[3]{\frac{z}{y}}+\sqrt[3]{\frac{x}{z}}\right)
$$
|
Expanding the left side we obtain
$$
x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z} \geq 2\left(\sqrt[3]{\frac{y}{x}}+\sqrt[3]{\frac{z}{y}}+\sqrt[3]{\frac{x}{z}}\right)
$$
As $\sqrt[3]{\frac{y}{x}} \leq \frac{1}{3}\left(y+\frac{1}{x}+1\right)$ etc., it suffices to prove that
$$
x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z} \geq \frac{2}{3}\left(x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)+2
$$
which follows from $a+\frac{1}{a} \geq 2$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x, y$ and $z$ be positive real numbers such that $x y z=1$. Prove that
$$
(1+x)(1+y)(1+z) \geq 2\left(1+\sqrt[3]{\frac{y}{x}}+\sqrt[3]{\frac{z}{y}}+\sqrt[3]{\frac{x}{z}}\right)
$$
|
Expanding the left side we obtain
$$
x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z} \geq 2\left(\sqrt[3]{\frac{y}{x}}+\sqrt[3]{\frac{z}{y}}+\sqrt[3]{\frac{x}{z}}\right)
$$
As $\sqrt[3]{\frac{y}{x}} \leq \frac{1}{3}\left(y+\frac{1}{x}+1\right)$ etc., it suffices to prove that
$$
x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z} \geq \frac{2}{3}\left(x+y+z+\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)+2
$$
which follows from $a+\frac{1}{a} \geq 2$.
|
{
"exam": "BalticWay",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"solution_match": "\nSolution 2:",
"tier": "T3",
"year": "2003"
}
|
Let $a, b, c$ be positive real numbers. Prove that
$$
\frac{2 a}{a^{2}+b c}+\frac{2 b}{b^{2}+c a}+\frac{2 c}{c^{2}+a b} \leq \frac{a}{b c}+\frac{b}{c a}+\frac{c}{a b} .
$$
|
First we prove that
$$
\frac{2 a}{a^{2}+b c} \leq \frac{1}{2}\left(\frac{1}{b}+\frac{1}{c}\right)
$$
which is equivalent to $0 \leq b(a-c)^{2}+c(a-b)^{2}$, and therefore holds true. Now we turn to the inequality
$$
\frac{1}{b}+\frac{1}{c} \leq \frac{1}{2}\left(\frac{2 a}{b c}+\frac{b}{c a}+\frac{c}{a b}\right),
$$
which by multiplying by $2 a b c$ is seen to be equivalent to $0 \leq(a-b)^{2}+(a-c)^{2}$. Hence we have proved that
Analogously we have
$$
\frac{2 a}{a^{2}+b c} \leq \frac{1}{4}\left(\frac{2 a}{b c}+\frac{b}{c a}+\frac{c}{a b}\right) .
$$
$$
\begin{aligned}
\frac{2 b}{b^{2}+c a} & \leq \frac{1}{4}\left(\frac{2 b}{c a}+\frac{c}{a b}+\frac{a}{b c}\right) \\
\frac{2 c}{c^{2}+a b} & \leq \frac{1}{4}\left(\frac{2 c}{a b}+\frac{a}{b c}+\frac{b}{c a}\right)
\end{aligned}
$$
and it suffices to sum the above three inequalities.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers. Prove that
$$
\frac{2 a}{a^{2}+b c}+\frac{2 b}{b^{2}+c a}+\frac{2 c}{c^{2}+a b} \leq \frac{a}{b c}+\frac{b}{c a}+\frac{c}{a b} .
$$
|
First we prove that
$$
\frac{2 a}{a^{2}+b c} \leq \frac{1}{2}\left(\frac{1}{b}+\frac{1}{c}\right)
$$
which is equivalent to $0 \leq b(a-c)^{2}+c(a-b)^{2}$, and therefore holds true. Now we turn to the inequality
$$
\frac{1}{b}+\frac{1}{c} \leq \frac{1}{2}\left(\frac{2 a}{b c}+\frac{b}{c a}+\frac{c}{a b}\right),
$$
which by multiplying by $2 a b c$ is seen to be equivalent to $0 \leq(a-b)^{2}+(a-c)^{2}$. Hence we have proved that
Analogously we have
$$
\frac{2 a}{a^{2}+b c} \leq \frac{1}{4}\left(\frac{2 a}{b c}+\frac{b}{c a}+\frac{c}{a b}\right) .
$$
$$
\begin{aligned}
\frac{2 b}{b^{2}+c a} & \leq \frac{1}{4}\left(\frac{2 b}{c a}+\frac{c}{a b}+\frac{a}{b c}\right) \\
\frac{2 c}{c^{2}+a b} & \leq \frac{1}{4}\left(\frac{2 c}{a b}+\frac{a}{b c}+\frac{b}{c a}\right)
\end{aligned}
$$
and it suffices to sum the above three inequalities.
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2003"
}
|
Let $a, b, c$ be positive real numbers. Prove that
$$
\frac{2 a}{a^{2}+b c}+\frac{2 b}{b^{2}+c a}+\frac{2 c}{c^{2}+a b} \leq \frac{a}{b c}+\frac{b}{c a}+\frac{c}{a b} .
$$
|
As $a^{2}+b c \geq 2 a \sqrt{b c}$ etc., it is sufficient to prove that
$$
\frac{1}{\sqrt{b c}}+\frac{1}{\sqrt{a c}}+\frac{1}{\sqrt{a b}} \leq \frac{a}{b c}+\frac{b}{c a}+\frac{c}{a b}
$$
which can be obtained by "inserting" $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$ between the left side and the right side.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers. Prove that
$$
\frac{2 a}{a^{2}+b c}+\frac{2 b}{b^{2}+c a}+\frac{2 c}{c^{2}+a b} \leq \frac{a}{b c}+\frac{b}{c a}+\frac{c}{a b} .
$$
|
As $a^{2}+b c \geq 2 a \sqrt{b c}$ etc., it is sufficient to prove that
$$
\frac{1}{\sqrt{b c}}+\frac{1}{\sqrt{a c}}+\frac{1}{\sqrt{a b}} \leq \frac{a}{b c}+\frac{b}{c a}+\frac{c}{a b}
$$
which can be obtained by "inserting" $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$ between the left side and the right side.
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"solution_match": "\nSolution 2:",
"tier": "T3",
"year": "2003"
}
|
A sequence $\left(a_{n}\right)$ is defined as follows: $a_{1}=\sqrt{2}, a_{2}=2$, and $a_{n+1}=a_{n} a_{n-1}^{2}$ for $n \geq 2$. Prove that for every $n \geq 1$ we have
$$
\left(1+a_{1}\right)\left(1+a_{2}\right) \cdots\left(1+a_{n}\right)<(2+\sqrt{2}) a_{1} a_{2} \cdots a_{n} .
$$
|
First we prove inductively that for $n \geq 1, a_{n}=2^{2^{n-2}}$. We have $a_{1}=2^{2^{-1}}$, $a_{2}=2^{2^{0}}$ and
$$
a_{n+1}=2^{2^{n-2}} \cdot\left(2^{2^{n-3}}\right)^{2}=2^{2^{n-2}} \cdot 2^{2^{n-2}}=2^{2^{n-1}} .
$$
Since $1+a_{1}=1+\sqrt{2}$, we must prove, that
$$
\left(1+a_{2}\right)\left(1+a_{3}\right) \cdots\left(1+a_{n}\right)<2 a_{2} a_{3} \cdots a_{n} .
$$
The right-hand side is equal to
$$
2^{1+2^{0}+2^{1}+\cdots+2^{n-2}}=2^{2^{n-1}}
$$
and the left-hand side
$$
\begin{aligned}
\left(1+2^{2^{0}}\right) & \left(1+2^{2^{1}}\right) \cdots\left(1+2^{2^{n-2}}\right) \\
& =1+2^{2^{0}}+2^{2^{1}}+2^{2^{0}+2^{1}}+2^{2^{2}}+\cdots+2^{2^{0}+2^{1}+\cdots+2^{n-2}} \\
& =1+2+2^{2}+2^{3}+\cdots+2^{2^{n-1}-1} \\
& =2^{2^{n-1}}-1 .
\end{aligned}
$$
The proof is complete.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
A sequence $\left(a_{n}\right)$ is defined as follows: $a_{1}=\sqrt{2}, a_{2}=2$, and $a_{n+1}=a_{n} a_{n-1}^{2}$ for $n \geq 2$. Prove that for every $n \geq 1$ we have
$$
\left(1+a_{1}\right)\left(1+a_{2}\right) \cdots\left(1+a_{n}\right)<(2+\sqrt{2}) a_{1} a_{2} \cdots a_{n} .
$$
|
First we prove inductively that for $n \geq 1, a_{n}=2^{2^{n-2}}$. We have $a_{1}=2^{2^{-1}}$, $a_{2}=2^{2^{0}}$ and
$$
a_{n+1}=2^{2^{n-2}} \cdot\left(2^{2^{n-3}}\right)^{2}=2^{2^{n-2}} \cdot 2^{2^{n-2}}=2^{2^{n-1}} .
$$
Since $1+a_{1}=1+\sqrt{2}$, we must prove, that
$$
\left(1+a_{2}\right)\left(1+a_{3}\right) \cdots\left(1+a_{n}\right)<2 a_{2} a_{3} \cdots a_{n} .
$$
The right-hand side is equal to
$$
2^{1+2^{0}+2^{1}+\cdots+2^{n-2}}=2^{2^{n-1}}
$$
and the left-hand side
$$
\begin{aligned}
\left(1+2^{2^{0}}\right) & \left(1+2^{2^{1}}\right) \cdots\left(1+2^{2^{n-2}}\right) \\
& =1+2^{2^{0}}+2^{2^{1}}+2^{2^{0}+2^{1}}+2^{2^{2}}+\cdots+2^{2^{0}+2^{1}+\cdots+2^{n-2}} \\
& =1+2+2^{2}+2^{3}+\cdots+2^{2^{n-1}-1} \\
& =2^{2^{n-1}}-1 .
\end{aligned}
$$
The proof is complete.
|
{
"exam": "BalticWay",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2003"
}
|
Let $n \geq 2$ and $d \geq 1$ be integers with $d \mid n$, and let $x_{1}, x_{2}, \ldots, x_{n}$ be real numbers such that $x_{1}+x_{2}+\cdots+x_{n}=0$. Prove that there are at least $\left(\begin{array}{l}n-1 \\ d-1\end{array}\right)$ choices of $d$ indices $1 \leq i_{1}<i_{2}<\cdots<i_{d} \leq n$ such that $x_{i_{1}}+x_{i_{2}}+\cdots+x_{i_{d}} \geq 0$.
|
Put $m=n / d$ and $[n]=\{1,2, \ldots, n\}$, and consider all partitions $[n]=A_{1} \cup$ $A_{2} \cup \cdots \cup A_{m}$ of $[n]$ into $d$-element subsets $A_{i}, i=1,2, \ldots, m$. The number of such partitions is denoted by $t$. Clearly, there are exactly $\left(\begin{array}{l}n \\ d\end{array}\right) d$-element subsets of $[n]$ each of which occurs in the same number of partitions. Hence, every $A \subseteq[n]$ with $|A|=d$ occurs in exactly $s:=t m /\left(\begin{array}{l}n \\ d\end{array}\right)$ partitions. On the other hand, every partition contains at least one $d$-element set $A$ such that $\sum_{i \in A} x_{i} \geq 0$. Consequently, the total number of sets with this property is at least $t / s=\left(\begin{array}{l}n \\ d\end{array}\right) / m=\frac{d}{n}\left(\begin{array}{l}n \\ d\end{array}\right)=\left(\begin{array}{l}n-1 \\ d-1\end{array}\right)$.
|
\left(\begin{array}{l}n-1 \\ d-1\end{array}\right)
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n \geq 2$ and $d \geq 1$ be integers with $d \mid n$, and let $x_{1}, x_{2}, \ldots, x_{n}$ be real numbers such that $x_{1}+x_{2}+\cdots+x_{n}=0$. Prove that there are at least $\left(\begin{array}{l}n-1 \\ d-1\end{array}\right)$ choices of $d$ indices $1 \leq i_{1}<i_{2}<\cdots<i_{d} \leq n$ such that $x_{i_{1}}+x_{i_{2}}+\cdots+x_{i_{d}} \geq 0$.
|
Put $m=n / d$ and $[n]=\{1,2, \ldots, n\}$, and consider all partitions $[n]=A_{1} \cup$ $A_{2} \cup \cdots \cup A_{m}$ of $[n]$ into $d$-element subsets $A_{i}, i=1,2, \ldots, m$. The number of such partitions is denoted by $t$. Clearly, there are exactly $\left(\begin{array}{l}n \\ d\end{array}\right) d$-element subsets of $[n]$ each of which occurs in the same number of partitions. Hence, every $A \subseteq[n]$ with $|A|=d$ occurs in exactly $s:=t m /\left(\begin{array}{l}n \\ d\end{array}\right)$ partitions. On the other hand, every partition contains at least one $d$-element set $A$ such that $\sum_{i \in A} x_{i} \geq 0$. Consequently, the total number of sets with this property is at least $t / s=\left(\begin{array}{l}n \\ d\end{array}\right) / m=\frac{d}{n}\left(\begin{array}{l}n \\ d\end{array}\right)=\left(\begin{array}{l}n-1 \\ d-1\end{array}\right)$.
|
{
"exam": "BalticWay",
"problem_label": "6",
"problem_match": "\n6.",
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2003"
}
|
Let $X$ be a subset of $\{1,2,3, \ldots, 10000\}$ with the following property: If $a, b \in X, a \neq b$, then $a \cdot b \notin X$. What is the maximal number of elements in $X$ ?
Answer: 9901.
|
If $X=\{100,101,102, \ldots, 9999,10000\}$, then for any two selected $a$ and $b, a \neq b$, $a \cdot b \geq 100 \cdot 101>10000$, so $a \cdot b \notin X$. So $X$ may have 9901 elements.
Suppose that $x_{1}<x_{2}<\cdots<x_{k}$ are all elements of $X$ that are less than 100. If there are none of them, no more than 9901 numbers can be in the set $X$. Otherwise, if $x_{1}=1$ no other number can be in the set $X$, so suppose $x_{1}>1$ and consider the pairs
$$
\begin{gathered}
200-x_{1},\left(200-x_{1}\right) \cdot x_{1} \\
200-x_{2},\left(200-x_{2}\right) \cdot x_{2} \\
\vdots \\
200-x_{k},\left(200-x_{k}\right) \cdot x_{k}
\end{gathered}
$$
Clearly $x_{1}<x_{2}<\cdots<x_{k}<100<200-x_{k}<200-x_{k-1}<\cdots<200-x_{2}<$ $200-x_{1}<200<\left(200-x_{1}\right) \cdot x_{1}<\left(200-x_{2}\right) \cdot x_{2}<\cdots<\left(200-x_{k}\right) \cdot x_{k}$. So all numbers in these pairs are different and greater than 100. So at most one from each pair is in the set $X$. Therefore, there are at least $k$ numbers greater than 100 and $99-k$ numbers less than 100 that are not in the set $X$, together at least 99 numbers out of 10000 not being in the set $X$.
|
9901
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $X$ be a subset of $\{1,2,3, \ldots, 10000\}$ with the following property: If $a, b \in X, a \neq b$, then $a \cdot b \notin X$. What is the maximal number of elements in $X$ ?
Answer: 9901.
|
If $X=\{100,101,102, \ldots, 9999,10000\}$, then for any two selected $a$ and $b, a \neq b$, $a \cdot b \geq 100 \cdot 101>10000$, so $a \cdot b \notin X$. So $X$ may have 9901 elements.
Suppose that $x_{1}<x_{2}<\cdots<x_{k}$ are all elements of $X$ that are less than 100. If there are none of them, no more than 9901 numbers can be in the set $X$. Otherwise, if $x_{1}=1$ no other number can be in the set $X$, so suppose $x_{1}>1$ and consider the pairs
$$
\begin{gathered}
200-x_{1},\left(200-x_{1}\right) \cdot x_{1} \\
200-x_{2},\left(200-x_{2}\right) \cdot x_{2} \\
\vdots \\
200-x_{k},\left(200-x_{k}\right) \cdot x_{k}
\end{gathered}
$$
Clearly $x_{1}<x_{2}<\cdots<x_{k}<100<200-x_{k}<200-x_{k-1}<\cdots<200-x_{2}<$ $200-x_{1}<200<\left(200-x_{1}\right) \cdot x_{1}<\left(200-x_{2}\right) \cdot x_{2}<\cdots<\left(200-x_{k}\right) \cdot x_{k}$. So all numbers in these pairs are different and greater than 100. So at most one from each pair is in the set $X$. Therefore, there are at least $k$ numbers greater than 100 and $99-k$ numbers less than 100 that are not in the set $X$, together at least 99 numbers out of 10000 not being in the set $X$.
|
{
"exam": "BalticWay",
"problem_label": "7",
"problem_match": "\n7.",
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2003"
}
|
There are 2003 pieces of candy on a table. Two players alternately make moves. A move consists of eating one candy or half of the candies on the table (the "lesser half" if there is an odd number of candies); at least one candy must be eaten at each move. The loser is the one who eats the last candy. Which player - the first or the second - has a winning strategy?
Answer: The second.
|
Let us prove inductively that for $2 n$ pieces of candy the first player has a winning strategy. For $n=1$ it is obvious. Suppose it is true for $2 n$ pieces, and let's consider $2 n+2$ pieces. If for $2 n+1$ pieces the second is the winner, then the first eats 1 piece and becomes the second in the game starting with $2 n+1$ pieces. So suppose that for $2 n+1$ pieces the first is the winner. His winning move for $2 n+1$ is not eating 1 piece (according to the inductive assumption). So his winning move is to eat $n$ pieces, leaving the second with $n+1$ pieces, when the second must lose. But the first can leave the second with $n+1$ pieces from the starting position with $2 n+2$ pieces, eating $n+1$ pieces; so $2 n+2$ is a winning position for the first.
Now if there are 2003 pieces of candy on the table, the first must eat either 1 or 1001 candies, leaving an even number of candies on the table. So the second player will be the first player in a game with even number of candies and therefore has a winning strategy.
In general, if there is an odd number $N$ of candies, write $N=2^{m} r+1$, where $r$ is odd. Then the first player wins if $m$ is even, and the second player wins if $m$ is odd: At each move, the player must avoid leaving the other with an even number of candies, so he must eat half of the candies. But this means that the number of candies descend as $2^{m} r+1,2^{m-1} r+1, \ldots, 2 r+1, r+1$, and eventually there is an even number of candies.
|
The second
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
There are 2003 pieces of candy on a table. Two players alternately make moves. A move consists of eating one candy or half of the candies on the table (the "lesser half" if there is an odd number of candies); at least one candy must be eaten at each move. The loser is the one who eats the last candy. Which player - the first or the second - has a winning strategy?
Answer: The second.
|
Let us prove inductively that for $2 n$ pieces of candy the first player has a winning strategy. For $n=1$ it is obvious. Suppose it is true for $2 n$ pieces, and let's consider $2 n+2$ pieces. If for $2 n+1$ pieces the second is the winner, then the first eats 1 piece and becomes the second in the game starting with $2 n+1$ pieces. So suppose that for $2 n+1$ pieces the first is the winner. His winning move for $2 n+1$ is not eating 1 piece (according to the inductive assumption). So his winning move is to eat $n$ pieces, leaving the second with $n+1$ pieces, when the second must lose. But the first can leave the second with $n+1$ pieces from the starting position with $2 n+2$ pieces, eating $n+1$ pieces; so $2 n+2$ is a winning position for the first.
Now if there are 2003 pieces of candy on the table, the first must eat either 1 or 1001 candies, leaving an even number of candies on the table. So the second player will be the first player in a game with even number of candies and therefore has a winning strategy.
In general, if there is an odd number $N$ of candies, write $N=2^{m} r+1$, where $r$ is odd. Then the first player wins if $m$ is even, and the second player wins if $m$ is odd: At each move, the player must avoid leaving the other with an even number of candies, so he must eat half of the candies. But this means that the number of candies descend as $2^{m} r+1,2^{m-1} r+1, \ldots, 2 r+1, r+1$, and eventually there is an even number of candies.
|
{
"exam": "BalticWay",
"problem_label": "8",
"problem_match": "\n8.",
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2003"
}
|
It is known that $n$ is a positive integer, $n \leq 144$. Ten questions of type "Is $n$ smaller than a?" are allowed. Answers are given with a delay: The answer to the $i$ 'th question is given only after the $(i+1)$ 'st question is asked, $i=1,2, \ldots, 9$. The answer to the tenth question is given immediately after it is asked. Find a strategy for identifying $n$.
|
Let the Fibonacci numbers be denoted $F_{0}=1, F_{1}=2, F_{2}=3$ etc. Then $F_{10}=144$. We will prove by induction on $k$ that using $k$ questions subject to the conditions of the problem, it is possible to determine any positive integer $n \leq F_{k}$. First, for $k=0$ it is trivial, since without asking we know that $n=1$. For $k=1$, we simply ask if $n$ is smaller than 2. For $k=2$, we ask if $n$ is smaller than 3 and if $n$ is smaller than 2; from the two answers we can determine $n$.
Now, in general, our first two questions will always be "Is $n$ smaller than $F_{k-1}+1$ ?" and "Is $n$ smaller than $F_{k-2}+1$ ". We then receive the answer to the first question. As long as we receive affirmative answers to the $i-1$ 'st question, the $i+1$ 'st question will be "Is $n$ smaller than $F_{k-(i+1)}+1$ ?". If at any point, say after asking the $j$ 'th question, we receive a negative answer to the $j-1$ 'st question, we then know that $F_{k-(j-1)}+1 \leq n \leq F_{k-(j-2)}$, so $n$ is one of $F_{k-(j-2)}-F_{k-(j-1)}=F_{k-j}$ consecutive integers, and by induction we may determine $n$ using the remaining $k-j$ questions. Otherwise, we receive affirmative answers to all the questions, the last being "Is $n$ smaller than $F_{k-k}+1=2$ ?"; so $n=1$ in that case.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
It is known that $n$ is a positive integer, $n \leq 144$. Ten questions of type "Is $n$ smaller than a?" are allowed. Answers are given with a delay: The answer to the $i$ 'th question is given only after the $(i+1)$ 'st question is asked, $i=1,2, \ldots, 9$. The answer to the tenth question is given immediately after it is asked. Find a strategy for identifying $n$.
|
Let the Fibonacci numbers be denoted $F_{0}=1, F_{1}=2, F_{2}=3$ etc. Then $F_{10}=144$. We will prove by induction on $k$ that using $k$ questions subject to the conditions of the problem, it is possible to determine any positive integer $n \leq F_{k}$. First, for $k=0$ it is trivial, since without asking we know that $n=1$. For $k=1$, we simply ask if $n$ is smaller than 2. For $k=2$, we ask if $n$ is smaller than 3 and if $n$ is smaller than 2; from the two answers we can determine $n$.
Now, in general, our first two questions will always be "Is $n$ smaller than $F_{k-1}+1$ ?" and "Is $n$ smaller than $F_{k-2}+1$ ". We then receive the answer to the first question. As long as we receive affirmative answers to the $i-1$ 'st question, the $i+1$ 'st question will be "Is $n$ smaller than $F_{k-(i+1)}+1$ ?". If at any point, say after asking the $j$ 'th question, we receive a negative answer to the $j-1$ 'st question, we then know that $F_{k-(j-1)}+1 \leq n \leq F_{k-(j-2)}$, so $n$ is one of $F_{k-(j-2)}-F_{k-(j-1)}=F_{k-j}$ consecutive integers, and by induction we may determine $n$ using the remaining $k-j$ questions. Otherwise, we receive affirmative answers to all the questions, the last being "Is $n$ smaller than $F_{k-k}+1=2$ ?"; so $n=1$ in that case.
|
{
"exam": "BalticWay",
"problem_label": "9",
"problem_match": "\n9.",
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2003"
}
|
A lattice point in the plane is a point whose coordinates are both integral. The centroid of four points $\left(x_{i}, y_{i}\right), i=1,2,3,4$, is the point $\left(\frac{x_{1}+x_{2}+x_{3}+x_{4}}{4}, \frac{y_{1}+y_{2}+y_{3}+y_{4}}{4}\right)$. Let $n$ be the largest natural number with the following property: There are $n$ distinct lattice points in the plane such that the centroid of any four of them is not a lattice point. Prove that $n=12$.
|
To prove $n \geq 12$, we have to show that there are 12 lattice points $\left(x_{i}, y_{i}\right)$, $i=1,2, \ldots, 12$, such that no four determine a lattice point centroid. This is guaranteed if we just choose the points such that $x_{i} \equiv 0(\bmod 4)$ for $i=1, \ldots, 6, x_{i} \equiv 1(\bmod 4)$ for
$i=7, \ldots, 12, y_{i} \equiv 0(\bmod 4)$ for $i=1,2,3,10,11,12, y_{i} \equiv 1(\bmod 4)$ for $i=4, \ldots, 9$.
Now let $P_{i}, i=1,2, \ldots, 13$, be lattice points. We have to show that some four of them determine a lattice point centroid. First observe that, by the Pigeonhole Principle, among any five of the points we find two such that their $x$-coordinates as well as their $y$-coordinates have the same parity. Consequently, among any five of the points there are two whose midpoint is a lattice point. Iterated application of this observation implies that among the 13 points in question we find five disjoint pairs of points whose midpoint is a lattice point. Among these five midpoints we again find two, say $M$ and $M^{\prime}$, such that their midpoint $C$ is a lattice point. Finally, if $M$ and $M^{\prime}$ are the midpoints of $P_{i} P_{j}$ and $P_{k} P_{\ell}$, respectively, $\{i, j, k, \ell\} \subseteq\{1,2, \ldots, 13\}$, then $C$ is the centroid of $P_{i}, P_{j}, P_{k}, P_{\ell}$.
|
12
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A lattice point in the plane is a point whose coordinates are both integral. The centroid of four points $\left(x_{i}, y_{i}\right), i=1,2,3,4$, is the point $\left(\frac{x_{1}+x_{2}+x_{3}+x_{4}}{4}, \frac{y_{1}+y_{2}+y_{3}+y_{4}}{4}\right)$. Let $n$ be the largest natural number with the following property: There are $n$ distinct lattice points in the plane such that the centroid of any four of them is not a lattice point. Prove that $n=12$.
|
To prove $n \geq 12$, we have to show that there are 12 lattice points $\left(x_{i}, y_{i}\right)$, $i=1,2, \ldots, 12$, such that no four determine a lattice point centroid. This is guaranteed if we just choose the points such that $x_{i} \equiv 0(\bmod 4)$ for $i=1, \ldots, 6, x_{i} \equiv 1(\bmod 4)$ for
$i=7, \ldots, 12, y_{i} \equiv 0(\bmod 4)$ for $i=1,2,3,10,11,12, y_{i} \equiv 1(\bmod 4)$ for $i=4, \ldots, 9$.
Now let $P_{i}, i=1,2, \ldots, 13$, be lattice points. We have to show that some four of them determine a lattice point centroid. First observe that, by the Pigeonhole Principle, among any five of the points we find two such that their $x$-coordinates as well as their $y$-coordinates have the same parity. Consequently, among any five of the points there are two whose midpoint is a lattice point. Iterated application of this observation implies that among the 13 points in question we find five disjoint pairs of points whose midpoint is a lattice point. Among these five midpoints we again find two, say $M$ and $M^{\prime}$, such that their midpoint $C$ is a lattice point. Finally, if $M$ and $M^{\prime}$ are the midpoints of $P_{i} P_{j}$ and $P_{k} P_{\ell}$, respectively, $\{i, j, k, \ell\} \subseteq\{1,2, \ldots, 13\}$, then $C$ is the centroid of $P_{i}, P_{j}, P_{k}, P_{\ell}$.
|
{
"exam": "BalticWay",
"problem_label": "10",
"problem_match": "\n10.",
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2003"
}
|
Is it possible to select 1000 points in a plane so that at least 6000 distances between two of them are equal?
Answer: Yes.
|
Let's start with configuration of 4 points and 5 distances equal to $d$, like in this figure:
$(\alpha)$
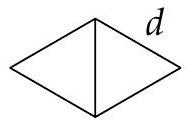
Now take $(\alpha)$ and two copies of it obtainable by parallel shifts along vectors $\vec{a}$ and $\vec{b},|\vec{a}|=|\vec{b}|=d$ and $\angle(\vec{a}, \vec{b})=60^{\circ}$. Vectors $\vec{a}$ and $\vec{b}$ should be chosen so that no two vertices of $(\alpha)$ and of the two copies coincide. We get $3 \cdot 4=12$ points and $3 \cdot 5+12=27$ distances. Proceeding in the same way, we get gradually
- $3 \cdot 12=36$ points and $3 \cdot 27+36=117$ distances;
- $3 \cdot 36=108$ points and $3 \cdot 117+108=459$ distances;
- $3 \cdot 108=324$ points and $3 \cdot 459+324=1701$ distances;
- $3 \cdot 324=972$ points and $3 \cdot 1701+972=6075$ distances.
|
6075
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Is it possible to select 1000 points in a plane so that at least 6000 distances between two of them are equal?
Answer: Yes.
|
Let's start with configuration of 4 points and 5 distances equal to $d$, like in this figure:
$(\alpha)$

Now take $(\alpha)$ and two copies of it obtainable by parallel shifts along vectors $\vec{a}$ and $\vec{b},|\vec{a}|=|\vec{b}|=d$ and $\angle(\vec{a}, \vec{b})=60^{\circ}$. Vectors $\vec{a}$ and $\vec{b}$ should be chosen so that no two vertices of $(\alpha)$ and of the two copies coincide. We get $3 \cdot 4=12$ points and $3 \cdot 5+12=27$ distances. Proceeding in the same way, we get gradually
- $3 \cdot 12=36$ points and $3 \cdot 27+36=117$ distances;
- $3 \cdot 36=108$ points and $3 \cdot 117+108=459$ distances;
- $3 \cdot 108=324$ points and $3 \cdot 459+324=1701$ distances;
- $3 \cdot 324=972$ points and $3 \cdot 1701+972=6075$ distances.
|
{
"exam": "BalticWay",
"problem_label": "11",
"problem_match": "\n11.",
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2003"
}
|
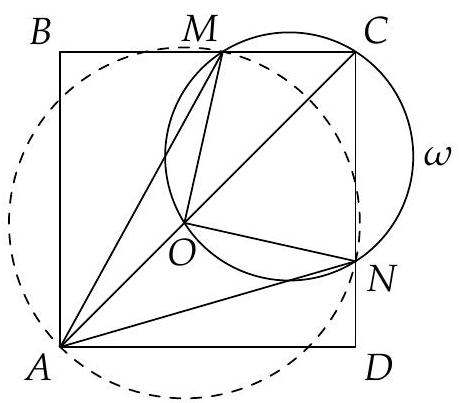
Let $A B C D$ be a square. Let $M$ be an inner point on side $B C$ and $N$ be an inner point on side $C D$ with $\angle M A N=45^{\circ}$. Prove that the circumcentre of $A M N$ lies on $A C$.
|
Draw a circle $\omega$ through $M, C, N$; let it intersect $A C$ at $O$. We claim that $O$ is the circumcentre of $A M N$.
Clearly $\angle M O N=180^{\circ}-\angle M C N=90^{\circ}$. If the radius of $\omega$ is $R$, then $O M=$ $2 R \sin 45^{\circ}=R \sqrt{2}$; similarly $O N=R \sqrt{2}$. Hence we get that $O M=O N$. Then the circle with centre $O$ and radius $R \sqrt{2}$ will pass through $A$, since $\angle M A N=\frac{1}{2} \angle M O N$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a square. Let $M$ be an inner point on side $B C$ and $N$ be an inner point on side $C D$ with $\angle M A N=45^{\circ}$. Prove that the circumcentre of $A M N$ lies on $A C$.
|
Draw a circle $\omega$ through $M, C, N$; let it intersect $A C$ at $O$. We claim that $O$ is the circumcentre of $A M N$.
Clearly $\angle M O N=180^{\circ}-\angle M C N=90^{\circ}$. If the radius of $\omega$ is $R$, then $O M=$ $2 R \sin 45^{\circ}=R \sqrt{2}$; similarly $O N=R \sqrt{2}$. Hence we get that $O M=O N$. Then the circle with centre $O$ and radius $R \sqrt{2}$ will pass through $A$, since $\angle M A N=\frac{1}{2} \angle M O N$.

|
{
"exam": "BalticWay",
"problem_label": "12",
"problem_match": "\n12.",
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2003"
}
|
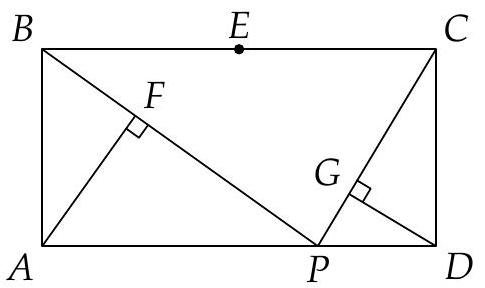
Let $A B C D$ be a rectangle and $B C=2 \cdot A B$. Let $E$ be the midpoint of $B C$ and $P$ an arbitrary inner point of $A D$. Let $F$ and $G$ be the feet of perpendiculars drawn correspondingly from $A$ to $B P$ and from $D$ to $C P$. Prove that the points $E, F, P, G$ are concyclic.
|
From rectangular triangle $B A P$ we have $B P \cdot B F=A B^{2}=B E^{2}$. Therefore the circumference through $F$ and $P$ touching the line $B C$ between $B$ and $C$ touches it at $E$.
Analogously, the circumference through $P$ and $G$ touching the line $B C$ between $B$ and $C$ touches it at $E$. But there is only one circumference touching $B C$ at $E$ and passing through $P$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a rectangle and $B C=2 \cdot A B$. Let $E$ be the midpoint of $B C$ and $P$ an arbitrary inner point of $A D$. Let $F$ and $G$ be the feet of perpendiculars drawn correspondingly from $A$ to $B P$ and from $D$ to $C P$. Prove that the points $E, F, P, G$ are concyclic.
|
From rectangular triangle $B A P$ we have $B P \cdot B F=A B^{2}=B E^{2}$. Therefore the circumference through $F$ and $P$ touching the line $B C$ between $B$ and $C$ touches it at $E$.
Analogously, the circumference through $P$ and $G$ touching the line $B C$ between $B$ and $C$ touches it at $E$. But there is only one circumference touching $B C$ at $E$ and passing through $P$.

|
{
"exam": "BalticWay",
"problem_label": "13",
"problem_match": "\n13.",
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2003"
}
|
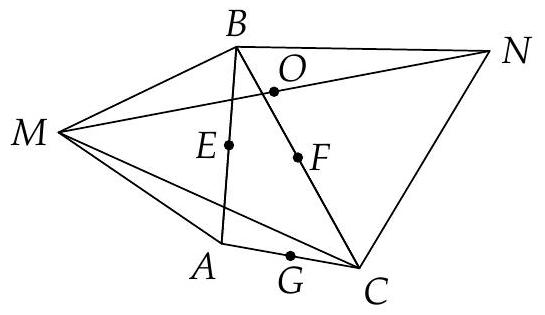
Let $A B C$ be an arbitrary triangle and $A M B, B N C, C K A$ regular triangles outward of $A B C$. Through the midpoint of $M N$ a perpendicular to $A C$ is constructed; similarly through the midpoints of $N K$ resp. KM perpendiculars to $A B$ resp. $B C$ are constructed. Prove that these three perpendiculars intersect at the same point.
|
Let $O$ be the midpoint of $M N$, and let $E$ and $F$ be the midpoints of $A B$ and $B C$, respectively. As triangle $M B C$ transforms into triangle $A B N$ when rotated $60^{\circ}$ around $B$ we get $M C=A N$ (it is also a well-known fact). Considering now the quadrangles $A M B N$ and $C M B N$ we get $O E=O F$ (from Eiler's formula $a^{2}+b^{2}+c^{2}+d^{2}=e^{2}+f^{2}+4 \cdot P Q^{2}$ or otherwise). As $E F \| A C$ we get from this that the perpendicular to $A C$ through $O$ passes through the circumcentre of $E F G$, as it is the perpendicular bisector of $E F$. The same holds for the other two perpendiculars.
First solution
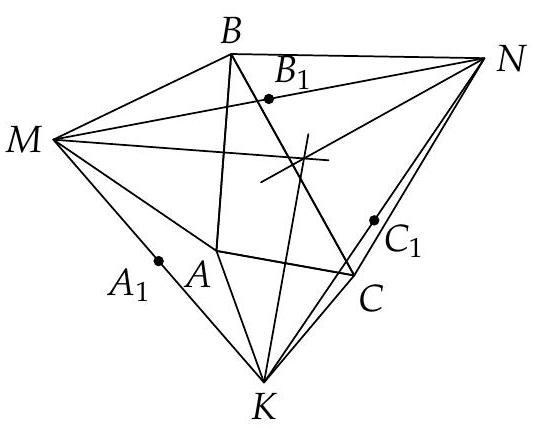
Second solution
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an arbitrary triangle and $A M B, B N C, C K A$ regular triangles outward of $A B C$. Through the midpoint of $M N$ a perpendicular to $A C$ is constructed; similarly through the midpoints of $N K$ resp. KM perpendiculars to $A B$ resp. $B C$ are constructed. Prove that these three perpendiculars intersect at the same point.
|
Let $O$ be the midpoint of $M N$, and let $E$ and $F$ be the midpoints of $A B$ and $B C$, respectively. As triangle $M B C$ transforms into triangle $A B N$ when rotated $60^{\circ}$ around $B$ we get $M C=A N$ (it is also a well-known fact). Considering now the quadrangles $A M B N$ and $C M B N$ we get $O E=O F$ (from Eiler's formula $a^{2}+b^{2}+c^{2}+d^{2}=e^{2}+f^{2}+4 \cdot P Q^{2}$ or otherwise). As $E F \| A C$ we get from this that the perpendicular to $A C$ through $O$ passes through the circumcentre of $E F G$, as it is the perpendicular bisector of $E F$. The same holds for the other two perpendiculars.

First solution

Second solution
|
{
"exam": "BalticWay",
"problem_label": "14",
"problem_match": "\n14.",
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2003"
}
|
Let $A B C$ be an arbitrary triangle and $A M B, B N C, C K A$ regular triangles outward of $A B C$. Through the midpoint of $M N$ a perpendicular to $A C$ is constructed; similarly through the midpoints of $N K$ resp. KM perpendiculars to $A B$ resp. $B C$ are constructed. Prove that these three perpendiculars intersect at the same point.
|
Let us denote the midpoints of the segments $M N, N K, K M$ by $B_{1}, C_{1}, A_{1}$, respectively. It is easy to see that triangle $A_{1} B_{1} C_{1}$ is homothetic to triangle $N K M$ via the homothety centered at the intersection of the medians of triangle $N M K$ and dilation $-\frac{1}{2}$. The perpendiculars through $M, N, K$ to $A B, B C, C A$, respectively, are also the perpendicular bisectors of these sides, so they intersect in the circumcentre of triangle $A B C$. The desired result follows now from the homothety, and we find that that the common point of intersection is the circumcentre of the image of triangle $A B C$ under the homothety; that is, the circumcentre of the triangle with vertices the midpoints of the sides $A B, B C, C A$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an arbitrary triangle and $A M B, B N C, C K A$ regular triangles outward of $A B C$. Through the midpoint of $M N$ a perpendicular to $A C$ is constructed; similarly through the midpoints of $N K$ resp. KM perpendiculars to $A B$ resp. $B C$ are constructed. Prove that these three perpendiculars intersect at the same point.
|
Let us denote the midpoints of the segments $M N, N K, K M$ by $B_{1}, C_{1}, A_{1}$, respectively. It is easy to see that triangle $A_{1} B_{1} C_{1}$ is homothetic to triangle $N K M$ via the homothety centered at the intersection of the medians of triangle $N M K$ and dilation $-\frac{1}{2}$. The perpendiculars through $M, N, K$ to $A B, B C, C A$, respectively, are also the perpendicular bisectors of these sides, so they intersect in the circumcentre of triangle $A B C$. The desired result follows now from the homothety, and we find that that the common point of intersection is the circumcentre of the image of triangle $A B C$ under the homothety; that is, the circumcentre of the triangle with vertices the midpoints of the sides $A B, B C, C A$.
|
{
"exam": "BalticWay",
"problem_label": "14",
"problem_match": "\n14.",
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"solution_match": "\nSolution 2:",
"tier": "T3",
"year": "2003"
}
|
Let $P$ be the intersection point of the diagonals $A C$ and $B D$ in a cyclic quadrilateral. $A$ circle through $P$ touches the side $C D$ in the midpoint $M$ of this side and intersects the segments $B D$ and $A C$ in the points $Q$ and $R$, respectively. Let $S$ be a point on the segment $B D$ such that $B S=D Q$. The parallel to $A B$ through $S$ intersects $A C$ at $T$. Prove that $A T=R C$.
|
With reference to the figure below we have $C R \cdot C P=D Q \cdot D P=C M^{2}=D M^{2}$, which is equivalent to $R C=\frac{D Q \cdot D P}{C P}$. We also have $\frac{A T}{B S}=\frac{A P}{B P}=\frac{A T}{D Q}$, so $A T=\frac{A P \cdot D Q}{B P}$. Since $A B C D$ is cyclic the result now comes from the fact that $D P \cdot B P=A P \cdot C P$ (due to a well-known theorem).
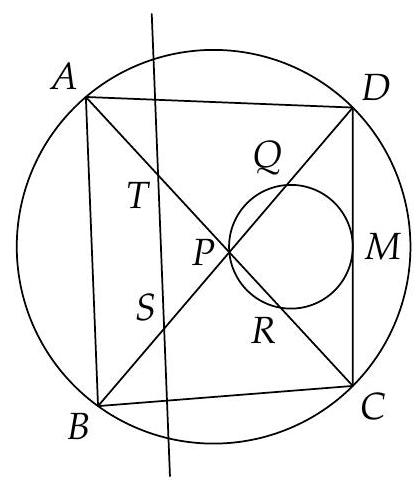
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $P$ be the intersection point of the diagonals $A C$ and $B D$ in a cyclic quadrilateral. $A$ circle through $P$ touches the side $C D$ in the midpoint $M$ of this side and intersects the segments $B D$ and $A C$ in the points $Q$ and $R$, respectively. Let $S$ be a point on the segment $B D$ such that $B S=D Q$. The parallel to $A B$ through $S$ intersects $A C$ at $T$. Prove that $A T=R C$.
|
With reference to the figure below we have $C R \cdot C P=D Q \cdot D P=C M^{2}=D M^{2}$, which is equivalent to $R C=\frac{D Q \cdot D P}{C P}$. We also have $\frac{A T}{B S}=\frac{A P}{B P}=\frac{A T}{D Q}$, so $A T=\frac{A P \cdot D Q}{B P}$. Since $A B C D$ is cyclic the result now comes from the fact that $D P \cdot B P=A P \cdot C P$ (due to a well-known theorem).

|
{
"exam": "BalticWay",
"problem_label": "15",
"problem_match": "\n15.",
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2003"
}
|
Find all pairs of positive integers $(a, b)$ such that $a-b$ is a prime and $a b$ is a perfect square. Answer: Pairs $(a, b)=\left(\left(\frac{p+1}{2}\right)^{2},\left(\frac{p-1}{2}\right)^{2}\right)$, where $p$ is a prime greater than 2 .
|
Let $p$ be a prime such that $a-b=p$ and let $a b=k^{2}$. Insert $a=b+p$ in the equation $a b=k^{2}$. Then
$$
k^{2}=(b+p) b=\left(b+\frac{p}{2}\right)^{2}-\frac{p^{2}}{4}
$$
which is equivalent to
$$
p^{2}=(2 b+p)^{2}-4 k^{2}=(2 b+p+2 k)(2 b+p-2 k) .
$$
Since $2 b+p+2 k>2 b+p-2 k$ and $p$ is a prime, we conclude $2 b+p+2 k=p^{2}$ and $2 b+p-2 k=1$. By adding these equations we get $2 b+p=\frac{p^{2}+1}{2}$ and then $b=\left(\frac{p-1}{2}\right)^{2}$, so $a=b+p=\left(\frac{p+1}{2}\right)^{2}$. By checking we conclude that all the solutions are $(a, b)=\left(\left(\frac{p+1}{2}\right)^{2},\left(\frac{p-1}{2}\right)^{2}\right)$ with $p$ a prime greater than 2 .
|
(a, b)=\left(\left(\frac{p+1}{2}\right)^{2},\left(\frac{p-1}{2}\right)^{2}\right)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all pairs of positive integers $(a, b)$ such that $a-b$ is a prime and $a b$ is a perfect square. Answer: Pairs $(a, b)=\left(\left(\frac{p+1}{2}\right)^{2},\left(\frac{p-1}{2}\right)^{2}\right)$, where $p$ is a prime greater than 2 .
|
Let $p$ be a prime such that $a-b=p$ and let $a b=k^{2}$. Insert $a=b+p$ in the equation $a b=k^{2}$. Then
$$
k^{2}=(b+p) b=\left(b+\frac{p}{2}\right)^{2}-\frac{p^{2}}{4}
$$
which is equivalent to
$$
p^{2}=(2 b+p)^{2}-4 k^{2}=(2 b+p+2 k)(2 b+p-2 k) .
$$
Since $2 b+p+2 k>2 b+p-2 k$ and $p$ is a prime, we conclude $2 b+p+2 k=p^{2}$ and $2 b+p-2 k=1$. By adding these equations we get $2 b+p=\frac{p^{2}+1}{2}$ and then $b=\left(\frac{p-1}{2}\right)^{2}$, so $a=b+p=\left(\frac{p+1}{2}\right)^{2}$. By checking we conclude that all the solutions are $(a, b)=\left(\left(\frac{p+1}{2}\right)^{2},\left(\frac{p-1}{2}\right)^{2}\right)$ with $p$ a prime greater than 2 .
|
{
"exam": "BalticWay",
"problem_label": "16",
"problem_match": "\n16.",
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2003"
}
|
Find all pairs of positive integers $(a, b)$ such that $a-b$ is a prime and $a b$ is a perfect square. Answer: Pairs $(a, b)=\left(\left(\frac{p+1}{2}\right)^{2},\left(\frac{p-1}{2}\right)^{2}\right)$, where $p$ is a prime greater than 2 .
|
Let $p$ be a prime such that $a-b=p$ and let $a b=k^{2}$. We have $(b+p) b=k^{2}$, so $\operatorname{gcd}(b, b+p)=\operatorname{gcd}(b, p)$ is equal either to 1 or $p$. If $\operatorname{gcd}(b, b+p)=p$, let $b=b_{1} p$. Then $p^{2} b_{1}\left(b_{1}+1\right)=k^{2}, b_{1}\left(b_{1}+1\right)=m^{2}$, but this equation has no solutions.
Hence $\operatorname{gcd}(b, b+p)=1$, and
$$
b=u^{2} \quad b+p=v^{2}
$$
so that $p=v^{2}-u^{2}=(v+u)(v-u)$. This in turn implies that $v-u=1$ and $v+u=p$, from which we finally obtain $a=\left(\frac{p+1}{2}\right)^{2}, b=\left(\frac{p-1}{2}\right)^{2}$, where $p$ must be an odd prime.
|
(a, b)=\left(\left(\frac{p+1}{2}\right)^{2},\left(\frac{p-1}{2}\right)^{2}\right)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all pairs of positive integers $(a, b)$ such that $a-b$ is a prime and $a b$ is a perfect square. Answer: Pairs $(a, b)=\left(\left(\frac{p+1}{2}\right)^{2},\left(\frac{p-1}{2}\right)^{2}\right)$, where $p$ is a prime greater than 2 .
|
Let $p$ be a prime such that $a-b=p$ and let $a b=k^{2}$. We have $(b+p) b=k^{2}$, so $\operatorname{gcd}(b, b+p)=\operatorname{gcd}(b, p)$ is equal either to 1 or $p$. If $\operatorname{gcd}(b, b+p)=p$, let $b=b_{1} p$. Then $p^{2} b_{1}\left(b_{1}+1\right)=k^{2}, b_{1}\left(b_{1}+1\right)=m^{2}$, but this equation has no solutions.
Hence $\operatorname{gcd}(b, b+p)=1$, and
$$
b=u^{2} \quad b+p=v^{2}
$$
so that $p=v^{2}-u^{2}=(v+u)(v-u)$. This in turn implies that $v-u=1$ and $v+u=p$, from which we finally obtain $a=\left(\frac{p+1}{2}\right)^{2}, b=\left(\frac{p-1}{2}\right)^{2}$, where $p$ must be an odd prime.
|
{
"exam": "BalticWay",
"problem_label": "16",
"problem_match": "\n16.",
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"solution_match": "\nSolution 2:",
"tier": "T3",
"year": "2003"
}
|
All the positive divisors of a positive integer $n$ are stored into an array in increasing order. Mary has to write a program which decides for an arbitrarily chosen divisor $d>1$ whether it is a prime. Let $n$ have $k$ divisors not greater than $d$. Mary claims that it suffices to check divisibility of $d$ by the first $\lceil k / 2\rceil$ divisors of $n$ : If a divisor of $d$ greater than 1 is found among them, then $d$ is composite, otherwise d is prime. Is Mary right?
Answer: Yes, Mary is right.
|
Let $d>1$ be a divisor of $n$. Suppose Mary's program outputs "composite" for $d$. That means it has found a divisor of $d$ greater than 1 . Since $d>1$, the array contains at least 2 divisors of $d$, namely 1 and $d$. Thus Mary's program does not check divisibility of $d$ by $d$ (the first half gets complete before reaching $d$ ) which means that the divisor found lays strictly between 1 and $d$. Hence $d$ is composite indeed.
Suppose now $d$ being composite. Let $p$ be its smallest prime divisor; then $\frac{d}{p} \geq p$ or, equivalently, $d \geq p^{2}$. As $p$ is a divisor of $n$, it occurs in the array. Let $a_{1}, \ldots, a_{k}$ all divisors of $n$ smaller than $p$. Then $p a_{1}, \ldots, p a_{k}$ are less than $p^{2}$ and hence less than $d$.
As $a_{1}, \ldots, a_{k}$ are all relatively prime with $p$, all the numbers $p a_{1}, \ldots, p a_{k}$ divide $n$. The numbers $a_{1}, \ldots, a_{k}, p a_{1}, \ldots, p a_{k}$ are pairwise different by construction. Thus there are at least $2 k+1$ divisors of $n$ not greater than $d$. So Mary's program checks divisibility of $d$ by at least $k+1$ smallest divisors of $n$, among which it finds $p$, and outputs "composite".
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
All the positive divisors of a positive integer $n$ are stored into an array in increasing order. Mary has to write a program which decides for an arbitrarily chosen divisor $d>1$ whether it is a prime. Let $n$ have $k$ divisors not greater than $d$. Mary claims that it suffices to check divisibility of $d$ by the first $\lceil k / 2\rceil$ divisors of $n$ : If a divisor of $d$ greater than 1 is found among them, then $d$ is composite, otherwise d is prime. Is Mary right?
Answer: Yes, Mary is right.
|
Let $d>1$ be a divisor of $n$. Suppose Mary's program outputs "composite" for $d$. That means it has found a divisor of $d$ greater than 1 . Since $d>1$, the array contains at least 2 divisors of $d$, namely 1 and $d$. Thus Mary's program does not check divisibility of $d$ by $d$ (the first half gets complete before reaching $d$ ) which means that the divisor found lays strictly between 1 and $d$. Hence $d$ is composite indeed.
Suppose now $d$ being composite. Let $p$ be its smallest prime divisor; then $\frac{d}{p} \geq p$ or, equivalently, $d \geq p^{2}$. As $p$ is a divisor of $n$, it occurs in the array. Let $a_{1}, \ldots, a_{k}$ all divisors of $n$ smaller than $p$. Then $p a_{1}, \ldots, p a_{k}$ are less than $p^{2}$ and hence less than $d$.
As $a_{1}, \ldots, a_{k}$ are all relatively prime with $p$, all the numbers $p a_{1}, \ldots, p a_{k}$ divide $n$. The numbers $a_{1}, \ldots, a_{k}, p a_{1}, \ldots, p a_{k}$ are pairwise different by construction. Thus there are at least $2 k+1$ divisors of $n$ not greater than $d$. So Mary's program checks divisibility of $d$ by at least $k+1$ smallest divisors of $n$, among which it finds $p$, and outputs "composite".
|
{
"exam": "BalticWay",
"problem_label": "17",
"problem_match": "\n17.",
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2003"
}
|
Every integer is coloured with exactly one of the colours BLUE, GREEN, RED, YELLOW. Can this be done in such a way that if $a, b, c, d$ are not all 0 and have the same colour, then $3 a-2 b \neq 2 c-3 d$ ?
Answer: Yes.
|
A colouring with the required property can be defined as follows. For a non-zero integer $k$ let $k^{*}$ be the integer uniquely defined by $k=5^{m} \cdot k^{*}$, where $m$ is a nonnegative integer and $5 \nmid k^{*}$. We also define $0^{*}=0$. Two non-zero integers $k_{1}, k_{2}$ receive the same colour if and only if $k_{1}^{*} \equiv k_{2}^{*}(\bmod 5)$; we assign 0 any colour.
Assume $a, b, c, d$ has the same colour and that $3 a-2 b=2 c-3 d$, which we rewrite as $3 a-2 b-2 c+3 d=0$. Dividing both sides by the largest power of 5 which simultaneously divides $a, b, c, d$ (this makes sense since not all of $a, b, c, d$ are 0 ), we obtain
$$
3 \cdot 5^{A} \cdot a^{*}-2 \cdot 5^{B} \cdot b^{*}-2 \cdot 5^{C} \cdot c^{*}+3 \cdot 5^{D} \cdot d^{*}=0,
$$
where $A, B, C, D$ are nonnegative integers at least one of which is equal to 0 . The above equality implies
$$
3\left(5^{A} \cdot a^{*}+5^{B} \cdot b^{*}+5^{C} \cdot c^{*}+5^{D} \cdot d^{*}\right) \equiv 0 \quad(\bmod 5) .
$$
Assume $a, b, c, d$ are all non-zero. Then $a^{*} \equiv b^{*} \equiv c^{*} \equiv d^{*} \not \equiv 0(\bmod 5)$. This implies
$$
5^{A}+5^{B}+5^{C}+5^{D} \equiv 0 \quad(\bmod 5)
$$
which is impossible since at least one of the numbers $A, B, C, D$ is equal to 0 . If one or more of $a, b, c, d$ are 0 , we simply omit the corresponding terms from (1), and the same conclusion holds.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Every integer is coloured with exactly one of the colours BLUE, GREEN, RED, YELLOW. Can this be done in such a way that if $a, b, c, d$ are not all 0 and have the same colour, then $3 a-2 b \neq 2 c-3 d$ ?
Answer: Yes.
|
A colouring with the required property can be defined as follows. For a non-zero integer $k$ let $k^{*}$ be the integer uniquely defined by $k=5^{m} \cdot k^{*}$, where $m$ is a nonnegative integer and $5 \nmid k^{*}$. We also define $0^{*}=0$. Two non-zero integers $k_{1}, k_{2}$ receive the same colour if and only if $k_{1}^{*} \equiv k_{2}^{*}(\bmod 5)$; we assign 0 any colour.
Assume $a, b, c, d$ has the same colour and that $3 a-2 b=2 c-3 d$, which we rewrite as $3 a-2 b-2 c+3 d=0$. Dividing both sides by the largest power of 5 which simultaneously divides $a, b, c, d$ (this makes sense since not all of $a, b, c, d$ are 0 ), we obtain
$$
3 \cdot 5^{A} \cdot a^{*}-2 \cdot 5^{B} \cdot b^{*}-2 \cdot 5^{C} \cdot c^{*}+3 \cdot 5^{D} \cdot d^{*}=0,
$$
where $A, B, C, D$ are nonnegative integers at least one of which is equal to 0 . The above equality implies
$$
3\left(5^{A} \cdot a^{*}+5^{B} \cdot b^{*}+5^{C} \cdot c^{*}+5^{D} \cdot d^{*}\right) \equiv 0 \quad(\bmod 5) .
$$
Assume $a, b, c, d$ are all non-zero. Then $a^{*} \equiv b^{*} \equiv c^{*} \equiv d^{*} \not \equiv 0(\bmod 5)$. This implies
$$
5^{A}+5^{B}+5^{C}+5^{D} \equiv 0 \quad(\bmod 5)
$$
which is impossible since at least one of the numbers $A, B, C, D$ is equal to 0 . If one or more of $a, b, c, d$ are 0 , we simply omit the corresponding terms from (1), and the same conclusion holds.
|
{
"exam": "BalticWay",
"problem_label": "18",
"problem_match": "\n18.",
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2003"
}
|
Let $a$ and $b$ be positive integers. Prove that if $a^{3}+b^{3}$ is the square of an integer, then $a+b$ is not a product of two different prime numbers.
|
Suppose $a+b=p q$, where $p \neq q$ are two prime numbers. We may assume that $p \neq 3$. Since
$$
a^{3}+b^{3}=(a+b)\left(a^{2}-a b+b^{2}\right)
$$
is a square, the number $a^{2}-a b+b^{2}=(a+b)^{2}-3 a b$ must be divisible by $p$ and $q$, whence $3 a b$ must be divisible by $p$ and $q$. But $p \neq 3$, so $p \mid a$ or $p \mid b$; but $p \mid a+b$, so $p \mid a$ and $p \mid b$. Write $a=p k, b=p \ell$ for some integers $k, \ell$. Notice that $q=3$, since otherwise, repeating the above argument, we would have $q|a, q| b$ and $a+b>p q)$. So we have
$$
3 p=a+b=p(k+\ell)
$$
and we conclude that $a=p, b=2 p$ or $a=2 p, b=p$. Then $a^{3}+b^{3}=9 p^{3}$ is obviously not a square, a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a$ and $b$ be positive integers. Prove that if $a^{3}+b^{3}$ is the square of an integer, then $a+b$ is not a product of two different prime numbers.
|
Suppose $a+b=p q$, where $p \neq q$ are two prime numbers. We may assume that $p \neq 3$. Since
$$
a^{3}+b^{3}=(a+b)\left(a^{2}-a b+b^{2}\right)
$$
is a square, the number $a^{2}-a b+b^{2}=(a+b)^{2}-3 a b$ must be divisible by $p$ and $q$, whence $3 a b$ must be divisible by $p$ and $q$. But $p \neq 3$, so $p \mid a$ or $p \mid b$; but $p \mid a+b$, so $p \mid a$ and $p \mid b$. Write $a=p k, b=p \ell$ for some integers $k, \ell$. Notice that $q=3$, since otherwise, repeating the above argument, we would have $q|a, q| b$ and $a+b>p q)$. So we have
$$
3 p=a+b=p(k+\ell)
$$
and we conclude that $a=p, b=2 p$ or $a=2 p, b=p$. Then $a^{3}+b^{3}=9 p^{3}$ is obviously not a square, a contradiction.
|
{
"exam": "BalticWay",
"problem_label": "19",
"problem_match": "\n19.",
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2003"
}
|
Let $n$ be a positive integer such that the sum of all the positive divisors of $n$ (except $n$ ) plus the number of these divisors is equal to $n$. Prove that $n=2 m^{2}$ for some integer $m$.
|
Let $t_{1}<t_{2}<\cdots<t_{s}$ be all positive odd divisors of $n$, and let $2^{k}$ be the maximal power of 2 that divides $n$. Then the full list of divisors of $n$ is the following:
$$
t_{1}, \ldots, t_{s}, 2 t_{1}, \ldots, 2 t_{s}, \ldots, 2^{k} t_{1}, \ldots, 2^{k} t_{s} .
$$
Hence,
$$
2 n=\left(2^{k+1}-1\right)\left(t_{1}+t_{2}+\cdots+t_{s}\right)+(k+1) s-1 .
$$
The right-hand side can be even only if both $k$ and $s$ are odd. In this case the number $n / 2^{k}$ has an odd number of divisors and therefore it is equal to a perfect square $r^{2}$. Writing $k=2 a+1$, we have $n=2^{k} r^{2}=2\left(2^{a} r\right)^{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ be a positive integer such that the sum of all the positive divisors of $n$ (except $n$ ) plus the number of these divisors is equal to $n$. Prove that $n=2 m^{2}$ for some integer $m$.
|
Let $t_{1}<t_{2}<\cdots<t_{s}$ be all positive odd divisors of $n$, and let $2^{k}$ be the maximal power of 2 that divides $n$. Then the full list of divisors of $n$ is the following:
$$
t_{1}, \ldots, t_{s}, 2 t_{1}, \ldots, 2 t_{s}, \ldots, 2^{k} t_{1}, \ldots, 2^{k} t_{s} .
$$
Hence,
$$
2 n=\left(2^{k+1}-1\right)\left(t_{1}+t_{2}+\cdots+t_{s}\right)+(k+1) s-1 .
$$
The right-hand side can be even only if both $k$ and $s$ are odd. In this case the number $n / 2^{k}$ has an odd number of divisors and therefore it is equal to a perfect square $r^{2}$. Writing $k=2 a+1$, we have $n=2^{k} r^{2}=2\left(2^{a} r\right)^{2}$.
|
{
"exam": "BalticWay",
"problem_label": "20",
"problem_match": "\n20.",
"resource_path": "BalticWay/segmented/en-bw03sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2003"
}
|
Given a sequence $a_{1}, a_{2}, a_{3}, \ldots$ of non-negative real numbers satisfying the conditions
(1) $a_{n}+a_{2 n} \geq 3 n$
(2) $a_{n+1}+n \leq 2 \sqrt{a_{n} \cdot(n+1)}$
for all indices $n=1,2 \ldots$
(a) Prove that the inequality $a_{n} \geq n$ holds for every $n \in \mathbb{N}$.
(b) Give an example of such a sequence.
|
(a) Note that the inequality
$$
\frac{a_{n+1}+n}{2} \geq \sqrt{a_{n+1} \cdot n}
$$
holds, which together with the second condition of the problem gives
$$
\sqrt{a_{n+1} \cdot n} \leq \sqrt{a_{n} \cdot(n+1)}
$$
This inequality simplifies to
$$
\frac{a_{n+1}}{a_{n}} \leq \frac{n+1}{n}
$$
Now, using the last inequality for the index $n$ replaced by $n, n+1, \ldots, 2 n-1$ and multiplying the results, we obtain
$$
\frac{a_{2 n}}{a_{n}} \leq \frac{2 n}{n}=2
$$
or $2 a_{n} \geq a_{2 n}$. Taking into account the first condition of the problem, we have
$$
3 a_{n}=a_{n}+2 a_{n} \geq a_{n}+a_{2 n} \geq 3 n
$$
which implies $a_{n} \geq n$. (b) The sequence defined by $a_{n}=n+1$ satisfies all the conditions of the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Given a sequence $a_{1}, a_{2}, a_{3}, \ldots$ of non-negative real numbers satisfying the conditions
(1) $a_{n}+a_{2 n} \geq 3 n$
(2) $a_{n+1}+n \leq 2 \sqrt{a_{n} \cdot(n+1)}$
for all indices $n=1,2 \ldots$
(a) Prove that the inequality $a_{n} \geq n$ holds for every $n \in \mathbb{N}$.
(b) Give an example of such a sequence.
|
(a) Note that the inequality
$$
\frac{a_{n+1}+n}{2} \geq \sqrt{a_{n+1} \cdot n}
$$
holds, which together with the second condition of the problem gives
$$
\sqrt{a_{n+1} \cdot n} \leq \sqrt{a_{n} \cdot(n+1)}
$$
This inequality simplifies to
$$
\frac{a_{n+1}}{a_{n}} \leq \frac{n+1}{n}
$$
Now, using the last inequality for the index $n$ replaced by $n, n+1, \ldots, 2 n-1$ and multiplying the results, we obtain
$$
\frac{a_{2 n}}{a_{n}} \leq \frac{2 n}{n}=2
$$
or $2 a_{n} \geq a_{2 n}$. Taking into account the first condition of the problem, we have
$$
3 a_{n}=a_{n}+2 a_{n} \geq a_{n}+a_{2 n} \geq 3 n
$$
which implies $a_{n} \geq n$. (b) The sequence defined by $a_{n}=n+1$ satisfies all the conditions of the problem.
|
{
"exam": "BalticWay",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2004"
}
|
Let $P(x)$ be a polynomial with non-negative coefficients. Prove that if $P\left(\frac{1}{x}\right) P(x) \geq 1$ for $x=1$, then the same inequality holds for each positive $x$.
|
For $x>0$ we have $P(x)>0$ (because at least one coefficient is non-zero). From the given condition we have $(P(1))^{2} \geq 1$. Further, let's denote $P(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+$ $\cdots+a_{0}$. Then
$$
\begin{aligned}
P(x) P\left(\frac{1}{x}\right) & =\left(a_{n} x^{n}+\cdots+a_{0}\right)\left(a_{n} x^{-n}+\cdots+a_{0}\right) \\
& =\sum_{i=0}^{n} a_{i}^{2}+\sum_{i=1}^{n} \sum_{j=0}^{i-1}\left(a_{i-j} a_{j}\right)\left(x^{i}+x^{-i}\right) \\
& \geq \sum_{i=0}^{n} a_{i}^{2}+2 \sum_{i>j} a_{i} a_{j} \\
& =(P(1))^{2} \geq 1 .
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $P(x)$ be a polynomial with non-negative coefficients. Prove that if $P\left(\frac{1}{x}\right) P(x) \geq 1$ for $x=1$, then the same inequality holds for each positive $x$.
|
For $x>0$ we have $P(x)>0$ (because at least one coefficient is non-zero). From the given condition we have $(P(1))^{2} \geq 1$. Further, let's denote $P(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+$ $\cdots+a_{0}$. Then
$$
\begin{aligned}
P(x) P\left(\frac{1}{x}\right) & =\left(a_{n} x^{n}+\cdots+a_{0}\right)\left(a_{n} x^{-n}+\cdots+a_{0}\right) \\
& =\sum_{i=0}^{n} a_{i}^{2}+\sum_{i=1}^{n} \sum_{j=0}^{i-1}\left(a_{i-j} a_{j}\right)\left(x^{i}+x^{-i}\right) \\
& \geq \sum_{i=0}^{n} a_{i}^{2}+2 \sum_{i>j} a_{i} a_{j} \\
& =(P(1))^{2} \geq 1 .
\end{aligned}
$$
|
{
"exam": "BalticWay",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2004"
}
|
Let $p, q, r$ be positive real numbers and $n \in \mathbb{N}$. Show that if $p q r=1$, then
$$
\frac{1}{p^{n}+q^{n}+1}+\frac{1}{q^{n}+r^{n}+1}+\frac{1}{r^{n}+p^{n}+1} \leq 1
$$
|
The key idea is to deal with the case $n=3$. Put $a=p^{n / 3}, b=q^{n / 3}$, and $c=r^{n / 3}$, so $a b c=(p q r)^{n / 3}=1$ and
$$
\frac{1}{p^{n}+q^{n}+1}+\frac{1}{q^{n}+r^{n}+1}+\frac{1}{r^{n}+p^{n}+1}=\frac{1}{a^{3}+b^{3}+1}+\frac{1}{b^{3}+c^{3}+1}+\frac{1}{c^{3}+a^{3}+1} .
$$
Now
$$
\frac{1}{a^{3}+b^{3}+1}=\frac{1}{(a+b)\left(a^{2}-a b+b^{2}\right)+1}=\frac{1}{(a+b)\left((a-b)^{2}+a b\right)+1} \leq \frac{1}{(a+b) a b+1} .
$$
Since $a b=c^{-1}$,
$$
\frac{1}{a^{3}+b^{3}+1} \leq \frac{1}{(a+b) a b+1}=\frac{c}{a+b+c}
$$
Similarly we obtain
$$
\frac{1}{b^{3}+c^{3}+1} \leq \frac{a}{a+b+c} \quad \text { and } \quad \frac{1}{c^{3}+a^{3}+1} \leq \frac{b}{a+b+c}
$$
Hence
$$
\frac{1}{a^{3}+b^{3}+1}+\frac{1}{b^{3}+c^{3}+1}+\frac{1}{c^{3}+a^{3}+1} \leq \frac{c}{a+b+c}+\frac{a}{a+b+c}+\frac{b}{a+b+c}=1,
$$
which was to be shown.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $p, q, r$ be positive real numbers and $n \in \mathbb{N}$. Show that if $p q r=1$, then
$$
\frac{1}{p^{n}+q^{n}+1}+\frac{1}{q^{n}+r^{n}+1}+\frac{1}{r^{n}+p^{n}+1} \leq 1
$$
|
The key idea is to deal with the case $n=3$. Put $a=p^{n / 3}, b=q^{n / 3}$, and $c=r^{n / 3}$, so $a b c=(p q r)^{n / 3}=1$ and
$$
\frac{1}{p^{n}+q^{n}+1}+\frac{1}{q^{n}+r^{n}+1}+\frac{1}{r^{n}+p^{n}+1}=\frac{1}{a^{3}+b^{3}+1}+\frac{1}{b^{3}+c^{3}+1}+\frac{1}{c^{3}+a^{3}+1} .
$$
Now
$$
\frac{1}{a^{3}+b^{3}+1}=\frac{1}{(a+b)\left(a^{2}-a b+b^{2}\right)+1}=\frac{1}{(a+b)\left((a-b)^{2}+a b\right)+1} \leq \frac{1}{(a+b) a b+1} .
$$
Since $a b=c^{-1}$,
$$
\frac{1}{a^{3}+b^{3}+1} \leq \frac{1}{(a+b) a b+1}=\frac{c}{a+b+c}
$$
Similarly we obtain
$$
\frac{1}{b^{3}+c^{3}+1} \leq \frac{a}{a+b+c} \quad \text { and } \quad \frac{1}{c^{3}+a^{3}+1} \leq \frac{b}{a+b+c}
$$
Hence
$$
\frac{1}{a^{3}+b^{3}+1}+\frac{1}{b^{3}+c^{3}+1}+\frac{1}{c^{3}+a^{3}+1} \leq \frac{c}{a+b+c}+\frac{a}{a+b+c}+\frac{b}{a+b+c}=1,
$$
which was to be shown.
|
{
"exam": "BalticWay",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2004"
}
|
Let $x_{1}, x_{2}, \ldots, x_{n}$ be real numbers with arithmetic mean $X$. Prove that there is a positive integer $K$ such that the arithmetic mean of each of the lists $\left\{x_{1}, x_{2}, \ldots, x_{K}\right\},\left\{x_{2}, x_{3}, \ldots, x_{K}\right\}$, $\ldots,\left\{x_{K-1}, x_{K}\right\},\left\{x_{K}\right\}$ is not greater than $X$.
|
Suppose the conclusion is false. This means that for every $K \in\{1,2, \ldots, n\}$, there exists a $k \leq K$ such that the arithmetic mean of $x_{k}, x_{k+1}, \ldots, x_{K}$ exceeds $X$. We now define a decreasing sequence $b_{1} \geq a_{1}>a_{1}-1=b_{2} \geq a_{2}>\cdots$ as follows: Put $b_{1}=n$, and for each $i$, let $a_{i}$ be the largest largest $k \leq b_{i}$ such that the arithmetic mean of $x_{a_{i}}, \ldots, x_{b_{i}}$ exceeds $X$; then put $b_{i+1}=a_{i}-1$ and repeat. Clearly for some $m, a_{m}=1$. Now, by construction, each of the sets $\left\{x_{a_{m}}, \ldots, x_{b_{m}}\right\},\left\{x_{a_{m-1}}, \ldots, x_{b_{m-1}}\right\}, \ldots,\left\{x_{a_{1}}, \ldots, x_{b_{1}}\right\}$ has arithmetic mean strictly greater than $X$, but then the union $\left\{x_{1}, x_{2}, \ldots, x_{n}\right\}$ of these sets has arithmetic mean strictly greater than $X$; a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $x_{1}, x_{2}, \ldots, x_{n}$ be real numbers with arithmetic mean $X$. Prove that there is a positive integer $K$ such that the arithmetic mean of each of the lists $\left\{x_{1}, x_{2}, \ldots, x_{K}\right\},\left\{x_{2}, x_{3}, \ldots, x_{K}\right\}$, $\ldots,\left\{x_{K-1}, x_{K}\right\},\left\{x_{K}\right\}$ is not greater than $X$.
|
Suppose the conclusion is false. This means that for every $K \in\{1,2, \ldots, n\}$, there exists a $k \leq K$ such that the arithmetic mean of $x_{k}, x_{k+1}, \ldots, x_{K}$ exceeds $X$. We now define a decreasing sequence $b_{1} \geq a_{1}>a_{1}-1=b_{2} \geq a_{2}>\cdots$ as follows: Put $b_{1}=n$, and for each $i$, let $a_{i}$ be the largest largest $k \leq b_{i}$ such that the arithmetic mean of $x_{a_{i}}, \ldots, x_{b_{i}}$ exceeds $X$; then put $b_{i+1}=a_{i}-1$ and repeat. Clearly for some $m, a_{m}=1$. Now, by construction, each of the sets $\left\{x_{a_{m}}, \ldots, x_{b_{m}}\right\},\left\{x_{a_{m-1}}, \ldots, x_{b_{m-1}}\right\}, \ldots,\left\{x_{a_{1}}, \ldots, x_{b_{1}}\right\}$ has arithmetic mean strictly greater than $X$, but then the union $\left\{x_{1}, x_{2}, \ldots, x_{n}\right\}$ of these sets has arithmetic mean strictly greater than $X$; a contradiction.
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2004"
}
|
Determine the range of the function $f$ defined for integers $k$ by
$$
f(k)=(k)_{3}+(2 k)_{5}+(3 k)_{7}-6 k
$$
where $(k)_{2 n+1}$ denotes the multiple of $2 n+1$ closest to $k$.
|
For odd $n$ we have
$$
(k)_{n}=k+\frac{n-1}{2}-\left[k+\frac{n-1}{2}\right]_{n^{\prime}}
$$
where $[m]_{n}$ denotes the principal remainder of $m$ modulo $n$. Hence we get
$$
f(k)=6-[k+1]_{3}-[2 k+2]_{5}-[3 k+3]_{7}
$$
The condition that the principal remainders take the values $a, b$ and $c$, respectively, may be written
$$
\begin{aligned}
k+1 \equiv a & (\bmod 3) \\
2 k+2 \equiv b & (\bmod 5) \\
3 k+3 & \equiv c \quad(\bmod 7)
\end{aligned}
$$
or
$$
\begin{aligned}
& k \equiv a-1 \quad(\bmod 3) \\
& k \equiv-2 b-1 \quad(\bmod 5) \\
& k \equiv-2 c-1 \quad(\bmod 7)
\end{aligned}
$$
By the Chinese Remainder Theorem, these congruences have a solution for any set of $a, b, c$. Hence $f$ takes all the integer values between $6-2-4-6=-6$ and $6-0-0-0=$ 6. (In fact, this proof also shows that $f$ is periodic with period $3 \cdot 5 \cdot 7=105$.)
|
-6 \text{ to } 6
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Determine the range of the function $f$ defined for integers $k$ by
$$
f(k)=(k)_{3}+(2 k)_{5}+(3 k)_{7}-6 k
$$
where $(k)_{2 n+1}$ denotes the multiple of $2 n+1$ closest to $k$.
|
For odd $n$ we have
$$
(k)_{n}=k+\frac{n-1}{2}-\left[k+\frac{n-1}{2}\right]_{n^{\prime}}
$$
where $[m]_{n}$ denotes the principal remainder of $m$ modulo $n$. Hence we get
$$
f(k)=6-[k+1]_{3}-[2 k+2]_{5}-[3 k+3]_{7}
$$
The condition that the principal remainders take the values $a, b$ and $c$, respectively, may be written
$$
\begin{aligned}
k+1 \equiv a & (\bmod 3) \\
2 k+2 \equiv b & (\bmod 5) \\
3 k+3 & \equiv c \quad(\bmod 7)
\end{aligned}
$$
or
$$
\begin{aligned}
& k \equiv a-1 \quad(\bmod 3) \\
& k \equiv-2 b-1 \quad(\bmod 5) \\
& k \equiv-2 c-1 \quad(\bmod 7)
\end{aligned}
$$
By the Chinese Remainder Theorem, these congruences have a solution for any set of $a, b, c$. Hence $f$ takes all the integer values between $6-2-4-6=-6$ and $6-0-0-0=$ 6. (In fact, this proof also shows that $f$ is periodic with period $3 \cdot 5 \cdot 7=105$.)
|
{
"exam": "BalticWay",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2004"
}
|
A positive integer is written on each of the six faces of a cube. For each vertex of the cube we compute the product of the numbers on the three adjacent faces. The sum of these products is 1001. What is the sum of the six numbers on the faces?
|
Let the numbers on the faces be $a_{1}, a_{2}, b_{1}, b_{2}, c_{1}, c_{2}$, placed so that $a_{1}$ and $a_{2}$ are on opposite faces etc. Then the sum of the eight products is equal to
$$
\left(a_{1}+a_{2}\right)\left(b_{1}+b_{2}\right)\left(c_{1}+c_{2}\right)=1001=7 \cdot 11 \cdot 13 .
$$
Hence the sum of the numbers on the faces is $a_{1}+a_{2}+b_{1}+b_{2}+c_{1}+c_{2}=7+11+13=$ 31.
|
31
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A positive integer is written on each of the six faces of a cube. For each vertex of the cube we compute the product of the numbers on the three adjacent faces. The sum of these products is 1001. What is the sum of the six numbers on the faces?
|
Let the numbers on the faces be $a_{1}, a_{2}, b_{1}, b_{2}, c_{1}, c_{2}$, placed so that $a_{1}$ and $a_{2}$ are on opposite faces etc. Then the sum of the eight products is equal to
$$
\left(a_{1}+a_{2}\right)\left(b_{1}+b_{2}\right)\left(c_{1}+c_{2}\right)=1001=7 \cdot 11 \cdot 13 .
$$
Hence the sum of the numbers on the faces is $a_{1}+a_{2}+b_{1}+b_{2}+c_{1}+c_{2}=7+11+13=$ 31.
|
{
"exam": "BalticWay",
"problem_label": "6",
"problem_match": "\n6.",
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2004"
}
|
Find all sets $X$ consisting of at least two positive integers such that for every pair $m, n \in X$, where $n>m$, there exists $k \in X$ such that $n=m k^{2}$.
Answer: The sets $\left\{m, m^{3}\right\}$, where $m>1$.
|
Let $X$ be a set satisfying the condition of the problem and let $n>m$ be the two smallest elements in the set $X$. There has to exist a $k \in X$ so that $n=m k^{2}$, but as $m \leq k \leq n$, either $k=n$ or $k=m$. The first case gives $m=n=1$, a contradiction; the second case implies $n=m^{3}$ with $m>1$.
Suppose there exists a third smallest element $q \in X$. Then there also exists $k_{0} \in X$, such that $q=m k_{0}^{2}$. We have $q>k_{0} \geq m$, but $k_{0}=m$ would imply $q=n$, thus $k_{0}=n=m^{3}$ and $q=m^{7}$. Now for $q$ and $n$ there has to exist $k_{1} \in X$ such that $q=n k_{1}^{2}$, which gives $k_{1}=m^{2}$. Since $m^{2} \notin X$, we have a contradiction.
Thus we see that the only possible sets are those of the form $\left\{m, m^{3}\right\}$ with $m>1$, and these are easily seen to satisfy the conditions of the problem.
|
\left\{m, m^{3}\right\}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all sets $X$ consisting of at least two positive integers such that for every pair $m, n \in X$, where $n>m$, there exists $k \in X$ such that $n=m k^{2}$.
Answer: The sets $\left\{m, m^{3}\right\}$, where $m>1$.
|
Let $X$ be a set satisfying the condition of the problem and let $n>m$ be the two smallest elements in the set $X$. There has to exist a $k \in X$ so that $n=m k^{2}$, but as $m \leq k \leq n$, either $k=n$ or $k=m$. The first case gives $m=n=1$, a contradiction; the second case implies $n=m^{3}$ with $m>1$.
Suppose there exists a third smallest element $q \in X$. Then there also exists $k_{0} \in X$, such that $q=m k_{0}^{2}$. We have $q>k_{0} \geq m$, but $k_{0}=m$ would imply $q=n$, thus $k_{0}=n=m^{3}$ and $q=m^{7}$. Now for $q$ and $n$ there has to exist $k_{1} \in X$ such that $q=n k_{1}^{2}$, which gives $k_{1}=m^{2}$. Since $m^{2} \notin X$, we have a contradiction.
Thus we see that the only possible sets are those of the form $\left\{m, m^{3}\right\}$ with $m>1$, and these are easily seen to satisfy the conditions of the problem.
|
{
"exam": "BalticWay",
"problem_label": "7",
"problem_match": "\n7.",
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2004"
}
|
Let $f$ be a non-constant polynomial with integer coefficients. Prove that there is an integer $n$ such that $f(n)$ has at least 2004 distinct prime factors.
|
Suppose the contrary. Choose an integer $n_{0}$ so that $f\left(n_{0}\right)$ has the highest number of prime factors. By translating the polynomial we may assume $n_{0}=0$. Setting $k=f(0)$, we have $f\left(w k^{2}\right) \equiv k\left(\bmod k^{2}\right)$, or $f\left(w k^{2}\right)=a k^{2}+k=(a k+1) k$. Since $\operatorname{gcd}(a k+1, k)=1$ and $k$ alone achieves the highest number of prime factors of $f$, we must have $a k+1= \pm 1$. This cannot happen for every $w$ since $f$ is non-constant, so we have a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $f$ be a non-constant polynomial with integer coefficients. Prove that there is an integer $n$ such that $f(n)$ has at least 2004 distinct prime factors.
|
Suppose the contrary. Choose an integer $n_{0}$ so that $f\left(n_{0}\right)$ has the highest number of prime factors. By translating the polynomial we may assume $n_{0}=0$. Setting $k=f(0)$, we have $f\left(w k^{2}\right) \equiv k\left(\bmod k^{2}\right)$, or $f\left(w k^{2}\right)=a k^{2}+k=(a k+1) k$. Since $\operatorname{gcd}(a k+1, k)=1$ and $k$ alone achieves the highest number of prime factors of $f$, we must have $a k+1= \pm 1$. This cannot happen for every $w$ since $f$ is non-constant, so we have a contradiction.
|
{
"exam": "BalticWay",
"problem_label": "8",
"problem_match": "\n8.",
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2004"
}
|
$A$ set $S$ of $n-1$ natural numbers is given ( $n \geq 3$ ). There exists at least two elements in this set whose difference is not divisible by $n$. Prove that it is possible to choose a non-empty subset of $S$ so that the sum of its elements is divisible by $n$.
|
Suppose to the contrary that there exists a set $X=\left\{a_{1}, a_{2}, \ldots, a_{n-1}\right\}$ violating the statement of the problem, and let $a_{n-2} \not \equiv a_{n-1}(\bmod n)$. Denote $S_{i}=a_{1}+a_{2}+$ $\cdots+a_{i}, i=1, \ldots, n-1$. The conditions of the problem imply that all the numbers $S_{i}$ must give different remainders when divided by $n$. Indeed, if for some $j<k$ we had $S_{j} \equiv S_{k}(\bmod n)$, then $a_{j+1}+a_{j+2}+\cdots+a_{k}=S_{k}-S_{j} \equiv 0(\bmod n)$. Consider now the sum $S^{\prime}=S_{n-3}+a_{n-1}$. We see that $S^{\prime}$ can not be congruent to any of the sums $S_{i}$ (for $i \neq n-2$ the above argument works and for $i=n-2$ we use the assumption $a_{n-2} \not \equiv a_{n-1}$ $(\bmod n))$. Thus we have $n$ sums that give pairwise different remainders when divided by $n$, consequently one of them has to give the remainder 0 , a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
$A$ set $S$ of $n-1$ natural numbers is given ( $n \geq 3$ ). There exists at least two elements in this set whose difference is not divisible by $n$. Prove that it is possible to choose a non-empty subset of $S$ so that the sum of its elements is divisible by $n$.
|
Suppose to the contrary that there exists a set $X=\left\{a_{1}, a_{2}, \ldots, a_{n-1}\right\}$ violating the statement of the problem, and let $a_{n-2} \not \equiv a_{n-1}(\bmod n)$. Denote $S_{i}=a_{1}+a_{2}+$ $\cdots+a_{i}, i=1, \ldots, n-1$. The conditions of the problem imply that all the numbers $S_{i}$ must give different remainders when divided by $n$. Indeed, if for some $j<k$ we had $S_{j} \equiv S_{k}(\bmod n)$, then $a_{j+1}+a_{j+2}+\cdots+a_{k}=S_{k}-S_{j} \equiv 0(\bmod n)$. Consider now the sum $S^{\prime}=S_{n-3}+a_{n-1}$. We see that $S^{\prime}$ can not be congruent to any of the sums $S_{i}$ (for $i \neq n-2$ the above argument works and for $i=n-2$ we use the assumption $a_{n-2} \not \equiv a_{n-1}$ $(\bmod n))$. Thus we have $n$ sums that give pairwise different remainders when divided by $n$, consequently one of them has to give the remainder 0 , a contradiction.
|
{
"exam": "BalticWay",
"problem_label": "9",
"problem_match": "\n9.",
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2004"
}
|
Is there an infinite sequence of prime numbers $p_{1}, p_{2}, \ldots$ such that $\left|p_{n+1}-2 p_{n}\right|=1$ for each $n \in \mathbb{N}$ ?
Answer: No, there is no such sequence.
|
Suppose the contrary. Clearly $p_{3}>3$. There are two possibilities: If $p_{3} \equiv 1$ $(\bmod 3)$ then necessarily $p_{4}=2 p_{3}-1\left(\right.$ otherwise $\left.p_{4} \equiv 0(\bmod 3)\right)$, so $p_{4} \equiv 1(\bmod 3)$. Analogously $p_{5}=2 p_{4}-1, p_{6}=2 p_{5}-1$ etc. By an easy induction we have
$$
p_{n+1}-1=2^{n-2}\left(p_{3}-1\right), \quad n=3,4,5, \ldots
$$
If we set $n=p_{3}+1$ we have $p_{p_{3}+2}-1=2^{p_{3}-1}\left(p_{3}-1\right)$, from which
$$
p_{p_{3}+2} \equiv 1+1 \cdot\left(p_{3}-1\right)=p_{3} \equiv 0 \quad\left(\bmod p_{3}\right)
$$
a contradiction. The case $p_{3} \equiv 2(\bmod 3)$ is treated analogously.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Is there an infinite sequence of prime numbers $p_{1}, p_{2}, \ldots$ such that $\left|p_{n+1}-2 p_{n}\right|=1$ for each $n \in \mathbb{N}$ ?
Answer: No, there is no such sequence.
|
Suppose the contrary. Clearly $p_{3}>3$. There are two possibilities: If $p_{3} \equiv 1$ $(\bmod 3)$ then necessarily $p_{4}=2 p_{3}-1\left(\right.$ otherwise $\left.p_{4} \equiv 0(\bmod 3)\right)$, so $p_{4} \equiv 1(\bmod 3)$. Analogously $p_{5}=2 p_{4}-1, p_{6}=2 p_{5}-1$ etc. By an easy induction we have
$$
p_{n+1}-1=2^{n-2}\left(p_{3}-1\right), \quad n=3,4,5, \ldots
$$
If we set $n=p_{3}+1$ we have $p_{p_{3}+2}-1=2^{p_{3}-1}\left(p_{3}-1\right)$, from which
$$
p_{p_{3}+2} \equiv 1+1 \cdot\left(p_{3}-1\right)=p_{3} \equiv 0 \quad\left(\bmod p_{3}\right)
$$
a contradiction. The case $p_{3} \equiv 2(\bmod 3)$ is treated analogously.
|
{
"exam": "BalticWay",
"problem_label": "10",
"problem_match": "\n10.",
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2004"
}
|
An $m \times n$ table is given, in each cell of which a number +1 or -1 is written. It is known that initially exactly one -1 is in the table, all the other numbers being +1 . During a move, it is allowed to choose any cell containing -1 , replace this -1 by 0 , and simultaneously multiply all the numbers in the neighboring cells by -1 (we say that two cells are neighboring if they have a common side). Find all $(m, n)$ for which using such moves one can obtain the table containing zeroes only, regardless of the cell in which the initial -1 stands.
Answer: Those $(m, n)$ for which at least one of $m, n$ is odd.
|
Let us erase a unit segment which is the common side of any two cells in which two zeroes appear. If the final table consists of zeroes only, all the unit segments (except those which belong to the boundary of the table) are erased. We must erase a total of
$$
m(n-1)+n(m-1)=2 m n-m-n
$$
such unit segments.
On the other hand, in order to obtain 0 in a cell with initial +1 one must first obtain -1 in this cell, that is, the sign of the number in this cell must change an odd number of times (namely, 1 or 3 ). Hence, any cell with -1 (except the initial one) has an odd number of neighboring zeroes. So, any time we replace -1 by 0 we erase an odd number of unit segments. That is, the total number of unit segments is congruent modulo 2 to the initial number of +1 's in the table. Therefore $2 m n-m-n \equiv m n-1$ $(\bmod 2)$, implying that $(m-1)(n-1) \equiv 0(\bmod 2)$, so at least one of $m, n$ is odd.
It remains to show that if, for example, $n$ is odd, we can obtain a zero table. First, if -1 is in the $i^{\prime}$ th row, we may easily make the $i^{\prime}$ th row contain only zeroes, while its one or two neighboring rows contain only -1 's. Next, in any row containing only -1 's, we first change the -1 in the odd-numbered columns (that is, the columns $1,3, \ldots, n$ ) to zeroes, resulting in a row consisting of alternating 0 and -1 (since the -1 's in the
even-numbered columns have been changed two times), and we then easily obtain an entire row of zeroes. The effect of this on the next neighboring row is to create a new row of -1 's, while the original row is clearly unchanged. In this way we finally obtain a zero table.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
An $m \times n$ table is given, in each cell of which a number +1 or -1 is written. It is known that initially exactly one -1 is in the table, all the other numbers being +1 . During a move, it is allowed to choose any cell containing -1 , replace this -1 by 0 , and simultaneously multiply all the numbers in the neighboring cells by -1 (we say that two cells are neighboring if they have a common side). Find all $(m, n)$ for which using such moves one can obtain the table containing zeroes only, regardless of the cell in which the initial -1 stands.
Answer: Those $(m, n)$ for which at least one of $m, n$ is odd.
|
Let us erase a unit segment which is the common side of any two cells in which two zeroes appear. If the final table consists of zeroes only, all the unit segments (except those which belong to the boundary of the table) are erased. We must erase a total of
$$
m(n-1)+n(m-1)=2 m n-m-n
$$
such unit segments.
On the other hand, in order to obtain 0 in a cell with initial +1 one must first obtain -1 in this cell, that is, the sign of the number in this cell must change an odd number of times (namely, 1 or 3 ). Hence, any cell with -1 (except the initial one) has an odd number of neighboring zeroes. So, any time we replace -1 by 0 we erase an odd number of unit segments. That is, the total number of unit segments is congruent modulo 2 to the initial number of +1 's in the table. Therefore $2 m n-m-n \equiv m n-1$ $(\bmod 2)$, implying that $(m-1)(n-1) \equiv 0(\bmod 2)$, so at least one of $m, n$ is odd.
It remains to show that if, for example, $n$ is odd, we can obtain a zero table. First, if -1 is in the $i^{\prime}$ th row, we may easily make the $i^{\prime}$ th row contain only zeroes, while its one or two neighboring rows contain only -1 's. Next, in any row containing only -1 's, we first change the -1 in the odd-numbered columns (that is, the columns $1,3, \ldots, n$ ) to zeroes, resulting in a row consisting of alternating 0 and -1 (since the -1 's in the
even-numbered columns have been changed two times), and we then easily obtain an entire row of zeroes. The effect of this on the next neighboring row is to create a new row of -1 's, while the original row is clearly unchanged. In this way we finally obtain a zero table.
|
{
"exam": "BalticWay",
"problem_label": "11",
"problem_match": "\n11.",
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2004"
}
|
There are $2 n$ different numbers in a row. By one move we can interchange any two numbers or interchange any three numbers cyclically (choose $a, b, c$ and place a instead of $b, b$ instead of $c$ and $c$ instead of $a$ ). What is the minimal number of moves that is always sufficient to arrange the numbers in increasing order?
|
If a number $y$ occupies the place where $x$ should be at the end, we draw an arrow $x \rightarrow y$. Clearly at the beginning all numbers are arranged in several cycles: Loops
$\bullet \bullet$, binary cycles $\bullet \rightleftarrows \bullet$ and "long" cycles $\bullet_{\nwarrow}^{\nearrow} \succeq \bullet$ (at least three numbers). Our aim is to obtain $2 n$ loops.
Clearly each binary cycle can be rearranged into two loops by one move. If there is a long cycle with a fragment $\cdots \rightarrow a \rightarrow b \rightarrow c \rightarrow \cdots$, interchange $a, b, c$ cyclically so that at least two loops, $a \oslash, b \oslash$, appear. By each of these moves, the number of loops increase by 2 , so at most $n$ moves are needed.
On the other hand, by checking all possible ways the two or three numbers can be distributed among disjoint cycles, it is easy to see that each of the allowed moves increases the number of disjoint cycles by at most two. Hence if the initial situation is one single loop, at least $n$ moves are needed.
|
n
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There are $2 n$ different numbers in a row. By one move we can interchange any two numbers or interchange any three numbers cyclically (choose $a, b, c$ and place a instead of $b, b$ instead of $c$ and $c$ instead of $a$ ). What is the minimal number of moves that is always sufficient to arrange the numbers in increasing order?
|
If a number $y$ occupies the place where $x$ should be at the end, we draw an arrow $x \rightarrow y$. Clearly at the beginning all numbers are arranged in several cycles: Loops
$\bullet \bullet$, binary cycles $\bullet \rightleftarrows \bullet$ and "long" cycles $\bullet_{\nwarrow}^{\nearrow} \succeq \bullet$ (at least three numbers). Our aim is to obtain $2 n$ loops.
Clearly each binary cycle can be rearranged into two loops by one move. If there is a long cycle with a fragment $\cdots \rightarrow a \rightarrow b \rightarrow c \rightarrow \cdots$, interchange $a, b, c$ cyclically so that at least two loops, $a \oslash, b \oslash$, appear. By each of these moves, the number of loops increase by 2 , so at most $n$ moves are needed.
On the other hand, by checking all possible ways the two or three numbers can be distributed among disjoint cycles, it is easy to see that each of the allowed moves increases the number of disjoint cycles by at most two. Hence if the initial situation is one single loop, at least $n$ moves are needed.
|
{
"exam": "BalticWay",
"problem_label": "12",
"problem_match": "\n12.",
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2004"
}
|
The 25 member states of the European Union set up a committee with the following rules: (1) the committee should meet daily; (2) at each meeting, at least one member state should be represented; (3) at any two different meetings, a different set of member states should be represented; and (4) at the $n$ 'th meeting, for every $k<n$, the set of states represented should include at least one state that was represented at the k'th meeting. For how many days can the committee have its meetings?
Answer: At most $2^{24}=16777216$ days.
|
If one member is always represented, rules 2 and 4 will be fulfilled. There are $2^{24}$ different subsets of the remaining 24 members, so there can be at least $2^{24}$ meetings. Rule 3 forbids complementary sets at two different meetings, so the maximal number of meetings cannot exceed $\frac{1}{2} \cdot 2^{25}=2^{24}$. So the maximal number of meetings for the committee is exactly $2^{24}=16777216$.
|
16777216
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
The 25 member states of the European Union set up a committee with the following rules: (1) the committee should meet daily; (2) at each meeting, at least one member state should be represented; (3) at any two different meetings, a different set of member states should be represented; and (4) at the $n$ 'th meeting, for every $k<n$, the set of states represented should include at least one state that was represented at the k'th meeting. For how many days can the committee have its meetings?
Answer: At most $2^{24}=16777216$ days.
|
If one member is always represented, rules 2 and 4 will be fulfilled. There are $2^{24}$ different subsets of the remaining 24 members, so there can be at least $2^{24}$ meetings. Rule 3 forbids complementary sets at two different meetings, so the maximal number of meetings cannot exceed $\frac{1}{2} \cdot 2^{25}=2^{24}$. So the maximal number of meetings for the committee is exactly $2^{24}=16777216$.
|
{
"exam": "BalticWay",
"problem_label": "13",
"problem_match": "\n13.",
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2004"
}
|
We say that a pile is a set of four or more nuts. Two persons play the following game. They start with one pile of $n \geq 4$ nuts. During a move a player takes one of the piles that they have and split it into two non-empty subsets (these sets are not necessarily piles, they can contain an arbitrary number of nuts). If the player cannot move, he loses. For which values of $n$ does the first player have a winning strategy?
Answer: The first player has a winning strategy when $n \equiv 0,1,2(\bmod 4)$; otherwise the second player has a winning strategy.
|
Let $n=4 k+r$, where $0 \leq r \leq 3$. We will prove the above answer by induction on $k$; clearly it holds for $k=1$. We are also going to need the following useful fact:
If at some point there are exactly two piles with $4 s+1$ and $4 t+1$ nuts, $s+t \leq k$, then the second player to move from that point wins.
This holds vacuously when $k=1$.
Now assume that we know the answer when the starting pile consists of at most $4 k-1$ nuts, and that the useful fact holds for $s+t \leq k$. We will prove the answer is
correct for $4 k, 4 k+1,4 k+2$ and $4 k+3$, and that the useful fact holds for $s+t \leq k+1$. For the sake of bookkeeping, we will refer to the first player as A and the second player as B.
If the pile consists of $4 k, 4 k+1$ or $4 k+2$ nuts, A simply makes one pile consisting of $4 k-1$ nuts, and another consisting of 1,2 or 3 nuts, respectively. This makes $A$ the second player in a game starting with $4 k-1 \equiv 3(\bmod 4)$ nuts, so A wins.
Now assume the pile contains $4 k+3$ nuts. A can split the pile in two ways: Either as $(4 p+1,4 q+2)$ or $(4 p, 4 q+3)$. In the former case, if either $p$ or $q$ is $0, \mathrm{~B}$ wins by the above paragraph. Otherwise, $\mathrm{B}$ removes one nut from the $4 q+2$ pile, making B the second player in a game where we may apply the useful fact (since $p+q=k$ ), so B wins. If A splits the original pile as $(4 p, 4 q+3)$, B removes one nut from the $4 p$ pile, so the situation is two piles with $4(p-1)+3$ and $4 q+3$ nuts. Then $\mathrm{B}$ can use the winning strategy for the second player just described on each pile seperately, ultimately making B the winner.
It remains to prove the useful fact when $s+t=k+1$. Due to symmetry, there are two possibilities for the first move: Assume the first player moves $(4 s+1,4 t+1) \rightarrow$ $(4 s+1,4 p, 4 q+1)$. The second player then splits the middle pile into $(4 p-1,1)$, so the situation is $(4 s+1,4 q+1,4 p-1)$. Since the second player has a winning strategy both when the initial situtation is $(4 s+1,4 q+1)$ and when it is $4 p-1$, he wins (this also holds when $p=1$ ).
Now assume the first player makes the move $(4 s+1,4 t+1) \rightarrow(4 s+1,4 p+2,4 q+3)$. If $p=0$, the second player splits the third pile as $4 q+3=(4 q+1)+2$ and wins by the useful fact. If $p>0$, the second player splits the second pile as $4 p+2=(4 p+1)+1$, and wins because he wins in each of the situations $(4 s+1,4 p+1)$ and $4 q+3$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
We say that a pile is a set of four or more nuts. Two persons play the following game. They start with one pile of $n \geq 4$ nuts. During a move a player takes one of the piles that they have and split it into two non-empty subsets (these sets are not necessarily piles, they can contain an arbitrary number of nuts). If the player cannot move, he loses. For which values of $n$ does the first player have a winning strategy?
Answer: The first player has a winning strategy when $n \equiv 0,1,2(\bmod 4)$; otherwise the second player has a winning strategy.
|
Let $n=4 k+r$, where $0 \leq r \leq 3$. We will prove the above answer by induction on $k$; clearly it holds for $k=1$. We are also going to need the following useful fact:
If at some point there are exactly two piles with $4 s+1$ and $4 t+1$ nuts, $s+t \leq k$, then the second player to move from that point wins.
This holds vacuously when $k=1$.
Now assume that we know the answer when the starting pile consists of at most $4 k-1$ nuts, and that the useful fact holds for $s+t \leq k$. We will prove the answer is
correct for $4 k, 4 k+1,4 k+2$ and $4 k+3$, and that the useful fact holds for $s+t \leq k+1$. For the sake of bookkeeping, we will refer to the first player as A and the second player as B.
If the pile consists of $4 k, 4 k+1$ or $4 k+2$ nuts, A simply makes one pile consisting of $4 k-1$ nuts, and another consisting of 1,2 or 3 nuts, respectively. This makes $A$ the second player in a game starting with $4 k-1 \equiv 3(\bmod 4)$ nuts, so A wins.
Now assume the pile contains $4 k+3$ nuts. A can split the pile in two ways: Either as $(4 p+1,4 q+2)$ or $(4 p, 4 q+3)$. In the former case, if either $p$ or $q$ is $0, \mathrm{~B}$ wins by the above paragraph. Otherwise, $\mathrm{B}$ removes one nut from the $4 q+2$ pile, making B the second player in a game where we may apply the useful fact (since $p+q=k$ ), so B wins. If A splits the original pile as $(4 p, 4 q+3)$, B removes one nut from the $4 p$ pile, so the situation is two piles with $4(p-1)+3$ and $4 q+3$ nuts. Then $\mathrm{B}$ can use the winning strategy for the second player just described on each pile seperately, ultimately making B the winner.
It remains to prove the useful fact when $s+t=k+1$. Due to symmetry, there are two possibilities for the first move: Assume the first player moves $(4 s+1,4 t+1) \rightarrow$ $(4 s+1,4 p, 4 q+1)$. The second player then splits the middle pile into $(4 p-1,1)$, so the situation is $(4 s+1,4 q+1,4 p-1)$. Since the second player has a winning strategy both when the initial situtation is $(4 s+1,4 q+1)$ and when it is $4 p-1$, he wins (this also holds when $p=1$ ).
Now assume the first player makes the move $(4 s+1,4 t+1) \rightarrow(4 s+1,4 p+2,4 q+3)$. If $p=0$, the second player splits the third pile as $4 q+3=(4 q+1)+2$ and wins by the useful fact. If $p>0$, the second player splits the second pile as $4 p+2=(4 p+1)+1$, and wins because he wins in each of the situations $(4 s+1,4 p+1)$ and $4 q+3$.
|
{
"exam": "BalticWay",
"problem_label": "14",
"problem_match": "\n14.",
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2004"
}
|
A circle is divided into 13 segments, numbered consecutively from 1 to 13. Five fleas called $A, B, C, D$ and $E$ are sitting in the segments 1,2,3,4 and 5. A flea is allowed to jump to an empty segment five positions away in either direction around the circle. Only one flea jumps at the same time, and two fleas cannot be in the same segment. After some jumps, the fleas are back in the segments 1,2,3,4,5, but possibly in some other order than they started. Which orders are possible?
|
Write the numbers from 1 to 13 in the order $\mathbf{1}, 6,11, \mathbf{3}, 8,13,5,10,2,7,12,4$, 9. Then each time a flea jumps it moves between two adjacent numbers or between the first and the last number in this row. Since a flea can never move past another flea, the possible permutations are
| 3 | 5 | 2 | 4 | | 1 | 2 | 3 | 4 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| C | $\mathrm{E}$ | B | $\mathrm{D}$ | | A | B | C | D |
| A | C | $\mathrm{E}$ | B | | $\mathrm{D}$ | $\mathrm{E}$ | A | B |
| D | A | C | E | or equivalently | B | C | $\mathrm{D}$ | E |
| B | $\mathrm{D}$ | A | C | | $\mathrm{E}$ | A | B | C |
| C E | B | $\mathrm{D}$ | A | | C | $\mathrm{D}$ | $\mathrm{E}$ | A |
that is, exactly the cyclic permutations of the original order.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A circle is divided into 13 segments, numbered consecutively from 1 to 13. Five fleas called $A, B, C, D$ and $E$ are sitting in the segments 1,2,3,4 and 5. A flea is allowed to jump to an empty segment five positions away in either direction around the circle. Only one flea jumps at the same time, and two fleas cannot be in the same segment. After some jumps, the fleas are back in the segments 1,2,3,4,5, but possibly in some other order than they started. Which orders are possible?
|
Write the numbers from 1 to 13 in the order $\mathbf{1}, 6,11, \mathbf{3}, 8,13,5,10,2,7,12,4$, 9. Then each time a flea jumps it moves between two adjacent numbers or between the first and the last number in this row. Since a flea can never move past another flea, the possible permutations are
| 3 | 5 | 2 | 4 | | 1 | 2 | 3 | 4 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| C | $\mathrm{E}$ | B | $\mathrm{D}$ | | A | B | C | D |
| A | C | $\mathrm{E}$ | B | | $\mathrm{D}$ | $\mathrm{E}$ | A | B |
| D | A | C | E | or equivalently | B | C | $\mathrm{D}$ | E |
| B | $\mathrm{D}$ | A | C | | $\mathrm{E}$ | A | B | C |
| C E | B | $\mathrm{D}$ | A | | C | $\mathrm{D}$ | $\mathrm{E}$ | A |
that is, exactly the cyclic permutations of the original order.
|
{
"exam": "BalticWay",
"problem_label": "15",
"problem_match": "\n15.",
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2004"
}
|
Through a point $P$ exterior to a given circle pass a secant and a tangent to the circle. The secant intersects the circle at $A$ and $B$, and the tangent touches the circle at $C$ on the same side of the diameter thorugh $P$ as $A$ and $B$. The projection of $C$ on the diameter is $Q$. Prove that $Q C$ bisects $\angle A Q B$.
|
Denoting the centre of the circle by $O$, we have $O Q \cdot O P=O A^{2}=O B^{2}$. Hence $\triangle O A Q \sim \triangle O P A$ and $\triangle O B Q \sim \triangle O P B$. Since $\triangle A O B$ is isosceles, we have
$\angle O A P+\angle O B P=180^{\circ}$, and therefore
$$
\begin{aligned}
\angle A Q P+\angle B Q P & =\angle A O P+\angle O A Q+\angle B O P+\angle O B Q \\
& =\angle A O P+\angle O P A+\angle B O P+\angle O P B \\
& =180^{\circ}-\angle O A P+180^{\circ}-\angle O B P \\
& =180^{\circ} .
\end{aligned}
$$
Thus $Q C$, being perpendicular to $Q P$, bisects $\angle A Q B$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Through a point $P$ exterior to a given circle pass a secant and a tangent to the circle. The secant intersects the circle at $A$ and $B$, and the tangent touches the circle at $C$ on the same side of the diameter thorugh $P$ as $A$ and $B$. The projection of $C$ on the diameter is $Q$. Prove that $Q C$ bisects $\angle A Q B$.
|
Denoting the centre of the circle by $O$, we have $O Q \cdot O P=O A^{2}=O B^{2}$. Hence $\triangle O A Q \sim \triangle O P A$ and $\triangle O B Q \sim \triangle O P B$. Since $\triangle A O B$ is isosceles, we have
$\angle O A P+\angle O B P=180^{\circ}$, and therefore
$$
\begin{aligned}
\angle A Q P+\angle B Q P & =\angle A O P+\angle O A Q+\angle B O P+\angle O B Q \\
& =\angle A O P+\angle O P A+\angle B O P+\angle O P B \\
& =180^{\circ}-\angle O A P+180^{\circ}-\angle O B P \\
& =180^{\circ} .
\end{aligned}
$$
Thus $Q C$, being perpendicular to $Q P$, bisects $\angle A Q B$.
|
{
"exam": "BalticWay",
"problem_label": "16",
"problem_match": "\n16.",
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2004"
}
|
Consider a rectangle with side lengths 3 and 4 , and pick an arbitrary inner point on each side. Let $x, y, z$ and $u$ denote the side lengths of the quadrilateral spanned by these points. Prove that $25 \leq x^{2}+y^{2}+z^{2}+u^{2} \leq 50$.
|
Let $a, b, c$ and $d$ be the distances of the chosen points from the midpoints of the sides of the rectangle (with $a$ and $c$ on the sides of length 3). Then
$$
\begin{aligned}
x^{2}+y^{2}+z^{2}+u^{2}= & \left(\frac{3}{2}+a\right)^{2}+\left(\frac{3}{2}-a\right)^{2}+\left(\frac{3}{2}+c\right)^{2}+\left(\frac{3}{2}-c\right)^{2} \\
& +(2+b)^{2}+(2-b)^{2}+(2+d)^{2}+(2-d)^{2} \\
= & 4 \cdot\left(\frac{3}{2}\right)^{2}+4 \cdot 2^{2}+2\left(a^{2}+b^{2}+c^{2}+d^{2}\right) \\
= & 25+2\left(a^{2}+b^{2}+c^{2}+d^{2}\right) .
\end{aligned}
$$
Since $0 \leq a^{2}, c^{2} \leq(3 / 2)^{2}, 0 \leq b^{2}, d^{2} \leq 2^{2}$, the desired inequalities follow.
|
25 \leq x^{2}+y^{2}+z^{2}+u^{2} \leq 50
|
Yes
|
Yes
|
proof
|
Geometry
|
Consider a rectangle with side lengths 3 and 4 , and pick an arbitrary inner point on each side. Let $x, y, z$ and $u$ denote the side lengths of the quadrilateral spanned by these points. Prove that $25 \leq x^{2}+y^{2}+z^{2}+u^{2} \leq 50$.
|
Let $a, b, c$ and $d$ be the distances of the chosen points from the midpoints of the sides of the rectangle (with $a$ and $c$ on the sides of length 3). Then
$$
\begin{aligned}
x^{2}+y^{2}+z^{2}+u^{2}= & \left(\frac{3}{2}+a\right)^{2}+\left(\frac{3}{2}-a\right)^{2}+\left(\frac{3}{2}+c\right)^{2}+\left(\frac{3}{2}-c\right)^{2} \\
& +(2+b)^{2}+(2-b)^{2}+(2+d)^{2}+(2-d)^{2} \\
= & 4 \cdot\left(\frac{3}{2}\right)^{2}+4 \cdot 2^{2}+2\left(a^{2}+b^{2}+c^{2}+d^{2}\right) \\
= & 25+2\left(a^{2}+b^{2}+c^{2}+d^{2}\right) .
\end{aligned}
$$
Since $0 \leq a^{2}, c^{2} \leq(3 / 2)^{2}, 0 \leq b^{2}, d^{2} \leq 2^{2}$, the desired inequalities follow.
|
{
"exam": "BalticWay",
"problem_label": "17",
"problem_match": "\n17.",
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2004"
}
|
A ray emanating from the vertex $A$ of the triangle $A B C$ intersects the side $B C$ at $X$ and the circumcircle of $A B C$ at $Y$. Prove that $\frac{1}{A X}+\frac{1}{X Y} \geq \frac{4}{B C}$.
|
From the GM-HM inequality we have
$$
\frac{1}{A X}+\frac{1}{X Y} \geq \frac{2}{\sqrt{A X \cdot X Y}}
$$
As $B C$ and $A Y$ are chords intersecting at $X$ we have $A X \cdot X Y=B X \cdot X C$. Therefore (1) transforms into
$$
\frac{1}{A X}+\frac{1}{X Y} \geq \frac{2}{\sqrt{B X \cdot X C}}
$$
We also have
$$
\sqrt{B X \cdot X C} \leq \frac{B X+X C}{2}=\frac{B C}{2}
$$
so from (2) the result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
A ray emanating from the vertex $A$ of the triangle $A B C$ intersects the side $B C$ at $X$ and the circumcircle of $A B C$ at $Y$. Prove that $\frac{1}{A X}+\frac{1}{X Y} \geq \frac{4}{B C}$.
|
From the GM-HM inequality we have
$$
\frac{1}{A X}+\frac{1}{X Y} \geq \frac{2}{\sqrt{A X \cdot X Y}}
$$
As $B C$ and $A Y$ are chords intersecting at $X$ we have $A X \cdot X Y=B X \cdot X C$. Therefore (1) transforms into
$$
\frac{1}{A X}+\frac{1}{X Y} \geq \frac{2}{\sqrt{B X \cdot X C}}
$$
We also have
$$
\sqrt{B X \cdot X C} \leq \frac{B X+X C}{2}=\frac{B C}{2}
$$
so from (2) the result follows.
|
{
"exam": "BalticWay",
"problem_label": "18",
"problem_match": "\n18.",
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2004"
}
|
$D$ is the midpoint of the side $B C$ of the given triangle $A B C . M$ is a point on the side $B C$ such that $\angle B A M=\angle D A C$. $L$ is the second intersection point of the circumcircle of the triangle $C A M$ with the side $A B . K$ is the second intersection point of the circumcircle of the triangle $B A M$ with the side $A C$. Prove that $K L \| B C$.
|
It is sufficient to prove that $C K: L B=A C: A B$.
The triangles $A B C$ and $M K C$ are similar beacuse they have common angle $C$ and $\angle C M K=180^{\circ}-\angle B M K=\angle K A B$ (the latter equality is due to the observation that $\angle B M K$ and $\angle K A B$ are the opposite angles in the insecribed quadrilateral $A K M B$ ).
By analogous reasoning the triangles $A B C$ and $M B L$ are similar. Therefore the triangles $M K C$ and $M B L$ are also similar and we have
$$
\frac{C K}{L B}=\frac{K M}{B M}=\frac{\frac{A M \sin K A M}{\sin A K M}}{\frac{A M \sin M A B}{\sin M B A}}=\frac{\sin K A M}{\sin M A B}=\frac{\sin D A B}{\sin D A C}=\frac{\frac{B D \sin B D A}{A B}}{\frac{C D \sin C D A}{A C}}=\frac{A C}{A B} .
$$
The second equality is due to the sinus theorem for triangles $A K M$ and $A B M$; the third is due to the equality $\angle A K M=180^{\circ}-\angle M B A$ in the inscribed quadrilateral $A K M B$; the fourth is due to the definition of the point $M$; and the fifth is due to the sinus theorem for triangles $A C D$ and $A B D$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
$D$ is the midpoint of the side $B C$ of the given triangle $A B C . M$ is a point on the side $B C$ such that $\angle B A M=\angle D A C$. $L$ is the second intersection point of the circumcircle of the triangle $C A M$ with the side $A B . K$ is the second intersection point of the circumcircle of the triangle $B A M$ with the side $A C$. Prove that $K L \| B C$.
|
It is sufficient to prove that $C K: L B=A C: A B$.
The triangles $A B C$ and $M K C$ are similar beacuse they have common angle $C$ and $\angle C M K=180^{\circ}-\angle B M K=\angle K A B$ (the latter equality is due to the observation that $\angle B M K$ and $\angle K A B$ are the opposite angles in the insecribed quadrilateral $A K M B$ ).
By analogous reasoning the triangles $A B C$ and $M B L$ are similar. Therefore the triangles $M K C$ and $M B L$ are also similar and we have
$$
\frac{C K}{L B}=\frac{K M}{B M}=\frac{\frac{A M \sin K A M}{\sin A K M}}{\frac{A M \sin M A B}{\sin M B A}}=\frac{\sin K A M}{\sin M A B}=\frac{\sin D A B}{\sin D A C}=\frac{\frac{B D \sin B D A}{A B}}{\frac{C D \sin C D A}{A C}}=\frac{A C}{A B} .
$$
The second equality is due to the sinus theorem for triangles $A K M$ and $A B M$; the third is due to the equality $\angle A K M=180^{\circ}-\angle M B A$ in the inscribed quadrilateral $A K M B$; the fourth is due to the definition of the point $M$; and the fifth is due to the sinus theorem for triangles $A C D$ and $A B D$.
|
{
"exam": "BalticWay",
"problem_label": "19",
"problem_match": "\n19.",
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2004"
}
|
Three circular arcs $w_{1}, w_{2}, w_{3}$ with common endpoints $A$ and $B$ are on the same side of the line $A B ; w_{2}$ lies between $w_{1}$ and $w_{3}$. Two rays emanating from $B$ intersect these arcs at $M_{1}, M_{2}, M_{3}$ and $K_{1}, K_{2}, K_{3}$, respectively. Prove that $\frac{M_{1} M_{2}}{M_{2} M_{3}}=\frac{K_{1} K_{2}}{K_{2} K_{3}}$.
|
From inscribed angles we have $\angle A K_{1} B=\angle A M_{1} B$ and $\angle A K_{2} B=\angle A M_{2} B$. From this it follows that $\triangle A K_{1} K_{2} \sim \triangle A M_{1} M_{2}$, so
$$
\frac{K_{1} K_{2}}{M_{1} M_{2}}=\frac{A K_{2}}{A M_{2}}
$$
Similarly $\triangle A K_{2} K_{3} \sim \triangle A M_{2} M_{3}$, so
$$
\frac{K_{2} K_{3}}{M_{2} M_{3}}=\frac{A K_{2}}{A M_{2}}
$$
From these equations we get $\frac{K_{1} K_{2}}{M_{1} M_{2}}=\frac{K_{2} K_{3}}{M_{2} M_{3}}$, from which the desired property follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Three circular arcs $w_{1}, w_{2}, w_{3}$ with common endpoints $A$ and $B$ are on the same side of the line $A B ; w_{2}$ lies between $w_{1}$ and $w_{3}$. Two rays emanating from $B$ intersect these arcs at $M_{1}, M_{2}, M_{3}$ and $K_{1}, K_{2}, K_{3}$, respectively. Prove that $\frac{M_{1} M_{2}}{M_{2} M_{3}}=\frac{K_{1} K_{2}}{K_{2} K_{3}}$.
|
From inscribed angles we have $\angle A K_{1} B=\angle A M_{1} B$ and $\angle A K_{2} B=\angle A M_{2} B$. From this it follows that $\triangle A K_{1} K_{2} \sim \triangle A M_{1} M_{2}$, so
$$
\frac{K_{1} K_{2}}{M_{1} M_{2}}=\frac{A K_{2}}{A M_{2}}
$$
Similarly $\triangle A K_{2} K_{3} \sim \triangle A M_{2} M_{3}$, so
$$
\frac{K_{2} K_{3}}{M_{2} M_{3}}=\frac{A K_{2}}{A M_{2}}
$$
From these equations we get $\frac{K_{1} K_{2}}{M_{1} M_{2}}=\frac{K_{2} K_{3}}{M_{2} M_{3}}$, from which the desired property follows.

|
{
"exam": "BalticWay",
"problem_label": "20",
"problem_match": "\n20.",
"resource_path": "BalticWay/segmented/en-bw04sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2004"
}
|
Let $a_{0}$ be a positive integer. Define the sequence $a_{n}, n \geq 0$, as follows: If
$$
a_{n}=\sum_{i=0}^{j} c_{i} 10^{i}
$$
where $c_{i}$ are integers with $0 \leq c_{i} \leq 9$, then
$$
a_{n+1}=c_{0}^{2005}+c_{1}^{2005}+\cdots+c_{j}^{2005} .
$$
Is it possible to choose $a_{0}$ so that all the terms in the sequence are distinct?
Answer: No, the sequence must contain two equal terms.
|
It is clear that there exists a smallest positive integer $k$ such that
$$
10^{k}>(k+1) \cdot 9^{2005} .
$$
We will show that there exists a positive integer $N$ such that $a_{n}$ consists of less than $k+1$ decimal digits for all $n \geq N$. Let $a_{i}$ be a positive integer which consists of exactly $j+1$ digits, that is,
$$
10^{j} \leq a_{i}<10^{j+1} .
$$
We need to prove two statements:
- $a_{i+1}$ has less than $k+1$ digits if $j<k$; and
- $a_{i}>a_{i+1}$ if $j \geq k$.
To prove the first statement, notice that
$$
a_{i+1} \leq(j+1) \cdot 9^{2005}<(k+1) \cdot 9^{2005}<10^{k}
$$
and hence $a_{i+1}$ consists of less than $k+1$ digits. To prove the second statement, notice that $a_{i}$ consists of $j+1$ digits, none of which exceeds 9 . Hence $a_{i+1} \leq(j+1) \cdot 9^{2005}$ and because $j \geq k$, we get $a_{i} \geq 10^{j}>(j+1) \cdot 9^{2005} \geq a_{i+1}$, which proves the second statement. It is now easy to derive the result from this statement. Assume that $a_{0}$ consists of $k+1$ or more digits (otherwise we are done, because then it follows inductively that all terms of the sequence consist of less than $k+1$ digits, by the first statement). Then the sequence starts with a strictly decreasing segment $a_{0}>a_{1}>a_{2}>\cdots$ by the second statement, so for some index $N$ the number $a_{N}$ has less than $k+1$ digits. Then, by the first statement, each number $a_{n}$ with $n \geq N$ consists of at most $k$ digits. By the Pigeonhole Principle, there are two different indices $n, m \geq N$ such that $a_{n}=a_{m}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a_{0}$ be a positive integer. Define the sequence $a_{n}, n \geq 0$, as follows: If
$$
a_{n}=\sum_{i=0}^{j} c_{i} 10^{i}
$$
where $c_{i}$ are integers with $0 \leq c_{i} \leq 9$, then
$$
a_{n+1}=c_{0}^{2005}+c_{1}^{2005}+\cdots+c_{j}^{2005} .
$$
Is it possible to choose $a_{0}$ so that all the terms in the sequence are distinct?
Answer: No, the sequence must contain two equal terms.
|
It is clear that there exists a smallest positive integer $k$ such that
$$
10^{k}>(k+1) \cdot 9^{2005} .
$$
We will show that there exists a positive integer $N$ such that $a_{n}$ consists of less than $k+1$ decimal digits for all $n \geq N$. Let $a_{i}$ be a positive integer which consists of exactly $j+1$ digits, that is,
$$
10^{j} \leq a_{i}<10^{j+1} .
$$
We need to prove two statements:
- $a_{i+1}$ has less than $k+1$ digits if $j<k$; and
- $a_{i}>a_{i+1}$ if $j \geq k$.
To prove the first statement, notice that
$$
a_{i+1} \leq(j+1) \cdot 9^{2005}<(k+1) \cdot 9^{2005}<10^{k}
$$
and hence $a_{i+1}$ consists of less than $k+1$ digits. To prove the second statement, notice that $a_{i}$ consists of $j+1$ digits, none of which exceeds 9 . Hence $a_{i+1} \leq(j+1) \cdot 9^{2005}$ and because $j \geq k$, we get $a_{i} \geq 10^{j}>(j+1) \cdot 9^{2005} \geq a_{i+1}$, which proves the second statement. It is now easy to derive the result from this statement. Assume that $a_{0}$ consists of $k+1$ or more digits (otherwise we are done, because then it follows inductively that all terms of the sequence consist of less than $k+1$ digits, by the first statement). Then the sequence starts with a strictly decreasing segment $a_{0}>a_{1}>a_{2}>\cdots$ by the second statement, so for some index $N$ the number $a_{N}$ has less than $k+1$ digits. Then, by the first statement, each number $a_{n}$ with $n \geq N$ consists of at most $k$ digits. By the Pigeonhole Principle, there are two different indices $n, m \geq N$ such that $a_{n}=a_{m}$.
|
{
"exam": "BalticWay",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2005"
}
|
Let $\alpha, \beta$ and $\gamma$ be three angles with $0 \leq \alpha, \beta, \gamma<90^{\circ}$ and $\sin \alpha+\sin \beta+\sin \gamma=1$. Show that
$$
\tan ^{2} \alpha+\tan ^{2} \beta+\tan ^{2} \gamma \geq \frac{3}{8}
$$
|
Since $\tan ^{2} x=1 / \cos ^{2} x-1$, the inequality to be proved is equivalent to
$$
\frac{1}{\cos ^{2} \alpha}+\frac{1}{\cos ^{2} \beta}+\frac{1}{\cos ^{2} \gamma} \geq \frac{27}{8}
$$
The AM-HM inequality implies
$$
\begin{aligned}
\frac{3}{\frac{1}{\cos ^{2} \alpha}+\frac{1}{\cos ^{2} \beta}+\frac{1}{\cos ^{2} \gamma}} & \leq \frac{\cos ^{2} \alpha+\cos ^{2} \beta+\cos ^{2} \gamma}{3} \\
& =\frac{3-\left(\sin ^{2} \alpha+\sin ^{2} \beta+\sin ^{2} \gamma\right)}{3} \\
& \leq 1-\left(\frac{\sin \alpha+\sin \beta+\sin \gamma}{3}\right)^{2} \\
& =\frac{8}{9}
\end{aligned}
$$
and the result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $\alpha, \beta$ and $\gamma$ be three angles with $0 \leq \alpha, \beta, \gamma<90^{\circ}$ and $\sin \alpha+\sin \beta+\sin \gamma=1$. Show that
$$
\tan ^{2} \alpha+\tan ^{2} \beta+\tan ^{2} \gamma \geq \frac{3}{8}
$$
|
Since $\tan ^{2} x=1 / \cos ^{2} x-1$, the inequality to be proved is equivalent to
$$
\frac{1}{\cos ^{2} \alpha}+\frac{1}{\cos ^{2} \beta}+\frac{1}{\cos ^{2} \gamma} \geq \frac{27}{8}
$$
The AM-HM inequality implies
$$
\begin{aligned}
\frac{3}{\frac{1}{\cos ^{2} \alpha}+\frac{1}{\cos ^{2} \beta}+\frac{1}{\cos ^{2} \gamma}} & \leq \frac{\cos ^{2} \alpha+\cos ^{2} \beta+\cos ^{2} \gamma}{3} \\
& =\frac{3-\left(\sin ^{2} \alpha+\sin ^{2} \beta+\sin ^{2} \gamma\right)}{3} \\
& \leq 1-\left(\frac{\sin \alpha+\sin \beta+\sin \gamma}{3}\right)^{2} \\
& =\frac{8}{9}
\end{aligned}
$$
and the result follows.
|
{
"exam": "BalticWay",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2005"
}
|
Consider the sequence $a_{k}$ defined by $a_{1}=1, a_{2}=\frac{1}{2}$,
$$
a_{k+2}=a_{k}+\frac{1}{2} a_{k+1}+\frac{1}{4 a_{k} a_{k+1}} \quad \text { for } k \geq 1
$$
Prove that
$$
\frac{1}{a_{1} a_{3}}+\frac{1}{a_{2} a_{4}}+\frac{1}{a_{3} a_{5}}+\cdots+\frac{1}{a_{98} a_{100}}<4
$$
|
Note that
$$
\frac{1}{a_{k} a_{k+2}}<\frac{2}{a_{k} a_{k+1}}-\frac{2}{a_{k+1} a_{k+2}}
$$
because this inequality is equivalent to the inequality
$$
a_{k+2}>a_{k}+\frac{1}{2} a_{k+1}
$$
which is evident for the given sequence. Now we have
$$
\begin{aligned}
\frac{1}{a_{1} a_{3}}+\frac{1}{a_{2} a_{4}} & +\frac{1}{a_{3} a_{5}}+\cdots+\frac{1}{a_{98} a_{100}} \\
& <\frac{2}{a_{1} a_{2}}-\frac{2}{a_{2} a_{3}}+\frac{2}{a_{2} a_{3}}-\frac{2}{a_{3} a_{4}}+\cdots \\
& <\frac{2}{a_{1} a_{2}}=4
\end{aligned}
$$
|
4
|
Yes
|
Yes
|
proof
|
Algebra
|
Consider the sequence $a_{k}$ defined by $a_{1}=1, a_{2}=\frac{1}{2}$,
$$
a_{k+2}=a_{k}+\frac{1}{2} a_{k+1}+\frac{1}{4 a_{k} a_{k+1}} \quad \text { for } k \geq 1
$$
Prove that
$$
\frac{1}{a_{1} a_{3}}+\frac{1}{a_{2} a_{4}}+\frac{1}{a_{3} a_{5}}+\cdots+\frac{1}{a_{98} a_{100}}<4
$$
|
Note that
$$
\frac{1}{a_{k} a_{k+2}}<\frac{2}{a_{k} a_{k+1}}-\frac{2}{a_{k+1} a_{k+2}}
$$
because this inequality is equivalent to the inequality
$$
a_{k+2}>a_{k}+\frac{1}{2} a_{k+1}
$$
which is evident for the given sequence. Now we have
$$
\begin{aligned}
\frac{1}{a_{1} a_{3}}+\frac{1}{a_{2} a_{4}} & +\frac{1}{a_{3} a_{5}}+\cdots+\frac{1}{a_{98} a_{100}} \\
& <\frac{2}{a_{1} a_{2}}-\frac{2}{a_{2} a_{3}}+\frac{2}{a_{2} a_{3}}-\frac{2}{a_{3} a_{4}}+\cdots \\
& <\frac{2}{a_{1} a_{2}}=4
\end{aligned}
$$
|
{
"exam": "BalticWay",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2005"
}
|
Find three different polynomials $P(x)$ with real coefficients such that $P\left(x^{2}+1\right)=P(x)^{2}+1$ for all real $x$.
Answer: For example, $P(x)=x, P(x)=x^{2}+1$ and $P(x)=x^{4}+2 x^{2}+2$.
|
Let $Q(x)=x^{2}+1$. Then the equation that $P$ must satisfy can be written $P(Q(x))=Q(P(x))$, and it is clear that this will be satisfied for $P(x)=x, P(x)=Q(x)$ and $P(x)=Q(Q(x))$.
|
P(x)=x, P(x)=x^{2}+1, P(x)=x^{4}+2x^{2}+2
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find three different polynomials $P(x)$ with real coefficients such that $P\left(x^{2}+1\right)=P(x)^{2}+1$ for all real $x$.
Answer: For example, $P(x)=x, P(x)=x^{2}+1$ and $P(x)=x^{4}+2 x^{2}+2$.
|
Let $Q(x)=x^{2}+1$. Then the equation that $P$ must satisfy can be written $P(Q(x))=Q(P(x))$, and it is clear that this will be satisfied for $P(x)=x, P(x)=Q(x)$ and $P(x)=Q(Q(x))$.
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2005"
}
|
Find three different polynomials $P(x)$ with real coefficients such that $P\left(x^{2}+1\right)=P(x)^{2}+1$ for all real $x$.
Answer: For example, $P(x)=x, P(x)=x^{2}+1$ and $P(x)=x^{4}+2 x^{2}+2$.
|
For all reals $x$ we have $P(x)^{2}+1=P\left(x^{2}+1\right)=P(-x)^{2}+1$ and consequently, $(P(x)+P(-x))(P(x)-P(-x))=0$. Now one of the three cases holds:
(a) If both $P(x)+P(-x)$ and $P(x)-P(-x)$ are not identically 0 , then they are nonconstant polynomials and have a finite numbers of roots, so this case cannot hold.
(b) If $P(x)+P(-x)$ is identically 0 then obviously, $P(0)=0$. Consider the infinite sequence of integers $a_{0}=0$ and $a_{n+1}=a_{n}^{2}+1$. By induction it is easy to see that $P\left(a_{n}\right)=a_{n}$ for all non-negative integers $n$. Also, $Q(x)=x$ has that property, so $P(x)-Q(x)$ is a polynomial with infinitely many roots, whence $P(x)=x$.
(c) If $P(x)-P(-x)$ is identically 0 then
$$
P(x)=x^{2 n}+b_{n-1} x^{2 n-2}+\cdots+b_{1} x^{2}+b_{0}
$$
for some integer $n$ since $P(x)$ is even and it is easy to see that the coefficient of $x^{2 n}$ must be 1 . Putting $n=1$ and $n=2$ yield the solutions $P(x)=x^{2}+1$ and $P(x)=x^{4}+2 x^{2}+2$.
Remark: For $n=3$ there is no solution, whereas for $n=4$ there is the unique solution $P(x)=x^{8}+6 x^{6}+8 x^{4}+8 x^{2}+5$.
|
P(x)=x, P(x)=x^{2}+1, P(x)=x^{4}+2 x^{2}+2
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find three different polynomials $P(x)$ with real coefficients such that $P\left(x^{2}+1\right)=P(x)^{2}+1$ for all real $x$.
Answer: For example, $P(x)=x, P(x)=x^{2}+1$ and $P(x)=x^{4}+2 x^{2}+2$.
|
For all reals $x$ we have $P(x)^{2}+1=P\left(x^{2}+1\right)=P(-x)^{2}+1$ and consequently, $(P(x)+P(-x))(P(x)-P(-x))=0$. Now one of the three cases holds:
(a) If both $P(x)+P(-x)$ and $P(x)-P(-x)$ are not identically 0 , then they are nonconstant polynomials and have a finite numbers of roots, so this case cannot hold.
(b) If $P(x)+P(-x)$ is identically 0 then obviously, $P(0)=0$. Consider the infinite sequence of integers $a_{0}=0$ and $a_{n+1}=a_{n}^{2}+1$. By induction it is easy to see that $P\left(a_{n}\right)=a_{n}$ for all non-negative integers $n$. Also, $Q(x)=x$ has that property, so $P(x)-Q(x)$ is a polynomial with infinitely many roots, whence $P(x)=x$.
(c) If $P(x)-P(-x)$ is identically 0 then
$$
P(x)=x^{2 n}+b_{n-1} x^{2 n-2}+\cdots+b_{1} x^{2}+b_{0}
$$
for some integer $n$ since $P(x)$ is even and it is easy to see that the coefficient of $x^{2 n}$ must be 1 . Putting $n=1$ and $n=2$ yield the solutions $P(x)=x^{2}+1$ and $P(x)=x^{4}+2 x^{2}+2$.
Remark: For $n=3$ there is no solution, whereas for $n=4$ there is the unique solution $P(x)=x^{8}+6 x^{6}+8 x^{4}+8 x^{2}+5$.
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"solution_match": "\nSolution 2:",
"tier": "T3",
"year": "2005"
}
|
Let $a, b, c$ be positive real numbers with $a b c=1$. Prove that
$$
\frac{a}{a^{2}+2}+\frac{b}{b^{2}+2}+\frac{c}{c^{2}+2} \leq 1
$$
|
For any positive real $x$ we have $x^{2}+1 \geq 2 x$. Hence
$$
\begin{aligned}
\frac{a}{a^{2}+2}+\frac{b}{b^{2}+2}+\frac{c}{c^{2}+2} & \leq \frac{a}{2 a+1}+\frac{b}{2 b+1}+\frac{c}{2 c+1} \\
& =\frac{1}{2+1 / a}+\frac{1}{2+1 / b}+\frac{1}{2+1 / c}=: R .
\end{aligned}
$$
$R \leq 1$ is equivalent to
$$
\left(2+\frac{1}{b}\right)\left(2+\frac{1}{c}\right)+\left(2+\frac{1}{a}\right)\left(2+\frac{1}{c}\right)+\left(2+\frac{1}{a}\right)\left(2+\frac{1}{b}\right) \leq\left(2+\frac{1}{a}\right)\left(2+\frac{1}{b}\right)\left(2+\frac{1}{c}\right)
$$
and to $4 \leq \frac{1}{a b}+\frac{1}{a c}+\frac{1}{b c}+\frac{1}{a b c}$. By $a b c=1$ and by the AM-GM inequality
$$
\frac{1}{a b}+\frac{1}{a c}+\frac{1}{b c} \geq 3 \sqrt[3]{\left(\frac{1}{a b c}\right)^{2}}=3
$$
the last inequality follows. Equality appears exactly when $a=b=c=1$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers with $a b c=1$. Prove that
$$
\frac{a}{a^{2}+2}+\frac{b}{b^{2}+2}+\frac{c}{c^{2}+2} \leq 1
$$
|
For any positive real $x$ we have $x^{2}+1 \geq 2 x$. Hence
$$
\begin{aligned}
\frac{a}{a^{2}+2}+\frac{b}{b^{2}+2}+\frac{c}{c^{2}+2} & \leq \frac{a}{2 a+1}+\frac{b}{2 b+1}+\frac{c}{2 c+1} \\
& =\frac{1}{2+1 / a}+\frac{1}{2+1 / b}+\frac{1}{2+1 / c}=: R .
\end{aligned}
$$
$R \leq 1$ is equivalent to
$$
\left(2+\frac{1}{b}\right)\left(2+\frac{1}{c}\right)+\left(2+\frac{1}{a}\right)\left(2+\frac{1}{c}\right)+\left(2+\frac{1}{a}\right)\left(2+\frac{1}{b}\right) \leq\left(2+\frac{1}{a}\right)\left(2+\frac{1}{b}\right)\left(2+\frac{1}{c}\right)
$$
and to $4 \leq \frac{1}{a b}+\frac{1}{a c}+\frac{1}{b c}+\frac{1}{a b c}$. By $a b c=1$ and by the AM-GM inequality
$$
\frac{1}{a b}+\frac{1}{a c}+\frac{1}{b c} \geq 3 \sqrt[3]{\left(\frac{1}{a b c}\right)^{2}}=3
$$
the last inequality follows. Equality appears exactly when $a=b=c=1$.
|
{
"exam": "BalticWay",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2005"
}
|
Let $K$ and $N$ be positive integers with $1 \leq K \leq N$. A deck of $N$ different playing cards is shuffled by repeating the operation of reversing the order of the $K$ topmost cards and moving these to the bottom of the deck. Prove that the deck will be back in its initial order after a number of operations not greater than $4 \cdot N^{2} / K^{2}$.
|
Let $N=q \cdot K+r, 0 \leq r<K$, and let us number the cards $1,2, \ldots, N$, starting from the one at the bottom of the deck. First we find out how the cards $1,2, \ldots K$ are moving in the deck.
If $i \leq r$ then the card $i$ is moving along the cycle
$$
\begin{aligned}
& i \rightarrow K+i \rightarrow 2 K+i \rightarrow \cdots \rightarrow q K+i \rightarrow(r+1-i) \rightarrow \\
& K+(r+1-i) \rightarrow \cdots \rightarrow q K+(r+1-i),
\end{aligned}
$$
because $N-K<q K+i \leq N$ and $N-K<q K+(r+1-i) \leq N$. The length of this cycle is $2 q+2$. In the special case of $i=r+i-1$, it actually consists of two smaller cycles of length $q+1$.
If $r<i \leq K$ then the card $i$ is moving along the cycle
$$
\begin{aligned}
i \rightarrow K+i \rightarrow 2 K+i \rightarrow & \cdots \rightarrow(q-1) K+i \rightarrow \\
& K+r+1-i \rightarrow K+(K+r+1-i) \rightarrow \\
& 2 K+(K+r+1-i) \rightarrow \cdots \rightarrow(q-1) K+(K+r+1-i),
\end{aligned}
$$
because $N-K<(q-1) K+i \leq N$ and $N-K<(q-1) K+(K+r+1-i) \leq N$. The length of this cycle is $2 q$. In the special case of $i=K+r+1-i$, it actually consists of two smaller cycles of length $q$.
Since these cycles cover all the numbers $1, \ldots, N$, we can say that every card returns to its initial position after either $2 q+2$ or $2 q$ operations. Therefore, all the cards are simultaneously at their initial position after at most $\operatorname{lcm}(2 q+2,2 q)=2 \operatorname{lcm}(q+1, q)=$ $2 q(q+1)$ operations. Finally,
$$
2 q(q+1) \leq(2 q)^{2}=4 q^{2} \leq 4\left(\frac{N}{K}\right)^{2}
$$
which concludes the proof.
|
4 \cdot \left(\frac{N}{K}\right)^{2}
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $K$ and $N$ be positive integers with $1 \leq K \leq N$. A deck of $N$ different playing cards is shuffled by repeating the operation of reversing the order of the $K$ topmost cards and moving these to the bottom of the deck. Prove that the deck will be back in its initial order after a number of operations not greater than $4 \cdot N^{2} / K^{2}$.
|
Let $N=q \cdot K+r, 0 \leq r<K$, and let us number the cards $1,2, \ldots, N$, starting from the one at the bottom of the deck. First we find out how the cards $1,2, \ldots K$ are moving in the deck.
If $i \leq r$ then the card $i$ is moving along the cycle
$$
\begin{aligned}
& i \rightarrow K+i \rightarrow 2 K+i \rightarrow \cdots \rightarrow q K+i \rightarrow(r+1-i) \rightarrow \\
& K+(r+1-i) \rightarrow \cdots \rightarrow q K+(r+1-i),
\end{aligned}
$$
because $N-K<q K+i \leq N$ and $N-K<q K+(r+1-i) \leq N$. The length of this cycle is $2 q+2$. In the special case of $i=r+i-1$, it actually consists of two smaller cycles of length $q+1$.
If $r<i \leq K$ then the card $i$ is moving along the cycle
$$
\begin{aligned}
i \rightarrow K+i \rightarrow 2 K+i \rightarrow & \cdots \rightarrow(q-1) K+i \rightarrow \\
& K+r+1-i \rightarrow K+(K+r+1-i) \rightarrow \\
& 2 K+(K+r+1-i) \rightarrow \cdots \rightarrow(q-1) K+(K+r+1-i),
\end{aligned}
$$
because $N-K<(q-1) K+i \leq N$ and $N-K<(q-1) K+(K+r+1-i) \leq N$. The length of this cycle is $2 q$. In the special case of $i=K+r+1-i$, it actually consists of two smaller cycles of length $q$.
Since these cycles cover all the numbers $1, \ldots, N$, we can say that every card returns to its initial position after either $2 q+2$ or $2 q$ operations. Therefore, all the cards are simultaneously at their initial position after at most $\operatorname{lcm}(2 q+2,2 q)=2 \operatorname{lcm}(q+1, q)=$ $2 q(q+1)$ operations. Finally,
$$
2 q(q+1) \leq(2 q)^{2}=4 q^{2} \leq 4\left(\frac{N}{K}\right)^{2}
$$
which concludes the proof.
|
{
"exam": "BalticWay",
"problem_label": "6",
"problem_match": "\n6.",
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2005"
}
|
A rectangular array has $n$ rows and six columns, where $n>2$. In each cell there is written either 0 or 1 . All rows in the array are different from each other. For each pair of rows $\left(x_{1}, x_{2}, \ldots, x_{6}\right)$ and $\left(y_{1}, y_{2}, \ldots, y_{6}\right)$, the row $\left(x_{1} y_{1}, x_{2} y_{2}, \ldots, x_{6} y_{6}\right)$ can also be found in the array. Prove that there is a column in which at least half of the entries are zeroes.
|
Clearly there must be rows with some zeroes. Consider the case when there is a row with just one zero; we can assume it is $(0,1,1,1,1,1)$. Then for each row $\left(1, x_{2}, x_{3}, x_{4}, x_{5}, x_{6}\right)$ there is also a row $\left(0, x_{2}, x_{3}, x_{4}, x_{5}, x_{6}\right)$; the conclusion follows. Consider the case when there is a row with just two zeroes; we can assume it is $(0,0,1,1,1,1)$. Let $n_{i j}$ be the number of rows with first two elements $i, j$. As in the first case $n_{00} \geq n_{11}$. Let $n_{01} \geq n_{10}$; the other subcase is analogous. Now there are $n_{00}+n_{01}$ zeroes in the first column and $n_{10}+n_{11}$ ones in the first column; the conclusion follows. Consider now the case when each row contains at least three zeroes (except $(1,1,1,1,1,1$ ), if such a row exists). Let us prove that it is impossible that each such row contains exactly three zeroes. Assume the opposite. As $n>2$ there are at least two rows with zeroes; they are different, so their product contains at least four zeroes, a contradiction. So there are more then $3(n-1)$ zeroes in the array; so in some column there are more than $(n-1) / 2$ zeroes; so there are at least $n / 2$ zeroes.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A rectangular array has $n$ rows and six columns, where $n>2$. In each cell there is written either 0 or 1 . All rows in the array are different from each other. For each pair of rows $\left(x_{1}, x_{2}, \ldots, x_{6}\right)$ and $\left(y_{1}, y_{2}, \ldots, y_{6}\right)$, the row $\left(x_{1} y_{1}, x_{2} y_{2}, \ldots, x_{6} y_{6}\right)$ can also be found in the array. Prove that there is a column in which at least half of the entries are zeroes.
|
Clearly there must be rows with some zeroes. Consider the case when there is a row with just one zero; we can assume it is $(0,1,1,1,1,1)$. Then for each row $\left(1, x_{2}, x_{3}, x_{4}, x_{5}, x_{6}\right)$ there is also a row $\left(0, x_{2}, x_{3}, x_{4}, x_{5}, x_{6}\right)$; the conclusion follows. Consider the case when there is a row with just two zeroes; we can assume it is $(0,0,1,1,1,1)$. Let $n_{i j}$ be the number of rows with first two elements $i, j$. As in the first case $n_{00} \geq n_{11}$. Let $n_{01} \geq n_{10}$; the other subcase is analogous. Now there are $n_{00}+n_{01}$ zeroes in the first column and $n_{10}+n_{11}$ ones in the first column; the conclusion follows. Consider now the case when each row contains at least three zeroes (except $(1,1,1,1,1,1$ ), if such a row exists). Let us prove that it is impossible that each such row contains exactly three zeroes. Assume the opposite. As $n>2$ there are at least two rows with zeroes; they are different, so their product contains at least four zeroes, a contradiction. So there are more then $3(n-1)$ zeroes in the array; so in some column there are more than $(n-1) / 2$ zeroes; so there are at least $n / 2$ zeroes.
|
{
"exam": "BalticWay",
"problem_label": "7",
"problem_match": "\n7.",
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2005"
}
|
Consider a grid of $25 \times 25$ unit squares. Draw with a red pen contours of squares of any size on the grid. What is the minimal number of squares we must draw in order to colour all the lines of the grid?
Answer: 48 squares.
|
Consider a diagonal of the square grid. For any grid vertex $A$ on this diagonal denote by $C$ the farthest endpoint of this diagonal. Let the square with the diagonal $A C$ be red. Thus, we have defined the set of 48 red squares (24 for each diagonal). It is clear that if we draw all these squares, all the lines in the grid will turn red.
In order to show that 48 is the minimum, consider all grid segments of length 1 that have exactly one endpoint on the border of the grid. Every horizontal and every vertical line that cuts the grid into two parts determines two such segments. So we have $4 \cdot 24=96$ segments. It is evident that every red square can contain at most two of these segments.
|
48
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Consider a grid of $25 \times 25$ unit squares. Draw with a red pen contours of squares of any size on the grid. What is the minimal number of squares we must draw in order to colour all the lines of the grid?
Answer: 48 squares.
|
Consider a diagonal of the square grid. For any grid vertex $A$ on this diagonal denote by $C$ the farthest endpoint of this diagonal. Let the square with the diagonal $A C$ be red. Thus, we have defined the set of 48 red squares (24 for each diagonal). It is clear that if we draw all these squares, all the lines in the grid will turn red.
In order to show that 48 is the minimum, consider all grid segments of length 1 that have exactly one endpoint on the border of the grid. Every horizontal and every vertical line that cuts the grid into two parts determines two such segments. So we have $4 \cdot 24=96$ segments. It is evident that every red square can contain at most two of these segments.
|
{
"exam": "BalticWay",
"problem_label": "8",
"problem_match": "\n8.",
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2005"
}
|
A rectangle is divided into $200 \times 3$ unit squares. Prove that the number of ways of splitting this rectangle into rectangles of size $1 \times 2$ is divisible by 3 .
|
Let us denote the number of ways to split some figure into dominos by a small picture of this figure with a sign \#. For example, $\# \boxplus=2$.
Let $N_{n}=\#$ ( $n$ rows) and $\gamma_{n}=\#$ ( $n-2$ full rows and one row with two cells).
We are going to find a recurrence relation for the numbers $N_{n}$.
Observe that

We can generalize our observations by writing the equalities
$$
\begin{aligned}
N_{n} & =2 \gamma_{n}+N_{n-2}, \\
2 \gamma_{n-2} & =N_{n-2}-N_{n-4}, \\
2 \gamma_{n} & =2 \gamma_{n-2}+2 N_{n-2} .
\end{aligned}
$$
If we sum up these equalities we obtain the desired recurrence
$$
N_{n}=4 N_{n-2}-N_{n-4}
$$
It is easy to find that $N_{2}=3, N_{4}=11$. Now by the recurrence relation it is trivial to check that $N_{6 k+2} \equiv 0(\bmod 3)$.
|
N_{6k+2} \equiv 0 \pmod{3}
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A rectangle is divided into $200 \times 3$ unit squares. Prove that the number of ways of splitting this rectangle into rectangles of size $1 \times 2$ is divisible by 3 .
|
Let us denote the number of ways to split some figure into dominos by a small picture of this figure with a sign \#. For example, $\# \boxplus=2$.
Let $N_{n}=\#$ ( $n$ rows) and $\gamma_{n}=\#$ ( $n-2$ full rows and one row with two cells).
We are going to find a recurrence relation for the numbers $N_{n}$.
Observe that

We can generalize our observations by writing the equalities
$$
\begin{aligned}
N_{n} & =2 \gamma_{n}+N_{n-2}, \\
2 \gamma_{n-2} & =N_{n-2}-N_{n-4}, \\
2 \gamma_{n} & =2 \gamma_{n-2}+2 N_{n-2} .
\end{aligned}
$$
If we sum up these equalities we obtain the desired recurrence
$$
N_{n}=4 N_{n-2}-N_{n-4}
$$
It is easy to find that $N_{2}=3, N_{4}=11$. Now by the recurrence relation it is trivial to check that $N_{6 k+2} \equiv 0(\bmod 3)$.
|
{
"exam": "BalticWay",
"problem_label": "9",
"problem_match": "\n9.",
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2005"
}
|
Let $m=30030=2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13$ and let $M$ be the set of its positive divisors which have exactly two prime factors. Determine the minimal integer $n$ with the following property: for any choice of numbers from $M$, there exist three numbers $a, b, c$ among them satisfying $a \cdot b \cdot c=m$.
Answer: $n=11$.
|
Taking the 10 divisors without the prime 13 shows that $n \geq 11$. Consider the following partition of the 15 divisors into five groups of three each with the property that the product of the numbers in every group equals $m$.
$$
\begin{array}{ll}
\{2 \cdot 3,5 \cdot 13,7 \cdot 11\}, & \{2 \cdot 5,3 \cdot 7,11 \cdot 13\}, \\
\{2 \cdot 11,3 \cdot 5,7 \cdot 13\}, & \{2 \cdot 13,3 \cdot 11,5 \cdot 7\} .
\end{array}
$$
If $n=11$, there is a group from which we take all three numbers, that is, their product equals $m$.
|
11
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $m=30030=2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13$ and let $M$ be the set of its positive divisors which have exactly two prime factors. Determine the minimal integer $n$ with the following property: for any choice of numbers from $M$, there exist three numbers $a, b, c$ among them satisfying $a \cdot b \cdot c=m$.
Answer: $n=11$.
|
Taking the 10 divisors without the prime 13 shows that $n \geq 11$. Consider the following partition of the 15 divisors into five groups of three each with the property that the product of the numbers in every group equals $m$.
$$
\begin{array}{ll}
\{2 \cdot 3,5 \cdot 13,7 \cdot 11\}, & \{2 \cdot 5,3 \cdot 7,11 \cdot 13\}, \\
\{2 \cdot 11,3 \cdot 5,7 \cdot 13\}, & \{2 \cdot 13,3 \cdot 11,5 \cdot 7\} .
\end{array}
$$
If $n=11$, there is a group from which we take all three numbers, that is, their product equals $m$.
|
{
"exam": "BalticWay",
"problem_label": "10",
"problem_match": "\n10.",
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2005"
}
|
Let the points $D$ and $E$ lie on the sides $B C$ and $A C$, respectively, of the triangle $A B C$, satisfying $B D=A E$. The line joining the circumcentres of the triangles $A D C$ and $B E C$ meets the lines $A C$ and $B C$ at $K$ and $L$, respectively. Prove that $K C=L C$.
|
Assume that the circumcircles of triangles $A D C$ and $B E C$ meet at $C$ and $P$. The problem is to show that the line $K L$ makes equal angles with the lines $A C$ and $B C$. Since the line joining the circumcentres of triangles $A D C$ and $B E C$ is perpendicular to the line $C P$, it suffices to show that $C P$ is the angle-bisector of $\angle A C B$.
Since the points $A, P, D, C$ are concyclic, we obtain $\angle E A P=\angle B D P$. Analogously, we have $\angle A E P=\angle D B P$. These two equalities together with $A E=B D$ imply that triangles $A P E$ and $D P B$ are congruent. This means that the distance from $P$ to $A C$ is equal to the distance from $P$ to $B C$, and thus $C P$ is the angle-bisector of $\angle A C B$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let the points $D$ and $E$ lie on the sides $B C$ and $A C$, respectively, of the triangle $A B C$, satisfying $B D=A E$. The line joining the circumcentres of the triangles $A D C$ and $B E C$ meets the lines $A C$ and $B C$ at $K$ and $L$, respectively. Prove that $K C=L C$.
|
Assume that the circumcircles of triangles $A D C$ and $B E C$ meet at $C$ and $P$. The problem is to show that the line $K L$ makes equal angles with the lines $A C$ and $B C$. Since the line joining the circumcentres of triangles $A D C$ and $B E C$ is perpendicular to the line $C P$, it suffices to show that $C P$ is the angle-bisector of $\angle A C B$.

Since the points $A, P, D, C$ are concyclic, we obtain $\angle E A P=\angle B D P$. Analogously, we have $\angle A E P=\angle D B P$. These two equalities together with $A E=B D$ imply that triangles $A P E$ and $D P B$ are congruent. This means that the distance from $P$ to $A C$ is equal to the distance from $P$ to $B C$, and thus $C P$ is the angle-bisector of $\angle A C B$, as desired.
|
{
"exam": "BalticWay",
"problem_label": "11",
"problem_match": "\n11.",
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2005"
}
|
Let $A B C D$ be a convex quadrilateral such that $B C=A D$. Let $M$ and $N$ be the midpoints of $A B$ and $C D$, respectively. The lines $A D$ and $B C$ meet the line $M N$ at $P$ and $Q$, respectively. Prove that $C Q=D P$.
|
Let $A^{\prime}, B^{\prime}, C^{\prime}, D^{\prime}$ be the feet of the perpendiculars from $A, B, C, D$, respectively, onto the line $M N$. Then
$$
A A^{\prime}=B B^{\prime} \quad \text { and } \quad C C^{\prime}=D D^{\prime} \text {. }
$$
Denote by $X, Y$ the feet of the perpendiculars from $C, D$ onto the lines $B B^{\prime}, A A^{\prime}$, respectively. We infer from the above equalities that $A Y=B X$. Since also $B C=A D$, the right-angled triangles $B X C$ and $A Y D$ are congruent. This shows that
$$
\angle C^{\prime} C Q=\angle B^{\prime} B Q=\angle A^{\prime} A P=\angle D^{\prime} D P .
$$
Therefore, since $C C^{\prime}=D D^{\prime}$, the triangles $C C^{\prime} Q$ and $D D^{\prime} P$ are congruent. Thus $C Q=$ $D P$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral such that $B C=A D$. Let $M$ and $N$ be the midpoints of $A B$ and $C D$, respectively. The lines $A D$ and $B C$ meet the line $M N$ at $P$ and $Q$, respectively. Prove that $C Q=D P$.
|
Let $A^{\prime}, B^{\prime}, C^{\prime}, D^{\prime}$ be the feet of the perpendiculars from $A, B, C, D$, respectively, onto the line $M N$. Then
$$
A A^{\prime}=B B^{\prime} \quad \text { and } \quad C C^{\prime}=D D^{\prime} \text {. }
$$
Denote by $X, Y$ the feet of the perpendiculars from $C, D$ onto the lines $B B^{\prime}, A A^{\prime}$, respectively. We infer from the above equalities that $A Y=B X$. Since also $B C=A D$, the right-angled triangles $B X C$ and $A Y D$ are congruent. This shows that
$$
\angle C^{\prime} C Q=\angle B^{\prime} B Q=\angle A^{\prime} A P=\angle D^{\prime} D P .
$$
Therefore, since $C C^{\prime}=D D^{\prime}$, the triangles $C C^{\prime} Q$ and $D D^{\prime} P$ are congruent. Thus $C Q=$ $D P$.

|
{
"exam": "BalticWay",
"problem_label": "12",
"problem_match": "\n12.",
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2005"
}
|
What is the smallest number of circles of radius $\sqrt{2}$ that are needed to cover a rectangle
(a) of size $6 \times 3$ ?
(b) of size $5 \times 3$ ?
Answer: (a) Six circles, (b) five circles.
|
(a) Consider the four corners and the two midpoints of the sides of length 6 . The distance between any two of these six points is 3 or more, so one circle cannot cover two of these points, and at least six circles are needed.
On the other hand one circle will cover a $2 \times 2$ square, and it is easy to see that six such squares can cover the rectangle.
(b) Consider the four corners and the centre of the rectangle. The minimum distance between any two of these points is the distance between the centre and one of the corners, which is $\sqrt{34} / 2$. This is greater than the diameter of the circle $(\sqrt{34 / 4}>\sqrt{32 / 4})$, so one circle cannot cover two of these points, and at least five circles are needed.
Partition the rectangle into three rectangles of size $5 / 3 \times 2$ and two rectangles of size $5 / 2 \times 1$ as shown on the right. It is easy to check that each has a diagonal of length less than $2 \sqrt{2}$, so five circles can cover the five small rectangles and hence the $5 \times 3$ rectangle.
|
5
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
What is the smallest number of circles of radius $\sqrt{2}$ that are needed to cover a rectangle
(a) of size $6 \times 3$ ?
(b) of size $5 \times 3$ ?
Answer: (a) Six circles, (b) five circles.
|
(a) Consider the four corners and the two midpoints of the sides of length 6 . The distance between any two of these six points is 3 or more, so one circle cannot cover two of these points, and at least six circles are needed.
On the other hand one circle will cover a $2 \times 2$ square, and it is easy to see that six such squares can cover the rectangle.
(b) Consider the four corners and the centre of the rectangle. The minimum distance between any two of these points is the distance between the centre and one of the corners, which is $\sqrt{34} / 2$. This is greater than the diameter of the circle $(\sqrt{34 / 4}>\sqrt{32 / 4})$, so one circle cannot cover two of these points, and at least five circles are needed.

Partition the rectangle into three rectangles of size $5 / 3 \times 2$ and two rectangles of size $5 / 2 \times 1$ as shown on the right. It is easy to check that each has a diagonal of length less than $2 \sqrt{2}$, so five circles can cover the five small rectangles and hence the $5 \times 3$ rectangle.
|
{
"exam": "BalticWay",
"problem_label": "13",
"problem_match": "\n13.",
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2005"
}
|
Let the medians of the triangle $A B C$ meet at $M$. Let $D$ and $E$ be different points on the line $B C$ such that $D C=C E=A B$, and let $P$ and $Q$ be points on the segments $B D$ and $B E$, respectively, such that $2 B P=P D$ and $2 B Q=Q E$. Determine $\angle P M Q$.
Answer: $\angle P M Q=90^{\circ}$.
|
Draw the parallelogram $A B C A^{\prime}$, with $A A^{\prime} \| B C$. Then $M$ lies on $B A^{\prime}$, and $B M=\frac{1}{3} B A^{\prime}$. So $M$ is on the homothetic image (centre $B$, dilation $1 / 3$ ) of the circle with centre $C$ and radius $A B$, which meets $B C$ at $D$ and $E$. The image meets $B C$ at $P$ and $Q$. So $\angle P M Q=90^{\circ}$.
|
90^{\circ}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let the medians of the triangle $A B C$ meet at $M$. Let $D$ and $E$ be different points on the line $B C$ such that $D C=C E=A B$, and let $P$ and $Q$ be points on the segments $B D$ and $B E$, respectively, such that $2 B P=P D$ and $2 B Q=Q E$. Determine $\angle P M Q$.
Answer: $\angle P M Q=90^{\circ}$.
|
Draw the parallelogram $A B C A^{\prime}$, with $A A^{\prime} \| B C$. Then $M$ lies on $B A^{\prime}$, and $B M=\frac{1}{3} B A^{\prime}$. So $M$ is on the homothetic image (centre $B$, dilation $1 / 3$ ) of the circle with centre $C$ and radius $A B$, which meets $B C$ at $D$ and $E$. The image meets $B C$ at $P$ and $Q$. So $\angle P M Q=90^{\circ}$.

|
{
"exam": "BalticWay",
"problem_label": "14",
"problem_match": "\n14.",
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2005"
}
|
Let the lines $e$ and $f$ be perpendicular and intersect each other at $O$. Let $A$ and $B$ lie on $e$ and $C$ and $D$ lie on $f$, such that all the five points $A, B, C, D$ and $O$ are distinct. Let the lines $b$ and $d$ pass through $B$ and $D$ respectively, perpendicularly to $A C$; let the lines $a$ and $c$ pass through $A$ and $C$ respectively, perpendicularly to $B D$. Let $a$ and $b$ intersect $a t X$ and $c$ and $d$ intersect at $Y$. Prove that $X Y$ passes through $O$.
|
Let $A_{1}$ be the intersection of $a$ with $B D, B_{1}$ the intersection of $b$ with $A C, C_{1}$ the intersection of $c$ with $B D$ and $D_{1}$ the intersection of $d$ with $A C$. It follows easily by the given right angles that the following three sets each are concyclic:
- $A, A_{1}, D, D_{1}, O$ lie on a circle $w_{1}$ with diameter $A D$.
- $B, B_{1}, C, C 1, O$ lie on a circle $w_{2}$ with diameter $B C$.
- $C, C_{1}, D, D_{1}$ lie on a circle $w_{3}$ with diameter $D C$.
We see that $O$ lies on the radical axis of $w_{1}$ and $w_{2}$. Also, $Y$ lies on the radical axis of $w_{1}$ and $w_{3}$, and on the radical axis of $w_{2}$ and $w_{3}$, so $Y$ is the radical centre of $w_{1}, w_{2}$ and $w_{3}$, so it lies on the radical axis of $w_{1}$ and $w_{2}$. Analogously we prove that $X$ lies on the radical axis of $w_{1}$ and $w_{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let the lines $e$ and $f$ be perpendicular and intersect each other at $O$. Let $A$ and $B$ lie on $e$ and $C$ and $D$ lie on $f$, such that all the five points $A, B, C, D$ and $O$ are distinct. Let the lines $b$ and $d$ pass through $B$ and $D$ respectively, perpendicularly to $A C$; let the lines $a$ and $c$ pass through $A$ and $C$ respectively, perpendicularly to $B D$. Let $a$ and $b$ intersect $a t X$ and $c$ and $d$ intersect at $Y$. Prove that $X Y$ passes through $O$.
|
Let $A_{1}$ be the intersection of $a$ with $B D, B_{1}$ the intersection of $b$ with $A C, C_{1}$ the intersection of $c$ with $B D$ and $D_{1}$ the intersection of $d$ with $A C$. It follows easily by the given right angles that the following three sets each are concyclic:
- $A, A_{1}, D, D_{1}, O$ lie on a circle $w_{1}$ with diameter $A D$.
- $B, B_{1}, C, C 1, O$ lie on a circle $w_{2}$ with diameter $B C$.
- $C, C_{1}, D, D_{1}$ lie on a circle $w_{3}$ with diameter $D C$.
We see that $O$ lies on the radical axis of $w_{1}$ and $w_{2}$. Also, $Y$ lies on the radical axis of $w_{1}$ and $w_{3}$, and on the radical axis of $w_{2}$ and $w_{3}$, so $Y$ is the radical centre of $w_{1}, w_{2}$ and $w_{3}$, so it lies on the radical axis of $w_{1}$ and $w_{2}$. Analogously we prove that $X$ lies on the radical axis of $w_{1}$ and $w_{2}$.

|
{
"exam": "BalticWay",
"problem_label": "15",
"problem_match": "\n15.",
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2005"
}
|
Let $p$ be a prime number and let $n$ be a positive integer. Let $q$ be a positive divisor of $(n+1)^{p}-n^{p}$. Show that $q-1$ is divisible by $p$.
|
It is sufficient to show the statement for $q$ prime. We need to prove that
$$
(n+1)^{p} \equiv n^{p} \quad(\bmod q) \Longrightarrow q \equiv 1 \quad(\bmod p) .
$$
It is obvious that $\operatorname{gcd}(n, q)=\operatorname{gcd}(n+1, q)=1$ (as $n$ and $n+1$ cannot be divisible by $q$ simultaneously). Hence there exists a positive integer $m$ such that $m n \equiv 1(\bmod q)$. In fact, $m$ is just the multiplicative inverse of $n(\bmod q)$. Take $s=m(n+1)$. It is easy to see that
$$
s^{p} \equiv 1 \quad(\bmod q)
$$
Let $t$ be the smallest positive integer which satisfies $s^{t} \equiv 1(\bmod q)(t$ is the order of $s(\bmod q)$ ). One can easily prove that $t$ divides $p$. Indeed, write $p=a t+b$ where $0 \leq b<t$. Then
$$
1 \equiv s^{p} \equiv s^{a t+b} \equiv\left(s^{t}\right)^{a} \cdot s^{b} \equiv s^{b} \quad(\bmod q) .
$$
By the definition of $t$, we must have $b=0$. Hence $t$ divides $p$. This means that $t=1$ or $t=p$. However, $t=1$ is easily seen to give a contradiction since then we would have
$$
m(n+1) \equiv 1 \quad(\bmod q) \quad \text { or } \quad n+1 \equiv n \quad(\bmod q)
$$
Therefore $t=p$, and $p$ is the order of $s(\bmod q)$. By Fermat's little theorem,
$$
s^{q-1} \equiv 1 \quad(\bmod q)
$$
Since $p$ is the order of $s(\bmod q)$, we have that $p$ divides $q-1$, and we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $p$ be a prime number and let $n$ be a positive integer. Let $q$ be a positive divisor of $(n+1)^{p}-n^{p}$. Show that $q-1$ is divisible by $p$.
|
It is sufficient to show the statement for $q$ prime. We need to prove that
$$
(n+1)^{p} \equiv n^{p} \quad(\bmod q) \Longrightarrow q \equiv 1 \quad(\bmod p) .
$$
It is obvious that $\operatorname{gcd}(n, q)=\operatorname{gcd}(n+1, q)=1$ (as $n$ and $n+1$ cannot be divisible by $q$ simultaneously). Hence there exists a positive integer $m$ such that $m n \equiv 1(\bmod q)$. In fact, $m$ is just the multiplicative inverse of $n(\bmod q)$. Take $s=m(n+1)$. It is easy to see that
$$
s^{p} \equiv 1 \quad(\bmod q)
$$
Let $t$ be the smallest positive integer which satisfies $s^{t} \equiv 1(\bmod q)(t$ is the order of $s(\bmod q)$ ). One can easily prove that $t$ divides $p$. Indeed, write $p=a t+b$ where $0 \leq b<t$. Then
$$
1 \equiv s^{p} \equiv s^{a t+b} \equiv\left(s^{t}\right)^{a} \cdot s^{b} \equiv s^{b} \quad(\bmod q) .
$$
By the definition of $t$, we must have $b=0$. Hence $t$ divides $p$. This means that $t=1$ or $t=p$. However, $t=1$ is easily seen to give a contradiction since then we would have
$$
m(n+1) \equiv 1 \quad(\bmod q) \quad \text { or } \quad n+1 \equiv n \quad(\bmod q)
$$
Therefore $t=p$, and $p$ is the order of $s(\bmod q)$. By Fermat's little theorem,
$$
s^{q-1} \equiv 1 \quad(\bmod q)
$$
Since $p$ is the order of $s(\bmod q)$, we have that $p$ divides $q-1$, and we are done.
|
{
"exam": "BalticWay",
"problem_label": "16",
"problem_match": "\n16.",
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2005"
}
|
A sequence $\left(x_{n}\right), n \geq 0$, is defined as follows: $x_{0}=a, x_{1}=2$ and $x_{n}=2 x_{n-1} x_{n-2}-$ $x_{n-1}-x_{n-2}+1$ for $n>1$. Find all integers a such that $2 x_{3 n}-1$ is a perfect square for all $n \geq 1$.
Answer: $a=\frac{(2 m-1)^{2}+1}{2}$ where $m$ is an arbitrary positive integer.
|
Let $y_{n}=2 x_{n}-1$. Then
$$
\begin{aligned}
y_{n} & =2\left(2 x_{n-1} x_{n-2}-x_{n-1}-x_{n-2}+1\right)-1 \\
& =4 x_{n-1} x_{n-2}-2 x_{n-1}-2 x_{n-2}+1 \\
& =\left(2 x_{n-1}-1\right)\left(2 x_{n-2}-1\right)=y_{n-1} y_{n-2}
\end{aligned}
$$
when $n>1$. Notice that $y_{n+3}=y_{n+2} y_{n+1}=y_{n+1}^{2} y_{n}$. We see that $y_{n+3}$ is a perfect square if and only if $y_{n}$ is a perfect square. Hence $y_{3 n}$ is a perfect square for all $n \geq 1$ exactly when $y_{0}$ is a perfect square. Since $y_{0}=2 a-1$, the result is obtained when $a=\frac{(2 m-1)^{2}+1}{2}$ for all positive integers $m$.
|
a=\frac{(2 m-1)^{2}+1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
A sequence $\left(x_{n}\right), n \geq 0$, is defined as follows: $x_{0}=a, x_{1}=2$ and $x_{n}=2 x_{n-1} x_{n-2}-$ $x_{n-1}-x_{n-2}+1$ for $n>1$. Find all integers a such that $2 x_{3 n}-1$ is a perfect square for all $n \geq 1$.
Answer: $a=\frac{(2 m-1)^{2}+1}{2}$ where $m$ is an arbitrary positive integer.
|
Let $y_{n}=2 x_{n}-1$. Then
$$
\begin{aligned}
y_{n} & =2\left(2 x_{n-1} x_{n-2}-x_{n-1}-x_{n-2}+1\right)-1 \\
& =4 x_{n-1} x_{n-2}-2 x_{n-1}-2 x_{n-2}+1 \\
& =\left(2 x_{n-1}-1\right)\left(2 x_{n-2}-1\right)=y_{n-1} y_{n-2}
\end{aligned}
$$
when $n>1$. Notice that $y_{n+3}=y_{n+2} y_{n+1}=y_{n+1}^{2} y_{n}$. We see that $y_{n+3}$ is a perfect square if and only if $y_{n}$ is a perfect square. Hence $y_{3 n}$ is a perfect square for all $n \geq 1$ exactly when $y_{0}$ is a perfect square. Since $y_{0}=2 a-1$, the result is obtained when $a=\frac{(2 m-1)^{2}+1}{2}$ for all positive integers $m$.
|
{
"exam": "BalticWay",
"problem_label": "17",
"problem_match": "\n17.",
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2005"
}
|
Let $x$ and $y$ be positive integers and assume that $z=4 x y /(x+y)$ is an odd integer. Prove that at least one divisor of $z$ can be expressed in the form $4 n-1$ where $n$ is a positive integer.
|
Let $x=2^{s} x_{1}$ and $y=2^{t} y_{1}$ where $x_{1}$ and $y_{1}$ are odd integers. Without loss of generality we can assume that $s \geq t$. We have
$$
z=\frac{2^{s+t+2} x_{1} y_{1}}{2^{t}\left(2^{s-t} x_{1}+y_{1}\right)}=\frac{2^{s+2} x_{1} y_{1}}{2^{s-t} x_{1}+y_{1}}
$$
If $s \neq t$, then the denominator is odd and therefore $z$ is even. So we have $s=t$ and $z=2^{s+2} x_{1} y_{1} /\left(x_{1}+y_{1}\right)$. Let $x_{1}=d x_{2}, y_{1}=d y_{2}$ with $\operatorname{gcd}\left(x_{2}, y_{2}\right)=1$. So $z=$ $2^{s+2} d x_{2} y_{2} /\left(x_{2}+y_{2}\right)$. As $z$ is odd, it must be that $x_{2}+y_{2}$ is divisible by $2^{s+2} \geq 4$, so $x_{2}+y_{2}$ is divisible by 4 . As $x_{2}$ and $y_{2}$ are odd integers, one of them, say $x_{2}$ is congruent to 3 modulo 4. But $\operatorname{gcd}\left(x_{2}, x_{2}+y_{2}\right)=1$, so $x_{2}$ is a divisor of $z$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $x$ and $y$ be positive integers and assume that $z=4 x y /(x+y)$ is an odd integer. Prove that at least one divisor of $z$ can be expressed in the form $4 n-1$ where $n$ is a positive integer.
|
Let $x=2^{s} x_{1}$ and $y=2^{t} y_{1}$ where $x_{1}$ and $y_{1}$ are odd integers. Without loss of generality we can assume that $s \geq t$. We have
$$
z=\frac{2^{s+t+2} x_{1} y_{1}}{2^{t}\left(2^{s-t} x_{1}+y_{1}\right)}=\frac{2^{s+2} x_{1} y_{1}}{2^{s-t} x_{1}+y_{1}}
$$
If $s \neq t$, then the denominator is odd and therefore $z$ is even. So we have $s=t$ and $z=2^{s+2} x_{1} y_{1} /\left(x_{1}+y_{1}\right)$. Let $x_{1}=d x_{2}, y_{1}=d y_{2}$ with $\operatorname{gcd}\left(x_{2}, y_{2}\right)=1$. So $z=$ $2^{s+2} d x_{2} y_{2} /\left(x_{2}+y_{2}\right)$. As $z$ is odd, it must be that $x_{2}+y_{2}$ is divisible by $2^{s+2} \geq 4$, so $x_{2}+y_{2}$ is divisible by 4 . As $x_{2}$ and $y_{2}$ are odd integers, one of them, say $x_{2}$ is congruent to 3 modulo 4. But $\operatorname{gcd}\left(x_{2}, x_{2}+y_{2}\right)=1$, so $x_{2}$ is a divisor of $z$.
|
{
"exam": "BalticWay",
"problem_label": "18",
"problem_match": "\n18.",
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2005"
}
|
Is it possible to find 2005 different positive square numbers such that their sum is also a square number?
Answer: Yes, it is possible.
|
Start with a simple Pythagorian identity such as $3^{2}+4^{2}=5^{2}$. Multiply it by $5^{2}$
$$
3^{2} \cdot 5^{2}+4^{2} \cdot 5^{2}=5^{2} \cdot 5^{2}
$$
and insert the identity for the first
$$
3^{2} \cdot\left(3^{2}+4^{2}\right)+4^{2} \cdot 5^{2}=5^{2} \cdot 5^{2}
$$
which gives
$$
3^{2} \cdot 3^{2}+3^{2} \cdot 4^{2}+4^{2} \cdot 5^{2}=5^{2} \cdot 5^{2} .
$$
Multiply again by $5^{2}$
$$
3^{2} \cdot 3^{2} \cdot 5^{2}+3^{2} \cdot 4^{2} \cdot 5^{2}+4^{2} \cdot 5^{2} \cdot 5^{2}=5^{2} \cdot 5^{2} \cdot 5^{2}
$$
and split the first term
$$
3^{2} \cdot 3^{2} \cdot\left(3^{2}+4^{2}\right)+3^{2} \cdot 4^{2} \cdot 5^{2}+4^{2} \cdot 5^{2} \cdot 5^{2}=5^{2} \cdot 5^{2} \cdot 5^{2}
$$
that is
$$
3^{2} \cdot 3^{2} \cdot 3^{2}+3^{2} \cdot 3^{2} \cdot 4^{2}+3^{2} \cdot 4^{2} \cdot 5^{2}+4^{2} \cdot 5^{2} \cdot 5^{2}=5^{2} \cdot 5^{2} \cdot 5^{2} .
$$
This (multiplying by $5^{2}$ and splitting the first term) can be repeated as often as needed, each time increasing the number of terms by one.
Clearly, each term is a square number and the terms are strictly increasing from left to right.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Is it possible to find 2005 different positive square numbers such that their sum is also a square number?
Answer: Yes, it is possible.
|
Start with a simple Pythagorian identity such as $3^{2}+4^{2}=5^{2}$. Multiply it by $5^{2}$
$$
3^{2} \cdot 5^{2}+4^{2} \cdot 5^{2}=5^{2} \cdot 5^{2}
$$
and insert the identity for the first
$$
3^{2} \cdot\left(3^{2}+4^{2}\right)+4^{2} \cdot 5^{2}=5^{2} \cdot 5^{2}
$$
which gives
$$
3^{2} \cdot 3^{2}+3^{2} \cdot 4^{2}+4^{2} \cdot 5^{2}=5^{2} \cdot 5^{2} .
$$
Multiply again by $5^{2}$
$$
3^{2} \cdot 3^{2} \cdot 5^{2}+3^{2} \cdot 4^{2} \cdot 5^{2}+4^{2} \cdot 5^{2} \cdot 5^{2}=5^{2} \cdot 5^{2} \cdot 5^{2}
$$
and split the first term
$$
3^{2} \cdot 3^{2} \cdot\left(3^{2}+4^{2}\right)+3^{2} \cdot 4^{2} \cdot 5^{2}+4^{2} \cdot 5^{2} \cdot 5^{2}=5^{2} \cdot 5^{2} \cdot 5^{2}
$$
that is
$$
3^{2} \cdot 3^{2} \cdot 3^{2}+3^{2} \cdot 3^{2} \cdot 4^{2}+3^{2} \cdot 4^{2} \cdot 5^{2}+4^{2} \cdot 5^{2} \cdot 5^{2}=5^{2} \cdot 5^{2} \cdot 5^{2} .
$$
This (multiplying by $5^{2}$ and splitting the first term) can be repeated as often as needed, each time increasing the number of terms by one.
Clearly, each term is a square number and the terms are strictly increasing from left to right.
|
{
"exam": "BalticWay",
"problem_label": "19",
"problem_match": "\n19.",
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2005"
}
|
Find all positive integers $n=p_{1} p_{2} \cdots p_{k}$ which divide $\left(p_{1}+1\right)\left(p_{2}+1\right) \cdots\left(p_{k}+1\right)$, where $p_{1} p_{2} \cdots p_{k}$ is the factorization of $n$ into prime factors (not necessarily distinct).
Answer: All numbers $2^{r} 3^{s}$ where $r$ and $s$ are non-negative integers and $s \leq r \leq 2 s$.
|
Let $m=\left(p_{1}+1\right)\left(p_{2}+1\right) \cdots\left(p_{k}+1\right)$. We may assume that $p_{k}$ is the largest prime factor. If $p_{k}>3$ then $p_{k}$ cannot divide $m$, because if $p_{k}$ divides $m$ it is a prime factor of $p_{i}+1$ for some $i$, but if $p_{i}=2$ then $p_{i}+1<p_{k}$, and otherwise $p_{i}+1$ is an even number with factors 2 and $\frac{1}{2}\left(p_{i}+1\right)$ which are both strictly smaller than $p_{k}$. Thus the only primes that can divide $n$ are 2 and 3 , so we can write $n=2^{r} 3^{s}$. Then $m=3^{r} 4^{s}=2^{2 s} 3^{r}$ which is divisible by $n$ if and only if $s \leq r \leq 2 s$.
|
All\ numbers\ 2^{r}3^{s}\ where\ r\ and\ s\ are\ non-negative\ integers\ and\ s \leq r \leq 2s
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all positive integers $n=p_{1} p_{2} \cdots p_{k}$ which divide $\left(p_{1}+1\right)\left(p_{2}+1\right) \cdots\left(p_{k}+1\right)$, where $p_{1} p_{2} \cdots p_{k}$ is the factorization of $n$ into prime factors (not necessarily distinct).
Answer: All numbers $2^{r} 3^{s}$ where $r$ and $s$ are non-negative integers and $s \leq r \leq 2 s$.
|
Let $m=\left(p_{1}+1\right)\left(p_{2}+1\right) \cdots\left(p_{k}+1\right)$. We may assume that $p_{k}$ is the largest prime factor. If $p_{k}>3$ then $p_{k}$ cannot divide $m$, because if $p_{k}$ divides $m$ it is a prime factor of $p_{i}+1$ for some $i$, but if $p_{i}=2$ then $p_{i}+1<p_{k}$, and otherwise $p_{i}+1$ is an even number with factors 2 and $\frac{1}{2}\left(p_{i}+1\right)$ which are both strictly smaller than $p_{k}$. Thus the only primes that can divide $n$ are 2 and 3 , so we can write $n=2^{r} 3^{s}$. Then $m=3^{r} 4^{s}=2^{2 s} 3^{r}$ which is divisible by $n$ if and only if $s \leq r \leq 2 s$.
|
{
"exam": "BalticWay",
"problem_label": "20",
"problem_match": "\n20.",
"resource_path": "BalticWay/segmented/en-bw05sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2005"
}
|
For a sequence $a_{1}, a_{2}, a_{3}, \ldots$ of real numbers it is known that
$$
a_{n}=a_{n-1}+a_{n+2} \quad \text { for } n=2,3,4, \ldots
$$
What is the largest number of its consecutive elements that can all be positive?
Answer: 5.
|
The initial segment of the sequence could be $1 ; 2 ; 3 ; 1 ; 1 ;-2 ; 0$. Clearly it is enough to consider only initial segments. For each sequence the first 6 elements are $a_{1} ; a_{2}$; $a_{3} ; a_{2}-a_{1} ; a_{3}-a_{2} ; a_{2}-a_{1}-a_{3}$. As we see, $a_{1}+a_{5}+a_{6}=a_{1}+\left(a_{3}-a_{2}\right)+\left(a_{2}-a_{1}-a_{3}\right)=$ 0 . So all the elements $a_{1}, a_{5}, a_{6}$ can not be positive simultaneously.
|
5
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
For a sequence $a_{1}, a_{2}, a_{3}, \ldots$ of real numbers it is known that
$$
a_{n}=a_{n-1}+a_{n+2} \quad \text { for } n=2,3,4, \ldots
$$
What is the largest number of its consecutive elements that can all be positive?
Answer: 5.
|
The initial segment of the sequence could be $1 ; 2 ; 3 ; 1 ; 1 ;-2 ; 0$. Clearly it is enough to consider only initial segments. For each sequence the first 6 elements are $a_{1} ; a_{2}$; $a_{3} ; a_{2}-a_{1} ; a_{3}-a_{2} ; a_{2}-a_{1}-a_{3}$. As we see, $a_{1}+a_{5}+a_{6}=a_{1}+\left(a_{3}-a_{2}\right)+\left(a_{2}-a_{1}-a_{3}\right)=$ 0 . So all the elements $a_{1}, a_{5}, a_{6}$ can not be positive simultaneously.
|
{
"exam": "BalticWay",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "BalticWay/segmented/en-bw06sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2006"
}
|
Suppose that the real numbers $a_{i} \in[-2,17], i=1,2, \ldots, 59$, satisfy $a_{1}+a_{2}+\cdots+a_{59}=0$. Prove that
$$
a_{1}^{2}+a_{2}^{2}+\cdots+a_{59}^{2} \leq 2006 .
$$
|
For convenience denote $m=-2$ and $M=17$. Then
$$
\left(a_{i}-\frac{m+M}{2}\right)^{2} \leq\left(\frac{M-m}{2}\right)^{2},
$$
because $m \leq a_{i} \leq M$. So we have
$$
\begin{aligned}
\sum_{i=1}^{59}\left(a_{i}-\frac{m+M}{2}\right)^{2} & =\sum_{i} a_{i}^{2}+59 \cdot\left(\frac{m+M}{2}\right)^{2}-(m+M) \sum_{i} a_{i} \\
& \leq 59 \cdot\left(\frac{M-m}{2}\right)^{2},
\end{aligned}
$$
and thus
$$
\sum_{i} a_{i}^{2} \leq 59 \cdot\left(\left(\frac{M-m}{2}\right)^{2}-\left(\frac{m+M}{2}\right)^{2}\right)=-59 \cdot m \cdot M=2006 .
$$
|
2006
|
Yes
|
Yes
|
proof
|
Inequalities
|
Suppose that the real numbers $a_{i} \in[-2,17], i=1,2, \ldots, 59$, satisfy $a_{1}+a_{2}+\cdots+a_{59}=0$. Prove that
$$
a_{1}^{2}+a_{2}^{2}+\cdots+a_{59}^{2} \leq 2006 .
$$
|
For convenience denote $m=-2$ and $M=17$. Then
$$
\left(a_{i}-\frac{m+M}{2}\right)^{2} \leq\left(\frac{M-m}{2}\right)^{2},
$$
because $m \leq a_{i} \leq M$. So we have
$$
\begin{aligned}
\sum_{i=1}^{59}\left(a_{i}-\frac{m+M}{2}\right)^{2} & =\sum_{i} a_{i}^{2}+59 \cdot\left(\frac{m+M}{2}\right)^{2}-(m+M) \sum_{i} a_{i} \\
& \leq 59 \cdot\left(\frac{M-m}{2}\right)^{2},
\end{aligned}
$$
and thus
$$
\sum_{i} a_{i}^{2} \leq 59 \cdot\left(\left(\frac{M-m}{2}\right)^{2}-\left(\frac{m+M}{2}\right)^{2}\right)=-59 \cdot m \cdot M=2006 .
$$
|
{
"exam": "BalticWay",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "BalticWay/segmented/en-bw06sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2006"
}
|
Prove that for every polynomial $P(x)$ with real coefficients there exist a positive integer $m$ and polynomials $P_{1}(x), P_{2}(x), \ldots, P_{m}(x)$ with real coefficients such that
$$
P(x)=\left(P_{1}(x)\right)^{3}+\left(P_{2}(x)\right)^{3}+\cdots+\left(P_{m}(x)\right)^{3} .
$$
|
We will prove by induction on the degree of $P(x)$ that all polynomials can be represented as a sum of cubes. This is clear for constant polynomials. Now we proceed to the inductive step. It is sufficient to show that if $P(x)$ is a polynomial of degree $n$, then there exist polynomials $Q_{1}(x), Q_{2}(x), \ldots, Q_{r}(x)$ such that the polynomial
$$
P(x)-\left(Q_{1}(x)\right)^{3}-\left(Q_{2}(x)\right)^{3}-\cdots-\left(Q_{r}(x)\right)^{3}
$$
has degree at most $n-1$. Assume that the coefficient of $x^{n}$ in $P(x)$ is equal to $c$. We consider three cases: If $n=3 k$, we put $r=1, Q_{1}(x)=\sqrt[3]{c} x^{k}$; if $n=3 k+1$ we put $r=3$,
$$
Q_{1}(x)=\sqrt[3]{\frac{c}{6}} x^{k}(x-1), \quad Q_{2}(x)=\sqrt[3]{\frac{c}{6}} x^{k}(x+1), \quad Q_{3}(x)=-\sqrt[3]{\frac{c}{3}} x^{k+1}
$$
and if $n=3 k+2$ we put $r=2$ and
$$
Q_{1}(x)=\sqrt[3]{\frac{c}{3}} x^{k}(x+1), \quad Q_{2}(x)=-\sqrt[3]{\frac{c}{3}} x^{k+1}
$$
This completes the induction.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Prove that for every polynomial $P(x)$ with real coefficients there exist a positive integer $m$ and polynomials $P_{1}(x), P_{2}(x), \ldots, P_{m}(x)$ with real coefficients such that
$$
P(x)=\left(P_{1}(x)\right)^{3}+\left(P_{2}(x)\right)^{3}+\cdots+\left(P_{m}(x)\right)^{3} .
$$
|
We will prove by induction on the degree of $P(x)$ that all polynomials can be represented as a sum of cubes. This is clear for constant polynomials. Now we proceed to the inductive step. It is sufficient to show that if $P(x)$ is a polynomial of degree $n$, then there exist polynomials $Q_{1}(x), Q_{2}(x), \ldots, Q_{r}(x)$ such that the polynomial
$$
P(x)-\left(Q_{1}(x)\right)^{3}-\left(Q_{2}(x)\right)^{3}-\cdots-\left(Q_{r}(x)\right)^{3}
$$
has degree at most $n-1$. Assume that the coefficient of $x^{n}$ in $P(x)$ is equal to $c$. We consider three cases: If $n=3 k$, we put $r=1, Q_{1}(x)=\sqrt[3]{c} x^{k}$; if $n=3 k+1$ we put $r=3$,
$$
Q_{1}(x)=\sqrt[3]{\frac{c}{6}} x^{k}(x-1), \quad Q_{2}(x)=\sqrt[3]{\frac{c}{6}} x^{k}(x+1), \quad Q_{3}(x)=-\sqrt[3]{\frac{c}{3}} x^{k+1}
$$
and if $n=3 k+2$ we put $r=2$ and
$$
Q_{1}(x)=\sqrt[3]{\frac{c}{3}} x^{k}(x+1), \quad Q_{2}(x)=-\sqrt[3]{\frac{c}{3}} x^{k+1}
$$
This completes the induction.
|
{
"exam": "BalticWay",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "BalticWay/segmented/en-bw06sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2006"
}
|
Let $a, b, c, d, e, f$ be non-negative real numbers satisfying $a+b+c+d+e+f=6$. Find the maximal possible value of
$$
a b c+b c d+c d e+d e f+e f a+f a b
$$
and determine all 6-tuples $(a, b, c, d, e, f)$ for which this maximal value is achieved.
Answer: 8 .
|
If we set $a=b=c=2, d=e=f=0$, then the given expression is equal to 8 . We will show that this is the maximal value. Applying the inequality between arithmetic and geometric mean we obtain
$$
\begin{aligned}
8 & =\left(\frac{(a+d)+(b+e)+(c+f)}{3}\right)^{3} \geq(a+d)(b+e)(c+f) \\
& =(a b c+b c d+c d e+d e f+e f a+f a b)+(a c e+b d f),
\end{aligned}
$$
so we see that $a b c+b c d+c d e+d e f+e f a+f a b \leq 8$ and the maximal value 8 is achieved when $a+d=b+e=c+f$ (and then the common value is 2 because $a+b+c+d+$ $e+f=6)$ and $a c e=b d f=0$, which can be written as $(a, b, c, d, e, f)=(a, b, c, 2-a, 2-$ $b, 2-c)$ with $a c(2-b)=b(2-a)(2-c)=0$. From this it follows that $(a, b, c)$ must have one of the forms $(0,0, t),(0, t, 2),(t, 2,2),(2,2, t),(2, t, 0)$ or $(t, 0,0)$. Therefore the maximum is achieved for the 6 -tuples $(a, b, c, d, e, f)=(0,0, t, 2,2,2-t)$, where $0 \leq t \leq 2$, and its cyclic permutations.
|
8
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Let $a, b, c, d, e, f$ be non-negative real numbers satisfying $a+b+c+d+e+f=6$. Find the maximal possible value of
$$
a b c+b c d+c d e+d e f+e f a+f a b
$$
and determine all 6-tuples $(a, b, c, d, e, f)$ for which this maximal value is achieved.
Answer: 8 .
|
If we set $a=b=c=2, d=e=f=0$, then the given expression is equal to 8 . We will show that this is the maximal value. Applying the inequality between arithmetic and geometric mean we obtain
$$
\begin{aligned}
8 & =\left(\frac{(a+d)+(b+e)+(c+f)}{3}\right)^{3} \geq(a+d)(b+e)(c+f) \\
& =(a b c+b c d+c d e+d e f+e f a+f a b)+(a c e+b d f),
\end{aligned}
$$
so we see that $a b c+b c d+c d e+d e f+e f a+f a b \leq 8$ and the maximal value 8 is achieved when $a+d=b+e=c+f$ (and then the common value is 2 because $a+b+c+d+$ $e+f=6)$ and $a c e=b d f=0$, which can be written as $(a, b, c, d, e, f)=(a, b, c, 2-a, 2-$ $b, 2-c)$ with $a c(2-b)=b(2-a)(2-c)=0$. From this it follows that $(a, b, c)$ must have one of the forms $(0,0, t),(0, t, 2),(t, 2,2),(2,2, t),(2, t, 0)$ or $(t, 0,0)$. Therefore the maximum is achieved for the 6 -tuples $(a, b, c, d, e, f)=(0,0, t, 2,2,2-t)$, where $0 \leq t \leq 2$, and its cyclic permutations.
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "BalticWay/segmented/en-bw06sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2006"
}
|
An occasionally unreliable professor has devoted his last book to a certain binary operation $*$. When this operation is applied to any two integers, the result is again an integer. The operation is known to satisfy the following axioms:
(a) $x *(x * y)=y$ for all $x, y \in \mathbb{Z}$;
(b) $(x * y) * y=x$ for all $x, y \in \mathbb{Z}$.
The professor claims in his book that
(C1) the operation $*$ is commutative: $x * y=y * x$ for all $x, y \in \mathbb{Z}$.
(C2) the operation $*$ is associative: $(x * y) * z=x *(y * z)$ for all $x, y, z \in \mathbb{Z}$.
Which of these claims follow from the stated axioms?
Answer: (C1) is true; (C2) is false.
|
Write $(x, y, z)$ for $x * y=z$. So the axioms can be formulated as
$$
\begin{aligned}
& (x, y, z) \Longrightarrow(x, z, y) \\
& (x, y, z) \Longrightarrow(z, y, x) .
\end{aligned}
$$
(C1) is proved by the sequence $(x, y, z) \xrightarrow{(2)}(z, y, x) \xrightarrow{(1)}(z, x, y) \xrightarrow{(2)}(y, x, z)$.
A counterexample for (C2) is the operation $x * y=-(x+y)$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
An occasionally unreliable professor has devoted his last book to a certain binary operation $*$. When this operation is applied to any two integers, the result is again an integer. The operation is known to satisfy the following axioms:
(a) $x *(x * y)=y$ for all $x, y \in \mathbb{Z}$;
(b) $(x * y) * y=x$ for all $x, y \in \mathbb{Z}$.
The professor claims in his book that
(C1) the operation $*$ is commutative: $x * y=y * x$ for all $x, y \in \mathbb{Z}$.
(C2) the operation $*$ is associative: $(x * y) * z=x *(y * z)$ for all $x, y, z \in \mathbb{Z}$.
Which of these claims follow from the stated axioms?
Answer: (C1) is true; (C2) is false.
|
Write $(x, y, z)$ for $x * y=z$. So the axioms can be formulated as
$$
\begin{aligned}
& (x, y, z) \Longrightarrow(x, z, y) \\
& (x, y, z) \Longrightarrow(z, y, x) .
\end{aligned}
$$
(C1) is proved by the sequence $(x, y, z) \xrightarrow{(2)}(z, y, x) \xrightarrow{(1)}(z, x, y) \xrightarrow{(2)}(y, x, z)$.
A counterexample for (C2) is the operation $x * y=-(x+y)$.
|
{
"exam": "BalticWay",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "BalticWay/segmented/en-bw06sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2006"
}
|
Determine the maximal size of a set of positive integers with the following properties:
(1) The integers consist of digits from the set $\{1,2,3,4,5,6\}$.
(2) No digit occurs more than once in the same integer.
(3) The digits in each integer are in increasing order.
(4) Any two integers have at least one digit in common (possibly at different positions).
(5) There is no digit which appears in all the integers.
Answer: 32.
|
Associate with any $a_{i}$ the set $M_{i}$ of its digits. By (??), (??) and (??) the numbers are uniquely determined by their associated subsets of $\{1,2, \ldots, 6\}$. By (??) the sets are intersecting. Partition the 64 subsets of $\{1,2, \ldots, 6\}$ into 32 pairs of complementary sets $(X,\{1,2, \ldots, 6\}-X)$. Obviously, at most one of the two sets in such a pair can be a $M_{i}$, since the two sets are non-intersecting. Hence, $n \leq 32$. Consider the 22 subsets with at least four elements and the 10 subsets with three elements containing 1 . Hence, $n=32$. 7. A photographer took some pictures at a party with 10 people. Each of the 45 possible pairs of people appears together on exactly one photo, and each photo depicts two or three people. What is the smallest possible number of photos taken?
Answer: 19.
|
32
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Determine the maximal size of a set of positive integers with the following properties:
(1) The integers consist of digits from the set $\{1,2,3,4,5,6\}$.
(2) No digit occurs more than once in the same integer.
(3) The digits in each integer are in increasing order.
(4) Any two integers have at least one digit in common (possibly at different positions).
(5) There is no digit which appears in all the integers.
Answer: 32.
|
Associate with any $a_{i}$ the set $M_{i}$ of its digits. By (??), (??) and (??) the numbers are uniquely determined by their associated subsets of $\{1,2, \ldots, 6\}$. By (??) the sets are intersecting. Partition the 64 subsets of $\{1,2, \ldots, 6\}$ into 32 pairs of complementary sets $(X,\{1,2, \ldots, 6\}-X)$. Obviously, at most one of the two sets in such a pair can be a $M_{i}$, since the two sets are non-intersecting. Hence, $n \leq 32$. Consider the 22 subsets with at least four elements and the 10 subsets with three elements containing 1 . Hence, $n=32$. 7. A photographer took some pictures at a party with 10 people. Each of the 45 possible pairs of people appears together on exactly one photo, and each photo depicts two or three people. What is the smallest possible number of photos taken?
Answer: 19.
|
{
"exam": "BalticWay",
"problem_label": "6",
"problem_match": "\n6.",
"resource_path": "BalticWay/segmented/en-bw06sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2006"
}
|
Determine the maximal size of a set of positive integers with the following properties:
(1) The integers consist of digits from the set $\{1,2,3,4,5,6\}$.
(2) No digit occurs more than once in the same integer.
(3) The digits in each integer are in increasing order.
(4) Any two integers have at least one digit in common (possibly at different positions).
(5) There is no digit which appears in all the integers.
Answer: 32.
|
Let $x$ be the number of triplet photos (depicting three people, that is, three pairs) and let $y$ be the number of pair photos (depicting two people, that is, one pair). Then $3 x+y=45$.
Each person appears with nine other people, and since 9 is odd, each person appears on at least one pair photo. Thus $y \geq 5$, so that $x \leq 13$. The total number of photos is $x+y=45-2 x \geq 45-2 \cdot 13=19$.
On the other hand, 19 photos will suffice. We number the persons $0,1, \ldots, 9$, and will proceed to specify 13 triplet photos. We start with making triplets without common pairs of the persons $1-8$ :
$$
123,345,567,781
$$
Think of the persons 1-8 as arranged in order around a circle. Then the persons in each triplet above are separated by at most one person. Next we make triplets containing 0 , avoiding previously mentioned pairs by combining 0 with two people among the persons $1-8$ separated by two persons:
$$
014,085,027,036
$$
Then we make triplets containing 9, again avoiding previously mentioned pairs by combining 9 with the other four possibilities of two people among 1-8 being separated by two persons:
$$
916,925,938,947
$$
Finally, we make our last triplet, again by combining people from 1-8: 246 . Here 2 and 4 , and 4 and 6 , are separated by one person, but those pairs were not accounted for in the first list, whereas 2 and 6 are separated by three persons, and have not been paired before. We now have 13 photos of 39 pairs. The remaining 6 pairs appear on 6 pair photos.
Remark: This problem is equivalent to asking how many complete 3-graphs can be packed (without common edges) into a complete 10-graph.
|
19
|
Yes
|
Problem not solved
|
math-word-problem
|
Combinatorics
|
Determine the maximal size of a set of positive integers with the following properties:
(1) The integers consist of digits from the set $\{1,2,3,4,5,6\}$.
(2) No digit occurs more than once in the same integer.
(3) The digits in each integer are in increasing order.
(4) Any two integers have at least one digit in common (possibly at different positions).
(5) There is no digit which appears in all the integers.
Answer: 32.
|
Let $x$ be the number of triplet photos (depicting three people, that is, three pairs) and let $y$ be the number of pair photos (depicting two people, that is, one pair). Then $3 x+y=45$.
Each person appears with nine other people, and since 9 is odd, each person appears on at least one pair photo. Thus $y \geq 5$, so that $x \leq 13$. The total number of photos is $x+y=45-2 x \geq 45-2 \cdot 13=19$.
On the other hand, 19 photos will suffice. We number the persons $0,1, \ldots, 9$, and will proceed to specify 13 triplet photos. We start with making triplets without common pairs of the persons $1-8$ :
$$
123,345,567,781
$$
Think of the persons 1-8 as arranged in order around a circle. Then the persons in each triplet above are separated by at most one person. Next we make triplets containing 0 , avoiding previously mentioned pairs by combining 0 with two people among the persons $1-8$ separated by two persons:
$$
014,085,027,036
$$
Then we make triplets containing 9, again avoiding previously mentioned pairs by combining 9 with the other four possibilities of two people among 1-8 being separated by two persons:
$$
916,925,938,947
$$
Finally, we make our last triplet, again by combining people from 1-8: 246 . Here 2 and 4 , and 4 and 6 , are separated by one person, but those pairs were not accounted for in the first list, whereas 2 and 6 are separated by three persons, and have not been paired before. We now have 13 photos of 39 pairs. The remaining 6 pairs appear on 6 pair photos.
Remark: This problem is equivalent to asking how many complete 3-graphs can be packed (without common edges) into a complete 10-graph.
|
{
"exam": "BalticWay",
"problem_label": "6",
"problem_match": "\n6.",
"resource_path": "BalticWay/segmented/en-bw06sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2006"
}
|
The director has found out that six conspiracies have been set up in his department, each of them involving exactly three persons. Prove that the director can split the department in two laboratories so that none of the conspirative groups is entirely in the same laboratory.
|
Let the department consist of $n$ persons. Clearly $n>4$ (because $\left(\begin{array}{l}4 \\ 3\end{array}\right)<6$ ). If $n=5$, take three persons who do not make a conspiracy and put them in one laboratory, the other two in another. If $n=6$, note that $\left(\begin{array}{l}6 \\ 3\end{array}\right)=20$, so we can find a three-person set such that neither it nor its complement is a conspiracy; this set will form one laboratory. If $n \geq 7$, use induction. We have $\left(\begin{array}{l}n \\ 2\end{array}\right) \geq\left(\begin{array}{l}7 \\ 2\end{array}\right)=21>6 \cdot 3$, so there are two persons $A$ and $B$ who are not together in any conspiracy. Replace $A$ and $B$ by a new person $A B$ and use the inductive hypothesis; then replace $A B$ by initial persons $A$ and $B$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
The director has found out that six conspiracies have been set up in his department, each of them involving exactly three persons. Prove that the director can split the department in two laboratories so that none of the conspirative groups is entirely in the same laboratory.
|
Let the department consist of $n$ persons. Clearly $n>4$ (because $\left(\begin{array}{l}4 \\ 3\end{array}\right)<6$ ). If $n=5$, take three persons who do not make a conspiracy and put them in one laboratory, the other two in another. If $n=6$, note that $\left(\begin{array}{l}6 \\ 3\end{array}\right)=20$, so we can find a three-person set such that neither it nor its complement is a conspiracy; this set will form one laboratory. If $n \geq 7$, use induction. We have $\left(\begin{array}{l}n \\ 2\end{array}\right) \geq\left(\begin{array}{l}7 \\ 2\end{array}\right)=21>6 \cdot 3$, so there are two persons $A$ and $B$ who are not together in any conspiracy. Replace $A$ and $B$ by a new person $A B$ and use the inductive hypothesis; then replace $A B$ by initial persons $A$ and $B$.
|
{
"exam": "BalticWay",
"problem_label": "8",
"problem_match": "\n8.",
"resource_path": "BalticWay/segmented/en-bw06sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2006"
}
|
To every vertex of a regular pentagon a real number is assigned. We may perform the following operation repeatedly: we choose two adjacent vertices of the pentagon and replace each of the two numbers assigned to these vertices by their arithmetic mean. Is it always possible to obtain the position in which all five numbers are zeroes, given that in the initial position the sum of all five numbers is equal to zero?
Answer: No.
|
We will show that starting from the numbers $-\frac{1}{5},-\frac{1}{5},-\frac{1}{5},-\frac{1}{5}, \frac{4}{5}$ we cannot get five zeroes. By adding $\frac{1}{5}$ to all vertices we see that our task is equivalent to showing that beginning from numbers $0,0,0,0,1$ and performing the same operations we can never get five numbers $\frac{1}{5}$. This we prove by noticing that in the initial position all the numbers are "binary rational" - that is, of the form $\frac{k}{2^{m}}$, where $k$ is an integer and $m$ is a non-negative integer - and an arithmetic mean of two binary rationals is also such a number, while the number $\frac{1}{5}$ is not of such form.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
To every vertex of a regular pentagon a real number is assigned. We may perform the following operation repeatedly: we choose two adjacent vertices of the pentagon and replace each of the two numbers assigned to these vertices by their arithmetic mean. Is it always possible to obtain the position in which all five numbers are zeroes, given that in the initial position the sum of all five numbers is equal to zero?
Answer: No.
|
We will show that starting from the numbers $-\frac{1}{5},-\frac{1}{5},-\frac{1}{5},-\frac{1}{5}, \frac{4}{5}$ we cannot get five zeroes. By adding $\frac{1}{5}$ to all vertices we see that our task is equivalent to showing that beginning from numbers $0,0,0,0,1$ and performing the same operations we can never get five numbers $\frac{1}{5}$. This we prove by noticing that in the initial position all the numbers are "binary rational" - that is, of the form $\frac{k}{2^{m}}$, where $k$ is an integer and $m$ is a non-negative integer - and an arithmetic mean of two binary rationals is also such a number, while the number $\frac{1}{5}$ is not of such form.
|
{
"exam": "BalticWay",
"problem_label": "9",
"problem_match": "\n9.",
"resource_path": "BalticWay/segmented/en-bw06sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2006"
}
|
162 pluses and 144 minuses are placed in a $30 \times 30$ table in such a way that each row and each column contains at most 17 signs. (No cell contains more than one sign.) For every plus we count the number of minuses in its row and for every minus we count the number of pluses in its column. Find the maximum of the sum of these numbers.
Answer: $1296=72 \cdot 18$.
|
In the statement of the problem there are two kinds of numbers: "horizontal" (that has been counted for pluses) and "vertical" (for minuses). We will show that the sum of numbers of each type reaches its maximum on the same configuration.
We restrict our attention to the horizontal numbers only. Consider an arbitrary row. Let it contains $p$ pluses and $m$ minuses, $m+p \leq 17$. Then the sum that has been counted for pluses in this row is equal to $m p$. Let us redistribute this sum between all signs in the row. More precisely, let us write the number $m p /(m+p)$ in every nonempty cell in the row. Now the whole "horizontal" sum equals to the sum of all 306 written numbers.
Now let us find the maximal possible contribution of each sign in this sum. That is, we ask about maximum of the expression $f(m, p)=m p /(m+p)$ where $m+p \leq 17$. Remark that $f(m, p)$ is an increasing function of $m$. Therefore if $m+p<17$ then increasing of $m$ will also increase the value of $f(m, p)$. Now if $m+p=17$ then $f(m, p)=m(17-m) / 17$ and, obviously, it has maximum $72 / 17$ when $m=8$ or $m=9$.
So all the 306 summands in the horizontal sum will be maximal if we find a configuration in which every non-empty row contains 9 pluses and 8 minuses. The similar statement holds for the vertical sum. In order to obtain the desired configuration take a square $18 \times 18$ and draw pluses on 9 generalized diagonals and minuses on 8 other generalized diagonals (the 18th generalized diagonal remains empty).
|
1296=72 \cdot 18
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
162 pluses and 144 minuses are placed in a $30 \times 30$ table in such a way that each row and each column contains at most 17 signs. (No cell contains more than one sign.) For every plus we count the number of minuses in its row and for every minus we count the number of pluses in its column. Find the maximum of the sum of these numbers.
Answer: $1296=72 \cdot 18$.
|
In the statement of the problem there are two kinds of numbers: "horizontal" (that has been counted for pluses) and "vertical" (for minuses). We will show that the sum of numbers of each type reaches its maximum on the same configuration.
We restrict our attention to the horizontal numbers only. Consider an arbitrary row. Let it contains $p$ pluses and $m$ minuses, $m+p \leq 17$. Then the sum that has been counted for pluses in this row is equal to $m p$. Let us redistribute this sum between all signs in the row. More precisely, let us write the number $m p /(m+p)$ in every nonempty cell in the row. Now the whole "horizontal" sum equals to the sum of all 306 written numbers.
Now let us find the maximal possible contribution of each sign in this sum. That is, we ask about maximum of the expression $f(m, p)=m p /(m+p)$ where $m+p \leq 17$. Remark that $f(m, p)$ is an increasing function of $m$. Therefore if $m+p<17$ then increasing of $m$ will also increase the value of $f(m, p)$. Now if $m+p=17$ then $f(m, p)=m(17-m) / 17$ and, obviously, it has maximum $72 / 17$ when $m=8$ or $m=9$.
So all the 306 summands in the horizontal sum will be maximal if we find a configuration in which every non-empty row contains 9 pluses and 8 minuses. The similar statement holds for the vertical sum. In order to obtain the desired configuration take a square $18 \times 18$ and draw pluses on 9 generalized diagonals and minuses on 8 other generalized diagonals (the 18th generalized diagonal remains empty).
|
{
"exam": "BalticWay",
"problem_label": "10",
"problem_match": "\n10.",
"resource_path": "BalticWay/segmented/en-bw06sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2006"
}
|
The altitudes of a triangle are 12,15 and 20. What is the area of the triangle?
Answer: 150.
|
Denote the sides of the triangle by $a, b$ and $c$ and its altitudes by $h_{a}, h_{b}$ and $h_{c}$. Then we know that $h_{a}=12, h_{b}=15$ and $h_{c}=20$. By the well known relation $a: b=h_{b}: h_{a}$ it follows $b=\frac{h_{a}}{h_{b}} a=\frac{12}{15} a=\frac{4}{5} a$. Analogously, $c=\frac{h_{a}}{h_{c}} a=\frac{12}{20} a=\frac{3}{5} a$. Thus half of the triangle's circumference is $s=\frac{1}{2}(a+b+c)=\frac{1}{2}\left(a+\frac{4}{5} a+\frac{3}{5} a\right)=\frac{6}{5} a$. For the area $\Delta$ of the triangle we have $\Delta=\frac{1}{2} a h_{a}=\frac{1}{2} a 12=6 a$, and also by the well known Heron formula $\Delta=\sqrt{s(s-a)(s-b)(s-c)}=\sqrt{\frac{6}{5} a \cdot \frac{1}{5} a \cdot \frac{2}{5} a \cdot \frac{3}{5} a}=\sqrt{\frac{6^{2}}{5^{4}} a^{4}}=\frac{6}{25} a^{2}$. Hence, $6 a=\frac{6}{25} a^{2}$, and we get $a=25(b=20, c=15)$ and consequently $\Delta=150$.
|
150
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
The altitudes of a triangle are 12,15 and 20. What is the area of the triangle?
Answer: 150.
|
Denote the sides of the triangle by $a, b$ and $c$ and its altitudes by $h_{a}, h_{b}$ and $h_{c}$. Then we know that $h_{a}=12, h_{b}=15$ and $h_{c}=20$. By the well known relation $a: b=h_{b}: h_{a}$ it follows $b=\frac{h_{a}}{h_{b}} a=\frac{12}{15} a=\frac{4}{5} a$. Analogously, $c=\frac{h_{a}}{h_{c}} a=\frac{12}{20} a=\frac{3}{5} a$. Thus half of the triangle's circumference is $s=\frac{1}{2}(a+b+c)=\frac{1}{2}\left(a+\frac{4}{5} a+\frac{3}{5} a\right)=\frac{6}{5} a$. For the area $\Delta$ of the triangle we have $\Delta=\frac{1}{2} a h_{a}=\frac{1}{2} a 12=6 a$, and also by the well known Heron formula $\Delta=\sqrt{s(s-a)(s-b)(s-c)}=\sqrt{\frac{6}{5} a \cdot \frac{1}{5} a \cdot \frac{2}{5} a \cdot \frac{3}{5} a}=\sqrt{\frac{6^{2}}{5^{4}} a^{4}}=\frac{6}{25} a^{2}$. Hence, $6 a=\frac{6}{25} a^{2}$, and we get $a=25(b=20, c=15)$ and consequently $\Delta=150$.
|
{
"exam": "BalticWay",
"problem_label": "11",
"problem_match": "\n11.",
"resource_path": "BalticWay/segmented/en-bw06sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2006"
}
|
Let $A B C$ be a triangle, let $B_{1}$ be the midpoint of the side $A B$ and $C_{1}$ the midpoint of the side $A C$. Let $P$ be the point of intersection, other than $A$, of the circumscribed circles around the triangles $A B C_{1}$ and $A B_{1} C$. Let $P_{1}$ be the point of intersection, other than $A$, of the line $A P$ with the circumscribed circle around the triangle $A B_{1} C_{1}$. Prove that $2 A P=3 A P_{1}$.
|
Since $\angle P B B_{1}=\angle P B A=180^{\circ}-\angle P C_{1} A=\angle P C_{1} C$ and $\angle P C C_{1}=\angle P C A=$ $180^{\circ}-\angle P B_{1} A=\angle P B_{1} B$ it follows that $\triangle P B B_{1}$ is similar to $\triangle P C_{1} C$. Let $B_{2}$ and $C_{2}$ be the midpoints of $B B_{1}$ and $C C_{1}$ respectively. It follows that $\angle B P B_{2}=\angle C_{1} P C_{2}$ and hence $\angle B_{2} P C_{2}=\angle B P C_{1}=180^{\circ}-\angle B A C$, which implies that $A B_{2} P C_{2}$ lie on a circle. By similarity it is now clear that $A P / A P_{1}=A B_{2} / A B_{1}=A C_{2} / A C_{1}=3 / 2$.

|
2 AP = 3 AP_1
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle, let $B_{1}$ be the midpoint of the side $A B$ and $C_{1}$ the midpoint of the side $A C$. Let $P$ be the point of intersection, other than $A$, of the circumscribed circles around the triangles $A B C_{1}$ and $A B_{1} C$. Let $P_{1}$ be the point of intersection, other than $A$, of the line $A P$ with the circumscribed circle around the triangle $A B_{1} C_{1}$. Prove that $2 A P=3 A P_{1}$.
|
Since $\angle P B B_{1}=\angle P B A=180^{\circ}-\angle P C_{1} A=\angle P C_{1} C$ and $\angle P C C_{1}=\angle P C A=$ $180^{\circ}-\angle P B_{1} A=\angle P B_{1} B$ it follows that $\triangle P B B_{1}$ is similar to $\triangle P C_{1} C$. Let $B_{2}$ and $C_{2}$ be the midpoints of $B B_{1}$ and $C C_{1}$ respectively. It follows that $\angle B P B_{2}=\angle C_{1} P C_{2}$ and hence $\angle B_{2} P C_{2}=\angle B P C_{1}=180^{\circ}-\angle B A C$, which implies that $A B_{2} P C_{2}$ lie on a circle. By similarity it is now clear that $A P / A P_{1}=A B_{2} / A B_{1}=A C_{2} / A C_{1}=3 / 2$.

|
{
"exam": "BalticWay",
"problem_label": "12",
"problem_match": "\n12.",
"resource_path": "BalticWay/segmented/en-bw06sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2006"
}
|
In a triangle $A B C$, points $D, E$ lie on sides $A B, A C$ respectively. The lines $B E$ and $C D$ intersect at $F$. Prove that if
$$
B C^{2}=B D \cdot B A+C E \cdot C A,
$$
then the points $A, D, F, E$ lie on a circle.
|
Let $G$ be a point on the segment $B C$ determined by the condition $B G \cdot B C=$ $B D \cdot B A$. (Such a point exists because $B D \cdot B A<B C^{2}$.) Then the points $A, D, G, C$ lie on a circle. Moreover, we have
$$
C E \cdot C A=B C^{2}-B D \cdot B A=B C \cdot(B G+C G)-B C \cdot B G=C B \cdot C G,
$$
hence the points $A, B, G, E$ lie on a circle as well. Therefore
$$
\angle D A G=\angle D C G, \quad \angle E A G=\angle E B G,
$$
which implies that
$$
\begin{aligned}
\angle D A E+\angle D F E & =\angle D A G+\angle E A G+\angle B F C \\
& =\angle D C G+\angle E B G+\angle B F C .
\end{aligned}
$$
But the sum on the right side is the sum of angles in $\triangle B F C$. Thus $\angle D A E+\angle D F E=180^{\circ}$, and the desired result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In a triangle $A B C$, points $D, E$ lie on sides $A B, A C$ respectively. The lines $B E$ and $C D$ intersect at $F$. Prove that if
$$
B C^{2}=B D \cdot B A+C E \cdot C A,
$$
then the points $A, D, F, E$ lie on a circle.
|
Let $G$ be a point on the segment $B C$ determined by the condition $B G \cdot B C=$ $B D \cdot B A$. (Such a point exists because $B D \cdot B A<B C^{2}$.) Then the points $A, D, G, C$ lie on a circle. Moreover, we have
$$
C E \cdot C A=B C^{2}-B D \cdot B A=B C \cdot(B G+C G)-B C \cdot B G=C B \cdot C G,
$$
hence the points $A, B, G, E$ lie on a circle as well. Therefore
$$
\angle D A G=\angle D C G, \quad \angle E A G=\angle E B G,
$$
which implies that
$$
\begin{aligned}
\angle D A E+\angle D F E & =\angle D A G+\angle E A G+\angle B F C \\
& =\angle D C G+\angle E B G+\angle B F C .
\end{aligned}
$$
But the sum on the right side is the sum of angles in $\triangle B F C$. Thus $\angle D A E+\angle D F E=180^{\circ}$, and the desired result follows.
|
{
"exam": "BalticWay",
"problem_label": "13",
"problem_match": "\n13.",
"resource_path": "BalticWay/segmented/en-bw06sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2006"
}
|
There are 2006 points marked on the surface of a sphere. Prove that the surface can be cut into 2006 congruent pieces so that each piece contains exactly one of these points inside it.
|
Choose a North Pole and a South Pole so that no two points are on the same parallel and no point coincides with either pole. Draw parallels through each point. Divide each of these parallels into 2006 equal arcs so that no point is the endpoint of any arc. In the sequel, "to connect two points" means to draw the smallest arc of the great circle passing through these points. Denote the points of division by $A_{i, j}$, where $i$ is the number of the parallel counting from North to South $(i=1,2, \ldots, 2006)$, and $A_{i, 1}, A_{i, 2}, \ldots, A_{i, 2006}$ are the points of division on the $i$ 'th parallel, where the numbering is chosen such that the marked point on the $i^{\prime}$ th parallel lies between $A_{i, i}$ and $A_{i, i+1}$.
Consider the lines connecting gradually
$$
\begin{gathered}
N-A_{1,1}-A_{2,1}-A_{3,1}-\cdots-A_{2006,1}-S \\
N-A_{1,2}-A_{2,2}-A_{3,2}-\cdots-A_{2006,2}-S \\
\vdots \\
N-A_{1,2006}-A_{2,2006}-A_{3,2006}-\cdots-A_{2006,2006}-S
\end{gathered}
$$
These lines divide the surface of the sphere into 2006 parts which are congruent by rotation; each part contains one of the given points.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
There are 2006 points marked on the surface of a sphere. Prove that the surface can be cut into 2006 congruent pieces so that each piece contains exactly one of these points inside it.
|
Choose a North Pole and a South Pole so that no two points are on the same parallel and no point coincides with either pole. Draw parallels through each point. Divide each of these parallels into 2006 equal arcs so that no point is the endpoint of any arc. In the sequel, "to connect two points" means to draw the smallest arc of the great circle passing through these points. Denote the points of division by $A_{i, j}$, where $i$ is the number of the parallel counting from North to South $(i=1,2, \ldots, 2006)$, and $A_{i, 1}, A_{i, 2}, \ldots, A_{i, 2006}$ are the points of division on the $i$ 'th parallel, where the numbering is chosen such that the marked point on the $i^{\prime}$ th parallel lies between $A_{i, i}$ and $A_{i, i+1}$.
Consider the lines connecting gradually
$$
\begin{gathered}
N-A_{1,1}-A_{2,1}-A_{3,1}-\cdots-A_{2006,1}-S \\
N-A_{1,2}-A_{2,2}-A_{3,2}-\cdots-A_{2006,2}-S \\
\vdots \\
N-A_{1,2006}-A_{2,2006}-A_{3,2006}-\cdots-A_{2006,2006}-S
\end{gathered}
$$
These lines divide the surface of the sphere into 2006 parts which are congruent by rotation; each part contains one of the given points.
|
{
"exam": "BalticWay",
"problem_label": "14",
"problem_match": "\n14.",
"resource_path": "BalticWay/segmented/en-bw06sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2006"
}
|
Let the medians of the triangle $A B C$ intersect at the point $M$. A line $t$ through $M$ intersects the circumcircle of $A B C$ at $X$ and $Y$ so that $A$ and $C$ lie on the same side of $t$. Prove that $B X \cdot B Y=A X \cdot A Y+C X \cdot C Y$.
|
Let us start with a lemma: If the diagonals of an inscribed quadrilateral $A B C D$ intersect at $O$, then $\frac{A B \cdot B C}{A D \cdot D C}=\frac{B O}{O D}$. Indeed,
$$
\frac{A B \cdot B C}{A D \cdot D C}=\frac{\frac{1}{2} A B \cdot B C \cdot \sin B}{\frac{1}{2} A D \cdot D C \cdot \sin D}=\frac{\operatorname{area}(A B C)}{\operatorname{area}(A D C)}=\frac{h_{1}}{h_{2}}=\frac{B O}{O D}
$$
Now we have (from the lemma) $\frac{A X \cdot A Y}{B X \cdot B Y}=\frac{A R}{R B}$ and $\frac{C X \cdot C Y}{B X \cdot B Y}=\frac{C S}{S B}$, so we have to prove $\frac{A R}{R B}+\frac{C S}{S B}=1$.
Suppose at first that the line $R S$ is not parallel to $A C$. Let $R S$ intersect $A C$ at $K$ and the line parallel to $A C$ through $B$ at $L$. So $\frac{A R}{R B}=\frac{A K}{B L}$ and $\frac{C S}{S B}=\frac{C K}{B L}$; we must prove that $A K+C K=B L$. But $A K+C K=2 K B_{1}$, and $B L=\frac{B M}{M B_{1}} \cdot K B_{1}=2 K B_{1}$, completing the proof.
If $R S \| A C$, the conclusion is trivial.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let the medians of the triangle $A B C$ intersect at the point $M$. A line $t$ through $M$ intersects the circumcircle of $A B C$ at $X$ and $Y$ so that $A$ and $C$ lie on the same side of $t$. Prove that $B X \cdot B Y=A X \cdot A Y+C X \cdot C Y$.
|
Let us start with a lemma: If the diagonals of an inscribed quadrilateral $A B C D$ intersect at $O$, then $\frac{A B \cdot B C}{A D \cdot D C}=\frac{B O}{O D}$. Indeed,
$$
\frac{A B \cdot B C}{A D \cdot D C}=\frac{\frac{1}{2} A B \cdot B C \cdot \sin B}{\frac{1}{2} A D \cdot D C \cdot \sin D}=\frac{\operatorname{area}(A B C)}{\operatorname{area}(A D C)}=\frac{h_{1}}{h_{2}}=\frac{B O}{O D}
$$

Now we have (from the lemma) $\frac{A X \cdot A Y}{B X \cdot B Y}=\frac{A R}{R B}$ and $\frac{C X \cdot C Y}{B X \cdot B Y}=\frac{C S}{S B}$, so we have to prove $\frac{A R}{R B}+\frac{C S}{S B}=1$.
Suppose at first that the line $R S$ is not parallel to $A C$. Let $R S$ intersect $A C$ at $K$ and the line parallel to $A C$ through $B$ at $L$. So $\frac{A R}{R B}=\frac{A K}{B L}$ and $\frac{C S}{S B}=\frac{C K}{B L}$; we must prove that $A K+C K=B L$. But $A K+C K=2 K B_{1}$, and $B L=\frac{B M}{M B_{1}} \cdot K B_{1}=2 K B_{1}$, completing the proof.

If $R S \| A C$, the conclusion is trivial.
|
{
"exam": "BalticWay",
"problem_label": "15",
"problem_match": "\n15.",
"resource_path": "BalticWay/segmented/en-bw06sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2006"
}
|
Are there four distinct positive integers such that adding the product of any two of them to 2006 yields a perfect square?
Answer: No, there are no such integers.
|
Suppose there are such integers. Let us consider the situation modulo 4 . Then each square is 0 or 1 . But $2006 \equiv 2(\bmod 4)$. So the product of each two supposed numbers must be $2(\bmod 4)$ or $3(\bmod 4)$. From this it follows that there are at least three odd numbers (because the product of two even numbers is $0(\bmod 4)$ ). Two of these odd numbers are congruent modulo 4 , so their product is $1(\bmod 4)$, which is a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Are there four distinct positive integers such that adding the product of any two of them to 2006 yields a perfect square?
Answer: No, there are no such integers.
|
Suppose there are such integers. Let us consider the situation modulo 4 . Then each square is 0 or 1 . But $2006 \equiv 2(\bmod 4)$. So the product of each two supposed numbers must be $2(\bmod 4)$ or $3(\bmod 4)$. From this it follows that there are at least three odd numbers (because the product of two even numbers is $0(\bmod 4)$ ). Two of these odd numbers are congruent modulo 4 , so their product is $1(\bmod 4)$, which is a contradiction.
|
{
"exam": "BalticWay",
"problem_label": "16",
"problem_match": "\n16.",
"resource_path": "BalticWay/segmented/en-bw06sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2006"
}
|
Determine all positive integers $n$ such that $3^{n}+1$ is divisible by $n^{2}$.
Answer: Only $n=1$ satisfies the given condition.
|
First observe that if $n^{2} \mid 3^{n}+1$, then $n$ must be odd, because if $n$ is even, then $3^{n}$ is a square of an odd integer, hence $3^{n}+1 \equiv 1+1=2(\bmod 4)$, so $3^{n}+1$ cannot be divisible by $n^{2}$ which is a multiple of 4 .
Assume that for some $n>1$ we have $n^{2} \mid 3^{n}+1$. Let $p$ be the smallest prime divisor of $n$. We have shown that $p>2$. It is also clear that $p \neq 3$, since $3^{n}+1$ is never divisible by 3. Therefore $p \geq 5$. We have $p \mid 3^{n}+1$, so also $p \mid 3^{2 n}-1$. Let $k$ be the smallest positive integer such that $p \mid 3^{k}-1$. Then we have $k \mid 2 n$, but also $k \mid p-1$ by Fermat's theorem. The numbers $3^{1}-1,3^{2}-1$ do not have prime divisors other than 2 , so $p \geq 5$ implies $k \geq 3$. This means that $\operatorname{gcd}(2 n, p-1) \geq k \geq 3$, and therefore $\operatorname{gcd}(n, p-1)>1$, which contradicts the fact that $p$ is the smallest prime divisor of $n$. This completes the proof.
|
1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Determine all positive integers $n$ such that $3^{n}+1$ is divisible by $n^{2}$.
Answer: Only $n=1$ satisfies the given condition.
|
First observe that if $n^{2} \mid 3^{n}+1$, then $n$ must be odd, because if $n$ is even, then $3^{n}$ is a square of an odd integer, hence $3^{n}+1 \equiv 1+1=2(\bmod 4)$, so $3^{n}+1$ cannot be divisible by $n^{2}$ which is a multiple of 4 .
Assume that for some $n>1$ we have $n^{2} \mid 3^{n}+1$. Let $p$ be the smallest prime divisor of $n$. We have shown that $p>2$. It is also clear that $p \neq 3$, since $3^{n}+1$ is never divisible by 3. Therefore $p \geq 5$. We have $p \mid 3^{n}+1$, so also $p \mid 3^{2 n}-1$. Let $k$ be the smallest positive integer such that $p \mid 3^{k}-1$. Then we have $k \mid 2 n$, but also $k \mid p-1$ by Fermat's theorem. The numbers $3^{1}-1,3^{2}-1$ do not have prime divisors other than 2 , so $p \geq 5$ implies $k \geq 3$. This means that $\operatorname{gcd}(2 n, p-1) \geq k \geq 3$, and therefore $\operatorname{gcd}(n, p-1)>1$, which contradicts the fact that $p$ is the smallest prime divisor of $n$. This completes the proof.
|
{
"exam": "BalticWay",
"problem_label": "17",
"problem_match": "\n17.",
"resource_path": "BalticWay/segmented/en-bw06sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2006"
}
|
For a positive integer $n$ let $a_{n}$ denote the last digit of $n^{\left(n^{n}\right)}$. Prove that the sequence $\left(a_{n}\right)$ is periodic and determine the length of the minimal period.
|
Let $b_{n}$ and $c_{n}$ denote the last digit of $n$ and $n^{n}$, respectively. Obviously, if $b_{n}=0,1,5,6$, then $c_{n}=0,1,5,6$ and $a_{n}=0,1,5,6$, respectively.
If $b_{n}=9$, then $n^{n} \equiv 1(\bmod 2)$ and consequently $a_{n}=9$. If $b_{n}=4$, then $n^{n} \equiv 0$ $(\bmod 2)$ and consequently $a_{n}=6$.
If $b_{n}=2,3,7$, or 8 , then the last digits of $n^{m}$ run through the periods: $2-4-8-6$, $3-9-7-1,7-9-3-1$ or $8-4-2-6$, respectively. If $b_{n}=2$ or $b_{n}=8$, then $n^{n} \equiv 0$ $(\bmod 4)$ and $a_{n}=6$.
In the remaining cases $b_{n}=3$ or $b_{n}=7$, if $n \equiv \pm 1(\bmod 4)$, then so is $n^{n}$.
If $b_{n}=3$, then $n \equiv 3(\bmod 20)$ or $n \equiv 13(\bmod 20)$ and $n^{n} \equiv 7(\bmod 20)$ or $n^{n} \equiv 13$ $(\bmod 20)$, so $a_{n}=7$ or $a_{n}=3$, respectively.
If $b_{n}=7$, then $n \equiv 7(\bmod 20)$ or $n \equiv 17(\bmod 20)$ and $n^{n} \equiv 3(\bmod 20)$ or $n^{n} \equiv 17$ $(\bmod 20)$, so $a_{n}=3$ or $a_{n}=7$, respectively.
Finally, we conclude that the sequence $\left(a_{n}\right)$ has the following period of length 20:
$$
1-6-7-6-5-6-3-6-9-0-1-6-3-6-5-6-7-6-9-0
$$
|
20
|
Yes
|
Yes
|
proof
|
Number Theory
|
For a positive integer $n$ let $a_{n}$ denote the last digit of $n^{\left(n^{n}\right)}$. Prove that the sequence $\left(a_{n}\right)$ is periodic and determine the length of the minimal period.
|
Let $b_{n}$ and $c_{n}$ denote the last digit of $n$ and $n^{n}$, respectively. Obviously, if $b_{n}=0,1,5,6$, then $c_{n}=0,1,5,6$ and $a_{n}=0,1,5,6$, respectively.
If $b_{n}=9$, then $n^{n} \equiv 1(\bmod 2)$ and consequently $a_{n}=9$. If $b_{n}=4$, then $n^{n} \equiv 0$ $(\bmod 2)$ and consequently $a_{n}=6$.
If $b_{n}=2,3,7$, or 8 , then the last digits of $n^{m}$ run through the periods: $2-4-8-6$, $3-9-7-1,7-9-3-1$ or $8-4-2-6$, respectively. If $b_{n}=2$ or $b_{n}=8$, then $n^{n} \equiv 0$ $(\bmod 4)$ and $a_{n}=6$.
In the remaining cases $b_{n}=3$ or $b_{n}=7$, if $n \equiv \pm 1(\bmod 4)$, then so is $n^{n}$.
If $b_{n}=3$, then $n \equiv 3(\bmod 20)$ or $n \equiv 13(\bmod 20)$ and $n^{n} \equiv 7(\bmod 20)$ or $n^{n} \equiv 13$ $(\bmod 20)$, so $a_{n}=7$ or $a_{n}=3$, respectively.
If $b_{n}=7$, then $n \equiv 7(\bmod 20)$ or $n \equiv 17(\bmod 20)$ and $n^{n} \equiv 3(\bmod 20)$ or $n^{n} \equiv 17$ $(\bmod 20)$, so $a_{n}=3$ or $a_{n}=7$, respectively.
Finally, we conclude that the sequence $\left(a_{n}\right)$ has the following period of length 20:
$$
1-6-7-6-5-6-3-6-9-0-1-6-3-6-5-6-7-6-9-0
$$
|
{
"exam": "BalticWay",
"problem_label": "18",
"problem_match": "\n18.",
"resource_path": "BalticWay/segmented/en-bw06sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2006"
}
|
Does there exist a sequence $a_{1}, a_{2}, a_{3}, \ldots$ of positive integers such that the sum of every $n$ consecutive elements is divisible by $n^{2}$ for every positive integer $n$ ?
Answer: Yes. One such sequence begins 1, 3, 5, 55, 561, 851, 63253, 110055,...
|
We will show that whenever we have positive integers $a_{1}, \ldots, a_{k}$ such that $n^{2} \mid a_{i+1}+\cdots+a_{i+n}$ for every $n \leq k$ and $i \leq k-n$, then it is possible to choose $a_{k+1}$ such that $n^{2} \mid a_{i+1}+\cdots+a_{i+n}$ for every $n \leq k+1$ and $i \leq k+1-n$. This directly implies the positive answer to the problem because we can start constructing the sequence from any single positive integer.
To obtain the necessary property, it is sufficient for $a_{k+1}$ to satisfy
$$
a_{k+1} \equiv-\left(a_{k-n+2}+\cdots+a_{k}\right) \quad\left(\bmod n^{2}\right)
$$
for every $n \leq k+1$. This is a system of $k+1$ congruences.
Note first that, for any prime $p$ and positive integer $l$ such that $p^{l} \leq k+1$, if the congruence with module $p^{2 l}$ is satisfied then also the congruence with module $p^{2(l-1)}$ is satisfied. To see this, group the last $p^{l}$ elements of $a_{1}, \ldots, a_{k+1}$ into $p$ groups of $p^{l-1}$ consecutive elements. By choice of $a_{1}, \ldots, a_{k}$, the sums computed for the first $p-1$ groups are all divisible by $p^{2(l-1)}$. By assumption, the sum of the elements in all $p$ groups is divisible by $p^{2 l}$. Hence the sum of the remaining $p^{l-1}$ elements, that is $a_{k-p^{l-1}+2}+\cdots+a_{k+1}$, is divisible by $p^{2(l-1)}$.
Secondly, note that, for any relatively prime positive integers $c, d$ such that $c d \leq k+1$, if the congruences both with module $c^{2}$ and module $d^{2}$ hold then also the congruence with module $(c d)^{2}$ holds. To see this, group the last $c d$ elements of $a_{1}, \ldots, a_{k+1}$ into $d$ groups of $c$ consecutive elements, as well as into $c$ groups of $d$ consecutive elements. Using the choice of $a_{1}, \ldots, a_{k}$ and the assumption together, we get that the sum of the last $c d$ elements of $a_{1}, \ldots, a_{k+1}$ is divisible by both $c^{2}$ and $d^{2}$. Hence this sum is divisible by $(c d)^{2}$.
The two observations let us reject all congruences except for the ones with module being the square of a prime power $p^{l}$ such that $p^{l+1}>k+1$. The resulting system has pairwise relatively prime modules and hence possesses a solution by the Chinese Remainder Theorem.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Does there exist a sequence $a_{1}, a_{2}, a_{3}, \ldots$ of positive integers such that the sum of every $n$ consecutive elements is divisible by $n^{2}$ for every positive integer $n$ ?
Answer: Yes. One such sequence begins 1, 3, 5, 55, 561, 851, 63253, 110055,...
|
We will show that whenever we have positive integers $a_{1}, \ldots, a_{k}$ such that $n^{2} \mid a_{i+1}+\cdots+a_{i+n}$ for every $n \leq k$ and $i \leq k-n$, then it is possible to choose $a_{k+1}$ such that $n^{2} \mid a_{i+1}+\cdots+a_{i+n}$ for every $n \leq k+1$ and $i \leq k+1-n$. This directly implies the positive answer to the problem because we can start constructing the sequence from any single positive integer.
To obtain the necessary property, it is sufficient for $a_{k+1}$ to satisfy
$$
a_{k+1} \equiv-\left(a_{k-n+2}+\cdots+a_{k}\right) \quad\left(\bmod n^{2}\right)
$$
for every $n \leq k+1$. This is a system of $k+1$ congruences.
Note first that, for any prime $p$ and positive integer $l$ such that $p^{l} \leq k+1$, if the congruence with module $p^{2 l}$ is satisfied then also the congruence with module $p^{2(l-1)}$ is satisfied. To see this, group the last $p^{l}$ elements of $a_{1}, \ldots, a_{k+1}$ into $p$ groups of $p^{l-1}$ consecutive elements. By choice of $a_{1}, \ldots, a_{k}$, the sums computed for the first $p-1$ groups are all divisible by $p^{2(l-1)}$. By assumption, the sum of the elements in all $p$ groups is divisible by $p^{2 l}$. Hence the sum of the remaining $p^{l-1}$ elements, that is $a_{k-p^{l-1}+2}+\cdots+a_{k+1}$, is divisible by $p^{2(l-1)}$.
Secondly, note that, for any relatively prime positive integers $c, d$ such that $c d \leq k+1$, if the congruences both with module $c^{2}$ and module $d^{2}$ hold then also the congruence with module $(c d)^{2}$ holds. To see this, group the last $c d$ elements of $a_{1}, \ldots, a_{k+1}$ into $d$ groups of $c$ consecutive elements, as well as into $c$ groups of $d$ consecutive elements. Using the choice of $a_{1}, \ldots, a_{k}$ and the assumption together, we get that the sum of the last $c d$ elements of $a_{1}, \ldots, a_{k+1}$ is divisible by both $c^{2}$ and $d^{2}$. Hence this sum is divisible by $(c d)^{2}$.
The two observations let us reject all congruences except for the ones with module being the square of a prime power $p^{l}$ such that $p^{l+1}>k+1$. The resulting system has pairwise relatively prime modules and hence possesses a solution by the Chinese Remainder Theorem.
|
{
"exam": "BalticWay",
"problem_label": "19",
"problem_match": "\n19.",
"resource_path": "BalticWay/segmented/en-bw06sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2006"
}
|
A 12-digit positive integer consisting only of digits 1,5 and 9 is divisible by 37. Prove that the sum of its digits is not equal to 76.
|
Let $N$ be the initial number. Assume that its digit sum is equal to 76 .
The key observation is that $3 \cdot 37=111$, and therefore $27 \cdot 37=999$. Thus we have a divisibility test similar to the one for divisibility by 9: for $x=a_{n} 10^{3 n}+a_{n-1} 10^{3(n-1)}+$ $\cdots+a_{1} 10^{3}+a_{0}$, we have $x \equiv a_{n}+a_{n-1}+\cdots+a_{0}(\bmod 37)$. In other words, if we take the digits of $x$ in groups of three and sum these groups, we obtain a number congruent to $x$ modulo 37 .
The observation also implies that $A=11111111111$ is divisible by 37 . Therefore the number $N-A$ is divisible by 37 , and since it consists of the digits 0,4 and 8 , it is divisible by 4 . The sum of the digits of $N-A$ equals $76-12=64$. Therefore the number $\frac{1}{4}(N-A)$ contains only the digits $0,1,2$; it is divisible by 37 ; and its digits sum to 16 . Applying our divisibility test to this number, we sum four three-digit groups consisting of the digits $0,1,2$ only. No digits will be carried, and each digit of the sum $S$ is at most 8 . Also $S$ is divisible by 37 , and its digits sum up to 16 . Since $S \equiv 16 \equiv 1(\bmod 3)$ and $37 \equiv 1(\bmod 3)$, we have $S / 37 \equiv 1(\bmod 3)$. Therefore $S=37(3 k+1)$, that is, $S$ is one of $037,148,259,370,481,592,703,814,925$; but each of these either contains the digit 9 or does not have a digit sum of 16 .
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
A 12-digit positive integer consisting only of digits 1,5 and 9 is divisible by 37. Prove that the sum of its digits is not equal to 76.
|
Let $N$ be the initial number. Assume that its digit sum is equal to 76 .
The key observation is that $3 \cdot 37=111$, and therefore $27 \cdot 37=999$. Thus we have a divisibility test similar to the one for divisibility by 9: for $x=a_{n} 10^{3 n}+a_{n-1} 10^{3(n-1)}+$ $\cdots+a_{1} 10^{3}+a_{0}$, we have $x \equiv a_{n}+a_{n-1}+\cdots+a_{0}(\bmod 37)$. In other words, if we take the digits of $x$ in groups of three and sum these groups, we obtain a number congruent to $x$ modulo 37 .
The observation also implies that $A=11111111111$ is divisible by 37 . Therefore the number $N-A$ is divisible by 37 , and since it consists of the digits 0,4 and 8 , it is divisible by 4 . The sum of the digits of $N-A$ equals $76-12=64$. Therefore the number $\frac{1}{4}(N-A)$ contains only the digits $0,1,2$; it is divisible by 37 ; and its digits sum to 16 . Applying our divisibility test to this number, we sum four three-digit groups consisting of the digits $0,1,2$ only. No digits will be carried, and each digit of the sum $S$ is at most 8 . Also $S$ is divisible by 37 , and its digits sum up to 16 . Since $S \equiv 16 \equiv 1(\bmod 3)$ and $37 \equiv 1(\bmod 3)$, we have $S / 37 \equiv 1(\bmod 3)$. Therefore $S=37(3 k+1)$, that is, $S$ is one of $037,148,259,370,481,592,703,814,925$; but each of these either contains the digit 9 or does not have a digit sum of 16 .
|
{
"exam": "BalticWay",
"problem_label": "20",
"problem_match": "\n20.",
"resource_path": "BalticWay/segmented/en-bw06sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2006"
}
|
Determine all polynomials $p(x)$ with real coefficients such that
$$
p\left((x+1)^{3}\right)=(p(x)+1)^{3}
$$
and
$$
p(0)=0
$$
Answer: $p(x)=x$.
|
Consider the sequence defined by
$$
\left\{\begin{array}{l}
a_{0}=0 \\
a_{n+1}=\left(a_{n}+1\right)^{3}
\end{array}\right.
$$
It follows inductively that $p\left(a_{n}\right)=a_{n}$. Since the polynomials $p$ and $x$ agree on infinitely many points, they must be equal, so $p(x)=x$.
|
p(x)=x
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Determine all polynomials $p(x)$ with real coefficients such that
$$
p\left((x+1)^{3}\right)=(p(x)+1)^{3}
$$
and
$$
p(0)=0
$$
Answer: $p(x)=x$.
|
Consider the sequence defined by
$$
\left\{\begin{array}{l}
a_{0}=0 \\
a_{n+1}=\left(a_{n}+1\right)^{3}
\end{array}\right.
$$
It follows inductively that $p\left(a_{n}\right)=a_{n}$. Since the polynomials $p$ and $x$ agree on infinitely many points, they must be equal, so $p(x)=x$.
|
{
"exam": "BalticWay",
"problem_label": "1",
"problem_match": "\nProblem 1.",
"resource_path": "BalticWay/segmented/en-bw08sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2008"
}
|
Prove that if the real numbers $a, b$ and $c$ satisfy $a^{2}+b^{2}+c^{2}=3$ then
$$
\frac{a^{2}}{2+b+c^{2}}+\frac{b^{2}}{2+c+a^{2}}+\frac{c^{2}}{2+a+b^{2}} \geq \frac{(a+b+c)^{2}}{12} .
$$
When does equality hold?
|
Let $2+b+c^{2}=u, 2+c+a^{2}=v, 2+a+b^{2}=w$. We note that it follows from $a^{2}+b^{2}+c^{2}=3$ that $a, b, c \geq-\sqrt{3}>-2$. Therefore, $u, v$ and $w$ are positive. From the Cauchy-Schwartz inequality we get then
$$
\begin{aligned}
(a+b+c)^{2} & =\left(\frac{a}{\sqrt{u}} \sqrt{u}+\frac{b}{\sqrt{v}} \sqrt{v}+\frac{c}{\sqrt{w}} \sqrt{w}\right)^{2} \\
& \leq\left(\frac{a^{2}}{u}+\frac{b^{2}}{v}+\frac{c^{2}}{w}\right)(u+v+w) .
\end{aligned}
$$
Here,
$$
u+v+w=6+a+b+c+a^{2}+b^{2}+c^{2}=9+a+b+c .
$$
Invoking once more the Cauchy-Schwartz inequality, we get
$$
(a+b+c)^{2}=(a \cdot 1+b \cdot 1+c \cdot 1)^{2} \leq\left(a^{2}+b^{2}+c^{2}\right)(1+1+1)=9,
$$
whence $a+b+c \leq 3$ and $u+v+w \leq 12$. The proposed inequality follows.
In the second application above of the Cauchy-Schwartz inequality, equality requires $a=b=c$. If this is satified, $u+v+w=12$, which is equivalent to $a+b+c=3$, requires $a=b=c=1$. It is seen by a direct check that equality holds in the proposed inequality in this case.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that if the real numbers $a, b$ and $c$ satisfy $a^{2}+b^{2}+c^{2}=3$ then
$$
\frac{a^{2}}{2+b+c^{2}}+\frac{b^{2}}{2+c+a^{2}}+\frac{c^{2}}{2+a+b^{2}} \geq \frac{(a+b+c)^{2}}{12} .
$$
When does equality hold?
|
Let $2+b+c^{2}=u, 2+c+a^{2}=v, 2+a+b^{2}=w$. We note that it follows from $a^{2}+b^{2}+c^{2}=3$ that $a, b, c \geq-\sqrt{3}>-2$. Therefore, $u, v$ and $w$ are positive. From the Cauchy-Schwartz inequality we get then
$$
\begin{aligned}
(a+b+c)^{2} & =\left(\frac{a}{\sqrt{u}} \sqrt{u}+\frac{b}{\sqrt{v}} \sqrt{v}+\frac{c}{\sqrt{w}} \sqrt{w}\right)^{2} \\
& \leq\left(\frac{a^{2}}{u}+\frac{b^{2}}{v}+\frac{c^{2}}{w}\right)(u+v+w) .
\end{aligned}
$$
Here,
$$
u+v+w=6+a+b+c+a^{2}+b^{2}+c^{2}=9+a+b+c .
$$
Invoking once more the Cauchy-Schwartz inequality, we get
$$
(a+b+c)^{2}=(a \cdot 1+b \cdot 1+c \cdot 1)^{2} \leq\left(a^{2}+b^{2}+c^{2}\right)(1+1+1)=9,
$$
whence $a+b+c \leq 3$ and $u+v+w \leq 12$. The proposed inequality follows.
In the second application above of the Cauchy-Schwartz inequality, equality requires $a=b=c$. If this is satified, $u+v+w=12$, which is equivalent to $a+b+c=3$, requires $a=b=c=1$. It is seen by a direct check that equality holds in the proposed inequality in this case.
|
{
"exam": "BalticWay",
"problem_label": "2",
"problem_match": "\nProblem 2.",
"resource_path": "BalticWay/segmented/en-bw08sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2008"
}
|
Does there exist an angle $\alpha \in(0, \pi / 2)$ such that $\sin \alpha, \cos \alpha, \tan \alpha$ and $\cot \alpha$, taken in some order, are consecutive terms of an arithmetic progression?
Answer: No.
|
Suppose that there is an $x$ such that $0<x<\frac{\pi}{2}$ and $\sin x, \cos x, \tan x, \cot x$ in some order are consecutive terms of an arithmetic progression.
Suppose $x \leq \frac{\pi}{4}$. Then $\sin x \leq \sin \frac{\pi}{4}=\cos \frac{\pi}{4} \leq \cos x<1 \leq \cot x$ and $\sin x<\frac{\sin x}{\cos x}=\tan x \leq 1 \leq \cot x$, hence $\sin x$ is the least and $\cot x$ is the greatest among the four terms. Thereby, $\sin x<\cot x$, therefore equalities do not occur.
Independently on whether the order of terms is $\sin x<\tan x<\cos x<\cot x$ or $\sin x<\cos x<\tan x<\cot x$, we have $\cos x-\sin x=\cot x-\tan x$. As
$$
\cot x-\tan x=\frac{\cos x}{\sin x}-\frac{\sin x}{\cos x}=\frac{\cos ^{2} x-\sin ^{2} x}{\cos x \sin x}=\frac{(\cos x-\sin x)(\cos x+\sin x)}{\cos x \sin x},
$$
we obtain $\cos x-\sin x=\frac{(\cos x-\sin x)(\cos x+\sin x)}{\cos x \sin x}$. As $\cos x>\sin x$, we can reduce by $\cos x-\sin x$ and get
$$
1=\frac{\cos x+\sin x}{\cos x \sin x}=\frac{1}{\sin x}+\frac{1}{\cos x} .
$$
But $0<\sin x<1$ and $0<\cos x<1$, hence $\frac{1}{\sin x}$ and $\frac{1}{\cos x}$ are greater than 1 and their sum cannot equal 1 , a contradiction.
If $x>\frac{\pi}{4}$ then $0<\frac{\pi}{2}-x<\frac{\pi}{4}$. As the sine, cosine, tangent and cotangent of $\frac{\pi}{2}-x$ are equal to the sine, cosine, tangent and cotangent of $x$ in some order, the contradiction carries over to this case, too.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Does there exist an angle $\alpha \in(0, \pi / 2)$ such that $\sin \alpha, \cos \alpha, \tan \alpha$ and $\cot \alpha$, taken in some order, are consecutive terms of an arithmetic progression?
Answer: No.
|
Suppose that there is an $x$ such that $0<x<\frac{\pi}{2}$ and $\sin x, \cos x, \tan x, \cot x$ in some order are consecutive terms of an arithmetic progression.
Suppose $x \leq \frac{\pi}{4}$. Then $\sin x \leq \sin \frac{\pi}{4}=\cos \frac{\pi}{4} \leq \cos x<1 \leq \cot x$ and $\sin x<\frac{\sin x}{\cos x}=\tan x \leq 1 \leq \cot x$, hence $\sin x$ is the least and $\cot x$ is the greatest among the four terms. Thereby, $\sin x<\cot x$, therefore equalities do not occur.
Independently on whether the order of terms is $\sin x<\tan x<\cos x<\cot x$ or $\sin x<\cos x<\tan x<\cot x$, we have $\cos x-\sin x=\cot x-\tan x$. As
$$
\cot x-\tan x=\frac{\cos x}{\sin x}-\frac{\sin x}{\cos x}=\frac{\cos ^{2} x-\sin ^{2} x}{\cos x \sin x}=\frac{(\cos x-\sin x)(\cos x+\sin x)}{\cos x \sin x},
$$
we obtain $\cos x-\sin x=\frac{(\cos x-\sin x)(\cos x+\sin x)}{\cos x \sin x}$. As $\cos x>\sin x$, we can reduce by $\cos x-\sin x$ and get
$$
1=\frac{\cos x+\sin x}{\cos x \sin x}=\frac{1}{\sin x}+\frac{1}{\cos x} .
$$
But $0<\sin x<1$ and $0<\cos x<1$, hence $\frac{1}{\sin x}$ and $\frac{1}{\cos x}$ are greater than 1 and their sum cannot equal 1 , a contradiction.
If $x>\frac{\pi}{4}$ then $0<\frac{\pi}{2}-x<\frac{\pi}{4}$. As the sine, cosine, tangent and cotangent of $\frac{\pi}{2}-x$ are equal to the sine, cosine, tangent and cotangent of $x$ in some order, the contradiction carries over to this case, too.
|
{
"exam": "BalticWay",
"problem_label": "3",
"problem_match": "\nProblem 3.",
"resource_path": "BalticWay/segmented/en-bw08sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2008"
}
|
Does there exist an angle $\alpha \in(0, \pi / 2)$ such that $\sin \alpha, \cos \alpha, \tan \alpha$ and $\cot \alpha$, taken in some order, are consecutive terms of an arithmetic progression?
Answer: No.
|
The case $x \leq \frac{\pi}{4}$ can also be handled as follows. Consider two cases according to the order of the intermediate two terms.
If the order is $\sin x<\tan x<\cos x<\cot x$ then using AM-GM gives
$$
\cos x=\frac{\tan x+\cot x}{2}>\sqrt{\tan x \cdot \cot x}=\sqrt{1}=1
$$
which is impossible.
Suppose the other case, $\sin x<\cos x<\tan x<\cot x$. From equalities
$$
\frac{\sin x+\tan x}{2}=\cos x \quad \text { and } \quad \frac{\cos x+\cot x}{2}=\tan x
$$
one gets
$$
\begin{aligned}
& \tan x(\cos x+1)=2 \cos x \\
& \cot x(\sin x+1)=2 \tan x,
\end{aligned}
$$
respectively. By multiplying the corresponding sides, one obtains $(\cos x+1)(\sin x+1)=4 \sin x$, leading to $\cos x \sin x+\cos x+1=3 \sin x$. On the other hand, using $\cos x>\sin x$ and AM-GM gives
$$
\cos x \sin x+\cos x+1>\sin ^{2} x+\sin x+1 \geq 2 \sin x+\sin x=3 \sin x
$$
a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Does there exist an angle $\alpha \in(0, \pi / 2)$ such that $\sin \alpha, \cos \alpha, \tan \alpha$ and $\cot \alpha$, taken in some order, are consecutive terms of an arithmetic progression?
Answer: No.
|
The case $x \leq \frac{\pi}{4}$ can also be handled as follows. Consider two cases according to the order of the intermediate two terms.
If the order is $\sin x<\tan x<\cos x<\cot x$ then using AM-GM gives
$$
\cos x=\frac{\tan x+\cot x}{2}>\sqrt{\tan x \cdot \cot x}=\sqrt{1}=1
$$
which is impossible.
Suppose the other case, $\sin x<\cos x<\tan x<\cot x$. From equalities
$$
\frac{\sin x+\tan x}{2}=\cos x \quad \text { and } \quad \frac{\cos x+\cot x}{2}=\tan x
$$
one gets
$$
\begin{aligned}
& \tan x(\cos x+1)=2 \cos x \\
& \cot x(\sin x+1)=2 \tan x,
\end{aligned}
$$
respectively. By multiplying the corresponding sides, one obtains $(\cos x+1)(\sin x+1)=4 \sin x$, leading to $\cos x \sin x+\cos x+1=3 \sin x$. On the other hand, using $\cos x>\sin x$ and AM-GM gives
$$
\cos x \sin x+\cos x+1>\sin ^{2} x+\sin x+1 \geq 2 \sin x+\sin x=3 \sin x
$$
a contradiction.
|
{
"exam": "BalticWay",
"problem_label": "3",
"problem_match": "\nProblem 3.",
"resource_path": "BalticWay/segmented/en-bw08sol.jsonl",
"solution_match": "\nSolution 2:",
"tier": "T3",
"year": "2008"
}
|
The polynomial $P$ has integer coefficients and $P(x)=5$ for five different integers $x$. Show that there is no integer $x$ such that $-6 \leq P(x) \leq 4$ or $6 \leq P(x) \leq 16$.
|
Assume $P\left(x_{k}\right)=5$ for different integers $x_{1}, x_{2}, \ldots, x_{5}$. Then
$$
P(x)-5=\prod_{k=1}^{5}\left(x-x_{k}\right) Q(x)
$$
where $Q$ is a polynomial with integral coefficients. Assume $n$ satisfies the condition in the problem. Then $|n-5| \leq 11$. If $P\left(x_{0}\right)=n$ for some integer $x_{0}$, then $n-5$ is a product of six non-zero integers, five of which are different. The smallest possible absolute value of a product of five different non-zero integers is $1^{2} \cdot 2^{2} \cdot 3=12$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
The polynomial $P$ has integer coefficients and $P(x)=5$ for five different integers $x$. Show that there is no integer $x$ such that $-6 \leq P(x) \leq 4$ or $6 \leq P(x) \leq 16$.
|
Assume $P\left(x_{k}\right)=5$ for different integers $x_{1}, x_{2}, \ldots, x_{5}$. Then
$$
P(x)-5=\prod_{k=1}^{5}\left(x-x_{k}\right) Q(x)
$$
where $Q$ is a polynomial with integral coefficients. Assume $n$ satisfies the condition in the problem. Then $|n-5| \leq 11$. If $P\left(x_{0}\right)=n$ for some integer $x_{0}$, then $n-5$ is a product of six non-zero integers, five of which are different. The smallest possible absolute value of a product of five different non-zero integers is $1^{2} \cdot 2^{2} \cdot 3=12$.
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "\nProblem 4.",
"resource_path": "BalticWay/segmented/en-bw08sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2008"
}
|
Suppose that Romeo and Juliet each have a regular tetrahedron to the vertices of which some positive real numbers are assigned. They associate each edge of their tetrahedra with the product of the two numbers assigned to its end points. Then they write on each face of their tetrahedra the sum of the three numbers associated to its three edges. The four numbers written on the faces of Romeo's tetrahedron turn out to coincide with the four numbers written on Juliet's tetrahedron. Does it follow that the four numbers assigned to the vertices of Romeo's tetrahedron are identical to the four numbers assigned to the vertices of Juliet's tetrahedron?
Answer: Yes.
|
Let us prove that this conclusion can in fact be drawn. For this purpose we denote the numbers assigned to the vertices of Romeo's tetrahedron by $r_{1}, r_{2}, r_{3}, r_{4}$ and the numbers assigned to the vertices of Juliette's tetrahedron by $j_{1}, j_{2}, j_{3}, j_{4}$ in such a way that
$$
\begin{aligned}
& r_{2} r_{3}+r_{3} r_{4}+r_{4} r_{2}=j_{2} j_{3}+j_{3} j_{4}+j_{4} j_{2} \\
& r_{1} r_{3}+r_{3} r_{4}+r_{4} r_{1}=j_{1} j_{3}+j_{3} j_{4}+j_{4} j_{1} \\
& r_{1} r_{2}+r_{2} r_{4}+r_{4} r_{1}=j_{1} j_{2}+j_{2} j_{4}+j_{4} j_{1} \\
& r_{1} r_{2}+r_{2} r_{3}+r_{3} r_{1}=j_{1} j_{2}+j_{2} j_{3}+j_{3} j_{1}
\end{aligned}
$$
We intend to show that $r_{1}=j_{1}, r_{2}=j_{2}, r_{3}=j_{3}$ and $r_{4}=j_{4}$, which clearly suffices to establish our claim. Now let
$$
R=\left\{i \mid r_{i}>j_{i}\right\}
$$
denote the set indices where Romeo's corresponding number is larger and define similarly
$$
J=\left\{i \mid r_{i}<j_{i}\right\}
$$
If we had $|R|>2$, then w.l.o.g. $\{1,2,3\} \subseteq R$, which easily contradicted (4). Therefore $|R| \leq 2$, so let us suppose for the moment that $|R|=2$. Then w.l.o.g. $R=\{1,2\}$, i.e. $r_{1}>j_{1}, r_{2}>j_{2}, r_{3} \leq j_{3}, r_{4} \leq j_{4}$. It follows that $r_{1} r_{2}-r_{3} r_{4}>j_{1} j_{2}-j_{3} j_{4}$, but (1) + (2) - (3) - (4) actually tells us that both sides of this strict inequality are equal. This contradiction yields $|R| \leq 1$ and replacing the roles Romeo and Juliet played in the argument just performed we similarly infer $|J| \leq 1$. For these reasons at least two of the four desired equalities hold, say $r_{1}=1_{1}$ and $r_{2}=j_{2}$. Now using (3) and (4) we easily get $r_{3}=j_{3}$ and $r_{4}=j_{4}$ as well.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Suppose that Romeo and Juliet each have a regular tetrahedron to the vertices of which some positive real numbers are assigned. They associate each edge of their tetrahedra with the product of the two numbers assigned to its end points. Then they write on each face of their tetrahedra the sum of the three numbers associated to its three edges. The four numbers written on the faces of Romeo's tetrahedron turn out to coincide with the four numbers written on Juliet's tetrahedron. Does it follow that the four numbers assigned to the vertices of Romeo's tetrahedron are identical to the four numbers assigned to the vertices of Juliet's tetrahedron?
Answer: Yes.
|
Let us prove that this conclusion can in fact be drawn. For this purpose we denote the numbers assigned to the vertices of Romeo's tetrahedron by $r_{1}, r_{2}, r_{3}, r_{4}$ and the numbers assigned to the vertices of Juliette's tetrahedron by $j_{1}, j_{2}, j_{3}, j_{4}$ in such a way that
$$
\begin{aligned}
& r_{2} r_{3}+r_{3} r_{4}+r_{4} r_{2}=j_{2} j_{3}+j_{3} j_{4}+j_{4} j_{2} \\
& r_{1} r_{3}+r_{3} r_{4}+r_{4} r_{1}=j_{1} j_{3}+j_{3} j_{4}+j_{4} j_{1} \\
& r_{1} r_{2}+r_{2} r_{4}+r_{4} r_{1}=j_{1} j_{2}+j_{2} j_{4}+j_{4} j_{1} \\
& r_{1} r_{2}+r_{2} r_{3}+r_{3} r_{1}=j_{1} j_{2}+j_{2} j_{3}+j_{3} j_{1}
\end{aligned}
$$
We intend to show that $r_{1}=j_{1}, r_{2}=j_{2}, r_{3}=j_{3}$ and $r_{4}=j_{4}$, which clearly suffices to establish our claim. Now let
$$
R=\left\{i \mid r_{i}>j_{i}\right\}
$$
denote the set indices where Romeo's corresponding number is larger and define similarly
$$
J=\left\{i \mid r_{i}<j_{i}\right\}
$$
If we had $|R|>2$, then w.l.o.g. $\{1,2,3\} \subseteq R$, which easily contradicted (4). Therefore $|R| \leq 2$, so let us suppose for the moment that $|R|=2$. Then w.l.o.g. $R=\{1,2\}$, i.e. $r_{1}>j_{1}, r_{2}>j_{2}, r_{3} \leq j_{3}, r_{4} \leq j_{4}$. It follows that $r_{1} r_{2}-r_{3} r_{4}>j_{1} j_{2}-j_{3} j_{4}$, but (1) + (2) - (3) - (4) actually tells us that both sides of this strict inequality are equal. This contradiction yields $|R| \leq 1$ and replacing the roles Romeo and Juliet played in the argument just performed we similarly infer $|J| \leq 1$. For these reasons at least two of the four desired equalities hold, say $r_{1}=1_{1}$ and $r_{2}=j_{2}$. Now using (3) and (4) we easily get $r_{3}=j_{3}$ and $r_{4}=j_{4}$ as well.
|
{
"exam": "BalticWay",
"problem_label": "5",
"problem_match": "\nProblem 5.",
"resource_path": "BalticWay/segmented/en-bw08sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2008"
}
|
Find all finite sets of positive integers with at least two elements such that for any two numbers $a, b(a>b)$ belonging to the set, the number $\frac{b^{2}}{a-b}$ belongs to the set, too.
Answer: $X=\{a, 2 a\}$, where $a$ is an arbitrary nonnegative integer.
|
Let $X$ be a set we seek for, and $a$ be its minimal element. For each other element $b$ we have $\frac{a^{2}}{b-a} \geq a$, hence $b \leq 2 a$. Therefore all the elements of $X$ belong to the interval $[a, 2 a]$. So the quotient of any two elements of $X$ is at most 2 .
Now consider two biggest elements $d$ and $c, c<d$. Since $d \leq 2 c$ we conclude that $\frac{c^{2}}{d-c} \geq c$. Hence $\frac{c^{2}}{d-c}=d$ or $\frac{c^{2}}{d-c}=c$. The first case is impossible because we obtain an equality $(c / d)^{2}+(c / d)-1=0$, which implies that $c / d$ is irrational. Therefore we have the second case and $c^{2}=d c-c^{2}$, i.e. $c=d / 2$. Thus the set $X$ could contain only one element except $d$, and this element should be equal to $d / 2$. It is clear that all these sets satisfy the condition of the problem.
|
X=\{a, 2a\}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all finite sets of positive integers with at least two elements such that for any two numbers $a, b(a>b)$ belonging to the set, the number $\frac{b^{2}}{a-b}$ belongs to the set, too.
Answer: $X=\{a, 2 a\}$, where $a$ is an arbitrary nonnegative integer.
|
Let $X$ be a set we seek for, and $a$ be its minimal element. For each other element $b$ we have $\frac{a^{2}}{b-a} \geq a$, hence $b \leq 2 a$. Therefore all the elements of $X$ belong to the interval $[a, 2 a]$. So the quotient of any two elements of $X$ is at most 2 .
Now consider two biggest elements $d$ and $c, c<d$. Since $d \leq 2 c$ we conclude that $\frac{c^{2}}{d-c} \geq c$. Hence $\frac{c^{2}}{d-c}=d$ or $\frac{c^{2}}{d-c}=c$. The first case is impossible because we obtain an equality $(c / d)^{2}+(c / d)-1=0$, which implies that $c / d$ is irrational. Therefore we have the second case and $c^{2}=d c-c^{2}$, i.e. $c=d / 2$. Thus the set $X$ could contain only one element except $d$, and this element should be equal to $d / 2$. It is clear that all these sets satisfy the condition of the problem.
|
{
"exam": "BalticWay",
"problem_label": "6",
"problem_match": "\nProblem 6.",
"resource_path": "BalticWay/segmented/en-bw08sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2008"
}
|
How many pairs $(m, n)$ of positive integers with $m<n$ fulfill the equation
$$
\frac{3}{2008}=\frac{1}{m}+\frac{1}{n} ?
$$
## Answer: 5.
|
Let $d$ be the greatest common divisor of $m$ and $n$, and let $m=d x$ and $n=d y$. Then the equation is equivalent to
$$
3 d x y=2008(x+y) \text {. }
$$
The numbers $x$ and $y$ are relatively prime and have no common divisors with $x+y$ and hence they are both divisors of 2008. Notice that $2008=8 \cdot 251$ and 251 is a prime. Then $x$ and $y$ fulfil:
1) They are both divisors of 2008 .
2) Only one of them can be even.
3) The number 251 can only divide none or one of them.
4) $x<y$.
That gives the following possibilities of $(x, y)$ :
$$
(1,2),(1,4),(1,8),(1,251),(1,2 \cdot 251),(1,4 \cdot 251),(1,8 \cdot 251),(2,251),(4,251),(8,251) \text {. }
$$
The number 3 does not divide 2008 and hence 3 divides $x+y$. That shortens the list down to
$$
(1,2),(1,8),(1,251),(1,4 \cdot 251),(4,251) \text {. }
$$
For every pair $(x, y)$ in the list determine the number $d=\frac{2008}{x y} \cdot \frac{x+y}{3}$. It is seen that $x y$ divides 2008 for all $(x, y)$ in the list and hence $d$ is an integer. Hence exactly 5 solutions exist to the equation.
|
5
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
How many pairs $(m, n)$ of positive integers with $m<n$ fulfill the equation
$$
\frac{3}{2008}=\frac{1}{m}+\frac{1}{n} ?
$$
## Answer: 5.
|
Let $d$ be the greatest common divisor of $m$ and $n$, and let $m=d x$ and $n=d y$. Then the equation is equivalent to
$$
3 d x y=2008(x+y) \text {. }
$$
The numbers $x$ and $y$ are relatively prime and have no common divisors with $x+y$ and hence they are both divisors of 2008. Notice that $2008=8 \cdot 251$ and 251 is a prime. Then $x$ and $y$ fulfil:
1) They are both divisors of 2008 .
2) Only one of them can be even.
3) The number 251 can only divide none or one of them.
4) $x<y$.
That gives the following possibilities of $(x, y)$ :
$$
(1,2),(1,4),(1,8),(1,251),(1,2 \cdot 251),(1,4 \cdot 251),(1,8 \cdot 251),(2,251),(4,251),(8,251) \text {. }
$$
The number 3 does not divide 2008 and hence 3 divides $x+y$. That shortens the list down to
$$
(1,2),(1,8),(1,251),(1,4 \cdot 251),(4,251) \text {. }
$$
For every pair $(x, y)$ in the list determine the number $d=\frac{2008}{x y} \cdot \frac{x+y}{3}$. It is seen that $x y$ divides 2008 for all $(x, y)$ in the list and hence $d$ is an integer. Hence exactly 5 solutions exist to the equation.
|
{
"exam": "BalticWay",
"problem_label": "7",
"problem_match": "\nProblem 7.",
"resource_path": "BalticWay/segmented/en-bw08sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2008"
}
|
Consider a set $A$ of positive integers such that the least element of $A$ equals 1001 and the product of all elements of $A$ is a perfect square. What is the least possible value of the greatest element of $A$ ?
Answer: 1040.
|
We first prove that max $A$ has to be at least 1040 .
As $1001=13 \cdot 77$ and $13 \nmid 77$, the set $A$ must contain a multiple of 13 that is greater than $13 \cdot 77$. Consider the following cases:
- $13 \cdot 78 \in$. But $13 \cdot 78=13^{2} \cdot 6$, hence $A$ must also contain some greater multiple of 13 .
- $13 \cdot 79 \in A$. As 79 is a prime, $A$ must contain another multiple of 79 , which is greater than 1040 as $14 \cdot 79>1040$ and $12 \cdot 79<1001$.
- $13 \cdot k \in A$ for $k \geq 80$. As $13 \cdot k \geq 13 \cdot 80=1040$, we are done.
Now take $A=\{1001,1008,1012,1035,1040\}$. The prime factorizations are $1001=7 \cdot 11 \cdot 13,1008=7 \cdot 2^{4} \cdot 3^{2}$, $1012=2^{2} \cdot 11 \cdot 23,1035=5 \cdot 3^{2} \cdot 23,1040=2^{4} \cdot 5 \cdot 13$. The sum of exponents of each prime occurring in these representations is even. Thus the product of elements of $A$ is a perfect square.
|
1040
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Consider a set $A$ of positive integers such that the least element of $A$ equals 1001 and the product of all elements of $A$ is a perfect square. What is the least possible value of the greatest element of $A$ ?
Answer: 1040.
|
We first prove that max $A$ has to be at least 1040 .
As $1001=13 \cdot 77$ and $13 \nmid 77$, the set $A$ must contain a multiple of 13 that is greater than $13 \cdot 77$. Consider the following cases:
- $13 \cdot 78 \in$. But $13 \cdot 78=13^{2} \cdot 6$, hence $A$ must also contain some greater multiple of 13 .
- $13 \cdot 79 \in A$. As 79 is a prime, $A$ must contain another multiple of 79 , which is greater than 1040 as $14 \cdot 79>1040$ and $12 \cdot 79<1001$.
- $13 \cdot k \in A$ for $k \geq 80$. As $13 \cdot k \geq 13 \cdot 80=1040$, we are done.
Now take $A=\{1001,1008,1012,1035,1040\}$. The prime factorizations are $1001=7 \cdot 11 \cdot 13,1008=7 \cdot 2^{4} \cdot 3^{2}$, $1012=2^{2} \cdot 11 \cdot 23,1035=5 \cdot 3^{2} \cdot 23,1040=2^{4} \cdot 5 \cdot 13$. The sum of exponents of each prime occurring in these representations is even. Thus the product of elements of $A$ is a perfect square.
|
{
"exam": "BalticWay",
"problem_label": "8",
"problem_match": "\nProblem 8.",
"resource_path": "BalticWay/segmented/en-bw08sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2008"
}
|
Suppose that the positive integers $a$ and $b$ satisfy the equation
$$
a^{b}-b^{a}=1008 .
$$
Prove that $a$ and $b$ are congruent modulo 1008.
|
Observe that $1008=2^{4} \cdot 3^{2} \cdot 7$. First we show that $a$ and $b$ cannot both be even. For suppose the largest of them were equal to $2 x$ and the smallest of them equal to $2 y$, where $x \geq y \geq 1$. Then
$$
\pm 1008=(2 x)^{2 y}-(2 y)^{2 x}
$$
so that $2^{2 y}$ divides 1008 . It follows that $y \leq 2$. If $y=2$, then $\pm 1008=(2 x)^{4}-4^{2 x}$, and
$$
\pm 63=x^{4}-4^{2 x-2}=\left(x^{2}+4^{x-1}\right)\left(x^{2}-4^{x-1}\right) \text {. }
$$
But $x^{2}-4^{x-1}$ is easily seen never to divide 63; already at $x=4$ it is too large. Suppose that $y=1$. Then $\pm 1008=(2 x)^{2}-2^{2 x}$, and
$$
\pm 252=x^{2}-2^{2 x-2}=\left(x+2^{x-1}\right)\left(x-2^{x-1}\right) .
$$
This equation has no solutions. Clearly $x$ must be even. $x=2,4,6,8$ do not work, and when $x \geq 10$, then $x+2^{x-1}>252$.
We see that $a$ and $b$ cannot both be even, so they must both be odd. They cannot both be divisible by 3 , for then $1008=a^{b}-b^{a}$ would be divisible by 27 ; therefore neither of them is. Likewise, none of them is divisible by 7 .
Everything will now follow from repeated use of the following fact, where $\varphi$ denotes Euler's totient function:
If $n \mid 1008, a$ and $b$ are relatively prime to both $n$ and $\varphi(n)$, and $a \equiv b \bmod \varphi(n)$, then also $a \equiv b \bmod n$.
To prove the fact, use Euler's Totient Theorem: $a^{\varphi(n)} \equiv b^{\varphi(n)} \equiv 1 \bmod n$. From $a \equiv b \equiv d \bmod \varphi(n)$, we get
$$
0 \equiv 1008=a^{b}-b^{a} \equiv a^{d}-b^{d} \bmod n,
$$
and since $d$ is invertible modulo $\varphi(n)$, we may deduce that $a \equiv b \bmod n$.
Now begin with $a \equiv b \equiv 1 \bmod 2$. From $\varphi(4)=2, \varphi(8)=4$ and $\varphi(16)=8$, we get congruence of $a$ and $b$ modulo 4, 8 and 16 in turn. We established that $a$ and $b$ are not divisible by 3 . Since $\varphi(3)=2$, we get $a \equiv b$ $\bmod 3$, then from $\varphi(9)=6$, deduce $a \equiv b \bmod 9$. Finally, since $a$ and $b$ are not divisible by 7 , and $\varphi(7)=6$, infer $a \equiv b \bmod 7$.
Consequently, $a \equiv b \bmod 1008$. We remark that the equation possesses at least one solution, namely $1009^{1}-1^{1009}=1008$. It is unknown whether there exist others.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Suppose that the positive integers $a$ and $b$ satisfy the equation
$$
a^{b}-b^{a}=1008 .
$$
Prove that $a$ and $b$ are congruent modulo 1008.
|
Observe that $1008=2^{4} \cdot 3^{2} \cdot 7$. First we show that $a$ and $b$ cannot both be even. For suppose the largest of them were equal to $2 x$ and the smallest of them equal to $2 y$, where $x \geq y \geq 1$. Then
$$
\pm 1008=(2 x)^{2 y}-(2 y)^{2 x}
$$
so that $2^{2 y}$ divides 1008 . It follows that $y \leq 2$. If $y=2$, then $\pm 1008=(2 x)^{4}-4^{2 x}$, and
$$
\pm 63=x^{4}-4^{2 x-2}=\left(x^{2}+4^{x-1}\right)\left(x^{2}-4^{x-1}\right) \text {. }
$$
But $x^{2}-4^{x-1}$ is easily seen never to divide 63; already at $x=4$ it is too large. Suppose that $y=1$. Then $\pm 1008=(2 x)^{2}-2^{2 x}$, and
$$
\pm 252=x^{2}-2^{2 x-2}=\left(x+2^{x-1}\right)\left(x-2^{x-1}\right) .
$$
This equation has no solutions. Clearly $x$ must be even. $x=2,4,6,8$ do not work, and when $x \geq 10$, then $x+2^{x-1}>252$.
We see that $a$ and $b$ cannot both be even, so they must both be odd. They cannot both be divisible by 3 , for then $1008=a^{b}-b^{a}$ would be divisible by 27 ; therefore neither of them is. Likewise, none of them is divisible by 7 .
Everything will now follow from repeated use of the following fact, where $\varphi$ denotes Euler's totient function:
If $n \mid 1008, a$ and $b$ are relatively prime to both $n$ and $\varphi(n)$, and $a \equiv b \bmod \varphi(n)$, then also $a \equiv b \bmod n$.
To prove the fact, use Euler's Totient Theorem: $a^{\varphi(n)} \equiv b^{\varphi(n)} \equiv 1 \bmod n$. From $a \equiv b \equiv d \bmod \varphi(n)$, we get
$$
0 \equiv 1008=a^{b}-b^{a} \equiv a^{d}-b^{d} \bmod n,
$$
and since $d$ is invertible modulo $\varphi(n)$, we may deduce that $a \equiv b \bmod n$.
Now begin with $a \equiv b \equiv 1 \bmod 2$. From $\varphi(4)=2, \varphi(8)=4$ and $\varphi(16)=8$, we get congruence of $a$ and $b$ modulo 4, 8 and 16 in turn. We established that $a$ and $b$ are not divisible by 3 . Since $\varphi(3)=2$, we get $a \equiv b$ $\bmod 3$, then from $\varphi(9)=6$, deduce $a \equiv b \bmod 9$. Finally, since $a$ and $b$ are not divisible by 7 , and $\varphi(7)=6$, infer $a \equiv b \bmod 7$.
Consequently, $a \equiv b \bmod 1008$. We remark that the equation possesses at least one solution, namely $1009^{1}-1^{1009}=1008$. It is unknown whether there exist others.
|
{
"exam": "BalticWay",
"problem_label": "9",
"problem_match": "\nProblem 9.",
"resource_path": "BalticWay/segmented/en-bw08sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2008"
}
|
For a positive integer $n$, let $S(n)$ denote the sum of its digits. Find the largest possible value of the expression $\frac{S(n)}{S(16 n)}$.
## Answer: 13
|
It is obvious that $S(a b) \leq S(a) S(b)$ for all positive integers $a$ and $b$. From here we get
$$
S(n)=S(n \cdot 10000)=S(16 n \cdot 625) \leq S(16 n) \cdot 13 \text {; }
$$
so we get $\frac{S(n)}{S(16 n)} \leq 13$.
For $n=625$ we have an equality. So the largest value is 13 .
|
13
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
For a positive integer $n$, let $S(n)$ denote the sum of its digits. Find the largest possible value of the expression $\frac{S(n)}{S(16 n)}$.
## Answer: 13
|
It is obvious that $S(a b) \leq S(a) S(b)$ for all positive integers $a$ and $b$. From here we get
$$
S(n)=S(n \cdot 10000)=S(16 n \cdot 625) \leq S(16 n) \cdot 13 \text {; }
$$
so we get $\frac{S(n)}{S(16 n)} \leq 13$.
For $n=625$ we have an equality. So the largest value is 13 .
|
{
"exam": "BalticWay",
"problem_label": "10",
"problem_match": "\nProblem 10.",
"resource_path": "BalticWay/segmented/en-bw08sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2008"
}
|
Consider a subset $A$ of 84 elements of the set $\{1,2, \ldots, 169\}$ such that no two elements in the set add up to 169 . Show that $A$ contains a perfect square.
|
If $169 \in A$, we are done. If not, then
$$
A \subset \bigcup_{k=1}^{84}\{k, 169-k\}
$$
Since the sum of the numbers in each of the sets in the union is 169, each set contains at most one element of $A$; on the other hand, as $A$ has 84 elements, each set in the union contains exactly one element of $A$. So there is an $a \in A$ such that $a \in\{25,144\}$. $a$ is a perfect square.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Consider a subset $A$ of 84 elements of the set $\{1,2, \ldots, 169\}$ such that no two elements in the set add up to 169 . Show that $A$ contains a perfect square.
|
If $169 \in A$, we are done. If not, then
$$
A \subset \bigcup_{k=1}^{84}\{k, 169-k\}
$$
Since the sum of the numbers in each of the sets in the union is 169, each set contains at most one element of $A$; on the other hand, as $A$ has 84 elements, each set in the union contains exactly one element of $A$. So there is an $a \in A$ such that $a \in\{25,144\}$. $a$ is a perfect square.
|
{
"exam": "BalticWay",
"problem_label": "11",
"problem_match": "\nProblem 11.",
"resource_path": "BalticWay/segmented/en-bw08sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2008"
}
|
In a school class with $3 n$ children, any two children make a common present to exactly one other child. Prove that for all odd $n$ it is possible that the following holds:
For any three children $A, B$ and $C$ in the class, if $A$ and $B$ make a present to $C$ then $A$ and $C$ make a present to $B$.
|
Assume there exists a set $\mathscr{S}$ of sets of three children such that any set of two children is a subset of exactly one member of $\mathscr{S}$, and assume that the children $A$ and $B$ make a common present to $C$ if and only if $\{A, B, C\} \in \mathscr{S}$. Then it is true that any two children $A$ and $B$ make a common present to exactly one other child $C$, namely the unique child such that $\{A, B, C\} \in \mathscr{S}$. Because $\{A, B, C\}=\{A, C, B\}$ it is also true that if $A$ and $B$ make a present to $C$ then $A$ and $C$ make a present to $B$. We shall construct such a set $\mathscr{S}$.
Let $A_{1}, \ldots, A_{n}, B_{1}, \ldots B_{n}, C_{1}, \ldots, C_{n}$ be the children, and let the following sets belong to $\mathscr{S}$. (1) $\left\{A_{i}, B_{i}, C_{i}\right\}$ for $1 \leq i \leq n$. (2) $\left\{A_{i}, A_{j}, B_{k}\right\},\left\{B_{i}, B_{j}, C_{k}\right\}$ and $\left\{C_{i}, C_{j}, A_{k}\right\}$ for $1 \leq i<j \leq n, 1 \leq k \leq n$ and $i+j \equiv 2 k(\bmod n)$. We note that because $n$ is odd, the congruence $i+j \equiv 2 k(\bmod n)$ has a unique solution with respect to $k$ in the interval $1 \leq k \leq n$. Hence for $1 \leq i<j \leq n$ the set $\left\{A_{i}, A_{j}\right\}$ is a subset of a unique set $\left\{A_{i}, A_{j}, B_{k}\right\} \in \mathscr{S}$, and similarly the sets $\left\{B_{i}, B_{j}\right\}$ and $\left\{C_{i}, C_{j}\right\}$. The relations $i+j \equiv 2 i(\bmod n)$ and $i+j \equiv 2 j(\bmod n)$ both imply $i \equiv j(\bmod n)$, which contradicts $1 \leq i<j \leq n$. Hence for $1 \leq i \leq n$, the set $\left\{A_{i}, B_{i}, C_{i}\right\}$ is the only set in $\mathscr{S}$ of which any of the sets $\left\{A_{i}, B_{i}\right\}\left\{A_{i}, C_{i}\right\}$ and $\left\{B_{i}, C_{i}\right\}$ is a subset. For $i \neq k$, the relations $i+j \equiv 2 k$ $(\bmod n)$ and $1 \leq j \leq n$ determine $j$ uniquely, and we have $i \neq j$ because otherwise $i+j \equiv 2 k(\bmod n)$ implies $i \equiv k(\bmod n)$, which contradicts $i \neq k$. Thus $\left\{A_{i}, B_{k}\right\}$ is a subset of the unique set $\left\{A_{i}, A_{j}, B_{k}\right\} \in \mathscr{S}$. Similarly $\left\{B_{i}, C_{k}\right\}$ and $\left\{A_{i}, C_{k}\right\}$. Altogether, each set of two children is thus a subset of a unique set in $\mathscr{S}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
In a school class with $3 n$ children, any two children make a common present to exactly one other child. Prove that for all odd $n$ it is possible that the following holds:
For any three children $A, B$ and $C$ in the class, if $A$ and $B$ make a present to $C$ then $A$ and $C$ make a present to $B$.
|
Assume there exists a set $\mathscr{S}$ of sets of three children such that any set of two children is a subset of exactly one member of $\mathscr{S}$, and assume that the children $A$ and $B$ make a common present to $C$ if and only if $\{A, B, C\} \in \mathscr{S}$. Then it is true that any two children $A$ and $B$ make a common present to exactly one other child $C$, namely the unique child such that $\{A, B, C\} \in \mathscr{S}$. Because $\{A, B, C\}=\{A, C, B\}$ it is also true that if $A$ and $B$ make a present to $C$ then $A$ and $C$ make a present to $B$. We shall construct such a set $\mathscr{S}$.
Let $A_{1}, \ldots, A_{n}, B_{1}, \ldots B_{n}, C_{1}, \ldots, C_{n}$ be the children, and let the following sets belong to $\mathscr{S}$. (1) $\left\{A_{i}, B_{i}, C_{i}\right\}$ for $1 \leq i \leq n$. (2) $\left\{A_{i}, A_{j}, B_{k}\right\},\left\{B_{i}, B_{j}, C_{k}\right\}$ and $\left\{C_{i}, C_{j}, A_{k}\right\}$ for $1 \leq i<j \leq n, 1 \leq k \leq n$ and $i+j \equiv 2 k(\bmod n)$. We note that because $n$ is odd, the congruence $i+j \equiv 2 k(\bmod n)$ has a unique solution with respect to $k$ in the interval $1 \leq k \leq n$. Hence for $1 \leq i<j \leq n$ the set $\left\{A_{i}, A_{j}\right\}$ is a subset of a unique set $\left\{A_{i}, A_{j}, B_{k}\right\} \in \mathscr{S}$, and similarly the sets $\left\{B_{i}, B_{j}\right\}$ and $\left\{C_{i}, C_{j}\right\}$. The relations $i+j \equiv 2 i(\bmod n)$ and $i+j \equiv 2 j(\bmod n)$ both imply $i \equiv j(\bmod n)$, which contradicts $1 \leq i<j \leq n$. Hence for $1 \leq i \leq n$, the set $\left\{A_{i}, B_{i}, C_{i}\right\}$ is the only set in $\mathscr{S}$ of which any of the sets $\left\{A_{i}, B_{i}\right\}\left\{A_{i}, C_{i}\right\}$ and $\left\{B_{i}, C_{i}\right\}$ is a subset. For $i \neq k$, the relations $i+j \equiv 2 k$ $(\bmod n)$ and $1 \leq j \leq n$ determine $j$ uniquely, and we have $i \neq j$ because otherwise $i+j \equiv 2 k(\bmod n)$ implies $i \equiv k(\bmod n)$, which contradicts $i \neq k$. Thus $\left\{A_{i}, B_{k}\right\}$ is a subset of the unique set $\left\{A_{i}, A_{j}, B_{k}\right\} \in \mathscr{S}$. Similarly $\left\{B_{i}, C_{k}\right\}$ and $\left\{A_{i}, C_{k}\right\}$. Altogether, each set of two children is thus a subset of a unique set in $\mathscr{S}$.
|
{
"exam": "BalticWay",
"problem_label": "12",
"problem_match": "\nProblem 12.",
"resource_path": "BalticWay/segmented/en-bw08sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2008"
}
|
For an upcoming international mathematics contest, the participating countries were asked to choose from nine combinatorics problems. Given how hard it usually is to agree, nobody was surprised that the following happened:
- Every country voted for exactly three problems.
- Any two countries voted for different sets of problems.
- Given any three countries, there was a problem none of them voted for.
Find the maximal possible number of participating countries.
## Answer: 56
|
Certainly, the 56 three-element subsets of the set $\{1,2, \ldots, 8\}$ would do. Now we prove that 56 is the maximum. Assume we have a maximal configuration. Let $Y$ be the family of the three-element subsets, which were chosen by the participating countries and $N$ be the family of the three-element subsets, which were not chosen by the participating countries. Then $|Y|+|N|=\left(\begin{array}{l}9 \\ 3\end{array}\right)=84$. Consider an $x \in Y$. There are $\left(\begin{array}{l}6 \\ 3\end{array}\right)=20$ three-element subsets disjoint to $x$, which can be partitioned into 10 pairs of complementary subsets. At least one of the two sets of those pairs of complementary sets have to belong to $N$, otherwise these two together with $x$ have the whole sets as union, i.e., three countries would have voted for all problems. Therefore, to any $x \in Y$ there are associated at least 10 sets of $N$. On the other hand, a set $y \in N$ can be associated not more than to 20 sets, since there are exactly 20 disjoint sets to $y$. Together we have $10 \cdot|Y| \leq 20 \cdot|N|$ and
$$
|Y|=\frac{2}{3}|Y|+\frac{1}{3}|Y| \leq \frac{2}{3}|Y|+\frac{2}{3}|N|=\frac{2}{3}(|Y|+|N|)=\frac{2}{3} \cdot 84=56 .
$$
Remark: The set of the 84 three-element subsets can be partitioned into 28 triples of pairwise disjoint sets. From any of those triples at most two can be chosen. The partition is not obvious, but possible.
|
56
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
For an upcoming international mathematics contest, the participating countries were asked to choose from nine combinatorics problems. Given how hard it usually is to agree, nobody was surprised that the following happened:
- Every country voted for exactly three problems.
- Any two countries voted for different sets of problems.
- Given any three countries, there was a problem none of them voted for.
Find the maximal possible number of participating countries.
## Answer: 56
|
Certainly, the 56 three-element subsets of the set $\{1,2, \ldots, 8\}$ would do. Now we prove that 56 is the maximum. Assume we have a maximal configuration. Let $Y$ be the family of the three-element subsets, which were chosen by the participating countries and $N$ be the family of the three-element subsets, which were not chosen by the participating countries. Then $|Y|+|N|=\left(\begin{array}{l}9 \\ 3\end{array}\right)=84$. Consider an $x \in Y$. There are $\left(\begin{array}{l}6 \\ 3\end{array}\right)=20$ three-element subsets disjoint to $x$, which can be partitioned into 10 pairs of complementary subsets. At least one of the two sets of those pairs of complementary sets have to belong to $N$, otherwise these two together with $x$ have the whole sets as union, i.e., three countries would have voted for all problems. Therefore, to any $x \in Y$ there are associated at least 10 sets of $N$. On the other hand, a set $y \in N$ can be associated not more than to 20 sets, since there are exactly 20 disjoint sets to $y$. Together we have $10 \cdot|Y| \leq 20 \cdot|N|$ and
$$
|Y|=\frac{2}{3}|Y|+\frac{1}{3}|Y| \leq \frac{2}{3}|Y|+\frac{2}{3}|N|=\frac{2}{3}(|Y|+|N|)=\frac{2}{3} \cdot 84=56 .
$$
Remark: The set of the 84 three-element subsets can be partitioned into 28 triples of pairwise disjoint sets. From any of those triples at most two can be chosen. The partition is not obvious, but possible.
|
{
"exam": "BalticWay",
"problem_label": "13",
"problem_match": "\nProblem 13.",
"resource_path": "BalticWay/segmented/en-bw08sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2008"
}
|
Is it possible to build a $4 \times 4 \times 4$ cube from blocks of the following shape consisting of 4 unit cubes?
Answer: Yes.
|
It is possible to put two blocks together to form a new block that covers an area of shape
whereby the part marked with crosses has two layers.
From two such new blocks, one can build figure
Taking two such figures, turning one of them upside down and rotating 90 degrees, leads to a $4 \times 4 \times 2$ block. Finally, two such blocks together form the desired cube.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
Is it possible to build a $4 \times 4 \times 4$ cube from blocks of the following shape consisting of 4 unit cubes?

Answer: Yes.
|
It is possible to put two blocks together to form a new block that covers an area of shape

whereby the part marked with crosses has two layers.
From two such new blocks, one can build figure

Taking two such figures, turning one of them upside down and rotating 90 degrees, leads to a $4 \times 4 \times 2$ block. Finally, two such blocks together form the desired cube.
|
{
"exam": "BalticWay",
"problem_label": "14",
"problem_match": "\nProblem 14.",
"resource_path": "BalticWay/segmented/en-bw08sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2008"
}
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.