problem
stringlengths 14
10.4k
| solution
stringlengths 1
24.1k
| answer
stringlengths 1
250
⌀ | problem_is_valid
stringclasses 4
values | solution_is_valid
stringclasses 3
values | question_type
stringclasses 4
values | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
10.4k
| solution_raw
stringlengths 1
24.1k
| metadata
dict |
|---|---|---|---|---|---|---|---|---|---|
Given positive real numbers $a, b, c, d$ that satisfy equalities
$$
a^{2}+d^{2}-a d=b^{2}+c^{2}+b c \quad \text { and } \quad a^{2}+b^{2}=c^{2}+d^{2}
$$
find all possible values of the expression $\frac{a b+c d}{a d+b c}$.
Answer: $\frac{\sqrt{3}}{2}$.
|
. Let $A_{1} B C_{1}$ be a triangle with $A_{1} B=b, B C_{1}=c$ and $\angle A_{1} B C_{1}=120^{\circ}$, and let $C_{2} D A_{2}$ be another triangle with $C_{2} D=d, D A_{2}=a$ and $\angle C_{2} D A_{2}=60^{\circ}$. By the law of cosines and the assumption $a^{2}+d^{2}-a d=b^{2}+c^{2}+b c$, we have $A_{1} C_{1}=A_{2} C_{2}$. Thus, the two triangles can be put together to form a quadrilateral $A B C D$ with $A B=b$, $B C=c, C D=d, D A=a$ and $\angle A B C=120^{\circ}, \angle C D A=60^{\circ}$. Then $\angle D A B+\angle B C D=$ $360^{\circ}-(\angle A B C+\angle C D A)=180^{\circ}$.
Suppose that $\angle D A B>90^{\circ}$. Then $\angle B C D<90^{\circ}$, whence $a^{2}+b^{2}<B D^{2}<c^{2}+d^{2}$, contradicting the assumption $a^{2}+b^{2}=c^{2}+d^{2}$. By symmetry, $\angle D A B<90^{\circ}$ also leads to a contradiction. Hence, $\angle D A B=\angle B C D=90^{\circ}$. Now, let us calculate the area of $A B C D$ in two ways: on one hand, it equals $\frac{1}{2} a d \sin 60^{\circ}+\frac{1}{2} b c \sin 120^{\circ}$ or $\frac{\sqrt{3}}{4}(a d+b c)$. On the other hand, it equals $\frac{1}{2} a b+\frac{1}{2} c d$ or $\frac{1}{2}(a b+c d)$. Consequently,
$$
\frac{a b+c d}{a d+b c}=\frac{\frac{\sqrt{3}}{4}}{\frac{1}{2}}=\frac{\sqrt{3}}{2}
$$
|
\frac{\sqrt{3}}{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Given positive real numbers $a, b, c, d$ that satisfy equalities
$$
a^{2}+d^{2}-a d=b^{2}+c^{2}+b c \quad \text { and } \quad a^{2}+b^{2}=c^{2}+d^{2}
$$
find all possible values of the expression $\frac{a b+c d}{a d+b c}$.
Answer: $\frac{\sqrt{3}}{2}$.
|
. Let $A_{1} B C_{1}$ be a triangle with $A_{1} B=b, B C_{1}=c$ and $\angle A_{1} B C_{1}=120^{\circ}$, and let $C_{2} D A_{2}$ be another triangle with $C_{2} D=d, D A_{2}=a$ and $\angle C_{2} D A_{2}=60^{\circ}$. By the law of cosines and the assumption $a^{2}+d^{2}-a d=b^{2}+c^{2}+b c$, we have $A_{1} C_{1}=A_{2} C_{2}$. Thus, the two triangles can be put together to form a quadrilateral $A B C D$ with $A B=b$, $B C=c, C D=d, D A=a$ and $\angle A B C=120^{\circ}, \angle C D A=60^{\circ}$. Then $\angle D A B+\angle B C D=$ $360^{\circ}-(\angle A B C+\angle C D A)=180^{\circ}$.
Suppose that $\angle D A B>90^{\circ}$. Then $\angle B C D<90^{\circ}$, whence $a^{2}+b^{2}<B D^{2}<c^{2}+d^{2}$, contradicting the assumption $a^{2}+b^{2}=c^{2}+d^{2}$. By symmetry, $\angle D A B<90^{\circ}$ also leads to a contradiction. Hence, $\angle D A B=\angle B C D=90^{\circ}$. Now, let us calculate the area of $A B C D$ in two ways: on one hand, it equals $\frac{1}{2} a d \sin 60^{\circ}+\frac{1}{2} b c \sin 120^{\circ}$ or $\frac{\sqrt{3}}{4}(a d+b c)$. On the other hand, it equals $\frac{1}{2} a b+\frac{1}{2} c d$ or $\frac{1}{2}(a b+c d)$. Consequently,
$$
\frac{a b+c d}{a d+b c}=\frac{\frac{\sqrt{3}}{4}}{\frac{1}{2}}=\frac{\sqrt{3}}{2}
$$
|
{
"exam": "BalticWay",
"problem_label": "5",
"problem_match": "# Problem 5",
"resource_path": "BalticWay/segmented/en-bw14sol.jsonl",
"solution_match": "\nSolution 1",
"tier": "T3",
"year": "2014"
}
|
Given positive real numbers $a, b, c, d$ that satisfy equalities
$$
a^{2}+d^{2}-a d=b^{2}+c^{2}+b c \quad \text { and } \quad a^{2}+b^{2}=c^{2}+d^{2}
$$
find all possible values of the expression $\frac{a b+c d}{a d+b c}$.
Answer: $\frac{\sqrt{3}}{2}$.
|
. Setting $T^{2}=a^{2}+b^{2}=c^{2}+d^{2}$, where $T>0$, we can write
$$
a=T \sin \alpha, \quad b=T \cos \alpha, \quad c=T \sin \beta, \quad d=T \cos \beta
$$
for some $\alpha, \beta \in(0, \pi / 2)$. With this notation, the first equality gives
$$
\sin ^{2} \alpha+\cos ^{2} \beta-\sin \alpha \cos \beta=\sin ^{2} \beta+\cos ^{2} \alpha+\cos \alpha \sin \beta .
$$
Hence, $\cos (2 \beta)-\cos (2 \alpha)=\sin (\alpha+\beta)$. Since $\cos (2 \beta)-\cos (2 \alpha)=2 \sin (\alpha-\beta) \sin (\alpha+\beta)$ and $\sin (\alpha+\beta) \neq 0$, this yields $\sin (\alpha-\beta)=1 / 2$. Thus, in view of $\alpha-\beta \in(-\pi / 2, \pi / 2)$ we deduce that $\cos (\alpha-\beta)=\sqrt{1-\sin ^{2}(\alpha-\beta)}=\sqrt{3} / 2$.
Now, observing that $a b+c d=\frac{T^{2}}{2}(\sin (2 \alpha)+\sin (2 \beta))=T^{2} \sin (\alpha+\beta) \cos (\alpha-\beta)$ and $a d+b c=T^{2} \sin (\alpha+\beta)$, we obtain $(a b+c d) /(a d+b c)=\cos (\alpha-\beta)=\sqrt{3} / 2$.
|
\frac{\sqrt{3}}{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Given positive real numbers $a, b, c, d$ that satisfy equalities
$$
a^{2}+d^{2}-a d=b^{2}+c^{2}+b c \quad \text { and } \quad a^{2}+b^{2}=c^{2}+d^{2}
$$
find all possible values of the expression $\frac{a b+c d}{a d+b c}$.
Answer: $\frac{\sqrt{3}}{2}$.
|
. Setting $T^{2}=a^{2}+b^{2}=c^{2}+d^{2}$, where $T>0$, we can write
$$
a=T \sin \alpha, \quad b=T \cos \alpha, \quad c=T \sin \beta, \quad d=T \cos \beta
$$
for some $\alpha, \beta \in(0, \pi / 2)$. With this notation, the first equality gives
$$
\sin ^{2} \alpha+\cos ^{2} \beta-\sin \alpha \cos \beta=\sin ^{2} \beta+\cos ^{2} \alpha+\cos \alpha \sin \beta .
$$
Hence, $\cos (2 \beta)-\cos (2 \alpha)=\sin (\alpha+\beta)$. Since $\cos (2 \beta)-\cos (2 \alpha)=2 \sin (\alpha-\beta) \sin (\alpha+\beta)$ and $\sin (\alpha+\beta) \neq 0$, this yields $\sin (\alpha-\beta)=1 / 2$. Thus, in view of $\alpha-\beta \in(-\pi / 2, \pi / 2)$ we deduce that $\cos (\alpha-\beta)=\sqrt{1-\sin ^{2}(\alpha-\beta)}=\sqrt{3} / 2$.
Now, observing that $a b+c d=\frac{T^{2}}{2}(\sin (2 \alpha)+\sin (2 \beta))=T^{2} \sin (\alpha+\beta) \cos (\alpha-\beta)$ and $a d+b c=T^{2} \sin (\alpha+\beta)$, we obtain $(a b+c d) /(a d+b c)=\cos (\alpha-\beta)=\sqrt{3} / 2$.
|
{
"exam": "BalticWay",
"problem_label": "5",
"problem_match": "# Problem 5",
"resource_path": "BalticWay/segmented/en-bw14sol.jsonl",
"solution_match": "\nSolution 2",
"tier": "T3",
"year": "2014"
}
|
In how many ways can we paint 16 seats in a row, each red or green, in such a way that the number of consecutive seats painted in the same colour is always odd?
Answer: 1974.
|
Let $g_{k}, r_{k}$ be the numbers of possible odd paintings of $k$ seats such that the first seat is painted green or red, respectively. Obviously, $g_{k}=r_{k}$ for any $k$. Note that $g_{k}=r_{k-1}+g_{k-2}=g_{k-1}+g_{k-2}$, since $r_{k-1}$ is the number of odd paintings with first seat green and second seat red and $g_{k-2}$ is the number of odd paintings with first and second seats green. Moreover, $g_{1}=g_{2}=1$, so $g_{k}$ is the $k$ th element of the Fibonacci sequence. Hence, the number of ways to paint $n$ seats in a row is $g_{n}+r_{n}=2 f_{n}$. Inserting $n=16$ we obtain $2 f_{16}=2 \cdot 987=1974$.
|
1974
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In how many ways can we paint 16 seats in a row, each red or green, in such a way that the number of consecutive seats painted in the same colour is always odd?
Answer: 1974.
|
Let $g_{k}, r_{k}$ be the numbers of possible odd paintings of $k$ seats such that the first seat is painted green or red, respectively. Obviously, $g_{k}=r_{k}$ for any $k$. Note that $g_{k}=r_{k-1}+g_{k-2}=g_{k-1}+g_{k-2}$, since $r_{k-1}$ is the number of odd paintings with first seat green and second seat red and $g_{k-2}$ is the number of odd paintings with first and second seats green. Moreover, $g_{1}=g_{2}=1$, so $g_{k}$ is the $k$ th element of the Fibonacci sequence. Hence, the number of ways to paint $n$ seats in a row is $g_{n}+r_{n}=2 f_{n}$. Inserting $n=16$ we obtain $2 f_{16}=2 \cdot 987=1974$.
|
{
"exam": "BalticWay",
"problem_label": "6",
"problem_match": "# Problem 6",
"resource_path": "BalticWay/segmented/en-bw14sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2014"
}
|
Let $p_{1}, p_{2}, \ldots, p_{30}$ be a permutation of the numbers $1,2, \ldots, 30$. For how many permutations does the equality $\sum_{k=1}^{30}\left|p_{k}-k\right|=450$ hold?
Answer: $(15 !)^{2}$.
|
Let us define pairs $\left(a_{i}, b_{i}\right)$ such that $\left\{a_{i}, b_{i}\right\}=\left\{p_{i}, i\right\}$ and $a_{i} \geqslant b_{i}$. Then for every $i=1, \ldots, 30$ we have $\left|p_{i}-i\right|=a_{i}-b_{i}$ and
$$
\sum_{i=1}^{30}\left|p_{i}-i\right|=\sum_{i=1}^{30}\left(a_{i}-b_{i}\right)=\sum_{i=1}^{30} a_{i}-\sum_{i=1}^{30} b_{i}
$$
It is clear that the sum $\sum_{i=1}^{30} a_{i}-\sum_{i=1}^{30} b_{i}$ is maximal when
$$
\left\{a_{1}, a_{2}, \ldots, a_{30}\right\}=\{16,17, \ldots, 30\} \quad \text { and } \quad\left\{b_{1}, b_{2}, \ldots, b_{30}\right\}=\{1,2, \ldots, 15\}
$$
where exactly two $a_{i}$ 's and two $b_{j}$ 's are equal, and the maximal value equals
$$
2(16+\cdots+30-1-\cdots-15)=450 .
$$
The number of such permutations is $(15 !)^{2}$.
|
(15 !)^{2}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $p_{1}, p_{2}, \ldots, p_{30}$ be a permutation of the numbers $1,2, \ldots, 30$. For how many permutations does the equality $\sum_{k=1}^{30}\left|p_{k}-k\right|=450$ hold?
Answer: $(15 !)^{2}$.
|
Let us define pairs $\left(a_{i}, b_{i}\right)$ such that $\left\{a_{i}, b_{i}\right\}=\left\{p_{i}, i\right\}$ and $a_{i} \geqslant b_{i}$. Then for every $i=1, \ldots, 30$ we have $\left|p_{i}-i\right|=a_{i}-b_{i}$ and
$$
\sum_{i=1}^{30}\left|p_{i}-i\right|=\sum_{i=1}^{30}\left(a_{i}-b_{i}\right)=\sum_{i=1}^{30} a_{i}-\sum_{i=1}^{30} b_{i}
$$
It is clear that the sum $\sum_{i=1}^{30} a_{i}-\sum_{i=1}^{30} b_{i}$ is maximal when
$$
\left\{a_{1}, a_{2}, \ldots, a_{30}\right\}=\{16,17, \ldots, 30\} \quad \text { and } \quad\left\{b_{1}, b_{2}, \ldots, b_{30}\right\}=\{1,2, \ldots, 15\}
$$
where exactly two $a_{i}$ 's and two $b_{j}$ 's are equal, and the maximal value equals
$$
2(16+\cdots+30-1-\cdots-15)=450 .
$$
The number of such permutations is $(15 !)^{2}$.
|
{
"exam": "BalticWay",
"problem_label": "7",
"problem_match": "# Problem 7",
"resource_path": "BalticWay/segmented/en-bw14sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2014"
}
|
Albert and Betty are playing the following game. There are 100 blue balls in a red bowl and 100 red balls in a blue bowl. In each turn a player must make one of the following moves:
a) Take two red balls from the blue bowl and put them in the red bowl.
b) Take two blue balls from the red bowl and put them in the blue bowl.
c) Take two balls of different colors from one bowl and throw the balls away.
They take alternate turns and Albert starts. The player who first takes the last red ball from the blue bowl or the last blue ball from the red bowl wins. Determine who has a winning strategy.
Answer: Betty has a winning strategy.
|
Betty follows the following strategy. If Albert makes move a), then Betty makes move b) and vice verse. If Albert makes move c) from one bowl, Betty makes move c) from the other bowl. The only exception of this rule is that if Betty can make a winning move, that is, a move where she removes the last blue ball from the red bowl, or the last red ball from the blue bowl, then she makes her winning move.
Firstly, we prove that it is possible to follow this strategy. Let
$$
\begin{aligned}
& b=(\# \text { red balls in the blue bowl, } \# \text { blue balls in the blue bowl }), \\
& r=(\# \text { blue balls in the red bowl, } \# \text { red balls in the red bowl }) .
\end{aligned}
$$
At the beginning $b=r=(100,0)$. If $b=r$ and Albert takes a move a), then it must be possible for Betty to take a move b) and again leave a situation with $b=r$ to Albert. The same happens when Albert takes a move b). If $b=r$ and Albert takes a move c) from one bowl, then it is possible for Betty to take a move c) from the other bowl and again leave a situation with $b=r$. Thus, by following this strategy, Betty always leaves to Albert a situation with $b=r$ if she is not taking a winning move. Notice that there is one situation from which no legal move is possible, that is, $b=r=(1,0)$, but this could not happen, because the number of balls in a bowl is always even. (It is either increased or decreased by 2 , or doesn't change.)
Now, we will prove that, by using this strategy, Betty wins. Assume that at some point Albert wins, that is, he takes a winning move. Since, before his move, we have $b=r$, the situation was either $b=r=(1, s), s \geqslant 1$, or $b=r=(2, t), t \geqslant 0$. But that means that either $b$ or $r$ was either $\left(1, s^{\prime}\right), s^{\prime} \geqslant 1$ (because $1+s^{\prime}$ is even), or $\left(2, t^{\prime}\right), t^{\prime} \geqslant 0$,
before Betty made her last move. This is a contradiction with Betty's strategy, because in this situation Betty would have taken a winning move, and the game would have stopped. Hence, Betty always wins.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Albert and Betty are playing the following game. There are 100 blue balls in a red bowl and 100 red balls in a blue bowl. In each turn a player must make one of the following moves:
a) Take two red balls from the blue bowl and put them in the red bowl.
b) Take two blue balls from the red bowl and put them in the blue bowl.
c) Take two balls of different colors from one bowl and throw the balls away.
They take alternate turns and Albert starts. The player who first takes the last red ball from the blue bowl or the last blue ball from the red bowl wins. Determine who has a winning strategy.
Answer: Betty has a winning strategy.
|
Betty follows the following strategy. If Albert makes move a), then Betty makes move b) and vice verse. If Albert makes move c) from one bowl, Betty makes move c) from the other bowl. The only exception of this rule is that if Betty can make a winning move, that is, a move where she removes the last blue ball from the red bowl, or the last red ball from the blue bowl, then she makes her winning move.
Firstly, we prove that it is possible to follow this strategy. Let
$$
\begin{aligned}
& b=(\# \text { red balls in the blue bowl, } \# \text { blue balls in the blue bowl }), \\
& r=(\# \text { blue balls in the red bowl, } \# \text { red balls in the red bowl }) .
\end{aligned}
$$
At the beginning $b=r=(100,0)$. If $b=r$ and Albert takes a move a), then it must be possible for Betty to take a move b) and again leave a situation with $b=r$ to Albert. The same happens when Albert takes a move b). If $b=r$ and Albert takes a move c) from one bowl, then it is possible for Betty to take a move c) from the other bowl and again leave a situation with $b=r$. Thus, by following this strategy, Betty always leaves to Albert a situation with $b=r$ if she is not taking a winning move. Notice that there is one situation from which no legal move is possible, that is, $b=r=(1,0)$, but this could not happen, because the number of balls in a bowl is always even. (It is either increased or decreased by 2 , or doesn't change.)
Now, we will prove that, by using this strategy, Betty wins. Assume that at some point Albert wins, that is, he takes a winning move. Since, before his move, we have $b=r$, the situation was either $b=r=(1, s), s \geqslant 1$, or $b=r=(2, t), t \geqslant 0$. But that means that either $b$ or $r$ was either $\left(1, s^{\prime}\right), s^{\prime} \geqslant 1$ (because $1+s^{\prime}$ is even), or $\left(2, t^{\prime}\right), t^{\prime} \geqslant 0$,
before Betty made her last move. This is a contradiction with Betty's strategy, because in this situation Betty would have taken a winning move, and the game would have stopped. Hence, Betty always wins.
|
{
"exam": "BalticWay",
"problem_label": "8",
"problem_match": "# Problem 8",
"resource_path": "BalticWay/segmented/en-bw14sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2014"
}
|
What is the least possible number of cells that can be marked on an $n \times n$ board such that for each $m>\frac{n}{2}$ both diagonals of any $m \times m$ sub-board contain a marked cell?
## Answer: $n$.
|
For any $n$ it is possible to set $n$ marks on the board and get the desired property, if they are simply put on every cell in row number $\left\lceil\frac{n}{2}\right\rceil$. We now show that $n$ is also the minimum amount of marks needed.
If $n$ is odd, then there are $2 n$ series of diagonal cells of length $>\frac{n}{2}$ and both end cells on the edge of the board, and, since every mark on the board can at most lie on two of these diagonals, it is necessary to set at least $n$ marks to have a mark on every one of them.
If $n$ is even, then there are $2 n-2$ series of diagonal cells of length $>\frac{n}{2}$ and both end cells on the edge of the board. We call one of these diagonals even if every coordinate $(x, y)$ on it satisfies $2 \mid x-y$ and odd else. It can be easily seen that this is well defined. Now, by symmetry, the number of odd and even diagonals is the same, so there are exactly $n-1$ of each of them. Any mark set on the board can at most sit on two diagonals and these two have to be of the same kind. Thus, we will need at least $\frac{n}{2}$ marks for the even diagonals, since there are $n-1$ of them and $2 \nmid n-1$, and, similarly, we need at least $\frac{n}{2}$ marks for the the odd diagonals. So we need at least $\frac{n}{2}+\frac{n}{2}=n$ marks to get the desired property.
|
n
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
What is the least possible number of cells that can be marked on an $n \times n$ board such that for each $m>\frac{n}{2}$ both diagonals of any $m \times m$ sub-board contain a marked cell?
## Answer: $n$.
|
For any $n$ it is possible to set $n$ marks on the board and get the desired property, if they are simply put on every cell in row number $\left\lceil\frac{n}{2}\right\rceil$. We now show that $n$ is also the minimum amount of marks needed.
If $n$ is odd, then there are $2 n$ series of diagonal cells of length $>\frac{n}{2}$ and both end cells on the edge of the board, and, since every mark on the board can at most lie on two of these diagonals, it is necessary to set at least $n$ marks to have a mark on every one of them.
If $n$ is even, then there are $2 n-2$ series of diagonal cells of length $>\frac{n}{2}$ and both end cells on the edge of the board. We call one of these diagonals even if every coordinate $(x, y)$ on it satisfies $2 \mid x-y$ and odd else. It can be easily seen that this is well defined. Now, by symmetry, the number of odd and even diagonals is the same, so there are exactly $n-1$ of each of them. Any mark set on the board can at most sit on two diagonals and these two have to be of the same kind. Thus, we will need at least $\frac{n}{2}$ marks for the even diagonals, since there are $n-1$ of them and $2 \nmid n-1$, and, similarly, we need at least $\frac{n}{2}$ marks for the the odd diagonals. So we need at least $\frac{n}{2}+\frac{n}{2}=n$ marks to get the desired property.
|
{
"exam": "BalticWay",
"problem_label": "9",
"problem_match": "# Problem 9",
"resource_path": "BalticWay/segmented/en-bw14sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2014"
}
|
In a country there are 100 airports. Super-Air operates direct flights between some pairs of airports (in both directions). The traffic of an airport is the number of airports it has a direct Super-Air connection with. A new company, Concur-Air, establishes a direct flight between two airports if and only if the sum of their traffics is at least 100. It turns out that there exists a round-trip of Concur-Air flights that lands in every airport exactly once. Show that then there also exists a round-trip of Super-Air flights that lands in every airport exactly once.
|
Let $G$ and $G^{\prime}$ be two graphs corresponding to the flights of Super-Air and Concur-Air, respectively. Then the traffic of an airport is simply the degree of a corresponding vertex, and the assertion means that the graph $G$ has a Hamiltonian cycle.
Lemma. Let a graph $H$ has 100 vertices and contains a Hamiltonian path (not cycle) that starts at the vertex $A$ and ends in $B$. If the sum of degrees of vertices $A$ and $B$ is at least 100, then the graph $H$ contains a Hamiltonian cycle.
Proof. Put $N=\operatorname{deg} A$. Then $\operatorname{deg} B \geqslant 100-N$. Let us enumarate the vertices along the Hamiltonian path: $C_{1}=A, C_{2}, \ldots, C_{100}=B$. Let $C_{p}, C_{q}, C_{r}, \ldots$ be the $N$ vertices which are connected directly to $A$. Consider $N$ preceding vertices: $C_{p-1}, C_{q-1}, C_{r-1}, \ldots$ Since the remaining part of the graph $H$ contains $100-N$ vertices (including $B$ ) and $\operatorname{deg} B \geqslant 100-N$, we conclude that at least one vertex under consideration, say $C_{r-1}$, is connected directly to $B$. Then
$$
A=C_{1} \rightarrow C_{2} \rightarrow \cdots \rightarrow C_{r-1} \rightarrow B=C_{100} \rightarrow C_{99} \rightarrow \cdots \rightarrow C_{r} \rightarrow A
$$
is a Hamiltonian cycle.
Now, let us solve the problem. Assume that the graph $G$ contains no Hamiltonian cycle. Consider arbitrary two vertices $A$ and $B$ not connected by an edge in the graph $G$ but connected in $G^{\prime}$. The latter means that $\operatorname{deg} A+\operatorname{deg} B \geqslant 100$ in the graph $G$. Let us add the edge $A B$ to the graph $G$. By the lemma, there was no Hamiltonian path from $A$ to $B$ in the graph $G$. Therefore, the graph $G$ still does not contain a Hamiltonian cycle after adding this new edge. By repeating this operation, we will obtain that all the vertices connected by an edge in the graph $G^{\prime}$ are also connected in the graph $G$ and at the same time the graph $G$ has no Hamiltonian cycle (in contrast to $G^{\prime}$ ). This is a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
In a country there are 100 airports. Super-Air operates direct flights between some pairs of airports (in both directions). The traffic of an airport is the number of airports it has a direct Super-Air connection with. A new company, Concur-Air, establishes a direct flight between two airports if and only if the sum of their traffics is at least 100. It turns out that there exists a round-trip of Concur-Air flights that lands in every airport exactly once. Show that then there also exists a round-trip of Super-Air flights that lands in every airport exactly once.
|
Let $G$ and $G^{\prime}$ be two graphs corresponding to the flights of Super-Air and Concur-Air, respectively. Then the traffic of an airport is simply the degree of a corresponding vertex, and the assertion means that the graph $G$ has a Hamiltonian cycle.
Lemma. Let a graph $H$ has 100 vertices and contains a Hamiltonian path (not cycle) that starts at the vertex $A$ and ends in $B$. If the sum of degrees of vertices $A$ and $B$ is at least 100, then the graph $H$ contains a Hamiltonian cycle.
Proof. Put $N=\operatorname{deg} A$. Then $\operatorname{deg} B \geqslant 100-N$. Let us enumarate the vertices along the Hamiltonian path: $C_{1}=A, C_{2}, \ldots, C_{100}=B$. Let $C_{p}, C_{q}, C_{r}, \ldots$ be the $N$ vertices which are connected directly to $A$. Consider $N$ preceding vertices: $C_{p-1}, C_{q-1}, C_{r-1}, \ldots$ Since the remaining part of the graph $H$ contains $100-N$ vertices (including $B$ ) and $\operatorname{deg} B \geqslant 100-N$, we conclude that at least one vertex under consideration, say $C_{r-1}$, is connected directly to $B$. Then
$$
A=C_{1} \rightarrow C_{2} \rightarrow \cdots \rightarrow C_{r-1} \rightarrow B=C_{100} \rightarrow C_{99} \rightarrow \cdots \rightarrow C_{r} \rightarrow A
$$
is a Hamiltonian cycle.
Now, let us solve the problem. Assume that the graph $G$ contains no Hamiltonian cycle. Consider arbitrary two vertices $A$ and $B$ not connected by an edge in the graph $G$ but connected in $G^{\prime}$. The latter means that $\operatorname{deg} A+\operatorname{deg} B \geqslant 100$ in the graph $G$. Let us add the edge $A B$ to the graph $G$. By the lemma, there was no Hamiltonian path from $A$ to $B$ in the graph $G$. Therefore, the graph $G$ still does not contain a Hamiltonian cycle after adding this new edge. By repeating this operation, we will obtain that all the vertices connected by an edge in the graph $G^{\prime}$ are also connected in the graph $G$ and at the same time the graph $G$ has no Hamiltonian cycle (in contrast to $G^{\prime}$ ). This is a contradiction.
|
{
"exam": "BalticWay",
"problem_label": "10",
"problem_match": "# Problem 10",
"resource_path": "BalticWay/segmented/en-bw14sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2014"
}
|
Let $\Gamma$ be the circumcircle of an acute triangle $A B C$. The perpendicular to $A B$ from $C$ meets $A B$ at $D$ and $\Gamma$ again at $E$. The bisector of angle $C$ meets $A B$ at $F$ and $\Gamma$ again at $G$. The line $G D$ meets $\Gamma$ again at $H$ and the line $H F$ meets $\Gamma$ again at $I$. Prove that $A I=E B$.
|
Since $C G$ bisects $\angle A C B$, we have $\angle A H G=\angle A C G=\angle G C B$. Thus, from the triangle $A D H$ we find that $\angle H D B=\angle H A B+\angle A H G=\angle H C B+\angle G C B=\angle G C H$. It follows that a pair of opposite angles in the quadrilateral $C F D H$ are supplementary, whence $C F D H$ is a cyclic quadrilateral. Thus, $\angle G C E=\angle F C D=\angle F H D=\angle I H G=$ $\angle I C G$. In view of $\angle A C G=\angle G C B$ we obtain $\angle A C I=\angle E C B$, which implies $A I=E B$.
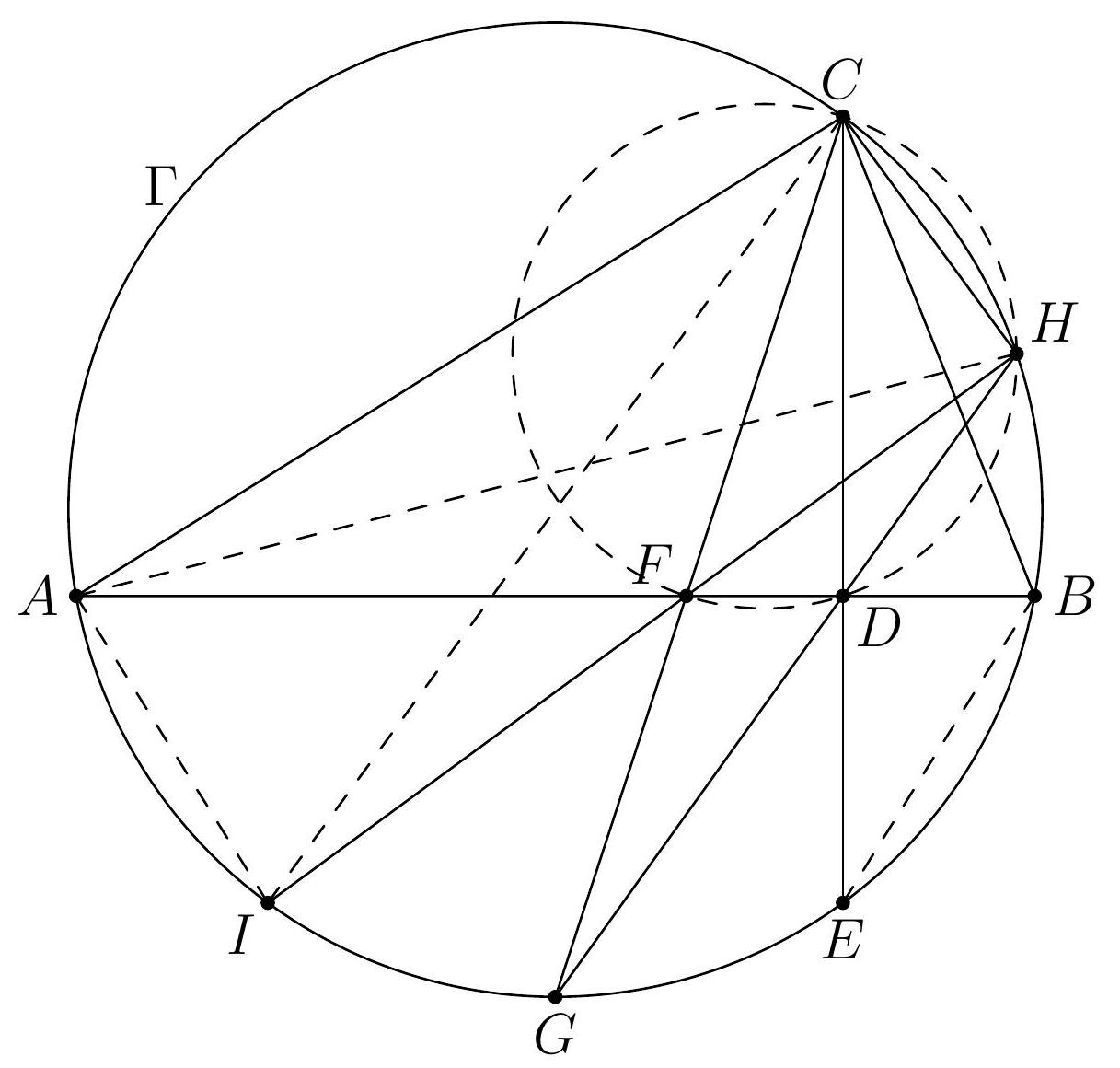
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\Gamma$ be the circumcircle of an acute triangle $A B C$. The perpendicular to $A B$ from $C$ meets $A B$ at $D$ and $\Gamma$ again at $E$. The bisector of angle $C$ meets $A B$ at $F$ and $\Gamma$ again at $G$. The line $G D$ meets $\Gamma$ again at $H$ and the line $H F$ meets $\Gamma$ again at $I$. Prove that $A I=E B$.
|
Since $C G$ bisects $\angle A C B$, we have $\angle A H G=\angle A C G=\angle G C B$. Thus, from the triangle $A D H$ we find that $\angle H D B=\angle H A B+\angle A H G=\angle H C B+\angle G C B=\angle G C H$. It follows that a pair of opposite angles in the quadrilateral $C F D H$ are supplementary, whence $C F D H$ is a cyclic quadrilateral. Thus, $\angle G C E=\angle F C D=\angle F H D=\angle I H G=$ $\angle I C G$. In view of $\angle A C G=\angle G C B$ we obtain $\angle A C I=\angle E C B$, which implies $A I=E B$.

|
{
"exam": "BalticWay",
"problem_label": "11",
"problem_match": "# Problem 11",
"resource_path": "BalticWay/segmented/en-bw14sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2014"
}
|
Triangle $A B C$ is given. Let $M$ be the midpoint of the segment $A B$ and $T$ be the midpoint of the arc $B C$ not containing $A$ of the circumcircle of $A B C$. The point $K$ inside the triangle $A B C$ is such that $M A T K$ is an isosceles trapezoid with $A T \| M K$. Show that $A K=K C$.
|
Assume that $T K$ intersects the circumcircle of $A B C$ at the point $S$ (where $S \neq T)$. Then $\angle A B S=\angle A T S=\angle B A T$, so $A S B T$ is a trapezoid. Hence, $M K\|A T\| S B$ and $M$ is the midpoint of $A B$. Thus, $K$ is the midpoint of $T S$. From $\angle T A C=\angle B A T=$ $\angle A T S$ we see that $A C T S$ is an inscribed trapezoid, so it is isosceles. Thus, $A K=K C$, since $K$ is the midpoint of $T S$.
|
A K=K C
|
Yes
|
Yes
|
proof
|
Geometry
|
Triangle $A B C$ is given. Let $M$ be the midpoint of the segment $A B$ and $T$ be the midpoint of the arc $B C$ not containing $A$ of the circumcircle of $A B C$. The point $K$ inside the triangle $A B C$ is such that $M A T K$ is an isosceles trapezoid with $A T \| M K$. Show that $A K=K C$.
|
Assume that $T K$ intersects the circumcircle of $A B C$ at the point $S$ (where $S \neq T)$. Then $\angle A B S=\angle A T S=\angle B A T$, so $A S B T$ is a trapezoid. Hence, $M K\|A T\| S B$ and $M$ is the midpoint of $A B$. Thus, $K$ is the midpoint of $T S$. From $\angle T A C=\angle B A T=$ $\angle A T S$ we see that $A C T S$ is an inscribed trapezoid, so it is isosceles. Thus, $A K=K C$, since $K$ is the midpoint of $T S$.
|
{
"exam": "BalticWay",
"problem_label": "12",
"problem_match": "# Problem 12",
"resource_path": "BalticWay/segmented/en-bw14sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2014"
}
|
Let $A B C D$ be a square inscribed in a circle $\omega$ and let $P$ be a point on the shorter arc $A B$ of $\omega$. Let $C P \cap B D=R$ and $D P \cap A C=S$. Show that triangles $A R B$ and $D S R$ have equal areas.
|
Let $T=P C \cap A B$. Then $\angle B T C=90^{\circ}-\angle P C B=90^{\circ}-\angle P D B=90^{\circ}-$ $\angle S B D=\angle B S C$, thus the points $B, S, T, C$ are concyclic. Hence $\angle T S C=90^{\circ}$, and, therefore, $T S \| B D$. It follows that
$$
[D S R]=[D T R]=[D T B]-[T B R]=[C T B]-[T B R]=[C R B]=[A R B]
$$
where $[\Delta]$ denotes the area of a triangle $\Delta$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a square inscribed in a circle $\omega$ and let $P$ be a point on the shorter arc $A B$ of $\omega$. Let $C P \cap B D=R$ and $D P \cap A C=S$. Show that triangles $A R B$ and $D S R$ have equal areas.
|
Let $T=P C \cap A B$. Then $\angle B T C=90^{\circ}-\angle P C B=90^{\circ}-\angle P D B=90^{\circ}-$ $\angle S B D=\angle B S C$, thus the points $B, S, T, C$ are concyclic. Hence $\angle T S C=90^{\circ}$, and, therefore, $T S \| B D$. It follows that
$$
[D S R]=[D T R]=[D T B]-[T B R]=[C T B]-[T B R]=[C R B]=[A R B]
$$
where $[\Delta]$ denotes the area of a triangle $\Delta$.
|
{
"exam": "BalticWay",
"problem_label": "13",
"problem_match": "# Problem 13",
"resource_path": "BalticWay/segmented/en-bw14sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2014"
}
|
Let $A B C D$ be a convex quadrilateral such that the line $B D$ bisects the angle $A B C$. The circumcircle of triangle $A B C$ intersects the sides $A D$ and $C D$ in the points $P$ and $Q$, respectively. The line through $D$ and parallel to $A C$ intersects the lines $B C$ and $B A$ at the points $R$ and $S$, respectively. Prove that the points $P, Q, R$ and $S$ lie on a common circle.
|
. Since $\angle S D P=\angle C A P=\angle R B P$, the quadrilateral $B R D P$ is cyclic (see Figure 1). Similarly, the quadrilateral $B S D Q$ is cyclic. Let $X$ be the second intersection point of the segment $B D$ with the circumcircle of the triangle $A B C$. Then
$$
\angle A X B=\angle A C B=\angle D R B,
$$
and, moreover, $\angle A B X=\angle D B R$. It means that triangles $A B X$ and $D B R$ are similar. Thus
$$
\angle R P B=\angle R D B=\angle X A B=\angle X P B,
$$
which implies that the points $R, X$ and $P$ are collinear. Analogously, we can show that the points $S, X$ and $Q$ are collinear.
Thus, we obtain $R X \cdot X P=D X \cdot X B=S X \cdot X Q$, which proves that the points $P$, $Q, R$ and $S$ lie on a common circle.
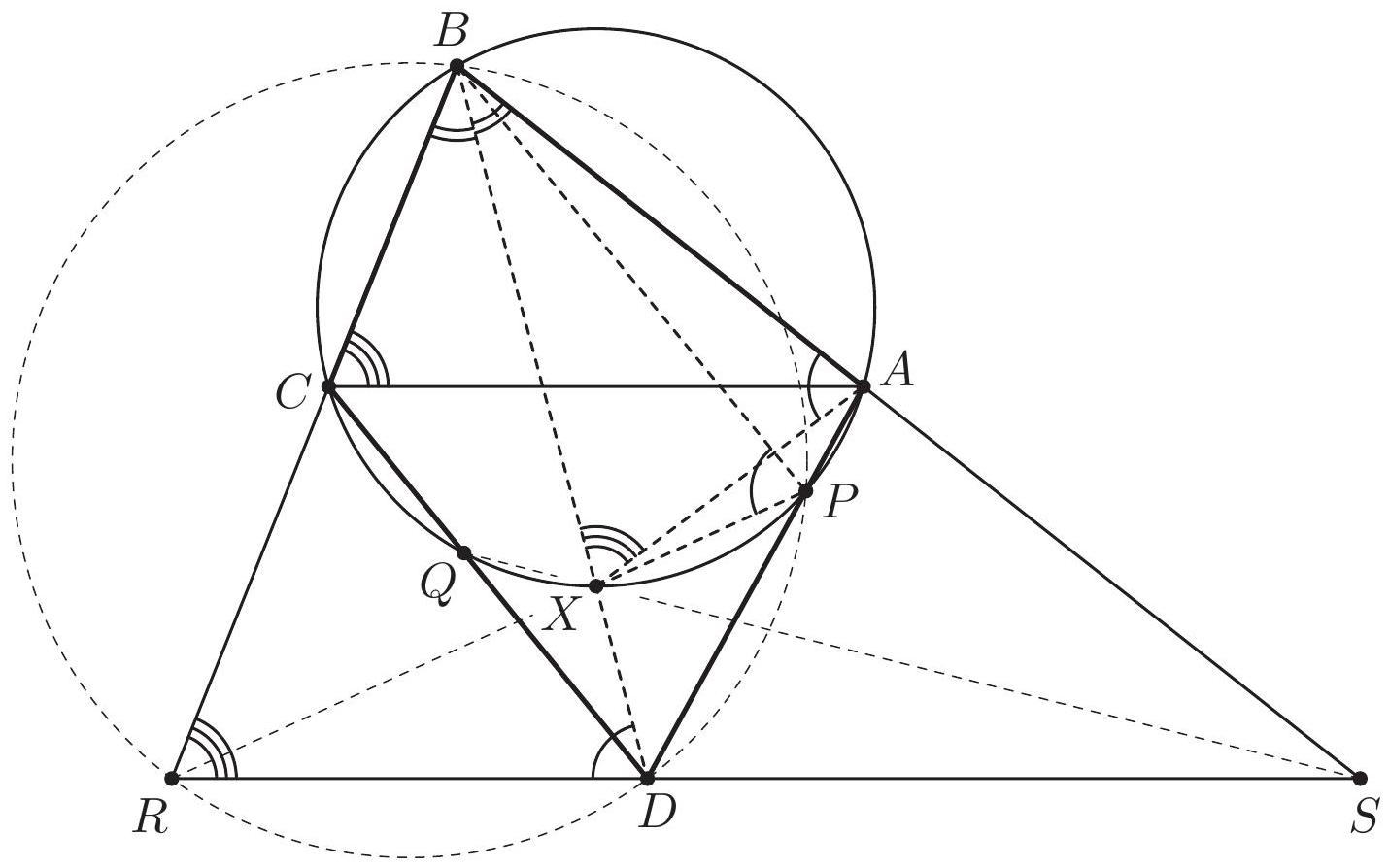
Figure 1
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral such that the line $B D$ bisects the angle $A B C$. The circumcircle of triangle $A B C$ intersects the sides $A D$ and $C D$ in the points $P$ and $Q$, respectively. The line through $D$ and parallel to $A C$ intersects the lines $B C$ and $B A$ at the points $R$ and $S$, respectively. Prove that the points $P, Q, R$ and $S$ lie on a common circle.
|
. Since $\angle S D P=\angle C A P=\angle R B P$, the quadrilateral $B R D P$ is cyclic (see Figure 1). Similarly, the quadrilateral $B S D Q$ is cyclic. Let $X$ be the second intersection point of the segment $B D$ with the circumcircle of the triangle $A B C$. Then
$$
\angle A X B=\angle A C B=\angle D R B,
$$
and, moreover, $\angle A B X=\angle D B R$. It means that triangles $A B X$ and $D B R$ are similar. Thus
$$
\angle R P B=\angle R D B=\angle X A B=\angle X P B,
$$
which implies that the points $R, X$ and $P$ are collinear. Analogously, we can show that the points $S, X$ and $Q$ are collinear.
Thus, we obtain $R X \cdot X P=D X \cdot X B=S X \cdot X Q$, which proves that the points $P$, $Q, R$ and $S$ lie on a common circle.

Figure 1
|
{
"exam": "BalticWay",
"problem_label": "14",
"problem_match": "# Problem 14",
"resource_path": "BalticWay/segmented/en-bw14sol.jsonl",
"solution_match": "\nSolution 1",
"tier": "T3",
"year": "2014"
}
|
Let $A B C D$ be a convex quadrilateral such that the line $B D$ bisects the angle $A B C$. The circumcircle of triangle $A B C$ intersects the sides $A D$ and $C D$ in the points $P$ and $Q$, respectively. The line through $D$ and parallel to $A C$ intersects the lines $B C$ and $B A$ at the points $R$ and $S$, respectively. Prove that the points $P, Q, R$ and $S$ lie on a common circle.
|
. If $A B=B C$, then the points $R$ and $S$ are symmetric to each other with respect to the line $B D$. Similarly, the points $P$ and $Q$ are symmetric to each other with respect to the line $B D$. Therefore, $R S P Q$ is an isosceles trapezoid, so the claim follows.
Assume that $A B \neq B C$. Denote by $\omega$ the circumcircle of the triangle $A B C$ (see Figure 2). Since the lines $A C$ and $S R$ are parallel, the dilation with center $B$, which takes $A$ to $S$, also takes $C$ to $R$ and the circle $\omega$ to the circumcircle $\omega_{1}$ of $B S R$. This implies that $\omega$ and $\omega_{1}$ are tangent at $B$.
Note that $\angle R D Q=\angle D C A=\angle D P Q$, which means that the circumcircle $\omega_{2}$ of the triangle $P Q D$ is tangent to the line $R S$ at $D$.
Denote by $K$ the intersection point of the line $R S$ with the common tangent to $\omega$ and $\omega_{1}$ at $B$. Then we have
$$
\angle K B D=\angle K B R+\angle C B D=\angle D S B+\angle S B D=\angle K D B,
$$
which implies that $K D=K B$. Therefore, the powers of the point $K$ with respect to the circles $\omega$ and $\omega_{2}$ are equal, so $K$ lies on their radical axis. This implies that the points $K, P$ and $Q$ are collinear. Finally, we obtain
$$
K R \cdot K S=K B^{2}=K D^{2}=K P \cdot K Q,
$$
which shows that the points $P, Q, R$ and $S$ lie on a common circle.

Figure 2
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral such that the line $B D$ bisects the angle $A B C$. The circumcircle of triangle $A B C$ intersects the sides $A D$ and $C D$ in the points $P$ and $Q$, respectively. The line through $D$ and parallel to $A C$ intersects the lines $B C$ and $B A$ at the points $R$ and $S$, respectively. Prove that the points $P, Q, R$ and $S$ lie on a common circle.
|
. If $A B=B C$, then the points $R$ and $S$ are symmetric to each other with respect to the line $B D$. Similarly, the points $P$ and $Q$ are symmetric to each other with respect to the line $B D$. Therefore, $R S P Q$ is an isosceles trapezoid, so the claim follows.
Assume that $A B \neq B C$. Denote by $\omega$ the circumcircle of the triangle $A B C$ (see Figure 2). Since the lines $A C$ and $S R$ are parallel, the dilation with center $B$, which takes $A$ to $S$, also takes $C$ to $R$ and the circle $\omega$ to the circumcircle $\omega_{1}$ of $B S R$. This implies that $\omega$ and $\omega_{1}$ are tangent at $B$.
Note that $\angle R D Q=\angle D C A=\angle D P Q$, which means that the circumcircle $\omega_{2}$ of the triangle $P Q D$ is tangent to the line $R S$ at $D$.
Denote by $K$ the intersection point of the line $R S$ with the common tangent to $\omega$ and $\omega_{1}$ at $B$. Then we have
$$
\angle K B D=\angle K B R+\angle C B D=\angle D S B+\angle S B D=\angle K D B,
$$
which implies that $K D=K B$. Therefore, the powers of the point $K$ with respect to the circles $\omega$ and $\omega_{2}$ are equal, so $K$ lies on their radical axis. This implies that the points $K, P$ and $Q$ are collinear. Finally, we obtain
$$
K R \cdot K S=K B^{2}=K D^{2}=K P \cdot K Q,
$$
which shows that the points $P, Q, R$ and $S$ lie on a common circle.

Figure 2
|
{
"exam": "BalticWay",
"problem_label": "14",
"problem_match": "# Problem 14",
"resource_path": "BalticWay/segmented/en-bw14sol.jsonl",
"solution_match": "\nSolution 2",
"tier": "T3",
"year": "2014"
}
|
Let $A B C D$ be a convex quadrilateral such that the line $B D$ bisects the angle $A B C$. The circumcircle of triangle $A B C$ intersects the sides $A D$ and $C D$ in the points $P$ and $Q$, respectively. The line through $D$ and parallel to $A C$ intersects the lines $B C$ and $B A$ at the points $R$ and $S$, respectively. Prove that the points $P, Q, R$ and $S$ lie on a common circle.
|
. Denote by $X^{\prime}$ the image of the point $X$ under some fixed inversion with center $B$. At the beginning of Solution 2 we noticed that the circumcircles of the triangles $A B C$ and $S B R$ are tangent at the point $B$. Therefore, the images of these two circles
under the considered inversion become two parallel lines $A^{\prime} C^{\prime}$ and $S^{\prime} R^{\prime}$ (see Figure 3).
Since $D$ lies on the line $R S$ and also on the angle bisector of the angle $A B C$, the point $D^{\prime}$ lies on the circumcircle of the triangle $B R^{\prime} S^{\prime}$ and also on the angle bisector of the angle $A^{\prime} B C^{\prime}$. Since the point $P$, other than $A$, is the intersection point of the line $A D$ and the circumcircle of the triangle $A B C$, the point $P^{\prime}$, other than $A^{\prime}$, is the intersection point of the circumcircle of the triangle $B A^{\prime} D^{\prime}$ and the line $A^{\prime} C^{\prime}$. Similarly, the point $Q^{\prime}$ is the intersection point of the circumcircle of the triangle $B C^{\prime} D^{\prime}$ and the line $A^{\prime} C^{\prime}$.
Therefore, we obtain
$$
\angle D^{\prime} Q^{\prime} P^{\prime}=\angle C^{\prime} B D^{\prime}=\angle A^{\prime} B D^{\prime}=\angle D^{\prime} P^{\prime} Q^{\prime}
$$
and
$$
\angle D^{\prime} R^{\prime} S^{\prime}=\angle D^{\prime} B S^{\prime}=\angle R^{\prime} B D^{\prime}=\angle R^{\prime} S^{\prime} D^{\prime} .
$$
This implies that the points $P^{\prime}$ and $S^{\prime}$ are symmetric to the points $Q^{\prime}$ and $R^{\prime}$ with respect to the line passing through $D^{\prime}$ and perpendicular to the lines $A^{\prime} C^{\prime}$ and $S^{\prime} R^{\prime}$. Thus $P^{\prime} S^{\prime} R^{\prime} Q^{\prime}$ is an isosceles trapezoid, so the points $P^{\prime}, S^{\prime}, R^{\prime}$ and $Q^{\prime}$ lie on a common circle. Therefore, the points $P, Q, R$ and $S$ also lie on a common circle.
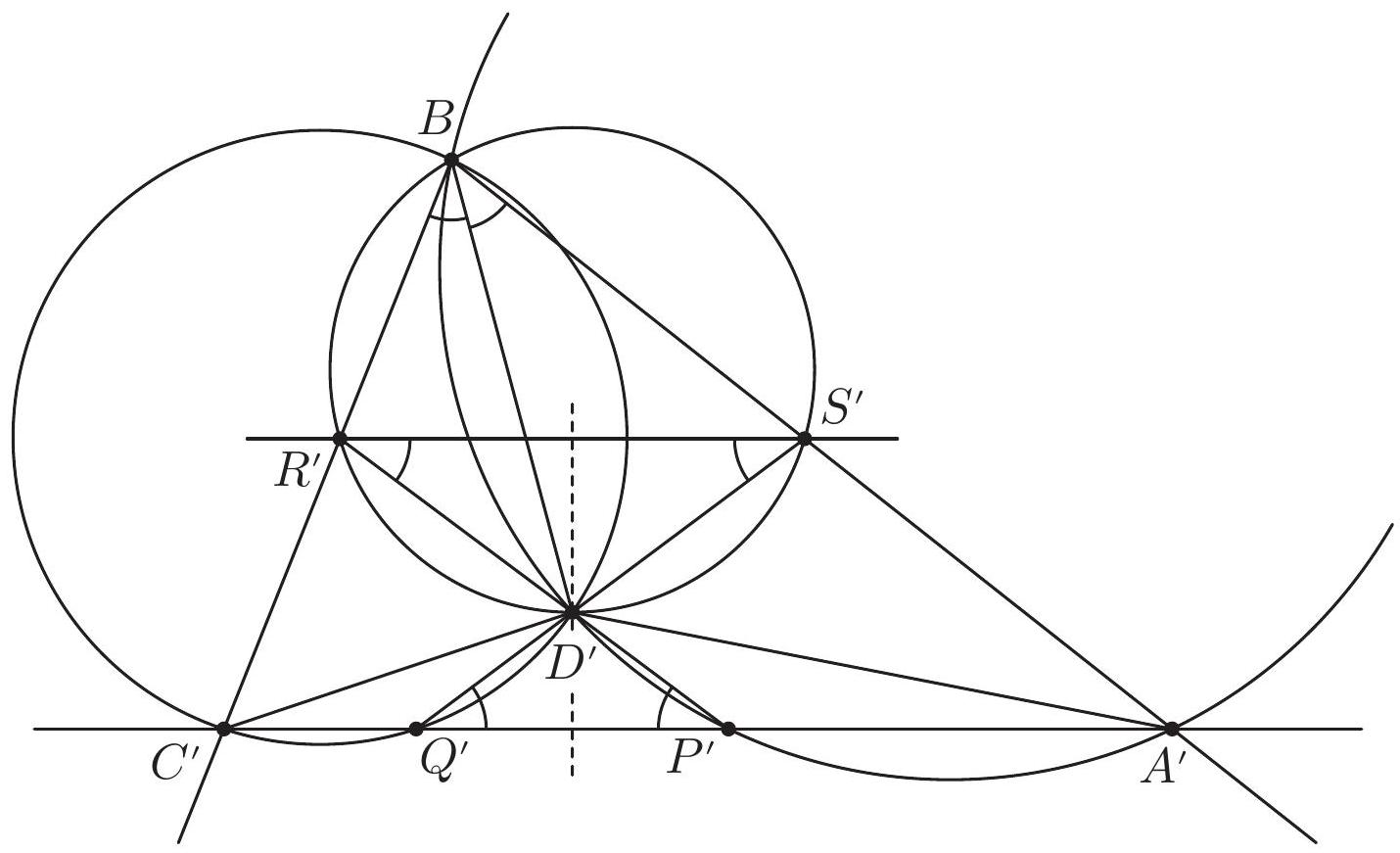
Figure 3
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral such that the line $B D$ bisects the angle $A B C$. The circumcircle of triangle $A B C$ intersects the sides $A D$ and $C D$ in the points $P$ and $Q$, respectively. The line through $D$ and parallel to $A C$ intersects the lines $B C$ and $B A$ at the points $R$ and $S$, respectively. Prove that the points $P, Q, R$ and $S$ lie on a common circle.
|
. Denote by $X^{\prime}$ the image of the point $X$ under some fixed inversion with center $B$. At the beginning of Solution 2 we noticed that the circumcircles of the triangles $A B C$ and $S B R$ are tangent at the point $B$. Therefore, the images of these two circles
under the considered inversion become two parallel lines $A^{\prime} C^{\prime}$ and $S^{\prime} R^{\prime}$ (see Figure 3).
Since $D$ lies on the line $R S$ and also on the angle bisector of the angle $A B C$, the point $D^{\prime}$ lies on the circumcircle of the triangle $B R^{\prime} S^{\prime}$ and also on the angle bisector of the angle $A^{\prime} B C^{\prime}$. Since the point $P$, other than $A$, is the intersection point of the line $A D$ and the circumcircle of the triangle $A B C$, the point $P^{\prime}$, other than $A^{\prime}$, is the intersection point of the circumcircle of the triangle $B A^{\prime} D^{\prime}$ and the line $A^{\prime} C^{\prime}$. Similarly, the point $Q^{\prime}$ is the intersection point of the circumcircle of the triangle $B C^{\prime} D^{\prime}$ and the line $A^{\prime} C^{\prime}$.
Therefore, we obtain
$$
\angle D^{\prime} Q^{\prime} P^{\prime}=\angle C^{\prime} B D^{\prime}=\angle A^{\prime} B D^{\prime}=\angle D^{\prime} P^{\prime} Q^{\prime}
$$
and
$$
\angle D^{\prime} R^{\prime} S^{\prime}=\angle D^{\prime} B S^{\prime}=\angle R^{\prime} B D^{\prime}=\angle R^{\prime} S^{\prime} D^{\prime} .
$$
This implies that the points $P^{\prime}$ and $S^{\prime}$ are symmetric to the points $Q^{\prime}$ and $R^{\prime}$ with respect to the line passing through $D^{\prime}$ and perpendicular to the lines $A^{\prime} C^{\prime}$ and $S^{\prime} R^{\prime}$. Thus $P^{\prime} S^{\prime} R^{\prime} Q^{\prime}$ is an isosceles trapezoid, so the points $P^{\prime}, S^{\prime}, R^{\prime}$ and $Q^{\prime}$ lie on a common circle. Therefore, the points $P, Q, R$ and $S$ also lie on a common circle.

Figure 3
|
{
"exam": "BalticWay",
"problem_label": "14",
"problem_match": "# Problem 14",
"resource_path": "BalticWay/segmented/en-bw14sol.jsonl",
"solution_match": "\nSolution 3",
"tier": "T3",
"year": "2014"
}
|
The sum of the angles $A$ and $C$ of a convex quadrilateral $A B C D$ is less than $180^{\circ}$. Prove that
$$
A B \cdot C D+A D \cdot B C<A C(A B+A D)
$$
|
. Let $\omega$ be the circumcircle $A B D$. Then the point $C$ is outside this circle, but inside the angle $B A D$. Let us ppply the inversion with the center $A$ and radius 1 . This inversion maps the circle $\omega$ to the line $\omega^{\prime}=B^{\prime} D^{\prime}$, where $B^{\prime}$ and $D^{\prime}$ are images of $B$ and $D$. The point $C$ goes to the point $C^{\prime}$ inside the triangle $A B^{\prime} D^{\prime}$. Therefore, $B^{\prime} C^{\prime}+C^{\prime} D^{\prime}<A B^{\prime}+A D^{\prime}$. Now, due to inversion properties, we have
$$
B^{\prime} C^{\prime}=\frac{B C}{A B \cdot A C}, \quad C^{\prime} D^{\prime}=\frac{C D}{A C \cdot A D}, \quad A B^{\prime}=\frac{1}{A B}, \quad A D^{\prime}=\frac{1}{A D} .
$$
Hence
$$
\frac{B C}{A B \cdot A C}+\frac{C D}{A C \cdot A D}<\frac{1}{A B}+\frac{1}{A D}
$$
Multiplying by $A B \cdot A C \cdot A D$, we obtain the desired inequality.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
The sum of the angles $A$ and $C$ of a convex quadrilateral $A B C D$ is less than $180^{\circ}$. Prove that
$$
A B \cdot C D+A D \cdot B C<A C(A B+A D)
$$
|
. Let $\omega$ be the circumcircle $A B D$. Then the point $C$ is outside this circle, but inside the angle $B A D$. Let us ppply the inversion with the center $A$ and radius 1 . This inversion maps the circle $\omega$ to the line $\omega^{\prime}=B^{\prime} D^{\prime}$, where $B^{\prime}$ and $D^{\prime}$ are images of $B$ and $D$. The point $C$ goes to the point $C^{\prime}$ inside the triangle $A B^{\prime} D^{\prime}$. Therefore, $B^{\prime} C^{\prime}+C^{\prime} D^{\prime}<A B^{\prime}+A D^{\prime}$. Now, due to inversion properties, we have
$$
B^{\prime} C^{\prime}=\frac{B C}{A B \cdot A C}, \quad C^{\prime} D^{\prime}=\frac{C D}{A C \cdot A D}, \quad A B^{\prime}=\frac{1}{A B}, \quad A D^{\prime}=\frac{1}{A D} .
$$
Hence
$$
\frac{B C}{A B \cdot A C}+\frac{C D}{A C \cdot A D}<\frac{1}{A B}+\frac{1}{A D}
$$
Multiplying by $A B \cdot A C \cdot A D$, we obtain the desired inequality.
|
{
"exam": "BalticWay",
"problem_label": "15",
"problem_match": "# Problem 15",
"resource_path": "BalticWay/segmented/en-bw14sol.jsonl",
"solution_match": "\nSolution 1",
"tier": "T3",
"year": "2014"
}
|
The sum of the angles $A$ and $C$ of a convex quadrilateral $A B C D$ is less than $180^{\circ}$. Prove that
$$
A B \cdot C D+A D \cdot B C<A C(A B+A D)
$$
|
. Consider an inscribed quadrilateral $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ with sides of the same lengths as $A B C D$ (such a quadrilateral exists, because we can draw these 4 sides in a big circle and afterwards continuously decrease its radius). Then $\angle B^{\prime}+\angle D^{\prime}=180^{\circ}<\angle B+\angle D$. Therefore, $\angle B^{\prime}<\angle B$ or $\angle D^{\prime}<\angle D$ and hence $A^{\prime} C^{\prime}<A C$, by the cosine theorem.
So the inequality under consideration for $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ is stronger than that for $A B C D$. However, the inequality for $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ follows immediately from Ptolemy's theorem.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
The sum of the angles $A$ and $C$ of a convex quadrilateral $A B C D$ is less than $180^{\circ}$. Prove that
$$
A B \cdot C D+A D \cdot B C<A C(A B+A D)
$$
|
. Consider an inscribed quadrilateral $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ with sides of the same lengths as $A B C D$ (such a quadrilateral exists, because we can draw these 4 sides in a big circle and afterwards continuously decrease its radius). Then $\angle B^{\prime}+\angle D^{\prime}=180^{\circ}<\angle B+\angle D$. Therefore, $\angle B^{\prime}<\angle B$ or $\angle D^{\prime}<\angle D$ and hence $A^{\prime} C^{\prime}<A C$, by the cosine theorem.
So the inequality under consideration for $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ is stronger than that for $A B C D$. However, the inequality for $A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ follows immediately from Ptolemy's theorem.
|
{
"exam": "BalticWay",
"problem_label": "15",
"problem_match": "# Problem 15",
"resource_path": "BalticWay/segmented/en-bw14sol.jsonl",
"solution_match": "\nSolution 2",
"tier": "T3",
"year": "2014"
}
|
Determine whether $712 !+1$ is a prime number.
Answer: It is composite.
|
We will show that 719 is a prime factor of given number (evidently, $719<$ $712 !+1$ ). All congruences are considered modulo 719 . By Wilson's theorem, $718 ! \equiv-1$. Furthermore,
$$
713 \cdot 714 \cdot 715 \cdot 716 \cdot 717 \cdot 718 \equiv(-6)(-5)(-4)(-3)(-2)(-1) \equiv 720 \equiv 1 .
$$
Hence $712 ! \equiv-1$, which means that $712 !+1$ is divisible by 719 .
We remark that 719 is the smallest prime greater then 712 , so 719 is the smallest prime divisor of $712 !+1$.
|
719
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Determine whether $712 !+1$ is a prime number.
Answer: It is composite.
|
We will show that 719 is a prime factor of given number (evidently, $719<$ $712 !+1$ ). All congruences are considered modulo 719 . By Wilson's theorem, $718 ! \equiv-1$. Furthermore,
$$
713 \cdot 714 \cdot 715 \cdot 716 \cdot 717 \cdot 718 \equiv(-6)(-5)(-4)(-3)(-2)(-1) \equiv 720 \equiv 1 .
$$
Hence $712 ! \equiv-1$, which means that $712 !+1$ is divisible by 719 .
We remark that 719 is the smallest prime greater then 712 , so 719 is the smallest prime divisor of $712 !+1$.
|
{
"exam": "BalticWay",
"problem_label": "16",
"problem_match": "# Problem 16",
"resource_path": "BalticWay/segmented/en-bw14sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2014"
}
|
Do there exist pairwise distinct rational numbers $x, y$ and $z$ such that
$$
\frac{1}{(x-y)^{2}}+\frac{1}{(y-z)^{2}}+\frac{1}{(z-x)^{2}}=2014 ?
$$
Answer: No.
|
Put $a=x-y$ and $b=y-z$. Then
$$
\begin{aligned}
\frac{1}{(x-y)^{2}}+\frac{1}{(y-z)^{2}}+\frac{1}{(z-x)^{2}} & =\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{(a+b)^{2}} \\
& =\frac{b^{2}(a+b)^{2}+a^{2}(a+b)^{2}+a^{2} b^{2}}{a^{2} b^{2}(a+b)^{2}} \\
& =\left(\frac{a^{2}+b^{2}+a b}{a b(a+b)}\right)^{2} .
\end{aligned}
$$
On the other hand, 2014 is not a square of a rational number. Hence, such numbers $x, y, z$ do not exist.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Do there exist pairwise distinct rational numbers $x, y$ and $z$ such that
$$
\frac{1}{(x-y)^{2}}+\frac{1}{(y-z)^{2}}+\frac{1}{(z-x)^{2}}=2014 ?
$$
Answer: No.
|
Put $a=x-y$ and $b=y-z$. Then
$$
\begin{aligned}
\frac{1}{(x-y)^{2}}+\frac{1}{(y-z)^{2}}+\frac{1}{(z-x)^{2}} & =\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{(a+b)^{2}} \\
& =\frac{b^{2}(a+b)^{2}+a^{2}(a+b)^{2}+a^{2} b^{2}}{a^{2} b^{2}(a+b)^{2}} \\
& =\left(\frac{a^{2}+b^{2}+a b}{a b(a+b)}\right)^{2} .
\end{aligned}
$$
On the other hand, 2014 is not a square of a rational number. Hence, such numbers $x, y, z$ do not exist.
|
{
"exam": "BalticWay",
"problem_label": "17",
"problem_match": "# Problem 17",
"resource_path": "BalticWay/segmented/en-bw14sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2014"
}
|
Let $p$ be a prime number, and let $n$ be a positive integer. Find the number of quadruples $\left(a_{1}, a_{2}, a_{3}, a_{4}\right)$ with $a_{i} \in\left\{0,1, \ldots, p^{n}-1\right\}$ for $i=1,2,3,4$ such that
$$
p^{n} \mid\left(a_{1} a_{2}+a_{3} a_{4}+1\right) .
$$
Answer: $p^{3 n}-p^{3 n-2}$.
|
We have $p^{n}-p^{n-1}$ choices for $a_{1}$ such that $p \nmid a_{1}$. In this case for any of the $p^{n} \cdot p^{n}$ choices of $a_{3}$ and $a_{4}$, there is a unique choice of $a_{2}$, namely,
$$
a_{2} \equiv a_{1}^{-1}\left(-1-a_{3} a_{4}\right) \quad \bmod p^{n}
$$
This gives $p^{2 n}\left(p^{n}-p^{n-1}\right)=p^{3 n-1}(p-1)$ of quadruples.
If $p \mid a_{1}$ then we obviously have $p \nmid a_{3}$, since otherwise the condition
$$
p^{n} \mid\left(a_{1} a_{2}+a_{3} a_{4}+1\right)
$$
is violated. Now, if $p \mid a_{1}, p \nmid a_{3}$, for any choice of $a_{2}$ there is a unique choice of $a_{4}$, namely,
$$
a_{4} \equiv a_{3}^{-1}\left(-1-a_{1} a_{2}\right) \quad \bmod p^{n}
$$
Thus, for these $p^{n-1}$ choices of $a_{1}$ and $p^{n}-p^{n-1}$ choices of $a_{3}$, we have for each of the $p^{n}$ choices of $a_{2}$ a unique $a_{4}$. So in this case there are $p^{n-1}\left(p^{n}-p^{n-1}\right) p^{n}=p^{3 n-2}(p-1)$ of quadruples.
Thus, the total number of quadruples is
$$
p^{3 n-1}(p-1)+p^{3 n-2}(p-1)=p^{3 n}-p^{3 n-2} \text {. }
$$
|
p^{3 n}-p^{3 n-2}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $p$ be a prime number, and let $n$ be a positive integer. Find the number of quadruples $\left(a_{1}, a_{2}, a_{3}, a_{4}\right)$ with $a_{i} \in\left\{0,1, \ldots, p^{n}-1\right\}$ for $i=1,2,3,4$ such that
$$
p^{n} \mid\left(a_{1} a_{2}+a_{3} a_{4}+1\right) .
$$
Answer: $p^{3 n}-p^{3 n-2}$.
|
We have $p^{n}-p^{n-1}$ choices for $a_{1}$ such that $p \nmid a_{1}$. In this case for any of the $p^{n} \cdot p^{n}$ choices of $a_{3}$ and $a_{4}$, there is a unique choice of $a_{2}$, namely,
$$
a_{2} \equiv a_{1}^{-1}\left(-1-a_{3} a_{4}\right) \quad \bmod p^{n}
$$
This gives $p^{2 n}\left(p^{n}-p^{n-1}\right)=p^{3 n-1}(p-1)$ of quadruples.
If $p \mid a_{1}$ then we obviously have $p \nmid a_{3}$, since otherwise the condition
$$
p^{n} \mid\left(a_{1} a_{2}+a_{3} a_{4}+1\right)
$$
is violated. Now, if $p \mid a_{1}, p \nmid a_{3}$, for any choice of $a_{2}$ there is a unique choice of $a_{4}$, namely,
$$
a_{4} \equiv a_{3}^{-1}\left(-1-a_{1} a_{2}\right) \quad \bmod p^{n}
$$
Thus, for these $p^{n-1}$ choices of $a_{1}$ and $p^{n}-p^{n-1}$ choices of $a_{3}$, we have for each of the $p^{n}$ choices of $a_{2}$ a unique $a_{4}$. So in this case there are $p^{n-1}\left(p^{n}-p^{n-1}\right) p^{n}=p^{3 n-2}(p-1)$ of quadruples.
Thus, the total number of quadruples is
$$
p^{3 n-1}(p-1)+p^{3 n-2}(p-1)=p^{3 n}-p^{3 n-2} \text {. }
$$
|
{
"exam": "BalticWay",
"problem_label": "18",
"problem_match": "# Problem 18",
"resource_path": "BalticWay/segmented/en-bw14sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2014"
}
|
Let $m$ and $n$ be relatively prime positive integers. Determine all possible values of
$$
\operatorname{gcd}\left(2^{m}-2^{n}, 2^{m^{2}+m n+n^{2}}-1\right) .
$$
Answer: 1 and 7 .
|
Without restriction of generality we may assume that $m \geqslant n$. It is well known that
$$
\operatorname{gcd}\left(2^{p}-1,2^{q}-1\right)=2^{\operatorname{gcd}(p, q)}-1,
$$
SO
$$
\begin{aligned}
\operatorname{gcd}\left(2^{m}-2^{n}, 2^{m^{2}+m n+n^{2}}-1\right) & =\operatorname{gcd}\left(2^{m-n}-1,2^{m^{2}+m n+n^{2}}-1\right) \\
& =2^{\operatorname{gcd}\left(m-n, m^{2}+m n+n^{2}\right)}-1 .
\end{aligned}
$$
Let $d \geqslant 1$ be a divisor of $m-n$. Clearly, $\operatorname{gcd}(m, d)=1$, since $m$ and $n$ are relatively prime. Assume that $d$ also divides $m^{2}+m n+n^{2}$. Then $d$ divides $3 m^{2}$. In view of $\operatorname{gcd}(m, d)=1$ the only choices for $d$ are $d=1$ and $d=3$. Hence $\operatorname{gcd}\left(m-n, m^{2}+m n+n^{2}\right)$ is either 1 or 3 . Consequently, $\operatorname{gcd}\left(2^{m}-2^{n}, 2^{m^{2}+m n+n^{2}}-1\right)$ may only assume the values $2^{1}-1=1$ and $2^{3}-1=7$.
Both values are attainable, since $m=2, n=1$ gives
$$
\operatorname{gcd}\left(2^{2}-2^{1}, 2^{2^{2}+2 \cdot 1+1^{2}}-1\right)=\operatorname{gcd}\left(2,2^{7}-1\right)=1
$$
whereas $m=1, n=1$ gives
$$
\operatorname{gcd}\left(2^{1}-2^{1}, 2^{1^{2}+1 \cdot 1+1^{2}}-1\right)=\operatorname{gcd}\left(0,2^{3}-1\right)=7
$$
|
1 \text{ and } 7
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $m$ and $n$ be relatively prime positive integers. Determine all possible values of
$$
\operatorname{gcd}\left(2^{m}-2^{n}, 2^{m^{2}+m n+n^{2}}-1\right) .
$$
Answer: 1 and 7 .
|
Without restriction of generality we may assume that $m \geqslant n$. It is well known that
$$
\operatorname{gcd}\left(2^{p}-1,2^{q}-1\right)=2^{\operatorname{gcd}(p, q)}-1,
$$
SO
$$
\begin{aligned}
\operatorname{gcd}\left(2^{m}-2^{n}, 2^{m^{2}+m n+n^{2}}-1\right) & =\operatorname{gcd}\left(2^{m-n}-1,2^{m^{2}+m n+n^{2}}-1\right) \\
& =2^{\operatorname{gcd}\left(m-n, m^{2}+m n+n^{2}\right)}-1 .
\end{aligned}
$$
Let $d \geqslant 1$ be a divisor of $m-n$. Clearly, $\operatorname{gcd}(m, d)=1$, since $m$ and $n$ are relatively prime. Assume that $d$ also divides $m^{2}+m n+n^{2}$. Then $d$ divides $3 m^{2}$. In view of $\operatorname{gcd}(m, d)=1$ the only choices for $d$ are $d=1$ and $d=3$. Hence $\operatorname{gcd}\left(m-n, m^{2}+m n+n^{2}\right)$ is either 1 or 3 . Consequently, $\operatorname{gcd}\left(2^{m}-2^{n}, 2^{m^{2}+m n+n^{2}}-1\right)$ may only assume the values $2^{1}-1=1$ and $2^{3}-1=7$.
Both values are attainable, since $m=2, n=1$ gives
$$
\operatorname{gcd}\left(2^{2}-2^{1}, 2^{2^{2}+2 \cdot 1+1^{2}}-1\right)=\operatorname{gcd}\left(2,2^{7}-1\right)=1
$$
whereas $m=1, n=1$ gives
$$
\operatorname{gcd}\left(2^{1}-2^{1}, 2^{1^{2}+1 \cdot 1+1^{2}}-1\right)=\operatorname{gcd}\left(0,2^{3}-1\right)=7
$$
|
{
"exam": "BalticWay",
"problem_label": "19",
"problem_match": "# Problem 19",
"resource_path": "BalticWay/segmented/en-bw14sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2014"
}
|
Consider a sequence of positive integers $a_{1}, a_{2}, a_{3}, \ldots$ such that for $k \geqslant 2$ we have
$$
a_{k+1}=\frac{a_{k}+a_{k-1}}{2015^{i}}
$$
where $2015^{i}$ is the maximal power of 2015 that divides $a_{k}+a_{k-1}$. Prove that if this sequence is periodic then its period is divisible by 3 .
|
If all the numbers in the sequence are even, then we can divide each element of the sequence by the maximal possible power of 2 . In this way we obtain a new sequence of integers which is determined by the same recurrence formula and has the same period, but now it contains an odd number. Consider this new sequence modulo 2. Since the number 2015 is odd, it has no influence to the calculations modulo 2 , so we may think that modulo 2 this sequence is given by the Fibonacci recurrence $a_{k+1} \equiv a_{k}+a_{k-1}$ with $a_{j} \equiv 1$ $(\bmod 2)$ for at least one $j$. Then it has the following form $\ldots, 1,1,0,1,1,0,1,1,0, \ldots$ (with period 3 modulo 2), so that the length of the original period of our sequence (if it is periodic!) must be divisible by 3 .
Remark. It is not known whether a periodic sequence of integers satisfying the recurrence condition of this problem exists. The solution of such a problem is apparently completely out of reach. See, e.g., the recent preprint
Brandon Avila and Tanya Khovanova, Free Fibonacci sequences, 2014, preprint at http://arxiv.org/pdf/1403.4614v1.pdf
for more information. (The problem given at the olympiad is Lemma 28 of this paper, where 2015 can be replaced by any odd integer greater than 1.)
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Consider a sequence of positive integers $a_{1}, a_{2}, a_{3}, \ldots$ such that for $k \geqslant 2$ we have
$$
a_{k+1}=\frac{a_{k}+a_{k-1}}{2015^{i}}
$$
where $2015^{i}$ is the maximal power of 2015 that divides $a_{k}+a_{k-1}$. Prove that if this sequence is periodic then its period is divisible by 3 .
|
If all the numbers in the sequence are even, then we can divide each element of the sequence by the maximal possible power of 2 . In this way we obtain a new sequence of integers which is determined by the same recurrence formula and has the same period, but now it contains an odd number. Consider this new sequence modulo 2. Since the number 2015 is odd, it has no influence to the calculations modulo 2 , so we may think that modulo 2 this sequence is given by the Fibonacci recurrence $a_{k+1} \equiv a_{k}+a_{k-1}$ with $a_{j} \equiv 1$ $(\bmod 2)$ for at least one $j$. Then it has the following form $\ldots, 1,1,0,1,1,0,1,1,0, \ldots$ (with period 3 modulo 2), so that the length of the original period of our sequence (if it is periodic!) must be divisible by 3 .
Remark. It is not known whether a periodic sequence of integers satisfying the recurrence condition of this problem exists. The solution of such a problem is apparently completely out of reach. See, e.g., the recent preprint
Brandon Avila and Tanya Khovanova, Free Fibonacci sequences, 2014, preprint at http://arxiv.org/pdf/1403.4614v1.pdf
for more information. (The problem given at the olympiad is Lemma 28 of this paper, where 2015 can be replaced by any odd integer greater than 1.)
|
{
"exam": "BalticWay",
"problem_label": "20",
"problem_match": "# Problem 20",
"resource_path": "BalticWay/segmented/en-bw14sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2014"
}
|
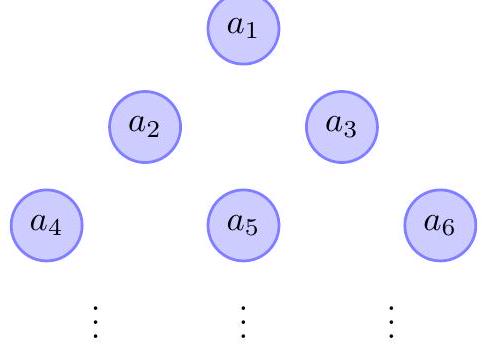
For $n \geq 2$, an equilateral triangle is divided into $n^{2}$ congruent smaller equilateral triangles. Determine all ways in which real numbers can be assigned to the $\frac{(n+1)(n+2)}{2}$ vertices so that three such numbers sum to zero whenever the three vertices form a triangle with edges parallel to the sides of the big triangle.
|
We label the vertices (and the corresponding real numbers) as follows.
For $n=2$, we see that
$$
a_{2}+a_{4}+a_{5}=0=a_{2}+a_{3}+a_{5}
$$
which shows that $a_{3}=a_{4}$ and similarly $a_{1}=a_{5}$ and $a_{2}=a_{6}$. Now the only additional requirement is $a_{1}+a_{2}+a_{3}=0$, so that all solutions are of the following form, for any $x, y$ and $z$ with $x+y+z=0$ :

For $n=3$, observe that $a_{1}=a_{7}=a_{10}$ since they all equal $a_{5}$. Since also $a_{1}+a_{7}+a_{10}=0$, they all equal zero. By considering the top triangle, we get $x=a_{2}=-a_{3}$ and this uniquely determines the rest. It is easily checked that, for any real $x$, this is actually a solution:

For $n \geq 3$ we can apply the same argument as above for any collection of 10 vertices. Any vertex not on the sides of the big triangle has to equal zero, since it is the centre of such a collection of 10 vertices. Any vertex $a$ on the sides of the big triangle forms some parallelogram similar to $a_{4}, a_{2}, a_{5}, a_{8}$, where the point opposite $a$ is in the interior of the big triangle. Since such opposite numbers are equal, all $a_{i}$ have to be zero in this case.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
For $n \geq 2$, an equilateral triangle is divided into $n^{2}$ congruent smaller equilateral triangles. Determine all ways in which real numbers can be assigned to the $\frac{(n+1)(n+2)}{2}$ vertices so that three such numbers sum to zero whenever the three vertices form a triangle with edges parallel to the sides of the big triangle.
|
We label the vertices (and the corresponding real numbers) as follows.

For $n=2$, we see that
$$
a_{2}+a_{4}+a_{5}=0=a_{2}+a_{3}+a_{5}
$$
which shows that $a_{3}=a_{4}$ and similarly $a_{1}=a_{5}$ and $a_{2}=a_{6}$. Now the only additional requirement is $a_{1}+a_{2}+a_{3}=0$, so that all solutions are of the following form, for any $x, y$ and $z$ with $x+y+z=0$ :

For $n=3$, observe that $a_{1}=a_{7}=a_{10}$ since they all equal $a_{5}$. Since also $a_{1}+a_{7}+a_{10}=0$, they all equal zero. By considering the top triangle, we get $x=a_{2}=-a_{3}$ and this uniquely determines the rest. It is easily checked that, for any real $x$, this is actually a solution:

For $n \geq 3$ we can apply the same argument as above for any collection of 10 vertices. Any vertex not on the sides of the big triangle has to equal zero, since it is the centre of such a collection of 10 vertices. Any vertex $a$ on the sides of the big triangle forms some parallelogram similar to $a_{4}, a_{2}, a_{5}, a_{8}$, where the point opposite $a$ is in the interior of the big triangle. Since such opposite numbers are equal, all $a_{i}$ have to be zero in this case.
|
{
"exam": "BalticWay",
"problem_label": "1",
"problem_match": "# Problem 1.",
"resource_path": "BalticWay/segmented/en-bw15sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2015"
}
|
Let $n$ be a positive integer and let $a_{1}, \ldots, a_{n}$ be real numbers satisfying $0 \leq a_{i} \leq 1$ for $i=1, \ldots, n$. Prove the inequality
$$
\left(1-a_{1}^{n}\right)\left(1-a_{2}^{n}\right) \cdots\left(1-a_{n}^{n}\right) \leq\left(1-a_{1} a_{2} \cdots a_{n}\right)^{n} .
$$
|
The numbers $1-a_{i}^{n}$ are positive by assumption. AM-GM gives
$$
\begin{aligned}
\left(1-a_{1}^{n}\right)\left(1-a_{2}^{n}\right) \cdots\left(1-a_{n}^{n}\right) & \leq\left(\frac{\left(1-a_{1}^{n}\right)+\left(1-a_{2}^{n}\right)+\cdots+\left(1-a_{n}^{n}\right)}{n}\right)^{n} \\
& =\left(1-\frac{a_{1}^{n}+\cdots+a_{n}^{n}}{n}\right)^{n} .
\end{aligned}
$$
By applying AM-GM again we obtain
$$
a_{1} a_{2} \cdots a_{n} \leq \frac{a_{1}^{n}+\cdots+a_{n}^{n}}{n} \Rightarrow\left(1-\frac{a_{1}^{n}+\cdots+a_{n}^{n}}{n}\right)^{n} \leq\left(1-a_{1} a_{2} \cdots a_{n}\right)^{n}
$$
and hence the desired inequality.
Remark. It is possible to use Jensen's inequality applied to $f(x)=\log \left(1-e^{x}\right)$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n$ be a positive integer and let $a_{1}, \ldots, a_{n}$ be real numbers satisfying $0 \leq a_{i} \leq 1$ for $i=1, \ldots, n$. Prove the inequality
$$
\left(1-a_{1}^{n}\right)\left(1-a_{2}^{n}\right) \cdots\left(1-a_{n}^{n}\right) \leq\left(1-a_{1} a_{2} \cdots a_{n}\right)^{n} .
$$
|
The numbers $1-a_{i}^{n}$ are positive by assumption. AM-GM gives
$$
\begin{aligned}
\left(1-a_{1}^{n}\right)\left(1-a_{2}^{n}\right) \cdots\left(1-a_{n}^{n}\right) & \leq\left(\frac{\left(1-a_{1}^{n}\right)+\left(1-a_{2}^{n}\right)+\cdots+\left(1-a_{n}^{n}\right)}{n}\right)^{n} \\
& =\left(1-\frac{a_{1}^{n}+\cdots+a_{n}^{n}}{n}\right)^{n} .
\end{aligned}
$$
By applying AM-GM again we obtain
$$
a_{1} a_{2} \cdots a_{n} \leq \frac{a_{1}^{n}+\cdots+a_{n}^{n}}{n} \Rightarrow\left(1-\frac{a_{1}^{n}+\cdots+a_{n}^{n}}{n}\right)^{n} \leq\left(1-a_{1} a_{2} \cdots a_{n}\right)^{n}
$$
and hence the desired inequality.
Remark. It is possible to use Jensen's inequality applied to $f(x)=\log \left(1-e^{x}\right)$.
|
{
"exam": "BalticWay",
"problem_label": "2",
"problem_match": "# Problem 2.",
"resource_path": "BalticWay/segmented/en-bw15sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2015"
}
|
Let $n>1$ be an integer. Find all non-constant real polynomials $P(x)$ satisfying, for any real $x$, the identity
$$
P(x) P\left(x^{2}\right) P\left(x^{3}\right) \cdots P\left(x^{n}\right)=P\left(x^{\frac{n(n+1)}{2}}\right) .
$$
|
Answer: $P(x)=x^{m}$ if $n$ is even; $P(x)= \pm x^{m}$ if $n$ is odd.
Consider first the case of a monomial $P(x)=a x^{m}$ with $a \neq 0$. Then
$$
a x^{\frac{m n(n+1)}{2}}=P\left(x^{\frac{n(n+1)}{2}}\right)=P(x) P\left(x^{2}\right) P\left(x^{3}\right) \cdots P\left(x^{n}\right)=a x^{m} \cdot a x^{2 m} \cdots a x^{n m}=a^{n} x^{\frac{m n(n+1)}{2}}
$$
implies $a^{n}=a$. Thus, $a=1$ when $n$ is even and $a= \pm 1$ when $n$ is odd. Obviously these polynomials satisfy the desired equality.
Suppose now that $P$ is not a monomial. Write $P(x)=a x^{m}+Q(x)$, where $Q$ is non-zero polynomial with $\operatorname{deg} Q=k<m$. We have
$$
\begin{aligned}
a x^{\frac{m n(n+1)}{2}}+Q & \left(x^{\frac{n(n+1)}{2}}\right)=P\left(x^{\frac{n(n+1)}{2}}\right) \\
& =P(x) P\left(x^{2}\right) P\left(x^{3}\right) \cdots P\left(x^{n}\right)=\left(a x^{m}+Q(x)\right)\left(a x^{2 m}+Q\left(x^{2}\right)\right) \cdots\left(a x^{n m}+Q\left(x^{n}\right)\right) .
\end{aligned}
$$
The highest degree of a monomial, on both sides of the equality, is $\frac{m n(n+1)}{2}$. The second highest degree in the right-hand side is
$$
2 m+3 m+\cdots+n m+k=\frac{m(n+2)(n-1)}{2}+k
$$
while in the left-hand side it is $\frac{k n(n+1)}{2}$. Thus
$$
\frac{m(n+2)(n-1)}{2}+k=\frac{k n(n+1)}{2}
$$
which leads to
$$
(m-k)(n+2)(n-1)=0
$$
and so $m=k$, contradicting the assumption that $m>k$. Consequently, no polynomial of the form $a x^{m}+Q(x)$ fulfils the given condition.
|
P(x)=x^{m} \text{ if } n \text{ is even; } P(x)= \pm x^{m} \text{ if } n \text{ is odd.}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $n>1$ be an integer. Find all non-constant real polynomials $P(x)$ satisfying, for any real $x$, the identity
$$
P(x) P\left(x^{2}\right) P\left(x^{3}\right) \cdots P\left(x^{n}\right)=P\left(x^{\frac{n(n+1)}{2}}\right) .
$$
|
Answer: $P(x)=x^{m}$ if $n$ is even; $P(x)= \pm x^{m}$ if $n$ is odd.
Consider first the case of a monomial $P(x)=a x^{m}$ with $a \neq 0$. Then
$$
a x^{\frac{m n(n+1)}{2}}=P\left(x^{\frac{n(n+1)}{2}}\right)=P(x) P\left(x^{2}\right) P\left(x^{3}\right) \cdots P\left(x^{n}\right)=a x^{m} \cdot a x^{2 m} \cdots a x^{n m}=a^{n} x^{\frac{m n(n+1)}{2}}
$$
implies $a^{n}=a$. Thus, $a=1$ when $n$ is even and $a= \pm 1$ when $n$ is odd. Obviously these polynomials satisfy the desired equality.
Suppose now that $P$ is not a monomial. Write $P(x)=a x^{m}+Q(x)$, where $Q$ is non-zero polynomial with $\operatorname{deg} Q=k<m$. We have
$$
\begin{aligned}
a x^{\frac{m n(n+1)}{2}}+Q & \left(x^{\frac{n(n+1)}{2}}\right)=P\left(x^{\frac{n(n+1)}{2}}\right) \\
& =P(x) P\left(x^{2}\right) P\left(x^{3}\right) \cdots P\left(x^{n}\right)=\left(a x^{m}+Q(x)\right)\left(a x^{2 m}+Q\left(x^{2}\right)\right) \cdots\left(a x^{n m}+Q\left(x^{n}\right)\right) .
\end{aligned}
$$
The highest degree of a monomial, on both sides of the equality, is $\frac{m n(n+1)}{2}$. The second highest degree in the right-hand side is
$$
2 m+3 m+\cdots+n m+k=\frac{m(n+2)(n-1)}{2}+k
$$
while in the left-hand side it is $\frac{k n(n+1)}{2}$. Thus
$$
\frac{m(n+2)(n-1)}{2}+k=\frac{k n(n+1)}{2}
$$
which leads to
$$
(m-k)(n+2)(n-1)=0
$$
and so $m=k$, contradicting the assumption that $m>k$. Consequently, no polynomial of the form $a x^{m}+Q(x)$ fulfils the given condition.
|
{
"exam": "BalticWay",
"problem_label": "3",
"problem_match": "# Problem 3.",
"resource_path": "BalticWay/segmented/en-bw15sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2015"
}
|
A family wears clothes of three colours: red, blue and green, with a separate, identical laundry bin for each colour. At the beginning of the first week, all bins are empty. Each week, the family generates a total of $10 \mathrm{~kg}$ of laundry (the proportion of each colour is subject to variation). The laundry is sorted by colour and placed in the bins. Next, the heaviest bin (only one of them, if there are several that are heaviest) is emptied and its contents washed. What is the minimal possible storing capacity required of the laundry bins in order for them never to overflow?
|
Answer: $25 \mathrm{~kg}$.
Each week, the accumulation of laundry increases the total amount by $K=10$, after which the washing decreases it by at least one third, because, by the pigeon-hole principle, the bin with the most laundry must contain at least a third of the total. Hence the amount of laundry post-wash after the $n$th week is bounded above by the sequence $a_{n+1}=\frac{2}{3}\left(a_{n}+K\right)$ with $a_{0}=0$, which is clearly bounded above by $2 K$. The total amount of laundry is less than $2 K$ post-wash and $3 K$ pre-wash.
Now suppose pre-wash state $(a, b, c)$ precedes post-wash state $(a, b, 0)$, which precedes pre-wash state $\left(a^{\prime}, b^{\prime}, c^{\prime}\right)$. The relations $a \leq c$ and $a^{\prime} \leq a+K$ lead to
$$
3 K>a+b+c \geq 2 a \geq 2\left(a^{\prime}-K\right)
$$
and similarly for $b^{\prime}$, whence $a^{\prime}, b^{\prime}<\frac{5}{2} K$. Since also $c^{\prime} \leq K$, a pre-wash bin, and a fortiori a post-wash bin, always contains less than $\frac{5}{2} K$.
Consider now the following scenario. For a start, we keep packing the three bins equally full before washing. Initialising at $(0,0,0)$, the first week will end at $\left(\frac{1}{3} K, \frac{1}{3} K, \frac{1}{3} K\right)$ pre-wash and $\left(\frac{1}{3} K, \frac{1}{3} K, 0\right)$ post-wash, the second week at $\left(\frac{5}{9} K, \frac{5}{9} K, \frac{5}{9} K\right)$ pre-wash and $\left(\frac{5}{9} K, \frac{5}{9} K, 0\right)$ post-wash, \&c. Following this scheme, we can get arbitrarily close to the state $(K, K, 0)$ after washing. Supposing this accomplished, placing $\frac{1}{2} K \mathrm{~kg}$ of laundry in each of the non-empty bins leaves us in a state close to $\left(\frac{3}{2} K, \frac{3}{2} K, 0\right)$ pre-wash and $\left(\frac{3}{2} K, 0,0\right)$ post-wash. Finally, the next week's worth of laundry is directed solely to the single non-empty bin. It may thus contain any amount of laundry below $\frac{5}{2} K \mathrm{~kg}$.
|
25 \mathrm{~kg}
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
A family wears clothes of three colours: red, blue and green, with a separate, identical laundry bin for each colour. At the beginning of the first week, all bins are empty. Each week, the family generates a total of $10 \mathrm{~kg}$ of laundry (the proportion of each colour is subject to variation). The laundry is sorted by colour and placed in the bins. Next, the heaviest bin (only one of them, if there are several that are heaviest) is emptied and its contents washed. What is the minimal possible storing capacity required of the laundry bins in order for them never to overflow?
|
Answer: $25 \mathrm{~kg}$.
Each week, the accumulation of laundry increases the total amount by $K=10$, after which the washing decreases it by at least one third, because, by the pigeon-hole principle, the bin with the most laundry must contain at least a third of the total. Hence the amount of laundry post-wash after the $n$th week is bounded above by the sequence $a_{n+1}=\frac{2}{3}\left(a_{n}+K\right)$ with $a_{0}=0$, which is clearly bounded above by $2 K$. The total amount of laundry is less than $2 K$ post-wash and $3 K$ pre-wash.
Now suppose pre-wash state $(a, b, c)$ precedes post-wash state $(a, b, 0)$, which precedes pre-wash state $\left(a^{\prime}, b^{\prime}, c^{\prime}\right)$. The relations $a \leq c$ and $a^{\prime} \leq a+K$ lead to
$$
3 K>a+b+c \geq 2 a \geq 2\left(a^{\prime}-K\right)
$$
and similarly for $b^{\prime}$, whence $a^{\prime}, b^{\prime}<\frac{5}{2} K$. Since also $c^{\prime} \leq K$, a pre-wash bin, and a fortiori a post-wash bin, always contains less than $\frac{5}{2} K$.
Consider now the following scenario. For a start, we keep packing the three bins equally full before washing. Initialising at $(0,0,0)$, the first week will end at $\left(\frac{1}{3} K, \frac{1}{3} K, \frac{1}{3} K\right)$ pre-wash and $\left(\frac{1}{3} K, \frac{1}{3} K, 0\right)$ post-wash, the second week at $\left(\frac{5}{9} K, \frac{5}{9} K, \frac{5}{9} K\right)$ pre-wash and $\left(\frac{5}{9} K, \frac{5}{9} K, 0\right)$ post-wash, \&c. Following this scheme, we can get arbitrarily close to the state $(K, K, 0)$ after washing. Supposing this accomplished, placing $\frac{1}{2} K \mathrm{~kg}$ of laundry in each of the non-empty bins leaves us in a state close to $\left(\frac{3}{2} K, \frac{3}{2} K, 0\right)$ pre-wash and $\left(\frac{3}{2} K, 0,0\right)$ post-wash. Finally, the next week's worth of laundry is directed solely to the single non-empty bin. It may thus contain any amount of laundry below $\frac{5}{2} K \mathrm{~kg}$.
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "# Problem 4.",
"resource_path": "BalticWay/segmented/en-bw15sol.jsonl",
"solution_match": "# Solution.",
"tier": "T3",
"year": "2015"
}
|
Find all functions $f: \mathbf{R} \rightarrow \mathbf{R}$ satisfying the equation
$$
|x| f(y)+y f(x)=f(x y)+f\left(x^{2}\right)+f(f(y))
$$
for all real numbers $x$ and $y$.
|
Answer: all functions $f(x)=c(|x|-x)$, where $c \geq 0$.
Choosing $x=y=0$, we find
$$
f(f(0))=-2 f(0)
$$
Denote $a=f(0)$, so that $f(a)=-2 a$, and choose $y=0$ in the initial equation:
$$
a|x|=a+f\left(x^{2}\right)+f(a)=a+f\left(x^{2}\right)-2 a \quad \Rightarrow \quad f\left(x^{2}\right)=a(|x|+1)
$$
In particular, $f(1)=2 a$. Choose $(x, y)=\left(z^{2}, 1\right)$ in the initial equation:
$$
\begin{aligned}
& z^{2} f(1)+f\left(z^{2}\right)=f\left(z^{2}\right)+f\left(z^{4}\right)+f(f(1)) \\
\Rightarrow & 2 a z^{2}=z^{2} f(1)=f\left(z^{4}\right)+f(f(1))=a\left(z^{2}+1\right)+f(2 a) \\
\Rightarrow & a z^{2}=a+f(2 a)
\end{aligned}
$$
The right-hand side is constant, while the left-hand side is a quadratic function in $z$, which can only happen if $a=0$. (Choose $z=1$ and then $z=0$.)
We now conclude that $f\left(x^{2}\right)=0$, and so $f(x)=0$ for all non-negative $x$. In particular, $f(0)=0$. Choosing $x=0$ in the initial equation, we find $f(f(y))=0$ for all $y$. Simplifying the original equation and swapping $x$ and $y$ leads to
$$
|x| f(y)+y f(x)=f(x y)=|y| f(x)+x f(y) .
$$
Choose $y=-1$ and put $c=\frac{f(-1)}{2}$ :
$$
|x| f(-1)-f(x)=f(x)+x f(-1) \Rightarrow f(x)=\frac{f(-1)}{2}(|x|-x)=c(|x|-x) \text {. }
$$
One easily verifies that these functions satisfy the functional equation for any parameter $c \geq 0$.
|
f(x)=c(|x|-x), \text{ where } c \geq 0
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all functions $f: \mathbf{R} \rightarrow \mathbf{R}$ satisfying the equation
$$
|x| f(y)+y f(x)=f(x y)+f\left(x^{2}\right)+f(f(y))
$$
for all real numbers $x$ and $y$.
|
Answer: all functions $f(x)=c(|x|-x)$, where $c \geq 0$.
Choosing $x=y=0$, we find
$$
f(f(0))=-2 f(0)
$$
Denote $a=f(0)$, so that $f(a)=-2 a$, and choose $y=0$ in the initial equation:
$$
a|x|=a+f\left(x^{2}\right)+f(a)=a+f\left(x^{2}\right)-2 a \quad \Rightarrow \quad f\left(x^{2}\right)=a(|x|+1)
$$
In particular, $f(1)=2 a$. Choose $(x, y)=\left(z^{2}, 1\right)$ in the initial equation:
$$
\begin{aligned}
& z^{2} f(1)+f\left(z^{2}\right)=f\left(z^{2}\right)+f\left(z^{4}\right)+f(f(1)) \\
\Rightarrow & 2 a z^{2}=z^{2} f(1)=f\left(z^{4}\right)+f(f(1))=a\left(z^{2}+1\right)+f(2 a) \\
\Rightarrow & a z^{2}=a+f(2 a)
\end{aligned}
$$
The right-hand side is constant, while the left-hand side is a quadratic function in $z$, which can only happen if $a=0$. (Choose $z=1$ and then $z=0$.)
We now conclude that $f\left(x^{2}\right)=0$, and so $f(x)=0$ for all non-negative $x$. In particular, $f(0)=0$. Choosing $x=0$ in the initial equation, we find $f(f(y))=0$ for all $y$. Simplifying the original equation and swapping $x$ and $y$ leads to
$$
|x| f(y)+y f(x)=f(x y)=|y| f(x)+x f(y) .
$$
Choose $y=-1$ and put $c=\frac{f(-1)}{2}$ :
$$
|x| f(-1)-f(x)=f(x)+x f(-1) \Rightarrow f(x)=\frac{f(-1)}{2}(|x|-x)=c(|x|-x) \text {. }
$$
One easily verifies that these functions satisfy the functional equation for any parameter $c \geq 0$.
|
{
"exam": "BalticWay",
"problem_label": "5",
"problem_match": "# Problem 5.",
"resource_path": "BalticWay/segmented/en-bw15sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2015"
}
|
Two players take alternate turns in the following game. At the outset there are two piles, containing 10,000 and 20,000 tokens, respectively. A move consists of removing any positive number of tokens from a single pile or removing $x>0$ tokens from one pile and $y>0$ tokens from the other, where $x+y$ is divisible by 2015. The player who cannot make a move loses. Which player has a winning strategy?
|
The first player wins.
He should present his opponent with one of the following positions:
$$
(0,0), \quad(1,1), \quad(2,2), \quad \ldots, \quad(2014,2014) .
$$
All these positions have different total numbers of tokens modulo 2015. Therefore, if the game starts from two piles of arbitrary sizes, it is possible to obtain one of these positions just by the first move. In our case
$$
10,000+20,000 \equiv 1790 \bmod 2015,
$$
and the first player can leave to his opponent the position $(895,895)$.
Now the second type of move can no longer be carried out. If the second player removes $n$ tokens from one pile, the first player may always respond be removing $n$ tokens from the other pile.
|
(895,895)
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Two players take alternate turns in the following game. At the outset there are two piles, containing 10,000 and 20,000 tokens, respectively. A move consists of removing any positive number of tokens from a single pile or removing $x>0$ tokens from one pile and $y>0$ tokens from the other, where $x+y$ is divisible by 2015. The player who cannot make a move loses. Which player has a winning strategy?
|
The first player wins.
He should present his opponent with one of the following positions:
$$
(0,0), \quad(1,1), \quad(2,2), \quad \ldots, \quad(2014,2014) .
$$
All these positions have different total numbers of tokens modulo 2015. Therefore, if the game starts from two piles of arbitrary sizes, it is possible to obtain one of these positions just by the first move. In our case
$$
10,000+20,000 \equiv 1790 \bmod 2015,
$$
and the first player can leave to his opponent the position $(895,895)$.
Now the second type of move can no longer be carried out. If the second player removes $n$ tokens from one pile, the first player may always respond be removing $n$ tokens from the other pile.
|
{
"exam": "BalticWay",
"problem_label": "6",
"problem_match": "# Problem 6.",
"resource_path": "BalticWay/segmented/en-bw15sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2015"
}
|
There are 100 members in a ladies' club. Each lady has had tea (in private) with exactly 56 of the other members of the club. The Board, consisting of the 50 most distinguished ladies, have all had tea with one another. Prove that the entire club may be split into two groups in such a way that, within each group, any lady has had tea with any other.
|
Each lady in the Board has had tea with 49 ladies within the Board, and 7 ladies without. Each lady not in the Board has had tea with at most 49 ladies not in the Board, and at least 7 ladies in the Board. Comparing these two observations, we conclude that each lady not in the Board has had tea with exactly 49 ladies not in the Board and exactly 7 ladies in the Board. Hence the club may be split into Board members and non-members.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
There are 100 members in a ladies' club. Each lady has had tea (in private) with exactly 56 of the other members of the club. The Board, consisting of the 50 most distinguished ladies, have all had tea with one another. Prove that the entire club may be split into two groups in such a way that, within each group, any lady has had tea with any other.
|
Each lady in the Board has had tea with 49 ladies within the Board, and 7 ladies without. Each lady not in the Board has had tea with at most 49 ladies not in the Board, and at least 7 ladies in the Board. Comparing these two observations, we conclude that each lady not in the Board has had tea with exactly 49 ladies not in the Board and exactly 7 ladies in the Board. Hence the club may be split into Board members and non-members.
|
{
"exam": "BalticWay",
"problem_label": "7",
"problem_match": "# Problem 7.",
"resource_path": "BalticWay/segmented/en-bw15sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2015"
}
|
With inspiration drawn from the rectilinear network of streets in New York, the Manhattan distance between two points $(a, b)$ and $(c, d)$ in the plane is defined to be
$$
|a-c|+|b-d| \text {. }
$$
Suppose only two distinct Manhattan distances occur between all pairs of distinct points of some point set. What is the maximal number of points in such a set?
|
Answer: nine.
Let
$$
\left\{\left(x_{1}, y_{1}\right), \ldots,\left(x_{m}, y_{m}\right)\right\}, \quad \text { where } \quad x_{1} \leq \cdots \leq x_{m}
$$
be the set, and suppose $m \geq 10$.
A special case of the Erdős-Szekeres Theorem asserts that a real sequence of length $n^{2}+1$ contains a monotonic subsequence of length $n+1$. (Proof: Given a sequence $a_{1} \ldots, a_{n^{2}+1}$, let $p_{i}$ denote the length of the longest increasing subsequence ending with $a_{i}$, and $q_{i}$ the length of the longest decreasing subsequence ending with $a_{i}$. If $i<j$ and $a_{i} \leq a_{j}$, then $p_{i}<p_{j}$. If $a_{i} \geq a_{j}$, then $q_{i}<q_{j}$. Hence all $n^{2}+1$ pairs $\left(p_{i}, q_{i}\right)$ are distinct. If all of them were to satisfy $1 \leq p_{i}, q_{i} \leq n$, it would violate the Pigeon-Hole Principle.)
Applied to the sequence $y_{1}, \ldots, y_{m}$, this will produce a subsequence
$$
y_{i} \leq y_{j} \leq y_{k} \leq y_{l} \quad \text { or } \quad y_{i} \geq y_{j} \geq y_{k} \geq y_{l}
$$
One of the shortest paths from $\left(x_{i}, y_{i}\right)$ to $\left(x_{l}, y_{l}\right)$ will pass through first $\left(x_{j}, y_{j}\right)$ and then $\left(x_{k}, y_{k}\right)$. At least three distinct Manhattan distances will occur.
Conversely, among the nine points
$$
(0,0), \quad( \pm 1, \pm 1), \quad( \pm 2,0), \quad(0, \pm 2),
$$
only the Manhattan distances 2 and 4 occur.
|
9
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
With inspiration drawn from the rectilinear network of streets in New York, the Manhattan distance between two points $(a, b)$ and $(c, d)$ in the plane is defined to be
$$
|a-c|+|b-d| \text {. }
$$
Suppose only two distinct Manhattan distances occur between all pairs of distinct points of some point set. What is the maximal number of points in such a set?
|
Answer: nine.
Let
$$
\left\{\left(x_{1}, y_{1}\right), \ldots,\left(x_{m}, y_{m}\right)\right\}, \quad \text { where } \quad x_{1} \leq \cdots \leq x_{m}
$$
be the set, and suppose $m \geq 10$.
A special case of the Erdős-Szekeres Theorem asserts that a real sequence of length $n^{2}+1$ contains a monotonic subsequence of length $n+1$. (Proof: Given a sequence $a_{1} \ldots, a_{n^{2}+1}$, let $p_{i}$ denote the length of the longest increasing subsequence ending with $a_{i}$, and $q_{i}$ the length of the longest decreasing subsequence ending with $a_{i}$. If $i<j$ and $a_{i} \leq a_{j}$, then $p_{i}<p_{j}$. If $a_{i} \geq a_{j}$, then $q_{i}<q_{j}$. Hence all $n^{2}+1$ pairs $\left(p_{i}, q_{i}\right)$ are distinct. If all of them were to satisfy $1 \leq p_{i}, q_{i} \leq n$, it would violate the Pigeon-Hole Principle.)
Applied to the sequence $y_{1}, \ldots, y_{m}$, this will produce a subsequence
$$
y_{i} \leq y_{j} \leq y_{k} \leq y_{l} \quad \text { or } \quad y_{i} \geq y_{j} \geq y_{k} \geq y_{l}
$$
One of the shortest paths from $\left(x_{i}, y_{i}\right)$ to $\left(x_{l}, y_{l}\right)$ will pass through first $\left(x_{j}, y_{j}\right)$ and then $\left(x_{k}, y_{k}\right)$. At least three distinct Manhattan distances will occur.
Conversely, among the nine points
$$
(0,0), \quad( \pm 1, \pm 1), \quad( \pm 2,0), \quad(0, \pm 2),
$$
only the Manhattan distances 2 and 4 occur.
|
{
"exam": "BalticWay",
"problem_label": "8",
"problem_match": "# Problem 8.",
"resource_path": "BalticWay/segmented/en-bw15sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2015"
}
|
Let $n>2$ be an integer. A deck contains $\frac{n(n-1)}{2}$ cards, numbered
$$
1,2,3, \ldots, \frac{n(n-1)}{2}
$$
Two cards form a magic pair if their numbers are consecutive, or if their numbers are 1 and $\frac{n(n-1)}{2}$.
For which $n$ is it possible to distribute the cards into $n$ stacks in such a manner that, among the cards in any two stacks, there is exactly one magic pair?
|
. Answer: for all odd $n$.
First assume a stack contains two cards that form a magic pair; say cards number $i$ and $i+1$. Among the cards in this stack and the stack with card number $i+2$ (they might be identical), there are two magic pairs - a contradiction. Hence no stack contains a magic pair.
Each card forms a magic pair with exactly two other cards. Hence if $n$ is even, each stack must contain at least $\left\lceil\frac{n-1}{2}\right\rceil=\frac{n}{2}$ cards, since there are $n-1$ other stacks. But then we need at least $n \frac{n}{2}>\frac{n(n-1)}{2}$ cards - a contradiction.
In the odd case we distribute the cards like this: Let $a_{1}, a_{2}, \ldots, a_{n}$ be the $n$ stacks and let $n=2 m+1$. Card number 1 is put into stack $a_{1}$. If card number $k m+i$, for $i=1,2, \ldots, m$, is put into stack $a_{j}$, then card number $k m+i+1$ is put into stack number $a_{j+i}$, where the indices are calculated modulo $n$.
There are
$$
\frac{n(n-1)}{2}=\frac{(2 m+1)(2 m)}{2}=m(2 m+1)
$$
cards. If we look at all the card numbers of the form $k m+1$, there are exactly $n=2 m+1$ of these, and we claim that there is exactly one in each stack. Card number 1 is in stack $a_{1}$, and card number $k m+1$ is in stack
$$
a_{1+k(1+2+3+\cdots+m)}
$$
Since
$$
1+2+3+\cdots+m=\frac{m(m+1)}{2}
$$
and $\operatorname{gcd}\left(2 m+1, \frac{m(m+1)}{2}\right)=1$, all the indices
$$
1+k(1+2+3+\cdots+m), \quad k=0,1,2, \ldots, 2 m
$$
are different modulo $n=2 m+1$. In the same way we see that each stack contains exactly one of the $2 m+1$ cards with the numbers $k m+i$ for a given $i=2,3, \ldots, m$.
Now look at two different stacks $a_{v}$ and $a_{u}$. Then, without loss of generality, we may assume that $u=v+i$ for some $i=1,2, \ldots, m$ (again we consider the index modulo $n=2 m+1$ ). Since there is a card in stack $a_{v}$ with number $k m+i$, the card $k m+i+1$ is in stack $a_{v+i}=a_{u}$. Hence among the cards in any two stacks there is at least one magic pair. Since there is the same number of pairs of stacks as of magic pairs, there must be exactly one magic pair among the cards of any two stacks.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n>2$ be an integer. A deck contains $\frac{n(n-1)}{2}$ cards, numbered
$$
1,2,3, \ldots, \frac{n(n-1)}{2}
$$
Two cards form a magic pair if their numbers are consecutive, or if their numbers are 1 and $\frac{n(n-1)}{2}$.
For which $n$ is it possible to distribute the cards into $n$ stacks in such a manner that, among the cards in any two stacks, there is exactly one magic pair?
|
. Answer: for all odd $n$.
First assume a stack contains two cards that form a magic pair; say cards number $i$ and $i+1$. Among the cards in this stack and the stack with card number $i+2$ (they might be identical), there are two magic pairs - a contradiction. Hence no stack contains a magic pair.
Each card forms a magic pair with exactly two other cards. Hence if $n$ is even, each stack must contain at least $\left\lceil\frac{n-1}{2}\right\rceil=\frac{n}{2}$ cards, since there are $n-1$ other stacks. But then we need at least $n \frac{n}{2}>\frac{n(n-1)}{2}$ cards - a contradiction.
In the odd case we distribute the cards like this: Let $a_{1}, a_{2}, \ldots, a_{n}$ be the $n$ stacks and let $n=2 m+1$. Card number 1 is put into stack $a_{1}$. If card number $k m+i$, for $i=1,2, \ldots, m$, is put into stack $a_{j}$, then card number $k m+i+1$ is put into stack number $a_{j+i}$, where the indices are calculated modulo $n$.
There are
$$
\frac{n(n-1)}{2}=\frac{(2 m+1)(2 m)}{2}=m(2 m+1)
$$
cards. If we look at all the card numbers of the form $k m+1$, there are exactly $n=2 m+1$ of these, and we claim that there is exactly one in each stack. Card number 1 is in stack $a_{1}$, and card number $k m+1$ is in stack
$$
a_{1+k(1+2+3+\cdots+m)}
$$
Since
$$
1+2+3+\cdots+m=\frac{m(m+1)}{2}
$$
and $\operatorname{gcd}\left(2 m+1, \frac{m(m+1)}{2}\right)=1$, all the indices
$$
1+k(1+2+3+\cdots+m), \quad k=0,1,2, \ldots, 2 m
$$
are different modulo $n=2 m+1$. In the same way we see that each stack contains exactly one of the $2 m+1$ cards with the numbers $k m+i$ for a given $i=2,3, \ldots, m$.
Now look at two different stacks $a_{v}$ and $a_{u}$. Then, without loss of generality, we may assume that $u=v+i$ for some $i=1,2, \ldots, m$ (again we consider the index modulo $n=2 m+1$ ). Since there is a card in stack $a_{v}$ with number $k m+i$, the card $k m+i+1$ is in stack $a_{v+i}=a_{u}$. Hence among the cards in any two stacks there is at least one magic pair. Since there is the same number of pairs of stacks as of magic pairs, there must be exactly one magic pair among the cards of any two stacks.
|
{
"exam": "BalticWay",
"problem_label": "9",
"problem_match": "# Problem 9.",
"resource_path": "BalticWay/segmented/en-bw15sol.jsonl",
"solution_match": "# Solution 1",
"tier": "T3",
"year": "2015"
}
|
Let $n>2$ be an integer. A deck contains $\frac{n(n-1)}{2}$ cards, numbered
$$
1,2,3, \ldots, \frac{n(n-1)}{2}
$$
Two cards form a magic pair if their numbers are consecutive, or if their numbers are 1 and $\frac{n(n-1)}{2}$.
For which $n$ is it possible to distribute the cards into $n$ stacks in such a manner that, among the cards in any two stacks, there is exactly one magic pair?
|
(found by Saint Petersburg). For the case of $n$ odd, consider the complete graph on the vertices $1, \ldots, n$ with $\frac{n(n-1)}{2}$ edges. The degree of each vertex is $n-1$, which is even, hence an Euler cycle $v_{1} v_{2} \cdots v_{\frac{n(n-1)}{2}} v_{1}$ exists. Place card number $i$ into stack number $v_{i}$. The magic pairs correspond to edges in the cycle.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n>2$ be an integer. A deck contains $\frac{n(n-1)}{2}$ cards, numbered
$$
1,2,3, \ldots, \frac{n(n-1)}{2}
$$
Two cards form a magic pair if their numbers are consecutive, or if their numbers are 1 and $\frac{n(n-1)}{2}$.
For which $n$ is it possible to distribute the cards into $n$ stacks in such a manner that, among the cards in any two stacks, there is exactly one magic pair?
|
(found by Saint Petersburg). For the case of $n$ odd, consider the complete graph on the vertices $1, \ldots, n$ with $\frac{n(n-1)}{2}$ edges. The degree of each vertex is $n-1$, which is even, hence an Euler cycle $v_{1} v_{2} \cdots v_{\frac{n(n-1)}{2}} v_{1}$ exists. Place card number $i$ into stack number $v_{i}$. The magic pairs correspond to edges in the cycle.
|
{
"exam": "BalticWay",
"problem_label": "9",
"problem_match": "# Problem 9.",
"resource_path": "BalticWay/segmented/en-bw15sol.jsonl",
"solution_match": "\nSolution 2",
"tier": "T3",
"year": "2015"
}
|
A subset $S$ of $\{1,2, \ldots, n\}$ is called balanced if for every $a \in S$ there exists some $b \in S, b \neq a$, such that $\frac{a+b}{2} \in S$ as well.
(a) Let $k>1$ be an integer and let $n=2^{k}$. Show that every subset $S$ of $\{1,2, \ldots, n\}$ with $|S|>\frac{3 n}{4}$ is balanced.
(b) Does there exist an $n=2^{k}$, with $k>1$ an integer, for which every subset $S$ of $\{1,2, \ldots, n\}$ with $|S|>\frac{2 n}{3}$ is balanced?
Solution of part (a). Let $m=n-|S|$, thus $m<\frac{n}{4}$ and (as $n$ is a multiple of 4 ) $m \leq \frac{n}{4}-1$. Let $a \in S$. There are $\frac{n}{2}-1$ elements in $\{1,2, \ldots, n\}$ distinct from $a$ and with the same parity as $a$. At most $m$ of those elements are not in $S$, hence at least $\frac{n}{2}-1-m \geq \frac{n}{4}$ of them are in $S$. For each such $b$, the number $\frac{a+b}{2}$ is an integer, and all of these at least $\frac{n}{4}$ numbers are distinct. But at most $m<\frac{n}{4}$ of them are not in $S$, so at least one is a member of $S$. Hence $S$ is balanced.
|
of part (b). For convenience we work with $\{0,1, \ldots, n-1\}$ rather than $\{1,2, \ldots, n\}$; this does not change the problem. We show that one can always find an unbalanced subset containing more than $\frac{2 n}{3}$ elements.
Let $\operatorname{ord}_{2}(i)$ denote the number of factors 2 occurring in the prime factorisation of $i$. We set
$$
T_{j}=\left\{i \in\{1,2, \ldots, n-1\} \mid \operatorname{ord}_{2}(i)=j\right\}
$$
Then we choose
$$
S=\{0,1,2, \ldots, n-1\} \backslash\left(T_{1} \cup T_{3} \cup \cdots \cup T_{l}\right), \quad \text { where } l= \begin{cases}k-1 & \text { if } k \text { even } \\ k-2 & \text { if } k \text { odd. }\end{cases}
$$
Observe that $\left|T_{j}\right|=\frac{n}{2^{j+1}}$, so
$$
|S|=n-\left(\frac{n}{4}+\frac{n}{16}+\cdots+\frac{n}{2^{l+1}}\right)=n-n \cdot \frac{\frac{1}{4}-\frac{1}{2^{l+3}}}{1-\frac{1}{4}}>n-\frac{n}{3}=\frac{2 n}{3} .
$$
We show that $S$ is not balanced. Take $a=0 \in S$, and consider a $0 \neq b \in S$. If $b$ is odd, then $\frac{0+b}{2}$ is not integral. If $b$ is even, then $b \in T_{2} \cup T_{4} \cup \cdots$, so $\frac{b}{2} \in T_{1} \cup T_{3} \cup \cdots$, hence $\frac{b}{2} \notin S$. Thus $S$ is not balanced.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A subset $S$ of $\{1,2, \ldots, n\}$ is called balanced if for every $a \in S$ there exists some $b \in S, b \neq a$, such that $\frac{a+b}{2} \in S$ as well.
(a) Let $k>1$ be an integer and let $n=2^{k}$. Show that every subset $S$ of $\{1,2, \ldots, n\}$ with $|S|>\frac{3 n}{4}$ is balanced.
(b) Does there exist an $n=2^{k}$, with $k>1$ an integer, for which every subset $S$ of $\{1,2, \ldots, n\}$ with $|S|>\frac{2 n}{3}$ is balanced?
Solution of part (a). Let $m=n-|S|$, thus $m<\frac{n}{4}$ and (as $n$ is a multiple of 4 ) $m \leq \frac{n}{4}-1$. Let $a \in S$. There are $\frac{n}{2}-1$ elements in $\{1,2, \ldots, n\}$ distinct from $a$ and with the same parity as $a$. At most $m$ of those elements are not in $S$, hence at least $\frac{n}{2}-1-m \geq \frac{n}{4}$ of them are in $S$. For each such $b$, the number $\frac{a+b}{2}$ is an integer, and all of these at least $\frac{n}{4}$ numbers are distinct. But at most $m<\frac{n}{4}$ of them are not in $S$, so at least one is a member of $S$. Hence $S$ is balanced.
|
of part (b). For convenience we work with $\{0,1, \ldots, n-1\}$ rather than $\{1,2, \ldots, n\}$; this does not change the problem. We show that one can always find an unbalanced subset containing more than $\frac{2 n}{3}$ elements.
Let $\operatorname{ord}_{2}(i)$ denote the number of factors 2 occurring in the prime factorisation of $i$. We set
$$
T_{j}=\left\{i \in\{1,2, \ldots, n-1\} \mid \operatorname{ord}_{2}(i)=j\right\}
$$
Then we choose
$$
S=\{0,1,2, \ldots, n-1\} \backslash\left(T_{1} \cup T_{3} \cup \cdots \cup T_{l}\right), \quad \text { where } l= \begin{cases}k-1 & \text { if } k \text { even } \\ k-2 & \text { if } k \text { odd. }\end{cases}
$$
Observe that $\left|T_{j}\right|=\frac{n}{2^{j+1}}$, so
$$
|S|=n-\left(\frac{n}{4}+\frac{n}{16}+\cdots+\frac{n}{2^{l+1}}\right)=n-n \cdot \frac{\frac{1}{4}-\frac{1}{2^{l+3}}}{1-\frac{1}{4}}>n-\frac{n}{3}=\frac{2 n}{3} .
$$
We show that $S$ is not balanced. Take $a=0 \in S$, and consider a $0 \neq b \in S$. If $b$ is odd, then $\frac{0+b}{2}$ is not integral. If $b$ is even, then $b \in T_{2} \cup T_{4} \cup \cdots$, so $\frac{b}{2} \in T_{1} \cup T_{3} \cup \cdots$, hence $\frac{b}{2} \notin S$. Thus $S$ is not balanced.
|
{
"exam": "BalticWay",
"problem_label": "10",
"problem_match": "# Problem 10.",
"resource_path": "BalticWay/segmented/en-bw15sol.jsonl",
"solution_match": "\nSolution 1",
"tier": "T3",
"year": "2015"
}
|
A subset $S$ of $\{1,2, \ldots, n\}$ is called balanced if for every $a \in S$ there exists some $b \in S, b \neq a$, such that $\frac{a+b}{2} \in S$ as well.
(a) Let $k>1$ be an integer and let $n=2^{k}$. Show that every subset $S$ of $\{1,2, \ldots, n\}$ with $|S|>\frac{3 n}{4}$ is balanced.
(b) Does there exist an $n=2^{k}$, with $k>1$ an integer, for which every subset $S$ of $\{1,2, \ldots, n\}$ with $|S|>\frac{2 n}{3}$ is balanced?
Solution of part (a). Let $m=n-|S|$, thus $m<\frac{n}{4}$ and (as $n$ is a multiple of 4 ) $m \leq \frac{n}{4}-1$. Let $a \in S$. There are $\frac{n}{2}-1$ elements in $\{1,2, \ldots, n\}$ distinct from $a$ and with the same parity as $a$. At most $m$ of those elements are not in $S$, hence at least $\frac{n}{2}-1-m \geq \frac{n}{4}$ of them are in $S$. For each such $b$, the number $\frac{a+b}{2}$ is an integer, and all of these at least $\frac{n}{4}$ numbers are distinct. But at most $m<\frac{n}{4}$ of them are not in $S$, so at least one is a member of $S$. Hence $S$ is balanced.
|
of part (b). We define the sets
$$
A_{j}=\left\{2^{j-1}+1,2^{j-1}+2, \ldots, 2^{j}\right\}
$$
and set
$$
S=A_{k} \cup A_{k-2} \cup \cdots \cup A_{l} \cup\{1\}, \quad \text { where } l= \begin{cases}2 & \text { if } k \text { even }, \\ 1 & \text { if } k \text { odd. }\end{cases}
$$
Note that $A_{j} \subseteq\{1,2, \ldots, n\}$ whenever $j \leq k$, and that $\left|A_{j}\right|=2^{j-1}$. We find
$$
|S|=2^{k-1}+2^{k-3}+\cdots+2^{l-1}+1=\frac{2^{l-1}-2^{k+1}}{1-4}+1=-\frac{2^{l-1}}{3}+\frac{2 n}{3}+1>\frac{2 n}{3} .
$$
We show that $S$ is not balanced. Take $a=1 \in S$, and consider a $1 \neq b \in S$. Then $b \in A_{j}$ for some $j$. If $b$ is even, then $\frac{1+b}{2}$ is not integral. If $b$ is odd, then also $1+b \in A_{j}$, so $\frac{1+b}{2} \in A_{j-1}$ and does not lie in $S$. Thus $S$ is not balanced.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A subset $S$ of $\{1,2, \ldots, n\}$ is called balanced if for every $a \in S$ there exists some $b \in S, b \neq a$, such that $\frac{a+b}{2} \in S$ as well.
(a) Let $k>1$ be an integer and let $n=2^{k}$. Show that every subset $S$ of $\{1,2, \ldots, n\}$ with $|S|>\frac{3 n}{4}$ is balanced.
(b) Does there exist an $n=2^{k}$, with $k>1$ an integer, for which every subset $S$ of $\{1,2, \ldots, n\}$ with $|S|>\frac{2 n}{3}$ is balanced?
Solution of part (a). Let $m=n-|S|$, thus $m<\frac{n}{4}$ and (as $n$ is a multiple of 4 ) $m \leq \frac{n}{4}-1$. Let $a \in S$. There are $\frac{n}{2}-1$ elements in $\{1,2, \ldots, n\}$ distinct from $a$ and with the same parity as $a$. At most $m$ of those elements are not in $S$, hence at least $\frac{n}{2}-1-m \geq \frac{n}{4}$ of them are in $S$. For each such $b$, the number $\frac{a+b}{2}$ is an integer, and all of these at least $\frac{n}{4}$ numbers are distinct. But at most $m<\frac{n}{4}$ of them are not in $S$, so at least one is a member of $S$. Hence $S$ is balanced.
|
of part (b). We define the sets
$$
A_{j}=\left\{2^{j-1}+1,2^{j-1}+2, \ldots, 2^{j}\right\}
$$
and set
$$
S=A_{k} \cup A_{k-2} \cup \cdots \cup A_{l} \cup\{1\}, \quad \text { where } l= \begin{cases}2 & \text { if } k \text { even }, \\ 1 & \text { if } k \text { odd. }\end{cases}
$$
Note that $A_{j} \subseteq\{1,2, \ldots, n\}$ whenever $j \leq k$, and that $\left|A_{j}\right|=2^{j-1}$. We find
$$
|S|=2^{k-1}+2^{k-3}+\cdots+2^{l-1}+1=\frac{2^{l-1}-2^{k+1}}{1-4}+1=-\frac{2^{l-1}}{3}+\frac{2 n}{3}+1>\frac{2 n}{3} .
$$
We show that $S$ is not balanced. Take $a=1 \in S$, and consider a $1 \neq b \in S$. Then $b \in A_{j}$ for some $j$. If $b$ is even, then $\frac{1+b}{2}$ is not integral. If $b$ is odd, then also $1+b \in A_{j}$, so $\frac{1+b}{2} \in A_{j-1}$ and does not lie in $S$. Thus $S$ is not balanced.
|
{
"exam": "BalticWay",
"problem_label": "10",
"problem_match": "# Problem 10.",
"resource_path": "BalticWay/segmented/en-bw15sol.jsonl",
"solution_match": "\nSolution 2",
"tier": "T3",
"year": "2015"
}
|
A subset $S$ of $\{1,2, \ldots, n\}$ is called balanced if for every $a \in S$ there exists some $b \in S, b \neq a$, such that $\frac{a+b}{2} \in S$ as well.
(a) Let $k>1$ be an integer and let $n=2^{k}$. Show that every subset $S$ of $\{1,2, \ldots, n\}$ with $|S|>\frac{3 n}{4}$ is balanced.
(b) Does there exist an $n=2^{k}$, with $k>1$ an integer, for which every subset $S$ of $\{1,2, \ldots, n\}$ with $|S|>\frac{2 n}{3}$ is balanced?
Solution of part (a). Let $m=n-|S|$, thus $m<\frac{n}{4}$ and (as $n$ is a multiple of 4 ) $m \leq \frac{n}{4}-1$. Let $a \in S$. There are $\frac{n}{2}-1$ elements in $\{1,2, \ldots, n\}$ distinct from $a$ and with the same parity as $a$. At most $m$ of those elements are not in $S$, hence at least $\frac{n}{2}-1-m \geq \frac{n}{4}$ of them are in $S$. For each such $b$, the number $\frac{a+b}{2}$ is an integer, and all of these at least $\frac{n}{4}$ numbers are distinct. But at most $m<\frac{n}{4}$ of them are not in $S$, so at least one is a member of $S$. Hence $S$ is balanced.
|
of part (b). Let us introduce the concept of lonely element as an $a \in S$ for which there does not exist a $b \in S$, distinct from $a$, such that $\frac{a+b}{2} \in S$.
We will construct an unbalanced set $S$ with $|S|>\frac{2 n}{3}$ for all $k$. For $n=4$ we can use $S=\{1,2,4\}$ (all elements are lonely), and for $n=8$ we can use $S=\{1,2,3,5,6,7\}$ (2 and 6 are lonely).
We now construct an unbalanced set $S \subseteq\{1,2, \ldots, 4 n\}$, given an unbalanced set $T \subseteq\{1,2, \ldots, n\}$ with $|T|>\frac{2 n}{3}$. Take
$$
S=\{i \in\{1,2, \ldots, 4 n\} \mid i \equiv 1 \bmod 2\} \cup\{4 t-2 \mid t \in T\}
$$
Then
$$
|S|=2 n+|T|>2 n+\frac{2 n}{3}=\frac{8 n}{3}=\frac{2 \cdot 4 n}{3} .
$$
Figure 1: Problem 11.
Supposing $a \in T$ is lonely, we will show that $4 a-2 \in S$ is lonely. Indeed, suppose $4 a-2 \neq b \in S$ with
$$
\frac{4 a-2+b}{2}=2 a-1+\frac{b}{2} \in S .
$$
Then $b$ must be even, so $b=4 t-2$ for some $a \neq t \in T$. But then
$$
\frac{4 a-2+4 t-2}{2}=4 \frac{a+t}{2}-2
$$
again an even element. However, as $a$ is lonely we know that $\frac{a+t}{2} \notin T$, and hence $4 \frac{a+t}{2}-2 \notin S$. We conclude that $4 a-2$ is lonely in $S$.
Thus $S$ is an unbalanced set, and by induction we can find an unbalanced set of size exceeding $\frac{2 n}{3}$ for all $k>1$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A subset $S$ of $\{1,2, \ldots, n\}$ is called balanced if for every $a \in S$ there exists some $b \in S, b \neq a$, such that $\frac{a+b}{2} \in S$ as well.
(a) Let $k>1$ be an integer and let $n=2^{k}$. Show that every subset $S$ of $\{1,2, \ldots, n\}$ with $|S|>\frac{3 n}{4}$ is balanced.
(b) Does there exist an $n=2^{k}$, with $k>1$ an integer, for which every subset $S$ of $\{1,2, \ldots, n\}$ with $|S|>\frac{2 n}{3}$ is balanced?
Solution of part (a). Let $m=n-|S|$, thus $m<\frac{n}{4}$ and (as $n$ is a multiple of 4 ) $m \leq \frac{n}{4}-1$. Let $a \in S$. There are $\frac{n}{2}-1$ elements in $\{1,2, \ldots, n\}$ distinct from $a$ and with the same parity as $a$. At most $m$ of those elements are not in $S$, hence at least $\frac{n}{2}-1-m \geq \frac{n}{4}$ of them are in $S$. For each such $b$, the number $\frac{a+b}{2}$ is an integer, and all of these at least $\frac{n}{4}$ numbers are distinct. But at most $m<\frac{n}{4}$ of them are not in $S$, so at least one is a member of $S$. Hence $S$ is balanced.
|
of part (b). Let us introduce the concept of lonely element as an $a \in S$ for which there does not exist a $b \in S$, distinct from $a$, such that $\frac{a+b}{2} \in S$.
We will construct an unbalanced set $S$ with $|S|>\frac{2 n}{3}$ for all $k$. For $n=4$ we can use $S=\{1,2,4\}$ (all elements are lonely), and for $n=8$ we can use $S=\{1,2,3,5,6,7\}$ (2 and 6 are lonely).
We now construct an unbalanced set $S \subseteq\{1,2, \ldots, 4 n\}$, given an unbalanced set $T \subseteq\{1,2, \ldots, n\}$ with $|T|>\frac{2 n}{3}$. Take
$$
S=\{i \in\{1,2, \ldots, 4 n\} \mid i \equiv 1 \bmod 2\} \cup\{4 t-2 \mid t \in T\}
$$
Then
$$
|S|=2 n+|T|>2 n+\frac{2 n}{3}=\frac{8 n}{3}=\frac{2 \cdot 4 n}{3} .
$$

Figure 1: Problem 11.
Supposing $a \in T$ is lonely, we will show that $4 a-2 \in S$ is lonely. Indeed, suppose $4 a-2 \neq b \in S$ with
$$
\frac{4 a-2+b}{2}=2 a-1+\frac{b}{2} \in S .
$$
Then $b$ must be even, so $b=4 t-2$ for some $a \neq t \in T$. But then
$$
\frac{4 a-2+4 t-2}{2}=4 \frac{a+t}{2}-2
$$
again an even element. However, as $a$ is lonely we know that $\frac{a+t}{2} \notin T$, and hence $4 \frac{a+t}{2}-2 \notin S$. We conclude that $4 a-2$ is lonely in $S$.
Thus $S$ is an unbalanced set, and by induction we can find an unbalanced set of size exceeding $\frac{2 n}{3}$ for all $k>1$.
|
{
"exam": "BalticWay",
"problem_label": "10",
"problem_match": "# Problem 10.",
"resource_path": "BalticWay/segmented/en-bw15sol.jsonl",
"solution_match": "\nSolution 3",
"tier": "T3",
"year": "2015"
}
|
The diagonals of the parallelogram $A B C D$ intersect at $E$. The bisectors of $\angle D A E$ and $\angle E B C$ intersect at $F$. Assume that $E C F D$ is a parallelogram. Determine the ratio $A B: A D$.
|
Since $E C F D$ is a parallelogram, we have $E D \| C F$ and $\angle C F B=\angle E B F=\angle F B C(B F$ bisects $\angle D B C$ ). So $C F B$ is an isosceles triangle and $B C=C F=E D$ (ECFD is a parallelogram). In a similar manner, $E C=A D$. But since $A B C D$ is a parallelogram, $A D=B C$, whence $E C=E D$. So the diagonals of $A B C D$ are equal, which means that $A B C D$ is in fact a rectangle. Also, the triangles $E D A$ and $E B C$ are equilateral, and so $A B$ is twice the altitude of $E D A$, or $A B=\sqrt{3} \cdot A D$.
|
A B=\sqrt{3} \cdot A D
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
The diagonals of the parallelogram $A B C D$ intersect at $E$. The bisectors of $\angle D A E$ and $\angle E B C$ intersect at $F$. Assume that $E C F D$ is a parallelogram. Determine the ratio $A B: A D$.
|
Since $E C F D$ is a parallelogram, we have $E D \| C F$ and $\angle C F B=\angle E B F=\angle F B C(B F$ bisects $\angle D B C$ ). So $C F B$ is an isosceles triangle and $B C=C F=E D$ (ECFD is a parallelogram). In a similar manner, $E C=A D$. But since $A B C D$ is a parallelogram, $A D=B C$, whence $E C=E D$. So the diagonals of $A B C D$ are equal, which means that $A B C D$ is in fact a rectangle. Also, the triangles $E D A$ and $E B C$ are equilateral, and so $A B$ is twice the altitude of $E D A$, or $A B=\sqrt{3} \cdot A D$.
|
{
"exam": "BalticWay",
"problem_label": "11",
"problem_match": "# Problem 11.",
"resource_path": "BalticWay/segmented/en-bw15sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2015"
}
|
A circle passes through vertex $B$ of the triangle $A B C$, intersects its sides $A B$ and $B C$ at points $K$ and $L$, respectively, and touches the side $A C$ at its midpoint $M$. The point $N$ on the $\operatorname{arc} B L$ (which does not contain $K)$ is such that $\angle L K N=\angle A C B$. Find $\angle B A C$ given that the triangle $C K N$ is equilateral.
|
Answer: $\angle B A C=75^{\circ}$.
Since $\angle A C B=\angle L K N=\angle L B N$, the lines $A C$ and $B N$ are parallel. Hence $A C N B$ is a trapezium. Moreover, $A C N B$ is an isosceles trapezium, because the segment $A C$ touches the circle $s$ in the midpoint (and so the trapezium is symmetrical with respect to the perpendicular bisectors of $B N$ ).
Figure 2: Problem 12.
Denote by $K^{\prime}$ the intersection point of $s$ and $C N$. Then the line $K K^{\prime}$ is parallel to the bases of the trapezium. Hence $M$ is the midpoint of $\operatorname{arc} K K^{\prime}$ and the line $N M$ is an angle bisector of the equilateral triangle $K N C$.
Thus we obtain that $M C=M K$. Therefore the length of median $K M$ of the triangle $A K C$ equals $\frac{1}{2} A C$; hence $\angle A K C=90^{\circ}$. We have
$$
2 \angle A=\angle K A C+\angle A C N=\angle K A C+\angle A C K+\angle K C N=90^{\circ}+60^{\circ}=150^{\circ} \text {, }
$$
and so $\angle A=75^{\circ}$.
|
75^{\circ}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A circle passes through vertex $B$ of the triangle $A B C$, intersects its sides $A B$ and $B C$ at points $K$ and $L$, respectively, and touches the side $A C$ at its midpoint $M$. The point $N$ on the $\operatorname{arc} B L$ (which does not contain $K)$ is such that $\angle L K N=\angle A C B$. Find $\angle B A C$ given that the triangle $C K N$ is equilateral.
|
Answer: $\angle B A C=75^{\circ}$.
Since $\angle A C B=\angle L K N=\angle L B N$, the lines $A C$ and $B N$ are parallel. Hence $A C N B$ is a trapezium. Moreover, $A C N B$ is an isosceles trapezium, because the segment $A C$ touches the circle $s$ in the midpoint (and so the trapezium is symmetrical with respect to the perpendicular bisectors of $B N$ ).

Figure 2: Problem 12.
Denote by $K^{\prime}$ the intersection point of $s$ and $C N$. Then the line $K K^{\prime}$ is parallel to the bases of the trapezium. Hence $M$ is the midpoint of $\operatorname{arc} K K^{\prime}$ and the line $N M$ is an angle bisector of the equilateral triangle $K N C$.
Thus we obtain that $M C=M K$. Therefore the length of median $K M$ of the triangle $A K C$ equals $\frac{1}{2} A C$; hence $\angle A K C=90^{\circ}$. We have
$$
2 \angle A=\angle K A C+\angle A C N=\angle K A C+\angle A C K+\angle K C N=90^{\circ}+60^{\circ}=150^{\circ} \text {, }
$$
and so $\angle A=75^{\circ}$.
|
{
"exam": "BalticWay",
"problem_label": "12",
"problem_match": "# Problem 12.",
"resource_path": "BalticWay/segmented/en-bw15sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2015"
}
|
Let $D$ be the footpoint of the altitude from $B$ in the triangle $A B C$, where $A B=1$. The incentre of triangle $B C D$ coincides with the centroid of triangle $A B C$. Find the lengths of $A C$ and $B C$.
|
Answer: $A C=B C=\sqrt{\frac{5}{2}}$.
The centroid of $A B C$ lies on the median $C C^{\prime}$. It will also, by the assumption, lie on the angle bisector through $C$. Since the median and the angle bisector coincide, $A B C$ is isosceles with $A C=$ $B C=a$.
Furthermore, the centroid lies on the median $B B^{\prime}$ and the bisector of $\angle D B C$, again by hypothesis. By the Angle Bisector Theorem,
$$
\frac{B^{\prime} D}{B D}=\frac{B^{\prime} C}{B C}=\frac{a / 2}{a}=\frac{1}{2}
$$
The triangles $A B D \sim A C C^{\prime}$ since they have equal angles, whence
$$
\frac{1}{a}=\frac{A B}{A C}=\frac{A D}{A C^{\prime}}=\frac{a / 2-B^{\prime} D}{1 / 2}=a-B D
$$
Using the fact that the length of the altitude $C C^{\prime}$ is $\sqrt{a^{2}-\frac{1}{4}}$, this leads to
$$
a^{2}-1=a B D=2|A B C|=\sqrt{a^{2}-\frac{1}{4}},
$$
or, equivalently,
$$
a^{2}-1=\sqrt{a^{2}-\frac{1}{4}}
$$
Clearly, $a>1$, and the only solution is $a=\sqrt{\frac{5}{2}}$.
|
A C=B C=\sqrt{\frac{5}{2}}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $D$ be the footpoint of the altitude from $B$ in the triangle $A B C$, where $A B=1$. The incentre of triangle $B C D$ coincides with the centroid of triangle $A B C$. Find the lengths of $A C$ and $B C$.
|
Answer: $A C=B C=\sqrt{\frac{5}{2}}$.
The centroid of $A B C$ lies on the median $C C^{\prime}$. It will also, by the assumption, lie on the angle bisector through $C$. Since the median and the angle bisector coincide, $A B C$ is isosceles with $A C=$ $B C=a$.
Furthermore, the centroid lies on the median $B B^{\prime}$ and the bisector of $\angle D B C$, again by hypothesis. By the Angle Bisector Theorem,
$$
\frac{B^{\prime} D}{B D}=\frac{B^{\prime} C}{B C}=\frac{a / 2}{a}=\frac{1}{2}
$$
The triangles $A B D \sim A C C^{\prime}$ since they have equal angles, whence
$$
\frac{1}{a}=\frac{A B}{A C}=\frac{A D}{A C^{\prime}}=\frac{a / 2-B^{\prime} D}{1 / 2}=a-B D
$$
Using the fact that the length of the altitude $C C^{\prime}$ is $\sqrt{a^{2}-\frac{1}{4}}$, this leads to
$$
a^{2}-1=a B D=2|A B C|=\sqrt{a^{2}-\frac{1}{4}},
$$
or, equivalently,
$$
a^{2}-1=\sqrt{a^{2}-\frac{1}{4}}
$$
Clearly, $a>1$, and the only solution is $a=\sqrt{\frac{5}{2}}$.
|
{
"exam": "BalticWay",
"problem_label": "13",
"problem_match": "# Problem 13.",
"resource_path": "BalticWay/segmented/en-bw15sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2015"
}
|
In the non-isosceles triangle $A B C$ the altitude from $A$ meets side $B C$ in $D$. Let $M$ be the midpoint of $B C$ and let $N$ be the reflection of $M$ in $D$. The circumcircle of the triangle $A M N$ intersects the side $A B$ in $P \neq A$ and the side $A C$ in $Q \neq A$. Prove that $A N, B Q$ and $C P$ are concurrent.
|
. Without loss of generality, we assume the order of the points on $B C$ to be $B, M, D, N$, $C$. This implies that $P$ is on the segment $A B$ and $Q$ is on the segment $A C$.
Since $D$ is the midpoint of $M N$ and $A D$ is perpendicular to $M N$, the line $A D$ is the perpendicular bisector of $M N$, which contains the circumcentre of $\triangle A M N$. As $A$ is on the perpendicular bisector of $M N$, we have $|A M|=|A N|$. We now have $\angle A P M=\angle A Q N$. Therefore
$$
\angle C Q N=180^{\circ}-\angle A Q N=180^{\circ}-\angle A P M=\angle B P M \text {. }
$$
Furthermore, as $N M P Q$ is cyclic, we have
$$
\angle N Q P=180^{\circ}-\angle N M P=\angle B M P \text {. }
$$
Hence
$$
\angle A Q P=180^{\circ}-\angle C Q N-\angle N Q P=180^{\circ}-\angle B P M-\angle B M P=\angle P B M=\angle A B C .
$$
Similarly,
$$
\angle A P Q=\angle B C A \text {. }
$$
Now we have $\triangle A P Q \sim \triangle A C B$. So
$$
\frac{|A P|}{|A Q|}=\frac{|A C|}{|A B|}
$$
Furthermore, $\angle M A B=\angle M A P=\angle M N P=\angle B N P$, so $\triangle B M A \sim \triangle B P N$, and hence
$$
\frac{|B N|}{|B P|}=\frac{|B A|}{|B M|}
$$
We also have $\angle C A M=\angle Q A M=180^{\circ}-\angle Q N M=\angle Q N C$. This implies $\triangle C M A \sim \triangle C Q N$, so
$$
\frac{|C Q|}{|C N|}=\frac{|C M|}{|C A|}
$$
Putting everything together, we find
$$
\frac{|B N|}{|B P|} \cdot \frac{|C Q|}{|C N|} \cdot \frac{|A P|}{|A Q|}=\frac{|B A|}{|B M|} \cdot \frac{|C M|}{|C A|} \cdot \frac{|A C|}{|A B|}
$$
As $|B M|=|C M|$, the right-hand side is equal to 1 . This means that
$$
\frac{|B N|}{|N C|} \cdot \frac{|C Q|}{|Q A|} \cdot \frac{|A P|}{|P B|}=1
$$
With Ceva's theorem we can conclude that $A N, B Q$ and $C P$ are concurrent.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In the non-isosceles triangle $A B C$ the altitude from $A$ meets side $B C$ in $D$. Let $M$ be the midpoint of $B C$ and let $N$ be the reflection of $M$ in $D$. The circumcircle of the triangle $A M N$ intersects the side $A B$ in $P \neq A$ and the side $A C$ in $Q \neq A$. Prove that $A N, B Q$ and $C P$ are concurrent.
|
. Without loss of generality, we assume the order of the points on $B C$ to be $B, M, D, N$, $C$. This implies that $P$ is on the segment $A B$ and $Q$ is on the segment $A C$.
Since $D$ is the midpoint of $M N$ and $A D$ is perpendicular to $M N$, the line $A D$ is the perpendicular bisector of $M N$, which contains the circumcentre of $\triangle A M N$. As $A$ is on the perpendicular bisector of $M N$, we have $|A M|=|A N|$. We now have $\angle A P M=\angle A Q N$. Therefore
$$
\angle C Q N=180^{\circ}-\angle A Q N=180^{\circ}-\angle A P M=\angle B P M \text {. }
$$
Furthermore, as $N M P Q$ is cyclic, we have
$$
\angle N Q P=180^{\circ}-\angle N M P=\angle B M P \text {. }
$$
Hence
$$
\angle A Q P=180^{\circ}-\angle C Q N-\angle N Q P=180^{\circ}-\angle B P M-\angle B M P=\angle P B M=\angle A B C .
$$
Similarly,
$$
\angle A P Q=\angle B C A \text {. }
$$
Now we have $\triangle A P Q \sim \triangle A C B$. So
$$
\frac{|A P|}{|A Q|}=\frac{|A C|}{|A B|}
$$
Furthermore, $\angle M A B=\angle M A P=\angle M N P=\angle B N P$, so $\triangle B M A \sim \triangle B P N$, and hence
$$
\frac{|B N|}{|B P|}=\frac{|B A|}{|B M|}
$$
We also have $\angle C A M=\angle Q A M=180^{\circ}-\angle Q N M=\angle Q N C$. This implies $\triangle C M A \sim \triangle C Q N$, so
$$
\frac{|C Q|}{|C N|}=\frac{|C M|}{|C A|}
$$
Putting everything together, we find
$$
\frac{|B N|}{|B P|} \cdot \frac{|C Q|}{|C N|} \cdot \frac{|A P|}{|A Q|}=\frac{|B A|}{|B M|} \cdot \frac{|C M|}{|C A|} \cdot \frac{|A C|}{|A B|}
$$
As $|B M|=|C M|$, the right-hand side is equal to 1 . This means that
$$
\frac{|B N|}{|N C|} \cdot \frac{|C Q|}{|Q A|} \cdot \frac{|A P|}{|P B|}=1
$$
With Ceva's theorem we can conclude that $A N, B Q$ and $C P$ are concurrent.
|
{
"exam": "BalticWay",
"problem_label": "14",
"problem_match": "# Problem 14.",
"resource_path": "BalticWay/segmented/en-bw15sol.jsonl",
"solution_match": "\nSolution 1",
"tier": "T3",
"year": "2015"
}
|
In the non-isosceles triangle $A B C$ the altitude from $A$ meets side $B C$ in $D$. Let $M$ be the midpoint of $B C$ and let $N$ be the reflection of $M$ in $D$. The circumcircle of the triangle $A M N$ intersects the side $A B$ in $P \neq A$ and the side $A C$ in $Q \neq A$. Prove that $A N, B Q$ and $C P$ are concurrent.
|
. We consider the same configuration as in Solution 1. Let $K$ be the second intersection of $A D$ with the circumcircle of $\triangle A M N$. Since $D$ is the midpoint of $M N$ and $A D$ is perpendicular to $M N$, the line $A D$ is the perpendicular bisector of $M N$, which contains the circumcentre of $\triangle A M N$. So $A K$ is a diameter of this circumcircle. Now we have $\angle B P K=90^{\circ}=\angle B D K$, so $B P D K$ is a cyclic quadrilateral. Also, $A, M, N, K, P$ and $Q$ are concyclic. Using both circles, we find
$$
180^{\circ}-\angle C Q P=\angle A Q P=\angle A K P=\angle D K P=\angle D B P=\angle C B P .
$$
This implies that $B P Q C$ is cyclic as well. Using the power theorem we find $A P \cdot A B=A Q \cdot A C$, with directed lengths. Also, $B N \cdot B M=B P \cdot B A$ and $C N \cdot C M=C Q \cdot C A$. Hence
$$
A P \cdot A B \cdot B N \cdot B M \cdot C Q \cdot C A=A Q \cdot A C \cdot B P \cdot B A \cdot C N \cdot C M
$$
Changing the signs of all six lengths on the right-hand side and replacing $M C$ by $B M$, we find
$$
A P \cdot A B \cdot B N \cdot B M \cdot C Q \cdot C A=Q A \cdot C A \cdot P B \cdot A B \cdot N C \cdot B M
$$
Cleaning this up, we have
$$
A P \cdot B N \cdot C Q=Q A \cdot P B \cdot N C,
$$
implying
$$
\frac{B N}{N C} \cdot \frac{C Q}{Q A} \cdot \frac{A P}{P B}=1
$$
With Ceva's theorem we can conclude that $A N, B Q$ and $C P$ are concurrent.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In the non-isosceles triangle $A B C$ the altitude from $A$ meets side $B C$ in $D$. Let $M$ be the midpoint of $B C$ and let $N$ be the reflection of $M$ in $D$. The circumcircle of the triangle $A M N$ intersects the side $A B$ in $P \neq A$ and the side $A C$ in $Q \neq A$. Prove that $A N, B Q$ and $C P$ are concurrent.
|
. We consider the same configuration as in Solution 1. Let $K$ be the second intersection of $A D$ with the circumcircle of $\triangle A M N$. Since $D$ is the midpoint of $M N$ and $A D$ is perpendicular to $M N$, the line $A D$ is the perpendicular bisector of $M N$, which contains the circumcentre of $\triangle A M N$. So $A K$ is a diameter of this circumcircle. Now we have $\angle B P K=90^{\circ}=\angle B D K$, so $B P D K$ is a cyclic quadrilateral. Also, $A, M, N, K, P$ and $Q$ are concyclic. Using both circles, we find
$$
180^{\circ}-\angle C Q P=\angle A Q P=\angle A K P=\angle D K P=\angle D B P=\angle C B P .
$$
This implies that $B P Q C$ is cyclic as well. Using the power theorem we find $A P \cdot A B=A Q \cdot A C$, with directed lengths. Also, $B N \cdot B M=B P \cdot B A$ and $C N \cdot C M=C Q \cdot C A$. Hence
$$
A P \cdot A B \cdot B N \cdot B M \cdot C Q \cdot C A=A Q \cdot A C \cdot B P \cdot B A \cdot C N \cdot C M
$$
Changing the signs of all six lengths on the right-hand side and replacing $M C$ by $B M$, we find
$$
A P \cdot A B \cdot B N \cdot B M \cdot C Q \cdot C A=Q A \cdot C A \cdot P B \cdot A B \cdot N C \cdot B M
$$
Cleaning this up, we have
$$
A P \cdot B N \cdot C Q=Q A \cdot P B \cdot N C,
$$
implying
$$
\frac{B N}{N C} \cdot \frac{C Q}{Q A} \cdot \frac{A P}{P B}=1
$$
With Ceva's theorem we can conclude that $A N, B Q$ and $C P$ are concurrent.
|
{
"exam": "BalticWay",
"problem_label": "14",
"problem_match": "# Problem 14.",
"resource_path": "BalticWay/segmented/en-bw15sol.jsonl",
"solution_match": "\nSolution 2",
"tier": "T3",
"year": "2015"
}
|
In triangle $A B C$, the interior and exterior angle bisectors of $\angle B A C$ intersect the line $B C$ in $D$ and $E$, respectively. Let $F$ be the second point of intersection of the line $A D$ with the circumcircle of the triangle $A B C$. Let $O$ be the circumcentre of the triangle $A B C$ and let $D^{\prime}$ be the reflection of $D$ in $O$. Prove that $\angle D^{\prime} F E=90^{\circ}$.
|
. Note that $A B \neq A C$, since otherwise the exterior angle bisector of $\angle B A C$ would be parallel to $B C$. So assume without loss of generality that $A B<A C$. Let $M$ be the midpoint of $B C$ and let $F^{\prime}$ the reflection of $F$ in $O$, which is also the second intersection of the line $A E$ with the circumcircle of $\triangle A B C$. We now have
$$
\angle D^{\prime} F O=\angle O F^{\prime} D \text {. }
$$
Since $\angle D M F^{\prime}=90^{\circ}=\angle D A F^{\prime}$, the quadrilateral $M D A F^{\prime}$ is cyclic, thus
$$
\angle O F^{\prime} D=\angle M F^{\prime} D=\angle M A D \text {. }
$$
Furthermore, $\angle F M E=90^{\circ}=\angle F A E$, so $F M A E$ is cyclic as well. This implies that
$$
\angle M A D=\angle M A F=\angle M E F .
$$
Combining these three equalities we find that $\angle D^{\prime} F O=\angle M E F$, thus
$$
\angle D^{\prime} F E=\angle D^{\prime} F O+\angle O F E=\angle M E F+\angle M F E=180^{\circ}-\angle E M F=90^{\circ} .
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In triangle $A B C$, the interior and exterior angle bisectors of $\angle B A C$ intersect the line $B C$ in $D$ and $E$, respectively. Let $F$ be the second point of intersection of the line $A D$ with the circumcircle of the triangle $A B C$. Let $O$ be the circumcentre of the triangle $A B C$ and let $D^{\prime}$ be the reflection of $D$ in $O$. Prove that $\angle D^{\prime} F E=90^{\circ}$.
|
. Note that $A B \neq A C$, since otherwise the exterior angle bisector of $\angle B A C$ would be parallel to $B C$. So assume without loss of generality that $A B<A C$. Let $M$ be the midpoint of $B C$ and let $F^{\prime}$ the reflection of $F$ in $O$, which is also the second intersection of the line $A E$ with the circumcircle of $\triangle A B C$. We now have
$$
\angle D^{\prime} F O=\angle O F^{\prime} D \text {. }
$$
Since $\angle D M F^{\prime}=90^{\circ}=\angle D A F^{\prime}$, the quadrilateral $M D A F^{\prime}$ is cyclic, thus
$$
\angle O F^{\prime} D=\angle M F^{\prime} D=\angle M A D \text {. }
$$
Furthermore, $\angle F M E=90^{\circ}=\angle F A E$, so $F M A E$ is cyclic as well. This implies that
$$
\angle M A D=\angle M A F=\angle M E F .
$$
Combining these three equalities we find that $\angle D^{\prime} F O=\angle M E F$, thus
$$
\angle D^{\prime} F E=\angle D^{\prime} F O+\angle O F E=\angle M E F+\angle M F E=180^{\circ}-\angle E M F=90^{\circ} .
$$
|
{
"exam": "BalticWay",
"problem_label": "15",
"problem_match": "# Problem 15.",
"resource_path": "BalticWay/segmented/en-bw15sol.jsonl",
"solution_match": "\nSolution 1",
"tier": "T3",
"year": "2015"
}
|
In triangle $A B C$, the interior and exterior angle bisectors of $\angle B A C$ intersect the line $B C$ in $D$ and $E$, respectively. Let $F$ be the second point of intersection of the line $A D$ with the circumcircle of the triangle $A B C$. Let $O$ be the circumcentre of the triangle $A B C$ and let $D^{\prime}$ be the reflection of $D$ in $O$. Prove that $\angle D^{\prime} F E=90^{\circ}$.
|
. Again, assume $A B<A C$ and define $F^{\prime}$ as in the previous solution. Let $G$ be the intersection of the lines $D F^{\prime}$ and $E F$.
We can easily see that $F A$ is perpendicular to $E F^{\prime}$, and $B C$ to $F F^{\prime}$. Now, in triangle $\triangle E F F^{\prime}$, we have that $F D$ and $E D$ are altitudes, so $D$ is the orthocentre of this triangle. Now, $F^{\prime} D$ is an altitude
as well and we find that $F^{\prime} G$ is perpendicular to $E F$. Since $F F^{\prime}$ is a diameter of the circumcircle of $\triangle A B C, G$ must lie on this circle as well.
We now find
$$
\angle E F A=\angle G F A=\angle G F^{\prime} A=\angle D F^{\prime} A \text {. }
$$
Also, $\angle D F^{\prime} F=\angle D^{\prime} F F^{\prime}$. This implies that
$$
\angle D^{\prime} F E=\angle D^{\prime} F F^{\prime}+\angle F^{\prime} F A+\angle A F E=\angle D F^{\prime} F+\angle F^{\prime} F A+\angle A F^{\prime} D=\angle F^{\prime} F A+\angle A F^{\prime} F \text {. }
$$
Now, in triangle $\triangle A F F^{\prime}$ we have
$$
\angle F^{\prime} F A+\angle A F^{\prime} F=180^{\circ}-\angle F A F^{\prime}=90^{\circ},
$$
as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In triangle $A B C$, the interior and exterior angle bisectors of $\angle B A C$ intersect the line $B C$ in $D$ and $E$, respectively. Let $F$ be the second point of intersection of the line $A D$ with the circumcircle of the triangle $A B C$. Let $O$ be the circumcentre of the triangle $A B C$ and let $D^{\prime}$ be the reflection of $D$ in $O$. Prove that $\angle D^{\prime} F E=90^{\circ}$.
|
. Again, assume $A B<A C$ and define $F^{\prime}$ as in the previous solution. Let $G$ be the intersection of the lines $D F^{\prime}$ and $E F$.
We can easily see that $F A$ is perpendicular to $E F^{\prime}$, and $B C$ to $F F^{\prime}$. Now, in triangle $\triangle E F F^{\prime}$, we have that $F D$ and $E D$ are altitudes, so $D$ is the orthocentre of this triangle. Now, $F^{\prime} D$ is an altitude
as well and we find that $F^{\prime} G$ is perpendicular to $E F$. Since $F F^{\prime}$ is a diameter of the circumcircle of $\triangle A B C, G$ must lie on this circle as well.
We now find
$$
\angle E F A=\angle G F A=\angle G F^{\prime} A=\angle D F^{\prime} A \text {. }
$$
Also, $\angle D F^{\prime} F=\angle D^{\prime} F F^{\prime}$. This implies that
$$
\angle D^{\prime} F E=\angle D^{\prime} F F^{\prime}+\angle F^{\prime} F A+\angle A F E=\angle D F^{\prime} F+\angle F^{\prime} F A+\angle A F^{\prime} D=\angle F^{\prime} F A+\angle A F^{\prime} F \text {. }
$$
Now, in triangle $\triangle A F F^{\prime}$ we have
$$
\angle F^{\prime} F A+\angle A F^{\prime} F=180^{\circ}-\angle F A F^{\prime}=90^{\circ},
$$
as required.
|
{
"exam": "BalticWay",
"problem_label": "15",
"problem_match": "# Problem 15.",
"resource_path": "BalticWay/segmented/en-bw15sol.jsonl",
"solution_match": "\nSolution 2",
"tier": "T3",
"year": "2015"
}
|
In triangle $A B C$, the interior and exterior angle bisectors of $\angle B A C$ intersect the line $B C$ in $D$ and $E$, respectively. Let $F$ be the second point of intersection of the line $A D$ with the circumcircle of the triangle $A B C$. Let $O$ be the circumcentre of the triangle $A B C$ and let $D^{\prime}$ be the reflection of $D$ in $O$. Prove that $\angle D^{\prime} F E=90^{\circ}$.
|
. Again, assume $A B<A C$. We first consider the case $\angle B A C=90^{\circ}$. Define $F^{\prime}$ as in the previous solution. Now $O$ and $D^{\prime}$ lie on $B C$, so $\triangle D^{\prime} F O$ and $\triangle D F O$ are mirror images with respect to $F F^{\prime}$, while $\triangle O F E$ and $\triangle O F^{\prime} E$ are mirror images with respect to $B C$. We find that
$$
\angle D^{\prime} F E=\angle D^{\prime} F O+\angle O F E=\angle D F O+\angle O F^{\prime} E=\angle A F F^{\prime}+\angle F F^{\prime} A=180^{\circ}-\angle F A F^{\prime}=90^{\circ} .
$$
Now assume that $\angle B A C \neq 90^{\circ}$. We consider the configuration where $\angle B A C<90^{\circ}$. Let $M$, $N$ and $L$ be the midpoints of the line segments $B C, D E$ and $D F$, respectively. Note that $N$ is the circumcentre of $\triangle A D E$, so we find
$$
\begin{aligned}
\angle N A F=\angle N A D=\angle N D A & =\angle D A C+\angle A C D \\
& =\frac{1}{2} \angle A+\angle A C D=\angle B A F+\angle A C D=\angle B C F+\angle A C D=\angle A C F .
\end{aligned}
$$
Hence $N A$ is tangent to the circumcircle of $\triangle A B C$, thus $N A \perp O A$. Furthermore, we have $N M \perp$ $O M$, so $A O M N$ is cyclic with $O N$ as diameter. Now, since $L$ is the circumcentre of $\triangle D M F$, we find
$$
\angle L M N=\angle L M D=\angle L D M=\angle A D N=\angle D A N=\angle L A N
$$
so $A N L M$ is cyclic. Combining this with what we found before, we now conclude that $A O M L N$ is cyclic with $O N$ as diameter, thus $\angle O L N=90^{\circ}$. Using a dilation with centre $D$ and factor 2 we now can conclude $\angle D^{\prime} F E=\angle O L N=90^{\circ}$.
In case $\angle B A C>90^{\circ}$, the proof is similar (the cyclic quadrilateral will this time be $A M O N$ ).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In triangle $A B C$, the interior and exterior angle bisectors of $\angle B A C$ intersect the line $B C$ in $D$ and $E$, respectively. Let $F$ be the second point of intersection of the line $A D$ with the circumcircle of the triangle $A B C$. Let $O$ be the circumcentre of the triangle $A B C$ and let $D^{\prime}$ be the reflection of $D$ in $O$. Prove that $\angle D^{\prime} F E=90^{\circ}$.
|
. Again, assume $A B<A C$. We first consider the case $\angle B A C=90^{\circ}$. Define $F^{\prime}$ as in the previous solution. Now $O$ and $D^{\prime}$ lie on $B C$, so $\triangle D^{\prime} F O$ and $\triangle D F O$ are mirror images with respect to $F F^{\prime}$, while $\triangle O F E$ and $\triangle O F^{\prime} E$ are mirror images with respect to $B C$. We find that
$$
\angle D^{\prime} F E=\angle D^{\prime} F O+\angle O F E=\angle D F O+\angle O F^{\prime} E=\angle A F F^{\prime}+\angle F F^{\prime} A=180^{\circ}-\angle F A F^{\prime}=90^{\circ} .
$$
Now assume that $\angle B A C \neq 90^{\circ}$. We consider the configuration where $\angle B A C<90^{\circ}$. Let $M$, $N$ and $L$ be the midpoints of the line segments $B C, D E$ and $D F$, respectively. Note that $N$ is the circumcentre of $\triangle A D E$, so we find
$$
\begin{aligned}
\angle N A F=\angle N A D=\angle N D A & =\angle D A C+\angle A C D \\
& =\frac{1}{2} \angle A+\angle A C D=\angle B A F+\angle A C D=\angle B C F+\angle A C D=\angle A C F .
\end{aligned}
$$
Hence $N A$ is tangent to the circumcircle of $\triangle A B C$, thus $N A \perp O A$. Furthermore, we have $N M \perp$ $O M$, so $A O M N$ is cyclic with $O N$ as diameter. Now, since $L$ is the circumcentre of $\triangle D M F$, we find
$$
\angle L M N=\angle L M D=\angle L D M=\angle A D N=\angle D A N=\angle L A N
$$
so $A N L M$ is cyclic. Combining this with what we found before, we now conclude that $A O M L N$ is cyclic with $O N$ as diameter, thus $\angle O L N=90^{\circ}$. Using a dilation with centre $D$ and factor 2 we now can conclude $\angle D^{\prime} F E=\angle O L N=90^{\circ}$.
In case $\angle B A C>90^{\circ}$, the proof is similar (the cyclic quadrilateral will this time be $A M O N$ ).
|
{
"exam": "BalticWay",
"problem_label": "15",
"problem_match": "# Problem 15.",
"resource_path": "BalticWay/segmented/en-bw15sol.jsonl",
"solution_match": "\nSolution 3",
"tier": "T3",
"year": "2015"
}
|
In triangle $A B C$, the interior and exterior angle bisectors of $\angle B A C$ intersect the line $B C$ in $D$ and $E$, respectively. Let $F$ be the second point of intersection of the line $A D$ with the circumcircle of the triangle $A B C$. Let $O$ be the circumcentre of the triangle $A B C$ and let $D^{\prime}$ be the reflection of $D$ in $O$. Prove that $\angle D^{\prime} F E=90^{\circ}$.
|
. We consider the configuration where $C, D, B$ and $E$ are on the line $B C$ in that order. The other configuration can be solved analogously. Let $P$ and $R$ be the feet of the perpendiculars from $D^{\prime}$ and $O$ to the line $A D$, respectively, and let $Q$ and $S$ be the feet of the perpendiculars from $D^{\prime}$ and $O$ to the line $C D$, respectively. Since $D^{\prime}$ is the reflection of $D$ with respect to $O$, we have $P R=R D$. Since we also have $O A=O F$ and therefore $R A=R F$, we obtain $A D=P F$. Similarly, $C D=B Q$. By Pythagoras's theorem,
$$
D^{\prime} F^{2}=D^{\prime} P^{2}+P F^{2}=4 O R^{2}+A D^{2}=4 O A^{2}-4 A R^{2}+A D^{2}=4 O A^{2}-A F^{2}+A D^{2}
$$
and
$$
D^{\prime} E^{2}=D^{\prime} Q^{2}+E Q^{2}=4 O S^{2}+E Q^{2}=4 O B^{2}-4 B S^{2}+E Q^{2}=4 O B^{2}-B C^{2}+(E B+C D)^{2} .
$$
And since $\angle E A F=90^{\circ}$ we have
$$
E F^{2}=A E^{2}+A F^{2} .
$$
As $O A=O B$, we conclude that
$$
\begin{array}{r}
D^{\prime} F^{2}+E F^{2}-D^{\prime} E^{2}=\left(4 O A^{2}-A F^{2}+A D^{2}\right)+\left(A E^{2}+A F^{2}\right)-\left(4 O B^{2}-B C^{2}+(E B+C D)^{2}\right) \\
=A E^{2}+A D^{2}+B C^{2}-(E B+C D)^{2}
\end{array}
$$
By Pythagoras's theorem again, we obtain $A E^{2}+A D^{2}=E D^{2}$, and hence
$$
D^{\prime} F^{2}+E F^{2}-D^{\prime} E^{2}=E D^{2}+B C^{2}-(E B+C D)^{2} .
$$
We have
$$
\begin{aligned}
E D^{2}+B C^{2} & =(E B+B D)^{2}+(B D+C D)^{2} \\
& =E B^{2}+B D^{2}+2 \cdot E B \cdot B D+B D^{2}+C D^{2}+2 \cdot B D \cdot C D \\
& =E B^{2}+C D^{2}+2 \cdot B D \cdot(E B+B D+C D) \\
& =E B^{2}+C D^{2}+2 \cdot B D \cdot E C .
\end{aligned}
$$
By the internal and external bisector theorems, we have
$$
\frac{B D}{C D}=\frac{B A}{C A}=\frac{B E}{C E},
$$
hence
$$
E D^{2}+B C^{2}=E B^{2}+C D^{2}+2 \cdot C D \cdot B E=(E B+C D)^{2} .
$$
So
$$
D^{\prime} F^{2}+E F^{2}-D^{\prime} E^{2}=0,
$$
which implies that $\angle D^{\prime} F E=90^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In triangle $A B C$, the interior and exterior angle bisectors of $\angle B A C$ intersect the line $B C$ in $D$ and $E$, respectively. Let $F$ be the second point of intersection of the line $A D$ with the circumcircle of the triangle $A B C$. Let $O$ be the circumcentre of the triangle $A B C$ and let $D^{\prime}$ be the reflection of $D$ in $O$. Prove that $\angle D^{\prime} F E=90^{\circ}$.
|
. We consider the configuration where $C, D, B$ and $E$ are on the line $B C$ in that order. The other configuration can be solved analogously. Let $P$ and $R$ be the feet of the perpendiculars from $D^{\prime}$ and $O$ to the line $A D$, respectively, and let $Q$ and $S$ be the feet of the perpendiculars from $D^{\prime}$ and $O$ to the line $C D$, respectively. Since $D^{\prime}$ is the reflection of $D$ with respect to $O$, we have $P R=R D$. Since we also have $O A=O F$ and therefore $R A=R F$, we obtain $A D=P F$. Similarly, $C D=B Q$. By Pythagoras's theorem,
$$
D^{\prime} F^{2}=D^{\prime} P^{2}+P F^{2}=4 O R^{2}+A D^{2}=4 O A^{2}-4 A R^{2}+A D^{2}=4 O A^{2}-A F^{2}+A D^{2}
$$
and
$$
D^{\prime} E^{2}=D^{\prime} Q^{2}+E Q^{2}=4 O S^{2}+E Q^{2}=4 O B^{2}-4 B S^{2}+E Q^{2}=4 O B^{2}-B C^{2}+(E B+C D)^{2} .
$$
And since $\angle E A F=90^{\circ}$ we have
$$
E F^{2}=A E^{2}+A F^{2} .
$$
As $O A=O B$, we conclude that
$$
\begin{array}{r}
D^{\prime} F^{2}+E F^{2}-D^{\prime} E^{2}=\left(4 O A^{2}-A F^{2}+A D^{2}\right)+\left(A E^{2}+A F^{2}\right)-\left(4 O B^{2}-B C^{2}+(E B+C D)^{2}\right) \\
=A E^{2}+A D^{2}+B C^{2}-(E B+C D)^{2}
\end{array}
$$
By Pythagoras's theorem again, we obtain $A E^{2}+A D^{2}=E D^{2}$, and hence
$$
D^{\prime} F^{2}+E F^{2}-D^{\prime} E^{2}=E D^{2}+B C^{2}-(E B+C D)^{2} .
$$
We have
$$
\begin{aligned}
E D^{2}+B C^{2} & =(E B+B D)^{2}+(B D+C D)^{2} \\
& =E B^{2}+B D^{2}+2 \cdot E B \cdot B D+B D^{2}+C D^{2}+2 \cdot B D \cdot C D \\
& =E B^{2}+C D^{2}+2 \cdot B D \cdot(E B+B D+C D) \\
& =E B^{2}+C D^{2}+2 \cdot B D \cdot E C .
\end{aligned}
$$
By the internal and external bisector theorems, we have
$$
\frac{B D}{C D}=\frac{B A}{C A}=\frac{B E}{C E},
$$
hence
$$
E D^{2}+B C^{2}=E B^{2}+C D^{2}+2 \cdot C D \cdot B E=(E B+C D)^{2} .
$$
So
$$
D^{\prime} F^{2}+E F^{2}-D^{\prime} E^{2}=0,
$$
which implies that $\angle D^{\prime} F E=90^{\circ}$.
|
{
"exam": "BalticWay",
"problem_label": "15",
"problem_match": "# Problem 15.",
"resource_path": "BalticWay/segmented/en-bw15sol.jsonl",
"solution_match": "\nSolution 4",
"tier": "T3",
"year": "2015"
}
|
Denote by $P(n)$ the greatest prime divisor of $n$. Find all integers $n \geq 2$ for which
$$
P(n)+\lfloor\sqrt{n}\rfloor=P(n+1)+\lfloor\sqrt{n+1}\rfloor .
$$
(Note: $\lfloor x\rfloor$ denotes the greatest integer less than or equal to $x$.)
|
Answer: The equality holds only for $n=3$.
It is easy to see that $P(n) \neq P(n+1)$. Therefore we need also that $\lfloor\sqrt{n}\rfloor \neq\lfloor\sqrt{n+1}\rfloor$ in order for equality to hold. This is only possible if $n+1$ is a perfect square. In this case,
$$
\lfloor\sqrt{n}\rfloor+1=\lfloor\sqrt{n+1}\rfloor
$$
and hence $P(n)=P(n+1)+1$. As both $P(n)$ and $P(n+1)$ are primes, it must be that $P(n)=3$ and $P(n+1)=2$.
It follows that $n=3^{a}$ and $n+1=2^{b}$, and we are required to solve the equation $3^{a}=2^{b}-1$. Calculating modulo 3 , we find that $b$ is even. Put $b=2 c$ :
$$
3^{a}=\left(2^{c}-1\right)\left(2^{c}+1\right) .
$$
As both factors cannot be divisible by 3 (their difference is 2 ), $2^{c}-1=1$. From this we get $c=1$, which leads to $n=3$.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Denote by $P(n)$ the greatest prime divisor of $n$. Find all integers $n \geq 2$ for which
$$
P(n)+\lfloor\sqrt{n}\rfloor=P(n+1)+\lfloor\sqrt{n+1}\rfloor .
$$
(Note: $\lfloor x\rfloor$ denotes the greatest integer less than or equal to $x$.)
|
Answer: The equality holds only for $n=3$.
It is easy to see that $P(n) \neq P(n+1)$. Therefore we need also that $\lfloor\sqrt{n}\rfloor \neq\lfloor\sqrt{n+1}\rfloor$ in order for equality to hold. This is only possible if $n+1$ is a perfect square. In this case,
$$
\lfloor\sqrt{n}\rfloor+1=\lfloor\sqrt{n+1}\rfloor
$$
and hence $P(n)=P(n+1)+1$. As both $P(n)$ and $P(n+1)$ are primes, it must be that $P(n)=3$ and $P(n+1)=2$.
It follows that $n=3^{a}$ and $n+1=2^{b}$, and we are required to solve the equation $3^{a}=2^{b}-1$. Calculating modulo 3 , we find that $b$ is even. Put $b=2 c$ :
$$
3^{a}=\left(2^{c}-1\right)\left(2^{c}+1\right) .
$$
As both factors cannot be divisible by 3 (their difference is 2 ), $2^{c}-1=1$. From this we get $c=1$, which leads to $n=3$.
|
{
"exam": "BalticWay",
"problem_label": "16",
"problem_match": "# Problem 16.",
"resource_path": "BalticWay/segmented/en-bw15sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2015"
}
|
Find all positive integers $n$ for which $n^{n-1}-1$ is divisible by $2^{2015}$, but not by $2^{2016}$.
|
Since $n$ must be odd, write $n=2^{d} u+1$, where $u, d \in \mathbf{N}$ and $u$ is odd. Now
$$
n^{n-1}-1=\left(n^{2^{d}}-1\right)(\underbrace{n^{2^{d} \cdot(u-1)}+\cdots+n^{2^{d} \cdot 1}+1}_{u}),
$$
and hence $2^{2015} \|\left(n^{n-1}-1\right)$ iff $2^{2015} \|\left(n^{2^{d}}-1\right)$. (The notation $p^{k} \| m$ denotes that $p^{k} \mid m$ and $p^{k+1} \nmid m$.)
We factorise once more:
$$
\begin{aligned}
n^{2^{d}}-1 & =(n-1)(n+1) \underbrace{\left(n^{2}+1\right) \cdots\left(n^{2^{d-1}}+1\right)}_{d-1} \\
& =2^{d} u \cdot 2\left(2^{d-1} u+1\right) \underbrace{\left(n^{2}+1\right) \cdots\left(n^{2^{d-1}}+1\right)}_{d-1} .
\end{aligned}
$$
If $k \geq 1$, then $2 \| n^{2^{k}}+1$, and so from the above
$$
2^{2 d} \| 2^{d} u \cdot 2 \cdot \underbrace{\left(n^{2}+1\right) \cdots\left(n^{2^{d-1}}+1\right)}_{d-1} \quad \text { and } \quad 2^{2015-2 d} \|\left(2^{d-1} u+1\right)
$$
It is easy to see that this is the case exactly when $d=1$ and $u=2^{2013} v-1$, where $v$ is odd.
Hence the required numbers are those of the form
$$
n=2\left(2^{2013} v-1\right)+1=2^{2014} v-1
$$
for $v$ a positive odd number.
|
n=2^{2014} v-1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all positive integers $n$ for which $n^{n-1}-1$ is divisible by $2^{2015}$, but not by $2^{2016}$.
|
Since $n$ must be odd, write $n=2^{d} u+1$, where $u, d \in \mathbf{N}$ and $u$ is odd. Now
$$
n^{n-1}-1=\left(n^{2^{d}}-1\right)(\underbrace{n^{2^{d} \cdot(u-1)}+\cdots+n^{2^{d} \cdot 1}+1}_{u}),
$$
and hence $2^{2015} \|\left(n^{n-1}-1\right)$ iff $2^{2015} \|\left(n^{2^{d}}-1\right)$. (The notation $p^{k} \| m$ denotes that $p^{k} \mid m$ and $p^{k+1} \nmid m$.)
We factorise once more:
$$
\begin{aligned}
n^{2^{d}}-1 & =(n-1)(n+1) \underbrace{\left(n^{2}+1\right) \cdots\left(n^{2^{d-1}}+1\right)}_{d-1} \\
& =2^{d} u \cdot 2\left(2^{d-1} u+1\right) \underbrace{\left(n^{2}+1\right) \cdots\left(n^{2^{d-1}}+1\right)}_{d-1} .
\end{aligned}
$$
If $k \geq 1$, then $2 \| n^{2^{k}}+1$, and so from the above
$$
2^{2 d} \| 2^{d} u \cdot 2 \cdot \underbrace{\left(n^{2}+1\right) \cdots\left(n^{2^{d-1}}+1\right)}_{d-1} \quad \text { and } \quad 2^{2015-2 d} \|\left(2^{d-1} u+1\right)
$$
It is easy to see that this is the case exactly when $d=1$ and $u=2^{2013} v-1$, where $v$ is odd.
Hence the required numbers are those of the form
$$
n=2\left(2^{2013} v-1\right)+1=2^{2014} v-1
$$
for $v$ a positive odd number.
|
{
"exam": "BalticWay",
"problem_label": "17",
"problem_match": "# Problem 17.",
"resource_path": "BalticWay/segmented/en-bw15sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2015"
}
|
Let $f(x)=x^{n}+a_{n-1} x^{n-1}+\cdots+a_{0}$ be a polynomial of degree $n \geq 1$ with $n$ (not necessarily distinct) integer roots. Assume that there exist distinct primes $p_{0}, p_{1}, \ldots, p_{n-1}$ such that $a_{i}>1$ is a power of $p_{i}$, for all $i=0, \ldots, n-1$. Find all possible values of $n$.
|
Obviously all the roots have to be negative by the positivity of the coefficients. If at least two of the roots are unequal to -1 , then both of them have to be powers of $p_{0}$. Now Vieta's formulæ yield $p_{0} \mid a_{1}$, which is a contradiction. Thus we can factor $f$ as
$$
f(x)=\left(x+a_{0}\right)(x+1)^{n-1}
$$
Expanding yields
$$
a_{2}=\left(\begin{array}{c}
n-1 \\
1
\end{array}\right)+a_{0}\left(\begin{array}{c}
n-1 \\
2
\end{array}\right) \quad \text { and } \quad a_{n-2}=a_{0}\left(\begin{array}{l}
n-1 \\
n-2
\end{array}\right)+\left(\begin{array}{l}
n-1 \\
n-3
\end{array}\right)
$$
If $n \geq 5$, we see that $2 \neq n-2$ and so the two coefficients above are relatively prime, being powers of two distinct primes. However, depending on the parity of $n$, we have that $a_{2}$ and $a_{n-2}$ are both divisible by $n-1$ or $\frac{n-1}{2}$, which is a contradiction.
For $n=1,2,3,4$, the following polynomials meet the requirements:
$$
\begin{aligned}
& f_{1}(x)=x+2 \\
& f_{2}(x)=(x+2)(x+1)=x^{2}+3 x+2 \\
& f_{3}(x)=(x+3)(x+1)^{2}=x^{3}+5 x^{2}+7 x+3 \\
& f_{4}(x)=(x+2)(x+1)^{3}=x^{4}+5 x^{3}+9 x^{2}+7 x+2
\end{aligned}
$$
|
n=1,2,3,4
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $f(x)=x^{n}+a_{n-1} x^{n-1}+\cdots+a_{0}$ be a polynomial of degree $n \geq 1$ with $n$ (not necessarily distinct) integer roots. Assume that there exist distinct primes $p_{0}, p_{1}, \ldots, p_{n-1}$ such that $a_{i}>1$ is a power of $p_{i}$, for all $i=0, \ldots, n-1$. Find all possible values of $n$.
|
Obviously all the roots have to be negative by the positivity of the coefficients. If at least two of the roots are unequal to -1 , then both of them have to be powers of $p_{0}$. Now Vieta's formulæ yield $p_{0} \mid a_{1}$, which is a contradiction. Thus we can factor $f$ as
$$
f(x)=\left(x+a_{0}\right)(x+1)^{n-1}
$$
Expanding yields
$$
a_{2}=\left(\begin{array}{c}
n-1 \\
1
\end{array}\right)+a_{0}\left(\begin{array}{c}
n-1 \\
2
\end{array}\right) \quad \text { and } \quad a_{n-2}=a_{0}\left(\begin{array}{l}
n-1 \\
n-2
\end{array}\right)+\left(\begin{array}{l}
n-1 \\
n-3
\end{array}\right)
$$
If $n \geq 5$, we see that $2 \neq n-2$ and so the two coefficients above are relatively prime, being powers of two distinct primes. However, depending on the parity of $n$, we have that $a_{2}$ and $a_{n-2}$ are both divisible by $n-1$ or $\frac{n-1}{2}$, which is a contradiction.
For $n=1,2,3,4$, the following polynomials meet the requirements:
$$
\begin{aligned}
& f_{1}(x)=x+2 \\
& f_{2}(x)=(x+2)(x+1)=x^{2}+3 x+2 \\
& f_{3}(x)=(x+3)(x+1)^{2}=x^{3}+5 x^{2}+7 x+3 \\
& f_{4}(x)=(x+2)(x+1)^{3}=x^{4}+5 x^{3}+9 x^{2}+7 x+2
\end{aligned}
$$
|
{
"exam": "BalticWay",
"problem_label": "18",
"problem_match": "# Problem 18.",
"resource_path": "BalticWay/segmented/en-bw15sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2015"
}
|
Three pairwise distinct positive integers $a, b, c$, with $\operatorname{gcd}(a, b, c)=1$, satisfy
$$
a\left|(b-c)^{2}, \quad b\right|(c-a)^{2} \quad \text { and } \quad c \mid(a-b)^{2} \text {. }
$$
Prove that there does not exist a non-degenerate triangle with side lengths $a, b, c$.
|
First observe that these numbers are pairwise coprime. Indeed, if, say, $a$ and $b$ are divisible by a prime $p$, then $p$ divides $b$, which divides $(a-c)^{2}$; hence $p$ divides $a-c$, and therefore $p$ divides $c$. Thus, $p$ is a common divisor of these three numbers, a contradiction.
Now consider the number
$$
M=2 a b+2 b c+2 a c-a^{2}-b^{2}-c^{2} .
$$
It is clear from the problem condition that $M$ is divisible by $a, b, c$, and therefore $M$ is divisible by $a b c$.
Assume that a triangle with sides $a, b, c$ exists. Then $a<b+c$, and so $a^{2}<a b+a c$. Analogously, we have $b^{2}<b c+b a$ and $c^{2}<c a+c b$. Summing these three inequalities leads to $M>0$, and hence $M \geq a b c$.
On the other hand,
$$
a^{2}+b^{2}+c^{2}>a b+b c+a c
$$
and therefore $M<a b+b c+a c$. Supposing, with no loss of generality, $a>b>c$, we must have $M<3 a b$. Taking into account the inequality $M \geq a b c$, we conclude that $c=1$ or $c=2$ are the only possibilities.
For $c=1$ we have $b<a<b+1$ (the first inequality is our assumption, the second is the triangle inequality), a contradiction.
For $c=2$ we have $b<a<b+2$, i.e. $a=b+1$. But then $1=(a-b)^{2}$ is not divisible by $c=2$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Three pairwise distinct positive integers $a, b, c$, with $\operatorname{gcd}(a, b, c)=1$, satisfy
$$
a\left|(b-c)^{2}, \quad b\right|(c-a)^{2} \quad \text { and } \quad c \mid(a-b)^{2} \text {. }
$$
Prove that there does not exist a non-degenerate triangle with side lengths $a, b, c$.
|
First observe that these numbers are pairwise coprime. Indeed, if, say, $a$ and $b$ are divisible by a prime $p$, then $p$ divides $b$, which divides $(a-c)^{2}$; hence $p$ divides $a-c$, and therefore $p$ divides $c$. Thus, $p$ is a common divisor of these three numbers, a contradiction.
Now consider the number
$$
M=2 a b+2 b c+2 a c-a^{2}-b^{2}-c^{2} .
$$
It is clear from the problem condition that $M$ is divisible by $a, b, c$, and therefore $M$ is divisible by $a b c$.
Assume that a triangle with sides $a, b, c$ exists. Then $a<b+c$, and so $a^{2}<a b+a c$. Analogously, we have $b^{2}<b c+b a$ and $c^{2}<c a+c b$. Summing these three inequalities leads to $M>0$, and hence $M \geq a b c$.
On the other hand,
$$
a^{2}+b^{2}+c^{2}>a b+b c+a c
$$
and therefore $M<a b+b c+a c$. Supposing, with no loss of generality, $a>b>c$, we must have $M<3 a b$. Taking into account the inequality $M \geq a b c$, we conclude that $c=1$ or $c=2$ are the only possibilities.
For $c=1$ we have $b<a<b+1$ (the first inequality is our assumption, the second is the triangle inequality), a contradiction.
For $c=2$ we have $b<a<b+2$, i.e. $a=b+1$. But then $1=(a-b)^{2}$ is not divisible by $c=2$.
|
{
"exam": "BalticWay",
"problem_label": "19",
"problem_match": "# Problem 19.",
"resource_path": "BalticWay/segmented/en-bw15sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2015"
}
|
For any integer $n \geq 2$, we define $A_{n}$ to be the number of positive integers $m$ with the following property: the distance from $n$ to the nearest non-negative multiple of $m$ is equal to the distance from $n^{3}$ to the nearest non-negative multiple of $m$. Find all integers $n \geq 2$ for which $A_{n}$ is odd.
(Note: The distance between two integers $a$ and $b$ is defined as $|a-b|$.)
|
For an integer $m$ we consider the distance $d$ from $n$ to the nearest multiple of $m$. Then $m \mid n \pm d$, which means $n \equiv \pm d \bmod m$. So if, for some $m$, the distance from $n$ to the nearest multiple of $m$ is equal to the distance from $n^{3}$ to the nearest multiple of $m$, then $n \equiv \pm n^{3} \bmod m$.
On the other hand, if $n \equiv \pm n^{3} \bmod m$, then there exists a $0 \leq d \leq \frac{1}{2} m$ such that $n \equiv \pm d \bmod m$ and $n^{3} \equiv \pm d \bmod m$, so the distance from $n$ to the nearest multiple of $m$ is equal to the distance from $n^{3}$ to the nearest multiple of $m$.
We conclude that we need to count the number of positive integers $m$ such that $n \equiv \pm n^{3} \bmod m$, or, equivalently, $m \mid n^{3}-n$ or $m \mid n^{3}+n$. That is,
$$
\begin{aligned}
& A_{n}=\mid\left\{m \in \mathbf{Z}^{+}|m| n^{3}-n \text { or } m \mid n^{3}+n\right\} \mid \\
& =\left|\left\{m \in \mathbf{Z}^{+}|m| n^{3}-n\right\}\right|+\left|\left\{m \in \mathbf{Z}^{+}|m| n^{3}+n\right\}\right|-\mid\left\{m \in \mathbf{Z}^{+}|m| n^{3}-n \text { and } m \mid n^{3}+n\right\} \mid \\
& =\left|\left\{m \in \mathbf{Z}^{+}|m| n^{3}-n\right\}\right|+\left|\left\{m \in \mathbf{Z}^{+}|m| n^{3}+n\right\}\right|-\left|\left\{m \in \mathbf{Z}^{+}|m| \operatorname{gcd}\left(n^{3}-n, n^{3}+n\right)\right\}\right| \\
& =\tau\left(n^{3}-n\right)+\tau\left(n^{3}+n\right)-\tau\left(\operatorname{gcd}\left(n^{3}-n, n^{3}+n\right)\right),
\end{aligned}
$$
where $\tau(k)$ denotes the number of (positive) divisors of a positive integer $k$.
Recall that $\tau(k)$ is odd if and only if $k$ is a square. Furthermore, we have
$$
\operatorname{gcd}\left(n, n^{2} \pm 1\right)=1
$$
So if $n^{3} \pm n$ were a square, then both $n$ and $n^{2} \pm 1$ would be squares. But $n^{2} \pm 1$ is not a square, since $n \geq 2$ and the only consecutive squares are 0,1 . Hence neither $n^{3}-n$ nor $n^{3}+n$ is a square, so the first two terms $\tau\left(n^{3}-n\right)$ and $\tau\left(n^{3}+n\right)$ are both even. Hence $A_{n}$ is odd if and only if $\operatorname{gcd}\left(n^{3}-n, n^{3}+n\right)$ is a square.
We have
$$
\operatorname{gcd}\left(n^{2}-1, n^{2}+1\right)=\operatorname{gcd}\left(n^{2}-1,2\right)= \begin{cases}1 & \text { if } n \text { even } \\ 2 & \text { if } n \text { odd }\end{cases}
$$
Hence,
$$
\operatorname{gcd}\left(n^{3}-n, n^{3}+n\right)= \begin{cases}n & \text { if } n \text { even } \\ 2 n & \text { if } n \text { odd }\end{cases}
$$
Note that $2 n$ for $n$ odd is never a square, since it has exactly one factor of 2 . We conclude that $A_{n}$ is odd if and only if $n$ is an even square.
|
n \text{ is an even square}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
For any integer $n \geq 2$, we define $A_{n}$ to be the number of positive integers $m$ with the following property: the distance from $n$ to the nearest non-negative multiple of $m$ is equal to the distance from $n^{3}$ to the nearest non-negative multiple of $m$. Find all integers $n \geq 2$ for which $A_{n}$ is odd.
(Note: The distance between two integers $a$ and $b$ is defined as $|a-b|$.)
|
For an integer $m$ we consider the distance $d$ from $n$ to the nearest multiple of $m$. Then $m \mid n \pm d$, which means $n \equiv \pm d \bmod m$. So if, for some $m$, the distance from $n$ to the nearest multiple of $m$ is equal to the distance from $n^{3}$ to the nearest multiple of $m$, then $n \equiv \pm n^{3} \bmod m$.
On the other hand, if $n \equiv \pm n^{3} \bmod m$, then there exists a $0 \leq d \leq \frac{1}{2} m$ such that $n \equiv \pm d \bmod m$ and $n^{3} \equiv \pm d \bmod m$, so the distance from $n$ to the nearest multiple of $m$ is equal to the distance from $n^{3}$ to the nearest multiple of $m$.
We conclude that we need to count the number of positive integers $m$ such that $n \equiv \pm n^{3} \bmod m$, or, equivalently, $m \mid n^{3}-n$ or $m \mid n^{3}+n$. That is,
$$
\begin{aligned}
& A_{n}=\mid\left\{m \in \mathbf{Z}^{+}|m| n^{3}-n \text { or } m \mid n^{3}+n\right\} \mid \\
& =\left|\left\{m \in \mathbf{Z}^{+}|m| n^{3}-n\right\}\right|+\left|\left\{m \in \mathbf{Z}^{+}|m| n^{3}+n\right\}\right|-\mid\left\{m \in \mathbf{Z}^{+}|m| n^{3}-n \text { and } m \mid n^{3}+n\right\} \mid \\
& =\left|\left\{m \in \mathbf{Z}^{+}|m| n^{3}-n\right\}\right|+\left|\left\{m \in \mathbf{Z}^{+}|m| n^{3}+n\right\}\right|-\left|\left\{m \in \mathbf{Z}^{+}|m| \operatorname{gcd}\left(n^{3}-n, n^{3}+n\right)\right\}\right| \\
& =\tau\left(n^{3}-n\right)+\tau\left(n^{3}+n\right)-\tau\left(\operatorname{gcd}\left(n^{3}-n, n^{3}+n\right)\right),
\end{aligned}
$$
where $\tau(k)$ denotes the number of (positive) divisors of a positive integer $k$.
Recall that $\tau(k)$ is odd if and only if $k$ is a square. Furthermore, we have
$$
\operatorname{gcd}\left(n, n^{2} \pm 1\right)=1
$$
So if $n^{3} \pm n$ were a square, then both $n$ and $n^{2} \pm 1$ would be squares. But $n^{2} \pm 1$ is not a square, since $n \geq 2$ and the only consecutive squares are 0,1 . Hence neither $n^{3}-n$ nor $n^{3}+n$ is a square, so the first two terms $\tau\left(n^{3}-n\right)$ and $\tau\left(n^{3}+n\right)$ are both even. Hence $A_{n}$ is odd if and only if $\operatorname{gcd}\left(n^{3}-n, n^{3}+n\right)$ is a square.
We have
$$
\operatorname{gcd}\left(n^{2}-1, n^{2}+1\right)=\operatorname{gcd}\left(n^{2}-1,2\right)= \begin{cases}1 & \text { if } n \text { even } \\ 2 & \text { if } n \text { odd }\end{cases}
$$
Hence,
$$
\operatorname{gcd}\left(n^{3}-n, n^{3}+n\right)= \begin{cases}n & \text { if } n \text { even } \\ 2 n & \text { if } n \text { odd }\end{cases}
$$
Note that $2 n$ for $n$ odd is never a square, since it has exactly one factor of 2 . We conclude that $A_{n}$ is odd if and only if $n$ is an even square.
|
{
"exam": "BalticWay",
"problem_label": "20",
"problem_match": "# Problem 20.",
"resource_path": "BalticWay/segmented/en-bw15sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2015"
}
|
Find all pairs of primes $(p, q)$ such that
$$
p^{3}-q^{5}=(p+q)^{2} .
$$
|
Assume first that neither of the numbers equals 3. Then, if $p \equiv q \bmod 3$, the left hand side is divisible by 3 , but the right hand side is not. But if $p \equiv-q \bmod 3$, the left hand side is not divisible by 3 , while the right hand side is. So this is not possible.
If $p=3$, then $q^{5}<27$, which is impossible. Therefore $q=3$, and the equation turns into $p^{3}-243=(p+3)^{2}$ or
$$
p\left(p^{2}-p-6\right)=252=7 \cdot 36 \text {. }
$$
As $p>3$ then $p^{2}-p-6$ is positive and increases with $p$. So the equation has at most one solution. It is easy to see that $p=7$ is the one and $(7,3)$ is a solution to the given equation.
|
(7,3)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all pairs of primes $(p, q)$ such that
$$
p^{3}-q^{5}=(p+q)^{2} .
$$
|
Assume first that neither of the numbers equals 3. Then, if $p \equiv q \bmod 3$, the left hand side is divisible by 3 , but the right hand side is not. But if $p \equiv-q \bmod 3$, the left hand side is not divisible by 3 , while the right hand side is. So this is not possible.
If $p=3$, then $q^{5}<27$, which is impossible. Therefore $q=3$, and the equation turns into $p^{3}-243=(p+3)^{2}$ or
$$
p\left(p^{2}-p-6\right)=252=7 \cdot 36 \text {. }
$$
As $p>3$ then $p^{2}-p-6$ is positive and increases with $p$. So the equation has at most one solution. It is easy to see that $p=7$ is the one and $(7,3)$ is a solution to the given equation.
|
{
"exam": "BalticWay",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "BalticWay/segmented/en-bw16sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2016"
}
|
Prove or disprove the following hypotheses.
a) For all $k \geq 2$, each sequence of $k$ consecutive positive integers contains a number that is not divisible by any prime number less than $k$.
b) For all $k \geq 2$, each sequence of $k$ consecutive positive integers contains a number that is relatively prime to all other members of the sequence.
|
We give a counterexample to both claims. So neither of them is true.
For a), a counterexample is the sequence $(2,3,4,5,6,7,8,9)$ of eight consecutive integers all of which are divisible by some prime less than 8 .
To construct a counterexample to b), we notice that by the Chinese Remainder Theorem, there exists an integer $x$ such that $x \equiv 0 \bmod 2, x \equiv 0 \bmod 5, x \equiv 0 \bmod 11, x \equiv 2 \bmod 3$, $x \equiv 5 \bmod 7$ and $x \equiv 10 \bmod 13$. The last three of these congruences mean that $x+16$ is a multiple of 3,7 , and 13 . Now consider the sequence $(x, x+1, \ldots, x+16)$ of 17 consequtive integers. Of these all numbers $x+2 k, 0 \leq k \leq 8$, are even and so have a common factor with some other. Of the remaining, $x+1, x+7$ and $x+13$ are divisible by $3, x+3$ is a multiple of 13 as is $x+16, x+5$ is divisible by 5 as $x, x+9$ is a multiple of 7 as $x+2$, $x+11$ a multiple of 11 as is $x$, and finally $x+15$ is a multiple of 5 as is $x$.
Remark. The counterexample given to either hypothesis is the shortest possible. The only counterexamples of length 8 to the first hypothesis are those where numbers give remainders $2,3, \ldots, 9 ; 3,4, \ldots, 10 ;-2,-3, \ldots,-9 ;$ or $-3,-4, \ldots,-10$ modulo 210 . The only counterexamples of length 17 to the second hypothesis are those where the numbers give remainders $2184,2185, \ldots, 2200$ or $-2184,-2185, \ldots,-2200$ modulo 30030.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove or disprove the following hypotheses.
a) For all $k \geq 2$, each sequence of $k$ consecutive positive integers contains a number that is not divisible by any prime number less than $k$.
b) For all $k \geq 2$, each sequence of $k$ consecutive positive integers contains a number that is relatively prime to all other members of the sequence.
|
We give a counterexample to both claims. So neither of them is true.
For a), a counterexample is the sequence $(2,3,4,5,6,7,8,9)$ of eight consecutive integers all of which are divisible by some prime less than 8 .
To construct a counterexample to b), we notice that by the Chinese Remainder Theorem, there exists an integer $x$ such that $x \equiv 0 \bmod 2, x \equiv 0 \bmod 5, x \equiv 0 \bmod 11, x \equiv 2 \bmod 3$, $x \equiv 5 \bmod 7$ and $x \equiv 10 \bmod 13$. The last three of these congruences mean that $x+16$ is a multiple of 3,7 , and 13 . Now consider the sequence $(x, x+1, \ldots, x+16)$ of 17 consequtive integers. Of these all numbers $x+2 k, 0 \leq k \leq 8$, are even and so have a common factor with some other. Of the remaining, $x+1, x+7$ and $x+13$ are divisible by $3, x+3$ is a multiple of 13 as is $x+16, x+5$ is divisible by 5 as $x, x+9$ is a multiple of 7 as $x+2$, $x+11$ a multiple of 11 as is $x$, and finally $x+15$ is a multiple of 5 as is $x$.
Remark. The counterexample given to either hypothesis is the shortest possible. The only counterexamples of length 8 to the first hypothesis are those where numbers give remainders $2,3, \ldots, 9 ; 3,4, \ldots, 10 ;-2,-3, \ldots,-9 ;$ or $-3,-4, \ldots,-10$ modulo 210 . The only counterexamples of length 17 to the second hypothesis are those where the numbers give remainders $2184,2185, \ldots, 2200$ or $-2184,-2185, \ldots,-2200$ modulo 30030.
|
{
"exam": "BalticWay",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "BalticWay/segmented/en-bw16sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2016"
}
|
For which integers $n=1, \ldots, 6$ does the equation
$$
a^{n}+b^{n}=c^{n}+n
$$
have a solution in integers?
|
A solution clearly exists for $n=1,2,3$ :
$$
1^{1}+0^{1}=0^{1}+1, \quad 1^{2}+1^{2}=0^{2}+2, \quad 1^{3}+1^{3}=(-1)^{3}+3 .
$$
We show that for $n=4,5,6$ there is no solution.
For $n=4$, the equation $a^{4}+b^{4}=c^{4}+4$ may be considered modulo 8 . Since each fourth power $x^{4} \equiv 0,1 \bmod 8$, the expression $a^{4}+b^{4}-c^{4}$ can never be congruent to 4 .
For $n=5$, consider the equation $a^{5}+b^{5}=c^{5}+5$ modulo 11 . As $x^{5} \equiv 0$ or $\equiv \pm 1 \bmod 11$ (This can be seen by Fermat's Little Theorem or by direct computation), $a^{5}+b^{5}-c^{5}$ cannot be congruent to 5 .
The case $n=6$ is similarly dismissed by considering the equation modulo 13 .
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
For which integers $n=1, \ldots, 6$ does the equation
$$
a^{n}+b^{n}=c^{n}+n
$$
have a solution in integers?
|
A solution clearly exists for $n=1,2,3$ :
$$
1^{1}+0^{1}=0^{1}+1, \quad 1^{2}+1^{2}=0^{2}+2, \quad 1^{3}+1^{3}=(-1)^{3}+3 .
$$
We show that for $n=4,5,6$ there is no solution.
For $n=4$, the equation $a^{4}+b^{4}=c^{4}+4$ may be considered modulo 8 . Since each fourth power $x^{4} \equiv 0,1 \bmod 8$, the expression $a^{4}+b^{4}-c^{4}$ can never be congruent to 4 .
For $n=5$, consider the equation $a^{5}+b^{5}=c^{5}+5$ modulo 11 . As $x^{5} \equiv 0$ or $\equiv \pm 1 \bmod 11$ (This can be seen by Fermat's Little Theorem or by direct computation), $a^{5}+b^{5}-c^{5}$ cannot be congruent to 5 .
The case $n=6$ is similarly dismissed by considering the equation modulo 13 .
|
{
"exam": "BalticWay",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "BalticWay/segmented/en-bw16sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2016"
}
|
Let $n$ be a positive integer and let $a, b, c, d$ be integers such that $n \mid a+b+c+d$ and $n \mid a^{2}+b^{2}+c^{2}+d^{2}$. Show that
$$
n \mid a^{4}+b^{4}+c^{4}+d^{4}+4 a b c d .
$$
|
. Consider the polynomial
$$
w(x)=(x-a)(x-b)(x-c)(x-d)=x^{4}+A x^{3}+B x^{2}+C x+D .
$$
It is clear that $w(a)=w(b)=w(c)=w(d)=0$. By adding these values we get
$$
\begin{gathered}
w(a)+w(b)+w(c)+w(d)=a^{4}+b^{4}+c^{4}+d^{4}+A\left(a^{3}+b^{3}+c^{3}+d^{3}\right)+ \\
+B\left(a^{2}+b^{2}+c^{2}+d^{2}\right)+C(a+b+c+d)+4 D=0 .
\end{gathered}
$$
Hence
$$
\begin{gathered}
a^{4}+b^{4}+c^{4}+d^{4}+4 D \\
=-A\left(a^{3}+b^{3}+c^{3}+d^{3}\right)-B\left(a^{2}+b^{2}+c^{2}+d^{2}\right)-C(a+b+c+d) .
\end{gathered}
$$
Using Vieta's formulas, we can see that $D=a b c d$ and $-A=a+b+c+d$. Therefore the right hand side of the equation above is divisible by $n$, and so is the left hand side.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ be a positive integer and let $a, b, c, d$ be integers such that $n \mid a+b+c+d$ and $n \mid a^{2}+b^{2}+c^{2}+d^{2}$. Show that
$$
n \mid a^{4}+b^{4}+c^{4}+d^{4}+4 a b c d .
$$
|
. Consider the polynomial
$$
w(x)=(x-a)(x-b)(x-c)(x-d)=x^{4}+A x^{3}+B x^{2}+C x+D .
$$
It is clear that $w(a)=w(b)=w(c)=w(d)=0$. By adding these values we get
$$
\begin{gathered}
w(a)+w(b)+w(c)+w(d)=a^{4}+b^{4}+c^{4}+d^{4}+A\left(a^{3}+b^{3}+c^{3}+d^{3}\right)+ \\
+B\left(a^{2}+b^{2}+c^{2}+d^{2}\right)+C(a+b+c+d)+4 D=0 .
\end{gathered}
$$
Hence
$$
\begin{gathered}
a^{4}+b^{4}+c^{4}+d^{4}+4 D \\
=-A\left(a^{3}+b^{3}+c^{3}+d^{3}\right)-B\left(a^{2}+b^{2}+c^{2}+d^{2}\right)-C(a+b+c+d) .
\end{gathered}
$$
Using Vieta's formulas, we can see that $D=a b c d$ and $-A=a+b+c+d$. Therefore the right hand side of the equation above is divisible by $n$, and so is the left hand side.
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "BalticWay/segmented/en-bw16sol.jsonl",
"solution_match": "\nSolution 1",
"tier": "T3",
"year": "2016"
}
|
Let $n$ be a positive integer and let $a, b, c, d$ be integers such that $n \mid a+b+c+d$ and $n \mid a^{2}+b^{2}+c^{2}+d^{2}$. Show that
$$
n \mid a^{4}+b^{4}+c^{4}+d^{4}+4 a b c d .
$$
|
. Since the numbers $(a+b+c+d)\left(a^{3}+b^{3}+c^{3}+d^{3}\right),\left(a^{2}+b^{2}+c^{2}+d^{2}\right)(a b+$ $a c+a d+b c+b d+c d)$ and $(a+b+c+d)(a b c+a c d+a b d+b c d)$ are divisible by $n$, then so is the number
$$
\begin{gathered}
(a+b+c+d)\left(a^{3}+b^{3}+c^{3}+d^{3}\right)-\left(a^{2}+b^{2}+c^{2}+d^{2}\right)(a b+a c+a d+b c+b d+c d)+ \\
+(a+b+c+d)(a b c+a c d+a b d+b c d)=a^{4}+b^{4}+c^{4}+d^{4}+4 a b c d .
\end{gathered}
$$
(Heiki Niglas, Estonia)
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n$ be a positive integer and let $a, b, c, d$ be integers such that $n \mid a+b+c+d$ and $n \mid a^{2}+b^{2}+c^{2}+d^{2}$. Show that
$$
n \mid a^{4}+b^{4}+c^{4}+d^{4}+4 a b c d .
$$
|
. Since the numbers $(a+b+c+d)\left(a^{3}+b^{3}+c^{3}+d^{3}\right),\left(a^{2}+b^{2}+c^{2}+d^{2}\right)(a b+$ $a c+a d+b c+b d+c d)$ and $(a+b+c+d)(a b c+a c d+a b d+b c d)$ are divisible by $n$, then so is the number
$$
\begin{gathered}
(a+b+c+d)\left(a^{3}+b^{3}+c^{3}+d^{3}\right)-\left(a^{2}+b^{2}+c^{2}+d^{2}\right)(a b+a c+a d+b c+b d+c d)+ \\
+(a+b+c+d)(a b c+a c d+a b d+b c d)=a^{4}+b^{4}+c^{4}+d^{4}+4 a b c d .
\end{gathered}
$$
(Heiki Niglas, Estonia)
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "BalticWay/segmented/en-bw16sol.jsonl",
"solution_match": "\nSolution 2",
"tier": "T3",
"year": "2016"
}
|
Let $p>3$ be a prime such that $p \equiv 3(\bmod 4)$. Given a positive integer $a_{0}$, define the sequence $a_{0}, a_{1}, \ldots$ of integers by $a_{n}=a_{n-1}^{2^{n}}$ for all $n=1,2, \ldots$ Prove that it is possible to choose $a_{0}$ such that the subsequence $a_{N}, a_{N+1}, a_{N+2}, \ldots$ is not constant modulo $p$ for any positive integer $N$.
|
Let $p$ be a prime with residue 3 modulo 4 and $p>3$. Then $p-1=u \cdot 2$ where $u>1$ is odd. Choose $a_{0}=2$. The order of 2 modulo $p$ (that is, the smallest positive integer $t$ such that $\left.2^{t} \equiv 1 \bmod p\right)$ is a divisor of $\phi(p)=p-1=u \cdot 2$, but not a divisor of 2 since $1<2^{2}<p$. Hence the order of 2 modulo $p$ is not a power of 2 . By definition we see that $a_{n}=a_{0}^{2^{1+2+\cdots+n}}$. Since the order of $a_{0}=2$ modulo $p$ is not a power of 2 , we know that $a_{n} \not \equiv 1 \quad(\bmod p)$ for all $n=1,2,3, \ldots$ We proof the statement by contradiction. Assume there exists a positive integer $N$ such that $a_{n} \equiv a_{N}(\bmod p)$ for all $n \geq N$. Let $d>1$ be the order of $a_{N}$ modulo $p$. Then $a_{N} \equiv a_{n} \equiv a_{n+1}=a_{n}^{2^{n+1}} \equiv a_{N}^{2^{n+1}} \quad(\bmod p)$, and hence $a_{N}^{2^{n+1}-1} \equiv 1 \quad(\bmod p)$ for all $n \geq N$. Now $d$ divides $2^{n+1}-1$ for all $n \geq N$, but this is a contradiction since
$\operatorname{gcd}\left(2^{n+1}-1,2^{n+2}-1\right)=\operatorname{gcd}\left(2^{n+1}-1,2^{n+2}-1-2\left(2^{n+1}-1\right)\right)=\operatorname{gcd}\left(2^{n+1}-1,1\right)=1$.
Hence there does not exist such an $N$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $p>3$ be a prime such that $p \equiv 3(\bmod 4)$. Given a positive integer $a_{0}$, define the sequence $a_{0}, a_{1}, \ldots$ of integers by $a_{n}=a_{n-1}^{2^{n}}$ for all $n=1,2, \ldots$ Prove that it is possible to choose $a_{0}$ such that the subsequence $a_{N}, a_{N+1}, a_{N+2}, \ldots$ is not constant modulo $p$ for any positive integer $N$.
|
Let $p$ be a prime with residue 3 modulo 4 and $p>3$. Then $p-1=u \cdot 2$ where $u>1$ is odd. Choose $a_{0}=2$. The order of 2 modulo $p$ (that is, the smallest positive integer $t$ such that $\left.2^{t} \equiv 1 \bmod p\right)$ is a divisor of $\phi(p)=p-1=u \cdot 2$, but not a divisor of 2 since $1<2^{2}<p$. Hence the order of 2 modulo $p$ is not a power of 2 . By definition we see that $a_{n}=a_{0}^{2^{1+2+\cdots+n}}$. Since the order of $a_{0}=2$ modulo $p$ is not a power of 2 , we know that $a_{n} \not \equiv 1 \quad(\bmod p)$ for all $n=1,2,3, \ldots$ We proof the statement by contradiction. Assume there exists a positive integer $N$ such that $a_{n} \equiv a_{N}(\bmod p)$ for all $n \geq N$. Let $d>1$ be the order of $a_{N}$ modulo $p$. Then $a_{N} \equiv a_{n} \equiv a_{n+1}=a_{n}^{2^{n+1}} \equiv a_{N}^{2^{n+1}} \quad(\bmod p)$, and hence $a_{N}^{2^{n+1}-1} \equiv 1 \quad(\bmod p)$ for all $n \geq N$. Now $d$ divides $2^{n+1}-1$ for all $n \geq N$, but this is a contradiction since
$\operatorname{gcd}\left(2^{n+1}-1,2^{n+2}-1\right)=\operatorname{gcd}\left(2^{n+1}-1,2^{n+2}-1-2\left(2^{n+1}-1\right)\right)=\operatorname{gcd}\left(2^{n+1}-1,1\right)=1$.
Hence there does not exist such an $N$.
|
{
"exam": "BalticWay",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "BalticWay/segmented/en-bw16sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2016"
}
|
The set $\{1,2, \ldots, 10\}$ is partitioned into three subsets $A, B$ and $C$. For each subset the sum of its elements, the product of its elements and the sum of the digits of all its elements are calculated. Is it possible that $A$ alone has the largest sum of elements, $B$ alone has the largest product of elements, and $C$ alone has the largest sum of digits?
|
It is indeed possible. Choose $A=\{1,9,10\}, B=\{3,7,8\}, C=\{2,4,5,6\}$. Then the sum of elements in $A, B$ and $C$, respectively, is 20,18 and 17 , the sum of digits 11, 18 and 17, while the product of elements is 90,168 and 240.
|
not found
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
The set $\{1,2, \ldots, 10\}$ is partitioned into three subsets $A, B$ and $C$. For each subset the sum of its elements, the product of its elements and the sum of the digits of all its elements are calculated. Is it possible that $A$ alone has the largest sum of elements, $B$ alone has the largest product of elements, and $C$ alone has the largest sum of digits?
|
It is indeed possible. Choose $A=\{1,9,10\}, B=\{3,7,8\}, C=\{2,4,5,6\}$. Then the sum of elements in $A, B$ and $C$, respectively, is 20,18 and 17 , the sum of digits 11, 18 and 17, while the product of elements is 90,168 and 240.
|
{
"exam": "BalticWay",
"problem_label": "6",
"problem_match": "\n6.",
"resource_path": "BalticWay/segmented/en-bw16sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2016"
}
|
Find all positive integers $n$ for which
$$
3 x^{n}+n(x+2)-3 \geq n x^{2}
$$
holds for all real numbers $x$.
|
We show that the inequality holds for even $n$ and only for them.
If $n$ is odd, the for $x=-1$ the left hand side of the inequality equals $n-6$ while the right hand side is $n$. So the inequality is not true for $x=-1$ for any odd $n$. So now assume that $n$ is even. Since $|x| \geq x$, it is enough to prove $3 x^{n}+2 n-3 \geq n x^{2}+n|x|$ for all $x$ or equivalently that $3 x^{n}+(2 n-3) \geq n x^{2}+n x$ for $x \geq 0$. Now the AGM-inequality gives
$$
2 x^{n}+(n-2)=x^{n}+x^{n}+1+\cdots+1 \geq n\left(x^{n} \cdot x^{n} \cdot 1^{n-2}\right)^{\frac{1}{n}}=n x^{2} \text {, }
$$
and similarly
$$
x^{n}+(n-1) \geq n\left(x^{n} \cdot 1^{n-1}\right)^{\frac{1}{n}}=n x \text {. }
$$
Adding (1) and (2) yields the claim.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Find all positive integers $n$ for which
$$
3 x^{n}+n(x+2)-3 \geq n x^{2}
$$
holds for all real numbers $x$.
|
We show that the inequality holds for even $n$ and only for them.
If $n$ is odd, the for $x=-1$ the left hand side of the inequality equals $n-6$ while the right hand side is $n$. So the inequality is not true for $x=-1$ for any odd $n$. So now assume that $n$ is even. Since $|x| \geq x$, it is enough to prove $3 x^{n}+2 n-3 \geq n x^{2}+n|x|$ for all $x$ or equivalently that $3 x^{n}+(2 n-3) \geq n x^{2}+n x$ for $x \geq 0$. Now the AGM-inequality gives
$$
2 x^{n}+(n-2)=x^{n}+x^{n}+1+\cdots+1 \geq n\left(x^{n} \cdot x^{n} \cdot 1^{n-2}\right)^{\frac{1}{n}}=n x^{2} \text {, }
$$
and similarly
$$
x^{n}+(n-1) \geq n\left(x^{n} \cdot 1^{n-1}\right)^{\frac{1}{n}}=n x \text {. }
$$
Adding (1) and (2) yields the claim.
|
{
"exam": "BalticWay",
"problem_label": "7",
"problem_match": "\n7.",
"resource_path": "BalticWay/segmented/en-bw16sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2016"
}
|
Find all real numbers a for which there exists a non-constant function $f: \mathbb{R} \rightarrow \mathbb{R}$ satisfying the following two equations for all $x \in \mathbb{R}$ :
i) $\quad f(a x)=a^{2} f(x)$ and
ii) $f(f(x))=a f(x)$.
|
The conditions of the problem give two representations for $f(f(f(x)))$ :
$$
f(f(f(x)))=a f(f(x))=a^{2} f(x)
$$
and
$$
f(f(f(x)))=f(a f(x))=a^{2} f(f(x))=a^{3} f(x) .
$$
So $a^{2} f(x)=a^{3} f(x)$ for all $x$, and if there is an $x$ such that $f(x) \neq 0$, the $a=0$ or $a=1$. Otherwise $f$ is the constant function $f(x)=0$ for all $x$. If $a=1$, the function $f(x)=x$ satisfies the conditions. For $a=0$, one possible solution is the function $f$,
$$
f(x)=\left\{\begin{array}{ll}
1 & \text { for } x<0 \\
0 & \text { for } x \geq 0
\end{array} .\right.
$$
|
a=0 \text{ or } a=1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all real numbers a for which there exists a non-constant function $f: \mathbb{R} \rightarrow \mathbb{R}$ satisfying the following two equations for all $x \in \mathbb{R}$ :
i) $\quad f(a x)=a^{2} f(x)$ and
ii) $f(f(x))=a f(x)$.
|
The conditions of the problem give two representations for $f(f(f(x)))$ :
$$
f(f(f(x)))=a f(f(x))=a^{2} f(x)
$$
and
$$
f(f(f(x)))=f(a f(x))=a^{2} f(f(x))=a^{3} f(x) .
$$
So $a^{2} f(x)=a^{3} f(x)$ for all $x$, and if there is an $x$ such that $f(x) \neq 0$, the $a=0$ or $a=1$. Otherwise $f$ is the constant function $f(x)=0$ for all $x$. If $a=1$, the function $f(x)=x$ satisfies the conditions. For $a=0$, one possible solution is the function $f$,
$$
f(x)=\left\{\begin{array}{ll}
1 & \text { for } x<0 \\
0 & \text { for } x \geq 0
\end{array} .\right.
$$
|
{
"exam": "BalticWay",
"problem_label": "8",
"problem_match": "\n8.",
"resource_path": "BalticWay/segmented/en-bw16sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2016"
}
|
Find all quadruples $(a, b, c, d)$ of real numbers that simultaneously satisfy the following equations:
$$
\left\{\begin{aligned}
a^{3}+c^{3} & =2 \\
a^{2} b+c^{2} d & =0 \\
b^{3}+d^{3} & =1 \\
a b^{2}+c d^{2} & =-6
\end{aligned}\right.
$$
|
. Consider the polynomial $P(x)=(a x+b)^{3}+(c x+d)^{3}=\left(a^{3}+b^{3}\right) x^{3}+3\left(a^{2} b+\right.$ $\left.c^{2} d\right) x^{2}+3\left(a b^{2}+c d^{2}\right) x+b^{3}+d^{3}$. By the conditions of the problem, $P(x)=2 x^{3}-18 x+1$. Clearly $P(0)>0, P(1)<0$ and $P(3)>0$. Thus $P$ has three distinct zeroes. But $P(x)=0$ implies $a x+b=-(c x+d)$ or $(a+c) x+b+d=0$. This equation has only one solution, unless $a=-c$ and $b=-d$. But since the conditions of the problem do not allow this, we infer that the system of equations in the problem has no solution.
|
not found
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all quadruples $(a, b, c, d)$ of real numbers that simultaneously satisfy the following equations:
$$
\left\{\begin{aligned}
a^{3}+c^{3} & =2 \\
a^{2} b+c^{2} d & =0 \\
b^{3}+d^{3} & =1 \\
a b^{2}+c d^{2} & =-6
\end{aligned}\right.
$$
|
. Consider the polynomial $P(x)=(a x+b)^{3}+(c x+d)^{3}=\left(a^{3}+b^{3}\right) x^{3}+3\left(a^{2} b+\right.$ $\left.c^{2} d\right) x^{2}+3\left(a b^{2}+c d^{2}\right) x+b^{3}+d^{3}$. By the conditions of the problem, $P(x)=2 x^{3}-18 x+1$. Clearly $P(0)>0, P(1)<0$ and $P(3)>0$. Thus $P$ has three distinct zeroes. But $P(x)=0$ implies $a x+b=-(c x+d)$ or $(a+c) x+b+d=0$. This equation has only one solution, unless $a=-c$ and $b=-d$. But since the conditions of the problem do not allow this, we infer that the system of equations in the problem has no solution.
|
{
"exam": "BalticWay",
"problem_label": "9",
"problem_match": "\n9.",
"resource_path": "BalticWay/segmented/en-bw16sol.jsonl",
"solution_match": "\nSolution 1",
"tier": "T3",
"year": "2016"
}
|
Find all quadruples $(a, b, c, d)$ of real numbers that simultaneously satisfy the following equations:
$$
\left\{\begin{aligned}
a^{3}+c^{3} & =2 \\
a^{2} b+c^{2} d & =0 \\
b^{3}+d^{3} & =1 \\
a b^{2}+c d^{2} & =-6
\end{aligned}\right.
$$
|
. If $0 \in\{a, b\}$, then one easily gets that $0 \in\{c, d\}$, which contradicts the equation $a b^{2}+c d^{2}=-6$. Similarly, if $0 \in\{c, d\}$, then $0 \in\{a, b\}$ and this contradicts $a b^{2}+c d^{2}=-6$ again. Hence $a, b, c, d \neq 0$.
Let the four equations in the problem be (i), (ii), (iii) and (iv), respectively. Then $(i)+3(i i)+3(i i i)+(i v)$ will give
$$
(a+b)^{3}+(c+d)^{3}=-15 .
$$
According to the equation (ii), $b$ and $d$ have different sign, and similarly (iv) yields that $a$ and $c$ have different sign.
First, consider the case $a>0, b>0$. Then $c<0$ and $d<0$. By $(i)$, we have $a>-c$ (i.e. $|a|>|c|)$ and (iii) gives $b>-d$. Hence $a+b>-(c+d)$ and so $(a+b)^{3}>-(c+d)^{3}$, thus $(a+b)^{3}+(c+d)^{3}>0$ which contradicts (1).
Next, consider the case $a>0, b<0$. Then $c<0$ and $d>0$. By $(i)$, we have $a>-c$ and by (iii), $d>-b$ (i.e. $b>-d$ ). Thus $a+b>-(c+d)$ and hence $(a+b)^{3}+(c+d)^{3}>0$ which contradicts (1).
The case $a<0, b<0$ leads to $c>0, d>0$. By (i), we have $c>-a$ and by (iii) $d>-b$. So $c+d>-(a+b)$ and hence $(c+d)^{3}+(a+b)^{3}>0$ which contradicts (1) again.
Finally, consider the case $a<0, b>0$. Then $c>0$ and $d<0$. By (i), $c>-a$ and by (iii) $b>-d$ which gives $c+d>-(a+b)$ and hence $(c+d)^{3}+(a+b)^{3}>0$ contradicting (1).
Hence there is no real solution to this system of equations. (Heiki Niglas)
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all quadruples $(a, b, c, d)$ of real numbers that simultaneously satisfy the following equations:
$$
\left\{\begin{aligned}
a^{3}+c^{3} & =2 \\
a^{2} b+c^{2} d & =0 \\
b^{3}+d^{3} & =1 \\
a b^{2}+c d^{2} & =-6
\end{aligned}\right.
$$
|
. If $0 \in\{a, b\}$, then one easily gets that $0 \in\{c, d\}$, which contradicts the equation $a b^{2}+c d^{2}=-6$. Similarly, if $0 \in\{c, d\}$, then $0 \in\{a, b\}$ and this contradicts $a b^{2}+c d^{2}=-6$ again. Hence $a, b, c, d \neq 0$.
Let the four equations in the problem be (i), (ii), (iii) and (iv), respectively. Then $(i)+3(i i)+3(i i i)+(i v)$ will give
$$
(a+b)^{3}+(c+d)^{3}=-15 .
$$
According to the equation (ii), $b$ and $d$ have different sign, and similarly (iv) yields that $a$ and $c$ have different sign.
First, consider the case $a>0, b>0$. Then $c<0$ and $d<0$. By $(i)$, we have $a>-c$ (i.e. $|a|>|c|)$ and (iii) gives $b>-d$. Hence $a+b>-(c+d)$ and so $(a+b)^{3}>-(c+d)^{3}$, thus $(a+b)^{3}+(c+d)^{3}>0$ which contradicts (1).
Next, consider the case $a>0, b<0$. Then $c<0$ and $d>0$. By $(i)$, we have $a>-c$ and by (iii), $d>-b$ (i.e. $b>-d$ ). Thus $a+b>-(c+d)$ and hence $(a+b)^{3}+(c+d)^{3}>0$ which contradicts (1).
The case $a<0, b<0$ leads to $c>0, d>0$. By (i), we have $c>-a$ and by (iii) $d>-b$. So $c+d>-(a+b)$ and hence $(c+d)^{3}+(a+b)^{3}>0$ which contradicts (1) again.
Finally, consider the case $a<0, b>0$. Then $c>0$ and $d<0$. By (i), $c>-a$ and by (iii) $b>-d$ which gives $c+d>-(a+b)$ and hence $(c+d)^{3}+(a+b)^{3}>0$ contradicting (1).
Hence there is no real solution to this system of equations. (Heiki Niglas)
|
{
"exam": "BalticWay",
"problem_label": "9",
"problem_match": "\n9.",
"resource_path": "BalticWay/segmented/en-bw16sol.jsonl",
"solution_match": "\nSolution 2",
"tier": "T3",
"year": "2016"
}
|
Find all quadruples $(a, b, c, d)$ of real numbers that simultaneously satisfy the following equations:
$$
\left\{\begin{aligned}
a^{3}+c^{3} & =2 \\
a^{2} b+c^{2} d & =0 \\
b^{3}+d^{3} & =1 \\
a b^{2}+c d^{2} & =-6
\end{aligned}\right.
$$
|
. As in Solution 2, we conclude that $a, b, c, d \neq 0$. The equation $a^{2} b+c^{2} d=0$ yields $a= \pm \sqrt{\frac{-d}{b}} c$. On the other hand, we have $a^{3}+c^{3}=2$ and $a b^{2}+c d^{2}=-6<0$ which implies that $\min \{a, c\}<0<\max \{a, c\}$ and thus $a=-\sqrt{\frac{-d}{b}} c$.
Let $x=-\sqrt{\frac{-d}{b}}$. Then $a=x c$ and so
$$
2=a^{3}+c^{3}=c^{3}\left(1+x^{3}\right) .
$$
Also $-6=a b^{2}+c d^{2}=c x b^{2}+c d^{2}$, which, using (2), gives
$$
\left(x b^{2}+d^{2}\right)^{3}=\frac{-6^{3}}{c^{3}}=-108\left(x^{3}+1\right) \text {. }
$$
Thus
$$
-108\left(1+x^{3}\right)=\left(d^{2}\left(x \frac{b^{2}}{d^{2}}+1\right)\right)^{3}=d^{6}\left(\frac{1}{x^{3}}+1\right)^{3}=d^{6}\left(\frac{1+x^{3}}{x^{3}}\right)^{3} .
$$
If $x^{3}+1=0$, then $x=-1$ and hence $a=-c$, which contradicts $a^{3}+c^{3}=2$. So $x^{3}+1 \neq 0$ and (3) gives
$$
d^{6}\left(1+x^{3}\right)^{2}=-108 x^{9} .
$$
Now note that
$$
x^{3}=\left(-\sqrt{\frac{-d}{b}}\right)^{3}=-\sqrt{\frac{-d^{3}}{b^{3}}}=-\sqrt{\frac{b^{3}-1}{b^{3}}}
$$
and hence (4) yields that
$$
\left(b^{3}-1\right)^{2}\left(1-\sqrt{\frac{b^{3}-1}{b^{3}}}\right)^{2}=108\left(\sqrt{\frac{b^{3}-1}{b^{3}}}\right)^{3} .
$$
Let $y=\sqrt{\frac{b^{3}-1}{b^{3}}}$. Then $b^{3}=\frac{1}{1-y^{2}}$ and so (5) implies
$$
\left(\frac{1}{1-y^{2}}-1\right)^{2}\left(1-y^{2}\right)^{2}=108 y^{3}
$$
i.e.
$$
\frac{y^{4}}{\left(1-y^{2}\right)^{2}}(1-y)^{2}=108 y^{3}
$$
If $y=0$, then $b=1$ and so $d=0$, a contradiction. So
$$
y(1-y)^{2}=108(1-y)^{2}(1+y)^{2}
$$
Clearly $y \neq 1$ and hence $y=108+108 y^{2}+216 y$, or $108 y^{2}+215 y+108=0$. The last equation has no real solutions and thus the initial system of equations has no real solutions.
Remark 1. Note that this solution worked because RHS of $a^{2} b+c^{2} d=0$ is zero. If instead it was, e.g., $a^{2} b+c^{2} d=0.1$ then this solution would not work out, but the first solution still would.
Remark 2. The advantage of this solution is that solving the last equation $108 y^{2}+$ $215 y+108=0$ one can find complex solutions of this system of equations. (Heiki Niglas)
|
not found
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all quadruples $(a, b, c, d)$ of real numbers that simultaneously satisfy the following equations:
$$
\left\{\begin{aligned}
a^{3}+c^{3} & =2 \\
a^{2} b+c^{2} d & =0 \\
b^{3}+d^{3} & =1 \\
a b^{2}+c d^{2} & =-6
\end{aligned}\right.
$$
|
. As in Solution 2, we conclude that $a, b, c, d \neq 0$. The equation $a^{2} b+c^{2} d=0$ yields $a= \pm \sqrt{\frac{-d}{b}} c$. On the other hand, we have $a^{3}+c^{3}=2$ and $a b^{2}+c d^{2}=-6<0$ which implies that $\min \{a, c\}<0<\max \{a, c\}$ and thus $a=-\sqrt{\frac{-d}{b}} c$.
Let $x=-\sqrt{\frac{-d}{b}}$. Then $a=x c$ and so
$$
2=a^{3}+c^{3}=c^{3}\left(1+x^{3}\right) .
$$
Also $-6=a b^{2}+c d^{2}=c x b^{2}+c d^{2}$, which, using (2), gives
$$
\left(x b^{2}+d^{2}\right)^{3}=\frac{-6^{3}}{c^{3}}=-108\left(x^{3}+1\right) \text {. }
$$
Thus
$$
-108\left(1+x^{3}\right)=\left(d^{2}\left(x \frac{b^{2}}{d^{2}}+1\right)\right)^{3}=d^{6}\left(\frac{1}{x^{3}}+1\right)^{3}=d^{6}\left(\frac{1+x^{3}}{x^{3}}\right)^{3} .
$$
If $x^{3}+1=0$, then $x=-1$ and hence $a=-c$, which contradicts $a^{3}+c^{3}=2$. So $x^{3}+1 \neq 0$ and (3) gives
$$
d^{6}\left(1+x^{3}\right)^{2}=-108 x^{9} .
$$
Now note that
$$
x^{3}=\left(-\sqrt{\frac{-d}{b}}\right)^{3}=-\sqrt{\frac{-d^{3}}{b^{3}}}=-\sqrt{\frac{b^{3}-1}{b^{3}}}
$$
and hence (4) yields that
$$
\left(b^{3}-1\right)^{2}\left(1-\sqrt{\frac{b^{3}-1}{b^{3}}}\right)^{2}=108\left(\sqrt{\frac{b^{3}-1}{b^{3}}}\right)^{3} .
$$
Let $y=\sqrt{\frac{b^{3}-1}{b^{3}}}$. Then $b^{3}=\frac{1}{1-y^{2}}$ and so (5) implies
$$
\left(\frac{1}{1-y^{2}}-1\right)^{2}\left(1-y^{2}\right)^{2}=108 y^{3}
$$
i.e.
$$
\frac{y^{4}}{\left(1-y^{2}\right)^{2}}(1-y)^{2}=108 y^{3}
$$
If $y=0$, then $b=1$ and so $d=0$, a contradiction. So
$$
y(1-y)^{2}=108(1-y)^{2}(1+y)^{2}
$$
Clearly $y \neq 1$ and hence $y=108+108 y^{2}+216 y$, or $108 y^{2}+215 y+108=0$. The last equation has no real solutions and thus the initial system of equations has no real solutions.
Remark 1. Note that this solution worked because RHS of $a^{2} b+c^{2} d=0$ is zero. If instead it was, e.g., $a^{2} b+c^{2} d=0.1$ then this solution would not work out, but the first solution still would.
Remark 2. The advantage of this solution is that solving the last equation $108 y^{2}+$ $215 y+108=0$ one can find complex solutions of this system of equations. (Heiki Niglas)
|
{
"exam": "BalticWay",
"problem_label": "9",
"problem_match": "\n9.",
"resource_path": "BalticWay/segmented/en-bw16sol.jsonl",
"solution_match": "\nSolution 3",
"tier": "T3",
"year": "2016"
}
|
Let $a_{0,1}, a_{0,2}, \ldots, a_{0,2016}$ be positive real numbers. For $n \geq 0$ and $1 \leq k<2016$ set
$$
a_{n+1, k}=a_{n, k}+\frac{1}{2 a_{n, k+1}} \quad \text { and } \quad a_{n+1,2016}=a_{n, 2016}+\frac{1}{2 a_{n, 1}} .
$$
Show that $\max _{1 \leq k \leq 2016} a_{2016, k}>44$.
|
We prove
$$
m_{n}^{2} \geq n
$$
for all $n$. The claim then follows from $44^{2}=1936<2016$. To prove (1), first notice that the inequality certainly holds for $n=0$. Assume (1) is true for $n$. There is a $k$ such that $a_{n, k}=m_{n}$. Also $a_{n, k+1} \leq m_{n}$ (or if $k=2016, a_{n, 1} \leq m_{n}$ ). Now (assuming $k<2016$ )
$$
a_{n+1, k}^{2}=\left(m_{n}+\frac{1}{2 a_{n, k+1}}\right)^{2}=m_{n}^{2}+\frac{m_{n}}{a_{n, k+1}}+\frac{1}{4 a_{n, k+1}^{2}}>n+1 .
$$
Since $m_{n+1}^{2} \geq a_{n+1, k}^{2}$, we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $a_{0,1}, a_{0,2}, \ldots, a_{0,2016}$ be positive real numbers. For $n \geq 0$ and $1 \leq k<2016$ set
$$
a_{n+1, k}=a_{n, k}+\frac{1}{2 a_{n, k+1}} \quad \text { and } \quad a_{n+1,2016}=a_{n, 2016}+\frac{1}{2 a_{n, 1}} .
$$
Show that $\max _{1 \leq k \leq 2016} a_{2016, k}>44$.
|
We prove
$$
m_{n}^{2} \geq n
$$
for all $n$. The claim then follows from $44^{2}=1936<2016$. To prove (1), first notice that the inequality certainly holds for $n=0$. Assume (1) is true for $n$. There is a $k$ such that $a_{n, k}=m_{n}$. Also $a_{n, k+1} \leq m_{n}$ (or if $k=2016, a_{n, 1} \leq m_{n}$ ). Now (assuming $k<2016$ )
$$
a_{n+1, k}^{2}=\left(m_{n}+\frac{1}{2 a_{n, k+1}}\right)^{2}=m_{n}^{2}+\frac{m_{n}}{a_{n, k+1}}+\frac{1}{4 a_{n, k+1}^{2}}>n+1 .
$$
Since $m_{n+1}^{2} \geq a_{n+1, k}^{2}$, we are done.
|
{
"exam": "BalticWay",
"problem_label": "10",
"problem_match": "\n10.",
"resource_path": "BalticWay/segmented/en-bw16sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2016"
}
|
The set $A$ consists of 2016 positive integers. All prime divisors of these numbers are smaller than 30. Prove that there are four distinct numbers $a, b, c$ and $d$ in $A$ such that abcd is a perfect square.
|
There are ten prime numbers $\leq 29$. Let us denote them as $p_{1}, p_{2}, \ldots, p_{10}$. To each number $n$ in $A$ we can assign a 10 -element sequence $\left(n_{1}, n_{2}, \ldots, n_{10}\right)$ such that $n_{i}=1$ $p_{i}$ has an odd exponent in the prime factorization of $n$, and $n_{i}=0$ otherwise. Two numbers to which identical sequences are assigned, multiply to a perfect square. There are only 1024 different 10-element $\{0,1\}$-sequences so there exist some two numbers $a$ and $b$ with identical sequencies, and after removing these from $A$ certainly two other numbers $c$ and $d$ with identical sequencies remain. These $a, b, c$ and $d$ satisfy the condition of the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
The set $A$ consists of 2016 positive integers. All prime divisors of these numbers are smaller than 30. Prove that there are four distinct numbers $a, b, c$ and $d$ in $A$ such that abcd is a perfect square.
|
There are ten prime numbers $\leq 29$. Let us denote them as $p_{1}, p_{2}, \ldots, p_{10}$. To each number $n$ in $A$ we can assign a 10 -element sequence $\left(n_{1}, n_{2}, \ldots, n_{10}\right)$ such that $n_{i}=1$ $p_{i}$ has an odd exponent in the prime factorization of $n$, and $n_{i}=0$ otherwise. Two numbers to which identical sequences are assigned, multiply to a perfect square. There are only 1024 different 10-element $\{0,1\}$-sequences so there exist some two numbers $a$ and $b$ with identical sequencies, and after removing these from $A$ certainly two other numbers $c$ and $d$ with identical sequencies remain. These $a, b, c$ and $d$ satisfy the condition of the problem.
|
{
"exam": "BalticWay",
"problem_label": "11",
"problem_match": "\n11.",
"resource_path": "BalticWay/segmented/en-bw16sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2016"
}
|
Does there exist a hexagon (not necessarily convex) with side lengths 1, 2, 3, 4, 5, 6 (not necessarily in this order) that can be tiled with a) 31 b) 32 equilateral triangles with side length 1 ?
|
The adjoining figure shows that question a) can be answered positively.
For a negative answer to b), we show that the number of triangles has to be odd. Assume there are $x$ triangles in the triangulation. They hav altogether $3 x$ sides. Of these, $1+2+3+4+6=21$ are on the perimeter of the hexagon. The remaining $3 x-21$ sides are in the interior, and they touch each other pairwise. So $3 x-21$ has to be even, which is only possible, if $x$ is odd.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Does there exist a hexagon (not necessarily convex) with side lengths 1, 2, 3, 4, 5, 6 (not necessarily in this order) that can be tiled with a) 31 b) 32 equilateral triangles with side length 1 ?
|
The adjoining figure shows that question a) can be answered positively.
For a negative answer to b), we show that the number of triangles has to be odd. Assume there are $x$ triangles in the triangulation. They hav altogether $3 x$ sides. Of these, $1+2+3+4+6=21$ are on the perimeter of the hexagon. The remaining $3 x-21$ sides are in the interior, and they touch each other pairwise. So $3 x-21$ has to be even, which is only possible, if $x$ is odd.
|
{
"exam": "BalticWay",
"problem_label": "12",
"problem_match": "\n12.",
"resource_path": "BalticWay/segmented/en-bw16sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2016"
}
|
Let $n$ numbers all equal to 1 be written on a blackboard. A move consists of replacing two numbers on
the board with two copies of their sum. It happens that after $h$ moves all $n$ numbers on the blackboard are equal to $m$. Prove that $h \leq \frac{1}{2} n \log _{2} m$.
|
Let the product of the numbers after the $k$-th move be $a_{k}$. Suppose the numbers involved in a move were $a$ and $b$. By the arithmetic-geometric mean inequality, $(a+b)(a+b) \geq 4 a b$. Therefore, regardless of the choice of the numbers in the move, $a_{k} \geq 4 a_{k-1}$, and since $a_{0}=1, a_{h}=m^{n}$, we have $m^{n} \geq 4^{h}=2^{2 h}$ and $h \leq \frac{1}{2} n \log _{2} m$.
|
h \leq \frac{1}{2} n \log _{2} m
|
Incomplete
|
Yes
|
proof
|
Number Theory
|
Let $n$ numbers all equal to 1 be written on a blackboard. A move consists of replacing two numbers on

the board with two copies of their sum. It happens that after $h$ moves all $n$ numbers on the blackboard are equal to $m$. Prove that $h \leq \frac{1}{2} n \log _{2} m$.
|
Let the product of the numbers after the $k$-th move be $a_{k}$. Suppose the numbers involved in a move were $a$ and $b$. By the arithmetic-geometric mean inequality, $(a+b)(a+b) \geq 4 a b$. Therefore, regardless of the choice of the numbers in the move, $a_{k} \geq 4 a_{k-1}$, and since $a_{0}=1, a_{h}=m^{n}$, we have $m^{n} \geq 4^{h}=2^{2 h}$ and $h \leq \frac{1}{2} n \log _{2} m$.
|
{
"exam": "BalticWay",
"problem_label": "13",
"problem_match": "\n13.",
"resource_path": "BalticWay/segmented/en-bw16sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2016"
}
|
A cube consists of $4^{3}$ unit cubes each containing an integer. At each move, you choose a unit cube and increase by 1 all the integers in the neighbouring cubes having a face in common with the chosen cube. Is it possible to reach a position where all the $4^{3}$ integers are divisible by 3 , no matter what the starting position is?
|
Two unit cubes with a common face are called neighbours. Colour the cubes either black or white in such a way that two neighbours always have different colours. Notice that the integers in the white cubes only change when a black cube is chosen. Now recolour the white cubes that have exactly 4 neighbours and make them green. If we look at a random black cube it has either 0,3 or 6 white neighbours. Hence if we look at the sum of the integers in the white cubes, it changes by 0,3 or 6 in each turn. From this it follows that if this sum is not divisible by 3 at the beginning, it will never be, and none of the integers in the white cubes is divisible by 3 at any state.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A cube consists of $4^{3}$ unit cubes each containing an integer. At each move, you choose a unit cube and increase by 1 all the integers in the neighbouring cubes having a face in common with the chosen cube. Is it possible to reach a position where all the $4^{3}$ integers are divisible by 3 , no matter what the starting position is?
|
Two unit cubes with a common face are called neighbours. Colour the cubes either black or white in such a way that two neighbours always have different colours. Notice that the integers in the white cubes only change when a black cube is chosen. Now recolour the white cubes that have exactly 4 neighbours and make them green. If we look at a random black cube it has either 0,3 or 6 white neighbours. Hence if we look at the sum of the integers in the white cubes, it changes by 0,3 or 6 in each turn. From this it follows that if this sum is not divisible by 3 at the beginning, it will never be, and none of the integers in the white cubes is divisible by 3 at any state.
|
{
"exam": "BalticWay",
"problem_label": "14",
"problem_match": "\n14.",
"resource_path": "BalticWay/segmented/en-bw16sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2016"
}
|
The Baltic Sea has 2016 harbours. There are two-way ferry connections between some of them. It is impossible to make a sequence of direct voyages $C_{1}-C_{2}-\cdots-C_{1062}$ where all the harbours $C_{1}, \ldots, C_{1062}$ are distinct. Prove that there exist two disjoint sets $A$ and $B$ of 477 harbours each, such that there is no harbour in $A$ with a direct ferry connection to a harbour in $B$.
|
Let $V$ be the set of all harbours. Take any harbour $C_{1}$ and set $U=V \backslash\left\{C_{1}\right\}$, $W=\emptyset$. If there is a ferry connection from $C$ to another harbour, say $C_{2}$ in $V$, consider the route $C_{1} C_{2}$ and remove $C_{2}$ from $U$. Extend it as long as possible. Since there is no route of length 1061, So we have a route from $C_{1}$ to some $C_{k}, k \leq 1061$, and no connection from $C_{k}$ to a harbor not already included in the route exists. There are at least $2016-1062$ harbours in $U$. Now we move $C_{k}$ from $U$ to $W$ and try to extend the route from $C_{k-1}$ onwards. The extension again terminates at some harbor, which we then move from $U$ to $W$. If no connection from $C_{1}$ to any harbour exists, we move $C_{1}$ to $W$ and start the process again from some other harbour. This algorithm produces two sets of harbours, $W$ and $U$, between which there are no direct connections. During the process, the number of harbours in $U$ always decreases by 1 and the number of harbours in $W$ increases by 1 . So at some point the number of harbours is the same, and it then is at least $\frac{1}{2}(2016-1062)=477$. By removing, if necessary, some harbours fron $U$ and $W$ we get sets of exactly 477 harbours.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
The Baltic Sea has 2016 harbours. There are two-way ferry connections between some of them. It is impossible to make a sequence of direct voyages $C_{1}-C_{2}-\cdots-C_{1062}$ where all the harbours $C_{1}, \ldots, C_{1062}$ are distinct. Prove that there exist two disjoint sets $A$ and $B$ of 477 harbours each, such that there is no harbour in $A$ with a direct ferry connection to a harbour in $B$.
|
Let $V$ be the set of all harbours. Take any harbour $C_{1}$ and set $U=V \backslash\left\{C_{1}\right\}$, $W=\emptyset$. If there is a ferry connection from $C$ to another harbour, say $C_{2}$ in $V$, consider the route $C_{1} C_{2}$ and remove $C_{2}$ from $U$. Extend it as long as possible. Since there is no route of length 1061, So we have a route from $C_{1}$ to some $C_{k}, k \leq 1061$, and no connection from $C_{k}$ to a harbor not already included in the route exists. There are at least $2016-1062$ harbours in $U$. Now we move $C_{k}$ from $U$ to $W$ and try to extend the route from $C_{k-1}$ onwards. The extension again terminates at some harbor, which we then move from $U$ to $W$. If no connection from $C_{1}$ to any harbour exists, we move $C_{1}$ to $W$ and start the process again from some other harbour. This algorithm produces two sets of harbours, $W$ and $U$, between which there are no direct connections. During the process, the number of harbours in $U$ always decreases by 1 and the number of harbours in $W$ increases by 1 . So at some point the number of harbours is the same, and it then is at least $\frac{1}{2}(2016-1062)=477$. By removing, if necessary, some harbours fron $U$ and $W$ we get sets of exactly 477 harbours.
|
{
"exam": "BalticWay",
"problem_label": "15",
"problem_match": "\n15.",
"resource_path": "BalticWay/segmented/en-bw16sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2016"
}
|
In triangle $A B C$, the points $D$ and $E$ are the intersections of the angular bisectors from $C$ and $B$ with the sides $A B$ and $A C$, respectively. Points $F$ and $G$ on the extensions of $A B$ and $A C$ beyond $B$ and $C$, respectively, satisfy $B F=C G=B C$. Prove that $F G \| D E$.
|
Since $B E$ and $C D$ are angle bisectors,
$$
\frac{A D}{A B}=\frac{A C}{A C+B C}, \quad \frac{A E}{A C}=\frac{A B}{A B+B C} .
$$
So
$$
\frac{A D}{A F}=\frac{A D}{A B} \cdot \frac{A B}{A F}=\frac{A C \cdot A B}{(A C+B C)(A B+B C)}
$$
and
$$
\frac{A E}{A G}=\frac{A E}{A C} \cdot \frac{A C}{A G}=\frac{A B \cdot A C}{(A B+A C)(A C+B C)}
$$
Since $\frac{A D}{A F}=\frac{A E}{A G}, D E$ and $F G$ are parallel.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In triangle $A B C$, the points $D$ and $E$ are the intersections of the angular bisectors from $C$ and $B$ with the sides $A B$ and $A C$, respectively. Points $F$ and $G$ on the extensions of $A B$ and $A C$ beyond $B$ and $C$, respectively, satisfy $B F=C G=B C$. Prove that $F G \| D E$.
|
Since $B E$ and $C D$ are angle bisectors,
$$
\frac{A D}{A B}=\frac{A C}{A C+B C}, \quad \frac{A E}{A C}=\frac{A B}{A B+B C} .
$$
So

$$
\frac{A D}{A F}=\frac{A D}{A B} \cdot \frac{A B}{A F}=\frac{A C \cdot A B}{(A C+B C)(A B+B C)}
$$
and
$$
\frac{A E}{A G}=\frac{A E}{A C} \cdot \frac{A C}{A G}=\frac{A B \cdot A C}{(A B+A C)(A C+B C)}
$$
Since $\frac{A D}{A F}=\frac{A E}{A G}, D E$ and $F G$ are parallel.
|
{
"exam": "BalticWay",
"problem_label": "16",
"problem_match": "\n16.",
"resource_path": "BalticWay/segmented/en-bw16sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2016"
}
|
Let $A B C D$ be a convex quadrilateral with $A B=A D$. Let $T$ be a point on the diagonal $A C$ such that $\angle A B T+\angle A D T=\angle B C D$. Prove that $A T+A C \geq A B+A D$.
|
On the segment $A C$, consider the unique point $T^{\prime}$ such that $A T^{\prime} \cdot A C=A B^{2}$. The triangles $A B C$ and $A T^{\prime} B$ are similar: they have the angle at $A$ common, and $A T^{\prime}: A B=A B: A C$. So $\angle A B T^{\prime}=\angle A C B$. Analogously, $\angle A D T^{\prime}=\angle A C D$. So $\angle A B T^{\prime}+\angle A D T^{\prime}=\angle B C D$. But $A B T^{\prime}+A D T^{\prime}$ increases strictly monotonously, as $T^{\prime}$ moves from $A$ towards $C$ on $A C$. The assumption on $T$ implies that $T^{\prime}=T$. So, by the arithmetic-geometric mean inequality,
$$
A B+A D=2 A B=2 \sqrt{A T \cdot A C} \leq A T+A C .
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral with $A B=A D$. Let $T$ be a point on the diagonal $A C$ such that $\angle A B T+\angle A D T=\angle B C D$. Prove that $A T+A C \geq A B+A D$.
|
On the segment $A C$, consider the unique point $T^{\prime}$ such that $A T^{\prime} \cdot A C=A B^{2}$. The triangles $A B C$ and $A T^{\prime} B$ are similar: they have the angle at $A$ common, and $A T^{\prime}: A B=A B: A C$. So $\angle A B T^{\prime}=\angle A C B$. Analogously, $\angle A D T^{\prime}=\angle A C D$. So $\angle A B T^{\prime}+\angle A D T^{\prime}=\angle B C D$. But $A B T^{\prime}+A D T^{\prime}$ increases strictly monotonously, as $T^{\prime}$ moves from $A$ towards $C$ on $A C$. The assumption on $T$ implies that $T^{\prime}=T$. So, by the arithmetic-geometric mean inequality,

$$
A B+A D=2 A B=2 \sqrt{A T \cdot A C} \leq A T+A C .
$$
|
{
"exam": "BalticWay",
"problem_label": "17",
"problem_match": "\n17.",
"resource_path": "BalticWay/segmented/en-bw16sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2016"
}
|
Let $A B C D$ be a parallelogram such that $\angle B A D=60^{\circ}$. Let $K$ and $L$ be the midpoints of $B C$ and $C D$, respectively. Assuming that $A B K L$ is a cyclic quadrilateral, find $\angle A B D$.
|
Let $\angle B A L=\alpha$. Since $A B K L$ is cyclic, $\angle K K C=\alpha$. Because $L K \| D B$ and $A B \| D C$, we further have $\angle D B C=\alpha$ and $\angle A D B=\alpha$. Let $B D$ and $A L$ intersect at $P$. The triangles $A B P$ and $D B A$ have two equal angles, and hence $A B P \sim D B A$. So
$$
\frac{A B}{D B}=\frac{B P}{A B}
$$
The triangles $A B P$ and $L D P$ are clearly similar with similarity ratio $2: 1$. Hence $B P=$ $\frac{2}{3} D B$. Inserting this into (1) we get
$$
A B=\sqrt{\frac{2}{3}} \cdot D B
$$
The sine theorem applied to $A B D$ (recall that $\angle D A B=60^{\circ}$ ) immediately gives
$$
\sin \alpha=\frac{A B}{B D} \sin 60^{\circ}=\sqrt{\frac{2}{3}} \cdot \frac{\sqrt{3}}{2}=\frac{\sqrt{2}}{2}=\sin 45^{\circ} .
$$
So $\angle A B D=180^{\circ}-60^{\circ}-45^{\circ}=75^{\circ}$.
|
75^{\circ}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C D$ be a parallelogram such that $\angle B A D=60^{\circ}$. Let $K$ and $L$ be the midpoints of $B C$ and $C D$, respectively. Assuming that $A B K L$ is a cyclic quadrilateral, find $\angle A B D$.
|
Let $\angle B A L=\alpha$. Since $A B K L$ is cyclic, $\angle K K C=\alpha$. Because $L K \| D B$ and $A B \| D C$, we further have $\angle D B C=\alpha$ and $\angle A D B=\alpha$. Let $B D$ and $A L$ intersect at $P$. The triangles $A B P$ and $D B A$ have two equal angles, and hence $A B P \sim D B A$. So
$$
\frac{A B}{D B}=\frac{B P}{A B}
$$

The triangles $A B P$ and $L D P$ are clearly similar with similarity ratio $2: 1$. Hence $B P=$ $\frac{2}{3} D B$. Inserting this into (1) we get
$$
A B=\sqrt{\frac{2}{3}} \cdot D B
$$
The sine theorem applied to $A B D$ (recall that $\angle D A B=60^{\circ}$ ) immediately gives
$$
\sin \alpha=\frac{A B}{B D} \sin 60^{\circ}=\sqrt{\frac{2}{3}} \cdot \frac{\sqrt{3}}{2}=\frac{\sqrt{2}}{2}=\sin 45^{\circ} .
$$
So $\angle A B D=180^{\circ}-60^{\circ}-45^{\circ}=75^{\circ}$.
|
{
"exam": "BalticWay",
"problem_label": "18",
"problem_match": "\n18.",
"resource_path": "BalticWay/segmented/en-bw16sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2016"
}
|
Consider triangles in the plane where each vertex has integer coordinates. Such a triangle can be legally transformed by moving one vertex parallel to the opposite side to a different point with integer coordinates. Show that if two triangles have the same area, then there exists a series of legal transformations that transforms one to the other.
|
We will first show that any such triangle can be transformed to a special triangle whose vertices are at $(0,0),(0,1)$ and $(n, 0)$. Since every transformation preserves the triangle's area, triangles with the same area will have the same value for $n$.
Define th $y$-span of a triangle to be the difference between the largest and the smallest $y$ coordinate of its vertices. First we show that a triangle with a $y$-span greater than one can be transformed to a triangle with a strictly lower $y$-span.
Assume $A$ has the highest and $C$ the lowest $y$ coordinate of $A B C$. Shifting $C$ to $C^{\prime}$ by the vector $\overrightarrow{B A}$ results in the new triangle $A B C^{\prime}$ where $C^{\prime}$ has larger $y$ coordinate than $C$ baut lower than $A$, and $C^{\prime}$ has integer coordinates. If $A C$ is parallel to the $x$-axis, a horizontal shift of $B$ can be made to transform $A B C$ into $A B^{\prime} C$ where $B^{\prime} C$ is vertical, and then $A$ can be vertically shifted so that the $y$ coordinate of $A$ is between those of $B^{\prime}$ and $C$. Then the $y$-span of $A B^{\prime} C$ can be reduced in the manner described above. Continuing the process, one necessarily arrives at a triangle with $y$-span equal to 1 . Such a triangle then necessarily has one side, say $A C$, horizontal. A legal horizontal move can take $B$ to the a position $B^{\prime}$ where $A B^{\prime}$ is horizontal and $C$ has the highest $x$-coordinate. If $B^{\prime}$ is above $A C$, perform a vertical and a horizontal legal move to take $B^{\prime}$ to the origin; the result is a special triangle. If $B^{\prime}$ is below $A C$, legal transformation again can bring $B^{\prime}$ to the origin, and a final horizontal transformation of one vertex produces the desired special triangle.
The inverse of a legal transformation is again a legal transformation. Hence any two triangles having vertices with integer coordinates and same area can be legally transformed into each other via a special triangle.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Consider triangles in the plane where each vertex has integer coordinates. Such a triangle can be legally transformed by moving one vertex parallel to the opposite side to a different point with integer coordinates. Show that if two triangles have the same area, then there exists a series of legal transformations that transforms one to the other.
|
We will first show that any such triangle can be transformed to a special triangle whose vertices are at $(0,0),(0,1)$ and $(n, 0)$. Since every transformation preserves the triangle's area, triangles with the same area will have the same value for $n$.
Define th $y$-span of a triangle to be the difference between the largest and the smallest $y$ coordinate of its vertices. First we show that a triangle with a $y$-span greater than one can be transformed to a triangle with a strictly lower $y$-span.
Assume $A$ has the highest and $C$ the lowest $y$ coordinate of $A B C$. Shifting $C$ to $C^{\prime}$ by the vector $\overrightarrow{B A}$ results in the new triangle $A B C^{\prime}$ where $C^{\prime}$ has larger $y$ coordinate than $C$ baut lower than $A$, and $C^{\prime}$ has integer coordinates. If $A C$ is parallel to the $x$-axis, a horizontal shift of $B$ can be made to transform $A B C$ into $A B^{\prime} C$ where $B^{\prime} C$ is vertical, and then $A$ can be vertically shifted so that the $y$ coordinate of $A$ is between those of $B^{\prime}$ and $C$. Then the $y$-span of $A B^{\prime} C$ can be reduced in the manner described above. Continuing the process, one necessarily arrives at a triangle with $y$-span equal to 1 . Such a triangle then necessarily has one side, say $A C$, horizontal. A legal horizontal move can take $B$ to the a position $B^{\prime}$ where $A B^{\prime}$ is horizontal and $C$ has the highest $x$-coordinate. If $B^{\prime}$ is above $A C$, perform a vertical and a horizontal legal move to take $B^{\prime}$ to the origin; the result is a special triangle. If $B^{\prime}$ is below $A C$, legal transformation again can bring $B^{\prime}$ to the origin, and a final horizontal transformation of one vertex produces the desired special triangle.
The inverse of a legal transformation is again a legal transformation. Hence any two triangles having vertices with integer coordinates and same area can be legally transformed into each other via a special triangle.
|
{
"exam": "BalticWay",
"problem_label": "19",
"problem_match": "\n19.",
"resource_path": "BalticWay/segmented/en-bw16sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2016"
}
|
Let $A B C D$ be a cyclic quadrilateral with $A B$ and $C D$ not parallel. Let $M$ be the midpoint of $C D$. Let $P$ be a point inside $A B C D$ such that $P A=P B=C M$. Prove that $A B, C D$ and the perpendicular bisector of $M P$ are concurrent.
|
Let $\omega$ be the circumcircle of $A B C D$. Let $A B$ and $C D$ intersect at $X$. Let $\omega_{1}$ and $\omega_{2}$ be the circles with centers $P$ and $M$ and with equal radius $P B=M C=r$. The power of $X$ with respect to $\omega$ and $\omega_{1}$ equals $X A \cdot X B$ and with respect to $\omega$ and $\omega_{2} X D \cdot X C$. The latter power also equals $(X M+$ $r)(X M-r)=X M^{2}-r^{2}$. Analogously, the first power is $X P^{2}-r^{2}$. But since $X A \cdot X B=X D \cdot X C$, we must have $X M^{2}=X P^{2}$ or $X M=X P . X$ indeed is on the perpendicular bisector of $P M$, and we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral with $A B$ and $C D$ not parallel. Let $M$ be the midpoint of $C D$. Let $P$ be a point inside $A B C D$ such that $P A=P B=C M$. Prove that $A B, C D$ and the perpendicular bisector of $M P$ are concurrent.
|
Let $\omega$ be the circumcircle of $A B C D$. Let $A B$ and $C D$ intersect at $X$. Let $\omega_{1}$ and $\omega_{2}$ be the circles with centers $P$ and $M$ and with equal radius $P B=M C=r$. The power of $X$ with respect to $\omega$ and $\omega_{1}$ equals $X A \cdot X B$ and with respect to $\omega$ and $\omega_{2} X D \cdot X C$. The latter power also equals $(X M+$ $r)(X M-r)=X M^{2}-r^{2}$. Analogously, the first power is $X P^{2}-r^{2}$. But since $X A \cdot X B=X D \cdot X C$, we must have $X M^{2}=X P^{2}$ or $X M=X P . X$ indeed is on the perpendicular bisector of $P M$, and we are done.

|
{
"exam": "BalticWay",
"problem_label": "20",
"problem_match": "\n20.",
"resource_path": "BalticWay/segmented/en-bw16sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2016"
}
|
Let $a_{0}, a_{1}, a_{2}, \ldots$ be an infinite sequence of real numbers satisfying $\frac{a_{n-1}+a_{n+1}}{2} \geq a_{n}$ for all positive integers $n$. Show that
$$
\frac{a_{0}+a_{n+1}}{2} \geq \frac{a_{1}+a_{2}+\ldots+a_{n}}{n}
$$
holds for all positive integers $n$.
|
From the inequality $\frac{a_{n-1}+a_{n+1}}{2} \geq a_{n}$ we get $a_{n+1}-a_{n} \geq a_{n}-a_{n-1}$. Inductively this yields that $a_{l+1}-a_{l} \geq a_{k+1}-a_{k}$ for any positive integers $l>k$, which rewrites as
$$
a_{l+1}+a_{k} \geq a_{l}+a_{k+1}
$$
Now fix $n$ and define $b_{m}=a_{m}+a_{n+1-m}$ for $m=0, \ldots n+1$. For $m<\frac{n}{2}$, we can apply the above for $(l, k)=(n-m, m)$ yielding
$$
b_{m}=a_{n+1-m}+a_{m} \geq a_{n-m}+a_{m+1}=b_{m+1}
$$
Also by symmetry $b_{m}=b_{n+1-m}$. Thus
$$
b_{0}=\max _{m=0, \ldots, n+1} b_{m} \geq \max _{m=1, \ldots, n} b_{m} \geq \frac{b_{1}+\cdots+b_{n}}{n}
$$
substituting back yields the desired inequality.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a_{0}, a_{1}, a_{2}, \ldots$ be an infinite sequence of real numbers satisfying $\frac{a_{n-1}+a_{n+1}}{2} \geq a_{n}$ for all positive integers $n$. Show that
$$
\frac{a_{0}+a_{n+1}}{2} \geq \frac{a_{1}+a_{2}+\ldots+a_{n}}{n}
$$
holds for all positive integers $n$.
|
From the inequality $\frac{a_{n-1}+a_{n+1}}{2} \geq a_{n}$ we get $a_{n+1}-a_{n} \geq a_{n}-a_{n-1}$. Inductively this yields that $a_{l+1}-a_{l} \geq a_{k+1}-a_{k}$ for any positive integers $l>k$, which rewrites as
$$
a_{l+1}+a_{k} \geq a_{l}+a_{k+1}
$$
Now fix $n$ and define $b_{m}=a_{m}+a_{n+1-m}$ for $m=0, \ldots n+1$. For $m<\frac{n}{2}$, we can apply the above for $(l, k)=(n-m, m)$ yielding
$$
b_{m}=a_{n+1-m}+a_{m} \geq a_{n-m}+a_{m+1}=b_{m+1}
$$
Also by symmetry $b_{m}=b_{n+1-m}$. Thus
$$
b_{0}=\max _{m=0, \ldots, n+1} b_{m} \geq \max _{m=1, \ldots, n} b_{m} \geq \frac{b_{1}+\cdots+b_{n}}{n}
$$
substituting back yields the desired inequality.
|
{
"exam": "BalticWay",
"problem_label": "1",
"problem_match": "\nProblem 1.",
"resource_path": "BalticWay/segmented/en-bw17sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2017"
}
|
Does there exist a finite set of real numbers such that their sum equals 2 , the sum of their squares equals 3 , the sum of their cubes equals 4 and the sum of their ninth powers equals 10 ?
|
Answer: no.
Assume that such a set of numbers $\left\{a_{1}, \ldots, a_{n}\right\}$ exists. Summing up the inequalities
$$
2 a_{i}^{3} \leq a_{i}^{2}+a_{i}^{4}
$$
for all $i$ we obtain the inequality $8 \leq 8$. Therefore all the inequalities are in fact equalities. This is possible for the cases $a_{i}=0$ or $a_{i}=1$ only, but the elements of a set are all different.
(Remark: Even if the $a_{i}$ 's are allowed to be equal it is clear that only 0's or only l's do not satisfy the problem conditions.)
|
no
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Does there exist a finite set of real numbers such that their sum equals 2 , the sum of their squares equals 3 , the sum of their cubes equals 4 and the sum of their ninth powers equals 10 ?
|
Answer: no.
Assume that such a set of numbers $\left\{a_{1}, \ldots, a_{n}\right\}$ exists. Summing up the inequalities
$$
2 a_{i}^{3} \leq a_{i}^{2}+a_{i}^{4}
$$
for all $i$ we obtain the inequality $8 \leq 8$. Therefore all the inequalities are in fact equalities. This is possible for the cases $a_{i}=0$ or $a_{i}=1$ only, but the elements of a set are all different.
(Remark: Even if the $a_{i}$ 's are allowed to be equal it is clear that only 0's or only l's do not satisfy the problem conditions.)
|
{
"exam": "BalticWay",
"problem_label": "2",
"problem_match": "\nProblem 2.",
"resource_path": "BalticWay/segmented/en-bw17sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2017"
}
|
Positive integers $x_{1}, \ldots, x_{m}$ (not necessarily distinct) are written on a blackboard. It is known that each of the numbers $F_{1}, \ldots, F_{2018}$ can be represented as a sum of one or more of the numbers on the blackboard. What is the smallest possible value of $m$ ?
(Here $F_{1}, \ldots, F_{2018}$ are the first 2018 Fibonacci numbers: $F_{1}=F_{2}=1, F_{k+1}=F_{k}+F_{k-1}$ for $k>1$.)
|
Answer: the minimal value for $m$ is 1009 .
Construction: Define $x_{i}=F_{2 i-1}$. This works since $F_{2 k}=F_{1}+F_{3}+\ldots+F_{2 k-1}$, for all $k$, which can easily be proved by induction. Minimality: Again by induction we get that $F_{k+2}=1+F_{1}+F_{2}+\ldots+F_{k}$, for all $k$, which means that
$$
F_{k+2}>F_{1}+F_{2}+\ldots+F_{k} .
$$
Consider the numbers that have been used for the representing the first $k$ Fibonacci numbers. Then the sum of these $x_{i}$ 's is less than $F_{k+2}$ due to $(*)$. Thus, at least one additional number is required to deal with $F_{k+2}$. This establishes the lower bound $m \leq 1009$.
|
1009
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Positive integers $x_{1}, \ldots, x_{m}$ (not necessarily distinct) are written on a blackboard. It is known that each of the numbers $F_{1}, \ldots, F_{2018}$ can be represented as a sum of one or more of the numbers on the blackboard. What is the smallest possible value of $m$ ?
(Here $F_{1}, \ldots, F_{2018}$ are the first 2018 Fibonacci numbers: $F_{1}=F_{2}=1, F_{k+1}=F_{k}+F_{k-1}$ for $k>1$.)
|
Answer: the minimal value for $m$ is 1009 .
Construction: Define $x_{i}=F_{2 i-1}$. This works since $F_{2 k}=F_{1}+F_{3}+\ldots+F_{2 k-1}$, for all $k$, which can easily be proved by induction. Minimality: Again by induction we get that $F_{k+2}=1+F_{1}+F_{2}+\ldots+F_{k}$, for all $k$, which means that
$$
F_{k+2}>F_{1}+F_{2}+\ldots+F_{k} .
$$
Consider the numbers that have been used for the representing the first $k$ Fibonacci numbers. Then the sum of these $x_{i}$ 's is less than $F_{k+2}$ due to $(*)$. Thus, at least one additional number is required to deal with $F_{k+2}$. This establishes the lower bound $m \leq 1009$.
|
{
"exam": "BalticWay",
"problem_label": "3",
"problem_match": "\nProblem 3.",
"resource_path": "BalticWay/segmented/en-bw17sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2017"
}
|
A linear form in $k$ variables is an expression of the form $P\left(x_{1}, \ldots, x_{k}\right)=a_{1} x_{1}+\ldots+a_{k} x_{k}$ with real constants $a_{1}, \ldots, a_{k}$. Prove that there exist a positive integer $n$ and linear forms $P_{1}, \ldots, P_{n}$ in 2017 variables such that the equation
$$
x_{1} \cdot x_{2} \cdot \ldots \cdot x_{2017}=P_{1}\left(x_{1}, \ldots, x_{2017}\right)^{2017}+\ldots+P_{n}\left(x_{1}, \ldots, x_{2017}\right)^{2017}
$$
holds for all real numbers $x_{1}, \ldots, x_{2017}$.
|
For every $\varepsilon=\left(\varepsilon_{1}, \ldots, \varepsilon_{n}\right) \in\{ \pm 1\}^{2017}$ let
$$
P_{\varepsilon}\left(X_{1}, \ldots, X_{2017}\right)=\varepsilon_{1} X_{1}+\cdots+\varepsilon_{2017} X_{2017}
$$
and $\beta_{\varepsilon}=\varepsilon_{1} \cdots \varepsilon_{2017}$. Consider
$$
\begin{aligned}
g\left(X_{1}, \ldots, X_{k}\right) & :=\sum_{\varepsilon}\left(\beta_{\varepsilon} P_{\varepsilon}\left(X_{1}, \ldots, X_{2017}\right)\right)^{2017} \\
& =\sum_{\varepsilon_{1}, \ldots, \varepsilon_{2017}} \varepsilon_{1} \cdots \varepsilon_{2017}\left(\varepsilon_{1} X_{1}+\cdots+\varepsilon_{2017} X_{2017}\right)^{2017}
\end{aligned}
$$
If we choose $X_{1}=0$, then every combination $\left(\varepsilon_{2} X_{2}+\cdots+\varepsilon_{2017} X_{2017}\right)^{2017}$ occurs exactly twice and with opposite signs in the above sum. Hence, $g\left(0, X_{2}, \ldots, X_{2017}\right) \equiv 0$. The analogous statements are true for all other variables. Consequently, $g$ is divisible by $X_{1} \ldots X_{2017}$, and thereby of the form $c X_{1} \ldots X_{2017}$ for some real constant $c$. If $c \neq 0$, then both sides can be divided by $c$, and we obtain a representation with $n=2^{2017}$ linear forms.
With $X_{1}=\cdots=X_{2017}=1$ we get
$$
\begin{aligned}
c & =\sum_{\varepsilon} \varepsilon_{1} \cdot \ldots \cdot \varepsilon_{2017}\left(\varepsilon_{1}+\ldots+\varepsilon_{2017}\right)^{2017} \\
& =\sum_{\varepsilon} \sum_{\substack{k_{1}, \ldots, k_{2017} \\
k_{1}+\ldots+k_{2017}=2017}}\left(\begin{array}{c}
2017 \\
k_{1}, \ldots, k_{2017}
\end{array}\right) \varepsilon_{1}^{k_{1}+1} \cdot \ldots \cdot \varepsilon_{2017}^{k_{2017}+1}
\end{aligned}
$$
The part of the sum with $k_{1}$ even is zero since
$$
\sum_{\substack{k_{1} \text { even,.,.,k } \\
k_{1}+\ldots+k_{2017}=2017}}\left(\begin{array}{c}
2017 \\
k_{1}, \ldots, k_{2017}
\end{array}\right)\left(\sum_{\varepsilon, \varepsilon_{1}=1} \varepsilon_{2}^{k_{2}+1} \cdot \ldots \cdot \varepsilon_{2017}^{k_{2017}+1}+\sum_{\varepsilon, \varepsilon_{1}=-1}(-1)^{k_{1}+1} \cdot \ldots \cdot \varepsilon_{2017}^{k_{2017}+1}\right)=0
$$
Now we may consider the part of the sum with $k_{1}$ odd. Similarly the part of this new sum with $k_{2}$ even equals 0 . Doing this for all the variables we get
$$
c=\sum_{\varepsilon=1} \sum_{\substack{k_{1} \text { odd, }, \ldots, k_{2017} \text { odd } \\
k_{1}+\ldots+k_{2017}=2017}}\left(\begin{array}{c}
2017 \\
k_{1}, \ldots, k_{2017}
\end{array}\right)=2^{2017}\left(\begin{array}{c}
2017 \\
1, \ldots, 1
\end{array}\right)=2^{2017} \cdot 2017 ! \neq 0
$$
forms.
Finally, we can even merge the two forms with opposite choices of the signs to obtain a representation with $2^{2016}$ linear
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
A linear form in $k$ variables is an expression of the form $P\left(x_{1}, \ldots, x_{k}\right)=a_{1} x_{1}+\ldots+a_{k} x_{k}$ with real constants $a_{1}, \ldots, a_{k}$. Prove that there exist a positive integer $n$ and linear forms $P_{1}, \ldots, P_{n}$ in 2017 variables such that the equation
$$
x_{1} \cdot x_{2} \cdot \ldots \cdot x_{2017}=P_{1}\left(x_{1}, \ldots, x_{2017}\right)^{2017}+\ldots+P_{n}\left(x_{1}, \ldots, x_{2017}\right)^{2017}
$$
holds for all real numbers $x_{1}, \ldots, x_{2017}$.
|
For every $\varepsilon=\left(\varepsilon_{1}, \ldots, \varepsilon_{n}\right) \in\{ \pm 1\}^{2017}$ let
$$
P_{\varepsilon}\left(X_{1}, \ldots, X_{2017}\right)=\varepsilon_{1} X_{1}+\cdots+\varepsilon_{2017} X_{2017}
$$
and $\beta_{\varepsilon}=\varepsilon_{1} \cdots \varepsilon_{2017}$. Consider
$$
\begin{aligned}
g\left(X_{1}, \ldots, X_{k}\right) & :=\sum_{\varepsilon}\left(\beta_{\varepsilon} P_{\varepsilon}\left(X_{1}, \ldots, X_{2017}\right)\right)^{2017} \\
& =\sum_{\varepsilon_{1}, \ldots, \varepsilon_{2017}} \varepsilon_{1} \cdots \varepsilon_{2017}\left(\varepsilon_{1} X_{1}+\cdots+\varepsilon_{2017} X_{2017}\right)^{2017}
\end{aligned}
$$
If we choose $X_{1}=0$, then every combination $\left(\varepsilon_{2} X_{2}+\cdots+\varepsilon_{2017} X_{2017}\right)^{2017}$ occurs exactly twice and with opposite signs in the above sum. Hence, $g\left(0, X_{2}, \ldots, X_{2017}\right) \equiv 0$. The analogous statements are true for all other variables. Consequently, $g$ is divisible by $X_{1} \ldots X_{2017}$, and thereby of the form $c X_{1} \ldots X_{2017}$ for some real constant $c$. If $c \neq 0$, then both sides can be divided by $c$, and we obtain a representation with $n=2^{2017}$ linear forms.
With $X_{1}=\cdots=X_{2017}=1$ we get
$$
\begin{aligned}
c & =\sum_{\varepsilon} \varepsilon_{1} \cdot \ldots \cdot \varepsilon_{2017}\left(\varepsilon_{1}+\ldots+\varepsilon_{2017}\right)^{2017} \\
& =\sum_{\varepsilon} \sum_{\substack{k_{1}, \ldots, k_{2017} \\
k_{1}+\ldots+k_{2017}=2017}}\left(\begin{array}{c}
2017 \\
k_{1}, \ldots, k_{2017}
\end{array}\right) \varepsilon_{1}^{k_{1}+1} \cdot \ldots \cdot \varepsilon_{2017}^{k_{2017}+1}
\end{aligned}
$$
The part of the sum with $k_{1}$ even is zero since
$$
\sum_{\substack{k_{1} \text { even,.,.,k } \\
k_{1}+\ldots+k_{2017}=2017}}\left(\begin{array}{c}
2017 \\
k_{1}, \ldots, k_{2017}
\end{array}\right)\left(\sum_{\varepsilon, \varepsilon_{1}=1} \varepsilon_{2}^{k_{2}+1} \cdot \ldots \cdot \varepsilon_{2017}^{k_{2017}+1}+\sum_{\varepsilon, \varepsilon_{1}=-1}(-1)^{k_{1}+1} \cdot \ldots \cdot \varepsilon_{2017}^{k_{2017}+1}\right)=0
$$
Now we may consider the part of the sum with $k_{1}$ odd. Similarly the part of this new sum with $k_{2}$ even equals 0 . Doing this for all the variables we get
$$
c=\sum_{\varepsilon=1} \sum_{\substack{k_{1} \text { odd, }, \ldots, k_{2017} \text { odd } \\
k_{1}+\ldots+k_{2017}=2017}}\left(\begin{array}{c}
2017 \\
k_{1}, \ldots, k_{2017}
\end{array}\right)=2^{2017}\left(\begin{array}{c}
2017 \\
1, \ldots, 1
\end{array}\right)=2^{2017} \cdot 2017 ! \neq 0
$$
forms.
Finally, we can even merge the two forms with opposite choices of the signs to obtain a representation with $2^{2016}$ linear
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "\nProblem 4.",
"resource_path": "BalticWay/segmented/en-bw17sol.jsonl",
"solution_match": "\nSolution 1:",
"tier": "T3",
"year": "2017"
}
|
A linear form in $k$ variables is an expression of the form $P\left(x_{1}, \ldots, x_{k}\right)=a_{1} x_{1}+\ldots+a_{k} x_{k}$ with real constants $a_{1}, \ldots, a_{k}$. Prove that there exist a positive integer $n$ and linear forms $P_{1}, \ldots, P_{n}$ in 2017 variables such that the equation
$$
x_{1} \cdot x_{2} \cdot \ldots \cdot x_{2017}=P_{1}\left(x_{1}, \ldots, x_{2017}\right)^{2017}+\ldots+P_{n}\left(x_{1}, \ldots, x_{2017}\right)^{2017}
$$
holds for all real numbers $x_{1}, \ldots, x_{2017}$.
|
We show by induction that for every integer $k \geq 1$ there exist an $n=n_{k}$, real numbers $\lambda_{1}, \ldots, \lambda_{n_{k}}$ and linear forms $P_{k, 1}, \ldots, P_{k, n_{k}}$ in $k$ variables such that
$$
x_{1} \ldots x_{k}=\lambda_{1} P_{k, 1}\left(x_{1}, \ldots, x_{k}\right)^{k}+\cdots+\lambda_{n_{k}} P_{k, n_{k}}\left(x_{1}, \ldots, x_{k}\right)^{k} .
$$
For $k=1$ we can choose $n=n_{1}=1$ and $P_{1,1}\left(x_{1}\right)=x_{1}$. Now for the induction step, we observe that
$$
x_{1} \ldots x_{k} y=\lambda_{1} P_{k, 1}\left(x_{1}, \ldots, x_{k}\right)^{k} y+\cdots+\lambda_{k} P_{k, n_{k}}\left(x_{1}, \ldots, x_{k}\right)^{k} y
$$
Thus it suffices to write $X^{k} Y$ as a linear combination of $(k+1)$-th powers of linear forms in $X$ and $Y$. The set-up
$$
X^{k} Y=\sum_{i=1}^{m} \alpha_{i}\left(X+\beta_{i} Y\right)^{k+1}
$$
leads to the equations $\sum_{i} \alpha_{i} \beta_{i}=\frac{1}{k+1}$ and $\sum_{i} \alpha_{i} \beta_{i}^{d}=0$ for $d=0,2,3, \ldots, k+1$. Choosing $m=k+2$ and distinct values for the $\beta_{i}$ 's, this becomes a system of $k+2$ linear equations in the $k+2$ variables $\alpha_{i}$. If the system had no solution, then the lefthand sides of the equations would be linearly dependent. On the other hand, given $c_{j}, j=0,1, \ldots, k+1$ with $\sum_{j} c_{j} \beta_{i}^{j}=0$ for all $i$, the polynomial $P(x)=\sum_{j} c_{j} x^{j}$ has degree at most $k+1$ and the $k+2$ distinct zeros $b_{1}, \ldots, b_{k+2}$ and, hence, is the zero polynomial. Consequently, the system has a solution, and we can choose $n_{k+1}=(k+2) n_{k}$ and the induction is complete.
The above gives us
$$
\begin{aligned}
x_{1} \ldots x_{2017} & =\lambda_{1} P_{2017,1}\left(x_{1}, \ldots, x_{2017}\right)^{2017}+\cdots+\lambda_{n_{2017}} P_{2017, n_{2017}}\left(x_{1}, \ldots, x_{2017}\right)^{2017} \\
& =\left(\lambda_{1}^{1 / 2017} P_{2017,1}\left(x_{1}, \ldots, x_{2017}\right)\right)^{2017}+\cdots+\left(\lambda_{n_{2017}}^{1 / 2017} P_{2017, n_{2017}}\left(x_{1}, \ldots, x_{2017}\right)\right)^{2017},
\end{aligned}
$$
as wanted.
Remark: Of course, the consistency of the system of linear equations also follows by the fact that the determinant of the coefficient matrix does not vanish as it is of Vandermonde's type.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
A linear form in $k$ variables is an expression of the form $P\left(x_{1}, \ldots, x_{k}\right)=a_{1} x_{1}+\ldots+a_{k} x_{k}$ with real constants $a_{1}, \ldots, a_{k}$. Prove that there exist a positive integer $n$ and linear forms $P_{1}, \ldots, P_{n}$ in 2017 variables such that the equation
$$
x_{1} \cdot x_{2} \cdot \ldots \cdot x_{2017}=P_{1}\left(x_{1}, \ldots, x_{2017}\right)^{2017}+\ldots+P_{n}\left(x_{1}, \ldots, x_{2017}\right)^{2017}
$$
holds for all real numbers $x_{1}, \ldots, x_{2017}$.
|
We show by induction that for every integer $k \geq 1$ there exist an $n=n_{k}$, real numbers $\lambda_{1}, \ldots, \lambda_{n_{k}}$ and linear forms $P_{k, 1}, \ldots, P_{k, n_{k}}$ in $k$ variables such that
$$
x_{1} \ldots x_{k}=\lambda_{1} P_{k, 1}\left(x_{1}, \ldots, x_{k}\right)^{k}+\cdots+\lambda_{n_{k}} P_{k, n_{k}}\left(x_{1}, \ldots, x_{k}\right)^{k} .
$$
For $k=1$ we can choose $n=n_{1}=1$ and $P_{1,1}\left(x_{1}\right)=x_{1}$. Now for the induction step, we observe that
$$
x_{1} \ldots x_{k} y=\lambda_{1} P_{k, 1}\left(x_{1}, \ldots, x_{k}\right)^{k} y+\cdots+\lambda_{k} P_{k, n_{k}}\left(x_{1}, \ldots, x_{k}\right)^{k} y
$$
Thus it suffices to write $X^{k} Y$ as a linear combination of $(k+1)$-th powers of linear forms in $X$ and $Y$. The set-up
$$
X^{k} Y=\sum_{i=1}^{m} \alpha_{i}\left(X+\beta_{i} Y\right)^{k+1}
$$
leads to the equations $\sum_{i} \alpha_{i} \beta_{i}=\frac{1}{k+1}$ and $\sum_{i} \alpha_{i} \beta_{i}^{d}=0$ for $d=0,2,3, \ldots, k+1$. Choosing $m=k+2$ and distinct values for the $\beta_{i}$ 's, this becomes a system of $k+2$ linear equations in the $k+2$ variables $\alpha_{i}$. If the system had no solution, then the lefthand sides of the equations would be linearly dependent. On the other hand, given $c_{j}, j=0,1, \ldots, k+1$ with $\sum_{j} c_{j} \beta_{i}^{j}=0$ for all $i$, the polynomial $P(x)=\sum_{j} c_{j} x^{j}$ has degree at most $k+1$ and the $k+2$ distinct zeros $b_{1}, \ldots, b_{k+2}$ and, hence, is the zero polynomial. Consequently, the system has a solution, and we can choose $n_{k+1}=(k+2) n_{k}$ and the induction is complete.
The above gives us
$$
\begin{aligned}
x_{1} \ldots x_{2017} & =\lambda_{1} P_{2017,1}\left(x_{1}, \ldots, x_{2017}\right)^{2017}+\cdots+\lambda_{n_{2017}} P_{2017, n_{2017}}\left(x_{1}, \ldots, x_{2017}\right)^{2017} \\
& =\left(\lambda_{1}^{1 / 2017} P_{2017,1}\left(x_{1}, \ldots, x_{2017}\right)\right)^{2017}+\cdots+\left(\lambda_{n_{2017}}^{1 / 2017} P_{2017, n_{2017}}\left(x_{1}, \ldots, x_{2017}\right)\right)^{2017},
\end{aligned}
$$
as wanted.
Remark: Of course, the consistency of the system of linear equations also follows by the fact that the determinant of the coefficient matrix does not vanish as it is of Vandermonde's type.
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "\nProblem 4.",
"resource_path": "BalticWay/segmented/en-bw17sol.jsonl",
"solution_match": "\nSolution 2:",
"tier": "T3",
"year": "2017"
}
|
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
f\left(x^{2} y\right)=f(x y)+y f(f(x)+y)
$$
for all real numbers $x$ and $y$.
|
Answer: $f(y)=0$.
By substituting $x=0$ into the original equation we obtain $f(0)=f(0)+y f(f(0)+y)$, which after simplifying yields $y f(f(0)+$ $y)=0$. This has to hold for every $y$.
Now let's substitute $y=-f(0)$. We get that $-(f(0))^{2}=0$, which gives us $f(0)=0$.
By plugging the last result into $y f(f(0)+y)=0$ we now get that $y f(y)=0$.
Therefore if $y \neq 0$ then $f(y)=0$.
Altogether we have shown that $f(y)=0$ for every $y$ is the only possible solution, and it clearly is a solution.
|
f(y)=0
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
f\left(x^{2} y\right)=f(x y)+y f(f(x)+y)
$$
for all real numbers $x$ and $y$.
|
Answer: $f(y)=0$.
By substituting $x=0$ into the original equation we obtain $f(0)=f(0)+y f(f(0)+y)$, which after simplifying yields $y f(f(0)+$ $y)=0$. This has to hold for every $y$.
Now let's substitute $y=-f(0)$. We get that $-(f(0))^{2}=0$, which gives us $f(0)=0$.
By plugging the last result into $y f(f(0)+y)=0$ we now get that $y f(y)=0$.
Therefore if $y \neq 0$ then $f(y)=0$.
Altogether we have shown that $f(y)=0$ for every $y$ is the only possible solution, and it clearly is a solution.
|
{
"exam": "BalticWay",
"problem_label": "5",
"problem_match": "\nProblem 5.",
"resource_path": "BalticWay/segmented/en-bw17sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2017"
}
|
Fifteen stones are placed on a $4 \times 4$ board, one in each cell, the remaining cell being empty. Whenever two stones are on neighbouring cells (having a common side), one may jump over the other to the opposite neighbouring cell, provided this cell is empty. The stone jumped over is removed from the board.

For which initial positions of the empty cell is it possible to end up with exactly one stone on the board?
|
There are three types of cells on the board: corner cells, edge cells and centre cells. Colour the cells in three distinct colours as follows.
$$
\begin{array}{|c|c|c|c|}
\hline \mathrm{A} & \mathrm{B} & \mathrm{C} & \mathrm{A} \\
\hline \mathrm{B} & \mathrm{C} & \mathrm{A} & \mathrm{B} \\
\hline \mathrm{C} & \mathrm{A} & \mathrm{B} & \mathrm{C} \\
\hline \mathrm{A} & \mathrm{B} & \mathrm{C} & \mathrm{A} \\
\hline
\end{array}
$$
Suppose there are initially $a, b, c$ stones on cells of colours A, B, C, respectively. With each move, one of these numbers will increase by 1 , while the other two will decrease by 1 . Because there are fourteen moves altogether, the game must end with $a, b, c$ of the same parity as they originally had. There are $6,5,5$ cells of each colour on the board, so if the game should end with a single stone remaining, the game must begin with
$$
a=6, b=5, c=4 \quad \text { or } \quad a=6, b=4, c=5 \text {. }
$$
The empty slot should thus have colour B or C. This excludes the corner cells and two of the centre cells. However, by symmetry (changing the colouring), the two remaining centre cells will also be excluded. Hence the empty space at the beginning must be at an edge cell. That the game is indeed winnable in this case can be seen from the sequence of moves here:
|
not found
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
Fifteen stones are placed on a $4 \times 4$ board, one in each cell, the remaining cell being empty. Whenever two stones are on neighbouring cells (having a common side), one may jump over the other to the opposite neighbouring cell, provided this cell is empty. The stone jumped over is removed from the board.

For which initial positions of the empty cell is it possible to end up with exactly one stone on the board?
|
There are three types of cells on the board: corner cells, edge cells and centre cells. Colour the cells in three distinct colours as follows.
$$
\begin{array}{|c|c|c|c|}
\hline \mathrm{A} & \mathrm{B} & \mathrm{C} & \mathrm{A} \\
\hline \mathrm{B} & \mathrm{C} & \mathrm{A} & \mathrm{B} \\
\hline \mathrm{C} & \mathrm{A} & \mathrm{B} & \mathrm{C} \\
\hline \mathrm{A} & \mathrm{B} & \mathrm{C} & \mathrm{A} \\
\hline
\end{array}
$$
Suppose there are initially $a, b, c$ stones on cells of colours A, B, C, respectively. With each move, one of these numbers will increase by 1 , while the other two will decrease by 1 . Because there are fourteen moves altogether, the game must end with $a, b, c$ of the same parity as they originally had. There are $6,5,5$ cells of each colour on the board, so if the game should end with a single stone remaining, the game must begin with
$$
a=6, b=5, c=4 \quad \text { or } \quad a=6, b=4, c=5 \text {. }
$$
The empty slot should thus have colour B or C. This excludes the corner cells and two of the centre cells. However, by symmetry (changing the colouring), the two remaining centre cells will also be excluded. Hence the empty space at the beginning must be at an edge cell. That the game is indeed winnable in this case can be seen from the sequence of moves here:

|
{
"exam": "BalticWay",
"problem_label": "6",
"problem_match": "\nProblem 6.",
"resource_path": "BalticWay/segmented/en-bw17sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2017"
}
|
Each edge of a complete graph on 30 vertices is coloured either red or blue. It is allowed to choose a nonmonochromatic triangle and change the colour of the two edges of the same colour to make the triangle monochromatic. Prove that by using this operation repeatedly it is possible to make the entire graph monochromatic.
(A complete graph is a graph where any two vertices are connected by an edge.)
|
The total number of edges is odd. Assume without loss of generality that the number of blue edges is odd, and the number of red edges is even. It is clear that the parity of the number of edges of each colour does not change by the operations.
Consider a graph with maximal number of blue edges that can be obtained by these operations. Suppose that not all of its edges are blue. Then it contains at least two red edges. Because of maximality, it is not possible to have a triangle with exactæy two red edges.
Case 1. It contains two red edges $A B$ and $B C$ sharing a common vertex. Then edge $A C$ is coloured in red, too. If there exists a vertex $D$ such that the edges $D A, D B, D C$ are not of the same colour, then wlog we can assume that $D A$ is red and $D B$ is blue, but then we have a triangle $A B D$ with exactly two red edges, a contradiction.
If some vertex $D$ is connected to $A, B$ and $C$ with blue edges, then perform the operation on the triangles $B C D, A B D$, $A C D$, and the number of blue edges increases, a contradiction.

Otherwise all the vertices are connected to $A, B$ and $C$ with red edges. Due to parity we have at least one blue edge. If $X$ and $Y$ are connected by a blue edge, then perform the operation on $A X Y$, and the number of blue edges increases, a contradiction.
Case 2. Every two red edges have no common vertex. Let $A B$ and $C D$ be red edges. Perform the operation in the triangles $A B D, B C D, A B D$. The number of blue edges increases.

|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Each edge of a complete graph on 30 vertices is coloured either red or blue. It is allowed to choose a nonmonochromatic triangle and change the colour of the two edges of the same colour to make the triangle monochromatic. Prove that by using this operation repeatedly it is possible to make the entire graph monochromatic.
(A complete graph is a graph where any two vertices are connected by an edge.)
|
The total number of edges is odd. Assume without loss of generality that the number of blue edges is odd, and the number of red edges is even. It is clear that the parity of the number of edges of each colour does not change by the operations.
Consider a graph with maximal number of blue edges that can be obtained by these operations. Suppose that not all of its edges are blue. Then it contains at least two red edges. Because of maximality, it is not possible to have a triangle with exactæy two red edges.
Case 1. It contains two red edges $A B$ and $B C$ sharing a common vertex. Then edge $A C$ is coloured in red, too. If there exists a vertex $D$ such that the edges $D A, D B, D C$ are not of the same colour, then wlog we can assume that $D A$ is red and $D B$ is blue, but then we have a triangle $A B D$ with exactly two red edges, a contradiction.

If some vertex $D$ is connected to $A, B$ and $C$ with blue edges, then perform the operation on the triangles $B C D, A B D$, $A C D$, and the number of blue edges increases, a contradiction.

Otherwise all the vertices are connected to $A, B$ and $C$ with red edges. Due to parity we have at least one blue edge. If $X$ and $Y$ are connected by a blue edge, then perform the operation on $A X Y$, and the number of blue edges increases, a contradiction.
Case 2. Every two red edges have no common vertex. Let $A B$ and $C D$ be red edges. Perform the operation in the triangles $A B D, B C D, A B D$. The number of blue edges increases.

|
{
"exam": "BalticWay",
"problem_label": "7",
"problem_match": "\nProblem 7.",
"resource_path": "BalticWay/segmented/en-bw17sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2017"
}
|
A chess knight has injured his leg and is limping. He alternates between a normal move and a short move where he moves to any diagonally neighbouring cell.
Normal move
Short move
The limping knight moves on a $5 \times 6$ cell chessboard starting with a normal move. What is the largest number of moves he can make if he is starting from a cell of his own choice and is not allowed to visit any cell (including the initial cell) more than once?
|
Answer: 25 moves.
Let us enumerate the rows of the chessboard with numbers 1 to 5 . We will consider only the short moves. Each short move connects two cells from rows of different parity and no two short moves has a common cell. Therefore there can be at most 12 short moves as there are just 12 cells in the rows of even parity (second and fourth). It means that the maximal number of moves is 12 short +13 normal $=25$ moves.
The figure shows that 25 moves indeed can be made.
| 19 | 5 | 7 | 9 | 11 | |
| :---: | :---: | :---: | :---: | :---: | :---: |
| 4 | 18 | 20 | 6 | 8 | 10 |
| | 2 | | 21 | 26 | 12 |
| 17 | 3 | 24 | 15 | 13 | 22 |
| 2 | 16 | 14 | 25 | 23 | |
|
25
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A chess knight has injured his leg and is limping. He alternates between a normal move and a short move where he moves to any diagonally neighbouring cell.

Normal move

Short move
The limping knight moves on a $5 \times 6$ cell chessboard starting with a normal move. What is the largest number of moves he can make if he is starting from a cell of his own choice and is not allowed to visit any cell (including the initial cell) more than once?
|
Answer: 25 moves.
Let us enumerate the rows of the chessboard with numbers 1 to 5 . We will consider only the short moves. Each short move connects two cells from rows of different parity and no two short moves has a common cell. Therefore there can be at most 12 short moves as there are just 12 cells in the rows of even parity (second and fourth). It means that the maximal number of moves is 12 short +13 normal $=25$ moves.
The figure shows that 25 moves indeed can be made.
| 19 | 5 | 7 | 9 | 11 | |
| :---: | :---: | :---: | :---: | :---: | :---: |
| 4 | 18 | 20 | 6 | 8 | 10 |
| | 2 | | 21 | 26 | 12 |
| 17 | 3 | 24 | 15 | 13 | 22 |
| 2 | 16 | 14 | 25 | 23 | |
|
{
"exam": "BalticWay",
"problem_label": "8",
"problem_match": "\nProblem 8.",
"resource_path": "BalticWay/segmented/en-bw17sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2017"
}
|
A positive integer $n$ is Danish if a regular hexagon can be partitioned into $n$ congruent polygons. Prove that there are infinitely many positive integers $n$ such that both $n$ and $2^{n}+n$ are Danish.
|
At first we note that $n=3 k$ is danish for any positive integer $k$, because a hexagon can be cut in 3 equal parallelograms each of which can afterwards be cut in $k$ equal parallelograms (Fig 1).
Furthermore a hexagon can be cut into two equal trapezoids (Fig. 2) each of which can afterwards be cut into 4 equal trapezoids of the same shape (Fig. 3) and so on. Therefore any number of the form $n=2 \cdot 4^{k}$ is also danish.
Figure 1
Figure 2
Figure 3
If we take any danish number $n=2 \cdot 4^{k}$ of the second type, then
$$
2^{n}+n=2^{2 \cdot 4^{k}}+2 \cdot 4^{k} \equiv 1+2 \equiv 0(\bmod 3)
$$
showing that $2^{n}+n$ is also a danish number.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
A positive integer $n$ is Danish if a regular hexagon can be partitioned into $n$ congruent polygons. Prove that there are infinitely many positive integers $n$ such that both $n$ and $2^{n}+n$ are Danish.
|
At first we note that $n=3 k$ is danish for any positive integer $k$, because a hexagon can be cut in 3 equal parallelograms each of which can afterwards be cut in $k$ equal parallelograms (Fig 1).
Furthermore a hexagon can be cut into two equal trapezoids (Fig. 2) each of which can afterwards be cut into 4 equal trapezoids of the same shape (Fig. 3) and so on. Therefore any number of the form $n=2 \cdot 4^{k}$ is also danish.

Figure 1

Figure 2

Figure 3
If we take any danish number $n=2 \cdot 4^{k}$ of the second type, then
$$
2^{n}+n=2^{2 \cdot 4^{k}}+2 \cdot 4^{k} \equiv 1+2 \equiv 0(\bmod 3)
$$
showing that $2^{n}+n$ is also a danish number.
|
{
"exam": "BalticWay",
"problem_label": "9",
"problem_match": "\nProblem 9.",
"resource_path": "BalticWay/segmented/en-bw17sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2017"
}
|
Maker and Breaker are building a wall. Maker has a supply of green cubical building blocks, and Breaker has a supply of red ones, all of the same size. On the ground, a row of $m$ squares has been marked in chalk as place-holders. Maker and Breaker now take turns in placing a block either directly on one of these squares, or on top of another block already in place, in such a way that the height of each column never exceeds $n$. Maker places the first block.
Maker bets that he can form a green row, i.e. all $m$ blocks at a certain height are green. Breaker bets that he can prevent Maker from achieving this. Determine all pairs $(m, n)$ of positive integers for which Maker can make sure he wins the bet.
|
Answer: Maker has a winning strategy if $m>1$ and $n>1$ are both odd, or if $m=1$.
Let us refer to the positions of the blocks in the wall by coordinates $(x, y)$ where $x \in\{0,1, \ldots, m-1\}$ refers to the column and $y \in\{0,1, \ldots, n-1\}$ to the height of the block. Consider the different cases according to the parity of the parameters. In addition, there are some exceptional trivial cases.
1) If $m=1$, then Maker trivially wins by the first move.
2) If $m>1$, but $n=1$, then Breaker obviously can break the only row.
3) Suppose $m$ is even. Then Breaker has a defensive strategy based on the horizontal reflection, i.e. if Maker places a block in $(x, y)$, then Breaker places a block in $(m-1-x, y)$. Note that this move is always available for Breaker, because $m$ is even. It is clear that this reflection strategy breaks all the green rows.
4) Suppose then $n$ is even but $m>1$ is odd. Then Breaker has the same defensive stra-tegy as above based on the horizontal reflection, with one modification: Whenever Maker places a block in the middle column, Breaker does too. Since $n$ is even, this middle column does not influence the rest of the construction. Hence this reflection strategy breaks all the green rows as above.
5) Suppose both $m$ and $n$ are odd, $m>1$ and $n>1$. Maker's strategy is the following: Maker starts with $(0,0)$. Maker pairs the positions $(2 i-1,0)$ and $(2 i, 0), i=1,2, \ldots, \frac{m-1}{2}$, so that if Breaker places a red block in one of the positions, Maker places a green block in the other position; otherwise Maker does not use the bottom row. Maker's reply to Breaker's $(x, y)$ with $y>0$ is $(x, y+1)$. This strategy builds a green row at the height 2 .
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Maker and Breaker are building a wall. Maker has a supply of green cubical building blocks, and Breaker has a supply of red ones, all of the same size. On the ground, a row of $m$ squares has been marked in chalk as place-holders. Maker and Breaker now take turns in placing a block either directly on one of these squares, or on top of another block already in place, in such a way that the height of each column never exceeds $n$. Maker places the first block.
Maker bets that he can form a green row, i.e. all $m$ blocks at a certain height are green. Breaker bets that he can prevent Maker from achieving this. Determine all pairs $(m, n)$ of positive integers for which Maker can make sure he wins the bet.
|
Answer: Maker has a winning strategy if $m>1$ and $n>1$ are both odd, or if $m=1$.
Let us refer to the positions of the blocks in the wall by coordinates $(x, y)$ where $x \in\{0,1, \ldots, m-1\}$ refers to the column and $y \in\{0,1, \ldots, n-1\}$ to the height of the block. Consider the different cases according to the parity of the parameters. In addition, there are some exceptional trivial cases.
1) If $m=1$, then Maker trivially wins by the first move.
2) If $m>1$, but $n=1$, then Breaker obviously can break the only row.
3) Suppose $m$ is even. Then Breaker has a defensive strategy based on the horizontal reflection, i.e. if Maker places a block in $(x, y)$, then Breaker places a block in $(m-1-x, y)$. Note that this move is always available for Breaker, because $m$ is even. It is clear that this reflection strategy breaks all the green rows.
4) Suppose then $n$ is even but $m>1$ is odd. Then Breaker has the same defensive stra-tegy as above based on the horizontal reflection, with one modification: Whenever Maker places a block in the middle column, Breaker does too. Since $n$ is even, this middle column does not influence the rest of the construction. Hence this reflection strategy breaks all the green rows as above.
5) Suppose both $m$ and $n$ are odd, $m>1$ and $n>1$. Maker's strategy is the following: Maker starts with $(0,0)$. Maker pairs the positions $(2 i-1,0)$ and $(2 i, 0), i=1,2, \ldots, \frac{m-1}{2}$, so that if Breaker places a red block in one of the positions, Maker places a green block in the other position; otherwise Maker does not use the bottom row. Maker's reply to Breaker's $(x, y)$ with $y>0$ is $(x, y+1)$. This strategy builds a green row at the height 2 .
|
{
"exam": "BalticWay",
"problem_label": "10",
"problem_match": "\nProblem 10.",
"resource_path": "BalticWay/segmented/en-bw17sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2017"
}
|
Let $H$ and $I$ be the orthocentre and incentre, respectively, of an acute angled triangle $A B C$. The circumcircle of the triangle $B C I$ intersects the segment $A B$ at the point $P$ different from $B$. Let $K$ be the projection of $H$ onto $A I$ and $Q$ the reflection of $P$ in $K$. Show that $B, H$ and $Q$ are collinear.
|
Let $H^{\prime}$ be the reflection of $H$ in $K$. The reflection about the point $K$ sends $Q$ to $P$, and the line $B H$ to the line through $H^{\prime}$ and orthogonal to $A C$. The reflection about the line $A I$ sends $P$ to $C$, and the line through $H^{\prime}$ orthogonal to $A C$ to the line through $H$ orthogonal to $A B$, but this is just $B H$. Since composition of the two reflections sends $B, H$ and $Q$ to the same line, it follows that $B, H$ and $Q$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $H$ and $I$ be the orthocentre and incentre, respectively, of an acute angled triangle $A B C$. The circumcircle of the triangle $B C I$ intersects the segment $A B$ at the point $P$ different from $B$. Let $K$ be the projection of $H$ onto $A I$ and $Q$ the reflection of $P$ in $K$. Show that $B, H$ and $Q$ are collinear.
|
Let $H^{\prime}$ be the reflection of $H$ in $K$. The reflection about the point $K$ sends $Q$ to $P$, and the line $B H$ to the line through $H^{\prime}$ and orthogonal to $A C$. The reflection about the line $A I$ sends $P$ to $C$, and the line through $H^{\prime}$ orthogonal to $A C$ to the line through $H$ orthogonal to $A B$, but this is just $B H$. Since composition of the two reflections sends $B, H$ and $Q$ to the same line, it follows that $B, H$ and $Q$ are collinear.

|
{
"exam": "BalticWay",
"problem_label": "11",
"problem_match": "\nProblem 11.",
"resource_path": "BalticWay/segmented/en-bw17sol.jsonl",
"solution_match": "\nSolution 1:",
"tier": "T3",
"year": "2017"
}
|
Let $H$ and $I$ be the orthocentre and incentre, respectively, of an acute angled triangle $A B C$. The circumcircle of the triangle $B C I$ intersects the segment $A B$ at the point $P$ different from $B$. Let $K$ be the projection of $H$ onto $A I$ and $Q$ the reflection of $P$ in $K$. Show that $B, H$ and $Q$ are collinear.
|
Let $\alpha=\frac{1}{2} \angle B A C, \beta=\frac{1}{2} \angle C B A$, and $\gamma=\frac{1}{2} \angle A C B$. Clearly then $\alpha+\beta+\gamma=90^{\circ}$, which yields $\angle B I C=180^{\circ}-\beta-\gamma=$ $90^{\circ}+\alpha$. From this we get $\angle C P A=180^{\circ}-\angle B P C=180^{\circ}-\angle B I C=90^{\circ}-\alpha$, so triangle $A P C$ is isosceles.
Now since $A I$ is the anglebisector of $\angle P A C$ it must also be the perpendicular bisector of $C P$. Hence $C K=P K=Q K$ so triangle $K C Q$ is isosceles. Additionally $A I$ bisects $P Q$ so $A I$ is the midline of triangle $P C Q$ parallel to $C Q$. Since $K H$ is perpendicular to $A I$, it is also perpendicular to $C Q$, so we may then conclude by symmetry that $H C Q$ is also isosceles. Moreover $\angle Q C A=\angle I A C=\alpha$, and $\angle A C H=90^{\circ}-2 \alpha$, so $\angle Q C H=\alpha+90^{\circ}-2 \alpha=90^{\circ}-\alpha$, which means that triangles $H C Q$ and $A P C$ are similar. In particular we have $\angle C H Q=2 \alpha$. Since also
$$
180^{\circ}-\angle B H C=\angle H C B+\angle C B H=90^{\circ}-2 \beta+90^{\circ}-2 \gamma=2 \alpha
$$
it follows that $B, H$, and $Q$ are collinear.
To prove that $Q$ always lies outside of triangle $A B C$ one could do the following: Since $P$ lies on $A B$, angle $C$ is larger than angle $B$ in triangle $A B C$. Thus angle $A D B$ is obtuse, where $D$ is the intersection point between $A I$ and $B C$. As $Q C$ and $A I$ are parallel, angle $Q C B$ is obtuse. Thus $Q$ lies outside of triangle $A B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $H$ and $I$ be the orthocentre and incentre, respectively, of an acute angled triangle $A B C$. The circumcircle of the triangle $B C I$ intersects the segment $A B$ at the point $P$ different from $B$. Let $K$ be the projection of $H$ onto $A I$ and $Q$ the reflection of $P$ in $K$. Show that $B, H$ and $Q$ are collinear.
|
Let $\alpha=\frac{1}{2} \angle B A C, \beta=\frac{1}{2} \angle C B A$, and $\gamma=\frac{1}{2} \angle A C B$. Clearly then $\alpha+\beta+\gamma=90^{\circ}$, which yields $\angle B I C=180^{\circ}-\beta-\gamma=$ $90^{\circ}+\alpha$. From this we get $\angle C P A=180^{\circ}-\angle B P C=180^{\circ}-\angle B I C=90^{\circ}-\alpha$, so triangle $A P C$ is isosceles.
Now since $A I$ is the anglebisector of $\angle P A C$ it must also be the perpendicular bisector of $C P$. Hence $C K=P K=Q K$ so triangle $K C Q$ is isosceles. Additionally $A I$ bisects $P Q$ so $A I$ is the midline of triangle $P C Q$ parallel to $C Q$. Since $K H$ is perpendicular to $A I$, it is also perpendicular to $C Q$, so we may then conclude by symmetry that $H C Q$ is also isosceles. Moreover $\angle Q C A=\angle I A C=\alpha$, and $\angle A C H=90^{\circ}-2 \alpha$, so $\angle Q C H=\alpha+90^{\circ}-2 \alpha=90^{\circ}-\alpha$, which means that triangles $H C Q$ and $A P C$ are similar. In particular we have $\angle C H Q=2 \alpha$. Since also
$$
180^{\circ}-\angle B H C=\angle H C B+\angle C B H=90^{\circ}-2 \beta+90^{\circ}-2 \gamma=2 \alpha
$$
it follows that $B, H$, and $Q$ are collinear.
To prove that $Q$ always lies outside of triangle $A B C$ one could do the following: Since $P$ lies on $A B$, angle $C$ is larger than angle $B$ in triangle $A B C$. Thus angle $A D B$ is obtuse, where $D$ is the intersection point between $A I$ and $B C$. As $Q C$ and $A I$ are parallel, angle $Q C B$ is obtuse. Thus $Q$ lies outside of triangle $A B C$.
|
{
"exam": "BalticWay",
"problem_label": "11",
"problem_match": "\nProblem 11.",
"resource_path": "BalticWay/segmented/en-bw17sol.jsonl",
"solution_match": "\nSolution 2:",
"tier": "T3",
"year": "2017"
}
|
Line $\ell$ touches circle $S_{1}$ in the point $X$ and circle $S_{2}$ in the point $Y$. We draw a line $m$ which is parallel to $\ell$ and intersects $S_{1}$ in a point $P$ and $S_{2}$ in a point $Q$. Prove that the ratio $X P / Y Q$ does not depend on the choice of $m$.
|
Let $T$ be the second intersection point of $P Q$ and $S_{1}$ and $R$ be the second intersection point of $P Q$ and $S_{2}$. Let $\angle P X T=\alpha$, $\angle R Y Q=\beta$. It is evident that $P X=X T, R Y=Y Q$. Calculate the ratio area ${ }_{P X T} /$ area $_{R Y Q}$ by two different ways. First,
$$
\frac{\operatorname{area}_{P X T}}{\operatorname{area}_{R Y Q}}=\frac{X P^{2} \sin \alpha}{Y Q^{2} \sin \beta}
$$
Second,
Equating these expressions we obtain
$$
\frac{\operatorname{area}_{P X T}}{\operatorname{area}_{R Y Q}}=\frac{P T}{R Q}=\frac{2 R_{1} \sin \alpha}{2 R_{2} \sin \beta}
$$
$$
\frac{X P}{Y Q}=\sqrt{\frac{R_{1}}{R_{2}}}
$$
|
\frac{X P}{Y Q}=\sqrt{\frac{R_{1}}{R_{2}}}
|
Yes
|
Yes
|
proof
|
Geometry
|
Line $\ell$ touches circle $S_{1}$ in the point $X$ and circle $S_{2}$ in the point $Y$. We draw a line $m$ which is parallel to $\ell$ and intersects $S_{1}$ in a point $P$ and $S_{2}$ in a point $Q$. Prove that the ratio $X P / Y Q$ does not depend on the choice of $m$.
|
Let $T$ be the second intersection point of $P Q$ and $S_{1}$ and $R$ be the second intersection point of $P Q$ and $S_{2}$. Let $\angle P X T=\alpha$, $\angle R Y Q=\beta$. It is evident that $P X=X T, R Y=Y Q$. Calculate the ratio area ${ }_{P X T} /$ area $_{R Y Q}$ by two different ways. First,
$$
\frac{\operatorname{area}_{P X T}}{\operatorname{area}_{R Y Q}}=\frac{X P^{2} \sin \alpha}{Y Q^{2} \sin \beta}
$$
Second,
Equating these expressions we obtain
$$
\frac{\operatorname{area}_{P X T}}{\operatorname{area}_{R Y Q}}=\frac{P T}{R Q}=\frac{2 R_{1} \sin \alpha}{2 R_{2} \sin \beta}
$$
$$
\frac{X P}{Y Q}=\sqrt{\frac{R_{1}}{R_{2}}}
$$
|
{
"exam": "BalticWay",
"problem_label": "12",
"problem_match": "\nProblem 12.",
"resource_path": "BalticWay/segmented/en-bw17sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2017"
}
|
Let $A B C$ be a triangle in which $\angle A B C=60^{\circ}$. Let $I$ and $O$ be the incentre and circumcentre of $A B C$, respectively. Let $M$ be the midpoint of the arc $B C$ of the circumcircle of $A B C$, which does not contain the point $A$. Determine $\angle B A C$ given that $M B=O I$.
|
Since $\angle A B C=60^{\circ}$, we have $\angle A I C=\angle A O C=120^{\circ}$. Let $I^{\prime}, O^{\prime}$ be the points symmetric to $I, O$ with respect to $A C$, respectively. Then $I^{\prime}$ and $O^{\prime}$ lie on the circumcircle of $A B C$. Since $O^{\prime} I^{\prime}=O I=M B$, the angles determined by arcs $O^{\prime} I^{\prime}$ and $M B$ are equal. It follows that $\angle M A B=\angle I^{\prime} A O^{\prime}$.
Now, denoting $\angle B A C=\alpha$, we have
$$
\angle I^{\prime} A O^{\prime}=\angle I A O=|\angle I A C-\angle O A C|=\left|\frac{\alpha}{2}-30^{\circ}\right|
$$
It follows that $\frac{\alpha}{2}=\angle M A B=\angle I^{\prime} A O^{\prime}=\left|\frac{\alpha}{2}-30^{\circ}\right|$, i.e. $\alpha=30^{\circ}$.
|
30^{\circ}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle in which $\angle A B C=60^{\circ}$. Let $I$ and $O$ be the incentre and circumcentre of $A B C$, respectively. Let $M$ be the midpoint of the arc $B C$ of the circumcircle of $A B C$, which does not contain the point $A$. Determine $\angle B A C$ given that $M B=O I$.
|
Since $\angle A B C=60^{\circ}$, we have $\angle A I C=\angle A O C=120^{\circ}$. Let $I^{\prime}, O^{\prime}$ be the points symmetric to $I, O$ with respect to $A C$, respectively. Then $I^{\prime}$ and $O^{\prime}$ lie on the circumcircle of $A B C$. Since $O^{\prime} I^{\prime}=O I=M B$, the angles determined by arcs $O^{\prime} I^{\prime}$ and $M B$ are equal. It follows that $\angle M A B=\angle I^{\prime} A O^{\prime}$.
Now, denoting $\angle B A C=\alpha$, we have
$$
\angle I^{\prime} A O^{\prime}=\angle I A O=|\angle I A C-\angle O A C|=\left|\frac{\alpha}{2}-30^{\circ}\right|
$$
It follows that $\frac{\alpha}{2}=\angle M A B=\angle I^{\prime} A O^{\prime}=\left|\frac{\alpha}{2}-30^{\circ}\right|$, i.e. $\alpha=30^{\circ}$.

|
{
"exam": "BalticWay",
"problem_label": "13",
"problem_match": "\nProblem 13.",
"resource_path": "BalticWay/segmented/en-bw17sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2017"
}
|
Let $P$ be a point inside the acute angle $\angle B A C$. Suppose that $\angle A B P=\angle A C P=90^{\circ}$. The points $D$ and $E$ are on the segments $B A$ and $C A$, respectively, such that $B D=B P$ and $C P=C E$. The points $F$ and $G$ are on the segments $A C$ and $A B$, respectively, such that $D F$ is perpendicular to $A B$ and $E G$ is perpendicular to $A C$. Show that $P F=P G$.
|
As $\triangle P B D$ is an isosceles right triangle $\angle G D P=\angle B D P=45^{\circ}$. Similarly $\angle P E C=45^{\circ}$, and thus $\angle P E G=45^{\circ}$. Therefore $P G D E$ is cyclic. As $\angle G D F$ and $\angle G E F$ are right $E F G D$ is cyclic. Therefore $D G P F E$ is a cyclic pentagon. Therefore $\angle G F P=\angle G E P=45^{\circ}$. Similarly $\angle F G P=45^{\circ}$. Therefore $\triangle F P G$ is a (right) isosceles triangle.
Remark: It can be shown given two intersecting lines $l$ and $m$, not perpendicular to one another and an point $P$. there exist unique points $F$ and $G$ on $l$ and $m$ respectively such that $\triangle F P G$ is an right isosceles triangle using similar constructions to above.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $P$ be a point inside the acute angle $\angle B A C$. Suppose that $\angle A B P=\angle A C P=90^{\circ}$. The points $D$ and $E$ are on the segments $B A$ and $C A$, respectively, such that $B D=B P$ and $C P=C E$. The points $F$ and $G$ are on the segments $A C$ and $A B$, respectively, such that $D F$ is perpendicular to $A B$ and $E G$ is perpendicular to $A C$. Show that $P F=P G$.
|
As $\triangle P B D$ is an isosceles right triangle $\angle G D P=\angle B D P=45^{\circ}$. Similarly $\angle P E C=45^{\circ}$, and thus $\angle P E G=45^{\circ}$. Therefore $P G D E$ is cyclic. As $\angle G D F$ and $\angle G E F$ are right $E F G D$ is cyclic. Therefore $D G P F E$ is a cyclic pentagon. Therefore $\angle G F P=\angle G E P=45^{\circ}$. Similarly $\angle F G P=45^{\circ}$. Therefore $\triangle F P G$ is a (right) isosceles triangle.

Remark: It can be shown given two intersecting lines $l$ and $m$, not perpendicular to one another and an point $P$. there exist unique points $F$ and $G$ on $l$ and $m$ respectively such that $\triangle F P G$ is an right isosceles triangle using similar constructions to above.
|
{
"exam": "BalticWay",
"problem_label": "14",
"problem_match": "\nProblem 14.",
"resource_path": "BalticWay/segmented/en-bw17sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2017"
}
|
Let $n \geq 3$ be an integer. What is the largest possible number of interior angles greater than $180^{\circ}$ in an $n$-gon in the plane, given that the $n$-gon does not intersect itself and all its sides have the same length?
|
Answer: 0 if $n=3,4$ and $n-3$ for $n \geq 5$.
If $n=3,4$ then any such $n$-gon is a triangle, resp. a rhombus, therefore the answer is 0 .
If $n=5$ then consider a triangle with side lengths 2,2,1. Now move the vertex between sides of length 2 towards the opposite side by 0.0000001 units. Consider the triangle as a closed physical chain of links of length 1 that are aluminium tubes and through them is a closed rubber string. So deform the chain on a level surface so that links of the chain move towards the inside of the triangle, by fixing the vertices of the triangle to the surface. Geometrically, the links which are on sides of length 2 are now distinct chords of a large circle, attached to each other by their endpoints.
If $n>5$ then first consider a triangle of integer sides lengths, with sides of as equal lengths as possible, so that the sum of side lengths is $n$. Imagine a closed aluminium chain on a rubber string, as in the previous case. Now move two of the vertices of the triangle towards the third one be 0.00000001 units each. Again consider the chain on a level surface and deform it so that its links move towards the interior of the triangle. Geometrically each side of a triangle is deformed into consecutive equal-length chords of a large circle with centre far away from the original triangle.
For $n \geq 5$ this gives an example of $n-3$ interior angles of more than $180^{\circ}$.
To see that $n-2$ or more such angles is not possible, note than the sum of interior angles of any $n$-gon (that does not cut itself) is equal to $(n-2) 180^{\circ}$, but already the sum of the 'large' angles would be greater than that if there were at least $n-2$ of 'large' angles of size greater than $180^{\circ}$.
|
n-3
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $n \geq 3$ be an integer. What is the largest possible number of interior angles greater than $180^{\circ}$ in an $n$-gon in the plane, given that the $n$-gon does not intersect itself and all its sides have the same length?
|
Answer: 0 if $n=3,4$ and $n-3$ for $n \geq 5$.
If $n=3,4$ then any such $n$-gon is a triangle, resp. a rhombus, therefore the answer is 0 .
If $n=5$ then consider a triangle with side lengths 2,2,1. Now move the vertex between sides of length 2 towards the opposite side by 0.0000001 units. Consider the triangle as a closed physical chain of links of length 1 that are aluminium tubes and through them is a closed rubber string. So deform the chain on a level surface so that links of the chain move towards the inside of the triangle, by fixing the vertices of the triangle to the surface. Geometrically, the links which are on sides of length 2 are now distinct chords of a large circle, attached to each other by their endpoints.
If $n>5$ then first consider a triangle of integer sides lengths, with sides of as equal lengths as possible, so that the sum of side lengths is $n$. Imagine a closed aluminium chain on a rubber string, as in the previous case. Now move two of the vertices of the triangle towards the third one be 0.00000001 units each. Again consider the chain on a level surface and deform it so that its links move towards the interior of the triangle. Geometrically each side of a triangle is deformed into consecutive equal-length chords of a large circle with centre far away from the original triangle.
For $n \geq 5$ this gives an example of $n-3$ interior angles of more than $180^{\circ}$.
To see that $n-2$ or more such angles is not possible, note than the sum of interior angles of any $n$-gon (that does not cut itself) is equal to $(n-2) 180^{\circ}$, but already the sum of the 'large' angles would be greater than that if there were at least $n-2$ of 'large' angles of size greater than $180^{\circ}$.
|
{
"exam": "BalticWay",
"problem_label": "15",
"problem_match": "\nProblem 15.",
"resource_path": "BalticWay/segmented/en-bw17sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2017"
}
|
Is it possible for any group of people to choose a positive integer $N$ and assign a positive integer to each person in the group such that the product of two persons' numbers is divisible by $N$ if and only if they are friends?
|
Answer: Yes, this is always possible.
Consider a graph with a vertex for each person in the group. For each pair of friends we join the corresponding vertices by a red edge. If a pair are not friends, we join their vertices with a blue edge.
Let us label blue edges with different primes $p_{1}, \ldots, p_{k}$. To a vertex $A$ we assign the number $n(A)=\frac{P^{2}}{P(A)}$, where $P=$ $p_{1} p_{2} \ldots p_{k}$, and $P(A)$ is the product of the primes on all blue edges starting from $A$ (for the empty set the product of all its elements equals 1). Now take $N=P^{3}$.
Let us check that all conditions are satisfied. If vertices $A$ and $B$ are connected by a red edge, then $P(A)$ and $P(B)$ are coprime, hence $P(A) P(B) \mid P$ and $P^{3} \left\lvert\, n(A) n(B)=\frac{P^{4}}{P(A) P(B)}\right.$. If vertices $A$ and $B$ are connected by a blue edge labelled with a prime $q$, then $q^{2}$ divides neither $n(A)$ nor $n(B)$. Hence $q^{3}$ does not divide $n(A) n(B)$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Is it possible for any group of people to choose a positive integer $N$ and assign a positive integer to each person in the group such that the product of two persons' numbers is divisible by $N$ if and only if they are friends?
|
Answer: Yes, this is always possible.
Consider a graph with a vertex for each person in the group. For each pair of friends we join the corresponding vertices by a red edge. If a pair are not friends, we join their vertices with a blue edge.
Let us label blue edges with different primes $p_{1}, \ldots, p_{k}$. To a vertex $A$ we assign the number $n(A)=\frac{P^{2}}{P(A)}$, where $P=$ $p_{1} p_{2} \ldots p_{k}$, and $P(A)$ is the product of the primes on all blue edges starting from $A$ (for the empty set the product of all its elements equals 1). Now take $N=P^{3}$.
Let us check that all conditions are satisfied. If vertices $A$ and $B$ are connected by a red edge, then $P(A)$ and $P(B)$ are coprime, hence $P(A) P(B) \mid P$ and $P^{3} \left\lvert\, n(A) n(B)=\frac{P^{4}}{P(A) P(B)}\right.$. If vertices $A$ and $B$ are connected by a blue edge labelled with a prime $q$, then $q^{2}$ divides neither $n(A)$ nor $n(B)$. Hence $q^{3}$ does not divide $n(A) n(B)$.
|
{
"exam": "BalticWay",
"problem_label": "16",
"problem_match": "\nProblem 16.",
"resource_path": "BalticWay/segmented/en-bw17sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2017"
}
|
Determine whether the equation
$$
x^{4}+y^{3}=z !+7
$$
has an infinite number of solutions in positive integers.
|
We consider the equation modulo 13 since both 3 and 4 divides $12=13-1$. Now $x^{4} \bmod 13 \in\{0,1,3,9\}$ and $y^{3} \bmod 13 \in$ $\{0,1,5,8,12\}$. We can verify that $x^{4}+y^{3} \not \equiv 7 \bmod 13$. However $z !+7 \equiv 7 \bmod 13$ if $z \geq 13$, what leads to a conclusion that this equation has no solutions with $z \geq 13$, what proves that it has finite number of solutions.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Determine whether the equation
$$
x^{4}+y^{3}=z !+7
$$
has an infinite number of solutions in positive integers.
|
We consider the equation modulo 13 since both 3 and 4 divides $12=13-1$. Now $x^{4} \bmod 13 \in\{0,1,3,9\}$ and $y^{3} \bmod 13 \in$ $\{0,1,5,8,12\}$. We can verify that $x^{4}+y^{3} \not \equiv 7 \bmod 13$. However $z !+7 \equiv 7 \bmod 13$ if $z \geq 13$, what leads to a conclusion that this equation has no solutions with $z \geq 13$, what proves that it has finite number of solutions.
|
{
"exam": "BalticWay",
"problem_label": "17",
"problem_match": "\nProblem 17.",
"resource_path": "BalticWay/segmented/en-bw17sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2017"
}
|
Let $p>3$ be a prime and let $a_{1}, a_{2}, \ldots, a_{\frac{p-1}{2}}$ be a permutation of $1,2, \ldots, \frac{p-1}{2}$. For which $p$ is it always possible to determine the sequence $a_{1}, a_{2}, \ldots, a_{\frac{p-1}{2}}$ if for all $i, j \in\left\{1,2, \ldots, \frac{p-1}{2}\right\}$ with $i \neq j$ the residue of $a_{i} a_{j}$ modulo $p$ is known?
|
Answer: For all primes $p>5$.
When $p=5$ it is clear that it is not possible to determine $a_{1}$ and $a_{2}$ from the residue of $a_{1} a_{2}$ modulo 5 .
Assume that $p>5$. Now $\frac{p-1}{2} \geq 3$. For all $i \in\left\{1,2, \ldots, \frac{p-1}{2}\right\}$ it is possible to choose $j, k \in\left\{1,2, \ldots, \frac{p-1}{2}\right\}$ such that $i, j$ and $k$ are different. Thus we know
$$
a_{i}^{2} \equiv\left(a_{i} a_{j}\right)\left(a_{i} a_{k}\right)\left(a_{j} a_{k}\right)^{-1}(\bmod p) .
$$
The equation $x^{2} \equiv a(\bmod p)$ has exactly one solution in $\left\{1,2, \ldots, \frac{p-1}{2}\right\}$, and hence it is possible to determine $a_{i}$ for all $i$.
|
For all primes p>5
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $p>3$ be a prime and let $a_{1}, a_{2}, \ldots, a_{\frac{p-1}{2}}$ be a permutation of $1,2, \ldots, \frac{p-1}{2}$. For which $p$ is it always possible to determine the sequence $a_{1}, a_{2}, \ldots, a_{\frac{p-1}{2}}$ if for all $i, j \in\left\{1,2, \ldots, \frac{p-1}{2}\right\}$ with $i \neq j$ the residue of $a_{i} a_{j}$ modulo $p$ is known?
|
Answer: For all primes $p>5$.
When $p=5$ it is clear that it is not possible to determine $a_{1}$ and $a_{2}$ from the residue of $a_{1} a_{2}$ modulo 5 .
Assume that $p>5$. Now $\frac{p-1}{2} \geq 3$. For all $i \in\left\{1,2, \ldots, \frac{p-1}{2}\right\}$ it is possible to choose $j, k \in\left\{1,2, \ldots, \frac{p-1}{2}\right\}$ such that $i, j$ and $k$ are different. Thus we know
$$
a_{i}^{2} \equiv\left(a_{i} a_{j}\right)\left(a_{i} a_{k}\right)\left(a_{j} a_{k}\right)^{-1}(\bmod p) .
$$
The equation $x^{2} \equiv a(\bmod p)$ has exactly one solution in $\left\{1,2, \ldots, \frac{p-1}{2}\right\}$, and hence it is possible to determine $a_{i}$ for all $i$.
|
{
"exam": "BalticWay",
"problem_label": "18",
"problem_match": "\nProblem 18.",
"resource_path": "BalticWay/segmented/en-bw17sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2017"
}
|
For an integer $n \geq 1$ let $a(n)$ denote the total number of carries which arise when adding 2017 and $n \cdot 2017$. The first few values are given by $a(1)=1, a(2)=1, a(3)=0$, which can be seen from the following:
| 001 | 001 | 000 |
| :---: | :---: | :---: |
| 2017 | 4034 | 6051 |
| +2017 | +2017 | +2017 |
| $=4034$ | $=6051$ | $=8068$ |
Prove that
$$
a(1)+a(2)+\ldots+a\left(10^{2017}-2\right)+a\left(10^{2017}-1\right)=10 \cdot \frac{10^{2017}-1}{9}
$$
|
Let $k(m)$ be the residue of $m$ when divided by $10^{k}$. There is a carry at the digit representing $10^{k}$ exactly when $k(2017)+k(n \cdot 2017)>10^{k}$. Thus the number of 10-, 100-, 1000- and 10000-carries are, respectively,
$$
\left\lfloor\frac{7 \cdot 10^{2017}}{10}\right\rfloor,\left\lfloor\frac{17 \cdot 10^{2017}}{100}\right\rfloor,\left\lfloor\frac{17 \cdot 10^{2017}}{1000}\right\rfloor,\left\lfloor\frac{2017 \cdot 10^{2017}}{10000}\right\rfloor
$$
and similarly for the rest of the carries. Thus
$$
\begin{aligned}
\sum_{n=1}^{10^{2017}-1} a(n) & =7 \cdot 10^{2016}+17 \cdot 10^{2015}+\ldots+2017+201+20+2 \\
& =(2+0+1+7) \cdot 10^{2016}+(2+0+1+7) \cdot 10^{2015}+\ldots+(2+0+1+7)=10 \cdot \frac{10^{2017}-1}{9}
\end{aligned}
$$
|
10 \cdot \frac{10^{2017}-1}{9}
|
Yes
|
Yes
|
proof
|
Number Theory
|
For an integer $n \geq 1$ let $a(n)$ denote the total number of carries which arise when adding 2017 and $n \cdot 2017$. The first few values are given by $a(1)=1, a(2)=1, a(3)=0$, which can be seen from the following:
| 001 | 001 | 000 |
| :---: | :---: | :---: |
| 2017 | 4034 | 6051 |
| +2017 | +2017 | +2017 |
| $=4034$ | $=6051$ | $=8068$ |
Prove that
$$
a(1)+a(2)+\ldots+a\left(10^{2017}-2\right)+a\left(10^{2017}-1\right)=10 \cdot \frac{10^{2017}-1}{9}
$$
|
Let $k(m)$ be the residue of $m$ when divided by $10^{k}$. There is a carry at the digit representing $10^{k}$ exactly when $k(2017)+k(n \cdot 2017)>10^{k}$. Thus the number of 10-, 100-, 1000- and 10000-carries are, respectively,
$$
\left\lfloor\frac{7 \cdot 10^{2017}}{10}\right\rfloor,\left\lfloor\frac{17 \cdot 10^{2017}}{100}\right\rfloor,\left\lfloor\frac{17 \cdot 10^{2017}}{1000}\right\rfloor,\left\lfloor\frac{2017 \cdot 10^{2017}}{10000}\right\rfloor
$$
and similarly for the rest of the carries. Thus
$$
\begin{aligned}
\sum_{n=1}^{10^{2017}-1} a(n) & =7 \cdot 10^{2016}+17 \cdot 10^{2015}+\ldots+2017+201+20+2 \\
& =(2+0+1+7) \cdot 10^{2016}+(2+0+1+7) \cdot 10^{2015}+\ldots+(2+0+1+7)=10 \cdot \frac{10^{2017}-1}{9}
\end{aligned}
$$
|
{
"exam": "BalticWay",
"problem_label": "19",
"problem_match": "\nProblem 19.",
"resource_path": "BalticWay/segmented/en-bw17sol.jsonl",
"solution_match": "\nSolution 1:",
"tier": "T3",
"year": "2017"
}
|
For an integer $n \geq 1$ let $a(n)$ denote the total number of carries which arise when adding 2017 and $n \cdot 2017$. The first few values are given by $a(1)=1, a(2)=1, a(3)=0$, which can be seen from the following:
| 001 | 001 | 000 |
| :---: | :---: | :---: |
| 2017 | 4034 | 6051 |
| +2017 | +2017 | +2017 |
| $=4034$ | $=6051$ | $=8068$ |
Prove that
$$
a(1)+a(2)+\ldots+a\left(10^{2017}-2\right)+a\left(10^{2017}-1\right)=10 \cdot \frac{10^{2017}-1}{9}
$$
|
Let $s(n)$ denote the digit sum of $n$. Then we claim the following.
Lemma. We have
$$
s(n+m)=s(n)+s(m)-9 a(n, m)
$$
where $a(n, m)$ denotes the total number of carries, which arises when adding $n$ and $m$.
Proof: We proceed by induction on the maximal number of digits $k$ of $n$ and $m$.
If both $n$ and $m$ are single digit numbers then we have just two cases. If $n+m<10$, then we have no carries and clearly $s(n+m)=n+m=s(n)+s(m)$. If on the other hand $n+m=10+k \geq 10$, then
$$
s(n+m)=1+k=1+(n+m-10)=s(n)+s(m)-9
$$
Assume that the claim holds for all pair with at most $k$ digits each. Let $n=n_{1}+a \cdot 10^{k+1}$ and $m=m_{1}+b \cdot 10^{k+1}$ where $n_{1}$ og $m_{1}$ are at most $k$ digit numbers. If there is no carry at the $k+1$ th digit, then $a(n, m)=a\left(n_{1}, m_{1}\right)$ and thus
$$
\begin{gathered}
s(n+m)=s\left(n_{1}+m_{1}\right)+a+b \\
=s\left(n_{1}\right)+a+s\left(m_{1}\right)+b-9 a\left(n_{1}, m_{1}\right)=s(n)+s(m)-9 a(n, m)
\end{gathered}
$$
If there is a carry then $a(n, m)=1+a\left(n_{1}, m_{1}\right)$ and thus
$$
s(n+m)=s\left(n_{1}+m_{1}\right)+a+b-9
$$
$$
=s\left(n_{1}\right)+a+s\left(m_{1}\right)+b-9\left(a\left(n_{1}, m_{1}\right)+1\right)=s(n)+s(m)-9 a(n, m)
$$
This finishes the induction and we are done.
Now observe that $s\left(2017 \cdot 10^{2017}\right)=2+1+7=10$. We now use (1) a total of $10^{2017}-1$ times which yields
$$
\begin{aligned}
10 & =s\left(2017 \cdot 10^{2017}\right)=s\left(2017 \cdot\left(10^{2017}-1\right)+2017\right) \\
& =s\left(2017 \cdot\left(10^{2017}-1\right)\right)+s(2017)-9 \cdot a\left(10^{2017}-1\right) \\
& \vdots \\
& =s(2017)+s(2017) \cdot\left(10^{2017}-1\right)-9 \cdot \sum_{n=1}^{10^{2017}-1} a(n) \\
& =10 \cdot 10^{2017}-9 \cdot \sum_{n=1}^{10^{2017}-1} a(n)
\end{aligned}
$$
Thus we arrive at
$$
\sum_{n=1}^{10^{2017}-1} a(n)=10 \cdot \frac{10^{2017}-1}{9}
$$
|
10 \cdot \frac{10^{2017}-1}{9}
|
Yes
|
Yes
|
proof
|
Number Theory
|
For an integer $n \geq 1$ let $a(n)$ denote the total number of carries which arise when adding 2017 and $n \cdot 2017$. The first few values are given by $a(1)=1, a(2)=1, a(3)=0$, which can be seen from the following:
| 001 | 001 | 000 |
| :---: | :---: | :---: |
| 2017 | 4034 | 6051 |
| +2017 | +2017 | +2017 |
| $=4034$ | $=6051$ | $=8068$ |
Prove that
$$
a(1)+a(2)+\ldots+a\left(10^{2017}-2\right)+a\left(10^{2017}-1\right)=10 \cdot \frac{10^{2017}-1}{9}
$$
|
Let $s(n)$ denote the digit sum of $n$. Then we claim the following.
Lemma. We have
$$
s(n+m)=s(n)+s(m)-9 a(n, m)
$$
where $a(n, m)$ denotes the total number of carries, which arises when adding $n$ and $m$.
Proof: We proceed by induction on the maximal number of digits $k$ of $n$ and $m$.
If both $n$ and $m$ are single digit numbers then we have just two cases. If $n+m<10$, then we have no carries and clearly $s(n+m)=n+m=s(n)+s(m)$. If on the other hand $n+m=10+k \geq 10$, then
$$
s(n+m)=1+k=1+(n+m-10)=s(n)+s(m)-9
$$
Assume that the claim holds for all pair with at most $k$ digits each. Let $n=n_{1}+a \cdot 10^{k+1}$ and $m=m_{1}+b \cdot 10^{k+1}$ where $n_{1}$ og $m_{1}$ are at most $k$ digit numbers. If there is no carry at the $k+1$ th digit, then $a(n, m)=a\left(n_{1}, m_{1}\right)$ and thus
$$
\begin{gathered}
s(n+m)=s\left(n_{1}+m_{1}\right)+a+b \\
=s\left(n_{1}\right)+a+s\left(m_{1}\right)+b-9 a\left(n_{1}, m_{1}\right)=s(n)+s(m)-9 a(n, m)
\end{gathered}
$$
If there is a carry then $a(n, m)=1+a\left(n_{1}, m_{1}\right)$ and thus
$$
s(n+m)=s\left(n_{1}+m_{1}\right)+a+b-9
$$
$$
=s\left(n_{1}\right)+a+s\left(m_{1}\right)+b-9\left(a\left(n_{1}, m_{1}\right)+1\right)=s(n)+s(m)-9 a(n, m)
$$
This finishes the induction and we are done.
Now observe that $s\left(2017 \cdot 10^{2017}\right)=2+1+7=10$. We now use (1) a total of $10^{2017}-1$ times which yields
$$
\begin{aligned}
10 & =s\left(2017 \cdot 10^{2017}\right)=s\left(2017 \cdot\left(10^{2017}-1\right)+2017\right) \\
& =s\left(2017 \cdot\left(10^{2017}-1\right)\right)+s(2017)-9 \cdot a\left(10^{2017}-1\right) \\
& \vdots \\
& =s(2017)+s(2017) \cdot\left(10^{2017}-1\right)-9 \cdot \sum_{n=1}^{10^{2017}-1} a(n) \\
& =10 \cdot 10^{2017}-9 \cdot \sum_{n=1}^{10^{2017}-1} a(n)
\end{aligned}
$$
Thus we arrive at
$$
\sum_{n=1}^{10^{2017}-1} a(n)=10 \cdot \frac{10^{2017}-1}{9}
$$
|
{
"exam": "BalticWay",
"problem_label": "19",
"problem_match": "\nProblem 19.",
"resource_path": "BalticWay/segmented/en-bw17sol.jsonl",
"solution_match": "\nSolution 2:",
"tier": "T3",
"year": "2017"
}
|
Let $S$ be the set of all ordered pairs $(a, b)$ of integers with $0<2 a<2 b<2017$ such that $a^{2}+b^{2}$ is a multiple of 2017. Prove that
$$
\sum_{(a, b) \in S} a=\frac{1}{2} \sum_{(a, b) \in S} b
$$
|
Let $A=\{a:(a, b) \in S\}$ and $B=\{b:(a, b) \in S\}$. The claim is equivalent to
$$
2 \sum_{a \in A} a=\sum_{b \in B} b
$$
Assume that for some $x, y, z \in\{1,2, \ldots, 1008\}$ both, $x^{2}+y^{2}$ and $x^{2}+z^{2}$, are multiples of 2017. By
$$
\left(x^{2}+y^{2}\right)-\left(x^{2}+z^{2}\right)=y^{2}-z^{2}=(y+z)(y-z) \equiv 0(\bmod 2017),
$$
$0<y+z<2017$ and the fact that 2017 is a prime number, it follows that $y=z$. Hence, $A$ and $B$ are disjoint, and there is a bijection $f: A \mapsto B$ such that for any $a \in A$ and $b \in B$ the pair $(a, b)$ is in $S$ if and only if $b=f(a)$.
We show that the mapping $g$ defined by $g(a)=f(a)-a$ for $a \in A$ is a bijection from $A$ to $A$. Then (2) follows by
$$
\sum_{a \in A} a=\sum_{a \in A} g(a)=\sum_{a \in A} f(a)-\sum_{a \in A} a=\sum_{b \in B} b-\sum_{a \in A} a
$$
Let $a \in A$, and let $h(a)=\min \{a+f(a), 2017-(a+f(a))\}$. Then $0<2 h(a)<2017$ and, by the definition of $g, 0<2 g(a)<$ 2017. Furthermore,
$$
g(a)^{2}+h(a)^{2} \equiv(a-f(a))^{2}+(a+f(a))^{2} \equiv 2\left(a^{2}+f(a)^{2}\right) \equiv 0(\bmod 2017) .
$$
If $a+f(a) \leq 1008$, then $g(a)=f(a)-a<f(a)+a=h(a)$. If $a+f(a)>1008$, then $g(a)=f(a)-a<(f(a)-a)+(2017-2 f(a))=$ $2017-(a+f(a))=h(a)$. Consequently, $g(a) \in A$ with $f(g(a))=h(a)$.
It remains to show that $g$ is injective. Assume that $g\left(a_{1}\right)=g\left(a_{2}\right)$ for some $a_{1}, a_{2} \in A$, i.e.,
$$
b_{1}-a_{1}=b_{2}-a_{2},
$$
where $b_{i}=f\left(a_{i}\right)$ for $i=1,2$. Clearly, we also have $h\left(a_{1}\right)=h\left(a_{2}\right)$ then. If $h\left(a_{1}\right)=a_{1}+b_{1}$ and $h\left(a_{2}\right)=a_{2}+b_{2}$, then subtracting (3) from $a_{1}+b_{1}=a_{2}+b_{2}$ gives $a_{1}=a_{2}$. Similarly, if $h_{1}\left(a_{1}\right)=2017-\left(a_{1}+b_{1}\right)$ and $h_{2}=2017-\left(a_{2}+b_{2}\right)$, then we obtain $a_{1}=a_{2}$. Finally, if $h\left(a_{1}\right)=a_{1}+b_{1}$ and $h_{2}=2017-\left(a_{2}+b_{2}\right)$, then $2\left(a_{1}+b_{2}\right)=2017$, a contradiction.
Remark: The proof as given above obviously works for any prime congruent to 1 modulo 4 in the place of 2017. With a little more effort, one can show that the statement is true for any positive odd $n$ (vacuously, if $n$ has a prime factor congruent to 3 modulo 4).
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $S$ be the set of all ordered pairs $(a, b)$ of integers with $0<2 a<2 b<2017$ such that $a^{2}+b^{2}$ is a multiple of 2017. Prove that
$$
\sum_{(a, b) \in S} a=\frac{1}{2} \sum_{(a, b) \in S} b
$$
|
Let $A=\{a:(a, b) \in S\}$ and $B=\{b:(a, b) \in S\}$. The claim is equivalent to
$$
2 \sum_{a \in A} a=\sum_{b \in B} b
$$
Assume that for some $x, y, z \in\{1,2, \ldots, 1008\}$ both, $x^{2}+y^{2}$ and $x^{2}+z^{2}$, are multiples of 2017. By
$$
\left(x^{2}+y^{2}\right)-\left(x^{2}+z^{2}\right)=y^{2}-z^{2}=(y+z)(y-z) \equiv 0(\bmod 2017),
$$
$0<y+z<2017$ and the fact that 2017 is a prime number, it follows that $y=z$. Hence, $A$ and $B$ are disjoint, and there is a bijection $f: A \mapsto B$ such that for any $a \in A$ and $b \in B$ the pair $(a, b)$ is in $S$ if and only if $b=f(a)$.
We show that the mapping $g$ defined by $g(a)=f(a)-a$ for $a \in A$ is a bijection from $A$ to $A$. Then (2) follows by
$$
\sum_{a \in A} a=\sum_{a \in A} g(a)=\sum_{a \in A} f(a)-\sum_{a \in A} a=\sum_{b \in B} b-\sum_{a \in A} a
$$
Let $a \in A$, and let $h(a)=\min \{a+f(a), 2017-(a+f(a))\}$. Then $0<2 h(a)<2017$ and, by the definition of $g, 0<2 g(a)<$ 2017. Furthermore,
$$
g(a)^{2}+h(a)^{2} \equiv(a-f(a))^{2}+(a+f(a))^{2} \equiv 2\left(a^{2}+f(a)^{2}\right) \equiv 0(\bmod 2017) .
$$
If $a+f(a) \leq 1008$, then $g(a)=f(a)-a<f(a)+a=h(a)$. If $a+f(a)>1008$, then $g(a)=f(a)-a<(f(a)-a)+(2017-2 f(a))=$ $2017-(a+f(a))=h(a)$. Consequently, $g(a) \in A$ with $f(g(a))=h(a)$.
It remains to show that $g$ is injective. Assume that $g\left(a_{1}\right)=g\left(a_{2}\right)$ for some $a_{1}, a_{2} \in A$, i.e.,
$$
b_{1}-a_{1}=b_{2}-a_{2},
$$
where $b_{i}=f\left(a_{i}\right)$ for $i=1,2$. Clearly, we also have $h\left(a_{1}\right)=h\left(a_{2}\right)$ then. If $h\left(a_{1}\right)=a_{1}+b_{1}$ and $h\left(a_{2}\right)=a_{2}+b_{2}$, then subtracting (3) from $a_{1}+b_{1}=a_{2}+b_{2}$ gives $a_{1}=a_{2}$. Similarly, if $h_{1}\left(a_{1}\right)=2017-\left(a_{1}+b_{1}\right)$ and $h_{2}=2017-\left(a_{2}+b_{2}\right)$, then we obtain $a_{1}=a_{2}$. Finally, if $h\left(a_{1}\right)=a_{1}+b_{1}$ and $h_{2}=2017-\left(a_{2}+b_{2}\right)$, then $2\left(a_{1}+b_{2}\right)=2017$, a contradiction.
Remark: The proof as given above obviously works for any prime congruent to 1 modulo 4 in the place of 2017. With a little more effort, one can show that the statement is true for any positive odd $n$ (vacuously, if $n$ has a prime factor congruent to 3 modulo 4).
|
{
"exam": "BalticWay",
"problem_label": "20",
"problem_match": "\nProblem 20.",
"resource_path": "BalticWay/segmented/en-bw17sol.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2017"
}
|
A finite collection of positive real numbers (not necessarily distinct) is balanced if each number is less than the sum of the others. Find all $m \geq 3$ such that every balanced finite collection of $m$ numbers can be split into three parts with the property that the sum of the numbers in each part is less than the sum of the numbers in the two other parts.
|
Answer: The partition is always possible precisely when $m \neq 4$.
For $m=3$ it is trivially possible, and for $m=4$ the four equal numbers $g, g, g, g$ provide a counter-example. Henceforth, we assume $m \geq 5$.
Among all possible partitions $A \sqcup B \sqcup C=\{1, \ldots, m\}$ such that
$$
S_{A} \leq S_{B} \leq S_{C},
$$
select one for which the difference $S_{C}-S_{A}$ is minimal. If there are several such, select one so as to maximise the number of elements in $C$. We will show that $S_{C}<S_{A}+S_{B}$, which is clearly sufficient.
If $C$ consists of a single element, this number is by assumption less than the sum of the remaining ones, hence $S_{C}<S_{A}+S_{B}$ holds true.
Suppose now $C$ contains at least two elements, and let $g_{c}$ be a minimal number indexed by a $c \in C$. We have the inequality
$$
S_{C}-S_{A} \leq g_{c} \leq \frac{1}{2} S_{C}
$$
The first is by the minimality of $S_{C}-S_{A}$, the second by the minimality of $g_{c}$. These two inequalities together yield
$$
S_{A}+S_{B} \geq 2 S_{A} \geq 2\left(S_{C}-g_{c}\right) \geq S_{C}
$$
If either of these inequalities is strict, we are finished.
Hence suppose all inequalities are in fact equalities, so that
$$
S_{A}=S_{B}=\frac{1}{2} S_{C}=g_{c}
$$
It follows that $C=\{c, d\}$, where $g_{d}=g_{c}$. If $A$ contained more than one element, we could increase the number of elements in $C$ by creating instead a partition
$$
\{1, \ldots, m\}=\{c\} \sqcup B \sqcup(A \cup\{d\}),
$$
resulting in the same sums. A similar procedure applies to $B$. Consequently, $A$ and $B$ must be singleton sets, whence
$$
m=|A|+|B|+|C|=4 \text {. }
$$
|
m \neq 4
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A finite collection of positive real numbers (not necessarily distinct) is balanced if each number is less than the sum of the others. Find all $m \geq 3$ such that every balanced finite collection of $m$ numbers can be split into three parts with the property that the sum of the numbers in each part is less than the sum of the numbers in the two other parts.
|
Answer: The partition is always possible precisely when $m \neq 4$.
For $m=3$ it is trivially possible, and for $m=4$ the four equal numbers $g, g, g, g$ provide a counter-example. Henceforth, we assume $m \geq 5$.
Among all possible partitions $A \sqcup B \sqcup C=\{1, \ldots, m\}$ such that
$$
S_{A} \leq S_{B} \leq S_{C},
$$
select one for which the difference $S_{C}-S_{A}$ is minimal. If there are several such, select one so as to maximise the number of elements in $C$. We will show that $S_{C}<S_{A}+S_{B}$, which is clearly sufficient.
If $C$ consists of a single element, this number is by assumption less than the sum of the remaining ones, hence $S_{C}<S_{A}+S_{B}$ holds true.
Suppose now $C$ contains at least two elements, and let $g_{c}$ be a minimal number indexed by a $c \in C$. We have the inequality
$$
S_{C}-S_{A} \leq g_{c} \leq \frac{1}{2} S_{C}
$$
The first is by the minimality of $S_{C}-S_{A}$, the second by the minimality of $g_{c}$. These two inequalities together yield
$$
S_{A}+S_{B} \geq 2 S_{A} \geq 2\left(S_{C}-g_{c}\right) \geq S_{C}
$$
If either of these inequalities is strict, we are finished.
Hence suppose all inequalities are in fact equalities, so that
$$
S_{A}=S_{B}=\frac{1}{2} S_{C}=g_{c}
$$
It follows that $C=\{c, d\}$, where $g_{d}=g_{c}$. If $A$ contained more than one element, we could increase the number of elements in $C$ by creating instead a partition
$$
\{1, \ldots, m\}=\{c\} \sqcup B \sqcup(A \cup\{d\}),
$$
resulting in the same sums. A similar procedure applies to $B$. Consequently, $A$ and $B$ must be singleton sets, whence
$$
m=|A|+|B|+|C|=4 \text {. }
$$
|
{
"exam": "BalticWay",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "BalticWay/segmented/en-bw18sol.jsonl",
"solution_match": "# Solution.",
"tier": "T3",
"year": "2018"
}
|
A $100 \times 100$ table is given. For each $k, 1 \leq k \leq 100$, the $k$-th row of the table contains the numbers $1,2, \ldots, k$ in increasing order (from left to right) but not necessarily in consecutive cells; the remaining $100-k$ cells are filled with zeroes. Prove that there exist two columns such that the sum of the numbers in one of the columns is at least 19 times as large as the sum of the numbers in the other column.
|
Observe that the sum of numbers in the first column is at most $1 \cdot 100=100$, the sum in the first and second columns is at most $1 \cdot 100+2 \cdot 99$, the sum in the first, second and third columns is at most $1 \cdot 100+2 \cdot 99+3 \cdot 98$, etc. But the sum of all nonzero numbers equals $\sum_{i=1}^{100} i(101-i)$, therefore the sum in the columns from $31^{\text {th }}$ to $100^{\text {th }}$ is at least
$$
\sum_{i=31}^{100} i(101-i)=\sum_{i=1}^{70} i(101-i)=101 \sum_{i=1}^{70} i-\sum_{i=1}^{70} i^{2}=35 \cdot 71(101-141 / 3)=70 \cdot 27 \cdot 71 .
$$
Therefore one of these columns has a sum at least $27 \cdot 71=1917$. Therefore the ratio of sums in this column and in the first one is more that 19.
|
1917
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A $100 \times 100$ table is given. For each $k, 1 \leq k \leq 100$, the $k$-th row of the table contains the numbers $1,2, \ldots, k$ in increasing order (from left to right) but not necessarily in consecutive cells; the remaining $100-k$ cells are filled with zeroes. Prove that there exist two columns such that the sum of the numbers in one of the columns is at least 19 times as large as the sum of the numbers in the other column.
|
Observe that the sum of numbers in the first column is at most $1 \cdot 100=100$, the sum in the first and second columns is at most $1 \cdot 100+2 \cdot 99$, the sum in the first, second and third columns is at most $1 \cdot 100+2 \cdot 99+3 \cdot 98$, etc. But the sum of all nonzero numbers equals $\sum_{i=1}^{100} i(101-i)$, therefore the sum in the columns from $31^{\text {th }}$ to $100^{\text {th }}$ is at least
$$
\sum_{i=31}^{100} i(101-i)=\sum_{i=1}^{70} i(101-i)=101 \sum_{i=1}^{70} i-\sum_{i=1}^{70} i^{2}=35 \cdot 71(101-141 / 3)=70 \cdot 27 \cdot 71 .
$$
Therefore one of these columns has a sum at least $27 \cdot 71=1917$. Therefore the ratio of sums in this column and in the first one is more that 19.
|
{
"exam": "BalticWay",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "BalticWay/segmented/en-bw18sol.jsonl",
"solution_match": "# Solution.",
"tier": "T3",
"year": "2018"
}
|
Let $a, b, c, d$ be positive real numbers such that $a b c d=1$. Prove the inequality
$$
\frac{1}{\sqrt{a+2 b+3 c+10}}+\frac{1}{\sqrt{b+2 c+3 d+10}}+\frac{1}{\sqrt{c+2 d+3 a+10}}+\frac{1}{\sqrt{d+2 a+3 b+10}} \leq 1 .
$$
|
Let $x, y, z, t$ be positive numbers such that $a=x^{4}, b=y^{4}, c=z^{4}, d=t^{4}$.
By AM-GM ineguality $x^{4}+y^{4}+z^{4}+1 \geq 4 x y z, y^{4}+z^{4}+1+1 \geq 4 y z$ and $z^{4}+1+1+1 \geq 4 z$. Therefore we have the following estimation for the first fraction
$$
\frac{1}{\sqrt{x^{4}+2 y^{4}+3 z^{4}+10}} \leq \frac{1}{\sqrt{4 x y z+4 y z+4 z+4}}=\frac{1}{2 \sqrt{x y z+y z+z+1}} .
$$
Transform analogous estimations for the other fractions:
$$
\begin{aligned}
& \frac{1}{\sqrt{b+2 c+3 d+10}} \leq \frac{1}{2 \sqrt{y z t+z t+t+1}}=\frac{1}{2 \sqrt{t} \sqrt{y z+z+1+x y z}}=\frac{\sqrt{x y z}}{2 \sqrt{x y z+y z+z+1}} \\
& \frac{1}{\sqrt{c+2 d+3 a+10}} \leq \frac{1}{2 \sqrt{z t x+t x+x+1}}=\frac{\sqrt{y z}}{2 \sqrt{t x} \sqrt{z+1+x y z+y z}}=\frac{1}{2 \sqrt{x y z+y z+z+1}} \\
& \frac{1}{\sqrt{d+2 a+3 b+10}} \leq \frac{1}{2 \sqrt{t x y+x y+y+1}}=\frac{\sqrt{z}}{2 \sqrt{t x y} \sqrt{1+x y z+y z+z}}=\frac{1}{2 \sqrt{x y z+y z+z+1}}
\end{aligned}
$$
Thus, the sum does not exceed
$$
\frac{1+\sqrt{x y z}+\sqrt{y z}+\sqrt{z}}{2 \sqrt{x y z+y z+z+1}} .
$$
It remains to apply inequality $\sqrt{\alpha}+\sqrt{\beta}+\sqrt{\gamma}+\sqrt{\delta} \leq 2 \sqrt{\alpha+\beta+\gamma+\delta}$, which can be easily proven by taking squares or derived from inequality between arithmetical and quadratic means.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c, d$ be positive real numbers such that $a b c d=1$. Prove the inequality
$$
\frac{1}{\sqrt{a+2 b+3 c+10}}+\frac{1}{\sqrt{b+2 c+3 d+10}}+\frac{1}{\sqrt{c+2 d+3 a+10}}+\frac{1}{\sqrt{d+2 a+3 b+10}} \leq 1 .
$$
|
Let $x, y, z, t$ be positive numbers such that $a=x^{4}, b=y^{4}, c=z^{4}, d=t^{4}$.
By AM-GM ineguality $x^{4}+y^{4}+z^{4}+1 \geq 4 x y z, y^{4}+z^{4}+1+1 \geq 4 y z$ and $z^{4}+1+1+1 \geq 4 z$. Therefore we have the following estimation for the first fraction
$$
\frac{1}{\sqrt{x^{4}+2 y^{4}+3 z^{4}+10}} \leq \frac{1}{\sqrt{4 x y z+4 y z+4 z+4}}=\frac{1}{2 \sqrt{x y z+y z+z+1}} .
$$
Transform analogous estimations for the other fractions:
$$
\begin{aligned}
& \frac{1}{\sqrt{b+2 c+3 d+10}} \leq \frac{1}{2 \sqrt{y z t+z t+t+1}}=\frac{1}{2 \sqrt{t} \sqrt{y z+z+1+x y z}}=\frac{\sqrt{x y z}}{2 \sqrt{x y z+y z+z+1}} \\
& \frac{1}{\sqrt{c+2 d+3 a+10}} \leq \frac{1}{2 \sqrt{z t x+t x+x+1}}=\frac{\sqrt{y z}}{2 \sqrt{t x} \sqrt{z+1+x y z+y z}}=\frac{1}{2 \sqrt{x y z+y z+z+1}} \\
& \frac{1}{\sqrt{d+2 a+3 b+10}} \leq \frac{1}{2 \sqrt{t x y+x y+y+1}}=\frac{\sqrt{z}}{2 \sqrt{t x y} \sqrt{1+x y z+y z+z}}=\frac{1}{2 \sqrt{x y z+y z+z+1}}
\end{aligned}
$$
Thus, the sum does not exceed
$$
\frac{1+\sqrt{x y z}+\sqrt{y z}+\sqrt{z}}{2 \sqrt{x y z+y z+z+1}} .
$$
It remains to apply inequality $\sqrt{\alpha}+\sqrt{\beta}+\sqrt{\gamma}+\sqrt{\delta} \leq 2 \sqrt{\alpha+\beta+\gamma+\delta}$, which can be easily proven by taking squares or derived from inequality between arithmetical and quadratic means.
|
{
"exam": "BalticWay",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "BalticWay/segmented/en-bw18sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2018"
}
|
Find all functions $f:[0,+\infty) \rightarrow[0,+\infty)$, such that for any positive integer $n$ and for any non-negative real numbers $x_{1}, \ldots, x_{n}$
$$
f\left(x_{1}^{2}+\cdots+x_{n}^{2}\right)=f\left(x_{1}\right)^{2}+\cdots+f\left(x_{n}\right)^{2} .
$$
|
Answer: the functions $f(x)=0$ and $f(x)=x$.
A first observation is that
$$
f(1)=f\left(1^{2}\right)=f(1)^{2}
$$
so that $f(1)$ is either 0 or 1 .
Assume first that $f(1)=0$. For each positive integer $n$, we find
$$
f(n)=f\left(n \cdot 1^{2}\right)=n f(1)^{2}=0 .
$$
Given an arbitrary $x$, find $y$ so that $x^{2}+y^{2}$ becomes a positive integer $n$. Then
$$
f(x)^{2}+f(y)^{2}=f\left(x^{2}+y^{2}\right)=f(n)=0 .
$$
Consequently, $f(x)=0$ for all $x$.
Now assume $f(1)=1$. We shall prove that $f(x)=x$ for all $x$. For each positive integer $n$, we find
$$
f(n)=f\left(n \cdot 1^{2}\right)=n f(1)^{2}=n .
$$
For a non-negative rational number $\frac{p}{q}$, we find
$$
p^{2}=f\left(p^{2}\right)=f\left(q^{2} \cdot\left(\frac{p}{q}\right)^{2}\right)=q^{2} f\left(\frac{p}{q}\right)^{2}
$$
hence $f(x)=x$ also for rational numbers.
Finally, let $x$ be an irrational number. Select a rational number $\frac{p}{q}>x$. Choosing $y$ so that $x^{2}+y^{2}=\frac{p^{2}}{q^{2}}$, we deduce
$$
\frac{p^{2}}{q^{2}}=f\left(\frac{p^{2}}{q^{2}}\right)=f\left(x^{2}+y^{2}\right)=f(x)^{2}+f(y)^{2} \geq f(x)^{2}
$$
hence $f(x) \leq \frac{p}{q}$. Next, select a (positive) rational number $\frac{r}{s}<\sqrt{x}$, i.e. $\frac{r^{2}}{s^{2}}<x$. Choosing $z$ so that $\frac{r^{2}}{s^{2}}+z^{2}=x$, we deduce
$$
f(x)=f\left(\frac{r^{2}}{s^{2}}+z^{2}\right)=f\left(\frac{r}{s}\right)^{2}+f(z)^{2}=\frac{r^{2}}{s^{2}}+f(z)^{2} \geq \frac{r^{2}}{s^{2}}
$$
hence $f(x) \geq \frac{r^{2}}{s^{2}}$. Together, these two bounds for $f(x)$ imply $f(x)=x$, and we are finished.
Remark of the Problem committee. The main part of this solution is the proof of well known fact that if an additive function is non negative (for non negative arguments) then it is linear.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all functions $f:[0,+\infty) \rightarrow[0,+\infty)$, such that for any positive integer $n$ and for any non-negative real numbers $x_{1}, \ldots, x_{n}$
$$
f\left(x_{1}^{2}+\cdots+x_{n}^{2}\right)=f\left(x_{1}\right)^{2}+\cdots+f\left(x_{n}\right)^{2} .
$$
|
Answer: the functions $f(x)=0$ and $f(x)=x$.
A first observation is that
$$
f(1)=f\left(1^{2}\right)=f(1)^{2}
$$
so that $f(1)$ is either 0 or 1 .
Assume first that $f(1)=0$. For each positive integer $n$, we find
$$
f(n)=f\left(n \cdot 1^{2}\right)=n f(1)^{2}=0 .
$$
Given an arbitrary $x$, find $y$ so that $x^{2}+y^{2}$ becomes a positive integer $n$. Then
$$
f(x)^{2}+f(y)^{2}=f\left(x^{2}+y^{2}\right)=f(n)=0 .
$$
Consequently, $f(x)=0$ for all $x$.
Now assume $f(1)=1$. We shall prove that $f(x)=x$ for all $x$. For each positive integer $n$, we find
$$
f(n)=f\left(n \cdot 1^{2}\right)=n f(1)^{2}=n .
$$
For a non-negative rational number $\frac{p}{q}$, we find
$$
p^{2}=f\left(p^{2}\right)=f\left(q^{2} \cdot\left(\frac{p}{q}\right)^{2}\right)=q^{2} f\left(\frac{p}{q}\right)^{2}
$$
hence $f(x)=x$ also for rational numbers.
Finally, let $x$ be an irrational number. Select a rational number $\frac{p}{q}>x$. Choosing $y$ so that $x^{2}+y^{2}=\frac{p^{2}}{q^{2}}$, we deduce
$$
\frac{p^{2}}{q^{2}}=f\left(\frac{p^{2}}{q^{2}}\right)=f\left(x^{2}+y^{2}\right)=f(x)^{2}+f(y)^{2} \geq f(x)^{2}
$$
hence $f(x) \leq \frac{p}{q}$. Next, select a (positive) rational number $\frac{r}{s}<\sqrt{x}$, i.e. $\frac{r^{2}}{s^{2}}<x$. Choosing $z$ so that $\frac{r^{2}}{s^{2}}+z^{2}=x$, we deduce
$$
f(x)=f\left(\frac{r^{2}}{s^{2}}+z^{2}\right)=f\left(\frac{r}{s}\right)^{2}+f(z)^{2}=\frac{r^{2}}{s^{2}}+f(z)^{2} \geq \frac{r^{2}}{s^{2}}
$$
hence $f(x) \geq \frac{r^{2}}{s^{2}}$. Together, these two bounds for $f(x)$ imply $f(x)=x$, and we are finished.
Remark of the Problem committee. The main part of this solution is the proof of well known fact that if an additive function is non negative (for non negative arguments) then it is linear.
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "BalticWay/segmented/en-bw18sol.jsonl",
"solution_match": "# Solution.",
"tier": "T3",
"year": "2018"
}
|
A polynomial $f(x)$ with real coefficients is called generating, if for each polynomial $\varphi(x)$ with real coefficients there exist a positive integer $k$ and polynomials $g_{1}(x), \ldots, g_{k}(x)$ with real coefficients such that
$$
\varphi(x)=f\left(g_{1}(x)\right)+\cdots+f\left(g_{k}(x)\right) .
$$
Find all generating polynomials.
|
Answer: the generating polynomials are exactly the polynomials of odd degree.
Take an arbitrary polynomial $f$. We call a polynomial good if it can pe represented as $\sum f\left(g_{i}(x)\right)$ for some polynomials $g_{i}$. It is clear that the sum of good polynomials is good, and if $\phi$ is a good polynomial then each polynomial of the form $\phi(g(x))$ is good also. Therefore for the proof that $f$ is generating it is sufficient to show that $x$ is good polynomial. Consider two cases.
1) Let the degree $n$ of $f$ is odd. Check that $x$ is good polynomial. Observe that by substitutions of the form $f(u x)$ we can obtain a good polynomial $\phi_{n}$ of degree $n$ with leading coefficient 1 , and a good polynomial $\psi_{n}$ of degree $n$ with leading coefficient -1 (because $n$ is odd). Then for each $a$ a polynomial $\phi_{n}(x+a)+\psi_{n}(x)$ is good. It is clear that its coefficient of $x^{n}$ equals 0 ; moreover, by choosing appropriate $a$ we can obtain a good polynomial $\phi_{n-1}$ of degree $n-1$ with leading coefficient 1 , and a good polynomial $\psi_{n-1}$ with leading coefficient -1 . Continuing in this way we will obtain a good poynomial $\phi_{1}(x)=x+c$. Then $\phi_{1}(x-c)=x$ is also good.
2) Let the degree $n$ of $f$ is even. Prove that $f(x)$ is not generating. It follows from the observation that the degree of every good polynomial is even in this case. Indeed, the degree of each polynomial $f\left(g_{i}\right)$ is even and the leading coefficient has the same sign as the leading coefficient of $f$. Therefore the degree of polynomial $\sum f\left(g_{i}(x)\right)$ is even.
## 2 Combinatorics
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
A polynomial $f(x)$ with real coefficients is called generating, if for each polynomial $\varphi(x)$ with real coefficients there exist a positive integer $k$ and polynomials $g_{1}(x), \ldots, g_{k}(x)$ with real coefficients such that
$$
\varphi(x)=f\left(g_{1}(x)\right)+\cdots+f\left(g_{k}(x)\right) .
$$
Find all generating polynomials.
|
Answer: the generating polynomials are exactly the polynomials of odd degree.
Take an arbitrary polynomial $f$. We call a polynomial good if it can pe represented as $\sum f\left(g_{i}(x)\right)$ for some polynomials $g_{i}$. It is clear that the sum of good polynomials is good, and if $\phi$ is a good polynomial then each polynomial of the form $\phi(g(x))$ is good also. Therefore for the proof that $f$ is generating it is sufficient to show that $x$ is good polynomial. Consider two cases.
1) Let the degree $n$ of $f$ is odd. Check that $x$ is good polynomial. Observe that by substitutions of the form $f(u x)$ we can obtain a good polynomial $\phi_{n}$ of degree $n$ with leading coefficient 1 , and a good polynomial $\psi_{n}$ of degree $n$ with leading coefficient -1 (because $n$ is odd). Then for each $a$ a polynomial $\phi_{n}(x+a)+\psi_{n}(x)$ is good. It is clear that its coefficient of $x^{n}$ equals 0 ; moreover, by choosing appropriate $a$ we can obtain a good polynomial $\phi_{n-1}$ of degree $n-1$ with leading coefficient 1 , and a good polynomial $\psi_{n-1}$ with leading coefficient -1 . Continuing in this way we will obtain a good poynomial $\phi_{1}(x)=x+c$. Then $\phi_{1}(x-c)=x$ is also good.
2) Let the degree $n$ of $f$ is even. Prove that $f(x)$ is not generating. It follows from the observation that the degree of every good polynomial is even in this case. Indeed, the degree of each polynomial $f\left(g_{i}\right)$ is even and the leading coefficient has the same sign as the leading coefficient of $f$. Therefore the degree of polynomial $\sum f\left(g_{i}(x)\right)$ is even.
## 2 Combinatorics
|
{
"exam": "BalticWay",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "BalticWay/segmented/en-bw18sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2018"
}
|
Let $n$ be a positive integer. Elfie the Elf travels in $\mathbb{R}^{3}$. She starts at the origin: $(0,0,0)$. In each turn she can teleport to any point with integer coordinates which lies at distance exactly $\sqrt{n}$ from her current location. However, teleportation is a complicated procedure. Elfie starts off normal but she turns strange with her first teleportation. Next time she teleports she becomes normal again, then strange again... etc.
For which $n$ can Elfie travel to any given point with integer coordinates and be normal when she gets there?
|
Answer: there are no such $n$.
We colour all the points in $\mathbb{Z}^{3}$ white and black: The point $(x, y, z)$ is colored white if $x+y+z \equiv_{2} 0$ and black if if $x+y+z \equiv_{2} 1$.
After the first move Elfie is at a point $(a, b, c)$ where $a^{2}+b^{2}+c^{2}=n$. Thus, $a+b+c \equiv_{2}$ $a^{2}+b^{2}+c^{2}=n$.
Now, if $n$ is even then $(a, b, c)$ is white. Thus, in that case Elfie only jumps between white points.
On the other hand, if $n$ is odd, then $(a, b, c)$ is certainly black. And one can easily see that Elfie alternates between black and white squares after each move. But since Elfie is normal after even number of moves, and is then on a white point, she can never reach any black point being normal. Thus, there no $n$ such that Elfie can travel to any given point and be normal when she gets there.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $n$ be a positive integer. Elfie the Elf travels in $\mathbb{R}^{3}$. She starts at the origin: $(0,0,0)$. In each turn she can teleport to any point with integer coordinates which lies at distance exactly $\sqrt{n}$ from her current location. However, teleportation is a complicated procedure. Elfie starts off normal but she turns strange with her first teleportation. Next time she teleports she becomes normal again, then strange again... etc.
For which $n$ can Elfie travel to any given point with integer coordinates and be normal when she gets there?
|
Answer: there are no such $n$.
We colour all the points in $\mathbb{Z}^{3}$ white and black: The point $(x, y, z)$ is colored white if $x+y+z \equiv_{2} 0$ and black if if $x+y+z \equiv_{2} 1$.
After the first move Elfie is at a point $(a, b, c)$ where $a^{2}+b^{2}+c^{2}=n$. Thus, $a+b+c \equiv_{2}$ $a^{2}+b^{2}+c^{2}=n$.
Now, if $n$ is even then $(a, b, c)$ is white. Thus, in that case Elfie only jumps between white points.
On the other hand, if $n$ is odd, then $(a, b, c)$ is certainly black. And one can easily see that Elfie alternates between black and white squares after each move. But since Elfie is normal after even number of moves, and is then on a white point, she can never reach any black point being normal. Thus, there no $n$ such that Elfie can travel to any given point and be normal when she gets there.
|
{
"exam": "BalticWay",
"problem_label": "6",
"problem_match": "\n6.",
"resource_path": "BalticWay/segmented/en-bw18sol.jsonl",
"solution_match": "# Solution.",
"tier": "T3",
"year": "2018"
}
|
On a $16 \times 16$ torus as shown all 512 edges are colored red or blue. A coloring is good if every vertex is an endpoint of an even number of red edges. A move consists of switching the color of each of the 4 edges of an arbitrary cell. What is the largest number of good colorings such that none of them can be converted to another by a sequence of moves?
|
Answer: 4. Representatives of the equivalence classes are: all blue, all blue with one longitudinal red ring, all blue with one transversal red ring, all blue with one longitudinal and one transversal red ring.
First, show that these four classes are non equivalent. Consider any ring transversal or longitudinal and count the number of red edges going out from vertices of this ring in the same halftorus. This number can not be changed mod 2.
Now we show that each configuration can be transformed to one of these four classes. We suggest two independent reasoning.
Scanning of the square.
Cut the torus up in a square $16 \times 16$. In order to restore the initial torus we will identify the opposite sides of the square, but we will do it in the end of solution. Now we will work with the square. It is clear that during all recolorings each vertex of torus has even red degree. The same is true for the degrees of the inner vertices of the $16 \times 16$ square when we deal with it instead of the torus.
Scan all cells of this square one by one from left to right and from bottom to top. For convenience we may think that in each moment the scanned area is colored grey. First we take bottom left corner cell ( $a 1$ in chess notations) and color it grey. Then we consider the next cell ( $b 1$ in chess notations) color it grey and if the edge between the cells $a 1$ and $b 1$ is red, change the colors of the cell $b 1$ edges.
We obtain a grey area with no red edges in its interior. After that when we scan each new cell we append this cell to the grey figure and if it is necessary change the colors of edges of the new cell to make the color of all new edges in the grey area blue.
The latter is always possible because the new cell have either one common edge with the grey figure (as in the case " $a 1-b 1$ " above) or two common edges. For example let grey figure consist of the first row of the square and $a 2$ cell. When we append the cell $b 2$ to the grey figure two edges of its lower left corner vertex already belong to the grey figure, they are blue. Therefore the other two edges $a 2-b 2$ and $b 1-b 2$ have the same color and we can make them both blue (if they are not) by recoloring the edges of cell $b 2$.
So by doing that with all cells of the square we obtain $16 \times 16$ square with blue edges inside it. Now its time to recall that the sides of the square should be identified, and the red degree of each vertex of torus is even. It follows that the whole (identified) vertical sides of the square are either red or blue, and the same for horizontal sides.
Deformations of red loops (sketch).
To see that any configuration can be made into one of the above four configurations it is most clear to cut the torus up in a square with opposite edges identified.
Since the red degree of each vertex is even we can always find a loop consisting of red edges only. Now, suppose that one can make a (simple) red loop that does not cross the boundary of the square. We can change the color of this loop by changing one by one the colors of unit squares inside it. In the remaining configuration every vertex is still an endpoint of an even number of red edges and we can repeat the operation. So by doing that to every red loop we are left with a configuration where one can not make red loops that do not intersect the boundary. Second, any red loop left that passes through more than one boundary vertex can be deformed into a loop containing only one boundary vertex. Finally, any two loops crossing the same side of the square can be removed by changing colors of all unit squares between these loops. Thus, we are left with only the four possibilities mentioned.
|
4
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On a $16 \times 16$ torus as shown all 512 edges are colored red or blue. A coloring is good if every vertex is an endpoint of an even number of red edges. A move consists of switching the color of each of the 4 edges of an arbitrary cell. What is the largest number of good colorings such that none of them can be converted to another by a sequence of moves?
|

Answer: 4. Representatives of the equivalence classes are: all blue, all blue with one longitudinal red ring, all blue with one transversal red ring, all blue with one longitudinal and one transversal red ring.
First, show that these four classes are non equivalent. Consider any ring transversal or longitudinal and count the number of red edges going out from vertices of this ring in the same halftorus. This number can not be changed mod 2.
Now we show that each configuration can be transformed to one of these four classes. We suggest two independent reasoning.
Scanning of the square.
Cut the torus up in a square $16 \times 16$. In order to restore the initial torus we will identify the opposite sides of the square, but we will do it in the end of solution. Now we will work with the square. It is clear that during all recolorings each vertex of torus has even red degree. The same is true for the degrees of the inner vertices of the $16 \times 16$ square when we deal with it instead of the torus.
Scan all cells of this square one by one from left to right and from bottom to top. For convenience we may think that in each moment the scanned area is colored grey. First we take bottom left corner cell ( $a 1$ in chess notations) and color it grey. Then we consider the next cell ( $b 1$ in chess notations) color it grey and if the edge between the cells $a 1$ and $b 1$ is red, change the colors of the cell $b 1$ edges.
We obtain a grey area with no red edges in its interior. After that when we scan each new cell we append this cell to the grey figure and if it is necessary change the colors of edges of the new cell to make the color of all new edges in the grey area blue.
The latter is always possible because the new cell have either one common edge with the grey figure (as in the case " $a 1-b 1$ " above) or two common edges. For example let grey figure consist of the first row of the square and $a 2$ cell. When we append the cell $b 2$ to the grey figure two edges of its lower left corner vertex already belong to the grey figure, they are blue. Therefore the other two edges $a 2-b 2$ and $b 1-b 2$ have the same color and we can make them both blue (if they are not) by recoloring the edges of cell $b 2$.
So by doing that with all cells of the square we obtain $16 \times 16$ square with blue edges inside it. Now its time to recall that the sides of the square should be identified, and the red degree of each vertex of torus is even. It follows that the whole (identified) vertical sides of the square are either red or blue, and the same for horizontal sides.
Deformations of red loops (sketch).
To see that any configuration can be made into one of the above four configurations it is most clear to cut the torus up in a square with opposite edges identified.
Since the red degree of each vertex is even we can always find a loop consisting of red edges only. Now, suppose that one can make a (simple) red loop that does not cross the boundary of the square. We can change the color of this loop by changing one by one the colors of unit squares inside it. In the remaining configuration every vertex is still an endpoint of an even number of red edges and we can repeat the operation. So by doing that to every red loop we are left with a configuration where one can not make red loops that do not intersect the boundary. Second, any red loop left that passes through more than one boundary vertex can be deformed into a loop containing only one boundary vertex. Finally, any two loops crossing the same side of the square can be removed by changing colors of all unit squares between these loops. Thus, we are left with only the four possibilities mentioned.
|
{
"exam": "BalticWay",
"problem_label": "7",
"problem_match": "\n7.",
"resource_path": "BalticWay/segmented/en-bw18sol.jsonl",
"solution_match": "# Solution.",
"tier": "T3",
"year": "2018"
}
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.