problem
stringlengths 14
10.4k
| solution
stringlengths 1
24.1k
| answer
stringlengths 1
250
⌀ | problem_is_valid
stringclasses 4
values | solution_is_valid
stringclasses 3
values | question_type
stringclasses 4
values | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
10.4k
| solution_raw
stringlengths 1
24.1k
| metadata
dict |
|---|---|---|---|---|---|---|---|---|---|
Suppose $a, b$ and $c$ are integers such that the greatest common divisor of $x^{2}+a x+b$ and $x^{2}+b x+c$ is $x+1$ (in the set of polynomials in $x$ with integer coefficients), and the least common multiple of $x^{2}+a x+b$ and $x^{2}+b x+c$ is $x^{3}-4 x^{2}+x+6$. Find $a+b+c$.
|
$\quad-6$
|
-6
|
Yes
|
Incomplete
|
math-word-problem
|
Algebra
|
Suppose $a, b$ and $c$ are integers such that the greatest common divisor of $x^{2}+a x+b$ and $x^{2}+b x+c$ is $x+1$ (in the set of polynomials in $x$ with integer coefficients), and the least common multiple of $x^{2}+a x+b$ and $x^{2}+b x+c$ is $x^{3}-4 x^{2}+x+6$. Find $a+b+c$.
|
$\quad-6$
|
{
"exam": "HMMT",
"problem_label": "5",
"problem_match": "\n5. [4]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
Suppose $a, b$ and $c$ are integers such that the greatest common divisor of $x^{2}+a x+b$ and $x^{2}+b x+c$ is $x+1$ (in the set of polynomials in $x$ with integer coefficients), and the least common multiple of $x^{2}+a x+b$ and $x^{2}+b x+c$ is $x^{3}-4 x^{2}+x+6$. Find $a+b+c$.
|
Since $x+1$ divides $x^{2}+a x+b$ and the constant term is $b$, we have $x^{2}+a x+b=(x+1)(x+b)$, and similarly $x^{2}+b x+c=(x+1)(x+c)$. Therefore, $a=b+1=c+2$. Furthermore, the least common
multiple of the two polynomials is $(x+1)(x+b)(x+b-1)=x^{3}-4 x^{2}+x+6$, so $b=-2$. Thus $a=-1$ and $c=-3$, and $a+b+c=-6$.
|
-6
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Suppose $a, b$ and $c$ are integers such that the greatest common divisor of $x^{2}+a x+b$ and $x^{2}+b x+c$ is $x+1$ (in the set of polynomials in $x$ with integer coefficients), and the least common multiple of $x^{2}+a x+b$ and $x^{2}+b x+c$ is $x^{3}-4 x^{2}+x+6$. Find $a+b+c$.
|
Since $x+1$ divides $x^{2}+a x+b$ and the constant term is $b$, we have $x^{2}+a x+b=(x+1)(x+b)$, and similarly $x^{2}+b x+c=(x+1)(x+c)$. Therefore, $a=b+1=c+2$. Furthermore, the least common
multiple of the two polynomials is $(x+1)(x+b)(x+b-1)=x^{3}-4 x^{2}+x+6$, so $b=-2$. Thus $a=-1$ and $c=-3$, and $a+b+c=-6$.
|
{
"exam": "HMMT",
"problem_label": "5",
"problem_match": "\n5. [4]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-gen2-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
In how many ways can you rearrange the letters of "HMMTHMMT" such that the consecutive substring "HMMT" does not appear?
|
361
|
361
|
Yes
|
Problem not solved
|
math-word-problem
|
Combinatorics
|
In how many ways can you rearrange the letters of "HMMTHMMT" such that the consecutive substring "HMMT" does not appear?
|
361
|
{
"exam": "HMMT",
"problem_label": "6",
"problem_match": "\n6. [4]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
In how many ways can you rearrange the letters of "HMMTHMMT" such that the consecutive substring "HMMT" does not appear?
|
There are $8!/(4!2!2!)=420$ ways to order the letters. If the permuted letters contain "HMMT", there are $5 \cdot 4!/ 2!=60$ ways to order the other letters, so we subtract these. However, we have subtracted "HMMTHMMT" twice, so we add it back once to obtain 361 possibilities.
|
361
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In how many ways can you rearrange the letters of "HMMTHMMT" such that the consecutive substring "HMMT" does not appear?
|
There are $8!/(4!2!2!)=420$ ways to order the letters. If the permuted letters contain "HMMT", there are $5 \cdot 4!/ 2!=60$ ways to order the other letters, so we subtract these. However, we have subtracted "HMMTHMMT" twice, so we add it back once to obtain 361 possibilities.
|
{
"exam": "HMMT",
"problem_label": "6",
"problem_match": "\n6. [4]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-gen2-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
Let $F_{n}$ be the Fibonacci sequence, that is, $F_{0}=0, F_{1}=1$, and $F_{n+2}=F_{n+1}+F_{n}$. Compute $\sum_{n=0}^{\infty} F_{n} / 10^{n}$.
|
$10 / 89$
|
\frac{10}{89}
|
Yes
|
Incomplete
|
math-word-problem
|
Algebra
|
Let $F_{n}$ be the Fibonacci sequence, that is, $F_{0}=0, F_{1}=1$, and $F_{n+2}=F_{n+1}+F_{n}$. Compute $\sum_{n=0}^{\infty} F_{n} / 10^{n}$.
|
$10 / 89$
|
{
"exam": "HMMT",
"problem_label": "7",
"problem_match": "\n7. [5]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
Let $F_{n}$ be the Fibonacci sequence, that is, $F_{0}=0, F_{1}=1$, and $F_{n+2}=F_{n+1}+F_{n}$. Compute $\sum_{n=0}^{\infty} F_{n} / 10^{n}$.
|
Write $F(x)=\sum_{n=0}^{\infty} F_{n} x^{n}$. Then the Fibonacci recursion tells us that $F(x)-x F(x)-$ $x^{2} F(x)=x$, so $F(x)=x /\left(1-x-x^{2}\right)$. Plugging in $x=1 / 10$ gives the answer.
|
\frac{10}{89}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $F_{n}$ be the Fibonacci sequence, that is, $F_{0}=0, F_{1}=1$, and $F_{n+2}=F_{n+1}+F_{n}$. Compute $\sum_{n=0}^{\infty} F_{n} / 10^{n}$.
|
Write $F(x)=\sum_{n=0}^{\infty} F_{n} x^{n}$. Then the Fibonacci recursion tells us that $F(x)-x F(x)-$ $x^{2} F(x)=x$, so $F(x)=x /\left(1-x-x^{2}\right)$. Plugging in $x=1 / 10$ gives the answer.
|
{
"exam": "HMMT",
"problem_label": "7",
"problem_match": "\n7. [5]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-gen2-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
The incircle $\omega$ of equilateral triangle $A B C$ has radius 1. Three smaller circles are inscribed tangent to $\omega$ and the sides of $A B C$, as shown. Three smaller circles are then inscribed tangent to the previous circles and to each of two sides of $A B C$. This process is repeated an infinite number of times. What is the total length of the circumferences of all the circles?
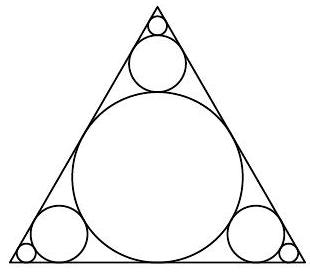
|
$5 \pi$
|
5 \pi
|
Yes
|
Incomplete
|
math-word-problem
|
Geometry
|
The incircle $\omega$ of equilateral triangle $A B C$ has radius 1. Three smaller circles are inscribed tangent to $\omega$ and the sides of $A B C$, as shown. Three smaller circles are then inscribed tangent to the previous circles and to each of two sides of $A B C$. This process is repeated an infinite number of times. What is the total length of the circumferences of all the circles?

|
$5 \pi$
|
{
"exam": "HMMT",
"problem_label": "8",
"problem_match": "\n8. [5]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
The incircle $\omega$ of equilateral triangle $A B C$ has radius 1. Three smaller circles are inscribed tangent to $\omega$ and the sides of $A B C$, as shown. Three smaller circles are then inscribed tangent to the previous circles and to each of two sides of $A B C$. This process is repeated an infinite number of times. What is the total length of the circumferences of all the circles?

|
One can find using the Pythagorean Theorem that, in each iteration, the new circles have radius $1 / 3$ of that of the previously drawn circles. Thus the total circumference is $2 \pi+3 \cdot 2 \pi\left(\frac{1}{1-1 / 3}-1\right)=$ $5 \pi$.
|
5\pi
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
The incircle $\omega$ of equilateral triangle $A B C$ has radius 1. Three smaller circles are inscribed tangent to $\omega$ and the sides of $A B C$, as shown. Three smaller circles are then inscribed tangent to the previous circles and to each of two sides of $A B C$. This process is repeated an infinite number of times. What is the total length of the circumferences of all the circles?

|
One can find using the Pythagorean Theorem that, in each iteration, the new circles have radius $1 / 3$ of that of the previously drawn circles. Thus the total circumference is $2 \pi+3 \cdot 2 \pi\left(\frac{1}{1-1 / 3}-1\right)=$ $5 \pi$.
|
{
"exam": "HMMT",
"problem_label": "8",
"problem_match": "\n8. [5]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-gen2-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
How many sequences of 5 positive integers $(a, b, c, d, e)$ satisfy $a b c d e \leq a+b+c+d+e \leq 10$ ?
|
116
|
116
|
Yes
|
Problem not solved
|
math-word-problem
|
Combinatorics
|
How many sequences of 5 positive integers $(a, b, c, d, e)$ satisfy $a b c d e \leq a+b+c+d+e \leq 10$ ?
|
116
|
{
"exam": "HMMT",
"problem_label": "9",
"problem_match": "\n9. [6]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
How many sequences of 5 positive integers $(a, b, c, d, e)$ satisfy $a b c d e \leq a+b+c+d+e \leq 10$ ?
|
We count based on how many 1's the sequence contains. If $a=b=c=d=e=1$ then this gives us 1 possibility. If $a=b=c=d=1$ and $e \neq 1, e$ can be $2,3,4,5,6$. Each such sequence $(1,1,1,1, e)$ can be arranged in 5 different ways, for a total of $5 \cdot 5=25$ ways in this case.
If three of the numbers are 1 , the last two can be $(2,2),(3,3),(2,3),(2,4)$, or $(2,5)$. Counting ordering, this gives a total of $2 \cdot 10+3 \cdot 20=80$ possibilities.
If two of the numbers are 1 , the other three must be equal to 2 for the product to be under 10 , and this yields 10 more possibilities.
Thus there are $1+25+80+10=116$ such sequences.
|
116
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
How many sequences of 5 positive integers $(a, b, c, d, e)$ satisfy $a b c d e \leq a+b+c+d+e \leq 10$ ?
|
We count based on how many 1's the sequence contains. If $a=b=c=d=e=1$ then this gives us 1 possibility. If $a=b=c=d=1$ and $e \neq 1, e$ can be $2,3,4,5,6$. Each such sequence $(1,1,1,1, e)$ can be arranged in 5 different ways, for a total of $5 \cdot 5=25$ ways in this case.
If three of the numbers are 1 , the last two can be $(2,2),(3,3),(2,3),(2,4)$, or $(2,5)$. Counting ordering, this gives a total of $2 \cdot 10+3 \cdot 20=80$ possibilities.
If two of the numbers are 1 , the other three must be equal to 2 for the product to be under 10 , and this yields 10 more possibilities.
Thus there are $1+25+80+10=116$ such sequences.
|
{
"exam": "HMMT",
"problem_label": "9",
"problem_match": "\n9. [6]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-gen2-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
Let $T$ be a right triangle with sides having lengths 3,4 , and 5 . A point $P$ is called awesome if $P$ is the center of a parallelogram whose vertices all lie on the boundary of $T$. What is the area of the set of awesome points?
|
$3 / 2$
|
\frac{3}{2}
|
Yes
|
Incomplete
|
math-word-problem
|
Geometry
|
Let $T$ be a right triangle with sides having lengths 3,4 , and 5 . A point $P$ is called awesome if $P$ is the center of a parallelogram whose vertices all lie on the boundary of $T$. What is the area of the set of awesome points?
|
$3 / 2$
|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n10. [6]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
Let $T$ be a right triangle with sides having lengths 3,4 , and 5 . A point $P$ is called awesome if $P$ is the center of a parallelogram whose vertices all lie on the boundary of $T$. What is the area of the set of awesome points?
|
The set of awesome points is the medial triangle, which has area $6 / 4=3 / 2$.
|
\frac{3}{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $T$ be a right triangle with sides having lengths 3,4 , and 5 . A point $P$ is called awesome if $P$ is the center of a parallelogram whose vertices all lie on the boundary of $T$. What is the area of the set of awesome points?
|
The set of awesome points is the medial triangle, which has area $6 / 4=3 / 2$.
|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n10. [6]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-gen2-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
A rectangular piece of paper with side lengths 5 by 8 is folded along the dashed lines shown below, so that the folded flaps just touch at the corners as shown by the dotted lines. Find the area of the resulting trapezoid.
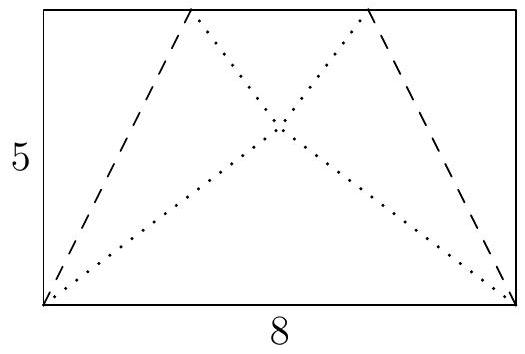
|
$55 / 2$
|
\frac{55}{2}
|
Incomplete
|
Yes
|
math-word-problem
|
Geometry
|
A rectangular piece of paper with side lengths 5 by 8 is folded along the dashed lines shown below, so that the folded flaps just touch at the corners as shown by the dotted lines. Find the area of the resulting trapezoid.

|
$55 / 2$
|
{
"exam": "HMMT",
"problem_label": "1",
"problem_match": "\n1. [3]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
A rectangular piece of paper with side lengths 5 by 8 is folded along the dashed lines shown below, so that the folded flaps just touch at the corners as shown by the dotted lines. Find the area of the resulting trapezoid.

|
Drawing the perpendiculars from the point of intersection of the corners to the bases of the trapezoid, we see that we have similar $3-4-5$ right triangles, and we can calculate that the length of the smaller base is 3 . Thus the area of the trapezoid is $\frac{8+3}{2} \cdot 5=55 / 2$.
|
\frac{55}{2}
|
Incomplete
|
Yes
|
math-word-problem
|
Geometry
|
A rectangular piece of paper with side lengths 5 by 8 is folded along the dashed lines shown below, so that the folded flaps just touch at the corners as shown by the dotted lines. Find the area of the resulting trapezoid.

|
Drawing the perpendiculars from the point of intersection of the corners to the bases of the trapezoid, we see that we have similar $3-4-5$ right triangles, and we can calculate that the length of the smaller base is 3 . Thus the area of the trapezoid is $\frac{8+3}{2} \cdot 5=55 / 2$.
|
{
"exam": "HMMT",
"problem_label": "1",
"problem_match": "\n1. [3]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
The corner of a unit cube is chopped off such that the cut runs through the three vertices adjacent to the vertex of the chosen corner. What is the height of the cube when the freshly-cut face is placed on a table?
|
$2 \sqrt{3} / 3$
|
\frac{2 \sqrt{3}}{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
The corner of a unit cube is chopped off such that the cut runs through the three vertices adjacent to the vertex of the chosen corner. What is the height of the cube when the freshly-cut face is placed on a table?
|
$2 \sqrt{3} / 3$
|
{
"exam": "HMMT",
"problem_label": "2",
"problem_match": "\n2. [3]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
The corner of a unit cube is chopped off such that the cut runs through the three vertices adjacent to the vertex of the chosen corner. What is the height of the cube when the freshly-cut face is placed on a table?
|
The major diagonal has a length of $\sqrt{3}$. The volume of the pyramid is $1 / 6$, and so its height $h$ satisfies $\frac{1}{3} \cdot h \cdot \frac{\sqrt{3}}{4}(\sqrt{2})^{2}=1 / 6$ since the freshly cut face is an equilateral triangle of side length $\sqrt{2}$. Thus $h=\sqrt{3} / 3$, and the answer follows.
|
\sqrt{3} / 3
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
The corner of a unit cube is chopped off such that the cut runs through the three vertices adjacent to the vertex of the chosen corner. What is the height of the cube when the freshly-cut face is placed on a table?
|
The major diagonal has a length of $\sqrt{3}$. The volume of the pyramid is $1 / 6$, and so its height $h$ satisfies $\frac{1}{3} \cdot h \cdot \frac{\sqrt{3}}{4}(\sqrt{2})^{2}=1 / 6$ since the freshly cut face is an equilateral triangle of side length $\sqrt{2}$. Thus $h=\sqrt{3} / 3$, and the answer follows.
|
{
"exam": "HMMT",
"problem_label": "2",
"problem_match": "\n2. [3]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
Let $T$ be a right triangle with sides having lengths 3,4 , and 5 . A point $P$ is called awesome if $P$ is the center of a parallelogram whose vertices all lie on the boundary of $T$. What is the area of the set of awesome points?
|
$3 / 2$
|
\frac{3}{2}
|
Yes
|
Incomplete
|
math-word-problem
|
Geometry
|
Let $T$ be a right triangle with sides having lengths 3,4 , and 5 . A point $P$ is called awesome if $P$ is the center of a parallelogram whose vertices all lie on the boundary of $T$. What is the area of the set of awesome points?
|
$3 / 2$
|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n3. [4]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
Let $T$ be a right triangle with sides having lengths 3,4 , and 5 . A point $P$ is called awesome if $P$ is the center of a parallelogram whose vertices all lie on the boundary of $T$. What is the area of the set of awesome points?
|
The set of awesome points is the medial triangle, which has area $6 / 4=3 / 2$.
|
\frac{3}{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $T$ be a right triangle with sides having lengths 3,4 , and 5 . A point $P$ is called awesome if $P$ is the center of a parallelogram whose vertices all lie on the boundary of $T$. What is the area of the set of awesome points?
|
The set of awesome points is the medial triangle, which has area $6 / 4=3 / 2$.
|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n3. [4]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
A kite is a quadrilateral whose diagonals are perpendicular. Let kite $A B C D$ be such that $\angle B=$ $\angle D=90^{\circ}$. Let $M$ and $N$ be the points of tangency of the incircle of $A B C D$ to $A B$ and $B C$ respectively. Let $\omega$ be the circle centered at $C$ and tangent to $A B$ and $A D$. Construct another kite $A B^{\prime} C^{\prime} D^{\prime}$ that is similar to $A B C D$ and whose incircle is $\omega$. Let $N^{\prime}$ be the point of tangency of $B^{\prime} C^{\prime}$ to $\omega$. If $M N^{\prime} \| A C$, then what is the ratio of $A B: B C$ ?
|
$\frac{1+\sqrt{5}}{2}$
|
\frac{1+\sqrt{5}}{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A kite is a quadrilateral whose diagonals are perpendicular. Let kite $A B C D$ be such that $\angle B=$ $\angle D=90^{\circ}$. Let $M$ and $N$ be the points of tangency of the incircle of $A B C D$ to $A B$ and $B C$ respectively. Let $\omega$ be the circle centered at $C$ and tangent to $A B$ and $A D$. Construct another kite $A B^{\prime} C^{\prime} D^{\prime}$ that is similar to $A B C D$ and whose incircle is $\omega$. Let $N^{\prime}$ be the point of tangency of $B^{\prime} C^{\prime}$ to $\omega$. If $M N^{\prime} \| A C$, then what is the ratio of $A B: B C$ ?
|
$\frac{1+\sqrt{5}}{2}$
|
{
"exam": "HMMT",
"problem_label": "4",
"problem_match": "\n4. [4]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
A kite is a quadrilateral whose diagonals are perpendicular. Let kite $A B C D$ be such that $\angle B=$ $\angle D=90^{\circ}$. Let $M$ and $N$ be the points of tangency of the incircle of $A B C D$ to $A B$ and $B C$ respectively. Let $\omega$ be the circle centered at $C$ and tangent to $A B$ and $A D$. Construct another kite $A B^{\prime} C^{\prime} D^{\prime}$ that is similar to $A B C D$ and whose incircle is $\omega$. Let $N^{\prime}$ be the point of tangency of $B^{\prime} C^{\prime}$ to $\omega$. If $M N^{\prime} \| A C$, then what is the ratio of $A B: B C$ ?
|
Let's focus on the right triangle $A B C$ and the semicircle inscribed in it since the situation is symmetric about $A C$. First we find the radius $a$ of circle $O$. Let $A B=x$ and $B C=y$. Drawing the radii $O M$ and $O N$, we see that $A M=x-a$ and $\triangle A M O \sim \triangle A B C$. In other words,
$$
\begin{aligned}
\frac{A M}{M O} & =\frac{A B}{B C} \\
\frac{x-a}{a} & =\frac{x}{y} \\
a & =\frac{x y}{x+y} .
\end{aligned}
$$
Now we notice that the situation is homothetic about $A$. In particular,
$$
\triangle A M O \sim \triangle O N C \sim \triangle C N^{\prime} C^{\prime}
$$
Also, $C B$ and $C N^{\prime}$ are both radii of circle $C$. Thus, when $M N^{\prime} \| A C^{\prime}$, we have
$$
\begin{aligned}
A M & =C N^{\prime}=C B \\
x-a & =y \\
a=\frac{x y}{x+y} & =x-y \\
x^{2}-x y-y^{2} & =0 \\
x & =\frac{y}{2} \pm \sqrt{\frac{y^{2}}{4}+y^{2}} \\
\frac{A B}{B C}=\frac{x}{y} & =\frac{1+\sqrt{5}}{2} .
\end{aligned}
$$
|
\frac{1+\sqrt{5}}{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A kite is a quadrilateral whose diagonals are perpendicular. Let kite $A B C D$ be such that $\angle B=$ $\angle D=90^{\circ}$. Let $M$ and $N$ be the points of tangency of the incircle of $A B C D$ to $A B$ and $B C$ respectively. Let $\omega$ be the circle centered at $C$ and tangent to $A B$ and $A D$. Construct another kite $A B^{\prime} C^{\prime} D^{\prime}$ that is similar to $A B C D$ and whose incircle is $\omega$. Let $N^{\prime}$ be the point of tangency of $B^{\prime} C^{\prime}$ to $\omega$. If $M N^{\prime} \| A C$, then what is the ratio of $A B: B C$ ?
|
Let's focus on the right triangle $A B C$ and the semicircle inscribed in it since the situation is symmetric about $A C$. First we find the radius $a$ of circle $O$. Let $A B=x$ and $B C=y$. Drawing the radii $O M$ and $O N$, we see that $A M=x-a$ and $\triangle A M O \sim \triangle A B C$. In other words,
$$
\begin{aligned}
\frac{A M}{M O} & =\frac{A B}{B C} \\
\frac{x-a}{a} & =\frac{x}{y} \\
a & =\frac{x y}{x+y} .
\end{aligned}
$$
Now we notice that the situation is homothetic about $A$. In particular,
$$
\triangle A M O \sim \triangle O N C \sim \triangle C N^{\prime} C^{\prime}
$$
Also, $C B$ and $C N^{\prime}$ are both radii of circle $C$. Thus, when $M N^{\prime} \| A C^{\prime}$, we have
$$
\begin{aligned}
A M & =C N^{\prime}=C B \\
x-a & =y \\
a=\frac{x y}{x+y} & =x-y \\
x^{2}-x y-y^{2} & =0 \\
x & =\frac{y}{2} \pm \sqrt{\frac{y^{2}}{4}+y^{2}} \\
\frac{A B}{B C}=\frac{x}{y} & =\frac{1+\sqrt{5}}{2} .
\end{aligned}
$$
|
{
"exam": "HMMT",
"problem_label": "4",
"problem_match": "\n4. [4]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
Circle $B$ has radius $6 \sqrt{7}$. Circle $A$, centered at point $C$, has radius $\sqrt{7}$ and is contained in $B$. Let $L$ be the locus of centers $C$ such that there exists a point $D$ on the boundary of $B$ with the following property: if the tangents from $D$ to circle $A$ intersect circle $B$ again at $X$ and $Y$, then $X Y$ is also tangent to $A$. Find the area contained by the boundary of $L$.
|
$168 \pi$
|
168 \pi
|
Yes
|
Incomplete
|
math-word-problem
|
Geometry
|
Circle $B$ has radius $6 \sqrt{7}$. Circle $A$, centered at point $C$, has radius $\sqrt{7}$ and is contained in $B$. Let $L$ be the locus of centers $C$ such that there exists a point $D$ on the boundary of $B$ with the following property: if the tangents from $D$ to circle $A$ intersect circle $B$ again at $X$ and $Y$, then $X Y$ is also tangent to $A$. Find the area contained by the boundary of $L$.
|
$168 \pi$
|
{
"exam": "HMMT",
"problem_label": "5",
"problem_match": "\n5. [4]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
Circle $B$ has radius $6 \sqrt{7}$. Circle $A$, centered at point $C$, has radius $\sqrt{7}$ and is contained in $B$. Let $L$ be the locus of centers $C$ such that there exists a point $D$ on the boundary of $B$ with the following property: if the tangents from $D$ to circle $A$ intersect circle $B$ again at $X$ and $Y$, then $X Y$ is also tangent to $A$. Find the area contained by the boundary of $L$.
|
The conditions imply that there exists a triangle such that $B$ is the circumcircle and $A$ is the incircle for the position of $A$. The distance between the circumcenter and incenter is given by $\sqrt{(R-2 r) R}$, where $R, r$ are the circumradius and inradius, respectively. Thus the locus of $C$ is a circle concentric to $B$ with radius $2 \sqrt{42}$. The conclusion follows.
|
2 \sqrt{42}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Circle $B$ has radius $6 \sqrt{7}$. Circle $A$, centered at point $C$, has radius $\sqrt{7}$ and is contained in $B$. Let $L$ be the locus of centers $C$ such that there exists a point $D$ on the boundary of $B$ with the following property: if the tangents from $D$ to circle $A$ intersect circle $B$ again at $X$ and $Y$, then $X Y$ is also tangent to $A$. Find the area contained by the boundary of $L$.
|
The conditions imply that there exists a triangle such that $B$ is the circumcircle and $A$ is the incircle for the position of $A$. The distance between the circumcenter and incenter is given by $\sqrt{(R-2 r) R}$, where $R, r$ are the circumradius and inradius, respectively. Thus the locus of $C$ is a circle concentric to $B$ with radius $2 \sqrt{42}$. The conclusion follows.
|
{
"exam": "HMMT",
"problem_label": "5",
"problem_match": "\n5. [4]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
Let $A B C$ be a triangle in the coordinate plane with vertices on lattice points and with $A B=1$. Suppose the perimeter of $A B C$ is less than 17 . Find the largest possible value of $1 / r$, where $r$ is the inradius of $A B C$.
|
$1+5 \sqrt{2}+\sqrt{65}$
|
1+5 \sqrt{2}+\sqrt{65}
|
Yes
|
Incomplete
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle in the coordinate plane with vertices on lattice points and with $A B=1$. Suppose the perimeter of $A B C$ is less than 17 . Find the largest possible value of $1 / r$, where $r$ is the inradius of $A B C$.
|
$1+5 \sqrt{2}+\sqrt{65}$
|
{
"exam": "HMMT",
"problem_label": "6",
"problem_match": "\n6. [4]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
Let $A B C$ be a triangle in the coordinate plane with vertices on lattice points and with $A B=1$. Suppose the perimeter of $A B C$ is less than 17 . Find the largest possible value of $1 / r$, where $r$ is the inradius of $A B C$.
|
Let $a$ denote the area of the triangle, $r$ the inradius, and $p$ the perimeter. Then $a=r p / 2$, so $r=2 a / p>2 a / 17$. Notice that $a=h / 2$ where $h$ is the height of the triangle from $C$ to $A B$, and $h$ is an integer since the vertices are lattice points. Thus we first guess that the inradius is minimized when $h=1$ and the area is $1 / 2$. In this case, we can now assume WLOG that $A=(0,0), B=(1,0)$, and $C=(n+1,1)$ for some nonnegative integer $n$. The perimeter of $A B C$ is $\sqrt{n^{2}+2 n+2}+\sqrt{n^{2}+1}+1$. Since $n=8$ yields a perimeter greater than 17 , the required triangle has $n=7$ and inradius $r=1 / p=$ $\frac{1}{1+5 \sqrt{2}+\sqrt{65}}$ which yields the answer of $1 / r=1+5 \sqrt{2}+\sqrt{65}$. We can now verify that this is indeed
minimal over all $h$ by noting that its perimeter is greater than $17 / 2$, which is the upper bound in the case $h \geq 2$.
|
1+5\sqrt{2}+\sqrt{65}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle in the coordinate plane with vertices on lattice points and with $A B=1$. Suppose the perimeter of $A B C$ is less than 17 . Find the largest possible value of $1 / r$, where $r$ is the inradius of $A B C$.
|
Let $a$ denote the area of the triangle, $r$ the inradius, and $p$ the perimeter. Then $a=r p / 2$, so $r=2 a / p>2 a / 17$. Notice that $a=h / 2$ where $h$ is the height of the triangle from $C$ to $A B$, and $h$ is an integer since the vertices are lattice points. Thus we first guess that the inradius is minimized when $h=1$ and the area is $1 / 2$. In this case, we can now assume WLOG that $A=(0,0), B=(1,0)$, and $C=(n+1,1)$ for some nonnegative integer $n$. The perimeter of $A B C$ is $\sqrt{n^{2}+2 n+2}+\sqrt{n^{2}+1}+1$. Since $n=8$ yields a perimeter greater than 17 , the required triangle has $n=7$ and inradius $r=1 / p=$ $\frac{1}{1+5 \sqrt{2}+\sqrt{65}}$ which yields the answer of $1 / r=1+5 \sqrt{2}+\sqrt{65}$. We can now verify that this is indeed
minimal over all $h$ by noting that its perimeter is greater than $17 / 2$, which is the upper bound in the case $h \geq 2$.
|
{
"exam": "HMMT",
"problem_label": "6",
"problem_match": "\n6. [4]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
In $\triangle A B C, D$ is the midpoint of $B C, E$ is the foot of the perpendicular from $A$ to $B C$, and $F$ is the foot of the perpendicular from $D$ to $A C$. Given that $B E=5, E C=9$, and the area of triangle $A B C$ is 84 , compute $|E F|$.
|
$\frac{6 \sqrt{37}}{5}, \frac{21}{205} \sqrt{7585}$
|
\frac{6 \sqrt{37}}{5}, \frac{21}{205} \sqrt{7585}
|
Yes
|
Problem not solved
|
math-word-problem
|
Geometry
|
In $\triangle A B C, D$ is the midpoint of $B C, E$ is the foot of the perpendicular from $A$ to $B C$, and $F$ is the foot of the perpendicular from $D$ to $A C$. Given that $B E=5, E C=9$, and the area of triangle $A B C$ is 84 , compute $|E F|$.
|
$\frac{6 \sqrt{37}}{5}, \frac{21}{205} \sqrt{7585}$
|
{
"exam": "HMMT",
"problem_label": "7",
"problem_match": "\n7. [5]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
In $\triangle A B C, D$ is the midpoint of $B C, E$ is the foot of the perpendicular from $A$ to $B C$, and $F$ is the foot of the perpendicular from $D$ to $A C$. Given that $B E=5, E C=9$, and the area of triangle $A B C$ is 84 , compute $|E F|$.
|
There are two possibilities for the triangle $A B C$ based on whether $E$ is between $B$ and $C$ or not. We first consider the former case.
We find from the area and the Pythagorean theorem that $A E=12, A B=13$, and $A C=15$. We can then use Stewart's theorem to obtain $A D=2 \sqrt{37}$.
Since the area of $\triangle A D C$ is half that of $A B C$, we have $\frac{1}{2} A C \cdot D F=42$, so $D F=14 / 5$. Also, $D C=14 / 2=7$ so $E D=9-7=2$.
Notice that $A E D F$ is a cyclic quadrilateral. By Ptolemy's theorem, we have $E F \cdot 2 \sqrt{37}=(28 / 5) \cdot 12+$ $2 \cdot(54 / 5)$. Thus $E F=\frac{6 \sqrt{37}}{5}$ as desired.
The latter case is similar.
|
\frac{6 \sqrt{37}}{5}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In $\triangle A B C, D$ is the midpoint of $B C, E$ is the foot of the perpendicular from $A$ to $B C$, and $F$ is the foot of the perpendicular from $D$ to $A C$. Given that $B E=5, E C=9$, and the area of triangle $A B C$ is 84 , compute $|E F|$.
|
There are two possibilities for the triangle $A B C$ based on whether $E$ is between $B$ and $C$ or not. We first consider the former case.
We find from the area and the Pythagorean theorem that $A E=12, A B=13$, and $A C=15$. We can then use Stewart's theorem to obtain $A D=2 \sqrt{37}$.
Since the area of $\triangle A D C$ is half that of $A B C$, we have $\frac{1}{2} A C \cdot D F=42$, so $D F=14 / 5$. Also, $D C=14 / 2=7$ so $E D=9-7=2$.
Notice that $A E D F$ is a cyclic quadrilateral. By Ptolemy's theorem, we have $E F \cdot 2 \sqrt{37}=(28 / 5) \cdot 12+$ $2 \cdot(54 / 5)$. Thus $E F=\frac{6 \sqrt{37}}{5}$ as desired.
The latter case is similar.
|
{
"exam": "HMMT",
"problem_label": "7",
"problem_match": "\n7. [5]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
Triangle $A B C$ has side lengths $A B=231, B C=160$, and $A C=281$. Point $D$ is constructed on the opposite side of line $A C$ as point $B$ such that $A D=178$ and $C D=153$. Compute the distance from $B$ to the midpoint of segment $A D$.
|
208
|
208
|
Yes
|
Incomplete
|
math-word-problem
|
Geometry
|
Triangle $A B C$ has side lengths $A B=231, B C=160$, and $A C=281$. Point $D$ is constructed on the opposite side of line $A C$ as point $B$ such that $A D=178$ and $C D=153$. Compute the distance from $B$ to the midpoint of segment $A D$.
|
208
|
{
"exam": "HMMT",
"problem_label": "8",
"problem_match": "\n8. [7]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
Triangle $A B C$ has side lengths $A B=231, B C=160$, and $A C=281$. Point $D$ is constructed on the opposite side of line $A C$ as point $B$ such that $A D=178$ and $C D=153$. Compute the distance from $B$ to the midpoint of segment $A D$.
|
Note that $\angle A B C$ is right since
$$
B C^{2}=160^{2}=50 \cdot 512=(A C-A B) \cdot(A C+A B)=A C^{2}-A B^{2}
$$
Construct point $B^{\prime}$ such that $A B C B^{\prime}$ is a rectangle, and construct $D^{\prime}$ on segment $B^{\prime} C$ such that $A D=A D^{\prime}$. Then
$$
B^{\prime} D^{\prime 2}=A D^{\prime 2}-A B^{\prime 2}=A D^{2}-B C^{2}=(A D-B C)(A D+B C)=18 \cdot 338=78^{2}
$$
It follows that $C D^{\prime}=B^{\prime} C-B^{\prime} D^{\prime}=153=C D$; thus, points $D$ and $D^{\prime}$ coincide, and $A B \| C D$. Let $M$ denote the midpoint of segment $A D$, and denote the orthogonal projections $M$ to lines $A B$ and $B C$ by $P$ and $Q$ respectively. Then $Q$ is the midpoint of $B C$ and $A P=39$, so that $P B=A B-A P=192$ and
$$
B M=P Q=\sqrt{80^{2}+192^{2}}=16 \sqrt{5^{2}+12^{2}}=208
$$
|
208
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Triangle $A B C$ has side lengths $A B=231, B C=160$, and $A C=281$. Point $D$ is constructed on the opposite side of line $A C$ as point $B$ such that $A D=178$ and $C D=153$. Compute the distance from $B$ to the midpoint of segment $A D$.
|
Note that $\angle A B C$ is right since
$$
B C^{2}=160^{2}=50 \cdot 512=(A C-A B) \cdot(A C+A B)=A C^{2}-A B^{2}
$$
Construct point $B^{\prime}$ such that $A B C B^{\prime}$ is a rectangle, and construct $D^{\prime}$ on segment $B^{\prime} C$ such that $A D=A D^{\prime}$. Then
$$
B^{\prime} D^{\prime 2}=A D^{\prime 2}-A B^{\prime 2}=A D^{2}-B C^{2}=(A D-B C)(A D+B C)=18 \cdot 338=78^{2}
$$
It follows that $C D^{\prime}=B^{\prime} C-B^{\prime} D^{\prime}=153=C D$; thus, points $D$ and $D^{\prime}$ coincide, and $A B \| C D$. Let $M$ denote the midpoint of segment $A D$, and denote the orthogonal projections $M$ to lines $A B$ and $B C$ by $P$ and $Q$ respectively. Then $Q$ is the midpoint of $B C$ and $A P=39$, so that $P B=A B-A P=192$ and
$$
B M=P Q=\sqrt{80^{2}+192^{2}}=16 \sqrt{5^{2}+12^{2}}=208
$$
|
{
"exam": "HMMT",
"problem_label": "8",
"problem_match": "\n8. [7]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
Let $A B C$ be a triangle with $A B=16$ and $A C=5$. Suppose the bisectors of angles $\angle A B C$ and $\angle B C A$ meet at point $P$ in the triangle's interior. Given that $A P=4$, compute $B C$.
|
14
|
14
|
Yes
|
Problem not solved
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle with $A B=16$ and $A C=5$. Suppose the bisectors of angles $\angle A B C$ and $\angle B C A$ meet at point $P$ in the triangle's interior. Given that $A P=4$, compute $B C$.
|
14
|
{
"exam": "HMMT",
"problem_label": "9",
"problem_match": "\n9. [7]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
Let $A B C$ be a triangle with $A B=16$ and $A C=5$. Suppose the bisectors of angles $\angle A B C$ and $\angle B C A$ meet at point $P$ in the triangle's interior. Given that $A P=4$, compute $B C$.
|
As the incenter of triangle $A B C$, point $P$ has many properties. Extend $A P$ past $P$ to its intersection with the circumcircle of triangle $A B C$, and call this intersection $M$. Now observe that
$$
\angle P B M=\angle P B C+\angle C B M=\angle P B C+\angle C A M=\beta+\alpha=90-\gamma
$$
where $\alpha, \beta$, and $\gamma$ are the half-angles of triangle $A B C$. Since
$$
\angle B M P=\angle B M A=\angle B C A=2 \gamma
$$
it follows that $B M=M P=C M$. Let $Q$ denote the intersection of $A M$ and $B C$, and observe that $\triangle A Q B \sim \triangle C Q M$ and $\triangle A Q C \sim \triangle B Q M$; some easy algebra gives
$$
A M / B C=(A B \cdot A C+B M \cdot C M) /(A C \cdot C M+A B \cdot B M)
$$
Writing $(a, b, c, d, x)=(B C, A C, A B, M P, A P)$, this is $(x+d) / a=\left(b c+d^{2}\right) /((b+c) d)$. Ptolemy's theorem applied to $A B C D$ gives $a(d+x)=d(b+c)$. Multiplying the two gives $(d+x)^{2}=b c+d^{2}$. We easily solve for $d=\left(b c-x^{2}\right) /(2 x)=8$ and $a=d(b+c) /(d+x)=14$.
|
14
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle with $A B=16$ and $A C=5$. Suppose the bisectors of angles $\angle A B C$ and $\angle B C A$ meet at point $P$ in the triangle's interior. Given that $A P=4$, compute $B C$.
|
As the incenter of triangle $A B C$, point $P$ has many properties. Extend $A P$ past $P$ to its intersection with the circumcircle of triangle $A B C$, and call this intersection $M$. Now observe that
$$
\angle P B M=\angle P B C+\angle C B M=\angle P B C+\angle C A M=\beta+\alpha=90-\gamma
$$
where $\alpha, \beta$, and $\gamma$ are the half-angles of triangle $A B C$. Since
$$
\angle B M P=\angle B M A=\angle B C A=2 \gamma
$$
it follows that $B M=M P=C M$. Let $Q$ denote the intersection of $A M$ and $B C$, and observe that $\triangle A Q B \sim \triangle C Q M$ and $\triangle A Q C \sim \triangle B Q M$; some easy algebra gives
$$
A M / B C=(A B \cdot A C+B M \cdot C M) /(A C \cdot C M+A B \cdot B M)
$$
Writing $(a, b, c, d, x)=(B C, A C, A B, M P, A P)$, this is $(x+d) / a=\left(b c+d^{2}\right) /((b+c) d)$. Ptolemy's theorem applied to $A B C D$ gives $a(d+x)=d(b+c)$. Multiplying the two gives $(d+x)^{2}=b c+d^{2}$. We easily solve for $d=\left(b c-x^{2}\right) /(2 x)=8$ and $a=d(b+c) /(d+x)=14$.
|
{
"exam": "HMMT",
"problem_label": "9",
"problem_match": "\n9. [7]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
Points $A$ and $B$ lie on circle $\omega$. Point $P$ lies on the extension of segment $A B$ past $B$. Line $\ell$ passes through $P$ and is tangent to $\omega$. The tangents to $\omega$ at points $A$ and $B$ intersect $\ell$ at points $D$ and $C$ respectively. Given that $A B=7, B C=2$, and $A D=3$, compute $B P$.
|
9
|
9
|
Yes
|
Problem not solved
|
math-word-problem
|
Geometry
|
Points $A$ and $B$ lie on circle $\omega$. Point $P$ lies on the extension of segment $A B$ past $B$. Line $\ell$ passes through $P$ and is tangent to $\omega$. The tangents to $\omega$ at points $A$ and $B$ intersect $\ell$ at points $D$ and $C$ respectively. Given that $A B=7, B C=2$, and $A D=3$, compute $B P$.
|
9
|
{
"exam": "HMMT",
"problem_label": "10",
"problem_match": "\n10. [8]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
Points $A$ and $B$ lie on circle $\omega$. Point $P$ lies on the extension of segment $A B$ past $B$. Line $\ell$ passes through $P$ and is tangent to $\omega$. The tangents to $\omega$ at points $A$ and $B$ intersect $\ell$ at points $D$ and $C$ respectively. Given that $A B=7, B C=2$, and $A D=3$, compute $B P$.
|
Say that $\ell$ be tangent to $\omega$ at point $T$. Observing equal tangents, write
$$
C D=C T+D T=B C+A D=5 .
$$
Let the tangents to $\omega$ at $A$ and $B$ intersect each other at $Q$. Working from Menelaus applied to triangle $C D Q$ and line $A B$ gives
$$
\begin{aligned}
-1 & =\frac{D A}{A Q} \cdot \frac{Q B}{B C} \cdot \frac{C P}{P D} \\
& =\frac{D A}{B C} \cdot \frac{C P}{P C+C D} \\
& =\frac{3}{2} \cdot \frac{C P}{P C+5},
\end{aligned}
$$
from which $P C=10$. By power of a point, $P T^{2}=A P \cdot B P$, or $12^{2}=B P \cdot(B P+7)$, from which $B P=9$.
|
9
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Points $A$ and $B$ lie on circle $\omega$. Point $P$ lies on the extension of segment $A B$ past $B$. Line $\ell$ passes through $P$ and is tangent to $\omega$. The tangents to $\omega$ at points $A$ and $B$ intersect $\ell$ at points $D$ and $C$ respectively. Given that $A B=7, B C=2$, and $A D=3$, compute $B P$.
|
Say that $\ell$ be tangent to $\omega$ at point $T$. Observing equal tangents, write
$$
C D=C T+D T=B C+A D=5 .
$$
Let the tangents to $\omega$ at $A$ and $B$ intersect each other at $Q$. Working from Menelaus applied to triangle $C D Q$ and line $A B$ gives
$$
\begin{aligned}
-1 & =\frac{D A}{A Q} \cdot \frac{Q B}{B C} \cdot \frac{C P}{P D} \\
& =\frac{D A}{B C} \cdot \frac{C P}{P C+C D} \\
& =\frac{3}{2} \cdot \frac{C P}{P C+5},
\end{aligned}
$$
from which $P C=10$. By power of a point, $P T^{2}=A P \cdot B P$, or $12^{2}=B P \cdot(B P+7)$, from which $B P=9$.
|
{
"exam": "HMMT",
"problem_label": "10",
"problem_match": "\n10. [8]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-geo-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
Compute
$$
1 \cdot 2^{2}+2 \cdot 3^{2}+3 \cdot 4^{2}+\cdots+19 \cdot 20^{2}
$$
|
41230 y Solution: We can write this as $\left(1^{3}+2^{3}+\cdots+20^{3}\right)-\left(1^{2}+2^{2}+\cdots+20^{2}\right)$, which is equal to $44100-2870=41230$.
|
41230
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Compute
$$
1 \cdot 2^{2}+2 \cdot 3^{2}+3 \cdot 4^{2}+\cdots+19 \cdot 20^{2}
$$
|
41230 y Solution: We can write this as $\left(1^{3}+2^{3}+\cdots+20^{3}\right)-\left(1^{2}+2^{2}+\cdots+20^{2}\right)$, which is equal to $44100-2870=41230$.
|
{
"exam": "HMMT",
"problem_label": "1",
"problem_match": "\n1. [5]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
Given that $\sin A+\sin B=1$ and $\cos A+\cos B=3 / 2$, what is the value of $\cos (A-B)$ ?
|
$5 / 8$
|
\frac{5}{8}
|
Yes
|
Incomplete
|
math-word-problem
|
Algebra
|
Given that $\sin A+\sin B=1$ and $\cos A+\cos B=3 / 2$, what is the value of $\cos (A-B)$ ?
|
$5 / 8$
|
{
"exam": "HMMT",
"problem_label": "2",
"problem_match": "\n2. [5]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
Given that $\sin A+\sin B=1$ and $\cos A+\cos B=3 / 2$, what is the value of $\cos (A-B)$ ?
|
Squaring both equations and add them together, one obtains $1+9 / 4=2+2(\cos (A) \cos (B)+$ $\sin (A) \sin (B))=2+2 \cos (A-B)$. Thus $\cos A-B=5 / 8$.
|
\frac{5}{8}
|
Yes
|
Incomplete
|
math-word-problem
|
Algebra
|
Given that $\sin A+\sin B=1$ and $\cos A+\cos B=3 / 2$, what is the value of $\cos (A-B)$ ?
|
Squaring both equations and add them together, one obtains $1+9 / 4=2+2(\cos (A) \cos (B)+$ $\sin (A) \sin (B))=2+2 \cos (A-B)$. Thus $\cos A-B=5 / 8$.
|
{
"exam": "HMMT",
"problem_label": "2",
"problem_match": "\n2. [5]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
Find all pairs of integer solutions $(n, m)$ to
$$
2^{3^{n}}=3^{2^{m}}-1
$$
|
$(0,0)$ and $(1,1)$
|
(0,0) \text{ and } (1,1)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all pairs of integer solutions $(n, m)$ to
$$
2^{3^{n}}=3^{2^{m}}-1
$$
|
$(0,0)$ and $(1,1)$
|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n3. [5]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
Find all pairs of integer solutions $(n, m)$ to
$$
2^{3^{n}}=3^{2^{m}}-1
$$
|
We find all solutions of $2^{x}=3^{y}-1$ for positive integers $x$ and $y$. If $x=1$, we obtain the solution $x=1, y=1$, which corresponds to $(n, m)=(0,0)$ in the original problem. If $x>1$, consider the equation modulo 4 . The left hand side is 0 , and the right hand side is $(-1)^{y}-1$, so $y$ is even. Thus we can write $y=2 z$ for some positive integer $z$, and so $2^{x}=\left(3^{z}-1\right)\left(3^{z}+1\right)$. Thus each of $3^{z}-1$ and $3^{z}+1$ is a power of 2 , but they differ by 2 , so they must equal 2 and 4 respectively. Therefore, the only other solution is $x=3$ and $y=2$, which corresponds to $(n, m)=(1,1)$ in the original problem.
$12^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
(n, m) = (0, 0), (1, 1)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all pairs of integer solutions $(n, m)$ to
$$
2^{3^{n}}=3^{2^{m}}-1
$$
|
We find all solutions of $2^{x}=3^{y}-1$ for positive integers $x$ and $y$. If $x=1$, we obtain the solution $x=1, y=1$, which corresponds to $(n, m)=(0,0)$ in the original problem. If $x>1$, consider the equation modulo 4 . The left hand side is 0 , and the right hand side is $(-1)^{y}-1$, so $y$ is even. Thus we can write $y=2 z$ for some positive integer $z$, and so $2^{x}=\left(3^{z}-1\right)\left(3^{z}+1\right)$. Thus each of $3^{z}-1$ and $3^{z}+1$ is a power of 2 , but they differ by 2 , so they must equal 2 and 4 respectively. Therefore, the only other solution is $x=3$ and $y=2$, which corresponds to $(n, m)=(1,1)$ in the original problem.
$12^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n3. [5]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
Simplify: $i^{0}+i^{1}+\cdots+i^{2009}$.
|
$1+i$
|
1+i
|
Yes
|
Incomplete
|
math-word-problem
|
Algebra
|
Simplify: $i^{0}+i^{1}+\cdots+i^{2009}$.
|
$1+i$
|
{
"exam": "HMMT",
"problem_label": "4",
"problem_match": "\n4. [6]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
Simplify: $i^{0}+i^{1}+\cdots+i^{2009}$.
|
By the geometric series formula, the sum is equal to $\frac{i^{2010}-1}{i-1}=\frac{-2}{i-1}=1+i$.
|
1+i
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Simplify: $i^{0}+i^{1}+\cdots+i^{2009}$.
|
By the geometric series formula, the sum is equal to $\frac{i^{2010}-1}{i-1}=\frac{-2}{i-1}=1+i$.
|
{
"exam": "HMMT",
"problem_label": "4",
"problem_match": "\n4. [6]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
In how many distinct ways can you color each of the vertices of a tetrahedron either red, blue, or green such that no face has all three vertices the same color? (Two colorings are considered the same if one coloring can be rotated in three dimensions to obtain the other.)
|
6
|
6
|
Yes
|
Problem not solved
|
math-word-problem
|
Combinatorics
|
In how many distinct ways can you color each of the vertices of a tetrahedron either red, blue, or green such that no face has all three vertices the same color? (Two colorings are considered the same if one coloring can be rotated in three dimensions to obtain the other.)
|
6
|
{
"exam": "HMMT",
"problem_label": "5",
"problem_match": "\n5. [6]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
In how many distinct ways can you color each of the vertices of a tetrahedron either red, blue, or green such that no face has all three vertices the same color? (Two colorings are considered the same if one coloring can be rotated in three dimensions to obtain the other.)
|
If only two colors are used, there is only one possible arrangement up to rotation, so this gives 3 possibilities. If all three colors are used, then one is used twice. There are 3 ways to choose the color that is used twice. Say this color is red. Then the red vertices are on a common edge, and the green and blue vertices are on another edge. We see that either choice of arrangement of the green and blue vertices is the same up to rotation. Thus there are 6 possibilities total.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In how many distinct ways can you color each of the vertices of a tetrahedron either red, blue, or green such that no face has all three vertices the same color? (Two colorings are considered the same if one coloring can be rotated in three dimensions to obtain the other.)
|
If only two colors are used, there is only one possible arrangement up to rotation, so this gives 3 possibilities. If all three colors are used, then one is used twice. There are 3 ways to choose the color that is used twice. Say this color is red. Then the red vertices are on a common edge, and the green and blue vertices are on another edge. We see that either choice of arrangement of the green and blue vertices is the same up to rotation. Thus there are 6 possibilities total.
|
{
"exam": "HMMT",
"problem_label": "5",
"problem_match": "\n5. [6]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
Let $A B C$ be a right triangle with hypotenuse $A C$. Let $B^{\prime}$ be the reflection of point $B$ across $A C$, and let $C^{\prime}$ be the reflection of $C$ across $A B^{\prime}$. Find the ratio of $\left[B C B^{\prime}\right]$ to $\left[B C^{\prime} B^{\prime}\right]$.
|
1 Solution: Since $C, B^{\prime}$, and $C^{\prime}$ are collinear, it is evident that $\left[B C B^{\prime}\right]=\frac{1}{2}\left[B C C^{\prime}\right]$. It immediately follows that $\left[B C B^{\prime}\right]=\left[B C^{\prime} B^{\prime}\right]$. Thus, the ratio is 1 .
$12^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
1
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a right triangle with hypotenuse $A C$. Let $B^{\prime}$ be the reflection of point $B$ across $A C$, and let $C^{\prime}$ be the reflection of $C$ across $A B^{\prime}$. Find the ratio of $\left[B C B^{\prime}\right]$ to $\left[B C^{\prime} B^{\prime}\right]$.
|
1 Solution: Since $C, B^{\prime}$, and $C^{\prime}$ are collinear, it is evident that $\left[B C B^{\prime}\right]=\frac{1}{2}\left[B C C^{\prime}\right]$. It immediately follows that $\left[B C B^{\prime}\right]=\left[B C^{\prime} B^{\prime}\right]$. Thus, the ratio is 1 .
$12^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
{
"exam": "HMMT",
"problem_label": "6",
"problem_match": "\n6. [6]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
How many perfect squares divide $2^{3} \cdot 3^{5} \cdot 5^{7} \cdot 7^{9}$ ?
|
120
|
120
|
Yes
|
Incomplete
|
math-word-problem
|
Number Theory
|
How many perfect squares divide $2^{3} \cdot 3^{5} \cdot 5^{7} \cdot 7^{9}$ ?
|
120
|
{
"exam": "HMMT",
"problem_label": "7",
"problem_match": "\n7. [6]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
How many perfect squares divide $2^{3} \cdot 3^{5} \cdot 5^{7} \cdot 7^{9}$ ?
|
The number of such perfect squares is $2 \cdot 3 \cdot 4 \cdot 5$, since the exponent of each prime can be any nonnegative even number less than the given exponent.
|
2 \cdot 3 \cdot 4 \cdot 5
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
How many perfect squares divide $2^{3} \cdot 3^{5} \cdot 5^{7} \cdot 7^{9}$ ?
|
The number of such perfect squares is $2 \cdot 3 \cdot 4 \cdot 5$, since the exponent of each prime can be any nonnegative even number less than the given exponent.
|
{
"exam": "HMMT",
"problem_label": "7",
"problem_match": "\n7. [6]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
Which is greater, $\log _{2008}(2009)$ or $\log _{2009}(2010)$ ?
|
$\log _{2008} 2009$.
|
\log _{2008} 2009
|
Yes
|
Problem not solved
|
math-word-problem
|
Algebra
|
Which is greater, $\log _{2008}(2009)$ or $\log _{2009}(2010)$ ?
|
$\log _{2008} 2009$.
|
{
"exam": "HMMT",
"problem_label": "8",
"problem_match": "\n8. [6]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
Which is greater, $\log _{2008}(2009)$ or $\log _{2009}(2010)$ ?
|
Let $f(x)=\log _{x}(x+1)$. Then $f^{\prime}(x)=\frac{x \ln x-(x+1) \ln (x+1)}{x(x+1) \ln ^{2} x}<0$ for any $x>1$, so $f$ is decreasing. Thus $\log _{2008}(2009)$ is greater.
|
\log _{2008}(2009) \text{ is greater}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Which is greater, $\log _{2008}(2009)$ or $\log _{2009}(2010)$ ?
|
Let $f(x)=\log _{x}(x+1)$. Then $f^{\prime}(x)=\frac{x \ln x-(x+1) \ln (x+1)}{x(x+1) \ln ^{2} x}<0$ for any $x>1$, so $f$ is decreasing. Thus $\log _{2008}(2009)$ is greater.
|
{
"exam": "HMMT",
"problem_label": "8",
"problem_match": "\n8. [6]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
An icosidodecahedron is a convex polyhedron with 20 triangular faces and 12 pentagonal faces. How many vertices does it have?
|
30
|
30
|
Yes
|
Problem not solved
|
math-word-problem
|
Geometry
|
An icosidodecahedron is a convex polyhedron with 20 triangular faces and 12 pentagonal faces. How many vertices does it have?
|
30
|
{
"exam": "HMMT",
"problem_label": "9",
"problem_match": "\n9. [6]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
An icosidodecahedron is a convex polyhedron with 20 triangular faces and 12 pentagonal faces. How many vertices does it have?
|
Since every edge is shared by exactly two faces, there are $(20 \cdot 3+12 \cdot 5) / 2=60$ edges. Using Euler's formula $v-e+f=2$, we see that there are 30 vertices.
$12^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
30
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
An icosidodecahedron is a convex polyhedron with 20 triangular faces and 12 pentagonal faces. How many vertices does it have?
|
Since every edge is shared by exactly two faces, there are $(20 \cdot 3+12 \cdot 5) / 2=60$ edges. Using Euler's formula $v-e+f=2$, we see that there are 30 vertices.
$12^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
{
"exam": "HMMT",
"problem_label": "9",
"problem_match": "\n9. [6]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
Let $a, b$, and $c$ be real numbers. Consider the system of simultaneous equations in variables $x$ and $y$ :
$$
\begin{aligned}
a x+b y & =c-1 \\
(a+5) x+(b+3) y & =c+1
\end{aligned}
$$
Determine the value(s) of $c$ in terms of $a$ such that the system always has a solution for any $a$ and $b$.
|
$$
2 a / 5+1 .\left(\text { or } \frac{2 a+5}{5}\right)
$$
|
\frac{2a+5}{5}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $a, b$, and $c$ be real numbers. Consider the system of simultaneous equations in variables $x$ and $y$ :
$$
\begin{aligned}
a x+b y & =c-1 \\
(a+5) x+(b+3) y & =c+1
\end{aligned}
$$
Determine the value(s) of $c$ in terms of $a$ such that the system always has a solution for any $a$ and $b$.
|
$$
2 a / 5+1 .\left(\text { or } \frac{2 a+5}{5}\right)
$$
|
{
"exam": "HMMT",
"problem_label": "10",
"problem_match": "\n10. [7]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer:\n\n",
"tier": "T4",
"year": "2009"
}
|
Let $a, b$, and $c$ be real numbers. Consider the system of simultaneous equations in variables $x$ and $y$ :
$$
\begin{aligned}
a x+b y & =c-1 \\
(a+5) x+(b+3) y & =c+1
\end{aligned}
$$
Determine the value(s) of $c$ in terms of $a$ such that the system always has a solution for any $a$ and $b$.
|
We have to only consider when the determinant of $\left(\begin{array}{cc}a \\ a+5 & b \\ b+3\end{array}\right)$ is zero. That is, when $b=3 a / 5$. Plugging in $b=3 a / 5$, we find that $(a+5)(c-1)=a(c+1)$ or that $c=2 a / 5+1$.
|
c=\frac{2a}{5}+1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $a, b$, and $c$ be real numbers. Consider the system of simultaneous equations in variables $x$ and $y$ :
$$
\begin{aligned}
a x+b y & =c-1 \\
(a+5) x+(b+3) y & =c+1
\end{aligned}
$$
Determine the value(s) of $c$ in terms of $a$ such that the system always has a solution for any $a$ and $b$.
|
We have to only consider when the determinant of $\left(\begin{array}{cc}a \\ a+5 & b \\ b+3\end{array}\right)$ is zero. That is, when $b=3 a / 5$. Plugging in $b=3 a / 5$, we find that $(a+5)(c-1)=a(c+1)$ or that $c=2 a / 5+1$.
|
{
"exam": "HMMT",
"problem_label": "10",
"problem_match": "\n10. [7]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
There are 2008 distinct points on a circle. If you connect two of these points to form a line and then connect another two points (distinct from the first two) to form another line, what is the probability that the two lines intersect inside the circle?
|
$1 / 3$
|
\frac{1}{3}
|
Yes
|
Incomplete
|
math-word-problem
|
Combinatorics
|
There are 2008 distinct points on a circle. If you connect two of these points to form a line and then connect another two points (distinct from the first two) to form another line, what is the probability that the two lines intersect inside the circle?
|
$1 / 3$
|
{
"exam": "HMMT",
"problem_label": "11",
"problem_match": "\n11. [7]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
There are 2008 distinct points on a circle. If you connect two of these points to form a line and then connect another two points (distinct from the first two) to form another line, what is the probability that the two lines intersect inside the circle?
|
Given four of these points, there are 3 ways in which to connect two of them and then connect the other two, and of these possibilities exactly one will intersect inside the circle. Thus $1 / 3$ of all the ways to connect two lines and then connect two others have an intersection point inside the circle.
|
\frac{1}{3}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There are 2008 distinct points on a circle. If you connect two of these points to form a line and then connect another two points (distinct from the first two) to form another line, what is the probability that the two lines intersect inside the circle?
|
Given four of these points, there are 3 ways in which to connect two of them and then connect the other two, and of these possibilities exactly one will intersect inside the circle. Thus $1 / 3$ of all the ways to connect two lines and then connect two others have an intersection point inside the circle.
|
{
"exam": "HMMT",
"problem_label": "11",
"problem_match": "\n11. [7]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
Bob is writing a sequence of letters of the alphabet, each of which can be either uppercase or lowercase, according to the following two rules:
- If he had just written an uppercase letter, he can either write the same letter in lowercase after it, or the next letter of the alphabet in uppercase.
- If he had just written a lowercase letter, he can either write the same letter in uppercase after it, or the preceding letter of the alphabet in lowercase.
For instance, one such sequence is $a A a A B C D d c b B C$. How many sequences of 32 letters can he write that start at (lowercase) $a$ and end at (lowercase) $z$ ? (The alphabet contains 26 letters from $a$ to $z$.)
|
376
|
376
|
Yes
|
Problem not solved
|
math-word-problem
|
Combinatorics
|
Bob is writing a sequence of letters of the alphabet, each of which can be either uppercase or lowercase, according to the following two rules:
- If he had just written an uppercase letter, he can either write the same letter in lowercase after it, or the next letter of the alphabet in uppercase.
- If he had just written a lowercase letter, he can either write the same letter in uppercase after it, or the preceding letter of the alphabet in lowercase.
For instance, one such sequence is $a A a A B C D d c b B C$. How many sequences of 32 letters can he write that start at (lowercase) $a$ and end at (lowercase) $z$ ? (The alphabet contains 26 letters from $a$ to $z$.)
|
376
|
{
"exam": "HMMT",
"problem_label": "12",
"problem_match": "\n12. [7]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
Bob is writing a sequence of letters of the alphabet, each of which can be either uppercase or lowercase, according to the following two rules:
- If he had just written an uppercase letter, he can either write the same letter in lowercase after it, or the next letter of the alphabet in uppercase.
- If he had just written a lowercase letter, he can either write the same letter in uppercase after it, or the preceding letter of the alphabet in lowercase.
For instance, one such sequence is $a A a A B C D d c b B C$. How many sequences of 32 letters can he write that start at (lowercase) $a$ and end at (lowercase) $z$ ? (The alphabet contains 26 letters from $a$ to $z$.)
|
The smallest possible sequence from $a$ to $z$ is $a A B C D \ldots Z z$, which has 28 letters. To insert 4 more letters, we can either switch two (not necessarily distinct) letters to lowercase and back again (as in $a A B C c C D E F f F G H \ldots Z z$ ), or we can insert a lowercase letter after its corresponding uppercase letter, insert the previous letter of the alphabet, switch back to uppercase, and continue the sequence (as in $a A B C c b B C D E \ldots Z z$ ). There are $\binom{27}{2}=13 \cdot 27$ sequences of the former type and 25 of the latter, for a total of 376 such sequences.
## $12^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
376
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Bob is writing a sequence of letters of the alphabet, each of which can be either uppercase or lowercase, according to the following two rules:
- If he had just written an uppercase letter, he can either write the same letter in lowercase after it, or the next letter of the alphabet in uppercase.
- If he had just written a lowercase letter, he can either write the same letter in uppercase after it, or the preceding letter of the alphabet in lowercase.
For instance, one such sequence is $a A a A B C D d c b B C$. How many sequences of 32 letters can he write that start at (lowercase) $a$ and end at (lowercase) $z$ ? (The alphabet contains 26 letters from $a$ to $z$.)
|
The smallest possible sequence from $a$ to $z$ is $a A B C D \ldots Z z$, which has 28 letters. To insert 4 more letters, we can either switch two (not necessarily distinct) letters to lowercase and back again (as in $a A B C c C D E F f F G H \ldots Z z$ ), or we can insert a lowercase letter after its corresponding uppercase letter, insert the previous letter of the alphabet, switch back to uppercase, and continue the sequence (as in $a A B C c b B C D E \ldots Z z$ ). There are $\binom{27}{2}=13 \cdot 27$ sequences of the former type and 25 of the latter, for a total of 376 such sequences.
## $12^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
{
"exam": "HMMT",
"problem_label": "12",
"problem_match": "\n12. [7]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
How many ordered quadruples $(a, b, c, d)$ of four distinct numbers chosen from the set $\{1,2,3, \ldots, 9\}$ satisfy $b<a, b<c$, and $d<c$ ?
|
630
|
630
|
Yes
|
Incomplete
|
math-word-problem
|
Combinatorics
|
How many ordered quadruples $(a, b, c, d)$ of four distinct numbers chosen from the set $\{1,2,3, \ldots, 9\}$ satisfy $b<a, b<c$, and $d<c$ ?
|
630
|
{
"exam": "HMMT",
"problem_label": "13",
"problem_match": "\n13. [8]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
How many ordered quadruples $(a, b, c, d)$ of four distinct numbers chosen from the set $\{1,2,3, \ldots, 9\}$ satisfy $b<a, b<c$, and $d<c$ ?
|
Given any 4 elements $p<q<r<s$ of $\{1,2, \ldots, 9\}$, there are 5 ways of rearranging them to satisfy the inequality: prqs, psqr, qspr, qrps, and rspq. This gives a total of $\binom{9}{4} \cdot 5=630$ quadruples.
|
630
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
How many ordered quadruples $(a, b, c, d)$ of four distinct numbers chosen from the set $\{1,2,3, \ldots, 9\}$ satisfy $b<a, b<c$, and $d<c$ ?
|
Given any 4 elements $p<q<r<s$ of $\{1,2, \ldots, 9\}$, there are 5 ways of rearranging them to satisfy the inequality: prqs, psqr, qspr, qrps, and rspq. This gives a total of $\binom{9}{4} \cdot 5=630$ quadruples.
|
{
"exam": "HMMT",
"problem_label": "13",
"problem_match": "\n13. [8]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
Compute
$$
\sum_{k=1}^{2009} k\left(\left\lfloor\frac{2009}{k}\right\rfloor-\left\lfloor\frac{2008}{k}\right\rfloor\right)
$$
|
2394
|
2394
|
Yes
|
Incomplete
|
math-word-problem
|
Number Theory
|
Compute
$$
\sum_{k=1}^{2009} k\left(\left\lfloor\frac{2009}{k}\right\rfloor-\left\lfloor\frac{2008}{k}\right\rfloor\right)
$$
|
2394
|
{
"exam": "HMMT",
"problem_label": "14",
"problem_match": "\n14. [8]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
Compute
$$
\sum_{k=1}^{2009} k\left(\left\lfloor\frac{2009}{k}\right\rfloor-\left\lfloor\frac{2008}{k}\right\rfloor\right)
$$
|
The summand is equal to $k$ if $k$ divides 2009 and 0 otherwise. Thus the sum is equal to the sum of the divisors of 2009 , or 2394.
|
2394
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Compute
$$
\sum_{k=1}^{2009} k\left(\left\lfloor\frac{2009}{k}\right\rfloor-\left\lfloor\frac{2008}{k}\right\rfloor\right)
$$
|
The summand is equal to $k$ if $k$ divides 2009 and 0 otherwise. Thus the sum is equal to the sum of the divisors of 2009 , or 2394.
|
{
"exam": "HMMT",
"problem_label": "14",
"problem_match": "\n14. [8]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
Stan has a stack of 100 blocks and starts with a score of 0 , and plays a game in which he iterates the following two-step procedure:
(a) Stan picks a stack of blocks and splits it into 2 smaller stacks each with a positive number of blocks, say $a$ and $b$. (The order in which the new piles are placed does not matter.)
(b) Stan adds the product of the two piles' sizes, $a b$, to his score.
The game ends when there are only 1-block stacks left. What is the expected value of Stan's score at the end of the game?
|
4950
|
4950
|
Yes
|
Incomplete
|
math-word-problem
|
Combinatorics
|
Stan has a stack of 100 blocks and starts with a score of 0 , and plays a game in which he iterates the following two-step procedure:
(a) Stan picks a stack of blocks and splits it into 2 smaller stacks each with a positive number of blocks, say $a$ and $b$. (The order in which the new piles are placed does not matter.)
(b) Stan adds the product of the two piles' sizes, $a b$, to his score.
The game ends when there are only 1-block stacks left. What is the expected value of Stan's score at the end of the game?
|
4950
|
{
"exam": "HMMT",
"problem_label": "15",
"problem_match": "\n15. [8]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
Stan has a stack of 100 blocks and starts with a score of 0 , and plays a game in which he iterates the following two-step procedure:
(a) Stan picks a stack of blocks and splits it into 2 smaller stacks each with a positive number of blocks, say $a$ and $b$. (The order in which the new piles are placed does not matter.)
(b) Stan adds the product of the two piles' sizes, $a b$, to his score.
The game ends when there are only 1-block stacks left. What is the expected value of Stan's score at the end of the game?
|
Let $E(n)$ be the expected value of the score for an $n$-block game. It suffices to show that the score is invariant regardless of how the game is played. We proceed by induction. We have $E(1)=0$ and $E(2)=1$. We require that $E(n)=E(n-k)+E(k)+(n-k) k$ for all $k$. Setting $k=1$, we hypothesize that $E(n)=n(n-1) / 2$. This satisfies the recursion and base cases so $E(100)=100 \cdot 99 / 2=4950$.
|
4950
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Stan has a stack of 100 blocks and starts with a score of 0 , and plays a game in which he iterates the following two-step procedure:
(a) Stan picks a stack of blocks and splits it into 2 smaller stacks each with a positive number of blocks, say $a$ and $b$. (The order in which the new piles are placed does not matter.)
(b) Stan adds the product of the two piles' sizes, $a b$, to his score.
The game ends when there are only 1-block stacks left. What is the expected value of Stan's score at the end of the game?
|
Let $E(n)$ be the expected value of the score for an $n$-block game. It suffices to show that the score is invariant regardless of how the game is played. We proceed by induction. We have $E(1)=0$ and $E(2)=1$. We require that $E(n)=E(n-k)+E(k)+(n-k) k$ for all $k$. Setting $k=1$, we hypothesize that $E(n)=n(n-1) / 2$. This satisfies the recursion and base cases so $E(100)=100 \cdot 99 / 2=4950$.
|
{
"exam": "HMMT",
"problem_label": "15",
"problem_match": "\n15. [8]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
A spider is making a web between $n>1$ distinct leaves which are equally spaced around a circle. He chooses a leaf to start at, and to make the base layer he travels to each leaf one at a time, making a straight line of silk between each consecutive pair of leaves, such that no two of the lines of silk cross each other and he visits every leaf exactly once. In how many ways can the spider make the base layer of the web? Express your answer in terms of $n$.
|
$n 2^{n-2}$
|
n 2^{n-2}
|
Yes
|
Problem not solved
|
math-word-problem
|
Combinatorics
|
A spider is making a web between $n>1$ distinct leaves which are equally spaced around a circle. He chooses a leaf to start at, and to make the base layer he travels to each leaf one at a time, making a straight line of silk between each consecutive pair of leaves, such that no two of the lines of silk cross each other and he visits every leaf exactly once. In how many ways can the spider make the base layer of the web? Express your answer in terms of $n$.
|
$n 2^{n-2}$
|
{
"exam": "HMMT",
"problem_label": "16",
"problem_match": "\n16. [9]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
A spider is making a web between $n>1$ distinct leaves which are equally spaced around a circle. He chooses a leaf to start at, and to make the base layer he travels to each leaf one at a time, making a straight line of silk between each consecutive pair of leaves, such that no two of the lines of silk cross each other and he visits every leaf exactly once. In how many ways can the spider make the base layer of the web? Express your answer in terms of $n$.
|
There are $n$ ways to choose a starting vertex, and at each vertex he has only two choices for where to go next: the nearest untouched leaf in the clockwise direction, and the nearest untouched leaf in the counterclockwise direction. For, if the spider visited a leaf which is not nearest in some direction, there are two untouched leaves which are separated by this line of silk, and so the silk would eventually cross itself. Thus, for the first $n-2$ choices there are 2 possibilities, and the $(n-1)$ st choice is then determined.
Note: This formula can also be derived recursively.
|
n \cdot 2^{n-2}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A spider is making a web between $n>1$ distinct leaves which are equally spaced around a circle. He chooses a leaf to start at, and to make the base layer he travels to each leaf one at a time, making a straight line of silk between each consecutive pair of leaves, such that no two of the lines of silk cross each other and he visits every leaf exactly once. In how many ways can the spider make the base layer of the web? Express your answer in terms of $n$.
|
There are $n$ ways to choose a starting vertex, and at each vertex he has only two choices for where to go next: the nearest untouched leaf in the clockwise direction, and the nearest untouched leaf in the counterclockwise direction. For, if the spider visited a leaf which is not nearest in some direction, there are two untouched leaves which are separated by this line of silk, and so the silk would eventually cross itself. Thus, for the first $n-2$ choices there are 2 possibilities, and the $(n-1)$ st choice is then determined.
Note: This formula can also be derived recursively.
|
{
"exam": "HMMT",
"problem_label": "16",
"problem_match": "\n16. [9]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
How many positive integers $n \leq 2009$ have the property that $\left\lfloor\log _{2}(n)\right\rfloor$ is odd?
|
682
|
682
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
How many positive integers $n \leq 2009$ have the property that $\left\lfloor\log _{2}(n)\right\rfloor$ is odd?
|
682
|
{
"exam": "HMMT",
"problem_label": "17",
"problem_match": "\n17. [9]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
How many positive integers $n \leq 2009$ have the property that $\left\lfloor\log _{2}(n)\right\rfloor$ is odd?
|
We wish to find $n$ such that there is some natural number $k$ for which $2 k-1 \leq \log _{2} n<$ $2 k$. Since $n \leq 2009$ we must have $k \leq 5$. This is equivalent to finding the number of positive integers $n \leq 2009$ satisfying $2^{2 k-1} \leq n<2^{2 k}$ for some $k \leq 5$, so the number of such integers is $2+2^{3}+2^{5}+2^{7}+2^{9}=682$.
|
682
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
How many positive integers $n \leq 2009$ have the property that $\left\lfloor\log _{2}(n)\right\rfloor$ is odd?
|
We wish to find $n$ such that there is some natural number $k$ for which $2 k-1 \leq \log _{2} n<$ $2 k$. Since $n \leq 2009$ we must have $k \leq 5$. This is equivalent to finding the number of positive integers $n \leq 2009$ satisfying $2^{2 k-1} \leq n<2^{2 k}$ for some $k \leq 5$, so the number of such integers is $2+2^{3}+2^{5}+2^{7}+2^{9}=682$.
|
{
"exam": "HMMT",
"problem_label": "17",
"problem_match": "\n17. [9]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
If $n$ is a positive integer such that $n^{3}+2 n^{2}+9 n+8$ is the cube of an integer, find $n$.
|
7
|
7
|
Yes
|
Problem not solved
|
math-word-problem
|
Algebra
|
If $n$ is a positive integer such that $n^{3}+2 n^{2}+9 n+8$ is the cube of an integer, find $n$.
|
7
|
{
"exam": "HMMT",
"problem_label": "18",
"problem_match": "\n18. [9]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
If $n$ is a positive integer such that $n^{3}+2 n^{2}+9 n+8$ is the cube of an integer, find $n$.
|
Since $n^{3}<n^{3}+2 n^{2}+9 n+8<(n+2)^{3}$, we must have $n^{3}+2 n^{2}+9 n+8=(n+1)^{3}$. Thus $n^{2}=6 n+7$, so $n=7$.
$\qquad$
$12^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
7
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
If $n$ is a positive integer such that $n^{3}+2 n^{2}+9 n+8$ is the cube of an integer, find $n$.
|
Since $n^{3}<n^{3}+2 n^{2}+9 n+8<(n+2)^{3}$, we must have $n^{3}+2 n^{2}+9 n+8=(n+1)^{3}$. Thus $n^{2}=6 n+7$, so $n=7$.
$\qquad$
$12^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
{
"exam": "HMMT",
"problem_label": "18",
"problem_match": "\n18. [9]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
Shelly writes down a vector $v=(a, b, c, d)$, where $0<a<b<c<d$ are integers. Let $\sigma(v)$ denote the set of 24 vectors whose coordinates are $a, b, c$, and $d$ in some order. For instance, $\sigma(v)$ contains $(b, c, d, a)$. Shelly notes that there are 3 vectors in $\sigma(v)$ whose sum is of the form $(s, s, s, s)$ for some $s$. What is the smallest possible value of $d$ ?
|
6
|
6
|
Yes
|
Problem not solved
|
math-word-problem
|
Combinatorics
|
Shelly writes down a vector $v=(a, b, c, d)$, where $0<a<b<c<d$ are integers. Let $\sigma(v)$ denote the set of 24 vectors whose coordinates are $a, b, c$, and $d$ in some order. For instance, $\sigma(v)$ contains $(b, c, d, a)$. Shelly notes that there are 3 vectors in $\sigma(v)$ whose sum is of the form $(s, s, s, s)$ for some $s$. What is the smallest possible value of $d$ ?
|
6
|
{
"exam": "HMMT",
"problem_label": "19",
"problem_match": "\n19. [10]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
Shelly writes down a vector $v=(a, b, c, d)$, where $0<a<b<c<d$ are integers. Let $\sigma(v)$ denote the set of 24 vectors whose coordinates are $a, b, c$, and $d$ in some order. For instance, $\sigma(v)$ contains $(b, c, d, a)$. Shelly notes that there are 3 vectors in $\sigma(v)$ whose sum is of the form $(s, s, s, s)$ for some $s$. What is the smallest possible value of $d$ ?
|
If $k=a+b+c+d$, first you notice $4 \mid 3 k$, and $k \geq 10$. So we try $k=12$, which works with $a, b, c, d=1,2,3,6$ and not $1,2,4,5$.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Shelly writes down a vector $v=(a, b, c, d)$, where $0<a<b<c<d$ are integers. Let $\sigma(v)$ denote the set of 24 vectors whose coordinates are $a, b, c$, and $d$ in some order. For instance, $\sigma(v)$ contains $(b, c, d, a)$. Shelly notes that there are 3 vectors in $\sigma(v)$ whose sum is of the form $(s, s, s, s)$ for some $s$. What is the smallest possible value of $d$ ?
|
If $k=a+b+c+d$, first you notice $4 \mid 3 k$, and $k \geq 10$. So we try $k=12$, which works with $a, b, c, d=1,2,3,6$ and not $1,2,4,5$.
|
{
"exam": "HMMT",
"problem_label": "19",
"problem_match": "\n19. [10]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
A positive integer is called jubilant if the number of 1's in its binary representation is even. For example, $6=110_{2}$ is a jubilant number. What is the 2009th smallest jubilant number?
|
4018
|
4018
|
Yes
|
Problem not solved
|
math-word-problem
|
Number Theory
|
A positive integer is called jubilant if the number of 1's in its binary representation is even. For example, $6=110_{2}$ is a jubilant number. What is the 2009th smallest jubilant number?
|
4018
|
{
"exam": "HMMT",
"problem_label": "20",
"problem_match": "\n20. [10]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
A positive integer is called jubilant if the number of 1's in its binary representation is even. For example, $6=110_{2}$ is a jubilant number. What is the 2009th smallest jubilant number?
|
Notice that for each pair of consecutive positive integers $2 k$ and $2 k+1$, their binary representation differs by exactly one 1 (in the units digit), so exactly one of 2 and 3 is jubilant, exactly one of 4 and 5 is jubilant, etc. It follows that there are exactly 2009 jubilant numbers less than or equal to 4019 . We now simply need to check whether 4018 or 4019 is jubilant. Since the binary representation of 4018 is 111110110010,4018 is the 2009 th jubilant number.
|
4018
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A positive integer is called jubilant if the number of 1's in its binary representation is even. For example, $6=110_{2}$ is a jubilant number. What is the 2009th smallest jubilant number?
|
Notice that for each pair of consecutive positive integers $2 k$ and $2 k+1$, their binary representation differs by exactly one 1 (in the units digit), so exactly one of 2 and 3 is jubilant, exactly one of 4 and 5 is jubilant, etc. It follows that there are exactly 2009 jubilant numbers less than or equal to 4019 . We now simply need to check whether 4018 or 4019 is jubilant. Since the binary representation of 4018 is 111110110010,4018 is the 2009 th jubilant number.
|
{
"exam": "HMMT",
"problem_label": "20",
"problem_match": "\n20. [10]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
Simplify
$$
2 \cos ^{2}(\ln (2009) i)+i \sin (\ln (4036081) i)
$$
|
$$
\begin{aligned}
& \text { Answer: } \begin{aligned}
& \frac{4036082}{4036081} \text { Solution: We have } \\
& \begin{aligned}
2 \cos ^{2}(\ln (2009) i)+i \sin (\ln (4036081) i) & =1+\cos (2 \ln (2009) i)+i \sin (\ln (4036081) i) \\
& =1+\cos (\ln (4036081) i)+i \sin (\ln (4036081) i) \\
& =1+e^{i^{2} \ln (4036081)} \\
& =1+\frac{1}{4036081} \\
& =\frac{4036082}{4036081}
\end{aligned}
\end{aligned} . \begin{array}{l}
\\
\end{array}
\end{aligned}
$$
as desired.
## $12^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
\frac{4036082}{4036081}
|
Incomplete
|
Yes
|
math-word-problem
|
Algebra
|
Simplify
$$
2 \cos ^{2}(\ln (2009) i)+i \sin (\ln (4036081) i)
$$
|
$$
\begin{aligned}
& \text { Answer: } \begin{aligned}
& \frac{4036082}{4036081} \text { Solution: We have } \\
& \begin{aligned}
2 \cos ^{2}(\ln (2009) i)+i \sin (\ln (4036081) i) & =1+\cos (2 \ln (2009) i)+i \sin (\ln (4036081) i) \\
& =1+\cos (\ln (4036081) i)+i \sin (\ln (4036081) i) \\
& =1+e^{i^{2} \ln (4036081)} \\
& =1+\frac{1}{4036081} \\
& =\frac{4036082}{4036081}
\end{aligned}
\end{aligned} . \begin{array}{l}
\\
\end{array}
\end{aligned}
$$
as desired.
## $12^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
{
"exam": "HMMT",
"problem_label": "21",
"problem_match": "\n21. [10]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nSolution:\n",
"tier": "T4",
"year": "2009"
}
|
A circle having radius $r_{1}$ centered at point $N$ is tangent to a circle of radius $r_{2}$ centered at $M$. Let $l$ and $j$ be the two common external tangent lines to the two circles. A circle centered at $P$ with radius $r_{2}$ is externally tangent to circle $N$ at the point at which $l$ coincides with circle $N$, and line $k$ is externally tangent to $P$ and $N$ such that points $M, N$, and $P$ all lie on the same side of $k$. For what ratio $r_{1} / r_{2}$ are $j$ and $k$ parallel?
|
3
|
3
|
Yes
|
Problem not solved
|
math-word-problem
|
Geometry
|
A circle having radius $r_{1}$ centered at point $N$ is tangent to a circle of radius $r_{2}$ centered at $M$. Let $l$ and $j$ be the two common external tangent lines to the two circles. A circle centered at $P$ with radius $r_{2}$ is externally tangent to circle $N$ at the point at which $l$ coincides with circle $N$, and line $k$ is externally tangent to $P$ and $N$ such that points $M, N$, and $P$ all lie on the same side of $k$. For what ratio $r_{1} / r_{2}$ are $j$ and $k$ parallel?
|
3
|
{
"exam": "HMMT",
"problem_label": "22",
"problem_match": "\n22. [10]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
A circle having radius $r_{1}$ centered at point $N$ is tangent to a circle of radius $r_{2}$ centered at $M$. Let $l$ and $j$ be the two common external tangent lines to the two circles. A circle centered at $P$ with radius $r_{2}$ is externally tangent to circle $N$ at the point at which $l$ coincides with circle $N$, and line $k$ is externally tangent to $P$ and $N$ such that points $M, N$, and $P$ all lie on the same side of $k$. For what ratio $r_{1} / r_{2}$ are $j$ and $k$ parallel?
|
Suppose the lines are parallel. Draw the other tangent line to $N$ and $P$ - since $M$ and $P$ have the same radius, it is tangent to all three circles. Let $j$ and $k$ meet circle $N$ at $A$ and $B$, respectively. Then by symmetry we see that $\angle A N M=\angle M N P=\angle P N B=60^{\circ}$ since $A, N$, and $B$ are collinear (perpendicular to $j$ and $k$ ). Let $D$ be the foot of the perpendicular from $M$ to $A N$. In $\triangle M D N$, we have $M N=2 D N$, so $r_{1}+r_{2}=2\left(r_{1}-r_{2}\right)$, and so $r_{1} / r_{2}=3$.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A circle having radius $r_{1}$ centered at point $N$ is tangent to a circle of radius $r_{2}$ centered at $M$. Let $l$ and $j$ be the two common external tangent lines to the two circles. A circle centered at $P$ with radius $r_{2}$ is externally tangent to circle $N$ at the point at which $l$ coincides with circle $N$, and line $k$ is externally tangent to $P$ and $N$ such that points $M, N$, and $P$ all lie on the same side of $k$. For what ratio $r_{1} / r_{2}$ are $j$ and $k$ parallel?
|
Suppose the lines are parallel. Draw the other tangent line to $N$ and $P$ - since $M$ and $P$ have the same radius, it is tangent to all three circles. Let $j$ and $k$ meet circle $N$ at $A$ and $B$, respectively. Then by symmetry we see that $\angle A N M=\angle M N P=\angle P N B=60^{\circ}$ since $A, N$, and $B$ are collinear (perpendicular to $j$ and $k$ ). Let $D$ be the foot of the perpendicular from $M$ to $A N$. In $\triangle M D N$, we have $M N=2 D N$, so $r_{1}+r_{2}=2\left(r_{1}-r_{2}\right)$, and so $r_{1} / r_{2}=3$.
|
{
"exam": "HMMT",
"problem_label": "22",
"problem_match": "\n22. [10]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
The roots of $z^{6}+z^{4}+z^{2}+1=0$ are the vertices of a convex polygon in the complex plane. Find the sum of the squares of the side lengths of the polygon.
|
$12-4 \sqrt{2}$
|
12-4 \sqrt{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
The roots of $z^{6}+z^{4}+z^{2}+1=0$ are the vertices of a convex polygon in the complex plane. Find the sum of the squares of the side lengths of the polygon.
|
$12-4 \sqrt{2}$
|
{
"exam": "HMMT",
"problem_label": "23",
"problem_match": "\n23. [10]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
The roots of $z^{6}+z^{4}+z^{2}+1=0$ are the vertices of a convex polygon in the complex plane. Find the sum of the squares of the side lengths of the polygon.
|
Factoring the polynomial as $\left(z^{4}+1\right)\left(z^{2}+1\right)=0$, we find that the 6 roots are $e^{ \pm i \pi / 4}$, $e^{ \pm i \pi / 2}, e^{ \pm i 3 \pi / 4}$. The calculation then follows from the Law of Cosines or the distance formula.
|
not found
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
The roots of $z^{6}+z^{4}+z^{2}+1=0$ are the vertices of a convex polygon in the complex plane. Find the sum of the squares of the side lengths of the polygon.
|
Factoring the polynomial as $\left(z^{4}+1\right)\left(z^{2}+1\right)=0$, we find that the 6 roots are $e^{ \pm i \pi / 4}$, $e^{ \pm i \pi / 2}, e^{ \pm i 3 \pi / 4}$. The calculation then follows from the Law of Cosines or the distance formula.
|
{
"exam": "HMMT",
"problem_label": "23",
"problem_match": "\n23. [10]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
Compute, in terms of $n$,
$$
\sum_{k=0}^{n}\binom{n-k}{k} 2^{k}
$$
Note that whenever $s<t,\binom{s}{t}=0$.
|
$$
\frac{2 \cdot 2^{n}+(-1)^{n}}{3}
$$
|
\frac{2 \cdot 2^{n}+(-1)^{n}}{3}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Compute, in terms of $n$,
$$
\sum_{k=0}^{n}\binom{n-k}{k} 2^{k}
$$
Note that whenever $s<t,\binom{s}{t}=0$.
|
$$
\frac{2 \cdot 2^{n}+(-1)^{n}}{3}
$$
|
{
"exam": "HMMT",
"problem_label": "24",
"problem_match": "\n24. [10]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer:\n\n",
"tier": "T4",
"year": "2009"
}
|
Compute, in terms of $n$,
$$
\sum_{k=0}^{n}\binom{n-k}{k} 2^{k}
$$
Note that whenever $s<t,\binom{s}{t}=0$.
|
Let $T_{n}=\sum_{k=0}^{n}\binom{n-k}{k} 2^{k}$. From Pascal's recursion for binomial coefficients, we can find $T_{n}=2 T_{n-2}+T_{n-1}$, with $T_{0}=1$ and $T_{1}=1$. The characteristic polynomial of this recursion is $x^{2}-x-2=0$, which has roots 2 and -1 . Thus $T_{n}=a \cdot 2^{n}+b \cdot(-1)^{n}$ for some $a$ and $b$. From the initial conditions we have $a+b=1$ and $2 a-b=1$. It follows that $a=2 / 3$ and $b=1 / 3$, from which the conclusion follows.
|
T_{n} = \frac{2}{3} \cdot 2^{n} + \frac{1}{3} \cdot (-1)^{n}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Compute, in terms of $n$,
$$
\sum_{k=0}^{n}\binom{n-k}{k} 2^{k}
$$
Note that whenever $s<t,\binom{s}{t}=0$.
|
Let $T_{n}=\sum_{k=0}^{n}\binom{n-k}{k} 2^{k}$. From Pascal's recursion for binomial coefficients, we can find $T_{n}=2 T_{n-2}+T_{n-1}$, with $T_{0}=1$ and $T_{1}=1$. The characteristic polynomial of this recursion is $x^{2}-x-2=0$, which has roots 2 and -1 . Thus $T_{n}=a \cdot 2^{n}+b \cdot(-1)^{n}$ for some $a$ and $b$. From the initial conditions we have $a+b=1$ and $2 a-b=1$. It follows that $a=2 / 3$ and $b=1 / 3$, from which the conclusion follows.
|
{
"exam": "HMMT",
"problem_label": "24",
"problem_match": "\n24. [10]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
Four points, $A, B, C$, and $D$, are chosen randomly on the circumference of a circle with independent uniform probability. What is the expected number of sides of triangle $A B C$ for which the projection of $D$ onto the line containing the side lies between the two vertices?
|
$3 / 2$
|
\frac{3}{2}
|
Yes
|
Incomplete
|
math-word-problem
|
Geometry
|
Four points, $A, B, C$, and $D$, are chosen randomly on the circumference of a circle with independent uniform probability. What is the expected number of sides of triangle $A B C$ for which the projection of $D$ onto the line containing the side lies between the two vertices?
|
$3 / 2$
|
{
"exam": "HMMT",
"problem_label": "25",
"problem_match": "\n25. [12]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
Four points, $A, B, C$, and $D$, are chosen randomly on the circumference of a circle with independent uniform probability. What is the expected number of sides of triangle $A B C$ for which the projection of $D$ onto the line containing the side lies between the two vertices?
|
By linearity of expectations, the answer is exactly 3 times the probability that the orthogonal projection of $D$ onto $A B$ lies interior to the segment. This happens exactly when either $\angle D A B$ or $\angle D B A$ is obtuse, which is equivalent to saying that $A$ and $B$ lie on the same side of the diameter through $D$. This happens with probability $1 / 2$. Therefore, desired answer is $3 / 2$.
|
\frac{3}{2}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Four points, $A, B, C$, and $D$, are chosen randomly on the circumference of a circle with independent uniform probability. What is the expected number of sides of triangle $A B C$ for which the projection of $D$ onto the line containing the side lies between the two vertices?
|
By linearity of expectations, the answer is exactly 3 times the probability that the orthogonal projection of $D$ onto $A B$ lies interior to the segment. This happens exactly when either $\angle D A B$ or $\angle D B A$ is obtuse, which is equivalent to saying that $A$ and $B$ lie on the same side of the diameter through $D$. This happens with probability $1 / 2$. Therefore, desired answer is $3 / 2$.
|
{
"exam": "HMMT",
"problem_label": "25",
"problem_match": "\n25. [12]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
Define the sequence $\left\{x_{i}\right\}_{i \geq 0}$ by $x_{0}=2009$ and $x_{n}=-\frac{2009}{n} \sum_{k=0}^{n-1} x_{k}$ for all $n \geq 1$. Compute the value of $\sum_{n=0}^{2009} 2^{n} x_{n}$.
|
2009
|
2009
|
Yes
|
Incomplete
|
math-word-problem
|
Algebra
|
Define the sequence $\left\{x_{i}\right\}_{i \geq 0}$ by $x_{0}=2009$ and $x_{n}=-\frac{2009}{n} \sum_{k=0}^{n-1} x_{k}$ for all $n \geq 1$. Compute the value of $\sum_{n=0}^{2009} 2^{n} x_{n}$.
|
2009
|
{
"exam": "HMMT",
"problem_label": "26",
"problem_match": "\n26. [12]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
Define the sequence $\left\{x_{i}\right\}_{i \geq 0}$ by $x_{0}=2009$ and $x_{n}=-\frac{2009}{n} \sum_{k=0}^{n-1} x_{k}$ for all $n \geq 1$. Compute the value of $\sum_{n=0}^{2009} 2^{n} x_{n}$.
|
We have
$$
-\frac{n x_{n}}{2009}=x_{n-1}+x_{n-2}+\ldots+x_{0}=x_{n-1}+\frac{(n-1) x_{n-1}}{2009}
$$
, which yields the recursion $x_{n}=\frac{n-2010}{n} x_{n-1}$. Unwinding this recursion, we find $x_{n}=(-1)^{n} \cdot 2009$. $\binom{2008}{n}$. Thus
$$
\begin{aligned}
\sum_{k=0}^{2009} 2^{n} x_{n} & =\sum_{k=0}^{2009}(-2)^{n} \cdot 2009 \cdot\binom{2008}{n} \\
& =2009 \sum_{k=0}^{2008}(-2)^{n}\binom{2008}{n} \\
& =2009(-2+1)^{2008}
\end{aligned}
$$
as desired.
|
2009
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Define the sequence $\left\{x_{i}\right\}_{i \geq 0}$ by $x_{0}=2009$ and $x_{n}=-\frac{2009}{n} \sum_{k=0}^{n-1} x_{k}$ for all $n \geq 1$. Compute the value of $\sum_{n=0}^{2009} 2^{n} x_{n}$.
|
We have
$$
-\frac{n x_{n}}{2009}=x_{n-1}+x_{n-2}+\ldots+x_{0}=x_{n-1}+\frac{(n-1) x_{n-1}}{2009}
$$
, which yields the recursion $x_{n}=\frac{n-2010}{n} x_{n-1}$. Unwinding this recursion, we find $x_{n}=(-1)^{n} \cdot 2009$. $\binom{2008}{n}$. Thus
$$
\begin{aligned}
\sum_{k=0}^{2009} 2^{n} x_{n} & =\sum_{k=0}^{2009}(-2)^{n} \cdot 2009 \cdot\binom{2008}{n} \\
& =2009 \sum_{k=0}^{2008}(-2)^{n}\binom{2008}{n} \\
& =2009(-2+1)^{2008}
\end{aligned}
$$
as desired.
|
{
"exam": "HMMT",
"problem_label": "26",
"problem_match": "\n26. [12]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
Circle $\Omega$ has radius 5. Points $A$ and $B$ lie on $\Omega$ such that chord $A B$ has length 6 . A unit circle $\omega$ is tangent to chord $A B$ at point $T$. Given that $\omega$ is also internally tangent to $\Omega$, find $A T \cdot B T$.
|
2
|
2
|
Yes
|
Problem not solved
|
math-word-problem
|
Geometry
|
Circle $\Omega$ has radius 5. Points $A$ and $B$ lie on $\Omega$ such that chord $A B$ has length 6 . A unit circle $\omega$ is tangent to chord $A B$ at point $T$. Given that $\omega$ is also internally tangent to $\Omega$, find $A T \cdot B T$.
|
2
|
{
"exam": "HMMT",
"problem_label": "27",
"problem_match": "\n27. [12]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
Circle $\Omega$ has radius 5. Points $A$ and $B$ lie on $\Omega$ such that chord $A B$ has length 6 . A unit circle $\omega$ is tangent to chord $A B$ at point $T$. Given that $\omega$ is also internally tangent to $\Omega$, find $A T \cdot B T$.
|
Let $M$ be the midpoint of chord $A B$ and let $O$ be the center of $\Omega$. Since $A M=B M=3$, Pythagoras on triangle $A M O$ gives $O M=4$. Now let $\omega$ be centered at $P$ and say that $\omega$ and $\Omega$ are tangent at $Q$. Because the diameter of $\omega$ exceeds 1 , points $P$ and $Q$ lie on the same side of $A B$. By tangency, $O, P$, and $Q$ are collinear, so that $O P=O Q-P Q=4$. Let $H$ be the orthogonal projection of $P$ onto $O M$; then $O H=O M-H M=O M-P T=3$. Pythagoras on $O H P$ gives $H P^{2}=7$. Finally,
$$
A T \cdot B T=A M^{2}-M T^{2}=A M^{2}-H P^{2}=9-7=2
$$
$12^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
2
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Circle $\Omega$ has radius 5. Points $A$ and $B$ lie on $\Omega$ such that chord $A B$ has length 6 . A unit circle $\omega$ is tangent to chord $A B$ at point $T$. Given that $\omega$ is also internally tangent to $\Omega$, find $A T \cdot B T$.
|
Let $M$ be the midpoint of chord $A B$ and let $O$ be the center of $\Omega$. Since $A M=B M=3$, Pythagoras on triangle $A M O$ gives $O M=4$. Now let $\omega$ be centered at $P$ and say that $\omega$ and $\Omega$ are tangent at $Q$. Because the diameter of $\omega$ exceeds 1 , points $P$ and $Q$ lie on the same side of $A B$. By tangency, $O, P$, and $Q$ are collinear, so that $O P=O Q-P Q=4$. Let $H$ be the orthogonal projection of $P$ onto $O M$; then $O H=O M-H M=O M-P T=3$. Pythagoras on $O H P$ gives $H P^{2}=7$. Finally,
$$
A T \cdot B T=A M^{2}-M T^{2}=A M^{2}-H P^{2}=9-7=2
$$
$12^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
{
"exam": "HMMT",
"problem_label": "27",
"problem_match": "\n27. [12]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
The vertices of a regular hexagon are labeled $\cos (\theta), \cos (2 \theta), \ldots, \cos (6 \theta)$. For every pair of vertices, Bob draws a blue line through the vertices if one of these functions can be expressed as a polynomial function of the other (that holds for all real $\theta$ ), and otherwise Roberta draws a red line through the
vertices. In the resulting graph, how many triangles whose vertices lie on the hexagon have at least one red and at least one blue edge?
|
14 Solution: The existence of the Chebyshev polynomials, which express $\cos (n \theta)$ as a polynomial in $\cos (\theta)$, imply that Bob draws a blue line between $\cos (\theta)$ and each other vertex, and also between $\cos (2 \theta)$ and $\cos (4 \theta)$, between $\cos (2 \theta)$ and $\cos (6 \theta)$, and between $\cos (3 \theta)$ and $\cos (6 \theta)$ (by substituting $\theta^{\prime}=2 \theta$ or $3 \theta$ as necessary). We now show that Roberta draws a red line through each other pair of vertices.
Let $m$ and $n$ be positive integers. Notice that $\cos (n \theta)$ is a periodic function with period $\frac{2 \pi}{n}$, and $\cos (m \theta)$ is periodic with period $\frac{2 \pi}{m}$. Thus, any polynomial in $\cos (m \theta)$ is also periodic of period $\frac{2 \pi}{m}$. This may not be the minimum period of the polynomial, however, so the minimum period is $\frac{2 \pi}{m k}$ for some $k$. Therefore, if $\cos (n \theta)$ can be expressed as a polynomial in $\cos (m \theta)$ then $\frac{2 \pi}{n}=\frac{2 \pi}{m k}$ for some $k$, so $m \mid n$. This shows that there is a blue line between two vertices $\cos (a \theta)$ and $\cos (b \theta)$ if and only if one of $a$ or $b$ divides the other.
Drawing the graph, one can easily count that there are 3 triangles with all blue edges, 3 triangles with all red edges, and $\binom{6}{3}=20$ triangles total. Thus there are $20-3-3=14$ triangles having at least one red and at least one blue edge.
|
14
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
The vertices of a regular hexagon are labeled $\cos (\theta), \cos (2 \theta), \ldots, \cos (6 \theta)$. For every pair of vertices, Bob draws a blue line through the vertices if one of these functions can be expressed as a polynomial function of the other (that holds for all real $\theta$ ), and otherwise Roberta draws a red line through the
vertices. In the resulting graph, how many triangles whose vertices lie on the hexagon have at least one red and at least one blue edge?
|
14 Solution: The existence of the Chebyshev polynomials, which express $\cos (n \theta)$ as a polynomial in $\cos (\theta)$, imply that Bob draws a blue line between $\cos (\theta)$ and each other vertex, and also between $\cos (2 \theta)$ and $\cos (4 \theta)$, between $\cos (2 \theta)$ and $\cos (6 \theta)$, and between $\cos (3 \theta)$ and $\cos (6 \theta)$ (by substituting $\theta^{\prime}=2 \theta$ or $3 \theta$ as necessary). We now show that Roberta draws a red line through each other pair of vertices.
Let $m$ and $n$ be positive integers. Notice that $\cos (n \theta)$ is a periodic function with period $\frac{2 \pi}{n}$, and $\cos (m \theta)$ is periodic with period $\frac{2 \pi}{m}$. Thus, any polynomial in $\cos (m \theta)$ is also periodic of period $\frac{2 \pi}{m}$. This may not be the minimum period of the polynomial, however, so the minimum period is $\frac{2 \pi}{m k}$ for some $k$. Therefore, if $\cos (n \theta)$ can be expressed as a polynomial in $\cos (m \theta)$ then $\frac{2 \pi}{n}=\frac{2 \pi}{m k}$ for some $k$, so $m \mid n$. This shows that there is a blue line between two vertices $\cos (a \theta)$ and $\cos (b \theta)$ if and only if one of $a$ or $b$ divides the other.
Drawing the graph, one can easily count that there are 3 triangles with all blue edges, 3 triangles with all red edges, and $\binom{6}{3}=20$ triangles total. Thus there are $20-3-3=14$ triangles having at least one red and at least one blue edge.
|
{
"exam": "HMMT",
"problem_label": "28",
"problem_match": "\n28. [15]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
The average of a set of distinct primes is 27 . What is the largest prime that can be in this set?
|
139 Solution: Denote the set of these primes by $A$ and the number of elements in $A$ by
$n$. There are 9 primes smaller than 27 , namely $2,3,5,7,11,13,17,19$ and 23 . Since 27 is odd and all primes except 2 are odd, $2 \notin A$. Thus the largest prime $p$ is at most $27 \cdot 9-3-5-7-11-13-17-19-23=145$, so $p \leq 141$. When the primes are $3,5,7,11,13,17,19,23,29,31$ and 139 , their average is 27 . Therefore $p=139$.
|
139
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
The average of a set of distinct primes is 27 . What is the largest prime that can be in this set?
|
139 Solution: Denote the set of these primes by $A$ and the number of elements in $A$ by
$n$. There are 9 primes smaller than 27 , namely $2,3,5,7,11,13,17,19$ and 23 . Since 27 is odd and all primes except 2 are odd, $2 \notin A$. Thus the largest prime $p$ is at most $27 \cdot 9-3-5-7-11-13-17-19-23=145$, so $p \leq 141$. When the primes are $3,5,7,11,13,17,19,23,29,31$ and 139 , their average is 27 . Therefore $p=139$.
|
{
"exam": "HMMT",
"problem_label": "29",
"problem_match": "\n29. [15]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
Let $f$ be a polynomial with integer coefficients such that the greatest common divisor of all its coefficients is 1 . For any $n \in \mathbb{N}, f(n)$ is a multiple of 85 . Find the smallest possible degree of $f$.
|
17 Solution: Notice that, if $p$ is a prime and $g$ is a polynomial with integer coefficients
such that $g(n) \equiv 0(\bmod p)$ for some $n$, then $g(n+m p)$ is divisible by $p$ as well for any integer multiple $m p$ of $p$. Therefore, it suffices to find the smallest possible degree of a polynomial $f$ for which $f(0), f(1), f(2), \ldots, f(16)$ are divisible by 17 and by 5 .
There is a polynomial of degree 17 with integer coefficients having $f(0)=f(1)=\cdots=f(16)=0$, namely $f(x)=(x)(x-1)(x-2) \cdots(x-16)$. Thus the minimal degree is no larger than 17 .
Now, let $f$ be such a polynomial and consider $f$ modulo 17 . The polynomial has 17 roots, so it must be at least degree 17 when taken modulo 17 . Thus $f$ has degree at least 17 as well.
## $12^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
17
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $f$ be a polynomial with integer coefficients such that the greatest common divisor of all its coefficients is 1 . For any $n \in \mathbb{N}, f(n)$ is a multiple of 85 . Find the smallest possible degree of $f$.
|
17 Solution: Notice that, if $p$ is a prime and $g$ is a polynomial with integer coefficients
such that $g(n) \equiv 0(\bmod p)$ for some $n$, then $g(n+m p)$ is divisible by $p$ as well for any integer multiple $m p$ of $p$. Therefore, it suffices to find the smallest possible degree of a polynomial $f$ for which $f(0), f(1), f(2), \ldots, f(16)$ are divisible by 17 and by 5 .
There is a polynomial of degree 17 with integer coefficients having $f(0)=f(1)=\cdots=f(16)=0$, namely $f(x)=(x)(x-1)(x-2) \cdots(x-16)$. Thus the minimal degree is no larger than 17 .
Now, let $f$ be such a polynomial and consider $f$ modulo 17 . The polynomial has 17 roots, so it must be at least degree 17 when taken modulo 17 . Thus $f$ has degree at least 17 as well.
## $12^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
{
"exam": "HMMT",
"problem_label": "30",
"problem_match": "\n30. [15]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
How many ways are there to win tic-tac-toe in $\mathbb{R}^{n}$ ? (That is, how many lines pass through three of the lattice points $\left(a_{1}, \ldots, a_{n}\right)$ in $\mathbb{R}^{n}$ with each coordinate $a_{i}$ in $\{1,2,3\} ?$ ) Express your answer in terms of $n$.
|
$\quad\left(5^{n}-3^{n}\right) / 2$ Solution: A line consists of three points. Each coordinate can do one of three things passing from the first point to the last point: increase by 1 each time, stay the same, or decrease by 1 each time. There are three ways to stay the same (three coordinates), one way to increase by 1 , and one way to decrease by 1 , so there are $5^{n}$ possible types of behavior. Determining this behavior uniquely determines the end point and start point except that we have traced every line exactly twice (forwards and backwards) and incorrectly counted the $3^{n}$ "lines" where each coordinate stays the same, so we subtract $3^{n}$ and divide by 2 .
|
\left(5^{n}-3^{n}\right) / 2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
How many ways are there to win tic-tac-toe in $\mathbb{R}^{n}$ ? (That is, how many lines pass through three of the lattice points $\left(a_{1}, \ldots, a_{n}\right)$ in $\mathbb{R}^{n}$ with each coordinate $a_{i}$ in $\{1,2,3\} ?$ ) Express your answer in terms of $n$.
|
$\quad\left(5^{n}-3^{n}\right) / 2$ Solution: A line consists of three points. Each coordinate can do one of three things passing from the first point to the last point: increase by 1 each time, stay the same, or decrease by 1 each time. There are three ways to stay the same (three coordinates), one way to increase by 1 , and one way to decrease by 1 , so there are $5^{n}$ possible types of behavior. Determining this behavior uniquely determines the end point and start point except that we have traced every line exactly twice (forwards and backwards) and incorrectly counted the $3^{n}$ "lines" where each coordinate stays the same, so we subtract $3^{n}$ and divide by 2 .
|
{
"exam": "HMMT",
"problem_label": "31",
"problem_match": "\n31. [18]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
Circle $\Omega$ has radius 13. Circle $\omega$ has radius 14 and its center $P$ lies on the boundary of circle $\Omega$. Points $A$ and $B$ lie on $\Omega$ such that chord $A B$ has length 24 and is tangent to $\omega$ at point $T$. Find $A T \cdot B T$.
|
56 Solution: Let $M$ be the midpoint of chord $A B$; then $A M=B M=12$ and Pythagoras on triangle $A M O$ gives $M O=5$. Note that $\angle A O M=\angle A O B / 2=\angle A P B=\angle A P T+\angle T P B$ or $\tan (\angle A O M)=\tan (\angle A P T+\angle T P B)$. Applying the tangent addition formula,
$$
\begin{aligned}
\frac{A M}{M O} & =\frac{\frac{A T}{T P}+\frac{B T}{T P}}{1-\frac{A T}{T P} \cdot \frac{B T}{T P}} \\
& =\frac{A B \cdot T P}{T P^{2}-A T \cdot B T}
\end{aligned}
$$
from which $A T \cdot B T=T P^{2}-A B \cdot T P \cdot M O / A M=14^{2}-24 \cdot 14 \cdot 5 / 12=56$.
|
56
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Circle $\Omega$ has radius 13. Circle $\omega$ has radius 14 and its center $P$ lies on the boundary of circle $\Omega$. Points $A$ and $B$ lie on $\Omega$ such that chord $A B$ has length 24 and is tangent to $\omega$ at point $T$. Find $A T \cdot B T$.
|
56 Solution: Let $M$ be the midpoint of chord $A B$; then $A M=B M=12$ and Pythagoras on triangle $A M O$ gives $M O=5$. Note that $\angle A O M=\angle A O B / 2=\angle A P B=\angle A P T+\angle T P B$ or $\tan (\angle A O M)=\tan (\angle A P T+\angle T P B)$. Applying the tangent addition formula,
$$
\begin{aligned}
\frac{A M}{M O} & =\frac{\frac{A T}{T P}+\frac{B T}{T P}}{1-\frac{A T}{T P} \cdot \frac{B T}{T P}} \\
& =\frac{A B \cdot T P}{T P^{2}-A T \cdot B T}
\end{aligned}
$$
from which $A T \cdot B T=T P^{2}-A B \cdot T P \cdot M O / A M=14^{2}-24 \cdot 14 \cdot 5 / 12=56$.
|
{
"exam": "HMMT",
"problem_label": "32",
"problem_match": "\n32. [18]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
Let $m$ be a positive integer. Let $d(n)$ denote the number of divisors of $n$, and define the function
$$
F(x)=\sum_{n=1}^{105^{m}} \frac{d(n)}{n^{x}}
$$
Define the numbers $a(n)$ to be the positive integers for which
$$
F(x)^{2}=\sum_{n=1}^{105^{2 m}} \frac{a(n)}{n^{x}}
$$
for all real $x$. Express $a\left(105^{m}\right)$ in terms of $m$.
|
$\left(\frac{m^{3}+6 m^{2}+11 m+6}{6}\right)^{3}$ OR $\binom{m+3}{3}^{3}$
(The expanded polynomial $\frac{1}{216}\left(216+1188 m+2826 m^{2}+3815 m^{3}+3222 m^{4}+1767 m^{5}+630 m^{6}+141 m^{7}+\right.$ $18 m^{8}+m^{9}$ ) is also an acceptable answer.)
|
\left(\frac{m^{3}+6 m^{2}+11 m+6}{6}\right)^{3}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $m$ be a positive integer. Let $d(n)$ denote the number of divisors of $n$, and define the function
$$
F(x)=\sum_{n=1}^{105^{m}} \frac{d(n)}{n^{x}}
$$
Define the numbers $a(n)$ to be the positive integers for which
$$
F(x)^{2}=\sum_{n=1}^{105^{2 m}} \frac{a(n)}{n^{x}}
$$
for all real $x$. Express $a\left(105^{m}\right)$ in terms of $m$.
|
$\left(\frac{m^{3}+6 m^{2}+11 m+6}{6}\right)^{3}$ OR $\binom{m+3}{3}^{3}$
(The expanded polynomial $\frac{1}{216}\left(216+1188 m+2826 m^{2}+3815 m^{3}+3222 m^{4}+1767 m^{5}+630 m^{6}+141 m^{7}+\right.$ $18 m^{8}+m^{9}$ ) is also an acceptable answer.)
|
{
"exam": "HMMT",
"problem_label": "33",
"problem_match": "\n33. [18]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
Let $m$ be a positive integer. Let $d(n)$ denote the number of divisors of $n$, and define the function
$$
F(x)=\sum_{n=1}^{105^{m}} \frac{d(n)}{n^{x}}
$$
Define the numbers $a(n)$ to be the positive integers for which
$$
F(x)^{2}=\sum_{n=1}^{105^{2 m}} \frac{a(n)}{n^{x}}
$$
for all real $x$. Express $a\left(105^{m}\right)$ in terms of $m$.
|
The denominator of a term in the expansion of $F(x)^{2}$ is equal to $n^{x}$ if and only if it is a product of two terms of $F$ of the form $\frac{d(n / k)}{(n / k)^{x}}$ and $\frac{d(k)}{k^{x}}$ for some divisor $k$ of $n$. Thus $a\left(105^{m}\right)=$ $\sum_{k \mid 105^{m}} d(k) d\left(\frac{105^{m}}{k}\right)$. We can write $k=3^{a} 5^{b} 7^{c}$ with $a, b, c \leq m$ for any divisor $k$ of $105^{m}$, and in this case $d(k)=(a+1)(b+1)(c+1)$. Thus the sum becomes
$$
\sum_{0 \leq a, b, c \leq m}(a+1)(b+1)(c+1)(m-a+1)(m-b+1)(m-c+1)
$$
For a fixed $b$ and $c$, we can factor out $(b+1)(c+1)(m-b+1)(m-c+1)$ from the terms having this $b$ and $c$ and find that the sum is equal to
$$
\begin{aligned}
a\left(105^{m}\right) & =\sum_{0 \leq b, c \leq m}(b+1)(c+1)(m-b+1)(m-c+1)\left(\sum_{a=1}^{m+1} a(m-a+2)\right) \\
& =\sum_{0 \leq b, c \leq m}(b+1)(c+1)(m-b+1)(m-c+1)\left((m+2) \frac{(m+1)(m+2)}{2}-\frac{(m+1)(m+2)(2 m+3)}{6}\right) \\
& =\sum_{0 \leq b, c \leq m}(b+1)(c+1)(m-b+1)(m-c+1)\left(\frac{(3 m+6-2 m-3)(m+1)(m+2)}{6}\right) \\
& =\sum_{0 \leq b, c \leq m}(b+1)(c+1)(m-b+1)(m-c+1)\binom{m+3}{3}
\end{aligned}
$$
Fixing $c$ and factoring out terms again, we find by a similar argument that $a\left(105^{m}\right)=\binom{m+3}{3}^{3}$.
$12^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
\binom{m+3}{3}^{3}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $m$ be a positive integer. Let $d(n)$ denote the number of divisors of $n$, and define the function
$$
F(x)=\sum_{n=1}^{105^{m}} \frac{d(n)}{n^{x}}
$$
Define the numbers $a(n)$ to be the positive integers for which
$$
F(x)^{2}=\sum_{n=1}^{105^{2 m}} \frac{a(n)}{n^{x}}
$$
for all real $x$. Express $a\left(105^{m}\right)$ in terms of $m$.
|
The denominator of a term in the expansion of $F(x)^{2}$ is equal to $n^{x}$ if and only if it is a product of two terms of $F$ of the form $\frac{d(n / k)}{(n / k)^{x}}$ and $\frac{d(k)}{k^{x}}$ for some divisor $k$ of $n$. Thus $a\left(105^{m}\right)=$ $\sum_{k \mid 105^{m}} d(k) d\left(\frac{105^{m}}{k}\right)$. We can write $k=3^{a} 5^{b} 7^{c}$ with $a, b, c \leq m$ for any divisor $k$ of $105^{m}$, and in this case $d(k)=(a+1)(b+1)(c+1)$. Thus the sum becomes
$$
\sum_{0 \leq a, b, c \leq m}(a+1)(b+1)(c+1)(m-a+1)(m-b+1)(m-c+1)
$$
For a fixed $b$ and $c$, we can factor out $(b+1)(c+1)(m-b+1)(m-c+1)$ from the terms having this $b$ and $c$ and find that the sum is equal to
$$
\begin{aligned}
a\left(105^{m}\right) & =\sum_{0 \leq b, c \leq m}(b+1)(c+1)(m-b+1)(m-c+1)\left(\sum_{a=1}^{m+1} a(m-a+2)\right) \\
& =\sum_{0 \leq b, c \leq m}(b+1)(c+1)(m-b+1)(m-c+1)\left((m+2) \frac{(m+1)(m+2)}{2}-\frac{(m+1)(m+2)(2 m+3)}{6}\right) \\
& =\sum_{0 \leq b, c \leq m}(b+1)(c+1)(m-b+1)(m-c+1)\left(\frac{(3 m+6-2 m-3)(m+1)(m+2)}{6}\right) \\
& =\sum_{0 \leq b, c \leq m}(b+1)(c+1)(m-b+1)(m-c+1)\binom{m+3}{3}
\end{aligned}
$$
Fixing $c$ and factoring out terms again, we find by a similar argument that $a\left(105^{m}\right)=\binom{m+3}{3}^{3}$.
$12^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 21 FEBRUARY 2009 - GUTS ROUND
|
{
"exam": "HMMT",
"problem_label": "33",
"problem_match": "\n33. [18]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
Descartes's Blackjack: How many integer lattice points (points of the form $(m, n)$ for integers $m$ and $n$ ) lie inside or on the boundary of the disk of radius 2009 centered at the origin?
If your answer is higher than the correct answer, you will receive 0 points. If your answer is $d$ less than the correct answer, your score on this problem will be the larger of 0 and $25-\lfloor d / 10\rfloor$.
|
12679605
|
12679605
|
Yes
|
Incomplete
|
math-word-problem
|
Geometry
|
Descartes's Blackjack: How many integer lattice points (points of the form $(m, n)$ for integers $m$ and $n$ ) lie inside or on the boundary of the disk of radius 2009 centered at the origin?
If your answer is higher than the correct answer, you will receive 0 points. If your answer is $d$ less than the correct answer, your score on this problem will be the larger of 0 and $25-\lfloor d / 10\rfloor$.
|
12679605
|
{
"exam": "HMMT",
"problem_label": "34",
"problem_match": "\n34. $[\\leq \\mathbf{2 5}]$",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
Von Neumann's Poker: The first step in Von Neumann's game is selecting a random number on $[0,1]$. To generate this number, Chebby uses the factorial base: the number $0 . A_{1} A_{2} A_{3} A_{4} \ldots$ stands for $\sum_{n=0}^{\infty} \frac{A_{n}}{(n+1)!}$, where each $A_{n}$ is an integer between 0 and $n$, inclusive.
Chebby has an infinite number of cards labeled $\mathbf{0}, \mathbf{1}, \mathbf{2}, \ldots$. He begins by putting cards $\mathbf{0}$ and $\mathbf{1}$ into a hat and drawing randomly to determine $A_{1}$. The card assigned $A_{1}$ does not get reused. Chebby then adds in card 2 and draws for $A_{2}$, and continues in this manner to determine the random number. At each step, he only draws one card from two in the hat.
Unfortunately, this method does not result in a uniform distribution. What is the expected value of Chebby's final number?
Your score on this problem will be the larger of 0 and $\lfloor 25(1-d)\rfloor$, where $d$ is the positive difference between your answer and the correct answer.
|
.57196
|
0.57196
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Von Neumann's Poker: The first step in Von Neumann's game is selecting a random number on $[0,1]$. To generate this number, Chebby uses the factorial base: the number $0 . A_{1} A_{2} A_{3} A_{4} \ldots$ stands for $\sum_{n=0}^{\infty} \frac{A_{n}}{(n+1)!}$, where each $A_{n}$ is an integer between 0 and $n$, inclusive.
Chebby has an infinite number of cards labeled $\mathbf{0}, \mathbf{1}, \mathbf{2}, \ldots$. He begins by putting cards $\mathbf{0}$ and $\mathbf{1}$ into a hat and drawing randomly to determine $A_{1}$. The card assigned $A_{1}$ does not get reused. Chebby then adds in card 2 and draws for $A_{2}$, and continues in this manner to determine the random number. At each step, he only draws one card from two in the hat.
Unfortunately, this method does not result in a uniform distribution. What is the expected value of Chebby's final number?
Your score on this problem will be the larger of 0 and $\lfloor 25(1-d)\rfloor$, where $d$ is the positive difference between your answer and the correct answer.
|
.57196
|
{
"exam": "HMMT",
"problem_label": "35",
"problem_match": "\n35. $[\\leq \\mathbf{2 5}]$",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
Euler's Bridge: The following figure is the graph of the city of Konigsburg in 1736 - vertices represent sections of the cities, edges are bridges. An Eulerian path through the graph is a path which moves from vertex to vertex, crossing each edge exactly once. How many ways could World War II bombers have knocked out some of the bridges of Konigsburg such that the Allied victory parade could trace an Eulerian path through the graph? (The order in which the bridges are destroyed matters.)
Your score on this problem will be the larger of 0 and $25-\lfloor d / 10\rfloor$, where $d$ is the positive difference between your answer and the correct answer.
|
13023
|
13023
|
Incomplete
|
Incomplete
|
math-word-problem
|
Combinatorics
|
Euler's Bridge: The following figure is the graph of the city of Konigsburg in 1736 - vertices represent sections of the cities, edges are bridges. An Eulerian path through the graph is a path which moves from vertex to vertex, crossing each edge exactly once. How many ways could World War II bombers have knocked out some of the bridges of Konigsburg such that the Allied victory parade could trace an Eulerian path through the graph? (The order in which the bridges are destroyed matters.)
Your score on this problem will be the larger of 0 and $25-\lfloor d / 10\rfloor$, where $d$ is the positive difference between your answer and the correct answer.

|
13023
|
{
"exam": "HMMT",
"problem_label": "36",
"problem_match": "\n36. [ $\\leq \\mathbf{2 5}$ ]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
Let $n \geq 3$ be a positive integer. A triangulation of a convex $n$-gon is a set of $n-3$ of its diagonals which do not intersect in the interior of the polygon. Along with the $n$ sides, these diagonals separate the polygon into $n-2$ disjoint triangles. Any triangulation can be viewed as a graph: the vertices of the graph are the corners of the polygon, and the $n$ sides and $n-3$ diagonals are the edges.
For a fixed $n$-gon, different triangulations correspond to different graphs. Prove that all of these graphs have the same chromatic number.
|
We will show that all triangulations have chromatic number 3, by induction on $n$. As a base case, if $n=3$, a triangle has chromatic number 3. Now, given a triangulation of an $n$-gon for $n>3$, every edge is either a side or a diagonal of the polygon. There are $n$ sides and only $n-3$ diagonals in the edge-set, so the Pigeonhole Principle guarentees a triangle with two side edges. These two sides must be adjacent, so we can remove this triangle to leave a triangulation of an ( $n-1$ )-gon, which has chromatic number 3 by the inductive hypothesis. Adding the last triangle adds only one new vertex with two neighbors, so we can color this vertex with one of the three colors not used on its neighbors.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n \geq 3$ be a positive integer. A triangulation of a convex $n$-gon is a set of $n-3$ of its diagonals which do not intersect in the interior of the polygon. Along with the $n$ sides, these diagonals separate the polygon into $n-2$ disjoint triangles. Any triangulation can be viewed as a graph: the vertices of the graph are the corners of the polygon, and the $n$ sides and $n-3$ diagonals are the edges.
For a fixed $n$-gon, different triangulations correspond to different graphs. Prove that all of these graphs have the same chromatic number.
|
We will show that all triangulations have chromatic number 3, by induction on $n$. As a base case, if $n=3$, a triangle has chromatic number 3. Now, given a triangulation of an $n$-gon for $n>3$, every edge is either a side or a diagonal of the polygon. There are $n$ sides and only $n-3$ diagonals in the edge-set, so the Pigeonhole Principle guarentees a triangle with two side edges. These two sides must be adjacent, so we can remove this triangle to leave a triangulation of an ( $n-1$ )-gon, which has chromatic number 3 by the inductive hypothesis. Adding the last triangle adds only one new vertex with two neighbors, so we can color this vertex with one of the three colors not used on its neighbors.
|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n1. [8]",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-team1-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
(a) [6] Let $P$ be a graph with one vertex $v_{n}$ for each positive integer $n$. If $a<b$, then an edge connects vertices $v_{a}$ and $v_{b}$ if and only if $\frac{b}{a}$ is a prime number. What is the chromatic number of $P$ ? Prove your answer.
|
2
|
2
|
Yes
|
Problem not solved
|
proof
|
Combinatorics
|
(a) [6] Let $P$ be a graph with one vertex $v_{n}$ for each positive integer $n$. If $a<b$, then an edge connects vertices $v_{a}$ and $v_{b}$ if and only if $\frac{b}{a}$ is a prime number. What is the chromatic number of $P$ ? Prove your answer.
|
2
|
{
"exam": "HMMT",
"problem_label": "2",
"problem_match": "\n2. ",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-team1-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
(a) [6] Let $P$ be a graph with one vertex $v_{n}$ for each positive integer $n$. If $a<b$, then an edge connects vertices $v_{a}$ and $v_{b}$ if and only if $\frac{b}{a}$ is a prime number. What is the chromatic number of $P$ ? Prove your answer.
|
At least two colors are needed in a good coloring of $P$. We show that two is sufficient. Write the positive integer $n$ as $p_{1}^{e_{1}} p_{2}^{e_{2}} \ldots p_{k}^{e_{k}}$, for distinct primes $p_{1}, p_{2}, \ldots p_{k}$, and let $f(n)=e_{1}+e_{2}+\ldots+e_{k}$. Notice that if $v_{a}$ and $v_{b}$ are connected, then $f(a)$ and $f(b)$ have opposite parity. So, if we color $v_{n}$ red if $f(n)$ is odd and blue otherwise, the two-coloring is good.
(b) [6] Let $T$ be a graph with one vertex $v_{n}$ for every integer $n$. An edge connects $v_{a}$ and $v_{b}$ if $|a-b|$ is a power of two. What is the chromatic number of $T$ ? Prove your answer.
|
2
|
Yes
|
Yes
|
proof
|
Combinatorics
|
(a) [6] Let $P$ be a graph with one vertex $v_{n}$ for each positive integer $n$. If $a<b$, then an edge connects vertices $v_{a}$ and $v_{b}$ if and only if $\frac{b}{a}$ is a prime number. What is the chromatic number of $P$ ? Prove your answer.
|
At least two colors are needed in a good coloring of $P$. We show that two is sufficient. Write the positive integer $n$ as $p_{1}^{e_{1}} p_{2}^{e_{2}} \ldots p_{k}^{e_{k}}$, for distinct primes $p_{1}, p_{2}, \ldots p_{k}$, and let $f(n)=e_{1}+e_{2}+\ldots+e_{k}$. Notice that if $v_{a}$ and $v_{b}$ are connected, then $f(a)$ and $f(b)$ have opposite parity. So, if we color $v_{n}$ red if $f(n)$ is odd and blue otherwise, the two-coloring is good.
(b) [6] Let $T$ be a graph with one vertex $v_{n}$ for every integer $n$. An edge connects $v_{a}$ and $v_{b}$ if $|a-b|$ is a power of two. What is the chromatic number of $T$ ? Prove your answer.
|
{
"exam": "HMMT",
"problem_label": "2",
"problem_match": "\n2. ",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-team1-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
(a) [6] Let $P$ be a graph with one vertex $v_{n}$ for each positive integer $n$. If $a<b$, then an edge connects vertices $v_{a}$ and $v_{b}$ if and only if $\frac{b}{a}$ is a prime number. What is the chromatic number of $P$ ? Prove your answer.
|
3
|
3
|
Yes
|
Problem not solved
|
proof
|
Combinatorics
|
(a) [6] Let $P$ be a graph with one vertex $v_{n}$ for each positive integer $n$. If $a<b$, then an edge connects vertices $v_{a}$ and $v_{b}$ if and only if $\frac{b}{a}$ is a prime number. What is the chromatic number of $P$ ? Prove your answer.
|
3
|
{
"exam": "HMMT",
"problem_label": "2",
"problem_match": "\n2. ",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-team1-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
(a) [6] Let $P$ be a graph with one vertex $v_{n}$ for each positive integer $n$. If $a<b$, then an edge connects vertices $v_{a}$ and $v_{b}$ if and only if $\frac{b}{a}$ is a prime number. What is the chromatic number of $P$ ? Prove your answer.
|
Since $v_{0}, v_{1}$, and $v_{2}$ are all connected to each other, three colors is necessary. Now, color $v_{n}$ red if $n \equiv 0(\bmod 3)$, blue if $n \equiv 1(\bmod 3)$, and green otherwise. Since $v_{a}$ and $v_{b}$ are the same color only if $3 \mid(a-b)$, no two connected vertices are the same color.
|
3
|
Yes
|
Incomplete
|
proof
|
Combinatorics
|
(a) [6] Let $P$ be a graph with one vertex $v_{n}$ for each positive integer $n$. If $a<b$, then an edge connects vertices $v_{a}$ and $v_{b}$ if and only if $\frac{b}{a}$ is a prime number. What is the chromatic number of $P$ ? Prove your answer.
|
Since $v_{0}, v_{1}$, and $v_{2}$ are all connected to each other, three colors is necessary. Now, color $v_{n}$ red if $n \equiv 0(\bmod 3)$, blue if $n \equiv 1(\bmod 3)$, and green otherwise. Since $v_{a}$ and $v_{b}$ are the same color only if $3 \mid(a-b)$, no two connected vertices are the same color.
|
{
"exam": "HMMT",
"problem_label": "2",
"problem_match": "\n2. ",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-team1-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
A graph is finite if it has a finite number of vertices.
(a) $[6]$ Let $G$ be a finite graph in which every vertex has degree $k$. Prove that the chromatic number of $G$ is at most $k+1$.
|
We find a good coloring with $k+1$ colors. Order the vertices and color them one by one. Since each vertex has at most $k$ neighbors, one of the $k+1$ colors has not been used on a neighbor, so there is always a good color for that vertex. In fact, we have shows that any graph in which every vertex has degree at most $k$ can be colored with $k+1$ colors.
(b) [10] In terms of $n$, what is the minimum number of edges a finite graph with chromatic number $n$ could have? Prove your answer.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A graph is finite if it has a finite number of vertices.
(a) $[6]$ Let $G$ be a finite graph in which every vertex has degree $k$. Prove that the chromatic number of $G$ is at most $k+1$.
|
We find a good coloring with $k+1$ colors. Order the vertices and color them one by one. Since each vertex has at most $k$ neighbors, one of the $k+1$ colors has not been used on a neighbor, so there is always a good color for that vertex. In fact, we have shows that any graph in which every vertex has degree at most $k$ can be colored with $k+1$ colors.
(b) [10] In terms of $n$, what is the minimum number of edges a finite graph with chromatic number $n$ could have? Prove your answer.
|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n3. ",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-team1-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2009"
}
|
A graph is finite if it has a finite number of vertices.
(a) $[6]$ Let $G$ be a finite graph in which every vertex has degree $k$. Prove that the chromatic number of $G$ is at most $k+1$.
|
$\frac{n(n-1)}{2}$
|
proof
|
Yes
|
Problem not solved
|
proof
|
Combinatorics
|
A graph is finite if it has a finite number of vertices.
(a) $[6]$ Let $G$ be a finite graph in which every vertex has degree $k$. Prove that the chromatic number of $G$ is at most $k+1$.
|
$\frac{n(n-1)}{2}$
|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n3. ",
"resource_path": "HarvardMIT/segmented/en-122-2009-feb-team1-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2009"
}
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.