problem
stringlengths 14
10.4k
| solution
stringlengths 1
24.1k
| answer
stringlengths 1
250
⌀ | problem_is_valid
stringclasses 4
values | solution_is_valid
stringclasses 3
values | question_type
stringclasses 4
values | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
10.4k
| solution_raw
stringlengths 1
24.1k
| metadata
dict |
|---|---|---|---|---|---|---|---|---|---|
By a tropical polynomial we mean a function of the form
$$
p(x)=a_{n} \odot x^{n} \oplus a_{n-1} \odot x^{n-1} \oplus \cdots \oplus a_{1} \odot x \oplus a_{0}
$$
where exponentiation is as defined in the previous problem.
Let $p$ be a tropical polynomial. Prove that
$$
p\left(\frac{x+y}{2}\right) \geq \frac{p(x)+p(y)}{2}
$$
for all $x, y \in \mathbb{R} \cup\{\infty\}$. (This means that all tropical polynomials are concave.)
|
First, note that for any $x_{1}, \ldots, x_{n}, y_{1}, \ldots, y_{n}$, we have
$$
\min \left\{x_{1}+y_{1}, x_{2}+y_{2}, \ldots, x_{n}+y_{n}\right\} \geq \min \left\{x_{1}, x_{2}, \ldots, x_{n}\right\}+\min \left\{y_{1}, y_{2}, \ldots, y_{n}\right\} .
$$
Indeed, suppose that $x_{m}+y_{m}=\min _{i}\left\{x_{i}+y_{i}\right\}$, then $x_{m} \geq \min _{i} x_{i}$ and $y_{m} \geq \min _{i} y_{i}$, and so $\min _{i}\left\{x_{i}+y_{i}\right\}=x_{m}+y_{m} \geq \min _{i} x_{i}+\min _{i} y_{i}$.
Now, let us write a tropical polynomial in a more familiar notation. We have
$$
p(x)=\min _{0 \leq k \leq n}\left\{a_{k}+k x\right\} .
$$
So
$$
\begin{aligned}
p\left(\frac{x+y}{2}\right) & =\min _{0 \leq k \leq n}\left\{a_{k}+k\left(\frac{x+y}{2}\right)\right\} \\
& =\frac{1}{2} \min _{0 \leq k \leq n}\left\{\left(a_{k}+k x\right)+\left(a_{k}+k y\right)\right\} \\
& \geq \frac{1}{2}\left(\min _{0 \leq k \leq n}\left\{a_{k}+k x\right\}+\min _{0 \leq k \leq n}\left\{a_{k}+k y\right\}\right) \\
& =\frac{1}{2}(p(x)+p(y)) .
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
By a tropical polynomial we mean a function of the form
$$
p(x)=a_{n} \odot x^{n} \oplus a_{n-1} \odot x^{n-1} \oplus \cdots \oplus a_{1} \odot x \oplus a_{0}
$$
where exponentiation is as defined in the previous problem.
Let $p$ be a tropical polynomial. Prove that
$$
p\left(\frac{x+y}{2}\right) \geq \frac{p(x)+p(y)}{2}
$$
for all $x, y \in \mathbb{R} \cup\{\infty\}$. (This means that all tropical polynomials are concave.)
|
First, note that for any $x_{1}, \ldots, x_{n}, y_{1}, \ldots, y_{n}$, we have
$$
\min \left\{x_{1}+y_{1}, x_{2}+y_{2}, \ldots, x_{n}+y_{n}\right\} \geq \min \left\{x_{1}, x_{2}, \ldots, x_{n}\right\}+\min \left\{y_{1}, y_{2}, \ldots, y_{n}\right\} .
$$
Indeed, suppose that $x_{m}+y_{m}=\min _{i}\left\{x_{i}+y_{i}\right\}$, then $x_{m} \geq \min _{i} x_{i}$ and $y_{m} \geq \min _{i} y_{i}$, and so $\min _{i}\left\{x_{i}+y_{i}\right\}=x_{m}+y_{m} \geq \min _{i} x_{i}+\min _{i} y_{i}$.
Now, let us write a tropical polynomial in a more familiar notation. We have
$$
p(x)=\min _{0 \leq k \leq n}\left\{a_{k}+k x\right\} .
$$
So
$$
\begin{aligned}
p\left(\frac{x+y}{2}\right) & =\min _{0 \leq k \leq n}\left\{a_{k}+k\left(\frac{x+y}{2}\right)\right\} \\
& =\frac{1}{2} \min _{0 \leq k \leq n}\left\{\left(a_{k}+k x\right)+\left(a_{k}+k y\right)\right\} \\
& \geq \frac{1}{2}\left(\min _{0 \leq k \leq n}\left\{a_{k}+k x\right\}+\min _{0 \leq k \leq n}\left\{a_{k}+k y\right\}\right) \\
& =\frac{1}{2}(p(x)+p(y)) .
\end{aligned}
$$
|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n3. [35]",
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team2-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2008"
}
|
(Fundamental Theorem of Algebra) Let $p$ be a tropical polynomial:
$$
p(x)=a_{n} \odot x^{n} \oplus a_{n-1} \odot x^{n-1} \oplus \cdots \oplus a_{1} \odot x \oplus a_{0}, \quad a_{n} \neq \infty
$$
Prove that we can find $r_{1}, r_{2}, \ldots, r_{n} \in \mathbb{R} \cup\{\infty\}$ so that
$$
p(x)=a_{n} \odot\left(x \oplus r_{1}\right) \odot\left(x \oplus r_{2}\right) \odot \cdots \odot\left(x \oplus r_{n}\right)
$$
for all $x$.
|
Again, we have
$$
p(x)=\min _{0 \leq k \leq n}\left\{a_{k}+k x\right\} .
$$
So the graph of $y=p(x)$ can be drawn as follows: first, draw all the lines $y=a_{k}+k x$, $k=0,1, \ldots, n$, then trace out the lowest broken line, which then is the graph of $y=p(x)$.
So $p(x)$ is piecewise linear and continuous, and has slopes from the set $\{0,1,2, \ldots, n\}$. We know from the previous problem that $p(x)$ is concave, and so its slope must be decreasing (this can also be observed simply from the drawing of the graph of $y=p(x)$ ). Then, let $r_{k}$ denote the $x$-coordinate of the leftmost kink such that the slope of the graph is less than $k$ to the right of this kink. Then, $r_{n} \leq r_{n-1} \leq \cdots \leq r_{1}$, and for $r_{k-1} \leq x \leq r_{k}$, the graph of $p$ is linear with slope $k$. Note that is if possible that $r_{k-1}=r_{k}$, if no segment of $p$ has slope $k$. Also, since $a_{n} \neq \infty$, the leftmost piece of $p(x)$ must have slope $n$, and thus $r_{n}$ exists, and thus all $r_{i}$ exist.
Now, compare $p(x)$ with
$$
\begin{aligned}
q(x) & =a_{n} \odot\left(x \oplus r_{1}\right) \odot\left(x \oplus r_{2}\right) \odot \cdots \odot\left(x \oplus r_{n}\right) \\
& =a_{n}+\min \left(x, r_{1}\right)+\min \left(x, r_{2}\right)+\cdots+\min \left(x, r_{n}\right) .
\end{aligned}
$$
For $r_{k-1} \leq x \leq r_{k}$, the slope of $q(x)$ is $k$, and for $x \leq r_{n}$ the slope of $q$ is $n$ and for $x \geq r_{1}$ the slope of $q$ is 0 . So $q$ is piecewise linear, and of course it is continuous. It follows that the graph of $q$ coincides with that of $p$ up to a translation. By taking any $x<r_{n}$, we see that $q(x)=a_{n}+n x=p(x)$, we see that the graphs of $p$ and $q$ coincide, and thus they must be the same function.
## Juggling [125]
A juggling sequence of length $n$ is a sequence $j(\cdot)$ of $n$ nonnegative integers, usually written as a string
$$
j(0) j(1) \ldots j(n-1)
$$
such that the mapping $f: \mathbb{Z} \rightarrow \mathbb{Z}$ defined by
$$
f(t)=t+j(\bar{t})
$$
is a permutation of the integers. Here $\bar{t}$ denotes the remainder of $t$ when divided by $n$. In this case, we say that $f$ is the corresponding juggling pattern.
For a juggling pattern $f$ (or its corresponding juggling sequence), we say that it has $b$ balls if the permutation induces $b$ infinite orbits on the set of integers. Equivalently, $b$ is the maximum number such that we can find a set of $b$ integers $\left\{t_{1}, t_{2}, \ldots, t_{b}\right\}$ so that the sets $\left\{t_{i}, f\left(t_{i}\right), f\left(f\left(t_{i}\right)\right), f\left(f\left(f\left(t_{i}\right)\right)\right), \ldots\right\}$ are all infinite and mutually disjoint (i.e. non-overlapping) for $i=1,2, \ldots, b$. (This definition will become clear in a second.)
Now is probably a good time to pause and think about what all this has to do with juggling. Imagine that we are juggling a number of balls, and at time $t$, we toss a ball from our hand up to a height $j(\bar{t})$. This ball stays up in the air for $j(\bar{t})$ units of time, so that it comes back to our hand at time $f(t)=t+j(\bar{t})$. Then, the juggling pattern presents a simplified model of how balls are juggled (for instance, we ignore information such as which hand we use to toss the ball). A throw height of 0 (i.e., $j(\bar{t})=0$ and $f(t)=t$ ) represents that no thrown takes place at time $t$, which could correspond to an empty hand. Then, $b$ is simply the minimum number of balls needed to carry out the juggling.
The following graphical representation may be helpful to you. On a horizontal line, an curve is drawn from $t$ to $f(t)$. For instance, the following diagram depicts the juggling sequence 441 (or the juggling sequences 414 and 144). Then $b$ is simply the number of contiguous "paths" drawn, which is 3 in this case.
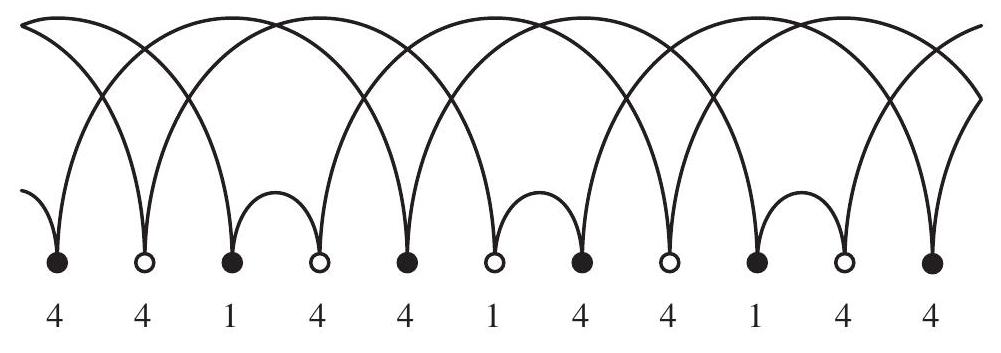
Figure 1: Juggling diagram of 441.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
(Fundamental Theorem of Algebra) Let $p$ be a tropical polynomial:
$$
p(x)=a_{n} \odot x^{n} \oplus a_{n-1} \odot x^{n-1} \oplus \cdots \oplus a_{1} \odot x \oplus a_{0}, \quad a_{n} \neq \infty
$$
Prove that we can find $r_{1}, r_{2}, \ldots, r_{n} \in \mathbb{R} \cup\{\infty\}$ so that
$$
p(x)=a_{n} \odot\left(x \oplus r_{1}\right) \odot\left(x \oplus r_{2}\right) \odot \cdots \odot\left(x \oplus r_{n}\right)
$$
for all $x$.
|
Again, we have
$$
p(x)=\min _{0 \leq k \leq n}\left\{a_{k}+k x\right\} .
$$
So the graph of $y=p(x)$ can be drawn as follows: first, draw all the lines $y=a_{k}+k x$, $k=0,1, \ldots, n$, then trace out the lowest broken line, which then is the graph of $y=p(x)$.
So $p(x)$ is piecewise linear and continuous, and has slopes from the set $\{0,1,2, \ldots, n\}$. We know from the previous problem that $p(x)$ is concave, and so its slope must be decreasing (this can also be observed simply from the drawing of the graph of $y=p(x)$ ). Then, let $r_{k}$ denote the $x$-coordinate of the leftmost kink such that the slope of the graph is less than $k$ to the right of this kink. Then, $r_{n} \leq r_{n-1} \leq \cdots \leq r_{1}$, and for $r_{k-1} \leq x \leq r_{k}$, the graph of $p$ is linear with slope $k$. Note that is if possible that $r_{k-1}=r_{k}$, if no segment of $p$ has slope $k$. Also, since $a_{n} \neq \infty$, the leftmost piece of $p(x)$ must have slope $n$, and thus $r_{n}$ exists, and thus all $r_{i}$ exist.
Now, compare $p(x)$ with
$$
\begin{aligned}
q(x) & =a_{n} \odot\left(x \oplus r_{1}\right) \odot\left(x \oplus r_{2}\right) \odot \cdots \odot\left(x \oplus r_{n}\right) \\
& =a_{n}+\min \left(x, r_{1}\right)+\min \left(x, r_{2}\right)+\cdots+\min \left(x, r_{n}\right) .
\end{aligned}
$$
For $r_{k-1} \leq x \leq r_{k}$, the slope of $q(x)$ is $k$, and for $x \leq r_{n}$ the slope of $q$ is $n$ and for $x \geq r_{1}$ the slope of $q$ is 0 . So $q$ is piecewise linear, and of course it is continuous. It follows that the graph of $q$ coincides with that of $p$ up to a translation. By taking any $x<r_{n}$, we see that $q(x)=a_{n}+n x=p(x)$, we see that the graphs of $p$ and $q$ coincide, and thus they must be the same function.
## Juggling [125]
A juggling sequence of length $n$ is a sequence $j(\cdot)$ of $n$ nonnegative integers, usually written as a string
$$
j(0) j(1) \ldots j(n-1)
$$
such that the mapping $f: \mathbb{Z} \rightarrow \mathbb{Z}$ defined by
$$
f(t)=t+j(\bar{t})
$$
is a permutation of the integers. Here $\bar{t}$ denotes the remainder of $t$ when divided by $n$. In this case, we say that $f$ is the corresponding juggling pattern.
For a juggling pattern $f$ (or its corresponding juggling sequence), we say that it has $b$ balls if the permutation induces $b$ infinite orbits on the set of integers. Equivalently, $b$ is the maximum number such that we can find a set of $b$ integers $\left\{t_{1}, t_{2}, \ldots, t_{b}\right\}$ so that the sets $\left\{t_{i}, f\left(t_{i}\right), f\left(f\left(t_{i}\right)\right), f\left(f\left(f\left(t_{i}\right)\right)\right), \ldots\right\}$ are all infinite and mutually disjoint (i.e. non-overlapping) for $i=1,2, \ldots, b$. (This definition will become clear in a second.)
Now is probably a good time to pause and think about what all this has to do with juggling. Imagine that we are juggling a number of balls, and at time $t$, we toss a ball from our hand up to a height $j(\bar{t})$. This ball stays up in the air for $j(\bar{t})$ units of time, so that it comes back to our hand at time $f(t)=t+j(\bar{t})$. Then, the juggling pattern presents a simplified model of how balls are juggled (for instance, we ignore information such as which hand we use to toss the ball). A throw height of 0 (i.e., $j(\bar{t})=0$ and $f(t)=t$ ) represents that no thrown takes place at time $t$, which could correspond to an empty hand. Then, $b$ is simply the minimum number of balls needed to carry out the juggling.
The following graphical representation may be helpful to you. On a horizontal line, an curve is drawn from $t$ to $f(t)$. For instance, the following diagram depicts the juggling sequence 441 (or the juggling sequences 414 and 144). Then $b$ is simply the number of contiguous "paths" drawn, which is 3 in this case.

Figure 1: Juggling diagram of 441.
|
{
"exam": "HMMT",
"problem_label": "4",
"problem_match": "\n4. [40]",
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team2-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2008"
}
|
Prove that 572 is not a juggling sequence.
|
We are given $j(0)=5, j(1)=7$ and $j(2)=2$. So $f(3)=3+j(0)=8$ and $f(1)=1+j(1)=8$. Thus $f(3)=f(1)$ and so $f$ is not a permutation of $\mathbb{Z}$, and hence 572 is not a juggling pattern. (In other words, there is a "collision" at times $t \equiv 2(\bmod 3)$.)
|
proof
|
Incomplete
|
Yes
|
proof
|
Number Theory
|
Prove that 572 is not a juggling sequence.
|
We are given $j(0)=5, j(1)=7$ and $j(2)=2$. So $f(3)=3+j(0)=8$ and $f(1)=1+j(1)=8$. Thus $f(3)=f(1)$ and so $f$ is not a permutation of $\mathbb{Z}$, and hence 572 is not a juggling pattern. (In other words, there is a "collision" at times $t \equiv 2(\bmod 3)$.)
|
{
"exam": "HMMT",
"problem_label": "5",
"problem_match": "\n5. [10]",
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team2-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2008"
}
|
Suppose that $j(0) j(1) \cdots j(n-1)$ is a valid juggling sequence. For $i=0,1, \ldots, n-1$, Let $a_{i}$ denote the remainder of $j(i)+i$ when divided by $n$. Prove that $\left(a_{0}, a_{1}, \ldots, a_{n-1}\right)$ is a permutation of $(0,1, \ldots, n-1)$.
|
Suppose that $a_{i}=j(i)+i-b_{i} n$, where $b_{i}$ is an integer. Note that $f\left(i-b_{i} n\right)=$ $i-b_{i} n+j(i)=a_{i}$. Since $\left\{i-b_{i} n \mid i=0,1, \ldots, n-1\right\}$ contains $n$ distinct integers (as their residue $\bmod n$ are all distinct), and $f$ is a permutation, we see that after applying the map $f$, the resulting set $\left\{a_{0}, a_{1}, \ldots, a_{n-1}\right\}$ is a set of $n$ distinct integers. Since $0 \leq a_{i}<n$ from definition, we see that ( $a_{0}, a_{1}, \ldots, a_{n-1}$ ) is a permutation of $(0,1, \ldots, n-1)$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Suppose that $j(0) j(1) \cdots j(n-1)$ is a valid juggling sequence. For $i=0,1, \ldots, n-1$, Let $a_{i}$ denote the remainder of $j(i)+i$ when divided by $n$. Prove that $\left(a_{0}, a_{1}, \ldots, a_{n-1}\right)$ is a permutation of $(0,1, \ldots, n-1)$.
|
Suppose that $a_{i}=j(i)+i-b_{i} n$, where $b_{i}$ is an integer. Note that $f\left(i-b_{i} n\right)=$ $i-b_{i} n+j(i)=a_{i}$. Since $\left\{i-b_{i} n \mid i=0,1, \ldots, n-1\right\}$ contains $n$ distinct integers (as their residue $\bmod n$ are all distinct), and $f$ is a permutation, we see that after applying the map $f$, the resulting set $\left\{a_{0}, a_{1}, \ldots, a_{n-1}\right\}$ is a set of $n$ distinct integers. Since $0 \leq a_{i}<n$ from definition, we see that ( $a_{0}, a_{1}, \ldots, a_{n-1}$ ) is a permutation of $(0,1, \ldots, n-1)$.
|
{
"exam": "HMMT",
"problem_label": "6",
"problem_match": "\n6. [40]",
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team2-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2008"
}
|
Determine the number of juggling sequences of length $n$ with exactly 1 ball.
|
$2^{n}-1$. Solution: With 1 ball, we simply need to decide at times should the ball land in our hand. That is, we need to choose a non-empty subset of $\{0,1,2, \ldots, n-1\}$ where the ball lands. It follows that the answer is $2^{n}-1$.
|
2^{n}-1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Determine the number of juggling sequences of length $n$ with exactly 1 ball.
|
$2^{n}-1$. Solution: With 1 ball, we simply need to decide at times should the ball land in our hand. That is, we need to choose a non-empty subset of $\{0,1,2, \ldots, n-1\}$ where the ball lands. It follows that the answer is $2^{n}-1$.
|
{
"exam": "HMMT",
"problem_label": "7",
"problem_match": "\n7. [30]",
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Prove that the number of balls $b$ in a juggling sequence $j(0) j(1) \cdots j(n-1)$ is simply the average
$$
b=\frac{j(0)+j(1)+\cdots+j(n-1)}{n} .
$$
|
Consider the corresponding juggling diagram. Say the length of an curve from $t$ to $f(t)$ is $f(t)-t$. Let us draw only the curves whose left endpoint lies inside $[0, M n-1]$. For every single ball, the sum of the lengths of the arrows drawn corresponding to that ball is between $M n-J$ and $M n+J$, where $J=\max \{j(0), j(1), \ldots, j(n-1)\}$. It follows that the sum of the lengths of the arrows drawn is between $b(M n-J)$ and $b(M n+J)$. Since the arrow drawn at $t$ has length $j(\bar{t})$, the sum of the lengths of the arrows drawn is $M(j(0)+j(1)+\cdots+j(n-1))$. It follows that
$$
b(M n-J) \leq M(j(0)+j(1)+\cdots+j(n-1)) \leq b(M n+J)
$$
Dividing by $M n$, we get
$$
b\left(1-\frac{J}{n M}\right) \leq \frac{j(0)+j(1)+\cdots+j(n-1)}{n} \leq b\left(1+\frac{J}{n M}\right)
$$
Since we can take $M$ to be arbitrarily large, we must have
$$
b=\frac{j(0)+j(1)+\cdots+j(n-1)}{n}
$$
as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Prove that the number of balls $b$ in a juggling sequence $j(0) j(1) \cdots j(n-1)$ is simply the average
$$
b=\frac{j(0)+j(1)+\cdots+j(n-1)}{n} .
$$
|
Consider the corresponding juggling diagram. Say the length of an curve from $t$ to $f(t)$ is $f(t)-t$. Let us draw only the curves whose left endpoint lies inside $[0, M n-1]$. For every single ball, the sum of the lengths of the arrows drawn corresponding to that ball is between $M n-J$ and $M n+J$, where $J=\max \{j(0), j(1), \ldots, j(n-1)\}$. It follows that the sum of the lengths of the arrows drawn is between $b(M n-J)$ and $b(M n+J)$. Since the arrow drawn at $t$ has length $j(\bar{t})$, the sum of the lengths of the arrows drawn is $M(j(0)+j(1)+\cdots+j(n-1))$. It follows that
$$
b(M n-J) \leq M(j(0)+j(1)+\cdots+j(n-1)) \leq b(M n+J)
$$
Dividing by $M n$, we get
$$
b\left(1-\frac{J}{n M}\right) \leq \frac{j(0)+j(1)+\cdots+j(n-1)}{n} \leq b\left(1+\frac{J}{n M}\right)
$$
Since we can take $M$ to be arbitrarily large, we must have
$$
b=\frac{j(0)+j(1)+\cdots+j(n-1)}{n}
$$
as desired.
|
{
"exam": "HMMT",
"problem_label": "8",
"problem_match": "\n8. [40]",
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team2-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2008"
}
|
Show that the converse of the previous statement is false by providing a non-juggling sequence $j(0) j(1) j(2)$ of length 3 where the average $\frac{1}{3}(j(0)+j(1)+j(2))$ is an integer. Show that your example works.
|
One such example is 210 . This is not a juggling sequence since $f(0)=f(1)=2$.
## Incircles [180]
In the following problems, $A B C$ is a triangle with incenter $I$. Let $D, E, F$ denote the points where the incircle of $A B C$ touches sides $B C, C A, A B$, respectively.
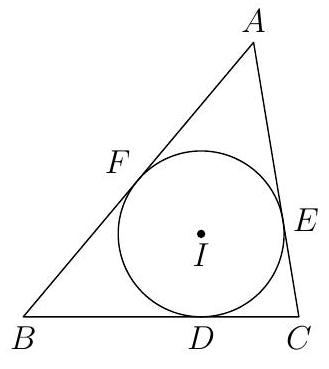
At the end of this section you can find some terminology and theorems that may be helpful to you.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Show that the converse of the previous statement is false by providing a non-juggling sequence $j(0) j(1) j(2)$ of length 3 where the average $\frac{1}{3}(j(0)+j(1)+j(2))$ is an integer. Show that your example works.
|
One such example is 210 . This is not a juggling sequence since $f(0)=f(1)=2$.
## Incircles [180]
In the following problems, $A B C$ is a triangle with incenter $I$. Let $D, E, F$ denote the points where the incircle of $A B C$ touches sides $B C, C A, A B$, respectively.

At the end of this section you can find some terminology and theorems that may be helpful to you.
|
{
"exam": "HMMT",
"problem_label": "9",
"problem_match": "\n9. [5]",
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team2-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2008"
}
|
Let $a, b, c$ denote the side lengths of $B C, C A, A B$. Find the lengths of $A E, B F, C D$ in terms of $a, b, c$.
|
Let $x=A E=A F, y=B D=B F, z=C D=C E$. Since $B C=B D+C D$, we have $a=x+y$. Similarly with the other sides, we arrive at the following system of equations:
$$
a=y+z, \quad b=x+z, \quad c=x+y .
$$
Solving this system gives us
$$
\begin{aligned}
& A E=x=\frac{b+c-a}{2}, \\
& B F=y=\frac{a+c-b}{2}, \\
& C D=z=\frac{a+b-c}{2}
\end{aligned}
$$
|
\begin{aligned}
& A E=\frac{b+c-a}{2}, \\
& B F=\frac{a+c-b}{2}, \\
& C D=\frac{a+b-c}{2}
\end{aligned}
|
Incomplete
|
Yes
|
math-word-problem
|
Geometry
|
Let $a, b, c$ denote the side lengths of $B C, C A, A B$. Find the lengths of $A E, B F, C D$ in terms of $a, b, c$.
|
Let $x=A E=A F, y=B D=B F, z=C D=C E$. Since $B C=B D+C D$, we have $a=x+y$. Similarly with the other sides, we arrive at the following system of equations:
$$
a=y+z, \quad b=x+z, \quad c=x+y .
$$
Solving this system gives us
$$
\begin{aligned}
& A E=x=\frac{b+c-a}{2}, \\
& B F=y=\frac{a+c-b}{2}, \\
& C D=z=\frac{a+b-c}{2}
\end{aligned}
$$
|
{
"exam": "HMMT",
"problem_label": "10",
"problem_match": "\n10. [15]",
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team2-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2008"
}
|
Show that lines $A D, B E, C F$ pass through a common point.
|
Using Ceva's theorem on triangle $A B C$, we see that it suffices to show that
$$
\frac{B D}{D C} \cdot \frac{C E}{E A} \cdot \frac{A F}{F B}=1
$$
Since $A F=A E, B D=B F$, and $C D=C E$ (due to equal tangents), we see that the LHS is indeed 1.
Remark: The point of concurrency is known as the Gergonne point.
|
proof
|
Incomplete
|
Yes
|
proof
|
Geometry
|
Show that lines $A D, B E, C F$ pass through a common point.
|
Using Ceva's theorem on triangle $A B C$, we see that it suffices to show that
$$
\frac{B D}{D C} \cdot \frac{C E}{E A} \cdot \frac{A F}{F B}=1
$$
Since $A F=A E, B D=B F$, and $C D=C E$ (due to equal tangents), we see that the LHS is indeed 1.
Remark: The point of concurrency is known as the Gergonne point.
|
{
"exam": "HMMT",
"problem_label": "11",
"problem_match": "\n11. [15]",
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team2-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2008"
}
|
Show that the incenter of triangle $A E F$ lies on the incircle of $A B C$.
|
Let segment $A I$ meet the incircle at $A_{1}$. Let us show that $A_{1}$ is the incenter of $A E F$.
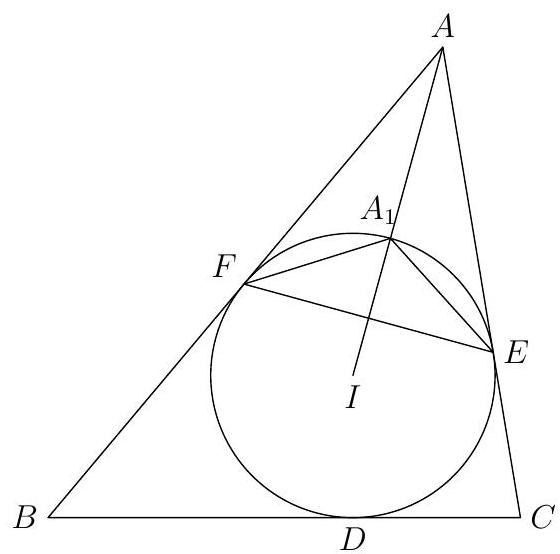
Since $A E=A F$ and $A A^{\prime}$ is the angle bisector of $\angle E A F$, we find that $A_{1} E=A_{1} F$. Using tangent-chord, we see that $\angle A F A_{1}=\angle A_{1} E F=\angle A_{1} F E$. Therefore, $A_{1}$ lies on the angle bisector of $\angle A F E$. Since $A_{1}$ also lies on the angle bisector of $\angle E A F, A_{1}$ must be the incenter of $A E F$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Show that the incenter of triangle $A E F$ lies on the incircle of $A B C$.
|
Let segment $A I$ meet the incircle at $A_{1}$. Let us show that $A_{1}$ is the incenter of $A E F$.

Since $A E=A F$ and $A A^{\prime}$ is the angle bisector of $\angle E A F$, we find that $A_{1} E=A_{1} F$. Using tangent-chord, we see that $\angle A F A_{1}=\angle A_{1} E F=\angle A_{1} F E$. Therefore, $A_{1}$ lies on the angle bisector of $\angle A F E$. Since $A_{1}$ also lies on the angle bisector of $\angle E A F, A_{1}$ must be the incenter of $A E F$, as desired.
|
{
"exam": "HMMT",
"problem_label": "12",
"problem_match": "\n12. [35]",
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team2-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2008"
}
|
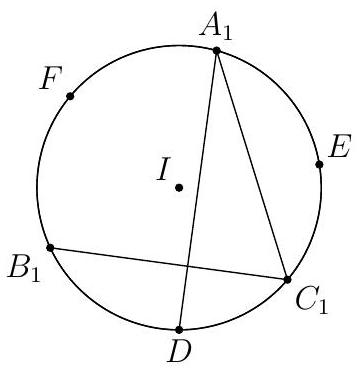
Let $A_{1}, B_{1}, C_{1}$ be the incenters of triangle $A E F, B D F, C D E$, respectively. Show that $A_{1} D, B_{1} E, C_{1} F$ all pass through the orthocenter of $A_{1} B_{1} C_{1}$.
|
Using the result from the previous problem, we see that $A_{1}, B_{1}, C_{1}$ are respectively the midpoints of the $\operatorname{arc} F E, F D, D F$ of the incircle. We have
$$
\begin{aligned}
\angle D A_{1} C_{1}+\angle B_{1} C_{1} A_{1} & =\frac{1}{2} \angle D I C_{1}+\frac{1}{2} \angle B_{1} I F+\frac{1}{2} \angle F I A_{1} \\
& =\frac{1}{4}(\angle E I D+\angle D I F+\angle F I E) \\
& =\frac{1}{4} \cdot 360^{\circ} \\
& =90^{\circ} .
\end{aligned}
$$
It follows that $A_{1} D$ is perpendicular to $B_{1} C_{1}$, and thus $A_{1} D$ passes through the orthocenter of $A_{1} B_{1} C_{1}$. Similarly, $A_{1} D, B_{1} E, C_{1} F$ all pass through the orthocenter of $A_{1} B_{1} C_{1}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A_{1}, B_{1}, C_{1}$ be the incenters of triangle $A E F, B D F, C D E$, respectively. Show that $A_{1} D, B_{1} E, C_{1} F$ all pass through the orthocenter of $A_{1} B_{1} C_{1}$.
|
Using the result from the previous problem, we see that $A_{1}, B_{1}, C_{1}$ are respectively the midpoints of the $\operatorname{arc} F E, F D, D F$ of the incircle. We have

$$
\begin{aligned}
\angle D A_{1} C_{1}+\angle B_{1} C_{1} A_{1} & =\frac{1}{2} \angle D I C_{1}+\frac{1}{2} \angle B_{1} I F+\frac{1}{2} \angle F I A_{1} \\
& =\frac{1}{4}(\angle E I D+\angle D I F+\angle F I E) \\
& =\frac{1}{4} \cdot 360^{\circ} \\
& =90^{\circ} .
\end{aligned}
$$
It follows that $A_{1} D$ is perpendicular to $B_{1} C_{1}$, and thus $A_{1} D$ passes through the orthocenter of $A_{1} B_{1} C_{1}$. Similarly, $A_{1} D, B_{1} E, C_{1} F$ all pass through the orthocenter of $A_{1} B_{1} C_{1}$.
|
{
"exam": "HMMT",
"problem_label": "13",
"problem_match": "\n13. [35]",
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team2-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2008"
}
|
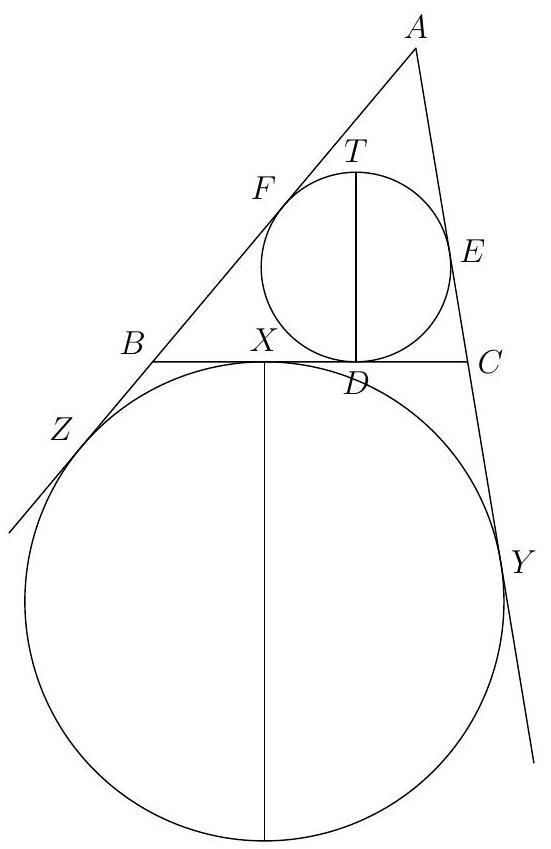
Let $X$ be the point on side $B C$ such that $B X=C D$. Show that the excircle $A B C$ opposite of vertex $A$ touches segment $B C$ at $X$.
|
Let the excircle touch lines $B C, A C$ and $A B$ at $X^{\prime}, Y$ and $Z$, respectively. Using the equal tangent property repeatedly, we have
$$
B X^{\prime}-X^{\prime} C=B Z-C Y=(E Y-C Y)-(F Z-B Z)=C E-B F=C D-B D .
$$
It follows that $B X^{\prime}=C D$, and thus $X^{\prime}=X$. So the excircle touches $B C$ at $X$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $X$ be the point on side $B C$ such that $B X=C D$. Show that the excircle $A B C$ opposite of vertex $A$ touches segment $B C$ at $X$.
|
Let the excircle touch lines $B C, A C$ and $A B$ at $X^{\prime}, Y$ and $Z$, respectively. Using the equal tangent property repeatedly, we have
$$
B X^{\prime}-X^{\prime} C=B Z-C Y=(E Y-C Y)-(F Z-B Z)=C E-B F=C D-B D .
$$
It follows that $B X^{\prime}=C D$, and thus $X^{\prime}=X$. So the excircle touches $B C$ at $X$.

|
{
"exam": "HMMT",
"problem_label": "14",
"problem_match": "\n14. [40]",
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team2-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2008"
}
|
Let $X$ be as in the previous problem. Let $T$ be the point diametrically opposite to $D$ on on the incircle of $A B C$. Show that $A, T, X$ are collinear.
|
Consider a dilation centered at $A$ that carries the incircle to the excircle. This dilation must send the diameter $D T$ to some the diameter of excircle that is perpendicular to $B C$. The only such diameter is the one goes through $X$. It follows that $T$ gets carried to $X$. Therefore, $A, T, X$ are collinear.
## Glossary and some possibly useful facts
- A set of points is collinear if they lie on a common line. A set of lines is concurrent if they pass through a common point.
- Given $A B C$ a triangle, the three angle bisectors are concurrent at the incenter of the triangle. The incenter is the center of the incircle, which is the unique circle inscribed in $A B C$, tangent to all three sides.
- The excircles of a triangle $A B C$ are the three circles on the exterior the triangle but tangent to all three lines $A B, B C, C A$.
- The orthocenter of a triangle is the point of concurrency of the three altitudes.
- Ceva's theorem states that given $A B C$ a triangle, and points $X, Y, Z$ on sides $B C, C A, A B$, respectively, the lines $A X, B Y, C Z$ are concurrent if and only if
$$
\frac{B X}{X B} \cdot \frac{C Y}{Y A} \cdot \frac{A Z}{Z B}=1
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $X$ be as in the previous problem. Let $T$ be the point diametrically opposite to $D$ on on the incircle of $A B C$. Show that $A, T, X$ are collinear.
|
Consider a dilation centered at $A$ that carries the incircle to the excircle. This dilation must send the diameter $D T$ to some the diameter of excircle that is perpendicular to $B C$. The only such diameter is the one goes through $X$. It follows that $T$ gets carried to $X$. Therefore, $A, T, X$ are collinear.
## Glossary and some possibly useful facts
- A set of points is collinear if they lie on a common line. A set of lines is concurrent if they pass through a common point.
- Given $A B C$ a triangle, the three angle bisectors are concurrent at the incenter of the triangle. The incenter is the center of the incircle, which is the unique circle inscribed in $A B C$, tangent to all three sides.
- The excircles of a triangle $A B C$ are the three circles on the exterior the triangle but tangent to all three lines $A B, B C, C A$.
- The orthocenter of a triangle is the point of concurrency of the three altitudes.
- Ceva's theorem states that given $A B C$ a triangle, and points $X, Y, Z$ on sides $B C, C A, A B$, respectively, the lines $A X, B Y, C Z$ are concurrent if and only if
$$
\frac{B X}{X B} \cdot \frac{C Y}{Y A} \cdot \frac{A Z}{Z B}=1
$$
|
{
"exam": "HMMT",
"problem_label": "15",
"problem_match": "\n15. [40]",
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-team2-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "2008"
}
|
Evaluate
$$
\sin \left(1998^{\circ}+237^{\circ}\right) \sin \left(1998^{\circ}-1653^{\circ}\right)
$$
|
$-\frac{1}{4}$. We have $\sin \left(1998^{\circ}+237^{\circ}\right) \sin \left(1998^{\circ}-1653^{\circ}\right)=\sin \left(2235^{\circ}\right) \sin \left(345^{\circ}\right)=\sin \left(75^{\circ}\right) \sin \left(-15^{\circ}\right)=$ $-\sin \left(75^{\circ}\right) \sin \left(15^{\circ}\right)=-\sin \left(15^{\circ}\right) \cos \left(15^{\circ}\right)=-\frac{\sin \left(30^{\circ}\right)}{2}=-\frac{1}{4}$.
|
-\frac{1}{4}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Evaluate
$$
\sin \left(1998^{\circ}+237^{\circ}\right) \sin \left(1998^{\circ}-1653^{\circ}\right)
$$
|
$-\frac{1}{4}$. We have $\sin \left(1998^{\circ}+237^{\circ}\right) \sin \left(1998^{\circ}-1653^{\circ}\right)=\sin \left(2235^{\circ}\right) \sin \left(345^{\circ}\right)=\sin \left(75^{\circ}\right) \sin \left(-15^{\circ}\right)=$ $-\sin \left(75^{\circ}\right) \sin \left(15^{\circ}\right)=-\sin \left(15^{\circ}\right) \cos \left(15^{\circ}\right)=-\frac{\sin \left(30^{\circ}\right)}{2}=-\frac{1}{4}$.
|
{
"exam": "HMMT",
"problem_label": "1",
"problem_match": "\n1. ",
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-adv-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "1998"
}
|
How many values of $x,-19<x<98$, satisfy
$$
\cos ^{2} x+2 \sin ^{2} x=1 ?
$$
|
38. For any $x, \sin ^{2} x+\cos ^{2} x=1$. Subtracting this from the given equation gives $\sin ^{2} x=0$, or $\sin x=0$. Thus $x$ must be a multiple of $\pi$, so $-19<k \pi<98$ for some integer $k$, or approximately $-6.1<k<31.2$. There are 32 values of $k$ that satisfy this, so there are 38 values of $x$ that satisfy $\cos ^{2} x+2 \sin ^{2} x=1$.
|
38
|
Yes
|
Incomplete
|
math-word-problem
|
Algebra
|
How many values of $x,-19<x<98$, satisfy
$$
\cos ^{2} x+2 \sin ^{2} x=1 ?
$$
|
38. For any $x, \sin ^{2} x+\cos ^{2} x=1$. Subtracting this from the given equation gives $\sin ^{2} x=0$, or $\sin x=0$. Thus $x$ must be a multiple of $\pi$, so $-19<k \pi<98$ for some integer $k$, or approximately $-6.1<k<31.2$. There are 32 values of $k$ that satisfy this, so there are 38 values of $x$ that satisfy $\cos ^{2} x+2 \sin ^{2} x=1$.
|
{
"exam": "HMMT",
"problem_label": "2",
"problem_match": "\n2. ",
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-adv-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "1998"
}
|
Find the sum of the infinite series
$$
1+2\left(\frac{1}{1998}\right)+3\left(\frac{1}{1998}\right)^{2}+4\left(\frac{1}{1998}\right)^{3}+\ldots
$$
|
$\left(\frac{1998}{1997}\right)^{2}$ or $\frac{3992004}{3988009}$. We can rewrite the sum as
$\left(1+\frac{1}{1998}+\left(\frac{1}{1998}\right)^{2}+\ldots\right)+\left(\frac{1}{1998}+\left(\frac{1}{1998}\right)^{2}+\left(\frac{1}{1998}\right)^{3}+\ldots\right)+\left(\left(\frac{1}{1998}\right)^{2}+\left(\frac{1}{1998}\right)^{3}+\ldots\right)+\ldots$.
Evaluating each of the infinite sums gives
$\frac{1}{1-\frac{1}{1998}}+\frac{\frac{1}{1998}}{1-\frac{1}{1998}}+\frac{\left(\frac{1}{1998}\right)^{2}}{1-\frac{1}{1998}}+\ldots=\frac{1998}{1997} \cdot\left(1+\frac{1}{1998}+\left(\frac{1}{1998}\right)^{2}+\ldots\right)=\frac{1998}{1997} \cdot\left(1+\frac{1}{1998}+\left(\frac{1}{1998}\right)^{2}+\ldots\right)$,
which is equal to $\left(\frac{1998}{1997}\right)^{2}$, or $\frac{3992004}{3988009}$, as desired.
|
\left(\frac{1998}{1997}\right)^{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find the sum of the infinite series
$$
1+2\left(\frac{1}{1998}\right)+3\left(\frac{1}{1998}\right)^{2}+4\left(\frac{1}{1998}\right)^{3}+\ldots
$$
|
$\left(\frac{1998}{1997}\right)^{2}$ or $\frac{3992004}{3988009}$. We can rewrite the sum as
$\left(1+\frac{1}{1998}+\left(\frac{1}{1998}\right)^{2}+\ldots\right)+\left(\frac{1}{1998}+\left(\frac{1}{1998}\right)^{2}+\left(\frac{1}{1998}\right)^{3}+\ldots\right)+\left(\left(\frac{1}{1998}\right)^{2}+\left(\frac{1}{1998}\right)^{3}+\ldots\right)+\ldots$.
Evaluating each of the infinite sums gives
$\frac{1}{1-\frac{1}{1998}}+\frac{\frac{1}{1998}}{1-\frac{1}{1998}}+\frac{\left(\frac{1}{1998}\right)^{2}}{1-\frac{1}{1998}}+\ldots=\frac{1998}{1997} \cdot\left(1+\frac{1}{1998}+\left(\frac{1}{1998}\right)^{2}+\ldots\right)=\frac{1998}{1997} \cdot\left(1+\frac{1}{1998}+\left(\frac{1}{1998}\right)^{2}+\ldots\right)$,
which is equal to $\left(\frac{1998}{1997}\right)^{2}$, or $\frac{3992004}{3988009}$, as desired.
|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n3. ",
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-adv-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "1998"
}
|
Find the range of
$$
f(A)=\frac{(\sin A)\left(3 \cos ^{2} A+\cos ^{4} A+3 \sin ^{2} A+\left(\sin ^{2} A\right)\left(\cos ^{2} A\right)\right)}{(\tan A)(\sec A-(\sin A)(\tan A))}
$$
if $A \neq \frac{n \pi}{2}$.
|
$(3,4)$. We factor the numerator and write the denominator in term of fractions to get
$$
\frac{(\sin A)\left(3+\cos ^{2} A\right)\left(\sin ^{2} A+\cos ^{2} A\right)}{\left(\frac{\sin A}{\cos A}\right)\left(\frac{1}{\cos A}-\frac{\sin ^{2} A}{\cos A}\right)}=\frac{(\sin A)\left(3+\cos ^{2} A\right)\left(\sin ^{2} A+\cos ^{2} A\right)}{\frac{(\sin A)\left(1-\sin ^{2} A\right)}{\cos ^{2} A}} .
$$
Because $\sin ^{2} A+\cos ^{2} A=1,1-\sin ^{2} A=\cos ^{2} A$, so the expression is simply equal to $3+\cos ^{2} A$. The range of $\cos ^{2} A$ is $(0,1)$ ( 0 and 1 are not included because $A \neq \frac{n \pi}{2}$, so the range of $3+\cos ^{2} A$ is $(3,4)$.
|
(3,4)
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find the range of
$$
f(A)=\frac{(\sin A)\left(3 \cos ^{2} A+\cos ^{4} A+3 \sin ^{2} A+\left(\sin ^{2} A\right)\left(\cos ^{2} A\right)\right)}{(\tan A)(\sec A-(\sin A)(\tan A))}
$$
if $A \neq \frac{n \pi}{2}$.
|
$(3,4)$. We factor the numerator and write the denominator in term of fractions to get
$$
\frac{(\sin A)\left(3+\cos ^{2} A\right)\left(\sin ^{2} A+\cos ^{2} A\right)}{\left(\frac{\sin A}{\cos A}\right)\left(\frac{1}{\cos A}-\frac{\sin ^{2} A}{\cos A}\right)}=\frac{(\sin A)\left(3+\cos ^{2} A\right)\left(\sin ^{2} A+\cos ^{2} A\right)}{\frac{(\sin A)\left(1-\sin ^{2} A\right)}{\cos ^{2} A}} .
$$
Because $\sin ^{2} A+\cos ^{2} A=1,1-\sin ^{2} A=\cos ^{2} A$, so the expression is simply equal to $3+\cos ^{2} A$. The range of $\cos ^{2} A$ is $(0,1)$ ( 0 and 1 are not included because $A \neq \frac{n \pi}{2}$, so the range of $3+\cos ^{2} A$ is $(3,4)$.
|
{
"exam": "HMMT",
"problem_label": "4",
"problem_match": "\n4. ",
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-adv-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "1998"
}
|
How many positive integers less than 1998 are relatively prime to 1547 ? (Two integers are relatively prime if they have no common factors besides 1.)
|
1487. The factorization of 1547 is $7 \cdot 13 \cdot 17$, so we wish to find the number of positive integers less than 1998 that are not divisible by 7,13 , or 17 . By the Principle of Inclusion-Exclusion, we first subtract the numbers that are divisible by one of 7,13 , and 17 , add back those that are divisible by two of 7,13 , and 17 , then subtract those divisible by three of them. That is,
$$
1997-\left\lfloor\frac{1997}{7}\right\rfloor-\left\lfloor\frac{1997}{13}\right\rfloor-\left\lfloor\frac{1997}{17}\right\rfloor+\left\lfloor\frac{1997}{7 \cdot 13}\right\rfloor+\left\lfloor\frac{1997}{7 \cdot 17}\right\rfloor+\left\lfloor\frac{1997}{13 \cdot 17}\right\rfloor-\left\lfloor\frac{1997}{7 \cdot 13 \cdot 17}\right\rfloor,
$$
or 1487.
|
1487
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
How many positive integers less than 1998 are relatively prime to 1547 ? (Two integers are relatively prime if they have no common factors besides 1.)
|
1487. The factorization of 1547 is $7 \cdot 13 \cdot 17$, so we wish to find the number of positive integers less than 1998 that are not divisible by 7,13 , or 17 . By the Principle of Inclusion-Exclusion, we first subtract the numbers that are divisible by one of 7,13 , and 17 , add back those that are divisible by two of 7,13 , and 17 , then subtract those divisible by three of them. That is,
$$
1997-\left\lfloor\frac{1997}{7}\right\rfloor-\left\lfloor\frac{1997}{13}\right\rfloor-\left\lfloor\frac{1997}{17}\right\rfloor+\left\lfloor\frac{1997}{7 \cdot 13}\right\rfloor+\left\lfloor\frac{1997}{7 \cdot 17}\right\rfloor+\left\lfloor\frac{1997}{13 \cdot 17}\right\rfloor-\left\lfloor\frac{1997}{7 \cdot 13 \cdot 17}\right\rfloor,
$$
or 1487.
|
{
"exam": "HMMT",
"problem_label": "5",
"problem_match": "\n5. ",
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-adv-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "1998"
}
|
In the diagram below, how many distinct paths are there from January 1 to December 31, moving from one adjacent dot to the next either to the right, down, or diagonally down to the right?
| Jan. $1->$ | * | * | * | * | * | * | * | * | * | * | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| | * | * | | * | * | | * | * | | * | |
| | * | * | * | * | * | * | * | * | * | * | |
| | * | | | * | | | * | * | | * | |
| | * | * | * | * | * | * | * | * | * | * | <-Dec. 31 |
|
372. For each dot in the diagram, we can count the number of paths from January 1 to it by adding the number of ways to get to the dots to the left of it, above it, and above and to the left of it, starting from the topmost leftmost dot. This yields the following numbers of paths:
| Jan. $1->$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ |
| ---: | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |$* 1$
So the number of paths from January 1 to December 31 is 372 .
|
372
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In the diagram below, how many distinct paths are there from January 1 to December 31, moving from one adjacent dot to the next either to the right, down, or diagonally down to the right?
| Jan. $1->$ | * | * | * | * | * | * | * | * | * | * | |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| | * | * | | * | * | | * | * | | * | |
| | * | * | * | * | * | * | * | * | * | * | |
| | * | | | * | | | * | * | | * | |
| | * | * | * | * | * | * | * | * | * | * | <-Dec. 31 |
|
372. For each dot in the diagram, we can count the number of paths from January 1 to it by adding the number of ways to get to the dots to the left of it, above it, and above and to the left of it, starting from the topmost leftmost dot. This yields the following numbers of paths:
| Jan. $1->$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ | $* 1$ |
| ---: | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |$* 1$
So the number of paths from January 1 to December 31 is 372 .
|
{
"exam": "HMMT",
"problem_label": "6",
"problem_match": "\n6. ",
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-adv-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "1998"
}
|
The Houson Association of Mathematics Educators decides to hold a grand forum on mathematics education and invites a number of politicians from the United States to participate. Around lunch time the politicians decide to play a game. In this game, players can score 19 points for pegging the coordinator of the gathering with a spit ball, 9 points for downing an entire cup of the forum's interpretation of coffee, or 8 points for quoting more than three consecutive words from the speech Senator Bobbo delivered before lunch. What is the product of the two greatest scores that a player cannot score in this game?
|
1209. Attainable scores are positive integers that can be written in the form $8 a+9 b+19 c$, where $a, b$, and $c$ are nonnegative integers. Consider attainable number of points modulo 8 .
Scores that are $0(\bmod 8)$ can be obtained with $8 a$ for positive $a$.
Scores that are $1(\bmod 8)$ greater than or equal to 9 can be obtained with $9+8 a$ for nonnegative $a$.
Scores that are $2(\bmod 8)$ greater than or equal to 18 can be obtained with $9 \cdot 2+8 a$.
Scores that are $3(\bmod 8)$ greater than or equal to 19 can be obtained with $19+8 a$.
Scores that are $4(\bmod 8)$ greater than or equal to $19+9=28$ can be obtained with $19+9+8 a$.
Scores that are $5(\bmod 8)$ greater than or equal to $19+9 \cdot 2=37$ can be obtained with $19+9 \cdot 2+8 a$.
Scores that are $6(\bmod 8)$ greater than or equal to $19 \cdot 2=38$ can be obtained with $19 \cdot 2+8 a$.
Scores that are $7(\bmod 8)$ greater than or equal to $19 \cdot 2+9=47$ can be obtained with $19 \cdot 2+9+8 a$.
So the largest two unachievable values are 39 and 31. Multiplying them gives 1209.
|
1209
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
The Houson Association of Mathematics Educators decides to hold a grand forum on mathematics education and invites a number of politicians from the United States to participate. Around lunch time the politicians decide to play a game. In this game, players can score 19 points for pegging the coordinator of the gathering with a spit ball, 9 points for downing an entire cup of the forum's interpretation of coffee, or 8 points for quoting more than three consecutive words from the speech Senator Bobbo delivered before lunch. What is the product of the two greatest scores that a player cannot score in this game?
|
1209. Attainable scores are positive integers that can be written in the form $8 a+9 b+19 c$, where $a, b$, and $c$ are nonnegative integers. Consider attainable number of points modulo 8 .
Scores that are $0(\bmod 8)$ can be obtained with $8 a$ for positive $a$.
Scores that are $1(\bmod 8)$ greater than or equal to 9 can be obtained with $9+8 a$ for nonnegative $a$.
Scores that are $2(\bmod 8)$ greater than or equal to 18 can be obtained with $9 \cdot 2+8 a$.
Scores that are $3(\bmod 8)$ greater than or equal to 19 can be obtained with $19+8 a$.
Scores that are $4(\bmod 8)$ greater than or equal to $19+9=28$ can be obtained with $19+9+8 a$.
Scores that are $5(\bmod 8)$ greater than or equal to $19+9 \cdot 2=37$ can be obtained with $19+9 \cdot 2+8 a$.
Scores that are $6(\bmod 8)$ greater than or equal to $19 \cdot 2=38$ can be obtained with $19 \cdot 2+8 a$.
Scores that are $7(\bmod 8)$ greater than or equal to $19 \cdot 2+9=47$ can be obtained with $19 \cdot 2+9+8 a$.
So the largest two unachievable values are 39 and 31. Multiplying them gives 1209.
|
{
"exam": "HMMT",
"problem_label": "7",
"problem_match": "\n7. ",
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-adv-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "1998"
}
|
Given any two positive real numbers $x$ and $y$, then $x \diamond y$ is a positive real number defined in terms of $x$ and $y$ by some fixed rule. Suppose the operation $x \diamond y$ satisfies the equations $(x \cdot y) \diamond y=x(y \diamond y)$ and $(x \diamond 1) \diamond x=x \diamond 1$ for all $x, y>0$. Given that $1 \diamond 1=1$, find $19 \diamond 98$.
|
19. Note first that $x \diamond 1=(x \cdot 1) \diamond 1=x \cdot(1 \diamond 1)=x \cdot 1=x$. Also, $x \diamond x=(x \diamond 1) \diamond x=x \diamond 1=x$. Now, we have $(x \cdot y) \diamond y=x \cdot(y \diamond y)=x \cdot y$. So $19 \diamond 98=\left(\frac{19}{98} \cdot 98\right) \diamond 98=\frac{19}{98} \cdot(98 \diamond 98)=\frac{19}{98} \cdot 98=19$.
|
19
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Given any two positive real numbers $x$ and $y$, then $x \diamond y$ is a positive real number defined in terms of $x$ and $y$ by some fixed rule. Suppose the operation $x \diamond y$ satisfies the equations $(x \cdot y) \diamond y=x(y \diamond y)$ and $(x \diamond 1) \diamond x=x \diamond 1$ for all $x, y>0$. Given that $1 \diamond 1=1$, find $19 \diamond 98$.
|
19. Note first that $x \diamond 1=(x \cdot 1) \diamond 1=x \cdot(1 \diamond 1)=x \cdot 1=x$. Also, $x \diamond x=(x \diamond 1) \diamond x=x \diamond 1=x$. Now, we have $(x \cdot y) \diamond y=x \cdot(y \diamond y)=x \cdot y$. So $19 \diamond 98=\left(\frac{19}{98} \cdot 98\right) \diamond 98=\frac{19}{98} \cdot(98 \diamond 98)=\frac{19}{98} \cdot 98=19$.
|
{
"exam": "HMMT",
"problem_label": "8",
"problem_match": "\n8. ",
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-adv-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "1998"
}
|
Bob's Rice ID number has six digits, each a number from 1 to 9 , and any digit can be used any number of times. The ID number satisfies the following property: the first two digits is a number divisible by 2 , the first three digits is a number divisible by 3 , etc. so that the ID number itself is divisible by 6 . One ID number that satisfies this condition is 123252 . How many different possibilities are there for Bob's ID number?
|
324 . We will count the number of possibilities for each digit in Bob's ID number, then multiply them to find the total number of possibilities for Bob's ID number. There are 3 possibilities for the first digit given any last 5 digits, because the entire number must be divisible by 3 , so the sum of the digits must be divisible by 3 . Because the first two digits are a number divisible by 2 , the second digit must be $2,4,6$, or 8 , which is 4 possibilities. Because the first five digits are a number divisible by 5 , the fifth digit must be a 5 . Now, if the fourth digit is a 2 , then the last digit has two choices, 2,8 , and the third digit has 5 choices, $1,3,5,7,9$. If the fourth digit is a 4 , then the last digit must be a 6 , and the third digit has 4 choices, $2,4,6,8$. If the fourth digit is a 6 , then the last digit must be a 4 , and the third digit has 5 choices, $1,3,5,7,9$. If the fourth digit is an 8 , then the last digit has two choices, 2,8 , and the third digit has 4 choices, $2,4,6,8$. So there are a total of $3 \cdot 4(2 \cdot 5+4+5+2 \cdot 4)=3 \cdot 4 \cdot 27=324$ possibilities for Bob's ID number.
|
324
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Bob's Rice ID number has six digits, each a number from 1 to 9 , and any digit can be used any number of times. The ID number satisfies the following property: the first two digits is a number divisible by 2 , the first three digits is a number divisible by 3 , etc. so that the ID number itself is divisible by 6 . One ID number that satisfies this condition is 123252 . How many different possibilities are there for Bob's ID number?
|
324 . We will count the number of possibilities for each digit in Bob's ID number, then multiply them to find the total number of possibilities for Bob's ID number. There are 3 possibilities for the first digit given any last 5 digits, because the entire number must be divisible by 3 , so the sum of the digits must be divisible by 3 . Because the first two digits are a number divisible by 2 , the second digit must be $2,4,6$, or 8 , which is 4 possibilities. Because the first five digits are a number divisible by 5 , the fifth digit must be a 5 . Now, if the fourth digit is a 2 , then the last digit has two choices, 2,8 , and the third digit has 5 choices, $1,3,5,7,9$. If the fourth digit is a 4 , then the last digit must be a 6 , and the third digit has 4 choices, $2,4,6,8$. If the fourth digit is a 6 , then the last digit must be a 4 , and the third digit has 5 choices, $1,3,5,7,9$. If the fourth digit is an 8 , then the last digit has two choices, 2,8 , and the third digit has 4 choices, $2,4,6,8$. So there are a total of $3 \cdot 4(2 \cdot 5+4+5+2 \cdot 4)=3 \cdot 4 \cdot 27=324$ possibilities for Bob's ID number.
|
{
"exam": "HMMT",
"problem_label": "9",
"problem_match": "\n9. ",
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-adv-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "1998"
}
|
In the fourth annual Swirled Series, the Oakland Alphas are playing the San Francisco Gammas. The first game is played in San Francisco and succeeding games alternate in location. San Francisco has a $50 \%$ chance of winning their home games, while Oakland has a probability of $60 \%$ of winning at home. Normally, the serios will stretch on forever until one team gets a three-game lead, in which case they are declared the winners. However, after each game in San Francisco there is a $50 \%$ chance of an earthquake, which will cause the series to end with the team that has won more games declared the winner. What is the probability that the Gammas will win?
|
| $\frac{34}{73} \cdot$ | Let $F(x)$ be the probability that the Gammas will win the series if they are ahead by |
| :--- | :--- | $x$ games and are about to play in San Francisco, and let $A(x)$ be the probability that the Gammas will win the series if they are ahead by $x$ games and are about to play in Oakland. Then we have
$$
\begin{gathered}
F(2)=\frac{3}{4}+\frac{A(1)}{4} \\
A(1)=\frac{6 F(0)}{10}+\frac{4 F(2)}{10} \\
F(0)=\frac{1}{4}+\frac{A(1)}{4}+\frac{A(-1)}{4} \\
A(-1)=\frac{6 F(-2)}{10}+\frac{4 F(0)}{10} \\
F(-2)=\frac{A(-1)}{4}
\end{gathered}
$$
Plugging $A(1)=\frac{6 F(0)}{10}+\frac{4 F(2)}{10}$ into $F(2)=\frac{3}{4}+\frac{A(1)}{4}$, we get
$$
\begin{gathered}
F(2)=\frac{3}{4}+\frac{1}{4}\left(\frac{6 F(0)}{10}+\frac{4 F(2)}{10}\right) \\
\frac{9 F(2)}{10}=\frac{3}{4}+\frac{6 F(0)}{40} \Leftrightarrow F(2)=\frac{5}{6}+\frac{F(0)}{6}
\end{gathered}
$$
Plugging $A(-1)=\frac{6 F(-2)}{10}+\frac{4 F(0)}{10}$ into $F(-2)=\frac{A(-1)}{4}$, we get
$$
\frac{34 A(-1)}{40}=\frac{4 F(0)}{10} \Leftrightarrow F(-2)=\frac{2 F(0)}{17}
$$
Now,
$$
F(0)=\frac{1}{4}+\frac{1}{4}\left(\frac{6 F(0)}{10}+\frac{4 F(2)}{10}\right)+\frac{1}{4}\left(\frac{6 F(-2)}{10}+\frac{4 F(0)}{10}\right)
$$
This simplifies to $F(0)=\frac{1}{4}+\frac{F(0)}{4}+\frac{F(2)}{10}+\frac{6 F(-2)}{40}$. Then, plugging our formulas in, we get
$$
\begin{gathered}
F(0)=\frac{1}{4}+\frac{F(0)}{4}+\frac{1}{10}\left(\frac{5}{6}+\frac{F(0)}{6}\right)+\frac{3 F(0)}{170} \\
\frac{73 F(0)}{102}=\frac{1}{3} \Leftrightarrow F(0)=\frac{34}{73}
\end{gathered}
$$
Since $F(0)$ is the situation before the Series has started, the probability that the Gammas will win is $\frac{34}{73}$.
|
\frac{34}{73}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In the fourth annual Swirled Series, the Oakland Alphas are playing the San Francisco Gammas. The first game is played in San Francisco and succeeding games alternate in location. San Francisco has a $50 \%$ chance of winning their home games, while Oakland has a probability of $60 \%$ of winning at home. Normally, the serios will stretch on forever until one team gets a three-game lead, in which case they are declared the winners. However, after each game in San Francisco there is a $50 \%$ chance of an earthquake, which will cause the series to end with the team that has won more games declared the winner. What is the probability that the Gammas will win?
|
| $\frac{34}{73} \cdot$ | Let $F(x)$ be the probability that the Gammas will win the series if they are ahead by |
| :--- | :--- | $x$ games and are about to play in San Francisco, and let $A(x)$ be the probability that the Gammas will win the series if they are ahead by $x$ games and are about to play in Oakland. Then we have
$$
\begin{gathered}
F(2)=\frac{3}{4}+\frac{A(1)}{4} \\
A(1)=\frac{6 F(0)}{10}+\frac{4 F(2)}{10} \\
F(0)=\frac{1}{4}+\frac{A(1)}{4}+\frac{A(-1)}{4} \\
A(-1)=\frac{6 F(-2)}{10}+\frac{4 F(0)}{10} \\
F(-2)=\frac{A(-1)}{4}
\end{gathered}
$$
Plugging $A(1)=\frac{6 F(0)}{10}+\frac{4 F(2)}{10}$ into $F(2)=\frac{3}{4}+\frac{A(1)}{4}$, we get
$$
\begin{gathered}
F(2)=\frac{3}{4}+\frac{1}{4}\left(\frac{6 F(0)}{10}+\frac{4 F(2)}{10}\right) \\
\frac{9 F(2)}{10}=\frac{3}{4}+\frac{6 F(0)}{40} \Leftrightarrow F(2)=\frac{5}{6}+\frac{F(0)}{6}
\end{gathered}
$$
Plugging $A(-1)=\frac{6 F(-2)}{10}+\frac{4 F(0)}{10}$ into $F(-2)=\frac{A(-1)}{4}$, we get
$$
\frac{34 A(-1)}{40}=\frac{4 F(0)}{10} \Leftrightarrow F(-2)=\frac{2 F(0)}{17}
$$
Now,
$$
F(0)=\frac{1}{4}+\frac{1}{4}\left(\frac{6 F(0)}{10}+\frac{4 F(2)}{10}\right)+\frac{1}{4}\left(\frac{6 F(-2)}{10}+\frac{4 F(0)}{10}\right)
$$
This simplifies to $F(0)=\frac{1}{4}+\frac{F(0)}{4}+\frac{F(2)}{10}+\frac{6 F(-2)}{40}$. Then, plugging our formulas in, we get
$$
\begin{gathered}
F(0)=\frac{1}{4}+\frac{F(0)}{4}+\frac{1}{10}\left(\frac{5}{6}+\frac{F(0)}{6}\right)+\frac{3 F(0)}{170} \\
\frac{73 F(0)}{102}=\frac{1}{3} \Leftrightarrow F(0)=\frac{34}{73}
\end{gathered}
$$
Since $F(0)$ is the situation before the Series has started, the probability that the Gammas will win is $\frac{34}{73}$.
|
{
"exam": "HMMT",
"problem_label": "10",
"problem_match": "\n10. ",
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-adv-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "1998"
}
|
The cost of 3 hamburgers, 5 milk shakes, and 1 order of fries at a certain fast food restaurant is $\$ 23.50$. At the same restaurant, the cost of 5 hamburgers, 9 milk shakes, and 1 order of fries is $\$ 39.50$. What is the cost of 2 hamburgers, 2 milk shakes ,and 2 orders of fries at this restaurant?
|
Let $H=$ hamburger, $M=$ milk shake, and $F=$ order of fries. Then $3 H+5 M+F=\$ 23.50$. Multiplying the equation by 2 yields $6 H+10 M+2 F=\$ 47$. Also, it is given that $5 H+9 M+F=\$ 39.50$. Then subtracting the following equations
$$
\begin{aligned}
& 6 H+10 M+2 F=\$ 47.00 \\
& 5 H+9 M+F=\$ 39.50
\end{aligned}
$$
yields $H+M+F=\$ 7.50$. Multiplying the equation by 2 yields $2 H+2 M+2 F=\$ 15$.
|
15
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
The cost of 3 hamburgers, 5 milk shakes, and 1 order of fries at a certain fast food restaurant is $\$ 23.50$. At the same restaurant, the cost of 5 hamburgers, 9 milk shakes, and 1 order of fries is $\$ 39.50$. What is the cost of 2 hamburgers, 2 milk shakes ,and 2 orders of fries at this restaurant?
|
Let $H=$ hamburger, $M=$ milk shake, and $F=$ order of fries. Then $3 H+5 M+F=\$ 23.50$. Multiplying the equation by 2 yields $6 H+10 M+2 F=\$ 47$. Also, it is given that $5 H+9 M+F=\$ 39.50$. Then subtracting the following equations
$$
\begin{aligned}
& 6 H+10 M+2 F=\$ 47.00 \\
& 5 H+9 M+F=\$ 39.50
\end{aligned}
$$
yields $H+M+F=\$ 7.50$. Multiplying the equation by 2 yields $2 H+2 M+2 F=\$ 15$.
|
{
"exam": "HMMT",
"problem_label": "1",
"problem_match": "\n1. Problem: ",
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-alg-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "1998"
}
|
Bobbo starts swimming at 2 feet/s across a 100 foot wide river with a current of 5 feet/s. Bobbo doesn't know that there is a waterfall 175 feet from where he entered the river. He realizes his predicament midway across the river. What is the minimum speed that Bobbo must increase to make it to the other side of the river safely?
|
When Bobbo is midway across the river, he has travelled 50 feet. Going at a speed of 2 feet $/ \mathrm{s}$, this means that Bobbo has already been in the river for $\frac{50 \text { feet }}{20 \text { feet } / \mathrm{s}}=25 \mathrm{~s}$. Then he has traveled 5 feet $/ \mathrm{s} \cdot 25 \mathrm{~s}=125$ feet down the river. Then he has 175 feet- 125 feet $=50$ feet left to travel downstream before he hits the waterfall.
Bobbo travels at a rate of 5 feet/s downstream. Thus there are $\frac{50 \mathrm{feet}}{5 \text { feet } / \mathrm{s}}=10 \mathrm{~s}$ before he hits the waterfall. He still has to travel 50 feet horizontally across the river. Thus he must travel at a speed of $\frac{50 \text { feet }}{10 \mathrm{~s}}=5$ feet $/ \mathrm{s}$. This is a 3 feet/s difference from Bobbo's original speed of 2 feet $/ \mathrm{s}$.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Bobbo starts swimming at 2 feet/s across a 100 foot wide river with a current of 5 feet/s. Bobbo doesn't know that there is a waterfall 175 feet from where he entered the river. He realizes his predicament midway across the river. What is the minimum speed that Bobbo must increase to make it to the other side of the river safely?
|
When Bobbo is midway across the river, he has travelled 50 feet. Going at a speed of 2 feet $/ \mathrm{s}$, this means that Bobbo has already been in the river for $\frac{50 \text { feet }}{20 \text { feet } / \mathrm{s}}=25 \mathrm{~s}$. Then he has traveled 5 feet $/ \mathrm{s} \cdot 25 \mathrm{~s}=125$ feet down the river. Then he has 175 feet- 125 feet $=50$ feet left to travel downstream before he hits the waterfall.
Bobbo travels at a rate of 5 feet/s downstream. Thus there are $\frac{50 \mathrm{feet}}{5 \text { feet } / \mathrm{s}}=10 \mathrm{~s}$ before he hits the waterfall. He still has to travel 50 feet horizontally across the river. Thus he must travel at a speed of $\frac{50 \text { feet }}{10 \mathrm{~s}}=5$ feet $/ \mathrm{s}$. This is a 3 feet/s difference from Bobbo's original speed of 2 feet $/ \mathrm{s}$.
|
{
"exam": "HMMT",
"problem_label": "2",
"problem_match": "\n2. Problem: ",
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-alg-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "1998"
}
|
Find the sum of every even positive integer less than 233 not divisible by 10 .
|
We find the sum of all positive even integers less than 233 and then subtract all the positive integers less than 233 that are divisible by 10 .
$2+4+\ldots+232=2(1+2+\ldots+116)=116 \cdot 117=13572$. The sum of all positive integers less than 233 that are divisible by 10 is $10+20+\ldots+230=10(1+2+\ldots+23)=2760$. Then our answer is $13572-2760=10812$.
|
10812
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the sum of every even positive integer less than 233 not divisible by 10 .
|
We find the sum of all positive even integers less than 233 and then subtract all the positive integers less than 233 that are divisible by 10 .
$2+4+\ldots+232=2(1+2+\ldots+116)=116 \cdot 117=13572$. The sum of all positive integers less than 233 that are divisible by 10 is $10+20+\ldots+230=10(1+2+\ldots+23)=2760$. Then our answer is $13572-2760=10812$.
|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n3. Problem: ",
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-alg-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "1998"
}
|
Given that $r$ and $s$ are relatively prime positive integers such that $\frac{r}{s}=\frac{2(\sqrt{2}+\sqrt{10})}{5(\sqrt{3+\sqrt{5}})}$, find $r$ and $s$.
|
Squaring both sides of the given equation yields $\frac{r^{2}}{s^{2}}=\frac{4(12+4 \sqrt{5})}{25(3+\sqrt{5})}=\frac{16(3+\sqrt{5})}{25(3+\sqrt{5})}=\frac{16}{25}$. Because $r$ and $s$ are positive and relatively prime, then by inspection, $r=4$ and $s=5$.
|
r=4, s=5
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Given that $r$ and $s$ are relatively prime positive integers such that $\frac{r}{s}=\frac{2(\sqrt{2}+\sqrt{10})}{5(\sqrt{3+\sqrt{5}})}$, find $r$ and $s$.
|
Squaring both sides of the given equation yields $\frac{r^{2}}{s^{2}}=\frac{4(12+4 \sqrt{5})}{25(3+\sqrt{5})}=\frac{16(3+\sqrt{5})}{25(3+\sqrt{5})}=\frac{16}{25}$. Because $r$ and $s$ are positive and relatively prime, then by inspection, $r=4$ and $s=5$.
|
{
"exam": "HMMT",
"problem_label": "4",
"problem_match": "\n4. Problem: ",
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-alg-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "1998"
}
|
A man named Juan has three rectangular solids, each having volume 128. Two of the faces of one solid have areas 4 and 32 . Two faces of another solid have areas 64 and 16 . Finally, two faces of the last solid have areas 8 and 32 . What is the minimum possible exposed surface area of the tallest tower Juan can construct by stacking his solids one on top of the other, face to face? (Assume that the base of the tower is not exposed).
|
Suppose that $x, y, z$ are the sides of the following solids. Then Volume $=x y z=128$. For the first solid, without loss of generality (with respect to assigning lengths to $x, y, z$ ), $x y=4$ and $y z=32$. Then $x y^{2} z=128$. Then $y=1$. Solving the remaining equations yields $x=4$ and $z=32$. Then the first solid has dimensions $4 \times 1 \times 32$.
For the second solid, without loss of generality, $x y=64$ and $y z=16$. Then $x y^{2} z=1024$. Then $y=8$. Solving the remaining equations yields $x=8$ and $z=2$. Then the second solid has dimensions $8 \times 8 \times 2$.
For the third solid, without loss of generality, $x y=8$ and $y z=32$. Then $y=2$. Solving the remaining equations yields $x=4$ and $z=16$. Then the third solid has dimensions $4 \times 2 \times 16$.
To obtain the tallest structure, Juan must stack the boxes such that the longest side of each solid is oriented vertically. Then for the first solid, the base must be $1 \times 4$, so that the side of length 32 can
contribute to the height of the structure. Similarly, for the second solid, the base must be $8 \times 2$, so that the side of length 8 can contribute to the height. Finally, for the third solid, the base must be $4 \times 2$. Thus the structure is stacked, from bottom to top: second solid, third solid, first solid. This order is necessary, so that the base of each solid will fit entirely on the top of the solid directly beneath it.
All the side faces of the solids contribute to the surface area of the final solid. The side faces of the bottom solid have area $8 \cdot(8+2+8+2)=160$. The side faces of the middle solid have area $16 \cdot(4+2+4+2)=192$. The sides faces of the top solid have area $32 \cdot(4+1+4+1)=320$.
Furthermore, the top faces of each of the solids are exposed. The top face of the bottom solid is partially obscured by the middle solid. Thus the total exposed area of the top face of the bottom solid is $8 \cdot 2-4 \cdot 2=8$. The top face of the middle solid is partially obscured by the top solid. Thus the total exposed area of the top face of the middle solid is $4 \cdot 2-4 \cdot 1=4$. The top face of the top solid is fully exposed. Thus the total exposed area of the top face of the top solid is $4 \cdot 1=4$.
Then the total surface area of the entire structure is $160+192+320+8+4+4=688$.
|
688
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A man named Juan has three rectangular solids, each having volume 128. Two of the faces of one solid have areas 4 and 32 . Two faces of another solid have areas 64 and 16 . Finally, two faces of the last solid have areas 8 and 32 . What is the minimum possible exposed surface area of the tallest tower Juan can construct by stacking his solids one on top of the other, face to face? (Assume that the base of the tower is not exposed).
|
Suppose that $x, y, z$ are the sides of the following solids. Then Volume $=x y z=128$. For the first solid, without loss of generality (with respect to assigning lengths to $x, y, z$ ), $x y=4$ and $y z=32$. Then $x y^{2} z=128$. Then $y=1$. Solving the remaining equations yields $x=4$ and $z=32$. Then the first solid has dimensions $4 \times 1 \times 32$.
For the second solid, without loss of generality, $x y=64$ and $y z=16$. Then $x y^{2} z=1024$. Then $y=8$. Solving the remaining equations yields $x=8$ and $z=2$. Then the second solid has dimensions $8 \times 8 \times 2$.
For the third solid, without loss of generality, $x y=8$ and $y z=32$. Then $y=2$. Solving the remaining equations yields $x=4$ and $z=16$. Then the third solid has dimensions $4 \times 2 \times 16$.
To obtain the tallest structure, Juan must stack the boxes such that the longest side of each solid is oriented vertically. Then for the first solid, the base must be $1 \times 4$, so that the side of length 32 can
contribute to the height of the structure. Similarly, for the second solid, the base must be $8 \times 2$, so that the side of length 8 can contribute to the height. Finally, for the third solid, the base must be $4 \times 2$. Thus the structure is stacked, from bottom to top: second solid, third solid, first solid. This order is necessary, so that the base of each solid will fit entirely on the top of the solid directly beneath it.
All the side faces of the solids contribute to the surface area of the final solid. The side faces of the bottom solid have area $8 \cdot(8+2+8+2)=160$. The side faces of the middle solid have area $16 \cdot(4+2+4+2)=192$. The sides faces of the top solid have area $32 \cdot(4+1+4+1)=320$.
Furthermore, the top faces of each of the solids are exposed. The top face of the bottom solid is partially obscured by the middle solid. Thus the total exposed area of the top face of the bottom solid is $8 \cdot 2-4 \cdot 2=8$. The top face of the middle solid is partially obscured by the top solid. Thus the total exposed area of the top face of the middle solid is $4 \cdot 2-4 \cdot 1=4$. The top face of the top solid is fully exposed. Thus the total exposed area of the top face of the top solid is $4 \cdot 1=4$.
Then the total surface area of the entire structure is $160+192+320+8+4+4=688$.
|
{
"exam": "HMMT",
"problem_label": "5",
"problem_match": "\n5. Problem: ",
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-alg-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "1998"
}
|
How many pairs of positive integers $(a, b)$ with $\leq b$ satisfy $\frac{1}{a}+\frac{1}{b}=\frac{1}{6}$ ?
|
$\frac{1}{a}+\frac{1}{b}=\frac{1}{6} \Rightarrow \frac{a+b}{a b}=\frac{1}{6} \Rightarrow a b=6 a+6 b \Rightarrow a b-6 a-6 b=0$. Factoring yields $(a-b)(b-6)-36=0$. Then $(a-6)(b-6)=36$. Because $a$ and $b$ are positive integers, only the factor pairs of 36 are possible values of $a-6$ and $b-6$. The possible pairs are:
$$
\begin{aligned}
& a-6=1, b-6=36 \\
& a-6=2, b-6=18 \\
& a-6=3, b-6=12 \\
& a-6=4, b-6=9 \\
& a-6=6, b-6=6
\end{aligned}
$$
Because $a \leq b$, the symmetric cases, such as $a-6=12, b-6=3$ are not applicable. Then there are 5 possible pairs.
|
5
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
How many pairs of positive integers $(a, b)$ with $\leq b$ satisfy $\frac{1}{a}+\frac{1}{b}=\frac{1}{6}$ ?
|
$\frac{1}{a}+\frac{1}{b}=\frac{1}{6} \Rightarrow \frac{a+b}{a b}=\frac{1}{6} \Rightarrow a b=6 a+6 b \Rightarrow a b-6 a-6 b=0$. Factoring yields $(a-b)(b-6)-36=0$. Then $(a-6)(b-6)=36$. Because $a$ and $b$ are positive integers, only the factor pairs of 36 are possible values of $a-6$ and $b-6$. The possible pairs are:
$$
\begin{aligned}
& a-6=1, b-6=36 \\
& a-6=2, b-6=18 \\
& a-6=3, b-6=12 \\
& a-6=4, b-6=9 \\
& a-6=6, b-6=6
\end{aligned}
$$
Because $a \leq b$, the symmetric cases, such as $a-6=12, b-6=3$ are not applicable. Then there are 5 possible pairs.
|
{
"exam": "HMMT",
"problem_label": "6",
"problem_match": "\n6. Problem: ",
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-alg-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "1998"
}
|
Given that three roots of $f(x)=x^{4}+a x^{2}+b x+c$ are $2,-3$, and 5 , what is the value of $a+b+c$ ?
|
By definition, the coefficient of $x^{3}$ is negative the sum of the roots. In $f(x)$, the coefficient of $x^{3}$ is 0 . Thus the sum of the roots of $f(x)$ is 0 . Then the fourth root is -4 . Then $f(x)=(x-2)(x+3)(x-5)(x+4)$. Notice that $f(1)$ is $1+a+b+c$. Thus our answer is $f(1)-1=(1-2)(1+3)(1-5)(1+4)-1=79$.
|
79
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Given that three roots of $f(x)=x^{4}+a x^{2}+b x+c$ are $2,-3$, and 5 , what is the value of $a+b+c$ ?
|
By definition, the coefficient of $x^{3}$ is negative the sum of the roots. In $f(x)$, the coefficient of $x^{3}$ is 0 . Thus the sum of the roots of $f(x)$ is 0 . Then the fourth root is -4 . Then $f(x)=(x-2)(x+3)(x-5)(x+4)$. Notice that $f(1)$ is $1+a+b+c$. Thus our answer is $f(1)-1=(1-2)(1+3)(1-5)(1+4)-1=79$.
|
{
"exam": "HMMT",
"problem_label": "7",
"problem_match": "\n7. Problem: ",
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-alg-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "1998"
}
|
Find the set of solutions for $x$ in the inequality $\frac{x+1}{x+2}>\frac{3 x+4}{2 x+9}$ when $x \neq-2, x \neq \frac{9}{2}$.
|
There are 3 possible cases of $x$ : 1) $\left.\left.-\frac{9}{2}<x, 2\right) \frac{9}{2} \leq x \leq-2,3\right)-2<x$. For the cases (1) and (3), $x+2$ and $2 x+9$ are both positive or negative, so the following operation can be carried out without changing the inequality sign:
$$
\begin{aligned}
\frac{x+1}{x+2} & >\frac{3 x+4}{2 x+9} \\
\Rightarrow 2 x^{2}+11 x+9 & >3 x^{2}+10 x+8 \\
\Rightarrow 0 & >x^{2}-x-1
\end{aligned}
$$
The inequality holds for all $\frac{1-\sqrt{5}}{2}<x<\frac{1+\sqrt{5}}{2}$. The initial conditions were $-\frac{9}{2}<x$ or $-2<x$. The intersection of these three conditions occurs when $\frac{1-\sqrt{5}}{2}<x<\frac{1+\sqrt{5}}{2}$.
Case (2) is $\frac{9}{2} \leq x \leq-2$. For all $x$ satisfying these conditions, $x+2<0$ and $2 x+9>0$. Then the following operations will change the direction of the inequality:
$$
\begin{aligned}
\frac{x+1}{x+2} & >\frac{3 x+4}{2 x+9} \\
\Rightarrow 2 x^{2}+11 x+9 & <3 x^{2}+10 x+8 \\
\Rightarrow 0 & <x^{2}-x-1
\end{aligned}
$$
The inequality holds for all $x<\frac{1-\sqrt{5}}{2}$ and $\frac{1+\sqrt{5}}{2}<x$. The initial condition was $\frac{-9}{2} \leq x \leq-2$. Hence the intersection of these conditions yields all $x$ such that $\frac{-9}{2} \leq x \leq-2$. Then all possible cases of $x$ are $\frac{-9}{2} \leq x \leq-2 \cup \frac{1-\sqrt{5}}{2}<x<\frac{1+\sqrt{5}}{2}$.
|
\frac{-9}{2} \leq x \leq-2 \cup \frac{1-\sqrt{5}}{2}<x<\frac{1+\sqrt{5}}{2}
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Find the set of solutions for $x$ in the inequality $\frac{x+1}{x+2}>\frac{3 x+4}{2 x+9}$ when $x \neq-2, x \neq \frac{9}{2}$.
|
There are 3 possible cases of $x$ : 1) $\left.\left.-\frac{9}{2}<x, 2\right) \frac{9}{2} \leq x \leq-2,3\right)-2<x$. For the cases (1) and (3), $x+2$ and $2 x+9$ are both positive or negative, so the following operation can be carried out without changing the inequality sign:
$$
\begin{aligned}
\frac{x+1}{x+2} & >\frac{3 x+4}{2 x+9} \\
\Rightarrow 2 x^{2}+11 x+9 & >3 x^{2}+10 x+8 \\
\Rightarrow 0 & >x^{2}-x-1
\end{aligned}
$$
The inequality holds for all $\frac{1-\sqrt{5}}{2}<x<\frac{1+\sqrt{5}}{2}$. The initial conditions were $-\frac{9}{2}<x$ or $-2<x$. The intersection of these three conditions occurs when $\frac{1-\sqrt{5}}{2}<x<\frac{1+\sqrt{5}}{2}$.
Case (2) is $\frac{9}{2} \leq x \leq-2$. For all $x$ satisfying these conditions, $x+2<0$ and $2 x+9>0$. Then the following operations will change the direction of the inequality:
$$
\begin{aligned}
\frac{x+1}{x+2} & >\frac{3 x+4}{2 x+9} \\
\Rightarrow 2 x^{2}+11 x+9 & <3 x^{2}+10 x+8 \\
\Rightarrow 0 & <x^{2}-x-1
\end{aligned}
$$
The inequality holds for all $x<\frac{1-\sqrt{5}}{2}$ and $\frac{1+\sqrt{5}}{2}<x$. The initial condition was $\frac{-9}{2} \leq x \leq-2$. Hence the intersection of these conditions yields all $x$ such that $\frac{-9}{2} \leq x \leq-2$. Then all possible cases of $x$ are $\frac{-9}{2} \leq x \leq-2 \cup \frac{1-\sqrt{5}}{2}<x<\frac{1+\sqrt{5}}{2}$.
|
{
"exam": "HMMT",
"problem_label": "8",
"problem_match": "\n8. Problem: ",
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-alg-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "1998"
}
|
Suppose $f(x)$ is a rational function such that $3 f\left(\frac{1}{x}\right)+\frac{2 f(x)}{x}=x^{2}$ for $x \neq 0$. Find $f(-2)$.
|
Let $x=\frac{-1}{2}$. Then
$$
\begin{aligned}
& 3 f(-2)+\frac{2 f\left(\frac{-1}{2}\right)}{\frac{-1}{2}}=\frac{1}{4} \\
& \Rightarrow 3 f(-2)-4 f\left(\frac{-1}{2}\right)= \frac{1}{4}
\end{aligned}
$$
Let $x=-2$. Then
$$
\begin{aligned}
& 3 f\left(\frac{-1}{2}\right)+\frac{2 f(-2)}{-2}=4 \\
\Rightarrow 3 f\left(\frac{-1}{2}\right)-f(-2) & =4
\end{aligned}
$$
Solving this system of equations $\{(1),(2)\}$ for $f(-2)$ yields $f(-2)=\frac{67}{20}$.
|
\frac{67}{20}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Suppose $f(x)$ is a rational function such that $3 f\left(\frac{1}{x}\right)+\frac{2 f(x)}{x}=x^{2}$ for $x \neq 0$. Find $f(-2)$.
|
Let $x=\frac{-1}{2}$. Then
$$
\begin{aligned}
& 3 f(-2)+\frac{2 f\left(\frac{-1}{2}\right)}{\frac{-1}{2}}=\frac{1}{4} \\
& \Rightarrow 3 f(-2)-4 f\left(\frac{-1}{2}\right)= \frac{1}{4}
\end{aligned}
$$
Let $x=-2$. Then
$$
\begin{aligned}
& 3 f\left(\frac{-1}{2}\right)+\frac{2 f(-2)}{-2}=4 \\
\Rightarrow 3 f\left(\frac{-1}{2}\right)-f(-2) & =4
\end{aligned}
$$
Solving this system of equations $\{(1),(2)\}$ for $f(-2)$ yields $f(-2)=\frac{67}{20}$.
|
{
"exam": "HMMT",
"problem_label": "9",
"problem_match": "\n9. Problem: ",
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-alg-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "1998"
}
|
G.H. Hardy once went to visit Srinivasa Ramanujan in the hospital, and he started the conversation with: "I came here in taxi-cab number 1729. That number seems dull to me, which I hope isn't a bad omen." "Nonsense," said Ramanujan. "The number isn't dull at all. It's quite interesting. It's the smallest number that can be expressed as the sum of two cubes in two different ways." Ramanujan had immediately seen that $1729=12^{3}+1^{3}=10^{3}+9^{3}$. What is the smallest positive integer representable as the sum of the cubes of three positive integers in two different ways?
|
Let this smallest positive integer be represented as $a^{3}+b^{3}+c^{3}=d^{3}+e^{3}+f^{3}$. By inspection, a solution is not possible with the first 4 cubes. We prove that it is impossible to write the same number as two different sums of the first 5 cubes. Because we necessarily need to use the 5 th cube (otherwise, this proof would be for the first 4 cubes), we have $5^{3}+b^{3}+c^{3}=d^{3}+e^{3}+f^{3}$. Without loss of generality, suppose $d=5$. By inspection, there is no solution to $b^{3}+c^{3}=e^{3}+f^{3}$, such that $b, c, e, f \leq 5$ and $b, c$ and $e, f$ are unique.
Then none of $d, e, f$ are 5 . Then at least two must be 4 , otherwise the RHS would be too small. Without loss of generality, suppose $d=e=4$. Then $b^{3}+c^{3}=3+f^{3}$. By inspection, there are no possible solutions if $b, c, f \leq 4$.
Thus if $a=5$, there are no solutions.
Suppose that there is a solution within the first 6 cubes. Then $a=6$. By the same analysis as above, $d=e=5$, otherwise the RHS would be too small. Then $b^{3}+c^{3}=34+f^{3}$. By inspection, we see that a possible solution is $b=3, c=2, f=1$. Then the desired integer is $6^{3}+3^{3}+2^{3}=251$.
|
251
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
G.H. Hardy once went to visit Srinivasa Ramanujan in the hospital, and he started the conversation with: "I came here in taxi-cab number 1729. That number seems dull to me, which I hope isn't a bad omen." "Nonsense," said Ramanujan. "The number isn't dull at all. It's quite interesting. It's the smallest number that can be expressed as the sum of two cubes in two different ways." Ramanujan had immediately seen that $1729=12^{3}+1^{3}=10^{3}+9^{3}$. What is the smallest positive integer representable as the sum of the cubes of three positive integers in two different ways?
|
Let this smallest positive integer be represented as $a^{3}+b^{3}+c^{3}=d^{3}+e^{3}+f^{3}$. By inspection, a solution is not possible with the first 4 cubes. We prove that it is impossible to write the same number as two different sums of the first 5 cubes. Because we necessarily need to use the 5 th cube (otherwise, this proof would be for the first 4 cubes), we have $5^{3}+b^{3}+c^{3}=d^{3}+e^{3}+f^{3}$. Without loss of generality, suppose $d=5$. By inspection, there is no solution to $b^{3}+c^{3}=e^{3}+f^{3}$, such that $b, c, e, f \leq 5$ and $b, c$ and $e, f$ are unique.
Then none of $d, e, f$ are 5 . Then at least two must be 4 , otherwise the RHS would be too small. Without loss of generality, suppose $d=e=4$. Then $b^{3}+c^{3}=3+f^{3}$. By inspection, there are no possible solutions if $b, c, f \leq 4$.
Thus if $a=5$, there are no solutions.
Suppose that there is a solution within the first 6 cubes. Then $a=6$. By the same analysis as above, $d=e=5$, otherwise the RHS would be too small. Then $b^{3}+c^{3}=34+f^{3}$. By inspection, we see that a possible solution is $b=3, c=2, f=1$. Then the desired integer is $6^{3}+3^{3}+2^{3}=251$.
|
{
"exam": "HMMT",
"problem_label": "10",
"problem_match": "\n10. Problem: ",
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-alg-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "1998"
}
|
Farmer Tim is lost in the densely-forested Cartesian plane. Starting from the origin he walks a sinusoidal path in search of home; that is, after $t$ minutes he is at position $(t, \sin t)$.
Five minutes after he sets out, Alex enters the forest at the origin and sets out in search of Tim. He walks in such a way that after he has been in the forest for $m$ minutes, his position is $(m, \cos t)$.
What is the greatest distance between Alex and Farmer Tim while they are walking in these paths?
|
At arbitrary time $t$, Farmer Tim is at position $(t, \sin t)$ and Alex is at position $(t-5, \cos t)$. Hence at time $t$, the distance, $d$, between Tim and Alex is $d=\sqrt{(\sin t-\cos t)^{2}+25}$. To find the maximum value of $d$, we solve for $t$ such that $\frac{d d}{d t}=0$.
$\frac{d d}{d t}=\frac{(\sin t-\cos t)(\cos t+\sin t)}{\sqrt{(\sin t-\cos t)^{2}+25}}$. Then $\frac{d d}{d t}=0 \Rightarrow \sin ^{2} t-\cos ^{2} t=0 \Rightarrow \sin ^{2} t=\cos ^{2} t$. Equality happens if $t$ is any constant multiple of $\frac{\pi}{4}$.
Notice that to maximize $d$, we need to maximize $(\sin t-\cos t)^{2}$. This is achieved when $\cos t=-\sin t$. Because we determined earlier that $t$ is a constant multiple of $\frac{\pi}{4}$, then with this new condition, we see that $t$ must be a constant multiple of $\frac{3 \pi}{4}$.
Then $(\sin t-\cos t)^{2}=2 \Rightarrow d=\sqrt{29}$.
|
\sqrt{29}
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Farmer Tim is lost in the densely-forested Cartesian plane. Starting from the origin he walks a sinusoidal path in search of home; that is, after $t$ minutes he is at position $(t, \sin t)$.
Five minutes after he sets out, Alex enters the forest at the origin and sets out in search of Tim. He walks in such a way that after he has been in the forest for $m$ minutes, his position is $(m, \cos t)$.
What is the greatest distance between Alex and Farmer Tim while they are walking in these paths?
|
At arbitrary time $t$, Farmer Tim is at position $(t, \sin t)$ and Alex is at position $(t-5, \cos t)$. Hence at time $t$, the distance, $d$, between Tim and Alex is $d=\sqrt{(\sin t-\cos t)^{2}+25}$. To find the maximum value of $d$, we solve for $t$ such that $\frac{d d}{d t}=0$.
$\frac{d d}{d t}=\frac{(\sin t-\cos t)(\cos t+\sin t)}{\sqrt{(\sin t-\cos t)^{2}+25}}$. Then $\frac{d d}{d t}=0 \Rightarrow \sin ^{2} t-\cos ^{2} t=0 \Rightarrow \sin ^{2} t=\cos ^{2} t$. Equality happens if $t$ is any constant multiple of $\frac{\pi}{4}$.
Notice that to maximize $d$, we need to maximize $(\sin t-\cos t)^{2}$. This is achieved when $\cos t=-\sin t$. Because we determined earlier that $t$ is a constant multiple of $\frac{\pi}{4}$, then with this new condition, we see that $t$ must be a constant multiple of $\frac{3 \pi}{4}$.
Then $(\sin t-\cos t)^{2}=2 \Rightarrow d=\sqrt{29}$.
|
{
"exam": "HMMT",
"problem_label": "1",
"problem_match": "\n1. Problem: ",
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-calc-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "1998"
}
|
A cube with sides 1 m in length is filled with water, and has a tiny hole through which the water drains into a cylinder of radius 1 m . If the water level in the cube is falling at a rate of $1 \mathrm{~cm} / \mathrm{s}$, at what rate is the water level in the cylinder rising?
|
The magnitude of the change in volume per unit time of the two solids is the same. The change in volume per unit time of the cube is $1 \mathrm{~cm} \cdot \mathrm{~m}^{2} / \mathrm{s}$. The change in volume per unit time of the cylinder is $\pi \cdot \frac{d h}{d t} \cdot m^{2}$, where $\frac{d h}{d t}$ is the rate at which the water level in the cylinder is rising.
Solving the equation $\pi \cdot \frac{d h}{d t} \cdot m^{2}=1 \mathrm{~cm} \cdot m^{2} / \mathrm{s}$ yields $\frac{1}{\pi} \mathrm{~cm} / \mathrm{s}$.
|
\frac{1}{\pi} \mathrm{~cm} / \mathrm{s}
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
A cube with sides 1 m in length is filled with water, and has a tiny hole through which the water drains into a cylinder of radius 1 m . If the water level in the cube is falling at a rate of $1 \mathrm{~cm} / \mathrm{s}$, at what rate is the water level in the cylinder rising?
|
The magnitude of the change in volume per unit time of the two solids is the same. The change in volume per unit time of the cube is $1 \mathrm{~cm} \cdot \mathrm{~m}^{2} / \mathrm{s}$. The change in volume per unit time of the cylinder is $\pi \cdot \frac{d h}{d t} \cdot m^{2}$, where $\frac{d h}{d t}$ is the rate at which the water level in the cylinder is rising.
Solving the equation $\pi \cdot \frac{d h}{d t} \cdot m^{2}=1 \mathrm{~cm} \cdot m^{2} / \mathrm{s}$ yields $\frac{1}{\pi} \mathrm{~cm} / \mathrm{s}$.
|
{
"exam": "HMMT",
"problem_label": "2",
"problem_match": "\n2. Problem: ",
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-calc-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "1998"
}
|
Find the area of the region bounded by the graphs of $y=x^{2}, y=x$, and $x=2$.
|
There are two regions to consider. First, there is the region bounded by $y=x^{2}$ and $y=x$, in the interval $[0,1]$. In this interval, the values of $y=x$ are greater than the values of $y=x^{2}$, thus the area is calculated by $\int_{0}^{1}\left(x-x^{2}\right) d x$.
Second, there is the region bounded by $y=x^{2}$ and $y=x$ and $x=2$, in the interval [1,2]. In this interval, the values of $y=x^{2}$ are greater than the values of $y=x$, thus the area is calculated by $\int_{1}^{2}\left(x^{2}-x\right) d x$. Then the total area of the region bounded by the three graphs is $\int_{0}^{1}\left(x-x^{2}\right) d x+\int_{1}^{2}\left(x^{2}-x\right) d x=1$.
|
1
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Find the area of the region bounded by the graphs of $y=x^{2}, y=x$, and $x=2$.
|
There are two regions to consider. First, there is the region bounded by $y=x^{2}$ and $y=x$, in the interval $[0,1]$. In this interval, the values of $y=x$ are greater than the values of $y=x^{2}$, thus the area is calculated by $\int_{0}^{1}\left(x-x^{2}\right) d x$.
Second, there is the region bounded by $y=x^{2}$ and $y=x$ and $x=2$, in the interval [1,2]. In this interval, the values of $y=x^{2}$ are greater than the values of $y=x$, thus the area is calculated by $\int_{1}^{2}\left(x^{2}-x\right) d x$. Then the total area of the region bounded by the three graphs is $\int_{0}^{1}\left(x-x^{2}\right) d x+\int_{1}^{2}\left(x^{2}-x\right) d x=1$.
|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n3. Problem: ",
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-calc-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "1998"
}
|
Let $f(x)=1+\frac{x}{2}+\frac{x^{2}}{4}+\frac{x^{3}}{8}+\ldots$, for $-1 \leq x \leq 1$. Find $\sqrt{e^{\int_{0}^{1} f(x) d x}}$.
|
Observe that $f(x)$ is merely an infinite geometric series. Thus $f(x)=\frac{1}{1-\frac{x}{2}}=\frac{2}{2-x}$. Then $\int_{0}^{1} \frac{2}{2-x}=2 \ln 2$. Then $\sqrt{e^{2 \ln 2}}=\sqrt{2^{2}}=2$.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Let $f(x)=1+\frac{x}{2}+\frac{x^{2}}{4}+\frac{x^{3}}{8}+\ldots$, for $-1 \leq x \leq 1$. Find $\sqrt{e^{\int_{0}^{1} f(x) d x}}$.
|
Observe that $f(x)$ is merely an infinite geometric series. Thus $f(x)=\frac{1}{1-\frac{x}{2}}=\frac{2}{2-x}$. Then $\int_{0}^{1} \frac{2}{2-x}=2 \ln 2$. Then $\sqrt{e^{2 \ln 2}}=\sqrt{2^{2}}=2$.
|
{
"exam": "HMMT",
"problem_label": "4",
"problem_match": "\n4. Problem: ",
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-calc-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "1998"
}
|
Edward, the author of this test, had to escape from prison to work in the grading room today. He stopped to rest at a place 1,875 feet from the prison and was spotted by a guard with a crossbow. The guard fired an arrow with an initial velocity of $100 \mathrm{ft} / \mathrm{s}$. At the same time, Edward started running away with an acceleration of $1 \mathrm{ft} / \mathrm{s}^{2}$. Assuming that air resistance causes the arrow to decelerate at $1 \mathrm{ft} / \mathrm{s}^{2}$ and that it does hit Edward, how fast was the arrow moving at the moment of impact (in $\mathrm{ft} / \mathrm{s}$ )?
|
We use the formula for distance, $d=\frac{1}{2} a t^{2}+v t+d_{0}$. Then after $t$ seconds, Edward is at location $1875+\frac{1}{2}(1)\left(t^{2}\right)$ from the prison. After $t$ seconds, the arrow is at location $\frac{1}{2}(-1)\left(t^{2}\right)+100 t$ from the prison. When the arrow hits Edward, both objects are at the same distance away from the tower. Hence $1875+\frac{1}{2}(1)\left(t^{2}\right)=\frac{1}{2}(-1)\left(t^{2}\right)+100 t$. Solving for $t$ yields $t^{2}-100 t+1875=0 \Rightarrow t=25$ or $t=75$. Then it must be $t=25$, because after the arrow hits Edward, he will stop running.
After 25 seconds, the arrow is moving at a velocity of $100-25(1)=75 \mathrm{ft} / \mathrm{s}$.
|
75
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Edward, the author of this test, had to escape from prison to work in the grading room today. He stopped to rest at a place 1,875 feet from the prison and was spotted by a guard with a crossbow. The guard fired an arrow with an initial velocity of $100 \mathrm{ft} / \mathrm{s}$. At the same time, Edward started running away with an acceleration of $1 \mathrm{ft} / \mathrm{s}^{2}$. Assuming that air resistance causes the arrow to decelerate at $1 \mathrm{ft} / \mathrm{s}^{2}$ and that it does hit Edward, how fast was the arrow moving at the moment of impact (in $\mathrm{ft} / \mathrm{s}$ )?
|
We use the formula for distance, $d=\frac{1}{2} a t^{2}+v t+d_{0}$. Then after $t$ seconds, Edward is at location $1875+\frac{1}{2}(1)\left(t^{2}\right)$ from the prison. After $t$ seconds, the arrow is at location $\frac{1}{2}(-1)\left(t^{2}\right)+100 t$ from the prison. When the arrow hits Edward, both objects are at the same distance away from the tower. Hence $1875+\frac{1}{2}(1)\left(t^{2}\right)=\frac{1}{2}(-1)\left(t^{2}\right)+100 t$. Solving for $t$ yields $t^{2}-100 t+1875=0 \Rightarrow t=25$ or $t=75$. Then it must be $t=25$, because after the arrow hits Edward, he will stop running.
After 25 seconds, the arrow is moving at a velocity of $100-25(1)=75 \mathrm{ft} / \mathrm{s}$.
|
{
"exam": "HMMT",
"problem_label": "6",
"problem_match": "\n6. Problem: ",
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-calc-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "1998"
}
|
A parabola is inscribed in equilateral triangle $A B C$ of side length 1 in the sense that $A C$ and $B C$ are tangent to the parabola at $A$ and $B$, respectively. Find the area between $A B$ and the parabola.
|
Suppose $A=(0,0), B=(1,0)$, and $C=\left(\frac{1}{2}, \frac{\sqrt{3}}{2}\right)$. Then the parabola in question goes through $(0,0)$ and $(1,0)$ and has tangents with slopes of $\sqrt{3}$ and $-\sqrt{3}$, respectively, at these points. Suppose the parabola has equation $y=a x^{2}+b x+c$. Then $\frac{d y}{d x}=2 a x+b$.
At point $(0,0), \frac{d y}{d x}=b$. Also the slope at $(0,0)$, as we determined earlier, is $\sqrt{3}$. Hence $b=\sqrt{3}$. Similarly, at point $(1,0), \frac{d y}{d x}=2 a+b$. The slope at $(1,0)$, as we determined earlier, is $-\sqrt{3}$. Then $a=-\sqrt{3}$.
Since the parabola goes through $(0,0), c=0$. Hence the equation of the parabola is $y=-\sqrt{3} x^{2}+\sqrt{3} x$. The desired area is simply the area under the parabolic curve in the interval $[0,1]$.
Hence $\int_{0}^{1}\left(-\sqrt{3} x^{2}+\sqrt{3} x\right) d x=\frac{\sqrt{3}}{6}$.
|
\frac{\sqrt{3}}{6}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A parabola is inscribed in equilateral triangle $A B C$ of side length 1 in the sense that $A C$ and $B C$ are tangent to the parabola at $A$ and $B$, respectively. Find the area between $A B$ and the parabola.
|
Suppose $A=(0,0), B=(1,0)$, and $C=\left(\frac{1}{2}, \frac{\sqrt{3}}{2}\right)$. Then the parabola in question goes through $(0,0)$ and $(1,0)$ and has tangents with slopes of $\sqrt{3}$ and $-\sqrt{3}$, respectively, at these points. Suppose the parabola has equation $y=a x^{2}+b x+c$. Then $\frac{d y}{d x}=2 a x+b$.
At point $(0,0), \frac{d y}{d x}=b$. Also the slope at $(0,0)$, as we determined earlier, is $\sqrt{3}$. Hence $b=\sqrt{3}$. Similarly, at point $(1,0), \frac{d y}{d x}=2 a+b$. The slope at $(1,0)$, as we determined earlier, is $-\sqrt{3}$. Then $a=-\sqrt{3}$.
Since the parabola goes through $(0,0), c=0$. Hence the equation of the parabola is $y=-\sqrt{3} x^{2}+\sqrt{3} x$. The desired area is simply the area under the parabolic curve in the interval $[0,1]$.
Hence $\int_{0}^{1}\left(-\sqrt{3} x^{2}+\sqrt{3} x\right) d x=\frac{\sqrt{3}}{6}$.
|
{
"exam": "HMMT",
"problem_label": "7",
"problem_match": "\n7. Problem: ",
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-calc-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "1998"
}
|
Find the slopes of all lines passing through the origin and tangent to the curve $y^{2}=x^{3}+39 x-35$.
|
Any line passing throug the origin has equation $y=m x$, where $m$ is the slope of the line. If a line is tangent to the given curve, then at the point of tangency, $(x, y), \frac{d y}{d x}=m$.
First, we calculate $\frac{d y}{d x}$ of the curve: $2 y d y=3 x^{2} d x+39 d x \Rightarrow \frac{d y}{d x}=\frac{3 x^{2}+39}{2 y}$. Substituting $m x$ for $y$, we get the following system of equations:
$$
\begin{aligned}
m^{2} x^{2} & =x^{3}+39 x-35 \\
m & =\frac{3 x^{2}+39}{2 m x}
\end{aligned}
$$
Solving for $x$ yields the equation $x^{3}-39 x+70=0 \Rightarrow(x-2)(x+7)(x-5)=0 \Rightarrow x=2$ or $x=-7$ or $x=5$. These solutions indicate the $x$-coordinate of the points at which the desired lines are tangent to the curve. Solving for the slopes of these lines, we get $m= \pm \frac{\sqrt{51}}{2}$ for $x=2$, no real solutions for $x=-7$, and $m= \pm \frac{\sqrt{285}}{5}$ for $x=5$. Thus $m= \pm \frac{\sqrt{51}}{2}, \pm \frac{\sqrt{285}}{5}$.
|
m= \pm \frac{\sqrt{51}}{2}, \pm \frac{\sqrt{285}}{5}
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Find the slopes of all lines passing through the origin and tangent to the curve $y^{2}=x^{3}+39 x-35$.
|
Any line passing throug the origin has equation $y=m x$, where $m$ is the slope of the line. If a line is tangent to the given curve, then at the point of tangency, $(x, y), \frac{d y}{d x}=m$.
First, we calculate $\frac{d y}{d x}$ of the curve: $2 y d y=3 x^{2} d x+39 d x \Rightarrow \frac{d y}{d x}=\frac{3 x^{2}+39}{2 y}$. Substituting $m x$ for $y$, we get the following system of equations:
$$
\begin{aligned}
m^{2} x^{2} & =x^{3}+39 x-35 \\
m & =\frac{3 x^{2}+39}{2 m x}
\end{aligned}
$$
Solving for $x$ yields the equation $x^{3}-39 x+70=0 \Rightarrow(x-2)(x+7)(x-5)=0 \Rightarrow x=2$ or $x=-7$ or $x=5$. These solutions indicate the $x$-coordinate of the points at which the desired lines are tangent to the curve. Solving for the slopes of these lines, we get $m= \pm \frac{\sqrt{51}}{2}$ for $x=2$, no real solutions for $x=-7$, and $m= \pm \frac{\sqrt{285}}{5}$ for $x=5$. Thus $m= \pm \frac{\sqrt{51}}{2}, \pm \frac{\sqrt{285}}{5}$.
|
{
"exam": "HMMT",
"problem_label": "8",
"problem_match": "\n8. Problem: ",
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-calc-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "1998"
}
|
Evaluate $\sum_{n=1}^{\infty} \frac{1}{n \cdot 2^{n-1}}$.
|
Note that if we take the integral of $f(x)$ in problem 4, we get the function $F(x)=x+\frac{x^{2}}{2 \cdot 2}+$ $\frac{x^{3}}{3 \cdot 2^{2}}+\ldots$. Evaluating this integral in the interval $[0,1]$, we get $1+\frac{1}{2 \cdot 2}+\frac{1}{3 \cdot 2^{2}}+\ldots$, which is the desired sum.
Hence $\int_{0}^{1} \frac{2}{2-x} d x=2 \ln 2$.
|
2 \ln 2
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Evaluate $\sum_{n=1}^{\infty} \frac{1}{n \cdot 2^{n-1}}$.
|
Note that if we take the integral of $f(x)$ in problem 4, we get the function $F(x)=x+\frac{x^{2}}{2 \cdot 2}+$ $\frac{x^{3}}{3 \cdot 2^{2}}+\ldots$. Evaluating this integral in the interval $[0,1]$, we get $1+\frac{1}{2 \cdot 2}+\frac{1}{3 \cdot 2^{2}}+\ldots$, which is the desired sum.
Hence $\int_{0}^{1} \frac{2}{2-x} d x=2 \ln 2$.
|
{
"exam": "HMMT",
"problem_label": "9",
"problem_match": "\n9. Problem: ",
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-calc-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "1998"
}
|
Let $S$ be the locus of all points $(x, y)$ in the first quadrant such that $\frac{x}{t}+\frac{y}{1-t}=1$ for some $t$ with $0<t<1$. Find the area of $S$.
|
Solving for $t$ in the given equation, we get $t^{2}+(y-x-1) t+x=0$. Using the quadratic equation, we get $t=\frac{(x+1-y) \pm \sqrt{(y-x-1)^{2}-4 x}}{2}$. For all valid combinations of $(x, y), t$ is positive and less than 1 (this is easy to see by inspection). All valid combinations of $(x, y)$ are those that make $(y-x-1)^{2}-4 x \geq 0$.
Solving for $y$ in the equation $(y-x-1)^{2}-4 x=0$ yields $y^{2}-(2 x+2) y+(x-1)^{2} \geq 0 \Rightarrow y=(x+1) \pm 2 \sqrt{x}$. In the original equation, it is given that $\frac{x}{t}+\frac{y}{1-t}=1$, and $0<t<1$. This implies that $x, y<1$. Then the only possible $y<1$ that satisfies $(y-x-1)^{2}-4 x=0$ is $y=x+1-2 \sqrt{x}$.
Then to satisfy the inequality $(y-x-1)^{2}-4 x \geq 0$, we must have $y \leq x+1-2 \sqrt{x}$. Recall that this is when $0<y<1$. Hence we integrate in the interval $[0,1]: \in_{0}^{1} x+1-2 \sqrt{x}=\frac{1}{6}$.
|
\frac{1}{6}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $S$ be the locus of all points $(x, y)$ in the first quadrant such that $\frac{x}{t}+\frac{y}{1-t}=1$ for some $t$ with $0<t<1$. Find the area of $S$.
|
Solving for $t$ in the given equation, we get $t^{2}+(y-x-1) t+x=0$. Using the quadratic equation, we get $t=\frac{(x+1-y) \pm \sqrt{(y-x-1)^{2}-4 x}}{2}$. For all valid combinations of $(x, y), t$ is positive and less than 1 (this is easy to see by inspection). All valid combinations of $(x, y)$ are those that make $(y-x-1)^{2}-4 x \geq 0$.
Solving for $y$ in the equation $(y-x-1)^{2}-4 x=0$ yields $y^{2}-(2 x+2) y+(x-1)^{2} \geq 0 \Rightarrow y=(x+1) \pm 2 \sqrt{x}$. In the original equation, it is given that $\frac{x}{t}+\frac{y}{1-t}=1$, and $0<t<1$. This implies that $x, y<1$. Then the only possible $y<1$ that satisfies $(y-x-1)^{2}-4 x=0$ is $y=x+1-2 \sqrt{x}$.
Then to satisfy the inequality $(y-x-1)^{2}-4 x \geq 0$, we must have $y \leq x+1-2 \sqrt{x}$. Recall that this is when $0<y<1$. Hence we integrate in the interval $[0,1]: \in_{0}^{1} x+1-2 \sqrt{x}=\frac{1}{6}$.
|
{
"exam": "HMMT",
"problem_label": "10",
"problem_match": "\n10. Problem: ",
"resource_path": "HarvardMIT/segmented/en-12-1998-feb-calc-solutions.jsonl",
"solution_match": "\nSolution: ",
"tier": "T4",
"year": "1998"
}
|
Find the minimum of $x^{2}-2 x$ over all real numbers $x$.
|
-1 Write $x^{2}-2 x=x^{2}-2 x+1-1=(x-1)^{2}-1$. Since $(x-1)^{2} \geq 0$, it is clear that the minimum is -1 .
Alternate method: The graph of $y=x^{2}-2 x$ is a parabola that opens up. Therefore, the minimum occurs at its vertex, which is at $\frac{-b}{2 a}=\frac{-(-2)}{2}=1$. But $1^{2}-2 \cdot 1=-1$, so the minimum is -1 .
|
-1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find the minimum of $x^{2}-2 x$ over all real numbers $x$.
|
-1 Write $x^{2}-2 x=x^{2}-2 x+1-1=(x-1)^{2}-1$. Since $(x-1)^{2} \geq 0$, it is clear that the minimum is -1 .
Alternate method: The graph of $y=x^{2}-2 x$ is a parabola that opens up. Therefore, the minimum occurs at its vertex, which is at $\frac{-b}{2 a}=\frac{-(-2)}{2}=1$. But $1^{2}-2 \cdot 1=-1$, so the minimum is -1 .
|
{
"exam": "HMMT",
"problem_label": "1",
"problem_match": "\n1. [2]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen1-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
What is the units digit of $7^{2009}$ ?
|
7 Note that the units digits of $7^{1}, 7^{2}, 7^{3}, 7^{4}, 7^{5}, 7^{6}, \ldots$ follows the pattern $7,9,3,1,7,9,3,1, \ldots$. The 2009th term in this sequence should be 7 .
Alternate method: Note that the units digit of $7^{4}$ is equal to 1 , so the units digit of $\left(7^{4}\right)^{502}$ is also 1. But $\left(7^{4}\right)^{502}=7^{2008}$, so the units digit of $7^{2008}$ is 1 , and therefore the units digit of $7^{2009}$ is 7 .
|
7
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
What is the units digit of $7^{2009}$ ?
|
7 Note that the units digits of $7^{1}, 7^{2}, 7^{3}, 7^{4}, 7^{5}, 7^{6}, \ldots$ follows the pattern $7,9,3,1,7,9,3,1, \ldots$. The 2009th term in this sequence should be 7 .
Alternate method: Note that the units digit of $7^{4}$ is equal to 1 , so the units digit of $\left(7^{4}\right)^{502}$ is also 1. But $\left(7^{4}\right)^{502}=7^{2008}$, so the units digit of $7^{2008}$ is 1 , and therefore the units digit of $7^{2009}$ is 7 .
|
{
"exam": "HMMT",
"problem_label": "2",
"problem_match": "\n2. [3]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen1-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
How many diagonals does a regular undecagon (11-sided polygon) have?
|
44 There are 8 diagonals coming from the first vertex, 8 more from the next, 7 from the next, 6 from the next, 5 from the next, etc., and 1 from the last, for $8+8+7+6+5+4+3+2+1=44$ total.
Third method: Each vertex has 8 diagonals touching it. There are 11 vertices. Since each diagonal touches two vertices, this counts every diagonal twice, so there are $\frac{8 \cdot 11}{2}=44$ diagonals.
|
44
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
How many diagonals does a regular undecagon (11-sided polygon) have?
|
44 There are 8 diagonals coming from the first vertex, 8 more from the next, 7 from the next, 6 from the next, 5 from the next, etc., and 1 from the last, for $8+8+7+6+5+4+3+2+1=44$ total.
Third method: Each vertex has 8 diagonals touching it. There are 11 vertices. Since each diagonal touches two vertices, this counts every diagonal twice, so there are $\frac{8 \cdot 11}{2}=44$ diagonals.
|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n3. [3]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen1-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
How many numbers between 1 and $1,000,000$ are perfect squares but not perfect cubes?
|
$9901000000=1000^{2}=10^{6}$. A number is both a perfect square and a perfect cube if and only if it is exactly a perfect sixth power. So, the answer is the number of perfect squares, minus the number of perfect sixth powers, which is $1000-10=990$.
|
990
|
Yes
|
Incomplete
|
math-word-problem
|
Number Theory
|
How many numbers between 1 and $1,000,000$ are perfect squares but not perfect cubes?
|
$9901000000=1000^{2}=10^{6}$. A number is both a perfect square and a perfect cube if and only if it is exactly a perfect sixth power. So, the answer is the number of perfect squares, minus the number of perfect sixth powers, which is $1000-10=990$.
|
{
"exam": "HMMT",
"problem_label": "4",
"problem_match": "\n4. [4]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen1-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Joe has a triangle with area $\sqrt{3}$. What's the smallest perimeter it could have?
|
6 The minimum occurs for an equilateral triangle. The area of an equilateral triangle with side-length $s$ is $\frac{\sqrt{3}}{4} s^{2}$, so if the area is $\sqrt{3}$ then $s=\sqrt{\sqrt{3} \frac{4}{\sqrt{3}}}=2$. Multiplying by 3 to get the perimeter yields the answer.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Joe has a triangle with area $\sqrt{3}$. What's the smallest perimeter it could have?
|
6 The minimum occurs for an equilateral triangle. The area of an equilateral triangle with side-length $s$ is $\frac{\sqrt{3}}{4} s^{2}$, so if the area is $\sqrt{3}$ then $s=\sqrt{\sqrt{3} \frac{4}{\sqrt{3}}}=2$. Multiplying by 3 to get the perimeter yields the answer.
|
{
"exam": "HMMT",
"problem_label": "5",
"problem_match": "\n5. [5]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen1-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
We say " $s$ grows to $r$ " if there exists some integer $n>0$ such that $s^{n}=r$. Call a real number $r$ "sparse" if there are only finitely many real numbers $s$ that grow to $r$. Find all real numbers that are sparse.
|
$-1,0,1$ For any number $x$, other than these $3, x, \sqrt[3]{x}, \sqrt[5]{x}, \sqrt[7]{x}, \ldots$ provide infinitely many possible values of $s$, so these are the only possible sparse numbers. On the other hand, -1 is the only possible value of $s$ for $r=-1,0$ is the only value for $r=0$, and -1 and 1 are the only values for $r=1$. Therefore, $-1,0$, and 1 are all sparse.
|
-1,0,1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
We say " $s$ grows to $r$ " if there exists some integer $n>0$ such that $s^{n}=r$. Call a real number $r$ "sparse" if there are only finitely many real numbers $s$ that grow to $r$. Find all real numbers that are sparse.
|
$-1,0,1$ For any number $x$, other than these $3, x, \sqrt[3]{x}, \sqrt[5]{x}, \sqrt[7]{x}, \ldots$ provide infinitely many possible values of $s$, so these are the only possible sparse numbers. On the other hand, -1 is the only possible value of $s$ for $r=-1,0$ is the only value for $r=0$, and -1 and 1 are the only values for $r=1$. Therefore, $-1,0$, and 1 are all sparse.
|
{
"exam": "HMMT",
"problem_label": "6",
"problem_match": "\n6. [5]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen1-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Find all ordered pairs $(x, y)$ such that
$$
(x-2 y)^{2}+(y-1)^{2}=0
$$
|
$(2,1)$ The square of a real number is always at least 0 , so to have equality we must have $(x-2 y)^{2}=0$ and $(y-1)^{2}=0$. Then $y=1$ and $x=2 y=2$.
|
(2,1)
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all ordered pairs $(x, y)$ such that
$$
(x-2 y)^{2}+(y-1)^{2}=0
$$
|
$(2,1)$ The square of a real number is always at least 0 , so to have equality we must have $(x-2 y)^{2}=0$ and $(y-1)^{2}=0$. Then $y=1$ and $x=2 y=2$.
|
{
"exam": "HMMT",
"problem_label": "7",
"problem_match": "\n7. [6]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen1-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
How many integers between 2 and 100 inclusive cannot be written as $m \cdot n$, where $m$ and $n$ have no common factors and neither $m$ nor $n$ is equal to 1 ? Note that there are 25 primes less than 100 .
|
35 A number cannot be written in the given form if and only if it is a power of a prime. We can see this by considering the prime factorization. Suppose that $k=p_{1}^{e_{1}} p_{2}^{e_{2}} \cdots p_{n}^{e_{n}}$, with $p_{1}, \ldots, p_{n}$ primes. Then we can write $m=p_{1}^{e_{1}}$ and $n=p_{2}^{e_{2}} \cdots p_{n}^{e_{n}}$. So, we want to find the powers of primes that are less than or equal to 100 . There are 25 primes, as given in the problem statement. The squares of primes are $2^{2}, 3^{2}, 5^{2}, 7^{2}$. The cubes of primes are $2^{3}, 3^{3}$. The fourth powers of primes are $2^{4}, 3^{4}$. The fifth powers of primes are $2^{5}$, The sixth powers of primes are $2^{6}$. There are no seventh or higher powers of primes between 2 and 100 . This adds 10 non-primes to the list, so that in total there are $10+25=35$ such integers.
|
35
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
How many integers between 2 and 100 inclusive cannot be written as $m \cdot n$, where $m$ and $n$ have no common factors and neither $m$ nor $n$ is equal to 1 ? Note that there are 25 primes less than 100 .
|
35 A number cannot be written in the given form if and only if it is a power of a prime. We can see this by considering the prime factorization. Suppose that $k=p_{1}^{e_{1}} p_{2}^{e_{2}} \cdots p_{n}^{e_{n}}$, with $p_{1}, \ldots, p_{n}$ primes. Then we can write $m=p_{1}^{e_{1}}$ and $n=p_{2}^{e_{2}} \cdots p_{n}^{e_{n}}$. So, we want to find the powers of primes that are less than or equal to 100 . There are 25 primes, as given in the problem statement. The squares of primes are $2^{2}, 3^{2}, 5^{2}, 7^{2}$. The cubes of primes are $2^{3}, 3^{3}$. The fourth powers of primes are $2^{4}, 3^{4}$. The fifth powers of primes are $2^{5}$, The sixth powers of primes are $2^{6}$. There are no seventh or higher powers of primes between 2 and 100 . This adds 10 non-primes to the list, so that in total there are $10+25=35$ such integers.
|
{
"exam": "HMMT",
"problem_label": "8",
"problem_match": "\n8. [7]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen1-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Find the product of all real $x$ for which
$$
2^{3 x+1}-17 \cdot 2^{2 x}+2^{x+3}=0
$$
|
-3 We can re-write the equation as $2^{x}\left(2 \cdot\left(2^{x}\right)^{2}-17 \cdot\left(2^{x}\right)+8\right)=0$, or $2 \cdot\left(2^{x}\right)^{2}-17 \cdot\left(2^{x}\right)+8=0$. Make the substitution $y=2^{x}$. Then we have $2 y^{2}-17 y+8=0$, which has solutions (by the quadratic formula) $y=\frac{17 \pm \sqrt{289-64}}{4}=\frac{17 \pm 15}{4}=8, \frac{1}{2}$, so $2^{x}=8, \frac{1}{2}$ and $x=3,-1$. The product of these numbers is -3 .
|
-3
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find the product of all real $x$ for which
$$
2^{3 x+1}-17 \cdot 2^{2 x}+2^{x+3}=0
$$
|
-3 We can re-write the equation as $2^{x}\left(2 \cdot\left(2^{x}\right)^{2}-17 \cdot\left(2^{x}\right)+8\right)=0$, or $2 \cdot\left(2^{x}\right)^{2}-17 \cdot\left(2^{x}\right)+8=0$. Make the substitution $y=2^{x}$. Then we have $2 y^{2}-17 y+8=0$, which has solutions (by the quadratic formula) $y=\frac{17 \pm \sqrt{289-64}}{4}=\frac{17 \pm 15}{4}=8, \frac{1}{2}$, so $2^{x}=8, \frac{1}{2}$ and $x=3,-1$. The product of these numbers is -3 .
|
{
"exam": "HMMT",
"problem_label": "9",
"problem_match": "\n9. [7]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen1-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Find the largest positive integer $n$ such that $n^{3}+4 n^{2}-15 n-18$ is the cube of an integer.
|
19 Note that the next cube after $n^{3}$ is $(n+1)^{3}=n^{3}+3 n^{2}+3 n+1$. After that, it is $(n+2)^{3}=n^{3}+6 n^{2}+12 n+8 . n^{3}+6 n^{3}+12 n+8$ is definitely bigger than $n^{3}+4 n^{2}-15 n-18$, so the largest cube that $n^{3}+4 n^{2}-15 n-18$ could be is $(n+1)^{3}$. On the other hand, for $n \geq 4, n^{3}+4 n^{2}-15 n-18$ is larger than $(n-2)^{3}=n^{3}-6 n^{2}+12 n-8$ (as $4 n^{2}-15 n-18>-6 n^{2}+12 n-8 \Longleftrightarrow 10 n^{2}-27 n-10>0$, which is true for $n \geq 4$ ).
So, we will check for all solutions to $n^{3}+4 n^{2}-15 n-18=(n-1)^{3}, n^{3},(n+1)^{3}$. The first case yields
$$
n^{3}+4 n^{2}-15 n-18=n^{3}-3 n^{2}+3 n-1 \Longleftrightarrow 7 n^{2}-18 n-17=0
$$
which has no integer solutions. The second case yields
$$
n^{3}+4 n^{2}-15 n-18=n^{3} \Longleftrightarrow 4 n^{2}-15 n-18=0
$$
which also has no integer solutions. The final case yields
$$
n^{3}+4 n^{2}-15 n-18=n^{3}+3 n^{2}+3 n+1 \Longleftrightarrow n^{2}-18 n-19=0
$$
which has integer solutions $n=-1,19$. So, the largest possible $n$ is 19 .
Remark: The easiest way to see that the first two polynomials have no integer solutions is using the Rational Root Theorem, which states that the rational solutions of a polynomial $a x^{n}+\ldots+b$ are all of the form $\pm \frac{b^{\prime}}{a^{\prime}}$, where $b^{\prime}$ divides $b$ and $a^{\prime}$ divides $a$.
|
19
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find the largest positive integer $n$ such that $n^{3}+4 n^{2}-15 n-18$ is the cube of an integer.
|
19 Note that the next cube after $n^{3}$ is $(n+1)^{3}=n^{3}+3 n^{2}+3 n+1$. After that, it is $(n+2)^{3}=n^{3}+6 n^{2}+12 n+8 . n^{3}+6 n^{3}+12 n+8$ is definitely bigger than $n^{3}+4 n^{2}-15 n-18$, so the largest cube that $n^{3}+4 n^{2}-15 n-18$ could be is $(n+1)^{3}$. On the other hand, for $n \geq 4, n^{3}+4 n^{2}-15 n-18$ is larger than $(n-2)^{3}=n^{3}-6 n^{2}+12 n-8$ (as $4 n^{2}-15 n-18>-6 n^{2}+12 n-8 \Longleftrightarrow 10 n^{2}-27 n-10>0$, which is true for $n \geq 4$ ).
So, we will check for all solutions to $n^{3}+4 n^{2}-15 n-18=(n-1)^{3}, n^{3},(n+1)^{3}$. The first case yields
$$
n^{3}+4 n^{2}-15 n-18=n^{3}-3 n^{2}+3 n-1 \Longleftrightarrow 7 n^{2}-18 n-17=0
$$
which has no integer solutions. The second case yields
$$
n^{3}+4 n^{2}-15 n-18=n^{3} \Longleftrightarrow 4 n^{2}-15 n-18=0
$$
which also has no integer solutions. The final case yields
$$
n^{3}+4 n^{2}-15 n-18=n^{3}+3 n^{2}+3 n+1 \Longleftrightarrow n^{2}-18 n-19=0
$$
which has integer solutions $n=-1,19$. So, the largest possible $n$ is 19 .
Remark: The easiest way to see that the first two polynomials have no integer solutions is using the Rational Root Theorem, which states that the rational solutions of a polynomial $a x^{n}+\ldots+b$ are all of the form $\pm \frac{b^{\prime}}{a^{\prime}}$, where $b^{\prime}$ divides $b$ and $a^{\prime}$ divides $a$.
|
{
"exam": "HMMT",
"problem_label": "10",
"problem_match": "\n10. [8]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen1-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
A triangle has sides of length 9,40 , and 41 . What is its area?
|
180 Observe that $9^{2}+40^{2}=41^{2}$, so this triangle is right and therefore has area $\frac{1}{2} \cdot 9 \cdot 40=$ 180.
|
180
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A triangle has sides of length 9,40 , and 41 . What is its area?
|
180 Observe that $9^{2}+40^{2}=41^{2}$, so this triangle is right and therefore has area $\frac{1}{2} \cdot 9 \cdot 40=$ 180.
|
{
"exam": "HMMT",
"problem_label": "1",
"problem_match": "\n1. [3]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Let $A B C$ be a triangle, and let $M$ be the midpoint of side $A B$. If $A B$ is 17 units long and $C M$ is 8 units long, find the maximum possible value of the area of $A B C$.
|
68 Let $h$ be the length of the altitude from $C$ to $A B$. Observe that $K=\frac{1}{2} \cdot h \cdot A B \leq$ $\frac{1}{2} \cdot C M \cdot A B=68$ and that equality is achieved when $C M \perp A B$.
|
68
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle, and let $M$ be the midpoint of side $A B$. If $A B$ is 17 units long and $C M$ is 8 units long, find the maximum possible value of the area of $A B C$.
|
68 Let $h$ be the length of the altitude from $C$ to $A B$. Observe that $K=\frac{1}{2} \cdot h \cdot A B \leq$ $\frac{1}{2} \cdot C M \cdot A B=68$ and that equality is achieved when $C M \perp A B$.
|
{
"exam": "HMMT",
"problem_label": "2",
"problem_match": "\n2. [4]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Let $D E F$ be a triangle and $H$ the foot of the altitude from $D$ to $E F$. If $D E=60, D F=35$, and $D H=21$, what is the difference between the minimum and the maximum possible values for the area of $D E F$ ?
|
588 Observe that the two possible configurations come from $D E F$ obtuse and $D E F$ acute. In either case, we have that $H F=\sqrt{35^{2}-21^{2}}=28$ and $E H=\sqrt{60^{2}-21^{2}}=9 \sqrt{39}$. This means that $H F-E H$, so in the two cases the values of $E F$ are $F H+E H$ and $E H-F H$. The difference in area is hence $\frac{1}{2} \cdot 2 \cdot F H \cdot D H=28 \cdot 21=588$.
|
588
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $D E F$ be a triangle and $H$ the foot of the altitude from $D$ to $E F$. If $D E=60, D F=35$, and $D H=21$, what is the difference between the minimum and the maximum possible values for the area of $D E F$ ?
|
588 Observe that the two possible configurations come from $D E F$ obtuse and $D E F$ acute. In either case, we have that $H F=\sqrt{35^{2}-21^{2}}=28$ and $E H=\sqrt{60^{2}-21^{2}}=9 \sqrt{39}$. This means that $H F-E H$, so in the two cases the values of $E F$ are $F H+E H$ and $E H-F H$. The difference in area is hence $\frac{1}{2} \cdot 2 \cdot F H \cdot D H=28 \cdot 21=588$.
|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n3. [5]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Right triangle $X Y Z$, with hypotenuse $Y Z$, has an incircle of radius $\frac{3}{8}$ and one leg of length 3. Find the area of the triangle.
|
$\quad \frac{21}{16}$ Let the other leg have length $x$. Then the tangents from $Y$ and $Z$ to the incircle have length $x-\frac{3}{8}$ and $3-\frac{3}{8}$. So the hypotenuse has length $x+\frac{9}{4}$, the semiperimeter of the triangle is $x+\frac{21}{8}$, and the area of the triangle is $\frac{3}{8}\left(x+\frac{21}{8}\right)$. But the area can also be calculated as $\frac{3 x}{2}$. Setting these expressions equal, we find $x=\frac{7}{8}$ and the area is $\frac{21}{16}$.
|
\frac{21}{16}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Right triangle $X Y Z$, with hypotenuse $Y Z$, has an incircle of radius $\frac{3}{8}$ and one leg of length 3. Find the area of the triangle.
|
$\quad \frac{21}{16}$ Let the other leg have length $x$. Then the tangents from $Y$ and $Z$ to the incircle have length $x-\frac{3}{8}$ and $3-\frac{3}{8}$. So the hypotenuse has length $x+\frac{9}{4}$, the semiperimeter of the triangle is $x+\frac{21}{8}$, and the area of the triangle is $\frac{3}{8}\left(x+\frac{21}{8}\right)$. But the area can also be calculated as $\frac{3 x}{2}$. Setting these expressions equal, we find $x=\frac{7}{8}$ and the area is $\frac{21}{16}$.
|
{
"exam": "HMMT",
"problem_label": "4",
"problem_match": "\n4. [6]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
A triangle has altitudes of length 15,21 , and 35 . Find its area.
|
$\quad 245 \sqrt{3}$ If $A$ is the area of the triangle, the sides are $\frac{2 A}{15}, \frac{2 A}{21}$, and $\frac{2 A}{35}$. So the triangle is similar to a $\frac{1}{15}, \frac{1}{21}, \frac{1}{35}$ triangle, which is similar to a $3,5,7$ triangle. Let the sides be $3 k, 5 k$, and $7 k$. Then the angle between the sides of length $3 k$ and $7 k$ is $120^{\circ}$, so the area is $\frac{15 \sqrt{3}}{4} k^{2}$. But the area can also be calculated as $\frac{(3 k)(35)}{2}=\frac{105 k}{2}$. Setting these values equal, $k=\frac{14 \sqrt{3}}{3}$ and the area is $245 \sqrt{3}$.
Chessboards [25]
Joe B. is playing with some chess pieces on a $6 \times 6$ chessboard. Help him find out some things.
|
245 \sqrt{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A triangle has altitudes of length 15,21 , and 35 . Find its area.
|
$\quad 245 \sqrt{3}$ If $A$ is the area of the triangle, the sides are $\frac{2 A}{15}, \frac{2 A}{21}$, and $\frac{2 A}{35}$. So the triangle is similar to a $\frac{1}{15}, \frac{1}{21}, \frac{1}{35}$ triangle, which is similar to a $3,5,7$ triangle. Let the sides be $3 k, 5 k$, and $7 k$. Then the angle between the sides of length $3 k$ and $7 k$ is $120^{\circ}$, so the area is $\frac{15 \sqrt{3}}{4} k^{2}$. But the area can also be calculated as $\frac{(3 k)(35)}{2}=\frac{105 k}{2}$. Setting these values equal, $k=\frac{14 \sqrt{3}}{3}$ and the area is $245 \sqrt{3}$.
Chessboards [25]
Joe B. is playing with some chess pieces on a $6 \times 6$ chessboard. Help him find out some things.
|
{
"exam": "HMMT",
"problem_label": "5",
"problem_match": "\n5. [7]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Joe B. first places the black king in one corner of the board. In how many of the 35 remaining squares can he place a white bishop so that it does not check the black king?
|
30 Any square not on the diagonal containing the corner is a possible location, and there are $36-6=30$ such squares.
|
30
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Joe B. first places the black king in one corner of the board. In how many of the 35 remaining squares can he place a white bishop so that it does not check the black king?
|
30 Any square not on the diagonal containing the corner is a possible location, and there are $36-6=30$ such squares.
|
{
"exam": "HMMT",
"problem_label": "1",
"problem_match": "\n1. [3]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Joe B. then places a white king in the opposite corner of the board. How many total ways can he place one black bishop and one white bishop so that neither checks the king of the opposite color?
|
876 Observe that either both bishops are on the diagonal containing both kings or neither are. If both are on the diagonal, each of the $\binom{4}{2}=6$ choices of pairs of squares yields one possible configuration, so there are 6 possibilities in this case. Off the diagonal, any pair of locations works, giving $30 \cdot 29=870$ possibilities in this case. Summing, we obtain $870+6=876$ total possibilities.
|
876
|
Incomplete
|
Yes
|
math-word-problem
|
Combinatorics
|
Joe B. then places a white king in the opposite corner of the board. How many total ways can he place one black bishop and one white bishop so that neither checks the king of the opposite color?
|
876 Observe that either both bishops are on the diagonal containing both kings or neither are. If both are on the diagonal, each of the $\binom{4}{2}=6$ choices of pairs of squares yields one possible configuration, so there are 6 possibilities in this case. Off the diagonal, any pair of locations works, giving $30 \cdot 29=870$ possibilities in this case. Summing, we obtain $870+6=876$ total possibilities.
|
{
"exam": "HMMT",
"problem_label": "2",
"problem_match": "\n2. [4]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Joe B. now clears the board. How many ways can he place 3 white rooks and 3 black rooks on the board so that no two rooks of opposite color can attack each other?
|
608 Consider first placing the white rooks. They will occupy either 3 columns and 1 row, 3 columns and 2 rows, 3 columns and 3 rows, 2 rows and 2 columns, 2 columns and 3 rows, or 1 column and 3 rows. First note that placing the black rooks is impossible in the second, third, and fifth cases. The first case can happen in 4.4 ways, and each leads to a unique way to place the black rooks. In the fourth case, we can choose the row with 2 rooks in 4 ways, place the rooks in $\binom{4}{2}$ ways, choose the column of the other rook in 2 ways, and place it in 3 ways, for a total of $4 \cdot\binom{4}{2} \cdot 2 \cdot 3=144$ ways to place the white rooks in this configuration; the black rooks can then be placed in any of 4 possible locations, and there are 4 ways to do this, leading to 576 possibilities in this case. Finally, the sixth case is analogous to the first, giving 16 possibilities. Summing, we find $16+576+16=608$ total placements.
|
608
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Joe B. now clears the board. How many ways can he place 3 white rooks and 3 black rooks on the board so that no two rooks of opposite color can attack each other?
|
608 Consider first placing the white rooks. They will occupy either 3 columns and 1 row, 3 columns and 2 rows, 3 columns and 3 rows, 2 rows and 2 columns, 2 columns and 3 rows, or 1 column and 3 rows. First note that placing the black rooks is impossible in the second, third, and fifth cases. The first case can happen in 4.4 ways, and each leads to a unique way to place the black rooks. In the fourth case, we can choose the row with 2 rooks in 4 ways, place the rooks in $\binom{4}{2}$ ways, choose the column of the other rook in 2 ways, and place it in 3 ways, for a total of $4 \cdot\binom{4}{2} \cdot 2 \cdot 3=144$ ways to place the white rooks in this configuration; the black rooks can then be placed in any of 4 possible locations, and there are 4 ways to do this, leading to 576 possibilities in this case. Finally, the sixth case is analogous to the first, giving 16 possibilities. Summing, we find $16+576+16=608$ total placements.
|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n3. [5]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Joe B. is frustrated with chess. He breaks the board, leaving a $4 \times 4$ board, and throws 3 black knights and 3 white kings at the board. Miraculously, they all land in distinct squares! What is the expected number of checks in the resulting position? (Note that a knight can administer multiple checks and a king can be checked by multiple knights.)
|
$\quad \frac{9}{5}$ We first compute the expected number of checks between a single knight-king pair. If the king is located at any of the 4 corners, the knight has 2 possible checks. If the king is located in one of the 8 squares on the side of the board but not in the corner, the knight has 3 possible checks. If the king is located in any of the 4 central squares, the knight has 4 possible checks. Summing up, $4 \cdot 2+8 \cdot 3+4 \cdot 4=48$ of the $16 \cdot 15$ knight-king positions yield a single check, so each pair yields $\frac{48}{16 \cdot 15}=\frac{1}{5}$ expected checks. Now, note that each of the 9 knight-king pairs is in each of $16 \cdot 15$ possible positions with equal probability, so by linearity of expectation the answer is $9 \cdot \frac{1}{5}=\frac{9}{5}$.
|
\frac{9}{5}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Joe B. is frustrated with chess. He breaks the board, leaving a $4 \times 4$ board, and throws 3 black knights and 3 white kings at the board. Miraculously, they all land in distinct squares! What is the expected number of checks in the resulting position? (Note that a knight can administer multiple checks and a king can be checked by multiple knights.)
|
$\quad \frac{9}{5}$ We first compute the expected number of checks between a single knight-king pair. If the king is located at any of the 4 corners, the knight has 2 possible checks. If the king is located in one of the 8 squares on the side of the board but not in the corner, the knight has 3 possible checks. If the king is located in any of the 4 central squares, the knight has 4 possible checks. Summing up, $4 \cdot 2+8 \cdot 3+4 \cdot 4=48$ of the $16 \cdot 15$ knight-king positions yield a single check, so each pair yields $\frac{48}{16 \cdot 15}=\frac{1}{5}$ expected checks. Now, note that each of the 9 knight-king pairs is in each of $16 \cdot 15$ possible positions with equal probability, so by linearity of expectation the answer is $9 \cdot \frac{1}{5}=\frac{9}{5}$.
|
{
"exam": "HMMT",
"problem_label": "4",
"problem_match": "\n4. [6]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Suppose that at some point Joe B. has placed 2 black knights on the original board, but gets bored of chess. He now decides to cover the 34 remaining squares with 17 dominos so that no two overlap and the dominos cover the entire rest of the board. For how many initial arrangements of the two pieces is this possible?
|
324 Color the squares of the board red and blue in a checkerboard pattern, and observe that any domino will cover exactly one red square and one blue square. Therefore, if the two knights cover squares of the same color, this is impossible. We now claim that it is always possible if they cover squares of opposite colors, which will give an answer of $18^{2}=324$. Consider the rectangle $R$ with the knights at its corners. Because the knights cover differently colored squares, $R$ must have one side length odd and one side length even. Therefore, the 4 lines bounding $R$ cut the original board into $R$ and up to 8 other rectangles, which can be put together into rectangles with at least one side even. These rectangles can be tiled, and it is easy to see that $R$ can be tiled, proving the claim.
|
324
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Suppose that at some point Joe B. has placed 2 black knights on the original board, but gets bored of chess. He now decides to cover the 34 remaining squares with 17 dominos so that no two overlap and the dominos cover the entire rest of the board. For how many initial arrangements of the two pieces is this possible?
|
324 Color the squares of the board red and blue in a checkerboard pattern, and observe that any domino will cover exactly one red square and one blue square. Therefore, if the two knights cover squares of the same color, this is impossible. We now claim that it is always possible if they cover squares of opposite colors, which will give an answer of $18^{2}=324$. Consider the rectangle $R$ with the knights at its corners. Because the knights cover differently colored squares, $R$ must have one side length odd and one side length even. Therefore, the 4 lines bounding $R$ cut the original board into $R$ and up to 8 other rectangles, which can be put together into rectangles with at least one side even. These rectangles can be tiled, and it is easy to see that $R$ can be tiled, proving the claim.
|
{
"exam": "HMMT",
"problem_label": "5",
"problem_match": "\n5. [7]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Find the sum of all solutions for $x$ :
$$
\begin{aligned}
x y & =1 \\
x+y & =3
\end{aligned}
$$
|
3 Substitute $3-x$ in for $y$ into the first equation:
$$
x(3-x)=1 \Leftrightarrow x^{2}-3 x+1=0
$$
This equation has two distinct roots, each of which corresponds to a possible solution $x$. The sum of the roots of the quadratic equation $a x^{2}+b x+c=0$ is $\frac{-b}{a}$, which in this case is 3 .
|
3
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find the sum of all solutions for $x$ :
$$
\begin{aligned}
x y & =1 \\
x+y & =3
\end{aligned}
$$
|
3 Substitute $3-x$ in for $y$ into the first equation:
$$
x(3-x)=1 \Leftrightarrow x^{2}-3 x+1=0
$$
This equation has two distinct roots, each of which corresponds to a possible solution $x$. The sum of the roots of the quadratic equation $a x^{2}+b x+c=0$ is $\frac{-b}{a}$, which in this case is 3 .
|
{
"exam": "HMMT",
"problem_label": "1",
"problem_match": "\n1. [5]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Evaluate the sum
$$
1-2+3-4+\cdots+2007-2008
$$
|
-1004 Every odd integer term can be paired with the next even integer, and this pair sums to -1 . There are 1004 such pairs, so the total sum is -1004 .
|
-1004
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Evaluate the sum
$$
1-2+3-4+\cdots+2007-2008
$$
|
-1004 Every odd integer term can be paired with the next even integer, and this pair sums to -1 . There are 1004 such pairs, so the total sum is -1004 .
|
{
"exam": "HMMT",
"problem_label": "2",
"problem_match": "\n2. [5]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
What is the largest $x$ such that $x^{2}$ divides $24 \cdot 35 \cdot 46 \cdot 57$ ?
|
12 We factor the product as $2^{4} \cdot 3^{2} \cdot 5 \cdot 7 \cdot 19 \cdot 23$. If $x^{2}$ divides this product, $x$ can have at most 2 factors of 2,1 factor of 3 , and no factors of any other prime. So $2^{2} \cdot 3=12$ is the largest value of $x$.
## $1^{\text {st }}$ HARVARD-MIT NOVEMBER TOURNAMENT, 8 SATURDAY 2008 - GUTS ROUND
|
12
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
What is the largest $x$ such that $x^{2}$ divides $24 \cdot 35 \cdot 46 \cdot 57$ ?
|
12 We factor the product as $2^{4} \cdot 3^{2} \cdot 5 \cdot 7 \cdot 19 \cdot 23$. If $x^{2}$ divides this product, $x$ can have at most 2 factors of 2,1 factor of 3 , and no factors of any other prime. So $2^{2} \cdot 3=12$ is the largest value of $x$.
## $1^{\text {st }}$ HARVARD-MIT NOVEMBER TOURNAMENT, 8 SATURDAY 2008 - GUTS ROUND
|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n3. [5]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
What is the smallest prime divisor of $5^{7^{10^{7^{10}}}}+1$ ?
|
2 Notice that 5 to any power is odd, so this number is even. Then 2 is a prime divisor. It also happens to be the smallest prime.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
What is the smallest prime divisor of $5^{7^{10^{7^{10}}}}+1$ ?
|
2 Notice that 5 to any power is odd, so this number is even. Then 2 is a prime divisor. It also happens to be the smallest prime.
|
{
"exam": "HMMT",
"problem_label": "4",
"problem_match": "\n4. [6]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
What is the sum of all integers $x$ such that $|x+2| \leq 10$ ?
|
$\quad-42$ The inequality $|x+2| \leq 10$ holds if and only if $x+2 \leq 10$ and $x+2 \geq-10$. So $x$ must be in the range $-12 \leq x \leq 8$. If we add up the integers in this range, each positive integer cancels with its additive inverse, so the sum is equal to $-12-11-10-9=-42$.
|
-42
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
What is the sum of all integers $x$ such that $|x+2| \leq 10$ ?
|
$\quad-42$ The inequality $|x+2| \leq 10$ holds if and only if $x+2 \leq 10$ and $x+2 \geq-10$. So $x$ must be in the range $-12 \leq x \leq 8$. If we add up the integers in this range, each positive integer cancels with its additive inverse, so the sum is equal to $-12-11-10-9=-42$.
|
{
"exam": "HMMT",
"problem_label": "5",
"problem_match": "\n5. [6]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Sarah is deciding whether to visit Russia or Washington, DC for the holidays. She makes her decision by rolling a regular 6 -sided die. If she gets a 1 or 2 , she goes to DC . If she rolls a 3,4 , or 5 , she goes to Russia. If she rolls a 6 , she rolls again. What is the probability that she goes to DC?
|
$\quad \frac{2}{5}$ On each roll, the probability that Sarah decides to go to Russia is $3 / 2$ times the probability she decides to go to DC. So, the total probability that she goes to Russia is $3 / 2$ times the total probability that she goes to DC. Since these probabilities sum to 1 (they are the only two eventual outcomes) Sarah goes to DC with probability $\frac{2}{5}$ and Russia with probability $\frac{3}{5}$.
## $1^{\text {st }}$ HARVARD-MIT NOVEMBER TOURNAMENT, 8 SATURDAY 2008 - GUTS ROUND
|
\frac{2}{5}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Sarah is deciding whether to visit Russia or Washington, DC for the holidays. She makes her decision by rolling a regular 6 -sided die. If she gets a 1 or 2 , she goes to DC . If she rolls a 3,4 , or 5 , she goes to Russia. If she rolls a 6 , she rolls again. What is the probability that she goes to DC?
|
$\quad \frac{2}{5}$ On each roll, the probability that Sarah decides to go to Russia is $3 / 2$ times the probability she decides to go to DC. So, the total probability that she goes to Russia is $3 / 2$ times the total probability that she goes to DC. Since these probabilities sum to 1 (they are the only two eventual outcomes) Sarah goes to DC with probability $\frac{2}{5}$ and Russia with probability $\frac{3}{5}$.
## $1^{\text {st }}$ HARVARD-MIT NOVEMBER TOURNAMENT, 8 SATURDAY 2008 - GUTS ROUND
|
{
"exam": "HMMT",
"problem_label": "6",
"problem_match": "\n6. [6]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Compute $2009^{2}-2008^{2}$.
|
4017 Factoring this product with difference of squares, we find it equals:
$$
(2009+2008)(2009-2008)=(4017)(1)=4017
$$
|
4017
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Compute $2009^{2}-2008^{2}$.
|
4017 Factoring this product with difference of squares, we find it equals:
$$
(2009+2008)(2009-2008)=(4017)(1)=4017
$$
|
{
"exam": "HMMT",
"problem_label": "7",
"problem_match": "\n7. [7]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Alice rolls two octahedral dice with the numbers $2,3,4,5,6,7,8,9$. What's the probability the two dice sum to 11 ?
|
$\frac{1}{8}$ No matter what comes up on the first die, there is exactly one number that could appear on the second die to make the sum 11 , because 2 can be paired with 9,3 with 8 , and so on. So, there is a $\frac{1}{8}$ chance of getting the correct number on the second die.
|
\frac{1}{8}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Alice rolls two octahedral dice with the numbers $2,3,4,5,6,7,8,9$. What's the probability the two dice sum to 11 ?
|
$\frac{1}{8}$ No matter what comes up on the first die, there is exactly one number that could appear on the second die to make the sum 11 , because 2 can be paired with 9,3 with 8 , and so on. So, there is a $\frac{1}{8}$ chance of getting the correct number on the second die.
|
{
"exam": "HMMT",
"problem_label": "8",
"problem_match": "\n8. [7]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Let $a_{0}=\frac{6}{7}$, and
$$
a_{n+1}= \begin{cases}2 a_{n} & \text { if } a_{n}<\frac{1}{2} \\ 2 a_{n}-1 & \text { if } a_{n} \geq \frac{1}{2}\end{cases}
$$
Find $a_{2008}$.
|
$\sqrt{\frac{5}{7}}$ We calculate the first few $a_{i}$ :
$$
a_{1}=\frac{5}{7}, a_{2}=\frac{3}{7}, a_{3}=\frac{6}{7}=a_{0}
$$
So this sequence repeats every three terms, so $a_{2007}=a_{0}=\frac{6}{7}$. Then $a_{2008}=\frac{5}{7}$.
```
$1^{\text {st }}$ HARVARD-MIT NOVEMBER TOURNAMENT, 8 SATURDAY 2008 - GUTS ROUND
```
|
\frac{5}{7}
|
Yes
|
Incomplete
|
math-word-problem
|
Algebra
|
Let $a_{0}=\frac{6}{7}$, and
$$
a_{n+1}= \begin{cases}2 a_{n} & \text { if } a_{n}<\frac{1}{2} \\ 2 a_{n}-1 & \text { if } a_{n} \geq \frac{1}{2}\end{cases}
$$
Find $a_{2008}$.
|
$\sqrt{\frac{5}{7}}$ We calculate the first few $a_{i}$ :
$$
a_{1}=\frac{5}{7}, a_{2}=\frac{3}{7}, a_{3}=\frac{6}{7}=a_{0}
$$
So this sequence repeats every three terms, so $a_{2007}=a_{0}=\frac{6}{7}$. Then $a_{2008}=\frac{5}{7}$.
```
$1^{\text {st }}$ HARVARD-MIT NOVEMBER TOURNAMENT, 8 SATURDAY 2008 - GUTS ROUND
```
|
{
"exam": "HMMT",
"problem_label": "9",
"problem_match": "\n9. [7]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Find the sum of all positive integers $n$ such that $n$ divides $n^{2}+n+2$.
|
3 Since $n$ always divides $n^{2}+n$, the only $n$ that work are divisors of 2 , because if $n$ divides $a$ and $n$ divides $b$, then $n$ divides $a+b$. So the solutions are 1 and 2 which sum to 3 .
|
3
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the sum of all positive integers $n$ such that $n$ divides $n^{2}+n+2$.
|
3 Since $n$ always divides $n^{2}+n$, the only $n$ that work are divisors of 2 , because if $n$ divides $a$ and $n$ divides $b$, then $n$ divides $a+b$. So the solutions are 1 and 2 which sum to 3 .
|
{
"exam": "HMMT",
"problem_label": "10",
"problem_match": "\n10. [8]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Al has a rectangle of integer side lengths $a$ and $b$, and area 1000 . What is the smallest perimeter it could have?
|
130 To minimize the sum of the side lengths, we need to keep the height and width as close as possible, because the square has the smallest perimeter of all rectangles with a fixed area. So, 40 and 25 multiply to 1000 and are as close as possible - the $40 \times 25$ rectangle has perimeter 130 .
|
130
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Al has a rectangle of integer side lengths $a$ and $b$, and area 1000 . What is the smallest perimeter it could have?
|
130 To minimize the sum of the side lengths, we need to keep the height and width as close as possible, because the square has the smallest perimeter of all rectangles with a fixed area. So, 40 and 25 multiply to 1000 and are as close as possible - the $40 \times 25$ rectangle has perimeter 130 .
|
{
"exam": "HMMT",
"problem_label": "11",
"problem_match": "\n11. [8]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Solve the following system of equations for $w$.
$$
\begin{aligned}
& 2 w+x+y+z=1 \\
& w+2 x+y+z=2 \\
& w+x+2 y+z=2 \\
& w+x+y+2 z=1
\end{aligned}
$$
|
$\quad \frac{-1}{5}$ Add all the equations together to find that $5 x+5 y+5 z+5 w=6$, or $x+y+z+w=\frac{6}{5}$. We can now subtract this equation from the first equation to see that $w=\frac{-1}{5}$.
|
\frac{-1}{5}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Solve the following system of equations for $w$.
$$
\begin{aligned}
& 2 w+x+y+z=1 \\
& w+2 x+y+z=2 \\
& w+x+2 y+z=2 \\
& w+x+y+2 z=1
\end{aligned}
$$
|
$\quad \frac{-1}{5}$ Add all the equations together to find that $5 x+5 y+5 z+5 w=6$, or $x+y+z+w=\frac{6}{5}$. We can now subtract this equation from the first equation to see that $w=\frac{-1}{5}$.
|
{
"exam": "HMMT",
"problem_label": "12",
"problem_match": "\n12. [8]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Find the number of distinct primes dividing $1 \cdot 2 \cdot 3 \cdots 9 \cdot 10$.
|
4 A prime divides this product if and only if it divides one of the multiplicands, so prime divisors of this product must be less than 10 . There are 4 primes less than 10 , namely, $2,3,5$, and 7 .
|
4
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the number of distinct primes dividing $1 \cdot 2 \cdot 3 \cdots 9 \cdot 10$.
|
4 A prime divides this product if and only if it divides one of the multiplicands, so prime divisors of this product must be less than 10 . There are 4 primes less than 10 , namely, $2,3,5$, and 7 .
|
{
"exam": "HMMT",
"problem_label": "13",
"problem_match": "\n13. [9]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
You have a $2 \times 3$ grid filled with integers between 1 and 9 . The numbers in each row and column are distinct, the first row sums to 23 , and the columns sum to 14,16 , and 17 respectively.
| | 14 | 16 | 17 |
| :---: | :---: | :---: | :---: |
| 23 | $a$ | $b$ | $c$ |
| | $x$ | $y$ | $z$ |
What is $x+2 y+3 z ?$
|
49 The sum of all 6 numbers is $14+16+17=47$, so $x+y+z=47-23=24$. If three distinct digits sum to 24 , they must be 7,8 , and 9 , because any other triple of digits would have a smaller sum. So, we try placing these digits in for $x, y$, and $z$, and the only arrangement that does not force equal digits in any row or column is $x=8, y=7, z=9$. In this case, $x+2 y+3 z=49$.
|
49
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
You have a $2 \times 3$ grid filled with integers between 1 and 9 . The numbers in each row and column are distinct, the first row sums to 23 , and the columns sum to 14,16 , and 17 respectively.
| | 14 | 16 | 17 |
| :---: | :---: | :---: | :---: |
| 23 | $a$ | $b$ | $c$ |
| | $x$ | $y$ | $z$ |
What is $x+2 y+3 z ?$
|
49 The sum of all 6 numbers is $14+16+17=47$, so $x+y+z=47-23=24$. If three distinct digits sum to 24 , they must be 7,8 , and 9 , because any other triple of digits would have a smaller sum. So, we try placing these digits in for $x, y$, and $z$, and the only arrangement that does not force equal digits in any row or column is $x=8, y=7, z=9$. In this case, $x+2 y+3 z=49$.
|
{
"exam": "HMMT",
"problem_label": "14",
"problem_match": "\n14. [9]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
A cat is going up a stairwell with ten stairs. However, instead of walking up the stairs one at a time, the cat jumps, going either two or three stairs up at each step (though if necessary, it will just walk the last step). How many different ways can the cat go from the bottom to the top?
|
12 The number of ways for the cat to get to the $i$ th step is the number of ways for the cat to get to step $i-2$ plus the number of ways to get to step $i-3$, because for each way to get to step $i$, we can undo the last move the cat made to go back to one of these two steps. The cat can get to step 1 in 0 ways, to step 2 in 1 way, and to step 3 in 1 way. Now we repeatedly use our formula for calculating the number of ways to get to the $i$ th step to see that the cat gets to:
| Step | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| Number of ways | 0 | 1 | 1 | 1 | 2 | 2 | 3 | 4 | 5 | 7 |
So our answer is $5+7=12$.
|
12
|
Yes
|
Incomplete
|
math-word-problem
|
Combinatorics
|
A cat is going up a stairwell with ten stairs. However, instead of walking up the stairs one at a time, the cat jumps, going either two or three stairs up at each step (though if necessary, it will just walk the last step). How many different ways can the cat go from the bottom to the top?
|
12 The number of ways for the cat to get to the $i$ th step is the number of ways for the cat to get to step $i-2$ plus the number of ways to get to step $i-3$, because for each way to get to step $i$, we can undo the last move the cat made to go back to one of these two steps. The cat can get to step 1 in 0 ways, to step 2 in 1 way, and to step 3 in 1 way. Now we repeatedly use our formula for calculating the number of ways to get to the $i$ th step to see that the cat gets to:
| Step | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| Number of ways | 0 | 1 | 1 | 1 | 2 | 2 | 3 | 4 | 5 | 7 |
So our answer is $5+7=12$.
|
{
"exam": "HMMT",
"problem_label": "15",
"problem_match": "\n15. [9]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
If $p$ and $q$ are positive integers and $\frac{2008}{2009}<\frac{p}{q}<\frac{2009}{2010}$, what is the minimum value of $p$ ?
|
4017 By multiplying out the fraction inequalities, we find that $2008 q+1 \leq 2009 p$ and $2010 p+\leq 2009 q$. Adding 2009 times the first inequality to 2008 times the second, we find that $2008 \cdot 2009 q+4017 \leq 2008 \cdot 2009 q+p$, or $p \geq 4017$. This minumum is attained when $\frac{p}{q}=\frac{4017}{4019}$.
|
4017
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
If $p$ and $q$ are positive integers and $\frac{2008}{2009}<\frac{p}{q}<\frac{2009}{2010}$, what is the minimum value of $p$ ?
|
4017 By multiplying out the fraction inequalities, we find that $2008 q+1 \leq 2009 p$ and $2010 p+\leq 2009 q$. Adding 2009 times the first inequality to 2008 times the second, we find that $2008 \cdot 2009 q+4017 \leq 2008 \cdot 2009 q+p$, or $p \geq 4017$. This minumum is attained when $\frac{p}{q}=\frac{4017}{4019}$.
|
{
"exam": "HMMT",
"problem_label": "16",
"problem_match": "\n16. [10]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Determine the last two digits of $17^{17}$, written in base 10 .
|
77 We are asked to find the remainder when $17^{17}$ is divided by 100 . Write the power as $(7+10)^{17}$ and expand with the binomial theorem:
$$
(7+10)^{17}=7^{17}+17 \cdot 7^{16} \cdot 10+\ldots
$$
We can ignore terms with more than one factor of 10 because these terms are divisible by 100 , so adding them does not change the last two digits. Now, $7^{4}=2401$, which has remainder $1 \bmod 100$, so $7^{17}$ has last two digits 07 and $7^{16} \cdot 10$ has last two digits 70 . We add these together.
|
77
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Determine the last two digits of $17^{17}$, written in base 10 .
|
77 We are asked to find the remainder when $17^{17}$ is divided by 100 . Write the power as $(7+10)^{17}$ and expand with the binomial theorem:
$$
(7+10)^{17}=7^{17}+17 \cdot 7^{16} \cdot 10+\ldots
$$
We can ignore terms with more than one factor of 10 because these terms are divisible by 100 , so adding them does not change the last two digits. Now, $7^{4}=2401$, which has remainder $1 \bmod 100$, so $7^{17}$ has last two digits 07 and $7^{16} \cdot 10$ has last two digits 70 . We add these together.
|
{
"exam": "HMMT",
"problem_label": "17",
"problem_match": "\n17. [10]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Find the coefficient of $x^{6}$ in the expansion of
$$
(x+1)^{6} \cdot \sum_{i=0}^{6} x^{i}
$$
|
64 Each term of $(x+1)^{6}$ can be multiplied by a unique power $x^{i}, 0 \leq i \leq 6$ to get a sixth degree term. So the answer is the sum of the coefficients of the terms of $(x+1)^{6}$, which is the same as substituting $x=1$ into this power to get $2^{6}=64$.
## $1^{\text {st }}$ HARVARD-MIT NOVEMBER TOURNAMENT, 8 SATURDAY 2008 - GUTS ROUND
|
64
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find the coefficient of $x^{6}$ in the expansion of
$$
(x+1)^{6} \cdot \sum_{i=0}^{6} x^{i}
$$
|
64 Each term of $(x+1)^{6}$ can be multiplied by a unique power $x^{i}, 0 \leq i \leq 6$ to get a sixth degree term. So the answer is the sum of the coefficients of the terms of $(x+1)^{6}$, which is the same as substituting $x=1$ into this power to get $2^{6}=64$.
## $1^{\text {st }}$ HARVARD-MIT NOVEMBER TOURNAMENT, 8 SATURDAY 2008 - GUTS ROUND
|
{
"exam": "HMMT",
"problem_label": "18",
"problem_match": "\n18. [10]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Let $P$ be a polynomial with $P(1)=P(2)=\cdots=P(2007)=0$ and $P(0)=2009$ !. $P(x)$ has leading coefficient 1 and degree 2008. Find the largest root of $P(x)$.
|
$4034072 P(0)$ is the constant term of $P(x)$, which is the product of all the roots of the polynomial, because its degree is even. So the product of all 2008 roots is 2009 ! and the product of the first 2007 is 2007!, which means the last root is $\frac{2009!}{2007!}=2009 \cdot 2008=4034072$.
|
4034072
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $P$ be a polynomial with $P(1)=P(2)=\cdots=P(2007)=0$ and $P(0)=2009$ !. $P(x)$ has leading coefficient 1 and degree 2008. Find the largest root of $P(x)$.
|
$4034072 P(0)$ is the constant term of $P(x)$, which is the product of all the roots of the polynomial, because its degree is even. So the product of all 2008 roots is 2009 ! and the product of the first 2007 is 2007!, which means the last root is $\frac{2009!}{2007!}=2009 \cdot 2008=4034072$.
|
{
"exam": "HMMT",
"problem_label": "19",
"problem_match": "\n19. [11]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
You have a die with faces labelled 1 through 6 . On each face, you draw an arrow to an adjacent face, such that if you start on a face and follow the arrows, after 6 steps you will have passed through every face once and will be back on your starting face. How many ways are there to draw the arrows so that this is true?
|
32 There are 4 choices for where to go from face 1 . Consider the 4 faces adjacent to 1 . We can visit either 1,2 , or 3 of them before visiting the face opposite 1 . If we only visit one of these adjacent faces, we have 4 choices for which one, then we visit face 6 , opposite face 1 , then we visit the remaining 3 faces in one of two orders - for a total of 8 ways. If we visit 2 adjacent faces first, there is 8 choices for these two faces, then 2 choices for the path back from face 6 to face 1 . Lastly, there are 8 ways to visit three of the adjacent faces before visiting the opposite face. These choices give 32 total.
|
32
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
You have a die with faces labelled 1 through 6 . On each face, you draw an arrow to an adjacent face, such that if you start on a face and follow the arrows, after 6 steps you will have passed through every face once and will be back on your starting face. How many ways are there to draw the arrows so that this is true?
|
32 There are 4 choices for where to go from face 1 . Consider the 4 faces adjacent to 1 . We can visit either 1,2 , or 3 of them before visiting the face opposite 1 . If we only visit one of these adjacent faces, we have 4 choices for which one, then we visit face 6 , opposite face 1 , then we visit the remaining 3 faces in one of two orders - for a total of 8 ways. If we visit 2 adjacent faces first, there is 8 choices for these two faces, then 2 choices for the path back from face 6 to face 1 . Lastly, there are 8 ways to visit three of the adjacent faces before visiting the opposite face. These choices give 32 total.
|
{
"exam": "HMMT",
"problem_label": "20",
"problem_match": "\n20. [11]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Call a number overweight if it has at least three positive integer divisors (including 1 and the number), and call a number obese if it has at least four positive integer divisors (including 1 and the number). How many positive integers between 1 and 200 are overweight, but not obese?
|
6 A positive integer is overweight, but not obese, if it has exactly 3 factors - this can only happen if that integer is the square of a prime. (If two primes, $p$ and $q$, divide the number, then $p, q$, $p q$, and 1 all divide it, making it at least obese). So, the integers less than 200 which are squares of a prime are the squares of $2,3,5,7,11$, and 13 .
## $1^{\text {st }}$ HARVARD-MIT NOVEMBER TOURNAMENT, 8 SATURDAY 2008 - GUTS ROUND
|
6
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Call a number overweight if it has at least three positive integer divisors (including 1 and the number), and call a number obese if it has at least four positive integer divisors (including 1 and the number). How many positive integers between 1 and 200 are overweight, but not obese?
|
6 A positive integer is overweight, but not obese, if it has exactly 3 factors - this can only happen if that integer is the square of a prime. (If two primes, $p$ and $q$, divide the number, then $p, q$, $p q$, and 1 all divide it, making it at least obese). So, the integers less than 200 which are squares of a prime are the squares of $2,3,5,7,11$, and 13 .
## $1^{\text {st }}$ HARVARD-MIT NOVEMBER TOURNAMENT, 8 SATURDAY 2008 - GUTS ROUND
|
{
"exam": "HMMT",
"problem_label": "21",
"problem_match": "\n21. [11]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Sandra the Maverick has 5 pairs of shoes in a drawer, each pair a different color. Every day for 5 days, Sandra takes two shoes out and throws them out the window. If they are the same color, she treats herself to a practice problem from a past HMMT. What is the expected value (average number) of practice problems she gets to do?
|
$\quad \frac{5}{9}$ On any given day, there is a $\frac{1}{9}$ chance that the second shoe that Sandra chooses makes a pair with the first shoe she chose. Thus the average number of problems she does in a day is $\frac{1}{9}$, so, by the linearity of expectation, she does $\frac{5}{9}$ problems total, on average.
|
\frac{5}{9}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Sandra the Maverick has 5 pairs of shoes in a drawer, each pair a different color. Every day for 5 days, Sandra takes two shoes out and throws them out the window. If they are the same color, she treats herself to a practice problem from a past HMMT. What is the expected value (average number) of practice problems she gets to do?
|
$\quad \frac{5}{9}$ On any given day, there is a $\frac{1}{9}$ chance that the second shoe that Sandra chooses makes a pair with the first shoe she chose. Thus the average number of problems she does in a day is $\frac{1}{9}$, so, by the linearity of expectation, she does $\frac{5}{9}$ problems total, on average.
|
{
"exam": "HMMT",
"problem_label": "22",
"problem_match": "\n22. [12]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
If $x$ and $y$ are real numbers such that $\frac{(x-4)^{2}}{4}+\frac{y^{2}}{9}=1$, find the largest possible value of $\frac{x^{2}}{4}+\frac{y^{2}}{9}$.
|
9 The first equation is an ellipse with major axis parallel to the y-axis. If the second expression is set equal to a certain value $c$, then it is also the equation of an ellipse with major axis parallel to the y-axis; further, it is similar to the first ellipse. So the largest value of $c$ occurs when both ellipse are tangent on the x-axis, at $x=6, y=0$, which gives 9 as the largest value of $c$.
|
9
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
If $x$ and $y$ are real numbers such that $\frac{(x-4)^{2}}{4}+\frac{y^{2}}{9}=1$, find the largest possible value of $\frac{x^{2}}{4}+\frac{y^{2}}{9}$.
|
9 The first equation is an ellipse with major axis parallel to the y-axis. If the second expression is set equal to a certain value $c$, then it is also the equation of an ellipse with major axis parallel to the y-axis; further, it is similar to the first ellipse. So the largest value of $c$ occurs when both ellipse are tangent on the x-axis, at $x=6, y=0$, which gives 9 as the largest value of $c$.
|
{
"exam": "HMMT",
"problem_label": "23",
"problem_match": "\n23. [12]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Let $f(x)=\frac{1}{1-x}$. Let $f^{k+1}(x)=f\left(f^{k}(x)\right)$, with $f^{1}(x)=f(x)$. What is $f^{2008}(2008)$ ?
|
$\frac{-1}{2007}$ Notice that, if $x \neq 0,1$, then $f^{2}(x)=\frac{1}{1-\frac{1}{1-x}}=\frac{x-1}{x}$, which means that $f^{3}(x)=$ $\frac{1}{1-\frac{x-1}{x}}=x$. So $f^{n}$ is periodic with period $n=3$, which means that $f^{2007}(x)=x$ so $f^{2008}(2008)=$ $f(2008)=\frac{-1}{2007}$.
$1^{\text {st }}$ HARVARD-MIT NOVEMBER TOURNAMENT, 8 SATURDAY 2008 - GUTS ROUND
|
\frac{-1}{2007}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $f(x)=\frac{1}{1-x}$. Let $f^{k+1}(x)=f\left(f^{k}(x)\right)$, with $f^{1}(x)=f(x)$. What is $f^{2008}(2008)$ ?
|
$\frac{-1}{2007}$ Notice that, if $x \neq 0,1$, then $f^{2}(x)=\frac{1}{1-\frac{1}{1-x}}=\frac{x-1}{x}$, which means that $f^{3}(x)=$ $\frac{1}{1-\frac{x-1}{x}}=x$. So $f^{n}$ is periodic with period $n=3$, which means that $f^{2007}(x)=x$ so $f^{2008}(2008)=$ $f(2008)=\frac{-1}{2007}$.
$1^{\text {st }}$ HARVARD-MIT NOVEMBER TOURNAMENT, 8 SATURDAY 2008 - GUTS ROUND
|
{
"exam": "HMMT",
"problem_label": "24",
"problem_match": "\n24. [12]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Evaluate the sum
$$
\cos \left(\frac{2 \pi}{18}\right)+\cos \left(\frac{4 \pi}{18}\right)+\cdots+\cos \left(\frac{34 \pi}{18}\right)
$$
|
-1 If $k<18$, then we can pair $\cos \left(\frac{k \pi}{18}\right)$ with $\cos \left(\frac{(18-k) \pi}{18}\right)$, and these two terms sum to 0 . If $k>18$, then the pair $\cos \left(\frac{k \pi}{18}\right)$ and $\cos \left(\frac{(36-k) \pi}{18}\right)$ also sums to 0 . So, the only term in this series that is left over is $\cos \left(\frac{18 \pi}{18}\right)=-1$.
|
-1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Evaluate the sum
$$
\cos \left(\frac{2 \pi}{18}\right)+\cos \left(\frac{4 \pi}{18}\right)+\cdots+\cos \left(\frac{34 \pi}{18}\right)
$$
|
-1 If $k<18$, then we can pair $\cos \left(\frac{k \pi}{18}\right)$ with $\cos \left(\frac{(18-k) \pi}{18}\right)$, and these two terms sum to 0 . If $k>18$, then the pair $\cos \left(\frac{k \pi}{18}\right)$ and $\cos \left(\frac{(36-k) \pi}{18}\right)$ also sums to 0 . So, the only term in this series that is left over is $\cos \left(\frac{18 \pi}{18}\right)=-1$.
|
{
"exam": "HMMT",
"problem_label": "25",
"problem_match": "\n25. [13]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
John M. is sitting at ( 0,0 ), looking across the aisle at his friends sitting at $(i, j)$ for each $1 \leq i \leq 10$ and $0 \leq j \leq 5$. Unfortunately, John can only see a friend if the line connecting them doesn't pass through any other friend. How many friends can John see?
|
36 The simplest method is to draw a picture and count which friends he can see. John can see the friend on point $(i, j)$ if and only if $i$ and $j$ are relatively prime.
|
36
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
John M. is sitting at ( 0,0 ), looking across the aisle at his friends sitting at $(i, j)$ for each $1 \leq i \leq 10$ and $0 \leq j \leq 5$. Unfortunately, John can only see a friend if the line connecting them doesn't pass through any other friend. How many friends can John see?
|
36 The simplest method is to draw a picture and count which friends he can see. John can see the friend on point $(i, j)$ if and only if $i$ and $j$ are relatively prime.
|
{
"exam": "HMMT",
"problem_label": "26",
"problem_match": "\n26. [13]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
$A B C D E$ is a regular pentagon inscribed in a circle of radius 1 . What is the area of the set of points inside the circle that are farther from $A$ than they are from any other vertex?
|
$\quad \frac{\pi}{5}$ Draw the perpendicular bisectors of all the sides and diagonals of the pentagon with one endpoint at $A$. These lines all intersect in the center of the circle, because they are the set of points equidistant from two points on the circle. Now, a given point is farther from $A$ than from point $X$ if it is on the $X$ side of the perpendicular bisector of segment $A X$. So, we want to find the area of the set of all points which are separated from $A$ by all of these perpendicular bisectors, which turns out to be a single $72^{\circ}$ sector of the circle, which has area $\frac{\pi}{5}$.
## $1^{\text {st }}$ HARVARD-MIT NOVEMBER TOURNAMENT, 8 SATURDAY 2008 - GUTS ROUND
|
\frac{\pi}{5}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
$A B C D E$ is a regular pentagon inscribed in a circle of radius 1 . What is the area of the set of points inside the circle that are farther from $A$ than they are from any other vertex?
|
$\quad \frac{\pi}{5}$ Draw the perpendicular bisectors of all the sides and diagonals of the pentagon with one endpoint at $A$. These lines all intersect in the center of the circle, because they are the set of points equidistant from two points on the circle. Now, a given point is farther from $A$ than from point $X$ if it is on the $X$ side of the perpendicular bisector of segment $A X$. So, we want to find the area of the set of all points which are separated from $A$ by all of these perpendicular bisectors, which turns out to be a single $72^{\circ}$ sector of the circle, which has area $\frac{\pi}{5}$.
## $1^{\text {st }}$ HARVARD-MIT NOVEMBER TOURNAMENT, 8 SATURDAY 2008 - GUTS ROUND
|
{
"exam": "HMMT",
"problem_label": "27",
"problem_match": "\n27. [13]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Johnny the grad student is typing all the integers from 1 to $\infty$, in order. The 2 on his computer is broken however, so he just skips any number with a 2 . What's the 2008th number he types?
|
3781 Write 2008 in base 9 as 2671, and interpret the result as a base 10 number such that the base 9 digits $2,3, \ldots 8$ correspond to the base 10 digits $3,4, \ldots 9$. This gives an answer of 3781 .
|
3781
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Johnny the grad student is typing all the integers from 1 to $\infty$, in order. The 2 on his computer is broken however, so he just skips any number with a 2 . What's the 2008th number he types?
|
3781 Write 2008 in base 9 as 2671, and interpret the result as a base 10 number such that the base 9 digits $2,3, \ldots 8$ correspond to the base 10 digits $3,4, \ldots 9$. This gives an answer of 3781 .
|
{
"exam": "HMMT",
"problem_label": "28",
"problem_match": "\n28. [14]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Let $p(x)$ be the polynomial of degree 4 with roots $1,2,3,4$ and leading coefficient 1 . Let $q(x)$ be the polynomial of degree 4 with roots $1, \frac{1}{2}, \frac{1}{3}$, and $\frac{1}{4}$ and leading coefficient 1 . Find $\lim _{x \rightarrow 1} \frac{p(x)}{q(x)}$.
|
-24 Consider the polynomial $f(x)=x^{4} q\left(\frac{1}{1}\right)(x)$ - it has the same roots, 1, 2, 3, and 4, as $p(x)$. But this polynomial also has the same coefficients as $q(x)$, just in reverse order. Its leading coefficient is $q(0)=1 \cdot \frac{1}{2} \cdot \frac{1}{3} \cdot \frac{1}{4}=\frac{1}{24}$. So $f(x)$ is $p(x)$ scaled by $\frac{1}{24}$, which means that $p(x) / f(x)$ goes to 24 as $x$ goes to 1 , and $f(x) / q(x)$ goes to -1 .
|
-24
|
Yes
|
Incomplete
|
math-word-problem
|
Algebra
|
Let $p(x)$ be the polynomial of degree 4 with roots $1,2,3,4$ and leading coefficient 1 . Let $q(x)$ be the polynomial of degree 4 with roots $1, \frac{1}{2}, \frac{1}{3}$, and $\frac{1}{4}$ and leading coefficient 1 . Find $\lim _{x \rightarrow 1} \frac{p(x)}{q(x)}$.
|
-24 Consider the polynomial $f(x)=x^{4} q\left(\frac{1}{1}\right)(x)$ - it has the same roots, 1, 2, 3, and 4, as $p(x)$. But this polynomial also has the same coefficients as $q(x)$, just in reverse order. Its leading coefficient is $q(0)=1 \cdot \frac{1}{2} \cdot \frac{1}{3} \cdot \frac{1}{4}=\frac{1}{24}$. So $f(x)$ is $p(x)$ scaled by $\frac{1}{24}$, which means that $p(x) / f(x)$ goes to 24 as $x$ goes to 1 , and $f(x) / q(x)$ goes to -1 .
|
{
"exam": "HMMT",
"problem_label": "29",
"problem_match": "\n29. [14]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Alice has an equilateral triangle $A B C$ of area 1. Put $D$ on $B C, E$ on $C A$, and $F$ on $A B$, with $B D=D C, C E=2 E A$, and $2 A F=F B$. Note that $A D, B E$, and $C F$ pass through a single point $M$. What is the area of triangle $E M C$ ?
|
$\frac{1}{6}$ Triangles $A C F$ and $B C F$ share a height, so the ratio of their areas is $A F / B F=1 / 2$. By the same method, the ratio of the areas of $A M F$ and $B M F$ is $1 / 2$. So, the ratio of the areas of
$A C M$ and $B C M$ is also $1 / 2$. Similarly, the ratio of the areas of $A B M$ and $B C M$ is $1 / 2$. But the sum of the areas of $A C M, B C M$, and $A B M$ is 1 , so the area of $A C M$ is $\frac{1}{4}$. Then the area of $E M C$ is $2 / 3$ the area of $A C M$, because they share heights, so their areas are in the same ratio as their bases. The area of $E M C$ is then $\frac{2 \cdot 1}{3 \cdot 4}=\frac{1}{6}$.
## $1^{\text {st }}$ HARVARD-MIT NOVEMBER TOURNAMENT, 8 SATURDAY 2008 - GUTS ROUND
|
\frac{1}{6}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Alice has an equilateral triangle $A B C$ of area 1. Put $D$ on $B C, E$ on $C A$, and $F$ on $A B$, with $B D=D C, C E=2 E A$, and $2 A F=F B$. Note that $A D, B E$, and $C F$ pass through a single point $M$. What is the area of triangle $E M C$ ?
|
$\frac{1}{6}$ Triangles $A C F$ and $B C F$ share a height, so the ratio of their areas is $A F / B F=1 / 2$. By the same method, the ratio of the areas of $A M F$ and $B M F$ is $1 / 2$. So, the ratio of the areas of
$A C M$ and $B C M$ is also $1 / 2$. Similarly, the ratio of the areas of $A B M$ and $B C M$ is $1 / 2$. But the sum of the areas of $A C M, B C M$, and $A B M$ is 1 , so the area of $A C M$ is $\frac{1}{4}$. Then the area of $E M C$ is $2 / 3$ the area of $A C M$, because they share heights, so their areas are in the same ratio as their bases. The area of $E M C$ is then $\frac{2 \cdot 1}{3 \cdot 4}=\frac{1}{6}$.
## $1^{\text {st }}$ HARVARD-MIT NOVEMBER TOURNAMENT, 8 SATURDAY 2008 - GUTS ROUND
|
{
"exam": "HMMT",
"problem_label": "30",
"problem_match": "\n30. [14]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Find the sum of all primes $p$ for which there exists a prime $q$ such that $p^{2}+p q+q^{2}$ is a square.
|
83 and 5 both work, because $3^{2}+3 \cdot 5+5^{2}=49$. Now, say $p^{2}+p q+q^{2}=k^{2}$, for a positive integer $k$. Then $(p+q)^{2}-k^{2}=p q$, or:
$$
(p+q+k)(p+q-k)=p q
$$
Since $p+q+k$ is a divisor of $p q$, and it is greater than $p$ and $q, p+q+k=p q$. Then $p+q-k=1$. So:
$$
2 p+2 q=p q+1 \Leftrightarrow p q-2 p-2 q+4=3 \Leftrightarrow(p-2)(q-2)=3
$$
This shows that one of $p$ and $q$ is 3 and the other is 5 .
|
83
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the sum of all primes $p$ for which there exists a prime $q$ such that $p^{2}+p q+q^{2}$ is a square.
|
83 and 5 both work, because $3^{2}+3 \cdot 5+5^{2}=49$. Now, say $p^{2}+p q+q^{2}=k^{2}$, for a positive integer $k$. Then $(p+q)^{2}-k^{2}=p q$, or:
$$
(p+q+k)(p+q-k)=p q
$$
Since $p+q+k$ is a divisor of $p q$, and it is greater than $p$ and $q, p+q+k=p q$. Then $p+q-k=1$. So:
$$
2 p+2 q=p q+1 \Leftrightarrow p q-2 p-2 q+4=3 \Leftrightarrow(p-2)(q-2)=3
$$
This shows that one of $p$ and $q$ is 3 and the other is 5 .
|
{
"exam": "HMMT",
"problem_label": "31",
"problem_match": "\n31. [15]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Pirate ships Somy and Lia are having a tough time. At the end of the year, they are both one pillage short of the minimum required for maintaining membership in the Pirate Guild, so they decide to pillage each other to bring their counts up. Somy by tradition only pillages $28 \cdot 3^{k}$ coins for integers $k$, and Lia by tradition only pillages $82 \cdot 3^{j}$ coins for integers $j$. Note that each pillage can have a different $k$ or $j$. Soma and Lia work out a system where Somy pillages Lia $n$ times, Lia pillages Somy $n$ times, and after both sets of pillages Somy and Lia are financially even.
What is the smallest $n$ can be?
|
2 Clearly, $n=1$ cannot be acheived, because $28 \cdot 3^{k}$ is never a multiple of 82 . However, two pillages is enough: Somy pillages 28 and $28 \cdot 81$ from Lia, and Lia pillages 81 and $81 \cdot 27$ from Somy. As is easily checked, both pillage $28 \cdot 82$.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Pirate ships Somy and Lia are having a tough time. At the end of the year, they are both one pillage short of the minimum required for maintaining membership in the Pirate Guild, so they decide to pillage each other to bring their counts up. Somy by tradition only pillages $28 \cdot 3^{k}$ coins for integers $k$, and Lia by tradition only pillages $82 \cdot 3^{j}$ coins for integers $j$. Note that each pillage can have a different $k$ or $j$. Soma and Lia work out a system where Somy pillages Lia $n$ times, Lia pillages Somy $n$ times, and after both sets of pillages Somy and Lia are financially even.
What is the smallest $n$ can be?
|
2 Clearly, $n=1$ cannot be acheived, because $28 \cdot 3^{k}$ is never a multiple of 82 . However, two pillages is enough: Somy pillages 28 and $28 \cdot 81$ from Lia, and Lia pillages 81 and $81 \cdot 27$ from Somy. As is easily checked, both pillage $28 \cdot 82$.
|
{
"exam": "HMMT",
"problem_label": "32",
"problem_match": "\n32. [15]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
The polynomial $a x^{2}-b x+c$ has two distinct roots $p$ and $q$, with $a, b$, and $c$ positive integers and with $0<p, q<1$. Find the minimum possible value of $a$.
|
5 Let $x$ and $y$ be the roots. Then:
$$
\begin{gathered}
\frac{b}{a}=x+y<2 \Rightarrow b<2 a \\
\frac{c}{a}=x y<1 \Rightarrow c<a \Rightarrow a>1 \\
b^{2}>4 a c>4 c^{2} \Rightarrow b>2 c
\end{gathered}
$$
Evaluated at 1 , the polynomial must be greater than 0 , so $a+c>b$. Then:
$$
\begin{gathered}
2 c<b<a+c \\
2 c+1 \leq b \leq a+c-1 \\
a \geq c+2 \geq 3
\end{gathered}
$$
If $a=3$, then $c=1$ and $b=3$, by the above bounds, but this polynomial has complex roots. Similarly, if $a=4$, then $c=1$ and $b$ is forced to be either 3 or 4 , again giving either 0 or 1 distinct real roots. So $a \geq 5$. But the polynomial $5 x^{2}-5 x+1$ satisfies the condition, so 5 is the answer.
|
5
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
The polynomial $a x^{2}-b x+c$ has two distinct roots $p$ and $q$, with $a, b$, and $c$ positive integers and with $0<p, q<1$. Find the minimum possible value of $a$.
|
5 Let $x$ and $y$ be the roots. Then:
$$
\begin{gathered}
\frac{b}{a}=x+y<2 \Rightarrow b<2 a \\
\frac{c}{a}=x y<1 \Rightarrow c<a \Rightarrow a>1 \\
b^{2}>4 a c>4 c^{2} \Rightarrow b>2 c
\end{gathered}
$$
Evaluated at 1 , the polynomial must be greater than 0 , so $a+c>b$. Then:
$$
\begin{gathered}
2 c<b<a+c \\
2 c+1 \leq b \leq a+c-1 \\
a \geq c+2 \geq 3
\end{gathered}
$$
If $a=3$, then $c=1$ and $b=3$, by the above bounds, but this polynomial has complex roots. Similarly, if $a=4$, then $c=1$ and $b$ is forced to be either 3 or 4 , again giving either 0 or 1 distinct real roots. So $a \geq 5$. But the polynomial $5 x^{2}-5 x+1$ satisfies the condition, so 5 is the answer.
|
{
"exam": "HMMT",
"problem_label": "33",
"problem_match": "\n33. [15]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Find $\max \{\operatorname{Perimeter}(T)\}$ for $T$ a triangle contained in a regular septagon (7-sided figure) of unit edge length. Write your answer $N$ to 2 places after the decimal. If the correct answer rounded to 2 decimal places is $A$, you will receive 0 points if $N<A$ and $\lfloor\max \{0,25-50 \cdot(N-A)\}\rfloor$ points otherwise.
|
5.85086 Let the septagon be $A_{0} A_{1} \ldots A_{6}$.
If $x$ is a point that can move along the x -axis, the distance from $x$ to a fixed point $p$ is a convex function in the x -coordinate. Therefore, the sum of the distances from $x$ to two other points is convex too, so if $x$ is constrained to lie on a closed line segment, its maximum value is attained at an endpoint. Therefore, the triangle of maximal perimeter has vertices at the vertices of the pentagon. The triangle with the largest such perimeter has almost evenly spaced vertices, so triangle $A_{0} A_{2} A_{4}$ has the maximal perimeter. It has area $5.85 \ldots$
|
5.85
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Find $\max \{\operatorname{Perimeter}(T)\}$ for $T$ a triangle contained in a regular septagon (7-sided figure) of unit edge length. Write your answer $N$ to 2 places after the decimal. If the correct answer rounded to 2 decimal places is $A$, you will receive 0 points if $N<A$ and $\lfloor\max \{0,25-50 \cdot(N-A)\}\rfloor$ points otherwise.
|
5.85086 Let the septagon be $A_{0} A_{1} \ldots A_{6}$.
If $x$ is a point that can move along the x -axis, the distance from $x$ to a fixed point $p$ is a convex function in the x -coordinate. Therefore, the sum of the distances from $x$ to two other points is convex too, so if $x$ is constrained to lie on a closed line segment, its maximum value is attained at an endpoint. Therefore, the triangle of maximal perimeter has vertices at the vertices of the pentagon. The triangle with the largest such perimeter has almost evenly spaced vertices, so triangle $A_{0} A_{2} A_{4}$ has the maximal perimeter. It has area $5.85 \ldots$
|
{
"exam": "HMMT",
"problem_label": "35",
"problem_match": "\n35. [25]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
How many numbers less than $1,000,000$ are the product of exactly 2 distinct primes? You will receive $\left\lfloor 25-50 \cdot\left|\frac{N}{A}-1\right|\right\rfloor$ points, if you submit $N$ and the correct answer is $A$.
|
209867 While it is difficult to compute this answer without writing a program or using a calculator, it can be approximated using the fact that the number of primes less than a positive integer $n$ is about $\frac{n}{\log n}$.
|
209867
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
How many numbers less than $1,000,000$ are the product of exactly 2 distinct primes? You will receive $\left\lfloor 25-50 \cdot\left|\frac{N}{A}-1\right|\right\rfloor$ points, if you submit $N$ and the correct answer is $A$.
|
209867 While it is difficult to compute this answer without writing a program or using a calculator, it can be approximated using the fact that the number of primes less than a positive integer $n$ is about $\frac{n}{\log n}$.
|
{
"exam": "HMMT",
"problem_label": "36",
"problem_match": "\n36. [25]",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
(a) Decompose 1 into unit fractions.
|
$\frac{1}{2}+\frac{1}{3}+\frac{1}{6}$
(b) Decompose $\frac{1}{4}$ into unit fractions.
|
\frac{1}{2}+\frac{1}{3}+\frac{1}{6}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
(a) Decompose 1 into unit fractions.
|
$\frac{1}{2}+\frac{1}{3}+\frac{1}{6}$
(b) Decompose $\frac{1}{4}$ into unit fractions.
|
{
"exam": "HMMT",
"problem_label": "1",
"problem_match": "\n1. ",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-team-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
(a) Decompose 1 into unit fractions.
|
$\frac{1}{8}+\frac{1}{12}+\frac{1}{24}$
(c) Decompose $\frac{2}{5}$ into unit fractions.
|
\frac{1}{8}+\frac{1}{12}+\frac{1}{24}
|
Yes
|
Problem not solved
|
math-word-problem
|
Number Theory
|
(a) Decompose 1 into unit fractions.
|
$\frac{1}{8}+\frac{1}{12}+\frac{1}{24}$
(c) Decompose $\frac{2}{5}$ into unit fractions.
|
{
"exam": "HMMT",
"problem_label": "1",
"problem_match": "\n1. ",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-team-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
(a) Decompose 1 into unit fractions.
|
$\frac{1}{5}+\frac{1}{10}+\frac{1}{15}+\frac{1}{30}$
|
\frac{1}{5}+\frac{1}{10}+\frac{1}{15}+\frac{1}{30}
|
Yes
|
Problem not solved
|
math-word-problem
|
Number Theory
|
(a) Decompose 1 into unit fractions.
|
$\frac{1}{5}+\frac{1}{10}+\frac{1}{15}+\frac{1}{30}$
|
{
"exam": "HMMT",
"problem_label": "1",
"problem_match": "\n1. ",
"resource_path": "HarvardMIT/segmented/en-121-2008-nov-team-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.