problem
stringlengths 14
10.4k
| solution
stringlengths 1
24.1k
| answer
stringlengths 1
250
⌀ | problem_is_valid
stringclasses 4
values | solution_is_valid
stringclasses 3
values | question_type
stringclasses 4
values | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
10.4k
| solution_raw
stringlengths 1
24.1k
| metadata
dict |
|---|---|---|---|---|---|---|---|---|---|
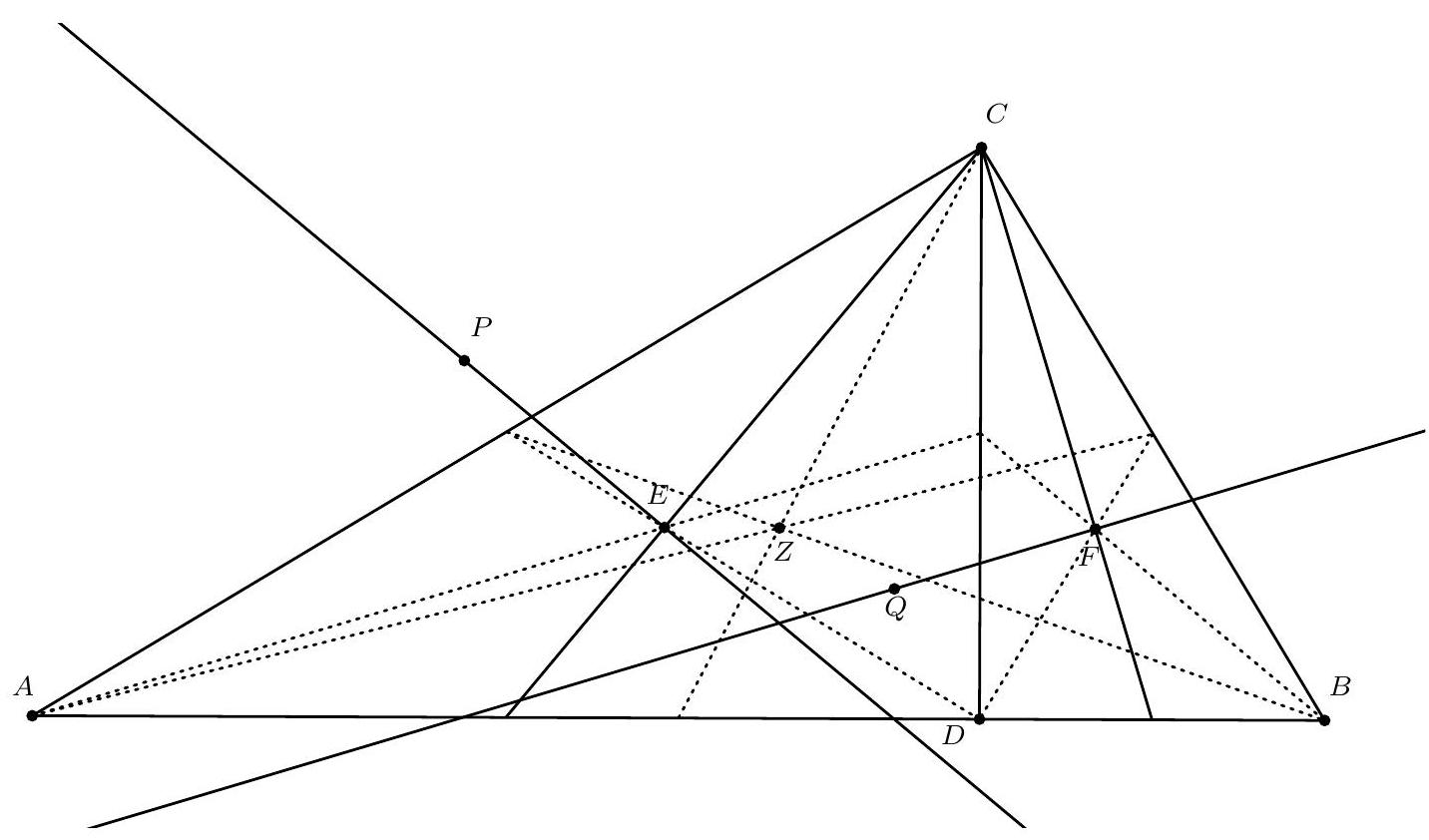
Let $A B C$ be a right triangle with $\angle C=90^{\circ}$ and let $D$ be the foot of the altitude from $C$. Let $E$ be the centroid of triangle $A C D$ and let $F$ be the centroid of triangle $B C D$. The point $P$ satisfies $\angle C E P=90^{\circ}$ and $|C P|=|A P|$, while the point $Q$ satisfies $\angle C F Q=90^{\circ}$ and $|C Q|=|B Q|$.
Show that $P Q$ passes through the centroid of triangle $A B C$.
|
Let $M, N, K$ and $L$ be the midpoints of sides $B C, C A, A B$ and $C D$, respectively. Let $Z$ be the centroid of $\triangle A B C$. Since $M L$ is a midline in triangle $B C D$, we have $M L \| B D$ and thus $M L \| A B$. Similarly, $N L \| A B$, so $M, N$ and $L$ lie on a line $\ell$ parallel to $A B$. Furthermore, because $M L \| B D$, $\triangle B D F \sim \triangle L M F$, and the scaling factor between these two triangles is 2. Therefore, the distance from $F$ to $\ell$ (which is the line $M L$) is half the distance from $F$ to $A B$ (which is the line $B D$). Similarly, the distance from $E$ to $\ell$ is half the distance from $E$ to $A B$, and the same applies to $Z$. Thus, $E, F$ and $Z$ all lie on a line parallel to $A B$ that is twice as far from $A B$ as from $\ell$.
(Another way to see this is by using the fact that centroids always lie at $\frac{1}{3}$ of the altitude from the corresponding vertex. The points $E, F$ and $Z$ all lie at $\frac{1}{3}$ of the altitude from $C$, which leads to the same conclusion.)
In particular, this implies that $\angle C Z E = \angle C K A$ (F-angles). We will use this to show that the points $Z, E, N$ and $C$ lie on a circle. For this, consider the similar triangles $\triangle A B C$ and $\triangle A C D$. We have $\frac{|A K|}{|A N|} = \frac{|A B|}{|A C|} = \frac{|A C|}{|A D|}$, so $\triangle A K C \sim \triangle A N D$ (SAS). This gives $\angle C K A = \angle D N A$. Altogether, we find
$$
\angle C Z E = \angle C K A = \angle D N A = 180^{\circ} - \angle D N C = 180^{\circ} - \angle E N C,
$$
so $C Z E N$ is a cyclic quadrilateral.
Since $|C P| = |A P|$, $P$ lies on the perpendicular bisector of $A C$. Therefore, $\angle C N P = 90^{\circ} = \angle C E P$, which means that $C, E, N$ and $P$ lie on a circle. We have just seen that $Z$ also lies on this circle. Thus, $\angle C Z P = \angle C E P = 90^{\circ}$. Similarly, $\angle C Z Q = 90^{\circ}$. Together, we can conclude that $P, Z$ and $Q$ lie on a line.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $A B C$ een rechthoekige driehoek met $\angle C=90^{\circ}$ en zij $D$ het voetpunt van de hoogtelijn uit $C$. Zij $E$ het zwaartepunt van driehoek $A C D$ en zij $F$ het zwaartepunt van driehoek $B C D$. Het punt $P$ voldoet aan $\angle C E P=90^{\circ}$ en $|C P|=|A P|$, terwijl het punt $Q$ voldoet aan $\angle C F Q=90^{\circ}$ en $|C Q|=|B Q|$.
Toon aan dat $P Q$ door het zwaartepunt van driehoek $A B C$ gaat.

|
Noem $M, N, K$ en $L$ de middens van respectievelijk zijden $B C, C A, A B$ en $C D$. Zij $Z$ het zwaartepunt van $\triangle A B C$. Omdat $M L$ een middenparallel in driehoek $B C D$ is, geldt $M L \| B D$ en dus $M L \| A B$. Zo is ook $N L \| A B$, dus $M, N$ en $L$ liggen op een lijn $\ell$ evenwijdig aan $A B$. Verder geldt vanwege $M L \| B D$ dat $\triangle B D F \sim \triangle L M F$, waarbij de vermenigvuldigingsfactor tussen deze twee driehoeken gelijk aan 2 is. Dus de afstand van $F$ tot $\ell$ (wat de lijn $M L$ is) is twee keer zo klein als de afstand van $F$ tot $A B$ (wat de lijn $B D$ is). Net zo is de afstand van $E$ tot $\ell$ twee keer zo klein als de afstand van $E$ tot $A B$, en hetzelfde geldt voor $Z$. Dus $E, F$ en $Z$ liggen allemaal op een lijn evenwijdig aan $A B$ die twee keer zo ver van $A B$ af ligt als van $\ell$.
(Een andere manier om dit in te zien, is door gebruik te maken van het feit dat zwaartepunten altijd op $\frac{1}{3}$ hoogte van een zwaartelijn liggen. De punten $E, F$ en $Z$ liggen allemaal op $\frac{1}{3}$ hoogte van de corresponderende zwaartelijnen uit $C$, waaruit het gestelde volgt.)
Hieruit volgt in het bijzonder dat $\angle C Z E=\angle C K A$ (F-hoeken). We gaan dit gebruiken om aan te tonen dat de punten $Z, E, N$ en $C$ samen op een cirkel liggen. Bekijk hiervoor eerst de gelijkvormige driehoeken $\triangle A B C$ en $\triangle A C D$. Er geldt nu $\frac{|A K|}{|A N|}=\frac{|A B|}{|A C|}=\frac{|A C|}{|A D|}$, dus $\triangle A K C \sim \triangle A N D$ (zhz). Hieruit volgt $\angle C K A=\angle D N A$. Al met al vinden we nu
$$
\angle C Z E=\angle C K A=\angle D N A=180^{\circ}-\angle D N C=180^{\circ}-\angle E N C,
$$
dus $C Z E N$ is een koordenvierhoek.
Omdat $|C P|=|A P|$ ligt $P$ op de middelloodlijn van $A C$. Er geldt dus $\angle C N P=90^{\circ}=$ $\angle C E P$, wat betekent dat $C, E, N$ en $P$ op een cirkel liggen. We hebben zojuist gezien dat $Z$ ook op deze cirkel ligt. Dus geldt $\angle C Z P=\angle C E P=90^{\circ}$. Analoog volgt $\angle C Z Q=90^{\circ}$. Samen kunnen we hieruit concluderen dat $P, Z$ en $Q$ op een lijn liggen.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2021-E2021_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2021"
}
|
Vind alle functies $f: \mathbb{R} \rightarrow \mathbb{R}$ met
$$
f(x+y f(x+y))=y^{2}+f(x) f(y)
$$
voor alle $x, y \in \mathbb{R}$.
|
Merk op dat de functie $f(x)=0$ voor alle $x$ niet voldoet. Er is dus een $a$ met $f(a) \neq 0$. Vul $x=a$ en $y=0$ in, dat geeft $f(a)=f(a) f(0)$, dus $f(0)=1$. Vul nu $x=1$ en $y=-1$ in, dat geeft $f(1-f(0))=1+f(1) f(-1)$. Omdat $f(0)=1$, staat hier $1=1+f(1) f(-1)$, dus $f(1)=0$ of $f(-1)=0$. We onderscheiden deze twee gevallen.
Stel eerst dat $f(1)=0$. Vul $x=t$ en $y=1-t$ in, en vervolgens $x=1-t$ en $y=t$, dan krijgen we de twee vergelijkingen
$$
\begin{aligned}
f(t) & =(1-t)^{2}+f(t) f(1-t) \\
f(1-t) & =t^{2}+f(t) f(1-t)
\end{aligned}
$$
Deze van elkaar afhalen geeft $f(t)-f(1-t)=(1-t)^{2}-t^{2}=1-2 t$, dus $f(1-t)=f(t)+2 t-1$. Dit invullen in de eerste van bovenstaande twee vergelijkingen geeft
$$
f(t)=(1-t)^{2}+f(t)^{2}+(2 t-1) f(t)
$$
wat we kunnen herschrijven tot
$$
f(t)^{2}+(2 t-2) f(t)+(1-t)^{2}=0
$$
oftewel $(f(t)-(1-t))^{2}=0$. We concluderen dat $f(t)=1-t$. Controleren van deze functie in de oorspronkelijke functievergelijking geeft links $1-(x+y(1-x-y))=1-$ $\left(x+y-x y-y^{2}\right)=1-x-y+x y+y^{2}$ en rechts $y^{2}+(1-x)(1-y)=y^{2}+1-x-y+x y$ en dat is hetzelfde, dus de functie voldoet.
Stel nu $f(-1)=0$. Vul $x=t$ en $y=-1-t$ in, en vervolgens $x=-1-t$ en $y=t$, dan krijgen we de twee vergelijkingen
$$
\begin{aligned}
f(t) & =(-1-t)^{2}+f(t) f(-1-t), \\
f(-1-t) & =t^{2}+f(t) f(-1-t)
\end{aligned}
$$
Deze van elkaar afhalen geeft $f(t)-f(-1-t)=(-1-t)^{2}-t^{2}=1+2 t$, dus $f(-1-t)=$ $f(t)-2 t-1$. Dit invullen in de eerste van bovenstaande twee vergelijkingen geeft
$$
f(t)=(-1-t)^{2}+f(t)^{2}+(-2 t-1) f(t)
$$
wat we kunnen herschrijven tot
$$
f(t)^{2}-(2 t+2) f(t)+(t+1)^{2}=0
$$
oftewel $(f(t)-(t+1))^{2}=0$. We concluderen dat $f(t)=t+1$. Controleren van deze functie in de oorspronkelijke functievergelijking geeft links $x+y(x+y+1)+1=x+x y+y^{2}+y+1$ en rechts $y^{2}+(x+1)(y+1)=y^{2}+x y+x+y+1$ en dat is hetzelfde, dus de functie voldoet.
We concluderen dat er precies twee oplossingen zijn: $f(x)=1-x$ voor alle $x$ en $f(x)=x+1$ voor alle $x$.
|
f(x)=1-x \text{ en } f(x)=x+1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Vind alle functies $f: \mathbb{R} \rightarrow \mathbb{R}$ met
$$
f(x+y f(x+y))=y^{2}+f(x) f(y)
$$
voor alle $x, y \in \mathbb{R}$.
|
Merk op dat de functie $f(x)=0$ voor alle $x$ niet voldoet. Er is dus een $a$ met $f(a) \neq 0$. Vul $x=a$ en $y=0$ in, dat geeft $f(a)=f(a) f(0)$, dus $f(0)=1$. Vul nu $x=1$ en $y=-1$ in, dat geeft $f(1-f(0))=1+f(1) f(-1)$. Omdat $f(0)=1$, staat hier $1=1+f(1) f(-1)$, dus $f(1)=0$ of $f(-1)=0$. We onderscheiden deze twee gevallen.
Stel eerst dat $f(1)=0$. Vul $x=t$ en $y=1-t$ in, en vervolgens $x=1-t$ en $y=t$, dan krijgen we de twee vergelijkingen
$$
\begin{aligned}
f(t) & =(1-t)^{2}+f(t) f(1-t) \\
f(1-t) & =t^{2}+f(t) f(1-t)
\end{aligned}
$$
Deze van elkaar afhalen geeft $f(t)-f(1-t)=(1-t)^{2}-t^{2}=1-2 t$, dus $f(1-t)=f(t)+2 t-1$. Dit invullen in de eerste van bovenstaande twee vergelijkingen geeft
$$
f(t)=(1-t)^{2}+f(t)^{2}+(2 t-1) f(t)
$$
wat we kunnen herschrijven tot
$$
f(t)^{2}+(2 t-2) f(t)+(1-t)^{2}=0
$$
oftewel $(f(t)-(1-t))^{2}=0$. We concluderen dat $f(t)=1-t$. Controleren van deze functie in de oorspronkelijke functievergelijking geeft links $1-(x+y(1-x-y))=1-$ $\left(x+y-x y-y^{2}\right)=1-x-y+x y+y^{2}$ en rechts $y^{2}+(1-x)(1-y)=y^{2}+1-x-y+x y$ en dat is hetzelfde, dus de functie voldoet.
Stel nu $f(-1)=0$. Vul $x=t$ en $y=-1-t$ in, en vervolgens $x=-1-t$ en $y=t$, dan krijgen we de twee vergelijkingen
$$
\begin{aligned}
f(t) & =(-1-t)^{2}+f(t) f(-1-t), \\
f(-1-t) & =t^{2}+f(t) f(-1-t)
\end{aligned}
$$
Deze van elkaar afhalen geeft $f(t)-f(-1-t)=(-1-t)^{2}-t^{2}=1+2 t$, dus $f(-1-t)=$ $f(t)-2 t-1$. Dit invullen in de eerste van bovenstaande twee vergelijkingen geeft
$$
f(t)=(-1-t)^{2}+f(t)^{2}+(-2 t-1) f(t)
$$
wat we kunnen herschrijven tot
$$
f(t)^{2}-(2 t+2) f(t)+(t+1)^{2}=0
$$
oftewel $(f(t)-(t+1))^{2}=0$. We concluderen dat $f(t)=t+1$. Controleren van deze functie in de oorspronkelijke functievergelijking geeft links $x+y(x+y+1)+1=x+x y+y^{2}+y+1$ en rechts $y^{2}+(x+1)(y+1)=y^{2}+x y+x+y+1$ en dat is hetzelfde, dus de functie voldoet.
We concluderen dat er precies twee oplossingen zijn: $f(x)=1-x$ voor alle $x$ en $f(x)=x+1$ voor alle $x$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2021-E2021_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2021"
}
|
Vind alle functies $f: \mathbb{R} \rightarrow \mathbb{R}$ met
$$
f(x+y f(x+y))=y^{2}+f(x) f(y)
$$
voor alle $x, y \in \mathbb{R}$.
|
Net als in de eerste oplossing leiden we af dat $f(0)=1$ en dat $f(1)=0$ of $f(-1)=0$.
Stel eerst dat $f(1)=0$. Invullen van $x=t-1$ en $y=1$ geeft $f(t-1+f(t))=1$. Anderzijds geldt ook $f(0)=1$. We laten nu zien dat $f(z)=1$ impliceert dat $z=0$. Stel $f(z)=1$. Invullen van $x=1$ en $y=z-1$ geeft $f(1+(z-1) f(z))=(z-1)^{2}$, dus $f(z)=(z-1)^{2}$, oftewel $1=(z-1)^{2}$. Dus $z=0$ of $z=2$. Stel $z=2$, dan geeft invullen van $x=0$ en $y=2$ dat $f(2 f(2))=4+f(0) f(2)$, wat met $f(2)=f(z)=1$ leidt tot $f(2)=5$, in tegenspraak met $f(2)=1$. Dus $z=0$. In het bijzonder volgt uit $f(t-1+f(t))=1$ dus dat $t-1+f(t)=0$, dus $f(t)=1-t$. Deze functie voldoet (zie eerste oplossing).
Stel nu dat $f(-1)=0$. Invullen van $x=t+1$ en $y=-1$ geeft $f(t+1-f(t))=1$. Anderzijds geldt ook $f(0)=1$. We laten nu wederom zien dat $f(z)=1$ impliceert dat $z=0$. Stel $f(z)=1$. Invullen van $x=-1$ en $y=z+1$ geeft $f(-1+(z+1) f(z))=(z+1)^{2}$, dus $f(z)=(z+1)^{2}$, oftewel $1=(z+1)^{2}$. Dus $z=0$ of $z=-2$. Stel $z=-2$, dan geeft invullen van $x=0$ en $y=-2$ dat $f(-2 f(-2))=4+f(0) f(-2)$, wat met $f(-2)=f(z)=1$ leidt tot $f(-2)=5$, in tegenspraak met $f(-2)=1$. Dus $z=0$. In het bijzonder volgt uit $f(t+1-f(t))=1$ dus dat $t+1-f(t)=0$, dus $f(t)=t+1$. Deze functie voldoet ook (zie eerste oplossing).
|
f(t)=1-t \text{ or } f(t)=t+1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Vind alle functies $f: \mathbb{R} \rightarrow \mathbb{R}$ met
$$
f(x+y f(x+y))=y^{2}+f(x) f(y)
$$
voor alle $x, y \in \mathbb{R}$.
|
Net als in de eerste oplossing leiden we af dat $f(0)=1$ en dat $f(1)=0$ of $f(-1)=0$.
Stel eerst dat $f(1)=0$. Invullen van $x=t-1$ en $y=1$ geeft $f(t-1+f(t))=1$. Anderzijds geldt ook $f(0)=1$. We laten nu zien dat $f(z)=1$ impliceert dat $z=0$. Stel $f(z)=1$. Invullen van $x=1$ en $y=z-1$ geeft $f(1+(z-1) f(z))=(z-1)^{2}$, dus $f(z)=(z-1)^{2}$, oftewel $1=(z-1)^{2}$. Dus $z=0$ of $z=2$. Stel $z=2$, dan geeft invullen van $x=0$ en $y=2$ dat $f(2 f(2))=4+f(0) f(2)$, wat met $f(2)=f(z)=1$ leidt tot $f(2)=5$, in tegenspraak met $f(2)=1$. Dus $z=0$. In het bijzonder volgt uit $f(t-1+f(t))=1$ dus dat $t-1+f(t)=0$, dus $f(t)=1-t$. Deze functie voldoet (zie eerste oplossing).
Stel nu dat $f(-1)=0$. Invullen van $x=t+1$ en $y=-1$ geeft $f(t+1-f(t))=1$. Anderzijds geldt ook $f(0)=1$. We laten nu wederom zien dat $f(z)=1$ impliceert dat $z=0$. Stel $f(z)=1$. Invullen van $x=-1$ en $y=z+1$ geeft $f(-1+(z+1) f(z))=(z+1)^{2}$, dus $f(z)=(z+1)^{2}$, oftewel $1=(z+1)^{2}$. Dus $z=0$ of $z=-2$. Stel $z=-2$, dan geeft invullen van $x=0$ en $y=-2$ dat $f(-2 f(-2))=4+f(0) f(-2)$, wat met $f(-2)=f(z)=1$ leidt tot $f(-2)=5$, in tegenspraak met $f(-2)=1$. Dus $z=0$. In het bijzonder volgt uit $f(t+1-f(t))=1$ dus dat $t+1-f(t)=0$, dus $f(t)=t+1$. Deze functie voldoet ook (zie eerste oplossing).
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2021-E2021_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2021"
}
|
Let $p>10$ be a prime number. Prove that there exist positive integers $m$ and $n$ with $m+n<p$ such that $p$ is a divisor of $5^{m} 7^{n}-1$.
|
Due to Fermat's little theorem, $a^{p-1} \equiv 1 \bmod p$ for all $a$ with $p \nmid a$. Since $p>10$, $p$ is odd, so $p-1$ is even. It holds that
$$
\left(a^{\frac{p-1}{2}}-1\right)\left(a^{\frac{p-1}{2}}+1\right)=a^{p-1}-1 \equiv 0 \quad \bmod p
$$
Thus $p \left\lvert\,\left(a^{\frac{p-1}{2}}-1\right)\left(a^{\frac{p-1}{2}}+1\right)\right.$, so $p$ is a divisor of at least one of the two factors. Therefore, $a^{\frac{p-1}{2}}$ is congruent to 1 or -1 modulo $p$.
We apply this to $a=5$ and $a=7$. Note that $p>10$ so $p \neq 5,7$. If $5^{\frac{p-1}{2}} \equiv 1$ $\bmod p$ and $7^{\frac{p-1}{2}} \equiv 1 \bmod p$, then we take $m=n=\frac{p-1}{2}$ and that satisfies. The same applies if they are both $-1 \bmod p$. The remaining case is when one is 1 and the other is -1. Assume $5^{\frac{p-1}{2}} \equiv 1 \bmod p$ and $7^{\frac{p-1}{2}} \equiv-1 \bmod p$. The case where it is the other way around proceeds analogously.
If there is an $n$ with $0<n<\frac{p-1}{2}$ and $7^{n} \equiv 1 \bmod p$, then we choose this $n$ and further $m=\frac{p-1}{2}$. That satisfies. Otherwise, there can also be no $n$ with $\frac{p-1}{2}<n<p-1$ and $7^{n} \equiv 1 \bmod p$, because then $7^{p-1-n} \equiv 7^{p-1} \cdot\left(7^{n}\right)^{-1} \equiv 1 \bmod p$, while $0<p-1-n<\frac{p-1}{2}$, a contradiction. Furthermore, there can now be no $i$ and $j$ with $1 \leq i<j \leq p-1$ such that $7^{i} \equiv 7^{j} \bmod p$, because if they did exist, then $7^{j-i} \equiv 1 \bmod p$ with $1 \leq j-i<p-1$. We conclude that $7^{i}$ with $1 \leq i \leq p-1$ all take different values modulo $p$, and the value 0 is not among them, so they are precisely all the values from 1 to $p-1$.
In particular, there is an $n$ such that $7^{n} \equiv 5^{-1} \bmod p$. It holds that $n \leq p-2$, because $7^{p-1} \equiv 1 \not \equiv 5^{-1}$ $\bmod p$. We now choose this $n$ and further $m=1$ and then $7^{n} \cdot 5^{m} \equiv 5^{-1} \cdot 5 \equiv 1 \bmod p$.
We see that it is possible in all cases to find $m$ and $n$ that satisfy the conditions.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Zij $p>10$ een priemgetal. Bewijs dat er positieve gehele getallen $m$ en $n$ met $m+n<p$ bestaan waarvoor $p$ een deler is van $5^{m} 7^{n}-1$.
|
Wegens de kleine stelling van Fermat geldt $a^{p-1} \equiv 1 \bmod p$ voor alle $a$ met $p \nmid a$. Omdat $p>10$ is $p$ oneven, dus $p-1$ is even. Er geldt
$$
\left(a^{\frac{p-1}{2}}-1\right)\left(a^{\frac{p-1}{2}}+1\right)=a^{p-1}-1 \equiv 0 \quad \bmod p
$$
Dus $p \left\lvert\,\left(a^{\frac{p-1}{2}}-1\right)\left(a^{\frac{p-1}{2}}+1\right)\right.$, dus $p$ is een deler van minstens één van beide factoren. Dus $a^{\frac{p-1}{2}}$ is modulo $p$ congruent aan 1 of -1 .
We passen dit toe op $a=5$ en $a=7$. Merk op dat $p>10$ dus $p \neq 5,7$. Als $5^{\frac{p-1}{2}} \equiv 1$ $\bmod p$ en $7^{\frac{p-1}{2}} \equiv 1 \bmod p$, dan nemen we $m=n=\frac{p-1}{2}$ en dat voldoet. Hetzelfde geldt als ze beide $-1 \bmod p$ zijn. Blijft over het geval dat één van beide 1 en de ander -1 is. Neem aan dat $5^{\frac{p-1}{2}} \equiv 1 \bmod p$ en $7^{\frac{p-1}{2}} \equiv-1 \bmod p$. Het geval waarin het andersom is, gaat precies analoog.
Als er een $n$ is met $0<n<\frac{p-1}{2}$ en $7^{n} \equiv 1 \bmod p$, dan kiezen we deze $n$ en verder $m=\frac{p-1}{2}$. Dat voldoet. Zo niet, dan kan er ook geen $n$ zijn met $\frac{p-1}{2}<n<p-1$ en $7^{n} \equiv 1 \bmod p$, want dan zou $7^{p-1-n} \equiv 7^{p-1} \cdot\left(7^{n}\right)^{-1} \equiv 1 \bmod p$, terwijl $0<p-1-n<\frac{p-1}{2}$, tegenspraak. Verder kunnen er nu geen $i$ en $j$ zijn met $1 \leq i<j \leq p-1$ zodat $7^{i} \equiv 7^{j} \bmod p$, want als die wel zouden bestaan, dan is $7^{j-i} \equiv 1 \bmod p$ met $1 \leq j-i<p-1$. We concluderen dat $7^{i}$ met $1 \leq i \leq p-1$ allemaal verschillende waarden aanneemt modulo $p$, en daar zit waarde 0 niet bij, dus het zijn precies alle waarden van 1 tot en met $p-1$.
In het bijzonder is er een $n$ zodat $7^{n} \equiv 5^{-1} \bmod p$. Er geldt $n \leq p-2$, want $7^{p-1} \equiv 1 \not \equiv 5^{-1}$ $\bmod p$. We kiezen nu deze $n$ en verder $m=1$ en dan geldt $7^{n} \cdot 5^{m} \equiv 5^{-1} \cdot 5 \equiv 1 \bmod p$.
We zien dat het in alle gevallen mogelijk is om $m$ en $n$ te vinden die aan de voorwaarden voldoen.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2021-E2021_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2021"
}
|
Let $p>10$ be a prime number. Prove that there exist positive integers $m$ and $n$ with $m+n<p$ such that $p$ is a divisor of $5^{m} 7^{n}-1$.
|
We consider all numbers of the form $5^{i} 7^{j}$ for $1 \leq i, j \leq p-1$. These are $(p-1)^{2}$ numbers. Modulo $p$ these numbers never take the value 0, because for $p>10$ we have $p \neq 5,7$. Therefore, modulo $p$ there are at most $p-1$ different values assumed. By the pigeonhole principle, there is now a value $k$ such that at least $\frac{(p-1)^{2}}{p-1}=p-1$ of these pairs $(i, j)$ satisfy $5^{i} 7^{j} \equiv k \bmod p$. We call these pairs $k$-valued.
Take such a $k$-valued pair $(i, j)=(a, b)$. We will first show that not all $k$-valued pairs are of the form $(x, b)$. For example, $(a+1, b)$ (and similarly $(a-1, b)$ if it happens that $a=p-1$) is not $k$-valued, because from $5^{a+1} 7^{b} \equiv 5^{a} 7^{b} \bmod p$ it would follow that $5 \equiv 1 \bmod p$ so $p \mid 4$, a contradiction. Since there are at least $p-1$ $k$-valued pairs, it follows that not all $k$-valued pairs can be of the form $(x, b)$. Therefore, there is a $k$-valued pair $(c, d)$ with $d \neq b$. Similarly, there is a $k$-valued pair $(e, f)$ with $e \neq a$. If $a \neq c$, then $(a, b)$ and $(c, d)$ are two pairs with two different numbers in the first component and two different numbers in the second component. If $b \neq f$, then $(a, b)$ and $(e, f)$ are such pairs. If $a=c$ and $b=f$, then precisely $(c, d)=(a, d)$ and $(e, f)=(e, b)$ are such pairs.
Thus, we can always find two $k$-valued pairs $\left(i_{1}, j_{1}\right)$ and $\left(i_{2}, j_{2}\right)$ with $i_{1} \neq i_{2}$ and $j_{1} \neq j_{2}$. It now follows that
$$
5^{i_{1}-i_{2}} 7^{j_{1}-j_{2}} \equiv 5^{i_{1}}\left(5^{i_{2}}\right)^{-1} \cdot 7^{j_{1}}\left(7^{j_{2}}\right)^{-1} \equiv k \cdot k^{-1} \equiv 1 \quad \bmod p .
$$
From Fermat's little theorem, it follows that $u^{p-1} \equiv 1 \bmod p$ if $u \in\{5,7\}$. For $t \in \mathbb{Z}$, we have $u^{p-1+t} \equiv u^{p-1} u^{t} \equiv u^{t} \bmod p$. Write $m^{\prime}=i_{1}-i_{2}$ if $i_{1}>i_{2}$ and $m^{\prime}=p-1+i_{1}-i_{2}$ if $i_{1}<i_{2}$, then $5^{m^{\prime}} \equiv 5^{i_{1}-i_{2}} \bmod p$. Furthermore, $1 \leq m^{\prime} \leq p-2$. Similarly, we define $n^{\prime}$ so that $7^{n^{\prime}} \equiv 7^{j_{1}-j_{2}} \bmod p$ and $1 \leq n^{\prime} \leq p-2$. We now have $5^{m^{\prime}} 7^{n^{\prime}} \equiv 1 \bmod p$.
If $n^{\prime}+m^{\prime}<p$, then we choose $m=m^{\prime}$ and $n=n^{\prime}$ and we are done. Otherwise, we choose $m=p-1-m^{\prime}$ and $n=p-1-n^{\prime}$ and it follows that $5^{m} 7^{n} \equiv 5^{p-1}\left(5^{m^{\prime}}\right)^{-1} \cdot 7^{p-1}\left(7^{n^{\prime}}\right)^{-1} \equiv 1 \cdot 1^{-1} \equiv 1$ $\bmod p$. Now $n+m=2(p-2)-\left(n^{\prime}+m^{\prime}\right) \leq 2 p-4-p=p-4$, so we are also done.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Zij $p>10$ een priemgetal. Bewijs dat er positieve gehele getallen $m$ en $n$ met $m+n<p$ bestaan waarvoor $p$ een deler is van $5^{m} 7^{n}-1$.
|
We bekijken alle getallen van de vorm $5^{i} 7^{j}$ voor $1 \leq i, j \leq p-1$. Dit zijn $(p-1)^{2}$ getallen. Modulo $p$ nemen deze getallen nooit de waarde 0 aan, want vanwege $p>10$ geldt $p \neq 5,7$. Dus modulo $p$ worden er hooguit $p-1$ verschillende waarden aangenomen. Vanwege het ladenprincipe is er nu een waarde $k$ zodat minstens $\frac{(p-1)^{2}}{p-1}=p-1$ van deze paren $(i, j)$ voldoen aan $5^{i} 7^{j} \equiv k \bmod p$. Noem deze paren $k$-waardig.
Neem zo'n $k$-waardig paar $(i, j)=(a, b)$. We gaan eerst laten zien dat niet alle $k$-waardige paren van de vorm $(x, b)$ zijn. Bijvoorbeeld $(a+1, b)$ (en net zo goed $(a-1, b)$ als net toevallig $a=p-1$ ) is niet $k$-waardig, want uit $5^{a+1} 7^{b} \equiv 5^{a} 7^{b} \bmod p$ zou volgen dat $5 \equiv 1$
$\bmod p$ dus $p \mid 4$, tegenspraak. Omdat er minstens $p-1$ paren $k$-waardig zijn, volgt nu dat niet alle $k$-waardige paren van de vorm $(x, b)$ kunnen zijn. Dus er is een $k$-waardig paar $(c, d)$ met $d \neq b$. Net zo bestaat er een $k$-waardig paar $(e, f)$ met $e \neq a$. Als nu $a \neq c$, dan zijn $(a, b)$ en $(c, d)$ twee paren met twee verschillende getallen in de eerste component en twee verschillende getallen in de tweede component. Als $b \neq f$, zijn $(a, b)$ en $(e, f)$ zulke paren. Als $a=c$ en $b=f$, dan zijn juist $(c, d)=(a, d)$ en $(e, f)=(e, b)$ zulke paren.
We kunnen dus altijd twee $k$-waardige paren $\left(i_{1}, j_{1}\right)$ en $\left(i_{2}, j_{2}\right)$ vinden met $i_{1} \neq i_{2}$ en $j_{1} \neq j_{2}$. Er geldt nu
$$
5^{i_{1}-i_{2}} 7^{j_{1}-j_{2}} \equiv 5^{i_{1}}\left(5^{i_{2}}\right)^{-1} \cdot 7^{j_{1}}\left(7^{j_{2}}\right)^{-1} \equiv k \cdot k^{-1} \equiv 1 \quad \bmod p .
$$
Uit de kleine stelling van Fermat volgt $u^{p-1} \equiv 1 \bmod p$ als $u \in\{5,7\}$. Voor $t \in \mathbb{Z}$ geldt nu $u^{p-1+t} \equiv u^{p-1} u^{t} \equiv u^{t} \bmod p$. Schrijf $m^{\prime}=i_{1}-i_{2}$ als $i_{1}>i_{2}$ en $m^{\prime}=p-1+i_{1}-i_{2}$ als $i_{1}<i_{2}$, dan geldt dus $5^{m^{\prime}} \equiv 5^{i_{1}-i_{2}} \bmod p$. Verder is $1 \leq m^{\prime} \leq p-2$. Analoog definiëren we $n^{\prime}$ zodat $7^{n^{\prime}} \equiv 7^{j_{1}-j_{2}} \bmod p$ en $1 \leq n^{\prime} \leq p-2$. We hebben nu $5^{m^{\prime}} 7^{n^{\prime}} \equiv 1 \bmod p$.
Als $n^{\prime}+m^{\prime}<p$, dan kiezen we $m=m^{\prime}$ en $n=n^{\prime}$ en zijn we klaar. Zo niet, dan kiezen we $m=p-1-m^{\prime}$ en $n=p-1-n^{\prime}$ en geldt $5^{m} 7^{n} \equiv 5^{p-1}\left(5^{m^{\prime}}\right)^{-1} \cdot 7^{p-1}\left(7^{n^{\prime}}\right)^{-1} \equiv 1 \cdot 1^{-1} \equiv 1$ $\bmod p$. Nu geldt $n+m=2(p-2)-\left(n^{\prime}+m^{\prime}\right) \leq 2 p-4-p=p-4$, dus zijn we ook klaar.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2021-E2021_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2021"
}
|
Find all functions $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}_{>0}$ for which $f(n) \mid f(m)-n$ if and only if $n \mid m$ for all positive integers $m$ and $n$.
|
When we substitute $m=n$, we find that $f(n) \mid f(n)-n$, so for all natural numbers, $f(n) \mid n$. If we use this again on the original functional condition, we find that $f(n) \mid f(m)$ if and only if $n \mid m$.
Now we prove that $f(n)=n$ by induction on the number of prime divisors of $n$ counted with multiplicity. As the base case, we have that $f(1) \mid 1$, so indeed $f(1)=1$. Suppose that $f(k)=k$ for all numbers $k$ with fewer divisors than $n$ and that $f(n) \mid n$ is a strict divisor of $n$. Then there exists a prime number $p$ such that $f(n) \mid n / p=f(n / p)$ by the induction hypothesis. But $n$ is not a divisor of $n / p$, so our assumption that $f(n) \neq n$ leads to a contradiction.
We check that $f(n)=n$ is indeed a solution: $n \mid m$ if and only if $n \mid m-n$.
|
f(n)=n
|
Yes
|
Yes
|
proof
|
Number Theory
|
Vind alle functies $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}_{>0}$ waarvoor geldt dat $f(n) \mid f(m)-n$ dan en slechts dan als $n \mid m$ voor alle natuurlijke getallen $m$ en $n$.
|
Als we $m=n$ invullen, dan vinden we dat $f(n) \mid f(n)-n$, dus voor alle natuurlijke getallen geldt $f(n) \mid n$. Als we dat weer gebruiken op de originele functievoorwaarde vinden we dat $f(n) \mid f(m)$ dan en slechts dan als $n \mid m$.
Nu bewijzen we dat $f(n)=n$ via inductie naar het aantal priemdelers van $n$ geteld met multipliciteit. Als inductiebasis hebben we dat $f(1) \mid 1$, dus inderdaad $f(1)=1$. Stel dat $f(k)=k$ voor alle getallen $k$ met minder delers dan $n$ en dat $f(n) \mid n$ een strikte deler is van $n$. Dan bestaat er dus een priemgetal $p$ zo dat $f(n) \mid n / p=f(n / p)$ door de inductiehypothese. Maar $n$ is geen deler van $n / p$, dus onze aanname dat $f(n) \neq n$ leidt tot een tegenspraak.
We controleren dat $f(n)=n$ inderdaad een oplossing is: $n \mid m$ dan en slechts dan als $n \mid m-n$.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2022-B2022_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2022"
}
|
Find all functions $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}_{>0}$ for which $f(n) \mid f(m)-n$ if and only if $n \mid m$ for all positive integers $m$ and $n$.
|
We can also perform strong induction on $n$. The base case is the same as above. Suppose that $f(k)=k$ for all $k<n$ (this is the induction hypothesis). To derive a contradiction, we also assume that $f(n)<n$. Then by taking $k=f(n)$, we have that $f(f(n))=f(n)$. In particular, this means that $f(n) \mid f(f(n))$. Since $f(n) \mid f(m)$ if and only if $n \mid m$, it follows that $n \mid f(n)$. But this is in contradiction with $f(n)<n$, so $f(n)=n$.
|
f(n)=n
|
Yes
|
Yes
|
proof
|
Number Theory
|
Vind alle functies $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}_{>0}$ waarvoor geldt dat $f(n) \mid f(m)-n$ dan en slechts dan als $n \mid m$ voor alle natuurlijke getallen $m$ en $n$.
|
We kunnen ook sterke inductie doen naar $n$. De basis is hetzelfde als hierboven. Stel dat $f(k)=k$ voor alle $k<n$ (dat is de inductiehypothese). Om een tegenspraak af te leiden stellen we ook dat $f(n)<n$. Dan geldt door $k=f(n)$ te nemen dat $f(f(n))=f(n)$. En in het bijzonder dus dat $f(n) \mid f(f(n))$. Doordat $f(n) \mid f(m)$ dan en slechts dan als $n \mid m$ volgt hieruit dat $n \mid f(n)$. Maar dat is in tegenspraak met $f(n)<n$, dus $f(n)=n$.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2022-B2022_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2022"
}
|
Let $A B C$ be an acute triangle with $D$ the foot of the altitude from $A$. The circle centered at $A$ passing through $D$ intersects the circumcircle of triangle $A B C$ at $X$ and $Y$, such that the order of the points on this circumcircle is: $A, X, B, C, Y$. Prove that $\angle B X D=\angle C Y D$.
|
Since the ray $A D$ is perpendicular to $B C$, $B C$ is tangent to the circumcircle of $\triangle D X Y$. Due to the tangent-secant theorem, the angle between the tangent and the chord $D X$ is equal to the inscribed angle on this chord, i.e., $\angle X D B = \angle X Y D$. Furthermore, we know that $B C Y X$ is a cyclic quadrilateral. This means that the opposite angles add up to $180^{\circ}$, so $\angle C B X + \angle X Y C = 180^{\circ}$. From the angle sum in $\triangle B D X$, we find that $\angle B X D = 180^{\circ} - \angle D B X - \angle X D B = (180^{\circ} - \angle C B X) - \angle X D B = \angle X Y C - \angle X Y D$, where we have used the two derived equations. We can simply subtract these two angles: $\angle X Y C - \angle X Y D = \angle D Y C$, from which it follows that $\angle B X D = \angle D Y C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $A B C$ een scherphoekige driehoek met $D$ het voetpunt van de hoogtelijn vanuit $A$. De cirkel met middelpunt $A$ die door $D$ gaat, snijdt de omgeschreven cirkel van driehoek $A B C$ in $X$ en $Y$, waarbij de volgorde van de punten op deze omgeschreven cirkel is: $A, X, B, C, Y$. Bewijs dat $\angle B X D=\angle C Y D$.
|
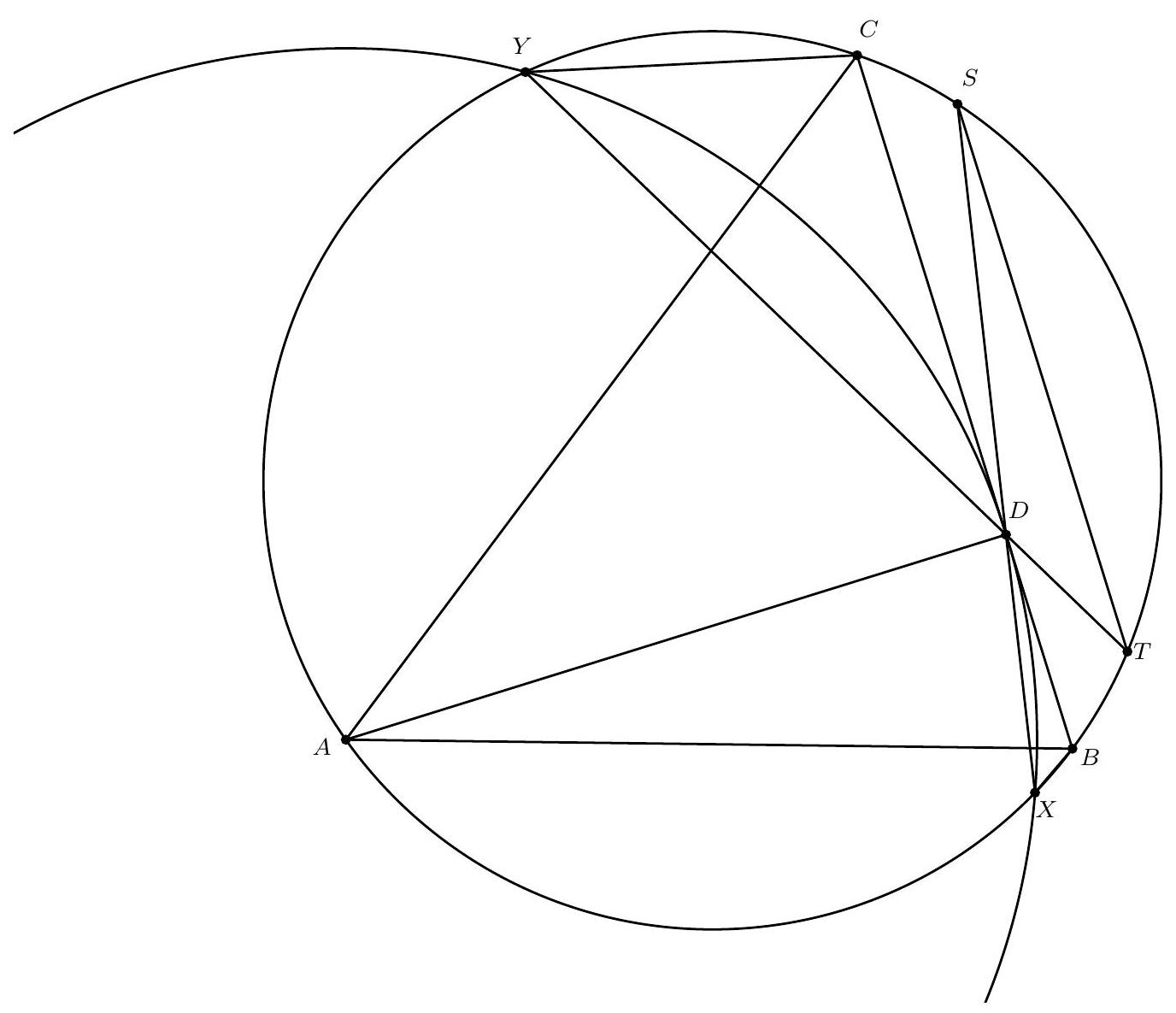
Omdat de straal $A D$ loodrecht staat op $B C$, raakt $B C$ aan de omgeschreven cirkel van $\triangle D X Y$. Wegens de raaklijn-omtrekshoekstelling geldt daardoor dat de hoek tussen de raaklijn en de koorde $D X$ gelijk is aan de omtrekshoek op deze koorde, oftewel $\angle X D B=$ $\angle X Y D$. Verder weten we dat $B C Y X$ een koordenvierkhoek is. Dat betekent dat de overstaande hoeken optellen tot $180^{\circ}$, dus $\angle C B X+\angle X Y C=180^{\circ}$. Vanwege de hoekensom in $\triangle B D X$ vinden we dan dat $\angle B X D=180^{\circ}-\angle D B X-\angle X D B=\left(180^{\circ}-\angle C B X\right)-$ $\angle X D B=\angle X Y C-\angle X Y D$ waar we de twee gevonden vergelijkingen hebben gebruikt. Deze laatste twee hoeken kunnen we gewoon van elkaar aftrekken: $\angle X Y C-\angle X Y D=$ $\angle D Y C$, waaruit volgt dat $\angle B X D=\angle D Y C$.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2022-B2022_uitwerkingen.jsonl",
"solution_match": "# Oplossing I.",
"tier": "T1",
"year": "2022"
}
|
Let $A B C$ be an acute triangle with $D$ the foot of the altitude from $A$. The circle centered at $A$ passing through $D$ intersects the circumcircle of triangle $A B C$ at $X$ and $Y$, such that the order of the points on this circumcircle is: $A, X, B, C, Y$. Prove that $\angle B X D=\angle C Y D$.
|
Let $S$ be the second intersection of $XD$ and the circumcircle of $\triangle ABC$. Let $T$ be the second intersection of $YD$ and the circumcircle of $\triangle ABC$. Then, $\angle DST = \angle XST = \angle XYT = \angle XYD$. Furthermore, $AD \perp BC$ and $A$ is the center of the circle through $D, X$, and $Y$, so $BC$ is tangent to this circle. Using the tangent-secant angle theorem, we find that $\angle XYD = \angle XDB$. Therefore, $\angle DST = \angle XDB$, from which it follows with F-angles that $BD$ is parallel to $ST$.
Thus, $BC$ and $ST$ are parallel, from which it follows by Julian's theorem that $|BS| = |CT|$. The inscribed angles on these chords are equal, that is, $\angle BXS = \angle CYT$. This means that $\angle BXD = \angle CYD$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $A B C$ een scherphoekige driehoek met $D$ het voetpunt van de hoogtelijn vanuit $A$. De cirkel met middelpunt $A$ die door $D$ gaat, snijdt de omgeschreven cirkel van driehoek $A B C$ in $X$ en $Y$, waarbij de volgorde van de punten op deze omgeschreven cirkel is: $A, X, B, C, Y$. Bewijs dat $\angle B X D=\angle C Y D$.
|
Zij $S$ het tweede snijpunt van $X D$ en de omgeschreven cirkel van $\triangle A B C$. Zij $T$ het tweede snijpunt van $Y D$ en de omgeschreven cirkel van $\triangle A B C$. Dan geldt $\angle D S T=\angle X S T=\angle X Y T=\angle X Y D$. Verder geldt $A D \perp B C$ en $A$ is het middelpunt van de cirkel door $D, X$ en $Y$, dus $B C$ raakt aan deze cirkel. Met de raaklijnomtrekshoekstelling vinden we dan $\angle X Y D=\angle X D B$. Dus $\angle D S T=\angle X D B$, waaruit met F-hoeken volgt dat $B D$ evenwijdig aan $S T$ is.
Dus $B C$ en $S T$ zijn evenwijdig, waaruit met de stelling van Julian volgt dat $|B S|=|C T|$. De omtrekshoeken op deze koorden zijn gelijk, oftewel $\angle B X S=\angle C Y T$. Dit betekent dat $\angle B X D=\angle C Y D$.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2022-B2022_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2022"
}
|
Find all pairs of prime numbers $(p, q)$ for which
$$
p\left(p^{2}-p-1\right)=q(2 q+3)
$$
|
Answer: the only solution is $(p, q)=(13,31)$.
If $p=q$, then it must also hold that $p^{2}-p-1=2 q+3=2 p+3$. This can be factored as $(p-4)(p+1)=0$. Since 4 and -1 are not prime numbers, this does not yield any solutions.
In the other case, we have $p \mid 2 q+3$ and $q \mid p^{2}-p-1$. Since $2 q+3$ and $p^{2}-p-1$ are positive, it follows that $p \leq 2 q+3$ and $q \leq p^{2}-p-1$. To find a sharper lower bound for $p$, we multiply the two relations
$$
\begin{aligned}
p q & \mid(2 q+3)\left(p^{2}-p-1\right) \\
& \mid 2 q p^{2}-2 q p-2 q+3\left(p^{2}-p-1\right) \\
& \mid 3\left(p^{2}-p-1\right)-2 q,
\end{aligned}
$$
where we have discarded terms with a factor of $p q$. Note now that $3\left(p^{2}-p-1\right)-2 q \geq$ $3 q-2 q=q>0$. This means that the above divisibility relation leads to
$$
\begin{aligned}
p q & \leq 3\left(p^{2}-p-1\right)-2 q \\
& =3 p^{2}-3 p-(2 q+3) \\
& \leq 3 p^{2}-3 p-p \\
& =3 p^{2}-4 p .
\end{aligned}
$$
If we move $4 p$ to the other side and divide by $p$, we find that $q+4 \leq 3 p$, or
$$
\frac{2 q+3}{6}<\frac{q+4}{3} \leq p
$$
Since $p$ is a divisor of $2 q+3$, we deduce that $2 q+3=k p$ with $k \in\{1,2,3,4,5\}$. If $k=1$, then we have $2 q+3=p$ and thus also $q=p^{2}-p-1$. But then it would hold that $p=2 q+3=2\left(p^{2}-p-1\right)+3=2 p^{2}-2 p+1$. This can be factored as $(2 p-1)(p-1)=0$, which has no solutions with $p$ prime. If $k=2$ or $k=4$, then $k p$ is even. But $2 q+3$ is odd, so these cases are ruled out. If $k=3$, then from $2 q+3=3 p$ it follows that $q$ must be a multiple of 3. Since $q$ is prime, we then have $q=3$, and thus also $p=(2 q+3) / 3=3$. Checking shows that this is not a solution to the original equation.
The last case is $k=5$. Then we have $5 p=2 q+3$ and from the original equation, we have $5 q=p^{2}-p-1$. If we substitute this, we get $25 p=5(2 q+3)=$ $2\left(p^{2}-p-1\right)+15=2 p^{2}-2 p+13$. This can be factored as $(p-13)(2 p-1)=0$. This gives the possible solution $p=13$ with $q=(5 p-3) / 2=31$. We check that $(p, q)=(13,31)$ is indeed a solution to the problem.
|
(13,31)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Vind alle paren priemgetallen $(p, q)$ waarvoor geldt dat
$$
p\left(p^{2}-p-1\right)=q(2 q+3)
$$
|
Antwoord: de enige oplossing is $(p, q)=(13,31)$.
Als $p=q$, dan moet ook gelden dat $p^{2}-p-1=2 q+3=2 p+3$. Dit kunnen we ontbinden als $(p-4)(p+1)=0$. Omdat 4 en -1 geen priemgetallen zijn, levert dit dus geen oplossingen op.
In het andere geval hebben we $p \mid 2 q+3$ en $q \mid p^{2}-p-1$. Omdat $2 q+3$ en $p^{2}-p-1$ positief zijn, volgt hieruit dat $p \leq 2 q+3$ en $q \leq p^{2}-p-1$. Om een scherpere ondergrens voor $p$ te vinden vermenigvuldigen we de twee relaties
$$
\begin{aligned}
p q & \mid(2 q+3)\left(p^{2}-p-1\right) \\
& \mid 2 q p^{2}-2 q p-2 q+3\left(p^{2}-p-1\right) \\
& \mid 3\left(p^{2}-p-1\right)-2 q,
\end{aligned}
$$
waarbij we termen met een factor $p q$ hebben weggegooid. Merk nu op dat $3\left(p^{2}-p-1\right)-2 q \geq$ $3 q-2 q=q>0$. Dat betekent dat de bovenstaande deelrelatie leidt tot
$$
\begin{aligned}
p q & \leq 3\left(p^{2}-p-1\right)-2 q \\
& =3 p^{2}-3 p-(2 q+3) \\
& \leq 3 p^{2}-3 p-p \\
& =3 p^{2}-4 p .
\end{aligned}
$$
Als we $4 p$ naar de andere kant halen en delen door $p$ vinden we dus dat $q+4 \leq 3 p$, oftewel
$$
\frac{2 q+3}{6}<\frac{q+4}{3} \leq p
$$
Aangezien $p$ een deler is van $2 q+3$ leiden we hieruit af dat $2 q+3=k p$ met $k \in\{1,2,3,4,5\}$. Als $k=1$, dan hebben we $2 q+3=p$ en dus ook $q=p^{2}-p-1$. Maar dan zou gelden dat $p=2 q+3=2\left(p^{2}-p-1\right)+3=2 p^{2}-2 p+1$. Dat kunnen we ontbinden als $(2 p-1)(p-1)=0$, wat geen oplossingen heeft met $p$ priem. Als $k=2$ of $k=4$, dan is $k p$ even. Maar $2 q+3$ is oneven, dus die vallen af. Als $k=3$, dan volgt uit $2 q+3=3 p$ dat $q$ een drievoud moet zijn. Omdat $q$ priem is, hebben we dan $q=3$, en dus ook $p=(2 q+3) / 3=3$. Controleren geeft dat dit geen oplossing is van de oorspronkelijke vergelijking.
Het laatste geval is $k=5$. Dan hebben we $5 p=2 q+3$ en wegens de oorspronkelijke vergelijking dus dat $5 q=p^{2}-p-1$. Als we dat invullen, vinden we $25 p=5(2 q+3)=$ $2\left(p^{2}-p-1\right)+15=2 p^{2}-2 p+13$. Dit kunnen we ontbinden als $(p-13)(2 p-1)=0$. Dit geeft als mogelijke oplossing $p=13$ met daarbij $q=(5 p-3) / 2=31$. We controleren dat $(p, q)=(13,31)$ inderdaad een oplossing is van de opgave.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2022-B2022_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2022"
}
|
Given positive real numbers $a_{1}, a_{2}, \ldots, a_{n}$ with $n \geq 2$ for which $a_{1} a_{2} \cdots a_{n}=1$. Prove that
$$
\left(\frac{a_{1}}{a_{2}}\right)^{n-1}+\left(\frac{a_{2}}{a_{3}}\right)^{n-1}+\ldots+\left(\frac{a_{n-1}}{a_{n}}\right)^{n-1}+\left(\frac{a_{n}}{a_{1}}\right)^{n-1} \geq a_{1}^{2}+a_{2}^{2}+\ldots+a_{n}^{2}
$$
and determine when equality holds.
|
We take the arithmetic-mean on $\frac{1}{2} n(n-1)$ terms:
$$
\begin{aligned}
\frac{(n-1)\left(\frac{a_{1}}{a_{2}}\right)^{n-1}+(n-2)\left(\frac{a_{2}}{a_{3}}\right)^{n-1}+\ldots+\left(\frac{a_{n-1}}{a_{n}}\right)^{n-1}}{\frac{1}{2} n(n-1)} & \geq\left(\left(\frac{a_{1}}{a_{2}}\right)^{(n-1)^{2}}\left(\frac{a_{2}}{a_{3}}\right)^{(n-1)(n-2)} \cdots\left(\frac{a_{n-1}}{a_{n}}\right)^{n-1}\right)^{\frac{2}{n(n-1)}} \\
& =\left(\left(\frac{a_{1}}{a_{2}}\right)^{n-1}\left(\frac{a_{2}}{a_{3}}\right)^{n-2} \cdots\left(\frac{a_{n-1}}{a_{n}}\right)\right)^{\frac{2}{n}} \\
& =\left(a_{1}^{n-1} a_{2}^{-1} a_{3}^{-1} \cdots a_{n}^{-1}\right)^{\frac{2}{n}} \\
& =a_{1}^{2}\left(a_{1}^{-1} a_{2}^{-1} a_{2}^{-1} \cdots a_{n}^{-1}\right)^{\frac{2}{n}}
\end{aligned}
$$
Since it is given that $a_{1} a_{2} \cdots a_{n}=1$, this is equal to $a_{1}^{2}$. By cyclically rotating this inequality, we get one inequality for each $a_{i}^{2}$. Adding these $n$ inequalities gives exactly what is required: the right-hand side is clearly $a_{1}^{2}+a_{2}^{2}+\ldots+a_{n}^{2}$, and on the left-hand side, we only have terms of the form $\left(\frac{a_{i}}{a_{i+1}}\right)^{n-1}$, each with a factor $\frac{1}{\frac{1}{2} n(n-1)}((n-1)+(n-2)+\ldots+1)=1$.
Equality holds if and only if equality holds for each of the $n$ inequalities. For each of these $n$ inequalities, equality holds when the $n-1$ different terms are equal. For $n=2$, this is trivially true, so equality holds for all $a_{1}, a_{2}$ with $a_{1} a_{2}=1$. For $n>2$, the equality cases are the cyclic permutations of $\frac{a_{1}}{a_{2}}=\frac{a_{2}}{a_{3}}=\ldots=\frac{a_{n-1}}{a_{n}}$. If we combine two permutations, we get $\frac{a_{1}}{a_{2}}=\frac{a_{2}}{a_{3}}=\ldots=\frac{a_{n}}{a_{1}}=a$ for some positive real $a$, and then the equality also holds for all permutations. The product of all these fractions can be calculated as $a^{n}=\frac{a_{1}}{a_{2}} \frac{a_{2}}{a_{3}} \cdots \frac{a_{n}}{a_{1}}=1$, so $a=1$. We conclude that all $a_{i}$ must be the same. Given the condition, they are all equal to 1.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Gegeven zijn positieve, reële getallen $a_{1}, a_{2}, \ldots, a_{n}$ met $n \geq 2$ waarvoor geldt dat $a_{1} a_{2} \cdots a_{n}=1$. Bewijs dat
$$
\left(\frac{a_{1}}{a_{2}}\right)^{n-1}+\left(\frac{a_{2}}{a_{3}}\right)^{n-1}+\ldots+\left(\frac{a_{n-1}}{a_{n}}\right)^{n-1}+\left(\frac{a_{n}}{a_{1}}\right)^{n-1} \geq a_{1}^{2}+a_{2}^{2}+\ldots+a_{n}^{2}
$$
en bepaal wanneer gelijkheid geldt.
|
We nemen het rekenkundig-meetkundig gemiddelde op $\frac{1}{2} n(n-1)$ termen:
$$
\begin{aligned}
\frac{(n-1)\left(\frac{a_{1}}{a_{2}}\right)^{n-1}+(n-2)\left(\frac{a_{2}}{a_{3}}\right)^{n-1}+\ldots+\left(\frac{a_{n-1}}{a_{n}}\right)^{n-1}}{\frac{1}{2} n(n-1)} & \geq\left(\left(\frac{a_{1}}{a_{2}}\right)^{(n-1)^{2}}\left(\frac{a_{2}}{a_{3}}\right)^{(n-1)(n-2)} \cdots\left(\frac{a_{n-1}}{a_{n}}\right)^{n-1}\right)^{\frac{2}{n(n-1)}} \\
& =\left(\left(\frac{a_{1}}{a_{2}}\right)^{n-1}\left(\frac{a_{2}}{a_{3}}\right)^{n-2} \cdots\left(\frac{a_{n-1}}{a_{n}}\right)\right)^{\frac{2}{n}} \\
& =\left(a_{1}^{n-1} a_{2}^{-1} a_{3}^{-1} \cdots a_{n}^{-1}\right)^{\frac{2}{n}} \\
& =a_{1}^{2}\left(a_{1}^{-1} a_{2}^{-1} a_{2}^{-1} \cdots a_{n}^{-1}\right)^{\frac{2}{n}}
\end{aligned}
$$
Aangezien gegeven is dat $a_{1} a_{2} \cdots a_{n}=1$ is dit gelijk aan $a_{1}^{2}$. Als we deze ongelijkheid cyclisch roteren krijgen we één ongelijkheid voor elke $a_{i}^{2}$. Het optellen van deze $n$ ongelijkheden geeft precies het gevraagde: de rechterkant is duidelijk $a_{1}^{2}+a_{2}^{2}+\ldots+a_{n}^{2}$ en aan de linkerkant krijgen hebben we alleen termen van de vorm $\left(\frac{a_{i}}{a_{i+1}}\right)^{n-1}$ elk met een factor $\frac{1}{\frac{1}{2} n(n-1)}((n-1)+(n-2)+\ldots+1)=1$.
Er geldt gelijkheid dan en slechts dan als er gelijkheid geldt voor elk van de $n$ ongelijkheden. Voor elk van deze $n$ ongelijkheden geldt gelijkheid wanneer de $n-1$ verschillende termen gelijk zijn. Voor $n=2$ is dit triviaal waar, dus geldt er gelijkheid voor alle $a_{1}, a_{2}$ met $a_{1} a_{2}=1$. Voor $n>2$ zijn de gelijkheidsgevallen de cyclische permutaties van $\frac{a_{1}}{a_{2}}=\frac{a_{2}}{a_{3}}=\ldots=\frac{a_{n-1}}{a_{n}}$. Als we twee permutaties combineren krijgen we $\frac{a_{1}}{a_{2}}=\frac{a_{2}}{a_{3}}=\ldots=\frac{a_{n}}{a_{1}}=a$ voor een zekere positieve reële $a$, en dan geldt de gelijkheid ook voor alle permutaties. Het product van al deze breuken kunnen we dan uitrekenen als $a^{n}=\frac{a_{1}}{a_{2}} \frac{a_{2}}{a_{3}} \cdots \frac{a_{n}}{a_{1}}=1$, dus $a=1$. We concluderen dat alle $a_{i}$ hetzelfde moeten zijn. Wegens de voorwaarde zijn ze dan allemaal gelijk aan 1.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2022-B2022_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2022"
}
|
At a fish market, there are 10 stalls, all selling the same 10 types of fish. All the fish are caught in either the North Sea or the Mediterranean Sea, and each stall has only one sea of origin for each type of fish. A number, $k$, of customers buy one fish from each stall such that they have one fish of each type. Furthermore, we know that each pair of customers has at least one fish of a different origin. We consider all possible ways to stock the stalls according to the above rules.
What is the maximum possible value of $k$?
|
The answer is $2^{10}-10$. First, we note that there are $2^{10}$ possible combinations for the origins of each fish species. We will show that there are always at least 10 exceptions (possibilities that are ruled out) and that there is a market setup where there are exactly 10 exceptions.
We order both the stalls and the fish from 1 to 10. For a stall $i$, we define the sequence $a_{i} \in\{M, N\}^{10}$ as the origins of the 10 fish species in this stall (for example, $a_{1}=(M, M, M, N, M, N, N, M, M, M)$). Let $c_{i}$ be the complement of this sequence: we replace all $M$ with $N$ and vice versa. Since every customer has bought a fish from stall $i$, no customer can have the sequence $c_{i}$. If the sequences $c_{i}$ with $1 \leq i \leq 10$ are all different, then we have 10 exceptions.
On the other hand, suppose that stalls $i$ and $j$ sell fish from exactly the same seas, i.e., $a_{i}=a_{j}$. Then also $c_{i}=c_{j}$. We define the sequences $d_{k}$ with $1 \leq k \leq 10$ by swapping the origin of fish $k$ in the sequence $c_{i}$. These are precisely the sequences that match the sequence $a_{i}=a_{j}$ in exactly one sea. If a customer has bought a sequence $d_{k}$, then there can be at most one fish from stall $i$ or $j$ in that sequence. This contradicts the fact that the customer has bought a fish from both stalls. We conclude that in this case, we also have at least 10 exceptions $d_{k}$ (and in fact also $c_{i}$).
We construct a market as follows where you can buy $2^{10}-10$ different combinations of fish origins as described in the problem: stall $i$ sells only fish from the North Sea, with the exception of fish $i$ from the Mediterranean Sea. Let $b \in\{M, N\}^{10}$ be a sequence of origins such that it does not contain exactly one $N$. We will show that we can buy 10 different fish from 10 different stalls so that $b$ is the sequence of origins. We split the fish in $b$ into a set $A$ from the Mediterranean Sea and a set $B$ from the North Sea, that is, $A$ is the set of indices where $b$ has an $M$ and $B$ is the set of indices where $b$ has an $N$. For $i \in A$, we buy fish species $i$ from stall $i$, so we indeed get a fish from the Mediterranean Sea. If $B$ is empty, then we are done. Otherwise, $B$ has at least two elements, and we write $B=\left\{i_{1}, \ldots, i_{n}\right\} \subset\{1, \ldots, 10\}$. For $i_{k} \in B$, we buy fish species $i_{k}$ from stall $i_{k+1}$, where we compute the indices modulo $n$. Since $n \neq 1$, it holds that $i_{k+1} \neq i_{k}$, so this fish indeed comes from the North Sea.
|
2^{10}-10
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Op een vismarkt staan 10 kraampjes die allemaal dezelfde 10 vissoorten verkopen. Alle vissen zijn gevangen in de Noordzee of de Middellandse Zee, en elk kraampje heeft per vissoort maar één zee van afkomst. Een aantal, $k$, klanten koopt van elk kraampje één vis zo dat ze één vis van elke soort hebben. Verder weten we dat elk tweetal klanten een vissoort hebben met verschillende afkomst. We beschouwen alle mogelijke manieren om de kraampjes te vullen volgens de bovenstaande spelregels.
Wat is de maximaal mogelijke waarde van $k$ ?
|
Het antwoord is $2^{10}-10$. Ten eerste merken we op dat er $2^{10}$ mogelijke combinaties zijn voor de afkomsten per vissoort. We gaan laten zien dat er altijd minstens 10 uitzonderingen zijn (mogelijkheden die afvallen) en dat er een marktopzet is waarbij er precies 10 uitzonderingen zijn.
We ordenen zowel de kraampjes als de vissen van 1 tot 10. Voor een kraampje $i$ definiëren we het rijtje $a_{i} \in\{M, N\}^{10}$ als de afkomsten van de 10 vissoorten in dit kraampje (bijvoorbeeld $a_{1}=(M, M, M, N, M, N, N, M, M, M)$ ). Zij $c_{i}$ het complement van dit rijtje: we vervangen alle $M$ door $N$ en vice versa. Aangezien elke klant een vis heeft gekocht van kraampje $i$ kan geen enkele klant het rijtje $c_{i}$ hebben. Als de rijtjes $c_{i}$ met $1 \leq i \leq 10$ allemaal verschillend zijn, dan hebben we dus 10 uitzonderingen.
Stel aan de andere kant dat kraampjes $i$ en $j$ vissen van precies dezelfde zeeën verkopen, oftewel $a_{i}=a_{j}$. Dan ook $c_{i}=c_{j}$. Dan definiëren we de rijtjes $d_{k}$ met $1 \leq k \leq 10$ door in het rijtje $c_{i}$ de afkomst van vis $k$ te wisselen. Dit zijn precies de rijtjes die één zee overeenkomstig hebben met het rijtje $a_{i}=a_{j}$. Als een klant een rijtje $d_{k}$ heeft ingekocht, dan kan daar dus maximaal één vis tussen zitten van kraampje $i$ of $j$. Dit is in tegenspraak met het feit dat de klant bij beide kraampjes een vis heeft gekocht. We concluderen dat we in dat geval ook minstens 10 uitzonderingen $d_{k}$ hebben (en in feite ook nog $c_{i}$ ).
We construeren als volgt een markt waar je $2^{10}-10$ verschillende combinaties van afkomsten van vissen kan kopen zoals in de opgave: kraampje $i$ verkoopt alleen vis uit de Noordzee met uitzondering van vis $i$ uit de Middellandse Zee. Zij $b \in\{M, N\}^{10}$ een rijtje afkomsten zo dat er niet precies één $N$ in voorkomt. We gaan laten zien dat we 10 verschillende vissen van 10 verschillende kraampjes kunnen kopen zo dat $b$ het rijtje afkomsten is. We splitsen de vissen in $b$ op in een verzameling $A$ uit de Middellandse Zee en een verzameling $B$ uit de Noordzee, dat wil zeggen $A$ is de verzameling indices waar in $b$ een $M$ staat en $B$ is de verzameling indices waar een $N$ staat. Voor $i \in A$ kopen we vissoort $i$ bij kraampje $i$, zodat we inderdaad een vis uit de Middellandse Zee krijgen. Als $B$ leeg is, dan zijn we klaar. Anders heeft $B$ minstens twee elementen en schrijven we $B=\left\{i_{1}, \ldots, i_{n}\right\} \subset\{1, \ldots, 10\}$. Voor $i_{k} \in B$ kopen we vissoort $i_{k}$ bij kraampje $i_{k+1}$, waarbij we de indices modulo $n$ rekenen. Omdat $n \neq 1$ geldt dat $i_{k+1} \neq i_{k}$, dus deze vis komt inderdaad uit de Noordzee.
|
{
"exam": "Dutch_TST",
"problem_label": "5",
"problem_match": "\nOpgave 5.",
"resource_path": "Dutch_TST/segmented/nl-2022-B2022_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2022"
}
|
Determine all positive integers $n \geq 2$ for which there exists a positive divisor $m \mid n$ such that
$$
n=d^{3}+m^{3},
$$
where $d$ is the smallest divisor of $n$ greater than 1.
|
The smallest divisor of $n$ greater than 1 is the smallest prime that is a divisor of $n$, so $d$ is prime. Furthermore, $d \mid n$, so $d \mid d^{3}+m^{3}$, thus $d \mid m^{3}$. This implies that $m>1$. On the other hand, $m \mid n$, so $m \mid d^{3}+m^{3}$, thus $m \mid d^{3}$. Since $d$ is prime and $m>1$, we see that $m$ is equal to $d, d^{2}$, or $d^{3}$.
In all cases, the parity of $m^{3}$ is the same as that of $d^{3}$, so $n=d^{3}+m^{3}$ is even. This means that the smallest divisor of $n$ greater than 1 is equal to 2, so $d=2$. We now find the possible solutions: in the case $m=d$, the number $n=2^{3}+2^{3}=16$; in the case $m=d^{2}$, the number $n=2^{3}+2^{6}=72$; and in the case $m=d^{3}$, the number $n=2^{3}+2^{9}=520$. These indeed satisfy the conditions: they are even, so $d=2$, and $2|16 ; 4| 72$ and $8 \mid 520$, so $m \mid n$.
|
16, 72, 520
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Bepaal alle positieve gehele getallen $n \geq 2$ waarvoor er een positieve deler $m \mid n$ bestaat met
$$
n=d^{3}+m^{3},
$$
waarbij $d$ de kleinste deler van $n$ groter dan 1 is.
|
De kleinste deler van $n$ groter dan 1 is het kleinste priemgetal dat een deler is dan $n$, dus $d$ is priem. Verder geldt dat $d \mid n$, dus $d \mid d^{3}+m^{3}$, dus $d \mid m^{3}$. Hieruit volgt dat $m>1$. Anderzijds is $m \mid n$, dus $m \mid d^{3}+m^{3}$, dus $m \mid d^{3}$. Omdat $d$ priem is en $m>1$, zien we nu dat $m$ gelijk is aan $d, d^{2}$ of $d^{3}$.
In alle gevallen is de pariteit van $m^{3}$ hetzelfde als die van $d^{3}$, dus $n=d^{3}+m^{3}$ is even. Dat betekent dat de kleinste deler van $n$ groter dan 1 gelijk is aan 2 , dus $d=2$. We vinden nu als mogelijke oplossingen in geval $m=d$ het getal $n=2^{3}+2^{3}=16$, in geval $m=d^{2}$ het getal $n=2^{3}+2^{6}=72$, en in geval $m=d^{3}$ het getal $n=2^{3}+2^{9}=520$. Deze voldoen daadwerkelijk: ze zijn even zodat inderdaad $d=2$, en $2|16 ; 4| 72$ en $8 \mid 520$, zodat inderdaad $m \mid n$.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2022-C2022_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2022"
}
|
Given are two circles $\Gamma_{1}$ and $\Gamma_{2}$ with centers $O_{1}$ and $O_{2}$ and common external tangents $\ell_{1}$ and $\ell_{2}$. The line $\ell_{1}$ is tangent to $\Gamma_{1}$ at $A$ and to $\Gamma_{2}$ at $B$. Let $X$ be a point on the segment $O_{1} O_{2}$, but not on $\Gamma_{1}$ or $\Gamma_{2}$. The segment $A X$ intersects $\Gamma_{1}$ at $Y \neq A$ and the segment $B X$ intersects $\Gamma_{2}$ at $Z \neq B$.
Prove that the tangent line at $Y$ to $\Gamma_{1}$ and the tangent line at $Z$ to $\Gamma_{2}$ intersect on $\ell_{2}$.
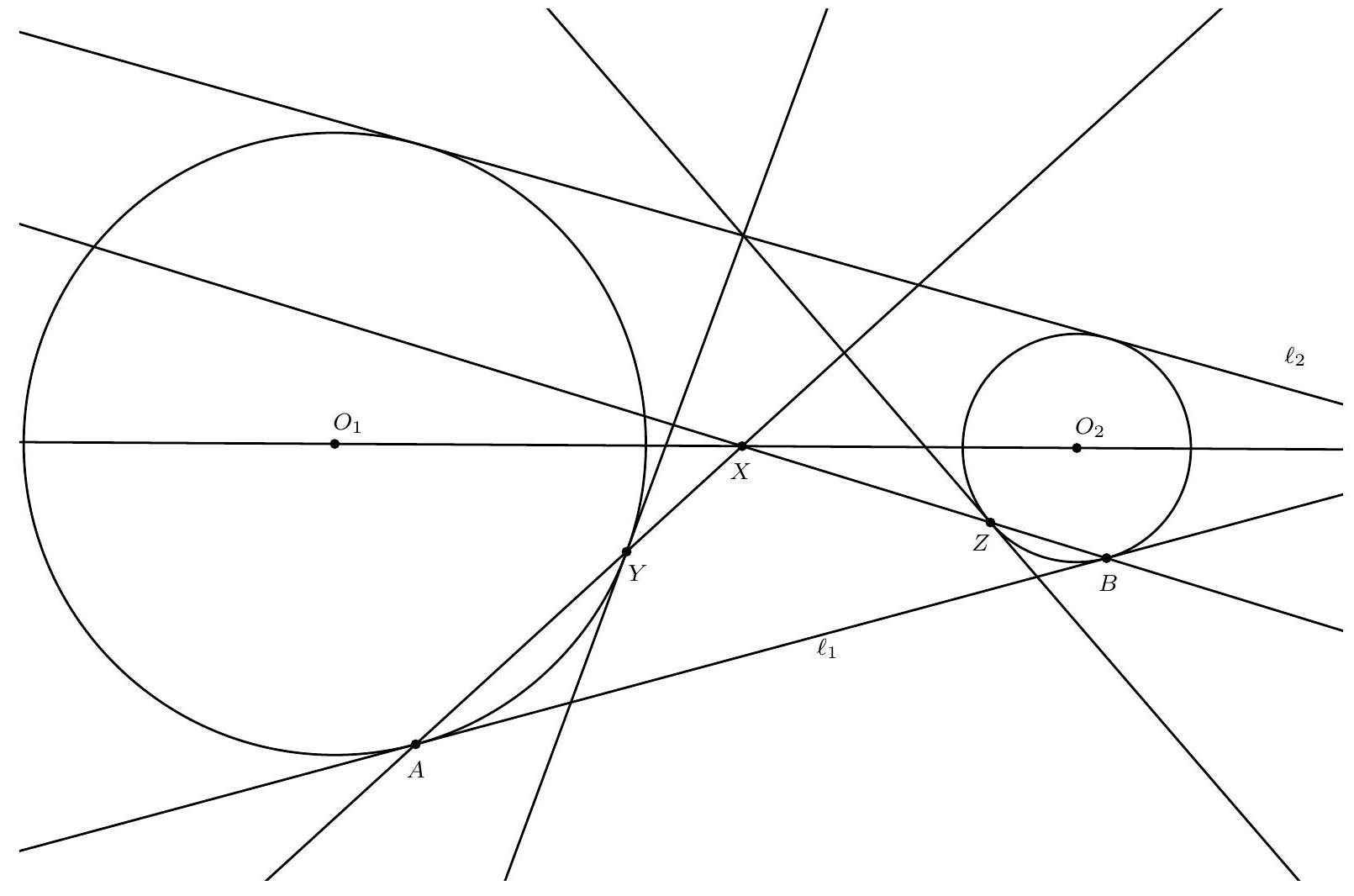
|
We consider the configuration where $Y$ lies between $A$ and $X$; other configurations proceed analogously. Let $C$ be the point of tangency of $\ell_{2}$ with $\Gamma_{1}$. Then $C$ is the reflection of $A$ in $O_{1} O_{2}$. We have
$$
\begin{array}{rrr}
\angle O_{1} Y X & =180^{\circ}-\angle O_{1} Y A & \text { (straight angle) } \\
& =180^{\circ}-\angle Y A O_{1} & \text { (isosceles triangle } \left.O_{1} Y A\right) \\
& =180^{\circ}-\angle X A O_{1} & \\
& =180^{\circ}-\angle X C O_{1} & \left(A \text { and } C \text { are reflections of each other in } O_{1} X\right)
\end{array}
$$
which implies that $O_{1} C X Y$ is a cyclic quadrilateral.
Now let $S$ be the intersection of the tangent to $\Gamma_{1}$ at $Y$ and $\ell_{2}$. Then both $S C$ and $S Y$ are tangent to $\Gamma_{1}$, so $\angle S C O_{1}=90^{\circ}=\angle S Y O_{1}$, hence $O_{1} C S Y$ is a cyclic quadrilateral.
We see that both $X$ and $S$ lie on the circle through $O_{1}, C$ and $Y$. Therefore, $\angle S X O_{1}=$ $\angle S Y O_{1}=90^{\circ}$. We conclude that $S X$ is perpendicular to $O_{1} O_{2}$. Analogously, for the intersection $S^{\prime}$ of the tangent to $\Gamma_{2}$ at $Z$ and $\ell_{2}$, we can deduce that $S^{\prime} X$ is perpendicular to $O_{1} O_{2}$. Since $S$ and $S^{\prime}$ both lie on $\ell_{2}$, it follows that $S=S^{\prime}$. Thus, the two tangents intersect on $\ell_{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Gegeven zijn twee cirkels $\Gamma_{1}$ en $\Gamma_{2}$ met middelpunten $O_{1}$ en $O_{2}$ en gemeenschappelijke uitwendige raaklijnen $\ell_{1}$ en $\ell_{2}$. De lijn $\ell_{1}$ raakt $\Gamma_{1}$ in $A$ en $\Gamma_{2}$ in $B$. Zij $X$ een punt op het lijnstuk $O_{1} O_{2}$, maar niet op $\Gamma_{1}$ of $\Gamma_{2}$. Het lijnstuk $A X$ snijdt $\Gamma_{1}$ in $Y \neq A$ en het lijnstuk $B X$ snijdt $\Gamma_{2}$ in $Z \neq B$.
Bewijs dat de raaklijn in $Y$ aan $\Gamma_{1}$ en de raaklijn in $Z$ aan $\Gamma_{2}$ elkaar snijden op $\ell_{2}$.

|
We bekijken de configuratie waarbij $Y$ tussen $A$ en $X$ ligt; andere configuraties gaan analoog. Zij $C$ het raakpunt van $\ell_{2}$ aan $\Gamma_{1}$. Dan is $C$ de spiegeling van $A$ in $O_{1} O_{2}$. Er geldt
$$
\begin{array}{rrr}
\angle O_{1} Y X & =180^{\circ}-\angle O_{1} Y A & \text { (gestrekte hoek) } \\
& =180^{\circ}-\angle Y A O_{1} & \text { (gelijkbenige driehoek } \left.O_{1} Y A\right) \\
& =180^{\circ}-\angle X A O_{1} & \\
& =180^{\circ}-\angle X C O_{1} & \left(A \text { en } C \text { elkaars gespiegelde in } O_{1} X\right)
\end{array}
$$
waaruit volgt dat $O_{1} C X Y$ een koordenvierhoek is.
Noem nu $S$ het snijpunt van de raaklijn aan $\Gamma_{1}$ in $Y$ en $\ell_{2}$. Dan raakt zowel $S C$ als $S Y$ aan $\Gamma_{1}$, dus geldt $\angle S C O_{1}=90^{\circ}=\angle S Y O_{1}$, dus $O_{1} C S Y$ is een koordenvierhoek.
We zien dat zowel $X$ als $S$ op de cirkel door $O_{1}, C$ en $Y$ ligt. Er geldt dus $\angle S X O_{1}=$ $\angle S Y O_{1}=90^{\circ}$. We concluderen dat $S X$ loodrecht op $O_{1} O_{2}$ staat. Analoog kunnen we nu voor het snijpunt $S^{\prime}$ van de raaklijn aan $\Gamma_{2}$ in $Z$ en $\ell_{2}$ afleiden dat $S^{\prime} X$ loodrecht op $O_{1} O_{2}$ staat. Aangezien $S$ en $S^{\prime}$ ook beide op $\ell_{2}$ liggen, geldt $S=S^{\prime}$. Dus de twee raaklijnen snijden elkaar op $\ell_{2}$.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2022-C2022_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2022"
}
|
For real numbers $x$ and $y$, we define $M(x, y)$ as the maximum of the three numbers $x y, (x-1)(y-1)$, and $x+y-2 x y$. Determine the smallest possible value of $M(x, y)$ over all real numbers $x$ and $y$ with $0 \leq x, y \leq 1$.
|
We show that the minimum value is $\frac{4}{9}$. This value can be achieved by taking $x=y=\frac{2}{3}$. Then we have $x y=\frac{4}{9}, (x-1)(y-1)=\frac{1}{9}$, and $x+y-2 x y=\frac{4}{9}$, so the maximum is indeed $\frac{4}{9}$.
Now we will prove that $M(x, y) \geq \frac{4}{9}$ for all $x$ and $y$. Let $a=x y, b=(x-1)(y-1)$, and $c=x+y-2 x y$. If we replace $x$ and $y$ with $1-x$ and $1-y$, then $a$ and $b$ are swapped and $c$ remains the same, because $(1-x)+(1-y)-2(1-x)(1-y)=2-x-y-2+2 x+2 y-2 x y=x+y-2 x y$. Thus, $M(1-x, 1-y)=M(x, y)$. We have $x+y=2-(1-x)-(1-y)$, so at least one of $x+y$ and $(1-x)+(1-y)$ is greater than or equal to 1, which means we can assume without loss of generality that $x+y \geq 1$.
Now write $x+y=1+t$ with $t \geq 0$. We also have $t \leq 1$, because $x, y \leq 1$ so $x+y \leq 2$. From the inequality of the arithmetic and geometric means, we get
$$
x y \leq\left(\frac{x+y}{2}\right)^{2}=\frac{(1+t)^{2}}{4}=\frac{t^{2}+2 t+1}{4}
$$
We have $b=x y-x-y+1=x y-(1+t)+1=x y-t=a-t$, so $b \leq a$. Furthermore,
$$
c=x+y-2 x y \geq(1+t)-2 \cdot \frac{t^{2}+2 t+1}{4}=\frac{2+2 t}{2}-\frac{t^{2}+2 t+1}{2}=\frac{1-t^{2}}{2}.
$$
If $t \leq \frac{1}{3}$, then $c \geq \frac{1-t^{2}}{2} \geq \frac{1-\frac{1}{9}}{2}=\frac{4}{9}$, and thus $M(x, y) \geq \frac{4}{9}$.
The remaining case is $t>\frac{1}{3}$. We have $c=x+y-2 x y=1+t-2 a>\frac{4}{3}-2 a$. We have $M(x, y) \geq \max \left(a, \frac{4}{3}-2 a\right)$, so
$$
3 M(x, y) \geq a+a+\left(\frac{4}{3}-2 a\right)=\frac{4}{3},
$$
which implies that $M(x, y) \geq \frac{4}{9}$.
We conclude that the minimum value of $M(x, y)$ is $\frac{4}{9}$.
|
\frac{4}{9}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Voor reële getallen $x$ en $y$ definiëren we $M(x, y)$ als het maximum van de drie getallen $x y,(x-1)(y-1)$ en $x+y-2 x y$. Bepaal de kleinst mogelijke waarde van $M(x, y)$ over alle reële getallen $x$ en $y$ met $0 \leq x, y \leq 1$.
|
We laten zien dat de minimale waarde $\frac{4}{9}$ is. Deze waarde kan bereikt worden door $x=y=\frac{2}{3}$ te nemen. Dan geldt $x y=\frac{4}{9},(x-1)(y-1)=\frac{1}{9}$ en $x+y-2 x y=\frac{4}{9}$, dus dan is het maximum inderdaad $\frac{4}{9}$.
Nu gaan we bewijzen dat $M(x, y) \geq \frac{4}{9}$ voor alle $x$ en $y$. Schrijf $a=x y, b=(x-1)(y-1)$ en $c=x+y-2 x y$. Als we $x$ en $y$ vervangen door $1-x$ en $1-y$, dan worden $a$ en $b$ verwisseld en blijft $c$ gelijk, omdat $(1-x)+(1-y)-2(1-x)(1-y)=2-x-y-2+2 x+2 y-2 x y=x+y-2 x y$. Dus $M(1-x, 1-y)=M(x, y)$. Er geldt $x+y=2-(1-x)-(1-y)$, dus minstens één $\operatorname{van} x+y$ en $(1-x)+(1-y)$ is groter of gelijk aan 1 , wat betekent dat we zonder verlies van algemeemheid mogen aannemen dat $x+y \geq 1$.
Schrijf nu $x+y=1+t$ met $t \geq 0$. Er geldt ook $t \leq 1$, want $x, y \leq 1$ dus $x+y \leq 2$. Uit de ongelijkheid van het rekenkundig en meetkundig gemiddelde volgt
$$
x y \leq\left(\frac{x+y}{2}\right)^{2}=\frac{(1+t)^{2}}{4}=\frac{t^{2}+2 t+1}{4}
$$
Er geldt $b=x y-x-y+1=x y-(1+t)+1=x y-t=a-t$, dus $b \leq a$. Verder is
$$
c=x+y-2 x y \geq(1+t)-2 \cdot \frac{t^{2}+2 t+1}{4}=\frac{2+2 t}{2}-\frac{t^{2}+2 t+1}{2}=\frac{1-t^{2}}{2} .
$$
Als nu $t \leq \frac{1}{3}$, dan geldt $c \geq \frac{1-t^{2}}{2} \geq \frac{1-\frac{1}{9}}{2}=\frac{4}{9}$ en dus ook $M(x, y) \geq \frac{4}{9}$.
Blijft over het geval $t>\frac{1}{3}$. Er geldt $c=x+y-2 x y=1+t-2 a>\frac{4}{3}-2 a$. Er geldt $M(x, y) \geq \max \left(a, \frac{4}{3}-2 a\right)$, dus
$$
3 M(x, y) \geq a+a+\left(\frac{4}{3}-2 a\right)=\frac{4}{3},
$$
waaruit volgt dat $M(x, y) \geq \frac{4}{9}$.
We concluderen dat de minimale waarde van $M(x, y)$ gelijk is aan $\frac{4}{9}$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2022-C2022_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2022"
}
|
For real numbers $x$ and $y$, we define $M(x, y)$ as the maximum of the three numbers $x y, (x-1)(y-1)$, and $x+y-2 x y$. Determine the smallest possible value of $M(x, y)$ over all real numbers $x$ and $y$ with $0 \leq x, y \leq 1$.
|
We show that the minimum value is $\frac{4}{9}$. Just like in the first solution, we see that this value can be achieved by taking $x=y=\frac{2}{3}$. Now we will prove that $M(x, y) \geq \frac{4}{9}$ for all $x$ and $y$. We do this by comparing the level curves on which the expressions $x y$, $(1-x)(1-y)$, and $x+y-2 x y$ take the value $\frac{4}{9}$.
First, we consider the case $0 \leq x<\frac{1}{2}$. Note that in this case $1-2 x>0$. If $(1-x)(1-y) \geq \frac{4}{9}$, then we are done. Suppose now that $(1-x)(1-y)<\frac{4}{9}$. Then $1-y<\frac{\frac{4}{9}}{1-x}$, so $y>1-\frac{\frac{4}{9}}{1-x}$. We now show that $1-\frac{\frac{4}{9}}{1-x} \geq \frac{\frac{4}{9}-x}{1-2 x}$. Since the denominators are positive, it suffices to prove that $\left(1-x-\frac{4}{9}\right)(1-2 x) \geq\left(\frac{4}{9}-x\right)(1-x)$, or equivalently $2 x^{2}-\frac{19}{9} x+\frac{5}{9} \geq x^{2}-\frac{13}{9} x+\frac{4}{9}$, which simplifies to $x^{2}-\frac{2}{3} x+\frac{1}{9} \geq 0$. The left side is $\left(x-\frac{1}{3}\right)^{2}$, which proves this inequality and thus the desired inequality. Now we are done, because from $y>1-\frac{\frac{4}{9}}{1-x}$ it follows that $y>\frac{\frac{4}{9}-x}{1-2 x}$, so $y(1-2 x)>\frac{4}{9}-x$, or equivalently $x+y-2 x y>\frac{4}{9}$. Therefore, in any case, $M(x, y) \geq \frac{4}{9}$.
If $x=\frac{1}{2}$, then $x+y-2 x y=\frac{1}{2}+y-2 \cdot \frac{1}{2} y=\frac{1}{2}>\frac{4}{9}$.
Finally, we consider the case $\frac{1}{2}<x \leq 1$. Note that in this case $2 x-1>0$. If $x y \geq \frac{4}{9}$, then we are done. Suppose now that $x y<\frac{4}{9}$. Then $y<\frac{\frac{4}{9}}{x}$. We now show that $\frac{\frac{4}{9}}{x} \leq \frac{x-\frac{4}{9}}{2 x-1}$. For this, it suffices to show that $\frac{4}{9}(2 x-1) \leq x\left(x-\frac{4}{9}\right)$, or equivalently $\frac{8}{9} x-\frac{4}{9} \leq x^{2}-\frac{4}{9} x$, which simplifies to $0 \leq x^{2}-\frac{4}{3} x+\frac{4}{9}$. The right side is $\left(x-\frac{2}{3}\right)^{2}$, which proves this inequality and thus the desired inequality. Now we are done, because from $y<\frac{x-\frac{4}{9}}{2 x-1}$ it follows that $y(2 x-1)<x-\frac{4}{9}$, or equivalently $x+y-2 x y>\frac{4}{9}$. Therefore, in any case, $M(x, y) \geq \frac{4}{9}$.
|
\frac{4}{9}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Voor reële getallen $x$ en $y$ definiëren we $M(x, y)$ als het maximum van de drie getallen $x y,(x-1)(y-1)$ en $x+y-2 x y$. Bepaal de kleinst mogelijke waarde van $M(x, y)$ over alle reële getallen $x$ en $y$ met $0 \leq x, y \leq 1$.
|
We laten zien dat de minimale waarde $\frac{4}{9}$ is. Net als in de eerste oplossing zien we dat deze waarde bereikt kan worden door $x=y=\frac{2}{3}$ te nemen. Nu gaan we bewijzen dat $M(x, y) \geq \frac{4}{9}$ voor alle $x$ en $y$. Dit doen we in feite door de niveaukrommen te vergelijken waarop de uitdrukkingen $x y,(1-x)(1-y)$ respectievelijk $x+y-2 x y$ de waarde $\frac{4}{9}$ aannemen.
We bekijken eerst het geval $0 \leq x<\frac{1}{2}$. Merk op dat nu geldt dat $1-2 x>0$. Als $(1-x)(1-y) \geq \frac{4}{9}$, dan zijn we klaar. Stel nu dat $(1-x)(1-y)<\frac{4}{9}$. Dan geldt $1-y<\frac{\frac{4}{9}}{1-x}$, dus $y>1-\frac{\frac{4}{9}}{1-x}$. We laten nu zien dat $1-\frac{\frac{4}{9}}{1-x} \geq \frac{\frac{4}{9}-x}{1-2 x}$. Omdat de noemers positief zijn, is het voldoende om te bewijzen dat $\left(1-x-\frac{4}{9}\right)(1-2 x) \geq\left(\frac{4}{9}-x\right)(1-x)$, oftewel $2 x^{2}-\frac{19}{9} x+\frac{5}{9} \geq x^{2}-\frac{13}{9} x+\frac{4}{9}$, wat neerkomt op $x^{2}-\frac{2}{3} x+\frac{1}{9} \geq 0$. Aan de linkerkant staat $\left(x-\frac{1}{3}\right)^{2}$, waarmee deze ongelijkheid en dus ook de gevraagde ongelijkheid bewezen is. Nu zijn we klaar, want hieruit volgt wegens $y>1-\frac{\frac{4}{9}}{1-x}$ dat $y>\frac{\frac{4}{9}-x}{1-2 x}$, dus $y(1-2 x)>\frac{4}{9}-x$, oftewel $x+y-2 x y>\frac{4}{9}$. Dus hoe dan ook geldt $M(x, y) \geq \frac{4}{9}$.
Als $x=\frac{1}{2}$, dan is $x+y-2 x y=\frac{1}{2}+y-2 \cdot \frac{1}{2} y=\frac{1}{2}>\frac{4}{9}$.
We bekijken ten slotte het geval $\frac{1}{2}<x \leq 1$. Merk op dat nu juist geldt dat $2 x-1>0$. Als $x y \geq \frac{4}{9}$, dan zijn we klaar. Stel nu dat $x y<\frac{4}{9}$. Dan geldt $y<\frac{\frac{4}{9}}{x}$. We laten nu zien dat $\frac{\frac{4}{9}}{x} \leq \frac{x-\frac{4}{9}}{2 x-1}$. Hiervoor is het voldoende om te laten zien dat $\frac{4}{9}(2 x-1) \leq x\left(x-\frac{4}{9}\right)$, oftewel $\frac{8}{9} x-\frac{4}{9} \leq x^{2}-\frac{4}{9} x$, wat neerkomt op $0 \leq x^{2}-\frac{4}{3} x+\frac{4}{9}$. Aan de rechterkant staat $\left(x-\frac{2}{3}\right)^{2}$, waarmee deze ongelijkheid en dus ook de gevraagde ongelijkheid bewezen is. Nu zijn we klaar, want hieruit volgt dat $y<\frac{x-\frac{4}{9}}{2 x-1}$, dus $y(2 x-1)<x-\frac{4}{9}$, oftewel $x+y-2 x y>\frac{4}{9}$. Dus ook nu geldt hoe dan ook $M(x, y) \geq \frac{4}{9}$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2022-C2022_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2022"
}
|
In a sequence of numbers $a_{1}, a_{2}, \ldots, a_{1000}$ consisting of 1000 different numbers, a pair $\left(a_{i}, a_{j}\right)$ with $i<j$ is called increasing if $a_{i}<a_{j}$ and decreasing if $a_{i}>a_{j}$. Determine the largest positive integer $k$ with the property that in any sequence of 1000 different numbers, there are at least $k$ non-overlapping increasing pairs or at least $k$ non-overlapping decreasing pairs.
|
We will prove that the largest $k$ is equal to 333. First, consider the sequence $1000, 999, 998, \ldots, 669, 668, 1, 2, 3, \ldots, 666, 667$. The first 333 numbers in the sequence are not usable in an increasing pair, because for each of these numbers, only larger numbers are to the left and only smaller numbers are to the right. Therefore, only the last 667 numbers are available for increasing pairs, and this yields at most 333 non-overlapping increasing pairs. For a decreasing pair $\left(a_{i}, a_{j}\right)$ with $i<j$, $a_{i}$ cannot be one of the numbers from 1 to 667, because for each of these numbers, only larger numbers are to the right. Thus, $a_{i}$ must be one of the first 333 numbers, which means there are at most 333 non-overlapping decreasing pairs. We conclude that $k>333$ cannot be satisfied.
Now we prove that for all $t \geq 1$, in a sequence of $3t-1$ different numbers, there are always at least $t$ non-overlapping increasing pairs or $t$ non-overlapping decreasing pairs. We prove this by induction on $t$. For $t=1$, the sequence has length 2, and this pair of numbers is either increasing or decreasing, so it holds. Now let $r \geq 1$ and assume the statement is true for $t=r$. We now consider $t=r+1$ and take an arbitrary sequence $a_{1}, a_{2}, \ldots, a_{3r+2}$ with $3r+2$ different numbers. If the sequence is completely increasing, we can divide the sequence into adjacent pairs, all of which are increasing. There are $\left\lfloor\frac{3r+2}{2}\right\rfloor \geq \frac{2r+2}{2}=r+1$ such pairs. If the sequence is completely decreasing, there are analogously at least $r+1$ decreasing pairs. If the sequence is neither completely increasing nor completely decreasing, there is a point in the sequence where it first increases and then decreases, or vice versa, i.e., there are numbers $a_{i}, a_{i+1}, a_{i+2}$ in the sequence with $a_{i}<a_{i+1}>a_{i+2}$ or $a_{i}>a_{i+1}<a_{i+2}$. In both cases, among these three numbers, there is both an increasing pair and a decreasing pair. Now apply the induction hypothesis to the sequence $a_{1}, a_{2}, \ldots, a_{i-1}, a_{i+3}, a_{i+4}, \ldots, a_{3r+2}$. This is a sequence with $3r+2-3=3r-1$ different numbers, so there are $r$ non-overlapping increasing pairs or $r$ non-overlapping decreasing pairs. In the first case, we add the increasing pair from $a_{i}, a_{i+1}, a_{i+2}$ to these, and in the second case, we add the decreasing pair. This gives us $r+1$ non-overlapping increasing pairs or $r+1$ non-overlapping decreasing pairs. This completes the induction.
Now substitute $t=333$ into this result: in a sequence of 998 different numbers, there are always at least 333 non-overlapping increasing pairs or at least 333 non-overlapping decreasing pairs. This also holds for a sequence of 1000 numbers (ignore the last two numbers in the sequence). Therefore, $k=333$ satisfies the condition and is thus the largest $k$ that satisfies it.
|
333
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In een getallenrij $a_{1}, a_{2}, \ldots, a_{1000}$ van 1000 verschillende getallen heet een paar $\left(a_{i}, a_{j}\right)$ met $i<j$ stijgend als $a_{i}<a_{j}$ en dalend als $a_{i}>a_{j}$. Bepaal de grootste positieve gehele $k$ met de eigenschap dat in elke rij van 1000 verschillende getallen ten minste $k$ niet-overlappende stijgende paren te vinden zijn of ten minste $k$ niet-overlappende dalende paren.
|
We gaan bewijzen dat de grootste $k$ gelijk aan 333 is. Bekijk ten eerste de rij $1000,999,998, \ldots, 669,668,1,2,3, \ldots, 666,667$. De eerste 333 getallen in de rij zijn niet bruikbaar in een stijgend paar, omdat voor elk van deze getallen geldt dat links van dit getal alleen maar grotere getallen staan en rechts van dit getal alleen maar kleinere getallen. Voor de stijgende paren zijn dus alleen de laatste 667 getallen beschikbaar en dat levert hooguit 333 niet-overlappende stijgende paren op. Voor een dalend paar $\left(a_{i}, a_{j}\right)$ met $i<j$ geldt dat $a_{i}$ niet één van de getallen 1 tot en met 667 kan zijn, want voor elk van deze getallen geldt dat er rechts van dit getal alleen maar grotere getallen staan. Dus $a_{i}$ moet één van de eerste 333 getallen zijn, waaruit volgt dat er hooguit 333 niet-overlappende dalende paren zijn. We concluderen dat $k>333$ niet kan voldoen.
Nu bewijzen we voor alle $t \geq 1$ dat er in een getallenrij van $3 t-1$ verschillende getallen altijd minstens $t$ niet-overlappende stijgende paren of $t$ niet-overlappende dalende paren te vinden zijn. We bewijzen dit met inductie naar $t$. Voor $t=1$ geldt dat de getallenrij lengte 2 heeft en dit paar getallen is ofwel stijgend ofwel dalend, dus het klopt. Zij nu $r \geq 1$ en veronderstel dat de bewering waar is voor $t=r$. We bekijken nu $t=r+1$ en nemen een willekeurige getallenrij $a_{1}, a_{2}, \ldots, a_{3 r+2}$ met $3 r+2$ verschillende getallen. Als de rij volledig stijgend is, dan kunnen we de rij opdelen in buurparen en die zijn allemaal stijgend. Dit zijn er $\left\lfloor\frac{3 r+2}{2}\right\rfloor \geq \frac{2 r+2}{2}=r+1$. Als de rij volledig dalend is, zijn er analoog minstens $r+1$ dalende paren. Als de rij niet volledig stijgend, maar ook niet volledig dalend is, dan is er een plek in de rij waar de rij eerst stijgt en dan daalt of andersom, oftewel: er zijn getallen $a_{i}, a_{i+1}, a_{i+2}$ in de rij met $a_{i}<a_{i+1}>a_{i+2}$ of $a_{i}>a_{i+1}<a_{i+2}$. In beide gevallen zit er in deze drie getallen zowel een stijgend paar als een dalend paar. Pas nu de inductiehypothese toe op de rij $a_{1}, a_{2}, \ldots, a_{i-1}, a_{i+3}, a_{i+4}, \ldots, a_{3 r+2}$. Dit is een rij met $3 r+2-3=3 r-1$ verschillende getallen, dus zijn er $r$ niet-overlappende stijgende paren te vinden of $r$ niet-overlappende dalende paren. In het eerste geval voegen we hier het stijgende paar uit $a_{i}, a_{i+1}, a_{i+2}$ aan toe en in het tweede geval juist het dalende paar. Daarmee hebben we dan $r+1$ niet-overlappende stijgende paren of $r+1$ niet-overlappende dalende paren gevonden. Dat voltooit de inductie.
Vul nu $t=333$ in dit resultaat in: in een rij van 998 verschillende getallen zijn altijd minstens 333 niet-overlappende stijgende paren of minstens 333 niet-overlappende dalende paren te vinden. In een rij van 1000 getallen geldt dit dus ook (negeer de laatste twee getallen in de rij). Dus $k=333$ voldoet en is daarmee de grootste $k$ die voldoet.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2022-C2022_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2022"
}
|
In an acute-angled triangle $ABC$, it holds that $|AB| > |CA| > |BC|$. The points $D, E$, and $F$ are the feet of the altitudes from $A, B$, and $C$ respectively. The line through $F$ parallel to $DE$ intersects $BC$ at $M$. The bisector of $\angle MFE$ intersects $DE$ at $N$. Prove that $F$ is the circumcenter of $\triangle DMN$ if and only if $B$ is the circumcenter of $\triangle FMN$.
|
Due to the length requirement in the problem, the configuration is fixed: $M$ lies on the ray $CB$ beyond $B$, and $N$ lies on the ray $ED$ beyond $D$. See the figure. Let $\alpha = \angle BAC$ and $\beta = \angle ABC$. Furthermore, let $H$ be the orthocenter of the triangle (i.e., the intersection of $AD$, $BE$, and $CF$). By Thales' theorem, $AFHE$, $BDHF$, $CEHD$, $ABDE$, $BCEF$, and $CAFD$ are cyclic quadrilaterals. Due to cyclic quadrilateral $ABDE$, $\angle CED = 180^\circ - \angle AED = \angle ABD = \beta$ and due to cyclic quadrilateral $BCEF$, $\angle AEF = 180^\circ - \angle CEF = \angle CBF = \beta$. Similarly, $\angle CDE$ and $\angle BDF$ are equal to $\alpha$.
From $\angle CED = \beta = \angle AEF$, it follows that $\angle DEH = 90^\circ - \beta = \angle FEH$. Therefore, $EH$ is the angle bisector of $\angle DEF$. Since $DE \parallel FM$, by alternate interior angles, $\angle MFE = 180^\circ - \angle FED = 180^\circ - 2(90^\circ - \beta) = 2\beta$. Since $FN$ is the angle bisector of $\angle MFE$, $\angle EFN = \frac{1}{2} \cdot 2\beta = \beta$. Given that $\angle FEH = 90^\circ - \beta$, we see that $FN$ and $EH$ are perpendicular to each other, so $EH$ is not only the angle bisector in $\triangle FEN$ but also the altitude. This line is thus the perpendicular bisector of $FN$. Since $B$ lies on this line, $|BF| = |BN|$.
We have previously seen that $\angle CDE = \alpha = \angle BDF$. Since $DE \parallel FM$, $\angle BMF = \angle CDE = \alpha$, so $\angle DMF = \angle BMF = \angle BDF = \angle MDF$. Therefore, $|FM| = |FD|$.
Let $S$ be the intersection of $AC$ and $MF$. Then $\angle BFM = \angle AFS$ and since $DE \parallel FM$, $\angle CED = \angle CSF$. By the exterior angle theorem in triangle $AFS$, we also have $\angle CSF = \angle SAF + \angle AFS = \alpha + \angle AFS$. Combining all this, we find $\angle CED = \alpha + \angle BFM$. On the other hand, we know that $\angle CED = \beta$, so $\angle BFM = \beta - \alpha$. We also know that $\angle BMF = \alpha$. We conclude that $|BF| = |BM|$ if and only if $\beta - \alpha = \alpha$ or if and only if $\beta = 2\alpha$. Since we already know that $|BF| = |BN|$, we have: $B$ is the circumcenter of $\triangle FMN$ if and only if $\beta = 2\alpha$.
We have previously seen that $EH$ is the angle bisector and altitude in triangle $EFN$, so this triangle is isosceles with vertex $E$, which implies that $\angle DNF = \angle ENF = \angle EFN = \beta$. We also know that $\angle CDE = \alpha = \angle BDF$, so $\angle NDF = \angle NDB + \angle BDF = \angle CDE + \angle BDF = 2\alpha$. Therefore, $|FD| = |FN|$ if and only if $\beta = 2\alpha$. Since we also know that $|FM| = |FD|$, we have: $F$ is the circumcenter of $\triangle DMN$ if and only if $\beta = 2\alpha$.
We conclude that $F$ is the circumcenter of $\triangle DMN$ if and only if $B$ is the circumcenter of $\triangle FMN$, because both properties are equivalent to $\beta = 2\alpha$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In een scherphoekige driehoek $A B C$ geldt $|A B|>|C A|>|B C|$. De punten $D, E$ en $F$ zijn de voetpunten van de hoogtelijnen vanuit respectievelijk $A, B$ en $C$. De lijn door $F$ evenwijdig aan $D E$ snijdt $B C$ in $M$. De bissectrice van $\angle M F E$ snijdt $D E$ in $N$. Bewijs dat $F$ het middelpunt van de omgeschreven cirkel van $\triangle D M N$ is dan en slechts dan als $B$ het middelpunt van de omgeschreven cirkel van $\triangle F M N$ is.
|
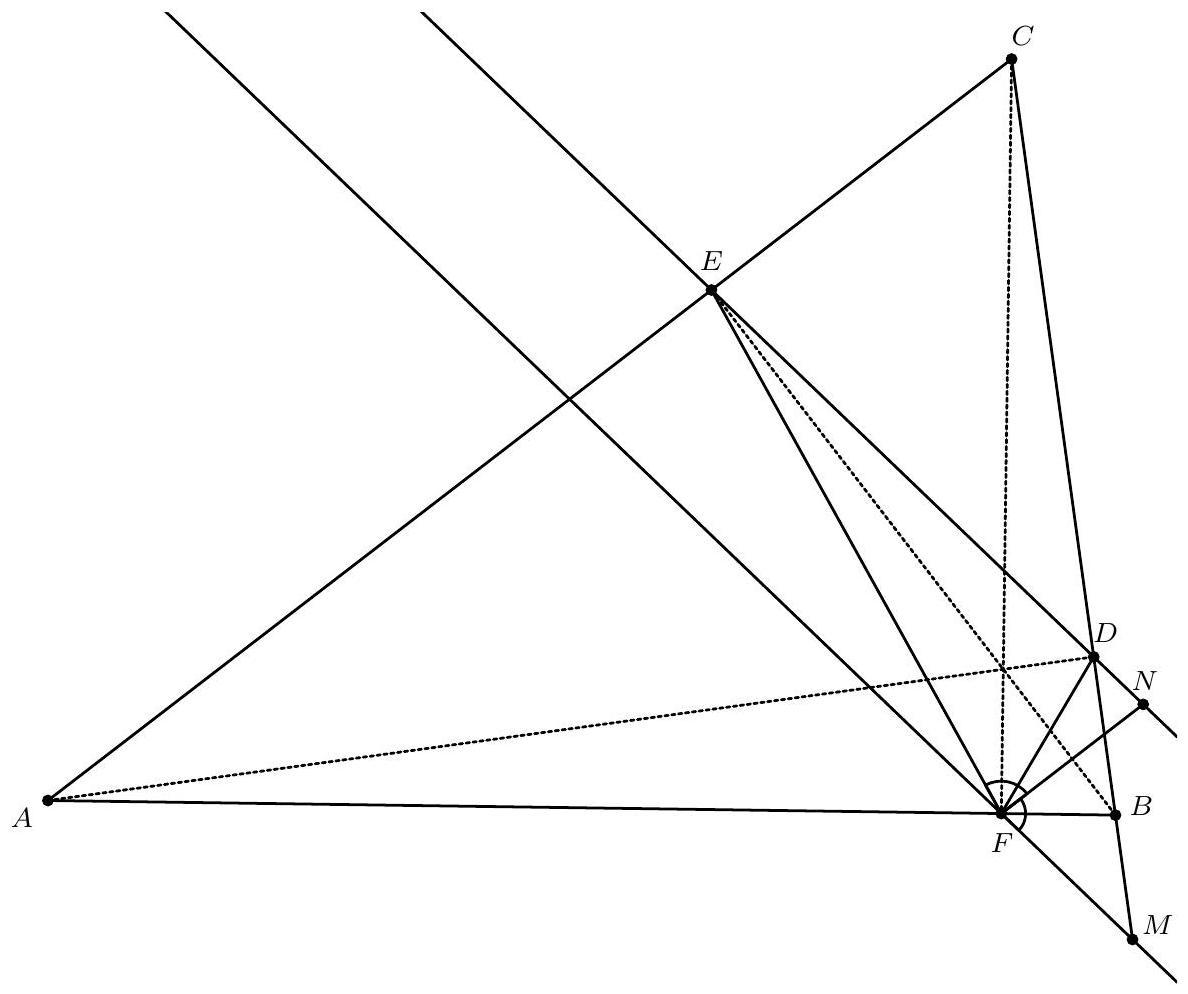
Vanwege de lengte-eis in de opgave ligt de configuratie vast: $M$ ligt op de halfrechte $C B$ voorbij $B$, en $N$ ligt op de halfrechte $E D$ voorbij $D$. Zie de figuur. Noem $\alpha=\angle B A C$ en $\beta=\angle A B C$. Noem verder $H$ het hoogtepunt van de driehoek (oftewel het snijpunt
van $A D, B E$ en $C F)$. Wegens Thales zijn $A F H E, B D H F, C E H D, A B D E, B C E F$ en $C A F D$ koordenvierhoeken. Vanwege koordenvierhoek $A B D E$ is $\angle C E D=180^{\circ}-$ $\angle A E D=\angle A B D=\beta$ en vanwege koordenvierhoek $B C E F$ is $\angle A E F=180^{\circ}-\angle C E F=$ $\angle C B F=\beta$. Analoog zijn $\angle C D E$ en $\angle B D F$ gelijk aan $\alpha$.
Uit $\angle C E D=\beta=\angle A E F$ volgt $\angle D E H=90^{\circ}-\beta=\angle F E H$. Dus $E H$ is de bissectrice van $\angle D E F$. Vanwege $D E \| F M$ geldt wegens U-hoeken verder $\angle M F E=180^{\circ}-\angle F E D=$ $180^{\circ}-2\left(90^{\circ}-\beta\right)=2 \beta$. Aangezien $F N$ de bissectrice van $\angle M F E$ is, is $\angle E F N=\frac{1}{2} \cdot 2 \beta=\beta$. Vanwege $\angle F E H=90^{\circ}-\beta$ zien we nu ook dat $F N$ en $E H$ loodrecht op elkaar staan, dus $E H$ is niet alleen bissectrice in $\triangle F E N$ maar ook hoogtelijn. Deze lijn is daarmee ook de middelloodlijn van $F N$. Omdat $B$ op deze lijn ligt, geldt $|B F|=|B N|$.
We hebben eerder gezien dat $\angle C D E=\alpha=\angle B D F$. Vanwege $D E \| F M$ geldt ook $\angle B M F=\angle C D E=\alpha$, dus $\angle D M F=\angle B M F=\angle B D F=\angle M D F$. Dus $|F M|=|F D|$.
Noem $S$ het snijpunt van $A C$ en $M F$. Dan is $\angle B F M=\angle A F S$ en wegens $D E \| F M$ is $\angle C E D=\angle C S F$. Met de buitenhoekstelling in driehoek $A F S$ zien we bovendien $\angle C S F=$ $\angle S A F+\angle A F S=\alpha+\angle A F S$. Als we dit alles combineren, vinden we $\angle C E D=\alpha+$ $\angle B F M$. Anderzijds wisten we dat $\angle C E D=\beta$, dus $\angle B F M=\beta-\alpha$. We weten daarnaast dat $\angle B M F=\alpha$. We concluderen dat $|B F|=|B M|$ dan en slechts dan als $\beta-\alpha=\alpha$ oftewel dan en slechts dan als $\beta=2 \alpha$. Omdat we al weten dat $|B F|=|B N|$ geldt nu: $B$ is het middelpunt van de omgeschreven cirkel van $\triangle F M N$ dan en slechts dan als $\beta=2 \alpha$.
We hebben eerder gezien dat $E H$ de bissectrice en hoogtelijn in driehoek $E F N$ is, dus deze driehoek is gelijkbenig met top $E$, waaruit volgt dat $\angle D N F=\angle E N F=\angle E F N=\beta$. Verder weten we dat $\angle C D E=\alpha=\angle B D F$, waaruit volgt dat $\angle N D F=\angle N D B+$ $\angle B D F=\angle C D E+\angle B D F=2 \alpha$. Dus $|F D|=|F N|$ dan en slechts dan als $\beta=2 \alpha$. Omdat we ook al wisten dat $|F M|=|F D|$, geldt nu: $F$ is het middelpunt van de omgeschreven cirkel van $\triangle D M N$ dan en slechts dan als $\beta=2 \alpha$.
We concluderen dat $F$ het middelpunt van de omgeschreven cirkel van $\triangle D M N$ is dan en slechts dan als $B$ het middelpunt van de omgeschreven cirkel van $\triangle F M N$ is, omdat beide eigenschappen equivalent zijn met $\beta=2 \alpha$.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2022-D2022_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2022"
}
|
Let $n$ be a positive integer. For a real number $x \geq 1$, it holds that $\left\lfloor x^{n+1}\right\rfloor$, $\left\lfloor x^{n+2}\right\rfloor, \ldots,\left\lfloor x^{4 n}\right\rfloor$ are all squares of positive integers. Prove that $\lfloor x\rfloor$ is also the square of a positive integer.
With $\lfloor z\rfloor$ we mean the greatest integer less than or equal to $z$.
|
We first prove this for $n=1$. Write $x=a+r$, with $a \geq 1$ an integer and $0 \leq r<1$. Suppose $\left\lfloor x^{2}\right\rfloor$, $\left\lfloor x^{3}\right\rfloor$ and $\left\lfloor x^{4}\right\rfloor$ are squares. It follows that $a \leq x<a+1$, from which we conclude that $a^{2} \leq x^{2}<(a+1)^{2}$. This pins $x^{2}$ between two consecutive squares. But $\left\lfloor x^{2}\right\rfloor$ is a square, so the only possibility is $\left\lfloor x^{2}\right\rfloor=a^{2}$. We conclude that $a^{2} \leq x^{2}<a^{2}+1$. Similarly, it follows that $\left(a^{2}\right)^{2} \leq x^{4}<\left(a^{2}+1\right)^{2}$ and thus $\left\lfloor x^{4}\right\rfloor=a^{4}$. We conclude that $a^{4} \leq x^{4}<a^{4}+1$.
Furthermore, $x^{3} \geq a^{3}$. Suppose now that $x^{3} \geq a^{3}+1$, then
$$
x^{4} \geq x\left(a^{3}+1\right)=(a+r)\left(a^{3}+1\right)=a^{4}+r a^{3}+a+r \geq a^{4}+a \geq a^{4}+1
$$
contradiction. Therefore, $x^{3}<a^{3}+1$, from which it follows that $\left\lfloor x^{3}\right\rfloor=a^{3}$. This is also a square, so $a$ must itself be a square. We see that $\lfloor x\rfloor$ is a square.
Now we prove the problem by induction on $n$. The base case has just been done. Let $k \geq 1$ and suppose we have proven the statement for $n=k$. Consider now a real number $x \geq 1$ with the property that $\left\lfloor x^{k+2}\right\rfloor,\left\lfloor x^{k+3}\right\rfloor, \ldots,\left\lfloor x^{4 k+4}\right\rfloor$ are all squares. In particular, $\left\lfloor x^{2(k+1)}\right\rfloor,\left\lfloor x^{3(k+1)}\right\rfloor$ and $\left\lfloor x^{4(k+1)}\right\rfloor$ are all squares. We can thus apply the case $n=1$ to $x^{k+1}$ (which is a real number greater than or equal to 1) and find that $\left\lfloor x^{k+1}\right\rfloor$ is also a square. Now we know that $\left\lfloor x^{k+1}\right\rfloor$, $\left\lfloor x^{k+2}\right\rfloor, \ldots,\left\lfloor x^{4 k}\right\rfloor$ are all squares and it follows from the induction hypothesis that $\lfloor x\rfloor$ is also a square. This completes the induction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Zij $n$ een positief geheel getal. Voor een reëel getal $x \geq 1$ geldt dat $\left\lfloor x^{n+1}\right\rfloor$, $\left\lfloor x^{n+2}\right\rfloor, \ldots,\left\lfloor x^{4 n}\right\rfloor$ allemaal kwadraten van positieve gehele getallen zijn. Bewijs dat $\lfloor x\rfloor$ ook het kwadraat van een positief geheel getal is.
Met $\lfloor z\rfloor$ bedoelen we het grootste gehele getal kleiner dan of gelijk aan z.
|
We bewijzen dit eerst voor $n=1$. Schrijf $x=a+r$, met $a \geq 1$ geheel en $0 \leq r<1$. Stel $\left\lfloor x^{2}\right\rfloor$, $\left\lfloor x^{3}\right\rfloor$ en $\left\lfloor x^{4}\right\rfloor$ zijn kwadraten. Er geldt dus $a \leq x<a+1$, waaruit volgt dat $a^{2} \leq x^{2}<(a+1)^{2}$. Daarmee hebben we $x^{2}$ ingeklemd tussen twee opeenvolgende kwadraten. Maar $\left\lfloor x^{2}\right\rfloor$ is een kwadraat, dus de enige mogelijkheid is $\left\lfloor x^{2}\right\rfloor=a^{2}$. We concluderen dat $a^{2} \leq x^{2}<a^{2}+1$. Volledig analoog volgt hieruit dat $\left(a^{2}\right)^{2} \leq x^{4}<\left(a^{2}+1\right)^{2}$ en dus $\left\lfloor x^{4}\right\rfloor=a^{4}$. We concluderen dat $a^{4} \leq x^{4}<a^{4}+1$.
Verder geldt $x^{3} \geq a^{3}$. Stel nu dat $x^{3} \geq a^{3}+1$, dan is
$$
x^{4} \geq x\left(a^{3}+1\right)=(a+r)\left(a^{3}+1\right)=a^{4}+r a^{3}+a+r \geq a^{4}+a \geq a^{4}+1
$$
tegenspraak. Dus $x^{3}<a^{3}+1$, waaruit volgt dat $\left\lfloor x^{3}\right\rfloor=a^{3}$. Dit is bovendien een kwadraat, dus $a$ moet zelf een kwadraat zijn. We zien dat $\lfloor x\rfloor$ een kwadraat is.
Nu gaan we de opgave bewijzen met inductie naar $n$. De inductiebasis hebben we zojuist gedaan. Zij nu $k \geq 1$ en veronderstel dat we de stelling bewezen hebben voor $n=k$. Bekijk nu een reëel getal $x \geq 1$ met de eigenschap dat $\left\lfloor x^{k+2}\right\rfloor,\left\lfloor x^{k+3}\right\rfloor, \ldots,\left\lfloor x^{4 k+4}\right\rfloor$ allemaal kwadraten zijn. In het bijzonder zijn dan $\left\lfloor x^{2(k+1)}\right\rfloor,\left\lfloor x^{3(k+1)}\right\rfloor$ en $\left\lfloor x^{4(k+1)}\right\rfloor$ allemaal kwadraten. We kunnen dus het geval $n=1$ toepassen op $x^{k+1}$ (dat is een reëel getal groter of gelijk aan 1) en vinden dat $\left\lfloor x^{k+1}\right\rfloor$ ook een kwadraat is. Nu weten we dus dat $\left\lfloor x^{k+1}\right\rfloor$, $\left\lfloor x^{k+2}\right\rfloor, \ldots,\left\lfloor x^{4 k}\right\rfloor$ allemaal kwadraten zijn en volgt uit de inductiehypothese dat $\lfloor x\rfloor$ ook een kwadraat is. Dit voltooit de inductie.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2022-D2022_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2022"
}
|
On the ceiling of a room hang 15 lamps, numbered from 1 to 15. Initially, all the lamps are off. In another room are 15 switches: one switch for lamp 1 and 2, one switch for lamp 2 and 3, one switch for lamp 3 and 4, and so on, up to a switch for lamp 15 and 1. When the switch for such a pair of lamps is flipped, the status of each of those two lamps changes (from on to off or vice versa). The switches are hung in a random order and all look identical. Raymond wants to find out which switch corresponds to which pair of lamps. From the room with the switches, he cannot see the lamps. He can, however, flip a number of switches and then go to the other room to see which lamps are on. He can do this multiple times. How many times must he minimally go to the other room to be certain of which switch corresponds to which pair of lamps?
|
With three rounds of walking, Raymond can never be certain. After all, if you note for each switch whether it is in the initial position or the flipped position in the three rounds, you can get $2^{3}=8$ different patterns. However, there are 15 switches, so there are multiple switches with the same pattern, and Raymond can never distinguish these switches from each other. Therefore, he must walk at least four times. We will prove that this is indeed sufficient.
Assume that Raymond, starting from the situation where all lights are off, flips a number of switches. If he flips all the switches or none at all, then all the lights will remain off afterward. Otherwise, there will always be a light that has been changed by only one flipped switch, so it will be on. Consider such a light $i$ that is on. Then the switch with $i-1$ and $i$ or the switch with $i$ and $i+1$ has been flipped. (Consider the light numbers modulo 15.) First, assume that the latter is the case. Now consider light $i+1$. If it is off, then the switch with $i+1$ and $i+2$ has also been flipped; if the light is on, then that switch has not been used. Next, we can deduce from the status of light $i+2$ whether the switch with $i+2$ and $i+3$ has been flipped or not. By continuing this process, we see that the status of all switches is determined. In the second case, if the switch with $i-1$ and $i$ has been flipped, then the status of all switches is also determined. Therefore, there are exactly two combinations of switches that result in the same status of the lights. If we choose one of these combinations and then flip all 15 switches again, the same lights will be on, so this must result in the second combination of switches. If the first combination of switches contains an even number of switches, then the second combination contains 15 minus that number, so an odd number of switches.
However, Raymond knows himself how many switches he has flipped. He can deduce from the status of the lights which two combinations of switches are possible, and only one of these can match the number of switches he has flipped. Therefore, he can precisely determine which lights the switches he has flipped correspond to; he only does not know which is which within that group of switches.
Write the numbers 1 to 15 in binary notation. For this, a maximum of 4 digits are needed; pad with zeros if necessary so that each number is written with exactly 4 digits. Raymond numbers the switches with these binary numbers. In the first round, he flips the switches whose numbers in binary notation start with a 1 and notes the 8 corresponding light pairs. In the second round, he first resets all switches and then selects the numbers that have a 1 in the second position in binary notation. Similarly, in the third round, he selects the third position in the binary notation, and in the fourth round, the fourth position. In each round, he can determine which light pairs the switches he used correspond to (only not which is which). Since each switch corresponds to a unique combination of rounds, he can then deduce from each switch which light pair it controls. For example, if a certain light pair is turned on in the first round, not in the second round, in the third round, and also in the fourth round, then it corresponds to the switch with binary code 1011, which is switch 11. Therefore, he can succeed in four rounds of walking.
|
4
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
Aan het plafond van een kamer hangen 15 lampen, genummerd van 1 tot en met 15. In het begin zijn de lampen allemaal uit. In een andere kamer zijn 15 schakelaars: een schakelaar voor lamp 1 en 2 , een schakelaar voor lamp 2 en 3 , een schakelaar voor lamp 3 en 4, enzovoorts, tot en met een schakelaar voor lamp 15 en 1. Als de schakelaar voor zo'n tweetal lampen wordt omgezet, verandert elk van die twee lampen van status (van aan naar uit of andersom). De schakelaars hangen in een willekeurige volgorde en zien er allemaal identiek uit. Raymond wil uitzoeken welke schakelaar bij welk tweetal lampen hoort. Vanuit de kamer met de schakelaars kan hij de lampen niet zien. Hij kan wel een aantal schakelaars omzetten en vervolgens naar de andere kamer lopen om te kijken welke lampen er aan staan. Dit kan hij meerdere keren doen. Hoe vaak moet hij minimaal naar de andere kamer lopen om van elke schakelaar zeker te weten bij welk tweetal lampen die hoort?
|
Met drie keer lopen kan Raymond het nooit met zekerheid weten. Immers, als je voor elke schakelaar noteert of hij in de drie rondes in de beginstand of juist de omgezette stand staat, dan kun je $2^{3}=8$ verschillende patronen krijgen. Er zijn echter 15 schakelaars, dus er zijn meerdere schakelaars met hetzelfde patroon en Raymond kan dan nooit deze schakelaars van elkaar onderscheiden. Hij moet dus minimaal vier keer lopen. We bewijzen dat dit inderdaad voldoende is.
Stel dat Raymond vanuit de situatie waarin alle lampen uit staan, een aantal schakelaars om zet. Als hij alle schakelaars om zet of helemaal geen, dan staan daarna alle lampen uit. Anders is er altijd een lamp die maar door één omgezette schakelaar van status is veranderd, dus die aan staat. Bekijk zo'n lamp $i$ die aan staat. Dan is de schakelaar met $i-1$ en $i$ of de schakelaar met $i$ en $i+1$ omgezet. (Reken de lampnummers modulo 15.) Neem eerst aan dat het het tweede is. Bekijk nu lamp $i+1$. Als die uit staat, dan is de schakelaar met $i+1$ en $i+2$ ook omgezet; staat de lamp aan, dan is die schakelaar juist niet gebruikt. Vervolgens kunnen we uit de status van lamp $i+2$ afleiden of de schakelaar met $i+2$ en $i+3$ wel of niet omgezet is. Door zo door te gaan, zien we dat van alle schakelaars vast ligt of ze wel of niet omgezet zijn. In het tweede geval, als juist de schakelaar met $i-1$ en $i$ omgezet is, dan ligt ook van alle schakelaars vast of ze wel of niet omgezet zijn. Er zijn dus precies twee combinaties van schakelaars die samen dezelfde status van de lampen opleveren. Als we één van die combinaties kiezen en vervolgens alle 15 schakelaars nogmaals omzetten, dan staan weer precies dezelfde lampen aan, dus dit moet precies de tweede combinatie van schakelaars opleveren. Als nu de eerste combinatie van schakelaars een even aantal schakelaars bevat, dan bevat de tweede combinatie 15 min dat aantal, dus een oneven aantal schakelaars.
Raymond weet echter zelf hoeveel schakelaars hij heeft omgezet. Hij kan aan de hand van de situatie van de lampen afleiden welke twee combinaties van schakelaars er mogelijk zijn en daarvan kan er maar één kloppen met het aantal schakelaars dat hij heeft omgezet. Hij kan dus precies achterhalen voor welke lampen de schakelaars zijn die hij heeft omgezet;
hij weet alleen binnen die groep schakelaars niet welke welke is.
Schrijf nu de getallen 1 tot en met 15 in binaire notatie. Daarvoor zijn maximaal 4 cijfers nodig; vul eventueel aan met nullen zodat elk getal met precies 4 cijfers geschreven wordt. Raymond nummert de schakelaars met deze binaire getallen. Vervolgens zet hij in de eerste ronde de schakelaars om waarvan het nummer in binaire notatie met een 1 begint en noteert hij de 8 bijbehorende lampentweetallen. In de tweede ronde zet hij eerst alle schakelaars weer terug en kiest hij vervolgens de nummers die in binaire notatie op de tweede positie een 1 hebben. Op dezelfde manier kiest hij in de derde ronde de derde positie in de binaire schrijfwijze en in de vierde ronde de vierde positie. In elke ronde kan hij achterhalen voor welke lampentweetallen de schakelaars zijn die hij heeft gebruikt (alleen niet welke welke is). Omdat elke schakelaar correspondeert met een unieke combinatie van rondes, kan hij vervolgens van elke schakelaar uitpuzzelen welk tweetal lampen die schakelaar bedient. Als bijvoorbeeld een bepaald lampentweetal wel in de eerste ronde, niet in de tweede ronde, wel in de derde en ook in de veride ronde wordt aangezet, dan hoort hier de schakelaar bij met binaire code 1011, dus schakelaar 11. Het lukt hem dus in vier keer lopen.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2022-D2022_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2022"
}
|
Determine all positive integers $d$ for which there exists a $k \geq 3$ such that the numbers $d, 2d, 3d, \ldots, kd$ can be arranged in a row in such a way that for each pair of adjacent numbers, the sum of those two numbers is a perfect square.
|
For $d=1$ we take $k=15$ and the sequence
$$
8,1,15,10,6,3,13,12,4,5,11,14,2,7,9
$$
Two neighboring numbers in this sequence always add up to 9, 16, or 25. For $d>1$ a square, we also take $k=15$ and the same sequence as above, but with all numbers multiplied by $d$. Two neighboring numbers in that sequence then always add up to $9d, 16d$ or $25d$, and these are all squares.
Now consider a $d$ that is not a square. We will show that this does not satisfy the condition. Suppose there exists such a $k$ with the corresponding sequence $a_{1}d, a_{2}d, \ldots, a_{k}d$, where $\left\{a_{1}, a_{2}, \ldots, a_{k}\right\} = \{1,2, \ldots, k\}$. Write $d = cm^2$ with $m$ positive and maximal, so that $c$ is not divisible by a square greater than 1. For all $i$ with $1 \leq i \leq k-1$, it holds that $a_{i}d + a_{i+1}d$ is a square and $d = cm^2 \mid a_{i}d + a_{i+1}d$, so $cd = c^2m^2 \mid a_{i}d + a_{i+1}d$, which implies that $c \mid a_{i} + a_{i+1}$. This gives $a_{i+1} \equiv -a_{i} \bmod c$ and thus $a_{i+2} \equiv -a_{i+1} \equiv a_{i} \bmod c$. Therefore, at most two different residue classes modulo $c$ occur among the $a_{i}$, namely those of $a_{1}$ and $a_{2}$. But $\left\{a_{1}, a_{2}, \ldots, a_{k}\right\} = \{1,2, \ldots, k\}$ and $k \geq 3$, so apparently $c \leq 2$. Since $d$ is not a square, $c=1$ is not possible, so $c=2$. But then $a_{i+1} \equiv -a_{i} \equiv a_{i} \bmod 2$, so only one residue class modulo 2 occurs in the sequence. Contradiction.
We conclude that the $d$ that satisfy the condition are precisely the squares.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Bepaal alle positieve gehele getallen $d$ waarvoor er een $k \geq 3$ bestaat zodat je de getallen $d, 2 d, 3 d, \ldots, k d$ op een rij kan zetten op zo'n manier dat voor elk tweetal buurgetallen geldt dat de som van die twee getallen een kwadraat is.
|
Voor $d=1$ nemen we $k=15$ en de rij
$$
8,1,15,10,6,3,13,12,4,5,11,14,2,7,9
$$
Twee buurgetallen in deze rij zijn samen altijd 9 , 16 of 25 . Voor $d>1$ een kwadraat nemen we ook $k=15$ en dezelfde rij als hierboven, maar dan met alle getallen vermenigvuldigd met $d$. Twee buurgetallen in die rij zijn dan altijd $9 d, 16 d$ of $25 d$ en dat zijn allemaal kwadraten.
Bekijk nu een $d$ die geen kwadraat is. We gaan laten zien dat deze niet voldoet. Stel dat er toch zo'n $k$ bestaat met bijbehorende rij $a_{1} d, a_{2} d, \ldots, a_{k} d$, waarbij $\left\{a_{1}, a_{2}, \ldots, a_{k}\right\}=$ $\{1,2, \ldots, k\}$. Schrijf $d=c m^{2}$ met $m$ positief geheel en maximaal, zodat $c$ niet deelbaar is door een kwadraat groter dan 1 . Er geldt voor alle $i$ met $1 \leq i \leq k-1$ dat $a_{i} d+a_{i+1} d$ een kwadraat is en $d=c m^{2} \mid a_{i} d+a_{i+1} d$, dus $c d=c^{2} m^{2} \mid a_{i} d+a_{i+1} d$, waaruit volgt dat $c \mid a_{i}+a_{i+1}$. Hieruit volgt $a_{i+1} \equiv-a_{i} \bmod c$ en dus $a_{i+2} \equiv-a_{i+1} \equiv a_{i} \bmod c$. Er komen dus maximaal twee verschillende restklassen modulo $c$ voor bij de $a_{i}$, namelijk die van $a_{1}$ en die van $a_{2}$. Maar $\left\{a_{1}, a_{2}, \ldots, a_{k}\right\}=\{1,2, \ldots, k\}$ en $k \geq 3$, dus kennelijk is $c \leq 2$. Omdat $d$ geen kwadraat is, kan $c=1$ niet, dus geldt $c=2$. Maar dan is $a_{i+1} \equiv-a_{i} \equiv a_{i} \bmod 2$ dus komt er maar één restklasse modulo 2 in de rij voor. Tegenspraak.
We concluderen dat de $d$ die voldoen precies de kwadraten zijn.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2022-D2022_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2022"
}
|
Find all quadruples $(a, b, c, d)$ of non-negative integers such that $a b = 2(1 + c d)$ and there exists a non-degenerate triangle with sides of length $a - c$, $b - d$, and $c + d$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
|
It holds that $a>c$ and $b>d$ because $a-c$ and $b-d$ must be sides of a triangle. Therefore, $a \geq c+1$ and $b \geq d+1$, since we are dealing with integers. We now distinguish two cases: $a>2c$ and $a \leq 2c$.
Suppose that $a>2c$ holds. Then $ab > 2bc \geq 2c \cdot (d+1) = 2cd + 2c$. On the other hand, $ab = 2 + 2cd$, so $2c < 2$. This means that $c=0$. We then find that $ab=2$ and that there exists a non-degenerate triangle with sides of length $a$, $b-d$, and $d$. There must then hold $d \geq 1$ and $b>d$, so $b \geq 2$. From $ab=2$ it follows that $a=1$, $b=2$. Therefore, $d=1$ and the triangle has sides of length 1, 1, and 1. Such a triangle indeed exists. Thus, the quadruple $(1,2,0,1)$ is indeed a solution.
Now suppose that $a \leq 2c$ holds. The triangle inequality says that $(a-c) + (b-d) > c + d$, so $a + b > 2(c + d)$. Since $a \leq 2c$, it follows that $b > 2d$. We also knew that $a \geq c+1$, so $ab > (c+1) \cdot 2d = 2cd + 2d$. On the other hand, $ab = 2 + 2cd$, so $2d < 2$. This means that $d=0$. Analogous to the case $c=0$, this results in the only solution being the quadruple $(2,1,1,0)$.
The only solutions are thus $(1,2,0,1)$ and $(2,1,1,0)$.
|
(1,2,0,1) \text{ and } (2,1,1,0)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Vind alle viertallen $(a, b, c, d)$ van niet-negatieve gehele getallen zodat $a b=$ $2(1+c d)$ en er een niet-ontaarde driehoek bestaat met zijden van lengte $a-c, b-d$ en $c+d$.
|
Er geldt $a>c$ en $b>d$ omdat $a-c$ en $b-d$ zijden van een driehoek moeten zijn. Dus $a \geq c+1$ en $b \geq d+1$, aangezien het om gehele getallen gaat. We onderscheiden nu twee gevallen: $a>2 c$ en $a \leq 2 c$.
Stel dat $a>2 c$ geldt. Dan is $a b>2 b c \geq 2 c \cdot(d+1)=2 c d+2 c$. Anderzijds is $a b=2+2 c d$, dus $2 c<2$. Dit betekent dat $c=0$. We vinden dan dat $a b=2$ en dat er een niet-ontaarde driehoek bestaat met zijden van lengte $a, b-d$ en $d$. Er moet dan gelden $d \geq 1$ en $b>d$, dus $b \geq 2$. Uit $a b=2$ volgt dan $a=1, b=2$. En dus geldt $d=1$ en heeft de driehoek zijden van lengte 1 , 1 en 1 . Zo'n driehoek bestaat inderdaad. Dus het viertal $(1,2,0,1)$ is inderdaad een oplossing.
Stel nu dat $a \leq 2 c$ geldt. De driehoeksongelijkheid zegt dat $(a-c)+(b-d)>c+d$, dus $a+b>2(c+d)$. Omdat $a \leq 2 c$ volgt hieruit dat $b>2 d$. We wisten ook dat $a \geq c+1$, dus geldt $a b>(c+1) \cdot 2 d=2 c d+2 d$. Anderzijds is $a b=2+2 c d$, dus $2 d<2$. Dit betekent dat $d=0$. Analoog aan het geval $c=0$ volgt hieruit als enige oplossing het viertal $(2,1,1,0)$.
De enige oplossingen zijn dus $(1,2,0,1)$ en $(2,1,1,0)$.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2022-E2022_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2022"
}
|
Find all quadruples $(a, b, c, d)$ of non-negative integers such that $a b = 2(1 + c d)$ and there exists a non-degenerate triangle with sides of length $a - c$, $b - d$, and $c + d$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
|
As stated above, $a \geq c+1$ because $a-c$ is a side. The triangle inequality gives that $(a-c)+(b-d)>c+d$. From this, it follows that $a+b \geq 2 c+2 d+1$. Multiplying these two inequalities, we get
$$
a^{2}+2(1+c d)=a(a+b) \geq(c+1)(2 c+2 d+1)
$$
which we expand to
$$
a^{2} \geq 2 c^{2}+3 c+2 d-1=2 c(c+1)+(c+d-1)+d \geq 2 c(c+1)
$$
since $c+d$ is a side of the triangle. Similarly, we get $b^{2} \geq 2 d(d+1)$. Multiplying these two inequalities again, we get
$$
4(1+c d)^{2}=a^{2} b^{2} \geq 2 c(c+1) 2 d(d+1)
$$
We rewrite this as $1 \geq c d(c+d-1)$, which means that $c=0, d=0$ or $(c, d)=(1,1)$. Checking yields the two solutions as mentioned above and that $(c, d)=(1,1)$ has no solutions.
| null |
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Vind alle viertallen $(a, b, c, d)$ van niet-negatieve gehele getallen zodat $a b=$ $2(1+c d)$ en er een niet-ontaarde driehoek bestaat met zijden van lengte $a-c, b-d$ en $c+d$.
|
Zoals hierboven geldt dat $a \geq c+1$ omdat $a-c$ een zijde is. De driehoeksongelijkheid geeft dat $(a-c)+(b-d)>c+d$. Hieruit volgt dat $a+b \geq 2 c+2 d+1$. Als we deze twee ongelijkheden vermenigvuldigen krijgen we
$$
a^{2}+2(1+c d)=a(a+b) \geq(c+1)(2 c+2 d+1)
$$
wat we uitwerken tot
$$
a^{2} \geq 2 c^{2}+3 c+2 d-1=2 c(c+1)+(c+d-1)+d \geq 2 c(c+1)
$$
aangezien $c+d$ een zijde is van de driehoek. Evenzo krijgen we $b^{2} \geq 2 d(d+1)$. Deze twee ongelijkheden vermenigvuldigen we weer tot
$$
4(1+c d)^{2}=a^{2} b^{2} \geq 2 c(c+1) 2 d(d+1)
$$
Dat herschrijven we tot $1 \geq c d(c+d-1)$ wat betekent dat $c=0, d=0$ of $(c, d)=(1,1)$. Controleren levert de twee oplossingen zoals hierboven en dat $(c, d)=(1,1)$ geen oplossingen heeft.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2022-E2022_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2022"
}
|
Find all quadruples $(a, b, c, d)$ of non-negative integers such that $a b = 2(1 + c d)$ and there exists a non-degenerate triangle with sides of length $a - c$, $b - d$, and $c + d$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
|
As stated above, $a \geq c+1$ because $a-c$ is a side, and $b \geq d+1$ because $b-d$ is a side. Due to the condition $ab=2(1+cd)$, we now have
$$
\begin{aligned}
& a=\frac{2(1+cd)}{b} \leq \frac{2(1+cd)}{d+1} \\
& b=\frac{2(1+cd)}{a} \leq \frac{2(1+cd)}{c+1}
\end{aligned}
$$
Adding these inequalities gives
$$
\begin{aligned}
\frac{a+b}{2} & \leq \frac{1+cd}{d+1}+\frac{1+cd}{c+1} \\
& =\frac{c(d+1)-c+1}{d+1}+\frac{d(c+1)-d+1}{c+1} \\
& =c+d+\frac{1-c}{d+1}+\frac{1-d}{c+1}
\end{aligned}
$$
On the other hand, the triangle inequality gives that $(a-c)+(b-d)>c+d$, which implies that $a+b>2c+2d$. Combining this with the previous inequality, we get
$$
c+d<\frac{a+b}{2} \leq c+d+\frac{1-c}{d+1}+\frac{1-d}{c+1} .
$$
From this, it follows that $1-c$ or $1-d$ is positive. Since they must be non-negative integers, it follows that $c=0$ or $d=0$. This gives the two solutions as in solution 1.
| null |
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Vind alle viertallen $(a, b, c, d)$ van niet-negatieve gehele getallen zodat $a b=$ $2(1+c d)$ en er een niet-ontaarde driehoek bestaat met zijden van lengte $a-c, b-d$ en $c+d$.
|
Zoals hierboven geldt dat $a \geq c+1$ omdat $a-c$ een zijde is en $b \geq d+1$ omdat $b-d$ een zijde is. Wegens de voorwaarde $a b=2(1+c d)$ volgt nu
$$
\begin{aligned}
& a=\frac{2(1+c d)}{b} \leq \frac{2(1+c d)}{d+1} \\
& b=\frac{2(1+c d)}{a} \leq \frac{2(1+c d)}{c+1}
\end{aligned}
$$
Optellen van deze ongelijkheden geeft
$$
\begin{aligned}
\frac{a+b}{2} & \leq \frac{1+c d}{d+1}+\frac{1+c d}{c+1} \\
& =\frac{c(d+1)-c+1}{d+1}+\frac{d(c+1)-d+1}{c+1} \\
& =c+d+\frac{1-c}{d+1}+\frac{1-d}{c+1}
\end{aligned}
$$
Anderzijds geeft de driehoeksongelijkheid dat $(a-c)+(b-d)>c+d$, waaruit volgt dat $a+b>2 c+2 d$. Als we dit combineren met de vorige ongelijkheid krijgen we
$$
c+d<\frac{a+b}{2} \leq c+d+\frac{1-c}{d+1}+\frac{1-d}{c+1} .
$$
Hieruit volgt dat $1-c$ of $1-d$ positief is. Omdat het niet-negatieve gehele getallen moeten zijn geldt dus dat $c=0$ of $d=0$. Dat geeft de twee oplossingen zoals in oplossing 1 .
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2022-E2022_uitwerkingen.jsonl",
"solution_match": "\nOplossing III.",
"tier": "T1",
"year": "2022"
}
|
Let $n>1$ be an integer. In a row, there are $n$ boxes, and we have $n+1$ identical stones. A distribution is a way to distribute the stones over the boxes, with each stone being in exactly one box. We say that two such distributions are a stone's throw away from each other if we can obtain one distribution from the other by moving exactly one stone to a different box. The sociability of a distribution $a$ is defined as the number of distributions that are a stone's throw away from $a$. Determine the average sociability over all possible distributions.
(Two distributions are the same if there are the same number of stones in the $i$-th box of both rows, for all $i \in\{1,2, \ldots, n\}$.)
Answer. $\frac{n^{2}-1}{2}$
In the solutions below, we call two distributions neighbors if they are a stone's throw away from each other.
|
We count the number, $N_{k}$, of distributions that contain exactly $k$ empty boxes with $0 \leq k \leq n-1$ (since not all boxes can be empty). There are $\binom{n}{k}$ ways to choose the empty boxes and by the stars and bars principle $\binom{(k+1)+(n-k)-1}{k+1}=\binom{n}{k+1}$ ways to fill the remaining $n-k$ boxes with $n+1=(n-k)+(k+1)$ stones such that each of these boxes contains at least one stone. This gives a total of $N_{k}=\binom{n}{k} \cdot\binom{n}{k+1}$ distributions with exactly $k$ empty boxes.
Given such a distribution, we can move a stone from one of the $n-k$ non-empty boxes to one of the other $n-1$ boxes. This means that there are $(n-k)(n-1)$ different distributions within one stone move. Thus, the sociability of each of these $N_{k}$ distributions is $(n-k)(n-1)$.
For $k^{\prime}=(n-1)-k$, the number of distributions with exactly $k^{\prime}$ empty boxes is $N_{k^{\prime}}=\binom{n}{k^{\prime}} \cdot\binom{n}{k^{\prime}+1}=\binom{n}{n-1-k} \cdot\binom{n}{n-k}=\binom{n}{k+1} \cdot\binom{n}{k}$, so $N_{k^{\prime}}=N_{k}$. The sociability of these $N_{k}$ distributions is $\left(n-k^{\prime}\right)(n-1)=(k+1)(n-1)$. Therefore, the average sociability of these two (possibly the same) sets of distributions is $\frac{(n-k)+(k+1)}{2}(n-1)=\frac{n+1}{2}(n-1)$. Since this is constant in $k$, it is also the overall average.
|
\frac{n^{2}-1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Zij $n>1$ een geheel getal. Op een rij staan $n$ dozen, en we hebben $n+1$ identieke stenen. Een verdeling is een manier om de stenen over de dozen te verdelen, waarbij elke steen in precies één doos zit. We zeggen dat twee van zulke verdelingen zich op een steenworp afstand van elkaar bevinden als we de ene verdeling uit de andere kunnen verkrijgen door precies één steen te verplaatsen naar een andere doos. De gezelligheid van een verdeling $a$ is gedefinieerd als het aantal verdelingen dat zich op een steenworp afstand van $a$ bevindt. Bepaal de gemiddelde gezelligheid over alle mogelijke verdelingen.
(Twee verdelingen zijn hetzelfde als er in de $i$-de doos van beide rijen evenveel stenen zitten, voor alle $i \in\{1,2, \ldots, n\}$.)
Antwoord. $\frac{n^{2}-1}{2}$
In de oplossingen hieronder noemen we twee verdelingen buren als ze op een steenworp afstand van elkaar liggen.
|
We tellen het aantal, $N_{k}$, verdelingen dat precies $k$ lege dozen bevat met $0 \leq k \leq n-1$ (aangezien niet alle dozen leeg kunnen zijn). Er zijn $\binom{n}{k}$ manieren om de lege dozen te kiezen en wegens het paaseierenprincipe $\binom{(k+1)+(n-k)-1}{k+1}=\binom{n}{k+1}$ manieren om de overige $n-k$ dozen te vullen met $n+1=(n-k)+(k+1)$ stenen zo dat elke van deze dozen minstens een steen bevat. Dit geeft een totaal van $N_{k}=\binom{n}{k} \cdot\binom{n}{k+1}$ verdelingen met precies $k$ lege dozen.
Gegeven zo'n verdeling kunnen we een steen van een van de de $n-k$ niet-lege dozen verplaatsen naar een van de andere $n-1$ dozen. Dit betekent dat er $(n-k)(n-1)$ verschillende verdelingen op steenworp afstand liggen. Dus de gezelligheid van elk van deze $N_{k}$ verdelingen is $(n-k)(n-1)$.
Voor $k^{\prime}=(n-1)-k$ is het aantal verdelingen met precies $k^{\prime}$ lege dozen gelijk aan $N_{k^{\prime}}=\binom{n}{k^{\prime}} \cdot\binom{n}{k^{\prime}+1}=\binom{n}{n-1-k} \cdot\binom{n}{n-k}=\binom{n}{k+1} \cdot\binom{n}{k}$, dus $N_{k^{\prime}}=N_{k}$. De gezelligheid van deze $N_{k}$ verdelingen is $\left(n-k^{\prime}\right)(n-1)=(k+1)(n-1)$. Dus de gemiddelde gezelligheid van deze twee (mogelijk dezelfde) verzamelingen verdelingen is $\frac{(n-k)+(k+1)}{2}(n-1)=\frac{n+1}{2}(n-1)$. Aangezien dit constant is in $k$, is dit ook het totale gemiddelde.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2022-E2022_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2022"
}
|
Let $n>1$ be an integer. In a row, there are $n$ boxes, and we have $n+1$ identical stones. A distribution is a way to distribute the stones over the boxes, with each stone being in exactly one box. We say that two such distributions are a stone's throw away from each other if we can obtain one distribution from the other by moving exactly one stone to a different box. The sociability of a distribution $a$ is defined as the number of distributions that are a stone's throw away from $a$. Determine the average sociability over all possible distributions.
(Two distributions are the same if there are the same number of stones in the $i$-th box of both rows, for all $i \in\{1,2, \ldots, n\}$.)
Answer. $\frac{n^{2}-1}{2}$
In the solutions below, we call two distributions neighbors if they are a stone's throw away from each other.
|
Let $V$ be the total number of distributions and let $E$ be the number of (ordered) pairs of distributions $(a, b)$ where $a$ and $b$ are neighbors. By the pigeonhole principle, we know that $V=\binom{(n+1)+n-1}{n+1}=\binom{2 n}{n+1}$.
Now take a pair of neighbors $(a, b)$ and assume that $b$ can be obtained from $a$ by moving a stone from box $i$ to box $j$ (with $i \neq j$). Let $c$ be the distribution of $n$ stones over $n$ boxes that you get by removing that stone from box $i$ of $a$, or equivalently by removing that stone from box $j$ of $b$. Conversely, you can construct the pair of neighbors $(a, b)$ from $c$ and the ordered pair $(i, j)$. We conclude that $E$ is equal to the number of distributions of $n$ stones over $n$ boxes multiplied by the number of ways to choose ordered pairs $(i, j)$ with $i \neq j$. This means that $E=\binom{n+n-1}{n} \cdot n(n-1)=n(n-1) \cdot\binom{2 n-1}{n}$.
Since $E$ is the sum of the sociability over all distributions, the average sociability is
$$
\begin{aligned}
\frac{E}{V} & =n(n-1) \cdot \frac{(2 n-1)!}{n!(n-1)!} \cdot \frac{(n+1)!(n-1)!}{(2 n)!}=n(n-1) \cdot \frac{(2 n-1)!}{(2 n)!} \cdot \frac{(n+1)!}{n!} \\
& =\frac{n(n-1)(n+1)}{2 n}=\frac{(n-1)(n+1)}{2}=\frac{n^{2}-1}{2}
\end{aligned}
$$
|
\frac{n^{2}-1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Zij $n>1$ een geheel getal. Op een rij staan $n$ dozen, en we hebben $n+1$ identieke stenen. Een verdeling is een manier om de stenen over de dozen te verdelen, waarbij elke steen in precies één doos zit. We zeggen dat twee van zulke verdelingen zich op een steenworp afstand van elkaar bevinden als we de ene verdeling uit de andere kunnen verkrijgen door precies één steen te verplaatsen naar een andere doos. De gezelligheid van een verdeling $a$ is gedefinieerd als het aantal verdelingen dat zich op een steenworp afstand van $a$ bevindt. Bepaal de gemiddelde gezelligheid over alle mogelijke verdelingen.
(Twee verdelingen zijn hetzelfde als er in de $i$-de doos van beide rijen evenveel stenen zitten, voor alle $i \in\{1,2, \ldots, n\}$.)
Antwoord. $\frac{n^{2}-1}{2}$
In de oplossingen hieronder noemen we twee verdelingen buren als ze op een steenworp afstand van elkaar liggen.
|
Zij $V$ het totale aantal verdelingen en zij $E$ het aantal (geordende) paren verdelingen $(a, b)$ waarvan $a$ en $b$ buren zijn. Wegens het paaseierenprincipe weten we dat $V=\binom{(n+1)+n-1}{n+1}=\binom{2 n}{n+1}$.
Neem nu een paar buren $(a, b)$ en stel dat $b$ verkregen kan worden uit $a$ door een steen van doos $i$ naar doos $j$ te gooien (met $i \neq j$ ). Laat $c$ de verdeling van $n$ stenen over $n$ dozen zijn die je krijgt door die steen uit doos $i$ van $a$ te halen, of equivalent door die steen uit doos $j$ van $b$ te halen. Andersom kun je vanuit $c$ en het geordende paar $(i, j)$ het paar buren $(a, b)$ construeren. We concluderen dat $E$ gelijk is aan het aantal verdelingen van $n$ stenen over $n$ dozen vermenigvuldigd met het aantal manieren om geordende paren $(i, j)$ met $i \neq j$. Dat betekent dat $E=\binom{n+n-1}{n} \cdot n(n-1)=n(n-1) \cdot\binom{2 n-1}{n}$.
Aangezien $E$ de som van de gezelligheid is over alle verdelingen is de gemiddelde gezelligheid
$$
\begin{aligned}
\frac{E}{V} & =n(n-1) \cdot \frac{(2 n-1)!}{n!(n-1)!} \cdot \frac{(n+1)!(n-1)!}{(2 n)!}=n(n-1) \cdot \frac{(2 n-1)!}{(2 n)!} \cdot \frac{(n+1)!}{n!} \\
& =\frac{n(n-1)(n+1)}{2 n}=\frac{(n-1)(n+1)}{2}=\frac{n^{2}-1}{2}
\end{aligned}
$$
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2022-E2022_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2022"
}
|
Let $n>1$ be an integer. In a row, there are $n$ boxes, and we have $n+1$ identical stones. A distribution is a way to distribute the stones over the boxes, with each stone being in exactly one box. We say that two such distributions are a stone's throw away from each other if we can obtain one distribution from the other by moving exactly one stone to a different box. The sociability of a distribution $a$ is defined as the number of distributions that are a stone's throw away from $a$. Determine the average sociability over all possible distributions.
(Two distributions are the same if there are the same number of stones in the $i$-th box of both rows, for all $i \in\{1,2, \ldots, n\}$.)
Answer. $\frac{n^{2}-1}{2}$
In the solutions below, we call two distributions neighbors if they are a stone's throw away from each other.
|
Just as in the first solution, we calculate that for each $0 \leq k \leq n-1$ there are exactly $N_{k}=\binom{n}{k} \cdot\binom{n}{k+1}$ distributions with sociability $(n-k)(n-1)$. To calculate the total sociability, we prove that
$$
\sum_{k=0}^{n-1}\binom{n}{k}(n-k)\binom{n}{k+1}=n\binom{2 n-1}{n}
$$
The right-hand side counts the number of ways to compile a handout from $n$ algebra problems and $n$ geometry problems with 1 algebra example problem and $n$ other problems. The left-hand side counts this as well, but as a sum over $k$ by first choosing $n-k$ algebra problems, then an example problem from these $n-k$, and then $k+1$ geometry problems. (This sum can also be calculated in other ways. For example, by rewriting $\binom{n}{k}(n-k)=\binom{n-1}{k} n$ and factoring out the $n$ from the sum. You then get $n$ times $\sum_{k=0}^{n-1}\binom{n-1}{k}\binom{n}{k+1}=\binom{2 n-1}{n}$, which follows from a similar story about a handout with $n-k-1$ algebra problems and $k+1$ geometry problems, without the example.)
We conclude that the total sociability is
$$
\sum_{k=0}^{n-1} N_{k}(n-k)(n-1)=n\binom{2 n-1}{n}(n-1)
$$
Just as in the second solution, we note that the number of distributions $V$ is equal to $\binom{2 n}{n+1}$. Therefore, the average sociability is $(n-1) n\binom{2 n-1}{n} /\binom{2 n}{n+1}=\frac{n^{2}-1}{2}$.
|
\frac{n^{2}-1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Zij $n>1$ een geheel getal. Op een rij staan $n$ dozen, en we hebben $n+1$ identieke stenen. Een verdeling is een manier om de stenen over de dozen te verdelen, waarbij elke steen in precies één doos zit. We zeggen dat twee van zulke verdelingen zich op een steenworp afstand van elkaar bevinden als we de ene verdeling uit de andere kunnen verkrijgen door precies één steen te verplaatsen naar een andere doos. De gezelligheid van een verdeling $a$ is gedefinieerd als het aantal verdelingen dat zich op een steenworp afstand van $a$ bevindt. Bepaal de gemiddelde gezelligheid over alle mogelijke verdelingen.
(Twee verdelingen zijn hetzelfde als er in de $i$-de doos van beide rijen evenveel stenen zitten, voor alle $i \in\{1,2, \ldots, n\}$.)
Antwoord. $\frac{n^{2}-1}{2}$
In de oplossingen hieronder noemen we twee verdelingen buren als ze op een steenworp afstand van elkaar liggen.
|
Net als in de eerste oplossing rekenen we uit dat er voor elke $0 \leq k \leq n-1$ precies $N_{k}=\binom{n}{k} \cdot\binom{n}{k+1}$ verdelingen zijn met gezelligheid $(n-k)(n-1)$. Om de totale gezelligheid uit te rekenen, bewijzen we dat
$$
\sum_{k=0}^{n-1}\binom{n}{k}(n-k)\binom{n}{k+1}=n\binom{2 n-1}{n}
$$
De rechterkant telt het aantal manieren om uit $n$ algebra problemen en $n$ meetkunde problemen een handout samen te stellen met 1 algebravoorbeeldopgave en $n$ andere opgaven. De linkerkant telt dit ook, maar dan als som over $k$ door eerst $n-k$ algebra opgaven te kiezen, dan een voorbeeldopgave uit deze $n-k$ en dan nog $k+1$ meetkunde opgaven. (Deze som kan ook op andere manieren worden uitgerekend. Bijvoorbeeld door het herschrijven van $\binom{n}{k}(n-k)=\binom{n-1}{k} n$ en de factor $n$ buiten de som te halen. Je krijgt dan $n$ keer $\sum_{k=0}^{n-1}\binom{n-1}{k}\binom{n}{k+1}=\binom{2 n-1}{n}$ wat volgt uit een soortgelijk verhaal over een handout met $n-k-1$ algebra opgaven en $k+1$ meetkunde opgaven, zonder voorbeeld.)
We concluderen dus dat de totale gezelligheid gelijk is aan
$$
\sum_{k=0}^{n-1} N_{k}(n-k)(n-1)=n\binom{2 n-1}{n}(n-1)
$$
Net als in de tweede oplossing merken we op dat het aantal verdelingen $V$ gelijk is aan $\binom{2 n}{n+1}$. Dus de gemiddelde gezelligheid is $(n-1) n\binom{2 n-1}{n} /\binom{2 n}{n+1}=\frac{n^{2}-1}{2}$.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2022-E2022_uitwerkingen.jsonl",
"solution_match": "\nOplossing III.",
"tier": "T1",
"year": "2022"
}
|
Let $n>1$ be an integer. In a row, there are $n$ boxes, and we have $n+1$ identical stones. A distribution is a way to distribute the stones over the boxes, with each stone being in exactly one box. We say that two such distributions are a stone's throw away from each other if we can obtain one distribution from the other by moving exactly one stone to a different box. The sociability of a distribution $a$ is defined as the number of distributions that are a stone's throw away from $a$. Determine the average sociability over all possible distributions.
(Two distributions are the same if there are the same number of stones in the $i$-th box of both rows, for all $i \in\{1,2, \ldots, n\}$.)
Answer. $\frac{n^{2}-1}{2}$
In the solutions below, we call two distributions neighbors if they are a stone's throw away from each other.
|
Define $f(a)$ as the number of non-empty boxes in a distribution $a$. Just like in the other solutions, each non-empty box $i$ of $a$ gives exactly $n-1$ neighbors of $a$, namely by throwing one stone from $i$ to any other box. Therefore, the average sociability is equal to $n-1$ times the average value of $f(a)$.
For $i \in\{1, \ldots, n\}$ and a distribution $a$, we define
$$
f_{i}(a)= \begin{cases}0 & \text { if box } i \text { is empty in } a \\ 1 & \text { otherwise. }\end{cases}
$$
Note that $f(a)=f_{1}(a)+\cdots+f_{n}(a)$. Let $V_{i}$ be the number of distributions where box $i$ is empty. If box $i$ is empty, then we need to distribute the $n+1$ stones over the other $n-1$ boxes, so $V_{i}=\binom{(n+1)+(n-1)-1}{n+1}=\binom{2 n-1}{n+1}$. Thus, the fraction of distributions where box $i$ is empty is equal to
$$
\frac{V_{i}}{V}=\frac{(2 n-1)!}{(n+1)!(n-2)!} \cdot \frac{(n+1)!(n-1)!}{(2 n)!}=\frac{(2 n-1)!}{(2 n)!} \cdot \frac{(n-1)!}{(n-2)!}=\frac{n-1}{2 n}
$$
The fraction of distributions where box $i$ is non-empty, or the average of $f_{i}(a)$, is thus equal to $1-\frac{n-1}{2 n}=\frac{n+1}{2 n}$. If we sum this over $i$, we find an average of $f(a)$ of $n \cdot \frac{n+1}{2 n}=\frac{n+1}{2}$. We conclude that the average sociability is equal to $(n-1) \cdot \frac{n+1}{2}=\frac{n^{2}-1}{2}$.
|
\frac{n^{2}-1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Zij $n>1$ een geheel getal. Op een rij staan $n$ dozen, en we hebben $n+1$ identieke stenen. Een verdeling is een manier om de stenen over de dozen te verdelen, waarbij elke steen in precies één doos zit. We zeggen dat twee van zulke verdelingen zich op een steenworp afstand van elkaar bevinden als we de ene verdeling uit de andere kunnen verkrijgen door precies één steen te verplaatsen naar een andere doos. De gezelligheid van een verdeling $a$ is gedefinieerd als het aantal verdelingen dat zich op een steenworp afstand van $a$ bevindt. Bepaal de gemiddelde gezelligheid over alle mogelijke verdelingen.
(Twee verdelingen zijn hetzelfde als er in de $i$-de doos van beide rijen evenveel stenen zitten, voor alle $i \in\{1,2, \ldots, n\}$.)
Antwoord. $\frac{n^{2}-1}{2}$
In de oplossingen hieronder noemen we twee verdelingen buren als ze op een steenworp afstand van elkaar liggen.
|
Definieer $f(a)$ als het aantal niet-lege dozen in een verdeling $a$. Net als in de andere oplossingen geeft elke niet-lege doos $i$ van $a$ geeft precies $n-1$ buren van $a$, namelijk door een een steen van $i$ naar een willekeurige andere doos te gooien. Dus de gemiddelde gezelligheid is gelijk aan $n-1$ maal de gemiddelde waarde van $f(a)$.
Voor $i \in\{1, \ldots, n\}$ en een verdeling $a$ definiëren we
$$
f_{i}(a)= \begin{cases}0 & \text { als doos } i \text { leeg is in } a \\ 1 & \text { anders. }\end{cases}
$$
Merk op dat $f(a)=f_{1}(a)+\cdots+f_{n}(a)$. Zij $V_{i}$ verder het aantal verdelingen waarvan doos $i$ leeg is. Als doos $i$ leeg is dan moeten we de $n+1$ stenen verdelen over de ander $n-1$ dozen, dus $V_{i}=\binom{(n+1)+(n-1)-1}{n+1}=\binom{2 n-1}{n+1}$. Dus de fractie van verdelingen waarvan doos $i$ leeg is gelijk aan
$$
\frac{V_{i}}{V}=\frac{(2 n-1)!}{(n+1)!(n-2)!} \cdot \frac{(n+1)!(n-1)!}{(2 n)!}=\frac{(2 n-1)!}{(2 n)!} \cdot \frac{(n-1)!}{(n-2)!}=\frac{n-1}{2 n}
$$
De fractie van verdelingen waarvan doos $i$ niet-leeg is, oftewel het gemiddelde van $f_{i}(a)$, is dus gelijk aan $1-\frac{n-1}{2 n}=\frac{n+1}{2 n}$. Als we dit sommeren over $i$ dan vinden we dus een gemiddelde van $f(a)$ van $n \cdot \frac{n+1}{2 n}=\frac{n+1}{2}$. We concluderen dat de gemiddelde gezelligheid gelijk is aan $(n-1) \cdot \frac{n+1}{2}=\frac{n^{2}-1}{2}$.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2022-E2022_uitwerkingen.jsonl",
"solution_match": "\nOplossing IV.",
"tier": "T1",
"year": "2022"
}
|
Find all natural numbers $n$ for which there exists an integer $a>2$ such that $a^{d}+2^{d} \mid a^{n}-2^{n}$ for all positive divisors $d \neq n$ of $n$.
|
Answer: $n$ is prime or a power of two (including $n=1$).
Indeed, if $n$ is an odd prime, then the only divisor is $d=1$. Choose $a=2^{k}-2$ with $3 \leq k \leq n+1$, for example $a=6$. Then we need to check that $2^{k}-2+2=2^{k}$ is a divisor of $\left(2^{k}-2\right)^{n}-2^{n}$. This is the difference between two terms that both have exactly $n$ factors of 2, so the difference has at least $n+1$ factors of 2.
In the second case, we have $n=2^{m}$ with $m \geq 0$. If $m=0$, then there are no positive divisors $d \neq n$, so the condition holds because the requirement is vacuously true. Note also that $m=1$ gives the even prime 2. For all divisors $d \neq n$, we now observe that
$$
a^{n}-2^{n}=a^{d e}-2^{d e} \equiv\left(-2^{d}\right)^{e}-2^{d e}=2^{n}\left((-1)^{e}-1\right) \quad \bmod a^{d}+2^{d}
$$
is zero for all $a$. Thus, $a^{n}-2^{n}$ is a multiple of $a^{d}+2^{d}$, or in other words, $a^{d}+2^{d} \mid a^{n}-2^{n}$. This checks both cases.
Now suppose that $n$ is neither a prime nor a power of two. Then we can write $n$ as $n=d e$ with $e \neq 1$ odd (since $n$ is not a power of two) and $d \neq 1$ (since $n$ is not a prime). Since $(-1)^{e}-1=2$, it follows from the above calculation that $a^{d}+2^{d} \mid 2^{n+1}$. This means that $a^{d}+2^{d}$ is a power of two, so $a^{d}=2^{k}-2^{d}$ for some $d<k \leq n+1$. Therefore, $a$ is divisible by 2 and $\left(\frac{a}{2}\right)^{d}=2^{k-d}-1$.
Now we distinguish between $d$ even and $d$ odd. In the first case, $2^{k-d}-1$ is a square. Since $a>2$, $\left(\frac{a}{2}\right)^{d}=2^{k-d}-1$ implies that $k-d \geq 2$. So this square is -1 modulo 4, which is impossible. If $d$ is odd, then we observe that
$$
2^{k-d}=\left(\frac{a}{2}\right)^{d}+1=\left(\frac{a}{2}+1\right)\left(\left(\frac{a}{2}\right)^{d-1}-\left(\frac{a}{2}\right)^{d-2}+\cdots+1\right).
$$
Since $d \neq 1$, $\frac{a}{2}+1$ is strictly less than $\left(\frac{a}{2}\right)^{d}+1$. The second factor in this product is a sum of an even number of terms with the parity of $\frac{a}{2}$ and a 1, so this factor is odd. Since the second factor is also greater than 1, this contradicts the fact that it must be a divisor of the power of two $2^{k-d}$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Vind alle natuurlijke getallen $n$ waarvoor er een geheel getal $a>2$ bestaat zo dat $a^{d}+2^{d} \mid a^{n}-2^{n}$ voor alle positieve delers $d \neq n$ van $n$.
|
Antwoord: $n$ is priem of een tweemacht (incl. $n=1$ ).
Inderdaad, als $n$ een oneven priemgetal is, dan is de enige deler $d=1$. Kies $a=2^{k}-2$ met $3 \leq k \leq n+1$, bijvoorbeeld $a=6$. Dan moeten we controleren dat $2^{k}-2+2=2^{k}$ een deler is $\left(2^{k}-2\right)^{n}-2^{n}$. Dit is het verschil tussen twee termen die allebei precies $n$ factoren 2 hebben, dus het verschil heeft minstens $n+1$ factoren 2 .
In het tweede geval hebben we $n=2^{m}$ met $m \geq 0$. Als $m=0$, dan zijn er geen positieve delers $d \neq n$, dus dan geldt de voorwaarde omdat de eis leeg is. Merk ook op dat $m=1$ het even priemgetal 2 geeft. Voor alle delers $d \neq n$ geldt nu dat $e=n / d$ even is. Dan merken we op dat
$$
a^{n}-2^{n}=a^{d e}-2^{d e} \equiv\left(-2^{d}\right)^{e}-2^{d e}=2^{n}\left((-1)^{e}-1\right) \quad \bmod a^{d}+2^{d}
$$
nul is voor alle $a$. Dus $a^{n}-2^{n}$ is een veelvoud van $a^{d}+2^{d}$, oftewel $a^{d}+2^{d} \mid a^{n}-2^{n}$. Hiermee hebben we beide gevallen gecontroleerd.
Stel nu dat $n$ geen priemgetal of tweemacht is. Dan kunnen we $n$ schrijven als $n=d e$ met $e \neq 1$ oneven (omdat $n$ geen tweemacht is) en $d \neq 1$ (omdat $n$ geen priemgetal is). Omdat $(-1)^{e}-1=2$ volgt uit de bovenstaande berekening nu dat $a^{d}+2^{d} \mid 2^{n+1}$. Dat betekent dat $a^{d}+2^{d}$ een tweemacht, dus $a^{d}=2^{k}-2^{d}$ voor een zekere $d<k \leq n+1$. Dus $a$ is deelbaar door 2 en $\left(\frac{a}{2}\right)^{d}=2^{k-d}-1$.
Nu maken we onderscheid tussen $d$ even en $d$ oneven. In het eerste geval is $2^{k-d}-1$ een kwadraat. Omdat $a>2$ impliceert $\left(\frac{a}{2}\right)^{d}=2^{k-d}-1$ echter dat $k-d \geq 2$. Dus dit kwadraat is -1 modulo 4 wat onmogelijk is. Als $d$ oneven is, dan merken we op dat
$$
2^{k-d}=\left(\frac{a}{2}\right)^{d}+1=\left(\frac{a}{2}+1\right)\left(\left(\frac{a}{2}\right)^{d-1}-\left(\frac{a}{2}\right)^{d-2}+\cdots+1\right) .
$$
Omdat $d \neq 1$ is $\frac{a}{2}+1$ strikt kleiner dan $\left(\frac{a}{2}\right)^{d}+1$. De tweede factor in dit product is een som van een even aantal termen met de pariteit van $\frac{a}{2}$ en een 1 , dus deze factor is oneven. Omdat de tweede factor ook groter dan 1 is, is dit in tegenspraak met de het feit dat het een deler moet zijn van de tweemacht $2^{k-d}$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2022-E2022_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2022"
}
|
Let $\triangle A B C$ be a right-angled triangle with a right angle at $C$ and $|A C|>|B C|$, let $I$ be the center of the inscribed circle, and let $H$ be the projection of $C$ onto the line segment $A B$. The incircle $\omega$ of $\triangle A B C$ touches the sides $B C, C A$, and $A B$ at points $A_{1}, B_{1}$, and $C_{1}$, respectively. Let $E$ and $F$ be the reflections of $C$ in the lines $A_{1} C_{1}$ and $B_{1} C_{1}$, respectively, and let $K$ and $L$ be the reflections of $H$ in the lines $A_{1} C_{1}$ and $B_{1} C_{1}$, respectively. Prove that the circumcircles of $\triangle A_{1} E I, \triangle B_{1} F I$, and $\triangle C_{1} K L$ pass through a common point.
|
Note that the line segments $B C_{1}$ and $B A_{1}$ are of equal length because they are tangents from $B$ to the same circle $\omega$. This means that $\triangle A_{1} B C_{1}$ is an isosceles triangle with vertex angle $B$. Since the angle bisector and the altitude in an isosceles triangle coincide, the angle bisector of $\angle A B C$ is perpendicular to the line $A_{1} C_{1}$.
From this, we can directly deduce that $A_{1} E \| A B$, but it can also be done with simple angle chasing: since $E$ is the reflection of $C$, we have $\angle E A_{1} C_{1} = \angle C A_{1} C_{1}$, and because $\triangle A_{1} B C_{1}$ is an isosceles triangle, $\angle C A_{1} C_{1} = \angle A C_{1} A_{1}$. Therefore, by Z-angles, we have $A_{1} E \| A B$. Similarly, we find that $C_{1} K \| B C$, because $\angle K C_{1} A_{1} = \angle H C_{1} A_{1} = \angle B C_{1} A_{1} = \angle B A_{1} C_{1}$ gives us Z-angles. Further, $|A_{1} E| = |A_{1} C| = r$ where $r$ is the radius of the inscribed circle $\omega$, because we have a right angle at $C$.
Since $E K$ is the reflection of $C H$ in $A_{1} C_{1}$, it also holds that $E K \perp B C$. Indeed, with $S$ the intersection of $E K$ and $B C$, we find that $\angle A_{1} E S = \angle B C H$ due to the reflection and $\angle E A_{1} S = \angle C B H$ due to Z-angles. Thus, the triangles $\triangle A_{1} E S$ and $\triangle B C H$ are similar, and the angle $\angle E S A_{1}$ is right, just like $\angle C H B$. Since $E K$ and $A C$ are both perpendicular to $B C$, we conclude that $E K \| A C$.
Similarly, it holds that $B_{1} F \| A B$, $C_{1} L \| A C$, $F L \| B C$, and $|B_{1} F| = r$.
Let $X$ be the intersection of the lines $E K$ and $F L$. We will show that this is the desired point. First, $C_{1} K X L$ is a rectangle and thus a cyclic quadrilateral.
Second, we will prove that $|X I| = r$, because $|A_{1} E| = |B_{1} F| = r$. Indeed, let $Y$ and $Z$ be the intersections of the line through $I$ parallel to $A B$ with the lines $E K$ and $F L$, respectively. Then $A_{1} E Y I$ and $B_{1} F Z I$ are parallelograms, so $|Y I| = r = |Z I|$. Furthermore, the angle $\angle Y X Z = 90^{\circ}$, so by the Thales' theorem, $|X I| = r$.
In particular, $X$ lies on the inscribed circle $\omega$. But more importantly, $A_{1} E X I$ and $B_{1} F X I$ are isosceles trapezoids, and thus cyclic quadrilaterals.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $\triangle A B C$ een driehoek met een rechte hoek in $C$ en $|A C|>|B C|$, zij $I$ het middelpunt van de ingeschreven cirkel en zij $H$ de projectie van $C$ op het lijnstuk $A B$. De ingeschreven cirkel $\omega$ van $\triangle A B C$ raakt de zijden $B C, C A$ en $A B$ in respectievelijk de punten $A_{1}, B_{1}$ en $C_{1}$. Laat $E$ en $F$ de reflectie zijn van $C$ in respectievelijk de lijnen $A_{1} C_{1}$ en $B_{1} C_{1}$, en laat $K$ en $L$ de reflectie zijn van $H$ in respectievelijk de lijnen $A_{1} C_{1}$ en $B_{1} C_{1}$. Bewijs de de omgeschreven cirkels van $A_{1} E I, B_{1} F I$ en $C_{1} K L$ door een gemeenschappelijk punt gaan.
|
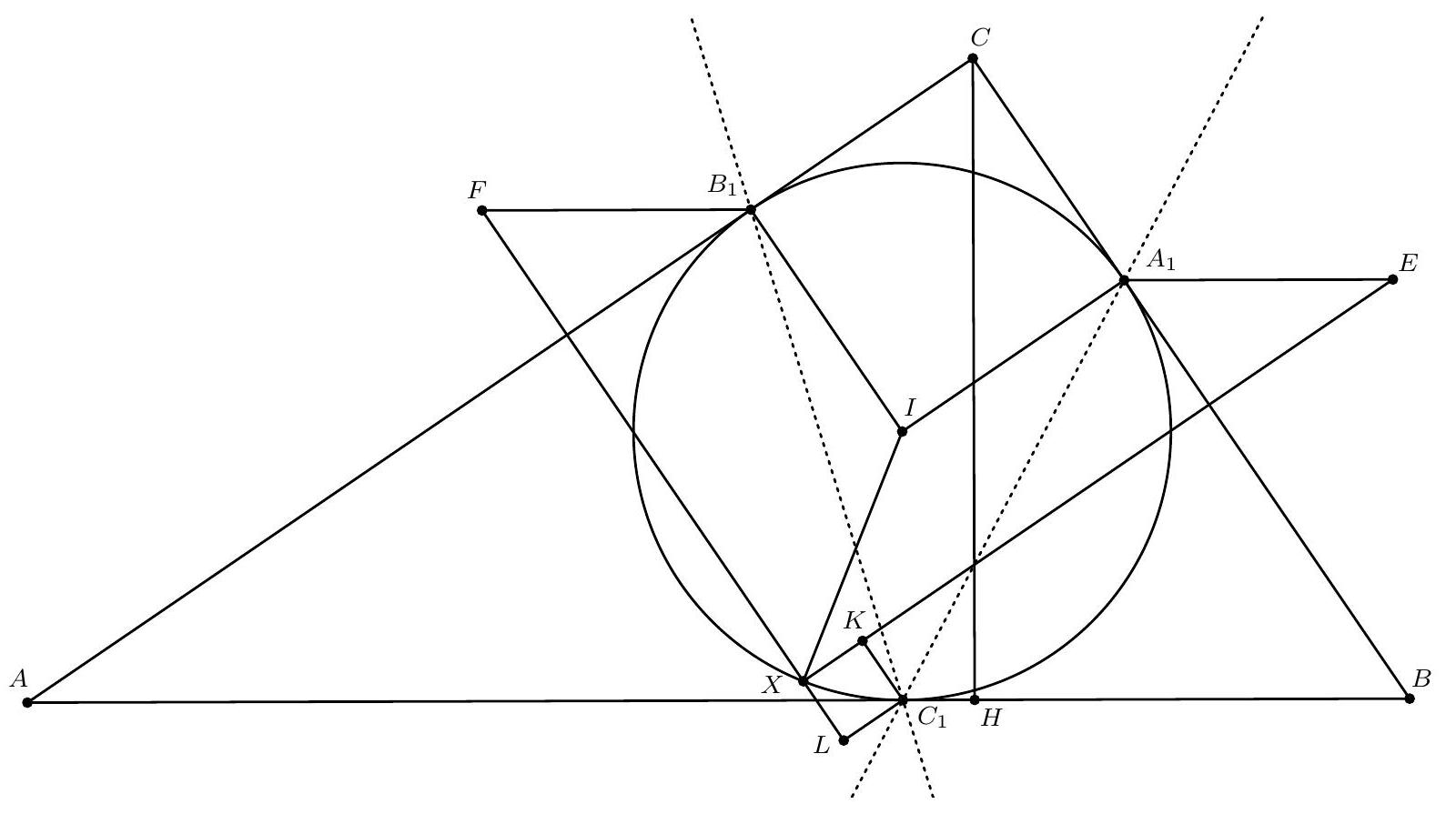
Merk op dat de lijnstukken $B C_{1}$ en $B A_{1}$ even lang zijn omdat het raaklijnen zijn vanuit $B$ aan de zelfde cirkel $\omega$. Dat betekent dat $\triangle A_{1} B C_{1}$ een gelijkbenige driehoek is met tophoek $B$. Omdat de bissectrice en hoogtelijn in een gelijkbenige driehoek samenvallen, staat de bissectrice van hoek $\angle A B C$ loodrecht op de lijn $A_{1} C_{1}$.
Hieruit kunnen we direct afleiden dat $A_{1} E \| A B$, maar het kan ook met eenvoudig hoekenjagen: aangezien $E$ de spiegeling is van $C$ geldt $\angle E A_{1} C_{1}=\angle C A_{1} C_{1}$ en wegens de gelijkbenige driehoek $\triangle A_{1} B C_{1}$ geldt $\angle C A_{1} C_{1}=\angle A C_{1} A_{1}$. Dus wegens Z-hoeken hebben we dat $A_{1} E \| A B$. Op dezelfde manier vinden we dat $C_{1} K \| B C$, omdat $\angle K C_{1} A_{1}=\angle H C_{1} A_{1}=$ $\angle B C_{1} A_{1}=\angle B A_{1} C_{1}$ ons Z-hoeken geven. Verder geldt $\left|A_{1} E\right|=\left|A_{1} C\right|=r$ waarbij $r$ de straal is van de ingeschreven cirkel $\omega$, omdat we een rechte hoek in $C$ hebben.
Omdat $E K$ de spiegeling is van $C H$ in $A_{1} C_{1}$ geldt ook dat $E K \perp B C$. Inderdaad, met
$S$ het snijpunt van $E K$ en $B C$, vinden we dat $\angle A_{1} E S=\angle B C H$ wegens de spiegeling en $\angle E A_{1} S=\angle C B H$ wegens Z-hoeken. Dus de driehoeken $\triangle A_{1} E S$ en $\triangle B C H$ zijn gelijkvormig, en de hoek $\angle E S A_{1}$ is recht net als $\angle C H B$. Omdat $E K$ en $A C$ nu allebei loodrecht op $B C$ staan concluderen we ook dat $E K \| A C$.
Evenzo geldt dat $B_{1} F\left\|A B, C_{1} L\right\| A C, F L \| B C$ en $\left|B_{1} F\right|=r$.
Zij $X$ het snijpunt van de lijnen $E K$ en $F L$. We gaan laten zien dat dit het gezochte punt is. Ten eerste is $C_{1} K X L$ een rechthoek en dus een koordenvierhoek.
Ten tweede gaan we bewijzen dat $|X I|=r$, omdat $\left|A_{1} E\right|=\left|B_{1} F\right|=r$. Inderdaad, laat $Y$ en $Z$ de snijpunten zijn van de lijn door $I$ evenwijdig aan $A B$ en respectievelijk de lijnen $E K$ en $F L$. Dan zijn $A_{1} E Y I$ en $B_{1} F Z I$ parallellogrammen, dus $|Y I|=r=|Z I|$. Verder is de hoek $\angle Y X Z=90^{\circ}$, dus wegens de stelling van Thales is ook $|X I|=r$.
In het bijzonder ligt $X$ dus op de ingeschreven cirkel $\omega$. Maar belangrijker is dat $A_{1} E X I$ en $B_{1} F X I$ gelijkbenige trapeziums zijn, en dus koordenvierhoeken.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2022-E2022_uitwerkingen.jsonl",
"solution_match": "# Oplossing I.",
"tier": "T1",
"year": "2022"
}
|
Let $\triangle A B C$ be a right-angled triangle with a right angle at $C$ and $|A C|>|B C|$, let $I$ be the center of the inscribed circle, and let $H$ be the projection of $C$ onto the line segment $A B$. The incircle $\omega$ of $\triangle A B C$ touches the sides $B C, C A$, and $A B$ at points $A_{1}, B_{1}$, and $C_{1}$, respectively. Let $E$ and $F$ be the reflections of $C$ in the lines $A_{1} C_{1}$ and $B_{1} C_{1}$, respectively, and let $K$ and $L$ be the reflections of $H$ in the lines $A_{1} C_{1}$ and $B_{1} C_{1}$, respectively. Prove that the circumcircles of $\triangle A_{1} E I, \triangle B_{1} F I$, and $\triangle C_{1} K L$ pass through a common point.
|
You can enter $X$ in several ways and complete the proof. Note that $CH$ intersects line segment $A_{1}C_{1}$ internally due to $|BC|<|AC|$. Therefore, $EK$ also intersects chord $A_{1}C_{1}$ of $\omega$ internally, as $EK$ is the reflection of $CH$. Define $X$ now, for example, as the intersection of $EK$ and $\omega$ on the same side of $A_{1}C_{1}$ as $K$. Then we know that $|XI|=r=|A_{1}E|$ and $EK \| A_{1}I$, so $A_{1}EXI$ is an isosceles trapezoid (and thus a cyclic quadrilateral). Since $\angle A_{1}IB_{1}=90^{\circ}$, we find $\angle B_{1}IX + \angle XIA_{1} = 270^{\circ}$. Since we also know that $FB_{1} \| AB \| A_{1}E$, we find $\angle FB_{1}I + \angle IA_{1}E = 270^{\circ}$. Since $\angle XIA_{1} = \angle IA_{1}E$ in the isosceles trapezoid, we conclude that $\angle B_{1}IX = \angle FB_{1}I$. And with $|XI| = r = |B_{1}F|$, we have that $B_{1}FXI$ is also an isosceles trapezoid (and thus a cyclic quadrilateral).
By definition, $X$ lies on $EK$. We now show that $X$ also lies on $FL$. Since $B_{1}FXI$ is an isosceles trapezoid, $FX \| B_{1}I$. And we already knew that $B_{1}I \| BC \| FL$. Therefore, $FX$ and $FL$ are parallel and both pass through $F$, so they coincide. Thus, $C_{1}KXL$ is a rectangle (and thus a cyclic quadrilateral).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $\triangle A B C$ een driehoek met een rechte hoek in $C$ en $|A C|>|B C|$, zij $I$ het middelpunt van de ingeschreven cirkel en zij $H$ de projectie van $C$ op het lijnstuk $A B$. De ingeschreven cirkel $\omega$ van $\triangle A B C$ raakt de zijden $B C, C A$ en $A B$ in respectievelijk de punten $A_{1}, B_{1}$ en $C_{1}$. Laat $E$ en $F$ de reflectie zijn van $C$ in respectievelijk de lijnen $A_{1} C_{1}$ en $B_{1} C_{1}$, en laat $K$ en $L$ de reflectie zijn van $H$ in respectievelijk de lijnen $A_{1} C_{1}$ en $B_{1} C_{1}$. Bewijs de de omgeschreven cirkels van $A_{1} E I, B_{1} F I$ en $C_{1} K L$ door een gemeenschappelijk punt gaan.
|
Je kan $X$ op verschillende manieren invoeren en het bewijs afmaken. Merk op dat $C H$ lijnstuk $A_{1} C_{1}$ inwendig snijdt wegens $|B C|<|A C|$. Dus $E K$ snijdt koorde $A_{1} C_{1}$ van $\omega$ ook inwendig, omdat $E K$ het spiegelbeeld is van $C H$. Definieer $X$ nu bijvoorbeeld als het snijpunt van $E K$ en $\omega$ aan dezelfde kant van $A_{1} C 1$ als $K$. Dan weten we dat $|X I|=r=\left|A_{1} E\right|$ en $E K \| A_{1} I$, dus $A_{1} E X I$ is een gelijkbenige trapezium (en dus een koordenvierhoek). Omdat $\angle A_{1} I B_{1}=90^{\circ}$ vinden we $\angle B_{1} I X+\angle X I A_{1}=270^{\circ}$. Omdat we ook weten dat $F B_{1}\|A B\| A_{1} E$, vinden we $\angle F B_{1} I+\angle I A_{1} E=270^{\circ}$. Aangezien $\angle X I A_{1}=$ $\angle I A_{1} E$ in het gelijkbenige trapezium, concluderen we dat ook $\angle B_{1} I X=\angle F B_{1} I$. En met $|X I|=r=\left|B_{1} F\right|$ hebben we dus dat ook $B_{1} F X I$ een gelijkbenig trapezium is (en dus een koordenvierhoek).
Per definitie ligt $X$ op $E K$. We laten nu zien dat $X$ ook op $F L$ ligt. Omdat $B_{1} F X I$ een gelijkbenig trapezium is, geldt $F X \| B_{1} I$. En we wisten al dat $B_{1} I\|B C\| F L$. Dus $F X$ en $F L$ zijn parallel en gaan beide door $F$, dus vallen ze samen. Dus is $C_{1} K X L$ een rechthoek (en dus een koordenvierhoek).
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2022-E2022_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2022"
}
|
Let $n \geq 1$ be an integer. Ruben creates a test with $n$ questions. Each question on this test is worth a different number of points. The first question is worth 1 point, the second question 2, the third 3, and so on, up to the last question which is worth $n$ points. Each question is either correct or incorrect. For a question, he either gets no points or all the points. Let $f(n)$ be the number of ways he can complete the test such that the number of points he scores is equal to the number of questions he got wrong.
Investigate whether there are infinitely many pairs $(a, b)$ with $a < b$ and $f(a) = f(b)$.
|
Ten overvloede merken we op dat $f(1)=0, f(2)=f(3)=f(4)=1$, $f(5)=f(6)=2, f(7)=f(8)=3, f(9)=f(10)=5$. Vanaf dat moment is $f(n)$ strikt stijgend als functie van $n$. Er zijn dus slechts een eindig aantal van de gezochte paren.
We translate the above text into English, preserving the original text's line breaks and formatting:
---
We observe that $f(1)=0, f(2)=f(3)=f(4)=1$, $f(5)=f(6)=2, f(7)=f(8)=3, f(9)=f(10)=5$. From that point onward, $f(n)$ is strictly increasing as a function of $n$. Therefore, there are only a finite number of the desired pairs.
Let $S_{n}$ be a set of good answers, seen as a subset of $\{1,2, \ldots, n\}$. Then $S_{n}$ is a solution to the condition if the sum of all elements of $S_{n}$ plus the number of elements of $S_{n}$ is equal to $n$. We first claim that $f(n)$ is at least non-decreasing. Indeed, if the subset $S_{n-1}$ of $\{1,2, \ldots, n-1\}$ satisfies the condition for $n-1$ and we increase the largest element of $S_{n-1}$ by 1, then we get a set $S_{n}$ with the same number of elements as $S_{n-1}$ and with a sum 1 higher than the sum of $S_{n-1}$. Thus, this gives a solution for $n$. This is an injective mapping from the set of solutions for $n-1$ to the set of solutions for $n$.
We now show that for $n \geq 11$ there is at least one other solution that does not lie in the image of this mapping. A set of at least two good answers where the largest and the second-largest elements differ by exactly 1 does not lie in the image. In a set that does lie in the image, the largest good answer has had 1 added to it. If $n=2 k+1$ with $k \geq 5$, then the set of good answers $S=\{1, k-2, k-1\}$ is a solution, because $1+(k-2)+(k-1)+|S|=2 k+1=n$. If $n=2 k$ with $k \geq 6$, then similarly $S=\{2, k-3, k-2\}$ is a solution, because $2+(k-3)+(k-2)+|S|=2 k=n$. We conclude that $f(n)>f(n-1)$ for all $n \geq 11$. $\square$
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Zij $n \geq 1$ een geheel getal. Ruben maakt een toets met $n$ vragen. Elke vraag op deze toets is een ander aantal punten waard. De eerste vraag is 1 punt waard, de tweede vraag 2 , de derde 3 en zo door tot en met de laatste vraag die $n$ punten waard is. Elke vraag is goed of fout. Voor een vraag krijgt hij dus óf geen, óf alle punten. Zij $f(n)$ het aantal manieren waarop hij de toets kan maken zodat het aantal punten dat hij gehaald heeft gelijk is aan het aantal vragen dat hij fout had.
Onderzoek of er oneindig veel paren $(a, b)$ bestaan met $a<b$ en $f(a)=f(b)$.
|
Ten overvloede merken we op dat $f(1)=0, f(2)=f(3)=f(4)=1$, $f(5)=f(6)=2, f(7)=f(8)=3, f(9)=f(10)=5$. Vanaf dat moment is $f(n)$ strikt stijgend als functie van $n$. Er zijn dus slechts een eindig aantal van de gezochte paren.
Zij $S_{n}$ een verzameling van goede antwoorden, gezien als deelverzameling van $\{1,2, \ldots, n\}$. Dan is $S_{n}$ een oplossing van de voorwaarde als de som van alle elementen van $S_{n}$ plus het aantal elementen van $S_{n}$ gelijk is aan $n$. We claimen eerst dat $f(n)$ in elk geval niet-dalend is. Inderdaad, als de deelverzameling $S_{n-1}$ van $\{1,2, \ldots, n-1\}$ voldoet voor $n-1$ en we verhogen het grootste element van $S_{n-1}$ met 1, dan krijgen we een verzameling $S_{n}$ met evenveel elementen als $S_{n-1}$ en met som 1 hoger dan de som van $S_{n-1}$. Dus dit geeft een oplossing voor $n$. Dit is een injectieve afbeelding van de verzameling van oplossingen voor $n-1$ naar de verzameling van oplossingen voor $n$.
We laten nu zien dat er voor $n \geq 11$ nog minstens één andere oplossing is die niet in het beeld van deze afbeelding ligt. Een verzameling van minstens twee goede antwoorden waarvan het grootste en het een-na-grootste element precies 1 van elkaar verschillen ligt in ieder geval niet in het beeld. Bij een verzameling die wel in het beeld ligt, is namelijk bij het grootste goede antwoord 1 opgeteld. Als $n=2 k+1$ met $k \geq 5$, dan is de verzameling goede antwoorden $S=\{1, k-2, k-1\}$ een oplossing, omdat $1+(k-2)+(k-1)+|S|=2 k+1=n$. Als $n=2 k$ met $k \geq 6$, dan is op dezelfde manier $S=\{2, k-3, k-2\}$ een oplossing, omdat $2+(k-3)+(k-2)+|S|=2 k=n$. We concluderen dat $f(n)>f(n-1)$ voor alle $n \geq 11 . \square$
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2023-B2023_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2023"
}
|
Let $n \geq 1$ be an integer. Ruben creates a test with $n$ questions. Each question on this test is worth a different number of points. The first question is worth 1 point, the second question 2, the third 3, and so on, up to the last question which is worth $n$ points. Each question is either correct or incorrect. For a question, he either gets no points or all the points. Let $f(n)$ be the number of ways he can complete the test such that the number of points he scores is equal to the number of questions he got wrong.
Investigate whether there are infinitely many pairs $(a, b)$ with $a < b$ and $f(a) = f(b)$.
|
When $n=2 k+1$ with $k \geq 2$ odd, the set of good answers $S=\{k-1, k\}$ is also a solution, because indeed $(k-1)+k+|S|=2 k+1=n$.
|
not found
|
Yes
|
Problem not solved
|
proof
|
Combinatorics
|
Zij $n \geq 1$ een geheel getal. Ruben maakt een toets met $n$ vragen. Elke vraag op deze toets is een ander aantal punten waard. De eerste vraag is 1 punt waard, de tweede vraag 2 , de derde 3 en zo door tot en met de laatste vraag die $n$ punten waard is. Elke vraag is goed of fout. Voor een vraag krijgt hij dus óf geen, óf alle punten. Zij $f(n)$ het aantal manieren waarop hij de toets kan maken zodat het aantal punten dat hij gehaald heeft gelijk is aan het aantal vragen dat hij fout had.
Onderzoek of er oneindig veel paren $(a, b)$ bestaan met $a<b$ en $f(a)=f(b)$.
|
Als $n=2 k+1$ met $k \geq 2$ oneven is, dan is de verzameling goede antwoorden $S=\{k-1, k\}$ ook een oplossing, omdat immers $(k-1)+k+|S|=2 k+1=n$.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2023-B2023_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2023"
}
|
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ for which
$$
f(a-b) f(c-d)+f(a-d) f(b-c) \leq(a-c) f(b-d)
$$
for all real numbers $a, b, c$ and $d$.
N.B. on the right-hand side of the inequality, there is only one $f$.
|
The solutions are $f(x)=0$ for all $x$ and $f(x)=x$ for all $x$. For $f(x)=0$, we easily find that equality always holds. For $f(x)=x$, we check that
$$
\begin{aligned}
(a-b)(c-d)+(a-d)(b-c) & =a c-a d-b c+b d+a b-a c-b d+c d \\
& =-a d-b c+a b+c d \\
& =(a-c)(b-d),
\end{aligned}
$$
so equality also holds in this case. Now we show that these are the only two solutions.
Substituting $a=b=c=d=0$ gives us that $2 f(0)^{2} \leq 0$, which means that $f(0)=0$.
Next, we substitute $b=a-x, c=a$ and $d=a-y$, so that $a-b=x, a-c=0$ and $a-d=y$. Then we find that
$$
f(y)(f(x)+f(-x)) \leq 0
$$
Suppose there is a $y$ such that $f(y) \neq 0$. If we then substitute $x=y$ into the equation above and move one of the terms to the right, we find that
$$
0<f(y)^{2} \leq-f(y) f(-y)
$$
This means that one of the two values $f(y)$ and $f(-y)$ is positive and the other is negative. Suppose without loss of generality that $f(y)$ is positive.
Given arbitrary $a$ and $y$, now substitute $b=a, c=0$ and $d=a-y$. Then we find that $f(y) f(a) \leq a f(y)$. Dividing by $f(y)$, we get $f(a) \leq a$. However, if we had substituted $b=a$, $c=0$ and $d=a+y$, we would have found that $f(-y) f(a) \leq a f(-y)$. Since $f(-y)$ is negative, the inequality sign flips when we divide by $f(-y)$, so we also find that $f(a) \geq a$. We conclude that $f(a)=a$ for all real $a$.
Thus, $f$ is the zero function or $f(a)=a$ for all real $a$, both of which we checked at the beginning.
Remark. By applying the argument of the last paragraph to equation (1), we can also find as an intermediate step that $f(x)=-f(-x)$ for all $x$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Vind alle functies $f: \mathbb{R} \rightarrow \mathbb{R}$ waarvoor geldt dat
$$
f(a-b) f(c-d)+f(a-d) f(b-c) \leq(a-c) f(b-d)
$$
voor alle reële getallen $a, b, c$ en $d$.
N.B. rechts van het ongelijkheidsteken staat dus maar één $f$.
|
De oplossingen zijn $f(x)=0$ voor alle $x$ en $f(x)=x$ voor alle $x$. Voor $f(x)=0$ vinden we eenvoudig dat altijd gelijkheid geldt. Voor $f(x)=x$ controleren we dat
$$
\begin{aligned}
(a-b)(c-d)+(a-d)(b-c) & =a c-a d-b c+b d+a b-a c-b d+c d \\
& =-a d-b c+a b+c d \\
& =(a-c)(b-d),
\end{aligned}
$$
dus ook in dat geval geldt gelijkheid. Nu laten we zien dat dit de enige twee oplossingen zijn.
Invullen van $a=b=c=d=0$ geeft ons dat $2 f(0)^{2} \leq 0$, wat betekent dat $f(0)=0$.
Vervolgens vullen we in $b=a-x, c=a$ en $d=a-y$, zodat $a-b=x, a-c=0$ en $a-d=y$. Dan vinden we dat
$$
f(y)(f(x)+f(-x)) \leq 0
$$
Stel dat er een $y$ is zo dat $f(y) \neq 0$. Als we dan in de vergelijking hierboven $x=y$ invullen en een van de termen naar rechts halen, vinden we dat
$$
0<f(y)^{2} \leq-f(y) f(-y)
$$
Dit betekent dat één van de twee waardes $f(y)$ en $f(-y)$ positief is en de ander negatief. Stel zonder verlies van algemeenheid dat $f(y)$ positief is.
Gegeven willekeurige $a$ en $y$, vul nu $b=a, c=0$ en $d=a-y$ in. Dan vinden we dat $f(y) f(a) \leq a f(y)$. Als we door $f(y)$ delen, krijgen we dus $f(a) \leq a$. Als we echter $b=a$, $c=0$ en $d=a+y$ hadden ingevuld, dan hadden we gevonden dat $f(-y) f(a) \leq a f(-y)$. Aangezien $f(-y)$ negatief is, klapt het teken om wanneer we delen door $f(-y)$ zodat we ook vinden dat $f(a) \geq a$. We concluderen dat $f(a)=a$ voor alle reële $a$.
Dus $f$ is de nulfunctie of $f(a)=a$ voor alle reële $a$, die we allebei aan het begin hebben gecontroleerd.
Opmerking. Door het argument van de laatste alinea toe te passen op vergelijking (1) kunnen we als tussenstap ook vinden dat $f(x)=-f(-x)$ voor alle $x$.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2023-B2023_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2023"
}
|
We play a game of musical chairs with $n$ chairs numbered 1 to $n$. You hang $n$ slips of paper, numbered 1 to $n$, on the chairs such that the number on a slip does not match the number on the chair.
Each chair has a player sitting on it. When you clap, each player looks at the number on the slip on their current chair and sits on the chair with that number. Prove that for every $m$ that is not a prime power with $1<m \leq n$, it is possible to hang the slips such that after $m$ claps, everyone is sitting on their own chair for the first time.
|
When $m=n$, you can hang the slip with number $i+1$ on chair $i$. Everyone then moves one chair over with each clap, and the first time someone is back in their own chair is after $n$ claps. And then everyone is back in their own chair. Now suppose that $m<n$.
Since $m$ is not a prime power, we can write $m$ as $m=k \ell$ with $\operatorname{ggd}(k, \ell)=1$. We claim that there are $a, b>0$ such that
$$
a k+b \ell=n
$$
The numbers $n-a k$ with $a \in\{1,2, \ldots, \ell\}$ are all different modulo $\ell$. If this were not the case, there would be $a_{1}$ and $a_{2}$ such that $n-a_{1} k \equiv n-a_{2} k \bmod \ell$, or $\left(a_{1}-a_{2}\right) k \equiv 0 \bmod \ell$. Since $\operatorname{ggd}(k, \ell)=1$, this would mean that $\ell \mid\left(a_{1}-a_{2}\right)$, which is not possible since these are two elements from $\{1,2, \ldots, \ell\}$. Therefore, the numbers $n-a k$ with $a \in\{1,2, \ldots, \ell\}$ are indeed all different modulo $\ell$. Thus, these are all $\ell$ different residue classes. Since $n-a k \geq n-\ell k=n-m>0$, these $\ell$ numbers are also all greater than 0. Choose now the $a$ for which $n-a k$ is congruent to 0 modulo $\ell$. Since $n-a k$ is greater than 0, there is now a $b>0$ such that $n-a k=b \ell$. This gives the $a, b>0$ such that $a k+b \ell=n$.
Now we divide the chairs into $a$ groups of $k$ chairs and $b$ groups of $\ell$ chairs. In each group, we hang the cards so that they cycle through. The players on a chair in a group of $k$ chairs are in their own chair every $k$ claps (and not otherwise). The players on a chair in a group of $\ell$ chairs are in their own chair every $\ell$ claps (and not otherwise). The first time everyone is back in their own chair is thus after $\mathrm{kgv}(k, \ell)$ claps. But
$$
\operatorname{kgv}(k, \ell)=k \ell=m
$$
$\operatorname{because} \operatorname{ggd}(k, \ell)=1$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
We spelen een spelletje stoelendans met $n$ stoelen genummerd 1 tot en met $n$. Je hangt $n$ blaadjes, genummerd 1 tot en met $n$, op de stoelen zodanig dat het nummer op een blaadje niet overeenkomt met het nummer op de stoel.
Op elke stoel zit een speler. Wanneer je klapt, kijkt elke speler naar het nummer op het blaadje aan zijn huidige stoel en gaat op de stoel zitten met dat nummer. Bewijs dat het voor elke $m$ die geen priem-macht is met $1<m \leq n$ mogelijk is om de blaadjes zo op te hangen dat na $m$ klappen voor het eerst iedereen weer op hun eigen stoel zit.
|
Als $m=n$, dan kan je op stoel $i$ het blaadje ophangen met nummer $i+1$. Iedereen schuift dan elke klap een stoel op en de eerste keer dat iemand weer op zijn eigen stoel zit is na $n$ klappen. En dan zit ook iedereen weer op zijn eigen stoel. Stel nu dat $m<n$.
Aangezien $m$ geen priemmacht is kunnen we $m$ schrijven als $m=k \ell$ met $\operatorname{ggd}(k, \ell)=1$. We claimen dat er $a, b>0$ zijn zo dat
$$
a k+b \ell=n
$$
De getallen $n-a k$ met $a \in\{1,2, \ldots, \ell\}$ zijn allemaal verschillend modulo $\ell$. Zou dat immers niet het geval zijn, dan zouden er $a_{1}$ en $a_{2}$ zijn zo dat $n-a_{1} k \equiv n-a_{2} k \bmod \ell$, oftewel $\left(a_{1}-a_{2}\right) k \equiv 0 \bmod \ell$. Aangezien $\operatorname{ggd}(k, \ell)=1$ zou dat betekenen dat $\ell \mid\left(a_{1}-a_{2}\right)$, wat niet kan aangezien dit twee elementen zijn uit $\{1,2, \ldots, \ell\}$. Dus de getallen $n-a k$ met $a \in\{1,2, \ldots, \ell\}$ zijn inderdaad allemaal verschillend modulo $\ell$. Daardoor zijn dit alle $\ell$ verschillende restklassen. Aangezien $n-a k \geq n-\ell k=n-m>0$, zijn deze $\ell$ getallen ook allemaal groter dan 0 . Kies nu de $a$ waarvoor geldt dat $n-a k$ congruent is aan 0 modulo $\ell$. Omdat $n-a k$ groter is dan 0 , is er nu een $b>0$ zodanig dat $n-a k=b \ell$. Dit geeft de $a, b>0$ zo dat $a k+b \ell=n$.
Nu delen we de stoelen op in $a$ groepjes van $k$ stoelen en $b$ groepjes van $\ell$ stoelen. In elk groepje hangen we de kaartjes op zo dat ze cyclisch doorschuiven. De spelers op een stoel in een groepje met $k$ stoelen, zitten op hun eigen stoel elke $k$ klappen (en anders niet). De spelers op een stoel in een groepje met $\ell$ stoelen, zitten op hun eigen stoel elke $\ell$ klappen (en anders niet). De eerste keer dat iedereen op hun eigen stoel zit, is dus na $\mathrm{kgv}(k, \ell)$ klappen. Maar
$$
\operatorname{kgv}(k, \ell)=k \ell=m
$$
$\operatorname{omdat} \operatorname{ggd}(k, \ell)=1$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2023-B2023_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2023"
}
|
We play a game of musical chairs with $n$ chairs numbered 1 to $n$. You hang $n$ slips of paper, numbered 1 to $n$, on the chairs such that the number on a slip does not match the number on the chair.
Each chair has a player sitting on it. When you clap, each player looks at the number on the slip on their current chair and sits on the chair with that number. Prove that for every $m$ that is not a prime power with $1<m \leq n$, it is possible to hang the slips such that after $m$ claps, everyone is sitting on their own chair for the first time.
|
We provide an alternative proof for the fact that there are $a, b>0$ such that $a k+b \ell=n$ when $n>m$. By Bézout, there are integers $a_{0}$ and $b_{0}$ such that $a_{0} k+b_{0} \ell=$
$\operatorname{gcd}(k, \ell)=1$. If we multiply this by $n$, we get $n a_{0} k+n b_{0} \ell=n$. This can be rewritten as
$$
\left(n a_{0}+\lambda \ell\right) k+\left(n b_{0}-\lambda k\right) \ell=n
$$
for all integers $\lambda$. We are looking for a $\lambda$ such that $a=n a_{0}+\lambda \ell>0$ and $b=n b_{0}-\lambda k>0$.
We know that $n>m=k \ell$, so
$$
\frac{n b_{0}}{k}-\frac{-n a_{0}}{\ell}=\frac{n b_{0} \ell+n a_{0} k}{k \ell}=\frac{n\left(b_{0} \ell+a_{0} k\right)}{k \ell}=\frac{n}{k \ell}>1 .
$$
This means that the distance between the two fractions $\frac{n b_{0}}{k}$ and $\frac{-n a_{0}}{\ell}$ is greater than 1, and thus there is an integer $\lambda$ such that $\frac{n b_{0}}{k}>\lambda>\frac{-n a_{0}}{\ell}$. This precisely implies that $a=n a_{0}+\lambda \ell>0$ and $b=n b_{0}-\lambda k>0$.
|
proof
|
Yes
|
Incomplete
|
proof
|
Combinatorics
|
We spelen een spelletje stoelendans met $n$ stoelen genummerd 1 tot en met $n$. Je hangt $n$ blaadjes, genummerd 1 tot en met $n$, op de stoelen zodanig dat het nummer op een blaadje niet overeenkomt met het nummer op de stoel.
Op elke stoel zit een speler. Wanneer je klapt, kijkt elke speler naar het nummer op het blaadje aan zijn huidige stoel en gaat op de stoel zitten met dat nummer. Bewijs dat het voor elke $m$ die geen priem-macht is met $1<m \leq n$ mogelijk is om de blaadjes zo op te hangen dat na $m$ klappen voor het eerst iedereen weer op hun eigen stoel zit.
|
We geven een alternatief bewijs voor het feit dat er $a, b>0$ zijn zo dat $a k+b \ell=n$ wanneer $n>m$. Wegens Bézout zijn er gehele $a_{0}$ en $b_{0}$ zodanig dat $a_{0} k+b_{0} \ell=$
$\operatorname{ggd}(k, \ell)=1$. Als we dit vermenigvuldigen met $n$, krijgen we $n a_{0} k+n b_{0} \ell=n$. Dit kunnen we herschrijven als
$$
\left(n a_{0}+\lambda \ell\right) k+\left(n b_{0}-\lambda k\right) \ell=n
$$
voor alle gehele $\lambda$. We zoeken dus een $\lambda$ zo dat $a=n a_{0}+\lambda \ell>0$ en $b=n b_{0}-\lambda k>0$.
We weten dat $n>m=k \ell$, dus
$$
\frac{n b_{0}}{k}-\frac{-n a_{0}}{\ell}=\frac{n b_{0} \ell+n a_{0} k}{k \ell}=\frac{n\left(b_{0} \ell+a_{0} k\right)}{k \ell}=\frac{n}{k \ell}>1 .
$$
Dat betekent dat de afstand tussen de twee breuken $\frac{n b_{0}}{k}$ en $\frac{-n a_{0}}{\ell}$ groter is dan 1 , en dat er dus een geheel getal $\lambda$ is zodat $\frac{n b_{0}}{k}>\lambda>\frac{-n a_{0}}{\ell}$. Hieruit volgt precies dat $a=n a_{0}+\lambda \ell>0$ en $b=n b_{0}-\lambda k>0$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2023-B2023_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2023"
}
|
In a triangle $\triangle ABC$ with $\angle ABC < \angle BCA$, we define $K$ as the center of the excircle opposite $AC$. The lines $AK$ and $BC$ intersect at a point $D$. Let $E$ be the center of the circumcircle of $\triangle BKC$. Prove that
$$
\frac{1}{|KA|} = \frac{1}{|KD|} + \frac{1}{|KE|}
$$
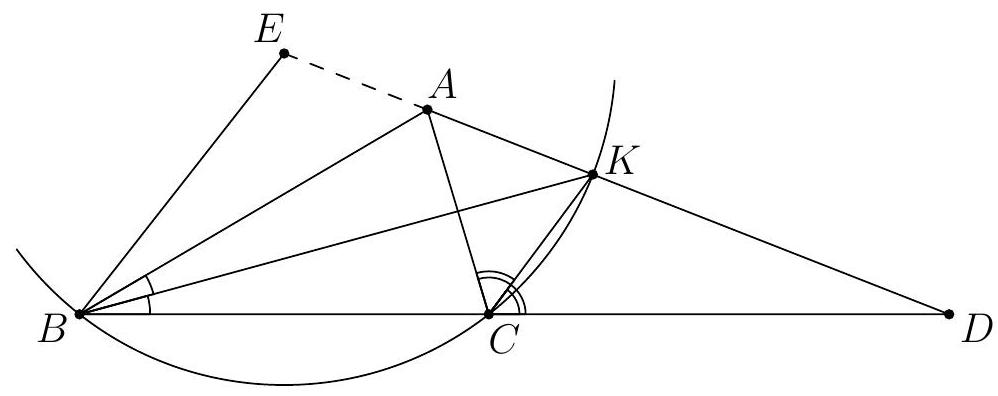
|
We use the notation $\angle C A B=2 \alpha, \angle A B C=2 \beta$ and $\angle B C A=2 \gamma$. Note that $\alpha+\beta+\gamma=\frac{1}{2}(\angle C A B+\angle A B C+\angle B C A)=\frac{1}{2} \cdot 180^{\circ}=90^{\circ}$.
We first prove that $K, A$ and $E$ are collinear. Since $K$ lies on the angle bisector of $\angle A B C$ and the external angle bisector of $\angle C A B$, we find that $\angle B K A=180^{\circ}-\angle K A B-\angle A B K=180^{\circ}-\left(90^{\circ}+\alpha\right)-\beta=90^{\circ}-\alpha-\beta=\gamma$. On the other hand, we know that $\angle B C K=90^{\circ}+\gamma>90^{\circ}$ is obtuse. Since $E$ is the circumcenter of $\triangle B K C$, $E$ must lie on the opposite side of $B K$ from $C$, and by the central angle theorem, we know that $\angle K E B=2 \cdot\left(180^{\circ}-\angle B C K\right)=2 \cdot\left(90^{\circ}-\gamma\right)=180^{\circ}-2 \gamma$. Since $E$ is the circumcenter of $\triangle B K C$, we also know that $\triangle B E K$ is isosceles with vertex angle $E$. Thus, $\angle B K E=\frac{1}{2}\left(180^{\circ}-\angle K E B\right)=\frac{1}{2} \cdot 2 \gamma=\gamma$. We conclude that $\angle B K A=\gamma=\angle B K E$, which implies that $K, A$ and $E$ are collinear.
Due to this collinearity, we find that $\angle A E B=\angle K E B=180^{\circ}-2 \gamma=180^{\circ}-\angle B C A$, so $A C B E$ is a cyclic quadrilateral. In particular, it follows that $\angle A E C=\angle A B C=\angle A B D$. Since also $\angle C A E=90^{\circ}+\alpha=\angle K A B=\angle D A B$, we find by (AA) that $\triangle A E C \sim \triangle A B D$.
The last two observations we need are that $|E C|=|E K|$ because $\triangle C E K$ is also isosceles with vertex angle $E$, and that $B K$ is a bisector of $\triangle A B D$. Now it follows that
$$
1-\frac{|K A|}{|K E|}=\frac{|K E|-|K A|}{|K E|}=\frac{|A E|}{|K E|}=\frac{|A E|}{|C E|}=\frac{|A B|}{|D B|}=\frac{|A K|}{|D K|}
$$
where we have used, respectively: the difference of fractions, that $K$, $A$ and $E$ are collinear, that $|E C|=|E K|$, that $\triangle A E C \sim \triangle A B D$, and the angle bisector theorem on $B K$ in $\triangle A B D$. The desired result now follows easily by moving $\frac{|K A|}{|K E|}$ to the other side and dividing by $|K A|$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In een driehoek $\triangle A B C$ met $\angle A B C<\angle B C A$ definiëren we $K$ als het middelpunt van de aangeschreven cirkel aan $A C$. De lijnen $A K$ en $B C$ snijden in een punt $D$. Laat $E$ het middelpunt zijn van de omgeschreven cirkel van $\triangle B K C$. Bewijs dat
$$
\frac{1}{|K A|}=\frac{1}{|K D|}+\frac{1}{|K E|}
$$

|
We gebruiken de notatie $\angle C A B=2 \alpha, \angle A B C=2 \beta$ en $\angle B C A=2 \gamma$. Merk op dat $\alpha+\beta+\gamma=\frac{1}{2}(\angle C A B+\angle A B C+\angle B C A)=\frac{1}{2} \cdot 180^{\circ}=90^{\circ}$.
We bewijzen eerst dat $K, A$ en $E$ collineair zijn. Omdat $K$ op de binnenbissectrice van $\angle A B C$ en de buitenbissectrice van hoek $\angle C A B$ ligt vinden we dat $\angle B K A=180^{\circ}-$ $\angle K A B-\angle A B K=180^{\circ}-\left(90^{\circ}+\alpha\right)-\beta=90^{\circ}-\alpha-\beta=\gamma$. Aan de andere kant weten we dat $\angle B C K=90^{\circ}+\gamma>90^{\circ}$ stomp is. Aangezien $E$ het middelpunt is van de omgeschreven cirkel van $\triangle B K C$, ligt $E$ dus aan de andere kant van $B K$ dan $C$, en met de middelpunt omtrekshoek weten we dat $\angle K E B=2 \cdot\left(180^{\circ}-\angle B C K\right)=2 \cdot\left(90^{\circ}-\gamma\right)=180^{\circ}-2 \gamma$. Omdat $E$ het middelpunt is van de omgeschreven cirkel van $\triangle B K C$ weten we echter ook dat $\triangle B E K$ gelijkbenig is met tophoek $E$. Dus $\angle B K E=\frac{1}{2}\left(180^{\circ}-\angle K E B\right)=\frac{1}{2} \cdot 2 \gamma=\gamma$. We concluderen dat $\angle B K A=\gamma=\angle B K E$, waaruit volgt dat $K, A$ en $E$ op één lijn liggen.
Wegens deze collineariteit vinden we dat $\angle A E B=\angle K E B=180^{\circ}-2 \gamma=180^{\circ}-\angle B C A$, dus $A C B E$ is een koordenvierhoek. In het bijzonder geldt dus dat $\angle A E C=\angle A B C=$ $\angle A B D$. Omdat ook $\angle C A E=90^{\circ}+\alpha=\angle K A B=\angle D A B$, vinden we met (hh) dat $\triangle A E C \sim \triangle A B D$.
De laatste twee observaties die we nodig hebben, zijn dat $|E C|=|E K|$ omdat ook $\triangle C E K$ gelijkbenig is met tophoek $E$, en dat $B K$ een bissectrice is van $\triangle A B D$. Nu volgt alles bij elkaar dat
$$
1-\frac{|K A|}{|K E|}=\frac{|K E|-|K A|}{|K E|}=\frac{|A E|}{|K E|}=\frac{|A E|}{|C E|}=\frac{|A B|}{|D B|}=\frac{|A K|}{|D K|}
$$
waarbij we respectievelijk het volgende hebben gebruikt: het verschil van breuken, dat $K$, $A$ en $E$ collineair zijn, dat $|E C|=|E K|$, dat $\triangle A E C \sim \triangle A B D$, en de bissectricestelling op $B K$ in $\triangle A B D$. Het gevraagde volgt nu eenvoudig door $\frac{|K A|}{|K E|}$ naar de ander kant te halen en te delen door $|K A|$.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2023-B2023_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2023"
}
|
Find all pairs of prime numbers $(p, q)$ for which
$$
2^{p}=2^{q-2}+q!
$$
|
Answer: the only pairs $(p, q)$ that satisfy are $(3,3)$ and $(7,5)$.
First, we will go through a few small cases. If $q=2$, then $2^{p}=1+2$ has no solution. If $q=3$, then $2^{p}=2+6$ gives $p=3$ as the only solution. If $q=5$, then $2^{p}=8+120$ gives $p=7$ as the only solution. Henceforth, we may assume that $q$ is at least 7.
Now we notice that we can rewrite the condition as
$$
q!=2^{p}-2^{q-2}=2^{q-2}\left(2^{p-q+2}-1\right)
$$
Since $q!$ is positive, the right-hand side is also positive. In particular, $2^{p-q+2}>1$, so $p-q+2>0$ and $2^{p-q+2}$ is an integer (and greater than 1). We conclude that $2^{p-q+2}-1$ is an integer and odd. Therefore, the right-hand side has exactly $q-2$ factors of 2. To count the number of factors on the left-hand side, let $\nu_{2}(a)$ be the function that counts how many factors an integer $a$ has. Since $q$ is a prime number greater than 2, it is odd. Then $\left\lfloor\frac{q}{2}\right\rfloor=\frac{q-1}{2}$ and in general $\left\lfloor\frac{q}{2^{i}}\right\rfloor=\left\lfloor\frac{q-1}{2^{i}}\right\rfloor$. Let $n$ now be the integer such that $2^{n}<q<2^{n+1}$. Then we calculate that
$$
\begin{aligned}
\nu_{2}(q!) & =\left\lfloor\frac{q}{2}\right\rfloor+\left\lfloor\frac{q}{4}\right\rfloor+\ldots+\left\lfloor\frac{q}{2^{n}}\right\rfloor \\
& =\left\lfloor\frac{q-1}{2}\right\rfloor+\left\lfloor\frac{q-1}{4}\right\rfloor+\ldots+\left\lfloor\frac{q-1}{2^{n}}\right\rfloor \\
& \leq(q-1)\left(\frac{1}{2}+\frac{1}{4}+\ldots+\frac{1}{2^{n}}\right) \\
& =(q-1)\left(1-\frac{1}{2^{n}}\right) \\
& =(q-1)-\frac{q-1}{2^{n}} \\
& \leq q-2 .
\end{aligned}
$$
In both inequalities above, equality holds if and only if $q=2^{n}+1$ (and we used in the second line that $q$ is odd). Due to the condition, equality must also hold, so $q=2^{n}+1$ for some natural number $n$.
Now that we have come a long way by looking at factors of 2, we would like to derive a contradiction from equation (2) using modular arithmetic since $q!$ has many prime factors. From our small examples, we know that this will not work modulo 3 or 5, so we try the next prime number: 7.
Since we have assumed that $q$ is at least 7, $q!$ is indeed divisible by 7. This means that $2^{p-q+2} \equiv 1 \bmod 7$. Since also $2^{3} \equiv 8 \equiv 1 \bmod 7$, this means that $2^{\operatorname{ggd}(p-q+2,3)} \equiv 1 \bmod 7$. But $2^{1} \not \equiv 1 \bmod 7$, so $\operatorname{ggd}(p-q+2,3)=3$ or $p-q+2 \equiv 0 \bmod 3$. We know, however, that $q=2^{n}+1$ is congruent to -1 or 0 modulo 3. Since we also know that $q$ is prime (and greater than 3), the second case is ruled out and we conclude that $q \equiv-1 \bmod 3$. But then the previous gives $p \equiv q-2 \equiv-1-2 \equiv 0 \bmod 3$. Since $p$ is also prime, we conclude that $p=3$. But $2^{q-2}+q!=2^{3}=8$ has no solutions for $q \geq 7$.
We conclude that the only pairs $(p, q)$ that satisfy are $(3,3)$ and $(7,5)$.
Remark. In general, if an arbitrary natural number $q$ in binary notation has $r$ digits 1, then
$$
\nu_{2}(q!)=\sum_{i=1}^{\infty}\left\lfloor\frac{q}{2^{i}}\right\rfloor=q-r
$$
So for $2^{n}<q<2^{n+1}$, it holds due to $r \geq 2$ that $\nu_{2}(q!) \leq q-2$ with equality if and only if $r=2$. If $q$ is also odd, then $q=2^{n}+1$ (because $q=2^{n}+2^{k}$ with $k \geq 1$ is even).
|
(3,3) \text{ and } (7,5)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Vind alle paren priemgetallen $(p, q)$ waarvoor geldt dat
$$
2^{p}=2^{q-2}+q!
$$
|
Antwoord: de enige paren $(p, q)$ die voldoen zijn $(3,3)$ en $(7,5)$.
Als eerste gaan we een paar kleine gevallen af. Als $q=2$, dan heeft $2^{p}=1+2$ geen oplossing. Als $q=3$, dan geeft $2^{p}=2+6$ dat $p=3$ de enige oplossing is. Als $q=5$, dan geeft $2^{p}=8+120$ dat $p=7$ de enige oplossing op. Hierna mogen we dus aannemen dat $q$ minstens 7 is.
Nu merken we op dat we de voorwaarde kunnen herschrijven als
$$
q!=2^{p}-2^{q-2}=2^{q-2}\left(2^{p-q+2}-1\right)
$$
Omdat $q$ ! positief is, is de rechterkant dat ook. In het bijzonder geldt dat $2^{p-q+2}>1$, dus $p-q+2>0$ en $2^{p-q+2}$ is geheel (en groter dan 1 ). We concluderen dat $2^{p-q+2}-1$ geheel en oneven is. Dus de rechterkant heeft precies $q-2$ factoren 2. Om het aantal factoren aan de linkerkant te tellen zij $\nu_{2}(a)$ de functie die telt hoeveel factoren een geheel getal $a$ heeft. Omdat $q$ een priemgetal groter dan 2, is het oneven. Dan geldt dat $\left\lfloor\frac{q}{2}\right\rfloor=\frac{q-1}{2}$ en in het algemeen $\left\lfloor\frac{q}{2^{i}}\right\rfloor=\left\lfloor\frac{q-1}{2^{i}}\right\rfloor$. Zij $n$ nu het gehele getal zo dat $2^{n}<q<2^{n+1}$. Dan berekenen we dat
$$
\begin{aligned}
\nu_{2}(q!) & =\left\lfloor\frac{q}{2}\right\rfloor+\left\lfloor\frac{q}{4}\right\rfloor+\ldots+\left\lfloor\frac{q}{2^{n}}\right\rfloor \\
& =\left\lfloor\frac{q-1}{2}\right\rfloor+\left\lfloor\frac{q-1}{4}\right\rfloor+\ldots+\left\lfloor\frac{q-1}{2^{n}}\right\rfloor \\
& \leq(q-1)\left(\frac{1}{2}+\frac{1}{4}+\ldots+\frac{1}{2^{n}}\right) \\
& =(q-1)\left(1-\frac{1}{2^{n}}\right) \\
& =(q-1)-\frac{q-1}{2^{n}} \\
& \leq q-2 .
\end{aligned}
$$
In beide ongelijkheden hierboven geldt gelijkheid dan en slechts dan als $q=2^{n}+1$ (en we hebben in de tweede regel dus gebruikt dat $q$ oneven is). Wegens de voorwaarde moet er ook gelijkheid gelden, dus $q=2^{n}+1$ voor een zeker natuurlijk getal $n$.
Nu we een heel eind zijn gekomen door naar factoren 2 te kijken, willen we graag een tegenspraak afleiden uit vergelijking (2) met modulo rekenen aangezien $q$ ! veel priemfactoren heeft. Uit onze kleine voorbeelden weten we dat dit niet gaat lukken modulo 3 of 5 , dus proberen het eerstvolgende priemgetal: 7 .
Aangezien we hebben aangenomen dat $q$ minstens 7 is, is $q$ ! inderdaad deelbaar door 7 . Dat betekent dat $2^{p-q+2} \equiv 1 \bmod 7$. Aangezien ook $2^{3} \equiv 8 \equiv 1 \bmod 7$, betekent dit dat $2^{\operatorname{ggd}(p-q+2,3)} \equiv 1 \bmod 7$. Maar $2^{1} \not \equiv 1 \bmod 7$, dus $\operatorname{ggd}(p-q+2,3)=3$ oftewel $p-q+2 \equiv 0$ $\bmod 3$. We weten echter dat $q=2^{n}+1$ congruent is aan -1 of 0 modulo 3 . Omdat we ook weten dat $q$ priem is (en groter dan 3), vervalt het tweede geval en concluderen we dat $q \equiv-1 \bmod 3$. Maar dan geeft het voorgaande dat $p \equiv q-2 \equiv-1-2 \equiv 0 \bmod 3$. Aangezien $p$ ook priem is, concluderen we dat $p=3$. Maar $2^{q-2}+q!=2^{3}=8$ heeft geen oplossingen voor $q \geq 7$.
We concluderen dat de enige paren $(p, q)$ die voldoen $(3,3)$ en $(7,5)$ zijn.
Opmerking. In het algemeen, als een willekeurig natuurlijk getal $q$ in binaire schrijfwijze $r$ cijfers 1 heeft, dan geldt dat
$$
\nu_{2}(q!)=\sum_{i=1}^{\infty}\left\lfloor\frac{q}{2^{i}}\right\rfloor=q-r
$$
Dus voor $2^{n}<q<2^{n+1}$ geldt wegens $r \geq 2$ dat $\nu_{2}(q!) \leq q-2$ met gelijkheid dan en slechts dan als $r=2$. Als $q$ bovendien oneven is, moet wel $q=2^{n}+1$ (want $q=2^{n}+2^{k}$ met $k \geq 1$ is even).
|
{
"exam": "Dutch_TST",
"problem_label": "5",
"problem_match": "\nOpgave 5.",
"resource_path": "Dutch_TST/segmented/nl-2023-B2023_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2023"
}
|
Let $\triangle A B C$ be a triangle with $|A B|<|A C|<|B C|$, and let $\Gamma$ be its circumcircle with center $O$. Let $\omega_{1}$ be the circle with center $B$ and radius $|A C|$, and let $\omega_{2}$ be the circle with center $C$ and radius $|A B|$. The circles $\omega_{1}$ and $\omega_{2}$ intersect at a point $E$ such that $A$ and $E$ lie on opposite sides of the line $B C$. The circles $\Gamma$ and $\omega_{1}$ intersect at a point $F$, and the circles $\Gamma$ and $\omega_{2}$ intersect at a point $G$, such that $F$ and $G$ lie on the same side of the line $B C$ as $E$.
Prove that the antipode $K$ of $A$ with respect to $\Gamma$ is the circumcenter of $\triangle E F G$.
The antipode $K$ of a point $A$ is the unique point on the circle such that $A K$ is a diameter.
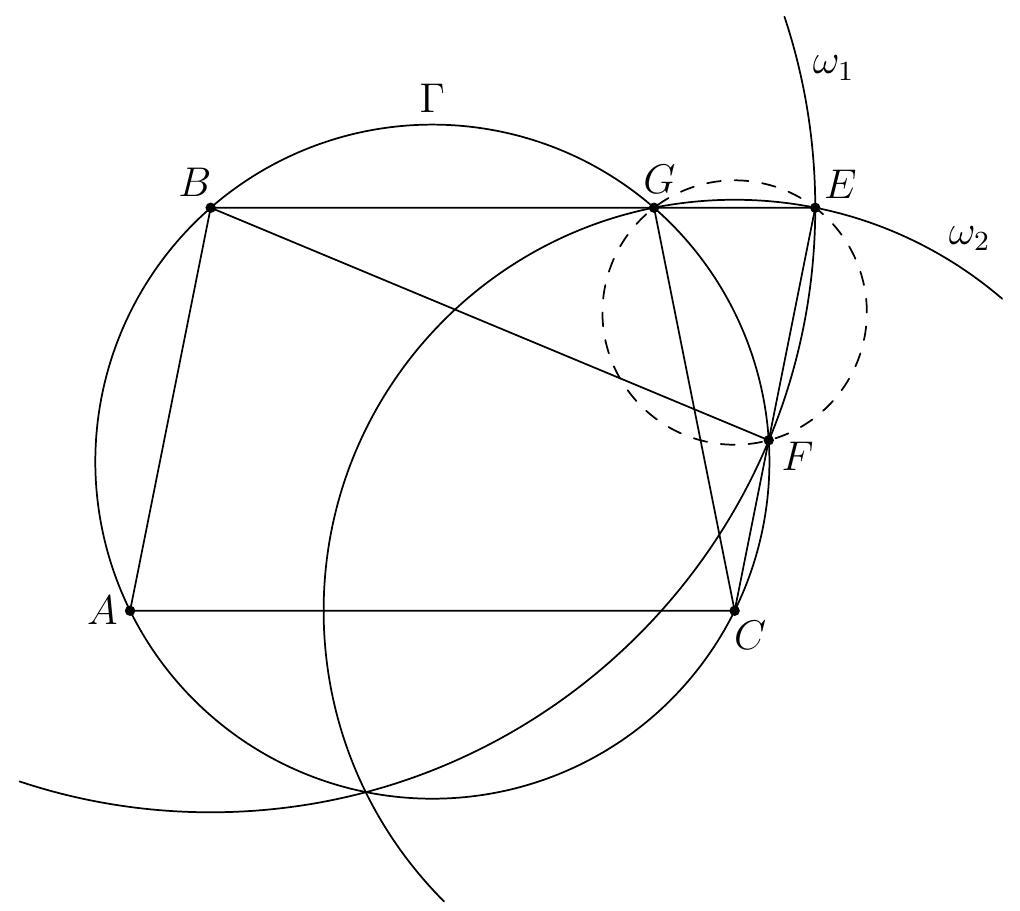
|
Since $|BE|=|AC|$ and $|CE|=|AB|$, $ABEC$ is a parallelogram. This means that $BE \| AC$. On the other hand, $ABGC$ is a cyclic quadrilateral with $|CG| = |AB|$. It follows that $ABGC$ is an isosceles trapezium with $BG \| AC$. In particular, $B, G$ and $E$ are collinear. Similarly, $C, F$ and $E$ are collinear.
Since $K$ is the antipodal point of $A$, $\angle ACK = 90^{\circ}$. Because $AC \| BE$ and $G$ lies on the line $BE$, $CK$ is also perpendicular to $GE$. But we also know that $|CE| = |AB| = |CG|$, so $\triangle ECG$ is isosceles and $CK$ is the perpendicular bisector of $EG$. Similarly, $BK$ is the perpendicular bisector of $EF$. Therefore, $K$ lies on the perpendicular bisectors of $EG$ and $EF$. We conclude that $K$ is the circumcenter of $\triangle EFG$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $\triangle A B C$ een driehoek met $|A B|<|A C|<|B C|$, omgeschreven cirkel $\Gamma$ met middelpunt $O$. Zij $\omega_{1}$ de cirkel met middelpunt $B$ en straal $|A C|$ en zij $\omega_{2}$ de cirkel met middelpunt $C$ en straal $|A B|$. De cirkels $\omega_{1}$ en $\omega_{2}$ snijden in een punt $E$ zodanig dat $A$ en $E$ aan verschillende kanten liggen van de lijn $B C$. De cirkels $\Gamma$ en $\omega_{1}$ snijden in een punt $F$ en de cirkels $\Gamma$ en $\omega_{2}$ snijden in een punt $G$, zodanig dat $F$ en $G$ aan dezelfde kant liggen van de lijn $B C$ als $E$.
Bewijs dat de antipode $K$ van $A$ ten opzichte van $\Gamma$ het middelpunt van de omgeschreven cirkel van $\triangle E F G$.
De antipode $K$ van een punt $A$ is het unieke punt op de cirkel zo dat $A K$ een diameter is.

|
Omdat $|B E|=|A C|$ en $|C E|=|A B|$ is $A B E C$ een parallellogram. Dat betekent dat $B E \| A C$. Aan de andere kant is $A B G C$ een koordenvierhoek met $|C G|=$ $|A B|$. Hieruit volgt dat $A B G C$ een gelijkbenig trapezium is met $B G \| A C$. In het bijzonder zijn $B, G$ en $E$ collineair. Geheel analoog zijn $C, F$ en $E$ collineair.
Aangezien $K$ het antipodale punt is van $A$ geldt dat $\angle A C K=90^{\circ}$. Omdat $A C \| B E$ en $G$ op de lijn $B E$ ligt, staat $C K$ dan ook loodrecht op $G E$. Maar we weten ook dat $|C E|=|A B|=|C G|$, dus $\triangle E C G$ is gelijkbenig en $C K$ is de middelloodlijn van $E G$. Evenzo is $B K$ de middelloodlijn van $E F$. Dus $K$ ligt op de middelloodlijnen van $E G$ en $E F$. We concluderen dat $K$ het middelpunt van de omgeschreven cirkel van $\triangle E F G$ is.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2023-C2023_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2023"
}
|
Determine the largest real number $M$ such that for every infinite sequence $x_{0}, x_{1}, x_{2}, \ldots$ of real numbers that satisfies
a) $x_{0}=1$ and $x_{1}=3$,
b) $x_{0}+x_{1}+\cdots+x_{n-1} \geq 3 x_{n}-x_{n+1}$,
it holds that
$$
\frac{x_{n+1}}{x_{n}}>M
$$
for all $n \geq 0$.
|
Answer: the largest possible constant for which this holds is $M=2$.
This problem is a typical example where it pays to take a stronger induction hypothesis than you strictly need: we show by induction that $x_{n+1}>2 x_{n}>x_{n}+x_{n-1}+\ldots+x_{0}$. For $n=0$, this translates to $x_{1}>2 x_{0}>x_{0}$, which, with the given initial values, translates to $3>2>1$. Now assume as the induction hypothesis that $x_{n+1}>2 x_{n}>x_{n}+x_{n-1}+\ldots+x_{0}$. Then for $x_{n+2}$, using the condition that
$$
\begin{aligned}
x_{n+2} & \geq 3 x_{n+1}-\left(x_{n}+\ldots+x_{0}\right) \\
& >2 x_{n+1} \\
& >x_{n+1}+x_{n}+\ldots+x_{0} .
\end{aligned}
$$
This completes the induction step. From this, it follows that for all possible sequences and all possible $n$, $\frac{x_{n+1}}{x_{n}}>2$.
To show that we cannot find a higher value for $M$, we look at the sequence for which equality holds in b), i.e., $x_{0}+x_{1}+\cdots+x_{n-1}=3 x_{n}-x_{n+1}$. Then we have
$$
\begin{aligned}
x_{n+1} & =3 x_{n}-\left(x_{n-1}+\ldots+x_{0}\right) \\
& =3 x_{n}-x_{n-1}-\left(x_{n-2}+\ldots+x_{0}\right) \\
& =3 x_{n}-x_{n-1}-\left(3 x_{n-1}-x_{n}\right) \\
& =4 x_{n}-4 x_{n-1} .
\end{aligned}
$$
The characteristic equation of this homogeneous recurrence relation is $\lambda^{2}-4 \lambda+4=(\lambda-2)^{2}=0$. Since this has a double root at $\lambda=2$, the two characteristic solutions are $2^{n}$ and $n 2^{n}$. Solving $x_{n}=B 2^{n}+C n 2^{n}$ for the given initial values, we get $B+0=x_{0}=1$ and $2 B+2 C=x_{1}=3$, so $B=1$ and $C=\frac{1}{2}$. The solution for these initial values is thus $x_{n}=1 \cdot 2^{n}+\frac{1}{2} n 2^{n}=(n+2) 2^{n-1}$.
Now that we have solved the recurrence relation, we simply calculate that
$$
\frac{x_{n+1}}{x_{n}}=\frac{(n+3) 2^{n}}{(n+2) 2^{n-1}}=2 \frac{n+3}{n+2}=2\left(1+\frac{1}{n+2}\right)
$$
For large $n$, this fraction approaches 2 arbitrarily closely. To make this precise: suppose $M=2+\epsilon$ with $\epsilon>0$. Then for this sequence and $n>\frac{2}{\epsilon}-2$, we have $\frac{x_{n+1}}{x_{n}}=2+\frac{2}{n+2}<2+\epsilon=M$. Therefore, such an $M$ does not satisfy the condition. The largest value of $M$ that can satisfy is thus 2, and we have seen above that this value does indeed satisfy.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Bepaal het grootste reële getal $M$ zodanig dat voor elke oneindige rij $x_{0}, x_{1}, x_{2}, \ldots$ van reële getallen die voldoet aan
a) $x_{0}=1$ en $x_{1}=3$,
b) $x_{0}+x_{1}+\cdots+x_{n-1} \geq 3 x_{n}-x_{n+1}$,
geldt dat
$$
\frac{x_{n+1}}{x_{n}}>M
$$
voor alle $n \geq 0$.
|
Antwoord: de grootst mogelijke constante waarvoor dit geldt is $M=2$.
Deze opgave is een typisch voorbeeld waarbij het baat om een sterkere inductiehypothese te nemen dan je strikt nodig hebt: we laten met inductie zien dat $x_{n+1}>2 x_{n}>x_{n}+x_{n-1}+$ $\ldots+x_{0}$. Voor $n=0$ staat hier dat $x_{1}>2 x_{0}>x_{0}$ wat zich met de gegeven beginwaarden vertaalt naar $3>2>1$. Stel nu als inductiehypothese dat $x_{n+1}>2 x_{n}>x_{n}+x_{n-1}+\ldots+x_{0}$. Dan vinden we voor $x_{n+2}$ met de voorwaarde dat
$$
\begin{aligned}
x_{n+2} & \geq 3 x_{n+1}-\left(x_{n}+\ldots+x_{0}\right) \\
& >2 x_{n+1} \\
& >x_{n+1}+x_{n}+\ldots+x_{0} .
\end{aligned}
$$
Dit voltooit de inductiestap. Hieruit volgt dat voor alle mogelijke rijtjes en alle mogelijk $n$ geldt dat $\frac{x_{n+1}}{x_{n}}>2$.
Om te laten zien dat we geen hogere waarde voor $M$ kunnen vinden, kijken we naar het rijtje waarvoor er gelijkheid geldt in b), oftewel $x_{0}+x_{1}+\cdots+x_{n-1}=3 x_{n}-x_{n+1}$. Dan geldt er dat
$$
\begin{aligned}
x_{n+1} & =3 x_{n}-\left(x_{n-1}+\ldots+x_{0}\right) \\
& =3 x_{n}-x_{n-1}-\left(x_{n-2}+\ldots+x_{0}\right) \\
& =3 x_{n}-x_{n-1}-\left(3 x_{n-1}-x_{n}\right) \\
& =4 x_{n}-4 x_{n-1} .
\end{aligned}
$$
De karakteristieke vergelijking van deze homogene recurrente betrekking is $\lambda^{2}-4 \lambda+4=$ $(\lambda-2)^{2}=0$. Aangezien dit een dubbel nulpunt heeft bij $\lambda=2$, zijn de twee karakteristieke oplossingen $2^{n}$ en $n 2^{n}$. Als we nu $x_{n}=B 2^{n}+C n 2^{n}$ oplossen voor de gegeven startwaarden vinden we $B+0=x_{0}=1$ en $2 B+2 C=x_{1}=3$, dus $B=1$ en $C=\frac{1}{2}$. De oplossing voor deze startwaarden is dus $x_{n}=1 \cdot 2^{n}+\frac{1}{2} n 2^{n}=(n+2) 2^{n-1}$.
Nu we de recurrente betrekking hebben opgelost rekenen we eenvoudig uit dat
$$
\frac{x_{n+1}}{x_{n}}=\frac{(n+3) 2^{n}}{(n+2) 2^{n-1}}=2 \frac{n+3}{n+2}=2\left(1+\frac{1}{n+2}\right)
$$
Voor grote $n$ gaat deze breuk dus willekeurig dicht naar 2. Om dat precies te maken: stel dat $M=2+\epsilon$ met $\epsilon>0$. Dan geldt er voor dit rijtje en $n>\frac{2}{\epsilon}-2$ dat $\frac{x_{n+1}}{x_{n}}=2+\frac{2}{n+2}<$ $2+\epsilon=M$. Dus zo'n $M$ voldoet niet. De grootste waarde van $M$ die kan voldoen is dus 2, en hierboven hebben we gezien dat die ook daadwerkelijk voldoet.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2023-C2023_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2023"
}
|
Find all positive integers $n$ for which there exist $n$ distinct natural numbers $a_{1}, a_{2}, \ldots, a_{n}$, none of which are greater than $n^{2}$, such that the sum
$$
\frac{1}{a_{1}}+\frac{1}{a_{2}}+\cdots+\frac{1}{a_{n}}=1 .
$$
|
The answer is all $n \neq 2$. For $n=1$, the set $\{1\}$ works. For $n=2$, no set satisfies the condition. If $a_{1}$ or $a_{2}$ is equal to 1, then $\frac{1}{a_{1}}+\frac{1}{a_{2}}>1$. If $a_{1}$ and $a_{2}$ are both at least two, then one is at least 2 and the other is at least 3. Thus $\frac{1}{a_{1}}+\frac{1}{a_{2}} \leq \frac{1}{2}+\frac{1}{3}<1$.
For $n \geq 3$, we use the identity
$$
\frac{1}{k}=\frac{1}{k+\ell}+\frac{1}{k(k+1)}+\frac{1}{(k+1)(k+2)}+\cdots+\frac{1}{(k+\ell-1)(k+\ell)}.
$$
Indeed, if we use $\frac{1}{k(k+1)}=\frac{1}{k}-\frac{1}{k+1}$, then the right-hand side is equal to
$\frac{1}{k+\ell}+\left(\frac{1}{k}-\frac{1}{k+1}\right)+\left(\frac{1}{k+1}-\frac{1}{k+2}\right)+\cdots+\left(\frac{1}{k+\ell-1}-\frac{1}{k+\ell}\right)=\frac{1}{k+\ell}+\frac{1}{k}-\frac{1}{k+\ell}$.
If we apply this with $k=1$ and $\ell=n-1$, we find the sum of $n$ fractions
$$
1=\frac{1}{n}+\frac{1}{1 \cdot 2}+\frac{1}{2 \cdot 3}+\frac{1}{3 \cdot 4}+\frac{1}{4 \cdot 5}+\cdots+\frac{1}{(n-1) \cdot n}
$$
all of which have a smaller denominator than $n^{2}$. This gives the desired sum as long as $n \neq k(k+1)$ for all $k$.
Suppose $n$ can be written as $k(k+1)$. Then we apply the substitutions $\frac{1}{n}+\frac{1}{(n-1) n}=\frac{1}{n-1}$ and $\frac{1}{6}=\frac{1}{10}+\frac{1}{15}$ to sum (2). Then we get the sum of $n$ fractions
$$
1=\frac{1}{n-1}+\frac{1}{2}+\frac{1}{10}+\frac{1}{15}+\frac{1}{3 \cdot 4}+\frac{1}{4 \cdot 5}+\cdots+\frac{1}{(n-2) \cdot(n-1)}
$$
Note that $k(k+1)$ is always even. Since $n$ is of the form $k(k+1)$, $n-1$ is odd and thus not of this form. Furthermore, $n-1$ is also not equal to 2, 10, and 15, because 3, 11, and 16 are not of the form $k(k+1)$. Also, 10 and 15 themselves are not of the form $k(k+1)$. Since $n=k(k+1)$ and $n \geq 3$, in this case $n \geq 6$, so $n^{2}>15$. The sum (3) is thus of the desired form.
|
all\ n \neq 2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Vind alle positieve gehele getallen $n$ waarvoor er $n$ verschillende natuurlijke getallen $a_{1}, a_{2}, \ldots, a_{n}$ bestaan, geen van alle groter dan $n^{2}$, zo dat de som
$$
\frac{1}{a_{1}}+\frac{1}{a_{2}}+\cdots+\frac{1}{a_{n}}=1 .
$$
|
Het antwoord is alle $n \neq 2$. Voor $n=1$, werkt de verzameling $\{1\}$. Voor $n=2$, voldoet geen enkele verzameling. Als $a_{1}$ of $a_{2}$ gelijk is aan 1 , dan is $\frac{1}{a_{1}}+\frac{1}{a_{2}}>1$. Als $a_{1}$ en $a_{2}$ allebei minstens twee zijn, dan is de één minstens 2 en de ander minstens 3. Dus $\frac{1}{a_{1}}+\frac{1}{a_{2}} \leq \frac{1}{2}+\frac{1}{3}<1$.
Voor $n \geq 3$ maken we gebruik van de identiteit
$$
\frac{1}{k}=\frac{1}{k+\ell}+\frac{1}{k(k+1)}+\frac{1}{(k+1)(k+2)}+\cdots+\frac{1}{(k+\ell-1)(k+\ell)} .
$$
Inderdaad als we gebruik maken van $\frac{1}{k(k+1)}=\frac{1}{k}-\frac{1}{k+1}$ dan is de rechterkant gelijk aan
$\frac{1}{k+\ell}+\left(\frac{1}{k}-\frac{1}{k+1}\right)+\left(\frac{1}{k+1}-\frac{1}{k+2}\right)+\cdots+\left(\frac{1}{k+\ell-1}-\frac{1}{k+\ell}\right)=\frac{1}{k+\ell}+\frac{1}{k}-\frac{1}{k+\ell}$.
Als we dit toepassen met $k=1$ en $\ell=n-1$, dan vinden we de som van $n$ breuken
$$
1=\frac{1}{n}+\frac{1}{1 \cdot 2}+\frac{1}{2 \cdot 3}+\frac{1}{3 \cdot 4}+\frac{1}{4 \cdot 5}+\cdots+\frac{1}{(n-1) \cdot n}
$$
die allemaal een kleinere noemer hebben dan $n^{2}$. Dit geeft de gewenste som zolang $n \neq$ $k(k+1)$ voor alle $k$.
Stel dat $n$ wel te schrijven is als $k(k+1)$. Dan passen we op som (2) de substituties $\frac{1}{n}+\frac{1}{(n-1) n}=\frac{1}{n-1}$ en $\frac{1}{6}=\frac{1}{10}+\frac{1}{15}$ toe. Dan krijgen we de som van $n$ breuken
$$
1=\frac{1}{n-1}+\frac{1}{2}+\frac{1}{10}+\frac{1}{15}+\frac{1}{3 \cdot 4}+\frac{1}{4 \cdot 5}+\cdots+\frac{1}{(n-2) \cdot(n-1)}
$$
Merk op dat $k(k+1)$ altijd even is. Aangezien $n$ van de vorm $k(k+1)$ is, is $n-1$ oneven en dus niet van deze vorm. Verder is $n-1$ ook ongelijk aan 2,10 en 15, omdat 3,11 en 16 niet van de vorm $k(k+1)$ zijn. Ook zijn 10 en 15 zelf niet van de vorm $k(k+1)$. Aangezien $n=k(k+1)$ en $n \geq 3$, geldt in dit geval dat $n \geq 6$, dus $n^{2}>15$. De som (3) is dus van de gewenste vorm.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2023-C2023_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2023"
}
|
Find all positive integers $n$ for which there exist $n$ distinct natural numbers $a_{1}, a_{2}, \ldots, a_{n}$, none of which are greater than $n^{2}$, such that the sum
$$
\frac{1}{a_{1}}+\frac{1}{a_{2}}+\cdots+\frac{1}{a_{n}}=1 .
$$
|
We provide an alternative solution in the case that $n$ can be written as $k(k+1)$. First, we note that $k(k+1)$ is even. Thus, we can combine the fractions
$\frac{1}{n}+\frac{1}{k(k+1)}=\frac{2}{k(k+1)}=\frac{1}{k(k+1) / 2}$. At the same time, we split $\frac{1}{6}=\frac{1}{8}+\frac{1}{24}$. Note that 8 and 24 are not of the form $\kappa(\kappa+1)$ or of the form $\kappa(\kappa+1) / 2$. If $k(k+1) / 2$ is not of the form $\ell(\ell+1)$, we are done since we have replaced three fractions with three different fractions that do not appear elsewhere.
If $k(k+1) / 2=\ell(\ell+1)$ for some $\ell$, then we can combine the fractions $\frac{1}{k(k+1) / 2}$ and $\frac{1}{\ell(\ell+1)}$ again to $\frac{1}{k(k+1) / 2}+\frac{1}{\ell(\ell+1)}=\frac{1}{\ell(\ell+1) / 2}$. At the same time, we split $\frac{1}{2}=\frac{1}{3}+\frac{1}{6}$. Note that $\frac{1}{3}$ and $\frac{1}{6}$ did not appear in our sum. (We had just replaced $\frac{1}{6}$ with $\frac{1}{8}+\frac{1}{24}$.) Furthermore, $\ell(\ell+1) / 2=k(k+1) / 4$ cannot be of the form $\kappa(\kappa+1)$ again. Otherwise, $4 \kappa(\kappa+1)=2 \kappa(2 \kappa+2)$ would be $k(k+1)$, but
$$
2 \kappa(2 \kappa+1)<2 \kappa(2 \kappa+2)<(2 \kappa+1)(2 \kappa+2)
$$
So as long as 3 and 6 are not equal to $k(k+1) / 2=n / 2$, we are done since we have once again replaced three fractions with three different fractions that do not appear elsewhere.
For $n=6$, $1=\frac{1}{2}+\frac{1}{3}+\frac{1}{18}+\frac{1}{20}+\frac{1}{30}+\frac{1}{36}$ and for $n=12$, $1=$ $\frac{1}{2}+\frac{1}{6}+\frac{1}{9}+\frac{1}{18}+\frac{1}{20}+\frac{1}{30}+\frac{1}{42}+\frac{1}{56}+\frac{1}{72}+\frac{1}{90}+\frac{1}{110}+\frac{1}{132}$.
Remark. Another way to find equations (2) and (3) is, for example, as follows. For $n=3$, we have $\frac{1}{2}+\frac{1}{3}+\frac{1}{6}=1$. If we apply the substitution (1) with $k=3$ and $\ell=n-3$, then we also find (2). Similarly, we can find (3) by applying (1) with $k=3$ and $\ell=n-4$ to $\frac{1}{2}+\frac{1}{3}+\frac{1}{10}+\frac{1}{15}=1$.
|
not found
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Vind alle positieve gehele getallen $n$ waarvoor er $n$ verschillende natuurlijke getallen $a_{1}, a_{2}, \ldots, a_{n}$ bestaan, geen van alle groter dan $n^{2}$, zo dat de som
$$
\frac{1}{a_{1}}+\frac{1}{a_{2}}+\cdots+\frac{1}{a_{n}}=1 .
$$
|
We geven een alternatieve oplossing voor het geval dat $n$ te schrijven is als $k(k+1)$. Als eerste merken we op dat $k(k+1)$ even is. Dus we kunnen de breuken
$\frac{1}{n}+\frac{1}{k(k+1)}=\frac{2}{k(k+1)}=\frac{1}{k(k+1) / 2}$ samennemen. Tegelijkertijd splitsen we $\frac{1}{6}=\frac{1}{8}+\frac{1}{24}$. Merk op dat 8 en 24 niet van de vorm $\kappa(\kappa+1)$ of van de vorm $\kappa(\kappa+1) / 2$ zijn. Als $k(k+1) / 2$ niet van de vorm $\ell(\ell+1)$ is, zijn we klaar aangezien we drie breuken hebben vervangen door drie verschillende breuken die verder niet voorkomen.
Als $k(k+1) / 2=\ell(\ell+1)$ voor een zekere $\ell$, dan kunnen we de breuken $\frac{1}{k(k+1) / 2}$ en $\frac{1}{\ell(\ell+1)}$ weer samennemen tot $\frac{1}{k(k+1) / 2}+\frac{1}{\ell(\ell+1)}=\frac{1}{\ell(\ell+1) / 2}$. Tegelijkertijd splitsen we $\frac{1}{2}=\frac{1}{3}+\frac{1}{6}$. Merk op dat $\frac{1}{3}$ en $\frac{1}{6}$ niet voorkwamen in onze som. (We hadden $\frac{1}{6}$ immers net vervangen door $\frac{1}{8}+\frac{1}{24}$.) Verder kan $\ell(\ell+1) / 2=k(k+1) / 4$ niet weer van de vorm $\kappa(\kappa+1)$ zijn. Dan zou $4 \kappa(\kappa+1)=2 \kappa(2 \kappa+2)$ immers $k(k+1)$ zijn, maar
$$
2 \kappa(2 \kappa+1)<2 \kappa(2 \kappa+2)<(2 \kappa+1)(2 \kappa+2)
$$
Dus zolang 3 en 6 niet gelijk zijn aan $k(k+1) / 2=n / 2$, zijn we klaar aangezien we nogmaals drie breuken hebben vervangen door drie verschillende breuken die verder niet voorkomen.
Voor $n=6$ voldoet $1=\frac{1}{2}+\frac{1}{3}+\frac{1}{18}+\frac{1}{20}+\frac{1}{30}+\frac{1}{36}$ en voor $n=12$ voldoet $1=$ $\frac{1}{2}+\frac{1}{6}+\frac{1}{9}+\frac{1}{18}+\frac{1}{20}+\frac{1}{30}+\frac{1}{42}+\frac{1}{56}+\frac{1}{72}+\frac{1}{90}+\frac{1}{110}+\frac{1}{132}$.
Opmerking. Een andere manier om de vergelijkingen (2) en (3) te vinden is bijvoorbeeld als volgt. Voor $n=3$ hebben we $\frac{1}{2}+\frac{1}{3}+\frac{1}{6}=1$. Als we hierop de substitutie (1) toepassen met $k=3$ en $\ell=n-3$, dan vinden we ook (2). Evenzo kunnen we (3) vinden door (1) toe te passen met $k=3$ en $\ell=n-4$ op $\frac{1}{2}+\frac{1}{3}+\frac{1}{10}+\frac{1}{15}=1$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2023-C2023_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2023"
}
|
Given a natural number $n$, we define $\tau(n)$ as the number of natural numbers that divide $n$, and we define $\sigma(n)$ as the sum of these divisors. Find all natural numbers $n$ for which
$$
\sigma(n)=\tau(n) \cdot\lceil\sqrt{n}\rceil .
$$
For a real number $x$, the notation $\lceil x\rceil$ denotes the smallest integer greater than or equal to $x$.
|
Answer: this only applies to 1, 3, 5, 6.
For these four cases, it indeed holds respectively that $1=1 \cdot 1, 4=2 \cdot\lceil\sqrt{3}\rceil, 6=2 \cdot\lceil\sqrt{5}\rceil$ and $12=4 \cdot\lceil\sqrt{6}\rceil$. From now on, we assume that $n \neq 1$.
If $n$ is a square, then $n$ has an odd number of divisors $1=d_{1}<d_{2}<\ldots<d_{2 k-1}=n$. The middle one of these is $d_{k}=\sqrt{n}$; all other divisors can be divided into $k-1$ pairs $\left(d_{i}, d_{2 k-i}\right)$ with $d_{i} d_{2 k-i}=n$. Using the arithmetic-geometric mean inequality, we find that
$$
\frac{\sigma(n)}{\tau(n)}=\frac{\sum_{i=1}^{2 k-1} d_{i}}{2 k-1}>\sqrt[2 k-1]{\prod_{i=1}^{2 k-1} d_{i}}=\sqrt[2 k-1]{\sqrt{n} \cdot n^{k-1}}=\sqrt{n}=\lceil\sqrt{n}\rceil,
$$
since we cannot have equality because $d_{1} \neq d_{2 k-1}$. Therefore, there are no solutions for $n$ being a square.
If $n$ is not a square, then $n$ has an even number of divisors. Indeed, if $n=p_{1}^{e_{1}} p_{2}^{e_{2}} \cdots p_{t}^{e_{t}}$ then $\tau(n)=\left(e_{1}+1\right)\left(e_{2}+1\right) \cdots\left(e_{t}+1\right)$ and at least one of the $e_{i}$ must be odd. We order the divisors again by size $1=d_{1}<d_{2}<\ldots<d_{2 k}=n$. For the middle two of these divisors, we find
$$
\frac{d_{k}+d_{k+1}+1}{2} \geq \frac{d_{k}+d_{k+1}}{2} \geq \sqrt{d_{k} d_{k+1}}=\sqrt{n} .
$$
Since $\frac{d_{k}+d_{k+1}+1}{2}$ or $\frac{d_{k}+d_{k+1}}{2}$ is an integer, we note that $\frac{d_{k}+d_{k+1}+1}{2}$ is greater than or equal to an integer greater than or equal to $\sqrt{n}$. We conclude from this that $\frac{d_{k}+d_{k+1}+1}{2} \geq \lceil\sqrt{n}\rceil$, which we can rewrite as $d_{k}+d_{k+1} \geq 2\lceil\sqrt{n}\rceil-1$.
Suppose we have two divisors of $n$ $d<e \leq \sqrt{n}$. Then the sequences $\left(d, \frac{n}{e}\right)$ and $\left(1, \frac{e}{d}\right)$ are both strictly increasing, because $d<\sqrt{n} \leq \frac{n}{e}$ and $1<\frac{e}{d}$. Using the rearrangement inequality, we find that $d+\frac{n}{d}>e+\frac{n}{e}$. Note that this is a strict inequality because both sequences are strictly increasing. With $e=d_{k}$, we find that $d+\frac{n}{d}>d_{k}+d_{k+1} \geq 2\lceil\sqrt{n}\rceil-1$. Thus, $d_{k-i}+d_{k+1+i}>2\lceil\sqrt{n}\rceil-1$, or $d_{k-i}+d_{k+1+i} \geq 2\lceil\sqrt{n}\rceil$ for all $1 \leq i \leq k-1$.
Now suppose that $n \geq 8$. Then we know that $(n-4)^{2} \geq 4^{2}>12$, or $n^{2}-8 n+16 \geq 12$. This can also be written as $n^{2}-4 n+4 \geq 4 n$ and then factored as $(n-2)^{2} \geq 4 n$. Taking the square root of this, we find that
$$
\frac{n-1}{2} \geq \frac{n-2}{2} \geq \sqrt{n}
$$
As before, we note that $\frac{n-1}{2}$ is now greater than or equal to an integer greater than or equal to $\sqrt{n}$, so $\frac{n-1}{2} \geq \lceil\sqrt{n}\rceil$. This can be rewritten as $n+1 \geq 2\lceil\sqrt{n}\rceil+2$.
For $n \geq 8$ and not a square, we conclude that
$$
\begin{aligned}
\sigma(n) & =\left(d_{k}+d_{k+1}\right)+\left(d_{k-1}+d_{k+2}\right)+\ldots+\left(d_{2}+d_{2 k-1}\right)+\left(d_{1}+d_{2 k}\right) \\
& \geq(2\lceil\sqrt{n}\rceil-1)+2\lceil\sqrt{n}\rceil+\ldots+2\lceil\sqrt{n}\rceil+(2\lceil\sqrt{n}\rceil+2) \\
& =2 k\lceil\sqrt{n}\rceil+1 \\
& =\tau(n) \cdot\lceil\sqrt{n}\rceil+1,
\end{aligned}
$$
which means there can be no solutions. It remains to check that for $n=2$ it holds that $3 \neq 2 \cdot\lceil\sqrt{2}\rceil$ and that for $n=7$ it holds that $8 \neq 2 \cdot\lceil\sqrt{7}\rceil$. The case $n=4$ was handled when we dealt with the squares.
|
1, 3, 5, 6
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Gegeven een natuurlijk getal $n$ definiëren we $\tau(n)$ als het aantal natuurlijke getallen dat $n$ deelt, en definiëren we $\sigma(n)$ als de som van deze delers. Vind alle natuurlijke getallen $n$ waarvoor geldt dat
$$
\sigma(n)=\tau(n) \cdot\lceil\sqrt{n}\rceil .
$$
Voor een reëel getal $x$ bedoelen we met de notatie $\lceil x\rceil$ het kleinste gehele getal groter of gelijk aan $x$.
|
Antwoord: dit geldt alleen voor 1, 3, 5, 6 .
Voor deze vier gevallen geldt inderdaad respectievelijk dat $1=1 \cdot 1,4=2 \cdot\lceil\sqrt{3}\rceil, 6=2 \cdot\lceil\sqrt{5}\rceil$ en $12=4 \cdot\lceil\sqrt{6}\rceil$. Vanaf nu nemen we aan dat $n \neq 1$.
Als $n$ een kwadraat is, dan heeft $n$ een oneven aantal delers $1=d_{1}<d_{2}<\ldots<d_{2 k-1}=n$. De middelste daarvan is $d_{k}=\sqrt{n}$; alle andere delers kunnen in $k-1$ paren $\left(d_{i}, d_{2 k-i}\right)$ worden verdeeld met $d_{i} d_{2 k-i}=n$. Met de ongelijkheid van het rekenkundig-meetkundig gemiddelde vinden we dan dat
$$
\frac{\sigma(n)}{\tau(n)}=\frac{\sum_{i=1}^{2 k-1} d_{i}}{2 k-1}>\sqrt[2 k-1]{\prod_{i=1}^{2 k-1} d_{i}}=\sqrt[2 k-1]{\sqrt{n} \cdot n^{k-1}}=\sqrt{n}=\lceil\sqrt{n}\rceil,
$$
aangezien we geen gelijkheid kunnen krijgen omdat $d_{1} \neq d_{2 k-1}$. Voor $n$ een kwadraat zijn er dus geen oplossingen.
Als $n$ geen kwadraat is, dan heeft $n$ een even aantal delers. Inderdaad, als $n=p_{1}^{e_{1}} p_{2}^{e_{2}} \cdots p_{t}^{e_{t}}$ dan is $\tau(n)=\left(e_{1}+1\right)\left(e_{2}+1\right) \cdots\left(e_{t}+1\right)$ en minstens een van de $e_{i}$ moet oneven zijn. We ordenen de delers weer op grootte $1=d_{1}<d_{2}<\ldots<d_{2 k}=n$. Voor de middelste twee van deze delers vinden we
$$
\frac{d_{k}+d_{k+1}+1}{2} \geq \frac{d_{k}+d_{k+1}}{2} \geq \sqrt{d_{k} d_{k+1}}=\sqrt{n} .
$$
Aangezien $\frac{d_{k}+d_{k+1}+1}{2}$ of $\frac{d_{k}+d_{k+1}}{2}$ geheel is, merken we dus op dat $\frac{d_{k}+d_{k+1}+1}{2}$ groter of gelijk is aan een natuurlijk getal groter of gelijk aan $\sqrt{n}$. We concluderen hieruit dat $\frac{d_{k}+d_{k+1}+1}{2} \geq$ $\lceil\sqrt{n}\rceil$, wat we kunnen herschrijven als $d_{k}+d_{k+1} \geq 2\lceil\sqrt{n}\rceil-1$.
Stel dat we twee delers van $n$ hebben $d<e \leq \sqrt{n}$. Dan zijn de rijtjes $\left(d, \frac{n}{e}\right)$ en $\left(1, \frac{e}{d}\right)$ beide strikt stijgend, want $d<\sqrt{n} \leq \frac{n}{e}$ en $1<\frac{e}{d}$. Met de herschikkingsongelijkheid vinden we dan dat $d+\frac{n}{d}>e+\frac{n}{e}$. Merk op dat dit een strikte ongelijkheid is omdat beide rijtjes strikt stijgend zijn. Met $e=d_{k}$ vinden we dan dat $d+\frac{n}{d}>d_{k}+d_{k+1} \geq 2\lceil\sqrt{n}\rceil-1$. Dus $d_{k-i}+d_{k+1+i}>2\lceil\sqrt{n}\rceil-1$, oftewel $d_{k-i}+d_{k+1+i} \geq 2\lceil\sqrt{n}\rceil$ voor alle $1 \leq i \leq k-1$.
Stel nu dat $n \geq 8$. Dan weten dat $(n-4)^{2} \geq 4^{2}>12$, oftewel $n^{2}-8 n+16 \geq 12$. Dit kunnen we ook schrijven als $n^{2}-4 n+4 \geq 4 n$ en dan ontbinden als $(n-2)^{2} \geq 4 n$. Als we
hiervan de wortel nemen vinden we dus dat
$$
\frac{n-1}{2} \geq \frac{n-2}{2} \geq \sqrt{n}
$$
Net als hiervoor merken we op dat $\frac{n-1}{2}$ nu groter of gelijk is aan een natuurlijk getal groter of gelijk aan $\sqrt{n}$, dus $\frac{n-1}{2} \geq\lceil\sqrt{n}\rceil$. Dit kunnen we herschrijven als $n+1 \geq 2\lceil\sqrt{n}\rceil+2$.
Voor $n \geq 8$ en geen kwadraat concluderen we dat
$$
\begin{aligned}
\sigma(n) & =\left(d_{k}+d_{k+1}\right)+\left(d_{k-1}+d_{k+2}\right)+\ldots+\left(d_{2}+d_{2 k-1}\right)+\left(d_{1}+d_{2 k}\right) \\
& \geq(2\lceil\sqrt{n}\rceil-1)+2\lceil\sqrt{n}\rceil+\ldots+2\lceil\sqrt{n}\rceil+(2\lceil\sqrt{n}\rceil+2) \\
& =2 k\lceil\sqrt{n}\rceil+1 \\
& =\tau(n) \cdot\lceil\sqrt{n}\rceil+1,
\end{aligned}
$$
waardoor er geen oplossingen kunnen zijn. Het rest ons nog te controleren dat voor $n=2$ geldt dat $3 \neq 2 \cdot\lceil\sqrt{2}\rceil$ en dat voor $n=7$ geldt dat $8 \neq 2 \cdot\lceil\sqrt{7}\rceil$. Het geval $n=4$ is afgehandeld toen we de kwadraten hebben afgeschoten.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2023-C2023_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2023"
}
|
Given a natural number $n$, we define $\tau(n)$ as the number of natural numbers that divide $n$, and we define $\sigma(n)$ as the sum of these divisors. Find all natural numbers $n$ for which
$$
\sigma(n)=\tau(n) \cdot\lceil\sqrt{n}\rceil .
$$
For a real number $x$, the notation $\lceil x\rceil$ denotes the smallest integer greater than or equal to $x$.
|
The case where $n$ is not a square can also be approached as follows. Instead of estimating the last pair $(1, n)$ for $n \geq 8$, we can repeatedly apply the rearrangement argument with respect to the previous pair (viewed from the middle): $d_{k-i}+d_{k+1+i}>d_{k-i+1}+d_{k+i}$. This yields the stronger inequality that $d_{k-i}+d_{k+1+i} \geq 2\lceil\sqrt{n}\rceil+i-1$ for all $0 \leq i \leq k-1$. Summing these inequalities, we get
\[
\begin{aligned}
\sigma(n) & =\left(d_{k}+d_{k+1}\right)+\left(d_{k-1}+d_{k+2}\right)+\left(d_{k-2}+d_{k+3}\right)+\ldots+\left(d_{1}+d_{2 k}\right) \\
& \geq(2\lceil\sqrt{n}\rceil-1)+2\lceil\sqrt{n}\rceil+(2\lceil\sqrt{n}\rceil+1)+\ldots+(2\lceil\sqrt{n}\rceil+k-2) \\
& =2 k\lceil\sqrt{n}\rceil+\frac{1}{2} k(k-3) \\
& =\tau(n) \cdot\lceil\sqrt{n}\rceil+\frac{1}{2} k(k-3) .
\end{aligned}
\]
The problem can only hold if $\frac{1}{2} k(k-3) \leq 0$, i.e., $k \leq 3$.
If $k=3$, equality must hold for each pair, and in particular for the last pair: $1+n=2\lceil\sqrt{n}\rceil+k-2=2\lceil\sqrt{n}\rceil+1<2(\sqrt{n}+1)+1=2 \sqrt{n}+3$. Thus, $(\sqrt{n}-1)^{2}=$ $n-2 \sqrt{n}+1<3$, which implies $\sqrt{n}<1+\sqrt{3}$. Therefore, $n<(1+\sqrt{3})^{2}=4+2 \sqrt{3}<8$. This means $n \leq 7$, but none of these numbers have $2 k=6$ divisors.
If $k=2$, then $n=p q$ for two distinct primes $p \neq q$, or $n=p^{3}$. If $n=p q$, the original equation states that
$4(\sqrt{p q}+1) \geq 4\lceil\sqrt{p q}\rceil=\tau(n) \cdot\lceil\sqrt{n}\rceil=\sigma(n)=(p+1)(q+1)=p q+p+q+1>p q+2 \sqrt{p q}+1$.
This implies $4>(\sqrt{p q}-1)^{2}$, so $n=p q<9$. The only possibility is $n=6$, and we have already verified that this is indeed a solution. If $n=p^{3}$, we write this as $n=p q$ with $q=p^{2}$. In this case, $\sigma(n)=p^{3}+p^{2}+p+1=p q+q+p+1=(p+1)(q+1)$ and $p \neq q$. The same inequality holds, and we find that $n=p^{3}<9$. The only possibility here is $n=8$, but this does not satisfy the condition.
If $k=1$, then $n=p$ for a prime $p$. The original equation states that
\[
2(\sqrt{p}+1)>2\lceil\sqrt{p}\rceil=\tau(n) \cdot\lceil\sqrt{n}\rceil=\sigma(n)=p+1
\]
This can be rewritten as $2>(\sqrt{p}-1)^{2}$. Thus, $\sqrt{p}<1+\sqrt{2}$. Therefore, $n=p<3+2 \sqrt{2}<6$. Checking 2, 3, and 5, we find that 2 is not a solution, but 3 and 5 are.
Remark. We write $n=p_{1}^{e_{1}} p_{2}^{e_{2}} \cdots p_{t}^{e^{t}}$. Then $\tau(n)=\left(e_{1}+1\right)\left(e_{2}+1\right) \cdots\left(e_{t}+1\right)$ and $\sigma(n)=\left(p_{1}^{e_{1}}+p_{1}^{e_{1}-1}+\ldots+1\right) \cdots\left(p_{t}^{e_{t}}+p_{t}^{e_{t}-1}+\ldots+1\right)$. Some arguments become easier by splitting them into different primes. For $e>1$ odd, we have
\[
\frac{p^{(e-1) / 2}+p^{(e+1) / 2}}{2} \geq\left\lceil\sqrt{p^{e}}\right\rceil
\]
because the fraction is an integer. Using the rearrangement argument, we find for all $e>1$ that
\[
p^{e}+p^{e-1}+\ldots+1 \geq(e+1)\left\lceil\sqrt{p^{e}}\right\rceil+1
\]
However, the case $e=1, p=2$ complicates matters because $2+1<2 \cdot\lceil\sqrt{2}\rceil$.
|
3, 5, 6
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Gegeven een natuurlijk getal $n$ definiëren we $\tau(n)$ als het aantal natuurlijke getallen dat $n$ deelt, en definiëren we $\sigma(n)$ als de som van deze delers. Vind alle natuurlijke getallen $n$ waarvoor geldt dat
$$
\sigma(n)=\tau(n) \cdot\lceil\sqrt{n}\rceil .
$$
Voor een reëel getal $x$ bedoelen we met de notatie $\lceil x\rceil$ het kleinste gehele getal groter of gelijk aan $x$.
|
Het geval dat $n$ geen kwadraat is kunnen we ook als volgt aanpakken. In plaats van het laatste paar $(1, n)$ af te schatten voor $n \geq 8$, kunnen we het herschikkingsargument ook herhaaldelijk toepassen in vergelijking met het vorige paar (gezien vanuit het midden): $d_{k-i}+d_{k+1+i}>d_{k-i+1}+d_{k+i}$. Hieruit volgt de sterkere ongelijkheid dat $d_{k-i}+d_{k+1+i} \geq 2\lceil\sqrt{n}\rceil+i-1$ voor alle $0 \leq i \leq k-1$. Als we deze ongelijkheden sommeren krijgen we dat
$$
\begin{aligned}
\sigma(n) & =\left(d_{k}+d_{k+1}\right)+\left(d_{k-1}+d_{k+2}\right)+\left(d_{k-2}+d_{k+3}\right)+\ldots+\left(d_{1}+d_{2 k}\right) \\
& \geq(2\lceil\sqrt{n}\rceil-1)+2\lceil\sqrt{n}\rceil+(2\lceil\sqrt{n}\rceil+1)+\ldots+(2\lceil\sqrt{n}\rceil+k-2) \\
& =2 k\lceil\sqrt{n}\rceil+\frac{1}{2} k(k-3) \\
& =\tau(n) \cdot\lceil\sqrt{n}\rceil+\frac{1}{2} k(k-3) .
\end{aligned}
$$
De opgave kan dus alleen gelden als $\frac{1}{2} k(k-3) \leq 0$, oftewel $k \leq 3$.
Als $k=3$ moet voor elk paar gelijkheid gelden, dus in het bijzonder voor het laatste paar: $1+n=2\lceil\sqrt{n}\rceil+k-2=2\lceil\sqrt{n}\rceil+1<2(\sqrt{n}+1)+1=2 \sqrt{n}+3$. Dus $(\sqrt{n}-1)^{2}=$ $n-2 \sqrt{n}+1<3$ waaruit volgt dat $\sqrt{n}<1+\sqrt{3}$. En dus $n<(1+\sqrt{3})^{2}=4+2 \sqrt{3}<8$. Dit betekent dat $n \leq 7$, maar geen van deze getallen heeft $2 k=6$ delers.
Als $k=2$, dan moet er gelden dat $n=p q$ voor twee priemgetallen $p \neq q$, of $n=p^{3}$. Als $n=p q$, dan zegt de oorspronkelijke vergelijking dat
$4(\sqrt{p q}+1) \geq 4\lceil\sqrt{p q}\rceil=\tau(n) \cdot\lceil\sqrt{n}\rceil=\sigma(n)=(p+1)(q+1)=p q+p+q+1>p q+2 \sqrt{p q}+1$.
Hieruit volgt dat $4>(\sqrt{p q}-1)^{2}$, dus $n=p q<9$. De enige mogelijkheid is $n=6$, en we hebben al gecontroleerd dat dit inderdaad een oplossing is. Als $n=p^{3}$, dan schrijven we dit als $n=p q$ met $q=p^{2}$. In dit geval geldt ook dat $\sigma(n)=p^{3}+p^{2}+p+1=p q+q+p+1=$ $(p+1)(q+1)$ en dat $p \neq q$. Dus dezelfde ongelijkheid geldt en we vinden dat $n=p^{3}<9$. De enige mogelijkheid in dit geval is $n=8$, maar die voldoet niet.
Als $k=1$, dan moet er gelden dat $n=p$ voor een priemgetal $p$. Dan zegt de oorspronkelijke vergelijking dat
$$
2(\sqrt{p}+1)>2\lceil\sqrt{p}\rceil=\tau(n) \cdot\lceil\sqrt{n}\rceil=\sigma(n)=p+1
$$
Dit kunnen we herschrijven als $2>(\sqrt{p}-1)^{2}$. Hieruit volgt $\sqrt{p}<1+\sqrt{2}$. Dus $n=p<3+2 \sqrt{2}<6$. Controleren van 2, 3 en 5 levert dat 2 geen oplossing is, maar 3 en 5 wel.
Opmerking. We schrijven $n=p_{1}^{e_{1}} p_{2}^{e_{2}} \cdots p_{t}^{e^{t}}$. Dan is $\tau(n)=\left(e_{1}+1\right)\left(e_{2}+1\right) \cdots\left(e_{t}+1\right)$ en $\sigma(n)=\left(p_{1}^{e_{1}}+p_{1}^{e_{1}-1}+\ldots+1\right) \cdots\left(p_{t}^{e_{t}}+p_{t}^{e_{t}-1}+\ldots+1\right)$. Een aantal argumenten wordt iets makkelijker door ze uit te splitsen naar de verschillende priemgetallen. Voor $e>1$ oneven hebben we bijvoorbeeld dat
$$
\frac{p^{(e-1) / 2}+p^{(e+1) / 2}}{2} \geq\left\lceil\sqrt{p^{e}}\right\rceil
$$
omdat de breuk geheel is. Met het herschikkingsargument vinden we dus voor alle $e>1$ dat
$$
p^{e}+p^{e-1}+\ldots+1 \geq(e+1)\left\lceil\sqrt{p^{e}}\right\rceil+1
$$
Het geval $e=1, p=2$ gooit echter roet in het eten, doordat $2+1<2 \cdot\lceil\sqrt{2}\rceil$.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2023-C2023_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2023"
}
|
Let $n$ be a positive integer. Prove that the numbers
$$
1^{1}, 3^{3}, 5^{5}, \ldots,\left(2^{n}-1\right)^{2^{n}-1}
$$
are in different residue classes modulo $2^{n}$.
|
We prove the requested statement by induction. For $n=1$, we only look at the number $1^{1}$, so the statement is trivially true.
Assume as the induction hypothesis that $1^{1}, 3^{3}, 5^{5}, \ldots,\left(2^{n}-1\right)^{2^{n}-1}$ are in different residue classes modulo $2^{n}$. First, these numbers are also in different residue classes modulo $2^{n+1}$. Since $\varphi\left(2^{n+1}\right)=2^{n}$, it holds that $a^{k} \equiv a^{\ell} \bmod 2^{n+1}$ if $k \equiv \ell \bmod 2^{n}$ and $a$ is odd.
The additional numbers we consider can be written as $\left(2^{n}+m\right)^{2^{n}+m}$ with $1 \leq m \leq 2^{n}-1$ and $m$ odd. If we expand $\left(2^{n}+m\right)^{2^{n}+m}$ using the binomial theorem, we notice that every term with at least two factors $2^{n}$ is congruent to 0 modulo $2^{n+1}$. Therefore, modulo $2^{n+1}$, we have
\[
\begin{aligned}
\left(2^{n}+m\right)^{2^{n}+m} & \equiv m^{2^{n}+m}+\left(2^{n}+m\right) m^{2^{n}+m-1} 2^{n}+\binom{2^{n}+m}{2} m^{2^{n}+m-2}\left(2^{n}\right)^{2}+\ldots \\
& \equiv m^{2^{n}+m}+\left(2^{n}+m\right) m^{2^{n}+m-1} 2^{n} \\
& \equiv m^{m}+\left(2^{2 n}+2^{n} m\right) m^{m-1} \\
& \equiv m^{m}+2^{n} \cdot m^{m} \\
& \equiv m^{m}+2^{n}
\end{aligned}
\]
where in the last step we used the fact that $m^{m}$ is odd. This means that we can write $m^{m}$ as $2a+1$, and then we find that $2^{n}(2a+1)=2^{n+1}a+2^{n} \equiv 2^{n} \bmod 2^{n+1}$.
Since the numbers $m^{m}$ from the first group are distinct modulo $2^{n+1}$, the numbers from the second group are also distinct modulo $2^{n+1}$. From this calculation, we also conclude that the numbers from the first group are different from the numbers from the second group. Suppose that $\left(2^{n}+m\right)^{2^{n}+m} \equiv k^{k} \bmod 2^{n+1}$ with $1 \leq k, m \leq 2^{n}-1$, then from this calculation it follows in particular that $m^{m} \equiv m^{m}+2^{n} \equiv k^{k} \bmod 2^{n}$. Therefore, by the induction hypothesis, we know that $m=k$. But in that case, it holds that $\left(2^{n}+m\right)^{2^{n}+m} \equiv m^{m}+2^{n} \not \equiv m^{m} \bmod 2^{n+1}$.
We conclude that no number from the groups $1^{1}, 3^{3}, 5^{5}, \ldots,\left(2^{n}-1\right)^{2^{n}-1}$ and $\left(2^{n}+1\right)^{2^{n}+1},\left(2^{n}+3\right)^{2^{n}+3}, \ldots,\left(2^{n+1}-1\right)^{2^{n+1}-1}$ has the same residue class as another number from these two groups. This completes the induction step, and by induction, the statement is true for all natural numbers $n$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Zij $n$ een positief geheel getal. Bewijs dat de getallen
$$
1^{1}, 3^{3}, 5^{5}, \ldots,\left(2^{n}-1\right)^{2^{n}-1}
$$
in verschillende restklassen zitten modulo $2^{n}$.
|
We bewijzen het gevraagde met inductie. Voor $n=1$ kijken we enkel naar het getal $1^{1}$, dus is het gevraagde triviaal waar.
Stel nu als inductiehypothese dat $1^{1}, 3^{3}, 5^{5}, \ldots,\left(2^{n}-1\right)^{2^{n}-1}$ in verschillende restklassen zitten modulo $2^{n}$. Ten eerste zitten deze getallen dan ook in verschillende restklassen modulo $2^{n+1}$. Aangezien $\varphi\left(2^{n+1}\right)=2^{n}$, geldt $a^{k} \equiv a^{\ell} \bmod 2^{n+1}$ als $k \equiv \ell \bmod 2^{n}$ en $a$ oneven.
De getallen die er bij komen, schrijven we als $\left(2^{n}+m\right)^{2^{n}+m}$ met $1 \leq m \leq 2^{n}-1$ en oneven. Als we de haakjes van $\left(2^{n}+m\right)^{2^{n}+m}$ gaan uitwerken met het binomium van Newton, dan merken we op dat elke term met minstens twee factoren $2^{n}$ congruent is aan 0 modulo $2^{n+1}$. We vinden dus modulo $2^{n+1}$ dat
$$
\begin{aligned}
\left(2^{n}+m\right)^{2^{n}+m} & \equiv m^{2^{n}+m}+\left(2^{n}+m\right) m^{2^{n}+m-1} 2^{n}+\binom{2^{n}+m}{2} m^{2^{n}+m-2}\left(2^{n}\right)^{2}+\ldots \\
& \equiv m^{2^{n}+m}+\left(2^{n}+m\right) m^{2^{n}+m-1} 2^{n} \\
& \equiv m^{m}+\left(2^{2 n}+2^{n} m\right) m^{m-1} \\
& \equiv m^{m}+2^{n} \cdot m^{m} \\
& \equiv m^{m}+2^{n}
\end{aligned}
$$
waarbij we in de laatste stap hebben gebruikt dat $m^{m}$ oneven is. Dit betekent immers dat we $m^{m}$ kunnen schrijven als $2 a+1$ en dan vinden we dat $2^{n}(2 a+1)=2^{n+1} a+2^{n} \equiv 2^{n}$ $\bmod 2^{n+1}$ 。
Aangezien de getallen $m^{m}$ uit de eerste groep onderling verschillend zijn modulo $2^{n+1}$, zijn de getallen uit de tweede groep nu ook onderling verschillend modulo $2^{n+1}$. Uit deze
berekening concluderen we bovendien dat de getallen van de eerste groep verschillend zijn van de getallen uit de tweede groep. Stel namelijk dat $\left(2^{n}+m\right)^{2^{n}+m} \equiv k^{k} \bmod 2^{n+1}$ met $1 \leq k, m \leq 2^{n}-1$, dan volgt uit deze berekening in het bijzonder dat $m^{m} \equiv m^{m}+2^{n} \equiv k^{k}$ $\bmod 2^{n}$. Dus wegens de inductiehypothese weten we dat $m=k$. Maar in dat geval geldt juist dat $\left(2^{n}+m\right)^{2^{n}+m} \equiv m^{m}+2^{n} \not \equiv m^{m} \bmod 2^{n+1}$.
We concluderen dus dat geen enkel getal uit de groepen $1^{1}, 3^{3}, 5^{5}, \ldots,\left(2^{n}-1\right)^{2^{n}-1}$ en $\left(2^{n}+1\right)^{2^{n}+1},\left(2^{n}+3\right)^{2^{n}+3}, \ldots,\left(2^{n+1}-1\right)^{2^{n+1}-1}$ dezelfde restklasse heeft als een ander getal uit deze twee groepen. Hiermee is de inductiestap afgerond, en met inductie volgt dus dat de stelling waar is voor alle natuurlijke getallen $n$.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2023-D2023_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2023"
}
|
Let $n$ be a positive integer. Prove that the numbers
$$
1^{1}, 3^{3}, 5^{5}, \ldots,\left(2^{n}-1\right)^{2^{n}-1}
$$
are in different residue classes modulo $2^{n}$.
|
To show that the numbers in the second group are different from each other, we can also do the following. These numbers are of the form $\left(2^{n+1}-k\right)^{2^{n+1}-k}$ with $1 \leq k \leq 2^{n}-1$ and odd. Since $\varphi\left(2^{n+1}\right)=2^{n}$, it holds that $a^{k} \equiv a^{l} \bmod 2^{n+1}$ if $k \equiv l$ $\bmod 2^{n}$. This means that $\left(2^{n+1}-k\right)^{2^{n+1}-k} \equiv(-k)^{-k} \equiv-\left(k^{k}\right)^{-1} \bmod 2^{n+1}$, where we also used that $k$ is odd. Since the numbers $k^{k}$ with $1 \leq k \leq 2^{n}-1$ and odd are different, the numbers $\left(2^{n+1}-k\right)^{2^{n+1}-k}$ are thus also different.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Zij $n$ een positief geheel getal. Bewijs dat de getallen
$$
1^{1}, 3^{3}, 5^{5}, \ldots,\left(2^{n}-1\right)^{2^{n}-1}
$$
in verschillende restklassen zitten modulo $2^{n}$.
|
Om te laten zien dat de getallen in de tweede groep verschillend van elkaar zijn, kunnen we ook het volgende doen. Deze getallen zijn van de vorm $\left(2^{n+1}-k\right)^{2^{n+1}-k}$ met $1 \leq k \leq 2^{n}-1$ en oneven. Aangezien $\varphi\left(2^{n+1}\right)=2^{n}$, geldt $a^{k} \equiv a^{l} \bmod 2^{n+1}$ als $k \equiv l$ $\bmod 2^{n}$. Dat betekent dat $\left(2^{n+1}-k\right)^{2^{n+1}-k} \equiv(-k)^{-k} \equiv-\left(k^{k}\right)^{-1} \bmod 2^{n+1}$ waarbij we ook hebben gebruikt dat $k$ oneven is. Aangezien de getallen $k^{k}$ met $1 \leq k \leq 2^{n}-1$ en oneven verschillend zijn, zijn de getallen $\left(2^{n+1}-k\right)^{2^{n+1}-k}$ dat dus ook.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2023-D2023_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2023"
}
|
Given is a triangle $ABC$ and a point $D$ on the line segment $AC$. Let $M$ be the midpoint of $CD$ and let $\Omega$ be the circle through $B$ and $D$ that is tangent to $AB$. Let $E$ be the point such that $\triangle M D B \sim \triangle M B E$ and such that $D$ and $E$ lie on opposite sides of the line $MB$.
Show that $E$ lies on $\Omega$ if and only if $\angle A B D = \angle M B C$.
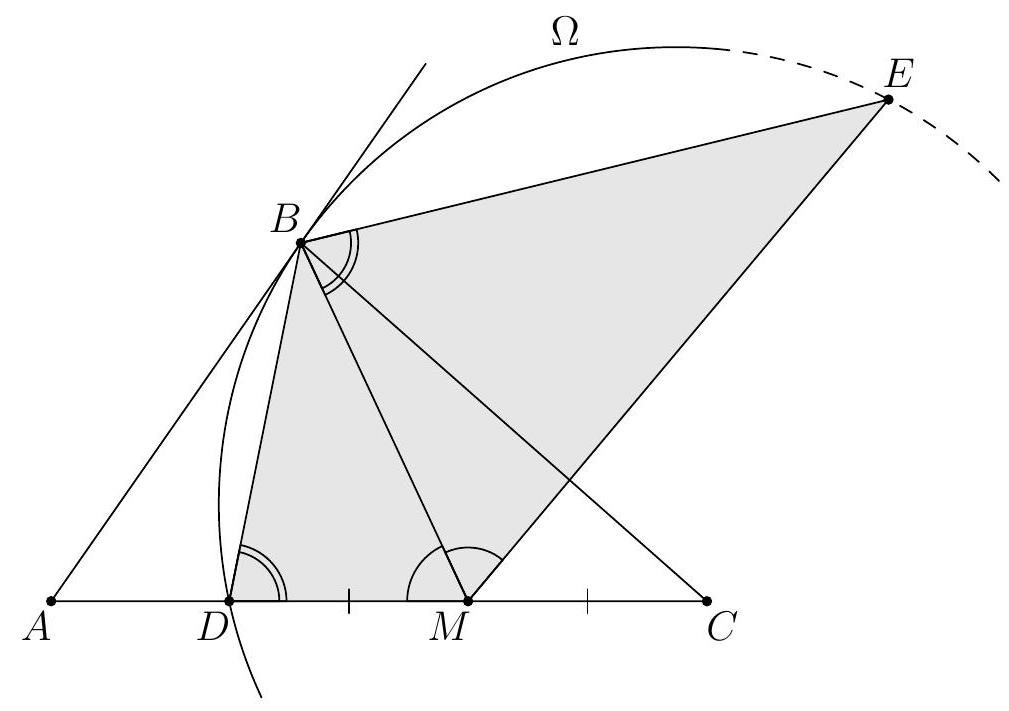
|
We first prove that $\triangle C M B \sim \triangle D B E$. Since $D$ and $E$ lie on opposite sides of $M B$, it follows that $\angle D B E=\angle D B M+\angle M B E=\angle D B M+\angle M D B=\angle C M B$ due to the given similarity and the exterior angle theorem. Secondly, it holds that
$$
\frac{|D B|}{|B E|}=\frac{|M D|}{|M B|}=\frac{|C M|}{|M B|}
$$
due to the given similarity and the fact that $M$ is the midpoint of $C D$. By SAS, it indeed follows that $\triangle C M B \sim \triangle D B E$. In particular, this implies that $\angle B E D = \angle M B C$. Therefore, $\angle A B D = \angle M B C$ if and only if $\angle A B D = \angle B E D$. By the tangent-secant theorem, this holds if and only if $A B$ is tangent to the circumcircle of $\triangle B D E$. The circle through $B$ and $D$ that is tangent to $A B$ is unique, with its center being the intersection of the perpendicular bisector of $B D$ and the line through $B$ perpendicular to $A B$. Thus, $A B$ is tangent to the circumcircle of $\triangle B D E$ if and only if $E$ lies on $\Omega$. $\square$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Gegeven is een driehoek $A B C$ en een punt $D$ op het lijnstuk $A C$. Zij $M$ het midden van $C D$ en zij $\Omega$ de cirkel door $B$ en $D$ die raakt aan $A B$. Zij $E$ het punt zodat $\triangle M D B \sim \triangle M B E$ en zodat $D$ en $E$ aan weerszijden van de lijn $M B$ liggen.
Toon aan dat $E$ op $\Omega$ ligt dan en slechts dan als $\angle A B D=\angle M B C$.

|
We bewijzen eerst dat $\triangle C M B \sim \triangle D B E$. Omdat $D$ en $E$ aan weerszijden van $M B$ liggen, geldt er dat $\angle D B E=\angle D B M+\angle M B E=\angle D B M+\angle M D B=\angle C M B$ vanwege de gegeven gelijkvormigheid en de buitenhoekstelling. Ten tweede geldt er dat
$$
\frac{|D B|}{|B E|}=\frac{|M D|}{|M B|}=\frac{|C M|}{|M B|}
$$
vanwege de gegeven gelijkvormigheid en het feit dat $M$ het midden is van $C D$. Met zhz volgt nu inderdaad dat $\triangle C M B \sim \triangle D B E$. In het bijzonder volgt hieruit dat $\angle B E D=$ $\angle M B C$. Er geldt dus dat $\angle A B D=\angle M B C$ dan en slechts dan als $\angle A B D=\angle B E D$. Wegens de raaklijn-omtrekhoekstelling geldt dit dan en slechts dan als $A B$ raakt aan de omgeschreven cirkel van $\triangle B D E$. De cirkel door $B$ en $D$ die raakt aan $A B$ is uniek, met als middelpunt het snijpunt van de middelloodlijn van $B D$ en de lijn door $B$ loodrecht op $A B$. Dus $A B$ raakt aan de omgeschreven cirkel van $\triangle B D E$ dan en slechts dan als $E$ op $\Omega$ ligt. $\square$
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2023-D2023_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2023"
}
|
Given is a triangle $ABC$ and a point $D$ on the line segment $AC$. Let $M$ be the midpoint of $CD$ and let $\Omega$ be the circle through $B$ and $D$ that is tangent to $AB$. Let $E$ be the point such that $\triangle M D B \sim \triangle M B E$ and such that $D$ and $E$ lie on opposite sides of the line $MB$.
Show that $E$ lies on $\Omega$ if and only if $\angle A B D = \angle M B C$.

|
Let $F$ be the reflection of $B$ in $M$. Then $B C F D$ is a parallelogram, so $\angle M B C=\angle M F D=\angle B F D$. Furthermore, since $M$ is the midpoint of $C D$ and $B F$ from $\triangle M D B \sim \triangle M B E$ it follows that $\triangle C D B \sim \triangle F B E$, because similarity transformations carry points along.
(To be precise, by SAS with $\frac{|F B|}{|B E|}=2 \frac{|M B|}{|B E|}=2 \frac{|M D|}{|D B|}=\frac{|C D|}{|D B|}$ and $\angle F B E=\angle C D B$.) Therefore, $\angle B E F=\angle D B C=180^{\circ}-\angle B D F$, from which it follows by the cyclic quadrilateral theorem that $B D F E$ is a cyclic quadrilateral.
Now, $E$ lies on $\Omega$ if and only if $F$ lies on $\Omega$. The latter holds by the tangent-secant theorem if and only if $\angle A B D=\angle B F D$ (just as in the first solution because the circle through $B D$ tangent to $A B$ is unique). Since $\angle M B C=\angle B F D$, this holds if and only if $\angle A B D=\angle M B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Gegeven is een driehoek $A B C$ en een punt $D$ op het lijnstuk $A C$. Zij $M$ het midden van $C D$ en zij $\Omega$ de cirkel door $B$ en $D$ die raakt aan $A B$. Zij $E$ het punt zodat $\triangle M D B \sim \triangle M B E$ en zodat $D$ en $E$ aan weerszijden van de lijn $M B$ liggen.
Toon aan dat $E$ op $\Omega$ ligt dan en slechts dan als $\angle A B D=\angle M B C$.

|
Zij $F$ de spiegeling van $B$ in $M$. Dan is $B C F D$ een parallellogram, dus $\angle M B C=\angle M F D=\angle B F D$. Verder volgt omdat $M$ het midden is van $C D$ en $B F$ uit $\triangle M D B \sim \triangle M B E$ dat $\triangle C D B \sim \triangle F B E$, want gelijkvormigheden nemen punten mee.
(Om precies te zijn, wegens zhz met $\frac{|F B|}{|B E|}=2 \frac{|M B|}{|B E|}=2 \frac{|M D|}{|D B|}=\frac{|C D|}{|D B|}$ en $\angle F B E=\angle C D B$.) Er geldt dus dat $\angle B E F=\angle D B C=180^{\circ}-\angle B D F$, waaruit met de koordenvierhoekstelling volgt dat $B D F E$ een koordenvierhoek is.
Er geldt nu dat $E$ op $\Omega$ ligt dan en slechts dan als $F$ op $\Omega$ ligt. Dat laatste geldt vanwege de raaklijn-omtrekhoekstelling dan en slechts dan als $\angle A B D=\angle B F D$ (net als in de eerste oplossing omdat de cirkel door $B D$ rakend aan $A B$ uniek is). Omdat $\angle M B C=\angle B F D$, geldt dit dan en slechts dan als $\angle A B D=\angle M B C$.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2023-D2023_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2023"
}
|
Given is a triangle $ABC$ and a point $D$ on the line segment $AC$. Let $M$ be the midpoint of $CD$ and let $\Omega$ be the circle through $B$ and $D$ that is tangent to $AB$. Let $E$ be the point such that $\triangle M D B \sim \triangle M B E$ and such that $D$ and $E$ lie on opposite sides of the line $MB$.
Show that $E$ lies on $\Omega$ if and only if $\angle A B D = \angle M B C$.

|
Let $H$ be the second intersection of $CD$ with $\Omega$. Then, due to the tangent-secant theorem, $\angle ABD = \angle BHD$.
If $\angle ABD = \angle MBC$, it follows that $\angle MBC = \angle BHD = \angle BHM$, and by AA similarity, $\triangle MBC \sim \triangle MHB$. From this, we conclude that
$$
\frac{|MB|}{|MH|} = \frac{|MC|}{|MB|} = \frac{|MD|}{|MB|} = \frac{|MB|}{|ME|}
$$
where we also use the fact that $M$ is the midpoint of $CD$ and that $\triangle MDB \sim \triangle MBE$. We conclude that $|ME| = |MH|$. By the exterior angle theorem in $\triangle MEH$, it follows that $\angle DHE = \angle MHE = \frac{1}{2} \angle DME = \angle DMB = 180^\circ - \angle MDB - \angle DBM = 180^\circ - \angle MBE - \angle DBM = 180^\circ - \angle DBE$, from which, by the cyclic quadrilateral theorem, it follows that $E$ lies on $\Omega$.
Conversely, if $E$ lies on $\Omega$, then $\angle MHE = \angle DHE = 180^\circ - \angle DBE = 180^\circ - \angle MBE - \angle DBM = 180^\circ - \angle MDB - \angle DBM = \angle DMB = \frac{1}{2} \angle DME$. Now, $\angle MHE + \angle MEH = \angle DME$, so also $\angle MEH = \frac{1}{2} \angle DME$. Thus, $|ME| = |MH|$ and subsequently,
$$
\frac{|MB|}{|MH|} = \frac{|MB|}{|ME|} = \frac{|MD|}{|MB|} = \frac{|MC|}{|MB|}.
$$
By SAS similarity, we now deduce that $\triangle MBC \sim \triangle MHB$, from which it follows that $\angle ABD = \angle BHD = \angle BHM = \angle MBC$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Gegeven is een driehoek $A B C$ en een punt $D$ op het lijnstuk $A C$. Zij $M$ het midden van $C D$ en zij $\Omega$ de cirkel door $B$ en $D$ die raakt aan $A B$. Zij $E$ het punt zodat $\triangle M D B \sim \triangle M B E$ en zodat $D$ en $E$ aan weerszijden van de lijn $M B$ liggen.
Toon aan dat $E$ op $\Omega$ ligt dan en slechts dan als $\angle A B D=\angle M B C$.

|
Zij $H$ het tweede snijpunt van $C D$ met $\Omega$. Dan geldt vanwege de raaklijnomtrekhoekstelling dat $\angle A B D=\angle B H D$.
Als $\angle A B D=\angle M B C$, geldt er dus dat $\angle M B C=\angle B H D=\angle B H M$, waaruit met hh volgt dat $\triangle M B C \sim \triangle M H B$. Daaruit volgt dat
$$
\frac{|M B|}{|M H|}=\frac{|M C|}{|M B|}=\frac{|M D|}{|M B|}=\frac{|M B|}{|M E|}
$$
waarbij we ook gebruiken dat $M$ het midden is van $C D$ en dat $\triangle M D B \sim \triangle M B E$. We concluderen dat $|M E|=|M H|$. Met de buitenhoekstelling in $\triangle M E H$ volgt nu dat $\angle D H E=\angle M H E=\frac{1}{2} \angle D M E=\angle D M B=180^{\circ}-\angle M D B-\angle D B M=180^{\circ}-\angle M B E-$ $\angle D B M=180^{\circ}-\angle D B E$, waaruit met de koordenvierhoekstelling volgt dat $E$ op $\Omega$ ligt.
Als andersom $E$ op $\Omega$ ligt, dan geldt dat $\angle M H E=\angle D H E=180^{\circ}-\angle D B E=180^{\circ}-$ $\angle M B E-\angle D B M=180^{\circ}-\angle M D B-\angle D B M=\angle D M B=\frac{1}{2} \angle D M E$. Nu zijn $\angle M H E+$ $\angle M E H=\angle D M E$, dus ook $\angle M E H=\frac{1}{2} \angle D M E$. Dus $|M E|=|M H|$ en vervolgens geldt dat
$$
\frac{|M B|}{|M H|}=\frac{|M B|}{|M E|}=\frac{|M D|}{|M B|}=\frac{|M C|}{|M B|} .
$$
Met zhz leiden we nu af dat $\triangle M B C \sim \triangle M H B$, waaruit volgt dat $\angle A B D=\angle B H D=$ $\angle B H M=\angle M B C$, zoals gewenst.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2023-D2023_uitwerkingen.jsonl",
"solution_match": "\nOplossing III.",
"tier": "T1",
"year": "2023"
}
|
Find the smallest possible value of
$$
x y+y z+z x+\frac{1}{x}+\frac{2}{y}+\frac{5}{z},
$$
for positive real numbers $x, y$ and $z$.
|
Answer: the smallest possible value is $3 \sqrt[3]{36}$.
Using the arithmetic-geometric mean inequality, we find
$$
\begin{aligned}
x y+\frac{1}{3 x}+\frac{1}{2 y} & \geq 3 \sqrt[3]{x y \frac{1}{3 x} \frac{1}{2 y}}=3 \sqrt[3]{\frac{1}{6}} \\
y z+\frac{3}{2 y}+\frac{3}{z} & \geq 3 \sqrt[3]{y z \frac{3}{2 y} \frac{3}{z}}=3 \sqrt[3]{\frac{9}{2}} \\
x z+\frac{2}{3 x}+\frac{2}{z} & \geq 3 \sqrt[3]{x z \frac{2}{3 x} \frac{2}{z}}=3 \sqrt[3]{\frac{4}{3}}
\end{aligned}
$$
When we add these three inequalities, we get
$$
x y+y z+z x+\frac{1}{x}+\frac{2}{y}+\frac{5}{z} \geq 3\left(\sqrt[3]{\frac{1}{6}}+\sqrt[3]{\frac{9}{2}}+\sqrt[3]{\frac{4}{3}}\right)=3\left(\frac{1}{6}+\frac{1}{2}+\frac{1}{3}\right) \sqrt[3]{36}=3 \sqrt[3]{36}
$$
For each of the three inequalities, equality holds when the three terms are equal. We arrive at an equality case for all three when $(x, y, z)=\left(\frac{1}{3} \sqrt[3]{6}, \frac{1}{2} \sqrt[3]{6}, \sqrt[3]{6}\right)$, which is also easy to verify. Then $x y+y z+z x+\frac{1}{x}+\frac{2}{y}+\frac{5}{z}$ is indeed equal to
$$
\frac{1}{6} \sqrt[3]{36}+\frac{1}{2} \sqrt[3]{36}+\frac{1}{3} \sqrt[3]{36}+3 \frac{1}{\sqrt[3]{6}}+4 \frac{1}{\sqrt[3]{6}}+5 \frac{1}{\sqrt[3]{6}}=\sqrt[3]{36}+12 \frac{1}{\sqrt[3]{6}}=\sqrt[3]{36}+2 \sqrt[3]{36}=3 \sqrt[3]{36}
$$
Remark. After deciding to split the inequality into three inequalities using the arithmetic-geometric mean (one for $x y$, one for $y z$, and one for $x z$), there are different ways to find the coefficients for $\frac{1}{x}, \frac{1}{y}$, and $\frac{1}{z}$. First, you can be guided by examples you have found in your search for the equality case. For example, the expression equals 10 for $(x, y, z)=\left(\frac{2}{3}, 1,2\right)$, and with $(x, y, z)=\left(\frac{3}{5}, \frac{9}{10}, \frac{9}{5}\right)$, you get $\frac{324}{100}+\frac{12}{18} \cdot 10=3.24+6.6666 \ldots=9.9066 \ldots$.
A more structured approach is to introduce variables $a, b, c, d, e, f$ for the inequalities on $x y+a \frac{1}{x}+b \frac{1}{y}, y z+c \frac{1}{y}+d \frac{1}{z}$, and $z x+e \frac{1}{z}+f \frac{1}{x}$. Since these three terms must add up to the desired expressions, we get the conditions
$$
\begin{aligned}
f+a & =1, \\
b+c & =2, \\
d+e & =5 .
\end{aligned}
$$
Furthermore, we want equality to hold for certain $x, y$, and $z$. So the system
$$
\begin{aligned}
& x y=a \frac{1}{x}=b \frac{1}{y} \\
& y z=c \frac{1}{y}=d \frac{1}{z} \\
& z x=e \frac{1}{z}=f \frac{1}{x}
\end{aligned}
$$
must have a solution for some $x, y$, and $z$. From the first equation, it follows that $\frac{x}{y}=\frac{a}{b}$. But using the last two equations, we can also write this as
$$
\frac{x}{y}=\frac{z x}{y z}=\frac{f / x}{c / y}=\frac{f y}{c x} .
$$
This means that $\frac{f}{c}=\frac{x^{2}}{y^{2}}=\frac{a^{2}}{b^{2}}$, or $a^{2} / f=b^{2} / c$. Similarly, $c^{2} / b=d^{2} / e$ and $e^{2} / d=f^{2} / a$ hold. Together with $f+a=1, b+c=2$, and $d+e=5$, we now have six equations in six variables. Although it is not easy to solve this system, it greatly simplifies the search because it is now easy to check whether $a, b, c, d, e, f$ satisfy the conditions. Other equations that can be derived from this system include $ace = bdf$ and $ad = be = cf$.
|
3 \sqrt[3]{36}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Vind de kleinst mogelijke waarde van
$$
x y+y z+z x+\frac{1}{x}+\frac{2}{y}+\frac{5}{z},
$$
voor positieve reële getallen $x, y$ en $z$.
|
Antwoord: de kleinst mogelijke waarde is $3 \sqrt[3]{36}$.
Met de ongelijkheid van het rekenkundig-meetkundig gemiddelde vinden we
$$
\begin{aligned}
x y+\frac{1}{3 x}+\frac{1}{2 y} & \geq 3 \sqrt[3]{x y \frac{1}{3 x} \frac{1}{2 y}}=3 \sqrt[3]{\frac{1}{6}} \\
y z+\frac{3}{2 y}+\frac{3}{z} & \geq 3 \sqrt[3]{y z \frac{3}{2 y} \frac{3}{z}}=3 \sqrt[3]{\frac{9}{2}} \\
x z+\frac{2}{3 x}+\frac{2}{z} & \geq 3 \sqrt[3]{x z \frac{2}{3 x} \frac{2}{z}}=3 \sqrt[3]{\frac{4}{3}}
\end{aligned}
$$
Wanneer we deze drie ongelijkheden optellen krijgen we
$$
x y+y z+z x+\frac{1}{x}+\frac{2}{y}+\frac{5}{z} \geq 3\left(\sqrt[3]{\frac{1}{6}}+\sqrt[3]{\frac{9}{2}}+\sqrt[3]{\frac{4}{3}}\right)=3\left(\frac{1}{6}+\frac{1}{2}+\frac{1}{3}\right) \sqrt[3]{36}=3 \sqrt[3]{36}
$$
Voor elke van de drie ongelijkheden geldt gelijkheid wanneer de drie termen gelijk zijn. We komen uit op een gelijkheidsgeval voor alledrie wanneer $(x, y, z)=\left(\frac{1}{3} \sqrt[3]{6}, \frac{1}{2} \sqrt[3]{6}, \sqrt[3]{6}\right)$, wat ook gemakkelijk te controleren is. Dan is $x y+y z+z x+\frac{1}{x}+\frac{2}{y}+\frac{5}{z}$ namelijk gelijk aan
$$
\frac{1}{6} \sqrt[3]{36}+\frac{1}{2} \sqrt[3]{36}+\frac{1}{3} \sqrt[3]{36}+3 \frac{1}{\sqrt[3]{6}}+4 \frac{1}{\sqrt[3]{6}}+5 \frac{1}{\sqrt[3]{6}}=\sqrt[3]{36}+12 \frac{1}{\sqrt[3]{6}}=\sqrt[3]{36}+2 \sqrt[3]{36}=3 \sqrt[3]{36}
$$
Opmerking. Nadat je hebt besloten om de ongelijkheid op te splitsen in drie ongelijkheden met het rekenkundig-meetkundig gemiddelde (één voor $x y$, één voor $y z$ en één voor $x z$ ), zijn er verschillende manieren om de coëfficiënten te vinden voor $\frac{1}{x}, \frac{1}{y}$ en $\frac{1}{z}$. Allereerst kun je je laten leiden door voorbeelden die je hebt gevonden in je zoektocht naar het gelijkheidsgeval. Zo wordt de uitdrukking gelijk aan 10 voor $(x, y, z)=\left(\frac{2}{3}, 1,2\right)$ en met $(x, y, z)=\left(\frac{3}{5}, \frac{9}{10}, \frac{9}{5}\right)$ krijg je $\frac{324}{100}+\frac{12}{18} \cdot 10=3,24+6,6666 \ldots=9,9066 \ldots$.
Een structurelere aanpak is het invoeren van variabelen $a, b, c, d, e, f$ voor de ongelijkheden op $x y+a \frac{1}{x}+b \frac{1}{y}, y z+c \frac{1}{y}+d \frac{1}{z}$ en $z x+e \frac{1}{z}+f \frac{1}{x}$. Omdat deze drie termen op moeten tellen
tot de gevraagde uitdrukkingen, krijgen we de voorwaarden
$$
\begin{aligned}
f+a & =1, \\
b+c & =2, \\
d+e & =5 .
\end{aligned}
$$
Verder willen we dat er gelijkheid geldt voor bepaalde $x, y$ en $z$. Dus het stelsel
$$
\begin{aligned}
& x y=a \frac{1}{x}=b \frac{1}{y} \\
& y z=c \frac{1}{y}=d \frac{1}{z} \\
& z x=e \frac{1}{z}=f \frac{1}{x}
\end{aligned}
$$
moet een oplossing hebben voor een zekere $x, y$ en $z$. Uit de eerste vergelijking volgt dan dat $\frac{x}{y}=\frac{a}{b}$. Maar met behulp van de laatste twee vergelijkingen kunnen we dat ook schrijven als
$$
\frac{x}{y}=\frac{z x}{y z}=\frac{f / x}{c / y}=\frac{f y}{c x} .
$$
Dat betekent dat $\frac{f}{c}=\frac{x^{2}}{y^{2}}=\frac{a^{2}}{b^{2}}$, oftewel $a^{2} / f=b^{2} / c$. Evenzo geldt er dat $c^{2} / b=d^{2} / e$ en $e^{2} / d=f^{2} / a$. Samen met $f+a=1, b+c=2$ en $d+e=5$ hebben we nu zes vergelijkingen in zes variabelen. Hoewel het nog niet eenvoudig is om dit stelsel op te lossen, versimpelt dat de zoektocht enorm doordat het nu makkelijk te controleren is of $a, b, c, d, e, f$ voldoet. Andere vergelijkingen die je uit dit stelsel kan afleiden zijn bijvoorbeeld ace $=b d f$ en $a d=b e=c f$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2023-D2023_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2023"
}
|
Let $n \geq 3$ be a fixed natural number. There are $n$ boxes $A_{1}, A_{2}, \ldots, A_{n}$, each containing a number of stones $a_{1}, a_{2}, \ldots, a_{n}$ such that $a_{1}+a_{2}+\cdots+a_{n}=3 n$. A move consists of the following actions:
choose a box and distribute all the stones in the box over the $n$ boxes (including the chosen box) such that for any two boxes, the number of added stones differs by at most 1.
For a distribution $a_{1}, a_{2}, \ldots, a_{n}$, we define $f\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ as the minimum number of moves required to get all the stones in one box. Let $M_{n}$ be the maximum of $f\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ for all possible distributions $a_{1}, a_{2}, \ldots, a_{n}$ such that $a_{1}+a_{2}+\cdots+a_{n}=3 n$. Determine $M_{n}$ and all distributions $a_{1}, a_{2}, \ldots, a_{n}$ for which $f\left(a_{1}, a_{2}, \ldots, a_{n}\right)=M_{n}$.
Example. If $n=4$ and the boxes contain 2, 6, 0, 4 stones, then we can distribute the 2 stones from box $A_{1}$ as 1,0,1,0. After this move, the number of stones per box is 1, 6, 1, 4.
|
Answer: $M=3 n-4$ and $f\left(a_{1}, a_{2}, \ldots, a_{n}\right)=3 n-4$ if and only if $a_{1}=a_{2}=\ldots=a_{n}=3$.
First, we note that for every distribution, there exists a move such that $\max \left(a_{1}, \ldots, a_{n}\right)$ increases by at least one, unless all stones are in one box. Indeed, choose a box where the maximum is achieved, choose another non-empty box, and distribute the stones from that box so that at least one stone goes to the first box. This implies that $f\left(a_{1}, a_{2}, \ldots, a_{n}\right) \leq 3 n-\max \left(a_{1}, \ldots, a_{n}\right)$. In particular, if $\max \left(a_{1}, \ldots, a_{n}\right) \geq 5$, then $f\left(a_{1}, a_{2}, \ldots, a_{n}\right) \leq 3 n-5$. The rest of the proof follows from four claims.
Claim 1. If $\max \left(a_{1}, \ldots, a_{n}\right)=4$, then $f\left(a_{1}, a_{2}, \ldots, a_{n}\right) \leq 3 n-5$.
Proof. Let $A_{1}$ be the box with the most stones, and $A_{2}$ the box with the second-highest number of stones. This means that $a_{1}=4$ and $a_{2} \geq \frac{3 n-4}{n-1}=3-\frac{1}{n-1}$. Since $a_{2}$ is an integer and $n \geq 3$, this means that $a_{2} \geq 3$. We distribute every other box with at least 2 stones so that $A_{1}$ and $A_{2}$ each receive one stone. We repeat this until there are no more boxes with at least 2 stones, except for $A_{1}$ and $A_{2}$. For this distribution $b_{1}, \ldots, b_{n}$, we have $b_{3}+\cdots+b_{n} \leq n-2$. This means that $b_{1}+b_{2} \geq 3 n-(n-2)=2 n+2$ and since $b_{1}-b_{2}=a_{1}-a_{2} \leq 1$, we find that $b_{2}=\frac{1}{2}\left(b_{2}+b_{2}\right) \geq \frac{1}{2}\left(b_{1}+b_{2}-1\right) \geq \frac{1}{2}(2 n+1)=n+\frac{1}{2}$. Since $b_{2}$ is an integer, we find that $b_{2} \geq n+1$. Now we can make a move where we distribute the stones from $A_{2}$, giving $A_{1}$ 2 stones. Then we finish with moves where $A_{1}$ receives at least one stone each time. Since $A_{1}$ receives at least one stone per move and a move involves at least two stones, the number of moves made is at most $3 n-5$.
Claim 2. If $\max \left(a_{1}, \ldots, a_{n}\right)=3$, then $f\left(a_{1}, a_{2}, \ldots, a_{n}\right) \leq 3 n-4$.
Proof. We make an arbitrary move and apply Claim 1 to the result. Then we are done in at most $1+(3 n-5)=3 n-4$ moves. Alternatively, we can give a concrete series of $3 n-4$ moves. If $\max \left(a_{1}, \ldots, a_{n}\right)=3$, each box has exactly 3 stones. We start with $n-2$ moves where we choose $A_{i}$ with $i \geq 3$ and distribute the three stones over $A_{1}, A_{2}$, and $A_{i}$. Then the first two boxes each have $n+1$ stones, so we can make a move where we distribute the $n+1$ stones from the second box so that the first box gets 2 stones. Since $A_{1}$ receives at least one stone per move and a move involves at least two stones, the number of moves made is at most $3 n-4$.
Claim 3. There are no moves such that the maximum $\max \left(a_{1}, \ldots, a_{n}\right)$ increases by 3 or more.
Proof. To make a move where a box receives more than 3 stones, the chosen box would need to contain at least $3 n+1$ stones. This contradicts the fact that there are only $3 n$ stones. To make a move where a box receives 3 stones, the chosen box must contain at least $2 n+1$ stones. A box that achieves the new maximum after this move must also contain at least $2 n+1$ stones. This is again a contradiction.
Claim 4. If $\max \left(a_{1}, \ldots, a_{n}\right)=3$, then $f\left(a_{1}, a_{2}, \ldots, a_{n}\right) \geq 3 n-4$.
Proof. Suppose we can get all the stones into one box in $3 n-5$ or fewer turns. By Claim 3, there are no moves where the maximum increases by 3 or more. This means that there are at least two moves where the maximum increases by 2. We call such moves large moves. Let the first large move be in turn $i$ and the last large move be in turn $j$. Since a large move can only be performed with a box containing at least $n+1$ stones and each box starts with 3 stones, we have $i-1 \geq(n+1)-3$ or $i \geq n-1$.
Let $m$ be the number of empty boxes at the start of move $j$. Since each box has at least 1 stone after move $i$, we must have made at least one move per empty box after that. This means that $(j-1)-i \geq m$. Since each box receives at least 1 stone, there are at most $m$ boxes with 1 stone after move $j$; the rest contain at least 2. Since we do not make any large moves after move $j$, it takes at least $m+2(n-1-m)=2(n-1)-m$ moves to empty $n-1$ boxes. The total number of moves is thus at least
$$
i+(j-i)+2(n-1)-m \geq(n-1)+(m+1)+2(n-1)-m=3 n-2,
$$
which contradicts our assumption that we could do it in $3 n-5$ moves.
|
M=3 n-4
|
Yes
|
Incomplete
|
math-word-problem
|
Combinatorics
|
Zij $n \geq 3$ een vast natuurlijk getal. Er zijn $n$ dozen $A_{1}, A_{2}, \ldots, A_{n}$, elk met een aantal stenen erin $a_{1}, a_{2}, \ldots, a_{n}$ zo dat $a_{1}+a_{2}+\cdots+a_{n}=3 n$. Een zet bestaat uit de volgende handelingen:
kies een doos en verdeel alle stenen in de doos over de $n$ dozen (inclusief de gekozen doos) zo dat voor elke twee dozen het aantal toegevoegde stenen hoogstens 1 verschilt.
Voor een verdeling $a_{1}, a_{2}, \ldots, a_{n}$ definiëren we $f\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ als het minste aantal benodigde zetten om alle stenen in één doos te krijgen. Zij $M_{n}$ het maximum van $f\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ voor alle mogelijk verdelingen $a_{1}, a_{2}, \ldots, a_{n}$ zo dat $a_{1}+a_{2}+\cdots+a_{n}=3 n$. Bepaal $M_{n}$ en alle verdelingen $a_{1}, a_{2}, \ldots, a_{n}$ waarvoor $f\left(a_{1}, a_{2}, \ldots, a_{n}\right)=M_{n}$.
Voorbeeld. Als $n=4$ en de dozen bevatten 2, 6, 0, 4 stenen, dan kunnen we de 2 stenen uit doos $A_{1}$ uitdelen als 1,0,1,0. Na deze zet is het aantal stenen per doos 1, 6, 1, 4.
|
Antwoord: $M=3 n-4$ en $f\left(a_{1}, a_{2}, \ldots, a_{n}\right)=3 n-4$ dan en slechts dan als $a_{1}=a_{2}=\ldots=a_{n}=3$.
Allereerst merken we op dat er voor elke verdeling een zet bestaat zo dat $\max \left(a_{1}, \ldots, a_{n}\right)$ minstens een omhoog gaat, tenzij alle stenen in één doos zitten. Inderdaad, kies een doos waar het maximum bereikt wordt, kies een andere niet-lege doos en verdeel de stenen van die doos zo dat minstens een steen in de eerste doos gaat. Hieruit volgt dat $f\left(a_{1}, a_{2}, \ldots, a_{n}\right) \leq 3 n-\max \left(a_{1}, \ldots, a_{n}\right)$. In het bijzonder, als $\max \left(a_{1}, \ldots, a_{n}\right) \geq 5$, dan geldt $f\left(a_{1}, a_{2}, \ldots, a_{n}\right) \leq 3 n-5$. De rest van het bewijs volgt uit vier claims.
Claim 1. Als $\max \left(a_{1}, \ldots, a_{n}\right)=4$, dan geldt $f\left(a_{1}, a_{2}, \ldots, a_{n}\right) \leq 3 n-5$.
Bewijs. Laat $A_{1}$ de doos zijn met de meeste stenen, en $A_{2}$ de doos met het op-een-nahoogste aantal stenen. Dit betekent dat $a_{1}=4$ en $a_{2} \geq \frac{3 n-4}{n-1}=3-\frac{1}{n-1}$. Omdat $a_{2}$ geheel is en $n \geq 3$, betekent dat dus dat $a_{2} \geq 3$. Elke andere doos met minstens 2 stenen verdelen we zo dat $A_{1}$ en $A_{2}$ allebei één steen krijgen. We herhalen dit totdat er geen dozen meer zijn met minstens 2 stenen, buiten $A_{1}$ en $A_{2}$. Voor deze verdeling $b_{1}, \ldots, b_{n}$ geldt dus dat $b_{3}+\cdots+b_{n} \leq n-2$. Dat betekent dat $b_{1}+b_{2} \geq 3 n-(n-2)=2 n+2$ en omdat $b_{1}-b_{2}=a_{1}-a_{2} \leq 1$ vinden we dus dat $b_{2}=\frac{1}{2}\left(b_{2}+b_{2}\right) \geq \frac{1}{2}\left(b_{1}+b_{2}-1\right) \geq \frac{1}{2}(2 n+1)=n+\frac{1}{2}$. Omdat $b_{2}$ geheel is, vinden we dus dat $b_{2} \geq n+1$. Nu kunnen we een zet doen waarbij we de stenen van $A_{2}$ verdelen, waarbij we $A_{1} 2$ stenen geven. Daarna maken we het af met zetten waarbij $A_{1}$ elke keer minstens een steen krijgt. Aangezien $A_{1}$ elke zet minstens een steen krijgt en een zet minstens twee, is het aantal gedane zetten hoogstens $3 n-5$.
Claim 2. Als $\max \left(a_{1}, \ldots, a_{n}\right)=3$, dan geldt $f\left(a_{1}, a_{2}, \ldots, a_{n}\right) \leq 3 n-4$.
Bewijs. We doen een willekeurige zet en passen Claim 1 toe op het resultaat. Dan zijn we klaar in hooguit $1+(3 n-5)=3 n-4$ zetten. Alternatief, kunnen we een concrete serie van $3 n-4$ zetten geven. Als $\max \left(a_{1}, \ldots, a_{n}\right)=3$ heeft elke doos precies 3 stenen. We beginnen met $n-2$ zetten waarbij we $A_{i}$ kiezen met $i \geq 3$ en de drie stenen verdelen over $A_{1}, A_{2}$ en $A_{i}$. Daarna hebben de eerste twee dozen beide $n+1$ stenen, dus kunnen we een zet doen waarbij we de $n+1$ stenen van de tweede doos verdelen zo dat de eerste doos er 2 krijgt. Aangezien $A_{1}$ elke zet minstens een steen krijgt en een zet minstens twee, is het aantal gedane zetten hoogstens $3 n-4$.
Claim 3. Er zijn geen zetten zodat het maximum $\max \left(a_{1}, \ldots, a_{n}\right)$ met 3 of meer omhoog gaat.
Bewijs. Om een zet te doen waarbij een doos meer dan 3 stenen krijgt, zou de gekozen doos minstens $3 n+1$ stenen moeten bevatten. Dit is in tegenspraak met het feit dat er maar $3 n$ stenen zijn. Om een zet te doen waarbij een doos 3 stenen krijgt, moet de gekozen doos minstens $2 n+1$ stenen bevatten. Een doos die na deze zet het nieuwe maximum bereikt moet dus ook minstens $2 n+1$ stenen bevatten. Dit is wederom een tegenspraak.
Claim 4. Als $\max \left(a_{1}, \ldots, a_{n}\right)=3$, dan geldt $f\left(a_{1}, a_{2}, \ldots, a_{n}\right) \geq 3 n-4$.
Bewijs. Stel dat we alle stenen in $3 n-5$ of minder beurten in één doos kunnen krijgen. Wegens Claim 3 zijn er geen zetten waarbij het maximum 3 of meer omhoog gaat. Dat betekent dat er minstens twee zetten zijn waarbij het maximum 2 omhoog gaat. Zulke zetten noemen we grote zetten. Merk op dat elke doos minstens 1 steen krijgt bij een grote zet. Zij de eerste grote zet in beurt $i$ en de laatste grote zet in beurt $j$. Aangezien een grote zet alleen uitgevoerd kan worden met een doos met minstens $n+1$ stenen en elke doos begint met 3 stenen, geldt $i-1 \geq(n+1)-3$ oftewel $i \geq n-1$.
Zij $m$ het aantal lege dozen aan het begin van zet $j$. Aangezien elke doos na zet $i$ minstens 1 steen bevat, moeten we daarna minstens een zet gedaan hebben per lege doos. Dat betekent dat $(j-1)-i \geq m$. Omdat elke doos weer minstens 1 steen krijgt, zijn er na zet $j$ maximaal $m$ dozen met 1 steen; de rest bevat er minstens 2 . Omdat we na zet $j$ geen grote zetten meer doen, kost het daarna dus nog minimaal $m+2(n-1-m)=2(n-1)-m$ zetten om $n-1$ dozen leeg te maken. Het totaal aantal zetten is dus minstens
$$
i+(j-i)+2(n-1)-m \geq(n-1)+(m+1)+2(n-1)-m=3 n-2,
$$
wat in tegenspraak is met onze aanname dat we het in $3 n-5$ zetten konden.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2023-D2023_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2023"
}
|
Find all prime numbers $p$ for which the natural number
$$
3^{p}+4^{p}+5^{p}+9^{p}-98
$$
has at most 6 positive divisors.
Note. You may use that 9049 is a prime number.
|
Answer: the only prime numbers for which this holds are 2, 3, and 5.
We write $f(p)=3^{p}+4^{p}+5^{p}+9^{p}-98$. Then we calculate the prime factorizations $f(2)=3 \cdot 11, f(3)=7 \cdot 11^{2}$ and $f(5)=7 \cdot 9049$. Thus, they have 4, 6, and 4 divisors, respectively. The number of divisors of $p_{1}^{e_{1}} p_{2}^{e_{2}} \cdots p_{n}^{e_{n}}$ is, after all, $\left(e_{1}+1\right)\left(e_{2}+1\right) \cdots\left(e_{n}+1\right)$.
Now suppose that $p>5$. Modulo 6, we then have only two possibilities for $p$, namely $p \equiv 1,-1 \bmod 6$, otherwise $p$ would have a factor 2 or 3. Fermat's little theorem tells us that $a^{6} \equiv 1 \bmod 7$ (as long as $a \not \equiv 0 \bmod 7$), so these two possibilities result in
$$
\begin{array}{r}
f(p) \equiv 3^{1}+4^{1}+5^{1}+9^{1}-98 \equiv 3+4+5+9+0 \equiv 0 \quad \bmod 7 \quad \begin{array}{c}
\text { if } p \equiv 1 \\
\bmod 6, \\
f(p) \equiv 3^{-1}+4^{-1}+5^{-1}+9^{-1}-98 \equiv 5+2+3+4+0 \equiv 0
\end{array} \quad \bmod 7
\end{array} \text { if } p \equiv-1 \quad \bmod 6 .
$$
The multiplicative inverses in the second line can be easily verified by multiplying them with the numbers in the row above. We conclude that $7 \mid f(p)$ for all $p>5$. Alternatively, modulo 7, $f(p) \equiv 3^{p}+(-3)^{p}+5^{p}+(-5)^{p}-0 \equiv 0$ for odd $p$.
Modulo 10, we have four possibilities for $p$, namely $p \equiv 1,3,-3,-1 \bmod 10$, otherwise $p$ would have a factor 2 or 5. Since $a^{10} \equiv 1 \bmod 11$ (as long as $a \not \equiv 0 \bmod 11$), these four possibilities result in
$$
\begin{array}{rrrrr}
3^{1}+4^{1}+5^{1}+9^{1}-98 \equiv 3+4+5+9+1 \equiv 0 & \bmod 11 & \text { if } p \equiv 1 & \bmod 10, \\
3^{3}+4^{3}+5^{3}+9^{3}-98 \equiv 5+9+4+3+1 \equiv 0 & \bmod 11 & \text { if } p \equiv 3 & \bmod 10, \\
3^{-3}+4^{-3}+5^{-3}+9^{-3}-98 \equiv 9+5+3+4+1 \equiv 0 & \bmod 11 & \text { if } p \equiv-3 & \bmod 10 \\
3^{-1}+4^{-1}+5^{-1}+9^{-1}-98 \equiv 4+3+9+5+1 \equiv 0 & \bmod 11 & \text { if } p \equiv-1 & \bmod 10
\end{array}
$$
For the second line, you just need to calculate the cubes, such as $5^{3}=125=$ $11 \cdot 11+4$. For the third and fourth lines, we can again easily find the multiplicative inverses. We conclude that $11 \mid f(p)$ for all $p>5$.
Now we note that for $p>5$ it holds that $f(p)>9^{5}=9 \cdot 81 \cdot 81>7 \cdot 11 \cdot 77$. So we can write $f(p)$ as $f(p)=7 \cdot 11 \cdot d$ with $d>77$. Then we have at least 8 different divisors, namely
$$
1<7<11<77<d<7 d<11 d<77 d
$$
So no prime number greater than 5 satisfies the condition.
|
2, 3, 5
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Vind alle priemgetallen $p$ waarvoor het natuurlijke getal
$$
3^{p}+4^{p}+5^{p}+9^{p}-98
$$
hoogstens 6 positieve delers heeft.
Opmerking. Je mag gebruiken dat 9049 een priemgetal is.
|
Antwoord: de enige priemgetallen waarvoor dit geldt zijn 2, 3 en 5.
We schrijven $f(p)=3^{p}+4^{p}+5^{p}+9^{p}-98$. Dan berekenen we de priemfactorisaties $f(2)=3 \cdot 11, f(3)=7 \cdot 11^{2}$ en $f(5)=7 \cdot 9049$. Die hebben dus respectievelijk 4,6 en 4 delers. Het aantal delers van $p_{1}^{e_{1}} p_{2}^{e_{2}} \cdots p_{n}^{e_{n}}$ is namelijk $\left(e_{1}+1\right)\left(e_{2}+1\right) \cdots\left(e_{n}+1\right)$.
Stel nu dat $p>5$. Modulo 6 hebben we dan maar twee mogelijkheden voor $p$ te weten $p \equiv 1,-1 \bmod 6$, anders zou $p$ een factor 2 of 3 hebben. De kleine stelling van Fermat vertelt ons dat $a^{6} \equiv 1 \bmod 7($ zolang $a \not \equiv 0 \bmod 7)$, dus deze twee mogelijkheden komen uit op
$$
\begin{array}{r}
f(p) \equiv 3^{1}+4^{1}+5^{1}+9^{1}-98 \equiv 3+4+5+9+0 \equiv 0 \quad \bmod 7 \quad \begin{array}{c}
\text { als } p \equiv 1 \\
\bmod 6, \\
f(p) \equiv 3^{-1}+4^{-1}+5^{-1}+9^{-1}-98 \equiv 5+2+3+4+0 \equiv 0
\end{array} \quad \bmod 7
\end{array} \text { als } p \equiv-1 \quad \bmod 6 .
$$
De multiplicatieve inverses in de tweede regel kunnen eenvoudig gecontroleerd worden door ze te vermenigvuldigen met de getallen in de rij erboven. We concluderen dat $7 \mid f(p)$ voor alle $p>5$. Alternatief geldt modulo 7 dat $f(p) \equiv 3^{p}+(-3)^{p}+5^{p}+(-5)^{p}-0 \equiv 0$ voor oneven $p$.
Modulo 10 hebben we vier mogelijkheden voor $p$ te weten $p \equiv 1,3,-3,-1 \bmod 10$, anders zou $p$ een factor 2 of 5 hebben. Aangezien $a^{10} \equiv 1 \bmod 11($ zolang $a \not \equiv 0 \bmod 11)$, komen
deze vier mogelijkheden uit op
$$
\begin{array}{rrrrr}
3^{1}+4^{1}+5^{1}+9^{1}-98 \equiv 3+4+5+9+1 \equiv 0 & \bmod 11 & \text { als } p \equiv 1 & \bmod 10, \\
3^{3}+4^{3}+5^{3}+9^{3}-98 \equiv 5+9+4+3+1 \equiv 0 & \bmod 11 & \text { als } p \equiv 3 & \bmod 10, \\
3^{-3}+4^{-3}+5^{-3}+9^{-3}-98 \equiv 9+5+3+4+1 \equiv 0 & \bmod 11 & \text { als } p \equiv-3 & \bmod 10 \\
3^{-1}+4^{-1}+5^{-1}+9^{-1}-98 \equiv 4+3+9+5+1 \equiv 0 & \bmod 11 & \text { als } p \equiv-1 & \bmod 10
\end{array}
$$
Voor de tweede regel moet je gewoon de derdemachten uitrekenen, zoals $5^{3}=125=$ $11 \cdot 11+4$. Voor de derde en vierde regel kunnen we weer eenvoudig de multiplicatieve inverses vinden. We concluderen dat $11 \mid f(p)$ voor alle $p>5$.
Nu merken we op dat voor $p>5$ geldt dat $f(p)>9^{5}=9 \cdot 81 \cdot 81>7 \cdot 11 \cdot 77$. Dus we kunnen $f(p)$ schrijven als $f(p)=7 \cdot 11 \cdot d$ met $d>77$. Dan hebben we minstens 8 verschillende delers, te weten
$$
1<7<11<77<d<7 d<11 d<77 d
$$
Dus geen enkel priemgetal groter dan 5 voldoet aan de voorwaarde.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2023-E2023_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2023"
}
|
Every student in the Netherlands receives a finite number of tickets. Each ticket has a real number in the interval $[0,1]$ written on it. (The numbers on different tickets do not have to be different.) Find the smallest real number $c>0$ for which the following holds, regardless of the numbers on the tickets that everyone has received.
Every student for whom the sum of the numbers on the tickets is at most 1000, can distribute the tickets over 100 boxes so that the sum of the numbers in each box is at most $c$.
|
Suppose one of the students has received 1001 tickets, each with the number $\frac{1000}{1001}$. Since the sum of the tickets is 1000, this student must be able to distribute the tickets over 100 boxes. By the pigeonhole principle, there is at least one box with 11 tickets. The sum of these 11 tickets is $11 \cdot \frac{1000}{1001}=11\left(1-\frac{1}{1001}\right)=11-\frac{11}{1001}=11-\frac{1}{91}$. We will now show that this is the smallest possible value, $c=11-\frac{1}{91}$.
For any given student, we first choose those distributions in which the maximum of the sums of the tickets per box is as low as possible, and from these distributions, we then choose a distribution in which the fewest number of boxes achieve this maximum. Let $d_{1} \leq d_{2} \leq \ldots \leq d_{100}$ be the total value of the 100 boxes in this distribution, ordered from low to high (where the last $k$ are equal to the maximum). Since the sum of all tickets is at most 1000, we note that
$$
99 d_{1}+d_{100} \leq d_{1}+d_{2}+\ldots+d_{100} \leq 1000
$$
On the other hand, moving a positive ticket from box (with sum) $d_{100}$ to box (with sum) $d_{1}$ should not result in a better distribution by assumption: thus, no distribution with a lower maximum or with fewer than $k$ boxes of this maximum value. This means that the new value of $d_{1}$ must be at least $d_{100}$. If $d_{100} \leq 10$, we are done, since $10<11-\frac{1}{91}$. We can therefore assume that $d_{100}>10$. Since each ticket is at most 1, this means that box $d_{100}$ contains at least 11 positive tickets. This, in turn, implies that there is a ticket in this box with a positive value of at most $\frac{d_{100}}{11}$. If we move this ticket to box $d_{1}$, then it must be true that
$$
d_{1}+\frac{d_{100}}{11} \geq \text { "new value of box } d_{1} " \geq d_{100}
$$
This can be rewritten as $11 d_{1} \geq 10 d_{100}$. If we combine this with the first equation, we find
$$
91 d_{100}=90 d_{100}+d_{100} \leq 99 d_{1}+d_{100} \leq 1000
$$
For every student, the lowest maximum of the sums of the tickets per box is thus $d_{100} \leq \frac{1000}{91}=\frac{1001}{91}-\frac{1}{91}=11-\frac{1}{91}$.
|
11-\frac{1}{91}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Elke scholier in Nederland krijgt een eindig aantal kaartjes. Op elk kaartje staat een reël getal in het interval $[0,1]$. (De getallen op verschillende kaartjes hoeven niet verschillend te zijn.) Vind het kleinste reële getal $c>0$ waarvoor het volgende geldt, onafhankelijk van de getallen op de kaartjes die iedereen heeft gekregen.
Elke scholier waarvan de som van de getallen op de kaartjes hoogstens 1000 is, kan de kaartjes over 100 dozen verdelen zo dat de som van de kaartjes in elke doos hoogstens $c$ is.
|
Stel dat een van de scholieren 1001 kaartjes heeft gekregen met elk het getal $\frac{1000}{1001}$. Aangezien de som van de kaartjes 1000 is, moet deze scholier de kaartjes over de 100 dozen kunnen verdelen. Wegens het ladenprincipe is er minstens een doos met 11 kaartjes. De som van deze 11 kaartjes is $11 \cdot \frac{1000}{1001}=11\left(1-\frac{1}{1001}\right)=11-\frac{11}{1001}=11-\frac{1}{91}$. We gaan nu laten zien dat dit de kleinst mogelijke waarde is, $c=11-\frac{1}{91}$.
Voor een willekeurige scholier kiezen we eerst die verdelingen waarbij het maximum van de sommen van de kaartjes per doos zo laag mogelijk is, en uit deze verdelingen kiezen we vervolgens een verdeling waarbij het minst aantal dozen dit maximum aanneemt. Laat $d_{1} \leq d_{2} \leq \ldots \leq d_{100}$ de totale waarde van de 100 dozen in deze verdeling zijn, geordend van laag naar hoog (waarbij de laatste $k$ gelijk zijn aan het maximum). Omdat de som van alle kaartjes hoogstens 1000 is, merken we op dat
$$
99 d_{1}+d_{100} \leq d_{1}+d_{2}+\ldots+d_{100} \leq 1000
$$
Aan de andere kant mag het verplaatsen van een positief kaartje van doos (met som) $d_{100}$ naar doos (met som) $d_{1}$ geen betere verdeling opleveren per aanname: dus geen verdeling met een lager maximum of met minder dan $k$ dozen van deze maximale waarde. Dit betekent dat de nieuwe waarde van $d_{1}$ minstens gelijk is aan $d_{100}$. Als $d_{100} \leq 10$ zijn we direct klaar, want $10<11-\frac{1}{91}$. We mogen dus aannemen dat $d_{100}>10$. Aangezien elk kaartje hoogstens 1 is, betekent dit dat doos $d_{100}$ minstens 11 positieve kaartjes bevat. Dit impliceert dan weer dat er een kaartje in deze doos zit met positieve waarde hoogstens $\frac{d_{100}}{11}$. Als we dit kaartje naar doos $d_{1}$ verplaatsen, dan moet er dus gelden dat
$$
d_{1}+\frac{d_{100}}{11} \geq \text { "nieuwe waarde van doos } d_{1} " \geq d_{100}
$$
Dit kunnen we herschrijven als $11 d_{1} \geq 10 d_{100}$. Als we dit combineren met de eerste vergelijking vinden we
$$
91 d_{100}=90 d_{100}+d_{100} \leq 99 d_{1}+d_{100} \leq 1000
$$
Voor elke scholier is het laagste maximum van de sommen van de kaartjes per doos dus $d_{100} \leq \frac{1000}{91}=\frac{1001}{91}-\frac{1}{91}=11-\frac{1}{91}$.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2023-E2023_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2023"
}
|
Let $\triangle A B C$ be an isosceles triangle with $|A B|=|A C|$. Given a point $P$ in $\triangle A B C$ different from the circumcenter of the triangle. Let $\omega$ be the circle through $C$ with center $P$. Given that the circle $\omega$ intersects the line segments $B C$ and $A C$ a second time at $D$ and $E$, respectively. Let $\Gamma$ be the circumcircle of $\triangle A E P$ and let $F$ be the second intersection point of $\omega$ and $\Gamma$. Prove that the circumcenter of $\triangle B D F$ lies on $\Gamma$.
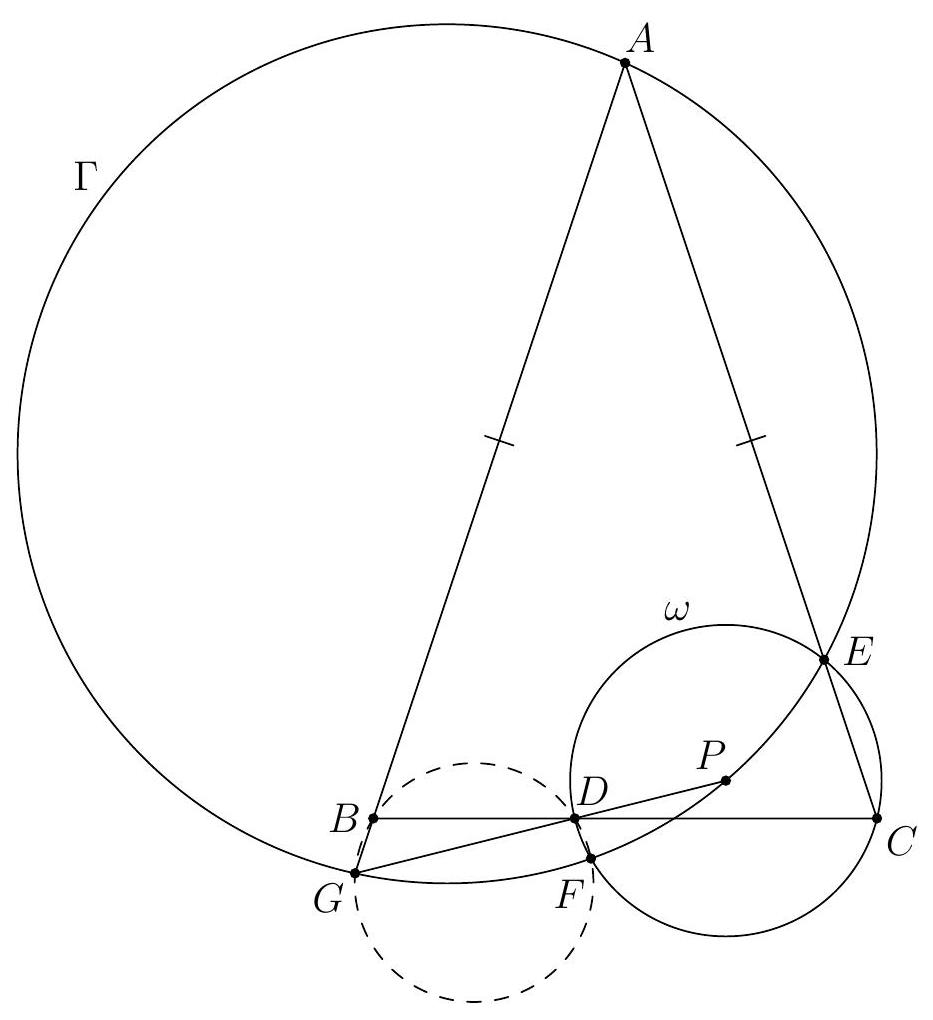
|
Since $|FP|=|PE|$, the angles subtended by these chords of $\Gamma$ are also equal: $\angle FAP = \angle PAE = \angle PAC$. Then, using cyclic quadrilateral $AEPF$, we find that $\angle PFA = 180^{\circ} - \angle PEA = \angle PEC$. Therefore, by the angle sum property,
$$
\begin{aligned}
\angle APF & = 180^{\circ} - \angle PFA - \angle FAP \\
& = 180^{\circ} - \angle PEC - \angle PAC \\
& = 180^{\circ} - \angle ECP - \angle PAC \\
& = \angle CPA.
\end{aligned}
$$
Since we also know that $|FP| = |PC|$ (and of course $|AP| = |AP|$), it follows from (SAS) that $\triangle AFP \simeq \triangle ACP$. From this, we conclude that $|AF| = |AC| = |AB|$. This means that $A$ is the circumcenter of $\triangle BCF$. It also means that $\triangle ABF$ is isosceles, and thus the perpendicular bisector of $BF$ is the same as the angle bisector of $\angle BAF$. On the other hand, $\triangle DPF$ is also isosceles, so the perpendicular bisector of $DF$ is the same as the angle bisector of $\angle DPF$. The intersection of the perpendicular bisectors of $BF$ and $DF$ is called $Q$. Since $A$ and $P$ are the circumcenters of the respective circumcircles, we get from the central angle-circumference angle theorem that
$$
\angle QAF = \frac{1}{2} \angle BAF = \angle BCF = \angle DCF = \frac{1}{2} \angle DPF = \angle QPF.
$$
Thus, $Q$ lies on $\Gamma$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $\triangle A B C$ een gelijkbenige driehoek met $|A B|=|A C|$. Gegeven is een punt $P$ in $\triangle A B C$ ongelijk aan het middelpunt van de omgeschreven cirkel. Zij $\omega$ de cirkel door $C$ met middelpunt $P$. Gegeven is dat de cirkel $\omega$ de lijnstukken $B C$ en $A C$ een tweede keer snijdt in respectievelijk $D$ en $E$. Zij $\Gamma$ de omgeschreven cirkel van $\triangle A E P$ en zij $F$ het tweede snijpunt van $\omega$ en $\Gamma$. Bewijs dat het middelpunt van de omgeschreven cirkel van $\triangle B D F$ op $\Gamma$ ligt.

|
Omdat $|F P|=|P E|$ zijn de hoeken op deze koorden van $\Gamma$ ook gelijk: $\angle F A P=\angle P A E=\angle P A C$. Dan vinden we met behulp van koordenvierhoek $A E P F$ dat $\angle P F A=180^{\circ}-\angle P E A=\angle P E C$. Dus met hoekensom volgt
$$
\begin{aligned}
\angle A P F & =180^{\circ}-\angle P F A-\angle F A P \\
& =180^{\circ}-\angle P E C-\angle P A C \\
& =180^{\circ}-\angle E C P-\angle P A C \\
& =\angle C P A .
\end{aligned}
$$
Aangezien we ook weten dat $|F P|=|P C|$ (en natuurlijk $|A P|=|A P|$ ) volgt uit (ZHZ) dat $\triangle A F P \simeq \triangle A C P$. Hieruit concluderen we dat $|A F|=|A C|=|A B|$. Dat betekent dat $A$ het middelpunt is van de omgeschreven cirkel van $\triangle B C F$. Het betekent ook dat $\triangle A B F$
gelijkbenig is en dus dat de middelloodlijn van $B F$ gelijk is aan de bissectrice van $\angle B A F$. Aan de andere kant is $\triangle D P F$ ook gelijkbenig, dus de middelloodlijn van $D F$ is gelijk aan de bissectrice van $\angle D P F$. Het snijpunt van de middellooddlijnen van $B F$ en $D F$ noemen we $Q$. Aangezien $A$ en $P$ de middelpunten zijn van de betreffende omgeschreven cirkels krijgen we met de middelpunt-omtrekshoekstelling dat
$$
\angle Q A F=\frac{1}{2} \angle B A F=\angle B C F=\angle D C F=\frac{1}{2} \angle D P F=\angle Q P F .
$$
Dus $Q$ ligt op $\Gamma$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2023-E2023_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2023"
}
|
Let $\triangle A B C$ be an isosceles triangle with $|A B|=|A C|$. Given a point $P$ in $\triangle A B C$ different from the circumcenter of the triangle. Let $\omega$ be the circle through $C$ with center $P$. Given that the circle $\omega$ intersects the line segments $B C$ and $A C$ a second time at $D$ and $E$, respectively. Let $\Gamma$ be the circumcircle of $\triangle A E P$ and let $F$ be the second intersection point of $\omega$ and $\Gamma$. Prove that the circumcenter of $\triangle B D F$ lies on $\Gamma$.

|
Let $G$ be the intersection of $DP$ and $AB$. Due to the isosceles property and that $P$ is the center of $\omega$, it holds that
$$
\begin{aligned}
\angle GAE & = \angle BAC \\
& = 180^{\circ} - 2 \angle ACB \\
& = 180^{\circ} - 2 \angle ECD \\
& = 180^{\circ} - \angle EPD \\
& = 180^{\circ} - \angle EPG.
\end{aligned}
$$
Thus, $G$ lies on $\Gamma$. Therefore, it also holds that
$$
\begin{aligned}
\angle BGF & = \angle AGF \\
& = 180^{\circ} - \angle AEF \\
& = \angle FEC \\
& = \angle FDC \\
& = 180^{\circ} - \angle BDF,
\end{aligned}
$$
which implies that $BDFG$ is a cyclic quadrilateral. The center of the circumcircle of $\triangle BDF$ is thus also the center of the circumcircle of $\triangle BDG$, which we call $Q$. Now we find that $\frac{1}{2} \angle DQG = \angle DFG = 180^{\circ} - \angleDBG = \angle DBA$. Therefore, $\angle GDQ = \frac{1}{2} \left(180^{\circ} - \angle DQG\right) = 90^{\circ} - \angle DBA = 90^{\circ} - \angle ACD = 90^{\circ} - \frac{1}{2} \angle EPD = \angle PDE$. Since $G, D$, and $P$ are collinear, $E, D$, and $Q$ are also collinear. We conclude that
$$
\angle QGP = \angle QGD = \angle GDQ = \angle PDE = \angle DEP = \angle QEP
$$
so $Q$ lies on $\Gamma$, since $G, E$, and $P$ also lie on it.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $\triangle A B C$ een gelijkbenige driehoek met $|A B|=|A C|$. Gegeven is een punt $P$ in $\triangle A B C$ ongelijk aan het middelpunt van de omgeschreven cirkel. Zij $\omega$ de cirkel door $C$ met middelpunt $P$. Gegeven is dat de cirkel $\omega$ de lijnstukken $B C$ en $A C$ een tweede keer snijdt in respectievelijk $D$ en $E$. Zij $\Gamma$ de omgeschreven cirkel van $\triangle A E P$ en zij $F$ het tweede snijpunt van $\omega$ en $\Gamma$. Bewijs dat het middelpunt van de omgeschreven cirkel van $\triangle B D F$ op $\Gamma$ ligt.

|
Zij $G$ het snijpunt van $D P$ en $A B$. Wegens de gelijkbenigheid en dat $P$ het middelpunt is van $\omega$ geldt dat
$$
\begin{aligned}
\angle G A E & =\angle B A C \\
& =180^{\circ}-2 \angle A C B \\
& =180^{\circ}-2 \angle E C D \\
& =180^{\circ}-\angle E P D \\
& =180^{\circ}-\angle E P G .
\end{aligned}
$$
Dus $G$ ligt op $\Gamma$. Daardoor geldt ook dat
$$
\begin{aligned}
\angle B G F & =\angle A G F \\
& =180^{\circ}-\angle A E F \\
& =\angle F E C \\
& =\angle F D C \\
& =180^{\circ}-\angle B D F,
\end{aligned}
$$
waaruit volgt dat $B D F G$ een koordenvierhoek is. Het middelpunt van de omgeschreven cirkel van $\triangle B D F$ is dus ook het middelpunt van de omgeschreven cirkel van $\triangle B D G$, dat we $Q$ noemen. Nu vinden we dat $\frac{1}{2} \angle D Q G=\angle D F G=180^{\circ}-\angle D B G=\angle D B A$. Dus $\angle G D Q=\frac{1}{2}\left(180^{\circ}-\angle D Q G\right)=90^{\circ}-\angle D B A=90^{\circ}-\angle A C D=90^{\circ}-\frac{1}{2} \angle E P D=\angle P D E$. Aangezien $G, D$ en $P$ collineair zijn, zijn $E, D$ en $Q$ dat nu ook. We concluderen dat
$$
\angle Q G P=\angle Q G D=\angle G D Q=\angle P D E=\angle D E P=\angle Q E P
$$
dus $Q$ ligt op $\Gamma$, omdat $G, E$ en $P$ daar ook op liggen.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2023-E2023_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2023"
}
|
Let $\triangle A B C$ be an isosceles triangle with $|A B|=|A C|$. Given a point $P$ in $\triangle A B C$ different from the circumcenter of the triangle. Let $\omega$ be the circle through $C$ with center $P$. Given that the circle $\omega$ intersects the line segments $B C$ and $A C$ a second time at $D$ and $E$, respectively. Let $\Gamma$ be the circumcircle of $\triangle A E P$ and let $F$ be the second intersection point of $\omega$ and $\Gamma$. Prove that the circumcenter of $\triangle B D F$ lies on $\Gamma$.

|
After we found in solution II that $B D F G$ is a cyclic quadrilateral and we introduced $Q$, we can also finish with the help of an arbitrary point $X$ on the arc $F G$ where $D$ does not lie. Then it holds that
$$
\angle G Q F=2 \angle G X F=2\left(180^{\circ}-\angle G D F\right)=2 \angle P D F=180^{\circ}-\angle D P F=180^{\circ}-\angle G P F
$$
since $\triangle P D F$ is isosceles. From this, it follows by the cyclic quadrilateral theorem that $G P F Q$ is a cyclic quadrilateral.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $\triangle A B C$ een gelijkbenige driehoek met $|A B|=|A C|$. Gegeven is een punt $P$ in $\triangle A B C$ ongelijk aan het middelpunt van de omgeschreven cirkel. Zij $\omega$ de cirkel door $C$ met middelpunt $P$. Gegeven is dat de cirkel $\omega$ de lijnstukken $B C$ en $A C$ een tweede keer snijdt in respectievelijk $D$ en $E$. Zij $\Gamma$ de omgeschreven cirkel van $\triangle A E P$ en zij $F$ het tweede snijpunt van $\omega$ en $\Gamma$. Bewijs dat het middelpunt van de omgeschreven cirkel van $\triangle B D F$ op $\Gamma$ ligt.

|
Nadat we in oplossing II gevonden hebben dat $B D F G$ een koordenvierhoek is en we $Q$ hebben geïntroduceerd, kunnen we het ook afmaken met behulp van een willekeurig punt $X$ op de boog $F G$ waar $D$ niet op ligt. Dan geldt dat
$$
\angle G Q F=2 \angle G X F=2\left(180^{\circ}-\angle G D F\right)=2 \angle P D F=180^{\circ}-\angle D P F=180^{\circ}-\angle G P F
$$
omdat $\triangle P D F$ gelijkbenig is. Hieruit volgt met de koordenvierhoekstelling dat $G P F Q$ een koordenvierhoek is.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2023-E2023_uitwerkingen.jsonl",
"solution_match": "\nOplossing III.",
"tier": "T1",
"year": "2023"
}
|
Find all functions $f: \mathbb{Q}^{+} \rightarrow \mathbb{Q}$ such that
$$
f(x)+f(y)=\left(f(x+y)+\frac{1}{x+y}\right)(1-x y+f(x y))
$$
for all $x, y \in \mathbb{Q}^{+}$.
|
The only function that satisfies is $f\left(\frac{m}{n}\right)=\frac{m}{n}-\frac{n}{m}$. This function indeed satisfies because
$$
\begin{aligned}
\left(f(x+y)+\frac{1}{x+y}\right)(1-x y+f(x y)) & =\left((x+y)-\frac{1}{x+y}+\frac{1}{x+y}\right)\left(1-x y+x y-\frac{1}{x y}\right) \\
& =(x+y)\left(1-\frac{1}{x y}\right) \\
& =x+y-\frac{1}{x}-\frac{1}{y} \\
& =f(x)+f(y) .
\end{aligned}
$$
When dealing with a function on $\mathbb{Q}^{+}$, it is often a good idea to first look at what happens with the natural numbers. The idea is to play products $x y$ against sums $x+y$, such as $2 \cdot 2=2+2$.
Lemma. It holds that $f(1)=0$.
Proof. If we substitute $x=y=1$, we get $2 f(1)=\left(f(2)+\frac{1}{2}\right) f(1)$. This means that $f(1)=0$ or $f(2)=\frac{3}{2}$.
Assume that $f(2)=\frac{3}{2}$. If we now substitute $x=y=2$, we get $2 f(2)=\left(f(4)+\frac{1}{4}\right)(f(4)-3)$. This simplifies to $3=f(4)^{2}-\frac{11}{4} f(4)-\frac{3}{4}$. After multiplying by 4, we can factorize this as $(f(4)+1)(4 f(4)-15)=0$. Thus, $f(4)=-1$ or $f(4)=\frac{15}{4}$.
If we substitute $y=1$ into the original equation, we find that
$$
f(x)+f(1)=\left(f(x+1)+\frac{1}{x+1}\right)(f(x)-x+1)
$$
If we substitute $x=2,3,4,5$ into this, we get respectively
$$
\begin{aligned}
\frac{3}{2}+f(1) & =\left(f(3)+\frac{1}{3}\right) \cdot \frac{1}{2} \\
f(3)+f(1) & =\left(f(4)+\frac{1}{4}\right)(f(3)-2) \\
f(4)+f(1) & =\left(f(5)+\frac{1}{5}\right)(f(4)-3) \\
f(5)+f(1) & =\left(f(6)+\frac{1}{6}\right)(f(5)-4)
\end{aligned}
$$
In the case that $f(4)=\frac{15}{4}$, the second equation gives $f(3)+f(1)=4(f(3)-2)$, so $3 f(3)=f(1)+8$. The first equation, however, gives $3 f(3)-6 f(1)=8$. We conclude that $f(1)+8=3 f(3)=6 f(1)+9-1=6 f(1)+8$. Thus, in this case, $f(1)=0$ as we wanted to prove.
On the other hand, assume that $f(4)=-1$. As we just saw, the first equation gives $3 f(3)-6 f(1)=8$. The second equation, in this case, gives $f(3)+f(1)=-\frac{3}{4}(f(3)-2)$, so $7 f(3)+4 f(1)=6$. If we solve this system (for example, by adding two times the first equation to three times the second), we find that $f(1)=-\frac{19}{27}$ and $f(3)=\frac{34}{27}$. If we substitute these into the third equation, we get $-1-\frac{19}{27}=-4\left(f(5)+\frac{1}{5}\right)$, or $f(5)=\frac{61}{270}$. Similarly, from the fourth equation, we get $\frac{61}{270}-\frac{19}{27}=\left(f(6)+\frac{1}{6}\right)\left(\frac{61}{270}-4\right)$, or $f(6)=-\frac{245}{6114}$.
We have now calculated 6 as $4+1+1$, but we can also do it as $2 \cdot 3$. If we substitute $x=2$ and $y=3$, we get
$$
f(2)+f(3)=\left(f(5)+\frac{1}{5}\right)(f(6)-5)
$$
If we substitute the calculated values of $f(2), f(3), f(5)$, and $f(6)$, we do not get an equality, because the left side is greater than zero and the right side is less than zero. We conclude that the case $f(4)=-1$ is not possible, and that $f(1)=0$.
Now we would like to use equation (1) for induction, but the base case with $x=1$ does not work because $f(1)=0$. As a new base case, we want to use the case $f(4)=\frac{15}{4}$ from above, which did not lead to a contradiction but rather to $f(1)=0$.
Lemma. It holds that $f(4)=\frac{15}{4}$.
Proof. We actually use the same trick as above to calculate $f(4)$, but now with the fact that we know $f(1)$ instead of $f(2)$. With $x=y=2$, we find again that $2 f(2)=\left(f(4)+\frac{1}{4}\right)(f(4)-3)$. By substituting $x=2$ into (1), we find $f(2)=\left(f(3)+\frac{1}{3}\right)(f(2)-1)$, and by substituting $x=3$ into (1), we find $f(3)=\left(f(4)+\frac{1}{4}\right)(f(3)-2)$. This system of three equations can be solved by rewriting the second equation as
$$
\begin{aligned}
f(3) & =\frac{f(2)}{f(2)-1}-\frac{1}{3} \\
& =\frac{f(2)-1+1}{f(2)-1}-\frac{1}{3} \\
& =1+\frac{1}{f(2)-1}-\frac{1}{3} \\
& =\frac{1}{f(2)-1}+\frac{2}{3}
\end{aligned}
$$
or $f(2)=\frac{1}{f(3)-\frac{2}{3}}+1$. Similarly, from the third equation, we get $f(4)=\frac{2}{f(3)-2}+\frac{3}{4}$, which we can rewrite as $f(3)-\frac{2}{3}=\frac{\frac{4}{3} f(4)+1}{f(4)-\frac{3}{4}}$. By combining everything, we find that
$$
\begin{aligned}
\left(f(4)+\frac{1}{4}\right)(f(4)-3) & =2 f(2) \\
& =2\left(\frac{1}{f(3)-\frac{2}{3}}+1\right) \\
& =2\left(\frac{f(4)-\frac{3}{4}}{\frac{4}{3} f(4)+1}+1\right) \\
& =\frac{2 f(4)-\frac{3}{2}+\frac{8}{3} f(4)+2}{\frac{4}{3} f(4)+1} \\
& =\frac{\frac{14}{3} f(4)+\frac{1}{2}}{\frac{4}{3} f(4)+1} .
\end{aligned}
$$
If we simplify this by multiplying by $12\left(\frac{4}{3} f(4)+1\right)$, we get a cubic equation. With $t=f(4)$, this is $16 t^{3}-32 t^{2}-101 t-15=0$. Fortunately, we already have a guess for a root, namely $t=\frac{15}{4}$. We can easily check that this is indeed a root and factorize
$$
0=16 t^{3}-32 t^{2}-101 t-15=(4 t-15)\left(4 t^{2}+7 t+1\right)
$$
The discriminant of $4 t^{2}+7 t+1$ is $D=7^{2}-4 \cdot 4=33$, which is not a square of a rational number. Thus, $t=\frac{15}{4}$ is the only rational root of the cubic equation and the only possibility for $f(4)$.
From the three equations we started with for the system for $f(4)$, it follows directly that $f(2)=\frac{3}{2}$ and $f(3)=\frac{8}{3}$. Altogether, we have a base case for induction for $f(n)=n-\frac{1}{n}$ for all natural numbers $n$. Assume as the induction hypothesis that this formula holds for $n$. Then from (1), we get
$$
\begin{aligned}
f(n+1) & =\frac{f(n)+f(1)}{f(n)-n+1}-\frac{1}{n+1} \\
& =\frac{n-\frac{1}{n}+0}{n-\frac{1}{n}-n+1}-\frac{1}{n+1} \\
& =\frac{n^{2}-1}{n-1}-\frac{1}{n+1} \\
& =(n+1)-\frac{1}{n+1}
\end{aligned}
$$
which completes the induction. If we now substitute $x=n$ and $y=\frac{1}{n}$, we find
$$
f(n)+f\left(\frac{1}{n}\right)=\left(f\left(n+\frac{1}{n}\right)+\frac{1}{n+\frac{1}{n}}\right)(1-1+0)=0 .
$$
From this, it follows that $f\left(\frac{1}{n}\right)=-f(n)=\frac{1}{n}-n$. Now we prove that $f\left(\frac{m}{n}\right)=\frac{m}{n}-\frac{n}{m}$ by induction on $m$. The base case with $m=1$ has just been proven. Assume now that this formula holds for a certain $m$ and all $n$. If we substitute $x=\frac{m}{n}$ and $y=\frac{1}{n}$, we get
$$
\begin{aligned}
f\left(\frac{m+1}{n}\right) & =\frac{f\left(\frac{m}{n}\right)+f\left(\frac{1}{n}\right)}{f\left(\frac{m}{n^{2}}\right)-\frac{m}{n^{2}}+1}-\frac{n}{m+1} \\
& =\frac{\frac{m}{n}-\frac{n}{m}+\frac{1}{n}-n}{\frac{m}{n^{2}}-\frac{n^{2}}{m}-\frac{m}{n^{2}}+1}-\frac{n}{m+1} \\
& =\frac{(m+1)\left(\frac{1}{n}-\frac{n}{m}\right)}{n\left(\frac{1}{n}-\frac{n}{m}\right)}-\frac{n}{m+1} \\
& =\frac{m+1}{n}-\frac{n}{m+1} .
\end{aligned}
$$
This completes the induction on $m$, and thus the complete proof.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Vind alle functies $f: \mathbb{Q}^{+} \rightarrow \mathbb{Q}$ zodanig dat
$$
f(x)+f(y)=\left(f(x+y)+\frac{1}{x+y}\right)(1-x y+f(x y))
$$
voor alle $x, y \in \mathbb{Q}^{+}$.
|
Antwoord: de enige functie die voldoet is $f\left(\frac{m}{n}\right)=\frac{m}{n}-\frac{n}{m}$. Deze functie voldoet inderdaad want
$$
\begin{aligned}
\left(f(x+y)+\frac{1}{x+y}\right)(1-x y+f(x y)) & =\left((x+y)-\frac{1}{x+y}+\frac{1}{x+y}\right)\left(1-x y+x y-\frac{1}{x y}\right) \\
& =(x+y)\left(1-\frac{1}{x y}\right) \\
& =x+y-\frac{1}{x}-\frac{1}{y} \\
& =f(x)+f(y) .
\end{aligned}
$$
Als functie op $\mathbb{Q}^{+}$is het vaak een goed idee om eerst te kijken wat er met de natuurlijke getallen gebeurt. Het idee is om producten $x y$ uit te spelen tegen sommen $x+y$, zoals bijvoorbeeld $2 \cdot 2=2+2$.
Lemma. Er geldt dat $f(1)=0$.
Bewijs. Als we $x=y=1$ invullen krijgen we $2 f(1)=\left(f(2)+\frac{1}{2}\right) f(1)$. Dit betekent dat $f(1)=0$ of $f(2)=\frac{3}{2}$.
Stel dat $f(2)=\frac{3}{2}$. Als we nu $x=y=2$ invullen krijgen we $2 f(2)=\left(f(4)+\frac{1}{4}\right)(f(4)-3)$. Dit werken we uit als $3=f(4)^{2}-\frac{11}{4} f(4)-\frac{3}{4}$. Na vermenigvuldigen met 4 zien we dat we dit kunnen ontbinden als $(f(4)+1)(4 f(4)-15)=0$. Dus $f(4)=-1$ of $f(4)=\frac{15}{4}$.
Als we $y=1$ invullen in de oorspronkelijke vergelijking vinden we dat
$$
f(x)+f(1)=\left(f(x+1)+\frac{1}{x+1}\right)(f(x)-x+1)
$$
Als we hier $x=2,3,4,5$ invullen krijgen we respectievelijk
$$
\begin{aligned}
\frac{3}{2}+f(1) & =\left(f(3)+\frac{1}{3}\right) \cdot \frac{1}{2} \\
f(3)+f(1) & =\left(f(4)+\frac{1}{4}\right)(f(3)-2) \\
f(4)+f(1) & =\left(f(5)+\frac{1}{5}\right)(f(4)-3) \\
f(5)+f(1) & =\left(f(6)+\frac{1}{6}\right)(f(5)-4)
\end{aligned}
$$
In het geval dat $f(4)=\frac{15}{4}$ levert de tweede vergelijking dat $f(3)+f(1)=4(f(3)-2)$ dus $3 f(3)=f(1)+8$. De eerste vergelijking levert echter dat $3 f(3)+1=3 \cdot 2 \cdot\left(\frac{3}{2}+f(1)\right)=$ $6 f(1)+9$. We concluderen dat $f(1)+8=3 f(3)=6 f(1)+9-1=6 f(1)+8$. Oftewel in dit geval geldt $f(1)=0$ zoals we wilden bewijzen.
Stel aan de andere kant dat $f(4)=-1$. Zoals we net gezien hebben levert de eerste vergelijking dat $3 f(3)-6 f(1)=8$. De tweede vergelijking levert in dit geval dat $f(3)+$ $f(1)=-\frac{3}{4}(f(3)-2)$ dus $7 f(3)+4 f(1)=6$. Als we dit stelsel oplossen (bijv. door twee keer de eerste vergelijking op te tellen bij drie keer de tweede), dan vinden we dat $f(1)=-\frac{19}{27}$ en $f(3)=\frac{34}{27}$. Als we dit in de derde vergelijking invullen krijgen we $-1-\frac{19}{27}=$ $-4\left(f(5)+\frac{1}{5}\right)$, oftewel $f(5)=\frac{61}{270}$. Evenzo krijgen we dan uit de vierde vergelijking dat $\frac{61}{270}-\frac{19}{27}=\left(f(6)+\frac{1}{6}\right)\left(\frac{61}{270}-4\right)$, oftewel $f(6)=-\frac{245}{6114}$.
We hebben nu 6 uitgerekend als $4+1+1$, maar we kunnen het natuurlijk ook doen als $2 \cdot 3$. Als we $x=2$ en $y=3$ invullen, dan krijgen we
$$
f(2)+f(3)=\left(f(5)+\frac{1}{5}\right)(f(6)-5)
$$
Als we hier de gevonden waarden van $f(2), f(3), f(5)$ en $f(6)$ invullen komt er echter geen gelijkheid uit, want de linkerkant is groter dan nul en de rechterkant kleiner dan nul. We concluderen dat het geval $f(4)=-1$ niet kan, en dat $f(1)=0$.
Nu zouden we graag vergelijking (1) gebruiken voor inductie, maar de basis met $x=1$ werkt niet, omdat $f(1)=0$. Als nieuwe basis willen we het geval $f(4)=\frac{15}{4}$ van hiervoor gebruiken, dat niet op een tegenspraak uitkwam maar juist op $f(1)=0$.
Lemma. Er geldt dat $f(4)=\frac{15}{4}$.
Bewijs. We gebruiken eigenlijk hetzelfde trucje als hierboven om $f(4)$ uit te reken, maar nu met het feit dat we $f(1)$ weten in plaats van $f(2)$. Met $x=y=2$ vinden we weer dat $2 f(2)=\left(f(4)+\frac{1}{4}\right)(f(4)-3)$. Door $x=2$ in te vullen in (1) vinden we $f(2)=$
$\left(f(3)+\frac{1}{3}\right)(f(2)-1)$ en door $x=3$ in te vullen in (1) vinden we $f(3)=\left(f(4)+\frac{1}{4}\right)(f(3)-$ 2 ). Dit stelsel van drie vergelijkingen kunnen we oplossen door de tweede vergelijking te herschrijven als
$$
\begin{aligned}
f(3) & =\frac{f(2)}{f(2)-1}-\frac{1}{3} \\
& =\frac{f(2)-1+1}{f(2)-1}-\frac{1}{3} \\
& =1+\frac{1}{f(2)-1}-\frac{1}{3} \\
& =\frac{1}{f(2)-1}+\frac{2}{3}
\end{aligned}
$$
oftewel $f(2)=\frac{1}{f(3)-\frac{2}{3}}+1$. Net zo volgt uit de derde vergelijking dat $f(4)=\frac{2}{f(3)-2}+\frac{3}{4}$ wat we kunnen herschrijven als $f(3)-\frac{2}{3}=\frac{\frac{4}{3} f(4)+1}{f(4)-\frac{3}{4}}$. Door alles te combineren, vinden we dat
$$
\begin{aligned}
\left(f(4)+\frac{1}{4}\right)(f(4)-3) & =2 f(2) \\
& =2\left(\frac{1}{f(3)-\frac{2}{3}}+1\right) \\
& =2\left(\frac{f(4)-\frac{3}{4}}{\frac{4}{3} f(4)+1}+1\right) \\
& =\frac{2 f(4)-\frac{3}{2}+\frac{8}{3} f(4)+2}{\frac{4}{3} f(4)+1} \\
& =\frac{\frac{14}{3} f(4)+\frac{1}{2}}{\frac{4}{3} f(4)+1} .
\end{aligned}
$$
Als we dit uitwerken door met $12\left(\frac{4}{3} f(4)+1\right)$ te vermenigvuldigen krijgen we een derdegraads vergelijking. Met $t=f(4)$ is dat $16 t^{3}-32 t^{2}-101 t-15=0$. Gelukkig hebben we al een vermoeden voor een nulpunt, namelijk $t=\frac{15}{4}$. We kunnen eenvoudig controleren dat dit inderdaad een nulpunt is en we factoriseren
$$
0=16 t^{3}-32 t^{2}-101 t-15=(4 t-15)\left(4 t^{2}+7 t+1\right)
$$
De discriminant van $4 t^{2}+7 t+1$ is $D=7^{2}-4 \cdot 4=33$ wat geen kwadraat is van een rationaal getal. Dus $t=\frac{15}{4}$ is het enige rationale nulpunt van de derdegraads vergelijking en de enige mogelijkheid voor $f(4)$.
Uit de drie vergelijkingen waar we het stelsel voor $f(4)$ mee begonnen, volgt nu direct dat $f(2)=\frac{3}{2}$ en $f(3)=\frac{8}{3}$. Al met al hebben we met $f(1), f(2), f(3)$ en $f(4)$ een inductiebasis voor $f(n)=n-\frac{1}{n}$ voor alle natuurlijke getallen $n$. Stel als inductiehypothese dat deze
formule geldt voor $n$. Dan volgt uit (1) dat
$$
\begin{aligned}
f(n+1) & =\frac{f(n)+f(1)}{f(n)-n+1}-\frac{1}{n+1} \\
& =\frac{n-\frac{1}{n}+0}{n-\frac{1}{n}-n+1}-\frac{1}{n+1} \\
& =\frac{n^{2}-1}{n-1}-\frac{1}{n+1} \\
& =(n+1)-\frac{1}{n+1}
\end{aligned}
$$
wat de inductie voltooit. Als we nu $x=n$ en $y=\frac{1}{n}$ invullen, dan vinden we
$$
f(n)+f\left(\frac{1}{n}\right)=\left(f\left(n+\frac{1}{n}\right)+\frac{1}{n+\frac{1}{n}}\right)(1-1+0)=0 .
$$
Hieruit volgt dat $f\left(\frac{1}{n}\right)=-f(n)=\frac{1}{n}-n$. Nu bewijzen we dat $f\left(\frac{m}{n}\right)=\frac{m}{n}-\frac{n}{m}$ met inductie naar $m$. De inductiebasis met $m=1$ hebben we net bewezen. Stel nu dus dat deze formule geldt voor een zekere $m$ en alle $n$. Nu vullen we $x=\frac{m}{n}$ en $y=\frac{1}{n}$ waaruit we krijgen dat
$$
\begin{aligned}
f\left(\frac{m+1}{n}\right) & =\frac{f\left(\frac{m}{n}\right)+f\left(\frac{1}{n}\right)}{f\left(\frac{m}{n^{2}}\right)-\frac{m}{n^{2}}+1}-\frac{n}{m+1} \\
& =\frac{\frac{m}{n}-\frac{n}{m}+\frac{1}{n}-n}{\frac{m}{n^{2}}-\frac{n^{2}}{m}-\frac{m}{n^{2}}+1}-\frac{n}{m+1} \\
& =\frac{(m+1)\left(\frac{1}{n}-\frac{n}{m}\right)}{n\left(\frac{1}{n}-\frac{n}{m}\right)}-\frac{n}{m+1} \\
& =\frac{m+1}{n}-\frac{n}{m+1} .
\end{aligned}
$$
Hiermee is de inductie naar $m$ voltooid, en daarmee ook het complete bewijs.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2023-E2023_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2023"
}
|
Find all pairs of prime numbers $(p, q)$ for which there exist positive integers $(m, n)$ such that
$$
(p+q)^{m}=(p-q)^{n}
$$
|
The only divisors that $p-q$ and $p+q$ can have in common are 2, because $p$ and $q$ are different prime numbers. Indeed, a divisor $d$ of $p+q$ and $p-q$ is also a divisor of $(p+q)+(p-q)=2p$ and of $(p+q)-(p-q)=2q$. And we know that $\operatorname{gcd}(2p, 2q)=2$, so $d$ must be a divisor of 2.
Since every prime factor of $|p-q|$ or $p+q$ must, due to the given equation, also be a prime factor of the other, we now know that $|p-q|$ and $p+q$ are both powers of 2 (not equal to 1). But the greatest common divisor is 2, so the smallest power of two of the two (and that must be $|p-q|$) is equal to 2. Thus, $|p-q|=2$ and $p+q$ is a power of 2. Therefore, there is exactly one number between $p$ and $q$, namely $\frac{p+q}{2}$. Since $p+q$ is a power of 2, $p+q$ is not divisible by 3. So $\frac{p+q}{2}$ is also not divisible by 3. Since one of three consecutive numbers must be divisible by 3, it follows that $p$ or $q$ is divisible by 3. Since 1 is not a prime number, the smaller of $p$ and $q$ must be 3 and the other 5. We find two solutions, $(p, q)=(3,5)$ and $(p, q)=(5,3)$, both of which satisfy the condition.
|
(3,5), (5,3)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Vind alle paren priemgetallen $(p, q)$ waarvoor er positieve gehele $(m, n)$ bestaan zodat
$$
(p+q)^{m}=(p-q)^{n}
$$
|
De enige deler die $p-q$ en $p+q$ gemeen kunnen hebben, is 2 , want $p$ en $q$ zijn verschillende priemgetallen. Inderdaad, een deler $d$ van $p+q$ en $p-q$ is ook een deler $\operatorname{van}(p+q)+(p-q)=2 p$ en $\operatorname{van}(p+q)-(p-q)=2 q$. En we weten dat $\operatorname{ggd}(2 p, 2 q)=2$, dus $d$ moet een deler zijn van 2 .
Aangezien elke priemfactor van $|p-q|$ of $p+q$ wegens de gegeven vergelijking ook een priemfactor van de ander moet zijn, weten we nu dat $|p-q|$ en $p+q$ allebei machten van 2 zijn (ongelijk aan 1). Maar de grootste gemeenschappelijke deler is 2, dus de kleinste tweemacht van de twee (en dat moet wel $|p-q|$ zijn) is gelijk aan 2. Dus $|p-q|=2$ en $p+q$ is een tweemacht. Er zit dus precies één getal tussen $p$ en $q$, namelijk $\frac{p+q}{2}$. Omdat $p+q$ is een tweemacht is, is $p+q$ niet deelbaar door 3. Dus $\frac{p+q}{2}$ is ook niet deelbaar door 3. Aangezien van drie opvolgende getallen er één deelbaar moet zijn door 3, volgt hieruit dat $p$ of $q$ deelbaar is door 3. Aangezien 1 geen priemgetal is, moet de kleinste van $p$ en $q$ gelijk zijn aan 3 en de ander aan 5 . We vinden twee oplossingen, $(p, q)=(3,5)$ en $(p, q)=(5,3)$, die beide voldoen.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2024-B2024_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2024"
}
|
We define a sequence with $a_{1}=850$ and
$$
a_{n+1}=\frac{a_{n}^{2}}{a_{n}-1}
$$
for $n \geq 1$. Determine all values of $n$ for which $\left\lfloor a_{n}\right\rfloor=2024$.
Here, the floor $\lfloor a\rfloor$ of a real number $a$ denotes the greatest integer less than or equal to $a$.
|
Answer: the only value that satisfies is $n=1175$.
First, we note that we can rewrite the recursion as
$$
a_{n+1}=\frac{a_{n}^{2}-1+1}{a_{n}-1}=\frac{a_{n}^{2}-1}{a_{n}-1}+\frac{1}{a_{n}-1}=a_{n}+1+\frac{1}{a_{n}-1} .
$$
Since the difference $a_{n+1}-a_{n}>1$, there is at most one value of $n$ that satisfies. Now we will show that $n=1175$ indeed satisfies. First, the above gives us
$$
\begin{aligned}
a_{1175} & =a_{1}+1174+\frac{1}{a_{1}-1}+\frac{1}{a_{2}-1}+\cdots+\frac{1}{a_{1174}-1} \\
& >850+1174 \\
& =2024
\end{aligned}
$$
More generally, it follows from (??) analogously that $a_{n} \geq 849+n$. From this, we deduce that
$$
\begin{aligned}
\frac{1}{a_{1}-1}+\cdots+\frac{1}{a_{1174}-1} & \leq \frac{1}{849}+\frac{1}{850}+\cdots+\frac{1}{2022} \\
& <51 \cdot \frac{1}{849}+100 \cdot \frac{1}{900}+200 \cdot \frac{1}{1000}+400 \cdot \frac{1}{1200}+400 \cdot \frac{1}{1600}+23 \cdot \frac{1}{2000} \\
& =\frac{17}{283}+\frac{1}{9}+\frac{1}{5}+\frac{1}{3}+\frac{1}{4}+\frac{23}{2000} \\
& =\frac{17}{283}+\frac{20+36+60+45}{180}+\frac{23}{2000} \\
& <\frac{11}{180}+\frac{161}{180}+\frac{3}{180} \\
& <1
\end{aligned}
$$
With this, we conclude that indeed
$$
a_{1175} \leq 850+1174+\frac{1}{849}+\frac{1}{850}+\cdots+\frac{1}{2022}<2024+1
$$
|
1175
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
We definiëren een rij met $a_{1}=850$ en
$$
a_{n+1}=\frac{a_{n}^{2}}{a_{n}-1}
$$
voor $n \geq 1$. Bepaal alle waarden van $n$ waarvoor geldt dat $\left\lfloor a_{n}\right\rfloor=2024$.
Hierbij staat de entier $\lfloor a\rfloor$ van een reëel getal a voor het grootste gehele getal kleiner of gelijk aan a.
|
Antwoord: de enige waarde die voldoet is $n=1175$.
Als eerst merken we op dat we de recursie kunnen herschrijven als
$$
a_{n+1}=\frac{a_{n}^{2}-1+1}{a_{n}-1}=\frac{a_{n}^{2}-1}{a_{n}-1}+\frac{1}{a_{n}-1}=a_{n}+1+\frac{1}{a_{n}-1} .
$$
Omdat het verschil van $a_{n+1}-a_{n}>1$, is er hoogstens één waarde van $n$ die voldoet. Nu gaan we laten zien dat $n=1175$ inderdaad voldoet. Ten eerste geeft het bovenstaande dat
$$
\begin{aligned}
a_{1175} & =a_{1}+1174+\frac{1}{a_{1}-1}+\frac{1}{a_{2}-1}+\cdots+\frac{1}{a_{1174}-1} \\
& >850+1174 \\
& =2024
\end{aligned}
$$
Algemener volgt uit (??) analoog dat $a_{n} \geq 849+n$. Hieruit leiden we af dat
$$
\begin{aligned}
\frac{1}{a_{1}-1}+\cdots+\frac{1}{a_{1174}-1} & \leq \frac{1}{849}+\frac{1}{850}+\cdots+\frac{1}{2022} \\
& <51 \cdot \frac{1}{849}+100 \cdot \frac{1}{900}+200 \cdot \frac{1}{1000}+400 \cdot \frac{1}{1200}+400 \cdot \frac{1}{1600}+23 \cdot \frac{1}{2000} \\
& =\frac{17}{283}+\frac{1}{9}+\frac{1}{5}+\frac{1}{3}+\frac{1}{4}+\frac{23}{2000} \\
& =\frac{17}{283}+\frac{20+36+60+45}{180}+\frac{23}{2000} \\
& <\frac{11}{180}+\frac{161}{180}+\frac{3}{180} \\
& <1
\end{aligned}
$$
Hiermee concluderen we dat inderdaad
$$
a_{1175} \leq 850+1174+\frac{1}{849}+\frac{1}{850}+\cdots+\frac{1}{2022}<2024+1
$$
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2024-B2024_uitwerkingen.jsonl",
"solution_match": "\nOplossing 1.",
"tier": "T1",
"year": "2024"
}
|
We define a sequence with $a_{1}=850$ and
$$
a_{n+1}=\frac{a_{n}^{2}}{a_{n}-1}
$$
for $n \geq 1$. Determine all values of $n$ for which $\left\lfloor a_{n}\right\rfloor=2024$.
Here, the floor $\lfloor a\rfloor$ of a real number $a$ denotes the greatest integer less than or equal to $a$.
|
In solution 1, we have estimated groups of consecutive fractions by the largest fraction in each group. Besides other groupings, we can also approach it differently by forming pairs of fractions from the middle. Then the sum of each pair of fractions is smaller than the pair of fractions at the ends. Indeed, for $0<x<1173$ we have
$$
(849+x)(2022-x)=849 \cdot 2022+1173 x-x^{2}=849 \cdot 2022+x(1173-x)>849 \cdot 2022
$$
If we apply this to the fractional part of $a_{1174}$, we get
$$
\begin{aligned}
\frac{1}{849}+\frac{1}{850}+\cdots+\frac{1}{2022} & =\left(\frac{1}{849}+\frac{1}{2022}\right)+\ldots+\left(\frac{1}{1435}+\frac{1}{1436}\right) \\
& =\frac{2871}{849 \cdot 2022}+\ldots+\frac{2871}{1435 \cdot 1436} \\
& <587 \cdot \frac{2871}{849 \cdot 2022}=\frac{587 \cdot 319}{283 \cdot 674} \\
& <\frac{587 \cdot 320}{280 \cdot 674}=\frac{587 \cdot 8}{7 \cdot 674} \\
& =\frac{4696}{4718} \\
& <1
\end{aligned}
$$
Remark. A fraction of products can often be estimated without calculating everything. For example, we could also do the last step using $7 \cdot 674=$ $7 \cdot 587+7 \cdot 87>7 \cdot 587+587=8 \cdot 587$.
|
not found
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
We definiëren een rij met $a_{1}=850$ en
$$
a_{n+1}=\frac{a_{n}^{2}}{a_{n}-1}
$$
voor $n \geq 1$. Bepaal alle waarden van $n$ waarvoor geldt dat $\left\lfloor a_{n}\right\rfloor=2024$.
Hierbij staat de entier $\lfloor a\rfloor$ van een reëel getal a voor het grootste gehele getal kleiner of gelijk aan a.
|
In oplossing 1 hebben we groepjes van opvolgende breuken afgeschat op de grootste breuk in elk groepje. Naast andere groepjes kunnen we het ook anders aanpakken door paren breuken te maken vanuit het midden. Dan is de som van elk paar breuken kleiner dan het paar van de breuken aan de uiteinden. Inderdaad, voor $0<x<1173$ geldt
$$
(849+x)(2022-x)=849 \cdot 2022+1173 x-x^{2}=849 \cdot 2022+x(1173-x)>849 \cdot 2022
$$
Als we dit toepassen op het fractionele deel van $a_{1174}$ vinden we
$$
\begin{aligned}
\frac{1}{849}+\frac{1}{850}+\cdots+\frac{1}{2022} & =\left(\frac{1}{849}+\frac{1}{2022}\right)+\ldots+\left(\frac{1}{1435}+\frac{1}{1436}\right) \\
& =\frac{2871}{849 \cdot 2022}+\ldots+\frac{2871}{1435 \cdot 1436} \\
& <587 \cdot \frac{2871}{849 \cdot 2022}=\frac{587 \cdot 319}{283 \cdot 674} \\
& <\frac{587 \cdot 320}{280 \cdot 674}=\frac{587 \cdot 8}{7 \cdot 674} \\
& =\frac{4696}{4718} \\
& <1
\end{aligned}
$$
Opmerking. Een breuk van producten kan je vaak afschatten zonder alles uit te rekenen. Zo zouden we de laatste stap bijvoorbeeld ook kunnen doen met behulp van $7 \cdot 674=$ $7 \cdot 587+7 \cdot 87>7 \cdot 587+587=8 \cdot 587$.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2024-B2024_uitwerkingen.jsonl",
"solution_match": "\nOplossing 2.",
"tier": "T1",
"year": "2024"
}
|
Find all pairs $(a, b)$ of positive integers such that $f(x)=x$ is the only function $f: \mathbb{R} \rightarrow \mathbb{R}$ satisfying
$$
f^{a}(x) f^{b}(y)+f^{b}(x) f^{a}(y)=2 x y
$$
for all $x, y \in \mathbb{R}$.
Here, $f^{n}(x)$ denotes the $n$-fold application of $f$ to $x$, so $f^{1}(x)=f(x)$ and $f^{n+1}(x)=$ $f\left(f^{n}(x)\right)$.
|
We will prove that exactly all pairs $(a, b)$ with $\operatorname{gcd}(a, b)=1$ and with $a+b$ odd satisfy.
First, assume that $\operatorname{gcd}(a, b)=n \neq 1$. Consider the function
$$
g(x)=\left\{\begin{array}{lll}
x+1 & \text { if }\lfloor x\rfloor \not \equiv 0 & \bmod n \\
x+1-n & \text { if }\lfloor x\rfloor \equiv 0 & \bmod n
\end{array}\right.
$$
This function is not equal to $\operatorname{id}_{\mathbb{R}}$ because $n \neq 1$. Then $\lfloor g(x)\rfloor \equiv\lfloor x\rfloor+1 \bmod n$. Therefore, the numbers $\lfloor x\rfloor,\lfloor g(x)\rfloor,\lfloor g(g(x))\rfloor, \ldots,\left\lfloor g^{n-1}(x)\right\rfloor$ have all residue classes $\bmod n$. Thus $g^{n}(x)=x+\underbrace{1+\ldots+1}_{n \text { times }}-n=x$. By induction, it follows that $g^{c n}(x)=x$ for all natural $c$, so since $n \mid a, b$ it also holds that $g^{a}(x)=x$ and $g^{b}(x)=x$. Therefore,
$$
g^{a}(x) g^{b}(y)+g^{b}(x) g^{a}(y)=x y+x y=2 x y
$$
Thus the function $f=g \neq \operatorname{id}_{\mathbb{R}}$ satisfies the functional equation in this case.
Now consider the case where $a+b$ is even. Take the function $h(x)=-x$. Then by simple induction, $h^{c}(x)=(-1)^{c} x$. Therefore,
$$
h^{a}(x) h^{b}(y)+h^{b}(x) h^{a}(y)=(-1)^{a+b} x y+(-1)^{a+b} x y=2 x y
$$
Thus the function $f=h \neq \operatorname{id}_{\mathbb{R}}$ satisfies the functional equation.
Now assume that $\operatorname{gcd}(a, b)=1$ and that $a+b$ is odd. With $x=y$ we see
$$
f^{a}(x) f^{b}(x)=x^{2}
$$
If we multiply the functional equation by $f^{a}(x) f^{a}(y)$, we get
$$
\begin{aligned}
2\left(x f^{a}(y)\right)\left(y f^{a}(x)\right) & =f^{a}(x) f^{b}(y) f^{a}(x) f^{a}(y)+f^{b}(x) f^{a}(y) f^{a}(x) f^{a}(y) \\
& =(\left(f^{a}(x)\right)^{2} \underbrace{f^{a}(y) f^{b}(y)}_{=y^{2}}+(\left(f^{a}(y)\right)^{2} \underbrace{f^{a}(x) f^{b}(x)}_{=x^{2}} \\
& =\left(y f^{a}(x)\right)^{2}+\left(x f^{a}(y)\right)^{2}
\end{aligned}
$$
This is the equality case of the arithmetic and geometric mean inequality. More beautifully, we can rewrite it as
$$
\left(y f^{a}(x)-x f^{a}(y)\right)^{2}=0
$$
Thus we conclude that $y f^{a}(x)=x f^{a}(y)$. With $y=1$ we see $f^{a}(x)=c_{1} x$ for some $c_{1} \in \mathbb{R}$. Similarly, multiplying by $f^{b}(x) f^{b}(y)$ gives $f^{b}(x)=c_{2} x$ for some $c_{2} \in \mathbb{R}$. If one of the constants were 0, then the left side of the functional equation would always be 0, but the right side would not. Therefore, both constants are not 0. Since $\operatorname{gcd}(a, b)=1$, there exist integers $p$ and $q$ such that $a p+b q=1$. Assume without loss of generality that $p$ is positive and $q$ is negative, and write $r=-q$. Then $a p=1+r b$ with $p$ and $r$ positive. We see
$$
\begin{aligned}
c_{1}^{p} x=\left(f^{a}\right)^{p}(x) & =f^{a p}(x) \\
& =f^{1+r b}(x) \\
& =f\left(\left(f^{b}\right)^{r}(x)\right) \\
& =f\left(c_{2}^{r} x\right)
\end{aligned}
$$
Thus $f(x)=\frac{c_{1}^{p}}{c_{2}^{r}} x=d x$. If we substitute this function, we see $2 d^{a+b} x y=2 x y$, so $d^{a+b}=1$. This implies $d=1$ because $a+b$ is odd. This means that $f(x)=x$ is the only function that potentially satisfies. It is easy to see that this function also actually satisfies, so all pairs $(a, b)$ of natural numbers for which $f(x)=x$ is the only function $f: \mathbb{R} \rightarrow \mathbb{R}$ that satisfies
$$
f^{a}(x) f^{b}(y)+f^{b}(x) f^{a}(y)=2 x y
$$
for all $x, y \in \mathbb{R}$ are exactly the pairs $(a, b)$ where $a+b$ is odd and $\operatorname{gcd}(a, b)=1$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Vind alle paren $(a, b)$ van positieve gehele getallen zodat $f(x)=x$ de enige functie $f: \mathbb{R} \rightarrow \mathbb{R}$ is die voldoet aan
$$
f^{a}(x) f^{b}(y)+f^{b}(x) f^{a}(y)=2 x y
$$
voor alle $x, y \in \mathbb{R}$.
Hierin staat $f^{n}(x)$ voor het $n$ keer toepassen van $f$ op $x$, dus $f^{1}(x)=f(x)$ en $f^{n+1}(x)=$ $f\left(f^{n}(x)\right)$.
|
We gaan bewijzen dat precies alle paren $(a, b)$ met $\operatorname{ggd}(a, b)=1$ en met $a+b$ oneven voldoen.
Neem eerst aan dat $\operatorname{ggd}(a, b)=n \neq 1$. Bekijk de functie
$$
g(x)=\left\{\begin{array}{lll}
x+1 & \text { als }\lfloor x\rfloor \not \equiv 0 & \bmod n \\
x+1-n & \text { als }\lfloor x\rfloor \equiv 0 & \bmod n
\end{array}\right.
$$
Deze functie is ongelijk aan $\operatorname{id}_{\mathbb{R}}$ omdat $n \neq 1$. Dan geldt $\lfloor g(x)\rfloor \equiv\lfloor x\rfloor+1 \bmod n$. Dus de getallen $\lfloor x\rfloor,\lfloor g(x)\rfloor,\lfloor g(g(x))\rfloor, \ldots,\left\lfloor g^{n-1}(x)\right\rfloor$ hebben alle restklassen $\bmod n$. Dus $g^{n}(x)=x+\underbrace{1+\ldots+1}_{n \text { keer }}-n=x$. Met inductie volgt hieruit $g^{c n}(x)=x$ voor alle natuurlijke $c$, dus omdat $n \mid a, b$ geldt ook $g^{a}(x)=x$ en $g^{b}(x)=x$. Dus
$$
g^{a}(x) g^{b}(y)+g^{b}(x) g^{a}(y)=x y+x y=2 x y
$$
Dus de functie $f=g \neq \operatorname{id}_{\mathbb{R}}$ voldoet aan de functievergelijking in dit geval.
We bekijken nu het geval dat $a+b$ even is. Neem dan de functie $h(x)=-x$. Dan volgt uit eenvoudige inductie dat $h^{c}(x)=(-1)^{c} x$. Dus
$$
h^{a}(x) h^{b}(y)+h^{b}(x) h^{a}(y)=(-1)^{a+b} x y+(-1)^{a+b} x y=2 x y
$$
Dus de functie $f=h \neq \operatorname{id}_{\mathbb{R}}$ voldoet aan de functievergelijking.
Neem nu aan dat $\operatorname{ggd}(a, b)=1$ en dat $a+b$ oneven is. Met $x=y$ zien we
$$
f^{a}(x) f^{b}(x)=x^{2}
$$
Als we de funcievergelijking met $f^{a}(x) f^{a}(y)$ vermenigvuldigen, krijgen we
$$
\begin{aligned}
2\left(x f^{a}(y)\right)\left(y f^{a}(x)\right) & =f^{a}(x) f^{b}(y) f^{a}(x) f^{a}(y)+f^{b}(x) f^{a}(y) f^{a}(x) f^{a}(y) \\
& =(\left(f^{a}(x)\right)^{2} \underbrace{f^{a}(y) f^{b}(y)}_{=y^{2}}+(\left(f^{a}(y)\right)^{2} \underbrace{f^{a}(x) f^{b}(x)}_{=x^{2}} \\
& =\left(y f^{a}(x)\right)^{2}+\left(x f^{a}(y)\right)^{2}
\end{aligned}
$$
Dit is het gelijkheidsgeval van de ongelijkheid van het rekenkundig en het meetkundig gemiddelde. Nog mooier zien we dat we het kunnen herschrijven als
$$
\left(y f^{a}(x)-x f^{a}(y)\right)^{2}=0
$$
Dus we concluderen dat $y f^{a}(x)=x f^{a}(y)$. Met $y=1$ zien we $f^{a}(x)=c_{1} x$ voor een zekere $c_{1} \in \mathbb{R}$. Analoog geeft vermenigvuldiging met $f^{b}(x) f^{b}(y)$ dat $f^{b}(x)=c_{2} x$ voor een zekere $c_{2} \in \mathbb{R}$. Als een van de constantes gelijk aan 0 zou zijn, dan is de linkerkant van de functievergelijking altijd gelijk aan 0 , maar rechts is dat niet. Beide constantes zijn dus niet gelijk aan 0 . Omdat $\operatorname{ggd}(a, b)=1$ bestaan er gehele $p$ en $q$ zodat $a p+b q=1$. Neem z.v.v.a. aan dat $p$ positief is en $q$ negatief en schrijf $r=-q$. Dan geldt $a p=1+r b$ met $p$ en $r$ positief. We zien
$$
\begin{aligned}
c_{1}^{p} x=\left(f^{a}\right)^{p}(x) & =f^{a p}(x) \\
& =f^{1+r b}(x) \\
& =f\left(\left(f^{b}\right)^{r}(x)\right) \\
& =f\left(c_{2}^{r} x\right)
\end{aligned}
$$
Dus $f(x)=\frac{c_{1}^{p}}{c_{2}^{r}} x=d x$. Als we deze functie invullen zien we $2 d^{a+b} x y=2 x y$, dus $d^{a+b}=1$. Hieruit volgt $d=1$ omdat $a+b$ oneven is. Dit betekent dat $f(x)=x$ de enige functie is die potentieel voldoet. Het is makkelijk te zien dat deze functie ook daadwerkelijk voldoet, dus alle paren $(a, b)$ van natuurlijke getallen waarvoor geldt dat $f(x)=x$ de enige functie $f: \mathbb{R} \rightarrow \mathbb{R}$ is die voldoet aan
$$
f^{a}(x) f^{b}(y)+f^{b}(x) f^{a}(y)=2 x y
$$
voor alle $x, y \in \mathbb{R}$ zijn precies de paren $(a, b)$ waarbij $a+b$ oneven is en $\operatorname{ggd}(a, b)=1$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2024-B2024_uitwerkingen.jsonl",
"solution_match": "\nOplossing 1.",
"tier": "T1",
"year": "2024"
}
|
Find all pairs $(a, b)$ of positive integers such that $f(x)=x$ is the only function $f: \mathbb{R} \rightarrow \mathbb{R}$ satisfying
$$
f^{a}(x) f^{b}(y)+f^{b}(x) f^{a}(y)=2 x y
$$
for all $x, y \in \mathbb{R}$.
Here, $f^{n}(x)$ denotes the $n$-fold application of $f$ to $x$, so $f^{1}(x)=f(x)$ and $f^{n+1}(x)=$ $f\left(f^{n}(x)\right)$.
|
From $f^{a}(x)=c_{1} x$ and $f^{b}(x)=c_{2} x$ we can also directly deduce that $c_{1}=$ $c_{2}=1$, even without using that the $\operatorname{gcd}(a, b)=1$. Indeed, if we substitute this into the original equation, we get $c_{1} x c_{2} y+c_{2} x c_{1} y=2 x y$. This implies that $c_{1} c_{2}=1$. Furthermore, $c_{1}^{b} x=\left(f^{a}\right)^{b}(x)=\left(f^{b}\right)^{a}(x)=c_{2}^{a} x=\frac{1}{c_{1}^{a}} x$, so $c_{1}^{a+b}=1$. Since $a+b$ is odd, we find that $c_{1}=1$, from which it also follows that $c_{2}=1$. We conclude that $f^{a}(x)=x$ and $f^{b}(x)=x$.
To deduce from this that $f(x)=x$, we now use $\operatorname{gcd}(a, b)=1$ to apply Bézout as in solution 1, or the Euclidean algorithm.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Vind alle paren $(a, b)$ van positieve gehele getallen zodat $f(x)=x$ de enige functie $f: \mathbb{R} \rightarrow \mathbb{R}$ is die voldoet aan
$$
f^{a}(x) f^{b}(y)+f^{b}(x) f^{a}(y)=2 x y
$$
voor alle $x, y \in \mathbb{R}$.
Hierin staat $f^{n}(x)$ voor het $n$ keer toepassen van $f$ op $x$, dus $f^{1}(x)=f(x)$ en $f^{n+1}(x)=$ $f\left(f^{n}(x)\right)$.
|
Uit $f^{a}(x)=c_{1} x$ en $f^{b}(x)=c_{2} x$ kunnen we ook direct afleiden dat $c_{1}=$ $c_{2}=1$, zelfs zonder te gebruiken dat de $\operatorname{ggd}(a, b)=1$. Inderdaad, als we dit invullen in de oorspronkelijke vergelijking, krijgen we $c_{1} x c_{2} y+c_{2} x c_{1} y=2 x y$. Hieruit volgt dat $c_{1} c_{2}=1$. Verder geldt $c_{1}^{b} x=\left(f^{a}\right)^{b}(x)=\left(f^{b}\right)^{a}(x)=c_{2}^{a} x=\frac{1}{c_{1}^{a}} x$, dus $c_{1}^{a+b}=1$. Omdat $a+b$ oneven is, vinden we dus dat $c_{1}=1$ waaruit ook volgt dat $c_{2}=1$. We concluderen dat $f^{a}(x)=x$ en $f^{b}(x)=x$.
Om hieruit af te leiden dat $f(x)=x$ gebruiken we nu alsnog $\operatorname{ggd}(a, b)=1$ zodat we Bézout kunnen toepassen zoals in oplossing 1 , of het algoritme van Euclides.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2024-B2024_uitwerkingen.jsonl",
"solution_match": "\nOplossing 2.",
"tier": "T1",
"year": "2024"
}
|
We have an $n \times n$ board with $n \geq 3$ where each cell can be colored either white or black individually. Each move changes the color of five chosen cells in the pentomino pattern
which can be rotated. Initially, all cells are white. Determine for which $n$ it is possible to make all cells black after a finite number of moves.
|
Answer: This is possible if and only if $n$ is divisible by 2 or 3, with the exception of 3 itself.
First, we show that for $n=3$, the recoloring is not possible. Consider the cells $A, B$, and $M$ in the following figure.
| | $B$ | |
| :---: | :---: | :---: |
| $A$ | $M$ | |
| | | |
Then, every pentomino contains cell $M$ and every pentomino contains $A$ or $B$. Since $A$ and $B$ must be chosen an odd number of times to turn them black, in such a case $M$ is chosen an odd + odd = even number of times. Thus, $M$ remains white, and we conclude that it is impossible to make all cells black simultaneously.
Now, assume that $n \geq 4$. If $n$ is divisible by 2, we repeatedly use the following procedure:

For this, we divide the board into $\left(\frac{1}{2} n\right)^{2}$ blocks of $2 \times 2$. Since $n \geq 4$, we can find a $4 \times 4$ block around each $2 \times 2$ block to apply the procedure.
If $n$ is divisible by 3 and not equal to 3 itself, then $n$ is at least 6. Using our work above, we have the following procedure for a $3 \times 3$ block with sufficient space:

To apply this repeatedly, we divide the board into $\left(\frac{1}{3} n\right)^{2}$ blocks of $3 \times 3$. Since $n \geq 6$, we can find the required $4 \times 5$ block around each $3 \times 3$ block to apply the procedure.
Now, suppose that $n$ is not divisible by 2 or 3. Then we color the columns cyclically with the colors $0, 1, 2 \bmod 3$. Each pentomino always has 3 cells of the same color and 1 cell of each of the other two colors. This means that each move changes an odd number of cells of each color between white and black. Therefore, the parity of the number of black cells is always the same for all three colors. Since $n$ is not divisible by 3, there is a color that has one more column than another color. The difference in the number of cells of these two colors is thus $n$, which is odd since $n$ is also not divisible by 2. We conclude that these two colors cannot both be entirely black.
|
proof
|
Incomplete
|
Yes
|
math-word-problem
|
Combinatorics
|
We hebben een $n \times n$-bord met $n \geq 3$ waarvan elk vakje afzonderlijk wit of zwart gekleurd kan worden. Elke zet veranderen we de kleur van vijf gekozen vakjes in het pentomino patroon

dat geroteerd mag worden. Aan het begin zijn alle vakjes wit. Bepaal voor welke $n$ het mogelijk is alle vakjes zwart te maken na een eindig aantal zetten.
|
Antwoord: dit kan precies als $n$ deelbaar is door 2 of 3 , met uizondering van 3 zelf.
We laten eerst zien dat voor $n=3$ de herkleuring niet mogelijk is. We beschouwen de vakjes $A, B$ en $M$ in het volgende figuur.
| | $B$ | |
| :---: | :---: | :---: |
| $A$ | $M$ | |
| | | |
Dan bevat elke pentomino vakje $M$ en elke pentomino bevat $A$ óf $B$. Aangezien $A$ en $B$ een ovenen aantal keer gekozen moeten worden om ze zwart te maken, is in zo'n geval $M$ een oneven + oneven $=$ even keer gekozen. Dus $M$ is dan wit en we concluderen dat we nooit alle vakjes tegelijk zwart kunnen maken.
Stel nu dat $n \geq 4$. Als $n$ deelbaar is door 2 dan gebruiken we herhaaldelijk de volgende procedure:

Hiervoor delen we het bord op in $\left(\frac{1}{2} n\right)^{2}$ blokken van $2 \times 2$. Omdat $n \geq 4$ kunnen we een $4 \times 4$-blok om elk $2 \times 2$-blok vinden zodat we de procedure kunnen toepassen.
Als $n$ deelbaar is door 3 en ongelijk aan 3 zelf dan is $n$ minstens 6 . Met behulp van ons werk hierboven hebben we de volgende procedure voor een $3 \times 3$-blok met voldoende ruimte:

Om dit herhaaldelijk toe te passen, delen we het bord op in $\left(\frac{1}{3} n\right)^{2}$ blokken van $3 \times 3$. Omdat $n \geq 6$ kunnen we om elk $3 \times 3$-blok het benodigde $4 \times 5$-blok vinden zodat we de procedure kunnen toepassen.
Stel nu dat $n$ niet deelbaar is door 2 of 3 . Dan kleuren we de kolommen cyclisch met de kleuren $0,1,2 \bmod 3$. Elke pentomino heeft altijd 3 vakjes van dezelfde kleur, en 1 vakje van beide andere kleuren. Dit betekent dat elke zet een oneven aantal vakjes van elke kleur wisselt tussen wit/zwart. Dus de pariteit van het aantal zwarte vakjes is altijd hetzelfde voor alledrie de kleuren. Omdat $n$ niet deelbaar is door 3 is er daarentegen een kleur die één kolom meer heeft dan een andere kleur. Het verschil tussen het aantal vakjes van deze twee kleuren is dus $n$, wat oneven is aangezien $n$ ook niet deelbaar is door 2 . We concluderen dat deze twee kleuren nooit beide alleen maar zwarte vakjes kunnen hebben.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2024-B2024_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2024"
}
|
Let $\triangle A B C$ be an acute triangle with $|A B|<|A C|$. Given are points $D$ and $E$ on the line segments $A B$ and $A C$, respectively. Let $P$ be a point such that $|P B|=|P D|$ and $|P C|=|P E|$. Let $X$ be a point on the arc $A C$ of the circumcircle of $\triangle A B C$ that does not contain $B$. The line $X A$ intersects the circumcircle of $\triangle A D E$ again at $Y$. Prove that $|P X|=|P Y|$.
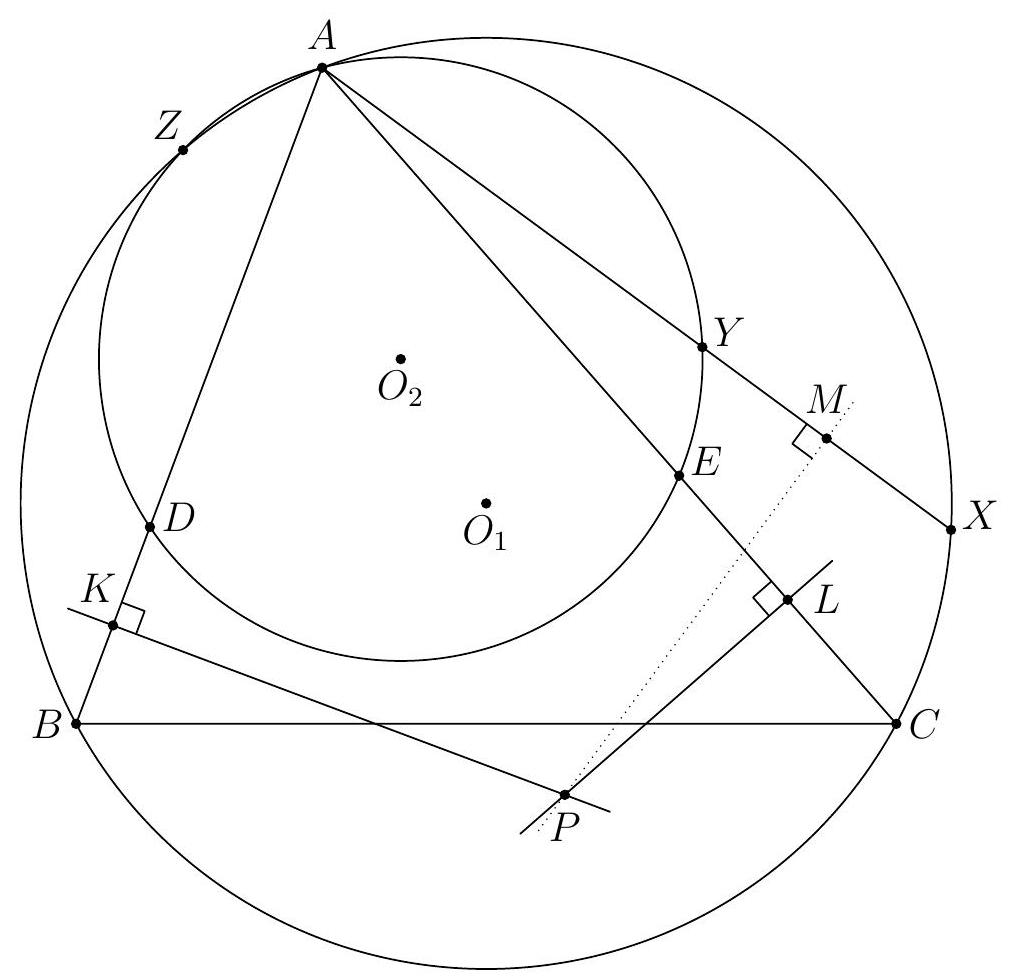
|
We consider the configuration as shown in the picture, where $Y$ lies on the arc $A E$. When $Y$ lies on the arc $A Z$, a corner folds over, but this case proceeds analogously. Let $Z$ be the second intersection point of the circumcircles of $\triangle A B C$ and $\triangle A D E$. Then, using directed angle chasing, we find that $\angle Z B C = \angle Z A C = \angle Z A E = \angle Z D E$ and similarly $\angle Z C B = \angle Z E D$. Therefore, $Z$ is the center of the spiral similarity $\triangle Z B C \sim \triangle Z D E$. Analogously, $\triangle Z C X \sim \triangle Z E Y$. Thus, we find $\triangle Z B D \sim \triangle Z C E \sim \triangle Z X Y$. These similarities carry the midpoints of the sides $B D, C E$, and $X Y$, which we denote as $K, L$, and $M$ respectively. This gives us that $\angle A K Z = \angle A L Z = \angle A M Z$, so $A Z K L M$ is a cyclic pentagon. Since $\angle A K P = \angle A L P = 90^{\circ}$, $P$ also lies on this circle. From this, we conclude that $\angle A M P = 90^{\circ}$, meaning that $P$ lies on the perpendicular bisector of $X Y$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $\triangle A B C$ een scherphoekige driehoek met $|A B|<|A C|$. Gegeven zijn punten $D$ en $E$ op respectievelijk de lijnstukken $A B$ en $A C$. Zij $P$ een punt zodanig dat $|P B|=|P D|$ en $|P C|=|P E|$. Zij $X$ een punt op de boog $A C$ van de omgeschreven cirkel van $\triangle A B C$ die niet $B$ bevat. De lijn $X A$ snijdt de omgeschreven cirkel van $\triangle A D E$ nogmaals in $Y$. Bewijs dat $|P X|=|P Y|$.

|
We bekijken de configuratie zoals in het plaatje waarbij $Y$ op de boog $A E$ ligt. Wanneer $Y$ op de boog $A Z$ ligt, klapt er een hoekje om maar dit geval gaat verder analoog. Zij $Z$ het tweede snijpunt van de omgeschreven cirkels van $\triangle A B C$ en $\triangle A D E$. Dan vinden vinden we met gericht hoekenjagen dat $\angle Z B C=\angle Z A C=$ $\angle Z A E=\angle Z D E$ en evenzo $\angle Z C B=\angle Z E D$. Dus is $Z$ het centrum van de draaivermenigvuldiging $\triangle Z B C \sim \triangle Z D E$. Analoog geldt $\triangle Z C X \sim \triangle Z E Y$. Dus vinden we $\triangle Z B D \sim \triangle Z C E \sim \triangle Z X Y$. Deze gelijkvormigheden nemen de middens mee van de zijden $B D, C E$ en $X Y$, die we respectievelijk $K, L$ en $M$ noemen. Hierdoor krijgen we dat $\angle A K Z=\angle A L Z=\angle A M Z$, dus $A Z K L M$ is een koordenvijfhoek. Aangezien $\angle A K P=\angle A L P=90^{\circ}$ ligt $P$ ook op deze cirkel. Hieruit concluderen we dan weer dat $\angle A M P=90^{\circ}$, oftewel dat $P$ op de middelloodlijn van $X Y$ ligt.
|
{
"exam": "Dutch_TST",
"problem_label": "5",
"problem_match": "\nOpgave 5.",
"resource_path": "Dutch_TST/segmented/nl-2024-B2024_uitwerkingen.jsonl",
"solution_match": "\nOplossing 1.",
"tier": "T1",
"year": "2024"
}
|
Let $\triangle A B C$ be an acute triangle with $|A B|<|A C|$. Given are points $D$ and $E$ on the line segments $A B$ and $A C$, respectively. Let $P$ be a point such that $|P B|=|P D|$ and $|P C|=|P E|$. Let $X$ be a point on the arc $A C$ of the circumcircle of $\triangle A B C$ that does not contain $B$. The line $X A$ intersects the circumcircle of $\triangle A D E$ again at $Y$. Prove that $|P X|=|P Y|$.

|
Let $O_{1}$ and $O_{2}$ be the centers of the circumcircles of $\triangle A B C$ and $\triangle A D E$, respectively. Let $O_{3}$ be the midpoint of $O_{1} O_{2}$, and let $\Gamma$ be the circle through $A$ with center $O_{3}$. We define $P$ as the antipode of $A$ in $\Gamma$. Now we project everything onto the line $B D$. Let $P_{1}, P_{2}$, and $P_{3}$ be the projections of $O_{1}, O_{2}$, and $O_{3}$, and let $K$ be the projection of $P$. Then it holds that
$$
|A K|=2\left|A P_{3}\right|=\left|A P_{1}\right|+\left|A P_{2}\right|=\frac{1}{2}(|A B|+|A D|)
$$
This means that $K$ is the midpoint of $B D$, or in other words, $P$ lies on the perpendicular bisector of $B D$. Similarly, $P$ lies on the perpendicular bisector of $C E$ and on the perpendicular bisector of $X Y$. Therefore, this is indeed the $P$ from the problem, and this point is equidistant from $X$ and $Y$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $\triangle A B C$ een scherphoekige driehoek met $|A B|<|A C|$. Gegeven zijn punten $D$ en $E$ op respectievelijk de lijnstukken $A B$ en $A C$. Zij $P$ een punt zodanig dat $|P B|=|P D|$ en $|P C|=|P E|$. Zij $X$ een punt op de boog $A C$ van de omgeschreven cirkel van $\triangle A B C$ die niet $B$ bevat. De lijn $X A$ snijdt de omgeschreven cirkel van $\triangle A D E$ nogmaals in $Y$. Bewijs dat $|P X|=|P Y|$.

|
Laat $O_{1}$ en $O_{2}$ de middelpunten zijn van de omgeschreven cirkels van respectievelijk $\triangle A B C$ en $\triangle A D E$. Zij $O_{3}$ nu het midden van $O_{1} O_{2}$ en zij $\Gamma$ de cirkel door
$A$ met middelpunt $O_{3}$. We definiëren $P$ als de antipode van $A$ in $\Gamma$. Nu projecteren we alles op de lijn $B D$. Laat $P_{1}, P_{2}$ en $P_{3}$ de projecties zijn van $O_{1}, O_{2}$ en $O_{3}$ en zij $K$ de projectie van $P$. Dan geldt dat
$$
|A K|=2\left|A P_{3}\right|=\left|A P_{1}\right|+\left|A P_{2}\right|=\frac{1}{2}(|A B|+|A D|)
$$
Dit betekent dat $K$ het midden is van $B D$, oftewel $P$ ligt op de middelloodlijn van $B D$. Net zo ligt $P$ op de middeloodlijn van $C E$ en op de middelloodlijn van $X Y$. Dus dit is inderdaad de $P$ van de opgave, en dit punt ligt even ver van $X$ als $Y$.
|
{
"exam": "Dutch_TST",
"problem_label": "5",
"problem_match": "\nOpgave 5.",
"resource_path": "Dutch_TST/segmented/nl-2024-B2024_uitwerkingen.jsonl",
"solution_match": "\nOplossing 2.",
"tier": "T1",
"year": "2024"
}
|
For a positive integer $n$, we define $\alpha(n)$ as the average of all positive divisors of $n$, and $\beta(n)$ as the average of all positive integers $k \leq n$ such that $\operatorname{gcd}(k, n)=1$.
Find all positive integers $n$ for which $\alpha(n)=\beta(n)$.
|
Answer: $n=1$ and $n=6$.
We first note that $n=1$ satisfies the condition.
We now prove that $\beta(n)=\frac{n}{2}$ for $n \geq 2$. Indeed, $\operatorname{gcd}(k, n)=\operatorname{gcd}(k-n, n)=\operatorname{gcd}(n-k, n)$, so $\operatorname{gcd}(k, n)=1$ if and only if $\operatorname{gcd}(n-k, n)=1$. This yields a partition of the positive integers $1 \leq k \leq n-1$ with $\operatorname{gcd}(k, n)=1$ into pairs $(k, n-k)$, which have an average of $\frac{n}{2}$. For $n \geq 2$, $\operatorname{gcd}(n, n)>1$, so we see that the average of all numbers $1 \leq k \leq n$ with $\operatorname{gcd}(k, n)=1$ is also equal to $\frac{n}{2}$. We have now possibly counted $\frac{n}{2}$ twice, but this does not matter since the average is exactly $\frac{n}{2}$.
Prime numbers do not satisfy the condition, because then $\alpha(n)=\frac{n+1}{2}$ and $\beta(n)=\frac{n}{2}$.
Suppose now that $d$ is a positive divisor of $n$ with $d$ not equal to 1 and $n$. Then $2 \leq d \leq \frac{n}{2}$, so $\left(\frac{n}{2}-d\right)(d-2) \geq 0$, so $\frac{n}{2} d+2 d \geq n+d^{2}$, so $\frac{n}{2}+2 \geq \frac{n}{d}+d$.
Suppose now that $n>6$ is composite. We can partition the positive divisors of $n$ into pairs $\left(d, \frac{n}{d}\right)$. The pair $(1, n)$ has an average of $\frac{n+1}{2}$, all other pairs have an average of $\frac{\frac{n}{d}+d}{2} \leq \frac{\frac{n}{2}+2}{2}<\frac{n-1}{2}$, or it is the single number $\sqrt{n} \leq \frac{n}{3}<\frac{n-2}{2}$ (in this case $n \geq 9$). If $n$ is not the square of a prime number, we have a pair with an average of $\frac{n+1}{2}$, a pair with an average less than $\frac{n-1}{2}$, and possibly more pairs (or a single number) with all averages less than $\frac{n-1}{2}$, resulting in a total average less than $\frac{n}{2}$. If $n$ is the square of a prime number, we find $\alpha(n)=\frac{1+\sqrt{n}+n}{3}<\frac{1+\frac{n-2}{2}+n}{3}=\frac{3 n}{6}=\frac{n}{2}$. Therefore, $n>6$ does not satisfy the condition.
Also, $n=4$ does not satisfy the condition, because $\alpha(4)=\frac{1+2+4}{3}=\frac{7}{3}$ while $\beta(4)=\frac{4}{2}=2$. Finally, we check that $n=1$ and $n=6$ indeed satisfy the condition:
- $n=1$: We have $\alpha(1)=\beta(1)=1$.
- $n=6$: We have $\alpha(3)=\frac{1+2+3+6}{4}=3$ and $\beta(6)=\frac{1+5}{2}=3$.
We conclude that $\alpha(n)=\beta(n)$ if and only if $n=1$ or $n=6$.
|
n=1 \text{ and } n=6
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Voor een positief geheel getal $n$ definieren we $\alpha(n)$ als het gemiddelde van alle positieve delers van $n$, en $\beta(n)$ als het gemiddelde van alle positieve gehele getallen $k \leq n$ zodat $\operatorname{ggd}(k, n)=1$.
Vind alle positieve gehele getallen $n$ waarvoor geldt dat $\alpha(n)=\beta(n)$.
|
Antwoord: $n=1$ en $n=6$.
We merken eerst op dat $n=1$ voldoet.
We bewijzen nu dat $\beta(n)=\frac{n}{2}$ voor $n \geq 2$. Er geldt namelijk $\operatorname{ggd}(k, n)=\operatorname{ggd}(k-n, n)=$ $\operatorname{ggd}(n-k, n)$, dus $\operatorname{ggd}(k, n)=1$ dan en slechts dan als $\operatorname{ggd}(n-k, n)=1$. Dit levert een opdeling van de positieve gehele getallen $1 \leq k \leq n-1$ met $\operatorname{ggd}(k, n)=1$ in paren $(k, n-k)$, die gemiddelde $\frac{n}{2}$ hebben. Voor $n \geq 2$ geldt $\operatorname{ggd}(n, n)>1$, dus we zien dat het gemiddelde van alle getallen $1 \leq k \leq n$ met $\operatorname{ggd}(k, n)=1$ ook gelijk is aan $\frac{n}{2}$. We hebben nu alleen $\frac{n}{2}$ mogelijk dubbel geteld, maar dat maakt niet uit aangezien het gemiddelde precies $\frac{n}{2}$ is.
Priemgetallen voldoen niet, want dan geldt er $\alpha(n)=\frac{n+1}{2}$ en $\beta(n)=\frac{n}{2}$.
Stel nu dat $d$ een positieve deler is van $n$ met $d$ ongelijk aan 1 en $n$. Dan geldt er $2 \leq d \leq \frac{n}{2}$, dus $\left(\frac{n}{2}-d\right)(d-2) \geq 0$, dus $\frac{n}{2} d+2 d \geq n+d^{2}$, dus $\frac{n}{2}+2 \geq \frac{n}{d}+d$.
Stel nu dat $n>6$ samengesteld is. We kunnen de positieve delers van $n$ opdelen in paren $\left(d, \frac{n}{d}\right)$. Het paar $(1, n)$ heeft gemiddelde $\frac{n+1}{2}$, alle andere paren hebben gemiddelde $\frac{\frac{n}{d}+d}{2} \leq \frac{\frac{n}{2}+2}{2}<\frac{n-1}{2}$, of het is alleen het getal $\sqrt{n} \leq \frac{n}{3}<\frac{n-2}{2}$ (in dit geval geldt $n \geq 9$ ). Als $n$ niet het kwadraat is van een priemgetal, hebben we een paar met gemiddelde $\frac{n+1}{2}$, een paar met gemiddelde kleiner dan $\frac{n-1}{2}$, en nog mogelijk meer paren (of een los getal) met allemaal een gemiddelde kleiner dan $\frac{n-1}{2}$, waardoor het totale gemiddelde kleiner is dan $\frac{n}{2}$. Als $n$ wel het kwadraat is van een priemgetal, vinden we $\alpha(n)=\frac{1+\sqrt{n}+n}{3}<\frac{1+\frac{n-2}{2}+n}{3}=\frac{3 n}{6}=\frac{n}{2}$. Dus $n>6$ voldoet niet.
Ook $n=4$ voldoet niet, want $\alpha(4)=\frac{1+2+4}{3}=\frac{7}{3}$ terwijl $\beta(4)=\frac{4}{2}=2$. Ten slotte controleren we dat $n=1$ en $n=6$ inderdaad voldoen:
- $n=1:$ Er geldt $\alpha(1)=\beta(1)=1$.
- $n=6$ : Er geldt $\alpha(3)=\frac{1+2+3+6}{4}=3$ en $\beta(6)=\frac{1+5}{2}=3$.
We concluderen dat $\alpha(n)=\beta(n)$ dan en slechts dan als $n=1$ of $n=6$.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2024-C2024_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2024"
}
|
Vind alle functies $f: \mathbb{R}_{\geq 0} \rightarrow \mathbb{R}$ die voldoen aan
$$
2 x^{3} z f(z)+y f(y) \geq 3 y z^{2} f(x)
$$
voor alle $x, y, z \in \mathbb{R}_{\geq 0}$.
|
Antwoord: alle functies van de vorm $f_{c, d}(x)=\left\{\begin{array}{ll}c x^{2} & \text { als } x>0 \\ d & \text { als } x=0\end{array}\right.$ met $c \geq 0$ en $d \leq 0$.
Invullen van $x=0$ en $y=1$ levert $f(1) \geq 3 f(0) z^{2}$ voor alle $z \geq 0$. Als $f(0)>0$, dan is de rechterkant van deze ongelijkheid onbegrensd, tegenspraak. Dus er geldt $f(0) \leq 0$.
Invullen van $z=0$ levert $y f(y) \geq 0$, dus $f(y) \geq 0$ voor alle $y>0$. In het bijzonder geldt $f(1) \geq 0$.
Invullen van $x=y$ en $z=1$ levert
$$
2 y^{3} f(1)+y f(y) \geq 3 y f(y)
$$
dus $2 y^{3} f(1) \geq 2 y f(y)$, dus $f(y) \leq y^{2} f(1)$ voor $y>0$.
Invullen van $z=y$ en $x=1$ levert
$$
2 y f(y)+y f(y) \geq 3 y^{3} f(1)
$$
dus $3 y f(y) \geq 3 y^{3} f(1)$, dus $f(y) \geq y^{2} f(1)$ voor $y>0$.
Samen levert dit $f(y)=y^{2} f(1)$ voor $y>0$.
Schrijf $c=f(1)$ en $d=f(0)$. Dan weten we nu dus dat $f(x)=\left\{\begin{array}{ll}c x^{2} & \text { als } x>0 \\ d & \text { als } x=0\end{array}\right.$ met $c \geq 0$ en $d \leq 0$. We gaan nu deze functies controleren.
Merk eerst op dat $x f(x) \geq 0$ voor alle $x \in \mathbb{R}_{\geq 0}$ : voor $x=0$ is dit triviaal en voor $x>0$ geldt er $x f(x)=c x^{3} \geq 0$ aangezien $c \geq 0$.
Voor $x=0$ staat er $y f(y) \geq 3 y z^{2} f(0)$, en dit klopt aangezien $y f(y) \geq 0$ en $3 y z^{2} f(0)=$ $3 y z^{2} d \leq 0$ voor $y, z \geq 0$.
Voor $y=0$ staat er $2 x^{3} z f(z) \geq 0$ en dit klopt. Voor $z=0$ staat er $y f(y) \geq 0$ en dit klopt.
Neem nu aan dat $x, y, z>0$. Dan geldt dus $f(x)=c x^{2}, f(y)=c y^{2}, f(z)=c z^{2}$ en moeten we bewijzen dat
$$
2 x^{3} z c z^{2}+y c y^{2} \geq 3 y z^{2} c x^{2}
$$
Aangezien $c \geq 0$ is het voldoende om te laten zien dat $2 x^{3} z^{3}+y^{3} \geq 3 y z^{2} x^{2}$ voor alle $x, y, z>0$. Dit volgt uit de ongelijkheid van het rekenkundig en meetkundig gemiddelde op de drie termen $x^{3} z^{3}, x^{3} z^{3}$ en $y^{3}$. Dus al deze functies voldoen.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Vind alle functies $f: \mathbb{R}_{\geq 0} \rightarrow \mathbb{R}$ die voldoen aan
$$
2 x^{3} z f(z)+y f(y) \geq 3 y z^{2} f(x)
$$
voor alle $x, y, z \in \mathbb{R}_{\geq 0}$.
|
Antwoord: alle functies van de vorm $f_{c, d}(x)=\left\{\begin{array}{ll}c x^{2} & \text { als } x>0 \\ d & \text { als } x=0\end{array}\right.$ met $c \geq 0$ en $d \leq 0$.
Invullen van $x=0$ en $y=1$ levert $f(1) \geq 3 f(0) z^{2}$ voor alle $z \geq 0$. Als $f(0)>0$, dan is de rechterkant van deze ongelijkheid onbegrensd, tegenspraak. Dus er geldt $f(0) \leq 0$.
Invullen van $z=0$ levert $y f(y) \geq 0$, dus $f(y) \geq 0$ voor alle $y>0$. In het bijzonder geldt $f(1) \geq 0$.
Invullen van $x=y$ en $z=1$ levert
$$
2 y^{3} f(1)+y f(y) \geq 3 y f(y)
$$
dus $2 y^{3} f(1) \geq 2 y f(y)$, dus $f(y) \leq y^{2} f(1)$ voor $y>0$.
Invullen van $z=y$ en $x=1$ levert
$$
2 y f(y)+y f(y) \geq 3 y^{3} f(1)
$$
dus $3 y f(y) \geq 3 y^{3} f(1)$, dus $f(y) \geq y^{2} f(1)$ voor $y>0$.
Samen levert dit $f(y)=y^{2} f(1)$ voor $y>0$.
Schrijf $c=f(1)$ en $d=f(0)$. Dan weten we nu dus dat $f(x)=\left\{\begin{array}{ll}c x^{2} & \text { als } x>0 \\ d & \text { als } x=0\end{array}\right.$ met $c \geq 0$ en $d \leq 0$. We gaan nu deze functies controleren.
Merk eerst op dat $x f(x) \geq 0$ voor alle $x \in \mathbb{R}_{\geq 0}$ : voor $x=0$ is dit triviaal en voor $x>0$ geldt er $x f(x)=c x^{3} \geq 0$ aangezien $c \geq 0$.
Voor $x=0$ staat er $y f(y) \geq 3 y z^{2} f(0)$, en dit klopt aangezien $y f(y) \geq 0$ en $3 y z^{2} f(0)=$ $3 y z^{2} d \leq 0$ voor $y, z \geq 0$.
Voor $y=0$ staat er $2 x^{3} z f(z) \geq 0$ en dit klopt. Voor $z=0$ staat er $y f(y) \geq 0$ en dit klopt.
Neem nu aan dat $x, y, z>0$. Dan geldt dus $f(x)=c x^{2}, f(y)=c y^{2}, f(z)=c z^{2}$ en moeten we bewijzen dat
$$
2 x^{3} z c z^{2}+y c y^{2} \geq 3 y z^{2} c x^{2}
$$
Aangezien $c \geq 0$ is het voldoende om te laten zien dat $2 x^{3} z^{3}+y^{3} \geq 3 y z^{2} x^{2}$ voor alle $x, y, z>0$. Dit volgt uit de ongelijkheid van het rekenkundig en meetkundig gemiddelde op de drie termen $x^{3} z^{3}, x^{3} z^{3}$ en $y^{3}$. Dus al deze functies voldoen.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2024-C2024_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2024"
}
|
Player Zero and Player One play a game on an $n \times n$ board $(n \geq 1)$. The columns of this $n \times n$ board are numbered with powers of two, so we have column 1, column 2, column 4, up to column $2^{n-1}$. Taking turns, the players place their own number (so Zero places a 0 and One places a 1) in one of the empty squares. Player 0 starts. When the board is full, the game ends and in each row a (reverse binary) number is formed by summing the values of the squares with a 1 in them. So if $n=4$, then a row with 0101 corresponds to the number $0 \cdot 1 + 1 \cdot 2 + 0 \cdot 4 + 1 \cdot 8 = 10$.
a) For which natural numbers $n$ can Player One always ensure that at least one of the rows is divisible by 4?
b) And for which natural numbers $n$ can Player One always ensure that at least one of the rows is divisible by 3?
a) Solution 1. First note that if $n=1$, the unique square gets a 0 because Player Zero starts, so in this case it is possible.
We will now prove that for all other $n$, Zero can prevent One from winning. Since $4 \mid 2^{k}$ for all $k \geq 2$, only the first two columns determine who wins. If there is a row with two zeros at the beginning, then Player One wins, and otherwise Player Zero wins. We will prove that for all $n>1$, Zero can prevent One from winning.
We say "Zero blocks One" if Zero places a 0 next to a 1 in the first two squares of a row. We call the first two columns the left area; the entire board except the first two columns is the right area.
If $n$ is odd, Zero places a 0 in the right area first. There are then still an even number of squares in both the right area and the left area. Zero plays in such a way that this property is maintained after each of his moves, and that in addition, the neighboring square of each empty square in the left area is also empty. (In each row, the first two squares are thus both empty or both occupied.) Each time One places a 1 in one of the areas, there is still at least 1 more empty square in that area, and Zero plays a 0 in the same area. For the left area, Zero does this by immediately blocking the 1 just played by One.
If $n$ is even, Zero places a 0 in the left area first. There are now an odd number of squares left on the left and an even number of squares on the right. If One plays a 1 on the right, Zero also plays a 0 on the right. If One plays a 1 on the left in a new row, Zero immediately blocks it. If One plays a 1 on the left in a row where a 0 already stands, then Zero starts a new row on the left again if possible by playing a 0 in the left area so that the adjacent square (in the left area) is still empty. If there is no new row, then all rows on the left are filled with 01 or 10, and Zero plays on the right.
|
Player Zero has the following strategy: do not place a 0 in the first two columns unless you have no other choice. In that case, place a 0 in a row where the other cell of the first two cells already contains a 1, if possible. If such a cell does not exist, place it in a row that does not yet have a 0 in the first two cells. We will show that Zero can continue to do this all the time, so that Zero wins because there will never be a row that starts with two 0s.
We claim that with this strategy, at any moment, there is at most one row whose first two cells are $(0, \emptyset)$. Suppose that Zero places a zero next to an empty cell. Then the right area is full due to the strategy. When One makes a move after this, it replaces the $(0, \emptyset)$-row with a $(0,1)$-row, or a $(1, \emptyset)$-row is created where Zero can/must play. Zero is thus never forced to create a second $(0, \emptyset)$-row, or a $(0,0)$-row.
b) Solution. Zero can only ensure that no row is divisible by 3 if $n \equiv 2 \bmod 4$.
First note that modulo 3 the columns are numbered $1,2,1,2, \ldots$. If $n$ is even, there are an even number of cells and One has the last turn; if $n$ is odd, there are an odd number of cells and Zero has the last turn.
If $n=4k$, both 1 and 2 appear an even number of times per row. Now One has the following strategy: mirror player Zero. If Zero places a zero in a cell with value 1, then One places a 1 in a cell in the same row that also has value 1. If Zero places a zero in a cell with value 2, then One places a 1 in a cell with value 2 in the same row. Since there is an even number of 1s and 2s in each row, One can always continue to do this. Now it holds that at the end $k$ cells with value 1 have the number 1 and $k$ cells with value 2 have the number 1 from One. So the sum of each row is $3k \equiv 0 \bmod 3$.
If $n=4k+1$, there are $2k+1$ cells with value 1 and $2k$ cells with value 2. One wants to create a row such that exactly $k$ cells with value 1 have a 1 and exactly $k$ cells with value 2. One now uses the mirror strategy again. However, if One cannot mirror, then One places a 1 in any cell with value 1. Only if this is also no longer possible does he place a 1 in a cell with value 2. Since there are exactly $2k$ cells per row with value 2, One can ensure with this strategy that in each row exactly $k$ cells with value 2 get the number 1. In addition, this strategy ensures that there is at least one row with $k+1$ zeros in cells with value 1 (and thus $k$ with the number 1). For this row, the sum is $k+2k=3k \equiv 0 \bmod 3$.
If $n=4k+3$, there are $2k+2$ cells with value 1 and $2k+1$ cells with value 2. One starts by placing a 1 in any cell with value 2 in one of the rows where Zero has not placed his first cell. One then applies the copy technique to this specific row. So if Zero places it outside, One does the same and if Zero places it inside, One also does this and places his 1 on a cell with the same value. Since there is now an odd number of empty cells outside this row, it can happen that One has to place a cell in the special row while Zero did not do so on the previous turn. There are still $2k$ cells with value 2 and $2k+2$ with value 1 for this move. By applying the copy technique again after this move (and the fact that Zero has the last move), One can ensure that both One and Zero choose $k$ cells with value 2 and $k+1$ cells with value 1. Now the special row has exactly $k+1$ cells with value 1 and $k+1$ with value 2, so the sum is $3(k+1) \equiv 0 \bmod 3$ and One wins.
If $n=4k+2$, there are $2k+1$ cells with value 1 and $2k+1$ cells with value 2. Then Zero can prevent One from winning. This time it is Zero who applies the copy technique from his second turn. However, if there are no more cells with the same value in the same row, then Zero places the cell in the same row with the other value. Since in this case One has the last turn, Zero can ensure with this strategy that both exactly $2k+1$ cells in each row are occupied and that Zero occupies at least $k$ cells with value 1 and $k$ cells with value 2 in the row. This means that the sum in each row is either $k+2(k+1) \equiv 2 \bmod 3$ or $k+1+2k \equiv 1 \bmod 3$. In this case, Zero can always prevent One from winning.
|
proof
|
Yes
|
Incomplete
|
proof
|
Combinatorics
|
Speler Zero en speler One spelen een spel op een $n \times n$-bord $(n \geq 1)$. De kolommen van dit $n \times n$-bord zijn genummerd met tweemachten, dus we hebben kolom 1 , kolom 2, kolom 4 tot en met kolom $2^{n-1}$. Om en om zetten de spelers hun eigen getal (dus Zero een 0 en One een 1) in één van de lege vakjes. Speler 0 begint. Als het bord vol is, eindigt het spel en ontstaat er in elke rij een (omgekeerd binair) getal door de waardes van de vakjes met een 1 erin bij elkaar op te tellen. Dus als $n=4$ dan hoort bij een rij met 0101 het getal $0 \cdot 1+1 \cdot 2+0 \cdot 4+1 \cdot 8=10$.
a) Voor welke natuurlijke getallen $n$ kan speler One er altijd voor zorgen dat minimaal één van de rijen deelbaar is door 4 ?
b) En voor welke natuurlijke getallen $n$ kan speler One er altijd voor zorgen dat minimaal één van de rijen deelbaar is door 3?
a) Oplossing 1. Merk eerst op dat als $n=1$, het unieke vakje een 0 krijgt omdat speler Zero begint, dus in dit geval is het mogelijk.
We gaan nu bewijzen dat voor alle andere $n$ Zero kan voorkomen dat One wint. Omdat $4 \mid 2^{k}$ voor alle $k \geq 2$, bepalen alleen de eerste twee kolommen wie er wint. Als er een rij is met twee nullen aan het begin, dan wint speler One en anders speler Zero. We gaan bewijzen dat voor alle $n>1$ Zero kan voorkomen dat One wint.
We zeggen "Zero blokkeert One" als Zero zijn 0 naast een 1 in de eerste twee vakjes van een rij zet. We noemen de eerste twee kolommen het linkergebied; het hele bord op de eerste twee kolommen na juist het rechtergebied.
Als $n$ oneven is, zet Zero als eerste een 0 in het rechtergebied. Er zijn dan nog een even aantal vakjes in zowel het rechtergebied als in het linkergebied. Zero speelt nu zo dat deze eigenschap behouden blijft na elke zet van hem, en dat bovendien het buurvakje van elk leeg vakje in het linkergebied ook leeg is. (In elke rij zijn de twee eerste vakjes dus beide leeg of beide bezet.) Elke keer als One een 1 zet in een van de gebieden, is er in dat gebied dus nog minstens 1 vakje meer leeg en speelt Zero een 0 in datzelfde gebied. Voor het linkergebied doet Zero dat door telkens de zojuist gespeelde 1 van One te blokkeren.
Als $n$ even is, zet Zero als eerste een 0 in het linkergebied. Er zijn nu links nog een oneven aantal vakjes en rechts een even aantal vakjes. Als One rechts een 1 speelt, speelt Zero ook rechts een 0 . Als One links een 1 speelt op een nieuwe rij, blokkeert Zero deze meteen. Als One links een 1 speelt in de rij waar al een 0 stond, dan begint Zero links weer een nieuwe rij als dat kan door een 0 te spelen in het linkergebied zodat het vakje daarnaast (in het linkergebied) nog leeg is. Als er geen nieuwe rij is,
dan zij alle rijen links gevuld met 01 of 10 en speelt Zero rechts.
|
Speler Zero heeft de volgende tactiek: zet geen 0 in de eerste twee kolommen tenzij je niets anders meer kan doen. Zet in dat geval een 0 in een rij waarbij het andere vakje van de eerste twee vakjes al een 1 bevat, indien mogelijk. Als zo'n vakje niet bestaat zet je hem in een rij, die nog geen 0 in de eerste twee vakjes heeft. We gaan laten zien dat Zero dit de hele tijd kan blijven doen, zodat Zero wint omdat er dan nooit een rij is die begint met twee keer een 0 .
We beweren dat er met deze tactiek op elk moment hoogstens één rij is waarvan de eerste twee vakjes $(0, \emptyset$ ) zijn. Stel namelijk dat Zero een nul neerzet, naast een leeg vakje. Dan is het rechtergebied vol wegens de tactiek. Wanneer One hierna een zet doet, vervangt dit de $(0, \emptyset)$-rij door een $(0,1)$-rij, of ontstaat er een $(1, \emptyset)$-rij waar Zero in kan/moet spelen. Zero wordt dus nooit geforceerd om een tweede $(0, \emptyset$ )-rij te creëren, of een $(0,0)$-rij.
b) Oplossing. Zero kan er alleen voor zorgen dat geen enkele rij deelbaar is door 3 als $n \equiv 2 \bmod 4$.
Merk allereerst op dat modulo 3 de kolommen als $1,2,1,2, \ldots$ genummerd zijn. Als $n$ even is, zijn er een even aantal vakjes en heeft One de laatste beurt; als $n$ echter oneven is, zijn er een oneven aantal vakjes en heeft Zero de laatste beurt.
Als $n=4 k$ komen zowel de 1 als de 2 een even aantal keer per rij voor. Nu heeft One de volgende tactiek: spiegel speler Zero. Als Zero een nul zet in een rij met waarde 1 dan zet One een 1 in een vakje in diezelfde rij die ook waarde 1 heeft. Als Zero een nul zet in een rij met waarde 2 , dan zet One een 1 in een vakje met waarde 2 in diezelfde rij. Omdat er in elke rij een even aantal 1-en en 2-en zijn, kan One dit altijd blijven doen. Nu geldt dat er op het einde $k$ vakjes met waarde 1 het getal 1 hebben en $k$ vakjes met waarde 2 die het getal 1 van One hebben gekregen. Dus is de som van elke rij $3 k \equiv 0 \bmod 3$.
Als $n=4 k+1$, zijn er $2 k+1$ vakjes met waarde 1 en $2 k$ vakjes met waarde 2 . One wil een rij maken zodat in exact $k$ vakjes van waarde 1 een 1 staat en in exact $k$ vakjes van waarde 2. One gebruikt nu opnieuw de spiegeltactiek. Als One echter niet kan spiegelen, dan zet One een 1 in een willekeurig vakje met waarde 1. Pas als dit ook niet meer kan zet hij een 1 neer in een vakje met waarde 2 . Omdat er exact $2 k$ vakjes per rij van waarde 2 zijn, kan One er met deze tactiek voor zorgen dat in elke rij exact $k$ vakjes met waarde 2 het getal 1 krijgen. Daarnaast zorgt deze tactiek ervoor dat er minimaal één rij is met $k+1$ nullen op vakjes met waarde 1 (en dus $k$ met het getal 1). Voor deze rij geldt dat de som gelijk is aan $k+2 k=3 k \equiv 0 \bmod 3$.
Als $n=4 k+3$, zijn er $2 k+2$ vakjes met waarde 1 en $2 k+1$ vakjes met waarde 2 . One begint een 1 te zetten in een willekeurig vakje van waarde 2 in een van de rijen waar Zero niet zijn eerste vakje heeft geplaatst. Vervolgens past One de kopieer techniek toe op deze specifieke rij. Dus als Zero erbuiten plaatst, doet One dat ook en als Zero erbinnen plaatst dan doet One dat ook en zet zijn 1 op een vakje met dezelfde waarde. Omdat er nu een oneven aantal lege vakjes buiten deze rij zijn, kan het zo zijn dat One een vakje in de speciale rij moet zetten, terwijl Zero de beurt daarvoor dat niet gedaan heeft. Er zijn voor deze zet nog $2 k$ vakjes met waarde 2 over en $2 k+2$ met waarde 1. Door de kopieertactiek na deze zet weer toe te passen (en het feit dat Zero de laatste zet heeft) kan One ervoor zorgen dat zowel One als Zero $k$ vakjes kiest met waarde 2 en $k+1$ vakjes met waarde 1 . Nu heeft de speciale rij exact $k+1$ vakjes met waarde 1 en $k+1$ met waarde 2, waardoor de som $3(k+1) \equiv 0 \bmod 3$ is en One wint.
Als $n=4 k+2$, zijn er $2 k+1$ vakjes met waarde 1 en $2 k+1$ vakjes met waarde 2. Dan kan Zero voorkomen dat One wint. Ditmaal is het juist Zero die vanaf zijn tweede beurt de kopieertactiek toepast. Als er echter geen vakjes meer zijn met dezelfde waarde in dezelfde rij, dan zet Zero het vakje in dezelfde rij met de andere waarde. Doordat in dit geval One de laatste beurt heeft, kan Zero er met deze tactiek voor zorgen dat beide exact $2 k+1$ vakjes in elke rij bezetten en dat Zero minimaal $k$ vakjes met waarde 1 en $k$ vakjes met waarde 2 in de rij bezet. Dit betekent dat de som in elke rij ofwel $k+2(k+1) \equiv 2 \bmod 3$ of $k+1+2 k \equiv 1 \bmod 3$ is. In dit geval kan Zero dus altijd voorkomen dat One wint.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2024-C2024_uitwerkingen.jsonl",
"solution_match": "\nOplossing 2.",
"tier": "T1",
"year": "2024"
}
|
Let $\triangle A B C$ be an acute triangle such that $|A B|<|A C|$ with circumcircle $\Gamma$ and center $O$. The points $D, E$, and $F$ are constructed as the feet of the altitudes from $A, B$, and $C$ respectively. The intersection of the tangents to $\Gamma$ at $B$ and $C$ is denoted as $P$. The line through $P$ perpendicular to $E F$ intersects the line $A D$ at point $Q$. Let $R$ be the orthogonal projection of $A$ onto $E F$.
Prove that the lines $D R$ and $O Q$ are parallel.
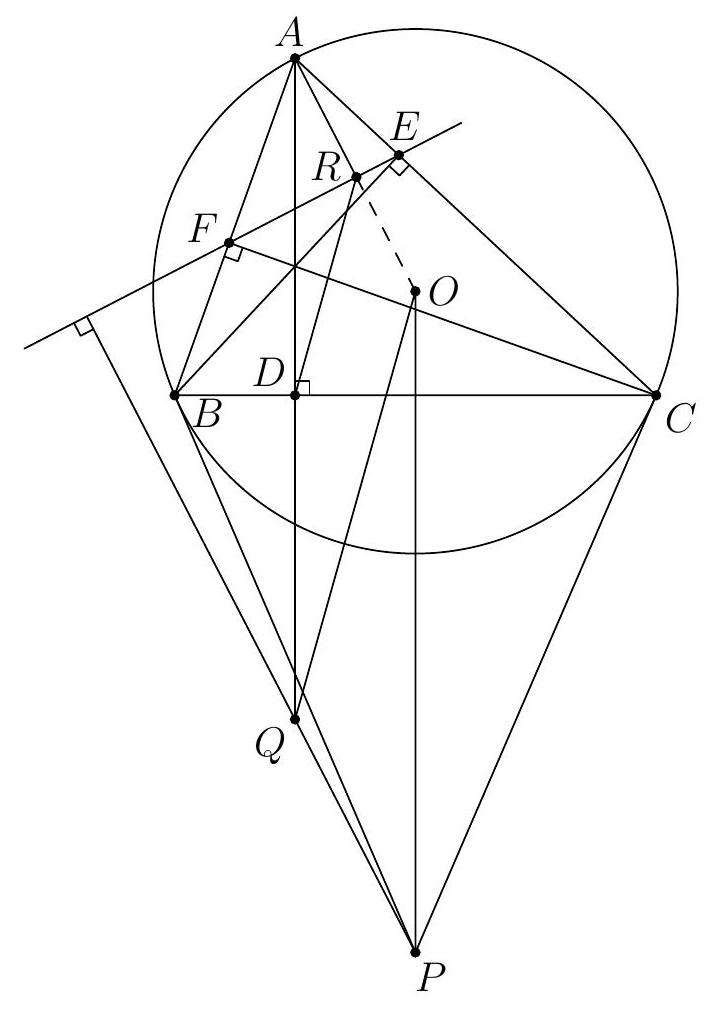
|
Since $O$ is the center of the circumscribed circle, we calculate that
$$
\begin{aligned}
\angle B A O & =\frac{1}{2}\left(180^{\circ}-\angle A O B\right) \\
& =90^{\circ}-\angle A C B \\
& =90^{\circ}-\angle E F A \\
& =\angle F A R,
\end{aligned}
$$
where we also used the fact that $B C E F$ is a cyclic quadrilateral due to Thales, and that $R$ is the orthogonal projection of $A$ onto $E F$. From this, we conclude that $A, R$, and $O$ are collinear. To show that $D R$ and $O Q$ are parallel, it is sufficient to show that $\frac{|A R|}{|A D|}=\frac{|A O|}{|A Q|}$.
Due to the cyclic quadrilateral $B C E F$, we have that $\triangle A E F \sim \triangle A B C$. Under this similarity, the altitude $A R$ maps to the altitude $A D$. (Alternatively, one can simply show that $\triangle A R E \sim \triangle A D B$.) From this, it follows that $\frac{|A R|}{|A D|}=\frac{|A E|}{|A B|}$.
On the other hand, we know that
$$
\angle P O B=\frac{1}{2} \angle C O B=\angle C A B=\angle E A B
$$
due to symmetry and the fact that $O$ is the center of the circumscribed circle. Also, $\angle O B P=90^{\circ}=\angle A E B$. Thus, we find that $\triangle P O B \sim \triangle B A E$, which implies that $\frac{|A E|}{|A B|}=\frac{|B O|}{|O P|}$.
Furthermore, the lines $A O$ and $P Q$ are parallel because they are both perpendicular to $E F$, and the lines $A Q$ and $O P$ are parallel because they are both perpendicular to $B C$. This means that $A O P Q$ is a parallelogram, and in particular, that $|O P|=|A Q|$. We also know that $|B O|=|A O|$. Therefore, we conclude that
$$
\frac{|A R|}{|A D|}=\frac{|A E|}{|A B|}=\frac{|B O|}{|O P|}=\frac{|A O|}{|A Q|}
$$
which implies that $D R$ and $O Q$ are parallel.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $\triangle A B C$ een scherphoekige driehoek zodanig dat $|A B|<|A C|$ met omgeschreven cirkel $\Gamma$ met middelpunt $O$. De punten $D, E$ en $F$ worden geconstrueerd als de voetpunten van de hoogtelijnen vanuit resp. $A, B$ en $C$. Het snijpunt van de raaklijnen aan $\Gamma$ door $B$ en $C$ noemen we $P$. De lijn door $P$ loodrecht op $E F$ snijdt de lijn $A D$ in het punt $Q$. Zij $R$ de loodrechte projectie van $A$ op $E F$.
Bewijs dat de lijnen $D R$ en $O Q$ parallel zijn.

|
Aangezien $O$ het middelpunt van de omgeschreven cirkel is, rekenen we uit dat
$$
\begin{aligned}
\angle B A O & =\frac{1}{2}\left(180^{\circ}-\angle A O B\right) \\
& =90^{\circ}-\angle A C B \\
& =90^{\circ}-\angle E F A \\
& =\angle F A R,
\end{aligned}
$$
waar we ook hebben gebruikt dat $B C E F$ een koordenvierhoek is wegens Thales en dat $R$ de loodrechte projectie is van $A$ op $E F$. Hieruit concluderen we dat $A, R$ en $O$ collineair zijn. Om te laten zien dat $D R$ en $O Q$ parallel zijn, is het dus voldoende om aan te tonen dat $\frac{|A R|}{|A D|}=\frac{|A O|}{|A Q|}$.
Wegens de koordenvierhoek $B C E F$ geldt dat $\triangle A E F \sim \triangle A B C$. Onder deze gelijkvormigheid gaat de hoogtelijn $A R$ over in de hoogtelijn $A D$. (Alternatief kan men gewoon laten zien dat $\triangle A R E \sim \triangle A D B$.) Hieruit volgt dat $\frac{|A R|}{|A D|}=\frac{|A E|}{|A B|}$.
Aan de andere kant weten we dat
$$
\angle P O B=\frac{1}{2} \angle C O B=\angle C A B=\angle E A B
$$
wegens symmetrie en het feit dat $O$ het middelpunt is van de omgeschreven cirkel. Ook geldt dat $\angle O B P=90^{\circ}=\angle A E B$. Dus we vinden dat $\triangle P O B \sim \triangle B A E$ waaruit volgt dat $\frac{|A E|}{|A B|}=\frac{|B O|}{|O P|}$
Verder zijn de lijnen $A O$ en $P Q$ evenwijdig omdat ze allebei loodrecht staan op $E F$, en zijn de lijnen $A Q$ en $O P$ evenwijdig omdat ze allebei loodrecht staan op $B C$. Dit betekent dat $A O P Q$ een parallellogram is, en in het bijzonder dat $|O P|=|A Q|$. Ook weten we natuurlijk dat $|B O|=|A O|$. We concluderen dus dat
$$
\frac{|A R|}{|A D|}=\frac{|A E|}{|A B|}=\frac{|B O|}{|O P|}=\frac{|A O|}{|A Q|}
$$
waaruit volgt dat $D R$ en $O Q$ parallel zijn.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2024-C2024_uitwerkingen.jsonl",
"solution_match": "\nOplossing 1.",
"tier": "T1",
"year": "2024"
}
|
Let $\triangle A B C$ be an acute triangle such that $|A B|<|A C|$ with circumcircle $\Gamma$ and center $O$. The points $D, E$, and $F$ are constructed as the feet of the altitudes from $A, B$, and $C$ respectively. The intersection of the tangents to $\Gamma$ at $B$ and $C$ is denoted as $P$. The line through $P$ perpendicular to $E F$ intersects the line $A D$ at point $Q$. Let $R$ be the orthogonal projection of $A$ onto $E F$.
Prove that the lines $D R$ and $O Q$ are parallel.

|
Just as in solution 1, $A, R$, and $O$ are collinear. We will again prove that $\frac{|A R|}{|A D|}=\frac{|A O|}{|A Q|}$.
Due to the cyclic quadrilateral $B C E F$, it holds that $\triangle A E F \sim \triangle A B C$. Under this similarity, the altitude $A R$ corresponds to the altitude $A D$. Let $M$ be the midpoint of $B C$. By Thales, $M$ is the center of the circumcircle of $B C E F$. Thus, we calculate that $\angle E F M=\angle F E M=\frac{1}{2}\left(180^{\circ}-\angle E M F\right)=90^{\circ}-\angle E C F=\angle B A C=\angle F A E$. From this, it follows that $E M$ and $F M$ are tangents to the circumcircle of $\triangle A E F$ (by the tangent-secant angle theorem). Therefore, $M$ corresponds to $P$ in the similarity between $\triangle A E F$ and $\triangle A B C$.
To find the point that corresponds to $Q$ in $\triangle A E F$, we need to construct the feet of the perpendiculars from $E$ and $F$ in this triangle. We call these points $B^{\prime}$ and $C^{\prime}$, respectively. Then, $\angle A B^{\prime} C^{\prime}=\angle A E F=\angle A B C$. Thus, $B^{\prime} C^{\prime} \| B C$. Note that $Q$ is defined with respect to $\triangle A B C$ as the intersection of $A D$ with the perpendicular from $P$ to $E F$. The corresponding point in $\triangle A E F$ is therefore the intersection of $A R$ with the perpendicular from $M$ to $B^{\prime} C^{\prime} \| B C$, which is the point $O$. The ratio of corresponding segments is the same, so
$$
\frac{|A R|}{|A D|}=\frac{|A O|}{|A Q|}
$$
from which it follows that $D R$ and $O Q$ are parallel.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $\triangle A B C$ een scherphoekige driehoek zodanig dat $|A B|<|A C|$ met omgeschreven cirkel $\Gamma$ met middelpunt $O$. De punten $D, E$ en $F$ worden geconstrueerd als de voetpunten van de hoogtelijnen vanuit resp. $A, B$ en $C$. Het snijpunt van de raaklijnen aan $\Gamma$ door $B$ en $C$ noemen we $P$. De lijn door $P$ loodrecht op $E F$ snijdt de lijn $A D$ in het punt $Q$. Zij $R$ de loodrechte projectie van $A$ op $E F$.
Bewijs dat de lijnen $D R$ en $O Q$ parallel zijn.

|
Net als in oplossing 1 geldt dat $A, R$ en $O$ collineair zijn. We gaan weer bewijzen dat $\frac{|A R|}{|A D|}=\frac{|A O|}{|A Q|}$.
Wegens de koordenvierhoek $B C E F$ geldt dat $\triangle A E F \sim \triangle A B C$. Onder deze gelijkvormigheid gaat de hoogtelijn $A R$ over in de hoogtelijn $A D$. Noem $M$ het midden van $B C$. Dat is wegens Thales het middelpunt van de omgeschreven cirkel van $B C E F$. Dus berekenen we dat $\angle E F M=\angle F E M=\frac{1}{2}\left(180^{\circ}-\angle E M F\right)=90^{\circ}-\angle E C F=\angle B A C=\angle F A E$. Hieruit volgt dat $E M$ en $F M$ raaklijnen zijn aan de omgeschreven cirkel van $\triangle A E F$ (wegens raaklijnomtrekshoekstelling). Dus correspondeert $M$ met $P$ in de gelijkvormigheid tussen $\triangle A E F$ en $\triangle A B C$.
Om het punt te vinden dat met $Q$ correspondeert in $\triangle A E F$ moeten we in deze driehoek nu de voetpunten van $E$ en $F$ construeren. Deze noemen we respectievelijk $B^{\prime}$ en $C^{\prime}$. Dan geldt dat $\angle A B^{\prime} C^{\prime}=\angle A E F=\angle A B C$. Dus $B^{\prime} C^{\prime} \| B C$. Bedenk dat $Q$ gedefinieerd t.o.v. $\triangle A B C$ is als het snijpunt van $A D$ met de loodlijn door $P$ op $E F$. Het corresponderende punt van $\triangle A E F$ is dus het snijpunt van $A R$ met de loodlijn door $M$ op $B^{\prime} C^{\prime} \| B C$, oftewel het punt $O$. De verhouding tussen corresponderende lijnstukken is hetzelfde, dus
$$
\frac{|A R|}{|A D|}=\frac{|A O|}{|A Q|}
$$
waaruit volgt dat $D R$ en $O Q$ parallel zijn.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2024-C2024_uitwerkingen.jsonl",
"solution_match": "\nOplossing 2.",
"tier": "T1",
"year": "2024"
}
|
Given triangle $\triangle A B C$ with orthocenter $H$, and circumcircle $\Gamma$. Let $D$ be the reflection of $A$ in $B$, and let $E$ be the reflection of $A$ in $C$. The midpoint of segment $D E$ is denoted as $M$.
Prove that the tangent to $\Gamma$ at $A$ is perpendicular to $H M$.
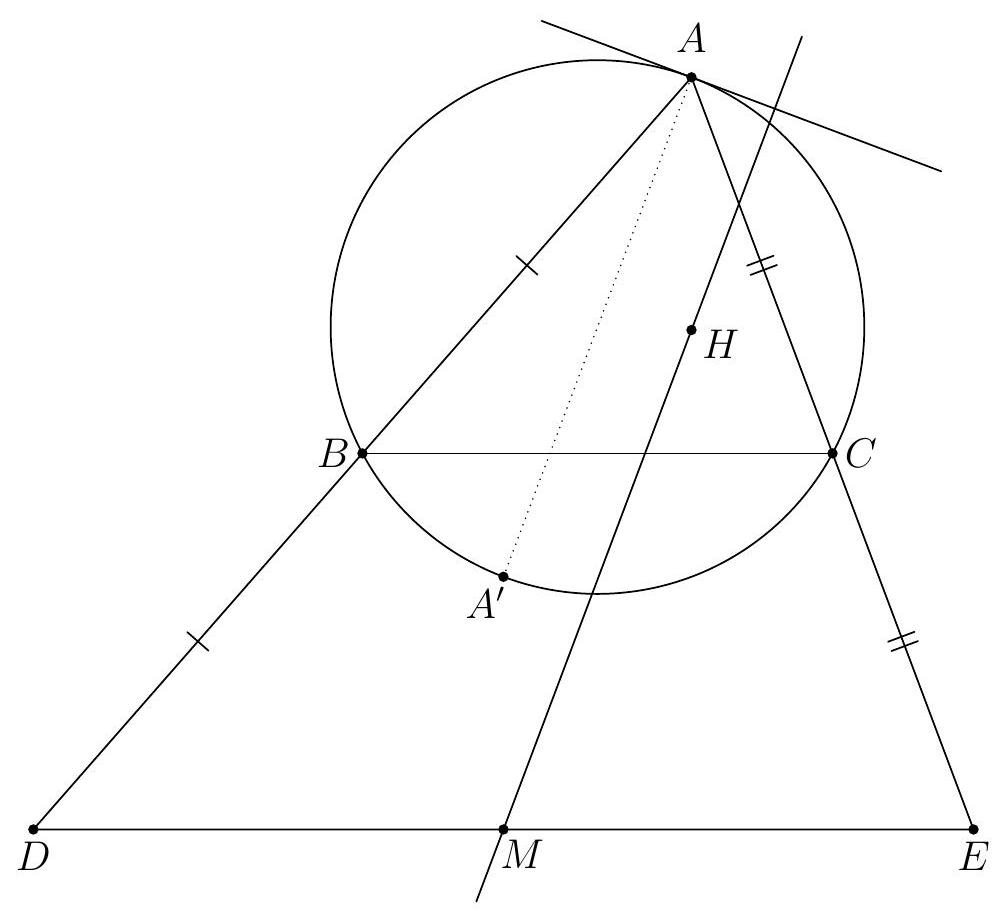
|
Let $A^{\prime}$ be the reflection of $H$ in the midpoint of $B C$. Since $A$ is the reflection of $M$ in the midpoint of $B C$, we note that $A^{\prime} A$ is parallel to $H M$ (since these line segments are point reflections of each other). Furthermore, $A^{\prime}$ is one of the so-called orthocentric points: $A^{\prime}$ lies on $\Gamma$ and is the antipode of $A$. Indeed, the first follows from the cyclic quadrilateral theorem, for which we calculate that
$$
\angle B A^{\prime} C=\angle C H B=180^{\circ}-\angle B C H-\angle H B C=\angle A B C+\angle B C A=\angle 180^{\circ}-\angle C A B .
$$
Similarly, the reflection $A^{\prime \prime}$ of $H$ in the line $B C$ lies on $\Gamma$. Since $A H$ and $H A^{\prime \prime}$ are both perpendicular to $B C$, $A, H$ and $A^{\prime \prime}$ are collinear and since $A^{\prime} A^{\prime \prime}$ is parallel to $B C$ we find that $A^{\prime} A^{\prime \prime} \perp A A^{\prime \prime}$. By Thales, this means that $A^{\prime} A$ is a diameter of $\Gamma$ and thus perpendicular to the tangent at $A$. Therefore, $H M$ is also perpendicular to this.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij gegeven driehoek $\triangle A B C$ met hoogtepunt $H$, en omgeschreven cirkel $\Gamma$. Zij verder $D$ de spiegeling van $A$ in $B$, en zij $E$ de spiegeling van $A$ in $C$. Het midden van lijnstuk $D E$ noemen we $M$.
Bewijs dat de raaklijn aan $\Gamma$ in $A$ loodrecht staat op $H M$.

|
Zij $A^{\prime}$ de spiegeling van $H$ in het midden van $B C$. Omdat $A$ de spiegeling is van $M$ in het midden van $B C$, merken we op dat $A^{\prime} A$ parallel is aan $H M$ (want deze lijnstukken zijn puntspiegelingen van elkaar). Verder is $A^{\prime}$ een van de zogenaamde dieptepunten: $A^{\prime}$ ligt op $\Gamma$ en is de antipodaal van $A$. Inderdaad, het eerste volgt uit de koordenvierhoekstelling waarvoor we uitrekenen dat
$$
\angle B A^{\prime} C=\angle C H B=180^{\circ}-\angle B C H-\angle H B C=\angle A B C+\angle B C A=\angle 180^{\circ}-\angle C A B .
$$
Evenzo ligt de spiegeling $A^{\prime \prime}$ van $H$ in de lijn $B C$ op $\Gamma$. Omdat $A H$ en $H A^{\prime \prime}$ allebei loodrecht op $B C$ staan, zijn $A, H$ en $A^{\prime \prime}$ collineair en omdat $A^{\prime} A^{\prime \prime}$ parallel is aan $B C$ vinden we dat $A^{\prime} A^{\prime \prime} \perp A A^{\prime \prime}$. Met Thales betekent dit dat $A^{\prime} A$ een diameter is van $\Gamma$ en dus loodrecht staat op de raaklijn in $A$. Dus $H M$ staat ook loodrecht hierop.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2024-D2024_uitwerkingen.jsonl",
"solution_match": "\nOplossing 1.",
"tier": "T1",
"year": "2024"
}
|
Given triangle $\triangle A B C$ with orthocenter $H$, and circumcircle $\Gamma$. Let $D$ be the reflection of $A$ in $B$, and let $E$ be the reflection of $A$ in $C$. The midpoint of segment $D E$ is denoted as $M$.
Prove that the tangent to $\Gamma$ at $A$ is perpendicular to $H M$.

|
Let $A^{\prime}$ be the reflection of $H$ in the midpoint of $B C$, just as in Solution 1. Let $O$ be the center of $\Gamma$ and $N$ the midpoint of $B C$. Due to the reflection, $A^{\prime}$ is also the orthocenter in $\triangle B C M$. Since $\triangle B C M$ is the medial triangle of $\triangle A D E$, $A^{\prime}$ is also the circumcenter of the circumcircle of $\triangle A D E$. Now we perform a homothety centered at $A$ with factor $\frac{1}{2}$ and a homothety centered at $A^{\prime}$ with factor 2. This gives
$$
\left|M A^{\prime}\right|=2|N O|=|H A|
$$
Now the segments $M A^{\prime}$ and $H A$ are of equal length, and they were already parallel (both perpendicular to $B C$). Therefore, $A H M A^{\prime}$ is a parallelogram (possibly degenerate). We conclude that $H M$ is parallel to $A A^{\prime}$ and thus perpendicular to the tangent at $A$. (If $A H M A^{\prime}$ is degenerate, then $H M$ coincides with $A A^{\prime}$, so it is already perpendicular to the tangent at $A$.)
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij gegeven driehoek $\triangle A B C$ met hoogtepunt $H$, en omgeschreven cirkel $\Gamma$. Zij verder $D$ de spiegeling van $A$ in $B$, en zij $E$ de spiegeling van $A$ in $C$. Het midden van lijnstuk $D E$ noemen we $M$.
Bewijs dat de raaklijn aan $\Gamma$ in $A$ loodrecht staat op $H M$.

|
Zij $A^{\prime}$ de spiegeling van $H$ in het midden van $B C$, net als in Oplossing 1. Zij $O$ verder het middelpunt van $\Gamma$ en $N$ het midden van $B C$. Wegens de spiegeling is $A^{\prime}$ ook het hoogtepunt in $\triangle B C M$. Aangezien $\triangle B C M$ de middendriehoek is van $\triangle A D E$ is $A^{\prime}$ daarmee ook het middelpunt van de omgeschreven cirkel van $\triangle A D E$. Nu doen we een puntvermenigvuldiging vanuit $A$ met factor $\frac{1}{2}$ en een puntvermenigvuldiging vanuit $A^{\prime}$ met factor 2. Dit geeft
$$
\left|M A^{\prime}\right|=2|N O|=|H A|
$$
Nu zijn de stukjes $M A^{\prime}$ en $H A$ dus even lang, en ze waren al evenwijdig (want allebei loodrecht op $B C$ ). Dus $A H M A^{\prime}$ is een parallellogram (mogelijk gedegenereerd). We concluderen dat $H M$ parallel is met $A A^{\prime}$ en dus loodrecht op de raaklijn in $A$ staat. (Als $A H M A^{\prime}$ gedegenereerd is, dan valt $H M$ samen met $A A^{\prime}$, dus staat die meteen al loodrecht op de raaklijn in $A$.)
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2024-D2024_uitwerkingen.jsonl",
"solution_match": "\nOplossing 2.",
"tier": "T1",
"year": "2024"
}
|
Given triangle $\triangle A B C$ with orthocenter $H$, and circumcircle $\Gamma$. Let $D$ be the reflection of $A$ in $B$, and let $E$ be the reflection of $A$ in $C$. The midpoint of segment $D E$ is denoted as $M$.
Prove that the tangent to $\Gamma$ at $A$ is perpendicular to $H M$.

|
It is given that $BC$ is parallel to $DE$ (since $BC$ is the midline of $\triangle ADE$), so the perpendicular from $A$ to $BC$ is also perpendicular to $DE$. Let $F$ be the foot of the perpendicular from $A$ to $DE$, and $H'$ be the orthocenter of $\triangle ADE$. Thus, we know that $A, H, H'$, and $F$ are collinear. Let $V$ be the intersection of $HM$ with the tangent to $\Gamma$ at $A$. We first consider the case that $V \neq A$. Assume without loss of generality that $V$ lies on the side of $C$. We want to show that $\angle AV M = 90^\circ$, and since $\angle AFM = 90^\circ$, it suffices to prove that $AMFV$ is a cyclic quadrilateral.
We will do this by showing that $\angle VAF = \angle VMF$. However, before we can begin, we need to introduce two new points: let $G$ be the foot of the altitude from $D$, and $I$ be the foot of the altitude from $E$. It follows that $\angle VAF = \angle VAC + \angle CAF = \angle ABC + 90^\circ - \angle AEF = \angle ADE + \angle GDE = 2\angle GDE + \angle ADG$. On the other hand, $\angle VMF = \angle VMG + \angle GMF$. Since $\angle EGD = 90^\circ$, $M$ is the center of the circle through $D, E$, and $G$. The inscribed angle theorem then states that $2\angle GDE = \angle GMF$, so we only need to prove that $\angle ADG = \angle VMG$.
Since $|AD| = 2|AB|$ and $|AE| = 2|AC|$, the triangle $ADE$ can be obtained by scaling triangle $ABC$ from $A$ by a factor of 2. This also means that $|AH'| = 2|AH|$, so $H$ is the midpoint of $AH'$. This implies that the nine-point circle of $ADE$ passes through $H$, and we also know that $B, M, F, G, C$, and $I$ lie on this circle. Together with the cyclic quadrilaterals $H'FEG (\angle EGH' = 90^\circ = \angle EFH')$ and $DEGI$ ($\angle EGD = 90^\circ = \angle EID$), we can complete the proof: $\angle VMG = \angle HMG = \angle HFG = \angle H'FG = \angle H'EG = \angle IEG = \angle IDG = \angle ADG$. This proves that $\angle ADG = \angle VMG$, from which it follows that $\angle VAF = 2\angle GDE + \angle ADG = \angle GMF + \angle VMG = \angle VMF$, so $AMFV$ is a cyclic quadrilateral, which implies that $HM$ is perpendicular to $AV$, exactly as we wanted to prove.
Now we have the case that $V = A$. Let the tangent to $\Gamma$ at $A$ be $\ell$. Then we find in the same way that $\angle(\ell, AF) = \angle(\ell, AC) + \angle CAF = \ldots = \angle VMF = \angle AMF$. Now we do not have a cyclic quadrilateral, but we see that $\ell$ is a tangent to the circumcircle of $\triangle AMF$. For this circumcircle, $AM$ is naturally a diameter (by Thales' theorem), so $\ell$ is perpendicular to $AM = HM$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij gegeven driehoek $\triangle A B C$ met hoogtepunt $H$, en omgeschreven cirkel $\Gamma$. Zij verder $D$ de spiegeling van $A$ in $B$, en zij $E$ de spiegeling van $A$ in $C$. Het midden van lijnstuk $D E$ noemen we $M$.
Bewijs dat de raaklijn aan $\Gamma$ in $A$ loodrecht staat op $H M$.

|
Er geldt dat $B C$ parallel is met $D E$ (want $B C$ is de middenparallel van $\triangle A D E$ ), dus de loodlijn vanuit $A$ op $B C$ staat ook loodrecht op $D E$. Zij $F$ het voetpunt van $A$ op $D E$, en $H^{\prime}$ het hoogtepunt van driehoek $A D E$, dan weten we dus dat $A, H$, $H^{\prime}$ en $F$ collinear zijn. Laat $V$ het snijpunt zijn van $H M$ met de raaklijn aan $\Gamma$ in $A$. We bekijken eerst het gaval dat $V \neq A$. Neem dan z.v.v.a. aan dat $V$ aan de kant van $C$ ligt. We willen laten zien dat $\angle A V M=90^{\circ}$, en omdat $\angle A F M=90^{\circ}$, voldoet het om de koordenvierhoek $A M F V$ te bewijzen.
Dit gaan we doen door $\angle V A F$ en $\angle V M F$ aan elkaar gelijk te praten. Alleen voordat we kunnen beginnen moeten we nog twee nieuwe punten introduceren: laat $G$ het voetpunt van de hoogtelijn uit $D$ zijn, en $I$ het voetpunt van de hoogtelijn uit $E$. Er geldt nu dat $\angle V A F=\angle V A C+\angle C A F=\angle A B C+90^{\circ}-\angle A E F=\angle A D E+\angle G D E=2 \angle G D E+$ $\angle A D G$. Aan de andere kant geldt dat $\angle V M F=\angle V M G+\angle G M F$. Omdat $\angle E G D=90^{\circ}$, is $M$ het middelpunt van de cirkel door $D, E$ en $G$. De middelpunt-omtrekshoekstelling zegt vervolgens dat $2 \angle G D E=\angle G M F$, waarmee we enkel nog hoeven te bewijzen dat $\angle A D G=\angle V M G$.
Omdat $|A D|=2|A B|$ en $|A E|=2|A C|$, geldt dat de driehoek $A D E$ verkregen kan worden door driehoek $A B C$ vanuit $A$ met een factor 2 te schalen. Hierdoor geldt ook dat $\left|A H^{\prime}\right|=$ $2|A H|$, dus $H$ is het midden van $A H^{\prime}$. Dit betekent dat de negenpuntcirkel van $A D E$ door $H$ gaat, en verder weten we ook dat $B, M, F, G, C$ en $I$ op deze cirkel liggen. Samen met de koordenvierhoeken $H^{\prime} F E G\left(\angle E G H^{\prime}=90^{\circ}=\angle E F H^{\prime}\right)$ en $D E G I$ ( $\angle E G D=$
$\left.90^{\circ}=\angle E I D\right)$ kunnen we de opgave afmaken: $\angle V M G=\angle H M G=\angle H F G=\angle H^{\prime} F G=$ $\angle H^{\prime} E G=\angle I E G=\angle I D G=\angle A D G$. Hiermee hebben we $\angle A D G=\angle V M G$ bewezen, waaruit volgt dat $\angle V A F=2 \angle G D E+\angle A D G=\angle G M F+\angle V M G=\angle V M F$, dus $A M F V$ is een koordenvierhoek, waaruit volgt dat $H M$ loodrecht staat op $A V$, precies zoals we wilden bewijzen.
Nu hebben we nog het geval dat $V=A$. Noem de raaklijn aan $\Gamma$ in $A$ even $\ell$. Dan vinden we op dezelfde manier dat $\angle(\ell, A F)=\angle(\ell, A C)+\angle C A F=\ldots=\angle V M F=\angle A M F$. Nu hebben we geen koordenvierhoek, maar we zien wel dat $\ell$ een raaklijn is aan de omgeschreven cirkel van $\triangle A M F$. Van die omgeschreven cirkel is $A M$ natuurlijk een diameter (wegens Thales), dus $\ell$ staat loodrecht op $A M=H M$.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2024-D2024_uitwerkingen.jsonl",
"solution_match": "\nOplossing 3.",
"tier": "T1",
"year": "2024"
}
|
Given triangle $\triangle A B C$ with orthocenter $H$, and circumcircle $\Gamma$. Let $D$ be the reflection of $A$ in $B$, and let $E$ be the reflection of $A$ in $C$. The midpoint of segment $D E$ is denoted as $M$.
Prove that the tangent to $\Gamma$ at $A$ is perpendicular to $H M$.

|
Note that $A B M C$ is a parallelogram. Therefore, if we reflect in the intersection of the diagonals, $A B M C$ maps onto itself. Let $X$ and $Y$ be the reflection points of $D$ and $E$ respectively (still in the intersection of the diagonals of $A B M C$), then we have a triangle $\triangle X Y M$, with medial triangle $\triangle A B C$. Since the center of the circumcircle is the orthocenter of the medial triangle, $H$ is the center of the circumcircle of $\triangle X Y M$.
Let $V$ be the intersection of $H M$ with the tangent to $\Gamma$ at $A$. We first consider the case that $V \neq A$. Assume without loss of generality that $V$ lies on the side of $C$. Then we have $\angle V A C=\angle A B C=\angle A X C=\angle Y X M$. Let $Z$ be the intersection of $A C$ with $M H$. Then $\angle V Z A=\angle H M Y$. By the inscribed angle theorem, $2 \angle Y X M+2 \angle H M Y=\angle Y H M+\angle H M Y+\angle H Y M=180^{\circ}$, so $\angle Y X M+\angle H M Y=90^{\circ}$. But we have $\angle A V Z=180^{\circ}-\angle V A C-\angle V Z A=180^{\circ}-(\angle Y X M+\angle H M Y)=$ $180^{\circ}-90^{\circ}=90^{\circ}$, which implies that $H M$ and $A V$ are perpendicular to each other.
In the case that $V=A$, we call the tangent to $\Gamma$ at $A$ again $\ell$. Then $\angle(\ell, A C)=\angle Y X M$ and $\angle M Z E=\angle H M Y$. Therefore, the angle $\angle(\ell, H M)=\angle(\ell, A C)+$ $\angle M A C=\angle(\ell, A C)+\angle M Z E=\angle Y X M+\angle H M Y=90^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij gegeven driehoek $\triangle A B C$ met hoogtepunt $H$, en omgeschreven cirkel $\Gamma$. Zij verder $D$ de spiegeling van $A$ in $B$, en zij $E$ de spiegeling van $A$ in $C$. Het midden van lijnstuk $D E$ noemen we $M$.
Bewijs dat de raaklijn aan $\Gamma$ in $A$ loodrecht staat op $H M$.

|
Merk op dat $A B M C$ een paralellogram is. Dus als we spiegelen in het snijpunt van de diagonalen gaat $A B M C$ in zichzelf over. Laat $X$ en $Y$ het spiegelpunt van resp. $D$ en $E$ zijn (nog steeds in het snijpunt van de diagonalen van $A B M C$ ), dan hebben we een driehoek $\triangle X Y M$, met middendriehoek $\triangle A B C$. Omdat het middelpunt van de omgeschreven cirkel het hoogtepunt van de middendriehoek is, is $H$ het middelpunt van de omgeschreven cirkel van $\triangle X Y M$.
Laat $V$ het snijpunt zijn van $H M$ met de raaklijn aan $\Gamma$ in $A$. We bekijken eerst het geval dat $V \neq A$. Neem dan z.v.v.a. aan dat $V$ aan de kant van $C$ ligt. Er geldt dan dat $\angle V A C=\angle A B C=\angle A X C=\angle Y X M$. Laat $Z$ het snijpunt zijn van $A C$ met $M H$. Dan geldt er $\angle V Z A=\angle H M Y$. Wegens de middelpuntomtrekshoekstelling geldt $2 \angle Y X M+2 \angle H M Y=\angle Y H M+\angle H M Y+\angle H Y M=180^{\circ}$, dus $\angle Y X M+\angle H M Y=90^{\circ}$. Maar we hebben $\angle A V Z=180^{\circ}-\angle V A C-\angle V Z A=180^{\circ}-(\angle Y X M+\angle H M Y)=$ $180^{\circ}-90^{\circ}=90^{\circ}$, waaruit volgt dat $H M$ en $A V$ loodrecht op elkaar staan.
In het geval dat $V=A$ noemen we de raaklijn aan $\Gamma$ in $A$ weer even $\ell$. Dan geldt $\angle(\ell, A C)=\angle Y X M$ en $\angle M Z E=\angle H M Y$. Dus de hoek $\angle(\ell, H M)=\angle(\ell, A C)+$ $\angle M A C=\angle(\ell, A C)+\angle M Z E=\angle Y X M+\angle H M Y=90^{\circ}$.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2024-D2024_uitwerkingen.jsonl",
"solution_match": "\nOplossing 4.",
"tier": "T1",
"year": "2024"
}
|
Find all functions $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}_{>0}$ such that for all positive integers $m$, $n$, and $a$ the following conditions hold:
a) $f(f(m) f(n))=m n$,
b) $f(2024 a+1)=2024 a+1$.
|
If we were allowed to plug in $a=0$, we would find $f(1)=1$. With $n=1$, we then get $f(f(m))=m$, so $f$ is bijective. Unfortunately, we are not allowed to plug in $a=0$, but it does put us on the right track.
We start by plugging in $n=1$. This gives us $f(f(m) f(1))=m$, which means that $f$ is bijective. Indeed, if $f(m)=f(n)$, then we directly get $m=f(f(m) f(1))=f(f(n) f(1))=n$ and for every $m$ there is an $a$ such that $f(a)=m$, namely $a=f(m) f(1)$. Now we plug in $m=n$, which gives us $f(f(m)^2)=m^2=f(f(m^2) f(1))$. Due to the injectivity of $f$, it follows that $f(m)^2=f(m^2) f(1)$. Choose now $m_1$ such that $f(m_1)=1$. (From our proof of surjectivity, we can choose $m_1=f(1)^2$, but that is not important.) If we plug in $m=m_1$ in the above, we get $1=f(m_1^2) f(1)$. In particular, $f(1)$ is a divisor of 1, and since it must be a natural number, we conclude that $f(1)=1$.
If we now plug in $n=1$ again, we find that $f(f(m))=m$. Now we can plug in $f(m)$ and $f(n)$ for $m$ and $n$ so that we get the more classical equation
$$
f(m n)=f(f(f(m)) f(f(n)))=f(m) f(n)
$$
This means that $f$ is determined by the values $f(p)$ with $p$ prime.
Suppose we have an arbitrary prime number $p$, and let $m$ and $n$ be natural numbers such that $f(p)=m n$. It follows that $f(m) f(n)=f(m n)=f(f(p))=p$. Since $f(m)$ and $f(n)$ are natural numbers, it must be that $f(m)=1$ or $f(n)=1$. Due to injectivity, the only $m$ for which $f(m)=1$ is the number $m=1$. Therefore, $m=1$ or $n=1$. We conclude that $f(p)$ is a prime number.
Now suppose that $p \nmid 2024$. In particular, this means that $\operatorname{gcd}(p, 2024)=1$, so $p$ has a multiplicative inverse modulo 2024. Let $b$ be a natural number in the residue class of the inverse, i.e., $b p \equiv 1 \bmod 2024$. Since $b p \geq p > 1$, it follows from the second equation that $f(b p)=b p$, but also that $f(b p + 2024 p)=b p + 2024 p$. From the previous paragraph, however, it follows that $f(b p)=f(b) f(p)$ and $f((b+2024) p)=f(b+2024) f(p)$. This means that $f(p)$ is a divisor of both $b p$ and $b p + 2024 p$. Now we calculate that
$$
\operatorname{gcd}(b p, b p + 2024 p) = \operatorname{gcd}(b p, 2024 p) = \operatorname{gcd}(b, 2024) p = p,
$$
since $b$ is the multiplicative inverse of $p$ modulo 2024. Due to injectivity, we know that $f(p) \neq 1$, so $f(p) \mid p$ implies that $f(p)=p$.
Suppose for a $p \mid 2024$ that $f(p)=q$, with $q \neq p$ another prime number. Then it follows that $f(q)=f(f(p))=p$. So all prime numbers that do not map to themselves by $f$ form pairs $(p, q)$ with $f(p)=q$ and $f(q)=p$. Since $2024=2^3 \cdot 11 \cdot 23$, we have four solutions:
- $f(p)=p$ for all prime numbers $p$. So $f$ is the identity,
- $f(2)=11, f(11)=2$ and $f(p)=p$ for all $p \notin \{2,11\}$,
- $f(2)=23, f(23)=2$ and $f(p)=p$ for all $p \notin \{2,23\}$,
- $f(11)=23, f(23)=11$ and $f(p)=p$ for all $p \notin \{11,23\}$.
It is easy to check that these functions also satisfy the conditions.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Vind alle functies $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}_{>0}$ zo dat voor alle positieve gehele getallen $m$, $n$ en $a$ geldt dat
a) $f(f(m) f(n))=m n$,
b) $f(2024 a+1)=2024 a+1$.
|
Als we $a=0$ zouden mogen invullen, vinden we $f(1)=1$. Met $n=1$ krijgen we dan $f(f(m))=m$, dus $f$ is bijectief. Helaas mogen we $a=0$ niet invullen, maar het zet ons wel op het goede spoor.
We beginnen met invullen van $n=1$. Dit geeft dat $f(f(m) f(1))=m$, wat betekent dat $f$ bijectief is. Inderdaad, als $f(m)=f(n)$ dan volgt direct $m=f(f(m) f(1))=$ $f(f(n) f(1))=n$ en voor elke $m$ is er een $a$ zo dat $f(a)=m$ namelijk $a=f(m) f(1)$. Nu vullen we $m=n$ in, waardoor we krijgen dat $f\left(f(m)^{2}\right)=m^{2}=f\left(f\left(m^{2}\right) f(1)\right)$. Wegens de injectiviteit van $f$ volgt hieruit dat $f(m)^{2}=f\left(m^{2}\right) f(1)$. Kies nu $m_{1}$ waarvoor geldt dat $f\left(m_{1}\right)=1$. (Uit ons bewijs voor surjectiviteit volgt dat we hiervoor $m_{1}=f(1)^{2}$ kunnen kiezen, maar dat is niet belangrijk.) Als we $m=m_{1}$ in het voorgaande invullen krijgen we dat $1=f\left(m_{1}^{2}\right) f(1)$. In het bijzonder is $f(1)$ een deler van 1 , en omdat het een natuurlijk getal moet zijn concluderen we dat $f(1)=1$.
Als we nu opnieuw $n=1$ invullen vinden we dus alsnog dat $f(f(m))=m$. Nu kunnen we $f(m)$ en $f(n)$ invullen voor $m$ en $n$ zodat we uitkomen op de klassiekere vergelijking
$$
f(m n)=f(f(f(m)) f(f(n)))=f(m) f(n)
$$
Dit betekent dat $f$ bepaald wordt door de waardes $f(p)$ met $p$ priem.
Stel dat we een willekeurig priemgetal $p$ hebben, en laat $m$ en $n$ naturlijke getallen zijn zo dat $f(p)=m n$. Dan volgt dat $f(m) f(n)=f(m n)=f(f(p))=p$. Aangezien $f(m)$ en $f(n)$ natuurlijke getallen zijn, moet er gelden dat $f(m)=1$ of $f(n)=1$. Wegens injectiviteit is de enige $m$ waarvoor $f(m)=1$ het getal $m=1$. Dus $m=1$ of $n=1$. We concluderen dat $f(p)$ een priemgetal is.
Stel nu dat er geldt dat $p \nmid 2024$. In het bijzonder betekent dit dat $\operatorname{ggd}(p, 2024)=1$, dus $p$ heeft een multiplicatieve inverse modulo 2024. Zij $b$ een natuurlijk getal in de restklasse van de inverse, oftewel $b p \equiv 1 \bmod 2024$. Omdat $b p \geq p>1$ volgt uit de tweede vergelijking dat $f(b p)=b p$, maar ook dat $f(b p+2024 p)=b p+2024 p$. Uit de vorige alinea volgt echter dat $f(b p)=f(b) f(p)$ en $f((b+2024) p)=f(b+2024) f(p)$. Dat betekent dat $f(p)$ een deler is van zowel $b p$ als $b p+2024 p$. Nu rekenen we uit dat
$$
\operatorname{ggd}(b p, b p+2024 p)=\operatorname{ggd}(b p, 2024 p)=\operatorname{ggd}(b, 2024) p=p,
$$
aangezien $b$ de multiplicatieve inverse is van $p$ modulo 2024. Wegens injectiviteit weten we dat $f(p) \neq 1$, dus dat $f(p) \mid p$ impliceert dat $f(p)=p$.
Stel voor een $p \mid 2024$ dat $f(p)=q$, met $q \neq p$ een ander priemgetal. Dan volgt dat $f(q)=f(f(p))=p$. Dus alle priemgetallen die niet naar zichzelf worden gestuurd door $f$ vormen paren $(p, q)$ met $f(p)=q$ en $f(q)=p$. Aangezien $2024=2^{3} \cdot 11 \cdot 23$ hebben we vier oplossingen:
- $f(p)=p$ voor alle priemgetallen $p$. Dus $f$ is de identiteit,
- $f(2)=11, f(11)=2$ en $f(p)=p$ voor alle $p \notin\{2,11\}$,
- $f(2)=23, f(23)=2$ en $f(p)=p$ voor alle $p \notin\{2,23\}$,
- $f(11)=23, f(23)=11$ en $f(p)=p$ voor alle $p \notin\{11,23\}$.
Het is eenvoudig te controleren dat deze functies ook daadwerkelijk voldoen.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2024-D2024_uitwerkingen.jsonl",
"solution_match": "\nOplossing 1.",
"tier": "T1",
"year": "2024"
}
|
Find all functions $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}_{>0}$ such that for all positive integers $m$, $n$, and $a$ the following conditions hold:
a) $f(f(m) f(n))=m n$,
b) $f(2024 a+1)=2024 a+1$.
|
We first prove that $f$ is injective. Suppose that $f(k)=f(\ell)$. Then it follows from a) that
$$
k=f(f(k) f(1))=f(f(\ell) f(1))=\ell
$$
Thus, $f$ is injective. Now, by b) with $a=1$, we have
$$
f(2025 f(1))=f(f(2025) f(1))=2025=f(2025)
$$
Therefore, by injectivity, $2025 f(1)=2025$, which means $f(1)=1$.
Now we have
$$
f(f(m) f(n))=m n=1 \cdot m n=f(f(1) f(m n))=f(f(m n)),
$$
which, with injectivity, leads to $f(m) f(n)=f(m n)$. By also substituting $m=1$ into a), we find $f(f(n))=n$. Thus, $f$ is even bijective.
Just like in the first solution, we see that $f$ is defined by its values on the prime numbers, and that $f$ maps prime numbers to prime numbers.
Now suppose that $p \nmid 2024$. Since $\operatorname{gcd}(p, 2024)=1$, we have $p^{\varphi(2024)} \equiv 1 \bmod 2024$. Thus, $p^{\varphi(2024)}=2024 a+1$ for some $a>0$. By b), this implies that $f\left(p^{\varphi(2024)}\right)=$ $p^{\varphi(2024)}$. Due to the multiplicativity $f(m n)=f(m) f(n)$, this means that $f(p)^{\varphi(2024)}=$ $p^{\varphi(2024)}$. Since these are powers of positive integers, it follows that $f(p)=p$.
Just like in solution 1, $f$ can only permute 2, 11, and 23, and the rest of the solution proceeds in the same way.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Vind alle functies $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}_{>0}$ zo dat voor alle positieve gehele getallen $m$, $n$ en $a$ geldt dat
a) $f(f(m) f(n))=m n$,
b) $f(2024 a+1)=2024 a+1$.
|
We bewijzen eerst dat $f$ injectief is. Stel dat $f(k)=f(\ell)$. Dan volgt uit a) dat
$$
k=f(f(k) f(1))=f(f(\ell) f(1))=\ell
$$
Dus $f$ is injectief. Nu geldt wegens b) met $a=1$ dat
$$
f(2025 f(1))=f(f(2025) f(1))=2025=f(2025)
$$
Dus wegens injectiviteit geldt $2025 f(1)=2025$, oftewel $f(1)=1$.
Nu geldt
$$
f(f(m) f(n))=m n=1 \cdot m n=f(f(1) f(m n))=f(f(m n)),
$$
wat met injectiviteit leidt tot $f(m) f(n)=f(m n)$. Door ook $m=1$ in a) in te vullen, vinden we $f(f(n))=n$. Dus $f$ is zelfs bijectief.
Net als in de eerste oplossing zien we nu dat $f$ gedefinieerd is door zijn waarden op de priemgetallen, en dat $f$ priemgetallen naar priemgetallen stuurt.
Stel nu dat er geldt dat $p \nmid 2024$. Omdat $\operatorname{ggd}(p, 2024)=1$, geldt $p^{\varphi(2024)} \equiv 1 \bmod 2024$. Dus $p^{\varphi(2024)}=2024 a+1$ voor een zekere $a>0$. Wegens b) volgt hieruit dat $f\left(p^{\varphi(2024)}\right)=$ $p^{\varphi(2024)}$. Wegens de multiplicativeit $f(m n)=f(m) f(n)$ betekent dit dat $f(p)^{\varphi(2024)}=$ $p^{\varphi(2024)}$. Omdat dit machten zijn van positieve gehele getallen volgt dan dat $f(p)=p$.
Net als in oplossing 1 kan $f$ dus alleen 2, 11 en 23 permuteren en de rest van de oplossing gaat hetzelfde.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2024-D2024_uitwerkingen.jsonl",
"solution_match": "\nOplossing 2.",
"tier": "T1",
"year": "2024"
}
|
Given real numbers $a, b$ and $c$ such that $0 \leq a \leq b \leq c$ and $a+b+c=1$. Prove that
$$
a b \sqrt{b-a}+b c \sqrt{c-b}+a c \sqrt{c-a}<\frac{1}{4}
$$
|
For every $x \leq y$ we have by the arithmetic-geometric mean inequality that $\sqrt{y-x} \leq \frac{y-x+1}{2}$ with equality if and only if $y-x=1$. Furthermore, we note that $1-a=b+c$ and the symmetric variants, because $a+b+c=1$. If we apply this to the roots on the left side, we get
\[
\begin{aligned}
a b \sqrt{b-a}+b c \sqrt{c-b}+a c \sqrt{c-a} & \leq a b \frac{b-a+1}{2}+b c \frac{c-b+1}{2}+a c \frac{c-a+1}{2} \\
& =\frac{1}{2}(a b(2 b+c)+b c(a+2 c)+c a(2 c+b)) \\
& =\frac{1}{4}\left(4 a b^{2}+4 b c^{2}+4 a c^{2}+6 a b c\right)
\end{aligned}
\]
where in the last step we have already factored out $\frac{1}{4}$ for convenience. Now we note that $a b^{2} \leq b^{3}$ and $a c^{2}+b c^{2} \leq 2 b c^{2}=2 b c \cdot c \leq (b^{2}+c^{2}) c=b^{2} c+c^{3}$. In these inequalities, equality holds respectively if $a=b$ and if $a=b=c$. If we apply this above, we get
\[
\begin{aligned}
4 a b^{2}+4 b c^{2}+4 a c^{2}+6 a b c & \leq 3 a b^{2}+b^{3}+3 b c^{2}+3 a c^{2}+b^{2} c+c^{3}+6 a b c \\
& \leq a^{3}+b^{3}+c^{3}+3 a^{2} b+3 a b^{2}+3 b^{2} c+3 b c^{2}+3 a^{2} c+3 a c^{2}+6 a b c \\
& =(a+b+c)^{3}=1
\end{aligned}
\]
In the last inequality, equality holds only if the terms $a^{3}, a^{2} b, b^{2} c$ and $a^{2} c$ that we added are all zero. In particular, this implies that $a=0$ and $b^{2} c=0$, from which it follows due to $b \leq c$ that $b=0$.
It is easy to see that not all equality cases can occur simultaneously. For example, for $a=b=0$, the left side of the original inequality is equal to zero.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Gegeven zijn reële getallen $a, b$ en $c$ waarvoor geldt dat $0 \leq a \leq b \leq c$ en $a+b+c=1$. Bewijs dat
$$
a b \sqrt{b-a}+b c \sqrt{c-b}+a c \sqrt{c-a}<\frac{1}{4}
$$
|
Voor elke $x \leq y$ hebben we wegens de rekenkundig-meetkundig gemiddelde ongelijkheid dat $\sqrt{y-x} \leq \frac{y-x+1}{2}$ met gelijkheid dan en slechts dan als $y-x=1$. Verder merken we op dat $1-a=b+c$ en de symmetrische varianten, omdat $a+b+c=1$. Als we dit toepassen op de wortels aan de linkerkant krijgen we
$$
\begin{aligned}
a b \sqrt{b-a}+b c \sqrt{c-b}+a c \sqrt{c-a} & \leq a b \frac{b-a+1}{2}+b c \frac{c-b+1}{2}+a c \frac{c-a+1}{2} \\
& =\frac{1}{2}(a b(2 b+c)+b c(a+2 c)+c a(2 c+b)) \\
& =\frac{1}{4}\left(4 a b^{2}+4 b c^{2}+4 a c^{2}+6 a b c\right)
\end{aligned}
$$
waarbij we in de laatste stap voor het gemak alvast $\frac{1}{4}$ hebben uitgedeeld. Nu merken we op dat $a b^{2} \leq b^{3}$ en $a c^{2}+b c^{2} \leq 2 b c^{2}=2 b c \cdot c \leq\left(b^{2}+c^{2}\right) c=b^{2} c+c^{3}$. In deze ongelijkheden geldt gelijkheid respectievelijk als $a=b$ en als $a=b=c$. Als we dit toepassen hierboven krijgen we
$$
\begin{aligned}
4 a b^{2}+4 b c^{2}+4 a c^{2}+6 a b c & \leq 3 a b^{2}+b^{3}+3 b c^{2}+3 a c^{2}+b^{2} c+c^{3}+6 a b c \\
& \leq a^{3}+b^{3}+c^{3}+3 a^{2} b+3 a b^{2}+3 b^{2} c+3 b c^{2}+3 a^{2} c+3 a c^{2}+6 a b c \\
& =(a+b+c)^{3}=1
\end{aligned}
$$
In de laatste ongelijkheid geldt alleen gelijkheid als de termen $a^{3}, a^{2} b, b^{2} c$ en $a^{2} c$ die we hebben toegevoegd allemaal nul zijn. In het bijzonder moet dan gelden dat $a=0$ en $b^{2} c=0$, waaruit wegens $b \leq c$ volgt dat $b=0$.
Het is eenvoudig te zien dat niet alle gelijkheidsgevallen tegelijk kunnen optreden. Zo is voor $a=b=0$ de linkerkant van de oorspronkelijke ongelijkheid gelijk aan nul.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2024-D2024_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2024"
}
|
Given a natural number $n$. There are $n$ islands with $n-1$ bridges between them such that you can get from any island to any other island. One afternoon, a fire breaks out on one of the islands. Every morning, the fire spreads to all neighboring islands (those islands connected by a bridge). To control the fire, every night a bridge is blown up, as long as the fire still has room to spread. Let $X$ be the minimum number of bridges that must be blown up for a given group of islands and fire origin. Find the maximum of $X$ over all possible island groups and fire origins.
|
The answer is $\lfloor\sqrt{n-1}\rfloor$.
For $n=k^{2}+1$, consider an archipelago with $k^{2}$ islands arranged in a $k \times k$ grid, where the islands are connected row by row, and all islands in the leftmost column are also connected to the last island, where the fire starts. After $\ell<k$ nights, there are still at least $k-\ell>0$ rows where no bridge has been blown up. In such a row, the fire consumes the $\ell^{\text{th}}$ island the next morning. This means that after that morning, there is still an unburned bridge (towards the $k^{\text{th}}$ island) to blow up. Therefore, in this archipelago, you need to blow up at least $k$ bridges. By randomly adding islands to this group, we find that $X \geq\lfloor\sqrt{n-1}\rfloor$.
Now we describe a strategy that shows that for any archipelago, the minimum is also at most $\lfloor\sqrt{n-1}\rfloor$. In this strategy, we blow up the bridge each night to cut off the most islands from the fire. We then consider the situation by collapsing all the islands that are on fire into a single point and forgetting about the isolated islands. This way, we have a situation with one fire source but fewer islands. We then finish it off with induction towards $k=\lfloor\sqrt{n-1}\rfloor$.
The base case $k=0$ gives the only possibility $n=1$, for which there is only one configuration and no bridges need to be blown up (since there are none). Assume as the induction hypothesis that in all groups with at most $k^{2}$ islands, at most $k-1$ bridges need to be blown up, and consider an archipelago with $n \leq(k+1)^{2}$ islands.
Suppose the fire source had a degree of $d$: the island is connected to $d$ other islands via a bridge. Then, by the pigeonhole principle, there is a branch from the fire source with at least $\frac{n-1}{d}$ islands. In the morning, with this strategy, at least $\frac{n-1}{d}$ islands are removed by blowing up a bridge, and the fire then takes over $d-1$ islands. By collapsing these islands, we thus get a graph with a number of islands that is less than or equal to
$$
n-\frac{n-1}{d}-(d-1)=n+1-\frac{n-1}{d}-d \leq n+1-2 \sqrt{n-1}=(\sqrt{n-1}-1)^{2}+1<k^{2}+1
$$
where the first inequality follows from the arithmetic-geometric mean inequality: $\frac{n-1}{d}+d \geq 2 \sqrt{n-1}$. Since the number of islands is an integer, it follows that there are at most $k^{2}$ islands. Therefore, the archipelago with $n$ islands needs to blow up $1+(k-1)=k$ bridges. This proves the induction step and thus concludes the proof. $\square$
|
\lfloor\sqrt{n-1}\rfloor
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Gegeven is een natuurlijk getal $n$. Er zijn $n$ eilanden met $n-1$ bruggen ertussen zo dat je van elk eiland bij elk ander eiland kan komen. Op een middag breekt er brand uit op een van de eilanden. Elke morgen verspreidt het vuur zich naar alle naburige eilanden (die eilanden die met een brug zijn verbonden). Om het vuur te controleren wordt elke nacht een brug opgeblazen, zolang het vuur nog ruimte heeft om zich te verspreiden. Zij $X$ het minimale aantal bruggen dat men moet opblazen voor een gegeven eilandengroep en brandhaard. Vind het maximum van $X$ over alle mogelijke eilandengroepen en brandhaarden.
|
Het antwoord is $\lfloor\sqrt{n-1}\rfloor$.
Voor $n=k^{2}+1$ beschouwen we de eilandengroep met $k^{2}$ eilanden in een $k \times k$-grid, waarin de eilanden per rij verbonden worden en alle eilanden in de meest linker kolom nog met het laatste eiland worden verbonden, waar ook de brand start. Dan zijn er na $\ell<k$ nachten nog minstens $k-\ell>0$ rijen over waarin nog geen brug is opgeblazen. In zo'n rij verslindt het vuur die morgen het $\ell^{\text {de }}$ eiland. Dat betekent dat er na die morgen nog een onverwoeste brug is (richting het $k^{\text {de }}$ eiland) om op te blazen. Je moet in deze eilandengroep dus minstens $k$ bruggen opblazen. Door random eilanden aan deze groep toe te voegen vinden we dat $X \geq\lfloor\sqrt{n-1}\rfloor$.
Nu beschrijven we een strategie waaruit blijkt dat voor elke eilandengroep het minimum ook hoogstens $\lfloor\sqrt{n-1}\rfloor$ is. In deze strategie blazen we elke nacht de brug op zo dat je de meeste eilanden afsnijdt van het vuur. We beschouwen daarna de situatie door alle eilanden die in brand staan, samen te trekken tot één punt en alle afgesneden eilanden te vergeten. Nu hebben we dus weer een situatie met één brandhaard, maar minder eilanden. Nu maken we het af met inductie naar $k=\lfloor\sqrt{n-1}\rfloor$.
De inductiebasis $k=0$, geeft als enige mogelijkheid $n=1$ waarvoor er maar één configuratie is en er inderdaad geen bruggen hoeven worden opgeblazen (want die zijn er niet). Stel nu als inductiehypothese dat in alle groepen met hoogstens $k^{2}$ eilanden hoogstens $k-1$ bruggen hoeven te worden opgeblazen en bekijk een eilandgroep met $n \leq(k+1)^{2}$ eilanden.
Stel dat de brandhaard een graad had gelijk aan $d$ : het eiland grenst aan $d$ eilanden middels een brug. Dan geldt wegens het ladenprincipe dat er een tak is van de brandhaard met minstens $\frac{n-1}{d}$ eilanden. In de ochtend zijn er met deze strategie dus minstens $\frac{n-1}{d}$ eilanden verwijderd door een brug op te blazen, en daarna heeft het vuur $d-1$ eilanden overgenomen. Met het samentrekken van deze eilanden krijgen we dus een graaf waarvan het aantal eilanden kleiner of gelijk is aan
$$
n-\frac{n-1}{d}-(d-1)=n+1-\frac{n-1}{d}-d \leq n+1-2 \sqrt{n-1}=(\sqrt{n-1}-1)^{2}+1<k^{2}+1
$$
waarbij de eerste ongelijkheid volgt uit de ongelijkheid van rekenkundig-meetkundig gemiddelde: $\frac{n-1}{d}+d \geq 2 \sqrt{n-1}$. Aangezien het aantal eilanden geheel is, volgt hieruit dat het er
hoogstens $k^{2}$ zijn. Dus de eilandgroep met $n$ eilanden heeft er genoeg aan om $1+(k-1)=k$ bruggen op te blazen. Dit bewijst de inductiestap en is daarmee het einde van het bewijs. $\square$
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2024-D2024_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2024"
}
|
On a $2023 \times 2023$ board, some squares contain a beetle, with at most one beetle per square. After one minute, each beetle moves one square to the left, right, up, or down. After each subsequent minute, each beetle moves one square further, but always makes a 90-degree turn. If a beetle moved left or right in one minute, it will move up or down in the next minute, and vice versa. What is the minimum number of beetles that must be on the board to ensure that at some point, two beetles will end up in the same square at the same time, regardless of where the beetles start and how they move (following the rules)?
|
The answer is $2022^{2}+1$.
First, let's show that $2022^{2}$ is indeed insufficient. For this, we divide a $2022 \times 2022$ sub-board into $2 \times 2$ boards. In each such board, we can place four beetles such that they walk in a small circle (square) clockwise.
Now, suppose we have more than $2022^{2}$ beetles. We want to prove that at some point, two will end up in the same square. To this end, we number the squares from $(1,1)$ to $(2023,2023)$ and color the board as follows: the squares in an odd row and odd column are colored $A$, an odd row and even column are colored $B$, an even row and even column are colored $C$, and an even row and odd column are colored $D$. Thus, half of the diagonals are colored with $A$ and $C$, and the other half with $B$ and $D$. Therefore, there are $1012^{2}$ squares $A$, there are $1011^{2}$ squares $C$, and there are $1011 \cdot 1012$ squares of both $B$ and $D$.
Then each beetle follows a cyclic path $A \rightarrow B \rightarrow C \rightarrow D \rightarrow A$ or $A \rightarrow D \rightarrow C \rightarrow B \rightarrow A$. We note that no more than $1011^{2}$ beetles can start in squares $C$, as there are only $1011^{2}$ of them. Since the number of beetles is greater than $2022^{2}$, there must be more than $1011^{2}$ beetles on squares $A$ or more than $2 \cdot 1011^{2}$ beetles on squares $B$ and $D$ together.
In the first case, after two minutes, there are more than $1011^{2}$ beetles in squares $C$, and we conclude that two beetles meet.
In the second case, after the first minute, there are more than $2 \cdot 1011^{2}$ beetles in the squares $A$ and $C$ together. Thus, two beetles meet in $C$ or we find more than $1011^{2}$ beetles on squares $A$. In that case, after the third minute, there are more than $1011^{2}$ beetles in squares $C$, and we conclude that two beetles meet anyway.
|
2022^{2}+1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Op een $2023 \times 2023$ bord staan er op sommige vakjes een kever, met hoogstens één kever per vakje. Na een minuut gaat elke kever een vakje naar links of rechts, of een vakje naar boven of beneden. Na elke volgende minuut gaat elke kever weer een vakje verder, maar ze maken altijd een bocht van 90 graden. Als een kever de ene minuut naar links of rechts ging dan gaat die dus de volgende minuut naar boven of beneden, en vice versa. Wat is het minimale aantal kevers dat er op het bord moet staan zodat je zeker weet dat er in de loop der tijd een keer twee kevers tegelijk in hetzelfde vakje terecht komen, ongeacht waar de kevers beginnen en hoe ze bewegen (de regels in acht nemende).
|
Het antwoord is $2022^{2}+1$.
Eerst laten we zien dat $2022^{2}$ inderdaad onvoldoende is. Hiervoor delen we een $2022 \times 2022$ deelbord op in $2 \times 2$ bordjes. In elk zo'n bordje kunnen we vier kevers plaatsen zodanig dat ze in een met de klok mee een cirkeltje (vierkantje) lopen.
Stel nu dat we meer dan $2022^{2}$ kevers hebben. We willen bewijzen dat er ooit twee op eenzelfde vakje terecht komen. Hiertoe nummeren we de vakjes van $(1,1) \mathrm{t} / \mathrm{m}(2023,2023)$ en kleuren we het bord als volgt: de vakjes in een oneven rij en oneven kolom kleuren we $A$, een oneven rij en een even kolom kleuren we $B$, een even rij en even kolom kleuren we $C$ en een even rij en oneven kolom kleuren we $D$. De helft van de diagonalen is dus gekleurd met $A$ en $C$ en de andere met $B$ en $D$. Dus er zijn $1012^{2}$ vakjes $A$, er zijn $1011^{2}$ vakjes $C$, en er zijn $1011 \cdot 1012$ vakjes van zowel $B$ als $D$.
Dan volgt elke kever een cyclisch pad $A \rightarrow B \rightarrow C \rightarrow D \rightarrow A$ of $A \rightarrow D \rightarrow C \rightarrow B \rightarrow A$. We merken op dat er niet meer dan $1011^{2}$ kevers in vakjes $C$ kunnen beginnen, want daar zijn er maar $1011^{2}$ van. Omdat het aantal kevers groter is dan $2022^{2}$, moeten er dus meer dan $1011^{2}$ kevers op vakjes $A$ zijn of meer dan $2 \cdot 1011^{2}$ kever op vakjes $B$ en $D$ samen.
In het eerste geval hebben we na twee minuten meer dan $1011^{2}$ kevers in vakjes $C$ en concluderen we dat er twee kevers samenkomen.
In het tweede geval zijn er na de eerste minuut meer dan $2 \cdot 1011^{2}$ kevers in de vakjes $A$ en
$C$ samen. Dan komen er dus twee kevers samen in $C$ of vinden we meer dan $1011^{2}$ kevers op vakjes $A$. In dat geval krijgen we na de derde minuut meer dan $1011^{2}$ kevers in vakjes $C$ en concluderen we alsnog dat er twee kevers samenkomen.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2024-E2024_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2024"
}
|
Let triangle $\triangle A B C$ be given. On segment $B C$ lies point $P$, such that the circle with diameter $B P$ passes through the incenter of $\triangle A B C$. Prove that
$$
\frac{|B P|}{|P C|}=\frac{c}{s-c}
$$
where $c$ is the length of segment $A B$, and $s$ is half the perimeter of $\triangle A B C$.
We introduce $I$ as the incenter of the incircle, and call the incircle itself $\omega$. By the given condition, it follows from Thales' theorem that $\angle B I P=90^{\circ}$.
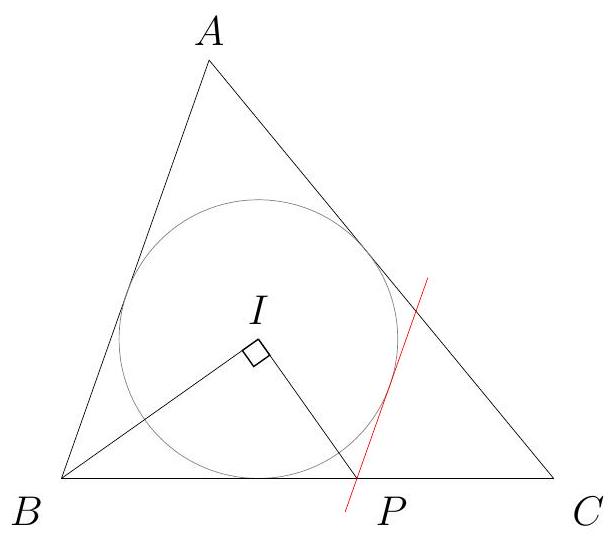
|
We introduce the second tangent line $\ell$ through $P$ to $\omega$ besides $B C$. Note that
$$
\angle A B P=2 \angle I B P=2\left(90^{\circ}-\angle B P I\right)=180^{\circ}-2 \angle B P I=180^{\circ}-\angle(B P, \ell)=\angle(C P, \ell),
$$
where we use the fact that $B I$ is the bisector of $\angle A B P$, and that $P I$ is the bisector of the angle between $P B$ and $\ell$. By F-angles, it follows that $A B \| \ell$. The distance between these two parallel lines is $2 r$ with $r$ being the radius of the inscribed circle.
If we denote the distance from $C$ to $A B$ as $h$, we see that the area of $\triangle A B C$ is on the one hand equal to $r s$, and on the other hand $\frac{1}{2} c h$. From $r s=\frac{1}{2} c h$ it follows that
$$
\frac{|B C|}{|B P|}=\frac{d(A B, C)}{d(A B, \ell)}=\frac{h}{2 r}=\frac{s}{c} .
$$
We conclude that
$$
\frac{|P C|}{|B P|}=\frac{|B C|-|B P|}{|B P|}=\frac{|B C|}{|B P|}-1=\frac{s}{c}-1=\frac{s-c}{c} .
$$
|
\frac{|B P|}{|P C|}=\frac{c}{s-c}
|
Yes
|
Yes
|
proof
|
Geometry
|
Laat driehoek $\triangle A B C$ gegeven zijn. Op lijnstuk $B C$ ligt punt $P$, zodanig dat de cirkel met middellijn $B P$ door het middelpunt van de ingeschreven cirkel van $\triangle A B C$ gaat. Bewijs dat
$$
\frac{|B P|}{|P C|}=\frac{c}{s-c}
$$
waarbij $c$ de lengte is van lijnstuk $A B$, en $s$ de helft van de omtrek van $\triangle A B C$.
We introduceren voor onze oplossingen uiteraard $I$ als het middelpunt van de ingeschreven cirkel, en noemen de ingeschreven cirkel zelf $\omega$. Wegens het gegeven geldt met Thales dat $\angle B I P=90^{\circ}$.

|
We introduceren de tweede raaklijn $\ell$ door $P$ aan $\omega$ naast $B C$. Merk op dat
$$
\angle A B P=2 \angle I B P=2\left(90^{\circ}-\angle B P I\right)=180^{\circ}-2 \angle B P I=180^{\circ}-\angle(B P, \ell)=\angle(C P, \ell),
$$
waarbij we gebruikmaken van het feit dat $B I$ bissectrice is van $\angle A B P$, en dat $P I$ de bissectrice is van de hoek tussen $P B$ en $\ell$. Met F-hoeken volgt hieruit dat $A B \| \ell$. De afstand tussen deze twee parallelle lijnen is $2 r$ met $r$ de straal van de ingeschreven cirkel.
Als we de afstand van $C$ tot $A B$ nu $h$ noemen, zien we dat de oppervlakte van $\triangle A B C$ enerzijds gelijk is aan $r s$, en anderzijds $\frac{1}{2} c h$. Uit $r s=\frac{1}{2} c h$ volgt nu dat
$$
\frac{|B C|}{|B P|}=\frac{d(A B, C)}{d(A B, \ell)}=\frac{h}{2 r}=\frac{s}{c} .
$$
We concluderen dat
$$
\frac{|P C|}{|B P|}=\frac{|B C|-|B P|}{|B P|}=\frac{|B C|}{|B P|}-1=\frac{s}{c}-1=\frac{s-c}{c} .
$$
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2024-E2024_uitwerkingen.jsonl",
"solution_match": "\nOplossing 1.",
"tier": "T1",
"year": "2024"
}
|
Let triangle $\triangle A B C$ be given. On segment $B C$ lies point $P$, such that the circle with diameter $B P$ passes through the incenter of $\triangle A B C$. Prove that
$$
\frac{|B P|}{|P C|}=\frac{c}{s-c}
$$
where $c$ is the length of segment $A B$, and $s$ is half the perimeter of $\triangle A B C$.
We introduce $I$ as the incenter of the incircle, and call the incircle itself $\omega$. By the given condition, it follows from Thales' theorem that $\angle B I P=90^{\circ}$.

|
Let $D$ be the point of tangency of $\omega$ with $BC$. We further define $I'$ as the center of the excircle of $\triangle ABC$ opposite to $C$. And let $D'$ be the projection of $I'$ onto $BC$. This is thus the point of tangency of the excircle with $BC$. As part of the Ravi transformation, we have that $\left|C D^{\prime}\right|=s$.
Now we note that $BI'$ is the external bisector and is therefore perpendicular to the internal bisector $BI$. Since $PI$ is also perpendicular to $BI$, this means that $BI' \| PI$. Now we observe that the point multiplication from $C$ that sends $I'$ to $I$ also sends $D'$ to $D$ and $B$ to $P$. From this it follows that
$$
|CP|=|CB| \cdot \frac{|CD|}{\left|C D^{\prime}\right|}=a \cdot \frac{s-c}{s}
$$
so
$$
|BP|=|BC|-|CP|=a-\frac{a(s-c)}{s}=\frac{ac}{s}.
$$
Now it follows that $\frac{|BC|}{|BP|}=\frac{a}{|BP|}=\frac{s}{c}$ and we can finish as in Solution 1.
|
\frac{|B P|}{|P C|}=\frac{c}{s-c}
|
Yes
|
Yes
|
proof
|
Geometry
|
Laat driehoek $\triangle A B C$ gegeven zijn. Op lijnstuk $B C$ ligt punt $P$, zodanig dat de cirkel met middellijn $B P$ door het middelpunt van de ingeschreven cirkel van $\triangle A B C$ gaat. Bewijs dat
$$
\frac{|B P|}{|P C|}=\frac{c}{s-c}
$$
waarbij $c$ de lengte is van lijnstuk $A B$, en $s$ de helft van de omtrek van $\triangle A B C$.
We introduceren voor onze oplossingen uiteraard $I$ als het middelpunt van de ingeschreven cirkel, en noemen de ingeschreven cirkel zelf $\omega$. Wegens het gegeven geldt met Thales dat $\angle B I P=90^{\circ}$.

|
Zij $D$ het raakpunt van $\omega$ met $B C$. We definiëren $I^{\prime}$ verder als het middelpunt van de aangeschreven cirkel van $\triangle A B C$ tegenover $C$. En zij $D^{\prime}$ de projectie van $I^{\prime}$ op $B C$. Dat is dus het raakpunt van de aangeschreven cirkel aan $B C$. Onderdeel van de Ravi-transformatie is dan dat $\left|C D^{\prime}\right|=s$.
Nu merken we op dat $B I^{\prime}$ de buitenbissectrice is en dus loodrecht staat op de binnenbissectrice $B I$. Aangezien $P I$ ook loodrecht op $B I$ staat, betekent dit dat $B I^{\prime} \| P I$. Nu merken we op dat de puntvermenigvuldiging vanuit $C$ die $I^{\prime}$ naar $I$ stuurt, ook $D^{\prime}$ naar $D$ stuurt en $B$ naar $P$. Hieruit volgt dat
$$
|C P|=|C B| \cdot \frac{|C D|}{\left|C D^{\prime}\right|}=a \cdot \frac{s-c}{s}
$$
dus
$$
|B P|=|B C|-|C P|=a-\frac{a(s-c)}{s}=\frac{a c}{s} .
$$
Nu volgt dat $\frac{|B C|}{|B P|}=\frac{a}{|B P|}=\frac{s}{c}$ en kunnen we het afmaken zoals in Oplossing 1.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2024-E2024_uitwerkingen.jsonl",
"solution_match": "\nOplossing 2.",
"tier": "T1",
"year": "2024"
}
|
Let triangle $\triangle A B C$ be given. On segment $B C$ lies point $P$, such that the circle with diameter $B P$ passes through the incenter of $\triangle A B C$. Prove that
$$
\frac{|B P|}{|P C|}=\frac{c}{s-c}
$$
where $c$ is the length of segment $A B$, and $s$ is half the perimeter of $\triangle A B C$.
We introduce $I$ as the incenter of the incircle, and call the incircle itself $\omega$. By the given condition, it follows from Thales' theorem that $\angle B I P=90^{\circ}$.

|
We will prove that $d(P, AB) = 2r$ with $r$ being the radius of $\omega$, so that we can either finish the problem as in Solution 1, or use the argument in this solution to complete the problem.
Project $I$ and $P$ onto $AB$ and call the images $F$ and $E$. Note that for the intersection point $Q$ of $PI$, in $\triangle BPQ$, $BI$ is both the angle bisector and the altitude, and thus $I$ is the midpoint of $PQ$. It immediately follows that $\triangle QIF \sim \triangle QPE$ is a dilation from $Q$ with a factor of 2. Therefore, $PE = 2 \cdot IF = 2r$.
We can now finish the problem as in Solution 1 by noting that
$$
\frac{|BC|}{|BP|} = \frac{d(C, AB)}{d(P, AB)} = \frac{d(C, AB)}{2r} = \frac{s}{c}.
$$
But we can also observe that in the right triangle $\triangle BPE$, we have
$$
|BP| = \frac{2r}{\sin \beta} = \frac{rs}{\frac{1}{2} \sin \beta \cdot ac} \cdot \frac{ac}{s} = \frac{ac}{s},
$$
and from this, we also get
$$
\frac{|BC|}{|BP|} = \frac{a}{\frac{ac}{s}} = \frac{s}{c}.
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Laat driehoek $\triangle A B C$ gegeven zijn. Op lijnstuk $B C$ ligt punt $P$, zodanig dat de cirkel met middellijn $B P$ door het middelpunt van de ingeschreven cirkel van $\triangle A B C$ gaat. Bewijs dat
$$
\frac{|B P|}{|P C|}=\frac{c}{s-c}
$$
waarbij $c$ de lengte is van lijnstuk $A B$, en $s$ de helft van de omtrek van $\triangle A B C$.
We introduceren voor onze oplossingen uiteraard $I$ als het middelpunt van de ingeschreven cirkel, en noemen de ingeschreven cirkel zelf $\omega$. Wegens het gegeven geldt met Thales dat $\angle B I P=90^{\circ}$.

|
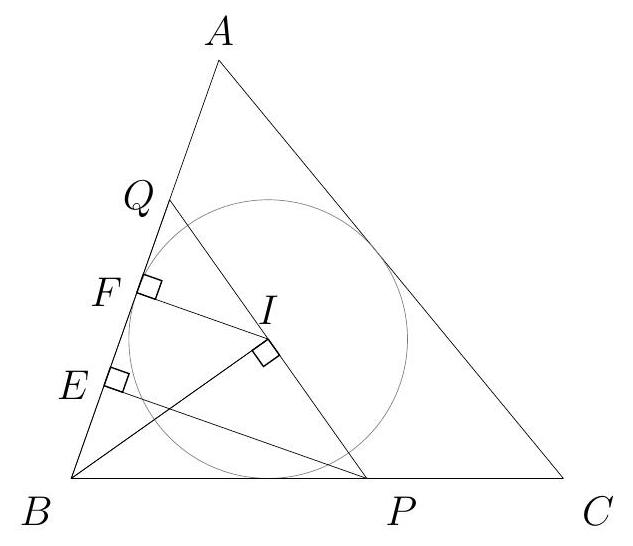
We gaan bewijzen dat $d(P, A B)=2 r$ met $r$ de straal van $\omega$, zodat we het ofwel af kunnen maken zoals in oplossing 1 , ofwel het argument in deze oplossing gebruiken om de opgave af te maken.
Projecteer $I$ en $P$ op $A B$ en noem de beelden $F$ en $E$. Merk voor het snijpunt $Q$ van $P I$ op dat in $\triangle B P Q$ nu $B I$ zowel bissectrice als hoogtelijn is, en dus $I$ het midden is van
$P Q$. Nu volgt onmiddellijk dat $\triangle Q I F \sim \triangle Q P E$ een puntvermenigvuldiging vanuit $Q$ met factor 2 is. Dus $P E=2 \cdot I F=2 r$.
We kunnen het nu afmaken zoals in oplossing 1 door op te merken dat nu
$$
\frac{|B C|}{|B P|}=\frac{d(C, A B)}{d(P, A B)}=\frac{d(C, A B)}{2 r}=\frac{s}{c} .
$$
Maar we kunnen nu ook opmerken dat in rechthoekige driehoek $\triangle B P E$ geldt dat
$$
|B P|=\frac{2 r}{\sin \beta}=\frac{r s}{\frac{1}{2} \sin \beta \cdot a c} \cdot \frac{a c}{s}=\frac{a c}{s},
$$
en hier volgt óók
$$
\frac{|B C|}{|B P|}=\frac{a}{\frac{a c}{s}}=\frac{s}{c}
$$
uit.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2024-E2024_uitwerkingen.jsonl",
"solution_match": "# Oplossing 3.",
"tier": "T1",
"year": "2024"
}
|
Let $P(x)$ be a polynomial with integer coefficients of degree $n>1$ for which $Q(x)=P(P(P(x)))-P(x)$ has exactly $n^{3}$ distinct real roots. Prove that the roots of $Q(x)$ can be divided into two groups whose arithmetic means are the same.
|
We write $\gamma_{i}$ with $1 \leq i \leq n^{3}$ for the different roots of $Q(x)$. This means that $P\left(P\left(P\left(\gamma_{i}\right)\right)\right)-P\left(\gamma_{i}\right)=0$, so $P\left(\gamma_{i}\right)$ is a root of the polynomial $P(P(x))-x$. The degree of $P(P(x))-x$ is $n^{2}$, so this polynomial has at most $n^{2}$ roots, which we denote by $\beta_{i}$. For each root $\beta_{i}$, the equation $P(x)=\beta_{i}$ has at most $n$ solutions. In total, we thus have at most $n^{2} \cdot n$ solutions $\gamma_{i}$ such that $P\left(\gamma_{i}\right)$ is a root of $P(P(x))-x$. Since this maximum is achieved, there are $n^{2}$ roots $\beta_{i}$ of $P(P(x))-x$ and for each $\beta_{i}$ we have exactly $n$ solutions of $P(x)=\beta_{i}$.
We write $P(x)=a x^{n}-b x^{n-1}+P^{\prime}(x)$ with $\operatorname{deg} P^{\prime}(x) \leq n-2$. On the other hand, for each $\beta_{i}$ we get a subset $\left\{\delta_{1}, \delta_{2}, \ldots, \delta_{n}\right\}$ of the roots $\left\{\gamma_{1}, \ldots, \gamma_{n^{3}}\right\}$ such that we can write $P(x)-\beta_{i}$ as $P(x)-\beta_{i}=a\left(x-\delta_{1}\right)\left(x-\delta_{2}\right) \cdots\left(x-\delta_{n}\right)$. Thus, $a x^{n}-b x^{n-1}+P^{\prime}(x)-\beta_{i}=a\left(x-\delta_{1}\right)\left(x-\delta_{2}\right) \cdots\left(x-\delta_{n}\right)$. Since $n \geq 2$, it follows from this that the sum $\delta_{1}+\delta_{2}+\ldots+\delta_{n}$ of the roots of $P(x)-\beta_{i}$ is equal to $b / a$. (This is actually Vieta's formula.) We conclude that we have $n^{2}$ groups of $n$ roots of $Q(x)$, each with the same mean $\frac{b}{n a}$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Zij $P(x)$ een polynoom met gehele coëfficienten van graad $n>1$ waarvoor geldt dat $Q(x)=P(P(P(x)))-P(x)$ precies $n^{3}$ verschillende reële nulpunten heeft. Bewijs dat de nulpunten $\operatorname{van} Q(x)$ in twee groepen verdeeld kunnen worden waarvan het rekenkundig gemiddelde hetzelfde is.
|
We schrijven $\gamma_{i}$ met $1 \leq i \leq n^{3}$ voor de verschillende wortels zijn van $Q(x)$. Dat betekent dat $P\left(P\left(P\left(\gamma_{i}\right)\right)\right)-P\left(\gamma_{i}\right)=0$, dus $P\left(\gamma_{i}\right)$ is een nulpunt van het polynoom $P(P(x))-x$. De graad van $P(P(x))-x$ is $n^{2}$, dus dit polynoom heeft maximaal $n^{2}$ nulpunten, die we noteren met $\beta_{i}$. Voor elk nulpunt $\beta_{i}$ heeft de vergelijking $P(x)=\beta_{i}$ maximaal $n$ oplossingen. In totaal hebben we dus maximaal $n^{2} \cdot n$ oplossingen $\gamma_{i}$ zo dat $P\left(\gamma_{i}\right)$ is een nulpunt van $P(P(x))-x$. Aangezien dit maximum bereikt wordt, zijn er $n^{2}$ nulpunten $\beta_{i}$ van $P(P(x))-x$ en hebben we voor elke $\beta_{i}$ precies $n$ oplossingen van $P(x)=\beta_{i}$.
We schrijven $P(x)=a x^{n}-b x^{n-1}+P^{\prime}(x)$ met $\operatorname{deg} P^{\prime}(x) \leq n-2$. Anderzijds krijgen we voor elke $\beta_{i}$ een deelverzameling $\left\{\delta_{1}, \delta_{2}, \ldots, \delta_{n}\right\}$ van de wortels $\left\{\gamma_{1}, \ldots, \gamma_{n^{3}}\right\}$ zo dat we $P(x)-\beta_{i}$ kunnen schrijven als $P(x)-\beta_{i}=a\left(x-\delta_{1}\right)\left(x-\delta_{2}\right) \cdots\left(x-\delta_{n}\right)$. Dus $a x^{n}-b x^{n-1}+P^{\prime}(x)-\beta_{i}=a\left(x-\delta_{1}\right)\left(x-\delta_{2}\right) \cdots\left(x-\delta_{n}\right)$. Omdat $n \geq 2$ volgt hieruit dat de som $\delta_{1}+\delta_{2}+\ldots+\delta_{n}$ van de nulpunten van $P(x)-\beta_{i}$ gelijk is aan $b / a$. (Dit is eigenlijk Viéta.) We concluderen dat we $n^{2}$ groepen hebben van $n$ nulpnten van $Q(x)$ met telkens hetzelfde gemiddelde $\frac{b}{n a}$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2024-E2024_uitwerkingen.jsonl",
"solution_match": "\nOplossing 1.",
"tier": "T1",
"year": "2024"
}
|
Let $P(x)$ be a polynomial with integer coefficients of degree $n>1$ for which $Q(x)=P(P(P(x)))-P(x)$ has exactly $n^{3}$ distinct real roots. Prove that the roots of $Q(x)$ can be divided into two groups whose arithmetic means are the same.
|
We begin with a small lemma: if $K(x)$ and $L(x)$ are two polynomials with integer coefficients such that for all integer $x$ it holds that $K(x) \mid L(x)$ as numbers, then $K(x) \mid L(x)$ as polynomials. For the proof, we write $L(x) = K(x) M(x) + r(x)$ for polynomials $M(x)$ and $r(x)$ such that the degree of $r(x)$ is smaller than the degree of $K(x)$. This condition implies that there exists an $N$ such that $|K(x)| > |r(x)|$ for all $x > N$. Since it also holds that $K(x) \mid L(x) - K(x) M(x) = r(x)$, it follows that $r(x) = 0$ for all $x > N$. Since $r(x)$ has infinitely many roots, we can conclude that $r(x) = 0$ for all $x$, thus proving the lemma.
In particular, it follows from $a - b \mid P(a) - P(b)$ with $a = P(x)$ and $b = x$ that $P(x) - x \mid P(P(x)) - P(x)$ for all $x$. Therefore, by the lemma, $P(x) - x \mid P(P(x)) - P(x)$ as polynomials. And if we substitute $P(x)$, we find that $P(P(x)) - P(x) \mid P(P(P(x))) - P(P(x))$.
Let $\alpha_{i}$ with $1 \leq i \leq n$ be the roots of $P(x) - x$, a priori possibly complex and with multiplicity. Then $Q(\alpha_{i}) = 0$, so $\alpha_{i}$ is real. If $\alpha_{i}$ had a multiplicity greater than one, then $(x - \alpha_{i})^2 \mid P(x) - x$. This implies, by the lemma, that $(x - \alpha_{i})^2 \mid P(P(x)) - P(x)$ and $(x - \alpha_{i})^2 \mid P(P(P(x))) - P(P(x))$. Adding the last two relations gives that $(x - \alpha_{i})^2 \mid Q(x)$, which contradicts the conditions of the problem.
Now let $\beta_{i}$ with $1 \leq i \leq n^2$ be the roots of $P(P(x)) - P(x)$, all real and distinct, such that $\alpha_{i} = \beta_{i}$ for $i \leq n$. (Note: these are not the same $\beta_{i}$ as in the first solution. We can also do this proof here with $P(P(x)) - x$ as in the first solution. Then the $\beta_{i}$ would coincide.) And let $\gamma_{i}$ with $1 \leq i \leq n^3$ be the roots of $Q(x)$ with $\beta_{i} = \gamma_{i}$ for $i \leq n^2$.
We write $P(x) = a x^n - b x^{n-1} + P'(x)$ with $\operatorname{deg} P'(x) \leq n-2$ such that $b = a (\alpha_1 + \cdots + \alpha_n)$. Then we easily compute that $P(P(x)) - P(x) = a^{n+1} x^{n^2} - n a^n b x^{n^2-1} + P''(x)$ with $\operatorname{deg} P''(x) \leq n^2 - 2$, so $n a^n b = a^{n+1} (\beta_1 + \cdots + \beta_{n^2})$. And similarly, $Q(x) = a^{n^2+n+1} x^{n^3} - n^2 a^{n^2+n} b x^{n^3-1} + P'''(x) \operatorname{deg} P'''(x) \leq n^2 - 2$, so $n^2 a^{n^2+n} b = a^{n^2+n+1} (\gamma_1 + \cdots + \gamma_{n^3})$. From this, it follows that
$$
\frac{\alpha_1 + \cdots + \alpha_n}{n} = \frac{\beta_1 + \cdots + \beta_{n^2}}{n^2} = \frac{\gamma_1 + \cdots + \gamma_{n^3}}{n^3} = \frac{b}{n a}.
$$
The set of $\alpha_i$ and its complement or the set of $\beta_i$ and its complement give the desired partition.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Zij $P(x)$ een polynoom met gehele coëfficienten van graad $n>1$ waarvoor geldt dat $Q(x)=P(P(P(x)))-P(x)$ precies $n^{3}$ verschillende reële nulpunten heeft. Bewijs dat de nulpunten $\operatorname{van} Q(x)$ in twee groepen verdeeld kunnen worden waarvan het rekenkundig gemiddelde hetzelfde is.
|
We beginnen met een klein lemma: als $K(x)$ en $L(x)$ twee polynomen zijn met gehele coëfficienten zo dat voor alle gehele $x$ geldt dat $K(x) \mid L(x)$ als getallen, dan geldt dat $K(x) \mid L(x)$ als polynomen. Voor het bewijs schrijven we $L(x)=K(x) M(x)+$ $r(x)$ voor polynomen $M(x)$ en $r(x)$ zo dat de graad van $r(x)$ kleiner is dan de graad van $K(x)$. Deze voorwaarde impliceert dat er een $N$ bestaat zo dat $|K(x)|>|r(x)|$ voor alle $x>N$. Aangezien ook geldt dat $K(x) \mid L(x)-K(x) M(x)=r(x)$, geldt dat $r(x)=0$ voor alle $x>N$. Aangezien $r(x)$ oneindig veel nulpunten heeft, kunnen we concluderen dat $r(x)=0$ voor alle $x$, waarmee we het lemma hebben bewezen.
In het bijzonder volgt uit $a-b \mid P(a)-P(b)$ met $a=P(x)$ en $b=x$ dat $P(x)-x \mid P(P(x))-$ $P(x)$ voor alle $x$. Dus uit het lemma volgt dat $P(x)-x \mid P(P(x))-P(x)$ als polynomen. En als we hier $P(x)$ invullen, vinden we dat ook $P(P(x))-P(x) \mid P(P(P(x)))-P(P(x))$
Schrijf $\alpha_{i}$ met $1 \leq i \leq n$ voor de wortels van van $P(x)-x$, a priori mogelijk complex en met multipliciteit. Dan geldt $Q\left(\alpha_{i}\right)=0$, dus $\alpha_{i}$ is reëel. Als $\alpha_{i}$ multipliciteit groter dan een zou hebben, dan geldt dus dat $\left(x-\alpha_{i}\right)^{2} \mid P(x)-x$. Hieruit volgt wegens het lemma dat $\left(x-\alpha_{i}\right)^{2} \mid P(P(x))-P(x)$ en $\left(x-\alpha_{i}\right)^{2} \mid P(P(P(x)))-P(P(x))$. Het optellen van de laatste twee relaties geeft dat $\left(x-\alpha_{i}\right)^{2} \mid Q(x)$ wat in tegenspraak is met de voorwaarden van de opgave.
Schrijf nu $\beta_{i}$ met $1 \leq i \leq n^{2}$ voor de wortels van $P(P(x))-P(x)$, alle ook reëel en verschillend, zo dat $\alpha_{i}=\beta_{i}$ voor $i \leq n$. (Let op: dit zijn niet dezelfde $\beta_{i}$ als in de eerste oplossing. We kunnen dit bewijs hier ook doen met $P(P(x))-x$ zoals in de eerste oplossing. Dan zouden de $\beta_{i}$ wel overeenkomen.) En laat $\gamma_{i}$ met $1 \leq i \leq n^{3}$ de wortels zijn van $Q(x)$ met $\beta_{i}=\gamma_{i}$ voor $i \leq n^{2}$.
We schrijven $P(x)=a x^{n}-b x^{n-1}+P^{\prime}(x)$ met $\operatorname{deg} P^{\prime}(x) \leq n-2$ zo dat $b=a\left(\alpha_{1}+\cdots+\alpha_{n}\right)$. Dan rekenen we gemakkelijk uit dat $P(P(x))-P(x)=a^{n+1} x^{n^{2}}-n a^{n} b x^{n^{2}-1}+P^{\prime \prime}(x)$ met $\operatorname{deg} P^{\prime \prime}(x) \leq n^{2}-2$, dus $n a^{n} b=a^{n+1}\left(\beta_{1}+\cdots+\beta_{n^{2}}\right)$. En evenzo $Q(x)=a^{n^{2}+n+1} x^{n^{3}}-$ $n^{2} a^{n^{2}+n} b x^{n^{3}-1}+P^{\prime \prime \prime}(x) \operatorname{deg} P^{\prime \prime}(x) \leq n^{2}-2$, dus $n^{2} a^{n^{2}+n} b=a^{n^{2}+n+1}\left(\gamma_{1}+\cdots+\gamma_{n^{3}}\right)$. Hieruit volgt dat
$$
\frac{\alpha_{1}+\cdots+\alpha_{n}}{n}=\frac{\beta_{1}+\cdots+\beta_{n^{2}}}{n^{2}}=\frac{\gamma_{1}+\cdots+\gamma_{n^{3}}}{n^{3}}=\frac{b}{n a} .
$$
De verzameling van $\alpha_{i}$ en zijn complement of de verzameling van $\beta_{i}$ en zijn complement geven de gevraagde splitsing.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2024-E2024_uitwerkingen.jsonl",
"solution_match": "\nOplossing 2.",
"tier": "T1",
"year": "2024"
}
|
Initially, there is a positive integer $N$ on the blackboard. We repeatedly replace the number according to the following rules:
- replace the number on the board with a positive multiple of itself,
- replace the number with a number having the same digits in a different order. (It is allowed for the new number to start with one or more zeros, which are then omitted.)
Determine for which values of $N$ it is possible to get 1 after a series of moves.
An example of valid moves is $5 \rightarrow 20 \rightarrow 140 \rightarrow 041=41$.
|
Answer: this is possible if and only if $N \not \equiv 0 \bmod 3$. Indeed, if 3 is a divisor of $N$, then this remains so after both steps: every multiple of $N$ is divisible by 3, and swapping the digits does not change the sum of the digits.
Now assume that $N \not \equiv 0 \bmod 3$. We will first show that we can replace $N$ with a number that has only ones as digits. Then we will show that such a number can be replaced by 1.
By multiplying $N$ by 10, we can add zeros, and by swapping the digits, we can remove zeros. To replace $N$ with a number that has only ones as digits, we first multiply $N$ by 2 a number of times until the first digit is equal to 1. By then placing the 1 in the last position, we get a number that is relatively prime to 10. By Euler-Fermat, for $n=\varphi(N)$, we have that $10^{k n} \equiv 1^{k} \equiv 1 \bmod N$ for all $k$. This implies that $10^{n}+10^{2 n}+\ldots+10^{N n} \equiv 0 \bmod N$. This is thus a multiple of $N$, and by removing the zeros, we get a number with exactly $N \not \equiv 0 \bmod 3$ ones.
For step 2, we write $A_{n}$ for the number with $n$ digits all equal to 1. Now we observe that $10^{n}=9 \cdot A_{n}+1$, so $10^{n} \equiv 1 \bmod A_{n}$. This means that
$$
10^{10 n}+10^{9 n}+\ldots+10^{n}+A_{n}-10 \equiv 1+1+\ldots+1+A_{n}-10=A_{n} \bmod A_{n}
$$
Therefore, the number on the left is a multiple of $A_{n}$, so we can obtain it from $A_{n}$ with step 1. It has 10 extra ones (at positions $10 n, 9 n$, etc., counting from the right, starting from the zeroth digit) and one 1 less (at the tens place). By applying step 2, we rewrite this to $A_{n+9}$. By repeating this step, we can obtain all $A_{m}$ with $m$ in the arithmetic sequence $n+9 k$, with $3 \nmid n$ and $k \geq 0$.
Now we consider the set of powers of two modulo 9. This is the repeating sequence $1,2,4,8,7,5,1, \ldots$ In particular, every residue class not equal to $0,3,6$ occurs infinitely often in this sequence. This means that there is a power of two greater than $n$ with the same residue as $n$ modulo 9. This power of two is thus in the arithmetic sequence: there are $k$ and $\ell$ such that $n+9 k=2^{\ell}$.
Finally, we claim that we can make steps from $A_{2 n}$ to $A_{n}$. For this, we look for a power of two whose digits can be grouped into two equal-sized groups (plus or minus 1 for an odd number of digits) with the same sum. We find this with $2^{13}=8192$. With this, we come to the following steps from $A_{2}$ to $A_{1}$:
$$
11 \rightarrow 11 \cdot 118=1298 \rightarrow 8192=2^{13} \rightarrow 10^{13} \rightarrow 1
$$
If we group the ones of $A_{2 n}$ into pairs with enough zeros in between and apply these steps simultaneously to each group, then this also gives a process from $A_{2 n}$ to $A_{n}$. If we repeatedly apply this to $A_{2^{\ell}}$, we eventually end up at $A_{1}$.
Remark. Instead of $A_{N}$, we can also make the smaller number $A_{S}$ with $S$ the sum of the digits of $N$ with a bit more work. Indeed, assume that the $m^{\text {th }}$ digit of $N$ is greater than 1 (counting from the right, starting from the zeroth digit). Now choose $k$ such that $k n+m$ is greater than the number of digits of $N$ with $n=\varphi(N)$. Then $10^{k n+m}-10^{m}+N$ is a multiple of $N$ where the $m^{\text {th }}$ digit is one less, and we have one additional digit 1 with some zeros. By removing the zeros and repeating this step, we get a number that consists only of ones. Since we started with $N \not \equiv 0 \bmod 3$, the number of ones is not divisible by 3.
|
N \not \equiv 0 \bmod 3
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Initieel staat er een positief geheel getal $N$ op het schoolbord. We vervangen het getal herhaaldelijk aan de hand van de volgende regels:
- vervang het getal op het bord door een positief veelvoud van zichzelf,
- vervang het getal door een getal met dezelfde cijfers in een andere volgorde. (Het is toegestaan dat het nieuwe getal met een of meerdere nullen begint, die dan worden weggelaten.)
Bepaal voor welke waarden van $N$ het mogelijk is om 1 te krijgen na een serie van zetten.
Een voorbeeld van geldige zetten is $5 \rightarrow 20 \rightarrow 140 \rightarrow 041=41$.
|
Antwoord: dit is mogelijk precies als $N \not \equiv 0 \bmod 3$. Inderdaad als 3 wel een deler is $N$, dan is dat na beide stappen nog zo: elk veelvoud van $N$ is deelbaar door 3 , en het verwisselen van de cijfers verandert de som van de cijfers niet.
Nu nemen we aan dat $N \not \equiv 0 \bmod 3$. We gaan nu eerst laten zien dat we $N$ met de stappen kunnen vervangen door een getal dat enkel enen heeft als cijfers. Daarna laten we zien dat zo'n getal te vervangen is door 1.
Door $N$ met 10 te vermenigvuldigen kunnen we nullen toevoegen, en door de cijfers te wisselen kunnen we nullen weghalen. Om $N$ te vervangen door een getal dat enkel enen heeft als cijfers, vermenigvuldigen we $N$ eerst een aantal keer met 2 tot het eerste cijfer gelijk is aan 1 . Door nu de 1 juist op de laatste plek te zetten krijgen we een getal relatief priem met 10 . Wegens Euler-Fermat geldt dan voor $n=\varphi(N)$ dat $10^{k n} \equiv 1^{k} \equiv 1 \bmod N$ voor alle $k$. Hieruit volgt dat $10^{n}+10^{2 n}+\ldots+10^{N n} \equiv 0 \bmod N$. Dat is dus een veelvoud $\operatorname{van} N$ en door de nullen weg te halen krijgen we een getal met precies $N \not \equiv 0 \bmod 3$ enen.
Voor stap 2 schrijven we $A_{n}$ voor het getal met $n$ cijfers welke allemaal gelijk zijn aan 1. Nu merken we op dat $10^{n}=9 \cdot A_{n}+1$, dus $10^{n} \equiv 1 \bmod A_{n}$. Dat betekent dat
$$
10^{10 n}+10^{9 n}+\ldots+10^{n}+A_{n}-10 \equiv 1+1+\ldots+1+A_{n}-10=A_{n} \bmod A_{n}
$$
Zodoende is het getal links een veelvoud van $A_{n}$ zodat we het kunnen verkrijgen uit $A_{n}$ met stap 1. Het heeft 10 extra enen (op plekken $10 n, 9 n$, etc. tellend vanaf rechts, beginnend bij het nulde cijfer) en één 1 minder (op de plek van de tientallen). Met stap 2 herschrijven we dit naar $A_{n+9}$. Door deze stap te herhalen kunnen we alle $A_{m}$ verkrijgen met $m$ in de rekenkundige rij $n+9 k$, met $3 \nmid n$ en $k \geq 0$.
Nu bekijken we de verzameling van tweemachten modulo 9. Dat is de repeterende rij $1,2,4,8,7,5,1, \ldots$ In het bijzonder komt elke restklasse ongelijk $0,3,6$ oneindig vaak
voor in deze rij. Dat betekent dat er een tweemacht is groter dan $n$ met dezelfde restklasse als $n$ modulo 9 . Deze tweemacht zit dus in de rekenkundige rij: er zijn $k$ en $\ell$ zodanig dat $n+9 k=2^{\ell}$.
Als laatste beweren we dat we stappen kunnen maken van $A_{2 n}$ naar $A_{n}$. Hiervoor gaan we op zoek naar een tweemacht waarvan we de cijfers kunnen groeperen in twee even grote groepen (plus-min 1 voor oneven aantal cijfers) met dezelfde som. Dat vinden we bij $2^{13}=8192$. Hiermee komen we bij de volgende stappen van $A_{2}$ naar $A_{1}$ :
$$
11 \rightarrow 11 \cdot 118=1298 \rightarrow 8192=2^{13} \rightarrow 10^{13} \rightarrow 1
$$
Als we groepjes van twee maken van de enen van $A_{2 n}$ met genoeg nullen ertussen en deze stappen tegelijk toepassen op elk groepje, dan geeft dit ook een proces van $A_{2 n}$ naar $A_{n}$. Als we dit herhaaldelijk toepassen op $A_{2^{\ell}}$ eindigen we uiteindelijk bij $A_{1}$.
Opmerking. In plaats van $A_{N}$ kunnen we met iets meer werk ook het kleinere getal $A_{S}$ maken met $S$ de som van de cijfers van $N$. Inderdaad, neem aan dat het $m^{\text {de }}$ cijfer van $N$ groter is dan 1 (tellend vanaf rechts, beginnend bij het nulde cijfer). Nu kiezen we $k$ zodanig dat $k n+m$ groter is dan het aantal cijfers van $N$ met $n=\varphi(N)$. Dan is $10^{k n+m}-10^{m}+N$ een veelvoud van $N$ waarbij het $m^{\text {de }}$ cijfer één kleiner is, en we één extra cijfer 1 hebben met een aantal nullen. Door de nullen weg te halen en deze stap te herhalen krijgen we een getal dat enkel uit enen bestaat. Aangezien we begonnen met $N \not \equiv 0 \bmod 3$ is het aantal enen niet deelbaar door 3.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2024-E2024_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2024"
}
|
For a five-digit number \(n = abcde\), we define the twisted sum of \(n\) as the value
\[bcdea + cdeab + deabc + eabcd.\]
The twisted sum of 20253, for example, is
\[05232 + 25320 + 53202 + 32025 = 113079.\]
Let \(m\) and \(n\) be two five-digit numbers with the same twisted sum. Prove that \(m = n\).
|
We define \(S(n)\) as the sum of the digits of \(n\) and \(T(n)\) as the twisted sum of \(n\). If we look at the five terms of \(T(n) + n\), we see that each digit of \(n\) appears exactly once in each of the places (ten-thousands, thousands, hundreds, tens, units). This means that
\[T(n) + n = (10000 + 1000 + 100 + 10 + 1)(a + b + c + d + e) = 11111 \cdot S(n).\]
Now suppose that \(T(m) = T(n)\). Then it follows that \(11111 \cdot S(m) - m = 11111 \cdot S(n) - n\), which we can rewrite as
\[11111 \cdot (S(m) - S(n)) = m - n.\]
In particular, this implies that \(11111 \mid m - n\). Furthermore, we know that \(S(n) \equiv n \mod 9\), so if we look at this equation modulo 9, we find \(5(m - n) \equiv m - n \mod 9\) hence \(9 \mid 4(m - n)\). Since \(\text{gcd}(4, 9) = 1\), this means that \(9 \mid m - n\). Therefore, given \(11111 \mid m - n\), we now conclude that \(99999 \mid m - n\), because \(\text{gcd}(11111, 9) = 1\). Since \(m\) and \(n\) are both five-digit numbers, we conclude that \(m = n\). \(\square\)
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Voor een getal van vijf cijfers \(n = abcde\) definiëren we de verdraaide som van \(n\) als de waarde
\[bcdea + cdeab + deabc + eabcd.\]
De verdraaide som van 20253 is bijvoorbeeld
\[05232 + 25320 + 53202 + 32025 = 113079.\]
Laat \(m\) en \(n\) twee vijfcijferige getallen zijn met dezelfde verdraaide som. Bewijs dat \(m = n\).
|
We definiëren \(S(n)\) als de som van de cijfers van \(n\) en \(T(n)\) als de verdraaide som van \(n\). Als we de vijf termen van \(T(n) + n\) bekijken, dan zien we dat elk cijfer van \(n\) precies één keer op elk van de plekken (tienduizendtal, duizendtal, honderdtal, tiental, eenheid) staat. Dit betekent dat
\[T(n) + n = (10000 + 1000 + 100 + 10 + 1)(a + b + c + d + e) = 11111 \cdot S(n).\]
Stel nu dat \(T(m) = T(n)\). Dan geldt dus dat \(11111 \cdot S(m) - m = 11111 \cdot S(n) - n\), wat we kunnen herschrijven als
\[11111 \cdot (S(m) - S(n)) = m - n.\]
In het bijzonder volgt hieruit dat \(11111 \mid m - n\). Daarbovenop weten we dat \(S(n) \equiv n \mod 9\), dus als we deze vergelijking modulo 9 bekijken, vinden we \(5(m - n) \equiv m - n \mod 9\) dus \(9 \mid 4(m - n)\). Omdat \(\text{gcd}(4, 9) = 1\) betekent dit dat \(9 \mid m - n\). Hieruit volgt wegens \(11111 \mid m - n\) nu dat \(99999 \mid m - n\), want \(\text{gcd}(11111, 9) = 1\). Aangezien \(m\) en \(n\) beide vijfcijferige getallen zijn, concluderen we dat \(m = n\). \(\square\)
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2025-B2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2025"
}
|
For a five-digit number \(n = abcde\), we define the twisted sum of \(n\) as the value
\[bcdea + cdeab + deabc + eabcd.\]
The twisted sum of 20253, for example, is
\[05232 + 25320 + 53202 + 32025 = 113079.\]
Let \(m\) and \(n\) be two five-digit numbers with the same twisted sum. Prove that \(m = n\).
|
As we know that \(11111 \cdot (S(m) - S(n)) = m - n\) and \(9 \mid m - n\), we can also conclude as follows (without using that \(\text{gcd}(11111, 9) = 1\)). From the second relation, we also know that \(S(m) \equiv m \equiv n \equiv S(n) \mod 9\), so \(9 \mid S(m) - S(n)\). From the first relation, it follows that \(11111 \cdot 9 = 99999\) is a divisor of \(m - n\). Since \(m\) and \(n\) are both five-digit numbers, we conclude that \(m = n\). \(\square\)
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Voor een getal van vijf cijfers \(n = abcde\) definiëren we de verdraaide som van \(n\) als de waarde
\[bcdea + cdeab + deabc + eabcd.\]
De verdraaide som van 20253 is bijvoorbeeld
\[05232 + 25320 + 53202 + 32025 = 113079.\]
Laat \(m\) en \(n\) twee vijfcijferige getallen zijn met dezelfde verdraaide som. Bewijs dat \(m = n\).
|
Als we weten dat \(11111 \cdot (S(m) - S(n)) = m - n\) en \(9 \mid m - n\), kunnen we het ook als volgt afmaken (zonder te gebruiken dat \(\text{gcd}(11111, 9) = 1\)). Wegens de tweede relatie weten we ook dat \(S(m) \equiv m \equiv n \equiv S(n) \mod 9\), dus \(9 \mid S(m) - S(n)\). Wegens de eerste relatie volgt hieruit dat \(11111 \cdot 9 = 99999\) een deler is van \(m - n\). Aangezien \(m\) en \(n\) beide vijfcijferige getallen zijn, concluderen we dat \(m = n\). \(\square\)
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2025-B2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2025"
}
|
Let \(n \ge 2\) be an integer, and let \(z_1, \dots, z_n\) be positive integers that satisfy:
- \(z_j \le j\) for \(j = 1, \dots, n\);
- \(z_1 + \dots + z_n\) is even.
Prove that there exist \(s_1, \dots, s_n \in \{-1, 1\}\) such that:
\[s_1 z_1 + s_2 z_2 + \dots + s_n z_n = 0.\]
|
We prove this by two-step induction on \(n\). For \(n = 2\), it follows from the conditions that \(z_1 = z_2 = 1\), and thus \(z_1 - z_2 = 0\). For \(n = 3\), it follows from the condition that \((z_1, z_2, z_3)\) is equal to \((1, 1, 2)\), \((1, 2, 1)\), or \((1, 2, 3)\). For these, we choose \((s_1, s_2, s_3)\) to be \((1, 1, -1)\), \((1, -1, 1)\), and \((1, 1, -1)\), respectively.
Now suppose we have proven the desired result for \(n = k\) and \(n = k-1\), where \(k \ge 2\). Let \(z_1, \dots, z_{k+1}\) be numbers that satisfy the conditions in the problem. We distinguish two cases. First, suppose \(z_k = z_{k+1}\). By applying the induction hypothesis for \(n = k-1\) to \(z_1, \dots, z_{k-1}\), we find \(s_1, \dots, s_{k-1}\) such that \(s_1 z_1 + \dots + s_{k-1} z_{k-1} = 0\). Now we also have
\[s_1 z_1 + \dots + s_{k-1} z_{k-1} + z_k - z_{k+1} = 0,\]
so the desired result follows. Now suppose \(z_k \neq z_{k+1}\). Then \(|z_k - z_{k+1}| \ge 1\). Additionally, we know that \(|z_k - z_{k+1}| \le k\) because \(1 \le z_k, z_{k+1} \le k+1\). Since \(|z_k - z_{k+1}| \equiv z_k + z_{k+1} \mod 2\), it also follows that \(z_1 + \dots + z_{k-1} + |z_k - z_{k+1}|\) is even. Therefore, we can apply the induction hypothesis for \(n = k\) to \(z_1, \dots, z_{k-1}, |z_k - z_{k+1}|\). This gives us \(s_1, \dots, s_k\) such that:
\[s_1 z_1 + \dots + s_{k-1} z_{k-1} + s_k |z_k - z_{k+1}| = 0.\]
Since \(|z_k - z_{k+1}| = \pm (z_k - z_{k+1})\), the desired result follows in this case as well.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Zij \(n \ge 2\) een geheel getal, en laat \(z_1, \dots, z_n\) positieve gehele getallen zijn die voldoen aan:
- \(z_j \le j\) voor \(j = 1, \dots, n\);
- \(z_1 + \dots + z_n\) is even.
Bewijs dat er \(s_1, \dots, s_n \in \{-1, 1\}\) bestaan zodat:
\[s_1 z_1 + s_2 z_2 + \dots + s_n z_n = 0.\]
|
We bewijzen dit met tweestapsinductie naar \(n\). Voor \(n = 2\) volgt uit de voorwaarden dat \(z_1 = z_2 = 1\), en dan geldt dus dat \(z_1 - z_2 = 0\). Voor \(n = 3\) volgt uit de voorwaarde dat \((z_1, z_2, z_3)\) gelijk is aan \((1, 1, 2)\), \((1, 2, 1)\) of \((1, 2, 3)\). Daarvoor kiezen we respectievelijk \((s_1, s_2, s_3)\) gelijk aan \((1, 1, -1)\), \((1, -1, 1)\) en \((1, 1, -1)\).
Stel nu dat we het gevraagde bewezen hebben voor \(n = k\) en \(n = k-1\), waarbij \(k \ge 2\). Laat \(z_1, \dots, z_{k+1}\) getallen zijn die voldoen aan de voorwaarden in de opgave. We onderscheiden twee gevallen. Stel eerst dat \(z_k = z_{k+1}\). Door de inductiehypothese voor \(n = k-1\) toe te passen op \(z_1, \dots, z_{k-1}\) vinden we \(s_1, \dots, s_{k-1}\) zodat \(s_1 z_1 + \dots + s_{k-1} z_{k-1} = 0\). Nu hebben we ook dat
\[s_1 z_1 + \dots + s_{k-1} z_{k-1} + z_k - z_{k+1} = 0,\]
dus volgt het gevraagde. Stel nu dat \(z_k \neq z_{k+1}\). Dan geldt dat \(|z_k - z_{k+1}| \ge 1\). Daarnaast weten we ook dat \(|z_k - z_{k+1}| \le k\) omdat \(1 \le z_k, z_{k+1} \le k+1\). Omdat \(|z_k - z_{k+1}| \equiv z_k + z_{k+1} \mod 2\), geldt ook dat \(z_1 + \dots + z_{k-1} + |z_k - z_{k+1}|\) even is. We kunnen dus de inductiehypothese voor \(n = k\) toepassen op \(z_1, \dots, z_{k-1}, |z_k - z_{k+1}|\). Hierdoor vinden we \(s_1, \dots, s_k\) zodanig dat:
\[s_1 z_1 + \dots + s_{k-1} z_{k-1} + s_k |z_k - z_{k+1}| = 0.\]
Omdat \(|z_k - z_{k+1}| = \pm (z_k - z_{k+1})\), volgt ook nu het gevraagde.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2025-B2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2025"
}
|
Let \(n \ge 2\) be an integer, and let \(z_1, \dots, z_n\) be positive integers that satisfy:
- \(z_j \le j\) for \(j = 1, \dots, n\);
- \(z_1 + \dots + z_n\) is even.
Prove that there exist \(s_1, \dots, s_n \in \{-1, 1\}\) such that:
\[s_1 z_1 + s_2 z_2 + \dots + s_n z_n = 0.\]
|
We construct \(s_n, s_{n-1}, \dots, s_1\) recursively in the following way. To begin with, we choose \(s_n = 1\). Next, consider a \(k \in \{2, \dots, n\}\) and suppose we have chosen \(s_k, \dots, s_n\). Define \(b_k = s_k z_k + \dots + s_n z_n\), and choose:
\[s_{k-1} = \begin{cases} -1 & \text{if } b_k \ge 0; \\ 1 & \text{if } b_k < 0. \end{cases}\]
Finally, define \(b_1 = s_1z_1 + \dots + s_nz_n\).
We claim that \(|b_k| \le k\) for \(k = 1, \dots, n\). We prove this by downward induction on \(k\). For \(k = n\), it is indeed true that \(|b_n| = |s_nz_n| = |z_n| \le n\). Suppose now that we have proven that \(|b_k| \le k\) for some \(k \in \{2, \dots, n\}\). If \(b_k \ge 0\), then \(b_{k-1} = b_k - z_{k-1}\). We have \(-(k-1) \le -z_{k-1} \le b_k - z_{k-1} \le b_k - 1 \le k-1\), so \(|b_{k-1}| = |b_k - z_{k-1}| \le k-1\). If \(b_k < 0\), then \(b_{k-1} = b_k + z_{k-1}\). In this case, we have \(-(k-1) \le b_k + 1 \le b_k + z_{k-1} < z_{k-1} \le k-1\), so it follows that \(|b_{k-1}| = |b_k + z_{k-1}| \le k-1\). This completes the induction.
In particular, we have \(|b_1| \le 1\). Additionally, we know that \(b_1 \equiv z_1 + \dots + z_n \equiv 0 \mod 2\), so \(b_1 = 0\), as desired. \(\square\)
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Zij \(n \ge 2\) een geheel getal, en laat \(z_1, \dots, z_n\) positieve gehele getallen zijn die voldoen aan:
- \(z_j \le j\) voor \(j = 1, \dots, n\);
- \(z_1 + \dots + z_n\) is even.
Bewijs dat er \(s_1, \dots, s_n \in \{-1, 1\}\) bestaan zodat:
\[s_1 z_1 + s_2 z_2 + \dots + s_n z_n = 0.\]
|
We construeren recursief \(s_n, s_{n-1}, \dots, s_1\), op de volgende manier. Om te beginnen kiezen we \(s_n = 1\). Bekijk vervolgens een \(k \in \{2, \dots, n\}\) en stel dat we \(s_k, \dots, s_n\) gekozen hebben. Definieer \(b_k = s_k z_k + \dots + s_n z_n\), en kies:
\[s_{k-1} = \begin{cases} -1 & \text{als } b_k \ge 0; \\ 1 & \text{als } b_k < 0. \end{cases}\]
Definieer ten slotte \(b_1 = s_1z_1 + \dots + s_nz_n\).
We beweren dat \(|b_k| \le k\) voor \(k = 1, \dots, n\). We bewijzen dit met neerwaartse inductie naar \(k\). Voor \(k = n\) geldt inderdaad dat \(|b_n| = |s_nz_n| = |z_n| \le n\). Stel nu dat we bewezen hebben dat \(|b_k| \le k\) voor een zekere \(k \in \{2, \dots, n\}\). Als \(b_k \ge 0\), dan geldt dat \(b_{k-1} = b_k - z_{k-1}\). We hebben \(-(k-1) \le -z_{k-1} \le b_k - z_{k-1} \le b_k - 1 \le k-1\), dus \(|b_{k-1}| = |b_k - z_{k-1}| \le k-1\). Als \(b_k < 0\), dan geldt dat \(b_{k-1} = b_k + z_{k-1}\). In dit geval hebben we \(-(k-1) \le b_k + 1 \le b_k + z_{k-1} < z_{k-1} \le k-1\), dus volgt ook dat \(|b_{k-1}| = |b_k + z_{k-1}| \le k-1\). Dit voltooit de inductie.
In het bijzonder geldt dat \(|b_1| \le 1\). Daarnaast weten we dat \(b_1 \equiv z_1 + \dots + z_n \equiv 0 \mod 2\), dus moet \(b_1 = 0\), zoals we wilden. \(\square\)
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2025-B2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2025"
}
|
Let \(n \ge 2\) be an integer, and let \(z_1, \dots, z_n\) be positive integers that satisfy:
- \(z_j \le j\) for \(j = 1, \dots, n\);
- \(z_1 + \dots + z_n\) is even.
Prove that there exist \(s_1, \dots, s_n \in \{-1, 1\}\) such that:
\[s_1 z_1 + s_2 z_2 + \dots + s_n z_n = 0.\]
|
We prove the following stronger claim, from which the problem follows by choosing \(m = \frac{1}{2}S\).
**Claim.** Let \(n\) be a positive integer, and let \(z_1, \dots, z_n\) be positive integers such that \(z_j \le j\) for \(j = 1, \dots, n\). Let \(S = z_1 + \dots + z_n\) (not necessarily even) and \(0 \le m \le S\). Then there exists a subset of \(\{z_1, \dots, z_n\}\) with sum \(m\).
We prove this by induction on \(n\). For \(n = 1\), the empty subset has sum 0 and the entire set \(\{z_1\}\) has sum 1.
Now suppose the claim is true for \(n = k\) and consider numbers \(z_1, \dots, z_{k+1}\) that satisfy the condition. We define \(Z = \max(z_1, \dots, z_{k+1})\) and let \(j\) be maximal such that \(z_j = Z\). This means that \(z_i < Z \le j\) for all \(i > j\).
If we remove \(z_j\), we get a set of \(k\) elements, defined as
\[ \text{for } i < j: \quad \tilde{z}_i = z_i \le i; \\ \text{for } i \ge j: \quad \tilde{z}_i = z_{i+1} < Z \le j \le i, \]
with sum \(\tilde{S} = \sum_{i=1}^n \tilde{z}_i = S-Z\). Note that \(Z \le j \le k+1\) and \(S-Z = \sum_{i=1; i \ne j}^{k+1} z_i \ge k \cdot 1 = k\), or equivalently \(Z \le S-k\). This means that \(2Z \le (k+1) + (S-k) = S+1\). Therefore, \(Z\) is at most half of the sum \(S\) rounded up, \(Z \le \lceil \frac{1}{2}S \rceil\), and \(\tilde{S}\) is at least half of \(S\) rounded down, \(\tilde{S} \ge \lfloor \frac{1}{2}S \rfloor\). With this, we can now apply the induction hypothesis.
- For \(0 \le m \le \lfloor \frac{1}{2}S \rfloor\), it follows that \(0 \le m \le \tilde{S}\). Then there is a subset of the \(\tilde{z}_i\) with sum \(m\), which immediately gives a subset of the \(z_i\) with the same sum.
- For \(\lceil \frac{1}{2}S \rceil \le m \le S\), it follows that \(0 \le m-Z \le S-Z = \tilde{S}\). So there is a subset of the \(\tilde{z}_i\) with sum \(m-Z\). If we add \(z_j\) to this, we get a subset of the \(z_i\) with sum \(m\).
With this, we have found for \(n = k + 1\) a subset for every \(0 \le m \le S\), and the induction is complete.
If the sum \(S\) is even, we can choose \(m = \frac{1}{2}S\). This gives a subset with sum \(\frac{1}{2}S\), and the sum of the remaining numbers is also equal to \(S - \frac{1}{2}S = \frac{1}{2}S\). Now take \(s_i = 1\) for the \(z_i\) in this subset, and all other \(s_i = -1\). Then it follows that \(s_1z_1 + s_2z_2 + \dots + s_nz_n = \frac{1}{2}S - \frac{1}{2}S = 0\). \(\square\)
Remark. With the substitution \(s_i = 2t_i - 1\), the problem is equivalent to a sequence \(t_1, \dots, t_n\) with \(t_i \in \{0, 1\}\) such that
\[t_1z_1 + t_2z_2 + \dots + t_nz_n = \frac{1}{2}S.\]
The strategy described in Solution 2 is to choose the \(t_i\) starting from \(i = n\) such that the sum \(t_i z_i + \dots + t_n z_n\) is not greater than \(\frac{1}{2}S\). The subset in Solution 3 is given by the \(i\) for which \(t_i = 1\).
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Zij \(n \ge 2\) een geheel getal, en laat \(z_1, \dots, z_n\) positieve gehele getallen zijn die voldoen aan:
- \(z_j \le j\) voor \(j = 1, \dots, n\);
- \(z_1 + \dots + z_n\) is even.
Bewijs dat er \(s_1, \dots, s_n \in \{-1, 1\}\) bestaan zodat:
\[s_1 z_1 + s_2 z_2 + \dots + s_n z_n = 0.\]
|
We bewijzen de volgende sterkere claim, waaruit de opgave volgt door voor \(m = \frac{1}{2}S\) te kiezen.
**Claim.** Zij \(n\) een positief geheel getal, en laat \(z_1, \dots, z_n\) positieve gehele getallen zo dat \(z_j \le j\) voor \(j = 1, \dots, n\). Zij \(S = z_1 + \dots + z_n\) (niet-noodzakelijk even) en \(0 \le m \le S\). Dan bestaat er een deelverzameling van \(\{z_1, \dots, z_n\}\) met som \(m\).
We bewijzen dit met inductie naar \(n\). Voor \(n = 1\), heeft de lege deelverzameling som 0 en de hele verzameling \(\{z_1\}\) som 1.
Stel nu dat de claim waar is voor \(n = k\) en beschouw getallen \(z_1, \dots, z_{k+1}\) die aan de voorwaarde voldoen. We definiëren \(Z = \max(z_1, \dots, z_{k+1})\) en zij \(j\) maximaal zo dat \(z_j = Z\). Dat betekent dat \(z_i < Z \le j\) voor alle \(i > j\).
Als we \(z_j\) weglaten krijgen we een verzameling van \(k\) elementen, gedefinieerd als
\[ \text{voor } i < j: \quad \tilde{z}_i = z_i \le i; \\ \text{voor } i \ge j: \quad \tilde{z}_i = z_{i+1} < Z \le j \le i, \]
met som \(\tilde{S} = \sum_{i=1}^n \tilde{z}_i = S-Z\). Merk op dat \(Z \le j \le k+1\) en \(S-Z = \sum_{i=1; i \ne j}^{k+1} z_i \ge k \cdot 1 = k\), oftewel \(Z \le S-k\). Dat betekent dat \(2Z \le (k+1) + (S-k) = S+1\). Dus \(Z\) is hoogstens de helft van de som \(S\) naar boven afgerond, \(Z \le \lceil \frac{1}{2}S \rceil\), en \(\tilde{S}\) is minstens de helft van \(S\) naar beneden afgerond, \(\tilde{S} \ge \lfloor \frac{1}{2}S \rfloor\). Hiermee kunnen we nu de inductiehypothese toepassen.
- Voor \(0 \le m \le \lfloor \frac{1}{2}S \rfloor\), geldt dus \(0 \le m \le \tilde{S}\). Dan is er een deelverzameling van de \(\tilde{z}_i\) met som \(m\), wat meteen een deelverzameling van de \(z_i\) geeft met dezelfde som.
- Voor \(\lceil \frac{1}{2}S \rceil \le m \le S\), geldt dat \(0 \le m-Z \le S-Z = \tilde{S}\). Dus er is een deelverzameling van de \(\tilde{z}_i\) met som \(m-Z\). Als we hier \(z_j\) aan toevoegen krijgen we een deelverzameling van de \(z_i\) met som \(m\).
Hiermee hebben we voor \(n = k + 1\) voor elke \(0 \le m \le S\) een deelverzameling gevonden met som \(m\), en is de inductie voltooid.
Als de som \(S\) even is, dan kunnen we \(m = \frac{1}{2}S\) kiezen. Dat geeft een deelverzameling met som \(\frac{1}{2}S\), en de som van de overige getallen is ook gelijk aan aan \(S - \frac{1}{2}S = \frac{1}{2}S\). Neem nu de bijbehorende \(s_i = 1\) voor de \(z_i\) in deze deelverzameling, en alle overige \(s_i = -1\). Dan geldt dus \(s_1z_1 + s_2z_2 + \dots + s_nz_n = \frac{1}{2}S - \frac{1}{2}S = 0\). \(\square\)
Opmerking. Met de substitutie \(s_i = 2t_i - 1\) wordt de vraag equivalent aan een reeks \(t_1, \dots, t_n\) met \(t_i \in \{0, 1\}\) zo dat
\[t_1z_1 + t_2z_2 + \dots + t_nz_n = \frac{1}{2}S.\]
Dan is de omschreven strategie van Oplossing 2 om de \(t_i\) te kiezen beginnende vanaf \(i = n\) zodanig dat de som \(t_i z_i + \dots + t_n z_n\) niet groter is dan \(\frac{1}{2}S\). En de deelverzameling van Oplossing 3 wordt gegeven door de \(i\) waarvoor \(t_i = 1\).
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2025-B2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing III.",
"tier": "T1",
"year": "2025"
}
|
A group of 4050 friends is playing a video game tournament. For this, there are 2025 computers in one room labeled \(a_1, \dots, a_{2025}\) and 2025 computers in another room labeled \(b_1, \dots, b_{2025}\). The player on computer \(a_i\) always plays against the players \(b_i\), \(b_{i+2}\), \(b_{i+3}\) and \(b_{i+4}\) (in particular, not against \(b_{i+1}\)), where the computers are numbered cyclically. After the first round, all players choose a computer within their room for the second round. Then they notice that everyone has the same opponents in the second round as in the first round.
Prove that if someone has chosen the same computer in both rounds, then everyone has chosen the same computer in both rounds.
|
For the opponent computers of \(a_i\), we look at which \(a_j\) they play against in the following table.
<table><tr><td>\(b_i\) :</td><td>\(a_{i-4}\)</td><td>\(a_{i-3}\)</td><td>\(a_{i-2}\)</td><td>\(a_i\)</td></tr></table>
<table><tr><td>\(b_{i+2}\) :</td><td>\(a_{i-2}\)</td><td>\(a_{i-1}\)</td><td>\(a_i\)</td><td>\(a_{i+2}\)</td></tr><tr><td>\(b_{i+3}\) :</td><td></td><td>\(a_{i-1}\)</td><td>\(a_i\)</td><td>\(a_{i+1}\)</td><td>\(a_{i+3}\)</td></tr><tr><td>\(b_{i+4}\) :</td><td></td><td></td><td>\(a_i\)</td><td>\(a_{i+1}\)</td><td>\(a_{i+2}\)</td><td>\(a_{i+4}\)</td></tr></table>
Note that the computers \(a_{i-2}\), \(a_{i-1}\), \(a_{i+1}\), and \(a_{i+2}\) each have two common opponent computers with \(a_i\). Furthermore, \(a_{i-4}\), \(a_{i-3}\), \(a_{i+3}\), and \(a_{i+4}\) each have one common opponent computer with \(a_i\). Only for the first two, \(a_{i-4}\) and \(a_{i-3}\), is the common opponent with \(a_i\) the same, namely \(b_i\).

Now suppose a player has remained stuck, say the player on \(a_{2025}\). We will now prove by induction that all players on \(a_i\) and \(b_i\) have remained stuck.
Assume by induction hypothesis that the player on a certain computer \(a_i\) is the same in both rounds. Since everyone has the same opponents in both rounds, the players on \(a_{i-4}\) and \(a_{i-3}\) each have one common opponent with \(a_i\), namely the player on \(b_i\). This means that the player on \(b_i\) has also remained stuck. Now we observe that only the player on \(a_{i-2}\) has another common opponent with \(a_i\) besides \(b_i\). Therefore, the same player has also remained stuck on \(a_{i-2}\).
Since 2025 is odd, it follows by induction that everyone has remained on the same computer if one person has remained stuck. □
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Een groep van 4050 vrienden speelt een videospel-toernooi. Daarvoor staan er 2025 computers in een zaal gelabeld \(a_1, \dots, a_{2025}\) en 2025 computers in een andere zaal gelabeld \(b_1, \dots, b_{2025}\). De speler op computer \(a_i\) speelt altijd tegen de spelers \(b_i\), \(b_{i+2}\), \(b_{i+3}\) en \(b_{i+4}\) (in het bijzonder dus juist niet tegen \(b_{i+1}\)), waarbij we de computers cyclisch doornummeren. Na de eerste ronde kiezen alle spelers een computer binnen hun zaal voor de tweede ronde. Daarna merken ze op dat iedereen in de tweede ronde dezelfde tegenstanders heeft als in de eerste ronde.
Bewijs dat als er iemand dezelfde computer heeft gekozen in beide rondes, dan iedereen dezelfde computer heeft gekozen in beide rondes.
|
Voor de tegenstandercomputers van \(a_i\) bekijken we tegen welke \(a_j\) zij spelen in de volgende tabel.
<table><tr><td>\(b_i\) :</td><td>\(a_{i-4}\)</td><td>\(a_{i-3}\)</td><td>\(a_{i-2}\)</td><td>\(a_i\)</td></tr></table>
<table><tr><td>\(b_{i+2}\) :</td><td>\(a_{i-2}\)</td><td>\(a_{i-1}\)</td><td>\(a_i\)</td><td>\(a_{i+2}\)</td></tr><tr><td>\(b_{i+3}\) :</td><td></td><td>\(a_{i-1}\)</td><td>\(a_i\)</td><td>\(a_{i+1}\)</td><td>\(a_{i+3}\)</td></tr><tr><td>\(b_{i+4}\) :</td><td></td><td></td><td>\(a_i\)</td><td>\(a_{i+1}\)</td><td>\(a_{i+2}\)</td><td>\(a_{i+4}\)</td></tr></table>
Merk op dat de computers \(a_{i-2}\), \(a_{i-1}\), \(a_{i+1}\) en \(a_{i+2}\) elk twee gemeenschappelijk tegenstandercomputers hebben met \(a_i\). Verder hebben \(a_{i-4}\), \(a_{i-3}\), \(a_{i+3}\) en \(a_{i+4}\) elk één gemeenschappelijke tegenstandercomputer met \(a_i\). Alleen voor de eerste twee, \(a_{i-4}\) en \(a_{i-3}\), is de gemeenschappelijk tegenstander met \(a_i\) hetzelfde, namelijk \(b_i\).

Stel nu dat er een speler is blijven zitten, zeg de speler op \(a_{2025}\). We gaan nu met inductie bewijzen dat alle spelers op \(a_i\) en \(b_i\) zijn blijven zitten.
Stel per inductiehypothese dat de speler op een zekere computer \(a_i\) in beide rondes hetzelfde is. Aangezien iedereen dezelfde tegenstanders heeft in beide rondes, hebben de spelers die op \(a_{i-4}\) en \(a_{i-3}\) zaten wederom elk één dezelfde gemeenschappelijke speler met
\(a_i\), namelijk de speler die op \(b_i\) zat. Dat betekent dat de speler op \(b_i\) ook is blijven zitten. Nu merken we op dat alleen de speler die op \(a_{i-2}\) zat naast \(b_i\) nog een tweede gemeenschappelijke tegenstander met \(a_i\) heeft. Dus ook op \(a_{i-2}\) is dezelfde speler blijven zitten.
Omdat 2025 oneven is, volgt nu met inductie eenvoudig dat iedereen op dezelfde computer is blijven zitten, als er één iemand is blijven zitten. □
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2025-B2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2025"
}
|
A group of 4050 friends is playing a video game tournament. For this, there are 2025 computers in one room labeled \(a_1, \dots, a_{2025}\) and 2025 computers in another room labeled \(b_1, \dots, b_{2025}\). The player on computer \(a_i\) always plays against the players \(b_i\), \(b_{i+2}\), \(b_{i+3}\) and \(b_{i+4}\) (in particular, not against \(b_{i+1}\)), where the computers are numbered cyclically. After the first round, all players choose a computer within their room for the second round. Then they notice that everyone has the same opponents in the second round as in the first round.
Prove that if someone has chosen the same computer in both rounds, then everyone has chosen the same computer in both rounds.
|
We call two computers *superconnected* if they have two common opponent computers. We note that the only computers superconnected with \(a_i\) are the computers \(a_{i-2}\), \(a_{i-1}\), \(a_{i+1}\), and \(a_{i+2}\). Now we look at triples that are superconnected.
- There are two computers superconnected with both \(a_i\) and \(a_{i+1}\), namely the computers \(a_{i-1}\) and \(a_{i+2}\).
- There is one computer superconnected with both \(a_i\) and \(a_{i+2}\), namely the computer \(a_{i+1}\).

So if a computer is superconnected with \(a_i\) and has two common superconnected computers with \(a_i\), then this computer is \(a_{i-1}\) or \(a_{i+1}\).
Since everyone has the same opponents in both rounds, it follows that if two friends played on superconnected computers in the first round, they will also play on superconnected computers in the second round. From the above, it follows that if two friends sat next to each other in the first round, they will also do so in the second round.
Assume now that the player on \(a_1\) is the same in both rounds. We further assume, for the sake of contradiction, that the player who sat on \(a_2\) in the first round sat on \(a_{2025}\) in the second round. Then, inductively, the players on \(a_3\), \(a_4\), and \(a_5\) must have moved to \(a_{2024}\), \(a_{2023}\), and \(a_{2022}\). So the player who sat on \(b_5\) in the first round (and played against \(a_1\), \(a_2\), \(a_3\), \(a_5\)) must, in the second round, play against the players on computers \(a_{2022}\), \(a_{2024}\), \(a_{2025}\), \(a_1\). But there is no computer with those opponents. We conclude that the player on \(a_2\) must have stayed put. This inductively shows that everyone in that room stayed on the same computer.
Since the players in the second room have the same opponents in both rounds, we now know that they also play against the same computers. This fixes the computers in the second room, so everyone in the second room also chose the same computer in both rounds. □
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Een groep van 4050 vrienden speelt een videospel-toernooi. Daarvoor staan er 2025 computers in een zaal gelabeld \(a_1, \dots, a_{2025}\) en 2025 computers in een andere zaal gelabeld \(b_1, \dots, b_{2025}\). De speler op computer \(a_i\) speelt altijd tegen de spelers \(b_i\), \(b_{i+2}\), \(b_{i+3}\) en \(b_{i+4}\) (in het bijzonder dus juist niet tegen \(b_{i+1}\)), waarbij we de computers cyclisch doornummeren. Na de eerste ronde kiezen alle spelers een computer binnen hun zaal voor de tweede ronde. Daarna merken ze op dat iedereen in de tweede ronde dezelfde tegenstanders heeft als in de eerste ronde.
Bewijs dat als er iemand dezelfde computer heeft gekozen in beide rondes, dan iedereen dezelfde computer heeft gekozen in beide rondes.
|
We noemen twee computers *superconnected* als ze twee tegenstandercomputers gemeen hebben. We merken op dat de enige computers superconnected met \(a_i\) de computers \(a_{i-2}\), \(a_{i-1}\), \(a_{i+1}\) en \(a_{i+2}\) zijn. Nu gaan we kijken naar drietallen die superconnected zijn.
- Er zijn twee computers superconnected met zowel \(a_i\) als \(a_{i+1}\), namelijk de computers \(a_{i-1}\) en \(a_{i+2}\).
- Er is één computer superconnected met zowel \(a_i\) als \(a_{i+2}\), namelijk de computer \(a_{i+1}\).

Dus als een computer zelf superconnected is met \(a_i\) en twee gemeenschappelijke superconnected computers met \(a_i\) heeft, dan is deze computer \(a_{i-1}\) of \(a_{i+1}\).
Aangezien iedereen dezelfde tegenstanders heeft in beide rondes, geldt dat als twee vrienden in de eerste ronde op superconnected computers speelden, ze in de tweede ronde ook op superconnected computers spelen. Uit het bovenstaande volgt dan dat, als twee vrienden in de eerste ronde naast elkaar zaten, ze dat in de tweede ronde ook doen.
Stel nu dat de speler op \(a_1\) beide rondes hetzelfde is. We nemen verder uit het ongerijmde aan dat de speler die de eerste ronde op \(a_2\) zat, in de tweede ronde op \(a_{2025}\) zat. Dan moeten inductief de spelers op \(a_3\), \(a_4\) en \(a_5\) verhuisd zijn naar \(a_{2024}\), \(a_{2023}\) en \(a_{2022}\). Dus de speler die in de eerste ronde op \(b_5\) zat (en tegen \(a_1\), \(a_2\), \(a_3\), \(a_5\) speelde), moet in de tweede ronde tegen de spelers op computers \(a_{2022}\), \(a_{2024}\), \(a_{2025}\), \(a_1\). Maar er is geen computer met die tegenstanders. We concluderen dus dat de speler op \(a_2\) wel moet zijn blijven zitten. Dit laat inductief zien dat iedereen in die zaal op dezelfde computer is blijven zitten.
Aangezien de spelers in de tweede zaal dezelfde tegenstanders hebben in beide rondes, weten we nu dat ze ook tegen dezelfde computers spelen. Dit legt de computers in de tweede zaal vast, dus iedereen in de tweede zaal heeft ook voor dezelfde computer gekozen in beide rondes. □
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2025-B2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2025"
}
|
Given is \(\triangle ABC\) with circumcircle \(\Gamma\). Let \(M\) be the midpoint of the arc \(BC\) of \(\Gamma\) that does not contain \(A\). The point \(N\) on \(\Gamma\) is the antipode of \(A\). The line through \(B\) perpendicular to \(AM\) intersects \(AM\) at point \(D\) and intersects \(\Gamma\) a second time at point \(P \neq B\). The line through \(D\) perpendicular to \(AC\) intersects \(AC\) at point \(E\) and intersects \(BC\) at point \(F\).
Prove that \(ND\), \(MF\), and \(PE\) are concurrent.

|
We denote half of the angle at \(A\) as \(\alpha = \frac{1}{2} \angle BAC = \angle BAM = \angle MAC\), because \(M\) is the midpoint of arc \(BC\). Then we observe that \(\angle ABP = \angle ABD = 90^\circ - \angle DAB = 90^\circ - \alpha\) and that \(\angle EDA = 90^\circ - \angle DAE = 90^\circ - \alpha\). We also calculate that, due to the straight angle \(\angle ADM\), \(\angle PDE = 180^\circ - \angle EDA - \angle MDP = 180^\circ - (90^\circ - \alpha) - 90^\circ = \alpha\).
Now we define \(K\) as the second intersection point of the circumcircle of \(\triangle ADE\) with \(\Gamma\) (besides \(A\)). Then we observe that \(\angle AKE = \angle ADE = 90^\circ - \alpha = \angle ABP = \angle AKP\), so \(K\), \(E\), and \(P\) are collinear. Similarly, \(\angle AKD = 180^\circ - \angle AED = 90^\circ = \angle AKN\), due to Thales' theorem because \(A\) and \(N\) are antipodes. Thus, \(K\), \(D\), and \(N\) are collinear.
For the last line, we claim that \(BFDK\) is also a cyclic quadrilateral. Indeed, \(\angle KBF = \angle KBC = 180^\circ - \angle KAC = 180^\circ - \angle KAE = \angle KDE = 180^\circ - \angle KDF\).
(Note that this is essentially Miquel's theorem in \(\triangle CEF\) and cyclic quadrilaterals \(AKBC\) and \(DEAK\).) From the inscribed angle theorem in the cyclic quadrilateral \(BFDK\), it follows that \(\angle BKF = \angle BDF = \angle PDE = \alpha = \angle BAM = \angle BKM\), so \(K\), \(F\), and \(M\) are collinear. We conclude that \(ND\), \(MF\), and \(PE\) are concurrent at point \(K\). \(\square\)
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Gegeven is \(\triangle ABC\) met omgeschreven cirkel \(\Gamma\). Zij \(M\) het midden van de boog \(BC\) van \(\Gamma\) waar \(A\) niet op ligt. Het punt \(N\) op \(\Gamma\) is de antipode van \(A\). De lijn door \(B\) loodrecht op \(AM\) snijdt \(AM\) in het punt \(D\) en snijdt \(\Gamma\) een tweede keer in het punt \(P \neq B\). De lijn door \(D\) loodrecht op \(AC\) snijdt \(AC\) in het punt \(E\) en snijdt \(BC\) in het punt \(F\).
Bewijs dat \(ND\), \(MF\) en \(PE\) concurrent zijn.

|
We noteren de helft van de hoek bij \(A\) als \(\alpha = \frac{1}{2} \angle BAC = \angle BAM = \angle MAC\), want \(M\) is het midden van boog \(BC\). Dan merken we op dat \(\angle ABP = \angle ABD = 90^\circ - \angle DAB = 90^\circ - \alpha\) en dat \(\angle EDA = 90^\circ - \angle DAE = 90^\circ - \alpha\). Ook rekenen we uit dat, wegens de gestrekte hoek \(\angle ADM\), geldt dat \(\angle PDE = 180^\circ - \angle EDA - \angle MDP = 180^\circ - (90^\circ - \alpha) - 90^\circ = \alpha\).
Nu definiëren we \(K\) als het tweede snijpunt van de omgeschreven cirkel van \(\triangle ADE\) met \(\Gamma\) (naast \(A\)). Dan merken we op dat \(\angle AKE = \angle ADE = 90^\circ - \alpha = \angle ABP = \angle AKP\), dus \(K\), \(E\) en \(P\) zijn collinear. Evenzo geldt dat \(\angle AKD = 180^\circ - \angle AED = 90^\circ = \angle AKN\), wegens Thales omdat \(A\) en \(N\) antipoden zijn. Dus \(K\), \(D\) en \(N\) zijn collinear.
Voor de laatste lijn claimen we dat \(BFDK\) ook een koordenvierhoek is. Inderdaad, \(\angle KBF = \angle KBC = 180^\circ - \angle KAC = 180^\circ - \angle KAE = \angle KDE = 180^\circ - \angle KDF\).
(Merk op dat dit in feite de stelling van Miquel is in \(\triangle CEF\) en koordenvierhoeken \(AKBC\) en \(DEAK\).) Uit de omtrekhoekstelling in de koordenvierhoek \(BFDK\) volgt dat \(\angle BKF = \angle BDF = \angle PDE = \alpha = \angle BAM = \angle BKM\), dus \(K\), \(F\) en \(M\) zijn collinear. We concluderen dat \(ND\), \(MF\) en \(PE\) concurrent zijn in het punt \(K\). \(\square\)
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2025-B2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2025"
}
|
Given is \(\triangle ABC\) with circumcircle \(\Gamma\). Let \(M\) be the midpoint of the arc \(BC\) of \(\Gamma\) that does not contain \(A\). The point \(N\) on \(\Gamma\) is the antipode of \(A\). The line through \(B\) perpendicular to \(AM\) intersects \(AM\) at point \(D\) and intersects \(\Gamma\) a second time at point \(P \neq B\). The line through \(D\) perpendicular to \(AC\) intersects \(AC\) at point \(E\) and intersects \(BC\) at point \(F\).
Prove that \(ND\), \(MF\), and \(PE\) are concurrent.

|
Just as in Solution I, we write \(\alpha = \frac{1}{2}\angle BAC\) and note that \(\angle ANP = \angle ABP = 90^\circ - \alpha = \angle ADE\). Since also \(\angle APN = 90^\circ = \angle AED\), we see that \(\triangle ANP \sim \triangle ADE\). Moreover, they are similarly oriented. From the theory of spiral similarities, it follows that \(\triangle AND \sim \triangle APE\) and that \(ND\) and \(PE\) intersect at the second intersection point of the circumcircles of \(\triangle ANP\) and \(\triangle ADE\), that is, at \(K\). Now we proceed as in Solution I to show that \(MF\) passes through \(K\). \(\square\)
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Gegeven is \(\triangle ABC\) met omgeschreven cirkel \(\Gamma\). Zij \(M\) het midden van de boog \(BC\) van \(\Gamma\) waar \(A\) niet op ligt. Het punt \(N\) op \(\Gamma\) is de antipode van \(A\). De lijn door \(B\) loodrecht op \(AM\) snijdt \(AM\) in het punt \(D\) en snijdt \(\Gamma\) een tweede keer in het punt \(P \neq B\). De lijn door \(D\) loodrecht op \(AC\) snijdt \(AC\) in het punt \(E\) en snijdt \(BC\) in het punt \(F\).
Bewijs dat \(ND\), \(MF\) en \(PE\) concurrent zijn.

|
Net als in Oplossing I schrijven we \(\alpha = \frac{1}{2}\angle BAC\) en merken we op dat \(\angle ANP = \angle ABP = 90^\circ - \alpha = \angle ADE\). Omdat ook \(\angle APN = 90^\circ = \angle AED\) zien we dat \(\triangle ANP \sim \triangle ADE\). Bovendien zijn ze gelijk georiënteerd. Uit de theorie van draaiver- menigvuldigingen volgt nu dat \(\triangle AND \sim \triangle APE\) en dat \(ND\) en \(PE\) elkaar snijden in het tweede snijpunt van de omgeschreven cirkels van \(\triangle ANP\) en \(\triangle ADE\), oftewel in \(K\). Nu gaan we verder zoals in Oplossing I om te laten zien dat \(MF\) door \(K\) gaat. \(\square\)
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2025-B2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2025"
}
|
Determine all natural numbers \(n\) for which all prime factors of \(2^n - 1\) are at most 7.
|
We observe that \(2 \nmid 2^n - 1\) for all \(n > 1\), so we are looking for all \(n\) such that 3, 5, and 7 are the only divisors, i.e., \(2^n - 1 = 3^a 5^b 7^c\). The answers are \(n = 1, 2, 3, 4, 6\), which we can easily verify with the results 1, 3, 7, 3 · 5, 3² · 7.
We calculate that \(2^2 \equiv 1 \mod 3\), \(2^4 \equiv 1 \mod 5\), and \(2^3 \equiv 1 \mod 7\), and that these are the smallest positive exponents for which \(2^n\) is congruent to 1. This means that \(3 \mid 2^n - 1\) if and only if \(2 \mid n\), \(5 \mid 2^n - 1\) if and only if \(4 \mid n\), and \(7 \mid 2^n - 1\) if and only if \(3 \mid n\).
If \(n\) is odd, it follows from the above that \(2^n - 1\) has no factors 3 or 5. We distinguish two cases. If \(3 \nmid n\) and \(n > 1\), then 7 is also not a divisor, while \(2^n - 1 > 1\). Therefore, \(2^n - 1\) must have a prime divisor greater than 7, and these \(n\) do not satisfy the condition. The other option for odd \(n\) is that \(3 \mid n\). To satisfy the condition, it must hold that \(2^n - 1 = 7^c\). If \(n \ge 4\), we then find the relation \(7^c \equiv -1 \mod 16\). However, this is in contradiction with the fact that \(7^c \equiv 7, 1 \mod 16\), since \(7^2 = 49 = 3 \cdot 16 + 1\). Thus, the only possibility is \(n = 3\).
We now provide a proof for even \(n \ge 8\) that \(2^n - 1\) has a prime factor greater than 7 using complete induction on \(n\). As the base case, we calculate that
\[
\begin{align*}
2^8 - 1 &= 3 \cdot 5 \cdot 17, \\
2^{10} - 1 &= 3 \cdot 11 \cdot 31, \\
2^{12} - 1 &= 3^2 \cdot 5 \cdot 7 \cdot 13.
\end{align*}
\]
Now suppose \(n = 2m\) with \(m \ge 7\), and suppose that for all even \(k\) with \(8 \le k < n\), \(2^k - 1\) has a prime factor greater than 7. Consider the factorization \(2^n - 1 = 2^{2m} - 1 = (2^m - 1)(2^m + 1)\). If \(m\) is odd, then the first factor has a prime factor greater than 7 since \(m \ge 7 > 3\). If \(m\) is even, then the same holds by the induction hypothesis since \(8 \le m < 2m = n\). This completes the induction. \(\square\)
|
n = 1, 2, 3, 4, 6
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Bepaal alle natuurlijke getallen \(n\) waarvoor geldt dat alle priemfactoren van \(2^n - 1\) hoogstens 7 zijn.
|
We merken op dat \(2 \nmid 2^n - 1\) voor alle \(n > 1\), dus we zijn op zoek naar alle \(n\) zodanig dat 3, 5 en 7 de enige delers zijn, oftewel \(2^n - 1 = 3^a 5^b 7^c\). De antwoorden zijn \(n = 1, 2, 3, 4, 6\), die we gemakkelijk controleren met uitkomsten 1, 3, 7, 3 · 5, 3² · 7.
We rekenen uit dat \(2^2 \equiv 1 \mod 3\), \(2^4 \equiv 1 \mod 5\) en \(2^3 \equiv 1 \mod 7\), én dat dit de kleinste positieve exponenten zijn waarvoor \(2^n\) congruent is aan 1. Dat betekent dat \(3 \mid 2^n - 1\) dan en slechts dan als \(2 \mid n\), dat \(5 \mid 2^n - 1\) dan en slechts dan als \(4 \mid n\) en dat \(7 \mid 2^n - 1\) dan en slechts dan als \(3 \mid n\).
Als \(n\) oneven is dan volgt uit het bovenstaande dat \(2^n - 1\) geen factoren 3 of 5 heeft. We onderscheiden twee gevallen. Als \(3 \nmid n\) en \(n > 1\), geldt dat ook 7 geen deler is, terwijl \(2^n - 1 > 1\). Dus \(2^n - 1\) moet wel een grotere priemdeler dan 7 hebben, en deze \(n\) voldoen niet. De andere optie voor oneven \(n\) is dat \(3 \mid n\). Om aan de voorwaarde te voldoen moet dan gelden dat \(2^n - 1 = 7^c\). Als \(n \ge 4\) vinden we dus de relatie \(7^c \equiv -1 \mod 16\). Dat is echter in tegenspraak met het feit dat \(7^c \equiv 7, 1 \mod 16\), want \(7^2 = 49 = 3 \cdot 16 + 1\). Dan is de enige mogelijkheid dus \(n = 3\).
We geven nu voor even \(n \ge 8\) een bewijs dat \(2^n - 1\) een priemfactor heeft groter dan 7 met volledige inductie naar \(n\). Als inductiebasis rekenen we uit dat
\[
\begin{align*}
2^8 - 1 &= 3 \cdot 5 \cdot 17, \\
2^{10} - 1 &= 3 \cdot 11 \cdot 31, \\
2^{12} - 1 &= 3^2 \cdot 5 \cdot 7 \cdot 13.
\end{align*}
\]
Stel nu dat \(n = 2m\) met \(m \ge 7\), en stel dat voor alle even \(k\) met \(8 \le k < n\) geldt dat \(2^k - 1\) een priemfactor groter dan 7 heeft. Beschouw de ontbinding \(2^n - 1 = 2^{2m} - 1 = (2^m - 1)(2^m + 1)\). Als \(m\) oneven is, dan heeft de eerst factor een priemfactor groter dan 7 aangezien \(m \ge 7 > 3\). Als \(m\) even is, dan geldt hetzelfde op basis van de inductiehypothese aangezien nu geldt dat \(8 \le m < 2m = n\). Dit voltooit de inductie. \(\square\)
|
{
"exam": "Dutch_TST",
"problem_label": "5",
"problem_match": "\nOpgave 5.",
"resource_path": "Dutch_TST/segmented/nl-2025-B2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2025"
}
|
Determine all natural numbers \(n\) for which all prime factors of \(2^n - 1\) are at most 7.
|
The proof that \(2^n - 1\) has a prime factor greater than 7 for odd \(n > 3\) proceeds similarly to the above. We provide an alternative proof that the only even \(n\) that satisfy the condition are 2, 4, and 6 by distinguishing three cases.
Suppose \(4 \mid n\). Then we write \(n = 4k\) and factorize \(2^n - 1\) as \(2^n - 1 = (2^{2k})^2 - 1 = (4^k - 1)(4^k + 1)\). Note that \(3 \nmid 4^k + 1\) because \(4^k + 1 \equiv 2 \mod 3\) for all \(k\), and note that \(7 \nmid 4^k + 1\) because the residue classes of \(4^k\) modulo 7 are 1, 4, and 2. Since \(2^n - 1\) must not have a prime factor greater than 7, it must hold that \(4^k + 1 = 5^d\), with \(d > 0\) because \(k > 0\). If \(k \ge 2\), then 16 must divide \(5^d - 1\). This implies that \(d\) is a multiple of 4, so we write \(d = 4d'\), with \(d' > 0\). In that case, we find that \(2^{2k} = 4^k = 5^{4d'} - 1 = (5^{2d'} - 1)(5^{2d'} + 1) = (25^{d'} - 1)(25^{d'} + 1)\). Since \(\text{gcd}(25^{d'} - 1, 25^{d'} + 1) = 2\), this means that at least one of the terms \((25^{d'} - 1\) or \(25^{d'} + 1)\) is less than or equal to 2. This is a contradiction with \(d' > 0\). Therefore, the only possibility in this case is \(k = 1\), i.e., \(n = 4\).
Suppose \(6 \mid n\), but \(4 \nmid n\). Then we write \(n = 6k\) with \(k\) odd, and factorize \(2^n - 1 = (2^{3k})^2 - 1 = (8^k - 1)(8^k + 1)\). Note that \(5 \nmid 8^k + 1\) because \(8^k \equiv 3, -3 \mod 5\) for odd \(k\), and note that \(7 \nmid 8^k + 1\) because \(8^k + 1 \equiv 2 \mod 7\). Now it must hold that \(8^k + 1 = 3^a\). Since \(8 \mid 3^a - 1\), \(a\) is even, which we write as \(a = 2a'\), with \(a' > 0\). Then we get \(8^k = (3^{a'} - 1)(3^{a'} + 1)\). Because \(\text{gcd}(3^{a'} - 1, 3^{a'} + 1) = 2\), it follows that one of the terms \((3^{a'} - 1\) or \(3^{a'} + 1)\) is less than or equal to 2. This can only happen if \(a' = 1\), i.e., \(a = 2\), \(k = 1\), and \(n = 6\).
The last case is that \(2 \mid n\), but \(4 \nmid n\) and \(3 \nmid n\). Then we write \(n = 2k\) and immediately find that \(3^a = 2^n - 1 = (2^k - 1)(2^k + 1)\). Since \(\text{gcd}(2^k - 1, 2^k + 1) = 1 < 3\), the only possibility is that \(2^k - 1 = 1\). Thus, \(k = 1\) and \(n = 2\). \(\square\)
|
2, 4, 6
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Bepaal alle natuurlijke getallen \(n\) waarvoor geldt dat alle priemfactoren van \(2^n - 1\) hoogstens 7 zijn.
|
Het bewijs dat \(2^n - 1\) een priemfactor groter dan 7 heeft voor oneven \(n > 3\) gaat hetzelfde als hierboven. We geven een alternatief bewijs dat de enige even \(n\) die voldoen 2, 4 en 6 zijn door drie gevallen te onderscheiden.
Stel dat \(4 \mid n\). Dan schrijven we \(n = 4k\) en ontbinden we \(2^n - 1\) als \(2^n - 1 = (2^{2k})^2 - 1 = (4^k - 1)(4^k + 1)\). Merk op dat \(3 \nmid 4^k + 1\) want \(4^k + 1 \equiv 2 \mod 3\) voor alle \(k\), en merk op dat \(7 \nmid 4^k + 1\) want de restklasses van \(4^k\) modulo 7 zijn 1, 4 en 2. Aangezien \(2^n - 1\)
geen priemfactor mag hebben groter dan 7, moet nu gelden dat \(4^k + 1 = 5^d\), met \(d > 0\) want \(k > 0\). Als \(k \ge 2\), dan krijgen we dus dat 16 een deler is van \(5^d - 1\). Hieruit volgt dan weer dat \(b\) een viervoud is, dus we schrijven \(b = 4d'\), met \(d' > 0\). In dat geval vinden we dus dat \(2^{2k} = 4^k = 5^{4d'} - 1 = (5^{2d'} - 1)(5^{2d'} + 1) = (25^{d'} - 1)(25^{d'} + 1)\). Aangezien \(\text{ggd}(25^{d'} - 1, 25^{d'} + 1) = 2\) betekent dit dan minstens één van de termen \((25^{d'} - 1\) of \(25^{d'} + 1)\) kleiner of gelijk is aan 2. Dat is een tegenspraak met \(d' > 0\). Dus de enige mogelijkheid in dit geval is \(k = 1\), oftewel \(n = 4\).
Stel dat 6 | \(n\), maar 4 \(\nmid\) \(n\). Dan schrijven we \(n = 6k\) met \(k\) oneven, en ontbinden we \(2^n - 1 = (2^{3k})^2 - 1 = (8^k - 1)(8^k + 1)\). Merk op dat \(5 \nmid 8^k + 1\) want \(8^k \equiv 3, -3 \mod 5\) voor oneven \(k\), en merk op dat \(7 \nmid 8^k + 1\) want \(8^k + 1 \equiv 2 \mod 7\). Nu moet dus gelden dat \(8^k + 1 = 3^a\). Aangezien nu \(8 \mid 3^a - 1\), is \(a\) even wat we schrijven als \(a = 2a'\), met \(a' > 0\). Dan krijgen we \(8^k = (3^{a'} - 1)(3^{a'} + 1)\). Omdat \(\text{ggd}(3^{a'} - 1, 3^{a'} + 1) = 2\) volgt hieruit dat één van de termen \((3^{a'} - 1\) of \(3^{a'} + 1)\) kleiner of gelijk is aan 2. Dat kan alleen als \(a' = 1\), oftewel \(a = 2\), \(k = 1\) en \(n = 6\).
Het laatste geval is dat 2 | \(n\), maar 4 \(\nmid\) \(n\) en 3 \(\nmid\) \(n\). Dan schrijven we \(n = 2k\) en vinden we meteen dat \(3^a = 2^n - 1 = (2^k - 1)(2^k + 1)\). Omdat \(\text{ggd}(2^k - 1, 2^k + 1) = 1 < 3\), is de enige mogelijkheid dat \(2^k - 1 = 1\). Oftewel \(k = 1\) en \(n = 2\). \(\square\)
|
{
"exam": "Dutch_TST",
"problem_label": "5",
"problem_match": "\nOpgave 5.",
"resource_path": "Dutch_TST/segmented/nl-2025-B2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2025"
}
|
Consider the sequence \(y_0, y_1, \ldots\) with \(y_0 = -\frac{1}{4}\) and \(y_1 = 0\) and which further satisfies
\[y_{n+1} + y_{n-1} = 4y_n + 1\]
for all \(n \ge 1\). Prove that for all \(n \ge 0\) the expression \(2y_{2n} + \frac{3}{2}\)
a) is a positive integer and
b) is the square of an integer.
|
We make the substitution \(x_n = 4y_n + 2\). Then the equation becomes homogeneous:
\[x_{n+1} + x_{n-1} = 4y_{n+1} + 2 + 4y_{n-1} + 2 = 4(4y_n + 1) + 4 = 16y_n + 8 = 4x_n,\]
with initial conditions \(x_0 = 4(-\frac{1}{4}) + 2 = 1\) and \(x_1 = 4 \cdot 0 + 2 = 2\). All numbers in the sequence \((x_i)\) are thus integers, and we see that \(x_{n+1}\) and \(x_{n-1}\) always have the same parity. In particular, \(x_{2n}\) is always odd. Therefore, \(2y_{2n} + \frac{3}{2} = \frac{4y_{2n}+3}{2} = \frac{x_{2n}+1}{2}\) is always an integer. To show that they are also positive, we prove by induction that \(x_n\) is a strictly increasing sequence of positive numbers. This is indeed true for \(x_1 > x_0 > 0\). Suppose as the induction hypothesis that \(x_n > x_{n-1} > 0\). Then we also find that \(x_{n+1} - x_n = 3x_n - x_{n-1} > x_n - x_{n-1} > 0\). With this, we conclude the proof of part (a).
For part (b), we note that the characteristic equation for the homogeneous part \(y_{n+1} + y_{n-1} = 4y_n\) is given by \(x^2 + 1 = 4x\). The solutions to this are \(x = 2 - \sqrt{3}\) and \(x = 2 + \sqrt{3}\). Now we choose a particular solution to the inhomogeneous equation, say \(y_n = -\frac{1}{2}\). Then the general solution is
\[y_n = A(2 - \sqrt{3})^n + B(2 + \sqrt{3})^n - \frac{1}{2}.\]
Solving this using \(n = 0\) and \(n = 1\), we find \(-\frac{1}{4} = A + B - \frac{1}{2}\) and \(0 = A(2 - \sqrt{3}) + B(2 + \sqrt{3}) - \frac{1}{2} = 2(A + B) + \sqrt{3}(B - A) - \frac{1}{2}\). This means that \(A + B = \frac{1}{4}\) and \(B - A = 0\), or \(A = B = \frac{1}{8}\). Thus,
\[y_n = \frac{1}{8}(2 - \sqrt{3})^n + \frac{1}{8}(2 + \sqrt{3})^n - \frac{1}{2}.\]
Since \((2 - \sqrt{3})(2 + \sqrt{3}) = 4 - 3 = 1\), we easily check that
\[
\begin{align*}
(4y_n + 2)^2 &= \left(\frac{1}{2}(2 - \sqrt{3})^n + \frac{1}{2}(2 + \sqrt{3})^n\right)^2 \\
&= \frac{1}{4}(2 - \sqrt{3})^{2n} + \frac{1}{4}(2 + \sqrt{3})^{2n} + \frac{1}{2}(2 - \sqrt{3})^n(2 + \sqrt{3})^n \\
&= \frac{1}{4}(2 - \sqrt{3})^{2n} + \frac{1}{4}(2 + \sqrt{3})^{2n} + \frac{1}{2} \\
&= 2y_{2n} + \frac{3}{2}.
\end{align*}
\]
This proves part (b), since \(4y_n + 2 = x_n\) is an integer. \(\square\)
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Beschouw de rij \(y_0, y_1, \ldots\) met \(y_0 = -\frac{1}{4}\) en \(y_1 = 0\) en die verder voldoet aan
\[y_{n+1} + y_{n-1} = 4y_n + 1\]
voor alle \(n \ge 1\). Bewijs dat voor alle \(n \ge 0\) de uitdrukking \(2y_{2n} + \frac{3}{2}\)
a) een positief geheel getal is en
b) het kwadraat van een geheel getal is.
|
We maken de substitutie \(x_n = 4y_n + 2\). Dan wordt de vergelijking homogeen:
\[x_{n+1} + x_{n-1} = 4y_{n+1} + 2 + 4y_{n-1} + 2 = 4(4y_n + 1) + 4 = 16y_n + 8 = 4x_n,\]
met beginvoorwaarden \(x_0 = 4(-\frac{1}{4}) + 2 = 1\) en \(x_1 = 4 \cdot 0 + 2 = 2\). Alle getallen in de rij \((x_i)\) zijn dus geheel en we zien dat \(x_{n+1}\) en \(x_{n-1}\) altijd dezelfde pariteit hebben. In het bijzonder is \(x_{2n}\) altijd oneven. Dus \(2y_{2n} + \frac{3}{2} = \frac{4y_{2n}+3}{2} = \frac{x_{2n}+1}{2}\) is altijd geheel. Om te laten zien dat ze ook positief zijn, bewijzen we met inductie dat \(x_n\) een stijgende rij positieve getallen is. Dit geldt inderdaad voor \(x_1 > x_0 > 0\). Stel nu als inductiehypothese dat \(x_n > x_{n-1} > 0\). Dan vinden we ook dat \(x_{n+1} - x_n = 3x_n - x_{n-1} > x_n - x_{n-1} > 0\). Hiermee concluderen we het bewijs van onderdeel (a).
Voor onderdeel (b) merken we op dat de karakteristieke vergelijking voor het homogene deel \(y_{n+1} + y_{n-1} = 4y_n\) wordt gegeven door \(x^2 + 1 = 4x\). Hiervan zijn de oplossingen \(x = 2 - \sqrt{3}\) en \(x = 2 + \sqrt{3}\). Nu kiezen we een oplossing voor de inhomogene vergelijking, zeg \(y_n = -\frac{1}{2}\). Dan is de algemene oplossing dus
\[y_n = A(2 - \sqrt{3})^n + B(2 + \sqrt{3})^n - \frac{1}{2}.\]
Als we dit oplossen met behulp van \(n = 0\) en \(n = 1\), dan vinden we \(-\frac{1}{4} = A + B - \frac{1}{2}\) en \(0 = A(2 - \sqrt{3}) + B(2 + \sqrt{3}) - \frac{1}{2} = 2(A + B) + \sqrt{3}(B - A) - \frac{1}{2}\). Dat betekent dat \(A + B = \frac{1}{4}\) en \(B - A = 0\), oftewel \(A = B = \frac{1}{8}\). Dus
\[y_n = \frac{1}{8}(2 - \sqrt{3})^n + \frac{1}{8}(2 + \sqrt{3})^n - \frac{1}{2}.\]
Aangezien \((2 - \sqrt{3})(2 + \sqrt{3}) = 4 - 3 = 1\) controleren we eenvoudig dat
\[
\begin{align*}
(4y_n + 2)^2 &= \left(\frac{1}{2}(2 - \sqrt{3})^n + \frac{1}{2}(2 + \sqrt{3})^n\right)^2 \\
&= \frac{1}{4}(2 - \sqrt{3})^{2n} + \frac{1}{4}(2 + \sqrt{3})^{2n} + \frac{1}{2}(2 - \sqrt{3})^n(2 + \sqrt{3})^n \\
&= \frac{1}{4}(2 - \sqrt{3})^{2n} + \frac{1}{4}(2 + \sqrt{3})^{2n} + \frac{1}{2} \\
&= 2y_{2n} + \frac{3}{2}.
\end{align*}
\]
Dit bewijst onderdeel (b), omdat \(4y_n + 2 = x_n\) geheel is. \(\square\)
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2025-C2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2025"
}
|
Consider the sequence \(y_0, y_1, \ldots\) with \(y_0 = -\frac{1}{4}\) and \(y_1 = 0\) and which further satisfies
\[y_{n+1} + y_{n-1} = 4y_n + 1\]
for all \(n \ge 1\). Prove that for all \(n \ge 0\) the expression \(2y_{2n} + \frac{3}{2}\)
a) is a positive integer and
b) is the square of an integer.
|
For an alternative approach to part (b), we calculate that
\[ x_{n+1}^2 - x_{n-1}^2 = (x_{n+1} + x_{n-1})(x_{n+1} - x_{n-1}) = 4x_n(x_{n+1} - x_{n-1}). \]
This means that \(x_{n+1}^2 - 4x_{n+1}x_n + x_n^2 = x_n^2 - 4x_nx_{n-1} + x_{n-1}^2\). By induction on \(n\), this implies that \(x_{n+1}^2 - 4x_{n+1}x_n + x_n^2 = -3\), because for \(n = 0\) we calculate that \(2^2 - 4 \cdot 2 \cdot 1 + 1^2 = -3\).
Now we prove by induction that \(x_{2n} = 2x_n^2 - 1\) for \(n \ge 0\). For \(n = 0\), this is true because \(1 = 2 \cdot 1^2 - 1\). Also for \(n = 1\), we calculate that \(x_2 = 4x_1 - x_0 = 7 = 2x_1^2 - 1\). Since we will use induction on odd numbers, we note that \(16x_n = 4x_{n-1} + 4x_{n+1} = x_{n-2} + 2x_n + x_{n+2}\), so \(14x_n = x_{n-2} + x_{n+2}\). Suppose now that the claim is true for \(n = k\) and \(n = k-1\). Then we calculate using the above that
\[
\begin{align*}
x_{2k+2} &= 14x_{2k} - x_{2k-2} \\
&\overset{\text{(IH)}}{=} 14(2x_k^2 - 1) - (2x_{k-1}^2 - 1) \\
&= 2(14x_k^2 - x_{k-1}^2 - 6) - 1 \\
&= 2(14x_k^2 - (4x_k - x_{k+1})^2 - 6) - 1 \\
&= 2(-2x_k^2 + 8x_kx_{k+1} - x_{k+1}^2 - 6) - 1 \\
&= 2x_{k+1}^2 - 1.
\end{align*}
\]
Thus, we have shown by induction that \(x_{2n} = 2x_n^2 - 1\), or equivalently,
\[ 2y_{2n} + \frac{3}{2} = \frac{x_{2n} + 1}{2} = x_n^2. \]
|
2y_{2n} + \frac{3}{2} = x_n^2
|
Yes
|
Yes
|
proof
|
Algebra
|
Beschouw de rij \(y_0, y_1, \ldots\) met \(y_0 = -\frac{1}{4}\) en \(y_1 = 0\) en die verder voldoet aan
\[y_{n+1} + y_{n-1} = 4y_n + 1\]
voor alle \(n \ge 1\). Bewijs dat voor alle \(n \ge 0\) de uitdrukking \(2y_{2n} + \frac{3}{2}\)
a) een positief geheel getal is en
b) het kwadraat van een geheel getal is.
|
Voor een alternatieve aanpak van onderdeel (b) rekenen we uit dat
\[ x_{n+1}^2 - x_{n-1}^2 = (x_{n+1} + x_{n-1})(x_{n+1} - x_{n-1}) = 4x_n(x_{n+1} - x_{n-1}). \]
Dit betekent dat \(x_{n+1}^2 - 4x_{n+1}x_n + x_n^2 = x_n^2 - 4x_nx_{n-1} + x_{n-1}^2\). Met inductie naar \(n\) betekent dit dat \(x_{n+1}^2 - 4x_{n+1}x_n + x_n^2 = -3\), want voor \(n = 0\) rekenen we uit dat \(2^2 - 4 \cdot 2 \cdot 1 + 1^2 = -3\).
Nu bewijzen we met inductie dat \(x_{2n} = 2x_n^2 - 1\) voor \(n \ge 0\). Voor \(n = 0\) is dit waar want \(1 = 2 \cdot 1^2 - 1\). Ook voor \(n = 1\) rekenen we uit dat \(x_2 = 4x_1 - x_0 = 7 = 2x_1^2 - 1\). Omdat we inductie gaan doen op oneven getallen merken we alvast op dat \(16x_n = 4x_{n-1} + 4x_{n+1} = x_{n-2} + 2x_n + x_{n+2}\), dus \(14x_n = x_{n-2} + x_{n+2}\). Stel nu dat de bewering waar is voor \(n = k\) en \(n = k-1\). Dan rekenen we met behulp van het voorgaande uit dat
\[
\begin{align*}
x_{2k+2} &= 14x_{2k} - x_{2k-2} \\
&\overset{\text{(IH)}}{=} 14(2x_k^2 - 1) - (2x_{k-1}^2 - 1) \\
&= 2(14x_k^2 - x_{k-1}^2 - 6) - 1 \\
&= 2(14x_k^2 - (4x_k - x_{k+1})^2 - 6) - 1 \\
&= 2(-2x_k^2 + 8x_kx_{k+1} - x_{k+1}^2 - 6) - 1 \\
&= 2x_{k+1}^2 - 1.
\end{align*}
\]
Nu hebben we dus met inductie laten zien dat \(x_{2n} = 2x_n^2 - 1\), oftewel
\[ 2y_{2n} + \frac{3}{2} = \frac{x_{2n} + 1}{2} = x_n^2. \]
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2025-C2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2025"
}
|
Consider the sequence \(y_0, y_1, \ldots\) with \(y_0 = -\frac{1}{4}\) and \(y_1 = 0\) and which further satisfies
\[y_{n+1} + y_{n-1} = 4y_n + 1\]
for all \(n \ge 1\). Prove that for all \(n \ge 0\) the expression \(2y_{2n} + \frac{3}{2}\)
a) is a positive integer and
b) is the square of an integer.
|
As an alternative to part (b), we claim by induction on \(m\) that
\[ x_{n-m} + x_{n+m} = 2x_m x_n, \]
for all numbers \(m\) and \(n\) with \(0 \le m \le n\). For \(m = 0\) and \(m = 1\), the equations \(x_n + x_n = 2x_n\) and \(x_{n-1} + x_{n+1} = 4x_n\) indeed hold. Suppose now that the claim is true for \(m = k\) and \(m = k-1\). Then for \(m = k+1\) we find that
\[
\begin{align*}
x_{n-k-1} + x_{n+k+1} &= (4x_{n-k} - x_{n-k+1}) + (4x_{n+k} - x_{n+k-1}) \\
&= 4(x_{n-k} + x_{n+k}) - (x_{n-k+1} + x_{n+k-1}) \\
&\overset{\text{(IH)}}{=} 8x_k x_n - 2x_{k-1} x_n \\
&= 2(4x_k - x_{k-1}) x_n \\
&= 2x_{k+1} x_n.
\end{align*}
\]
This completes the induction. If we now set \(m = n\), we find \(1 + x_{2n} = 2x_n^2\).
Thus, we conclude that \(2y_{2n} + \frac{3}{2} = \frac{x_{2n+1}}{2} = x_n^2\). \(\square\)
Remark. For the odd indices, we have \(x_{2n+1} = 3\left(\frac{x_{n+1}+x_n}{3}\right)^2 - 1\).
|
2y_{2n} + \frac{3}{2} = x_n^2
|
Yes
|
Yes
|
proof
|
Algebra
|
Beschouw de rij \(y_0, y_1, \ldots\) met \(y_0 = -\frac{1}{4}\) en \(y_1 = 0\) en die verder voldoet aan
\[y_{n+1} + y_{n-1} = 4y_n + 1\]
voor alle \(n \ge 1\). Bewijs dat voor alle \(n \ge 0\) de uitdrukking \(2y_{2n} + \frac{3}{2}\)
a) een positief geheel getal is en
b) het kwadraat van een geheel getal is.
|
Als alternatief voor onderdeel (b) claimen we met inductie naar \(m\) dat
\[ x_{n-m} + x_{n+m} = 2x_m x_n, \]
voor alle getallen \(m\) en \(n\) met \(0 \le m \le n\). Voor \(m = 0\) en \(m = 1\), voldoen de vergelijkingen \(x_n + x_n = 2x_n\) en \(x_{n-1} + x_{n+1} = 4x_n\) inderdaad. Stel nu dat de bewering waar is voor \(m = k\) en \(m = k-1\). Dan vinden we voor \(m = k+1\) dat
\[
\begin{align*}
x_{n-k-1} + x_{n+k+1} &= (4x_{n-k} - x_{n-k+1}) + (4x_{n+k} - x_{n+k-1}) \\
&= 4(x_{n-k} + x_{n+k}) - (x_{n-k+1} + x_{n+k-1}) \\
&\overset{\text{(IH)}}{=} 8x_k x_n - 2x_{k-1} x_n \\
&= 2(4x_k - x_{k-1}) x_n \\
&= 2x_{k+1} x_n.
\end{align*}
\]
Hiermee is de inductie voltooid. Als we nu \(m = n\) invullen, dan vinden we \(1 + x_{2n} = 2x_n^2\).
Dus we concluderen dat \(2y_{2n} + \frac{3}{2} = \frac{x_{2n+1}}{2} = x_n^2\). \(\square\)
Opmerking. Voor de oneven indices geldt \(x_{2n+1} = 3\left(\frac{x_{n+1}+x_n}{3}\right)^2 - 1\).
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2025-C2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing III.",
"tier": "T1",
"year": "2025"
}
|
Consider a rectangular board of \(m \times n\) squares with \(m, n \ge 1\). The vertices of the squares form an \((m+1) \times (n+1)\)-grid. We call a triangle with vertices being points of the grid *low* if it has at least one side that is parallel to a side of the board such that the height of the triangle on that side is 1. We call a low triangle *special* if it has two sides that are parallel to a side of the board. We partition the board into low triangles.
Determine the minimum number of special triangles over all possible partitions of the \(m \times n\)-board.
|
When \(m, n \ge 2\) and at least one of them is even, then the answer is 0. Otherwise (at least one of them is 1, or they are both odd), the answer is 2.
We first draw an example for \(n = 1\) and \(m \ge 1\) with two special triangles, an example for \(n = 2\) and \(m \ge 3\) with zero special triangles, and the special case \(n = 2\), \(m = 2\) with zero special triangles again.

If \(m = 1\) or \(n = 1\), then there is a partitioning with two special triangles. Now suppose \(m, n \ge 2\).
If at least one of \(m\) and \(n\) is even, we can cut the rectangle into strips of width 2, so we can create a partitioning with zero special triangles. If they are both odd, then we cut the rectangle into strips of width 2 plus one strip of width 1. This way, we create a partitioning with two special triangles. Now we need to show that this upper bound is the best we can do.
For every partitioning, we now create the following picture. We place a red dot in the middle of each slanted side of each triangle, and if there are two slanted sides, we connect the two red dots with a red line. Note that each triangle has at most two slanted sides, and only special triangles have just one.

At each red dot, at most two red lines meet. So these red lines form closed cycles or open paths, and the special triangles are precisely the ends of the open paths. Here, we have an open path of length zero, and a closed cycle formed by 6 red segments. A red path can only change direction at a slanted side that has "height" 1 in both directions (i.e., it belongs to two triangles that have height 1 in different directions). Such a slanted side must therefore be the diagonal of a cell. In particular, a red path only changes direction at the center of cells. (Alternatively, you can say that the red sides never run along the grid lines, because the height of each triangle is 1 and the red lines run at half height. So you can never change direction on the grid lines.)
Now we have open and closed paths of orthogonal red lines that only change direction at the center of the cells. If we color the cells in a checkerboard pattern, then the cells through which the path passes are alternately black and white. A closed cycle thus always passes through an even number of cells. If the board has an odd number of cells, then there is at least one open path. And this open path has two special triangles at its ends. □
|
2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Beschouw een rechthoekig bord van \(m \times n\) vakjes met \(m, n \ge 1\). De hoekpunten van de vakjes vormen een \((m+1) \times (n+1)\)-grid. We noemen een driehoek met hoekpunten punten van het grid *laag* als die minstens één zijde heeft die parallel is met een zijde van het bord zo dat de hoogte van de driehoek op die zijde 1 is. We noemen een lage driehoek *bijzonder* als die twee zijden heeft die parallel zijn met een zijde van het bord. We partitioneren het bord in lage driehoeken.
Bepaal het minimale aantal bijzondere driehoeken over alle mogelijke partitioneringen van het \(m \times n\)-bord.
|
Als \(m, n \ge 2\) en minstens één van de twee is even, dan is het antwoord 0. Anders (minstens één van de twee is 1, of ze zijn beide oneven) is het antwoord 2.
We tekenen eerst een voorbeeld voor \(n = 1\) en \(m \ge 1\) met twee bijzondere driehoeken, een voorbeeld voor \(n = 2\) en \(m \ge 3\) met nul bijzondere driehoeken, en het speciale geval \(n = 2\), \(m = 2\) met wederom nul bijzondere driehoeken.

Als \(m = 1\) of \(n = 1\), dan is er dus een partitionering met twee bijzondere driehoeken. Stel nu dat \(m, n \ge 2\).
Als minstens één van \(m\) en \(n\) even is, kunnen we de rechthoek opknippen in stroken van breedte 2, dus dan kunnen we een partitionering maken met nul bijzondere driehoeken. Als ze beide oneven zijn, dan knippen we de rechthoek op in stroken van breedte 2 plus één strook van breedte 1. Zo maken we een partitionering met twee bijzondere driehoeken. Nu moeten we nog laten zien dat deze bovengrens het beste is wat we kunnen doen.
Voor elke partitionering maken we nu het volgende plaatje. We zetten een rood punt in het midden van elke schuine zijde van elke driehoek, en als er twee schuine zijden zijn dan verbinden we de twee rode punten met een rode lijn. Merk op dat elke driehoek hoogstens twee schuine zijden heeft, en alleen bijzondere driehoeken hebben er maar één.

In elk rood punt komen nu hoogstens twee rode lijnen samen. Dus deze rode lijnen vormen gesloten cykels of open paden, en de bijzondere driehoeken zijn precies de eindes van de de open paden. Zo hebben we hierboven een open pad van lengte nul, en een gesloten cykel gevormd door 6 rode segmenten. Een rood pad kan alleen van richting veranderen op een schuine zijde die in beide richtingen “hoogte” 1 heeft (oftewel die hoort bij twee driehoeken die in verschillende richtingen hoogte 1 hebben). Zo’n schuine zijde moet dus precies de diagonaal zijn van een vakje. In het bijzonder verandert een rood pad alleen van richting in het midden van vakjes. (Alternatief kun je zeggen dat de rode zijden nooit over de roosterlijnen lopen, want de hoogte van elke driehoek is 1 en de rode lijnen lopen op halve hoogte. Dus je kan nooit van richting veranderen op de roosterlijnen.)
Nu hebben we dus open en gesloten paden van orthogonale rode lijnen die alleen van richt- ing veranderen in het midden van de vakjes. Als we de vakjes in een schaakbordpatroon kleuren, dan zijn de vakjes waardoor het pad loopt om-en-om zwart en wit. Een gesloten cykel gaat dus altijd door een even aantal vakjes. Als het bord een oneven aantal vak- jes heeft, dan is er dus minstens één open pad. En dit open pad heeft twee bijzondere driehoeken aan de uiteindes. □
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2025-C2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2025"
}
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.