problem
stringlengths 14
10.4k
| solution
stringlengths 1
24.1k
| answer
stringlengths 1
250
⌀ | problem_is_valid
stringclasses 4
values | solution_is_valid
stringclasses 3
values | question_type
stringclasses 4
values | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
10.4k
| solution_raw
stringlengths 1
24.1k
| metadata
dict |
|---|---|---|---|---|---|---|---|---|---|
Let $a_{1}, a_{2}, \ldots, a_{n}$ be a sequence of real numbers such that $a_{1}+\cdots+a_{n}=0$ and define $b_{i}=a_{1}+\cdots+a_{i}$ for $1 \leq i \leq n$. Suppose that $b_{i}\left(a_{j+1}-a_{i+1}\right) \geq 0$ for all $1 \leq i \leq j \leq n-1$. Prove that
$$
\max _{1 \leq \ell \leq n}\left|a_{\ell}\right| \geq \max _{1 \leq m \leq n}\left|b_{m}\right|
$$
|
Just as in solution I, we find that from $b_{i}>0$ it follows that $a_{i+1}<0$ and from $b_{i}<0$ it follows that $a_{i+1}>0$. Let now $M=\max _{1 \leq \ell \leq n}\left|a_{\ell}\right|$. We prove by induction on $t$ that $\left|b_{t}\right| \leq M$ for $1 \leq t \leq n$. For $t=1$ we have $\left|b_{1}\right|=\left|a_{1}\right| \leq M$. Let now $r \geq 1$ and assume that $\left|b_{r}\right| \leq M$. We now prove that $\left|b_{r+1}\right| \leq M$. We distinguish three cases. If $b_{r}=0$, then $\left|b_{r+1}\right|=\left|b_{r}+a_{r+1}\right|=\left|a_{r+1}\right| \leq M$. Now suppose $b_{r}>0$. Then we know $a_{r+1}<0$, so $b_{r+1}=b_{r}+a_{r+1}$, hence $a_{r+1}<b_{r+1}<b_{r}$. By the induction hypothesis, $b_{r} \leq M$ and further we know $a_{r+1} \geq-M$, so $-M<b_{r+1}<M$, which means that $\left|b_{r+1}\right| \leq M$. Finally, suppose that $b_{r}<0$. Then we know $a_{r+1}>0$, so we see in the same way as above $-M \leq b_{r}<b_{r+1}<a_{r+1} \leq M$, thus $\left|b_{r+1}\right| \leq M$. This completes the induction. We conclude that $\left|b_{t}\right| \leq M$ for all $t$ and from this the desired result follows directly.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
$\mathrm{Zij} a_{1}, a_{2}, \ldots, a_{n}$ een rijtje reële getallen zodat $a_{1}+\cdots+a_{n}=0$ en definieer $b_{i}=a_{1}+\cdots+a_{i}$ voor $1 \leq i \leq n$. Veronderstel dat $b_{i}\left(a_{j+1}-a_{i+1}\right) \geq 0$ voor alle $1 \leq i \leq$ $j \leq n-1$. Bewijs dat
$$
\max _{1 \leq \ell \leq n}\left|a_{\ell}\right| \geq \max _{1 \leq m \leq n}\left|b_{m}\right|
$$
|
Net als in oplossing I vinden we dat uit $b_{i}>0$ volgt dat $a_{i+1}<0$ en uit $b_{i}<0$ volgt $a_{i+1}>0$. Zij nu $M=\max _{1 \leq \ell \leq n}\left|a_{\ell}\right|$. We bewijzen met inductie naar $t$ dat $\left|b_{t}\right| \leq M$ voor $1 \leq t \leq n$. Voor $t=1$ geldt $\left|b_{1}\right|=\left|a_{1}\right| \leq M$. Zij nu $r \geq 1$ en neem aan dat $\left|b_{r}\right| \leq M$. Nu bewijzen we dat $\left|b_{r+1}\right| \leq M$. We onderscheiden drie gevallen. Als $b_{r}=0$, dan geldt $\left|b_{r+1}\right|=\left|b_{r}+a_{r+1}\right|=\left|a_{r+1}\right| \leq M$. Stel nu $b_{r}>0$. Dan weten we $a_{r+1}<0$, dan geldt $b_{r+1}=b_{r}+a_{r+1}$, dus $a_{r+1}<b_{r+1}<b_{r}$. Vanwege de inductiehypothese is $b_{r} \leq M$ en verder weten we $a_{r+1} \geq-M$, dus $-M<b_{r+1}<M$, wat betekent dat $\left|b_{r+1}\right| \leq M$. Stel ten slotte dat $b_{r}<0$. Dan weten we $a_{r+1}>0$, dus zien we op dezelfde manier als hierboven $-M \leq b_{r}<b_{r+1}<a_{r+1} \leq M$, dus $\left|b_{r+1}\right| \leq M$. Dit voltooit de inductie. We concluderen dat $\left|b_{t}\right| \leq M$ voor alle $t$ en daaruit volgt direct het gevraagde.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2017-E_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2017"
}
|
Determine the product of all positive integers $n$ for which $3(n!+1)$ is divisible by $2 n-5$.
将上面的文本翻译成英文,请保留源文本的换行和格式,直接输出翻译结果。
However, it seems there is a note or an additional request in Chinese at the end of your message. If you need the Chinese text translated as well, please let me know! For now, I'll assume you only need the provided Dutch text translated to English. If that's correct, the translation is as above.
|
The numbers $n=1$ to $n=4$ satisfy the condition, because $2n-5$ is then equal to $-3, -1, 1$, and $3$, respectively, and is always a divisor of $3(n!+1)$. From now on, we only consider $n>4$ and then $2n-5>3$.
We first prove that if $n$ satisfies the condition, then $2n-5$ must be prime. We distinguish two cases. Suppose first that $2n-5$ is not prime and has a prime divisor $p>3$. Since $p \neq 2n-5$ and since $2n-5$ is odd, it follows that $p \leq \frac{2n-5}{3} < n$. Therefore, $p \mid n!$, but then $p \nmid n!+1$ and thus also $p \nmid 3(n!+1)$ since $p \neq 3$. Therefore, $2n-5 \nmid 3(n!+1)$, which means that $n$ does not satisfy the condition. Now suppose that $2n-5$ is not prime but has only prime divisors 3; then it is a power of 3 greater than 3. However, for $n>4$, $3 \nmid n!+1$, so $3(n!+1)$ is divisible by exactly one factor of 3 and no more. We see that $n$ cannot satisfy the condition in this case either.
For an $n>4$ that satisfies the condition, we now know that $2n-5$ is a prime number greater than 3. Let $q=2n-5$. Then $q \mid n!+1$, or $n! \equiv -1 \pmod{q}$. Furthermore, Wilson's theorem states that $(q-1)! \equiv -1 \pmod{q}$. Therefore,
$$
\begin{aligned}
-1 & \equiv (2n-6)! \\
& \equiv (2n-6)(2n-7) \cdots (n+1) \cdot n! \\
& \equiv (-1) \cdot (-2) \cdots (-n+6) \cdot n! \\
& \equiv (-1)^{n-6} \cdot (n-6)! \cdot n! \\
& \equiv (-1)^{n} \cdot (n-6)! \cdot -1 \quad \pmod{q}.
\end{aligned}
$$
Thus, $(n-6)! \equiv (-1)^{n} \pmod{q}$. Since $n! \equiv -1 \pmod{q}$, it follows that $n \cdot (n-1) \cdots (n-5) \equiv (-1)^{n-1} \pmod{q}$. We multiply this by $2^6$:
$$
2n \cdot (2n-2) \cdot (2n-4) \cdot (2n-6) \cdot (2n-8) \cdot (2n-10) \equiv (-1)^{n-1} \cdot 64 \pmod{q}.
$$
Modulo $q=2n-5$, the left side is $5 \cdot 3 \cdot 1 \cdot -1 \cdot -3 \cdot -5 = -225$.
Suppose $n$ is odd. Then we have $-225 \equiv 64 \pmod{q}$, so $q \mid -225-64 = -289 = -17^2$. Therefore, $q=17$ and then $n=\frac{17+5}{2}=11$. Now suppose $n$ is even. Then we have $-225 \equiv -64 \pmod{q}$, so $q \mid -225+64 = -161 = -7 \cdot 23$. Therefore, $q=7$ or $q=23$, which gives $n=6$ and $n=14$, respectively.
We check these three possibilities. For $n=11$ and $2n-5=17$:
$$
\begin{aligned}
11! & = 1 \cdot (2 \cdot 9) \cdot (3 \cdot 6) \cdot (5 \cdot 7) \cdot 4 \cdot 8 \cdot 10 \cdot 11 \\
& \equiv 4 \cdot 8 \cdot 10 \cdot 11 = 88 \cdot 40 \equiv 3 \cdot 6 \equiv 1 \quad \pmod{17}
\end{aligned}
$$
so $n=11$ does not satisfy the condition. For $n=14$ and $2n-5=23$:
$$
\begin{aligned}
14! & = 1 \cdot (2 \cdot 12) \cdot (3 \cdot 8) \cdot (4 \cdot 6) \cdot (5 \cdot 14) \cdot (7 \cdot 10) \cdot 9 \cdot 11 \cdot 13 \\
& \equiv 9 \cdot 11 \cdot 13 = 117 \cdot 11 \equiv 2 \cdot 11 \equiv -1 \quad \pmod{23}
\end{aligned}
$$
so $n=14$ satisfies the condition. For $n=6$ and $2n-5=7$, it follows from Wilson's theorem that $6! \equiv -1 \pmod{7}$, so $n=6$ also satisfies the condition.
We conclude that the numbers $n$ that satisfy the condition are: $1, 2, 3, 4, 6$, and 14. The product of these is 2016.
|
2016
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Bepaal het product van alle positieve gehele getallen $n$ waarvoor $3(n!+1)$ deelbaar is door $2 n-5$.
|
De getallen $n=1$ tot en met $n=4$ voldoen, want $2 n-5$ is dan gelijk aan respectievelijk $-3,-1,1$ en 3 , dus altijd een deler dan $3(n!+1)$. Vanaf nu bekijken we alleen $n>4$ en dan is $2 n-5>3$.
We bewijzen eerst dat als $n$ voldoet, dan $2 n-5$ priem moet zijn. We onderscheiden twee gevallen. Stel eerst dat $2 n-5$ niet priem is en een priemdeler $p>3$ heeft. Omdat $p \neq 2 n-5$ en omdat $2 n-5$ oneven is, geldt $p \leq \frac{2 n-5}{3}<n$. Dus $p \mid n!$, maar dan $p \nmid n!+1$ en dus ook $p \nmid 3(n!+1)$ aangezien $p \neq 3$. Dus $2 n-5 \nmid 3(n!+1)$, wat betekent dat $n$ niet voldoet. Stel nu dat $2 n-5$ niet priem is, maar alleen priemdelers 3 heeft; dan is het dus een driemacht groter dan 3. Echter, voor $n>4$ is $3 \nmid n!+1$, dus $3(n!+1)$ is deelbaar door precies één factor 3 en niet meer. We zien dat $n$ ook in dit geval niet kan voldoen.
Voor een $n>4$ die voldoet, weten we nu dat $2 n-5$ een priemgetal groter dan 3 is. Schrijf $q=2 n-5$. Dan $q \mid n!+1$, oftewel $n!\equiv-1 \bmod q$. Verder zegt de stelling van Wilson dat $(q-1)!\equiv-1 \bmod q$. Dus
$$
\begin{aligned}
-1 & \equiv(2 n-6)! \\
& \equiv(2 n-6)(2 n-7) \cdots(n+1) \cdot n! \\
& \equiv(-1) \cdot(-2) \cdots \cdots(-n+6) \cdot n! \\
& \equiv(-1)^{n-6} \cdot(n-6)!\cdot n! \\
& \equiv(-1)^{n} \cdot(n-6)!\cdot-1 \quad \bmod q .
\end{aligned}
$$
Dus $(n-6)!\equiv(-1)^{n} \bmod q$. Omdat $n!\equiv-1 \bmod q$, volgt daaruit $n \cdot(n-1) \cdots \cdot \cdot(n-5) \equiv$ $(-1)^{n-1} \bmod q$. We vermenigvuldigen dit met $2^{6}$ :
$$
2 n \cdot(2 n-2) \cdot(2 n-4) \cdot(2 n-6) \cdot(2 n-8) \cdot(2 n-10) \equiv(-1)^{n-1} \cdot 64 \bmod q .
$$
Modulo $q=2 n-5$ staat links $5 \cdot 3 \cdot 1 \cdot-1 \cdot-3 \cdot-5=-225$.
Stel $n$ is oneven. Dan hebben we dus $-225 \equiv 64 \bmod q$, dus $q \mid-225-64=-289=-17^{2}$. Dus $q=17$ en dan $n=\frac{17+5}{2}=11$. Stel nu $n$ is even. Dan hebben we $-225 \equiv-64 \bmod q$, dus $q \mid-225+64=-161=-7 \cdot 23$. Dus $q=7$ of $q=23$ en dat geeft respectievelijk $n=6$ en $n=14$.
We controleren deze drie mogelijkheden. Voor $n=11$ en $2 n-5=17$ :
$$
\begin{aligned}
11! & =1 \cdot(2 \cdot 9) \cdot(3 \cdot 6) \cdot(5 \cdot 7) \cdot 4 \cdot 8 \cdot 10 \cdot 11 \\
& \equiv 4 \cdot 8 \cdot 10 \cdot 11=88 \cdot 40 \equiv 3 \cdot 6 \equiv 1 \quad \bmod 17
\end{aligned}
$$
dus $n=11$ voldoet niet. Voor $n=14$ en $2 n-5=23$ :
$$
\begin{aligned}
14! & =1 \cdot(2 \cdot 12) \cdot(3 \cdot 8) \cdot(4 \cdot 6) \cdot(5 \cdot 14) \cdot(7 \cdot 10) \cdot 9 \cdot 11 \cdot 13 \\
& \equiv 9 \cdot 11 \cdot 13=117 \cdot 11 \equiv 2 \cdot 11 \equiv-1 \quad \bmod 23
\end{aligned}
$$
dus $n=14$ voldoet. Voor $n=6$ en $2 n-5=7$ ten slotte volgt $6!\equiv-1 \bmod 7$ uit de stelling van Wilson, dus $n=6$ voldoet ook.
We concluderen dat de getallen $n$ die voldoen, zijn: $1,2,3,4,6$ en 14. Het product daarvan is 2016.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2017-E_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2017"
}
|
Let $n \geq 2$ be an integer. Determine the smallest positive integer $m$ such that: given $n$ points in the plane, no three on a line, there are $m$ lines to be found, such that no line passes through any of the given points and such that for each pair of given points $X \neq Y$ there is a line such that $X$ and $Y$ lie on opposite sides of the line.
|
We prove that the smallest $m$ is equal to $\frac{n}{2}$ if $n$ is even and $\frac{n+1}{2}$ if $n$ is odd. Choose the $n$ points all on the same circle and call them $P_{1}, P_{2}, \ldots, P_{n}$ in the order in which they lie on the circle. The $n$ line segments $P_{1} P_{2}, P_{2} P_{3}, \ldots, P_{n} P_{1}$ must all be intersected by at least one line. Each line can intersect at most two such line segments, since each line intersects the circle at most twice. Therefore, the number of lines is at least $\frac{n}{2}$ and thus for odd $n$ at least $\frac{n+1}{2}$.
Now we prove that this is sufficient. First, we show that given four distinct points $P_{1}, P_{2}$ and $Q_{1}, Q_{2}$, there always exists a line such that $P_{1}$ and $P_{2}$ lie on opposite sides of the line and $Q_{1}$ and $Q_{2}$ also. For this, take the line through the midpoint of $P_{1} P_{2}$ and through the midpoint of $Q_{1} Q_{2}$. Suppose this line passes through $P_{1}$. Then it also passes through $P_{2}$, but not through $Q_{1}$ or $Q_{2}$, because no three points lie on a line. Shift it slightly so that it no longer passes through the midpoint of $Q_{1} Q_{2}$, but still through the midpoint of $P_{1} P_{2}$, then it no longer passes through any of these four points. Similarly, if the line passes through one of the other three points. If the now chosen line passes through one of the other given points in the plane, shift it (even) a little bit so that it no longer does. Since there are only finitely many points, this is always possible. This line now has $P_{1}$ and $P_{2}$ on opposite sides and $Q_{1}$ and $Q_{2}$ also.
Now assume that $n$ is even; if $n$ is odd, add an arbitrary point (not on a line with two of the other points). The lines we then construct also work if you remove the extra point. We now need to construct $\frac{n}{2}$ lines. Choose a random line in a direction such that no line through two of the given points is parallel to this line (this is possible because there are only finitely many points and thus also finitely many pairs, while there are infinitely many directions to choose from). Now shift the chosen line. In doing so, it encounters the given points one by one. There is thus a moment when there are no points on the line and there are exactly $\frac{n}{2}$ points on either side of the line. We fix this first line at that moment.
The plane is now divided into two regions, let's say the left and right regions. We will now add lines so that each line creates a new subregion in both the left and right regions. (We only count subregions in which at least one point lies.) For this, we always take two points in the left region that are not yet separated by a line and two points in the right region that are not yet separated by a line. We now choose a line such that the two points on the left lie on opposite sides of this line and the two points on the right also; we have shown earlier that this is possible. There is now at least one additional subregion on both the left and right sides, because the subregion with the two points in it is split into two. If at some point there are no two points left on one of the two sides that are not yet separated by a line, we only use points on the other side. Eventually, after adding $\frac{n}{2}-1$ lines, there are at least $\frac{n}{2}$ subregions with at least one point in each on both the left and right sides; there must therefore be exactly one point in each subregion. Each point thus lies in its own subregion, so the condition is satisfied. In total, we have used $\frac{n}{2}$ lines. So with $\frac{n}{2}$ lines, it is always possible to satisfy the condition.
|
m = \frac{n}{2} \text{ if } n \text{ is even and } m = \frac{n+1}{2} \text{ if } n \text{ is odd}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Zij $n \geq 2$ een geheel getal. Bepaal de kleinste positieve gehele $m$ zodat geldt: gegeven $n$ punten in het vlak, geen drie op een lijn, zijn er $m$ lijnen te vinden, zodat geen enkele lijn door één van de gegeven punten gaat en zodat voor elk tweetal gegeven punten $X \neq Y$ geldt dat er een lijn is waarvan $X$ en $Y$ aan weerszijden liggen.
|
We bewijzen dat de kleinste $m$ gelijk is aan $\frac{n}{2}$ als $n$ even is en $\frac{n+1}{2}$ als $n$ oneven. Kies de $n$ punten allemaal op dezelfde cirkel en noem ze $P_{1}, P_{2}, \ldots, P_{n}$ in de volgorde waarin ze op de cirkel liggen. De $n$ lijnstukken $P_{1} P_{2}, P_{2} P_{3}, \ldots, P_{n} P_{1}$ moeten allemaal gesneden worden door minstens één lijn. Elke lijn snijdt hoogstens twee van zulke lijnstukken, aangezien elke lijn de cirkel hoogstens twee keer snijdt. Dus het aantal lijnen is minstens $\frac{n}{2}$ en dus voor oneven $n$ minstens $\frac{n+1}{2}$.
Nu bewijzen we dat dit voldoende is. Eerst laten we zien dat gegeven vier verschillende punten $P_{1}, P_{2}$ en $Q_{1}, Q_{2}$ er altijd een lijn bestaat zodat $P_{1}$ en $P_{2}$ aan weerszijden van de lijn liggen en $Q_{1}$ en $Q_{2}$ ook. Neem hiervoor de lijn door het midden van $P_{1} P_{2}$ en door het midden van $Q_{1} Q_{2}$. Stel dat deze lijn door $P_{1}$ heen gaat. Dan gaat hij ook door $P_{2}$ heen, maar niet door $Q_{1}$ of $Q_{2}$, omdat er nooit drie punten op een lijn liggen. Schuif hem dan een klein stukje op zodat hij net niet door het midden van $Q_{1} Q_{2}$ heen gaat, maar nog wel door het midden van $P_{1} P_{2}$, dan gaat hij niet meer door één van deze vier punten heen. Analoog als de lijn door één van de andere drie punten heen zou gaan. Als de nu gekozen lijn door één van de overige gegeven punten in het vlak gaat, schuif je hem (nog) een heel klein beetje op zodat dat niet meer zo is. Omdat er maar eindig veel punten zijn, lukt dit altijd. Deze lijn heeft nu $P_{1}$ en $P_{2}$ aan weerszijden en $Q_{1}$ en $Q_{2}$ ook.
Neem nu aan dat $n$ even is; als $n$ oneven is, voegen we een willekeurig punt (niet op een lijn met twee van de andere punten) toe. De lijnen die we dan construeren, werken ook als je het extra punt weer weglaat. We moeten dus nu $\frac{n}{2}$ lijnen construeren. Kies een willekeurige lijn in een richting zodat geen enkele lijn door twee van de gegeven punten evenwijdig aan deze lijn loopt (dat kan omdat er maar eindig veel punten zijn en dus ook maar eindig veel tweetallen, terwijl er oneindig veel richtingen te kiezen zijn). Schuif nu de gekozen lijn op. Hierbij komt hij één voor één de gegeven punten tegen. Er is dus een moment dat er geen punten op de lijn liggen en er aan weerszijden van de lijn precies $\frac{n}{2}$ punten liggen. Daar leggen we deze eerste lijn vast.
Het vlak wordt nu in twee gebieden verdeeld, laten we zeggen het linker- en rechtergebied. We gaan nu lijnen toevoegen zodat elke lijn een nieuw deelgebied creëert in zowel het linker- als het rechtergebied. (We tellen alleen deelgebieden waarin minstens één punt ligt.) Hiervoor nemen we steeds twee punten in het linkergebied die nog niet gescheiden worden door een lijn en twee punten in het rechtergebied die nog niet gescheiden worden door een lijn. We kiezen nu een lijn zodat de twee punten links aan weerszijden van deze lijn liggen en de twee punten rechts ook; we hebben eerder laten zien dat dit kan. Er is nu zowel links als rechts minstens één extra deelgebied ontstaan, want het deelgebied met de twee punten erin is in tweeën gesplitst. Mochten er op een gegeven moment aan één van beide kanten geen twee punten meer zijn waar nog geen lijn tussendoor loopt, dan gebruiken we alleen nog punten aan de andere kant. Uiteindelijk hebben we na het toevoegen van $\frac{n}{2}-1$ lijnen
zowel links als rechts minstens $\frac{n}{2}$ deelgebieden met elk minstens één punt erin; er moet dus wel precies één punt in elk deelgebied zitten. Elk punt ligt dus in zijn eigen deelgebied, waardoor aan de voorwaarde voldaan wordt. In totaal hebben we $\frac{n}{2}$ lijnen gebruikt. Dus met $\frac{n}{2}$ lijnen lukt het altijd om aan de voorwaarde te voldoen.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2017-E_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2017"
}
|
We have 1000 balls in 40 different colors, with exactly 25 balls of each color. Determine the smallest value of $n$ with the following property: if you randomly arrange the 1000 balls in a circle, there will always be $n$ consecutive balls where at least 20 different colors appear.
|
Consider the circle of balls where 25 balls of one color are always next to each other. To have 20 different colors, you need to take at least 18 of these groups plus one ball on one side and one ball on the other side. In total, you need at least \(18 \cdot 25 + 2 = 452\) balls next to each other. Therefore, \(n \geq 452\). Now we prove that in any circle of balls, you need at most 452 balls next to each other to get 20 different colors. For this, consider any random circle of balls and all possible series of balls next to each other that together have exactly 20 colors. (There is at least one such series: take a random ball and add the balls next to it one by one until you have exactly 20 colors.) Take a series with the minimum number of balls. Say the first ball in this series is white. If there is another white ball in the series, we could have omitted the first ball to get a series with the same number of colors but fewer balls. This contradicts the minimality of the series. Therefore, there is no other white ball. In particular, the last ball in the series is not white; say it is black. We see in the same way that no other ball in the series is black. So there is one white ball, one black ball, and balls in 18 other colors, with at most 25 of each color. Together, this is at most \(18 \cdot 25 + 2 = 452\) balls. Therefore, you can always find a series of 452 balls next to each other that contains at least 20 different colors. We conclude that the required minimum \(n\) is 452.
|
452
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
We hebben 1000 ballen in 40 verschillende kleuren, waarbij er van elke kleur precies 25 ballen zijn. Bepaal de kleinste waarde van $n$ met de volgende eigenschap: als je de 1000 ballen willekeurig in een cirkel legt, zijn er altijd $n$ ballen naast elkaar te vinden waarbij minstens 20 verschillende kleuren voorkomen.
|
Bekijk de cirkel van ballen waarbij de 25 ballen van één kleur steeds allemaal naast elkaar liggen. Om nu 20 verschillende kleuren te hebben, moet je minstens 18 van deze groepen nemen plus nog een bal aan de ene kant daarvan en een bal aan de andere kant. Totaal heb je dus minimaal $18 \cdot 25+2=452$ ballen naast elkaar nodig. Dus $n \geq 452$. Nu bewijzen we dat je in elke cirkel van ballen genoeg hebt aan 452 ballen naast elkaar om 20 verschillende kleuren te krijgen. Bekijk daarvoor een willekeurige cirkel van ballen en alle mogelijke series van ballen naast elkaar die samen precies 20 kleuren hebben. (Er bestaat minstens één zo'n serie: pak een willekeurige bal en voeg de ballen ernaast één voor één toe, totdat je precies 20 kleuren hebt.) Neem een serie daarvan met zo min mogelijk ballen erin. Zeg dat de eerste bal daarvan wit is. Als er nog een bal in de serie wit is, dan hadden we de eerste bal kunnen weglaten om een serie te krijgen met evenveel kleuren, maar minder ballen. Dat is een tegenspraak met de minimaliteit van de serie. Dus er is geen enkele andere bal wit. In het bijzonder is ook de laatste bal van de serie niet wit; zeg dat deze zwart is. We zien op dezelfde manier dat geen enkele andere bal in de serie zwart is. Dus er is één witte bal, één zwarte bal en daarnaast nog ballen in 18 andere kleuren, hooguit 25 per kleur. Samen zijn dat hooguit $18 \cdot 25+2=452$ ballen. Dus inderdaad kun je altijd een serie van 452 ballen naast elkaar vinden met daarin minstens 20 verschillende kleuren. We concluderen dat de gevraagde minimale $n$ gelijk is aan 452 .
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2018-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2018"
}
|
We have 1000 balls in 40 different colors, with exactly 25 balls of each color. Determine the smallest value of $n$ with the following property: if you randomly arrange the 1000 balls in a circle, there will always be $n$ consecutive balls where at least 20 different colors appear.
|
We provide an alternative proof for the second part of the solution. We do this by contradiction. Suppose we have a circle of balls where every series of 452 balls contains at most 19 colors. Since $452=18 \cdot 25+2$, each such series then contains exactly 19 colors, and there are at least two balls of each color. Now consider such a series and shift it one ball at a time. With each shift, one ball leaves the series, say ball $A$, and one ball joins, say ball $B$. The color of ball $A$ appears at least once more in the series, so the color of ball $A$ does not disappear. However, no new color can be added, so ball $B$ must be of a color that is already in the series. Each time we shift by one, the set of colors present in the series remains the same set of 19 colors. If we go around the entire circle this way, we thus encounter only 19 different colors, while there are 40 different colors. Contradiction. Therefore, there is a series of 452 balls with at least 20 different colors.
|
452
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
We hebben 1000 ballen in 40 verschillende kleuren, waarbij er van elke kleur precies 25 ballen zijn. Bepaal de kleinste waarde van $n$ met de volgende eigenschap: als je de 1000 ballen willekeurig in een cirkel legt, zijn er altijd $n$ ballen naast elkaar te vinden waarbij minstens 20 verschillende kleuren voorkomen.
|
We geven een alternatief bewijs voor het tweede deel van de oplossing. We doen dit uit het ongerijmde. Stel dat we een cirkel van ballen hebben waar elke serie van 452 ballen hooguit 19 kleuren bevat. Omdat $452=18 \cdot 25+2$ bevat elk zo'n serie dan precies 19 kleuren en zitten er van elke kleur minstens twee ballen in. Bekijk nu zo'n serie en schuif hem steeds één bal op. Bij zo'n verschuiving verdwijnt één bal uit de serie, zeg bal $A$, en komt er ook eentje bij, zeg bal $B$. De kleur van bal $A$ komt minstens nog een keer voor in de serie, dus de kleur van bal $A$ verdwijnt niet. Maar er mag ook geen extra kleur bijkomen, dus bal $B$ moet van een kleur zijn die al in de serie zat. Elke keer dat we één opschuiven, blijft de verzameling van kleuren die voorkomen in de serie, dus dezelfde verzameling van 19 kleuren. Als we zo de hele cirkel rondgaan, komen we dus maar 19
verschillende kleuren tegen, terwijl er 40 verschillende kleuren zijn. Tegenspraak. Dus er is een serie van 452 ballen met minstens 20 verschillende kleuren.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2018-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2018"
}
|
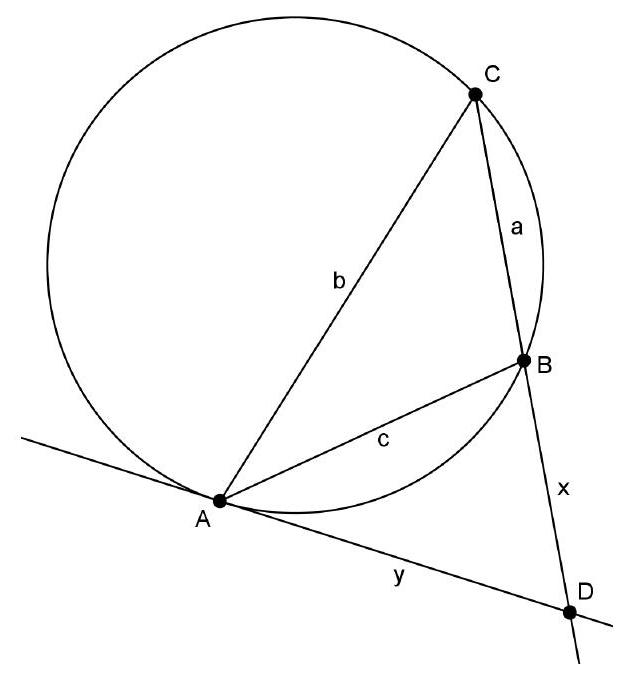
Let $\triangle A B C$ be a triangle with side lengths that are positive integers and pairwise relatively prime. The tangent at $A$ to the circumcircle intersects the line $B C$ at $D$. Prove that $|B D|$ is not an integer.
|
There are two possible configurations. Without loss of generality, assume that $B$ lies between $D$ and $C$. Let $a=|B C|, b=|C A|, c=|A B|, x=|B D|$, and $y=|A D|$. By the tangent-secant angle theorem, $\angle B A D=\angle A C B=\angle A C D$, so $\triangle A B D \sim \triangle C A D(\mathrm{AA})$, hence $\frac{|B D|}{|A D|}=\frac{|A B|}{|C A|}=\frac{|A D|}{|C D|}$, or $\frac{x}{y}=\frac{c}{b}=\frac{y}{a+x}$. From this, we get $y c=b x$ and $a c+x c=b y$, so also $b y c=b^{2} x$ and $a c^{2}+x c^{2}=b y c$. Combining these gives $b^{2} x=a c^{2}+x c^{2}$, or $x\left(b^{2}-c^{2}\right)=a c^{2}$.
Now assume for the sake of contradiction that $x$ is an integer. Then $b^{2}-c^{2}$ is a divisor of $a c^{2}$. But we know $\operatorname{gcd}(b, c)=1$, so also $\operatorname{gcd}\left(b^{2}-c^{2}, c\right)=\operatorname{gcd}\left(b^{2}, c\right)=1$. Therefore, $b^{2}-c^{2}$ must be a divisor of $a$. This implies $b^{2}-c^{2} \leq a$. Note that $b^{2}-c^{2}>0$ since $x\left(b^{2}-c^{2}\right)=a c^{2}$; thus, $b-c>0$ as well. Therefore, $b^{2}-c^{2}=(b-c)(b+c) \geq 1 \cdot(b+c)$ because $b$ and $c$ are positive integers. Hence, $a \geq b+c$, which contradicts the triangle inequality. Therefore, $x=|B D|$ cannot be an integer.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $\triangle A B C$ een driehoek waarvan de zijdelengtes positieve gehele getallen zijn die paarsgewijs relatief priem zijn. De raaklijn in $A$ aan de omgeschreven cirkel snijdt de lijn $B C$ in $D$. Bewijs dat $|B D|$ geen geheel getal is.

|
Er zijn twee configuraties mogelijk. Neem zonder verlies van algemeenheid aan dat $B$ tussen $D$ en $C$ ligt. Schrijf $a=|B C|, b=|C A|, c=|A B|, x=|B D|$ en $y=|A D|$. Vanwege de raaklijnomtrekshoekstelling geldt $\angle B A D=\angle A C B=\angle A C D$, dus $\triangle A B D \sim \triangle C A D(\mathrm{hh})$, dus $\frac{|B D|}{|A D|}=\frac{|A B|}{|C A|}=\frac{|A D|}{|C D|}$, oftewel $\frac{x}{y}=\frac{c}{b}=\frac{y}{a+x}$. We vinden hieruit $y c=b x$ en $a c+x c=b y$, dus ook byc $=b^{2} x$ en $a c^{2}+x c^{2}=b y c$. Dit combineren geeft $b^{2} x=a c^{2}+x c^{2}$, oftewel $x\left(b^{2}-c^{2}\right)=a c^{2}$.
Stel nu uit het ongerijmde dat $x$ geheel is. Dan is $b^{2}-c^{2}$ een deler van $a c^{2}$. Maar we weten $\operatorname{ggd}(b, c)=1$, dus ook $\operatorname{ggd}\left(b^{2}-c^{2}, c\right)=\operatorname{ggd}\left(b^{2}, c\right)=1$. Dus $b^{2}-c^{2}$ moet een deler zijn van $a$. Daaruit volgt $b^{2}-c^{2} \leq a$. Merk op dat $b^{2}-c^{2}>0$ aangezien $x\left(b^{2}-c^{2}\right)=a c^{2}$; er geldt dus ook $b-c>0$. Dus $b^{2}-c^{2}=(b-c)(b+c) \geq 1 \cdot(b+c)$ omdat $b$ en $c$ positieve gehele getallen zijn. Dus $a \geq b+c$, wat in tegenspraak is met de driehoeksongelijkheid. Dus $x=|B D|$ kan niet geheel zijn.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2018-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2018"
}
|
Let $p$ be a prime number. Prove that it is possible to choose a permutation $a_{1}, a_{2}, \ldots, a_{p}$ of $1,2, \ldots, p$ such that the numbers $a_{1}, a_{1} a_{2}, a_{1} a_{2} a_{3}, \ldots, a_{1} a_{2} a_{3} \cdots a_{p}$ all give different remainders when divided by $p$.
|
Let $b_{i}=a_{1} a_{2} \cdots a_{i}$, for $1 \leq i \leq p$. We prove that it is possible to choose the permutation such that $b_{i} \equiv i \bmod p$ for all $i$. For $i \geq 2$, $a_{i} \equiv b_{i} \cdot b_{i-1}^{-1} \bmod p$ if $b_{i-1} \not \equiv 0 \bmod p$. We now choose $a_{1}=1$ and $a_{i} \equiv i \cdot(i-1)^{-1} \bmod p$ for $2 \leq i \leq p$. It is now sufficient to prove that $a_{i} \not \equiv 1 \bmod p$ for all $2 \leq i \leq p$ and $a_{i} \not \equiv a_{j} \bmod p$ for all $2 \leq j<i \leq p$.
Assume for the sake of contradiction that $a_{i} \equiv 1 \bmod p$ for some $2 \leq i \leq p$. Then $i \cdot(i-1)^{-1} \equiv 1 \bmod p$, so $i \equiv i-1 \bmod p$, so $0 \equiv -1 \bmod p$. Since $p \geq 2$, this is a contradiction. Now assume that $a_{i} \equiv a_{j} \bmod p$ for some $2 \leq j<i \leq p$. Then $i \cdot(i-1)^{-1} \equiv j \cdot(j-1)^{-1} \bmod p$ so $i(j-1) \equiv j(i-1) \bmod p$ so $ij - i \equiv ij - j \bmod p$ so $-i \equiv -j \bmod p$. But we had $2 \leq j < i \leq p$, so this cannot be.
We conclude that if we choose the $a_{i}$ as indicated above, all $a_{i}$ will be distinct, making it indeed a permutation of $1, 2, \ldots, p$. Furthermore, by definition, $a_{1} a_{2} \cdots a_{i} \equiv i \bmod p$, so the second condition is also satisfied.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Zij $p$ een priemgetal. Bewijs dat het mogelijk is om een permutatie $a_{1}, a_{2}, \ldots, a_{p}$ van $1,2, \ldots, p$ te kiezen zodat de getallen $a_{1}, a_{1} a_{2}, a_{1} a_{2} a_{3}, \ldots, a_{1} a_{2} a_{3} \cdots a_{p}$ allemaal verschillende resten geven na deling door $p$.
|
Noem $b_{i}=a_{1} a_{2} \cdots a_{i}$, voor $1 \leq i \leq p$. We bewijzen dat het mogelijk is de permutatie zo te kiezen dat $b_{i} \equiv i \bmod p$ voor alle $i$. Voor $i \geq 2$ is $a_{i} \equiv b_{i} \cdot b_{i-1}^{-1} \bmod p$ als $b_{i-1} \not \equiv 0 \bmod p$. We kiezen nu dus $a_{1}=1$ en $a_{i} \equiv i \cdot(i-1)^{-1} \bmod p$ voor $2 \leq i \leq p$. Het is nu voldoende te bewijzen dat $a_{i} \not \equiv 1 \bmod p$ voor alle $2 \leq i \leq p$ en $a_{i} \not \equiv a_{j} \bmod p$ voor alle $2 \leq j<i \leq p$.
Stel uit het ongerijmde dat $a_{i} \equiv 1 \bmod p$ voor zekere $2 \leq i \leq p$. Dan is $i \cdot(i-1)^{-1} \equiv 1$ $\bmod p$, dus $i \equiv i-1 \bmod p$, dus $0 \equiv-1 \bmod p$. Omdat $p \geq 2$ is dit een tegenspraak. Stel nu dat $a_{i} \equiv a_{j} \bmod p$ voor zekere $2 \leq j<i \leq p$. Dan geldt $i \cdot(i-1)^{-1} \equiv j \cdot(j-1)^{-1}$ $\bmod p$ dus $i(j-1) \equiv j(i-1) \bmod p$ dus $i j-i \equiv i j-j \bmod p$ dus $-i \equiv-j \bmod p$. Maar we hadden $2 \leq j<i \leq p$, dus dit kan niet.
We concluderen dat als we de $a_{i}$ kiezen zoals hierboven aangegeven, alle $a_{i}$ verschillend worden, zodat het inderdaad een permutatie van $1,2, \ldots, p$ is. Verder geldt nu per definitie dat $a_{1} a_{2} \cdots a_{i} \equiv i \bmod p$, zodat ook aan de tweede eis is voldaan.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2018-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2018"
}
|
In a non-equilateral triangle $\triangle ABC$, $\angle BAC = 60^{\circ}$. Let $D$ be the intersection of the angle bisector of $\angle BAC$ with side $BC$, $O$ the circumcenter of $\triangle ABC$, and $E$ the intersection of $AO$ with $BC$. Prove that $\angle AED + \angle ADO = 90^{\circ}$.
|
Let $M$ be the second intersection of $A D$ with the circumcircle of $\triangle A B C$. Then $M$ is the midpoint of the arc $B C$ not containing $A$. It now holds that $\angle C O M = \frac{1}{2} \angle C O B = \angle C A B = 60^{\circ}$. Of course, $|O C| = |O M|$, so $\triangle O C M$ is isosceles with a top angle of $60^{\circ}$. This means it is equilateral, so $|C M| = |C O|$. Since $O M$ is perpendicular to $B C$, it follows that $M$ is the reflection of $O$ in side $B C$, and thus $\angle D O M = \angle D M O$.
Furthermore, $\angle D M O = \angle A M O = \angle M A O$ due to $|O A| = |O M|$. We now find $\angle O D E = 90^{\circ} - \angle D O M = 90^{\circ} - \angle D M O = 90^{\circ} - \angle M A O = 90^{\circ} - \angle D A E$. Therefore, $\angle O D E + \angle D A E = 90^{\circ}$. In triangle $A D E$, $180^{\circ} = \angle D A E + \angle A E D + \angle O D E + \angle A D O$, so we conclude that $\angle A E D + \angle A D O = 90^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In een niet-gelijkbenige driehoek $\triangle A B C$ geldt $\angle B A C=60^{\circ}$. Zij $D$ het snijpunt van de bissectrice van $\angle B A C$ met de zijde $B C, O$ het middelpunt van de omgeschreven cirkel van $\triangle A B C$ en $E$ het snijpunt van $A O$ met $B C$. Bewijs dat $\angle A E D+\angle A D O=90^{\circ}$.

|
Zij $M$ het tweede snijpunt van $A D$ met de omgeschreven cirkel van $\triangle A B C$. Dan is $M$ het midden van de boog $B C$ waar $A$ niet op ligt. Er geldt nu $\angle C O M=$ $\frac{1}{2} \angle C O B=\angle C A B=60^{\circ}$. Verder is natuurlijk $|O C|=|O M|$, dus $\triangle O C M$ is gelijkbenig met een tophoek van $60^{\circ}$. Dat betekent dat hij gelijkzijdig is, dus $|C M|=|C O|$. Omdat $O M$ loodrecht op $B C$ staat, volgt hieruit dat $M$ de spiegeling is van $O$ in zijde $B C$, en dus $\angle D O M=\angle D M O$.
Verder geldt $\angle D M O=\angle A M O=\angle M A O$ vanwege $|O A|=|O M|$. We vinden nu $\angle O D E=90^{\circ}-\angle D O M=90^{\circ}-\angle D M O=90^{\circ}-\angle M A O=90^{\circ}-\angle D A E$. Dus $\angle O D E+\angle D A E=90^{\circ}$. In driehoek $A D E$ geldt $180^{\circ}=\angle D A E+\angle A E D+\angle O D E+\angle A D O$, dus we concluderen dat $\angle A E D+\angle A D O=90^{\circ}$.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2018-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2018"
}
|
Given a positive integer $n$. Determine all positive real numbers $x$ such that
$$
n x^{2}+\frac{2^{2}}{x+1}+\frac{3^{2}}{x+2}+\ldots+\frac{(n+1)^{2}}{x+n}=n x+\frac{n(n+3)}{2} .
$$
|
For $1 \leq i \leq n$ we have
$\frac{(i+1)^{2}}{x+i}=i+1+\frac{(i+1)^{2}-(i+1)(x+i)}{x+i}=i+1+\frac{i+1-(i+1) x}{x+i}=i+1+\frac{(i+1)(1-x)}{x+i}$,
so we can rewrite the left side of the given equation to
$$
n x^{2}+2+3+\ldots+(n+1)+\frac{2(1-x)}{x+1}+\frac{3(1-x)}{x+2}+\ldots+\frac{(n+1)(1-x)}{x+n}
$$
It holds that $2+3+\ldots+(n+1)=\frac{1}{2} n(n+3)$, so this sum cancels out with $\frac{n(n+3)}{2}$ on the right side of the given equation. Furthermore, we can move $n x^{2}$ to the other side and factor out $1-x$ in all fractions. The equation can thus be rewritten as
$$
(1-x) \cdot\left(\frac{2}{x+1}+\frac{3}{x+2}+\ldots+\frac{n+1}{x+n}\right)=n x-n x^{2} .
$$
The right side can be factored as $n x(1-x)$. We now see that $x=1$ is a solution to this equation. If there were another solution $x \neq 1$, then it would have to satisfy
$$
\frac{2}{x+1}+\frac{3}{x+2}+\ldots+\frac{n+1}{x+n}=n x .
$$
However, for $0<x<1$ we have
$$
\frac{2}{x+1}+\frac{3}{x+2}+\ldots+\frac{n+1}{x+n}>\frac{2}{2}+\frac{3}{3}+\ldots+\frac{n+1}{n+1}=n>n x
$$
while for $x>1$ we have
$$
\frac{2}{x+1}+\frac{3}{x+2}+\ldots+\frac{n+1}{x+n}<\frac{2}{2}+\frac{3}{3}+\ldots+\frac{n+1}{n+1}=n<n x .
$$
Therefore, there are no solutions with $x \neq 1$. We conclude that for all $n$, the only solution is $x=1$.
|
x=1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Gegeven is een positief geheel getal $n$. Bepaal alle positieve reële getallen $x$ met
$$
n x^{2}+\frac{2^{2}}{x+1}+\frac{3^{2}}{x+2}+\ldots+\frac{(n+1)^{2}}{x+n}=n x+\frac{n(n+3)}{2} .
$$
|
Voor $1 \leq i \leq n$ geldt
$\frac{(i+1)^{2}}{x+i}=i+1+\frac{(i+1)^{2}-(i+1)(x+i)}{x+i}=i+1+\frac{i+1-(i+1) x}{x+i}=i+1+\frac{(i+1)(1-x)}{x+i}$,
dus kunnen we de linkerkant van de gegeven vergelijking herschrijven tot
$$
n x^{2}+2+3+\ldots+(n+1)+\frac{2(1-x)}{x+1}+\frac{3(1-x)}{x+2}+\ldots+\frac{(n+1)(1-x)}{x+n}
$$
Er geldt $2+3+\ldots+(n+1)=\frac{1}{2} n(n+3)$ dus deze som valt weg tegen $\frac{n(n+3)}{2}$ aan de rechterkant van de gegeven vergelijking. Verder kunnen we $n x^{2}$ naar de andere kant halen en in alle breuken $1-x$ buiten haakjes halen. De vergelijking laat zich dus herschrijven tot
$$
(1-x) \cdot\left(\frac{2}{x+1}+\frac{3}{x+2}+\ldots+\frac{n+1}{x+n}\right)=n x-n x^{2} .
$$
De rechterkant kunnen we ontbinden als $n x(1-x)$. We zien nu dat $x=1$ een oplossing is van deze vergelijking. Als er nog een oplossing $x \neq 1$ zou zijn, dan moet die voldoen aan
$$
\frac{2}{x+1}+\frac{3}{x+2}+\ldots+\frac{n+1}{x+n}=n x .
$$
Voor $0<x<1$ geldt echter
$$
\frac{2}{x+1}+\frac{3}{x+2}+\ldots+\frac{n+1}{x+n}>\frac{2}{2}+\frac{3}{3}+\ldots+\frac{n+1}{n+1}=n>n x
$$
terwijl voor $x>1$ juist geldt
$$
\frac{2}{x+1}+\frac{3}{x+2}+\ldots+\frac{n+1}{x+n}<\frac{2}{2}+\frac{3}{3}+\ldots+\frac{n+1}{n+1}=n<n x .
$$
Er zijn dus geen oplossingen met $x \neq 1$. We concluderen dat voor alle $n$ de enige oplossing $x=1$ is.
|
{
"exam": "Dutch_TST",
"problem_label": "5",
"problem_match": "\nOpgave 5.",
"resource_path": "Dutch_TST/segmented/nl-2018-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2018"
}
|
Given is a board with $2 m$ rows and $2 n$ columns, where $m$ and $n$ are positive integers. You may place one pawn on a square of this board, but not on the bottom-left square or the top-right square. Then a snail starts a walk over the board. The snail starts in the bottom-left square and may move horizontally and vertically. The snail does not land on the square with the pawn, but wants to visit every other square exactly once, with the top-right square being its endpoint. On which squares can you place the pawn so that the snail can succeed in its plan?
|
Number the rows from bottom to top with 1 to $2 m$ and number the columns from left to right with 1 to $2 n$. The snail thus starts in square $(1,1)$ and ends in square $(2 m, 2 n)$. Color the squares like a chessboard, where square $(i, j)$ is black if $i+j$ is even and white if $i+j$ is odd. Since $2 m$ and $2 n$ are even, there are as many black as white squares. The snail starts and ends on a black square and visits black and white squares alternately during its walk. The number of black squares it visits is therefore 1 more than the number of white squares it visits. Therefore, the pawn must stand on a white square, i.e., a square $(i, j)$ with $i+j$ odd.
We now show that if the pawn stands on such a square, the snail can always make its walk. Let $1 \leq k \leq m$ and $1 \leq l \leq n$ such that the pawn is in one of the rows $2 k-1$ and $2 k$ and in one of the columns $2 l-1$ and $2 l$. Let the snail run through all rows with row number less than $2 k-1$ in their entirety: the odd rows from left to right, then one square up and the even rows from right to left back. Then one square up again and he is on an odd row again. At some point, the snail arrives in row $2 k-1$ and is then on the far left square. As long as the snail is still in the columns with number less than $2 l-1$, it visits each $2 \times 2$ square (in rows $2 k-1,2 k$) in the order bottom-left-top-left-top-right-bottom-right. And then he arrives at the bottom-left again in the next $2 \times 2$ square. At some point, he arrives in column $2 l-1$. He is then on square $(2 k-1,2 l-1)$ and the pawn cannot stand there, because $2 k-1+2 l-1$ is even. In this $2 \times 2$ square, the pawn stands either top-left or bottom-right. In the first case, the snail walks bottom-left-bottom-right-top-right and in the second case, he walks bottom-left-top-left-top-right. In both cases, he ends up in this $2 \times 2$ square in the top-right square. The rest of the $2 \times 2$ squares in these rows he can visit in the order top-left-bottom-left-bottom-right-top-right. He always ends up top-right. When he eventually arrives in the last column, he goes one row up, to row $2 k+1$. There he arrives at the bottom-right. The remaining rows he runs through again in their entirety: the odd rows from right to left, then one square up and the even rows from left to right back. In row $2 m$ he ends up top-right, exactly as required. We conclude that the pawn can be placed on the squares $(i, j)$ with $i+j$ odd.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Gegeven is een bord met $2 m$ rijen en $2 n$ kolommen, waarbij $m$ en $n$ positieve gehele getallen zijn. Je mag één pion plaatsen op een vakje van dit bord, maar niet het vakje linksonder of het vakje rechtsboven. Vervolgens begint een slak een wandeling te maken over het bord. De slak begint in het vakje linksonder en mag horizontaal en verticaal bewegen. De slak komt niet op het vakje met de pion, maar wil verder elk vakje precies één keer aandoen, waarbij het vakje rechtsboven zijn eindpunt is. Op welke vakjes kun je de pion neerzetten zodat de slak in zijn opzet kan slagen?
|
Nummer de rijen van beneden naar boven met 1 tot en met $2 m$ en nummer de kolommen van links naar rechts met 1 tot en met $2 n$. De slak begint dus in vakje $(1,1)$ en eindigt in vakje $(2 m, 2 n)$. Kleur nu de vakjes als een schaakbord, waarbij vakje $(i, j)$ zwart wordt als $i+j$ even is en wit als $i+j$ oneven is. Omdat $2 m$ en $2 n$ even zijn, zijn er evenveel zwarte als witte vakjes. De slak begint en eindigt op een zwart vakje en bezoekt tijdens zijn wandeling om en om zwarte en witte vakjes. Het aantal zwarte vakjes waar hij komt, is dus 1 groter dan het aantal witte vakjes waar hij komt. Daarom moet de pion wel op een wit vakje staan, dus een vakje $(i, j)$ met $i+j$ oneven.
We laten nu zien dat als de pion op zo'n vakje staat, de slak altijd zijn wandeling kan maken. Zij $1 \leq k \leq m$ en $1 \leq l \leq n$ zo dat de pion in één van de rijen $2 k-1$ en $2 k$ staat en in één van de kolommen $2 l-1$ en $2 l$. Laat de slak alle rijen met rijnummer kleiner dan $2 k-1$ in zijn geheel aflopen: de oneven rijen van links naar rechts, dan één vakje omhoog en de even rijen van rechts naar links terug. Vervolgens weer één vakje omhoog en dan is hij weer op een oneven rij. Op een gegeven moment komt de slak aan in rij $2 k-1$ en staat dan op het vakje helemaal links. Zolang de slak nog in de kolommen met nummer kleiner dan $2 l-1$ zit, bezoekt hij elk $2 \times 2$-vierkantje (in rijen $2 k-1,2 k$ ) in de volgorde linksonder-linksboven-rechtsboven-rechtsonder. En dan komt hij linksonder weer aan in het volgende $2 \times 2$-vierkantje. Op een gegeven moment arriveert hij in kolom $2 l-1$. Hij staat dan op vakje $(2 k-1,2 l-1)$ en daar kan de pion niet staan, want $2 k-1+2 l-1$ is even. In dit $2 \times 2$-vierkantje staat de pion ofwel linksboven ofwel rechtsonder. In het eerste geval loopt de slak linksonder-rechtsonder-rechtsboven en in het tweede geval loopt hij linksonder-linksboven-rechtsboven. In beide gevallen eindigt hij in dit $2 \times 2$-vierkantje in het vakje rechtsboven. De rest van de $2 \times 2$-vierkantjes in deze rijen kan hij dus in de volgorde linksboven-linksonder-rechtsonder-rechtsboven bezoeken. Steeds eindigt hij rechtsboven. Als hij uiteindelijk in de laatste kolom is aangekomen, gaat hij een rij omhoog, naar rij $2 k+1$. Daar komt hij dus rechtsonderin aan. De overige rijen loopt hij weer in z'n geheel af: de oneven rijen van rechts naar links, dan een vakje omhoog en de even rijen van links
naar rechts terug. In rij $2 m$ eindigt hij dus rechtsboven, precies zoals gevraagd. We concluderen dat de pion op de vakjes $(i, j)$ met $i+j$ oneven neergezet kan worden.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2018-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2018"
}
|
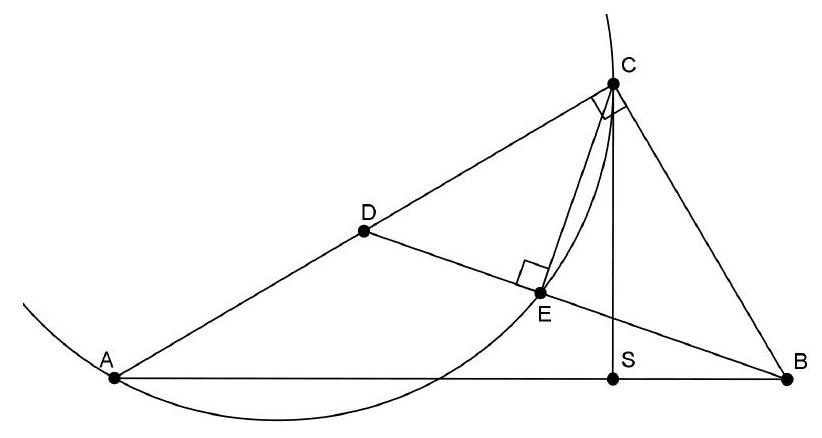
Given is a triangle $\triangle A B C$ with $\angle C=90^{\circ}$. The midpoint of $A C$ is called $D$ and the perpendicular projection of $C$ on $B D$ is called $E$. Prove that the tangent at $C$ to the circumcircle of $\triangle A E C$ is perpendicular to $A B$.
|
Let $S$ be the intersection of the tangent line and $AB$. We need to prove that $\angle BSC=90^{\circ}$.
Since $\angle BCD=90^{\circ}=\angle CED$, we have $\triangle BCD \sim \triangle CED$, so $\frac{|DC|}{|DB|}=\frac{|DE|}{|DC|}$. Because $|DA|=|DC|$, it follows that $\frac{|DA|}{|DB|}=\frac{|DE|}{|DA|}$. Together with $\angle BDA=\angle EDA$, this gives $\triangle ADE \sim \triangle BDA$ (side-angle-side). Therefore, $\angle ABD=\angle EAD$. Since $SC$ is a tangent to the circumcircle of $\triangle AEC$, by the tangent-secant theorem, we also have $\angle EAD=\angle EAC=\angle SCE$. Thus, $\angle SCE=\angle ABD=\angle SBE$. This implies that $SBCE$ is a cyclic quadrilateral. Therefore, $\angle BSC=\angle BEC=90^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Gegeven is een driehoek $\triangle A B C$ met $\angle C=90^{\circ}$. Het midden van $A C$ noemen we $D$ en de loodrechte projectie van $C$ op $B D$ noemen we $E$. Bewijs dat de raaklijn in $C$ aan de omgeschreven cirkel van $\triangle A E C$ loodrecht op $A B$ staat.

|
Noem $S$ het snijpunt van de raaklijn en $A B$. We moeten dus bewijzen dat $\angle B S C=90^{\circ}$.
Vanwege $\angle B C D=90^{\circ}=\angle C E D$ geldt $\triangle B C D \sim \triangle C E D$, dus $\frac{|D C|}{|D B|}=\frac{|D E|}{|D C|}$. Omdat $|D A|=|D C|$ volgt hieruit $\frac{|D A|}{|D B|}=\frac{|D E|}{|D A|}$. Samen met $\angle B D A=\angle E D A$ geeft dit $\triangle A D E \sim \triangle B D A$ (zhz). Dus $\angle A B D=\angle E A D$. Omdat $S C$ een raaklijn is aan de omgeschreven cirkel van $\triangle A E C$ geldt vanwege de raaklijnomtrekshoekstelling ook dat $\angle E A D=\angle E A C=\angle S C E$. Dus $\angle S C E=\angle A B D=\angle S B E$. Hieruit volgt dat $S B C E$ een koordenvierhoek is. Dus $\angle B S C=\angle B E C=90^{\circ}$.

|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2018-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2018"
}
|
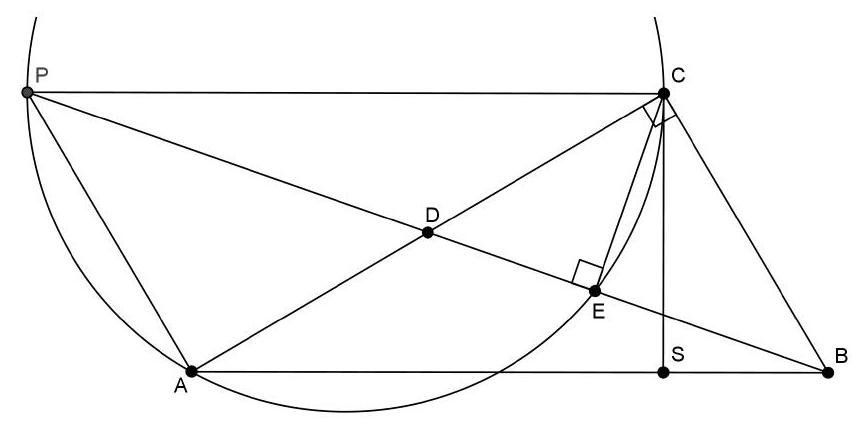
Given is a triangle $\triangle A B C$ with $\angle C=90^{\circ}$. The midpoint of $A C$ is called $D$ and the perpendicular projection of $C$ on $B D$ is called $E$. Prove that the tangent at $C$ to the circumcircle of $\triangle A E C$ is perpendicular to $A B$.

|
Let $P$ be the reflection of $B$ in $D$. Then $AC$ and $PB$ bisect each other, so $CBAP$ is a parallelogram. Therefore, $\angle CAP = \angle ACB = 90^{\circ} = \angle CEP$. This means that $CEAP$ is a cyclic quadrilateral and that $CP$ is a diameter of its circumscribed circle. The tangent at $C$ to this circumscribed circle is perpendicular to the diameter $CP$. Since in the parallelogram $AB \parallel CP$, the tangent is also perpendicular to $AB$.
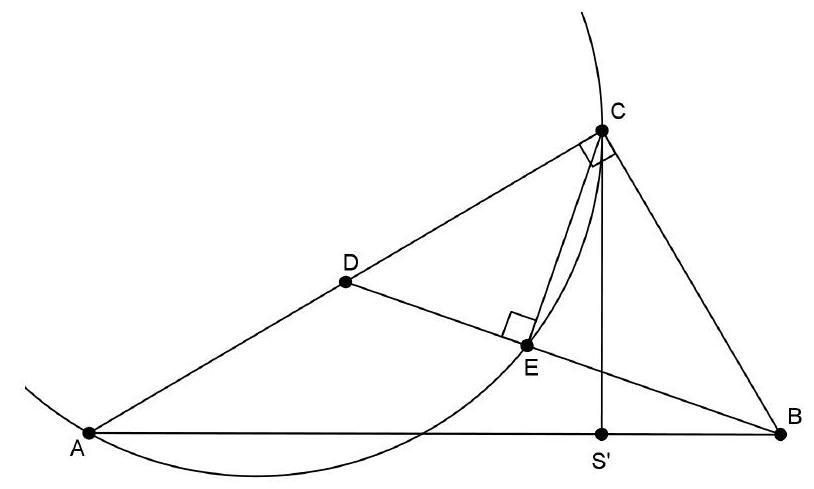
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Gegeven is een driehoek $\triangle A B C$ met $\angle C=90^{\circ}$. Het midden van $A C$ noemen we $D$ en de loodrechte projectie van $C$ op $B D$ noemen we $E$. Bewijs dat de raaklijn in $C$ aan de omgeschreven cirkel van $\triangle A E C$ loodrecht op $A B$ staat.

|
Zij $P$ de spiegeling van $B$ in $D$. Dan snijden $A C$ en $P B$ elkaar middendoor, dus is $C B A P$ een parallellogram. Dus $\angle C A P=\angle A C B=90^{\circ}=\angle C E P$. Dit betekent dat $C E A P$ een koordenvierhoek is en dat $C P$ een middellijn van zijn omgeschreven cirkel is. De raaklijn in $C$ aan deze omgeschreven cirkel staat loodrecht op de middellijn $C P$. Aangezien in het parallellogram $A B \| C P$, staat de raaklijn dus ook loodrecht op $A B$.

|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2018-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2018"
}
|
Given is a triangle $\triangle A B C$ with $\angle C=90^{\circ}$. The midpoint of $A C$ is called $D$ and the perpendicular projection of $C$ on $B D$ is called $E$. Prove that the tangent at $C$ to the circumcircle of $\triangle A E C$ is perpendicular to $A B$.

|
Let $S^{\prime}$ be the orthogonal projection of $C$ on $AB$. Then $\angle B S^{\prime} C = 90^{\circ} = \angle B E C$, so $B C S^{\prime} E$ is a cyclic quadrilateral. It follows that $\angle E D C = 90^{\circ} - \angle E C D = \angle E C B = 180^{\circ} - \angle E S^{\prime} C = \angle E S^{\prime} A$, so $\angle E D A = 180^{\circ} - \angle E D C = 180^{\circ} - \angle E S^{\prime} A$, which implies that $A D E S^{\prime}$ is a cyclic quadrilateral. Now, $\angle S^{\prime} A E = \angle S^{\prime} D E$. Furthermore, by Thales' theorem, $D$ is the center of the circle through $A, C$, and $S^{\prime}$, so $\angle D S^{\prime} A = \angle S^{\prime} A D$. These two results together give $\angle E A C = \angle S^{\prime} A C - \angle S^{\prime} A E = \angle S^{\prime} A D - \angle S^{\prime} A E = \angle D S^{\prime} A - \angle S^{\prime} D E$. By the exterior angle theorem in triangle $D S^{\prime} B$, this is equal to $\angle S^{\prime} B D = \angle S^{\prime} B E$, and by the cyclic quadrilateral $B C S^{\prime} E$, this is again equal to $\angle S^{\prime} C E$. Therefore, $\angle E A C = \angle S^{\prime} C E$. By the tangent-secant theorem, it follows that $S^{\prime} C$ is tangent to the circumcircle of $\triangle E A C$. This tangent $S^{\prime} C$ is indeed perpendicular to $AB$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Gegeven is een driehoek $\triangle A B C$ met $\angle C=90^{\circ}$. Het midden van $A C$ noemen we $D$ en de loodrechte projectie van $C$ op $B D$ noemen we $E$. Bewijs dat de raaklijn in $C$ aan de omgeschreven cirkel van $\triangle A E C$ loodrecht op $A B$ staat.

|
Zij $S^{\prime}$ de loodrechte projectie van $C$ op $A B$. Er geldt dan $\angle B S^{\prime} C=$ $90^{\circ}=\angle B E C$, dus $B C S^{\prime} E$ is een koordenvierhoek. Er volgt dat $\angle E D C=90^{\circ}-\angle E C D=$ $\angle E C B=180^{\circ}-\angle E S^{\prime} C=\angle E S^{\prime} A$, dus $\angle E D A=180^{\circ}-\angle E D C=180^{\circ}-\angle E S^{\prime} A$, waaruit volgt dat $A D E S^{\prime}$ een koordenvierhoek is. Nu is $\angle S^{\prime} A E=\angle S^{\prime} D E$. Verder is vanwege Thales $D$ het middelpunt van de cirkel door $A, C$ en $S^{\prime}$, dus is $\angle D S^{\prime} A=\angle S^{\prime} A D$. Deze twee resultaten samen geven $\angle E A C=\angle S^{\prime} A C-\angle S^{\prime} A E=\angle S^{\prime} A D-\angle S^{\prime} A E=\angle D S^{\prime} A-$ $\angle S^{\prime} D E$. Met de buitenhoekstelling in driehoek $D S^{\prime} B$ is dit gelijk aan $\angle S^{\prime} B D=\angle S^{\prime} B E$ en vanwege koordenvierhoek $B C S^{\prime} E$ is dat weer gelijk aan $\angle S^{\prime} C E$. Dus $\angle E A C=\angle S^{\prime} C E$. Met de raaklijnomtrekshoekstelling volgt hieruit dat $S^{\prime} C$ raakt aan de omgeschreven cirkel van $\triangle E A C$. Deze raaklijn $S^{\prime} C$ staat dus inderdaad loodrecht op $A B$.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2018-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing III.",
"tier": "T1",
"year": "2018"
}
|
Let $n \geq 0$ be an integer. A sequence $a_{0}, a_{1}, a_{2}, \ldots$ of integers is defined as follows: $a_{0}=n$ and for $k \geq 1$, $a_{k}$ is the smallest integer greater than $a_{k-1}$ such that $a_{k}+a_{k-1}$ is the square of an integer. Prove that there are exactly $\lfloor\sqrt{2 n}\rfloor$ positive integers that cannot be written in the form $a_{k}-a_{\ell}$ with $k>\ell \geq 0$.
|
Let $m=\lfloor\sqrt{2 n}\rfloor$. We first prove that the sequence of squares $a_{0}+a_{1}, a_{1}+a_{2}$, ... is exactly the sequence $(m+1)^{2},(m+2)^{2}, \ldots$. Then we show that the differences $a_{i}-a_{i-1}$ form a sequence of consecutive even numbers and a sequence of consecutive odd numbers. With this, we can then prove the desired result.
Note that $a_{0}+a_{1}$ is the smallest square greater than $2 n$. Therefore, $a_{0}+a_{1}=(m+1)^{2}$. We now prove by induction on $i$ that $a_{i-1}+a_{i}=(m+i)^{2}$. For $i=1$, we have just proven this. Suppose that $a_{j-1}+a_{j}=(m+j)^{2}$. This means that $a_{j-1} \geq \frac{(m+j-1)^{2}}{2}$ (otherwise, $a_{j}$ could have been chosen such that $a_{j-1}+a_{j}=(m+j-1)^{2}$) and thus
$$
\begin{aligned}
a_{j} & =(m+j)^{2}-a_{j-1} \\
& \leq(m+j)^{2}-\frac{(m+j-1)^{2}}{2} \\
& =\frac{2 m^{2}+4 m j+2 j^{2}-\left(m^{2}+2 m j+j^{2}+1-2 m-2 j\right)}{2} \\
& =\frac{m^{2}+2 m j+j^{2}-1+2 m+2 j}{2} \\
& <\frac{m^{2}+2 m j+j^{2}+1+2 m+2 j}{2} \\
& =\frac{(m+j+1)^{2}}{2} .
\end{aligned}
$$
From this, it follows that $a_{j}+a_{j+1} \leq(m+j+1)^{2}$. Moreover, $a_{j}+a_{j+1}>a_{j-1}+a_{j}=(m+j)^{2}$, so $a_{j}+a_{j+1}=(m+j+1)^{2}$. This completes the induction.
Define now $b_{i}=a_{i}-a_{i-1}$ for all $i \geq 1$. Then we have
$$
\begin{aligned}
b_{i+2}-b_{i} & =a_{i+2}-a_{i+1}-a_{i}+a_{i-1} \\
& =\left(a_{i+2}+a_{i+1}\right)+\left(a_{i}+a_{i-1}\right)-2\left(a_{i+1}+a_{i}\right) \\
& =(m+i+2)^{2}+(m+i)^{2}-2(m+i+1)^{2} \\
& =(m+i)^{2}+4(m+i)+4+(m+i)^{2}-2(m+i)^{2}-4(m+i)-2 \\
& =2
\end{aligned}
$$
for all $i \geq 1$. We now see that
$$
\left(b_{1}, b_{3}, b_{5}, \ldots\right)=\left(b_{1}, b_{1}+2, b_{1}+4, \ldots\right), \quad\left(b_{2}, b_{4}, b_{6}, \ldots\right)=\left(b_{2}, b_{2}+2, b_{2}+4, \ldots\right)
$$
We have $b_{1}+b_{2}=\left(a_{2}-a_{1}\right)+\left(a_{1}-a_{0}\right)=\left(a_{2}+a_{1}\right)-\left(a_{1}+a_{0}\right)=(m+2)^{2}-(m+1)^{2}=2 m+3$. In particular, $b_{1}$ and $b_{2}$ have different parities. Now, at least all numbers with the same parity as $b_{1}$ and at least as large as $b_{1}$ can be written as $a_{k}-a_{k-1}$ for some $k$. The same holds for the numbers with the same parity as $b_{2}$ and at least as large as $b_{2}$. All numbers of the form $a_{k}-a_{\ell}$ with $k \geq \ell+2$ are at least as large as $b_{k}+b_{k-1} \geq b_{1}+b_{2}$ and thus larger than $b_{1}$ and larger than $b_{2}$. In this way, we can no longer create new numbers. The numbers that cannot be written as $a_{k}-a_{\ell}$ with $k>\ell \geq 0$ are therefore exactly the numbers with the same parity as $b_{1}$ and smaller than $b_{1}$ and the numbers with the same parity as $b_{2}$ and smaller than $b_{2}$. There are in total
$$
\left\lfloor\frac{b_{1}-1}{2}\right\rfloor+\left\lfloor\frac{b_{2}-1}{2}\right\rfloor
$$
numbers, where within the brackets of the floor function, exactly one of the two times is an integer. We can thus write this as
$$
\frac{b_{1}-1}{2}+\frac{b_{2}-1}{2}-\frac{1}{2}=\frac{b_{1}+b_{2}-3}{2}=\frac{2 m}{2}=m \text {. }
$$
There are thus exactly $m=\lfloor\sqrt{2 n}\rfloor$ positive integers that cannot be written in the desired form.
|
\lfloor\sqrt{2 n}\rfloor
|
Yes
|
Yes
|
proof
|
Number Theory
|
Zij $n \geq 0$ een geheel getal. Een rij $a_{0}, a_{1}, a_{2}, \ldots$ van gehele getallen wordt als volgt gedefinieerd: er geldt $a_{0}=n$ en voor $k \geq 1$ is $a_{k}$ het kleinste gehele getal groter dan $a_{k-1}$ waarvoor $a_{k}+a_{k-1}$ het kwadraat van een geheel getal is. Bewijs dat er precies $\lfloor\sqrt{2 n}\rfloor$ positieve gehele getallen zijn die niet te schrijven zijn in de vorm $a_{k}-a_{\ell}$ met $k>\ell \geq 0$.
|
Zij $m=\lfloor\sqrt{2 n}\rfloor$. We bewijzen eerst dat de rij kwadraten $a_{0}+a_{1}, a_{1}+a_{2}$, ... precies de rij $(m+1)^{2},(m+2)^{2}, \ldots$ is. Vervolgens laten we zien dat de verschillen $a_{i}-a_{i-1}$ een rij opeenvolgende even getallen en een rij opeenvolgende oneven getallen vormen. Hiermee kunnen we daarna het gevraagde bewijzen.
Merk op dat $a_{0}+a_{1}$ het kleinste kwadraat is dat groter is dan $2 n$. Er geldt dus $a_{0}+a_{1}=$ $(m+1)^{2}$. We bewijzen nu met inductie naar $i$ dat $a_{i-1}+a_{i}=(m+i)^{2}$. Voor $i=1$ hebben we dit zojuist bewezen. Stel dat $a_{j-1}+a_{j}=(m+j)^{2}$. Dat betekent dat $a_{j-1} \geq \frac{(m+j-1)^{2}}{2}$ (anders had $a_{j}$ zo gekozen kunnen worden dat $\left.a_{j-1}+a_{j}=(m+j-1)^{2}\right)$ en dus
$$
\begin{aligned}
a_{j} & =(m+j)^{2}-a_{j-1} \\
& \leq(m+j)^{2}-\frac{(m+j-1)^{2}}{2} \\
& =\frac{2 m^{2}+4 m j+2 j^{2}-\left(m^{2}+2 m j+j^{2}+1-2 m-2 j\right)}{2} \\
& =\frac{m^{2}+2 m j+j^{2}-1+2 m+2 j}{2} \\
& <\frac{m^{2}+2 m j+j^{2}+1+2 m+2 j}{2} \\
& =\frac{(m+j+1)^{2}}{2} .
\end{aligned}
$$
Hieruit volgt dat $a_{j}+a_{j+1} \leq(m+j+1)^{2}$. Er geldt bovendien $a_{j}+a_{j+1}>a_{j-1}+a_{j}=(m+j)^{2}$, dus $a_{j}+a_{j+1}=(m+j+1)^{2}$. Dit voltooit de inductie.
Definieer nu $b_{i}=a_{i}-a_{i-1}$ voor alle $i \geq 1$. Dan geldt
$$
\begin{aligned}
b_{i+2}-b_{i} & =a_{i+2}-a_{i+1}-a_{i}+a_{i-1} \\
& =\left(a_{i+2}+a_{i+1}\right)+\left(a_{i}+a_{i-1}\right)-2\left(a_{i+1}+a_{i}\right) \\
& =(m+i+2)^{2}+(m+i)^{2}-2(m+i+1)^{2} \\
& =(m+i)^{2}+4(m+i)+4+(m+i)^{2}-2(m+i)^{2}-4(m+i)-2 \\
& =2
\end{aligned}
$$
voor alle $i \geq 1$. We zien nu dat
$$
\left(b_{1}, b_{3}, b_{5}, \ldots\right)=\left(b_{1}, b_{1}+2, b_{1}+4, \ldots\right), \quad\left(b_{2}, b_{4}, b_{6}, \ldots\right)=\left(b_{2}, b_{2}+2, b_{2}+4, \ldots\right)
$$
Er geldt $b_{1}+b_{2}=\left(a_{2}-a_{1}\right)+\left(a_{1}-a_{0}\right)=\left(a_{2}+a_{1}\right)-\left(a_{1}+a_{0}\right)=(m+2)^{2}-(m+1)^{2}=2 m+3$. In het bijzonder hebben $b_{1}$ en $b_{2}$ verschillende pariteit. Nu kunnen in elk geval alle getallen
met dezelfde pariteit als $b_{1}$ en minstens gelijk aan $b_{1}$ geschreven worden als $a_{k}-a_{k-1}$ voor zekere $k$. Hetzelfde geldt voor de getallen met dezelfde pariteit als $b_{2}$ en minstens gelijk aan $b_{2}$. Alle getallen van de vorm $a_{k}-a_{\ell}$ met $k \geq \ell+2$ zijn minstens gelijk aan $b_{k}+b_{k-1} \geq b_{1}+b_{2}$ en dus groter dan $b_{1}$ en groter dan $b_{2}$. We kunnen op deze manier dus geen nieuwe getallen meer maken. De getallen die niet te schrijven zijn als $a_{k}-a_{\ell}$ met $k>\ell \geq 0$ zijn dus precies de getallen met dezelfde pariteit als $b_{1}$ en kleiner dan $b_{1}$ en de getallen met dezelfde pariteit als $b_{2}$ en kleiner dan $b_{2}$. Dit zijn in totaal
$$
\left\lfloor\frac{b_{1}-1}{2}\right\rfloor+\left\lfloor\frac{b_{2}-1}{2}\right\rfloor
$$
getallen, waarbij binnen de haken van de entierfunctie precies één van beide keren een geheel getal staat. We kunnen dit dus schrijven als
$$
\frac{b_{1}-1}{2}+\frac{b_{2}-1}{2}-\frac{1}{2}=\frac{b_{1}+b_{2}-3}{2}=\frac{2 m}{2}=m \text {. }
$$
Er zijn dus precies $m=\lfloor\sqrt{2 n}\rfloor$ positieve gehele getallen die niet op de gevraagde manier te schrijven zijn.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2018-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2018"
}
|
Gegeven is een verzameling $A$ van functies $f: \mathbb{R} \rightarrow \mathbb{R}$. Voor alle $f_{1}, f_{2} \in A$ bestaat er een $f_{3} \in A$ zodat
$$
f_{1}\left(f_{2}(y)-x\right)+2 x=f_{3}(x+y)
$$
voor alle $x, y \in \mathbb{R}$. Bewijs dat voor alle $f \in A$ geldt:
$$
f(x-f(x))=0
$$
voor alle $x \in \mathbb{R}$.
|
Invullen van $x=0$ geeft
$$
f_{1}\left(f_{2}(y)\right)=f_{3}(y)
$$
dus de $f_{3}$ die bij $f_{1}$ en $f_{2}$ hoort, is blijkbaar de samenstelling $f_{3}(x)=f_{1}\left(f_{2}(x)\right)$. Invullen van $x=-y$ geeft nu dat voor alle $f_{1}, f_{2} \in A$
$$
f_{1}\left(f_{2}(y)+y\right)-2 y=f_{3}(0)=f_{1}\left(f_{2}(0)\right)
$$
voor alle $y \in \mathbb{R}$.
Invullen van $x=f_{2}(y)$ geeft dat er voor alle $f_{1}, f_{2} \in A$ een $f_{3} \in A$ bestaat met
$$
f_{1}(0)+2 f_{2}(y)=f_{3}\left(f_{2}(y)+y\right)
$$
voor alle $y \in \mathbb{R}$. We hebben hiervoor gezien dat we $f_{3}\left(f_{2}(y)+y\right)$ kunnen schrijven als $2 y+f_{3}\left(f_{2}(0)\right)$. Dus
$$
2 f_{2}(y)=2 y+f_{3}\left(f_{2}(0)\right)-f_{1}(0)
$$
voor alle $y \in \mathbb{R}$. We concluderen dat er een $d \in \mathbb{R}$ is, onafhankelijk van $y$, zodat $f_{2}(y)=y+d$ voor alle $y \in \mathbb{R}$.
Dus elke $f \in A$ is van de vorm $f(x)=x+d$ met $d$ een constante. Er geldt dan
$$
f(x-f(x))=f(x-(x+d))=f(-d)=-d+d=0
$$
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Gegeven is een verzameling $A$ van functies $f: \mathbb{R} \rightarrow \mathbb{R}$. Voor alle $f_{1}, f_{2} \in A$ bestaat er een $f_{3} \in A$ zodat
$$
f_{1}\left(f_{2}(y)-x\right)+2 x=f_{3}(x+y)
$$
voor alle $x, y \in \mathbb{R}$. Bewijs dat voor alle $f \in A$ geldt:
$$
f(x-f(x))=0
$$
voor alle $x \in \mathbb{R}$.
|
Invullen van $x=0$ geeft
$$
f_{1}\left(f_{2}(y)\right)=f_{3}(y)
$$
dus de $f_{3}$ die bij $f_{1}$ en $f_{2}$ hoort, is blijkbaar de samenstelling $f_{3}(x)=f_{1}\left(f_{2}(x)\right)$. Invullen van $x=-y$ geeft nu dat voor alle $f_{1}, f_{2} \in A$
$$
f_{1}\left(f_{2}(y)+y\right)-2 y=f_{3}(0)=f_{1}\left(f_{2}(0)\right)
$$
voor alle $y \in \mathbb{R}$.
Invullen van $x=f_{2}(y)$ geeft dat er voor alle $f_{1}, f_{2} \in A$ een $f_{3} \in A$ bestaat met
$$
f_{1}(0)+2 f_{2}(y)=f_{3}\left(f_{2}(y)+y\right)
$$
voor alle $y \in \mathbb{R}$. We hebben hiervoor gezien dat we $f_{3}\left(f_{2}(y)+y\right)$ kunnen schrijven als $2 y+f_{3}\left(f_{2}(0)\right)$. Dus
$$
2 f_{2}(y)=2 y+f_{3}\left(f_{2}(0)\right)-f_{1}(0)
$$
voor alle $y \in \mathbb{R}$. We concluderen dat er een $d \in \mathbb{R}$ is, onafhankelijk van $y$, zodat $f_{2}(y)=y+d$ voor alle $y \in \mathbb{R}$.
Dus elke $f \in A$ is van de vorm $f(x)=x+d$ met $d$ een constante. Er geldt dan
$$
f(x-f(x))=f(x-(x+d))=f(-d)=-d+d=0
$$
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2018-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2018"
}
|
a) If $c\left(a^{3}+b^{3}\right)=a\left(b^{3}+c^{3}\right)=b\left(c^{3}+a^{3}\right)$ for positive real numbers $a, b, c$, does it necessarily follow that $a=b=c$?
b) If $a\left(a^{3}+b^{3}\right)=b\left(b^{3}+c^{3}\right)=c\left(c^{3}+a^{3}\right)$ for positive real numbers $a, b, c$, does it necessarily follow that $a=b=c$?
|
a) We claim that $(a, b, c)=(2,2,-1+\sqrt{5})$ satisfies the given equalities. In this triplet, all numbers are positive real and they are not all equal, so the answer to the question is then no.
We calculate $c^{3}=(-1+\sqrt{5})^{3}=-1+3 \cdot \sqrt{5}-3 \cdot 5+5 \sqrt{5}=-16+8 \sqrt{5}$. Now, $c\left(a^{3}+b^{3}\right)=(-1+\sqrt{5}) \cdot 2 \cdot 8=-16+16 \sqrt{5}$ and $a\left(b^{3}+c^{3}\right)=b\left(c^{3}+a^{3}\right)=$ $2 \cdot(-16+8 \sqrt{5}+8)=-16+16 \sqrt{5}$. The given equalities indeed hold.
Here is a possible approach to find this triplet. Assume without loss of generality that $c \leq a, b$. Rewrite $a\left(b^{3}+c^{3}\right)=b\left(c^{3}+a^{3}\right)$ as $a b\left(b^{2}-a^{2}\right)=c^{3}(b-a)$. If $a \neq b$, we can divide by $b-a$ and get $a b(a+b)=c^{3}$. But $c \leq a, b$ and everything is positive, so $c^{3}<2 c^{3} \leq a^{2} b+a b^{2}=a b(a+b)$, a contradiction. Therefore, it must be that $a=b$. Now we can rewrite $c\left(a^{3}+b^{3}\right)=a\left(b^{3}+c^{3}\right)$ as $a^{3} c-a c^{3}=a^{4}-a^{3} c$ and then further to $ac \left(a^{2}-c^{2}\right)=a^{3}(a-c)$. Now, $a=c$ (and thus $a=b=c$) or $a c(a+c)=a^{3}$. This second is a quadratic equation in $c$. Solving this gives $c=\left(-\frac{1}{2}+\frac{1}{2} \sqrt{5}\right) a$. This way we find infinitely many triplets that satisfy the conditions.
b) We will prove that it must always be that $a=b=c$. Assume without loss of generality that $c \leq a, b$. There are two cases (since the given equalities are cyclic but not symmetric).
First, assume that $a \geq b \geq c$. Then,
$$
a\left(a^{3}+b^{3}\right) \geq c\left(a^{3}+b^{3}\right) \geq c\left(a^{3}+c^{3}\right)=a\left(a^{3}+b^{3}\right)
$$
so equality must always hold. Since everything is positive, this implies $a=c$ from the first inequality and $b=c$ from the second. Thus, $a=b=c$.
Now, assume that $b \geq a \geq c$. Then,
$$
b\left(b^{3}+c^{3}\right) \geq c\left(b^{3}+c^{3}\right) \geq c\left(a^{3}+c^{3}\right)=b\left(b^{3}+c^{3}\right)
$$
so equality must always hold. We find $b=c$ from the first inequality and $b=a$ from the second, thus $a=b=c$.
Solution II for b). Assume without loss of generality that $a \geq b, c$. Then,
$$
a\left(a^{3}+b^{3}\right) \geq b\left(a^{3}+b^{3}\right) \geq b\left(c^{3}+b^{3}\right)=a\left(a^{3}+b^{3}\right)
$$
so equality must always hold. Since everything is positive, this implies $a=b$ from the first inequality and $a=c$ from the second. Thus, $a=b=c$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
a) Als $c\left(a^{3}+b^{3}\right)=a\left(b^{3}+c^{3}\right)=b\left(c^{3}+a^{3}\right)$ voor positieve reële getallen $a, b, c$, geldt dan noodzakelijk $a=b=c$ ?
b) Als $a\left(a^{3}+b^{3}\right)=b\left(b^{3}+c^{3}\right)=c\left(c^{3}+a^{3}\right)$ voor positieve reële getallen $a, b, c$, geldt dan noodzakelijk $a=b=c$ ?
|
a) We beweren dat $(a, b, c)=(2,2,-1+\sqrt{5})$ aan de gegeven gelijkheden voldoet. In dit drietal zijn alle getallen positief reëel en ze zijn niet allemaal gelijk, dus het antwoord op de vraag is dan nee.
We berekenen $c^{3}=(-1+\sqrt{5})^{3}=-1+3 \cdot \sqrt{5}-3 \cdot 5+5 \sqrt{5}=-16+8 \sqrt{5}$. Nu geldt $c\left(a^{3}+b^{3}\right)=(-1+\sqrt{5}) \cdot 2 \cdot 8=-16+16 \sqrt{5}$ en $a\left(b^{3}+c^{3}\right)=b\left(c^{3}+a^{3}\right)=$ $2 \cdot(-16+8 \sqrt{5}+8)=-16+16 \sqrt{5}$. De gegeven gelijkheden gelden dus inderdaad.
Hier een mogelijke aanpak om dit drietal te vinden. Neem zonder verlies van algemeenheid aan dat $c \leq a, b$. Herschrijf $a\left(b^{3}+c^{3}\right)=b\left(c^{3}+a^{3}\right)$ tot $a b\left(b^{2}-a^{2}\right)=c^{3}(b-a)$. Als $a \neq b$ kunnen we delen door $b-a$ en volgt $a b(a+b)=c^{3}$. Maar $c \leq a, b$ en alles is positief, dus $c^{3}<2 c^{3} \leq a^{2} b+a b^{2}=a b(a+b)$, tegenspraak. Er moet dus wel gelden $a=b$. Nu kunnen we $c\left(a^{3}+b^{3}\right)=a\left(b^{3}+c^{3}\right)$ herschrijven tot $a^{3} c-a c^{3}=a^{4}-a^{3} c$ en dan verder tot ac $\left(a^{2}-c^{2}\right)=a^{3}(a-c)$. Nu geldt $a=c$ (en dus $a=b=c$ ) of $a c(a+c)=a^{3}$. Dit tweede is een kwadratische vergelijking in $c$. Dit oplossen geeft dat $c=\left(-\frac{1}{2}+\frac{1}{2} \sqrt{5}\right) a$. Zo vinden we oneindig veel drietallen die voldoen.
b) We gaan bewijzen dat altijd moet gelden dat $a=b=c$. Neem zonder verlies van algemeenheid aan dat $c \leq a, b$. Nu zijn er twee gevallen (want de gegeven gelijkheden zijn slechts cyclisch en niet symmetrisch).
Stel eerst dat $a \geq b \geq c$. Dan geldt
$$
a\left(a^{3}+b^{3}\right) \geq c\left(a^{3}+b^{3}\right) \geq c\left(a^{3}+c^{3}\right)=a\left(a^{3}+b^{3}\right)
$$
dus er moet steeds gelijkheid gelden. Omdat alles positief is, volgt daaruit $a=c$ bij de eerste ongelijkheid en $b=c$ bij de tweede. Dus $a=b=c$.
Stel nu dat $b \geq a \geq c$. Dan geldt
$$
b\left(b^{3}+c^{3}\right) \geq c\left(b^{3}+c^{3}\right) \geq c\left(a^{3}+c^{3}\right)=b\left(b^{3}+c^{3}\right)
$$
dus ook hier moet steeds gelijkheid gelden. We vinden nu $b=c$ bij de eerste ongelijkheid en $b=a$ bij de tweede, dus $a=b=c$.
Oplossing II voor b). Neem zonder verlies van algemeenheid aan dat $a \geq b, c$. Dan geldt
$$
a\left(a^{3}+b^{3}\right) \geq b\left(a^{3}+b^{3}\right) \geq b\left(c^{3}+b^{3}\right)=a\left(a^{3}+b^{3}\right)
$$
dus er moet steeds gelijkheid gelden. Omdat alles positief is, volgt daaruit $a=b$ bij de eerste ongelijkheid en $a=c$ bij de tweede. Dus $a=b=c$.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "# Opgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2018-D_uitwerkingen.jsonl",
"solution_match": "# Oplossing I.",
"tier": "T1",
"year": "2018"
}
|
Find all positive integers $n$ for which there exists a positive integer $k$ such that for every positive divisor $d$ of $n$, $d-k$ is also a (not necessarily positive) divisor of $n$.
|
When $n=1$ or $n$ is a prime number, the only positive divisors of $n$ are 1 and $n$ (which coincide in the case $n=1$). Now take $k=n+1$, then $1-(n+1)=-n$ and $n-(n+1)=-1$ must also be divisors of $n$. This is exactly correct. So $n=1$ and $n$ being prime satisfy the condition with $k=n+1$. If $n=4$, the positive divisors are 1, 2, and 4. We choose $k=3$, so $-2, -1$, and 1 must be divisors of 4, and this is correct. So $n=4$ satisfies the condition with $k=3$. If $n=6$, then the positive divisors are $1, 2, 3$, and 6. We choose $k=4$, so $-3, -2, -1$, and 2 must also be divisors of 6, and this is correct. So $n=6$ satisfies the condition with $k=4$. In summary, we now know that $n \leq 6$ and all prime numbers $n$ satisfy the condition.
Now assume $n>6$ and $n$ is not prime. Suppose $n$ satisfies the condition. Since $n$ is a positive divisor of $n$, $n-k$ is also a divisor of $n$. The largest divisor less than $n$ is at most $\frac{1}{2} n$, so $n-k \leq \frac{1}{2} n$, thus $k \geq \frac{1}{2} n$. Furthermore, 1 is a positive divisor of $n$, so $1-k$ is a divisor of $n$. We now know $1-k \leq 1-\frac{1}{2} n$. Since $n>6$, $\frac{1}{6} n>1$, so $\frac{1}{2} n-\frac{1}{3} n>1$, thus $-\frac{1}{3} n>1-\frac{1}{2} n$. The only divisors that are at most $1-\frac{1}{2} n$ are $-n$ and (if $n$ is even) $-\frac{1}{2} n$. We conclude that $1-k=-n$ or $1-k=-\frac{1}{2} n$.
In the latter case, $k=\frac{1}{2} n+1$, so $n-k=\frac{1}{2} n-1$. However, similarly to the above, there is no divisor equal to $\frac{1}{2} n-1$ for $n>6$ (since after $\frac{1}{2} n$, the next possible divisor is $\frac{1}{3} n$, which is already smaller than $\frac{1}{2} n-1$). Contradiction, because $n-k$ must be a divisor of $n$.
We are left with the case $1-k=-n$. So $k=n+1$. Since $n$ is not prime, there is a divisor $d$ with $1<d<n$. Therefore, $d-k=d-n-1$ is also a divisor. But $d \leq \frac{1}{2} n$, so $d-n-1 \leq -\frac{1}{2} n-1$, and the only divisor less than or equal to $-\frac{1}{2} n-1$ is $-n$. We see that $d-n-1=-n$, so $d=1$, contradiction.
We conclude that all $n$ with $n>6$ and $n$ not prime do not satisfy the condition, so the only solutions are all $n$ with $n \leq 6$ and all $n$ that are prime.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Vind alle positieve gehele getallen $n$ waarvoor er een positief geheel getal $k$ bestaat zodat voor iedere positieve deler $d$ van $n$ geldt dat ook $d-k$ een (niet noodzakelijk positieve) deler van $n$ is.
|
Als $n=1$ of $n$ is een priemgetal, dan zijn de enige positieve delers van $n$ gelijk aan 1 en $n$ (die samenvallen in het geval $n=1$ ). Neem nu $k=n+1$, dan moeten $1-(n+1)=-n$ en $n-(n+1)=-1$ ook delers zijn van $n$. Dat klopt precies. Dus $n=1$ en $n$ is priem voldoen met $k=n+1$. Als $n=4$, zijn de positieve delers 1,2 en 4 . We kiezen $k=3$, waardoor $-2,-1$ en 1 delers van 4 moeten zijn en dat klopt. Dus $n=4$ voldoet met $k=3$. Als $n=6$, dan zijn de positieve delers $1,2,3$ en 6 . We kiezen $k=4$, waardoor $-3,-2,-1$ en 2 ook delers van 6 moeten zijn en dat klopt. Dus $n=6$ voldoet met $k=4$. Al met al weten we nu dat $n \leq 6$ en alle priemgetallen $n$ voldoen.
Stel nu dat $n>6$ en $n$ is niet priem. Neem aan dat $n$ voldoet. Omdat $n$ een positieve deler is van $n$, is $n-k$ ook een deler van $n$. De grootste deler kleiner dan $n$ is hoogstens $\frac{1}{2} n$, dus $n-k \leq \frac{1}{2} n$, dus $k \geq \frac{1}{2} n$. Verder is 1 een positieve deler van $n$, dus is $1-k$ een deler van $n$. We weten nu $1-k \leq 1-\frac{1}{2} n$. Aangezien $n>6$, is $\frac{1}{6} n>1$, dus $\frac{1}{2} n-\frac{1}{3} n>1$, dus $-\frac{1}{3} n>1-\frac{1}{2} n$. De enige delers die hoogstens $1-\frac{1}{2} n$ zijn, zijn dus $-n$ en (als $n$ even is) $-\frac{1}{2} n$. We concluderen dat $1-k=-n$ of $1-k=-\frac{1}{2} n$.
In het laatste geval geldt $k=\frac{1}{2} n+1$, dus $n-k=\frac{1}{2} n-1$. Echter, analoog aan het voorgaande is er voor $n>6$ geen deler gelijk aan $\frac{1}{2} n-1$ (want na $\frac{1}{2} n$ is de volgende mogelijke deler $\frac{1}{3} n$ en die is al kleiner dan $\frac{1}{2} n-1$ ). Tegenspraak, want $n-k$ moet een deler van $n$ zijn.
We houden het geval $1-k=-n$ over. Dus $k=n+1$. Omdat $n$ niet priem is, is er een deler $d$ met $1<d<n$. Daarom is $d-k=d-n-1$ ook een deler. Maar $d \leq \frac{1}{2} n$, dus $d-n-1 \leq-\frac{1}{2} n-1$, maar de enige deler kleiner dan of gelijk aan $-\frac{1}{2} n-1$ is $-n$. We zien dat $d-n-1=-n$, dus $d=1$, tegenspraak.
We concluderen dat alle $n$ met $n>6$ en $n$ niet priem niet voldoen, dus de enige oplossingen zijn alle $n$ met $n \leq 6$ en alle $n$ die priem zijn.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2018-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2018"
}
|
Find all positive integers $n$ for which there exists a positive integer $k$ such that for every positive divisor $d$ of $n$, $d-k$ is also a (not necessarily positive) divisor of $n$.
|
Consider an $n \geq 2$ that satisfies the condition. Since 1 is a positive divisor of $n$, $1-k$ is a divisor of $n$. This must be a negative divisor, since $k$ is a positive integer. If we write this divisor as $-d$ with $d$ a positive divisor of $n$, we have $1-k=-d$, so $d+1=k$. Since $n$ is a positive divisor of $n$, $n-k=n-d-1$ is also a divisor of $n$. Note that $\operatorname{gcd}(d, n-d-1)=\operatorname{gcd}(d,-1)=1$ because $d \mid n$. This means that $d(n-d-1)$ is also a divisor of $n$. Therefore, $d(n-d-1) \leq n$.
Suppose $d=n$. Consider the smallest prime divisor $p$ of $n$ and write $n=p m$ with $m$ a positive integer. Now, $m$ is the largest divisor of $n$ that is smaller than $n$, and $p-k=p-d-1=p-n-1$ is a divisor of $n$. But $p-n-1>-n$ and $p-n-1=p-p m-1=p(1-m)-1 \leq 2(1-m)-1=-2 m+1 \leq -m$. However, there are no divisors between $-n$ and $-m$, so equality must hold in the last inequality. This can only happen if $m=1$, which means $n$ is prime.
Now suppose $d<n$. Then $2 d \leq n$. From $d(n-d-1) \leq n$ we get $-d^{2}-d \leq n-d n$, so $d^{2}+d \geq n(d-1) \geq 2 d(d-1)=2 d^{2}-2 d$. This implies $d^{2} \leq 3 d$ or $d \leq 3$. Now $n-d-1 \geq n-4$. Since $n-d-1$ is a divisor of $n$ smaller than $n$, we have $2(n-4) \leq 2(n-d-1) \leq n$, so $n \leq 8$.
We now know that if $n$ satisfies the condition, then $n$ is prime or $n \leq 8$ (this also includes the case $n=1$, which we initially overlooked). We consider $n=8$. The divisors 1 and 2 of 8 are consecutive, so $1-k$ and $2-k$ must also be consecutive. These must be -2 and -1, so $k=3$. But $8-3=5$ is not a divisor of $n$, a contradiction. Therefore, if $n$ satisfies the condition, then $n$ must be prime or $n \leq 6$. Just as in Solution I, we can show that all these values of $n$ satisfy the condition.
|
n \text{ is prime or } n \leq 6
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Vind alle positieve gehele getallen $n$ waarvoor er een positief geheel getal $k$ bestaat zodat voor iedere positieve deler $d$ van $n$ geldt dat ook $d-k$ een (niet noodzakelijk positieve) deler van $n$ is.
|
Bekijk een $n \geq 2$ die voldoet. Omdat 1 een positieve deler van $n$ is, is $1-k$ een deler van $n$. Dit moet een negatieve deler zijn, aangezien $k$ positief geheel is. Als we deze deler als $-d$ schrijven met $d$ een positieve deler van $n$, geldt $1-k=-d$, dus $d+1=k$. Omdat $n$ een positieve deler van $n$ is, is ook $n-k=n-d-1$ een deler van $n$. Merk op dat $\operatorname{ggd}(d, n-d-1)=\operatorname{ggd}(d,-1)=1$ omdat $d \mid n$. Dit betekent dat $d(n-d-1)$ ook een deler van $n$ is. Er geldt dan $d(n-d-1) \leq n$.
Stel $d=n$. Bekijk de kleinste priemdeler $p$ van $n$ en schrijf $n=p m$ met $m$ positief geheel. Er geldt nu dat $m$ de grootste deler van $n$ is die kleiner is dan $n$, en verder is $p-k=p-d-1=p-n-1$ een deler van $n$. Maar $p-n-1>-n$ en $p-n-1=$ $p-p m-1=p(1-m)-1 \leq 2(1-m)-1=-2 m+1 \leq-m$. Er zijn echter geen delers tussen $-n$ en $-m$, dus moet in de laatste ongelijkheid wel gelijkheid gelden. Dat kan alleen als $m=1$ en dat betekent dat $n$ priem is.
Stel nu $d<n$. Dan geldt $2 d \leq n$. Uit $d(n-d-1) \leq n$ volgt $-d^{2}-d \leq n-d n$, dus $d^{2}+d \geq n(d-1) \geq 2 d(d-1)=2 d^{2}-2 d$. Hieruit volgt dat $d^{2} \leq 3 d$ oftewel $d \leq 3$. Nu is $n-d-1 \geq n-4$. Omdat $n-d-1$ een deler van $n$ kleiner dan $n$ is, geldt $2(n-4) \leq 2(n-d-1) \leq n$, dus $n \leq 8$.
We weten nu dat als $n$ voldoet, dat dan $n$ priem is of $n \leq 8$ (hier valt ook het geval $n=1$ onder, dat we in eerste instantie hadden overgeslagen). We bekijken $n=8$. De delers 1 en 2 van 8 zijn opeenvolgend, dus moeten $1-k$ en $2-k$ ook opeenvolgend zijn. Dat moeten dan wel -2 en -1 zijn, dus $k=3$. Maar $8-3=5$ is geen deler van $n$, tegenspraak. Dus als $n$ voldoet, dan moet $n$ priem zijn of $n \leq 6$. Net als in oplossing I kunnen we laten zien dat al deze waarden van $n$ voldoen.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2018-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2018"
}
|
Let $A B C$ be an acute triangle and let $D$ be the foot of the altitude from $A$. On $A D$ lie different points $E$ and $F$ such that $|A E|=|B E|$ and $|A F|=|C F|$. A point $T \neq D$ satisfies $\angle B T E=\angle C T F=90^{\circ}$. Show that $|T A|^{2}=|T B| \cdot|T C|$.
We consider the configuration with the order of the points as shown in the picture.
|
Let $M$ be the midpoint of $AB$ and $N$ the midpoint of $AC$. From the given information, it follows that $E$ lies on the perpendicular bisector of $AB$, so $\angle BME = 90^{\circ}$. Since also $\angle BTE = 90^{\circ}$ and $\angle BDE = 90^{\circ}$, $BDTEM$ is a cyclic pentagon by Thales' theorem. Similarly, $CFDTN$ is a cyclic pentagon. It now holds that $\angle NTM = 360^{\circ} - \angle DTN - \angle MTD = (180^{\circ} - \angle DTN) + (180^{\circ} - \angle MTD) = \angle DCN + \angle MBD = \angle BCA + \angle ABC = 180^{\circ} - \angle CAB = 180^{\circ} - \angle NAM$. Therefore, $AMTN$ is a cyclic quadrilateral. (This also follows directly from Miquel's theorem.) Using only angle chasing, we will now prove that $\triangle TBA \sim \triangle TAC$. It holds that $\angle NTC = \angle NFC = 90^{\circ} - \angle FCN$ because $\angle FNC = 90^{\circ}$. Furthermore, $\angle FCN = \angle FCA = \angle CAF$ due to $|AF| = |CF|$, so $\angle NTC = 90^{\circ} - \angle CAF = 90^{\circ} - \angle CAD = \angle DCA = \angle BCA$. Now we get $\angle ACT = \angle NCT = 180^{\circ} - \angle NTC - \angle CNT = 180^{\circ} - \angle BCA - \angle CNT$. Since $MN$ is a midline in triangle $ABC$, it follows that $MN \| BC$ and by alternate interior angles, $180^{\circ} - \angle BCA = \angle CNM$. Therefore, $\angle ACT = \angle CNM - \angle CNT = \angle TNM = \angle TAM = \angle TAB$, where we also used cyclic quadrilateral $AMTN$. Similarly, $\angle ABT = \angle TAC$, so $\triangle TBA \sim \triangle TAC$. This implies that $\frac{|TB|}{|TA|} = \frac{|TA|}{|TC|}$, hence $|TA|^2 = |TB| \cdot |TC|$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $A B C$ een scherphoekige driehoek en zij $D$ het voetpunt van de hoogtelijn uit $A$. Op $A D$ liggen verschillende punten $E$ en $F$ zodat $|A E|=|B E|$ en $|A F|=|C F|$. Een punt $T \neq D$ voldoet aan $\angle B T E=\angle C T F=90^{\circ}$. Toon aan dat $|T A|^{2}=|T B| \cdot|T C|$.

We bekijken de configuratie met de volgorde van de punten zoals in het plaatje.
|
Zij $M$ het midden van $A B$ en zij $N$ het midden van $A C$. Uit de gegevens volgt dat $E$ op de middelloodlijn van $A B$ ligt, dus $\angle B M E=90^{\circ}$. Omdat ook $\angle B T E=90^{\circ}$ en $\angle B D E=90^{\circ}$, is $B D T E M$ een koordenvijfhoek wegens Thales. Zo ook is $C F D T N$ een koordenvijfhoek. Er geldt nu $\angle N T M=360^{\circ}-\angle D T N-\angle M T D=\left(180^{\circ}-\angle D T N\right)+$ $\left(180^{\circ}-\angle M T D\right)=\angle D C N+\angle M B D=\angle B C A+\angle A B C=180^{\circ}-\angle C A B=180^{\circ}-\angle N A M$. Dus $A M T N$ is een koordenvierhoek. (Dit laatste volgt ook direct uit de stelling van Miquel.) Met alleen hoekenjagen gaan we nu bewijzen dat $\triangle T B A \sim \triangle T A C$. Er geldt $\angle N T C=$ $\angle N F C=90^{\circ}-\angle F C N$ omdat $\angle F N C=90^{\circ}$. Verder is $\angle F C N=\angle F C A=\angle C A F$ vanwege $|A F|=|C F|$, dus $\angle N T C=90^{\circ}-\angle C A F=90^{\circ}-\angle C A D=\angle D C A=\angle B C A$. Nu krijgen we $\angle A C T=\angle N C T=180^{\circ}-\angle N T C-\angle C N T=180^{\circ}-\angle B C A-\angle C N T$. Omdat $M N$ een middenparallel in driehoek $A B C$ is, geldt $M N \| B C$ en met U-hoeken volgt daaruit $180^{\circ}-\angle B C A=\angle C N M$. Dus $\angle A C T=\angle C N M-\angle C N T=\angle T N M=$ $\angle T A M=\angle T A B$, waarbij we ook koordenvierhoek $A M T N$ nog gebruikt hebben. Analoog geldt $\angle A B T=\angle T A C$, dus $\triangle T B A \sim \triangle T A C$. Hieruit volgt dat $\frac{|T B|}{|T A|}=\frac{|T A|}{|T C|}$, dus $|T A|^{2}=$ $|T B| \cdot|T C|$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2018-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2018"
}
|
Let $A B C$ be an acute triangle and let $D$ be the foot of the altitude from $A$. On $A D$ lie different points $E$ and $F$ such that $|A E|=|B E|$ and $|A F|=|C F|$. A point $T \neq D$ satisfies $\angle B T E=\angle C T F=90^{\circ}$. Show that $|T A|^{2}=|T B| \cdot|T C|$.

We consider the configuration with the order of the points as shown in the picture.
|
We follow solution I up to the claim that $A M T N$ is a cyclic quadrilateral.
Since $M N$ is a midline in triangle $A B C$, $A D$ is perpendicular to $M N$ and is bisected by $M N$. Therefore, $D$ is the reflection of $A$ in $M N$. It follows that
$\angle D M N=\angle A M N=\angle A B C=\angle M B D$, so by the tangent-secant angle theorem, we can now conclude that $M N$ is tangent to the circle through $B, D, T, E$ and $M$. We now find that $\angle T A C=\angle T A N=\angle T M N=\angle T B M=\angle T B A$. Similarly, $\angle T C A=\angle T A B$, so $\triangle T B A \sim \triangle T A C$. It follows that $\frac{|T B|}{|T A|}=\frac{|T A|}{|T C|}$, hence $|T A|^{2}=|T B| \cdot|T C|$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $A B C$ een scherphoekige driehoek en zij $D$ het voetpunt van de hoogtelijn uit $A$. Op $A D$ liggen verschillende punten $E$ en $F$ zodat $|A E|=|B E|$ en $|A F|=|C F|$. Een punt $T \neq D$ voldoet aan $\angle B T E=\angle C T F=90^{\circ}$. Toon aan dat $|T A|^{2}=|T B| \cdot|T C|$.

We bekijken de configuratie met de volgorde van de punten zoals in het plaatje.
|
We volgen oplossing I tot en met de bewering dat $A M T N$ een koordenvierhoek is.
Omdat $M N$ een middenparallel in driehoek $A B C$ is, staat $A D$ loodrecht op $M N$ en wordt hij door $M N$ doormidden gedeeld. Daarom is $D$ de spiegeling van $A$ in $M N$. Hieruit volgt
dat $\angle D M N=\angle A M N=\angle A B C=\angle M B D$, dus vanwege de raaklijnomtrekshoekstelling kunnen we nu concluderen dat $M N$ raakt aan de cirkel door $B, D, T, E$ en $M$. We vinden nu dat $\angle T A C=\angle T A N=\angle T M N=\angle T B M=\angle T B A$. Analoog geldt $\angle T C A=\angle T A B$, dus $\triangle T B A \sim \triangle T A C$. Hieruit volgt dat $\frac{|T B|}{|T A|}=\frac{|T A|}{|T C|}$, dus $|T A|^{2}=|T B| \cdot|T C|$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2018-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2018"
}
|
In a class of at least four people, the following applies: if four of them sit down at a round table, there is always someone who knows both of their neighbors or does not know both of their neighbors. Prove that it is possible to divide the people into two groups (one of which may be empty) such that in one group everyone knows each other and in the other group no one knows each other.
(If person $A$ knows person $B$, then $B$ also knows $A$.)
|
Of all possible groups of people we can form in this class, we consider the groups in which everyone knows each other, and from these we take one with as many people as possible. (This largest group exists: there are finitely many people and there is at least a group of people who all know each other, namely a group consisting of one person.) Call this group $X$. We prove that the group $X$ and the group consisting of the rest of the people satisfy the condition.
Since everyone in $X$ knows each other, we only need to prove that all people outside $X$ do not know each other. Suppose there are $A$ and $B$ outside $X$ who do know each other. Since $X$ is as large as possible, $X$ contains a person $A^{\prime}$ who is not an acquaintance of $A$. Similarly, $X$ contains a person $B^{\prime}$ who is not an acquaintance of $B$. We now first prove that we can choose $A^{\prime}$ and $B^{\prime}$ to be different from each other. If not, there is a unique person $C=A^{\prime}=B^{\prime}$ in $X$ who does not know $A$ and $B$. For all other people in $X$, it then holds that they know both $A$ and $B$. Now consider the set $(X \backslash C) \cup\{A, B\}$. In this group of people, everyone knows each other: the people from $X$ know each other, $A$ and $B$ know each other, and everyone in $X$ knows both $A$ and $B$. This group is, however, larger than $X$, a contradiction.
Therefore, we may assume that $A^{\prime}$ and $B^{\prime}$ are different people. Note that $A^{\prime}$ and $B^{\prime}$ know each other, as they are both in $X$. If now $A, B, B^{\prime}$, and $A^{\prime}$ sit down at a round table in that order, everyone knows exactly one of their neighbors: $A$ and $B$ know each other and $A^{\prime}$ and $B^{\prime}$ know each other, but $A$ and $A^{\prime}$ do not know each other, and the same goes for $B$ and $B^{\prime}$. This is a contradiction to the given condition. We conclude that the division into $X$ and the rest of the people satisfies the condition.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
In een klas van minstens vier mensen geldt het volgende: als er vier van hen aan een ronde tafel gaan zitten, is er altijd iemand die allebei zijn buren kent of allebei zijn buren niet kent. Bewijs dat het mogelijk is om de mensen over twee groepen (waarvan er eentje leeg mag zijn) te verdelen, zodat in de ene groep iedereen elkaar kent en in de andere groep juist niemand elkaar kent.
(Als persoon $A$ persoon $B$ kent, dan kent $B$ ook $A$.)
|
Van alle mogelijke groepen mensen die we in deze klas kunnen maken, bekijken we de groepen waarin iedereen elkaar kent en daarvan nemen we er eentje met zoveel mogelijk mensen erin. (Deze grootste groep bestaat: er zijn eindig veel mensen en er is in elk geval een groep van mensen die elkaar allemaal kennen, namelijk een groep bestaande uit één persoon.) Noem deze groep $X$. We bewijzen dat de groep $X$ en de groep bestaande uit de rest van de mensen aan de voorwaarde voldoet.
Omdat in $X$ alle mensen elkaar kennen, hoeven we alleen te bewijzen dat alle mensen buiten $X$ elkaar niet kennen. Stel dat er wel $A$ en $B$ buiten $X$ bestaan die elkaar kennen. Omdat $X$ zo groot mogelijk is, bevat $X$ een persoon $A^{\prime}$ die geen kennis van $A$ is. Net zo bevat $X$ een persoon $B^{\prime}$ die geen kennis van $B$ is. We bewijzen nu eerst dat we $A^{\prime}$ en $B^{\prime}$ verschillend van elkaar kunnen kiezen. Zo niet, is er in $X$ een unieke persoon $C=A^{\prime}=B^{\prime}$ die $A$ en $B$ niet kent. Voor alle andere mensen in $X$ geldt dan dat ze $A$ en $B$ wel kennen. Bekijk nu de verzameling $(X \backslash C) \cup\{A, B\}$. In deze groep mensen kent iedereen elkaar: de mensen uit $X$ kennen elkaar, $A$ en $B$ kennen elkaar en iedereen in $X$ kent zowel $A$ als $B$. Deze groep is echter groter dan $X$, tegenspraak.
Dus we mogen aannemen dat $A^{\prime}$ en $B^{\prime}$ verschillende personen zijn. Merk op dat $A^{\prime}$ en $B^{\prime}$ elkaar kennen, want ze zitten allebei in $X$. Als nu $A, B, B^{\prime}$ en $A^{\prime}$ in die volgorde aan een ronde tafel gaan zitten, kent iedereen precies één van zijn buren: $A$ en $B$ kennen elkaar en $A^{\prime}$ en $B^{\prime}$ kennen elkaar, maar $A$ en $A^{\prime}$ kennen elkaar juist niet en hetzelfde geldt voor $B$ en $B^{\prime}$. Dit is een tegenspraak met het gegeven. We concluderen dat de opdeling in $X$ en de rest van de mensen voldoet.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2018-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2018"
}
|
In a class of at least four people, the following applies: if four of them sit down at a round table, there is always someone who knows both of their neighbors or does not know both of their neighbors. Prove that it is possible to divide the people into two groups (one of which may be empty) such that in one group everyone knows each other and in the other group no one knows each other.
(If person $A$ knows person $B$, then $B$ also knows $A$.)
|
We prove this by induction on the number of people $n$ in the class. We take $n=3$ as the base case; the given condition about four people at a table is then an empty requirement. We divide the three people arbitrarily into a group of one and a group of two. These two people either know each other or they don't; in both cases, it holds. Suppose now that we have proven it for all classes of $n$ people. Consider a class of $n+1$ people. Call one of them $N$. We divide the remaining $n$ people into two groups according to the induction hypothesis. Let group $\mathcal{K}$ be the group of people who all know each other and group $\mathcal{L}$ be the group of people who all do not know each other. If $N$ knows everyone in $\mathcal{K}$, we can add $N$ to $\mathcal{K}$. If $N$ knows no one in $\mathcal{L}$, we can add $N$ to $\mathcal{L}$. In the other cases, $N$ does not know at least one person in $\mathcal{K}$ and knows at least one person in $\mathcal{L}$.
Suppose that he does not know at least two people $K_{1}$ and $K_{2}$ in $\mathcal{K}$, while he knows at least two people $L_{1}$ and $L_{2}$ in $\mathcal{L}$. If $K_{1}$ and $L_{1}$ know each other, then we place $K_{1}, L_{1}, L_{2}, N$ around a round table in that order; contradiction. If $K_{1}$ and $L_{1}$ do not know each other,
then we place $K_{1}, L_{1}, N, K_{2}$ around a round table in that order; contradiction. This case is thus impossible.
Suppose that $N$ does not know at least two people $K_{1}$ and $K_{2}$ in $\mathcal{K}$, while he knows exactly one person $L$ in $\mathcal{L}$. Take a random $K$ in $\mathcal{K}$. Then we place $K, L, N$ and $K_{i}$ around a round table in that order, where $i$ is 1 or 2, so that $K \neq K_{i}$. Now we see that if $K$ and $L$ do not know each other, this gives a contradiction, so $K$ and $L$ know each other. Thus, $L$ knows everyone in $\mathcal{K}$. Now we add $L$ to $\mathcal{K}$. Since $N$ knows no one else in $\mathcal{L}$, we can then add $N$ to $\mathcal{L}$.
Suppose that $N$ does not know exactly one person in $\mathcal{K}$, while he knows at least two people in $\mathcal{L}$. Then we can make the group division analogously to the previous case.
Finally, suppose that $N$ does not know exactly one person $K_{1}$ in $\mathcal{K}$, while he knows exactly one person $L$ in $\mathcal{L}$. Without loss of generality, assume that $K_{1}$ and $L$ know each other. Take a random $K \neq K_{1}$ in $\mathcal{K}$. Then we place $K, L, N$ and $K_{1}$ around a round table in that order. Now we see that if $K$ and $L$ do not know each other, this gives a contradiction, so $K$ and $L$ know each other. Thus, $L$ knows everyone in $\mathcal{K}$. Now we add $L$ to $\mathcal{K}$. Since $N$ knows no one else in $\mathcal{L}$, we can then add $N$ to $\mathcal{L}$.
In all cases, it is thus possible to make a group division with $n+1$ people. This completes the induction.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
In een klas van minstens vier mensen geldt het volgende: als er vier van hen aan een ronde tafel gaan zitten, is er altijd iemand die allebei zijn buren kent of allebei zijn buren niet kent. Bewijs dat het mogelijk is om de mensen over twee groepen (waarvan er eentje leeg mag zijn) te verdelen, zodat in de ene groep iedereen elkaar kent en in de andere groep juist niemand elkaar kent.
(Als persoon $A$ persoon $B$ kent, dan kent $B$ ook $A$.)
|
We bewijzen dit met inductie naar het aantal mensen $n$ in de klas. We nemen $n=3$ als inductiebasis; het gegeven over vier mensen aan een tafel is dan een lege eis. We delen de drie mensen willekeurig in in een groep van één en een groep van twee. Die twee mensen kennen elkaar wel of niet; in beide gevallen klopt het. Stel nu dat we het voor alle klassen van $n$ mensen bewezen hebben. Bekijk een klas van $n+1$ mensen. Noem er eentje $N$. De overige $n$ mensen delen we in twee groepen op volgens de inductiehypothese. Noem groep $\mathcal{K}$ de groep mensen die elkaar allemaal kennen en groep $\mathcal{L}$ de groep mensen die elkaar allemaal niet kennen. Als $N$ iedereen in $\mathcal{K}$ kent, kunnen we $N$ aan $\mathcal{K}$ toevoegen. Als $N$ niemand in $\mathcal{L}$ kent, kunnen we $N$ aan $\mathcal{L}$ toevoegen. In de andere gevallen kent $N$ minstens één iemand in $\mathcal{K}$ niet en kent hij minstens één iemand in $\mathcal{L}$ wel.
Stel dat hij in $\mathcal{K}$ minstens twee mensen $K_{1}$ en $K_{2}$ niet kent, terwijl hij in $\mathcal{L}$ minstens twee mensen $L_{1}$ en $L_{2}$ wel kent. Als nu $K_{1}$ en $L_{1}$ elkaar kennen, dan zetten we $K_{1}, L_{1}, L_{2}, N$ in die volgorde om een ronde tafel; tegenspraak. Als juiste $K_{1}$ en $L_{1}$ elkaar niet kennen,
dan zetten we $K_{1}, L_{1}, N, K_{2}$ in die volgorde om een ronde tafel; tegenspraak. Dit geval is dus onmogelijk.
Stel dat $N$ in $\mathcal{K}$ minstens twee mensen $K_{1}$ en $K_{2}$ niet kent, terwijl hij in $\mathcal{L}$ precies één persoon $L$ wel kent. Neem een willekeurige $K$ in $\mathcal{K}$. Dan zetten we $K, L, N$ en $K_{i}$ in die volgorde aan een ronde tafel, waarbij $i$ gelijk is aan 1 of 2 , zodat $K \neq K_{i}$. Nu zien we dat als $K$ en $L$ elkaar niet kennen, dit een tegenspraak geeft, dus $K$ en $L$ kennen elkaar wel. Dus $L$ kent iedereen in $\mathcal{K}$. Nu voegen $L$ aan $\mathcal{K}$ toe. Omdat $N$ verder niemand in $\mathcal{L}$ kent, kunnen we dan $N$ bij $\mathcal{L}$ zetten.
Stel dat $N$ in $\mathcal{K}$ precies één persoon niet kent, terwijl hij in $\mathcal{L}$ minstens twee personen wel kent. Dan kunnen we analoog aan het vorige geval de groepsindeling maken.
Stel ten slotte dat $N$ in $\mathcal{K}$ precies één persoon $K_{1}$ niet kent, terwijl hij in $\mathcal{L}$ precies één persoon $L$ wel kent. Zonder verlies van algemeenheid nemen we aan dat $K_{1}$ en $L$ elkaar kennen. Neem een willekeurige $K \neq K_{1}$ in $\mathcal{K}$. Dan zetten we $K, L, N$ en $K_{1}$ in die volgorde aan een ronde tafel. Nu zien we dat als $K$ en $L$ elkaar niet kennen, dit een tegenspraak geeft, dus $K$ en $L$ kennen elkaar wel. Dus $L$ kent iedereen in $\mathcal{K}$. Nu voegen $L$ aan $\mathcal{K}$ toe. Omdat $N$ verder niemand in $\mathcal{L}$ kent, kunnen we dan $N$ bij $\mathcal{L}$ zetten.
In alle gevallen lukt het dus om een groepsindeling te maken met $n+1$ personen. Dit voltooit de inductie.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2018-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2018"
}
|
A collection of lines in the plane is called beautiful if each line in the collection intersects an odd number of the other lines in the collection.
Determine the smallest integer $k \geq 0$ with the following property: for any 2018 distinct lines $\ell_{1}, \ell_{2}, \ldots, \ell_{2018}$ in the plane, there exist lines $\ell_{2018+1}, \ell_{2018+2}, \ldots$, $\ell_{2018+k}$ such that the lines $\ell_{1}, \ell_{2}, \ldots, \ell_{2018+k}$ are all distinct and form a beautiful collection.
|
We first prove that in a beautiful collection, the number of lines must be even. Suppose the number of lines is odd. Then on each of the odd number of lines, there lies an odd number of intersection points, so the total number of intersection points is also odd. However, each intersection point is counted twice (once for each line it lies on), so the total should be even. Contradiction. Therefore, the number of lines in a beautiful collection must be even. In particular, $2018+k$ must also be even, so $k$ must be even.
Now assume there are 1009 directions such that in each direction, two of the original lines lie. Then each line is parallel to exactly one other line. If $k<1010$, then $k \leq 1008$, so there must be a direction in which we do not add a line. Consider an original line $\ell$ in this direction. It intersects all lines except itself and the line it is parallel to. This is an even number. Therefore, the resulting collection is not beautiful. Thus, there is an example where at least 1010 lines are needed.
We now show that it is possible to add exactly 1010 lines so that the total collection is ultimately beautiful. We consider all directions in which an even number (greater than 0) of the original lines lie. There are at most 1009 such directions. For each of these directions, we add a line. Each line is then parallel to an even number (possibly 0) of other lines. Suppose first that the total number of lines is now even. Then each line intersects an odd number of lines (the total minus itself and an even number of other lines). Suppose now that the total number of lines is now odd. Then each line intersects an even number of lines. We add a line in a new direction that thus intersects all lines (an odd number), so that afterwards each line intersects an odd number of other lines.
Now the collection is beautiful and we have added at most $1009+1=1010$ lines. It is possible that there are really fewer than 1010. In that case, the number of added lines is even, because the total number of lines in a beautiful collection is always even. We choose a direction in which at least one line already runs. We now add pairs of lines in the same direction. These lines intersect all lines in other directions; that is a total of an odd number. The other lines each gain two intersection points,
so they still have an odd number of intersection points. This is also true for the lines that were already in the chosen direction, as they gain zero new intersection points. The collection thus remains beautiful. We keep adding such pairs until we have added a total of 1010 lines.
We conclude that the minimal $k$ that satisfies is $k=1010$.
|
1010
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Een verzameling lijnen in het vlak noemen we mooi indien elke lijn in de verzameling een oneven aantal van de andere lijnen in de verzameling snijdt.
Bepaal het kleinste gehele getal $k \geq 0$ met de volgende eigenschap: voor iedere 2018 verschillende lijnen $\ell_{1}, \ell_{2}, \ldots, \ell_{2018}$ in het vlak bestaan er lijnen $\ell_{2018+1}, \ell_{2018+2}, \ldots$, $\ell_{2018+k}$ zodat de lijnen $\ell_{1}, \ell_{2}, \ldots, \ell_{2018+k}$ allemaal verschillend zijn en een mooie verzameling vormen.
|
We bewijzen eerst dat in een mooie verzameling het aantal lijnen even moet zijn. Stel namelijk dat het aantal lijnen oneven zou zijn. Dan ligt op elk van het oneven aantal lijnen een oneven aantal snijpunten, dus het totale aantal snijpunten is dan ook oneven. Elk snijpunt wordt hier echter twee keer geteld (één keer voor elke lijn waar hij op ligt), dus het totaal zou even moeten zijn. Tegenspraak. Dus het aantal lijnen in een mooie verzameling moet even zijn. In het bijzonder moet $2018+k$ ook even zijn, dus $k$ moet even zijn.
Stel nu dat er 1009 richtingen zijn zodat er in elke richting twee van de oorspronkelijke lijnen liggen. Dan is elke lijn evenwijdig met precies één andere lijn. Als $k<1010$ is $k \leq 1008$, dus moet er een richting zijn waarin we geen lijn toevoegen. Bekijk een oorspronkelijke lijn $\ell$ in deze richting. Die snijdt in de uiteindelijke verzameling alle lijnen behalve zichzelf en de lijn waar hij evenwijdig mee was. Dit is een even aantal. Dus dan is de resulterende verzameling niet mooi. Er is dus een voorbeeld waarbij minstens 1010 lijnen nodig zijn.
We laten nu zien dat het mogelijk is om precies 1010 lijnen toe te voegen zodat de totale verzameling uiteindelijk mooi is. We bekijken alle richtingen waarin een even aantal (groter dan 0) van de oorspronkelijke lijnen liggen. Er zijn hoogstens 1009 van zulke richtingen. Voor elk van deze richtingen voegen we een lijn toe. Elke lijn loopt dan evenwijdig aan een even aantal (mogelijk 0) andere lijnen. Stel eerst dat het totaal aantal lijnen nu even is. Dan snijdt elke lijn een oneven aantal lijnen (het totaal minus zichzelf en een even aantal andere lijnen). Stel nu dat het totaal aantal lijnen nu oneven is. Dan snijdt elke lijn een even aantal lijnen. We voegen een lijn toe in een nieuwe richting die dus alle lijnen snijdt (een oneven aantal), zodat daarna elke lijn een oneven aantal andere lijnen snijdt.
Nu is de verzameling mooi en we hebben hooguit $1009+1=1010$ lijnen toegevoegd. Mogelijk zijn het er echt nog minder dan 1010. In dat geval is het aantal toegevoegde lijnen wel even, want het totaal aantal lijnen van een mooie verzameling is altijd even. We kiezen een richting waarin al minstens één lijn loopt. We voegen nu steeds een tweetal lijnen in diezelfde richting toe. Deze lijnen snijden alle lijnen in andere richtingen; dat is totaal een oneven aantal. Die andere lijnen hebben er elk twee snijpunten bijgekregen,
dus zij houden een oneven aantal snijpunten. Dat laatste geldt ook voor de lijnen die er al waren in de gekozen richting, want zij krijgen nul nieuwe snijpunten. De verzameling blijft dus mooi. We voegen net zo lang zulke tweetallen toe totdat we in totaal 1010 lijnen hebben toegevoegd.
We concluderen dat de minimale $k$ die voldoet $k=1010$ is.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2018-E_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2018"
}
|
Vind alle functies $f: \mathbb{R} \rightarrow \mathbb{R}$ waarvoor
$$
f\left(x^{2}\right)-f\left(y^{2}\right) \leq(f(x)+y)(x-f(y))
$$
voor alle $x, y \in \mathbb{R}$.
|
Invullen van $x=y=0$ geeft $0 \leq f(0) \cdot-f(0)$. Maar kwadraten zijn nietnegatief, dus hieruit volgt $f(0)^{2}=0$ en daarmee $f(0)=0$. Nu geeft $x=0$ en $y=t$ dat $-f\left(t^{2}\right) \leq t \cdot-f(t)$, terwijl $x=t$ en $y=0$ geeft dat $f\left(t^{2}\right) \leq f(t) \cdot t$. We vinden $t f(t) \leq f\left(t^{2}\right) \leq t f(t)$, dus $f\left(t^{2}\right)=t f(t)$ voor alle $t \in \mathbb{R}$. We kunnen nu links in de functieongelijkheid $f\left(x^{2}\right)-f\left(y^{2}\right)$ vervangen door $x f(x)-y f(y)$. Door rechts haakjes uit te werken krijgen we daar $x f(x)-y f(y)+x y-f(x) f(y)$, dus krijgen we
$$
f(x) f(y) \leq x y
$$
Uit $f\left(t^{2}\right)=t f(t)$ volgt $f(1)=-f(-1)$. Door nu eerst $y=1$ te nemen en daarna $y=-1$, krijgen we voor alle $x \in \mathbb{R}$ :
$$
x \geq f(x) f(1)=-f(x) f(-1) \geq-x \cdot-1=x
$$
Dus er moet steeds gelijkheid gelden, wat betekent dat $f(x) f(1)=x$. Hieruit volgt in het bijzonder $f(1)^{2}=1$, dus $f(1)=1$ of $f(1)=-1$. In het eerste geval krijgen we $f(x)=x$ voor alle $x$ en in het tweede geval $f(x)=-x$ voor alle $x$.
Als we $f(x)=x$ controleren in de oorspronkelijke functieongelijkheid, komt er links $x^{2}-y^{2}$ en rechts $(x+y)(x-y)=x^{2}-y^{2}$, dus deze functie voldoet. Als we $f(x)=-x$ controleren, komt er links $-x^{2}+y^{2}$ en rechts $(-x+y)(x+y)=-x^{2}+y^{2}$, dus deze functie voldoet ook. We concluderen dat de oplossingen zijn: $f(x)=x$ voor alle $x \in \mathbb{R}$ en $f(x)=-x$ voor alle $x \in \mathbb{R}$.
|
f(x)=x \text{ voor alle } x \in \mathbb{R} \text{ en } f(x)=-x \text{ voor alle } x \in \mathbb{R}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Vind alle functies $f: \mathbb{R} \rightarrow \mathbb{R}$ waarvoor
$$
f\left(x^{2}\right)-f\left(y^{2}\right) \leq(f(x)+y)(x-f(y))
$$
voor alle $x, y \in \mathbb{R}$.
|
Invullen van $x=y=0$ geeft $0 \leq f(0) \cdot-f(0)$. Maar kwadraten zijn nietnegatief, dus hieruit volgt $f(0)^{2}=0$ en daarmee $f(0)=0$. Nu geeft $x=0$ en $y=t$ dat $-f\left(t^{2}\right) \leq t \cdot-f(t)$, terwijl $x=t$ en $y=0$ geeft dat $f\left(t^{2}\right) \leq f(t) \cdot t$. We vinden $t f(t) \leq f\left(t^{2}\right) \leq t f(t)$, dus $f\left(t^{2}\right)=t f(t)$ voor alle $t \in \mathbb{R}$. We kunnen nu links in de functieongelijkheid $f\left(x^{2}\right)-f\left(y^{2}\right)$ vervangen door $x f(x)-y f(y)$. Door rechts haakjes uit te werken krijgen we daar $x f(x)-y f(y)+x y-f(x) f(y)$, dus krijgen we
$$
f(x) f(y) \leq x y
$$
Uit $f\left(t^{2}\right)=t f(t)$ volgt $f(1)=-f(-1)$. Door nu eerst $y=1$ te nemen en daarna $y=-1$, krijgen we voor alle $x \in \mathbb{R}$ :
$$
x \geq f(x) f(1)=-f(x) f(-1) \geq-x \cdot-1=x
$$
Dus er moet steeds gelijkheid gelden, wat betekent dat $f(x) f(1)=x$. Hieruit volgt in het bijzonder $f(1)^{2}=1$, dus $f(1)=1$ of $f(1)=-1$. In het eerste geval krijgen we $f(x)=x$ voor alle $x$ en in het tweede geval $f(x)=-x$ voor alle $x$.
Als we $f(x)=x$ controleren in de oorspronkelijke functieongelijkheid, komt er links $x^{2}-y^{2}$ en rechts $(x+y)(x-y)=x^{2}-y^{2}$, dus deze functie voldoet. Als we $f(x)=-x$ controleren, komt er links $-x^{2}+y^{2}$ en rechts $(-x+y)(x+y)=-x^{2}+y^{2}$, dus deze functie voldoet ook. We concluderen dat de oplossingen zijn: $f(x)=x$ voor alle $x \in \mathbb{R}$ en $f(x)=-x$ voor alle $x \in \mathbb{R}$.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2018-E_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2018"
}
|
Vind alle functies $f: \mathbb{R} \rightarrow \mathbb{R}$ waarvoor
$$
f\left(x^{2}\right)-f\left(y^{2}\right) \leq(f(x)+y)(x-f(y))
$$
voor alle $x, y \in \mathbb{R}$.
|
Net als in oplossing I leiden we af dat $f(0)=0$ en $f\left(t^{2}\right)=t f(t)$ voor alle $t \in \mathbb{R}$. Daaruit volgt
$$
t f(t)=f\left(t^{2}\right)=f\left((-t)^{2}\right)=-t f(-t)
$$
dus voor $t \neq 0$ geldt $f(-t)=-f(t)$. We wisten al $f(0)=0$, dus dit geldt ook voor $t=0$. Vul nu $y=-x$ in in de functieongelijkheid:
$$
0 \leq(f(x)-x)(x-f(-x))=(f(x)-x)(x+f(x))=f(x)^{2}-x^{2}
$$
dus $f(x)^{2} \geq x^{2}$. Anderzijds volgt uit het invullen van $y=x$ dat
$$
0 \leq(f(x)+x)(x-f(x))=x^{2}-f(x)^{2}
$$
dus ook $f(x)^{2} \leq x^{2}$. We concluderen dat $f(x)^{2}=x^{2}$ en dus dat $f(x)= \pm x$ voor alle $x \in \mathbb{R}$. We hebben nu in elk geval de kandidaatoplossingen $f(x)=x$ voor alle $x$ en $f(x)=-x$ voor alle $x$ en deze voldoen (zoals in oplossing I). Nu willen we nog de mixfuncties uitsluiten.
Stel dat er $x \neq y$, allebei ongelijk aan 0 , bestaan met $f(x)=x$ en $f(y)=-y$. Dan geldt $f\left(x^{2}\right)=x f(x)=x^{2}$ en $f\left(y^{2}\right)=y f(y)=-y^{2}$, zodat de functieongelijkheid geeft:
$$
x^{2}+y^{2} \leq(x+y)(x--y)=x^{2}+2 x y+y^{2} .
$$
Dus $2 x y \geq 0$. Maar $x$ en $y$ waren ongelijk aan 0 , dus $x$ en $y$ zijn beide positief of beide negatief. Zeg zonder verlies van algemeenheid dat ze beide positief zijn. Neem vervolgens een $z<0$. Dan geldt $f(z)=z$ of $f(z)=-z$, dus bovenstaande redenering kunnen we ook toepassen op het tweetal $(z, x)$ (als $f(z)=-z$ ) of juist op $(z, y)$ (als $f(z)=z$ ). Daaruit volgt dat $z$ en $x$ (of juist $z$ en $y$ ) hetzelfde teken hebben, maar dat is een tegenspraak.
We concluderen dat voor alle $x, y \neq 0$ geldt dat $f(x)=x$ en $f(y)=y$ of juist $f(x)=-x$ en $f(y)=-y$. Omdat $f(0)=0=-0$ geldt dus voor alle $x \in \mathbb{R}$ dat $f(x)=x$ of voor alle $x \in \mathbb{R}$ dat $f(x)=-x$. Dus dit zijn de twee oplossingen.
|
f(x)=x \text{ or } f(x)=-x
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Vind alle functies $f: \mathbb{R} \rightarrow \mathbb{R}$ waarvoor
$$
f\left(x^{2}\right)-f\left(y^{2}\right) \leq(f(x)+y)(x-f(y))
$$
voor alle $x, y \in \mathbb{R}$.
|
Net als in oplossing I leiden we af dat $f(0)=0$ en $f\left(t^{2}\right)=t f(t)$ voor alle $t \in \mathbb{R}$. Daaruit volgt
$$
t f(t)=f\left(t^{2}\right)=f\left((-t)^{2}\right)=-t f(-t)
$$
dus voor $t \neq 0$ geldt $f(-t)=-f(t)$. We wisten al $f(0)=0$, dus dit geldt ook voor $t=0$. Vul nu $y=-x$ in in de functieongelijkheid:
$$
0 \leq(f(x)-x)(x-f(-x))=(f(x)-x)(x+f(x))=f(x)^{2}-x^{2}
$$
dus $f(x)^{2} \geq x^{2}$. Anderzijds volgt uit het invullen van $y=x$ dat
$$
0 \leq(f(x)+x)(x-f(x))=x^{2}-f(x)^{2}
$$
dus ook $f(x)^{2} \leq x^{2}$. We concluderen dat $f(x)^{2}=x^{2}$ en dus dat $f(x)= \pm x$ voor alle $x \in \mathbb{R}$. We hebben nu in elk geval de kandidaatoplossingen $f(x)=x$ voor alle $x$ en $f(x)=-x$ voor alle $x$ en deze voldoen (zoals in oplossing I). Nu willen we nog de mixfuncties uitsluiten.
Stel dat er $x \neq y$, allebei ongelijk aan 0 , bestaan met $f(x)=x$ en $f(y)=-y$. Dan geldt $f\left(x^{2}\right)=x f(x)=x^{2}$ en $f\left(y^{2}\right)=y f(y)=-y^{2}$, zodat de functieongelijkheid geeft:
$$
x^{2}+y^{2} \leq(x+y)(x--y)=x^{2}+2 x y+y^{2} .
$$
Dus $2 x y \geq 0$. Maar $x$ en $y$ waren ongelijk aan 0 , dus $x$ en $y$ zijn beide positief of beide negatief. Zeg zonder verlies van algemeenheid dat ze beide positief zijn. Neem vervolgens een $z<0$. Dan geldt $f(z)=z$ of $f(z)=-z$, dus bovenstaande redenering kunnen we ook toepassen op het tweetal $(z, x)$ (als $f(z)=-z$ ) of juist op $(z, y)$ (als $f(z)=z$ ). Daaruit volgt dat $z$ en $x$ (of juist $z$ en $y$ ) hetzelfde teken hebben, maar dat is een tegenspraak.
We concluderen dat voor alle $x, y \neq 0$ geldt dat $f(x)=x$ en $f(y)=y$ of juist $f(x)=-x$ en $f(y)=-y$. Omdat $f(0)=0=-0$ geldt dus voor alle $x \in \mathbb{R}$ dat $f(x)=x$ of voor alle $x \in \mathbb{R}$ dat $f(x)=-x$. Dus dit zijn de twee oplossingen.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2018-E_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2018"
}
|
Determine all pairs $(a, b)$ of positive integers such that $(a+b)^{3}-2 a^{3}-2 b^{3}$ is a perfect square.
|
We first determine the pairs $(a, b)$ with $\operatorname{gcd}(a, b)=1$. It holds that
$$
\begin{aligned}
(a+b)^{3}-2 a^{3}-2 b^{3} & =a^{3}+3 a^{2} b+3 a b^{2}+b^{3}-2 a^{3}-2 b^{3} \\
& =-a^{3}-b^{3}+3 a b(a+b) \\
& =-(a+b)\left(a^{2}-a b+b^{2}\right)+3 a b(a+b) \\
& =(a+b)\left(-a^{2}+a b-b^{2}+3 a b\right) \\
& =(a+b)\left(-a^{2}-b^{2}+4 a b\right) .
\end{aligned}
$$
This must be a perfect square. Since $a+b$ is positive, the other factor must also be positive, and thus both are perfect squares. Because $\operatorname{gcd}(a, b)=1$, at least one of $a$ and $b$ is odd. Then $a^{2}+b^{2}$ is congruent to 1 or 2 modulo 4, so $-a^{2}-b^{2}+4 a b$ is congruent to 3 or 2 modulo 4. It must, however, be a perfect square, so the number 3 modulo 4 is impossible, and in the case of 2 modulo 4, it can only be equal to 2. We conclude that $-a^{2}-b^{2}+4 a b=2$.
Suppose that $a+b$ is at least 8. Since it is a perfect square, it is then divisible by 8, so we can write $b=8 m-a$ for some positive integer $m$. Then it holds that
$$
\begin{aligned}
2 & =-a^{2}-b^{2}+4 a b \\
& =-a^{2}-(8 m-a)^{2}+4 a(8 m-a) \\
& =-a^{2}-64 m^{2}+16 m a-a^{2}+32 m a-4 a^{2} \\
& =-6 a^{2}+48 m a-64 m^{2},
\end{aligned}
$$
so
$$
1=-3 a^{2}+24 m a-32 m^{2}
$$
Now, modulo 8, this is $1 \equiv-3 a^{2}$. If $a$ is even, then the right side is even, and if $a$ is odd, then the right side is -3 modulo 8. In both cases, this equation does not hold modulo 8. We conclude that $a+b$ is not at least 8. Since $a$ and $b$ are both at least 1, $a+b$ must then be equal to 2 or 4.
- If $a+b=2$, then $a=b=1$. Now $-a^{2}-b^{2}+4 a b=2$, so the product of the two factors is indeed a perfect square (namely 4). Thus $(1,1)$ is a solution.
- If $a+b=4$, then because $\operatorname{gcd}(a, b)=1$, it must hold that $a=1$ and $b=3$ or vice versa. Now $-a^{2}-b^{2}+4 a b=2$, so the product of the two factors is also a perfect square (namely 8). Thus $(1,3)$ and $(3,1)$ are solutions.
Now consider a solution $(a, b)$ with $\operatorname{gcd}(a, b)=d>1$. Then $d$ is a divisor of $(a+b)^{3}-2 a^{3}-2 b^{3}$, so $d$ must itself be a perfect square. We now see that $\left(\frac{a}{d}, \frac{b}{d}\right)$ is also a solution, because the perfect square $(a+b)^{3}-2 a^{3}-2 b^{3}$ is divided by $d^{3}$, leaving another perfect square. Thus $\left(\frac{a}{d}, \frac{b}{d}\right)$ must be one of the three previously found pairs. Conversely, each of those three pairs, multiplied by any arbitrary perfect square, gives another solution. We conclude that all solutions are given by
$$
(a, b)=\left(2^{k}, 2^{k}\right), \quad(a, b)=\left(2^{k}, 3 \cdot 2^{k}\right), \quad \text { and } \quad(a, b)=\left(3 \cdot 2^{k}, 2^{k}\right),
$$
where $k$ varies over the non-negative integers.
|
(a, b)=\left(2^{k}, 2^{k}\right), (a, b)=\left(2^{k}, 3 \cdot 2^{k}\right), (a, b)=\left(3 \cdot 2^{k}, 2^{k}\right)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Bepaal alle paren $(a, b)$ van positieve gehele getallen zodat $(a+b)^{3}-2 a^{3}-2 b^{3}$ een tweemacht is.
|
We bepalen eerst de paren $(a, b)$ met $\operatorname{ggd}(a, b)=1$. Er geldt
$$
\begin{aligned}
(a+b)^{3}-2 a^{3}-2 b^{3} & =a^{3}+3 a^{2} b+3 a b^{2}+b^{3}-2 a^{3}-2 b^{3} \\
& =-a^{3}-b^{3}+3 a b(a+b) \\
& =-(a+b)\left(a^{2}-a b+b^{2}\right)+3 a b(a+b) \\
& =(a+b)\left(-a^{2}+a b-b^{2}+3 a b\right) \\
& =(a+b)\left(-a^{2}-b^{2}+4 a b\right) .
\end{aligned}
$$
Dit moet een tweemacht zijn. Omdat $a+b$ positief is, moet de andere factor ook positief zijn en zijn het dus beide tweemachten. Vanwege $\operatorname{ggd}(a, b)=1$ is minstens één van $a$ en $b$ oneven. Dan is $a^{2}+b^{2}$ congruent aan 1 of 2 modulo 4 , dus $-a^{2}-b^{2}+4 a b$ is congruent aan 3 of 2 modulo 4 . Het moet echter een tweemacht zijn, dus het getal 3 modulo 4 is onmogelijk en in het geval 2 modulo 4 kan het alleen gelijk aan 2 zijn. We concluderen dat $-a^{2}-b^{2}+4 a b=2$.
Stel dat $a+b$ minstens 8 is. Omdat het een tweemacht is, is het dan deelbaar door 8 , dus kunnen we $b=8 m-a$ schrijven voor zekere positieve gehele $m$. Er geldt dan
$$
\begin{aligned}
2 & =-a^{2}-b^{2}+4 a b \\
& =-a^{2}-(8 m-a)^{2}+4 a(8 m-a) \\
& =-a^{2}-64 m^{2}+16 m a-a^{2}+32 m a-4 a^{2} \\
& =-6 a^{2}+48 m a-64 m^{2},
\end{aligned}
$$
dus
$$
1=-3 a^{2}+24 m a-32 m^{2}
$$
Modulo 8 staat hier nu $1 \equiv-3 a^{2}$. Als $a$ even is, dan staat er rechts iets wat even is, en als $a$ oneven is, dan staat er rechts -3 modulo 8 . In beide gevallen klopt deze vergelijking niet modulo 8 . We concluderen dat $a+b$ niet minstens 8 is. Omdat $a$ en $b$ beide minstens 1 zijn, moet $a+b$ dan gelijk zijn aan 2 of aan 4 .
- Als $a+b=2$, dan geldt $a=b=1 . \mathrm{Nu}$ is $-a^{2}-b^{2}+4 a b=2$, dus het product van de twee factoren is inderdaad een tweemacht (namelijk 4). Dus $(1,1)$ is een oplossing.
- Als $a+b=4$, dan moet wegens $\operatorname{ggd}(a, b)=1$ gelden dat $a=1$ en $b=3$ of andersom. Nu is $-a^{2}-b^{2}+4 a b=2$, dus ook nu is het product van de twee factoren een tweemacht (namelijk 8). Dus $(1,3)$ en $(3,1)$ zijn oplossingen.
Bekijk nu een oplossing $(a, b)$ met $\operatorname{ggd}(a, b)=d>1$. Dan is $d$ een deler van $(a+b)^{3}-2 a^{3}-$ $2 b^{3}$, dus $d$ moet zelf een tweemacht zijn. We zien nu dat $\left(\frac{a}{d}, \frac{b}{d}\right)$ ook een oplossing is, want
uit de tweemacht $(a+b)^{3}-2 a^{3}-2 b^{3}$ wordt $d^{3}$ weggedeeld, waardoor er weer een tweemacht overblijft. Dus $\left(\frac{a}{d}, \frac{b}{d}\right)$ moet één van de drie eerder gevonden paren zijn. Andersom geeft elk van die drie paren vermenigvuldigd met een willekeurige tweemacht weer een oplossing. We concluderen dat alle oplossingen gegeven worden door
$$
(a, b)=\left(2^{k}, 2^{k}\right), \quad(a, b)=\left(2^{k}, 3 \cdot 2^{k}\right), \quad \text { en } \quad(a, b)=\left(3 \cdot 2^{k}, 2^{k}\right),
$$
waarbij $k$ varieert over de niet-negatieve gehele getallen.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2018-E_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2018"
}
|
In a non-isosceles triangle $ABC$, $I$ is the center of the inscribed circle. The angle bisector of $\angle BAC$ intersects the circumcircle of $\triangle ABC$ again at $D$. The line through $I$ perpendicular to $AD$ intersects $BC$ at $F$. The midpoint of arc $BC$ that contains $A$ is denoted as $M$. The line $MI$ intersects the circle through $B, I$, and $C$ again at $N$. Prove that $FN$ is tangent to the circle through $B, I$, and $C$.
We consider the configuration where $|AB| > |AC|$ so that $C$ lies between $B$ and $F$. Other configurations proceed analogously.
|
Since $\angle D A C=\angle B A D$, $D$ is the midpoint of the arc $B C$ where $A$ does not lie. The line $D M$ is thus a diameter of the circle. By Thales' theorem, we then have $\angle D B M=90^{\circ}$. Let $K$ be the intersection of $B C$ and $D M$. Since $D M$ is the perpendicular bisector of $B C$, we now have $\angle B K M=90^{\circ}=\angle D B M$. Therefore, $\triangle M K B \sim \triangle M B D$ (AA). This implies $\frac{|M B|}{|M K|}=\frac{|M D|}{|M B|}$, so $|M D| \cdot|M K|=|M B|^{2}$. Since $K$ lies internally on $M D$, this equality also holds in a directed sense: $M D \cdot M K=M B^{2}$.
Since $D$ is the midpoint of the arc $B C$, we have $|D B|=|D C|$. Furthermore, $\angle C D I=\angle C D A=\angle C B A$ and $\angle D C I=\angle D C B+\angle B C I=\angle D A B+\angle B C I=\frac{1}{2} \angle C A B+\frac{1}{2} \angle B C A$. By the angle sum in triangle $D C I$, we now see that $\angle D I C=180^{\circ}-\angle C B A-\frac{1}{2} \angle C A B-\frac{1}{2} \angle B C A=\frac{1}{2} \angle C A B+\frac{1}{2} \angle B C A=\angle D C I$. Therefore, triangle $D C I$ is isosceles with $|D C|=|D I|$. We conclude that $D$ is the center of the circle through $B, C$, and $I$. (This is also known as the incircle.) Now, $D B$ is a radius of this circle and $D B$ is perpendicular to $M B$, which implies that $M B$ is a tangent. By the power of a point theorem, we know $M B^{2}=M I \cdot M N$. Together with the previous result, we conclude that $M D \cdot M K=M I \cdot M N$. Therefore, by the power of a point theorem, $N D K I$ is a cyclic quadrilateral.
We also know that $\angle F I D=90^{\circ}=\angle F K D$, so $D K I F$ is a cyclic quadrilateral. We conclude that $N D K I F$ is a cyclic pentagon. This implies $\angle D N F=180^{\circ}-\angle D I F=90^{\circ}$.
Thus, $N F$ is perpendicular to the radius $D N$ of the circle through $B, I$, and $C$; this means that $F N$ is tangent to this circle.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In een niet-gelijkbenige driehoek $A B C$ is $I$ het middelpunt van de ingeschreven cirkel. De bissectrice van $\angle B A C$ snijdt de omgeschreven cirkel van $\triangle A B C$ nogmaals in $D$. De lijn door $I$ loodrecht op $A D$ snijdt $B C$ in $F$. Het midden van boog $B C$ waar $A$ op ligt, noemen we $M$. De lijn $M I$ snijdt de cirkel door $B, I$ en $C$ nogmaals in $N$. Bewijs dat $F N$ raakt aan de cirkel door $B, I$ en $C$.

We bekijken de configuratie waar $|A B|>|A C|$ zodat $C$ tussen $B$ en $F$ ligt. Andere configuraties gaan analoog.
|
Omdat $\angle D A C=\angle B A D$ is $D$ het midden van de boog $B C$ waar $A$ niet op ligt. De lijn $D M$ is dus een middellijn van de cirkel. Met Thales zien we dan dat $\angle D B M=90^{\circ}$. Zij nu $K$ het snijpunt van $B C$ en $D M$. Omdat $D M$ de middelloodlijn van $B C$ is, geldt nu $\angle B K M=90^{\circ}=\angle D B M$. Dus $\triangle M K B \sim \triangle M B D$ (hh). Hieruit volgt $\frac{|M B|}{|M K|}=\frac{|M D|}{|M B|}$, dus $|M D| \cdot|M K|=|M B|^{2}$. Omdat $K$ inwendig op $M D$ ligt, geldt deze gelijkheid ook gericht: $M D \cdot M K=M B^{2}$.
Omdat $D$ het midden van boog $B C$ is, geldt $|D B|=|D C|$. Verder is $\angle C D I=\angle C D A=$ $\angle C B A$ en $\angle D C I=\angle D C B+\angle B C I=\angle D A B+\angle B C I=\frac{1}{2} \angle C A B+\frac{1}{2} \angle B C A$. Met de hoekensom in driehoek $D C I$ zien we nu dat $\angle D I C=180^{\circ}-\angle C B A-\frac{1}{2} \angle C A B-\frac{1}{2} \angle B C A=$ $\frac{1}{2} \angle C A B+\frac{1}{2} \angle B C A=\angle D C I$. Dus driehoek $D C I$ is gelijkbenig met $|D C|=|D I|$. We conluderen dat $D$ het middelpunt is van de cirkel door $B, C$ en $I$. (Dit noemen we ook wel de tussengeschreven cirkel.) Nu is $D B$ een straal van deze cirkel en $D B$ staat loodrecht op $M B$, waaruit volgt dat $M B$ een raaklijn is. Met de machtstelling weten we nu $M B^{2}=M I \cdot M N$. Samen met het voorgaande concluderen we dat $M D \cdot M K=M I \cdot M N$. Dus vanwege de machtstelling is $N D K I$ een koordenvierhoek.
We weten ook dat $\angle F I D=90^{\circ}=\angle F K D$, dus $D K I F$ is een koordenvierhoek. We concluderen dat $N D K I F$ een koordenvijfhoek is. Hieruit volgt $\angle D N F=180^{\circ}-\angle D I F=90^{\circ}$.
Dus $N F$ staat loodrecht op de straal $D N$ van de cirkel door $B, I$ en $C$; dat betekent dat $F N$ raakt aan deze cirkel.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2018-E_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2018"
}
|
In a non-isosceles triangle $ABC$, $I$ is the center of the inscribed circle. The angle bisector of $\angle BAC$ intersects the circumcircle of $\triangle ABC$ again at $D$. The line through $I$ perpendicular to $AD$ intersects $BC$ at $F$. The midpoint of arc $BC$ that contains $A$ is denoted as $M$. The line $MI$ intersects the circle through $B, I$, and $C$ again at $N$. Prove that $FN$ is tangent to the circle through $B, I$, and $C$.

We consider the configuration where $|AB| > |AC|$ so that $C$ lies between $B$ and $F$. Other configurations proceed analogously.
|
We define, just as in solution I, point $K$ as the intersection of $B C$ and $D M$ and deduce that $\angle B K M=90^{\circ}$. Furthermore, by Thales, $\angle D C M=90^{\circ}=\angle C K D$, so $\triangle D C M \sim \triangle D K C$ (hh). Thus $\frac{|D C|}{|D M|}=\frac{|D K|}{|D C|}$, hence $|D C|^{2}=|D M| \cdot|D K|$. Also, just as in solution I, we see that $D$ is the center of the circle through $B, C$, and $I$. In particular, $|D I|=|D C|$, so $|D I|^{2}=|D M| \cdot|D K|$. Since $K$ lies internally on $M D$, this equality also holds in a directed sense: $D I^{2}=D M \cdot D K$. From the power of a point theorem, it follows that $D I$ is tangent to the circle through $I, K$, and $M$. The tangent-secant angle theorem then states that $\angle I M K=\angle D I K$.
Furthermore, $\angle D I F=90^{\circ}=\angle D K F$, so $D K I F$ is a cyclic quadrilateral. Thus $\angle D I K=\angle D F K$, and together with the previous result, we have $\angle I M K=\angle D F K$. Define $X$ as the intersection of $D F$ and $N M$. Then we see $\angle X M K=\angle I M K=\angle D F K=\angle X F K$, which means that $X K M F$ is a cyclic quadrilateral. Now we see $\angle F X M=\angle F K M=90^{\circ}$.
Thus $F D$ is perpendicular to $I N$. Since $D$ is the center of the circle with chord $I N$, $F D$ is the perpendicular bisector of $I N$. Therefore, $I$ and $N$ are each other's reflection in $F D$. Under this reflection, the circle through $B, I$, and $C$ maps to itself, so the tangent line $F I$ maps to the tangent line $F N$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In een niet-gelijkbenige driehoek $A B C$ is $I$ het middelpunt van de ingeschreven cirkel. De bissectrice van $\angle B A C$ snijdt de omgeschreven cirkel van $\triangle A B C$ nogmaals in $D$. De lijn door $I$ loodrecht op $A D$ snijdt $B C$ in $F$. Het midden van boog $B C$ waar $A$ op ligt, noemen we $M$. De lijn $M I$ snijdt de cirkel door $B, I$ en $C$ nogmaals in $N$. Bewijs dat $F N$ raakt aan de cirkel door $B, I$ en $C$.

We bekijken de configuratie waar $|A B|>|A C|$ zodat $C$ tussen $B$ en $F$ ligt. Andere configuraties gaan analoog.
|
We definiëren net als in oplossing I punt $K$ als het snijpunt van $B C$ en $D M$ en leiden af dat $\angle B K M=90^{\circ}$. Verder geldt wegens Thales dat $\angle D C M=90^{\circ}=\angle C K D$, dus $\triangle D C M \sim \triangle D K C$ (hh). Dus $\frac{|D C|}{|D M|}=\frac{|D K|}{|D C|}$, dus $|D C|^{2}=|D M| \cdot|D K|$. Ook net als in oplossing I zien we dat $D$ het middelpunt is van de cirkel door $B, C$ en $I$. In het bijzonder geldt $|D I|=|D C|$, dus $|D I|^{2}=|D M| \cdot|D K|$. Omdat $K$ inwendig op $M D$ ligt, geldt deze gelijkheid ook gericht: $D I^{2}=D M \cdot D K$. Met de machtstelling volgt hieruit dat $D I$ raakt aan de cirkel door $I, K$ en $M$. De raaklijnomtrekshoekstelling zegt dan dat $\angle I M K=\angle D I K$.
Verder geldt $\angle D I F=90^{\circ}=\angle D K F$, dus $D K I F$ is een koordenvierhoek. Dus $\angle D I K=$ $\angle D F K$ en samen met het voorgaande geeft dat $\angle I M K=\angle D F K$. Definieer nu $X$ als het snijpunt van $D F$ en $N M$. Dan zien we $\angle X M K=\angle I M K=\angle D F K=\angle X F K$, wat betekent dat $X K M F$ een koordenvierhoek is. Nu zien we $\angle F X M=\angle F K M=90^{\circ}$.
Dus $F D$ staat loodrecht op $I N$. Omdat $D$ het middelpunt is van de cirkel met koorde $I N$, is $F D$ de middelloodlijn van $I N$. Dus $I$ en $N$ zijn elkaars gespiegelde in $F D$. Bij deze spiegeling gaat de cirkel door $B, I$ en $C$ in zichzelf over, dus raaklijn $F I$ gaat over in raaklijn $F N$.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2018-E_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2018"
}
|
Prove that for every positive integer $n$ there are at most two pairs $(a, b)$ of positive integers with the following two properties:
(i) $a^{2}+b=n$,
(ii) $a+b$ is a power of two, i.e., there is an integer $k \geq 0$ with $a+b=2^{k}$.
|
Suppose there are three or more such pairs for the same $n$. Then, by the pigeonhole principle, there are at least two, say $(a, b)$ and $(c, d)$, such that $a \equiv c \bmod 2$. Write $a+b=2^{k}$ and $c+d=2^{\ell}$ with $k$ and $\ell$ positive integers. Without loss of generality, assume that $\ell \geq k$. We see that
$$
\begin{aligned}
2^{\ell}-2^{k} & =(c+d)-(a+b) \\
& =\left(c+n-c^{2}\right)-\left(a+n-a^{2}\right)=c-a-c^{2}+a^{2}=(a+c-1)(a-c) .
\end{aligned}
$$
Since $\ell \geq k$, $2^{k}$ is a divisor of $2^{\ell}-2^{k}$. Since $a \equiv c \bmod 2$, $a+c-1$ is odd, so $2^{k}$ must be a divisor of $a-c$. Since $2^{\ell}-2^{k} \geq 0$ and $a+c-1>0$, we have $a-c \geq 0$. On the other hand, $a-c<a+b=2^{k}$, so $0 \leq a-c<2^{k}$, while $2^{k} \mid a-c$. We conclude that $a-c=0$, so $a=c$. Now $b=n-a^{2}=n-c^{2}=d$, so the pairs $(a, b)$ and $(c, d)$ are identical. Contradiction. Therefore, there are at most two pairs $(a, b)$ that satisfy the condition.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Bewijs dat er voor elke positieve gehele $n$ hoogstens twee paren $(a, b)$ van positieve gehele getallen bestaan met de volgende twee eigenschappen:
(i) $a^{2}+b=n$,
(ii) $a+b$ is een tweemacht, d.w.z. er is een gehele $k \geq 0$ met $a+b=2^{k}$.
|
Stel dat er drie of meer zulke paren bestaan bij dezelfde $n$. Dan zijn er wegens het ladenprincipe minstens twee, zeg $(a, b)$ en $(c, d)$, zodat $a \equiv c \bmod 2$. Schrijf $a+b=2^{k}$ en $c+d=2^{\ell}$ met $k$ en $\ell$ positieve gehele getallen. Neem zonder verlies van algemeenheid aan dat $\ell \geq k$. We zien dat
$$
\begin{aligned}
2^{\ell}-2^{k} & =(c+d)-(a+b) \\
& =\left(c+n-c^{2}\right)-\left(a+n-a^{2}\right)=c-a-c^{2}+a^{2}=(a+c-1)(a-c) .
\end{aligned}
$$
Omdat $\ell \geq k$ is $2^{k}$ een deler van $2^{\ell}-2^{k}$. Omdat $a \equiv c \bmod 2$, is $a+c-1$ oneven, dus moet $2^{k}$ een deler zijn van $a-c$. Omdat $2^{\ell}-2^{k} \geq 0$ en $a+c-1>0$ is $a-c \geq 0$. Anderzijds geldt $a-c<a+b=2^{k}$, dus $0 \leq a-c<2^{k}$, terwijl $2^{k} \mid a-c$. We concluderen dat $a-c=0$, dus $a=c$. Nu geldt $b=n-a^{2}=n-c^{2}=d$, dus de paren $(a, b)$ en $(c, d)$ zijn identiek. Tegenspraak. Er zijn dus hoogstens twee paren $(a, b)$ die voldoen.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2019-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2019"
}
|
Let $A B C$ be a triangle and let $I$ be the center of the inscribed circle of this triangle. The line through $I$ perpendicular to $A I$ intersects the circumcircle of $\triangle A B C$ at points $P$ and $Q$, where $P$ is on the same side of $A I$ as $B$. Let $S$ be the second intersection point of the circumcircles of $\triangle B I P$ and $\triangle C I Q$. Prove that $S I$ is the bisector of $\angle P S Q$.
We consider the configuration where $S$ and $A$ are on opposite sides of $P Q$. The configuration where $S$ and $A$ are on the same side of $P Q$ is analogous.
|
Let $M$ and $N$ be the intersection points of $B I$ and $C I$ with the circumcircle of $\triangle A B C$. Further, let $\angle C A B=2 \alpha, \angle A B C=2 \beta$, and $\angle B C A=2 \gamma$. Then, by the inscribed angle theorem,
$$
\angle A M N=\angle A C N=\angle A C I=\gamma
$$
and
$$
\angle M A C=\angle M B C=\angle I B C=\beta,
$$
so that
$$
\angle A M N+\angle M A I=\gamma+\angle M A C+\angle C A I=\gamma+\beta+\alpha=90^{\circ} .
$$
From this, it follows that $M N \perp A I$. Since it is given that $P Q \perp A I$ as well, we have $M N \| P Q$. Therefore, quadrilateral $M N P Q$ is an isosceles trapezoid, and in it, the diagonals are equal in length, so $|M P|=|N Q|$. This implies $\angle P B M=\angle N C Q$. Using the inscribed angle theorem twice more, we find
$$
\angle P S I=\angle P B I=\angle P B M=\angle N C Q=\angle I C Q=\angle I S Q
$$
We conclude that $S I$ is the angle bisector of $\angle P S Q$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $A B C$ een driehoek en zij $I$ het middelpunt van de ingeschreven cirkel van deze driehoek. De lijn door $I$ loodrecht op $A I$ snijdt de omgeschreven cirkel van $\triangle A B C$ in de punten $P$ en $Q$, waarbij $P$ aan dezelfde kant van $A I$ ligt als $B$. Zij $S$ het tweede snijpunt van de omgeschreven cirkels van $\triangle B I P$ en $\triangle C I Q$. Bewijs dat $S I$ de bissectrice $\operatorname{van} \angle P S Q$ is.

We bekijken de configuratie waarin $S$ en $A$ aan verschillende kanten van $P Q$ liggen. De configuratie waarin $S$ en $A$ aan dezelfde kant van $P Q$ liggen, gaat analoog.
|
Laat $M$ en $N$ de snijpunten zijn van respectievelijk $B I$ en $C I$ met de omgeschreven cirkel van $\triangle A B C$. Schrijf verder $\angle C A B=2 \alpha, \angle A B C=2 \beta$ en $\angle B C A=$ $2 \gamma$. Dan geldt vanwege de omtrekshoekstelling
$$
\angle A M N=\angle A C N=\angle A C I=\gamma
$$
en
$$
\angle M A C=\angle M B C=\angle I B C=\beta,
$$
zodat
$$
\angle A M N+\angle M A I=\gamma+\angle M A C+\angle C A I=\gamma+\beta+\alpha=90^{\circ} .
$$
Hieruit volgt dat $M N \perp A I$. Aangezien gegeven is dat ook $P Q \perp A I$, geldt $M N \| P Q$. Koordenvierhoek $M N P Q$ is dus een gelijkbenig trapezium en daarin zijn de diagonalen even lang, dus $|M P|=|N Q|$. Hieruit volgt $\angle P B M=\angle N C Q$. Met nog twee keer omtrekshoekstelling vinden we nu
$$
\angle P S I=\angle P B I=\angle P B M=\angle N C Q=\angle I C Q=\angle I S Q
$$
We concluderen dat $S I$ de bissectrice van $\angle P S Q$ is.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2019-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2019"
}
|
Let $A B C$ be a triangle and let $I$ be the center of the inscribed circle of this triangle. The line through $I$ perpendicular to $A I$ intersects the circumcircle of $\triangle A B C$ at points $P$ and $Q$, where $P$ is on the same side of $A I$ as $B$. Let $S$ be the second intersection point of the circumcircles of $\triangle B I P$ and $\triangle C I Q$. Prove that $S I$ is the bisector of $\angle P S Q$.

We consider the configuration where $S$ and $A$ are on opposite sides of $P Q$. The configuration where $S$ and $A$ are on the same side of $P Q$ is analogous.
|
Write $\angle C A B=2 \alpha, \angle A B C=2 \beta$ and $\angle B C A=2 \gamma$. Due to the angle sum in $\triangle A I B$, we have
$$
\angle B I A=180^{\circ}-\angle I A B-\angle A B I=180^{\circ}-\alpha-\beta=90^{\circ}+\gamma,
$$
so
$$
\angle B I P=\angle B I A-\angle A I P=90^{\circ}+\gamma-90^{\circ}=\gamma=\angle B C I .
$$
Furthermore, using the cyclic quadrilateral theorem, we have
$$
180^{\circ}-\angle B P I=180^{\circ}-\angle B P Q=\angle B C Q=\angle B C I+\angle I C Q \text {. }
$$
If we now consider the angle sum in triangle $B P I$ and use both results above, we find
$$
\angle P B I=180^{\circ}-\angle B P I-\angle B I P=\angle B C I+\angle I C Q-\angle B C I=\angle I C Q
$$
Using the inscribed angle theorem twice more, we get
$$
\angle P S I=\angle P B I=\angle I C Q=\angle I S Q
$$
so $S I$ is the bisector of angle $P S Q$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $A B C$ een driehoek en zij $I$ het middelpunt van de ingeschreven cirkel van deze driehoek. De lijn door $I$ loodrecht op $A I$ snijdt de omgeschreven cirkel van $\triangle A B C$ in de punten $P$ en $Q$, waarbij $P$ aan dezelfde kant van $A I$ ligt als $B$. Zij $S$ het tweede snijpunt van de omgeschreven cirkels van $\triangle B I P$ en $\triangle C I Q$. Bewijs dat $S I$ de bissectrice $\operatorname{van} \angle P S Q$ is.

We bekijken de configuratie waarin $S$ en $A$ aan verschillende kanten van $P Q$ liggen. De configuratie waarin $S$ en $A$ aan dezelfde kant van $P Q$ liggen, gaat analoog.
|
Schrijf $\angle C A B=2 \alpha, \angle A B C=2 \beta$ en $\angle B C A=2 \gamma$. Er geldt vanwege de hoekensom in $\triangle A I B$ dat
$$
\angle B I A=180^{\circ}-\angle I A B-\angle A B I=180^{\circ}-\alpha-\beta=90^{\circ}+\gamma,
$$
dus
$$
\angle B I P=\angle B I A-\angle A I P=90^{\circ}+\gamma-90^{\circ}=\gamma=\angle B C I .
$$
Verder geldt met behulp van de koordenvierhoekstelling
$$
180^{\circ}-\angle B P I=180^{\circ}-\angle B P Q=\angle B C Q=\angle B C I+\angle I C Q \text {. }
$$
Als we nu de hoekensom in driehoek $B P I$ bekijken en beide resultaten hierboven gebruiken, vinden we
$$
\angle P B I=180^{\circ}-\angle B P I-\angle B I P=\angle B C I+\angle I C Q-\angle B C I=\angle I C Q
$$
Met nog twee keer omtrekshoekstelling volgt nu
$$
\angle P S I=\angle P B I=\angle I C Q=\angle I S Q
$$
dus $S I$ is de bissectrice van hoek $P S Q$.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2019-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2019"
}
|
Let $x$ and $y$ be positive real numbers.
a) Prove: if $x^{3}-y^{3} \geq 4 x$, then $x^{2}>2 y$.
b) Prove: if $x^{5}-y^{3} \geq 2 x$, then $x^{3} \geq 2 y$.
|
a) It holds that $x^{3}-4 x \geq y^{3}>0$, so $x\left(x^{2}-4\right)>0$. Since $x$ is positive, it follows that $x^{2}-4>0$, hence $x^{2}>4$. This means $x>2$. Furthermore, $x^{3}-y^{3} \geq 4 x>0$, so $x>y$. Combining these two results (which is allowed because both $x$ and $y$ are positive) gives $x^{2}=x \cdot x>2 \cdot y=2 y$.
b) It holds that $\left(x^{4}-4\right)^{2} \geq 0$. Expanding this gives $x^{8}-8 x^{4}+16 \geq 0$. Since $x$ is positive, we can multiply this by $x$ without changing the sign, so it also holds that $x^{9} \geq 8 x^{5}-16 x$. From the given inequality, it follows that $x^{5}-2 x \geq y^{3}$. Combining this with the previous result, we get $x^{9} \geq 8\left(x^{5}-2 x\right) \geq 8 y^{3}$. This implies $x^{3} \geq 2 y$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Laat $x$ en $y$ positieve reële getallen zijn.
a) Bewijs: als $x^{3}-y^{3} \geq 4 x$, dan geldt $x^{2}>2 y$.
b) Bewijs: als $x^{5}-y^{3} \geq 2 x$, dan geldt $x^{3} \geq 2 y$.
|
a) Er geldt $x^{3}-4 x \geq y^{3}>0$, dus $x\left(x^{2}-4\right)>0$. Omdat $x$ positief is, volgt hieruit dat $x^{2}-4>0$, dus $x^{2}>4$. Dat betekent $x>2$. Verder geldt $x^{3}-y^{3} \geq 4 x>0$, dus $x>y$. Combineren van deze twee resultaten (wat mag omdat $x$ en $y$ beide positief zijn) geeft $x^{2}=x \cdot x>2 \cdot y=2 y$.
b) Er geldt $\left(x^{4}-4\right)^{2} \geq 0$. Uitwerken geeft $x^{8}-8 x^{4}+16 \geq 0$. Omdat $x$ positief is, kunnen we dit met $x$ vermenigvuldigen zonder dat het teken omklapt, dus geldt ook $x^{9} \geq 8 x^{5}-16 x$. Uit de gegeven ongelijkheid volgt $x^{5}-2 x \geq y^{3}$. Als we dat combineren met het voorgaande, krijgen we $x^{9} \geq 8\left(x^{5}-2 x\right) \geq 8 y^{3}$. Hieruit volgt $x^{3} \geq 2 y$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2019-B_uitwerkingen.jsonl",
"solution_match": "# Oplossing.",
"tier": "T1",
"year": "2019"
}
|
Does there exist a positive integer $k$ and a non-constant sequence $a_{1}, a_{2}, a_{3}, \ldots$ of positive integers such that $a_{n}=\operatorname{gcd}\left(a_{n+k}, a_{n+k+1}\right)$ for all positive integers $n$?
|
There do not exist such a $k$ and corresponding sequence. We prove this by contradiction, so assume that they do exist. Note that $a_{n} \mid a_{n+k}$ and $a_{n} \mid a_{n+k+1}$ for all $n \geq 1$. By a simple induction, it also follows that $a_{n} \mid a_{n+\ell k}$ and $a_{n} \mid a_{n+\ell k+\ell}$ for all $l \geq 0$. We now prove by induction on $m$ that $a_{n} \mid a_{n+m k+(m+1)}$ for all $0 \leq m \leq k-1$. For $m=k-1$, this follows from $a_{n} \mid a_{n+k \cdot k}=a_{n+(k-1) k+k}$. Now assume that for some $m$ with $1 \leq m \leq k-1$ it holds that $a_{n} \mid a_{n+m k+(m+1)}$. We also know that $a_{n} \mid a_{n+m k+m}$, so because $a_{n+(m-1) k+m}=\operatorname{gcd}\left(a_{n+m k+m}, a_{n+m k+m+1}\right)$, it also holds that $a_{n} \mid a_{n+(m-1) k+m}$. This completes the induction step. Substituting $m=0$ now gives $a_{n} \mid a_{n+1}$.
Since $a_{n} \mid a_{n+1}$, it also holds that $\operatorname{gcd}\left(a_{n}, a_{n+1}\right)=a_{n}$ for all $n$. Thus, $a_{n}=a_{n-k}$ for all $n \geq k+1$. We now have $a_{n-k}\left|a_{n-k+1}\right| a_{n-k+2}|\ldots| a_{n}=a_{n-k}$. Since these are all positive integers, $a_{n-k}, a_{n-k+1}, \ldots, a_{n}$ must all be equal. This holds for all $n \geq k+1$, so the sequence is constant. Contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Bestaan er een positief geheel getal $k$ en een niet-constante rij $a_{1}, a_{2}, a_{3}, \ldots$ van positieve gehele getallen zodat $a_{n}=\operatorname{ggd}\left(a_{n+k}, a_{n+k+1}\right)$ voor alle positieve gehele getallen $n$ ?
|
Zo'n $k$ en bijbehorende rij bestaan niet. We bewijzen dit uit het ongerijmde, dus stel dat ze wel bestaan. Merk op dat $a_{n} \mid a_{n+k}$ en $a_{n} \mid a_{n+k+1}$ voor alle $n \geq 1$. Met een eenvoudige inductie volgt ook dat $a_{n} \mid a_{n+\ell k}$ en $a_{n} \mid a_{n+\ell k+\ell}$ voor alle $l \geq 0$. We bewijzen nu met inductie naar $m$ dat $a_{n} \mid a_{n+m k+(m+1)}$ voor alle $0 \leq m \leq k-1$. Voor $m=k-1$ volgt dit uit $a_{n} \mid a_{n+k \cdot k}=a_{n+(k-1) k+k}$. Stel nu dat voor zekere $m$ met $1 \leq m \leq k-1$ geldt dat $a_{n} \mid a_{n+m k+(m+1)}$. We weten ook dat $a_{n} \mid a_{n+m k+m}$, dus vanwege $a_{n+(m-1) k+m}=\operatorname{ggd}\left(a_{n+m k+m}, a_{n+m k+m+1}\right)$ geldt ook $a_{n} \mid a_{n+(m-1) k+m}$. Dit voltooit de inductiestap. Invulen van $m=0$ geeft nu $a_{n} \mid a_{n+1}$.
Omdat $a_{n} \mid a_{n+1}$, geldt ook $\operatorname{ggd}\left(a_{n}, a_{n+1}\right)=a_{n}$ voor alle $n$. Dus $a_{n}=a_{n-k}$ voor alle $n \geq k+1$. We hebben nu $a_{n-k}\left|a_{n-k+1}\right| a_{n-k+2}|\ldots| a_{n}=a_{n-k}$. Omdat het om allemaal positieve gehele getallen gaat, moeten $a_{n-k}, a_{n-k+1}, \ldots, a_{n}$ allemaal gelijk zijn. Dit geldt voor alle $n \geq k+1$, dus de rij is constant. Tegenspraak.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2019-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2019"
}
|
Does there exist a positive integer $k$ and a non-constant sequence $a_{1}, a_{2}, a_{3}, \ldots$ of positive integers such that $a_{n}=\operatorname{gcd}\left(a_{n+k}, a_{n+k+1}\right)$ for all positive integers $n$?
|
There do not exist $k$ and the corresponding sequence. We prove this by contradiction, so assume that they do exist. Note that $a_{n} \mid a_{n+k}$ and $a_{n} \mid a_{n+k+1}$ for all $n \geq 1$. Let now $0 \leq \ell \leq k$ be an integer. Then $k^{2}+\ell=(k-\ell) \cdot k+\ell \cdot(k+1)$. By applying the first divisibility $k-\ell$ times and then the second $\ell$ times, we find that $a_{n} \mid a_{n+k^{2}+\ell}$. Therefore, $a_{n} \mid a_{n+k^{2}+\ell}$ for all $0 \leq \ell \leq k$.
We now prove that if $a_{n} \mid a_{i}, a_{i+1}, \ldots, a_{i+k}$, then $a_{n} \mid a_{i-1}$. We have $a_{i-1} = \gcd\left(a_{i+k-1}, a_{i+k}\right)$. Since $a_{n}$ is also a common divisor of $a_{i+k-1}$ and $a_{i+k}$, it must be that $a_{n} \mid a_{i-1}$.
We know $a_{n} \mid a_{n+k^{2}}, a_{n+k^{2}+1}, \ldots, a_{n+k^{2}+k}$, so by applying the above, we find $a_{n} \mid a_{n+k^{2}-1}$. By induction, we get $a_{n} \mid a_{n+k^{2}-m}$ for all $m<n+k^{2}$. In particular, we find $a_{n} \mid a_{n+1}$ for all $n$, but also $a_{n} \mid a_{n-1}$ for all $n \geq 2$. Therefore, for all positive integers $j$, both $a_{j} \mid a_{j+1}$ and $a_{j+1} \mid a_{j}$ hold. Thus, $a_{j}=a_{j+1}$ for all $j$, so the sequence is constant. Contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Bestaan er een positief geheel getal $k$ en een niet-constante rij $a_{1}, a_{2}, a_{3}, \ldots$ van positieve gehele getallen zodat $a_{n}=\operatorname{ggd}\left(a_{n+k}, a_{n+k+1}\right)$ voor alle positieve gehele getallen $n$ ?
|
Zo'n $k$ en bijbehorende rij bestaan niet. We bewijzen dit uit het ongerijmde, dus stel dat ze wel bestaan. Merk op dat $a_{n} \mid a_{n+k}$ en $a_{n} \mid a_{n+k+1}$ voor alle $n \geq 1$. Zij nu $0 \leq \ell \leq k$ een geheel getal. Dan geldt $k^{2}+\ell=(k-\ell) \cdot k+\ell \cdot(k+1)$. Door de eerste deelbaarheid $k-\ell$ keer toe te passen en vervolgens de tweede $\ell$ keer, vinden we hiermee dat $a_{n} \mid a_{n+k^{2}+\ell}$. Er geldt dus $a_{n} \mid a_{n+k^{2}+\ell}$ voor alle $0 \leq \ell \leq k$.
We bewijzen nu dat als $a_{n} \mid a_{i}, a_{i+1}, \ldots, a_{i+k}$, dat dan ook $a_{n} \mid a_{i-1}$. Er geldt $a_{i-1}=$ $\operatorname{ggd}\left(a_{i+k-1}, a_{i+k}\right)$. Omdat $a_{n}$ ook een gemeenschappelijke deler van $a_{i+k-1}$ en $a_{i+k}$ is, moet er gelden dat $a_{n} \mid a_{i-1}$.
We weten $a_{n} \mid a_{n+k^{2}}, a_{n+k^{2}+1}, \ldots, a_{n+k^{2}+k}$, dus door het bovenstaande toe te passen, vinden we $a_{n} \mid a_{n+k^{2}-1}$. Met inductie krijgen we nu $a_{n} \mid a_{n+k^{2}-m}$ voor alle $m<n+k^{2}$. In het bijzonder vinden we $a_{n} \mid a_{n+1}$ voor alle $n$, maar ook $a_{n} \mid a_{n-1}$ voor alle $n \geq 2$. Dus geldt voor alle positieve gehele $j$ zowel $a_{j} \mid a_{j+1}$ als $a_{j+1} \mid a_{j}$. Er geldt dus $a_{j}=a_{j+1}$ voor alle $j$, dus de rij is constant. Tegenspraak.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2019-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2019"
}
|
In a country, there are 2018 cities, some of which are connected by roads. Each city is connected to at least three other cities. It is possible to travel from any arbitrary city to any other arbitrary city via one or more roads. Consider for each pair of cities the shortest route between these two cities. What is the maximum number of roads that could appear in such a shortest route?
|
The largest number of roads that can appear in a shortest route is 1511. We first give a country for which this number is assumed. Divide the cities into 504 groups: two groups of five cities $\left(A_{0}, B_{0}, C_{0}, D_{0}, E_{0}\right)$ and $\left(A_{503}, B_{503}, C_{503}, D_{503}, E_{503}\right)$ and further groups of four cities $\left(A_{i}, B_{i}, C_{i}, D_{i}\right)$ for $1 \leq i \leq 502$. For all $i$ with $0 \leq i \leq 503$: connect $A_{i}$ to $B_{i}$, connect $A_{i}$ to $C_{i}$, connect $B_{i}$ to $D_{i}$, and connect $C_{i}$ to $D_{i}$. Further, connect $E_{0}$ to $A_{0}, B_{0}$, and $C_{0}$. Connect $E_{503}$ to $B_{503}, C_{503}$, and $D_{503}$. For $1 \leq i \leq 502$: connect $B_{i}$ to $C_{i}$. Finally, for $0 \leq i \leq 502$: connect $D_{i}$ to $A_{i+1}$. Now every city is connected to exactly three other cities.
If we now want to go from $A_{0}$ to $D_{503}$, then this must be via all $A_{i}$ and $D_{i}$, because these are the only connections between the different groups and each group is only connected to the previous and next group. Furthermore, for $0 \leq i \leq 503$ the city $A_{i}$ is not connected to $D_{i}$, so the route within group $i$ must go via $B_{i}$ or $C_{i}$. At least three of the four or five cities in such a group are thus visited on the route. In total, the route thus contains at least $3 \cdot 504=1512$ cities and therefore at least 1511 roads.
We then show that a shortest route between two cities never goes through more than 1511 roads. Consider such a shortest route where the cities $A_{0}, A_{1}$, $\ldots, A_{k}$ are visited in sequence. Each of the cities $A_{i}$ is connected to at least one other city besides its neighbors $A_{i-1}$ and $A_{i+1}$, say to $B_{i}$ (here $B_{0}, B_{1}, \ldots, B_{k}$ do not have to be all different cities). Furthermore, $A_{0}$ and $A_{k}$ are also connected to a third city, say $C_{0} \neq B_{0}$ and $C_{k} \neq B_{k}$. If one of the cities $B_{i}$ or $C_{i}$ is equal to one of the cities $A_{j}$, then we could have found a shorter route by going directly from $A_{i}$ to $A_{j}$ (or vice versa), contradiction. Therefore, the cities $B_{i}$ and $C_{i}$ are all different from all cities $A_{j}$.
If one of the cities $B_{i}$ is connected to four cities $A_{j}$, say $B_{i}$ is connected to $A_{i}, A_{m}, A_{n}$, and $A_{p}$ with $i<m<n<p$, then we could shorten the route by going from $A_{i}$ to $B_{i}$ and then to $A_{p}$. We would then skip at least two cities from the original route (namely $A_{m}$ and $A_{n}$) and visit only $B_{i}$ in addition, so this new route would be shorter. Contradiction. The cities $B_{i}$ with $3 \leq i \leq k-3$ are thus at least $\frac{k-5}{3}$ different cities. For $B_{0}$ and $C_{0}$, we can shorten the route if one of these cities is equal to $B_{i}$ with $i \geq 3$. That would be a contradiction, so $B_{0}$ and $C_{0}$ are two different cities different from $B_{i}$ with $i \geq 3$. Similarly, $B_{k}$ and $C_{k}$ are two different cities different from $B_{i}$ with $i \leq k-3$. In total, we have $k+1$ cities on the route itself and at least $\frac{k-5}{3}+2+2$ other cities. So $\frac{k-5}{3}+k+5 \leq 2018$, so $4 k-5+15 \leq 3 \cdot 2018=6054$, so $4 k \leq 6044$, so $k \leq 1511$.
We conclude that the largest possible number of roads in a shortest route is 1511.
|
1511
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In een land zijn 2018 steden, waarvan sommige met elkaar verbonden zijn door wegen. Elke stad is verbonden met ten minste drie andere steden. Het is mogelijk om van elke willekeurige stad naar elke andere willekeurige stad te reizen via één of meer wegen. Bekijk voor elk tweetal steden de kortste route tussen deze twee steden. Wat is het grootste aantal wegen dat in zo'n kortste route zou kunnen voorkomen?
|
Het grootste aantal wegen dat in een kortste route kan voorkomen, is 1511. We geven eerst een land waarvoor dit aantal aangenomen wordt. Deel de steden op in 504 groepen: twee groepen van vijf steden $\left(A_{0}, B_{0}, C_{0}, D_{0}, E_{0}\right)$ en $\left(A_{503}, B_{503}, C_{503}, D_{503}, E_{503}\right)$ en verder groepen van vier steden $\left(A_{i}, B_{i}, C_{i}, D_{i}\right)$ voor $1 \leq i \leq 502$. Voor alle $i$ met $0 \leq i \leq 503$ : verbind $A_{i}$ met $B_{i}$, verbind $A_{i}$ met $C_{i}$, verbind $B_{i}$ met $D_{i}$ en verbind $C_{i}$ met $D_{i}$. Verbind verder $E_{0}$ met $A_{0}, B_{0}$ en $C_{0}$. Verbind $E_{503}$ met $B_{503}, C_{503}$ en $D_{503}$. Voor $1 \leq i \leq 502$ : verbind $B_{i}$ met $C_{i}$. Ten slotte voor $0 \leq i \leq 502$ : verbind $D_{i}$ met $A_{i+1}$. Nu is elke stad met precies drie andere steden verbonden.
Als we nu van $A_{0}$ naar $D_{503}$ willen, dan moet dat via alle $A_{i}$ en $D_{i}$, omdat daar de enige verbindingen tussen de verschillende groepen lopen en elke groep alleen verbonden is met de vorige en volgende groep. Verder is voor $0 \leq i \leq 503$ de stad $A_{i}$ niet verbonden met $D_{i}$, dus de route binnen groep $i$ moet via $B_{i}$ of $C_{i}$ lopen. Minstens drie van de vier of vijf steden in zo'n groep worden dus aangedaan op de route. In totaal bevat de route dus minstens $3 \cdot 504=1512$ steden en daarmee minstens 1511 wegen.
We laten vervolgens zien dat een kortste route tussen twee steden nooit meer dan 1511 wegen kan doorlopen. Bekijk zo'n korste route waarbij achtereenvolgens de steden $A_{0}, A_{1}$, $\ldots, A_{k}$ worden aangedaan. Elk van de steden $A_{i}$ is behalve met zijn buren $A_{i-1}$ en $A_{i+1}$ nog met minstens één andere stad verbonden, zeg met $B_{i}$ (hierbij hoeven $B_{0}, B_{1}, \ldots, B_{k}$ niet allemaal verschillende steden te zijn). Verder zijn $A_{0}$ en $A_{k}$ nog met een derde stad verbonden, zeg $C_{0} \neq B_{0}$ en $C_{k} \neq B_{k}$. Als één van de steden $B_{i}$ of $C_{i}$ gelijk is aan één van de steden $A_{j}$, dan hadden we een kortere route kunnen vinden door direct van $A_{i}$ naar $A_{j}$ te lopen (of andersom), tegenspraak. Dus de steden $B_{i}$ en $C_{i}$ zijn allemaal ongelijk aan alle steden $A_{j}$.
Als één van de steden $B_{i}$ in totaal met vier steden $A_{j}$ verbonden is, zeg $B_{i}$ is verbonden met $A_{i}, A_{m}, A_{n}$ en $A_{p}$ met $i<m<n<p$, dan zouden we de route kunnen inkorten door van $A_{i}$ naar $B_{i}$ en dan naar $A_{p}$ te lopen. We slaan dan minimaal twee steden uit de oorspronkelijke route over (namelijk $A_{m}$ en $A_{n}$ ) en bezoeken in plaats daarvan alleen $B_{i}$ extra, dus deze nieuwe route is korter. Tegenspraak. De steden $B_{i}$ met $3 \leq i \leq k-3$ zijn dus minstens $\frac{k-5}{3}$ verschillende steden. Voor $B_{0}$ en $C_{0}$ geldt dat we de route kunnen inkorten als één van deze steden gelijk is aan $B_{i}$ met $i \geq 3$. Dat zou een tegenspraak zijn, dus $B_{0}$ en $C_{0}$ zijn twee verschillende steden ongelijk aan $B_{i}$ met $i \geq 3$. Zo ook zijn $B_{k}$ en $C_{k}$ twee verschillende steden ongelijk aan $B_{i}$ met $i \leq k-3$. Al met al hebben we op de route zelf $k+1$ steden en daarnaast nog minstens $\frac{k-5}{3}+2+2$ andere steden. Dus $\frac{k-5}{3}+k+5 \leq 2018$, dus $4 k-5+15 \leq 3 \cdot 2018=6054$, dus $4 k \leq 6044$, dus $k \leq 1511$.
We concluderen dat het grootst mogelijke aantal wegen in een kortste route gelijk aan 1511.
|
{
"exam": "Dutch_TST",
"problem_label": "5",
"problem_match": "\nOpgave 5.",
"resource_path": "Dutch_TST/segmented/nl-2019-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2019"
}
|
Gegeven is een kwadratisch polynoom $P(x)$ met twee verschillende reële nulpunten. Voor alle reële getallen $a$ en $b$ met $|a|,|b| \geq 2017$ geldt dat $P\left(a^{2}+b^{2}\right) \geq P(2 a b)$. Bewijs dat minstens één van de nulpunten van $P$ negatief is.
|
Schrijf $P(x)=c(x-d)(x-e)$, waarbij $d$ en $e$ de nulpunten zijn, dus $d \neq e$. Verder geldt $c \neq 0$, anders is $P$ niet kwadratisch. Voor $|a|,|b| \geq 2017$ volgt nu uit $P\left(a^{2}+b^{2}\right) \geq P(2 a b)$ dat
$$
c\left(a^{2}+b^{2}-d\right)\left(a^{2}+b^{2}-e\right) \geq c(2 a b-d)(2 a b-e)
$$
We werken haakjes uit en strepen links en rechts de term cde weg:
$$
c\left(\left(a^{2}+b^{2}\right)^{2}-(d+e)\left(a^{2}+b^{2}\right)\right) \geq c\left((2 a b)^{2}-(d+e) \cdot 2 a b\right) .
$$
We halen $c(2 a b)^{2}$ naar links, zodat daar een merkwaardig product ontstaat; en we zetten de termen met een factor $(d+e)$ samen rechts. Nu vinden we
$$
c\left(a^{2}+b^{2}-2 a b\right)\left(a^{2}+b^{2}+2 a b\right) \geq c(d+e)\left(a^{2}+b^{2}-2 a b\right)
$$
We factoriseren beide kanten:
$$
c(a-b)^{2}(a+b)^{2} \geq c(d+e)(a-b)^{2}
$$
Voor $a \neq b$ is $(a-b)^{2}>0$, dus kunnen we daardoor delen, zonder dat het teken omklapt. We krijgen
$$
c(a+b)^{2} \geq c(d+e)
$$
We onderscheiden nu twee gevallen. Stel eerst dat $c>0$. Dan kunnen we links en rechts door $c$ delen en klapt het teken niet om. Als we vervolgens kiezen voor $a=2017, b=-2017$ krijgen we $0 \geq d+e$. Omdat $d \neq e$ volgt hieruit dat minstens één van $d$ en $e$ negatief moet zijn.
Nu het tweede geval: $c<0$. Dan klapt het teken om bij deling door $c$ en krijgen we $(a+b)^{2} \leq d+e$ voor alle $a \neq b$ met $|a|,|b| \geq 2017$. Door het variëren van $a$ en $b$ kan de linkerkant willekeurig groot worden, terwijl de rechterkant constant is. Tegenspraak.
We concluderen dat het eerste geval moet gelden en dus minstens één van de nulpunten van $P$ negatief is.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Gegeven is een kwadratisch polynoom $P(x)$ met twee verschillende reële nulpunten. Voor alle reële getallen $a$ en $b$ met $|a|,|b| \geq 2017$ geldt dat $P\left(a^{2}+b^{2}\right) \geq P(2 a b)$. Bewijs dat minstens één van de nulpunten van $P$ negatief is.
|
Schrijf $P(x)=c(x-d)(x-e)$, waarbij $d$ en $e$ de nulpunten zijn, dus $d \neq e$. Verder geldt $c \neq 0$, anders is $P$ niet kwadratisch. Voor $|a|,|b| \geq 2017$ volgt nu uit $P\left(a^{2}+b^{2}\right) \geq P(2 a b)$ dat
$$
c\left(a^{2}+b^{2}-d\right)\left(a^{2}+b^{2}-e\right) \geq c(2 a b-d)(2 a b-e)
$$
We werken haakjes uit en strepen links en rechts de term cde weg:
$$
c\left(\left(a^{2}+b^{2}\right)^{2}-(d+e)\left(a^{2}+b^{2}\right)\right) \geq c\left((2 a b)^{2}-(d+e) \cdot 2 a b\right) .
$$
We halen $c(2 a b)^{2}$ naar links, zodat daar een merkwaardig product ontstaat; en we zetten de termen met een factor $(d+e)$ samen rechts. Nu vinden we
$$
c\left(a^{2}+b^{2}-2 a b\right)\left(a^{2}+b^{2}+2 a b\right) \geq c(d+e)\left(a^{2}+b^{2}-2 a b\right)
$$
We factoriseren beide kanten:
$$
c(a-b)^{2}(a+b)^{2} \geq c(d+e)(a-b)^{2}
$$
Voor $a \neq b$ is $(a-b)^{2}>0$, dus kunnen we daardoor delen, zonder dat het teken omklapt. We krijgen
$$
c(a+b)^{2} \geq c(d+e)
$$
We onderscheiden nu twee gevallen. Stel eerst dat $c>0$. Dan kunnen we links en rechts door $c$ delen en klapt het teken niet om. Als we vervolgens kiezen voor $a=2017, b=-2017$ krijgen we $0 \geq d+e$. Omdat $d \neq e$ volgt hieruit dat minstens één van $d$ en $e$ negatief moet zijn.
Nu het tweede geval: $c<0$. Dan klapt het teken om bij deling door $c$ en krijgen we $(a+b)^{2} \leq d+e$ voor alle $a \neq b$ met $|a|,|b| \geq 2017$. Door het variëren van $a$ en $b$ kan de linkerkant willekeurig groot worden, terwijl de rechterkant constant is. Tegenspraak.
We concluderen dat het eerste geval moet gelden en dus minstens één van de nulpunten van $P$ negatief is.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2019-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2019"
}
|
Gegeven is een kwadratisch polynoom $P(x)$ met twee verschillende reële nulpunten. Voor alle reële getallen $a$ en $b$ met $|a|,|b| \geq 2017$ geldt dat $P\left(a^{2}+b^{2}\right) \geq P(2 a b)$. Bewijs dat minstens één van de nulpunten van $P$ negatief is.
|
Schrijf $P(x)=c(x-d)(x-e)$, waarbij $d$ en $e$ de nulpunten zijn, dus $d \neq e$. Verder geldt $c \neq 0$, anders is $P$ niet kwadratisch. We onderscheiden twee gevallen. Stel eerst dat $c>0$. We nemen $b=-a=2017$ in $P\left(a^{2}+b^{2}\right) \geq P(2 a b)$, waardoor we krijgen $P\left(2 a^{2}\right) \geq P\left(-2 a^{2}\right)$, dus
$$
c\left(2 a^{2}-d\right)\left(2 a^{2}-e\right) \geq c\left(-2 a^{2}-d\right)\left(-2 a^{2}-2\right)
$$
We delen door $c>0$, werken haakjes uit en strepen links en rechts de termen $4 a^{4}$ en de weg:
$$
-(d+e) \cdot 2 a^{2} \geq(d+e) \cdot 2 a^{2}
$$
oftewel
$$
4 a^{2}(d+e) \leq 0
$$
We kunnen delen door $4 a^{2}=4 \cdot 2017^{2}$, zodat we vinden dat $d+e \leq 0$. Omdat de twee nulpunten verschillend zijn, moet nu minstens één van beide negatief zijn.
Stel nu dat $c<0$. Dan hebben we te maken met een bergparabool, die rechts voorbij de top dalend is. Kies nu $a \neq b$ met $a, b \geq 2017$ en $a$ en $b$ rechts van de top, dan geldt volgens de ongelijkheid van het rekenkundig-meetkundig $a^{2}+b^{2}>2 a b$ (geen gelijkheid want $a \neq b$ ). Omdat $a$ en $b$ positief en groter dan 1 zijn en rechts van de top liggen, geldt $2 a b>a$, dus ligt ook $2 a b$ rechts van de top (en daarmee $a^{2}+b^{2}$ ook). Dus omdat $P$ dalend is, geldt $P\left(a^{2}+b^{2}\right)<P(2 a b)$, in tegenspraak met het gegeven.
We concluderen dat het eerste geval moet gelden en dus minstens één van de nulpunten van $P$ negatief is.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Gegeven is een kwadratisch polynoom $P(x)$ met twee verschillende reële nulpunten. Voor alle reële getallen $a$ en $b$ met $|a|,|b| \geq 2017$ geldt dat $P\left(a^{2}+b^{2}\right) \geq P(2 a b)$. Bewijs dat minstens één van de nulpunten van $P$ negatief is.
|
Schrijf $P(x)=c(x-d)(x-e)$, waarbij $d$ en $e$ de nulpunten zijn, dus $d \neq e$. Verder geldt $c \neq 0$, anders is $P$ niet kwadratisch. We onderscheiden twee gevallen. Stel eerst dat $c>0$. We nemen $b=-a=2017$ in $P\left(a^{2}+b^{2}\right) \geq P(2 a b)$, waardoor we krijgen $P\left(2 a^{2}\right) \geq P\left(-2 a^{2}\right)$, dus
$$
c\left(2 a^{2}-d\right)\left(2 a^{2}-e\right) \geq c\left(-2 a^{2}-d\right)\left(-2 a^{2}-2\right)
$$
We delen door $c>0$, werken haakjes uit en strepen links en rechts de termen $4 a^{4}$ en de weg:
$$
-(d+e) \cdot 2 a^{2} \geq(d+e) \cdot 2 a^{2}
$$
oftewel
$$
4 a^{2}(d+e) \leq 0
$$
We kunnen delen door $4 a^{2}=4 \cdot 2017^{2}$, zodat we vinden dat $d+e \leq 0$. Omdat de twee nulpunten verschillend zijn, moet nu minstens één van beide negatief zijn.
Stel nu dat $c<0$. Dan hebben we te maken met een bergparabool, die rechts voorbij de top dalend is. Kies nu $a \neq b$ met $a, b \geq 2017$ en $a$ en $b$ rechts van de top, dan geldt volgens de ongelijkheid van het rekenkundig-meetkundig $a^{2}+b^{2}>2 a b$ (geen gelijkheid want $a \neq b$ ). Omdat $a$ en $b$ positief en groter dan 1 zijn en rechts van de top liggen, geldt $2 a b>a$, dus ligt ook $2 a b$ rechts van de top (en daarmee $a^{2}+b^{2}$ ook). Dus omdat $P$ dalend is, geldt $P\left(a^{2}+b^{2}\right)<P(2 a b)$, in tegenspraak met het gegeven.
We concluderen dat het eerste geval moet gelden en dus minstens één van de nulpunten van $P$ negatief is.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2019-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2019"
}
|
Write $S_{n}$ for the set $\{1,2, \ldots, n\}$. Determine all positive integers $n$ for which there exist functions $f: S_{n} \rightarrow S_{n}$ and $g: S_{n} \rightarrow S_{n}$ such that for every $x$ exactly one of the equalities $f(g(x))=x$ and $g(f(x))=x$ holds.
|
We first show that if $n=2m$ for some positive integer $m$, then such functions do exist. Define
$$
f(x)=\left\{\begin{array}{ll}
x & \text { if } 1 \leq x \leq m, \\
x-m & \text { if } m+1 \leq x \leq 2 m,
\end{array} \quad g(x)= \begin{cases}x+m & \text { if } 1 \leq x \leq m \\
x & \text { if } m+1 \leq x \leq 2 m\end{cases}\right.
$$
Note that all prescribed function values fall within $S_{n}$, so these are indeed functions from $S_{n}$ to $S_{n}$. Furthermore, the range of $f$ is $\{1,2, \ldots, m\}$ and that of $g$ is $\{m+1, m+2, \ldots, 2 m\}$. Thus, $f(g(x)) \neq x$ if $x \geq m+1$ and $g(f(x)) \neq x$ if $x \leq m$. For $x \leq m$, we also have $f(g(x))=f(x+m)=x+m-m=x$ and for $x \geq m+1$, we have $g(f(x))=g(x-m)=x-m+m=x$. We see that for every $x$, exactly one of $g(f(x))=x$ and $f(g(x))=x$ is satisfied. Therefore, $n=2m$ satisfies the condition.
Now suppose that $n$ is odd, say $n=2m+1$, and suppose that $f$ and $g$ are functions that satisfy the conditions. Then, without loss of generality, $f(g(x))=x$ at least $m+1$ times, say for $x_{1}, \ldots, x_{m+1}$. Suppose now that for some $i, j$ with $1 \leq i, j \leq m+1$, we have $g(x_{i})=x_{j}$. Then $f(x_{j})=f(g(x_{i}))=x_{i}$, so $g(f(x_{j}))=g(x_{i})=x_{j}$. But now both $f(g(x))=x$ and $g(f(x))=x$ hold for $x=x_{j}$, which is not allowed. Therefore, for all $i$ with $1 \leq i \leq m+1$, $g(x_{i})$ is not one of the numbers $x_{j}$ with $1 \leq j \leq m+1$. However, there are only $m$ other numbers in $S_{n}$, while there are $m+1$ possible values of $i$, so two of the function values must be equal. Say $g(x_{k})=g(x_{l})$ for $1 \leq k<l \leq m+1$. But then $x_{k}=f(g(x_{k}))=f(g(x_{l}))=x_{l}$, a contradiction. Therefore, no functions can exist that satisfy the condition for odd $n$.
We conclude that all even $n$ satisfy the condition and all odd $n$ do not.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Schrijf $S_{n}$ voor de verzameling $\{1,2, \ldots, n\}$. Bepaal alle positieve gehele $n$ waarvoor er functies $f: S_{n} \rightarrow S_{n}$ en $g: S_{n} \rightarrow S_{n}$ bestaan zodat voor elke $x$ precies één van de gelijkheden $f(g(x))=x$ en $g(f(x))=x$ waar is.
|
We laten eerst zien dat als $n=2 m$ voor zekere positieve gehele $m$, er dan zulke functies bestaan. Definieer
$$
f(x)=\left\{\begin{array}{ll}
x & \text { als } 1 \leq x \leq m, \\
x-m & \text { als } m+1 \leq x \leq 2 m,
\end{array} \quad g(x)= \begin{cases}x+m & \text { als } 1 \leq x \leq m \\
x & \text { als } m+1 \leq x \leq 2 m\end{cases}\right.
$$
Merk op dat alle voorgeschreven functiewaarden in $S_{n}$ vallen, dus dit zijn inderdaad functies van $S_{n}$ naar $S_{n}$. Verder is het bereik van $f$ gelijk aan $\{1,2, \ldots, m\}$ en dat van $g$ aan $\{m+1, m+2, \ldots, 2 m\}$. Dus $f(g(x)) \neq x$ als $x \geq m+1$ en $g(f(x)) \neq x$ als $x \leq m$. Voor $x \leq m$ geldt daarnaast $f(g(x))=f(x+m)=x+m-m=x$ en vor $x \geq m+1$ geldt juist $g(f(x))=g(x-m)=x-m+m=x$. We zien dat voor elke $x$ inderdaad aan precies één van $g(f(x))=x$ en $f(g(x))=x$ voldaan wordt. Dus $n=2 m$ voldoet.
Stel nu dat $n$ oneven is, zeg $n=2 m+1$, en stel dat $f$ en $g$ functies zijn die aan de voorwaarden voldoen. Dan geldt zonder verlies van algemeenheid minstens $m+1$ keer $f(g(x))=x$, zeg voor $x_{1}, \ldots, x_{m+1}$. Stel nu dat voor een zekere $i, j$ met $1 \leq i, j \leq m+1$ geldt dat $g\left(x_{i}\right)=x_{j}$. Dan is $f\left(x_{j}\right)=f\left(g\left(x_{i}\right)\right)=x_{i}$, dus $g\left(f\left(x_{j}\right)\right)=g\left(x_{i}\right)=x_{j}$. Maar nu geldt zowel $f(g(x))=x$ als $g(f(x))=x$ voor $x=x_{j}$ en dat mag niet. Dus voor alle $i$ met $1 \leq i \leq m+1$ geldt dat $g\left(x_{i}\right)$ niet één van de getallen $x_{j}$ met $1 \leq j \leq m+1$ is. Er zijn echter nog slechts $m$ andere getallen in $S_{n}$, terwijl er $m+1$ waarden van $i$ mogelijk zijn, dus twee van de functiewaarden moeten gelijk zijn. Zeg $g\left(x_{k}\right)=g\left(x_{l}\right)$ voor $1 \leq k<l \leq m+1$. Maar nu is $x_{k}=f\left(g\left(x_{k}\right)\right)=f\left(g\left(x_{l}\right)\right)=x_{l}$, tegenspraak. Voor oneven $n$ kunnen dus geen functies bestaan die aan de voorwaarde voldoen.
We concluderen dat alle even $n$ voldoen en alle oneven $n$ niet.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2019-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2019"
}
|
Write $S_{n}$ for the set $\{1,2, \ldots, n\}$. Determine all positive integers $n$ for which there exist functions $f: S_{n} \rightarrow S_{n}$ and $g: S_{n} \rightarrow S_{n}$ such that for every $x$ exactly one of the equalities $f(g(x))=x$ and $g(f(x))=x$ holds.
|
Every $x \in S_{n}$ is a fixed point of exactly one of the functions $f \circ g$ and $g \circ f$. We first show that if $x$ is a fixed point of $f \circ g$, then $x$ is not a fixed point of $g$. Indeed, if both $f(g(x))=x$ and $g(x)=x$ were true, then $f(x)=f(g(x))=x$, and thus $g(f(x))=g(x)=x$, which is a contradiction. Therefore, if $x$ is a fixed point of $f \circ g$, then $g(x) \neq x$. Let now $y=g(x)$. Then $f(y)=f(g(x))=x$, so $g(f(y))=g(x)=y$, hence $y$ is a fixed point of $g \circ f$. For each fixed point $x$ of $f \circ g$, there is thus a fixed point $y=g(x)$ of $g \circ f$. Similarly, for each fixed point $y$ of $g \circ f$, there is also a fixed point $x^{\prime}=f(y)$ of $f \circ g$; moreover, $x^{\prime}=x$ because we already saw that $f(y)=x$. We can thus partition the numbers in $S_{n}$ into pairs $(x, y)$ where $x$ is a fixed point of $f \circ g$ and $y$ is a fixed point of $g \circ f$, and for which $x \neq y$. The number of elements in $S_{n}$ must therefore be even, so $n$ is even. For even $n$, we can then show, as in solution I, that such functions exist.
|
n \text{ is even}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Schrijf $S_{n}$ voor de verzameling $\{1,2, \ldots, n\}$. Bepaal alle positieve gehele $n$ waarvoor er functies $f: S_{n} \rightarrow S_{n}$ en $g: S_{n} \rightarrow S_{n}$ bestaan zodat voor elke $x$ precies één van de gelijkheden $f(g(x))=x$ en $g(f(x))=x$ waar is.
|
Elke $x \in S_{n}$ is een dekpunt van precies één van de functies $f \circ g$ en $g \circ f$. We laten nu eerst zien dat als $x$ een dekpunt van $f \circ g$ is, dat dan $x$ geen dekpunt van $g$ is. Immers, als wel zou gelden $f(g(x))=x$ en $g(x)=x$, dan is ook $f(x)=f(g(x))=x$, dus $g(f(x))=g(x)=x$, tegenspraak. Dus als $x$ een dekpunt van $f \circ g$ is, dan geldt $g(x) \neq x$. Noem nu $y=g(x)$. Dan is $f(y)=f(g(x))=x$, dus $g(f(y))=g(x)=y$, dus $y$ is een dekpunt van $g \circ f$. Bij elk dekpunt $x$ van $f \circ g$ hoort dus een dekpunt $y=g(x)$ van $g \circ f$. Analoog hoort bij dat dekpunt $y$ van $g \circ f$ ook weer een dekpunt $x^{\prime}=f(y)$ van $f \circ g$; bovendien geldt $x^{\prime}=x$ want we hadden al gezien dat $f(y)=x$. We kunnen dus de getallen in $S_{n}$ opdelen in paren $(x, y)$ waarbij $x$ een dekpunt van $f \circ g$ is en $y$ een dekpunt van $g \circ f$ en waarvoor geldt $x \neq y$. Het aantal elementen van $S_{n}$ moet dus even zijn, dus $n$ is even. Voor even $n$ kunnen we vervolgens net als in oplossing I laten zien dat zulke functies bestaan.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2019-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2019"
}
|
Given a positive integer $n$. Determine the maximum value of $\operatorname{gcd}(a, b)+\operatorname{gcd}(b, c)+\operatorname{gcd}(c, a)$, under the condition that $a, b$ and $c$ are positive integers with $a+b+c=5 n$.
|
Write $G=\operatorname{gcd}(a, b)+\operatorname{gcd}(b, c)+\operatorname{gcd}(c, a)$. Without loss of generality, we assume that $a \leq b \leq c$. Now, $\operatorname{gcd}(a, b) \leq a, \operatorname{gcd}(b, c) \leq b$ and $\operatorname{gcd}(c, a) \leq a$. Therefore,
$$
G \leq a+b+a \leq a+b+c=5 n
$$
If $3 \mid n$, then $G=5 n$ is achievable, namely with $a=b=c=\frac{5}{3} n$. All three gcds are then equal to $\frac{5}{3} n$, so $G=3 \cdot \frac{5}{3} n=5 n$.
Now suppose further that $3 \nmid n$. Then we know that $a, b$ and $c$ cannot all be equal. We distinguish several cases:
Case 1a: $b=c$ and $b \leq 2 n$. Since now $a \neq b$, we have $\operatorname{gcd}(a, b)=\operatorname{gcd}(a, b-a) \leq b-a$. Thus $G \leq(b-a)+b+a=2 b \leq 4 n$.
Case 1b: $b=c$ and $b>2 n$. We have $a+2 b=5 n$, so $a=5 n-2 b$, which implies that $G \leq a+b+a=10 n-4 b+b=10 n-3 b<10 n-6 n=4 n$.
Case 2a: $b \neq c$ and $c-a \geq n$. Now, $G \leq a+b+a=(a+b+c)-(c-a)=5 n-(c-a) \leq 5 n-n=4 n$.
Case 2b: $b \neq c$ and $c-a<n$. Since $a \leq b \leq c$, we also have $c-b<n$. Furthermore, $b \neq c$ and thus $a \neq c$. So $\operatorname{gcd}(c, a)=\operatorname{gcd}(c-a, a) \leq c-a<n$ and $\operatorname{gcd}(b, c)=\operatorname{gcd}(b, c-b) \leq c-b<n$. In addition, $a \leq \frac{5 n}{3}$. We conclude that $G<\frac{5 n}{3}+n+n<4 n$.
We see that in all cases $G \leq 4 n$. The value $G=4 n$ is achievable with $a=n, b=2 n$ and $c=2 n$, because then $\operatorname{gcd}(a, b)=\operatorname{gcd}(c, a)=n$ and $\operatorname{gcd}(b, c)=2 n$.
Thus, the maximum value of $G$ is $5 n$ if $3 \mid n$ and $4 n$ if $3 \nmid n$.
|
5 n \text{ if } 3 \mid n, \text{ and } 4 n \text{ if } 3 \nmid n
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Gegeven is een positief geheel getal $n$. Bepaal de maximale waarde van $\operatorname{ggd}(a, b)+\operatorname{ggd}(b, c)+\operatorname{ggd}(c, a)$, onder de voorwaarde dat $a, b$ en $c$ positieve gehele getallen zijn met $a+b+c=5 n$.
|
Schrijf $G=\operatorname{ggd}(a, b)+\operatorname{ggd}(b, c)+\operatorname{ggd}(c, a)$. Zonder verlies van algemeenheid nemen we aan dat $a \leq b \leq c$. Nu geldt $\operatorname{ggd}(a, b) \leq a, \operatorname{ggd}(b, c) \leq b$ en $\operatorname{ggd}(c, a) \leq a$. Dus
$$
G \leq a+b+a \leq a+b+c=5 n
$$
Als $3 \mid n$, dan is $G=5 n$ haalbaar, namelijk met $a=b=c=\frac{5}{3} n$. Alle drie de ggd's zijn dan gelijk aan $\frac{5}{3} n$, dus $G=3 \cdot \frac{5}{3} n=5 n$.
Stel nu verder dat $3 \nmid n$. Dan weten we dat $a, b$ en $c$ niet allemaal gelijk kunnen zijn. We onderscheiden een aantal gevallen:
Geval 1a: $b=c$ en $b \leq 2 n$. Omdat nu $a \neq b$, geldt $\operatorname{ggd}(a, b)=\operatorname{ggd}(a, b-a) \leq b-a$. Dus $G \leq(b-a)+b+a=2 b \leq 4 n$.
Geval 1b: $b=c$ en $b>2 n$. Er geldt $a+2 b=5 n$, dus $a=5 n-2 b$, waaruit volgt dat $G \leq a+b+a=10 n-4 b+b=10 n-3 b<10 n-6 n=4 n$.
Geval 2a: $b \neq c$ en $c-a \geq n$. Nu geldt $G \leq a+b+a=(a+b+c)-(c-a)=5 n-(c-a) \leq$ $5 n-n=4 n$.
Geval 2b: $b \neq c$ en $c-a<n$. Omdat $a \leq b \leq c$ geldt nu ook $c-b<n$. Verder is $b \neq c$ en dus ook $a \neq c$. Dus $\operatorname{ggd}(c, a)=\operatorname{ggd}(c-a, a) \leq c-a<n$ en $\operatorname{ggd}(b, c)=\operatorname{ggd}(b, c-b) \leq c-b<n$. Daarnaast is $a \leq \frac{5 n}{3}$. We conluderen dat $G<\frac{5 n}{3}+n+n<4 n$.
We zien dat in alle gevallen $G \leq 4 n$. De waarde $G=4 n$ is haalbaar met $a=n, b=2 n$ en $c=2 n$, want dan geldt $\operatorname{ggd}(a, b)=\operatorname{ggd}(c, a)=n$ en $\operatorname{ggd}(b, c)=2 n$.
Dus de maximale waarde van $G$ is $5 n$ als $3 \mid n$ en $4 n$ als $3 \nmid n$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2019-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2019"
}
|
Given a positive integer $n$. Determine the maximum value of $\operatorname{gcd}(a, b)+\operatorname{gcd}(b, c)+\operatorname{gcd}(c, a)$, under the condition that $a, b$ and $c$ are positive integers with $a+b+c=5 n$.
|
We prove in an alternative way that $G \leq 4 n$ for the case $3 \nmid n$. Initially, we do not assume that $a \leq b \leq c$. We distinguish two cases.
Case 1: two of $a, b$, and $c$ are equal, say $a=b$. Let $d=\operatorname{gcd}(a, c)$. Then $G=a+d+d$. Furthermore, $5 n=a+b+c=2 a+c$. Since $d \mid a$ and $d \mid c$, it also holds that $d \mid 5 n$ and moreover $3 d \leq 2 a+c=5 n$. Therefore, there is a $k \geq 3$ such that $k d=5 n$. But $3 \nmid n$, so $k=3$ is not possible. We now distinguish two subcases:
Case 1a: $k=4$. Then $4 d=5 n=2 a+c$, while $a$ and $c$ are both multiples of $d$. Then $a<2 d$, so $a=d$. We now find $G=a+2 d=3 d=\frac{3}{4} \cdot 5 n=\frac{15}{4} n<4 n$.
Case 1b: $k \geq 5$. Then $5 n=k d \geq 5 d$, so $n \geq d$. Furthermore, $c \geq d$, so $G=a+2 d=\frac{5 n-c}{2}+2 d \leq \frac{5 n-d}{2}+2 d=\frac{5}{2} n+\frac{3}{2} d \leq \frac{5}{2} n+\frac{3}{2} n=4 n$.
Case 2: $a, b$, and $c$ are all different. Without loss of generality, assume that $a<b<c$. Now $\operatorname{gcd}(a, b) \leq \frac{b}{2}, \operatorname{gcd}(b, c) \leq \frac{c}{2}$, and $\operatorname{gcd}(c, a) \leq a$, so $6 G \leq 3 b+3 c+6 a<3 b+3 c+4 a+b+c=4 a+4 b+4 c=20 n$, thus $G<\frac{20 n}{6}<4 n$.
|
4 n
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Gegeven is een positief geheel getal $n$. Bepaal de maximale waarde van $\operatorname{ggd}(a, b)+\operatorname{ggd}(b, c)+\operatorname{ggd}(c, a)$, onder de voorwaarde dat $a, b$ en $c$ positieve gehele getallen zijn met $a+b+c=5 n$.
|
We bewijzen op een alternatieve manier dat $G \leq 4 n$ voor het geval $3 \nmid n$. We nemen hier in eerste instantie niet aan dat $a \leq b \leq c$. We onderscheiden twee gevallen.
Geval 1: twee van $a, b$ en $c$ zijn gelijk, zeg $a=b$. Schrijf $d=\operatorname{ggd}(a, c)$. Dan geldt $G=a+d+d$. Verder is $5 n=a+b+c=2 a+c$. Omdat $d \mid a$ en $d \mid c$ geldt ook $d \mid 5 n$ en bovendien $3 d \leq 2 a+c=5 n$. Er is dus een $k \geq 3$ met $k d=5 n$. Maar $3 \nmid n$, dus $k=3$ kan niet. We onderscheiden nu weer twee gevallen:
Geval 1a: $k=4$. Dan is $4 d=5 n=2 a+c$, terwijl $a$ en $c$ beide veelvouden van $d$ zijn. Dan geldt $a<2 d$, dus $a=d$. We vinden nu $G=a+2 d=3 d=\frac{3}{4} \cdot 5 n=\frac{15}{4} n<4 n$.
Geval 1b: $k \geq 5$. Dan geldt $5 n=k d \geq 5 d$, dus $n \geq d$. Verder is $c \geq d$, dus $G=a+2 d=$ $\frac{5 n-c}{2}+2 d \leq \frac{5 n-d}{2}+2 d=\frac{5}{2} n+\frac{3}{2} d \leq \frac{5}{2} n+\frac{3}{2} n=4 n$.
Geval 2: $a, b$ en $c$ zijn allemaal verschillend. Neem zonder verlies van algemeenheid aan dat $a<b<c$. Er geldt nu $\operatorname{ggd}(a, b) \leq \frac{b}{2}, \operatorname{ggd}(b, c) \leq \frac{c}{2}$ en $\operatorname{ggd}(c, a) \leq a$, dus $6 G \leq 3 b+3 c+6 a<3 b+3 c+4 a+b+c=4 a+4 b+4 c=20 n$, dus $G<\frac{20 n}{6}<4 n$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2019-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2019"
}
|
Given is a triangle $ABC$. On side $AC$ lie points $D$ and $E$ such that the order of points on this line is $A, E, D, C$. The line through $E$ parallel to $BC$ intersects the circumcircle of $\triangle ABD$ at a point $F$, where $E$ and $F$ lie on opposite sides of $AB$. The line through $E$ parallel to $AB$ intersects the circumcircle of $\triangle BCD$ at a point $G$, where $E$ and $G$ lie on opposite sides of $BC$. Prove that $DEFG$ is a cyclic quadrilateral.
|
Let $G^{\prime}$ be the intersection of line $B F$ and the circumcircle of $\triangle B C D$. We prove that $D E F G^{\prime}$ is a cyclic quadrilateral and subsequently that $G=G^{\prime}$, completing the proof.
Since $E F \| B C$, we have $180^{\circ}-\angle D E F=\angle A E F=\angle A C B$ and due to the cyclic quadrilateral $B D C G^{\prime}$, $\angle A C B=\angle D C B=\angle D G^{\prime} B=\angle D G^{\prime} F$, thus $180^{\circ}-\angle D E F=\angle D G^{\prime} F$. This implies that $D E F G^{\prime}$ is a cyclic quadrilateral. This means that $\angle D E G^{\prime}=\angle D F G^{\prime}=\angle D F B$. Due to the cyclic quadrilateral $A D B F$, $\angle D F B=\angle D A B$, so $\angle D E G^{\prime}=\angle D A B$, which means that $E G^{\prime} \| A B$. Since $G^{\prime}$ also lies on the circumcircle of $\triangle B C D$, it must be that $G=G^{\prime}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Gegeven is een driehoek $A B C$. Op zijde $A C$ liggen punten $D$ en $E$ zodat de volgorde van punten op deze lijn $A, E, D, C$ is. De lijn door $E$ evenwijdig aan $B C$ snijdt de omgeschreven cirkel van $\triangle A B D$ in een punt $F$, waarbij $E$ en $F$ aan weerszijden van $A B$ liggen. De lijn door $E$ evenwijdig aan $A B$ snijdt de omgeschreven cirkel van $\triangle B C D$ in een punt $G$, waarbij $E$ en $G$ aan weerszijden van $B C$ liggen. Bewijs dat $D E F G$ een koordenvierhoek is.

|
Zij $G^{\prime}$ het snijpunt van de lijn $B F$ en de omgeschreven cirkel van $\triangle B C D$. We bewijzen dat $D E F G^{\prime}$ een koordenvierhoek is en vervolgens dat $G=G^{\prime}$, waarmee het bewijs compleet is.
Wegens $E F \| B C$ geldt $180^{\circ}-\angle D E F=\angle A E F=\angle A C B$ en vanwege koordenvierhoek $B D C G^{\prime}$ is $\angle A C B=\angle D C B=\angle D G^{\prime} B=\angle D G^{\prime} F$, dus $180^{\circ}-\angle D E F=\angle D G^{\prime} F$. Hieruit volgt dat $D E F G^{\prime}$ een koordenvierhoek is. Dit betekent dat $\angle D E G^{\prime}=\angle D F G^{\prime}=\angle D F B$. Vanwege koordenvierhoek $A D B F$ geldt $\angle D F B=\angle D A B$, dus $\angle D E G^{\prime}=\angle D A B$, wat betekent dat $E G^{\prime} \| A B$. Omdat $G^{\prime}$ ook op de omgeschreven cirkel van $\triangle B C D$ ligt, moet nu $G=G^{\prime}$.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2019-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2019"
}
|
In a middle school, each class has an odd number of students. Furthermore, each student has a best friend (possibly from a different class). Everyone is the best friend of their best friend. On the city trip, every student goes to either Rome or Paris. Prove that the students can be distributed over the two destinations such that
(i) every student goes on the city trip with their best friend;
(ii) for every class, the absolute difference between the number of students going to Rome and the number of students going to Paris is equal to 1.
|
A loose student is a student whose best friend is in a different class. We will now first assign a destination to all loose students. Start with a random loose student $A_{1}$ and send this student to Paris together with his best friend $A_{2}$. Choose another loose student $A_{3}$ (if possible) in the class of $A_{2}$ and send this student to Rome together with his best friend $A_{4}$. Then continue in the class of student $A_{4}$, and so on. More precisely: if we have chosen students $A_{1}$ to $A_{2 k}$ with $k \geq 1$, then we choose a new loose student $A_{2 k+1}$ (if possible) in the class of $A_{2 k}$ and send this student to the other destination than $A_{2 k}$, together with his best friend $A_{2 k+2}$. We continue this process until we reach a $k \geq 1$ for which there are no more loose students in the class of $A_{2 k}$ that have not been chosen. We then continue in the class of $A_{1}$ and choose another new loose student $A_{0}$ (if possible), who goes to Rome together with his best friend $A_{-1}$ (since $A_{1}$ went to Paris). Thus, we also extend the chain in this direction, until we reach a $m \leq 0$ for which there are no more loose students in the class of $A_{2 m+1}$ that have not been chosen. Note that this cannot be the class of $A_{2 k}$ again, as there were no more loose students there. We now have students $A_{2 m+1}, A_{2 m+2}, \ldots, A_{2 k-1}, A_{2 k}$ such that $A_{2 i-1}$ and $A_{2 i}$ are best friends and $A_{2 i}$ and $A_{2 i+1}$ are in the same class but do not go to the same destination. In every class except the class of $A_{2 m+1}$ and that of $A_{2 k}$, an equal number of students have been assigned to Paris as to Rome. In the class of $A_{2 m+1}$ and of $A_{2 k}$, one more student goes to one destination than to the other, but in these classes, we have already assigned a destination to all loose students. We repeat this process until all loose students have a destination. All students without a destination now have a best friend in their own class, so in every class, there is still an even number of students without a destination, and an odd number of students have received a destination. Therefore, every class must have appeared as the end of a chain once (and that was the last time this class was in a chain). In every class, there is therefore exactly one more loose student going to one destination than to the other. Now consider a random class and say that one more loose student goes to Paris than to Rome. We now assign destinations to the students in the class who have their best friend in the same class. If there is an even number of such pairs, we send half of the pairs to Paris and the other half to Rome. If there is an odd number of such pairs, we send one more pair to Rome than to Paris. Since one more loose student went to Paris, now in total, one more student goes to Rome in this class. We see that in all cases, the difference between the number of Paris-bound and Rome-bound students in a class is in absolute value equal to 1.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Op een middelbare school zit in elke klas een oneven aantal leerlingen. Verder heeft elke leerling een beste vriend (mogelijk uit een andere klas). Iedereen is de beste vriend van zijn of haar beste vriend. Bij de stedenreis gaat elke leerling naar Rome of Parijs. Bewijs dat de leerlingen over de twee bestemmingen kunnen worden verdeeld zodat
(i) iedere leerling samen met zijn beste vriend op stedenreis gaat;
(ii) voor iedere klas het absolute verschil tussen het aantal leerlingen dat naar Rome gaat en het aantal leerlingen dat naar Parijs gaat gelijk is aan 1.
|
Noem een losse leerling een leerling van wie de beste vriend in een andere klas zit. We gaan nu eerst alle losse leerlingen een bestemming geven. Begin met een willekeurige losse leerling $A_{1}$ en stuur deze naar Parijs samen met zijn beste vriend $A_{2}$. Kies in de klas van $A_{2}$ een andere losse leerling $A_{3}$ (als dat mogelijk is) en stuur deze naar Rome samen met zijn beste vriend $A_{4}$. Ga nu verder in de klas van leerling $A_{4}$, enzovoorts. Preciezer: als we leerlingen $A_{1}$ tot en met $A_{2 k}$ gekozen hebben met $k \geq 1$, dan kiezen we in de klas van $A_{2 k}$ nog een nieuwe losse leerling $A_{2 k+1}$ (als dat kan) en sturen deze naar de andere bestemming dan $A_{2 k}$, samen met zijn beste vriend $A_{2 k+2}$. Zo gaan we door totdat we bij een $k \geq 1$ komen waarvoor er in de klas van $A_{2 k}$ geen losse leerlingen meer zijn die nog niet gekozen zijn. We gaan dan verder in de klas van $A_{1}$ en kiezen daar nog een nieuwe losse leerling $A_{0}$ (als dat kan), die samen met zijn beste vriend $A_{-1}$ naar Rome gaat (want $A_{1}$ ging naar Parijs). Zo breiden we de keten ook in deze richting uit, totdat we bij een $m \leq 0$ komen waarvoor in de klas van $A_{2 m+1}$ geen losse leerlingen meer zijn die nog niet gekozen zijn. Merk op dat dit niet opnieuw klas $A_{2 k}$ kan zijn, want daar waren geen losse leerlingen meer. We hebben nu leerlingen $A_{2 m+1}, A_{2 m+2}, \ldots, A_{2 k-1}, A_{2 k}$ zodat steeds $A_{2 i-1}$ en $A_{2 i}$ beste vrienden zijn en zodat steeds $A_{2 i}$ en $A_{2 i+1}$ in dezelfde klas zitten maar niet naar dezelfde bestemming gaan. In elke klas behalve de klas van $A_{2 m+1}$ en die van $A_{2 k}$ hebben nu evenveel leerlingen bestemming Parijs als bestemming Rome gekregen. In de klas van $A_{2 m+1}$ en van $A_{2 k}$ gaat één leerling meer naar de ene bestemming dan naar de andere, maar in deze klassen hebben we alle losse leerlingen al een bestemming gegeven. We herhalen dit proces totdat alle losse leerlingen een bestemming hebben. Alle leerlingen zonder bestemming hebben nu een beste vriend in hun eigen klas, dus in elke klas is nog een even aantal leerlingen zonder bestemming en heeft een oneven aantal leerlingen een bestemming gekregen. Dan moet elke klas een keer als einde van een keten voorgekomen zijn (en dat was meteen de laatste keer dat deze klas in een keten zat). In elke klas is er
daarom precies één losse leerling meer voor de ene bestemming dan voor de andere. Bekijk nu een willekeurige klas en zeg dat er één losse leerling meer naar Parijs gaat dan naar Rome. We geven nu bestemmingen aan de leerlingen in de klas die met hun beste vriend in dezelfde klas zitten. Als er een even aantal van dit soort paren is, sturen we de helft van de paren naar Parijs en de andere helft naar Rome. Als er een oneven aantal van dit soort paren is, sturen we één paar meer naar Rome dan naar Parijs. Omdat van de losse leerlingen juist één leerling meer naar Parijs ging, gaat nu in totaal in deze klas één leerling meer naar Rome. We zien dat in alle gevallen het verschil tussen het aantal Parijsgangers en het aantal Romegangers in een klas in absolute waarde gelijk aan 1 is.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2019-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2019"
}
|
Determine all quadruples $(a, b, c, d)$ of positive real numbers that satisfy $a+b+c+d=1$ and
$$
\max \left(\frac{a^{2}}{b}, \frac{b^{2}}{a}\right) \cdot \max \left(\frac{c^{2}}{d}, \frac{d^{2}}{c}\right)=(\min (a+b, c+d))^{4}
$$
|
If $a \geq b$ then $\frac{a}{b} \geq \frac{b}{a}$ and if just $a \leq b$ then $\frac{a}{b} \leq \frac{b}{a}$, so the sequence $(a, b)$ and the sequence $\left(\frac{a}{b}, \frac{b}{a}\right)$ are equally ordered. The rearrangement inequality now says that
$$
a \cdot \frac{a}{b}+b \cdot \frac{b}{a} \geq a \cdot \frac{b}{a}+b \cdot \frac{a}{b}
$$
We can rewrite this as $\frac{a^{2}}{b}+\frac{b^{2}}{a} \geq a+b$. If we combine this with $\max \left(\frac{a^{2}}{b}, \frac{b^{2}}{a}\right) \geq$ $\frac{\frac{a^{2}}{b}+\frac{b^{2}}{a}}{2}$, then we see
$$
\max \left(\frac{a^{2}}{b}, \frac{b^{2}}{a}\right) \geq \frac{a+b}{2} .
$$
Similarly, we also have
$$
\max \left(\frac{c^{2}}{d}, \frac{d^{2}}{d}\right) \geq \frac{c+d}{2}
$$
so
$$
\max \left(\frac{a^{2}}{b}, \frac{b^{2}}{a}\right) \cdot \max \left(\frac{c^{2}}{d}, \frac{d^{2}}{c}\right) \geq \frac{(a+b)(c+d)}{4}
$$
Without loss of generality, we assume that $\min (a+b, c+d)=a+b$. Since $a+b+c+d=1$, we have $a+b \leq \frac{1}{2}$. Therefore,
$$
\frac{(a+b)(c+d)}{4} \geq \frac{1}{4} \cdot(a+b)^{2} \geq(a+b)^{2} \cdot(a+b)^{2}=(a+b)^{4}
$$
We conclude that
$$
\max \left(\frac{a^{2}}{b}, \frac{b^{2}}{a}\right) \cdot \max \left(\frac{c^{2}}{d}, \frac{d^{2}}{c}\right) \geq(a+b)^{4}
$$
Given that equality holds here, equality must hold everywhere in the above steps. In particular, $a+b=\frac{1}{2}$ and $\max \left(\frac{a^{2}}{b}, \frac{b^{2}}{a}\right)=\frac{\frac{a^{2}}{b}+\frac{b^{2}}{a}}{2}$, so $\frac{a^{2}}{b}=\frac{b^{2}}{a}$, which implies $a^{3}=b^{3}$, hence $a=b$. This means that $a=b=\frac{1}{4}$. Since $c+d=1-(a+b)=\frac{1}{2}$, we can similarly deduce that $c=d=\frac{1}{4}$.
The only quadruple that can satisfy this is thus $(a, b, c, d)=\left(\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right)$. Substituting this into the given equality shows that both sides are $\frac{1}{16}$, so this quadruple satisfies the equality.
|
\left(\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right)
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Bepaal alle viertallen $(a, b, c, d)$ van positieve reële getallen die voldoen aan $a+b+c+d=1$ en
$$
\max \left(\frac{a^{2}}{b}, \frac{b^{2}}{a}\right) \cdot \max \left(\frac{c^{2}}{d}, \frac{d^{2}}{c}\right)=(\min (a+b, c+d))^{4}
$$
|
Als $a \geq b$ dan $\frac{a}{b} \geq \frac{b}{a}$ en als juist $a \leq b$ dan $\frac{a}{b} \leq \frac{b}{a}$, dus het rijtje $(a, b)$ en het rijtje $\left(\frac{a}{b}, \frac{b}{a}\right)$ zijn gelijk geordend. De herschikkingsongelijkheid zegt nu dat
$$
a \cdot \frac{a}{b}+b \cdot \frac{b}{a} \geq a \cdot \frac{b}{a}+b \cdot \frac{a}{b}
$$
We kunnen dit herschrijven tot $\frac{a^{2}}{b}+\frac{b^{2}}{a} \geq a+b$. Als we dit combineren met $\max \left(\frac{a^{2}}{b}, \frac{b^{2}}{a}\right) \geq$ $\frac{\frac{a^{2}}{b}+\frac{b^{2}}{a}}{2}$, dan zien we
$$
\max \left(\frac{a^{2}}{b}, \frac{b^{2}}{a}\right) \geq \frac{a+b}{2} .
$$
Analoog geldt ook
$$
\max \left(\frac{c^{2}}{d}, \frac{d^{2}}{d}\right) \geq \frac{c+d}{2}
$$
dus
$$
\max \left(\frac{a^{2}}{b}, \frac{b^{2}}{a}\right) \cdot \max \left(\frac{c^{2}}{d}, \frac{d^{2}}{c}\right) \geq \frac{(a+b)(c+d)}{4}
$$
Zonder verlies van algemeenheid nemen we aan dat $\min (a+b, c+d)=a+b$. Vanwege $a+b+c+d=1$ geldt dan $a+b \leq \frac{1}{2}$. Dus
$$
\frac{(a+b)(c+d)}{4} \geq \frac{1}{4} \cdot(a+b)^{2} \geq(a+b)^{2} \cdot(a+b)^{2}=(a+b)^{4}
$$
We concluderen dat
$$
\max \left(\frac{a^{2}}{b}, \frac{b^{2}}{a}\right) \cdot \max \left(\frac{c^{2}}{d}, \frac{d^{2}}{c}\right) \geq(a+b)^{4}
$$
Gegeven is dat hier juist gelijkheid geldt. Omdat alles positief is, moet dan hiervoor overal ook gelijkheid gelden. In het bijzonder moet $a+b=\frac{1}{2}$ en verder moet $\max \left(\frac{a^{2}}{b}, \frac{b^{2}}{a}\right)=\frac{\frac{a^{2}}{b}+\frac{b^{2}}{a}}{a}$, dus $\frac{a^{2}}{b}=\frac{b^{2}}{a}$, waaruit volgt dat $a^{3}=b^{3}$, dus $a=b$. Dat betekent dat $a=b=\frac{1}{4}$. Omdat $c+d=1-(a+b)=\frac{1}{2}$ kunnen we op een vergelijkbare manier afleiden dat $c=d=\frac{1}{4}$.
Het enige viertal dat kan voldoen, is dus $(a, b, c, d)=\left(\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right)$. Dit invullen laat zien dat in de gegeven gelijkheid dan zowel links als rechts $\frac{1}{16}$ staat, dus dit viertal voldoet.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2019-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2019"
}
|
Bepaal alle viertallen $(a, b, c, d)$ van positieve reële getallen die voldoen aan $a+b+c+d=1$ en
$$
\max \left(\frac{a^{2}}{b}, \frac{b^{2}}{a}\right) \cdot \max \left(\frac{c^{2}}{d}, \frac{d^{2}}{c}\right)=(\min (a+b, c+d))^{4}
$$
|
Zonder verlies van algemeenheid nemen we aan dat $a+b \leq c+d$, aangezien $a$ en $b$ samen te verwisselen zijn met $c$ en $d$ zonder dat de opgave verandert. Ook kunnen
we aannemen dat $a \leq b$ en $c \leq d$, omdat $a$ en $b$ onderling te verwisselen en zijn en $c$ en $d$ onderling ook. Nu geldt $a^{3} \leq b^{3}$ dus $\frac{a^{2}}{b} \leq \frac{b^{2}}{a}$, en analoog $\frac{c^{2}}{d} \leq \frac{d^{2}}{c}$. De gegeven gelijkheid wordt nu
$$
\frac{b^{2}}{a} \cdot \frac{d^{2}}{c}=(a+b)^{4}
$$
Er geldt $\frac{b^{2}}{a} \geq b$ en $\frac{d^{2}}{c} \geq d$, dus de linkerkant is minstens $b d$. We gaan nu bewijzen dat $b d \geq(a+b)^{4}$ is, waaruit dan volgt dat overal gelijkheid moet gelden.
Vanwege $a \leq b$ geldt $b \geq \frac{1}{2}(a+b)$ en analoog is $d \geq \frac{1}{2}(c+d)$ en omdat $c+d \geq a+b$ volgt daaruit $d \geq \frac{1}{2}(a+b)$. Verder volgt uit $a+b+c+d=1$ en $a+b \leq c+d$ dat $a+b \leq \frac{1}{2}$, dus
$$
b d \geq \frac{1}{4}(a+b)^{2} \geq(a+b)^{2}(a+b)^{2}=(a+b)^{4} .
$$
Nu moet dus in alle gebruikte ongelijkheden gelijkheid gelden. In $\frac{b^{2}}{a} \geq b$ betekent dat dat $a=b$ en analoog geldt ook $c=d$. En in $a+b \leq \frac{1}{2}$ betekent dat $a+b=\frac{1}{2}$. Dus volgt nu $a=b=\frac{1}{4}$ en ook $c=d=\frac{1}{4}$.
Het enige viertal dat kan voldoen, is dus $(a, b, c, d)=\left(\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right)$. Dit invullen laat zien dat in de gegeven gelijkheid dan zowel links als rechts $\frac{1}{16}$ staat, dus dit viertal voldoet.
|
\left(\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right)
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Bepaal alle viertallen $(a, b, c, d)$ van positieve reële getallen die voldoen aan $a+b+c+d=1$ en
$$
\max \left(\frac{a^{2}}{b}, \frac{b^{2}}{a}\right) \cdot \max \left(\frac{c^{2}}{d}, \frac{d^{2}}{c}\right)=(\min (a+b, c+d))^{4}
$$
|
Zonder verlies van algemeenheid nemen we aan dat $a+b \leq c+d$, aangezien $a$ en $b$ samen te verwisselen zijn met $c$ en $d$ zonder dat de opgave verandert. Ook kunnen
we aannemen dat $a \leq b$ en $c \leq d$, omdat $a$ en $b$ onderling te verwisselen en zijn en $c$ en $d$ onderling ook. Nu geldt $a^{3} \leq b^{3}$ dus $\frac{a^{2}}{b} \leq \frac{b^{2}}{a}$, en analoog $\frac{c^{2}}{d} \leq \frac{d^{2}}{c}$. De gegeven gelijkheid wordt nu
$$
\frac{b^{2}}{a} \cdot \frac{d^{2}}{c}=(a+b)^{4}
$$
Er geldt $\frac{b^{2}}{a} \geq b$ en $\frac{d^{2}}{c} \geq d$, dus de linkerkant is minstens $b d$. We gaan nu bewijzen dat $b d \geq(a+b)^{4}$ is, waaruit dan volgt dat overal gelijkheid moet gelden.
Vanwege $a \leq b$ geldt $b \geq \frac{1}{2}(a+b)$ en analoog is $d \geq \frac{1}{2}(c+d)$ en omdat $c+d \geq a+b$ volgt daaruit $d \geq \frac{1}{2}(a+b)$. Verder volgt uit $a+b+c+d=1$ en $a+b \leq c+d$ dat $a+b \leq \frac{1}{2}$, dus
$$
b d \geq \frac{1}{4}(a+b)^{2} \geq(a+b)^{2}(a+b)^{2}=(a+b)^{4} .
$$
Nu moet dus in alle gebruikte ongelijkheden gelijkheid gelden. In $\frac{b^{2}}{a} \geq b$ betekent dat dat $a=b$ en analoog geldt ook $c=d$. En in $a+b \leq \frac{1}{2}$ betekent dat $a+b=\frac{1}{2}$. Dus volgt nu $a=b=\frac{1}{4}$ en ook $c=d=\frac{1}{4}$.
Het enige viertal dat kan voldoen, is dus $(a, b, c, d)=\left(\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right)$. Dit invullen laat zien dat in de gegeven gelijkheid dan zowel links als rechts $\frac{1}{16}$ staat, dus dit viertal voldoet.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2019-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2019"
}
|
Let $A B C$ be an acute triangle with $O$ the center of the circumcircle. Point $Q$ lies on the circumcircle of $\triangle B O C$ such that $O Q$ is a diameter. Point $M$ lies on $C Q$ and point $N$ lies internally on segment $B C$ such that $A N C M$ is a parallelogram. Prove that the circumcircle of $\triangle B O C$ and the lines $A Q$ and $N M$ intersect at one point.
|
Define $T$ as the intersection of the circumcircle of $\triangle B O C$ and the line $A Q$. We will prove that $T$ lies on $N M$. Let $\alpha=\angle B A C$. Then $\angle B O C=2 \alpha$ due to the central angle theorem. Since $|O B|=|O C|$ and $\angle O C Q=90^{\circ}=\angle O B Q$ by Thales, we have $\triangle O B Q \cong \triangle O C Q$ (SAS). Therefore, $\angle C O Q=\angle B O Q=\alpha$. Due to the parallelogram $A N C M$, we have $\angle A M C=180^{\circ}-\angle M C N=\angle Q C N=\angle Q C B=\angle Q O B=\alpha$, so also $\angle C N A=\angle A M C=\alpha$. Now we see that $\angle Q T B=\angle Q O B=\alpha=\angle C N A$, which implies $\angle A T B=180^{\circ}-\angle Q T B=180^{\circ}-\angle C N A=\angle A N B$. This means that $A T N B$ is a cyclic quadrilateral. Also, $A T C M$ is a cyclic quadrilateral because $\angle A M C=\alpha=\angle C O Q=\angle C T Q=180^{\circ}-\angle A T C$.
Cyclic quadrilateral $A T C M$ gives $\angle A T M=\angle A C M=180^{\circ}-\angle Q C B-\angle B C A$ due to the straight angle at $C$. We know $\angle Q C B=\angle Q O B=\alpha=\angle C A B$, so using the angle sum in triangle $A B C$ we get $\angle A T M=180^{\circ}-\angle C A B-\angle B C A=\angle A B C$. Now we use cyclic quadrilateral $A T N B$ to find that $\angle A B C=\angle A B N=180^{\circ}-\angle A T N$, so in total $\angle A T M=180^{\circ}-\angle A T N$. This means that $M, T$ and $N$ lie on a line, as we wanted to prove.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $A B C$ een scherphoekige driehoek met $O$ het middelpunt van de omgeschreven cirkel. Punt $Q$ ligt op de omgeschreven cirkel van $\triangle B O C$ zodat $O Q$ een middellijn is. Punt $M$ ligt op $C Q$ en punt $N$ ligt inwendig op lijnstuk $B C$ zodat $A N C M$ een parallellogram is. Bewijs dat de omgeschreven cirkel van $\triangle B O C$ en de lijnen $A Q$ en $N M$ door één punt gaan.

|
Definieer $T$ als het snijpunt van de omgeschreven cirkel van $\triangle B O C$ en de lijn $A Q$. We gaan bewijzen dat $T$ op $N M$ ligt. Schrijf $\alpha=\angle B A C$. Dan geldt $\angle B O C=2 \alpha$ vanwege de middelpuntsomtrekshoekstelling. Aangezien $|O B|=|O C|$ en $\angle O C Q=90^{\circ}=$ $\angle O B Q$ wegens Thales, geldt $\triangle O B Q \cong \triangle O C Q$ (ZZR). Dus geldt $\angle C O Q=\angle B O Q=\alpha$. Vanwege parallellogram $A N C M$ geldt $\angle A M C=180^{\circ}-\angle M C N=\angle Q C N=\angle Q C B=$ $\angle Q O B=\alpha$, dus ook $\angle C N A=\angle A M C=\alpha$. Nu zien we dat $\angle Q T B=\angle Q O B=\alpha=$ $\angle C N A$, waaruit volgt dat $\angle A T B=180^{\circ}-\angle Q T B=180^{\circ}-\angle C N A=\angle A N B$. Dit betekent dat $A T N B$ een koordenvierhoek is. Ook is $A T C M$ een koordenvierhoek omdat $\angle A M C=\alpha=\angle C O Q=\angle C T Q=180^{\circ}-\angle A T C$.
Koordenvierhoek $A T C M$ geeft $\angle A T M=\angle A C M=180^{\circ}-\angle Q C B-\angle B C A$ vanwege de gestrekte hoek bij $C$. We weten $\angle Q C B=\angle Q O B=\alpha=\angle C A B$, dus met een hoekensom in driehoek $A B C$ krijgen we $\angle A T M=180^{\circ}-\angle C A B-\angle B C A=\angle A B C$. Nu gebruiken we koordenvierhoek $A T N B$ om te vinden dat $\angle A B C=\angle A B N=180^{\circ}-\angle A T N$, zodat al met al geldt $\angle A T M=180^{\circ}-\angle A T N$. Dit betekent dat $M, T$ en $N$ op een lijn liggen, zoals we wilden bewijzen.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2019-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2019"
}
|
Vind alle functies $f: \mathbb{Z} \rightarrow \mathbb{Z}$ die voldoen aan
- $f(p)>0$ voor alle priemgetallen $p$,
- $p \mid(f(x)+f(p))^{f(p)}-x$ voor alle $x \in \mathbb{Z}$ en alle priemgetallen $p$.
|
Vul $x=p$ in: $p \mid(2 f(p))^{f(p)}-p$ en $p$ is priem, dus $p \mid 2 f(p)$. We zien dat $p=2$ of $p \mid f(p)$. Vul nu $x=0$ in: $p \mid(f(0)+f(p))^{f(p)}-0$ en $p$ is priem, dus $p \mid f(0)+f(p)$. Aangezien $p \mid f(p)$ voor $p \neq 2$, zien we nu ook $p \mid f(0)$ voor $p \neq 2$. Dus $f(0)$ is deelbaar door oneindig veel priemgetallen en moet daarom wel 0 zijn. Nu volgt uit $2 \mid f(0)+f(2)$ ook dat $2 \mid f(2)$, dus $p \mid f(p)$ voor alle priemgetallen $p$.
De gegeven deelrelatie laat zich nu vertalen tot $f(x)^{f(p)} \equiv x \bmod p$ voor alle gehele getallen $x$ en priemgetallen $p$. We zien dat $p \mid f(x)$ dan en slechts dan als $p \mid x$. Als we dit nu toepassen voor $x=q$ met $q$ een priemgetal ongelijk aan $p$, dan zien we dat $f(q)$ door geen enkele $p \neq q$ deelbaar is en dus wel een macht van $q$ moet zijn. De kleine stelling van Fermat zegt voor alle priemgetallen $p$ en gehele getallen $n$ dat $n^{p} \equiv n \bmod p$, dus ook $n^{p^{t}} \equiv n \bmod p$ voor alle positieve gehele $t$. Nu is $f(p)$ voor alle priemgetallen $p$ van de vorm $p^{t}$ met $t$ positief geheel, dus uit de gegeven deelrelatie kunnen we nu concluderen dat $f(x) \equiv x \bmod p$ voor alle gehele getallen $x$ en priemgetallen $p$. Dus $p \mid f(x)-x$ voor alle $x$ en $p$. Dus voor een vaste $x \in \mathbb{Z}$ geldt dat $f(x)-x$ deelbaar is door oneindig veel priemgetallen $p$, waaruit volgt dat $f(x)-x=0$. Dus $f(x)=x$ voor alle $x$.
We controleren deze functie. Er geldt inderdaad $f(p)>0$ voor priemgetallen $p$. En verder is
$$
(f(x)+f(p))^{f(p)}-x=(x+p)^{p}-x \equiv x^{p}-x \equiv 0 \quad \bmod p
$$
voor alle $x \in \mathbb{Z}$ en alle priemgetallen $p$. Dus de functie $f(x)=x$ voldoet.
|
f(x)=x
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Vind alle functies $f: \mathbb{Z} \rightarrow \mathbb{Z}$ die voldoen aan
- $f(p)>0$ voor alle priemgetallen $p$,
- $p \mid(f(x)+f(p))^{f(p)}-x$ voor alle $x \in \mathbb{Z}$ en alle priemgetallen $p$.
|
Vul $x=p$ in: $p \mid(2 f(p))^{f(p)}-p$ en $p$ is priem, dus $p \mid 2 f(p)$. We zien dat $p=2$ of $p \mid f(p)$. Vul nu $x=0$ in: $p \mid(f(0)+f(p))^{f(p)}-0$ en $p$ is priem, dus $p \mid f(0)+f(p)$. Aangezien $p \mid f(p)$ voor $p \neq 2$, zien we nu ook $p \mid f(0)$ voor $p \neq 2$. Dus $f(0)$ is deelbaar door oneindig veel priemgetallen en moet daarom wel 0 zijn. Nu volgt uit $2 \mid f(0)+f(2)$ ook dat $2 \mid f(2)$, dus $p \mid f(p)$ voor alle priemgetallen $p$.
De gegeven deelrelatie laat zich nu vertalen tot $f(x)^{f(p)} \equiv x \bmod p$ voor alle gehele getallen $x$ en priemgetallen $p$. We zien dat $p \mid f(x)$ dan en slechts dan als $p \mid x$. Als we dit nu toepassen voor $x=q$ met $q$ een priemgetal ongelijk aan $p$, dan zien we dat $f(q)$ door geen enkele $p \neq q$ deelbaar is en dus wel een macht van $q$ moet zijn. De kleine stelling van Fermat zegt voor alle priemgetallen $p$ en gehele getallen $n$ dat $n^{p} \equiv n \bmod p$, dus ook $n^{p^{t}} \equiv n \bmod p$ voor alle positieve gehele $t$. Nu is $f(p)$ voor alle priemgetallen $p$ van de vorm $p^{t}$ met $t$ positief geheel, dus uit de gegeven deelrelatie kunnen we nu concluderen dat $f(x) \equiv x \bmod p$ voor alle gehele getallen $x$ en priemgetallen $p$. Dus $p \mid f(x)-x$ voor alle $x$ en $p$. Dus voor een vaste $x \in \mathbb{Z}$ geldt dat $f(x)-x$ deelbaar is door oneindig veel priemgetallen $p$, waaruit volgt dat $f(x)-x=0$. Dus $f(x)=x$ voor alle $x$.
We controleren deze functie. Er geldt inderdaad $f(p)>0$ voor priemgetallen $p$. En verder is
$$
(f(x)+f(p))^{f(p)}-x=(x+p)^{p}-x \equiv x^{p}-x \equiv 0 \quad \bmod p
$$
voor alle $x \in \mathbb{Z}$ en alle priemgetallen $p$. Dus de functie $f(x)=x$ voldoet.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2019-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2019"
}
|
In quadrilateral $A B C D$, $E$ is the intersection of the diagonals. A line through $E$, not equal to $A C$ or $B D$, intersects $A B$ at $P$ and $B C$ at $Q$. The circle that is tangent to $P Q$ at $E$ and also passes through $D$, intersects the circumcircle of $A B C D$ again at point $R$. Prove that $B, P, R$ and $Q$ lie on a circle.
We consider the configuration where $P$ lies internally on $A B$ and $Q$ lies externally on $B C$; other configurations proceed analogously.
|
For the cyclic quadrilateral $D B C R$, we have $\angle Q C R=180^{\circ}-\angle B C R=\angle B D R$. Since $E Q$ is tangent to the circle through $E, D$, and $R$, we have $\angle B D R=\angle E D R=\angle Q E R$, so $\angle Q C R=\angle Q E R$. This means that $E R Q C$ is a cyclic quadrilateral. Similarly, $E P A R$ is also a cyclic quadrilateral.
We now find $\angle P R Q=\angle P R E+\angle E R Q=\angle P A E+180^{\circ}-\angle E C Q=\angle B A E+\angle E C B$. Due to the angle sum in $\triangle A B C$, this is equal to $180^{\circ}-\angle A B C=180^{\circ}-\angle P B Q$. Therefore, $\angle P R Q=180^{\circ}-\angle P B Q$, and it follows that $B P R Q$ is a cyclic quadrilateral.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In koordenvierhoek $A B C D$ is $E$ het snijpunt van de diagonalen. Een lijn door $E$, ongelijk aan $A C$ of $B D$, snijdt $A B$ in $P$ en $B C$ in $Q$. De cirkel die raakt aan $P Q$ in $E$ en verder door $D$ gaat, snijdt de omgeschreven cirkel van $A B C D$ nogmaals in punt $R$. Bewijs dat $B, P, R$ en $Q$ op een cirkel liggen.

We bekijken de configuratie waar $P$ inwendig op $A B$ ligt en $Q$ uitwendig op $B C$; andere configuraties gaan analoog.
|
Vanwege koordenvierhoek $D B C R$ geldt $\angle Q C R=180^{\circ}-\angle B C R=\angle B D R$. Omdat $E Q$ raakt aan de cirkel door $E, D$ en $R$ geldt $\angle B D R=\angle E D R=\angle Q E R$, dus $\angle Q C R=\angle Q E R$. Dit betekent dat $E R Q C$ een koordenvierhoek is. Analoog is ook $E P A R$ een koordenvierhoek.
We vinden nu $\angle P R Q=\angle P R E+\angle E R Q=\angle P A E+180^{\circ}-\angle E C Q=\angle B A E+\angle E C B$. Vanwege de hoekensom in $\triangle A B C$ is dit gelijk aan $180^{\circ}-\angle A B C=180^{\circ}-\angle P B Q$. Dus $\angle P R Q=180^{\circ}-\angle P B Q$ en daaruit volgt dat $B P R Q$ een koordenvierhoek is.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2019-E_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2019"
}
|
In quadrilateral $A B C D$, $E$ is the intersection of the diagonals. A line through $E$, not equal to $A C$ or $B D$, intersects $A B$ at $P$ and $B C$ at $Q$. The circle that is tangent to $P Q$ at $E$ and also passes through $D$, intersects the circumcircle of $A B C D$ again at point $R$. Prove that $B, P, R$ and $Q$ lie on a circle.

We consider the configuration where $P$ lies internally on $A B$ and $Q$ lies externally on $B C$; other configurations proceed analogously.
|
Analogous to solution I, we prove that $E P A R$ is a cyclic quadrilateral. (In this solution, we do not need cyclic quadrilateral $E R Q C$.) We now find $\angle B R P = \angle B R A - \angle P R A = \angle B C A - \angle P E A = (180^{\circ} - \angle Q C E) - (180^{\circ} - \angle Q E A) = \angle Q E A - \angle Q C E$. By the exterior angle theorem in triangle $Q C E$, this is equal to $\angle E Q C = \angle P Q B$. Therefore, $\angle B R P = \angle P Q B$, which implies that $B P R Q$ is a cyclic quadrilateral.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In koordenvierhoek $A B C D$ is $E$ het snijpunt van de diagonalen. Een lijn door $E$, ongelijk aan $A C$ of $B D$, snijdt $A B$ in $P$ en $B C$ in $Q$. De cirkel die raakt aan $P Q$ in $E$ en verder door $D$ gaat, snijdt de omgeschreven cirkel van $A B C D$ nogmaals in punt $R$. Bewijs dat $B, P, R$ en $Q$ op een cirkel liggen.

We bekijken de configuratie waar $P$ inwendig op $A B$ ligt en $Q$ uitwendig op $B C$; andere configuraties gaan analoog.
|
Analoog aan oplossing I bewijzen we dat $E P A R$ een koordenvierhoek is. (In deze oplossing hebben we koordenvierhoek $E R Q C$ niet nodig.) We vinden nu $\angle B R P=$ $\angle B R A-\angle P R A=\angle B C A-\angle P E A=\left(180^{\circ}-\angle Q C E\right)-\left(180^{\circ}-\angle Q E A\right)=\angle Q E A-\angle Q C E$. Vanwege de buitenhoekstelling in driehoek $Q C E$ is dit gelijk aan $\angle E Q C=\angle P Q B$. Dus $\angle B R P=\angle P Q B$, waaruit volgt dat $B P R Q$ een koordenvierhoek is.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2019-E_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2019"
}
|
Let $n$ be a positive integer. Prove that $n^{2}+n+1$ cannot be written as the product of two positive integers that differ by less than $2 \sqrt{n}$.
Translate the above text into English, keep the original text's line breaks and format, and output the translation result directly.
|
Suppose $a$ and $b$ are positive integers with $a b=n^{2}+n+1$. We will prove that $|a-b| \geq 2 \sqrt{n}$. Note that $(a-b)^{2} \geq 0$. Adding $4 a b$ to both sides gives
$$
(a+b)^{2}=(a-b)^{2}+4 a b \geq 4 a b=4 n^{2}+4 n+4>4 n^{2}+4 n+1=(2 n+1)^{2} .
$$
Since $(a+b)^{2}$ is a square, we have $(a+b)^{2} \geq(2 n+2)^{2}$. Then it follows that
$$
(a-b)^{2}=(a+b)^{2}-4 a b \geq(2 n+2)^{2}-4\left(n^{2}+n+1\right)=4 n
$$
so $|a-b| \geq 2 \sqrt{n}$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Zij $n$ een positief geheel getal. Bewijs dat $n^{2}+n+1$ niet te schrijven is als het product van twee positieve gehele getallen die minder dan $2 \sqrt{n}$ van elkaar verschillen.
|
Stel dat $a$ en $b$ positieve gehele getallen zijn met $a b=n^{2}+n+1$. We gaan bewijzen dat $|a-b| \geq 2 \sqrt{n}$. Merk op dat $(a-b)^{2} \geq 0$. Aan beide kanten $4 a b$ optellen geeft
$$
(a+b)^{2}=(a-b)^{2}+4 a b \geq 4 a b=4 n^{2}+4 n+4>4 n^{2}+4 n+1=(2 n+1)^{2} .
$$
Omdat $(a+b)^{2}$ een kwadraat is, geldt $(a+b)^{2} \geq(2 n+2)^{2}$. Dan volgt
$$
(a-b)^{2}=(a+b)^{2}-4 a b \geq(2 n+2)^{2}-4\left(n^{2}+n+1\right)=4 n
$$
dus $|a-b| \geq 2 \sqrt{n}$.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2019-E_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2019"
}
|
Let $n$ be a positive integer. Prove that $n^{2}+n+1$ cannot be written as the product of two positive integers that differ by less than $2 \sqrt{n}$.
Translate the above text into English, keep the original text's line breaks and format, and output the translation result directly.
|
Suppose $n^{2}+n+1$ is the product of two positive integers and call the smallest $n-a$ with $a$ an integer. Since $(n+1)^{2}=n^{2}+2 n+1>n^{2}+n+1$, it follows that $n-a \leq n$, so $a \geq 0$. Now, $(n-a)(n+a+1)=n^{2}+n-a(a+1)<n^{2}+n+1$, so this product is too small; the second factor is therefore at least $n+a+2$. If $n>(a+1)^{2}$, then
$$
\begin{gathered}
(n-a)(n+a+2)=n^{2}+2 n-a(a+2)>n^{2}+n+(a+1)^{2}-a(a+2) \\
=n^{2}+n+a^{2}+2 a+1-a^{2}-2 a=n^{2}+n+1,
\end{gathered}
$$
so this product is already too large, a contradiction. Therefore, $n \leq(a+1)^{2}$, which can be written as $a+1 \geq \sqrt{n}$. The difference between the two factors is then at least
$$
(n+a+2)-(n-a)=2 a+2 \geq 2 \sqrt{n}
$$
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Zij $n$ een positief geheel getal. Bewijs dat $n^{2}+n+1$ niet te schrijven is als het product van twee positieve gehele getallen die minder dan $2 \sqrt{n}$ van elkaar verschillen.
|
Stel dat $n^{2}+n+1$ het product van twee positieve gehele getallen is en noem de kleinste $n-a$ met $a$ geheel. Omdat $(n+1)^{2}=n^{2}+2 n+1>n^{2}+n+1$, is $n-a \leq n$, dus $a \geq 0$. Nu geldt $(n-a)(n+a+1)=n^{2}+n-a(a+1)<n^{2}+n+1$, dus dit product is te klein; de tweede factor is daarom minstens $n+a+2$. Als $n>(a+1)^{2}$ geldt
$$
\begin{gathered}
(n-a)(n+a+2)=n^{2}+2 n-a(a+2)>n^{2}+n+(a+1)^{2}-a(a+2) \\
=n^{2}+n+a^{2}+2 a+1-a^{2}-2 a=n^{2}+n+1,
\end{gathered}
$$
dus dit product is al te groot, tegenspraak. Er geldt dus $n \leq(a+1)^{2}$, wat te schrijven is als $a+1 \geq \sqrt{n}$. Het verschil tussen de twee factoren is dan minstens
$$
(n+a+2)-(n-a)=2 a+2 \geq 2 \sqrt{n}
$$
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2019-E_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2019"
}
|
Let $n$ be a positive integer. Prove that $n^{2}+n+1$ cannot be written as the product of two positive integers that differ by less than $2 \sqrt{n}$.
Translate the above text into English, keep the original text's line breaks and format, and output the translation result directly.
|
Suppose $a$ and $b$ are positive integers with $ab = n^2 + n + 1$. We will prove that $|a - b| \geq 2 \sqrt{n}$. Without loss of generality, assume that $b$ is the smallest. Since $(n+1)^2 = n^2 + 2n + 1 > n^2 + n + 1$, it follows that $b \leq n$. Write $b = n + 1 - c$ with $c \geq 1$ an integer. Modulo $b$, we now have $n \equiv c - 1$. Therefore,
$$
n^2 + n + 1 \equiv (c-1)^2 + (c-1) + 1 = c^2 - 2c + 1 + c - 1 + 1 = c^2 - c + 1 \pmod{b}.
$$
On the other hand, since $b$ is a divisor of $n^2 + n + 1$, we have $n^2 + n + 1 \equiv 0 \pmod{b}$. Thus, $c^2 - c \equiv -1 \pmod{b}$. However, the left-hand side is non-negative because $c \geq 1$, so it is at least $-1 + b = -1 + (n + 1 - c) = n - c$. Therefore, $c^2 - c \geq n - c$, which implies $c^2 \geq n$, and thus $c \geq \sqrt{n}$.
Notice now that $n^2 + n + 1 = (n - \sqrt{n} + 1)(n + \sqrt{n} + 1)$. We know that $b = n + 1 - c \leq n - \sqrt{n} + 1$, so $a \geq n + \sqrt{n} + 1$. The difference between the two factors is therefore at least $2 \sqrt{n}$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Zij $n$ een positief geheel getal. Bewijs dat $n^{2}+n+1$ niet te schrijven is als het product van twee positieve gehele getallen die minder dan $2 \sqrt{n}$ van elkaar verschillen.
|
Stel dat $a$ en $b$ positieve gehele getallen zijn met $a b=n^{2}+n+1$. We gaan bewijzen dat $|a-b| \geq 2 \sqrt{n}$. Neem zonder verlies van algemeenheid aan dat $b$ de kleinste is. Omdat $(n+1)^{2}=n^{2}+2 n+1>n^{2}+n+1$, is $b \leq n$. Schrijf $b=n+1-c$ met $c \geq 1$ geheel. Modulo $b$ geldt nu $n \equiv c-1$. Dus
$$
n^{2}+n+1 \equiv(c-1)^{2}+(c-1)+1=c^{2}-2 c+1+c-1+1=c^{2}-c+1 \bmod b .
$$
Anderzijds is $b$ een deler van $n^{2}+n+1$, dus geldt $n^{2}+n+1 \equiv 0 \bmod b$. Dus $c^{2}-c \equiv-1$ $\bmod b$. Maar de linkerkant is niet-negatief want $c \geq 1$, dus het is minstens gelijk aan $-1+b=-1+(n+1-c)=n-c$. Dus $c^{2}-c \geq n-c$, waaruit volgt dat $c^{2} \geq n$, dus $c \geq \sqrt{n}$.
Merk nu op dat $n^{2}+n+1=(n-\sqrt{n}+1)(n+\sqrt{n}+1)$. We weten nu $b=n+1-c \leq n-\sqrt{n}+1$, dus $a \geq n+\sqrt{n}+1$. Het verschil tussen de twee factoren is daarom minstens $2 \sqrt{n}$.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2019-E_uitwerkingen.jsonl",
"solution_match": "\nOplossing III.",
"tier": "T1",
"year": "2019"
}
|
Find all functions $f: \mathbb{Z} \rightarrow \mathbb{Z}$ that satisfy the following two conditions:
(i) for all integers $x$, $f(f(x))=x$;
(ii) for all integers $x$ and $y$ such that $x+y$ is odd, $f(x)+f(y) \geq x+y$.
|
The function $f(x)=x$ for all $x$ satisfies. Now assume that not for all $x$ it holds that $f(x)=x$. Due to (i), there is then both a value of $x$ with $f(x)>x$ and a value of $x$ with $f(x)<x$. We now take an $a \in \mathbb{Z}$ with $f(a)<a$ and consider an arbitrary $x$ with $x \not \equiv a \bmod 2$. It holds that $f(x)+f(a) \geq x+a$, so $f(x) \geq x+a-f(a)>x$. Write $w=f(x)$, then it holds that $f(w)=f(f(x))=x<f(x)=w$. If $w \not \equiv a \bmod 2$, it would follow that $f(w)>w$, a contradiction. Therefore, $f(x)=w \equiv a \bmod 2$ and thus also $f(x) \not \equiv x$.
Now take an $x_{1}$ and an $x_{2}$ that both do not have the same parity as $a$. Then they both also do not have the same parity as their function values, so $x_{1}+f\left(x_{2}\right)$ and $x_{2}+f\left(x_{1}\right)$ are odd. By substituting $x=x_{1}, y=f\left(x_{2}\right)$ and also $x=x_{2}, y=f\left(x_{1}\right)$, we see that
$$
f\left(x_{1}\right)+x_{2}=f\left(x_{1}\right)+f\left(f\left(x_{2}\right)\right) \geq x_{1}+f\left(x_{2}\right)=f\left(f\left(x_{1}\right)\right)+f\left(x_{2}\right) \geq f\left(x_{1}\right)+x_{1}
$$
Equality must hold everywhere, so $f\left(x_{1}\right)+x_{2}=x_{1}+f\left(x_{2}\right)$. Fix $x_{1}$ and write $c=f\left(x_{1}\right)-x_{1}$, then it holds that $f\left(x_{2}\right)=x_{2}+c$ for all $x_{2}$ that do not have the same parity as $a$. We further know that $c$ is odd. Write $z=x_{2}+c$, then $z$ can take all possible values that do not have the same parity as $x_{2}$ and thus do have the same as $a$. It holds that
$$
f(z)=f\left(x_{2}+c\right)=f\left(f\left(x_{2}\right)\right)=x_{2}=z-c
$$
Now write $d=c$ if $a$ is odd and $d=-c$ if $a$ is even, then the function satisfies
$$
f(x)= \begin{cases}x+d & \text { if } x \text { is even } \\ x-d & \text { if } x \text { is odd }\end{cases}
$$
We now check functions of this form for an arbitrary odd $d$. We see that $f(x)$ and $x$ never have the same parity, so $f(f(x))=x+d-d=x$, thus satisfying (i). Furthermore, if $x+y$ is odd, then $x$ and $y$ have different parities, so $f(x)+f(y)=x+y+d-d=x+y \geq x+y$, thus also satisfying (ii). We conclude that the functions of this form together with the function $f(x)=x$ for all $x$ are the solutions.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Vind alle functies $f: \mathbb{Z} \rightarrow \mathbb{Z}$ die voldoen aan de volgende twee voorwaarden:
(i) voor alle gehele getallen $x$ geldt $f(f(x))=x$;
(ii) voor alle gehele getallen $x$ en $y$ zodat $x+y$ oneven is geldt er dat $f(x)+f(y) \geq x+y$.
|
De functie $f(x)=x$ voor alle $x$ voldoet. Neem nu verder aan dat niet voor alle $x$ geldt $f(x)=x$. Vanwege (i) is er dan zowel een waarde van $x$ met $f(x)>x$ als een waarde van $x$ met $f(x)<x$. We nemen nu een $a \in \mathbb{Z}$ met $f(a)<a$ en bekijken een willekeurige $x$ met $x \not \equiv a \bmod 2$. Er geldt dat $f(x)+f(a) \geq x+a$, dus $f(x) \geq x+a-f(a)>x$. Schrijf $w=f(x)$, dan geldt $f(w)=f(f(x))=x<f(x)=w$. Als $w \not \equiv a \bmod 2$, zou juist $f(w)>w$, tegenspraak. Dus $f(x)=w \equiv a \bmod 2$ en dus ook $f(x) \not \equiv x$.
Neem nu een $x_{1}$ en een $x_{2}$ die beide niet dezelfde pariteit als $a$ hebben. Dan hebben ze beide ook niet dezelfde pariteit als hun functiewaarden, dus $x_{1}+f\left(x_{2}\right)$ en $x_{2}+f\left(x_{1}\right)$ zijn oneven. Door $x=x_{1}, y=f\left(x_{2}\right)$ en ook $x=x_{2}, y=f\left(x_{1}\right)$ in te vullen, zien we dat
$$
f\left(x_{1}\right)+x_{2}=f\left(x_{1}\right)+f\left(f\left(x_{2}\right)\right) \geq x_{1}+f\left(x_{2}\right)=f\left(f\left(x_{1}\right)\right)+f\left(x_{2}\right) \geq f\left(x_{1}\right)+x_{1}
$$
Er moet nu overal gelijkheid gelden, dus $f\left(x_{1}\right)+x_{2}=x_{1}+f\left(x_{2}\right)$. Fixeer $x_{1}$ en schrijf $c=f\left(x_{1}\right)-x_{1}$, dan geldt $f\left(x_{2}\right)=x_{2}+c$ voor alle $x_{2}$ die niet dezelfde pariteit hebben als $a$. We weten verder dat $c$ oneven is. Schrijf $z=x_{2}+c$, dan kan $z$ alle mogelijke waarden aannemen die niet dezelfde pariteit hebben als $x_{2}$ en dus wel dezelfde als $a$. Er geldt
$$
f(z)=f\left(x_{2}+c\right)=f\left(f\left(x_{2}\right)\right)=x_{2}=z-c
$$
Schrijf nu $d=c$ als $a$ oneven en $d=-c$ als $a$ even, dan voldoet de functie aan
$$
f(x)= \begin{cases}x+d & \text { als } x \text { even } \\ x-d & \text { als } x \text { oneven }\end{cases}
$$
We controleren nu functies van deze vorm voor een willekeurige oneven $d$. We zien dat $f(x)$ en $x$ nooit dezelfde pariteit hebben, dus $f(f(x))=x+d-d=x$, waarmee aan (i) voldaan wordt. Verder geldt als $x+y$ oneven is dat $x$ en $y$ verschillende pariteiten hebben, dus $f(x)+f(y)=x+y+d-d=x+y \geq x+y$, waarmee ook aan (ii) voldaan wordt. We concluderen dat de functies van deze vorm samen met de functie $f(x)=x$ voor alle $x$ de oplossingen zijn.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2019-E_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2019"
}
|
In a mathematics competition, 300 participants take part. After the competition, some participants play chess. Each pair of participants plays at most one game against each other. There are no three participants at this competition who all play against each other. Determine the maximum $n$ for which it is possible to satisfy the following conditions simultaneously: each participant plays at most $n$ chess games, and for every $m$ with $1 \leq m \leq n$ there is a participant who plays exactly $m$ chess games.
|
We show that $n$ is at most 200. First, we give an example where $n=200$. Consider players $A_{1}, A_{2}, \ldots, A_{200}$ and $B_{1}, B_{2}, \ldots, B_{100}$. This makes a total of 300 players. Let $B_{i}$ play chess against the players $A_{j}$ with $1 \leq j \leq i+100$, while no other participants play against each other. Then $B_{i}$ plays exactly $100+i$ other participants, so for $101 \leq m \leq 200$ there is a participant who plays exactly $m$ games. Furthermore, $A_{j}$ for $j>100$ plays against the participants $B_{i}$ with $i \geq j-100$; there are $100-(j-101)=201-j$ of them. Since $j$ can vary from 101 to 200, this number varies from 100 to 1. Thus, for $1 \leq m \leq 100$ there is also a participant who plays exactly $m$ games. Finally, $A_{j}$ for $j \leq 100$ plays against all $B_{i}$; there are 100 of them. Therefore, there are no participants who play more than 200 games. We see that this example meets the requirements for $n=200$.
Now we prove that $n>200$ is not possible. We do this by contradiction, so assume that $n>200$. Then there is at least one participant $A$ who plays exactly 201 games, against players $B_{1}, B_{2}, \ldots, B_{201}$. There are a total of 300 participants, so apart from them and $A$, there are still $300-1-201=98$ other participants, which we call $C_{1}, \ldots, C_{98}$. If a participant $B_{i}$ plays against another participant $B_{j}$, they form a trio with $A$ who play three games among themselves; this is not allowed. Therefore, $B_{i}$ does not play against another participant $B_{j}$. So he plays at most $1+98=99$ games. This means that the participants who play exactly $m$ other participants with $100 \leq m \leq 200$ must all be among the participants $C_{i}$. However, there are only 98 different people, a contradiction. We conclude that $n>200$ is not possible and that $n=200$ is the maximum.
|
200
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Aan een wiskundewedstrijd doen 300 deelnemers mee. Na de wedstrijd spelen sommige deelnemers wat potjes schaak. Elke twee deelnemers spelen hooguit één keer tegen elkaar. Er zijn geen drie deelnemers bij deze wedstrijd die onderling allemaal tegen elkaar schaken. Bepaal de maximale $n$ waarvoor het mogelijk is dat aan de volgende voorwaarden tegelijk voldaan wordt: elke deelnemer speelt hooguit $n$ potjes schaak, en voor elke $m$ met $1 \leq m \leq n$ is er een deelnemer die precies $m$ potjes schaak speelt.
|
We laten zien dat $n$ maximaal 200 is. We geven eerst een voorbeeld waarin $n=200$ geldt. Bekijk spelers $A_{1}, A_{2}, \ldots, A_{200}$ en $B_{1}, B_{2}, \ldots, B_{100}$. Dit zijn 300 spelers in totaal. Laat $B_{i}$ schaak spelen tegen de spelers $A_{j}$ met $1 \leq j \leq i+100$, terwijl verder geen andere deelnemers tegen elkaar schaken. Dan schaakt $B_{i}$ tegen precies $100+i$ andere deelnemers, dus voor $101 \leq m \leq 200$ is er een deelnemer die precies $m$ potjes schaak speelt. Verder schaakt $A_{j}$ voor $j>100$ tegen de deelnemers $B_{i}$ met $i \geq j-100$; dat zijn er $100-(j-101)=201-j$. Omdat $j$ hier kan variëren van 101 tot en met 200, varieert dit getal van 100 tot en met 1 . Voor $1 \leq m \leq 100$ is er dus ook een deelnemer die precies $m$ potjes schaak speelt. Ten slotte schaakt $A_{j}$ voor $j \leq 100$ tegen alle $B_{i}$; dat zijn er 100. Er zijn dus geen deelnemers die meer dan 200 potjes schaak spelen. We zien dat dit voorbeeld aan de eisen voldoet voor $n=200$.
Nu bewijzen we dat $n>200$ niet kan. Dit doen we uit het ongerijmde, dus stel dat $n>200$. Dan is er in elk geval een deelnemer $A$ die precies 201 potjes schaak speelt, tegen spelers $B_{1}, B_{2}, \ldots, B_{201}$. Er zijn in totaal 300 deelnemers, dus naast hen en $A$ zijn er nog $300-1-201=98$ andere deelnemers, die we $C_{1}, \ldots, C_{98}$ noemen. Als een deelnemer $B_{i}$ schaakt tegen een andere deelnemer $B_{j}$, vormen zij samen met $A$ een drietal dat onderling drie potjes schaakt; dat mag niet. Dus $B_{i}$ schaakt niet tegen een andere deelnemer $B_{j}$. Hij speelt dus hooguit $1+98=99$ potjes schaak. Dat betekent dat de deelnemers die tegen precies $m$ andere deelnemers schaken met $100 \leq m \leq 200$ allemaal onder de deelnemers $C_{i}$ te vinden moeten zijn. Echter, dat zijn maar 98 verschillende mensen, tegenspraak. We concluderen dat $n>200$ niet kan en dat dus $n=200$ maximaal is.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2019-E_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2019"
}
|
For an integer $n \geq 3$ we consider a circle with $n$ points on it. We place a positive integer at each point, where the numbers do not necessarily have to be distinct. Such a placement of numbers is called stable if three consecutive numbers always have the product $n$. For how many values of $n$ with $3 \leq n \leq 2020$ is it possible to place numbers in a stable manner?
|
Suppose $n$ is not a multiple of 3 and we have a stable placement of the numbers $a_{1}, a_{2}, \ldots, a_{n}$, which lie in that order on the circle. Then it holds that $a_{i} a_{i+1} a_{i+2}=3$ for all $i$, where we compute the indices modulo $n$. Thus,
$$
a_{i+1} a_{i+2} a_{i+3}=n=a_{i} a_{i+1} a_{i+2}
$$
from which it follows that $a_{i+3}=a_{i}$ (since all numbers are positive). By induction, we find that for all $k \geq 0$ integers, $a_{3 k+1}=a_{1}$. Since $n$ is not a multiple of 3, the numbers $3 k+1$ for $k \geq 0$ take on all values modulo $n$: indeed, 3 has a multiplicative inverse modulo $n$, so $k \equiv 3^{-1} \cdot(b-1)$ gives $3 k+1 \equiv b \bmod n$ for all $b$. We conclude that all numbers on the circle are equal to $a_{1}$. Therefore, it must hold that $a_{1}^{3}=n$, where $a_{1}$ is a positive integer. Thus, if $n$ is not a multiple of 3, then $n$ must be a cube.
If $n$ is a multiple of 3, then we place the numbers $1,1, n, 1,1, n, \ldots$ consecutively on the circle. The product of three consecutive numbers is now always $1 \cdot 1 \cdot n=n$. If $n$ is a cube, say $n=m^{3}$, then we place the numbers $m, m, m, \ldots$ on the circle. The product of three consecutive numbers is now always $m^{3}=n$.
We conclude that a stable placement is possible if and only if $n$ is a multiple of 3 or a cube. We now need to count this number. The multiples of 3 $n$ with $3 \leq n \leq 2020$ are $3,6,9, \ldots, 2019$ and there are $\frac{2019}{3}=673$ of them. The cubes $n$ with $3 \leq n \leq 2020$ are $2^{3}, 3^{3}, \ldots, 12^{3}$, since $12^{3}=1728 \leq 2020$ and $13^{3}=2197>2020$. This is 11 cubes, of which 4 are divisible by 3, so there are 7 cubes that are not multiples of 3. In total, there are $673+7=680$ values of $n$ that satisfy the condition.
|
680
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Voor een geheel getal $n \geq 3$ bekijken we een cirkel met $n$ punten erop. We plaatsen een positief geheel getal bij elk punt, waarbij de getallen niet noodzakelijk verschillend hoeven te zijn. Zo'n plaatsing van getallen heet stabiel als drie getallen naast elkaar altijd product $n$ hebben. Voor hoeveel waarden van $n$ met $3 \leq n \leq 2020$ is het mogelijk om getallen op een stabiele manier te plaatsen?
|
Stel dat $n$ geen veelvoud van 3 is en dat we een stabiele plaatsing hebben van de getallen $a_{1}, a_{2}, \ldots, a_{n}$, die in die volgorde op de cirkel liggen. Er geldt dan $a_{i} a_{i+1} a_{i+2}=3$ voor alle $i$, waarbij we de indices modulo $n$ rekenen. Dus
$$
a_{i+1} a_{i+2} a_{i+3}=n=a_{i} a_{i+1} a_{i+2}
$$
waaruit volgt dat $a_{i+3}=a_{i}$ (aangezien alle getallen positief zijn). Met inductie vinden we dat voor alle $k \geq 0$ geheel geldt $a_{3 k+1}=a_{1}$. Omdat $n$ geen drievoud is, nemen de getallen $3 k+1$ voor $k \geq 0$ alle waarden modulo $n$ aan: immers, 3 heeft een multiplicatieve inverse modulo $n$, dus $k \equiv 3^{-1} \cdot(b-1)$ geeft $3 k+1 \equiv b \bmod n$ voor alle $b$. We concluderen dat alle getallen op de cirkel gelijk zijn aan $a_{1}$. Er moet dus gelden dat $a_{1}^{3}=n$, waarbij $a_{1}$ positief geheel is. Dus als $n$ geen drievoud is, dan moet $n$ een derdemacht zijn.
Als $n$ een drievoud is, dan zetten we achteraanvolgens de getallen $1,1, n, 1,1, n, \ldots$ neer op de cirkel. Het product van drie getallen naast elkaar is nu altijd $1 \cdot 1 \cdot n=n$. Als $n$ een derdemacht is, zeg $n=m^{3}$, dan zetten we de getallen $m, m, m, \ldots$ neer op de cirkel. Het product van drie getallen naast elkaar is nu altijd $m^{3}=n$.
We conluderen dat er een stabiele plaatsing mogelijk is dan en slechts dan als $n$ een drievoud of een derdemacht is. We moeten nu nog dit aantal tellen. De drievouden $n$ met $3 \leq n \leq 2020$ zijn $3,6,9, \ldots, 2019$ en dat zijn er $\frac{2019}{3}=673$. De derdemachten $n$ met $3 \leq n \leq 2020$ zijn $2^{3}, 3^{3}, \ldots, 12^{3}$, want $12^{3}=1728 \leq 2020$ en $13^{3}=2197>2020$. Dit zijn 11 derdemachten, waarvan er 4 deelbaar zijn door 3 , dus er zijn 7 derdemachten die geen drievoud zijn. Alles bij elkaar zijn er $673+7=680$ waarden van $n$ die voldoen.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2020-B2020_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2020"
}
|
In an acute triangle $ABC$, $D$ is the foot of the altitude from $A$. Let $D_{1}$ and $D_{2}$ be the reflections of $D$ in $AB$ and $AC$, respectively. The intersection of $BC$ and the line through $D_{1}$ parallel to $AB$ is called $E_{1}$. The intersection of $BC$ and the line through $D_{2}$ parallel to $AC$ is called $E_{2}$. Prove that $D_{1}, D_{2}, E_{1}$, and $E_{2}$ lie on a circle whose center lies on the circumcircle of $\triangle ABC$.
|
We call the midpoint of $D D_{1}$ $K$ and the midpoint of $D D_{2}$ $L$. Then $K$ lies on $A B$ and $L$ lies on $A C$. Since $\angle A K D=90^{\circ}=\angle A L D$, $A K D L$ is a cyclic quadrilateral. Therefore, $\angle D L K=\angle D A K=\angle D A B=90^{\circ}-\angle A B C$. Furthermore, $K L$ is a midline in triangle $D D_{1} D_{2}$, so $\angle D L K=\angle D D_{2} D_{1}$. We conclude that $\angle D D_{2} D_{1}=90^{\circ}-\angle A B C$.
Since $A C \perp D D_{2}$ and $D_{2} E_{2} \| A C$, we have $\angle D D_{2} E_{2}=90^{\circ}$. Thus, $\angle D_{1} D_{2} E_{2}=\angle D_{1} D_{2} D + \angle D D_{2} E_{2}=90^{\circ}-\angle A B C+90^{\circ}=180^{\circ}-\angle A B C$. On the other hand, because $D_{1} E_{1} \| A B$, we have $\angle D_{1} E_{1} E_{2}=\angle A B C$, so we see $\angle D_{1} D_{2} E_{2}=180^{\circ}-\angle D_{1} E_{1} E_{2}$. We conclude that $D_{1} E_{1} E_{2} D_{2}$ is a cyclic quadrilateral.
Now let $M$ be the point such that $A M$ is a diameter of the circumcircle of $\triangle A B C$. By Thales' theorem, $\angle A C M=90^{\circ}$. Therefore, $C M \perp A C$, which implies $C M \perp D_{2} E_{2}$ and $C M \| D D_{2}$. Furthermore, $L$ is the midpoint of $D D_{2}$ and $L C \| D_{2} E_{2}$, so $L C$ is a midline in triangle $D D_{2} E_{2}$. This means that $C$ is the midpoint of $D E_{2}$. Since $C M \| D D_{2}$, it follows that $C M$ is also a midline, so $C M$ bisects $D_{2} E_{2}$. Because $C M \perp D_{2} E_{2}$, $C M$ is the perpendicular bisector of $D_{2} E_{2}$. Similarly, $B M$ is the perpendicular bisector of $D_{1} E_{1}$. Therefore, $M$ is the intersection of the perpendicular bisectors of two of the chords of the circle through $D_{1}, D_{2}, E_{1}$, and $E_{2}$, and is thus the center of this circle.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In een scherphoekige driehoek $A B C$ is $D$ het voetpunt van de hoogtelijn vanuit $A$. Laat $D_{1}$ en $D_{2}$ de spiegelbeelden zijn van $D$ in respectievelijk $A B$ en $A C$. Het snijpunt van $B C$ en de lijn door $D_{1}$ evenwijdig aan $A B$, noemen we $E_{1}$. Het snijpunt van $B C$ en de lijn door $D_{2}$ evenwijdig aan $A C$, noemen we $E_{2}$. Bewijs dat $D_{1}, D_{2}, E_{1}$ en $E_{2}$ op een cirkel liggen waarvan het middelpunt op de omgeschreven cirkel van $\triangle A B C$ ligt.

|
Het midden van $D D_{1}$ noemen we $K$ en het midden van $D D_{2}$ noemen we $L$. Dan ligt $K$ op $A B$ en $L$ op $A C$. Wegens $\angle A K D=90^{\circ}=\angle A L D$ is $A K D L$ een koordenvierhoek. Dus $\angle D L K=\angle D A K=\angle D A B=90^{\circ}-\angle A B C$. Verder is $K L$ een middenparallel in driehoek $D D_{1} D_{2}$, dus $\angle D L K=\angle D D_{2} D_{1}$. We concluderen dat $\angle D D_{2} D_{1}=90^{\circ}-\angle A B C$.
Omdat $A C \perp D D_{2}$ en $D_{2} E_{2} \| A C$, geldt $\angle D D_{2} E_{2}=90^{\circ}$. Dus $\angle D_{1} D_{2} E_{2}=\angle D_{1} D_{2} D+$ $\angle D D_{2} E_{2}=90^{\circ}-\angle A B C+90^{\circ}=180^{\circ}-\angle A B C$. Anderzijds geldt vanwege $D_{1} E_{1} \| A B$ dat $\angle D_{1} E_{1} E_{2}=\angle A B C$, dus we zien $\angle D_{1} D_{2} E_{2}=180^{\circ}-\angle D_{1} E_{1} E_{2}$. We concluderen dat $D_{1} E_{1} E_{2} D_{2}$ een koordenvierhoek is.
Noem nu $M$ het punt zodat $A M$ een middellijn is van de omgeschreven cirkel van $\triangle A B C$. Wegens Thales geldt dan $\angle A C M=90^{\circ}$. Dus $C M \perp A C$, waaruit volgt dat $C M \perp D_{2} E_{2}$ en $C M \| D D_{2}$. Verder is $L$ het midden van $D D_{2}$ en geldt $L C \| D_{2} E_{2}$, dus $L C$ is een middenparallel in driehoek $D D_{2} E_{2}$. Dit betekent dat $C$ het midden van $D E_{2}$ is. Aangezien $C M \| D D_{2}$ volgt nu dat $C M$ ook een middenparallel is, dus $C M$ snijdt $D_{2} E_{2}$ middendoor. Omdat ook $C M \perp D_{2} E_{2}$, is $C M$ de middelloodlijn van $D_{2} E_{2}$. Analoog geldt dat $B M$ de middelloodlijn van $D_{1} E_{1}$ is. Dus $M$ is het snijpunt van de middelloodlijnen van twee van de koorden van de cirkel door $D_{1}, D_{2}, E_{1}$ en $E_{2}$ en is daarmee het middelpunt van deze cirkel.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2020-B2020_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2020"
}
|
Vind alle functies $f: \mathbb{R} \rightarrow \mathbb{R}$ die voldoen aan
$$
f\left(x^{2} y\right)+2 f\left(y^{2}\right)=\left(x^{2}+f(y)\right) \cdot f(y)
$$
voor alle $x, y \in \mathbb{R}$.
|
Invullen van $x=1$ geeft $f(y)+2 f\left(y^{2}\right)=(1+f(y)) f(y)$, dus
$$
2 f\left(y^{2}\right)=f(y)^{2}
$$
We kunnen hiermee in de oorspronkelijke functievergelijking de term $2 f\left(y^{2}\right)$ links wegstrepen tegen $f(y)^{2}$ rechts:
$$
f\left(x^{2} y\right)=x^{2} f(y) .
$$
Invullen van $y=1$ hierin geeft $f\left(x^{2}\right)=x^{2} f(1)$ en invullen van $y=-1$ geeft $f\left(-x^{2}\right)=$ $x^{2} f(-1)$. Omdat $x^{2}$ alle niet-negatieve getallen aanneemt als $x \in \mathbb{R}$, geldt nu
$$
f(x)= \begin{cases}c x & \text { als } x \geq 0 \\ d x & \text { als } x<0\end{cases}
$$
met $c=f(1)$ en $d=-f(-1)$. Vul nu $y=1$ in bij (1), dat geeft $2 f(1)=f(1)^{2}$, dus $2 c=c^{2}$. Hieruit volgt $c=0$ of $c=2$. Vullen we juist $y=-1$ in bij (1), dan vinden we $2 f(1)=f(-1)^{2}$, dus $2 c=(-d)^{2}$. Voor $c=0$ geeft dit $d=0$ en voor $c=2$ geeft dit $d=2$ of $d=-2$. We hebben dus drie gevallen:
- $c=0, d=0$ : dan is $f(x)=0$ voor alle $x$;
- $c=2, d=2$ : dan is $f(x)=2 x$ voor alle $x$;
- $c=2, d=-2$ : dan is $f(x)=2 x$ voor $x \geq 0$ en $f(x)=-2 x$ voor $x<0$, oftewel $f(x)=2|x|$ voor alle $x$.
Met de eerste functie komt er in de functievergelijking links en rechts 0 , dus deze voldoet. Met de tweede functie komt er in de functievergelijking links $2 x^{2} y+4 y^{2}$ en rechts $\left(x^{2}+2 y\right)$. $2 y=2 x^{2} y+4 y^{2}$, dus die functie voldoet. Met de derde functie komt er links $2\left|x^{2} y\right|+4\left|y^{2}\right|=$ $2 x^{2}|y|+4 y^{2}$ en rechts $\left(x^{2}+2|y|\right) \cdot 2|y|=2 x^{2}|y|+4|y|^{2}=2 x^{2}|y|+4 y^{2}$, dus die functie voldoet ook.
Al met al hebben we drie oplossingen gevonden: $f(x)=0, f(x)=2 x$ en $f(x)=2|x|$.
|
f(x)=0, f(x)=2 x, f(x)=2|x|
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Vind alle functies $f: \mathbb{R} \rightarrow \mathbb{R}$ die voldoen aan
$$
f\left(x^{2} y\right)+2 f\left(y^{2}\right)=\left(x^{2}+f(y)\right) \cdot f(y)
$$
voor alle $x, y \in \mathbb{R}$.
|
Invullen van $x=1$ geeft $f(y)+2 f\left(y^{2}\right)=(1+f(y)) f(y)$, dus
$$
2 f\left(y^{2}\right)=f(y)^{2}
$$
We kunnen hiermee in de oorspronkelijke functievergelijking de term $2 f\left(y^{2}\right)$ links wegstrepen tegen $f(y)^{2}$ rechts:
$$
f\left(x^{2} y\right)=x^{2} f(y) .
$$
Invullen van $y=1$ hierin geeft $f\left(x^{2}\right)=x^{2} f(1)$ en invullen van $y=-1$ geeft $f\left(-x^{2}\right)=$ $x^{2} f(-1)$. Omdat $x^{2}$ alle niet-negatieve getallen aanneemt als $x \in \mathbb{R}$, geldt nu
$$
f(x)= \begin{cases}c x & \text { als } x \geq 0 \\ d x & \text { als } x<0\end{cases}
$$
met $c=f(1)$ en $d=-f(-1)$. Vul nu $y=1$ in bij (1), dat geeft $2 f(1)=f(1)^{2}$, dus $2 c=c^{2}$. Hieruit volgt $c=0$ of $c=2$. Vullen we juist $y=-1$ in bij (1), dan vinden we $2 f(1)=f(-1)^{2}$, dus $2 c=(-d)^{2}$. Voor $c=0$ geeft dit $d=0$ en voor $c=2$ geeft dit $d=2$ of $d=-2$. We hebben dus drie gevallen:
- $c=0, d=0$ : dan is $f(x)=0$ voor alle $x$;
- $c=2, d=2$ : dan is $f(x)=2 x$ voor alle $x$;
- $c=2, d=-2$ : dan is $f(x)=2 x$ voor $x \geq 0$ en $f(x)=-2 x$ voor $x<0$, oftewel $f(x)=2|x|$ voor alle $x$.
Met de eerste functie komt er in de functievergelijking links en rechts 0 , dus deze voldoet. Met de tweede functie komt er in de functievergelijking links $2 x^{2} y+4 y^{2}$ en rechts $\left(x^{2}+2 y\right)$. $2 y=2 x^{2} y+4 y^{2}$, dus die functie voldoet. Met de derde functie komt er links $2\left|x^{2} y\right|+4\left|y^{2}\right|=$ $2 x^{2}|y|+4 y^{2}$ en rechts $\left(x^{2}+2|y|\right) \cdot 2|y|=2 x^{2}|y|+4|y|^{2}=2 x^{2}|y|+4 y^{2}$, dus die functie voldoet ook.
Al met al hebben we drie oplossingen gevonden: $f(x)=0, f(x)=2 x$ en $f(x)=2|x|$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2020-B2020_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2020"
}
|
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ that satisfy
$$
f\left(x^{2} y\right)+2 f\left(y^{2}\right)=\left(x^{2}+f(y)\right) \cdot f(y)
$$
for all $x, y \in \mathbb{R}$.
|
Substituting $y=0$ gives $f(0)+2 f(0)=\left(x^{2}+f(0)\right) f(0)$. Thus, $f(0)=0$ or $3=x^{2}+f(0)$ for all $x \in \mathbb{R}$. The latter cannot be true, so $f(0)=0$.
Now substitute $x=0, y=1$. Then we get $f(0)+2 f(1)=f(1)^{2}$, so $2 f(1)=f(1)^{2}$, thus $f(1)=0$ or $f(1)=2$. Subsequently, substituting $y=1$ gives $f\left(x^{2}\right)+2 f(1)=\left(x^{2}+f(1)\right) \cdot f(1)$, which with the two possible values of $f(1)$ yields:
$$
f\left(x^{2}\right)= \begin{cases}0 & \text { if } f(1)=0 \\ 2 x^{2} & \text { if } f(1)=2\end{cases}
$$
Since $x^{2}$ takes on all non-negative values as $x \in \mathbb{R}$, the function values of all non-negative numbers are now determined. Note that the term $2 f\left(y^{2}\right)$ in the functional equation can now be calculated for all $y$.
First, consider the case where $f(1)=0$. Thus, $f(x)=0$ for all $x \geq 0$. Substitute $x=1$, which gives $f(y)+0=(1+f(y)) f(y)$, so $0=f(y)^{2}$, thus $f(y)=0$ for all $y \in \mathbb{R}$. The function $f(x)=0$ for all $x$ indeed satisfies the functional equation and is thus a solution.
Now consider the case where $f(1)=2$. Thus, $f(x)=2 x$ for all $x \geq 0$. Substitute $x=1$, which gives $f(y)+4 y^{2}=(1+f(y)) f(y)$, so $4 y^{2}=f(y)^{2}$. We find that for all $y$, $f(y)=2 y$ or $f(y)=-2 y$. For $y \geq 0$, we already know that the first always holds. We now want to rule out that both possibilities occur for $y<0$. So take $a, b<0$ with $a \neq b$ such that $f(a)=2 a$ and $f(b)=-2 b$. Choose $y=b$ and $x^{2}=\frac{a}{b}$, which is possible because $\frac{a}{b}>0$. Then $x^{2} y=a$, so substituting into the functional equation gives
$$
2 a+2 f\left(b^{2}\right)=\left(\frac{a}{b}-2 b\right) \cdot-2 b,
$$
or $2 f\left(b^{2}\right)=-4 a+4 b^{2}$. We know that $f\left(b^{2}\right)$ equals $2 b^{2}$, because $f(x)=2 x$ for $x \geq 0$. Thus, $4 b^{2}=-4 a+4 b^{2}$, or $-4 a=0$, a contradiction with $a<0$. We conclude that either for all $y<0$, $f(y)=2 y$, or for all $y<0$, $f(y)=-2 y$.
This gives two more possible functions: $f(x)=2 x$ for all $x$ and $f(x)=2|x|$ for all $x$. With the first function, the left side of the functional equation is $2 x^{2} y+4 y^{2}$ and the right side is $\left(x^{2}+2 y\right) \cdot 2 y=2 x^{2} y+4 y^{2}$, so this function satisfies. With the second function, the left side is $2\left|x^{2} y\right|+4\left|y^{2}\right|=2 x^{2}|y|+4 y^{2}$ and the right side is $\left(x^{2}+2|y|\right) \cdot 2|y|=2 x^{2}|y|+4|y|^{2}=2 x^{2}|y|+4 y^{2}$, so this function also satisfies.
In total, we have found three solutions: $f(x)=0, f(x)=2 x$, and $f(x)=2|x|$.
|
f(x)=0, f(x)=2 x, f(x)=2|x|
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Vind alle functies $f: \mathbb{R} \rightarrow \mathbb{R}$ die voldoen aan
$$
f\left(x^{2} y\right)+2 f\left(y^{2}\right)=\left(x^{2}+f(y)\right) \cdot f(y)
$$
voor alle $x, y \in \mathbb{R}$.
|
Invullen van $y=0$ geeft $f(0)+2 f(0)=\left(x^{2}+f(0)\right) f(0)$. Dus $f(0)=0$ of $3=x^{2}+f(0)$ voor alle $x \in \mathbb{R}$. Dat laatste kan niet waar zijn, dus $f(0)=0$.
Vul nu in $x=0, y=1$. Dan krijgen we $f(0)+2 f(1)=f(1)^{2}$, dus $2 f(1)=f(1)^{2}$, dus $f(1)=0$ of $f(1)=2$. Vervolgens geeft $y=1$ dat $f\left(x^{2}\right)+2 f(1)=\left(x^{2}+f(1)\right) \cdot f(1)$, wat met de twee mogelijke waarden van $f(1)$ oplevert:
$$
f\left(x^{2}\right)= \begin{cases}0 & \text { als } f(1)=0 \\ 2 x^{2} & \text { als } f(1)=2\end{cases}
$$
Omdat $x^{2}$ alle niet-negatieve getallen aanneemt als $x \in \mathbb{R}$, zijn nu de functiewaarden van alle niet-negatieve getallen bepaald. Merk op dat de term $2 f\left(y^{2}\right)$ in de functievergelijking nu ook voor alle $y$ uitgerekend kan worden.
Bekijk nu eerst het geval dat $f(1)=0$. Er geldt dus $f(x)=0$ voor alle $x \geq 0$. Vul $x=1$ in, dat geeft $f(y)+0=(1+f(y)) f(y)$, dus $0=f(y)^{2}$, dus $f(y)=0$ voor alle $y \in \mathbb{R}$. De functie $f(x)=0$ voor alle $x$ voldoet inderdaad aan de functievergelijking en is dus een oplossing.
Bekijk nu het geval dat $f(1)=2$. Er geldt dus $f(x)=2 x$ voor alle $x \geq 0$. Vul $x=1$ in, dat geeft $f(y)+4 y^{2}=(1+f(y)) f(y)$, dus $4 y^{2}=f(y)^{2}$. We vinden nu voor alle $y$ dat $f(y)=2 y$ of $f(y)=-2 y$. Voor $y \geq 0$ weten we al dat altijd het eerste geldt. We willen nu uitsluiten dat voor $y<0$ allebei de mogelijkheden voorkomen. Neem dus een $a, b<0$ met $a \neq b$ zodat $f(a)=2 a$ en $f(b)=-2 b$. Kies $y=b$ en $x^{2}=\frac{a}{b}$, wat kan omdat $\frac{a}{b}>0$. Dan geldt $x^{2} y=a$, dus invullen in de functievergelijking geeft
$$
2 a+2 f\left(b^{2}\right)=\left(\frac{a}{b}-2 b\right) \cdot-2 b,
$$
oftewel $2 f\left(b^{2}\right)=-4 a+4 b^{2}$. We weten dat $f\left(b^{2}\right)$ gelijk is aan $2 b^{2}$, want $f(x)=2 x$ voor $x \geq 0$. Dus $4 b^{2}=-4 a+4 b^{2}$, oftewel $-4 a=0$, tegenspraak met $a<0$. We concluderen dat ofwel voor alle $y<0$ geldt dat $f(y)=2 y$, ofwel voor alle $y<0$ geldt dat $f(y)=-2 y$.
Dat geeft nog twee mogelijke functies: $f(x)=2 x$ voor alle $x$ en $f(x)=2|x|$ voor alle $x$. Met de eerste functie komt er in de functievergelijking links $2 x^{2} y+4 y^{2}$ en rechts $\left(x^{2}+2 y\right) \cdot 2 y=2 x^{2} y+4 y^{2}$, dus die functie voldoet. Met de tweede functie komt er links $2\left|x^{2} y\right|+4\left|y^{2}\right|=2 x^{2}|y|+4 y^{2}$ en rechts $\left(x^{2}+2|y|\right) \cdot 2|y|=2 x^{2}|y|+4|y|^{2}=2 x^{2}|y|+4 y^{2}$, dus die functie voldoet ook.
Al met al hebben we drie oplossingen gevonden: $f(x)=0, f(x)=2 x$ en $f(x)=2|x|$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2020-B2020_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2020"
}
|
On a circle with center $M$ lie three different points $A, B$, and $C$ such that $|A B|=|B C|$. Point $D$ lies inside the circle in such a way that $\triangle B C D$ is equilateral. The second intersection of $A D$ with the circle we call $F$. Prove that $|F D|=|F M|$.
|
We will prove that $|F D|=|F C|$ and that $|F C|=|F M|$, from which the required result follows.
In cyclic quadrilateral $A B C F$, $\angle B C F=180^{\circ}-\angle B A F$. Since $|A B|=|B C|=|B D|$, we further have $\angle B A F=\angle B A D=\angle A D B$, so $\angle B D F=180^{\circ}-\angle A D B=180^{\circ}-\angle B A F$. We see that $\angle B C F=\angle B D F$. Furthermore, $\angle D F B=\angle A F B$ and $\angle C F B$ are inscribed angles subtended by the equal chords $A B$ and $B C$, so $\angle D F B=\angle C F B$. Triangles $B C F$ and $B D F$ thus have two pairs of equal angles; since they also share side $B F$, they are congruent by AAS. We conclude that $|F C|=|F D|$ and that $\angle D B F=\angle C B F$.
By the central angle-inscribed angle theorem, $\angle C M F=2 \angle C B F$. From the equality $\angle D B F=\angle C B F$ we just found, it follows that $2 \angle C B F=\angle C B D=60^{\circ}$, so $\angle C M F=60^{\circ}$. Furthermore, $|M C|=|M F|$ (radius of the circle), so $\triangle C M F$ is isosceles with a vertex angle of $60^{\circ}$, which means it is equilateral. This implies that $|F C|=|F M|$.
With this, we have proven that $|F D|=|F C|=|F M|$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Op een cirkel met middelpunt $M$ liggen drie verschillende punten $A, B$ en $C$ zodat $|A B|=|B C|$. Punt $D$ ligt binnen de cirkel op zo'n manier dat $\triangle B C D$ gelijkzijdig is. Het tweede snijpunt van $A D$ met de cirkel noemen we $F$. Bewijs dat $|F D|=|F M|$.

|
We gaan bewijzen dat $|F D|=|F C|$ en dat $|F C|=|F M|$, waaruit het gevraagde volgt.
In koordenvierhoek $A B C F$ is $\angle B C F=180^{\circ}-\angle B A F$. Wegens $|A B|=|B C|=|B D|$ geldt verder $\angle B A F=\angle B A D=\angle A D B$, dus $\angle B D F=180^{\circ}-\angle A D B=180^{\circ}-\angle B A F$. We zien dat $\angle B C F=\angle B D F$. Verder zijn $\angle D F B=\angle A F B$ en $\angle C F B$ omtrekshoeken op de gelijke koorden $A B$ en $B C$, dus $\angle D F B=\angle C F B$. Driehoeken $B C F$ en $B D F$ hebben dus twee paren hoeken gelijk; omdat ze ook nog zijde $B F$ gemeenschappelijk hebben, zijn ze congruent wegens ZHH. We concluderen dat $|F C|=|F D|$ en dat $\angle D B F=\angle C B F$.
Vanwege de middelpunt-omtrekhoekstelling geldt $\angle C M F=2 \angle C B F$. Uit de zojuist gevonden gelijkheid $\angle D B F=\angle C B F$ volgt dat $2 \angle C B F=\angle C B D=60^{\circ}$, dus $\angle C M F=$ $60^{\circ}$. Verder is $|M C|=|M F|$ (straal van de cirkel) dus $\triangle C M F$ is gelijkbenig met een tophoek van $60^{\circ}$, waaruit volgt dat hij gelijkzijdig is. Dit betekent dat $|F C|=|F M|$.
Hiermee hebben we bewezen dat $|F D|=|F C|=|F M|$.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2020-B2020_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2020"
}
|
A set $S$ consisting of 2019 (distinct) positive integers has the following property: the product of any 100 elements of $S$ is a divisor of the product of the remaining 1919 elements. What is the maximum number of prime numbers that $S$ can contain?
|
The maximum number of prime numbers is 1819.
We start with the construction. Choose different prime numbers \( p_{1}, p_{2}, \ldots, p_{1819} \) and let \( P = p_{1} p_{2} \cdots p_{1819} \). Take
\[
S = \left\{ p_{1}, p_{2}, \ldots, p_{1819}, P, P \cdot p_{1}, \ldots, P \cdot p_{199} \right\}
\]
For each \( p_{i} \), there are 201 numbers in \( S \) that are divisible by \( p_{i} \) (namely \( p_{i} \) and all numbers divisible by \( P \)). Of these, at most one number has two factors \( p_{i} \); the rest have one factor \( p_{i} \). If we take 100 numbers from \( S \), then their product contains at most 101 factors \( p_{i} \). Among the remaining numbers, there are still at least 101 numbers divisible by \( p_{i} \), so their product has at least 101 factors \( p_{i} \). Since this holds for every \( p_{i} \) and the numbers in \( S \) have no other prime factors, this means that \( S \) has the desired property.
We now prove that \( S \) cannot contain more than 1819 prime numbers. Consider a prime divisor \( q \) of a number in \( S \). Suppose that at most 199 numbers in \( S \) are divisible by \( q \). Then we take the 100 elements of \( S \) with the most factors \( q \); these always have more factors \( q \) than the remaining elements, contradicting the condition in the problem. Therefore, there must be at least 200 numbers in \( S \) that are divisible by \( q \). If there are exactly 200, it follows that the number of prime factors \( q \) in all these numbers must be the same, otherwise we get a contradiction if we choose the 100 elements with the most factors \( p \).
We now see that \( S \) must contain at least 199 non-prime numbers, because a prime number \( p \) in \( S \) divides at least 199 other elements of \( S \). Suppose now that \( S \) contains exactly 199 non-prime numbers. Then the prime factor \( p \) appears in each of these 199 non-prime numbers exactly once (the same number of times as in the prime number \( p \)). Furthermore, numbers in \( S \) cannot be divisible by a prime number \( r \) that is not in \( S \), because then there must be at least 200 multiples of \( r \) in \( S \), which would be 200 non-prime numbers, a contradiction. This implies that each of the 199 non-prime numbers in \( S \) must be the product of the prime numbers in \( S \) and in particular these 199 numbers are not distinct from each other. This is a contradiction, so \( S \) must contain at least 200 non-prime numbers and thus at most 1819 prime numbers.
|
1819
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Een verzameling $S$ die bestaat uit 2019 (verschillende) positieve gehele getallen heeft de volgende eigenschap: het product van elke 100 elementen van $S$ is een deler van het product van de overige 1919 elementen. Wat is het maximale aantal priemgetallen dat $S$ kan bevatten?
|
Het maximale aantal priemgetallen is 1819.
We beginnen met de constructie. Kies verschillende priemgetallen $p_{1}, p_{2}, \ldots, p_{1819}$ en zij $P=p_{1} p_{2} \cdots p_{1819}$. Neem
$$
S=\left\{p_{1}, p_{2}, \ldots, p_{1819}, P, P \cdot p_{1}, \ldots, P \cdot p_{199}\right\}
$$
Voor elke $p_{i}$ geldt dat er 201 getallen in $S$ zijn die deelbaar zijn door $p_{i}$ (namelijk $p_{i}$ en alle getallen deelbaar door $P$ ). Hiervan is er hoogstens één getal met twee factoren $p_{i}$; de rest heeft één factor $p_{i}$. Nemen we nu 100 getallen uit $S$, dan zitten in hun product hoogstens 101 factoren $p_{i}$. Bij de overige getallen zitten nog minstens 101 getallen deelbaar door $p_{i}$, dus hun product heeft minstens 101 factoren $p_{i}$. Omdat dit voor elke $p_{i}$ geldt en de getallen uit $S$ geen andere priemfactoren hebben, betekent dit dat $S$ de gewenste eigenschap heeft.
We bewijzen nu dat $S$ niet meer dan 1819 priemgetallen kan bevatten. Bekijk een priemdeler $q$ van een getal in $S$. Stel dat hooguit 199 getallen in $S$ deelbaar zijn door $q$. Dan nemen we de 100 elementen van $S$ met de meeste factoren $q$ erin; die hebben samen altijd meer factoren $q$ dan de overige elemenenten, tegenspraak met de voorwaarde in de opgave. Dus er zijn minstens 200 getallen in $S$ deelbaar door $q$. Als het er precies 200 zijn, volgt bovendien dat het aantal priemfactoren $q$ in al deze getallen gelijk moet zijn, anders krijgen we weer een tegenspraak als we de 100 elementen met de meeste factoren $p$ kiezen.
We zien nu dat $S$ minstens 199 niet-priemgetallen moet bevatten, want een priemgetal $p$ in $S$ deelt nog minstens 199 andere elementen van $S$. Stel nu dat $S$ precies 199 nietpriemgetallen bevat. Dan komt de priemfactor $p$ in elk van deze 199 niet-priemgetallen precies één keer voor (namelijk net zo vaak als in het priemgetal $p$ ). Verder kunnen getallen in $S$ nu niet deelbaar zijn door een priemgetal $r$ dat zelf niet in $S$ zit, want dan moeten er wel in totaal minstens 200 veelvouden van $r$ in $S$ zitten en dat zijn dan 200 niet-priemgetallen, tegenspraak. Hieruit volgt dat elk van de 199 niet-priemgetallen in $S$ het product moet zijn van de priemgetallen in $S$ en in het bijzonder zijn deze 199 getallen dus niet verschillend van elkaar. Dit is een tegenspraak, dus $S$ moet minstens 200 niet-priemgetallen bevatten en daarmee hoogstens 1819 priemgetallen.
|
{
"exam": "Dutch_TST",
"problem_label": "5",
"problem_match": "\nOpgave 5.",
"resource_path": "Dutch_TST/segmented/nl-2020-B2020_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2020"
}
|
In an acute triangle $A B C$, $I$ is the center of the inscribed circle, and it is given that $|A C|+|A I|=|B C|$. Prove that $\angle B A C=2 \angle A B C$.
|
Define a point $D$ on side $B C$ such that $|C D|=|A C|$. Given that $|B C|=|A C|+|A I|$, $D$ lies internally on side $B C$ and $|B D|=|A I|$. Since triangle $A C D$ is now isosceles, bisector $C I$ is also the perpendicular bisector of $A D$, so $A$ and $D$ are each other's reflection in $C I$. This implies $\angle C D I=\angle C A I=\angle I A B$, so $180^{\circ}-\angle B D I=\angle I A B$, which means that $A B D I$ is a cyclic quadrilateral. In this cyclic quadrilateral, $B D$ and $A I$ are of equal length. According to Julian's theorem, $A B$ and $I D$ are then parallel. Therefore, $A B D I$ is an isosceles trapezoid and the base angles of this trapezoid are equal. Thus, $\angle C B A=\angle D B A=\angle B A I=\frac{1}{2} \angle B A C$, from which the desired result follows directly.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In scherphoekige driehoek $A B C$ is $I$ het middelpunt van de ingeschreven cirkel en geldt $|A C|+|A I|=|B C|$. Bewijs dat $\angle B A C=2 \angle A B C$.

|
Definieer een punt $D$ op zijde $B C$ zodat $|C D|=|A C|$. Vanwege het gegeven dat $|B C|=|A C|+|A I|$ ligt $D$ dan inwendig op zijde $B C$ en geldt $|B D|=|A I|$. Omdat driehoek $A C D$ nu gelijkbenig is, is bissectrice $C I$ ook middelloodlijn van $A D$, dus zijn $A$ en $D$ elkaars gespiegelde in $C I$. Hieruit volgt $\angle C D I=\angle C A I=\angle I A B$, dus $180^{\circ}-\angle B D I=\angle I A B$, wat betekent dat $A B D I$ een koordenvierhoek is. In deze koordenvierhoek zijn $B D$ en $A I$ even lang. Volgens de stelling van Julian zijn dan $A B$ en $I D$ evenwijdig. Dus $A B D I$ is een gelijkbenig trapezium en daarvan zijn de basishoeken gelijk. Dus $\angle C B A=\angle D B A=\angle B A I=\frac{1}{2} \angle B A C$, waaruit het gevraagde direct volgt.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2020-C2020_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2020"
}
|
In an acute triangle $A B C$, $I$ is the center of the inscribed circle, and it is given that $|A C|+|A I|=|B C|$. Prove that $\angle B A C=2 \angle A B C$.

|
Define a point $E$ on line $A C$ such that $A$ lies between $E$ and $C$ and $|A E|=|A I|$. Given that $|B C|=|A C|+|A I|$, it follows that $|B C|=|C E|$. Therefore, triangles $E C I$ and $B C I$ have sides $|B C|=|C E|$ and $|C I|$ of equal length, and $\angle E C I=\angle B C I$ due to the angle bisector $C I$. Thus, $\triangle E C I \cong \triangle B C I$ (SAS). In isosceles triangle $E A I$,
$\angle I E A=\frac{1}{2}\left(180^{\circ}-\angle E A I\right)=\frac{1}{2} \angle C A I$. Therefore, $\angle A B C=2 \angle I B C=2 \angle I E C=2 \angle I E A=$
$\angle C A I=\frac{1}{2} \angle B A C$, from which the desired result directly follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In scherphoekige driehoek $A B C$ is $I$ het middelpunt van de ingeschreven cirkel en geldt $|A C|+|A I|=|B C|$. Bewijs dat $\angle B A C=2 \angle A B C$.

|
Definieer een punt $E$ op lijn $A C$ zodat $A$ tussen $E$ en $C$ ligt en $|A E|=|A I|$. Vanwege het gegeven dat $|B C|=|A C|+|A I|$ geldt dan $|B C|=|C E|$. Dus driehoeken $E C I$ en $B C I$ hebben zijden $|B C|=|C E|$ en $|C I|$ even lang en er geldt $\angle E C I=\angle B C I$ vanwege de bissectrice $C I$. Dus $\triangle E C I \cong \triangle B C I$ (ZHZ). In gelijkbenige driehoek $E A I$
geldt $\angle I E A=\frac{1}{2}\left(180^{\circ}-\angle E A I\right)=\frac{1}{2} \angle C A I$. Dus $\angle A B C=2 \angle I B C=2 \angle I E C=2 \angle I E A=$ $\angle C A I=\frac{1}{2} \angle B A C$, waaruit het gevraagde direct volgt.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2020-C2020_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2020"
}
|
Determine all polynomials $P(x)$ with real coefficients for which
$$
P\left(x^{2}\right)+2 P(x)=P(x)^{2}+2 .
$$
|
Rewrite the given equation to
$$
P\left(x^{2}\right)-1=(P(x)-1)^{2} \text {. }
$$
Let $Q(x)=P(x)-1$, then $Q$ is a polynomial with real coefficients for which
$$
Q\left(x^{2}\right)=Q(x)^{2}
$$
Suppose $Q$ is constant, say $Q(x)=c$ with $c \in \mathbb{R}$. Then $c=c^{2}$, so $c=0$ or $c=1$. Both possibilities satisfy the equation. We can now assume that $Q$ is not constant, so we can write $Q(x)=b x^{n}+R(x)$ with $n \geq 1, b \neq 0$ and $R(x)$ a polynomial with real coefficients of degree at most $n-1$. The polynomial equation now becomes
$$
b x^{2 n}+R\left(x^{2}\right)=b^{2} x^{2 n}+2 b x^{n} \cdot R(x)+R(x)^{2} .
$$
By comparing the coefficients of $x^{2 n}$ on both sides, we get $b=b^{2}$. Since $b \neq 0$, it follows that $b=1$. If we now subtract $x^{2 n}$ from both sides, we find
$$
R\left(x^{2}\right)=2 x^{n} \cdot R(x)+R(x)^{2} .
$$
If $R$ is not the zero polynomial, then it has a degree $m \geq 0$. It holds that $m<n$. The left side of this equation then has degree $2 m$ and the right side has degree $m+n$, since $m+n>2 m$. Contradiction. Therefore, $R$ must be the zero polynomial, which implies that $Q(x)=x^{n}$. This indeed satisfies the polynomial equation for $Q$.
This gives for $P$ the solutions $P(x)=1, P(x)=2$ and $P(x)=x^{n}+1$ with $n \geq 1$.
|
P(x)=1, P(x)=2, P(x)=x^n+1 \text{ with } n \geq 1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Bepaal alle polynomen $P(x)$ met reële coëfficiënten waarvoor geldt
$$
P\left(x^{2}\right)+2 P(x)=P(x)^{2}+2 .
$$
|
Herschrijf de gegeven vergelijking naar
$$
P\left(x^{2}\right)-1=(P(x)-1)^{2} \text {. }
$$
Schrijf $Q(x)=P(x)-1$, dan is $Q$ een polynoom met reële coëfficiënten waarvoor geldt dat
$$
Q\left(x^{2}\right)=Q(x)^{2}
$$
Stel dat $Q$ constant is, zeg $Q(x)=c$ met $c \in \mathbb{R}$. Dan geldt $c=c^{2}$, dus $c=0$ of $c=1$. Beide mogelijkheden voldoen. We kunnen nu verder aannemen dat $Q$ niet constant is, dus kunnen we schrijven $Q(x)=b x^{n}+R(x)$ met $n \geq 1, b \neq 0$ en $R(x)$ een polynoom met reële coëfficiënten van graad hoogstens $n-1$. De polynoomvergelijking wordt nu
$$
b x^{2 n}+R\left(x^{2}\right)=b^{2} x^{2 n}+2 b x^{n} \cdot R(x)+R(x)^{2} .
$$
Door de coëfficiënten van $x^{2 n}$ links en rechts te vergelijken, krijgen we $b=b^{2}$. Aangezien $b \neq 0$ volgt daaruit dat $b=1$. Als we nu links en rechts $x^{2 n}$ aftrekken, vinden we
$$
R\left(x^{2}\right)=2 x^{n} \cdot R(x)+R(x)^{2} .
$$
Als $R$ niet het nulpolynoom is, dan heeft hij een graad $m \geq 0$. Er geldt $m<n$. De linkerkant van deze vergelijking heeft dan graad $2 m$ en de rechterkant graad $m+n$, want $m+n>2 m$. Tegenspraak. Dus $R$ moet het nulpolynoom zijn, waaruit volgt dat $Q(x)=x^{n}$. Dit voldoet inderdaad aan de polynoomvergelijking voor $Q$.
Dit geeft voor $P$ de oplossingen $P(x)=1, P(x)=2$ en $P(x)=x^{n}+1$ met $n \geq 1$.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2020-C2020_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2020"
}
|
Determine all polynomials $P(x)$ with real coefficients for which
$$
P\left(x^{2}\right)+2 P(x)=P(x)^{2}+2 .
$$
|
Suppose $P$ is constant, say $P(x)=c$ with $c \in \mathbb{R}$. Then $c+2c=c^2+2$, so $c^2-3c+2=0$, thus $(c-2)(c-1)=0$, hence $c=2$ or $c=1$. Both possibilities satisfy the equation. We can now assume that $P$ is not constant, so we can write $P(x)=a_n x^n + a_{n-1} x^{n-1} + \ldots + a_1 x + a_0$ with $n \geq 1$ and $a_n \neq 0$. By comparing the coefficients of $x^{2n}$ on both sides, we see that $a_n = a_n^2$. Since $a_n \neq 0$, it follows that $a_n = 1$.
We now prove by induction on $k$ that $a_k = 0$ for all $1 \leq k \leq n-1$. As the induction hypothesis, we assume that for some $k$ with $1 \leq k \leq n-1$, $a_i = 0$ for all $k < i \leq n-1$. (We don't need an induction base; if $k=n-1$, the induction hypothesis is an empty statement.) In $P(x^2)$, the first term after $x^{2n}$ that might not be 0 is the one with $x^{2k}$. Since $k \leq n-1$, the coefficient of $x^{n+k}$ is certainly 0. The term $2P(x)$ cannot contribute to this coefficient because $k \geq 1$. Therefore, the coefficient of $x^{n+k}$ on the left is 0. On the right, the 2 is irrelevant because $n+k > 0$. In $P(x)^2$, the coefficient of $x^{n+k}$ is $\sum_{j=k}^{n} a_j a_{n+k-j}$. Since $a_i = 0$ for $k < i \leq n-1$, this sum is equal to $a_k a_n + a_n a_k$. We conclude that $2a_n a_k = 0$, which means that $a_k = 0$. This completes the induction.
We now know that $P$ is of the form $P(x) = x^n + c$. By substituting $x=0$ into the given polynomial equation, we see that $c + 2c = c^2 + 2$. We have already seen that this equation gives $c=1$ or $c=2$. We now check the two possible solutions $P(x) = x^n + 1$ and $P(x) = x^n + 2$. In the first case, on the left we have $(x^{2n} + 1) + 2(x^n + 1)$ and on the right $(x^n + 1)^2 + 2$, which are both equal to $x^{2n} + 2x^n + 3$, so this polynomial satisfies the equation. In the second case, on the left we have $(x^{2n} + 2) + 2(x^n + 2) = x^{2n} + 2x^n + 6$ and on the right $(x^n + 2)^2 + 2 = x^{2n} + 4x^n + 6$, which are not equal, so this polynomial does not satisfy the equation.
We conclude that the solutions are: $P(x) = 1$, $P(x) = 2$, and $P(x) = x^n + 1$ with $n \geq 1$.
|
P(x) = 1, P(x) = 2, P(x) = x^n + 1 \text{ with } n \geq 1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Bepaal alle polynomen $P(x)$ met reële coëfficiënten waarvoor geldt
$$
P\left(x^{2}\right)+2 P(x)=P(x)^{2}+2 .
$$
|
Stel dat $P$ constant is, zeg $P(x)=c$ met $c \in \mathbb{R}$. Dan geldt $c+2 c=c^{2}+2$, dus $c^{2}-3 c+2=0$, dus $(c-2)(c-1)=0$, dus $c=2$ of $c=1$. Beide mogelijkheden voldoen. We kunnen nu verder aannemen dat $P$ niet constant is, dus kunnen we schrijven $P(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\ldots+a_{1} x+a_{0}$ met $n \geq 1$ en $a_{n} \neq 0$. Door nu links en rechts de coëfficiënten van $x^{2 n}$ te vergelijken, zien we dat $a_{n}=a_{n}^{2}$. Omdat $a_{n} \neq 0$, volgt hieruit dat $a_{n}=1$.
We bewijzen nu met inductie naar $k$ dat $a_{k}=0$ voor alle $1 \leq k \leq n-1$. Als inductiehypothese nemen we aan dat voor zekere $k$ met $1 \leq k \leq n-1$ geldt dat $a_{i}=0$ voor alle
$k<i \leq n-1$. (We hebben nu geen inductiebasis nodig; als $k=n-1$ is de inductiehypothese een lege bewering.) In $P\left(x^{2}\right)$ is de eerste term na $x^{2 n}$ die mogelijk niet 0 is, die met $x^{2 k}$. Omdat $k \leq n-1$, is de coëfficiënt van $x^{n+k}$ dus zeker gelijk aan 0 . De term $2 P(x)$ kan niet aan deze coëfficiënt bijdragen, want $k \geq 1$. Dus links is de coëfficiënt van $x^{n+k}$ gelijk aan 0 . Rechts is de 2 niet relevant omdat $n+k>0$. In $P(x)^{2}$ is de coëfficiënt van $x^{n+k}$ gelijk aan $\sum_{j=k}^{n} a_{j} a_{n+k-j}$. Omdat $a_{i}=0$ voor $k<i \leq n-1$ is deze som gelijk aan $a_{k} a_{n}+a_{n} a_{k}$. We concluderen dat $2 a_{n} a_{k}=0$, wat betekent dat $a_{k}=0$. Dit voltooit de inductie.
We weten nu dat $P$ van de vorm $P(x)=x^{n}+c$ is. Door $x=0$ in te vullen in de gegeven polynoomvergelijking zien we bovendien dat $c+2 c=c^{2}+2$. We hebben eerder al gezien dat deze vergelijking $c=1$ of $c=2$ geeft. We controleren nu dus de twee mogelijke oplossingen $P(x)=x^{n}+1$ en $P(x)=x^{n}+2$. In het eerste geval staat er links $\left(x^{2 n}+1\right)+2\left(x^{n}+1\right)$ en rechts $\left(x^{n}+1\right)^{2}+2$, wat allebei gelijk is aan $x^{2 n}+2 x^{n}+3$, dus dit polynoom voldoet. In het tweede geval staat er links $\left(x^{2 n}+2\right)+2\left(x^{n}+2\right)=x^{2 n}+2 x^{n}+6$ en rechts $\left(x^{n}+2\right)^{2}+2=x^{2 n}+4 x^{n}+6$, wat niet gelijk is aan elkaar, dus dit polynoom voldoet niet.
We concluderen dat de oplossingen zijn: $P(x)=1, P(x)=2$ en $P(x)=x^{n}+1$ met $n \geq 1$.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2020-C2020_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2020"
}
|
For a positive integer $n$, we consider an $n \times n$ board and tiles with dimensions $1 \times 1, 1 \times 2, \ldots, 1 \times n$. In how many ways can exactly $\frac{1}{2} n(n+1)$ squares of the board be colored red, such that the red squares can all be covered by the $n$ tiles placed horizontally, and also by the $n$ tiles placed vertically? Two colorings that are not identical but can be transformed into each other by rotating or reflecting the board are counted as different.
|
The number of red squares is exactly equal to the total number of squares that can be covered by the $n$ tiles, so the tiles are placed only on red squares. Consider a coloring of the board and the corresponding horizontal covering of the tiles (where all tiles lie horizontally) and the vertical covering. We derive several properties of the coloring and then count the number of possibilities. Let the tile with dimensions $1 \times k$ be the $k$-tile.
Since the horizontal covering contains an $n$-tile, each column must contain at least one red square. Therefore, in the vertical covering, there must be at least one tile in each column; since there are exactly $n$ tiles, this means that there must be exactly one tile in each column. Similarly, there must be exactly one tile in each row in the horizontal covering. Number the rows and columns based on the number of the tile that lies in them: so row $i$ is the row in which the $i$-tile lies in the horizontal covering, and analogously for the columns.
We now prove that the square in row $i$ and column $j$ (call this square $(i, j)$) is red if and only if $i+j \geq n+1$. We prove this by induction on $i$. In row 1, there is only one red square, and it must be in the column where the $n$-tile lies in the vertical covering, so in column $n$. Thus, the square $(1, j)$ is red if and only if $j=n$, or equivalently, if and only if $1+j \geq n+1$. Now let $k \geq 1$ and assume we have proven this for all $i \leq k$. We want to prove it for $i=k+1$, that is, that a square $(k+1, j)$ is red if and only if $k+1+j \geq n+1$, or equivalently, if $j \geq n-k$. Consider a column $j \geq n-k$. By the induction hypothesis, we know exactly how many red squares this column has in rows $1,2, \ldots, k$: the square $(i, j)$ is red if and only if $i+j \geq n+1$, or $i \geq n+1-j$, so there are $k-(n-j)=j+k-n$ such squares. In the remaining $n-k$ rows, this column needs $j-(j+k-n)=n-k$ more red squares. Therefore, this column has a red square in each of those rows and in particular also in row $i=k+1$. In row $i=k+1$, the squares $(i, j)$ with $j \geq n-k$ are all red, and there are $k+1$ such squares. Thus, these are exactly all the red squares in row $i=k+1$, so the square $(i, j)$ is red if and only if $j \geq n-k$, or equivalently, if and only if $i+j \geq n-k+k+1=n+1$. This completes the induction.
Now consider two rows directly above each other with row numbers $a$ and $b$, with $a>b$. In column $n-b$, there is a red square in row $a$ (since $a+n-b>n$) but not in row $b$. In the row directly on the other side of row $b$ (if it exists), there should therefore be no red square in column $n-b$, otherwise the red squares in column $n-b$ would not be contiguous and the tile with number $n-b$ could not lie here. The row number of this row must therefore be less than $b$. We conclude that the row numbers cannot first decrease and then increase again. Above and below row $n$, there must be a row with a smaller number (or no more rows at all), so the row numbers must decrease on both sides from there. We see that the row numbers must first be increasing up to row $n$ and then decreasing. The same can be proven for the column numbers.
Conversely, we need to prove that if the row and column numbers are first increasing and then decreasing, we can place both the horizontal and vertical tiles. For this, we color the square $(i, j)$ red if and only if $i+j \geq n+1$. For a fixed $i$, the red squares are thus the squares $(i, j)$ with $j \geq n+1-i$; due to the shape of the column numbers, these columns are contiguous. Therefore, the red squares in each row are contiguous. We can thus place the horizontal tiles exactly on the red squares. The same works for the vertical tiles. We could not have chosen a different coloring with the same row and column numbers that would allow the tiling, because we already know that in every valid tiling, $(i, j)$ is red if and only if $i+j \geq n+1$.
In total, we are looking for the number of ways to choose both the row and column numbers in an order that is first increasing and then decreasing; for each of these choices, there is exactly one way to color the red squares that satisfies the condition. The number of ways to arrange the numbers 1 to $n$ in an order that is first increasing and then decreasing is equal to the number of subsets of $\{1,2, \ldots, n-1\}$, namely the subset of numbers that come before the number $n$; these can be sorted in only one way (increasing) and the rest of the numbers must be sorted in decreasing order and placed after $n$. The number of subsets is $2^{n-1}$. Therefore, the total number of colorings that satisfy the problem is $\left(2^{n-1}\right)^{2}=2^{2 n-2}$.
|
2^{2n-2}
|
Yes
|
Incomplete
|
math-word-problem
|
Combinatorics
|
Voor een positief geheel getal $n$ bekijken we een $n \times n$-bord en tegels met afmetingen $1 \times 1,1 \times 2, \ldots, 1 \times n$. Op hoeveel manieren kunnen er precies $\frac{1}{2} n(n+1)$ vakjes van het bord rood worden gekleurd, zodat de rode vakjes allemaal bedekt kunnen worden door de $n$ tegels allemaal horizontaal te plaatsen, maar ook door de $n$ tegels allemaal verticaal te plaatsen? Twee kleuringen die niet identiek zijn, maar door draaiing of spiegeling van het bord in elkaar overgaan, tellen als verschillend.
|
Het aantal rode vakjes is het precies gelijk aan het totaal aantal vakjes dat door de $n$ tegels bedekt kan worden, dus de tegels worden alleen op rode vakjes gelegd. Bekijk een kleuring van het bord en de bijbehorende horizontale bedekking van de tegels (waarin alle tegels horizontaal liggen) en verticale bedekking. We leiden een aantal eigenschappen van de kleuring af en tellen daarna hoeveel mogelijkheden er zijn. Noem de tegel met afmetingen $1 \times k$ de $k$-tegel.
Omdat de horizontale bedekking een $n$-tegel bevat, bevat elke kolom minstens één rood vakje. In de verticale bedekking moet daarom in elke kolom minstens één tegel liggen; omdat er precies $n$ tegels zijn, betekent dat dat er in elke kolom precies één tegel moet liggen. Net zo moet er in de horizontale bedekking in elke rij precies één tegel liggen. Nummer nu de rijen en kolommen afhankelijk van het nummer van de tegel die daarin ligt: dus rij $i$ is de rij waarin de $i$-tegel ligt in de horizontale bedekking, en analoog voor de kolommen.
We bewijzen nu eerst dat het vakje in rij $i$ en kolom $j$ (noem dit vakje $(i, j)$ ) rood is dan en slechts dan als $i+j \geq n+1$. We bewijzen dit met inductie naar $i$. In rij 1 is er slechts één rood vakje en dat moet wel in de kolom zijn waar de $n$-tegel ligt in de verticale bedekking, dus in kolom $n$. Dus het vakje $(1, j)$ is rood dan en slechts als $j=n$, oftewel dan en slechts dan als $1+j \geq n+1$. Zij nu $k \geq 1$ en neem aan dat we dit bewezen hebben voor alle $i \leq k$. We willen het nu bewijzen voor $i=k+1$, dus dat een vakje $(k+1, j)$ rood is dan en slechts dan als $k+1+j \geq n+1$, oftewel als $j \geq n-k$. Bekijk dus een kolom $j \geq n-k$. We weten wegens de inductiehypothese precies hoeveel rode vakjes deze kolom heeft in de rijen $1,2, \ldots, k$ : het vakje $(i, j)$ is namelijk rood dan en slechts dan als $i+j \geq n+1$, oftewel $i \geq n+1-j$, dus dat zijn er $k-(n-j)=j+k-n$. In de overige $n-k$ rijen heeft deze kolom dus nog $j-(j+k-n)=n-k$ rode vakjes nodig. Dus deze kolom heeft een rood vakje in elk van die rijen en in het bijzonder ook in rij $i=k+1$. In rij $i=k+1$ zijn dus de vakjes $(i, j)$ met $j \geq n-k$ allemaal rood en dat zijn er $k+1$. Dus dit zijn precies alle rode vakjes in rij $i=k+1$, dus het vakje $(i, j)$ is rood dan en slechts dan als $j \geq n-k$, oftewel dan en slechts dan als $i+j \geq n-k+k+1=n+1$. Dit voltooit de inductie.
Bekijk nu twee rijen direct boven elkaar met rijnummers $a$ en $b$, met $a>b$. In kolom $n-b$ zit een rood vakje in rij $a$ (want $a+n-b>n$ ) maar niet in rij $b$. In de rij direct aan de andere kant van rij $b$ (als deze bestaat) mag daarom geen rood vakje in kolom $n-b$ zitten, want anders zouden de rode vakjes in kolom $n-b$ niet aaneengesloten zijn en kan de
tegel met nummer $n-b$ hier niet liggen. Het rijnummer van deze rij moet daarom kleiner dan $b$ zijn. We concluderen dat de rijnummers niet eerst kunnen dalen en daarna weer stijgen. Boven en onder rij $n$ moet wel een rij met een kleiner nummer zitten (of helemaal geen rij meer) dus dalen vanaf daar de rijnummers allebei de kanten op. We zien dat de rijnummers van boven naar beneden eerst oplopend moeten zijn tot aan rij $n$ en daarna aflopend. Hetzelfde kunnen we bewijzen voor de kolomnummers.
Andersom moeten we bewijzen dat als de rijnummers en kolomnummers eerst oplopend en dan aflopend zijn, dat we dan de horizontale en verticale tegels allebei neer kunnen leggen. Hiervoor kleuren we de vakje $(i, j)$ rood dan en slechts dan als $i+j \geq n+1$. Voor vaste $i$ zijn de rode vakjes dus de vakjes $(i, j)$ met $j \geq n+1-i$; vanwege de vorm van de kolomnummers zijn die kolommen aaneengesloten. Dus in elke rij zijn de rode vakjes aaneengesloten. We kunnen dus de horizontale tegels precies op de rode vakjes leggen. Net zo goed lukt dit met de verticale tegels. We hadden bij dezelfde rij- en kolomnummers niet een andere kleuring kunnen kiezen waarvoor de betegeling werkt, want we weten al dat bij elke goede betegeling geldt dat $(i, j)$ rood is dan en slechts dan als $i+j \geq n+1$.
Al met al zijn we dus op zoek naar het aantal manieren om zowel de rij- als de kolomnummers te kiezen in een volgorde die eerst oplopend en daarna aflopend is; bij elk van die keuzes hoort precies één manier om de rode vakjes te kleuren die aan de voorwaarde voldoet. Het aantal manieren om de getallen 1 tot en met $n$ in een volgorde te zetten die eerst oplopend en dan aflopend is, is gelijk aan het aantal deelverzamelingen van $\{1,2, \ldots, n-1\}$, namelijk de deelverzameling van getallen die vóór het getal $n$ komen; deze kunnen maar op één manier gesorteerd worden (oplopend) en de rest van de getallen moet juist aflopend gesorteerd worden en na $n$ neergezet worden. Het aantal deelverzamelingen is $2^{n-1}$. Dus het totaal aantal kleuringen dat aan de opgave voldoet is $\left(2^{n-1}\right)^{2}=2^{2 n-2}$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2020-C2020_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2020"
}
|
For a positive integer $n$, we consider an $n \times n$ board and tiles with dimensions $1 \times 1, 1 \times 2, \ldots, 1 \times n$. In how many ways can exactly $\frac{1}{2} n(n+1)$ squares of the board be colored red, such that the red squares can all be covered by the $n$ tiles placed horizontally, and also by the $n$ tiles placed vertically? Two colorings that are not identical but can be transformed into each other by rotating or reflecting the board are counted as different.
|
Just as in Solution I, we deduce that in the horizontal tiling, there must be exactly one tile in each row, and in the vertical tiling, there must be exactly one tile in each column. First, consider an order for the tiles in the vertical tiling. We will derive the conditions this order must satisfy and how many possibilities there are per order to place the tiles (and thus choose the coloring).
Consider the column with the $n$-tile. This tile can only lie in one way in this column. Now consider an arbitrary other tile with length $i$. This tile covers $i$ cells in its column. In each row, the red cells must be contiguous, so in the $i$ rows where the $i$-tile lies, there are red cells from the column with the $i$-tile to the column with the $n$-tile. Therefore, the tiles between these columns must have a length of at least $i$. We see that the tile numbers must be increasing from left to right up to the $n$-tile and then decreasing. The number of ways to choose the vertical tiles in such an order is $2^{n-1}$ (see the end of Solution I).
Now consider one of these orders. We will place the vertical tiles in the columns and simultaneously color the cells they cover red. The $(n-1)$-tile can lie in its column in two ways. The only row where it does not lie must be the row where there is only one red cell, because all other rows already have at least two red cells. In this row (the top or bottom), no more tiles can be placed; we call this row complete. There are then two ways to place the $(n-2)$-tile in its column, as it must lie within the $n-1$ rows of the $(n-1)$-tile. After placing the $(n-2)$-tile, a second row is complete, namely the second row where this tile does not lie and where there are exactly two red cells. These two red cells are now automatically contiguous. The remaining rows (which are not yet complete) now have at least three red cells. Next, the $(n-3)$-tile must lie within the $n-2$ rows of the $(n-2)$-tile, making a third row complete, namely the one with exactly three red cells. These red cells are also contiguous. And so on. For each subsequent tile, there are exactly two options for placing it. In total, this gives $2^{n-1}$ possibilities. After making a choice for each tile, the number of red cells per row is exactly the numbers $1, 2, 3, \ldots, n$, and the red cells in all rows are contiguous. This means it is possible to place the horizontal tiles exactly on the red cells. We have a total of $2^{n-1} \cdot 2^{n-1} = 2^{2n-2}$ possible ways to color the board. Each of these ways satisfies all the conditions. Therefore, the total number of colorings that satisfy the problem is $2^{2n-2}$.
|
2^{2n-2}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Voor een positief geheel getal $n$ bekijken we een $n \times n$-bord en tegels met afmetingen $1 \times 1,1 \times 2, \ldots, 1 \times n$. Op hoeveel manieren kunnen er precies $\frac{1}{2} n(n+1)$ vakjes van het bord rood worden gekleurd, zodat de rode vakjes allemaal bedekt kunnen worden door de $n$ tegels allemaal horizontaal te plaatsen, maar ook door de $n$ tegels allemaal verticaal te plaatsen? Twee kleuringen die niet identiek zijn, maar door draaiing of spiegeling van het bord in elkaar overgaan, tellen als verschillend.
|
Net als in oplossing I leiden we af dat er in de horizontale bedekking in elke rij precies één tegel moet liggen en in de verticale bedekking in elke kolom precies één tegel. Bekijk nu eerst een volgorde voor de tegels in de verticale bedekking. We gaan afleiden aan welke eisen deze volgorde moet voldoen en hoeveel mogelijkheden er per volgorde zijn om de tegels neer te leggen (en daarmee de kleuring te kiezen).
Bekijk de kolom met de $n$-tegel. Deze tegel kan maar op één manier in deze kolom liggen. Bekijk vervolgens een willekeurige andere tegel met lengte $i$. Deze bedekt $i$ vakjes in zijn kolom. In elke rij moeten de rode vakjes aaneengesloten zijn, dus in de $i$ rijen waarin de $i$-tegel ligt, zijn er rode vakjes vanaf de kolom met de $i$-tegel tot en met de kolom met de $n$-tegel. In de kolommen daartussen liggen dus tegels met lengte minstens $i$. We zien dus dat de tegelnummers van links naar rechts oplopend moeten zijn tot aan de $n$-tegel en daarna juist aflopend. Het aantal manieren om de verticale tegels in zo'n volgorde te kiezen, is $2^{n-1}$ (zie het einde van oplossing I).
We bekijken nu één van deze volgordes. We gaan de verticale tegels in de kolommen leggen en tegelijkertijd de vakjes die ze bedekken, rood kleuren. De $(n-1)$-tegel kan op twee manieren in zijn kolom liggen. De enige rij waarin hij niet ligt, moet nu wel de rij zijn waarin maar één rood vakje komt, want alle andere rijen hebben al minstens twee rode vakjes. In deze rij (de bovenste of onderste) mag dus geen tegel meer gelegd worden; we noemen deze rij klaar. Vervolgens zijn er daardoor twee manieren om de $(n-2)$-tegel in zijn kolom te leggen, want die moet binnen de $n-1$ rijen van de $(n-1)$-tegel vallen. Na het neerleggen van de ( $n-2$ )-tegel is er een tweede rij klaar, namelijk de tweede rij waar deze tegel niet in ligt en waar dus precies twee rode vakjes zijn. Deze twee rode vakjes zijn nu automatisch aaneengesloten. De rest van de rijen (die nog niet klaar zijn) hebben nu minstens drie rode vakjes. Hierna moet de $(n-3)$-tegel binnen de $n-2$ rijen van de $(n-2)$-tegel liggen, waardoor er een derde rij klaar is, namelijk die met precies drie rode vakjes. Deze rode vakjes zijn ook weer aaneengesloten. Enzovoorts. Voor elke volgende tegel zijn er dus precies twee opties om hem neer te leggen. In totaal geeft dit $2^{n-1}$ mogelijkheden. Nadat we voor elke tegel een keuze hebben gemaakt, zijn de aantallen rode vakjes per rij precies de getallen $1,2,3, \ldots, n$ en liggen in alle rijen de rode vakjes aaneengesloten. Dit betekent dat het lukt om de horizontale tegels precies op de rode vakjes te leggen. We hebben in totaal $2^{n-1} \cdot 2^{n-1}=2^{2 n-2}$ mogelijke manieren waarop we nu het bord gekleurd hebben. Elk van deze manieren voldoet aan alle voorwaarden. Dus het totaal aantal kleuringen dat aan de opgave voldoet is $2^{2 n-2}$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2020-C2020_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2020"
}
|
Let $\mathrm{a}, \mathrm{b} \geq 2$ be positive integers with $\operatorname{gcd}(\mathrm{a}, \mathrm{b})=1$. Let $r$ be the smallest positive value assumed by an expression of the form $\frac{a}{b}-\frac{c}{d}$, where $c$ and $d$ are positive integers satisfying $\mathbf{c} \leq \mathrm{a}$ and $\mathrm{d} \leq \mathrm{b}$. Prove that $\frac{1}{r}$ is an integer.
|
We first show that it is possible to choose $\mathbf{C}$ and $\mathbf{d}$ such that $\frac{a}{b}-\frac{c}{d}=\frac{1}{b d}$.
Since $\operatorname{gcd}(\mathrm{a}, \mathrm{b})=1$, there exists a multiplicative inverse $\mathrm{b}^{-1}$ of b modulo a. Choose now c with $1 \leq \mathrm{c} \leq \mathrm{a}$ such that $\mathrm{c} \equiv-\mathrm{b}^{-1} \bmod \mathrm{a}$. Then $\mathrm{b} \equiv-1 \bmod \mathrm{a}$, so $\mathrm{a} \mid \mathrm{bc}+1$. Define $\mathrm{d}=\frac{b c+1}{a}$, then d is a positive integer. It holds that $\mathrm{d}=\frac{b c+1}{a} \leq \frac{b a+1}{a}=\mathrm{b}+\frac{1}{a}$. Since $\mathrm{a} \geq 2$ and d is an integer, it follows that $\mathrm{d} \leq \mathrm{b}$. Therefore, all conditions are satisfied. Now we have $\frac{a}{b}-\frac{c}{d}=\frac{a d-b c}{b d}=\frac{b c+1-b c}{b d}=\frac{1}{b d}$.
If this is the smallest possible positive result, then we are done, because then $\frac{1}{r}=\mathrm{bd}$ and that is an integer. We want to show that there is no smaller positive result. Take C and d as above and assume that there exist positive integers $\mathrm{c}^{\prime} \leq \mathrm{a}$ and $\mathrm{d}^{\prime} \leq \mathrm{b}$ such that $0<\frac{a}{b}-\frac{c^{\prime}}{d^{\prime}}<\frac{1}{b d}$. We will derive a contradiction.
Let $\mathbf{x}=\mathrm{ad}-\mathrm{bc}^{\prime}$, then $\frac{a}{b}-\frac{c^{\prime}}{d^{\prime}}=\frac{x}{b d^{\prime}}$, so $\mathbf{x b d}<\mathrm{bd}$, which implies that $\mathbf{x d}<\mathrm{d}^{\prime}$. We also know that $x>0$. Therefore, $0<x d<d^{\prime} \leq \mathrm{b}$, which means that $x d$ and $d^{\prime}$ are two different numbers with a difference less than b. Furthermore, from $\mathrm{x}=\mathrm{ad}-\mathrm{bc}^{\prime}$, it follows that $\mathbf{x} \equiv \mathbf{a d} \bmod \mathbf{b}$. On the other hand, we know that $\mathbf{a d}-\mathbf{b}=1$, so $\mathbf{a d} \equiv 1 \bmod \mathbf{b}$, thus $\mathbf{x a d} \equiv \mathbf{x} \bmod \mathbf{b}$. Combining these gives $\mathrm{ad} \equiv \mathrm{xad} \bmod \mathbf{b}$. Since $\operatorname{gcd}(\mathrm{a}, \mathrm{b})=1$, we can divide by $a$, so $\mathrm{d}^{\prime} \equiv x d \bmod \mathbf{b}$. However, we had seen that $d^{\prime}$ and $x d$ are different numbers with a difference less than b, so this is impossible.
We conclude that the chosen $\mathbf{C}$ and $\mathbf{d}$ indeed give the smallest result and that $\frac{1}{r}$ is an integer.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Laat $\mathrm{a}, \mathrm{b} \geq 2$ positieve gehele getallen met $\operatorname{ggd}(\mathrm{a}, \mathrm{b})=1$ zijn. Zij r de kleinste positieve waarde die aangenomen wordt bij een uitdrukking van de vorm $\frac{a}{b}-\frac{c}{d}$, met C en d positieve gehele getallen die voldoen aan $\mathbf{c} \leq \mathrm{a}$ en $\mathrm{d} \leq \mathrm{b}$ Bewijs dat $\frac{1}{r}$ geheel is.
|
We laten eerst zien dat het mogelijk is om $\mathbf{C}$ en $\mathbf{d}$ zo te kiezen dat $\frac{a}{b}-\frac{c}{d}=\frac{1}{b d}$.
Omdat $\operatorname{ggd}(\mathrm{a}, \mathrm{b})=1$, bestaat er een multiplicatieve inverse $\mathrm{b}^{-1}$ van b modulo a . Kies nu c met $1 \leq \mathrm{c} \leq \mathrm{a}$ zo dat $\mathrm{c} \equiv-\mathrm{b}^{-1} \bmod \mathrm{a}$. Er geldt dan $\mathrm{b} \equiv-1 \bmod \mathrm{a}$, dus $\mathrm{a} \mid \mathrm{bc}+1$. Definieer vervolgens $\mathrm{d}=\frac{b c+1}{a}$, dan is d een positief geheel getal. Er geldt $\mathrm{d}=\frac{b c+1}{a} \leq \frac{b a+1}{a}=\mathrm{b}+\frac{1}{a}$. Omdat $\mathrm{a} \geq 2$ en d een geheel getal is, volgt hieruit $\mathrm{d} \leq \mathrm{b}$ Aan alle voorwaarden is daarom voldaan. Er geldt nu $\frac{a}{b}-\frac{c}{d}=\frac{a d-b c}{b d}=\frac{b c+1-b c}{b d}=\frac{1}{b d}$.
Als dit de kleinst mogelijke uitkomst positieve is, dan zijn we klaar, want dan geldt $\frac{1}{r}=\mathrm{bd}$ en dat is geheel. We willen dus laten zien dat er geen kleinere positieve uitkomst mogelijk is. Neem C en d zoals hierboven en stel dat er positieve gehele getallen $\mathrm{c}^{\prime} \leq \mathrm{a}$ en $\mathrm{d}^{\prime} \leq \mathrm{b}$ bestaan zodat $0<\frac{a}{b}-\frac{c^{\prime}}{d^{\prime}}<\frac{1}{b d}$. We gaan een tegenspraak afleiden.
Schrijf $\mathbf{x}=\mathrm{ad}-\mathrm{bc}^{\prime}$, dan geldt $\frac{a}{b}-\frac{c^{\prime}}{d^{\prime}}=\frac{x}{b d^{\prime}}$, dus $\mathbf{x b d}<\mathrm{bd}$, waaruit volgt dat $\mathbf{x d}<\mathrm{d}^{\prime}$. We weten verder dat $x>0$. Dus $0<x d<d^{\prime} \leq \mathrm{b}$ wat betekent dat $x d$ en $d^{\prime}$ twee verschillende getallen zijn met verschil kleiner dan b . Verder volgt uit $\mathrm{x}=\mathrm{ad}$ - $\mathrm{bc}^{\prime}$ dat $\mathbf{x} \equiv \mathbf{a d} \bmod \mathbf{b}$. Anderzijds weten we dat $\mathbf{a d}-\mathbf{b}=1$, dus $\mathbf{a d} \equiv 1 \bmod \mathbf{b}$ dus $\mathbf{x a d} \equiv \mathbf{x}$ $\bmod \mathbf{b} . \quad$ Dit combineren geeft $\mathrm{ad} \equiv \mathrm{xad} \bmod \mathbf{b}$ Omdat $\operatorname{ggd}(\mathrm{a}, \mathrm{b})=1$ mogen we delen door $a$, dus $\mathrm{d}^{\prime} \equiv x d \bmod \mathbf{b}$ Echter, we hadden gezien dat $d^{\prime}$ en $x d$ verschillende getallen zijn met verschil kleiner dan b dus dit is onmogelijk.
We concluderen dat de gevonden $\mathbf{C}$ en $\mathbf{d}$ inderdaad de kleinste uitkomst geven en dat dus $\frac{1}{r}$ geheel is.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2020-C2020_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2020"
}
|
Given are real numbers $a_{1}, a_{2}, \ldots, a_{2020}$, not necessarily distinct. For every $n \geq 2020$, $a_{n+1}$ is now defined as the smallest real root of the polynomial
$$
P_{n}(x)=x^{2 n}+a_{1} x^{2 n-2}+a_{2} x^{2 n-4}+\ldots+a_{n-1} x^{2}+a_{n}
$$
if it exists. Suppose that $a_{n+1}$ exists for all $n \geq 2020$. Prove that $a_{n+1} \leq a_{n}$ for all $n \geq 2021$.
|
If $x=\alpha$ is a root of $P_{n}$, then $x=-\alpha$ is also a root, since all terms in $P_{n}(x)$ have an even degree. The smallest root of $P_{n}$ can therefore never be positive. Therefore, $a_{n} \leq 0$ for all $n>2020$. Given that $P_{n+1}(x)=x^{2} \cdot P_{n}(x)+a_{n+1}$, substitute $x=a_{n+1}$: we know that this is a root of $P_{n}$, so $P_{n+1}\left(a_{n+1}\right)=0+a_{n+1} \leq 0$.
Since the term in $P_{n}(x)$ with the highest degree is $x^{2 n}$, there is an $N<0$ such that $P_{n}(x)>0$ for all $x<N$. For example, take $-N=\max \left(2,\left|a_{1}\right|+\left|a_{2}\right|+\ldots+\left|a_{n}\right|\right)$, then for $x<N$ it holds that $x^{2 i-2} \leq x^{2 n-2}$ for $1 \leq i \leq n$ and thus
$$
\begin{aligned}
\mid a_{1} x^{2 n-2}+a_{2} x^{2 n-4}+ & \ldots+a_{n-1} x^{2}+a_{n} \mid \\
& \leq\left|a_{1} x^{2 n-2}\right|+\left|a_{2} x^{2 n-4}\right|+\ldots+\left|a_{n-1} x^{2}\right|+\left|a_{n}\right| \\
& \leq\left|a_{1}\right| x^{2 n-2}+\left|a_{2}\right| x^{2 n-2}+\ldots+\left|a_{n-1}\right| x^{2 n-2}+\left|a_{n}\right| x^{2 n-2} \\
& \leq\left(\left|a_{1}\right|+\left|a_{2}\right|+\ldots+\left|a_{n}\right|\right) x^{2 n-2} \\
& \leq-N \cdot x^{2 n-2} \\
& <x^{2 n},
\end{aligned}
$$
so $x^{2 n}+a_{1} x^{2 n-2}+a_{2} x^{2 n-4}+\ldots+a_{n-1} x^{2}+a_{n}>0$. Therefore, for $n \geq 2021$ there is a certain $N<0$ such that $P_{n}(x)>0$ for $x<N$, while $P_{n}\left(a_{n}\right) \leq 0$. This means that $P_{n}(x)$ has a root less than or equal to $a_{n}$. Since $a_{n+1}$ is the smallest root, it follows that $a_{n+1} \leq a_{n}$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Gegeven zijn reële getallen $a_{1}, a_{2}, \ldots, a_{2020}$, niet noodzakelijk verschillend. Voor elke $n \geq 2020$ wordt nu $a_{n+1}$ gedefinieerd als het kleinste reële nulpunt van het polynoom
$$
P_{n}(x)=x^{2 n}+a_{1} x^{2 n-2}+a_{2} x^{2 n-4}+\ldots+a_{n-1} x^{2}+a_{n}
$$
als dat bestaat. Veronderstel dat $a_{n+1}$ bestaat voor alle $n \geq 2020$. Bewijs dat $a_{n+1} \leq a_{n}$ voor alle $n \geq 2021$.
|
Als $x=\alpha$ een nulpunt van $P_{n}$ is, dan is $x=-\alpha$ ook een nulpunt, aangezien alle termen in $P_{n}(x)$ een even graad hebben. Het kleinste nulpunt van $P_{n}$ kan dus nooit positief zijn. Er geldt daarom $a_{n} \leq 0$ voor alle $n>2020$. Er geldt $P_{n+1}(x)=x^{2} \cdot P_{n}(x)+a_{n+1}$. Vul nu $x=a_{n+1}$ in: we weten dat dat een nulpunt van $P_{n}$ is, dus $P_{n+1}\left(a_{n+1}\right)=0+a_{n+1} \leq 0$.
Omdat de term in $P_{n}(x)$ met de hoogste graad $x^{2 n}$ is, is er een $N<0$ zodat $P_{n}(x)>0$ voor alle $x<N$. Neem bijvoorbeeld $-N=\max \left(2,\left|a_{1}\right|+\left|a_{2}\right|+\ldots+\left|a_{n}\right|\right)$, dan geldt voor $x<N$ dat $x^{2 i-2} \leq x^{2 n-2}$ voor $1 \leq i \leq n$ en dus
$$
\begin{aligned}
\mid a_{1} x^{2 n-2}+a_{2} x^{2 n-4}+ & \ldots+a_{n-1} x^{2}+a_{n} \mid \\
& \leq\left|a_{1} x^{2 n-2}\right|+\left|a_{2} x^{2 n-4}\right|+\ldots+\left|a_{n-1} x^{2}\right|+\left|a_{n}\right| \\
& \leq\left|a_{1}\right| x^{2 n-2}+\left|a_{2}\right| x^{2 n-2}+\ldots+\left|a_{n-1}\right| x^{2 n-2}+\left|a_{n}\right| x^{2 n-2} \\
& \leq\left(\left|a_{1}\right|+\left|a_{2}\right|+\ldots+\left|a_{n}\right|\right) x^{2 n-2} \\
& \leq-N \cdot x^{2 n-2} \\
& <x^{2 n},
\end{aligned}
$$
dus $x^{2 n}+a_{1} x^{2 n-2}+a_{2} x^{2 n-4}+\ldots+a_{n-1} x^{2}+a_{n}>0$. Dus voor $n \geq 2021$ is er een zekere $N<0$ met $P_{n}(x)>0$ voor $x<N$, terwijl $P_{n}\left(a_{n}\right) \leq 0$. Dat betekent dat $P_{n}(x)$ een nulpunt heeft kleiner dan of gelijk aan $a_{n}$. Aangezien $a_{n+1}$ het kleinste nulpunt is, geldt $a_{n+1} \leq a_{n}$.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2020-D2020_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2020"
}
|
Ward and Gabriëlle are playing a game on a large sheet of paper. At the beginning, there are 999 ones written on the paper. Ward and Gabriëlle take turns, with Ward starting. A player whose turn it is may choose two numbers $a$ and $b$ from the paper for which $\operatorname{ggd}(a, b)=1$, erase these numbers, and write the number $a+b$ on the paper. The first one who cannot make a move loses. Determine who of Ward and Gabriëlle can certainly win this game.
|
Gabriëlle can win with the following strategy: she always chooses the two largest numbers on the paper as $a$ and $b$. We prove by induction on $k$ that she can always do this and that after her $k$-th move, the number $2k+1$ and further $998-2k$ ones are on the paper.
In Ward's first turn, he can only choose $a=b=1$. After that, the number 2 and 997 ones are on the paper. Gabriëlle now chooses the two largest numbers, so $a=2$ and $b=1$, resulting in the number 3 and 996 ones. This proves the base case $k=1$. Suppose now that for some $m \geq 1$, after Gabriëlle's $m$-th turn, the number $2m+1$ and $998-2m$ ones are on the paper. If $998-2m=0$, then Ward cannot make a move. Otherwise, Ward has two options: choosing $a=b=1$ or $a=2m+1$ and $b=1$. We consider these two cases separately:
- If Ward chooses $a=b=1$, the situation becomes: the number $2m+1$, the number 2, and $996-2m$ ones. Gabriëlle now chooses the two largest numbers again, so $a=2m+1$ and $b=2$ (this is allowed because the gcd is 1). After her move, the number $2m+3=2(m+1)+1$ and $996-2m=998-2(m+1)$ ones remain.
- If Ward chooses $a=2m+1$ and $b=1$, the situation becomes: the number $2m+2$ and $997-2m$ ones. Gabriëlle now chooses the two largest numbers again, so $a=2m+2$ and $b=1$ (this is allowed because the gcd is 1). Note that there is still a 1 available, as $997-2m$ cannot be 0 because it is odd. After her move, the number $2m+3=2(m+1)+1$ and $996-2m=998-2(m+1)$ ones remain.
This completes the induction.
We see that Gabriëlle can always make a move. After Gabriëlle's 499th move, the paper contains only the number 999, so Ward cannot make a move and Gabriëlle wins.
|
Gabriëlle
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Ward en Gabriëlle spelen een spel op een groot vel papier. In het begin staan er 999 enen op het papier geschreven. Ward en Gabriëlle zijn om en om aan de beurt, waarbij Ward begint. Een speler die aan de beurt is, mag twee getallen $a$ en $b$ van het papier uitkiezen waarvoor geldt $\operatorname{ggd}(a, b)=1$, deze getallen weggummen en het getal $a+b$ erbij schrijven. De eerste die geen zet meer kan doen, verliest. Bepaal wie van Ward en Gabriëlle dit spel met zekerheid kan winnen.
|
Gabriëlle kan winnen met de volgende strategie: ze kiest steeds de grootste twee getallen op het papier als $a$ en $b$. We bewijzen met inductie naar $k$ dat ze dit altijd mag doen en dat na haar $k$-de zet het getal $2 k+1$ en verder $998-2 k$ enen op het papier staan.
In de eerste beurt van Ward kan hij alleen maar $a=b=1$ kiezen. Daarna staat er op het papier het getal 2 en verder 997 enen. Gabriëlle kiest nu de twee grootste getallen, dus $a=2$ en $b=1$ en komt uit op het getal 3 en verder 996 enen. Dit bewijst de inductiebasis $k=1$. Stel nu dat voor zekere $m \geq 1$ geldt dat na de $m$-de beurt van Gabriëlle op het papier het getal $2 m+1$ en verder $998-2 m$ enen staan. Als $998-2 m=0$, dan kan Ward geen zet doen. Zo niet, dan kan Ward twee dingen doen: $a=b=1$ kiezen of $a=2 m+1$ en $b=1$. We bekijken deze twee gevallen apart:
- Als Ward $a=b=1$ kiest, dan wordt de situatie daarna: het getal $2 m+1$, het getal 2 en verder $996-2 m$ enen. Gabriëlle kiest nu weer de grootste twee getallen, dus $a=2 m+1$ en $b=2$ (dit mag want de ggd is 1 ). Na haar zet staat er dan het getal $2 m+3=2(m+1)+1$ en verder $996-2 m=998-2(m+1)$ enen.
- Als Ward $a=2 m+1$ en $b=1$ kiest, dan wordt de situatie daarna: het getal $2 m+2$ en verder $997-2 m$ enen. Gabriëlle kiest nu weer de grootste twee getallen, dus $a=2 m+2$ en $b=1$ (dit mag want de ggd is 1 ). Merk op dat er nog een 1 beschikbaar is, want $997-2 m$ kan niet gelijk aan 0 zijn aangezien het oneven is. Na haar zet staat er dan het getal $2 m+3=2(m+1)+1$ en verder $996-2 m=998-2(m+1)$ enen.
Dit voltooit de inductie.
We zien dat Gabriëlle altijd een zet kan doen. Na zet nummer 499 van Gabriëlle bevat het papier alleen nog het getal 999, dus kan Ward geen zet meer doen en wint Gabriëlle.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2020-D2020_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2020"
}
|
Determine all pairs $(a, b)$ of positive integers for which
$$
a+b=\varphi(a)+\varphi(b)+\operatorname{gcd}(a, b) .
$$
Here, $\varphi(n)$ is the number of integers $k$ in $\{1,2, \ldots, n\}$ such that $\operatorname{gcd}(n, k)=1$.
|
First, let $a=1$. It holds that $\varphi(1)=1$. For all positive integers $b$, we have $\operatorname{ggd}(a, b)=1$, so the equation becomes $1+b=1+\varphi(b)+1$, thus $\varphi(b)=b-1$. Therefore, there is exactly one number in $\{1,2, \ldots, b\}$ that is not coprime with $b$; this must be $b$ itself (since $\operatorname{ggd}(b, b)>1$ unless $b=1$, but in that case $\varphi(b)=b$). This implies that $b$ is a prime number. The equation holds for all prime numbers. We conclude that $(1, p)$ is a solution for all prime numbers $p$. Similarly, $b=1$ gives the solutions $(p, 1)$.
Now, we assume that $a, b \geq 2$. Since $\operatorname{ggd}(b, b)>1$, it follows that $\varphi(b) \leq b-1$. Therefore,
$$
\operatorname{ggd}(a, b)=a+b-\varphi(a)-\varphi(b) \geq a-\varphi(a)+1
$$
Let $p$ be the smallest prime divisor of $a$ (which exists, since $a \geq 2$). Since for all multiples of $p$, $t p \leq a$, we have $\operatorname{ggd}(t p, a)>1$, it follows that $a-\varphi(a) \geq \frac{1}{p} \cdot a$. Therefore,
$$
\operatorname{ggd}(a, b) \geq a-\varphi(a)+1 \geq \frac{a}{p}+1
$$
The largest two divisors of $a$ are $a$ and $\frac{a}{p}$. Since $\operatorname{ggd}(a, b)$ is a divisor of $a$ that is at least $\frac{a}{p}+1$, it must be equal to $a$. Thus, $\operatorname{ggd}(a, b)=a$. By a completely analogous argument, we can prove that $\operatorname{ggd}(a, b)=b$. Therefore, $a=b$.
Now the equation becomes $2 a=2 \varphi(a)+a$, or $a=2 \varphi(a)$. We see that $2 \mid a$. Therefore, write $a=2^{k} \cdot m$ with $k \geq 1$ and $m$ odd. Then, by a known property of the $\varphi$-function, we have $\varphi(a)=\varphi\left(2^{k}\right) \varphi(m)=2^{k-1} \cdot \varphi(m)$, so the equation becomes $2^{k} \cdot m=2 \cdot 2^{k-1} \cdot \varphi(m)$, or $m=\varphi(m)$. This implies $m=1$. Therefore, $a=b=2^{k}$, and the equation indeed holds.
We conclude that the solutions are: $(1, p)$ and $(p, 1)$ for all prime numbers $p$, and $\left(2^{k}, 2^{k}\right)$ for all positive integers $k$.
|
(1, p) \text{ and } (p, 1) \text{ for all prime numbers } p, \text{ and } \left(2^{k}, 2^{k}\right) \text{ for all positive integers } k
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Bepaal alle paren $(a, b)$ van positieve gehele getallen waarvoor
$$
a+b=\varphi(a)+\varphi(b)+\operatorname{ggd}(a, b) .
$$
Hier is $\varphi(n)$ het aantal getallen $k$ uit $\{1,2, \ldots, n\}$ met $\operatorname{ggd}(n, k)=1$.
|
Stel eerst dat $a=1$. Er geldt $\varphi(1)=1$. Voor alle positieve gehele $b$ is nu $\operatorname{ggd}(a, b)=1$, dus de vergelijking wordt $1+b=1+\varphi(b)+1$, dus $\varphi(b)=b-1$. Er is dus precies één getal uit $\{1,2, \ldots, b\}$ dat niet copriem met $b$ is; dat moet $b$ zelf zijn (want $\operatorname{ggd}(b, b)>1$ tenzij $b=1$, maar in dat geval geldt $\varphi(b)=b$ ). Hieruit volgt dat $b$ een priemgetal is. Voor alle priemgetallen klopt de vergelijking. We concluderen dat $(1, p)$ een oplossing is voor alle priemgetallen $p$. Net zo goed geeft $b=1$ de oplossingen $(p, 1)$.
We nemen nu verder aan dat $a, b \geq 2$. Omdat $\operatorname{ggd}(b, b)>1$ geldt $\varphi(b) \leq b-1$. Dus
$$
\operatorname{ggd}(a, b)=a+b-\varphi(a)-\varphi(b) \geq a-\varphi(a)+1
$$
Zij nu $p$ de kleinste priemdeler van $a$ (die bestaat, want $a \geq 2$ ). Omdat voor alle $p$-vouden $t p \leq a$ geldt dat $\operatorname{ggd}(t p, a)>1$, is $a-\varphi(a) \geq \frac{1}{p} \cdot a$. Er geldt dus
$$
\operatorname{ggd}(a, b) \geq a-\varphi(a)+1 \geq \frac{a}{p}+1
$$
De grootste twee delers van $a$ zijn $a$ en $\frac{a}{p}$. Omdat $\operatorname{ggd}(a, b)$ een deler van $a$ is die minstens $\frac{a}{p}+1$ is, moet hij gelijk zijn aan $a$. Dus $\operatorname{ggd}(a, b)=a$. Volkomen analoog kunnen we bewijzen dat $\operatorname{ggd}(a, b)=b$. Dus $a=b$.
Nu gaat de vergelijking over in $2 a=2 \varphi(a)+a$, oftewel $a=2 \varphi(a)$. We zien dat $2 \mid a$. Schrijf daarom $a=2^{k} \cdot m$ met $k \geq 1$ en $m$ oneven. Dan geldt wegens een bekende eigenschap van de $\varphi$-functie dat $\varphi(a)=\varphi\left(2^{k}\right) \varphi(m)=2^{k-1} \cdot \varphi(m)$, dus de vergelijking gaat over in $2^{k} \cdot m=2 \cdot 2^{k-1} \cdot \varphi(m)$, oftewel $m=\varphi(m)$. Hieruit volgt $m=1$. Dus $a=b=2^{k}$ en dan klopt de vergelijking inderdaad.
We concluderen dat de oplossingen zijn: $(1, p)$ en $(p, 1)$ voor alle priemgetallen $p$, en $\left(2^{k}, 2^{k}\right)$ voor alle positieve gehele $k$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2020-D2020_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2020"
}
|
Determine all pairs $(a, b)$ of positive integers for which
$$
a+b=\varphi(a)+\varphi(b)+\operatorname{gcd}(a, b) .
$$
Here, $\varphi(n)$ is the number of integers $k$ in $\{1,2, \ldots, n\}$ such that $\operatorname{gcd}(n, k)=1$.
|
Write $a=x d, b=y d$ with $d=\operatorname{gcd}(a, b)$. Then the equation becomes
$$
x d+y d=\varphi(x d)+\varphi(y d)+d
$$
Of the numbers $\{1,2, \ldots, x\}$, there are $\varphi(x)$ that are coprime with $x$, so at most $\varphi(x)$ are coprime with $x d$. The same applies to the numbers $\{x+1, x+2, \ldots, 2 x\}$ and more
generally to the numbers $\{t x+1, t x+2, \ldots,(t+1) x\}$. By dividing the numbers $\{1,2, \ldots, x d\}$ into $d$ such groups, we see that at most $d \cdot \varphi(x)$ of these numbers are coprime with $x d$. Thus $\varphi(x d) \leq d \cdot \varphi(x)$. Similarly, $\varphi(y d) \leq d \cdot \varphi(y)$. Therefore, we get
$$
x d+y d \leq d \cdot \varphi(x)+d \cdot \varphi(y)+d
$$
Dividing by $d$ gives
$$
x+y \leq \varphi(x)+\varphi(y)+1
$$
If $x, y \geq 2$, then $\varphi(x) \leq x-1, \varphi(y) \leq y-1$, and this cannot be true. Therefore, at least one of $x$ and $y$ must be equal to 1.
Suppose $x=y=1$. Then $a=b$. Just like in the first solution, we deduce that then $a=b=2^{k}$ with $k \geq 1$.
Now suppose $x=1$ and $y \neq 1$. Then $\varphi(y) \geq y-1$ must hold, so $y$ must be a prime number. Furthermore, equality must hold in $\varphi(x d) \leq d \cdot \varphi(x)$. Substituting $x=1$ gives $\varphi(d)=d \cdot \varphi(1)=d$. This can only be true if $d=1$. We find $(a, b)=(1, p)$ for a prime number $p$. Similarly, from $x \neq 1$ and $y=1$, the solution $(p, 1)$ follows.
We conclude that the solutions are: $(1, p)$ and $(p, 1)$ for all prime numbers $p$, and $\left(2^{k}, 2^{k}\right)$ for all positive integers $k$.
|
(1, p) \text{ and } (p, 1) \text{ for all prime numbers } p, \text{ and } \left(2^{k}, 2^{k}\right) \text{ for all positive integers } k
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Bepaal alle paren $(a, b)$ van positieve gehele getallen waarvoor
$$
a+b=\varphi(a)+\varphi(b)+\operatorname{ggd}(a, b) .
$$
Hier is $\varphi(n)$ het aantal getallen $k$ uit $\{1,2, \ldots, n\}$ met $\operatorname{ggd}(n, k)=1$.
|
Schrijf $a=x d, b=y d$ met $d=\operatorname{ggd}(a, b)$. Dan gaat de vergelijking over in
$$
x d+y d=\varphi(x d)+\varphi(y d)+d
$$
Van de getallen $\{1,2, \ldots, x\}$ zijn er $\varphi(x)$ die copriem zijn met $x$, dus hooguit $\varphi(x)$ die copriem zijn met $x d$. Hetzelfde geldt voor de getallen $\{x+1, x+2, \ldots, 2 x\}$ en meer
algemeen voor de getallen $\{t x+1, t x+2, \ldots,(t+1) x\}$. Door de getallen $\{1,2, \ldots, x d\}$ in $d$ van dit soort groepjes op te delen, zien we dat hooguit $d \cdot \varphi(x)$ van deze getallen copriem zijn met $x d$. Dus $\varphi(x d) \leq d \cdot \varphi(x)$. Analoog geldt $\varphi(y d) \leq d \cdot \varphi(y)$. Dus krijgen we
$$
x d+y d \leq d \cdot \varphi(x)+d \cdot \varphi(y)+d
$$
Delen door $d$ geeft
$$
x+y \leq \varphi(x)+\varphi(y)+1
$$
Als $x, y \geq 2$ geldt $\varphi(x) \leq x-1, \varphi(y) \leq y-1$ en kan dit niet waar zijn. Dus minstens één van $x$ en $y$ is gelijk aan 1.
Stel dat $x=y=1$. Dan geldt $a=b$. Net als in de eerste oplossing leiden we af dat dan $a=b=2^{k}$ met $k \geq 1$.
Stel nu dat $x=1$ en $y \neq 1$. Dan moet gelden $\varphi(y) \geq y-1$, dus $y$ moet dan een priemgetal zijn. Verder moet er gelijkheid gelden in $\varphi(x d) \leq d \cdot \varphi(x)$. Invullen van $x=1$ geeft dus $\varphi(d)=d \cdot \varphi(1)=d$. Dat kan alleen als $d=1$. We vinden $(a, b)=(1, p)$ voor een priemgetal $p$. Analoog volgt uit $x \neq 1$ en $y=1$ de oplossing $(p, 1)$.
We concluderen dat de oplossingen zijn: $(1, p)$ en $(p, 1)$ voor alle priemgetallen $p$, en $\left(2^{k}, 2^{k}\right)$ voor alle positieve gehele $k$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2020-D2020_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2020"
}
|
Let $A B C$ be an acute triangle and let $P$ be the intersection of the tangents at $B$ and $C$ to the circumcircle of $\triangle A B C$. The line through $A$ perpendicular to $A B$ and the line through $C$ perpendicular to $A C$ intersect at $X$. The line through $A$ perpendicular to $A C$ and the line through $B$ perpendicular to $A B$ intersect at $Y$. Show that $A P \perp X Y$.
|
Let $M$ be the center of the circumcircle of $\triangle ABC$ and write $\alpha = \angle BAC$. First, we prove that $\triangle BYA \sim \triangle BMP$ and then that $\triangle YBM \sim \triangle ABP$. By the central angle theorem, we have $\angle BMC = 2 \angle BAC = 2\alpha$. Quadrilateral $PBMC$ is a kite with symmetry axis $PM$ (due to equal radii $|MB| = |MC|$ and equal tangent segments $|PB| = |PC|$), so $MP$ bisects angle $\angle BMC$. We conclude that $\angle BMP = \frac{1}{2} \angle BMC = \alpha$. Furthermore, $\angle PBM = 90^\circ$ (the tangent is perpendicular to the radius) and thus, by the angle sum, $\angle MPB = 90^\circ - \alpha$. On the other hand, $\angle ABY = 90^\circ$ (given) and $\angle YAB = \angle YAC - \angle BAC = 90^\circ - \alpha$. Therefore, $\angle ABY = \angle PBM$ and $\angle YAB = \angle MPB$, which implies that $\triangle BYA \sim \triangle BMP$. From this similarity, it follows that $\frac{|YB|}{|AB|} = \frac{|MB|}{|PB|}$. Combining this with the angle equality
$$
\angle YBM = \angle YBA + \angle ABM = 90^\circ + \angle ABM = \angle ABM + \angle MBP = \angle ABP
$$
we see that $\triangle YBM \sim \triangle ABP$ as well. Let $T$ be the intersection of $AP$ and $YM$, then we see that
$$
\angle BYT = \angle BYM = \angle BAP = \angle BAT
$$
which implies that $BYAT$ is a cyclic quadrilateral. We conclude that $\angle ATY = \angle ABY = 90^\circ$, so $AP \perp YM$. Similarly, we find that $AP \perp XM$. But this means that the lines $YM$ and $XM$ coincide and that $AP \perp XY$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $A B C$ een scherphoekige driehoek en zij $P$ het snijpunt van de raaklijnen in $B$ en $C$ aan de omgeschreven cirkel van $\triangle A B C$. De lijn door $A$ loodrecht op $A B$ en de lijn door $C$ loodrecht op $A C$ snijden in $X$. De lijn door $A$ loodrecht op $A C$ en de lijn door $B$ loodrecht op $A B$ snijden in $Y$. Toon aan dat $A P \perp X Y$.

|
Zij $M$ het midden van de omgeschreven cirkel van $\triangle A B C$ en schrijf $\alpha=$ $\angle B A C$. We bewijzen eerst dat $\triangle B Y A \sim \triangle B M P$ en vervolgens dat $\triangle Y B M \sim \triangle A B P$. Wegens de middelpunt-omtrekshoekstelling geldt $\angle B M C=2 \angle B A C=2 \alpha$. Vierhoek $P B M C$ is een vlieger met symmetrie-as $P M$ (wegens gelijke stralen $|M B|=|M C|$ en gelijke raaklijnstukjes $|P B|=|P C|$ ), dus $M P$ deelt hoek $\angle B M C$ in tweeën. We concluderen dat $\angle B M P=\frac{1}{2} \angle B M C=\alpha$. Verder geldt $\angle P B M=90^{\circ}$ (raaklijn staat loodrecht op de straal) en dus wegens hoekensom dat $\angle M P B=90^{\circ}-\alpha$. Anderzijds geldt dat $\angle A B Y=90^{\circ}$ (gegeven) en dat $\angle Y A B=\angle Y A C-\angle B A C=90^{\circ}-\alpha$. Dus $\angle A B Y=\angle P B M$ en $\angle Y A B=\angle M P B$, waaruit volgt dat $\triangle B Y A \sim \triangle B M P$. Uit deze gelijkvormigheid volgt dat $\frac{|Y B|}{|A B|}=\frac{|M B|}{|P B|}$. Combineren we dit met de hoekengelijkheid
$$
\angle Y B M=\angle Y B A+\angle A B M=90^{\circ}+\angle A B M=\angle A B M+\angle M B P=\angle A B P
$$
dan zien we dat bovendien $\triangle Y B M \sim \triangle A B P$. Noemen we nu $T$ het snijpunt van $A P$ en $Y M$, dan zien we dus dat
$$
\angle B Y T=\angle B Y M=\angle B A P=\angle B A T
$$
waaruit volgt dat $B Y A T$ een koordenvierhoek is. We concluderen dat $\angle A T Y=\angle A B Y=$ $90^{\circ}$, dus dat $A P \perp Y M$. Analoog vinden we dat $A P \perp X M$. Maar dat betekent dat de
lijnen $Y M$ en $X M$ samenvallen en dat $A P \perp X Y$.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2020-D2020_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2020"
}
|
Let $A B C$ be an acute triangle and let $P$ be the intersection of the tangents at $B$ and $C$ to the circumcircle of $\triangle A B C$. The line through $A$ perpendicular to $A B$ and the line through $C$ perpendicular to $A C$ intersect at $X$. The line through $A$ perpendicular to $A C$ and the line through $B$ perpendicular to $A B$ intersect at $Y$. Show that $A P \perp X Y$.

|
Let $S$ be the intersection of $CX$ and $BY$. The lines $AX$ and $BY$ are both perpendicular to $AB$, so $AX \parallel BY$, and similarly $AY \parallel CX$. Therefore, $AXSY$ is a parallelogram. Moreover, $\angle ABS = 90^{\circ} = \angle ACS$, so by Thales' theorem, $AS$ is a diameter of the circumcircle of $\triangle ABC$. The center $M$ of this circle is therefore the midpoint of $AS$. The diagonals of a parallelogram bisect each other, so $XY$ passes through the midpoint of $AS$, and thus through $M$.
Let $T$ be on $XY$ such that $\angle ATX = 90^{\circ}$. Then $\angle ATX = \angle ACX$, so $ATCX$ is a cyclic quadrilateral. Similarly, $ATBY$ is a cyclic quadrilateral. Now, $\angle ATC = 180^{\circ} - \angle AXC$, and since $AC \perp CX$ and $AB \perp AX$, we have $\angle AXC = 90^{\circ} - \angle CAX = \angle CAB$. Therefore, $\angle ATC = 180^{\circ} - \angle CAB$. Similarly, $\angle ATB = 180^{\circ} - \angle CAB$. Thus, $\angle BTC = 360^{\circ} - (180^{\circ} - \angle CAB) - (180^{\circ} - \angle CAB) = 2 \angle CAB$. By the inscribed angle theorem, $\angle BMC = 2 \angle BAC$, so $\angle BTC = \angle BMC$. This implies that $BMTC$ is a cyclic quadrilateral.
Since $BP$ and $CP$ are tangents to the circumcircle of $\triangle ABC$, $\angle MBP = 90^{\circ} = \angle MCP$, so $MBPC$ is a cyclic quadrilateral with diameter $MP$. But we have just seen that $T$ also lies on this circle. Therefore, $\angle MTP = \angle MBP = 90^{\circ}$. Since $\angle ATM + \angle MTP = 180^{\circ}$, $T$ lies on $AP$. We conclude that $AP \perp XY$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $A B C$ een scherphoekige driehoek en zij $P$ het snijpunt van de raaklijnen in $B$ en $C$ aan de omgeschreven cirkel van $\triangle A B C$. De lijn door $A$ loodrecht op $A B$ en de lijn door $C$ loodrecht op $A C$ snijden in $X$. De lijn door $A$ loodrecht op $A C$ en de lijn door $B$ loodrecht op $A B$ snijden in $Y$. Toon aan dat $A P \perp X Y$.

|
Zij $S$ het snijpunt van $C X$ en $B Y$. De lijnen $A X$ en $B Y$ staan allebei loodrecht op $A B$, dus geldt $A X \| B Y$, en analoog $A Y \| C X$. Dus $A X S Y$ is een parallellogram. Daarnaast geldt $\angle A B S=90^{\circ}=\angle A C S$, dus wegens Thales is $A S$ een middellijn van de omgeschreven cirkel van $\triangle A B C$. Het middelpunt $M$ van deze cirkel is daarom het midden van $A S$. De diagonalen van een parallellogram snijden elkaar middendoor, dus $X Y$ gaat door het midden van $A S$, dus door $M$.
Zij nu $T$ op $X Y$ zodat $\angle A T X=90^{\circ}$. Er geldt dan $\angle A T X=\angle A C X$, dus $A T C X$ is een koordenvierhoek. Net zo is $A T B Y$ een koordenvierhoek. Nu geldt $\angle A T C=180^{\circ}-\angle A X C$, en wegens $A C \perp C X$ en $A B \perp A X$ geldt $\angle A X C=90^{\circ}-\angle C A X=\angle C A B$. Dus $\angle A T C=180^{\circ}-\angle C A B$. Analoog geldt ook $\angle A T B=180^{\circ}-\angle C A B$. Dus $\angle B T C=360^{\circ}-$ $\left(180^{\circ}-\angle C A B\right)-\left(180^{\circ}-\angle C A B\right)=2 \angle C A B$. Wegens de middelpuntsomtrekshoekstelling geldt bovendien $\angle B M C=2 \angle B A C$, dus $\angle B T C=\angle B M C$. Hieruit volgt dat $B M T C$ een koordenvierhoek is.
Omdat $B P$ en $C P$ raaklijnen aan de omgeschreven cirkel van $\triangle A B C$ zijn, geldt $\angle M B P=$ $90^{\circ}=\angle M C P$, dus $M B P C$ is een koordenvierhoek met middellijn $M P$. Maar we hebben net gezien dat $T$ ook op deze cirkel ligt. Er geldt dus $\angle M T P=\angle M B P=90^{\circ}$. Aangezien nu $\angle A T M+\angle M T P=180^{\circ}$, ligt $T$ dus op $A P$. We concluderen dat $A P \perp X Y$.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2020-D2020_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2020"
}
|
For a positive number $n$, we write $d(n)$ for the number of positive divisors of $n$. Determine all positive integers $k$ for which there exist positive integers $a$ and $b$ with the property
$$
k=d(a)=d(b)=d(2 a+3 b)
$$
|
For $i \geq 0$ we choose $a=2 \cdot 5^{i}$ and $b=3 \cdot 5^{i}$. Then $a$ and $b$ each have $2(i+1)$ divisors. Furthermore, $2a + 3b = 4 \cdot 5^{i} + 9 \cdot 5^{i} = 13 \cdot 5^{i}$, and this also has $2(i+1)$ divisors. Thus, this satisfies the condition with $k=2(i+1)$. We see that all even values of $k$ satisfy the condition.
Now suppose that $k$ is odd. Then $a$ has an odd number of divisors and is thus a square, say $a=x^{2}$. Similarly, $b$ is a square, say $b=y^{2}$, and $2a + 3b$ is a square, say $2a + 3b = z^{2}$. Therefore, we have
$$
2x^{2} + 3y^{2} = z^{2}
$$
We prove that this equation has no solutions in the positive integers. Suppose there are such solutions, and choose the solution $(x, y, z) = (u, v, w)$ with the minimal value of $x + y + z$. Thus, $2u^{2} + 3v^{2} = w^{2}$. If we consider this equation modulo 3, we get $2u^{2} = w^{2}$. If $u$ is not divisible by 3, then $u^{2} \equiv 1 \bmod 3$, so $w^{2} = 2u^{2} \equiv 2 \bmod 3$, which is impossible. Therefore, $u$ is divisible by 3, and then $w$ is also divisible by 3. Now $2u^{2}$ is divisible by 9 and $w^{2}$ is also divisible by 9, so $3v^{2}$ is divisible by 9. This implies that $v$ is also divisible by 3. However, $(x, y, z) = \left(\frac{u}{3}, \frac{v}{3}, \frac{w}{3}\right)$ is also a solution to the equation, while this solution has a smaller value of $x + y + z$. Contradiction. Therefore, there are no solutions in the positive integers.
From this, it follows that an odd value of $k$ can never satisfy the condition. The only solutions are thus all even numbers.
Alternatively for the second part. As in the solution above, we consider the equation $2x^{2} + 3y^{2} = z^{2}$. We will show that this equation has no solutions in the positive integers. First, consider the equation modulo 2. Then we have $3y^{2} \equiv z^{2}$, so $y$ and $z$ are both even or both odd. Suppose they are both odd. Then consider the equation modulo 8. We know $y^{2} \equiv z^{2} \equiv 1 \bmod 8$, so $2x^{2} \equiv 1 - 3 \equiv 6 \bmod 8$. This implies $x^{2} \equiv 3 \bmod 4$, which is impossible. We conclude that $y$ and $z$ cannot both be odd, so they must both be even. Now the right-hand side of the equation is divisible by 4, so the left-hand side must also be divisible by 4. Also, $3y^{2}$ is divisible by 4, so $2x^{2}$ must be divisible by 4. This implies that $x$ is even. We see that for every solution $(x, y, z)$, $x$, $y$, and $z$ are all even. Now we can start with a solution $(x, y, z) = (u, v, w)$ with the minimal value of $x + y + z$. Then $(x, y, z) = \left(\frac{u}{2}, \frac{v}{2}, \frac{w}{2}\right)$ is also a solution to the equation with a smaller value of $x + y + z$, contradiction.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Voor een positief getal $n$ schrijven we $d(n)$ voor het aantal positieve delers van $n$. Bepaal alle positieve gehele getallen $k$ waarvoor er positieve gehele getallen $a$ en $b$ bestaan met de eigenschap
$$
k=d(a)=d(b)=d(2 a+3 b)
$$
|
Voor $i \geq 0$ kiezen we $a=2 \cdot 5^{i}$ en $b=3 \cdot 5^{i}$. Dan hebben $a$ en $b$ elk $2(i+1)$ delers. Verder is $2 a+3 b=4 \cdot 5^{i}+9 \cdot 5^{i}=13 \cdot 5^{i}$ en dat heeft ook $2(i+1)$ delers. Dus dit voldoet met $k=2(i+1)$. We zien dat alle even waarden van $k$ voldoen.
Stel nu dat $k$ oneven is. Dan heeft $a$ een oneven aantal delers en is dus een kwadraat, zeg $a=x^{2}$. Net zo is $b$ een kwadraat, zeg $b=y^{2}$, en is $2 a+3 b$ een kwadraat, zeg $2 a+3 b=z^{2}$. Er geldt dus
$$
2 x^{2}+3 y^{2}=z^{2}
$$
We bewijzen dat deze vergelijking geen oplossingen in de positieve gehele getallen heeft. Stel er bestaan wel zulke oplossing, kies dan de oplossing $(x, y, z)=(u, v, w)$ met de minimale waarde van $x+y+z$. Er geldt dus $2 u^{2}+3 v^{2}=w^{2}$. Als we deze vergelijking modulo 3 bekijken, staat er $2 u^{2}=w^{2}$. Als $u$ niet deelbaar door 3 is, dan is $u^{2} \equiv 1 \bmod 3$, dus $w^{2}=2 u^{2} \equiv 2 \bmod 3$, maar dat kan niet. Dus $u$ is deelbaar door 3 en dan volgt dat $w$ ook deelbaar door 3 is. Nu is $2 u^{2}$ deelbaar door 9 en $w^{2}$ ook, dus $3 v^{2}$ is deelbaar door 9 . Daaruit volgt dat $v$ ook deelbaar door 3 is. Nu voldoet echter $(x, y, z)=\left(\frac{u}{3}, \frac{v}{3}, \frac{w}{3}\right)$ ook aan de vergelijking, terwijl deze oplossing een kleinere waarde van $x+y+z$ heeft. Tegenspraak. Er bestaan dus geen oplossingen in de positieve gehele getallen.
Daaruit volgt dat een oneven waarde van $k$ nooit kan voldoen. De enige oplossingen zijn dus alle even getallen.
Alternatief voor het tweede deel. Net als in de oplossing hierboven bekijken we de vergelijking $2 x^{2}+3 y^{2}=z^{2}$. We gaan laten zien dat deze vergelijking geen oplossing in de positieve gehele getallen heeft. Bekijk de vergelijking eerst modulo 2. Dan staat er
$3 y^{2} \equiv z^{2}$, dus $y$ en $z$ zijn beide even of beide oneven. Stel dat ze beide oneven zijn. Bekijk dan de vergelijking modulo 8 . We weten dan $y^{2} \equiv z^{2} \equiv 1 \bmod 8$, dus $2 x^{2} \equiv 1-3 \equiv 6$ $\bmod 8$. Hieruit volgt $x^{2} \equiv 3 \bmod 4$, maar dat kan niet. We concluderen dat $y$ en $z$ niet allebei oneven kunnen zijn, dus moeten ze allebei even zijn. Nu is de rechterkant van de vergelijking deelbaar door 4 , dus de linkerkant ook. Ook $3 y^{2}$ is deelbaar door 4 , dus $2 x^{2}$ moet deelbaar door 4 zijn. Hieruit volgt dat $x$ even is. We zien dat voor elke oplossing $(x, y, z)$ geldt dat $x, y$ en $z$ alle drie even zijn. Nu kunnen we net als in de oplossing hierboven beginnen met een oplossing $(x, y, z)=(u, v, w)$ met minimale waarde van $x+y+z$. Dan is $(x, y, z)=\left(\frac{u}{2}, \frac{v}{2}, \frac{w}{2}\right)$ ook een oplossing van de vergelijking met een kleinere waarde van $x+y+z$, tegenspraak.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2020-E2020_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2020"
}
|
Given is a triangle $ABC$ with its circumcircle and with $|AC| < |AB|$. On the shorter arc $AC$ lies a variable point $D$ not equal to $A$. Let $E$ be the reflection of $A$ in the angle bisector of $\angle BDC$. Prove that the line $DE$ passes through a fixed point, independent of the position of $D$.
|
Let $M$ be the intersection of the angle bisector of $\angle B D C$ with the circumcircle of $\triangle A B C$. Since $D$ lies on the short arc $A C$, $M$ lies on the arc $B C$ where $A$ does not lie. We have $\angle B D M=\angle M D C$ because $D M$ is the angle bisector of $\angle B D C$, so arcs $B M$ and $C M$ are of equal length. This implies that the position of $M$ does not depend on the position of $D$.
Let $S$ be the intersection of $D E$ and the circumcircle of $\triangle A B C$. We will prove that $S$ does not depend on the position of $D$. Since $S$ and $M$ lie on the circumcircle of $\triangle A B C$, we have $\angle A M D=\angle A S D=\angle A S E$. Since $E$ is the reflection of $A$ in $D M$, we now see that $\angle A M E=2 \angle A M D=2 \angle A S E$. Consider the circle with center $M$ passing through $A$. Due to the reflection, $|M A|=|M E|$, so this circle also passes through $E$. The central angle theorem now tells us that from $\angle A M E=2 \angle A S E$ it follows that $S$ also lies on this circle. We see that $S$ is the second intersection of the circumcircle of $\triangle A B C$ and the circle with center $M$ passing through $A$. This fixes $S$, independently of the position of $D$. Since $D E$ passes through $S$, $S$ is the desired point.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Gegeven is een driehoek $A B C$ met zijn omgeschreven cirkel en met $|A C|<$ $|A B|$. Op de korte boog $A C$ ligt een variabel punt $D$ ongelijk aan $A$. Zij $E$ de spiegeling van $A$ in de binnenbissectrice van $\angle B D C$. Bewijs dat de lijn $D E$ door een vast punt gaat, onafhankelijk van de plek van $D$.

|
Zij $M$ het snijpunt van de binnenbissectrice van $\angle B D C$ met de omgeschreven cirkel van $\triangle A B C$. Omdat $D$ op de korte boog $A C$ ligt, ligt $M$ op de boog $B C$ waar $A$ niet op ligt. Er geldt $\angle B D M=\angle M D C$ omdat $D M$ de binnenbissectrice van $\angle B D C$ is, dus bogen $B M$ en $C M$ zijn even lang. Hieruit volgt dat de plek van $M$ niet afhangt van de plek van $D$.
Zij $S$ het snijpunt van $D E$ en de omgeschreven cirkel van $\triangle A B C$. We gaan bewijzen dat $S$ niet afhangt van de plek van $D$. Omdat $S$ en $M$ op de omgeschreven cirkel van $\triangle A B C$ liggen, geldt $\angle A M D=\angle A S D=\angle A S E$. Omdat $E$ de spiegeling van $A$ in $D M$ is, zien we nu $\angle A M E=2 \angle A M D=2 \angle A S E$. Bekijk de cirkel met middelpunt $M$ die door $A$ heen gaat. Vanwege opnieuw de spiegeling is $|M A|=|M E|$, dus deze cirkel gaat ook door $E$. De middelpunt-omtrekshoekstelling zegt nu dat uit $\angle A M E=2 \angle A S E$ volgt dat $S$ ook op deze cirkel ligt. We zien dat $S$ het tweede snijpunt is van de omgeschreven cirkel van $\triangle A B C$ en de cirkel met middelpunt $M$ die door $A$ gaat. Dat legt $S$ vast, onafhankelijk van de plek van $D$. Omdat $D E$ door $S$ heen gaat, is $S$ het gevraagde punt.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2020-E2020_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2020"
}
|
Given is a triangle $ABC$ with its circumcircle and with $|AC| < |AB|$. On the shorter arc $AC$ lies a variable point $D$ not equal to $A$. Let $E$ be the reflection of $A$ in the angle bisector of $\angle BDC$. Prove that the line $DE$ passes through a fixed point, independent of the position of $D$.

|
Let $T$ be the reflection of $A$ in the perpendicular bisector of $B C$. This point does not depend on $D$. We will prove that $D E$ always passes through $T$. We do this by showing that $\angle E D C + \angle C D B + \angle B D T = 180^{\circ}$.
Point $T$ lies on the circumcircle of $\triangle A B C$, because this circle maps onto itself when reflected in the perpendicular bisector of $B C$. Therefore, $\angle B D T = \angle B C T$. Due to the reflection in the perpendicular bisector of $B C$, $A C B T$ is an isosceles trapezoid with base $B C$, and thus $\angle B C T = \angle C B A$. Therefore, $\angle B D T = \angle C B A$.
Furthermore, when reflecting in the angle bisector of $\angle B D C$, point $A$ maps to point $E$ and line $B D$ to line $C D$, so $\angle E D C = \angle A D B$. By the inscribed angle theorem, $\angle A D B = \angle A C B$, so $\angle E D C = \angle A C B$.
Finally, $\angle C D B = \angle C A B$. We thus find
$$
\angle E D C + \angle C D B + \angle B D T = \angle A C B + \angle C A B + \angle C B A = 180^{\circ}.
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Gegeven is een driehoek $A B C$ met zijn omgeschreven cirkel en met $|A C|<$ $|A B|$. Op de korte boog $A C$ ligt een variabel punt $D$ ongelijk aan $A$. Zij $E$ de spiegeling van $A$ in de binnenbissectrice van $\angle B D C$. Bewijs dat de lijn $D E$ door een vast punt gaat, onafhankelijk van de plek van $D$.

|
Zij $T$ het spiegelbeeld van $A$ in de middelloodlijn van $B C$. Dit punt hangt
niet af van $D$. We gaan bewijzen dat $D E$ altijd door $T$ heen gaat. We doen dit door te laten zien dat $\angle E D C+\angle C D B+\angle B D T=180^{\circ}$.
Punt $T$ ligt op de omgeschreven cirkel van $\triangle A B C$, want deze cirkel gat in zichzelf over bij spiegeling in de middelloodlijn van $B C$. Dus $\angle B D T=\angle B C T$. Wegens de spiegeling in de middelloodlijn van $B C$ is $A C B T$ een gelijkbenig trapezium met basis $B C$ en dus is $\angle B C T=\angle C B A$. Dus $\angle B D T=\angle C B A$.
Verder gaat bij spiegeling in de bissectrice van $\angle B D C$ punt $A$ over in punt $E$ en lijn $B D$ in lijn $C D$, dus $\angle E D C=\angle A D B$. Vanwege de omtrekshoekstelling is $\angle A D B=\angle A C B$, dus $\angle E D C=\angle A C B$.
Ten slotte is $\angle C D B=\angle C A B$. We vinden dus
$$
\angle E D C+\angle C D B+\angle B D T=\angle A C B+\angle C A B+\angle C B A=180^{\circ} .
$$
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2020-E2020_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2020"
}
|
Vind alle functies $f: \mathbb{Z} \rightarrow \mathbb{Z}$ die voldoen aan
$$
f(-f(x)-f(y))=1-x-y
$$
voor alle $x, y \in \mathbb{Z}$.
|
Invullen van $x=y=1$ geeft $f(-2 f(1))=-1$. Invullen van $x=n, y=1$ geeft $f(-f(n)-f(1))=-n$. Nu kiezen we $x=-f(n)-f(1)$ en $y=-2 f(1)$, dat geeft
$$
f(-f(-f(n)-f(1))-f(-2 f(1)))=1-(-f(n)-f(1))-(-2 f(1))
$$
waarbij we de linkerkant verder kunnen uitrekenen als $f(--n--1)=f(n+1)$ en de rechterkant verder als $1+f(n)+f(1)+2 f(1)=f(n)+3 f(1)+1$. Schrijf nu $3 f(1)+1=c$, dan staat er
$$
f(n+1)=f(n)+c
$$
Met inductie twee kanten op volgt dat $f(n+k)=f(n)+c k$ voor alle $k \in \mathbb{Z}$, waarna $n=0$ geeft dat $f(k)=f(0)+c k$ voor alle $k \in \mathbb{Z}$, dus $f$ is een lineaire functie.
Om te controleren vullen we $f(x)=a x+b$ in met $a, b \in \mathbb{Z}$. Dan wordt de linkerkant van de functievergelijking
$$
f(-f(x)-f(y))=a(-a x-b-a y-b)+b=-a^{2} x-a^{2} y-2 a b+b
$$
Dit moet voor alle $x$ en $y$ gelijk zijn aan $1-x-y$. De coëfficiënt voor de $x$ moet daarom gelijk zijn (want met $y$ vast moet aan beide kanten dezelfde functie van $x$ staan) dus $-a^{2}=-1$, dus $a=1$ of $a=-1$. Met $a=-1$ en $x=y=0$ krijgen we $2 b+b=1$, wat geen gehele $b$ oplevert. Met $a=1$ en $x=y=0$ krijgen we $-2 b+b=1$ dus $b=-1$. Inderdaad komt er voor $a=1$ en $b=-1$ links ook $1-x-y$ te staan, dus de enige functie die voldoet is $f(x)=x-1$.
|
f(x)=x-1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Vind alle functies $f: \mathbb{Z} \rightarrow \mathbb{Z}$ die voldoen aan
$$
f(-f(x)-f(y))=1-x-y
$$
voor alle $x, y \in \mathbb{Z}$.
|
Invullen van $x=y=1$ geeft $f(-2 f(1))=-1$. Invullen van $x=n, y=1$ geeft $f(-f(n)-f(1))=-n$. Nu kiezen we $x=-f(n)-f(1)$ en $y=-2 f(1)$, dat geeft
$$
f(-f(-f(n)-f(1))-f(-2 f(1)))=1-(-f(n)-f(1))-(-2 f(1))
$$
waarbij we de linkerkant verder kunnen uitrekenen als $f(--n--1)=f(n+1)$ en de rechterkant verder als $1+f(n)+f(1)+2 f(1)=f(n)+3 f(1)+1$. Schrijf nu $3 f(1)+1=c$, dan staat er
$$
f(n+1)=f(n)+c
$$
Met inductie twee kanten op volgt dat $f(n+k)=f(n)+c k$ voor alle $k \in \mathbb{Z}$, waarna $n=0$ geeft dat $f(k)=f(0)+c k$ voor alle $k \in \mathbb{Z}$, dus $f$ is een lineaire functie.
Om te controleren vullen we $f(x)=a x+b$ in met $a, b \in \mathbb{Z}$. Dan wordt de linkerkant van de functievergelijking
$$
f(-f(x)-f(y))=a(-a x-b-a y-b)+b=-a^{2} x-a^{2} y-2 a b+b
$$
Dit moet voor alle $x$ en $y$ gelijk zijn aan $1-x-y$. De coëfficiënt voor de $x$ moet daarom gelijk zijn (want met $y$ vast moet aan beide kanten dezelfde functie van $x$ staan) dus $-a^{2}=-1$, dus $a=1$ of $a=-1$. Met $a=-1$ en $x=y=0$ krijgen we $2 b+b=1$, wat geen gehele $b$ oplevert. Met $a=1$ en $x=y=0$ krijgen we $-2 b+b=1$ dus $b=-1$. Inderdaad komt er voor $a=1$ en $b=-1$ links ook $1-x-y$ te staan, dus de enige functie die voldoet is $f(x)=x-1$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2020-E2020_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2020"
}
|
Find all functions $f: \mathbb{Z} \rightarrow \mathbb{Z}$ that satisfy
$$
f(-f(x)-f(y))=1-x-y
$$
for all $x, y \in \mathbb{Z}$.
|
Suppose there are $a, b \in \mathbb{Z}$ such that $f(a)=f(b)$. Then substituting $y=0$ and first $x=a$ and then $x=b$ gives
$$
1-a=f(-f(a)-f(0))=f(-f(b)-f(0))=1-b
$$
so $a=b$. We conclude that $f$ is injective.
Now substitute first $x=n, y=1$ and then $x=n+1, y=0$, which gives
$$
f(-f(n)-f(1))=1-n-1=1-(n+1)-0=f(-f(n+1)-f(0))
$$
from which, by injectivity, it follows that $-f(n)-f(1)=-f(n+1)-f(0)$, or equivalently $f(n+1)=f(n)+f(1)-f(0)$. It follows, just as in the previous solution, that $f$ is a linear function, and checking shows that the only solution is $f(x)=x-1$.
|
f(x)=x-1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Vind alle functies $f: \mathbb{Z} \rightarrow \mathbb{Z}$ die voldoen aan
$$
f(-f(x)-f(y))=1-x-y
$$
voor alle $x, y \in \mathbb{Z}$.
|
Stel dat er $a, b \in \mathbb{Z}$ zijn met $f(a)=f(b)$. Dan geeft $y=0$ invullen en vervolgens eerst $x=a$ en dan $x=b$ dat
$$
1-a=f(-f(a)-f(0))=f(-f(b)-f(0))=1-b
$$
dus $a=b$. We conluderen dat $f$ injectief is.
Vul nu eerst $x=n, y=1$ in en daarna $x=n+1, y=0$, dat geeft
$$
f(-f(n)-f(1))=1-n-1=1-(n+1)-0=f(-f(n+1)-f(0))
$$
waaruit wegens de injectiviteit volgt dat $-f(n)-f(1)=-f(n+1)-f(0)$, oftewel $f(n+1)=f(n)+f(1)-f(0)$. Nu volgt net als in de vorige oplossing dat $f$ een lineaire functie is, waarna controleren laat zien dat de enige oplossing $f(x)=x-1$ is.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2020-E2020_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2020"
}
|
Given are two positive integers $k$ and $n$ with $k \leq n \leq 2 k-1$. Julian has a large stack of rectangular $k \times 1$-tiles. Merlin names a positive integer $m$ and receives $m$ tiles from Julian to place on an $n \times n$ board. On each tile, Julian first writes whether it must be a horizontal or a vertical tile. Tiles must not overlap on the board and they must not stick out. What is the largest number $m$ that Merlin can name if he wants to be sure that he can place all the tiles according to Julian's instructions on the board?
|
We prove that the largest $m$ that Merlin can name is equal to $\min (n, 3(n-k)+1)$. First, we prove that $m \leq \min (n, 3(n-k)+1)$. If Merlin orders $n+1$ tiles, Julian can label all of them as horizontal. Since $n \leq 2k-1$, it is not possible to place more than one horizontal tile in the same row, so Merlin would need $n+1$ rows, which is a contradiction. Therefore, it must hold that $m \leq n$.
Now suppose that Merlin orders $3(n-k)+2$ tiles. Julian can then make $n-k+1$ tiles vertical and $2n-2k+1$ tiles horizontal. Vertical tiles can cover squares from the top $k$ rows, the bottom $k$ rows, or $k$ rows in between, but in all cases, they cover squares from the $k-(n-k)=2k-n \geq 1$ rows in the middle of the board. In each of these middle rows, the vertical tiles cover at least $n-k+1$ squares, leaving $k-1$ squares for the horizontal tiles. No horizontal tile can fit in these $2k-n$ middle rows, so all horizontal tiles must be in the remaining $n-(2k-n)=2n-2k$ rows. However, there are $2n-2k+1$ horizontal tiles, which is a contradiction. Therefore, it must hold that $m \leq 3(n-k)+1$. Altogether, we have $m \leq \min (n, 3(n-k)+1)$.
Now we prove that it is always possible to place a collection of $\min (n, 3(n-k)+1)$ tiles on the board. We first consider two special configurations. Place $n-k$ horizontal tiles in the bottom-left corner, covering a rectangle of height $n-k$ and width $k$. To the right of this, exactly $n-k$ vertical tiles can fit (as far down as possible), covering a rectangle of width $n-k$ and height $k$. Above this, exactly $n-k$ horizontal tiles can fit (as far to the right as possible), and there is space left in the top-left corner for $n-k$ vertical tiles. Thus, we can place $2(n-k)$ horizontal and $2(n-k)$ vertical tiles. Another way to cover the board is as follows. Place $n$ vertical tiles at the top, covering a rectangle of width $n$ and height $k$. There is then space below for $n-k$ horizontal tiles (each in its own row; the exact placement does not matter). It is therefore also possible to place $n$ vertical and $n-k$ horizontal tiles.
Now suppose that Merlin receives $A$ horizontal tiles and $B$ vertical tiles from Julian. Then $A+B \leq n$ and $A+B \leq 3(n-k)+1$. Without loss of generality, assume that $A \leq B$. If $A \leq n-k$, then Merlin uses the second special configuration and removes tiles as needed. Since $B \leq n$, this works. On the other hand, if $A \geq n-k+1$,
then $B \leq 3(n-k)+1-A \leq 3(n-k)+1-(n-k+1)=2(n-k)$. Since $A \leq B$, it also holds that $A \leq B \leq 2(n-k)$. Therefore, Merlin can use the first special configuration and remove tiles as needed. Thus, Merlin can always place $\min (n, 3(n-k)+1)$ tiles on the board.
|
\min (n, 3(n-k)+1)
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Gegeven zijn twee positieve gehele getallen $k$ en $n$ met $k \leq n \leq 2 k-1$. Julian heeft een grote stapel rechthoekige $k \times 1$-tegels. Merlijn noemt een positief geheel getal $m$ en ontvangt van Julian $m$ tegels om op een $n \times n$-bord te plaatsen. Op elke tegel schrijft Julian eerst of het een horizontale of een verticale tegel moet worden. Tegels mogen op het bord niet overlappen en ze mogen ook niet uitsteken. Wat is het grootste getal $m$ dat Merlijn kan noemen als hij zeker wil weten dat hij alle tegels volgens het voorschrift van Julian kwijt kan op het bord?
|
We bewijzen dat de grootste $m$ die Merlijn kan noemen, gelijk is aan $\min (n, 3(n-$ $k)+1$. Eerst bewijzen we dat $m \leq \min (n, 3(n-k)+1)$. Als Merlijn $n+1$ tegels bestelt, kan Julian ze allemaal als horizontaal bestempelen. Aangezien $n \leq 2 k-1$ is het niet mogelijk om meer dan één horizontale tegel in dezelfde rij te plaatsen, dus heeft Merlijn $n+1$ rijen nodig, tegenspraak. Er moet dus gelden $m \leq n$.
Stel nu dat Merlijn 3( $n-k)+2$ tegels bestelt. Julian kan nu $n-k+1$ tegels verticaal maken en $2 n-2 k+1$ tegels horizontaal. Verticale tegels kunnen vakjes uit de bovenste $k$ rijen bedekken of uit de onderste $k$ rijen of uit $k$ rijen ergens daartussenin, maar in alle gevallen bedekken ze vakjes uit de $k-(n-k)=2 k-n \geq 1$ rijen in het midden van het bord. In elk van deze middelste rijen bedekken de verticale tegels dus minimaal $n-k+1$ vakjes, waardoor er nog $k-1$ vakjes over zijn voor de horizontale tegels. Daar past geen horizontale tegel meer in, dus de $2 k-n$ middelste rijen bevatten geen horizontale tegels. Alle horizontale tegels liggen daarom in de overige $n-(2 k-n)=2 n-2 k$ rijen, maar er zijn $2 n-2 k+1$ horizontale tegels, tegenspraak. Er moet dus gelden $m \leq 3(n-k)+1$. Al met al geldt $m \leq \min (n, 3(n-k)+1)$.
Nu bewijzen we dat het altijd mogelijk is om een collectie van $\min (n, 3(n-k)+1)$ tegels op het bord te plaatsen. We bekijken eerst twee speciale configuraties. Leg $n-k$ horizontale tegels linksonder, die een rechthoek van $n-k$ hoog en $k$ breed bedekken. Rechts daarnaast passen dan nog precies $n-k$ verticale tegels (zo ver mogelijk naar beneden geschoven), die een rechthoek van $n-k$ breed en $k$ hoog bedekken. Vervolgens kunnen daarboven nog precies $n-k$ horizontale tegels (zo ver mogelijk naar rechts geschoven) en blijft er linksboven ruimte over voor $n-k$ verticale tegels. We kunnen dus $2(n-k)$ horizontale en $2(n-k)$ verticale tegels kwijt. Een andere manier om het bord te bedekken is als volgt. Leg $n$ verticale tegels bovenin, die een rechthoek van $n$ breed en $k$ hoog bedekken. Er is daaronder dan nog ruimte voor $n-k$ horizontale tegels (elk op hun eigen rij; de precieze plaatsing maakt verder niet uit). Het is dus ook mogelijk om $n$ verticale en $n-k$ horizontale tegels te plaatsen.
Stel nu dat Merlijn $A$ horizontale tegels van Julian krijgt en $B$ verticale. Dan geldt $A+B \leq n$ en $A+B \leq 3(n-k)+1$. Zonder verlies van algemeenheid nemen we aan dat $A \leq B$. Als nu $A \leq n-k$, dan gebruikt Merlijn de tweede speciale configuratie en laat daar indien nodig nog tegels weg. Omdat $B \leq n$, lukt dit. Stel anderzijds dat $A \geq n-k+1$.

Dan is $B \leq 3(n-k)+1-A \leq 3(n-k)+1-(n-k+1)=2(n-k)$. Omdat $A \leq B$ geldt ook $A \leq B \leq 2(n-k)$. Dus Merlijn kan de eerste speciale configuratie gebruiken, waarin hij indien nodig nog wat tegels weglaat. Het lukt Merlijn dus altijd om $\min (n, 3(n-k)+1)$ tegels op het bord te leggen.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2020-E2020_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2020"
}
|
Given is a cyclic quadrilateral $A B C D$ with $|A B|=|B C|$. Point $E$ lies on the arc $C D$ where $A$ and $B$ do not lie. The intersection of $B E$ and $C D$ is called $P$, and the intersection of $A E$ and $B D$ is called $Q$. Prove that $P Q \| A C$.
|
Since $|A B|=|B C|$, it follows that $\angle A E B=\angle B D C$, so $\angle Q E P=\angle A E B=$ $\angle B D C=\angle Q D P$, from which it follows that $Q P E D$ is a cyclic quadrilateral. Therefore, $\angle Q P D=$ $\angle Q E D=\angle A E D=\angle A C D$. This means, by corresponding angles, that $Q P$ and $A C$ are parallel.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Gegeven is een koordenvierhoek $A B C D$ met $|A B|=|B C|$. Punt $E$ ligt op de boog $C D$ waar $A$ en $B$ niet op liggen. Het snijpunt van $B E$ en $C D$ noemen we $P$, het snijpunt van $A E$ en $B D$ noemen we $Q$. Bewijs dat $P Q \| A C$.

|
Omdat $|A B|=|B C|$ geldt $\angle A E B=\angle B D C$, dus $\angle Q E P=\angle A E B=$ $\angle B D C=\angle Q D P$, waaruit volgt dat $Q P E D$ een koordenvierhoek is. Dus $\angle Q P D=$ $\angle Q E D=\angle A E D=\angle A C D$. Dit betekent wegens F-hoeken dat $Q P$ en $A C$ evenwijdig zijn.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2021-B2021_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2021"
}
|
Determine all triples $(x, y, z)$ of real numbers for which
$$
\begin{aligned}
& x^{2}-y z=|y-z|+1, \\
& y^{2}-z x=|z-x|+1, \\
& z^{2}-x y=|x-y|+1
\end{aligned}
$$
|
The system of equations is symmetric: if you swap, for example, $x$ and $y$, the third equation remains the same, and the first two equations switch places. We can therefore assume without loss of generality that $x \geq y \geq z$. The system then becomes:
$$
\begin{aligned}
& x^{2}-y z=y-z+1, \\
& y^{2}-z x=x-z+1 \\
& z^{2}-x y=x-y+1
\end{aligned}
$$
Subtracting the first two equations gives $x^{2}-y^{2}+z(x-y)=y-x$, or $(x-y)(x+y+z+1)=0$. This implies $x=y$ or $x+y+z=-1$. Subtracting the second and third equations gives $y^{2}-z^{2}+x(y-z)=y-z$, or $(y-z)(y+z+x-1)=0$. This implies $y=z$ or $x+y+z=1$.
We now distinguish two cases: $x=y$ and $x \neq y$. In the first case, $y \neq z$, because otherwise $x=y=z$ and this would give $0=1$ in the first equation, a contradiction. Therefore, $x+y+z=1$, or $2x+z=1$. Substituting $y=x$ and $z=1-2x$ into the first equation gives $x^{2}-x(1-2x)=x-(1-2x)+1$, which simplifies to $3x^{2}-x=3x$, or $3x^{2}=4x$. This gives $x=0$ or $x=\frac{4}{3}$. With $x=0$, we find $y=0, z=1$, but this does not satisfy our assumption $x \geq y \geq z$. Therefore, we only have the option $x=\frac{4}{3}$, which gives the triplet $\left(\frac{4}{3}, \frac{4}{3},-\frac{5}{3}\right)$. Checking shows that this is a solution.
Now consider the case $x \neq y$. Then $x+y+z=-1$, so it cannot also be true that $x+y+z=1$, so we see that $y=z$. Now $x+y+z=-1$ gives $x+2z=-1$, so $x=-1-2z$. The first equation becomes $(-1-2z)^{2}-z^{2}=1$, which simplifies to $3z^{2}+4z=0$. This gives $z=0$ or $z=-\frac{4}{3}$. With $z=0$, we find $y=0, x=-1$, but this does not satisfy our assumption $x \geq y \geq z$. Therefore, we only have the option $z=-\frac{4}{3}$, which gives the triplet $\left(\frac{5}{3},-\frac{4}{3},-\frac{4}{3}\right)$. Checking shows that this is a solution.
By including the permutations of these two solutions, we find a total of six solutions: $\left(\frac{4}{3}, \frac{4}{3},-\frac{5}{3}\right),\left(\frac{4}{3},-\frac{5}{3}, \frac{4}{3}\right),\left(-\frac{5}{3}, \frac{4}{3}, \frac{4}{3}\right),\left(\frac{5}{3},-\frac{4}{3},-\frac{4}{3}\right),\left(-\frac{4}{3}, \frac{5}{3},-\frac{4}{3}\right)$, and $\left(-\frac{4}{3},-\frac{4}{3}, \frac{5}{3}\right)$.
| null |
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Bepaal alle drietallen $(x, y, z)$ van reële getallen waarvoor geldt
$$
\begin{aligned}
& x^{2}-y z=|y-z|+1, \\
& y^{2}-z x=|z-x|+1, \\
& z^{2}-x y=|x-y|+1
\end{aligned}
$$
|
Het stelsel vergelijkingen is symmetrisch: verwissel je bijvoorbeeld $x$ en $y$, dan blijft de derde vergelijking hetzelfde en wisselen de eerste twee vergelijkingen om. We kunnen dus zonder verlies van algemeenheid aannemen dat $x \geq y \geq z$. Dan wordt het stelsel:
$$
\begin{aligned}
& x^{2}-y z=y-z+1, \\
& y^{2}-z x=x-z+1 \\
& z^{2}-x y=x-y+1
\end{aligned}
$$
De eerste twee vergelijkingen van elkaar afhalen geeft $x^{2}-y^{2}+z(x-y)=y-x$, oftewel $(x-y)(x+y+z+1)=0$. Hieruit volgt $x=y$ of $x+y+z=-1$. De tweede en derde vergelijking van elkaar afhalen geeft $y^{2}-z^{2}+x(y-z)=y-z$, oftewel $(y-z)(y+z+x-1)=0$. Hieruit volgt $y=z$ of $x+y+z=1$.
We onderscheiden nu twee gevallen: $x=y$ en $x \neq y$. In het eerste geval geldt $y \neq z$, want anders zou $x=y=z$ en dat geeft in de eerste vergelijking $0=1$, tegenspraak. Er volgt dus nu $x+y+z=1$, oftewel $2 x+z=1$. Invullen van $y=x$ en $z=1-2 x$ in de eerste vergelijking geeft $x^{2}-x(1-2 x)=x-(1-2 x)+1$, wat we herleiden tot $3 x^{2}-x=3 x$, oftewel $3 x^{2}=4 x$. Dit geeft $x=0$ of $x=\frac{4}{3}$. Met $x=0$ vinden we $y=0, z=1$, maar dit voldoet niet aan onze aanname $x \geq y \geq z$. We houden dus alleen de optie $x=\frac{4}{3}$ over en dat geeft het drietal $\left(\frac{4}{3}, \frac{4}{3},-\frac{5}{3}\right)$. Controleren laat zien dat dit een oplossing is.
Nu het geval $x \neq y$. Dan geldt $x+y+z=-1$, dus kan niet ook gelden $x+y+z=1$, dus we zien dat $y=z$. Nu geeft $x+y+z=-1$ dat $x+2 z=-1$, dus $x=-1-2 z$. De eerste vergelijking wordt nu $(-1-2 z)^{2}-z^{2}=1$, wat we herleiden tot $3 z^{2}+4 z=0$. Hieruit vinden we $z=0$ of $z=-\frac{4}{3}$. Met $z=0$ vinden we $y=0, x=-1$, maar dit voldoet niet aan onze aanname $x \geq y \geq z$. We houden dus alleen de optie $z=-\frac{4}{3}$ over en dat geeft het drietal $\left(\frac{5}{3},-\frac{4}{3},-\frac{4}{3}\right)$. Controleren laat zien dat dit een oplossing is.
Door de permutaties van deze twee oplossingen ook mee te nemen, vinden we al met al zes oplossingen: $\left(\frac{4}{3}, \frac{4}{3},-\frac{5}{3}\right),\left(\frac{4}{3},-\frac{5}{3}, \frac{4}{3}\right),\left(-\frac{5}{3}, \frac{4}{3}, \frac{4}{3}\right),\left(\frac{5}{3},-\frac{4}{3},-\frac{4}{3}\right),\left(-\frac{4}{3}, \frac{5}{3},-\frac{4}{3}\right)$ en $\left(-\frac{4}{3},-\frac{4}{3}, \frac{5}{3}\right)$.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2021-B2021_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2021"
}
|
Let $p$ be a prime number greater than 2. Patricia wants to assign 7 not necessarily distinct numbers from $\{1,2, \ldots, p\}$ to the black dots in the figure below, in such a way that the product of the three numbers on a line or circle always has the same remainder when divided by $p$.
(a) Suppose Patricia uses the number $p$ at least once. How many times does she minimally need the number $p$ in total?
(b) Suppose Patricia does not use the number $p$. In how many ways can she then assign the numbers? (Two ways are different if different numbers are assigned to at least one black dot. The figure is not rotated or reflected.)
|
(a) By 'lines' we mean in the following part of this section the six lines and the circle. Whenever the number $p$ is used somewhere, there is a 'line' with a product divisible by $p$, so with a remainder of 0 after division by $p$. Then all 'lines' must give a remainder of 0, so all 'lines' must contain $p$ at least once. This can be achieved by assigning the number $p$ to the bottom three dots. Suppose it can also be done with at most two $p$s. Each dot lies on exactly three 'lines', so then there are at most six 'lines' on which a number $p$ lies. However, there are seven 'lines', so this is not possible. We conclude that it needs $p$ at least three times in total.
(b) Let the bottom three numbers from left to right be $a, b$, and $c$. Let the number in the middle of the left side of the triangle be $d$. We can now calculate all numbers modulo $p$; note that all numbers are invertible modulo $p$ because $p$ itself does not participate and $p$ is prime. The bottom line has the product $a b c$. The left side of the triangle also does, so the number at the very top is congruent modulo $p$ to $a b c(a d)^{-1}=b c d^{-1}$. If we look at the line from the bottom right to the middle of the left side, we see that the middle number must be congruent to $a b c(c d)^{-1}=a b d^{-1}$. By looking at the circle, we find that the number on the right in the middle is $a b c(b d)^{-1} = a c d^{-1}$.
On the right side, we now get the equation $b c d^{-1} \cdot a c d^{-1} \cdot c \equiv a b c \bmod p$, so $c^{2} \equiv d^{2} \bmod p$. Similarly, we find on the vertical line $b^{2} \equiv d^{2}$ and on the line from the bottom left to the middle right $a^{2} \equiv d^{2} \bmod p$. We conclude that the numbers $a, b, c$, and $d$ must all have the same square. From $x^{2} \equiv y^{2}$ follows $(x-y)(x+y) \equiv 0 \bmod p$, so $p \mid x-y$ or $p \mid x+y$, because $p$ is prime. Thus, $x \equiv y$ or $x \equiv -y$. There are two options, because if $y \equiv -y$, then $2 y \equiv 0$, so $p \mid 2 y$, so $p \mid y$ due to $p>2$; contradiction. Therefore, the numbers $b, c$, and $d$ must all be congruent to $a$ or $-a$. If this condition is met, then $a^{2} \equiv b^{2} \equiv c^{2} \equiv d^{2}$ and then it follows from the above that on all six lines and on the circle the product is congruent to $a b c$.
There are $p-1$ possibilities for the number $a$ and then 2 possibilities for each of the numbers $b, c$, and $d$. So in total, there are $8(p-1)$ ways to assign the numbers.
|
8(p-1)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Zij $p$ een priemgetal groter dan 2. Patricia wil 7 niet-noodzakelijk verschillende getallen uit $\{1,2, \ldots, p\}$ aan de zwarte stippen in onderstaande figuur toekennen, op zo'n manier dat het product van drie getallen op een lijn of cirkel altijd dezelfde rest bij deling door $p$ heeft.

(a) Stel dat Patricia het getal $p$ minstens één keer gebruikt. Hoe vaak heeft ze het getal $p$ dan in totaal minimaal nodig?
(b) Stel dat Patricia het getal $p$ niet gebruikt. Op hoeveel manieren kan zij dan de getallen toekennen? (Twee manieren zijn verschillend als er aan minstens één zwarte stip verschillende getallen zijn toegekend. De figuur wordt niet gedraaid of gespiegeld.)
|
(a) Met 'lijnen' bedoelen we in het vervolg van dit onderdeel de zes lijnen en de cirkel. Zodra het getal $p$ ergens gebruikt wordt, is er een 'lijn' met product deelbaar door $p$, dus met rest 0 na deling door $p$. Alle 'lijnen' moeten dan rest 0 geven, dus alle 'lijnen' bevatten minstens één keer $p$. Dit kunnen we bereiken door het getal $p$ aan de onderste drie stippen toe te kennen. Stel dat het ook al kan met hooguit twee keer $p$. Elke stip ligt op precies drie 'lijnen', dus dan zijn er hooguit zes 'lijnen' waar een getal $p$ op ligt. Er zijn echter zeven 'lijnen', dus dit kan niet. We concluderen dat ze $p$ in totaal minimaal drie keer nodig heeft.
(b) Noem de onderste drie getallen van links naar rechts $a, b$ en $c$. Noem het getal midden op de linkerzijkant van de driehoek $d$. We kunnen nu alle getallen modulo $p$ uitrekenen; merk op dat alle getallen inverteerbaar zijn modulo $p$ omdat $p$ zelf niet meedoet en $p$ priem is. De onderste lijn heeft product $a b c$. De linkerzijde van de driehoek dus ook, dus het getal helemaal bovenin is modulo $p$ congruent aan $a b c(a d)^{-1}=b c d^{-1}$. Als we de lijn van rechtsonder naar het midden van de linkerzijde bekijken, zien we dat het middelste getal congruent moet zijn aan $a b c(c d)^{-1}=a b d^{-1}$. Door de cirkel te bekijken, vinden we dat het getal rechts in het midden $a b c(b d)^{-1}=$ $a c d^{-1}$ is.
Op de rechterzijde krijgen we nu de vergelijking $b c d^{-1} \cdot a c d^{-1} \cdot c \equiv a b c \bmod p$, dus $c^{2} \equiv d^{2} \bmod p$. Analoog vinden we op de verticale lijn $b^{2} \equiv d^{2}$ en op de lijn van linksonder naar rechts midden $a^{2} \equiv d^{2} \bmod p$. We concluderen dat de getallen $a, b, c$ en $d$ allemaal hetzelfde kwadraat moeten hebben. Uit $x^{2} \equiv y^{2} \operatorname{volgt}(x-y)(x+y) \equiv 0$ $\bmod p$, dus $p \mid x-y$ of $p \mid x+y$, want $p$ is priem. Dus geldt $x \equiv y$ of $x \equiv-y$. Dat zijn twee opties, want zou $y \equiv-y$, dan $2 y \equiv 0$, dus $p \mid 2 y$, dus $p \mid y$ wegens $p>2$; tegenspraak. Er geldt dus dat de getallen $b, c$ en $d$ allemaal congruent aan $a$ of $-a$ moeten zijn. Als aan deze voorwaarde voldaan is, dan geldt $a^{2} \equiv b^{2} \equiv c^{2} \equiv d^{2}$ en dan volgt uit het voorgaande dat op alle zes de lijnen en op de cirkel het product congruent aan $a b c$ is.
Er zijn $p-1$ mogelijkheden voor het getal $a$ en daarna 2 mogelijkheden voor elk van de getallen $b, c$ en $d$. Dus totaal zijn er $8(p-1)$ manieren om de getallen toe te kennen.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2021-B2021_uitwerkingen.jsonl",
"solution_match": "# Oplossing I.",
"tier": "T1",
"year": "2021"
}
|
Let $p$ be a prime number greater than 2. Patricia wants to assign 7 not necessarily distinct numbers from $\{1,2, \ldots, p\}$ to the black dots in the figure below, in such a way that the product of the three numbers on a line or circle always has the same remainder when divided by $p$.

(a) Suppose Patricia uses the number $p$ at least once. How many times does she minimally need the number $p$ in total?
(b) Suppose Patricia does not use the number $p$. In how many ways can she then assign the numbers? (Two ways are different if different numbers are assigned to at least one black dot. The figure is not rotated or reflected.)
|
As an alternative solution for part (b), let's show that either all seven numbers are the same, or there is a 'line' $k$ such that the three points on it have value $x$, while the remaining four points have value $-x$. Note that $-x \not \equiv x$ due to $p>2$.
Note that these assignments certainly satisfy the conditions: in the first case, the product of the three points on each 'line' is obviously the same; in the second case, it is $x^{3}$ for 'line' $k$, and $x(-x)^{2}=x^{3}$ for each of the six other lines, using the fact that each of these other lines has exactly one point in common with $k$. The number of ways this can be done is $p-1$ in the first case, and $7(p-1)$ in the second case (namely 7 choices for the 'line' $k$ and for each choice then $p-1$ choices for $x$), so in total $(p-1)+7(p-1)=8(p-1)$.
Given two different points with values $x$ and $y$. Let the value at the third point on the line through $x$ and $y$ now be $z$ and the other four values $a, b, c, d$, then (w.l.o.g.) we have $x a b \equiv x c d \equiv y c b \equiv y a d \equiv z a c \equiv z b d \equiv x y z$. Thus $x^{2} a b c d=(x a b)(x c d) \equiv(y c d)(y a d)=y^{2}(a b c d)$, so $x^{2} \equiv y^{2}$, since we can divide by $a b c d \not \equiv 0$. From $p \mid x^{2}-y^{2}=(x-y)(x+y)$ it follows that $p \mid x-y$ or $p \mid x+y$, so $y \equiv x$ or $y \equiv-x$. If we fix a point with value $x$, then every other point thus has value $x$ or $-x$.
Assume that not all points have the same value. Then both $x$ and $y \equiv-x$ occur, so there is a line with the points $x, y$ and (w.l.o.g.) $z=y$. This has product $x y^{2}=-y^{3}$. Since $y^{3} \not \equiv-y^{3}$ (otherwise $p \mid 2 y^{3}$ so $p \mid y$), each line now contains exactly 1 or 3 points with value $x$. The products we find for the remaining six 'lines' are $x a b \equiv x c d \equiv y c b \equiv y a d \equiv y a c \equiv y b d$. The last four products cannot consist of three times the factor $x$, so they contain exactly one $x$, so w.l.o.g. $(a, b, c, d)=(x, x, y, y)$. This means that $(x, a, b)=(x, x, x)$, while the points that do not lie on this line all have value $y \equiv-x$, as we wanted to prove.
|
8(p-1)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Zij $p$ een priemgetal groter dan 2. Patricia wil 7 niet-noodzakelijk verschillende getallen uit $\{1,2, \ldots, p\}$ aan de zwarte stippen in onderstaande figuur toekennen, op zo'n manier dat het product van drie getallen op een lijn of cirkel altijd dezelfde rest bij deling door $p$ heeft.

(a) Stel dat Patricia het getal $p$ minstens één keer gebruikt. Hoe vaak heeft ze het getal $p$ dan in totaal minimaal nodig?
(b) Stel dat Patricia het getal $p$ niet gebruikt. Op hoeveel manieren kan zij dan de getallen toekennen? (Twee manieren zijn verschillend als er aan minstens één zwarte stip verschillende getallen zijn toegekend. De figuur wordt niet gedraaid of gespiegeld.)
|
Als alternatieve oplossing voor onderdeel (b) laten we zien dat ofwel alle zeven getallen hetzelfde zijn, dan wel dat er een 'lijn' $k$ is waarvan de drie punten waarde $x$ hebben terwijl de overige vier punten waarde $-x$ hebben. Merk op dat $-x \not \equiv x$ wegens $p>2$.
Merk op dat deze toekenningen in ieder geval voldoen: in het eerste geval is het product van de drie punten op elke 'lijn' uiteraard hetzelfde; in het tweede geval is het $x^{3}$ voor 'lijn' $k$, en $x(-x)^{2}=x^{3}$ voor elk van de zes andere lijnen, waarbij we gebruiken dat elk van deze andere lijnen precies één punt met $k$ gemeen heeft. Het aantal manieren waarop ze dit kan doen is $p-1$ in het eerste geval, en $7(p-1)$ in het tweede geval (namelijk 7 keuzes voor de 'lijn' $k$ en per keuze vervolgens $p-1$ keuzes voor $x)$, dus in totaal $(p-1)+7(p-1)=8(p-1)$.
Gegeven twee verschillende stippen met waarden $x$ en $y$. Noem de waarde bij de derde stip op de lijn door $x$ en $y$ nu $z$ en de andere vier waarden $a, b, c, d$, dan geldt (z.b.d.a.) dat $x a b \equiv x c d \equiv y c b \equiv y a d \equiv z a c \equiv z b d \equiv x y z$. Dus $x^{2} a b c d=(x a b)(x c d) \equiv(y c d)(y a d)=$ $y^{2}(a b c d)$, dus $x^{2} \equiv y^{2}$, omdat we mogen delen door $a b c d \not \equiv 0$. Uit $p \mid x^{2}-y^{2}=(x-y)(x+y)$ volgt dat $p \mid x-y$ of $p \mid x+y$, dus $y \equiv x$ of $y \equiv-x$. Houden we een punt met waarde $x$ vast, dan zien we dat elk ander punt dus waarde $x$ of $-x$ heeft.
Stel dat niet alle punten dezelfde waarde hebben. Dan komen $x$ en $y \equiv-x$ dus beide voor, dus is er een lijn met daarop de punten $x, y$ en (z.b.d.a.) $z=y$. Deze heeft product $x y^{2}=-y^{3}$. Omdat $y^{3} \not \equiv-y^{3}$ (anders zou $p \mid 2 y^{3}$ dus $p \mid y$ ), bevat nu elke lijn precies 1 of 3 keer een punt met waarde $x$. De producten die we voor de overige zes 'lijnen' vinden zijn $x a b \equiv x c d \equiv y c b \equiv y a d \equiv y a c \equiv y b d$. De laatste vier producten kunnen niet uit drie maal factor $x$ bestaan, dus bevatten precies één $x$, dus geldt z.b.d.a. $(a, b, c, d)=(x, x, y, y)$. Dat betekent dat $(x, a, b)=(x, x, x)$, terwijl de punten die niet op deze lijn liggen allemaal waarde $y \equiv-x$ hebben, zoals we wilden bewijzen.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2021-B2021_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2021"
}
|
Jesse and Tjeerd are playing a game. Jesse has $n \geq 2$ stones at his disposal. There are two boxes: the black box has space for half of the stones (rounded down) and the white box has space for half of the stones (rounded up). Jesse and Tjeerd take turns, with Jesse starting. In his turn, Jesse picks up one new stone, writes a positive real number on the stone, and places it in one of the boxes that is not yet full. Tjeerd sees all the numbers on the stones in the boxes and can, in his turn, move one stone of his choice from one box to the other if it is not yet full, but he can also choose to do nothing. The game stops as soon as both boxes are full. If the total value of the stones in the black box is greater than the total value of the stones in the white box, Jesse wins; otherwise, Tjeerd wins. Determine for every $n \geq 2$ who can win with certainty (and provide a corresponding winning strategy).
|
When $n$ is even, an equal number of stones end up in both boxes. Jesse can now win by giving the first $n-1$ stones a value of 2 and placing them in a random box. Tjeerd may move a stone after each of Jesse's moves. If Jesse's last stone must go into the black box, he gives this stone a value of 3. Then he wins, because the total value in the black box is then 1 greater than in the white box. If his last stone must go into the white box, he gives this stone a value of 1. In this case, the total value in the black box is also 1 greater than in the white box, so Jesse wins.
Now consider the case where $n$ is odd, say $n=2m+1$ with $m \geq 1$. In the black box, there can be $m$ stones, and in the white box, there can be $m+1$ stones. Jesse can win again. The first $n-2$ stones he gives a value of 1 and places them in a random box. Tjeerd may again move a stone after each of Jesse's moves. We now distinguish two cases for the moment when Jesse's turn comes and there are still two empty spots in the boxes.
- Case 1: the black box is full. The value of the black box is now $m$, and that of the white box is $m-1$. Jesse now places a stone with a value of $\frac{1}{4}$ in the white box. If Tjeerd does not move a stone, Jesse gives the last stone a value of $\frac{1}{4}$. The total value in the white box is then $(m-1)+\frac{1}{4}+\frac{1}{4}=m-\frac{1}{2}$, which is less than the total value in the black box. If Tjeerd does move a stone, it must be a stone from the black box to the white box (since the black box is full). This makes the value in the white box $(m-1)+\frac{1}{4}+1=m+\frac{1}{4}$ and that in the black box $m-1$. Jesse now places the last stone with a value of 2 in the black box, so the total value in the black box becomes $(m-1) \cdot 1+1 \cdot 2=m+1$.
- Case 2: the black box is not yet full. Jesse now places a stone with a value of 3 in the black box. If Tjeerd does not move this stone, Jesse gives the last stone a value of 1. Then the total value in the white box is $m+1$ and in the black box $(m-1) \cdot 1+1 \cdot 3=m+2$. If Tjeerd does move the stone with a value of 3, then a spot becomes free in the black box, so Jesse places his last stone there and gives it a value of 5. The total value in the white box is now $m \cdot 1+1 \cdot 3=m+3$ and the total value in the black box $(m-1) \cdot 1+1 \cdot 5=m+4$.
We see that Jesse can always ensure that the total value in the black box is greater than that in the white box, so Jesse always wins.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Jesse en Tjeerd spelen een spelletje. Jesse heeft de beschikking over $n \geq 2$ stenen. Er zijn twee dozen: in de zwarte doos is ruimte voor de helft van de stenen (naar beneden afgerond) en in de witte doos is ruimte voor de helft van de stenen (naar boven afgerond). Jesse en Tjeerd zijn om en om aan de beurt, waarbij Jesse begint. Jesse pakt in zijn beurt steeds één nieuwe steen, schrijft een positief reëel getal op de steen en legt hem in één van de dozen die nog niet vol is. Tjeerd ziet al deze getallen op de stenen in de dozen en mag in zijn beurt één steen naar keuze uit een doos verplaatsen naar de andere doos als die nog niet vol is, maar hij mag er ook voor kiezen om niets te doen. Het spel stopt zodra beide dozen vol zijn. Als dan de totale waarde van de stenen in de zwarte doos groter is dan de totale waarde van de stenen in de witte doos, wint Jesse; anders wint Tjeerd. Bepaal voor elke $n \geq 2$ wie er met zekerheid kan winnen (en geef een bijbehorende winnende strategie).
|
Als $n$ even is, komen er in allebei de dozen precies evenveel stenen. Jesse kan nu winnen door de eerste $n-1$ stenen allemaal waarde 2 te geven en ze in een willekeurige doos te stoppen. Tjeerd verplaatst na elke zet van Jesse eventueel een steen. Als Jesse's laatste steen in de zwarte doos moet, geeft hij deze steen waarde 3. Dan wint hij, want de totale waarde in de zwarte doos is dan 1 groter dan in de witte doos. Als zijn laatste steen in de witte doos moet, geeft hij deze steen waarde 1 . Ook nu is de totale waarde in de zwarte doos 1 groter dan in de witte doos, dus Jesse wint.
Bekijk nu het geval dat $n$ oneven is, zeg $n=2 m+1$ met $m \geq 1$. In de zwarte doos kunnen $m$ stenen en in de witte kunnen $m+1$ stenen. Jesse kan nu weer winnen. De eerste $n-2$ stenen geeft hij allemaal waarde 1 en legt hij in een willekeurige doos. Tjeerd verplaatst na elke zet van Jesse weer eventueel een steen. We onderscheiden nu twee gevallen voor het moment dat Jesse aan de beurt is en er nog twee lege plekken in de dozen zijn.
- Geval 1: de zwarte doos is vol. De waarde van de zwarte doos is nu $m$, die van de witte doos $m-1$. Jesse legt nu een steen met waarde $\frac{1}{4}$ in de witte doos. Als Tjeerd vervolgens niet een steen verplaatst, geeft Jesse de laatste steen ook waarde $\frac{1}{4}$. De totale waarde van de witte doos is dan $(m-1)+\frac{1}{4}+\frac{1}{4}=m-\frac{1}{2}$ en dat is kleiner dan de totale waarde in de zwarte doos. Als Tjeerd wel iets verplaatst, dan moet dat een steen uit de zwarte doos zijn die naar de witte doos gaat (immers, de zwarte doos is vol). Daarmee is de waarde in de witte doos $(m-1)+\frac{1}{4}+1=m+\frac{1}{4}$ geworden en die in de zwarte doos $m-1$. Jesse legt nu de laatste steen met waarde 2 in de zwarte doos, zodat de totale waarde in de zwarte doos $(m-1) \cdot 1+1 \cdot 2=m+1$ wordt.
- Geval 2: de zwarte doos is nog niet vol. Jesse legt nu een steen met waarde 3 in de zwarte doos. Als Tjeerd deze steen niet verplaatst, geeft Jesse de laatste steen waarde 1. Dan is de totale waarde in de witte doos $m+1$ en in de zwarte doos $(m-1) \cdot 1+1 \cdot 3=m+2$. Als Tjeerd de steen met waarde 3 wel verplaatst, dan komt er een plek vrij in de zwarte doos, dus daar legt Jesse zijn laatste steen en deze
geeft hij waarde 5 . De totale waarde van de witte doos is nu $m \cdot 1+1 \cdot 3=m+3$ en de totale waarde van de zwarte doos $(m-1) \cdot 1+1 \cdot 5=m+4$.
We zien dat Jesse in alle gevallen ervoor kan zorgen dat de totale waarde in de zwarte doos groter is dan die in de witte doos, dus Jesse wint altijd.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2021-B2021_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2021"
}
|
Jesse and Tjeerd are playing a game. Jesse has $n \geq 2$ stones at his disposal. There are two boxes: the black box has space for half of the stones (rounded down) and the white box has space for half of the stones (rounded up). Jesse and Tjeerd take turns, with Jesse starting. In his turn, Jesse picks up one new stone, writes a positive real number on the stone, and places it in one of the boxes that is not yet full. Tjeerd sees all the numbers on the stones in the boxes and can, in his turn, move one stone of his choice from one box to the other if it is not yet full, but he can also choose to do nothing. The game stops as soon as both boxes are full. If the total value of the stones in the black box is greater than the total value of the stones in the white box, Jesse wins; otherwise, Tjeerd wins. Determine for every $n \geq 2$ who can win with certainty (and provide a corresponding winning strategy).
|
The following solution shows that it does not matter how large the capacity of the two boxes is, as long as the total capacity is $n$ (and at least 1 each). Jesse can always win and does so by first playing the power of two $2^{0}=1$, and then always playing the next smaller or larger power of two. So if at some point he has already played
$$
2^{-i}, 2^{-(i-1)}, \ldots, 2^{-1}, 2^{0}, 2^{1}, \ldots, 2^{j-1}, 2^{j}
$$
he will play in the next turn either $2^{-(i+1)}$ or $2^{j+1}$.
Jesse can ensure through clever play that the largest power of two among the played stones is always in the black box after his turn. We prove this claim by induction. On his first move, he places the stone with value $2^{0}$ in the black box, and the claim holds; this proves the base case. If it is his turn again and Tjeerd has moved the largest power of two so far, which according to the induction hypothesis was in the black box, to the white box, then there is now a free space in the black box and Jesse can place the next larger power of two there, and the claim holds again. If Tjeerd has moved something else or done nothing, then the largest power of two so far is still in the black box, and Jesse plays the next smaller power of two; it does not matter where he places it. The claim holds again in this case as well. This proves the induction step, and thus we have proven the claim.
After playing the last stone, the largest played power of two is therefore in the black box. This is greater than the sum of all smaller powers of two $\left(2^{j}>2^{j}-2^{-i}=\right.$ $\left.2^{j-1}+2^{j-2}+\cdots+2^{-(i-1)}+2^{-i}\right)$, and thus certainly greater than the sum of all powers of two in the white box. Therefore, the total value of the black box is greater than the total value of the white box.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Jesse en Tjeerd spelen een spelletje. Jesse heeft de beschikking over $n \geq 2$ stenen. Er zijn twee dozen: in de zwarte doos is ruimte voor de helft van de stenen (naar beneden afgerond) en in de witte doos is ruimte voor de helft van de stenen (naar boven afgerond). Jesse en Tjeerd zijn om en om aan de beurt, waarbij Jesse begint. Jesse pakt in zijn beurt steeds één nieuwe steen, schrijft een positief reëel getal op de steen en legt hem in één van de dozen die nog niet vol is. Tjeerd ziet al deze getallen op de stenen in de dozen en mag in zijn beurt één steen naar keuze uit een doos verplaatsen naar de andere doos als die nog niet vol is, maar hij mag er ook voor kiezen om niets te doen. Het spel stopt zodra beide dozen vol zijn. Als dan de totale waarde van de stenen in de zwarte doos groter is dan de totale waarde van de stenen in de witte doos, wint Jesse; anders wint Tjeerd. Bepaal voor elke $n \geq 2$ wie er met zekerheid kan winnen (en geef een bijbehorende winnende strategie).
|
De volgende oplossing laat zien dat het niet uitmaakt hoe groot de capaciteit van de twee dozen is, als de capaciteit in totaal maar $n$ is (en minstens 1 per stuk). Jesse kan altijd winnen en doet dat door eerst de tweemacht $2^{0}=1$ te spelen, en vervolgens telkens de eerstvolgende kleinere of grotere tweemacht. Dus als hij op zeker moment al
$$
2^{-i}, 2^{-(i-1)}, \ldots, 2^{-1}, 2^{0}, 2^{1}, \ldots, 2^{j-1}, 2^{j}
$$
heeft gespeeld, speelt hij in de volgende beurt ofwel $2^{-(i+1)}$, dan wel $2^{j+1}$.
Jesse kan er door handig te spelen voor zorgen dat de grootste tweemacht onder de gespeelde stenen na zijn beurt altijd in de zwarte doos zit. We bewijzen deze claim met inductie. Bij zijn eerste zet plaatst hij de steen met waarde $2^{0}$ in de zwarte doos en klopt de claim; dit bewijst de inductiebasis. Als hij later weer aan de beurt is en Tjeerd heeft in de vorige zet de tot dan toe grootste tweemacht, die volgens de inductiehypothese in de zwarte doos zat, verplaatst naar de witte doos, dan is er in de zwarte doos een plek vrijgekomen en kan Jesse daar de volgende grotere tweemacht neerzetten en klopt de claim weer. Als Tjeerd iets anders heeft verplaatst of niets heeft gedaan, dan staat de tot dan toe grootste tweemacht nog altijd in de zwarte doos en speelt Jesse juist de volgende kleinere tweemacht; het maakt niet uit waar hij die neerzet. Ook nu klopt de claim weer. Dit bewijst de inductiestap, waarmee we de claim hebben bewezen.
Na het spelen van de laatste steen staat de grootste gespeelde tweemacht dus in de zwarte doos. Die is groter dan de som van alle gespeelde kleinere tweemachten $\left(2^{j}>2^{j}-2^{-i}=\right.$ $\left.2^{j-1}+2^{j-2}+\cdots+2^{-(i-1)}+2^{-i}\right)$, dus zeker groter dan de som van alle tweemachten in de witte doos. Dus de totale waarde van de zwarte doos is groter dan de totale waarde van de witte doos.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2021-B2021_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2021"
}
|
Given is a triangle $ABC$ with the property that $|AB|+|AC|=3|BC|$. Let $T$ be the point on line segment $AC$ such that $|AC|=4|AT|$. Let $K$ and $L$ be points on the interior of line segments $AB$ and $AC$ respectively, such that first, $KL \parallel BC$ and second, $KL$ is tangent to the incircle of $\triangle ABC$. Let $S$ be the intersection of $BT$ and $KL$. Determine the ratio $\frac{|SL|}{|KL|}$.
|
The quadrilateral $K B C L$ touches all its sides to the inscribed circle of $\triangle A B C$. At each vertex, there are two equal tangent segments. Two opposite sides of the quadrilateral consist precisely of the four different tangent segments, so $|K B|+|L C|=|K L|+|B C|$.
Given $K L \| B C$, we have $\triangle A K L \sim \triangle A B C$. Let $t$ be the scaling factor of this similarity, so $|A K|=t|A B|,|A L|=t|A C|$, and $|K L|=t|B C|$. Then $|B K| = |A B| - |A K| = |A B| - t|A B| = (1-t)|A B|$. Similarly, $|C L| = (1-t)|A C|$. Now we have
$t|B C| + |B C| = |K L| + |B C| = |K B| + |L C| = (1-t)|A B| + (1-t)|A C| = 3(1-t)|B C|$,
where the last equality holds due to the given condition in the problem. Dividing by $|B C|$ gives $1 + t = 3 - 3t$, or $4t = 2$, thus $t = \frac{1}{2}$. We conclude that $K$ is the midpoint of $A B$ and $L$ is the midpoint of $A C$.
We already knew $\triangle A K L \sim \triangle A B C$, which implies $\frac{|K L|}{|B C|} = \frac{|A L|}{|A C|}$. Given $K L \| B C$, we also have $\triangle T S L \sim \triangle T B C$, so $\frac{|S L|}{|B C|} = \frac{|T L|}{|T C|}$. Combining these ratios, we get
$$
\frac{|S L|}{|K L|} = \frac{|S L|}{|B C|} \cdot \frac{|B C|}{|K L|} = \frac{|T L|}{|T C|} \cdot \frac{|A C|}{|A L|}.
$$
We know that $\frac{|A C|}{|A L|} = 2$, since $L$ is the midpoint of $A C$. This also means that $T$ is the midpoint of $A L$, as $4|A T| = |A C| = 2|A L|$. Thus, $\frac{|T L|}{|T C|} = \frac{\frac{1}{4}|A C|}{\frac{3}{4}|A C|} = \frac{1}{3}$. We conclude that $\frac{|S L|}{|K L|} = \frac{1}{3} \cdot 2 = \frac{2}{3}$.
|
\frac{2}{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Gegeven is een driehoek $A B C$ met de eigenschap dat $|A B|+|A C|=3|B C|$. Zij $T$ het punt op lijnstuk $A C$ zodat $|A C|=4|A T|$. Laat $K$ en $L$ punten zijn op het inwendige van respectievelijk lijnstukken $A B$ en $A C$ zodat ten eerste $K L \| B C$ en ten tweede $K L$ raakt aan de ingeschreven cirkel van $\triangle A B C$. $\mathrm{Zij} S$ het snijpunt van $B T$ en $K L$. Bepaal de verhouding $\frac{|S L|}{|K L|}$.

|
De vierhoek $K B C L$ raakt met alle zijden aan de ingeschreven cirkel van $\triangle A B C$. Bij elk hoekpunt zitten twee gelijke raaklijnstukjes. Twee overstaande zijden van de vierhoek bestaan samen precies uit de vier verschillende raaklijnstukjes, dus geldt $|K B|+|L C|=|K L|+|B C|$.
Vanwege $K L \| B C$ geldt $\triangle A K L \sim \triangle A B C$. Noem $t$ de vermenigvuldigingsfactor van deze gelijkvormigheid, dus $|A K|=t|A B|,|A L|=t|A C|$ en $|K L|=t|B C|$. Dan is $|B K|=$ $|A B|-|A K|=|A B|-t|A B|=(1-t)|A B|$. Analoog geldt $|C L|=(1-t)|A C|$. Er geldt nu
$t|B C|+|B C|=|K L|+|B C|=|K B|+|L C|=(1-t)|A B|+(1-t)|A C|=3(1-t)|B C|$,
waarbij de laatste gelijkheid geldt vanwege het gegeven in de opgave. Delen door $|B C|$ geeft nu $1+t=3-3 t$, oftewel $4 t=2$ dus $t=\frac{1}{2}$. We concluderen dat $K$ het midden van $A B$ is en $L$ het midden van $A C$.
We wisten al $\triangle A K L \sim \triangle A B C$, waaruit volgt $\frac{|K L|}{|B C|}=\frac{|A L|}{|A C|}$. Er geldt wegens $K L \| B C$ ook $\triangle T S L \sim \triangle T B C$, dus $\frac{|S L|}{|B C|}=\frac{|T L|}{|T C|}$. Combineren we deze verhoudingen, dan krijgen we
$$
\frac{|S L|}{|K L|}=\frac{|S L|}{|B C|} \cdot \frac{|B C|}{|K L|}=\frac{|T L|}{|T C|} \cdot \frac{|A C|}{|A L|} .
$$
We weten dat $\frac{|A C|}{|A L|}=2$, omdat $L$ het midden van $A C$ is. Dit betekent ook dat $T$ het midden van $A L$ is, aangezien $4|A T|=|A C|=2|A L|$. Dus $\frac{|T L|}{|T C|}=\frac{\frac{1}{4}|A C|}{\frac{3}{4}|A C|}=\frac{1}{3}$. We concluderen dat $\frac{|S L|}{|K L|}=\frac{1}{3} \cdot 2=\frac{2}{3}$.
|
{
"exam": "Dutch_TST",
"problem_label": "5",
"problem_match": "\nOpgave 5.",
"resource_path": "Dutch_TST/segmented/nl-2021-B2021_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2021"
}
|
Given is a triangle $ABC$ with the property that $|AB|+|AC|=3|BC|$. Let $T$ be the point on line segment $AC$ such that $|AC|=4|AT|$. Let $K$ and $L$ be points on the interior of line segments $AB$ and $AC$ respectively, such that first, $KL \parallel BC$ and second, $KL$ is tangent to the incircle of $\triangle ABC$. Let $S$ be the intersection of $BT$ and $KL$. Determine the ratio $\frac{|SL|}{|KL|}$.

|
Let $r$ be the radius of the inscribed circle of $\triangle ABC$. The area of triangle $ABC$ can be written as
$$
\frac{1}{2}|AB| \cdot r+\frac{1}{2}|BC| \cdot r+\frac{1}{2}|AC|=\frac{1}{2} r \cdot(3|BC|+|BC|)=2 r|BC| .
$$
On the other hand, the area of triangle $ABC$ is equal to $\frac{1}{2} h|BC|$ with $h$ the height from $A$. Thus, $h=4 r$. Since the distance from $KL$ to $BC$ is exactly $2 r$, the distance from $A$ to $KL$ is also $2 r$. Triangles $AKL$ and $ABC$ are similar due to $KL \| BC$, with the heights from $A$ being $2 r$ and $4 r$ respectively, so the scaling factor is exactly 2. Therefore, $K$ is the midpoint of $AB$ and $L$ is the midpoint of $AC$.
For point $T$, we have $|AC|=4|AT|$, so $|AT|=\frac{1}{4}|AC|=\frac{1}{2}|AL|$, thus $T$ is the midpoint of $AL$. Now consider triangle $ABL$. In this triangle, $BT$ is a median because $T$ is the midpoint of $AL$. Also, $LK$ is a median because $K$ is the midpoint of $AB$. Therefore, their intersection $S$ is the centroid, from which it follows that $\frac{|SL|}{|KL|}=\frac{2}{3}$.
|
\frac{2}{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Gegeven is een driehoek $A B C$ met de eigenschap dat $|A B|+|A C|=3|B C|$. Zij $T$ het punt op lijnstuk $A C$ zodat $|A C|=4|A T|$. Laat $K$ en $L$ punten zijn op het inwendige van respectievelijk lijnstukken $A B$ en $A C$ zodat ten eerste $K L \| B C$ en ten tweede $K L$ raakt aan de ingeschreven cirkel van $\triangle A B C$. $\mathrm{Zij} S$ het snijpunt van $B T$ en $K L$. Bepaal de verhouding $\frac{|S L|}{|K L|}$.

|
Noem $r$ de straal van de ingeschreven cirkel van $\triangle A B C$. De oppervlakte van driehoek $A B C$ is te schrijven als
$$
\frac{1}{2}|A B| \cdot r+\frac{1}{2}|B C| \cdot r+\frac{1}{2}|A C|=\frac{1}{2} r \cdot(3|B C|+|B C|)=2 r|B C| .
$$
Anderzijds is de oppervlakte van driehoek $A B C$ gelijk aan $\frac{1}{2} h|B C|$ met $h$ de hoogte vanuit $A$. Dus $h=4 r$. Omdat de afstand van $K L$ tot $B C$ precies $2 r$ is, is de afstand van $A$ tot $K L$ ook $2 r$. Driehoek $A K L$ en $A B C$ zijn gelijkvormig wegens $K L \| B C$, met de hoogtes vanuit $A$ gelijk aan respectievelijk $2 r$ en $4 r$, dus de vermenigvuldigingsfactor is precies 2. Dus $K$ is het midden van $A B$ en $L$ is het midden van $A C$.
Voor punt $T$ geldt $|A C|=4|A T|$, dus $|A T|=\frac{1}{4}|A C|=\frac{1}{2}|A L|$, dus $T$ is het midden van $A L$. Bekijk nu driehoek $A B L$. Hierin is $B T$ een zwaartelijn, want $T$ is het midden van $A L$. Ook is $L K$ een zwaartelijn, want $K$ is het midden van $A B$. Dus hun snijpunt $S$ is het zwaartepunt, waaruit volgt dat $\frac{|S L|}{|K L|}=\frac{2}{3}$.
|
{
"exam": "Dutch_TST",
"problem_label": "5",
"problem_match": "\nOpgave 5.",
"resource_path": "Dutch_TST/segmented/nl-2021-B2021_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2021"
}
|
The sequence of positive integers $a_{0}, a_{1}, a_{2}, \ldots$ is defined by $a_{0}=3$ and
$$
a_{n+1}-a_{n}=n\left(a_{n}-1\right)
$$
for all $n \geq 0$. Determine all integers $m \geq 2$ for which $\operatorname{gcd}\left(m, a_{n}\right)=1$ for all $n \geq 0$.
|
A direct formula for the sequence is given by $a_{n}=2 \cdot n!+1$ for $n \geq 0$. (We use the common definition $0!=1$, which satisfies $1!=1 \cdot 0!$, and for larger $n$ it holds that $n!=n \cdot(n-1)!$.) We prove the direct formula by induction. It holds that $a_{0}=3$ and that is equal to $2 \cdot 0!+1$. Suppose now that for some $k \geq 0$ it holds that $a_{k}=2 \cdot k!+1$, then
$$
a_{k+1}=a_{k}+k \left(a_{k}-1\right)=2 \cdot k!+1+k \cdot 2 \cdot k!=2 \cdot k! \cdot (1+k)+1=2 \cdot (k+1)!+1
$$
This completes the induction.
We see that $a_{n}$ is always odd, so $\operatorname{gcd}\left(2, a_{n}\right)=1$ for all $n$. It follows that $\operatorname{gcd}\left(2^{i}, a_{n}\right)=1$ for all $i \geq 1$. Therefore, $m=2^{i}$ with $i \geq 1$ satisfies. Now take an $m \geq 2$ that is not a power of two. Then $m$ has an odd prime divisor, say $p$. We show that $p$ is a divisor of $a_{p-3}$. By Wilson's theorem, it holds that $(p-1)!\equiv-1 \bmod p$. Thus,
$2 \cdot(p-3)!\equiv 2 \cdot(p-1)!\cdot((p-2)(p-1))^{-1} \equiv 2 \cdot-1 \cdot(-2 \cdot-1)^{-1} \equiv 2 \cdot-1 \cdot 2^{-1} \equiv-1 \quad \bmod p$.
Therefore, indeed $a_{p-3}=2 \cdot(p-3)!+1 \equiv 0 \bmod p$. We conclude that $m$ does not satisfy. Therefore, the only values of $m$ that satisfy are the powers of two.
|
m=2^i \text{ with } i \geq 1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
De rij positieve gehele getallen $a_{0}, a_{1}, a_{2}, \ldots$ is gedefinieerd door $a_{0}=3$ en
$$
a_{n+1}-a_{n}=n\left(a_{n}-1\right)
$$
voor alle $n \geq 0$. Bepaal alle gehele getallen $m \geq 2$ waarvoor geldt dat $\operatorname{ggd}\left(m, a_{n}\right)=1$ voor alle $n \geq 0$.
|
Een directe formule voor de rij wordt gegeven door $a_{n}=2 \cdot n!+1$ voor $n \geq 0$. (We gebruiken de gangbare definitie $0!=1$, die voldoet aan $1!=1 \cdot 0$ !, zoals ook voor grotere $n$ geldt $n!=n \cdot(n-1)!$.) We bewijzen de directe formule met inductie. Er geldt $a_{0}=3$ en dat is gelijk aan $2 \cdot 0!+1$. Stel nu dat voor zekere $k \geq 0$ geldt $a_{k}=2 \cdot k!+1$, dan is
$$
a_{k+1}=a_{k}+k\left(a_{k}-1\right)=2 \cdot k!+1+k \cdot 2 \cdot k!=2 \cdot k!\cdot(1+k)+1=2 \cdot(k+1)!+1
$$
Dit voltooit de inductie.
We zien dat $a_{n}$ altijd oneven is, dus $\operatorname{ggd}\left(2, a_{n}\right)=1$ voor alle $n$. Daaruit volgt ook dat $\operatorname{ggd}\left(2^{i}, a_{n}\right)=1$ voor alle $i \geq 1$. Dus $m=2^{i}$ met $i \geq 1$ voldoet. Neem nu een $m \geq 2$ die geen tweemacht is. Dan heeft $m$ een oneven priemdeler, zeg $p$. We laten zien dat $p$ een deler is van $a_{p-3}$. Wegens de stelling van Wilson geldt $(p-1)!\equiv-1 \bmod p$. Dus
$2 \cdot(p-3)!\equiv 2 \cdot(p-1)!\cdot((p-2)(p-1))^{-1} \equiv 2 \cdot-1 \cdot(-2 \cdot-1)^{-1} \equiv 2 \cdot-1 \cdot 2^{-1} \equiv-1 \quad \bmod p$.
Dus inderdaad geldt $a_{p-3}=2 \cdot(p-3)!+1 \equiv 0 \bmod p$. We concluderen dat $m$ niet voldoet. Dus de enige waarden van $m$ die voldoen zijn de tweemachten.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2021-C2021_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2021"
}
|
Find all quadruples $\left(x_{1}, x_{2}, x_{3}, x_{4}\right)$ of real numbers such that the following six equalities hold:
$$
\begin{aligned}
& x_{1}+x_{2}=x_{3}^{2}+x_{4}^{2}+6 x_{3} x_{4}, \\
& x_{1}+x_{3}=x_{2}^{2}+x_{4}^{2}+6 x_{2} x_{4}, \\
& x_{1}+x_{4}=x_{2}^{2}+x_{3}^{2}+6 x_{2} x_{3}, \\
& x_{2}+x_{3}=x_{1}^{2}+x_{4}^{2}+6 x_{1} x_{4}, \\
& x_{2}+x_{4}=x_{1}^{2}+x_{3}^{2}+6 x_{1} x_{3}, \\
& x_{3}+x_{4}=x_{1}^{2}+x_{2}^{2}+6 x_{1} x_{2} .
\end{aligned}
$$
|
Subtracting the first two equations from each other gives $x_{2}-x_{3}=x_{3}^{2}-x_{2}^{2}+6 x_{4}(x_{3}-x_{2})$, which we can factor as $0=(x_{3}-x_{2})(x_{3}+x_{2}+1+6 x_{4})$. We see that $x_{2}=x_{3}$ or $x_{2}+x_{3}+1+6 x_{4}=0$. Similarly, it also holds that $x_{2}=x_{3}$ or $x_{2}+x_{3}+1+6 x_{1}=0$. Therefore, if $x_{2} \neq x_{3}$, then in both cases the second equality holds; subtracting these from each other gives $x_{1}=x_{4}$. We conclude that $x_{2}=x_{3}$ or $x_{1}=x_{4}$. Similarly, for any permutation $(i, j, k, l)$ of $(1,2,3,4)$, it holds that $x_{i}=x_{j}$ or $x_{k}=x_{l}$.
We now prove that at least three of the $x_{i}$ are equal. If they are all equal, this is obviously true. Otherwise, there are two that are unequal, say without loss of generality $x_{1} \neq x_{2}$. Then $x_{3}=x_{4}$. If now $x_{1}=x_{3}$, then there are three elements equal. Otherwise, $x_{1} \neq x_{3}$, so $x_{2}=x_{4}$ and again there are three elements equal. The quadruple $(x_{1}, x_{2}, x_{3}, x_{4})$ is thus, up to order, of the form $(x, x, x, y)$, where it may be that $x=y$.
Substituting this into the given equations gives $x+y=8 x^{2}$ and $2 x=x^{2}+y^{2}+6 x y$. Adding these two equations: $3 x+y=9 x^{2}+y^{2}+6 x y$. The right-hand side can be factored as $(3 x+y)^{2}$. With $s=3 x+y$ we thus have $s=s^{2}$, from which it follows that $s=0$ or $s=1$. It holds that $s=3 x+y=2 x+(x+y)=2 x+8 x^{2}$. Therefore, $8 x^{2}+2 x=0$ or $8 x^{2}+2 x=1$.
In the first case, $x=0$ or $x=-\frac{1}{4}$. We find $y=0-3 x=0$ respectively $y=0-3 x=\frac{3}{4}$. In the second case, we can factor the equation as $(4 x-1)(2 x+1)=0$, so $x=\frac{1}{4}$ or $x=-\frac{1}{2}$. We find $y=1-3 x=\frac{1}{4}$ respectively $y=1-3 x=\frac{5}{2}$.
All together, we have found the following quadruples: $(0,0,0,0),\left(-\frac{1}{4},-\frac{1}{4},-\frac{1}{4}, \frac{3}{4}\right)$ and the permutations thereof, $\left(\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right)$ and $\left(-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}, \frac{5}{2}\right)$ and the permutations thereof. Checking shows that all these quadruples satisfy the equations.
| null |
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Vind alle viertallen $\left(x_{1}, x_{2}, x_{3}, x_{4}\right)$ van reële getallen zodat de volgende zes gelijkheden gelden:
$$
\begin{aligned}
& x_{1}+x_{2}=x_{3}^{2}+x_{4}^{2}+6 x_{3} x_{4}, \\
& x_{1}+x_{3}=x_{2}^{2}+x_{4}^{2}+6 x_{2} x_{4}, \\
& x_{1}+x_{4}=x_{2}^{2}+x_{3}^{2}+6 x_{2} x_{3}, \\
& x_{2}+x_{3}=x_{1}^{2}+x_{4}^{2}+6 x_{1} x_{4}, \\
& x_{2}+x_{4}=x_{1}^{2}+x_{3}^{2}+6 x_{1} x_{3}, \\
& x_{3}+x_{4}=x_{1}^{2}+x_{2}^{2}+6 x_{1} x_{2} .
\end{aligned}
$$
|
De eerste twee vergelijkingen van elkaar afhalen geeft $x_{2}-x_{3}=x_{3}^{2}-x_{2}^{2}+$ $6 x_{4}\left(x_{3}-x_{2}\right)$, wat we kunnen ontbinden als $0=\left(x_{3}-x_{2}\right)\left(x_{3}+x_{2}+1+6 x_{4}\right)$. We zien dat $x_{2}=x_{3}$ of $x_{2}+x_{3}+1+6 x_{4}=0$. Analoog geldt ook dat $x_{2}=x_{3}$ of $x_{2}+x_{3}+1+6 x_{1}=0$. Dus als $x_{2} \neq x_{3}$, dan geldt in beide gevallen de tweede gelijkheid; die van elkaar afhalen geeft $x_{1}=x_{4}$. We conluderen dat $x_{2}=x_{3}$ of $x_{1}=x_{4}$. Analoog geldt voor elke permutatie $(i, j, k, l) \operatorname{van}(1,2,3,4)$ dat $x_{i}=x_{j}$ of $x_{k}=x_{l}$.
We bewijzen nu dat minstens drie van de $x_{i}$ gelijk aan elkaar zijn. Als ze alle vier gelijk zijn, is dat natuurlijk waar. Anders zijn er twee die ongelijk zijn, zeg zonder verlies van algemeenheid $x_{1} \neq x_{2}$. Dan geldt $x_{3}=x_{4}$. Als nu $x_{1}=x_{3}$, dan zijn er drie elementen aan elkaar gelijk. Anders is $x_{1} \neq x_{3}$, dus $x_{2}=x_{4}$ en ook dan zijn er drie elementen aan elkaar gelijk. Het viertal $\left(x_{1}, x_{2}, x_{3}, x_{4}\right)$ is dus op volgorde na van de vorm $(x, x, x, y)$, waarbij eventueel mag gelden dat $x=y$.
Dit invullen in de gegeven vergelijkingen geeft $x+y=8 x^{2}$ en $2 x=x^{2}+y^{2}+6 x y$. Tel deze twee vergelijkingen bij elkaar op: $3 x+y=9 x^{2}+y^{2}+6 x y$. De rechterkant is te ontbinden als $(3 x+y)^{2}$. Met $s=3 x+y$ staat er dus $s=s^{2}$, waaruit volgt $s=0$ of $s=1$. Er geldt $s=3 x+y=2 x+(x+y)=2 x+8 x^{2}$. Dus $8 x^{2}+2 x=0$ of $8 x^{2}+2 x=1$.
In het eerste geval geldt $x=0$ of $x=-\frac{1}{4}$. We vinden $y=0-3 x=0$ respectievelijk $y=$ $0-3 x=\frac{3}{4}$. In het tweede geval kunnen we de vergelijking ontbinden als $(4 x-1)(2 x+1)=0$, dus $x=\frac{1}{4}$ of $x=-\frac{1}{2}$. We vinden $y=1-3 x=\frac{1}{4}$ respectievelijk $y=1-3 x=\frac{5}{2}$.
Alles bij elkaar hebben we de volgende viertallen gevonden: $(0,0,0,0),\left(-\frac{1}{4},-\frac{1}{4},-\frac{1}{4}, \frac{3}{4}\right)$ en de permutaties hiervan, $\left(\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right)$ en $\left(-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}, \frac{5}{2}\right)$ en de permutaties hiervan. Controleren laat zien dat al deze viertallen voldoen.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2021-C2021_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2021"
}
|
Find all quadruples $\left(x_{1}, x_{2}, x_{3}, x_{4}\right)$ of real numbers such that the following six equalities hold:
$$
\begin{aligned}
& x_{1}+x_{2}=x_{3}^{2}+x_{4}^{2}+6 x_{3} x_{4}, \\
& x_{1}+x_{3}=x_{2}^{2}+x_{4}^{2}+6 x_{2} x_{4}, \\
& x_{1}+x_{4}=x_{2}^{2}+x_{3}^{2}+6 x_{2} x_{3}, \\
& x_{2}+x_{3}=x_{1}^{2}+x_{4}^{2}+6 x_{1} x_{4}, \\
& x_{2}+x_{4}=x_{1}^{2}+x_{3}^{2}+6 x_{1} x_{3}, \\
& x_{3}+x_{4}=x_{1}^{2}+x_{2}^{2}+6 x_{1} x_{2} .
\end{aligned}
$$
|
Adding all the equalities gives
$$
3\left(x_{1}+x_{2}+x_{3}+x_{4}\right)=3\left(x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}\right)+6\left(x_{1} x_{2}+x_{1} x_{3}+x_{1} x_{4}+x_{2} x_{3}+x_{2} x_{4}+x_{3} x_{4}\right) .
$$
The right-hand side can be factored as $3\left(x_{1}+x_{2}+x_{3}+x_{4}\right)^{2}$. Let $s=x_{1}+x_{2}+x_{3}+x_{4}$, then we now have the equation $3 s=3 s^{2}$ with solutions $s=0$ and $s=1$.
Let $(i, j, k, l)$ be a permutation of $(1,2,3,4)$. Then we have
$$
s-\left(x_{i}+x_{j}\right)=x_{k}+x_{l}=x_{i}^{2}+x_{j}^{2}+6 x_{i} x_{j}
$$
so
$$
x_{i}^{2}+x_{j}^{2}+6 x_{i} x_{j}+x_{i}+x_{j}-s=0 .
$$
For a fixed $j$, this is a quadratic equation in $x_{i}$, with at most two solutions. For a fixed $j$, we can choose three different values for $i$, so by the pigeonhole principle, two of these possible $x_{i}$ must be equal. For each $x_{j}$, therefore, two of $x_{i}, x_{k}$, and $x_{l}$ must be equal.
In particular, two of $x_{2}, x_{3}$, and $x_{4}$ must be equal, say $x_{3}=x_{4}$. Now we take $j=3$ and see that two of $x_{1}, x_{2}$, and $x_{4}$ must be equal. If $x_{4}$ is included, we have three equal elements. If $x_{4}$ is not included, then $x_{1}=x_{2}$ and $x_{3}=x_{4}$. Therefore, the quadruples must be of the form $(x, x, x, y)$ or $(x, x, y, y)$. Substitute $x_{i}=x$ and $x_{j}=x$ into (1). Then we have $8 x^{2}+2 x-s=0$. We will now distinguish cases based on $s$.
Suppose $s=0$. Then $8 x^{2}+2 x=0$, so $x=0$ or $x=-\frac{1}{4}$. If $x=0$, then two or three of the elements must be equal to 0. We also know that the sum of the four elements must be zero and that if there are two remaining elements, they must have the same value. We see that only $(0,0,0,0)$ is possible. If $x=-\frac{1}{4}$, then we substitute $x$ and $y$ into (1). This gives $y^{2}+\frac{1}{16}-\frac{6}{4} y+y-\frac{1}{4}=0$, or $y^{2}-\frac{1}{2} y-\frac{3}{16}=0$. This can be rewritten as $\left(y+\frac{1}{4}\right)\left(y-\frac{3}{4}\right)=0$, so $y=-\frac{1}{4}$ or $y=\frac{3}{4}$. Since the sum of the four elements must be 0, only ( $-\frac{1}{4},-\frac{1}{4},-\frac{1}{4}, \frac{3}{4}$ ) is possible.
Suppose $s=1$. Then $8 x^{2}+2 x-1=0$, which can be written as $(4 x-1)(2 x+1)=0$, so $x=\frac{1}{4}$ or $x=-\frac{1}{2}$. If $x=\frac{1}{4}$, then we substitute $x$ and $y$ into (1). This gives $y^{2}+\frac{1}{16}+\frac{6}{4} y+y+\frac{1}{4}-1=0$, or $y^{2}+\frac{5}{2} y-\frac{11}{16}=0$. This can be rewritten as $\left(y-\frac{1}{4}\right)\left(y+\frac{11}{4}\right)=0$, so $y=\frac{1}{4}$ or $y=-\frac{11}{4}$. Since the sum of the four elements must be 1, only $\left(\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right)$ is possible. If $x=-\frac{1}{2}$, then we substitute $x$ and $y$ into (1). This gives $y^{2}+\frac{1}{4}-3 y+y-\frac{1}{2}-1=0$, or $y^{2}-2 y-\frac{5}{4}=0$. This can be rewritten as $\left(y+\frac{1}{2}\right)\left(y-\frac{5}{2}\right)=0$, so $y=-\frac{1}{2}$ or $y=\frac{5}{2}$. Since the sum of the four elements must be 1, only $\left(-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}, \frac{5}{2}\right)$ is possible.
In total, we have found the following quadruples: $(0,0,0,0),\left(-\frac{1}{4},-\frac{1}{4},-\frac{1}{4}, \frac{3}{4}\right)$ and their permutations, $\left(\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right)$, and $\left(-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}, \frac{5}{2}\right)$ and their permutations. Checking shows that all these quadruples satisfy the conditions.
|
(0,0,0,0),\left(-\frac{1}{4},-\frac{1}{4},-\frac{1}{4}, \frac{3}{4}\right) \text{ and their permutations}, \left(\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right), \left(-\frac{1}{2},-\frac{1}{2},
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Vind alle viertallen $\left(x_{1}, x_{2}, x_{3}, x_{4}\right)$ van reële getallen zodat de volgende zes gelijkheden gelden:
$$
\begin{aligned}
& x_{1}+x_{2}=x_{3}^{2}+x_{4}^{2}+6 x_{3} x_{4}, \\
& x_{1}+x_{3}=x_{2}^{2}+x_{4}^{2}+6 x_{2} x_{4}, \\
& x_{1}+x_{4}=x_{2}^{2}+x_{3}^{2}+6 x_{2} x_{3}, \\
& x_{2}+x_{3}=x_{1}^{2}+x_{4}^{2}+6 x_{1} x_{4}, \\
& x_{2}+x_{4}=x_{1}^{2}+x_{3}^{2}+6 x_{1} x_{3}, \\
& x_{3}+x_{4}=x_{1}^{2}+x_{2}^{2}+6 x_{1} x_{2} .
\end{aligned}
$$
|
Alle gelijkheden optellen geeft
$$
3\left(x_{1}+x_{2}+x_{3}+x_{4}\right)=3\left(x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}\right)+6\left(x_{1} x_{2}+x_{1} x_{3}+x_{1} x_{4}+x_{2} x_{3}+x_{2} x_{4}+x_{3} x_{4}\right) .
$$
De rechterkant laat zich ontbinden als $3\left(x_{1}+x_{2}+x_{3}+x_{4}\right)^{2}$. Schrijf $s=x_{1}+x_{2}+x_{3}+x_{4}$, dan vinden we dus nu de vergelijking $3 s=3 s^{2}$ met oplossingen $s=0$ en $s=1$.
Zij $(i, j, k, l)$ een permutatie van $(1,2,3,4)$. Dan geldt
$$
s-\left(x_{i}+x_{j}\right)=x_{k}+x_{l}=x_{i}^{2}+x_{j}^{2}+6 x_{i} x_{j}
$$
dus
$$
x_{i}^{2}+x_{j}^{2}+6 x_{i} x_{j}+x_{i}+x_{j}-s=0 .
$$
Voor een vaste $j$ is dit een kwadratische vergelijking in $x_{i}$, met maximaal twee oplossingen. Bij een vaste $j$ kunnen we voor $i$ drie verschillende waarden kiezen, dus volgens het ladenprincipe zijn twee van die mogelijke $x_{i}$ gelijk aan elkaar. Voor elke $x_{j}$ geldt dus dat van $x_{i}, x_{k}$ en $x_{l}$ er twee gelijk aan elkaar zijn.
In het bijzonder zijn twee van $x_{2}, x_{3}$ en $x_{4}$ gelijk aan elkaar, zeg $x_{3}=x_{4}$. Nu nemen we $j=3$ en zien we dat van $x_{1}, x_{2}$ en $x_{4}$ er twee gelijk aan elkaar zijn. Als $x_{4}$ daarbij zit, hebben we drie gelijke elementen. Als $x_{4}$ er niet bij zit, geldt $x_{1}=x_{2}$ en $x_{3}=x_{4}$. Op volgorde na moeten de viertallen dus van de vorm $(x, x, x, y)$ of $(x, x, y, y)$ zijn. Vul nu in (1) $x_{i}=x$ en $x_{j}=x$ in. Dan staat er $8 x^{2}+2 x-s=0$. We gaan nu gevallen naar $s$ onderscheiden.
Stel dat $s=0$. Dan geldt er $8 x^{2}+2 x=0$, dus $x=0$ of $x=-\frac{1}{4}$. Als $x=0$, dan zijn dus twee of drie van de elementen gelijk aan 0 . Verder weten we dat de som van de vier elementen nul moet zijn en dat als er nog twee elementen over zijn, die gelijke waarde moeten hebben. We zien dat alleen $(0,0,0,0)$ mogelijk is. Als $x=-\frac{1}{4}$, dan vullen we $x$ en $y$ in in (1). Dat geeft $y^{2}+\frac{1}{16}-\frac{6}{4} y+y-\frac{1}{4}=0$, oftewel $y^{2}-\frac{1}{2} y-\frac{3}{16}=0$. Dit kunnen we herschrijven als $\left(y+\frac{1}{4}\right)\left(y-\frac{3}{4}\right)=0$, dus $y=-\frac{1}{4}$ of $y=\frac{3}{4}$. Omdat de som van de vier elementen 0 moet zijn, kan (op volgorde na) alleen ( $-\frac{1}{4},-\frac{1}{4},-\frac{1}{4}, \frac{3}{4}$ ).
Stel dat $s=1$. Dan geldt er $8 x^{2}+2 x-1=0$, wat te schrijven is als $(4 x-1)(2 x+1)=0$, dus $x=\frac{1}{4}$ of $x=-\frac{1}{2}$. Als $x=\frac{1}{4}$, dan vullen we $x$ en $y$ in in (1). Dat geeft $y^{2}+\frac{1}{16}+\frac{6}{4} y+y+\frac{1}{4}-1=$ 0 , oftewel $y^{2}+\frac{5}{2} y-\frac{11}{16}=0$. Dit kunnen we herschrijven als $\left(y-\frac{1}{4}\right)\left(y+\frac{11}{4}\right)=0$, dus $y=\frac{1}{4}$ of $y=-\frac{11}{4}$. Omdat de som van de vier elementen 1 moet zijn, kan alleen $\left(\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right)$. Als $x=-\frac{1}{2}$, dan vullen we $x$ en $y$ in in (1). Dat geeft $y^{2}+\frac{1}{4}-3 y+y-\frac{1}{2}-1=0$, oftewel $y^{2}-2 y-\frac{5}{4}=0$. Dit kunnen we herschrijven als $\left(y+\frac{1}{2}\right)\left(y-\frac{5}{2}\right)=0$, dus $y=-\frac{1}{2}$ of $y=\frac{5}{2}$. Omdat de som van de vier elementen 1 moet zijn, kan (op volgorde na) alleen $\left(-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}, \frac{5}{2}\right)$.
Alles bij elkaar hebben we de volgende viertallen gevonden: $(0,0,0,0),\left(-\frac{1}{4},-\frac{1}{4},-\frac{1}{4}, \frac{3}{4}\right)$ en de permutaties hiervan, $\left(\frac{1}{4}, \frac{1}{4}, \frac{1}{4}, \frac{1}{4}\right)$ en $\left(-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}, \frac{5}{2}\right)$ en de permutaties hiervan. Controleren laat zien dat al deze viertallen voldoen.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2021-C2021_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2021"
}
|
Let $A B C$ be an acute and non-isosceles triangle with orthocenter $H$. Let $O$ be the circumcenter of triangle $A B C$ and let $K$ be the circumcenter of triangle $A H O$. Prove that the reflection of $K$ in $O H$ lies on $B C$.
|
We consider the configuration as shown in the figure. Other configurations proceed analogously. Let $D$ be the second intersection of $A H$ with the circumcircle of $\triangle A B C$. Let $S$ be the second intersection of the circumcircle of $A B C$ and the circumcircle of $A H O$. (Since $\triangle A B C$ is acute, $O$ and $H$ lie inside $\triangle A B C$ and thus also inside its circumcircle, so $D$ and $S$ both exist.)
We have
$$
\angle O S H=\angle O A H=\angle O A D=\angle O D A=\angle O D H,
$$
where we use that $|O A|=|O D|$. Furthermore, we have
$$
\angle O H D=180^{\circ}-\angle O H A=180^{\circ}-\angle O S A=180^{\circ}-\angle O A S=\angle O H S,
$$
where we use that $|O A|=|O S|$. We conclude that $\triangle O H S \cong \triangle O H D$ (SAS). It follows that $D$ and $S$ are each other's reflections in $O H$.
If we reflect the center $K$ of the circumcircle of $\triangle O H S$ in $O H$, we get the center $L$ of the circumcircle of $\triangle O H D$. We need to prove that $L$ lies on $B C$.
Point $D$ is the reflection of $H$ in $B C$. This is a known fact, which we can prove as follows: $\angle D B C=\angle D A C=\angle H A C=90^{\circ}-\angle A C B=\angle H B C$ and similarly $\angle D C B=\angle H C B$, so $\triangle D B C \cong \triangle H B C(\mathrm{SAS})$. Therefore, $D$ is indeed the reflection of $H$ in $B C$, which means that $B C$ is the perpendicular bisector of $H D$. Since $L$ lies on the perpendicular bisector of $H D$, $L$ lies on $B C$, and that is what we wanted to prove.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $A B C$ een scherphoekige en niet-gelijkbenige driehoek met hoogtepunt $H$. Zij $O$ het middelpunt van de omgeschreven cirkel van driehoek $A B C$ en zij $K$ het middelpunt van de omgeschreven cirkel van driehoek $A H O$. Bewijs dat de spiegeling van $K$ in $O H$ op $B C$ ligt.

|
We bekijken de configuratie zoals in de figuur. Andere configuraties gaan analoog. Noem $D$ het tweede snijpunt van $A H$ met de omgeschreven cirkel van $\triangle A B C$. Noem $S$ het tweede snijpunt van de omgeschreven cirkel van $A B C$ en de omgeschreven cirkel van $A H O$. (Omdat $\triangle A B C$ scherphoekig is, liggen $O$ en $H$ inwendig in driehoek $A B C$ en dus ook in zijn omgeschreven cirkel, dus $D$ en $S$ bestaan allebei.)
Er geldt
$$
\angle O S H=\angle O A H=\angle O A D=\angle O D A=\angle O D H,
$$
waarbij we gebruiken dat $|O A|=|O D|$. Verder geldt
$$
\angle O H D=180^{\circ}-\angle O H A=180^{\circ}-\angle O S A=180^{\circ}-\angle O A S=\angle O H S,
$$
waarbij we gebruiken dat $|O A|=|O S|$. We concluderen nu dat $\triangle O H S \cong \triangle O H D$ (ZHH). Hieruit volgt dat $D$ en $S$ elkaars gespiegelde in $O H$ zijn.
Als we het middelpunt $K$ van de omgeschreven cirkel van $\triangle O H S$ spiegelen in $O H$, krijgen we dus het middelpunt $L$ van de omgeschreven cirkel van $\triangle O H D$. We moeten nu bewijzen dat $L$ op $B C$ ligt.
Punt $D$ is de spiegeling van $H$ in $B C$. Dit is een bekend feit, dat we als volgt kunnen bewijzen: $\angle D B C=\angle D A C=\angle H A C=90^{\circ}-\angle A C B=\angle H B C$ en analoog is $\angle D C B=\angle H C B$, dus $\triangle D B C \cong \triangle H B C(\mathrm{HZH})$. Dus inderdaad is $D$ de spiegeling van $H$ in $B C$, waaruit volgt dat $B C$ de middelloodlijn van $H D$ is. Omdat $L$ op de middelloodlijn van $H D$ ligt, ligt $L$ op $B C$ en dat is wat we wilden bewijzen.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2021-C2021_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2021"
}
|
On a rectangular board with $m \times n$ squares ($m, n \geq 3$), dominoes ($2 \times 1$ or $1 \times 2$ tiles) are placed such that they do not overlap and do not extend beyond the board. Each domino covers exactly two squares of the board. Assume that the tiling with dominoes has the property that no additional domino can be placed on the board, and that not all four corner squares of the board are empty. Prove that at least $\frac{2}{3}$ of the squares of the board are covered by dominoes.
|
Pair each empty cell with the domino that is directly to the right of this cell (unless the cell is at the right edge of the board). Suppose now that two empty cells are paired with the same domino, then this domino must be placed vertically and both cells to its left are empty. However, then there would be room for an additional domino, contradiction. Therefore, no two empty cells are paired with the same domino.
The empty cells at the right edge of the board have not yet been paired. We try to pair these cells each with a domino that has no empty cell directly to its left (and thus has not yet been paired). First, assume that it is possible to pair all empty cells at the right edge in this way with different dominoes. We have then paired all empty cells on the board with a domino, without using any domino more than once. Since each domino covers two cells of the board, for each empty cell there are two covered cells, and thus at most $\frac{1}{3}$ of the cells on the board are empty. Then we are done.
We will now show that this pairing always works. Let $k$ be the number of empty cells at the right edge and $\ell$ be the number of empty cells at the left edge. The empty cells at the left edge must not be adjacent, so there are at least $\ell-1$ dominoes at the left edge, and none of these have an empty cell to their left. If $\ell > k$, then there are enough dominoes at the left edge to pair with all empty cells at the right edge. If $\ell < k$, then we could flip the entire situation and pair all empty cells with the domino to their left, and we could also prove that at most $\frac{1}{3}$ of the cells on the board are empty. The only situation that remains is if $\ell = k$ and there are exactly $k-1$ dominoes at both edges. In this case, there is an empty cell between every two dominoes at both edges, and there is also an empty cell in the corners. But this contradicts the condition in the problem that not all corner cells are empty. This situation cannot occur.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Op een rechthoekig bord met $m \times n$ vakjes ( $m, n \geq 3$ ) liggen domino's ( $2 \times 1$ of $1 \times 2$-tegels), die elkaar niet overlappen en niet uitsteken buiten het bord. Elke domino bedekt precies twee vakjes van het bord. Neem aan dat de bedekking met domino's de eigenschap heeft dat er geen enkele domino meer bijgeplaatst kan worden op het bord en dat de vier hoekvakjes van het bord niet allemaal leeg zijn. Bewijs dat minstens $\frac{2}{3}$ van de vakjes van het bord bedekt zijn met domino's.
|
Koppel elk leeg vakje aan de domino die direct rechts van dit vakje ligt (tenzij het vakje aan de rechterrand van het bord ligt). Stel dat er nu twee lege vakjes aan dezelfde domino gekoppeld worden, dan moet deze domino verticaal liggen en zijn beide vakjes links van hem leeg. Echter, dan zou er daar nog een extra domino passen, tegenspraak. Dus er worden geen twee lege vakjes aan dezelfde domino gekoppeld.
De lege vakjes aan de rechterrand van het bord zijn nog niet gekoppeld. We proberen deze vakjes elk te koppelen aan een domino die direct links van zich geen leeg vakje heeft (en dus nog niet gekoppeld was). Neem eerst even aan dat het lukt om alle lege vakjes van de rechterrand op deze manier te koppelen aan verschillende domino's. We hebben dan alle lege vakjes van het bord gekoppeld aan een domino, waarbij geen domino twee keer gebruikt wordt. Omdat elke domino twee vakjes van het bord bedekt, zijn er voor elk leeg vakje twee bedekte vakjes en is dus hooguit $\frac{1}{3}$ van de vakjes van het bord leeg. Dan zijn we klaar.
We gaan nu laten zien dat deze koppeling altijd lukt. Noem $k$ het aantal lege vakjes aan de rechterrand en $\ell$ het aantal lege vakjes aan de linkerrand. De lege vakjes aan de linkerrand mogen niet naast elkaar liggen, dus liggen er minstens $\ell-1$ domino's aan de linkerrand en deze hebben allemaal geen leeg vakje links van zich. Als $\ell>k$, dan liggen er dus genoeg domino's aan de linkerrand liggen om alle lege vakjes van de rechterrand te koppelen. Als $\ell<k$, dan zouden we de hele situatie kunnen omdraaien en juist alle lege vakjes koppelen aan de domino links daarvan en zouden we daarmee ook kunnen bewijzen dat hooguit $\frac{1}{3}$ van de vakjes van het bord leeg is. De enige situatie die nog over is, is als $\ell=k$ en er zowel links als rechts precies $k-1$ domino's aan de rand liggen. Aan beide randen geldt dan dat er tussen elke twee domino's een leeg vakje zit en er ook een leeg vakje in de hoeken zit. Maar dit is in tegenspraak met de voorwaarde in de opgave dat niet alle hoekvakjes leeg zijn. Deze situatie kan dus niet voorkomen.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2021-C2021_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2021"
}
|
Let $\Gamma$ be the circumcircle of a triangle $ABC$ and let $D$ be a point on line segment $BC$. The circle through $B$ and $D$ that is tangent to $\Gamma$ and the circle through $C$ and $D$ that is tangent to $\Gamma$ intersect at a point $E \neq D$. The line $DE$ intersects $\Gamma$ at two points $X$ and $Y$. Prove that $|EX|=|EY|$.
|
We consider the configuration as shown in the figure, where $E$ is at least as close to $B$ as to $C$. The configuration where this is reversed is analogous. Let $O$ be the center of $\Gamma$. The angle between the line $B C$ and the common tangent at $B$ is, according to the tangent-secant angle theorem, on the one hand equal to $\angle B E D$ and on the other hand to $\angle B A C$. Therefore, $\angle B E D = \angle B A C$. Similarly, $\angle C E D = \angle B A C$, so $\angle B E C = \angle B E D + \angle C E D = 2 \angle B A C = \angle B O C$, where in the last step we use the central angle theorem. It follows that $E$ lies on the circle through $B, O$, and $C$. If $E = O$, then we are done, because $|E X|$ and $|E Y|$ are both the radius of the circle. If not, then (in our configuration) $B E O C$ is a cyclic quadrilateral.
Thus, $\angle B E O = 180^{\circ} - \angle B C O$. Furthermore, in isosceles triangle $B O C$, we have $\angle B C O = 90^{\circ} - \frac{1}{2} \angle B O C = 90^{\circ} - \angle B A C$, so $\angle B E O = 180^{\circ} - (90^{\circ} - \angle B A C) = 90^{\circ} + \angle B A C$. From this, we find $\angle D E O = \angle B E O - \angle B E D = 90^{\circ} + \angle B A C - \angle B A C = 90^{\circ}$. Therefore, $E O$ is perpendicular to $D E$ and thus also perpendicular to chord $X Y$, which implies that $E$ is the midpoint of $X Y$. Hence, $|E X| = |E Y|$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $\Gamma$ de omgeschreven cirkel van een driehoek $A B C$ en zij $D$ een punt op lijnstuk $B C$. De cirkel door $B$ en $D$ die raakt aan $\Gamma$ en de cirkel door $C$ en $D$ die raakt aan $\Gamma$ snijden in een punt $E \neq D$. De lijn $D E$ snijdt $\Gamma$ in twee punten $X$ en $Y$. Bewijs dat $|E X|=|E Y|$.
|
We bekijken de configuratie zoals in de figuur, waarbij $E$ minstens zo dicht bij $B$ ligt als bij $C$. De configuratie waarbij dit andersom is, gaat analoog. Zij $O$ het middelpunt van $\Gamma$. De hoek tussen de lijn $B C$ en de gemeenschappelijke raaklijn in $B$ is volgens de raaklijnomtrekshoekstelling enerzijds gelijk aan $\angle B E D$ en anderzijds aan $\angle B A C$. Dus $\angle B E D=\angle B A C$. Analoog geldt $\angle C E D=\angle B A C$, dus $\angle B E C=\angle B E D+\angle C E D=2 \angle B A C=\angle B O C$, waarbij we in de laatste stap de middelpuntomtrekshoekstelling gebruiken. Nu volgt dat $E$ op de cirkel door $B, O$ en $C$ ligt. Als $E=O$, dan zijn we direct klaar, want dan zijn $|E X|$ en $|E Y|$ beide de straal van de cirkel. Zo niet, dan is (in onze configuratie) $B E O C$ een koordenvierhoek.
Dus $\angle B E O=180^{\circ}-\angle B C O$. Verder geldt in gelijkbenige driehoek $B O C$ dat $\angle B C O=$ $90^{\circ}-\frac{1}{2} \angle B O C=90^{\circ}-\angle B A C$, dus $\angle B E O=180^{\circ}-\left(90^{\circ}-\angle B A C\right)=90^{\circ}+\angle B A C$. Hiermee vinden we $\angle D E O=\angle B E O-\angle B E D=90^{\circ}+\angle B A C-\angle B A C=90^{\circ}$. Dus $E O$ staat loodrecht op $D E$ en daarmee ook loodrecht op koorde $X Y$, waaruit volgt dat $E$ het midden van $X Y$ is. Dus $|E X|=|E Y|$.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2021-D2021_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2021"
}
|
Let $\Gamma$ be the circumcircle of a triangle $ABC$ and let $D$ be a point on line segment $BC$. The circle through $B$ and $D$ that is tangent to $\Gamma$ and the circle through $C$ and $D$ that is tangent to $\Gamma$ intersect at a point $E \neq D$. The line $DE$ intersects $\Gamma$ at two points $X$ and $Y$. Prove that $|EX|=|EY|$.
|
Let $O$ be the center of $\Gamma$, let $\Gamma_{B}$ be the circle through $B, D$, and $E$, and let $\Gamma_{C}$ be the circle through $C, D$, and $E$. The common tangent of $\Gamma$ and $\Gamma_{B}$ is the power line of these two circles; similarly, the tangent at $C$ is the power line of $\Gamma$ and $\Gamma_{C}$. Let $P$ be the intersection of the two tangents; then $P$ is the power point of the three circles. Since $DE$ is the power line of $\Gamma_{B}$ and $\Gamma_{C}$, $P$ lies on $DE$. Let $M$ be the midpoint of $BC$. Then $OM$ is the perpendicular bisector of $BC$ and passes through the intersection of the tangents at $B$ and $C$, so $P$ also lies on $OM$. We have $\angle PBO = 90^{\circ}$ because $PB$ is tangent to $\Gamma$. But then $PB$ is also tangent to the circle with diameter $OB$, which passes through $M$ due to Thales' theorem since $\angle OMB = 90^{\circ}$. Using the power of a point theorem, we find $PB^2 = PM \cdot PO$, while the power of a point theorem on $\Gamma_{B}$ gives $PB^2 = PD \cdot PE$. Therefore, $PM \cdot PO = PD \cdot PE$, which implies that $D, M, O$, and $E$ lie on a circle. Since $\angle DMO = 90^{\circ}$, $OM$ is a diameter of this circle. If $E = O$, then we are done, as $|EX|$ and $|EY|$ are both the radius of the circle. Otherwise, $\angle DEO = 90^{\circ}$. Thus, $EO$ is perpendicular to $DE$ and therefore also perpendicular to the chord $XY$, which implies that $E$ is the midpoint of $XY$. Hence, $|EX| = |EY|$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $\Gamma$ de omgeschreven cirkel van een driehoek $A B C$ en zij $D$ een punt op lijnstuk $B C$. De cirkel door $B$ en $D$ die raakt aan $\Gamma$ en de cirkel door $C$ en $D$ die raakt aan $\Gamma$ snijden in een punt $E \neq D$. De lijn $D E$ snijdt $\Gamma$ in twee punten $X$ en $Y$. Bewijs dat $|E X|=|E Y|$.
|
Zij $O$ het middelpunt van $\Gamma$, zij $\Gamma_{B}$ de cirkel door $B, D$ en $E$ en zij $\Gamma_{C}$ de cirkel door $C$, $D$ en $E$. De gemeenschappelijke raaklijn van $\Gamma$ en $\Gamma_{B}$ is de machtlijn van deze twee cirkels; zo ook is de raaklijn in $C$ de machtlijn van $\Gamma$ en $\Gamma_{C}$. Noem $P$ het snijpunt van de twee raaklijnen; dan is $P$ het machtpunt van de drie cirkels. Aangezien $D E$ de machtlijn van $\Gamma_{B}$ en $\Gamma_{C}$ is, ligt $P$ op $D E$. Zij nu $M$ het midden van $B C$. Dan is $O M$ de middelloodlijn van $B C$ en die gaat door het snijpunt van de raaklijnen in $B$ en $C$, dus $P$ ligt ook op $O M$. Er geldt $\angle P B O=90^{\circ}$ omdat $P B$ de raaklijn aan $\Gamma$ is. Maar dan raakt $P B$ ook aan de cirkel met middellijn $O B$, die wegens Thales door $M$ gaat aangezien $\angle O M B=90^{\circ}$. Met de machtstelling vinden we nu $P B^{2}=P M \cdot P O$, terwijl de machtstelling op $\Gamma_{B}$ geeft dat $P B^{2}=P D \cdot P E$. Dus $P M \cdot P O=P D \cdot P E$, waaruit volgt dat $D, M, O$ en $E$ op een cirkel liggen. Omdat $\angle D M O=90^{\circ}$ is $O M$ een middellijn van deze cirkel. Als $E=O$, dan zijn we direct klaar, want dan zijn $|E X|$ en $|E Y|$ beide de straal van de cirkel. Zo niet, dan geldt $\angle D E O=90^{\circ}$. Dus $E O$ staat loodrecht op $D E$ en daarmee ook loodrecht op koorde $X Y$, waaruit volgt dat $E$ het midden van $X Y$ is. Dus $|E X|=|E Y|$.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2021-D2021_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2021"
}
|
Stekel and Prik are playing a game on an $m \times n$ board, where $m$ and $n$ are positive integers. They take turns alternately, with Stekel starting. Stekel always places a pawn on a square that does not yet have a pawn in his turn. Prik does the same in his turn, but his pawn must always be placed in a square that shares a side with the square where Stekel placed a pawn in his previous turn. Prik wins if the entire board is filled with pawns. Stekel wins if Prik cannot place a pawn in his turn, even though there is still at least one empty square on the board. Determine for all pairs $(m, n)$ who has a winning strategy.
|
When $m$ (the number of rows) is even, we pair the squares on the board in pairs: in each column, the top two squares form a pair, and the third and fourth squares, and so on. Because there is an even number of rows, this works. Prik can now follow the following strategy: if Stekel occupies a square of such a pair, he places a pawn in the other square of this pair. After each move by Prik, all pairs are thus occupied with either zero or two pawns, so he can continue to follow this strategy. He automatically meets the condition that his pawn is adjacent to the pawn Stekel just placed. Prik can thus ensure that the entire board is filled with pawns and wins. If $n$ is even, Prik also has a winning strategy in a similar way.
If $m=n=1$, Prik doesn't need to place any pawns to win. If $m=1$ and $n=3$ or vice versa, Prik places his first pawn on a square adjacent to the square where Stekel just placed a pawn; this is always possible. The board is then full after Stekel's next move, so Prik wins.
Now consider the case where $m=n=3$. Stekel can follow the following strategy. He places his first pawn in the middle square. Prik must place a pawn in the same row or the same column; without loss of generality, we assume that Prik's pawn is in the same column. Stekel then places a pawn in the third square of this column. At this point, the left and right columns are still completely empty. Prik must place a pawn in one of these two columns. Stekel then chooses the other column: there are still three empty squares there. He places a pawn there and forces Prik to also place a pawn in that column; the squares in the middle column are already all occupied. Stekel then places a pawn in the last square of that column, after which Prik can no longer move. So Stekel wins.
What remains is the case where $m$ and $n$ are both odd and $m \geq 5$ or $n \geq 5$ (or both). We consider the case where $n$ (the number of columns) is at least 5. The other case is analogous. Stekel can now follow the following strategy. He always places his pawns in the middle column, until that column is full. When it is Stekel's turn again, there is an even number of pawns on the board, all in the middle three columns, with the middle column being at least completely full. The left and right columns are still completely empty. There is still an odd number of empty squares, so either the area to the left of the middle column or the area to the right of the middle column contains an odd number of empty squares.
Stekel chooses that area and then places all his pawns there, in arbitrary positions. Because the middle column is completely full, Prik must also place all his pawns in that area. There was an odd number of empty squares in this area, so Stekel essentially occupies the last square. Prik can no longer move after that, so Stekel wins. If Prik cannot move in an earlier turn, Stekel also wins.
We conclude that Stekel wins if $m$ and $n$ are both odd and $m \geq 5$, if $m$ and $n$ are both odd and $n \geq 5$, and if $m=n=3$. Prik wins in all other cases: if $m$ is even, if $n$ is even, if $m=n=1$, if $m=1$ and $n=3$, and if $m=3$ and $n=1$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Stekel en Prik spelen een spel op een $m \times n$-bord, waarbij $m$ en $n$ positieve gehele getallen zijn. Ze zijn afwisselend aan de beurt, waarbij Stekel begint. Stekel zet in zijn beurt steeds een pion op een vakje waar nog geen pion staat. Prik doet in zijn beurt hetzelde, maar zijn pion moet altijd komen in een vakje dat met een zijde grenst aan het vakje waar Stekel net in zijn vorige beurt een pion in gezet heeft. Prik wint als het hele bord vol met pionnen staat. Stekel wint als Prik geen pion meer kan zetten in zijn beurt, terwijl er nog wel minstens een leeg vakje op het bord is. Bepaal voor alle paren $(m, n)$ wie er een winnende strategie heeft.
|
Als $m$ (het aantal rijen) even is, dan koppelen we de vakjes van het bord in tweetallen aan elkaar: in elke kolom vormen de bovenste twee vakjes een tweetal, en het derde en vierde vakje, enzovoorts. Omdat er een even aantal rijen is, lukt dit. Prik kan nu de volgende strategie hanteren: als Stekel een vakje van zo'n tweetal bezet, zet hij een pion in het andere vakje van dit tweetal. Na elke zet van Prik zijn op deze manier alle tweetallen met nul of met twee pionnen bezet, dus hij kan deze strategie steeds blijven uitvoeren. Hij voldoet automatisch aan de voorwaarde dat zijn pion grenst aan de pion die Stekel net heeft neergezet. Prik kan dus zorgen dat het hele bord vol met pionnen komt en wint. Als $n$ even is, heeft Prik analoog ook een winnende strategie.
Als $m=n=1$ hoeft Prik geen enkele pion te zetten om te winnen. Als $m=1$ en $n=3$ of andersom, zet Prik zijn eerste pion op een vakje dat grenst aan het vakje waar Stekel net een pion heeft neergezet; dat lukt altijd. Het bord is dan na de volgende zet van Stekel vol, dus Prik wint.
Bekijk nu het geval dat $m=n=3$. Stekel kan de volgende strategie volgen. Hij zet zijn eerste pion in het middelste vakje. Prik moet in dezelfde rij of in dezelfde kolom een pion zetten; zonder verlies van algemeenheid nemen we aan dat de pion van Prik in dezelfde kolom komt. Stekel zet nu in het derde vakje van deze kolom een pion. Op dat moment zijn de linker- en rechterkolom nog helemaal leeg. Prik moet in één van beide een pion zetten. Stekel kiest vervolgens de andere kolom: daar zijn nog drie vakjes leeg. Hij plaatst daar een pion en dwingt Prik daarmee om ook in die kolom een pion te zetten; de vakjes in de middelste kolom zijn immmers allemaal al vol. Stekel plaatst vervolgens een pion in het laatste vakje van die kolom, waarna Prik niet meer kan. Dus Stekel wint.
Blijft over het geval dat $m$ en $n$ allebei oneven zijn en dat $m \geq 5$ of $n \geq 5$ (of allebei). We bekijken het geval dat $n$ (het aantal kolommen) minstens 5 is. Het andere geval gaat analoog. Stekel kan nu de volgende strategie volgen. Hij zet zijn pionnen steeds in de middelste kolom, totdat die kolom vol is. Als Stekel vervolgens weer aan de beurt is, staat er een even aantal pionnen op het bord, allemaal in de middelste drie kolommen, waarbij de middelste kolom in elk geval helemaal vol is. De linker- en rechterkolom zijn nog helemaal leeg. Er is nog een oneven aantal vakjes open, dus ofwel het gebied links van de middelste kolom ofwel het gebied rechts van de middelste kolom bevat een oneven aantal lege vakjes.
Stekel kiest dat gebied en plaatst vervolgens al zijn pionnen daar, op willekeurige plekken. Omdat de middelste kolom helemaal vol is, moet Prik nu ook al zijn pionnen in dat gebied zetten. Er was een oneven aantal vakjes leeg in dit gebied, dus Stekel bezet in principe het laatste vakje. Prik kan daarna niet meer zetten, dus Stekel wint. Mocht Prik al in een eerdere beurt niet meer kunnen zetten, dan wint Stekel ook.
We concluderen dat Stekel wint als $m$ en $n$ oneven zijn en $m \geq 5$, als $m$ en $n$ oneven zijn en $n \geq 5$, en als $m=n=3$. Prik wint in alle overige gevallen: als $m$ even is, als $n$ even is, als $m=n=1$, als $m=1$ en $n=3$ en als $m=3$ en $n=1$.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2021-D2021_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2021"
}
|
Prove that for every positive integer $n$ there exist positive integers $a$ and $b$ such that
$$
n \mid 4 a^{2}+9 b^{2}-1
$$
|
For $n=1$, every choice of $a$ and $b$ satisfies the condition. Now suppose $n>1$ and let $p$ be a prime divisor of $n$. Let $k$ be the number of factors $p$ in $n$. We give a condition for $a$ and $b$ modulo $p^{k}$ that guarantees $p^{k} \mid 4 a^{2}+9 b^{2}-1$. By doing this for each prime divisor of $n$, we obtain a system of requirements for $a$ and $b$ modulo the different prime powers. The Chinese Remainder Theorem then tells us that there is an $n$ that satisfies all these requirements simultaneously.
If $p \neq 2$, we take the condition that $2 a \equiv 1 \bmod p^{k}$ and $b \equiv 0 \bmod p^{k}$. Since 2 has a multiplicative inverse modulo $p^{k}$, this is possible. We now see that
$$
4 a^{2}+9 b^{2}-1=(2 a)^{2}+9 b^{2}-1 \equiv 1^{2}+9 \cdot 0-1=0 \quad \bmod p^{k} .
$$
So this choice for $a$ and $b$ satisfies the condition.
If $p=2$, we take the condition $a \equiv 0 \bmod 2^{k}$ and $3 b \equiv 1 \bmod 2^{k}$. Since 3 has a multiplicative inverse modulo $2^{k}$, this is possible. We now see that
$$
4 a^{2}+9 b^{2}-1=4 a^{2}+(3 b)^{2}-1 \equiv 4 \cdot 0+1^{2}-1=0 \quad \bmod 2^{k}
$$
So this choice for $a$ and $b$ satisfies the condition.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Bewijs dat voor elk positief geheel getal $n$ er positieve gehele getallen $a$ en $b$ bestaan met
$$
n \mid 4 a^{2}+9 b^{2}-1
$$
|
Voor $n=1$ voldoet elke keuze van $a$ en $b$. Stel nu dat $n>1$ en zij $p$ een priemdeler van $n$. Zij $k$ het aantal factoren $p$ in $n$. We geven een voorwaarde voor $a$ en $b$ modulo $p^{k}$ die garandeert dat $p^{k} \mid 4 a^{2}+9 b^{2}-1$. Door dit voor elke priemdeler van $n$ te doen, krijgen we een stelsel van eisen voor $a$ en $b$ modulo de verschillende priemmachten. De Chinese reststelling vertelt ons vervolgens dat er nu een $n$ te vinden is die aan alle eisen tegelijk voldoet.
Als $p \neq 2$ nemen we als voorwaarde dat $2 a \equiv 1 \bmod p^{k}$ en $b \equiv 0 \bmod p^{k}$. Omdat 2 een multiplicatieve inverse heeft modulo $p^{k}$, is dit mogelijk. We zien nu dat
$$
4 a^{2}+9 b^{2}-1=(2 a)^{2}+9 b^{2}-1 \equiv 1^{2}+9 \cdot 0-1=0 \quad \bmod p^{k} .
$$
Dus deze keuze voor $a$ en $b$ voldoet.
Als $p=2$ nemen we als voorwaarde $a \equiv 0 \bmod 2^{k}$ en $3 b \equiv 1 \bmod 2^{k}$. Omdat 3 een multiplicatieve inverse heeft modulo $2^{k}$, is dit mogelijk. We zien nu dat
$$
4 a^{2}+9 b^{2}-1=4 a^{2}+(3 b)^{2}-1 \equiv 4 \cdot 0+1^{2}-1=0 \quad \bmod 2^{k}
$$
Dus deze keuze voor $a$ en $b$ voldoet.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2021-D2021_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2021"
}
|
Determine all positive integers $n$ with the following property: for every triple $(a, b, c)$ of positive real numbers, there is a triple $(k, \ell, m)$ of non-negative integers such that $a n^{k}, b n^{\ell}$ and $c n^{m}$ are the lengths of the sides of a (non-degenerate) triangle.
|
It is clear that $n=1$ does not work, because not every three positive real numbers $a, b,$ and $c$ are the lengths of a triangle. We now first prove that $n \geq 5$ does not work by considering the triplet $(1,2,3)$. Suppose there exist $k, \ell, m$ such that $n^{k}, 2 n^{\ell},$ and $3 n^{m}$ are the lengths of the sides of a triangle. First, note that no two of these three numbers can be equal, since $n \neq 2,3$. By possibly scaling the triangle by a factor of $n$ several times, we can assume that one of the numbers $k, \ell,$ and $m$ is equal to 0. Suppose the other two are both positive, then the corresponding side lengths are both multiples of $n$. Their difference is thus at least $n$, while the third side is at most 3. This contradicts the triangle inequality. Therefore, at least two of $k, \ell,$ and $m$ must be equal to 0. The corresponding two side lengths have a sum of at most 5, so the third side must be less than 5. From $n \geq 5$ it follows that this third side also does not have a factor of $n$ in its length. Thus, $k, \ell,$ and $m$ are all equal to 0, but then 1, 2, and 3 would have to be the lengths of the sides of a triangle, while $3=2+1$. Contradiction. We conclude that $n \geq 5$ does not work.
Now consider $n=2,3,4$. We construct $(k, \ell, m)$ as follows. Take a triplet $(a, b, c)$. If these are already the sides of a triangle, we take $k=\ell=m=0$. Otherwise, there is a triangle inequality that does not hold, say without loss of generality that $a \geq b+c$. Now multiply the smallest of $b$ and $c$ by $n$. If this does not make the right-hand side greater than $a$, multiply the smallest (of the new two terms) by $n$ again. Generally, if $a \geq n^{i} b+n^{j} c$, then multiply the smallest of $n^{i} b$ and $n^{j} c$ by $n$ and check again if the inequality holds. This process is guaranteed to stop, because there is an $i$ such that $n^{i}>a$. Now consider the $i$ and $j$ such that $a \geq n^{i} b+n^{j} c$ and this is the last step where this inequality holds. Without loss of generality, assume that $n^{i} b \leq n^{j} c$, then $a < n^{i+1} b + n^{j} c$. We claim that we can take $(k, \ell, m)$ to be one of $(0, i+1, j)$ and $(0, i+1, j+1)$.
By definition, $a < n^{i+1} b + n^{j} c$ and further, $n^{j} c < n^{i} b + n^{j} c \leq a < a + n^{i+1} b$, so if $(0, i+1, j)$ does not work, it must be because $n^{i+1} b \geq a + n^{j} c$. Furthermore, $n^{i} b \leq n^{j} c$, so $n^{i+1} b \leq n^{j+1} c < a + n^{j+1} c$. Also, of course, $a < n^{i+1} b + n^{j+1} c$, so if $(0, i+1, j+1)$ does not work, it must be because $n^{j+1} c \geq a + n^{i+1} b$. We will derive a contradiction in the case that both triplets do not work. We then know that both $n^{i+1} b \geq a + n^{j} c$ and $n^{j+1} c \geq a + n^{i+1} b$.
Adding these inequalities and canceling $n^{i+1} b$ on both sides gives $n^{j+1} c \geq 2a + n^{j} c$, or $(n-1) n^{j} c \geq 2a$. Thus,
$$
n^{i+1} b \geq a + n^{j} c \geq a + \frac{2a}{n-1} = \left(1 + \frac{2}{n-1}\right) a
$$
which implies
$$
a \geq n^{i} b + n^{j} c \geq \frac{1}{n} \left(1 + \frac{2}{n-1}\right) a + \frac{2}{n-1} a = \frac{(n-1) + 2 + 2n}{n(n-1)} a = \frac{3n + 1}{n(n-1)} a.
$$
Thus, $3n + 1 \leq n(n-1)$. For $n=2,3,4$, this gives $7 \leq 2$, $10 \leq 6$, and $13 \leq 12$, respectively, which are contradictions in all cases.
We conclude that the values of $n$ that work are exactly $n=2,3,4$.
Alternative solution for the first part. We prove in a different way that $n \geq 5$ does not work. We consider the triplet $(1,2,3)$ again. Suppose there exist $k, \ell, m$ such that $n^{k}, 2 n^{\ell},$ and $3 n^{m}$ are the lengths of the sides of a triangle. From the triangle inequality, we have
$$
\begin{aligned}
n^{k} & < 2 n^{\ell} + 3 n^{m} \\
2 n^{\ell} & < n^{k} + 3 n^{m} \\
3 n^{m} & < n^{k} + 2 n^{\ell}
\end{aligned}
$$
If $m \leq \ell-1$ and $k \leq \ell$, then
$$
n^{k} + 3 n^{m} \leq n^{\ell} + \frac{3}{n} n^{\ell} = \left(1 + \frac{3}{n}\right) \cdot n^{\ell} \leq 2 n^{\ell}
$$
which contradicts the second triangle inequality. Therefore, $m \geq \ell$ or $k \geq \ell+1$. Similarly, from the first triangle inequality, we can deduce that $\ell \geq k$ or $m \geq k$, and from the third that $k \geq m+1$ or $\ell \geq m+1$.
We now distinguish two cases: $m \geq \ell$ or $k \geq \ell+1$. Suppose first that $m \geq \ell$. Then $\ell \geq m+1$ does not hold, so $k \geq m+1$ must hold. But then $m \geq k$ does not hold, so $\ell \geq k$ must hold. We find $m \geq \ell \geq k \geq m+1$, a contradiction. Suppose next that $k \geq \ell+1$. Then $\ell \geq k$ does not hold, so $m \geq k$ must hold. But then $k \geq m+1$ does not hold, so $\ell \geq m+1$ must hold. We find $k \geq \ell+1 \geq m+2 \geq k+2$, a contradiction. We conclude that $n \geq 5$ does not work.
|
2,3,4
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Bepaal alle positieve gehele getallen $n$ met de volgende eigenschap: voor ieder drietal $(a, b, c)$ van positieve reële getallen is er een drietal $(k, \ell, m)$ van niet-negatieve gehele getallen zodat dat $a n^{k}, b n^{\ell}$ en $c n^{m}$ de lengtes van de zijden van een (niet-gedegenereerde) driehoek vormen.
|
Het is duidelijk dat $n=1$ niet voldoet, want niet elke drie positieve reële getallen $a, b$ en $c$ zijn de lengtes van een driehoek. We bewijzen nu eerst dat $n \geq 5$ niet voldoet door het drietal $(1,2,3)$ te bekijken. Stel dat er $k, \ell, m$ bestaan zodat $n^{k}, 2 n^{\ell}$ en $3 n^{m}$ de lengtes van de zijden van een driehoek vormen. Merk allereerst op dat geen twee van deze drie getallen gelijk aan elkaar kunnen zijn, aangezien $n \neq 2,3$. Door de driehoek eventueel een aantal keer met een factor $n$ te verkleinen, kunnen we verder aannemen dat één van de getallen $k$, $\ell$ en $m$ gelijk aan 0 is. Stel dat de andere twee allebei positief zijn, dan zijn de bijbehorende zijdelengtes allebei een veelvoud van $n$. Hun verschil is dus ook tenminste $n$, terwijl de derde zijde hooguit 3 is. Dit is in tegenspraak met de driehoeksongelijkheid. Dus van $k, \ell$ en $m$ moeten er minstens twee gelijk aan 0 zijn. De bijbehorende twee zijdelengtes hebben som hoogstens 5 , dus de derde zijde moet kleiner dan 5 zijn. Uit $n \geq 5$ volgt dan dat die derde zijde ook geen factor $n$ in zijn lengte heeft. Dus $k$, $\ell$ en $m$ zijn alle drie gelijk aan 0 , maar dan zouden 1,2 en 3 de lengtes van de zijden van een driehoek moeten zijn, terwijl $3=2+1$. Tegenspraak. We concluderen dat $n \geq 5$ niet voldoet.
Bekijk nu $n=2,3,4$. We construeren $(k, \ell, m)$ als volgt. Neem een drietal $(a, b, c)$. Als dit al de zijden van een driehoek zijn, nemen we $k=\ell=m=0$. Anders is er een driehoeksongelijkheid die niet geldt, zeg zonder verlies van algemeenheid dat er geldt $a \geq$ $b+c$. Vermenigvuldig nu de kleinste van $b$ en $c$ met $n$. Als daarmee de rechterkant nog niet groter dan $a$ is, vermenigvuldigen we nog een keer de kleinste (van de nieuwe twee termen) met $n$. Algemeen geldt dus: als $a \geq n^{i} b+n^{j} c$, dan vermenigvuldigen we de kleinste van $n^{i} b$ en $n^{j} c$ met $n$ en kijken dan opnieuw of de ongelijkheid nog geldt. Dit proces stopt gegarandeerd, want er is een $i$ zodat $n^{i}>a$. Bekijk nu de $i$ en $j$ zodat $a \geq n^{i} b+n^{j} c$ en dit de laatste stap is waarin deze ongelijkheid geldt. Neem zonder verlies van algemeenheid aan dat $n^{i} b \leq n^{j} c$, dan geldt dus $a<n^{i+1} b+n^{j} c$. We beweren nu dat we ( $k, \ell, m$ ) gelijk kunnen nemen aan een van $(0, i+1, j)$ en $(0, i+1, j+1)$.
Per definitie geldt $a<n^{i+1} b+n^{j} c$ en verder is $n^{j} c<n^{i} b+n^{j} c \leq a<a+n^{i+1} b$, dus als $(0, i+1, j)$ niet voldoet, dan moet dat komen omdat $n^{i+1} b \geq a+n^{j} c$. Verder is $n^{i} b \leq n^{j} c$, dus $n^{i+1} b \leq n^{j+1} c<a+n^{j+1} c$. Ook is natuurlijk $a<n^{i+1} b+n^{j+1} c$, dus als $(0, i+1, j+1)$ niet voldoet, dan moet dat komen omdat $n^{j+1} c \geq a+n^{i+1} b$. We gaan een tegenspraak afleiden in het geval dat beide drietallen niet voldoen. We weten dan dus dat zowel $n^{i+1} b \geq a+n^{j} c$ als $n^{j+1} c \geq a+n^{i+1} b$.
Deze ongelijkheden bij elkaar optellen en links en rechts $n^{i+1} b$ wegstrepen geeft $n^{j+1} c \geq$
$2 a+n^{j} c$, oftewel $(n-1) n^{j} c \geq 2 a$. Dus
$$
n^{i+1} b \geq a+n^{j} c \geq a+\frac{2 a}{n-1}=\left(1+\frac{2}{n-1}\right) a
$$
waaruit volgt dat
$$
a \geq n^{i} b+n^{j} c \geq \frac{1}{n}\left(1+\frac{2}{n-1}\right) a+\frac{2}{n-1} a=\frac{(n-1)+2+2 n}{n(n-1)} a=\frac{3 n+1}{n(n-1)} a .
$$
Dus $3 n+1 \leq n(n-1)$. Voor $n=2,3,4$ staat hier respectievelijk $7 \leq 2,10 \leq 6$ en $13 \leq 12$, wat in alle gevallen een tegenspraak is.
We concluderen dat de waarden van $n$ die voldoen, precies $n=2,3,4$ zijn.
Alternatieve oplossing voor het eerste deel. We bewijzen op een andere manier dat $n \geq 5$ niet voldoet. We bekijken weer het drietal $(1,2,3)$. Stel dat er $k, \ell, m$ bestaan zodat $n^{k}, 2 n^{\ell}$ en $3 n^{m}$ de lengtes van de zijden van een driehoek vormen. Uit de driehoeksongelijkheid volgt
$$
\begin{aligned}
n^{k} & <2 n^{\ell}+3 n^{m} \\
2 n^{\ell} & <n^{k}+3 n^{m} \\
3 n^{m} & <n^{k}+2 n^{\ell}
\end{aligned}
$$
Als $m \leq \ell-1$ en $k \leq \ell$, dan volgt
$$
n^{k}+3 n^{m} \leq n^{\ell}+\frac{3}{n} n^{\ell}=\left(1+\frac{3}{n}\right) \cdot n^{\ell} \leq 2 n^{\ell}
$$
wat in tegenspraak is met de tweede driehoeksongelijkheid. Dus $m \geq \ell$ of $k \geq \ell+1$. Analoog kunnen we uit de eerste driehoeksongelijkheid afleiden dat $\ell \geq k$ of $m \geq k$ en uit de derde dat $k \geq m+1$ of $\ell \geq m+1$.
We onderscheiden nu twee gevallen: $m \geq \ell$ of $k \geq \ell+1$. Stel eerst dat $m \geq \ell$. Dan geldt niet $\ell \geq m+1$, dus moet wel $k \geq m+1$. Maar dan geldt niet $m \geq k$, dus moet wel $\ell \geq k$. We vinden nu $m \geq \ell \geq k \geq m+1$, tegenspraak. Stel vervolgens dat juist $k \geq \ell+1$. Dan geldt niet $\ell \geq k$, dus wel $m \geq k$. Maar dan geldt niet $k \geq m+1$, dus wel $\ell \geq m+1$. We vinden nu $k \geq \ell+1 \geq m+2 \geq k+2$, tegenspraak. We concluderen dat $n \geq 5$ niet voldoet.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2021-D2021_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2021"
}
|
Let $m$ and $n$ be natural numbers with $mn$ even. Jetze is going to cover an $m \times n$ board (consisting of $m$ rows and $n$ columns) with dominoes, such that each domino covers exactly two squares, dominoes do not stick out or overlap, and all squares are covered by a domino. Merlijn will then color all the dominoes on the board red or blue. Determine the smallest non-negative integer $V$ (depending on $m$ and $n$) such that Merlijn can always ensure that in each row the number of squares covered by a red domino and the number of squares covered by a blue domino differ by at most $V$, no matter how Jetze covers the board.
|
First, assume that $n$ is odd. Then it is clear that $V \geq 1$; the difference is always odd. We show that $V=1$ is always possible. To do this, color the vertical dominoes in odd columns red and the vertical dominoes in even columns blue. Since in each row, each horizontal domino covers one cell in an even and one cell in an odd column, there is now one more cell covered by a red domino than by a blue domino in each row. Now color the horizontal dominoes in each row alternately blue, red, blue, red, .... If the number of horizontal dominoes is even, there will ultimately be one more red cell; if the number of horizontal dominoes is odd, there will ultimately be one more blue cell. The difference is thus always 1.
If $n \equiv 2 \bmod 4$, then $V \geq 2$ if Jetze places every domino horizontally; then there are an odd number of dominoes in each row. We now show that $V=2$ is always possible. Use the same strategy as in the odd case. After coloring the vertical dominoes, there are an equal number of red and blue cells in each row. If we then color the horizontal dominoes alternately red and blue in each row, the difference between the number of red and blue cells in each row is 0 or 2.
Finally, we consider the case where $n \equiv 0 \bmod 4$. We show that $V=0$ is always possible. Number the rows from top to bottom from 1 to $m$ and let $b_{i}$ be the number of vertical dominoes whose top cell is in row $i$. By induction on $i$, we can easily show that $b_{i}$ is even, using the fact that a horizontal domino always covers an even number of cells in a row. We color the vertical dominoes in row $i$ and row $i+1$ as follows: if $b_{i} \equiv 0 \bmod 4$, we color half red and half blue, and if $b_{i} \equiv 2 \bmod 4$, we color two more red than blue if $i$ is even, and two more blue than red if $i$ is odd. We now show that we can color the horizontal dominoes in each row $k$ so that this row has an equal number of red and blue cells. If $b_{k-1} \equiv b_{k} \equiv 0 \bmod 4$, then the vertical dominoes in row $k$ cover an equal number of red and blue cells. Moreover, the number of horizontal dominoes in row $k$ is now even, so we simply color half red and half blue. If $b_{k-1} \equiv b_{k} \equiv 2 \bmod 4$, then the vertical dominoes in row $k$ again cover an equal number of red and blue cells, because one of $k-1$ and $k$ is even and the other is odd. Furthermore, the number of horizontal dominoes in row $k$ is again even, so we can again color half red and half blue. If $b_{k-1} \not \equiv b_{k} \bmod 4$, the difference between the number of red and blue cells covered by vertical dominoes is 2. The number of horizontal dominoes in row $k$ is now odd. We can therefore color the horizontal dominoes so that ultimately there are an equal number of red and blue cells.
We conclude that the minimal values are: $V=1$ if $n$ is odd, $V=2$ if $n \equiv 2 \bmod 4$, and $V=0$ if $n \equiv 0 \bmod 4$.
|
V=1 \text{ if } n \text{ is odd, } V=2 \text{ if } n \equiv 2 \bmod 4, \text{ and } V=0 \text{ if } n \equiv 0 \bmod 4
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Laat $m$ en $n$ natuurlijke getallen zijn met $m n$ even. Jetze gaat een $m \times n$ bord (dus bestaande uit $m$ rijen en $n$ kolommen) bedekken met dominostenen, zodat elke dominosteen precies twee vakjes bedekt, dominostenen niet uitsteken of overlappen, en alle vakjes bedekt worden door een dominosteen. Merlijn gaat vervolgens alle dominostenen op het bord rood of blauw kleuren. Bepaal het kleinste niet-negatieve gehele getal $V$ (afhankelijk van $m$ en $n$ ) zodat Merlijn er altijd voor kan zorgen dat in elke rij het aantal vakjes bedekt door een rode dominosteen en het aantal vakjes bedekt door een blauwe dominosteen ten hoogste $V$ van elkaar verschillen, hoe Jetze het bord ook bedekt.
|
Stel eerst dat $n$ oneven is. Dan is het duidelijk dat $V \geq 1$; het verschil is immers altijd oneven. We laten zien dat $V=1$ altijd mogelijk is. Kleur hiertoe de verticale dominostenen in oneven kolommen rood en de verticale dominostenen in even kolommen blauw. Omdat in elke rij elke horizontale dominosteen een vakje in een even en een vakje in een oneven kolom bedekt, is er nu in elke rij één vakje meer door een rode dominosteen dan door een blauwe dominosteen bedekt. Kleur de horizontale dominostenen in elke rij nu afwisselend blauw, rood, blauw, rood, .... Als het aantal horizontale domino's even is, is er uiteindelijk één rood vakje meer; is het aantal horizontale domino's oneven, dan is er uiteindelijk één blauw vakje meer. Het verschil is dus altijd 1.
Als $n \equiv 2 \bmod 4$ geldt er dat $V \geq 2$ als Jetze elke dominosteen horizontaal legt; dan liggen er in elke rij immers een oneven aantal dominostenen. We laten nu zien dat $V=2$ altijd mogelijk is. Gebruik daartoe dezelfde strategie als in het oneven geval. Na het kleuren van de verticale dominostenen zijn er in elke rij evenveel vakjes rood als blauw. Als we daarna weer de horizontale dominostenen per rij afwisselend rood en blauw kleuren, is in elke rij het verschil tussen het aantal rode en blauwe vakjes gelijk aan 0 of 2 .
We bekijken ten slotte het geval waarin $n \equiv 0 \bmod 4$. We laten daarin zien dat $V=0$ altijd mogelijk is. Nummer de rijen van boven naar beneden van 1 tot en met $m$ en zij $b_{i}$ het aantal verticale dominostenen waarvan het bovenste vakje in rij $i$ ligt. Met inductie naar $i$ laten we eenvoudig zien dat $b_{i}$ even is, waarbij we gebruiken dat een horizontale dominosteen altijd een even aantal vakjes in een rij bedekt. We kleuren de verticale dominostenen in rij $i$ en rij $i+1 \mathrm{nu}$ als volgt: als $b_{i} \equiv 0 \bmod 4$ kleuren we de helft rood en
de helft blauw, en als $b_{i} \equiv 2$ mod 4 kleuren we er twee meer rood dan blauw als $i$ even is, en twee meer blauw dan rood als $i$ oneven is. We laten nu zien dat we in elke rij $k$ de horizontale dominostenen zo kunnen kleuren dat deze rij evenveel rode als blauwe vakjes heeft. Als $b_{k-1} \equiv b_{k} \equiv 0 \bmod 4$ dan bedekken verticale dominostenen in rij $k$ evenveel rode als blauwe vakjes. Bovendien is het aantal horizontale dominostenen in rij $k$ nu even, dus we kleuren simpelweg de helft rood en de helft blauw. Als $b_{k-1} \equiv b_{k} \equiv 2 \bmod 4$ geldt wederom dat de verticale dominostenen in rij $k$ evenveel rode als blauwe vakjes bedekken, omdat er van $k-1$ en $k$ één even en één oneven is. Verder is het aantal horizontale dominostenen in rij $k$ weer even, dus kunnen we weer de helft rood en de helft blauw kleuren. Als $b_{k-1} \not \equiv b_{k} \bmod 4$ is het verschil tussen rode en blauwe vakjes bedekt door verticale dominostenen gelijk aan 2. Het aantal horizontale dominostenen in rij $k$ is nu oneven. We kunnen dus de horizontale dominostenen zo kleuren dat uiteindelijk evenveel vakjes rood als blauw zijn.
We concluderen dat de minimale waarden zijn: $V=1$ als $n$ oneven is, $V=2$ als $n \equiv 2$ $\bmod 4$ en $V=0$ als $n \equiv 0 \bmod 4$.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2021-E2021_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2021"
}
|
Let $m$ and $n$ be natural numbers with $mn$ even. Jetze is going to cover an $m \times n$ board (consisting of $m$ rows and $n$ columns) with dominoes, such that each domino covers exactly two squares, dominoes do not stick out or overlap, and all squares are covered by a domino. Merlijn will then color all the dominoes on the board red or blue. Determine the smallest non-negative integer $V$ (depending on $m$ and $n$) such that Merlijn can always ensure that in each row the number of squares covered by a red domino and the number of squares covered by a blue domino differ by at most $V$, no matter how Jetze covers the board.
|
Number the rows from top to bottom from 1 to $m$ and let $b_{i}$ $(1 \leq i \leq m-1)$ be the number of vertical dominoes whose top square is in row $i$ and whose bottom square is in row $i+1$. Define $b_{0}=0$ and $b_{m}=0$.
First, assume that $n$ is odd. Write $n=\frac{1}{2}(n-1)+\frac{1}{2}(n+1)$; exactly one of these two terms is even and the other is odd; write $n_{\mathrm{e}}$ for the even term and $n_{\mathrm{o}}$ for the odd term. We now have $n=n_{\mathrm{e}}+n_{\mathrm{o}}$ while $n_{\mathrm{e}}$ and $n_{\mathrm{o}}$ differ by exactly 1. It is clear first that $V \geq 1$; the difference is always odd. We show that $V=1$ is always possible. By induction on $i$, we easily show that $b_{i}$ is odd for odd $i$ and even for even $i$, using the fact that a horizontal domino always covers an even number of squares. For odd $i$, we have in row $i$ an odd number $b_{i}$ of vertical dominoes that stick down, an even number of squares covered by horizontal dominoes, and an even number $b_{i-1}$ that stick up. Now color the squares in row $i$ as follows: of these dominoes, in the order just listed, color the first $n_{\mathrm{o}}$ squares red and the last $n_{\mathrm{e}}$ squares blue. For even $i$, we have in row $i$ an odd number $b_{i-1}$ of vertical dominoes that stick up, an even number of squares covered by horizontal dominoes, and an even number $b_{i}$ that stick down. Now color the squares in row $i$ as follows: of these dominoes, in the order just listed, color the first $n_{\mathrm{o}}$ squares red and the last $n_{\mathrm{e}}$ squares blue. In this way, in each row, at least each horizontal domino is monochromatic (the two squares have the same color), while for two consecutive rows, the squares on the vertical dominoes in both rows also have the same color. The coloring is thus correct and satisfies $V=1$.
If $n \equiv 2 \bmod 4$, then $\frac{1}{2} n$ is odd and we write $\frac{1}{2} n=n_{\mathrm{e}}+n_{\mathrm{o}}$ with $n_{\mathrm{e}}$ and $n_{\mathrm{o}}$ even and odd numbers that differ by exactly 1. It holds that $V \geq 2$ if Jetze places every domino horizontally; then there are an odd number of dominoes in each row. We now show that $V=2$ is always possible. To this end, use the same strategy as in the odd case. By induction on $i$, we easily show that $b_{i}$ is even for all $i$. For odd $i$, we have in row $i$ an even number $b_{i}$ of vertical dominoes that stick down, an even number of squares covered by horizontal dominoes, and an even number $b_{i-1}$ that stick up. Now color the squares in row $i$ as follows: of these dominoes, in the order just listed, color the first $2 n_{\mathrm{o}}$ squares red and the last $2 n_{\mathrm{e}}$ squares blue. For even $i$, we have in row $i$ an even number $b_{i-1}$ of vertical dominoes that stick up, an even number of squares covered by horizontal dominoes, and an even number $b_{i}$ that stick down. Now color the squares in row $i$ as follows: of these dominoes, in the order just listed, color the first $2 n_{\mathrm{o}}$ squares red and the last $2 n_{\mathrm{e}}$ squares blue. In this way, in each row, at least each horizontal domino is monochromatic (the two squares have the same color), while for two consecutive rows, the squares on the vertical dominoes in both rows also have the same color. The coloring is thus correct and satisfies $V=2$.
If $n \equiv 0 \bmod 4$, then $\frac{1}{2} n$ is even and we write $\frac{1}{2} n=2 n_{0}$. We now show that $V=0$ is always possible. To this end, use the same strategy as in the previous case. By induction on $i$, we easily show that $b_{i}$ is even for all $i$. For odd $i$, we have in row $i$ an even number $b_{i}$ of vertical dominoes that stick down, an even number of squares covered by horizontal dominoes, and an even number $b_{i-1}$ that stick up. Now color the squares in row $i$ as follows: of these dominoes, in the order just listed, color the first $2 n_{0}$ squares red and the last $2 n_{0}$ squares blue. For even $i$, we have in row $i$ an even number $b_{i-1}$ of vertical dominoes that stick up, an even number of squares covered by horizontal dominoes, and an even number $b_{i}$ that stick down. Now color the squares in row $i$ as follows: of these dominoes, in the order just listed, color the first $2 n_{0}$ squares red and the last $2 n_{0}$ squares blue. In this way, in each row, at least each horizontal domino is monochromatic (the two squares have the same color), while for two consecutive rows, the squares on the vertical dominoes in both rows also have the same color. The coloring is thus correct and satisfies $V=0$.
|
V=1 \text{ or } V=2
|
Yes
|
Incomplete
|
math-word-problem
|
Combinatorics
|
Laat $m$ en $n$ natuurlijke getallen zijn met $m n$ even. Jetze gaat een $m \times n$ bord (dus bestaande uit $m$ rijen en $n$ kolommen) bedekken met dominostenen, zodat elke dominosteen precies twee vakjes bedekt, dominostenen niet uitsteken of overlappen, en alle vakjes bedekt worden door een dominosteen. Merlijn gaat vervolgens alle dominostenen op het bord rood of blauw kleuren. Bepaal het kleinste niet-negatieve gehele getal $V$ (afhankelijk van $m$ en $n$ ) zodat Merlijn er altijd voor kan zorgen dat in elke rij het aantal vakjes bedekt door een rode dominosteen en het aantal vakjes bedekt door een blauwe dominosteen ten hoogste $V$ van elkaar verschillen, hoe Jetze het bord ook bedekt.
|
Nummer de rijen van boven naar beneden van 1 tot en met $m$ en zij $b_{i}$ $(1 \leq i \leq m-1)$ het aantal verticale dominostenen waarvan het bovenste vakje in rij $i$ ligt en het onderste vakje in rij $i+1$. Definieer $b_{0}=0$ en $b_{m}=0$.
Stel eerst dat $n$ oneven is. Schrijf $n=\frac{1}{2}(n-1)+\frac{1}{2}(n+1)$; precies een van deze twee termen is even en de ander is oneven; schrijf $n_{\mathrm{e}}$ voor de even term en $n_{\mathrm{o}}$ voor de oneven term. We hebben nu dus $n=n_{\mathrm{e}}+n_{\mathrm{o}}$ terwijl $n_{\mathrm{e}}$ en $n_{\mathrm{o}}$ precies 1 verschillen. Het is allereerst duidelijk dat $V \geq 1$; het verschil is immers altijd oneven. We laten zien dat $V=1$ altijd mogelijk is. Met inductie naar $i$ laten we eenvoudig zien dat $b_{i}$ oneven is voor oneven $i$ en even voor even $i$, waarbij we gebruiken dat een horizontale dominosteen altijd een even aantal vakjes in een rij bedekt. Voor oneven $i$ hebben we in rij $i$ te maken met een oneven aantal $b_{i}$ verticale stenen die naar beneden uitsteken, een aantal horizontale dominostenen die een even aantal vakjes bedekken, en een even aantal $b_{i-1}$ die naar boven uitsteken. Kleur nu de vakjes in rij $i$ als volgt: van deze dominostenen, in de volgorde zoals zojuist opgesomd, kleur je de eerste $n_{\mathrm{o}}$ vakjes rood en juist de laatste $n_{\mathrm{e}}$ vakjes blauw. Voor even $i$ hebben we in rij $i$ te maken met een oneven aantal $b_{i-1}$ verticale stenen die naar boven uitsteken, een aantal horizontale dominostenen die een even aantal vakjes bedekken, en een even aantal $b_{i}$ die naar beneden uitsteken. Kleur nu de vakjes in rij $i$ als volgt: van deze dominostenen, in de volgorde zoals zojuist opgesomd, kleur je de eerste $n_{\mathrm{o}}$ vakjes rood en juist de laatste $n_{\mathrm{e}}$ vakjes blauw. Op deze manier is in elke rij in ieder geval elke horizontale dobbelsteen monochroom (de twee vakjes hebben dezelfde kleur), terwijl we voor twee opeenvolgende rijen de vakjes op de verticale dominostenen in beide rijen ook dezelfde kleur hebben gegeven. De kleuring is dus correct en voldoet aan $V=1$.
Als $n \equiv 2 \bmod 4$ is $\frac{1}{2} n$ oneven en schrijven we $\frac{1}{2} n=n_{\mathrm{e}}+n_{\mathrm{o}}$ met $n_{\mathrm{e}}$ en $n_{\mathrm{o}}$ even en oneven
getallen die precies 1 verschillen. Er geldt dat $V \geq 2$ als Jetze elke dominosteen horizontaal legt; dan liggen er in elke rij immers een oneven aantal dominostenen. We laten nu zien dat $V=2$ altijd mogelijk is. Gebruik daartoe dezelfde strategie als in het oneven geval. Met inductie naar $i$ laten we eenvoudig zien dat $b_{i}$ even is voor alle $i$. Voor oneven $i$ hebben we in rij $i$ te maken met een even aantal $b_{i}$ verticale stenen die naar beneden uitsteken, een aantal horizontale dominostenen die een even aantal vakjes bedekken, en een even aantal $b_{i-1}$ die naar boven uitsteken. Kleur nu de vakjes in rij $i$ als volgt: van deze dominostenen, in de volgorde zoals zojuist opgesomd, kleur je de eerste $2 n_{\mathrm{o}}$ vakjes rood en juist de laatste $2 n_{\mathrm{e}}$ vakjes blauw. Voor even $i$ hebben we in rij $i$ te maken met een even aantal $b_{i-1}$ verticale stenen die naar boven uitsteken, een aantal horizontale dominostenen die een even aantal vakjes bedekken, en een even aantal $b_{i}$ die naar beneden uitsteken. Kleur nu de vakjes in rij $i$ als volgt: van deze dominostenen, in de volgorde zoals zojuist opgesomd, kleur je de eerste $2 n_{\mathrm{o}}$ vakjes rood en juist de laatste $2 n_{\mathrm{e}}$ vakjes blauw. Op deze manier is in elke rij in ieder geval elke horizontale dobbelsteen monochroom (de twee vakjes hebben dezelfde kleur), terwijl we voor twee opeenvolgende rijen de vakjes op de verticale dominostenen in beide rijen ook dezelfde kleur hebben gegeven. De kleuring is dus correct en voldoet aan $V=2$.
Als $n \equiv 0 \bmod 4$ is $\frac{1}{2} n$ even en schrijven we $\frac{1}{2} n=2 n_{0}$. We laten nu zien dat $V=0$ altijd mogelijk is. Gebruik daartoe dezelfde strategie als in het vorige geval. Met inductie naar $i$ laten we eenvoudig zien dat $b_{i}$ even is voor alle $i$. Voor oneven $i$ hebben we in rij $i$ te maken met een even aantal $b_{i}$ verticale stenen die naar beneden uitsteken, een aantal horizontale dominostenen die een even aantal vakjes bedekken, en een even aantal $b_{i-1}$ die naar boven uitsteken. Kleur nu de vakjes in rij $i$ als volgt: van deze dominostenen, in de volgorde zoals zojuist opgesomd, kleur je de eerste $2 n_{0}$ vakjes rood en juist de laatste $2 n_{0}$ vakjes blauw. Voor even $i$ hebben we in rij $i$ te maken met een even aantal $b_{i-1}$ verticale stenen die naar boven uitsteken, een aantal horizontale dominostenen die een even aantal vakjes bedekken, en een even aantal $b_{i}$ die naar beneden uitsteken. Kleur nu de vakjes in rij $i$ als volgt: van deze dominostenen, in de volgorde zoals zojuist opgesomd, kleur je de eerste $2 n_{0}$ vakjes rood en juist de laatste $2 n_{0}$ vakjes blauw. Op deze manier is in elke rij in ieder geval elke horizontale dobbelsteen monochroom (de twee vakjes hebben dezelfde kleur), terwijl we voor twee opeenvolgende rijen de vakjes op de verticale dominostenen in beide rijen ook dezelfde kleur hebben gegeven. De kleuring is dus correct en voldoet aan $V=0$.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2021-E2021_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2021"
}
|
Let $A B C$ be a right triangle with $\angle C=90^{\circ}$ and let $D$ be the foot of the altitude from $C$. Let $E$ be the centroid of triangle $A C D$ and let $F$ be the centroid of triangle $B C D$. The point $P$ satisfies $\angle C E P=90^{\circ}$ and $|C P|=|A P|$, while the point $Q$ satisfies $\angle C F Q=90^{\circ}$ and $|C Q|=|B Q|$.
Show that $P Q$ passes through the centroid of triangle $A B C$.
|
Let $M, N, R$ and $S$ be the midpoints of sides $B C, C A, B D$ and $A D$ respectively. Let $Z$ be the centroid of $\triangle A B C$. Quadrilateral $Q F M C$ is a cyclic quadrilateral due to the right angles $\angle Q F C=90^{\circ}=\angle Q M C$. Note that $C Q$ is thus the diameter of the circumscribed circle. Similarly, we see that $P N E C$ is a cyclic quadrilateral, with $C P$ being the diameter of the circumscribed circle.
We now prove that $Z$ also lies on these cyclic quadrilaterals. Triangle $C Z M$ transforms under the similarity $\triangle B C A \sim \triangle B D C$ into triangle $D F R$, because $C$ maps to $D$, the centroid $Z$ maps to the centroid $F$, and the midpoint $M$ of $B C$ maps to the midpoint of $B D$, which is $R$. Thus, $\triangle C Z M \sim \triangle D F R$, from which it particularly follows that $\angle C Z M=\angle D F R=\angle C F M$ due to vertically opposite angles. Therefore, $Z$ lies on the cyclic quadrilateral $Q F M C$. Similarly, it follows that $\angle C Z N=\angle D E S=\angle C E N$, which means that $Z$ lies on the cyclic quadrilateral $P N E C$.
We can now prove that $Z$ lies on $P Q$. Since $C Q$ is the diameter of the circle through $Q, F, M, C, Z$, we have $\angle Q Z C=90^{\circ}$. Since $C P$ is the diameter of the circle through $P, N, E, Z, C$, we also have $\angle C Z P=90^{\circ}$. Together, we can conclude from this that $P, Z$ and $Q$ lie on a straight line.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $A B C$ een rechthoekige driehoek met $\angle C=90^{\circ}$ en zij $D$ het voetpunt van de hoogtelijn uit $C$. Zij $E$ het zwaartepunt van driehoek $A C D$ en zij $F$ het zwaartepunt van driehoek $B C D$. Het punt $P$ voldoet aan $\angle C E P=90^{\circ}$ en $|C P|=|A P|$, terwijl het punt $Q$ voldoet aan $\angle C F Q=90^{\circ}$ en $|C Q|=|B Q|$.
Toon aan dat $P Q$ door het zwaartepunt van driehoek $A B C$ gaat.

|
Noem $M, N, R$ en $S$ de middens van respectievelijk zijden $B C, C A, B D$ en $A D$. Zij $Z$ het zwaartepunt van $\triangle A B C$. Vierhoek $Q F M C$ is een koordenveriehoek wegens rechte hoeken $\angle Q F C=90^{\circ}=\angle Q M C$. Merk op dat $C Q$ dus de middellijn van de omgeschreven cirkel is. Analoog zien we dat $P N E C$ een koordenvierhoek is, met $C P$ de middellijn van de omgeschreven cirkel.
We bewijzen nu dat $Z$ ook op deze koordenvierhoeken ligt. Driehoek $C Z M$ gaat onder de gelijkvormigheid $\triangle B C A \sim \triangle B D C$ over in driehoek $D F R$, want $C$ gaat naar $D$, het zwaartepunt $Z$ gaat naar het zwaartepunt $F$, en het midden $M$ van $B C$ gaat naar het midden van $B D$ en dat is $R$. Dus $\triangle C Z M \sim \triangle D F R$, waaruit in het bijzonder volgt dat $\angle C Z M=\angle D F R=\angle C F M$ wegens overstaande hoeken. Dus $Z$ ligt op koordenvierhoek $Q F M C$. Analoog volgt dat $\angle C Z N=\angle D E S=\angle C E N$, waaruit volgt dat $Z$ op koordenvierhoek $P N E C$ ligt.
We kunnen nu bewijzen dat $Z$ op $P Q$ ligt. Omdat $C Q$ de middellijn is van de cirkel door $Q, F, M, C, Z$, geldt $\angle Q Z C=90^{\circ}$. Omdat $C P$ de middellijn is van de cirkel door $P, N, E, Z, C$, geldt ook $\angle C Z P=90^{\circ}$. Samen kunnen we hieruit concluderen dat $P, Z$ en $Q$ op een lijn liggen.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2021-E2021_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2021"
}
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.