problem
stringlengths 14
10.4k
| solution
stringlengths 1
24.1k
| answer
stringlengths 1
250
⌀ | problem_is_valid
stringclasses 4
values | solution_is_valid
stringclasses 3
values | question_type
stringclasses 4
values | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
10.4k
| solution_raw
stringlengths 1
24.1k
| metadata
dict |
|---|---|---|---|---|---|---|---|---|---|
Let \(\triangle ABC\) be an acute triangle such that \(|AB| + |BC| = 4|AC|\) and \(|AB| < |BC|\). Let \(D\) be the intersection of the angle bisector of \(\angle ABC\) with the side \(AC\). Points \(P\) and \(Q\) lie on the line segment \(BD\) such that \(|BP| = 2|DQ|\). Let \(\ell\) be the line through \(P\) parallel to \(AC\). The line through \(Q\) perpendicular to \(BD\) intersects the line segments \(AB\) and \(BC\) at points \(X\) and \(Y\), respectively. Assume that \(X\) and \(Y\) lie on the opposite side of \(\ell\) from \(B\).
A ant starts its journey at \(X\) and from there goes to a point on \(AC\), then to a point on \(\ell\), then back to a (possibly different) point on \(AC\), and finally to \(Y\). Prove that the length of the shortest possible route of the ant is equal to \(4|XY|\).

|
Let \(R\), \(S\), and \(T\) be the points where the ant first reaches \(AC\), first reaches \(\ell\), and secondly reaches \(AC\) again, respectively. Let \(\ell'\) and \(S'\) be the reflections of \(\ell\) and \(S\) in \(AC\), and let \(Y'\) be the reflection of \(Y\) in \(\ell'\). Then, by the triangle inequality for the total length of the ant's path, we have
\[
\begin{align*}
|XR| + |RS| + |ST| + |TY| &= |XR| + |RS'| + |S'T| + |TY| \\
&\ge |XS'| + |S'Y| \\
&= |XS'| + |S'Y'| \\
&\ge |XY'|,
\end{align*}
\]
with equality if \(S'\) lies on \(XY'\), \(R\) lies on \(XS'\), and \(T\) lies on \(S'Y\). Therefore, it remains to prove that \(|XY'| = 4|XY|\).
Now, redefine \(S'\) as the intersection of \(XY'\) and \(\ell'\). By definition, \(\ell'\) is the external angle bisector of \(\angle XS'Y\). We also define \(B'\) as the intersection of \(BQ\) with \(\ell'\). Then \(B'\) also lies on the perpendicular bisector of \(XY\), so \(B'\) is the second Brocard point of \(\triangle XYS'\). (Note that \(BQ\) is neither parallel to \(\ell'\) nor perpendicular to it, because \(\ell' \parallel AC\) and \(\triangle BAC\) is not isosceles. Thus, this Brocard point is well-defined and distinct from \(S'\).) In particular, \(XYB'S'\) is a cyclic quadrilateral. By our definition of \(\ell'\), \(B'\) is also the reflection of
\(P\) in \(D\). Therefore, together with the condition that \(2|QD| = |BP|\), we calculate that
\[
\begin{align*}
|QB'| &= |QD| + |DB'| \\
&= |QD| + |PD| \\
&= |QD| + |PQ| + |QD| \\
&= |BP| + |PQ| \\
&= |BQ|.
\end{align*}
\]
Since \(Q\) is also the midpoint of \(XY\) and the diagonals are perpendicular to each other, we conclude that \(BXB'Y\) is a rhombus. Now we will angle chase with this cyclic quadrilateral, this rhombus, and F-angles:
\[
\begin{align*}
\angle S'XY &= \angle S'B'Y \\
&= \angle S'B'B - \angle YB'B \\
&= \angle CDB - \angle YBB' \\
&= (180^\circ - \frac{1}{2}\angle CBA - \angle ACB) - \frac{1}{2}\angle CBA \\
&= \angle BAC.
\end{align*}
\]
Similarly, \(\angle S'YX = \angle BCA\). Therefore, \(\triangle XYS' \sim \triangle ACB\), and the condition \(|AB| + |BC| = 4|AC|\) also holds in \(\triangle XYS'\). We conclude that \(|XY'| = |XS'| + |S'Y| = 4|XY|\), which is exactly what we sought. \(\square\)
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij \(\triangle ABC\) een scherphoekige driehoek zo dat \(|AB| + |BC| = 4|AC|\) en \(|AB| < |BC|\). Zij \(D\) het snijpunt van de bissectrice van \(\angle ABC\) met de zijde \(AC\). Punten \(P\) en \(Q\) liggen op het lijnstuk \(BD\) zo dat \(|BP| = 2|DQ|\). Zij \(\ell\) de lijn door \(P\) parallel aan \(AC\). De lijn door \(Q\) loodrecht op \(BD\) snijdt de lijnstukken \(AB\) en \(BC\) in respectievelijk \(X\) en \(Y\). Stel dat \(X\) en \(Y\) aan de andere kant liggen van \(\ell\) dan \(B\).
Een mier begint zijn reis in \(X\) en gaat vanaf daar naar een punt op \(AC\), dan een punt op \(\ell\), dan weer terug naar een (eventueel ander) punt op \(AC\) en uiteindelijk naar \(Y\). Bewijs dat de lengte van de kortst mogelijke route van de mier gelijk is aan \(4|XY|\).

|
Laat \(R\), \(S\) en \(T\) respectievelijk de punten zijn waar de mier de eerste keer op \(AC\) is, op \(\ell\) is en de tweede keer op \(AC\) is. Laat \(\ell'\) en \(S'\) de spiegelingen van \(\ell\) en \(S\) in \(AC\) zijn, en zij \(Y'\) de spiegeling van \(Y\) in \(\ell'\). Dan geldt wegens de driehoekongelijkheid voor de totale lengte van het pad van de mier dat
\[
\begin{align*}
|XR| + |RS| + |ST| + |TY| &= |XR| + |RS'| + |S'T| + |TY| \\
&\ge |XS'| + |S'Y| \\
&= |XS'| + |S'Y'| \\
&\ge |XY'|,
\end{align*}
\]
met gelijkheid als \(S'\) op \(XY'\) ligt, \(R\) op \(XS'\) en \(T\) op \(S'Y\). Dus nu rest ons te bewijzen dat \(|XY'| = 4|XY|\).
Nu herdefiniëren we \(S'\) als het snijpunt van \(XY'\) en \(\ell'\). Dan is \(\ell'\) per definitie de buiten-bissectrice van \(\angle XS'Y\). We definiëren ook \(B'\) als het snijpunt van \(BQ\) met \(\ell'\). Dan ligt \(B'\) ook op de middelloodlijn van \(XY\), dus \(B'\) is het tweede BOM-punt van \(\triangle XYS'\). (Merk op dat \(BQ\) niet parallel is aan \(\ell'\) of er loodrecht op staat, want \(\ell' \parallel AC\) en \(\triangle BAC\) is niet gelijkbenig. Dus dit BOM-punt is goed gedefinieerd en ongelijk aan \(S'\).) In het bijzonder is \(XYB'S'\) een koordenvierhoek. Wegens onze definitie van \(\ell'\) is \(B'\) ook de spiegeling van
\(P\) in \(D\). Dus samen met de voorwaarde dat \(2|QD| = |BP|\) rekenen we uit dat
\[
\begin{align*}
|QB'| &= |QD| + |DB'| \\
&= |QD| + |PD| \\
&= |QD| + |PQ| + |QD| \\
&= |BP| + |PQ| \\
&= |BQ|.
\end{align*}
\]
Omdat \(Q\) ook het midden is van \(XY\) en de diagonalen loodrecht op elkaar staan, concludeer en we dat \(BXB'Y\) een ruit is. Nu gaan we hoekenjagen met deze koordenvierhoek, deze ruit en F-hoeken:
\[
\begin{align*}
\angle S'XY &= \angle S'B'Y \\
&= \angle S'B'B - \angle YB'B \\
&= \angle CDB - \angle YBB' \\
&= (180^\circ - \frac{1}{2}\angle CBA - \angle ACB) - \frac{1}{2}\angle CBA \\
&= \angle BAC.
\end{align*}
\]
Analog geldt dat \(\angle S'YX = \angle BCA\). Dus \(\triangle XYS' \sim \triangle ACB\), waardoor de voorwaarde \(|AB| + |BC| = 4|AC|\) ook in \(\triangle XYS'\) geldt. We concluderen dat \(|XY'| = |XS'| + |S'Y| = 4|XY'|\), wat precies is wat we zochten. \(\square\)
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2025-C2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2025"
}
|
Let \(\triangle ABC\) be an acute triangle such that \(|AB| + |BC| = 4|AC|\) and \(|AB| < |BC|\). Let \(D\) be the intersection of the angle bisector of \(\angle ABC\) with the side \(AC\). Points \(P\) and \(Q\) lie on the line segment \(BD\) such that \(|BP| = 2|DQ|\). Let \(\ell\) be the line through \(P\) parallel to \(AC\). The line through \(Q\) perpendicular to \(BD\) intersects the line segments \(AB\) and \(BC\) at points \(X\) and \(Y\), respectively. Assume that \(X\) and \(Y\) lie on the opposite side of \(\ell\) from \(B\).
A ant starts its journey at \(X\) and from there goes to a point on \(AC\), then to a point on \(\ell\), then back to a (possibly different) point on \(AC\), and finally to \(Y\). Prove that the length of the shortest possible route of the ant is equal to \(4|XY|\).

|
We provide an alternative to the (subtle use of the) BOM-lemma. Define \(B'\) again as the intersection of \(BQ\) with \(\ell'\). Since \(BXB'Y\) is a rhombus and \(Y'\) is the reflection of \(Y\), it follows that \(|B'X| = |B'Y| = |B'Y'|\). Therefore, \(B'\) is the circumcenter of \(\triangle XYY'\). From this, it follows that \(\angle XYY' = \frac{1}{2}\angle XB'Y\). Thus, by the exterior angle theorem, we have \(\angle XS'Y = \angle XYY' + \angle Y'YS' = 2\angle XYY' = \angle XB'Y\). Therefore, \(XYB'S'\) is a cyclic quadrilateral. From here, we proceed as in Solution I. \(\square\)
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij \(\triangle ABC\) een scherphoekige driehoek zo dat \(|AB| + |BC| = 4|AC|\) en \(|AB| < |BC|\). Zij \(D\) het snijpunt van de bissectrice van \(\angle ABC\) met de zijde \(AC\). Punten \(P\) en \(Q\) liggen op het lijnstuk \(BD\) zo dat \(|BP| = 2|DQ|\). Zij \(\ell\) de lijn door \(P\) parallel aan \(AC\). De lijn door \(Q\) loodrecht op \(BD\) snijdt de lijnstukken \(AB\) en \(BC\) in respectievelijk \(X\) en \(Y\). Stel dat \(X\) en \(Y\) aan de andere kant liggen van \(\ell\) dan \(B\).
Een mier begint zijn reis in \(X\) en gaat vanaf daar naar een punt op \(AC\), dan een punt op \(\ell\), dan weer terug naar een (eventueel ander) punt op \(AC\) en uiteindelijk naar \(Y\). Bewijs dat de lengte van de kortst mogelijke route van de mier gelijk is aan \(4|XY|\).

|
We geven een alternatief voor het (subtiele gebruik van het) BOM-lemma. Definieer \(B'\) weer als het snijpunt van \(BQ\) met \(\ell'\). Omdat \(BXB'Y\) een ruit is en \(Y'\) de spiegeling van \(Y\), geldt dat \(|B'X| = |B'Y| = |B'Y'|\). Dus \(B'\) is het middelpunt van de omgeschreven cirkel van \(\triangle XYY'\). Daaruit volgt dat \(\angle XYY' = \frac{1}{2}\angle XB'Y\). Dus met de buitenhoekstelling geldt nu dat \(\angle XS'Y = \angle XYY' + \angle Y'YS' = 2\angle XYY' = \angle XB'Y\). Dus \(XYB'S'\) is een koordenvierhoek. Vanaf hier gaan we weer verder als Oplossing I. \(\square\)
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2025-C2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2025"
}
|
Determine all integers \(n \ge 2\) for which \(n\) is a divisor of \(\binom{2n-3}{n-1}\).
|
We will prove that the answer is: all \(n \ge 2\) that are not powers of 2. It holds that
\[ \binom{2n-3}{n-1} = \frac{(2n-3)!}{(n-1)!(n-2)!} = \frac{(2n-3)(2n-4)\cdots(n+1)n}{(n-2)(n-3)\cdots2\cdot1}. \qquad (1) \]
Let \(p\) be a prime factor of \(n\) and assume that \(p > 2\). We know that the following expression is an integer:
\[ \binom{2n-3}{n} = \frac{(2n-3)!}{n!(n-3)!} = \frac{(2n-3)(2n-4)\cdots(n+1)}{(n-3)(n-4)\cdots2\cdot1}. \]
Let \(e_p(N)\) denote the number of factors \(p\) in an integer \(N\). Now we see that
\[ e_p((2n-3)(2n-4)\cdots(n+1)) \ge e_p((n-3)(n-4)\cdots2\cdot1). \]
Furthermore, since \(p \mid n\) and \(p > 2\), it follows that \(p \nmid n-2\), so multiplying by \(n-2\) does not add any factor \(p\). We conclude that
\[ e_p((2n-3)(2n-4)\cdots(n+1)n) - e_p((n-2)(n-3)\cdots2\cdot1) \ge e_p(n). \]
Thus, \(\binom{2n-3}{n-1}\) contains at least \(e_p(n)\) factors \(p\). Now, \(n\) is a divisor of \(\binom{2n-3}{n-1}\) if and only if this result also holds for \(p = 2\).
In a product \(a_1a_2\cdots a_m\), the total number of factors 2 is equal to the sum of the number of \(a_i\) divisible by 2, the number of \(a_i\) divisible by 4, the number of \(a_i\) divisible by 8, etc. Consider now \(n = 2^k\) with \(k \ge 1\). In (1), the numerator is the product of \(2^k, 2^k+1, 2^k+2, \ldots, 2^{k+1}-3\), while the denominator is the product of \(1, 2, 3, \ldots, 2^k-2\). For \(1 \le i \le k-1\), the number of integers from \(1, 2, 3, \ldots, 2^k-2\) divisible by \(2^i\) is exactly the same as the number of integers from \(2^k+1, 2^k+2, 2^k+3, \ldots, 2^{k+1}-2\) divisible by \(2^i\). For \(i \ge k\), both counts are 0. Therefore,
\[ e_2(1 \cdot 2 \cdot 3 \cdots (2^k-2)) = e_2((2^k+1)(2^k+2)(2^k+3) \cdots (2^{k+1}-2)). \]
On the right side, we divide the product by \(2^{k+1}-2\) (one factor 2) and multiply by \(2^k\) (\(k\) factors 2) to get the product in the numerator. We conclude
\[ e_2(2^k(2^k+1)(2^k+2)(2^k+3)\cdots(2^{k+1}-3)) - e_2(1 \cdot 2 \cdot 3 \cdots (2^k-2)) = k-1, \]
and thus \(\binom{2n-3}{n-1}\) contains exactly \(k-1\) factors 2, which is not enough to be divisible by \(n\). Therefore, \(n = 2^k\) does not satisfy the condition.
Now consider the case where \(n\) is not a power of 2. Let \(2^k\) be the largest power of 2 less than \(n\). We know that \(\binom{2n-3}{n-1}\) is an integer, so for odd \(n\) it holds that
\[ e_2((2n-3)(2n-4)\cdots(n+1)n) - e_2((n-2)(n-3)\cdots 2\cdot 1) \ge 0 = e_2(n). \]
If \(n\) is even, then there is a maximum \(\ell\) such that \(2^\ell \mid n\). Since \(n\) is not a power of 2, we note that \(2^{\ell+1} < 3 \cdot 2^\ell \le n < 2^{k+1}\). This means that \(\ell < k\). Furthermore, \(2^k \le n-2\) and thus \(n < 2^{k+1} \le 2n-4\), so the numerator in (1) contains \(2^{k+1}\). Now we consider for each \(i\) the number of factors in the numerator and the denominator divisible by \(2^i\):
- \(i = 1\): there are \(n-2\) integers in each of the products, and \(n\) is even, so the number of integers in the product divisible by 2 is the same in the numerator and the denominator.
- \(2 \le i \le \ell\): in the denominator, there are \(\lfloor \frac{n-2}{2^i} \rfloor\) numbers divisible by \(2^i\); in the numerator, there are \(\lceil \frac{n-2}{2^i} \rceil\) numbers divisible by \(2^i\) since the smallest number is divisible by \(2^i\); therefore, there is one more in the numerator than in the denominator.
- \(\ell+1 \le i \le k\): in the denominator, there are \(\lfloor \frac{n-2}{2^i} \rfloor\) numbers divisible by \(2^i\); in the numerator, there are at least as many.
- \(i = k+1\): in the denominator, no number is divisible by \(2^{k+1}\); in the numerator, there is exactly one.
- \(i > k+1\): both the numerator and the denominator contain no numbers divisible by \(2^i\).
All together, we conclude that
\[ e_2((2n-3)(2n-4)\cdots(n+1)n) - e_2((n-2)(n-3)\cdots 2\cdot 1) \ge \ell - 1 + 1 = \ell = e_2(n). \]
Thus, \(n\) divides \(\binom{2n-3}{n-1}\). The answer to the question is therefore: all \(n \ge 2\) that are not powers of 2. \(\square\)
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Bepaal alle gehele getallen \(n \ge 2\) waarvoor \(n\) een deler is van \(\binom{2n-3}{n-1}\).
|
We gaan bewijzen dat het antwoord is: alle \(n \ge 2\) die geen macht van 2 zijn. Er geldt
\[ \binom{2n-3}{n-1} = \frac{(2n-3)!}{(n-1)!(n-2)!} = \frac{(2n-3)(2n-4)\cdots(n+1)n}{(n-2)(n-3)\cdots2\cdot1}. \qquad (1) \]
Zij \(p\) een priemfactor van \(n\) en stel dat \(p > 2\). We weten dat de volgende uitdrukking geheel is:
\[ \binom{2n-3}{n} = \frac{(2n-3)!}{n!(n-3)!} = \frac{(2n-3)(2n-4)\cdots(n+1)}{(n-3)(n-4)\cdots2\cdot1}. \]
Schrijf \(e_p(N)\) voor het aantal factoren \(p\) in een geheel getal \(N\). Nu zien we dat
\[ e_p((2n-3)(2n-4)\cdots(n+1)) \ge e_p((n-3)(n-4)\cdots2\cdot1). \]
Verder geldt, aangezien \(p \mid n\) en \(p > 2\), dat \(p \nmid n-2\), dus vermenigvuldigen met \(n-2\) voegt geen factor \(p\) toe. We concluderen dat
\[ e_p((2n-3)(2n-4)\cdots(n+1)n) - e_p((n-2)(n-3)\cdots2\cdot1) \ge e_p(n). \]
Dus \(\binom{2n-3}{n-1}\) bevat minstens \(e_p(n)\) factoren \(p\). Nu is \(n\) een deler van \(\binom{2n-3}{n-1}\) dan en slechts dan als dit resultaat ook geldt voor \(p = 2\).
In een product \(a_1a_2\cdots a_m\) is het totaal aantal factoren 2 gelijk aan de som van het aantal \(a_i\) deelbaar door 2, het aantal \(a_i\) deelbaar door 4, het aantal \(a_i\) deelbaar door 8, ... Bekijk nu eerst \(n = 2^k\) met \(k \ge 1\). Dan is in (1) de teller het product van \(2^k, 2^k+1, 2^k+2, \ldots, 2^{k+1}-3\), terwijl de noemer het product is van \(1, 2, 3, \ldots, 2^k-2\). Voor \(1 \le i \le k-1\) is het aantal getallen uit \(1, 2, 3, \ldots, 2^k-2\) deelbaar door \(2^i\) precies gelijk aan het aantal getallen uit \(2^k+1, 2^k+2, 2^k+3, \ldots, 2^{k+1}-2\) deelbaar door \(2^i\). Voor \(i \ge k\) zijn beide aantallen 0. Dus
\[ e_2(1 \cdot 2 \cdot 3 \cdots (2^k-2)) = e_2((2^k+1)(2^k+2)(2^k+3) \cdots (2^{k+1}-2)). \]
Aan de rechterkant delen we het product door \(2^{k+1}-2\) (één factor 2) en vermenigvuldigen met \(2^k\) (\(k\) factoren 2) om het product uit de teller te krijgen. We concluderen
\[ e_2(2^k(2^k+1)(2^k+2)(2^k+3)\cdots(2^{k+1}-3)) - e_2(1 \cdot 2 \cdot 3 \cdots (2^k-2)) = k-1, \]
en dus bevat \(\binom{2n-3}{n-1}\) precies \(k-1\) factoren 2, wat niet genoeg is om deelbaar te zijn door \(n\). Dus \(n = 2^k\) voldoet niet.
Bekijk nu het geval dat \(n\) geen macht van 2 is. Zij \(2^k\) de grootste macht van 2 kleiner dan \(n\). We weten dat \(\binom{2n-3}{n-1}\) geheel is, dus voor oneven \(n\) geldt dat
\[e_2((2n-3)(2n-4)\cdots(n+1)n) - e_2((n-2)(n-3)\cdots 2\cdot 1) \ge 0 = e_2(n).\]
Als \(n\) even is, dan is er een maximale \(\ell\) zo dat \(2^\ell \mid n\). Aangezien \(n\) geen tweemacht is, merken we op dat \(2^{\ell+1} < 3 \cdot 2^\ell \le n < 2^{k+1}\). Dat betekent dat \(\ell < k\). Verder is \(2^k \le n-2\) en dus \(n < 2^{k+1} \le 2n-4\), dus de teller van (1) bevat \(2^{k+1}\). Nu bekijken we voor elke \(i\) het aantal factoren in de teller en de noemer deelbaar door \(2^i\):
- \(i = 1\): er zijn \(n-2\) gehele getallen in elk van de producten, en \(n\) is even, dus het aantal getallen in het product deelbaar door 2 is in teller en noemer gelijk.
- \(2 \le i \le \ell\): in de noemer zijn \(\lfloor \frac{n-2}{2^i} \rfloor\) getallen deelbaar door \(2^i\); in de teller zijn er \(\lceil \frac{n-2}{2^i} \rceil\) deelbaar door \(2^i\) aangezien het kleinste getal deelbaar is door \(2^i\); daarom is er in de teller één meer dan in de noemer.
- \(\ell+1 \le i \le k\): in de noemer zijn \(\lfloor \frac{n-2}{2^i} \rfloor\) getallen deelbaar door \(2^i\); in de teller zijn het er minstens zoveel.
- \(i = k+1\): in de noemer is geen getal deelbaar door \(2^{k+1}\); in de teller is het er precies één.
- \(i > k+1\): zowel teller als noemer bevatten geen getallen deelbaar door \(2^i\).
Alles bij elkaar concluderen we dat
\[e_2((2n-3)(2n-4)\cdots(n+1)n) - e_2((n-2)(n-3)\cdots 2\cdot 1) \ge \ell - 1 + 1 = \ell = e_2(n).\]
Dus \(n\) deelt \(\binom{2n-3}{n-1}\). Het antwoord op de vraag is dus: alle \(n \ge 2\) die geen macht van 2 zijn. \(\square\)
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2025-C2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2025"
}
|
Determine all integers \(n \ge 2\) for which \(n\) is a divisor of \(\binom{2n-3}{n-1}\).
|
We first note that the number of ways to distribute \(n-2\) identical balls into \(n\) different boxes is equal to \(\binom{(n-2)+(n-1)}{n-1} = \binom{2n-3}{n-1}\) by the stars and bars principle for \(n \ge 2\). We will examine the symmetries in the set of distributions.
Denote a distribution as \((x_1, x_2, \ldots, x_n)\) with \(x_k\) the number of balls in the \(k\)-th box. The smallest \(1 \le p \le n\) such that \((x_{1+p}, x_{2+p}, \ldots, x_{n+p}) = (x_1, x_2, \ldots, x_n)\) is called the *period* of this distribution, where indices are taken modulo \(n\). Since you return to the original distribution after \(n\) rotations and \(p\) is minimal with this property, \(p\) is a divisor of \(n\). We write \(d = n/p\) and the distribution now consists of \(d\) identical
parts \((x_1, \ldots, x_p) = (x_{p+1}, \ldots, x_{2p}) = \ldots = (x_{n-p+1}, \ldots, x_n)\). In particular, each part contains the same number of balls, so \(d\) is also a divisor of \(n-2\). Since \(\text{gcd}(n, n-2) = \text{gcd}(n, 2)\), \(d\) is equal to 1, or possibly 2 if \(n\) is even.
Let \(A\) be the set of ways to distribute \(n-2\) identical balls into \(n\) different boxes, and let \(A_p\) be the subset of these ways with period \(p\). Then we can summarize the above as follows: for \(n \ge 2\), \(|A| = \binom{2n-3}{n-1}\), if \(n\) is odd, then \(A = A_n\), and if \(n\) is even, then \(A = A_n \cup A_{n/2}\). The crux of the solution is now that for a distribution \((x_1, x_2, \ldots, x_n)\) with period \(p\), the distributions \((x_{1+i}, x_{2+i}, \ldots, x_{n+i})\) for \(0 \le i \le p-1\) are distinct and unique (while \(i = p\) gives the same distribution as \(i = 0\)). Thus, \(p \mid |A_p|\). In particular, \(n \mid |A_n|\), and for all odd \(n \ge 3\), \(n\) is a divisor of \(|A_n| = |A| = \binom{2n-3}{n-1}\).
Now suppose \(n\) is even, and write \(n = 2m\). Let \(B\) be the set of ways to distribute \(m-1\) identical balls into \(m\) different boxes. Then the restriction \((x_1, x_2, \ldots, x_{2m}) \mapsto (x_1, x_2, \ldots, x_m)\) to the first \(m\) boxes is a function from \(A_m\) to \(B\). The function \((x_1, x_2, \ldots, x_m) \mapsto (x_1, x_2, \ldots, x_m, x_1, \ldots, x_m)\) that repeats the first \(m\) boxes is a two-sided inverse. Thus, we have a bijection between these two sets. This means that \(|A_m| = |B|\), and
\[|A| = |A_n| + |A_m| \equiv |A_m| = |B| \mod n.\]
Now we calculate using the stars and bars principle that
\[|B| = \binom{2m-2}{m-1} = \binom{2m-3}{m-2} + \binom{2m-3}{m-1} = 2\binom{2m-3}{m-1}.\]
We conclude that \(n\) is a divisor of \(|A| = \binom{2n-3}{n-1}\) if and only if \(n = 2m\) is a divisor of \(|B| = 2\binom{2m-3}{m-1}\), if and only if \(m\) is a divisor of \(\binom{2m-3}{m-1}\).
We had already proven that \(n\) is a divisor of \(\binom{2n-3}{n-1}\) for all odd \(n \ge 3\). By repeatedly applying the conclusion from the previous paragraph, we now find that \(n\) is a divisor of \(\binom{2n-3}{n-1}\) for all \(n\) with an odd divisor greater than or equal to 3. On the other hand, for \(n = 2\), we calculate that \(\binom{2n-3}{n-1} = \binom{1}{1} = 1\), which clearly is not divisible by 2. Thus, by repeatedly applying the conclusion from the previous paragraph, \(n\) is not a divisor of \(\binom{2n-3}{n-1}\) when \(n\) is a power of 2. \(\square\)
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Bepaal alle gehele getallen \(n \ge 2\) waarvoor \(n\) een deler is van \(\binom{2n-3}{n-1}\).
|
We merken als eerste op dat het aantal manieren om \(n-2\) identieke ballen te verdelen over \(n\) verschillende vakjes gelijk is aan \(\binom{(n-2)+(n-1)}{n-1} = \binom{2n-3}{n-1}\) wegens het paaseierenprincipe voor \(n \ge 2\). We gaan kijken naar de symmetrieën in de verzameling van manieren.
Noteer een verdeling als \((x_1, x_2, \ldots, x_n)\) met \(x_k\) het aantal ballen in het \(k\)-de vakje. De kleinste \(1 \le p \le n\) zo dat \((x_{1+p}, x_{2+p}, \ldots, x_{n+p}) = (x_1, x_2, \ldots, x_n)\) noemen we de *periode* van deze verdeling, waarbij we de indices modulo \(n\) rekenen. Omdat je na \(n\) keer doordraaien ook weer bij de oorspronkelijke verdeling uitkomt en \(p\) minimaal is met deze eigenschap, geldt dat \(p\) een deler is van \(n\). We schrijven \(d = n/p\) en de verdeling bestaat nu uit \(d\) gelijke
delen \((x_1, \ldots, x_p) = (x_{p+1}, \ldots, x_{2p}) = \ldots = (x_{n-p+1}, \ldots, x_n)\). In het bijzonder heeft elk deel evenveel ballen, dus \(d\) is ook een deler van \(n-2\). Aangezien \(\text{gcd}(n, n-2) = \text{gcd}(n, 2)\) is \(d\) gelijk aan 1, of eventueel 2 als \(n\) even is.
Zij \(A\) de verzameling van manieren om \(n-2\) identieke ballen te verdelen over \(n\) verschillende vakjes, en zij \(A_p\) de deelverzameling van deze manieren met periode \(p\). Dan kunnen we het bovenstaande als volgt samenvatten: voor \(n \ge 2\) geldt \(|A| = \binom{2n-3}{n-1}\), als \(n\) oneven is geldt \(A = A_n\), en als \(n\) even is dan \(A = A_n \cup A_{n/2}\). De crux van de oplossing is nu dat voor een verdeling \((x_1, x_2, \ldots, x_n)\) met periode \(p\) de verdelingen \((x_{1+i}, x_{2+i}, \ldots, x_{n+i})\) voor \(0 \le i \le p-1\) verschillende unieke verdelingen zijn (terwijl \(i = p\) dus juist dezelfde verdeling geeft als \(i = 0\)). Dus \(p \mid |A_p|\). In het bijzonder geldt \(n \mid |A_n|\), en voor alle oneven \(n \ge 3\) dat \(n\) een deler is van \(|A_n| = |A| = \binom{2n-3}{n-1}\).
Stel nu dat \(n\) even is, en schrijf \(n = 2m\). Zij \(B\) de verzameling van manieren om \(m-1\) identieke ballen te verdelen over \(m\) verschillende vakjes. Dan is de restrictie \((x_1, x_2, \ldots, x_{2m}) \mapsto (x_1, x_2, \ldots, x_m)\) tot de eerste \(m\) vakjes een functie van \(A_m\) naar \(B\). De functie \((x_1, x_2, \ldots, x_m) \mapsto (x_1, x_2, \ldots, x_m, x_1, \ldots, x_m)\) die de eerste \(m\) vakjes herhaalt, is een tweezijdige inverse. Dus we hebben een bijectie tussen deze twee verzamelingen. Dit betekent dat \(|A_m| = |B|\), en
\[|A| = |A_n| + |A_m| \equiv |A_m| = |B| \mod n.\]
Nu rekenen we met het paaseirenprincipe uit dat
\[|B| = \binom{2m-2}{m-1} = \binom{2m-3}{m-2} + \binom{2m-3}{m-1} = 2\binom{2m-3}{m-1}.\]
We concluderen dat \(n\) een deler is van \(|A| = \binom{2n-3}{n-1}\), dan en slechts dan als \(n = 2m\) een deler is van \(|B| = 2\binom{2m-3}{m-1}\), dan en slechts dan als \(m\) een deler is van \(\binom{2m-3}{m-1}\).
We hadden al bewezen dat \(n\) een deler is van \(\binom{2n-3}{n-1}\) voor alle oneven \(n \ge 3\). Door de conclusie van de vorige alinea herhaaldelijk toe te passen vinden we nu dus dat \(n\) een deler is van \(\binom{2n-3}{n-1}\) voor alle \(n\) met een oneven deler groter of gelijk aan 3. Aan de andere kant rekenen we voor \(n = 2\) uit dat \(\binom{2n-3}{n-1} = \binom{1}{1} = 1\), waarvan 2 duidelijk geen deler is. Dus met herhaaldelijk toepassen van de conclusie van de vorige alinea is \(n\) géén deler van \(\binom{2n-3}{n-1}\) wanneer \(n\) een tweemacht is. \(\square\)
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2025-C2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2025"
}
|
Determine all integers \(n \ge 2\) for which \(n\) is a divisor of \(\binom{2n-3}{n-1}\).
|
We use the notation of solution II. We provide an alternative to the induction for even \(n = 2m\) starting from the realization that \(|A| \equiv |B| \mod n\).
Since \(\text{gcd}(m, m-1) = 1\), there is no partition in \(B\) with a period smaller than \(m\). Thus, \(m \mid |B|\). This means that \(b = |B|/m\) is an integer, and \(n \mid |A|\) if and only if \(b\) is even. Now we compute that
\[b = \frac{1}{m} \binom{2m-2}{m-1} = \frac{1}{m} \frac{(2m-2)!}{(m-1)!(m-1)!} = \frac{1}{(2m-1)} \frac{(2m-1)!}{m!(m-1)!} = \frac{1}{(2m-1)} \binom{2m-1}{m-1}.\]
Since \(b\) is an integer, it follows that \(2m-1\) is a divisor of \(\binom{2m-1}{m-1}\). And since \(2m-1\) is odd, \(b\) is even if and only if \(\binom{2m-1}{m-1}\) is even. We rewrite this as \(\binom{2m-1}{m-1} = \frac{(2m-1)!}{m!(m-1)!} = \frac{m}{2m} \frac{(2m)!}{m!m!} = \frac{1}{2} \binom{2m}{m}\). Thus, \(\binom{2m-1}{m-1}\) is even if and only if 4 is a divisor of \(\binom{2m}{m}\). Let \(2^k\) be the largest power of 2 less than or equal to \(m\). Using the notation of solution I, we compute
\[e_2(\binom{2m}{m}) = e_2(2m!) - 2e_2(m!)\] \[= \sum_{i=1}^{k+1} \left\lfloor \frac{2m}{2^i} \right\rfloor - 2 \sum_{i=1}^{k} \left\lfloor \frac{m}{2^i} \right\rfloor\] \[= \left( \left\lfloor \frac{2m}{2} \right\rfloor + \sum_{i=2}^{k+1} \left\lfloor \frac{2m}{2^i} \right\rfloor \right) - 2 \sum_{i=1}^{k} \left\lfloor \frac{m}{2^i} \right\rfloor\] \[= \left( m + \sum_{i=1}^{k} \left\lfloor \frac{m}{2^i}\right\rfloor \right) - 2 \sum_{i=1}^{k} \left\lfloor \frac{m}{2^i} \right\rfloor\] \[= m - \sum_{i=1}^{k} \left\lfloor \frac{m}{2^i}\right\rfloor\] \[\geq m - \sum_{i=1}^{k} \frac{m}{2^i} = \frac{m}{2^k} \geq 1.\]
The two inequalities in the last line hold with equality if and only if \(m = 2^k\), and thus \(n = 2^{k+1}\). Since 4 is a divisor of \(\binom{2m}{m}\) if and only if \(e_2(\binom{2m}{m}) > 1\), this holds if and only if \(n\) is not a power of 2. \(\square\)
Remark. The formula \(m - \sum_{i=1}^{k} \left\lfloor \frac{m}{2^i} \right\rfloor\) gives the number of ones in the binary representation of \(m\).
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Bepaal alle gehele getallen \(n \ge 2\) waarvoor \(n\) een deler is van \(\binom{2n-3}{n-1}\).
|
We gebruiken de notatie van oplossing II. We geven een alternatief voor de inductie voor even \(n = 2m\) vanaf de realisatie dat \(|A| \equiv |B| \mod n\).
Omdat \(\text{gcd}(m, m-1) = 1\), is er geen enkele verdeling in \(B\) met een periode kleiner dan \(m\). Dus \(m \mid |B|\). Dat betekent dat \(b = |B|/m\) geheel is, en \(n \mid |A|\) dan en slechts dan als \(b\)
even is. Nu rekenen we uit dat
\[b = \frac{1}{m} \binom{2m-2}{m-1} = \frac{1}{m} \frac{(2m-2)!}{(m-1)!(m-1)!} = \frac{1}{(2m-1)} \frac{(2m-1)!}{m!(m-1)!} = \frac{1}{(2m-1)} \binom{2m-1}{m-1}.\]
Aangezien \(b\) geheel is, volgt hieruit dat \(2m-1\) een deler is van \(\binom{2m-1}{m-1}\). En omdat \(2m-1\) oneven is, is \(b\) even dan en slechts dan als \(\binom{2m-1}{m-1}\) even is. Dit herschrijven we nog een keer als \(\binom{2m-1}{m-1} = \frac{(2m-1)!}{m!(m-1)!} = \frac{m}{2m} \frac{(2m)!}{m!m!} = \frac{1}{2} \binom{2m}{m}\). Dus \(\binom{2m-1}{m-1}\) is even dan en slechts dan als 4 een deler is van \(\binom{2m}{m}\). Zij \(2^k\) de grootste macht van 2 kleiner dan of gelijk aan \(m\). Met de notatie van oplossing I rekenen we dan uit
\[e_2(\binom{2m}{m}) = e_2(2m!) - 2e_2(m!)\] \[= \sum_{i=1}^{k+1} \left\lfloor \frac{2m}{2^i} \right\rfloor - 2 \sum_{i=1}^{k} \left\lfloor \frac{m}{2^i} \right\rfloor\] \[= \left( \left\lfloor \frac{2m}{2} \right\rfloor + \sum_{i=2}^{k+1} \left\lfloor \frac{2m}{2^i} \right\rfloor \right) - 2 \sum_{i=1}^{k} \left\lfloor \frac{m}{2^i} \right\rfloor\] \[= \left( m + \sum_{i=1}^{k} \left\lfloor \frac{m}{2^i}\right\rfloor \right) - 2 \sum_{i=1}^{k} \left\lfloor \frac{m}{2^i} \right\rfloor\] \[= m - \sum_{i=1}^{k} \left\lfloor \frac{m}{2^i}\right\rfloor\] \[\geq m - \sum_{i=1}^{k} \frac{m}{2^i} = \frac{m}{2^k} \geq 1.\]
In de twee ongelijkheden van de laatste regel geldt gelijkheid dan en slechts dan als \(m = 2^k\), en dus \(n = 2^{k+1}\). Aangezien 4 is een deler van \(\binom{2m}{m}\) dan en slechts dan als \(e_2(\binom{2m}{m}) > 1\), geldt dat dus dan en slechts dan als \(n\) géén tweemacht is. \(\square\)
Opmerking. De formule \(m - \sum_{i=1}^{k} \left\lfloor \frac{m}{2^i} \right\rfloor\) geeft het aantal enen in de binaire notatie van \(m\).
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2025-C2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing III.",
"tier": "T1",
"year": "2025"
}
|
Can a number of the form 44...41, with an odd number of fours followed by a 1, be a square?
|
No. We can write such a number 44...41 as \(4 \cdot \frac{10^{2m}-1}{9} - 3\), with \(m \ge 1\) an integer. Suppose this is a square. Write \(4 \cdot \frac{10^{2m}-1}{9} - 3 = n^2\) with \(n\) a positive integer. Multiplying by 9 gives \(4(10^{2m} - 1) - 27 = 9n^2\), so \(4 \cdot 10^{2m} = 9n^2 + 31\), or \((2 \cdot 10^m)^2 - (3n)^2 = 31\). Write \(x = 2 \cdot 10^m\) and \(y = 3n\), then we get \(x^2 - y^2 = 31\). This can be factored as \((x - y)(x + y) = 31\). So \(x + y \mid 31\), and since \(x + y \ge 2\) we get \(x + y = 31\) and \(x - y = 1\). This yields \(x = 16\), but that is not of the form \(2 \cdot 10^m\). We conclude that a number of the form 44...41 with an odd number of fours cannot be a square. \(\square\)
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Kan een getal van de vorm 44...41, met een oneven aantal vieren gevolgd door een 1, een kwadraat zijn?
|
Nee. We kunnen zo'n getal 44...41 schrijven als \(4 \cdot \frac{10^{2m}-1}{9} - 3\), met \(m \ge 1\) geheel. Stel dat dit een kwadraat is. Schrijf \(4 \cdot \frac{10^{2m}-1}{9} - 3 = n^2\) met \(n\) positief geheel. Vermenigvuldigen met 9 geeft \(4(10^{2m} - 1) - 27 = 9n^2\), dus \(4 \cdot 10^{2m} = 9n^2 + 31\), ofwel \((2 \cdot 10^m)^2 - (3n)^2 = 31\). Schrijf nu \(x = 2 \cdot 10^m\) en \(y = 3n\), dan krijgen we dus \(x^2 - y^2 = 31\). Dit kunnen we ontbinden als \((x - y)(x + y) = 31\). Dus \(x + y \mid 31\), en omdat \(x + y \ge 2\) krijgen we dus \(x + y = 31\) en \(x - y = 1\). Dit levert \(x = 16\), maar dat is niet van de vorm \(2 \cdot 10^m\). We concluderen dat een getal van de vorm 44...41 met een oneven aantal vieren geen kwadraat kan zijn. \(\square\)
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2025-D2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2025"
}
|
Can a number of the form 44...41, with an odd number of fours followed by a 1, be a square?
|
We observe that the residue classes of squares modulo 11 are respectively 0, 1, 4, 9, 5, 3, 3, 5, 9, 4, 1. On the other hand, we can compute the residue class of 44...41 by repeatedly subtracting two fours from the number, which does not change the residue class due to \(44 \cdot 10^\ell \equiv 0 \mod 11\). Since the given number has an odd number of fours, it is thus equal to
\[44...41 \equiv 41 \equiv 8 \mod 11.\]
This is not one of the quadratic residue classes, so none of these numbers is a square. \(\square\)
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Kan een getal van de vorm 44...41, met een oneven aantal vieren gevolgd door een 1, een kwadraat zijn?
|
We merken op dat de restklassen van kwadraten modulo 11 gelijk zijn aan respectievelijk 0, 1, 4, 9, 5, 3, 3, 5, 9, 4, 1. Aan de andere kant kunnen we de restklasse van 44...41 uitrekenen door steeds twee vieren van het getal af te halen, waardoor de restklasse niet verandert wegens \(44 \cdot 10^\ell \equiv 0 \mod 11\). Omdat het gegeven getal een oneven aantal vieren heeft, is het dus gelijk aan
\[44...41 \equiv 41 \equiv 8 \mod 11.\]
Dit is niet een van de kwadratische restklassen, dus geen van deze getallen is een kwadraat. \(\square\)
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2025-D2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2025"
}
|
Let \(\triangle ABC\) be an acute triangle with \(|AB| > |AC|\), and let \(\omega\) be the circumcircle of \(\triangle ABC\) with center \(O\). The altitude from \(A\) intersects \(BC\) at \(D\) and intersects \(\omega\) again at \(P\). Define \(H\) as the orthocenter of \(\triangle ABC\) and let \(K\) be the point on segment \(BC\) such that \(|BD| = |KC|\). The circumcircle of \(\triangle PKH\) intersects \(\omega\) again at \(Q\) and intersects line \(BC\) again at \(N\). Let \(T\) be the point on line \(AD\) such that \(TN \perp PQ\).
Prove that the line \(KT\) passes through \(O\).

|
Let \(O\) be the center of \(\omega\). Since \(|BD| = |KC|\), the perpendicular bisectors of \(BC\) and \(KD\) coincide, and in particular, \(|OK| = |OD|\). Let \(T'\) be the reflection of \(K\) in \(O\). By Thales' theorem, \(\angle KDT' = 90^\circ\), so \(T'\) lies on \(AD\).
It is a standard fact that the reflection of \(H\) in \(BC\) lies on the circumcircle. (This can be easily proven by calculating \(\angle BHC\).) This implies that \(\triangle PKH\) maps to itself under reflection in \(BC\). This means that the center \(M\) of the circumcircle of \(\triangle PKH\) lies on \(BC\), and that \(M\) is the midpoint of \(KN\). By definition, \(O\) is the midpoint of \(KT'\), so \(OM\) is a midline in \(\triangle KNT'\); in particular, \(OM \parallel NT'\). Since \(P\) and \(Q\) both lie on \(\omega\) and the circumcircle of \(\triangle PKH\), \(OM\) is the perpendicular bisector of \(PQ\), so \(OM \perp PQ\). It follows that \(NT' \perp PQ\), and we can conclude that \(T'\) is equal to \(T\). \(\square\)
Remark. Let \(\ell\) be the line through \(N\) perpendicular to \(PQ\). For completeness, we show that \(\ell\) is not parallel to \(AD\) and in particular does not coincide (so that \(T\) exists and is unique). Note that \(H\) lies inside \(\triangle ABC\) because it is an acute triangle. This implies that \(D \neq N\), and thus \(\ell\) does not coincide with \(AD\). Since \(D \neq N\) and \(M\) is the midpoint of \(KN\), \(M\) is not the midpoint of \(KD\). Therefore, \(M\) is not the midpoint of \(BC\). Hence, \(OM\) is not perpendicular to \(BC\). Since \(OM \parallel \ell\) and \(AD \perp BC\), we conclude that \(\ell\) is not parallel to \(AD\).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij \(\triangle ABC\) een scherphoekige driehoek met \(|AB| > |AC|\), zij \(\omega\) de omgeschreven cirkel van \(\triangle ABC\) met middelpunt \(O\). De hoogtelijn vanuit \(A\) snijdt \(BC\) in \(D\) en snijdt \(\omega\) een tweede keer in \(P\). Definieer \(H\) als het hoogtepunt van \(\triangle ABC\) en zij \(K\) het punt op het lijnstuk \(BC\) zodanig dat \(|BD| = |KC|\). De omgeschreven cirkel van \(\triangle PKH\) snijdt \(\omega\) een tweede keer in \(Q\) en snijdt de lijn \(BC\) een tweede keer in \(N\). Zij \(T\) het punt op de lijn \(AD\) zodanig dat \(TN \perp PQ\).
Bewijs dat de lijn \(KT\) door \(O\) gaat.

|
Zij \(O\) het middelpunt van \(\omega\). Wegens \(|BD| = |KC|\) vallen de middelloodlijnen van \(BC\) en \(KD\) samen en in het bijzonder geldt dus dat \(|OK| = |OD|\). Zij \(T'\) de spiegeling van \(K\) in \(O\). Wegens Thales geldt dan dat \(\angle KDT' = 90^\circ\), dus \(T'\) ligt op \(AD\).
Het is een standaardplaatje dat de spiegeling van \(H\) in \(BC\) op de omgeschreven cirkel ligt. (Eenvoudig te bewijzen door \(\angle BHC\) uit te rekenen.) Hieruit volgt dat \(\triangle PKH\) in zichzelf overgaat onder spiegeling in \(BC\). Dit betekent dat het middelpunt \(M\) van de omgeschreven cirkel van \(\triangle PKH\) op \(BC\) ligt, en dat \(M\) het midden van \(KN\) is. Per definitie is \(O\) het midden van \(KT'\), dus \(OM\) is een middenparallel in \(\triangle KNT'\); in het bijzonder geldt \(OM \parallel NT'\). Omdat \(P\) en \(Q\) beide op zowel \(\omega\) als de omgeschreven cirkel
van \(\triangle PKH\) liggen, is \(OM\) de middelloodlijn van \(PQ\), dus \(OM \perp PQ\). Nu volgt dat ook \(NT' \perp PQ\), en kunnen we concluderen dat \(T'\) gelijk is aan \(T\). \(\square\)
Opmerking. Zij \(\ell\) de lijn door \(N\) loodrecht op \(PQ\). We laten voor de volledigheid zien dat \(\ell\) niet evenwijdig is met \(AD\) en in het bijzonder niet samenvalt (zodat \(T\) bestaat en uniek vastligt). Merk op dat \(H\) binnen \(\triangle ABC\) ligt, omdat dit een scherphoekige driehoek is. Hieruit volgt dat \(D \neq N\), en dus dat \(\ell\) niet samenvalt met \(AD\). Omdat \(D \neq N\) en \(M\) het midden is van \(KN\), is \(M\) niet het midden van \(KD\). Dus \(M\) is niet het midden van \(BC\). Hierdoor staat \(OM\) niet loodrecht op \(BC\). Omdat \(OM \parallel \ell\) en \(AD \perp BC\) concluderen we dat \(\ell\) niet evenwijdig is met \(AD\).
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2025-D2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2025"
}
|
Let \(\triangle ABC\) be an acute triangle with \(|AB| > |AC|\), and let \(\omega\) be the circumcircle of \(\triangle ABC\) with center \(O\). The altitude from \(A\) intersects \(BC\) at \(D\) and intersects \(\omega\) again at \(P\). Define \(H\) as the orthocenter of \(\triangle ABC\) and let \(K\) be the point on segment \(BC\) such that \(|BD| = |KC|\). The circumcircle of \(\triangle PKH\) intersects \(\omega\) again at \(Q\) and intersects line \(BC\) again at \(N\). Let \(T\) be the point on line \(AD\) such that \(TN \perp PQ\).
Prove that the line \(KT\) passes through \(O\).

|
For a more direct version of the previous solution, we again note that \(OM \perp PQ \perp TN\). Thus, \(OM \parallel TN\), and since \(M\) is the midpoint of \(KN\), the line \(OM\) is the midline of \(\triangle KNT\) (but \(O\) a priori is not yet on \(KT\)). Therefore, \(OM\) passes through the midpoint of \(KT\), say \(O'\). Furthermore, the perpendicular bisector of \(KD\) is a midline in \(\triangle KDT\), as it passes through the midpoint of \(KD\) and is parallel to \(DT\). Thus, it also passes through \(O'\). The perpendicular bisector of \(KD\) is the same as the perpendicular bisector of \(BC\). This also passes through \(O\), since \(BC\) is a chord of \(\omega\). Since both \(MO\) and the perpendicular bisector of \(BC\) pass through both \(O\) and \(O'\), we conclude that \(O' = O\). Therefore, \(KT\) passes through \(O\). \(\square\)
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij \(\triangle ABC\) een scherphoekige driehoek met \(|AB| > |AC|\), zij \(\omega\) de omgeschreven cirkel van \(\triangle ABC\) met middelpunt \(O\). De hoogtelijn vanuit \(A\) snijdt \(BC\) in \(D\) en snijdt \(\omega\) een tweede keer in \(P\). Definieer \(H\) als het hoogtepunt van \(\triangle ABC\) en zij \(K\) het punt op het lijnstuk \(BC\) zodanig dat \(|BD| = |KC|\). De omgeschreven cirkel van \(\triangle PKH\) snijdt \(\omega\) een tweede keer in \(Q\) en snijdt de lijn \(BC\) een tweede keer in \(N\). Zij \(T\) het punt op de lijn \(AD\) zodanig dat \(TN \perp PQ\).
Bewijs dat de lijn \(KT\) door \(O\) gaat.

|
Voor een directere versie van de vorige oplossing, merken we wederom op dat \(OM \perp PQ \perp TN\). Dus \(OM \parallel TN\), en omdat \(M\) het midden is van \(KN\) is de lijn \(OM\) dus de middenparallel van \(\triangle KNT\) (maar \(O\) ligt a priori nog niet op \(KT\)). Dus \(OM\) gaat door het midden van \(KT\), zeg \(O'\). Verder is de middelloodlijn van \(KD\) een middenparallel in \(\triangle KDT\), want hij gaat door het midden van \(KD\) en is evenwijdig aan \(DT\). Dus deze gaat ook door \(O'\). De middelloodlijn van \(KD\) is gelijk aan de middelloodlijn van \(BC\). Deze gaat ook door \(O\), omdat \(BC\) een koorde is van \(\omega\). Omdat \(MO\) en de middelloodlijn van \(BC\) beide door zowel \(O\) als \(O'\) gaan, concluderen we dat \(O' = O\). Dus \(KT\) gaat door \(O\). \(\square\)
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2025-D2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2025"
}
|
Johan and Quintijn play the following game, taking turns with Johan starting. At the beginning, the numbers \(1, 2, \dots, 2024\) are written on a board. In each turn, the player whose turn it is erases two numbers \(a\) and \(b\) that are on the board, and writes the (possibly negative) difference \(a - b\) on the board. The game ends when only one number remains on the board. If this number is divisible by 3, Johan wins; otherwise, Quintijn wins.
Determine which of the two players has a winning strategy.
|
We will prove that Quintijn has a winning strategy. First, note that only the number of numbers in each residue class modulo 3 is relevant. If \(a \equiv i \mod 3\), \(b \equiv j \mod 3\) and \(a - b \equiv k \mod 3\), we denote the move with \(a\) and \(b\) as \((i, j) \to k\). Let \(x\) be the number of numbers on the board that are *not* divisible by 3. Note that \(x\) can decrease by at most 2 in each turn.
Quintijn can play the game arbitrarily until at the beginning of his turn, \(1 \le x \le 4\). From that point on, he follows the following strategy.
- If \(x = 4\), then Quintijn always makes a move that ensures \(x\) remains 4. To show that this is always possible, note that Quintijn always has an odd number of numbers left at the beginning of his turn. If \(x = 4\), there must also be at least one number on the board that is divisible by 3. Now Quintijn can make a move of the form \((i, 0) \to i\) with \(i \in \{1, 2\}\), and the value of \(x\) does not change.
If Quintijn follows this strategy, Johan must eventually make a move that results in \(x \in \{2, 3\}\), and we are in one of the following cases.
- If \(x = 3\), then without loss of generality, there are two numbers on the board that are congruent to 1 modulo 3. With the move \((1, 1) \to 0\), Quintijn can ensure that \(x = 1\), and there will always be exactly one number that is not divisible by 3 on the board. Therefore, the last number will also not be divisible by 3, and Quintijn wins.
- If \(x = 2\), then we distinguish two subcases.
- The two numbers are in different residue classes modulo 3. Then Quintijn can make the move \((2, 1) \to 1\) so that \(x = 1\), and as we have seen, he wins then.
- The two numbers are in the same residue class modulo 3, say they are both congruent to 1 modulo 3. Since there is an odd number left, there is also a number on the board that is divisible by 3. With the move \((0, 1) \to 2\), Quintijn leaves a situation where \(x = 2\) again, and the numbers are not congruent to each other modulo 3. Now Johan cannot ensure that \(x\) becomes 0, so he leaves a situation where \(x = 1\) or \(x = 2\). If Quintijn follows this strategy, Johan must eventually make a move that leads to the previous subcase or the case \(x = 1\), and thus Quintijn wins.
- If \(x = 1\), then as stated, there will always be one number that is not divisible by 3 on the board, so Quintijn wins.
We conclude that Quintijn indeed has a winning strategy.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Johan en Quintijn spelen het volgende spel, waarbij ze om en om aan de beurt zijn en Johan begint. Aan het begin staan op een bord de getallen \(1, 2, \dots, 2024\) geschreven. In elke beurt veegt de speler die aan de beurt is twee getallen \(a\) en \(b\) die op het bord staan uit, en schrijft het (mogelijk negatieve) verschil \(a - b\) op het bord. Het spel eindigt als er nog maar één getal op het bord staat. Als dit getal deelbaar is door 3, dan wint Johan, en anders wint Quintijn.
Bepaal welke van de twee spelers een winnende strategie heeft.
|
We gaan bewijzen dat Quintijn een winnende strategie heeft. Merk allereerst op dat alleen het aantal getallen in elke restklasse modulo 3 van belang is. Als \(a \equiv i \mod 3\), \(b \equiv j \mod 3\) en \(a - b \equiv k \mod 3\), dan noteren we de zet met \(a\) en \(b\) als \((i, j) \to k\). Zij \(x\) het aantal getallen op het bord die *niet* deelbaar zijn door 3. Merk op dat \(x\) in elke beurt met hoogstens 2 kan afnemen.
Quintijn kan het spel willekeurig spelen totdat aan het begin van zijn beurt geldt dat \(1 \le x \le 4\). Vanaf dat moment houdt hij de volgende strategie aan.
- Als \(x = 4\), dan doet Quintijn altijd een zet die er voor zorgt dat \(x\) gelijk blijft aan 4. Om aan te tonen dat dit altijd kan, merken we op dat Quintijn aan het begin van zijn beurt altijd een oneven aantal getallen over heeft. Als \(x = 4\), moet er dus ook nog minstens één getal op het bord staan dat deelbaar is door 3. Nu kan Quintijn dus een zet doen van de vorm \((i, 0) \to i\) met \(i \in \{1, 2\}\), en verandert de waarde van \(x\) dus niet.
Als Quintijn deze strategie aanhoudt, moet Johan dus op een gegeven moment een zet doen waardoor \(x \in \{2, 3\}\), en bevinden we ons in één van de volgende gevallen.
- Als \(x = 3\), dan staan er zonder verlies van algemeenheid twee getallen op het bord die congruent zijn aan 1 modulo 3. Met de zet \((1, 1) \to 0\) kan Quintijn er voor zorgen dat \(x = 1\), en dan blijft er altijd exact 1 getal dat niet deelbaar is door 3 op het bord staan. Dus is uiteindelijk ook het laatste getal niet deelbaar door 3, en wint Quintijn.
- Als \(x = 2\), dan onderscheiden we twee deelgevallen.
- De twee getallen zitten in verschillende restklassen modulo 3. Dan kan Quintijn de zet \((2, 1) \to 1\) doen zodat \(x = 1\), en zoals we al zagen wint hij dan.
- De twee getallen zitten in dezelfde restklass modulo 3, zeg dat ze beide congruent zijn aan 1 modulo 3. Omdat er een oneven aantal overgebleven is, staat er ook nog een getal op het bord dat deelbaar is door 3. Met de zet \((0, 1) \to 2\) laat Quintijn een situatie over waarin opnieuw \(x = 2\), en de getallen niet congruent aan elkaar zijn modulo 3. Nu kan Johan er niet voor zorgen dat \(x\) gelijk wordt
aan 0, dus laat hij een situatie over waarin \(x = 1\) of \(x = 2\). Als Quintijn deze strategie aanhoudt, dan moet Johan uiteindelijk een zet doen waardoor we in het vorige deelgeval of in het geval \(x = 1\) terecht komen, en dus wint Quintijn.
* Als \(x = 1\), dan blijft er zoals gezegd altijd een getal dat niet deelbaar is door 3 op het bord staan, dus wint Quintijn.
We concluderen dat Quintijn inderdaad een winnende strategie heeft.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2025-D2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2025"
}
|
Johan and Quintijn play the following game, taking turns with Johan starting. At the beginning, the numbers \(1, 2, \dots, 2024\) are written on a board. In each turn, the player whose turn it is erases two numbers \(a\) and \(b\) that are on the board, and writes the (possibly negative) difference \(a - b\) on the board. The game ends when only one number remains on the board. If this number is divisible by 3, Johan wins; otherwise, Quintijn wins.
Determine which of the two players has a winning strategy.
|
For \(i = 0, 1, 2\), we denote the number of numbers on the board that are congruent to \(i\) modulo 3 by \(x_i\). Note that Johan can only play the remaining numbers that are not divisible by 3 if \(x_1 = 2\) and \(x_2 = 0\), or \(x_1 = 0\) and \(x_2 = 2\). We claim that if \(x_1\) and \(x_2\) are not both equal to 0, Quintijn can always make a move that ensures at least one of \(x_1\) and \(x_2\) is odd. As we just saw, Johan cannot then play all the numbers that are not divisible by 3; and in his first turn, this is of course also not possible. By following this strategy, Quintijn wins.
To prove the claim, first assume that both \(x_1\) and \(x_2\) are even. Then at least one of the two must be at least 2, say \(x_1 \ge 2\). Since Quintijn always has an odd number of numbers left at the beginning of his turn, there must also be a number on the board that is divisible by 3. With the move \((0, 1) \to 2\), Quintijn ensures that \(x_1\) decreases by 1 and \(x_2\) increases by 1. After this turn, both \(x_1\) and \(x_2\) are thus odd.
Now assume that at least one of \(x_1\) and \(x_2\) is odd. If there are at least 4 numbers left, then there is an \(i\) with \(x_i \ge 2\). By making the move \((i, i) \to 0\), \(x_1\) and \(x_2\) do not change modulo 2, so the claim follows. The last case is that there are exactly 3 numbers left (since Quintijn always has an odd number of numbers left at the beginning of his turn). Then it must be that \(x_0 = x_1 = x_2 = 1\), and Quintijn can make the move \((1, 0) \to 1\).
This completes the proof of the claim, so Quintijn indeed has a winning strategy.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Johan en Quintijn spelen het volgende spel, waarbij ze om en om aan de beurt zijn en Johan begint. Aan het begin staan op een bord de getallen \(1, 2, \dots, 2024\) geschreven. In elke beurt veegt de speler die aan de beurt is twee getallen \(a\) en \(b\) die op het bord staan uit, en schrijft het (mogelijk negatieve) verschil \(a - b\) op het bord. Het spel eindigt als er nog maar één getal op het bord staat. Als dit getal deelbaar is door 3, dan wint Johan, en anders wint Quintijn.
Bepaal welke van de twee spelers een winnende strategie heeft.
|
Voor \(i = 0, 1, 2\) noteren we het aantal getallen op het bord dat congruent is aan \(i\) modulo 3 met \(x_i\). Merk op dat Johan de laatst overgebleven getallen die niet deelbaar zijn door 3 alleen weg kan spelen als \(x_1 = 2\) en \(x_2 = 0\), of \(x_1 = 0\) en \(x_2 = 2\). We beweren nu dat, als \(x_1\) en \(x_2\) niet beide gelijk zijn aan 0, Quintijn altijd een zet kan doen die er voor zorgt dat minstens één van \(x_1\) en \(x_2\) oneven is. Zoals we net zagen, kan Johan dan niet alle getallen die niet deelbaar zijn door 3 wegspelen; en in zijn eerste beurt lukt dit natuurlijk ook niet. Door deze strategie te volgen, wint Quintijn dus.
Om de bewering te bewijzen, stel eerst dat \(x_1\) en \(x_2\) beide even zijn. Dan moet minstens één van de twee minstens gelijk zijn aan 2, zeg \(x_1 \ge 2\). Omdat Quintijn aan het begin van zijn beurt altijd een oneven aantal getallen over heeft, moet er ook nog een getal op het bord staan dat deelbaar is door 3. Met de zet \((0, 1) \to 2\) zorgt Quintijn ervoor dat \(x_1\) met 1 afneemt en \(x_2\) met 1 toeneemt. Na deze beurt zijn \(x_1\) en \(x_2\) dus beide oneven.
Stel nu dat minstens één van \(x_1\) en \(x_2\) oneven is. Als er nog minstens 4 getallen over zijn, dan is er een \(i\) met \(x_i \ge 2\). Door de zet \((i, i) \to 0\) veranderen \(x_1\) en \(x_2\) niet modulo 2, dus volgt de bewering. Het laatste geval is dat er precies 3 getallen over zijn (want Quintijn heeft aan het begin van zijn beurt altijd een oneven aantal getallen over). Dan moet gelden dat \(x_0 = x_1 = x_2 = 1\), en kan Quintijn de zet \((1, 0) \to 1\) doen.
Dit voltooit het bewijs van de bewering, dus Quintijn heeft inderdaad een winnende strategie.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2025-D2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2025"
}
|
Find all functions \(f: \mathbb{Z}_{>0} \to \mathbb{Z}_{>0}\) such that for all positive integers \(m, n\) it holds that
\[(f(m))^2 + 2mf(n) + f(n^2)\]
is the square of an integer.
|
Let \(m = n = 1\), then \(f(1)^2 + 3f(1)\) must be a square. Since
\[(f(1) + 1)^2 \le f(1)^2 + 3f(1) < (f(1) + 2)^2,\]
there must be equality on the left, and thus \(f(1) = 1\). Now let \(p = 2k+1\) be an odd prime and substitute \(m = k = (p-1)/2\) and \(n = 1\). Then we see that \(f(k)^2 + p\) must be a square, say \(a^2\) for some positive integer \(a\). This gives \(p = a^2 - f(k)^2 = (a - f(k))(a + f(k))\), and this has the only solution \(a - f(k) = 1\) and \(a + f(k) = p = 2k + 1\). Taking the difference of these gives \(f(k) = k\).
Now we only substitute \(m = k\) (again so that \(2k + 1\) is an odd prime, so \(f(k) = k\)), then we see that \(k^2 + 2kf(n) + f(n^2) = (k + f(n))^2 + f(n^2) - f(n)^2\) is a square. If we choose \(k\) large enough (for a given \(n\)) so that \(1 - 2k - 2f(n) < f(n^2) - f(n)^2 < 1 + 2k + 2f(n)\), then we see that
\[(k + f(n) - 1)^2 < (k + f(n))^2 + f(n^2) - f(n)^2 < (k + f(n) + 1)^2.\]
The middle expression is a square and must therefore be equal to \((k + f(n))^2\), which means that \(f(n^2) = f(n)^2\) for all \(n\). Finally, we substitute \(n = k\), and see that \(f(m)^2 + 2mk + k^2 = (k + m)^2 + f(m)^2 - m^2\) is a square. If we now choose \(k\) large enough again (for a given \(m\)), we see with the same reasoning that \(f(m)^2 = m^2\), so \(f(m) = m\) for all \(m\).
The function \(f(m) = m\) indeed satisfies, because then the desired expression is \((m+n)^2\). □
|
f(m) = m
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Vind alle functies \(f: \mathbb{Z}_{>0} \to \mathbb{Z}_{>0}\) zo dat voor alle positieve gehele getallen \(m, n\) geldt dat
\[(f(m))^2 + 2mf(n) + f(n^2)\]
het kwadraat van een geheel getal is.
|
Vul in \(m = n = 1\), dan moet \(f(1)^2 + 3f(1)\) een kwadraat zijn. Aangezien
\[(f(1) + 1)^2 \le f(1)^2 + 3f(1) < (f(1) + 2)^2,\]
moet er links gelijkheid gelden, en dus is \(f(1) = 1\). Laat nu \(p = 2k+1\) een oneven priemgetal en vul in \(m = k = (p-1)/2\) en \(n = 1\). Dan zien we dat \(f(k)^2 + p\) een kwadraat moet zijn, zeg \(a^2\) voor een positieve gehele \(a\). Dat geeft \(p = a^2 - f(k)^2 = (a - f(k))(a + f(k))\), en dit heeft als enige oplossing \(a - f(k) = 1\) en \(a + f(k) = p = 2k + 1\). Hiervan het verschil nemen geeft \(f(k) = k\).
Nu vullen we alleen \(m = k\) in (weer zodat \(2k + 1\) een oneven priemgetal is, dus zodat \(f(k) = k\)), dan zien we dat \(k^2 + 2kf(n) + f(n^2) = (k + f(n))^2 + f(n^2) - f(n)^2\) een kwadraat is. Als we \(k\) groot genoeg kiezen (voor gegeven \(n\)) zodat \(1 - 2k - 2f(n) < f(n^2) - f(n)^2 < 1 + 2k + 2f(n)\), dan zien we dat
\[(k + f(n) - 1)^2 < (k + f(n))^2 + f(n^2) - f(n)^2 < (k + f(n) + 1)^2.\]
De middelste uitdrukking is een kwadraat en moet dus gelijk zijn aan \((k + f(n))^2\), dat betekent dat \(f(n^2) = f(n)^2\) voor alle \(n\). Tot slot vullen we \(n = k\) in, en zien we dat \(f(m)^2 + 2mk + k^2 = (k + m)^2 + f(m)^2 - m^2\) een kwadraat is. Als we nu \(k\) weer groot genoeg kiezen (voor gegeven \(m\)), zien we met dezelfde redenering dat \(f(m)^2 = m^2\), dus \(f(m) = m\) voor alle \(m\).
De functie \(f(m) = m\) voldoet inderdaad, want dan is het gevraagde gelijk aan \((m+n)^2\). □
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2025-D2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2025"
}
|
Let \(ABCD\) be a parallelogram and let \(M\) be the intersection of the diagonals. The circumcircle of \(\triangle ABM\) intersects the line segment \(AD\) at \(E \neq A\) and the circumcircle of \(\triangle EMD\) intersects the line segment \(BE\) at the point \(F \neq E\).
Prove that \(\angle ACB = \angle DCF\).

|
We first show that \(CBFD\) is a cyclic quadrilateral. It holds that
\[
\begin{align*}
\angle BCD &= \angle BAD = \angle BAE \quad (\text{parallelogram}) \\
&= 180^\circ - \angle EMB \quad (\text{cyclic quadrilateral theorem in } EABM) \\
&= \angle EMD \quad (\text{straight angle}) \\
&= \angle EFD \quad (\text{inscribed angle theorem in } EFMD) \\
&= 180^\circ - \angle BFD \quad (\text{straight angle}).
\end{align*}
\]
Thus, by the cyclic quadrilateral theorem, \(CBFD\) is a cyclic quadrilateral. With this, we find that
\[
\begin{align*}
\angle ACD &= \angle CAB = \angle MAB \tag{Z-angles} \\
&= \angle MEB = \angle MEF \tag{inscribed angle theorem in EABM} \\
&= \angle MDF = \angle BDF \tag{inscribed angle theorem in EFMD} \\
&= \angle BCF \tag{inscribed angle theorem in CBFD}.
\end{align*}
\]
Thus, \(\angle ACF + \angle FCD = \angle ACD = \angle BCF = \angle BCA + \angle ACF\). If we subtract \(\angle ACF\) from both sides, we find that \(\angle ACB = \angle DCF\), which is what we wanted to prove. \(\square\)
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij \(ABCD\) een parallellogram en zij \(M\) het snijpunt van de diagonalen. De omgeschreven cirkel van \(\triangle ABM\) snijdt het lijnstuk \(AD\) in \(E \neq A\) en de omgeschreven cirkel van \(\triangle EMD\) snijdt het lijnstuk \(BE\) in het punt \(F \neq E\).
Bewijs dat \(\angle ACB = \angle DCF\).

|
We laten eerst zien dat \(CBFD\) een koordenvierhoek is. Er geldt
\[
\begin{align*}
\angle BCD &= \angle BAD = \angle BAE \quad (\text{parallellogram}) \\
&= 180^\circ - \angle EMB \quad (\text{koordenvierhoekstelling in } EABM) \\
&= \angle EMD \quad (\text{gestrekte hoek}) \\
&= \angle EFD \quad (\text{omtrekshoekstelling in } EFMD) \\
&= 180^\circ - \angle BFD \quad (\text{gestrekte hoek}).
\end{align*}
\]
Dus wegens de koordenvierhoekstelling is \(CBFD\) een koordenvierhoek. Daarmee vinden
we dat
\[
\begin{align*}
\angle ACD &= \angle CAB = \angle MAB \tag{Z-hoeken} \\
&= \angle MEB = \angle MEF \tag{omtrekshoekstelling in EABM} \\
&= \angle MDF = \angle BDF \tag{omtrekshoekstelling in EFMD} \\
&= \angle BCF \tag{omtrekshoekstelling in CBFD}.
\end{align*}
\]
Dus \(\angle ACF + \angle FCD = \angle ACD = \angle BCF = \angle BCA + \angle ACF\). Als we hier \(\angle ACF\) van af
halen vinden we dat \(\angle ACB = \angle DCF\), wat we wilden bewijzen. \(\square\)
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2025-E2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2025"
}
|
We call an integer \(n \ge 3\) polypythagorean if there are \(n\) distinct positive numbers that can be placed around a circle such that the sum of the squares of each pair of consecutive numbers is a square. For example, 3 is a polypythagorean number because you can use 44, 117, and 240, for which \(44^2 + 117^2 = 125^2\), \(117^2 + 240^2 = 267^2\), and \(240^2 + 44^2 = 244^2\).
Find all polypythagorean numbers.
|
We prove by induction that all integers greater than or equal to 2 are polypythagorean, where we extend the definition to \(n = 2\) in the logical way. As the base case, we take (3, 4) for \(n = 2\) and (44, 117, 240) from the example for \(n = 3\).
Suppose now that \(n\) is polypythagorean with witness numbers \((a_1, a_2, \dots, a_n)\). Choose a prime \(p\) that does not divide any of the \(a_i\). Then define \(x = p^2 - 1\) and \(y = 2p\). For these, we have that \(x^2 + y^2 = (p^2 - 1)^2 + (2p)^2 = (p^2 + 1)^2\). By multiplying our \(n\)-tuple by \(x\), we can now insert two numbers:
\[(x a_1, x a_2, \dots, x a_n, y a_n, y a_1).\]
We easily check that
\[
\begin{align*} (x a_i)^2 + (x a_{i+1})^2 &= x^2 (a_i^2 + a_{i+1}^2), \\ (x a_n)^2 + (y a_n)^2 &= (x^2 + y^2) a_n, \\ (y a_n)^2 + (y a_1)^2 &= y^2 (a_n^2 + a_1^2), \\ (y a_1)^2 + (x a_1)^2 &= (y^2 + x^2) a_1^2, \end{align*}
\]
are indeed all squares by the induction hypothesis and the definition of \(x\) and \(y\). Since the numbers \(a_1, a_2, \dots, a_n\) are all distinct, the numbers \(x a_1, x a_2, \dots, x a_n\) are also all distinct. The numbers \(y a_n\) and \(y a_1\) are also distinct from each other. And since \(y\) is divisible by \(p\), but \(x\) and \(a_i\) are not, \(y a_n\) or \(y a_1\) cannot be equal to any of the \(x a_i\). We conclude that \(x a_1, x a_2, \dots, x a_n, y a_n, y a_1\) are all distinct, so \(n + 2\) is polypythagorean.
Since our base case consisted of \(n = 2, 3\), this proves by steps of two that all numbers are polypythagorean. \(\square\)
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
We noemen een geheel getal \(n \ge 3\) polypythagorees als er \(n\) verschillende positieve getallen zijn die je een cirkel achter elkaar kan zetten zo dat de som van de kwadraten van elk paar opvolgende getallen een kwadraat is. Zo is 3 een polypythagorees getal omdat je bijvoorbeeld met 44, 117 en 240 een drietal hebt waarvoor geldt dat \(44^2 + 117^2 = 125^2\), \(117^2 + 240^2 = 267^2\) en \(240^2 + 44^2 = 244^2\).
Vind alle polypythagorees getallen.
|
We bewijzen met inductie dat alle gehele getallen groter of gelijk aan 2 polypythagorees zijn, waarbij we de definitie uitbreiden naar \(n = 2\) op de logische manier. Als inductiebasis nemen we (3, 4) voor \(n = 2\) en (44, 117, 240) uit het voorbeeld voor \(n = 3\).
Stel nu dat \(n\) polypythagorees is met als getuige de getallen \((a_1, a_2, \dots, a_n)\). Kies nu een priemgetal \(p\) dat geen enkele van de \(a_i\) deelt. Dan definiëren we \(x = p^2 - 1\) en \(y = 2p\). Hiervoor geldt dat \(x^2 + y^2 = (p^2 - 1)^2 + (2p)^2 = (p^2 + 1)^2\). Door ons \(n\)-tal met \(x\) te vermenigvuldigen kunnen hiermee nu twee getallen invoegen:
\[(x a_1, x a_2, \dots, x a_n, y a_n, y a_1).\]
We controleren eenvoudig dat
\[
\begin{align*} (x a_i)^2 + (x a_{i+1})^2 &= x^2 (a_i^2 + a_{i+1}^2), \\ (x a_n)^2 + (y a_n)^2 &= (x^2 + y^2) a_n, \\ (y a_n)^2 + (y a_1)^2 &= y^2 (a_n^2 + a_1^2), \\ (y a_1)^2 + (x a_1)^2 &= (y^2 + x^2) a_1^2, \end{align*}
\]
inderdaad allemaal kwadraten zijn wegens de inductiehypothese en de definitie van \(x\) en \(y\). Omdat de getallen \(a_1, a_2, \dots, a_n\) allemaal verschillend zijn, zijn de getallen \(x a_1, x a_2, \dots, x a_n\) ook allemaal verschillend. De getallen \(y a_n\) en \(y a_1\) zijn ook verschillend van elkaar. En omdat \(y\) deelbaar is door \(p\), maar \(x\) en \(a_i\) niet, kunnen \(y a_n\) of \(y a_1\) niet gelijk zijn aan een van de \(x a_i\). We concluderen dat \(x a_1, x a_2, \dots, x a_n, y a_n, y a_1\) allemaal verschillend zijn, dus \(n + 2\) is polypythagorees.
Aangezien onze inductiebasis bestond uit \(n = 2, 3\) bewijst dit met stappen van twee dat alle getallen polypythagorees zijn. \(\square\)
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2025-E2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2025"
}
|
Determine all triples \((x, y, p)\) of positive integers such that \(p\) is a prime number, \(x^2 = p - 1\), and \(y^2 = 2p^2 - 1\).
|
The only triplet that satisfies the condition is \((2, 7, 5)\).
First, we calculate that
\[ (y + x)(y - x) = y^2 - x^2 = (2p^2 - 1) - (p - 1) = 2p^2 - p = p(2p - 1). \quad (1) \]
This means in particular that \(p \mid x + y\) or \(p \mid x - y\).
Assume that \(p \mid y + x\). Then \(y = kp - x\) for some \(k \in \mathbb{Z}\). From the given conditions, however, \(2p > y > p\) and \(x < p\). Therefore, \(2p > y = kp - x > kp - p = (k - 1)p\) and \(kp > kp - x = y > p\), from which we conclude that \(k = 2\). Thus, \(y = 2p - x\). Substituting this into (1) gives us
\[ 2p(2p - x - x) = p(2p - 1). \]
Distributing \(p\) leaves us with \(4(p - x) = 2p - 1\). This is impossible since the left side is even and the right side is odd.
Now assume that \(p \mid y - x\). Then we have \(y = kp + x\). From the given conditions, \(2p > y = kp + x > kp\) and \((k + 1)p = kp + p > kp + x = y > p\). This implies that \(k = 1\), so \(y - x = p\), and from (1) also that \(y + x = 2p - 1\). Solving these, we find \(2x = (y + x) - (y - x) = (2p - 1) - p = p - 1\). We conclude that \(4(p - 1) = 4x^2 = (2x)^2 = (p - 1)^2\). As a quadratic equation in \(p - 1\), this has the solutions \(p - 1 = 0\) and \(p - 1 = 4\). Only in the second case is \(p\) a prime number, namely \(p = 5\). This gives \(x = (p-1)/2 = 2\) and \(y = p + x = 5 + 2 = 7\). This satisfies the condition. \(\square\)
|
(2, 7, 5)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Bepaal alle drietallen \((x, y, p)\) van positieve gehele getallen zo dat \(p\) een
priemgetal is, \(x^2 = p - 1\) en \(y^2 = 2p^2 - 1\).
|
Het enige drietal dat voldoet is \((2, 7, 5)\).
We rekenen eerst uit dat
\[ (y + x)(y - x) = y^2 - x^2 = (2p^2 - 1) - (p - 1) = 2p^2 - p = p(2p - 1). \quad (1) \]
Dat betekent in het bijzonder dat \(p \mid x + y\) of \(p \mid x - y\).
Stel dat \(p \mid y + x\). Dan geldt dat \(y = kp - x\) voor een zekere \(k \in \mathbb{Z}\). Uit het gegeven volgt echter dat \(2p > y > p\) en \(x < p\). Dus \(2p > y = kp - x > kp - p = (k - 1)p\) en \(kp > kp - x = y > p\), waaruit we concluderen dat \(k = 2\). Dus \(y = 2p - x\). Als we dat invullen in (1) krijgen we
\[ 2p(2p - x - x) = p(2p - 1). \]
Als we \(p\) uitdelen, dan houden we over dat \(4(p - x) = 2p - 1\). Dit is onmogelijk aangezien de linkerkant even is en de rechterkant oneven.
Stel nu dat \(p \mid y - x\). Dan hebben we \(y = kp + x\). Uit het gegeven volgt dan \(2p > y = kp + x > kp\) en \((k + 1)p = kp + p > kp + x = y > p\). Hieruit volgt dat \(k = 1\), dus \(y - x = p\), en wegens (1) ook dat \(y + x = 2p - 1\). Als we dat oplossen vinden we \(2x = (y + x) - (y - x) = (2p - 1) - p = p - 1\). We concluderen dat \(4(p - 1) = 4x^2 = (2x)^2 = (p - 1)^2\). Als kwadratische vergelijking in \(p - 1\) heeft dit de oplossingen \(p - 1 = 0\) en \(p - 1 = 4\). Alleen in het tweede geval is \(p\) een priemgetal, namelijk \(p = 5\). Dat geeft verder \(x = (p-1)/2 = 2\) en \(y = p+x = 5+2 = 7\). Deze voldoet. \(\square\)
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2025-E2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2025"
}
|
We say that a sequence \(a_1, \dots, a_n\) of real numbers is decreasingly increasing if for all \(1 < i < n\) it holds that \(0 < a_{i+1} - a_i < a_i - a_{i-1}\). Find for each positive integer \(m\) the smallest positive integer \(k\) for which there exists a decreasingly increasing sequence of length \(k\) such that 1 can be written as the difference of two elements \(a_i\) and \(a_j\) from the sequence in at least \(m\) different ways.
|
We first prove that \(k \ge 2m\). We define \(b_i = a_{i+1} - a_i\). Then \(b_1, b_2, \dots, b_{k-1}\) is a decreasing sequence of positive real numbers. Each of the ways to write 1 in this form is a sum of consecutive elements in this sequence \(b_j + b_{j+1} + \dots + b_{j+t-1} = a_{j+t} - a_j = 1\) with \(1 \le j\), \(1 \le t\) and \(j + t \le k\). No two of these ways can start at the same position, because their difference would then be the sum of the last few \(b_i\) of the longer sequence, contradicting that the difference \(1 - 1 = 0\) must be. Also, no two of these ways can be of the same length. In fact, if we order the ways by \(1 \le j_1 < j_2 < \dots < j_m\), then \(1 \le t_1 < t_2 < \dots < t_m\) because the terms in the sequence starting with \(j_h\) are each greater than the terms of the way starting with \(j_{h+1}\). This means that
\[k \ge j_m + t_m \ge m + m = 2m.\]
Now we construct an example for \(k = 2m\). We define the last \(m\) terms of the sequence \(b_1, \dots, b_{2m-1}\) as \(b_{m+i} = \frac{2(m-1)-i}{\frac{3}{2}m(m-1)}\) for \(0 \le i \le m-1\). Then this is clearly a decreasing sequence and it holds that
\[b_m + b_{m+1} + \dots + b_{2m-1} = \frac{1}{\frac{3}{2}m(m-1)} \left((2m-2) + (2m-3) + \dots + m + (m-1)\right) = 1.\]
Now we define recursively \(b_{m-1}, \dots, b_1\) as \(b_i = b_{2i} + b_{2i+1}\). Then we find in particular that
\[b_{m-1} = b_{m+(m-2)} + b_{m+(m-1)} = \frac{m}{\frac{3}{2}m(m-1)} + \frac{m-1}{\frac{3}{2}m(m-1)} = \frac{2m-1}{\frac{3}{2}m(m-1)} > \frac{2m-2}{\frac{3}{2}m(m-1)} = b_m.\]
And for \(i < m-1\) it holds recursively that \(b_i > b_{i+1}\), because this expression is equivalent to \(b_{2i} + b_{2i+1} > b_{2i+2} + b_{2i+3}\). We conclude that \(b_1, \dots, b_{2m-1}\) is a decreasing sequence. We now prove by induction on \(j\) (decreasing) that
\[b_j + b_{j+1} + \dots + b_{2j-1} = 1\]
for all \(1 \le j \le m\). For the base case, we take \(b_m + b_{m+1} + \dots + b_{2m-1} = 1\). For the inductive step, we note that \(b_{j-1} + b_j + \dots + b_{2j-3} = b_j + b_{j+1} + \dots + b_{2j-1}\). So if the formula holds for \(j\) then it also holds for \(j-1\). \(\square\)
|
2m
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
We zeggen dat een rij \(a_1, \dots, a_n\) van reële getallen afnemend stijgend is als voor alle \(1 < i < n\) geldt dat \(0 < a_{i+1} - a_i < a_i - a_{i-1}\). Vind voor elk positief geheel getal \(m\) het kleinste positieve gehele getal \(k\) waarvoor er een afnemend stijgende rij bestaat van lengte \(k\) zo dat 1 op zijn minst op \(m\) verschillende manieren geschreven kan worden als het verschil van twee elementen \(a_i\) en \(a_j\) uit de rij.
|
We bewijzen eerst dat \(k \ge 2m\). We definiëren \(b_i = a_{i+1} - a_i\). Dan is \(b_1, b_2, \dots, b_{k-1}\) een dalende rij positieve reële getallen. En elk van de manieren om 1 te schrijven is in deze schrijfwijze een som van opvolgende elementen in deze rij \(b_j + b_{j+1} + \dots + b_{j+t-1} = a_{j+t} - a_j = 1\) met \(1 \le j\), \(1 \le t\) en \(j + t \le k\). Geen twee van deze manieren kunnen op dezelfde plek beginnen, want hun verschil is dan de som van de laatste paar \(b_i\) van de langere reeks, in tegenspraak met dat het verschil \(1 - 1 = 0\) moet zijn. Ook geen twee van deze manieren kunnen even lang zijn. Sterker nog als we de manieren ordenen op \(1 \le j_1 < j_2 < \dots < j_m\), dan geldt \(1 \le t_1 < t_2 < \dots < t_m\) want de termen in de reeks beginnend met \(j_h\) zijn stuk voor stuk groter dan de termen van de manier beginnend met \(j_{h+1}\). Dit betekent dat
\[k \ge j_m + t_m \ge m + m = 2m.\]
Nu construeren we een voorbeeld voor \(k = 2m\). We definiëren de laatste \(m\) termen van de rij \(b_1, \dots, b_{2m-1}\) als \(b_{m+i} = \frac{2(m-1)-i}{\frac{3}{2}m(m-1)}\) voor \(0 \le i \le m-1\). Dan is dit duidelijk een dalende rij en geldt er dat
\[b_m + b_{m+1} + \dots + b_{2m-1} = \frac{1}{\frac{3}{2}m(m-1)} \left((2m-2) + (2m-3) + \dots + m + (m-1)\right) = 1.\]
Nu definiëren recursief \(b_{m-1}, \dots, b_1\) als \(b_i = b_{2i} + b_{2i+1}\). Dan vinden we in het bijzonder dat
\[b_{m-1} = b_{m+(m-2)} + b_{m+(m-1)} = \frac{m}{\frac{3}{2}m(m-1)} + \frac{m-1}{\frac{3}{2}m(m-1)} = \frac{2m-1}{\frac{3}{2}m(m-1)} > \frac{2m-2}{\frac{3}{2}m(m-1)} = b_m.\]
En voor \(i < m-1\) geldt recursief dat \(b_i > b_{i+1}\), omdat deze uitdrukking equivalent is met \(b_{2i} + b_{2i+1} > b_{2i+2} + b_{2i+3}\). We concluderen we dat \(b_1, \dots, b_{2m-1}\) een dalende rij is. We bewijzen nu met inductie naar \(j\) (aflopend) dat
\[b_j + b_{j+1} + \dots + b_{2j-1} = 1\]
voor alle \(1 \le j \le m\). Voor de inductiebasis nemen we \(b_m + b_{m+1} + \dots + b_{2m-1} = 1\). Voor de inductiestap merken we op dat \(b_{j-1} + b_j + \dots + b_{2j-3} = b_j + b_{j+1} + \dots + b_{2j-1}\). Dus als de formule geldt voor \(j\) dan geldt die ook voor \(j-1\). \(\square\)
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2025-E2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2025"
}
|
We say that a sequence \(a_1, \dots, a_n\) of real numbers is decreasingly increasing if for all \(1 < i < n\) it holds that \(0 < a_{i+1} - a_i < a_i - a_{i-1}\). Find for each positive integer \(m\) the smallest positive integer \(k\) for which there exists a decreasingly increasing sequence of length \(k\) such that 1 can be written as the difference of two elements \(a_i\) and \(a_j\) from the sequence in at least \(m\) different ways.
|
We present an alternative example. We first choose \(b_1 = 1\). Now we take a \(0 < \epsilon_1 < \frac{1}{6}\) and define \(b_2 = \frac{1}{2} + \epsilon_1\) and \(b_3 = \frac{1}{2} - \epsilon_1\). Then it holds that \(0 < \epsilon_1 < \frac{b_1 - b_2}{2}\).
We define the rest of the sequence recursively. Suppose that for some \(2 \le i \le m-1\) it holds that \(b_1, b_2, \dots, b_{2i-1}\) is a decreasing sequence and that \(0 < \epsilon_{i-1} < \frac{b_{i-1}-b_i}{2}\). Then we choose \(\epsilon_i\) with \(0 < \epsilon_i < \frac{b_i-b_{i+1}}{2}\) and \(\epsilon_i < \frac{b_{i-1}-b_i}{2} - \epsilon_{i-1}\), and define \(b_{2i} = \frac{b_i}{2} + \epsilon_i\) and \(b_{2i+1} = \frac{b_i}{2} - \epsilon_i\). Then both \(b_{2i}\) and \(b_{2i+1}\) are positive. We also see that \(b_{2i-1} = \frac{b_{i-1}}{2} - \epsilon_{i-1} > \frac{b_i}{2} + \epsilon_i = b_{2i}\) and \(b_{2i} = b_{2i+1} + 2\epsilon_i > b_{2i+1}\), so the sequence \(b_1, b_2, \dots, b_{2i+1}\) is decreasing.
Again, it holds that \(b_{2i} + b_{2i+1} = b_i\). If we apply this to \(b_1 = 1\), then we find by induction that
\[b_j + b_{j+1} + \ldots + b_{2j-1} = 1\]
for all \(1 \le j \le m\).
|
not found
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
We zeggen dat een rij \(a_1, \dots, a_n\) van reële getallen afnemend stijgend is als voor alle \(1 < i < n\) geldt dat \(0 < a_{i+1} - a_i < a_i - a_{i-1}\). Vind voor elk positief geheel getal \(m\) het kleinste positieve gehele getal \(k\) waarvoor er een afnemend stijgende rij bestaat van lengte \(k\) zo dat 1 op zijn minst op \(m\) verschillende manieren geschreven kan worden als het verschil van twee elementen \(a_i\) en \(a_j\) uit de rij.
|
We presenteren een alternatief voorbeeld. We kiezen eerst \(b_1 = 1\). Nu nemen we een \(0 < \epsilon_1 < \frac{1}{6}\) en definiëren we \(b_2 = \frac{1}{2} + \epsilon_1\) en \(b_3 = \frac{1}{2} - \epsilon_1\). Dan geldt er dat \(0 < \epsilon_1 < \frac{b_1 - b_2}{2}\).
We definièren de rest van de rij recursief. Stel dat voor een zekere \(2 \le i \le m-1\) geldt dat \(b_1, b_2, \dots, b_{2i-1}\) een dalende rij is en dat \(0 < \epsilon_{i-1} < \frac{b_{i-1}-b_i}{2}\). Dan kiezen we \(\epsilon_i\) met \(0 < \epsilon_i < \frac{b_i-b_{i+1}}{2}\) en \(\epsilon_i < \frac{b_{i-1}-b_i}{2} - \epsilon_{i-1}\), en definièren we \(b_{2i} = \frac{b_i}{2} + \epsilon_i\) en \(b_{2i+1} = \frac{b_i}{2} - \epsilon_i\). Dan zijn zowel \(b_{2i}\) als \(b_{2i+1}\) positief. Ook zien we dat \(b_{2i-1} = \frac{b_{i-1}}{2} - \epsilon_{i-1} > \frac{b_i}{2} + \epsilon_i = b_{2i}\) en \(b_{2i} = b_{2i+1} + 2\epsilon_i > b_{2i+1}\), dus de rij \(b_1, b_2, \dots, b_{2i+1}\) is dalend.
Wederom geldt dat \(b_{2i} + b_{2i+1} = b_i\). Als we dat toepassen op \(b_1 = 1\), dan vinden we met inductie dat
\[b_j + b_{j+1} + \ldots + b_{2j-1} = 1\]
voor alle \(1 \le j \le m\).
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2025-E2025_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2025"
}
|
Let $A B C$ be a triangle with circumcentre $O$. The points $D, E$ and $F$ lie in the interiors of the sides $B C, C A$ and $A B$ respectively, such that $D E$ is perpendicular to $C O$ and $D F$ is perpendicular to $B O$. (By interior we mean, for example, that the point $D$ lies on the line $B C$ and $D$ is between $B$ and $C$ on that line.)
Let $K$ be the circumcentre of triangle $A F E$. Prove that the lines $D K$ and $B C$ are perpendicular.
Origin. Netherlands (Merlijn Staps).
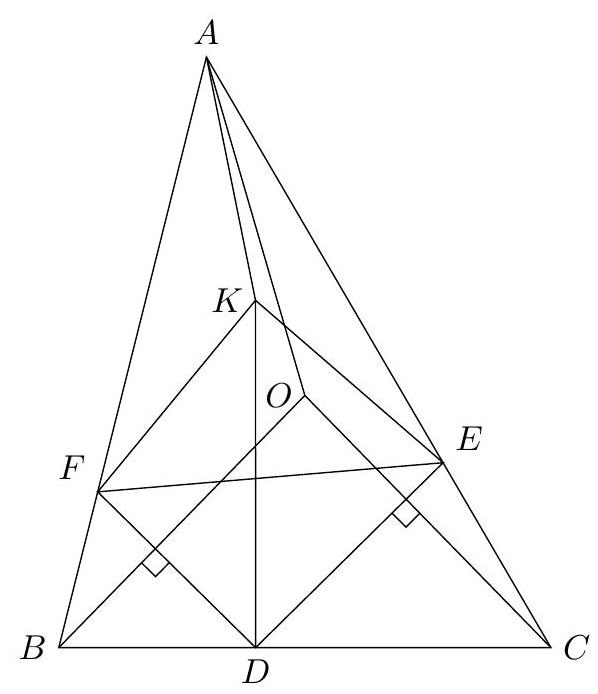
|
Let $\ell_{C}$ be the tangent at $C$ to the circumcircle of $\triangle A B C$. As $C O \perp \ell_{C}$, the lines $D E$ and $\ell_{C}$ are parallel. Now we find that
$$
\angle C D E=\angle\left(B C, \ell_{C}\right)=\angle B A C,
$$
hence the quadrilateral $B D E A$ is cyclic. Analogously, we find that the quadrilateral $C D F A$ is cyclic. As we now have $\angle C D E=\angle A=\angle F D B$, we conclude that the line $B C$ is the external angle bisector of $\angle E D F$. Furthermore, $\angle E D F=180^{\circ}-2 \angle A$. Since $K$ is the circumcentre of $\triangle A E F, \angle F K E=2 \angle F A E=2 \angle A$. So $\angle F K E+\angle E D F=180^{\circ}$, hence $K$ lies on the circumcircle of $\triangle D E F$. As $|K E|=|K F|$, we have that $K$ is the midpoint of the arc $E F$ of this circumcircle. It is well known that this point lies on the internal angle bisector of $\angle E D F$. We conclude that $D K$ is the internal angle bisector of $\angle E D F$. Together with the fact that $B C$ is the external angle bisector of $\angle E D F$, this yields that $D K \perp B C$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcentre $O$. The points $D, E$ and $F$ lie in the interiors of the sides $B C, C A$ and $A B$ respectively, such that $D E$ is perpendicular to $C O$ and $D F$ is perpendicular to $B O$. (By interior we mean, for example, that the point $D$ lies on the line $B C$ and $D$ is between $B$ and $C$ on that line.)
Let $K$ be the circumcentre of triangle $A F E$. Prove that the lines $D K$ and $B C$ are perpendicular.
Origin. Netherlands (Merlijn Staps).

|
Let $\ell_{C}$ be the tangent at $C$ to the circumcircle of $\triangle A B C$. As $C O \perp \ell_{C}$, the lines $D E$ and $\ell_{C}$ are parallel. Now we find that
$$
\angle C D E=\angle\left(B C, \ell_{C}\right)=\angle B A C,
$$
hence the quadrilateral $B D E A$ is cyclic. Analogously, we find that the quadrilateral $C D F A$ is cyclic. As we now have $\angle C D E=\angle A=\angle F D B$, we conclude that the line $B C$ is the external angle bisector of $\angle E D F$. Furthermore, $\angle E D F=180^{\circ}-2 \angle A$. Since $K$ is the circumcentre of $\triangle A E F, \angle F K E=2 \angle F A E=2 \angle A$. So $\angle F K E+\angle E D F=180^{\circ}$, hence $K$ lies on the circumcircle of $\triangle D E F$. As $|K E|=|K F|$, we have that $K$ is the midpoint of the arc $E F$ of this circumcircle. It is well known that this point lies on the internal angle bisector of $\angle E D F$. We conclude that $D K$ is the internal angle bisector of $\angle E D F$. Together with the fact that $B C$ is the external angle bisector of $\angle E D F$, this yields that $D K \perp B C$, as desired.
|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "\nProblem 1.",
"resource_path": "EGMO/segmented/en-2012-solutions-day1.jsonl",
"solution_match": "\nSolution 1 (submitter).",
"tier": "T2",
"year": "2012"
}
|
Let $A B C$ be a triangle with circumcentre $O$. The points $D, E$ and $F$ lie in the interiors of the sides $B C, C A$ and $A B$ respectively, such that $D E$ is perpendicular to $C O$ and $D F$ is perpendicular to $B O$. (By interior we mean, for example, that the point $D$ lies on the line $B C$ and $D$ is between $B$ and $C$ on that line.)
Let $K$ be the circumcentre of triangle $A F E$. Prove that the lines $D K$ and $B C$ are perpendicular.
Origin. Netherlands (Merlijn Staps).

|
As in the previous solution, we show that the quadrilaterals $B D E A$ and $C D F A$ are both cyclic. Denote by $M$ and $L$ respectively the circumcentres of these quadrilaterals. We will show that the quadrilateral $K L O M$ is a parallelogram. The lines $K L$ and $M O$ are the perpendicular bisectors of the line segments $A F$ and $A B$, respectively. Hence both $K L$ and $M O$ are perpendicular to $A B$, which yields $K L \| M O$. In the same way we can show that the lines $K M$ and $L O$ are both perpendicular to $A C$ and hence parallel as well. We conclude that $K L O M$ is indeed a parallelogram. Now, let $K^{\prime}, L^{\prime}, O^{\prime}$ and $M^{\prime}$ be the respective projections of $K, L, O$ and $M$ to $B C$. We have to show that $K^{\prime}=D$. As $L$ lies on the perpendicular bisector of $C D$, we have that $L^{\prime}$ is the midpoint of $C D$. Similarly, $M^{\prime}$ is the midpoint of $B D$ and $O^{\prime}$ is the midpoint of $B C$. Now we are going to use directed lengths. Since $K L O M$ is a parallelogram, $M^{\prime} K^{\prime}=O^{\prime} L^{\prime}$. As
$$
O^{\prime} L^{\prime}=O^{\prime} C-L^{\prime} C=\frac{1}{2} \cdot(B C-D C)=\frac{1}{2} \cdot B D=M^{\prime} D
$$
we find that $M^{\prime} K^{\prime}=M^{\prime} D$, hence $K^{\prime}=D$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcentre $O$. The points $D, E$ and $F$ lie in the interiors of the sides $B C, C A$ and $A B$ respectively, such that $D E$ is perpendicular to $C O$ and $D F$ is perpendicular to $B O$. (By interior we mean, for example, that the point $D$ lies on the line $B C$ and $D$ is between $B$ and $C$ on that line.)
Let $K$ be the circumcentre of triangle $A F E$. Prove that the lines $D K$ and $B C$ are perpendicular.
Origin. Netherlands (Merlijn Staps).

|
As in the previous solution, we show that the quadrilaterals $B D E A$ and $C D F A$ are both cyclic. Denote by $M$ and $L$ respectively the circumcentres of these quadrilaterals. We will show that the quadrilateral $K L O M$ is a parallelogram. The lines $K L$ and $M O$ are the perpendicular bisectors of the line segments $A F$ and $A B$, respectively. Hence both $K L$ and $M O$ are perpendicular to $A B$, which yields $K L \| M O$. In the same way we can show that the lines $K M$ and $L O$ are both perpendicular to $A C$ and hence parallel as well. We conclude that $K L O M$ is indeed a parallelogram. Now, let $K^{\prime}, L^{\prime}, O^{\prime}$ and $M^{\prime}$ be the respective projections of $K, L, O$ and $M$ to $B C$. We have to show that $K^{\prime}=D$. As $L$ lies on the perpendicular bisector of $C D$, we have that $L^{\prime}$ is the midpoint of $C D$. Similarly, $M^{\prime}$ is the midpoint of $B D$ and $O^{\prime}$ is the midpoint of $B C$. Now we are going to use directed lengths. Since $K L O M$ is a parallelogram, $M^{\prime} K^{\prime}=O^{\prime} L^{\prime}$. As
$$
O^{\prime} L^{\prime}=O^{\prime} C-L^{\prime} C=\frac{1}{2} \cdot(B C-D C)=\frac{1}{2} \cdot B D=M^{\prime} D
$$
we find that $M^{\prime} K^{\prime}=M^{\prime} D$, hence $K^{\prime}=D$, as desired.
|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "\nProblem 1.",
"resource_path": "EGMO/segmented/en-2012-solutions-day1.jsonl",
"solution_match": "\nSolution 2 (submitter).",
"tier": "T2",
"year": "2012"
}
|
Let $A B C$ be a triangle with circumcentre $O$. The points $D, E$ and $F$ lie in the interiors of the sides $B C, C A$ and $A B$ respectively, such that $D E$ is perpendicular to $C O$ and $D F$ is perpendicular to $B O$. (By interior we mean, for example, that the point $D$ lies on the line $B C$ and $D$ is between $B$ and $C$ on that line.)
Let $K$ be the circumcentre of triangle $A F E$. Prove that the lines $D K$ and $B C$ are perpendicular.
Origin. Netherlands (Merlijn Staps).

|
Denote by $\ell_{A}, \ell_{B}$ and $\ell_{C}$ the tangents at $A, B$ and $C$ to the circumcircle of $\triangle A B C$. Let $A^{\prime}$ be the point of intersection of $\ell_{B}$ and $\ell_{C}$ and define $B^{\prime}$ and $C^{\prime}$ analogously. As in the first solution, we find that $D E \| \ell_{C}$ and $D F \| \ell_{B}$. Now, let $Q$ be the point of intersection of $D E$ and $\ell_{A}$ and let $R$ be the point of intersection of $D F$ and $\ell_{A}$. We easily find $\triangle A Q E \sim \triangle A B^{\prime} C$. As $\left|B^{\prime} A\right|=\left|B^{\prime} C\right|$, we must have $|Q A|=|Q E|$, hence $\triangle A Q E$ is isosceles. Therefore the perpendicular bisector of $A E$ is the internal angle bisector of $\angle E Q A=\angle D Q R$. Analogously, the perpendicular bisector of $A F$ is the internal angle bisector of $\angle D R Q$. We conclude that $K$ is the incentre of $\triangle D Q R$, thus $D K$ is the angle bisector of $\angle Q D R$. Because the sides of the triangles $\triangle Q D R$ and $\triangle B^{\prime} A^{\prime} C^{\prime}$ are pairwise parallel, the angle bisector $D K$ of $\angle Q D R$ is parallel to the angle bisector of $\angle B^{\prime} A^{\prime} C^{\prime}$. Finally, as the angle bisector of $\angle B^{\prime} A^{\prime} C^{\prime}$ is easily seen to be perpendicular to $B C$ (as it is the perpendicular bisector of this segment), we find that $D K \perp B C$, as desired.
Remark (submitter). The fact that the quadrilateral $B D E A$ is cyclic (which is an essential part of the first two solutions) can be proven in various ways. Another possibility is as follows. Let $P$ be the midpoint of $B C$. Then, as $\angle C P O=90^{\circ}$, we have $\angle P O C=90^{\circ}-\angle O C P$. Let $X$ be the point of intersection of $D E$ and $C O$, then we have that $\angle C D E=\angle C D X=90^{\circ}-\angle X C D=90^{\circ}-\angle O C P$. Hence $\angle C D E=\angle P O C=\frac{1}{2} \angle B O C=\angle B A C$. From this we can conclude that $B D E A$ is cyclic.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcentre $O$. The points $D, E$ and $F$ lie in the interiors of the sides $B C, C A$ and $A B$ respectively, such that $D E$ is perpendicular to $C O$ and $D F$ is perpendicular to $B O$. (By interior we mean, for example, that the point $D$ lies on the line $B C$ and $D$ is between $B$ and $C$ on that line.)
Let $K$ be the circumcentre of triangle $A F E$. Prove that the lines $D K$ and $B C$ are perpendicular.
Origin. Netherlands (Merlijn Staps).

|
Denote by $\ell_{A}, \ell_{B}$ and $\ell_{C}$ the tangents at $A, B$ and $C$ to the circumcircle of $\triangle A B C$. Let $A^{\prime}$ be the point of intersection of $\ell_{B}$ and $\ell_{C}$ and define $B^{\prime}$ and $C^{\prime}$ analogously. As in the first solution, we find that $D E \| \ell_{C}$ and $D F \| \ell_{B}$. Now, let $Q$ be the point of intersection of $D E$ and $\ell_{A}$ and let $R$ be the point of intersection of $D F$ and $\ell_{A}$. We easily find $\triangle A Q E \sim \triangle A B^{\prime} C$. As $\left|B^{\prime} A\right|=\left|B^{\prime} C\right|$, we must have $|Q A|=|Q E|$, hence $\triangle A Q E$ is isosceles. Therefore the perpendicular bisector of $A E$ is the internal angle bisector of $\angle E Q A=\angle D Q R$. Analogously, the perpendicular bisector of $A F$ is the internal angle bisector of $\angle D R Q$. We conclude that $K$ is the incentre of $\triangle D Q R$, thus $D K$ is the angle bisector of $\angle Q D R$. Because the sides of the triangles $\triangle Q D R$ and $\triangle B^{\prime} A^{\prime} C^{\prime}$ are pairwise parallel, the angle bisector $D K$ of $\angle Q D R$ is parallel to the angle bisector of $\angle B^{\prime} A^{\prime} C^{\prime}$. Finally, as the angle bisector of $\angle B^{\prime} A^{\prime} C^{\prime}$ is easily seen to be perpendicular to $B C$ (as it is the perpendicular bisector of this segment), we find that $D K \perp B C$, as desired.
Remark (submitter). The fact that the quadrilateral $B D E A$ is cyclic (which is an essential part of the first two solutions) can be proven in various ways. Another possibility is as follows. Let $P$ be the midpoint of $B C$. Then, as $\angle C P O=90^{\circ}$, we have $\angle P O C=90^{\circ}-\angle O C P$. Let $X$ be the point of intersection of $D E$ and $C O$, then we have that $\angle C D E=\angle C D X=90^{\circ}-\angle X C D=90^{\circ}-\angle O C P$. Hence $\angle C D E=\angle P O C=\frac{1}{2} \angle B O C=\angle B A C$. From this we can conclude that $B D E A$ is cyclic.
|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "\nProblem 1.",
"resource_path": "EGMO/segmented/en-2012-solutions-day1.jsonl",
"solution_match": "\nSolution 3 (submitter).",
"tier": "T2",
"year": "2012"
}
|
Let $A B C$ be a triangle with circumcentre $O$. The points $D, E$ and $F$ lie in the interiors of the sides $B C, C A$ and $A B$ respectively, such that $D E$ is perpendicular to $C O$ and $D F$ is perpendicular to $B O$. (By interior we mean, for example, that the point $D$ lies on the line $B C$ and $D$ is between $B$ and $C$ on that line.)
Let $K$ be the circumcentre of triangle $A F E$. Prove that the lines $D K$ and $B C$ are perpendicular.
Origin. Netherlands (Merlijn Staps).

|
This is a simplified variant of Solution 1. $\angle C O B=2 \angle A$ (angle at centre of circle $A B C$ ) and $O B=O C$ so $\angle O B C=\angle B C O=90^{\circ}-\angle A$. Likewise $\angle E K F=2 \angle A$ and $\angle K F E=\angle F E K=90^{\circ}-\angle A$. Now because $D E \perp C O, \angle E D C=90^{\circ}-\angle D C O=90^{\circ}-\angle B C O=\angle A$ and similarly $\angle B D F=\angle A$, so $\angle F D E=180^{\circ}-2 \angle A$. So quadrilateral $K F D E$ is cyclic (opposite angles), so (same segment) $\angle K D E=$ $\angle K F E=90^{\circ}-\angle A$, so $\angle K D C=90^{\circ}$ and $D K$ is perpendicular to $B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcentre $O$. The points $D, E$ and $F$ lie in the interiors of the sides $B C, C A$ and $A B$ respectively, such that $D E$ is perpendicular to $C O$ and $D F$ is perpendicular to $B O$. (By interior we mean, for example, that the point $D$ lies on the line $B C$ and $D$ is between $B$ and $C$ on that line.)
Let $K$ be the circumcentre of triangle $A F E$. Prove that the lines $D K$ and $B C$ are perpendicular.
Origin. Netherlands (Merlijn Staps).

|
This is a simplified variant of Solution 1. $\angle C O B=2 \angle A$ (angle at centre of circle $A B C$ ) and $O B=O C$ so $\angle O B C=\angle B C O=90^{\circ}-\angle A$. Likewise $\angle E K F=2 \angle A$ and $\angle K F E=\angle F E K=90^{\circ}-\angle A$. Now because $D E \perp C O, \angle E D C=90^{\circ}-\angle D C O=90^{\circ}-\angle B C O=\angle A$ and similarly $\angle B D F=\angle A$, so $\angle F D E=180^{\circ}-2 \angle A$. So quadrilateral $K F D E$ is cyclic (opposite angles), so (same segment) $\angle K D E=$ $\angle K F E=90^{\circ}-\angle A$, so $\angle K D C=90^{\circ}$ and $D K$ is perpendicular to $B C$.
|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "\nProblem 1.",
"resource_path": "EGMO/segmented/en-2012-solutions-day1.jsonl",
"solution_match": "\nSolution 4 (PSC).",
"tier": "T2",
"year": "2012"
}
|
Let $n$ be a positive integer. Find the greatest possible integer $m$, in terms of $n$, with the following property: a table with $m$ rows and $n$ columns can be filled with real numbers in such a manner that for any two different rows $\left[a_{1}, a_{2}, \ldots, a_{n}\right]$ and $\left[b_{1}, b_{2}, \ldots, b_{n}\right]$ the following holds:
$$
\max \left(\left|a_{1}-b_{1}\right|,\left|a_{2}-b_{2}\right|, \ldots,\left|a_{n}-b_{n}\right|\right)=1
$$
Origin. Poland (Tomasz Kobos).
|
The largest possible $m$ is equal to $2^{n}$.
In order to see that the value $2^{n}$ can be indeed achieved, consider all binary vectors of length $n$ as rows of the table. We now proceed with proving that this is the maximum value.
Let $\left[a_{k}^{i}\right]$ be a feasible table, where $i=1, \ldots, m$ and $k=1, \ldots, n$. Let us define undirected graphs $G_{1}, G_{2}$, $\ldots, G_{n}$, each with vertex set $\{1,2, \ldots, m\}$, where $i j \in E\left(G_{k}\right)$ if and only if $\left|a_{k}^{i}-a_{k}^{j}\right|=1$ (by $E\left(G_{k}\right)$ we denote the edge set of the graph $G_{k}$ ). Observe the following two properties.
(1) Each graph $G_{k}$ is bipartite. Indeed, if it contained a cycle of odd length, then the sum of $\pm 1$ along this cycle would need to be equal to 0 , which contradicts the length of the cycle being odd.
(2) For every $i \neq j, i j \in E\left(G_{k}\right)$ for some $k$. This follows directly from the problem statement.
For every graph $G_{k}$ fix some bipartition $\left(A_{k}, B_{k}\right)$ of $\{1,2, \ldots, m\}$, i.e., a partition of $\{1,2, \ldots, m\}$ into two disjoint sets $A_{k}, B_{k}$ such that the edges of $G_{k}$ traverse only between $A_{k}$ and $B_{k}$. If $m>2^{n}$, then there are two distinct indices $i, j$ such that they belong to exactly the same parts $A_{k}, B_{k}$, that is, $i \in A_{k}$ if and only if $j \in A_{k}$ for all $k=1,2, \ldots, n$. However, this means that the edge $i j$ cannot be present in any of the graphs $G_{1}, G_{2}$, $\ldots, G_{n}$, which contradicts (2). Therefore, $m \leq 2^{n}$.
|
2^n
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be a positive integer. Find the greatest possible integer $m$, in terms of $n$, with the following property: a table with $m$ rows and $n$ columns can be filled with real numbers in such a manner that for any two different rows $\left[a_{1}, a_{2}, \ldots, a_{n}\right]$ and $\left[b_{1}, b_{2}, \ldots, b_{n}\right]$ the following holds:
$$
\max \left(\left|a_{1}-b_{1}\right|,\left|a_{2}-b_{2}\right|, \ldots,\left|a_{n}-b_{n}\right|\right)=1
$$
Origin. Poland (Tomasz Kobos).
|
The largest possible $m$ is equal to $2^{n}$.
In order to see that the value $2^{n}$ can be indeed achieved, consider all binary vectors of length $n$ as rows of the table. We now proceed with proving that this is the maximum value.
Let $\left[a_{k}^{i}\right]$ be a feasible table, where $i=1, \ldots, m$ and $k=1, \ldots, n$. Let us define undirected graphs $G_{1}, G_{2}$, $\ldots, G_{n}$, each with vertex set $\{1,2, \ldots, m\}$, where $i j \in E\left(G_{k}\right)$ if and only if $\left|a_{k}^{i}-a_{k}^{j}\right|=1$ (by $E\left(G_{k}\right)$ we denote the edge set of the graph $G_{k}$ ). Observe the following two properties.
(1) Each graph $G_{k}$ is bipartite. Indeed, if it contained a cycle of odd length, then the sum of $\pm 1$ along this cycle would need to be equal to 0 , which contradicts the length of the cycle being odd.
(2) For every $i \neq j, i j \in E\left(G_{k}\right)$ for some $k$. This follows directly from the problem statement.
For every graph $G_{k}$ fix some bipartition $\left(A_{k}, B_{k}\right)$ of $\{1,2, \ldots, m\}$, i.e., a partition of $\{1,2, \ldots, m\}$ into two disjoint sets $A_{k}, B_{k}$ such that the edges of $G_{k}$ traverse only between $A_{k}$ and $B_{k}$. If $m>2^{n}$, then there are two distinct indices $i, j$ such that they belong to exactly the same parts $A_{k}, B_{k}$, that is, $i \in A_{k}$ if and only if $j \in A_{k}$ for all $k=1,2, \ldots, n$. However, this means that the edge $i j$ cannot be present in any of the graphs $G_{1}, G_{2}$, $\ldots, G_{n}$, which contradicts (2). Therefore, $m \leq 2^{n}$.
|
{
"exam": "EGMO",
"problem_label": "2",
"problem_match": "\nProblem 2.",
"resource_path": "EGMO/segmented/en-2012-solutions-day1.jsonl",
"solution_match": "\nSolution 1 (submitter).",
"tier": "T2",
"year": "2012"
}
|
Let $n$ be a positive integer. Find the greatest possible integer $m$, in terms of $n$, with the following property: a table with $m$ rows and $n$ columns can be filled with real numbers in such a manner that for any two different rows $\left[a_{1}, a_{2}, \ldots, a_{n}\right]$ and $\left[b_{1}, b_{2}, \ldots, b_{n}\right]$ the following holds:
$$
\max \left(\left|a_{1}-b_{1}\right|,\left|a_{2}-b_{2}\right|, \ldots,\left|a_{n}-b_{n}\right|\right)=1
$$
Origin. Poland (Tomasz Kobos).
|
In any table with the given property, the least and greatest values in a column cannot differ by more than 1 . Thus, if each value that is neither least nor greatest in its column is changed to be equal to either the least or the greatest value in its column (arbitrarily), this does not affect any $\left|a_{i}-b_{i}\right|=1$, nor does it increase any difference above 1 , so the table still has that given property. But after such a change, for any choice of what the least and greatest values in each column are, there are only two possible choices for each entry in the table (either the least or the greatest value in its column); that is, only $2^{n}$ possible distinct rows, and the given property implies that all rows must be distinct. As in the previous solution, we see that this number can be achieved.
|
2^n
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be a positive integer. Find the greatest possible integer $m$, in terms of $n$, with the following property: a table with $m$ rows and $n$ columns can be filled with real numbers in such a manner that for any two different rows $\left[a_{1}, a_{2}, \ldots, a_{n}\right]$ and $\left[b_{1}, b_{2}, \ldots, b_{n}\right]$ the following holds:
$$
\max \left(\left|a_{1}-b_{1}\right|,\left|a_{2}-b_{2}\right|, \ldots,\left|a_{n}-b_{n}\right|\right)=1
$$
Origin. Poland (Tomasz Kobos).
|
In any table with the given property, the least and greatest values in a column cannot differ by more than 1 . Thus, if each value that is neither least nor greatest in its column is changed to be equal to either the least or the greatest value in its column (arbitrarily), this does not affect any $\left|a_{i}-b_{i}\right|=1$, nor does it increase any difference above 1 , so the table still has that given property. But after such a change, for any choice of what the least and greatest values in each column are, there are only two possible choices for each entry in the table (either the least or the greatest value in its column); that is, only $2^{n}$ possible distinct rows, and the given property implies that all rows must be distinct. As in the previous solution, we see that this number can be achieved.
|
{
"exam": "EGMO",
"problem_label": "2",
"problem_match": "\nProblem 2.",
"resource_path": "EGMO/segmented/en-2012-solutions-day1.jsonl",
"solution_match": "\nSolution 2 (PSC).",
"tier": "T2",
"year": "2012"
}
|
Let $n$ be a positive integer. Find the greatest possible integer $m$, in terms of $n$, with the following property: a table with $m$ rows and $n$ columns can be filled with real numbers in such a manner that for any two different rows $\left[a_{1}, a_{2}, \ldots, a_{n}\right]$ and $\left[b_{1}, b_{2}, \ldots, b_{n}\right]$ the following holds:
$$
\max \left(\left|a_{1}-b_{1}\right|,\left|a_{2}-b_{2}\right|, \ldots,\left|a_{n}-b_{n}\right|\right)=1
$$
Origin. Poland (Tomasz Kobos).
|
We prove by induction on $n$ that $m \leq 2^{n}$.
First suppose $n=1$. If real numbers $x$ and $y$ have $|x-y|=1$ then $\lfloor x\rfloor$ and $\lfloor y\rfloor$ have opposite parities and hence it is impossible to find three real numbers with all differences 1 . Thus $m \leq 2$.
Suppose instead $n>1$. Let $a$ be the smallest number appearing in the first column of the table; then every entry in the first column of the table lies in the interval $[a, a+1]$. Let $A$ be the collection of rows with first entry $a$ and $B$ be the collection of rows with first entry in $(a, a+1]$. No two rows in $A$ differ by 1 in their first entries, so if we list the rows in $A$ and delete their first entries we obtain a table satisfying the conditions of the problem with $n$ replaced by $n-1$; thus, by the induction hypothesis, there are at most $2^{n-1}$ rows in $A$. Similarly, there are at most $2^{n-1}$ rows in $B$. Hence $m \leq 2^{n-1}+2^{n-1}=2^{n}$. As before, this number can be achieved.
|
2^n
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be a positive integer. Find the greatest possible integer $m$, in terms of $n$, with the following property: a table with $m$ rows and $n$ columns can be filled with real numbers in such a manner that for any two different rows $\left[a_{1}, a_{2}, \ldots, a_{n}\right]$ and $\left[b_{1}, b_{2}, \ldots, b_{n}\right]$ the following holds:
$$
\max \left(\left|a_{1}-b_{1}\right|,\left|a_{2}-b_{2}\right|, \ldots,\left|a_{n}-b_{n}\right|\right)=1
$$
Origin. Poland (Tomasz Kobos).
|
We prove by induction on $n$ that $m \leq 2^{n}$.
First suppose $n=1$. If real numbers $x$ and $y$ have $|x-y|=1$ then $\lfloor x\rfloor$ and $\lfloor y\rfloor$ have opposite parities and hence it is impossible to find three real numbers with all differences 1 . Thus $m \leq 2$.
Suppose instead $n>1$. Let $a$ be the smallest number appearing in the first column of the table; then every entry in the first column of the table lies in the interval $[a, a+1]$. Let $A$ be the collection of rows with first entry $a$ and $B$ be the collection of rows with first entry in $(a, a+1]$. No two rows in $A$ differ by 1 in their first entries, so if we list the rows in $A$ and delete their first entries we obtain a table satisfying the conditions of the problem with $n$ replaced by $n-1$; thus, by the induction hypothesis, there are at most $2^{n-1}$ rows in $A$. Similarly, there are at most $2^{n-1}$ rows in $B$. Hence $m \leq 2^{n-1}+2^{n-1}=2^{n}$. As before, this number can be achieved.
|
{
"exam": "EGMO",
"problem_label": "2",
"problem_match": "\nProblem 2.",
"resource_path": "EGMO/segmented/en-2012-solutions-day1.jsonl",
"solution_match": "\nSolution 3 (Coordinators).",
"tier": "T2",
"year": "2012"
}
|
Let $n$ be a positive integer. Find the greatest possible integer $m$, in terms of $n$, with the following property: a table with $m$ rows and $n$ columns can be filled with real numbers in such a manner that for any two different rows $\left[a_{1}, a_{2}, \ldots, a_{n}\right]$ and $\left[b_{1}, b_{2}, \ldots, b_{n}\right]$ the following holds:
$$
\max \left(\left|a_{1}-b_{1}\right|,\left|a_{2}-b_{2}\right|, \ldots,\left|a_{n}-b_{n}\right|\right)=1
$$
Origin. Poland (Tomasz Kobos).
|
Consider the rows of the table as points of $\mathbb{R}^{n}$. As the values in each column differ by at most 1 , these points must lie in some $n$-dimensional unit cube $C$. Consider the unit cubes centred on each of the $m$ points. The conditions of the problem imply that the interiors of these unit cubes are pairwise disjoint. But now $C$ has volume 1, and each of these cubes intersects $C$ in volume at least $2^{-n}$ : indeed, if the unit cube centred on a point of $C$ is divided into $2^{n}$ cubes of equal size then one of these cubes must lie entirely within $C$. Hence $m \leq 2^{n}$. As before, this number can be achieved.
|
2^n
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be a positive integer. Find the greatest possible integer $m$, in terms of $n$, with the following property: a table with $m$ rows and $n$ columns can be filled with real numbers in such a manner that for any two different rows $\left[a_{1}, a_{2}, \ldots, a_{n}\right]$ and $\left[b_{1}, b_{2}, \ldots, b_{n}\right]$ the following holds:
$$
\max \left(\left|a_{1}-b_{1}\right|,\left|a_{2}-b_{2}\right|, \ldots,\left|a_{n}-b_{n}\right|\right)=1
$$
Origin. Poland (Tomasz Kobos).
|
Consider the rows of the table as points of $\mathbb{R}^{n}$. As the values in each column differ by at most 1 , these points must lie in some $n$-dimensional unit cube $C$. Consider the unit cubes centred on each of the $m$ points. The conditions of the problem imply that the interiors of these unit cubes are pairwise disjoint. But now $C$ has volume 1, and each of these cubes intersects $C$ in volume at least $2^{-n}$ : indeed, if the unit cube centred on a point of $C$ is divided into $2^{n}$ cubes of equal size then one of these cubes must lie entirely within $C$. Hence $m \leq 2^{n}$. As before, this number can be achieved.
|
{
"exam": "EGMO",
"problem_label": "2",
"problem_match": "\nProblem 2.",
"resource_path": "EGMO/segmented/en-2012-solutions-day1.jsonl",
"solution_match": "\nSolution 4 (Coordinators).",
"tier": "T2",
"year": "2012"
}
|
Let $n$ be a positive integer. Find the greatest possible integer $m$, in terms of $n$, with the following property: a table with $m$ rows and $n$ columns can be filled with real numbers in such a manner that for any two different rows $\left[a_{1}, a_{2}, \ldots, a_{n}\right]$ and $\left[b_{1}, b_{2}, \ldots, b_{n}\right]$ the following holds:
$$
\max \left(\left|a_{1}-b_{1}\right|,\left|a_{2}-b_{2}\right|, \ldots,\left|a_{n}-b_{n}\right|\right)=1
$$
Origin. Poland (Tomasz Kobos).
|
Again consider the rows of the table as points of $\mathbb{R}^{n}$. The conditions of the problem imply that these points must all lie in some $n$-dimensional unit cube $C$, but no two of the points lie in any smaller cube. Thus if $C$ is divided into $2^{n}$ equally-sized subcubes, each of these subcubes contains at most one row of the table, giving $m \leq 2^{n}$. As before, this number can be achieved.
|
2^n
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be a positive integer. Find the greatest possible integer $m$, in terms of $n$, with the following property: a table with $m$ rows and $n$ columns can be filled with real numbers in such a manner that for any two different rows $\left[a_{1}, a_{2}, \ldots, a_{n}\right]$ and $\left[b_{1}, b_{2}, \ldots, b_{n}\right]$ the following holds:
$$
\max \left(\left|a_{1}-b_{1}\right|,\left|a_{2}-b_{2}\right|, \ldots,\left|a_{n}-b_{n}\right|\right)=1
$$
Origin. Poland (Tomasz Kobos).
|
Again consider the rows of the table as points of $\mathbb{R}^{n}$. The conditions of the problem imply that these points must all lie in some $n$-dimensional unit cube $C$, but no two of the points lie in any smaller cube. Thus if $C$ is divided into $2^{n}$ equally-sized subcubes, each of these subcubes contains at most one row of the table, giving $m \leq 2^{n}$. As before, this number can be achieved.
|
{
"exam": "EGMO",
"problem_label": "2",
"problem_match": "\nProblem 2.",
"resource_path": "EGMO/segmented/en-2012-solutions-day1.jsonl",
"solution_match": "\nSolution 5 (Coordinators).",
"tier": "T2",
"year": "2012"
}
|
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
f(y f(x+y)+f(x))=4 x+2 y f(x+y)
$$
for all $x, y \in \mathbb{R}$.
Origin. Netherlands (Birgit van Dalen).
|
Setting $y=0$ yields
$$
f(f(x))=4 x
$$
from which we derive that $f$ is a bijective function. Also, we find that
$$
f(0)=f(4 \cdot 0)=f(f(f(0)))=4 f(0)
$$
hence $f(0)=0$. Now set $x=0$ and $y=1$ in the given equation and use (1) again:
$$
4=f(f(1))=2 f(1)
$$
so $f(1)=2$ and therefore also $f(2)=f(f(1))=4$. Finally substitute $y=1-x$ in the equation:
$$
f(2(1-x)+f(x))=4 x+4(1-x)=4=f(2) \quad \text { for all } x \in \mathbb{R}
$$
As $f$ is injective, from this it follows that $f(x)=2-2(1-x)=2 x$. It is easy to see that this function satisfies the original equation. Hence the only solution is the function defined by $f(x)=2 x$ for all $x \in \mathbb{R}$.
|
f(x)=2x
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
f(y f(x+y)+f(x))=4 x+2 y f(x+y)
$$
for all $x, y \in \mathbb{R}$.
Origin. Netherlands (Birgit van Dalen).
|
Setting $y=0$ yields
$$
f(f(x))=4 x
$$
from which we derive that $f$ is a bijective function. Also, we find that
$$
f(0)=f(4 \cdot 0)=f(f(f(0)))=4 f(0)
$$
hence $f(0)=0$. Now set $x=0$ and $y=1$ in the given equation and use (1) again:
$$
4=f(f(1))=2 f(1)
$$
so $f(1)=2$ and therefore also $f(2)=f(f(1))=4$. Finally substitute $y=1-x$ in the equation:
$$
f(2(1-x)+f(x))=4 x+4(1-x)=4=f(2) \quad \text { for all } x \in \mathbb{R}
$$
As $f$ is injective, from this it follows that $f(x)=2-2(1-x)=2 x$. It is easy to see that this function satisfies the original equation. Hence the only solution is the function defined by $f(x)=2 x$ for all $x \in \mathbb{R}$.
|
{
"exam": "EGMO",
"problem_label": "3",
"problem_match": "\nProblem 3.",
"resource_path": "EGMO/segmented/en-2012-solutions-day1.jsonl",
"solution_match": "\nSolution 1 (submitter).",
"tier": "T2",
"year": "2012"
}
|
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
f(y f(x+y)+f(x))=4 x+2 y f(x+y)
$$
for all $x, y \in \mathbb{R}$.
Origin. Netherlands (Birgit van Dalen).
|
Setting $y=0$ in the equation we see
$$
f(f(x))=4 x
$$
so $f$ is a bijection. Let $\kappa=f^{-1}(2)$ and set $x+y=\kappa$ in the original equation to see
$$
f(2 \kappa-2 x+f(x))=4 \kappa
$$
As the right hand side is independent of $x$ and $f$ is injective, $2 \kappa-2 x+f(x)$ is constant, i.e. $f(x)=2 x+\alpha$.
Substituting this into the original equation, we see that $2 x+\alpha$ is a solution to the original equation if and only if $4\left(y^{2}+x y+x\right)+(3+2 y) \alpha=4\left(y^{2}+x y+x\right)+2 y \alpha$ for all $x, y$, i.e. if and only if $\alpha=0$. Thus the unique solution to the equation is $f(x)=2 x$.
|
f(x)=2x
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
f(y f(x+y)+f(x))=4 x+2 y f(x+y)
$$
for all $x, y \in \mathbb{R}$.
Origin. Netherlands (Birgit van Dalen).
|
Setting $y=0$ in the equation we see
$$
f(f(x))=4 x
$$
so $f$ is a bijection. Let $\kappa=f^{-1}(2)$ and set $x+y=\kappa$ in the original equation to see
$$
f(2 \kappa-2 x+f(x))=4 \kappa
$$
As the right hand side is independent of $x$ and $f$ is injective, $2 \kappa-2 x+f(x)$ is constant, i.e. $f(x)=2 x+\alpha$.
Substituting this into the original equation, we see that $2 x+\alpha$ is a solution to the original equation if and only if $4\left(y^{2}+x y+x\right)+(3+2 y) \alpha=4\left(y^{2}+x y+x\right)+2 y \alpha$ for all $x, y$, i.e. if and only if $\alpha=0$. Thus the unique solution to the equation is $f(x)=2 x$.
|
{
"exam": "EGMO",
"problem_label": "3",
"problem_match": "\nProblem 3.",
"resource_path": "EGMO/segmented/en-2012-solutions-day1.jsonl",
"solution_match": "\nSolution 2 (Coordinators).",
"tier": "T2",
"year": "2012"
}
|
A set $A$ of integers is called sum-full if $A \subseteq A+A$, i.e. each element $a \in A$ is the sum of some pair of (not necessarily different) elements $b, c \in A$. A set $A$ of integers is said to be zero-sum-free if 0 is the only integer that cannot be expressed as the sum of the elements of a finite nonempty subset of $A$.
Does there exist a sum-full zero-sum-free set of integers?
Origin. Romania (Dan Schwarz).
Remark. The original formulation of this problem had a weaker definition of zero-sum-free that did not require all nonzero integers to be sums of finite nonempty subsets of $A$.
|
The set $A=\left\{F_{2 n}: n=1,2, \ldots\right\} \cup\left\{-F_{2 n+1}: n=1,2, \ldots\right\}$, where $F_{k}$ is the $k^{\text {th }}$ Fibonacci number $\left(F_{1}=1, F_{2}=1, F_{k+2}=F_{k+1}+F_{k}\right.$ for $k \geq 1$ ) qualifies for an example. We then have $F_{2 n}=F_{2 n+2}+\left(-F_{2 n+1}\right)$ and $-F_{2 n+1}=\left(-F_{2 n+3}\right)+F_{2 n+2}$ for all $n \geq 1$, so $A$ is sum-full (and even with unique representations). On the other hand, we can never have
$$
0=\sum_{i=1}^{s} F_{2 n_{i}}-\sum_{j=1}^{t} F_{2 n_{j}+1}
$$
owing to the fact that Zeckendorf representations are known to be unique.
It remains to be shown that all nonzero values can be represented as sums of distinct numbers $1,-2,3$, $-5,8,-13,21, \ldots$. This may be done using a greedy algorithm: when representing $n$, the number largest in magnitude that is used is the element $m= \pm F_{k}$ of $A$ that is closest to 0 subject to having the same sign as $n$ and $|m| \geq|n|$. That this algorithm terminates without using any member of $A$ twice is a straightforward induction on $k$; the base case is $k=2(m=1)$ and the induction hypothesis is that for all $n$ for which the above algorithm starts with $\pm F_{\ell}$ with $\ell \leq k$, it terminates without having used any member of $A$ twice and without having used any $\pm F_{j}$ with $j>\ell$.
Remark (James Aaronson and Adam P Goucher). Let $n$ be a positive integer, and write $u=2^{n}$; we claim that the set
$$
\left\{1,2,4, \ldots, 2^{n-1},-u, u+1,-(2 u+1), 3 u+2,-(5 u+3), 8 u+5, \ldots\right\}
$$
is a sum-full zero-sum-free set. The proof is similar to that used for the standard examples.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
A set $A$ of integers is called sum-full if $A \subseteq A+A$, i.e. each element $a \in A$ is the sum of some pair of (not necessarily different) elements $b, c \in A$. A set $A$ of integers is said to be zero-sum-free if 0 is the only integer that cannot be expressed as the sum of the elements of a finite nonempty subset of $A$.
Does there exist a sum-full zero-sum-free set of integers?
Origin. Romania (Dan Schwarz).
Remark. The original formulation of this problem had a weaker definition of zero-sum-free that did not require all nonzero integers to be sums of finite nonempty subsets of $A$.
|
The set $A=\left\{F_{2 n}: n=1,2, \ldots\right\} \cup\left\{-F_{2 n+1}: n=1,2, \ldots\right\}$, where $F_{k}$ is the $k^{\text {th }}$ Fibonacci number $\left(F_{1}=1, F_{2}=1, F_{k+2}=F_{k+1}+F_{k}\right.$ for $k \geq 1$ ) qualifies for an example. We then have $F_{2 n}=F_{2 n+2}+\left(-F_{2 n+1}\right)$ and $-F_{2 n+1}=\left(-F_{2 n+3}\right)+F_{2 n+2}$ for all $n \geq 1$, so $A$ is sum-full (and even with unique representations). On the other hand, we can never have
$$
0=\sum_{i=1}^{s} F_{2 n_{i}}-\sum_{j=1}^{t} F_{2 n_{j}+1}
$$
owing to the fact that Zeckendorf representations are known to be unique.
It remains to be shown that all nonzero values can be represented as sums of distinct numbers $1,-2,3$, $-5,8,-13,21, \ldots$. This may be done using a greedy algorithm: when representing $n$, the number largest in magnitude that is used is the element $m= \pm F_{k}$ of $A$ that is closest to 0 subject to having the same sign as $n$ and $|m| \geq|n|$. That this algorithm terminates without using any member of $A$ twice is a straightforward induction on $k$; the base case is $k=2(m=1)$ and the induction hypothesis is that for all $n$ for which the above algorithm starts with $\pm F_{\ell}$ with $\ell \leq k$, it terminates without having used any member of $A$ twice and without having used any $\pm F_{j}$ with $j>\ell$.
Remark (James Aaronson and Adam P Goucher). Let $n$ be a positive integer, and write $u=2^{n}$; we claim that the set
$$
\left\{1,2,4, \ldots, 2^{n-1},-u, u+1,-(2 u+1), 3 u+2,-(5 u+3), 8 u+5, \ldots\right\}
$$
is a sum-full zero-sum-free set. The proof is similar to that used for the standard examples.
|
{
"exam": "EGMO",
"problem_label": "4",
"problem_match": "\nProblem 4.",
"resource_path": "EGMO/segmented/en-2012-solutions-day1.jsonl",
"solution_match": "\nSolution (submitter, adapted).",
"tier": "T2",
"year": "2012"
}
|
The numbers $p$ and $q$ are prime and satisfy
$$
\frac{p}{p+1}+\frac{q+1}{q}=\frac{2 n}{n+2}
$$
for some positive integer $n$. Find all possible values of $q-p$.
Origin. Luxembourg (Pierre Haas).
|
Rearranging the equation, $2 q n(p+1)=(n+2)(2 p q+p+q+1)$. The left hand side is even, so either $n+2$ or $p+q+1$ is even, so either $p=2$ or $q=2$ since $p$ and $q$ are prime, or $n$ is even.
If $p=2,6 q n=(n+2)(5 q+3)$, so $(q-3)(n-10)=36$. Considering the divisors of 36 for which $q$ is prime, we find the possible solutions $(p, q, n)$ in this case are $(2,5,28)$ and $(2,7,19)$ (both of which satisfy the equation).
If $q=2,4 n(p+1)=(n+2)(5 p+3)$, so $n=p n+10 p+6$, a contradiction since $n<p n$, so there is no solution with $q=2$.
Finally, suppose that $n=2 k$ is even. We may suppose also that $p$ and $q$ are odd primes. The equation becomes $2 k q(p+1)=(k+1)(2 p q+p+q+1)$. The left hand side is even and $2 p q+p+q+1$ is odd, so $k+1$ is even, so $k=2 \ell+1$ is odd. We now have
$$
q(p+1)(2 \ell+1)=(\ell+1)(2 p q+p+q+1)
$$
or equivalently
$$
\ell q(p+1)=(\ell+1)(p q+p+1)
$$
Note that $q \mid p q+p+1$ if and only if $q \mid p+1$. Furthermore, because $(p, p+1)=1$ and $q$ is prime, $(p+1, p q+p+1)=(p+1, p q)=(p+1, q)>1$ if and only if $q \mid p+1$.
Since $(\ell, \ell+1)$, we see that, if $q \nmid p+1$, then $\ell=p q+p+1$ and $\ell+1=q(p+1)$, so $q=p+2$ (and $\left(p, p+2,2\left(2 p^{2}+6 p+3\right)\right)$ satisfies the original equation). In the contrary case, suppose $p+1=r q$, so $\ell(p+1)=(\ell+1)(p+r)$, a contradiction since $\ell<\ell+1$ and $p+1 \leq p+r$.
Thus the possible values of $q-p$ are 2,3 and 5 .
|
2, 3, 5
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
The numbers $p$ and $q$ are prime and satisfy
$$
\frac{p}{p+1}+\frac{q+1}{q}=\frac{2 n}{n+2}
$$
for some positive integer $n$. Find all possible values of $q-p$.
Origin. Luxembourg (Pierre Haas).
|
Rearranging the equation, $2 q n(p+1)=(n+2)(2 p q+p+q+1)$. The left hand side is even, so either $n+2$ or $p+q+1$ is even, so either $p=2$ or $q=2$ since $p$ and $q$ are prime, or $n$ is even.
If $p=2,6 q n=(n+2)(5 q+3)$, so $(q-3)(n-10)=36$. Considering the divisors of 36 for which $q$ is prime, we find the possible solutions $(p, q, n)$ in this case are $(2,5,28)$ and $(2,7,19)$ (both of which satisfy the equation).
If $q=2,4 n(p+1)=(n+2)(5 p+3)$, so $n=p n+10 p+6$, a contradiction since $n<p n$, so there is no solution with $q=2$.
Finally, suppose that $n=2 k$ is even. We may suppose also that $p$ and $q$ are odd primes. The equation becomes $2 k q(p+1)=(k+1)(2 p q+p+q+1)$. The left hand side is even and $2 p q+p+q+1$ is odd, so $k+1$ is even, so $k=2 \ell+1$ is odd. We now have
$$
q(p+1)(2 \ell+1)=(\ell+1)(2 p q+p+q+1)
$$
or equivalently
$$
\ell q(p+1)=(\ell+1)(p q+p+1)
$$
Note that $q \mid p q+p+1$ if and only if $q \mid p+1$. Furthermore, because $(p, p+1)=1$ and $q$ is prime, $(p+1, p q+p+1)=(p+1, p q)=(p+1, q)>1$ if and only if $q \mid p+1$.
Since $(\ell, \ell+1)$, we see that, if $q \nmid p+1$, then $\ell=p q+p+1$ and $\ell+1=q(p+1)$, so $q=p+2$ (and $\left(p, p+2,2\left(2 p^{2}+6 p+3\right)\right)$ satisfies the original equation). In the contrary case, suppose $p+1=r q$, so $\ell(p+1)=(\ell+1)(p+r)$, a contradiction since $\ell<\ell+1$ and $p+1 \leq p+r$.
Thus the possible values of $q-p$ are 2,3 and 5 .
|
{
"exam": "EGMO",
"problem_label": "5",
"problem_match": "\nProblem 5.",
"resource_path": "EGMO/segmented/en-2012-solutions-day2.jsonl",
"solution_match": "\nSolution 1 (submitter).",
"tier": "T2",
"year": "2012"
}
|
The numbers $p$ and $q$ are prime and satisfy
$$
\frac{p}{p+1}+\frac{q+1}{q}=\frac{2 n}{n+2}
$$
for some positive integer $n$. Find all possible values of $q-p$.
Origin. Luxembourg (Pierre Haas).
|
Subtracting 2 and multiplying by -1 , the condition is equivalent to
$$
\frac{1}{p+1}-\frac{1}{q}=\frac{4}{n+2}
$$
Thus $q>p+1$. Rearranging,
$$
q-p-1=\frac{4(p+1) q}{n+2}
$$
The expression on the right is a positive integer, and $q$ must cancel into $n+2$ else $q$ would divide $p+1<q$. Let $(n+2) / q=u$ a positive integer.
Now
so
$$
q-p-1=\frac{4(p+1)}{u}
$$
$$
u q-u(p+1)=4(p+1)
$$
so $p+1$ divides $u q$. However, $q$ is prime and $p+1<q$, therefore $p+1$ divides $u$. Let $v$ be the integer $u /(p+1)$. Now
$$
q-p=1+\frac{4}{v} \in\{2,3,5\}
$$
All three cases can occur, where $(p, q, n)$ is $(3,5,78),(2,5,28)$ or $(2,7,19)$. Note that all pairs of twin primes $q=p+2$ yield solutions $\left(p, p+2,2\left(2 p^{2}+6 p+3\right)\right)$.
|
q-p \in \{2,3,5\}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
The numbers $p$ and $q$ are prime and satisfy
$$
\frac{p}{p+1}+\frac{q+1}{q}=\frac{2 n}{n+2}
$$
for some positive integer $n$. Find all possible values of $q-p$.
Origin. Luxembourg (Pierre Haas).
|
Subtracting 2 and multiplying by -1 , the condition is equivalent to
$$
\frac{1}{p+1}-\frac{1}{q}=\frac{4}{n+2}
$$
Thus $q>p+1$. Rearranging,
$$
q-p-1=\frac{4(p+1) q}{n+2}
$$
The expression on the right is a positive integer, and $q$ must cancel into $n+2$ else $q$ would divide $p+1<q$. Let $(n+2) / q=u$ a positive integer.
Now
so
$$
q-p-1=\frac{4(p+1)}{u}
$$
$$
u q-u(p+1)=4(p+1)
$$
so $p+1$ divides $u q$. However, $q$ is prime and $p+1<q$, therefore $p+1$ divides $u$. Let $v$ be the integer $u /(p+1)$. Now
$$
q-p=1+\frac{4}{v} \in\{2,3,5\}
$$
All three cases can occur, where $(p, q, n)$ is $(3,5,78),(2,5,28)$ or $(2,7,19)$. Note that all pairs of twin primes $q=p+2$ yield solutions $\left(p, p+2,2\left(2 p^{2}+6 p+3\right)\right)$.
|
{
"exam": "EGMO",
"problem_label": "5",
"problem_match": "\nProblem 5.",
"resource_path": "EGMO/segmented/en-2012-solutions-day2.jsonl",
"solution_match": "\nSolution 2 (PSC).",
"tier": "T2",
"year": "2012"
}
|
The numbers $p$ and $q$ are prime and satisfy
$$
\frac{p}{p+1}+\frac{q+1}{q}=\frac{2 n}{n+2}
$$
for some positive integer $n$. Find all possible values of $q-p$.
Origin. Luxembourg (Pierre Haas).
|
Subtract 2 from both sides to get
$$
\frac{1}{p+1}-\frac{1}{q}=\frac{4}{n+2}
$$
From this, since $n$ is positive, we have that $q>p+1$. Therefore $q$ and $p+1$ are coprime, since $q$ is prime.
Group the terms on the LHS to get
$$
\frac{q-p-1}{q(p+1)}=\frac{4}{n+2}
$$
Now $(q, q-p-1)=(q, p+1)=1$ and $(p+1, q-p-1)=(p+1, q)=1$ so the fraction on the left is in lowest terms. Therefore the numerator must divide the numerator on the right, which is 4 . Since $q-p-1$ is positive, it must be 1,2 or 4 , so that $q-p$ must be 2,3 or 5 . All of these can be attained, by $(p, q, n)=(3,5,78)$, $(2,5,28)$ and $(2,7,19)$ respectively.
|
2, 3, 5
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
The numbers $p$ and $q$ are prime and satisfy
$$
\frac{p}{p+1}+\frac{q+1}{q}=\frac{2 n}{n+2}
$$
for some positive integer $n$. Find all possible values of $q-p$.
Origin. Luxembourg (Pierre Haas).
|
Subtract 2 from both sides to get
$$
\frac{1}{p+1}-\frac{1}{q}=\frac{4}{n+2}
$$
From this, since $n$ is positive, we have that $q>p+1$. Therefore $q$ and $p+1$ are coprime, since $q$ is prime.
Group the terms on the LHS to get
$$
\frac{q-p-1}{q(p+1)}=\frac{4}{n+2}
$$
Now $(q, q-p-1)=(q, p+1)=1$ and $(p+1, q-p-1)=(p+1, q)=1$ so the fraction on the left is in lowest terms. Therefore the numerator must divide the numerator on the right, which is 4 . Since $q-p-1$ is positive, it must be 1,2 or 4 , so that $q-p$ must be 2,3 or 5 . All of these can be attained, by $(p, q, n)=(3,5,78)$, $(2,5,28)$ and $(2,7,19)$ respectively.
|
{
"exam": "EGMO",
"problem_label": "5",
"problem_match": "\nProblem 5.",
"resource_path": "EGMO/segmented/en-2012-solutions-day2.jsonl",
"solution_match": "\nSolution 3 (Coordinators).",
"tier": "T2",
"year": "2012"
}
|
There are infinitely many people registered on the social network Mugbook. Some pairs of (different) users are registered as friends, but each person has only finitely many friends. Every user has at least one friend. (Friendship is symmetric; that is, if $A$ is a friend of $B$, then $B$ is a friend of $A$.)
Each person is required to designate one of their friends as their best friend. If $A$ designates $B$ as her best friend, then (unfortunately) it does not follow that $B$ necessarily designates $A$ as her best friend. Someone designated as a best friend is called a 1-best friend. More generally, if $n>1$ is a positive integer, then a user is an $n$-best friend provided that they have been designated the best friend of someone who is an $(n-1)$-best friend. Someone who is a $k$-best friend for every positive integer $k$ is called popular.
(a) Prove that every popular person is the best friend of a popular person.
(b) Show that if people can have infinitely many friends, then it is possible that a popular person is not the best friend of a popular person.
Origin. Romania (Dan Schwarz) (rephrasing by Geoff Smith).
Remark. The original formulation of this problem was:
Given a function $f: X \rightarrow X$, let us use the notations $f^{0}(X):=X, f^{n+1}(X):=f\left(f^{n}(X)\right)$ for $n \geq 0$, and also $f^{\omega}(X):=\bigcap_{n \geq 0} f^{n}(X)$. Let us now impose on $f$ that all its fibres $f^{-1}(y):=\{x \in X \mid f(x)=y\}$, for $y \in f(X)$, are finite. Prove that $f\left(f^{\omega}(X)\right)=f^{\omega}(X)$.
|
For any person $A$, let $f^{0}(x)=x$, let $f(A)$ be $A$ 's best friend, and define $f^{k+1}(A)=f\left(f^{k}(A)\right)$, so any person who is a $k$-best friend is $f^{k}(A)$ for some person $A$; clearly a $k$-best friend is also an $\ell$-best friend for all $\ell<k$. Let $X$ be a popular person. For each positive integer $k$, let $x_{k}$ be a person with $f^{k}\left(x_{k}\right)=X$. Because $X$ only has finitely many friends, infinitely many of the $f^{k-1}\left(x_{k}\right)$ (all of whom designated $X$ as best friend) must be the same person, who must be popular.
If people can have infinitely many friends, consider people $X_{i}$ for positive integers $i$ and $P_{i, j}$ for $i<j$ positive integers. $X_{i}$ designates $X_{i+1}$ as her best friend; $P_{i, i}$ designates $X_{1}$ as her best friend; $P_{i, j}$ designates $P_{i+1, j}$ as her best friend if $i<j$. Then all $X_{i}$ are popular, but $X_{1}$ is not the best friend of a popular person.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
There are infinitely many people registered on the social network Mugbook. Some pairs of (different) users are registered as friends, but each person has only finitely many friends. Every user has at least one friend. (Friendship is symmetric; that is, if $A$ is a friend of $B$, then $B$ is a friend of $A$.)
Each person is required to designate one of their friends as their best friend. If $A$ designates $B$ as her best friend, then (unfortunately) it does not follow that $B$ necessarily designates $A$ as her best friend. Someone designated as a best friend is called a 1-best friend. More generally, if $n>1$ is a positive integer, then a user is an $n$-best friend provided that they have been designated the best friend of someone who is an $(n-1)$-best friend. Someone who is a $k$-best friend for every positive integer $k$ is called popular.
(a) Prove that every popular person is the best friend of a popular person.
(b) Show that if people can have infinitely many friends, then it is possible that a popular person is not the best friend of a popular person.
Origin. Romania (Dan Schwarz) (rephrasing by Geoff Smith).
Remark. The original formulation of this problem was:
Given a function $f: X \rightarrow X$, let us use the notations $f^{0}(X):=X, f^{n+1}(X):=f\left(f^{n}(X)\right)$ for $n \geq 0$, and also $f^{\omega}(X):=\bigcap_{n \geq 0} f^{n}(X)$. Let us now impose on $f$ that all its fibres $f^{-1}(y):=\{x \in X \mid f(x)=y\}$, for $y \in f(X)$, are finite. Prove that $f\left(f^{\omega}(X)\right)=f^{\omega}(X)$.
|
For any person $A$, let $f^{0}(x)=x$, let $f(A)$ be $A$ 's best friend, and define $f^{k+1}(A)=f\left(f^{k}(A)\right)$, so any person who is a $k$-best friend is $f^{k}(A)$ for some person $A$; clearly a $k$-best friend is also an $\ell$-best friend for all $\ell<k$. Let $X$ be a popular person. For each positive integer $k$, let $x_{k}$ be a person with $f^{k}\left(x_{k}\right)=X$. Because $X$ only has finitely many friends, infinitely many of the $f^{k-1}\left(x_{k}\right)$ (all of whom designated $X$ as best friend) must be the same person, who must be popular.
If people can have infinitely many friends, consider people $X_{i}$ for positive integers $i$ and $P_{i, j}$ for $i<j$ positive integers. $X_{i}$ designates $X_{i+1}$ as her best friend; $P_{i, i}$ designates $X_{1}$ as her best friend; $P_{i, j}$ designates $P_{i+1, j}$ as her best friend if $i<j$. Then all $X_{i}$ are popular, but $X_{1}$ is not the best friend of a popular person.
|
{
"exam": "EGMO",
"problem_label": "6",
"problem_match": "\nProblem 6.",
"resource_path": "EGMO/segmented/en-2012-solutions-day2.jsonl",
"solution_match": "\nSolution 1 (submitter, adapted).",
"tier": "T2",
"year": "2012"
}
|
There are infinitely many people registered on the social network Mugbook. Some pairs of (different) users are registered as friends, but each person has only finitely many friends. Every user has at least one friend. (Friendship is symmetric; that is, if $A$ is a friend of $B$, then $B$ is a friend of $A$.)
Each person is required to designate one of their friends as their best friend. If $A$ designates $B$ as her best friend, then (unfortunately) it does not follow that $B$ necessarily designates $A$ as her best friend. Someone designated as a best friend is called a 1-best friend. More generally, if $n>1$ is a positive integer, then a user is an $n$-best friend provided that they have been designated the best friend of someone who is an $(n-1)$-best friend. Someone who is a $k$-best friend for every positive integer $k$ is called popular.
(a) Prove that every popular person is the best friend of a popular person.
(b) Show that if people can have infinitely many friends, then it is possible that a popular person is not the best friend of a popular person.
Origin. Romania (Dan Schwarz) (rephrasing by Geoff Smith).
Remark. The original formulation of this problem was:
Given a function $f: X \rightarrow X$, let us use the notations $f^{0}(X):=X, f^{n+1}(X):=f\left(f^{n}(X)\right)$ for $n \geq 0$, and also $f^{\omega}(X):=\bigcap_{n \geq 0} f^{n}(X)$. Let us now impose on $f$ that all its fibres $f^{-1}(y):=\{x \in X \mid f(x)=y\}$, for $y \in f(X)$, are finite. Prove that $f\left(f^{\omega}(X)\right)=f^{\omega}(X)$.
|
For any set $S$ of people, let $f^{-1}(S)$ be the set of people who designated someone in $S$ as their best friend. Since each person has only finitely many friends, if $S$ is finite then $f^{-1}(S)$ is finite.
Let $X$ be a popular person and put $V_{0}=\{X\}$ and $V_{k}=f^{-1}\left(V_{k-1}\right)$. All $V_{i}$ are finite and (since $X$ is popular) nonempty.
If any two sets $V_{i}, V_{j}$, with $0 \leq i<j$ are not disjoint, define $f^{i}(x)$ for positive integers $i$ as in Solution 1 . It follows $\emptyset \neq f^{i}\left(V_{i} \cap V_{j}\right) \subseteq f^{i}\left(V_{i}\right) \cap f^{i}\left(V_{j}\right) \subseteq V_{0} \cap V_{j-i}$, thus $X \in V_{j-i}$. But this means that $f^{j-i}(X)=X$, therefore $f^{n(j-i)}(X)=X$. Furthermore, if $Y=f^{j-i-1}(X)$, then $f(Y)=X$ and $f^{n(j-i)}(Y)=Y$, so $X$ is the best friend of $Y$, who is popular.
If all sets $V_{n}$ are disjoint, by König's infinity lemma there exists an infinite sequence of (distinct) $x_{i}, i \geq 0$, with $x_{i} \in V_{i}$ and $x_{i}=f\left(x_{i+1}\right)$ for all $i$. Now $x_{1}$ is popular and her best friend is $x_{0}=X$.
If people can have infinitely many friends, proceed as in Solution 1.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
There are infinitely many people registered on the social network Mugbook. Some pairs of (different) users are registered as friends, but each person has only finitely many friends. Every user has at least one friend. (Friendship is symmetric; that is, if $A$ is a friend of $B$, then $B$ is a friend of $A$.)
Each person is required to designate one of their friends as their best friend. If $A$ designates $B$ as her best friend, then (unfortunately) it does not follow that $B$ necessarily designates $A$ as her best friend. Someone designated as a best friend is called a 1-best friend. More generally, if $n>1$ is a positive integer, then a user is an $n$-best friend provided that they have been designated the best friend of someone who is an $(n-1)$-best friend. Someone who is a $k$-best friend for every positive integer $k$ is called popular.
(a) Prove that every popular person is the best friend of a popular person.
(b) Show that if people can have infinitely many friends, then it is possible that a popular person is not the best friend of a popular person.
Origin. Romania (Dan Schwarz) (rephrasing by Geoff Smith).
Remark. The original formulation of this problem was:
Given a function $f: X \rightarrow X$, let us use the notations $f^{0}(X):=X, f^{n+1}(X):=f\left(f^{n}(X)\right)$ for $n \geq 0$, and also $f^{\omega}(X):=\bigcap_{n \geq 0} f^{n}(X)$. Let us now impose on $f$ that all its fibres $f^{-1}(y):=\{x \in X \mid f(x)=y\}$, for $y \in f(X)$, are finite. Prove that $f\left(f^{\omega}(X)\right)=f^{\omega}(X)$.
|
For any set $S$ of people, let $f^{-1}(S)$ be the set of people who designated someone in $S$ as their best friend. Since each person has only finitely many friends, if $S$ is finite then $f^{-1}(S)$ is finite.
Let $X$ be a popular person and put $V_{0}=\{X\}$ and $V_{k}=f^{-1}\left(V_{k-1}\right)$. All $V_{i}$ are finite and (since $X$ is popular) nonempty.
If any two sets $V_{i}, V_{j}$, with $0 \leq i<j$ are not disjoint, define $f^{i}(x)$ for positive integers $i$ as in Solution 1 . It follows $\emptyset \neq f^{i}\left(V_{i} \cap V_{j}\right) \subseteq f^{i}\left(V_{i}\right) \cap f^{i}\left(V_{j}\right) \subseteq V_{0} \cap V_{j-i}$, thus $X \in V_{j-i}$. But this means that $f^{j-i}(X)=X$, therefore $f^{n(j-i)}(X)=X$. Furthermore, if $Y=f^{j-i-1}(X)$, then $f(Y)=X$ and $f^{n(j-i)}(Y)=Y$, so $X$ is the best friend of $Y$, who is popular.
If all sets $V_{n}$ are disjoint, by König's infinity lemma there exists an infinite sequence of (distinct) $x_{i}, i \geq 0$, with $x_{i} \in V_{i}$ and $x_{i}=f\left(x_{i+1}\right)$ for all $i$. Now $x_{1}$ is popular and her best friend is $x_{0}=X$.
If people can have infinitely many friends, proceed as in Solution 1.
|
{
"exam": "EGMO",
"problem_label": "6",
"problem_match": "\nProblem 6.",
"resource_path": "EGMO/segmented/en-2012-solutions-day2.jsonl",
"solution_match": "\nSolution 2 (submitter, adapted).",
"tier": "T2",
"year": "2012"
}
|
Let $A B C$ be an acute-angled triangle with circumcircle $\Gamma$ and orthocentre $H$. Let $K$ be a point of $\Gamma$ on the other side of $B C$ from $A$. Let $L$ be the reflection of $K$ in the line $A B$, and let $M$ be the reflection of $K$ in the line $B C$. Let $E$ be the second point of intersection of $\Gamma$ with the circumcircle of triangle $B L M$. Show that the lines $K H, E M$ and $B C$ are concurrent. (The orthocentre of a triangle is the point on all three of its altitudes.)
Origin. Luxembourg (Pierre Haas).
|
Since the quadrilateral $B M E L$ is cyclic, we have $\angle B E M=\angle B L M$. By construction, $|B K|=|B L|=|B M|$, and so (using directed angles)
$$
\begin{aligned}
\angle B L M & =90^{\circ}-\frac{1}{2} \angle M B L=90^{\circ}-\left(180^{\circ}-\frac{1}{2} \angle L B K-\frac{1}{2} \angle K B M\right) \\
& =\left(\frac{1}{2} \angle L B K+\frac{1}{2} \angle K B M\right)-90^{\circ}=\left(180^{\circ}-\angle B\right)-90^{\circ}=90^{\circ}-B .
\end{aligned}
$$
We see also that $\angle B E M=\angle B A H$, and so the point $N$ of intersection of $E M$ and $A H$ lies on $\Gamma$.
Let $X$ be the point of intersection of $K H$ and $B C$, and let $N^{\prime}$ be the point of intersection of $M X$ and $A H$. Since $B C$ bisects the segment $K M$ by construction, the triangle $K X M$ is isosceles; as $A H \| M K, H X N^{\prime}$ is isosceles. Since $A H \perp B C, N^{\prime}$ is the reflection of $H$ in the line $B C$. It is well known that this reflection lies on $\Gamma$, and so $N^{\prime}=N$. Thus $E, M, N$ and $M, X, N^{\prime}$ all lie on the same line $M N$; that is, $E M$ passes through $X$.
Remark (submitter). The condition that $K$ lies on the circumcircle of $A B C$ is not necessary; indeed, the solution above does not use it. However, together with the fact that the triangle $A B C$ is acute-angled, this condition implies that $M$ is in the interior of $\Gamma$, which is necessary to avoid dealing with different configurations including coincident points or the point of concurrence being at infinity.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute-angled triangle with circumcircle $\Gamma$ and orthocentre $H$. Let $K$ be a point of $\Gamma$ on the other side of $B C$ from $A$. Let $L$ be the reflection of $K$ in the line $A B$, and let $M$ be the reflection of $K$ in the line $B C$. Let $E$ be the second point of intersection of $\Gamma$ with the circumcircle of triangle $B L M$. Show that the lines $K H, E M$ and $B C$ are concurrent. (The orthocentre of a triangle is the point on all three of its altitudes.)
Origin. Luxembourg (Pierre Haas).
|
Since the quadrilateral $B M E L$ is cyclic, we have $\angle B E M=\angle B L M$. By construction, $|B K|=|B L|=|B M|$, and so (using directed angles)
$$
\begin{aligned}
\angle B L M & =90^{\circ}-\frac{1}{2} \angle M B L=90^{\circ}-\left(180^{\circ}-\frac{1}{2} \angle L B K-\frac{1}{2} \angle K B M\right) \\
& =\left(\frac{1}{2} \angle L B K+\frac{1}{2} \angle K B M\right)-90^{\circ}=\left(180^{\circ}-\angle B\right)-90^{\circ}=90^{\circ}-B .
\end{aligned}
$$
We see also that $\angle B E M=\angle B A H$, and so the point $N$ of intersection of $E M$ and $A H$ lies on $\Gamma$.
Let $X$ be the point of intersection of $K H$ and $B C$, and let $N^{\prime}$ be the point of intersection of $M X$ and $A H$. Since $B C$ bisects the segment $K M$ by construction, the triangle $K X M$ is isosceles; as $A H \| M K, H X N^{\prime}$ is isosceles. Since $A H \perp B C, N^{\prime}$ is the reflection of $H$ in the line $B C$. It is well known that this reflection lies on $\Gamma$, and so $N^{\prime}=N$. Thus $E, M, N$ and $M, X, N^{\prime}$ all lie on the same line $M N$; that is, $E M$ passes through $X$.

Remark (submitter). The condition that $K$ lies on the circumcircle of $A B C$ is not necessary; indeed, the solution above does not use it. However, together with the fact that the triangle $A B C$ is acute-angled, this condition implies that $M$ is in the interior of $\Gamma$, which is necessary to avoid dealing with different configurations including coincident points or the point of concurrence being at infinity.
|
{
"exam": "EGMO",
"problem_label": "7",
"problem_match": "\nProblem 7.",
"resource_path": "EGMO/segmented/en-2012-solutions-day2.jsonl",
"solution_match": "\nSolution 1 (submitter).",
"tier": "T2",
"year": "2012"
}
|
Let $A B C$ be an acute-angled triangle with circumcircle $\Gamma$ and orthocentre $H$. Let $K$ be a point of $\Gamma$ on the other side of $B C$ from $A$. Let $L$ be the reflection of $K$ in the line $A B$, and let $M$ be the reflection of $K$ in the line $B C$. Let $E$ be the second point of intersection of $\Gamma$ with the circumcircle of triangle $B L M$. Show that the lines $K H, E M$ and $B C$ are concurrent. (The orthocentre of a triangle is the point on all three of its altitudes.)
Origin. Luxembourg (Pierre Haas).
|
We work with directed angles. Let $H K$ meet $B C$ at $X$. Let $M X$ meet $A H$ at $H_{A}$ on $\Gamma$ (where $H_{A}$ is the reflection of $H$ in $B C$ ). Define $E^{\prime}$ to be where $H_{A} M$ meets $\Gamma$ (again). Our task is to show that $\angle M E^{\prime} B=\angle M L B$.
Observe that
$$
\begin{aligned}
\angle M E^{\prime} B & =\angle H_{A} A B & \text { (angles in same segment) } \\
& =B^{c} &
\end{aligned}
$$
Now
$$
\begin{aligned}
\angle M L B & =\angle H L B \\
& =\angle B K H_{C} \\
& =\angle B C H_{C} \\
& =B^{c} .
\end{aligned}
$$
(Simson line, doubled)
(reflecting in the line $A B$ )
(angles in the same segment)
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute-angled triangle with circumcircle $\Gamma$ and orthocentre $H$. Let $K$ be a point of $\Gamma$ on the other side of $B C$ from $A$. Let $L$ be the reflection of $K$ in the line $A B$, and let $M$ be the reflection of $K$ in the line $B C$. Let $E$ be the second point of intersection of $\Gamma$ with the circumcircle of triangle $B L M$. Show that the lines $K H, E M$ and $B C$ are concurrent. (The orthocentre of a triangle is the point on all three of its altitudes.)
Origin. Luxembourg (Pierre Haas).
|
We work with directed angles. Let $H K$ meet $B C$ at $X$. Let $M X$ meet $A H$ at $H_{A}$ on $\Gamma$ (where $H_{A}$ is the reflection of $H$ in $B C$ ). Define $E^{\prime}$ to be where $H_{A} M$ meets $\Gamma$ (again). Our task is to show that $\angle M E^{\prime} B=\angle M L B$.
Observe that
$$
\begin{aligned}
\angle M E^{\prime} B & =\angle H_{A} A B & \text { (angles in same segment) } \\
& =B^{c} &
\end{aligned}
$$
Now
$$
\begin{aligned}
\angle M L B & =\angle H L B \\
& =\angle B K H_{C} \\
& =\angle B C H_{C} \\
& =B^{c} .
\end{aligned}
$$
(Simson line, doubled)
(reflecting in the line $A B$ )
(angles in the same segment)
|
{
"exam": "EGMO",
"problem_label": "7",
"problem_match": "\nProblem 7.",
"resource_path": "EGMO/segmented/en-2012-solutions-day2.jsonl",
"solution_match": "\nSolution 2 (PSC).",
"tier": "T2",
"year": "2012"
}
|
A word is a finite sequence of letters from some alphabet. A word is repetitive if it is a concatenation of at least two identical subwords (for example, $a b a b a b$ and $a b c a b c$ are repetitive, but $a b a b a$ and $a a b b$ are not). Prove that if a word has the property that swapping any two adjacent letters makes the word repetitive, then all its letters are identical. (Note that one may swap two adjacent identical letters, leaving a word unchanged.)
## Origin. Romania (Dan Schwarz).
|
In this and the subsequent solutions we refer to a word with all letters identical as constant.
Let us consider a nonconstant word $W$, of length $|W|=w$, and reach a contradiction. Since the word $W$ must contain two distinct adjacent letters, be it $W=A a b B$ with $a \neq b$, we may assume $B=c C$ to be non-empty, and so $W=A a b c C$. By the proper transpositions we get the repetitive words $W^{\prime}=A b a c C=P^{w / p}$, of a period $P$ of length $p \mid w, 1<p<w$, and $W^{\prime \prime}=A a c b C=Q^{w / q}$, of a period $Q$ of length $q \mid w, 1<q<w$. However, if a word $U V$ is repetitive, then the word $V U$ is also repetitive, of a same period length; therefore we can work in the sequel with the repetitive words $W_{0}^{\prime}=C A b a c$, of a period $P^{\prime}$ of length $p$, and $W_{0}^{\prime \prime}=C A a c b$, of a period $Q^{\prime}$ of length $q$. The main idea now is that the common prefix of two repetitive words cannot be too long.
Now, if a word $a_{1} a_{2} \ldots a_{w}=T^{w / t}$ is repetitive, of a period $T$ of length $t \mid w, 1 \leq t<w$, then the word (and any subword of it) is $t$-periodic, i.e. $a_{k}=a_{k+t}$, for all $1 \leq k \leq w-t$. Therefore the word $C A$ is both $p$-periodic and $q$-periodic.
We now use the following classical result:
Wilf-Fine Theorem. Let $p, q$ be positive integers, and let $N$ be a word of length $n$, which is both p-periodic and $q$-periodic. If $n \geq p+q-\operatorname{gcd}(p, q)$ then the word $N$ is $\operatorname{gcd}(p, q)$-periodic (but this need not be the case if instead $n \leq p+q-\operatorname{gcd}(p, q)-1)$.
By this we need $|C A| \leq p+q-\operatorname{gcd}(p, q)-1 \leq p+q-2$, hence $w \leq p+q+1$, otherwise $W_{0}^{\prime}$ and $W_{0}^{\prime \prime}$ would be identical, absurd. Since $p \mid w$ and $1<p<w$, we have $2 p \leq w \leq p+q+1$, and so $p \leq q+1$; similarly we have $q \leq p+1$.
If $p=q$, then $|C A| \leq p+p-\operatorname{gcd}(p, p)-1=p-1$, so $2 p \leq w \leq p+2$, implying $p \leq 2$. But the three-letter suffix $a c b$ is not periodic (not even for $c=a$ or $c=b$ ), thus must be contained in $Q^{\prime}$, forcing $q \geq 3$, contradiction.
If $p \neq q$, then $\max (p, q)=\min (p, q)+1$, so $3 \min (p, q) \leq w \leq 2 \min (p, q)+2$, hence $\min (p, q) \leq 2$, forcing $\min (p, q)=2$ and $\max (p, q)=3$; by an above observation, we may even say $q=3$ and $p=2$, leading to $c=b$. It follows $6=3 \min (p, q) \leq w \leq 2 \min (p, q)+2=6$, forcing $w=6$. This leads to $C A=a b a=a b b$, contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A word is a finite sequence of letters from some alphabet. A word is repetitive if it is a concatenation of at least two identical subwords (for example, $a b a b a b$ and $a b c a b c$ are repetitive, but $a b a b a$ and $a a b b$ are not). Prove that if a word has the property that swapping any two adjacent letters makes the word repetitive, then all its letters are identical. (Note that one may swap two adjacent identical letters, leaving a word unchanged.)
## Origin. Romania (Dan Schwarz).
|
In this and the subsequent solutions we refer to a word with all letters identical as constant.
Let us consider a nonconstant word $W$, of length $|W|=w$, and reach a contradiction. Since the word $W$ must contain two distinct adjacent letters, be it $W=A a b B$ with $a \neq b$, we may assume $B=c C$ to be non-empty, and so $W=A a b c C$. By the proper transpositions we get the repetitive words $W^{\prime}=A b a c C=P^{w / p}$, of a period $P$ of length $p \mid w, 1<p<w$, and $W^{\prime \prime}=A a c b C=Q^{w / q}$, of a period $Q$ of length $q \mid w, 1<q<w$. However, if a word $U V$ is repetitive, then the word $V U$ is also repetitive, of a same period length; therefore we can work in the sequel with the repetitive words $W_{0}^{\prime}=C A b a c$, of a period $P^{\prime}$ of length $p$, and $W_{0}^{\prime \prime}=C A a c b$, of a period $Q^{\prime}$ of length $q$. The main idea now is that the common prefix of two repetitive words cannot be too long.
Now, if a word $a_{1} a_{2} \ldots a_{w}=T^{w / t}$ is repetitive, of a period $T$ of length $t \mid w, 1 \leq t<w$, then the word (and any subword of it) is $t$-periodic, i.e. $a_{k}=a_{k+t}$, for all $1 \leq k \leq w-t$. Therefore the word $C A$ is both $p$-periodic and $q$-periodic.
We now use the following classical result:
Wilf-Fine Theorem. Let $p, q$ be positive integers, and let $N$ be a word of length $n$, which is both p-periodic and $q$-periodic. If $n \geq p+q-\operatorname{gcd}(p, q)$ then the word $N$ is $\operatorname{gcd}(p, q)$-periodic (but this need not be the case if instead $n \leq p+q-\operatorname{gcd}(p, q)-1)$.
By this we need $|C A| \leq p+q-\operatorname{gcd}(p, q)-1 \leq p+q-2$, hence $w \leq p+q+1$, otherwise $W_{0}^{\prime}$ and $W_{0}^{\prime \prime}$ would be identical, absurd. Since $p \mid w$ and $1<p<w$, we have $2 p \leq w \leq p+q+1$, and so $p \leq q+1$; similarly we have $q \leq p+1$.
If $p=q$, then $|C A| \leq p+p-\operatorname{gcd}(p, p)-1=p-1$, so $2 p \leq w \leq p+2$, implying $p \leq 2$. But the three-letter suffix $a c b$ is not periodic (not even for $c=a$ or $c=b$ ), thus must be contained in $Q^{\prime}$, forcing $q \geq 3$, contradiction.
If $p \neq q$, then $\max (p, q)=\min (p, q)+1$, so $3 \min (p, q) \leq w \leq 2 \min (p, q)+2$, hence $\min (p, q) \leq 2$, forcing $\min (p, q)=2$ and $\max (p, q)=3$; by an above observation, we may even say $q=3$ and $p=2$, leading to $c=b$. It follows $6=3 \min (p, q) \leq w \leq 2 \min (p, q)+2=6$, forcing $w=6$. This leads to $C A=a b a=a b b$, contradiction.
|
{
"exam": "EGMO",
"problem_label": "8",
"problem_match": "\nProblem 8.",
"resource_path": "EGMO/segmented/en-2012-solutions-day2.jsonl",
"solution_match": "\nSolution 1 (submitter).",
"tier": "T2",
"year": "2012"
}
|
A word is a finite sequence of letters from some alphabet. A word is repetitive if it is a concatenation of at least two identical subwords (for example, $a b a b a b$ and $a b c a b c$ are repetitive, but $a b a b a$ and $a a b b$ are not). Prove that if a word has the property that swapping any two adjacent letters makes the word repetitive, then all its letters are identical. (Note that one may swap two adjacent identical letters, leaving a word unchanged.)
## Origin. Romania (Dan Schwarz).
|
We will take over from the solution above, just before invoking the Wilf-Fine Theorem, by replacing it with a weaker lemma, also built upon a seminal result of combinatorics on words.
Lemma. Let $p, q$ be positive integers, and let $N$ be a word of length $n$, which is both $p$-periodic and $q$ periodic. If $n \geq p+q$ then the word $N$ is $\operatorname{gcd}(p, q)$-periodic.
Proof. Let us first prove that two not-null words $U, V$ commute, i.e. $U V=V U$, if and only if there exists a word $W$ with $|W|=\operatorname{gcd}(|U|,|V|)$, such that $U=W^{|U| /|W|}, V=W^{|V| /|W|}$. The "if" part being trivial, we will prove the "only if" part, by strong induction on $|U|+|V|$. Indeed, for the base step $|U|+|V|=2$ we have $|U|=|V|=1$, and so clearly we can take $W=U=V$. Now, for $|U|+|V|>2$, if $|U|=|V|$ it follows $U=V$, and so we can again take $W=U=V$. If not, assume without loss of generality $|U|<|V|$; then $V=U V^{\prime}$, so $U U V^{\prime}=U V^{\prime} U$, whence $U V^{\prime}=V^{\prime} U$. Since $\left|V^{\prime}\right|<|V|$, it follows $2 \leq|U|+\left|V^{\prime}\right|<|U|+|V|$, so by the induction hypothesis there exists a suitable word $W$ such that $U=W^{|U| /|W|}, V^{\prime}=W^{\left|V^{\prime}\right| /|W|}$, so $V=U V^{\prime}=W^{|U| /|W|} W^{\left|V^{\prime}\right| /|W|}=W^{\left(|U|+\left|V^{\prime}\right|\right) /|W|}=W^{|V| /|W|}$.
Now, assuming without loss of generality $p \leq q, q=k p+r$, we have $N=Q P S$, with $|Q|=q,|P|=p$. If $r=0$ all is clear; otherwise it follows we can write $P=U V, Q=V(U V)^{k}$, with $|V|=r$, whence $U V=V U$, implying $P Q=Q P$, and so by the above result there will exist a word $W$ of length $\operatorname{gcd}(p, q)$ such that $P=W^{p / \operatorname{gcd}(p, q)}$, $Q=W^{q / \operatorname{gcd}(p, q)}$, therefore $N$ is $\operatorname{gcd}(p, q)$-periodic.
By this we need $|C A| \leq p+q-1$, hence $w \leq p+q+2$, otherwise by the previous lemma $W_{0}^{\prime}$ and $W_{0}^{\prime \prime}$ would be identical, absurd. Since $p \mid w$ and $1<p<w$, we have $2 p \leq w \leq p+q+2$, and so $p \leq q+2$; similarly we have $q \leq p+2$. That implies $\max (p, q) \leq \min (p, q)+2$. Now, from $k \max (p, q)=w \leq p+q+2 \leq 2 \max (p, q)+2$ we will have $(k-2) \max (p, q) \leq 2$; but $\max (p, q) \leq 2$ is impossible, since the three-letter suffix $a c b$ is not periodic (not even for $c=a$ or $c=b$ ), thus must be contained in $Q^{\prime}$, forcing $q \geq 3$. Therefore $k=2$, and so $w=2 \max (p, q)$.
If $\max (p, q)=\min (p, q)$, then $w=2 p=2 q$, for a quick contradiction.
If $\max (p, q)=\min (p, q)+1$, it follows $3 \min (p, q) \leq w=2 \max (p, q)=2 \min (p, q)+2$, hence $\min (p, q) \leq 2$, forcing $\min (p, q)=2$ and $\max (p, q)=3$; by an above observation, we may even say $q=3$ and $p=2$, leading to $c=b$. It follows $w=2 \max (p, q)=6$, leading to $C A=a b a=a b b$, contradiction.
If $\max (p, q)=\min (p, q)+2$, it follows $3 \min (p, q) \leq w=2 \max (p, q)=2 \min (p, q)+4$, hence $\min (p, q) \leq 4$. From $\min (p, q) \mid w=2 \max (p, q)$ then follows either $\min (p, q)=2$ and $\max (p, q)=4$, thus $w=8$, clearly contradictory, or else $\min (p, q)=4$ and $\max (p, q)=6$, thus $w=12$, which also leads to contradiction, by just a little deeper analysis.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A word is a finite sequence of letters from some alphabet. A word is repetitive if it is a concatenation of at least two identical subwords (for example, $a b a b a b$ and $a b c a b c$ are repetitive, but $a b a b a$ and $a a b b$ are not). Prove that if a word has the property that swapping any two adjacent letters makes the word repetitive, then all its letters are identical. (Note that one may swap two adjacent identical letters, leaving a word unchanged.)
## Origin. Romania (Dan Schwarz).
|
We will take over from the solution above, just before invoking the Wilf-Fine Theorem, by replacing it with a weaker lemma, also built upon a seminal result of combinatorics on words.
Lemma. Let $p, q$ be positive integers, and let $N$ be a word of length $n$, which is both $p$-periodic and $q$ periodic. If $n \geq p+q$ then the word $N$ is $\operatorname{gcd}(p, q)$-periodic.
Proof. Let us first prove that two not-null words $U, V$ commute, i.e. $U V=V U$, if and only if there exists a word $W$ with $|W|=\operatorname{gcd}(|U|,|V|)$, such that $U=W^{|U| /|W|}, V=W^{|V| /|W|}$. The "if" part being trivial, we will prove the "only if" part, by strong induction on $|U|+|V|$. Indeed, for the base step $|U|+|V|=2$ we have $|U|=|V|=1$, and so clearly we can take $W=U=V$. Now, for $|U|+|V|>2$, if $|U|=|V|$ it follows $U=V$, and so we can again take $W=U=V$. If not, assume without loss of generality $|U|<|V|$; then $V=U V^{\prime}$, so $U U V^{\prime}=U V^{\prime} U$, whence $U V^{\prime}=V^{\prime} U$. Since $\left|V^{\prime}\right|<|V|$, it follows $2 \leq|U|+\left|V^{\prime}\right|<|U|+|V|$, so by the induction hypothesis there exists a suitable word $W$ such that $U=W^{|U| /|W|}, V^{\prime}=W^{\left|V^{\prime}\right| /|W|}$, so $V=U V^{\prime}=W^{|U| /|W|} W^{\left|V^{\prime}\right| /|W|}=W^{\left(|U|+\left|V^{\prime}\right|\right) /|W|}=W^{|V| /|W|}$.
Now, assuming without loss of generality $p \leq q, q=k p+r$, we have $N=Q P S$, with $|Q|=q,|P|=p$. If $r=0$ all is clear; otherwise it follows we can write $P=U V, Q=V(U V)^{k}$, with $|V|=r$, whence $U V=V U$, implying $P Q=Q P$, and so by the above result there will exist a word $W$ of length $\operatorname{gcd}(p, q)$ such that $P=W^{p / \operatorname{gcd}(p, q)}$, $Q=W^{q / \operatorname{gcd}(p, q)}$, therefore $N$ is $\operatorname{gcd}(p, q)$-periodic.
By this we need $|C A| \leq p+q-1$, hence $w \leq p+q+2$, otherwise by the previous lemma $W_{0}^{\prime}$ and $W_{0}^{\prime \prime}$ would be identical, absurd. Since $p \mid w$ and $1<p<w$, we have $2 p \leq w \leq p+q+2$, and so $p \leq q+2$; similarly we have $q \leq p+2$. That implies $\max (p, q) \leq \min (p, q)+2$. Now, from $k \max (p, q)=w \leq p+q+2 \leq 2 \max (p, q)+2$ we will have $(k-2) \max (p, q) \leq 2$; but $\max (p, q) \leq 2$ is impossible, since the three-letter suffix $a c b$ is not periodic (not even for $c=a$ or $c=b$ ), thus must be contained in $Q^{\prime}$, forcing $q \geq 3$. Therefore $k=2$, and so $w=2 \max (p, q)$.
If $\max (p, q)=\min (p, q)$, then $w=2 p=2 q$, for a quick contradiction.
If $\max (p, q)=\min (p, q)+1$, it follows $3 \min (p, q) \leq w=2 \max (p, q)=2 \min (p, q)+2$, hence $\min (p, q) \leq 2$, forcing $\min (p, q)=2$ and $\max (p, q)=3$; by an above observation, we may even say $q=3$ and $p=2$, leading to $c=b$. It follows $w=2 \max (p, q)=6$, leading to $C A=a b a=a b b$, contradiction.
If $\max (p, q)=\min (p, q)+2$, it follows $3 \min (p, q) \leq w=2 \max (p, q)=2 \min (p, q)+4$, hence $\min (p, q) \leq 4$. From $\min (p, q) \mid w=2 \max (p, q)$ then follows either $\min (p, q)=2$ and $\max (p, q)=4$, thus $w=8$, clearly contradictory, or else $\min (p, q)=4$ and $\max (p, q)=6$, thus $w=12$, which also leads to contradiction, by just a little deeper analysis.
|
{
"exam": "EGMO",
"problem_label": "8",
"problem_match": "\nProblem 8.",
"resource_path": "EGMO/segmented/en-2012-solutions-day2.jsonl",
"solution_match": "\nSolution 2 (submitter).",
"tier": "T2",
"year": "2012"
}
|
A word is a finite sequence of letters from some alphabet. A word is repetitive if it is a concatenation of at least two identical subwords (for example, $a b a b a b$ and $a b c a b c$ are repetitive, but $a b a b a$ and $a a b b$ are not). Prove that if a word has the property that swapping any two adjacent letters makes the word repetitive, then all its letters are identical. (Note that one may swap two adjacent identical letters, leaving a word unchanged.)
## Origin. Romania (Dan Schwarz).
|
We define the distance between two words of the same length to be the number of positions in which those two words have different letters. Any two words related by a transposition have distance 0 or 2 ; any two words related by a sequence of two transpositions have distance $0,2,3$ or 4 .
Say the period of a repetitive word is the least $k$ such that the word is the concatenation of two or more identical subwords of length $k$. We use the following lemma on distances between repetitive words.
Lemma. Consider a pair of distinct, nonconstant repetitive words with periods ga and gb, where $(a, b)=1$ and $a, b>1$, the first word is made up of $k b$ repetitions of the subword of length ga and the second word is made up of ka repetitions of the subword of length gb . These two words have distance at least $\max (k a, k b)$.
Proof. We may assume $k=1$, since the distance between the words is $k$ times the distance between their initial subwords of length $g a b$. Without loss of generality suppose $b>a$.
For each positive integer $m$, look at the subsequence in each word of letters in positions congruent to $m$ $(\bmod g)$. Those subsequences (of length $a b)$ have periods dividing $a$ and $b$ respectively. If they are equal, then they are constant (since each letter is equal to those $a$ and $b$ before and after it, mod $a b$, and $(a, b)=1$ ). Because $a>1$, there is some $m$ for which the first subsequence is not constant, and so is unequal to the second subsequence. Restrict attention to those subsequences.
We now have two distinct repetitive words, one (nonconstant) made up of $b$ repetitions of a subword of length $a$ and one made up of $a$ repetitions of a subword of length $b$. Looking at the first of those words, for any $1 \leq t \leq b$ consider the letters in positions $t, t+b, \ldots, t+(a-1) b$. These letters cover every position (mod $a)$; since the first word is not constant, the letters are not all equal, but the letters in the corresponding positions in the second word are all equal. At least one of these letters in the first word must change to make them all equal to those in the corresponding positions in the second word; repeating for each $t$, at least $b$ letters must change, so the words have distance at least $b$.
In the original problem, consider all the words (which we suppose to be repetitive) obtained by a transposition of two adjacent letters from the original nonconstant word; say that word has length $n$. Suppose those words include two distinct words with periods $n / a$ and $n / b$; those words have distance at most 4 . If $a>4$ or $b>4$, we have a contradiction unless $a \mid b$ or $b \mid a$. If $a>4$ is the greatest number of repetitions in any of the words ( $n / a$ is the smallest period), then unless all the numbers of repetitions divide each other there must be words with 2 or 4 repetitions, words with 3 repetitions and all larger numbers of repetitions must divide each other and be divisible by 6 .
We now divide into three cases: all the numbers of repetitions may divide either other; or there may be words with (multiples of) 2,3 and 6 repetitions; or all words may have at most 4 repetitions, with at least one word having 3 repetitions and at least one having 2 or 4 repetitions.
Case 1. Suppose all the numbers of repetitions divide each other. Let $k$ be the least number of repetitions. Consider the word as being divided into $k$ blocks, each of $\ell$ letters; any transposition of two adjacent letters leaves those blocks identical. If any two adjacent letters within a block are the same, then this means all the blocks are already identical; since the word is not constant, the letters in the first block are not all identical, so there are two distinct adjacent letters in the first block, and transposing them leaves it distinct from the other blocks, a contradiction. Otherwise, all pairs of adjacent letters within each block are distinct; transposing any adjacent pair within the first block leaves it identical to the second block. If the first block has more than two letters, this is impossible since transposing the first two letters has a different result from transposing the second two. So the blocks all have length 2 ; similarly, there are just two blocks, the arrangement is $a b b a$ but transposing the adjacent letters $b b$ does not leave the word repetitive.
Case 2. Suppose some word resulting from a transposition is made of (a multiple of) 6 repetitions, some of 3 repetitions and some of 2 repetitions (or 4 repetitions, counted as 2 ). Consider it as a sequence of 6 blocks, each of length $\ell$. If the six blocks are already identical, then as the word is not constant, there are some two distinct adjacent letters within the first block; transposing them leaves a result where the blocks form a
pattern $B A A A A A$, which cannot have two, three or six repetitions. So the six blocks are not already identical. If a transposition within a block results in them being identical, the blocks form a pattern (without loss of generality) $B A A A A A, A B A A A A$ or $A A B A A A$. In any of these cases, apply the same transposition (that converts between $A$ and $B$ ) to an $A$ block adjacent to the $B$ block, and the result cannot have two, three or six repetitions. Finally, consider the case where some transposition between two adjacent blocks results in all six blocks being identical. The patterns are $B C A A A A, A B C A A A$ and $A A B C A A$ (and considering the letters at the start and end of each block shows $B \neq C$ ). In all cases, transposing two adjacent distinct letters within an $A$ block produces a result that cannot have two, three or six repetitions.
Case 3. In the remaining case, all words have at most 4 repetitions, at least one has 3 repetitions and at least one has 2 or 4 repetitions. For the purposes of this case we will think of 4 -repetition words as being 2 -repetition words. The number of each letter is a multiple of 6 , so $n \geq 12$; consider the word as made of six blocks of length $\ell$.
If the word is already repetitive with 2 repetitions, pattern $A B C A B C$, any transposition between two distinct letters leaves it no longer repetitive with two repetitions, so it must instead have three repetitions after the transposition. If $A B$ is not all one letter, transposing two adjacent letters within $A B$ implies that $C A=B C$, so $A=B=C$, the word has pattern $A A A A A A$ but transposing within the initial $A A$ means it no longer has 3 repetitions. This implies that $A B$ is all one letter, but similarly $B C$ must also be all one letter and so the word is constant, a contradiction.
If the word is already repetitive with 3 repetitions, it has pattern $A B A B A B$ and any transposition leaves it no longer having 3 repetitions, so having 2 repetitions instead. $A B A$ is not made all of one letter (since the word is not constant) and any transposition between two adjacent distinct letters therein turns it into $B A B$; such a transposition affects at most two of the blocks, so $A=B$, the word has pattern $A A A A A A$ and transposing two adjacent distinct letters within the first half cannot leave it with two repetitions.
So the word is not already repetitive, and so no two adjacent letters are the same; all transpositions give distinct strings. Consider transpositions of adjacent letters within the first four letters; three different words result, of which at most one is periodic with two repetitions (it must be made of two copies of the second half of the word) and at most one is periodic with three repetitions, a contradiction.
|
proof
|
Yes
|
Incomplete
|
proof
|
Combinatorics
|
A word is a finite sequence of letters from some alphabet. A word is repetitive if it is a concatenation of at least two identical subwords (for example, $a b a b a b$ and $a b c a b c$ are repetitive, but $a b a b a$ and $a a b b$ are not). Prove that if a word has the property that swapping any two adjacent letters makes the word repetitive, then all its letters are identical. (Note that one may swap two adjacent identical letters, leaving a word unchanged.)
## Origin. Romania (Dan Schwarz).
|
We define the distance between two words of the same length to be the number of positions in which those two words have different letters. Any two words related by a transposition have distance 0 or 2 ; any two words related by a sequence of two transpositions have distance $0,2,3$ or 4 .
Say the period of a repetitive word is the least $k$ such that the word is the concatenation of two or more identical subwords of length $k$. We use the following lemma on distances between repetitive words.
Lemma. Consider a pair of distinct, nonconstant repetitive words with periods ga and gb, where $(a, b)=1$ and $a, b>1$, the first word is made up of $k b$ repetitions of the subword of length ga and the second word is made up of ka repetitions of the subword of length gb . These two words have distance at least $\max (k a, k b)$.
Proof. We may assume $k=1$, since the distance between the words is $k$ times the distance between their initial subwords of length $g a b$. Without loss of generality suppose $b>a$.
For each positive integer $m$, look at the subsequence in each word of letters in positions congruent to $m$ $(\bmod g)$. Those subsequences (of length $a b)$ have periods dividing $a$ and $b$ respectively. If they are equal, then they are constant (since each letter is equal to those $a$ and $b$ before and after it, mod $a b$, and $(a, b)=1$ ). Because $a>1$, there is some $m$ for which the first subsequence is not constant, and so is unequal to the second subsequence. Restrict attention to those subsequences.
We now have two distinct repetitive words, one (nonconstant) made up of $b$ repetitions of a subword of length $a$ and one made up of $a$ repetitions of a subword of length $b$. Looking at the first of those words, for any $1 \leq t \leq b$ consider the letters in positions $t, t+b, \ldots, t+(a-1) b$. These letters cover every position (mod $a)$; since the first word is not constant, the letters are not all equal, but the letters in the corresponding positions in the second word are all equal. At least one of these letters in the first word must change to make them all equal to those in the corresponding positions in the second word; repeating for each $t$, at least $b$ letters must change, so the words have distance at least $b$.
In the original problem, consider all the words (which we suppose to be repetitive) obtained by a transposition of two adjacent letters from the original nonconstant word; say that word has length $n$. Suppose those words include two distinct words with periods $n / a$ and $n / b$; those words have distance at most 4 . If $a>4$ or $b>4$, we have a contradiction unless $a \mid b$ or $b \mid a$. If $a>4$ is the greatest number of repetitions in any of the words ( $n / a$ is the smallest period), then unless all the numbers of repetitions divide each other there must be words with 2 or 4 repetitions, words with 3 repetitions and all larger numbers of repetitions must divide each other and be divisible by 6 .
We now divide into three cases: all the numbers of repetitions may divide either other; or there may be words with (multiples of) 2,3 and 6 repetitions; or all words may have at most 4 repetitions, with at least one word having 3 repetitions and at least one having 2 or 4 repetitions.
Case 1. Suppose all the numbers of repetitions divide each other. Let $k$ be the least number of repetitions. Consider the word as being divided into $k$ blocks, each of $\ell$ letters; any transposition of two adjacent letters leaves those blocks identical. If any two adjacent letters within a block are the same, then this means all the blocks are already identical; since the word is not constant, the letters in the first block are not all identical, so there are two distinct adjacent letters in the first block, and transposing them leaves it distinct from the other blocks, a contradiction. Otherwise, all pairs of adjacent letters within each block are distinct; transposing any adjacent pair within the first block leaves it identical to the second block. If the first block has more than two letters, this is impossible since transposing the first two letters has a different result from transposing the second two. So the blocks all have length 2 ; similarly, there are just two blocks, the arrangement is $a b b a$ but transposing the adjacent letters $b b$ does not leave the word repetitive.
Case 2. Suppose some word resulting from a transposition is made of (a multiple of) 6 repetitions, some of 3 repetitions and some of 2 repetitions (or 4 repetitions, counted as 2 ). Consider it as a sequence of 6 blocks, each of length $\ell$. If the six blocks are already identical, then as the word is not constant, there are some two distinct adjacent letters within the first block; transposing them leaves a result where the blocks form a
pattern $B A A A A A$, which cannot have two, three or six repetitions. So the six blocks are not already identical. If a transposition within a block results in them being identical, the blocks form a pattern (without loss of generality) $B A A A A A, A B A A A A$ or $A A B A A A$. In any of these cases, apply the same transposition (that converts between $A$ and $B$ ) to an $A$ block adjacent to the $B$ block, and the result cannot have two, three or six repetitions. Finally, consider the case where some transposition between two adjacent blocks results in all six blocks being identical. The patterns are $B C A A A A, A B C A A A$ and $A A B C A A$ (and considering the letters at the start and end of each block shows $B \neq C$ ). In all cases, transposing two adjacent distinct letters within an $A$ block produces a result that cannot have two, three or six repetitions.
Case 3. In the remaining case, all words have at most 4 repetitions, at least one has 3 repetitions and at least one has 2 or 4 repetitions. For the purposes of this case we will think of 4 -repetition words as being 2 -repetition words. The number of each letter is a multiple of 6 , so $n \geq 12$; consider the word as made of six blocks of length $\ell$.
If the word is already repetitive with 2 repetitions, pattern $A B C A B C$, any transposition between two distinct letters leaves it no longer repetitive with two repetitions, so it must instead have three repetitions after the transposition. If $A B$ is not all one letter, transposing two adjacent letters within $A B$ implies that $C A=B C$, so $A=B=C$, the word has pattern $A A A A A A$ but transposing within the initial $A A$ means it no longer has 3 repetitions. This implies that $A B$ is all one letter, but similarly $B C$ must also be all one letter and so the word is constant, a contradiction.
If the word is already repetitive with 3 repetitions, it has pattern $A B A B A B$ and any transposition leaves it no longer having 3 repetitions, so having 2 repetitions instead. $A B A$ is not made all of one letter (since the word is not constant) and any transposition between two adjacent distinct letters therein turns it into $B A B$; such a transposition affects at most two of the blocks, so $A=B$, the word has pattern $A A A A A A$ and transposing two adjacent distinct letters within the first half cannot leave it with two repetitions.
So the word is not already repetitive, and so no two adjacent letters are the same; all transpositions give distinct strings. Consider transpositions of adjacent letters within the first four letters; three different words result, of which at most one is periodic with two repetitions (it must be made of two copies of the second half of the word) and at most one is periodic with three repetitions, a contradiction.
|
{
"exam": "EGMO",
"problem_label": "8",
"problem_match": "\nProblem 8.",
"resource_path": "EGMO/segmented/en-2012-solutions-day2.jsonl",
"solution_match": "\nSolution 3 (PSC).",
"tier": "T2",
"year": "2012"
}
|
The side $B C$ of the triangle $A B C$ is extended beyond $C$ to $D$ so that $C D=B C$. The side $C A$ is extended beyond $A$ to $E$ so that $A E=2 C A$.
Prove that if $A D=B E$, then the triangle $A B C$ is right-angled.
|
Define $F$ so that $A B F D$ is a parallelogram. Then $E, A, C, F$ are collinear (as diagonals of a parallelogram bisect each other) and $B F=A D=B E$. Further, $A$ is the midpoint of $E F$, since $A F=2 A C$, and thus $A B$ is an altitude of the isosceles triangle $E B F$ with apex $B$. Therefore $A B \perp A C$.
A Variant. Let $P$ be the midpoint of $[A E]$, so that $A P=A B$ because $A E=2 A B$. Let $Q$ be the midpoint of $[A B]$. Then $P Q=\frac{1}{2} B E=\frac{1}{2} A D=C Q$. Hence $P A$ is a median of the isosceles triangle $C P Q$. In other words, $P A \perp A B$, which completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The side $B C$ of the triangle $A B C$ is extended beyond $C$ to $D$ so that $C D=B C$. The side $C A$ is extended beyond $A$ to $E$ so that $A E=2 C A$.
Prove that if $A D=B E$, then the triangle $A B C$ is right-angled.
|
Define $F$ so that $A B F D$ is a parallelogram. Then $E, A, C, F$ are collinear (as diagonals of a parallelogram bisect each other) and $B F=A D=B E$. Further, $A$ is the midpoint of $E F$, since $A F=2 A C$, and thus $A B$ is an altitude of the isosceles triangle $E B F$ with apex $B$. Therefore $A B \perp A C$.

A Variant. Let $P$ be the midpoint of $[A E]$, so that $A P=A B$ because $A E=2 A B$. Let $Q$ be the midpoint of $[A B]$. Then $P Q=\frac{1}{2} B E=\frac{1}{2} A D=C Q$. Hence $P A$ is a median of the isosceles triangle $C P Q$. In other words, $P A \perp A B$, which completes the proof.

|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "\nProblem 1. (Proposed by David Monk, United Kingdom)\n",
"resource_path": "EGMO/segmented/en-2013-solutions.jsonl",
"solution_match": "\nSolution 1: ",
"tier": "T2",
"year": "2013"
}
|
The side $B C$ of the triangle $A B C$ is extended beyond $C$ to $D$ so that $C D=B C$. The side $C A$ is extended beyond $A$ to $E$ so that $A E=2 C A$.
Prove that if $A D=B E$, then the triangle $A B C$ is right-angled.
|
Notice that $A$ is the centroid of triangle $B D E$, since $C$ is the midpoint of $[B D]$ and $A E=2 C A$. Let $M$ be the midpoint of $[B E]$. Then $M, A, D$ lie on a line, and further, $A M=\frac{1}{2} A D=\frac{1}{2} B E$. This implies that $\angle E A B=90^{\circ}$.
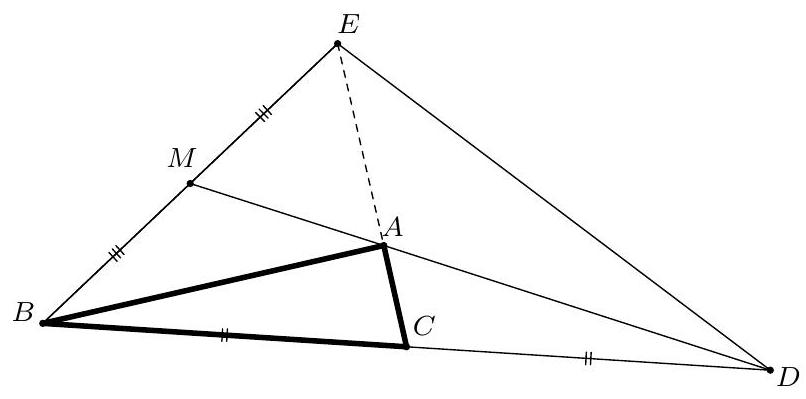
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The side $B C$ of the triangle $A B C$ is extended beyond $C$ to $D$ so that $C D=B C$. The side $C A$ is extended beyond $A$ to $E$ so that $A E=2 C A$.
Prove that if $A D=B E$, then the triangle $A B C$ is right-angled.
|
Notice that $A$ is the centroid of triangle $B D E$, since $C$ is the midpoint of $[B D]$ and $A E=2 C A$. Let $M$ be the midpoint of $[B E]$. Then $M, A, D$ lie on a line, and further, $A M=\frac{1}{2} A D=\frac{1}{2} B E$. This implies that $\angle E A B=90^{\circ}$.

|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "\nProblem 1. (Proposed by David Monk, United Kingdom)\n",
"resource_path": "EGMO/segmented/en-2013-solutions.jsonl",
"solution_match": "\nSolution 2: ",
"tier": "T2",
"year": "2013"
}
|
The side $B C$ of the triangle $A B C$ is extended beyond $C$ to $D$ so that $C D=B C$. The side $C A$ is extended beyond $A$ to $E$ so that $A E=2 C A$.
Prove that if $A D=B E$, then the triangle $A B C$ is right-angled.
|
Let $P$ be the midpoint $[A E]$. Since $C$ is the midpoint of $[B D]$, and, moreover, $A C=E P$, we have
$$
[A C D]=[A B C]=[E B P]
$$
But $A D=B E$, and, as mentioned previously, $A C=E P$, so this implies that
$$
\angle B E P=\angle C A D \text { or } \angle B E P=180^{\circ}-\angle C A D .
$$
But $\angle B E P<\angle B A C$ and $\angle B A C+\angle C A D=\angle B A D<180^{\circ}$, so we must be in the first case, i.e. $\angle B E P=\angle C A D$. It follows that triangles $B E P$ and $D A C$ are congruent, and thus $\angle B P A=\angle A C B$. But $A P=A C$, so $B A$ is a median of the isosceles triangle $B C P$. Thus $A B \perp P C$, completing the proof.
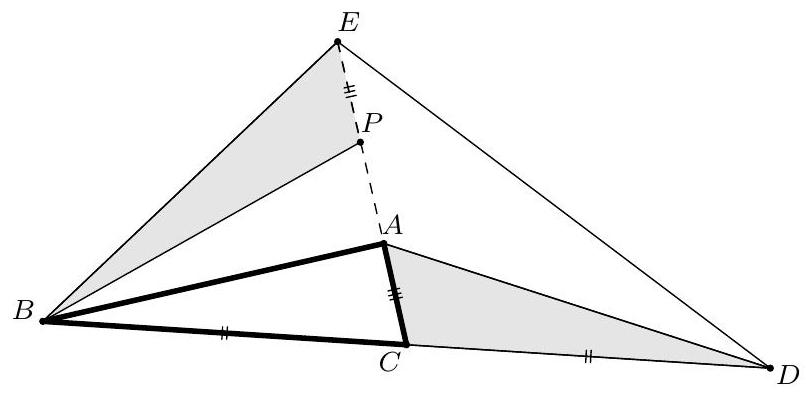
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The side $B C$ of the triangle $A B C$ is extended beyond $C$ to $D$ so that $C D=B C$. The side $C A$ is extended beyond $A$ to $E$ so that $A E=2 C A$.
Prove that if $A D=B E$, then the triangle $A B C$ is right-angled.
|
Let $P$ be the midpoint $[A E]$. Since $C$ is the midpoint of $[B D]$, and, moreover, $A C=E P$, we have
$$
[A C D]=[A B C]=[E B P]
$$
But $A D=B E$, and, as mentioned previously, $A C=E P$, so this implies that
$$
\angle B E P=\angle C A D \text { or } \angle B E P=180^{\circ}-\angle C A D .
$$
But $\angle B E P<\angle B A C$ and $\angle B A C+\angle C A D=\angle B A D<180^{\circ}$, so we must be in the first case, i.e. $\angle B E P=\angle C A D$. It follows that triangles $B E P$ and $D A C$ are congruent, and thus $\angle B P A=\angle A C B$. But $A P=A C$, so $B A$ is a median of the isosceles triangle $B C P$. Thus $A B \perp P C$, completing the proof.

|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "\nProblem 1. (Proposed by David Monk, United Kingdom)\n",
"resource_path": "EGMO/segmented/en-2013-solutions.jsonl",
"solution_match": "\nSolution 3: ",
"tier": "T2",
"year": "2013"
}
|
The side $B C$ of the triangle $A B C$ is extended beyond $C$ to $D$ so that $C D=B C$. The side $C A$ is extended beyond $A$ to $E$ so that $A E=2 C A$.
Prove that if $A D=B E$, then the triangle $A B C$ is right-angled.
|
Write $\beta=\angle E C B$, and let $x=A C, y=B C=C D, z=B E=A D$. Notice that $E C=3 x$. Then, using the cosine theorem,
$$
\begin{array}{ll}
z^{2}=x^{2}+y^{2}+2 x y \cos \beta & \text { in triangle } A C D ; \\
z^{2}=9 x^{2}+y^{2}-6 x y \cos \beta & \text { in triangle } B C E .
\end{array}
$$
Hence $4 z^{2}=12 x^{2}+4 y^{2}$ or $z^{2}-y^{2}=3 x^{2}$. Let $H$ be the foot of the perpendicular through $B$ to $A C$, and write $h=B H$. Then
$$
y^{2}-h^{2}=C H^{2}, z^{2}-h^{2}=E H^{2}
$$
Hence $z^{2}-y^{2}=E H^{2}-C H^{2}$. Substituting from the above,
$$
E H^{2}-C H^{2}=3 x^{2}=E A^{2}-C A^{2} .
$$
Thus $H=A$, and hence the triangle $A B C$ is right-angled at $A$.
Remark. It is possible to conclude directly from $z^{2}-y^{2}=3 x^{2}=(2 x)^{2}-x^{2}$ using Carnot's theorem.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The side $B C$ of the triangle $A B C$ is extended beyond $C$ to $D$ so that $C D=B C$. The side $C A$ is extended beyond $A$ to $E$ so that $A E=2 C A$.
Prove that if $A D=B E$, then the triangle $A B C$ is right-angled.
|
Write $\beta=\angle E C B$, and let $x=A C, y=B C=C D, z=B E=A D$. Notice that $E C=3 x$. Then, using the cosine theorem,
$$
\begin{array}{ll}
z^{2}=x^{2}+y^{2}+2 x y \cos \beta & \text { in triangle } A C D ; \\
z^{2}=9 x^{2}+y^{2}-6 x y \cos \beta & \text { in triangle } B C E .
\end{array}
$$
Hence $4 z^{2}=12 x^{2}+4 y^{2}$ or $z^{2}-y^{2}=3 x^{2}$. Let $H$ be the foot of the perpendicular through $B$ to $A C$, and write $h=B H$. Then
$$
y^{2}-h^{2}=C H^{2}, z^{2}-h^{2}=E H^{2}
$$
Hence $z^{2}-y^{2}=E H^{2}-C H^{2}$. Substituting from the above,
$$
E H^{2}-C H^{2}=3 x^{2}=E A^{2}-C A^{2} .
$$
Thus $H=A$, and hence the triangle $A B C$ is right-angled at $A$.
Remark. It is possible to conclude directly from $z^{2}-y^{2}=3 x^{2}=(2 x)^{2}-x^{2}$ using Carnot's theorem.
|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "\nProblem 1. (Proposed by David Monk, United Kingdom)\n",
"resource_path": "EGMO/segmented/en-2013-solutions.jsonl",
"solution_match": "\nSolution 4: ",
"tier": "T2",
"year": "2013"
}
|
The side $B C$ of the triangle $A B C$ is extended beyond $C$ to $D$ so that $C D=B C$. The side $C A$ is extended beyond $A$ to $E$ so that $A E=2 C A$.
Prove that if $A D=B E$, then the triangle $A B C$ is right-angled.
|
Writing $a=B C, b=C A, c=A B$, we have
$$
\left.\begin{array}{rlrl}
a^{2} & =b^{2}+c^{2}-2 b c \cos \angle A \\
c^{2} & =a^{2}+b^{2}-2 a b \cos \angle C
\end{array}\right\} \quad \begin{array}{ll}
\text { in triangle } A B C ; \\
E B^{2} & =4 b^{2}+c^{2}+4 b c \cos \angle A \\
A D^{2} & =a^{2}+b^{2}+2 a b \cos \angle C
\end{array} \quad \begin{aligned}
& \text { in triangle } A E B ; \\
& \text { in triangle } A C D .
\end{aligned}
$$
Thus
$$
\begin{aligned}
6 b^{2}+3 c^{2}-2 a^{2} & =4 b^{2}+c^{2}+4 b c \cos \angle A=E B^{2}=A D^{2} \\
& =a^{2}+b^{2}+2 a b \cos \angle C=2 a^{2}+2 b^{2}-c^{2}
\end{aligned}
$$
which gives $a^{2}=b^{2}+c^{2}$. Therefore $\angle B A C$ is a right angle by the converse of the theorem of Pythagoras.
|
a^{2}=b^{2}+c^{2}
|
Yes
|
Yes
|
proof
|
Geometry
|
The side $B C$ of the triangle $A B C$ is extended beyond $C$ to $D$ so that $C D=B C$. The side $C A$ is extended beyond $A$ to $E$ so that $A E=2 C A$.
Prove that if $A D=B E$, then the triangle $A B C$ is right-angled.
|
Writing $a=B C, b=C A, c=A B$, we have
$$
\left.\begin{array}{rlrl}
a^{2} & =b^{2}+c^{2}-2 b c \cos \angle A \\
c^{2} & =a^{2}+b^{2}-2 a b \cos \angle C
\end{array}\right\} \quad \begin{array}{ll}
\text { in triangle } A B C ; \\
E B^{2} & =4 b^{2}+c^{2}+4 b c \cos \angle A \\
A D^{2} & =a^{2}+b^{2}+2 a b \cos \angle C
\end{array} \quad \begin{aligned}
& \text { in triangle } A E B ; \\
& \text { in triangle } A C D .
\end{aligned}
$$
Thus
$$
\begin{aligned}
6 b^{2}+3 c^{2}-2 a^{2} & =4 b^{2}+c^{2}+4 b c \cos \angle A=E B^{2}=A D^{2} \\
& =a^{2}+b^{2}+2 a b \cos \angle C=2 a^{2}+2 b^{2}-c^{2}
\end{aligned}
$$
which gives $a^{2}=b^{2}+c^{2}$. Therefore $\angle B A C$ is a right angle by the converse of the theorem of Pythagoras.
|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "\nProblem 1. (Proposed by David Monk, United Kingdom)\n",
"resource_path": "EGMO/segmented/en-2013-solutions.jsonl",
"solution_match": "\nSolution 5: ",
"tier": "T2",
"year": "2013"
}
|
The side $B C$ of the triangle $A B C$ is extended beyond $C$ to $D$ so that $C D=B C$. The side $C A$ is extended beyond $A$ to $E$ so that $A E=2 C A$.
Prove that if $A D=B E$, then the triangle $A B C$ is right-angled.
|
Let $\overrightarrow{A C}=\vec{x}$ and $\overrightarrow{A B}=\vec{y}$. Now $\overrightarrow{A D}=2 \vec{x}-\vec{y}$ and $\overrightarrow{E B}=2 \vec{x}+\vec{y}$. Then
$$
\overrightarrow{B E} \cdot \overrightarrow{B E}=\overrightarrow{A D} \cdot \overrightarrow{A D} \quad \Longleftrightarrow \quad(2 \vec{x}+\vec{y})^{2}=(2 \vec{x}-\vec{y})^{2} \quad \Longleftrightarrow \quad \vec{x} \cdot \vec{y}=0
$$
and thus $A C \perp A B$, whence triangle $A B C$ is right-angled at $A$.
Remark. It is perhaps more natural to introduce $\overrightarrow{C A}=\vec{a}$ and $\overrightarrow{C B}=\vec{b}$. Then we have the equality
$$
(3 \vec{a}-\vec{b})^{2}=(\vec{a}+\vec{b})^{2} \quad \Longrightarrow \quad \vec{a} \cdot(\vec{a}-\vec{b})=0
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The side $B C$ of the triangle $A B C$ is extended beyond $C$ to $D$ so that $C D=B C$. The side $C A$ is extended beyond $A$ to $E$ so that $A E=2 C A$.
Prove that if $A D=B E$, then the triangle $A B C$ is right-angled.
|
Let $\overrightarrow{A C}=\vec{x}$ and $\overrightarrow{A B}=\vec{y}$. Now $\overrightarrow{A D}=2 \vec{x}-\vec{y}$ and $\overrightarrow{E B}=2 \vec{x}+\vec{y}$. Then
$$
\overrightarrow{B E} \cdot \overrightarrow{B E}=\overrightarrow{A D} \cdot \overrightarrow{A D} \quad \Longleftrightarrow \quad(2 \vec{x}+\vec{y})^{2}=(2 \vec{x}-\vec{y})^{2} \quad \Longleftrightarrow \quad \vec{x} \cdot \vec{y}=0
$$
and thus $A C \perp A B$, whence triangle $A B C$ is right-angled at $A$.
Remark. It is perhaps more natural to introduce $\overrightarrow{C A}=\vec{a}$ and $\overrightarrow{C B}=\vec{b}$. Then we have the equality
$$
(3 \vec{a}-\vec{b})^{2}=(\vec{a}+\vec{b})^{2} \quad \Longrightarrow \quad \vec{a} \cdot(\vec{a}-\vec{b})=0
$$
|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "\nProblem 1. (Proposed by David Monk, United Kingdom)\n",
"resource_path": "EGMO/segmented/en-2013-solutions.jsonl",
"solution_match": "\nSolution 6: ",
"tier": "T2",
"year": "2013"
}
|
The side $B C$ of the triangle $A B C$ is extended beyond $C$ to $D$ so that $C D=B C$. The side $C A$ is extended beyond $A$ to $E$ so that $A E=2 C A$.
Prove that if $A D=B E$, then the triangle $A B C$ is right-angled.
|
Let $a, b, c, d, e$ denote the complex co-ordinates of the points $A, B, C, D$, $E$ and take the unit circle to be the circumcircle of $A B C$. We have
$$
d=b+2(c-b)=2 c-b \quad \text { and } \quad e=c+3(a-c)=3 a-2 c .
$$
Thus $b-e=(d-a)+2(b-a)$, and hence
$$
\begin{aligned}
B E=A D & \Longleftrightarrow(b-e)(\overline{b-e})=(d-a)(\overline{d-a}) \\
& \Longleftrightarrow 2(d-a)(\overline{b-a})+2(\overline{d-a})(b-a)+4(b-a)(\overline{b-a})=0 \\
& \Longleftrightarrow 2(d-a)(a-b)+2(\overline{d-a})(b-a) a b+4(b-a)(a-b)=0 \\
& \Longleftrightarrow(d-a)-(\overline{d-a}) a b+2(b-a)=0 \\
& \Longleftrightarrow 2 c-b-a-2 \bar{c} a b+a+b+2(b-a)=0 \\
& \Longleftrightarrow c^{2}-a b+b c-a c=0 \\
& \Longleftrightarrow(b+c)(c-a)=0,
\end{aligned}
$$
implying $c=-b$ and that triangle $A B C$ is right-angled at $A$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The side $B C$ of the triangle $A B C$ is extended beyond $C$ to $D$ so that $C D=B C$. The side $C A$ is extended beyond $A$ to $E$ so that $A E=2 C A$.
Prove that if $A D=B E$, then the triangle $A B C$ is right-angled.
|
Let $a, b, c, d, e$ denote the complex co-ordinates of the points $A, B, C, D$, $E$ and take the unit circle to be the circumcircle of $A B C$. We have
$$
d=b+2(c-b)=2 c-b \quad \text { and } \quad e=c+3(a-c)=3 a-2 c .
$$
Thus $b-e=(d-a)+2(b-a)$, and hence
$$
\begin{aligned}
B E=A D & \Longleftrightarrow(b-e)(\overline{b-e})=(d-a)(\overline{d-a}) \\
& \Longleftrightarrow 2(d-a)(\overline{b-a})+2(\overline{d-a})(b-a)+4(b-a)(\overline{b-a})=0 \\
& \Longleftrightarrow 2(d-a)(a-b)+2(\overline{d-a})(b-a) a b+4(b-a)(a-b)=0 \\
& \Longleftrightarrow(d-a)-(\overline{d-a}) a b+2(b-a)=0 \\
& \Longleftrightarrow 2 c-b-a-2 \bar{c} a b+a+b+2(b-a)=0 \\
& \Longleftrightarrow c^{2}-a b+b c-a c=0 \\
& \Longleftrightarrow(b+c)(c-a)=0,
\end{aligned}
$$
implying $c=-b$ and that triangle $A B C$ is right-angled at $A$.
|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "\nProblem 1. (Proposed by David Monk, United Kingdom)\n",
"resource_path": "EGMO/segmented/en-2013-solutions.jsonl",
"solution_match": "\nSolution 7: ",
"tier": "T2",
"year": "2013"
}
|
The side $B C$ of the triangle $A B C$ is extended beyond $C$ to $D$ so that $C D=B C$. The side $C A$ is extended beyond $A$ to $E$ so that $A E=2 C A$.
Prove that if $A D=B E$, then the triangle $A B C$ is right-angled.
|
We use areal co-ordinates with reference to the triangle $A B C$. Recall that if $\left(x_{1}, y_{1}, z_{1}\right)$ and $\left(x_{2}, y_{2}, z_{2}\right)$ are points in the plane, then the square of the distance between these two points is $-a^{2} v w-b^{2} w u-c^{2} u v$, where $(u, v, w)=\left(x_{1}-x_{2}, y_{1}-y_{2}, z_{1}-z_{2}\right)$.
In our case $A=(1,0,0), B=(0,1,0), C=(0,0,1)$, so $E=(3,0,2)$ and, introducing point $F$ as in the first solution, $F=(-1,0,2)$. Then
$$
B E^{2}=A D^{2} \quad \Longleftrightarrow \quad-2 a^{2}+6 b^{2}+3 c^{2}=2 a^{2}+2 b^{2}-c^{2},
$$
and thus $a^{2}=b^{2}+c^{2}$. Therefore $\angle B A C$ is a right angle by the converse of the theorem of Pythagoras.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The side $B C$ of the triangle $A B C$ is extended beyond $C$ to $D$ so that $C D=B C$. The side $C A$ is extended beyond $A$ to $E$ so that $A E=2 C A$.
Prove that if $A D=B E$, then the triangle $A B C$ is right-angled.
|
We use areal co-ordinates with reference to the triangle $A B C$. Recall that if $\left(x_{1}, y_{1}, z_{1}\right)$ and $\left(x_{2}, y_{2}, z_{2}\right)$ are points in the plane, then the square of the distance between these two points is $-a^{2} v w-b^{2} w u-c^{2} u v$, where $(u, v, w)=\left(x_{1}-x_{2}, y_{1}-y_{2}, z_{1}-z_{2}\right)$.
In our case $A=(1,0,0), B=(0,1,0), C=(0,0,1)$, so $E=(3,0,2)$ and, introducing point $F$ as in the first solution, $F=(-1,0,2)$. Then
$$
B E^{2}=A D^{2} \quad \Longleftrightarrow \quad-2 a^{2}+6 b^{2}+3 c^{2}=2 a^{2}+2 b^{2}-c^{2},
$$
and thus $a^{2}=b^{2}+c^{2}$. Therefore $\angle B A C$ is a right angle by the converse of the theorem of Pythagoras.
|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "\nProblem 1. (Proposed by David Monk, United Kingdom)\n",
"resource_path": "EGMO/segmented/en-2013-solutions.jsonl",
"solution_match": "\nSolution 8: ",
"tier": "T2",
"year": "2013"
}
|
Determine all integers $m$ for which the $m \times m$ square can be dissected into five rectangles, the side lengths of which are the integers $1,2,3, \ldots, 10$ in some order.
|
The solution naturally divides into three different parts: we first obtain some bounds on $m$. We then describe the structure of possible dissections, and finally, we deal with the few remaining cases.
In the first part of the solution, we get rid of the cases with $m \leqslant 10$ or $m \geqslant 14$. Let $\ell_{1}, \ldots, \ell_{5}$ and $w_{1}, \ldots, w_{5}$ be the lengths and widths of the five rectangles. Then the rearrangement inequality yields the lower bound
$$
\begin{aligned}
\ell_{1} w_{1} & +\ell_{2} w_{2}+\ell_{3} w_{3}+\ell_{4} w_{4}+\ell_{5} w_{5} \\
& =\frac{1}{2}\left(\ell_{1} w_{1}+\ell_{2} w_{2}+\ell_{3} w_{3}+\ell_{4} w_{4}+\ell_{5} w_{5}+w_{1} \ell_{1}+w_{2} \ell_{2}+w_{3} \ell_{3}+w_{3} \ell_{4}+w_{5} \ell_{5}\right) \\
& \geqslant \frac{1}{2}(1 \cdot 10+2 \cdot 9+3 \cdot 8+\cdots+8 \cdot 3+9 \cdot 2+10 \cdot 1)=110
\end{aligned}
$$
and the upper bound
$$
\begin{aligned}
\ell_{1} w_{1} & +\ell_{2} w_{2}+\ell_{3} w_{3}+\ell_{4} w_{4}+\ell_{5} w_{5} \\
& =\frac{1}{2}\left(\ell_{1} w_{1}+\ell_{2} w_{2}+\ell_{3} w_{3}+\ell_{4} w_{4}+\ell_{5} w_{5}+w_{1} \ell_{1}+w_{2} \ell_{2}+w_{3} \ell_{3}+w_{3} \ell_{4}+w_{5} \ell_{5}\right) \\
& \leqslant \frac{1}{2}(1 \cdot 1+2 \cdot 2+3 \cdot 3+\cdots+8 \cdot 8+9 \cdot 9+10 \cdot 10)=192.5
\end{aligned}
$$
As the area of the square is sandwiched between 110 and 192.5, the only possible candidates for $m$ are 11,12 , and 13 .
In the second part of the solution, we show that a dissection of the square into five rectangles must consist of a single inner rectangle and four outer rectangles that each cover one of the four corners of the square. Indeed, if one of the sides the square had three rectangles adjacent to it, removing these three rectangles would leave a polygon with eight vertices, which is clearly not the union of two rectangles. Moreover, since $m>10$, each side of the square has at least two adjacent rectangles. Hence each side of the square has precisely two adjacent rectangles, and thus the only way of partitionning the square into five rectangles is to have a single inner rectangle and four outer rectangles each covering of the four corners of the square, as claimed.
Let us now show that a square of size $12 \times 12$ cannot be dissected in the desired way. Let $R_{1}, R_{2}, R_{3}$ and $R_{4}$ be the outer rectangles (in clockwise orientation along the
boundary of the square). If an outer rectangle has a side of length $s$, then some adjacent outer rectangle must have a side of length $12-s$. Therefore, neither of $s=1$ or $s=6$ can be sidelengths of an outer rectangle, so the inner rectangle must have dimensions $1 \times 6$. One of the outer rectangles (say $R_{1}$ ) must have dimensions $10 \times x$, and an adjacent rectangle (say $R_{2}$ ) must thus have dimensions $2 \times y$. Rectangle $R_{3}$ then has dimensions $(12-y) \times z$, and rectangle $R_{4}$ has dimensions $(12-z) \times(12-x)$. Note that exactly one of the three numbers $x, y, z$ is even (and equals 4 or 8 ), while the other two numbers are odd. Now, the total area of all five rectangles is
$$
144=6+10 x+2 y+(12-y) z+(12-z)(12-x),
$$
which simplifies to $(y-x)(z-2)=6$. As exactly one of the three numbers $x, y, z$ is even, the factors $y-x$ and $z-2$ are either both even or both odd, so their product cannot equal 6 , and thus there is no solution with $m=12$.
Finally, we handle the cases $m=11$ and $m=13$, which indeed are solutions. The corresponding rectangle sets are $10 \times 5,1 \times 9,8 \times 2,7 \times 4$ and $3 \times 6$ for $m=11$, and $10 \times 5,9 \times 8,4 \times 6,3 \times 7$ and $1 \times 2$ for $m=13$. These sets can be found by trial and error. The corresponding partitions are shown in the figure below.
Remark. The configurations for $m=11$ and $m=13$ given above are not unique.
A Variant for Obtaining Bounds. We first exclude the cases $m \leqslant 9$ by the observation that one of the small rectangles has a side of length 10 and must fit into the square; hence $m \geqslant 10$.
To exclude the cases $m \geqslant 14$, we work via the perimeter: as every rectangle has at most two sides on the boundary of the $m \times m$ square, the perimeter $4 m$ of the square is bounded by $1+2+3+4+5+6+7+8+9+10=55$; hence $m \leqslant 13$.
We are left to deal with the case $m=10$ : clearly, the rectangle with side length 10 must have one its sides of length 10 along the boundary of the square. The remaining rectangle $R$ of dimensions $10 \times s$, say, would have to be divided into four rectangles with different sidelengths strictly less than 10 . If there were at least two rectangles adjacent to one of the sides of length $s$ of $R$, removing these two rectangles from $R$ would leave a polygon with at least six vertices (since the sidelengths of the rectangles partitioning $R$ are strictly less than 10). It is clearly impossible to partition such a polygon into no more than two rectangles with different sidelengths. Hence, given a side of length $s$ of $R$, there is only one rectangle adjacent to that side, so the rectangles adjacent to the sides of length $s$ of $R$ would have to have the same length $s$, a contradiction.
Remark. Note that the argument of the second part of the main solution cannot be directly applied to the case $m=10$.
A Variant for Dealing with $\boldsymbol{m}=12$. As in the previous solution, we show that the inner rectangle must have dimensions $1 \times 6$. Since the area of the square and the area of the inner rectangle are even, the areas of the four outer rectangles must sum to an even number. Now the four sides of the square are divided into segments of lengths 2 and 10, 3 and 9,4 and 8 , and 5 and 7 . Hence the sides with adjacent segments of lengths 3 and 9 , and 5 and 7 must be opposite sides of the square (otherwise, exactly one of the outer rectangles would have odd area). However, the difference of two rectangle side lengths on opposite sides of the square must be 1 or 6 (in order to accomodate the inner rectangle). This is not the case, so there is no solution with $m=12$.
Remark. In the case $m=12$, having shown that the inner rectangle must have dimensions $1 \times 6$, this case can also be dealt with by listing the remaining configurations one by one.
|
not found
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Determine all integers $m$ for which the $m \times m$ square can be dissected into five rectangles, the side lengths of which are the integers $1,2,3, \ldots, 10$ in some order.
|
The solution naturally divides into three different parts: we first obtain some bounds on $m$. We then describe the structure of possible dissections, and finally, we deal with the few remaining cases.
In the first part of the solution, we get rid of the cases with $m \leqslant 10$ or $m \geqslant 14$. Let $\ell_{1}, \ldots, \ell_{5}$ and $w_{1}, \ldots, w_{5}$ be the lengths and widths of the five rectangles. Then the rearrangement inequality yields the lower bound
$$
\begin{aligned}
\ell_{1} w_{1} & +\ell_{2} w_{2}+\ell_{3} w_{3}+\ell_{4} w_{4}+\ell_{5} w_{5} \\
& =\frac{1}{2}\left(\ell_{1} w_{1}+\ell_{2} w_{2}+\ell_{3} w_{3}+\ell_{4} w_{4}+\ell_{5} w_{5}+w_{1} \ell_{1}+w_{2} \ell_{2}+w_{3} \ell_{3}+w_{3} \ell_{4}+w_{5} \ell_{5}\right) \\
& \geqslant \frac{1}{2}(1 \cdot 10+2 \cdot 9+3 \cdot 8+\cdots+8 \cdot 3+9 \cdot 2+10 \cdot 1)=110
\end{aligned}
$$
and the upper bound
$$
\begin{aligned}
\ell_{1} w_{1} & +\ell_{2} w_{2}+\ell_{3} w_{3}+\ell_{4} w_{4}+\ell_{5} w_{5} \\
& =\frac{1}{2}\left(\ell_{1} w_{1}+\ell_{2} w_{2}+\ell_{3} w_{3}+\ell_{4} w_{4}+\ell_{5} w_{5}+w_{1} \ell_{1}+w_{2} \ell_{2}+w_{3} \ell_{3}+w_{3} \ell_{4}+w_{5} \ell_{5}\right) \\
& \leqslant \frac{1}{2}(1 \cdot 1+2 \cdot 2+3 \cdot 3+\cdots+8 \cdot 8+9 \cdot 9+10 \cdot 10)=192.5
\end{aligned}
$$
As the area of the square is sandwiched between 110 and 192.5, the only possible candidates for $m$ are 11,12 , and 13 .
In the second part of the solution, we show that a dissection of the square into five rectangles must consist of a single inner rectangle and four outer rectangles that each cover one of the four corners of the square. Indeed, if one of the sides the square had three rectangles adjacent to it, removing these three rectangles would leave a polygon with eight vertices, which is clearly not the union of two rectangles. Moreover, since $m>10$, each side of the square has at least two adjacent rectangles. Hence each side of the square has precisely two adjacent rectangles, and thus the only way of partitionning the square into five rectangles is to have a single inner rectangle and four outer rectangles each covering of the four corners of the square, as claimed.
Let us now show that a square of size $12 \times 12$ cannot be dissected in the desired way. Let $R_{1}, R_{2}, R_{3}$ and $R_{4}$ be the outer rectangles (in clockwise orientation along the
boundary of the square). If an outer rectangle has a side of length $s$, then some adjacent outer rectangle must have a side of length $12-s$. Therefore, neither of $s=1$ or $s=6$ can be sidelengths of an outer rectangle, so the inner rectangle must have dimensions $1 \times 6$. One of the outer rectangles (say $R_{1}$ ) must have dimensions $10 \times x$, and an adjacent rectangle (say $R_{2}$ ) must thus have dimensions $2 \times y$. Rectangle $R_{3}$ then has dimensions $(12-y) \times z$, and rectangle $R_{4}$ has dimensions $(12-z) \times(12-x)$. Note that exactly one of the three numbers $x, y, z$ is even (and equals 4 or 8 ), while the other two numbers are odd. Now, the total area of all five rectangles is
$$
144=6+10 x+2 y+(12-y) z+(12-z)(12-x),
$$
which simplifies to $(y-x)(z-2)=6$. As exactly one of the three numbers $x, y, z$ is even, the factors $y-x$ and $z-2$ are either both even or both odd, so their product cannot equal 6 , and thus there is no solution with $m=12$.
Finally, we handle the cases $m=11$ and $m=13$, which indeed are solutions. The corresponding rectangle sets are $10 \times 5,1 \times 9,8 \times 2,7 \times 4$ and $3 \times 6$ for $m=11$, and $10 \times 5,9 \times 8,4 \times 6,3 \times 7$ and $1 \times 2$ for $m=13$. These sets can be found by trial and error. The corresponding partitions are shown in the figure below.

Remark. The configurations for $m=11$ and $m=13$ given above are not unique.
A Variant for Obtaining Bounds. We first exclude the cases $m \leqslant 9$ by the observation that one of the small rectangles has a side of length 10 and must fit into the square; hence $m \geqslant 10$.
To exclude the cases $m \geqslant 14$, we work via the perimeter: as every rectangle has at most two sides on the boundary of the $m \times m$ square, the perimeter $4 m$ of the square is bounded by $1+2+3+4+5+6+7+8+9+10=55$; hence $m \leqslant 13$.
We are left to deal with the case $m=10$ : clearly, the rectangle with side length 10 must have one its sides of length 10 along the boundary of the square. The remaining rectangle $R$ of dimensions $10 \times s$, say, would have to be divided into four rectangles with different sidelengths strictly less than 10 . If there were at least two rectangles adjacent to one of the sides of length $s$ of $R$, removing these two rectangles from $R$ would leave a polygon with at least six vertices (since the sidelengths of the rectangles partitioning $R$ are strictly less than 10). It is clearly impossible to partition such a polygon into no more than two rectangles with different sidelengths. Hence, given a side of length $s$ of $R$, there is only one rectangle adjacent to that side, so the rectangles adjacent to the sides of length $s$ of $R$ would have to have the same length $s$, a contradiction.
Remark. Note that the argument of the second part of the main solution cannot be directly applied to the case $m=10$.
A Variant for Dealing with $\boldsymbol{m}=12$. As in the previous solution, we show that the inner rectangle must have dimensions $1 \times 6$. Since the area of the square and the area of the inner rectangle are even, the areas of the four outer rectangles must sum to an even number. Now the four sides of the square are divided into segments of lengths 2 and 10, 3 and 9,4 and 8 , and 5 and 7 . Hence the sides with adjacent segments of lengths 3 and 9 , and 5 and 7 must be opposite sides of the square (otherwise, exactly one of the outer rectangles would have odd area). However, the difference of two rectangle side lengths on opposite sides of the square must be 1 or 6 (in order to accomodate the inner rectangle). This is not the case, so there is no solution with $m=12$.
Remark. In the case $m=12$, having shown that the inner rectangle must have dimensions $1 \times 6$, this case can also be dealt with by listing the remaining configurations one by one.
|
{
"exam": "EGMO",
"problem_label": "2",
"problem_match": "\nProblem 2. (Proposed by Matti Lehtinen, Finland)\n",
"resource_path": "EGMO/segmented/en-2013-solutions.jsonl",
"solution_match": "\nSolution:",
"tier": "T2",
"year": "2013"
}
|
Let $\boldsymbol{n}$ be a positive integer.
(a) Prove that there exists a set $S$ of $6 n$ pairwise different positive integers, such that the least common multiple of any two elements of $S$ is no larger than $32 n^{2}$.
(b) Prove that every set $T$ of $6 n$ pairwise different positive integers contains two elements the least common multiple of which is larger than $9 \boldsymbol{n}^{2}$.
|
(a) Let the set $A$ consist of the $4 n$ integers $1,2, \ldots, 4 n$ and let the set $B$ consist of the $2 n$ even integers $4 n+2,4 n+4, \ldots, 8 n$. We claim that the $6 n$-element set $S=A \cup B$ has the desired property.
Indeed, the least common multiple of two (even) elements of $B$ is no larger than $8 n \cdot(8 n / 2)=32 n^{2}$, and the least common multiple of some element of $A$ and some element of $A \cup B$ is at most their product, which is at most $4 n \cdot 8 n=32 n^{2}$.
(b) We prove the following lemma: "If a set $U$ contains $m+1$ integers, where $m \geqslant 2$, that are all not less than $m$, then some two of its elements have least common multiple strictly larger than $m^{2}$."
Let the elements of $U$ be $u_{1}>u_{2}>\cdots>u_{m+1} \geqslant m$. Note that $1 / u_{1} \leqslant 1 / u_{i} \leqslant 1 / m$ for $1 \leqslant i \leqslant m+1$. We partition the interval $\left[1 / u_{1} ; 1 / m\right]$ into $m$ subintervals of equal length. By the pigeonhole principle, there exist indices $i, j$ with $1 \leqslant i<j \leqslant m+1$ such that $1 / u_{i}$ and $1 / u_{j}$ belong to the same subinterval. Hence
$$
0<\frac{1}{u_{j}}-\frac{1}{u_{i}} \leqslant \frac{1}{m}\left(\frac{1}{m}-\frac{1}{u_{1}}\right)<\frac{1}{m^{2}} .
$$
Now $1 / u_{j}-1 / u_{i}$ is a positive fraction with denominator $\operatorname{lcm}\left(u_{i}, u_{j}\right)$. The above thus yields the lower bound $\operatorname{lcm}\left(u_{i}, u_{j}\right)>m^{2}$, completing the proof of the lemma.
Applying the lemma with $m=3 n$ to the $3 n+1$ largest elements of $T$, which are all not less than $3 n$, we arrive at the desired statement.
A Variant. Alternatively, for part (b), we prove the following lemma: "If a set $U$ contains $m \geqslant 2$ integers that all are greater than $m$, then some two of its elements have least common multiple strictly larger than $m^{2}$."
Let $u_{1}>u_{2}>\cdots>u_{m}$ be the elements of $U$. Since $u_{m}>m=m^{2} / m$, there exists a smallest index $k$ such that $u_{k}>m^{2} / k$. If $k=1$, then $u_{1}>m^{2}$, and the least common multiple of $u_{1}$ and $u_{2}$ is strictly larger than $m^{2}$. So let us suppose $k>1$ from now on, so that we have $u_{k}>m^{2} / k$ and $u_{k-1} \leqslant m^{2} /(k-1)$. The greatest common divisor $d$ of $u_{k-1}$ and $u_{k}$ satisfies
$$
d \leqslant u_{k-1}-u_{k}<\frac{m^{2}}{k-1}-\frac{m^{2}}{k}=\frac{m^{2}}{(k-1) k}
$$
This implies $m^{2} /(d k)>k-1$ and $u_{k} / d>k-1$, and hence $u_{k} / d \geqslant k$. But then the least common multiple of $u_{k-1}$ and $u_{k}$ equals
$$
\frac{u_{k-1} u_{k}}{d} \geqslant u_{k} \cdot \frac{u_{k}}{d}>\frac{m^{2}}{k} \cdot k=m^{2}
$$
and the proof of the lemma is complete.
If we remove the $3 n$ smallest elements from set $T$ and apply the lemma with $m=3 n$ to the remaining elements, we arrive at the desired statement.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $\boldsymbol{n}$ be a positive integer.
(a) Prove that there exists a set $S$ of $6 n$ pairwise different positive integers, such that the least common multiple of any two elements of $S$ is no larger than $32 n^{2}$.
(b) Prove that every set $T$ of $6 n$ pairwise different positive integers contains two elements the least common multiple of which is larger than $9 \boldsymbol{n}^{2}$.
|
(a) Let the set $A$ consist of the $4 n$ integers $1,2, \ldots, 4 n$ and let the set $B$ consist of the $2 n$ even integers $4 n+2,4 n+4, \ldots, 8 n$. We claim that the $6 n$-element set $S=A \cup B$ has the desired property.
Indeed, the least common multiple of two (even) elements of $B$ is no larger than $8 n \cdot(8 n / 2)=32 n^{2}$, and the least common multiple of some element of $A$ and some element of $A \cup B$ is at most their product, which is at most $4 n \cdot 8 n=32 n^{2}$.
(b) We prove the following lemma: "If a set $U$ contains $m+1$ integers, where $m \geqslant 2$, that are all not less than $m$, then some two of its elements have least common multiple strictly larger than $m^{2}$."
Let the elements of $U$ be $u_{1}>u_{2}>\cdots>u_{m+1} \geqslant m$. Note that $1 / u_{1} \leqslant 1 / u_{i} \leqslant 1 / m$ for $1 \leqslant i \leqslant m+1$. We partition the interval $\left[1 / u_{1} ; 1 / m\right]$ into $m$ subintervals of equal length. By the pigeonhole principle, there exist indices $i, j$ with $1 \leqslant i<j \leqslant m+1$ such that $1 / u_{i}$ and $1 / u_{j}$ belong to the same subinterval. Hence
$$
0<\frac{1}{u_{j}}-\frac{1}{u_{i}} \leqslant \frac{1}{m}\left(\frac{1}{m}-\frac{1}{u_{1}}\right)<\frac{1}{m^{2}} .
$$
Now $1 / u_{j}-1 / u_{i}$ is a positive fraction with denominator $\operatorname{lcm}\left(u_{i}, u_{j}\right)$. The above thus yields the lower bound $\operatorname{lcm}\left(u_{i}, u_{j}\right)>m^{2}$, completing the proof of the lemma.
Applying the lemma with $m=3 n$ to the $3 n+1$ largest elements of $T$, which are all not less than $3 n$, we arrive at the desired statement.
A Variant. Alternatively, for part (b), we prove the following lemma: "If a set $U$ contains $m \geqslant 2$ integers that all are greater than $m$, then some two of its elements have least common multiple strictly larger than $m^{2}$."
Let $u_{1}>u_{2}>\cdots>u_{m}$ be the elements of $U$. Since $u_{m}>m=m^{2} / m$, there exists a smallest index $k$ such that $u_{k}>m^{2} / k$. If $k=1$, then $u_{1}>m^{2}$, and the least common multiple of $u_{1}$ and $u_{2}$ is strictly larger than $m^{2}$. So let us suppose $k>1$ from now on, so that we have $u_{k}>m^{2} / k$ and $u_{k-1} \leqslant m^{2} /(k-1)$. The greatest common divisor $d$ of $u_{k-1}$ and $u_{k}$ satisfies
$$
d \leqslant u_{k-1}-u_{k}<\frac{m^{2}}{k-1}-\frac{m^{2}}{k}=\frac{m^{2}}{(k-1) k}
$$
This implies $m^{2} /(d k)>k-1$ and $u_{k} / d>k-1$, and hence $u_{k} / d \geqslant k$. But then the least common multiple of $u_{k-1}$ and $u_{k}$ equals
$$
\frac{u_{k-1} u_{k}}{d} \geqslant u_{k} \cdot \frac{u_{k}}{d}>\frac{m^{2}}{k} \cdot k=m^{2}
$$
and the proof of the lemma is complete.
If we remove the $3 n$ smallest elements from set $T$ and apply the lemma with $m=3 n$ to the remaining elements, we arrive at the desired statement.
|
{
"exam": "EGMO",
"problem_label": "3",
"problem_match": "\nProblem 3. (Proposed by Dan Schwarz, Romania)\n",
"resource_path": "EGMO/segmented/en-2013-solutions.jsonl",
"solution_match": "\nSolution:",
"tier": "T2",
"year": "2013"
}
|
Find all positive integers $a$ and $b$ for which there are three consecutive integers at which the polynomial
$$
P(n)=\frac{n^{5}+a}{b}
$$
## takes integer values.
|
Denote the three consecutive integers by $x-1, x$, and $x+1$, so that
$$
(x-1)^{5}+a \equiv 0 \quad(\bmod b), \quad x^{5}+a \equiv 0 \quad(\bmod b), \quad(x+1)^{5}+a \equiv 0 \quad(\bmod b) .
$$
By computing the differences of the equations in (1) we get
$$
\begin{aligned}
A & :=(x+1)^{5}-(x-1)^{5}=10 x^{4}+20 x^{2}+2 \equiv 0 \quad(\bmod b) \\
B & :=(x+1)^{5}-x^{5}=5 x^{4}+10 x^{3}+10 x^{2}+5 x+1 \equiv 0 \quad(\bmod b)
\end{aligned}
$$
Adding the first and third equation in (1) and subtracting twice the second equation yields
$$
C:=(x+1)^{5}+(x-1)^{5}-2 x^{5}=20 x^{3}+10 x \equiv 0 \quad(\bmod b) .
$$
Next, (2) and (4) together yield
$$
D:=4 x A-\left(2 x^{2}+3\right) C=-22 x \equiv 0(\bmod b) .
$$
Finally we combine (3) and (5) to derive
$$
22 B+\left(5 x^{3}+10 x^{2}+10 x+5\right) D=22 \equiv 0(\bmod b) .
$$
As the positive integer $b$ divides 22 , we are left with the four cases $b=1, b=2, b=11$ and $b=22$.
If $b$ is even (i.e. $b=2$ or $b=22$ ), then we get a contradiction from (3), because the integer $B=2\left(5 x^{3}+5 x^{2}\right)+5\left(x^{4}+x\right)+1$ is odd, and hence not divisible by any even integer.
For $b=1$, it is trivial to see that a polynomial of the form $P(n)=n^{5}+a$, with $a$ any positive integer, has the desired property.
For $b=11$, we note that
$$
\begin{aligned}
& n \equiv 0,1,2,3,4,5,6,7,8,9,10 \quad(\bmod 11) \\
& \Longrightarrow \quad n^{5} \equiv 0,1,-1,1,1,1,-1,-1,-1,1,-1 \quad(\bmod 11)
\end{aligned}
$$
Hence a polynomial of the form $P(n)=\left(n^{5}+a\right) / 11$ has the desired property if and only if $a \equiv \pm 1(\bmod 11)$. This completes the proof.
A Variant. We start by following the first solution up to equation (4). We note that $b=1$ is a trivial solution, and assume from now on that $b \geqslant 2$. As $(x-1)^{5}+a$ and $x^{5}+a$ have different parity, $b$ must be odd. As $B$ in (3) is a multiple of $b$, we conclude that (i) $b$ is not divisible by 5 and that (ii) $b$ and $x$ are relatively prime. As $C=10 x\left(2 x^{2}+1\right)$ in (4) is divisible by $b$, we altogether derive
$$
E:=2 x^{2}+1 \equiv 0(\bmod b)
$$
Together with (2) this implies that
$$
5 E^{2}+10 E-2 A=11 \equiv 0 \quad(\bmod b)
$$
Hence $b=11$ is the only remaining candidate, and it is handled as in the first solution.
|
a \equiv \pm 1(\bmod 11)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all positive integers $a$ and $b$ for which there are three consecutive integers at which the polynomial
$$
P(n)=\frac{n^{5}+a}{b}
$$
## takes integer values.
|
Denote the three consecutive integers by $x-1, x$, and $x+1$, so that
$$
(x-1)^{5}+a \equiv 0 \quad(\bmod b), \quad x^{5}+a \equiv 0 \quad(\bmod b), \quad(x+1)^{5}+a \equiv 0 \quad(\bmod b) .
$$
By computing the differences of the equations in (1) we get
$$
\begin{aligned}
A & :=(x+1)^{5}-(x-1)^{5}=10 x^{4}+20 x^{2}+2 \equiv 0 \quad(\bmod b) \\
B & :=(x+1)^{5}-x^{5}=5 x^{4}+10 x^{3}+10 x^{2}+5 x+1 \equiv 0 \quad(\bmod b)
\end{aligned}
$$
Adding the first and third equation in (1) and subtracting twice the second equation yields
$$
C:=(x+1)^{5}+(x-1)^{5}-2 x^{5}=20 x^{3}+10 x \equiv 0 \quad(\bmod b) .
$$
Next, (2) and (4) together yield
$$
D:=4 x A-\left(2 x^{2}+3\right) C=-22 x \equiv 0(\bmod b) .
$$
Finally we combine (3) and (5) to derive
$$
22 B+\left(5 x^{3}+10 x^{2}+10 x+5\right) D=22 \equiv 0(\bmod b) .
$$
As the positive integer $b$ divides 22 , we are left with the four cases $b=1, b=2, b=11$ and $b=22$.
If $b$ is even (i.e. $b=2$ or $b=22$ ), then we get a contradiction from (3), because the integer $B=2\left(5 x^{3}+5 x^{2}\right)+5\left(x^{4}+x\right)+1$ is odd, and hence not divisible by any even integer.
For $b=1$, it is trivial to see that a polynomial of the form $P(n)=n^{5}+a$, with $a$ any positive integer, has the desired property.
For $b=11$, we note that
$$
\begin{aligned}
& n \equiv 0,1,2,3,4,5,6,7,8,9,10 \quad(\bmod 11) \\
& \Longrightarrow \quad n^{5} \equiv 0,1,-1,1,1,1,-1,-1,-1,1,-1 \quad(\bmod 11)
\end{aligned}
$$
Hence a polynomial of the form $P(n)=\left(n^{5}+a\right) / 11$ has the desired property if and only if $a \equiv \pm 1(\bmod 11)$. This completes the proof.
A Variant. We start by following the first solution up to equation (4). We note that $b=1$ is a trivial solution, and assume from now on that $b \geqslant 2$. As $(x-1)^{5}+a$ and $x^{5}+a$ have different parity, $b$ must be odd. As $B$ in (3) is a multiple of $b$, we conclude that (i) $b$ is not divisible by 5 and that (ii) $b$ and $x$ are relatively prime. As $C=10 x\left(2 x^{2}+1\right)$ in (4) is divisible by $b$, we altogether derive
$$
E:=2 x^{2}+1 \equiv 0(\bmod b)
$$
Together with (2) this implies that
$$
5 E^{2}+10 E-2 A=11 \equiv 0 \quad(\bmod b)
$$
Hence $b=11$ is the only remaining candidate, and it is handled as in the first solution.
|
{
"exam": "EGMO",
"problem_label": "4",
"problem_match": "\nProblem 4. (Proposed by Vesna Iršič, Slovenia)\n",
"resource_path": "EGMO/segmented/en-2013-solutions.jsonl",
"solution_match": "\nSolution 1: ",
"tier": "T2",
"year": "2013"
}
|
Find all positive integers $a$ and $b$ for which there are three consecutive integers at which the polynomial
$$
P(n)=\frac{n^{5}+a}{b}
$$
## takes integer values.
|
Let $p$ be a prime such that $p$ divides $b$. For some integer $x$, we have
$$
(x-1)^{5} \equiv x^{5} \equiv(x+1)^{5} \quad(\bmod p)
$$
Now, there is a primitive root $g$ modulo $p$, so there exist $u, v, w$ such that
$$
x-1 \equiv g^{u} \quad(\bmod p), \quad x \equiv g^{v} \quad(\bmod p), \quad x+1 \equiv g^{w} \quad(\bmod p)
$$
The condition of the problem is thus
$$
g^{5 u} \equiv g^{5 v} \equiv g^{5 w} \quad(\bmod p) \quad \Longrightarrow \quad 5 u \equiv 5 v \equiv 5 w \quad(\bmod p-1)
$$
If $p \not \equiv 1(\bmod 5)$, then 5 is invertible modulo $p-1$ and thus $u \equiv v \equiv w(\bmod p-1)$, i.e. $x-1 \equiv x \equiv x+1(\bmod p)$. This is a contradiction. Hence $p \equiv 1(\bmod 5)$ and thus $u \equiv v \equiv w\left(\bmod \frac{p-1}{5}\right)$. Thus, from (6), there exist integers $k, \ell$ such that
$$
\left.\begin{array}{rl}
x-1 & \equiv g^{v+k \frac{p-1}{5}} \equiv x t^{k} \quad(\bmod p) \\
x+1 & \equiv g^{v+\ell \frac{p-1}{5}} \\
\equiv x t^{\ell} & (\bmod p)
\end{array}\right\} \quad \text { where } t=g^{\frac{p-1}{5}}
$$
Let $r=t^{k}$ and $s=t^{\ell}$. In particular, the above yields $r, s \not \equiv 1(\bmod p)$, and thus
$$
x \equiv-(r-1)^{-1} \equiv(s-1)^{-1} \quad(\bmod p)
$$
It follows that
$$
(r-1)^{-1}+(s-1)^{-1} \equiv 0 \quad(\bmod p) \quad \Longrightarrow \quad r+s \equiv 2 \quad(\bmod p)
$$
Now $t^{5} \equiv 1(\bmod p)$, so $r$ and $s$ must be congruent, modulo $p$, to some of the non-trivial fifth roots of unity $t, t^{2}, t^{3}, t^{4}$. Observe that, for any pair of these non-trivial roots of unity,
either one is the other's inverse, or one is the other's square. In the first case, we have $r+r^{-1} \equiv 2(\bmod p)$, implying $r \equiv 1(\bmod p)$, a contradiction. Hence
$$
r+r^{2} \equiv 2 \quad(\bmod p) \quad \Longrightarrow \quad(r-1)(r+2) \equiv 0 \quad(\bmod p),
$$
or
$$
s^{2}+s \equiv 2 \quad(\bmod p) \quad \Longrightarrow \quad(s-1)(s+2) \equiv 0 \quad(\bmod p)
$$
Thus, since $r, s \not \equiv 1(\bmod p)$, we have $r \equiv-2(\bmod p)$ or $s \equiv-2(\bmod p)$, and thus $1 \equiv r^{5} \equiv-32(\bmod p)$ or an analogous equation obtained from $s$. Hence $p \mid 33$. Since $p \equiv 1(\bmod 5)$, it follows that $p=11$, i.e. $b$ is a power of 11 .
Examining the fifth powers modulo 11 , we see that $b=11$ is indeed a solution with $a \equiv \pm 1(\bmod 11)$ and, correspondingly, $x \equiv \pm 4(\bmod 11)$. Now suppose, for the sake of contradiction, that $11^{2}$ divides $b$. Then, for some integer $m$, we must have
$$
(x-1, x, x+1) \equiv \pm(3+11 m, 4+11 m, 5+11 m) \quad(\bmod 121)
$$
and thus, substituting into the condition of the problem,
$$
\begin{aligned}
3^{5}+55 \cdot 3^{4} m & \equiv 4^{5}+55 \cdot 4^{4} m \equiv 5^{5}+55 \cdot 5^{4} m \quad(\bmod 121) \\
& \Longrightarrow \quad 1-22 m \equiv 56+44 m \equiv-21+11 m \quad(\bmod 121)
\end{aligned}
$$
Hence $33 m \equiv 22(\bmod 121)$ and $33 m \equiv 44(\bmod 121)$, so $22 \equiv 0(\bmod 121)$, a contradiction. It follows that $b \mid 11$.
Finally, we conclude that the positive integers satisfying the original condition are $b=11$, with $a \equiv \pm 1(\bmod 11)$, and $b=1$, for any positive integer $a$.
|
b=11, a \equiv \pm 1(\bmod 11) \text{ and } b=1, \text{ for any positive integer } a
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all positive integers $a$ and $b$ for which there are three consecutive integers at which the polynomial
$$
P(n)=\frac{n^{5}+a}{b}
$$
## takes integer values.
|
Let $p$ be a prime such that $p$ divides $b$. For some integer $x$, we have
$$
(x-1)^{5} \equiv x^{5} \equiv(x+1)^{5} \quad(\bmod p)
$$
Now, there is a primitive root $g$ modulo $p$, so there exist $u, v, w$ such that
$$
x-1 \equiv g^{u} \quad(\bmod p), \quad x \equiv g^{v} \quad(\bmod p), \quad x+1 \equiv g^{w} \quad(\bmod p)
$$
The condition of the problem is thus
$$
g^{5 u} \equiv g^{5 v} \equiv g^{5 w} \quad(\bmod p) \quad \Longrightarrow \quad 5 u \equiv 5 v \equiv 5 w \quad(\bmod p-1)
$$
If $p \not \equiv 1(\bmod 5)$, then 5 is invertible modulo $p-1$ and thus $u \equiv v \equiv w(\bmod p-1)$, i.e. $x-1 \equiv x \equiv x+1(\bmod p)$. This is a contradiction. Hence $p \equiv 1(\bmod 5)$ and thus $u \equiv v \equiv w\left(\bmod \frac{p-1}{5}\right)$. Thus, from (6), there exist integers $k, \ell$ such that
$$
\left.\begin{array}{rl}
x-1 & \equiv g^{v+k \frac{p-1}{5}} \equiv x t^{k} \quad(\bmod p) \\
x+1 & \equiv g^{v+\ell \frac{p-1}{5}} \\
\equiv x t^{\ell} & (\bmod p)
\end{array}\right\} \quad \text { where } t=g^{\frac{p-1}{5}}
$$
Let $r=t^{k}$ and $s=t^{\ell}$. In particular, the above yields $r, s \not \equiv 1(\bmod p)$, and thus
$$
x \equiv-(r-1)^{-1} \equiv(s-1)^{-1} \quad(\bmod p)
$$
It follows that
$$
(r-1)^{-1}+(s-1)^{-1} \equiv 0 \quad(\bmod p) \quad \Longrightarrow \quad r+s \equiv 2 \quad(\bmod p)
$$
Now $t^{5} \equiv 1(\bmod p)$, so $r$ and $s$ must be congruent, modulo $p$, to some of the non-trivial fifth roots of unity $t, t^{2}, t^{3}, t^{4}$. Observe that, for any pair of these non-trivial roots of unity,
either one is the other's inverse, or one is the other's square. In the first case, we have $r+r^{-1} \equiv 2(\bmod p)$, implying $r \equiv 1(\bmod p)$, a contradiction. Hence
$$
r+r^{2} \equiv 2 \quad(\bmod p) \quad \Longrightarrow \quad(r-1)(r+2) \equiv 0 \quad(\bmod p),
$$
or
$$
s^{2}+s \equiv 2 \quad(\bmod p) \quad \Longrightarrow \quad(s-1)(s+2) \equiv 0 \quad(\bmod p)
$$
Thus, since $r, s \not \equiv 1(\bmod p)$, we have $r \equiv-2(\bmod p)$ or $s \equiv-2(\bmod p)$, and thus $1 \equiv r^{5} \equiv-32(\bmod p)$ or an analogous equation obtained from $s$. Hence $p \mid 33$. Since $p \equiv 1(\bmod 5)$, it follows that $p=11$, i.e. $b$ is a power of 11 .
Examining the fifth powers modulo 11 , we see that $b=11$ is indeed a solution with $a \equiv \pm 1(\bmod 11)$ and, correspondingly, $x \equiv \pm 4(\bmod 11)$. Now suppose, for the sake of contradiction, that $11^{2}$ divides $b$. Then, for some integer $m$, we must have
$$
(x-1, x, x+1) \equiv \pm(3+11 m, 4+11 m, 5+11 m) \quad(\bmod 121)
$$
and thus, substituting into the condition of the problem,
$$
\begin{aligned}
3^{5}+55 \cdot 3^{4} m & \equiv 4^{5}+55 \cdot 4^{4} m \equiv 5^{5}+55 \cdot 5^{4} m \quad(\bmod 121) \\
& \Longrightarrow \quad 1-22 m \equiv 56+44 m \equiv-21+11 m \quad(\bmod 121)
\end{aligned}
$$
Hence $33 m \equiv 22(\bmod 121)$ and $33 m \equiv 44(\bmod 121)$, so $22 \equiv 0(\bmod 121)$, a contradiction. It follows that $b \mid 11$.
Finally, we conclude that the positive integers satisfying the original condition are $b=11$, with $a \equiv \pm 1(\bmod 11)$, and $b=1$, for any positive integer $a$.
|
{
"exam": "EGMO",
"problem_label": "4",
"problem_match": "\nProblem 4. (Proposed by Vesna Iršič, Slovenia)\n",
"resource_path": "EGMO/segmented/en-2013-solutions.jsonl",
"solution_match": "\nSolution 2: ",
"tier": "T2",
"year": "2013"
}
|
Find all positive integers $a$ and $b$ for which there are three consecutive integers at which the polynomial
$$
P(n)=\frac{n^{5}+a}{b}
$$
## takes integer values.
|
Denote the three consecutive integers by $x-1, x$, and $x+1$ as in Solution 1. By computing the differences in (1), we find
$$
\begin{aligned}
& F:=(x+1)^{5}-x^{5}=5 x^{4}+10 x^{3}+10 x^{2}+5 x+1 \equiv 0 \quad(\bmod b), \\
& G:=x^{5}-(x-1)^{5}=5 x^{4}-10 x^{3}+10 x^{2}-5 x+1 \equiv 0 \quad(\bmod b) .
\end{aligned}
$$
By determining the polynomial greatest divisor of $F(x)$ and $G(x)$ using the Euclidean algorithm, we find that
$$
p(x) F(x)+q(x) G(x)=22
$$
where
$$
\begin{aligned}
& p(x)=-15 x^{3}+30 x^{2}-28 x+11 \\
& q(x)=15 x^{3}+30 x^{2}+28 x+11
\end{aligned}
$$
Since $b \mid F(x)$ and $b \mid G(x)$, it follows from (7) that $b \mid 22$. We now finish off the problem as in Solution 1.
|
b \mid 22
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all positive integers $a$ and $b$ for which there are three consecutive integers at which the polynomial
$$
P(n)=\frac{n^{5}+a}{b}
$$
## takes integer values.
|
Denote the three consecutive integers by $x-1, x$, and $x+1$ as in Solution 1. By computing the differences in (1), we find
$$
\begin{aligned}
& F:=(x+1)^{5}-x^{5}=5 x^{4}+10 x^{3}+10 x^{2}+5 x+1 \equiv 0 \quad(\bmod b), \\
& G:=x^{5}-(x-1)^{5}=5 x^{4}-10 x^{3}+10 x^{2}-5 x+1 \equiv 0 \quad(\bmod b) .
\end{aligned}
$$
By determining the polynomial greatest divisor of $F(x)$ and $G(x)$ using the Euclidean algorithm, we find that
$$
p(x) F(x)+q(x) G(x)=22
$$
where
$$
\begin{aligned}
& p(x)=-15 x^{3}+30 x^{2}-28 x+11 \\
& q(x)=15 x^{3}+30 x^{2}+28 x+11
\end{aligned}
$$
Since $b \mid F(x)$ and $b \mid G(x)$, it follows from (7) that $b \mid 22$. We now finish off the problem as in Solution 1.
|
{
"exam": "EGMO",
"problem_label": "4",
"problem_match": "\nProblem 4. (Proposed by Vesna Iršič, Slovenia)\n",
"resource_path": "EGMO/segmented/en-2013-solutions.jsonl",
"solution_match": "\nSolution 3: ",
"tier": "T2",
"year": "2013"
}
|
Let $\Omega$ be the circumcircle of the triangle $A B C$. The circle $\omega$ is tangent to the sides $A C$ and $B C$, and it is internally tangent to $\Omega$ at the point $P$. A line parallel to $A B$ and intersecting the interior of triangle $A B C$ is tangent to $\omega$ at $Q$.
Prove that $\angle A C P=\angle Q C B$.
|
Assume that $\omega$ is tangent to $A C$ and $B C$ at $E$ and $F$, respectively and let $P E, P F, P Q$ meet $\Omega$ at $K, L, M$, respectively. Let $I$ and $O$ denote the respective centres of $\omega$ and $\Omega$, and consider the homethety $\mathscr{H}$ that maps $\omega$ onto $\Omega$. Now $K$ is the image of $E$ under $\mathscr{H}$, and $E I \perp A C$. Hence $O K \perp A C$, and thus $K$ is the midpoint of the $\operatorname{arc} C A$. Similarly, $L$ is the midpoint of the arc $B C$ and $M$ is the midpoint of the arc $B A$. It follows that arcs $L M$ and $C K$ are equal, because
$$
\begin{aligned}
\overparen{B M}=\overparen{M A} & \Longrightarrow \overparen{B L}+\overparen{L M}=\overparen{M K}+\overparen{K A} \Longrightarrow \overparen{L C}+\overparen{L M}=\overparen{M K}+\overparen{C K} \\
& \Longrightarrow 2 \overparen{L M}+\overparen{M C}=\overparen{M C}+2 \overparen{C K}
\end{aligned}
$$
Thus arcs $F Q$ and $D E$ of $\omega$ are equal, too, where $D$ is the intersection of $C P$ with $\omega$. Since $C E$ and $C F$ are tangents to $\omega$, this implies that $\angle D E C=\angle C F Q$. Further, $C E=C F$, and thus triangles $C E D$ and $C F Q$ are congruent. In particular, $\angle E C D=\angle Q C F$, as required.
A Variant. As above, we show that $\operatorname{arcs} F Q$ and $D E$ of $\omega$ are equal, which implies that $D E F Q$ is an isoceles trapezoid, and so we have $\angle F E D=\angle Q F E$. Together with $|F Q|=|D E|$, this implies that, since $E$ and $F$ are images of each other under reflection in the angle bisector $C I$ of $\angle C$, so are the segments $[E Q]$ and $[F D]$, and, in particular, $D$ and $Q$. In turn, this yields $\angle E C D=\angle Q C F$, as required.
Remark. Let $J$ denote the incentre of $A B C$. By Sawayama's theorem, $J$ is the midpoint of $[E F]$, i.e. $P J$ is a median of $P F E$. Since $C$ is the intersection of the tangents $A C$ and $B C$ to the circumcircle of $P F E$ at $E$ and $F$, respectively, $P C$ is a symmedian of $P F E$. Thus $\angle C P E=\angle F P J$. But, since the arcs $F Q$ and $D E$ of $\omega$ are equal, $\angle C P E=\angle F P Q$. This shows that $J$ lies on the line $P Q$.
Another Variant. We show that $\operatorname{arcs} Q E$ and $F D$ are equal, and then finish as in the main solution. Let $B P$ meet $\omega$ again at $Z$. Consider the homothety $\mathscr{H}$ that maps $\omega$ onto $\Omega$. Under $\mathscr{H}, D \mapsto C$ and $Z \mapsto B$, so $D Z \| C B$. (This also follows by considering the common tangent to $\omega$ and $\Omega$, and tangential angles.) Now, by power of a point,
$$
B F^{2}=B Z \cdot B P, \quad C F^{2}=C D \cdot C P
$$
Now $D Z \| C B$ implies $B Z / B P=C D / C P$, and so, dividing the two previous equations by each other, and taking square roots, $B F / C F=B P / C P$. Hence $P F$ bissects angle $\angle B P C$. Now let $\angle B P F=\angle F P C=\beta$. By tangential angles, it follows that $\angle C F D=\beta$. Further, $\angle B A C=\angle B P C=2 \beta$. Let the tangent to $\omega$ through $Q$ and parallel to $A B$ meet $A C$ at $X$. Then $\angle Q X C=2 \beta$, so, since $X Q=X E$ by tangency, $\angle Q E X=\beta$. By tangential angles, it follows that $\operatorname{arcs} F D$ and $Q E$ are equal, as claimed.
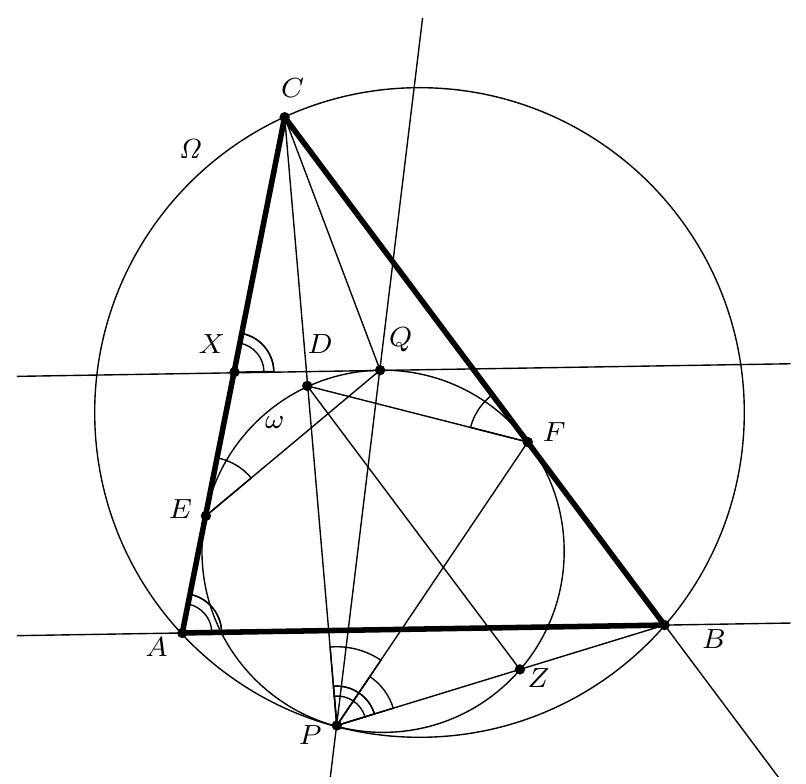
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\Omega$ be the circumcircle of the triangle $A B C$. The circle $\omega$ is tangent to the sides $A C$ and $B C$, and it is internally tangent to $\Omega$ at the point $P$. A line parallel to $A B$ and intersecting the interior of triangle $A B C$ is tangent to $\omega$ at $Q$.
Prove that $\angle A C P=\angle Q C B$.
|
Assume that $\omega$ is tangent to $A C$ and $B C$ at $E$ and $F$, respectively and let $P E, P F, P Q$ meet $\Omega$ at $K, L, M$, respectively. Let $I$ and $O$ denote the respective centres of $\omega$ and $\Omega$, and consider the homethety $\mathscr{H}$ that maps $\omega$ onto $\Omega$. Now $K$ is the image of $E$ under $\mathscr{H}$, and $E I \perp A C$. Hence $O K \perp A C$, and thus $K$ is the midpoint of the $\operatorname{arc} C A$. Similarly, $L$ is the midpoint of the arc $B C$ and $M$ is the midpoint of the arc $B A$. It follows that arcs $L M$ and $C K$ are equal, because
$$
\begin{aligned}
\overparen{B M}=\overparen{M A} & \Longrightarrow \overparen{B L}+\overparen{L M}=\overparen{M K}+\overparen{K A} \Longrightarrow \overparen{L C}+\overparen{L M}=\overparen{M K}+\overparen{C K} \\
& \Longrightarrow 2 \overparen{L M}+\overparen{M C}=\overparen{M C}+2 \overparen{C K}
\end{aligned}
$$
Thus arcs $F Q$ and $D E$ of $\omega$ are equal, too, where $D$ is the intersection of $C P$ with $\omega$. Since $C E$ and $C F$ are tangents to $\omega$, this implies that $\angle D E C=\angle C F Q$. Further, $C E=C F$, and thus triangles $C E D$ and $C F Q$ are congruent. In particular, $\angle E C D=\angle Q C F$, as required.

A Variant. As above, we show that $\operatorname{arcs} F Q$ and $D E$ of $\omega$ are equal, which implies that $D E F Q$ is an isoceles trapezoid, and so we have $\angle F E D=\angle Q F E$. Together with $|F Q|=|D E|$, this implies that, since $E$ and $F$ are images of each other under reflection in the angle bisector $C I$ of $\angle C$, so are the segments $[E Q]$ and $[F D]$, and, in particular, $D$ and $Q$. In turn, this yields $\angle E C D=\angle Q C F$, as required.
Remark. Let $J$ denote the incentre of $A B C$. By Sawayama's theorem, $J$ is the midpoint of $[E F]$, i.e. $P J$ is a median of $P F E$. Since $C$ is the intersection of the tangents $A C$ and $B C$ to the circumcircle of $P F E$ at $E$ and $F$, respectively, $P C$ is a symmedian of $P F E$. Thus $\angle C P E=\angle F P J$. But, since the arcs $F Q$ and $D E$ of $\omega$ are equal, $\angle C P E=\angle F P Q$. This shows that $J$ lies on the line $P Q$.
Another Variant. We show that $\operatorname{arcs} Q E$ and $F D$ are equal, and then finish as in the main solution. Let $B P$ meet $\omega$ again at $Z$. Consider the homothety $\mathscr{H}$ that maps $\omega$ onto $\Omega$. Under $\mathscr{H}, D \mapsto C$ and $Z \mapsto B$, so $D Z \| C B$. (This also follows by considering the common tangent to $\omega$ and $\Omega$, and tangential angles.) Now, by power of a point,
$$
B F^{2}=B Z \cdot B P, \quad C F^{2}=C D \cdot C P
$$
Now $D Z \| C B$ implies $B Z / B P=C D / C P$, and so, dividing the two previous equations by each other, and taking square roots, $B F / C F=B P / C P$. Hence $P F$ bissects angle $\angle B P C$. Now let $\angle B P F=\angle F P C=\beta$. By tangential angles, it follows that $\angle C F D=\beta$. Further, $\angle B A C=\angle B P C=2 \beta$. Let the tangent to $\omega$ through $Q$ and parallel to $A B$ meet $A C$ at $X$. Then $\angle Q X C=2 \beta$, so, since $X Q=X E$ by tangency, $\angle Q E X=\beta$. By tangential angles, it follows that $\operatorname{arcs} F D$ and $Q E$ are equal, as claimed.

|
{
"exam": "EGMO",
"problem_label": "5",
"problem_match": "\nProblem 5. (Proposed by Waldemar Pompe, Poland)\n",
"resource_path": "EGMO/segmented/en-2013-solutions.jsonl",
"solution_match": "\nSolution 1: ",
"tier": "T2",
"year": "2013"
}
|
Let $\Omega$ be the circumcircle of the triangle $A B C$. The circle $\omega$ is tangent to the sides $A C$ and $B C$, and it is internally tangent to $\Omega$ at the point $P$. A line parallel to $A B$ and intersecting the interior of triangle $A B C$ is tangent to $\omega$ at $Q$.
Prove that $\angle A C P=\angle Q C B$.
|
Let $I$ and $O$ denote the respective centres of $\omega$ and $\Omega$. Observe that $C I$ is the angle bisector of angle $\angle C$, because $\omega$ is tangent to $A C$ and $B C$. Consider the homethety $\mathscr{H}$ that maps $\omega$ onto $\Omega$. Let $M$ be the image of $Q$ under $\mathscr{H}$. By construction, $I Q \perp A B$, so $O M \perp A B$. Thus the diameter $O M$ of $\Omega$ passes through the midpoint of the $\operatorname{arc} A B$ of $\Omega$, which also lies on the angle bisector $C I$. This implies that $\angle I C M=90^{\circ}$. We next show that $P, I, Q, C$ lie on a circle. Notice that
$$
\begin{aligned}
\angle P Q I & =90^{\circ}-\frac{1}{2} \angle Q I P=90^{\circ}-\frac{1}{2} \angle M O P=90^{\circ}-\left(180^{\circ}-\angle P C M\right) \\
& =(\angle P C I+\angle I C M)-90^{\circ}=\angle P C I
\end{aligned}
$$
Hence $P, I, Q, C$ lie on a circle. But $P I=I Q$, so $C I$ is the angle bisector of $\angle P C Q$. Since $C I$ is also the angle bisector of angle $\angle C$, it follows that $\angle A C P=\angle Q C B$, as required.
A Variant. We show that $P I Q C$ is cyclic by chasing angles. Define $\alpha=\angle B A C$, $\beta=\angle C B A$ and $\gamma=\angle A C P$. For convenience, we consider the configuration where $A$ and $P$ lie one the same side of the angle bisector $C I$ of $\angle C$. In this configuration,
$$
\angle P C I=\frac{1}{2} \angle A C B-\angle A C P=90^{\circ}-\frac{1}{2} \alpha-\frac{1}{2} \beta-\gamma .
$$
Now notice that $\angle P B A=\angle A C P=\gamma$, and therefore $\angle C A P=180^{\circ}-\beta-\gamma$, whence $\angle P A B=180^{\circ}-\alpha-\beta-\gamma$. Further, $P O$ is a diameter of $\Omega$, and therefore $\angle A P O=90^{\circ}-\gamma$. Let $A B$ and $P O$ intersect at $T$. Then
$$
\angle B T O=180^{\circ}-\angle P A B-\angle A P O=\alpha+\beta+2 \gamma-90^{\circ}
$$
But $Q I \perp A B$ by construction, and thus
$$
\begin{aligned}
& \angle O I Q=90^{\circ}-\angle B T O=180^{\circ}-\alpha-\beta-2 \gamma \\
& \Longrightarrow \quad \angle Q I P=180^{\circ}-\angle O I Q=\alpha+\beta+2 \gamma \\
& \Longrightarrow \quad \angle P Q I=90^{\circ}-\frac{1}{2} \alpha-\frac{1}{2} \beta-\gamma .
\end{aligned}
$$
Hence $\angle I C Q=\angle P Q I$, and thus $P I Q C$ is cyclic. Since $P I=Q I$, it follows that $C I$ is the angle bisector of $\angle P C Q$, which completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\Omega$ be the circumcircle of the triangle $A B C$. The circle $\omega$ is tangent to the sides $A C$ and $B C$, and it is internally tangent to $\Omega$ at the point $P$. A line parallel to $A B$ and intersecting the interior of triangle $A B C$ is tangent to $\omega$ at $Q$.
Prove that $\angle A C P=\angle Q C B$.
|
Let $I$ and $O$ denote the respective centres of $\omega$ and $\Omega$. Observe that $C I$ is the angle bisector of angle $\angle C$, because $\omega$ is tangent to $A C$ and $B C$. Consider the homethety $\mathscr{H}$ that maps $\omega$ onto $\Omega$. Let $M$ be the image of $Q$ under $\mathscr{H}$. By construction, $I Q \perp A B$, so $O M \perp A B$. Thus the diameter $O M$ of $\Omega$ passes through the midpoint of the $\operatorname{arc} A B$ of $\Omega$, which also lies on the angle bisector $C I$. This implies that $\angle I C M=90^{\circ}$. We next show that $P, I, Q, C$ lie on a circle. Notice that
$$
\begin{aligned}
\angle P Q I & =90^{\circ}-\frac{1}{2} \angle Q I P=90^{\circ}-\frac{1}{2} \angle M O P=90^{\circ}-\left(180^{\circ}-\angle P C M\right) \\
& =(\angle P C I+\angle I C M)-90^{\circ}=\angle P C I
\end{aligned}
$$
Hence $P, I, Q, C$ lie on a circle. But $P I=I Q$, so $C I$ is the angle bisector of $\angle P C Q$. Since $C I$ is also the angle bisector of angle $\angle C$, it follows that $\angle A C P=\angle Q C B$, as required.

A Variant. We show that $P I Q C$ is cyclic by chasing angles. Define $\alpha=\angle B A C$, $\beta=\angle C B A$ and $\gamma=\angle A C P$. For convenience, we consider the configuration where $A$ and $P$ lie one the same side of the angle bisector $C I$ of $\angle C$. In this configuration,
$$
\angle P C I=\frac{1}{2} \angle A C B-\angle A C P=90^{\circ}-\frac{1}{2} \alpha-\frac{1}{2} \beta-\gamma .
$$
Now notice that $\angle P B A=\angle A C P=\gamma$, and therefore $\angle C A P=180^{\circ}-\beta-\gamma$, whence $\angle P A B=180^{\circ}-\alpha-\beta-\gamma$. Further, $P O$ is a diameter of $\Omega$, and therefore $\angle A P O=90^{\circ}-\gamma$. Let $A B$ and $P O$ intersect at $T$. Then
$$
\angle B T O=180^{\circ}-\angle P A B-\angle A P O=\alpha+\beta+2 \gamma-90^{\circ}
$$
But $Q I \perp A B$ by construction, and thus
$$
\begin{aligned}
& \angle O I Q=90^{\circ}-\angle B T O=180^{\circ}-\alpha-\beta-2 \gamma \\
& \Longrightarrow \quad \angle Q I P=180^{\circ}-\angle O I Q=\alpha+\beta+2 \gamma \\
& \Longrightarrow \quad \angle P Q I=90^{\circ}-\frac{1}{2} \alpha-\frac{1}{2} \beta-\gamma .
\end{aligned}
$$
Hence $\angle I C Q=\angle P Q I$, and thus $P I Q C$ is cyclic. Since $P I=Q I$, it follows that $C I$ is the angle bisector of $\angle P C Q$, which completes the proof.
|
{
"exam": "EGMO",
"problem_label": "5",
"problem_match": "\nProblem 5. (Proposed by Waldemar Pompe, Poland)\n",
"resource_path": "EGMO/segmented/en-2013-solutions.jsonl",
"solution_match": "\nSolution 2: ",
"tier": "T2",
"year": "2013"
}
|
Let $\Omega$ be the circumcircle of the triangle $A B C$. The circle $\omega$ is tangent to the sides $A C$ and $B C$, and it is internally tangent to $\Omega$ at the point $P$. A line parallel to $A B$ and intersecting the interior of triangle $A B C$ is tangent to $\omega$ at $Q$.
Prove that $\angle A C P=\angle Q C B$.
|
Let $I$ and $O$ denote the respective centres of $\omega$ and $\Omega$. Let $D$ be the second point of intersection of $C P$ with $\omega$, and let $\ell$ denote the tangent to $\omega$ at $D$, which meets $A C$ at $S$. Hence $I D \perp \ell$. By construction, $P, I, O$ lie one a line, and hence the isosceles triangles $P I D$ and $P O C$ are similar. In particular, it follows that $O C \perp \ell$, so $C$ is the midpoint of the arc of $\Omega$ defined by the points of intersection of $\ell$ with $\Omega$. It is easy to see that this implies that
$$
\angle D S C=\angle A B C
$$
Under reflection in the angle bisector $C I$ of $\angle C, \ell$ is thus mapped to a tangent to $\omega$ parallel to $A B$ and intersecting the interior of $A B C$, since $\omega$ is mapped to itself under this reflection. In particular, $D$ is mapped to $Q$, and thus $\angle Q C B=\angle A C D$, as required.
Remark. Conceptually, this solution is similar to Solution 1, but here, we proceed more directly via the reflectional symmetry. Therefore, this solution links Solution 1 to Solution 4, in which we use an inversion.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\Omega$ be the circumcircle of the triangle $A B C$. The circle $\omega$ is tangent to the sides $A C$ and $B C$, and it is internally tangent to $\Omega$ at the point $P$. A line parallel to $A B$ and intersecting the interior of triangle $A B C$ is tangent to $\omega$ at $Q$.
Prove that $\angle A C P=\angle Q C B$.
|
Let $I$ and $O$ denote the respective centres of $\omega$ and $\Omega$. Let $D$ be the second point of intersection of $C P$ with $\omega$, and let $\ell$ denote the tangent to $\omega$ at $D$, which meets $A C$ at $S$. Hence $I D \perp \ell$. By construction, $P, I, O$ lie one a line, and hence the isosceles triangles $P I D$ and $P O C$ are similar. In particular, it follows that $O C \perp \ell$, so $C$ is the midpoint of the arc of $\Omega$ defined by the points of intersection of $\ell$ with $\Omega$. It is easy to see that this implies that
$$
\angle D S C=\angle A B C
$$
Under reflection in the angle bisector $C I$ of $\angle C, \ell$ is thus mapped to a tangent to $\omega$ parallel to $A B$ and intersecting the interior of $A B C$, since $\omega$ is mapped to itself under this reflection. In particular, $D$ is mapped to $Q$, and thus $\angle Q C B=\angle A C D$, as required.

Remark. Conceptually, this solution is similar to Solution 1, but here, we proceed more directly via the reflectional symmetry. Therefore, this solution links Solution 1 to Solution 4, in which we use an inversion.
|
{
"exam": "EGMO",
"problem_label": "5",
"problem_match": "\nProblem 5. (Proposed by Waldemar Pompe, Poland)\n",
"resource_path": "EGMO/segmented/en-2013-solutions.jsonl",
"solution_match": "\nSolution 3: ",
"tier": "T2",
"year": "2013"
}
|
Let $\Omega$ be the circumcircle of the triangle $A B C$. The circle $\omega$ is tangent to the sides $A C$ and $B C$, and it is internally tangent to $\Omega$ at the point $P$. A line parallel to $A B$ and intersecting the interior of triangle $A B C$ is tangent to $\omega$ at $Q$.
Prove that $\angle A C P=\angle Q C B$.
|
Let the tangent to $\omega$ at $Q$ meet $A C$ and $B C$ at $X$ and $Y$, respectively. Then $A C / X C=B C / Y C$, and thus there is a radius $r$ such that $r^{2}=A C \cdot Y C=B C \cdot X C$. Let $\Gamma$ denote the circle with centre $C$ and radius $r$, and consider the inversion $\mathscr{I}$ in the circle $\Gamma$. Under $\mathscr{I}$,
$A \longmapsto A^{\prime}$, the point on the ray $C A$ satisfying $C A^{\prime}=C Y$;
$B \longmapsto B^{\prime}$, the point on the ray $C B$ satisfying $C B^{\prime}=C X$;
$\Omega \longmapsto$ the line $A^{\prime} B^{\prime}$;
$\omega \longmapsto \omega^{\prime}$, the excircle of $C A^{\prime} B^{\prime}$ opposite $C$;
$P \longmapsto P^{\prime}$, the point where $\omega^{\prime}$ touches $A^{\prime} B^{\prime}$;
In particular, $\omega^{\prime}$, the image of $\omega$, is a circle tangent to $A C, B C$ and $A^{\prime} B^{\prime}$, so it is either the excircle of $C A^{\prime} B^{\prime}$ opposite $C$, or the incircle of $C A^{\prime} B^{\prime}$. Let $\omega$ be tangent to $B C$ at $F$, and let $F^{\prime}$ be the image of $F$ under $\mathscr{I}$. Then $C F \cdot C F^{\prime}=B C \cdot X C$. Now $C F<B C$, so $C F^{\prime}>C X=C B^{\prime}$. Hence $\omega^{\prime}$ cannot be the incircle, so $\omega^{\prime}$ is indeed the excircle of $C A^{\prime} B^{\prime}$ opposite $C$.
Now note that $\omega$ is the excircle of $C X Y$ opposite $C$. The reflection about the angle bisector of $\angle C$ maps $X$ to $B^{\prime}, Y$ to $A^{\prime}$. It thus maps the triangle $C X Y$ to $C B^{\prime} A^{\prime}, \omega$ to $\omega^{\prime}$ and, finally, $Q$ to $P^{\prime}$. It follows that $\angle A C P=\angle A C P^{\prime}=\angle Q C B$, as required.
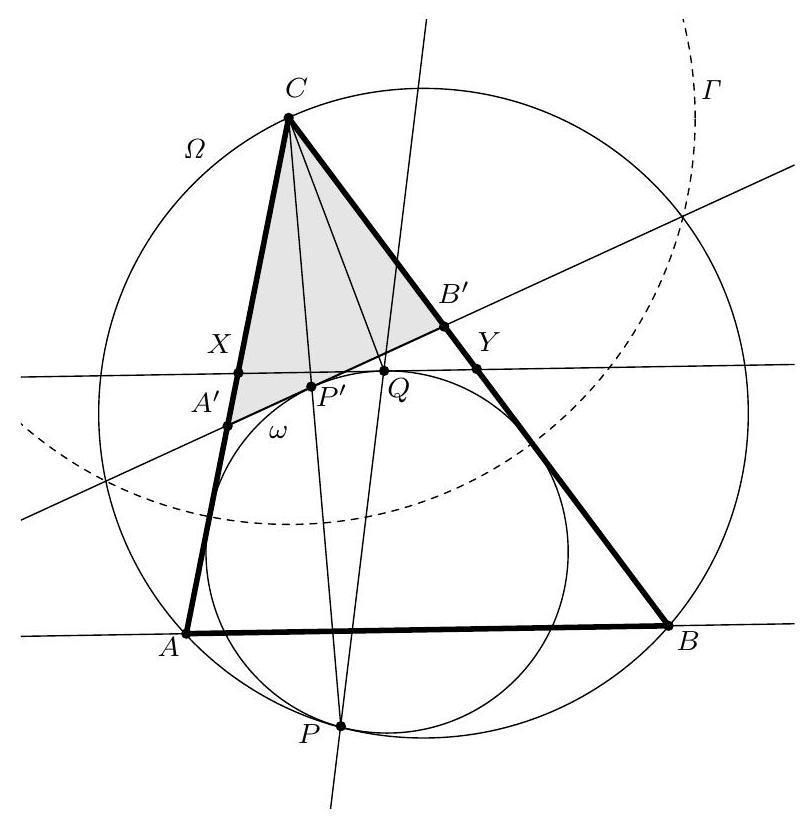
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\Omega$ be the circumcircle of the triangle $A B C$. The circle $\omega$ is tangent to the sides $A C$ and $B C$, and it is internally tangent to $\Omega$ at the point $P$. A line parallel to $A B$ and intersecting the interior of triangle $A B C$ is tangent to $\omega$ at $Q$.
Prove that $\angle A C P=\angle Q C B$.
|
Let the tangent to $\omega$ at $Q$ meet $A C$ and $B C$ at $X$ and $Y$, respectively. Then $A C / X C=B C / Y C$, and thus there is a radius $r$ such that $r^{2}=A C \cdot Y C=B C \cdot X C$. Let $\Gamma$ denote the circle with centre $C$ and radius $r$, and consider the inversion $\mathscr{I}$ in the circle $\Gamma$. Under $\mathscr{I}$,
$A \longmapsto A^{\prime}$, the point on the ray $C A$ satisfying $C A^{\prime}=C Y$;
$B \longmapsto B^{\prime}$, the point on the ray $C B$ satisfying $C B^{\prime}=C X$;
$\Omega \longmapsto$ the line $A^{\prime} B^{\prime}$;
$\omega \longmapsto \omega^{\prime}$, the excircle of $C A^{\prime} B^{\prime}$ opposite $C$;
$P \longmapsto P^{\prime}$, the point where $\omega^{\prime}$ touches $A^{\prime} B^{\prime}$;
In particular, $\omega^{\prime}$, the image of $\omega$, is a circle tangent to $A C, B C$ and $A^{\prime} B^{\prime}$, so it is either the excircle of $C A^{\prime} B^{\prime}$ opposite $C$, or the incircle of $C A^{\prime} B^{\prime}$. Let $\omega$ be tangent to $B C$ at $F$, and let $F^{\prime}$ be the image of $F$ under $\mathscr{I}$. Then $C F \cdot C F^{\prime}=B C \cdot X C$. Now $C F<B C$, so $C F^{\prime}>C X=C B^{\prime}$. Hence $\omega^{\prime}$ cannot be the incircle, so $\omega^{\prime}$ is indeed the excircle of $C A^{\prime} B^{\prime}$ opposite $C$.
Now note that $\omega$ is the excircle of $C X Y$ opposite $C$. The reflection about the angle bisector of $\angle C$ maps $X$ to $B^{\prime}, Y$ to $A^{\prime}$. It thus maps the triangle $C X Y$ to $C B^{\prime} A^{\prime}, \omega$ to $\omega^{\prime}$ and, finally, $Q$ to $P^{\prime}$. It follows that $\angle A C P=\angle A C P^{\prime}=\angle Q C B$, as required.

|
{
"exam": "EGMO",
"problem_label": "5",
"problem_match": "\nProblem 5. (Proposed by Waldemar Pompe, Poland)\n",
"resource_path": "EGMO/segmented/en-2013-solutions.jsonl",
"solution_match": "\nSolution 4: ",
"tier": "T2",
"year": "2013"
}
|
Let $\Omega$ be the circumcircle of the triangle $A B C$. The circle $\omega$ is tangent to the sides $A C$ and $B C$, and it is internally tangent to $\Omega$ at the point $P$. A line parallel to $A B$ and intersecting the interior of triangle $A B C$ is tangent to $\omega$ at $Q$.
Prove that $\angle A C P=\angle Q C B$.
|
Let $r$ be the radius such that $r^{2}=A C \cdot B C$. Let $\mathscr{J}$ denote the composition of the inversion $\mathscr{I}$ in the circle of centre $C$ and radius $r$, followed by the reflection in the
angle bisector of $\angle C$. Under $\mathscr{J}$,
$A \longmapsto B, B \mapsto A ;$
$\Omega \longmapsto$ the line $A B$;
$\omega \longmapsto \omega^{\prime}$, the excircle of $A B C$ opposite the vertex $C$;
$P \longmapsto Q^{\prime}$, the point where $\omega^{\prime}$ touches $A B$;
In particular, note that the image $\omega^{\prime}$ of $\omega$ under $\mathscr{J}$ is a circle tangent to $A C, B C$ and $A B$, so it is either the incircle of $A B C$, or the excircle opposite vertex $C$. Observe that $r \geqslant \min \{A C, B C\}$, so the image of the points of tangency of $\omega$ must lie outside $A B C$, and thus $\omega^{\prime}$ cannot be the incircle. Thus $\omega^{\prime}$ is the excircle opposite vertex $C$ as claimed. Further, the point of tangency $P$ is mapped to $Q^{\prime}$.
Now, since the line $C P$ is mapped to itself under the inversion $\mathscr{I}$, and mapped onto $C Q^{\prime}$ under $\mathscr{J}, C P$ and $C Q^{\prime}$ are images of each other under reflection in the angle bisector of $\angle C$. But $C, Q, Q^{\prime}$ lie on a line for there is a homothety with centre $C$ that maps $\omega$ onto the excircle $\omega^{\prime}$. This completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\Omega$ be the circumcircle of the triangle $A B C$. The circle $\omega$ is tangent to the sides $A C$ and $B C$, and it is internally tangent to $\Omega$ at the point $P$. A line parallel to $A B$ and intersecting the interior of triangle $A B C$ is tangent to $\omega$ at $Q$.
Prove that $\angle A C P=\angle Q C B$.
|
Let $r$ be the radius such that $r^{2}=A C \cdot B C$. Let $\mathscr{J}$ denote the composition of the inversion $\mathscr{I}$ in the circle of centre $C$ and radius $r$, followed by the reflection in the
angle bisector of $\angle C$. Under $\mathscr{J}$,
$A \longmapsto B, B \mapsto A ;$
$\Omega \longmapsto$ the line $A B$;
$\omega \longmapsto \omega^{\prime}$, the excircle of $A B C$ opposite the vertex $C$;
$P \longmapsto Q^{\prime}$, the point where $\omega^{\prime}$ touches $A B$;
In particular, note that the image $\omega^{\prime}$ of $\omega$ under $\mathscr{J}$ is a circle tangent to $A C, B C$ and $A B$, so it is either the incircle of $A B C$, or the excircle opposite vertex $C$. Observe that $r \geqslant \min \{A C, B C\}$, so the image of the points of tangency of $\omega$ must lie outside $A B C$, and thus $\omega^{\prime}$ cannot be the incircle. Thus $\omega^{\prime}$ is the excircle opposite vertex $C$ as claimed. Further, the point of tangency $P$ is mapped to $Q^{\prime}$.
Now, since the line $C P$ is mapped to itself under the inversion $\mathscr{I}$, and mapped onto $C Q^{\prime}$ under $\mathscr{J}, C P$ and $C Q^{\prime}$ are images of each other under reflection in the angle bisector of $\angle C$. But $C, Q, Q^{\prime}$ lie on a line for there is a homothety with centre $C$ that maps $\omega$ onto the excircle $\omega^{\prime}$. This completes the proof.

|
{
"exam": "EGMO",
"problem_label": "5",
"problem_match": "\nProblem 5. (Proposed by Waldemar Pompe, Poland)\n",
"resource_path": "EGMO/segmented/en-2013-solutions.jsonl",
"solution_match": "\nSolution 5: ",
"tier": "T2",
"year": "2013"
}
|
Let $\Omega$ be the circumcircle of the triangle $A B C$. The circle $\omega$ is tangent to the sides $A C$ and $B C$, and it is internally tangent to $\Omega$ at the point $P$. A line parallel to $A B$ and intersecting the interior of triangle $A B C$ is tangent to $\omega$ at $Q$.
Prove that $\angle A C P=\angle Q C B$.
|
Assume that $\omega$ is tangent to $A C$ and $B C$ at $E$ and $F$, respectively. Assume that $C P$ meets $\omega$ at $D$. Let $I$ and $O$ denote the respective centres of $\omega$ and $\Omega$. To set up a solution in the complex plane, we take the circle $\omega$ as the unit circle centered at the origin of the complex plane, and let $P O$ be the real axis with $o>0$, where we use the convention that lowercase letters denote complex coordinates of corresponding points in the plane denoted by uppercase letters.
Now, a point $Z$ on the circle $\Omega$ satisfies
$$
|z-o|^{2}=(o+1)^{2} \quad \Longleftrightarrow \quad z z^{*}-o\left(z+z^{*}\right)-2 o-1=0
$$
The triangle $A B C$ is defined by the points $E$ and $F$ on $\omega$, the intersection $C$ of the corresponding tangents lying on $\Omega$. Thus $c=2 e f /(e+f)$, and further
$$
|c-o|^{2}=(o+1)^{2} \quad \Longleftrightarrow \quad c c^{*}-o\left(c+c^{*}\right)-2 o-1=0,
$$
and this is the equality defining $o$. The points $A$ and $B$ are the second intersection points of $\Omega$ with the tangents to $\omega$ at $E$ and $F$ respectively. A point $Z$ on the tangent through $E$ is given by $z=2 e-e^{2} z^{*}$, and thus $A$ and $C$ satisfy
$$
\begin{aligned}
\left(2 e-e^{2} z^{*}\right) z^{*} & -o\left(2 e-e^{2} z^{*}+z^{*}\right)-2 o-1=0 \\
& \Longleftrightarrow-e^{2} z^{* 2}+\left(2 e+o e^{2}-o\right) z^{*}-(2 e o+2 o+1)=0 \\
& \Longleftrightarrow z^{* 2}-\left(2 e^{*}+o-o e^{* 2}\right) z^{*}+\left(2 e^{*} o+2 o e^{* 2}+e^{* 2}\right)=0
\end{aligned}
$$
since $|e|=1$. Thus
$$
a^{*}+c^{*}=2 e^{*}+o-o e^{* 2} \quad \Longrightarrow \quad a^{*}=\frac{2 e^{*} f}{e+f}+o\left(1-e^{* 2}\right)
$$
and similarly
$$
b^{*}=\frac{2 f^{*} e}{f+e}+o\left(1-f^{* 2}\right)
$$
Then
$$
\begin{aligned}
b^{*}-a^{*} & =\frac{2\left(e f^{*}-e^{*} f\right)}{e+f}+o\left(e^{* 2}-f^{* 2}\right) \\
& =\frac{2 e f\left(f^{* 2}-e^{* 2}\right)}{e+f}+o\left(e^{* 2}-f^{* 2}\right) \\
& =\left(f^{* 2}-e^{* 2}\right)\left(\frac{2 e f}{e+f}-o\right)=\left(f^{* 2}-e^{* 2}\right)(c-o) .
\end{aligned}
$$
Now let $Z$ be a point on the tangent to $\omega$ parallel to $A B$ passing through $Q$. Then
$$
z=2 q-q^{2} z^{*} \quad \Longleftrightarrow \quad z-q=q-q^{2} z^{*}=-q^{2}\left(z^{*}-q^{*}\right)
$$
for $|q|=1$, and thus
$$
\frac{b-a}{b^{*}-a^{*}}=\frac{z-q}{z^{*}-q^{*}}=\frac{-q^{2}\left(z^{*}-q^{*}\right)}{z^{*}-q^{*}}=-q^{2} .
$$
It follows that
$$
\begin{aligned}
q^{2} & =-\frac{b-a}{b^{*}-a^{*}}=-\frac{\left(f^{2}-e^{2}\right)\left(c^{*}-o\right)}{\left(f^{* 2}-e^{* 2}\right)(c-o)}=e^{2} f^{2} \frac{c^{*}-o}{c-o} \\
& =e^{2} f^{2} \frac{\left(c^{*}-o\right)^{2}}{|c-o|^{2}}=e^{2} f^{2} \frac{\left(c^{*}-o\right)^{2}}{(1+o)^{2}}
\end{aligned}
$$
where we have used (1). In particular,
$$
q=e f \frac{c^{*}-o}{1+o}
$$
where the choice of sign is to be justified a posteriori. Further, the point $D$ satisfies
$$
-d p=\frac{d-p}{d^{*}-p^{*}}=\frac{c-p}{c^{*}-p^{*}} \quad \Longrightarrow \quad d=-\frac{c-p}{c^{*} p-1}=\frac{c+1}{c^{*}+1},
$$
using $p=-1$ to obtain the final equality.
Now, it suffices to show that (i) $D Q \| E F \perp C I$ and (ii) the midpoint of $[D Q]$ is on $C I$. The desired equality then follows by symmetry with respect to the angle bisector of the angle $\angle A C B$. Notice that (i) is equivalent with
$$
\frac{d-q}{d^{*}-q^{*}}=\frac{e-f}{e^{*}-f^{*}} \quad \Longleftrightarrow \quad d q=e f
$$
for $[D Q]$ and $[E F]$ are chords of $\omega$. But
$$
\begin{aligned}
d q=e f & \Longleftrightarrow \frac{c+1}{c^{*}+1} e f \frac{c^{*}-o}{1+o}=e f \quad \Longleftrightarrow \quad(c+1)\left(c^{*}-o\right)=\left(c^{*}+1\right)(1+o) \\
& \Longleftrightarrow c c^{*}-o\left(c+c^{*}\right)-2 o-1=0 .
\end{aligned}
$$
The last equality is precisely the defining relation for $o,(1)$. This proves (i). Further, the midpoint of $[D Q]$ is $\frac{1}{2}(d+q)$, so it remains to check that
$$
d q=\frac{d+q}{d^{*}+q^{*}}=\frac{c}{c^{*}}=e f
$$
where the first equality expresses that $[D Q]$ is a chord of $\omega$ (obviously) containing its midpoint, the second equality expresses the alignment of the midpoint of $[D Q], C$ and $I$, and the third equality follows from the expression for $c$. But we have just shown that $d q=e f$. This proves (ii), justifies the choice of sign for $q$ a posteriori, and thus completes the solution of the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\Omega$ be the circumcircle of the triangle $A B C$. The circle $\omega$ is tangent to the sides $A C$ and $B C$, and it is internally tangent to $\Omega$ at the point $P$. A line parallel to $A B$ and intersecting the interior of triangle $A B C$ is tangent to $\omega$ at $Q$.
Prove that $\angle A C P=\angle Q C B$.
|
Assume that $\omega$ is tangent to $A C$ and $B C$ at $E$ and $F$, respectively. Assume that $C P$ meets $\omega$ at $D$. Let $I$ and $O$ denote the respective centres of $\omega$ and $\Omega$. To set up a solution in the complex plane, we take the circle $\omega$ as the unit circle centered at the origin of the complex plane, and let $P O$ be the real axis with $o>0$, where we use the convention that lowercase letters denote complex coordinates of corresponding points in the plane denoted by uppercase letters.
Now, a point $Z$ on the circle $\Omega$ satisfies
$$
|z-o|^{2}=(o+1)^{2} \quad \Longleftrightarrow \quad z z^{*}-o\left(z+z^{*}\right)-2 o-1=0
$$
The triangle $A B C$ is defined by the points $E$ and $F$ on $\omega$, the intersection $C$ of the corresponding tangents lying on $\Omega$. Thus $c=2 e f /(e+f)$, and further
$$
|c-o|^{2}=(o+1)^{2} \quad \Longleftrightarrow \quad c c^{*}-o\left(c+c^{*}\right)-2 o-1=0,
$$
and this is the equality defining $o$. The points $A$ and $B$ are the second intersection points of $\Omega$ with the tangents to $\omega$ at $E$ and $F$ respectively. A point $Z$ on the tangent through $E$ is given by $z=2 e-e^{2} z^{*}$, and thus $A$ and $C$ satisfy
$$
\begin{aligned}
\left(2 e-e^{2} z^{*}\right) z^{*} & -o\left(2 e-e^{2} z^{*}+z^{*}\right)-2 o-1=0 \\
& \Longleftrightarrow-e^{2} z^{* 2}+\left(2 e+o e^{2}-o\right) z^{*}-(2 e o+2 o+1)=0 \\
& \Longleftrightarrow z^{* 2}-\left(2 e^{*}+o-o e^{* 2}\right) z^{*}+\left(2 e^{*} o+2 o e^{* 2}+e^{* 2}\right)=0
\end{aligned}
$$
since $|e|=1$. Thus
$$
a^{*}+c^{*}=2 e^{*}+o-o e^{* 2} \quad \Longrightarrow \quad a^{*}=\frac{2 e^{*} f}{e+f}+o\left(1-e^{* 2}\right)
$$
and similarly
$$
b^{*}=\frac{2 f^{*} e}{f+e}+o\left(1-f^{* 2}\right)
$$
Then
$$
\begin{aligned}
b^{*}-a^{*} & =\frac{2\left(e f^{*}-e^{*} f\right)}{e+f}+o\left(e^{* 2}-f^{* 2}\right) \\
& =\frac{2 e f\left(f^{* 2}-e^{* 2}\right)}{e+f}+o\left(e^{* 2}-f^{* 2}\right) \\
& =\left(f^{* 2}-e^{* 2}\right)\left(\frac{2 e f}{e+f}-o\right)=\left(f^{* 2}-e^{* 2}\right)(c-o) .
\end{aligned}
$$
Now let $Z$ be a point on the tangent to $\omega$ parallel to $A B$ passing through $Q$. Then
$$
z=2 q-q^{2} z^{*} \quad \Longleftrightarrow \quad z-q=q-q^{2} z^{*}=-q^{2}\left(z^{*}-q^{*}\right)
$$
for $|q|=1$, and thus
$$
\frac{b-a}{b^{*}-a^{*}}=\frac{z-q}{z^{*}-q^{*}}=\frac{-q^{2}\left(z^{*}-q^{*}\right)}{z^{*}-q^{*}}=-q^{2} .
$$
It follows that
$$
\begin{aligned}
q^{2} & =-\frac{b-a}{b^{*}-a^{*}}=-\frac{\left(f^{2}-e^{2}\right)\left(c^{*}-o\right)}{\left(f^{* 2}-e^{* 2}\right)(c-o)}=e^{2} f^{2} \frac{c^{*}-o}{c-o} \\
& =e^{2} f^{2} \frac{\left(c^{*}-o\right)^{2}}{|c-o|^{2}}=e^{2} f^{2} \frac{\left(c^{*}-o\right)^{2}}{(1+o)^{2}}
\end{aligned}
$$
where we have used (1). In particular,
$$
q=e f \frac{c^{*}-o}{1+o}
$$
where the choice of sign is to be justified a posteriori. Further, the point $D$ satisfies
$$
-d p=\frac{d-p}{d^{*}-p^{*}}=\frac{c-p}{c^{*}-p^{*}} \quad \Longrightarrow \quad d=-\frac{c-p}{c^{*} p-1}=\frac{c+1}{c^{*}+1},
$$
using $p=-1$ to obtain the final equality.
Now, it suffices to show that (i) $D Q \| E F \perp C I$ and (ii) the midpoint of $[D Q]$ is on $C I$. The desired equality then follows by symmetry with respect to the angle bisector of the angle $\angle A C B$. Notice that (i) is equivalent with
$$
\frac{d-q}{d^{*}-q^{*}}=\frac{e-f}{e^{*}-f^{*}} \quad \Longleftrightarrow \quad d q=e f
$$
for $[D Q]$ and $[E F]$ are chords of $\omega$. But
$$
\begin{aligned}
d q=e f & \Longleftrightarrow \frac{c+1}{c^{*}+1} e f \frac{c^{*}-o}{1+o}=e f \quad \Longleftrightarrow \quad(c+1)\left(c^{*}-o\right)=\left(c^{*}+1\right)(1+o) \\
& \Longleftrightarrow c c^{*}-o\left(c+c^{*}\right)-2 o-1=0 .
\end{aligned}
$$
The last equality is precisely the defining relation for $o,(1)$. This proves (i). Further, the midpoint of $[D Q]$ is $\frac{1}{2}(d+q)$, so it remains to check that
$$
d q=\frac{d+q}{d^{*}+q^{*}}=\frac{c}{c^{*}}=e f
$$
where the first equality expresses that $[D Q]$ is a chord of $\omega$ (obviously) containing its midpoint, the second equality expresses the alignment of the midpoint of $[D Q], C$ and $I$, and the third equality follows from the expression for $c$. But we have just shown that $d q=e f$. This proves (ii), justifies the choice of sign for $q$ a posteriori, and thus completes the solution of the problem.
|
{
"exam": "EGMO",
"problem_label": "5",
"problem_match": "\nProblem 5. (Proposed by Waldemar Pompe, Poland)\n",
"resource_path": "EGMO/segmented/en-2013-solutions.jsonl",
"solution_match": "\nSolution 6: ",
"tier": "T2",
"year": "2013"
}
|
Snow White and the Seven Dwarves are living in their house in the forest. On each of 16 consecutive days, some of the dwarves worked in the diamond mine while the remaining dwarves collected berries in the forest. No dwarf performed both types of work on the same day. On any two different (not necessarily consecutive) days, at least three dwarves each performed both types of work. Further, on the first day, all seven dwarves worked in the diamond mine.
Prove that, on one of these 16 days, all seven dwarves were collecting berries.
|
We define $V$ as the set of all 128 vectors of length 7 with entries in $\{0,1\}$. Every such vector encodes the work schedule of a single day: if the $i$-th entry is 0 then the $i$-th dwarf works in the mine, and if this entry is 1 then the $i$-th dwarf collects berries. The 16 working days correspond to 16 vectors $d_{1}, \ldots, d_{16}$ in $V$, which we will call dayvectors. The condition imposed on any pair of distinct days means that any two distinct day-vectors $d_{i}$ and $d_{j}$ differ in at least three positions.
We say that a vector $x \in V$ covers some vector $y \in V$, if $x$ and $y$ differ in at most one position; note that every vector in $V$ covers exactly eight vectors. For each of the 16 day-vectors $d_{i}$ we define $B_{i} \subset V$ as the set of the eight vectors that are covered by $d_{i}$. As, for $i \neq j$, the day-vectors $d_{i}$ and $d_{j}$ differ in at least three positions, their corresponding sets $B_{i}$ and $B_{j}$ are disjoint. As the sets $B_{1}, \ldots, B_{16}$ together contain $16 \cdot 8=128=|V|$ distinct elements, they form a partition of $V$; in other words, every vector in $V$ is covered by precisely one day-vector.
The weight of a vector $v \in V$ is defined as the number of 1-entries in $v$. For $k=0,1, \ldots, 7$, the set $V$ contains $\binom{7}{k}$ vectors of weight $k$. Let us analyse the 16 dayvectors $d_{1}, \ldots, d_{16}$ by their weights, and let us discuss how the vectors in $V$ are covered by them.
1. As all seven dwarves work in the diamond mine on the first day, the first day-vector is $d_{1}=(0000000)$. This day-vector covers all vectors in $V$ with weight 0 or 1.
2. No day-vector can have weight 2 , as otherwise it would differ from $d_{1}$ in at most two positions. Hence each of the $\binom{7}{2}=21$ vectors of weight 2 must be covered by some day-vector of weight 3 . As every vector of weight 3 covers three vectors of weight 2 , exactly $21 / 3=7$ day-vectors have weight 3 .
3. How are the $\binom{7}{3}=35$ vectors of weight 3 covered by the day-vectors? Seven of them are day-vectors, and the remaining 28 ones must be covered by day-vectors of weight 4 . As every vector of weight 4 covers four vectors of weight 3 , exactly $28 / 4=7$ day-vectors have weight 4.
To summarize, one day-vector has weight 0 , seven have weight 3 , and seven have weight 4 . None of these 15 day-vectors covers any vector of weight 6 or 7 , so that the eight heavyweight vectors in $V$ must be covered by the only remaining day-vector; and this remaining vector must be (1111111). On the day corresponding to (1111111) all seven dwarves are collecting berries, and that is what we wanted to show.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Snow White and the Seven Dwarves are living in their house in the forest. On each of 16 consecutive days, some of the dwarves worked in the diamond mine while the remaining dwarves collected berries in the forest. No dwarf performed both types of work on the same day. On any two different (not necessarily consecutive) days, at least three dwarves each performed both types of work. Further, on the first day, all seven dwarves worked in the diamond mine.
Prove that, on one of these 16 days, all seven dwarves were collecting berries.
|
We define $V$ as the set of all 128 vectors of length 7 with entries in $\{0,1\}$. Every such vector encodes the work schedule of a single day: if the $i$-th entry is 0 then the $i$-th dwarf works in the mine, and if this entry is 1 then the $i$-th dwarf collects berries. The 16 working days correspond to 16 vectors $d_{1}, \ldots, d_{16}$ in $V$, which we will call dayvectors. The condition imposed on any pair of distinct days means that any two distinct day-vectors $d_{i}$ and $d_{j}$ differ in at least three positions.
We say that a vector $x \in V$ covers some vector $y \in V$, if $x$ and $y$ differ in at most one position; note that every vector in $V$ covers exactly eight vectors. For each of the 16 day-vectors $d_{i}$ we define $B_{i} \subset V$ as the set of the eight vectors that are covered by $d_{i}$. As, for $i \neq j$, the day-vectors $d_{i}$ and $d_{j}$ differ in at least three positions, their corresponding sets $B_{i}$ and $B_{j}$ are disjoint. As the sets $B_{1}, \ldots, B_{16}$ together contain $16 \cdot 8=128=|V|$ distinct elements, they form a partition of $V$; in other words, every vector in $V$ is covered by precisely one day-vector.
The weight of a vector $v \in V$ is defined as the number of 1-entries in $v$. For $k=0,1, \ldots, 7$, the set $V$ contains $\binom{7}{k}$ vectors of weight $k$. Let us analyse the 16 dayvectors $d_{1}, \ldots, d_{16}$ by their weights, and let us discuss how the vectors in $V$ are covered by them.
1. As all seven dwarves work in the diamond mine on the first day, the first day-vector is $d_{1}=(0000000)$. This day-vector covers all vectors in $V$ with weight 0 or 1.
2. No day-vector can have weight 2 , as otherwise it would differ from $d_{1}$ in at most two positions. Hence each of the $\binom{7}{2}=21$ vectors of weight 2 must be covered by some day-vector of weight 3 . As every vector of weight 3 covers three vectors of weight 2 , exactly $21 / 3=7$ day-vectors have weight 3 .
3. How are the $\binom{7}{3}=35$ vectors of weight 3 covered by the day-vectors? Seven of them are day-vectors, and the remaining 28 ones must be covered by day-vectors of weight 4 . As every vector of weight 4 covers four vectors of weight 3 , exactly $28 / 4=7$ day-vectors have weight 4.
To summarize, one day-vector has weight 0 , seven have weight 3 , and seven have weight 4 . None of these 15 day-vectors covers any vector of weight 6 or 7 , so that the eight heavyweight vectors in $V$ must be covered by the only remaining day-vector; and this remaining vector must be (1111111). On the day corresponding to (1111111) all seven dwarves are collecting berries, and that is what we wanted to show.
|
{
"exam": "EGMO",
"problem_label": "6",
"problem_match": "\nProblem 6. (Proposed by Emil Kolev, Bulgaria)\n",
"resource_path": "EGMO/segmented/en-2013-solutions.jsonl",
"solution_match": "\nSolution 1: ",
"tier": "T2",
"year": "2013"
}
|
Snow White and the Seven Dwarves are living in their house in the forest. On each of 16 consecutive days, some of the dwarves worked in the diamond mine while the remaining dwarves collected berries in the forest. No dwarf performed both types of work on the same day. On any two different (not necessarily consecutive) days, at least three dwarves each performed both types of work. Further, on the first day, all seven dwarves worked in the diamond mine.
Prove that, on one of these 16 days, all seven dwarves were collecting berries.
|
If a dwarf $X$ performs the same type of work on three days $D_{1}, D_{2}, D_{3}$, then we say that this triple of days is monotonous for $X$. We claim that the following configuration cannot occur: There are three dwarves $X_{1}, X_{2}, X_{3}$ and three days $D_{1}, D_{2}$, $D_{3}$, such that the triple $\left(D_{1}, D_{2}, D_{3}\right)$ is monotonous for each of the dwarves $X_{1}, X_{2}, X_{3}$.
(Proof: Suppose that such a configuration occurs. Then among the remaining dwarves there exist three dwarves $Y_{1}, Y_{2}, Y_{3}$ that performed both types of work on day $D_{1}$ and on day $D_{2}$; without loss of generality these three dwarves worked in the mine on day $D_{1}$ and collected berries on day $D_{2}$. On day $D_{3}$, two of $Y_{1}, Y_{2}, Y_{3}$ performed the same type of work, and without loss of generality $Y_{1}$ and $Y_{2}$ worked in the mine. But then on days $D_{1}$ and $D_{3}$, each of the five dwarves $X_{1}, X_{2}, X_{3}, Y_{1}, Y_{2}$ performed only one type of work; this is in contradiction with the problem statement.)
Next we consider some fixed triple $X_{1}, X_{2}, X_{3}$ of dwarves. There are eight possible working schedules for $X_{1}, X_{2}, X_{3}$ (like mine-mine-mine, mine-mine-berries, mine-berriesmine, etc). As the above forbidden configuration does not occur, each of these eight working schedules must occur on exactly two of the sixteen days. In particular this implies that every dwarf worked exactly eight times in the mine and exactly eight times in the forest.
For $0 \leqslant k \leqslant 7$ we denote by $d(k)$ the number of days on which exactly $k$ dwarves were collecting berries. Since on the first day all seven dwarves were in the mine, on each of the remaining days at least three dwarves collected berries. This yields $d(0)=1$ and $d(1)=d(2)=0$. We assume, for the sake of contradiction, that $d(7)=0$ and hence
$$
d(3)+d(4)+d(5)+d(6)=15
$$
As every dwarf collected berries exactly eight times, we get that, further,
$$
3 d(3)+4 d(4)+5 d(5)+6 d(6)=7 \cdot 8=56
$$
Next, let us count the number $q$ of quadruples $\left(X_{1}, X_{2}, X_{3}, D\right)$ for which $X_{1}, X_{2}, X_{3}$ are three pairwise distinct dwarves that all collected berries on day $D$. As there are $7 \cdot 6 \cdot 5=210$ triples of pairwise distinct dwarves, and as every working schedule for three fixed dwarves occurs on exactly two days, we get $q=420$. As every day on which $k$ dwarves collect berries contributes $k(k-1)(k-2)$ such quadruples, we also have
$$
3 \cdot 2 \cdot 1 \cdot d(3)+4 \cdot 3 \cdot 2 \cdot d(4)+5 \cdot 4 \cdot 3 \cdot d(5)+6 \cdot 5 \cdot 4 \cdot d(6)=q=420
$$
which simplifies to
$$
d(3)+4 d(4)+10 d(5)+20 d(6)=70
$$
Finally, we count the number $r$ of quadruples $\left(X_{1}, X_{2}, X_{3}, D\right)$ for which $X_{1}, X_{2}, X_{3}$ are three pairwise distinct dwarves that all worked in the mine on day $D$. Similarly as above we see that $r=420$ and that
$$
7 \cdot 6 \cdot 5 \cdot d(0)+4 \cdot 3 \cdot 2 \cdot d(3)+3 \cdot 2 \cdot 1 \cdot d(4)=r=420
$$
which simplifies to
$$
4 d(3)+d(4)=35
$$
Multiplying (1) by -40 , multiplying (2) by 10 , multiplying (3) by -1 , multiplying (4) by 4 , and then adding up the four resulting equations yields $5 d(3)=30$ and hence $d(3)=6$. Then (4) yields $d(4)=11$. As $d(3)+d(4)=17$, the total number of days cannot be 16 . We have reached the desired contradiction.
A Variant. We follow the second solution up to equation (3). Multiplying (1) by 8 , multiplying (2) by -3 , and adding the two resulting equations to (3) yields
$$
3 d(5)+10 d(6)=22
$$
As $d(5)$ and $d(6)$ are positive integers, (5) implies $0 \leqslant d(6) \leqslant 2$. Only the case $d(6)=1$ yields an integral value $d(5)=4$. The equations (1) and (2) then yield $d(3)=10$ and $d(4)=0$.
Now let us look at the $d(3)=10$ special days on which exactly three dwarves were collecting berries. One of the dwarves collected berries on at least five special days (if every dwarf collected berries on at most four special days, this would allow at most $7 \cdot 4 / 3<10$ special days); we call this dwarf $X$. On at least two out of these five special days, some dwarf $Y$ must have collected berries together with $X$. Then these two days contradict the problem statement. We have reached the desired contradiction.
Comment. Up to permutations of the dwarves, there exists a unique set of day-vectors (as introduced in the first solution) that satisfies the conditions of the problem statement:
| 0000000 | 1110000 | 1001100 | 1000011 | 0101010 | 0100101 | 0010110 | 0011001 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 1111111 | 0001111 | 0110011 | 0111100 | 1010101 | 1011010 | 1101001 | 1100110 |
|
proof
|
Yes
|
Incomplete
|
proof
|
Combinatorics
|
Snow White and the Seven Dwarves are living in their house in the forest. On each of 16 consecutive days, some of the dwarves worked in the diamond mine while the remaining dwarves collected berries in the forest. No dwarf performed both types of work on the same day. On any two different (not necessarily consecutive) days, at least three dwarves each performed both types of work. Further, on the first day, all seven dwarves worked in the diamond mine.
Prove that, on one of these 16 days, all seven dwarves were collecting berries.
|
If a dwarf $X$ performs the same type of work on three days $D_{1}, D_{2}, D_{3}$, then we say that this triple of days is monotonous for $X$. We claim that the following configuration cannot occur: There are three dwarves $X_{1}, X_{2}, X_{3}$ and three days $D_{1}, D_{2}$, $D_{3}$, such that the triple $\left(D_{1}, D_{2}, D_{3}\right)$ is monotonous for each of the dwarves $X_{1}, X_{2}, X_{3}$.
(Proof: Suppose that such a configuration occurs. Then among the remaining dwarves there exist three dwarves $Y_{1}, Y_{2}, Y_{3}$ that performed both types of work on day $D_{1}$ and on day $D_{2}$; without loss of generality these three dwarves worked in the mine on day $D_{1}$ and collected berries on day $D_{2}$. On day $D_{3}$, two of $Y_{1}, Y_{2}, Y_{3}$ performed the same type of work, and without loss of generality $Y_{1}$ and $Y_{2}$ worked in the mine. But then on days $D_{1}$ and $D_{3}$, each of the five dwarves $X_{1}, X_{2}, X_{3}, Y_{1}, Y_{2}$ performed only one type of work; this is in contradiction with the problem statement.)
Next we consider some fixed triple $X_{1}, X_{2}, X_{3}$ of dwarves. There are eight possible working schedules for $X_{1}, X_{2}, X_{3}$ (like mine-mine-mine, mine-mine-berries, mine-berriesmine, etc). As the above forbidden configuration does not occur, each of these eight working schedules must occur on exactly two of the sixteen days. In particular this implies that every dwarf worked exactly eight times in the mine and exactly eight times in the forest.
For $0 \leqslant k \leqslant 7$ we denote by $d(k)$ the number of days on which exactly $k$ dwarves were collecting berries. Since on the first day all seven dwarves were in the mine, on each of the remaining days at least three dwarves collected berries. This yields $d(0)=1$ and $d(1)=d(2)=0$. We assume, for the sake of contradiction, that $d(7)=0$ and hence
$$
d(3)+d(4)+d(5)+d(6)=15
$$
As every dwarf collected berries exactly eight times, we get that, further,
$$
3 d(3)+4 d(4)+5 d(5)+6 d(6)=7 \cdot 8=56
$$
Next, let us count the number $q$ of quadruples $\left(X_{1}, X_{2}, X_{3}, D\right)$ for which $X_{1}, X_{2}, X_{3}$ are three pairwise distinct dwarves that all collected berries on day $D$. As there are $7 \cdot 6 \cdot 5=210$ triples of pairwise distinct dwarves, and as every working schedule for three fixed dwarves occurs on exactly two days, we get $q=420$. As every day on which $k$ dwarves collect berries contributes $k(k-1)(k-2)$ such quadruples, we also have
$$
3 \cdot 2 \cdot 1 \cdot d(3)+4 \cdot 3 \cdot 2 \cdot d(4)+5 \cdot 4 \cdot 3 \cdot d(5)+6 \cdot 5 \cdot 4 \cdot d(6)=q=420
$$
which simplifies to
$$
d(3)+4 d(4)+10 d(5)+20 d(6)=70
$$
Finally, we count the number $r$ of quadruples $\left(X_{1}, X_{2}, X_{3}, D\right)$ for which $X_{1}, X_{2}, X_{3}$ are three pairwise distinct dwarves that all worked in the mine on day $D$. Similarly as above we see that $r=420$ and that
$$
7 \cdot 6 \cdot 5 \cdot d(0)+4 \cdot 3 \cdot 2 \cdot d(3)+3 \cdot 2 \cdot 1 \cdot d(4)=r=420
$$
which simplifies to
$$
4 d(3)+d(4)=35
$$
Multiplying (1) by -40 , multiplying (2) by 10 , multiplying (3) by -1 , multiplying (4) by 4 , and then adding up the four resulting equations yields $5 d(3)=30$ and hence $d(3)=6$. Then (4) yields $d(4)=11$. As $d(3)+d(4)=17$, the total number of days cannot be 16 . We have reached the desired contradiction.
A Variant. We follow the second solution up to equation (3). Multiplying (1) by 8 , multiplying (2) by -3 , and adding the two resulting equations to (3) yields
$$
3 d(5)+10 d(6)=22
$$
As $d(5)$ and $d(6)$ are positive integers, (5) implies $0 \leqslant d(6) \leqslant 2$. Only the case $d(6)=1$ yields an integral value $d(5)=4$. The equations (1) and (2) then yield $d(3)=10$ and $d(4)=0$.
Now let us look at the $d(3)=10$ special days on which exactly three dwarves were collecting berries. One of the dwarves collected berries on at least five special days (if every dwarf collected berries on at most four special days, this would allow at most $7 \cdot 4 / 3<10$ special days); we call this dwarf $X$. On at least two out of these five special days, some dwarf $Y$ must have collected berries together with $X$. Then these two days contradict the problem statement. We have reached the desired contradiction.
Comment. Up to permutations of the dwarves, there exists a unique set of day-vectors (as introduced in the first solution) that satisfies the conditions of the problem statement:
| 0000000 | 1110000 | 1001100 | 1000011 | 0101010 | 0100101 | 0010110 | 0011001 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 1111111 | 0001111 | 0110011 | 0111100 | 1010101 | 1011010 | 1101001 | 1100110 |
|
{
"exam": "EGMO",
"problem_label": "6",
"problem_match": "\nProblem 6. (Proposed by Emil Kolev, Bulgaria)\n",
"resource_path": "EGMO/segmented/en-2013-solutions.jsonl",
"solution_match": "\nSolution 2: ",
"tier": "T2",
"year": "2013"
}
|
Determine all real constants $t$ such that whenever $a, b, c$ are the lengths of the sides of a triangle, then so are $a^{2}+b c t, b^{2}+c a t, c^{2}+a b t$.
Proposed by S. Khan, UNK
The answer is the interval $[2 / 3,2]$.
|
If $t<2 / 3$, take a triangle with sides $c=b=1$ and $a=2-\epsilon$. Then $b^{2}+c a t+c^{2}+$ $a b t-a^{2}-b c t=3 t-2+\epsilon(4-2 t-\epsilon) \leq 0$ for small positive $\epsilon$; for instance, for any $0<\epsilon<(2-3 t) /(4-2 t)$.
On the other hand, if $t>2$, then take a triangle with sides $b=c=1$ and $a=\epsilon$. Then $b^{2}+c a t+c^{2}+a b t-a^{2}-b c t=2-t+\epsilon(2 t-\epsilon) \leq 0$ for small positive $\epsilon$; for instance, for any $0<\epsilon<(t-2) /(2 t)$.
Now assume that $2 / 3 \leq t \leq 2$ and $b+c>a$. Then using $(b+c)^{2} \geq 4 b c$ we obtain
$$
\begin{aligned}
b^{2}+c a t+c^{2}+a b t-a^{2}-b c t & =(b+c)^{2}+a t(b+c)-(2+t) b c-a^{2} \\
& \geq(b+c)^{2}+a t(b+c)-\frac{1}{4}(2+t)(b+c)^{2}-a^{2} \\
& \geq \frac{1}{4}(2-t)(b+c)^{2}+a t(b+c)-a^{2}
\end{aligned}
$$
As $2-t \geq 0$ and $t>0$, this last expression is an increasing function of $b+c$, and hence using $b+c>a$ we obtain
$$
b^{2}+c a t+c^{2}+a b t-a^{2}-b c t>\frac{1}{4}(2-t) a^{2}+t a^{2}-a^{2}=\frac{3}{4}\left(t-\frac{2}{3}\right) a^{2} \geq 0
$$
as $t \geq 2 / 3$. The other two inequalities follow by symmetry.
|
[2 / 3, 2]
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Determine all real constants $t$ such that whenever $a, b, c$ are the lengths of the sides of a triangle, then so are $a^{2}+b c t, b^{2}+c a t, c^{2}+a b t$.
Proposed by S. Khan, UNK
The answer is the interval $[2 / 3,2]$.
|
If $t<2 / 3$, take a triangle with sides $c=b=1$ and $a=2-\epsilon$. Then $b^{2}+c a t+c^{2}+$ $a b t-a^{2}-b c t=3 t-2+\epsilon(4-2 t-\epsilon) \leq 0$ for small positive $\epsilon$; for instance, for any $0<\epsilon<(2-3 t) /(4-2 t)$.
On the other hand, if $t>2$, then take a triangle with sides $b=c=1$ and $a=\epsilon$. Then $b^{2}+c a t+c^{2}+a b t-a^{2}-b c t=2-t+\epsilon(2 t-\epsilon) \leq 0$ for small positive $\epsilon$; for instance, for any $0<\epsilon<(t-2) /(2 t)$.
Now assume that $2 / 3 \leq t \leq 2$ and $b+c>a$. Then using $(b+c)^{2} \geq 4 b c$ we obtain
$$
\begin{aligned}
b^{2}+c a t+c^{2}+a b t-a^{2}-b c t & =(b+c)^{2}+a t(b+c)-(2+t) b c-a^{2} \\
& \geq(b+c)^{2}+a t(b+c)-\frac{1}{4}(2+t)(b+c)^{2}-a^{2} \\
& \geq \frac{1}{4}(2-t)(b+c)^{2}+a t(b+c)-a^{2}
\end{aligned}
$$
As $2-t \geq 0$ and $t>0$, this last expression is an increasing function of $b+c$, and hence using $b+c>a$ we obtain
$$
b^{2}+c a t+c^{2}+a b t-a^{2}-b c t>\frac{1}{4}(2-t) a^{2}+t a^{2}-a^{2}=\frac{3}{4}\left(t-\frac{2}{3}\right) a^{2} \geq 0
$$
as $t \geq 2 / 3$. The other two inequalities follow by symmetry.
|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "EGMO/segmented/en-2014-solutions-day1.jsonl",
"solution_match": "# Solution 1.",
"tier": "T2",
"year": "2014"
}
|
Determine all real constants $t$ such that whenever $a, b, c$ are the lengths of the sides of a triangle, then so are $a^{2}+b c t, b^{2}+c a t, c^{2}+a b t$.
Proposed by S. Khan, UNK
The answer is the interval $[2 / 3,2]$.
|
After showing that $t$ must be in the interval $[2 / 3,2]$ as in Solution 1, we let $x=$ $(c+a-b) / 2, y=(a+b-c) / 2$ and $z=(b+c-a) / 2$ so that $a=x+y, b=y+z$, $c=z+x$. Then we have:
$b^{2}+c a t+c^{2}+a b t-a^{2}-b c t=\left(x^{2}+y^{2}-z^{2}+x y+x z+y z\right) t+2\left(z^{2}+x z+y z-x y\right)$
Since this linear function of $t$ is positive both at $t=2 / 3$ where
$\frac{2}{3}\left(x^{2}+y^{2}-z^{2}+x y+x z+y z\right)+2\left(z^{2}+x z+y z-x y\right)=\frac{2}{3}\left((x-y)^{2}+4(x+y) z+2 z^{2}\right)>0$
and at $t=2$ where
$2\left(x^{2}+y^{2}-z^{2}+x y+x z-y z\right)+2\left(z^{2}+x z+y z+x y\right)=2\left(x^{2}+y^{2}\right)+4(x+y) z>0$,
it is positive on the entire interval $[2 / 3,2]$.
|
[2 / 3,2]
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Determine all real constants $t$ such that whenever $a, b, c$ are the lengths of the sides of a triangle, then so are $a^{2}+b c t, b^{2}+c a t, c^{2}+a b t$.
Proposed by S. Khan, UNK
The answer is the interval $[2 / 3,2]$.
|
After showing that $t$ must be in the interval $[2 / 3,2]$ as in Solution 1, we let $x=$ $(c+a-b) / 2, y=(a+b-c) / 2$ and $z=(b+c-a) / 2$ so that $a=x+y, b=y+z$, $c=z+x$. Then we have:
$b^{2}+c a t+c^{2}+a b t-a^{2}-b c t=\left(x^{2}+y^{2}-z^{2}+x y+x z+y z\right) t+2\left(z^{2}+x z+y z-x y\right)$
Since this linear function of $t$ is positive both at $t=2 / 3$ where
$\frac{2}{3}\left(x^{2}+y^{2}-z^{2}+x y+x z+y z\right)+2\left(z^{2}+x z+y z-x y\right)=\frac{2}{3}\left((x-y)^{2}+4(x+y) z+2 z^{2}\right)>0$
and at $t=2$ where
$2\left(x^{2}+y^{2}-z^{2}+x y+x z-y z\right)+2\left(z^{2}+x z+y z+x y\right)=2\left(x^{2}+y^{2}\right)+4(x+y) z>0$,
it is positive on the entire interval $[2 / 3,2]$.
|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "EGMO/segmented/en-2014-solutions-day1.jsonl",
"solution_match": "# Solution 2.",
"tier": "T2",
"year": "2014"
}
|
Determine all real constants $t$ such that whenever $a, b, c$ are the lengths of the sides of a triangle, then so are $a^{2}+b c t, b^{2}+c a t, c^{2}+a b t$.
Proposed by S. Khan, UNK
The answer is the interval $[2 / 3,2]$.
|
After the point in Solution 2 where we obtain
$b^{2}+c a t+c^{2}+a b t-a^{2}-b c t=\left(x^{2}+y^{2}-z^{2}+x y+x z+y z\right) t+2\left(z^{2}+x z+y z-x y\right)$
we observe that the right hand side can be rewritten as
$$
(2-t) z^{2}+(x-y)^{2} t+(3 t-2) x y+z(x+y)(2+t)
$$
As the first three terms are non-negative and the last term is positive, the result follows.
|
[2 / 3,2]
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Determine all real constants $t$ such that whenever $a, b, c$ are the lengths of the sides of a triangle, then so are $a^{2}+b c t, b^{2}+c a t, c^{2}+a b t$.
Proposed by S. Khan, UNK
The answer is the interval $[2 / 3,2]$.
|
After the point in Solution 2 where we obtain
$b^{2}+c a t+c^{2}+a b t-a^{2}-b c t=\left(x^{2}+y^{2}-z^{2}+x y+x z+y z\right) t+2\left(z^{2}+x z+y z-x y\right)$
we observe that the right hand side can be rewritten as
$$
(2-t) z^{2}+(x-y)^{2} t+(3 t-2) x y+z(x+y)(2+t)
$$
As the first three terms are non-negative and the last term is positive, the result follows.
|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "EGMO/segmented/en-2014-solutions-day1.jsonl",
"solution_match": "# Solution 3.",
"tier": "T2",
"year": "2014"
}
|
Determine all real constants $t$ such that whenever $a, b, c$ are the lengths of the sides of a triangle, then so are $a^{2}+b c t, b^{2}+c a t, c^{2}+a b t$.
Proposed by S. Khan, UNK
The answer is the interval $[2 / 3,2]$.
|
First we show that $t$ must be in the interval $[2 / 3,2]$ as in Solution 1. Then:
Case 1: If $a \geq b, c$, then $a b+a c-b c>0,2\left(b^{2}+c^{2}\right) \geq(b+c)^{2}>a^{2}$ and $t \geq 2 / 3$ implies:
$$
\begin{aligned}
b^{2}+c a t+c^{2}+a b t-a^{2}-b c t & =b^{2}+c^{2}-a^{2}+(a b+a c-b c) t \\
& \geq\left(b^{2}+c^{2}-a^{2}\right)+\frac{2}{3}(a b+a c-b c) \\
& \geq \frac{1}{3}\left(3 b^{2}+3 c^{2}-3 a^{2}+2 a b+2 a c-2 b c\right) \\
& \geq \frac{1}{3}\left[\left(2 b^{2}+2 c^{2}-a^{2}\right)+(b-c)^{2}+2 a(b+c-a)\right] \\
& >0
\end{aligned}
$$
Case 2: If $b \geq a, c$, then $b^{2}+c^{2}-a^{2}>0$. If also $a b+a c-b c \geq 0$, then $b^{2}+c a t+$ $c^{2}+a b t-a^{2}-b c t>0$. If, on the other hand, $a b+a c-b c \leq 0$, then since $t \leq 2$, we have:
$$
\begin{aligned}
b^{2}+c a t+c^{2}+a b t-a^{2}-b c t & \geq b^{2}+c^{2}-a^{2}+2(a b+a c-b c) \\
& \geq(b-c)^{2}+a(b+c-a)+a(b+c) \\
& >0
\end{aligned}
$$
By symmetry, we are done.
|
[2 / 3,2]
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Determine all real constants $t$ such that whenever $a, b, c$ are the lengths of the sides of a triangle, then so are $a^{2}+b c t, b^{2}+c a t, c^{2}+a b t$.
Proposed by S. Khan, UNK
The answer is the interval $[2 / 3,2]$.
|
First we show that $t$ must be in the interval $[2 / 3,2]$ as in Solution 1. Then:
Case 1: If $a \geq b, c$, then $a b+a c-b c>0,2\left(b^{2}+c^{2}\right) \geq(b+c)^{2}>a^{2}$ and $t \geq 2 / 3$ implies:
$$
\begin{aligned}
b^{2}+c a t+c^{2}+a b t-a^{2}-b c t & =b^{2}+c^{2}-a^{2}+(a b+a c-b c) t \\
& \geq\left(b^{2}+c^{2}-a^{2}\right)+\frac{2}{3}(a b+a c-b c) \\
& \geq \frac{1}{3}\left(3 b^{2}+3 c^{2}-3 a^{2}+2 a b+2 a c-2 b c\right) \\
& \geq \frac{1}{3}\left[\left(2 b^{2}+2 c^{2}-a^{2}\right)+(b-c)^{2}+2 a(b+c-a)\right] \\
& >0
\end{aligned}
$$
Case 2: If $b \geq a, c$, then $b^{2}+c^{2}-a^{2}>0$. If also $a b+a c-b c \geq 0$, then $b^{2}+c a t+$ $c^{2}+a b t-a^{2}-b c t>0$. If, on the other hand, $a b+a c-b c \leq 0$, then since $t \leq 2$, we have:
$$
\begin{aligned}
b^{2}+c a t+c^{2}+a b t-a^{2}-b c t & \geq b^{2}+c^{2}-a^{2}+2(a b+a c-b c) \\
& \geq(b-c)^{2}+a(b+c-a)+a(b+c) \\
& >0
\end{aligned}
$$
By symmetry, we are done.
|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "EGMO/segmented/en-2014-solutions-day1.jsonl",
"solution_match": "# Solution 4.",
"tier": "T2",
"year": "2014"
}
|
Let $D$ and $E$ be two points on the sides $A B$ and $A C$, respectively, of a triangle $A B C$, such that $D B=B C=C E$, and let $F$ be the point of intersection of the lines $C D$ and $B E$. Prove that the incenter $I$ of the triangle $A B C$, the orthocenter $H$ of the triangle $D E F$ and the midpoint $M$ of the $\operatorname{arc} B A C$ of the circumcircle of the triangle $A B C$ are collinear.
Proposed by Danylo Khilko, UKR
|
As $D B=B C=C E$ we have $B I \perp C D$ and $C I \perp B E$. Hence $I$ is orthocenter of triangle $B F C$. Let $K$ be the point of intersection of the lines $B I$ and $C D$, and let $L$ be the point of intersection of the lines $C I$ and $B E$. Then we have the power relation $I B \cdot I K=I C \cdot I L$. Let $U$ and $V$ be the feet of the perpendiculars from $D$ to $E F$ and $E$ to $D F$, respectively. Now we have the power relation $D H \cdot H U=E H \cdot H V$.
Let $\omega_{1}$ and $\omega_{2}$ be the circles with diameters $B D$ and $C E$, respectively. From the power relations above we conclude that $I H$ is the radical axis of the circles $\omega_{1}$ and $\omega_{2}$.
Let $O_{1}$ and $O_{2}$ be centers of $\omega_{1}$ and $\omega_{2}$, respectively. Then $M B=M C, B O_{1}=C O_{2}$ and $\angle M B O_{1}=\angle M C O_{2}$, and the triangles $M B O_{1}$ and $M C O_{2}$ are congruent. Hence $M O_{1}=M O_{2}$. Since radii of $\omega_{1}$ and $\omega_{2}$ are equal, this implies that $M$ lies on the radical axis of $\omega_{1}$ and $\omega_{2}$ and $M, I, H$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $D$ and $E$ be two points on the sides $A B$ and $A C$, respectively, of a triangle $A B C$, such that $D B=B C=C E$, and let $F$ be the point of intersection of the lines $C D$ and $B E$. Prove that the incenter $I$ of the triangle $A B C$, the orthocenter $H$ of the triangle $D E F$ and the midpoint $M$ of the $\operatorname{arc} B A C$ of the circumcircle of the triangle $A B C$ are collinear.
Proposed by Danylo Khilko, UKR
|
As $D B=B C=C E$ we have $B I \perp C D$ and $C I \perp B E$. Hence $I$ is orthocenter of triangle $B F C$. Let $K$ be the point of intersection of the lines $B I$ and $C D$, and let $L$ be the point of intersection of the lines $C I$ and $B E$. Then we have the power relation $I B \cdot I K=I C \cdot I L$. Let $U$ and $V$ be the feet of the perpendiculars from $D$ to $E F$ and $E$ to $D F$, respectively. Now we have the power relation $D H \cdot H U=E H \cdot H V$.

Let $\omega_{1}$ and $\omega_{2}$ be the circles with diameters $B D$ and $C E$, respectively. From the power relations above we conclude that $I H$ is the radical axis of the circles $\omega_{1}$ and $\omega_{2}$.
Let $O_{1}$ and $O_{2}$ be centers of $\omega_{1}$ and $\omega_{2}$, respectively. Then $M B=M C, B O_{1}=C O_{2}$ and $\angle M B O_{1}=\angle M C O_{2}$, and the triangles $M B O_{1}$ and $M C O_{2}$ are congruent. Hence $M O_{1}=M O_{2}$. Since radii of $\omega_{1}$ and $\omega_{2}$ are equal, this implies that $M$ lies on the radical axis of $\omega_{1}$ and $\omega_{2}$ and $M, I, H$ are collinear.
|
{
"exam": "EGMO",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "EGMO/segmented/en-2014-solutions-day1.jsonl",
"solution_match": "# Solution 1. ",
"tier": "T2",
"year": "2014"
}
|
Let $D$ and $E$ be two points on the sides $A B$ and $A C$, respectively, of a triangle $A B C$, such that $D B=B C=C E$, and let $F$ be the point of intersection of the lines $C D$ and $B E$. Prove that the incenter $I$ of the triangle $A B C$, the orthocenter $H$ of the triangle $D E F$ and the midpoint $M$ of the $\operatorname{arc} B A C$ of the circumcircle of the triangle $A B C$ are collinear.
Proposed by Danylo Khilko, UKR
|
Let the points $K, L, U, V$ be as in Solution 1. Le $P$ be the point of intersection of $D U$ and $E I$, and let $Q$ be the point of intersection of $E V$ and $D I$.
Since $D B=B C=C E$, the points $C I$ and $B I$ are perpendicular to $B E$ and $C D$, respectively. Hence the lines $B I$ and $E V$ are parallel and $\angle I E B=\angle I B E=$ $\angle U E H$. Similarly, the lines $C I$ and $D U$ are parallel and $\angle I D C=\angle I C D=\angle V D H$. Since $\angle U E H=\angle V D H$, the points $D, Q, F, P, E$ are concyclic. Hence $I P \cdot I E=$ $I Q \cdot I D$.
Let $R$ be the second point intersection of the circumcircle of triangle $H E P$ and the line $H I$. As $I H \cdot I R=I P \cdot I E=I Q \cdot I D$, the points $D, Q, H, R$ are also concyclic. We have $\angle D Q H=\angle E P H=\angle D F E=\angle B F C=180^{\circ}-\angle B I C=90^{\circ}-\angle B A C / 2$. Now using the concylicity of $D, Q, H, R$, and $E, P, H, R$ we obtain $\angle D R H=$ $\angle E R H=\angle 180^{\circ}-\left(90^{\circ}-\angle B A C / 2\right)=90^{\circ}+\angle B A C / 2$. Hence $R$ is inside the triangle $D E H$ and $\angle D R E=360^{\circ}-\angle D R H-\angle E R H=180^{\circ}-\angle B A C$ and it follows that the points $A, D, R, E$ are concyclic.
As $M B=M C, B D=C E, \angle M B D=\angle M C E$, the triangles $M B D$ and $M C E$ are congruent and $\angle M D A=\angle M E A$. Hence the points $M, D, E, A$ are concylic. Therefore the points $M, D, R, E, A$ are concylic. Now we have $\angle M R E=180^{\circ}-$ $\angle M A E=180^{\circ}-\left(90^{\circ}+\angle B A C / 2\right)=90^{\circ}-\angle B A C / 2$ and since $\angle E R H=90^{\circ}+$ $\angle B A C / 2$, we conclude that the points $I, H, R, M$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $D$ and $E$ be two points on the sides $A B$ and $A C$, respectively, of a triangle $A B C$, such that $D B=B C=C E$, and let $F$ be the point of intersection of the lines $C D$ and $B E$. Prove that the incenter $I$ of the triangle $A B C$, the orthocenter $H$ of the triangle $D E F$ and the midpoint $M$ of the $\operatorname{arc} B A C$ of the circumcircle of the triangle $A B C$ are collinear.
Proposed by Danylo Khilko, UKR
|
Let the points $K, L, U, V$ be as in Solution 1. Le $P$ be the point of intersection of $D U$ and $E I$, and let $Q$ be the point of intersection of $E V$ and $D I$.
Since $D B=B C=C E$, the points $C I$ and $B I$ are perpendicular to $B E$ and $C D$, respectively. Hence the lines $B I$ and $E V$ are parallel and $\angle I E B=\angle I B E=$ $\angle U E H$. Similarly, the lines $C I$ and $D U$ are parallel and $\angle I D C=\angle I C D=\angle V D H$. Since $\angle U E H=\angle V D H$, the points $D, Q, F, P, E$ are concyclic. Hence $I P \cdot I E=$ $I Q \cdot I D$.
Let $R$ be the second point intersection of the circumcircle of triangle $H E P$ and the line $H I$. As $I H \cdot I R=I P \cdot I E=I Q \cdot I D$, the points $D, Q, H, R$ are also concyclic. We have $\angle D Q H=\angle E P H=\angle D F E=\angle B F C=180^{\circ}-\angle B I C=90^{\circ}-\angle B A C / 2$. Now using the concylicity of $D, Q, H, R$, and $E, P, H, R$ we obtain $\angle D R H=$ $\angle E R H=\angle 180^{\circ}-\left(90^{\circ}-\angle B A C / 2\right)=90^{\circ}+\angle B A C / 2$. Hence $R$ is inside the triangle $D E H$ and $\angle D R E=360^{\circ}-\angle D R H-\angle E R H=180^{\circ}-\angle B A C$ and it follows that the points $A, D, R, E$ are concyclic.

As $M B=M C, B D=C E, \angle M B D=\angle M C E$, the triangles $M B D$ and $M C E$ are congruent and $\angle M D A=\angle M E A$. Hence the points $M, D, E, A$ are concylic. Therefore the points $M, D, R, E, A$ are concylic. Now we have $\angle M R E=180^{\circ}-$ $\angle M A E=180^{\circ}-\left(90^{\circ}+\angle B A C / 2\right)=90^{\circ}-\angle B A C / 2$ and since $\angle E R H=90^{\circ}+$ $\angle B A C / 2$, we conclude that the points $I, H, R, M$ are collinear.
|
{
"exam": "EGMO",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "EGMO/segmented/en-2014-solutions-day1.jsonl",
"solution_match": "# Solution 2.",
"tier": "T2",
"year": "2014"
}
|
Let $D$ and $E$ be two points on the sides $A B$ and $A C$, respectively, of a triangle $A B C$, such that $D B=B C=C E$, and let $F$ be the point of intersection of the lines $C D$ and $B E$. Prove that the incenter $I$ of the triangle $A B C$, the orthocenter $H$ of the triangle $D E F$ and the midpoint $M$ of the $\operatorname{arc} B A C$ of the circumcircle of the triangle $A B C$ are collinear.
Proposed by Danylo Khilko, UKR
|
Suppose that we have a coordinate system and $\left(b_{x}, b_{y}\right),\left(c_{x}, c_{y}\right),\left(d_{x}, d_{y}\right),\left(e_{x}, e_{y}\right)$ are the coordinates of the points $B, C, D, E$, respectively. From $\overrightarrow{B I} \cdot \overrightarrow{C D}=0, \overrightarrow{C I} \cdot \overrightarrow{B E}=$ $0, \overrightarrow{E H} \cdot \overrightarrow{C D}=0, \overrightarrow{D H} \cdot \overrightarrow{B E}=0$ we obtain $\overrightarrow{I H} \cdot(\vec{B}-\vec{C}-\vec{E}+\vec{D})=0$. Hence the slope of the line $I H$ is $\left(c_{x}+e_{x}-b_{x}-d_{x}\right) /\left(b_{y}+d_{y}-c_{y}-e_{y}\right)$.
Assume that the $x$-axis lies along the line $B C$, and let $\alpha=\angle B A C, \beta=\angle A B C$, $\theta=\angle A C B$. Since $D B=B C=C E$, we have $c_{x}-b_{x}=B C, e_{x}-d_{x}=B C-$ $B C \cos \beta-B C \cos \theta, b_{y}=c_{y}=0, d_{y}-e_{y}=B C \sin \beta-B C \sin \theta$. Therefore the slope of $I H$ is $(2-\cos \beta-\cos \theta) /(\sin \beta-\sin \theta)$.
Now we will show that the slope of the line $M I$ is the same. Let $r$ and $R$ be the inradius and circumradius of the triangle $A B C$, respectively. As $\angle B M C=$ $\angle B A C=\alpha$ and $B M=M C$, we have
$$
m_{y}-i_{y}=\frac{B C}{2} \cot \left(\frac{\alpha}{2}\right)-r \text { and } m_{x}-i_{x}=\frac{A C-A B}{2}
$$
where $\left(m_{x}, m_{y}\right)$ and $\left(i_{x}, i_{y}\right)$ are the coordinates of $M$ and $I$, respectively. Therefore the slope of $M I$ is $(B C \cot (\alpha / 2)-2 r) /(A C-A B)$.
Now the equality of these slopes follows using
$$
\frac{B C}{\sin \alpha}=\frac{A C}{\sin \beta}=\frac{A B}{\sin \theta}=2 R
$$
hence
$$
B C \cot \left(\frac{\alpha}{2}\right)=4 R \cos ^{2}\left(\frac{\alpha}{2}\right)=2 R(1+\cos \alpha)
$$
and
$$
\frac{r}{R}=\cos \alpha+\cos \beta+\cos \theta-1
$$
as
$$
\frac{B C \cot (\alpha / 2)-2 r}{A C-A B}=\frac{2 R(1+\cos \alpha)-2 r}{2 R(\sin \beta-\sin \theta)}=\frac{2-\cos \beta-\cos \theta}{\sin \beta-\sin \theta}
$$
giving the collinearity of the points $I, H, M$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $D$ and $E$ be two points on the sides $A B$ and $A C$, respectively, of a triangle $A B C$, such that $D B=B C=C E$, and let $F$ be the point of intersection of the lines $C D$ and $B E$. Prove that the incenter $I$ of the triangle $A B C$, the orthocenter $H$ of the triangle $D E F$ and the midpoint $M$ of the $\operatorname{arc} B A C$ of the circumcircle of the triangle $A B C$ are collinear.
Proposed by Danylo Khilko, UKR
|
Suppose that we have a coordinate system and $\left(b_{x}, b_{y}\right),\left(c_{x}, c_{y}\right),\left(d_{x}, d_{y}\right),\left(e_{x}, e_{y}\right)$ are the coordinates of the points $B, C, D, E$, respectively. From $\overrightarrow{B I} \cdot \overrightarrow{C D}=0, \overrightarrow{C I} \cdot \overrightarrow{B E}=$ $0, \overrightarrow{E H} \cdot \overrightarrow{C D}=0, \overrightarrow{D H} \cdot \overrightarrow{B E}=0$ we obtain $\overrightarrow{I H} \cdot(\vec{B}-\vec{C}-\vec{E}+\vec{D})=0$. Hence the slope of the line $I H$ is $\left(c_{x}+e_{x}-b_{x}-d_{x}\right) /\left(b_{y}+d_{y}-c_{y}-e_{y}\right)$.
Assume that the $x$-axis lies along the line $B C$, and let $\alpha=\angle B A C, \beta=\angle A B C$, $\theta=\angle A C B$. Since $D B=B C=C E$, we have $c_{x}-b_{x}=B C, e_{x}-d_{x}=B C-$ $B C \cos \beta-B C \cos \theta, b_{y}=c_{y}=0, d_{y}-e_{y}=B C \sin \beta-B C \sin \theta$. Therefore the slope of $I H$ is $(2-\cos \beta-\cos \theta) /(\sin \beta-\sin \theta)$.
Now we will show that the slope of the line $M I$ is the same. Let $r$ and $R$ be the inradius and circumradius of the triangle $A B C$, respectively. As $\angle B M C=$ $\angle B A C=\alpha$ and $B M=M C$, we have
$$
m_{y}-i_{y}=\frac{B C}{2} \cot \left(\frac{\alpha}{2}\right)-r \text { and } m_{x}-i_{x}=\frac{A C-A B}{2}
$$
where $\left(m_{x}, m_{y}\right)$ and $\left(i_{x}, i_{y}\right)$ are the coordinates of $M$ and $I$, respectively. Therefore the slope of $M I$ is $(B C \cot (\alpha / 2)-2 r) /(A C-A B)$.
Now the equality of these slopes follows using
$$
\frac{B C}{\sin \alpha}=\frac{A C}{\sin \beta}=\frac{A B}{\sin \theta}=2 R
$$
hence
$$
B C \cot \left(\frac{\alpha}{2}\right)=4 R \cos ^{2}\left(\frac{\alpha}{2}\right)=2 R(1+\cos \alpha)
$$
and
$$
\frac{r}{R}=\cos \alpha+\cos \beta+\cos \theta-1
$$
as
$$
\frac{B C \cot (\alpha / 2)-2 r}{A C-A B}=\frac{2 R(1+\cos \alpha)-2 r}{2 R(\sin \beta-\sin \theta)}=\frac{2-\cos \beta-\cos \theta}{\sin \beta-\sin \theta}
$$
giving the collinearity of the points $I, H, M$.
|
{
"exam": "EGMO",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "EGMO/segmented/en-2014-solutions-day1.jsonl",
"solution_match": "# Solution 3.",
"tier": "T2",
"year": "2014"
}
|
Let $D$ and $E$ be two points on the sides $A B$ and $A C$, respectively, of a triangle $A B C$, such that $D B=B C=C E$, and let $F$ be the point of intersection of the lines $C D$ and $B E$. Prove that the incenter $I$ of the triangle $A B C$, the orthocenter $H$ of the triangle $D E F$ and the midpoint $M$ of the $\operatorname{arc} B A C$ of the circumcircle of the triangle $A B C$ are collinear.
Proposed by Danylo Khilko, UKR
|
Let the bisectors $B I$ and $C I$ meet the circumcircle of $A B C$ again at $P$ and $Q$, respectively. Let the altitude of $D E F$ belonging to $D$ meet $B I$ at $R$ and the one belonging to $E$ meet $C I$ at $S$.
Since $B I$ is angle bisector of the iscosceles triangle $C B D, B I$ and $C D$ are perpendicular. Since $E H$ and $D F$ are also perpendicular, $H S$ and $R I$ are parallel. Similarly, $H R$ and $S I$ are parallel, and hence $H S I R$ is a parallelogram.
On the other hand, as $M$ is the midpoint of the $\operatorname{arc} B A C$, we have $\angle M P I=$ $\angle M P B=\angle M Q C=\angle M Q I$, and $\angle P I Q=(\widehat{P A}+\widehat{C B}+\widehat{A Q}) / 2=(\widehat{P C}+\widehat{C B}+$ $\widehat{B Q}) / 2=\angle P M Q$. Therefore $M P I Q$ is a parallelogram.
Since $C I$ is angle bisector of the iscosceles triangle $B C E$, the triangle $B S E$ is also isosceles. Hence $\angle F B S=\angle E B S=\angle S E B=\angle H E F=\angle H D F=\angle R D F=$ $\angle F C S$ and $B, S, F, C$ are concyclic. Similarly, $B, F, R, C$ are concyclic. Therefore $B, S, R, C$ are concyclic. As $B, Q, P, C$ are also concyclic, $S R$ an $Q P$ are parallel.
Now it follows that HSIR and MQIP are homothetic parallelograms, and therefore $M, H, I$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $D$ and $E$ be two points on the sides $A B$ and $A C$, respectively, of a triangle $A B C$, such that $D B=B C=C E$, and let $F$ be the point of intersection of the lines $C D$ and $B E$. Prove that the incenter $I$ of the triangle $A B C$, the orthocenter $H$ of the triangle $D E F$ and the midpoint $M$ of the $\operatorname{arc} B A C$ of the circumcircle of the triangle $A B C$ are collinear.
Proposed by Danylo Khilko, UKR
|
Let the bisectors $B I$ and $C I$ meet the circumcircle of $A B C$ again at $P$ and $Q$, respectively. Let the altitude of $D E F$ belonging to $D$ meet $B I$ at $R$ and the one belonging to $E$ meet $C I$ at $S$.
Since $B I$ is angle bisector of the iscosceles triangle $C B D, B I$ and $C D$ are perpendicular. Since $E H$ and $D F$ are also perpendicular, $H S$ and $R I$ are parallel. Similarly, $H R$ and $S I$ are parallel, and hence $H S I R$ is a parallelogram.
On the other hand, as $M$ is the midpoint of the $\operatorname{arc} B A C$, we have $\angle M P I=$ $\angle M P B=\angle M Q C=\angle M Q I$, and $\angle P I Q=(\widehat{P A}+\widehat{C B}+\widehat{A Q}) / 2=(\widehat{P C}+\widehat{C B}+$ $\widehat{B Q}) / 2=\angle P M Q$. Therefore $M P I Q$ is a parallelogram.
Since $C I$ is angle bisector of the iscosceles triangle $B C E$, the triangle $B S E$ is also isosceles. Hence $\angle F B S=\angle E B S=\angle S E B=\angle H E F=\angle H D F=\angle R D F=$ $\angle F C S$ and $B, S, F, C$ are concyclic. Similarly, $B, F, R, C$ are concyclic. Therefore $B, S, R, C$ are concyclic. As $B, Q, P, C$ are also concyclic, $S R$ an $Q P$ are parallel.
Now it follows that HSIR and MQIP are homothetic parallelograms, and therefore $M, H, I$ are collinear.

|
{
"exam": "EGMO",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "EGMO/segmented/en-2014-solutions-day1.jsonl",
"solution_match": "# Solution 4.",
"tier": "T2",
"year": "2014"
}
|
We denote the number of positive divisors of a positive integer $m$ by $d(m)$ and the number of distinct prime divisors of $m$ by $\omega(m)$. Let $k$ be a positive integer. Prove that there exist infinitely many positive integers $n$ such that $\omega(n)=k$ and $d(n)$ does not divide $d\left(a^{2}+b^{2}\right)$ for any positive integers $a, b$ satisfying $a+b=n$.
Proposed by JPN
|
We will show that any number of the form $n=2^{p-1} m$ where $m$ is a positive integer that has exactly $k-1$ prime factors all of which are greater than 3 and $p$ is a prime number such that $(5 / 4)^{(p-1) / 2}>m$ satisfies the given condition.
Suppose that $a$ and $b$ are positive integers such that $a+b=n$ and $d(n) \mid d\left(a^{2}+b^{2}\right)$. Then $p \mid d\left(a^{2}+b^{2}\right)$. Hence $a^{2}+b^{2}=q^{c p-1} r$ where $q$ is a prime, $c$ is a positive integer and $r$ is a positive integer not divisible by $q$. If $q \geq 5$, then
$$
2^{2 p-2} m^{2}=n^{2}=(a+b)^{2}>a^{2}+b^{2}=q^{c p-1} r \geq q^{p-1} \geq 5^{p-1}
$$
gives a contradiction. So $q$ is 2 or 3 .
If $q=3$, then $a^{2}+b^{2}$ is divisible by 3 and this implies that both $a$ and $b$ are divisible by 3 . This means $n=a+b$ is divisible by 3 , a contradiction. Hence $q=2$.
Now we have $a+b=2^{p-1} m$ and $a^{2}+b^{2}=2^{c p-1} r$. If the highest powers of 2 dividing $a$ and $b$ are different, then $a+b=2^{p-1} m$ implies that the smaller one must be $2^{p-1}$ and this makes $2^{2 p-2}$ the highest power of 2 dividing $a^{2}+b^{2}=2^{c p-1} r$, or equivalently, $c p-1=2 p-2$, which is not possible. Therefore $a=2^{t} a_{0}$ and $b=2^{t} b_{0}$ for some positive integer $t<p-1$ and odd integers $a_{0}$ and $b_{0}$. Then $a_{0}^{2}+b_{0}^{2}=2^{c p-1-2 t} r$. The left side of this equality is congruent to 2 modulo 4 , therefore $c p-1-2 t$ must be 1. But then $t<p-1$ gives $(c / 2) p=t+1<p$, which is not possible either.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
We denote the number of positive divisors of a positive integer $m$ by $d(m)$ and the number of distinct prime divisors of $m$ by $\omega(m)$. Let $k$ be a positive integer. Prove that there exist infinitely many positive integers $n$ such that $\omega(n)=k$ and $d(n)$ does not divide $d\left(a^{2}+b^{2}\right)$ for any positive integers $a, b$ satisfying $a+b=n$.
Proposed by JPN
|
We will show that any number of the form $n=2^{p-1} m$ where $m$ is a positive integer that has exactly $k-1$ prime factors all of which are greater than 3 and $p$ is a prime number such that $(5 / 4)^{(p-1) / 2}>m$ satisfies the given condition.
Suppose that $a$ and $b$ are positive integers such that $a+b=n$ and $d(n) \mid d\left(a^{2}+b^{2}\right)$. Then $p \mid d\left(a^{2}+b^{2}\right)$. Hence $a^{2}+b^{2}=q^{c p-1} r$ where $q$ is a prime, $c$ is a positive integer and $r$ is a positive integer not divisible by $q$. If $q \geq 5$, then
$$
2^{2 p-2} m^{2}=n^{2}=(a+b)^{2}>a^{2}+b^{2}=q^{c p-1} r \geq q^{p-1} \geq 5^{p-1}
$$
gives a contradiction. So $q$ is 2 or 3 .
If $q=3$, then $a^{2}+b^{2}$ is divisible by 3 and this implies that both $a$ and $b$ are divisible by 3 . This means $n=a+b$ is divisible by 3 , a contradiction. Hence $q=2$.
Now we have $a+b=2^{p-1} m$ and $a^{2}+b^{2}=2^{c p-1} r$. If the highest powers of 2 dividing $a$ and $b$ are different, then $a+b=2^{p-1} m$ implies that the smaller one must be $2^{p-1}$ and this makes $2^{2 p-2}$ the highest power of 2 dividing $a^{2}+b^{2}=2^{c p-1} r$, or equivalently, $c p-1=2 p-2$, which is not possible. Therefore $a=2^{t} a_{0}$ and $b=2^{t} b_{0}$ for some positive integer $t<p-1$ and odd integers $a_{0}$ and $b_{0}$. Then $a_{0}^{2}+b_{0}^{2}=2^{c p-1-2 t} r$. The left side of this equality is congruent to 2 modulo 4 , therefore $c p-1-2 t$ must be 1. But then $t<p-1$ gives $(c / 2) p=t+1<p$, which is not possible either.
|
{
"exam": "EGMO",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "EGMO/segmented/en-2014-solutions-day1.jsonl",
"solution_match": "# Solution.",
"tier": "T2",
"year": "2014"
}
|
Determine all integers $n \geq 2$ for which there exist integers $x_{1}, x_{2}, \ldots, x_{n-1}$ satisfying the condition that if $0<i<n, 0<j<n, i \neq j$ and $n$ divides $2 i+j$, then $x_{i}<x_{j}$.
Proposed by Merlijn Staps, NLD
The answer is that $n=2^{k}$ with $k \geq 1$ or $n=3 \cdot 2^{k}$ where $k \geq 0$.
|
Suppose that $n$ has one of these forms. For an integer $i$, let $x_{i}$ be the largest integer such that $2^{x_{i}}$ divides $i$. Now assume that $0<i<n, 0<j<n, i \neq j, n$ divides $2 i+j$ and $x_{i} \geq x_{j}$. Then the highest power of 2 dividing $2 i+j$ is $2^{x_{j}}$ and therefore $k \leq x_{j}$ and $2^{k} \leq j$. Since $0<j<n$, this is possible only if $n=3 \cdot 2^{k}$ and either $j=2^{k}$ or $j=2^{k+1}$. In the first case, $i \neq j$ and $x_{i} \geq x_{j}$ imply $i=2^{k+1}$ leading to the contradiction $3 \cdot 2^{k}=n \mid 2 i+j=5 \cdot 2^{k}$. The second case is not possible as $i \neq j$ and $x_{i} \geq x_{j}$ now imply $i \geq 2^{k+2}>n$.
Now suppose that $n$ does not have one of these forms and $x_{1}, x_{2}, \ldots, x_{n-1}$ satisfying the given condition exist. For any positive integer $m$, let $a_{m}$ be the remainder of the division of $(-2)^{m}$ by $n$. Then none of $a_{m}$ is 0 as $n$ is not a power of 2. Also $a_{m} \neq a_{m+1}$ for any $m \geq 1$ as $a_{m}=a_{m+1}$ would lead to $n$ dividing $3 \cdot 2^{m}$. Moreover $n$ divides $2 a_{m}+a_{m+1}$. Hence we must have $x_{a_{1}}<x_{a_{2}}<x_{a_{3}}<\ldots$ which is not possible as $a_{m}$ 's can take on only finitely many values.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Determine all integers $n \geq 2$ for which there exist integers $x_{1}, x_{2}, \ldots, x_{n-1}$ satisfying the condition that if $0<i<n, 0<j<n, i \neq j$ and $n$ divides $2 i+j$, then $x_{i}<x_{j}$.
Proposed by Merlijn Staps, NLD
The answer is that $n=2^{k}$ with $k \geq 1$ or $n=3 \cdot 2^{k}$ where $k \geq 0$.
|
Suppose that $n$ has one of these forms. For an integer $i$, let $x_{i}$ be the largest integer such that $2^{x_{i}}$ divides $i$. Now assume that $0<i<n, 0<j<n, i \neq j, n$ divides $2 i+j$ and $x_{i} \geq x_{j}$. Then the highest power of 2 dividing $2 i+j$ is $2^{x_{j}}$ and therefore $k \leq x_{j}$ and $2^{k} \leq j$. Since $0<j<n$, this is possible only if $n=3 \cdot 2^{k}$ and either $j=2^{k}$ or $j=2^{k+1}$. In the first case, $i \neq j$ and $x_{i} \geq x_{j}$ imply $i=2^{k+1}$ leading to the contradiction $3 \cdot 2^{k}=n \mid 2 i+j=5 \cdot 2^{k}$. The second case is not possible as $i \neq j$ and $x_{i} \geq x_{j}$ now imply $i \geq 2^{k+2}>n$.
Now suppose that $n$ does not have one of these forms and $x_{1}, x_{2}, \ldots, x_{n-1}$ satisfying the given condition exist. For any positive integer $m$, let $a_{m}$ be the remainder of the division of $(-2)^{m}$ by $n$. Then none of $a_{m}$ is 0 as $n$ is not a power of 2. Also $a_{m} \neq a_{m+1}$ for any $m \geq 1$ as $a_{m}=a_{m+1}$ would lead to $n$ dividing $3 \cdot 2^{m}$. Moreover $n$ divides $2 a_{m}+a_{m+1}$. Hence we must have $x_{a_{1}}<x_{a_{2}}<x_{a_{3}}<\ldots$ which is not possible as $a_{m}$ 's can take on only finitely many values.
|
{
"exam": "EGMO",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "EGMO/segmented/en-2014-solutions-day2.jsonl",
"solution_match": "# Solution 1.",
"tier": "T2",
"year": "2014"
}
|
Determine all integers $n \geq 2$ for which there exist integers $x_{1}, x_{2}, \ldots, x_{n-1}$ satisfying the condition that if $0<i<n, 0<j<n, i \neq j$ and $n$ divides $2 i+j$, then $x_{i}<x_{j}$.
Proposed by Merlijn Staps, NLD
The answer is that $n=2^{k}$ with $k \geq 1$ or $n=3 \cdot 2^{k}$ where $k \geq 0$.
|
Let $E=\{n / 3, n / 2,2 n / 3\} \cap\{1,2, \ldots, n-1\}, D=\{1,2, \ldots, n-1\} \backslash E$, and let $f: D \rightarrow\{1,2, \ldots, n-1\}$ be the function sending $i$ in $D$ to the unique $f(i)$ in $\{1,2, \ldots, n-1\}$ such that $f(i) \equiv-2 i(\bmod n)$.
Then the condition of the problem is that $x_{i}<x_{f(i)}$ for each $i$ in $D$. Since $D$ is a finite set, the integers $x_{1}, x_{2}, \ldots, x_{n-1}$ exist if and only if for each $i$ in $D$ there exists a positive integer $k(i)$ such that $f^{k(i)}(i)$ belongs to $E$. This can be seen as follows:
- If $f^{k}(i)$ does not belong to $E$ for any $k>0$ for some $i$, then there exists $k_{2}>k_{1}>0$ such that $f^{k_{1}}(i)=f^{k_{2}}(i)$, leading to the contradiction $x_{f^{k_{1}(i)}}<$ $x_{f^{k_{2}(i)}}=x_{f^{k_{1}(i)}}$.
- On the other hand, if such $k(i)$ exists for each $i$ in $D$, and if $k_{0}(i)$ denotes the smallest such, then the condition of the problem is satisfied by letting $x_{i}=-k_{0}(i)$ for $i$ in $D$, and $x_{i}=0$ for $i$ in $E$.
In other words, the integers $x_{1}, x_{2}, \ldots, x_{n-1}$ exist if and only if for each $i$ in $D$ there exists a positive integer $k(i)$ such that $(-2)^{k(i)} i \equiv n / 3, n / 2$ or $2 n / 3(\bmod n)$. For $i=1$, this implies that $n=2^{k}$ with $k \geq 1$ or $n=3 \cdot 2^{k}$ with $k \geq 0$. On the other hand, if $n$ has one of these forms, letting $k(i)=k$ does the trick for all $i$ in $D$.
|
n=2^{k} \text{ with } k \geq 1 \text{ or } n=3 \cdot 2^{k} \text{ where } k \geq 0
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Determine all integers $n \geq 2$ for which there exist integers $x_{1}, x_{2}, \ldots, x_{n-1}$ satisfying the condition that if $0<i<n, 0<j<n, i \neq j$ and $n$ divides $2 i+j$, then $x_{i}<x_{j}$.
Proposed by Merlijn Staps, NLD
The answer is that $n=2^{k}$ with $k \geq 1$ or $n=3 \cdot 2^{k}$ where $k \geq 0$.
|
Let $E=\{n / 3, n / 2,2 n / 3\} \cap\{1,2, \ldots, n-1\}, D=\{1,2, \ldots, n-1\} \backslash E$, and let $f: D \rightarrow\{1,2, \ldots, n-1\}$ be the function sending $i$ in $D$ to the unique $f(i)$ in $\{1,2, \ldots, n-1\}$ such that $f(i) \equiv-2 i(\bmod n)$.
Then the condition of the problem is that $x_{i}<x_{f(i)}$ for each $i$ in $D$. Since $D$ is a finite set, the integers $x_{1}, x_{2}, \ldots, x_{n-1}$ exist if and only if for each $i$ in $D$ there exists a positive integer $k(i)$ such that $f^{k(i)}(i)$ belongs to $E$. This can be seen as follows:
- If $f^{k}(i)$ does not belong to $E$ for any $k>0$ for some $i$, then there exists $k_{2}>k_{1}>0$ such that $f^{k_{1}}(i)=f^{k_{2}}(i)$, leading to the contradiction $x_{f^{k_{1}(i)}}<$ $x_{f^{k_{2}(i)}}=x_{f^{k_{1}(i)}}$.
- On the other hand, if such $k(i)$ exists for each $i$ in $D$, and if $k_{0}(i)$ denotes the smallest such, then the condition of the problem is satisfied by letting $x_{i}=-k_{0}(i)$ for $i$ in $D$, and $x_{i}=0$ for $i$ in $E$.
In other words, the integers $x_{1}, x_{2}, \ldots, x_{n-1}$ exist if and only if for each $i$ in $D$ there exists a positive integer $k(i)$ such that $(-2)^{k(i)} i \equiv n / 3, n / 2$ or $2 n / 3(\bmod n)$. For $i=1$, this implies that $n=2^{k}$ with $k \geq 1$ or $n=3 \cdot 2^{k}$ with $k \geq 0$. On the other hand, if $n$ has one of these forms, letting $k(i)=k$ does the trick for all $i$ in $D$.
|
{
"exam": "EGMO",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "EGMO/segmented/en-2014-solutions-day2.jsonl",
"solution_match": "# Solution 2.",
"tier": "T2",
"year": "2014"
}
|
Determine all integers $n \geq 2$ for which there exist integers $x_{1}, x_{2}, \ldots, x_{n-1}$ satisfying the condition that if $0<i<n, 0<j<n, i \neq j$ and $n$ divides $2 i+j$, then $x_{i}<x_{j}$.
Proposed by Merlijn Staps, NLD
The answer is that $n=2^{k}$ with $k \geq 1$ or $n=3 \cdot 2^{k}$ where $k \geq 0$.
|
Suppose that $x_{1}, x_{2}, \ldots, x_{k-1}$ satisfy the condition of the problem for $n=k$. Let $y_{2 i}=x_{i}$ for $1 \leq i \leq k-1$ and choose $y_{2 i-1}$ for $1 \leq i \leq k$ to be less than $\min \left\{x_{1}, x_{2}, \ldots, x_{k-1}\right\}$. Now suppose that for $n=2 k$ we have $0<i<n, 0<j<n$, $i \neq j, n$ divides $2 i+j$. Then $j$ is even. If $i$ is also even, then $0<i / 2<k, 0<j / 2<k$ and $k$ divides $2(i / 2)+(j / 2)$; hence $y_{i}=x_{i / 2}<x_{j / 2}=y_{j}$. On the other hand, if $i$ is odd, then $y_{i}<\min \left\{x_{1}, x_{2}, \ldots, x_{k-1}\right\} \leq x_{j / 2}=y_{j}$. Therefore, $y_{1}, y_{2}, \ldots, y_{2 k-1}$ satisfy the condition of the problem for $n=2 k$.
Since the condition is vacuous for $n=2$ and $n=3$, it follows that $x_{1}, x_{2}, \ldots, x_{n-1}$ satisfying the condition exist for all $n=2^{k}$ with $k \geq 1$ and $n=3 \cdot 2^{k}$ with $k \geq 0$.
Now suppose that $x_{1}, x_{2}, \ldots, x_{n-1}$ satisfying the condition of the problem exist for $n=2^{k} m$ where $k$ is a nonnegative integer and $m>3$ is an odd number. Let $b_{0}=2^{k}$ and let $b_{i+1}$ be the remainder of the division of $(-2) b_{i}$ by $n$ for $i \geq 0$. No terms of this sequence is 0 and no two consecutive terms are both equal to $b_{1}$ as $m>3$. On the other hand, as $(-2)^{\phi(m)} \equiv 1(\bmod m)$, we have $b_{\phi(m)} \equiv(-2)^{\phi(m)} 2^{k} \equiv 2^{k} \equiv b_{0}$ $(\bmod n)$, and hence $b_{\phi(m)}=b_{0}$. Since $2 b_{i}+b_{i+1}$ is divisible by $n$ for all $i \geq 0$, we have $x_{b_{0}}<x_{b_{1}}<\cdots<x_{b_{\phi(m)}}=x_{b_{0}}$, a contradiction.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Determine all integers $n \geq 2$ for which there exist integers $x_{1}, x_{2}, \ldots, x_{n-1}$ satisfying the condition that if $0<i<n, 0<j<n, i \neq j$ and $n$ divides $2 i+j$, then $x_{i}<x_{j}$.
Proposed by Merlijn Staps, NLD
The answer is that $n=2^{k}$ with $k \geq 1$ or $n=3 \cdot 2^{k}$ where $k \geq 0$.
|
Suppose that $x_{1}, x_{2}, \ldots, x_{k-1}$ satisfy the condition of the problem for $n=k$. Let $y_{2 i}=x_{i}$ for $1 \leq i \leq k-1$ and choose $y_{2 i-1}$ for $1 \leq i \leq k$ to be less than $\min \left\{x_{1}, x_{2}, \ldots, x_{k-1}\right\}$. Now suppose that for $n=2 k$ we have $0<i<n, 0<j<n$, $i \neq j, n$ divides $2 i+j$. Then $j$ is even. If $i$ is also even, then $0<i / 2<k, 0<j / 2<k$ and $k$ divides $2(i / 2)+(j / 2)$; hence $y_{i}=x_{i / 2}<x_{j / 2}=y_{j}$. On the other hand, if $i$ is odd, then $y_{i}<\min \left\{x_{1}, x_{2}, \ldots, x_{k-1}\right\} \leq x_{j / 2}=y_{j}$. Therefore, $y_{1}, y_{2}, \ldots, y_{2 k-1}$ satisfy the condition of the problem for $n=2 k$.
Since the condition is vacuous for $n=2$ and $n=3$, it follows that $x_{1}, x_{2}, \ldots, x_{n-1}$ satisfying the condition exist for all $n=2^{k}$ with $k \geq 1$ and $n=3 \cdot 2^{k}$ with $k \geq 0$.
Now suppose that $x_{1}, x_{2}, \ldots, x_{n-1}$ satisfying the condition of the problem exist for $n=2^{k} m$ where $k$ is a nonnegative integer and $m>3$ is an odd number. Let $b_{0}=2^{k}$ and let $b_{i+1}$ be the remainder of the division of $(-2) b_{i}$ by $n$ for $i \geq 0$. No terms of this sequence is 0 and no two consecutive terms are both equal to $b_{1}$ as $m>3$. On the other hand, as $(-2)^{\phi(m)} \equiv 1(\bmod m)$, we have $b_{\phi(m)} \equiv(-2)^{\phi(m)} 2^{k} \equiv 2^{k} \equiv b_{0}$ $(\bmod n)$, and hence $b_{\phi(m)}=b_{0}$. Since $2 b_{i}+b_{i+1}$ is divisible by $n$ for all $i \geq 0$, we have $x_{b_{0}}<x_{b_{1}}<\cdots<x_{b_{\phi(m)}}=x_{b_{0}}$, a contradiction.
|
{
"exam": "EGMO",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "EGMO/segmented/en-2014-solutions-day2.jsonl",
"solution_match": "# Solution 3.",
"tier": "T2",
"year": "2014"
}
|
Let $n$ be a positive integer. We have $n$ boxes where each box contains a nonnegative number of pebbles. In each move we are allowed to take two pebbles from a box we choose, throw away one of the pebbles and put the other pebble in another box we choose. An initial configuration of pebbles is called solvable if it is possible to reach a configuration with no empty box, in a finite (possibly zero) number of moves. Determine all initial configurations of pebbles which are not solvable, but become solvable when an additional pebble is added to a box, no matter which box is chosen.
Proposed by Dan Schwarz, ROU
The answer is any configuration with $2 n-2$ pebbles which has even numbers of pebbles in each box.
|
Number the boxes from 1 through $n$ and denote a configuration by $x=\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ where $x_{i}$ is the number of pebbles in the $i$ th box. Let
$$
D(x)=\sum_{i=1}^{n}\left\lfloor\frac{x_{i}-1}{2}\right\rfloor
$$
for a configuration $x$. We can rewrite this in the form
$$
D(x)=\frac{1}{2} N(x)-n+\frac{1}{2} O(x)
$$
where $N(x)$ is the total number of pebbles and $O(x)$ is the number of boxes with an odd number of pebbles for the configuration $x$.
Note that a move either leaves $D$ the same (if it is made into a box containing an even number of pebbles) or decreases it by 1 (if it is made into a box with an odd number of pebbles). As $D$ is nonnegative for any configuration which does not have any empty boxes, it is also nonnegative for any solvable configuration. On the other hand, if a configuration has nonnegative $D$, then making $m_{i}=\left\lfloor\left(x_{i}-1\right) / 2\right\rfloor$ moves from the $i$ th box into $m_{i}$ empty boxes for each $i$ with $m_{i}>0$ fills all boxes as $D(x) \geq 0$ means $\sum_{m_{i}>0} m_{i} \geq$ (number of empty boxes).
As $N(x)$ and $O(x)$ have the same parity, a configuration $x$ is solvable exactly when $O(x) \geq 2 n-N(x)$, and unsolvable exactly when $O(x) \leq 2 n-2-N(x)$. In particular, any configuration with $2 n-1$ pebbles is solvable, and a configuration with $2 n-2$ pebbles is unsolvable if and only if all boxes contain even numbers of pebbles.
Suppose that $x^{\prime}$ is obtained from $x$ by adding a pebble in some box. Then $O\left(x^{\prime}\right)=$ $O(x)+1$ or $O\left(x^{\prime}\right)=O(x)-1$. If $x$ is unsolvable and $x^{\prime}$ is solvable, then we must have $O(x) \leq 2 n-2-N(x)$ and $O\left(x^{\prime}\right) \geq 2 n-N\left(x^{\prime}\right)=2 n-1-N(x)$, and hence $O\left(x^{\prime}\right)=O(x)+1$. That is, the pebble must be added to a box with an even number of pebbles. This can be the case irrespective of where the pebble is added only if all boxes contain even numbers of pebbles, and $0=O(x) \leq 2 n-2-N(x)$ and $1=O\left(x^{\prime}\right) \geq 2 n-1-N(x)$; that is, $N(x)=2 n-2$.
|
N(x)=2 n-2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be a positive integer. We have $n$ boxes where each box contains a nonnegative number of pebbles. In each move we are allowed to take two pebbles from a box we choose, throw away one of the pebbles and put the other pebble in another box we choose. An initial configuration of pebbles is called solvable if it is possible to reach a configuration with no empty box, in a finite (possibly zero) number of moves. Determine all initial configurations of pebbles which are not solvable, but become solvable when an additional pebble is added to a box, no matter which box is chosen.
Proposed by Dan Schwarz, ROU
The answer is any configuration with $2 n-2$ pebbles which has even numbers of pebbles in each box.
|
Number the boxes from 1 through $n$ and denote a configuration by $x=\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ where $x_{i}$ is the number of pebbles in the $i$ th box. Let
$$
D(x)=\sum_{i=1}^{n}\left\lfloor\frac{x_{i}-1}{2}\right\rfloor
$$
for a configuration $x$. We can rewrite this in the form
$$
D(x)=\frac{1}{2} N(x)-n+\frac{1}{2} O(x)
$$
where $N(x)$ is the total number of pebbles and $O(x)$ is the number of boxes with an odd number of pebbles for the configuration $x$.
Note that a move either leaves $D$ the same (if it is made into a box containing an even number of pebbles) or decreases it by 1 (if it is made into a box with an odd number of pebbles). As $D$ is nonnegative for any configuration which does not have any empty boxes, it is also nonnegative for any solvable configuration. On the other hand, if a configuration has nonnegative $D$, then making $m_{i}=\left\lfloor\left(x_{i}-1\right) / 2\right\rfloor$ moves from the $i$ th box into $m_{i}$ empty boxes for each $i$ with $m_{i}>0$ fills all boxes as $D(x) \geq 0$ means $\sum_{m_{i}>0} m_{i} \geq$ (number of empty boxes).
As $N(x)$ and $O(x)$ have the same parity, a configuration $x$ is solvable exactly when $O(x) \geq 2 n-N(x)$, and unsolvable exactly when $O(x) \leq 2 n-2-N(x)$. In particular, any configuration with $2 n-1$ pebbles is solvable, and a configuration with $2 n-2$ pebbles is unsolvable if and only if all boxes contain even numbers of pebbles.
Suppose that $x^{\prime}$ is obtained from $x$ by adding a pebble in some box. Then $O\left(x^{\prime}\right)=$ $O(x)+1$ or $O\left(x^{\prime}\right)=O(x)-1$. If $x$ is unsolvable and $x^{\prime}$ is solvable, then we must have $O(x) \leq 2 n-2-N(x)$ and $O\left(x^{\prime}\right) \geq 2 n-N\left(x^{\prime}\right)=2 n-1-N(x)$, and hence $O\left(x^{\prime}\right)=O(x)+1$. That is, the pebble must be added to a box with an even number of pebbles. This can be the case irrespective of where the pebble is added only if all boxes contain even numbers of pebbles, and $0=O(x) \leq 2 n-2-N(x)$ and $1=O\left(x^{\prime}\right) \geq 2 n-1-N(x)$; that is, $N(x)=2 n-2$.
|
{
"exam": "EGMO",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "EGMO/segmented/en-2014-solutions-day2.jsonl",
"solution_match": "\nSolution 1. ",
"tier": "T2",
"year": "2014"
}
|
Let $n$ be a positive integer. We have $n$ boxes where each box contains a nonnegative number of pebbles. In each move we are allowed to take two pebbles from a box we choose, throw away one of the pebbles and put the other pebble in another box we choose. An initial configuration of pebbles is called solvable if it is possible to reach a configuration with no empty box, in a finite (possibly zero) number of moves. Determine all initial configurations of pebbles which are not solvable, but become solvable when an additional pebble is added to a box, no matter which box is chosen.
Proposed by Dan Schwarz, ROU
The answer is any configuration with $2 n-2$ pebbles which has even numbers of pebbles in each box.
|
Let $x$ be a configuration and $\tilde{x}$ be another configuration obtained from $x$ by removing two pebbles from a box and depositing them in another box.
Claim 1: $\tilde{x}$ is solvable if and only if $x$ is solvable.
Let us call two configurations equivalent if they have the same total number of pebbles and parities of the number of pebbles in the corresponding boxes are the same. (It does not matter whether we consider this equivalence for a fixed ordering of the boxes or up to permutation.) From Claim 1 it follows that two equivalent configurations are both solvable or both unsolvable. In particular, any configuration with $2 n-1$ or more pebbles is solvable, because it is equivalent to a configuration with no empty boxes.
Let us a call a configuration with all boxes containing two or fewer pebbles scant. Every unsolvable configuration is equivalent to a scant configuration.
Claim 2: A scant configuration is solvable if and only if it contains no empty boxes.
By Claim 1 and Claim 2, addition of a pebble to a scant unsolvable configuration makes it solvable if and only if the configuration has exactly one empty box and the pebble is added to the empty box or to a box containing two pebbles. Hence, the addition of a pebble makes an unsolvable scant configuration into a solvable configuration irrespective of where it is added if and only if all boxes have even numbers of pebbles and exactly one of them is empty. Therefore, the addition of a pebble makes an unsolvable configuration into a solvable one irrespective of where the pebble is added if and only if the configuration has $2 n-2$ pebbles and all boxes have even numbers of pebbles.
Proof of Claim 1: Suppose that the two pebbles were moved from box $B$ in $x$ to box $\tilde{B}$ in $\tilde{x}$, and $x$ is solvable. Then we perform exactly the same sequence of moves for $\tilde{x}$ as we did for $x$ except that instead of the first move that is made out of $B$ we make a move from $\tilde{B}$ (into the same box), and if there was no move from $B$, then at the end we make a move from $\tilde{B}$ to $B$ in case $B$ is now empty.
Proof of Claim 2: Any move from a scant configuration either leaves the number of empty boxes the same and the resulting configuration is also scant (if it is made into an empty box), or increases the number of empty boxes by one (if it is made into a nonempty box). In the second case, if the move was made into a box containing one pebble, then the resulting configuration is still scant. On the other hand, if it is made into a box containing two pebbles, then the resulting configuration is equivalent to the scant configuration which has one pebble in the box the move was made into and exactly the same number of pebbles in all other boxes as the original configuration. Therefore, any sequence of move from a scant configuration results in a configuration with more or the same number of empty boxes.
|
2 n-2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be a positive integer. We have $n$ boxes where each box contains a nonnegative number of pebbles. In each move we are allowed to take two pebbles from a box we choose, throw away one of the pebbles and put the other pebble in another box we choose. An initial configuration of pebbles is called solvable if it is possible to reach a configuration with no empty box, in a finite (possibly zero) number of moves. Determine all initial configurations of pebbles which are not solvable, but become solvable when an additional pebble is added to a box, no matter which box is chosen.
Proposed by Dan Schwarz, ROU
The answer is any configuration with $2 n-2$ pebbles which has even numbers of pebbles in each box.
|
Let $x$ be a configuration and $\tilde{x}$ be another configuration obtained from $x$ by removing two pebbles from a box and depositing them in another box.
Claim 1: $\tilde{x}$ is solvable if and only if $x$ is solvable.
Let us call two configurations equivalent if they have the same total number of pebbles and parities of the number of pebbles in the corresponding boxes are the same. (It does not matter whether we consider this equivalence for a fixed ordering of the boxes or up to permutation.) From Claim 1 it follows that two equivalent configurations are both solvable or both unsolvable. In particular, any configuration with $2 n-1$ or more pebbles is solvable, because it is equivalent to a configuration with no empty boxes.
Let us a call a configuration with all boxes containing two or fewer pebbles scant. Every unsolvable configuration is equivalent to a scant configuration.
Claim 2: A scant configuration is solvable if and only if it contains no empty boxes.
By Claim 1 and Claim 2, addition of a pebble to a scant unsolvable configuration makes it solvable if and only if the configuration has exactly one empty box and the pebble is added to the empty box or to a box containing two pebbles. Hence, the addition of a pebble makes an unsolvable scant configuration into a solvable configuration irrespective of where it is added if and only if all boxes have even numbers of pebbles and exactly one of them is empty. Therefore, the addition of a pebble makes an unsolvable configuration into a solvable one irrespective of where the pebble is added if and only if the configuration has $2 n-2$ pebbles and all boxes have even numbers of pebbles.
Proof of Claim 1: Suppose that the two pebbles were moved from box $B$ in $x$ to box $\tilde{B}$ in $\tilde{x}$, and $x$ is solvable. Then we perform exactly the same sequence of moves for $\tilde{x}$ as we did for $x$ except that instead of the first move that is made out of $B$ we make a move from $\tilde{B}$ (into the same box), and if there was no move from $B$, then at the end we make a move from $\tilde{B}$ to $B$ in case $B$ is now empty.
Proof of Claim 2: Any move from a scant configuration either leaves the number of empty boxes the same and the resulting configuration is also scant (if it is made into an empty box), or increases the number of empty boxes by one (if it is made into a nonempty box). In the second case, if the move was made into a box containing one pebble, then the resulting configuration is still scant. On the other hand, if it is made into a box containing two pebbles, then the resulting configuration is equivalent to the scant configuration which has one pebble in the box the move was made into and exactly the same number of pebbles in all other boxes as the original configuration. Therefore, any sequence of move from a scant configuration results in a configuration with more or the same number of empty boxes.
|
{
"exam": "EGMO",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "EGMO/segmented/en-2014-solutions-day2.jsonl",
"solution_match": "\nSolution 2. ",
"tier": "T2",
"year": "2014"
}
|
Determine all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ satisfying the condition
$$
f\left(y^{2}+2 x f(y)+f(x)^{2}\right)=(y+f(x))(x+f(y))
$$
for all real numbers $x$ and $y$.
Proposed by Daniël Kroes, NLD
The answer is the functions $f(x)=x, f(x)=-x$ and $f(x)=\frac{1}{2}-x$.
|
It can be easily checked that the functions $f(x)=x, f(x)=-x$ and $f(x)=\frac{1}{2}-x$ satisfy the given condition. We will show that these are the only functions doing so. Let $y=-f(x)$ in the original equation to obtain
$$
f\left(2 f(x)^{2}+2 x f(-f(x))\right)=0
$$
for all $x$. In particular, 0 is a value of $f$. Suppose that $u$ and $v$ are such that $f(u)=0=f(v)$. Plugging $x=u$ or $v$ and $y=u$ or $v$ in the original equations we get $f\left(u^{2}\right)=u^{2}, f\left(u^{2}\right)=u v, f\left(v^{2}\right)=u v$ and $f\left(v^{2}\right)=v^{2}$. We conclude that $u^{2}=u v=v^{2}$ and hence $u=v$. So there is exactly one $a$ mapped to 0 , and
$$
f(x)^{2}+x f(-f(x))=\frac{a}{2}
$$
for all $x$.
Suppose that $f\left(x_{1}\right)=f\left(x_{2}\right) \neq 0$ for some $x_{1}$ and $x_{2}$. Using (*) we obtain $x_{1} f\left(-f\left(x_{1}\right)\right)=x_{2} f\left(-f\left(x_{2}\right)\right)=x_{2} f\left(-f\left(x_{1}\right)\right)$ and hence either $x_{1}=x_{2}$ or $f\left(x_{1}\right)=$ $f\left(x_{2}\right)=-a$. In the second case, letting $x=a$ and $y=x_{1}$ in the original equation we get $f\left(x_{1}^{2}-2 a^{2}\right)=0$, hence $x_{1}^{2}-2 a^{2}=a$. Similarly, $x_{2}^{2}-2 a^{2}=a$, and it follows that $x_{1}=x_{2}$ or $x_{1}=-x_{2}$ in this case.
Using the symmetry of the original equation we have
$$
f\left(f(x)^{2}+y^{2}+2 x f(y)\right)=(x+f(y))(y+f(x))=f\left(f(y)^{2}+x^{2}+2 y f(x)\right)
$$
for all $x$ and $y$. Suppose $f(x)^{2}+y^{2}+2 x f(y) \neq f(y)^{2}+x^{2}+2 y f(x)$ for some $x$ and $y$. Then by the observations above, $(x+f(y))(y+f(x)) \neq 0$ and $f(x)^{2}+y^{2}+2 x f(y)=$ $-\left(f(y)^{2}+x^{2}+2 y f(x)\right)$. But these conditions are contradictory as the second one can be rewritten as $(f(x)+y)^{2}+(f(y)+x)^{2}=0$.
Therefore from $\left({ }^{* *}\right)$ now it follows that
$$
f(x)^{2}+y^{2}+2 x f(y)=f(y)^{2}+x^{2}+2 y f(x)
$$
for all $x$ and $y$. In particular, letting $y=0$ we obtain $f(x)^{2}=(f(0)-x)^{2}$ for all $x$. Let $f(x)=s(x)(f(0)-x)$ where $s: \mathbf{R} \rightarrow\{1,-1\}$. Plugging this in $\left({ }^{* * *}\right)$ gives
$$
x(y s(y)+f(0)(1-s(y))=y(x s(x)+f(0)(1-s(x)))
$$
for all $x$ and $y$. So $s(x)+f(0)(1-s(x)) / x$ must be constant for $x \neq 0$.
If $f(0)=0$ it follows that $s(x)$ is constant for $x \neq 0$, and therefore either $f(x)=x$ for all $x$ or $f(x)=-x$ for all $x$. Suppose that $f(0) \neq 0$. If $s(x)$ is -1 for all $x \neq 0$, then $-1+2 f(0) / x$ must be constant for all $x \neq 0$, which is not possible. On the other hand, if there exist nonzero $x$ and $y$ such that $s(x)=-1$ and $s(y)=1$, then $-1+2 f(0) / x=1$. That is, there can be only one such $x$, that $x$ is $f(0)$, and hence $f(x)=f(0)-x$ for all $x$. Putting this back in the original equation gives $2 f(0)^{2}=f(0)$ and hence $f(0)=1 / 2$. We are done.
## Remark:
The following line of reasoning or a variant of it can be used between $\left({ }^{*}\right)$ and $\left({ }^{* * *}\right)$ :
Suppose that $f\left(x_{1}\right)=f\left(x_{2}\right) \neq 0$ for some $x_{1}$ and $x_{2}$. Then from $\left(^{*}\right)$ it follows that $x_{1} f\left(-f\left(x_{1}\right)\right)=x_{2} f\left(-f\left(x_{2}\right)\right)=x_{2} f\left(-f\left(x_{1}\right)\right)$ and hence either $x_{1}=x_{2}$ or $f\left(x_{1}\right)=$ $f\left(x_{2}\right)=-a$. In the second case, using $\left(^{*}\right)$ again we obtain $a^{2}=a / 2$ and therefore $a=$ $1 / 2$. Now letting $x=1 / 2$ in the original equation gives $f\left(y^{2}+f(y)\right)=y(f(y)+1 / 2)$ for all $y$. From this letting $y=0$ we obtain $f(0)=1 / 2$, and letting $f(y)=-1 / 2$ we obtain $f\left(y^{2}-1 / 2\right)=0$ and $y^{2}=1$. To summarize, $f\left(x_{1}\right)=f\left(x_{2}\right) \neq 0$ implies either $x_{1}=x_{2}$ or $x_{1}, x_{2} \in\{1,-1\}$ and $f(1)=f(-1)=-1 / 2, f(1 / 2)=0, f(0)=1 / 2$.
Using the symmetry of the original equation we have
$$
f\left(f(x)^{2}+y^{2}+2 x f(y)\right)=(x+f(y))(y+f(x))=f\left(f(y)^{2}+x^{2}+2 y f(x)\right)
$$
for all $x$ and $y$. Let $y=0$. Then
$$
f\left(f(x)^{2}+2 x f(0)\right)=f\left(f(0)^{2}+x^{2}\right)
$$
for all $x$. If $f(x)^{2}+2 x f(0) \neq f(0)^{2}+x^{2}$ for some $x$, then by the observation above we must have $f(1 / 2)=0, f(0)=1 / 2$ and $f(x)^{2}+2 x f(0)=-\left(f(0)^{2}+x^{2}\right)$. We can rewrite this as $f(x)^{2}+(f(0)+x)^{2}=0$ to obtain $x=1 / 2$ and $f(0)=-x=-1 / 2$, which contradicts $f(0)=1 / 2$. So we conclude that $f(x)^{2}+2 x f(0)=f(0)^{2}+x^{2}$ for all $x$. This implies $f(x)^{2}=(f(0)-x)^{2}$ for all $x$. In particular, the second case considered above is not possible as $(f(0)-1)^{2}=f(1)=f(-1)=(f(0)+1)^{2}$ means $f(0)=0$, contradicting $f(0)=1 / 2$. Therefore $f$ is injective and from $\left({ }^{* *}\right)$ now it follows that
$$
f(x)^{2}+y^{2}+2 x f(y)=f(y)^{2}+x^{2}+2 y f(x)
$$
for all $x$ and $y$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Determine all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ satisfying the condition
$$
f\left(y^{2}+2 x f(y)+f(x)^{2}\right)=(y+f(x))(x+f(y))
$$
for all real numbers $x$ and $y$.
Proposed by Daniël Kroes, NLD
The answer is the functions $f(x)=x, f(x)=-x$ and $f(x)=\frac{1}{2}-x$.
|
It can be easily checked that the functions $f(x)=x, f(x)=-x$ and $f(x)=\frac{1}{2}-x$ satisfy the given condition. We will show that these are the only functions doing so. Let $y=-f(x)$ in the original equation to obtain
$$
f\left(2 f(x)^{2}+2 x f(-f(x))\right)=0
$$
for all $x$. In particular, 0 is a value of $f$. Suppose that $u$ and $v$ are such that $f(u)=0=f(v)$. Plugging $x=u$ or $v$ and $y=u$ or $v$ in the original equations we get $f\left(u^{2}\right)=u^{2}, f\left(u^{2}\right)=u v, f\left(v^{2}\right)=u v$ and $f\left(v^{2}\right)=v^{2}$. We conclude that $u^{2}=u v=v^{2}$ and hence $u=v$. So there is exactly one $a$ mapped to 0 , and
$$
f(x)^{2}+x f(-f(x))=\frac{a}{2}
$$
for all $x$.
Suppose that $f\left(x_{1}\right)=f\left(x_{2}\right) \neq 0$ for some $x_{1}$ and $x_{2}$. Using (*) we obtain $x_{1} f\left(-f\left(x_{1}\right)\right)=x_{2} f\left(-f\left(x_{2}\right)\right)=x_{2} f\left(-f\left(x_{1}\right)\right)$ and hence either $x_{1}=x_{2}$ or $f\left(x_{1}\right)=$ $f\left(x_{2}\right)=-a$. In the second case, letting $x=a$ and $y=x_{1}$ in the original equation we get $f\left(x_{1}^{2}-2 a^{2}\right)=0$, hence $x_{1}^{2}-2 a^{2}=a$. Similarly, $x_{2}^{2}-2 a^{2}=a$, and it follows that $x_{1}=x_{2}$ or $x_{1}=-x_{2}$ in this case.
Using the symmetry of the original equation we have
$$
f\left(f(x)^{2}+y^{2}+2 x f(y)\right)=(x+f(y))(y+f(x))=f\left(f(y)^{2}+x^{2}+2 y f(x)\right)
$$
for all $x$ and $y$. Suppose $f(x)^{2}+y^{2}+2 x f(y) \neq f(y)^{2}+x^{2}+2 y f(x)$ for some $x$ and $y$. Then by the observations above, $(x+f(y))(y+f(x)) \neq 0$ and $f(x)^{2}+y^{2}+2 x f(y)=$ $-\left(f(y)^{2}+x^{2}+2 y f(x)\right)$. But these conditions are contradictory as the second one can be rewritten as $(f(x)+y)^{2}+(f(y)+x)^{2}=0$.
Therefore from $\left({ }^{* *}\right)$ now it follows that
$$
f(x)^{2}+y^{2}+2 x f(y)=f(y)^{2}+x^{2}+2 y f(x)
$$
for all $x$ and $y$. In particular, letting $y=0$ we obtain $f(x)^{2}=(f(0)-x)^{2}$ for all $x$. Let $f(x)=s(x)(f(0)-x)$ where $s: \mathbf{R} \rightarrow\{1,-1\}$. Plugging this in $\left({ }^{* * *}\right)$ gives
$$
x(y s(y)+f(0)(1-s(y))=y(x s(x)+f(0)(1-s(x)))
$$
for all $x$ and $y$. So $s(x)+f(0)(1-s(x)) / x$ must be constant for $x \neq 0$.
If $f(0)=0$ it follows that $s(x)$ is constant for $x \neq 0$, and therefore either $f(x)=x$ for all $x$ or $f(x)=-x$ for all $x$. Suppose that $f(0) \neq 0$. If $s(x)$ is -1 for all $x \neq 0$, then $-1+2 f(0) / x$ must be constant for all $x \neq 0$, which is not possible. On the other hand, if there exist nonzero $x$ and $y$ such that $s(x)=-1$ and $s(y)=1$, then $-1+2 f(0) / x=1$. That is, there can be only one such $x$, that $x$ is $f(0)$, and hence $f(x)=f(0)-x$ for all $x$. Putting this back in the original equation gives $2 f(0)^{2}=f(0)$ and hence $f(0)=1 / 2$. We are done.
## Remark:
The following line of reasoning or a variant of it can be used between $\left({ }^{*}\right)$ and $\left({ }^{* * *}\right)$ :
Suppose that $f\left(x_{1}\right)=f\left(x_{2}\right) \neq 0$ for some $x_{1}$ and $x_{2}$. Then from $\left(^{*}\right)$ it follows that $x_{1} f\left(-f\left(x_{1}\right)\right)=x_{2} f\left(-f\left(x_{2}\right)\right)=x_{2} f\left(-f\left(x_{1}\right)\right)$ and hence either $x_{1}=x_{2}$ or $f\left(x_{1}\right)=$ $f\left(x_{2}\right)=-a$. In the second case, using $\left(^{*}\right)$ again we obtain $a^{2}=a / 2$ and therefore $a=$ $1 / 2$. Now letting $x=1 / 2$ in the original equation gives $f\left(y^{2}+f(y)\right)=y(f(y)+1 / 2)$ for all $y$. From this letting $y=0$ we obtain $f(0)=1 / 2$, and letting $f(y)=-1 / 2$ we obtain $f\left(y^{2}-1 / 2\right)=0$ and $y^{2}=1$. To summarize, $f\left(x_{1}\right)=f\left(x_{2}\right) \neq 0$ implies either $x_{1}=x_{2}$ or $x_{1}, x_{2} \in\{1,-1\}$ and $f(1)=f(-1)=-1 / 2, f(1 / 2)=0, f(0)=1 / 2$.
Using the symmetry of the original equation we have
$$
f\left(f(x)^{2}+y^{2}+2 x f(y)\right)=(x+f(y))(y+f(x))=f\left(f(y)^{2}+x^{2}+2 y f(x)\right)
$$
for all $x$ and $y$. Let $y=0$. Then
$$
f\left(f(x)^{2}+2 x f(0)\right)=f\left(f(0)^{2}+x^{2}\right)
$$
for all $x$. If $f(x)^{2}+2 x f(0) \neq f(0)^{2}+x^{2}$ for some $x$, then by the observation above we must have $f(1 / 2)=0, f(0)=1 / 2$ and $f(x)^{2}+2 x f(0)=-\left(f(0)^{2}+x^{2}\right)$. We can rewrite this as $f(x)^{2}+(f(0)+x)^{2}=0$ to obtain $x=1 / 2$ and $f(0)=-x=-1 / 2$, which contradicts $f(0)=1 / 2$. So we conclude that $f(x)^{2}+2 x f(0)=f(0)^{2}+x^{2}$ for all $x$. This implies $f(x)^{2}=(f(0)-x)^{2}$ for all $x$. In particular, the second case considered above is not possible as $(f(0)-1)^{2}=f(1)=f(-1)=(f(0)+1)^{2}$ means $f(0)=0$, contradicting $f(0)=1 / 2$. Therefore $f$ is injective and from $\left({ }^{* *}\right)$ now it follows that
$$
f(x)^{2}+y^{2}+2 x f(y)=f(y)^{2}+x^{2}+2 y f(x)
$$
for all $x$ and $y$.
|
{
"exam": "EGMO",
"problem_label": "6",
"problem_match": "\n6.",
"resource_path": "EGMO/segmented/en-2014-solutions-day2.jsonl",
"solution_match": "# Solution.",
"tier": "T2",
"year": "2014"
}
|
Let $\triangle A B C$ be an acute-angled triangle, and let $D$ be the foot of the altitude from $C$. The angle bisector of $\angle A B C$ intersects $C D$ at $E$ and meets the circumcircle $\omega$ of triangle $\triangle A D E$ again at $F$. If $\angle A D F=45^{\circ}$, show that $C F$ is tangent to $\omega$.
(Luxembourg)

|
Since $\angle C D F=90^{\circ}-45^{\circ}=45^{\circ}$, the line $D F$ bisects $\angle C D A$, and so $F$ lies on the perpendicular bisector of segment $A E$, which meets $A B$ at $G$. Let $\angle A B C=2 \beta$. Since $A D E F$ is cyclic, $\angle A F E=90^{\circ}$, and hence $\angle F A E=45^{\circ}$. Further, as $B F$ bisects $\angle A B C$, we have $\angle F A B=90^{\circ}-\beta$, and thus
$$
\angle E A B=\angle A E G=45^{\circ}-\beta, \quad \text { and } \quad \angle A E D=45^{\circ}+\beta,
$$
so $\angle G E D=2 \beta$. This implies that right-angled triangles $\triangle E D G$ and $\triangle B D C$ are similar, and so we have $|G D| /|C D|=|D E| /|D B|$. Thus the right-angled triangles $\triangle D E B$ and $\triangle D G C$ are similar, whence $\angle G C D=\angle D B E=\beta$. But $\angle D F E=\angle D A E=45^{\circ}-$ $\beta$, then $\angle G F D=45^{\circ}-\angle D F E=\beta$. Hence $G D C F$ is cyclic, so $\angle G F C=90^{\circ}$, whence $C F$ is perpendicular to the radius $F G$ of $\omega$. It follows that $C F$ is a tangent to $\omega$, as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\triangle A B C$ be an acute-angled triangle, and let $D$ be the foot of the altitude from $C$. The angle bisector of $\angle A B C$ intersects $C D$ at $E$ and meets the circumcircle $\omega$ of triangle $\triangle A D E$ again at $F$. If $\angle A D F=45^{\circ}$, show that $C F$ is tangent to $\omega$.
(Luxembourg)

|
Since $\angle C D F=90^{\circ}-45^{\circ}=45^{\circ}$, the line $D F$ bisects $\angle C D A$, and so $F$ lies on the perpendicular bisector of segment $A E$, which meets $A B$ at $G$. Let $\angle A B C=2 \beta$. Since $A D E F$ is cyclic, $\angle A F E=90^{\circ}$, and hence $\angle F A E=45^{\circ}$. Further, as $B F$ bisects $\angle A B C$, we have $\angle F A B=90^{\circ}-\beta$, and thus
$$
\angle E A B=\angle A E G=45^{\circ}-\beta, \quad \text { and } \quad \angle A E D=45^{\circ}+\beta,
$$
so $\angle G E D=2 \beta$. This implies that right-angled triangles $\triangle E D G$ and $\triangle B D C$ are similar, and so we have $|G D| /|C D|=|D E| /|D B|$. Thus the right-angled triangles $\triangle D E B$ and $\triangle D G C$ are similar, whence $\angle G C D=\angle D B E=\beta$. But $\angle D F E=\angle D A E=45^{\circ}-$ $\beta$, then $\angle G F D=45^{\circ}-\angle D F E=\beta$. Hence $G D C F$ is cyclic, so $\angle G F C=90^{\circ}$, whence $C F$ is perpendicular to the radius $F G$ of $\omega$. It follows that $C F$ is a tangent to $\omega$, as required.
|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "\nProblem 1.",
"resource_path": "EGMO/segmented/en-2015-solutions.jsonl",
"solution_match": "\nSolution 1: ",
"tier": "T2",
"year": "2015"
}
|
Let $\triangle A B C$ be an acute-angled triangle, and let $D$ be the foot of the altitude from $C$. The angle bisector of $\angle A B C$ intersects $C D$ at $E$ and meets the circumcircle $\omega$ of triangle $\triangle A D E$ again at $F$. If $\angle A D F=45^{\circ}$, show that $C F$ is tangent to $\omega$.
(Luxembourg)

|
As $\angle A D F=45^{\circ}$ line $D F$ is an exterior bisector of $\angle C D B$. Since $B F$ bisects $\angle D B C$ line $C F$ is an exterior bisector of $\angle B C D$. Let $\angle A B C=2 \beta$, so $\angle E C F=(\angle D B C+\angle C D B) / 2=45^{\circ}+\beta$. Hence $\angle C F E=180^{\circ}-\angle E C F-\angle B C E-\angle E B C=180^{\circ}-\left(45^{\circ}+\beta+90^{\circ}-2 \beta+\beta\right)=45^{\circ}$. It follows that $\angle F D C=\angle C F E$, then $C F$ is tangent to $\omega$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\triangle A B C$ be an acute-angled triangle, and let $D$ be the foot of the altitude from $C$. The angle bisector of $\angle A B C$ intersects $C D$ at $E$ and meets the circumcircle $\omega$ of triangle $\triangle A D E$ again at $F$. If $\angle A D F=45^{\circ}$, show that $C F$ is tangent to $\omega$.
(Luxembourg)

|
As $\angle A D F=45^{\circ}$ line $D F$ is an exterior bisector of $\angle C D B$. Since $B F$ bisects $\angle D B C$ line $C F$ is an exterior bisector of $\angle B C D$. Let $\angle A B C=2 \beta$, so $\angle E C F=(\angle D B C+\angle C D B) / 2=45^{\circ}+\beta$. Hence $\angle C F E=180^{\circ}-\angle E C F-\angle B C E-\angle E B C=180^{\circ}-\left(45^{\circ}+\beta+90^{\circ}-2 \beta+\beta\right)=45^{\circ}$. It follows that $\angle F D C=\angle C F E$, then $C F$ is tangent to $\omega$.
|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "\nProblem 1.",
"resource_path": "EGMO/segmented/en-2015-solutions.jsonl",
"solution_match": "\nSolution 2: ",
"tier": "T2",
"year": "2015"
}
|
Let $\triangle A B C$ be an acute-angled triangle, and let $D$ be the foot of the altitude from $C$. The angle bisector of $\angle A B C$ intersects $C D$ at $E$ and meets the circumcircle $\omega$ of triangle $\triangle A D E$ again at $F$. If $\angle A D F=45^{\circ}$, show that $C F$ is tangent to $\omega$.
(Luxembourg)

|
Note that $A E$ is diameter of circumcircle of $\triangle A B C$ since $\angle C D F=90^{\circ}$. From $\angle A E F=\angle A D F=45^{\circ}$ it follows that triangle $\triangle A F E$ is right-angled and isosceles. Without loss of generality, let points $A, E$ and $F$ have coordinates $(-1,0),(1,0)$ and $(0,1)$ respectively. Points $F, E$, $B$ are collinear, hence $B$ have coordinates $(b, 1-b)$ for some $b \neq-1$. Let point $C^{\prime}$ be intersection of line tangent to circumcircle of $\triangle A F E$ at $F$ with line $E D$. Thus $C^{\prime}$ have coordinates $(c, 1)$ and from $\overline{C^{\prime} E} \perp \overline{A B}$ we get $c=2 b /(b+1)$. Now vector $\overline{B C^{\prime}}=(2 b /(b+1)-b, b)=b /(b+1) \cdot(1-b, b+1)$, vector $\overline{B F}=(-b, b)=(-1,1) \cdot b$ and vector $\overline{B A}=(-(b+1),-(1-b))$. Its clear that $(1-b, b+1)$ and $(-(b+1),-(1-b))$ are symmetric with respect to $\overline{F E}=(-1,1)$, hence $B F$ bisects $\angle C^{\prime} B A$ and $C^{\prime}=C$ which completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\triangle A B C$ be an acute-angled triangle, and let $D$ be the foot of the altitude from $C$. The angle bisector of $\angle A B C$ intersects $C D$ at $E$ and meets the circumcircle $\omega$ of triangle $\triangle A D E$ again at $F$. If $\angle A D F=45^{\circ}$, show that $C F$ is tangent to $\omega$.
(Luxembourg)

|
Note that $A E$ is diameter of circumcircle of $\triangle A B C$ since $\angle C D F=90^{\circ}$. From $\angle A E F=\angle A D F=45^{\circ}$ it follows that triangle $\triangle A F E$ is right-angled and isosceles. Without loss of generality, let points $A, E$ and $F$ have coordinates $(-1,0),(1,0)$ and $(0,1)$ respectively. Points $F, E$, $B$ are collinear, hence $B$ have coordinates $(b, 1-b)$ for some $b \neq-1$. Let point $C^{\prime}$ be intersection of line tangent to circumcircle of $\triangle A F E$ at $F$ with line $E D$. Thus $C^{\prime}$ have coordinates $(c, 1)$ and from $\overline{C^{\prime} E} \perp \overline{A B}$ we get $c=2 b /(b+1)$. Now vector $\overline{B C^{\prime}}=(2 b /(b+1)-b, b)=b /(b+1) \cdot(1-b, b+1)$, vector $\overline{B F}=(-b, b)=(-1,1) \cdot b$ and vector $\overline{B A}=(-(b+1),-(1-b))$. Its clear that $(1-b, b+1)$ and $(-(b+1),-(1-b))$ are symmetric with respect to $\overline{F E}=(-1,1)$, hence $B F$ bisects $\angle C^{\prime} B A$ and $C^{\prime}=C$ which completes the proof.

|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "\nProblem 1.",
"resource_path": "EGMO/segmented/en-2015-solutions.jsonl",
"solution_match": "\nSolution 3: ",
"tier": "T2",
"year": "2015"
}
|
Let $\triangle A B C$ be an acute-angled triangle, and let $D$ be the foot of the altitude from $C$. The angle bisector of $\angle A B C$ intersects $C D$ at $E$ and meets the circumcircle $\omega$ of triangle $\triangle A D E$ again at $F$. If $\angle A D F=45^{\circ}$, show that $C F$ is tangent to $\omega$.
(Luxembourg)

|
Again $F$ lies on the perpendicular bisector of segment
$A E$, so $\triangle A F E$ is right-angled and isosceles. Let $M$ be an intersection of $B C$ and $A F$. Note that $\triangle A M B$ is isosceles since $B F$ is a bisector and altitude in this triangle. Thus $B F$ is a symmetry line of $\triangle A M B$. Then $\angle F D A=\angle F E A=\angle M E F=45^{\circ}, A F=F E=F M$ and $\angle D A E=\angle E M C$. Let us show that $E C=C M$. Indeed,
$$
\begin{aligned}
\angle C E M & =180^{\circ}-(\angle A E D+\angle F E A+\angle M E F)=90^{\circ}-\angle A E D= \\
& =\angle D A E=\angle E M C .
\end{aligned}
$$
It follows that $F M C E$ is a kite, since $E F=F M$ and $M C=C E$. Hence $\angle E F C=\angle C F M=\angle E D F=45^{\circ}$, so $F C$ is tangent to $\omega$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\triangle A B C$ be an acute-angled triangle, and let $D$ be the foot of the altitude from $C$. The angle bisector of $\angle A B C$ intersects $C D$ at $E$ and meets the circumcircle $\omega$ of triangle $\triangle A D E$ again at $F$. If $\angle A D F=45^{\circ}$, show that $C F$ is tangent to $\omega$.
(Luxembourg)

|
Again $F$ lies on the perpendicular bisector of segment
$A E$, so $\triangle A F E$ is right-angled and isosceles. Let $M$ be an intersection of $B C$ and $A F$. Note that $\triangle A M B$ is isosceles since $B F$ is a bisector and altitude in this triangle. Thus $B F$ is a symmetry line of $\triangle A M B$. Then $\angle F D A=\angle F E A=\angle M E F=45^{\circ}, A F=F E=F M$ and $\angle D A E=\angle E M C$. Let us show that $E C=C M$. Indeed,
$$
\begin{aligned}
\angle C E M & =180^{\circ}-(\angle A E D+\angle F E A+\angle M E F)=90^{\circ}-\angle A E D= \\
& =\angle D A E=\angle E M C .
\end{aligned}
$$
It follows that $F M C E$ is a kite, since $E F=F M$ and $M C=C E$. Hence $\angle E F C=\angle C F M=\angle E D F=45^{\circ}$, so $F C$ is tangent to $\omega$.
|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "\nProblem 1.",
"resource_path": "EGMO/segmented/en-2015-solutions.jsonl",
"solution_match": "\nSolution 4: ",
"tier": "T2",
"year": "2015"
}
|
Let $\triangle A B C$ be an acute-angled triangle, and let $D$ be the foot of the altitude from $C$. The angle bisector of $\angle A B C$ intersects $C D$ at $E$ and meets the circumcircle $\omega$ of triangle $\triangle A D E$ again at $F$. If $\angle A D F=45^{\circ}$, show that $C F$ is tangent to $\omega$.
(Luxembourg)

|
Let the tangent to $\omega$ at $F$ intersect $C D$ at $C^{\prime}$. Let $\angle A B F=$ $\angle F B C=\beta$. It follows that $\angle C^{\prime} F E=45^{\circ}$ since $C^{\prime} F$ is tangent. We have
$$
\frac{\sin \angle B D C}{\sin \angle C D F} \cdot \frac{\sin \angle D F C^{\prime}}{\sin \angle C^{\prime} F B} \cdot \frac{\sin \angle F B C}{\sin \angle C B D}=\frac{\sin 90^{\circ}}{\sin 45^{\circ}} \cdot \frac{\sin \left(90^{\circ}-\beta\right)}{\sin 45^{\circ}} \cdot \frac{\sin \beta}{\sin 2 \beta}=\frac{2 \sin \beta \cos \beta}{\sin 2 \beta}=1 .
$$
So by trig Ceva on triangle $\triangle B D F$, lines $F C^{\prime}, D C$ and $B C$ are concurrent (at $C$ ), so $C=C^{\prime}$. Hence $C F$ is tangent to $\omega$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\triangle A B C$ be an acute-angled triangle, and let $D$ be the foot of the altitude from $C$. The angle bisector of $\angle A B C$ intersects $C D$ at $E$ and meets the circumcircle $\omega$ of triangle $\triangle A D E$ again at $F$. If $\angle A D F=45^{\circ}$, show that $C F$ is tangent to $\omega$.
(Luxembourg)

|
Let the tangent to $\omega$ at $F$ intersect $C D$ at $C^{\prime}$. Let $\angle A B F=$ $\angle F B C=\beta$. It follows that $\angle C^{\prime} F E=45^{\circ}$ since $C^{\prime} F$ is tangent. We have
$$
\frac{\sin \angle B D C}{\sin \angle C D F} \cdot \frac{\sin \angle D F C^{\prime}}{\sin \angle C^{\prime} F B} \cdot \frac{\sin \angle F B C}{\sin \angle C B D}=\frac{\sin 90^{\circ}}{\sin 45^{\circ}} \cdot \frac{\sin \left(90^{\circ}-\beta\right)}{\sin 45^{\circ}} \cdot \frac{\sin \beta}{\sin 2 \beta}=\frac{2 \sin \beta \cos \beta}{\sin 2 \beta}=1 .
$$
So by trig Ceva on triangle $\triangle B D F$, lines $F C^{\prime}, D C$ and $B C$ are concurrent (at $C$ ), so $C=C^{\prime}$. Hence $C F$ is tangent to $\omega$.
|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "\nProblem 1.",
"resource_path": "EGMO/segmented/en-2015-solutions.jsonl",
"solution_match": "\nSolution 5: ",
"tier": "T2",
"year": "2015"
}
|
A domino is a $2 \times 1$ or $1 \times 2$ tile. Determine in how many ways exactly $n^{2}$ dominoes can be placed without overlapping on a $2 n \times 2 n$ chessboard so that every $2 \times 2$ square contains at least two uncovered unit squares which lie in the same row or column.
(Turkey)
|
The answer is $\binom{2 n}{n}^{2}$.
Divide the schessboard into $2 \times 2$ squares. There are exactly $n^{2}$ such squares on the chessboard. Each of these squares can have at most two unit squares covered by the dominos. As the dominos cover exactly $2 n^{2}$ squares, each of them must have exactly two unit squares which are covered, and these squares must lie in the same row or column.
We claim that these two unit squares are covered by the same domino tile. Suppose that this is not the case for some $2 \times 2$ square and one of the tiles covering one of its unit squares sticks out to the left. Then considering one of the leftmost $2 \times 2$ squares in this division with this property gives a contradiction.
Now consider this $n \times n$ chessboard consisting of $2 \times 2$ squares of the original board. Define $A, B$, $C, D$ as the following configurations on the original chessboard, where the gray squares indicate the domino tile, and consider the covering this $n \times n$ chessboard with the letters $A, B, C, D$ in such a

way that the resulting configuration on the original chessboard satisfies the condition of the question.
Note that then a square below or to the right of one containing an $A$ or $B$ must also contain an $A$ or $B$. Therefore the (possibly empty) region consisting of all squares containing an $A$ or $B$ abuts the lower right corner of the chessboard and is separated from the (possibly empty) region consisting of all squares containing a $C$ or $D$ by a path which goes from the lower left corner to the upper right corner of this chessboard and which moves up or right at each step.
A similar reasoning shows that the (possibly empty) region consisting of all squares containing an $A$ or $D$ abuts the lower left corner of the chessboard and is separated from the (possibly empty) region consisting of all squares containing a $B$ or $C$ by a path which goes from the upper left corner to the lower right corner of this chessboard and which moves down or right at each step.
| $D$ | $D$ | $C$ | $C$ | $C$ | $C$ |
| :---: | :---: | :---: | :---: | :---: | :---: |
| $D$ | $D$ | $C$ | $C$ | $C$ | $B$ |
| $D$ | $D$ | $D$ | $B$ | $B$ | $B$ |
| $D$ | $D$ | $D$ | $A$ | $A$ | $B$ |
| $D$ | $D$ | $D$ | $A$ | $A$ | $B$ |
| $D$ | $A$ | $A$ | $A$ | $A$ | $B$ |

Therefore the $n \times n$ chessboard is divided by these two paths into four (possibly empty) regions that consist respectively of all squares containing $A$ or $B$ or $C$ or $D$. Conversely, choosing two such paths and filling the four regions separated by them with $A \mathrm{~s}, B \mathrm{~s}, C \mathrm{~s}$ and $D \mathrm{~s}$ counterclockwise starting at the bottom results in a placement of the dominos on the original board satisfying the condition of the question.
As each of these paths can be chosen in $\binom{2 n}{n}$ ways, there are $\binom{2 n}{n}^{2}$ ways the dominos can be placed.
|
\binom{2 n}{n}^{2}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A domino is a $2 \times 1$ or $1 \times 2$ tile. Determine in how many ways exactly $n^{2}$ dominoes can be placed without overlapping on a $2 n \times 2 n$ chessboard so that every $2 \times 2$ square contains at least two uncovered unit squares which lie in the same row or column.
(Turkey)
|
The answer is $\binom{2 n}{n}^{2}$.
Divide the schessboard into $2 \times 2$ squares. There are exactly $n^{2}$ such squares on the chessboard. Each of these squares can have at most two unit squares covered by the dominos. As the dominos cover exactly $2 n^{2}$ squares, each of them must have exactly two unit squares which are covered, and these squares must lie in the same row or column.
We claim that these two unit squares are covered by the same domino tile. Suppose that this is not the case for some $2 \times 2$ square and one of the tiles covering one of its unit squares sticks out to the left. Then considering one of the leftmost $2 \times 2$ squares in this division with this property gives a contradiction.
Now consider this $n \times n$ chessboard consisting of $2 \times 2$ squares of the original board. Define $A, B$, $C, D$ as the following configurations on the original chessboard, where the gray squares indicate the domino tile, and consider the covering this $n \times n$ chessboard with the letters $A, B, C, D$ in such a

way that the resulting configuration on the original chessboard satisfies the condition of the question.
Note that then a square below or to the right of one containing an $A$ or $B$ must also contain an $A$ or $B$. Therefore the (possibly empty) region consisting of all squares containing an $A$ or $B$ abuts the lower right corner of the chessboard and is separated from the (possibly empty) region consisting of all squares containing a $C$ or $D$ by a path which goes from the lower left corner to the upper right corner of this chessboard and which moves up or right at each step.
A similar reasoning shows that the (possibly empty) region consisting of all squares containing an $A$ or $D$ abuts the lower left corner of the chessboard and is separated from the (possibly empty) region consisting of all squares containing a $B$ or $C$ by a path which goes from the upper left corner to the lower right corner of this chessboard and which moves down or right at each step.
| $D$ | $D$ | $C$ | $C$ | $C$ | $C$ |
| :---: | :---: | :---: | :---: | :---: | :---: |
| $D$ | $D$ | $C$ | $C$ | $C$ | $B$ |
| $D$ | $D$ | $D$ | $B$ | $B$ | $B$ |
| $D$ | $D$ | $D$ | $A$ | $A$ | $B$ |
| $D$ | $D$ | $D$ | $A$ | $A$ | $B$ |
| $D$ | $A$ | $A$ | $A$ | $A$ | $B$ |

Therefore the $n \times n$ chessboard is divided by these two paths into four (possibly empty) regions that consist respectively of all squares containing $A$ or $B$ or $C$ or $D$. Conversely, choosing two such paths and filling the four regions separated by them with $A \mathrm{~s}, B \mathrm{~s}, C \mathrm{~s}$ and $D \mathrm{~s}$ counterclockwise starting at the bottom results in a placement of the dominos on the original board satisfying the condition of the question.
As each of these paths can be chosen in $\binom{2 n}{n}$ ways, there are $\binom{2 n}{n}^{2}$ ways the dominos can be placed.
|
{
"exam": "EGMO",
"problem_label": "2",
"problem_match": "\nProblem 2.",
"resource_path": "EGMO/segmented/en-2015-solutions.jsonl",
"solution_match": "\nSolution:",
"tier": "T2",
"year": "2015"
}
|
Let $n, m$ be integers greater than 1 , and let $a_{1}, a_{2}, \ldots, a_{m}$ be positive integers not greater than $n^{m}$. Prove that there exist positive integers $b_{1}, b_{2}, \ldots, b_{m}$ not greater than $n$, such that
$$
\operatorname{gcd}\left(a_{1}+b_{1}, a_{2}+b_{2}, \ldots, a_{m}+b_{m}\right)<n
$$
where $\operatorname{gcd}\left(x_{1}, x_{2}, \ldots, x_{m}\right)$ denotes the greatest common divisor of $x_{1}, x_{2}, \ldots, x_{m}$.
|
Suppose without loss of generality that $a_{1}$ is the smallest of the $a_{i}$. If $a_{1} \geq n^{m}-1$, then the problem is simple: either all the $a_{i}$ are equal, or $a_{1}=n^{m}-1$ and $a_{j}=n^{m}$ for some $j$. In the first case, we can take (say) $b_{1}=1, b_{2}=2$, and the rest of the $b_{i}$ can be arbitrary, and we have
$$
\operatorname{gcd}\left(a_{1}+b_{1}, a_{2}+b_{2}, \ldots, a_{m}+b_{m}\right) \leq \operatorname{gcd}\left(a_{1}+b_{1}, a_{2}+b_{2}\right)=1
$$
In the second case, we can take $b_{1}=1, b_{j}=1$, and the rest of the $b_{i}$ arbitrary, and again
$$
\operatorname{gcd}\left(a_{1}+b_{1}, a_{2}+b_{2}, \ldots, a_{m}+b_{m}\right) \leq \operatorname{gcd}\left(a_{1}+b_{1}, a_{j}+b_{j}\right)=1
$$
So from now on we can suppose that $a_{1} \leq n^{m}-2$.
Now, let us suppose the desired $b_{1}, \ldots, b_{m}$ do not exist, and seek a contradiction. Then, for any choice of $b_{1}, \ldots, b_{m} \in\{1, \ldots, n\}$, we have
$$
\operatorname{gcd}\left(a_{1}+b_{1}, a_{2}+b_{2}, \ldots, a_{m}+b_{m}\right) \geq n
$$
Also, we have
$$
\operatorname{gcd}\left(a_{1}+b_{1}, a_{2}+b_{2}, \ldots, a_{m}+b_{m}\right) \leq a_{1}+b_{1} \leq n^{m}+n-2
$$
Thus there are at most $n^{m}-1$ possible values for the greatest common divisor. However, there are $n^{m}$ choices for the $m$-tuple $\left(b_{1}, \ldots, b_{m}\right)$. Then, by the pigeonhole principle, there are two $m$-tuples that yield the same values for the greatest common divisor, say $d$. But since $d \geq n$, for each $i$ there can be at most one choice of $b_{i} \in\{1,2, \ldots, n\}$ such that $a_{i}+b_{i}$ is divisible by $d$ - and therefore there can be at most one $m$-tuple $\left(b_{1}, b_{2}, \ldots, b_{m}\right)$ yielding $d$ as the greatest common divisor. This is the desired contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n, m$ be integers greater than 1 , and let $a_{1}, a_{2}, \ldots, a_{m}$ be positive integers not greater than $n^{m}$. Prove that there exist positive integers $b_{1}, b_{2}, \ldots, b_{m}$ not greater than $n$, such that
$$
\operatorname{gcd}\left(a_{1}+b_{1}, a_{2}+b_{2}, \ldots, a_{m}+b_{m}\right)<n
$$
where $\operatorname{gcd}\left(x_{1}, x_{2}, \ldots, x_{m}\right)$ denotes the greatest common divisor of $x_{1}, x_{2}, \ldots, x_{m}$.
|
Suppose without loss of generality that $a_{1}$ is the smallest of the $a_{i}$. If $a_{1} \geq n^{m}-1$, then the problem is simple: either all the $a_{i}$ are equal, or $a_{1}=n^{m}-1$ and $a_{j}=n^{m}$ for some $j$. In the first case, we can take (say) $b_{1}=1, b_{2}=2$, and the rest of the $b_{i}$ can be arbitrary, and we have
$$
\operatorname{gcd}\left(a_{1}+b_{1}, a_{2}+b_{2}, \ldots, a_{m}+b_{m}\right) \leq \operatorname{gcd}\left(a_{1}+b_{1}, a_{2}+b_{2}\right)=1
$$
In the second case, we can take $b_{1}=1, b_{j}=1$, and the rest of the $b_{i}$ arbitrary, and again
$$
\operatorname{gcd}\left(a_{1}+b_{1}, a_{2}+b_{2}, \ldots, a_{m}+b_{m}\right) \leq \operatorname{gcd}\left(a_{1}+b_{1}, a_{j}+b_{j}\right)=1
$$
So from now on we can suppose that $a_{1} \leq n^{m}-2$.
Now, let us suppose the desired $b_{1}, \ldots, b_{m}$ do not exist, and seek a contradiction. Then, for any choice of $b_{1}, \ldots, b_{m} \in\{1, \ldots, n\}$, we have
$$
\operatorname{gcd}\left(a_{1}+b_{1}, a_{2}+b_{2}, \ldots, a_{m}+b_{m}\right) \geq n
$$
Also, we have
$$
\operatorname{gcd}\left(a_{1}+b_{1}, a_{2}+b_{2}, \ldots, a_{m}+b_{m}\right) \leq a_{1}+b_{1} \leq n^{m}+n-2
$$
Thus there are at most $n^{m}-1$ possible values for the greatest common divisor. However, there are $n^{m}$ choices for the $m$-tuple $\left(b_{1}, \ldots, b_{m}\right)$. Then, by the pigeonhole principle, there are two $m$-tuples that yield the same values for the greatest common divisor, say $d$. But since $d \geq n$, for each $i$ there can be at most one choice of $b_{i} \in\{1,2, \ldots, n\}$ such that $a_{i}+b_{i}$ is divisible by $d$ - and therefore there can be at most one $m$-tuple $\left(b_{1}, b_{2}, \ldots, b_{m}\right)$ yielding $d$ as the greatest common divisor. This is the desired contradiction.
|
{
"exam": "EGMO",
"problem_label": "3",
"problem_match": "\nProblem 3.",
"resource_path": "EGMO/segmented/en-2015-solutions.jsonl",
"solution_match": "\nSolution 1: ",
"tier": "T2",
"year": "2015"
}
|
Let $n, m$ be integers greater than 1 , and let $a_{1}, a_{2}, \ldots, a_{m}$ be positive integers not greater than $n^{m}$. Prove that there exist positive integers $b_{1}, b_{2}, \ldots, b_{m}$ not greater than $n$, such that
$$
\operatorname{gcd}\left(a_{1}+b_{1}, a_{2}+b_{2}, \ldots, a_{m}+b_{m}\right)<n
$$
where $\operatorname{gcd}\left(x_{1}, x_{2}, \ldots, x_{m}\right)$ denotes the greatest common divisor of $x_{1}, x_{2}, \ldots, x_{m}$.
|
Similarly to Solution 1 suppose that $a_{1} \leq n^{m}-2$. The gcd of $a_{1}+1, a_{2}+1, a_{3}+1, \ldots, a_{m}+1$ is co-prime with the gcd of $a_{1}+1, a_{2}+2, a_{3}+1, \ldots, a_{m}+1$, thus $a_{1}+1 \geq n^{2}$. Now change another 1 into 2 and so on. After $m-1$ changes we get $a_{1}+1 \geq n^{m}$ which gives us a contradiction.
|
proof
|
Yes
|
Incomplete
|
proof
|
Number Theory
|
Let $n, m$ be integers greater than 1 , and let $a_{1}, a_{2}, \ldots, a_{m}$ be positive integers not greater than $n^{m}$. Prove that there exist positive integers $b_{1}, b_{2}, \ldots, b_{m}$ not greater than $n$, such that
$$
\operatorname{gcd}\left(a_{1}+b_{1}, a_{2}+b_{2}, \ldots, a_{m}+b_{m}\right)<n
$$
where $\operatorname{gcd}\left(x_{1}, x_{2}, \ldots, x_{m}\right)$ denotes the greatest common divisor of $x_{1}, x_{2}, \ldots, x_{m}$.
|
Similarly to Solution 1 suppose that $a_{1} \leq n^{m}-2$. The gcd of $a_{1}+1, a_{2}+1, a_{3}+1, \ldots, a_{m}+1$ is co-prime with the gcd of $a_{1}+1, a_{2}+2, a_{3}+1, \ldots, a_{m}+1$, thus $a_{1}+1 \geq n^{2}$. Now change another 1 into 2 and so on. After $m-1$ changes we get $a_{1}+1 \geq n^{m}$ which gives us a contradiction.
|
{
"exam": "EGMO",
"problem_label": "3",
"problem_match": "\nProblem 3.",
"resource_path": "EGMO/segmented/en-2015-solutions.jsonl",
"solution_match": "\nSolution 2: ",
"tier": "T2",
"year": "2015"
}
|
Let $n, m$ be integers greater than 1 , and let $a_{1}, a_{2}, \ldots, a_{m}$ be positive integers not greater than $n^{m}$. Prove that there exist positive integers $b_{1}, b_{2}, \ldots, b_{m}$ not greater than $n$, such that
$$
\operatorname{gcd}\left(a_{1}+b_{1}, a_{2}+b_{2}, \ldots, a_{m}+b_{m}\right)<n
$$
where $\operatorname{gcd}\left(x_{1}, x_{2}, \ldots, x_{m}\right)$ denotes the greatest common divisor of $x_{1}, x_{2}, \ldots, x_{m}$.
|
We will prove stronger version of this problem:
For $m, n>1$, let $a_{1}, \ldots, a_{m}$ be positive integers with at least one $a_{i} \leq n^{2^{m-1}}$. Then there are integers $b_{1}, \ldots, b_{m}$, each equal to 1 or 2 , such that $\operatorname{gcd}\left(a_{1}+b_{1}, \ldots, a_{m}+b_{m}\right)<n$.
Proof: Suppose otherwise. Then the $2^{m-1}$ integers $\operatorname{gcd}\left(a_{1}+b_{1}, \ldots, a_{m}+b_{m}\right)$ with $b_{1}=1$ and $b_{i}=1$ or 2 for $i>1$ are all pairwise coprime, since for any two of them, there is some $i>1$ with $a_{i}+1$ appearing in one and $a_{i}+2$ in the other. Since each of these $2^{m-1}$ integers divides $a_{1}+1$, and each is $\geq n$ with at most one equal to $n$, it follows that $a_{1}+1 \geq n(n+1)^{2^{m-1}-1}$ so $a_{1} \geq n^{2^{m-1}}$. The same is true for each $a_{i}, i=1, \ldots, n$, a contradiction.
Remark: Clearly the $n^{2^{m-1}}$ bound can be strengthened as well.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n, m$ be integers greater than 1 , and let $a_{1}, a_{2}, \ldots, a_{m}$ be positive integers not greater than $n^{m}$. Prove that there exist positive integers $b_{1}, b_{2}, \ldots, b_{m}$ not greater than $n$, such that
$$
\operatorname{gcd}\left(a_{1}+b_{1}, a_{2}+b_{2}, \ldots, a_{m}+b_{m}\right)<n
$$
where $\operatorname{gcd}\left(x_{1}, x_{2}, \ldots, x_{m}\right)$ denotes the greatest common divisor of $x_{1}, x_{2}, \ldots, x_{m}$.
|
We will prove stronger version of this problem:
For $m, n>1$, let $a_{1}, \ldots, a_{m}$ be positive integers with at least one $a_{i} \leq n^{2^{m-1}}$. Then there are integers $b_{1}, \ldots, b_{m}$, each equal to 1 or 2 , such that $\operatorname{gcd}\left(a_{1}+b_{1}, \ldots, a_{m}+b_{m}\right)<n$.
Proof: Suppose otherwise. Then the $2^{m-1}$ integers $\operatorname{gcd}\left(a_{1}+b_{1}, \ldots, a_{m}+b_{m}\right)$ with $b_{1}=1$ and $b_{i}=1$ or 2 for $i>1$ are all pairwise coprime, since for any two of them, there is some $i>1$ with $a_{i}+1$ appearing in one and $a_{i}+2$ in the other. Since each of these $2^{m-1}$ integers divides $a_{1}+1$, and each is $\geq n$ with at most one equal to $n$, it follows that $a_{1}+1 \geq n(n+1)^{2^{m-1}-1}$ so $a_{1} \geq n^{2^{m-1}}$. The same is true for each $a_{i}, i=1, \ldots, n$, a contradiction.
Remark: Clearly the $n^{2^{m-1}}$ bound can be strengthened as well.
|
{
"exam": "EGMO",
"problem_label": "3",
"problem_match": "\nProblem 3.",
"resource_path": "EGMO/segmented/en-2015-solutions.jsonl",
"solution_match": "\nSolution 3: ",
"tier": "T2",
"year": "2015"
}
|
Determine whether there exists an infinite sequence $a_{1}, a_{2}, a_{3}, \ldots$ of positive integers which satisfies the equality
$$
a_{n+2}=a_{n+1}+\sqrt{a_{n+1}+a_{n}}
$$
for every positive integer n.
(Japan)
|
The answer is no.
Suppose that there exists a sequence $\left(a_{n}\right)$ of positive integers satisfying the given condition. We will show that this will lead to a contradiction.
For each $n \geq 2$ define $b_{n}=a_{n+1}-a_{n}$. Then, by assumption, for $n \geq 2$ we get $b_{n}=\sqrt{a_{n}+a_{n-1}}$ so that we have
$$
b_{n+1}^{2}-b_{n}^{2}=\left(a_{n+1}+a_{n}\right)-\left(a_{n}+a_{n-1}\right)=\left(a_{n+1}-a_{n}\right)+\left(a_{n}-a_{n-1}\right)=b_{n}+b_{n-1} .
$$
Since each $a_{n}$ is a positive integer we see that $b_{n}$ is positive integer for $n \geq 2$ and the sequence $\left(b_{n}\right)$ is strictly increasing for $n \geq 3$. Thus $b_{n}+b_{n-1}=\left(b_{n+1}-b_{n}\right)\left(b_{n+1}+b_{n}\right) \geq b_{n+1}+b_{n}$, whence $b_{n-1} \geq b_{n+1}$ - a contradiction to increasing of the sequence $\left(b_{i}\right)$.
Thus we conclude that there exists no sequence $\left(a_{n}\right)$ of positive integers satisfying the given condition of the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Determine whether there exists an infinite sequence $a_{1}, a_{2}, a_{3}, \ldots$ of positive integers which satisfies the equality
$$
a_{n+2}=a_{n+1}+\sqrt{a_{n+1}+a_{n}}
$$
for every positive integer n.
(Japan)
|
The answer is no.
Suppose that there exists a sequence $\left(a_{n}\right)$ of positive integers satisfying the given condition. We will show that this will lead to a contradiction.
For each $n \geq 2$ define $b_{n}=a_{n+1}-a_{n}$. Then, by assumption, for $n \geq 2$ we get $b_{n}=\sqrt{a_{n}+a_{n-1}}$ so that we have
$$
b_{n+1}^{2}-b_{n}^{2}=\left(a_{n+1}+a_{n}\right)-\left(a_{n}+a_{n-1}\right)=\left(a_{n+1}-a_{n}\right)+\left(a_{n}-a_{n-1}\right)=b_{n}+b_{n-1} .
$$
Since each $a_{n}$ is a positive integer we see that $b_{n}$ is positive integer for $n \geq 2$ and the sequence $\left(b_{n}\right)$ is strictly increasing for $n \geq 3$. Thus $b_{n}+b_{n-1}=\left(b_{n+1}-b_{n}\right)\left(b_{n+1}+b_{n}\right) \geq b_{n+1}+b_{n}$, whence $b_{n-1} \geq b_{n+1}$ - a contradiction to increasing of the sequence $\left(b_{i}\right)$.
Thus we conclude that there exists no sequence $\left(a_{n}\right)$ of positive integers satisfying the given condition of the problem.
|
{
"exam": "EGMO",
"problem_label": "4",
"problem_match": "\nProblem 4.",
"resource_path": "EGMO/segmented/en-2015-solutions.jsonl",
"solution_match": "\nSolution 1: ",
"tier": "T2",
"year": "2015"
}
|
Determine whether there exists an infinite sequence $a_{1}, a_{2}, a_{3}, \ldots$ of positive integers which satisfies the equality
$$
a_{n+2}=a_{n+1}+\sqrt{a_{n+1}+a_{n}}
$$
for every positive integer n.
(Japan)
|
Suppose that such a sequence exists. We will calculate its members one by one and get a contradiction.
From the equality $a_{3}=a_{2}+\sqrt{a_{2}+a_{1}}$ it follows that $a_{3}>a_{2}$. Denote positive integers $\sqrt{a_{3}+a_{2}}$ by $b$ and $a_{3}$ by $a$, then we have $\sqrt{2 a}>b$. Since $a_{4}=a+b$ and $a_{5}=a+b+\sqrt{2 a+b}$ are positive integers, then $\sqrt{2 a+b}$ is positive integer.
Consider $a_{6}=a+b+\sqrt{2 a+b}+\sqrt{2 a+2 b+\sqrt{2 a+b}}$. Number $c=\sqrt{2 a+2 b+\sqrt{2 a+b}}$ must be positive integer, obviously it is greater than $\sqrt{2 a+b}$. But
$$
(\sqrt{2 a+b}+1)^{2}=2 a+b+2 \sqrt{2 a+b}+1=2 a+2 b+\sqrt{2 a+b}+(\sqrt{2 a+b}-b)+1>c^{2} .
$$
So $\sqrt{2 a+b}<c<\sqrt{2 a+b}+1$ which is impossible.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Determine whether there exists an infinite sequence $a_{1}, a_{2}, a_{3}, \ldots$ of positive integers which satisfies the equality
$$
a_{n+2}=a_{n+1}+\sqrt{a_{n+1}+a_{n}}
$$
for every positive integer n.
(Japan)
|
Suppose that such a sequence exists. We will calculate its members one by one and get a contradiction.
From the equality $a_{3}=a_{2}+\sqrt{a_{2}+a_{1}}$ it follows that $a_{3}>a_{2}$. Denote positive integers $\sqrt{a_{3}+a_{2}}$ by $b$ and $a_{3}$ by $a$, then we have $\sqrt{2 a}>b$. Since $a_{4}=a+b$ and $a_{5}=a+b+\sqrt{2 a+b}$ are positive integers, then $\sqrt{2 a+b}$ is positive integer.
Consider $a_{6}=a+b+\sqrt{2 a+b}+\sqrt{2 a+2 b+\sqrt{2 a+b}}$. Number $c=\sqrt{2 a+2 b+\sqrt{2 a+b}}$ must be positive integer, obviously it is greater than $\sqrt{2 a+b}$. But
$$
(\sqrt{2 a+b}+1)^{2}=2 a+b+2 \sqrt{2 a+b}+1=2 a+2 b+\sqrt{2 a+b}+(\sqrt{2 a+b}-b)+1>c^{2} .
$$
So $\sqrt{2 a+b}<c<\sqrt{2 a+b}+1$ which is impossible.
|
{
"exam": "EGMO",
"problem_label": "4",
"problem_match": "\nProblem 4.",
"resource_path": "EGMO/segmented/en-2015-solutions.jsonl",
"solution_match": "\nSolution 2: ",
"tier": "T2",
"year": "2015"
}
|
Determine whether there exists an infinite sequence $a_{1}, a_{2}, a_{3}, \ldots$ of positive integers which satisfies the equality
$$
a_{n+2}=a_{n+1}+\sqrt{a_{n+1}+a_{n}}
$$
for every positive integer n.
(Japan)
|
3: We will show that there is no sequence $\left(a_{n}\right)$ of positive integers which consists of $N>5$ members and satisfies
$$
a_{n+2}=a_{n+1}+\sqrt{a_{n+1}+a_{n}}
$$
for all $n=1, \ldots, N-2$. Moreover, we will describe all such sequences with five members.
Since every $a_{i}$ is a positive integer it follows from (1) that there exists such positive integer $k$ (obviously $k$ depends on $n$ ) that
$$
a_{n+1}+a_{n}=k^{2} .
$$
From (1) we have $\left(a_{n+2}-a_{n+1}\right)^{2}=a_{n+1}+a_{n}$, consider this equality as a quadratic equation with respect to $a_{n+1}$ :
$$
a_{n+1}^{2}-\left(2 a_{n+2}+1\right) a_{n+1}+a_{n+2}^{2}-a_{n}=0 .
$$
Obviously its solutions are $\left(a_{n+1}\right)_{1,2}=\frac{2 a_{n+2}+1 \pm \sqrt{D}}{2}$, where
$$
D=4\left(a_{n}+a_{n+2}\right)+1
$$
Since $a_{n+2}>a_{n+1}$ we have
$$
a_{n+1}=\frac{2 a_{n+2}+1-\sqrt{D}}{2} .
$$
From the last equality, using that $a_{n+1}$ and $a_{n+2}$ are positive integers, we conclude that $D$ is a square of some odd number i.e. $D=(2 m+1)^{2}$ for some positive integer $m \in \mathbb{N}$, substitute this into (3):
$$
a_{n}+a_{n+2}=m(m+1) \text {. }
$$
Now adding $a_{n}$ to both sides of (1) and using (2) and (4) we get $m(m+1)=k^{2}+k$ whence $m=k$. So
$$
\left\{\begin{array}{l}
a_{n}+a_{n+1}=k^{2}, \\
a_{n}+a_{n+2}=k^{2}+k
\end{array}\right.
$$
for some positive integer $k$ (recall that $k$ depends on $n$ ).
Write equations (5) for $n=2$ and $n=3$, then for some positive integers $k$ and $\ell$ we get
$$
\left\{\begin{array}{l}
a_{2}+a_{3}=k^{2}, \\
a_{2}+a_{4}=k^{2}+k, \\
a_{3}+a_{4}=\ell^{2} \\
a_{3}+a_{5}=\ell^{2}+\ell
\end{array}\right.
$$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Determine whether there exists an infinite sequence $a_{1}, a_{2}, a_{3}, \ldots$ of positive integers which satisfies the equality
$$
a_{n+2}=a_{n+1}+\sqrt{a_{n+1}+a_{n}}
$$
for every positive integer n.
(Japan)
|
3: We will show that there is no sequence $\left(a_{n}\right)$ of positive integers which consists of $N>5$ members and satisfies
$$
a_{n+2}=a_{n+1}+\sqrt{a_{n+1}+a_{n}}
$$
for all $n=1, \ldots, N-2$. Moreover, we will describe all such sequences with five members.
Since every $a_{i}$ is a positive integer it follows from (1) that there exists such positive integer $k$ (obviously $k$ depends on $n$ ) that
$$
a_{n+1}+a_{n}=k^{2} .
$$
From (1) we have $\left(a_{n+2}-a_{n+1}\right)^{2}=a_{n+1}+a_{n}$, consider this equality as a quadratic equation with respect to $a_{n+1}$ :
$$
a_{n+1}^{2}-\left(2 a_{n+2}+1\right) a_{n+1}+a_{n+2}^{2}-a_{n}=0 .
$$
Obviously its solutions are $\left(a_{n+1}\right)_{1,2}=\frac{2 a_{n+2}+1 \pm \sqrt{D}}{2}$, where
$$
D=4\left(a_{n}+a_{n+2}\right)+1
$$
Since $a_{n+2}>a_{n+1}$ we have
$$
a_{n+1}=\frac{2 a_{n+2}+1-\sqrt{D}}{2} .
$$
From the last equality, using that $a_{n+1}$ and $a_{n+2}$ are positive integers, we conclude that $D$ is a square of some odd number i.e. $D=(2 m+1)^{2}$ for some positive integer $m \in \mathbb{N}$, substitute this into (3):
$$
a_{n}+a_{n+2}=m(m+1) \text {. }
$$
Now adding $a_{n}$ to both sides of (1) and using (2) and (4) we get $m(m+1)=k^{2}+k$ whence $m=k$. So
$$
\left\{\begin{array}{l}
a_{n}+a_{n+1}=k^{2}, \\
a_{n}+a_{n+2}=k^{2}+k
\end{array}\right.
$$
for some positive integer $k$ (recall that $k$ depends on $n$ ).
Write equations (5) for $n=2$ and $n=3$, then for some positive integers $k$ and $\ell$ we get
$$
\left\{\begin{array}{l}
a_{2}+a_{3}=k^{2}, \\
a_{2}+a_{4}=k^{2}+k, \\
a_{3}+a_{4}=\ell^{2} \\
a_{3}+a_{5}=\ell^{2}+\ell
\end{array}\right.
$$
|
{
"exam": "EGMO",
"problem_label": "4",
"problem_match": "\nProblem 4.",
"resource_path": "EGMO/segmented/en-2015-solutions.jsonl",
"solution_match": "\nSolutions",
"tier": "T2",
"year": "2015"
}
|
Determine whether there exists an infinite sequence $a_{1}, a_{2}, a_{3}, \ldots$ of positive integers which satisfies the equality
$$
a_{n+2}=a_{n+1}+\sqrt{a_{n+1}+a_{n}}
$$
for every positive integer n.
(Japan)
|
of this linear system is
$$
a_{2}=\frac{2 k^{2}-\ell^{2}+k}{2}, \quad a_{3}=\frac{\ell^{2}-k}{2}, \quad a_{4}=\frac{\ell^{2}+k}{2}, \quad a_{5}=\frac{\ell^{2}+2 \ell+k}{2} .
$$
From $a_{2}<a_{4}$ we obtain $k^{2}<\ell^{2}$ hence $k<\ell$.
Consider $a_{6}$ :
$$
a_{6}=a_{5}+\sqrt{a_{5}+a_{4}}=a_{5}+\sqrt{\ell^{2}+\ell+k} .
$$
Since $0<k<l$ we have $\ell^{2}<\ell^{2}+\ell+k<(\ell+1)^{2}$. So $a_{6}$ cannot be integer i.e. there is no such sequence with six or more members.
To find all required sequences with five members we must find positive integers $a_{2}, a_{3}, a_{4}$ and $a_{5}$ which satisfy (7) for some positive integers $k<\ell$. Its clear that $k$ and $\ell$ must be of the same parity. Vise versa, let positive integers $k, \ell$ be of the same parity and satisfy $k<\ell$ then from (7) we get integers $a_{2}, a_{3}, a_{4}$ and $a_{5}$ then $a_{1}=\left(a_{3}-a_{2}\right)^{2}-a_{2}$ and it remains to verify that $a_{1}$ and $a_{2}$ are positive i.e. $2 k^{2}+k>\ell^{2}$ and $2\left(\ell^{2}-k^{2}-k\right)^{2}>2 k^{2}-\ell^{2}+k$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Determine whether there exists an infinite sequence $a_{1}, a_{2}, a_{3}, \ldots$ of positive integers which satisfies the equality
$$
a_{n+2}=a_{n+1}+\sqrt{a_{n+1}+a_{n}}
$$
for every positive integer n.
(Japan)
|
of this linear system is
$$
a_{2}=\frac{2 k^{2}-\ell^{2}+k}{2}, \quad a_{3}=\frac{\ell^{2}-k}{2}, \quad a_{4}=\frac{\ell^{2}+k}{2}, \quad a_{5}=\frac{\ell^{2}+2 \ell+k}{2} .
$$
From $a_{2}<a_{4}$ we obtain $k^{2}<\ell^{2}$ hence $k<\ell$.
Consider $a_{6}$ :
$$
a_{6}=a_{5}+\sqrt{a_{5}+a_{4}}=a_{5}+\sqrt{\ell^{2}+\ell+k} .
$$
Since $0<k<l$ we have $\ell^{2}<\ell^{2}+\ell+k<(\ell+1)^{2}$. So $a_{6}$ cannot be integer i.e. there is no such sequence with six or more members.
To find all required sequences with five members we must find positive integers $a_{2}, a_{3}, a_{4}$ and $a_{5}$ which satisfy (7) for some positive integers $k<\ell$. Its clear that $k$ and $\ell$ must be of the same parity. Vise versa, let positive integers $k, \ell$ be of the same parity and satisfy $k<\ell$ then from (7) we get integers $a_{2}, a_{3}, a_{4}$ and $a_{5}$ then $a_{1}=\left(a_{3}-a_{2}\right)^{2}-a_{2}$ and it remains to verify that $a_{1}$ and $a_{2}$ are positive i.e. $2 k^{2}+k>\ell^{2}$ and $2\left(\ell^{2}-k^{2}-k\right)^{2}>2 k^{2}-\ell^{2}+k$.
|
{
"exam": "EGMO",
"problem_label": "4",
"problem_match": "\nProblem 4.",
"resource_path": "EGMO/segmented/en-2015-solutions.jsonl",
"solution_match": "\nSolution ",
"tier": "T2",
"year": "2015"
}
|
Determine whether there exists an infinite sequence $a_{1}, a_{2}, a_{3}, \ldots$ of positive integers which satisfies the equality
$$
a_{n+2}=a_{n+1}+\sqrt{a_{n+1}+a_{n}}
$$
for every positive integer n.
(Japan)
|
It is easy to see that $\left(a_{n}\right)$ is increasing for large enough $n$. Hence
$$
a_{n+1}<a_{n}+\sqrt{2 a_{n}}
$$
and
$$
a_{n}<a_{n-1}+\sqrt{2 a_{n-1}} .
$$
Lets define $b_{n}=a_{n}+a_{n-1}$. Using AM-QM inequality we have
$$
\frac{\sqrt{2 a_{n}}+\sqrt{2 a_{n-1}}}{2} \leq \sqrt{\frac{2 a_{n}+2 a_{n-1}}{2}}
$$
Adding (1), (2) and using (3):
$$
b_{n+1}<b_{n}+\sqrt{2 a_{n}}+\sqrt{2 a_{n-1}} \leq b_{n}+2 \sqrt{b_{n}} .
$$
Let $b_{n}=m^{2}$. Since $\left(b_{n}\right)$ is increasing for large enough $n$, we have:
$$
m^{2}<b_{n+1}<m^{2}+2 m<(m+1)^{2}
$$
So, $b_{n+1}$ can't be a perfect square, so we get contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Determine whether there exists an infinite sequence $a_{1}, a_{2}, a_{3}, \ldots$ of positive integers which satisfies the equality
$$
a_{n+2}=a_{n+1}+\sqrt{a_{n+1}+a_{n}}
$$
for every positive integer n.
(Japan)
|
It is easy to see that $\left(a_{n}\right)$ is increasing for large enough $n$. Hence
$$
a_{n+1}<a_{n}+\sqrt{2 a_{n}}
$$
and
$$
a_{n}<a_{n-1}+\sqrt{2 a_{n-1}} .
$$
Lets define $b_{n}=a_{n}+a_{n-1}$. Using AM-QM inequality we have
$$
\frac{\sqrt{2 a_{n}}+\sqrt{2 a_{n-1}}}{2} \leq \sqrt{\frac{2 a_{n}+2 a_{n-1}}{2}}
$$
Adding (1), (2) and using (3):
$$
b_{n+1}<b_{n}+\sqrt{2 a_{n}}+\sqrt{2 a_{n-1}} \leq b_{n}+2 \sqrt{b_{n}} .
$$
Let $b_{n}=m^{2}$. Since $\left(b_{n}\right)$ is increasing for large enough $n$, we have:
$$
m^{2}<b_{n+1}<m^{2}+2 m<(m+1)^{2}
$$
So, $b_{n+1}$ can't be a perfect square, so we get contradiction.
|
{
"exam": "EGMO",
"problem_label": "4",
"problem_match": "\nProblem 4.",
"resource_path": "EGMO/segmented/en-2015-solutions.jsonl",
"solution_match": "\nSolution 4: ",
"tier": "T2",
"year": "2015"
}
|
Let $m, n$ be positive integers with $m>1$. Anastasia partitions the integers $1,2, \ldots, 2 m$ into $m$ pairs. Boris then chooses one integer from each pair and finds the sum of these chosen integers. Prove that Anastasia can select the pairs so that Boris cannot make his sum equal to $n$.
(Netherlands)
|
1A: Define the following ordered partitions:
$$
\begin{aligned}
& P_{1}=(\{1,2\},\{3,4\}, \ldots,\{2 m-1,2 m\}), \\
& P_{2}=(\{1, m+1\},\{2, m+2\}, \ldots,\{m, 2 m\}), \\
& P_{3}=(\{1,2 m\},\{2, m+1\},\{3, m+2\}, \ldots,\{m, 2 m-1\})
\end{aligned}
$$
For each $P_{j}$ we will compute the possible values for the expression $s=a_{1}+\ldots+a_{m}$, where $a_{i} \in P_{j, i}$ are the chosen integers. Here, $P_{j, i}$ denotes the $i$-th coordinate of the ordered partition $P_{j}$.
We will denote by $\sigma$ the number $\sum_{i=1}^{m} i=\left(m^{2}+m\right) / 2$.
- Consider the partition $P_{1}$ and a certain choice with corresponding sum $s$. We find that
$$
m^{2}=\sum_{i=1}^{m}(2 i-1) \leq s \leq \sum_{i=1}^{m} 2 i=m^{2}+m
$$
Hence, if $n<m^{2}$ or $n>m^{2}+m$, this partition gives a positive answer.
- Consider the partition $P_{2}$ and a certain choice with corresponding $s$. We find that
$$
s \equiv \sum_{i=1}^{m} i \equiv \sigma \quad(\bmod m)
$$
Hence, if $m^{2} \leq n \leq m^{2}+m$ and $n \not \equiv \sigma(\bmod m)$, this partition solves the problem.
- Consider the partition $P_{3}$ and a certain choice with corresponding $s$. We set
$$
d_{i}= \begin{cases}0 & \text { if } a_{i}=i \\ 1, & \text { if } a_{i} \neq i\end{cases}
$$
We also put $d=\sum_{i=1}^{m} d_{i}$, and note that $0 \leq d \leq m$. Note also that if $a_{i} \neq i$, then $a_{i} \equiv i-1$ $(\bmod m)$. Hence, for all $a_{i} \in P_{3, i}$ it holds that
$$
a_{i} \equiv i-d_{i} \quad(\bmod m)
$$
Hence,
$$
s \equiv \sum_{i=1}^{m} a_{i} \equiv \sum_{i=1}^{m}\left(i-d_{i}\right) \equiv \sigma-d \quad(\bmod m),
$$
which can only be congruent to $\sigma$ modulo $m$ if all $d_{i}$ are equal, which forces $s=\left(m^{2}+m\right) / 2$ or $s=\left(3 m^{2}+m\right) / 2$. Since $m>1$, it holds that
$$
\frac{m^{2}+m}{2}<m^{2}<m^{2}+m<\frac{3 m^{2}+m}{2} .
$$
Hence if $m^{2} \leq n \leq m^{2}+m$ and $n \equiv \sigma(\bmod m)$, then $s$ cannot be equal to $n$, so partition $P_{3}$ suffices for such $n$.
Note that all $n$ are treated in one of the cases above, so we are done.
Common notes for solutions 1B and 1C: Given the analysis of $P_{1}$ and $P_{2}$ as in the solution 1A, we may conclude (noting that $\sigma \equiv m(m+1) / 2(\bmod m)$ ) that if $m$ is odd then $m^{2}$ and $m^{2}+m$ are the only candidates for counterexamples $n$, while if $m$ is even then $m^{2}+\frac{m}{2}$ is the only candidate.
There are now various ways to proceed as alternatives to the partition $P_{3}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $m, n$ be positive integers with $m>1$. Anastasia partitions the integers $1,2, \ldots, 2 m$ into $m$ pairs. Boris then chooses one integer from each pair and finds the sum of these chosen integers. Prove that Anastasia can select the pairs so that Boris cannot make his sum equal to $n$.
(Netherlands)
|
1A: Define the following ordered partitions:
$$
\begin{aligned}
& P_{1}=(\{1,2\},\{3,4\}, \ldots,\{2 m-1,2 m\}), \\
& P_{2}=(\{1, m+1\},\{2, m+2\}, \ldots,\{m, 2 m\}), \\
& P_{3}=(\{1,2 m\},\{2, m+1\},\{3, m+2\}, \ldots,\{m, 2 m-1\})
\end{aligned}
$$
For each $P_{j}$ we will compute the possible values for the expression $s=a_{1}+\ldots+a_{m}$, where $a_{i} \in P_{j, i}$ are the chosen integers. Here, $P_{j, i}$ denotes the $i$-th coordinate of the ordered partition $P_{j}$.
We will denote by $\sigma$ the number $\sum_{i=1}^{m} i=\left(m^{2}+m\right) / 2$.
- Consider the partition $P_{1}$ and a certain choice with corresponding sum $s$. We find that
$$
m^{2}=\sum_{i=1}^{m}(2 i-1) \leq s \leq \sum_{i=1}^{m} 2 i=m^{2}+m
$$
Hence, if $n<m^{2}$ or $n>m^{2}+m$, this partition gives a positive answer.
- Consider the partition $P_{2}$ and a certain choice with corresponding $s$. We find that
$$
s \equiv \sum_{i=1}^{m} i \equiv \sigma \quad(\bmod m)
$$
Hence, if $m^{2} \leq n \leq m^{2}+m$ and $n \not \equiv \sigma(\bmod m)$, this partition solves the problem.
- Consider the partition $P_{3}$ and a certain choice with corresponding $s$. We set
$$
d_{i}= \begin{cases}0 & \text { if } a_{i}=i \\ 1, & \text { if } a_{i} \neq i\end{cases}
$$
We also put $d=\sum_{i=1}^{m} d_{i}$, and note that $0 \leq d \leq m$. Note also that if $a_{i} \neq i$, then $a_{i} \equiv i-1$ $(\bmod m)$. Hence, for all $a_{i} \in P_{3, i}$ it holds that
$$
a_{i} \equiv i-d_{i} \quad(\bmod m)
$$
Hence,
$$
s \equiv \sum_{i=1}^{m} a_{i} \equiv \sum_{i=1}^{m}\left(i-d_{i}\right) \equiv \sigma-d \quad(\bmod m),
$$
which can only be congruent to $\sigma$ modulo $m$ if all $d_{i}$ are equal, which forces $s=\left(m^{2}+m\right) / 2$ or $s=\left(3 m^{2}+m\right) / 2$. Since $m>1$, it holds that
$$
\frac{m^{2}+m}{2}<m^{2}<m^{2}+m<\frac{3 m^{2}+m}{2} .
$$
Hence if $m^{2} \leq n \leq m^{2}+m$ and $n \equiv \sigma(\bmod m)$, then $s$ cannot be equal to $n$, so partition $P_{3}$ suffices for such $n$.
Note that all $n$ are treated in one of the cases above, so we are done.
Common notes for solutions 1B and 1C: Given the analysis of $P_{1}$ and $P_{2}$ as in the solution 1A, we may conclude (noting that $\sigma \equiv m(m+1) / 2(\bmod m)$ ) that if $m$ is odd then $m^{2}$ and $m^{2}+m$ are the only candidates for counterexamples $n$, while if $m$ is even then $m^{2}+\frac{m}{2}$ is the only candidate.
There are now various ways to proceed as alternatives to the partition $P_{3}$.
|
{
"exam": "EGMO",
"problem_label": "5",
"problem_match": "\nProblem 5.",
"resource_path": "EGMO/segmented/en-2015-solutions.jsonl",
"solution_match": "\nSolution ",
"tier": "T2",
"year": "2015"
}
|
Let $m, n$ be positive integers with $m>1$. Anastasia partitions the integers $1,2, \ldots, 2 m$ into $m$ pairs. Boris then chooses one integer from each pair and finds the sum of these chosen integers. Prove that Anastasia can select the pairs so that Boris cannot make his sum equal to $n$.
(Netherlands)
|
1B: Consider the partition $(\{1, m+2\},\{2, m+3\}, \ldots,\{m-1,2 m\},\{m, m+1\})$. We consider possible sums mod $m+1$. For the first $m-1$ pairs, the elements of each pair are congruent mod $m+1$, so the sum of one element of each pair is $(\bmod m+1)$ congruent to $\frac{1}{2} m(m+1)-m$, which is congruent to 1 if $m+1$ is odd and $1+\frac{m+1}{2}$ if $m+1$ is even. Now the elements of the last pair are congruent to -1 and 0 , so any achievable value of $n$ is congruent to 0 or 1 if $m+1$ is odd, and to 0 or 1 plus $\frac{m+1}{2}$ if $m+1$ is even. If $m$ is even then $m^{2}+\frac{m}{2} \equiv 1+\frac{m}{2}$, which is not congruent to 0 or 1 . If $m$ is odd then $m^{2} \equiv 1$ and $m^{2}+m \equiv 0$, neither of which can equal 0 or 1 plus $\frac{m+1}{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $m, n$ be positive integers with $m>1$. Anastasia partitions the integers $1,2, \ldots, 2 m$ into $m$ pairs. Boris then chooses one integer from each pair and finds the sum of these chosen integers. Prove that Anastasia can select the pairs so that Boris cannot make his sum equal to $n$.
(Netherlands)
|
1B: Consider the partition $(\{1, m+2\},\{2, m+3\}, \ldots,\{m-1,2 m\},\{m, m+1\})$. We consider possible sums mod $m+1$. For the first $m-1$ pairs, the elements of each pair are congruent mod $m+1$, so the sum of one element of each pair is $(\bmod m+1)$ congruent to $\frac{1}{2} m(m+1)-m$, which is congruent to 1 if $m+1$ is odd and $1+\frac{m+1}{2}$ if $m+1$ is even. Now the elements of the last pair are congruent to -1 and 0 , so any achievable value of $n$ is congruent to 0 or 1 if $m+1$ is odd, and to 0 or 1 plus $\frac{m+1}{2}$ if $m+1$ is even. If $m$ is even then $m^{2}+\frac{m}{2} \equiv 1+\frac{m}{2}$, which is not congruent to 0 or 1 . If $m$ is odd then $m^{2} \equiv 1$ and $m^{2}+m \equiv 0$, neither of which can equal 0 or 1 plus $\frac{m+1}{2}$.
|
{
"exam": "EGMO",
"problem_label": "5",
"problem_match": "\nProblem 5.",
"resource_path": "EGMO/segmented/en-2015-solutions.jsonl",
"solution_match": "\nSolution ",
"tier": "T2",
"year": "2015"
}
|
Let $m, n$ be positive integers with $m>1$. Anastasia partitions the integers $1,2, \ldots, 2 m$ into $m$ pairs. Boris then chooses one integer from each pair and finds the sum of these chosen integers. Prove that Anastasia can select the pairs so that Boris cannot make his sum equal to $n$.
(Netherlands)
|
1C: Similarly, consider the partition $(\{1, m\},\{2, m+1\}, \ldots,\{m-1,2 m-2\},\{2 m-1,2 m\})$, this time considering sums of elements of pairs $\bmod m-1$. If $m-1$ is odd, the sum is congruent to 1 or 2 ; if $m-1$ is even, to 1 or 2 plus $\frac{m-1}{2}$. If $m$ is even then $m^{2}+\frac{m}{2} \equiv 1+\frac{m}{2}$, and this can only be congruent to 1 or 2 when $m=2$. If $m$ is odd, $m^{2}$ and $m^{2}+m$ are congruent to 1 and 2 , and these can only be congruent to 1 or 2 plus $\frac{m-1}{2}$ when $m=3$. Now the cases of $m=2$ and $m=3$ need considering separately (by finding explicit partitions excluding each $n$ ).
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $m, n$ be positive integers with $m>1$. Anastasia partitions the integers $1,2, \ldots, 2 m$ into $m$ pairs. Boris then chooses one integer from each pair and finds the sum of these chosen integers. Prove that Anastasia can select the pairs so that Boris cannot make his sum equal to $n$.
(Netherlands)
|
1C: Similarly, consider the partition $(\{1, m\},\{2, m+1\}, \ldots,\{m-1,2 m-2\},\{2 m-1,2 m\})$, this time considering sums of elements of pairs $\bmod m-1$. If $m-1$ is odd, the sum is congruent to 1 or 2 ; if $m-1$ is even, to 1 or 2 plus $\frac{m-1}{2}$. If $m$ is even then $m^{2}+\frac{m}{2} \equiv 1+\frac{m}{2}$, and this can only be congruent to 1 or 2 when $m=2$. If $m$ is odd, $m^{2}$ and $m^{2}+m$ are congruent to 1 and 2 , and these can only be congruent to 1 or 2 plus $\frac{m-1}{2}$ when $m=3$. Now the cases of $m=2$ and $m=3$ need considering separately (by finding explicit partitions excluding each $n$ ).
|
{
"exam": "EGMO",
"problem_label": "5",
"problem_match": "\nProblem 5.",
"resource_path": "EGMO/segmented/en-2015-solutions.jsonl",
"solution_match": "\nSolution ",
"tier": "T2",
"year": "2015"
}
|
Let $m, n$ be positive integers with $m>1$. Anastasia partitions the integers $1,2, \ldots, 2 m$ into $m$ pairs. Boris then chooses one integer from each pair and finds the sum of these chosen integers. Prove that Anastasia can select the pairs so that Boris cannot make his sum equal to $n$.
(Netherlands)
|
This solution does not use modulo arguments. Use only $P_{1}$ from the solution 1A to conclude that $m^{2} \leq n \leq m^{2}+m$. Now consider the partition $(\{1,2 m\},\{2,3\},\{4,5\}, \ldots,\{2 m-$ $2,2 m-1\})$. If 1 is chosen from the first pair, the sum is at most $m^{2}$; if $2 m$ is chosen, the sum is at least $m^{2}+m$. So either $n=m^{2}$ or $n=m^{2}+m$. Now consider the partition ( $\{1,2 m-$ $1\},\{2,2 m\},\{3,4\},\{5,6\}, \ldots,\{2 m-3,2 m-2\})$. Sums of one element from each of the last $m-2$ pairs are in the range from $(m-2) m=m^{2}-2 m$ to $(m-2)(m+1)=m^{2}-m-2$ inclusive. Sums of one element from each of the first two pairs are $3,2 m+1$ and $4 m-1$. In the first case we have $n \leq m^{2}-m+1<m^{2}$, in the second $m^{2}+1 \leq n \leq m^{2}+m-1$ and in the third $n \geq m^{2}+2 m-1>m^{2}+m$. So these three partitions together have eliminated all $n$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $m, n$ be positive integers with $m>1$. Anastasia partitions the integers $1,2, \ldots, 2 m$ into $m$ pairs. Boris then chooses one integer from each pair and finds the sum of these chosen integers. Prove that Anastasia can select the pairs so that Boris cannot make his sum equal to $n$.
(Netherlands)
|
This solution does not use modulo arguments. Use only $P_{1}$ from the solution 1A to conclude that $m^{2} \leq n \leq m^{2}+m$. Now consider the partition $(\{1,2 m\},\{2,3\},\{4,5\}, \ldots,\{2 m-$ $2,2 m-1\})$. If 1 is chosen from the first pair, the sum is at most $m^{2}$; if $2 m$ is chosen, the sum is at least $m^{2}+m$. So either $n=m^{2}$ or $n=m^{2}+m$. Now consider the partition ( $\{1,2 m-$ $1\},\{2,2 m\},\{3,4\},\{5,6\}, \ldots,\{2 m-3,2 m-2\})$. Sums of one element from each of the last $m-2$ pairs are in the range from $(m-2) m=m^{2}-2 m$ to $(m-2)(m+1)=m^{2}-m-2$ inclusive. Sums of one element from each of the first two pairs are $3,2 m+1$ and $4 m-1$. In the first case we have $n \leq m^{2}-m+1<m^{2}$, in the second $m^{2}+1 \leq n \leq m^{2}+m-1$ and in the third $n \geq m^{2}+2 m-1>m^{2}+m$. So these three partitions together have eliminated all $n$.
|
{
"exam": "EGMO",
"problem_label": "5",
"problem_match": "\nProblem 5.",
"resource_path": "EGMO/segmented/en-2015-solutions.jsonl",
"solution_match": "\nSolution 2: ",
"tier": "T2",
"year": "2015"
}
|
Let $H$ be the orthocenter and $G$ be the centroid of acute-angled triangle $\triangle A B C$ with $A B \neq A C$. The line $A G$ intersects the circumcircle of $\triangle A B C$ at $A$ and $P$. Let $P^{\prime}$ be the reflection of $P$ in the line $B C$. Prove that $\angle C A B=60^{\circ}$ if and only if $H G=G P^{\prime}$.
(Ukraine)
|
Let $\omega$ be the circumcircle of $\triangle A B C$. Reflecting $\omega$ in line $B C$, we obtain circle $\omega^{\prime}$ which, obviously, contains points $H$ and $P^{\prime}$. Let $M$ be the midpoint of $B C$. As triangle $\triangle A B C$ is acute-angled, then $H$ and $O$ lie inside this triangle.
Let us assume that $\angle C A B=60^{\circ}$. Since
$$
\angle C O B=2 \angle C A B=120^{\circ}=180^{\circ}-60^{\circ}=180^{\circ}-\angle C A B=\angle C H B,
$$
hence $O$ lies on $\omega^{\prime}$. Reflecting $O$ in line $B C$, we obtain point $O^{\prime}$ which lies on $\omega$ and this point is the center of $\omega^{\prime}$. Then $O O^{\prime}=2 O M=2 R \cos \angle C A B=A H$, so $A H=O O^{\prime}=H O^{\prime}=A O=R$, where $R$ is the radius of $\omega$ and, naturally, of $\omega^{\prime}$. Then quadrilateral $A H O^{\prime} O$ is a rhombus, so $A$ and $O^{\prime}$ are symmetric to each other with respect to $H O$. As $H, G$ and $O$ are collinear (Euler line), then $\angle G A H=\angle H O^{\prime} G$. Diagonals of quadrilateral $G O P O^{\prime}$ intersects at $M$. Since $\angle B O M=60^{\circ}$, so
$$
O M=M O^{\prime}=\operatorname{ctg} 60^{\circ} \cdot M B=\frac{M B}{\sqrt{3}} .
$$
As $3 M O \cdot M O^{\prime}=M B^{2}=M B \cdot M C=M P \cdot M A=3 M G \cdot M P$, then $G O P O^{\prime}$ is a cyclic. Since $B C$ is a perpendicular bisector of $O O^{\prime}$, so the circumcircle of quadrilateral $G O P O^{\prime}$ is symmetrical with respect to $B C$. Thus $P^{\prime}$ also belongs to the circumcircle of $G O P O^{\prime}$, hence $\angle G O^{\prime} P^{\prime}=\angle G P P^{\prime}$. Note that $\angle G P P^{\prime}=\angle G A H$ since $A H \| P P^{\prime}$. And as it was proved $\angle G A H=\angle H O^{\prime} G$, then $\angle H O^{\prime} G=\angle G O^{\prime} P^{\prime}$. Thus triangles $\triangle H O^{\prime} G$ and $\triangle G O^{\prime} P^{\prime}$ are equal and hence $H G=G P^{\prime}$.
Now we will prove that if $H G=G P^{\prime}$ then $\angle C A B=60^{\circ}$. Reflecting $A$ with respect to $M$, we get $A^{\prime}$. Then, as it was said in the first part of solution, points $B, C, H$ and $P^{\prime}$ belong to $\omega^{\prime}$. Also it is clear that $A^{\prime}$ belongs to $\omega^{\prime}$. Note that $H C \perp C A^{\prime}$ since $A B \| C A^{\prime}$ and hence $H A^{\prime}$ is a diameter of $\omega^{\prime}$. Obviously, the center $O^{\prime}$ of circle $\omega^{\prime}$ is midpoint of $H A^{\prime}$. From $H G=G P^{\prime}$ it follows that $\triangle H G O^{\prime}$ is equal to $\triangle P^{\prime} G O^{\prime}$. Therefore $H$ and $P^{\prime}$ are symmetric with respect to $G O^{\prime}$. Hence $G O^{\prime} \perp H P^{\prime}$ and $G O^{\prime} \| A^{\prime} P^{\prime}$. Let $H G$ intersect $A^{\prime} P^{\prime}$ at $K$ and $K \not \equiv O$ since $A B \neq A C$. We conclude that $H G=G K$, because line $G O^{\prime}$ is midline of the triangle $\triangle H K A^{\prime}$. Note that $2 G O=H G$. since $H O$ is Euler line of triangle $A B C$. So $O$ is midpoint of segment $G K$. Because of $\angle C M P=\angle C M P^{\prime}$, then $\angle G M O=\angle O M P^{\prime}$. Line $O M$, that passes through $O^{\prime}$, is an external angle bisector of $\angle P^{\prime} M A^{\prime}$. Also we know that $P^{\prime} O^{\prime}=O^{\prime} A^{\prime}$, then $O^{\prime}$ is the midpoint of arc $P^{\prime} M A^{\prime}$ of the circumcircle of triangle $\triangle P^{\prime} M A^{\prime}$. It
follows that quadrilateral $P^{\prime} M O^{\prime} A^{\prime}$ is cyclic, then $\angle O^{\prime} M A^{\prime}=\angle O^{\prime} P^{\prime} A^{\prime}=\angle O^{\prime} A^{\prime} P^{\prime}$. Let $O M$ and $P^{\prime} A^{\prime}$ intersect at $T$. Triangles $\triangle T O^{\prime} A^{\prime}$ and $\triangle A^{\prime} O^{\prime} M$ are similar, hence $O^{\prime} A^{\prime} / O^{\prime} M=O^{\prime} T / O^{\prime} A^{\prime}$. In the other words, $O^{\prime} M \cdot O^{\prime} T=O^{\prime} A^{\prime 2}$. Using Menelaus' theorem for triangle $\triangle H K A^{\prime}$ and line $T O^{\prime}$, we obtain that
$$
\frac{A^{\prime} O^{\prime}}{O^{\prime} H} \cdot \frac{H O}{O K} \cdot \frac{K T}{T A^{\prime}}=3 \cdot \frac{K T}{T A^{\prime}}=1
$$
It follows that $K T / T A^{\prime}=1 / 3$ and $K A^{\prime}=2 K T$. Using Menelaus' theorem for triangle $T O^{\prime} A^{\prime}$ and line $H K$ we get that
$$
1=\frac{O^{\prime} H}{H A^{\prime}} \cdot \frac{A^{\prime} K}{K T} \cdot \frac{T O}{O O^{\prime}}=\frac{1}{2} \cdot 2 \cdot \frac{T O}{O O^{\prime}}=\frac{T O}{O O^{\prime}} .
$$
It means that $T O=O O^{\prime}$, so $O^{\prime} A^{2}=O^{\prime} M \cdot O^{\prime} T=O O^{\prime 2}$. Hence $O^{\prime} A^{\prime}=O O^{\prime}$ and, consequently, $O \in \omega^{\prime}$. Finally we conclude that $2 \angle C A B=\angle B O C=180^{\circ}-\angle C A B$, so $\angle C A B=60^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $H$ be the orthocenter and $G$ be the centroid of acute-angled triangle $\triangle A B C$ with $A B \neq A C$. The line $A G$ intersects the circumcircle of $\triangle A B C$ at $A$ and $P$. Let $P^{\prime}$ be the reflection of $P$ in the line $B C$. Prove that $\angle C A B=60^{\circ}$ if and only if $H G=G P^{\prime}$.
(Ukraine)

|
Let $\omega$ be the circumcircle of $\triangle A B C$. Reflecting $\omega$ in line $B C$, we obtain circle $\omega^{\prime}$ which, obviously, contains points $H$ and $P^{\prime}$. Let $M$ be the midpoint of $B C$. As triangle $\triangle A B C$ is acute-angled, then $H$ and $O$ lie inside this triangle.
Let us assume that $\angle C A B=60^{\circ}$. Since
$$
\angle C O B=2 \angle C A B=120^{\circ}=180^{\circ}-60^{\circ}=180^{\circ}-\angle C A B=\angle C H B,
$$
hence $O$ lies on $\omega^{\prime}$. Reflecting $O$ in line $B C$, we obtain point $O^{\prime}$ which lies on $\omega$ and this point is the center of $\omega^{\prime}$. Then $O O^{\prime}=2 O M=2 R \cos \angle C A B=A H$, so $A H=O O^{\prime}=H O^{\prime}=A O=R$, where $R$ is the radius of $\omega$ and, naturally, of $\omega^{\prime}$. Then quadrilateral $A H O^{\prime} O$ is a rhombus, so $A$ and $O^{\prime}$ are symmetric to each other with respect to $H O$. As $H, G$ and $O$ are collinear (Euler line), then $\angle G A H=\angle H O^{\prime} G$. Diagonals of quadrilateral $G O P O^{\prime}$ intersects at $M$. Since $\angle B O M=60^{\circ}$, so
$$
O M=M O^{\prime}=\operatorname{ctg} 60^{\circ} \cdot M B=\frac{M B}{\sqrt{3}} .
$$
As $3 M O \cdot M O^{\prime}=M B^{2}=M B \cdot M C=M P \cdot M A=3 M G \cdot M P$, then $G O P O^{\prime}$ is a cyclic. Since $B C$ is a perpendicular bisector of $O O^{\prime}$, so the circumcircle of quadrilateral $G O P O^{\prime}$ is symmetrical with respect to $B C$. Thus $P^{\prime}$ also belongs to the circumcircle of $G O P O^{\prime}$, hence $\angle G O^{\prime} P^{\prime}=\angle G P P^{\prime}$. Note that $\angle G P P^{\prime}=\angle G A H$ since $A H \| P P^{\prime}$. And as it was proved $\angle G A H=\angle H O^{\prime} G$, then $\angle H O^{\prime} G=\angle G O^{\prime} P^{\prime}$. Thus triangles $\triangle H O^{\prime} G$ and $\triangle G O^{\prime} P^{\prime}$ are equal and hence $H G=G P^{\prime}$.
Now we will prove that if $H G=G P^{\prime}$ then $\angle C A B=60^{\circ}$. Reflecting $A$ with respect to $M$, we get $A^{\prime}$. Then, as it was said in the first part of solution, points $B, C, H$ and $P^{\prime}$ belong to $\omega^{\prime}$. Also it is clear that $A^{\prime}$ belongs to $\omega^{\prime}$. Note that $H C \perp C A^{\prime}$ since $A B \| C A^{\prime}$ and hence $H A^{\prime}$ is a diameter of $\omega^{\prime}$. Obviously, the center $O^{\prime}$ of circle $\omega^{\prime}$ is midpoint of $H A^{\prime}$. From $H G=G P^{\prime}$ it follows that $\triangle H G O^{\prime}$ is equal to $\triangle P^{\prime} G O^{\prime}$. Therefore $H$ and $P^{\prime}$ are symmetric with respect to $G O^{\prime}$. Hence $G O^{\prime} \perp H P^{\prime}$ and $G O^{\prime} \| A^{\prime} P^{\prime}$. Let $H G$ intersect $A^{\prime} P^{\prime}$ at $K$ and $K \not \equiv O$ since $A B \neq A C$. We conclude that $H G=G K$, because line $G O^{\prime}$ is midline of the triangle $\triangle H K A^{\prime}$. Note that $2 G O=H G$. since $H O$ is Euler line of triangle $A B C$. So $O$ is midpoint of segment $G K$. Because of $\angle C M P=\angle C M P^{\prime}$, then $\angle G M O=\angle O M P^{\prime}$. Line $O M$, that passes through $O^{\prime}$, is an external angle bisector of $\angle P^{\prime} M A^{\prime}$. Also we know that $P^{\prime} O^{\prime}=O^{\prime} A^{\prime}$, then $O^{\prime}$ is the midpoint of arc $P^{\prime} M A^{\prime}$ of the circumcircle of triangle $\triangle P^{\prime} M A^{\prime}$. It

follows that quadrilateral $P^{\prime} M O^{\prime} A^{\prime}$ is cyclic, then $\angle O^{\prime} M A^{\prime}=\angle O^{\prime} P^{\prime} A^{\prime}=\angle O^{\prime} A^{\prime} P^{\prime}$. Let $O M$ and $P^{\prime} A^{\prime}$ intersect at $T$. Triangles $\triangle T O^{\prime} A^{\prime}$ and $\triangle A^{\prime} O^{\prime} M$ are similar, hence $O^{\prime} A^{\prime} / O^{\prime} M=O^{\prime} T / O^{\prime} A^{\prime}$. In the other words, $O^{\prime} M \cdot O^{\prime} T=O^{\prime} A^{\prime 2}$. Using Menelaus' theorem for triangle $\triangle H K A^{\prime}$ and line $T O^{\prime}$, we obtain that
$$
\frac{A^{\prime} O^{\prime}}{O^{\prime} H} \cdot \frac{H O}{O K} \cdot \frac{K T}{T A^{\prime}}=3 \cdot \frac{K T}{T A^{\prime}}=1
$$
It follows that $K T / T A^{\prime}=1 / 3$ and $K A^{\prime}=2 K T$. Using Menelaus' theorem for triangle $T O^{\prime} A^{\prime}$ and line $H K$ we get that
$$
1=\frac{O^{\prime} H}{H A^{\prime}} \cdot \frac{A^{\prime} K}{K T} \cdot \frac{T O}{O O^{\prime}}=\frac{1}{2} \cdot 2 \cdot \frac{T O}{O O^{\prime}}=\frac{T O}{O O^{\prime}} .
$$
It means that $T O=O O^{\prime}$, so $O^{\prime} A^{2}=O^{\prime} M \cdot O^{\prime} T=O O^{\prime 2}$. Hence $O^{\prime} A^{\prime}=O O^{\prime}$ and, consequently, $O \in \omega^{\prime}$. Finally we conclude that $2 \angle C A B=\angle B O C=180^{\circ}-\angle C A B$, so $\angle C A B=60^{\circ}$.

|
{
"exam": "EGMO",
"problem_label": "6",
"problem_match": "\nProblem 6.",
"resource_path": "EGMO/segmented/en-2015-solutions.jsonl",
"solution_match": "\nSolution 1: ",
"tier": "T2",
"year": "2015"
}
|
Let $H$ be the orthocenter and $G$ be the centroid of acute-angled triangle $\triangle A B C$ with $A B \neq A C$. The line $A G$ intersects the circumcircle of $\triangle A B C$ at $A$ and $P$. Let $P^{\prime}$ be the reflection of $P$ in the line $B C$. Prove that $\angle C A B=60^{\circ}$ if and only if $H G=G P^{\prime}$.
(Ukraine)

|
Let $O^{\prime}$ and $G^{\prime}$ denote the reflection of $O$ and $G$, respectively, with respect to the line $B C$. We then need to show $\angle C A B=60^{\circ}$ iff $G^{\prime} H^{\prime}=G^{\prime} P$. Note that $\triangle H^{\prime} O P$ is isosceles and hence
$G^{\prime} H^{\prime}=G^{\prime} P$ is equivalent to $G^{\prime}$ lying on the bisector $\angle H^{\prime} O P$. Let $\angle H^{\prime} A P=\varepsilon$. By the assumption $A B \neq A C$, we have $\varepsilon \neq 0$. Then $\angle H^{\prime} O P=2 \angle H^{\prime} A P=2 \varepsilon$, hence $G^{\prime} H^{\prime}=G^{\prime} P$ iff $\angle G^{\prime} O H^{\prime}=\varepsilon$. But $\angle G O^{\prime} H=\angle G^{\prime} O H^{\prime}$. Let $D$ be the midpoint of $O O^{\prime}$. It is known that $\angle G D O=\angle G A H=\varepsilon$. Let $F$ be the midpoint of $H G$. Then $H G=F O$ (Euler line). Let $\angle G O^{\prime} H=\delta$. We then have to show $\delta=\varepsilon$ iff $\angle C A B=60^{\circ}$. But by similarity ( $\triangle G D O \sim \triangle F O^{\prime} O$ ) we have $\angle F O^{\prime} O=\varepsilon$. Consider the circumcircles of the triangles $F O^{\prime} O$ and $G O^{\prime} H$. By the sine law and since the segments $H G$ and $F O$ are of equal length we deduce that the circumcircles of the triangles $F O^{\prime} O$ and $G O^{\prime} H$ are symmetric with respect to the perpendicular bisector of the segment $F G$ iff $\delta=\varepsilon$. Obviously, $O^{\prime}$ is the common point of these two circles. Hence $O^{\prime}$ must be fixed after the symmetry about the perpendicular bisector of the segment $F G$ iff $\delta=\varepsilon$ so we have $\varepsilon=\delta$ iff $\triangle H O O^{\prime}$ is isosceles. But $H O^{\prime}=H^{\prime} O=R$, and so
$$
\varepsilon=\delta \Longleftrightarrow O O^{\prime}=R \Longleftrightarrow O D=\frac{R}{2} \Longleftrightarrow \cos \angle C A B=\frac{1}{2} \Longleftrightarrow \angle C A B=60^{\circ}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $H$ be the orthocenter and $G$ be the centroid of acute-angled triangle $\triangle A B C$ with $A B \neq A C$. The line $A G$ intersects the circumcircle of $\triangle A B C$ at $A$ and $P$. Let $P^{\prime}$ be the reflection of $P$ in the line $B C$. Prove that $\angle C A B=60^{\circ}$ if and only if $H G=G P^{\prime}$.
(Ukraine)

|
Let $O^{\prime}$ and $G^{\prime}$ denote the reflection of $O$ and $G$, respectively, with respect to the line $B C$. We then need to show $\angle C A B=60^{\circ}$ iff $G^{\prime} H^{\prime}=G^{\prime} P$. Note that $\triangle H^{\prime} O P$ is isosceles and hence
$G^{\prime} H^{\prime}=G^{\prime} P$ is equivalent to $G^{\prime}$ lying on the bisector $\angle H^{\prime} O P$. Let $\angle H^{\prime} A P=\varepsilon$. By the assumption $A B \neq A C$, we have $\varepsilon \neq 0$. Then $\angle H^{\prime} O P=2 \angle H^{\prime} A P=2 \varepsilon$, hence $G^{\prime} H^{\prime}=G^{\prime} P$ iff $\angle G^{\prime} O H^{\prime}=\varepsilon$. But $\angle G O^{\prime} H=\angle G^{\prime} O H^{\prime}$. Let $D$ be the midpoint of $O O^{\prime}$. It is known that $\angle G D O=\angle G A H=\varepsilon$. Let $F$ be the midpoint of $H G$. Then $H G=F O$ (Euler line). Let $\angle G O^{\prime} H=\delta$. We then have to show $\delta=\varepsilon$ iff $\angle C A B=60^{\circ}$. But by similarity ( $\triangle G D O \sim \triangle F O^{\prime} O$ ) we have $\angle F O^{\prime} O=\varepsilon$. Consider the circumcircles of the triangles $F O^{\prime} O$ and $G O^{\prime} H$. By the sine law and since the segments $H G$ and $F O$ are of equal length we deduce that the circumcircles of the triangles $F O^{\prime} O$ and $G O^{\prime} H$ are symmetric with respect to the perpendicular bisector of the segment $F G$ iff $\delta=\varepsilon$. Obviously, $O^{\prime}$ is the common point of these two circles. Hence $O^{\prime}$ must be fixed after the symmetry about the perpendicular bisector of the segment $F G$ iff $\delta=\varepsilon$ so we have $\varepsilon=\delta$ iff $\triangle H O O^{\prime}$ is isosceles. But $H O^{\prime}=H^{\prime} O=R$, and so
$$
\varepsilon=\delta \Longleftrightarrow O O^{\prime}=R \Longleftrightarrow O D=\frac{R}{2} \Longleftrightarrow \cos \angle C A B=\frac{1}{2} \Longleftrightarrow \angle C A B=60^{\circ}
$$
|
{
"exam": "EGMO",
"problem_label": "6",
"problem_match": "\nProblem 6.",
"resource_path": "EGMO/segmented/en-2015-solutions.jsonl",
"solution_match": "\nSolution 2: ",
"tier": "T2",
"year": "2015"
}
|
Let $H$ be the orthocenter and $G$ be the centroid of acute-angled triangle $\triangle A B C$ with $A B \neq A C$. The line $A G$ intersects the circumcircle of $\triangle A B C$ at $A$ and $P$. Let $P^{\prime}$ be the reflection of $P$ in the line $B C$. Prove that $\angle C A B=60^{\circ}$ if and only if $H G=G P^{\prime}$.
(Ukraine)

|
Let $H^{\prime}$ and $G^{\prime}$ denote the reflection of points $H$ and $G$ with respect to the line $B C$. It is known that $H^{\prime}$ belongs to the circumcircle of $\triangle A B C$. The equality $H G=G P^{\prime}$ is equivalent to $H^{\prime} G^{\prime}=G^{\prime} P$. As in the Solution 2, it is equivalent to the statement that point $G^{\prime}$ belongs to the perpendicular bisector of $H^{\prime} P$, which is equivalent to $O G^{\prime} \perp H^{\prime} P$, where $O$ is the circumcenter of $\triangle A B C$.
Let points $A(a), B(b)$, and $C(c=-\bar{b})$ belong to the unit circle in the complex plane. Point $G$ have coordinate $g=(a+b-\bar{b}) / 3$. Since $B C$ is parallel to the real axis point $H^{\prime}$ have coordinate $h^{\prime}=\bar{a}=1 / a$.
Point $P(p)$ belongs to the unit circle, so $\bar{p}=1 / p$. Since $a, p, g$ are collinear we have $\frac{p-a}{g-a}=$ $\overline{\left(\frac{p-a}{g-a}\right)}$. After computation we get $p=\frac{g-a}{1-\bar{g} a}$. Since $G^{\prime}(g)$ is the reflection of $G$ with respect to the chord $B C$, we have $g^{\prime}=b+(-\bar{b})-b(-\bar{b}) \bar{g}=b-\bar{b}+\bar{g}$. Let $b-\bar{b}=d$. We have $\bar{d}=-d$. So
$$
g=\frac{a+d}{3}, \quad \bar{g}=\frac{\bar{a}-d}{3}, \quad g^{\prime}=d+\bar{g}=\frac{\bar{a}+2 d}{3}, \quad \overline{g^{\prime}}=\frac{a-2 d}{3} \quad \text { and } \quad p=\frac{g-a}{1-\bar{g} a}=\frac{d-2 a}{2+a d} .
$$
It is easy to see that $O G^{\prime} \perp H^{\prime} P^{\prime}$ is equivalent to
$$
\frac{g^{\prime}}{h^{\prime}-p}=-\overline{\left(\frac{g^{\prime}}{h^{\prime}-p}\right)}=-\frac{g^{\prime}}{\frac{1}{h^{\prime}}-\frac{1}{p}}=\frac{\overline{g^{\prime}} h^{\prime} p}{h^{\prime}-p}
$$
since $h^{\prime}$ and $p$ belong to the unit circle (note that $H^{\prime} \neq P$ because $A B \neq A C$ ). This is equivalent to $g^{\prime}=\overline{g^{\prime}} h^{\prime} p$ and from (1), after easy computations, this is equivalent to $a^{2} g^{2}+a^{2}+d^{2}+1=$ $\left(a^{2}+1\right)\left(d^{2}+1\right)=0$.
We cannot have $a^{2}+1=0$, because then $a= \pm i$, but $A B \neq A C$. Hence $d=b-\bar{b}= \pm i$, and the pair $\{b, c=-\bar{b}\}$ is either $\{-\sqrt{3} / 2+i / 2, \sqrt{3} / 2+i / 2\}$ or $\{-\sqrt{3} / 2-i / 2, \sqrt{3} / 2-i / 2\}$. Both cases are equivalent to $\angle B A C=60^{\circ}$ which completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $H$ be the orthocenter and $G$ be the centroid of acute-angled triangle $\triangle A B C$ with $A B \neq A C$. The line $A G$ intersects the circumcircle of $\triangle A B C$ at $A$ and $P$. Let $P^{\prime}$ be the reflection of $P$ in the line $B C$. Prove that $\angle C A B=60^{\circ}$ if and only if $H G=G P^{\prime}$.
(Ukraine)

|
Let $H^{\prime}$ and $G^{\prime}$ denote the reflection of points $H$ and $G$ with respect to the line $B C$. It is known that $H^{\prime}$ belongs to the circumcircle of $\triangle A B C$. The equality $H G=G P^{\prime}$ is equivalent to $H^{\prime} G^{\prime}=G^{\prime} P$. As in the Solution 2, it is equivalent to the statement that point $G^{\prime}$ belongs to the perpendicular bisector of $H^{\prime} P$, which is equivalent to $O G^{\prime} \perp H^{\prime} P$, where $O$ is the circumcenter of $\triangle A B C$.
Let points $A(a), B(b)$, and $C(c=-\bar{b})$ belong to the unit circle in the complex plane. Point $G$ have coordinate $g=(a+b-\bar{b}) / 3$. Since $B C$ is parallel to the real axis point $H^{\prime}$ have coordinate $h^{\prime}=\bar{a}=1 / a$.
Point $P(p)$ belongs to the unit circle, so $\bar{p}=1 / p$. Since $a, p, g$ are collinear we have $\frac{p-a}{g-a}=$ $\overline{\left(\frac{p-a}{g-a}\right)}$. After computation we get $p=\frac{g-a}{1-\bar{g} a}$. Since $G^{\prime}(g)$ is the reflection of $G$ with respect to the chord $B C$, we have $g^{\prime}=b+(-\bar{b})-b(-\bar{b}) \bar{g}=b-\bar{b}+\bar{g}$. Let $b-\bar{b}=d$. We have $\bar{d}=-d$. So
$$
g=\frac{a+d}{3}, \quad \bar{g}=\frac{\bar{a}-d}{3}, \quad g^{\prime}=d+\bar{g}=\frac{\bar{a}+2 d}{3}, \quad \overline{g^{\prime}}=\frac{a-2 d}{3} \quad \text { and } \quad p=\frac{g-a}{1-\bar{g} a}=\frac{d-2 a}{2+a d} .
$$
It is easy to see that $O G^{\prime} \perp H^{\prime} P^{\prime}$ is equivalent to
$$
\frac{g^{\prime}}{h^{\prime}-p}=-\overline{\left(\frac{g^{\prime}}{h^{\prime}-p}\right)}=-\frac{g^{\prime}}{\frac{1}{h^{\prime}}-\frac{1}{p}}=\frac{\overline{g^{\prime}} h^{\prime} p}{h^{\prime}-p}
$$
since $h^{\prime}$ and $p$ belong to the unit circle (note that $H^{\prime} \neq P$ because $A B \neq A C$ ). This is equivalent to $g^{\prime}=\overline{g^{\prime}} h^{\prime} p$ and from (1), after easy computations, this is equivalent to $a^{2} g^{2}+a^{2}+d^{2}+1=$ $\left(a^{2}+1\right)\left(d^{2}+1\right)=0$.
We cannot have $a^{2}+1=0$, because then $a= \pm i$, but $A B \neq A C$. Hence $d=b-\bar{b}= \pm i$, and the pair $\{b, c=-\bar{b}\}$ is either $\{-\sqrt{3} / 2+i / 2, \sqrt{3} / 2+i / 2\}$ or $\{-\sqrt{3} / 2-i / 2, \sqrt{3} / 2-i / 2\}$. Both cases are equivalent to $\angle B A C=60^{\circ}$ which completes the proof.
|
{
"exam": "EGMO",
"problem_label": "6",
"problem_match": "\nProblem 6.",
"resource_path": "EGMO/segmented/en-2015-solutions.jsonl",
"solution_match": "\nSolution 3: ",
"tier": "T2",
"year": "2015"
}
|
Let $n$ be an odd positive integer, and let $x_{1}, x_{2}, \ldots, x_{n}$ be non-negative real numbers. Show that
$$
\min _{i=1, \ldots, n}\left(x_{i}^{2}+x_{i+1}^{2}\right) \leq \max _{j=1, \ldots, n}\left(2 x_{j} x_{j+1}\right)
$$
where $x_{n+1}=x_{1}$.
|
In what follows, indices are reduced modulo $n$. Consider the $n$ differences $x_{k+1}-x_{k}, k=1, \ldots, n$. Since $n$ is odd, there exists an index $j$ such that $\left(x_{j+1}-x_{j}\right)\left(x_{j+2}-x_{j+1}\right) \geq 0$. Without loss of generality, we may and will assume both factors non-negative, so $x_{j} \leq x_{j+1} \leq x_{j+2}$. Consequently,
$$
\min _{k=1, \ldots, n}\left(x_{k}^{2}+x_{k+1}^{2}\right) \leq x_{j}^{2}+x_{j+1}^{2} \leq 2 x_{j+1}^{2} \leq 2 x_{j+1} x_{j+2} \leq \max _{k=1, \ldots, n}\left(2 x_{k} x_{k+1}\right)
$$
Remark. If $n \geq 3$ is odd, and one of the $x_{k}$ is negative, then the conclusion may no longer hold. This is the case if, for instance, $x_{1}=-b$, and $x_{2 k}=a$, $x_{2 k+1}=b, k=1, \ldots,(n-1) / 2$, where $0 \leq a<b$, so the string of numbers is
$$
-b, b, a, b, a, \ldots, b, a
$$
If $n$ is even, the conclusion may again no longer hold, as shown by any string of alternate real numbers: $a, b, a, b, \ldots, a, b$, where $a \neq b$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n$ be an odd positive integer, and let $x_{1}, x_{2}, \ldots, x_{n}$ be non-negative real numbers. Show that
$$
\min _{i=1, \ldots, n}\left(x_{i}^{2}+x_{i+1}^{2}\right) \leq \max _{j=1, \ldots, n}\left(2 x_{j} x_{j+1}\right)
$$
where $x_{n+1}=x_{1}$.
|
In what follows, indices are reduced modulo $n$. Consider the $n$ differences $x_{k+1}-x_{k}, k=1, \ldots, n$. Since $n$ is odd, there exists an index $j$ such that $\left(x_{j+1}-x_{j}\right)\left(x_{j+2}-x_{j+1}\right) \geq 0$. Without loss of generality, we may and will assume both factors non-negative, so $x_{j} \leq x_{j+1} \leq x_{j+2}$. Consequently,
$$
\min _{k=1, \ldots, n}\left(x_{k}^{2}+x_{k+1}^{2}\right) \leq x_{j}^{2}+x_{j+1}^{2} \leq 2 x_{j+1}^{2} \leq 2 x_{j+1} x_{j+2} \leq \max _{k=1, \ldots, n}\left(2 x_{k} x_{k+1}\right)
$$
Remark. If $n \geq 3$ is odd, and one of the $x_{k}$ is negative, then the conclusion may no longer hold. This is the case if, for instance, $x_{1}=-b$, and $x_{2 k}=a$, $x_{2 k+1}=b, k=1, \ldots,(n-1) / 2$, where $0 \leq a<b$, so the string of numbers is
$$
-b, b, a, b, a, \ldots, b, a
$$
If $n$ is even, the conclusion may again no longer hold, as shown by any string of alternate real numbers: $a, b, a, b, \ldots, a, b$, where $a \neq b$.
|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "\nProblem 1.",
"resource_path": "EGMO/segmented/en-2016-solutions.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2016"
}
|
Let $A B C D$ be a cyclic quadrilateral, and let diagonals $A C$ and $B D$ intersect at $X$. Let $C_{1}, D_{1}$ and $M$ be the midpoints of segments $C X$, $D X$ and $C D$, respectively. Lines $A D_{1}$ and $B C_{1}$ intersect at $Y$, and line $M Y$ intersects diagonals $A C$ and $B D$ at different points $E$ and $F$, respectively. Prove that line $X Y$ is tangent to the circle through $E, F$ and $X$.
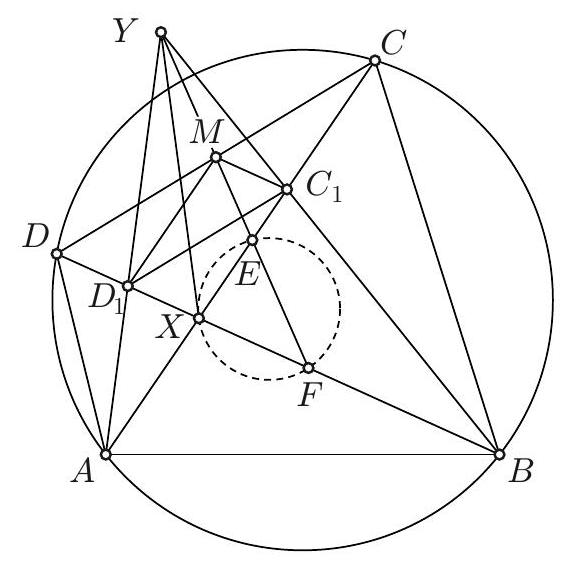
|
We are to prove that $\angle E X Y=\angle E F X$; alternatively, but equivalently, $\angle A Y X+\angle X A Y=\angle B Y F+\angle X B Y$.
Since the quadrangle $A B C D$ is cyclic, the triangles $X A D$ and $X B C$ are similar, and since $A D_{1}$ and $B C_{1}$ are corresponding medians in these triangles, it follows that $\angle X A Y=\angle X A D_{1}=\angle X B C_{1}=\angle X B Y$.
Finally, $\angle A Y X=\angle B Y F$, since $X$ and $M$ are corresponding points in the similar triangles $A B Y$ and $C_{1} D_{1} Y$ : indeed, $\angle X A B=\angle X D C=\angle M C_{1} D_{1}$, and $\angle X B A=\angle X C D=\angle M D_{1} C_{1}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral, and let diagonals $A C$ and $B D$ intersect at $X$. Let $C_{1}, D_{1}$ and $M$ be the midpoints of segments $C X$, $D X$ and $C D$, respectively. Lines $A D_{1}$ and $B C_{1}$ intersect at $Y$, and line $M Y$ intersects diagonals $A C$ and $B D$ at different points $E$ and $F$, respectively. Prove that line $X Y$ is tangent to the circle through $E, F$ and $X$.

|
We are to prove that $\angle E X Y=\angle E F X$; alternatively, but equivalently, $\angle A Y X+\angle X A Y=\angle B Y F+\angle X B Y$.
Since the quadrangle $A B C D$ is cyclic, the triangles $X A D$ and $X B C$ are similar, and since $A D_{1}$ and $B C_{1}$ are corresponding medians in these triangles, it follows that $\angle X A Y=\angle X A D_{1}=\angle X B C_{1}=\angle X B Y$.
Finally, $\angle A Y X=\angle B Y F$, since $X$ and $M$ are corresponding points in the similar triangles $A B Y$ and $C_{1} D_{1} Y$ : indeed, $\angle X A B=\angle X D C=\angle M C_{1} D_{1}$, and $\angle X B A=\angle X C D=\angle M D_{1} C_{1}$.
|
{
"exam": "EGMO",
"problem_label": "2",
"problem_match": "\nProblem 2.",
"resource_path": "EGMO/segmented/en-2016-solutions.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2016"
}
|
Let $m$ be a positive integer. Consider a $4 m \times 4 m$ array of square unit cells. Two different cells are related to each other if they are in either the same row or in the same column. No cell is related to itself. Some cells are coloured blue, such that every cell is related to at least two blue cells. Determine the minimum number of blue cells.
|
The required minimum is 6 m and is achieved by a diagonal string of $m 4 \times 4$ blocks of the form below (bullets mark centres of blue cells):
In particular, this configuration shows that the required minimum does not exceed 6 m .
We now show that any configuration of blue cells satisfying the condition in the statement has cardinality at least 6 m .
Fix such a configuration and let $m_{1}^{r}$ be the number of blue cells in rows containing exactly one such, let $m_{2}^{r}$ be the number of blue cells in rows containing exactly two such, and let $m_{3}^{r}$ be the number of blue cells in rows containing at least three such; the numbers $m_{1}^{c}, m_{2}^{c}$ and $m_{3}^{c}$ are defined similarly.
Begin by noticing that $m_{3}^{c} \geq m_{1}^{r}$ and, similarly, $m_{3}^{r} \geq m_{1}^{c}$. Indeed, if a blue cell is alone in its row, respectively column, then there are at least two other blue cells in its column, respectively row, and the claim follows.
Suppose now, if possible, the total number of blue cells is less than 6 m . We will show that $m_{1}^{r}>m_{3}^{r}$ and $m_{1}^{c}>m_{3}^{c}$, and reach a contradiction by the preceding: $m_{1}^{r}>m_{3}^{r} \geq m_{1}^{c}>m_{3}^{c} \geq m_{1}^{r}$.
We prove the first inequality; the other one is dealt with similarly. To this end, notice that there are no empty rows - otherwise, each column would contain at least two blue cells, whence a total of at least $8 m>6 m$ blue cells, which is a contradiction. Next, count rows to get $m_{1}^{r}+m_{2}^{r} / 2+m_{3}^{r} / 3 \geq 4 m$,
and count blue cells to get $m_{1}^{r}+m_{2}^{r}+m_{3}^{r}<6 m$. Subtraction of the latter from the former multiplied by $3 / 2$ yields $m_{1}^{r}-m_{3}^{r}>m_{2}^{r} / 2 \geq 0$, and the conclusion follows.
|
6m
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $m$ be a positive integer. Consider a $4 m \times 4 m$ array of square unit cells. Two different cells are related to each other if they are in either the same row or in the same column. No cell is related to itself. Some cells are coloured blue, such that every cell is related to at least two blue cells. Determine the minimum number of blue cells.
|
The required minimum is 6 m and is achieved by a diagonal string of $m 4 \times 4$ blocks of the form below (bullets mark centres of blue cells):
In particular, this configuration shows that the required minimum does not exceed 6 m .
We now show that any configuration of blue cells satisfying the condition in the statement has cardinality at least 6 m .
Fix such a configuration and let $m_{1}^{r}$ be the number of blue cells in rows containing exactly one such, let $m_{2}^{r}$ be the number of blue cells in rows containing exactly two such, and let $m_{3}^{r}$ be the number of blue cells in rows containing at least three such; the numbers $m_{1}^{c}, m_{2}^{c}$ and $m_{3}^{c}$ are defined similarly.
Begin by noticing that $m_{3}^{c} \geq m_{1}^{r}$ and, similarly, $m_{3}^{r} \geq m_{1}^{c}$. Indeed, if a blue cell is alone in its row, respectively column, then there are at least two other blue cells in its column, respectively row, and the claim follows.
Suppose now, if possible, the total number of blue cells is less than 6 m . We will show that $m_{1}^{r}>m_{3}^{r}$ and $m_{1}^{c}>m_{3}^{c}$, and reach a contradiction by the preceding: $m_{1}^{r}>m_{3}^{r} \geq m_{1}^{c}>m_{3}^{c} \geq m_{1}^{r}$.
We prove the first inequality; the other one is dealt with similarly. To this end, notice that there are no empty rows - otherwise, each column would contain at least two blue cells, whence a total of at least $8 m>6 m$ blue cells, which is a contradiction. Next, count rows to get $m_{1}^{r}+m_{2}^{r} / 2+m_{3}^{r} / 3 \geq 4 m$,
and count blue cells to get $m_{1}^{r}+m_{2}^{r}+m_{3}^{r}<6 m$. Subtraction of the latter from the former multiplied by $3 / 2$ yields $m_{1}^{r}-m_{3}^{r}>m_{2}^{r} / 2 \geq 0$, and the conclusion follows.
|
{
"exam": "EGMO",
"problem_label": "3",
"problem_match": "\nProblem 3.",
"resource_path": "EGMO/segmented/en-2016-solutions.jsonl",
"solution_match": "\nSolution 1 (Israel).",
"tier": "T2",
"year": "2016"
}
|
Let $m$ be a positive integer. Consider a $4 m \times 4 m$ array of square unit cells. Two different cells are related to each other if they are in either the same row or in the same column. No cell is related to itself. Some cells are coloured blue, such that every cell is related to at least two blue cells. Determine the minimum number of blue cells.
|
To prove that a minimal configuration of blue cells satisfying the condition in the statement has cardinality at least 6 m , consider a bipartite graph whose vertex parts are the rows and the columns of the array, respectively, a row and a column being joined by an edge if and only if the two cross at a blue cell. Clearly, the number of blue cells is equal to the number of edges of this graph, and the relationship condition in the statement reads: for every row $r$ and every column $c$, $\operatorname{deg} r+\operatorname{deg} c-\epsilon(r, c) \geq 2$, where $\epsilon(r, c)=2$ if $r$ and $c$ are joined by an edge, and $\epsilon(r, c)=0$ otherwise.
Notice that there are no empty rows/columns, so the graph has no isolated vertices. By the preceding, the cardinality of every connected component of the graph is at least 4 , so there are at most $2 \cdot 4 m / 4=2 m$ such and, consequently, the graph has at least $8 m-2 m=6 m$ edges. This completes the proof.
Remarks. The argument in the first solution shows that equality to 6 m is possible only if $m_{1}^{r}=m_{3}^{r}=m_{1}^{c}=m_{3}^{c}=3 m, m_{2}^{r}=m_{2}^{c}=0$, and there are no rows, respectively columns, containing four blue cells or more.
Consider the same problem for an $n \times n$ array. The argument in the second solution shows that the corresponding minimum is $3 n / 2$ if $n$ is divisible by 4 , and $3 n / 2+1 / 2$ if $n$ is odd; if $n \equiv 2(\bmod 4)$, the minimum in question is $3 n / 2+1$. To describe corresponding minimal configurations $C_{n}$, refer to the minimal configurations $C_{2}, C_{3}, C_{4}, C_{5}$ below:

The case $n \equiv 0(\bmod 4)$ was dealt with above: a $C_{n}$ consists of a diagonal string of $n / 4$ blocks $C_{4}$. If $n \equiv r(\bmod 4), r=2,3$, a $C_{n}$ consists of a diagonal string of $\lfloor n / 4\rfloor$ blocks $C_{4}$ followed by a $C_{r}$, and if $n \equiv 1(\bmod 4)$, a $C_{n}$ consists of a diagonal string of $\lfloor n / 4\rfloor-1$ blocks $C_{4}$ followed by a $C_{5}$.
Minimal configurations are not necessarily unique (two configurations being equivalent if one is obtained from the other by permuting the rows and/or the columns). For instance, if $n=6$, the configurations below are both minimal:

## EGMO 2016, Day 2 - Solutions
|
6m
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $m$ be a positive integer. Consider a $4 m \times 4 m$ array of square unit cells. Two different cells are related to each other if they are in either the same row or in the same column. No cell is related to itself. Some cells are coloured blue, such that every cell is related to at least two blue cells. Determine the minimum number of blue cells.
|
To prove that a minimal configuration of blue cells satisfying the condition in the statement has cardinality at least 6 m , consider a bipartite graph whose vertex parts are the rows and the columns of the array, respectively, a row and a column being joined by an edge if and only if the two cross at a blue cell. Clearly, the number of blue cells is equal to the number of edges of this graph, and the relationship condition in the statement reads: for every row $r$ and every column $c$, $\operatorname{deg} r+\operatorname{deg} c-\epsilon(r, c) \geq 2$, where $\epsilon(r, c)=2$ if $r$ and $c$ are joined by an edge, and $\epsilon(r, c)=0$ otherwise.
Notice that there are no empty rows/columns, so the graph has no isolated vertices. By the preceding, the cardinality of every connected component of the graph is at least 4 , so there are at most $2 \cdot 4 m / 4=2 m$ such and, consequently, the graph has at least $8 m-2 m=6 m$ edges. This completes the proof.
Remarks. The argument in the first solution shows that equality to 6 m is possible only if $m_{1}^{r}=m_{3}^{r}=m_{1}^{c}=m_{3}^{c}=3 m, m_{2}^{r}=m_{2}^{c}=0$, and there are no rows, respectively columns, containing four blue cells or more.
Consider the same problem for an $n \times n$ array. The argument in the second solution shows that the corresponding minimum is $3 n / 2$ if $n$ is divisible by 4 , and $3 n / 2+1 / 2$ if $n$ is odd; if $n \equiv 2(\bmod 4)$, the minimum in question is $3 n / 2+1$. To describe corresponding minimal configurations $C_{n}$, refer to the minimal configurations $C_{2}, C_{3}, C_{4}, C_{5}$ below:

The case $n \equiv 0(\bmod 4)$ was dealt with above: a $C_{n}$ consists of a diagonal string of $n / 4$ blocks $C_{4}$. If $n \equiv r(\bmod 4), r=2,3$, a $C_{n}$ consists of a diagonal string of $\lfloor n / 4\rfloor$ blocks $C_{4}$ followed by a $C_{r}$, and if $n \equiv 1(\bmod 4)$, a $C_{n}$ consists of a diagonal string of $\lfloor n / 4\rfloor-1$ blocks $C_{4}$ followed by a $C_{5}$.
Minimal configurations are not necessarily unique (two configurations being equivalent if one is obtained from the other by permuting the rows and/or the columns). For instance, if $n=6$, the configurations below are both minimal:

## EGMO 2016, Day 2 - Solutions
|
{
"exam": "EGMO",
"problem_label": "3",
"problem_match": "\nProblem 3.",
"resource_path": "EGMO/segmented/en-2016-solutions.jsonl",
"solution_match": "\nSolution 2. ",
"tier": "T2",
"year": "2016"
}
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.