problem
stringlengths 14
10.4k
| solution
stringlengths 1
24.1k
| answer
stringlengths 1
250
⌀ | problem_is_valid
stringclasses 4
values | solution_is_valid
stringclasses 3
values | question_type
stringclasses 4
values | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
10.4k
| solution_raw
stringlengths 1
24.1k
| metadata
dict |
|---|---|---|---|---|---|---|---|---|---|
Given is a triangle $ABC$. Let $\Gamma_{1}$ be the circle through $B$ that is tangent to side $AC$ at $A$. Let $\Gamma_{2}$ be the circle through $C$ that is tangent to side $AB$ at $A$. The second intersection point of $\Gamma_{1}$ and $\Gamma_{2}$ is called $D$. The line $AD$ intersects the circumcircle of $\triangle ABC$ again at $E$. Prove that $D$ is the midpoint of $AE$.
|
Due to the tangent-secant angle theorem in $\Gamma_{1}$, we have $\angle D A C=\angle D B A$. Due to the tangent-secant angle theorem in $\Gamma_{2}$, we have $\angle D A B=\angle D C A$. Therefore, $\triangle A B D \sim \triangle C A D(\mathrm{hh})$. Now let $M$ be the midpoint of $A B$ and $N$ the midpoint of $A C$. Then $D M$ is a median in $\triangle D B A$ and $D N$ is the corresponding median in $\triangle D A C$. Therefore, we know that $\angle B D M=\angle A D N$. Thus,
$$
\begin{array}{rlr}
\angle M D N & =\angle M D A+\angle A D N & \text { (splitting the angle) } \\
& =\angle M D A+\angle B D M & \text { (equality from above) } \\
& =\angle B D A & \text { (adding angles) } \\
& =180^{\circ}-\angle A B D-\angle B A D & \text { (angle sum in } \triangle A B D) \\
& =180^{\circ}-\angle C A D-\angle B A D & \text { (similarity of } \triangle A B D \sim \triangle C A D) \\
& =180^{\circ}-\angle C A B & \text { (adding angles) } \\
& =180^{\circ}-\angle N A M & \text { (same angle.) }
\end{array}
$$
We conclude that $M D N A$ is a cyclic quadrilateral. Therefore, $\angle M D A=\angle M N A$. Since $M N$ is a midline in $\triangle A B C$, $\angle M N A=\angle B C A$ and that is equal to $\angle B E A$ by the inscribed angle theorem. Altogether, we have $\angle M D A=\angle B E A$, which means that $M D$ is parallel to $B E$. Since $M$ is the midpoint of $A B$, $D$ must also be the midpoint of $A E$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Gegeven is een driehoek $A B C . \mathrm{Zij} \Gamma_{1}$ de cirkel door $B$ die raakt aan zijde $A C$ in $A$. Zij $\Gamma_{2}$ de cirkel door $C$ die raakt aan zijde $A B$ in $A$. Het tweede snijpunt van $\Gamma_{1}$ en $\Gamma_{2}$ noemen we $D$. De lijn $A D$ snijdt de omgeschreven cirkel van $\triangle A B C$ nog een keer in $E$. Bewijs dat $D$ het midden is van $A E$.
|
Vanwege de raaklijnomtrekshoekstelling in $\Gamma_{1}$ geldt $\angle D A C=\angle D B A$. Vanwege de raaklijnomtrekshoekstelling in $\Gamma_{2}$ geldt $\angle D A B=\angle D C A$. Er geldt dus $\triangle A B D \sim \triangle C A D(\mathrm{hh})$. Noem nu $M$ het midden van $A B$ en $N$ het midden van $A C$. Dan is $D M$ een zwaartelijn in $\triangle D B A$ en is $D N$ de corresponderende zwaartelijn in $\triangle D A C$. Daardoor weten we dat $\angle B D M=\angle A D N$. Dus
$$
\begin{array}{rlr}
\angle M D N & =\angle M D A+\angle A D N & \text { (opsplitsen hoek) } \\
& =\angle M D A+\angle B D M & \text { (gelijkheid van hiervoor) } \\
& =\angle B D A & \text { (optellen hoeken) } \\
& =180^{\circ}-\angle A B D-\angle B A D & \text { (hoekensom } \triangle A B D) \\
& =180^{\circ}-\angle C A D-\angle B A D & \text { (gelijkvormigheid } \triangle A B D \sim \triangle C A D) \\
& =180^{\circ}-\angle C A B & \text { (optellen hoeken) } \\
& =180^{\circ}-\angle N A M & \text { (zelfde hoek.) }
\end{array}
$$
We concluderen dat $M D N A$ een koordenvierhoek is. Dus $\angle M D A=\angle M N A$. Omdat $M N$ een middenparallel in $\triangle A B C$ is, is $\angle M N A=\angle B C A$ en dat is wegens de omtrekshoekstelling weer gelijk aan $\angle B E A$. Al met al hebben we $\angle M D A=\angle B E A$, wat betekent dat $M D$ evenwijdig is met $B E$. Aangezien $M$ het midden van $A B$ is, moet nu $D$ ook het midden van $A E$ zijn.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2013-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing III.",
"tier": "T1",
"year": "2013"
}
|
Let $n \geq 3$ be an integer and consider an $n \times n$ board, divided into $n^{2}$ unit squares. We have for each $m \geq 1$ arbitrarily many $1 \times m$ rectangles (type I) and arbitrarily many $m \times 1$ rectangles (type II) available. We cover the board with $N$ of these rectangles, which do not overlap and do not extend beyond the board. The total number of type I rectangles on the board must be equal to the total number of type II rectangles on the board. (Note that a $1 \times 1$ rectangle is both of type I and of type II.) What is the smallest value of $N$ for which this is possible?
|
We prove that the minimal value $N=2n-1$. First, we construct an example by induction.
Base case. For $n=3$, $N=5$ is possible, by placing a $1 \times 1$ rectangle in the middle field and covering the remaining fields with four $2 \times 1$ and $1 \times 2$ rectangles. There are then three rectangles with height 1 (type I) and three rectangles with width 1 (type II), where the $1 \times 1$ rectangle is counted twice.
Inductive step. Let $k \geq 3$ and assume that we can cover a $k \times k$ board with $2k-1$ rectangles such that all conditions are met. Consider a $(k+1) \times (k+1)$ board and cover the $k \times k$ sub-square at the bottom right according to the inductive hypothesis. Then cover the left column with a rectangle of width 1 and height $k+1$, and cover the remaining space with a rectangle of height 1 and width $k$. We have now used one more rectangle with width 1 and one more rectangle with height 1, so the condition is satisfied and we have used $2k-1+2=2(k+1)-1$ rectangles. This constructs an example for $n=k+1$.
This proves that it is possible to cover the board with $N=2n-1$ rectangles. We now want to prove that it cannot be done with fewer rectangles. Let $k$ be the number of rectangles with width 1 and height greater than 1. Then the number of rectangles with height 1 and width greater than 1 is also $k$. Let $l$ be the number of $1 \times 1$ rectangles. Thus, $N=2k+l$. If $k \geq n$, then $N \geq 2n$, so there is nothing to prove in this case. We therefore assume that $k < n$ and we will prove that then $l \geq 2n-2k-1$, so that $N \geq 2n-1$.
Each rectangle with width 1 can only cover fields in one column. Therefore, there are $n-k$ columns in which no field is covered by a rectangle with width 1 and height greater than 1. Similarly, there are $n-k$ rows in which no field is covered by a rectangle with height 1 and width greater than 1. Consider the $(n-k)^2$ fields that lie in both such a row and such a column. These fields must be covered by $1 \times 1$ rectangles. Thus, $l \geq (n-k)^2$.
We have $(k-n+1)^2 \geq 0$, so $k^2 + n^2 + 1 - 2kn + 2k - 2n \geq 0$, and thus $n^2 - 2kn + k^2 \geq 2n - 2k - 1$. We conclude that $l \geq (n-k)^2 \geq 2n - 2k - 1$, which is exactly what we wanted to prove. Therefore, in all cases, $N \geq 2n-1$, and this proves that the minimal value of $N$ is $2n-1$.
|
2n-1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Zij $n \geq 3$ een geheel getal en bekijk een $n \times n$-bord, opgedeeld in $n^{2}$ eenheidsvierkantjes. We hebben voor elke $m \geq 1$ willekeurig veel $1 \times m$-rechthoeken (type I) en willekeurig veel $m \times 1$-rechthoeken (type II) beschikbaar. We bedekken het bord met $N$ van deze rechthoeken, die elkaar niet overlappen en niet uitsteken buiten het bord. Het totaal aantal rechthoeken van type I op het bord moet hierbij gelijk zijn aan het totaal aantal rechthoeken van type II op het bord. (Merk op dat een $1 \times 1$-rechthoek zowel van type I als van type II is.) Wat is de kleinste waarde van $N$ waarvoor dit mogelijk is?
|
We bewijzen dat de minimale waarde $N=2 n-1$ is. We construeren eerst een voorbeeld door middel van inductie.
Inductiebasis. Voor $n=3$ is $N=5$ mogelijk, door in het middelste veld een $1 \times 1$-rechthoek te leggen en de overige velden te bedekken met vier $2 \times 1$ - en $1 \times 2$-rechthoeken. Er zijn dan drie rechthoeken met hoogte 1 (type I) en drie rechthoeken met breedte 1 (type II), waarbij de $1 \times 1$-rechthoek twee keer geteld wordt.
Inductiestap. Zij $k \geq 3$ en neem aan dat we een $k \times k$-bord kunnen bedekken met $2 k-1$ rechthoeken zodat aan alle voorwaarden is voldaan. Bekijk een $(k+1) \times(k+1)$-bord en bedek het $k \times k$-deelvierkant rechtsonder volgens de inductiehypothese. Bedek vervolgens de linkerkolom met een rechthoek met breedte 1 en hoogte $k+1$ en vervolgens de overgebleven ruimte met een rechthoek met hoogte 1 en breedte $k$. We hebben nu één rechthoek met breedte 1 en één rechthoek met hoogte 1 meer gebruikt, dus aan de voorwaarde is voldaan en we hebben $2 k-1+2=2(k+1)-1$ rechthoeken gebruikt. Hiermee hebben we een voorbeeld voor $n=k+1$ geconstrueerd.
Hiermee is bewezen dat het mogelijk is om het bord te bedekken met $N=2 n-1$ rechthoeken. We willen nu nog bewijzen dat het niet met minder rechthoeken kan. Zij $k$ het aantal rechthoeken met breedte 1 en hoogte groter dan 1 . Dan is ook het aantal rechthoeken met hoogte 1 en breedte groter dan 1 , gelijk aan $k$. Zij verder $l$ het aantal rechthoeken van $1 \times 1$. Er geldt dus $N=2 k+l$. Als $k \geq n$, geldt $N \geq 2 n$, dus in dit geval is er niets te bewijzen. We nemen dus aan dat $k<n$ en we gaan bewijzen dat dan $l \geq 2 n-2 k-1$, zodat $N \geq 2 n-1$.
Elke rechthoek met breedte 1 kan alleen velden in één kolom bedekken. Er zijn dus $n-k$ kolommen waarin geen enkel veld wordt bedekt door een rechthoek met breedte 1 en hoogte groter dan 1. Zo ook zijn er $n-k$ rijen waarin geen enkel veld wordt bedekt door een rechthoek met hoogte 1 en breedte groter dan 1. Bekijk de $(n-k)^{2}$ velden die in zowel zo'n rij als zo'n kolom liggen. Deze velden moeten bedekt worden door $1 \times 1$-rechthoeken. Dus $l \geq(n-k)^{2}$.
Er geldt $(k-n+1)^{2} \geq 0$, dus $k^{2}+n^{2}+1-2 k n+2 k-2 n \geq 0$, dus $n^{2}-2 k n+k^{2} \geq 2 n-2 k-1$. We concluderen dat $l \geq(n-k)^{2} \geq 2 n-2 k-1$ en dat is precies wat we wilden bewijzen. Dus in alle gevallen is $N \geq 2 n-1$ en dat bewijst dat de minimale waarde van $N$ gelijk is aan $2 n-1$.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2013-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2013"
}
|
Let $a, b$ and $c$ be positive real numbers with $a b c=1$. Prove that
$$
a+b+c \geq \sqrt{\frac{(a+2)(b+2)(c+2)}{3}}
$$
|
Let $x, y$ and $z$ be positive real numbers such that $x^{3}=a, y^{3}=b$ and $z^{3}=c$. Then $x^{3} y^{3} z^{3}=1$, so also $x y z=1$. We can now write $a+2$ as $x^{3}+2 x y z=x\left(x^{2}+2 y z\right)$, and similarly we can rewrite $b+2$ and $c+2$, which gives us
\[
(a+2)(b+2)(c+2)=x y z\left(x^{2}+2 y z\right)\left(y^{2}+2 z x\right)\left(z^{2}+2 x y\right)=\left(x^{2}+2 y z\right)\left(y^{2}+2 z x\right)\left(z^{2}+2 x y\right).
\]
Now we apply the arithmetic mean-geometric mean inequality to the positive terms $x^{2}+2 y z, y^{2}+2 z x$ and $z^{2}+2 x y$:
\[
\left(x^{2}+2 y z\right)\left(y^{2}+2 z x\right)\left(z^{2}+2 x y\right) \leq\left(\frac{x^{2}+2 y z+y^{2}+2 z x+z^{2}+2 x y}{3}\right)^{3}=\left(\frac{(x+y+z)^{2}}{3}\right)^{3}.
\]
So far, we have found:
\[
(a+2)(b+2)(c+2) \leq \frac{1}{27}\left((x+y+z)^{3}\right)^{2}
\]
We will now prove that $(x+y+z)^{3} \leq 9\left(x^{3}+y^{3}+z^{3}\right)$. For those familiar with power means: this follows directly from the inequality between the arithmetic mean and the cubic mean. We have
\[
(x+y+z)^{3}=x^{3}+y^{3}+z^{3}+3\left(x^{2} y+y^{2} z+z^{2} x+x y^{2}+y z^{2}+z x^{2}\right)+6 x y z.
\]
Using the arithmetic mean-geometric mean inequality on only positive terms, we know that
\[
2 x^{3}+y^{3}=x^{3}+x^{3}+y^{3} \geq 3 \sqrt[3]{x^{6} y^{3}}=3 x^{2} y
\]
and similarly $x^{3}+2 y^{3} \geq 3 x y^{2}$. If we cyclically permute these two inequalities, we find
\[
3\left(x^{2} y+y^{2} z+z^{2} x+x y^{2}+y z^{2}+z x^{2}\right) \leq 6\left(x^{3}+y^{3}+z^{3}\right).
\]
We also know $x^{3}+y^{3}+z^{3} \geq 3 \sqrt[3]{x^{3} y^{3} z^{3}}=3 x y z$, so altogether we get
\[
(x+y+z)^{3} \leq\left(x^{3}+y^{3}+z^{3}\right)+6\left(x^{3}+y^{3}+z^{3}\right)+2\left(x^{3}+y^{3}+z^{3}\right)=9\left(x^{3}+y^{3}+z^{3}\right).
\]
Combining this with (4) we now get
\[
(a+2)(b+2)(c+2) \leq \frac{1}{27}\left(9\left(x^{3}+y^{3}+z^{3}\right)\right)^{2}=3(a+b+c)^{2}.
\]
Dividing both sides by 3 and then taking the square root (both sides are positive) gives us exactly the desired result.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Laat $a, b$ en $c$ positieve reële getallen zijn met $a b c=1$. Bewijs dat
$$
a+b+c \geq \sqrt{\frac{(a+2)(b+2)(c+2)}{3}}
$$
|
Laat $x, y$ en $z$ positieve reële getallen zijn zodat $x^{3}=a, y^{3}=b$ en $z^{3}=c$. Dan geldt $x^{3} y^{3} z^{3}=1$, dus ook $x y z=1$. We kunnen nu $a+2$ schrijven als $x^{3}+2 x y z=x\left(x^{2}+2 y z\right)$, en analoog kunnen we $b+2$ en $c+2$ herschrijven, waarmee we krijgen
$(a+2)(b+2)(c+2)=x y z\left(x^{2}+2 y z\right)\left(y^{2}+2 z x\right)\left(z^{2}+2 x y\right)=\left(x^{2}+2 y z\right)\left(y^{2}+2 z x\right)\left(z^{2}+2 x y\right)$.
Nu passen we rekenkundig-meetkundig toe op de positieve termen $x^{2}+2 y z, y^{2}+2 z x$ en $z^{2}+2 x y:$
$\left(x^{2}+2 y z\right)\left(y^{2}+2 z x\right)\left(z^{2}+2 x y\right) \leq\left(\frac{x^{2}+2 y z+y^{2}+2 z x+z^{2}+2 x y}{3}\right)^{3}=\left(\frac{(x+y+z)^{2}}{3}\right)^{3}$.
We hebben tot nu toe dus gevonden:
$$
(a+2)(b+2)(c+2) \leq \frac{1}{27}\left((x+y+z)^{3}\right)^{2}
$$
We gaan nu bewijzen dat $(x+y+z)^{3} \leq 9\left(x^{3}+y^{3}+z^{3}\right)$. Voor wie het machtsgemiddelde kent: dit volgt direct uit de ongelijkheid van het rekenkundig gemiddelde en het derdemachtsgemiddelde. Er geldt
$$
(x+y+z)^{3}=x^{3}+y^{3}+z^{3}+3\left(x^{2} y+y^{2} z+z^{2} x+x y^{2}+y z^{2}+z x^{2}\right)+6 x y z .
$$
Met rekenkundig-meetkundig op alleen maar positieve termen weten we dat
$$
2 x^{3}+y^{3}=x^{3}+x^{3}+y^{3} \geq 3 \sqrt[3]{x^{6} y^{3}}=3 x^{2} y
$$
en analoog $x^{3}+2 y^{3} \geq 3 x y^{2}$. Als we deze beide ongelijkheden cyclisch doordraaien, vinden we
$$
3\left(x^{2} y+y^{2} z+z^{2} x+x y^{2}+y z^{2}+z x^{2}\right) \leq 6\left(x^{3}+y^{3}+z^{3}\right) .
$$
We weten natuurlijk ook $x^{3}+y^{3}+z^{3} \geq 3 \sqrt[3]{x^{3} y^{3} z^{3}}=3 x y z$, dus al met al krijgen we
$$
(x+y+z)^{3} \leq\left(x^{3}+y^{3}+z^{3}\right)+6\left(x^{3}+y^{3}+z^{3}\right)+2\left(x^{3}+y^{3}+z^{3}\right)=9\left(x^{3}+y^{3}+z^{3}\right) .
$$
Gecombineerd met (4) krijgen we nu
$$
(a+2)(b+2)(c+2) \leq \frac{1}{27}\left(9\left(x^{3}+y^{3}+z^{3}\right)\right)^{2}=3(a+b+c)^{2}
$$
Links en rechts delen door 3 en daarna de worteltrekken (beide kanten zijn positief) geeft nu precies het gevraagde.
|
{
"exam": "Dutch_TST",
"problem_label": "5",
"problem_match": "\nOpgave 5.",
"resource_path": "Dutch_TST/segmented/nl-2013-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2013"
}
|
Let $a, b$ and $c$ be positive real numbers with $a b c=1$. Prove that
$$
a+b+c \geq \sqrt{\frac{(a+2)(b+2)(c+2)}{3}}
$$
|
Note that $a, b$ and $c$ are positive, so we can always apply the arithmetic-geometric mean inequality below. First, we apply the arithmetic-geometric mean to $a^{2}$ and 1:
$$
a^{2}+1 \geq 2 \sqrt{a^{2}}=2 a
$$
We can cyclically permute and add, so we find:
$$
a^{2}+b^{2}+c^{2}+3 \geq 2 a+2 b+2 c
$$
Furthermore, we apply the arithmetic-geometric mean to $b c, c a$ and $a b$:
$$
b c+c a+a b \geq 3 \sqrt[3]{a^{2} b^{2} c^{2}}=3
$$
where we have used that $a b c=1$. Also, we apply the arithmetic-geometric mean to $a^{2}, b^{2}$ and $c^{2}$:
$$
a^{2}+b^{2}+c^{2} \geq 3 \sqrt[3]{a^{2} b^{2} c^{2}}=3
$$
Now we take 2 times (5), 4 times (6), and 1 time (7) and add them up. Then we get:
$$
2 a^{2}+2 b^{2}+2 c^{2}+6+4 b c+4 c a+4 a b+a^{2}+b^{2}+c^{2} \geq 4 a+4 b+4 c+12+3
$$
Combining like terms, subtracting 6 from both sides, and adding $2 a b+2 b c+2 c a$ to both sides gives:
$$
3 a^{2}+3 b^{2}+3 c^{2}+6 a b+6 b c+6 c a \geq 2 a b+2 b c+2 c a+4 a+4 b+4 c+9
$$
Now, on the left, we have $3\left(a^{2}+b^{2}+c^{2}+2 a b+2 b c+2 c a\right)=3(a+b+c)^{2}$. On the right, we can write 9 as $8+a b c$, and then we have exactly $(a+2)(b+2)(c+2)$. Finally, dividing both sides by 3 and taking the square root (everything is still positive), we get
$$
a+b+c \geq \sqrt{\frac{(a+2)(b+2)(c+2)}{3}}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Laat $a, b$ en $c$ positieve reële getallen zijn met $a b c=1$. Bewijs dat
$$
a+b+c \geq \sqrt{\frac{(a+2)(b+2)(c+2)}{3}}
$$
|
Merk op dat $a, b$ en $c$ positief zijn, zodat we hieronder steeds rekenkundigmeetkundig mogen toepassen. Allereerst passen we rekenkundig-meetkundig toe op $a^{2}$ en 1 :
$$
a^{2}+1 \geq 2 \sqrt{a^{2}}=2 a
$$
Dit kunnen we cyclisch doordraaien en optellen, zodat we vinden:
$$
a^{2}+b^{2}+c^{2}+3 \geq 2 a+2 b+2 c
$$
Verder passen we rekenkundig-meetkundig toe op $b c, c a$ en $a b$ :
$$
b c+c a+a b \geq 3 \sqrt[3]{a^{2} b^{2} c^{2}}=3
$$
waarbij we gebruikt hebben dat $a b c=1$. Ook passen we rekenkundig-meetkundig toe op $a^{2}, b^{2}$ en $c^{2}$ :
$$
a^{2}+b^{2}+c^{2} \geq 3 \sqrt[3]{a^{2} b^{2} c^{2}}=3
$$
Nu nemen we 2 keer (5), 4 keer (6) en 1 keer (7) en tellen dat op. Dan krijgen we:
$$
2 a^{2}+2 b^{2}+2 c^{2}+6+4 b c+4 c a+4 a b+a^{2}+b^{2}+c^{2} \geq 4 a+4 b+4 c+12+3
$$
Gelijke termen bij elkaar nemen, links en rechts 6 aftrekken en links en rechts $2 a b+2 b c+2 c a$ optellen geeft:
$$
3 a^{2}+3 b^{2}+3 c^{2}+6 a b+6 b c+6 c a \geq 2 a b+2 b c+2 c a+4 a+4 b+4 c+9
$$
Nu staat links $3\left(a^{2}+b^{2}+c^{2}+2 a b+2 b c+2 c a\right)=3(a+b+c)^{2}$. Rechts kunnen we 9 schrijven als $8+a b c$ en dan staat daar precies $(a+2)(b+2)(c+2)$. Als we dan ten slotte links en rechts delen door 3 en de wortel trekken (alles is nog steeds positief) dan krijgen we
$$
a+b+c \geq \sqrt{\frac{(a+2)(b+2)(c+2)}{3}}
$$
|
{
"exam": "Dutch_TST",
"problem_label": "5",
"problem_match": "\nOpgave 5.",
"resource_path": "Dutch_TST/segmented/nl-2013-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2013"
}
|
Prove that
$$
\sum_{n=0}^{2013} \frac{4026!}{(n!(2013-n)!)^{2}}
$$
is the square of an integer.
|
By replacing 2013 with 1, 2, 3, and 4 and then calculating the sum, you get a hunch for which number squared this sum yields. The factorials suggest that you should look in the binomial coefficients. We prove something more general:
$$
\sum_{n=0}^{m} \frac{(2 m)!}{(n!(m-n)!)^{2}}=\binom{2 m}{m}^{2}
$$
From this, the desired result follows.
It holds that
$$
\frac{(2 m)!}{(n!(m-n)!)^{2}}=\frac{(m!)^{2}}{(n!(m-n)!)^{2}} \cdot \frac{(2 m)!}{(m!)^{2}}=\binom{m}{n}^{2} \cdot\binom{2 m}{m}
$$
Thus, it is sufficient to prove that
$$
\sum_{n=0}^{m}\binom{m}{n}^{2}=\binom{2 m}{m}
$$
We do this combinatorially. Consider $2 m$ balls numbered from 1 to $2 m$, where the balls from 1 to $m$ are colored blue and the balls from $m+1$ to $2 m$ are colored red. You want to choose a total of $m$ balls. This can be done in $\binom{2 m}{m}$ ways. On the other hand, we can also first choose $n$ blue balls, with $0 \leq n \leq m$, and then choose $m-n$ red balls. This is equivalent to first choosing $n$ blue balls and then not choosing $n$ red balls. Thus, the number of ways to choose $m$ balls is also equal to
$$
\sum_{n=0}^{m}\binom{m}{n}^{2}
$$
Therefore, this sum is equal to $\binom{2 m}{m}$. And with that, we have proven (1).
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Bewijs dat
$$
\sum_{n=0}^{2013} \frac{4026!}{(n!(2013-n)!)^{2}}
$$
het kwadraat van een geheel getal is.
|
Door 2013 te vervangen door 1, 2, 3 en 4 en de som dan uit te rekenen, krijg je een vermoeden voor welk getal in het kwadraat deze som oplevert. De faculteiten suggereren dat je het in de binomiaalcoëfficiënten moet zoeken. We bewijzen iets algemeners:
$$
\sum_{n=0}^{m} \frac{(2 m)!}{(n!(m-n)!)^{2}}=\binom{2 m}{m}^{2}
$$
Hieruit volgt het gevraagde.
Er geldt
$$
\frac{(2 m)!}{(n!(m-n)!)^{2}}=\frac{(m!)^{2}}{(n!(m-n)!)^{2}} \cdot \frac{(2 m)!}{(m!)^{2}}=\binom{m}{n}^{2} \cdot\binom{2 m}{m}
$$
Het is dus voldoende te bewijzen dat
$$
\sum_{n=0}^{m}\binom{m}{n}^{2}=\binom{2 m}{m}
$$
We doen dit combinatorisch. Bekijk $2 m$ ballen genummerd van 1 tot en met $2 m$, waarbij de ballen van 1 tot en met $m$ blauw gekleurd zijn en de ballen van $m+1$ tot en met $2 m$ rood gekleurd zijn. Je wilt hier totaal $m$ ballen van uitkiezen. Dat kan op $\binom{2 m}{m}$ manieren. Anderzijds kunnen we ook eerst $n$ blauwe ballen uitkiezen, met $0 \leq n \leq m$, en vervolgens $m-n$ rode ballen. Dat komt op hetzelfde neer als eerst $n$ blauwe ballen uitkiezen en daarna $n$ rode ballen niet uitkiezen. Dus het aantal manieren om $m$ ballen uit te kiezen is ook gelijk aan
$$
\sum_{n=0}^{m}\binom{m}{n}^{2}
$$
Dus deze som is gelijk aan $\binom{2 m}{m}$. En daarmee hebben we (1) bewezen.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2013-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2013"
}
|
Let $P$ be the intersection of the diagonals of a convex quadrilateral $ABCD$. Let $X, Y$, and $Z$ be points on the interior of $AB, BC$, and $CD$ respectively, such that
$$
\frac{|AX|}{|XB|}=\frac{|BY|}{|YC|}=\frac{|CZ|}{|ZD|}=2
$$
Suppose moreover that $XY$ is tangent to the circumcircle of $\triangle CYZ$ and that $YZ$ is tangent to the circumcircle of $\triangle BXY$. Prove that $\angle APD = \angle XYZ$.
|
Due to the tangent-chord angle theorem, $\angle C Z Y = \angle B Y X$ and $\angle B X Y = \angle C Y Z$. From this, it follows first that
$$
\angle X Y Z = 180^{\circ} - \angle B Y X - \angle C Y Z = 180^{\circ} - \angle B Y X - \angle B X Y = \angle X B Y = \angle A B C.
$$
Secondly, we see that $\triangle X B Y \sim \triangle Y C Z$ (AA). This means
$$
\frac{|X B|}{|B Y|} = \frac{|Y C|}{|C Z|}
$$
Given that $|X B| = \frac{1}{3}|A B|$, $|B Y| = \frac{2}{3}|B C|$, $|Y C| = \frac{1}{3}|B C|$, and $|C Z| = \frac{2}{3}|C D|$. Substituting these values gives
$$
\frac{\frac{1}{3}|A B|}{\frac{2}{3}|B C|} = \frac{\frac{1}{3}|B C|}{\frac{2}{3}|C D|}
$$
and thus
$$
\frac{|A B|}{|B C|} = \frac{|B C|}{|C D|}
$$
From the similarity, it also follows that $\angle A B C = \angle X B Y = \angle Y C Z = \angle B C D$. Combining this with the found ratio, we get a new similarity: $\triangle A B C \sim \triangle B C D$ (SAS). Therefore, $\angle C A B = \angle D B C$. This gives
$$
\angle P A B + \angle A B P = \angle C A B + \angle A B D = \angle D B C + \angle A B D = \angle A B C.
$$
We already knew that $\angle A B C = \angle X Y Z$. Using the exterior angle theorem in triangle $A B P$, we now get
$$
\angle B P C = \angle P A B + \angle A B P = \angle A B C = \angle X Y Z.
$$
Since $\angle B P C = \angle A P D$, it follows that $\angle A P D = \angle X Y Z$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $P$ het snijpunt van de diagonalen van een convexe vierhoek $A B C D$. Laat $X, Y$ en $Z$ punten op het inwendige van respectievelijk $A B, B C$ en $C D$ zijn zodat
$$
\frac{|A X|}{|X B|}=\frac{|B Y|}{|Y C|}=\frac{|C Z|}{|Z D|}=2
$$
Veronderstel bovendien dat $X Y$ raakt aan de omgeschreven cirkel van $\triangle C Y Z$ en dat $Y Z$ raakt aan de omgeschreven cirkel van $\triangle B X Y$. Bewijs dat $\angle A P D=\angle X Y Z$.
|
Vanwege de raaklijnomtrekshoekstelling is $\angle C Z Y=\angle B Y X$ en $\angle B X Y=$ $\angle C Y Z$. Hieruit volgt ten eerste dat
$$
\angle X Y Z=180^{\circ}-\angle B Y X-\angle C Y Z=180^{\circ}-\angle B Y X-\angle B X Y=\angle X B Y=\angle A B C .
$$
Ten tweede zien we dat $\triangle X B Y \sim \triangle Y C Z$ (hh). Dit betekent
$$
\frac{|X B|}{|B Y|}=\frac{|Y C|}{|C Z|}
$$
Gegeven is dat $|X B|=\frac{1}{3}|A B|,|B Y|=\frac{2}{3}|B C|,|Y C|=\frac{1}{3}|B C|$ en $|C Z|=\frac{2}{3}|C D|$. Dit invullen geeft
$$
\frac{\frac{1}{3}|A B|}{\frac{2}{3}|B C|}=\frac{\frac{1}{3}|B C|}{\frac{2}{3}|C D|}
$$
en dus
$$
\frac{|A B|}{|B C|}=\frac{|B C|}{|C D|}
$$
Uit de gelijkvormigheid volgt ook $\angle A B C=\angle X B Y=\angle Y C Z=\angle B C D$. Als we dit combineren met de gevonden verhouding, krijgen we een nieuwe gelijkvormigheid: $\triangle A B C \sim \triangle B C D$ (zhz). Dus $\angle C A B=\angle D B C$. Dit geeft
$$
\angle P A B+\angle A B P=\angle C A B+\angle A B D=\angle D B C+\angle A B D=\angle A B C .
$$
We wisten al dat $\angle A B C=\angle X Y Z$. Met de buitenhoekstelling in driehoek $A B P$ krijgen we nu
$$
\angle B P C=\angle P A B+\angle A B P=\angle A B C=\angle X Y Z .
$$
Aangezien $\angle B P C=\angle A P D$, geldt $\angle A P D=\angle X Y Z$.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2013-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2013"
}
|
Gegeven is een onbekende rij $a_{1}, a_{2}, a_{3}, \ldots$ van gehele getallen die voldoet aan de volgende eigenschap: voor elk priemgetal $p$ en elk positief geheel getal $k$ geldt
$$
a_{p k+1}=p a_{k}-3 a_{p}+13
$$
Bepaal alle mogelijke waarden van $a_{2013}$.
|
Laat $q$ en $t$ priemgetallen zijn. Vul in $k=q, p=t$ :
$$
a_{q t+1}=t a_{q}-3 a_{t}+13
$$
Vul ook in $k=t, p=q$ :
$$
a_{q t+1}=q a_{t}-3 a_{q}+13
$$
Beide uitdrukkingen rechts zijn dus gelijk aan elkaar, waaruit volgt
$$
t a_{q}-3 a_{t}=q a_{t}-3 a_{q}
$$
oftewel
$$
(t+3) a_{q}=(q+3) a_{t}
$$
In het bijzonder geldt $5 a_{3}=6 a_{2}$ en $5 a_{7}=10 a_{2}$. Vul nu $k=3, p=2$ in:
$$
a_{7}=2 a_{3}-3 a_{2}+13=2 \cdot \frac{6}{5} a_{2}-3 a_{2}+13
$$
Omdat $a_{7}=\frac{10}{5} a_{2}$, vinden we nu
$$
\frac{13}{5} a_{2}=13
$$
dus $a_{2}=5$. Nu geldt voor elk priemgetal $p$ dat $a_{p}=\frac{(p+3) a_{2}}{5}=p+3$.
Vul in $k=4, p=3$ :
$$
a_{13}=3 a_{4}-3 a_{3}+13
$$
We weten dat $a_{13}=16$ en $a_{3}=6$, dus dit geeft $3 a_{4}=21$, oftewel $a_{4}=7$.
Vul ten slotte $k=4$ en $p=503$ in:
$a_{2013}=a_{4 \cdot 503+1}=503 \cdot a_{4}-3 a_{503}+13=503 \cdot 7-3 \cdot(503+3)+13=503 \cdot 4-9+13=2016$.
Dus $a_{2013}=2016$ en dit is de enige mogelijke waarde.
|
2016
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Gegeven is een onbekende rij $a_{1}, a_{2}, a_{3}, \ldots$ van gehele getallen die voldoet aan de volgende eigenschap: voor elk priemgetal $p$ en elk positief geheel getal $k$ geldt
$$
a_{p k+1}=p a_{k}-3 a_{p}+13
$$
Bepaal alle mogelijke waarden van $a_{2013}$.
|
Laat $q$ en $t$ priemgetallen zijn. Vul in $k=q, p=t$ :
$$
a_{q t+1}=t a_{q}-3 a_{t}+13
$$
Vul ook in $k=t, p=q$ :
$$
a_{q t+1}=q a_{t}-3 a_{q}+13
$$
Beide uitdrukkingen rechts zijn dus gelijk aan elkaar, waaruit volgt
$$
t a_{q}-3 a_{t}=q a_{t}-3 a_{q}
$$
oftewel
$$
(t+3) a_{q}=(q+3) a_{t}
$$
In het bijzonder geldt $5 a_{3}=6 a_{2}$ en $5 a_{7}=10 a_{2}$. Vul nu $k=3, p=2$ in:
$$
a_{7}=2 a_{3}-3 a_{2}+13=2 \cdot \frac{6}{5} a_{2}-3 a_{2}+13
$$
Omdat $a_{7}=\frac{10}{5} a_{2}$, vinden we nu
$$
\frac{13}{5} a_{2}=13
$$
dus $a_{2}=5$. Nu geldt voor elk priemgetal $p$ dat $a_{p}=\frac{(p+3) a_{2}}{5}=p+3$.
Vul in $k=4, p=3$ :
$$
a_{13}=3 a_{4}-3 a_{3}+13
$$
We weten dat $a_{13}=16$ en $a_{3}=6$, dus dit geeft $3 a_{4}=21$, oftewel $a_{4}=7$.
Vul ten slotte $k=4$ en $p=503$ in:
$a_{2013}=a_{4 \cdot 503+1}=503 \cdot a_{4}-3 a_{503}+13=503 \cdot 7-3 \cdot(503+3)+13=503 \cdot 4-9+13=2016$.
Dus $a_{2013}=2016$ en dit is de enige mogelijke waarde.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2013-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2013"
}
|
Given is an unknown sequence $a_{1}, a_{2}, a_{3}, \ldots$ of integers that satisfies the following property: for every prime number $p$ and every positive integer $k$ it holds that
$$
a_{p k+1}=p a_{k}-3 a_{p}+13
$$
Determine all possible values of $a_{2013}$.
|
Leid net als in oplossing I af dat $a_{2}=5$ en $a_{p}=p+3$ voor alle priemgetallen $p$. Dan geldt dus $a_{3}=6$. Invullen van $k=1$ en $p=2$ geeft
$$
a_{3}=2 a_{1}-3 a_{2}+13=2 a_{1}-2,
$$
dus $2 a_{1}=a_{3}+2=8$, dus $a_{1}=4$. Nu hebben we $a_{1}$ en $a_{2}$ berekend. Voor $n \geq 3$ geldt dat er altijd een priemgetal $p$ is met $p \mid n-1$, dus dat we altijd $p$ en $k$ kunnen vinden zodat
$n=k p+1$. Dus ligt de waarde van $a_{n}$ vast als we alle waarden $a_{m}$ met $1 \leq m<n$ al kennen. Er kan dus maar één rij zijn die voldoet. We proberen nu of $a_{n}=n+3$ voldoet. Dan geldt
$$
p a_{k}-3 a_{p}+13=p(k+3)-3(p+3)+13=p k+3 p-3 p-9+13=p k+4=a_{p k+1}
$$
Dus dit voldoet inderdaad. De enige rij die voldoet is dus degene met $a_{n}=n+3$ voor alle $n \geq 1$, waaruit volgt dat de enige mogelijke waarde voor $a_{2013}$ gelijk is aan 2016.
Translate the above text into English, keeping the original text's line breaks and formatting:
From the solution I, we can deduce that $a_{2}=5$ and $a_{p}=p+3$ for all prime numbers $p$. Therefore, $a_{3}=6$. Substituting $k=1$ and $p=2$ gives
$$
a_{3}=2 a_{1}-3 a_{2}+13=2 a_{1}-2,
$$
so $2 a_{1}=a_{3}+2=8$, hence $a_{1}=4$. Now we have calculated $a_{1}$ and $a_{2}$. For $n \geq 3$, there is always a prime number $p$ such that $p \mid n-1$, so we can always find $p$ and $k$ such that
$n=k p+1$. Therefore, the value of $a_{n}$ is fixed if we already know all values $a_{m}$ with $1 \leq m<n$. Thus, there can only be one sequence that satisfies the condition. We now try to see if $a_{n}=n+3$ satisfies the condition. Then we have
$$
p a_{k}-3 a_{p}+13=p(k+3)-3(p+3)+13=p k+3 p-3 p-9+13=p k+4=a_{p k+1}
$$
So this indeed satisfies the condition. The only sequence that satisfies the condition is the one with $a_{n}=n+3$ for all $n \geq 1$, which implies that the only possible value for $a_{2013}$ is 2016.
|
2016
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Gegeven is een onbekende rij $a_{1}, a_{2}, a_{3}, \ldots$ van gehele getallen die voldoet aan de volgende eigenschap: voor elk priemgetal $p$ en elk positief geheel getal $k$ geldt
$$
a_{p k+1}=p a_{k}-3 a_{p}+13
$$
Bepaal alle mogelijke waarden van $a_{2013}$.
|
Leid net als in oplossing I af dat $a_{2}=5$ en $a_{p}=p+3$ voor alle priemgetallen $p$. Dan geldt dus $a_{3}=6$. Invullen van $k=1$ en $p=2$ geeft
$$
a_{3}=2 a_{1}-3 a_{2}+13=2 a_{1}-2,
$$
dus $2 a_{1}=a_{3}+2=8$, dus $a_{1}=4$. Nu hebben we $a_{1}$ en $a_{2}$ berekend. Voor $n \geq 3$ geldt dat er altijd een priemgetal $p$ is met $p \mid n-1$, dus dat we altijd $p$ en $k$ kunnen vinden zodat
$n=k p+1$. Dus ligt de waarde van $a_{n}$ vast als we alle waarden $a_{m}$ met $1 \leq m<n$ al kennen. Er kan dus maar één rij zijn die voldoet. We proberen nu of $a_{n}=n+3$ voldoet. Dan geldt
$$
p a_{k}-3 a_{p}+13=p(k+3)-3(p+3)+13=p k+3 p-3 p-9+13=p k+4=a_{p k+1}
$$
Dus dit voldoet inderdaad. De enige rij die voldoet is dus degene met $a_{n}=n+3$ voor alle $n \geq 1$, waaruit volgt dat de enige mogelijke waarde voor $a_{2013}$ gelijk is aan 2016.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2013-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2013"
}
|
Determine all integers $n \geq 2$ for which
$$
i+j \equiv\binom{n}{i}+\binom{n}{j} \quad \bmod 2
$$
for all $i$ and $j$ with $0 \leq i \leq j \leq n$.
|
We first show that $n$ satisfies the condition if and only if $\binom{n}{i} \equiv i+1 \bmod 2$ for all $i$ with $0 \leq i \leq n$. Suppose that $\binom{n}{i} \equiv i+1 \bmod 2$ for all $i$, then $\binom{n}{i}+\binom{n}{j} \equiv i+1+j+1 \equiv i+j \bmod 2$ for all $i$ and $j$. Thus, $n$ satisfies the condition in the problem. Conversely, suppose that $n$ satisfies the condition. Since $\binom{n}{0}=1$, it follows that $i \equiv 1+\binom{n}{i} \bmod 2$ for all $i$, so $\binom{n}{i} \equiv i-1 \equiv i+1 \bmod 2$ for all $i$.
Write $n$ as $n=2^{k}+m$ with $0 \leq m<2^{k}$. Since $n \geq 2$, we may assume $k \geq 1$. Consider
$$
\binom{n}{2^{k}-2}=\binom{2^{k}+m}{2^{k}-2}=\frac{\left(2^{k}+m\right)\left(2^{k}+m-1\right) \cdots(m+4)(m+3)}{\left(2^{k}-2\right)\left(2^{k}-3\right) \cdots 2 \cdot 1} .
$$
The product in the denominator contains $\left\lfloor\frac{2^{k}-2}{2}\right\rfloor$ factors divisible by $2$, $\left\lfloor\frac{2^{k}-2}{4}\right\rfloor$ factors divisible by $4$, ..., $\left\lfloor\frac{2^{k}-2}{2^{k-1}}\right\rfloor$ factors divisible by $2^{k-1}$, and no factors divisible by $2^{k}$. The product in the numerator consists of $2^{k}-2$ consecutive factors and therefore contains at least $\left\lfloor\frac{2^{k}-2}{2}\right\rfloor$ factors divisible by $2$, at least $\left\lfloor\frac{2^{k}-2}{4}\right\rfloor$ factors divisible by $4$, ..., at least $\left\lfloor\frac{2^{k}-2}{2^{k-1}}\right\rfloor$ factors divisible by $2^{k-1}$. Thus, the product in the numerator contains at least as many factors of $2$ as the product in the denominator. The product in the numerator certainly has more factors of $2$ than the product in the denominator if $2^{k}$ appears as a factor in the numerator. This is the case if $m+3 \leq 2^{k}$, or equivalently if $m \leq 2^{k}-3$. Therefore, if $m \leq 2^{k}-3$, then $\binom{n}{2^{k}-2}$ is even, while $2^{k}-2$ is also even. Thus, $n=2^{k}+m$ does not satisfy the condition.
Therefore, $n$ can only satisfy the condition if there is a $k \geq 2$ such that $2^{k}-2 \leq n \leq 2^{k}-1$. If $n$ is odd, then $\binom{n}{0}+\binom{n}{1}=1+n \equiv 0 \bmod 2$, so $n$ does not satisfy the condition. Therefore, $n$ can only satisfy the condition if it is of the form $n=2^{k}-2$ with $k \geq 2$. Now suppose that $n$ is indeed of this form. We will show that $n$ satisfies the condition. We have
$$
\binom{2^{k}-2}{c}=\frac{\left(2^{k}-2\right)\left(2^{k}-3\right) \cdots\left(2^{k}-c\right)\left(2^{k}-c-1\right)}{c \cdot(c-1) \cdots 2 \cdot 1} .
$$
The number of factors of $2$ in $2^{k}-i$ is equal to the number of factors of $2$ in $i$ for $1 \leq i \leq 2^{k}-1$. Therefore, the number of factors of $2$ in the numerator is equal to the number of factors of $2$ in the product $(c+1) \cdot c \cdot(c-1) \cdots 2$, which is the number of factors of $2$ in the denominator plus the number of factors of $2$ in $c+1$. Thus, $\binom{2^{k}-2}{c}$ is even if and only if $c$ is odd. This means that $n=2^{k}-2$ satisfies the condition.
We conclude that $n$ satisfies the condition if and only if $n=2^{k}-2$ with $k \geq 2$.
|
n=2^{k}-2 \text{ with } k \geq 2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Bepaal alle gehele getallen $n \geq 2$ waarvoor geldt dat
$$
i+j \equiv\binom{n}{i}+\binom{n}{j} \quad \bmod 2
$$
voor alle $i$ en $j$ met $0 \leq i \leq j \leq n$.
|
We laten eerst zien dat $n$ voldoet dan en slechts dan als $\binom{n}{i} \equiv i+1 \bmod 2$ voor alle $i$ met $0 \leq i \leq n$. Stel dat $\binom{n}{i} \equiv i+1 \bmod 2$ voor alle $i$, dan geldt $\binom{n}{i}+\binom{n}{j} \equiv$ $i+1+j+1 \equiv i+j \bmod 2$ voor alle $i$ en $j$. Dus $n$ voldoet dan aan de voorwaarde in de opgave. Stel andersom dat $n$ voldoet. Omdat $\binom{n}{0}=1$, geldt dan $i \equiv 1+\binom{n}{i} \bmod 2$ voor alle $i$, dus $\binom{n}{i} \equiv i-1 \equiv i+1 \bmod 2$ voor alle $i$.
Schrijf nu $n$ als $n=2^{k}+m$ met $0 \leq m<2^{k}$. Omdat $n \geq 2$, mogen we aannemen $k \geq 1$. Bekijk
$$
\binom{n}{2^{k}-2}=\binom{2^{k}+m}{2^{k}-2}=\frac{\left(2^{k}+m\right)\left(2^{k}+m-1\right) \cdots(m+4)(m+3)}{\left(2^{k}-2\right)\left(2^{k}-3\right) \cdots 2 \cdot 1} .
$$
Het product in de noemer bevat $\left\lfloor\frac{2^{k}-2}{2}\right\rfloor$ factoren deelbaar door $2,\left\lfloor\frac{2^{k}-2}{4}\right\rfloor$ factoren deelbaar door $4, \ldots,\left\lfloor\frac{2^{k}-2}{2^{k-1}}\right\rfloor$ factoren deelbaar door $2^{k-1}$ en geen factoren deelbaar door $2^{k}$. Het product in de teller bestaat uit $2^{k}-2$ opeenvolgende factoren en bevat daarom minstens $\left\lfloor\frac{2^{k}-2}{2}\right\rfloor$ factoren deelbaar door 2 , minstens $\left\lfloor\frac{2^{k}-2}{4}\right\rfloor$ factoren deelbaar door $4, \ldots$, minstens $\left\lfloor\frac{2^{k}-2}{2^{k-1}}\right\rfloor$ factoren deelbaar door $2^{k-1}$. Het product in de teller bevat dus minstens evenveel factoren 2 als het product in de noemer. Het product in de teller bevat zeker meer factoren 2 dan het product in de noemer als $2^{k}$ voorkomt als factor in de teller. Dat is zo als $m+3 \leq 2^{k}$, oftewel als $m \leq 2^{k}-3$. Dus als $m \leq 2^{k}-3$, dan is $\binom{n}{2^{k}-2}$ even, terwijl $2^{k}-2$ ook even is. Dan voldoet $n=2^{k}+m$ dus niet.
Dus $n$ kan alleen voldoen als er een $k \geq 2$ is met $2^{k}-2 \leq n \leq 2^{k}-1$. Als $n$ oneven is, geldt $\binom{n}{0}+\binom{n}{1}=1+n \equiv 0 \bmod 2$, dus dan voldoet $n$ niet. Dus $n$ kan alleen voldoen als hij van de vorm $n=2^{k}-2$ met $k \geq 2$ is. Stel nu dat $n$ inderdaad van die vorm is. We gaan laten zien dat $n$ voldoet. Er geldt
$$
\binom{2^{k}-2}{c}=\frac{\left(2^{k}-2\right)\left(2^{k}-3\right) \cdots\left(2^{k}-c\right)\left(2^{k}-c-1\right)}{c \cdot(c-1) \cdots 2 \cdot 1} .
$$
Het aantal factoren 2 in $2^{k}-i$ is gelijk aan het aantal factoren 2 in $i$ voor $1 \leq i \leq 2^{k}-1$. Dus het aantal factoren 2 in de teller is gelijk aan het aantal factoren 2 in het product $(c+1) \cdot c \cdot(c-1) \cdots 2$, oftewel het aantal factoren 2 in de noemer plus het aantal factoren 2 in $c+1$. Dus $\binom{2^{k}-2}{c}$ is even dan en slechts dan als $c$ oneven is. Dit betekent dat $n=2^{k}-2$ voldoet.
We concluderen dat $n$ voldoet dan en slechts dan als $n=2^{k}-2$ met $k \geq 2$.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2013-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2013"
}
|
In a cyclic hexagon $A B C D E F$, $A B \perp B D$ and $|B C|=|E F|$. Let $P$ be the intersection of $B C$ and $A D$ and let $Q$ be the intersection of $E F$ and $A D$. Assume that $P$ and $Q$ both lie on the side of $D$ where $A$ does not lie. Let $S$ be the midpoint of $A D$. Let $K$ and $L$ be the centers of the inscribed circles of $\triangle B P S$ and $\triangle E Q S$, respectively. Prove that $\angle K D L=90^{\circ}$.
|
It is useful for this task to analyze what happens when you slide points. You can, for example, slide line segment EF without affecting $K$. Therefore, $L$ can move independently of $K$. Apparently, $L$ always moves along a line through D that is perpendicular to KD. The angle $\angle L D S$ is apparently independent of the position of line segment EF. Since we are dealing with a circle, this suggests that $\angle L D S$ might be equal to a certain inscribed angle. Then $\angle K D S$ would also be equal to an inscribed angle, and these two inscribed angles together would be $90^{\circ}$. In this way, you can get ideas to ultimately arrive at the following proof.
The configuration is fixed by the given order of points $A$ through $F$ on the circle and by the given positions of points $P$ and $Q$ on line $A D$. Therefore, we do not need to distinguish between different configurations. (The points $P$ and $Q$ can be swapped on line $A D$, but this is not relevant.)
First, note that $S$ is the center of the circle, since $\angle A B D=90^{\circ}$, line $A D$ is a diameter, and $S$ is the midpoint of $A D$. We will now prove that $\angle K D S=\angle K B S$. We know that $K S$ is a bisector, so $\angle B S K=\angle K S D$. Furthermore, $|S D|=|S B|$, since both lengths are equal to the radius of the circle. Since also $|S K|=|S K|$, we find $\triangle D S K \cong \triangle B S K$ (SAS). Therefore, $\angle K D S=\angle K B S$.
Since $B K$ is also a bisector, $\angle K B S=\angle C B K=\frac{1}{2} \angle C B S$. Thus, $\angle K D S=$ $\frac{1}{2} \angle C B S$.
Analogously, we derive that $\angle L D S=\frac{1}{2} \angle Q E S$, which implies that $\angle L D S=\frac{1}{2} \left(180^{\circ}-\angle F E S\right)=90^{\circ}-\frac{1}{2} \angle F E S$. Therefore, $\angle L D S+\angle K D S=90^{\circ}-\frac{1}{2} \angle F E S+\frac{1}{2} \angle C B S$. Furthermore, note that $\triangle S B C \cong \triangle S E F$ (SSS), so $\angle F E S=\angle C B S$. Now we can conclude that $\angle K D L=\angle L D S+\angle K D S=90^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In een koordenzeshoek $A B C D E F$ geldt $A B \perp B D$ en $|B C|=|E F|$. Noem $P$ het snijpunt van $B C$ en $A D$ en noem $Q$ het snijpunt van $E F$ en $A D$. Neem aan dat $P$ en $Q$ allebei aan de kant van $D$ liggen waar $A$ niet ligt. Zij $S$ het midden van $A D$. Laat $K$ en $L$ de middelpunten zijn van de ingeschreven cirkels van respectievelijk $\triangle B P S$ en $E Q S$. Bewijs dat $\angle K D L=90^{\circ}$.
|
Het is bij deze opgave nuttig om te analyseren wat er gebeurt als je met punten schuift. Je kunt namelijk lijnstuk EF verschuiven zonder dat dat invloed op $K$ heeft. Dus L kan onafhankelijk van $K$ bewegen. Kennelijk beweegt $L$ dan wel altijd over een lijn door D die loodrecht op KD staat. De hoek $\angle L D S$ is blijkbaar onafhankelijk van de positie van lijnstuk EF. Omdat we met een cirkel te maken hebben, suggereert dit dat $\angle L D S$ misschien gelijk is aan een bepaalde omtrekshoek. Dan zou $\angle K D S$ ook gelijk aan een omtrekshoek worden, en wel zo dat die twee omtrekshoeken samen $90^{\circ}$ zijn. Op deze manier kun je ideeën krijgen om uiteindelijk tot het volgende bewijs te komen.
De configuratie ligt vast door de gegeven volgorde van de punten $A$ tot en met $F$ op de cirkel en door het gegeven over de punten $P$ en $Q$ op de lijn $A D$. We hoeven dus geen verschillende configuraties te onderscheiden. (De punten $P$ en $Q$ kunnen wel verwisseld worden op de lijn $A D$, maar dat is niet relevant.)
Merk eerst op dat $S$ het middelpunt van de cirkel is, aangezien vanwege $\angle A B D=90^{\circ}$ de lijn $A D$ middellijn is, en $S$ het midden van $A D$ is. We gaan nu bewijzen dat $\angle K D S=\angle K B S$. We weten dat $K S$ een bissectrice is, dus $\angle B S K=\angle K S D$. Verder is $|S D|=|S B|$, omdat beide lengtes gelijk zijn aan de straal van de cirkel. Omdat ook $|S K|=|S K|$, vinden we $\triangle D S K \cong \triangle B S K$ (ZHZ). Dus $\angle K D S=\angle K B S$.
Omdat ook $B K$ een bissectrice is, geldt $\angle K B S=\angle C B K=\frac{1}{2} \angle C B S$. Dus $\angle K D S=$ $\frac{1}{2} \angle C B S$.
Helemaal analoog leiden we af dat $\angle L D S=\frac{1}{2} \angle Q E S$, waaruit volgt dat $\angle L D S=\frac{1}{2}$. $\left(180^{\circ}-\angle F E S\right)=90^{\circ}-\frac{1}{2} \angle F E S$. Dus $\angle L D S+\angle K D S=90^{\circ}-\frac{1}{2} \angle F E S+\frac{1}{2} \angle C B S$. Merk nu verder op dat $\triangle S B C \cong \triangle S E F$ (ZZZ), zodat $\angle F E S=\angle C B S$. Nu kunnen we concluderen dat $\angle K D L=\angle L D S+\angle K D S=90^{\circ}$.
|
{
"exam": "Dutch_TST",
"problem_label": "5",
"problem_match": "\nOpgave 5.",
"resource_path": "Dutch_TST/segmented/nl-2013-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2013"
}
|
Find all non-negative integers $n$ for which there exist integers $a$ and $b$ such that $n^{2}=a+b$ and $n^{3}=a^{2}+b^{2}$.
|
Due to the inequality of the arithmetic and geometric mean, applied to $a^{2}$ and $b^{2}$, it holds that $a^{2}+b^{2} \geq 2 a b$. Since $2 a b=(a+b)^{2}-(a^{2}+b^{2})$, it follows that $n^{3} \geq (n^{2})^{2}-n^{3}$, or equivalently $2 n^{3} \geq n^{4}$. This means $n=0$ or $2 \geq n$. Therefore, $n=0, n=1$ and $n=2$ are the only possibilities. For $n=0$ we find $a=b=0$ as a solution, for $n=1$ we find $a=0, b=1$ as a solution, and for $n=2$ we find $a=b=2$ as a solution. The numbers $n$ that satisfy this are thus precisely $n=0, n=1$, and $n=2$.
|
n=0, n=1, n=2
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Vind alle niet-negatieve gehele getallen $n$ waarvoor er gehele getallen $a$ en $b$ bestaan met $n^{2}=a+b$ en $n^{3}=a^{2}+b^{2}$.
|
Vanwege de ongelijkheid van het rekenkundig en meetkundig gemiddelde, toegepast op $a^{2}$ en $b^{2}$, geldt $a^{2}+b^{2} \geq 2 a b$. Aangezien $2 a b=(a+b)^{2}-\left(a^{2}+b^{2}\right)$, volgt hieruit $n^{3} \geq\left(n^{2}\right)^{2}-n^{3}$, oftewel $2 n^{3} \geq n^{4}$. Dit betekent $n=0$ of $2 \geq n$. Dus $n=0, n=1$ en $n=2$ zijn de enige mogelijkheden. Voor $n=0$ vinden we $a=b=0$ als oplossing, voor $n=1$ vinden we $a=0, b=1$ als oplossing en voor $n=2$ vinden we $a=b=2$ als oplossing. De getallen $n$ die voldoen zijn dus precies $n=0, n=1$ en $n=2$.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2014-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2014"
}
|
Find all non-negative integers $n$ for which there exist integers $a$ and $b$ such that $n^{2}=a+b$ and $n^{3}=a^{2}+b^{2}$.
|
Write $b=n^{2}-a$ and substitute it in:
$$
n^{3}=a^{2}+b^{2}=a^{2}+\left(n^{2}-a\right)^{2}=a^{2}+n^{4}-2 a n^{2}+a^{2} .
$$
So
$$
2 a^{2}-2 n^{2} a+n^{4}-n^{3}=0 .
$$
This is a quadratic equation in $a$, whose discriminant is equal to
$$
D=\left(-2 n^{2}\right)^{2}-4 \cdot 2 \cdot\left(n^{4}-n^{3}\right)=-4 n^{4}+8 n^{3}=4 n^{2}\left(-n^{2}+2 n\right) .
$$
For $n \geq 3$, we have $-n^{2}+2 n \leq-3 n+2 n=-n<0$, so there is no solution for $a$. Therefore, we must have $n \leq 2$. For $n=0$, we find $a=b=0$ as a solution, for $n=1$, we find $a=0, b=1$ as a solution, and for $n=2$, we find $a=b=2$ as a solution. The numbers $n$ that satisfy the condition are thus precisely $n=0, n=1$, and $n=2$.
|
n=0, n=1, n=2
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Vind alle niet-negatieve gehele getallen $n$ waarvoor er gehele getallen $a$ en $b$ bestaan met $n^{2}=a+b$ en $n^{3}=a^{2}+b^{2}$.
|
Schrijf $b=n^{2}-a$ en vul dat in:
$$
n^{3}=a^{2}+b^{2}=a^{2}+\left(n^{2}-a\right)^{2}=a^{2}+n^{4}-2 a n^{2}+a^{2} .
$$
Dus
$$
2 a^{2}-2 n^{2} a+n^{4}-n^{3}=0 .
$$
Dit is een kwadratische vergelijking in $a$, waarvan de discriminant gelijk is aan
$$
D=\left(-2 n^{2}\right)^{2}-4 \cdot 2 \cdot\left(n^{4}-n^{3}\right)=-4 n^{4}+8 n^{3}=4 n^{2}\left(-n^{2}+2 n\right) .
$$
Voor $n \geq 3$ geldt $-n^{2}+2 n \leq-3 n+2 n=-n<0$, dus dan is er geen oplossing voor $a$. Er moet dus gelden $n \leq 2$. Voor $n=0$ vinden we $a=b=0$ als oplossing, voor $n=1$ vinden we $a=0, b=1$ als oplossing en voor $n=2$ vinden we $a=b=2$ als oplossing. De getallen $n$ die voldoen zijn dus precies $n=0, n=1$ en $n=2$.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2014-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2014"
}
|
Vind alle functies $f: \mathbb{R} \backslash\{0\} \rightarrow \mathbb{R}$ waarvoor geldt:
$$
x f(x y)+f(-y)=x f(x)
$$
voor alle reële $x, y$ ongelijk aan 0 .
|
Vul in $x=1$, dat geeft $f(y)+f(-y)=f(1)$, oftewel $f(-y)=f(1)-f(y)$ voor alle $y$. Vul nu in $y=-1$, dat geeft $x f(-x)+f(1)=x f(x)$. Als we hierin $f(-x)=$ $f(1)-f(x)$ invullen, krijgen we $x(f(1)-f(x))+f(1)=x f(x)$, dus $x f(1)+f(1)=2 x f(x)$. We zien dat $f$ van de vorm $f(x)=c+\frac{c}{x}$ is voor zekere $c \in \mathbb{R}$. Deze familie van functies controleren we. Links staat dan $x f(x y)+f(-y)=x\left(c+\frac{c}{x y}\right)+c+\frac{c}{-y}=x c+c$ en rechts staat $x f(x)=x\left(c+\frac{c}{x}\right)=x c+c$. Deze twee zijn aan elkaar gelijk, dus deze functie voldoet voor alle $c \in \mathbb{R}$.
|
f(x)=c+\frac{c}{x}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Vind alle functies $f: \mathbb{R} \backslash\{0\} \rightarrow \mathbb{R}$ waarvoor geldt:
$$
x f(x y)+f(-y)=x f(x)
$$
voor alle reële $x, y$ ongelijk aan 0 .
|
Vul in $x=1$, dat geeft $f(y)+f(-y)=f(1)$, oftewel $f(-y)=f(1)-f(y)$ voor alle $y$. Vul nu in $y=-1$, dat geeft $x f(-x)+f(1)=x f(x)$. Als we hierin $f(-x)=$ $f(1)-f(x)$ invullen, krijgen we $x(f(1)-f(x))+f(1)=x f(x)$, dus $x f(1)+f(1)=2 x f(x)$. We zien dat $f$ van de vorm $f(x)=c+\frac{c}{x}$ is voor zekere $c \in \mathbb{R}$. Deze familie van functies controleren we. Links staat dan $x f(x y)+f(-y)=x\left(c+\frac{c}{x y}\right)+c+\frac{c}{-y}=x c+c$ en rechts staat $x f(x)=x\left(c+\frac{c}{x}\right)=x c+c$. Deze twee zijn aan elkaar gelijk, dus deze functie voldoet voor alle $c \in \mathbb{R}$.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2014-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2014"
}
|
In triangle $A B C$, $I$ is the center of the inscribed circle. A circle is tangent to $A I$ at $I$ and also passes through $B$. This circle intersects $A B$ again at $P$ and $B C$ again at $Q$. The line $Q I$ intersects $A C$ at $R$. Prove that $|A R| \cdot|B Q|=|P I|^{2}$.
|
There is only one configuration. The following applies:
$$
\begin{array}{rlr}
\angle A I P & =\angle I B P & \text { (tangent-secant angle theorem) } \\
& =\angle I B Q & (I B \text { is bisector) } \\
& =\angle I P Q & \text { (cyclic quadrilateral } P B Q I \text { ) }
\end{array}
$$
Thus, due to Z-angles, $A I \| P Q$. This means $\angle I A B=\angle Q P B=\angle Q I B$, where the last equality holds due to the cyclic quadrilateral. We had already seen that $\angle A I P=\angle I B Q$, so $\triangle I A P \sim \triangle B I Q$ (AA). Therefore,
$$
\frac{|A P|}{|P I|}=\frac{|Q I|}{|B Q|}
$$
Moreover, $\angle R I A$ is the opposite angle of a tangent angle and is therefore equal to $\angle I P Q$, which we already knew is equal to $\angle A I P$. Thus, $\angle R I A=\angle A I P$. Due to the bisector $A I$, it also holds that $\angle R A I=\angle P A I$, so $\triangle R A I \cong \triangle P A I$ (ASA). This implies $|A R|=|A P|$. Furthermore, $I$ is the midpoint of arc $P Q$, since $B I$ is a bisector, so $|P I|=|Q I|$. We substitute these two into (1):
$$
\frac{|A R|}{|P I|}=\frac{|P I|}{|B Q|}
$$
which implies $|A R| \cdot|B Q|=|P I|^{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In driehoek $A B C$ is $I$ het middelpunt van de ingeschreven cirkel. Een cirkel raakt aan $A I$ in $I$ en gaat verder door $B$. Deze cirkel snijdt $A B$ nogmaals in $P$ en $B C$ nogmaals in $Q$. De lijn $Q I$ snijdt $A C$ in $R$. Bewijs dat $|A R| \cdot|B Q|=|P I|^{2}$.
|
Er is maar één configuratie. Er geldt
$$
\begin{array}{rlr}
\angle A I P & =\angle I B P & \text { (raaklijn-omtrekshoekstelling) } \\
& =\angle I B Q & (I B \text { is bissectrice) } \\
& =\angle I P Q & \text { (koordenvierhoek } P B Q I \text { ) }
\end{array}
$$
dus vanwege Z-hoeken geldt nu $A I \| P Q$. Dit betekent $\angle I A B=\angle Q P B=\angle Q I B$, waarbij de laatste gelijkheid geldt vanwege de koordenvierhoek. We hadden al gezien dat $\angle A I P=\angle I B Q$, dus $\triangle I A P \sim \triangle B I Q$ (hh). Dus
$$
\frac{|A P|}{|P I|}=\frac{|Q I|}{|B Q|}
$$
Daarnaast is $\angle R I A$ de overstaande hoek van een raaklijnhoek en daarom gelijk aan $\angle I P Q$, waarvan we al wisten dat die gelijk is aan $\angle A I P$. Dus $\angle R I A=\angle A I P$. Vanwege de bissectrice $A I$ geldt ook $\angle R A I=\angle P A I$, dus $\triangle R A I \cong \triangle P A I$ (HZH). Hieruit volgt $|A R|=|A P|$. Verder is $I$ het midden van boog $P Q$, aangezien $B I$ een bissectrice is, dus $|P I|=|Q I|$. Deze twee dingen vullen we in in (1):
$$
\frac{|A R|}{|P I|}=\frac{|P I|}{|B Q|}
$$
waaruit volgt $|A R| \cdot|B Q|=|P I|^{2}$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2014-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2014"
}
|
Let $m \geq 3$ and $n$ be positive integers with $n > m(m-2)$. Find the largest positive integer $d$ such that $d \mid n!$ and $k \nmid d$ for all $k \in \{m, m+1, \ldots, n\}$.
|
We will prove that $d=m-1$ is the largest that satisfies. First, note that $m-1 \mid n$ ! and for $k \geq m$ we have $k \nmid m-1$, so $d=m-1$ indeed satisfies.
Suppose now that for some $d$ we have: $d \mid n$ ! and $k \nmid d$ for all $k \in\{m, m+1, \ldots, n\}$. We will prove that $d \leq m-1$. Write $d=p_{1} p_{2} \cdots p_{t}$ with $p_{i}$ prime for all $i$ (not necessarily all distinct). If $t=0$, then $d=1 \leq m-1$, so we may assume $t \geq 1$. From the first condition on $d$ it follows that $p_{i} \leq n$ for all $i$. From the second condition on $d$ it follows that $p_{i} \notin\{m, m+1, \ldots, n\}$ for all $i$. Thus $p_{i} \leq m-1$ for all $i$. Now consider the numbers $p_{1}, p_{1} p_{2}, \ldots, p_{1} p_{2} \cdots p_{t}$. These are all divisors of $d$ and therefore all different from numbers in $\{m, m+1, \ldots, n\}$. Furthermore, we know that $p_{1} \leq m-1$. Now consider the largest $j \leq t$ for which $p_{1} p_{2} \cdots p_{j} \leq m-1$. If $j<t$ then
$$
p_{1} p_{2} \cdots p_{j} p_{j+1} \leq(m-1) p_{j+1} \leq(m-1)(m-1)=m(m-2)+1 \leq n
$$
But that means that $p_{1} p_{2} \cdots p_{j} p_{j+1} \leq m-1$ as well. Contradiction with the maximality of $j$. So it must be that $j=t$, i.e., $d=p_{1} p_{2} \cdots p_{t} \leq m-1$.
We conclude that $d=m-1$ is indeed the largest $d$ that satisfies the conditions.
|
m-1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Laat $m \geq 3$ en $n$ positieve gehele getallen zijn met $n>m(m-2)$. Vind het grootste positieve gehele getal $d$ zodat $d \mid n$ ! en $k \nmid d$ voor alle $k \in\{m, m+1, \ldots, n\}$.
|
We gaan bewijzen dat $d=m-1$ de grootste is die voldoet. Merk eerst op dat $m-1 \mid n$ ! en dat voor $k \geq m$ geldt $k \nmid m-1$, dus $d=m-1$ voldoet inderdaad.
Stel nu dat voor zekere $d$ geldt: $d \mid n$ ! en $k \nmid d$ voor alle $k \in\{m, m+1, \ldots, n\}$. We gaan bewijzen dat $d \leq m-1$. Schrijf $d=p_{1} p_{2} \cdots p_{t}$ met $p_{i}$ priem voor alle $i$ (niet noodzakelijk allemaal verschillend). Als $t=0$, is $d=1 \leq m-1$, dus we mogen aannemen $t \geq 1$. Uit de eerste voorwaarde op $d$ volgt $p_{i} \leq n$ voor alle $i$. Uit de tweede voorwaarde op $d$ volgt dat $p_{i} \notin\{m, m+1, \ldots, n\}$ voor alle $i$. Dus $p_{i} \leq m-1$ voor alle $i$. Bekijk nu de getallen $p_{1}, p_{1} p_{2}, \ldots, p_{1} p_{2} \cdots p_{t}$. Dit zijn allemaal delers van $d$ en daarom allemaal ongelijk aan getallen uit $\{m, m+1, \ldots, n\}$. Verder weten we dat $p_{1} \leq m-1$. Bekijk nu de grootste $j \leq t$ waarvoor geldt dat $p_{1} p_{2} \cdots p_{j} \leq m-1$. Als $j<t$ geldt
$$
p_{1} p_{2} \cdots p_{j} p_{j+1} \leq(m-1) p_{j+1} \leq(m-1)(m-1)=m(m-2)+1 \leq n
$$
Maar dat betekent dat ook $p_{1} p_{2} \cdots p_{j} p_{j+1} \leq m-1$. Tegenspraak met de maximaliteit van $j$. Dus moet gelden $j=t$, oftewel $d=p_{1} p_{2} \cdots p_{t} \leq m-1$.
We concluderen dat $d=m-1$ inderdaad de grootste $d$ is die aan de eisen voldoet.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2014-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2014"
}
|
Let $n$ be a positive integer. Daniel and Merlijn are playing a game. Daniel has $k$ sheets of paper lying next to each other on the table, where $k$ is a positive integer. He writes a number from 1 to $n$ on each sheet (no number is allowed, all numbers are allowed too). On the back of each sheet, he writes exactly the remaining numbers from 1 to $n$. When Daniel is done, Merlijn may flip some of the sheets to show the back (he may also choose not to flip any or to flip all of them). If he can make all the numbers from 1 to $n$ visible at the same time (where duplicates are allowed), he wins.
Determine the smallest $k$ for which Merlijn can always win, regardless of what Daniel does.
|
We give all of Daniel's sheets of paper a different color. Furthermore, we have $n$ boxes with the numbers 1 to $n$ on them. We also provide enough tokens in exactly the colors of Daniel's sheets of paper. For each sheet, he looks at the numbers on the front of the sheet and puts a token of the color of this sheet in each of those boxes. Each box then contains the tokens in the colors of the sheets of paper on which that number is on the front, and precisely not the tokens in the colors of the sheets of paper on which that number is on the back.
If Merlin has laid the sheets of paper he desires with the back side up, he picks from the supply exactly the tokens in the colors of those sheets. A number is not visible on the table precisely if the sheets on which this number is on the front are the sheets that Merlin has turned over, or in other words, precisely if the set of tokens in his hand is equal to the set of tokens in the box of this number. Merlin wins then and only then if the set of tokens in his hand does not occur in any of the boxes, because then all numbers are visible. We claim now that Merlin can win if and only if $2^{k}>n$. The smallest $k$ for which Merlin wins is thus the smallest $k$ with $2^{k}>n$.
Assume that $2^{k}>n$. The number of possible sets of colors is $2^{k}$ and therefore greater than $n$. There are $n$ boxes, so not all sets of colors can be exactly the colors of tokens in a box. Merlin can thus choose a set of colors that does not occur in a box and lay the sheets of those colors with the back side up. Then he wins. Now assume that $2^{k} \leq n$. Daniel first fills the boxes with sets of tokens so that every possible set occurs in a box. This is possible because the number of possible sets is $2^{k}$ and we have at least $2^{k}$ boxes. Now Daniel writes on each colored sheet of paper on the front exactly the numbers of the boxes that contain a token of the correct color, and on the back the rest. In this way, the tokens in the boxes again correspond exactly to the numbers on the front of the sheets. No matter which set of colors Merlin chooses, there is always a box with exactly that set of colors. Merlin can therefore not win.
|
k = \lceil \log_2(n+1) \rceil
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Zij $n$ een positief geheel getal. Daniël en Merlijn spelen een spel. Daniël heeft $k$ vellen papier die naast elkaar op tafel liggen, waarbij $k$ een positief geheel getal is. Hij schrijft op elk vel papier een aantal van de getallen 1 tot en met $n$ (geen enkel getal mag ook, alle getallen mag ook). Op de achterkant van elk vel papier schrijft hij juiste de overige getallen van 1 tot en met $n$. Als Daniël klaar is, mag Merlijn een aantal vellen papier met de achterkant boven leggen (hij mag dit ook bij geen enkel vel of juist alle vellen doen). Als het hem lukt om de getallen 1 tot en met $n$ allemaal tegelijk zichtbaar te maken (waarbij dubbele mogen voorkomen), dan wint hij.
Bepaal de kleinste $k$ waarvoor Merlijn altijd kan winnen, wat Daniël ook doet.
|
We geven de vellen papier van Daniël allemaal een andere kleur. Verder hebben we $n$ doosjes met daarop de getallen 1 tot en met $n$. We zorgen ook voor voldoende beschikbare fiches in precies de kleuren van de vellen papier van Daniël. Per vel bekijkt hij de getallen op de voorkant van het vel en stopt een fiche met de kleur van dit vel in elk van die doosjes. Elk doosje bevat daarna dus de fiches in de kleuren van de vellen papier waar dat getal op de voorkant staat, en juist niet de fiches in de kleuren van de vellen papier waar dat getal op de achterkant staat.
Als Merlijn de door hem gewenste vellen papier met de achterkant boven heeft gelegd, pakt hij uit de voorraad precies de fiches in de kleuren van die vellen. Een getal is niet zichtbaar op tafel precies als de vellen waar dit getal op de voorkant staat, de vellen zijn die Merlijn omgedraaid heeft, oftewel precies als de verzameling fiches in zijn hand gelijk is aan de verzameling fiches in het doosje van dit getal. Merlijn wint dus dan en slechts dan als de verzameling fiches in zijn hand niet voorkomt in één van de doosjes, want dan zijn alle getallen zichtbaar. We beweren nu dat Merlijn kan winnen dan en slechts dan als $2^{k}>n$. De kleinste $k$ waarvoor Merlijn wint, is dan dus de kleinste $k$ met $2^{k}>n$.
Stel dat $2^{k}>n$. Het aantal mogelijke verzamelingen van kleuren is $2^{k}$ en daarom groter dan $n$. Er zijn $n$ doosjes, dus niet alle verzamelingen van kleuren kunnen precies de kleuren van fiches in een doosje zijn. Merlijn kan dus een verzameling kleuren kiezen die niet in een doosje voorkomt en de vellen daarvan met de achterkant boven leggen. Dan wint hij. Stel nu dat $2^{k} \leq n$. Daniël vult nu eerst de doosjes met verzamelingen fiches, zodat elke mogelijke verzameling voorkomt in een doosje. Dat kan, want het aantal mogelijke verzamelingen is $2^{k}$ en we hebben minstens $2^{k}$ doosjes. Nu schrijft Daniël op elk vel gekleurd papier op de voorkant precies de getallen van de doosjes waar een fiche van de juiste kleur in zit, en op de achterkant de rest. Op deze manier corresponderen de fiches in de doosjes weer precies met de getallen op de voorkant van de vellen. Welke verzameling kleuren Merlijn nu ook uitkiest, er is altijd een doosje met precies die verzameling kleuren. Merlijn kan dus niet winnen.
|
{
"exam": "Dutch_TST",
"problem_label": "5",
"problem_match": "\nOpgave 5.",
"resource_path": "Dutch_TST/segmented/nl-2014-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2014"
}
|
Let $n$ be a positive integer. Daniel and Merlijn are playing a game. Daniel has $k$ sheets of paper lying next to each other on the table, where $k$ is a positive integer. He writes a number from 1 to $n$ on each sheet (no number is allowed, all numbers are allowed too). On the back of each sheet, he writes exactly the remaining numbers from 1 to $n$. When Daniel is done, Merlijn may flip some of the sheets to show the back (he may also choose not to flip any or to flip all of them). If he can make all the numbers from 1 to $n$ visible at the same time (where duplicates are allowed), he wins.
Determine the smallest $k$ for which Merlijn can always win, regardless of what Daniel does.
|
We will show that Merlijn can win if and only if $2^{k}>n$. The smallest $k$ for which Merlijn wins is thus the smallest $k$ with $2^{k}>n$.
Suppose that $2^{k}>n$. Merlijn chooses one by one for each sheet whether to flip it or not. For the first sheet, he places the side with the most numbers on top (so at least half of the numbers from 1 to $n$). For each subsequent sheet, he places the side with as many numbers as possible that he has not yet made visible on earlier sheets. Let $b_{j}$ be the number of numbers that are still not visible on sheets 1 to $j$ after Merlijn has made his choices for these sheets. Then $b_{1} \leq \frac{1}{2} n$ and $b_{j} \leq \frac{1}{2} b_{j-1}$ for $j \geq 2$. Thus, $b_{j} \leq \left(\frac{1}{2}\right)^{j} n$ and in particular $b_{k} \leq \left(\frac{1}{2}\right)^{k} n$. Since $2^{k}>n$, it follows that $\left(\frac{1}{2}\right)^{k} n<1$, so $b_{k}<1$. Since $b_{k}$ must be an integer, $b_{k}=0$. Therefore, after Merlijn's choice for all $k$ sheets, there are no numbers left that are not visible.
Now we prove that for $2^{k} \leq n$ Daniël can ensure that Merlijn cannot win. We do this by induction on $k$. For $k=1$, we have $n \geq 2$. Daniël writes the number 1 on one side of the sheet and all other numbers (there is at least one) on the other side. Merlijn cannot now turn this sheet in such a way that he can win. This is the base case of the induction. Now let $k \geq 1$ and assume that Daniël can describe $k$ sheets with $n \geq 2^{k}$ numbers such that Merlijn cannot win. We now consider $k+1$ sheets. Describe the first $k$ sheets in such a way with the numbers 1 to $2^{k}$ that Merlijn cannot win with only these numbers; this is possible according to the induction hypothesis. Then write the same numbers on each sheet again, but increased by $2^{k}$, so that these numbers run from $2^{k}+1$ to $2^{k+1}$. Finally, write all numbers $m$ with $2^{k+1}<m \leq n$ on the back of each sheet. Now each of these $k$ sheets contains the numbers 1 to $n$. On sheet number $k+1$, write the numbers 1 to $2^{k}$ on the front and the numbers $2^{k}+1$ to $n$ on the back. Suppose Merlijn leaves the last sheet with the front side up. Then he must at least make the numbers $2^{k}+1$ to $2^{k+1}$ visible on the first $k$ sheets, but this is not possible according to the induction hypothesis. Suppose Merlijn lays the last sheet with the back side up. Then he must make the numbers 1 to $2^{k}$ visible on the first $k$ sheets, but this is also not possible according to the induction hypothesis. Merlijn can therefore not win with these sheets. This completes the proof.
|
2^{k}>n
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Zij $n$ een positief geheel getal. Daniël en Merlijn spelen een spel. Daniël heeft $k$ vellen papier die naast elkaar op tafel liggen, waarbij $k$ een positief geheel getal is. Hij schrijft op elk vel papier een aantal van de getallen 1 tot en met $n$ (geen enkel getal mag ook, alle getallen mag ook). Op de achterkant van elk vel papier schrijft hij juiste de overige getallen van 1 tot en met $n$. Als Daniël klaar is, mag Merlijn een aantal vellen papier met de achterkant boven leggen (hij mag dit ook bij geen enkel vel of juist alle vellen doen). Als het hem lukt om de getallen 1 tot en met $n$ allemaal tegelijk zichtbaar te maken (waarbij dubbele mogen voorkomen), dan wint hij.
Bepaal de kleinste $k$ waarvoor Merlijn altijd kan winnen, wat Daniël ook doet.
|
We gaan laten zien dat Merlijn kan winnen dan en slechts dan als $2^{k}>n$. De kleinste $k$ waarvoor Merlijn wint, is dan dus de kleinste $k$ met $2^{k}>n$.
Stel dat $2^{k}>n$. Merlijn kiest één voor één bij elk vel of hij het wel of niet omdraait. Bij het eerste vel legt hij de kant boven waar de meeste getallen op staan (dus minstens de
helft van de getallen 1 tot en met $n$ ). Bij elk volgende vel legt hij de kant naar boven waar zoveel mogelijk getallen op staan die hij nog niet op eerdere vellen zichtbaar had liggen. Laat $b_{j}$ het aantal getallen zijn dat nog niet zichtbaar is op de vellen 1 tot en met $j$ nadat Merlijn voor deze vellen een keuze heeft gemaakt. Dan is $b_{1} \leq \frac{1}{2} n$ en $b_{j} \leq \frac{1}{2} b_{j-1}$ voor $j \geq 2$. Dus $b_{j} \leq\left(\frac{1}{2}\right)^{j} n$ en in het bijzonder $b_{k} \leq\left(\frac{1}{2}\right)^{k} n$. Omdat $2^{k}>n$, is $\left(\frac{1}{2}\right)^{k} n<1$, dus $b_{k}<1$. Omdat $b_{k}$ geheel moet zijn, geldt $b_{k}=0$. Dus na Merlijns keuze voor alle $k$ vellen zijn er geen getallen meer onzichtbaar.
Nu bewijzen we dat voor $2^{k} \leq n$ Daniël kan zorgen dat Merlijn niet kan winnen. Dit doen we met inductie naar $k$. Voor $k=1$ geldt $n \geq 2$. Daniël schrijft nu het getal 1 op de ene kant van het vel en alle andere getallen (dat is er minstens één) op de andere kant. Merlijn kan dit vel nu niet zo draaien dat hij kan winnen. Dat is de inductiebasis. Zij nu $k \geq 1$ en neem aan dat Daniël $k$ vellen zo kan beschrijven met $n \geq 2^{k}$ getallen dat Merlijn niet kan winnen. We bekijken nu $k+1$ vellen. Beschrijf de eerste $k$ vellen op zo'n manier met de getallen 1 tot en met $2^{k}$ dat Merlijn met alleen die getallen niet kan winnen; dit kan volgens de inductiehypothese. Schrijf vervolgens op elk vel weer dezelfde getallen voor en achter, maar dan verhoogd met $2^{k}$, zodat deze getallen van $2^{k}+1$ tot en met $2^{k+1}$ lopen. Schrijf ten slotte alle getallen $m$ met $2^{k+1}<m \leq n$ op de achterkant van elk vel. Nu bevat elk van deze $k$ vellen de getallen 1 tot en met $n$. Op vel nummer $k+1$ schrijven we aan de voorkant de getallen 1 tot en met $2^{k}$ en aan de achterkant de getallen $2^{k}+1$ tot en met $n$. Stel dat Merlijn het laatste vel met de voorkant boven laat liggen. Dan moet hij in ieder geval de getallen $2^{k}+1$ tot en met $2^{k+1}$ nog zichtbaar maken op de eerste $k$ vellen, maar dat kan niet volgens de inductiehypothese. Stel dat Merlijn het laatste vel juist met de achterkant boven legt. Dan moet hij de getallen 1 tot en met $2^{k}$ nog zichtbaar maken op de eerste $k$ vellen, maar dat kan ook weer niet volgens de inductiehypothese. Merlijn kan dus met deze vellen niet winnen. Dit voltooit het bewijs.
|
{
"exam": "Dutch_TST",
"problem_label": "5",
"problem_match": "\nOpgave 5.",
"resource_path": "Dutch_TST/segmented/nl-2014-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2014"
}
|
Determine all pairs $(a, b)$ of positive integers for which
$$
a^{2}+b \mid a^{2} b+a \quad \text { and } \quad b^{2}-a \mid a b^{2}+b .
$$
|
From $a^{2}+b \mid a^{2} b+a$ it follows
$$
a^{2}+b \mid\left(a^{2} b+a\right)-b\left(a^{2}+b\right)=a-b^{2}
$$
From $b^{2}-a \mid a b^{2}+b$ it follows
$$
b^{2}-a \mid\left(a b^{2}+b\right)-a\left(b^{2}-a\right)=b+a^{2} .
$$
We see that $a^{2}+b\left|a-b^{2}\right| a^{2}+b$. This means that $a^{2}+b$ is equal to $a-b^{2}$ up to a sign. Therefore, we have two cases: $a^{2}+b=b^{2}-a$ and $a^{2}+b=a-b^{2}$. In the second case, $a^{2}+b^{2}=a-b$. But $a^{2} \geq a$ and $b^{2} \geq b>-b$, so this is impossible. Therefore, we must have the first case: $a^{2}+b=b^{2}-a$. This gives $a^{2}-b^{2}=-a-b$, so $(a+b)(a-b)=-(a+b)$. Since $a+b$ is positive, we can divide by it and get $a-b=-1$, so $b=a+1$. All pairs that can satisfy the conditions are thus of the form $(a, a+1)$ for a positive integer $a$.
We check these pairs. We have $a^{2}+b=a^{2}+a+1$ and $a^{2} b+a=a^{2}(a+1)+a=$ $a^{3}+a^{2}+a=a\left(a^{2}+a+1\right)$, so the first divisibility relation is satisfied. Furthermore, $b^{2}-a=(a+1)^{2}-a=a^{2}+a+1$ and $a b^{2}+b=a(a+1)^{2}+(a+1)=a^{3}+2 a^{2}+2 a+1=$ $a\left(a^{2}+a+1\right)+a^{2}+a+1=(a+1)\left(a^{2}+a+1\right)$, so the second divisibility relation is also satisfied. The pairs $(a, a+1)$ thus satisfy the conditions and are therefore the exact solutions.
|
(a, a+1)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Bepaal alle paren $(a, b)$ van positieve gehele getallen waarvoor
$$
a^{2}+b \mid a^{2} b+a \quad \text { en } \quad b^{2}-a \mid a b^{2}+b .
$$
|
Uit $a^{2}+b \mid a^{2} b+a$ volgt
$$
a^{2}+b \mid\left(a^{2} b+a\right)-b\left(a^{2}+b\right)=a-b^{2}
$$
Uit $b^{2}-a \mid a b^{2}+b$ volgt
$$
b^{2}-a \mid\left(a b^{2}+b\right)-a\left(b^{2}-a\right)=b+a^{2} .
$$
We zien dus dat $a^{2}+b\left|a-b^{2}\right| a^{2}+b$. Dat betekent dat $a^{2}+b$ op eventueel het teken na gelijk is aan $a-b^{2}$. We krijgen dus twee gevallen: $a^{2}+b=b^{2}-a$ en $a^{2}+b=a-b^{2}$. In het tweede geval geldt $a^{2}+b^{2}=a-b$. Maar $a^{2} \geq a$ en $b^{2} \geq b>-b$, dus dit is onmogelijk. We moeten dus wel het eerste geval hebben: $a^{2}+b=b^{2}-a$. Hieruit volgt $a^{2}-b^{2}=-a-b$, dus $(a+b)(a-b)=-(a+b)$. Aangezien $a+b$ positief is, mogen we erdoor delen en krijgen we $a-b=-1$, dus $b=a+1$. Alle paren die kunnen voldoen zijn dus van de vorm $(a, a+1)$ voor een positieve gehele $a$.
We controleren deze paren. Er geldt $a^{2}+b=a^{2}+a+1$ en $a^{2} b+a=a^{2}(a+1)+a=$ $a^{3}+a^{2}+a=a\left(a^{2}+a+1\right)$, dus aan de eerste deelbaarheidsrelatie wordt voldaan. Verder is $b^{2}-a=(a+1)^{2}-a=a^{2}+a+1$ en $a b^{2}+b=a(a+1)^{2}+(a+1)=a^{3}+2 a^{2}+2 a+1=$ $a\left(a^{2}+a+1\right)+a^{2}+a+1=(a+1)\left(a^{2}+a+1\right)$, dus aan de tweede deelbaarheidsrelatie wordt ook voldoen. De paren $(a, a+1)$ voldoen dus en zijn daarmee precies de oplossingen.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2014-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2014"
}
|
Let $\triangle A B C$ be a triangle. Let $M$ be the midpoint of $B C$ and let $D$ be a point on the interior of side $A B$. The intersection of $A M$ and $C D$ we call $E$. Suppose that $|A D|=|D E|$. Prove that $|A B|=|C E|$.
|
There is only one configuration. Let $N$ be the midpoint of $AC$. Then $MN$ is a midline. Due to Z-angles, $\angle EAD = \angle MAB = \angle AMN$, but also $\angle EAD = \angle DEA = \angle MEC$. Therefore, $\angle AMN = \angle CEM$. If $S$ is the intersection of $MN$ and $CE$, then $\triangle SEM$ is isosceles with $|SE| = |SM|$. Furthermore, $SM$ is a midline in triangle $CDB$, so $2|SM| = |DB|$ and $S$ is the midpoint of $CD$, such that $|CS| = |SD|$. Combining all this, we find
$$
|CE| = |CS| + |SE| = |SD| + |SE| = 2|SE| + |DE| = 2|SM| + |AD| = |DB| + |AD| = |AB|.
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $\triangle A B C$ een driehoek. Zij $M$ het midden van $B C$ en zij $D$ een punt op het inwendige van zijde $A B$. Het snijpunt van $A M$ en $C D$ noemen we $E$. Veronderstel dat $|A D|=|D E|$. Bewijs dat $|A B|=|C E|$.
|
Er is maar één configuratie. Zij $N$ het midden van $A C$. Dan is $M N$ een middenparallel. Wegens Z-hoeken is $\angle E A D=\angle M A B=\angle A M N$, maar ook geldt $\angle E A D=\angle D E A=\angle M E C$. Dus $\angle A M N=\angle C E M$. Als nu $S$ het snijpunt van $M N$ en $C E$ is, dan is $\triangle S E M$ dus gelijkbenig met $|S E|=|S M|$. Verder is $S M$ een middenparallel in driehoek $C D B$, dus $2|S M|=|D B|$ en is $S$ dan het midden van $C D$, zodat $|C S|=|S D|$. Als we dit alles combineren, vinden we
$$
|C E|=|C S|+|S E|=|S D|+|S E|=2|S E|+|D E|=2|S M|+|A D|=|D B|+|A D|=|A B| .
$$
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2014-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2014"
}
|
Let $\triangle A B C$ be a triangle. Let $M$ be the midpoint of $B C$ and let $D$ be a point on the interior of side $A B$. The intersection of $A M$ and $C D$ we call $E$. Suppose that $|A D|=|D E|$. Prove that $|A B|=|C E|$.
|
There is only one configuration. Let $K$ be a point on $A M$ such that $M$ is the midpoint of line segment $A K$. Then $A K$ and $B C$ bisect each other, so $A B K C$ is a parallelogram. This means
$$
\angle C K A=\angle K A B=\angle E A D=\angle D E A=\angle C E K
$$
so triangle $C K E$ is isosceles with vertex angle at $C$. It follows that $|C E|=|C K|$. Due to the parallelogram, $|C K|=|A B|$, so $|C E|=|A B|$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $\triangle A B C$ een driehoek. Zij $M$ het midden van $B C$ en zij $D$ een punt op het inwendige van zijde $A B$. Het snijpunt van $A M$ en $C D$ noemen we $E$. Veronderstel dat $|A D|=|D E|$. Bewijs dat $|A B|=|C E|$.
|
Er is maar één configuratie. Zij $K$ een punt op $A M$ zodat $M$ het midden van lijnstuk $A K$ is. Dan snijden $A K$ en $B C$ elkaar middendoor, dus $A B K C$ is een parallellogram. Dat betekent
$$
\angle C K A=\angle K A B=\angle E A D=\angle D E A=\angle C E K
$$
dus driehoek $C K E$ is gelijkbenig met tophoek $C$. Daaruit volgt $|C E|=|C K|$. Vanwege het parallellogram is $|C K|=|A B|$, dus $|C E|=|A B|$.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2014-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2014"
}
|
Let $\triangle A B C$ be a triangle. Let $M$ be the midpoint of $B C$ and let $D$ be a point on the interior of side $A B$. The intersection of $A M$ and $C D$ we call $E$. Suppose that $|A D|=|D E|$. Prove that $|A B|=|C E|$.
|
We apply Menelaos to the line through $A, E$, and $M$ in triangle $B C D$. Therefore, we have
$$
\frac{|B M|}{|M C|} \cdot \frac{|C E|}{|E D|} \cdot \frac{|D A|}{|A B|}=1 .
$$
Since $M$ is the midpoint of $B C$, $\frac{|B M|}{|M C|}=1$. And it is given that $|A D|=|D E|$. This together implies that $|C E|=|A B|$.
|
|C E|=|A B|
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $\triangle A B C$ een driehoek. Zij $M$ het midden van $B C$ en zij $D$ een punt op het inwendige van zijde $A B$. Het snijpunt van $A M$ en $C D$ noemen we $E$. Veronderstel dat $|A D|=|D E|$. Bewijs dat $|A B|=|C E|$.
|
We passen Menelaos toe op de lijn door $A, E$ en $M$ in driehoek $B C D$. Er geldt dus
$$
\frac{|B M|}{|M C|} \cdot \frac{|C E|}{|E D|} \cdot \frac{|D A|}{|A B|}=1 .
$$
Omdat $M$ het midden van $B C$ is, is $\frac{|B M|}{|M C|}=1$. En gegeven is dat $|A D|=|D E|$. Dit geeft samen dat $|C E|=|A B|$.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2014-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing III.",
"tier": "T1",
"year": "2014"
}
|
Let $\triangle A B C$ be a triangle. Let $M$ be the midpoint of $B C$ and let $D$ be a point on the interior of side $A B$. The intersection of $A M$ and $C D$ we call $E$. Suppose that $|A D|=|D E|$. Prove that $|A B|=|C E|$.
|
We first prove that $A$ and $B$ lie on the same side of the perpendicular bisector of $BC$. Suppose that $A$ and $C$ lie on the same side or $A$ lies on the perpendicular bisector. Then $|AB| \geq |AC|$, and the angle bisector theorem says that the bisector from angle $A$ intersects side $BC$ between $M$ and $C$. Thus, $\angle BAM \leq \angle CAM$. But
$$
\begin{aligned}
\angle AEC & =180^{\circ}-\angle AED=180^{\circ}-\angle DAE=180^{\circ}-\angle BAM \\
& \geq 180^{\circ}-\angle CAM=\angle AEC+\angle ACE>\angle AEC.
\end{aligned}
$$
Contradiction. This proves our claim.
Now reflect $A$ in the perpendicular bisector of $BC$ and call the image $A'$. Then $\angle MA'C = \angle MAB = \angle EAD$. Due to the isosceles property, $\angle EAD = \angle DEA = \angle MEC$, so $\angle MA'C = \angle MEC$. Since $A'$ and $C$ lie on the same side of the perpendicular bisector of $BC$ and $E$ lies on the other side (since $E$ lies on $AM$), this means that $MCA'E$ is a cyclic quadrilateral. Therefore,
$$
\angle EA'C = 180^{\circ} - \angle EMC = \angle EMB = \angle AMB = \angle A'MC = \angle A'EC,
$$
where we have also used the reflection again. Thus, triangle $A'EC$ is isosceles with vertex $C$. Therefore, $|CE| = |CA'| = |BA|$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $\triangle A B C$ een driehoek. Zij $M$ het midden van $B C$ en zij $D$ een punt op het inwendige van zijde $A B$. Het snijpunt van $A M$ en $C D$ noemen we $E$. Veronderstel dat $|A D|=|D E|$. Bewijs dat $|A B|=|C E|$.
|
We bewijzen eerst dat $A$ en $B$ aan dezelfde kant van de middelloodlijn van $B C$ liggen. Stel namelijk dat $A$ en $C$ juist aan dezelfde kant liggen of $A$ op de middelloodlijn ligt. Dan geldt $|A B| \geq|A C|$ en zegt de bissectricestelling dus dat de bissectrice vanuit hoek $A$ de zijde $B C$ snijdt tussen $M$ en $C$. Dus $\angle B A M \leq \angle C A M$. Maar
$$
\begin{aligned}
\angle A E C & =180^{\circ}-\angle A E D=180^{\circ}-\angle D A E=180^{\circ}-\angle B A M \\
& \geq 180^{\circ}-\angle C A M=\angle A E C+\angle A C E>\angle A E C .
\end{aligned}
$$
Tegenspraak. Dit bewijst onze claim.
Spiegel nu $A$ in de middelloodlijn van $B C$ en noem het beeld $A^{\prime}$. Dan is $\angle M A^{\prime} C=$ $\angle M A B=\angle E A D$. Vanwege de gelijkbenigheid is $\angle E A D=\angle D E A=\angle M E C$, dus $\angle M A^{\prime} C=\angle M E C$. Omdat $A^{\prime}$ en $C$ aan dezelfde kant van de middelloodlijn van $B C$ liggen en $E$ juist aan de andere kant (want $E$ ligt op $A M$ ), betekent dat dat $M C A^{\prime} E$ een koordenvierhoek is. Daarom is
$$
\angle E A^{\prime} C=180^{\circ}-\angle E M C=\angle E M B=\angle A M B=\angle A^{\prime} M C=\angle A^{\prime} E C,
$$
waarbij we ook de spiegeling nogmaals gebruikt hebben. Dus is driehoek $A^{\prime} E C$ gelijkbenig met top $C$. Dus $|C E|=\left|C A^{\prime}\right|=|B A|$.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2014-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing IV.",
"tier": "T1",
"year": "2014"
}
|
Let $\triangle A B C$ be a triangle. Let $M$ be the midpoint of $B C$ and let $D$ be a point on the interior of side $A B$. The intersection of $A M$ and $C D$ we call $E$. Suppose that $|A D|=|D E|$. Prove that $|A B|=|C E|$.
|
The sine rule in triangle $MAB$ gives
$$
\frac{|MB|}{\sin \angle MAB}=\frac{|AB|}{\sin \angle AMB}=\frac{|AB|}{\sin \angle AMC},
$$
where the last $=$ sign holds because $\angle AMB + \angle AMC = 180^{\circ}$. The sine rule in triangle EMC gives
$$
\frac{|MC|}{\sin \angle MEC}=\frac{|EC|}{\sin \angle EMC}.
$$
It is given that $|MB| = |MC|$ and $\angle AMC = \angle EMC$. Also, $\angle MAB = \angle EAD = \angle DEA = \angle MEC$. Combining all this gives
$$
\frac{|AB|}{\sin \angle AMC}=\frac{|MB|}{\sin \angle MAB}=\frac{|MC|}{\sin \angle MEC}=\frac{|EC|}{\sin \angle EMC}=\frac{|EC|}{\sin \angle AMC},
$$
thus $|AB| = |EC|$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $\triangle A B C$ een driehoek. Zij $M$ het midden van $B C$ en zij $D$ een punt op het inwendige van zijde $A B$. Het snijpunt van $A M$ en $C D$ noemen we $E$. Veronderstel dat $|A D|=|D E|$. Bewijs dat $|A B|=|C E|$.
|
De sinusregel in driehoek $M A B$ geeft
$$
\frac{|M B|}{\sin \angle M A B}=\frac{|A B|}{\sin \angle A M B}=\frac{|A B|}{\sin \angle A M C},
$$
waarbij het laatste $=$-teken geldt omdat $\angle A M B+\angle A M C=180^{\circ}$. De sinusregel in driehoek EMC geeft
$$
\frac{|M C|}{\sin \angle M E C}=\frac{|E C|}{\sin \angle E M C} .
$$
Er geldt $|M B|=|M C|$ en $\angle A M C=\angle E M C$. Ook is $\angle M A B=\angle E A D=\angle D E A=$ $\angle M E C$. Dit alles combineren geeft
$$
\frac{|A B|}{\sin \angle A M C}=\frac{|M B|}{\sin \angle M A B}=\frac{|M C|}{\sin \angle M E C}=\frac{|E C|}{\sin \angle E M C}=\frac{|E C|}{\sin \angle A M C},
$$
dus $|A B|=|E C|$.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2014-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing V.",
"tier": "T1",
"year": "2014"
}
|
Let $a, b$ and $c$ be rational numbers for which $a+b c, b+a c$ and $a+b$ are all not equal to 0 and for which it holds that
$$
\frac{1}{a+b c}+\frac{1}{b+a c}=\frac{1}{a+b}
$$
Prove that $\sqrt{(c-3)(c+1)}$ is rational.
|
It holds that
$$
\frac{1}{a+b c}+\frac{1}{b+a c}=\frac{(b+a c)+(a+b c)}{(a+b c)(b+a c)}=\frac{(a+b)+(a+b) c}{a b+a^{2} c+b^{2} c+a b c^{2}}
$$
From the given equality, it follows that
$$
(a+b)((a+b)+(a+b) c)=a b+a^{2} c+b^{2} c+a b c^{2}
$$
or
$$
\begin{aligned}
(a+b)^{2} & =a b+a^{2} c+b^{2} c+a b c^{2}-(a+b)^{2} c \\
& =a b+a b c^{2}-2 a b c \\
& =a b(c-1)^{2}
\end{aligned}
$$
Thus, $(c-1)^{2}=0$ or $a b$ is the square of a rational number. If $(c-1)^{2}=0$, then $c=1$ and the original equation becomes
$$
\frac{1}{a+b}+\frac{1}{a+b}=\frac{1}{a+b}
$$
which cannot be true. Therefore, $(c-1)^{2} \neq 0$, which implies that $a b$ is the square of a rational number.
Furthermore, we see that
$$
\begin{aligned}
(a-b)^{2} & =(a+b)^{2}-4 a b \\
& =a b+a b c^{2}-2 a b c-4 a b \\
& =a b c^{2}-2 a b c-3 a b \\
& =a b(c-3)(c+1) .
\end{aligned}
$$
Thus, $a=0$ or $b=0$ or $(c-3)(c+1)$ is the square of a rational number. If $a=0$, the original equation becomes
$$
\frac{1}{b c}+\frac{1}{b}=\frac{1}{b}
$$
which cannot be true. Therefore, $a \neq 0$ and similarly, we see that $b \neq 0$. Thus, $(c-3)(c+1)$ is the square of a rational number.
|
(c-3)(c+1) \text{ is the square of a rational number}
|
Yes
|
Yes
|
proof
|
Algebra
|
Laat $a, b$ en $c$ rationale getallen zijn waarvoor $a+b c, b+a c$ en $a+b$ allemaal ongelijk aan 0 zijn en waarvoor geldt dat
$$
\frac{1}{a+b c}+\frac{1}{b+a c}=\frac{1}{a+b}
$$
Bewijs dat $\sqrt{(c-3)(c+1)}$ rationaal is.
|
Er geldt
$$
\frac{1}{a+b c}+\frac{1}{b+a c}=\frac{(b+a c)+(a+b c)}{(a+b c)(b+a c)}=\frac{(a+b)+(a+b) c}{a b+a^{2} c+b^{2} c+a b c^{2}}
$$
Uit de gegeven gelijkheid volgt dus
$$
(a+b)((a+b)+(a+b) c)=a b+a^{2} c+b^{2} c+a b c^{2}
$$
oftewel
$$
\begin{aligned}
(a+b)^{2} & =a b+a^{2} c+b^{2} c+a b c^{2}-(a+b)^{2} c \\
& =a b+a b c^{2}-2 a b c \\
& =a b(c-1)^{2}
\end{aligned}
$$
Dus $(c-1)^{2}=0$ of $a b$ is het kwadraat van een rationaal getal. Als $(c-1)^{2}=0$, dan is $c=1$ en staat er in de oorspronkelijke vergelijking
$$
\frac{1}{a+b}+\frac{1}{a+b}=\frac{1}{a+b}
$$
wat niet waar kan zijn. Dus $(c-1)^{2} \neq 0$, waaruit volgt dat $a b$ het kwadraat van een rationaal getal is.
Verder zien we dat
$$
\begin{aligned}
(a-b)^{2} & =(a+b)^{2}-4 a b \\
& =a b+a b c^{2}-2 a b c-4 a b \\
& =a b c^{2}-2 a b c-3 a b \\
& =a b(c-3)(c+1) .
\end{aligned}
$$
Dus $a=0$ of $b=0$ of $(c-3)(c+1)$ is het kwadraat van een rationaal getal. Als $a=0$ staat er in de oorspronkelijke vergelijking
$$
\frac{1}{b c}+\frac{1}{b}=\frac{1}{b}
$$
wat niet waar kan zijn. Dus $a \neq 0$ en op vergelijkbare manier zien we dat $b \neq 0$. Dus $(c-3)(c+1)$ is het kwadraat van een rationaal getal.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2014-C_uitwerkingen.jsonl",
"solution_match": "# Oplossing I.",
"tier": "T1",
"year": "2014"
}
|
Let $a, b$ and $c$ be rational numbers for which $a+b c, b+a c$ and $a+b$ are all not equal to 0 and for which it holds that
$$
\frac{1}{a+b c}+\frac{1}{b+a c}=\frac{1}{a+b}
$$
Prove that $\sqrt{(c-3)(c+1)}$ is rational.
|
It holds that
$$
\frac{1}{a+b c}+\frac{1}{b+a c}=\frac{(b+a c)+(a+b c)}{(a+b c)(b+a c)}=\frac{a+b+a c+b c}{a b+a^{2} c+b^{2} c+a b c^{2}}.
$$
From the given equality, it follows that
$$
(a+b)(a+b+a c+b c)=a b+a^{2} c+b^{2} c+a b c^{2}
$$
or equivalently,
$$
a^{2}+a b+a^{2} c+a b c+a b+b^{2}+a b c+b^{2} c=a b+a^{2} c+b^{2} c+a b c^{2}
$$
or equivalently,
$$
a^{2}+2 a b c+a b-a b c^{2}+b^{2}=0
$$
We can view this as a quadratic equation in $a$, for which we know it has a rational solution. The discriminant of this equation must therefore be the square of a rational number. This discriminant is equal to
$$
\begin{aligned}
D & =\left(2 b c+b-b c^{2}\right)^{2}-4 b^{2} \\
& =\left(2 b c+b-b c^{2}-2 b\right)\left(2 b c+b-b c^{2}+2 b\right) \\
& =b^{2}\left(2 c-1-c^{2}\right)\left(2 c+3-c^{2}\right) \\
& =b^{2}(c^{2}-2 c+1)(c^{2}-2 c-3) \\
& =b^{2}(c-1)^{2}(c+1)(c-3).
\end{aligned}
$$
Just as in the previous solution, we see that $b=0$ and $c=1$ do not provide solutions, so it follows from this that
$$
(c-3)(c+1)=\frac{D}{b^{2}(c-1)^{2}}
$$
is the square of a rational number.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Laat $a, b$ en $c$ rationale getallen zijn waarvoor $a+b c, b+a c$ en $a+b$ allemaal ongelijk aan 0 zijn en waarvoor geldt dat
$$
\frac{1}{a+b c}+\frac{1}{b+a c}=\frac{1}{a+b}
$$
Bewijs dat $\sqrt{(c-3)(c+1)}$ rationaal is.
|
Er geldt
$$
\frac{1}{a+b c}+\frac{1}{b+a c}=\frac{(b+a c)+(a+b c)}{(a+b c)(b+a c)}=\frac{a+b+a c+b c}{a b+a^{2} c+b^{2} c+a b c^{2}} .
$$
Uit de gegeven gelijkheid volgt dus
$$
(a+b)(a+b+a c+b c)=a b+a^{2} c+b^{2} c+a b c^{2}
$$
oftewel
$$
a^{2}+a b+a^{2} c+a b c+a b+b^{2}+a b c+b^{2} c=a b+a^{2} c+b^{2} c+a b c^{2}
$$
oftewel
$$
a^{2}+2 a b c+a b-a b c^{2}+b^{2}=0
$$
We kunnen dit zien als kwadratische vergelijking in $a$, waarvan we weten dat het een rationale oplossing heeft. De discriminant van deze vergelijking moet dus het kwadraat van een rationaal getal zijn. Deze discriminant is gelijk aan
$$
\begin{aligned}
D & =\left(2 b c+b-b c^{2}\right)^{2}-4 b^{2} \\
& =\left(2 b c+b-b c^{2}-2 b\right)\left(2 b c+b-b c^{2}+2 b\right) \\
& =b^{2}\left(2 c-1-c^{2}\right)\left(2 c+3-c^{2}\right) \\
& =b^{2}\left(c^{2}-2 c+1\right)\left(c^{2}-2 c-3\right) \\
& =b^{2}(c-1)^{2}(c+1)(c-3) .
\end{aligned}
$$
Net als in de vorige oplossing zien we dat $b=0$ en $c=1$ geen oplossingen geven, dus volgt hieruit dat
$$
(c-3)(c+1)=\frac{D}{b^{2}(c-1)^{2}}
$$
het kwadraat van een rationaal getal is.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2014-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2014"
}
|
Let $\triangle A B C$ be a triangle with $|A C|=2|A B|$, and let $O$ be the center of the circumscribed circle. Let $D$ be the intersection of the angle bisector of $\angle A$ with $B C$. Let $E$ be the orthogonal projection of $O$ on $A D$, and let $F \neq D$ be the point on $A D$ for which $|C D|=|C F|$. Prove that $\angle E B F=\angle E C F$.
|
When $E=F$, angles $E B F$ and $E C F$ are both 0, hence equal to each other. We therefore assume from now on that $E \neq F$. Let $G$ be the second intersection of $A D$ and the circumcircle of $\triangle A B C$. There are multiple configurations possible. We consider the configuration where the points on line $A D$ are in the order $A, E, D, G, F$, with the possibility that $D=E$ and $F=G$. Other configurations proceed analogously.
Let $M$ be the midpoint of $A C$. Since $|A B|=\frac{|A C|}{2}=|A M|$ and $A D$ is the bisector of $\angle B A M$, $M$ is the image of $B$ under reflection in $A D$. Therefore, $\angle E B F=\angle E M F$, so to prove that $\angle E B F=\angle E C F$, it suffices to prove that $\angle E M F=\angle E C F$. This is equivalent to the points $E, M, C$, and $F$ lying on a circle, since $M$ and $C$ lie on the same side of $E F$.
To prove this, we show that $\angle E F C + \angle E M C = 180^{\circ}$, or equivalently, that $\angle E F C = \angle A M E$. Since $\triangle C D F$ is isosceles, we find
$$
\angle E F C = \angle D F C = \angle F D C = 180^{\circ} - \angle A D C = \angle D A C + \angle A C D = \frac{\angle A}{2} + \angle C.
$$
Furthermore, the perpendicular bisector of a chord passes through the center of the corresponding circle, so $M O$ is perpendicular to $A C$. This means, by Thales' theorem, that $E$ and $M$ both lie on the circle with diameter $A O$. This implies that $\angle A M E = \angle A O E$. Then, $\triangle A O G$ is isosceles, so the altitude $O E$ is also the bisector in this triangle. We thus find, using the inscribed angle theorem, that
$$
\angle A O E = \frac{\angle A O G}{2} = \angle A C G = \angle A C B + \angle B C G = \angle A C B + \angle B A G = \angle C + \frac{\angle A}{2}.
$$
Therefore,
$$
\angle A M E = \angle A O E = \angle C + \frac{\angle A}{2} = \angle E F C,
$$
precisely what we needed to prove.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $\triangle A B C$ een driehoek met $|A C|=2|A B|$ en zij $O$ het middelpunt van de omgeschreven cirkel. Zij $D$ het snijpunt van de bissectrice van $\angle A$ met $B C$. Zij $E$ de loodrechte projectie van $O$ op $A D$ en zij $F \neq D$ het punt op $A D$ waarvoor $|C D|=|C F|$. Bewijs dat $\angle E B F=\angle E C F$.
|
Als $E=F$ zijn hoeken $E B F$ en $E C F$ beide 0 , dus aan elkaar gelijk. We nemen dus verder aan dat $E \neq F$. Zij $G$ het tweede snijpunt van $A D$ en de omgeschreven cirkel van $\triangle A B C$. Er zijn meerdere configuraties mogelijk. We bekijken de configuratie waarbij de punten op de lijn $A D$ in de volgorde $A, E, D, G, F$ liggen, waarbij eventueel mag gelden $D=E$ en $F=G$. Andere configuraties gaan analoog.
Zij $M$ het midden van $A C$. Omdat $|A B|=\frac{|A C|}{2}=|A M|$ en omdat $A D$ de bissectrice van $\angle B A M$ is, is $M$ het beeld van $B$ onder spiegeling in $A D$. Er geldt dus $\angle E B F=\angle E M F$, dus om te bewijzen dat $\angle E B F=\angle E C F$ is het voldoende om te bewijzen dat $\angle E M F=$ $\angle E C F$. Dat is equivalent met dat de punten $E, M, C$ en $F$ op een cirkel liggen, aangezien $M$ en $C$ aan dezelfde kant van $E F$ liggen.
Om dit te bewijzen laten we zien dat $\angle E F C+\angle E M C=180^{\circ}$, oftewel dat $\angle E F C=$ $\angle A M E$. Omdat $\triangle C D F$ gelijkbenig is, vinden we
$$
\angle E F C=\angle D F C=\angle F D C=180^{\circ}-\angle A D C=\angle D A C+\angle A C D=\frac{\angle A}{2}+\angle C .
$$
Verder geldt dat de middelloodlijn van een koorde door het middelpunt van de bijbehorende cirkel gaat, dus $M O$ staat loodrecht op $A C$. Dit betekent met Thales dat $E$ en $M$ beide op de cirkel met middellijn $A O$ liggen. Hieruit volgt dat $\angle A M E=\angle A O E$. Dan is $\triangle A O G$ gelijkbenig, dus hoogtelijn $O E$ is in deze driehoek ook bissectrice. We vinden dus met de middelpunt-omtrekhoeksstelling dat
$$
\angle A O E=\frac{\angle A O G}{2}=\angle A C G=\angle A C B+\angle B C G=\angle A C B+\angle B A G=\angle C+\frac{\angle A}{2} .
$$
Er geldt dus
$$
\angle A M E=\angle A O E=\angle C+\frac{\angle A}{2}=\angle E F C,
$$
precies wat we moesten bewijzen.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2014-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2014"
}
|
Let $\triangle A B C$ be a triangle with $|A C|=2|A B|$, and let $O$ be the center of the circumscribed circle. Let $D$ be the intersection of the angle bisector of $\angle A$ with $B C$. Let $E$ be the orthogonal projection of $O$ on $A D$, and let $F \neq D$ be the point on $A D$ for which $|C D|=|C F|$. Prove that $\angle E B F=\angle E C F$.
|
Let $G \neq A$ be the intersection of $A D$ with the circumcircle of $\triangle A B C$. Then $|A G|=2|A E|$ because the projection of the center of a circle onto a chord of that circle is the midpoint of that chord. Let $M$ be the midpoint of $A C$. Since $|A B|=\frac{|A C|}{2}=|A M|$ and since $A D$ is the bisector of $\angle B A M$, $M$ is the image of $B$ under reflection in $A D$. Now, $\angle D G C=\angle A G C=\angle A B C=\angle A B D=$ $\angle D M A=180^{\circ}-\angle D M C$, so $D M C G$ is a cyclic quadrilateral. Now, $A M^{2}=\frac{A M \cdot A C}{2}=$ $\frac{A D \cdot A G}{2}=A D \cdot A E$, so $\triangle A M E \sim \triangle A D M$ (sas). Now, $180^{\circ}-\angle E M C=\angle E M A=$ $\angle M D A=\angle B D A=\angle C D F=\angle D F C=\angle E F C$, so $E M C F$ is a cyclic quadrilateral. Now, $\angle E B F=\angle E M F=\angle E C F$, which is exactly what we had to prove.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $\triangle A B C$ een driehoek met $|A C|=2|A B|$ en zij $O$ het middelpunt van de omgeschreven cirkel. Zij $D$ het snijpunt van de bissectrice van $\angle A$ met $B C$. Zij $E$ de loodrechte projectie van $O$ op $A D$ en zij $F \neq D$ het punt op $A D$ waarvoor $|C D|=|C F|$. Bewijs dat $\angle E B F=\angle E C F$.
|
Zij $G \neq A$ het snijpunt van $A D$ met de omgeschreven cirkel van $\triangle A B C$. Dan geldt $|A G|=2|A E|$ omdat de projectie van het middelpunt van een cirkel op een koorde van die cirkel het midden van die koorde is. Zij $M$ het midden van $A C$. Omdat $|A B|=\frac{|A C|}{2}=|A M|$ en omdat $A D$ de bissectrice van $\angle B A M$ is, is $M$ het beeld van $B$ onder spiegeling in $A D$. Nu geldt er $\angle D G C=\angle A G C=\angle A B C=\angle A B D=$ $\angle D M A=180^{\circ}-\angle D M C$, dus $D M C G$ is een koordenvierhoek. Nu is $A M^{2}=\frac{A M \cdot A C}{2}=$ $\frac{A D \cdot A G}{2}=A D \cdot A E$, dus $\triangle A M E \sim \triangle A D M$ (zhz). Nu geldt $180^{\circ}-\angle E M C=\angle E M A=$ $\angle M D A=\angle B D A=\angle C D F=\angle D F C=\angle E F C$, dus $E M C F$ is een koordenvierhoek. Nu is $\angle E B F=\angle E M F=\angle E C F$, precies wat we moesten bewijzen.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2014-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2014"
}
|
On a $2014 \times 2014$ board, each of the $2014^{2}$ squares contains a lamp. Lamps can be on or off. In the initial situation, some of the lamps are on. In a move, you choose a row or column in which at least 1007 lamps are on and change the status of all 2014 lamps in that row or column (from on to off and from off to on). Find the smallest non-negative integer $k$ such that the following holds: from any initial situation, you can reach a situation in a finite number of steps where at most $k$ lamps are on.
|
Number the rows from 1 to 2014 and the columns as well. Consider the following initial situation: in row $i$, the lamps in columns $i, i+1, \ldots, i+1005$ are on and the rest are off, where we calculate the column numbers modulo 2014. Now, in each row and each column, exactly 1006 lamps are on. Therefore, no move is possible. It is thus not always possible to reach a situation with fewer than 2014 • 1006 lamps on.
Now we show that we can always reach a situation with at most 2014 • 1006 lamps on. Suppose, for the sake of contradiction, that in a certain situation there are at least 2014•1006+1 lamps on and it is not possible to reduce the number of lamps on. If there is a row or column with 1008 or more lamps on, we can change the status of the lamps in this row or column, and there will be fewer lamps on afterward, a contradiction. Therefore, in every row and column, there are at most 1007 lamps on.
Let $I$ be the set of rows with exactly 1007 lamps on, and let $J_{1}$ be the set of columns with exactly 1007 lamps on. We plan to change the status of the lamps in all rows in $I$. This is called the big plan. If after executing the big plan, a column has 1008 or more lamps on, we get a contradiction again, so we assume that this does not happen. Let $J_{2}$ be the set of columns that will have exactly 1007 lamps on after executing the big plan. If there is a cell $(i, j)$ with $i \in I$ and $j \in J_{1}$ where the lamp is off, I can change row $i$ and get more than 1007 lamps on in column $j$, a contradiction. Therefore, every lamp at $(i, j)$ with $i \in I$ and $j \in J_{1}$ is on. If there is a cell $(i, j)$ with $i \in I$ and $j \in J_{2}$ where the lamp is off after executing the big plan, I get a contradiction in the same way. Therefore, every lamp at $(i, j)$ with $i \in I$ and $j \in J_{2}$ is on after executing the big plan. Since the columns in $J_{2}$ each have exactly 1007 lamps on after executing the big plan, they had $1007-|I|$ lamps on before the big plan. (The notation $|X|$ denotes the number of elements in the set $X$.) The columns in $J_{1}$ each have exactly 1007 lamps on, and this also means that $J_{1}$ and $J_{2}$ are disjoint (no overlapping columns). The remaining columns have at most 1006 lamps on. The total number of lamps on before the big plan is thus at most
$(1007-|I|)|J_{2}| + 1007|J_{1}| + 1006(2014 - |J_{1}| - |J_{2}|) = 1006 \cdot 2014 + |J_{1}| + |J_{2}| - |I| \cdot |J_{2}|$.
This must be at least $1006 \cdot 2014 + 1$, so $|J_{1}| + |J_{2}| - |I| \cdot |J_{2}| \geq 1$. This implies $|J_{1}| > (|I| - 1)|J_{2}|$. If $|I| \geq 2$, then $|J_{1}| > |J_{2}|$. By executing the big plan, the number of columns with 1007 lamps on is thus reduced. But then we have a situation again with $|I|$ rows with 1007 lamps on, where $J_{1}$ and $J_{2}$ are exactly swapped. So we can execute a new big plan, which again reduces the number of columns with 1007 lamps on. Contradiction, because we are back in the initial situation. We conclude that $|I| = 1$ must hold.
We thus have the situation that there is exactly one row with exactly 1007 lamps on. Similarly, we can show that there must also be exactly one column with exactly 1007 lamps on. Since there are $1006 \cdot 2014 + 1$ lamps on, there must be exactly 1006 lamps on in every other row and column. Now change the status of the lamps in the row with 1007 lamps on. In 1007 columns, there will then be $1006 + 1 = 1007$ lamps on. We have already seen that in this situation, the number of lamps that are on can be reduced.
We see that if there are more than 1006 • 2014 lamps on, it is always possible to reduce this number. Therefore, the smallest $k$ is $1006 \cdot 2014$.
|
1006 \cdot 2014
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Op een $2014 \times 2014$-bord staat op elk van de $2014^{2}$ vakjes een lamp. Lampen kunnen aan of uit staan. In de beginsituatie is een aantal van de lampen aan. In een zet kies je een rij of kolom waarin minstens 1007 lampen aan staan en verander je van alle 2014 lampen in die rij of kolom de status (van aan naar uit en van uit naar aan). Vind de kleinste niet-negatieve gehele $k$ zodat geldt: vanuit elke beginsituatie kun je in een eindig aantal stappen naar een situatie waarin hoogstens $k$ lampen aan staan.
|
Nummer de rijen van 1 tot en met 2014 en de kolommen ook. Bekijk de volgende beginsituatie: in rij $i$ zijn de lampen in de kolommen $i, i+1, \ldots, i+1005$ aan en de rest uit, waarbij we de kolomnummers modulo 2014 rekenen. Nu zijn in elke rij en in elke kolom precies 1006 lampen aan. Er is dus geen zet mogelijk. Het is dus niet altijd mogelijk om naar een situatie met minder dan 2014 • 1006 lampen aan toe te gaan.
Nu laten we zien dat we wel altijd naar een situatie met hoogstens 2014 • 1006 lampen aan toe kunnen. Stel uit het ongerijmde dat er in een bepaalde situatie minstens 2014•1006+1 lampen aan staan en het toch niet mogelijk is om naar minder lampen aan toe te gaan. Als er een rij of kolom is met 1008 of meer lampen aan, dan kunnen we de status van de lampen in deze rij of kolom veranderen en zijn er daarna minder lampen aan, tegenspraak. Dus in elke rij en kolom staan hoogstens 1007 lampen aan.
Zij $I$ de verzameling rijen met precies 1007 lampen aan en zij $J_{1}$ de verzameling kolommen met precies 1007 lampen aan. We zijn van plan om de status van de lampen in alle rijen in $I$ om te zetten. Dit noemen we het grote plan. Als na het uitvoeren van het grote plan een kolom ontstaat met 1008 of meer lampen aan, krijgen we weer een tegenspraak, dus we nemen aan dat dat niet zo is. $\mathrm{Zij} J_{2}$ de verzameling kolommen die na het uitvoeren van het grote plan precies 1007 lampen aan zullen hebben. Als er een vakje $(i, j)$ bestaat met $i \in I$ en $j \in J_{1}$ waarvan de lamp uit staat, kan ik rij $i$ omzetten en krijg ik in kolom $j$ meer dan 1007 lampen aan, tegenspraak. Dus elke lamp op $(i, j)$ met $i \in I$ en $j \in J_{1}$ is aan. Als er een vakje $(i, j)$ bestaat met $i \in I$ en $j \in J_{2}$ waarvan de lamp na het uitvoeren van het grote plan uit staat, krijg ik op dezelfde manier een tegenspraak. Dus elke lamp op $(i, j)$ met $i \in I$ en $j \in J_{2}$ staat na het uitvoeren van het grote plan aan. Omdat de kolommen in $J_{2}$ na het uitvoeren van het grote plan elk precies 1007 lampen aan hebben, hebben ze vóór het uitvoeren van het grote plan dus $1007-|I|$ lampen aan. (De notatie $|X|$ geeft het aantal elementen in de verzameling $X$ aan.) De kolommen in $J_{1}$ hebben precies 1007 lampen aan en dit betekent ook dat $J_{1}$ en $J_{2}$ disjunct zijn (geen overlappende kolommen hebben). De overige kolommen hebben hoogstens 1006 lampen aan. Het totaal aantal lampen aan vóór het grote plan is dus hoogstens
$(1007-|I|)\left|J_{2}\right|+1007\left|J_{1}\right|+1006\left(2014-\left|J_{1}\right|-\left|J_{2}\right|\right)=1006 \cdot 2014+\left|J_{1}\right|+\left|J_{2}\right|-|I| \cdot\left|J_{2}\right|$.
Dit moet minstens $1006 \cdot 2014+1$ zijn, dus $\left|J_{1}\right|+\left|J_{2}\right|-|I| \cdot\left|J_{2}\right| \geq 1$. Hieruit volgt $\left|J_{1}\right|>(|I|-1)\left|J_{2}\right|$. Als $|I| \geq 2$, dan $\left|J_{1}\right|>\left|J_{2}\right|$. Door het uitvoeren van het grote plan wordt dan dus het aantal kolommen met 1007 lampen aan verkleind. Maar daarna hebben we weer een situatie met $|I|$ rijen met 1007 lampen aan, waarbij $J_{1}$ en $J_{2}$ precies verwisseld zijn. Dus kunnen we hier een nieuw groot plan uitvoeren waardoor het aantal kolommen
met 1007 lampen aan weer kleiner wordt. Tegenspraak, want we zijn nu weer terug in de uitgangssituatie. We concluderen dat moet gelden $|I|=1$.
We hebben dus de situatie dat er precies één rij is met precies 1007 lampen aan. Analoog kunnen we laten zien dat er ook één kolom moet zijn met precies 1007 lampen aan. Omdat er $1006 \cdot 2014+1$ lampen aan staan, moeten er in elke andere rij en kolom precies 1006 lampen aan staan. Verander nu de status van lampen in de rij met 1007 lampen aan. In 1007 kolommen staan vervolgens $1006+1=1007$ lampen aan. We hebben al gezien dat we in deze situatie het aantal lampen dat aan staat, kunnen verminderen.
We zien dat als er meer dan 1006 • 2014 lampen aan staan, het altijd mogelijk is om dit aantal te verminderen. Dus de kleinste $k$ is $1006 \cdot 2014$.
|
{
"exam": "Dutch_TST",
"problem_label": "5",
"problem_match": "\nOpgave 5.",
"resource_path": "Dutch_TST/segmented/nl-2014-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2014"
}
|
Let $f: \mathbb{Z}_{>0} \rightarrow \mathbb{R}$ be a function for which it holds that for all $n>1$ there is a prime divisor $p$ of $n$ such that
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)
$$
Moreover, it is given that $f\left(2^{2014}\right)+f\left(3^{2015}\right)+f\left(5^{2016}\right)=2013$.
Calculate $f\left(2014^{2}\right)+f\left(2015^{3}\right)+f\left(2016^{5}\right)$.
|
When $n=q$ with $q$ prime, there is only one prime divisor of $n$, namely $q$, so it must hold that $f(q)=f(1)-f(q)$, thus $f(q)=\frac{1}{2} f(1)$. If $n=q^{2}$ with $q$ prime, then $n$ also has only one prime divisor, so $f\left(q^{2}\right)=f(q)-f(q)=0$. We now prove by induction on $k$ that $f\left(q^{k}\right)=\frac{2-k}{2} f(1)$ if $q$ is a prime number and $k$ is a positive integer. For $k=1$ and $k=2$, we have already shown this. Suppose now that $f\left(q^{k}\right)=\frac{2-k}{2} f(1)$ for some $k \geq 2$ and substitute $n=q^{k+1}$. It holds that
$$
f\left(q^{k+1}\right)=f\left(q^{k}\right)-f(q)=\frac{2-k}{2} f(1)-\frac{1}{2} f(1)=\frac{2-(k+1)}{2} f(1)
$$
This completes the induction.
Now we use our second given. It holds that
$$
\begin{aligned}
2013 & =f\left(2^{2014}\right)+f\left(3^{2015}\right)+f\left(5^{2016}\right) \\
& =\frac{2-2014}{2} f(1)+\frac{2-2015}{2} f(1)+\frac{2-2016}{2} f(1) \\
& =-\frac{6039}{2} f(1)
\end{aligned}
$$
so $f(1)=\frac{2013 \cdot 2}{-6039}=-\frac{2}{3}$. And then for any prime number $q$, it holds that $f(q)=\frac{1}{2} f(1)=-\frac{1}{3}$.
We then prove that if $n=p_{1} p_{2} \cdots p_{m}$ with $p_{1}, p_{2}, \ldots, p_{m}$ not necessarily distinct primes and $m \geq 0$, then $f(n)=\frac{m-2}{3}$. We do this by induction on $m$. For $m=0$, $n=1$ and $f(1)=-\frac{2}{3}=\frac{0-2}{3}$, so it holds for this case. Suppose now that we have proven it for some $m \geq 0$. Consider any $n$ of the form $n=p_{1} p_{2} \cdots p_{m+1}$. Then $n>1$, so there is a prime factor $p \mid n$ for which $f(n)=f\left(\frac{n}{p}\right)-f(p)$; without loss of generality, this is $p=p_{m+1}$. It follows that
$$
f(n)=f\left(p_{1} p_{2} \cdots p_{m}\right)-f\left(p_{m+1}\right)=\frac{m-2}{3}--\frac{1}{3}=\frac{(m+1)-2}{3} .
$$
This completes the induction.
We can now calculate the desired result. The prime factorizations of 2014, 2015, and 2016 are $2014=2 \cdot 19 \cdot 53, 2015=5 \cdot 13 \cdot 31$, and $2016=2^{5} \cdot 3^{2} \cdot 7$, so
$$
f\left(2014^{2}\right)+f\left(2015^{3}\right)+f\left(2016^{5}\right)=\frac{6-2}{3}+\frac{9-2}{3}+\frac{40-2}{3}=\frac{49}{3} .
$$
|
\frac{49}{3}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Zij $f: \mathbb{Z}_{>0} \rightarrow \mathbb{R}$ een functie waarvoor geldt: voor alle $n>1$ is er een priemdeler $p$ van $n$ zodat
$$
f(n)=f\left(\frac{n}{p}\right)-f(p)
$$
Bovendien is gegeven dat $f\left(2^{2014}\right)+f\left(3^{2015}\right)+f\left(5^{2016}\right)=2013$.
Bereken $f\left(2014^{2}\right)+f\left(2015^{3}\right)+f\left(2016^{5}\right)$.
|
Als $n=q$ met $q$ priem, dan is er maar één priemdeler van $n$, namelijk $q$, dus moet gelden dat $f(q)=f(1)-f(q)$, dus $f(q)=\frac{1}{2} f(1)$. Als $n=q^{2}$ met $q$ priem, dan heeft $n$ ook maar één priemdeler, dus geldt $f\left(q^{2}\right)=f(q)-f(q)=0$. We bewijzen nu met inductie naar $k$ dat $f\left(q^{k}\right)=\frac{2-k}{2} f(1)$ als $q$ een priemgetal is en $k$ een positief geheel getal. Voor $k=1$ en $k=2$ hebben we dit al laten zien. Stel nu dat $f\left(q^{k}\right)=\frac{2-k}{2} f(1)$ voor zekere $k \geq 2$ en vul in $n=q^{k+1}$. Er geldt
$$
f\left(q^{k+1}\right)=f\left(q^{k}\right)-f(q)=\frac{2-k}{2} f(1)-\frac{1}{2} f(1)=\frac{2-(k+1)}{2} f(1)
$$
Dit voltooit de inductie.
Nu gebruiken we ons tweede gegeven. Er geldt
$$
\begin{aligned}
2013 & =f\left(2^{2014}\right)+f\left(3^{2015}\right)+f\left(5^{2016}\right) \\
& =\frac{2-2014}{2} f(1)+\frac{2-2015}{2} f(1)+\frac{2-2016}{2} f(1) \\
& =-\frac{6039}{2} f(1)
\end{aligned}
$$
dus $f(1)=\frac{2013 \cdot 2}{-6039}=-\frac{2}{3}$. En dan geldt voor elk priemgetal $q$ dat $f(q)=\frac{1}{2} f(1)=-\frac{1}{3}$.
We bewijzen vervolgens dat als $n=p_{1} p_{2} \cdots p_{m}$ met $p_{1}, p_{2}, \ldots, p_{m}$ niet noodzakelijk verschillende priemgetallen en $m \geq 0$, dat dan geldt $f(n)=\frac{m-2}{3}$. Dit doen we met inductie naar $m$. Voor $m=0$ is $n=1$ en $f(1)=-\frac{2}{3}=\frac{0-2}{3}$, dus hiervoor klopt het. Stel nu dat we het bewezen hebben voor zekere $m \geq 0$. Bekijk een willekeurige $n$ van de vorm $n=p_{1} p_{2} \cdots p_{m+1}$. Dan is $n>1$, dus is er een priemfactor $p \mid n$ waarvoor geldt $f(n)=f\left(\frac{n}{p}\right)-f(p)$; zonder verlies van algemeenheid is dit $p=p_{m+1}$. Nu volgt
$$
f(n)=f\left(p_{1} p_{2} \cdots p_{m}\right)-f\left(p_{m+1}\right)=\frac{m-2}{3}--\frac{1}{3}=\frac{(m+1)-2}{3} .
$$
Dit voltooit de inductie.
We kunnen nu het gevraagde berekenen. De priemfactorisaties van 2014, 2015 en 2016 zijn $2014=2 \cdot 19 \cdot 53,2015=5 \cdot 13 \cdot 31$ en $2016=2^{5} \cdot 3^{2} \cdot 7$, dus
$$
f\left(2014^{2}\right)+f\left(2015^{3}\right)+f\left(2016^{5}\right)=\frac{6-2}{3}+\frac{9-2}{3}+\frac{40-2}{3}=\frac{49}{3} .
$$
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2014-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2014"
}
|
The sets $A$ and $B$ are subsets of the positive integers. The sum of any two different elements from $A$ is an element of $B$. The quotient of any two different elements from $B$ (where we divide the largest by the smallest) is an element of $A$. Determine the maximum number of elements in $A \cup B$.
|
Suppose $A$ contains at least three elements, say $a<b<c$. Then $B$ contains the three distinct elements $a+b<a+c<b+c$. So $A$ contains the element $\frac{b+c}{a+c}$. This fraction is clearly an integer, so $a+c \mid b+c$. But then it follows that $a+c \mid (b+c)-(a+c)=b-a$. We know $b>a$, so $b-a$ is positive, and thus $a+c \leq b-a$. This gives $c \leq b-2a < b$, a contradiction with $c>b$. Therefore, $A$ contains at most two elements.
Suppose $B$ contains at least four elements, say $a<b<c<d$. Then $A$ contains the three distinct elements $\frac{d}{a}, \frac{d}{b}$, and $\frac{d}{c}$. But $A$ cannot contain three distinct elements, a contradiction. Therefore, $B$ contains at most three elements.
In total, $A \cup B$ contains at most 5 elements. This is possible, for example, with $A=\{2,4\}$ and $B=\{3,6,12\}$. Now, $2+4=6 \in B$ and $\frac{12}{6}=\frac{6}{3}=2 \in A$ and $\frac{12}{3}=4 \in A$, so this pair of sets satisfies the conditions. We conclude that $A \cup B$ contains at most 5 elements.
Finding a pair of sets that satisfies the conditions can be done as follows. Suppose $B$ contains the elements $a<b<c$. Then $A$ contains the elements $\frac{c}{b}, \frac{b}{a}$, and $\frac{c}{a}$, with $\frac{c}{a}$ being the largest. Since $A$ contains only two elements, it must be that $\frac{c}{b}=\frac{b}{a}$. Furthermore, the sum of the two elements in $A$ must be in $B$, so $\frac{b}{a}+\frac{c}{a} \in B$. Write $b=ta$, then $c=tb=t^2a$ and $\frac{b}{a}+\frac{c}{a}=t+t^2$. Now you see that $b$ can equal $t+t^2$ by choosing $a=t+1$. With $t=1$, you get $b=a$, so that does not work; with $t=2$, you get the solution mentioned above.
|
5
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
De verzamelingen $A$ en $B$ zijn deelverzamelingen van de positieve gehele getallen. De som van elke twee verschillende elementen uit $A$ is een element van $B$. Het quotiënt van elke twee verschillende elementen van $B$ (waarbij we de grootste door de kleinste delen) is een element van $A$. Bepaal het maximale aantal elementen in $A \cup B$.
|
Stel dat $A$ minstens drie elementen bevat, zeg $a<b<c$. Dan bevat $B$ de drie verschillende elementen $a+b<a+c<b+c$. Dus $A$ bevat in elk geval het element $\frac{b+c}{a+c}$. Deze breuk is kennelijk geheel, dus $a+c \mid b+c$. Maar dan volgt $a+c \mid(b+c)-(a+c)=b-a$. We weten $b>a$, dus $b-a$ is positief, dus moet gelden $a+c \leq b-a$. Dit geeft $c \leq b-2 a<b$, een tegenspraak met $c>b$. Dus $A$ bevat hoogstens twee elementen.
Stel dat $B$ minstens vier elementen bevat, zeg $a<b<c<d$. Dan bevat $A$ de drie verschillende elementen $\frac{d}{a}, \frac{d}{b}$ en $\frac{d}{c}$. Maar $A$ kan geen drie verschillende elementen bevatten, tegenspraak. Dus $B$ bevat hoogstens drie elementen.
In totaal bevat $A \cup B$ dus hoogstens 5 elementen. Dit is mogelijk, bijvoorbeeld met $A=\{2,4\}$ en $B=\{3,6,12\}$. Nu is $2+4=6 \in B$ en $\frac{12}{6}=\frac{6}{3}=2 \in A$ en $\frac{12}{3}=4 \in A$, dus dit paar verzamelingen voldoet. We concluderen dat $A \cup B$ maximaal 5 elementen bevat.
Het vinden van een paar verzamelingen dat voldoet, kan bijvoorbeeld als volgt. Stel B bevat de elementen $a<b<c$. Dan bevat $A$ de elementen $\frac{c}{b}, \frac{b}{a}$ en $\frac{c}{a}$, waarvan $\frac{c}{a}$ in elk geval de grootste is. Omdat A maar twee elementen bevat, moet wel gelden $\frac{c}{b}=\frac{b}{a}$. Verder moet de som van de twee elementen in $A$ weer in $B$ zitten, dus $\frac{b}{a}+\frac{c}{a} \in B$. Schrijf $b=t a$, dan $c=t b=t^{2} a$ en $\frac{b}{a}+\frac{c}{a}=t+t^{2}$. Nu zie je dat $b$ gelijk kan zijn aan $t+t^{2}$ door $a=t+1$ te kiezen. Met $t=1$ krijg je $b=a$, dus die voldoet niet; met $t=2$ krijg je bovenstaande oplossing.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2014-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2014"
}
|
Let $H$ be the orthocenter of an acute triangle $ABC$. The line through $A$ perpendicular to $AC$ and the line through $B$ perpendicular to $BC$ intersect at $D$. The circle with center $C$ passing through $H$ intersects the circumcircle of triangle $ABC$ at points $E$ and $F$. Prove that $|DE|=|DF|=|AB|$.
|
The triangle is acute, so $H$ lies inside the triangle. This means that $E$ and $F$ lie on the shorter arcs $A C$ and $B C$. Assume that $E$ lies on the shorter arc $A C$ and $F$ on the shorter arc $B C$.
If we reflect $H$ in $A C$, the reflection $H^{\prime}$ lands on the circumcircle of $\triangle A B C$. (This is a known fact, provable by angle chasing to show that $\angle A H C=180^{\circ}-\angle A B C$.) On the other hand, this reflection also lies on the circle with center $C$ through $H$, since $\left|C H^{\prime}\right|=|C H|$. Therefore, $H^{\prime}$ is the intersection of the two circles and that is $E$. We conclude that $E$ is the reflection of $H$ under reflection in $A C$.
This means that $E H$ is perpendicular to $A C$ and thus the same line as $B H$. Since $A D$ is also perpendicular to $A C$, $B E$ and $A D$ are parallel. Furthermore, $D$ lies on the circumcircle of $\triangle A B C$ because $\angle C A D+\angle C B D=90^{\circ}+90^{\circ}=180^{\circ}$. We had already seen that $E$ lies on the shorter arc $A C$, so $E A D B$ is a cyclic quadrilateral in that order. Now, $\angle B E A+\angle E A D=180^{\circ}$ due to alternate segment theorem, but also $\angle E B D+\angle E A D=180^{\circ}$ because of the cyclic quadrilateral. Thus, $\angle B E A=\angle E B D$, so the corresponding chords $B A$ and $E D$ are equal in length.
Similarly, we can prove that $|A B|=|D F|$, which completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $H$ het hoogtepunt van een scherphoekige driehoek $A B C$. De lijn door $A$ loodrecht op $A C$ en de lijn door $B$ loodrecht op $B C$ snijden elkaar in $D$. De cirkel met middelpunt $C$ door $H$ snijdt de omgeschreven cirkel van driehoek $A B C$ in de punten $E$ en $F$. Bewijs dat $|D E|=|D F|=|A B|$.
|
De driehoek is scherphoekig, dus $H$ ligt binnen de driehoek. Dat betekent dat $E$ en $F$ op de korte bogen $A C$ en $B C$ liggen. Neem aan dat $E$ op de korte boog $A C$ ligt en $F$ op de korte boog $B C$.
Als we $H$ spiegelen in $A C$, komt het spiegelbeeld $H^{\prime}$ op de omgeschreven cirkel van $\triangle A B C$ terecht. (Dit is een bekend feit, te bewijzen door met wat hoekenjagen te laten zien dat $\angle A H C=180^{\circ}-\angle A B C$.) Anderzijds ligt dit spiegelbeeld ook op de cirkel met middelpunt $C$ door $H$, aangezien $\left|C H^{\prime}\right|=|C H|$. Dus $H^{\prime}$ is het snijpunt van de twee cirkels en dat is $E$. We concluderen dat $E$ het spiegelbeeld van $H$ is onder spiegeling in $A C$.
Dit betekent dat $E H$ loodrecht op $A C$ staat en dus dezelfde lijn is als $B H$. Omdat $A D$ ook loodrecht op $A C$ staat, zijn $B E$ en $A D$ evenwijdig. Verder ligt $D$ op de omgeschreven cirkel van $\triangle A B C$ omdat $\angle C A D+\angle C B D=90^{\circ}+90^{\circ}=180^{\circ}$. We hadden al gezien dat $E$ op de korte boog $A C$ ligt, dus is $E A D B$ een koordenvierhoek in die volgorde. Nu is $\angle B E A+\angle E A D=180^{\circ}$ wegens U-hoeken, maar ook $\angle E B D+\angle E A D=180^{\circ}$ vanwege de koordenvierhoek. Dus $\angle B E A=\angle E B D$, dus de bijbehorende koorden $B A$ en $E D$ zijn even lang.
Analoog kunnen we bewijzen dat $|A B|=|D F|$, waarmee het gevraagde bewezen is.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2014-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2014"
}
|
Let $H$ be the orthocenter of an acute triangle $ABC$. The line through $A$ perpendicular to $AC$ and the line through $B$ perpendicular to $BC$ intersect at $D$. The circle with center $C$ passing through $H$ intersects the circumcircle of triangle $ABC$ at points $E$ and $F$. Prove that $|DE|=|DF|=|AB|$.
|
In the same way as in the first solution, we show that $E$ is the reflection of $H$ in $AC$ and that $E A D B$ is a cyclic quadrilateral in that order. Due to the reflection, $|A E|=|A H|$. Since both $B D$ and $A H$ are perpendicular to $B C$, they are parallel. Similarly, $A D$ and $B H$ are also parallel, so $A D B H$ is a parallelogram. Therefore, $|A H|=|B D|$, which means $|A E|=|B D|$. We now have a chord $E A$ next to a chord $A D$, and further a chord $B D$ (of the same length as $E A$) next to the same chord $A D$. We now show that the intersecting chords $E D$ and $A B$ are therefore equal. It holds that $\angle A E D=\angle A B D$. And since $|A E|=|B D|$, it follows that $\angle A D E=\angle B A D$. Thus, $\triangle E A D \cong \triangle B D A(\mathrm{ASA})$, from which it follows that $|D E|=|A B|$.
Similarly, we can prove that $|A B|=|D F|$, which completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $H$ het hoogtepunt van een scherphoekige driehoek $A B C$. De lijn door $A$ loodrecht op $A C$ en de lijn door $B$ loodrecht op $B C$ snijden elkaar in $D$. De cirkel met middelpunt $C$ door $H$ snijdt de omgeschreven cirkel van driehoek $A B C$ in de punten $E$ en $F$. Bewijs dat $|D E|=|D F|=|A B|$.
|
Op dezelfde manier als in de eerste oplossing laten we zien dat $E$ het spiegelbeeld van $H$ is onder spiegeling in $A C$ en dat $E A D B$ een koordenvierhoek is in die volgorde. Vanwege de spiegeling is $|A E|=|A H|$. Omdat zowel $B D$ als $A H$ loodrecht op $B C$ staan, zijn ze evenwijdig. Analoog zijn ook $A D$ en $B H$ evenwijdig, dus is $A D B H$ een parallellogram. Dus is $|A H|=|B D|$, waarmee we zien dat $|A E|=|B D|$. We hebben nu een koorde $E A$ naast een koorde $A D$, en verder een koorde $B D$ (even lang als $E A$ ) naast weer dezelfde koorde $A D$. We laten nu zien dat de overspannende koorden $E D$ en $A B$ daarom gelijk zijn. Er geldt $\angle A E D=\angle A B D$. En omdat $|A E|=|B D|$ geldt $\angle A D E=\angle B A D$. Dus $\triangle E A D \cong \triangle B D A(\mathrm{ZHH})$, waaruit volgt $|D E|=|A B|$.
Analoog kunnen we bewijzen dat $|A B|=|D F|$, waarmee het gevraagde bewezen is.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2014-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2014"
}
|
Determine all pairs $(p, q)$ of prime numbers for which $p^{q+1}+q^{p+1}$ is a square.
Find all pairs $(p, q)$ of prime numbers for which $p^{q+1}+q^{p+1}$ is a square.
|
First, assume that $p$ and $q$ are both odd. Then, in $p^{q+1}+q^{p+1}$, both exponents are even, which implies that both terms are congruent to $1 \bmod 4$. The sum is thus congruent to 2 $\bmod 4$, but that is never a square.
Now assume that $p$ and $q$ are both even. Then they are both equal to 2. This gives $p^{q+1}+q^{p+1}=$ $2^{3}+2^{3}=16=4^{2}$, so this pair satisfies the condition.
Finally, assume that one of them, say $p$, is even and the other is odd. We then have $p=2$ and $2^{q+1}+q^{3}=a^{2}$ for some positive integer $a$. Write $q+1=2 b$ with $b$ a positive integer, then we have $2^{2 b}+q^{3}=a^{2}$, or equivalently
$$
q^{3}=a^{2}-2^{2 b}=\left(a-2^{b}\right)\left(a+2^{b}\right)
$$
Both factors on the right must now be a $q$-power, say $a-2^{b}=q^{k}$ and $a+2^{b}=q^{l}$ with $l>k \geq 0$. Both factors are divisible by $q^{k}$, so their difference is also divisible by it. Thus $q^{k} \mid 2 \cdot 2^{b}=2^{b+1}$. But $q$ is an odd prime, so the only $q$-power that is a divisor of a power of two is 1. Therefore, $k=0$. We now get $q^{3}=a+2^{b}$ and $a-2^{b}=1$, so $q^{3}=\left(2^{b}+1\right)+2^{b}=2^{b+1}+1$. From this, it follows that
$$
2^{b+1}=q^{3}-1=(q-1)\left(q^{2}+q+1\right)
$$
However, $q^{2}+q+1 \equiv 1 \bmod 2$ and further, $q^{2}+q+1>1$, so this can never be a power of two. Contradiction.
We conclude that the only solution is $(p, q)=(2,2)$.
|
(2,2)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Bepaal alle paren $(p, q)$ van priemgetallen waarvoor $p^{q+1}+q^{p+1}$ een kwadraat is.
|
Stel eerst dat $p$ en $q$ beide oneven zijn. Dan zijn in $p^{q+1}+q^{p+1}$ beide exponenten even, waaruit volgt dat beide termen congruent $1 \bmod 4$ zijn. De som is dus congruent 2 $\bmod 4$, maar dat is nooit een kwadraat.
Stel nu dat $p$ en $q$ beide even zijn. Dan zijn ze beide gelijk aan 2 . Dat geeft $p^{q+1}+q^{p+1}=$ $2^{3}+2^{3}=16=4^{2}$, dus dit tweetal voldoet.
Stel ten slotte dat één beide, zeg $p$, even is en de ander oneven. We hebben dan dus $p=2$ en $2^{q+1}+q^{3}=a^{2}$ voor een zeker positief geheel getal $a$. Schrijf $q+1=2 b$ met $b$ positief geheel, dan staat er $2^{2 b}+q^{3}=a^{2}$, oftewel
$$
q^{3}=a^{2}-2^{2 b}=\left(a-2^{b}\right)\left(a+2^{b}\right)
$$
Beide factoren rechts moeten nu een $q$-macht zijn, zeg $a-2^{b}=q^{k}$ en $a+2^{b}=q^{l}$ met $l>k \geq 0$. Beide factoren zijn deelbaar door $q^{k}$, dus ook het verschil is daardoor deelbaar. Dus $q^{k} \mid 2 \cdot 2^{b}=2^{b+1}$. Maar $q$ is een oneven priemgetal, dus de enige $q$-macht die een deler van een tweemacht is, is 1 . Dus $k=0$. We krijgen nu $q^{3}=a+2^{b}$ en $a-2^{b}=1$, dus $q^{3}=\left(2^{b}+1\right)+2^{b}=2^{b+1}+1$. Daaruit volgt
$$
2^{b+1}=q^{3}-1=(q-1)\left(q^{2}+q+1\right)
$$
Echter, $q^{2}+q+1 \equiv 1 \bmod 2$ en verder is $q^{2}+q+1>1$, dus dit kan nooit een tweemacht zijn. Tegenspraak.
We concluderen dat de enige oplossing $(p, q)=(2,2)$ is.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2014-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2014"
}
|
Let $P(x)$ be a polynomial with integer coefficients and degree $n \leq 10$ for which it holds that for every $k \in\{1,2, \ldots, 10\}$ there is an integer $m$ such that $P(m)=k$. Furthermore, it is given that $|P(10)-P(0)|<1000$. Prove that for every integer $k$ there is an integer $m$ such that $P(m)=k$.
|
Let for $i=1,2, \ldots, 10$ the integer $c_{i}$ be such that $P\left(c_{i}\right)=i$. It holds for $i \in\{1,2, \ldots, 9\}$ that
$$
c_{i+1}-c_{i} \mid P\left(c_{i+1}\right)-P\left(c_{i}\right)=(i+1)-i=1
$$
so $c_{i+1}-c_{i}= \pm 1$ for all $i \in\{1,2, \ldots, 9\}$. Furthermore, $c_{i} \neq c_{j}$ for $i \neq j$, because $P\left(c_{i}\right)=i \neq j=P\left(c_{j}\right)$. We conclude that $c_{1}, c_{2}, \ldots, c_{10}$ are ten consecutive numbers, either increasing or decreasing. Thus, we distinguish two cases:
(A) $c_{i}=c_{1}-1+i$ for $i=1,2, \ldots, 10$ (so $c_{1}, c_{2}, \ldots, c_{10}$ is an increasing sequence of consecutive numbers),
(B) $c_{i}=c_{1}+1-i$ for $i=1,2, \ldots, 10$ (so $c_{1}, c_{2}, \ldots, c_{10}$ is a decreasing sequence of consecutive numbers).
First, consider case (A). Define $Q(x)=1+x-c_{1}$. Then for $1 \leq i \leq 10$ it holds that
$$
Q\left(c_{i}\right)=Q\left(c_{1}-1+i\right)=1+\left(c_{1}-1+i\right)-c_{1}=i=P\left(c_{i}\right)
$$
so $P\left(c_{i}\right)-Q\left(c_{i}\right)=0$. Therefore, we can write
$$
P(x)-Q(x)=R(x) \cdot \prod_{i=1}^{10}\left(x-c_{i}\right)
$$
or equivalently
$$
P(x)=1+x-c_{1}+R(x) \cdot \prod_{i=1}^{10}\left(x-c_{i}\right)
$$
Since the degree of $P$ is at most 10, the degree of $R$ cannot be greater than 0. Thus, $R(x)$ is a constant, say $R(x)=a$ with $a \in \mathbb{Z}$. We then get
$$
P(x)=1+x-c_{1}+a \cdot \prod_{i=1}^{10}\left(x-c_{i}\right)
$$
Now we substitute $x=10$ and $x=0$:
$$
\begin{gathered}
P(10)-P(0)=1+10-c_{1}+a \cdot \prod_{i=1}^{10}\left(10-c_{i}\right)-\left(1+0-c_{1}\right)-a \cdot \prod_{i=1}^{10}\left(0-c_{i}\right) \\
=10+a \cdot\left(\prod_{i=1}^{10}\left(10-c_{i}\right)-\prod_{i=1}^{10}\left(0-c_{i}\right)\right)
\end{gathered}
$$
The numbers $10-c_{1}, 10-c_{2}, \ldots, 10-c_{10}$ are ten consecutive numbers and the numbers $0-c_{1}, 0-c_{2}, \ldots, 0-c_{10}$ follow them exactly. Thus, there is an $N$ such that
$$
\prod_{i=1}^{10}\left(10-c_{i}\right)-\prod_{i=1}^{10}\left(0-c_{i}\right)=(N+20)(N+19) \cdots(N+11)-(N+10)(N+9) \cdots(N+1)
$$
We will estimate this. First, assume that $N+1>0$. Then it holds that
$$
\begin{aligned}
(N+20)( & N+19) \cdots(N+11)-(N+10)(N+9) \cdots(N+1) \\
& >(N+20)(N+9) \cdots(N+1)-(N+10)(N+9) \cdots(N+1) \\
& =10 \cdot(N+9)(N+8) \cdots(N+1) \\
& \geq 10!.
\end{aligned}
$$
If just $N+20<0$, all factors are negative. Analogously, the absolute difference is again greater than 10!. If $N+20 \geq 0$ and $N+1 \leq 0$, there is a 0 among the factors. Thus, exactly one of the two terms is 0 and the other has an absolute value of at least 10!. We conclude that the absolute difference is always at least 10!. Therefore, if $a \neq 0$, $|P(10)-P(0)| \geq 10!-10>1000$. However, it is given that $|P(10)-P(0)|<1000$, so apparently $a=0$ must hold. Now we find that
$$
P(x)=1+x-c_{1} .
$$
Let $k \in \mathbb{Z}$ be arbitrary and choose $m=k-1+c_{1}$. Then $P(m)=1+\left(k-1+c_{1}\right)-c_{1}=k$. Thus, for every integer $k$ there is an integer $m$ such that $P(m)=k$.
Now consider case (B). We can follow exactly the same reasoning, where we now define $Q(x)=1-x+c_{1}$ and ultimately get that
$$
P(x)=1-x+c_{1}+a \cdot \prod_{i=1}^{10}\left(x-c_{i}\right)
$$
We derive in the same way that $a=0$, so
$$
P(x)=1-x+c_{1} .
$$
And again, it follows that for every integer $k$ there is an integer $m$ such that $P(m)=k$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Zij $P(x)$ een polynoom met gehele coëfficiënten en graad $n \leq 10$ waarvoor geldt dat er voor elke $k \in\{1,2, \ldots, 10\}$ een gehele $m$ is met $P(m)=k$. Verder is gegeven dat $|P(10)-P(0)|<1000$. Bewijs dat er voor elke gehele $k$ een gehele $m$ is met $P(m)=k$.
|
Laat voor $i=1,2, \ldots, 10$ het gehele getal $c_{i}$ zo zijn dat $P\left(c_{i}\right)=i$. Er geldt voor $i \in\{1,2, \ldots, 9\}$ dat
$$
c_{i+1}-c_{i} \mid P\left(c_{i+1}\right)-P\left(c_{i}\right)=(i+1)-i=1
$$
dus $c_{i+1}-c_{i}= \pm 1$ voor alle $i \in\{1,2, \ldots, 9\}$. Verder geldt dat $c_{i} \neq c_{j}$ voor $i \neq j$, want $P\left(c_{i}\right)=i \neq j=P\left(c_{j}\right)$. We concluderen dat $c_{1}, c_{2}, \ldots, c_{10}$ tien opeenvolgende getallen zijn, ofwel stijgend ofwel dalend. We onderscheiden dus twee gevallen:
(A) $c_{i}=c_{1}-1+i$ voor $i=1,2, \ldots, 10$ (dus $c_{1}, c_{2}, \ldots, c_{10}$ is een stijgend rijtje opeenvolgende getallen),
(B) $c_{i}=c_{1}+1-i$ voor $i=1,2, \ldots, 10$ (dus $c_{1}, c_{2}, \ldots, c_{10}$ is een dalend rijtje opeenvolgende getallen).
Bekijk eerst geval (A). Definieer $Q(x)=1+x-c_{1}$. Dan geldt voor $1 \leq i \leq 10$ dat
$$
Q\left(c_{i}\right)=Q\left(c_{1}-1+i\right)=1+\left(c_{1}-1+i\right)-c_{1}=i=P\left(c_{i}\right)
$$
dus $P\left(c_{i}\right)-Q\left(c_{i}\right)=0$. Dus kunnen we schrijven
$$
P(x)-Q(x)=R(x) \cdot \prod_{i=1}^{10}\left(x-c_{i}\right)
$$
oftewel
$$
P(x)=1+x-c_{1}+R(x) \cdot \prod_{i=1}^{10}\left(x-c_{i}\right)
$$
Omdat de graad van $P$ hoogstens 10 is, mag de graad van $R$ niet groter dan 0 zijn. Dus $R(x)$ is een constante, zeg $R(x)=a$ met $a \in \mathbb{Z}$. We krijgen dan
$$
P(x)=1+x-c_{1}+a \cdot \prod_{i=1}^{10}\left(x-c_{i}\right)
$$
We vullen nu $x=10$ en $x=0$ in:
$$
\begin{gathered}
P(10)-P(0)=1+10-c_{1}+a \cdot \prod_{i=1}^{10}\left(10-c_{i}\right)-\left(1+0-c_{1}\right)-a \cdot \prod_{i=1}^{10}\left(0-c_{i}\right) \\
=10+a \cdot\left(\prod_{i=1}^{10}\left(10-c_{i}\right)-\prod_{i=1}^{10}\left(0-c_{i}\right)\right)
\end{gathered}
$$
De getallen $10-c_{1}, 10-c_{2}, \ldots, 10-c_{10}$ zijn tien opeenvolgende getallen en de getallen $0-c_{1}, 0-c_{2}, \ldots, 0-c_{10}$ volgen daar weer precies op. Dus er is een $N$ zodat
$$
\prod_{i=1}^{10}\left(10-c_{i}\right)-\prod_{i=1}^{10}\left(0-c_{i}\right)=(N+20)(N+19) \cdots(N+11)-(N+10)(N+9) \cdots(N+1)
$$
We gaan dit afschatten. We nemen eerst aan dat $N+1>0$. Dan geldt
$$
\begin{aligned}
(N+20)( & N+19) \cdots(N+11)-(N+10)(N+9) \cdots(N+1) \\
& >(N+20)(N+9) \cdots(N+1)-(N+10)(N+9) \cdots(N+1) \\
& =10 \cdot(N+9)(N+8) \cdots(N+1) \\
& \geq 10!.
\end{aligned}
$$
Als juist $N+20<0$, zijn alle factoren negatief. Helemaal analoog is het absolute verschil ook weer groter dan 10 !. Als $N+20 \geq 0$ en $N+1 \leq 0$, zit er dus ergens een 0 tussen de factoren. Dus precies één van de twee termen is gelijk aan 0 en de ander is in absolute waarde minstens 10 !. We concluderen dat het absolute verschil altijd minstens 10 ! is. Dus als $a \neq 0$ is $|P(10)-P(0)| \geq 10!-10>1000$. Gegeven is echter dat $|P(10)-P(0)|<1000$, dus blijkbaar moet gelden dat $a=0$. Nu vinden we dat
$$
P(x)=1+x-c_{1} .
$$
Zij $k \in \mathbb{Z}$ willekeurig en kies $m=k-1+c_{1}$. Dan geldt $P(m)=1+\left(k-1+c_{1}\right)-c_{1}=k$. Dus voor elke gehele $k$ is er een gehele $m$ met $P(m)=k$.
Bekijk nu geval (B). We kunnen precies dezelfde redenering volgen, waarbij we nu $Q(x)=$ $1-x+c_{1}$ definiëren en uiteindelijk krijgen dat
$$
P(x)=1-x+c_{1}+a \cdot \prod_{i=1}^{10}\left(x-c_{i}\right)
$$
We leiden op dezelfde manier af dat $a=0$, zodat
$$
P(x)=1-x+c_{1} .
$$
En nu volgt weer dat er voor elke gehele $k$ een gehele $m$ is met $P(m)=k$.
|
{
"exam": "Dutch_TST",
"problem_label": "5",
"problem_match": "\nOpgave 5.",
"resource_path": "Dutch_TST/segmented/nl-2014-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2014"
}
|
Let $m$ and $n$ be positive integers such that $5m + n$ is a divisor of $5n + m$. Prove that $m$ is a divisor of $n$.
|
There is a positive integer $k$ with $(5 m+n) k=5 n+m$. So $5 k m-m=5 n-k n$, or $(5 k-1) m=(5-k) n$. The left side is positive, so the right side is also positive, which implies that $k<5$. If $k=1$, then $4 m=4 n$, so $m=n$, thus $m \mid n$. If $k=2$, then $9 m=3 n$, so $3 m=n$, thus $m \mid n$. If $k=3$, then $14 m=2 n$, so $7 m=n$, thus $m \mid n$. If $k=4$, then $19 m=n$, thus $m \mid n$. We see that in all cases, $m \mid n$. $\square$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Laat $m$ en $n$ positieve gehele getallen zijn zodat $5 m+n$ een deler is van $5 n+m$. Bewijs dat $m$ een deler is van $n$.
|
Er is een positieve gehele $k$ met $(5 m+n) k=5 n+m$. Dus $5 k m-m=5 n-k n$, oftewel $(5 k-1) m=(5-k) n$. De linkerkant is positief, dus de rechterkant ook, waaruit volgt dat $k<5$. Als $k=1$, dan is $4 m=4 n$, dus $m=n$, dus $m \mid n$. Als $k=2$, dan is $9 m=3 n$, dus $3 m=n$, dus $m \mid n$. Als $k=3$, dan is $14 m=2 n$, dus $7 m=n$, dus $m \mid n$. Als $k=4$, dan is $19 m=n$, dus $m \mid n$. We zien dat in alle gevallen geldt dat $m \mid n$. $\square$
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2015-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2015"
}
|
Let $m$ and $n$ be positive integers such that $5m + n$ is a divisor of $5n + m$. Prove that $m$ is a divisor of $n$.
|
Let $d=\operatorname{gcd}(m, n)$ and write $m=a d, n=b d$. Then $a$ and $b$ are positive integers with $\operatorname{gcd}(a, b)=1$. From $5 m+n \mid 5 n+m$ it follows that $5 a d+b d \mid 5 b d+a d$, so $5 a+b \mid 5 b+a$. Now it also holds that
$$
5 a+b \mid (5 b+a)-5(5 a+b)=-24 a
$$
and
$$
5 a+b \mid 5(5 b+a)-(5 a+b)=24 b
$$
Thus $5 a+b \mid \operatorname{gcd}(24 a, 24 b)=24$. If $a=1$, then $a \mid b$ always holds. If $a \geq 2$, then $5 a+b \geq 11$, so $5 a+b$ can only be equal to 12 or 24. If $5 a+b=12$, then $a=2$ and $b=2$, but these are not coprime, contradiction. If $5 a+b=24$, then $a=2$ and $b=14$ or $a=3$ and $b=9$ or $a=4$ and $b=4$. In all three cases, $a$ and $b$ are not coprime, contradiction. Therefore, only $a=1$ can hold, and then $a \mid b$, which implies $a d \mid b d$, so $m \mid n$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Laat $m$ en $n$ positieve gehele getallen zijn zodat $5 m+n$ een deler is van $5 n+m$. Bewijs dat $m$ een deler is van $n$.
|
Zij $d=\operatorname{ggd}(m, n)$ en schrijf $m=a d, n=b d$. Dan zijn $a$ en $b$ positieve gehele getallen met $\operatorname{ggd}(a, b)=1$. Uit $5 m+n \mid 5 n+m$ volgt $5 a d+b d \mid 5 b d+a d$, dus $5 a+b \mid 5 b+a$. Nu geldt ook
$$
5 a+b \mid(5 b+a)-5(5 a+b)=-24 a
$$
en
$$
5 a+b \mid 5(5 b+a)-(5 a+b)=24 b
$$
Dus $5 a+b \mid \operatorname{ggd}(24 a, 24 b)=24$. Als $a=1$ geldt altijd $a \mid b$. Als $a \geq 2$ is $5 a+b \geq 11$, dus kan $5 a+b$ alleen gelijk zijn aan 12 of 24 . Als $5 a+b=12$, dan moet gelden $a=2$ en $b=2$, maar die zijn niet copriem, tegenspraak. Als $5 a+b=24$, dan moet $a=2$ en $b=14$ of $a=3$ en $b=9$ of $a=4$ en $b=4$. In alle drie zijn $a$ en $b$ niet copriem, tegenspraak. Dus alleen $a=1$ kan gelden en dan is $a \mid b$, waaruit volgt $a d \mid b d$, dus $m \mid n$.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2015-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2015"
}
|
Given are positive integers $r$ and $k$ and an infinite sequence of positive integers $a_{1} \leq a_{2} \leq \ldots$ such that $\frac{r}{a_{r}}=k+1$. Prove that there is a $t$ such that $\frac{t}{a_{t}}=k$.
|
We prove this by contradiction. Suppose such a $t$ does not exist. If $a_{k}=1$, then $\frac{k}{a_{k}}=k$, contradicting our assumption. Therefore, $a_{k} \geq 2$. We now prove by induction on $i$ that $a_{i k} \geq i+1$. The base case has just been established. Suppose now that for some $i \geq 1$ it holds that $a_{i k} \geq i+1$. Then also $a_{(i+1) k} \geq i+1$. If $a_{(i+1) k}=i+1$, then $\frac{(i+1) k}{a_{(i+1) k}}=k$, a contradiction. Therefore, $a_{(i+1) k} \geq i+2$. This completes the induction step. Now take $i=a_{r}$, then $a_{a_{r} k} \geq a_{r}+1$. And since $r=a_{r}(k+1)$, it follows that $a_{r}=a_{a_{r}(k+1)} \geq a_{a_{r} k} \geq a_{r}+1$, a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Gegeven zijn positieve gehele getallen $r$ en $k$ en een oneindige rij positieve gehele getallen $a_{1} \leq a_{2} \leq \ldots$ zodat $\frac{r}{a_{r}}=k+1$. Bewijs dat er een $t$ is met $\frac{t}{a_{t}}=k$.
|
We bewijzen dit uit het ongerijmde. Stel dat zo'n $t$ niet bestaat. Als $a_{k}=1$, dan zou $\frac{k}{a_{k}}=k$, tegenspraak met onze aanname. Dus $a_{k} \geq 2$. We bewijzen nu met inductie naar $i$ dat $a_{i k} \geq i+1$. De inductiebasis hebben we zojuist gedaan. Stel nu dat voor zekere $i \geq 1$ geldt dat $a_{i k} \geq i+1$. Dan is ook $a_{(i+1) k} \geq i+1$. Als $a_{(i+1) k}=i+1$, dan is $\frac{(i+1) k}{a_{(i+1) k}}=k$, tegenspraak. Dus $a_{(i+1) k} \geq i+2$. Dit voltooit de inductiestap. Neem nu $i=a_{r}$, dan is dus $a_{a_{r} k} \geq a_{r}+1$. En omdat $r=a_{r}(k+1)$ geldt $a_{r}=a_{a_{r}(k+1)} \geq a_{a_{r} k} \geq a_{r}+1$, tegenspraak.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2015-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2015"
}
|
Let $n \geq 2$ be a positive integer. Each cell of an $n \times n$ board is colored red or blue. We place dominoes on the board, each covering two cells. We call a domino plain if it lies on two red or two blue cells, and colorful if it lies on one red and one blue cell. Find the largest positive integer $k$ with the following property: no matter how the red/blue coloring of the board is done, it is always possible to place $k$ non-overlapping dominoes on the board that are either all plain or all colorful.
|
We prove that $k=\left\lfloor\frac{n^{2}}{4}\right\rfloor$ is the largest possible value.
Suppose $n$ is even. Then it is possible to cover the board with $\frac{n^{2}}{2}$ dominoes (ignoring colors). Since there are $\frac{n^{2}}{2}$ dominoes, all of which are either colorful or plain, there are at least $\left\lfloor\frac{n^{2}}{4}\right\rfloor=\frac{n^{2}}{4}$ colorful or at least $\left\lfloor\frac{n^{2}}{4}\right\rfloor=\frac{n^{2}}{4}$ plain dominoes. If $n$ is odd, we can cover the board with $\frac{n^{2}-1}{2}$ dominoes. (Note that this number is an even integer.) Of these dominoes, there are at least $\frac{n^{2}-1}{4}=\left\lfloor\frac{n^{2}}{4}\right\rfloor$ colorful or at least $\frac{n^{2}-1}{4}=\left\lfloor\frac{n^{2}}{4}\right\rfloor$ plain. This proves that it is always possible to place at least $\left\lfloor\frac{n^{2}}{4}\right\rfloor$ colorful dominoes or at least $\left\lfloor\frac{n^{2}}{4}\right\rfloor$ plain dominoes on the board. We now prove that it is possible to choose the coloring of the squares in red and blue such that there are no more than $\left\lfloor\frac{n^{2}}{4}\right\rfloor$ plain and also no more than $\left\lfloor\frac{n^{2}}{4}\right\rfloor$ colorful dominoes that can be placed.
Color the squares of the board black and white like a chessboard, so that the bottom-left square is white. If $n$ is even, there are as many white as black squares, namely $\frac{n^{2}}{2}$. If $n$ is odd, there is one fewer black square, and the number of black squares is $\frac{n^{2}-1}{2}=\left\lfloor\frac{n^{2}}{2}\right\rfloor$. In both cases, this is an even number of squares, since for odd $n$ we have $n^{2} \equiv 1$ mod 4. Color half of the black squares red and all other squares blue. Then there are $\left\lfloor\frac{n^{2}}{4}\right\rfloor$ red squares, so we can place at most $\left\lfloor\frac{n^{2}}{4}\right\rfloor$ non-overlapping colorful dominoes on the board: each of these dominoes covers a red square. A plain domino cannot cover two red squares, as no two adjacent squares are red. It must therefore cover two blue squares. At least one of these is a black-blue square, so the number of plain dominoes is at most the number of black-blue squares, which is $\left\lfloor\frac{n^{2}}{4}\right\rfloor$. Therefore, both the colorful and the plain dominoes can have at most $\left\lfloor\frac{n^{2}}{4}\right\rfloor$ placed on the board simultaneously.
We conclude that the maximum $k$ is indeed $k=\left\lfloor\frac{n^{2}}{4}\right\rfloor$.
|
\left\lfloor\frac{n^{2}}{4}\right\rfloor
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Zij $n \geq 2$ een positief geheel getal. Ieder vakje van een $n \times n$-bord wordt rood of blauw gekleurd. We leggen dominostenen op het bord, die elk twee vakjes bedekken. We noemen een dominosteen effen als hij op twee rode of twee blauwe vakjes ligt en kleurrijk als hij op een rood en een blauw vakje ligt. Vind het grootste positieve gehele getal $k$ met de volgende eigenschap: hoe de rood/blauw-kleuring van het bord ook gebeurt, het is altijd mogelijk om $k$ niet-overlappende dominostenen op het bord te leggen die ofwel allemaal effen zijn ofwel allemaal kleurrijk.
|
We bewijzen dat $k=\left\lfloor\frac{n^{2}}{4}\right\rfloor$ de grootst mogelijke waarde is.
Stel dat $n$ even is. Dan is het mogelijk om het bord te bedekken met $\frac{n^{2}}{2}$ dominostenen (zonder op kleuren te letten). Omdat er $\frac{n^{2}}{2}$ dominostenen zijn die allemaal kleurrijk of effen zijn, zijn er of minstens $\left\lfloor\frac{n^{2}}{4}\right\rfloor=\frac{n^{2}}{4}$ kleurrijke of minstens $\left\lfloor\frac{n^{2}}{4}\right\rfloor=\frac{n^{2}}{4}$ effen dominostenen. Als $n$ oneven is, kunnen we het bord bedekken met $\frac{n^{2}-1}{2}$ dominostenen. (Merk op dat dit getal geheel en even is.) Van deze dominostenen zijn er of minstens $\frac{n^{2}-1}{4}=\left\lfloor\frac{n^{2}}{4}\right\rfloor$ kleurrijk, of minstens $\frac{n^{2}-1}{4}=\left\lfloor\frac{n^{2}}{4}\right\rfloor$ effen. Dit bewijst dat het altijd mogelijk is om op het bord minstens $\left\lfloor\frac{n^{2}}{4}\right\rfloor$ kleurrijke dominostenen of minstens $\left\lfloor\frac{n^{2}}{4}\right\rfloor$ effen dominostenen neer te leggen. We bewijzen nu dat het mogelijk is om de kleuring in rode en blauwe vakjes zo te kiezen, dat er niet meer dan $\left\lfloor\frac{n^{2}}{4}\right\rfloor$ effen en ook niet meer dan $\left\lfloor\frac{n^{2}}{4}\right\rfloor$ kleurrijke dominostenen neer te leggen zijn.
Kleur de vakjes van het bord zwart-wit als op een schaakbord, zodat het vakje linksonder wit is. Als $n$ even is, zijn er evenveel witte als zwarte vakjes, namelijk $\frac{n^{2}}{2}$. Als $n$ oneven is, is er een zwart vakje minder en is het aantal zwarte vakjes gelijk aan $\frac{n^{2}-1}{2}=\left\lfloor\frac{n^{2}}{2}\right\rfloor$. In beide gevallen is dit een even aantal vakjes, aangezien voor oneven $n$ geldt dat $n^{2} \equiv 1$ mod 4. Kleur de helft van de zwarte vakjes rood en alle andere vakjes blauw. Dan zijn er $\left\lfloor\frac{n^{2}}{4}\right\rfloor$ rode vakjes, dus we kunnen maximaal $\left\lfloor\frac{n^{2}}{4}\right\rfloor$ niet-overlappende kleurrijke dominostenen op het bord leggen: elk van deze dominostenen bedekt immers een rood vakje. Een effen dominosteen kan geen twee rode vakjes bedekken, want er zijn geen twee vakjes naast elkaar rood gekleurd. Hij moet dus wel twee blauwe vakjes bedekken. Daar zit in elk geval een zwart vakje bij, dus het aantal effen dominostenen is hoogstens het aantal zwart-blauwe vakjes en dat is $\left\lfloor\frac{n^{2}}{4}\right\rfloor$. Dus zowel van de kleurrijke als van de effen dominostenen kunnen er hooguit $\left\lfloor\frac{n^{2}}{4}\right\rfloor$ tegelijk op het bord worden gelegd.
We concluderen dat de maximale $k$ inderdaad $k=\left\lfloor\frac{n^{2}}{4}\right\rfloor$ is.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2015-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2015"
}
|
In a triangle $ABC$, $D$ is the intersection of the internal bisector of $\angle BAC$ with side $BC$. Let $P$ be the second intersection of the external bisector of $\angle BAC$ with the circumcircle of $\triangle ABC$. A circle through $A$ and $P$ intersects segment $BP$ internally at $E$ and segment $CP$ internally at $F$. Prove that $\angle DEP = \angle DFP$.
|
We consider the configuration where the points $A, C, B$ and $P$ lie on the circumcircle in that order. The other case is analogous.
Due to the inscribed angle theorem in the circumcircle of $\triangle A B C$, we have
$$
\angle A B E=\angle A B P=\angle A C P=\angle A C F .
$$
Furthermore, by the inscribed angle theorem in the circle through $A, P, E$ and $F$:
$$
\angle A E B=180^{\circ}-\angle A E P=180^{\circ}-\angle A F P=\angle A F C .
$$
With (AA) we conclude that $\triangle A B E \sim \triangle A C F$. From this it follows that
$$
\frac{|A B|}{|A C|}=\frac{|B E|}{|C F|}
$$
According to the angle bisector theorem, we have
$$
\frac{|A B|}{|A C|}=\frac{|D B|}{|D C|}
$$
so together this gives
$$
\frac{|B E|}{|C F|}=\frac{|D B|}{|D C|}
$$
Choose $Z$ on $P A$ such that $A$ lies between $P$ and $Z$. Since $A P$ is the external angle bisector of $\angle B A C$, we have $\angle P A B=\angle Z A C=180^{\circ}-\angle P A C$. Thus, using the inscribed angle theorem and the cyclic quadrilateral theorem, we now get
$$
\angle D C F=\angle P C B=\angle P A B=180^{\circ}-\angle P A C=\angle P B C=\angle E B D .
$$
(Alternative proof for $\angle D C F=\angle E B D$: Let $Q$ be the second intersection of the internal angle bisector of $\angle B A C$ with the circumcircle of $\triangle A B C$. Since $\angle C A Q=\angle B A Q$, the arcs $B Q$ and $C Q$ are of equal length. The external and internal angle bisectors are perpendicular to each other, so by Thales' theorem we see that $P Q$ is a diameter of the circumcircle. From this it follows that the arcs $B P$ and $C P$ are also of equal length. Thus $|B P|=|C P|$ and therefore
$$
\angle E B D=\angle P B C=\angle B C P=\angle D C F
$$
which is what we wanted to prove.)
Combined with (1) we now get $\triangle B E D \sim \triangle C F D$ (AA). From this it follows that $\angle B E D=$ $\angle C F D$ and thus also $\angle D E P=180^{\circ}-\angle B E D=180^{\circ}-\angle C F D=\angle D F P$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In een driehoek $A B C$ is $D$ het snijpunt van de binnenbissectrice van $\angle B A C$ met zijde $B C$. Zij $P$ het tweede snijpunt van de buitenbissectrice van $\angle B A C$ met de omgeschreven cirkel van $\triangle A B C$. Een cirkel door $A$ en $P$ snijdt lijnstuk $B P$ inwendig in $E$ en lijnstuk $C P$ inwendig in $F$. Bewijs dat $\angle D E P=\angle D F P$.
|
We bekijken de configuratie waarbij de punten $A, C, B$ en $P$ in die volgorde op de omgeschreven cirkel liggen. Het andere geval gaat analoog.
Vanwege de omtrekshoekstelling in de omgeschreven cirkel van $\triangle A B C$ geldt
$$
\angle A B E=\angle A B P=\angle A C P=\angle A C F .
$$
Verder is wegens de omtrekshoekstelling in de cirkel door $A, P, E$ en $F$ :
$$
\angle A E B=180^{\circ}-\angle A E P=180^{\circ}-\angle A F P=\angle A F C .
$$
Met (hh) concluderen we dat $\triangle A B E \sim \triangle A C F$. Hieruit volgt
$$
\frac{|A B|}{|A C|}=\frac{|B E|}{|C F|}
$$
Volgens de bissectricestelling geldt
$$
\frac{|A B|}{|A C|}=\frac{|D B|}{|D C|}
$$
dus samen geeft dit
$$
\frac{|B E|}{|C F|}=\frac{|D B|}{|D C|}
$$
Kies $Z$ op $P A$ zodat $A$ tussen $P$ en $Z$ ligt. Omdat $A P$ de buitenbissectrice van $\angle B A C$ is, geldt $\angle P A B=\angle Z A C=180^{\circ}-\angle P A C$. Dus met behulp van de omtrekshoekstelling en koordenvierhoekstelling krijgen we nu
$$
\angle D C F=\angle P C B=\angle P A B=180^{\circ}-\angle P A C=\angle P B C=\angle E B D .
$$
(Alternatief voor het bewijs $\angle D C F=\angle E B D$ : noem $Q$ het tweede snijpunt van de binnenbissectrice van $\angle B A C$ met de omgeschreven cirkel van $\triangle A B C$. Omdat $\angle C A Q=\angle B A Q$, zijn de bogen $B Q$ en $C Q$ even lang. De buitenbissectrice en de binnenbissectrice staan loodrecht op elkaar, dus met Thales zien we dat $P Q$ een middellijn van de omgeschreven cirkel is. Daaruit volgt dat ook de bogen $B P$ en $C P$ even lang zijn. Dus $|B P|=|C P|$ en daarmee ook
$$
\angle E B D=\angle P B C=\angle B C P=\angle D C F
$$
wat we wilden bewijzen.)
Gecombineerd met (1) krijgen we nu $\triangle B E D \sim \triangle C F D$ (zhz). Hieruit volgt dat $\angle B E D=$ $\angle C F D$ en dus ook $\angle D E P=180^{\circ}-\angle B E D=180^{\circ}-\angle C F D=\angle D F P$.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2015-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2015"
}
|
Vind alle functies $f: \mathbb{R} \rightarrow \mathbb{R}$ met
$$
\left(x^{2}+y^{2}\right) f(x y)=f(x) f(y) f\left(x^{2}+y^{2}\right)
$$
voor alle reële $x$ en $y$.
|
Vul in $x=y=0$, dan staat er $0=f(0)^{3}$, dus $f(0)=0$. We bekijken nu twee gevallen: $f$ is nog ergens anders ook 0 of juist niet. Voor het eerste geval nemen we dus aan dat er nog een $a \neq 0$ is zodat $f(a)=0$. Dan geeft $x=a$ invullen dat $\left(a^{2}+y^{2}\right) f(a y)=0$ voor alle $y$. Omdat $a^{2}+y^{2}>0$ aangezien $a \neq 0$, is $f(a y)=0$ voor alle $y$. Maar $a y$ kan alle waarden in $\mathbb{R}$ aannemen, dus $f(x)=0$ voor alle $x$. Dit is meteen een kandidaatfunctie en deze voldoet.
We bekijken nu verder het tweede geval: $f(x) \neq 0$ voor alle $x \neq 0$. Neem nu $x \neq 0$ en $y=1$. Dan geldt $\left(x^{2}+1\right) f(x)=f(x) f(1) f\left(x^{2}+1\right)$ en $f(x) \neq 0$, dus we kunnen hier delen door $f(x)$. We krijgen $\left(x^{2}+1\right)=f(1) f\left(x^{2}+1\right)$. Noem $f(1)=c$. We weten $c \neq 0$, dus $f\left(x^{2}+1\right)=\frac{x^{2}+1}{c}$. Omdat $x^{2}+1$ alle reële waarden groter dan 1 kan aannemen, geldt nu $f(x)=\frac{x}{c}$ voor alle $x>1$.
Neem $x=y=2$ en vul dit in: $(4+4) f(4)=f(2) f(2) f(4+4)$. Voor $x>1$ weten we de functiewaarde, dus in het bijzonder weten we ook $f(2), f(4)$ en $f(8)$. Dus $8 \cdot \frac{4}{c}=\frac{2}{c} \cdot \frac{2}{c} \cdot \frac{8}{c}$, oftewel $\frac{1}{c}=\frac{1}{c^{3}}$. We zien dat $c^{2}=1$, dus $c=1$ of $c=-1$. Omdat $c^{2}=1$, kunnen we nu ook schrijven $f(x)=c x$ voor alle $x \geq 1$.
Neem $x>1$ en vul $y=\frac{1}{x}$ in. Dat geeft $\left(x^{2}+\frac{1}{x^{2}}\right) f(1)=f(x) f\left(\frac{1}{x}\right) f\left(x^{2}+\frac{1}{x^{2}}\right)$. Omdat $x>1$, is ook $x^{2}+\frac{1}{x^{2}}>1$, dus hier staat $\left(x^{2}+\frac{1}{x^{2}}\right) c=x c \cdot f\left(\frac{1}{x}\right) \cdot c\left(x^{2}+\frac{1}{x^{2}}\right)$, oftewel $1=x c \cdot f\left(\frac{1}{x}\right)$. Dus $f\left(\frac{1}{x}\right)=\frac{1}{x c}=c \cdot \frac{1}{x}$. We concluderen dat $f(x)=c x$ voor alle $x>0$ met $x \neq 1$. Maar ook voor $x=1$ geldt $f(x)=c x$, want $f(1)=c$. Dus $f(x)=c x$ voor alle $x>0$.
Vul nu $x=y=-1 \mathrm{in}$. Dat geeft $2 f(1)=f(-1)^{2} f(2)$. We weten $f(1)=c$ en $f(2)=2 c$, dus $2 c=f(-1)^{2} \cdot 2 c$, oftewel $f(-1)^{2}=1$ aangezien $c \neq 0$. Dus $f(-1)=1$ of $f(-1)=-1$. Neem $x>0$ en $y=-1$. Dat geeft $\left(x^{2}+1\right) f(-x)=f(x) f(-1) f\left(x^{2}+1\right)$, dus $\left(x^{2}+1\right) f(-x)=$ $c x \cdot f(-1) \cdot c\left(x^{2}+1\right)$, oftewel $f(-x)=c^{2} x f(-1)=x f(-1)$. Als we $d=f(-1)$ noemen, geldt dus $f(x)=-d x$ voor alle $x<0$, met $d^{2}=1$.
We concluderen dat er vier mogelijke kandidaatfuncties zijn (naast $f(x)=0$, die we al gecontroleerd hadden): $f(x)=x, f(x)=-x, f(x)=|x|$ en $f(x)=-|x|$. We controleren eerst $f(x)=t x$ met $t= \pm 1$. Dan staat er links $\left(x^{2}+y^{2}\right) \cdot t x y$ en rechts $t x \cdot t y \cdot t\left(x^{2}+y^{2}\right)$. Omdat $t^{2}=1$, staat links en rechts hetzelfde. Dus deze twee functies voldoen. Nu controleren we $f(x)=t|x|$, waarbij weer $t= \pm 1$. Nu staat links $\left(x^{2}+y^{2}\right) \cdot t|x y|$ en rechts $t|x| \cdot t|y| \cdot t\left|x^{2}+y^{2}\right|$. Omdat $x^{2}+y^{2}=\left|x^{2}+y^{2}\right|$ en $|x y|=|x||y|$, staat links en rechts hetzelfde. Dus ook deze twee functies voldoen.
Er zijn dus vijf oplossingen: $f(x)=0, f(x)=x, f(x)=-x, f(x)=|x|$ en $f(x)=-|x|$.
|
f(x)=0, f(x)=x, f(x)=-x, f(x)=|x|, f(x)=-|x|
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Vind alle functies $f: \mathbb{R} \rightarrow \mathbb{R}$ met
$$
\left(x^{2}+y^{2}\right) f(x y)=f(x) f(y) f\left(x^{2}+y^{2}\right)
$$
voor alle reële $x$ en $y$.
|
Vul in $x=y=0$, dan staat er $0=f(0)^{3}$, dus $f(0)=0$. We bekijken nu twee gevallen: $f$ is nog ergens anders ook 0 of juist niet. Voor het eerste geval nemen we dus aan dat er nog een $a \neq 0$ is zodat $f(a)=0$. Dan geeft $x=a$ invullen dat $\left(a^{2}+y^{2}\right) f(a y)=0$ voor alle $y$. Omdat $a^{2}+y^{2}>0$ aangezien $a \neq 0$, is $f(a y)=0$ voor alle $y$. Maar $a y$ kan alle waarden in $\mathbb{R}$ aannemen, dus $f(x)=0$ voor alle $x$. Dit is meteen een kandidaatfunctie en deze voldoet.
We bekijken nu verder het tweede geval: $f(x) \neq 0$ voor alle $x \neq 0$. Neem nu $x \neq 0$ en $y=1$. Dan geldt $\left(x^{2}+1\right) f(x)=f(x) f(1) f\left(x^{2}+1\right)$ en $f(x) \neq 0$, dus we kunnen hier delen door $f(x)$. We krijgen $\left(x^{2}+1\right)=f(1) f\left(x^{2}+1\right)$. Noem $f(1)=c$. We weten $c \neq 0$, dus $f\left(x^{2}+1\right)=\frac{x^{2}+1}{c}$. Omdat $x^{2}+1$ alle reële waarden groter dan 1 kan aannemen, geldt nu $f(x)=\frac{x}{c}$ voor alle $x>1$.
Neem $x=y=2$ en vul dit in: $(4+4) f(4)=f(2) f(2) f(4+4)$. Voor $x>1$ weten we de functiewaarde, dus in het bijzonder weten we ook $f(2), f(4)$ en $f(8)$. Dus $8 \cdot \frac{4}{c}=\frac{2}{c} \cdot \frac{2}{c} \cdot \frac{8}{c}$, oftewel $\frac{1}{c}=\frac{1}{c^{3}}$. We zien dat $c^{2}=1$, dus $c=1$ of $c=-1$. Omdat $c^{2}=1$, kunnen we nu ook schrijven $f(x)=c x$ voor alle $x \geq 1$.
Neem $x>1$ en vul $y=\frac{1}{x}$ in. Dat geeft $\left(x^{2}+\frac{1}{x^{2}}\right) f(1)=f(x) f\left(\frac{1}{x}\right) f\left(x^{2}+\frac{1}{x^{2}}\right)$. Omdat $x>1$, is ook $x^{2}+\frac{1}{x^{2}}>1$, dus hier staat $\left(x^{2}+\frac{1}{x^{2}}\right) c=x c \cdot f\left(\frac{1}{x}\right) \cdot c\left(x^{2}+\frac{1}{x^{2}}\right)$, oftewel $1=x c \cdot f\left(\frac{1}{x}\right)$. Dus $f\left(\frac{1}{x}\right)=\frac{1}{x c}=c \cdot \frac{1}{x}$. We concluderen dat $f(x)=c x$ voor alle $x>0$ met $x \neq 1$. Maar ook voor $x=1$ geldt $f(x)=c x$, want $f(1)=c$. Dus $f(x)=c x$ voor alle $x>0$.
Vul nu $x=y=-1 \mathrm{in}$. Dat geeft $2 f(1)=f(-1)^{2} f(2)$. We weten $f(1)=c$ en $f(2)=2 c$, dus $2 c=f(-1)^{2} \cdot 2 c$, oftewel $f(-1)^{2}=1$ aangezien $c \neq 0$. Dus $f(-1)=1$ of $f(-1)=-1$. Neem $x>0$ en $y=-1$. Dat geeft $\left(x^{2}+1\right) f(-x)=f(x) f(-1) f\left(x^{2}+1\right)$, dus $\left(x^{2}+1\right) f(-x)=$ $c x \cdot f(-1) \cdot c\left(x^{2}+1\right)$, oftewel $f(-x)=c^{2} x f(-1)=x f(-1)$. Als we $d=f(-1)$ noemen, geldt dus $f(x)=-d x$ voor alle $x<0$, met $d^{2}=1$.
We concluderen dat er vier mogelijke kandidaatfuncties zijn (naast $f(x)=0$, die we al gecontroleerd hadden): $f(x)=x, f(x)=-x, f(x)=|x|$ en $f(x)=-|x|$. We controleren eerst $f(x)=t x$ met $t= \pm 1$. Dan staat er links $\left(x^{2}+y^{2}\right) \cdot t x y$ en rechts $t x \cdot t y \cdot t\left(x^{2}+y^{2}\right)$. Omdat $t^{2}=1$, staat links en rechts hetzelfde. Dus deze twee functies voldoen. Nu controleren we $f(x)=t|x|$, waarbij weer $t= \pm 1$. Nu staat links $\left(x^{2}+y^{2}\right) \cdot t|x y|$ en rechts $t|x| \cdot t|y| \cdot t\left|x^{2}+y^{2}\right|$. Omdat $x^{2}+y^{2}=\left|x^{2}+y^{2}\right|$ en $|x y|=|x||y|$, staat links en rechts hetzelfde. Dus ook deze twee functies voldoen.
Er zijn dus vijf oplossingen: $f(x)=0, f(x)=x, f(x)=-x, f(x)=|x|$ en $f(x)=-|x|$.
|
{
"exam": "Dutch_TST",
"problem_label": "5",
"problem_match": "\nOpgave 5.",
"resource_path": "Dutch_TST/segmented/nl-2015-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2015"
}
|
For quadrilateral $A B C D$, it holds that $\angle A=\angle C=90^{\circ}$. Let $E$ be a point inside the quadrilateral. Let $M$ be the midpoint of $B E$. Prove that $\angle A D B=\angle E D C$ if and only if $|M A|=|M C|$.
|
Let $N$ be the midpoint of $BD$. By Thales, the circle with diameter $BD$ also passes through $A$ and $C$, and point $N$ is the center of this circle. Furthermore, it holds that $MN \| DE$: if $E$ does not lie on $BD$, then $MN$ is a midline in triangle $BDE$, and if $E$ does lie on $BD$, then $MN$ and $DE$ are the same line.
The statement $|AM|=|CM|$ is equivalent to $M$ lying on the perpendicular bisector of $AC$. Since this perpendicular bisector passes through the center $N$ of the circle, this is equivalent to the statement $MN \perp AC$. And this is the case if and only if $DE \perp AC$. Let $T$ be the intersection of $DE$ and $AC$, then we have: $|AM|=|CM|$ if and only if $\angle DTC=90^{\circ}$.
Using the angle sum, we find $\angle DTC=180^{\circ}-\angle TDC-\angle DCT=180^{\circ}-\angle EDC-\angle DCA$. It holds that $\angle DCA=90^{\circ}-\angle ACB=90^{\circ}-\angle ADB$, where we used the cyclic quadrilateral $ABCD$ for the last equality. Thus, $\angle DTC=180^{\circ}-\angle EDC-(90^{\circ}-\angle ADB)=$ $90^{\circ}-\angle EDC+\angle ADB$. It immediately follows that $\angle ADB=\angle EDC$ if and only if $\angle DTC=90^{\circ}$, and we had already seen that the latter is equivalent to $|AM|=|CM|$. Note that this proof holds in any configuration.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Voor vierhoek $A B C D$ geldt $\angle A=\angle C=90^{\circ}$. Zij $E$ een punt binnen de vierhoek. Zij $M$ het midden van $B E$. Bewijs dat $\angle A D B=\angle E D C$ dan en slechts dan als $|M A|=|M C|$.
|
Zij $N$ het midden van $B D$. Wegens Thales gaat de cirkel met middellijn $B D$ ook door $A$ en $C$ en punt $N$ is hiervan het middelpunt. Verder geldt dat $M N \| D E$ : als $E$ niet op $B D$ ligt, is $M N$ een middenparallel in driehoek $B D E$, en als $E$ wel op $B D$ ligt, dan zijn $M N$ en $D E$ dezelfde lijn.
De bewering $|A M|=|C M|$ is equivalent met dat $M$ op de middelloodlijn van $A C$ ligt. Omdat die middelloodlijn door het middelpunt $N$ van de cirkel gaat, is dit dus equivalent met de bewering $M N \perp A C$. En dat is het geval dan en slechts dan als $D E \perp A C$. Noem $T$ het snijpunt van $D E$ en $A C$, dan geldt dus: $|A M|=|C M|$ dan en slechts dan als $\angle D T C=90^{\circ}$.
Met de hoekensom vinden we $\angle D T C=180^{\circ}-\angle T D C-\angle D C T=180^{\circ}-\angle E D C-\angle D C A$. Er geldt $\angle D C A=90^{\circ}-\angle A C B=90^{\circ}-\angle A D B$, waarbij we voor de laatste gelijkheid de koordenvierhoek $A B C D$ hebben gebruikt. Dus $\angle D T C=180^{\circ}-\angle E D C-\left(90^{\circ}-\angle A D B\right)=$ $90^{\circ}-\angle E D C+\angle A D B$. Nu volgt onmiddelijk dat $\angle A D B=\angle E D C$ dan en slechts dan als $\angle D T C=90^{\circ}$ en we hadden al gezien dat dat laatste equivalent was met $|A M|=|C M|$. Merk op dat dit bewijs geldt in iedere configuratie.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2015-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2015"
}
|
Bepaal alle polynomen $P(x)$ met reële coëfficiënten waarvoor het polynoom
$$
Q(x)=(x+1) P(x-1)-(x-1) P(x)
$$
constant is.
|
Stel dat $P(x)$ een constant polynoom is, zeg $P(x)=a$ met $a \in \mathbb{R}$. Dan is
$$
Q(x)=(x+1) a-(x-1) a=a x+a-a x+a=2 a,
$$
en dat is constant. Dus elk constant polynoom $P(x)$ voldoet.
We nemen nu verder aan dat $P$ niet constant is. We kunnen dan schrijven $P(x)=a_{n} x^{n}+$ $a_{n-1} x^{n-1}+\ldots+a_{1} x+a_{0}$ met $n \geq 1$ en $a_{n} \neq 0$. Bekijk de coëfficiënt van $x^{n}$ in $Q(x)$. Deze is de som van de coëfficiënten van $x^{n}$ in $x P(x-1), P(x-1),-x P(x)$ en $P(x)$. In de eerste is deze coëfficiënt gelijk aan $a_{n-1}-n a_{n}$, in de tweede aan $a_{n}$, in de derde aan $-a_{n-1}$ en in de vierde aan $a_{n}$. Samen is dat
$$
a_{n-1}-n a_{n}+a_{n}-a_{n-1}+a_{n}=(2-n) a_{n} .
$$
Maar in $Q(x)$ moet deze coëfficiënt gelijk zijn aan 0 . Omdat $a_{n} \neq 0$, volgt hieruit $n=2$. Dus $P(x)=a_{2} x^{2}+a_{1} x+a_{0}$ met $a_{2} \neq 0$.
Bekijk nu de constante coëfficiënt van $Q(x)$. Deze is de som van de constante coëfficiënten van $x P(x-1), P(x-1),-x P(x)$ en $P(x)$. Dit zijn achtereenvolgens $0, a_{2}-a_{1}+a_{0}, 0$ en $a_{0}$. Samen is dat $a_{2}-a_{1}+2 a_{0}$. Anderzijds kunnen we $Q(1)$ uitrekenen:
$$
Q(1)=2 P(0)-0=2 a_{0}
$$
Omdat $Q$ constant is, is $Q(1)$ gelijk aan de constante coëfficiënt van $Q$, dus $2 a_{0}=a_{2}-a_{1}+$ $2 a_{0}$. We zien dat $a_{2}=a_{1}$. Dus $P(x)$ is van de vorm $P(x)=b x^{2}+b x+a=b x(x+1)+a$ met $a, b \in \mathbb{R}$ en $b \neq 0$. Om te kijken of alle polynomen van deze vorm voldoen, vullen we dit in:
$$
\begin{aligned}
Q(x) & =(x+1)(b(x-1) x+a)-(x-1)(b x(x+1)+a) \\
& =(x-1) x(x+1) b+(x+1) a-(x-1) x(x+1) b-(x-1) a \\
& =2 a
\end{aligned}
$$
Dat is inderdaad constant, dus alle polynomen van deze vorm voldoen. In feite is elk constant polynoom ook van deze vorm, maar dan met $b=0$. We concluderen dat de oplossingen zijn: alle polynomen van de vorm $P(x)=b x^{2}+b x+a$ met $a, b \in \mathbb{R}$.
|
P(x)=b x^{2}+b x+a
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Bepaal alle polynomen $P(x)$ met reële coëfficiënten waarvoor het polynoom
$$
Q(x)=(x+1) P(x-1)-(x-1) P(x)
$$
constant is.
|
Stel dat $P(x)$ een constant polynoom is, zeg $P(x)=a$ met $a \in \mathbb{R}$. Dan is
$$
Q(x)=(x+1) a-(x-1) a=a x+a-a x+a=2 a,
$$
en dat is constant. Dus elk constant polynoom $P(x)$ voldoet.
We nemen nu verder aan dat $P$ niet constant is. We kunnen dan schrijven $P(x)=a_{n} x^{n}+$ $a_{n-1} x^{n-1}+\ldots+a_{1} x+a_{0}$ met $n \geq 1$ en $a_{n} \neq 0$. Bekijk de coëfficiënt van $x^{n}$ in $Q(x)$. Deze is de som van de coëfficiënten van $x^{n}$ in $x P(x-1), P(x-1),-x P(x)$ en $P(x)$. In de eerste is deze coëfficiënt gelijk aan $a_{n-1}-n a_{n}$, in de tweede aan $a_{n}$, in de derde aan $-a_{n-1}$ en in de vierde aan $a_{n}$. Samen is dat
$$
a_{n-1}-n a_{n}+a_{n}-a_{n-1}+a_{n}=(2-n) a_{n} .
$$
Maar in $Q(x)$ moet deze coëfficiënt gelijk zijn aan 0 . Omdat $a_{n} \neq 0$, volgt hieruit $n=2$. Dus $P(x)=a_{2} x^{2}+a_{1} x+a_{0}$ met $a_{2} \neq 0$.
Bekijk nu de constante coëfficiënt van $Q(x)$. Deze is de som van de constante coëfficiënten van $x P(x-1), P(x-1),-x P(x)$ en $P(x)$. Dit zijn achtereenvolgens $0, a_{2}-a_{1}+a_{0}, 0$ en $a_{0}$. Samen is dat $a_{2}-a_{1}+2 a_{0}$. Anderzijds kunnen we $Q(1)$ uitrekenen:
$$
Q(1)=2 P(0)-0=2 a_{0}
$$
Omdat $Q$ constant is, is $Q(1)$ gelijk aan de constante coëfficiënt van $Q$, dus $2 a_{0}=a_{2}-a_{1}+$ $2 a_{0}$. We zien dat $a_{2}=a_{1}$. Dus $P(x)$ is van de vorm $P(x)=b x^{2}+b x+a=b x(x+1)+a$ met $a, b \in \mathbb{R}$ en $b \neq 0$. Om te kijken of alle polynomen van deze vorm voldoen, vullen we dit in:
$$
\begin{aligned}
Q(x) & =(x+1)(b(x-1) x+a)-(x-1)(b x(x+1)+a) \\
& =(x-1) x(x+1) b+(x+1) a-(x-1) x(x+1) b-(x-1) a \\
& =2 a
\end{aligned}
$$
Dat is inderdaad constant, dus alle polynomen van deze vorm voldoen. In feite is elk constant polynoom ook van deze vorm, maar dan met $b=0$. We concluderen dat de oplossingen zijn: alle polynomen van de vorm $P(x)=b x^{2}+b x+a$ met $a, b \in \mathbb{R}$.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2015-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2015"
}
|
Determine all polynomials $P(x)$ with real coefficients for which the polynomial
$$
Q(x)=(x+1) P(x-1)-(x-1) P(x)
$$
is constant.
|
It holds that
$$
Q(1)=2 P(0)-0=2 P(0)
$$
and
$$
Q(-1)=0--2 P(-1)=2 P(-1)
$$
Since $Q$ is constant, it follows that $P(0)=P(-1)$. Let $P(0)=c$ and consider the polynomial $P(x)-c$. This polynomial has roots at $x=0$ and $x=-1$, so
$$
P(x)-c=x(x+1) R(x)
$$
for some polynomial $R(x)$ with real coefficients. Thus, $P(x)=x(x+1) R(x)+c$ and we substitute this in:
$$
\begin{aligned}
Q(x) & =(x+1)((x-1) x R(x-1)+c)-(x-1)(x(x+1) R(x)+c) \\
& =(x-1) x(x+1) R(x-1)+(x+1) c-(x-1) x(x+1) R(x)-(x-1) c \\
& =(x-1) x(x+1)(R(x-1)-R(x))+2 c
\end{aligned}
$$
This must be constant, so $R(x-1)-R(x)$ must be the zero polynomial. Thus, $R(x-1)=R(x)$ for all $x$. In particular, $R(0)=R(1)=R(2)=\ldots$, so $R$ takes the same value at infinitely many points. This means that $R$ must be a constant polynomial, say $R(x)=d$. Then we have
$$
P(x)=x(x+1) d+c=d x^{2}+d x+c .
$$
Just as in the first solution, we verify that all polynomials of this form, with $c, d \in \mathbb{R}$, satisfy the condition.
|
P(x)=dx^2+dx+c
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Bepaal alle polynomen $P(x)$ met reële coëfficiënten waarvoor het polynoom
$$
Q(x)=(x+1) P(x-1)-(x-1) P(x)
$$
constant is.
|
Er geldt
$$
Q(1)=2 P(0)-0=2 P(0)
$$
en
$$
Q(-1)=0--2 P(-1)=2 P(-1)
$$
Omdat $Q$ constant is, volgt hieruit $P(0)=P(-1)$. Schrijf $P(0)=c$ en bekijk het polynoom $P(x)-c$. Dit polynoom heeft nulpunten bij $x=0$ en $x=-1$, dus
$$
P(x)-c=x(x+1) R(x)
$$
voor een zeker polynoom $R(x)$ met reële coëfficiënten. Dus $P(x)=x(x+1) R(x)+c$ en dit vullen we in:
$$
\begin{aligned}
Q(x) & =(x+1)((x-1) x R(x-1)+c)-(x-1)(x(x+1) R(x)+c) \\
& =(x-1) x(x+1) R(x-1)+(x+1) c-(x-1) x(x+1) R(x)-(x-1) c \\
& =(x-1) x(x+1)(R(x-1)-R(x))+2 c
\end{aligned}
$$
Dit moet constant zijn, dus $R(x-1)-R(x)$ moet het nulpolynoom zijn. Dus $R(x-1)=$ $R(x)$ voor alle $x$. In het bijzonder geldt $R(0)=R(1)=R(2)=\ldots$, dus $R$ neemt dezelfde waarde aan op oneindig veel punten. Dat betekent dat $R$ gelijk moet zijn aan een constant polynoom, zeg $R(x)=d$. Dan geldt
$$
P(x)=x(x+1) d+c=d x^{2}+d x+c .
$$
Net als in de eerste oplossing controleren we dat alle polynomen van deze vorm, met $c, d \in \mathbb{R}$, voldoen.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2015-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2015"
}
|
Determine all polynomials $P(x)$ with real coefficients for which the polynomial
$$
Q(x)=(x+1) P(x-1)-(x-1) P(x)
$$
is constant.
|
We denote $p=P(1)$ and $q$ the constant value that $Q(x)$ assumes. We prove by induction on $m$ that $P(m)=\frac{1}{2} m(m+1) p-\left(\frac{1}{2} m(m+1)-1\right) \cdot \frac{q}{2}$ for all integers $m \geq 1$.
For $m=1$, we have $P(1)=\frac{1}{2} \cdot 1 \cdot 2 \cdot p-\left(\frac{1}{2} \cdot 1 \cdot 2-1\right) \cdot \frac{q}{2}=p-0=P(1)$, so this is correct. Now let $k \geq 1$ and assume that we have proven the claim for $m=k$. From the given equation, for $x \neq 1$:
$$
P(x)=\frac{(x+1) P(x-1)-q}{x-1} .
$$
Substitute $x=k+1$ (note that $x \neq 1$, since $k \geq 1$):
$$
\begin{aligned}
P(k+1) & =\frac{(k+2) P(k)-q}{k} \\
& =\frac{(k+2) \cdot\left(\frac{1}{2} k(k+1) p-\left(\frac{1}{2} k(k+1)-1\right) \cdot \frac{q}{2}\right)-q}{k} \\
& =(k+2) \cdot\left(\frac{1}{2}(k+1) p-\left(\frac{1}{2}(k+1)-\frac{1}{k}\right) \cdot \frac{q}{2}\right)-\frac{q}{k} \\
& =\frac{1}{2}(k+1)(k+2) p-\frac{1}{2}(k+1)(k+2) \cdot \frac{q}{2}+\frac{k+2}{k} \cdot \frac{q}{2}-\frac{q}{k} \\
& =\frac{1}{2}(k+1)(k+2) p-\frac{1}{2}(k+1)(k+2) \cdot \frac{q}{2}+\frac{q}{2}+\frac{2}{k} \cdot \frac{q}{2}-\frac{q}{k} \\
& =\frac{1}{2}(k+1)(k+2) p-\left(\frac{1}{2}(k+1)(k+2)-1\right) \cdot \frac{q}{2} .
\end{aligned}
$$
This completes the induction step.
Thus, $P(x)$ coincides at infinitely many points (namely all positive integers) with the polynomial $\frac{1}{2} x(x+1) p-\left(\frac{1}{2} x(x+1)-1\right) \cdot \frac{q}{2}$. Therefore, it must be equal to this polynomial. Rewriting this in standard notation, we get
$$
P(x)=\left(\frac{1}{2} p-\frac{1}{4} q\right) \cdot x^{2}+\left(\frac{1}{2} p-\frac{1}{4} q\right) \cdot x+\frac{q}{2} .
$$
This is of the form $P(x)=b x^{2}+b x+a$ with $a$ and $b$ constants in $\mathbb{R}$. Just like in the first solution, we check that all polynomials of this form satisfy the condition.
|
P(x)=\left(\frac{1}{2} p-\frac{1}{4} q\right) \cdot x^{2}+\left(\frac{1}{2} p-\frac{1}{4} q\right) \cdot x+\frac{q}{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Bepaal alle polynomen $P(x)$ met reële coëfficiënten waarvoor het polynoom
$$
Q(x)=(x+1) P(x-1)-(x-1) P(x)
$$
constant is.
|
We noemen $p=P(1)$ en $q$ de constante waarde die $Q(x)$ aanneemt. We bewijzen met inductie naar $m$ dat $P(m)=\frac{1}{2} m(m+1) p-\left(\frac{1}{2} m(m+1)-1\right) \cdot \frac{q}{2}$ voor alle gehele $m \geq 1$.
Voor $m=1$ staat er $P(1)=\frac{1}{2} \cdot 1 \cdot 2 \cdot p-\left(\frac{1}{2} \cdot 1 \cdot 2-1\right) \cdot \frac{q}{2}=p-0=P(1)$, dus dat klopt. Zij nu $k \geq 1$ en neem aan dat we de claim bewezen hebben voor $m=k$. Uit de gegeven vergelijking volgt voor $x \neq 1$ :
$$
P(x)=\frac{(x+1) P(x-1)-q}{x-1} .
$$
Vul nu $x=k+1$ in (merk op dat $x \neq 1$, want $k \geq 1$ ):
$$
\begin{aligned}
P(k+1) & =\frac{(k+2) P(k)-q}{k} \\
& =\frac{(k+2) \cdot\left(\frac{1}{2} k(k+1) p-\left(\frac{1}{2} k(k+1)-1\right) \cdot \frac{q}{2}\right)-q}{k} \\
& =(k+2) \cdot\left(\frac{1}{2}(k+1) p-\left(\frac{1}{2}(k+1)-\frac{1}{k}\right) \cdot \frac{q}{2}\right)-\frac{q}{k} \\
& =\frac{1}{2}(k+1)(k+2) p-\frac{1}{2}(k+1)(k+2) \cdot \frac{q}{2}+\frac{k+2}{k} \cdot \frac{q}{2}-\frac{q}{k} \\
& =\frac{1}{2}(k+1)(k+2) p-\frac{1}{2}(k+1)(k+2) \cdot \frac{q}{2}+\frac{q}{2}+\frac{2}{k} \cdot \frac{q}{2}-\frac{q}{k} \\
& =\frac{1}{2}(k+1)(k+2) p-\left(\frac{1}{2}(k+1)(k+2)-1\right) \cdot \frac{q}{2} .
\end{aligned}
$$
Dit voltooit de inductiestap.
Dus $P(x)$ valt op oneindig veel punten (namelijk alle positieve gehele getallen) samen met het polynoom $\frac{1}{2} x(x+1) p-\left(\frac{1}{2} x(x+1)-1\right) \cdot \frac{q}{2}$. Daarom moet hij gelijk zijn aan dit polynoom. Als we dit herschrijven tot de standaardnotatie, krijgen we
$$
P(x)=\left(\frac{1}{2} p-\frac{1}{4} q\right) \cdot x^{2}+\left(\frac{1}{2} p-\frac{1}{4} q\right) \cdot x+\frac{q}{2} .
$$
Dit is van de vorm $P(x)=b x^{2}+b x+a$ met $a$ en $b$ constanten in $\mathbb{R}$. Net als in de eerste oplossing controleren we dat alle polynomen van deze vorm voldoen.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2015-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing III.",
"tier": "T1",
"year": "2015"
}
|
Let $n$ be a positive integer. We consider sequences of numbers $a_{0}, a_{1}, \ldots, a_{k}$ and $b_{0}, b_{1}, \ldots, b_{k}$ that satisfy $a_{0}=b_{0}=1$ and $a_{k}=b_{k}=n$ and for every $i$ with $1 \leq i \leq k$ it holds that $\left(a_{i}, b_{i}\right)$ is either $\left(1+a_{i-1}, b_{i-1}\right)$ or $\left(a_{i-1}, 1+b_{i-1}\right)$. Define for $1 \leq i \leq k$ the number
$$
c_{i}= \begin{cases}a_{i} & \text { if } a_{i}=a_{i-1} \\ b_{i} & \text { if } b_{i}=b_{i-1}\end{cases}
$$
Prove that $c_{1}+c_{2}+\cdots+c_{k}=n^{2}-1$.
|
We prove by induction on $j$ that $c_{1}+\ldots+c_{j}=a_{j} b_{j}-1$. For $j=1$, this reads $c_{1}=a_{1} b_{1}-1$ and this is true since $\left(a_{1}, b_{1}\right) \in\{(1,2),(2,1)\}$. Now assume that $c_{1}+\ldots+c_{i-1}=a_{i-1} b_{i-1}-1$. Without loss of generality, assume that $\left(a_{i}, b_{i}\right)=$ $\left(a_{i-1}, 1+b_{i-1}\right)$, so that $a_{i}=a_{i-1}$ and thus $c_{i}=a_{i-1}$. We now have
$$
\left(c_{1}+\ldots+c_{i-1}\right)+c_{i}=\left(a_{i-1} b_{i-1}-1\right)+a_{i-1}=a_{i-1}\left(b_{i-1}+1\right)-1=a_{i} b_{i}-1
$$
which completes the induction. For $j=k$ we now see that $c_{1}+\ldots+c_{k}=a_{k} b_{k}-1=n^{2}-1$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Zij $n$ een positief geheel getal. We bekijken rijtjes getallen $a_{0}, a_{1}, \ldots, a_{k}$ en $b_{0}, b_{1}, \ldots, b_{k}$ die voldoen aan $a_{0}=b_{0}=1$ en $a_{k}=b_{k}=n$ en waarbij voor elke $i$ met $1 \leq i \leq k$ geldt dat $\left(a_{i}, b_{i}\right)$ gelijk is aan ofwel $\left(1+a_{i-1}, b_{i-1}\right)$ ofwel $\left(a_{i-1}, 1+b_{i-1}\right)$. Definieer voor $1 \leq i \leq k$ het getal
$$
c_{i}= \begin{cases}a_{i} & \text { als } a_{i}=a_{i-1} \\ b_{i} & \text { als } b_{i}=b_{i-1}\end{cases}
$$
Bewijs dat $c_{1}+c_{2}+\cdots+c_{k}=n^{2}-1$.
|
We bewijzen met inductie naar $j$ dat $c_{1}+\ldots+c_{j}=a_{j} b_{j}-1$. Voor $j=1$ staat hier $c_{1}=a_{1} b_{1}-1$ en dat is waar aangezien $\left(a_{1}, b_{1}\right) \in\{(1,2),(2,1)\}$. Stel nu dat $c_{1}+\ldots+c_{i-1}=a_{i-1} b_{i-1}-1$. Neem zonder verlies van algemeenheid aan dat $\left(a_{i}, b_{i}\right)=$ $\left(a_{i-1}, 1+b_{i-1}\right)$, zodat $a_{i}=a_{i-1}$ en dus $c_{i}=a_{i-1}$. Er geldt nu
$$
\left(c_{1}+\ldots+c_{i-1}\right)+c_{i}=\left(a_{i-1} b_{i-1}-1\right)+a_{i-1}=a_{i-1}\left(b_{i-1}+1\right)-1=a_{i} b_{i}-1
$$
wat de inductie voltooit. Voor $j=k$ zien we nu dat $c_{1}+\ldots+c_{k}=a_{k} b_{k}-1=n^{2}-1$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2015-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2015"
}
|
Let $n$ be a positive integer. We consider sequences of numbers $a_{0}, a_{1}, \ldots, a_{k}$ and $b_{0}, b_{1}, \ldots, b_{k}$ that satisfy $a_{0}=b_{0}=1$ and $a_{k}=b_{k}=n$ and for every $i$ with $1 \leq i \leq k$ it holds that $\left(a_{i}, b_{i}\right)$ is either $\left(1+a_{i-1}, b_{i-1}\right)$ or $\left(a_{i-1}, 1+b_{i-1}\right)$. Define for $1 \leq i \leq k$ the number
$$
c_{i}= \begin{cases}a_{i} & \text { if } a_{i}=a_{i-1} \\ b_{i} & \text { if } b_{i}=b_{i-1}\end{cases}
$$
Prove that $c_{1}+c_{2}+\cdots+c_{k}=n^{2}-1$.
|
We define a sequence of $k$ letters: the $i$-th letter in the sequence is equal to $A$ if $a_{i}=1+a_{i-1}$ and equal to $B$ if $b_{i}=1+b_{i-1}$. Since both sequences $a_{i}$ and $b_{i}$ go from 1 to $n$, there must be $n-1$ $A$s and $n-1$ $B$s in the sequence. If for some $i$ the $i$-th letter is equal to $A$, then $c_{i}=b_{i}$, which is equal to 1 plus the number of $B$s that appear earlier in the sequence (since $b_{0}=1$ and for each $B$, $b_{j}$ increases by 1, while for each $A$, $b_{j}$ remains unchanged). Conversely, if the $i$-th letter is a $B$, then $c_{i}$ is equal to 1 plus the number of $A$s that appear earlier in the sequence.
Now consider an old situation where the $i$-th letter is equal to $A$ and the $(i+1)$-st letter is equal to $B$, and a new situation where this is exactly reversed. The $c_{j}$ corresponding to the letter $A$ is 1 greater in the new situation than in the old one, because there is one more $B$ preceding the $A$. The $c_{j}$ corresponding to the letter $B$ is exactly 1 less. The rest of the $c_{j}$s remain unchanged, so the sum of the $c_{j}$s is also unchanged. Swapping $A B$ to $B A$ thus has no effect on the sum of the $c_{j}$s. We can now repeatedly replace $A B$ with $B A$ until the letter sequence consists of $n-1$ $B$s followed by $n-1$ $A$s. The corresponding $c_{j}$s are then $1, 1, \ldots, 1, n, n, \ldots, n$, where 1 appears exactly $n-1$ times and $n$ also appears $n-1$ times. The sum of these is $(n-1)(n+1)=n^{2}-1$, and this also holds for the sum of the $c_{j}$s in the original sequence.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Zij $n$ een positief geheel getal. We bekijken rijtjes getallen $a_{0}, a_{1}, \ldots, a_{k}$ en $b_{0}, b_{1}, \ldots, b_{k}$ die voldoen aan $a_{0}=b_{0}=1$ en $a_{k}=b_{k}=n$ en waarbij voor elke $i$ met $1 \leq i \leq k$ geldt dat $\left(a_{i}, b_{i}\right)$ gelijk is aan ofwel $\left(1+a_{i-1}, b_{i-1}\right)$ ofwel $\left(a_{i-1}, 1+b_{i-1}\right)$. Definieer voor $1 \leq i \leq k$ het getal
$$
c_{i}= \begin{cases}a_{i} & \text { als } a_{i}=a_{i-1} \\ b_{i} & \text { als } b_{i}=b_{i-1}\end{cases}
$$
Bewijs dat $c_{1}+c_{2}+\cdots+c_{k}=n^{2}-1$.
|
We definiëren een rijtje van $k$ letters: de $i$-de letter in het rijtje is gelijk aan $A$ als $a_{i}=1+a_{i-1}$ en gelijk aan $B$ als $b_{i}=1+b_{i-1}$. Omdat de rijtjes $a_{i}$ en $b_{i}$ beide van 1 naar $n$ gaan, moet er $n-1$ keer een $A$ staan en $n-1$ keer een $B$. Als voor zekere $i$ de $i$-de letter gelijk is aan $A$, dan is $c_{i}=b_{i}$ en dat is gelijk aan 1 plus het aantal letters $B$ dat eerder in het rijtje staat (want $b_{0}=1$ en voor elke $B$ is $b_{j}$ met 1 omhoog gegaan en bij elke $A$ is $b_{j}$ niet veranderd). En andersom geldt dat als de $i$-de letter een $B$ is, dan $c_{i}$ gelijk is aan 1 plus het aantal letters $A$ dat eerder in het rijtje staat.
Bekijk nu een oude situatie met de $i$-de letter gelijk aan $A$ en de $i+1$-ste letter gelijk aan $B$ en een nieuwe situatie waarin dit precies andersom is. De $c_{j}$ die hoort bij de letter $A$ is in de nieuwe situatie 1 groter dan in de oude, omdat er een keer $B$ extra voorafgaat aan de $A$. De $c_{j}$ die hoort bij de letter $B$ is juist 1 kleiner geworden. De rest van de $c_{j}$ 's is ongewijzigd, dus de som van de $c_{j}$ 's is ook ongewijzigd. Een verwisseling van $A B$ naar $B A$ heeft dus geen invloed op de som van de $c_{j}$ 's. We kunnen nu net zo lang $A B$ vervangen door $B A$ tot het letterrijtje bestaat uit eerst $n-1$ keer $B$ en daarna $n-1$ keer $A$. De bijbehorende $c_{j}$ 's zijn dan achtereenvolgens $1,1, \ldots, 1, n, n, \ldots, n$, waarbij de 1 precies $n-1$ keer voorkomt en de $n$ ook. De som hiervan is $(n-1)(n+1)=n^{2}-1$ en dat geldt dus ook voor de som van $c_{j}$ 's in het oorspronkelijke rijtje.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2015-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2015"
}
|
Let $n$ be a positive integer. We consider sequences of numbers $a_{0}, a_{1}, \ldots, a_{k}$ and $b_{0}, b_{1}, \ldots, b_{k}$ that satisfy $a_{0}=b_{0}=1$ and $a_{k}=b_{k}=n$ and for every $i$ with $1 \leq i \leq k$ it holds that $\left(a_{i}, b_{i}\right)$ is either $\left(1+a_{i-1}, b_{i-1}\right)$ or $\left(a_{i-1}, 1+b_{i-1}\right)$. Define for $1 \leq i \leq k$ the number
$$
c_{i}= \begin{cases}a_{i} & \text { if } a_{i}=a_{i-1} \\ b_{i} & \text { if } b_{i}=b_{i-1}\end{cases}
$$
Prove that $c_{1}+c_{2}+\cdots+c_{k}=n^{2}-1$.
|
We define a sequence of $k$ letters: the $i$-th letter in the sequence is equal to $A$ if $a_{i}=1+a_{i-1}$ and equal to $B$ if $b_{i}=1+b_{i-1}$. Furthermore, we define for $1 \leq i \leq k$
$$
d_{i}= \begin{cases}b_{i} & \text { if } a_{i}=a_{i-1} \\ a_{i} & \text { if } b_{i}=b_{i-1}\end{cases}
$$
If for some $i$ the $i$-th letter is equal to $A$, then $d_{i}=a_{i}$ and that is equal to 1 plus the number of letters $A$ that stand up to this position in the sequence (since $a_{0}=1$ and for each $A$, $a_{j}$ increases by 1 and for each $B$, $a_{j}$ does not change). The $d_{i}$ that correspond to the positions where an $A$ stands are thus exactly the numbers 2 to $n$. The $d_{i}$ that correspond to the positions where a $B$ stands are also exactly the numbers 2 to $n$. Therefore, the sum of all $d_{i}$ is equal to $(n-1)(n+2)=n^{2}+n-2$.
For every $i$, $c_{i}+d_{i}=a_{i}+b_{i}=1+\left(a_{i-1}+b_{i-1}\right)$ and $c_{1}+d_{1}=1+2=3$, so with a simple induction $c_{i}+d_{i}=i+2$. The total sum of all $c_{i}$ and $d_{i}$ together is thus $3+4+\ldots+2 n=\frac{1}{2}(2 n+3)(2 n-2)=(2 n+3)(n-1)=2 n^{2}+n-3$. We conclude that the sum of the $c_{i}$ is equal to $\left(2 n^{2}+n-3\right)-\left(n^{2}+n-2\right)=n^{2}-1$.
|
n^{2}-1
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Zij $n$ een positief geheel getal. We bekijken rijtjes getallen $a_{0}, a_{1}, \ldots, a_{k}$ en $b_{0}, b_{1}, \ldots, b_{k}$ die voldoen aan $a_{0}=b_{0}=1$ en $a_{k}=b_{k}=n$ en waarbij voor elke $i$ met $1 \leq i \leq k$ geldt dat $\left(a_{i}, b_{i}\right)$ gelijk is aan ofwel $\left(1+a_{i-1}, b_{i-1}\right)$ ofwel $\left(a_{i-1}, 1+b_{i-1}\right)$. Definieer voor $1 \leq i \leq k$ het getal
$$
c_{i}= \begin{cases}a_{i} & \text { als } a_{i}=a_{i-1} \\ b_{i} & \text { als } b_{i}=b_{i-1}\end{cases}
$$
Bewijs dat $c_{1}+c_{2}+\cdots+c_{k}=n^{2}-1$.
|
We definiëren een rijtje van $k$ letters: de $i$-de letter in het rijtje is gelijk aan $A$ als $a_{i}=1+a_{i-1}$ en gelijk aan $B$ als $b_{i}=1+b_{i-1}$. Verder definiëren we voor $1 \leq i \leq k$
$$
d_{i}= \begin{cases}b_{i} & \text { als } a_{i}=a_{i-1} \\ a_{i} & \text { als } b_{i}=b_{i-1}\end{cases}
$$
Als voor zekere $i$ de $i$-de letter gelijk is aan $A$, dan is $d_{i}=a_{i}$ en dat is gelijk aan 1 plus het aantal letters $A$ dat tot en met deze plek in het rijtje staat (want $a_{0}=1$ en voor elke $A$ is $a_{j}$ met 1 omhoog gegaan en bij elke $B$ is $a_{j}$ niet veranderd). De $d_{i}$ die corresponderen met de plekken waar een $A$ staat, zijn dus precies de getallen 2 tot en met $n$. De $d_{i}$ die corresponderen met de plekken waar een $B$ staat, zijn ook precies de getallen 2 tot en met $n$. Dus de som van alle $d_{i}$ is gelijk aan $(n-1)(n+2)=n^{2}+n-2$.
Voor elke $i$ geldt $c_{i}+d_{i}=a_{i}+b_{i}=1+\left(a_{i-1}+b_{i-1}\right)$ en $c_{1}+d_{1}=1+2=3$, dus met een simpele inductie $c_{i}+d_{i}=i+2$. De totale som van alle $c_{i}$ en $d_{i}$ bij elkaar is dus $3+4+\ldots+2 n=\frac{1}{2}(2 n+3)(2 n-2)=(2 n+3)(n-1)=2 n^{2}+n-3$. We concluderen dat de som van de $c_{i}$ gelijk is aan $\left(2 n^{2}+n-3\right)-\left(n^{2}+n-2\right)=n^{2}-1$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2015-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing III.",
"tier": "T1",
"year": "2015"
}
|
Let circles $\Gamma_{1}$ and $\Gamma_{2}$, with centers $O_{1}$ and $O_{2}$ respectively, intersect at two distinct points $A$ and $B$. The line $O_{1} A$ intersects $\Gamma_{2}$ again at $C$ and the line $O_{2} A$ intersects $\Gamma_{1}$ again at $D$. The line through $B$ parallel to $A D$ intersects $\Gamma_{1}$ again at $E$. Suppose that $O_{1} A$ is parallel to $D E$. Prove that $C D$ is perpendicular to $O_{2} C$.
|
In all solutions, we consider the configuration where $A, B, E$ and $D$ lie on a circle in that order, $O_{1}, A$ and $C$ lie on a line in that order, and $O_{2}, A$ and $D$ lie on a line in that order. The other configurations proceed analogously.
Due to cyclic quadrilateral $A B E D$, we have $\angle B E D=180^{\circ}-\angle D A B$. Furthermore, because of the two parallel lines, $\angle B E D=\angle D A O_{1}$, and since $\left|O_{1} A\right|=\left|O_{1} D\right|$, it follows that $\angle D A O_{1}=\angle A D O_{1}$. We conclude that $180^{\circ}-\angle D A B=\angle A D O_{1}$. By Z-angles, it follows that $D O_{1}$ and $A B$ are parallel.
We had already observed that $\angle A D O_{1}=\angle D A O_{1}$. Due to vertically opposite angles and the fact that $\left|O_{2} A\right|=\left|O_{2} C\right|$, we have $\angle D A O_{1}=\angle O_{2} A C=\angle O_{2} C A$. Thus, $\angle O_{2} D O_{1}=\angle A D O_{1}=\angle O_{2} C A=\angle O_{2} C O_{1}$, which means that $O_{1} D C O_{2}$ is a cyclic quadrilateral.
The line $O_{1} O_{2}$ is the perpendicular bisector of $A B$ and is therefore also perpendicular to $D O_{1}$, since the latter is parallel to $A B$. Thus, $\angle O_{2} O_{1} D=90^{\circ}$. Since $O_{1} D C O_{2}$ is a cyclic quadrilateral, it follows that $\angle O_{2} C D=90^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Laat cirkels $\Gamma_{1}$ en $\Gamma_{2}$, met middelpunten respectievelijk $O_{1}$ en $O_{2}$, elkaar snijden in twee verschillende punten $A$ en $B$. De lijn $O_{1} A$ snijdt $\Gamma_{2}$ nogmaals in $C$ en de lijn $O_{2} A$ snijdt $\Gamma_{1}$ nogmaals in $D$. De lijn door $B$ evenwijdig met $A D$ snijdt $\Gamma_{1}$ nogmaals in $E$. Veronderstel dat $O_{1} A$ evenwijdig is met $D E$. Bewijs dat $C D$ loodrecht op $O_{2} C$ staat.
|
In alle oplossingen bekijken we de configuratie waarin $A, B, E$ en $D$ in die volgorde op een cirkel liggen, $O_{1}, A$ en $C$ in die volgorde op een lijn en $O_{2}, A$ en $D$ in die volgorde op een lijn. De andere configuraties gaan analoog.
Vanwege koordenvierhoek $A B E D$ geldt $\angle B E D=180^{\circ}-\angle D A B$. Verder geldt wegens de twee evenwijdigheden dat $\angle B E D=\angle D A O_{1}$ en omdat $\left|O_{1} A\right|=\left|O_{1} D\right|$ geldt $\angle D A O_{1}=$ $\angle A D O_{1}$. We concluderen dat $180^{\circ}-\angle D A B=\angle A D O_{1}$. Met U-hoeken volgt nu dat $D O_{1}$ en $A B$ evenwijdig zijn.
We hadden al gezien dat $\angle A D O_{1}=\angle D A O_{1}$. Vanwege overstaande hoeken en het feit dat $\left|O_{2} A\right|=\left|O_{2} C\right|$ geldt $\angle D A O_{1}=\angle O_{2} A C=\angle O_{2} C A$. Dus $\angle O_{2} D O_{1}=\angle A D O_{1}=$ $\angle O_{2} C A=\angle O_{2} C O_{1}$, wat betekent dat $O_{1} D C O_{2}$ een koordenvierhoek is.
De lijn $O_{1} O_{2}$ is de middelloodlijn van $A B$ en staat dus ook loodrecht op $D O_{1}$, omdat die evenwijdig aan $A B$ is. Dus $\angle O_{2} O_{1} D=90^{\circ}$. Omdat $O_{1} D C O_{2}$ een koordenvierhoek is, is nu ook $\angle O_{2} C D=90^{\circ}$.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2015-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2015"
}
|
Let circles $\Gamma_{1}$ and $\Gamma_{2}$, with centers $O_{1}$ and $O_{2}$ respectively, intersect at two distinct points $A$ and $B$. The line $O_{1} A$ intersects $\Gamma_{2}$ again at $C$ and the line $O_{2} A$ intersects $\Gamma_{1}$ again at $D$. The line through $B$ parallel to $A D$ intersects $\Gamma_{1}$ again at $E$. Suppose that $O_{1} A$ is parallel to $D E$. Prove that $C D$ is perpendicular to $O_{2} C$.
|
Let $\alpha=\angle D E B$. Let $S$ be the intersection of $B E$ and $A C$, so that $E S A D$ is a parallelogram. Therefore, $\angle D A O_{1}=\angle D A S=\angle D E S=\angle D E B=\alpha$. Since triangle $A O_{1} D$ is isosceles with apex $O_{1}$, we have $\angle O_{1} A D=\angle D A O_{1}=\alpha$. Due to vertical angles and the isosceles property of $\triangle C O_{2} A$, we also have $\angle O_{2} C A=\angle C A O_{2}=\angle O_{1} A D=\alpha$. Because of the cyclic quadrilateral $B A D E$, we further have $\angle O_{2} A B=180^{\circ}-\angle D A B=\angle D E B=\alpha$, and due to the isosceles property of $\triangle A O_{2} B$, we also have $\angle O_{2} B A=\angle O_{2} A B=\alpha$. Now, $\triangle A O_{2} B$ and $\triangle A O_{2} C$ are two triangles with two angles equal to $\alpha$ and a common side $A O_{2}$, so they are congruent (ASA), which implies $|A B|=|A C|$.
A cyclic quadrilateral with two parallel sides is an isosceles trapezoid (Julian's theorem), so $|D E|=|A B|$. Together with the previous equality, we now have $|D E|=|A C|$. Since $D E$ and $A C$ are also parallel, we find a parallelogram $A C D E$. This means that $\angle D C A=\angle A E D$. By the inscribed angle theorem, $\angle A E D=\frac{1}{2} \angle A O_{1} D=90^{\circ}-\angle O_{1} A D=90^{\circ}-\alpha$. Thus, $\angle D C A=90^{\circ}-\alpha$. Now, $\angle D C O_{2}=\angle D C A+\angle O_{2} C A=90^{\circ}-\alpha+\alpha=90^{\circ}$, which is what we needed to prove.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Laat cirkels $\Gamma_{1}$ en $\Gamma_{2}$, met middelpunten respectievelijk $O_{1}$ en $O_{2}$, elkaar snijden in twee verschillende punten $A$ en $B$. De lijn $O_{1} A$ snijdt $\Gamma_{2}$ nogmaals in $C$ en de lijn $O_{2} A$ snijdt $\Gamma_{1}$ nogmaals in $D$. De lijn door $B$ evenwijdig met $A D$ snijdt $\Gamma_{1}$ nogmaals in $E$. Veronderstel dat $O_{1} A$ evenwijdig is met $D E$. Bewijs dat $C D$ loodrecht op $O_{2} C$ staat.
|
Noem $\alpha=\angle D E B$. Zij $S$ het snijpunt van $B E$ en $A C$, zodat $E S A D$ een parallellogram is. Dus is $\angle D A O_{1}=\angle D A S=\angle D E S=\angle D E B=\alpha$. Omdat driehoek $A O_{1} D$ gelijkbenig is met top $O_{1}$, geldt $\angle O_{1} A D=\angle D A O_{1}=\alpha$. Wegens overstaande hoeken en de gelijkbenigheid van $\triangle C O_{2} A$ geldt nu ook $\angle O_{2} C A=\angle C A O_{2}=\angle O_{1} A D=\alpha$. Wegens koordenvierhoek $B A D E$ geldt verder $\angle O_{2} A B=180^{\circ}-\angle D A B=\angle D E B=\alpha$, en vanwege de gelijkbenigheid van $\triangle A O_{2} B$ geldt ook $\angle O_{2} B A=\angle O_{2} A B=\alpha$. Nu zijn $\triangle A O_{2} B$ en $\triangle A O_{2} C$ twee driehoeken met twee hoeken gelijk aan $\alpha$ en een gemeenschappelijke zijde $A O_{2}$, dus ze zijn congruent (ZHH), waaruit volgt $|A B|=|A C|$.
Een koordenvierhoek met twee evenwijdige zijden is een gelijkbenig trapezium (stelling van Julian) dus $|D E|=|A B|$. Samen met de vorige gelijkheid krijgen we nu $|D E|=$ $|A C|$. Omdat $D E$ en $A C$ ook evenwijdig zijn, vinden we een parallellogram $A C D E$. Dit betekent dat $\angle D C A=\angle A E D$. Wegens de middelpunt-omtrekhoekstelling geldt $\angle A E D=\frac{1}{2} \angle A O_{1} D=90^{\circ}-\angle O_{1} A D=90^{\circ}-\alpha$. Dus $\angle D C A=90^{\circ}-\alpha . \mathrm{Nu}$ is $\angle D C O_{2}=\angle D C A+\angle O_{2} C A=90^{\circ}-\alpha+\alpha=90^{\circ}$, wat we moesten bewijzen.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2015-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2015"
}
|
Let circles $\Gamma_{1}$ and $\Gamma_{2}$, with centers $O_{1}$ and $O_{2}$ respectively, intersect at two distinct points $A$ and $B$. The line $O_{1} A$ intersects $\Gamma_{2}$ again at $C$ and the line $O_{2} A$ intersects $\Gamma_{1}$ again at $D$. The line through $B$ parallel to $A D$ intersects $\Gamma_{1}$ again at $E$. Suppose that $O_{1} A$ is parallel to $D E$. Prove that $C D$ is perpendicular to $O_{2} C$.
|
Let $S$ be the intersection of $BE$ and $AC$, so that $ESAD$ is a parallelogram. Let $T$ be the intersection of $BE$ and $CO_2$. We have $\angle CST = \angle ASB = \angle DAS$ due to $BE \| AD$ and $\angle DAS = \angle O_2AC = \angle O_2CA = \angle TCS$ because $|O_2A| = |O_2C|$. Thus, $\angle CST = \angle TCS$, which means that $|TS| = |TC|$. Furthermore, now $\angle BTC = \angle STC = 180^\circ - 2\angle O_2CA$. We had already seen that $\angle O_2CA = \angle O_2AC = \angle DAS$. Due to the parallelogram, $\angle DAS = \angle DES = \angle DEB = 180^\circ - \angle DAB = \angle O_2AB$. Therefore, $\angle O_2CA = \angle O_2AB$. With this, we see that $\angle BTC = 180^\circ - 2\angle O_2CA = 180^\circ - \angle O_2AC - \angle O_2AB = 180^\circ - \angle BAC$.
Thus, $BACT$ is a cyclic quadrilateral, or $T$ lies on $\Gamma_2$. By Thales' theorem, we now find $\angle TAC = 90^\circ$. But $TSC$ is isosceles and the line $TA$ is an altitude from the vertex, so it is also a median. Thus, $A$ is the midpoint of $SC$.
A cyclic quadrilateral with two parallel sides is an isosceles trapezoid (Julian's theorem), so $|DE| = |AB|$. Due to the parallelogram, $|DE| = |SA|$, so $|AB| = |SA| = |AC|$. Thus, $A$ lies on the perpendicular bisector of $BC$. This perpendicular bisector also passes through the center of the circle of which $BC$ is a chord and is thus the line $O_2A$. Therefore, $D$ also lies on this perpendicular bisector, so $|DC| = |DB|$. In particular, the median $DA$ in triangle $BCD$ is also an angle bisector, so $\angle CDB = 2\angle ADB$. By the inscribed angle theorem, $\angle AO_1B = 2\angle ADB$ as well. Thus, triangles $CDB$ and $AO_1B$ are isosceles with the same vertex angle, making them similar. Therefore, $\angle O_1AB = \angle DCB$. Since the inscribed angle theorem gives $\angle BAT = \angle BCT$, we now have
$$
\angle DCO_2 = \angle DCT = \angle DCB + \angle BCT = \angle O_1AB + \angle BAT = \angle O_1AT = 90^\circ.
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Laat cirkels $\Gamma_{1}$ en $\Gamma_{2}$, met middelpunten respectievelijk $O_{1}$ en $O_{2}$, elkaar snijden in twee verschillende punten $A$ en $B$. De lijn $O_{1} A$ snijdt $\Gamma_{2}$ nogmaals in $C$ en de lijn $O_{2} A$ snijdt $\Gamma_{1}$ nogmaals in $D$. De lijn door $B$ evenwijdig met $A D$ snijdt $\Gamma_{1}$ nogmaals in $E$. Veronderstel dat $O_{1} A$ evenwijdig is met $D E$. Bewijs dat $C D$ loodrecht op $O_{2} C$ staat.
|
Zij $S$ het snijpunt van $B E$ en $A C$, zodat $E S A D$ een parallellogram is. Zij $T$ het snijpunt van $B E$ en $C O_{2}$. Er geldt $\angle C S T=\angle A S B=\angle D A S$ vanwege $B E \| A D$ en $\angle D A S=\angle O_{2} A C=\angle O_{2} C A=\angle T C S$ omdat $\left|O_{2} A\right|=\left|O_{2} C\right|$. Dus $\angle C S T=\angle T C S$, wat betekent dat $|T S|=|T C|$. Verder is nu $\angle B T C=\angle S T C=180^{\circ}-2 \angle O_{2} C A$. Daarnaast hadden we al gezien dat $\angle O_{2} C A=\angle O_{2} A C=\angle D A S$. Vanwege het parallellogram geldt $\angle D A S=\angle D E S=\angle D E B=180^{\circ}-\angle D A B=\angle O_{2} A B$. Dus $\angle O_{2} C A=\angle O_{2} A B$. Hiermee zien we dat $\angle B T C=180^{\circ}-2 \angle O_{2} C A=180^{\circ}-\angle O_{2} A C-\angle O_{2} A B=180^{\circ}-\angle B A C$.
Dus $B A C T$ is een koordenvierhoek, oftewel $T$ ligt op $\Gamma_{2}$. Wegens Thales vinden we nu $\angle T A C=90^{\circ}$. Maar $T S C$ is gelijkbenig en de lijn $T A$ is een hoogtelijn vanuit de top, dus ook een zwaartelijn. Dus $A$ is het midden van $S C$.
Een koordenvierhoek met twee evenwijdige zijden is een gelijkbenig trapezium (stelling van Julian) dus $|D E|=|A B|$. Vanwege het parallellogram is ook $|D E|=|S A|$, dus $|A B|=|S A|=|A C|$. Dus $A$ ligt op de middelloodlijn van $B C$. Die middelloodlijn gaat ook door het middelpunt van de cirkel waar $B C$ een koorde van is en is dus de lijn $O_{2} A$. Dus $D$ ligt ook op deze middelloodlijn, zodat $|D C|=|D B|$. In het bijzonder is nu zwaartelijn $D A$ in driehoek $B C D$ ook een bissectrice, dus $\angle C D B=2 \angle A D B$. Met de middelpuntsomtrekshoekstelling is ook $\angle A O_{1} B=2 \angle A D B$. Dus driehoeken $C D B$ en $A O_{1} B$ zijn gelijkbenig met dezelfde tophoek, waardoor ze gelijkvormig zijn. Dus $\angle O_{1} A B=$ $\angle D C B$. Omdat met de omtrekshoekstelling geldt $\angle B A T=\angle B C T$, geldt nu
$$
\angle D C O_{2}=\angle D C T=\angle D C B+\angle B C T=\angle O_{1} A B+\angle B A T=\angle O_{1} A T=90^{\circ} .
$$
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2015-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing III.",
"tier": "T1",
"year": "2015"
}
|
For a positive integer $n$, we define $D_{n}$ as the largest number that divides $a^{n}+(a+1)^{n}+(a+2)^{n}$ for all positive integers $a$.
a) Prove that for every positive integer $n$, the number $D_{n}$ is of the form $3^{k}$ with $k \geq 0$.
b) Prove that for every $k \geq 0$, there exists a positive integer $n$ such that $D_{n}=3^{k}$.
|
a) Let $p$ be a prime and suppose that $p$ is a divisor of $D_{n}$. Then $p$ is a divisor of
$$
\left((a+1)^{n}+(a+2)^{n}+(a+3)^{n}\right)-\left(a^{n}+(a+1)^{n}+(a+2)^{n}\right)=(a+3)^{n}-a^{n}
$$
for all positive integers $a$. Choose now $a=p$, then $p \mid(p+3)^{n}-p^{n}$, or $(p+3)^{n}-p^{n} \equiv 0 \bmod p$. This is simply $3 \equiv 0 \bmod p$, so $p=3$. We conclude that $D_{n}$ only contains prime factors 3 and thus is of the form $3^{k}$ with $k \geq 0$.
b) For $k=0$ we take $n=2$. It holds that $1^{2}+2^{2}+3^{2}=14$ and $2^{2}+3^{2}+4^{2}=29$ and these two have no prime factors in common, so $D_{2}=1$. Now assume that $k \geq 1$. We will prove that $D_{n}=3^{k}$ for $n=3^{k-1}$.
First, we show that $1^{n}+2^{n}+3^{n}$ for $n=3^{k-1}$ is divisible by $3^{k}$, but not by $3^{k+1}$. For $k=1$ it is $n=1$ and indeed $1+2+3=6$ is divisible by 3, but not by $3^{2}$. For $k \geq 2$ it holds that $n>k$ and thus $3^{n}$ is divisible by $3^{k+1}$. What we need to prove is thus equivalent to: $1+2^{n}$ for $n=3^{k-1}$ is divisible by $3^{k}$ but not by $3^{k+1}$. We prove this by induction on $k$. For $k=2$ it is $n=3$ and indeed $1+8=9$ is divisible by 9, but not by 27. Let $m \geq 2$ and assume we have proven this for $k=m$. Take $n=3^{m-1}$. We know that $1+2^{n}$ is divisible by $3^{m}$, but not by $3^{m+1}$. We want to show that $1+2^{3 n}$ is divisible by $3^{m+1}$, but not by $3^{m+2}$. Write $1+2^{n}=3^{m} c$ with $3 \nmid c$. Then $2^{n}=3^{m} c-1$, so
$$
1+2^{3 n}=1+\left(3^{m} c-1\right)^{3}=3^{3 m} c^{3}-3 \cdot 3^{2 m} c^{2}+3 \cdot 3^{m} c
$$
Modulo $3^{m+2}$ this is congruent to $3^{m+1} c$ and since $3 \nmid c$ it follows that this is divisible by $3^{m+1}$, but not by $3^{m+2}$, as we wanted to prove. This completes the induction. Now we show that for $n=3^{k-1}$ it holds that $(a+3)^{n}-a^{n}$ is divisible by $3^{k}$ for all positive integers $a$. We prove this again by induction on $k$. For $k=1$ it is $n=1$ and indeed $(a+3)-a=3$ is divisible by 3. Now let $m \geq 1$ and assume we have proven this for $k=m$. Take $n=3^{m-1}$. Then we know that $(a+3)^{n}-a^{n}$ is divisible by $3^{m}$, so we can write $(a+3)^{n}=a^{n}+3^{m} c$ for some integer $c$. Taking the third power on both sides gives
$$
(a+3)^{3 n}=a^{3 n}+3 a^{2 n} \cdot 3^{m} c+3 a^{n} \cdot 3^{2 m} c^{2}+3^{3 m} c^{3},
$$
so
$$
(a+3)^{3 n}-a^{3 n}=a^{2 n} \cdot 3^{m+1} c+a^{n} \cdot 3^{2 m+1} c^{2}+3^{3 m} c^{3} .
$$
This is divisible by $3^{m+1}$, which completes the induction.
We have now proven for $n=3^{k-1}$ that $3^{k} \mid 1^{n}+2^{n}+3^{n}$ and $3^{k} \mid(a+3)^{n}-a^{n}$ for all positive integers $a$, from which it follows directly by induction on $a$ that $3^{k} \mid a^{n}+(a+1)^{n}+(a+2)^{n}$ for all $a$. Thus $3^{k} \mid D_{n}$. Since $3^{k+1} \nmid 1^{n}+2^{n}+3^{n}$ it also holds that $3^{k+1} \nmid D_{n}$. Therefore, $D_{n}=3^{k}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Voor een positief geheel getal $n$ definiëren we $D_{n}$ als het grootste getal dat een deler is van $a^{n}+(a+1)^{n}+(a+2)^{n}$ voor alle positieve gehele $a$.
a) Bewijs dat voor elke positieve gehele $n$ het getal $D_{n}$ van de vorm $3^{k}$ is met $k \geq 0$.
b) Bewijs dat er voor elke $k \geq 0$ een positieve gehele $n$ bestaat zodat $D_{n}=3^{k}$.
|
a) $\mathrm{Zij} p$ een priemgetal en stel dat $p$ een deler is van $D_{n}$. Dan is $p$ een deler van
$$
\left((a+1)^{n}+(a+2)^{n}+(a+3)^{n}\right)-\left(a^{n}+(a+1)^{n}+(a+2)^{n}\right)=(a+3)^{n}-a^{n}
$$
voor alle positieve gehele $a$. Kies nu $a=p$, dan $p \mid(p+3)^{n}-p^{n}$, oftewel $(p+3)^{n}-p^{n} \equiv$ $0 \bmod p$. Hier staat gewoon $3 \equiv 0 \bmod p$, dus $p=3$. We concluderen dat $D_{n}$ alleen priemfactoren 3 bevat en dus van de vorm $3^{k}$ is met $k \geq 0$.
b) Voor $k=0$ nemen we $n=2$. Er geldt $1^{2}+2^{2}+3^{2}=14$ en $2^{2}+3^{2}+4^{2}=29$ en die twee hebben geen enkele priemfactor gemeenschappelijk, dus $D_{2}=1$. Neem nu verder aan dat $k \geq 1$. We gaan bewijzen dat $D_{n}=3^{k}$ voor $n=3^{k-1}$.
Eerst laten we zien dat $1^{n}+2^{n}+3^{n}$ voor $n=3^{k-1}$ deelbaar is door $3^{k}$, maar niet door $3^{k+1}$. Voor $k=1$ is $n=1$ en geldt inderdaad dat $1+2+3=6$ deelbaar is door 3 , maar niet door $3^{2}$. Voor $k \geq 2$ geldt dat $n>k$ en dus dat $3^{n}$ deelbaar is door $3^{k+1}$. Het te bewijzen is dus equivalent aan: $1+2^{n}$ voor $n=3^{k-1}$ is deelbaar door $3^{k}$ maar niet door $3^{k+1}$. We bewijzen dit met inductie naar $k$. Voor $k=2$ is $n=3$ en geldt inderdaad dat $1+8=9$ deelbaar is door 9 , maar niet door 27 . Zij $m \geq 2$ en stel dat we dit hebben bewezen voor $k=m$. Neem $n=3^{m-1}$. We weten dat $1+2^{n}$ deelbaar is door $3^{m}$, maar niet door $3^{m+1}$. We willen laten zien dat $1+2^{3 n}$ deelbaar is door $3^{m+1}$, maar niet door $3^{m+2}$. Schrijf $1+2^{n}=3^{m} c$ met $3 \nmid c$. Dan is $2^{n}=3^{m} c-1$, dus
$$
1+2^{3 n}=1+\left(3^{m} c-1\right)^{3}=3^{3 m} c^{3}-3 \cdot 3^{2 m} c^{2}+3 \cdot 3^{m} c
$$
Modulo $3^{m+2}$ is dit congruent aan $3^{m+1} c$ en omdat $3 \nmid c$ volgt hieruit dat dit deelbaar is door $3^{m+1}$, maar niet door $3^{m+2}$, zoals we wilden bewijzen. Dit voltooit de inductie. Nu laten we zien dat voor $n=3^{k-1}$ geldt dat $(a+3)^{n}-a^{n}$ deelbaar is door $3^{k}$ voor alle positieve gehele $a$. We bewijzen dit weer met inductie naar $k$. Voor $k=1$ is $n=1$ en geldt inderdaad dat $(a+3)-a=3$ deelbaar is door 3 . Zij nu $m \geq 1$ en neem aan dat we dit bewezen hebben voor $k=m$. Neem $n=3^{m-1}$. Dan weten we dat $(a+3)^{n}-a^{n}$ deelbaar is door $3^{m}$, dus we kunnen schrijven $(a+3)^{n}=a^{n}+3^{m} c$ voor een zekere gehele $c$. Links en rechts de derde macht nemen geeft dan
$$
(a+3)^{3 n}=a^{3 n}+3 a^{2 n} \cdot 3^{m} c+3 a^{n} \cdot 3^{2 m} c^{2}+3^{3 m} c^{3},
$$
dus
$$
(a+3)^{3 n}-a^{3 n}=a^{2 n} \cdot 3^{m+1} c+a^{n} \cdot 3^{2 m+1} c^{2}+3^{3 m} c^{3} .
$$
Dit is deelbaar door $3^{m+1}$, wat de inductie voltooit.
We hebben nu voor $n=3^{k-1}$ bewezen dat $3^{k} \mid 1^{n}+2^{n}+3^{n}$ en $3^{k} \mid(a+3)^{n}-a^{n}$ voor alle positieve gehele $a$, waaruit met inductie naar $a$ direct volgt dat $3^{k} \mid a^{n}+$ $(a+1)^{n}+(a+2)^{n}$ voor alle $a$. Dus $3^{k} \mid D_{n}$. Omdat $3^{k+1} \nmid 1^{n}+2^{n}+3^{n}$ geldt ook $3^{k+1} \nmid D_{n}$. Dus $D_{n}=3^{k}$.
|
{
"exam": "Dutch_TST",
"problem_label": "5",
"problem_match": "\nOpgave 5.",
"resource_path": "Dutch_TST/segmented/nl-2015-C_uitwerkingen.jsonl",
"solution_match": "# Oplossing.",
"tier": "T1",
"year": "2015"
}
|
Let $a$ and $b$ be two positive integers that satisfy $\operatorname{gcd}(a, b)=1$. Consider a pawn standing on grid point $(x, y)$. A step of type A consists of moving the pawn to one of the following fields: $(x+a, y+a),(x+a, y-a),(x-$ $a, y+a)$ or $(x-a, y-a)$. A step of type B consists of moving the pawn to $(x+b, y+b),(x+b, y-b),(x-b, y+b)$ or $(x-b, y-b)$.
Now place a pawn on $(0,0)$. You may perform a (finite) number of steps, alternating between steps of type A and type B, starting with a step of type A. You may perform an even or odd number of steps, so the last step can be either of type A or of type B. Determine the set of all grid points $(x, y)$ that can be reached with such a series of steps.
|
We will prove that a grid point $(x, y)$ is reachable if and only if $x+y \equiv 0 \bmod 2$.
If we move the pawn from $(x, y)$ to $(x \pm a, y \pm a)$, then the sum of the new coordinates will be $x+y+2a$, $x+y$, or $x+y-2a$, thus congruent modulo 2 to the sum of the old coordinates. The same applies when performing a step of type B. Since the pawn starts at $(0,0)$, at any moment (after performing a number of steps), the sum of the coordinates of the point it stands on is even. The points $(x, y)$ with $x+y \equiv 1 \bmod 2$ are therefore not reachable.
Now we will show that all other points are reachable. Since $\operatorname{gcd}(a, b)=1$, there exist integers $m, n$ such that $m a + n b = 1$. Then $2 m a + 2 n b = 2$. Of the numbers $m$ and $n$, one must be positive and the other negative. We assume that $m$ is positive. The other case is analogous. We will now first perform $2 m$ steps of type A and $2 m$ steps of type B. For the steps of type A, we choose $m$ times $(x, y) \mapsto (x+a, y+a)$ and $m$ times $(x, y) \mapsto (x+a, y-a)$. For the steps of type B, we choose $m$ times $(x, y) \mapsto (x+b, y+b)$ and $m$ times $(x, y) \mapsto (x-b, y-b)$. The combined effect of all these steps is that the $x$-coordinate increases by $2 m a$ and the $y$-coordinate remains the same (in fact, the B-steps do nothing). After this, we perform another $2|n|$ steps of type A and $2|n|$ steps of type B. For the steps of type A, we choose $|n|$ times $(x, y) \mapsto (x+a, y+a)$ and $|n|$ times $(x, y) \mapsto (x-a, y-a)$. For the steps of type B, we choose $|n|$ times $(x, y) \mapsto (x-b, y+b)$ and $|n|$ times $(x, y) \mapsto (x-b, y-b)$. The combined effect of all these steps is that the $x$-coordinate decreases by $2|n| b$ and the $y$-coordinate remains the same (in fact, the A-steps do nothing now). In total, after these $4 m + 4|n|$ steps, the pawn has been moved from an initial point $(x, y)$ to the point $(x + 2 m a - 2|n| b, y) = (x + 2, y)$. We can construct an analogous series of steps that moves the pawn from $(x, y)$ to $(x, y+2)$, and also analogous series of steps that move the pawn from $(x, y)$ to $(x-2, y)$ and $(x, y-2)$. Each of these series starts with a step of type A and ends with a step of type B.
By concatenating such series, we can move the pawn from $(0,0)$ to any point $(x, y)$ with $x \equiv y \equiv 0 \bmod 2$. Now consider a point $(x, y)$ with $x \equiv y \equiv 1 \bmod 2$. Since $\operatorname{gcd}(a, b)=1$, at least one of $a$ and $b$ is odd. Suppose $a$ is odd. Then the point $(x-a, y-a)$ is a point with two even coordinates, to which we can construct a series of steps that ends with a step of type B. We now add a step of type A to this series to move from $(x-a, y-a)$ to $(x, y)$. Suppose instead that $a$ is even. Then $b$ is odd. The point $(x-b, y-b)$ now has two even coordinates, so this point can be reached with a series of steps that ends with a step of type B. We then perform three more steps:
$$
(x-b, y-b) \stackrel{\mathrm{A}}{\longmapsto} (x-b-a, y-b-a) \stackrel{\mathrm{B}}{\longmapsto} (x-a, y-a) \stackrel{\mathrm{A}}{\longmapsto} (x, y).
$$
Thus, we can also reach the point $(x, y)$.
We conclude that we can reach all points $(x, y)$ with $x+y \equiv 0 \bmod 2$ and none of the other points.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Laat $a$ en $b$ twee positieve gehele getallen zijn die voldoen aan $\operatorname{ggd}(a, b)=1$. Beschouw een pion die op roosterpunt $(x, y)$ staat. Een stap van type A bestaat uit het verplaatsen van de pion naar één van de volgende velden: $(x+a, y+a),(x+a, y-a),(x-$ $a, y+a)$ of $(x-a, y-a)$. Een stap van type B bestaat uit het verplaatsen van de pion naar $(x+b, y+b),(x+b, y-b),(x-b, y+b)$ of $(x-b, y-b)$.
Zet nu een pion op $(0,0)$. Je mag een (eindig) aantal stappen uitvoeren, en wel om en om stappen van type A en type B, beginnend met een stap van type A. Je mag een even aantal of een oneven aantal stappen uitvoeren, dus de laatste stap mag zowel van type A als van type B zijn. Bepaal de verzameling van alle roosterpunten $(x, y)$ die je met zo'n serie van stappen kunt bereiken.
|
We gaan bewijzen dat een roosterpunt $(x, y)$ bereikbaar is dan en slechts dan als $x+y \equiv 0 \bmod 2$.
Als we de pion verplaatsen van $(x, y)$ naar $(x \pm a, y \pm a)$, dan wordt de som van de nieuwe coördinaten gelijk aan $x+y+2 a, x+y$ of $x+y-2 a$, dus modulo 2 congruent aan de som van de oude coördinaten. Hetzelfde geldt bij het doen van een stap van type B. Omdat de pion begint op $(0,0)$, geldt op elk moment (na het uitvoeren van een aantal stappen) dat de som van de coördinaten van het punt waar hij op staat, even is. De punten $(x, y)$ met $x+y \equiv 1 \bmod 2$ zijn dus niet te bereiken.
Nu laten we zien dat alle andere punten wel te bereiken zijn. Omdat $\operatorname{ggd}(a, b)=1$, bestaan er gehele getallen $m, n$ met $m a+n b=1$. Dan geldt $2 m a+2 n b=2$. Van de getallen $m$ en $n$ moet er eentje positief en eentje negatief zijn. We nemen aan dat $m$ positief is. Het andere geval gaat analoog. We gaan nu eerst $2 m$ stappen van type A en $2 m$ stappen van type B doen. Voor de stappen van type A kiezen we $m$ keer $(x, y) \mapsto(x+a, y+a)$ en $m$ keer $(x, y) \mapsto(x+a, y-a)$. Voor de stappen van type B kiezen we $m$ keer $(x, y) \mapsto(x+b, y+b)$ en $m$ keer $(x, y) \mapsto(x-b, y-b)$. Het effect van al deze stappen samen is dat de $x$ coördinaat $2 m a$ groter wordt en de $y$-coördinaat gelijk blijft (in feite doen de B-stappen helemaal niets). Hierna doen we nog $2|n|$ stappen van type A en $2|n|$ stappen van type B. Voor de stappen van type A kiezen we $|n|$ keer $(x, y) \mapsto(x+a, y+a)$ en $|n|$ keer $(x, y) \mapsto(x-a, y-a)$. Voor de stappen van type B kiezen we $|n|$ keer $(x, y) \mapsto(x-b, y+b)$ en $|n|$ keer $(x, y) \mapsto(x-b, y-b)$. Het effect van al deze stappen samen is dat de $x$-coördinaat $2|n| b$ kleiner wordt en de $y$-coördinaat gelijk blijft (in feite doen nu de A-stappen helemaal niets). Al met al hebben we na deze $4 m+4|n|$ stappen de pion verplaatst van een beginpunt $(x, y)$ naar het punt $(x+2 m a-2|n| b, y)=(x+2, y)$. We kunnen een analoge serie stappen construeren die de pion van $(x, y)$ naar $(x, y+2)$ verplaatst, en ook analoge series stappen
die de pion van $(x, y)$ verplaatsen naar $(x-2, y)$ en $(x, y-2)$. Elk van deze series begint met een stap van type A en eindigt met een stap van type B.
Door dit soort series achter elkaar te plakken, kunnen we de pion van $(0,0)$ verplaatsen naar elk punt $(x, y)$ met $x \equiv y \equiv 0 \bmod 2$. Bekijk nu een punt $(x, y)$ met $x \equiv y \equiv 1$ $\bmod 2$. Omdat $\operatorname{ggd}(a, b)=1$, is minstens één van $a$ en $b$ oneven. Stel dat $a$ oneven is. Dan is het punt $(x-a, y-a)$ een punt met twee even coördinaten, waarnaartoe we dus een serie stappen kunnen construeren, die eindigt op een stap van type B. We voegen hierachter nu een stap van type A toe waarmee we van $(x-a, y-a)$ op $(x, y)$ komen. Stel vervolgens dat $a$ even is. Dan is $b$ oneven. Het punt $(x-b, y-b)$ heeft nu twee even coördinaten, dus dit punt kunnen we bereiken met een serie stappen die eindigt op een stap van type B. We voeren nog drie stappen hierna uit:
$$
(x-b, y-b) \stackrel{\mathrm{A}}{\longmapsto}(x-b-a, y-b-a) \stackrel{\mathrm{B}}{\longmapsto}(x-a, y-a) \stackrel{\mathrm{A}}{\longmapsto}(x, y) .
$$
Zo kunnen we het punt $(x, y)$ dus ook bereiken.
We concluderen dat we alle punten $(x, y)$ met $x+y \equiv 0 \bmod 2$ kunnen bereiken en alle overige punten niet.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2015-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2015"
}
|
Determine all positive integers $n$ for which there exist positive integers $a_{1}, a_{2}, \ldots, a_{n}$ such that
$$
a_{1}+2 a_{2}+3 a_{3}+\ldots+n a_{n}=6 n
$$
and
$$
\frac{1}{a_{1}}+\frac{2}{a_{2}}+\frac{3}{a_{3}}+\ldots+\frac{n}{a_{n}}=2+\frac{1}{n}
$$
|
When we apply the inequality of the arithmetic and harmonic mean to $a_{1}$, twice $a_{2}$, three times $a_{3}, \ldots, n$ times $a_{n}$, we find
$$
\frac{6 n}{\frac{1}{2} n(n+1)}=\frac{a_{1}+2 a_{2}+3 a_{3}+\ldots+n a_{n}}{\frac{1}{2} n(n+1)} \geq \frac{\frac{1}{2} n(n+1)}{\frac{1}{a_{1}}+\frac{2}{a_{2}}+\frac{3}{a_{3}}+\ldots+\frac{n}{a_{n}}}=\frac{\frac{1}{2} n(n+1)}{2+\frac{1}{n}}
$$
We have
$$
\frac{6 n}{\frac{1}{2} n(n+1)}=\frac{12}{n+1}<\frac{12}{n}
$$
and
$$
\frac{\frac{1}{2} n(n+1)}{2+\frac{1}{n}}=\frac{\frac{1}{2} n^{2}(n+1)}{2 n+1}>\frac{\frac{1}{2} n^{2}(n+1)}{2 n+2}=\frac{1}{4} n^{2}
$$
Putting everything together, we find $\frac{12}{n}>\frac{1}{4} n^{2}$, or $48>n^{3}$, from which it follows that $n \leq 3$.
With $n=1$, we get $a_{1}=6$ and $\frac{1}{a_{1}}=3$, which contradicts each other. So $n=1$ is not possible.
With $n=2$, we get $a_{1}+2 a_{2}=12$ and $\frac{1}{a_{1}}+\frac{2}{a_{2}}=2+\frac{1}{2}$. If $a_{2} \geq 2$, then $\frac{1}{a_{1}}+\frac{2}{a_{2}} \leq 1+1$ and that is too small. So $a_{2}$ must be $1$, but then we find $a_{1}=12-2=10$ and thus $\frac{1}{a_{1}}+\frac{2}{a_{2}}=\frac{1}{10}+2$, a contradiction. So $n=2$ is not possible.
For $n=3$, there is a solution, namely $a_{1}=6, a_{2}=3$ and $a_{3}=2$ (substitution shows that this satisfies the conditions). So $n=3$ is possible and we conclude that $n=3$ is the only solution.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Bepaal alle positieve gehele getallen $n$ waarvoor er positieve gehele getallen $a_{1}, a_{2}, \ldots, a_{n}$ bestaan met
$$
a_{1}+2 a_{2}+3 a_{3}+\ldots+n a_{n}=6 n
$$
en
$$
\frac{1}{a_{1}}+\frac{2}{a_{2}}+\frac{3}{a_{3}}+\ldots+\frac{n}{a_{n}}=2+\frac{1}{n}
$$
|
Als we de ongelijkheid van het rekenkundig en harmonisch gemiddelde toepassen op $a_{1}$, twee keer $a_{2}$, drie keer $a_{3}, \ldots, n$ keer $a_{n}$, dan vinden we
$$
\frac{6 n}{\frac{1}{2} n(n+1)}=\frac{a_{1}+2 a_{2}+3 a_{3}+\ldots+n a_{n}}{\frac{1}{2} n(n+1)} \geq \frac{\frac{1}{2} n(n+1)}{\frac{1}{a_{1}}+\frac{2}{a_{2}}+\frac{3}{a_{3}}+\ldots+\frac{n}{a_{n}}}=\frac{\frac{1}{2} n(n+1)}{2+\frac{1}{n}}
$$
Er geldt
$$
\frac{6 n}{\frac{1}{2} n(n+1)}=\frac{12}{n+1}<\frac{12}{n}
$$
en
$$
\frac{\frac{1}{2} n(n+1)}{2+\frac{1}{n}}=\frac{\frac{1}{2} n^{2}(n+1)}{2 n+1}>\frac{\frac{1}{2} n^{2}(n+1)}{2 n+2}=\frac{1}{4} n^{2}
$$
Alles bij elkaar vinden we $\frac{12}{n}>\frac{1}{4} n^{2}$, oftewel $48>n^{3}$, waaruit volgt $n \leq 3$.
Met $n=1$ krijgen we $a_{1}=6$ en $\frac{1}{a_{1}}=3$, wat in tegenspraak met elkaar is. Dus $n=1$ kan niet.
Met $n=2$ krijgen we $a_{1}+2 a_{2}=12$ en $\frac{1}{a_{1}}+\frac{2}{a_{2}}=2+\frac{1}{2}$. Als $a_{2} \geq 2$ geldt $\frac{1}{a_{1}}+\frac{2}{a_{2}} \leq 1+1$ en dat is te klein. Dus moet $a_{2}=1$, maar dan vinden we $a_{1}=12-2=10$ en dus $\frac{1}{a_{1}}+\frac{2}{a_{2}}=\frac{1}{10}+2$, tegenspraak. Dus $n=2$ kan niet.
Bij $n=3$ is er een oplossing, namelijk $a_{1}=6, a_{2}=3$ en $a_{3}=2$ (invullen laat zien dat deze voldoet). Dus $n=3$ kan wel en we concluderen dat $n=3$ de enige oplossing is.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2015-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2015"
}
|
Given is an equilateral triangle $A B C$. On the line through $B$ parallel to $A C$ lies a point $D$, such that $D$ and $C$ are on the same side of line $A B$. The perpendicular bisector of $C D$ intersects the line $A B$ at $E$. Prove that triangle $C D E$ is equilateral.
|
We consider in all solutions the configuration where $E$ lies between $A$ and $B$. The case where $B$ lies between $A$ and $E$ is analogous. (And due to the condition that $D$ and $C$ lie on the same side of $AB$, $A$ cannot lie between $B$ and $E$, so we have covered all cases.)
Since $E$ lies on the perpendicular bisector of $CD$, it follows that $|EC|=|ED|$. It is therefore sufficient to prove that the vertex angle $\angle CED=60^{\circ}$. First, assume that $E=B$. Then $\angle CED=\angle CBD=\angle ACB=60^{\circ}$ due to Z-angles, so we are done. Now assume that $E \neq B$.
Since $BD$ is parallel to $AC$, it follows that $\angle CBD=\angle ACB=60^{\circ}=\angle CBA$. The point $E$ is thus the intersection of the perpendicular bisector of $CD$ and the external angle bisector of $\angle CBD$. This means that $E$ lies on the circumcircle of triangle $CDB$. (This is a known fact, but it can also be proven as follows. Let $E'$ be the intersection of the external angle bisector of $\angle CBD$ and the circumcircle of $\triangle CDB$. Since $BE'$ is the external angle bisector, $\angle CBE'=180^{\circ}-\angle DBE'$. Therefore, chords $CE'$ and $DE'$ are of equal length, which means that $E'$ lies on the perpendicular bisector of $CD$.) We conclude that $CEBD$ is a cyclic quadrilateral. Thus, $\angle CED=\angle CBD=60^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Gegeven is een gelijkzijdige driehoek $A B C$. Op de lijn door $B$ evenwijdig aan $A C$ ligt een punt $D$, zodat $D$ en $C$ aan dezelfde kant van lijn $A B$ liggen. De middelloodlijn van $C D$ snijdt de lijn $A B$ in $E$. Bewijs dat driehoek $C D E$ gelijkzijdig is.
|
We bekijken in alle oplossingen de configuratie waarin $E$ tussen $A$ en $B$ ligt. Het geval dat $B$ tussen $A$ en $E$ ligt gaat analoog. (En vanwege de voorwaarde dat $D$ en $C$ aan dezelfde kant van $A B$ liggen, kan $A$ niet tussen $B$ en $E$ liggen, dus hebben we zo alle gevallen gehad.)
Omdat $E$ op de middelloodlijn van $C D$ ligt, geldt $|E C|=|E D|$. Het is dus voldoende om te bewijzen dat tophoek $\angle C E D=60^{\circ}$. Stel eerst dat $E=B$. Dan is $\angle C E D=\angle C B D=$ $\angle A C B=60^{\circ}$ wegens Z-hoeken, dus zijn we klaar. Stel nu dat $E \neq B$.
Omdat $B D$ evenwijdig aan $A C$ is, geldt $\angle C B D=\angle A C B=60^{\circ}=\angle C B A$. Het punt $E$ is dus het snijpunt van de middelloodlijn van $C D$ en de buitenbissectrice van $\angle C B D$. Dat betekent dat $E$ op de omgeschreven cirkel van driehoek $C D B$ ligt. (Dit is een bekend feit, maar het is ook als volgt te bewijzen. Zij $E^{\prime}$ het snijpunt van de buitenbissectrice van $\angle C B D$ en de omgeschreven cirkel van $\triangle C B D$. Omdat $B E^{\prime}$ de buitenbissectrice is, geldt $\angle C B E^{\prime}=180^{\circ}-\angle D B E^{\prime}$. Dus koorden $C E^{\prime}$ en $D E^{\prime}$ zijn even lang, wat betekent dat $E^{\prime}$ op de middelloodlijn van $C D$ ligt.) We concluderen dat $C E B D$ een koordenvierhoek is. Dus $\angle C E D=\angle C B D=60^{\circ}$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2015-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2015"
}
|
Given is an equilateral triangle $A B C$. On the line through $B$ parallel to $A C$ lies a point $D$, such that $D$ and $C$ are on the same side of line $A B$. The perpendicular bisector of $C D$ intersects the line $A B$ at $E$. Prove that triangle $C D E$ is equilateral.
|
Let $E^{\prime}$ be the second intersection of $AB$ with the circumcircle of $\triangle BCD$. Due to cyclic quadrilateral $BE^{\prime}CD$, we have $\angle E^{\prime}DC = \angle E^{\prime}BC = \angle ABC = 60^{\circ}$ and $\angle E^{\prime}CD = 180^{\circ} - \angle E^{\prime}BD = 60^{\circ}$ due to the parallelism. Therefore, triangle $CDE^{\prime}$ has two angles of $60^{\circ}$ and is thus equilateral. Because of this equilateral property, $E^{\prime}$ lies on the perpendicular bisector of $CD$, so $E^{\prime} = E$. Hence, $\triangle CDE$ is equilateral.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Gegeven is een gelijkzijdige driehoek $A B C$. Op de lijn door $B$ evenwijdig aan $A C$ ligt een punt $D$, zodat $D$ en $C$ aan dezelfde kant van lijn $A B$ liggen. De middelloodlijn van $C D$ snijdt de lijn $A B$ in $E$. Bewijs dat driehoek $C D E$ gelijkzijdig is.
|
Zij $E^{\prime}$ het tweede snijpunt van $A B$ met de omgeschreven cirkel van $\triangle B C D$. Wegens koordenvierhoek $B E^{\prime} C D$ geldt dan $\angle E^{\prime} D C=\angle E^{\prime} B C=\angle A B C=60^{\circ}$ en $\angle E^{\prime} C D=180^{\circ}-\angle E^{\prime} B D=60^{\circ}$ wegens de evenwijdigheid. Dus driehoek $C D E^{\prime}$ heeft twee hoeken van $60^{\circ}$ en is daarom gelijkzijdig. Vanwege deze gelijkzijdigheid ligt verder $E^{\prime}$ op de middelloodlijn van $C D$, dus $E^{\prime}=E$. Dus $\triangle C D E$ is gelijkzijdig.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2015-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2015"
}
|
Given is an equilateral triangle $A B C$. On the line through $B$ parallel to $A C$ lies a point $D$, such that $D$ and $C$ are on the same side of line $A B$. The perpendicular bisector of $C D$ intersects the line $A B$ at $E$. Prove that triangle $C D E$ is equilateral.
|
Let $E^{\prime}$ be a point on $A B$ with $\left|A E^{\prime}\right|=|B D|$, so that $E^{\prime}$ and $B$ are on the same side of $A$. It is given that $|A C|=|B C|$ and $\angle C A E=60^{\circ}=\angle C B D$ due to Z-angles and the equilateral property. Therefore, $\triangle C A E^{\prime} \cong \triangle C B D$ (SAS). From this, it follows that $\left|C E^{\prime}\right|=|C D|$ and $\angle E^{\prime} C A=\angle D C B$. From the latter, we get $\angle E^{\prime} C D=\angle E^{\prime} C B+\angle B C D=\angle E^{\prime} C B+$ $\angle E^{\prime} C A=\angle A C B=60^{\circ}$. Thus, triangle $C D E^{\prime}$ is isosceles with vertex angle $60^{\circ}$, hence equilateral. Due to this equilateral property, $E^{\prime}$ lies on the perpendicular bisector of $C D$, so $E^{\prime}=E$. Therefore, $\triangle C D E$ is equilateral.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Gegeven is een gelijkzijdige driehoek $A B C$. Op de lijn door $B$ evenwijdig aan $A C$ ligt een punt $D$, zodat $D$ en $C$ aan dezelfde kant van lijn $A B$ liggen. De middelloodlijn van $C D$ snijdt de lijn $A B$ in $E$. Bewijs dat driehoek $C D E$ gelijkzijdig is.
|
Zij $E^{\prime}$ een punt op $A B$ met $\left|A E^{\prime}\right|=|B D|$, zodat $E^{\prime}$ en $B$ aan dezelfde kant van $A$ liggen. Er geldt $|A C|=|B C|$ en $\angle C A E=60^{\circ}=\angle C B D$ wegens Z-hoeken en de gelijkzijdigheid. Dus $\triangle C A E^{\prime} \cong \triangle C B D$ (ZHZ). Hieruit volgt $\left|C E^{\prime}\right|=|C D|$ en $\angle E^{\prime} C A=\angle D C B$. Uit het laatste volgt $\angle E^{\prime} C D=\angle E^{\prime} C B+\angle B C D=\angle E^{\prime} C B+$ $\angle E^{\prime} C A=\angle A C B=60^{\circ}$. Dus driehoek $C D E^{\prime}$ is gelijkbenig met tophoek $60^{\circ}$, dus gelijkzijdig. Vanwege deze gelijkzijdigheid ligt verder $E^{\prime}$ op de middelloodlijn van $C D$, dus $E^{\prime}=E$. Dus $\triangle C D E$ is gelijkzijdig.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2015-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing III.",
"tier": "T1",
"year": "2015"
}
|
You may assign a color to each of the numbers from 1 to 2014, with exactly half being red and the other half blue. Then you examine the number $k$ of positive integers that can be written as the sum of a red and a blue number. Determine the maximum value of $k$ that you can achieve.
|
Let $n=2014$. We will prove that the maximum $k$ is equal to $2n-5$. The smallest number that can be written as the sum of a red and a blue number is $1+2=3$ and the largest number is $(n-1)+n=2n-1$. Therefore, there are at most $2n-3$ numbers that can be written as the sum of a red and a blue number.
Assume that the numbers can be colored in such a way that there are $2n-3$ or $2n-4$ numbers that can be written as the sum of a red and a blue number. There is now at most one number from 3 to $2n-1$ that cannot be written as such. We will first show that we can assume without loss of generality that this number is at least $n+1$. We can create a second coloring where a number $i$ is blue if and only if $n+1-i$ was blue in the first coloring. Then a number $m$ can be written as the sum of red and blue in the second coloring if and only if $2n+2-m$ could be written as the sum of red and blue in the first coloring. Therefore, if a number less than $n+1$ could not be written as the sum of red and blue in the first coloring, then in the second coloring, precisely a number greater than $2n+2-(n+1)=n+1$ cannot be written as the sum of red and blue.
Thus, we can assume that the numbers from 3 to $n$ can all be written as the sum of red and blue. Since red and blue are interchangeable, we can also assume without loss of generality that 1 is colored blue. Since 3 can be written as the sum of red and blue and this can only be $3=1+2$, 2 must be red. Now suppose we know that 2 to $l$ are red, for some $l$ with $2 \leq l \leq n-2$. Then in all possible sums $a+b=l+2$ with $a, b \geq 2$, both numbers are colored red, but we know that we can write $l+2$ as the sum of red and blue (since $l+2 \leq n$), so it must be $1+(l+1)$. Therefore, $l+1$ is also red. By induction, we see that the numbers from 2 to $n-1$ are all red. That is $n-2=2012$ numbers. But there are only $\frac{1}{2}n=1007$ red numbers, contradiction.
We conclude that there are at least two numbers from 3 to $2n-1$ that cannot be written as the sum of a red and a blue number. We will now show that we can color the numbers in such a way that all numbers from 4 to $2n-2$ can be written as the sum of a red and a blue number, so that the maximum $k$ is equal to $2n-5$.
For this, color all even numbers except $n$ blue and also the number 1. All odd numbers except 1 are colored red, and also the number $n$. By adding 1 to an odd number (not equal to 1), we can write all even numbers from 4 to $n$ as the sum of a red and a blue number. By adding 2 to an odd number (not equal to 1), we can write all odd numbers from 5 to $n+1$ as the sum of a red and a blue number. By adding $n-1$ to an even number (not equal to $n$), we can write all odd numbers from $n+1$ to $2n-3$ as the sum of a red and a blue number. By adding $n$ to an even number (not equal to $n$), we can write all even numbers from $n+2$ to $2n-2$ as the sum of a red and a blue number. In total, we can thus write all numbers from 4 to $2n-2$ as the sum of a red and a blue number.
We conclude that the maximum $k$ is equal to $2n-5=4023$.
|
4023
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Je mag elk van de getallen 1 tot en met 2014 een kleur geven, waarbij precies de helft rood moet worden en de andere helft blauw. Vervolgens bekijk je het aantal $k$ van positieve gehele getallen die te schrijven zijn als de som van een rood en een blauw getal. Bepaal de maximale waarde van $k$ die je kunt bereiken.
|
Noem $n=2014$. We gaan bewijzen dat de maximale $k$ gelijk is aan $2 n-5$. Het kleinste getal dat je zou kunnen schrijven als de som van een rood en een blauw getal is $1+2=3$ en het grootste getal is $(n-1)+n=2 n-1$. Er zijn dus hoogstens $2 n-3$ getallen te schrijven als de som van een rood en een blauw getal.
Stel dat de getallen zo gekleurd kunnen worden dat er $2 n-3$ of $2 n-4$ getallen te schrijven zijn als som van een rood en een blauw getal. Er is nu hooguit één getal van 3 tot en met $2 n-1$ dat niet zo te schrijven is. We laten nu eerst zien dat we zonder verlies van algemeenheid mogen aannemen dat dit getal minstens $n+1$ is. We kunnen namelijk een tweede kleuring maken waarbij een getal $i$ blauw is dan en slechts dan als in de eerste kleuring $n+1-i$ blauw was. Dan is een getal $m$ bij de tweede kleuring te schrijven als som van rood en blauw dan en slechts dan als $2 n+2-m$ in de eerste kleuring te schrijven was als som van rood en blauw. Dus als in de eerste kleuring een getal kleiner dan $n+1$ niet te schrijven was als som van rood en blauw, dan is in de tweede kleuring juist een getal groter dan $2 n+2-(n+1)=n+1$ niet te schrijven als som van rood en blauw.
We mogen dus aannemen dat de getallen 3 tot en met $n$ allemaal te schrijven zijn als som van rood en blauw. Omdat rood en blauw verwisselbaar zijn, mogen we ook nog zonder verlies van algemeenheid aannemen dat 1 blauw gekleurd is. Omdat 3 te schrijven is als som van rood en blauw en dat alleen $3=1+2$ kan zijn, moet 2 rood zijn. Stel nu dat we weten dat 2 tot en met $l$ rood zijn, voor zekere $l$ met $2 \leq l \leq n-2$. Dan zijn in alle mogelijke sommen $a+b=l+2$ met $a, b \geq 2$ beide getallen rood gekleurd, maar we weten dat we $l+2$ kunnen schrijven als som van rood en blauw (want $l+2 \leq n$ ), dus moet dat wel $1+(l+1)$ zijn. Dus $l+1$ is ook rood gekleurd. Met inductie zien we nu dus dat de getallen 2 tot en met $n-1$ allemaal rood zijn. Dat zijn $n-2=2012$ getallen. Maar er zijn slechts $\frac{1}{2} n=1007$ getallen rood, tegenspraak.
We concluderen dat er minstens twee getallen van 3 tot en met $2 n-1$ niet te schrijven zijn als som van een rood en een blauw getal. We laten nu zien dat we de getallen zo kunnen kleuren dat alle getallen van 4 tot en met $2 n-2$ te schrijven zijn als som van een rood en een blauw getal, zodat de maximale $k$ gelijk is aan $2 n-5$.
Kleur hiervoor alle even getallen behalve $n$ blauw en verder ook nog het getal 1. Alle oneven getallen behalve 1 kleuren we rood en verder ook nog het getal $n$. Door 1 op te tellen bij een oneven getal (ongelijk aan 1) kunnen we alle even getallen van 4 tot en met $n$ schrijven als som van een rood en een blauw getal. Door 2 op te tellen bij een oneven getal (ongelijk aan 1) kunnen we alle oneven getallen van 5 tot en met $n+1$ schrijven als som van een rood en een blauw getal. Door $n-1$ op te tellen bij een even getal (ongelijk aan $n$ ) kunnen we alle oneven getallen van $n+1$ tot en met $2 n-3$ schrijven als som van een rood en een blauw getal. Door $n$ op te tellen bij een even getal (ongelijk aan $n$ ) kunnen we alle even getallen van $n+2$ tot en met $2 n-2$ schrijven als som van een rood en een
blauw getal. Al met al kunnen we dus alle getallen van 4 tot en met $2 n-2$ schrijven als som van een rood en een blauw getal.
We concluderen dat de maximale $k$ gelijk is aan $2 n-5=4023$.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2015-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2015"
}
|
Vind alle functies $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}_{>0}$ zodat $f(1)=2$ en zodat voor alle $m, n \in \mathbb{Z}_{>0}$ geldt dat $\min (2 m+2 n, f(m+n)+1)$ deelbaar is door $\max (f(m)+f(n), m+n)$.
|
Invullen van $m=n$ geeft dat $\min (4 n, f(2 n)+1)$ deelbaar is door $\max (2 f(n), 2 n)$. Een getal hoogstens gelijk aan $4 n$ is dus deelbaar door een getal minstens gelijk aan $2 f(n)$. Daaruit volgt $4 n \geq 2 f(n)$, dus $f(n) \leq 2 n$ voor alle $n$.
Invullen van $m=n=1$ geeft dat $\min (4, f(2)+1)$ deelbaar is door $\max (2 f(1), 2)=$ $\max (4,2)=4$. Dus $\min (4, f(2)+1)$ kan niet kleiner dan 4 zijn, dus $f(2)+1 \geq 4$. Maar we hebben net ook al gezien dat $f(2) \leq 2 \cdot 2=4$, dus $f(2)=3$ of $f(2)=4$.
Stel eerst dat $f(2)=3$. We bewijzen met inductie naar $n$ dat $f(n)=n+1$ voor alle $n$. Stel namelijk dat dit waar is voor $n=r-1$ voor zekere $r \geq 3$ en vul in $m=1$ en $n=r-1$. Dan krijgen we dat $\min (2 r, f(r)+1)$ deelbaar is door $\max (f(1)+f(r-1), r)=$ $\max (r+2, r)=r+2$. Aangezien $\min (2 r, f(r)+1) \leq 2 r<2(r+2)$ moet er gelden dat $\min (2 r, f(r)+1)=r+2$. Omdat $r \geq 3$ is $2 r>r+2$, dus er geldt $f(r)+1=r+2$ oftewel $f(r)=r+1$. Dit voltooit de inductie. We krijgen dus de kandidaatfunctie $f(n)=n+1$. We controleren meteen of deze functie voldoet. Er geldt dan voor alle $m, n \in \mathbb{N}$ dat $\min (2 m+2 n, f(m+n)+1)=\min (2 m+2 n, m+n+2)=m+n+2$ omdat $m, n \geq 1$, en $\max (f(m)+f(n), m+n)=\max (m+n+2, m+n)=m+n+2$. Het eerste is deelbaar door het tweede (want gelijk aan het tweede), dus deze functie voldoet.
Stel nu dat $f(2)=4$. We bewijzen met inductie naar $n$ dat $f(n)=2 n$ voor alle $n$. Stel namelijk dat dit waar is voor $n=r-1$ voor zekere $r \geq 3$. We bewijzen dat ook $f(r)=2 r$. Vul eerst $m=1$ en $n=r-1$ in. Dan vinden we dat $\min (2 r, f(r)+1)$ deelbaar is door $\max (f(1)+f(r-1), 1+r-1)=\max (2 r, r)=2 r$. Dus $\min (2 r, f(r)+1)$ kan niet kleiner dan $2 r$ zijn, dus $f(r) \geq 2 r-1$. Maar we wisten ook al dat $f(r) \leq 2 r$, dus $f(r) \in\{2 r-1,2 r\}$. Veronderstel dat $f(r)=2 r-1$. Vul dan $m=1$ en $n=r$ in. Dan vinden we dat $\min (2(r+$ 1), $f(r+1)+1)$ deelbaar is door $\max (f(1)+f(r), 1+r)=\max (2+2 r-1, r+1)=2 r+1$. Omdat $2 r+1 \nmid 2(r+1)$, kan $2(r+1)$ niet het minimum zijn, dus moet $f(r+1)+1<2 r+2$ en het moet ook deelbaar zijn door $2 r+1$, dus $f(r+1)=2 r$. Vul ook $m=2$ en $n=r-1$ in. Dan vinden we dat $\min (2(r+1), f(r+1)+1)=\min (2 r+2,2 r+1)=2 r+1$ deelbaar is door $\max (f(2)+f(r-1), 1+r)=\max (4+2 r-2, r+1)=2 r+2$, tegenspraak. We concluderen dat $f(r)=2 r$, waarmee de inductie voltooid is. We krijgen hiermee de kandidaatfunctie $f(n)=2 n$ voor alle $n$. We controleren of deze functie voldoet. Voor alle $m, n$ geldt dan dat $\min (2 m+2 n, f(m+n)+1)=\min (2 m+2 n, 2 m+2 n+1)=2 m+2 n$ en $\max (f(m)+f(n), m+n)=\max (2 m+2 n, m+n)=2 m+2 n$. Het eerste is deelbaar door het tweede (want gelijk aan het tweede), dus deze functie voldoet.
We concluderen dat er precies twee oplossingen zijn: de functie $f(n)=n+1$ voor alle $n$ en de functie $f(n)=2 n$ voor alle $n$.
|
f(n)=n+1 \text{ and } f(n)=2n
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Vind alle functies $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}_{>0}$ zodat $f(1)=2$ en zodat voor alle $m, n \in \mathbb{Z}_{>0}$ geldt dat $\min (2 m+2 n, f(m+n)+1)$ deelbaar is door $\max (f(m)+f(n), m+n)$.
|
Invullen van $m=n$ geeft dat $\min (4 n, f(2 n)+1)$ deelbaar is door $\max (2 f(n), 2 n)$. Een getal hoogstens gelijk aan $4 n$ is dus deelbaar door een getal minstens gelijk aan $2 f(n)$. Daaruit volgt $4 n \geq 2 f(n)$, dus $f(n) \leq 2 n$ voor alle $n$.
Invullen van $m=n=1$ geeft dat $\min (4, f(2)+1)$ deelbaar is door $\max (2 f(1), 2)=$ $\max (4,2)=4$. Dus $\min (4, f(2)+1)$ kan niet kleiner dan 4 zijn, dus $f(2)+1 \geq 4$. Maar we hebben net ook al gezien dat $f(2) \leq 2 \cdot 2=4$, dus $f(2)=3$ of $f(2)=4$.
Stel eerst dat $f(2)=3$. We bewijzen met inductie naar $n$ dat $f(n)=n+1$ voor alle $n$. Stel namelijk dat dit waar is voor $n=r-1$ voor zekere $r \geq 3$ en vul in $m=1$ en $n=r-1$. Dan krijgen we dat $\min (2 r, f(r)+1)$ deelbaar is door $\max (f(1)+f(r-1), r)=$ $\max (r+2, r)=r+2$. Aangezien $\min (2 r, f(r)+1) \leq 2 r<2(r+2)$ moet er gelden dat $\min (2 r, f(r)+1)=r+2$. Omdat $r \geq 3$ is $2 r>r+2$, dus er geldt $f(r)+1=r+2$ oftewel $f(r)=r+1$. Dit voltooit de inductie. We krijgen dus de kandidaatfunctie $f(n)=n+1$. We controleren meteen of deze functie voldoet. Er geldt dan voor alle $m, n \in \mathbb{N}$ dat $\min (2 m+2 n, f(m+n)+1)=\min (2 m+2 n, m+n+2)=m+n+2$ omdat $m, n \geq 1$, en $\max (f(m)+f(n), m+n)=\max (m+n+2, m+n)=m+n+2$. Het eerste is deelbaar door het tweede (want gelijk aan het tweede), dus deze functie voldoet.
Stel nu dat $f(2)=4$. We bewijzen met inductie naar $n$ dat $f(n)=2 n$ voor alle $n$. Stel namelijk dat dit waar is voor $n=r-1$ voor zekere $r \geq 3$. We bewijzen dat ook $f(r)=2 r$. Vul eerst $m=1$ en $n=r-1$ in. Dan vinden we dat $\min (2 r, f(r)+1)$ deelbaar is door $\max (f(1)+f(r-1), 1+r-1)=\max (2 r, r)=2 r$. Dus $\min (2 r, f(r)+1)$ kan niet kleiner dan $2 r$ zijn, dus $f(r) \geq 2 r-1$. Maar we wisten ook al dat $f(r) \leq 2 r$, dus $f(r) \in\{2 r-1,2 r\}$. Veronderstel dat $f(r)=2 r-1$. Vul dan $m=1$ en $n=r$ in. Dan vinden we dat $\min (2(r+$ 1), $f(r+1)+1)$ deelbaar is door $\max (f(1)+f(r), 1+r)=\max (2+2 r-1, r+1)=2 r+1$. Omdat $2 r+1 \nmid 2(r+1)$, kan $2(r+1)$ niet het minimum zijn, dus moet $f(r+1)+1<2 r+2$ en het moet ook deelbaar zijn door $2 r+1$, dus $f(r+1)=2 r$. Vul ook $m=2$ en $n=r-1$ in. Dan vinden we dat $\min (2(r+1), f(r+1)+1)=\min (2 r+2,2 r+1)=2 r+1$ deelbaar is door $\max (f(2)+f(r-1), 1+r)=\max (4+2 r-2, r+1)=2 r+2$, tegenspraak. We concluderen dat $f(r)=2 r$, waarmee de inductie voltooid is. We krijgen hiermee de kandidaatfunctie $f(n)=2 n$ voor alle $n$. We controleren of deze functie voldoet. Voor alle $m, n$ geldt dan dat $\min (2 m+2 n, f(m+n)+1)=\min (2 m+2 n, 2 m+2 n+1)=2 m+2 n$ en $\max (f(m)+f(n), m+n)=\max (2 m+2 n, m+n)=2 m+2 n$. Het eerste is deelbaar door het tweede (want gelijk aan het tweede), dus deze functie voldoet.
We concluderen dat er precies twee oplossingen zijn: de functie $f(n)=n+1$ voor alle $n$ en de functie $f(n)=2 n$ voor alle $n$.
|
{
"exam": "Dutch_TST",
"problem_label": "5",
"problem_match": "\nOpgave 5.",
"resource_path": "Dutch_TST/segmented/nl-2015-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2015"
}
|
For a positive integer $n$ that is not a power of two, we define $t(n)$ as the greatest odd divisor of $n$ and $r(n)$ as the smallest positive odd divisor of $n$ that is not equal to 1. Determine all positive integers $n$ that are not powers of two and for which
$$
n=3 t(n)+5 r(n)
$$
|
When $n$ is odd, $t(n)=n$ so $3 t(n)$ is greater than $n$, contradiction. If $n$ is divisible by 2 but not by 4, then $t(n)=\frac{1}{2} n$ and $3 t(n)$ is again greater than $n$, contradiction again. We can conclude that $n$ must be divisible by 4 at least. If $n$ is divisible by 16, then $t(n) \leq \frac{1}{16} n$. Furthermore, $r(n) \leq t(n)$, so $3 t(n)+5 r(n) \leq 8 t(n) \leq \frac{1}{2} n < n$, contradiction. Therefore, $n$ is not divisible by 16. We can thus write $n=4 m$ or $n=8 m$ with $m \geq 3$ odd.
Suppose $n=4 m$ with $m \geq 3$ odd. Then $t(n)=m$, so $4 m=3 m+5 r(n)$, hence $5 r(n)=m$. Since $r(n)$ is equal to the smallest odd prime divisor of $n$, which is also the smallest prime divisor of $m$, $m$ must be of the form $m=5 p$ with $p \leq 5$ an odd prime number. Thus, $m=15$ or $m=25$, which gives $n=60$ or $n=100$. Both solutions are valid.
Suppose $n=8 m$ with $m \geq 3$ odd. Again, $t(n)=m$, so $8 m=3 m+5 r(n)$, hence $5 r(n)=5 m$, or $r(n)=m$. We see that $m$ is prime. Thus, $n=8 p$ with $p$ an odd prime number. This family of solutions is also valid.
We find the solutions to be $n=60, n=100$ and $n=8 p$ with $p$ an odd prime number.
|
n=60, n=100 \text{ and } n=8 p \text{ with } p \text{ an odd prime number}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Voor een positief geheel getal $n$ dat geen tweemacht is, definiëren we $t(n)$ als de grootste oneven deler van $n$ en $r(n)$ als de kleinste positieve oneven deler van $n$ die ongelijk aan 1 is. Bepaal alle positieve gehele getallen $n$ die geen tweemacht zijn en waarvoor geldt
$$
n=3 t(n)+5 r(n)
$$
|
Als $n$ oneven is, geldt $t(n)=n$ dus is $3 t(n)$ groter dan $n$, tegenspraak. Als $n$ deelbaar door 2 is maar niet deelbaar door 4 , dan geldt $t(n)=\frac{1}{2} n$ en is $3 t(n)$ weer groter dan $n$, opnieuw tegenspraak. We kunnen concluderen dat $n$ in elk geval deelbaar door 4 moet zijn. Als $n$ deelbaar door 16 is, dan is $t(n) \leq \frac{1}{16} n$. Verder is $r(n) \leq t(n)$, dus $3 t(n)+5 r(n) \leq 8 t(n) \leq \frac{1}{2} n<n$, tegenspraak. Dus $n$ is niet deelbaar door 16 . We kunnen dus schrijven $n=4 m$ of $n=8 m$ met $m \geq 3$ oneven.
Stel $n=4 m$ met $m \geq 3$ oneven. Dan geldt $t(n)=m$, dus $4 m=3 m+5 r(n)$, dus $5 r(n)=m$. Omdat $r(n)$ gelijk is aan de kleinste oneven priemdeler van $n$, wat ook de kleinste priemdeler van $m$ is, moet nu $m$ van de vorm $m=5 p$ zijn met $p \leq 5$ een oneven priemgetal. Dus $m=15$ of $m=25$, wat $n=60$ of $n=100$ geeft. Beide oplossingen voldoen.
Stel dat $n=8 m$ met $m \geq 3$ oneven. Opnieuw geldt $t(n)=m$, dus $8 m=3 m+5 r(n)$, dus $5 r(n)=5 m$, oftewel $r(n)=m$. We zien dat $m$ priem is. Dus $n=8 p$ met $p$ een oneven priemgetal. Deze familie van oplossingen voldoet ook.
We vinden als oplossingen dus $n=60, n=100$ en $n=8 p$ met $p$ een oneven priemgetal.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2016-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2016"
}
|
For a positive integer $n$ that is not a power of two, we define $t(n)$ as the greatest odd divisor of $n$ and $r(n)$ as the smallest positive odd divisor of $n$ that is not equal to 1. Determine all positive integers $n$ that are not powers of two and for which
$$
n=3 t(n)+5 r(n)
$$
|
Let $p$ be the smallest odd prime divisor of $n$. Then $r(n)=p$. We can now write $n=2^{t} m p$ with $m$ odd and $t \geq 0$. It follows that $t(n)=p m$, so the given equality becomes $2^{t} m p=3 p m+5 p$, or equivalently $\left(2^{t}-3\right) m p=5 p$, thus $\left(2^{t}-3\right) m=5$. We see that $m$ must be a divisor of 5, so $m=1$ or $m=5$. If $m=1$, then $2^{t}=8$, so $t=3$. We get $n=8 p$ with $p$ an odd prime. This solution works for all odd prime numbers $p$. If $m=5$, then $2^{t}=4$, so $t=2$. We get $n=4 \cdot 5 \cdot p$ with $p$ an odd prime. This solution only works if $p$ is the smallest odd prime divisor, so if $p=3$ or $p=5$. This gives us two more solutions: $n=60$ and $n=100$.
|
n=8p \text{ with } p \text{ an odd prime}, \, n=60, \, n=100
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Voor een positief geheel getal $n$ dat geen tweemacht is, definiëren we $t(n)$ als de grootste oneven deler van $n$ en $r(n)$ als de kleinste positieve oneven deler van $n$ die ongelijk aan 1 is. Bepaal alle positieve gehele getallen $n$ die geen tweemacht zijn en waarvoor geldt
$$
n=3 t(n)+5 r(n)
$$
|
Noem $p$ de kleinste oneven priemdeler van $n$. Dan is $r(n)=p$. We kunnen nu schrijven $n=2^{t} m p$ met $m$ oneven en $t \geq 0$. Er geldt dan $t(n)=p m$, dus de gegeven gelijkheid gaat over in $2^{t} m p=3 p m+5 p$, oftewel $\left(2^{t}-3\right) m p=5 p$, dus $\left(2^{t}-3\right) m=5$. We zien dat $m$ een deler van 5 moet zijn, dus $m=1$ of $m=5$. Als $m=1$ geldt $2^{t}=8$, dus $t=3$. We krijgen dan $n=8 p$ met $p$ een oneven priem. Deze oplossing voldoet voor alle oneven priemgetallen $p$. Als $m=5$ geldt $2^{t}=4$, dus $t=2$. We krijgen dan $n=4 \cdot 5 \cdot p$ met $p$ een oneven priem. Deze oplossing voldoet alleen als $p$ de kleinste oneven priemdeler is, dus als $p=3$ of $p=5$. Zo vinden we nog twee oplossingen: $n=60$ en $n=100$.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2016-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2016"
}
|
Determine all triples $(x, y, z)$ of non-negative real numbers that satisfy the system of equations
$$
\begin{aligned}
& x^{2}-y=(z-1)^{2} \\
& y^{2}-z=(x-1)^{2} \\
& z^{2}-x=(y-1)^{2}
\end{aligned}
$$
|
Expanding the brackets and adding everything together gives
$$
x^{2}+y^{2}+z^{2}-(x+y+z)=x^{2}+y^{2}+z^{2}-2(x+y+z)+3,
$$
so $x+y+z=3$. Without loss of generality, we assume that $x \leq y, z$. Then $0 \leq x \leq 1$. Therefore, $x^{2} \leq x$, so $x^{2}-y \leq x-y \leq 0$. On the other hand, $x^{2}-y=(z-1)^{2} \geq 0$. Thus, equality must hold in both $x^{2} \leq x$ and $x-y \leq 0$. From the first equality, we get $x=0$ or $x=1$, and from the second, $x=y$. Suppose $x=y=0$, then from $x+y+z=3$ we get $z=3$. But then $x^{2}-y=(z-1)^{2}$ does not hold, a contradiction. We are left with the case that $x=y=1$. Then $z=3-1-1=1$. This triplet indeed satisfies the conditions and is therefore the only solution.
|
(1, 1, 1)
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Bepaal alle drietallen $(x, y, z)$ van niet-negatieve reële getallen die voldoen aan het stelsel vergelijkingen
$$
\begin{aligned}
& x^{2}-y=(z-1)^{2} \\
& y^{2}-z=(x-1)^{2} \\
& z^{2}-x=(y-1)^{2}
\end{aligned}
$$
|
Haakjes uitwerken en alles bij elkaar optellen geeft
$$
x^{2}+y^{2}+z^{2}-(x+y+z)=x^{2}+y^{2}+z^{2}-2(x+y+z)+3,
$$
dus $x+y+z=3$. Zonder verlies van algemeenheid nemen we aan dat $x \leq y, z$. Dan geldt $0 \leq x \leq 1$. Dus $x^{2} \leq x$, dus $x^{2}-y \leq x-y \leq 0$. Anderzijds is $x^{2}-y=(z-1)^{2} \geq 0$. Dus moet gelijkheid gelden in o.a. $x^{2} \leq x$ en $x-y \leq 0$. Uit de eerste gelijkheid volgt $x=0$ of $x=1$ en uit de tweede $x=y$. Stel $x=y=0$, dan volgt uit $x+y+z=3$ dat $z=3$. Maar dan geldt niet $x^{2}-y=(z-1)^{2}$, tegenspraak. We houden alleen het geval over dat $x=y=1$. Dan geldt $z=3-1-1=1$. Dit drietal voldoet inderdaad en is daarmee de enige oplossing.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2016-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2016"
}
|
Let $\triangle A B C$ be a right triangle with $\angle A=90^{\circ}$ and circumcircle $\Gamma$. The incircle touches $B C$ at a point $D$. Let $E$ be the midpoint of the arc $A B$ of $\Gamma$ that does not contain $C$ and let $F$ be the midpoint of the arc $A C$ of $\Gamma$ that does not contain $B$.
a) Prove that $\triangle A B C \sim \triangle D E F$.
b) Prove that $E F$ passes through the points where the incircle touches $A B$ and $A C$.
|
a) The midpoint $E$ of arc $AB$ where $C$ does not lie, lies on the bisector $CI$. Similarly, $F$ lies on $BI$. It holds that $\angle IFC = \angle BFC = \angle BAC = 90^{\circ}$ because $ABCF$ is a cyclic quadrilateral and $\angle IDC = 90^{\circ}$ because $D$ is the tangency point of the inscribed circle with $BC$. Therefore, $\angle IFC + \angle IDC = 180^{\circ}$, which implies that $FIDC$ is a cyclic quadrilateral. Now, $\angle DFI = \angle DCI = \frac{1}{2} \angle ACB$, while also $\angle IFE = \angle BFE = \angle BCE = \frac{1}{2} \angle ACB$. Thus, $\angle DFE = \frac{1}{2} \angle ACB + \frac{1}{2} \angle ACB = \angle ACB$. Similarly, $\angle DEF = \angle ABC$. Together, this gives $\triangle DEF \sim \triangle ABC$.
b) Let $S$ be the intersection of $EF$ with $AB$. In the previous part, we have seen that $BF$ is the bisector of $\angle DFE = \angle DFS$. Also, $BF$ is the bisector of $\angle ABC = \angle SBD$. Therefore, $\triangle BDF \cong \triangle BSF$ by (SAS). This means that $|BD| = |BS|$. On the other hand, the distances from $B$ to the tangency points of the inscribed circle with $BC$ and $BA$ are equal, and one of these tangency points is $D$, so the other tangency point must be $S$. Thus, $EF$ passes through the tangency point of the inscribed circle with $AB$. Similarly, it also passes through the tangency point of the inscribed circle with $AC$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $\triangle A B C$ een rechthoekige driehoek met $\angle A=90^{\circ}$ en omgeschreven cirkel $\Gamma$. De ingeschreven cirkel raakt aan $B C$ in een punt $D$. Zij $E$ het midden van de boog $A B$ van $\Gamma$ waar $C$ niet op ligt en zij $F$ het midden van de boog $A C$ van $\Gamma$ waar $B$ niet op ligt.
a) Bewijs dat $\triangle A B C \sim \triangle D E F$.
b) Bewijs dat $E F$ door de raakpunten van de ingeschreven cirkel aan $A B$ en $A C$ gaat.
|
a) Het midden $E$ van boog $A B$ waar $C$ niet op ligt, ligt op de bissectrice $C I$. Net zo ligt $F$ op $B I$. Er geldt $\angle I F C=\angle B F C=\angle B A C=90^{\circ}$ omdat $A B C F$ een koordenvierhoek is en $\angle I D C=90^{\circ}$ omdat $D$ het raakpunt van de ingeschreven cirkel aan $B C$ is. Dus $\angle I F C+\angle I D C=180^{\circ}$, waaruit volgt dat $F I D C$ een koordenvierhoek is. Nu geldt $\angle D F I=\angle D C I=\frac{1}{2} \angle A C B$, terwijl ook $\angle I F E=\angle B F E=\angle B C E=$ $\frac{1}{2} \angle A C B$. Dus $\angle D F E=\frac{1}{2} \angle A C B+\frac{1}{2} \angle A C B=\angle A C B$. Analoog is $\angle D E F=\angle A B C$. Samen geeft dit $\triangle D E F \sim \triangle A B C$.
b) $\mathrm{Zij} S$ het snijpunt van $E F$ met $A B$. In het vorige onderdeel hebben we gezien dat $B F$ de bissectrice is van $\angle D F E=\angle D F S$. Ook is $B F$ de bissectrice van $\angle A B C=$ $\angle S B D$. Dus $\triangle B D F \cong \triangle B S F$ vanwege (HZH). Dit betekent dat $|B D|=|B S|$. Anderzijds zijn de afstanden van $B$ tot de raakpunten van de ingeschreven cirkel aan $B C$ en $B A$ gelijk en het ene raakpunt is $D$, dus het andere raakpunt moet $S$ zijn. Dus $E F$ gaat door het raakpunt van de ingeschreven cirkel aan $A B$. Analoog gaat hij ook door het raakpunt van de ingeschreven cirkel aan $A C$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2016-B_uitwerkingen.jsonl",
"solution_match": "# Oplossing I.",
"tier": "T1",
"year": "2016"
}
|
Let $\triangle A B C$ be a right triangle with $\angle A=90^{\circ}$ and circumcircle $\Gamma$. The incircle touches $B C$ at a point $D$. Let $E$ be the midpoint of the arc $A B$ of $\Gamma$ that does not contain $C$ and let $F$ be the midpoint of the arc $A C$ of $\Gamma$ that does not contain $B$.
a) Prove that $\triangle A B C \sim \triangle D E F$.
b) Prove that $E F$ passes through the points where the incircle touches $A B$ and $A C$.
|
a) As in the first solution, we prove that FIDC is a cyclic quadrilateral. Due to the external angle theorem, $\angle C I F=\angle I C B+\angle I B C=\frac{1}{2} \angle A C B+\frac{1}{2} \angle A B C=90^{\circ}-$ $\frac{1}{2} \angle B A C=45^{\circ}$. Therefore, $\angle C D F=\angle C I F=45^{\circ}$. Similarly, $\angle B D E=45^{\circ}$, so $\angle E D F=180^{\circ}-45^{\circ}-45^{\circ}=90^{\circ}$. Let $M$ be the midpoint of $B C$. Then $M$ is also the center of the circumcircle of $\triangle A B C$, so $M F$ is perpendicular to $A C$. This means that $M F \| A B$. Similarly, $M E \| A C$. Thus, $\angle E M F=90^{\circ}$. We see that $\angle E M F=\angle E D F$, so $D, E, F$, and $M$ lie on one circle. We now distinguish two cases.
If $D=M$, then $45^{\circ}=\angle C D F=\angle C M F=\angle C B A$ due to alternate segment theorem, so $\triangle A B C$ is an isosceles right triangle. Since $M$ is the center of the circumcircle, on which $E$ and $F$ also lie, $|M E|=|M F|$, so $\triangle M E F$ is also an isosceles right triangle. Therefore, $\triangle A B C \sim \triangle M E F=\triangle D E F$.
In the other case, $D \neq M$. Without loss of generality, assume that $D$ is closer to $C$ than $M$. Then $\angle D E F=\angle D M F=\angle C B A$ due to alternate segment theorem and $\angle D F E=180^{\circ}-\angle D M E=\angle B M E=\angle B C A$ due to alternate segment theorem. Thus, by AA similarity, $\triangle D E F \sim \triangle A B C$.
b) Let $L$ be the point of tangency of the incircle with $A C$. We have already seen that $F I D C$ is a cyclic quadrilateral because $\angle I D C=90^{\circ}=\angle I F C$. Since also $\angle I L C=$ $90^{\circ}$, $L$ lies on the same circle. Therefore,
$$
\angle L F B=\angle L F I=\angle L C I=\angle A C E=\angle E C B=\angle E F B,
$$
which implies that $E, F$, and $L$ lie on a straight line. Thus, $E F$ passes through the point of tangency $L$. Similarly, $E F$ also passes through the point of tangency of the incircle with $A B$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $\triangle A B C$ een rechthoekige driehoek met $\angle A=90^{\circ}$ en omgeschreven cirkel $\Gamma$. De ingeschreven cirkel raakt aan $B C$ in een punt $D$. Zij $E$ het midden van de boog $A B$ van $\Gamma$ waar $C$ niet op ligt en zij $F$ het midden van de boog $A C$ van $\Gamma$ waar $B$ niet op ligt.
a) Bewijs dat $\triangle A B C \sim \triangle D E F$.
b) Bewijs dat $E F$ door de raakpunten van de ingeschreven cirkel aan $A B$ en $A C$ gaat.
|
a) Zoals in de eerste oplossing bewijzen we dat FIDC een koordenvierhoek is. Vanwege de buitenhoekstelling is $\angle C I F=\angle I C B+\angle I B C=\frac{1}{2} \angle A C B+\frac{1}{2} \angle A B C=90^{\circ}-$ $\frac{1}{2} \angle B A C=45^{\circ}$. Dus $\angle C D F=\angle C I F=45^{\circ}$. Analoog is $\angle B D E=45^{\circ}$, zodat $\angle E D F=180^{\circ}-45^{\circ}-45^{\circ}=90^{\circ}$. Zij nu $M$ het midden van $B C$. Dan is $M$ ook het midden van de omgeschreven cirkel van $\triangle A B C$ dus staat $M F$ loodrecht op $A C$. Dat betekent dat $M F \| A B$. Zo ook is $M E \| A C$. Dus $\angle E M F=90^{\circ}$. We zien dat $\angle E M F=\angle E D F$, dus $D, E, F$ en $M$ liggen op één cirkel. We onderscheiden nu twee gevallen.
Als $D=M$, dan geldt $45^{\circ}=\angle C D F=\angle C M F=\angle C B A$ wegens $F$-hoeken, dus $\triangle A B C$ is een gelijkbenige rechthoekige driehoek. Omdat $M$ het middelpunt van de omgeschreven cirkel is, waar ook $E$ en $F$ op liggen, is $|M E|=|M F|$, dus ook $\triangle M E F$ is een gelijkbenige rechthoekige driehoek. Dus $\triangle A B C \sim \triangle M E F=\triangle D E F$.
In het andere geval geldt $D \neq M$. Zonder verlies van algemeenheid nemen we aan dat $D$ dichter bij $C$ ligt dan $M$. Dan geldt $\angle D E F=\angle D M F=\angle C B A$ wegens F-hoeken en $\angle D F E=180^{\circ}-\angle D M E=\angle B M E=\angle B C A$ wegens F-hoeken. Dus met (hh) is nu ook $\triangle D E F \sim \triangle A B C$.
b) $\mathrm{Zij} L$ het raakpunt van de ingeschreven cirkel aan $A C$. We hebben al gezien dat $F I D C$ een koordenvierhoek is wegens $\angle I D C=90^{\circ}=\angle I F C$. Omdat ook $\angle I L C=$ $90^{\circ}$, ligt $L$ op dezelfde cirkel. Dus
$$
\angle L F B=\angle L F I=\angle L C I=\angle A C E=\angle E C B=\angle E F B,
$$
waaruit volgt dat $E, F$ en $L$ op een lijn liggen. Dus $E F$ gaat door het raakpunt $L$. Analoog gaat $E F$ ook door het raakpunt van de ingeschreven cirkel aan $A B$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2016-B_uitwerkingen.jsonl",
"solution_match": "# Oplossing II.",
"tier": "T1",
"year": "2016"
}
|
Let $\triangle A B C$ be a right triangle with $\angle A=90^{\circ}$ and circumcircle $\Gamma$. The incircle touches $B C$ at a point $D$. Let $E$ be the midpoint of the arc $A B$ of $\Gamma$ that does not contain $C$ and let $F$ be the midpoint of the arc $A C$ of $\Gamma$ that does not contain $B$.
a) Prove that $\triangle A B C \sim \triangle D E F$.
b) Prove that $E F$ passes through the points where the incircle touches $A B$ and $A C$.
|
a) As in the previous solution, we prove that $\angle C D F=45^{\circ}=\angle B D E$. Let $F^{\prime}$ be the reflection of $F$ in $B C$. Since $B C$ is the diameter of $\Gamma$, $F^{\prime}$ lies on $\Gamma$ again. Furthermore, $\angle C D F^{\prime}=\angle C D F=45^{\circ}$ and $\angle C D E=180^{\circ}-\angle B D E=135^{\circ}$, so $\angle C D F^{\prime}+\angle C D E=180^{\circ}$, which implies that $F^{\prime}, D$ and $E$ lie on a straight line. We see that
$$
\angle F E D=\angle F E F^{\prime}=\angle F B F^{\prime}=2 \angle F B C=2 \cdot \frac{1}{2} \angle A B C=\angle A B C .
$$
Similarly, $\angle E F D=\angle A C B$, so by (AA) similarity, $\triangle D E F \sim \triangle A B C$.
b) Let $K$ and $L$ be the points of tangency of the incircle with $A B$ and $A C$, respectively. Since $\angle A K I=\angle A L I=90^{\circ}$ and also $\angle K A L=90^{\circ}$, $A K I L$ is a rectangle. It is even a square, since $|I K|=|I L|$. Thus, diagonal $K L$ is the perpendicular bisector of $A I$. We will now prove that $E F$ is also the perpendicular bisector of $A I$, so that $E F$ coincides with $K L$ and the desired result is proven.
We have
$$
\angle F A I=\angle F A C+\angle C A I=\angle F B C+\angle C A I=\frac{1}{2} \angle A B C+\frac{1}{2} \angle B A C
$$
and further, by the exterior angle theorem in $\triangle A B I$,
$$
\angle A I F=\angle I A B+\angle I B A=\frac{1}{2} \angle A B C+\frac{1}{2} \angle B A C .
$$
Thus, $\angle F A I=\angle A I F$, which implies $|A F|=|I F|$. This means that $F$ lies on the perpendicular bisector of $A I$. Similarly, we can show that $E$ also lies on the perpendicular bisector of $A I$. Therefore, $E F$ is indeed the perpendicular bisector of $A I$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $\triangle A B C$ een rechthoekige driehoek met $\angle A=90^{\circ}$ en omgeschreven cirkel $\Gamma$. De ingeschreven cirkel raakt aan $B C$ in een punt $D$. Zij $E$ het midden van de boog $A B$ van $\Gamma$ waar $C$ niet op ligt en zij $F$ het midden van de boog $A C$ van $\Gamma$ waar $B$ niet op ligt.
a) Bewijs dat $\triangle A B C \sim \triangle D E F$.
b) Bewijs dat $E F$ door de raakpunten van de ingeschreven cirkel aan $A B$ en $A C$ gaat.
|
a) Zoals in de vorige oplossing bewijzen we dat $\angle C D F=45^{\circ}=\angle B D E$. Zij nu $F^{\prime}$ de spiegeling van $F$ in $B C$. Omdat $B C$ de middellijn van $\Gamma$ is, ligt $F^{\prime}$ weer op $\Gamma$. Verder is $\angle C D F^{\prime}=\angle C D F=45^{\circ}$ en $\angle C D E=180^{\circ}-\angle B D E=135^{\circ}$, dus $\angle C D F^{\prime}+\angle C D E=180^{\circ}$, waaruit volgt dat $F^{\prime}, D$ en $E$ op een lijn liggen. We zien dat
$$
\angle F E D=\angle F E F^{\prime}=\angle F B F^{\prime}=2 \angle F B C=2 \cdot \frac{1}{2} \angle A B C=\angle A B C .
$$
Analoog geldt $\angle E F D=\angle A C B$, dus met (hh) geldt $\triangle D E F \sim \triangle A B C$.
b) Laat $K$ en $L$ de raakpunten zijn van de inschreven cirkel aan respectievelijk $A B$ en $A C$. Omdat $\angle A K I=\angle A L I=90^{\circ}$ en ook $\angle K A L=90^{\circ}$, is $A K I L$ een rechthoek. Het is zelfs een vierkant, aangezien $|I K|=|I L|$. Dus diagonaal $K L$ is de middelloodlijn van $A I$. We gaan nu bewijzen dat $E F$ ook de middelloodlijn van $A I$ is, zodat $E F$ samenvalt met $K L$ en het gevraagde bewezen is.
Er geldt
$$
\angle F A I=\angle F A C+\angle C A I=\angle F B C+\angle C A I=\frac{1}{2} \angle A B C+\frac{1}{2} \angle B A C
$$
en verder, wegens de buitenhoekstelling in $\triangle A B I$,
$$
\angle A I F=\angle I A B+\angle I B A=\frac{1}{2} \angle A B C+\frac{1}{2} \angle B A C .
$$
Dus $\angle F A I=\angle A I F$, waaruit volgt $|A F|=|I F|$. Dat betekent dat $F$ op de middelloodlijn van $A I$ ligt. Analoog kunnen we laten zien dat ook $E$ op de middelloodlijn van $A I$ ligt. Dus $E F$ is inderdaad de middelloodlijn van $A I$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2016-B_uitwerkingen.jsonl",
"solution_match": "# Oplossing III.",
"tier": "T1",
"year": "2016"
}
|
The Facebook group Olympiad Training has at least five members. There is a certain number $k$ with the property: for any $k$-member group, there is at least one member of that $k$-member group who is friends with the other $k-1$. (Friendship is mutual: if $A$ is friends with $B$, then $B$ is also friends with $A$.)
a) Let $k=4$. Can you be certain that the Facebook group has a member who is friends with all other members?
b) Let $k=5$. Can you be certain that the Facebook group has a member who is friends with all other members?
|
a) Yes, that's possible. If everyone is friends with everyone, then we are done. So, let's assume there are two members, say $A$ and $B$, who are not friends with each other. If we look at a group of four including $A, B$, and two other members, then one of those other two must be friends with the other and with $A$ and $B$. In particular, those two others are friends with each other. This applies to any two members (different from $A$ and $B$) that we choose, so every pair without $A$ and $B$ is friends with each other. Now take $A, B, C$, and $D$ and say that $C$ is friends with $A, B$, and $D$. He is also friends with all other members of the group, so $C$ is someone who is friends with everyone.
b) No, that's not possible. We provide a counterexample. Suppose the Facebook group has six members, namely $A, B, C, D, E$, and $F$. They are all friends with each other, except for the pair $(A, B)$, the pair $(C, D)$, and the pair $(E, F)$. This means that there is no member who is friends with all other members. If we take a group of five, then without loss of generality, it is $A, B, C, D$, and $E$. Here, someone who is friends with the other four is, for example, $E$. So the condition is satisfied.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
De Facebookgroep Olympiadetraining heeft minstens vijf leden. Er is een zeker getal $k$ met de eigenschap: voor elk $k$-tal leden geldt dat er minstens één lid van dat $k$-tal bevriend is met de andere $k-1$. (Vriendschap is wederzijds: als $A$ bevriend is met $B$, dan is $B$ ook bevriend met $A$.)
a) Stel $k=4$. Kun je met zekerheid zeggen dat de Facebookgroep een lid heeft dat vrienden is met alle andere leden?
b) Stel $k=5$. Kun je met zekerheid zeggen dat de Facebookgroep een lid heeft dat vrienden is met alle andere leden?
|
a) Ja, dat kan. Als iedereen bevriend is met iedereen, dan zijn we klaar. Stel dus dat er twee leden zijn, zeg $A$ en $B$, die geen vrienden met elkaar zijn. Als we een groep van vier bekijken met $A, B$ en twee andere leden, dan moet één van die andere twee bevriend zijn met de ander en met $A$ en $B$. In het bijzonder zijn die twee anderen bevriend met elkaar. Dit geldt voor elke twee leden (ongelijk aan $A$ en $B$ ) die we kiezen, dus elk tweetal zonder $A$ en $B$ is bevriend met elkaar. Neem nu $A, B, C$ en $D$ en zeg dat $C$ bevriend is met $A, B$ en $D$. Hij is verder ook bevriend met alle andere leden van de groep, dus $C$ is iemand die bevriend is met iedereen.
b) Nee, dat kan niet. We geven een tegenvoorbeeld. Stel dat de Facebookgroep zes leden heeft, namelijk $A, B, C, D, E$ en $F$. Zij zijn allemaal vrienden van elkaar, behalve het paar $(A, B)$, het paar $(C, D)$ en het paar $(E, F)$. Dat betekent dat er geen enkel lid vrienden is van alle andere leden. Als we een groep van vijf nemen, dan is dat zonder verlies van algemeenheid $A, B, C, D$ en $E$. Hierbij is iemand die vrienden is met de andere vier, namelijk $E$. Dus aan de voorwaarde is voldaan.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2016-B_uitwerkingen.jsonl",
"solution_match": "# Oplossing.",
"tier": "T1",
"year": "2016"
}
|
Determine all pairs $(m, n)$ of positive integers for which
$$
(m+n)^{3} \mid 2 n\left(3 m^{2}+n^{2}\right)+8
$$
|
Suppose the quotient of $2 n\left(3 m^{2}+n^{2}\right)+8$ and $(m+n)^{3}$ is not equal to 1. Then it is at least 2, so we have
$$
(m+n)^{3} \leq n\left(3 m^{2}+n^{2}\right)+4
$$
or equivalently,
$$
m^{3}+3 m^{2} n+3 m n^{2}+n^{3} \leq 3 m^{2} n+n^{3}+4
$$
or equivalently,
$$
m^{3}+3 m n^{2} \leq 4
$$
From this, it immediately follows that $m<2$, so $m=1$. Then we have $1+3 n^{2} \leq 4$, so also $n=1$. The pair $(m, n)=(1,1)$ is indeed a solution, as $2^{3} \mid 2 \cdot 4+8$.
The other possibility is that the quotient is exactly 1. Then we have
$$
(m+n)^{3}=2 n\left(3 m^{2}+n^{2}\right)+8
$$
or equivalently,
$$
m^{3}+3 m^{2} n+3 m n^{2}+n^{3}=6 m^{2} n+2 n^{3}+8
$$
or equivalently,
$$
m^{3}-3 m^{2} n+3 m n^{2}-n^{3}=8
$$
The left side can be factored as $(m-n)^{3}$. So we have $m-n=2$, or equivalently, $m=n+2$. From the previous calculations, it follows directly that $(m, n)=(n+2, n)$ is indeed a solution for all positive integers $n$.
We conclude that the solutions are: $(m, n)=(1,1)$ and $(m, n)=(n+2, n)$ for $n \geq 1$.
|
(m, n)=(1,1) \text{ and } (m, n)=(n+2, n) \text{ for } n \geq 1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Bepaal alle paren $(m, n)$ van positieve gehele getallen waarvoor
$$
(m+n)^{3} \mid 2 n\left(3 m^{2}+n^{2}\right)+8
$$
|
Stel dat het quotiënt van $2 n\left(3 m^{2}+n^{2}\right)+8$ en $(m+n)^{3}$ niet gelijk aan 1 is. Dan is het minstens 2, dus geldt
$$
(m+n)^{3} \leq n\left(3 m^{2}+n^{2}\right)+4
$$
oftewel
$$
m^{3}+3 m^{2} n+3 m n^{2}+n^{3} \leq 3 m^{2} n+n^{3}+4
$$
oftewel
$$
m^{3}+3 m n^{2} \leq 4
$$
Hieruit volgt meteen $m<2$, dus $m=1$. Dan staat er $1+3 n^{2} \leq 4$, dus ook $n=1$. Het paar $(m, n)=(1,1)$ is inderdaad een oplossing, want er geldt $2^{3} \mid 2 \cdot 4+8$.
De andere mogelijkheid is dat het quotiënt juist wel gelijk aan 1 is. Dan geldt
$$
(m+n)^{3}=2 n\left(3 m^{2}+n^{2}\right)+8
$$
oftewel
$$
m^{3}+3 m^{2} n+3 m n^{2}+n^{3}=6 m^{2} n+2 n^{3}+8
$$
oftewel
$$
m^{3}-3 m^{2} n+3 m n^{2}-n^{3}=8
$$
De linkerkant kunnen we ontbinden als $(m-n)^{3}$. Dus er geldt $m-n=2$, oftewel $m=n+2$. Uit de voorgaande berekeningen volgt direct ook dat $(m, n)=(n+2, n)$ inderdaad een oplossing is voor alle positieve gehele $n$.
We concluderen dat de oplossingen zijn: $(m, n)=(1,1)$ en $(m, n)=(n+2, n)$ voor $n \geq 1$.
|
{
"exam": "Dutch_TST",
"problem_label": "5",
"problem_match": "\nOpgave 5.",
"resource_path": "Dutch_TST/segmented/nl-2016-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2016"
}
|
Let $\mathrm{Zij} ABC$ be an acute triangle. Let $\mathrm{Zij} H$ be the foot of the altitude from $C$ to $AB$. Suppose that $|AH|=3|BH|$. Let $M$ and $N$ be the midpoints of $AB$ and $AC$, respectively. Let $P$ be a point such that $|NP|=|NC|$ and $|CP|=|CB|$, and such that $B$ and $P$ lie on opposite sides of the line $AC$.
Prove that $\angle APM = \angle PBA$.
|
There is only one configuration. Since $N$ is the midpoint of $A C$, $|N C|=|N A|$. It was also given that $|N P|=|N C|$, so $N$ is the center of a circle through $A, C$, and $P$. From Thales' theorem, it follows that $\angle A P C=90^{\circ}$. Since $|A H|=3|B H|$ and $M$ is the midpoint of $A B$, it follows that $|M H|=|B H|$. Since $\angle C H B=90^{\circ}=\angle C H M$, triangles $C H B$ and $C H M$ are congruent, from which it follows that $|C M|=|C B|$. It was further given that $|C P|=|C B|$, so $C$ is the center of a circle through $P, M$, and $B$. Since $\angle A P C=90^{\circ}$, $A P$ is a tangent to this circle. Using the tangent-secant angle theorem, we now get $\angle A P M=\angle P B M=\angle P B A$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
$\mathrm{Zij} A B C$ een scherphoekige driehoek. $\mathrm{Zij} H$ het voetpunt van de hoogtelijn vanuit $C$ op $A B$. Veronderstel dat $|A H|=3|B H|$. Laat $M$ en $N$ de middens van respectievelijk $A B$ en $A C$ zijn. Zij $P$ een punt zodat $|N P|=|N C|$ en $|C P|=|C B|$ en zodat $B$ en $P$ aan verschillende kanten van de lijn $A C$ liggen.
Bewijs dat $\angle A P M=\angle P B A$.
|
Er is maar één configuratie. Omdat $N$ het midden van $A C$ is, is $|N C|=|N A|$. Gegeven was ook dat $|N P|=|N C|$, dus $N$ is het middelpunt van een cirkel door $A, C$ en $P$. Met de stelling van Thales volgt hieruit dat $\angle A P C=90^{\circ}$. Omdat $|A H|=3|B H|$ en $M$ het midden van $A B$ is, geldt $|M H|=|B H|$. Omdat ook nog $\angle C H B=90^{\circ}=\angle C H M$ zijn driehoeken $C H B$ en $C H M$ congruent, waaruit volgt dat $|C M|=|C B|$. Gegeven was verder dat $|C P|=|C B|$, dus $C$ is het middelpunt van een cirkel door $P, M$ en $B$. Omdat $\angle A P C=90^{\circ}$, is $A P$ een raaklijn aan deze cirkel. Met de raaklijnomtrekshoekstelling krijgen we nu $\angle A P M=\angle P B M=\angle P B A$.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2016-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2016"
}
|
Let $n$ be a positive integer and consider a square with dimensions $2^{n} \times 2^{n}$. We cover this square with a number (at least 2) of non-overlapping rectangles, such that each rectangle has integer dimensions and a power of two as its area. Prove that two of the rectangles in the covering have the same dimensions. (Two rectangles have the same dimensions if they have the same width and the same height, where they cannot be rotated.)
|
First note that a rectangle with integer dimensions has a power of two as its area if and only if both dimensions are powers of two.
Consider a covering in which no two rectangles have the same dimensions. We first prove that there are then no rectangles with width 1. Suppose, for the sake of contradiction, that such a rectangle does exist. Color all cells blue that are covered by a rectangle with width 1. Let $M$ be the total number of blue cells. This is the sum of the heights of all rectangles with width 1, so the sum of different powers of two (at least one). Let $2^{k}$ be the largest power of two that is included. Since $2^{k}-1=2^{k-1}+$ $2^{k-2}+\ldots+2+1$, there are fewer than $2^{k}$ blue cells outside the one rectangle with height $2^{k}$, so there is at least one row where only a blue cell from that rectangle with height $2^{k}$ is present and no other blue cell. But in this row, there are then still an odd number of cells left, which must be covered with rectangles all having an even width (the width must then be a power of two greater than 1). Contradiction. Therefore, there are no rectangles with width 1. Similarly, there are no rectangles with height 1 in the covering. Thus, all rectangles have an even width and height.
Now consider the smallest $n$ for which such a covering exists in which no two rectangles have the same dimensions. Since all rectangles have an even width and height, we can divide all dimensions (of both the square and the rectangles) by 2 and get a square that is twice as small, covered by rectangles with integer dimensions, each having a power of two as its area. Contradiction with the minimality of $n$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Zij $n$ een positief geheel getal en bekijk een vierkant met afmetingen $2^{n} \times 2^{n}$. We bedekken dit vierkant met een aantal (minstens 2) niet-overlappende rechthoeken, zodat elke rechthoek gehele afmetingen heeft en een tweemacht als oppervlakte. Bewijs dat twee van de rechthoeken in de bedekking dezelfde afmetingen hebben. (Twee rechthoeken hebben dezelfde afmetingen als ze dezelfde breedte en dezelfde hoogte hebben, waarbij ze niet gedraaid mogen worden.)
|
Merk eerst op dat een rechthoek met gehele afmetingen een tweemacht als oppervlakte heeft precies dan als de afmetingen beide tweemachten zijn.
Bekijk een bedekking waarin geen twee rechthoeken met dezelfde afmetingen voorkomen. We bewijzen eerst dat er dan geen rechthoeken met breedte 1 voorkomen. Stel namelijk dat er wel zo'n rechthoek voorkomt. Kleur alle vakjes blauw die bedekt worden door een rechthoek met breedte 1. Noem $M$ het totaal aantal blauwe vakjes. Dit is de som van de hoogtes van alle rechthoeken met breedte 1, dus de som van verschillende tweemachten (minstens één). Noem $2^{k}$ de grootste tweemacht die daarbij zit. Omdat $2^{k}-1=2^{k-1}+$ $2^{k-2}+\ldots+2+1$, zijn er minder dan $2^{k}$ blauwe vakjes buiten die ene rechthoek met hoogte $2^{k}$, dus is er minstens één rij waar alleen een blauw vakje van die rechthoek met hoogte $2^{k}$ zit en geen ander blauw vakje. Maar in deze rij is er dan nog een oneven aantal vakjes over, die bedekt moeten worden met allemaal rechthoeken met een even breedte (de breedte moet dan immers een tweemacht groter dan 1 zijn). Tegenspraak. Dus er zijn geen rechthoeken met breedte 1. Analoog komen er in de bedekking geen rechthoeken met hoogte 1 voor. Dus alle rechthoeken hebben een even breedte en hoogte.
Bekijk nu de kleinste $n$ waarvoor zo'n bedekking bestaat waarin geen twee rechthoeken met dezelfde afmetingen voorkomen. Omdat alle rechthoeken een even breedte en hoogte hebben, kunnen we alle afmetingen (van zowel het vierkant als de rechthoeken) door 2 delen en krijgen we een twee keer zo klein vierkant dat bedekt is door rechthoeken met gehele afmetingen die elk een tweemacht als oppervlakte hebben. Tegenspraak met de minimaliteit van $n$.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2016-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2016"
}
|
Let $n$ be a positive integer and consider a square with dimensions $2^{n} \times 2^{n}$. We cover this square with a number (at least 2) of non-overlapping rectangles, such that each rectangle has integer dimensions and a power of two as its area. Prove that two of the rectangles in the covering have the same dimensions. (Two rectangles have the same dimensions if they have the same width and the same height, where they cannot be rotated.)
|
We provide an alternative way to prove that there are no rectangles with width 1 in a covering where no two rectangles have the same dimensions. The rest of the proof proceeds as in Solution I. Suppose there is a rectangle with width 1. Now color all odd columns blue and all even columns red. Then there are $2^{2 n-1}$ blue and $2^{2 n-1}$ red cells. Every rectangle with width at least 2 covers an equal number of blue and red cells. The rectangles with width 1 together thus also cover an equal number of red and blue cells; let this number of red cells be $V$. Consider the rectangle with width 1 and the smallest height $2^{\ell}$. Without loss of generality, assume this rectangle covers red cells. Every other rectangle with width 1 in a red column has height at least $2^{\ell+1}$ and thus covers a number of red cells that is 0 modulo $2^{\ell+1}$. Therefore, $V \equiv 2^{\ell} \bmod 2^{\ell+1}$. But all rectangles with width 1 in a blue column also have height at least $2^{\ell+1}$, so the number of blue cells covered by rectangles with width 1 is 0 modulo $2^{\ell+1}$. Thus, $0 \equiv V \equiv 2^{\ell} \bmod 2^{\ell+1}$, a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Zij $n$ een positief geheel getal en bekijk een vierkant met afmetingen $2^{n} \times 2^{n}$. We bedekken dit vierkant met een aantal (minstens 2) niet-overlappende rechthoeken, zodat elke rechthoek gehele afmetingen heeft en een tweemacht als oppervlakte. Bewijs dat twee van de rechthoeken in de bedekking dezelfde afmetingen hebben. (Twee rechthoeken hebben dezelfde afmetingen als ze dezelfde breedte en dezelfde hoogte hebben, waarbij ze niet gedraaid mogen worden.)
|
We geven een alternatieve manier om te bewijzen dat er geen rechthoeken met breedte 1 voorkomen in een bedekking waarin geen twee rechthoeken met dezelfde afmetingen voorkomen. De rest van het bewijs gaat hetzelfde als in oplossing I. Stel dus er wel een rechthoek met breedte 1 voorkomt. Kleur nu alle oneven kolommen blauw en alle even kolommen rood. Dan zijn er $2^{2 n-1}$ blauwe en $2^{2 n-1}$ rode vakjes. Iedere rechthoek met breedte minstens 2 bedekt evenveel blauwe als rode vakjes. De rechthoeken met breedte 1 bedekken samen dus ook evenveel rode als blauwe vakjes; noem dit aantal rode vakjes $V$. Bekijk de rechthoek met breedte 1 met de kleinste hoogte $2^{\ell}$. Stel zonder verlies van algemeenheid dat deze rode vakjes bedekt. Iedere andere rechthoek met breedte 1 in een rode kolom heeft hoogte minstens $2^{\ell+1}$ en bedekt dus een aantal rode vakjes dat 0 is modulo $2^{\ell+1}$. Dus $V \equiv 2^{\ell} \bmod 2^{\ell+1}$. Maar alle rechthoeken met breedte 1 in een blauwe kolom hebben ook hoogte minstens $2^{\ell+1}$, dus het aantal blauwe vakjes dat door rechthoeken met breedte 1 wordt bedekt, is 0 modulo $2^{\ell+1}$. Dus $0 \equiv V \equiv 2^{\ell} \bmod 2^{\ell+1}$, tegenspraak.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2016-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2016"
}
|
Find all positive integers $k$ for which the equation
$$
\operatorname{lcm}(m, n)-\operatorname{gcd}(m, n)=k(m-n)
$$
has no positive integer solutions $(m, n)$ with $m \neq n$.
|
Let $d=\operatorname{ggd}(m, n)$ and write $m=d a$ and $n=d b$. It holds that $\operatorname{kgv}(m, n) \cdot \operatorname{ggd}(m, n)=m n$, so we can write the given equation as
$$
\frac{d a \cdot d b}{d}-d=k(d a-d b)
$$
or equivalently
$$
a b-1=k(a-b) .
$$
From now on, we will look at the equivalent problem: find all positive integer $k$ for which this new equation has no positive integer solutions $(a, b)$ with $a \neq b$ and $\operatorname{ggd}(a, b)=1$. Note that if a pair $(a, b)$ satisfies this equation, it automatically follows that $\operatorname{ggd}(a, b)=1$. Suppose that $t \mid a$ and $t \mid b$, then $t \mid a b$ and $t \mid a-b$, so $t \mid 1$, so $a$ and $b$ have no common divisor greater than 1.
Suppose first that $k \geq 3$. We claim that $(a, b)=\left(k^{2}-k-1, k-1\right)$ is a solution. Then we have
$$
a b-1=a(k-1)-1=k a-a-1=k a-k^{2}+k+1-1=k a-k^{2}+k=k(a-k+1)=k(a-b).
$$
We have already seen that this immediately implies that $\operatorname{ggd}(a, b)=1$. We still need to check that $a$ and $b$ are positive and that they are not equal. Since $k \geq 3$, we have $b=k-1 \geq 2$ and $a=k^{2}-k-1 \geq 2 k-k-1=k-1 \geq 2$, so they are both positive. Suppose that $a=b$, then $k^{2}-k-1=k-1$, or $k^{2}=2 k$, or $k=2$, a contradiction. So our pair $(a, b)$ satisfies all the conditions. For every $k \geq 3$, the equation thus has at least one solution $(a, b)$ with $a \neq b$ and $\operatorname{ggd}(a, b)=1$.
Now suppose that $k=1$. We claim that $(a, b)=(2,1)$ is a solution. Clearly, $a$ and $b$ are positive and not equal. Furthermore, we have
$$
a b-1=2-1=1=1 \cdot(2-1)=k(a-b)
$$
So for $k=1$, the equation also has at least one solution $(a, b)$ with $a \neq b$ and $\operatorname{ggd}(a, b)=1$.
Finally, suppose that $k=2$. The equation becomes
$$
a b-1=2(a-b) .
$$
The right-hand side is at most $2 a-2$ because $b$ is positive and integer, so $a b-1 \leq 2 a-2$, so $a b<2 a$, so $b<2$. Therefore, we must have $b=1$. The equation then becomes $a-1=2(a-1)$, which implies $a-1=0$. We then have $a=1$ and $b=1$, so $a=b$. We conclude that there are no solutions $(a, b)$ with $a \neq b$.
Thus, the only $k$ for which the original equation has no positive integer solutions $(m, n)$ with $m \neq n$ is $k=2$.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Vind alle positieve gehele $k$ waarvoor de vergelijking
$$
\operatorname{kgv}(m, n)-\operatorname{ggd}(m, n)=k(m-n)
$$
geen positieve gehele oplossingen $(m, n)$ met $m \neq n$ heeft.
|
Noem $d=\operatorname{ggd}(m, n)$ en schrijf $m=d a$ en $n=d b$. Er geldt $\operatorname{kgv}(m, n)$. $\operatorname{ggd}(m, n)=m n$, dus we kunnen de gegeven vergelijking schrijven als
$$
\frac{d a \cdot d b}{d}-d=k(d a-d b)
$$
oftewel
$$
a b-1=k(a-b) .
$$
We kijken vanaf nu naar het equivalente vraagstuk: vind alle positieve gehele $k$ waarvoor deze nieuwe vergelijking geen positieve gehele oplossingen $(a, b)$ met $a \neq b$ en $\operatorname{ggd}(a, b)=1$ heeft. Merk op dat als een paar $(a, b)$ aan deze vergelijking voldoet, automatisch geldt dat $\operatorname{ggd}(a, b)=1$. Stel namelijk dat $t \mid a$ en $t \mid b$, dan geldt $t \mid a b$ en $t \mid a-b$, dus $t \mid 1$, dus $a$ en $b$ hebben geen gemeenschappelijke deler groter dan 1.
Stel eerst dat $k \geq 3$. We beweren dat $(a, b)=\left(k^{2}-k-1, k-1\right)$ een oplossing is. Er geldt dan namelijk
$a b-1=a(k-1)-1=k a-a-1=k a-k^{2}+k+1-1=k a-k^{2}+k=k(a-k+1)=k(a-b)$.
We hebben al gezien dat nu direct volgt dat $\operatorname{ggd}(a, b)=1$. We moeten nog checken dat $a$ en $b$ positief zijn en dat ze ongelijk aan elkaar zijn. Omdat $k \geq 3$, is $b=k-1 \geq 2$ en is $a=k^{2}-k-1 \geq 2 k-k-1=k-1 \geq 2$, dus ze zijn allebei positief. Stel dat $a=b$, dan geldt $k^{2}-k-1=k-1$, oftewel $k^{2}=2 k$, oftewel $k=2$, tegenspraak. Dus ons paar $(a, b)$ voldoet aan alle eisen. Voor elke $k \geq 3$ heeft de vergelijking dus minstens één oplossing $(a, b)$ met $a \neq b$ en $\operatorname{ggd}(a, b)=1$.
Stel nu dat $k=1$. We beweren dat $(a, b)=(2,1)$ een oplossing is. Overduidelijk zijn $a$ en $b$ positief en ongelijk aan elkaar. Verder geldt
$$
a b-1=2-1=1=1 \cdot(2-1)=k(a-b)
$$
Dus voor $k=1$ heeft de vergelijking ook minstens één oplossing $(a, b)$ met $a \neq b$ en $\operatorname{ggd}(a, b)=1$.
Stel ten slotte dat $k=2$. De vergelijking wordt dan
$$
a b-1=2(a-b) .
$$
De rechterkant is hooguit $2 a-2$ omdat $b$ positief en geheel is, dus $a b-1 \leq 2 a-2$, dus $a b<2 a$, dus $b<2$. Er moet dus gelden $b=1$. De vergelijking wordt dan $a-1=2(a-1)$, waaruit volgt $a-1=0$. We hebben dan $a=1$ en $b=1$, dus $a=b$. We concluderen dat er geen oplossingen $(a, b)$ met $a \neq b$ zijn.
Dus de enige $k$ waarvoor de oorspronkelijke vergelijking geen positieve gehele oplossingen $(m, n)$ met $m \neq n$ heeft, is $k=2$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2016-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2016"
}
|
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ that satisfy
$$
f(x y-1)+f(x) f(y)=2 x y-1
$$
for all $x, y \in \mathbb{R}$.
|
If $f$ is constant, the left side is always the same, while the right side can vary, a contradiction. Therefore, $f$ is not constant. Now, substitute $x=0$: $f(-1)+f(0) f(y)=-1$, so $f(0) f(y)$ takes the same value for all $y \in \mathbb{R}$. Since $f$ is not constant, this gives $f(0)=0$. We can then immediately conclude that $f(-1)=-1$. Now, substitute $x=y=1$: $f(0)+f(1)^{2}=1$, so $f(1)=1$ or $f(1)=-1$.
Substituting $y=1+\frac{1}{x}$ with $x \neq 0$ gives $f(x+1-1)+f(x) f\left(1+\frac{1}{x}\right)=2 x+2-1$, so
$$
f(x) f\left(1+\frac{1}{x}\right)=2 x+1-f(x) \quad \text { for all } x \neq 0
$$
Substituting $y=\frac{1}{x}$ with $x \neq 0$ gives $f(1-1)+f(x) f\left(\frac{1}{x}\right)=2-1$, so
$$
f(x) f\left(\frac{1}{x}\right)=1 \quad \text { for all } x \neq 0
$$
Substituting $y=1, x=z+1$ gives $f(z+1-1)+f(z+1) f(1)=2 z+2-1$, so
$$
f(z)+f(z+1) f(1)=2 z+1 \quad \text { for all } z
$$
We now choose $z=\frac{1}{x}$ with $x \neq 0$ in this equation and multiply the whole by $f(x)$:
$$
f(x) f\left(\frac{1}{x}\right)+f\left(\frac{1}{x}+1\right) f(1) f(x)=\frac{2}{x} f(x)+f(x) \quad \text { for all } x \neq 0
$$
We rewrite the first and second terms using (2) and (1) respectively, so we get:
$$
1+2 x f(1)+f(1)-f(x) f(1)=\frac{2}{x} f(x)+f(x) \quad \text { for all } x \neq 0
$$
This can be rewritten as
$$
f(x) \cdot\left(\frac{2}{x}+1+f(1)\right)=1+2 x f(1)+f(1) \quad \text { for all } x \neq 0
$$
If the second factor on the left is not 0, we can divide by it, so:
$$
f(x)=\frac{1+2 x f(1)+f(1)}{\frac{2}{x}+1+f(1)} \quad \text { if } x \neq 0 \text { and } \frac{2}{x}+1+f(1) \neq 0 \text {. }
$$
We had two possible values for $f(1)$. First, let $f(1)=1$. Then we have
$$
f(x)=\frac{2+2 x}{\frac{2}{x}+2}=x \quad \text { if } x \neq 0 \text { and } \frac{2}{x}+2 \neq 0
$$
$\frac{2}{x}+2=0$ only if $x=-1$, but we already knew that $f(-1)=-1$. Also, we already had $f(0)=0$. We see that $f(x)=x$ for all $x$. We check this function: in the original functional equation, we get $x y-1+x y=2 x y-1$ on the left, so it works.
On the other hand, let $f(1)=-1$. Then we have
$$
f(x)=\frac{-2 x}{\frac{2}{x}}=-x^{2} \quad \text { if } x \neq 0 \text { and } \frac{2}{x} \neq 0
$$
Since $\frac{2}{x}=0$ cannot occur, we conclude that $f(x)=-x^{2}$ for all $x \neq 0$. Also, $f(0)=0$ satisfies this formula. We check the function $f(x)=-x^{2}$ for all $x$: in the original functional equation, we get $-x^{2} y^{2}-1+2 x y+x^{2} y^{2}=2 x y-1$ on the left, so it works.
We conclude that there are two solutions, namely $f(x)=x$ for all $x$ and $f(x)=-x^{2}$ for all $x$.
|
f(x)=x \text{ or } f(x)=-x^2
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Vind alle functies $f: \mathbb{R} \rightarrow \mathbb{R}$ die voldoen aan
$$
f(x y-1)+f(x) f(y)=2 x y-1
$$
voor alle $x, y \in \mathbb{R}$.
|
Als $f$ constant is, staat links altijd hetzelfde, terwijl rechts kan variëren, tegenspraak. Dus $f$ is niet constant. Vul nu $x=0$ in: $f(-1)+f(0) f(y)=-1$, dus $f(0) f(y)$ neemt voor alle $y \in \mathbb{R}$ dezelfde waarde aan. Omdat $f$ niet constant is, geeft dit $f(0)=0$. We kunnen dan ook onmiddellijk concluderen dat $f(-1)=-1$. Vul nu $x=y=1$ in: $f(0)+f(1)^{2}=1$, dus $f(1)=1$ of $f(1)=-1$.
Invullen van $y=1+\frac{1}{x}$ met $x \neq 0$ geeft $f(x+1-1)+f(x) f\left(1+\frac{1}{x}\right)=2 x+2-1$, dus
$$
f(x) f\left(1+\frac{1}{x}\right)=2 x+1-f(x) \quad \text { voor alle } x \neq 0
$$
Invullen van $y=\frac{1}{x}$ met $x \neq 0$ geeft $f(1-1)+f(x) f\left(\frac{1}{x}\right)=2-1$, dus
$$
f(x) f\left(\frac{1}{x}\right)=1 \quad \text { voor alle } x \neq 0
$$
Invullen van $y=1, x=z+1$ geeft $f(z+1-1)+f(z+1) f(1)=2 z+2-1$, dus
$$
f(z)+f(z+1) f(1)=2 z+1 \quad \text { voor alle } z
$$
We kiezen in deze vergelijking nu $z=\frac{1}{x}$ met $x \neq 0$ en vermenigvuldigen het geheel met $f(x)$ :
$$
f(x) f\left(\frac{1}{x}\right)+f\left(\frac{1}{x}+1\right) f(1) f(x)=\frac{2}{x} f(x)+f(x) \quad \text { voor alle } x \neq 0
$$
We herschrijven de eerste en tweede term met behulp van respectievelijk (2) en (1), zodat we krijgen:
$$
1+2 x f(1)+f(1)-f(x) f(1)=\frac{2}{x} f(x)+f(x) \quad \text { voor alle } x \neq 0
$$
Dit kunnen we herschrijven tot
$$
f(x) \cdot\left(\frac{2}{x}+1+f(1)\right)=1+2 x f(1)+f(1) \quad \text { voor alle } x \neq 0
$$
Als de tweede factor links niet 0 is, kunnen we erdoor delen, dus:
$$
f(x)=\frac{1+2 x f(1)+f(1)}{\frac{2}{x}+1+f(1)} \quad \text { als } x \neq 0 \text { en } \frac{2}{x}+1+f(1) \neq 0 \text {. }
$$
We hadden twee mogelijke waarden voor $f(1)$. Stel eerst $f(1)=1$. Dan staat hier
$$
f(x)=\frac{2+2 x}{\frac{2}{x}+2}=x \quad \text { als } x \neq 0 \text { en } \frac{2}{x}+2 \neq 0
$$
Er geldt alleen $\frac{2}{x}+2=0$ als $x=-1$, maar we wisten al dat $f(-1)=-1$. Ook hadden we al $f(0)=0$. We zien dus dat $f(x)=x$ voor alle $x$. We controleren deze functie: in
de oorspronkelijke functievergelijking krijgen we dan links $x y-1+x y=2 x y-1$, dus het klopt.
Stel anderzijds juist $f(1)=-1$. Dan staat hier
$$
f(x)=\frac{-2 x}{\frac{2}{x}}=-x^{2} \quad \text { als } x \neq 0 \text { en } \frac{2}{x} \neq 0
$$
Omdat $\frac{2}{x}=0$ niet kan voorkomen, concluderen we dat $f(x)=-x^{2}$ voor alle $x \neq 0$. Ook $f(0)=0$ voldoet aan deze formule. We controleren de functie $f(x)=-x^{2}$ voor alle $x$ : in de oorspronkelijke functievergelijking krijgen we dan links $-x^{2} y^{2}-1+2 x y+x^{2} y^{2}=2 x y-1$, dus het klopt.
We concluderen dat er twee oplossingen zijn, namelijk $f(x)=x$ voor alle $x$ en $f(x)=-x^{2}$ voor alle $x$.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2016-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2016"
}
|
Prove that for all positive real numbers $a, b, c$:
$$
a+\sqrt{a b}+\sqrt[3]{a b c} \leq \frac{4}{3}(a+b+c)
$$
|
We can write $\sqrt[3]{a b c}$ as $\sqrt[3]{\frac{a}{4} \cdot b \cdot 4 c}$. Applying the arithmetic mean-geometric mean inequality to the (positive) terms $\frac{a}{4}, b$ and $4 c$ gives
$$
\sqrt[3]{a b c}=\sqrt[3]{\frac{a}{4} \cdot b \cdot 4 c} \leq \frac{\frac{a}{4}+b+4 c}{3}=\frac{a}{12}+\frac{b}{3}+\frac{4 c}{3} .
$$
Furthermore, we apply the arithmetic mean-geometric mean inequality to $\frac{a}{2}$ and $2 b$:
$$
\sqrt{a b}=\sqrt{\frac{a}{2} \cdot 2 b} \leq \frac{\frac{a}{2}+2 b}{2}=\frac{a}{4}+b .
$$
We add these two inequalities together and also add $a$:
$$
a+\sqrt{a b}+\sqrt[3]{a b c} \leq a+\frac{a}{4}+b+\frac{a}{12}+\frac{b}{3}+\frac{4 c}{3}=\frac{4}{3}(a+b+c) .
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Bewijs dat voor alle positieve reële getallen $a, b, c$ geldt:
$$
a+\sqrt{a b}+\sqrt[3]{a b c} \leq \frac{4}{3}(a+b+c)
$$
|
We kunnen $\sqrt[3]{a b c}$ schrijven als $\sqrt[3]{\frac{a}{4} \cdot b \cdot 4 c}$. Toepassen van de ongelijkheid van het rekenkundig en meetkundig gemiddelde op de (positieve) termen $\frac{a}{4}, b$ en $4 c$ geeft dan
$$
\sqrt[3]{a b c}=\sqrt[3]{\frac{a}{4} \cdot b \cdot 4 c} \leq \frac{\frac{a}{4}+b+4 c}{3}=\frac{a}{12}+\frac{b}{3}+\frac{4 c}{3} .
$$
Daarnaast passen we rekenkundig-meetkundig toe op $\frac{a}{2}$ en $2 b$ :
$$
\sqrt{a b}=\sqrt{\frac{a}{2} \cdot 2 b} \leq \frac{\frac{a}{2}+2 b}{2}=\frac{a}{4}+b .
$$
Deze twee ongelijkheden tellen we bij elkaar op en we tellen er ook nog $a$ bij op:
$$
a+\sqrt{a b}+\sqrt[3]{a b c} \leq a+\frac{a}{4}+b+\frac{a}{12}+\frac{b}{3}+\frac{4 c}{3}=\frac{4}{3}(a+b+c) .
$$
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2016-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2016"
}
|
Determine all pairs $(a, b)$ of integers with the following property: there is an integer $d \geq 2$ such that $a^{n}+b^{n}+1$ is divisible by $d$ for all positive integers $n$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
|
Consider a few $(a, b)$ that satisfy the condition, along with the corresponding $d$. Let $p$ be a prime divisor of $d$ (which exists because $d \geq 2$). Since $d \mid a^{n}+b^{n}+1$ for all $n$, it also follows that $p \mid a^{n}+b^{n}+1$ for all $n$. Now consider $n=p-1$. Then $a^{n} \equiv 0 \bmod p$ if $p \mid a$ and $a^{n} \equiv 1 \bmod p$ if $p \nmid a$, by Fermat's Little Theorem. The same applies to $b$. Therefore, $a^{n}+b^{n}+1$ can take the values 1, 2, and 3 modulo $p$. Since it must also be 0 modulo $p$, we see that $p=2$ or $p=3$. We thus distinguish two cases.
Suppose that $p=3$. Then $3 \nmid a$ and $3 \nmid b$ must hold. The case $n=1$ further gives that $3 \mid a+b+1$, so $a+b \equiv 2 \bmod 3$. These two conditions together imply that $a \equiv b \equiv 1 \bmod 3$. In this case, for all positive integers $n$, $a^{n}+b^{n}+1 \equiv 1+1+1 \equiv 0 \bmod 3$, so every such pair satisfies the condition, with $d=3$.
Now suppose that $p=2$. Then 2 must be a divisor of exactly one of $a$ and $b$. In this case, for all positive integers $n$, $a^{n}+b^{n}+1 \equiv 0+1+1 \equiv 0 \bmod 2$, so every such pair satisfies the condition, with $d=2$.
We conclude that the pairs that satisfy the condition are: $(a, b)$ with $a \equiv b \equiv 1 \bmod 3$, $(a, b)$ with $a \equiv 1, b \equiv 0 \bmod 2$, and $(a, b)$ with $a \equiv 0, b \equiv 1 \bmod 2$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Bepaal alle paren $(a, b)$ van gehele getallen met de volgende eigenschap: er is een gehele $d \geq 2$ zodat $a^{n}+b^{n}+1$ deelbaar is door $d$ voor alle positieve gehele getallen $n$.
|
Bekijk een paar $(a, b)$ dat voldoet, met bijbehorende $d$. Zij $p$ een priemdeler van $d$ (die bestaat omdat $d \geq 2$ ). Omdat $d \mid a^{n}+b^{n}+1$ voor alle $n$, geldt ook $p \mid a^{n}+b^{n}+1$ voor alle $n$. Bekijk nu $n=p-1$. Dan geldt $a^{n} \equiv 0 \bmod p$ als $p \mid a$ en $a^{n} \equiv 1 \bmod p$ als $p \nmid a$, wegens de kleine stelling van Fermat. Hetzelfde geldt voor $b$. Dus $a^{n}+b^{n}+1$ kan modulo $p$ de waarden 1 , 2 en 3 aannemen. Omdat het anderzijds 0 modulo $p$ moet zijn, zien we dat $p=2$ of $p=3$. We onderscheiden dus twee gevallen.
Stel dat $p=3$. Dan moet dus $3 \nmid a, 3 \nmid b$. Het geval $n=1$ geeft verder dat $3 \mid a+b+1$, dus $a+b \equiv 2 \bmod 3$. Die twee eisen samen betekenen dat $a \equiv b \equiv 1 \bmod 3$. In dit geval geldt voor alle positieve gehele $n$ dat $a^{n}+b^{n}+1 \equiv 1+1+1 \equiv 0 \bmod 3$, dus elk zo'n tweetal voldoet, met $d=3$.
Stel nu dat $p=2$. Dan moet 2 een deler zijn van precies één van $a$ en $b$. In dat geval geldt voor alle positieve gehele $n$ dat $a^{n}+b^{n}+1 \equiv 0+1+1 \equiv 0 \bmod 2$, dus elk zo'n tweetal voldoet, met $d=2$.
We concluderen dat dit de paren zijn die voldoen: $(a, b)$ met $a \equiv b \equiv 1 \bmod 3,(a, b)$ met $a \equiv 1, b \equiv 0 \bmod 2$, en $(a, b)$ met $a \equiv 0, b \equiv 1 \bmod 2$.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2016-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2016"
}
|
Let $\triangle A B C$ be an isosceles triangle with $|A B|=|A C|$. Let $D, E$ and $F$ be points on the respective line segments $B C, C A$ and $A B$ such that $|B F|=|B E|$ and such that $E D$ is the angle bisector of $\angle B E C$.
Prove that $|B D|=|E F|$ if and only if $|A F|=|E C|$.
|
From the given and the Angle Bisector Theorem, it follows that
$$
\frac{|B F|}{|B D|}=\frac{|B E|}{|B D|}=\frac{|C E|}{|C D|}
$$
Due to the isosceles property of $\triangle A B C$, we further have $\angle F B D=\angle E C D$, which together implies that $\triangle B F D \sim \triangle C E D$. This leads to $\angle B F D=\angle C E D=\angle B E D$, so $B D E F$ is a cyclic quadrilateral. By Julian's Theorem, $|B D|=|E F|$ if and only if $D E \| B F$. It holds that $|A F|=|E C|$ if and only if $|B F|=|A E|$ (since $|A B|=|A C|$), which is equivalent to $|E A|=|E B|$, and that holds if and only if $\angle B A E=\angle A B E$. Since $2 \angle B E D=\angle B E C=\angle B A E+\angle A B E$ by the exterior angle theorem, $\angle B A E=\angle A B E$ is equivalent to $\angle B E D=\angle A B E$ and that is again equivalent to $D E \| B F$. In short, $|B D|=|E F|$ if and only if $D E \| B F$ and that holds if and only if $|A F|=|E C|$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $\triangle A B C$ een gelijkbenige driehoek met $|A B|=|A C|$. Laat $D, E$ en $F$ punten zijn op de respectievelijke lijnstukken $B C, C A$ en $A B$ zodat $|B F|=|B E|$ en zodat $E D$ de binnenbissectrice van $\angle B E C$ is.
Bewijs dat $|B D|=|E F|$ dan en slechts dan als $|A F|=|E C|$.
|
Uit het gegeven en de bissectricestelling volgt dat
$$
\frac{|B F|}{|B D|}=\frac{|B E|}{|B D|}=\frac{|C E|}{|C D|}
$$
Vanwege de gelijkbenigheid van $\triangle A B C$ geldt verder $\angle F B D=\angle E C D$, wat samen geeft dat $\triangle B F D \sim \triangle C E D$. Hieruit volgt dat $\angle B F D=\angle C E D=\angle B E D$, dus $B D E F$ is een koordenvierhoek. Met de stelling van Julian geldt dus $|B D|=|E F|$ dan en slechts dan als $D E \| B F$. Er geldt $|A F|=|E C|$ dan en slechts dan als $|B F|=|A E|$ (aangezien $|A B|=|A C|$ ), oftewel dan en slechts dan als $|E A|=|E B|$, en dat geldt dan en slechts dan als $\angle B A E=\angle A B E$. Aangezien $2 \angle B E D=\angle B E C=\angle B A E+\angle A B E$ vanwege de buitenhoekstelling, is $\angle B A E=\angle A B E$ equivalent met $\angle B E D=\angle A B E$ en dat is weer equivalent met $D E \| B F$. Kortom, $|B D|=|E F|$ dan en slechts dan als $D E \| B F$ en dat geldt dan en slechts dan als $|A F|=|E C|$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2016-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2016"
}
|
Let $\triangle A B C$ be an isosceles triangle with $|A B|=|A C|$. Let $D, E$ and $F$ be points on the respective line segments $B C, C A$ and $A B$ such that $|B F|=|B E|$ and such that $E D$ is the angle bisector of $\angle B E C$.
Prove that $|B D|=|E F|$ if and only if $|A F|=|E C|$.
|
First, let $|BD|=|EF|$. Due to the exterior angle theorem and the given that $|BF|=|BE|$, we have $\angle AEF = \angle BFE - \angle FAE = \angle BEF - \angle FAE$. Therefore,
\[ 180^{\circ} - 2 \angle BED = \angle AEF + \angle BEF = 2 \angle BEF - \angle FAE = 2 \angle BEF - (180^{\circ} - 2 \angle ABC). \]
From this, it follows that
\[ 180^{\circ} = \angle BED + \angle BEF + \angle ABC = \angle DEF + \angle FBD, \]
so $BDEF$ is a cyclic quadrilateral. Due to $|BD|=|EF|$, we get from Julian's theorem that $BF \parallel DE$. Therefore,
\[ \angle BFD = \angle BED = \angle DEC = \angle BAC, \]
which means that $FD \parallel AC$. Thus, $FAED$ is a parallelogram. Furthermore, triangles $BFD$ and $BAC$ are now similar due to equal angles at $A$ and $F$, so $BFD$ is also isosceles. Therefore, $|AE|=|FD|=|FB|$. From $|AB|=|AC|$, it follows that $|EC|=|AF|$. Now, assume conversely that $|EC|=|AF|$. This means $|AE|=|BF|=|BE|$, so $\triangle AEB$ is isosceles. From this, it follows that $\angle BAC = \angle ABE$, so the isosceles triangles $\triangle ABC$ and $\triangle BEF$ have the same vertex angle. Let the vertex angle of these triangles be $\alpha$ and the base angle be $\beta$. Then $\angle DBE = \angle DBA - \angle EBF = \beta - \alpha = \angle AEF$ due to the exterior angle theorem in $\triangle AFE$. Furthermore, $\angle BED = \frac{1}{2} \angle BEC = \frac{1}{2} \cdot 2 \alpha = \alpha$ due to the exterior angle theorem in $\triangle AEB$. Triangles $\triangle AFE$ and $\triangle EDB$ thus have two pairs of equal angles. In addition, $|AE|=|EB|$, so these triangles are congruent. From this, it follows that $|DB|=|EF|$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Zij $\triangle A B C$ een gelijkbenige driehoek met $|A B|=|A C|$. Laat $D, E$ en $F$ punten zijn op de respectievelijke lijnstukken $B C, C A$ en $A B$ zodat $|B F|=|B E|$ en zodat $E D$ de binnenbissectrice van $\angle B E C$ is.
Bewijs dat $|B D|=|E F|$ dan en slechts dan als $|A F|=|E C|$.
|
Stel eerst $|B D|=|E F|$. Vanwege de buitenhoekstelling en het gegeven dat $|B F|=|B E|$ geldt $\angle A E F=\angle B F E-\angle F A E=\angle B E F-\angle F A E$. Dus
$180^{\circ}-2 \angle B E D=\angle A E F+\angle B E F=2 \angle B E F-\angle F A E=2 \angle B E F-\left(180^{\circ}-2 \angle A B C\right)$.
Hieruit volgt
$$
180^{\circ}=\angle B E D+\angle B E F+\angle A B C=\angle D E F+\angle F B D,
$$
dus $B D E F$ is een koordenvierhoek. Vanwege $|B D|=|E F|$ krijgen we met de stelling van Julian dat $B F \| D E$. Dus
$$
\angle B F D=\angle B E D=\angle D E C=\angle B A C,
$$
wat betekent dat $F D \| A C$. Dus $F A E D$ is een parallellogram. Verder zijn driehoeken $B F D$ en $B A C$ nu gelijkvormig wegens gelijke hoeken bij $A$ en $F$, dus $B F D$ is ook gelijkbenig. Dus geldt $|A E|=|F D|=|F B|$. Vanwege $|A B|=|A C|$ volgt daaruit $|E C|=|A F|$. Stel nu andersom dat $|E C|=|A F|$. Dat betekent $|A E|=|B F|=|B E|$, dus $\triangle A E B$ is gelijkbenig. Hieruit volgt $\angle B A C=\angle A B E$, dus hebben de gelijkbenige driehoeken $\triangle A B C$ en $\triangle B E F$ dezelfde tophoek. Dat maakt dat ze gelijkvormig zijn. Noem de tophoek van deze driehoeken even $\alpha$ en de basishoek $\beta$. Dan is $\angle D B E=\angle D B A-\angle E B F=\beta-\alpha=\angle A E F$ vanwege de buitenhoekstelling in $\triangle A F E$. Verder is $\angle B E D=\frac{1}{2} \angle B E C=\frac{1}{2} \cdot 2 \alpha=\alpha$ vanwege de buitenhoekstelling in $\triangle A E B$. Driehoeken $\triangle A F E$ en $\triangle E D B$ hebben dus twee paren gelijke hoeken. Daarnaast is $|A E|=|E B|$, dus deze driehoeken zijn congruent. Daaruit volgt $|D B|=|E F|$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2016-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2016"
}
|
Determine the number of sets $A=\left\{a_{1}, a_{2}, \ldots, a_{1000}\right\}$ of positive integers with $a_{1}<a_{2}<\ldots<a_{1000} \leq 2014$, for which the set
$$
S=\left\{a_{i}+a_{j} \mid 1 \leq i, j \leq 1000 \text { and } i+j \in A\right\}
$$
is a subset of $A$.
|
We prove that there are $2^{14}$ such sets. In particular, we prove that the sets $A$ that satisfy the conditions are of the form $B \cup C$, with $C$ a subset of $\{2001, \ldots, 2014\}$ and $B=\{1,2, \ldots, 1000-|C|\}$. Call sets of this form "nice". Since there are $2^{14}$ subsets of $\{2001, \ldots, 2014\}$, there are $2^{14}$ nice sets. We first show that every nice set $A$ satisfies the conditions. Suppose that $i, j \leq 1000$ with $i+j \in A$. Then $i+j \leq 2000$, so $i+j \in B$. There thus exists a $k$ with $k \leq 1000-|C|$ such that $i+j=a_{k}(=k)$. Since $a_{k} \leq 1000-|C|$, it also holds that $i, j \leq 1000-|C|$, so $a_{i}=i$ and $a_{j}=j$. This means $a_{i}+a_{j}=i+j=a_{k}$ and that is an element of $A$. Therefore, every element of $S$ is an element of $A$, which implies that $A$ satisfies the conditions.
We now show that every set $A$ that satisfies the conditions is nice. Suppose first that there exists a $k$ with $1 \leq k \leq 1000$ such that $a_{k} \in\{1001, \ldots, 2000\}$. Then $a_{k}=1000+i$ for some $i$ with $i \leq 1000$, so $a_{1000}+a_{i}$ is an element of $S$ and must therefore also be an element of $A$. However, $a_{1000}+a_{i}>a_{1000}$, a contradiction. Therefore, such an $a_{k}$ cannot occur. This means that $A$ can be written as the disjoint union $B \cup C$, with $C \subseteq\{2001, \ldots, 2014\}$ and $B \subseteq\{1,2, \ldots, 1000\}$. Let $b$ be the number of elements of $B$. Then $b \geq 986$, because $C$ has at most 14 elements. To prove that $A$ is nice, we need to prove that $B=\{1,2, \ldots, b\}$. It is sufficient to prove that $a_{b}$, the largest element of $B$, is equal to $b$. Therefore, assume for the sake of contradiction that $a_{b}>b$. For $i$ with $i=a_{b}-b$ it then holds that $b+i=a_{b} \leq 1000$, so $i \leq 1000-b \leq 14<b$. Therefore, $a_{i} \leq 1000$ and thus $a_{b}+a_{i} \leq$ 2000. Since $i+b=a_{b} \in A$, it follows that $a_{b}+a_{i} \in S \subset A$, but then $a_{b}+a_{i}$ is a larger element of $B$ than $a_{b}$, the maximal element. Contradiction. Therefore, $a_{b}=b$, which implies that $B=\{1,2, \ldots, b\}$. Thus, $A$ is nice.
|
2^{14}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Bepaal het aantal verzamelingen $A=\left\{a_{1}, a_{2}, \ldots, a_{1000}\right\}$ van positieve gehele getallen met $a_{1}<a_{2}<\ldots<a_{1000} \leq 2014$, waarvoor geldt dat de verzameling
$$
S=\left\{a_{i}+a_{j} \mid 1 \leq i, j \leq 1000 \text { en } i+j \in A\right\}
$$
een deelverzameling is van $A$.
|
We bewijzen dat er $2^{14}$ zulke verzamelingen zijn. We bewijzen in het bijzonder dat de verzamelingen $A$ die voldoen van de vorm $B \cup C$ zijn, met $C$ een deelverzameling van $\{2001, \ldots, 2014\}$ en $B=\{1,2, \ldots, 1000-|C|\}$. Noem verzamelingen van die vorm "leuk". Omdat er $2^{14}$ deelverzamelingen van $\{2001, \ldots, 2014\}$ zijn, zijn er $2^{14}$ leuke verzamelingen. We laten eerst zien dat iedere leuke verzameling $A$ voldoet. Stel dat $i, j \leq 1000$ met $i+j \in A$. Dan is $i+j \leq 2000$, dus $i+j \in B$. Er bestaat dan dus een $k$ met $k \leq 1000-|C|$ zodat $i+j=a_{k}(=k)$. Omdat $a_{k} \leq 1000-|C|$ geldt ook $i, j \leq 1000-|C|$, dus $a_{i}=i$ en $a_{j}=j$. Dat betekent $a_{i}+a_{j}=i+j=a_{k}$ en dat is een element van $A$. Dus elk element van $S$ is een element van $A$, waaruit volgt dat $A$ voldoet.
We laten nu zien dat iedere verzameling $A$ die voldoet, leuk is. Stel allereerst dat er een $k$ met $1 \leq k \leq 1000$ bestaat zodat $a_{k} \in\{1001, \ldots, 2000\}$. Dan is $a_{k}=1000+i$ voor zekere $i$ met $i \leq 1000$, dus $a_{1000}+a_{i}$ is een element van $S$ en moet daarom ook een element van $A$ zijn. Er geldt echter $a_{1000}+a_{i}>a_{1000}$, tegenspraak. Dus zo'n $a_{k}$ kan niet voorkomen. Dit betekent dat $A$ te schrijven is als de disjuncte vereniging $B \cup C$, met $C \subseteq\{2001, \ldots, 2014\}$ en $B \subseteq\{1,2, \ldots, 1000\}$. Zij $b$ het aantal elementen van $B$. Dan is $b \geq 986$, want $C$ heeft hoogstens 14 elementen. Om te bewijzen dat $A$ leuk is, moeten we bewijzen dat $B=\{1,2, \ldots, b\}$. Hiertoe is het voldoende om te bewijzen dat $a_{b}$, het grootste element van $B$, gelijk is aan $b$. Stel daarom uit het ongerijmde dat $a_{b}>b$. Voor $i$ met $i=a_{b}-b$ geldt dan $b+i=a_{b} \leq 1000$, dus $i \leq 1000-b \leq 14<b$. Daarom is $a_{i} \leq 1000$ en dus $a_{b}+a_{i} \leq$ 2000. Omdat $i+b=a_{b} \in A$, geldt $a_{b}+a_{i} \in S \subset A$, maar dan is $a_{b}+a_{i}$ een groter element van $B$ dan $a_{b}$, het maximale element. Tegenspraak. Dus $a_{b}=b$, waaruit volgt dat $B=\{1,2, \ldots, b\}$. Dus $A$ is leuk.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2016-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2016"
}
|
Let $n$ be a natural number. In a village, there live $n$ boys and $n$ girls. For the annual ball, $n$ dance pairs need to be formed, each consisting of one boy and one girl. Each girl provides a list containing the name of the boy she would most like to dance with, plus zero or more names of other boys she would also be willing to dance with. It turns out that it is possible to form $n$ dance pairs such that each girl dances with a boy whose name is on her list.
Prove that it is possible to form $n$ dance pairs such that each girl dances with a boy whose name is on her list and at least one girl dances with the boy she would most like to dance with.
|
For each girl, name the boy she would most like to dance with, her favorite boy. We prove the statement by induction on $n$. If $n=1$, then the girl dances with the only boy, so she dances with her favorite boy. Now let $k \geq 1$ and assume we have proven the statement for $n=k$. Consider the case $n=k+1$. We distinguish two cases. First, assume that each boy is named exactly once as a favorite boy. Then we pair each girl with her favorite boy, forming $n$ dance couples. This case is thus resolved. Now consider the other case: not every boy is named exactly once as a favorite boy. There are $n$ favorite boys named and there are $n$ boys, so there must be a boy, say boy $X$, who is not named as a favorite (and another who is named more often). We now take the dance couples that exist according to the statement, where each girl dances with a boy on her list. In this pairing, boy $X$ dances with girl $Y$. We now remove boy $X$ and girl $Y$ from the village. There remain $k$ boys and $k$ girls. The same pairing still has the property that each girl dances with a boy on her list. Furthermore, it is still the case that each girl has chosen one of the $k$ boys as her favorite (since no one chose boy $X$). We can thus apply the induction hypothesis to form a pairing of $k$ dance couples where at least one girl dances with her favorite boy. We then add the couple $X-Y$ back, and the requirement is satisfied. This completes the induction.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Zij $n$ een natuurlijk getal. In een dorp wonen $n$ jongens en $n$ meisjes. Voor het jaarlijkse bal moeten $n$ danskoppels worden gevormd, die elk uit één jongen en één meisje bestaan. Elk meisje geeft een lijstje door, bestaande uit de naam van de jongen met wie ze het liefst zou willen dansen, plus nul of meer namen van andere jongens met wie ze ook wel zou willen dansen. Het blijkt dat er $n$ danskoppels kunnen worden gevormd zodat elk meisje danst met een jongen die op haar lijstje staat.
Bewijs dat het mogelijk is om $n$ danskoppels te vormen zodat elk meisje danst met een jongen die op haar lijstje staat en waarbij ten minste één meisje danst met de jongen met wie ze het liefst wil dansen.
|
Noem bij elk meisje de jongen met wie ze het liefst zou willen dansen, haar lievelingsjongen. We bewijzen de opgave met inductie naar $n$. Als $n=1$, dan danst het meisje met de enige jongen, dus danst ze met haar lievelingsjongen. Zij nu $k \geq 1$ en neem aan dat we de opgave bewezen hebben voor $n=k$. Bekijk vervolgens het geval $n=k+1$. We onderscheiden twee gevallen. Stel eerst dat elke jongen precies één keer voorkomt als lievelingsjongen. Dan koppelen we elk meisjes aan haar lievelingsjongens en vormen zo $n$ danskoppels. Dit geval is hiermee afgehandeld. Bekijk nu het andere geval: niet elke jongen komt precies één keer voor als lievelingsjongen. Er worden $n$ lievelingsjongens genoemd en er zijn $n$ jongens, dus dan is er een jongen, zeg jongen $X$, die helemaal niet genoemd wordt als lievelingsjongen (en een ander die vaker genoemd wordt). We nemen nu de danskoppels die volgens de opgave bestaan, waarin elk meisje danst met een jongen van haar lijstje. In deze koppeling danst jongen $X$ met meisje $Y$. We verwijderen nu jongen $X$ en meisje $Y$ uit het dorp. Er blijven $k$ jongens en $k$ meisjes over. Dezelfde koppeling heeft nog steeds de eigenschap dat elk meisje danst met een jongen die op haar lijstje staat. Verder is het nog steeds zo dat elk meisje één van de $k$ jongens heeft uitverkoren als lievelingsjongen (want niemand had jongen $X$ gekozen). We kunnen dus de inductiehypothese toepassen om een koppeling te maken van $k$ danskoppels waarbij minstens één meisje danst met haar lievelingsjongen. Vervolgens voegen we het koppel $X-Y$ weer toe en dan wordt aan het gevraagde voldaan. Dit voltooit de inductie.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2016-E_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2016"
}
|
For real numbers $a_{1}, a_{2}, \ldots, a_{n}$, all distinct, we compute the $\frac{n(n-1)}{2}$ sums $a_{i}+a_{j}$ with $1 \leq i<j \leq n$ and then sort these in ascending order. Determine all integers $n \geq 3$ for which there exist $a_{1}, a_{2}, \ldots, a_{n}$ such that this sequence of $\frac{n(n-1)}{2}$ sums forms an arithmetic progression (i.e., the difference between consecutive terms is always the same).
|
For $n=3$ we consider $\left(a_{1}, a_{2}, a_{3}\right)=(1,2,3)$. The sums of any two elements are 3, 4, and 5, thus forming an arithmetic sequence. For $n=4$ we consider $\left(a_{1}, a_{2}, a_{3}, a_{4}\right)=(1,3,4,5)$. The sums of any two elements are 4, 5, 6, 7, 8, and 9, thus forming an arithmetic sequence.
Now take $n \geq 5$ and assume that $a_{1}, a_{2}, \ldots, a_{n}$ satisfies the condition. Without loss of generality, assume that $a_{1}<a_{2}<\ldots<a_{n}$. Let $d$ be the difference between two consecutive terms of the corresponding arithmetic sequence. The smallest sum is $a_{1}+a_{2}$ and the second smallest is $a_{1}+a_{3}$. There is a difference of $d$ between them, so $a_{3}-a_{2}=d$. The largest sum is $a_{n}+a_{n-1}$ and the second largest is $a_{n}+a_{n-2}$, so also $a_{n-1}-a_{n-2}=d$. This means that
$$
a_{2}+a_{n-1}=\left(a_{3}-d\right)+\left(a_{n-2}+d\right)=a_{3}+a_{n-2} .
$$
If $n \geq 6$, the left and right sides here are two different sums $a_{i}+a_{j}$ with $i \neq j$, but the difference between two different such sums should be at least $d$. Contradiction. Therefore, there is no solution for $n \geq 6$.
For $n=5$, we have that $a_{3}-a_{2}=d$ and $a_{4}-a_{3}=d$. This means that the third smallest sum must be equal to $a_{1}+a_{4}$ (since it is $d$ larger than $a_{1}+a_{3}$) and the third largest sum must be equal to $a_{5}+a_{2}$. In between, there are the sums $a_{2}+a_{3}<a_{2}+a_{4}<a_{3}+a_{4}$, each with a difference of $d$, and also $a_{1}+a_{5}$. So $a_{1}+a_{5}$ is the fourth sum in the sequence, either from the smallest or from the largest. Without loss of generality, assume it is from the smallest. We then have
$a_{1}+a_{2}<a_{1}+a_{3}<a_{1}+a_{4}<a_{1}+a_{5}<a_{2}+a_{3}<a_{2}+a_{4}<a_{3}+a_{4}<a_{2}+a_{5}<a_{3}+a_{5}<a_{4}+a_{5}$.
Thus, $\left(a_{5}+a_{2}\right)-\left(a_{3}+a_{4}\right)=d$, which implies $a_{5}-a_{4}=d+a_{3}-a_{2}=d+d$. On the other hand, we also know that $\left(a_{1}+a_{5}\right)-\left(a_{1}+a_{4}\right)=d$, so $a_{5}-a_{4}=d$. Contradiction. Therefore, $n=5$ does not satisfy the condition either.
We conclude that there exist $a_{1}, a_{2}, \ldots, a_{n}$ that satisfy the condition for $n=3$ and $n=4$, but not for $n \geq 5$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Voor reële getallen $a_{1}, a_{2}, \ldots, a_{n}$, allemaal verschillend, berekenen we de $\frac{n(n-1)}{2}$ sommen $a_{i}+a_{j}$ met $1 \leq i<j \leq n$ en sorteren deze vervolgens van klein naar groot. Bepaal alle gehele $n \geq 3$ waarvoor er $a_{1}, a_{2}, \ldots, a_{n}$ bestaan zodat dit rijtje van $\frac{n(n-1)}{2}$ sommen een rekenkundige rij vormt (d.w.z. dat het verschil tussen twee opeenvolgende termen steeds hetzelfde is).
|
Voor $n=3$ bekijken we $\left(a_{1}, a_{2}, a_{3}\right)=(1,2,3)$. De sommen van steeds twee elementen zijn gelijk aan 3,4 en 5 , dus die vormen een rekenkundige rij. Voor $n=4$ bekijken we $\left(a_{1}, a_{2}, a_{3}, a_{4}\right)=(1,3,4,5)$. De sommen van steeds twee elementen zijn gelijk aan $4,5,6,7,8$ en 9 , dus die vormen een rekenkundige rij.
Neem nu $n \geq 5$ en stel dat $a_{1}, a_{2}, \ldots, a_{n}$ voldoet. Zonder verlies van algemeenheid nemen we aan dat $a_{1}<a_{2}<\ldots<a_{n}$. $\mathrm{Zij} d$ het verschil van twee opeenvolgende termen van de bijbehorende rekenkundige rij. De kleinste som is $a_{1}+a_{2}$ en de op een na kleinste is $a_{1}+a_{3}$. Hier zit een verschil $d$ tussen, dus $a_{3}-a_{2}=d$. De grootste som is $a_{n}+a_{n-1}$ en de op een na grootste is $a_{n}+a_{n-2}$, dus ook $a_{n-1}-a_{n-2}=d$. Dit betekent dat
$$
a_{2}+a_{n-1}=\left(a_{3}-d\right)+\left(a_{n-2}+d\right)=a_{3}+a_{n-2} .
$$
Als $n \geq 6$ staan hier links en rechts twee verschillende sommen $a_{i}+a_{j}$ met $i \neq j$, maar het verschil tussen twee verschillende zulke sommen zou minstens $d$ moeten zijn. Tegenspraak. Dus voor $n \geq 6$ is er geen oplossing.
Voor $n=5$ hebben we dat $a_{3}-a_{2}=d$ en $a_{4}-a_{3}=d$. Dat betekent dat de op twee na kleinste som gelijk moet zijn aan $a_{1}+a_{4}$ (want die is $d$ groter dan $a_{1}+a_{3}$ ) en de op twee na grootste som gelijk aan $a_{5}+a_{2}$. Hiertussen zitten de sommen $a_{2}+a_{3}<a_{2}+a_{4}<a_{3}+a_{4}$, steeds met verschil $d$, en verder nog $a_{1}+a_{5}$. Dus $a_{1}+a_{5}$ is de vierde som in het rijtje, ofwel vanaf de kleinste kant geteld ofwel vanaf de grootste kant. Neem zonder verlies van algemeenheid aan dat het vanaf de kleinste kant is. We hebben dan
$a_{1}+a_{2}<a_{1}+a_{3}<a_{1}+a_{4}<a_{1}+a_{5}<a_{2}+a_{3}<a_{2}+a_{4}<a_{3}+a_{4}<a_{2}+a_{5}<a_{3}+a_{5}<a_{4}+a_{5}$.
Dan geldt dus $\left(a_{5}+a_{2}\right)-\left(a_{3}+a_{4}\right)=d$, waaruit volgt $a_{5}-a_{4}=d+a_{3}-a_{2}=d+d$. Anderzijds weten we ook dat $\left(a_{1}+a_{5}\right)-\left(a_{1}+a_{4}\right)=d$, dus $a_{5}-a_{4}=d$. Tegenspraak. Dus ook $n=5$ voldoet niet.
We concluderen dat er $a_{1}, a_{2}, \ldots, a_{n}$ bestaan die aan de voorwaarde voldoen voor $n=3$ en $n=4$, maar niet voor $n \geq 5$.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2016-E_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2016"
}
|
Zij $k$ een positief geheel getal en geef de som van de cijfers van een positief geheel getal $n$ aan met $s(n)$. Bewijs dat er onder de positieve gehele getallen met $k$ cijfers evenveel getallen $n$ zijn die voldoen aan $s(n)<s(2 n)$ als getallen $n$ die voldoen aan $s(n)>s(2 n)$.
|
We bewijzen dat er onder de positieve gehele getallen met hoogstens $k$ cijfers evenveel getallen $n$ zijn die voldoen aan $s(n)<s(2 n)$ als getallen die voldoen aan $s(n)>s(2 n)$. Het gevraagde volgt hieruit door dit resultaat voor $k$ en voor $k-1$ te combineren.
We gaan nu elk getal $n$ met hoogstens $k$ cijfers koppelen aan een ander getal $m$ met hoogstens $k$ cijfers. Definieer $m$ als $999 \cdots 999-n$, waarbij het eerste getal uit $k$ negens bestaat. Nu heeft $m$ hoogstens $k$ cijfers. We gaan bewijzen dat $s(m)-s(2 m)=s(2 n)-s(n)$. Om $m$ uit te rekenen, trekken we $n$ af van $999 \cdots 999$, waarbij elk cijfer van $n$ natuurlijk hooguit 9 is. Dus elk cijfer van $m$ is gelijk aan 9 min het bijbehorende cijfer van $n$ (zonder dat er ergens iets overgedragen wordt). Hierbij beschouwen we $m$ en $n$ beide als getallen van precies $k$ cijfers, door eventueel vooraan nullen aan te vullen. We zien dus dat $s(m)+s(n)=s(999 \cdots 999)=9 k$. Nu bekijken we $2 m$ en $2 n$. Er geldt $2 m=$ 1999...998-2n (met $k-1$ negens). We beschouwen $2 m$ en $2 n$ nu als getallen met precies $k+1$ cijfers, waarbij het eerste cijfer van $2 n$ een 0 of 1 is. Als we dat afhalen van $1999 \cdots 998$ wordt het eerste cijfer van $2 m$ dus $1-1=0$ of $1-0=1$. Het laatste cijfer van $2 m$ wordt 8 min het laatste cijfer van $2 n$, dat geen 9 kan zijn omdat $2 n$ even is. Alle overige cijfers van $2 m$ zijn gelijk aan 9 min het bijbehorende cijfer van $2 n$. Al met al zien we dat $s(2 m)+s(2 n)=s(1999 \cdots 998)=1+9(k-1)+9=9 k$. We concluderen dat $s(m)+s(n)=s(2 m)+s(2 n)$, zodat $s(m)-s(2 m)=s(2 n)-s(n)$.
Nu zien we dat $s(m)>s(2 m)$ dan en slechts dan als $s(n)<s(2 n)$. Merk verder op dat geen enkel getal aan zichzelf wordt gekoppeld omdat $999 \cdots 99$ oneven is. Er zijn dus precies evenveel getallen met $s(n)<s(2 n)$ als getallen met $s(n)>s(2 n)$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Zij $k$ een positief geheel getal en geef de som van de cijfers van een positief geheel getal $n$ aan met $s(n)$. Bewijs dat er onder de positieve gehele getallen met $k$ cijfers evenveel getallen $n$ zijn die voldoen aan $s(n)<s(2 n)$ als getallen $n$ die voldoen aan $s(n)>s(2 n)$.
|
We bewijzen dat er onder de positieve gehele getallen met hoogstens $k$ cijfers evenveel getallen $n$ zijn die voldoen aan $s(n)<s(2 n)$ als getallen die voldoen aan $s(n)>s(2 n)$. Het gevraagde volgt hieruit door dit resultaat voor $k$ en voor $k-1$ te combineren.
We gaan nu elk getal $n$ met hoogstens $k$ cijfers koppelen aan een ander getal $m$ met hoogstens $k$ cijfers. Definieer $m$ als $999 \cdots 999-n$, waarbij het eerste getal uit $k$ negens bestaat. Nu heeft $m$ hoogstens $k$ cijfers. We gaan bewijzen dat $s(m)-s(2 m)=s(2 n)-s(n)$. Om $m$ uit te rekenen, trekken we $n$ af van $999 \cdots 999$, waarbij elk cijfer van $n$ natuurlijk hooguit 9 is. Dus elk cijfer van $m$ is gelijk aan 9 min het bijbehorende cijfer van $n$ (zonder dat er ergens iets overgedragen wordt). Hierbij beschouwen we $m$ en $n$ beide als getallen van precies $k$ cijfers, door eventueel vooraan nullen aan te vullen. We zien dus dat $s(m)+s(n)=s(999 \cdots 999)=9 k$. Nu bekijken we $2 m$ en $2 n$. Er geldt $2 m=$ 1999...998-2n (met $k-1$ negens). We beschouwen $2 m$ en $2 n$ nu als getallen met precies $k+1$ cijfers, waarbij het eerste cijfer van $2 n$ een 0 of 1 is. Als we dat afhalen van $1999 \cdots 998$ wordt het eerste cijfer van $2 m$ dus $1-1=0$ of $1-0=1$. Het laatste cijfer van $2 m$ wordt 8 min het laatste cijfer van $2 n$, dat geen 9 kan zijn omdat $2 n$ even is. Alle overige cijfers van $2 m$ zijn gelijk aan 9 min het bijbehorende cijfer van $2 n$. Al met al zien we dat $s(2 m)+s(2 n)=s(1999 \cdots 998)=1+9(k-1)+9=9 k$. We concluderen dat $s(m)+s(n)=s(2 m)+s(2 n)$, zodat $s(m)-s(2 m)=s(2 n)-s(n)$.
Nu zien we dat $s(m)>s(2 m)$ dan en slechts dan als $s(n)<s(2 n)$. Merk verder op dat geen enkel getal aan zichzelf wordt gekoppeld omdat $999 \cdots 99$ oneven is. Er zijn dus precies evenveel getallen met $s(n)<s(2 n)$ als getallen met $s(n)>s(2 n)$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2016-E_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2016"
}
|
Let $k$ be a positive integer and denote the sum of the digits of a positive integer $n$ by $s(n)$. Prove that among the positive integers with $k$ digits, there are as many numbers $n$ that satisfy $s(n)<s(2 n)$ as there are numbers $n$ that satisfy $s(n)>s(2 n)$.
|
We prove here in an alternative way that $s(m)-s(2 m)=s(2 n)-s(n)$. Let $t(n)$ be the number of digits greater than or equal to 5 in the number $n$. When we add $n$ to itself, in this addition, a 1 is carried over to the next digit for some digits and not for others. This carrying over happens if and only if the relevant digit in $n$ is 5 or higher. Whether something is carried over from the previous digit has no influence on this. If something is carried over, then in the sum, not the double of the digit is written, but a digit 10 less than that, while the next digit becomes 1 larger. Therefore, for each time 1 is carried over, the sum of the digits of $2 n$ is exactly 9 less than if each digit were simply doubled. This gives $s(2 n)=2 s(n)-9 t(n)$.
As in the previous solution, we see that each digit of $m$ is equal to 9 minus the corresponding digit of $n$. So $s(m)=9 k-s(n)$ and $t(m)=k-t(n)$. We have
$$
\begin{aligned}
s(m)-s(2 m) & =s(m)-(2 s(m)-9 t(m)) \\
& =s(m)-(2 s(m)-9 k+9 t(n)) \\
& =-s(m)+9 k-9 t(n) \\
& =-9 k+s(n)+9 k-9 t(n) \\
& =s(n)-9 t(n) \\
& =s(2 n)-s(n)
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Zij $k$ een positief geheel getal en geef de som van de cijfers van een positief geheel getal $n$ aan met $s(n)$. Bewijs dat er onder de positieve gehele getallen met $k$ cijfers evenveel getallen $n$ zijn die voldoen aan $s(n)<s(2 n)$ als getallen $n$ die voldoen aan $s(n)>s(2 n)$.
|
We bewijzen hier op een alternatieve manier dat $s(m)-s(2 m)=s(2 n)-$ $s(n)$. Zij $t(n)$ het aantal cijfers groter of gelijk aan 5 in het getal $n$. Als we $n$ bij zichzelf optellen, dan wordt er in deze optelling bij sommige cijfers wel een 1 overgedragen aan het volgende cijfer en bij sommige cijfers niet. Dit overgedragen gebeurt dan en slechts dan als het betreffende cijfer in $n$ een 5 of hoger is. Of er bij het vorige cijfer iets overgedragen is, is hierop niet van invloed. Als er iets overgedragen wordt, dan komt in de som niet het dubbele van het cijfer te staan, maar een cijfer 10 kleiner dan dat, terwijl anderzijds het volgende cijfer juist 1 groter wordt. Dus voor elke keer 1 overdragen wordt de som van de cijfers van $2 n$ precies 9 kleiner dan wanneer gewoon elk cijfer verdubbeld zou worden. Dat geeft dus $s(2 n)=2 s(n)-9 t(n)$.
Zoals in de vorige oplossing zien we dat elk cijfer van $m$ gelijk is aan 9 min het bijbehorende
cijfer van $n$. Dus $s(m)=9 k-s(n)$ en $t(m)=k-t(n)$. Er geldt
$$
\begin{aligned}
s(m)-s(2 m) & =s(m)-(2 s(m)-9 t(m)) \\
& =s(m)-(2 s(m)-9 k+9 t(n)) \\
& =-s(m)+9 k-9 t(n) \\
& =-9 k+s(n)+9 k-9 t(n) \\
& =s(n)-9 t(n) \\
& =s(2 n)-s(n)
\end{aligned}
$$
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2016-E_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2016"
}
|
Given are circles $\Gamma_{1}$ with center $A$ and $\Gamma_{2}$ with center $B$, where $A$ lies on $\Gamma_{2}$. On $\Gamma_{2}$, there is a variable point $P$, not on $A B$. A line through $P$ that is tangent to $\Gamma_{1}$ at $S$, intersects $\Gamma_{2}$ again at $Q$, where $P$ and $Q$ lie on the same side of $A B$. Another line through $Q$ is tangent to $\Gamma_{1}$ at $T$. Let $M$ be the foot of the perpendicular from $P$ to $A B$. Let $N$ be the intersection of $A Q$ and $M T$. Prove that $N$ lies on a line that is independent of the position of $P$ on $\Gamma_{2}$.
|
Point $P$ lies outside $\Gamma_{1}$, otherwise there would be no tangent line $P S$ to $\Gamma_{1}$. Since $P$ and $Q$ are on the same side of $A B$, $S$ lies on the part of $\Gamma_{1}$ on that same side of $A B$ that is outside $\Gamma_{2}$. (In the extreme case that $P$ lies on $A B$, $S$ would end up at the intersection of $\Gamma_{1}$ and $\Gamma_{2}$ due to Thales.) We consider the configuration where $Q$ is between $P$ and $S$; thus $Q$ also lies on the short arc $A P$. The other configuration is analogous. (Note that $P \neq Q$ according to the problem.)
We prove that $N$ lies on the power line of $\Gamma_{1}$ and $\Gamma_{2}$. It holds that $\angle A S P=90^{\circ}=\angle A M P$, so $A S P M$ is a cyclic quadrilateral due to Thales. From this it follows
$$
\angle P S M=\angle P A M=\angle P A B=90^{\circ}-\frac{1}{2} \angle A B P=90^{\circ}-\left(180^{\circ}-\angle A Q P\right)=90^{\circ}-\angle A Q S,
$$
where in the penultimate step we applied the central angle theorem. Furthermore, due to the angle sum in $\triangle A Q S$, we have $90^{\circ}-\angle A Q S=\angle Q A S$. Since $A S Q T$ is a cyclic quadrilateral with $|Q T|=|Q S|$ (equal tangent segments), $\angle Q A S=\angle Q T S=\angle Q S T$. Altogether, we find $\angle P S M=90^{\circ}-\angle A Q S=\angle Q A S=\angle Q S T=\angle P S T$. Therefore, $S, T$, and $M$ lie on a line.
From this it follows that $N$ is the intersection of $S T$ and $A Q$. In cyclic quadrilateral $A S Q T$, we find with the power of a point theorem that $N T \cdot N S=N A \cdot N Q$. But on the left, we also have the power of $N$ with respect to $\Gamma_{1}$ and on the right, the power of $N$ with respect to $\Gamma_{2}$. Thus $N$ lies on the power line of $\Gamma_{1}$ and $\Gamma_{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Gegeven zijn cirkels $\Gamma_{1}$ met middelpunt $A$ en $\Gamma_{2}$ met middelpunt $B$, waarbij $A$ op $\Gamma_{2}$ ligt. Op $\Gamma_{2}$ ligt verder een variabel punt $P$, niet op $A B$. Een lijn door $P$ die $\Gamma_{1}$ raakt in $S$, snijdt $\Gamma_{2}$ nogmaals in $Q$, waarbij $P$ en $Q$ aan dezelfde kant van $A B$ liggen. Een andere lijn door $Q$ raakt $\Gamma_{1}$ in $T$. Zij verder $M$ het voetpunt van de loodlijn vanuit $P$ op $A B$. Zij $N$ het snijpunt van $A Q$ en $M T$. Bewijs dat $N$ op een lijn ligt die onafhankelijk is van de plaats van $P$ op $\Gamma_{2}$.
|
Punt $P$ ligt buiten $\Gamma_{1}$, omdat er anders geen raaklijn $P S$ aan $\Gamma_{1}$ bestaat. Aangezien $P$ en $Q$ aan dezelfde kant van $A B$ liggen, ligt $S$ op het deel van $\Gamma_{1}$ aan diezelfde kant van $A B$ dat buiten $\Gamma_{2}$ ligt. (In het extreme geval dat $P$ op $A B$ zou liggen, zou $S$ namelijk in het snijpunt van $\Gamma_{1}$ en $\Gamma_{2}$ terecht komen wegens Thales.) We bekijken de configuratie waarin $Q$ tussen $P$ en $S$ ligt; daarmee ligt $Q$ ook op de korte boog $A P$. De andere configuratie gaat analoog. (Merk op dat $P \neq Q$ volgens de opgave.)
We bewijzen dat $N$ op de machtlijn van $\Gamma_{1}$ en $\Gamma_{2}$ ligt. Er geldt $\angle A S P=90^{\circ}=\angle A M P$, dus $A S P M$ is een koordenvierhoek vanwege Thales. Hieruit volgt
$$
\angle P S M=\angle P A M=\angle P A B=90^{\circ}-\frac{1}{2} \angle A B P=90^{\circ}-\left(180^{\circ}-\angle A Q P\right)=90^{\circ}-\angle A Q S,
$$
waarbij we in de eennalaatste stap de middelpunts-omtrekshoekstelling toegepast hebben. Verder geldt wegens de hoekensom in $\triangle A Q S$ dat $90^{\circ}-\angle A Q S=\angle Q A S$. Omdat $A S Q T$ een koordenvierhoek is met $|Q T|=|Q S|$ (gelijke raaklijnstukjes) is $\angle Q A S=\angle Q T S=\angle Q S T$. Al met al vinden we $\angle P S M=90^{\circ}-\angle A Q S=\angle Q A S=\angle Q S T=\angle P S T$. Dus $S, T$ en $M$ liggen op een lijn.
Daaruit volgt dat $N$ het snijpunt is van $S T$ en $A Q$. In koordenvierhoek $A S Q T$ vinden we met de machtstelling nu $N T \cdot N S=N A \cdot N Q$. Maar links staat ook de macht van $N$ ten opzichte van $\Gamma_{1}$ en rechts de macht van $N$ ten opzichte van $\Gamma_{2}$. Dus $N$ ligt op de machtlijn $\operatorname{van} \Gamma_{1}$ en $\Gamma_{2}$.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2016-E_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2016"
}
|
Given are circles $\Gamma_{1}$ with center $A$ and $\Gamma_{2}$ with center $B$, where $A$ lies on $\Gamma_{2}$. On $\Gamma_{2}$, there is a variable point $P$, not on $A B$. A line through $P$ that is tangent to $\Gamma_{1}$ at $S$, intersects $\Gamma_{2}$ again at $Q$, where $P$ and $Q$ lie on the same side of $A B$. Another line through $Q$ is tangent to $\Gamma_{1}$ at $T$. Let $M$ be the foot of the perpendicular from $P$ to $A B$. Let $N$ be the intersection of $A Q$ and $M T$. Prove that $N$ lies on a line that is independent of the position of $P$ on $\Gamma_{2}$.
|
We consider the same configuration as in the first solution. We provide an alternative proof for the fact that $S, T$, and $M$ lie on a line; then you can finish it as in Solution I.
Let $R$ be the reflection of $P$ in the line $A B$. Then $R$ also lies on $\Gamma_{2}$ and $\angle P B A = \angle R B A$. By the inscribed angle theorem, $\angle R Q A = \frac{1}{2} \angle R B A$ and $180^{\circ} - \angle P Q A = \frac{1}{2} \angle P B A$. Therefore, $\angle R Q A = 180^{\circ} - \angle P Q A = \angle S Q A$. Due to equal tangent segments, $\angle S Q A = \angle T Q A$, from which we conclude $\angle R Q A = \angle T Q A$. This means that $R, Q$, and $T$ lie on a line.
Now we consider triangle $P Q R$ and the point $A$ on its circumcircle. The perpendiculars from $A$ to the sides of the triangle have feet $S, T$, and $M$. This is a Simson line, so $S, T$, and $M$ lie on a line.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Gegeven zijn cirkels $\Gamma_{1}$ met middelpunt $A$ en $\Gamma_{2}$ met middelpunt $B$, waarbij $A$ op $\Gamma_{2}$ ligt. Op $\Gamma_{2}$ ligt verder een variabel punt $P$, niet op $A B$. Een lijn door $P$ die $\Gamma_{1}$ raakt in $S$, snijdt $\Gamma_{2}$ nogmaals in $Q$, waarbij $P$ en $Q$ aan dezelfde kant van $A B$ liggen. Een andere lijn door $Q$ raakt $\Gamma_{1}$ in $T$. Zij verder $M$ het voetpunt van de loodlijn vanuit $P$ op $A B$. Zij $N$ het snijpunt van $A Q$ en $M T$. Bewijs dat $N$ op een lijn ligt die onafhankelijk is van de plaats van $P$ op $\Gamma_{2}$.
|
We bekijken dezelfde configuratie als in de eerste oplossing. We geven een alternatief bewijs voor het feit dat $S, T$ en $M$ op een lijn liggen; daarna kun je het afmaken zoals in oplossing I.
Noem $R$ het spiegelbeeld van $P$ in de lijn $A B$. Dan ligt $R$ ook op $\Gamma_{2}$ en geldt $\angle P B A=$ $\angle R B A$. Vanwege de middelpuntsomtrekshoekstelling is $\angle R Q A=\frac{1}{2} \angle R B A$ en $180^{\circ}-$ $\angle P Q A=\frac{1}{2} \angle P B A$. Dus $\angle R Q A=180^{\circ}-\angle P Q A=\angle S Q A$. Vanwege gelijke raaklijnstukjes is $\angle S Q A=\angle T Q A$, waaruit we concluderen $\angle R Q A=\angle T Q A$. Dat betekent dat $R, Q$ en $T$ op een lijn liggen.
Nu bekijken we driehoek $P Q R$ en het punt $A$ op zijn omgeschreven cirkel. De loodlijnen vanuit $A$ op de zijden van de driehoek hebben voetpunten $S, T$ en $M$. Dit is een Simsonlijn, dus $S, T$ en $M$ liggen op een lijn.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2016-E_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2016"
}
|
Let $n$ be an even positive integer. A sequence of $n$ real numbers is called complete if for every integer $m$ with $1 \leq m \leq n$, the sum of the first $m$ terms or the sum of the last $m$ terms of the sequence is an integer. Determine the minimum number of integers in a complete sequence of $n$ numbers.
|
We prove that the minimum number of integers in a complete sequence is equal to 2. First, consider the case $n=2$. Let $a_{1}$ and $a_{2}$ be the numbers in the sequence. Then $a_{1}$ or $a_{2}$ is an integer, say without loss of generality $a_{1}$. Furthermore, $a_{1}+a_{2}$ is an integer, but then $a_{2}$ is also an integer. Therefore, the sequence contains at least two integers.
Now consider the case $n>2$. Write $n=2k$ (since $n$ is even) with $k \geq 2$. Then $a_{1}+a_{2}+\ldots+a_{k}$ or $a_{k+1}+a_{k+2}+\ldots+a_{2k}$ is an integer. Since the sum of both expressions is also an integer, they are both integers. Furthermore, $a_{1}+a_{2}+\ldots+a_{k-1}$ or $a_{k+2}+a_{k+3}+\ldots+a_{2k}$ is an integer. This implies that $a_{k}$ or $a_{k+1}$ is an integer. Additionally, we know that $a_{1}$ or $a_{2k}$ is an integer, and these do not coincide with $a_{k}$ or $a_{k+1}$ because $k \geq 2$. Therefore, at least two different numbers are integers.
Finally, we show that for every even $n$ it is possible to construct a complete sequence with exactly two integers. Write $n=2k$ again. If $k$ is odd, we take $a_{1}=a_{k+1}=1$ and all other terms equal to $\frac{1}{2}$. The sum of all numbers in the sequence is an integer, so it suffices to show that the sum of the first or last $m$ terms is an integer with $1 \leq m \leq k$; the cases with $m>k$ follow directly. For odd $m \leq k$, the sum of the first $m$ terms is an integer, and for even $m<k$, the sum of the last $m$ terms is an integer. If $k$ is even, we take $a_{1}=a_{k}=1$ and all other terms equal to $\frac{1}{2}$. Now, for odd $m<k$, the sum of the first $m$ terms is an integer, and for even $m \leq k$, the sum of the last $m$ terms is an integer. Furthermore, the sum of all terms together is an integer, so the required result also follows for $m>k$.
We conclude that the minimum number of integers in a complete sequence of $n$ numbers is 2.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Zij $n$ een even positief geheel getal. Een rijtje van $n$ reële getallen noemen we volledig als voor elke gehele $m$ met $1 \leq m \leq n$ geldt dat de som van de eerste $m$ termen of de som van de laatste $m$ termen van het rijtje geheel is. Bepaal het minimale aantal gehele getallen in een volledig rijtje van $n$ getallen.
|
We bewijzen dat het minimale aantal gehele getallen in een volledig rijtje gelijk aan 2 is. Bekijk eerst het geval $n=2$. Noem $a_{1}$ en $a_{2}$ de getallen in het rijtje. Dan is $a_{1}$ of $a_{2}$ geheel, zeg zonder verlies van algemeenheid $a_{1}$. Verder is $a_{1}+a_{2}$ geheel, maar dan is ook $a_{2}$ geheel. Dus het rijtje bevat minstens twee gehele getallen.
Bekijk nu het geval $n>2$. Schrijf $n=2 k$ (want $n$ is even) met $k \geq 2$. Dan is $a_{1}+a_{2}+\ldots+a_{k}$ of $a_{k+1}+a_{k+2}+\ldots+a_{2 k}$ geheel. Maar omdat de som van beide uitdrukkingen ook geheel is, zijn ze allebei geheel. Verder is $a_{1}+a_{2}+\ldots+a_{k-1}$ of $a_{k+2}+a_{k+3}+\ldots+a_{2 k}$ geheel. Hieruit volgt dat $a_{k}$ of $a_{k+1}$ geheel is. Daarnaast weten we dat $a_{1}$ of $a_{2 k}$ geheel is en die vallen niet samen met $a_{k}$ of $a_{k+1}$ omdat $k \geq 2$. Dus minstens twee verschillende getallen zijn geheel.
Ten slotte laten we zien dat het voor elke even $n$ mogelijk is om een volledig rijtje met precies twee gehele getallen te maken. Schrijf weer $n=2 k$. Als $k$ oneven is, nemen we $a_{1}=a_{k+1}=1$ en alle overige termen gelijk aan $\frac{1}{2}$. De som van alle getallen in het rijtje is geheel, dus het is voldoende om nog te laten zien dat de som van de eerste of laatste $m$ termen geheel is met $1 \leq m \leq k$; de gevallen met $m>k$ volgen dan direct. Voor oneven $m \leq k$ zijn de eerste $m$ termen samen geheel, voor even $m<k$ juist de laatste $m$ termen. Als $k$ even is, nemen we juist $a_{1}=a_{k}=1$ en alle overige termen gelijk aan $\frac{1}{2}$. Nu is voor oneven $m<k$ de som van de eerste $m$ termen geheel en voor even $m \leq k$ de som van de laatste $m$ termen. Verder is de som van alle termen bij elkaar geheel, dus het gevraagde volgt ook voor $m>k$.
We concluderen dat het minimale aantal gehele getallen in een volledig rijtje van $n$ getallen 2 is.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2017-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2017"
}
|
Given is the function $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}$ that satisfies the properties:
(i) $f(p)=1$ for all prime numbers $p$,
(ii) $f(x y)=y f(x)+x f(y)$ for all $x, y \in \mathbb{Z}_{>0}$.
Determine the smallest $n \geq 2016$ with $f(n)=n$.
|
We first prove that for prime numbers $p$ and positive integers $k$, it holds that $f\left(p^{k}\right)=k p^{k-1}$. We do this by induction on $k$. For $k=1$, we have $f(p)=1$ and this is given. Now let $l \geq 1$ and assume we have proven it for $k=l$. Consider $k=l+1$. Then we apply the second property with $x=p$ and $y=p^{l}$:
$$
f\left(p^{l+1}\right)=f\left(p \cdot p^{l}\right)=p^{l} \cdot f(p)+p \cdot f\left(p^{l}\right)=p^{l}+p \cdot l p^{l-1}=(l+1) p^{l} .
$$
This completes the induction. Now we prove that for different prime numbers $p_{1}, p_{2}, \ldots$, $p_{t}$ and positive integers $a_{1}, a_{2}, \ldots, a_{t}$, it holds that
$$
f\left(p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{t}^{a_{t}}\right)=p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{t}^{a_{t}} \cdot\left(\frac{a_{1}}{p_{1}}+\frac{a_{2}}{p_{2}}+\cdots+\frac{a_{t}}{p_{t}}\right) .
$$
We prove this by induction on $t$. For $t=1$, it is exactly the formula we proved earlier. Now let $r \geq 1$ and assume we have proven it for $t=r$. Then we apply the second property again:
$$
\begin{aligned}
f\left(p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}} \cdot p_{r+1}^{a_{r+1}}\right) & =p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}} \cdot f\left(p_{r+1}^{a_{r+1}}\right)+p_{r+1}^{a_{r+1}} \cdot f\left(p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}}\right) \\
& =p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}} \cdot a_{r+1} p_{r+1}^{a_{r+1}-1}+p_{r+1}^{a_{r+1}} \cdot p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}} \cdot\left(\frac{a_{1}}{p_{1}}+\frac{a_{2}}{p_{2}}+\cdots+\frac{a_{r}}{p_{r}}\right) \\
& =p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}} p_{r+1}^{a_{r+1}} \cdot \frac{a_{r+1}}{p_{r+1}}+p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}} p_{r+1}^{a_{r+1}} \cdot\left(\frac{a_{1}}{p_{1}}+\frac{a_{2}}{p_{2}}+\cdots+\frac{a_{r}}{p_{r}}\right) \\
& =p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}} p_{r+1}^{a_{r+1}} \cdot\left(\frac{a_{1}}{p_{1}}+\frac{a_{2}}{p_{2}}+\cdots+\frac{a_{r}}{p_{r}}+\frac{a_{r+1}}{p_{r+1}}\right) .
\end{aligned}
$$
This completes the induction.
For an integer $n>1$ of the form $n=p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{t}^{a_{t}}$ with the $p_{i}$ different prime numbers, the property $f(n)=n$ is thus equivalent to
$$
p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{t}^{a_{t}} \cdot\left(\frac{a_{1}}{p_{1}}+\frac{a_{2}}{p_{2}}+\cdots+\frac{a_{t}}{p_{t}}\right)=p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{t}^{a_{t}}
$$
or equivalently
$$
\frac{a_{1}}{p_{1}}+\frac{a_{2}}{p_{2}}+\cdots+\frac{a_{t}}{p_{t}}=1 .
$$
Multiplying by $p_{1} p_{2} \cdots p_{t}$ gives
$$
a_{1} p_{2} p_{3} \cdots p_{t}+a_{2} p_{1} p_{3} \cdots p_{t}+\ldots+a_{t} p_{1} p_{2} \cdots p_{t-1}=p_{1} p_{2} \cdots p_{t}
$$
Assume without loss of generality that $p_{1}$ is the smallest prime number that occurs in the prime factorization of $n$. In the expression above, $p_{1}$ is a divisor of the right-hand side and of every term on the left-hand side except possibly the first. But then $p_{1}$ must also be a divisor of the first term. Since $p_{2}, \ldots, p_{t}$ are all prime numbers different from $p_{1}$, this can only be if $p_{1} \mid a_{1}$. In particular, then $a_{1} \geq p_{1}$, so $\frac{a_{1}}{p_{1}} \geq 1$. We now see that equality must hold and that $t=1$, because the sum of all $\frac{a_{i}}{p_{i}}$ would otherwise be greater than 1. Thus $n=p^{p}$ for some prime number $p$.
We are looking for the smallest $n \geq 2016$ of the form $n=p^{p}$. We have $3^{3}=27$ and $5^{5}=3125$, so the desired $n$ is equal to 3125.
|
3125
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Gegeven is de functie $f: \mathbb{Z}_{>0} \rightarrow \mathbb{Z}$ die voldoet aan de eigenschappen:
(i) $f(p)=1$ voor alle priemgetallen $p$,
(ii) $f(x y)=y f(x)+x f(y)$ voor alle $x, y \in \mathbb{Z}_{>0}$.
Bepaal de kleinste $n \geq 2016$ met $f(n)=n$.
|
We bewijzen allereerst dat voor priemgetallen $p$ en positieve gehele getallen $k$ geldt dat $f\left(p^{k}\right)=k p^{k-1}$. Dit doen we met inductie naar $k$. Voor $k=1$ staat er $f(p)=1$ en dat is gegeven. Zij nu $l \geq 1$ en stel dat we het bewezen hebben voor $k=l$. Bekijk $k=l+1$. Dan passen we de tweede eigenschap toe met $x=p$ en $y=p^{l}$ :
$$
f\left(p^{l+1}\right)=f\left(p \cdot p^{l}\right)=p^{l} \cdot f(p)+p \cdot f\left(p^{l}\right)=p^{l}+p \cdot l p^{l-1}=(l+1) p^{l} .
$$
Dit voltooit de inductie. Nu bewijzen we dat voor verschillende priemgetallen $p_{1}, p_{2}, \ldots$, $p_{t}$ en positieve gehele getallen $a_{1}, a_{2}, \ldots, a_{t}$ geldt dat
$$
f\left(p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{t}^{a_{t}}\right)=p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{t}^{a_{t}} \cdot\left(\frac{a_{1}}{p_{1}}+\frac{a_{2}}{p_{2}}+\cdots+\frac{a_{t}}{p_{t}}\right) .
$$
We bewijzen dit met inductie naar $t$. Voor $t=1$ is het precies de formule die we hiervoor bewezen hebben. Zij nu $r \geq 1$ en stel dat we het bewezen hebben voor $t=r$. Dan passen we weer de tweede eigenschap toe:
$$
\begin{aligned}
f\left(p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}} \cdot p_{r+1}^{a_{r+1}}\right) & =p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}} \cdot f\left(p_{r+1}^{a_{r+1}}\right)+p_{r+1}^{a_{r+1}} \cdot f\left(p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}}\right) \\
& =p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}} \cdot a_{r+1} p_{r+1}^{a_{r+1}-1}+p_{r+1}^{a_{r+1}} \cdot p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}} \cdot\left(\frac{a_{1}}{p_{1}}+\frac{a_{2}}{p_{2}}+\cdots+\frac{a_{r}}{p_{r}}\right) \\
& =p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}} p_{r+1}^{a_{r+1}} \cdot \frac{a_{r+1}}{p_{r+1}}+p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}} p_{r+1}^{a_{r+1}} \cdot\left(\frac{a_{1}}{p_{1}}+\frac{a_{2}}{p_{2}}+\cdots+\frac{a_{r}}{p_{r}}\right) \\
& =p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{r}^{a_{r}} p_{r+1}^{a_{r+1}} \cdot\left(\frac{a_{1}}{p_{1}}+\frac{a_{2}}{p_{2}}+\cdots+\frac{a_{r}}{p_{r}}+\frac{a_{r+1}}{p_{r+1}}\right) .
\end{aligned}
$$
Dit voltooit de inductie.
Voor een geheel getal $n>1$ van de vorm $n=p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{t}^{a_{t}}$ met de $p_{i}$ verschillende priemgetallen, is de eigenschap $f(n)=n$ dus equivalent met
$$
p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{t}^{a_{t}} \cdot\left(\frac{a_{1}}{p_{1}}+\frac{a_{2}}{p_{2}}+\cdots+\frac{a_{t}}{p_{t}}\right)=p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{t}^{a_{t}}
$$
oftewel
$$
\frac{a_{1}}{p_{1}}+\frac{a_{2}}{p_{2}}+\cdots+\frac{a_{t}}{p_{t}}=1 .
$$
Vermenigvuldigen met $p_{1} p_{2} \cdots p_{t}$ geeft
$$
a_{1} p_{2} p_{3} \cdots p_{t}+a_{2} p_{1} p_{3} \cdots p_{t}+\ldots+a_{t} p_{1} p_{2} \cdots p_{t-1}=p_{1} p_{2} \cdots p_{t}
$$
Neem zonder verlies van algemeenheid aan dat $p_{1}$ het kleinste priemgetal is dat voorkomt in de priemfactorisatie van $n$. In de uitdrukking hierboven is $p_{1}$ een deler van de rechterkant en van elke term aan de linkerkant behalve eventueel de eerste. Maar dan moet $p_{1}$ ook een deler van de eerste term zijn. Aangezien $p_{2}, \ldots, p_{t}$ allemaal priemgetallen ongelijk aan $p_{1}$ zijn, kan dat alleen als $p_{1} \mid a_{1}$. In het bijzonder geldt dan $a_{1} \geq p_{1}$, zodat $\frac{a_{1}}{p_{1}} \geq 1$. We zien nu dat hier gelijkheid moet gelden en dat $t=1$, omdat de som van alle $\frac{a_{i}}{p_{i}}$ anders groter dan 1 wordt. Dus $n=p^{p}$ voor een zeker priemgetal $p$.
We zoeken dus de kleinste $n \geq 2016$ van de vorm $n=p^{p}$. Er geldt $3^{3}=27$ en $5^{5}=3125$, dus de gevraagde $n$ is gelijk aan 3125 .
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2017-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2017"
}
|
Let $A B C$ be a triangle with $\angle A=90^{\circ}$ and let $D$ be the foot of the altitude from $A$. The midpoints of $A D$ and $A C$ are called $E$ and $F$ respectively. Let $M$ be the center of the circumcircle of $\triangle B E F$. Prove that $A C \| B M$.
Translate the above text into English, please retain the original text's line breaks and format, and output the translation result directly.
|
Due to the right angles at $A$ and $D$, we have $\triangle A D B \sim \triangle C A B$ (hh). From this, it follows that $\frac{|A D|}{|A B|}=\frac{|C A|}{|C B|}$. Since $|A E|=\frac{1}{2}|A D|$ and $|C F|=\frac{1}{2}|C A|$, it also follows that $\frac{|A E|}{|A B|}=\frac{|C F|}{|C B|}$. From the previous similarity, we also get $\angle B A E=\angle B A D=\angle B C A=\angle B C F$, so with (zhz) we now have $\triangle A E B \sim \triangle C F B$. This implies $\angle A B E=\angle C B F$.
Furthermore, $E F$ is a midline in triangle $A D C$, so $E F \| B C$. With Z-angles, this gives $\angle C B F=\angle B F E$. Due to the inscribed angle theorem and subsequently the angle sum in isosceles triangle $E B M$, we have $\angle B F E=\frac{1}{2} \angle B M E=90^{\circ}-\angle E B M$. Therefore, $\angle A B E=\angle C B F=90^{\circ}-\angle E B M$. We conclude that $\angle A B M=\angle A B E+\angle E B M=90^{\circ}$. Thus, $A C \| B M$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Zij $A B C$ een driehoek met $\angle A=90^{\circ}$ en zij $D$ het voetpunt van de hoogtelijn vanuit $A$. De middens van $A D$ en $A C$ noemen we respectievelijk $E$ en $F$. Zij $M$ het middelpunt van de omschreven cirkel van $\triangle B E F$. Bewijs dat $A C \| B M$.
|
Vanwege de rechte hoeken bij $A$ en $D$ geldt $\triangle A D B \sim \triangle C A B$ (hh). Hieruit volgt $\frac{|A D|}{|A B|}=\frac{|C A|}{|C B|}$. Omdat $|A E|=\frac{1}{2}|A D|$ en $|C F|=\frac{1}{2}|C A|$ geldt ook $\frac{|A E|}{|A B|}=\frac{|C F|}{|C B|}$. Uit de vorige gelijkvormigheid volgt ook dat $\angle B A E=\angle B A D=\angle B C A=\angle B C F$, dus met (zhz) krijgen we nu $\triangle A E B \sim \triangle C F B$. Hieruit volgt $\angle A B E=\angle C B F$.
Verder is $E F$ een middenparallel in driehoek $A D C$, dus $E F \| B C$. Met Z-hoeken geeft dit $\angle C B F=\angle B F E$. Vanwege de middelpunts-omtrekshoekstelling en vervolgens de hoekensom in gelijkbenige driehoek $E B M$ geldt $\angle B F E=\frac{1}{2} \angle B M E=90^{\circ}-\angle E B M$. Dus $\angle A B E=\angle C B F=90^{\circ}-\angle E B M$. We concluderen dat $\angle A B M=\angle A B E+\angle E B M=90^{\circ}$. Dus $A C \| B M$.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2017-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2017"
}
|
A quadruple $(a, b, c, d)$ of positive integers with $a \leq b \leq c \leq d$ is called good if we can color each integer red, blue, green, or purple such that
- in every $a$ consecutive integers, at least one is red;
- in every $b$ consecutive integers, at least one is blue;
- in every $c$ consecutive integers, at least one is green;
- in every $d$ consecutive integers, at least one is purple.
Determine all good quadruples with $a=2$.
|
We are always looking at quadruples $(a, b, c, d)$ of positive integers with $a \leq b \leq c \leq d$. Every quadruple with $b \geq 6$ satisfies: we color the even numbers red and the odd numbers alternately blue, green, purple, blue, green, purple, etc. Furthermore, every quadruple with $b \geq 4$ and $c \geq 8$ satisfies: we color the even numbers red, the numbers $1 \mod 4$ blue, the numbers $3 \mod 8$ green, and the numbers $7 \mod 8$ purple. We will prove that these are the only possibilities.
Suppose $(2, b, c, d)$ is good. We consider a purple number. The neighbors of this number must be red, so then we have 3 consecutive numbers with no blue. Therefore, $b \geq 4$. If $b \geq 6$, then the quadruple satisfies, as we have seen. Now suppose that $b=4$ or $b=5$. We consider a purple number. This has two red neighbors. On at least one of both sides, there is a blue number, say on the left. To the left of that, there is a red number. So we have $R B R P R$. The next two numbers in the sequence contain at least one red and at least one blue, so certainly no green. We thus have 7 consecutive numbers without green, so $c \geq 8$. We have already seen that this case satisfies.
We conclude that the following quadruples $(2, b, c, d)$ are the good quadruples: those with $b \geq 6$ and those with $b \geq 4$ and $c \geq 8$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Een viertal $(a, b, c, d)$ van positieve gehele getallen met $a \leq b \leq c \leq d$ noemen we goed indien we ieder geheel getal rood, blauw, groen of paars kunnen kleuren zodat
- van iedere $a$ opeenvolgende getallen er tenminste één rood is;
- van iedere $b$ opeenvolgende getallen er tenminste één blauw is;
- van iedere $c$ opeenvolgende getallen er tenminste één groen is;
- van iedere $d$ opeenvolgende getallen er tenminste één paars is.
Bepaal alle goede viertallen met $a=2$.
|
We bekijken steeds alleen viertallen $(a, b, c, d)$ van positieve gehele getallen met $a \leq b \leq c \leq d$. Ieder viertal met $b \geq 6$ voldoet: we kleuren dan de even getallen rood en de oneven getallen achtereenvolgens blauw, groen, paars, blauw, groen, paars, etc. Verder voldoet ieder viertal met $b \geq 4$ en $c \geq 8$ : we kleuren dan de even getallen rood, de getallen $1 \bmod 4$ blauw, de getallen $3 \bmod 8$ groen en de getallen $7 \bmod 8$ paars. We gaan bewijzen dat dit de enige mogelijkheden zijn.
Stel $(2, b, c, d)$ is goed. We bekijken een paars getal. De buren van dit getal moeten rood zijn, dus dan hebben we 3 opeenvolgende getallen waarvan er geen blauw is. Dus $b \geq 4$. Als $b \geq 6$, dan voldoet het viertal, zoals we hebben gezien. Stel nu dus dat $b=4$ of $b=5$. We bekijken een paars getal. Deze heeft twee rode buren. Aan minstens één van beide kanten staat een blauw getal, zeg links. Daar weer links van komt een rood getal. Dus we hebben $R B R P R$. Bij de volgende twee getallen in het rijtje zit in elk geval een rode en in elk geval een blauwe, dus zeker geen groene. We hebben daarmee 7 opeenvolgende getallen zonder groene, dus $c \geq 8$. We hebben al gezien dat dit geval voldoet.
We concluderen dat de volgende viertallen $(2, b, c, d)$ de goede viertallen zijn: die met $b \geq 6$ en die met $b \geq 4$ en $c \geq 8$.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2017-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2017"
}
|
Determine all pairs of prime numbers $(p, q)$ such that $p^{2}+5 p q+4 q^{2}$ is the square of an integer.
|
Write $p^{2}+5 p q+4 q^{2}=a^{2}$, with $a \geq 0$ an integer. The left side is equal to $(p+2 q)^{2}+p q$, so we can rewrite this as $p q=a^{2}-(p+2 q)^{2}$, or $p q=(a-p-2 q)(a+p+2 q)$. The second factor on the right is greater than $p$ and greater than $q$, but it is a divisor of $p q$. Since $p$ and $q$ are prime, it must be equal to $p q$, so $a+p+2 q=p q$. And then $a-p-2 q=1$. Subtract these two: $p q-1=(a+p+2 q)-(a-p-2 q)=2(p+2 q)$, or $p q-2 p-4 q-1=0$. This can be rewritten as $(p-4)(q-2)=9$. The factor $q-2$ cannot be negative, so $p-4$ cannot be negative either. The factors must therefore be equal to 1 and 9 or 9 and 1 or 3 and 3. This gives for $(p, q)$ the possibilities $(5,11),(13,3)$ and $(7,5)$. Checking shows that $p^{2}+5 p q+4 q^{2}$ is a square in each of these cases, namely $28^{2}, 20^{2}$ and $18^{2}$. So these three pairs are the solutions.
|
(5,11),(13,3),(7,5)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Bepaal alle paren priemgetallen $(p, q)$ zodat $p^{2}+5 p q+4 q^{2}$ het kwadraat van een geheel getal is.
|
Schrijf $p^{2}+5 p q+4 q^{2}=a^{2}$, met $a \geq 0$ een geheel getal. De linkerkant is gelijk aan $(p+2 q)^{2}+p q$, dus we kunnen dit herschrijven tot $p q=a^{2}-(p+2 q)^{2}$, oftewel $p q=(a-p-2 q)(a+p+2 q)$. De tweede factor rechts is groter dan $p$ en groter dan $q$, maar het is wel een deler van $p q$. Omdat $p$ en $q$ priem zijn, moet het wel gelijk zijn aan $p q$, dus $a+p+2 q=p q$. En dan is $a-p-2 q=1$. Trek deze twee van elkaar af: $p q-1=(a+p+2 q)-(a-p-2 q)=2(p+2 q)$, oftewel $p q-2 p-4 q-1=0$. Dit kunnen we herschrijven tot $(p-4)(q-2)=9$. De factor $q-2$ kan niet negatief zijn, dus is $p-4$ dat ook niet. De factoren moeten dus gelijk zijn aan 1 en 9 of aan 9 en 1 of aan 3 en 3. Dit geeft respectievelijk voor $(p, q)$ de mogelijkheden $(5,11),(13,3)$ en $(7,5)$. Controleren laat zien dat $p^{2}+5 p q+4 q^{2}$ in elk van die gevallen een kwadraat is, namelijk respectievelijk $28^{2}, 20^{2}$ en $18^{2}$. Dus deze drie tweetallen zijn de oplossingen.
|
{
"exam": "Dutch_TST",
"problem_label": "5",
"problem_match": "\nOpgave 5.",
"resource_path": "Dutch_TST/segmented/nl-2017-B_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2017"
}
|
Let $n$ be a positive integer. Given are circular discs with radii $1, 2, \ldots, n$. For each size, we have two discs: a transparent one and an opaque one. Each disc has a hole in the middle, allowing us to stack the discs on a vertical rod. We want to create stacks that meet the following conditions:
- Exactly one disc of each size is on the stack.
- When viewed from directly above, the outer edges of all $n$ discs on the stack can be seen. (This means that if there is an opaque disc on the stack, then no smaller discs may lie below it.)
Determine the number of different stacks that can be made under these conditions. (Two stacks are different if they do not use exactly the same set of discs, but also if they do use exactly the same set of discs but not in the same order.)
|
A stack is considered valid if it meets the conditions. Let $a_{n}$ be the number of valid stacks with $n$ disks (with radii $1, 2, \ldots, n$). We prove by induction that $a_{n}=(n+1)!$. For $n=1$, we can make two stacks: one with the transparent disk of radius 1 and one with the opaque disk of radius 1, so $a_{1}=2=2!$. Suppose now that for some $n \geq 1$ we have proven that $a_{n}=(n+1)!$. Consider a valid stack with $n+1$ disks. If we remove the disk with radius $n+1$, all remaining disks are still visible from above, so we are left with a valid stack of $n$ disks. Every valid stack with $n+1$ disks can thus be created by inserting the disk with radius $n+1$ into a valid stack of $n$ disks at a suitable position. In principle, there are $n+1$ positions where we can insert the disk with radius $n+1$: above the top disk, above the second disk, ..., above the bottom disk, and also below the bottom disk. The disk with radius $n+1$ itself is always visible, regardless of where we insert it. If we insert the disk with radius $n+1$ below the bottom disk, it can be either transparent or opaque; in both cases, the view of the other disks is not blocked. Thus, there are $2 a_{n}$ valid stacks where the disk with radius $n+1$ is at the bottom. However, if we insert an opaque disk with radius $n+1$ at any other position, it blocks the view of the disks below it. Therefore, we can only insert the transparent disk with radius $n+1$ at the other $n$ positions. Thus, there are $n a_{n}$ valid stacks where the disk with radius $n+1$ is not at the bottom. We find
$$
a_{n+1}=2 a_{n}+n a_{n}=(n+2) a_{n}=(n+2)(n+1)!=(n+2)!
$$
This completes the induction.
|
(n+1)!
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Zij $n$ een positief geheel getal. Gegeven zijn cirkelvormige schijven met stralen $1,2, \ldots, n$. Van elke grootte hebben we twee schijven: een doorzichtige en een ondoorzichtige. In elke schijf zit een gaatje, precies in het midden, waarmee we de schijven op een rechtopstaand staafje kunnen stapelen. We willen nu stapels maken die aan de volgende voorwaarden voldoen:
- Van elke grootte ligt er precies één schijf op de stapel.
- Als we recht van boven kijken, kunnen we de buitenranden van alle $n$ schijven op de stapel zien. (Dat wil zeggen, als er een ondoorzichtige schijf op de stapel ligt, dan mogen daaronder geen kleinere schijven liggen.)
Bepaal het aantal verschillende stapels dat we kunnen maken onder deze voorwaarden. (Twee stapels zijn verschillend als ze niet precies dezelfde verzameling schijven gebruiken, maar ook als ze wel precies dezelfde verzameling schijven gebruiken maar niet in dezelfde volgorde.)
|
Noem een stapel geldig als hij aan de voorwaarden voldoet. Zij $a_{n}$ het aantal geldige stapels met $n$ schijven (met straal $1,2, \ldots, n$ ). We bewijzen met inductie dat $a_{n}=(n+1)!$. Voor $n=1$ kunnen we twee stapels maken: met de doorzichtige schijf met straal 1 en met de ondoorzichtige schijf met straal 1 , dus $a_{1}=2=2$. Stel nu dat we voor zekere $n \geq 1$ bewezen hebben dat $a_{n}=(n+1)$ !. Bekijk een geldige stapel met $n+1$ schijven. Als we de schijf met straal $n+1$ weghalen, zijn nog steeds alle schijven van bovenaf zichtbaar, dus we houden een geldige stapel met $n$ schijven over. Elke geldige stapel met $n+1$ schijven is dus te maken door in een geldige stapel met $n$ schijven de schijf met straal $n+1$ op een geschikte plek in te voegen. In principe zijn er $n+1$ posities waarop we de schijf met straal $n+1$ kunnen invoegen: boven de bovenste schijf, boven de tweede schijf, ..., boven de onderste schijf en ook nog onder de onderste schijf. De schijf met straal $n+1$ zelf is altijd zichtbaar, waar we hem ook invoegen. Als we de schijf met straal $n+1$ invoegen onder de onderste schijf, dan mag hij zowel doorzichtig als ondoorzichtig zijn; in beide gevallen wordt het zicht op de andere schijven niet geblokkeerd. Er zijn dus $2 a_{n}$ geldige stapels waarbij de schijf met straal $n+1$ onderop liggen. Als we echter op een andere positie een ondoorzichtige schijf met straal $n+1$ invoegen, dan blokkeert hij het zicht op de schijven eronder. We kunnen dus op de andere $n$ posities alleen de doorzichtige schijf met straal $n+1$ invoegen. Er zijn dus $n a_{n}$ geldige stapels waarbij de schijf met straal
$n+1$ niet onderop ligt. Zo vinden we
$$
a_{n+1}=2 a_{n}+n a_{n}=(n+2) a_{n}=(n+2)(n+1)!=(n+2)!
$$
Dit voltooit de inductie.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2017-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2017"
}
|
Let $n \geq 4$ be an integer. Consider a regular $2n$-gon where each vertex is assigned an integer, which we call the value of that vertex. If four distinct vertices of this $2n$-gon form a rectangle, then we call the sum of the values of these vertices a rectangle sum.
Determine for which integers (not necessarily positive) $m$ we can assign the numbers $m+1, m+2$, $\ldots, m+2n$ as values to the vertices (in some order) so that every rectangle sum is a prime number. (Prime numbers are by definition positive.)
|
Number the vertices of the $2n$-gon clockwise from 1 to $2n$ and let $a_{i}$ be the value of vertex $i$. Since the number of vertices of the polygon is even, we can pair each vertex with the one directly opposite it. We add the values of each pair of opposite vertices and thus obtain the numbers $s_{i}=a_{i}+a_{i+n}$ with $1 \leq i \leq n$.
If four vertices $A, B, C$ and $D$ form a rectangle in that order, then $\angle ABC = 90^{\circ}$ and $\angle ADC = 90^{\circ}$, so $B$ and $D$ lie on the circle with diameter $AC$ according to Thales. Since all vertices of the polygon lie on its circumscribed circle, $AC$ is apparently a diameter of the circumscribed circle. Thus, $A$ and $C$ are opposite vertices, and the same applies to $B$ and $D$. Conversely, if $A$ and $C$ are opposite vertices and $B$ and $D$ are also, then $ABCD$ is a rectangle, also by Thales. In short, four points form a rectangle if and only if they belong to two pairs of opposite vertices.
Therefore, it must hold that $s_{i} + s_{j}$ is prime for all $1 \leq i < j \leq n$. Suppose that at least three of the numbers $s_{i}$ have the same parity, say $s_{j}, s_{k}$, and $s_{l}$. Then the sum of any two of these three is even, but also prime, so this sum must be 2 in all cases. Thus, $s_{j} + s_{k} = s_{k} + s_{l} = s_{j} + s_{l}$, which implies $s_{j} = s_{k} = s_{l}$. But since $s_{j} + s_{k} = 2$, this gives $s_{j} = s_{k} = s_{l} = 1$. We conclude that at most two of the numbers $s_{i}$ are even, and if there are three or more odd ones, they must all be equal to 1.
The total sum of all $s_{i}$ is equal to the sum of all the numbers at the vertices, which is
$$
(m+1) + (m+2) + \ldots + (m+2n) = 2mn + \frac{1}{2} \cdot 2n \cdot (2n+1) = 2mn + n(2n+1)
$$
Modulo 2, this sum is congruent to $n$. On the other hand, this sum must be congruent modulo 2 to the number of odd $s_{i}$. Therefore, the number of odd $s_{i}$ has the same parity as $n$. Since there are a total of $n$ numbers $s_{i}$, the number of even $s_{i}$ is even. We have already seen that there are at most two, so there are zero or two.
Suppose $n=4$ and suppose that two $s_{i}$ are even and thus also two $s_{i}$ are odd. Then the sum of the two even $s_{i}$ is 2 and the sum of the two odd $s_{i}$ is also 2, so the total sum of the $s_{i}$ is $4=n$. Now suppose $n \geq 5$ and suppose that two $s_{i}$ are even. Then there are $n-2 \geq 3$ of the $s_{i}$ that are odd, so all the odd $s_{i}$ are equal to 1. The two even $s_{i}$ together are equal to 2. So the total sum of the $s_{i}$ is $(n-2) + 2 = n$. (You can also prove that the case with exactly two even $s_{i}$ is impossible.) Now suppose that there are no even $s_{i}$. Then all $s_{i}$ are odd and thus all equal to 1, so the total sum of the $s_{i}$ is $n$.
In all cases, the total sum of the $s_{i}$ is thus $n$. We have also seen that this sum is equal to $2mn + n(2n+1)$. So $2mn + n(2n+1) = n$, from which it follows after division by $n \neq 0$ that $2m + 2n + 1 = 1$, so $m = -n$.
We now show that if $m = -n$, there is indeed a solution. Take $a_{i} = i$ and $a_{n+i} = 1 - i$ for $1 \leq i \leq n$. Then the numbers $1, 2, \ldots, n$ and the numbers $0, -1, \ldots, -n+1$ are used, and these are precisely the numbers $m+1, m+2, \ldots, m+2n$. Furthermore, $s_{i} = i + (1 - i) = 1$ for all $i$. So every rectangle sum is equal to 2, which is a prime number.
We conclude that $m = -n$ is the only value of $m$ that satisfies the condition.
|
m = -n
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Zij $n \geq 4$ een geheel getal. Bekijk een regelmatige $2 n$-hoek waarbij aan elk hoekpunt een geheel getal is toegekend, wat we de waarde van dat hoekpunt noemen. Als vier verschillende hoekpunten van deze $2 n$-hoek een rechthoek vormen, dan noemen we de som van de waarden van deze hoekpunten een rechthoekssom.
Bepaal voor welke gehele (niet-noodzakelijk positieve) $m$ we de getallen $m+1, m+2$, $\ldots, m+2 n$ als waarden kunnen toekennen aan de hoekpunten (in een of andere volgorde) zodat elke rechthoekssom een priemgetal is. (Priemgetallen zijn per definitie positief.)
|
Nummer de hoekpunten van de $2 n$-hoek met de klok mee 1 tot en met $2 n$ en zij $a_{i}$ de waarde van hoekpunt $i$. Omdat het aantal hoekpunten van de veelhoek even is, kunnen we elk hoekpunt koppelen aan het punt er precies tegenover. We tellen de waarden van elk tweetal tegenoverliggende hoekpunten bij elkaar op en verkrijgen zo de getallen $s_{i}=a_{i}+a_{i+n}$ met $1 \leq i \leq n$.
Als vier hoekpunten $A, B, C$ en $D$ in die volgorde een rechthoek vormen, dan is $\angle A B C=$ $90^{\circ}$ en $\angle A D C=90^{\circ}$, dus $B$ en $D$ liggen volgens Thales op de cirkel met middellijn $A C$. Omdat alle hoekpunten van de veelhoek op zijn omgeschreven cirkel liggen, is $A C$ blijkbaar een middellijn van de omgeschreven cirkel. Dus $A$ en $C$ zijn tegenoverliggende hoekpunten en hetzelfde geldt voor $B$ en $D$. Andersom geldt dat als $A$ en $C$ tegenoverliggende hoekpunten zijn en $B$ en $D$ ook, dat dan $A B C D$ een rechthoek is, ook wegens Thales. Kortom, vier punten vormen een rechthoek dan en slechts dan als ze tot twee paren tegenoverliggende hoekpunten behoren.
Er moet dus gelden dat $s_{i}+s_{j}$ priem is voor alle $1 \leq i<j \leq n$. Stel dat minstens drie van de getallen $s_{i}$ dezelfde pariteit hebben, zeg $s_{j}, s_{k}$ en $s_{l}$. Dan is de som van elke twee van die drie even, maar tegelijkertijd priem, dus die som moet in alle gevallen gelijk aan 2 zijn. Dus $s_{j}+s_{k}=s_{k}+s_{l}=s_{j}+s_{l}$, waaruit volgt dat $s_{j}=s_{k}=s_{l}$. Maar omdat $s_{j}+s_{k}=2$, geeft dit $s_{j}=s_{k}=s_{l}=1$. We concluderen dat hoogstens twee van de getallen $s_{i}$ even zijn, en dat als er drie of meer oneven zijn, deze allemaal gelijk moeten zijn aan 1.
De totale som van alle $s_{i}$ is gelijk aan de som van alle getallen bij de hoekpunten, dus gelijk aan
$$
(m+1)+(m+2)+\ldots+(m+2 n)=2 m n+\frac{1}{2} \cdot 2 n \cdot(2 n+1)=2 m n+n(2 n+1)
$$
Modulo 2 is deze som congruent aan $n$. Anderzijds moet deze som modulo 2 congruent zijn aan het aantal oneven $s_{i}$. Dus het aantal oneven $s_{i}$ heeft dezelfde pariteit als $n$. Omdat er totaal $n$ getallen $s_{i}$ zijn, is het aantal even $s_{i}$ dus even. We hebben al gezien dat dat er hoogstens twee zijn, dus het zijn er nul of twee.
Stel dat $n=4$ en stel dat er twee $s_{i}$ even zijn en dus ook twee $s_{i}$ oneven. Dan is de som van de twee even $s_{i}$ gelijk aan 2 en de som van de twee oneven $s_{i}$ ook gelijk aan 2, dus de totale som van de $s_{i}$ is $4=n$. Stel nu dat $n \geq 5$ en stel dat er twee $s_{i}$ even zijn. Dan zijn er $n-2 \geq 3$ van de $s_{i}$ oneven, dus alle oneven $s_{i}$ zijn gelijk aan 1 . De twee even $s_{i}$ samen zijn gelijk aan 2. Dus de totale som van de $s_{i}$ is $(n-2)+2=n$. (Je kunt ook bewijzen dat het geval met precies twee even $s_{i}$ onmogelijk is.) Stel nu dat er geen even $s_{i}$ zijn. Dan
zijn alle $s_{i}$ oneven en dus ook allemaal gelijk aan 1, dus is de totale som van de $s_{i}$ gelijk aan $n$.
In alle gevallen is de totale som van de $s_{i}$ dus $n$. We hebben ook gezien dat deze som gelijk is aan $2 m n+n(2 n+1)$. Dus $2 m n+n(2 n+1)=n$, waaruit na deling door $n \neq 0$ volgt $2 m+2 n+1=1$, dus $m=-n$.
We laten nu zien dat als $m=-n$, er inderdaad een oplossing bestaat. Neem $a_{i}=i$ en $a_{n+i}=1-i$ voor $1 \leq i \leq n$. Dan worden de getallen $1,2, \ldots, n$ en de getallen $0,-1, \ldots,-n+1$ gebruikt en dat zijn samen precies de getallen $m+1, m+2, \ldots, m+2 n$. Verder geldt $s_{i}=i+(1-i)=1$ voor alle $i$. Dus elke rechthoekssom is gelijk aan 2 en dat is een priemgetal.
We concluderen dat $m=-n$ de enige waarde van $m$ is die voldoet.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2017-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2017"
}
|
Determine all possible values of $\frac{1}{x}+\frac{1}{y}$ if $x$ and $y$ are real numbers (not equal to $0$) that satisfy $x^{3}+y^{3}+3 x^{2} y^{2}=x^{3} y^{3}$.
|
We rewrite the given to $x^{3}+y^{3}-x^{3} y^{3}=-3 x^{2} y^{2}$, from which we find
$$
\begin{aligned}
(x+y)^{3}-x^{3} y^{3} & =x^{3}+3 x^{2} y+3 x y^{2}+y^{3}-x^{3} y^{3} \\
& =-3 x^{2} y^{2}+3 x^{2} y+3 x y^{2}=3 x y(-x y+x+y)
\end{aligned}
$$
By using that $a^{3}-b^{3}=(a-b)\left(a^{2}+a b+b^{2}\right)$, we can also write
$$
\begin{aligned}
(x+y)^{3}-x^{3} y^{3} & =(x+y-x y)\left((x+y)^{2}+x y(x+y)+(x y)^{2}\right) \\
& =(x+y-x y)\left(x^{2}+y^{2}+2 x y+x^{2} y+x y^{2}+x^{2} y^{2}\right)
\end{aligned}
$$
If we now equate the two right-hand sides, we see that either $x+y-x y=0$ or $x^{2}+y^{2}+2 x y+x^{2} y+x y^{2}+x^{2} y^{2}=3 x y$. The latter case can be rewritten as
$$
\begin{aligned}
0 & =x^{2}+y^{2}-x y+x^{2} y+x y^{2}+x^{2} y^{2} \\
& =\frac{1}{2}(x-y)^{2}+\frac{1}{2} x^{2}\left(y^{2}+2 y+1\right)+\frac{1}{2} y^{2}\left(x^{2}+2 x+1\right) \\
& =\frac{1}{2}(x-y)^{2}+\frac{1}{2} x^{2}(y+1)^{2}+\frac{1}{2} y^{2}(x+1)^{2} .
\end{aligned}
$$
The sum of three squares must therefore be 0, which implies that each of the squares must be 0. Thus, $x=y=-1$. In this case, the given equation is indeed satisfied and $\frac{1}{x}+\frac{1}{y}=-2$.
In the other case, $x+y-x y=0$, so $\frac{1}{y}+\frac{1}{x}-1=0$, from which it follows that $\frac{1}{x}+\frac{1}{y}=1$. This is satisfied, for example, for $x=y=2$.
We conclude that the desired values are -2 and 1.
Alternative approach. It is also possible to find the desired form of the given relation with less algebraic manipulation. We describe a possible approach here.
Dividing by $x^{3} y^{3}$ gives
$$
\frac{1}{x^{3}}+\frac{1}{y^{3}}+\frac{3}{x y}=1
$$
Here we already see something with $\frac{1}{x}$ and $\frac{1}{y}$ in it. We substitute $a=\frac{1}{x}$ and $b=\frac{1}{y}$ to make the notation easier. Then we have
$$
a^{3}+b^{3}+3 a b=1
$$
and we are looking for the value of $a+b$. There are probably solutions with $a=b$. We get $2 a^{3}+3 a^{2}=1$. Trying numbers or factoring this gives that $a=-1$ and $a=\frac{1}{2}$ satisfy it. Now $a+b$ is equal to -2 or 1. We can now guess that perhaps all pairs $(a, b)$ with $a+b=-2$ or all pairs $(a, b)$ with $a+b=1$ work;
then the expression would be divisible by $a+b+2$ or $a+b-1$, respectively. Trying shows that the latter is indeed the case. We can rewrite it as
$$
(a+b-1)\left(a^{2}+b^{2}-a b+a+b+1\right)=0
$$
We also know by now that $a+b=-2$ does not give a solution for all $a$ and $b$, but does for $a=b=-1$. So we would want something with $a+1$ and $b+1$ for the right factor. It is now easy to see that the right factor is the sum of three squares. We can now finish it (similar to above).
|
-2 \text{ and } 1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Bepaal alle mogelijke waarden van $\frac{1}{x}+\frac{1}{y}$ als $x$ en $y$ reële getallen (ongelijk aan $0)$ zijn die voldoen aan $x^{3}+y^{3}+3 x^{2} y^{2}=x^{3} y^{3}$.
|
We herschrijven het gegeven naar $x^{3}+y^{3}-x^{3} y^{3}=-3 x^{2} y^{2}$, waarmee we vinden
$$
\begin{aligned}
(x+y)^{3}-x^{3} y^{3} & =x^{3}+3 x^{2} y+3 x y^{2}+y^{3}-x^{3} y^{3} \\
& =-3 x^{2} y^{2}+3 x^{2} y+3 x y^{2}=3 x y(-x y+x+y)
\end{aligned}
$$
Door te gebruiken dat $a^{3}-b^{3}=(a-b)\left(a^{2}+a b+b^{2}\right)$ kunnen we anderzijds ook schrijven
$$
\begin{aligned}
(x+y)^{3}-x^{3} y^{3} & =(x+y-x y)\left((x+y)^{2}+x y(x+y)+(x y)^{2}\right) \\
& =(x+y-x y)\left(x^{2}+y^{2}+2 x y+x^{2} y+x y^{2}+x^{2} y^{2}\right)
\end{aligned}
$$
Als we nu de twee rechterkanten aan elkaar gelijk stellen, dan zien we dat ofwel $x+y-x y=0$ ofwel $x^{2}+y^{2}+2 x y+x^{2} y+x y^{2}+x^{2} y^{2}=3 x y$. Het laatste geval laat zich herschrijven tot
$$
\begin{aligned}
0 & =x^{2}+y^{2}-x y+x^{2} y+x y^{2}+x^{2} y^{2} \\
& =\frac{1}{2}(x-y)^{2}+\frac{1}{2} x^{2}\left(y^{2}+2 y+1\right)+\frac{1}{2} y^{2}\left(x^{2}+2 x+1\right) \\
& =\frac{1}{2}(x-y)^{2}+\frac{1}{2} x^{2}(y+1)^{2}+\frac{1}{2} y^{2}(x+1)^{2} .
\end{aligned}
$$
De som van drie kwadraten moet dus 0 zijn, waaruit volgt dat elk van de kwadraten 0 moet zijn. Dus $x=y=-1$. In dit geval wordt inderdaad aan de gegeven vergelijking voldaan en geldt $\frac{1}{x}+\frac{1}{y}=-2$.
In het andere geval is $x+y-x y=0$, dus $\frac{1}{y}+\frac{1}{x}-1=0$, waaruit volgt dat $\frac{1}{x}+\frac{1}{y}=1$. Dit wordt bijvoorbeeld aangenomen voor $x=y=2$.
We concluderen dat de gevraagde waarden -2 en 1 zijn.
Alternatieve aanpak. Ook met minder algebraïsch gegoochel is het mogelijk de gewenste vorm van de gegeven relatie te vinden. We beschrijven hier een mogelijke aanpak.
Delen door $x^{3} y^{3}$ geeft
$$
\frac{1}{x^{3}}+\frac{1}{y^{3}}+\frac{3}{x y}=1
$$
Hier zien we alvast iets met $\frac{1}{x}$ en $\frac{1}{y}$ in terug. We substitueren $a=\frac{1}{x}$ en $b=\frac{1}{y}$ om de notatie makkelijker te maken. Dan staat er
$$
a^{3}+b^{3}+3 a b=1
$$
en zijn we op zoek naar de waarde van $a+b$. Waarschijnlijk zijn er wel oplossingen met $a=b$. We krijgen dan $2 a^{3}+3 a^{2}=1$. Getalletjes proberen of dit ontbinden geeft dat $a=-1$ en $a=\frac{1}{2}$ voldoen. Nu wordt $a+b$ gelijk aan -2 of 1 . We kunnen nu gokken dat misschien wel alle paren $(a, b)$ met $a+b=-2$ of alle paren $(a, b)$ met $a+b=1$ werken;
dan zou de uitdrukking deelbaar zijn door $a+b+2$ respectievelijk $a+b-1$. Proberen laat zien dat het laatste inderdaad het geval is. We kunnen herschrijven tot
$$
(a+b-1)\left(a^{2}+b^{2}-a b+a+b+1\right)=0
$$
We weten inmiddels ook dat $a+b=-2$ niet voor alle $a$ en $b$ een oplossing geeft, maar wel voor $a=b=-1$. Dus zouden we voor de rechterfactor iets met $a+1$ en $b+1$ willen. Het is nu makkelijk te zien dat de rechterfactor de som is van drie kwadraten. We kunnen het nu verder afmaken (vergelijkbaar met hierboven).
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2017-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2017"
}
|
In triangle $A B C$, $M$ is the midpoint of $A B$ and $N$ is the midpoint of $C M$. Let $X$ be a point such that $\angle X M C = \angle M B C$ and $\angle X C M = \angle M C B$, so that $X$ and $B$ lie on opposite sides of $C M$. Let $\Omega$ be the circumcircle of triangle $A M X$.
a) Prove that $C M$ is tangent to $\Omega$.
b) Prove that the lines $N X$ and $A C$ intersect on $\Omega$.
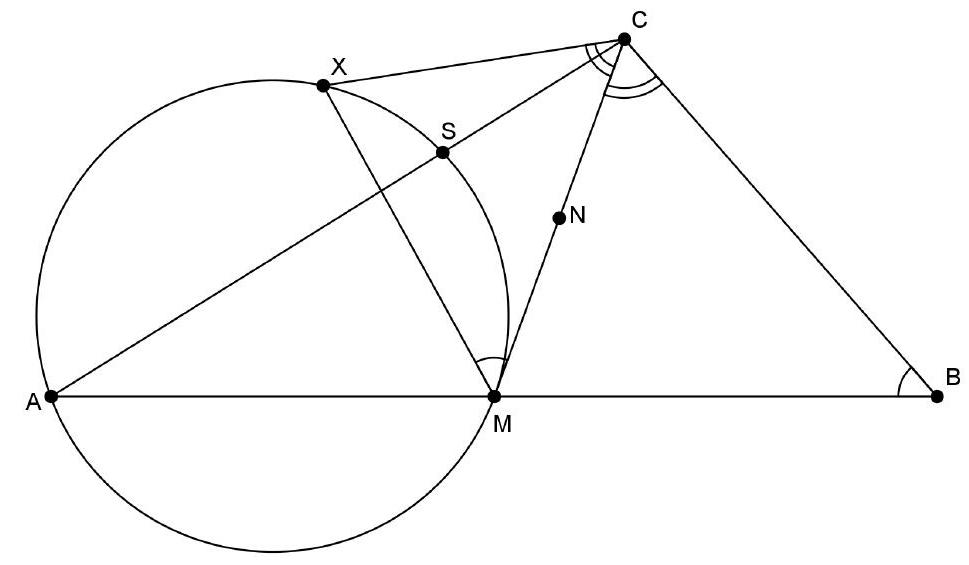
|
We examine the configuration in the figure; other configurations proceed analogously.
a) From the given data, it follows that $\triangle X M C \sim \triangle M B C$. Now, $\angle A M X=180^{\circ}-\angle X M C-\angle B M C=180^{\circ}-\angle X M C-\angle M X C=\angle M C X$ and
$$
\frac{|A M|}{|M X|}=\frac{|B M|}{|M X|}=\frac{|M C|}{|C X|}
$$
thus, by SAS (Side-Angle-Side), we see that $\triangle A M X \sim \triangle M C X$. From this, it follows that $\angle X A M=\angle X M C$, and by the converse of the tangent-secant angle theorem, we see that $C M$ is tangent to $\Omega$.
b) Let $S$ be the second intersection point of $A C$ and $\Omega$ (or the tangency point of $A C$ and $\Omega$; that is, $A$). We need to prove that $S$ lies on $N X$. By the tangent-secant angle theorem, $\angle S M C=\angle S A M=\angle C A M$. (If $S=A$, then $\angle S M C=\angle C A M$ follows from the fact that $C A$ and $C M$ are both tangent segments, making $\triangle C A M$ isosceles.) From this, it follows that $\triangle C S M \sim \triangle C M A$ (AA), so $\frac{|C M|}{|C A|}=\frac{|S M|}{|M A|}$. Since $|C M|=2|M N|$ and $|M A|=\frac{1}{2}|A B|$, it also follows that $\frac{|M N|}{|C A|}=\frac{|S M|}{|A B|}$. Together with $\angle S M N=\angle S M C=\angle C A M=\angle C A B$, this means $\triangle S N M \sim \triangle B C A$. Thus, $\angle M S N=\angle A B C$. Furthermore, $\angle X S M=180^{\circ}-\angle X A M$. In the previous part, we saw that $\angle X A M=\angle X M C=\angle M B C=\angle A B C$, so $\angle X S M=180^{\circ}-\angle A B C=180^{\circ}-\angle M S N$. From this, it follows that $S$ lies on $X N$.
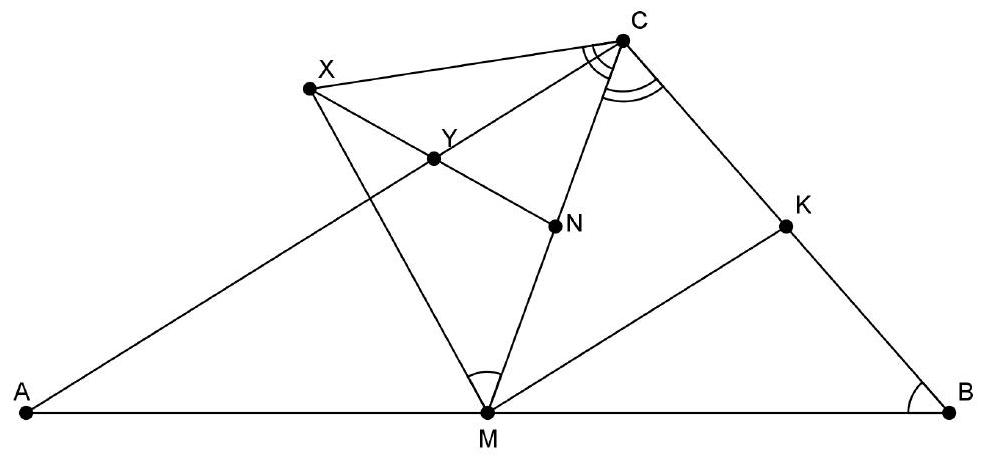
Solution II for part b Let $K$ be the midpoint of $B C$. From the similarity $\triangle X M C \sim \triangle M B C$, it also follows that $\triangle X M N \sim \triangle M B K$. Since line $X M$ and line $B M$ form an angle of $\angle A M X$, the other sides $N X$ and $K M$ are not parallel. Since $K M$ is a midline in triangle $A B C$, $K M$ is parallel to $A C$. Therefore, $N X$ and $A C$ have an intersection point $Y$. We now see that $\angle B M K=\angle M X N=\angle M X Y$. By the midline, it further follows that $\angle M A Y=\angle M A C=\angle B M K$. Thus, $\angle M X Y=\angle M A Y$, which means that $Y$ lies on $\Omega$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
In driehoek $A B C$ is $M$ het midden van $A B$ en $N$ het midden van $C M$. Zij $X$ een punt dat voldoet aan $\angle X M C=\angle M B C$ en $\angle X C M=\angle M C B$, zo dat $X$ en $B$ aan verschillende kanten van $C M$ liggen. $\mathrm{Zij} \Omega$ de omgeschreven cirkel van driehoek $A M X$.
a) Bewijs dat $C M$ raakt aan $\Omega$.
b) Bewijs dat de lijnen $N X$ en $A C$ snijden op $\Omega$.

|
We bekijken de configuratie in de figuur; andere configuraties gaan analoog.
a) Uit de gegevens volgt dat $\triangle X M C \sim \triangle M B C$. Er geldt nu $\angle A M X=180^{\circ}-$ $\angle X M C-\angle B M C=180^{\circ}-\angle X M C-\angle M X C=\angle M C X$ en
$$
\frac{|A M|}{|M X|}=\frac{|B M|}{|M X|}=\frac{|M C|}{|C X|}
$$
dus met zhz zien we dat $\triangle A M X \sim \triangle M C X$. Hieruit volgt dat $\angle X A M=\angle X M C$, dus met de omgekeerde raaklijnomtrekhoekstelling zien we dat $C M$ raakt aan $\Omega$.
b) Zij $S$ het tweede snijpunt van $A C$ en $\Omega$ (of het raakpunt van $A C$ en $\Omega$; dat is dan A). We moeten bewijzen dat $S$ op $N X$ ligt. Vanwege de raaklijnomtrekshoekstelling geldt $\angle S M C=\angle S A M=\angle C A M$. (Als $S=A$, dan volgt $\angle S M C=\angle C A M$ uit het feit dat $C A$ en $C M$ beide raaklijnstukjes zijn en dus $\triangle C A M$ gelijkbenig is.) Hieruit volgt $\triangle C S M \sim \triangle C M A$ (hh), dus $\frac{|C M|}{|C A|}=\frac{|S M|}{|M A|}$. Aangezien $|C M|=2|M N|$ en $|M A|=\frac{1}{2}|A B|$, geldt ook $\frac{|M N|}{|C A|}=\frac{|S M|}{|A B|}$. Samen met $\angle S M N=\angle S M C=\angle C A M=$ $\angle C A B$ betekent dit $\triangle S N M \sim \triangle B C A$. Dus $\angle M S N=\angle A B C$. Verder is $\angle X S M=$ $180^{\circ}-\angle X A M$. In het vorige onderdeel hebben we gezien dat $\angle X A M=\angle X M C=$ $\angle M B C=\angle A B C$, dus $\angle X S M=180^{\circ}-\angle A B C=180^{\circ}-\angle M S N$. Hieruit volgt dat $S$ op $X N$ ligt.

Oplossing II voor deel b Zij $K$ het midden van $B C$. Uit de gelijkvormigheid $\triangle X M C \sim$ $\triangle M B C$ volgt ook dat $\triangle X M N \sim \triangle M B K$. Omdat lijn $X M$ en lijn $B M$ een hoek van $\angle A M X$ maken, zijn de andere zijden $N X$ en $K M$ niet evenwijdig. Aangezien $K M$ een middenparallel is in driehoek $A B C$, is $K M$ evenwijdig aan $A C$. Dus hebben $N X$ en $A C$ een snijpunt $Y$. We zien nu dat $\angle B M K=\angle M X N=\angle M X Y$. Vanwege de middenparallel geldt verder $\angle M A Y=\angle M A C=\angle B M K$. Dus $\angle M X Y=\angle M A Y$, waaruit volgt dat $Y$ op $\Omega$ ligt.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2017-C_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2017"
}
|
Let $a, b$ and $c$ be positive integers, all distinct, and suppose that $p=ab+bc+ca$ is a prime number.
a) Prove that $a^{2}, b^{2}$ and $c^{2}$ give different remainders when divided by $p$.
b) Prove that $a^{3}, b^{3}$ and $c^{3}$ give different remainders when divided by $p$.
|
a) We prove this by contradiction. Assume that two of $a^{2}, b^{2}$, and $c^{2}$ give the same remainder when divided by $p$, say that $a^{2} \equiv b^{2} \bmod p$. Then $p \mid a^{2}-b^{2}=(a-b)(a+b)$, so $p \mid a-b$ or $p \mid a+b$. In the latter case, $p \leq a+b \leq c(a+b)<a b+b c+c a=p$, contradiction. In the former case, because $a \neq b$, we have $p \leq|a-b| \leq a+b<p$, contradiction.
b) We prove this by contradiction. Assume that two of $a^{3}, b^{3}$, and $c^{3}$ give the same remainder when divided by $p$, say that $a^{3} \equiv b^{3} \bmod p$. Then $p \mid a^{3}-b^{3}=(a-b)\left(a^{2}+a b+b^{2}\right)$, so $p \mid a-b$ or $p \mid a^{2}+a b+b^{2}$. The first case gives a contradiction just like in (a). We consider the other case: $p \mid a^{2}+a b+b^{2}$. From this, it follows that $p \mid a^{2}+a b+b^{2}+$ $(a b+b c+c a)=(a+b)(a+b+c)$ and thus $p \mid a+b$ or $p \mid a+b+c$. However, $a+b<a+b+c<a b+b c+c a$ because $a, b$, and $c$ cannot all be equal to 1. Therefore, $p$ is not a divisor of $a+b$ or $a+b+c$, contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Laat $a, b$ en $c$ positieve gehele getallen zijn, allemaal verschillend, en veronderstel dat $p=a b+b c+c a$ een priemgetal is.
a) Bewijs dat $a^{2}, b^{2}$ en $c^{2}$ verschillende resten geven bij deling door $p$.
b) Bewijs dat $a^{3}, b^{3}$ en $c^{3}$ verschillende resten geven bij deling door $p$.
|
a) We bewijzen dit uit het ongerijmde. Stel dat twee van $a^{2}, b^{2}$ en $c^{2}$ dezelfde rest geven bij deling door $p$, zeg dat $a^{2} \equiv b^{2} \bmod p$. Dan geldt $p \mid a^{2}-b^{2}=(a-b)(a+b)$, dus $p \mid a-b$ of $p \mid a+b$. In het laatste geval geldt $p \leq a+b \leq c(a+b)<a b+b c+c a=p$, tegenspraak. In het eerste geval geldt vanwege $a \neq b$ dat $p \leq|a-b| \leq a+b<p$, tegenspraak.
b) We bewijzen dit uit het ongerijmde. Stel dat twee van $a^{3}, b^{3}$ en $c^{3}$ dezelfde rest geven bij deling door $p$, zeg dat $a^{3} \equiv b^{3} \bmod p$. Dan geldt $p \mid a^{3}-b^{3}=(a-b)\left(a^{2}+a b+b^{2}\right)$, dus $p \mid a-b$ of $p \mid a^{2}+a b+b^{2}$. Het eerste geval geeft net als bij (a) een tegenspraak. We bekijken het andere geval: $p \mid a^{2}+a b+b^{2}$. Daaruit volgt dat $p \mid a^{2}+a b+b^{2}+$ $(a b+b c+c a)=(a+b)(a+b+c)$ en dus $p \mid a+b$ of $p \mid a+b+c$. Er geldt echter $a+b<a+b+c<a b+b c+c a$ omdat $a, b$ en $c$ niet allemaal gelijk kunnen zijn aan 1. Dus $p$ is geen deler van $a+b$ of $a+b+c$, tegenspraak.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2017-D_uitwerkingen.jsonl",
"solution_match": "# Oplossing.",
"tier": "T1",
"year": "2017"
}
|
The incircle of a non-isosceles triangle $\triangle A B C$ has center $I$ and touches $B C$ and $C A$ at $D$ and $E$, respectively. Let $H$ be the orthocenter of $\triangle A B I$, let $K$ be the intersection of $A I$ and $B H$, and let $L$ be the intersection of $B I$ and $A H$. Prove that the circumcircles of $\triangle D K H$ and $\triangle E L H$ intersect on the incircle of $\triangle A B C$.
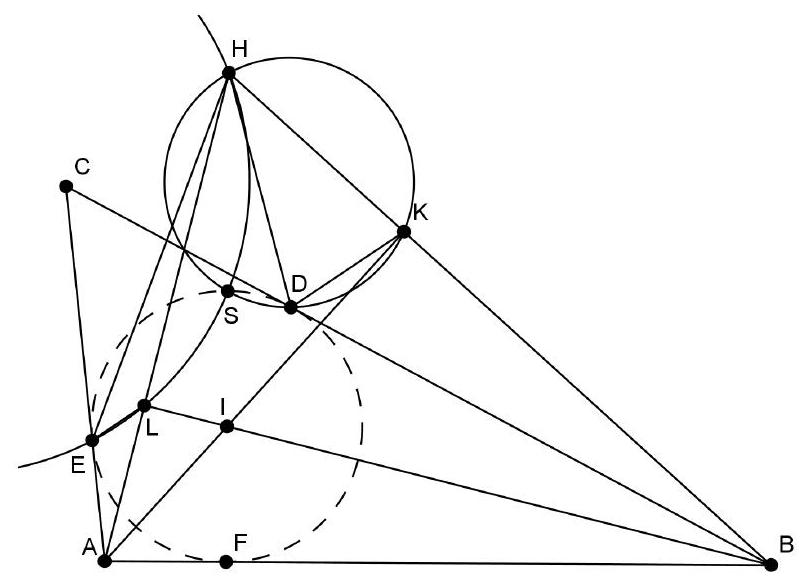
|
We examine the configuration in the figure; other configurations proceed analogously. It holds that $\angle I D B=90^{\circ}=\angle I K B$, so $B K D I$ is a cyclic quadrilateral. Furthermore, $\angle A L B=90^{\circ}=\angle A K B$, so $B K L A$ is also a cyclic quadrilateral. Therefore,
$$
\angle B K D=180^{\circ}-\angle B I D=180^{\circ}-\left(90^{\circ}-\frac{1}{2} \angle A B C\right)=180^{\circ}-\angle B A L=\angle B K L.
$$
From this, it follows that $K, D$, and $L$ lie on a straight line. Analogously, $K, E$, and $L$ also lie on a straight line, and this is the same line, so $D$ lies on it as well.
Let $S$ be the second intersection point of the circumcircles of $\triangle D K H$ and $\triangle E L H$. Then it holds that
$$
\begin{gathered}
\angle D S E=360^{\circ}-\angle D S H-\angle H S E=\angle D K H+180^{\circ}-\angle H L E=\angle L K H+\angle H L K \\
=180^{\circ}-\angle K H L .
\end{gathered}
$$
Since $H L I K$ is also a cyclic quadrilateral (due to two right angles), it holds that
$180^{\circ}-\angle K H L=\angle K I L=\angle A I B=180^{\circ}-\angle I B A-\angle I A B=180^{\circ}-\frac{1}{2} \angle C B A-\frac{1}{2} \angle C A B$.
Thus, $\angle D S E=180^{\circ}-\frac{1}{2} \angle C B A-\frac{1}{2} \angle C A B$. Now let $F$ be the tangency point of the incircle with side $A B$, then $A F I E$ and $B F I D$ are also cyclic quadrilaterals (both due to two right angles). Therefore, it holds that
$$
\angle D F E=\angle D F I+\angle I F E=\angle D B I+\angle I A E=\frac{1}{2} \angle C B A+\frac{1}{2} \angle C A B.
$$
We conclude that $\angle D F E+\angle D S E=180^{\circ}$, which implies that $S$ lies on the circumcircle of $\triangle D E F$, which is precisely the incircle of $\triangle A B C$.
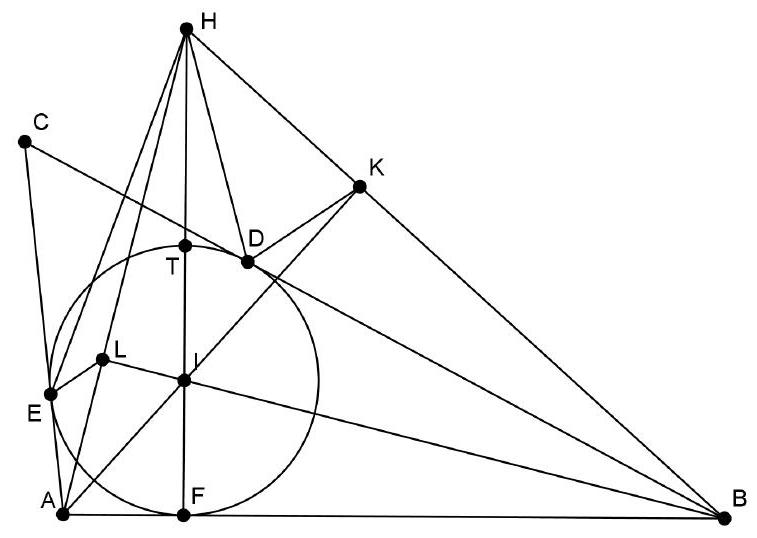
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
De ingeschreven cirkel van een niet-gelijkbenige driehoek $\triangle A B C$ heeft middelpunt $I$ en raakt aan $B C$ en $C A$ in respectievelijk $D$ en $E$. Zij $H$ het hoogtepunt van $\triangle A B I$, zij $K$ het snijpunt van $A I$ en $B H$ en zij $L$ het snijpunt van $B I$ en $A H$. Bewijs dat de omgeschreven cirkels van $\triangle D K H$ en $\triangle E L H$ snijden op de ingeschreven cirkel van $\triangle A B C$.

|
We bekijken de configuratie in de figuur; andere configuraties gaan analoog. Er geldt $\angle I D B=90^{\circ}=\angle I K B$, dus $B K D I$ is een koordenvierhoek. Verder is $\angle A L B=$ $90^{\circ}=\angle A K B$, dus ook $B K L A$ is een koordenvierhoek. Dus
$$
\angle B K D=180^{\circ}-\angle B I D=180^{\circ}-\left(90^{\circ}-\frac{1}{2} \angle A B C\right)=180^{\circ}-\angle B A L=\angle B K L .
$$
Hieruit volgt dat $K, D$ en $L$ op een lijn liggen. Analoog liggen ook $K, E$ en $L$ op een lijn en dat is dezelfde lijn, dus $D$ ligt hier ook op.
Zij $S$ het tweede snijpunt van de omgeschreven cirkels van $\triangle D K H$ en $\triangle E L H$. Dan geldt
$$
\begin{gathered}
\angle D S E=360^{\circ}-\angle D S H-\angle H S E=\angle D K H+180^{\circ}-\angle H L E=\angle L K H+\angle H L K \\
=180^{\circ}-\angle K H L .
\end{gathered}
$$
Omdat ook HLIK een koordenvierhoek is (wegens twee rechte hoeken) geldt
$180^{\circ}-\angle K H L=\angle K I L=\angle A I B=180^{\circ}-\angle I B A-\angle I A B=180^{\circ}-\frac{1}{2} \angle C B A-\frac{1}{2} \angle C A B$.
Dus $\angle D S E=180^{\circ}-\frac{1}{2} \angle C B A-\frac{1}{2} \angle C A B$. Noem nu $F$ het raakpunt van de ingeschreven cirkel aan zijde $A B$, dan zijn $A F I E$ en $B F I D$ ook koordenvierhoeken (allebei wegens twee rechte hoeken). Dus geldt
$$
\angle D F E=\angle D F I+\angle I F E=\angle D B I+\angle I A E=\frac{1}{2} \angle C B A+\frac{1}{2} \angle C A B .
$$
We concluderen dat $\angle D F E+\angle D S E=180^{\circ}$, waaruit volgt dat $S$ op de omgeschreven cirkel van $\triangle D E F$ ligt en dat is precies de ingeschreven cirkel van $\triangle A B C$.

|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2017-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2017"
}
|
The incircle of a non-isosceles triangle $\triangle A B C$ has center $I$ and touches $B C$ and $C A$ at $D$ and $E$, respectively. Let $H$ be the orthocenter of $\triangle A B I$, let $K$ be the intersection of $A I$ and $B H$, and let $L$ be the intersection of $B I$ and $A H$. Prove that the circumcircles of $\triangle D K H$ and $\triangle E L H$ intersect on the incircle of $\triangle A B C$.

|
We prove, just as in solution I, that $K, D, E$ and $L$ lie on a line. Let $T \neq F$ be the intersection of $H I$ and the incircle. If $T=H$, there is nothing to prove. Now assume $T \neq H$. It is sufficient to show that $KDTH$ and $ELTH$ are cyclic quadrilaterals. Due to the cyclic quadrilaterals $ETDF$ (incircle) and $E I F A$ (two right angles), we have: $\angle E D T=\angle E F T=\angle E F I=\angle E A I=\frac{1}{2} \angle C A B$. And due to the cyclic quadrilateral $H K F A$ (two right angles), we further have $\angle K H T=\angle K H F=$ $\angle K A F=\frac{1}{2} \angle C A B$. Therefore, $\angle K H T=\angle E D T=180^{\circ}-\angle K D T$ since $K, D$ and $E$ lie on a line. We conclude that $K D T H$ is a cyclic quadrilateral. The other cyclic quadrilateral follows analogously.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
De ingeschreven cirkel van een niet-gelijkbenige driehoek $\triangle A B C$ heeft middelpunt $I$ en raakt aan $B C$ en $C A$ in respectievelijk $D$ en $E$. Zij $H$ het hoogtepunt van $\triangle A B I$, zij $K$ het snijpunt van $A I$ en $B H$ en zij $L$ het snijpunt van $B I$ en $A H$. Bewijs dat de omgeschreven cirkels van $\triangle D K H$ en $\triangle E L H$ snijden op de ingeschreven cirkel van $\triangle A B C$.

|
We bewijzen net als in oplossing I dat $K, D, E$ en $L$ op een lijn liggen. Noem nu $T \neq F$ het snijpunt van $H I$ en de ingeschreven cirkel. Als $T=H$, dan is er niets te bewijzen. Neem nu aan $T \neq H$. Dan is het voldoende te laten zien dat KDTH en ELTH koordenvierhoeken zijn. Wegens koordenvierhoeken ETDF (ingeschreven cirkel) en $E I F A$ (twee rechte hoeken) geldt: $\angle E D T=\angle E F T=\angle E F I=\angle E A I=\frac{1}{2} \angle C A B$. En vanwege koordenvierhoek $H K F A$ (twee rechte hoeken) geldt verder $\angle K H T=\angle K H F=$ $\angle K A F=\frac{1}{2} \angle C A B$. Dus $\angle K H T=\angle E D T=180^{\circ}-\angle K D T$ aangezien $K, D$ en $E$ op een lijn liggen. We concluderen dat $K D T H$ een koordenvierhoek is. De andere koordenvierhoek gaat analoog.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2017-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2017"
}
|
Let $k>2$ be an integer. A positive integer $\ell$ is called $k$-able if we can partition the numbers $1,3,5, \ldots, 2 k-1$ into two sets $A$ and $B$ such that the sum of the elements of $A$ is exactly $\ell$ times the sum of the elements of $B$. Prove that the smallest $k$-able number is relatively prime to $k$.
|
We will prove that if $p$ is the smallest prime divisor of $k$, then $p-1$ is the smallest $k$-pable number. This implies the desired result, as it then follows that $\operatorname{ggd}(p-1, k)=1$. We know that $1+3+5+\ldots+(2 k-1)=k^{2}$. If $\ell$ is a $k$-pable number and $s$ is the sum of the elements in $B$, then the sum of the elements in $A$ is $\ell s$, so the total sum is $(\ell+1) s$ and this must equal $k^{2}$. Thus, $\ell+1 \mid k^{2}$. Since $\ell+1 \geq 2$, it follows that $\ell+1 \geq p$, where $p$ is the smallest prime divisor of $k$. Therefore, $\ell \geq p-1$. We will now prove that $\ell=p-1$ is a $k$-pable number, which immediately implies that it is the smallest $k$-pable number. And we are done, because $\operatorname{ggd}(k, p-1)=1$ since there are no prime divisors smaller than $p$ in $k$.
First, assume that $k$ is even, so $p=2$. We need to prove that we can partition the set $\{1,3, \ldots, 2 k-1\}$ into two sets with equal sums of the elements. We prove this by induction on $k$. For $k=4$ and $k=6$, we have $\{1,7\},\{3,5\}$ and $\{1,3,5,9\},\{7,11\}$, respectively. If we can partition the set $\{1,3, \ldots, 2 k-1\}$ in this way, we can also do it for the set $\{1,3, \ldots, 2(k+4)-1\}$ by placing the new elements $\{2 k+1,2 k+3,2 k+5,2 k+7\}$ into the sets such that $2 k+1$ and $2 k+7$ go into one set and $2 k+3$ and $2 k+5$ go into the other. This completes the induction. Now assume that $k$ is odd. Write $k=p m$. It is sufficient to find a subset $B$ of $\{1,3, \ldots, 2 k-1\}$ whose sum of elements is $p m^{2}$, because then the sum of the elements in the set $A=\{1,3, \ldots, 2 k-1\} \backslash B$ is $k^{2}-p m^{2}=p^{2} m^{2}-p m^{2}=(p-1) p m^{2}$, which is exactly $(p-1)$ times the sum of the elements in $B$. Consider the set $B=\{p, 3 p, \ldots,(2 m-1) p\} \subset\{1,3, \ldots, 2 k-1\}$. Then the sum of the elements in $B$ is
$$
p+3 p+\cdots+(2 m-1) p=p(1+3+\cdots+(2 m-1))=p m^{2}
$$
exactly as intended.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Zij $k>2$ een geheel getal. Een positief geheel getal $\ell$ noemen we $k$-pabel als we de getallen $1,3,5, \ldots, 2 k-1$ kunnen opdelen in twee verzamelingen $A$ en $B$ zodat de som van de elementen van $A$ precies $\ell$ keer zo groot is als de som van de elementen van $B$. Bewijs dat het kleinste $k$-pabele getal relatief priem is met $k$.
|
We gaan bewijzen dat als $p$ de kleinste priemdeler van $k$ is, dat dan $p-1$ het kleinste $k$-pabele getal is. Hieruit volgt het gevraagde, want er geldt dan $\operatorname{ggd}(p-1, k)=1$. Er geldt $1+3+5+\ldots+(2 k-1)=k^{2}$. Als $\ell$ een $k$-pabel getal is en $s$ is de bijbehorende som van de elementen uit $B$, dan is de som van de elementen uit $A$ gelijk aan $\ell s$, dus is de totale som $(\ell+1) s$ en dat moet gelijk zijn aan $k^{2}$. Dus $\ell+1 \mid k^{2}$. Omdat $\ell+1 \geq 2$ geldt nu $\ell+1 \geq p$, waarbij $p$ de kleinste priemdeler van $k$ is. Dus $\ell \geq p-1$. We gaan nu bewijzen dat $\ell=p-1$ een $k$-pabel getal is, waaruit dan onmiddellijk volgt dat het het kleinste $k$-pabele getal is. En daarmee zijn we klaar, want $\operatorname{ggd}(k, p-1)=1$ omdat er geen priemdelers kleiner dan $p$ in $k$ zitten.
Stel eerst dat $k$ even is, zodat $p=2$. Dan moeten we dus bewijzen dat we de verzameling $\{1,3, \ldots, 2 k-1\}$ kunnen opdelen in twee verzamelingen met gelijke som van de elementen. Dit bewijzen we met inductie naar $k$. Voor $k=4$ en $k=6$ hebben we respectievelijk $\{1,7\},\{3,5\}$ en $\{1,3,5,9\},\{7,11\}$. Als we de verzameling $\{1,3, \ldots, 2 k-1\}$ zo kunnen opdelen, kan dat ook voor de verzameling $\{1,3, \ldots, 2(k+4)-1\}$ door van de nieuwe elementen $\{2 k+1,2 k+3,2 k+5,2 k+7\}$ de elementen $2 k+1$ en $2 k+7$ in de ene verzameling te stoppen en de elementen $2 k+3$ en $2 k+5$ in de andere. Dat voltooit de inductie. Stel nu dat $k$ oneven is. Schrijf $k=p m$. Dan is het voldoende dat we een deelverzameling $B$ van $\{1,3, \ldots, 2 k-1\}$ kunnen vinden waarvan de som van de elementen gelijk is aan $p m^{2}$, want dan is de som van de elementen in de verzameling $A=\{1,3, \ldots, 2 k-1\} \backslash B$ gelijk aan $k^{2}-p m^{2}=p^{2} m^{2}-p m^{2}=(p-1) p m^{2}$ en dus precies $p-1$ keer zo groot als de som van de elementen in $B$. Bekijk de verzameling $B=\{p, 3 p, \ldots,(2 m-1) p\} \subset\{1,3, \ldots, 2 k-1\}$. Dan is de som van de elementen in $B$ gelijk aan
$$
p+3 p+\cdots+(2 m-1) p=p(1+3+\cdots+(2 m-1))=p m^{2}
$$
precies wat de bedoeling was.
|
{
"exam": "Dutch_TST",
"problem_label": "3",
"problem_match": "\nOpgave 3.",
"resource_path": "Dutch_TST/segmented/nl-2017-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing.",
"tier": "T1",
"year": "2017"
}
|
Bepaal alle functies $f: \mathbb{R} \rightarrow \mathbb{R}$ zodat
$$
(y+1) f(x)+f(x f(y)+f(x+y))=y
$$
voor alle $x, y \in \mathbb{R}$.
|
Invullen van $x=0$ geeft $(y+1) f(0)+f(f(y))=y$, dus $f(f(y))=y \cdot(1-$ $f(0))-f(0)$. Als $f(0) \neq 1$, is de rechterkant een bijectieve functie in $y$ en de linkerkant dus ook. Daarmee is in dit geval $f$ bijectief.
We gaan nu laten zien dat in het geval $f(0)=1$ ook geldt dat $f$ bijectief is. Dus stel $f(0)=1$. Dan krijgen we $f(f(y))=-1$ voor alle $y \in \mathbb{R}$. Invullen van $y=0$ geeft $f(x)+f(x+f(x))=0$, dus $f(x+f(x))=-f(x)$. Vul vervolgens $x=f(z)$ en $y=z$ in en vervang $f(f(z))$ door -1 :
$$
(z+1) \cdot-1+f(f(z) f(z)+f(z+f(z)))=z
$$
dus, als we ook nog gebruiken dat $f(z+f(z))=-f(z)$,
$$
f\left(f(z)^{2}-f(z)\right)=2 z+1
$$
Hieruit volgt direct dat $f$ surjectief is. Als er $a$ en $b$ zijn met $f(a)=f(b)$, dan geeft $z=a$ en daarna $z=b$ invullen in deze laatste vergelijking links twee keer hetzelfde, terwijl er rechts eerst $2 a+1$ en daarna $2 b+1$ staat. Dus $a=b$, waaruit volgt dat $f$ injectief is. We zien dat $f$ ook in dit geval bijectief is.
We kunnen dus vanaf nu aannemen dat $f$ bijectief is, waarbij we de aanname $f(0)=1$ weer laten vallen. We weten $f(f(y))=y \cdot(1-f(0))-f(0)$ en dus vinden we met $y=-1$ dat $f(f(-1))=-1$. Invullen van $y=-1$ in de oorspronkelijke vergelijking geeft
$$
f(x f(-1)+f(x-1))=-1=f(f(-1))
$$
Omdat $f$ injectief is, volgt hieruit dat $x f(-1)+f(x-1)=f(-1)$, dus $f(x-1)=$ $f(-1) \cdot(1-x)$. Als we nu $x=z+1$ nemen, zien we dat $f(z)=-f(-1) z$ voor alle $z \in \mathbb{R}$. Dus de functie is van de vorm $f(x)=c x$ voor $x \in \mathbb{R}$, waarbij $c \in \mathbb{R}$ een constante is. We controleren deze functie. Er geldt
$(y+1) f(x)+f(x f(y)+f(x+y))=(y+1) c x+c(x c y+c x+c y)=c x y+c x+c^{2} x y+c^{2} x+c^{2} y$.
Dit moet gelijk zijn aan $y$ voor alle $x, y \in \mathbb{R}$. Met $y=0$ en $x=1$ staat er $c+c^{2}=0$, dus $c=0$ of $c=-1$. Met $x=0$ en $y=1$ staat er $c^{2}=1$, dus $c=1$ of $c=-1$. We concluderen dat $c=-1$ en dan zien we dat deze functie inderdaad voldoet. Dus de enige oplossing is $f(x)=-x$ voor $x \in \mathbb{R}$.
|
f(x)=-x
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Bepaal alle functies $f: \mathbb{R} \rightarrow \mathbb{R}$ zodat
$$
(y+1) f(x)+f(x f(y)+f(x+y))=y
$$
voor alle $x, y \in \mathbb{R}$.
|
Invullen van $x=0$ geeft $(y+1) f(0)+f(f(y))=y$, dus $f(f(y))=y \cdot(1-$ $f(0))-f(0)$. Als $f(0) \neq 1$, is de rechterkant een bijectieve functie in $y$ en de linkerkant dus ook. Daarmee is in dit geval $f$ bijectief.
We gaan nu laten zien dat in het geval $f(0)=1$ ook geldt dat $f$ bijectief is. Dus stel $f(0)=1$. Dan krijgen we $f(f(y))=-1$ voor alle $y \in \mathbb{R}$. Invullen van $y=0$ geeft $f(x)+f(x+f(x))=0$, dus $f(x+f(x))=-f(x)$. Vul vervolgens $x=f(z)$ en $y=z$ in en vervang $f(f(z))$ door -1 :
$$
(z+1) \cdot-1+f(f(z) f(z)+f(z+f(z)))=z
$$
dus, als we ook nog gebruiken dat $f(z+f(z))=-f(z)$,
$$
f\left(f(z)^{2}-f(z)\right)=2 z+1
$$
Hieruit volgt direct dat $f$ surjectief is. Als er $a$ en $b$ zijn met $f(a)=f(b)$, dan geeft $z=a$ en daarna $z=b$ invullen in deze laatste vergelijking links twee keer hetzelfde, terwijl er rechts eerst $2 a+1$ en daarna $2 b+1$ staat. Dus $a=b$, waaruit volgt dat $f$ injectief is. We zien dat $f$ ook in dit geval bijectief is.
We kunnen dus vanaf nu aannemen dat $f$ bijectief is, waarbij we de aanname $f(0)=1$ weer laten vallen. We weten $f(f(y))=y \cdot(1-f(0))-f(0)$ en dus vinden we met $y=-1$ dat $f(f(-1))=-1$. Invullen van $y=-1$ in de oorspronkelijke vergelijking geeft
$$
f(x f(-1)+f(x-1))=-1=f(f(-1))
$$
Omdat $f$ injectief is, volgt hieruit dat $x f(-1)+f(x-1)=f(-1)$, dus $f(x-1)=$ $f(-1) \cdot(1-x)$. Als we nu $x=z+1$ nemen, zien we dat $f(z)=-f(-1) z$ voor alle $z \in \mathbb{R}$. Dus de functie is van de vorm $f(x)=c x$ voor $x \in \mathbb{R}$, waarbij $c \in \mathbb{R}$ een constante is. We controleren deze functie. Er geldt
$(y+1) f(x)+f(x f(y)+f(x+y))=(y+1) c x+c(x c y+c x+c y)=c x y+c x+c^{2} x y+c^{2} x+c^{2} y$.
Dit moet gelijk zijn aan $y$ voor alle $x, y \in \mathbb{R}$. Met $y=0$ en $x=1$ staat er $c+c^{2}=0$, dus $c=0$ of $c=-1$. Met $x=0$ en $y=1$ staat er $c^{2}=1$, dus $c=1$ of $c=-1$. We concluderen dat $c=-1$ en dan zien we dat deze functie inderdaad voldoet. Dus de enige oplossing is $f(x)=-x$ voor $x \in \mathbb{R}$.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2017-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2017"
}
|
Determine all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
(y+1) f(x)+f(x f(y)+f(x+y))=y
$$
for all $x, y \in \mathbb{R}$.
|
We provide an alternative proof for the case $f(0)=1$. Just like in the first solution, we find $f(f(y))=-1$ for all $y \in \mathbb{R}$. Now substitute $x=f(0)=1$:
$$
(y+1) f(f(0))+f(f(y)+f(1+y))=y
$$
We have $f(f(0))=-1$, so
$$
f(f(y)+f(1+y))=2 y+1
$$
If we now apply $f$ to both sides, we get
$$
f(f(f(y)+f(1+y)))=f(2 y+1)
$$
The left side is simply -1, so $f$ is everywhere equal to -1, but this contradicts $f(0)=1$. In this case, there are therefore no solutions.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Bepaal alle functies $f: \mathbb{R} \rightarrow \mathbb{R}$ zodat
$$
(y+1) f(x)+f(x f(y)+f(x+y))=y
$$
voor alle $x, y \in \mathbb{R}$.
|
We geven een alternatief bewijs voor het geval $f(0)=1$. Net als in de eerste oplossing vinden we $f(f(y))=-1$ voor alle $y \in \mathbb{R}$. Vul nu $x=f(0)=1$ in:
$$
(y+1) f(f(0))+f(f(y)+f(1+y))=y
$$
Er geldt $f(f(0))=-1$, dus
$$
f(f(y)+f(1+y))=2 y+1
$$
Als we nu links en rechts $f$ toepassen, vinden we
$$
f(f(f(y)+f(1+y)))=f(2 y+1)
$$
Links staat hier gewoon -1 , dus $f$ is overal gelijk aan -1 , maar dat is een tegenspraak met $f(0)=1$. In dit geval zijn er dus geen oplossingen.
|
{
"exam": "Dutch_TST",
"problem_label": "4",
"problem_match": "\nOpgave 4.",
"resource_path": "Dutch_TST/segmented/nl-2017-D_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2017"
}
|
Given is circle $\omega$ with diameter $A K$. Point $M$ lies inside the circle, not on line $A K$. The line $A M$ intersects $\omega$ again at $Q$. The tangent to $\omega$ at $Q$ intersects the line through $M$ perpendicular to $A K$ at $P$. Point $L$ lies on $\omega$ such that $P L$ is a tangent, with $L \neq Q$. Prove that $K, L$, and $M$ lie on a line.
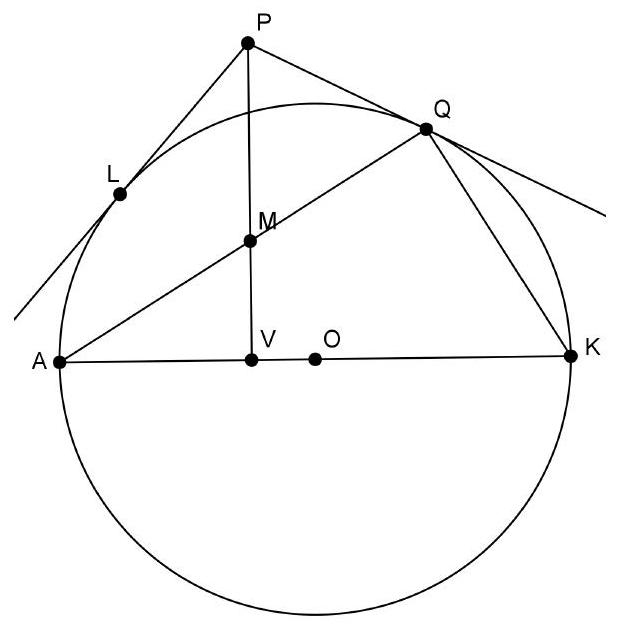
|
Let $O$ be the center of $\omega$ and let $V$ be the intersection of $M P$ with $A K$. We first prove that $\angle P V L=\angle P O L$. If $V$ and $O$ coincide, there is nothing to prove. If $V$ and $O$ do not coincide, then $\angle O V P=90^{\circ}=\angle O L P$, so $O V P L$ or $V O P L$ is a cyclic quadrilateral. (In fact, $Q$ also lies on the corresponding circumscribed circle.) From this, it follows that $\angle P V L=\angle P O L$. We now have in all cases $\angle M V L=\angle P V L=\angle P O L$. Since $P L$ and $P Q$ are tangents to $\omega$, $\triangle O Q P \cong \triangle O L P$, so $\angle P O L=\frac{1}{2} \angle Q O L$. By the central angle theorem applied to $\omega$, this angle is also equal to $\angle Q A L$. Altogether, we find
$$
\angle M V L=\angle P O L=\angle Q A L=\angle M A L
$$
which implies that $M V A L$ is a cyclic quadrilateral. Therefore, $\angle A L M=180^{\circ}-\angle A V M=90^{\circ}$. Furthermore, by Thales' theorem, $\angle A L K=90^{\circ}$, so $\angle A L M=\angle A L K$, which means that $L$, $M$, and $K$ lie on a straight line.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Gegeven is cirkel $\omega$ met middellijn $A K$. Punt $M$ ligt binnen de cirkel, niet op lijn $A K$. De lijn $A M$ snijdt $\omega$ nogmaals in $Q$. De raaklijn aan $\omega$ in $Q$ snijdt de lijn door $M$ loodrecht op $A K$ in $P$. Punt $L$ ligt op $\omega$ zodat $P L$ een raaklijn is, met $L \neq Q$. Bewijs dat $K, L$ en $M$ op een lijn liggen.

|
Noem $O$ het middelpunt van $\omega$ en zij $V$ het snijpunt van $M P$ met $A K$. We bewijzen nu eerst dat $\angle P V L=\angle P O L$. Als $V$ en $O$ samenvallen, dan is er niets te bewijzen. Als $V$ en $O$ niet samenvallen, dan geldt $\angle O V P=90^{\circ}=\angle O L P$, dus $O V P L$ of $V O P L$ is een koordenvierhoek. (In feite ligt $Q$ ook nog op de bijbehorende omgeschreven cirkel.) Hieruit volgt dat $\angle P V L=\angle P O L$. We hebben nu in alle gevallen $\angle M V L=\angle P V L=\angle P O L$. Omdat $P L$ en $P Q$ raken aan $\omega$, geldt $\triangle O Q P \cong \triangle O L P$, dus $\angle P O L=\frac{1}{2} \angle Q O L$. Vanwege de middelpuntsomtrekshoekstelling toegepast op $\omega$ is die hoek bovendien gelijk aan $\angle Q A L$. Al met al vinden we
$$
\angle M V L=\angle P O L=\angle Q A L=\angle M A L
$$
waaruit volgt dat $M V A L$ een koordenvierhoek is. Dus $\angle A L M=180^{\circ}-\angle A V M=90^{\circ}$. Verder geldt wegens Thales dat $\angle A L K=90^{\circ}$, dus $\angle A L M=\angle A L K$, wat betekent dat $L$, $M$ en $K$ op een lijn liggen.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2017-E_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2017"
}
|
Given is circle $\omega$ with diameter $A K$. Point $M$ lies inside the circle, not on line $A K$. The line $A M$ intersects $\omega$ again at $Q$. The tangent to $\omega$ at $Q$ intersects the line through $M$ perpendicular to $A K$ at $P$. Point $L$ lies on $\omega$ such that $P L$ is a tangent, with $L \neq Q$. Prove that $K, L$, and $M$ lie on a line.

|
We define $V$ as in the first solution. By Thales, $\angle M Q K=90^{\circ}=\angle M V K$, so $M Q K V$ is a cyclic quadrilateral. Therefore, $\angle P M Q=180^{\circ}-$
$\angle V M Q=\angle V K Q=\angle A K Q$. Since $P Q$ is tangent to $\omega$, we have $\angle A K Q=\angle A Q P=\angle M Q P$. Altogether, $\angle P M Q=\angle M Q P$, which means that $\triangle M Q P$ is isosceles with $|P M|=|P Q|$. Due to equal tangent segments, $|P Q|=|P L|$ as well, so $P$ is the center of the circle through $M, Q$, and $L$. It follows that
$$
\angle Q L M=\frac{1}{2} \angle Q P M=90^{\circ}-\angle M Q P=90^{\circ}-\angle A K Q=\angle Q A K=\angle Q L K
$$
We conclude that $L, M$, and $K$ lie on a straight line.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Gegeven is cirkel $\omega$ met middellijn $A K$. Punt $M$ ligt binnen de cirkel, niet op lijn $A K$. De lijn $A M$ snijdt $\omega$ nogmaals in $Q$. De raaklijn aan $\omega$ in $Q$ snijdt de lijn door $M$ loodrecht op $A K$ in $P$. Punt $L$ ligt op $\omega$ zodat $P L$ een raaklijn is, met $L \neq Q$. Bewijs dat $K, L$ en $M$ op een lijn liggen.

|
We definiëren $V$ als in de eerste oplossing. Er geldt wegens Thales dat $\angle M Q K=90^{\circ}=\angle M V K$, dus $M Q K V$ is een koordenvierhoek. Dus $\angle P M Q=180^{\circ}-$
$\angle V M Q=\angle V K Q=\angle A K Q$. Omdat $P Q$ raakt aan $\omega$ geldt $\angle A K Q=\angle A Q P=\angle M Q P$. Al met al geldt dus $\angle P M Q=\angle M Q P$, wat betekent dat $\triangle M Q P$ gelijkbenig is met $|P M|=|P Q|$. Vanwege gelijke raaklijnstukjes is ook $|P Q|=|P L|$, dus $P$ is het middelpunt van de cirkel door $M, Q$ en $L$. Daaruit volgt
$$
\angle Q L M=\frac{1}{2} \angle Q P M=90^{\circ}-\angle M Q P=90^{\circ}-\angle A K Q=\angle Q A K=\angle Q L K
$$
We concluderen dat $L, M$ en $K$ op een lijn liggen.
|
{
"exam": "Dutch_TST",
"problem_label": "1",
"problem_match": "\nOpgave 1.",
"resource_path": "Dutch_TST/segmented/nl-2017-E_uitwerkingen.jsonl",
"solution_match": "\nOplossing II.",
"tier": "T1",
"year": "2017"
}
|
Let $a_{1}, a_{2}, \ldots, a_{n}$ be a sequence of real numbers such that $a_{1}+\cdots+a_{n}=0$ and define $b_{i}=a_{1}+\cdots+a_{i}$ for $1 \leq i \leq n$. Suppose that $b_{i}\left(a_{j+1}-a_{i+1}\right) \geq 0$ for all $1 \leq i \leq j \leq n-1$. Prove that
$$
\max _{1 \leq \ell \leq n}\left|a_{\ell}\right| \geq \max _{1 \leq m \leq n}\left|b_{m}\right|
$$
|
Given $b_{n}=0$. Suppose there is an $i \leq n-1$ with $b_{i}>0$ and $a_{i+1} \geq 0$. Then it follows from $b_{i}\left(a_{j+1}-a_{i+1}\right) \geq 0$ that $a_{j+1} \geq a_{i+1} \geq 0$ for all $i \leq j \leq n-1$. Thus $b_{n}=b_{i}+a_{i+1}+a_{i+2}+\ldots+a_{n} \geq b_{i}>0$, a contradiction. We conclude that if $b_{i}>0$, then $a_{i+1}<0$. And similarly: if $b_{i}<0$, then $a_{i+1}>0$.
Now let $k$ be such that $\left|b_{k}\right|=\max _{1 \leq m \leq n}\left|b_{m}\right|$. We can assume without loss of generality that $b_{k}>0$ (otherwise we multiply all $a_{i}$ by -1). If $k=1$, then $b_{k}=a_{1}$, so $\left|b_{k}\right|=\left|a_{1}\right| \leq \max _{1 \leq \ell \leq n}\left|a_{\ell}\right|$ and we are done. Now suppose $k>1$. If $b_{k-1}>0$, then according to the above, $a_{k}<0$. On the other hand, $a_{k}=b_{k}-b_{k-1} \geq 0$ because $b_{k}$ was maximal, a contradiction. Therefore, $b_{k-1} \leq 0$. Now $a_{k}=b_{k}-b_{k-1}=b_{k}+\left|b_{k-1}\right| \geq b_{k}$, so $\left|b_{k}\right| \leq\left|a_{k}\right| \leq \max _{1 \leq \ell \leq n}\left|a_{\ell}\right|$, which is what we needed to prove.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
$\mathrm{Zij} a_{1}, a_{2}, \ldots, a_{n}$ een rijtje reële getallen zodat $a_{1}+\cdots+a_{n}=0$ en definieer $b_{i}=a_{1}+\cdots+a_{i}$ voor $1 \leq i \leq n$. Veronderstel dat $b_{i}\left(a_{j+1}-a_{i+1}\right) \geq 0$ voor alle $1 \leq i \leq$ $j \leq n-1$. Bewijs dat
$$
\max _{1 \leq \ell \leq n}\left|a_{\ell}\right| \geq \max _{1 \leq m \leq n}\left|b_{m}\right|
$$
|
Er geldt $b_{n}=0$. Stel dat er een $i \leq n-1$ is met $b_{i}>0$ en $a_{i+1} \geq 0$. Dan volgt uit $b_{i}\left(a_{j+1}-a_{i+1}\right) \geq 0$ dat $a_{j+1} \geq a_{i+1} \geq 0$ voor alle $i \leq j \leq n-1$. Dus $b_{n}=b_{i}+a_{i+1}+a_{i+2}+\ldots+a_{n} \geq b_{i}>0$, tegenspraak. We concluderen dat uit $b_{i}>0$ volgt dat $a_{i+1}<0$. En analoog: als $b_{i}<0$, dan geldt $a_{i+1}>0$.
Zij nu $k$ zo dat $\left|b_{k}\right|=\max _{1 \leq m \leq n}\left|b_{m}\right|$. We kunnen zonder verlies van algemeenheid aannemen dat $b_{k}>0$ (anders vermenigvuldigen we alle $a_{i}$ met -1 ). Als $k=1$, dan geldt $b_{k}=a_{1}$, dus $\left|b_{k}\right|=\left|a_{1}\right| \leq \max _{1 \leq \ell \leq n}\left|a_{\ell}\right|$ en dan zijn we klaar. Stel nu $k>1$. Als $b_{k-1}>0$, dan geldt volgens bovenstaande dat $a_{k}<0$. Anderzijds is $a_{k}=b_{k}-b_{k-1} \geq 0$ omdat $b_{k}$ maximaal was, tegenspraak. Dus $b_{k-1} \leq 0$. Nu is $a_{k}=b_{k}-b_{k-1}=b_{k}+\left|b_{k-1}\right| \geq b_{k}$, dus $\left|b_{k}\right| \leq\left|a_{k}\right| \leq \max _{1 \leq \ell \leq n}\left|a_{\ell}\right|$, wat we moesten bewijzen.
|
{
"exam": "Dutch_TST",
"problem_label": "2",
"problem_match": "\nOpgave 2.",
"resource_path": "Dutch_TST/segmented/nl-2017-E_uitwerkingen.jsonl",
"solution_match": "\nOplossing I.",
"tier": "T1",
"year": "2017"
}
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.