problem
stringlengths 14
10.4k
| solution
stringlengths 1
24.1k
| answer
stringlengths 1
250
⌀ | problem_is_valid
stringclasses 4
values | solution_is_valid
stringclasses 3
values | question_type
stringclasses 4
values | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
10.4k
| solution_raw
stringlengths 1
24.1k
| metadata
dict |
|---|---|---|---|---|---|---|---|---|---|
There are $n \geqslant 3$ positive real numbers $a_{1}, a_{2}, \ldots, a_{n}$. For each $1 \leqslant i \leqslant n$ we let $b_{i}=\frac{a_{i-1}+a_{i+1}}{a_{i}}$ (here we define $a_{0}$ to be $a_{n}$ and $a_{n+1}$ to be $a_{1}$ ). Assume that for all $i$ and $j$ in the range 1 to $n$, we have $a_{i} \leqslant a_{j}$ if and only if $b_{i} \leqslant b_{j}$.
Prove that $a_{1}=a_{2}=\cdots=a_{n}$.
|
Choose an arbitrary index $i$ and assume without loss of generality that $a_{i} \leqslant a_{i+1}$. (If the opposite inequality holds, reverse all the inequalities below.) By induction we will show that for each $k \in \mathbb{N}_{0}$ the following two inequalities hold
$$
\begin{gathered}
a_{i+1+k} \geqslant a_{i-k} \\
a_{i+1+k} a_{i+1-k} \geqslant a_{i-k} a_{i+k}
\end{gathered}
$$
(where all indices are cyclic modulo $n$ ). Both inequalities trivially hold for $k=0$.
Assume now that both inequalities hold for some $k \geqslant 0$. The inequality $a_{i+1+k} \geqslant a_{i-k}$ implies $b_{i+1+k} \geqslant b_{i-k}$, so
$$
\frac{a_{i+k}+a_{i+2+k}}{a_{i+1+k}} \geqslant \frac{a_{i-1-k}+a_{i+1-k}}{a_{i-k}} .
$$
We may rearrange this inequality by making $a_{i+2+k}$ the subject so
$$
a_{i+2+k} \geqslant \frac{a_{i+1+k} a_{i-1-k}}{a_{i-k}}+\frac{a_{i+1-k} a_{i+1+k}-a_{i+k} a_{i-k}}{a_{i-k}} \geqslant \frac{a_{i+1+k} a_{i-1-k}}{a_{i-k}},
$$
where the last inequality holds by (2). It follows that
$$
a_{(i+1)+(k+1)} a_{(i+1)-(k+1)} \geqslant a_{i+(k+1)} a_{i-(k+1)},
$$
i.e. the inequality (2) holds also for $k+1$. Using (1) we now get
$$
a_{(i+1)+(k+1)} \geqslant \frac{a_{i+k+1}}{a_{i-k}} a_{i-(k+1)} \geqslant a_{i-(k+1)},
$$
i.e. (1) holds for $k+1$.
Now we use the inequality (1) for $k=n-1$. We get $a_{i} \geqslant a_{i+1}$, and since at the beginning we assumed $a_{i} \leqslant a_{i+1}$, we get that any two consecutive $a$ 's are equal, so all of them are equal.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
There are $n \geqslant 3$ positive real numbers $a_{1}, a_{2}, \ldots, a_{n}$. For each $1 \leqslant i \leqslant n$ we let $b_{i}=\frac{a_{i-1}+a_{i+1}}{a_{i}}$ (here we define $a_{0}$ to be $a_{n}$ and $a_{n+1}$ to be $a_{1}$ ). Assume that for all $i$ and $j$ in the range 1 to $n$, we have $a_{i} \leqslant a_{j}$ if and only if $b_{i} \leqslant b_{j}$.
Prove that $a_{1}=a_{2}=\cdots=a_{n}$.
|
Choose an arbitrary index $i$ and assume without loss of generality that $a_{i} \leqslant a_{i+1}$. (If the opposite inequality holds, reverse all the inequalities below.) By induction we will show that for each $k \in \mathbb{N}_{0}$ the following two inequalities hold
$$
\begin{gathered}
a_{i+1+k} \geqslant a_{i-k} \\
a_{i+1+k} a_{i+1-k} \geqslant a_{i-k} a_{i+k}
\end{gathered}
$$
(where all indices are cyclic modulo $n$ ). Both inequalities trivially hold for $k=0$.
Assume now that both inequalities hold for some $k \geqslant 0$. The inequality $a_{i+1+k} \geqslant a_{i-k}$ implies $b_{i+1+k} \geqslant b_{i-k}$, so
$$
\frac{a_{i+k}+a_{i+2+k}}{a_{i+1+k}} \geqslant \frac{a_{i-1-k}+a_{i+1-k}}{a_{i-k}} .
$$
We may rearrange this inequality by making $a_{i+2+k}$ the subject so
$$
a_{i+2+k} \geqslant \frac{a_{i+1+k} a_{i-1-k}}{a_{i-k}}+\frac{a_{i+1-k} a_{i+1+k}-a_{i+k} a_{i-k}}{a_{i-k}} \geqslant \frac{a_{i+1+k} a_{i-1-k}}{a_{i-k}},
$$
where the last inequality holds by (2). It follows that
$$
a_{(i+1)+(k+1)} a_{(i+1)-(k+1)} \geqslant a_{i+(k+1)} a_{i-(k+1)},
$$
i.e. the inequality (2) holds also for $k+1$. Using (1) we now get
$$
a_{(i+1)+(k+1)} \geqslant \frac{a_{i+k+1}}{a_{i-k}} a_{i-(k+1)} \geqslant a_{i-(k+1)},
$$
i.e. (1) holds for $k+1$.
Now we use the inequality (1) for $k=n-1$. We get $a_{i} \geqslant a_{i+1}$, and since at the beginning we assumed $a_{i} \leqslant a_{i+1}$, we get that any two consecutive $a$ 's are equal, so all of them are equal.
|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "\nProblem 1.",
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"solution_match": "\nSolution 7. ",
"tier": "T2",
"year": "2023"
}
|
There are $n \geqslant 3$ positive real numbers $a_{1}, a_{2}, \ldots, a_{n}$. For each $1 \leqslant i \leqslant n$ we let $b_{i}=\frac{a_{i-1}+a_{i+1}}{a_{i}}$ (here we define $a_{0}$ to be $a_{n}$ and $a_{n+1}$ to be $a_{1}$ ). Assume that for all $i$ and $j$ in the range 1 to $n$, we have $a_{i} \leqslant a_{j}$ if and only if $b_{i} \leqslant b_{j}$.
Prove that $a_{1}=a_{2}=\cdots=a_{n}$.
|
We first prove the following claim by induction:
Claim 1: If $a_{k} a_{k+2}<a_{k+1}^{2}$ and $a_{k}<a_{k+1}$, then $a_{j} a_{j+2}<a_{j+1}^{2}$ and $a_{j}<a_{j+1}$ for all $j$.
We assume that $a_{i} a_{i+2}<a_{i+1}^{2}$ and $a_{i}<a_{i+1}$, and then show that $a_{i-1} a_{i+1}<a_{i}^{2}$ and $a_{i-1}<a_{i}$.
Since $a_{i} \leq a_{i+1}$ we have that $b_{i} \leq b_{i+1}$. By plugging in the definition of $b_{i}$ and $b_{i+1}$ we have that
$$
a_{i+1} a_{i-1}+a_{i+1}^{2} \leq a_{i}^{2}+a_{i+2} a_{i}
$$
Using $a_{i} a_{i+2}<a_{i+1}^{2}$ we get that
$$
a_{i+1} a_{i-1}<a_{i}^{2} .
$$
Since $a_{i}<a_{i+1}$ we have that $a_{i-1}<a_{i}$, which concludes the induction step and hence proves the claim.
We cannot have that $a_{j}<a_{j+1}$ for all indices $j$. Similar as in the above claim, one can prove that if $a_{k} a_{k+2}<a_{k+1}^{2}$ and $a_{k+2}<a_{k+1}$, then $a_{j+1}<a_{j}$ for all $j$, which also cannot be the case. Thus we have that $a_{k} a_{k+2} \geq a_{k+1}^{2}$ for all indices $k$.
Next observe (e.g. by taking the product over all indices) that this implies $a_{k} a_{k+2}=a_{k+1}^{2}$ for all indices $k$, which is equivalent to $b_{k}=b_{k+1}$ for all $k$ and hence $a_{k+1}=a_{k}$ for all $k$.
|
a_{1}=a_{2}=\cdots=a_{n}
|
Yes
|
Yes
|
proof
|
Algebra
|
There are $n \geqslant 3$ positive real numbers $a_{1}, a_{2}, \ldots, a_{n}$. For each $1 \leqslant i \leqslant n$ we let $b_{i}=\frac{a_{i-1}+a_{i+1}}{a_{i}}$ (here we define $a_{0}$ to be $a_{n}$ and $a_{n+1}$ to be $a_{1}$ ). Assume that for all $i$ and $j$ in the range 1 to $n$, we have $a_{i} \leqslant a_{j}$ if and only if $b_{i} \leqslant b_{j}$.
Prove that $a_{1}=a_{2}=\cdots=a_{n}$.
|
We first prove the following claim by induction:
Claim 1: If $a_{k} a_{k+2}<a_{k+1}^{2}$ and $a_{k}<a_{k+1}$, then $a_{j} a_{j+2}<a_{j+1}^{2}$ and $a_{j}<a_{j+1}$ for all $j$.
We assume that $a_{i} a_{i+2}<a_{i+1}^{2}$ and $a_{i}<a_{i+1}$, and then show that $a_{i-1} a_{i+1}<a_{i}^{2}$ and $a_{i-1}<a_{i}$.
Since $a_{i} \leq a_{i+1}$ we have that $b_{i} \leq b_{i+1}$. By plugging in the definition of $b_{i}$ and $b_{i+1}$ we have that
$$
a_{i+1} a_{i-1}+a_{i+1}^{2} \leq a_{i}^{2}+a_{i+2} a_{i}
$$
Using $a_{i} a_{i+2}<a_{i+1}^{2}$ we get that
$$
a_{i+1} a_{i-1}<a_{i}^{2} .
$$
Since $a_{i}<a_{i+1}$ we have that $a_{i-1}<a_{i}$, which concludes the induction step and hence proves the claim.
We cannot have that $a_{j}<a_{j+1}$ for all indices $j$. Similar as in the above claim, one can prove that if $a_{k} a_{k+2}<a_{k+1}^{2}$ and $a_{k+2}<a_{k+1}$, then $a_{j+1}<a_{j}$ for all $j$, which also cannot be the case. Thus we have that $a_{k} a_{k+2} \geq a_{k+1}^{2}$ for all indices $k$.
Next observe (e.g. by taking the product over all indices) that this implies $a_{k} a_{k+2}=a_{k+1}^{2}$ for all indices $k$, which is equivalent to $b_{k}=b_{k+1}$ for all $k$ and hence $a_{k+1}=a_{k}$ for all $k$.
|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "\nProblem 1.",
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"solution_match": "\nSolution 8. ",
"tier": "T2",
"year": "2023"
}
|
There are $n \geqslant 3$ positive real numbers $a_{1}, a_{2}, \ldots, a_{n}$. For each $1 \leqslant i \leqslant n$ we let $b_{i}=\frac{a_{i-1}+a_{i+1}}{a_{i}}$ (here we define $a_{0}$ to be $a_{n}$ and $a_{n+1}$ to be $a_{1}$ ). Assume that for all $i$ and $j$ in the range 1 to $n$, we have $a_{i} \leqslant a_{j}$ if and only if $b_{i} \leqslant b_{j}$.
Prove that $a_{1}=a_{2}=\cdots=a_{n}$.
|
Define $c_{i}:=\frac{a_{i}}{a_{i+1}}$, then $b_{i}=c_{i-1}+1 / c_{i}$. Assume that not all $c_{i}$ are equal to 1. Since, $\prod_{i=1}^{n} c_{i}=1$ there exists a $k$ such that $c_{k} \geqslant 1$. From the condition given in the problem statement for $(i, j)=(k, k+1)$ we have
$$
c_{k} \geqslant 1 \Longleftrightarrow c_{k-1}+\frac{1}{c_{k}} \geqslant c_{k}+\frac{1}{c_{k+1}} \Longleftrightarrow c_{k-1} c_{k} c_{k+1}+c_{k+1} \geqslant c_{k}^{2} c_{k+1}+c_{k}
$$
Now since $c_{k+1} \leqslant c_{k}^{2} c_{k+1}$, it follows that
$$
c_{i-1} c_{i} c_{i+1} \geqslant c_{i} \Longrightarrow\left(c_{i-1} \geqslant 1 \text { or } c_{i+1} \geqslant 1\right) .
$$
So there exist a set of at least 2 consecutive integers, such that the corresponding $c_{i}$ are greater or equal to one. By the innitial assumption there must exist an index $\ell$, such that $c_{\ell-1}, c_{\ell} \geqslant 1$ and $c_{\ell+1}<1$. We distinguish two cases:
Case 1: $c_{\ell}>c_{\ell-1} \geqslant 1$
From $c_{\ell-1} c_{\ell} c_{\ell+1}<c_{\ell}^{2} c_{\ell+1}$ and the inequality (5), we get that $c_{\ell+1}>c_{\ell} \geqslant 1$, which is a contradiction to our choice of $\ell$.
Case 2: $c_{\ell-1} \geqslant c_{\ell} \geqslant 1$
Once again looking at the inequality (5) we can find that
$$
c_{\ell-2} c_{\ell-1} c_{\ell} \geqslant c_{\ell-1}^{2} c_{\ell} \Longrightarrow c_{\ell-2} \geqslant c_{\ell-1} .
$$
Note that we only needed $c_{\ell-1} \geqslant c_{\ell} \geqslant 1$ to show $c_{\ell-2} \geqslant c_{\ell-1} \geqslant 1$. So using induction we can easily show $c_{\ell-s-1} \geqslant c_{\ell-s}$ for all $s$.
So
$$
c_{1} \leqslant c_{2} \leqslant \cdots \leqslant c_{n} \leqslant c_{1}
$$
a contradiction to our innitial assumption.
So our innitial assumtion must have been wrong, which implies that all the $a_{i}$ must have been equal from the start.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
There are $n \geqslant 3$ positive real numbers $a_{1}, a_{2}, \ldots, a_{n}$. For each $1 \leqslant i \leqslant n$ we let $b_{i}=\frac{a_{i-1}+a_{i+1}}{a_{i}}$ (here we define $a_{0}$ to be $a_{n}$ and $a_{n+1}$ to be $a_{1}$ ). Assume that for all $i$ and $j$ in the range 1 to $n$, we have $a_{i} \leqslant a_{j}$ if and only if $b_{i} \leqslant b_{j}$.
Prove that $a_{1}=a_{2}=\cdots=a_{n}$.
|
Define $c_{i}:=\frac{a_{i}}{a_{i+1}}$, then $b_{i}=c_{i-1}+1 / c_{i}$. Assume that not all $c_{i}$ are equal to 1. Since, $\prod_{i=1}^{n} c_{i}=1$ there exists a $k$ such that $c_{k} \geqslant 1$. From the condition given in the problem statement for $(i, j)=(k, k+1)$ we have
$$
c_{k} \geqslant 1 \Longleftrightarrow c_{k-1}+\frac{1}{c_{k}} \geqslant c_{k}+\frac{1}{c_{k+1}} \Longleftrightarrow c_{k-1} c_{k} c_{k+1}+c_{k+1} \geqslant c_{k}^{2} c_{k+1}+c_{k}
$$
Now since $c_{k+1} \leqslant c_{k}^{2} c_{k+1}$, it follows that
$$
c_{i-1} c_{i} c_{i+1} \geqslant c_{i} \Longrightarrow\left(c_{i-1} \geqslant 1 \text { or } c_{i+1} \geqslant 1\right) .
$$
So there exist a set of at least 2 consecutive integers, such that the corresponding $c_{i}$ are greater or equal to one. By the innitial assumption there must exist an index $\ell$, such that $c_{\ell-1}, c_{\ell} \geqslant 1$ and $c_{\ell+1}<1$. We distinguish two cases:
Case 1: $c_{\ell}>c_{\ell-1} \geqslant 1$
From $c_{\ell-1} c_{\ell} c_{\ell+1}<c_{\ell}^{2} c_{\ell+1}$ and the inequality (5), we get that $c_{\ell+1}>c_{\ell} \geqslant 1$, which is a contradiction to our choice of $\ell$.
Case 2: $c_{\ell-1} \geqslant c_{\ell} \geqslant 1$
Once again looking at the inequality (5) we can find that
$$
c_{\ell-2} c_{\ell-1} c_{\ell} \geqslant c_{\ell-1}^{2} c_{\ell} \Longrightarrow c_{\ell-2} \geqslant c_{\ell-1} .
$$
Note that we only needed $c_{\ell-1} \geqslant c_{\ell} \geqslant 1$ to show $c_{\ell-2} \geqslant c_{\ell-1} \geqslant 1$. So using induction we can easily show $c_{\ell-s-1} \geqslant c_{\ell-s}$ for all $s$.
So
$$
c_{1} \leqslant c_{2} \leqslant \cdots \leqslant c_{n} \leqslant c_{1}
$$
a contradiction to our innitial assumption.
So our innitial assumtion must have been wrong, which implies that all the $a_{i}$ must have been equal from the start.
|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "\nProblem 1.",
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"solution_match": "\nSolution 9. ",
"tier": "T2",
"year": "2023"
}
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
Let $M$ be the midpoint of $K L$. We will prove that $M$ is the orthocentre of $A B C$. Since $D K$ and $D L$ are tangent to the same circle, $|D K|=|D L|$ and hence $D M \perp K L$. The theorem of Thales in circle $A B C$ also gives $D B \perp B A$ and $D C \perp C A$. The right angles then give that quadrilaterals $B D M K$ and $D M L C$ are cyclic.
If $\angle B A C=\alpha$, then clearly $\angle D K M=\angle M L D=\alpha$ by angle in the alternate segment of circle $A K L$, and so $\angle M D K=\angle L D M=\frac{\pi}{2}-\alpha$, which thanks to cyclic quadrilaterals gives $\angle M B K=\angle L C M=\frac{\pi}{2}-\alpha$. From this, we have $B M \perp A C$ and $C M \perp A B$, and so $M$ indeed is the orthocentre of $A B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
Let $M$ be the midpoint of $K L$. We will prove that $M$ is the orthocentre of $A B C$. Since $D K$ and $D L$ are tangent to the same circle, $|D K|=|D L|$ and hence $D M \perp K L$. The theorem of Thales in circle $A B C$ also gives $D B \perp B A$ and $D C \perp C A$. The right angles then give that quadrilaterals $B D M K$ and $D M L C$ are cyclic.
If $\angle B A C=\alpha$, then clearly $\angle D K M=\angle M L D=\alpha$ by angle in the alternate segment of circle $A K L$, and so $\angle M D K=\angle L D M=\frac{\pi}{2}-\alpha$, which thanks to cyclic quadrilaterals gives $\angle M B K=\angle L C M=\frac{\pi}{2}-\alpha$. From this, we have $B M \perp A C$ and $C M \perp A B$, and so $M$ indeed is the orthocentre of $A B C$.
|
{
"exam": "EGMO",
"problem_label": "2",
"problem_match": "\nProblem 2.",
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"solution_match": "\nSolution 1. ",
"tier": "T2",
"year": "2023"
}
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
Preliminaries
Let $A B C$ be a triangle with circumcircle $\Gamma$. Let $X$ be a point in the plane. The Simson line (Wallace-Simson line) is defined via the following theorem. Drop perpendiculars from $X$ to each of the three side lines of $A B C$. The feet of these perpendiculars are collinear (on
the Simson line of $X$ ) if and only if $X$ lies of $\Gamma$. The Simson line of $X$ in the circumcircle bisects the line segment $X H$ where $H$ is the orthocentre of triangle $A B C$. See Figure 2
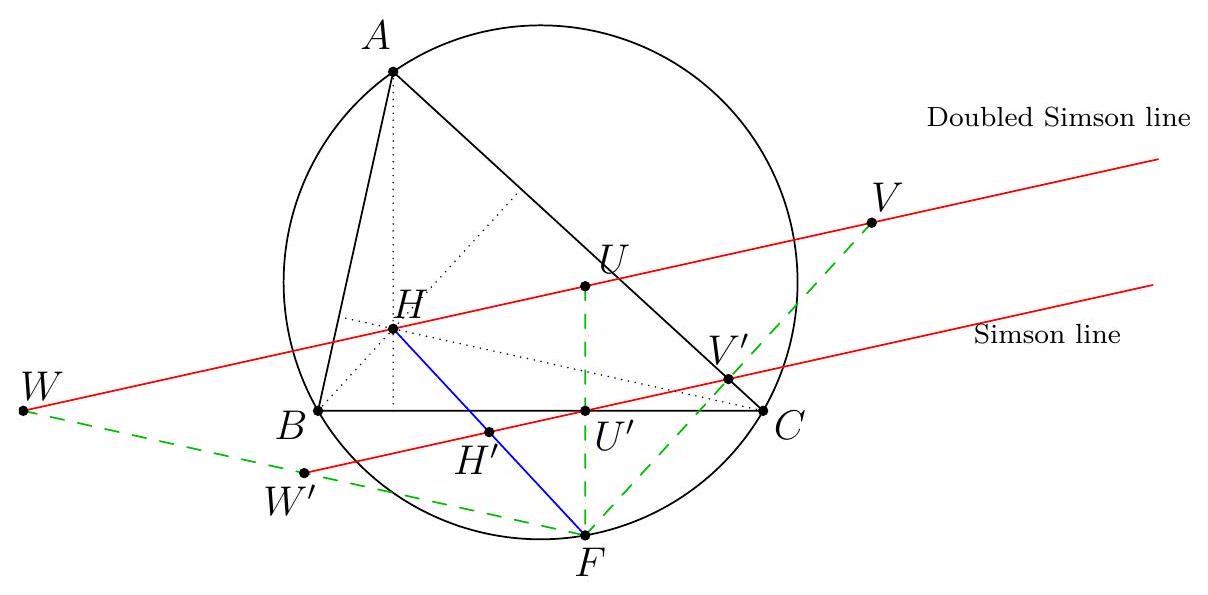
Figure 2: The Wallace-Simson configuration
When $X$ is on $\Gamma$, we can enlarge from $X$ with scale factor 2 (a homothety) to take the Simson line to the doubled Simson line which passes through the orthocentre $H$ and contains the reflections of $X$ in each of the three sides of $A B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
Preliminaries
Let $A B C$ be a triangle with circumcircle $\Gamma$. Let $X$ be a point in the plane. The Simson line (Wallace-Simson line) is defined via the following theorem. Drop perpendiculars from $X$ to each of the three side lines of $A B C$. The feet of these perpendiculars are collinear (on
the Simson line of $X$ ) if and only if $X$ lies of $\Gamma$. The Simson line of $X$ in the circumcircle bisects the line segment $X H$ where $H$ is the orthocentre of triangle $A B C$. See Figure 2

Figure 2: The Wallace-Simson configuration
When $X$ is on $\Gamma$, we can enlarge from $X$ with scale factor 2 (a homothety) to take the Simson line to the doubled Simson line which passes through the orthocentre $H$ and contains the reflections of $X$ in each of the three sides of $A B C$.
|
{
"exam": "EGMO",
"problem_label": "2",
"problem_match": "\nProblem 2.",
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"solution_match": "# Solution 2. ",
"tier": "T2",
"year": "2023"
}
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
of the problem
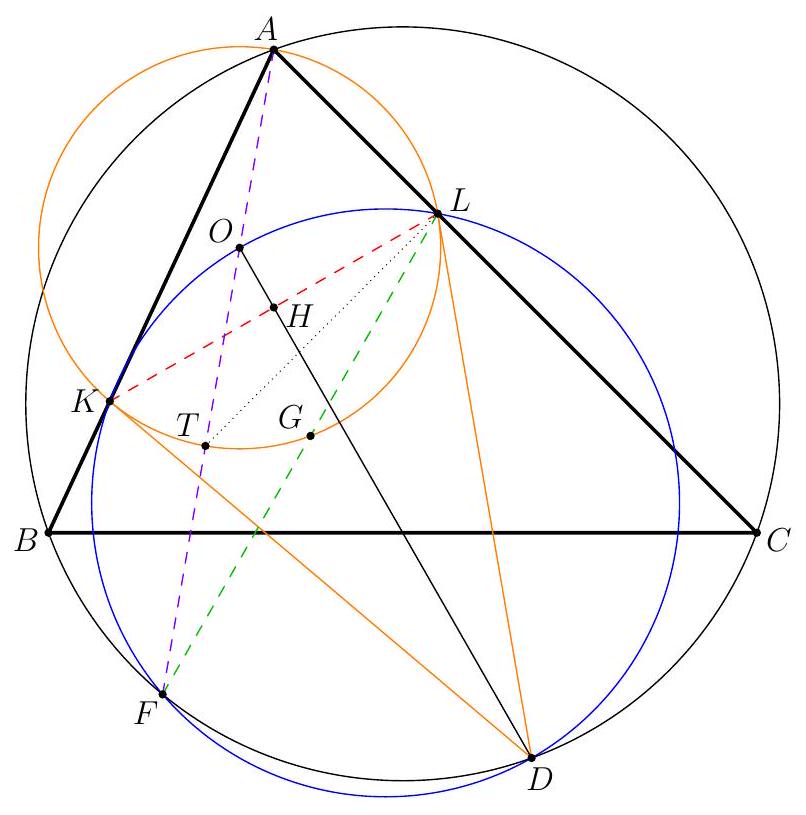
Figure 3: Three circles do the work
Let $\Gamma$ be the circle $A B C, \Sigma$ be the circle $A K L$ with centre $O$, and $\Omega$ be the circle on diameter $O D$ so $K$ and $L$ are on this circle by converse of Thales. Let $\Omega$ and $\Gamma$ meet at $D$ and $F$. By Thales in both circles, $\angle A F D$ and $\angle O F D$ are both right angles so $A O F$ is a line. Let $A F$ meet $\Sigma$ again at $T$ so $A T$ (containing $O$ ) is a diameter of this circle and by Thales, $T L \perp A C$.
Let $G$ (on $\Sigma$ ) be the reflection of $K$ in $A F$. Now $A T$ is the internal angle bisector of $\angle G A K$ so, by an upmarket use of angles in the same segment (of $\Sigma$ ), $T L$ is the internal
angle bisector of $\angle G L K$. Thus the line $G L$ is the reflection of the line $K L$ in $T L$, and so also the reflection of $K L$ in the line $A C$ (internal and external angle bisectors).
Our next project is to show that $L G F$ are collinear. Well $\angle F L K=\angle F O K$ (angles in the same segment of $\Omega$ ) and $\angle G L K=\angle G A K$ (angles in the same segment of $\Sigma$ ) $=2 \angle O A K$ ( $A K G$ is isosceles with apex $A)=\angle T O K$ (since $O A K$ is isosceles with apex $O$, and this is an external angle at $O$ ). The point $T$ lies in the interior of the line segment $F O$ so $\angle T O K=\angle F O K$. Therefore $\angle F L K=\angle G L K$ so $L G F$ is a line.
Now from the second paragraph, $F$ is on the reflection of $K L$ in $A C$. By symmetry, $F$ is also on the reflection of $K L$ in $A B$. Therefore the reflections of $F$ in $A B$ and $A C$ are both on $K L$ which must therefore be the doubled Wallace-Simson line of $F$. Therefore the orthocentre of $A B C$ lies on $K L$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
of the problem

Figure 3: Three circles do the work
Let $\Gamma$ be the circle $A B C, \Sigma$ be the circle $A K L$ with centre $O$, and $\Omega$ be the circle on diameter $O D$ so $K$ and $L$ are on this circle by converse of Thales. Let $\Omega$ and $\Gamma$ meet at $D$ and $F$. By Thales in both circles, $\angle A F D$ and $\angle O F D$ are both right angles so $A O F$ is a line. Let $A F$ meet $\Sigma$ again at $T$ so $A T$ (containing $O$ ) is a diameter of this circle and by Thales, $T L \perp A C$.
Let $G$ (on $\Sigma$ ) be the reflection of $K$ in $A F$. Now $A T$ is the internal angle bisector of $\angle G A K$ so, by an upmarket use of angles in the same segment (of $\Sigma$ ), $T L$ is the internal
angle bisector of $\angle G L K$. Thus the line $G L$ is the reflection of the line $K L$ in $T L$, and so also the reflection of $K L$ in the line $A C$ (internal and external angle bisectors).
Our next project is to show that $L G F$ are collinear. Well $\angle F L K=\angle F O K$ (angles in the same segment of $\Omega$ ) and $\angle G L K=\angle G A K$ (angles in the same segment of $\Sigma$ ) $=2 \angle O A K$ ( $A K G$ is isosceles with apex $A)=\angle T O K$ (since $O A K$ is isosceles with apex $O$, and this is an external angle at $O$ ). The point $T$ lies in the interior of the line segment $F O$ so $\angle T O K=\angle F O K$. Therefore $\angle F L K=\angle G L K$ so $L G F$ is a line.
Now from the second paragraph, $F$ is on the reflection of $K L$ in $A C$. By symmetry, $F$ is also on the reflection of $K L$ in $A B$. Therefore the reflections of $F$ in $A B$ and $A C$ are both on $K L$ which must therefore be the doubled Wallace-Simson line of $F$. Therefore the orthocentre of $A B C$ lies on $K L$.
|
{
"exam": "EGMO",
"problem_label": "2",
"problem_match": "\nProblem 2.",
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"solution_match": "# Solution ",
"tier": "T2",
"year": "2023"
}
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
Let $H$ be the orthocentre of triangle $A B C$ and $\Sigma$ the circumcircle of $A K L$ with centre $O$. Let $\Omega$ be the circle with diameter $O D$, which contains $K$ and $L$ by Thales, and let $\Gamma$ be the circumcircle of $A B C$ containing $D$. Denote the second intersection of $\Omega$ and $\Gamma$ by $F$. Since $O D$ and $A D$ are diameters of $\Omega$ and $\Gamma$ we have $\angle O F D=\frac{\pi}{2}=\angle A F D$, so the points $A, O, F$ are collinear. Let $M$ and $N$ be the second intersections of $C H$ and $B H$ with $\Gamma$, respectively. It is well-known that $M$ and $N$ are the reflections of $H$ in $A B$ and $A C$, respectively (because $\angle N C A=\angle N B A=\angle A C M=\angle A B M$ ). By collinearity of $A, O, F$ and the angles in $\Gamma$ we have
$$
\angle N F O=\angle N F A=\angle N B A=\frac{\pi}{2}-\angle B A C=\frac{\pi}{2}-\angle K A L
$$
Since $D L$ is tangent to $\Sigma$ we obtain
$$
\angle N F O=\frac{\pi}{2}-\angle K L D=\angle L D O,
$$
where the last equality follows from the fact that $O D$ is bisector of $\angle L D K$ since $L D$
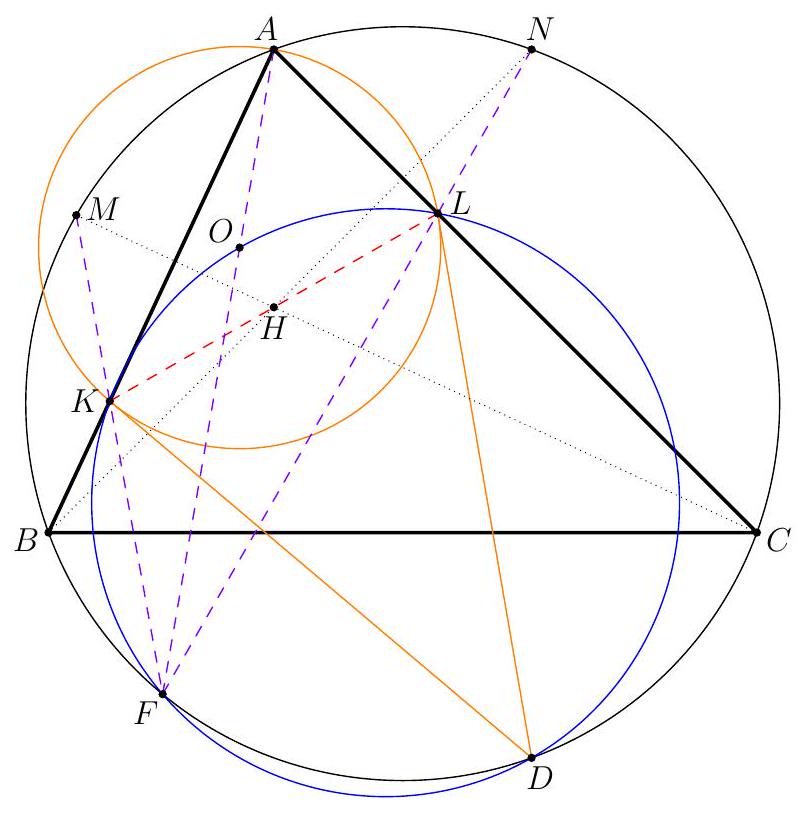
Figure 4: Diagram to Solution 3
and $K D$ are tangent to $\Sigma$. Furthermore, $\angle L D O=\angle L F O$ since these are angles in $\Omega$. Hence, $\angle N F O=\angle L F O$, which implies that points $N, L, F$ are collinear. Similarly points $M, K, F$ are collinear. Since $N$ and $M$ are reflections of $H$ in $A C$ and $A B$ we have
$$
\angle L H N=\angle H N L=\angle B N F=\angle B M F=\angle B M K=\angle K H B .
$$
Hence,
$$
\angle L H K=\angle L H N+\angle N H K=\angle K H B+\angle N H K=\pi
$$
and the points $L, H, K$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
Let $H$ be the orthocentre of triangle $A B C$ and $\Sigma$ the circumcircle of $A K L$ with centre $O$. Let $\Omega$ be the circle with diameter $O D$, which contains $K$ and $L$ by Thales, and let $\Gamma$ be the circumcircle of $A B C$ containing $D$. Denote the second intersection of $\Omega$ and $\Gamma$ by $F$. Since $O D$ and $A D$ are diameters of $\Omega$ and $\Gamma$ we have $\angle O F D=\frac{\pi}{2}=\angle A F D$, so the points $A, O, F$ are collinear. Let $M$ and $N$ be the second intersections of $C H$ and $B H$ with $\Gamma$, respectively. It is well-known that $M$ and $N$ are the reflections of $H$ in $A B$ and $A C$, respectively (because $\angle N C A=\angle N B A=\angle A C M=\angle A B M$ ). By collinearity of $A, O, F$ and the angles in $\Gamma$ we have
$$
\angle N F O=\angle N F A=\angle N B A=\frac{\pi}{2}-\angle B A C=\frac{\pi}{2}-\angle K A L
$$
Since $D L$ is tangent to $\Sigma$ we obtain
$$
\angle N F O=\frac{\pi}{2}-\angle K L D=\angle L D O,
$$
where the last equality follows from the fact that $O D$ is bisector of $\angle L D K$ since $L D$

Figure 4: Diagram to Solution 3
and $K D$ are tangent to $\Sigma$. Furthermore, $\angle L D O=\angle L F O$ since these are angles in $\Omega$. Hence, $\angle N F O=\angle L F O$, which implies that points $N, L, F$ are collinear. Similarly points $M, K, F$ are collinear. Since $N$ and $M$ are reflections of $H$ in $A C$ and $A B$ we have
$$
\angle L H N=\angle H N L=\angle B N F=\angle B M F=\angle B M K=\angle K H B .
$$
Hence,
$$
\angle L H K=\angle L H N+\angle N H K=\angle K H B+\angle N H K=\pi
$$
and the points $L, H, K$ are collinear.
|
{
"exam": "EGMO",
"problem_label": "2",
"problem_match": "\nProblem 2.",
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"solution_match": "\nSolution 3. ",
"tier": "T2",
"year": "2023"
}
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
As in Solution 3 let $M$ and $N$ be the reflections of the orthocentre in $A B$ and $A C$. Let $\angle B A C=\alpha$. Then $\angle N D M=\pi-\angle M A N=\pi-2 \alpha$.
Let $M K$ and $N L$ intersect at $F$. See Figure 3.
Claim. $\angle N F M=\pi-2 \alpha$, so $F$ lies on the circumcircle.
Proof. Since $K D$ and $L D$ are tangents to circle $A K L$, we have $|D K|=|D L|$ and $\angle D K L=\angle K L D=\alpha$, so $\angle L D K=\pi-2 \alpha$.
By definition of $M, N$ and $D, \angle M N D=\angle A N D-\angle A N M=\frac{\pi}{2}-\left(\frac{\pi}{2}-\alpha\right)=\alpha$ and analogously $\angle D M N=\alpha$. Hence $|D M|=|D N|$.
From $\angle N D M=\angle L D K=\pi-2 \alpha$ if follows that $\angle L D N=\angle K D M$. Since $|D K|=|D L|$ and $|D M|=|D N|$, triangles $M D K$ and $N D L$ are related by a rotation about $D$ through angle $\pi-2 \alpha$, and hence the angle between $M K$ and $N L$ is $\pi-2 \alpha$, which proved the claim.
We now finish as in Solution 3:
$$
\begin{gathered}
\angle M H K=\angle K M H=\angle F M C=\angle F A C \\
\angle L H N=\angle H N L=\angle B N F=\angle B A F
\end{gathered}
$$
As $\angle B A F+\angle F A C=\alpha$, we have $\angle L H K=\alpha+\angle N H M=\alpha+\pi-\alpha=\pi$, so $H$ lies on $K L$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
As in Solution 3 let $M$ and $N$ be the reflections of the orthocentre in $A B$ and $A C$. Let $\angle B A C=\alpha$. Then $\angle N D M=\pi-\angle M A N=\pi-2 \alpha$.
Let $M K$ and $N L$ intersect at $F$. See Figure 3.
Claim. $\angle N F M=\pi-2 \alpha$, so $F$ lies on the circumcircle.
Proof. Since $K D$ and $L D$ are tangents to circle $A K L$, we have $|D K|=|D L|$ and $\angle D K L=\angle K L D=\alpha$, so $\angle L D K=\pi-2 \alpha$.
By definition of $M, N$ and $D, \angle M N D=\angle A N D-\angle A N M=\frac{\pi}{2}-\left(\frac{\pi}{2}-\alpha\right)=\alpha$ and analogously $\angle D M N=\alpha$. Hence $|D M|=|D N|$.
From $\angle N D M=\angle L D K=\pi-2 \alpha$ if follows that $\angle L D N=\angle K D M$. Since $|D K|=|D L|$ and $|D M|=|D N|$, triangles $M D K$ and $N D L$ are related by a rotation about $D$ through angle $\pi-2 \alpha$, and hence the angle between $M K$ and $N L$ is $\pi-2 \alpha$, which proved the claim.
We now finish as in Solution 3:
$$
\begin{gathered}
\angle M H K=\angle K M H=\angle F M C=\angle F A C \\
\angle L H N=\angle H N L=\angle B N F=\angle B A F
\end{gathered}
$$
As $\angle B A F+\angle F A C=\alpha$, we have $\angle L H K=\alpha+\angle N H M=\alpha+\pi-\alpha=\pi$, so $H$ lies on $K L$.
|
{
"exam": "EGMO",
"problem_label": "2",
"problem_match": "\nProblem 2.",
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"solution_match": "\nSolution 4. ",
"tier": "T2",
"year": "2023"
}
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
Since $A D$ is a diameter, it is well known that $D B H C$ is a parallelogram (indeed, both $B D$ and $C H$ are perpendicular to $A B$, hence parallel, and similarly for $D C \| B H)$. Let $B^{\prime}, C^{\prime}$ be the reflections of $D$ in lines $A K B$ and $A L C$, respectively; since $A B D$ and $A C D$ are right angles, these are also the factor-2 homotheties of $B$ and $C$ with respect to $D$, hence $H$ is the midpoint of $B^{\prime} C^{\prime}$. We will prove that $B^{\prime} K C^{\prime} L$ is a parallelogram: it will then follow that the midpoint of $B^{\prime} C^{\prime}$, which is $H$, is also the midpoint of $K L$, and in particular is on the line, as we wanted to show.
We will prove $B^{\prime} K C^{\prime} L$ is a parallelogram by showing that $B^{\prime} K$ and $C^{\prime} L$ are the same length and direction. Indeed, for lengths we have $K B^{\prime}=K D=L D=L C^{\prime}$, where the first and last equalities arise from the reflections defining $B^{\prime}$ and $C^{\prime}$, and the middle one
is equality of tangents. For directions, let $\alpha, \beta, \gamma$ denote the angles of triangle $A K L$. Immediate angle chasing in the circle $A K L$, and the properties of the reflections, yield
$$
\begin{aligned}
\angle C^{\prime} L C & =\angle C L D=\angle A K L=\beta \\
\angle B K B^{\prime} & =\angle D K B=\angle K L A=\gamma \\
& \angle L D K=2 \alpha-\pi
\end{aligned}
$$
and therefore in directed angles $(\bmod 2 \pi)$ we have
$\angle\left(C^{\prime} L, B^{\prime} K\right)=\angle C^{\prime} L C+\angle C L D+\angle L D K+\angle D K B+\angle B K B^{\prime}=2 \alpha+2 \beta+2 \gamma-\pi=\pi$
and hence $C^{\prime} L$ and $B^{\prime} K$ are parallel and in opposite directions, i.e. $C^{\prime} L$ and $K B^{\prime}$ are in the same direction, as claimed.
Comment. While not necessary for the final solution, the following related observation motivates how the fact that $H$ is the midpoint of $K L$ (and therefore $B^{\prime} K C^{\prime} L$ is a parallelogram) was first conjectured. We have $A B^{\prime}=A D=A C^{\prime}$ by the reflections, i.e. $B^{\prime} A C^{\prime}$ is an isosceles triangle with $H$ being the midpoint of the base. Thus $A H$ is the median, altitude and angle bisector in $B^{\prime} A C^{\prime}$, thus $\angle B^{\prime} A K+\angle K A H=\angle H A L+\angle L A C^{\prime}$. Since from the reflections we also have $\angle B^{\prime} A K=\angle K A D$ and $\angle D A L=\angle L A C^{\prime}$ it follows that $\angle H A L=\angle K A D$ and $\angle K A H=\angle D A L$. Since $D$ is the symmedian point in $A K L$, the angle conjugation implies $A H$ is the median line of $K L$. Thus, if $H$ is indeed on $K L$ (as the problem assures us), it can only be the midpoint of $K L$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
Since $A D$ is a diameter, it is well known that $D B H C$ is a parallelogram (indeed, both $B D$ and $C H$ are perpendicular to $A B$, hence parallel, and similarly for $D C \| B H)$. Let $B^{\prime}, C^{\prime}$ be the reflections of $D$ in lines $A K B$ and $A L C$, respectively; since $A B D$ and $A C D$ are right angles, these are also the factor-2 homotheties of $B$ and $C$ with respect to $D$, hence $H$ is the midpoint of $B^{\prime} C^{\prime}$. We will prove that $B^{\prime} K C^{\prime} L$ is a parallelogram: it will then follow that the midpoint of $B^{\prime} C^{\prime}$, which is $H$, is also the midpoint of $K L$, and in particular is on the line, as we wanted to show.
We will prove $B^{\prime} K C^{\prime} L$ is a parallelogram by showing that $B^{\prime} K$ and $C^{\prime} L$ are the same length and direction. Indeed, for lengths we have $K B^{\prime}=K D=L D=L C^{\prime}$, where the first and last equalities arise from the reflections defining $B^{\prime}$ and $C^{\prime}$, and the middle one
is equality of tangents. For directions, let $\alpha, \beta, \gamma$ denote the angles of triangle $A K L$. Immediate angle chasing in the circle $A K L$, and the properties of the reflections, yield
$$
\begin{aligned}
\angle C^{\prime} L C & =\angle C L D=\angle A K L=\beta \\
\angle B K B^{\prime} & =\angle D K B=\angle K L A=\gamma \\
& \angle L D K=2 \alpha-\pi
\end{aligned}
$$
and therefore in directed angles $(\bmod 2 \pi)$ we have
$\angle\left(C^{\prime} L, B^{\prime} K\right)=\angle C^{\prime} L C+\angle C L D+\angle L D K+\angle D K B+\angle B K B^{\prime}=2 \alpha+2 \beta+2 \gamma-\pi=\pi$
and hence $C^{\prime} L$ and $B^{\prime} K$ are parallel and in opposite directions, i.e. $C^{\prime} L$ and $K B^{\prime}$ are in the same direction, as claimed.
Comment. While not necessary for the final solution, the following related observation motivates how the fact that $H$ is the midpoint of $K L$ (and therefore $B^{\prime} K C^{\prime} L$ is a parallelogram) was first conjectured. We have $A B^{\prime}=A D=A C^{\prime}$ by the reflections, i.e. $B^{\prime} A C^{\prime}$ is an isosceles triangle with $H$ being the midpoint of the base. Thus $A H$ is the median, altitude and angle bisector in $B^{\prime} A C^{\prime}$, thus $\angle B^{\prime} A K+\angle K A H=\angle H A L+\angle L A C^{\prime}$. Since from the reflections we also have $\angle B^{\prime} A K=\angle K A D$ and $\angle D A L=\angle L A C^{\prime}$ it follows that $\angle H A L=\angle K A D$ and $\angle K A H=\angle D A L$. Since $D$ is the symmedian point in $A K L$, the angle conjugation implies $A H$ is the median line of $K L$. Thus, if $H$ is indeed on $K L$ (as the problem assures us), it can only be the midpoint of $K L$.
|
{
"exam": "EGMO",
"problem_label": "2",
"problem_match": "\nProblem 2.",
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"solution_match": "\nSolution 5. ",
"tier": "T2",
"year": "2023"
}
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
There are a number of "phantom point" arguments which define $K^{\prime}$ and $L^{\prime}$ in terms of angles and then deduce that these points are actually $K$ and $L$.
Note: In these solutions it is necessary to show that $K$ and $L$ are uniquely determined by the conditions of the problem. One example of doing this is the following:
To prove uniqueness of $K$ and $L$, let us consider that there exist two other points $K^{\prime}$ and $L^{\prime}$ that satisfy the same properties ( $K^{\prime}$ on $A B$ and $L^{\prime}$ on $A C$ such that $D K^{\prime}$ and $D L^{\prime}$ are tangent to the circle $\left.A K^{\prime} L^{\prime}\right)$.
Then, we have that $D K=D L$ and $D K^{\prime}=D L^{\prime}$. We also have that $\angle K D L=\angle K^{\prime} D L^{\prime}=$ $\pi-2 \angle A$. Hence, we deduce $\angle K D K^{\prime}=\angle K D L-\angle K^{\prime} D L=\angle K^{\prime} D L^{\prime}-\angle K^{\prime} D L=\angle L D L^{\prime}$ Thus we have that $\triangle K D K^{\prime} \equiv \triangle L D L^{\prime}$, so we deduce $\angle D K A=\angle D K K^{\prime}=\angle D L L^{\prime}=$ $\pi-\angle A L D$. This implies that $A K D L$ is concyclic, which is clearly a contradiction since $\angle K A L+\angle K D L=\pi-\angle B A C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
There are a number of "phantom point" arguments which define $K^{\prime}$ and $L^{\prime}$ in terms of angles and then deduce that these points are actually $K$ and $L$.
Note: In these solutions it is necessary to show that $K$ and $L$ are uniquely determined by the conditions of the problem. One example of doing this is the following:
To prove uniqueness of $K$ and $L$, let us consider that there exist two other points $K^{\prime}$ and $L^{\prime}$ that satisfy the same properties ( $K^{\prime}$ on $A B$ and $L^{\prime}$ on $A C$ such that $D K^{\prime}$ and $D L^{\prime}$ are tangent to the circle $\left.A K^{\prime} L^{\prime}\right)$.
Then, we have that $D K=D L$ and $D K^{\prime}=D L^{\prime}$. We also have that $\angle K D L=\angle K^{\prime} D L^{\prime}=$ $\pi-2 \angle A$. Hence, we deduce $\angle K D K^{\prime}=\angle K D L-\angle K^{\prime} D L=\angle K^{\prime} D L^{\prime}-\angle K^{\prime} D L=\angle L D L^{\prime}$ Thus we have that $\triangle K D K^{\prime} \equiv \triangle L D L^{\prime}$, so we deduce $\angle D K A=\angle D K K^{\prime}=\angle D L L^{\prime}=$ $\pi-\angle A L D$. This implies that $A K D L$ is concyclic, which is clearly a contradiction since $\angle K A L+\angle K D L=\pi-\angle B A C$.
|
{
"exam": "EGMO",
"problem_label": "2",
"problem_match": "\nProblem 2.",
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"solution_match": "\nSolution 6. ",
"tier": "T2",
"year": "2023"
}
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
We will use the usual complex number notation, where we will use a capital letter (like $Z$ ) to denote the point associated to a complex number (like z). Consider $\triangle A K L$ on the unit circle. So, we have $a \cdot \bar{a}=k \cdot \bar{k}=l \cdot \bar{l}=1 \quad$ As point $D$ is the intersection of the tangents to the unit circle at $K$ and $L$, we have that
$$
d=\frac{2 k l}{k+l} \text { and } \bar{d}=\frac{2}{k+l}
$$
Defining $B$ as the foot of the perpendicular from $D$ on the line $A K$, and $C$ as the foot of the perpendicular from $D$ on the line $A L$, we have the formulas:
$$
b=\frac{1}{2}\left(d+\frac{(a-k) \bar{d}+\bar{a} k-a \bar{k}}{\bar{a}-\bar{k}}\right)
$$
$$
c=\frac{1}{2}\left(d+\frac{(a-l) \bar{d}+\bar{a} l-a \bar{l}}{\bar{a}-\bar{l}}\right)
$$
Simplyfing these formulas, we get:
$$
\begin{gathered}
b=\frac{1}{2}\left(d+\frac{(a-k) \frac{2}{k+l}+\frac{k}{a}-\frac{a}{k}}{\frac{1}{a}-\frac{1}{k}}\right)=\frac{1}{2}\left(d+\frac{\frac{2(a-k)}{k+l}+\frac{k^{2}-a^{2}}{a k}}{\frac{k-a}{a k}}\right) \\
b=\frac{1}{2}\left(\frac{2 k l}{k+l}-\frac{2 a k}{k+l}+(a+k)\right)=\frac{k(l-a)}{k+l}+\frac{1}{2}(k+a) \\
c=\frac{1}{2}\left(d+\frac{(a-l) \frac{2}{k+l}+\frac{l}{a}-\frac{a}{l}}{\frac{1}{a}-\frac{1}{l}}\right)=\frac{1}{2}\left(d+\frac{\frac{2(a-l)}{k+l}+\frac{l^{2}-a^{2}}{a l}}{\frac{l-a}{a l}}\right) \\
c=\frac{1}{2}\left(\frac{2 k l}{k+l}-\frac{2 a l}{k+l}+(a+l)\right)=\frac{l(k-a)}{k+l}+\frac{1}{2}(l+a)
\end{gathered}
$$
Let $O$ be the the circumcenter of triangle $\triangle A B C$. As $A D$ is the diameter of this circle, we have that:
$$
o=\frac{a+d}{2}
$$
Defining $H$ as the orthocentre of the $\triangle A B C$, we get that:
$$
\begin{gathered}
h=a+b+c-2 \cdot o=a+\left(\frac{k(l-a)}{k+l}+\frac{1}{2}(k+a)\right)+\left(\frac{l(k-a)}{k+l}+\frac{1}{2}(l+a)\right)-(a+d) \\
h=a+\frac{2 k l}{k+l}-\frac{a(k+l)}{k+l}+\frac{1}{2} k++\frac{1}{2} l++a-\left(a+\frac{2 k l}{k+l}\right) \\
h=\frac{1}{2}(k+l)
\end{gathered}
$$
Hence, we conclude that $H$ is the midpoint of $K L$, so $H, K, L$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
We will use the usual complex number notation, where we will use a capital letter (like $Z$ ) to denote the point associated to a complex number (like z). Consider $\triangle A K L$ on the unit circle. So, we have $a \cdot \bar{a}=k \cdot \bar{k}=l \cdot \bar{l}=1 \quad$ As point $D$ is the intersection of the tangents to the unit circle at $K$ and $L$, we have that
$$
d=\frac{2 k l}{k+l} \text { and } \bar{d}=\frac{2}{k+l}
$$
Defining $B$ as the foot of the perpendicular from $D$ on the line $A K$, and $C$ as the foot of the perpendicular from $D$ on the line $A L$, we have the formulas:
$$
b=\frac{1}{2}\left(d+\frac{(a-k) \bar{d}+\bar{a} k-a \bar{k}}{\bar{a}-\bar{k}}\right)
$$
$$
c=\frac{1}{2}\left(d+\frac{(a-l) \bar{d}+\bar{a} l-a \bar{l}}{\bar{a}-\bar{l}}\right)
$$
Simplyfing these formulas, we get:
$$
\begin{gathered}
b=\frac{1}{2}\left(d+\frac{(a-k) \frac{2}{k+l}+\frac{k}{a}-\frac{a}{k}}{\frac{1}{a}-\frac{1}{k}}\right)=\frac{1}{2}\left(d+\frac{\frac{2(a-k)}{k+l}+\frac{k^{2}-a^{2}}{a k}}{\frac{k-a}{a k}}\right) \\
b=\frac{1}{2}\left(\frac{2 k l}{k+l}-\frac{2 a k}{k+l}+(a+k)\right)=\frac{k(l-a)}{k+l}+\frac{1}{2}(k+a) \\
c=\frac{1}{2}\left(d+\frac{(a-l) \frac{2}{k+l}+\frac{l}{a}-\frac{a}{l}}{\frac{1}{a}-\frac{1}{l}}\right)=\frac{1}{2}\left(d+\frac{\frac{2(a-l)}{k+l}+\frac{l^{2}-a^{2}}{a l}}{\frac{l-a}{a l}}\right) \\
c=\frac{1}{2}\left(\frac{2 k l}{k+l}-\frac{2 a l}{k+l}+(a+l)\right)=\frac{l(k-a)}{k+l}+\frac{1}{2}(l+a)
\end{gathered}
$$
Let $O$ be the the circumcenter of triangle $\triangle A B C$. As $A D$ is the diameter of this circle, we have that:
$$
o=\frac{a+d}{2}
$$
Defining $H$ as the orthocentre of the $\triangle A B C$, we get that:
$$
\begin{gathered}
h=a+b+c-2 \cdot o=a+\left(\frac{k(l-a)}{k+l}+\frac{1}{2}(k+a)\right)+\left(\frac{l(k-a)}{k+l}+\frac{1}{2}(l+a)\right)-(a+d) \\
h=a+\frac{2 k l}{k+l}-\frac{a(k+l)}{k+l}+\frac{1}{2} k++\frac{1}{2} l++a-\left(a+\frac{2 k l}{k+l}\right) \\
h=\frac{1}{2}(k+l)
\end{gathered}
$$
Hence, we conclude that $H$ is the midpoint of $K L$, so $H, K, L$ are collinear.
|
{
"exam": "EGMO",
"problem_label": "2",
"problem_match": "\nProblem 2.",
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"solution_match": "\nSolution 7. ",
"tier": "T2",
"year": "2023"
}
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
Let us employ the barycentric coordinates. Set $A(1,0,0), K(0,1,0), L(0,0,1)$.
The tangent at $K$ of $(A K L)$ is $a^{2} z+c^{2} x=0$, and the tangent of of $L$ at $(A K L)$ is $a^{2} y+b^{2} x=0$. Their intersection is
$$
D\left(-a^{2}: b^{2}: c^{2}\right)
$$
Since $B \in A K$, we can let $B(1-t, t, 0)$. Solving for $\overrightarrow{A B} \cdot \overrightarrow{B D}=0$ gives
$$
t=\frac{3 b^{2}+c^{2}-a^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)} \Longrightarrow B=\left(\frac{-a^{2}-b^{2}+c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}, \frac{-a^{2}+3 b^{2}+c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}, 0\right)
$$
Likewise, $C$ has the coordinate
$$
C=\left(\frac{-a^{2}+b^{2}-c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}, 0, \frac{-a^{2}+b^{2}+3 c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}\right) .
$$
The altitude from $B$ for triangle $A B C$ is
$$
-b^{2}\left(x-z-\frac{-a^{2}-b^{2}+c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}\right)+\left(c^{2}-a^{2}\right)\left(y-\frac{-a^{2}+3 b^{2}+c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}\right)=0
$$
Also the altitude from $C$ for triangle $A B C$ is
$$
-c^{2}\left(x-y-\frac{-a^{2}+b^{2}-c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}\right)+\left(a^{2}-b^{2}\right)\left(z-\frac{-a^{2}+b^{2}+3 c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}\right)=0
$$
The intersection of these two altitudes, which is the orthocenter of triangle $A B C$, has the barycentric coordinate
$$
H=(0,1 / 2,1 / 2)
$$
which is the midpoint of the segment $K L$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
We are given an acute triangle $A B C$. Let $D$ be the point on its circumcircle such that $A D$ is a diameter. Suppose that points $K$ and $L$ lie on segments $A B$ and $A C$, respectively, and that $D K$ and $D L$ are tangent to circle $A K L$.
Show that line $K L$ passes through the orthocentre of $A B C$.
The altitudes of a triangle meet at its orthocentre.

Figure 1: Diagram to solution 1
|
Let us employ the barycentric coordinates. Set $A(1,0,0), K(0,1,0), L(0,0,1)$.
The tangent at $K$ of $(A K L)$ is $a^{2} z+c^{2} x=0$, and the tangent of of $L$ at $(A K L)$ is $a^{2} y+b^{2} x=0$. Their intersection is
$$
D\left(-a^{2}: b^{2}: c^{2}\right)
$$
Since $B \in A K$, we can let $B(1-t, t, 0)$. Solving for $\overrightarrow{A B} \cdot \overrightarrow{B D}=0$ gives
$$
t=\frac{3 b^{2}+c^{2}-a^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)} \Longrightarrow B=\left(\frac{-a^{2}-b^{2}+c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}, \frac{-a^{2}+3 b^{2}+c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}, 0\right)
$$
Likewise, $C$ has the coordinate
$$
C=\left(\frac{-a^{2}+b^{2}-c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}, 0, \frac{-a^{2}+b^{2}+3 c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}\right) .
$$
The altitude from $B$ for triangle $A B C$ is
$$
-b^{2}\left(x-z-\frac{-a^{2}-b^{2}+c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}\right)+\left(c^{2}-a^{2}\right)\left(y-\frac{-a^{2}+3 b^{2}+c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}\right)=0
$$
Also the altitude from $C$ for triangle $A B C$ is
$$
-c^{2}\left(x-y-\frac{-a^{2}+b^{2}-c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}\right)+\left(a^{2}-b^{2}\right)\left(z-\frac{-a^{2}+b^{2}+3 c^{2}}{2\left(b^{2}+c^{2}-a^{2}\right)}\right)=0
$$
The intersection of these two altitudes, which is the orthocenter of triangle $A B C$, has the barycentric coordinate
$$
H=(0,1 / 2,1 / 2)
$$
which is the midpoint of the segment $K L$.
|
{
"exam": "EGMO",
"problem_label": "2",
"problem_match": "\nProblem 2.",
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"solution_match": "\nSolution 8. ",
"tier": "T2",
"year": "2023"
}
|
Let $k$ be a positive integer. Lexi has a dictionary $\mathcal{D}$ consisting of some $k$-letter strings containing only the letters $A$ and $B$. Lexi would like to write either the letter $A$ or the letter $B$ in each cell of a $k \times k$ grid so that each column contains a string from $\mathcal{D}$ when read from top-to-bottom and each row contains a string from $\mathcal{D}$ when read from left-to-right.
What is the smallest integer $m$ such that if $\mathcal{D}$ contains at least $m$ different strings, then Lexi can fill her grid in this manner, no matter what strings are in $\mathcal{D}$ ?
|
We claim the minimum value of $m$ is $2^{k-1}$.
Firstly, we provide a set $\mathcal{S}$ of size $2^{k-1}-1$ for which Lexi cannot fill her grid. Consider the set of all length- $k$ strings containing only $A$ s and $B$ shich end with a $B$, and remove the string consisting of $k B$ s. Clearly there are 2 independent choices for each of the first $k-1$ letters and 1 for the last letter, and since exactly one string is excluded, there must be exactly $2^{k-1}-1$ strings in this set.
Suppose Lexi tries to fill her grid. For each row to have a valid string, it must end in a $B$. But then the right column would necessarily contain $k B \mathrm{~s}$, and not be in our set. Thus, Lexi cannot fill her grid with our set, and we must have $m \geqslant 2^{k-1}$.
Now, consider any set $\mathcal{S}$ with at least $2^{k-1}$ strings. Clearly, if $\mathcal{S}$ contained either the uniform string with $k A$ s or the string with $k B \mathrm{~s}$, then Lexi could fill her grid with all of the relevant letters and each row and column would contain that string.
Consider the case where $\mathcal{S}$ contains neither of those strings. Among all $2^{k}$ possible length$k$ strings with $A \mathrm{~s}$ and $B \mathrm{~s}$, each has a complement which corresponds to the string with $B$ s in every position where first string had $A$ s and vice-versa. Clearly, the string with all $A$ s is paired with the string with all $B$ s. We may assume that we do not take the two uniform strings and thus applying the pigeonhole principle to the remaining set of strings, we must have two strings which are complementary.
Let this pair of strings be $\ell, \ell^{\prime} \in \mathcal{S}$ in some order. Define the set of indices $\mathcal{J}$ corresponding to the $A$ s in $\ell$ and thus the $B \mathrm{~s}$ in $\ell^{\prime}$, and all other indices (not in $\mathcal{J}$ ) correspond to $B \mathrm{~s}$ in $\ell$ (and thus $A$ s in $\ell^{\prime}$ ). Then, we claim that Lexi puts an $A$ in the cell in row $r$, column $c$ if $r, c \in \mathcal{J}$ or $r, c \notin \mathcal{J}$, and a $B$ otherwise, each row and column contains a string in $\mathcal{S}$.
We illustrate this with a simple example: If $k=6$ and we have that $A A A B A B$ and $B B B A B A$ are both in the dictionary, then Lexi could fill the table as follows:
| A | A | A | B | A | B |
| :---: | :---: | :---: | :---: | :---: | :---: |
| A | A | A | B | A | B |
| A | A | A | B | A | B |
| B | B | B | A | B | A |
| A | A | A | B | A | B |
| B | B | B | A | B | A |
Suppose we are looking at row $i$ or column $i$ for $i \in \mathcal{J}$. Then by construction the string in this row/column contains $A$ s at indices $k$ with $k \in \mathcal{J}$ and $B$ s elsewhere, and thus is precisely $\ell$. Suppose instead we are looking at row $i$ or column $i$ for $i \notin \mathcal{J}$. Then again
by construction the string in this row/column contains $A$ s at indices $k$ with $k \notin \mathcal{J}$ and $B$ s elsewhere, and thus is precisely $\ell^{\prime}$. So each row and column indeed contains a string in $\mathcal{S}$.
Thus, for any $\mathcal{S}$ with $|\mathcal{S}| \geqslant 2^{k-1}$, Lexi can definitely fill the grid appropriately. Since we know $m \geqslant 2^{k-1}$, $2^{k-1}$ is the minimum possible value of $m$ as claimed.
|
2^{k-1}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $k$ be a positive integer. Lexi has a dictionary $\mathcal{D}$ consisting of some $k$-letter strings containing only the letters $A$ and $B$. Lexi would like to write either the letter $A$ or the letter $B$ in each cell of a $k \times k$ grid so that each column contains a string from $\mathcal{D}$ when read from top-to-bottom and each row contains a string from $\mathcal{D}$ when read from left-to-right.
What is the smallest integer $m$ such that if $\mathcal{D}$ contains at least $m$ different strings, then Lexi can fill her grid in this manner, no matter what strings are in $\mathcal{D}$ ?
|
We claim the minimum value of $m$ is $2^{k-1}$.
Firstly, we provide a set $\mathcal{S}$ of size $2^{k-1}-1$ for which Lexi cannot fill her grid. Consider the set of all length- $k$ strings containing only $A$ s and $B$ shich end with a $B$, and remove the string consisting of $k B$ s. Clearly there are 2 independent choices for each of the first $k-1$ letters and 1 for the last letter, and since exactly one string is excluded, there must be exactly $2^{k-1}-1$ strings in this set.
Suppose Lexi tries to fill her grid. For each row to have a valid string, it must end in a $B$. But then the right column would necessarily contain $k B \mathrm{~s}$, and not be in our set. Thus, Lexi cannot fill her grid with our set, and we must have $m \geqslant 2^{k-1}$.
Now, consider any set $\mathcal{S}$ with at least $2^{k-1}$ strings. Clearly, if $\mathcal{S}$ contained either the uniform string with $k A$ s or the string with $k B \mathrm{~s}$, then Lexi could fill her grid with all of the relevant letters and each row and column would contain that string.
Consider the case where $\mathcal{S}$ contains neither of those strings. Among all $2^{k}$ possible length$k$ strings with $A \mathrm{~s}$ and $B \mathrm{~s}$, each has a complement which corresponds to the string with $B$ s in every position where first string had $A$ s and vice-versa. Clearly, the string with all $A$ s is paired with the string with all $B$ s. We may assume that we do not take the two uniform strings and thus applying the pigeonhole principle to the remaining set of strings, we must have two strings which are complementary.
Let this pair of strings be $\ell, \ell^{\prime} \in \mathcal{S}$ in some order. Define the set of indices $\mathcal{J}$ corresponding to the $A$ s in $\ell$ and thus the $B \mathrm{~s}$ in $\ell^{\prime}$, and all other indices (not in $\mathcal{J}$ ) correspond to $B \mathrm{~s}$ in $\ell$ (and thus $A$ s in $\ell^{\prime}$ ). Then, we claim that Lexi puts an $A$ in the cell in row $r$, column $c$ if $r, c \in \mathcal{J}$ or $r, c \notin \mathcal{J}$, and a $B$ otherwise, each row and column contains a string in $\mathcal{S}$.
We illustrate this with a simple example: If $k=6$ and we have that $A A A B A B$ and $B B B A B A$ are both in the dictionary, then Lexi could fill the table as follows:
| A | A | A | B | A | B |
| :---: | :---: | :---: | :---: | :---: | :---: |
| A | A | A | B | A | B |
| A | A | A | B | A | B |
| B | B | B | A | B | A |
| A | A | A | B | A | B |
| B | B | B | A | B | A |
Suppose we are looking at row $i$ or column $i$ for $i \in \mathcal{J}$. Then by construction the string in this row/column contains $A$ s at indices $k$ with $k \in \mathcal{J}$ and $B$ s elsewhere, and thus is precisely $\ell$. Suppose instead we are looking at row $i$ or column $i$ for $i \notin \mathcal{J}$. Then again
by construction the string in this row/column contains $A$ s at indices $k$ with $k \notin \mathcal{J}$ and $B$ s elsewhere, and thus is precisely $\ell^{\prime}$. So each row and column indeed contains a string in $\mathcal{S}$.
Thus, for any $\mathcal{S}$ with $|\mathcal{S}| \geqslant 2^{k-1}$, Lexi can definitely fill the grid appropriately. Since we know $m \geqslant 2^{k-1}$, $2^{k-1}$ is the minimum possible value of $m$ as claimed.
|
{
"exam": "EGMO",
"problem_label": "3",
"problem_match": "\nProblem 3.",
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2023"
}
|
Turbo the snail sits on a point on a circle with circumference 1. Given an infinite sequence of positive real numbers $c_{1}, c_{2}, c_{3}, \ldots$, Turbo successively crawls distances $c_{1}, c_{2}, c_{3}, \ldots$ around the circle, each time choosing to crawl either clockwise or counterclockwise.
For example, if the sequence $c_{1}, c_{2}, c_{3}, \ldots$ is $0.4,0.6,0.3, \ldots$, then Turbo may start crawling as follows:

Determine the largest constant $C>0$ with the following property: for every sequence of positive real numbers $c_{1}, c_{2}, c_{3}, \ldots$ with $c_{i}<C$ for all $i$, Turbo can (after studying the sequence) ensure that there is some point on the circle that it will never visit or crawl across.
|
The largest possible $C$ is $C=\frac{1}{2}$.
For $0<C \leqslant \frac{1}{2}$, Turbo can simply choose an arbitrary point $P$ (different from its starting point) to avoid. When Turbo is at an arbitrary point $A$ different from $P$, the two arcs $A P$ have total length 1 ; therefore, the larger of the two the arcs (or either arc in case $A$ is diametrically opposite to $P$ ) must have length $\geqslant \frac{1}{2}$. By always choosing this larger arc (or either arc in case $A$ is diametrically opposite to $P$ ), Turbo will manage to avoid the point $P$ forever.
For $C>\frac{1}{2}$, we write $C=\frac{1}{2}+a$ with $a>0$, and we choose the sequence
$$
\frac{1}{2}, \quad \frac{1+a}{2}, \quad \frac{1}{2}, \quad \frac{1+a}{2}, \quad \frac{1}{2}, \quad \ldots
$$
In other words, $c_{i}=\frac{1}{2}$ if $i$ is odd and $c_{i}=\frac{1+a}{2}<C$ when $i$ is even. We claim Turbo must eventually visit all points on the circle. This is clear when it crawls in the same direction two times in a row; after all, we have $c_{i}+c_{i+1}>1$ for all $i$. Therefore, we are left with the case that Turbo alternates crawling clockwise and crawling counterclockwise. If it, without loss of generality, starts by going clockwise, then it will always crawl a distance $\frac{1}{2}$ clockwise followed by a distance $\frac{1+a}{2}$ counterclockwise. The net effect is that it crawls a distance $\frac{a}{2}$ counterclockwise. Because $\frac{a}{2}$ is positive, there exists a positive integer $N$ such that $\frac{a}{2} \cdot N>1$. After $2 N$ crawls, Turbo will have crawled a distance $\frac{a}{2}$ counterclockwise $N$ times, therefore having covered a total distance of $\frac{a}{2} \cdot N>1$, meaning that it must have crawled over all points on the circle.
Note: Every sequence of the form $c_{i}=x$ if $i$ is odd, and $c_{i}=y$ if $i$ is even, where $0<x, y<C$, such that $x+y \geqslant 1$, and $x \neq y$ satisfies the conditions with the same argument. There might be even more possible examples.
|
\frac{1}{2}
|
Incomplete
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
Turbo the snail sits on a point on a circle with circumference 1. Given an infinite sequence of positive real numbers $c_{1}, c_{2}, c_{3}, \ldots$, Turbo successively crawls distances $c_{1}, c_{2}, c_{3}, \ldots$ around the circle, each time choosing to crawl either clockwise or counterclockwise.
For example, if the sequence $c_{1}, c_{2}, c_{3}, \ldots$ is $0.4,0.6,0.3, \ldots$, then Turbo may start crawling as follows:

Determine the largest constant $C>0$ with the following property: for every sequence of positive real numbers $c_{1}, c_{2}, c_{3}, \ldots$ with $c_{i}<C$ for all $i$, Turbo can (after studying the sequence) ensure that there is some point on the circle that it will never visit or crawl across.
|
The largest possible $C$ is $C=\frac{1}{2}$.
For $0<C \leqslant \frac{1}{2}$, Turbo can simply choose an arbitrary point $P$ (different from its starting point) to avoid. When Turbo is at an arbitrary point $A$ different from $P$, the two arcs $A P$ have total length 1 ; therefore, the larger of the two the arcs (or either arc in case $A$ is diametrically opposite to $P$ ) must have length $\geqslant \frac{1}{2}$. By always choosing this larger arc (or either arc in case $A$ is diametrically opposite to $P$ ), Turbo will manage to avoid the point $P$ forever.
For $C>\frac{1}{2}$, we write $C=\frac{1}{2}+a$ with $a>0$, and we choose the sequence
$$
\frac{1}{2}, \quad \frac{1+a}{2}, \quad \frac{1}{2}, \quad \frac{1+a}{2}, \quad \frac{1}{2}, \quad \ldots
$$
In other words, $c_{i}=\frac{1}{2}$ if $i$ is odd and $c_{i}=\frac{1+a}{2}<C$ when $i$ is even. We claim Turbo must eventually visit all points on the circle. This is clear when it crawls in the same direction two times in a row; after all, we have $c_{i}+c_{i+1}>1$ for all $i$. Therefore, we are left with the case that Turbo alternates crawling clockwise and crawling counterclockwise. If it, without loss of generality, starts by going clockwise, then it will always crawl a distance $\frac{1}{2}$ clockwise followed by a distance $\frac{1+a}{2}$ counterclockwise. The net effect is that it crawls a distance $\frac{a}{2}$ counterclockwise. Because $\frac{a}{2}$ is positive, there exists a positive integer $N$ such that $\frac{a}{2} \cdot N>1$. After $2 N$ crawls, Turbo will have crawled a distance $\frac{a}{2}$ counterclockwise $N$ times, therefore having covered a total distance of $\frac{a}{2} \cdot N>1$, meaning that it must have crawled over all points on the circle.
Note: Every sequence of the form $c_{i}=x$ if $i$ is odd, and $c_{i}=y$ if $i$ is even, where $0<x, y<C$, such that $x+y \geqslant 1$, and $x \neq y$ satisfies the conditions with the same argument. There might be even more possible examples.
|
{
"exam": "EGMO",
"problem_label": "4",
"problem_match": "\nProblem 4.",
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"solution_match": "\nSolution 1. ",
"tier": "T2",
"year": "2023"
}
|
Turbo the snail sits on a point on a circle with circumference 1. Given an infinite sequence of positive real numbers $c_{1}, c_{2}, c_{3}, \ldots$, Turbo successively crawls distances $c_{1}, c_{2}, c_{3}, \ldots$ around the circle, each time choosing to crawl either clockwise or counterclockwise.
For example, if the sequence $c_{1}, c_{2}, c_{3}, \ldots$ is $0.4,0.6,0.3, \ldots$, then Turbo may start crawling as follows:

Determine the largest constant $C>0$ with the following property: for every sequence of positive real numbers $c_{1}, c_{2}, c_{3}, \ldots$ with $c_{i}<C$ for all $i$, Turbo can (after studying the sequence) ensure that there is some point on the circle that it will never visit or crawl across.
|
Alternative solution (to show that $C \leqslant \frac{1}{2}$ )
We consider the following related problem:
We assume instead that the snail Chet is moving left and right on the real line. Find the size $M$ of the smallest (closed) interval, that we cannot force Chet out of, using a sequence of real numbers $d_{i}$ with $0<d_{i}<1$ for all $i$.
Then $C=1 / M$. Indeed if for every sequence $c_{1}, c_{2}, \ldots$, with $c_{i}<C$ there exists a point that Turbo can avoid, then the circle can be cut open at the avoided point and mapped to an interval of size $M$ such that Chet can stay inside this interval for any sequence of the from $c_{1} / C, c_{2} / C, \ldots$, see Figure 5 . However, all sequences $d_{1}, d_{2}, \ldots$ with $d_{i}<1$ can be written in this form. Similarly if for every sequence $d_{1}, d_{2}, \ldots$, there exists an interval of length smaller or equal $M$ that we cannot force Chet out of, this projects to a subset of the circle, that we cannot force Turbo out of using any sequence of the form $d_{1} / M, d_{2} / M, \ldots$. These are again exactly all the sequences with elements in $[0, C)$.
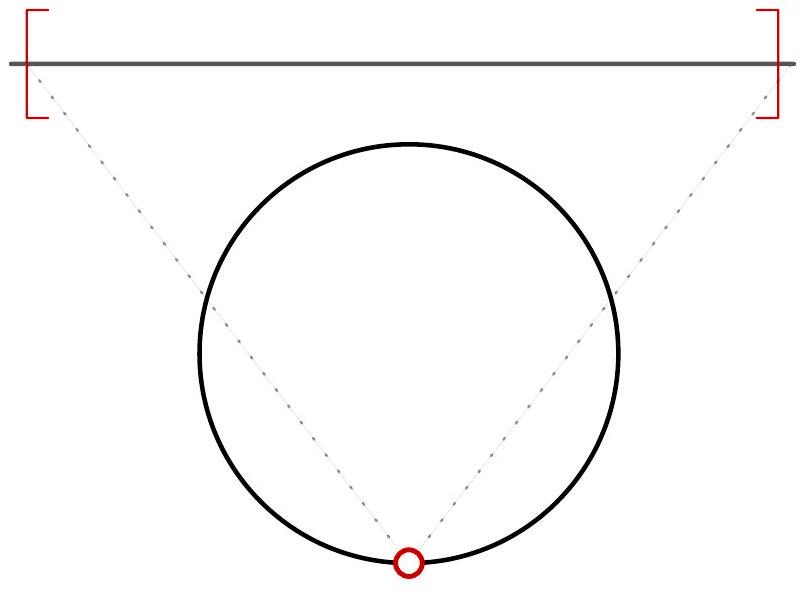
Figure 5: Chet and Turbo equivalence
Claim: $M \geqslant 2$.
Proof. Suppose not, so $M<2$. Say $M=2-2 \varepsilon$ for some $\varepsilon>0$ and let $[-1+\varepsilon, 1-\varepsilon]$ be a minimal interval, that Chet cannot be forced out of. Then we can force Chet arbitrarily close to $\pm(1-\varepsilon)$. In partiular, we can force Chet out of $\left[-1+\frac{4}{3} \varepsilon, 1-\frac{4}{3} \varepsilon\right]$ by minimality of $M$. This means that there exists a sequence $d_{1}, d_{2}, \ldots$ for which Chet has to leave $\left[-1+\frac{4}{3} \varepsilon, 1-\frac{4}{3} \varepsilon\right]$, which means he ends up either in the interval $\left[-1+\varepsilon,-1+\frac{4}{3} \varepsilon\right)$ or in the interval $\left(1-\frac{4}{3} \varepsilon, 1-\varepsilon\right]$.
Now consider the sequence,
$$
d_{1}, \quad 1-\frac{7}{6} \varepsilon, \quad 1-\frac{2}{3} \varepsilon, \quad 1-\frac{2}{3} \varepsilon, 1-\frac{7}{6} \varepsilon, \quad d_{2}, 1-\frac{7}{6} \varepsilon, 1-\frac{2}{3} \varepsilon, 1-\frac{2}{3} \varepsilon, 1-\frac{7}{6} \varepsilon, d_{3}, \ldots
$$
obtained by adding the sequence $1-\frac{7}{6} \varepsilon, \quad 1-\frac{2}{3} \varepsilon, \quad 1-\frac{2}{3} \varepsilon, \quad 1-\frac{7}{6} \varepsilon$ in between every two steps. We claim that this sequence forces Chet to leave the larger interval $[-1+\varepsilon, 1-\varepsilon]$. Indeed no two consecutive elements in the sequence $1-\frac{7}{6} \varepsilon, \quad 1-\frac{2}{3} \varepsilon, \quad 1-\frac{2}{3} \varepsilon, \quad 1-\frac{7}{6} \varepsilon$ can
have the same sign, because the sum of any two consecutive terms is larger than $2-2 \varepsilon$ and Chet would leave the interval $[-1+\varepsilon, 1-\varepsilon]$. It follows that the $\left(1-\frac{7}{6} \varepsilon\right.$ )'s and the ( $1-\frac{2}{3} \varepsilon$ )'s cancel out, so the position after $d_{k}$ is the same as before $d_{k+1}$. Hence, the positions after each $d_{k}$ remain the same as in the original sequence. Thus, Chet is also forced to the boundary in the new sequence.
If Chet is outside the interval $\left[-1+\frac{4}{3} \varepsilon, 1-\frac{4}{3} \varepsilon\right]$, then Chet has to move $1-\frac{7}{6} \varepsilon$ towards 0 , and ends in $\left[-\frac{1}{6} \varepsilon, \frac{1}{6} \varepsilon\right]$. Chet then has to move by $1-\frac{2}{3} \varepsilon$, which means that he has to leave the interval $[-1+\varepsilon, 1-\varepsilon]$. Indeed the absolute value of the final position is at least $1-\frac{5}{6} \varepsilon$. This contradicts the assumption, that we cannot force Chet out of $[-1+\varepsilon, 1-\varepsilon]$. Hence $M \geqslant 2$ as needed.
|
C \leqslant \frac{1}{2}
|
Incomplete
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
Turbo the snail sits on a point on a circle with circumference 1. Given an infinite sequence of positive real numbers $c_{1}, c_{2}, c_{3}, \ldots$, Turbo successively crawls distances $c_{1}, c_{2}, c_{3}, \ldots$ around the circle, each time choosing to crawl either clockwise or counterclockwise.
For example, if the sequence $c_{1}, c_{2}, c_{3}, \ldots$ is $0.4,0.6,0.3, \ldots$, then Turbo may start crawling as follows:

Determine the largest constant $C>0$ with the following property: for every sequence of positive real numbers $c_{1}, c_{2}, c_{3}, \ldots$ with $c_{i}<C$ for all $i$, Turbo can (after studying the sequence) ensure that there is some point on the circle that it will never visit or crawl across.
|
Alternative solution (to show that $C \leqslant \frac{1}{2}$ )
We consider the following related problem:
We assume instead that the snail Chet is moving left and right on the real line. Find the size $M$ of the smallest (closed) interval, that we cannot force Chet out of, using a sequence of real numbers $d_{i}$ with $0<d_{i}<1$ for all $i$.
Then $C=1 / M$. Indeed if for every sequence $c_{1}, c_{2}, \ldots$, with $c_{i}<C$ there exists a point that Turbo can avoid, then the circle can be cut open at the avoided point and mapped to an interval of size $M$ such that Chet can stay inside this interval for any sequence of the from $c_{1} / C, c_{2} / C, \ldots$, see Figure 5 . However, all sequences $d_{1}, d_{2}, \ldots$ with $d_{i}<1$ can be written in this form. Similarly if for every sequence $d_{1}, d_{2}, \ldots$, there exists an interval of length smaller or equal $M$ that we cannot force Chet out of, this projects to a subset of the circle, that we cannot force Turbo out of using any sequence of the form $d_{1} / M, d_{2} / M, \ldots$. These are again exactly all the sequences with elements in $[0, C)$.

Figure 5: Chet and Turbo equivalence
Claim: $M \geqslant 2$.
Proof. Suppose not, so $M<2$. Say $M=2-2 \varepsilon$ for some $\varepsilon>0$ and let $[-1+\varepsilon, 1-\varepsilon]$ be a minimal interval, that Chet cannot be forced out of. Then we can force Chet arbitrarily close to $\pm(1-\varepsilon)$. In partiular, we can force Chet out of $\left[-1+\frac{4}{3} \varepsilon, 1-\frac{4}{3} \varepsilon\right]$ by minimality of $M$. This means that there exists a sequence $d_{1}, d_{2}, \ldots$ for which Chet has to leave $\left[-1+\frac{4}{3} \varepsilon, 1-\frac{4}{3} \varepsilon\right]$, which means he ends up either in the interval $\left[-1+\varepsilon,-1+\frac{4}{3} \varepsilon\right)$ or in the interval $\left(1-\frac{4}{3} \varepsilon, 1-\varepsilon\right]$.
Now consider the sequence,
$$
d_{1}, \quad 1-\frac{7}{6} \varepsilon, \quad 1-\frac{2}{3} \varepsilon, \quad 1-\frac{2}{3} \varepsilon, 1-\frac{7}{6} \varepsilon, \quad d_{2}, 1-\frac{7}{6} \varepsilon, 1-\frac{2}{3} \varepsilon, 1-\frac{2}{3} \varepsilon, 1-\frac{7}{6} \varepsilon, d_{3}, \ldots
$$
obtained by adding the sequence $1-\frac{7}{6} \varepsilon, \quad 1-\frac{2}{3} \varepsilon, \quad 1-\frac{2}{3} \varepsilon, \quad 1-\frac{7}{6} \varepsilon$ in between every two steps. We claim that this sequence forces Chet to leave the larger interval $[-1+\varepsilon, 1-\varepsilon]$. Indeed no two consecutive elements in the sequence $1-\frac{7}{6} \varepsilon, \quad 1-\frac{2}{3} \varepsilon, \quad 1-\frac{2}{3} \varepsilon, \quad 1-\frac{7}{6} \varepsilon$ can
have the same sign, because the sum of any two consecutive terms is larger than $2-2 \varepsilon$ and Chet would leave the interval $[-1+\varepsilon, 1-\varepsilon]$. It follows that the $\left(1-\frac{7}{6} \varepsilon\right.$ )'s and the ( $1-\frac{2}{3} \varepsilon$ )'s cancel out, so the position after $d_{k}$ is the same as before $d_{k+1}$. Hence, the positions after each $d_{k}$ remain the same as in the original sequence. Thus, Chet is also forced to the boundary in the new sequence.
If Chet is outside the interval $\left[-1+\frac{4}{3} \varepsilon, 1-\frac{4}{3} \varepsilon\right]$, then Chet has to move $1-\frac{7}{6} \varepsilon$ towards 0 , and ends in $\left[-\frac{1}{6} \varepsilon, \frac{1}{6} \varepsilon\right]$. Chet then has to move by $1-\frac{2}{3} \varepsilon$, which means that he has to leave the interval $[-1+\varepsilon, 1-\varepsilon]$. Indeed the absolute value of the final position is at least $1-\frac{5}{6} \varepsilon$. This contradicts the assumption, that we cannot force Chet out of $[-1+\varepsilon, 1-\varepsilon]$. Hence $M \geqslant 2$ as needed.
|
{
"exam": "EGMO",
"problem_label": "4",
"problem_match": "\nProblem 4.",
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"solution_match": "\nSolution 2. ",
"tier": "T2",
"year": "2023"
}
|
We are given a positive integer $s \geqslant 2$. For each positive integer $k$, we define its twist $k^{\prime}$ as follows: write $k$ as $a s+b$, where $a, b$ are non-negative integers and $b<s$, then $k^{\prime}=b s+a$. For the positive integer $n$, consider the infinite sequence $d_{1}, d_{2}, \ldots$ where $d_{1}=n$ and $d_{i+1}$ is the twist of $d_{i}$ for each positive integer $i$.
Prove that this sequence contains 1 if and only if the remainder when $n$ is divided by $s^{2}-1$ is either 1 or $s$.
|
First, we consider the difference $k-k^{\prime \prime}$. If $k=a s+b$ as in the problem statement, then $k^{\prime}=b s+a$. We write $a=l s+m$ with $m, l$ non-negative numbers and $m \leq s-1$. This gives $k^{\prime \prime}=m s+(b+l)$ and hence $k-k^{\prime \prime}=(a-m) s-l=l\left(s^{2}-1\right)$.
We conclude
Fact 1.1. $k \geq k^{\prime \prime}$ for every every $k \geq 1$
Fact 1.2. $s^{2}-1$ divides the difference $k-k^{\prime \prime}$.
Fact 1.2 implies that the sequences $d_{1}, d_{3}, d_{5}, \ldots$ and $d_{2}, d_{4}, d_{6}, \ldots$ are constant modulo $s^{2}-1$. Moreover, Fact 1.1 says that the sequences are (weakly) decreasing and hence eventually constant. In other words, the sequence $d_{1}, d_{2}, d_{3}, \ldots$ is 2 -periodic modulo $s^{2}-1$ (from the start) and is eventually 2-periodic.
Now, assume that some term in the sequence is equal to 1 . The next term is equal to $1^{\prime}=s$ and since the sequence is 2 -periodic from the start modulo $s^{2}-1$, we conclude that $d_{1}$ is either equal to 1 or $s$ modulo $s^{2}-1$. This proves the first implication.
To prove the other direction, assume that $d_{1}$ is congruent to 1 or $s$ modulo $s^{2}-1$. We need the observation that once one of the sequences $d_{1}, d_{3}, d_{5}, \ldots$ or $d_{2}, d_{4}, d_{6}, \ldots$ stabilises, then their value is less than $s^{2}$. This is implied by the following fact.
Fact 1.3. If $k=k^{\prime \prime}$, then $k=k^{\prime \prime}<s^{2}$.
Proof. We use the expression for $k-k^{\prime \prime}$ found before. If $k=k^{\prime \prime}$, then $l=0$, and so $k^{\prime \prime}=m s+b$. Both $m$ and $b$ are reminders after division by $s$, so they are both $\leq s-1$. This gives $k^{\prime \prime} \leq(s-1) s+(s-1)<s^{2}$.
Using Fact 1.2, it follows that the sequence $d_{1}, d_{3}, d_{5}, \ldots$ is constant to 1 or $s$ modulo $s^{2}-1$ and stabilises to 1 or $s$ by Fact 1.3. Since $s^{\prime}=1$, we conclude that the sequence contains a 1.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
We are given a positive integer $s \geqslant 2$. For each positive integer $k$, we define its twist $k^{\prime}$ as follows: write $k$ as $a s+b$, where $a, b$ are non-negative integers and $b<s$, then $k^{\prime}=b s+a$. For the positive integer $n$, consider the infinite sequence $d_{1}, d_{2}, \ldots$ where $d_{1}=n$ and $d_{i+1}$ is the twist of $d_{i}$ for each positive integer $i$.
Prove that this sequence contains 1 if and only if the remainder when $n$ is divided by $s^{2}-1$ is either 1 or $s$.
|
First, we consider the difference $k-k^{\prime \prime}$. If $k=a s+b$ as in the problem statement, then $k^{\prime}=b s+a$. We write $a=l s+m$ with $m, l$ non-negative numbers and $m \leq s-1$. This gives $k^{\prime \prime}=m s+(b+l)$ and hence $k-k^{\prime \prime}=(a-m) s-l=l\left(s^{2}-1\right)$.
We conclude
Fact 1.1. $k \geq k^{\prime \prime}$ for every every $k \geq 1$
Fact 1.2. $s^{2}-1$ divides the difference $k-k^{\prime \prime}$.
Fact 1.2 implies that the sequences $d_{1}, d_{3}, d_{5}, \ldots$ and $d_{2}, d_{4}, d_{6}, \ldots$ are constant modulo $s^{2}-1$. Moreover, Fact 1.1 says that the sequences are (weakly) decreasing and hence eventually constant. In other words, the sequence $d_{1}, d_{2}, d_{3}, \ldots$ is 2 -periodic modulo $s^{2}-1$ (from the start) and is eventually 2-periodic.
Now, assume that some term in the sequence is equal to 1 . The next term is equal to $1^{\prime}=s$ and since the sequence is 2 -periodic from the start modulo $s^{2}-1$, we conclude that $d_{1}$ is either equal to 1 or $s$ modulo $s^{2}-1$. This proves the first implication.
To prove the other direction, assume that $d_{1}$ is congruent to 1 or $s$ modulo $s^{2}-1$. We need the observation that once one of the sequences $d_{1}, d_{3}, d_{5}, \ldots$ or $d_{2}, d_{4}, d_{6}, \ldots$ stabilises, then their value is less than $s^{2}$. This is implied by the following fact.
Fact 1.3. If $k=k^{\prime \prime}$, then $k=k^{\prime \prime}<s^{2}$.
Proof. We use the expression for $k-k^{\prime \prime}$ found before. If $k=k^{\prime \prime}$, then $l=0$, and so $k^{\prime \prime}=m s+b$. Both $m$ and $b$ are reminders after division by $s$, so they are both $\leq s-1$. This gives $k^{\prime \prime} \leq(s-1) s+(s-1)<s^{2}$.
Using Fact 1.2, it follows that the sequence $d_{1}, d_{3}, d_{5}, \ldots$ is constant to 1 or $s$ modulo $s^{2}-1$ and stabilises to 1 or $s$ by Fact 1.3. Since $s^{\prime}=1$, we conclude that the sequence contains a 1.
|
{
"exam": "EGMO",
"problem_label": "5",
"problem_match": "\nProblem 5.",
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"solution_match": "\nSolution 1. ",
"tier": "T2",
"year": "2023"
}
|
We are given a positive integer $s \geqslant 2$. For each positive integer $k$, we define its twist $k^{\prime}$ as follows: write $k$ as $a s+b$, where $a, b$ are non-negative integers and $b<s$, then $k^{\prime}=b s+a$. For the positive integer $n$, consider the infinite sequence $d_{1}, d_{2}, \ldots$ where $d_{1}=n$ and $d_{i+1}$ is the twist of $d_{i}$ for each positive integer $i$.
Prove that this sequence contains 1 if and only if the remainder when $n$ is divided by $s^{2}-1$ is either 1 or $s$.
|
We make a number of initial observations. Let $k$ be a positive integer.
Fact 2.1. If $k \geq s^{2}$, then $k^{\prime}<k$.
Proof. Write $k=a s+b$, as in the problem statement. If $k \geq s^{2}$, then $a \geq s$ because $b<s$. So, $k^{\prime}=b s+a \leq(s-1) s+a \leq a s \leq a s+b=k$. Moreover, we cannot have equality since that would imply $s-1=b=0$.
Fact 2.2. If $k \leq s^{2}-1$, then $k^{\prime} \leq s^{2}-1$ and $k^{\prime \prime}=k$.
Proof. Write $k=a s+b$, as in the problem statement. If $k<s^{2}$, then it must hold $1 \leq a, b<s$, hence $k^{\prime}=b s+a<s^{2}$ and $k^{\prime \prime}=(b s+a)^{\prime}=a s+b=k$.
Fact 2.3. We have $k^{\prime} \equiv s k\left(\bmod s^{2}-1\right)\left(\right.$ or equivalently $\left.k \equiv s k^{\prime}\left(\bmod s^{2}-1\right)\right)$.
Proof. We write $k=a s+b$, as in the problem statement. Now,
$$
s k-k^{\prime}=s(a s+b)-(b s+a)=a\left(s^{2}-1\right) \equiv 0 \quad\left(\bmod s^{2}-1\right),
$$
as desired.
Combining Facts 2.1 and 2.2 , we find that the sequence $d_{1}, d_{2}, d_{3} \ldots$ is eventually periodic with period 2, starting at the first value less than $s^{2}$. From Fact 2.3, it follows that
$$
k^{\prime \prime} \equiv s k^{\prime} \equiv s^{2} k \equiv k \quad\left(\bmod s^{2}-1\right)
$$
and hence the sequence is periodic modulo $s^{2}-1$ from the start with period 2 .
Now, if the sequence contains 1 , the sequence eventually alternates between 1 and $s$ since the twist of 1 is $s$ and vice versa. Using periodicity modulo $s^{2}-1$, we must have $n \equiv 1, s$ $\left(\bmod s^{2}-1\right)$. Conversely, if $n \equiv 1, s\left(\bmod s^{2}-1\right)$ then the eventual period must contain at least one value congruent to either 1 or $s$ modulo $s^{2}-1$. Since these values must be less than $s^{2}$, this implies that the sequence eventually alternates between 1 and $s$, showing that it contains a 1 .
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
We are given a positive integer $s \geqslant 2$. For each positive integer $k$, we define its twist $k^{\prime}$ as follows: write $k$ as $a s+b$, where $a, b$ are non-negative integers and $b<s$, then $k^{\prime}=b s+a$. For the positive integer $n$, consider the infinite sequence $d_{1}, d_{2}, \ldots$ where $d_{1}=n$ and $d_{i+1}$ is the twist of $d_{i}$ for each positive integer $i$.
Prove that this sequence contains 1 if and only if the remainder when $n$ is divided by $s^{2}-1$ is either 1 or $s$.
|
We make a number of initial observations. Let $k$ be a positive integer.
Fact 2.1. If $k \geq s^{2}$, then $k^{\prime}<k$.
Proof. Write $k=a s+b$, as in the problem statement. If $k \geq s^{2}$, then $a \geq s$ because $b<s$. So, $k^{\prime}=b s+a \leq(s-1) s+a \leq a s \leq a s+b=k$. Moreover, we cannot have equality since that would imply $s-1=b=0$.
Fact 2.2. If $k \leq s^{2}-1$, then $k^{\prime} \leq s^{2}-1$ and $k^{\prime \prime}=k$.
Proof. Write $k=a s+b$, as in the problem statement. If $k<s^{2}$, then it must hold $1 \leq a, b<s$, hence $k^{\prime}=b s+a<s^{2}$ and $k^{\prime \prime}=(b s+a)^{\prime}=a s+b=k$.
Fact 2.3. We have $k^{\prime} \equiv s k\left(\bmod s^{2}-1\right)\left(\right.$ or equivalently $\left.k \equiv s k^{\prime}\left(\bmod s^{2}-1\right)\right)$.
Proof. We write $k=a s+b$, as in the problem statement. Now,
$$
s k-k^{\prime}=s(a s+b)-(b s+a)=a\left(s^{2}-1\right) \equiv 0 \quad\left(\bmod s^{2}-1\right),
$$
as desired.
Combining Facts 2.1 and 2.2 , we find that the sequence $d_{1}, d_{2}, d_{3} \ldots$ is eventually periodic with period 2, starting at the first value less than $s^{2}$. From Fact 2.3, it follows that
$$
k^{\prime \prime} \equiv s k^{\prime} \equiv s^{2} k \equiv k \quad\left(\bmod s^{2}-1\right)
$$
and hence the sequence is periodic modulo $s^{2}-1$ from the start with period 2 .
Now, if the sequence contains 1 , the sequence eventually alternates between 1 and $s$ since the twist of 1 is $s$ and vice versa. Using periodicity modulo $s^{2}-1$, we must have $n \equiv 1, s$ $\left(\bmod s^{2}-1\right)$. Conversely, if $n \equiv 1, s\left(\bmod s^{2}-1\right)$ then the eventual period must contain at least one value congruent to either 1 or $s$ modulo $s^{2}-1$. Since these values must be less than $s^{2}$, this implies that the sequence eventually alternates between 1 and $s$, showing that it contains a 1 .
|
{
"exam": "EGMO",
"problem_label": "5",
"problem_match": "\nProblem 5.",
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"solution_match": "\nSolution 2. ",
"tier": "T2",
"year": "2023"
}
|
We are given a positive integer $s \geqslant 2$. For each positive integer $k$, we define its twist $k^{\prime}$ as follows: write $k$ as $a s+b$, where $a, b$ are non-negative integers and $b<s$, then $k^{\prime}=b s+a$. For the positive integer $n$, consider the infinite sequence $d_{1}, d_{2}, \ldots$ where $d_{1}=n$ and $d_{i+1}$ is the twist of $d_{i}$ for each positive integer $i$.
Prove that this sequence contains 1 if and only if the remainder when $n$ is divided by $s^{2}-1$ is either 1 or $s$.
|
We give an alternate proof of the direct implication: if the sequence contains a 1 , then the first term is 1 or $s$ modulo $s^{2}-1$. We prove the following fact, which is a combination of Facts 2.1 and 2.3.
Fact 3.1. For all $k \geq s^{2}$, we have $\left(k-s^{2}+1\right)^{\prime} \in\left\{k^{\prime}, k^{\prime}-s^{2}+1\right\}$.
Proof. We write $k=a s+b$, as in the problem statement. Since $k \geq s^{2}$, we have $a \geq s$. If $b<s-1$, then
$$
\left(k-s^{2}+1\right)^{\prime}=((a-s) s+(b+1))^{\prime}=(b+1) s+(a-s)=b s+a=k^{\prime}
$$
On the other hand, if $b=s-1$, then
$$
\left(k-s^{2}+1\right)^{\prime}=((a-s+1) s+0)^{\prime}=0 s+(a-s+1)=a-s+1=k^{\prime}-s^{2}+1
$$
Now assume $n \geq s^{2}$ and the sequence $d_{1}, d_{2}, \ldots$ contains a 1 . Denote by $e_{1}, e_{2}, \ldots$ the sequence constructed as in the problem statement, but with initial value $e_{1}=n-s^{2}+1$. Using the above fact, we deduce that $e_{i} \equiv d_{i}\left(\bmod s^{2}-1\right)$ and $e_{i} \leq d_{i}$ for all $i \geq 1$ by induction on $i$. Hence, the sequence $e_{1}, e_{2}, \ldots$ also contains a 1 .
Since the conclusion we are trying to reach only depends on the residue of $d_{1}$ modulo $s^{2}-1$, we conclude that without loss of generality we can assume $n<s^{2}$.
Using Fact 2.2, it now follows that the sequence $d_{1}, d_{2}, \ldots$ is periodic with period two. Since 1 and $s$ are twists of each other, it follows that if this sequence contains a 1 , it must be alternating between 1 and $s$. Hence, $d_{1} \equiv 1, s\left(\bmod s^{2}-1\right)$ as desired.
For the other direction we can make a similar argument, observing that the second of the two cases in the proof of Fact 3.1 can only apply to finitely many terms of the sequence $d_{1}, d_{2}, d_{3}, \ldots$, allowing us to also go the other way.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
We are given a positive integer $s \geqslant 2$. For each positive integer $k$, we define its twist $k^{\prime}$ as follows: write $k$ as $a s+b$, where $a, b$ are non-negative integers and $b<s$, then $k^{\prime}=b s+a$. For the positive integer $n$, consider the infinite sequence $d_{1}, d_{2}, \ldots$ where $d_{1}=n$ and $d_{i+1}$ is the twist of $d_{i}$ for each positive integer $i$.
Prove that this sequence contains 1 if and only if the remainder when $n$ is divided by $s^{2}-1$ is either 1 or $s$.
|
We give an alternate proof of the direct implication: if the sequence contains a 1 , then the first term is 1 or $s$ modulo $s^{2}-1$. We prove the following fact, which is a combination of Facts 2.1 and 2.3.
Fact 3.1. For all $k \geq s^{2}$, we have $\left(k-s^{2}+1\right)^{\prime} \in\left\{k^{\prime}, k^{\prime}-s^{2}+1\right\}$.
Proof. We write $k=a s+b$, as in the problem statement. Since $k \geq s^{2}$, we have $a \geq s$. If $b<s-1$, then
$$
\left(k-s^{2}+1\right)^{\prime}=((a-s) s+(b+1))^{\prime}=(b+1) s+(a-s)=b s+a=k^{\prime}
$$
On the other hand, if $b=s-1$, then
$$
\left(k-s^{2}+1\right)^{\prime}=((a-s+1) s+0)^{\prime}=0 s+(a-s+1)=a-s+1=k^{\prime}-s^{2}+1
$$
Now assume $n \geq s^{2}$ and the sequence $d_{1}, d_{2}, \ldots$ contains a 1 . Denote by $e_{1}, e_{2}, \ldots$ the sequence constructed as in the problem statement, but with initial value $e_{1}=n-s^{2}+1$. Using the above fact, we deduce that $e_{i} \equiv d_{i}\left(\bmod s^{2}-1\right)$ and $e_{i} \leq d_{i}$ for all $i \geq 1$ by induction on $i$. Hence, the sequence $e_{1}, e_{2}, \ldots$ also contains a 1 .
Since the conclusion we are trying to reach only depends on the residue of $d_{1}$ modulo $s^{2}-1$, we conclude that without loss of generality we can assume $n<s^{2}$.
Using Fact 2.2, it now follows that the sequence $d_{1}, d_{2}, \ldots$ is periodic with period two. Since 1 and $s$ are twists of each other, it follows that if this sequence contains a 1 , it must be alternating between 1 and $s$. Hence, $d_{1} \equiv 1, s\left(\bmod s^{2}-1\right)$ as desired.
For the other direction we can make a similar argument, observing that the second of the two cases in the proof of Fact 3.1 can only apply to finitely many terms of the sequence $d_{1}, d_{2}, d_{3}, \ldots$, allowing us to also go the other way.
|
{
"exam": "EGMO",
"problem_label": "5",
"problem_match": "\nProblem 5.",
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"solution_match": "\nSolution 3. ",
"tier": "T2",
"year": "2023"
}
|
We are given a positive integer $s \geqslant 2$. For each positive integer $k$, we define its twist $k^{\prime}$ as follows: write $k$ as $a s+b$, where $a, b$ are non-negative integers and $b<s$, then $k^{\prime}=b s+a$. For the positive integer $n$, consider the infinite sequence $d_{1}, d_{2}, \ldots$ where $d_{1}=n$ and $d_{i+1}$ is the twist of $d_{i}$ for each positive integer $i$.
Prove that this sequence contains 1 if and only if the remainder when $n$ is divided by $s^{2}-1$ is either 1 or $s$.
|
First assume that $d_{k}=1$ for some $k$. Let $k$ be the smallest such index. If $k=1$ then $n=1$, so we may assume $k \geqslant 2$.
Then $d_{k-1}=a s+b$ for some non-negative integers $a, b$ satisfying $b<s$ and $b s+a=1$. The only solution is $b=0, a=1$, so $d_{k-1}=s$. So, if $k=2$, then $n=s$, so we may assume $k \geqslant 3$.
Then there exist non-negative integers $c, d$ satisfying $d_{k-2}=c s+d, d<s$ and $d s+c=s$. We have two solutions: $d=0, c=s$ and $d=1, c=0$. However, in the second case we get $d_{k-2}=1$, which contradicts the minimality of $k$. Hence, $d_{k-2}=s^{2}$. If $k=3$, then $n=d_{1}=s^{2}$, which gives remainder 1 when divided by $s^{2}-1$.
Assume now that $k \geqslant 4$. We will show that for each $m \in\{3,4, \ldots, k-1\}$ there exist $b_{1}, b_{2}, \ldots, b_{m-2} \in\{0,1, \ldots, s-1\}$ such that
$$
d_{k-m}=s^{m}-\sum_{i=1}^{m-2} b_{i}\left(s^{m-i}-s^{m-i-2}\right) .
$$
We will prove this equality by induction on $m$. If $m=3$, then $d_{k-3}=a_{1} s+b_{1}$ for some non-negative integers $a_{1}, b_{1}$ satisfying $b_{1}<s$ and $b_{1} s+a_{1}=d_{k-2}=s^{2}$. Then $a_{1}=s^{2}-b_{1} s$, so $d_{k-3}=s^{3}-b_{1}\left(s^{2}-1\right)$, which proves (9) for $m=3$.
Assume that (9) holds for some $m$ and consider $d_{k-(m+1)}$. There exist non-negative integers $a_{m-1}, b_{m-1}$ such that $d_{k-(m+1)}=a_{m-1} s+b_{m-1}, b_{m-1}<s$ and $d_{k-m}=b_{m-1} s+a_{m-1}$. Using the inductive assumption we get
$$
a_{m-1}=d_{k-m}-b_{m-1} s=s^{m}-\sum_{i=1}^{m-2} b_{i}\left(s^{m-i}-s^{m-i-2}\right)-b_{m-1} s,
$$
therefore
$$
\begin{aligned}
d_{k-(m+1)} & =a_{m-1} s+b_{m-1}=s^{m+1}-\sum_{i=1}^{m-2} b_{i}\left(s^{m-i}-s^{m-i-2}\right) s-b_{m-1} s^{2}+b_{m-1} \\
& =s^{m+1}-\sum_{i=1}^{m-1} b_{i}\left(s^{m+1-i}-s^{m-i-1}\right)
\end{aligned}
$$
which completes the proof of (9). In particular, for $m=k-1$ we get
$$
d_{1}=s^{k-1}-\sum_{i=1}^{k-3} b_{i}\left(s^{k-i-1}-s^{k-i-3}\right) .
$$
The above sum is clearly divisible by $s^{2}-1$, and it is clear that the remainder of $s^{k-1}$ when divided by $s^{2}-1$ is 1 when $k$ is odd, and $s$ when $k$ is even. It follows that the remainder when $n=d_{1}$ is divided by $s^{2}-1$ is either 1 or $s$.
To prove the other implication, assume that $n$ gives remainder 1 or $s$ when divided by $s^{2}-1$. If $n \in\left\{1, s, s^{2}\right\}$, then one of the numbers $d_{1}, d_{2}$ and $d_{3}$ is 1 . We therefore assume that $n>s^{2}$. Since the reminder when a power of $s$ is divided by $s^{2}-1$ is either 1 or $s$, there exists a positive integer $m$ such that $s^{m}-n$ is non-negative and divisible by $s^{2}-1$. By our assumption $m \geqslant 3$. We also take the smallest such $m$, so that $n>s^{m-2}$. The quotient $\frac{s^{m}-n}{s^{2}-1}$ is therefore smaller than $s^{m-2}$, so there exist $b_{1}, \ldots, b_{m-2} \in\{0,1, \ldots, s-1\}$ such that $\frac{s^{m}-n}{s^{2}-1}=\sum_{i=1}^{m-2} b_{i} s^{i-1}$. It follows that
$$
n=s^{m}-\sum_{i=1}^{m-2} b_{i}\left(s^{i+1}-s^{i-1}\right) .
$$
We now show that
$$
d_{j}=s^{m+1-j}-\sum_{i=1}^{m-1-j} b_{i}\left(s^{i+1}-s^{i-1}\right)
$$
for $j=1,2, \ldots, m-2$ by induction on $j$. For $j=1$ this follows from $d_{1}=n$. Assume now that (10) holds for some $j<m-2$. Then
$$
d_{j}=\left(s^{m-j}-\sum_{i=2}^{m-1-j} b_{i}\left(s^{i}-s^{i-2}\right)-b_{1} s\right) s+b_{1}
$$
As $d_{j}$ is positive and $b_{1} \in\{0,1, \ldots, s-1\}$, the expression $s^{m-j}-\sum_{i=2}^{m-1-j} b_{i}\left(s^{i}-s^{i-2}\right)-b_{1} s$ has to be non-negative, so we can compute the twist of $d_{j}$ as
$$
d_{j+1}=b_{1} s+s^{m-j}-\sum_{i=2}^{m-1-j} b_{i}\left(s^{i}-s^{i-2}\right)-b_{1} s=s^{m-j}-\sum_{i=1}^{m-2-j} b_{i}\left(s^{i+1}-s^{i-1}\right),
$$
which finishes the induction.
Now we use (10) for $j=m-2$ and get $d_{m-2}=s^{3}-b_{1}\left(s^{2}-1\right)=\left(s^{2}-b_{1} s\right)+b_{1}$. Then $d_{m-1}=b_{1} s+s^{2}-b_{1} s=s^{2}=s \cdot s+0, d_{m}=0 \cdot s+s=s=1 \cdot s+0$ and $d_{m+1}=0 \cdot s+1=1$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
We are given a positive integer $s \geqslant 2$. For each positive integer $k$, we define its twist $k^{\prime}$ as follows: write $k$ as $a s+b$, where $a, b$ are non-negative integers and $b<s$, then $k^{\prime}=b s+a$. For the positive integer $n$, consider the infinite sequence $d_{1}, d_{2}, \ldots$ where $d_{1}=n$ and $d_{i+1}$ is the twist of $d_{i}$ for each positive integer $i$.
Prove that this sequence contains 1 if and only if the remainder when $n$ is divided by $s^{2}-1$ is either 1 or $s$.
|
First assume that $d_{k}=1$ for some $k$. Let $k$ be the smallest such index. If $k=1$ then $n=1$, so we may assume $k \geqslant 2$.
Then $d_{k-1}=a s+b$ for some non-negative integers $a, b$ satisfying $b<s$ and $b s+a=1$. The only solution is $b=0, a=1$, so $d_{k-1}=s$. So, if $k=2$, then $n=s$, so we may assume $k \geqslant 3$.
Then there exist non-negative integers $c, d$ satisfying $d_{k-2}=c s+d, d<s$ and $d s+c=s$. We have two solutions: $d=0, c=s$ and $d=1, c=0$. However, in the second case we get $d_{k-2}=1$, which contradicts the minimality of $k$. Hence, $d_{k-2}=s^{2}$. If $k=3$, then $n=d_{1}=s^{2}$, which gives remainder 1 when divided by $s^{2}-1$.
Assume now that $k \geqslant 4$. We will show that for each $m \in\{3,4, \ldots, k-1\}$ there exist $b_{1}, b_{2}, \ldots, b_{m-2} \in\{0,1, \ldots, s-1\}$ such that
$$
d_{k-m}=s^{m}-\sum_{i=1}^{m-2} b_{i}\left(s^{m-i}-s^{m-i-2}\right) .
$$
We will prove this equality by induction on $m$. If $m=3$, then $d_{k-3}=a_{1} s+b_{1}$ for some non-negative integers $a_{1}, b_{1}$ satisfying $b_{1}<s$ and $b_{1} s+a_{1}=d_{k-2}=s^{2}$. Then $a_{1}=s^{2}-b_{1} s$, so $d_{k-3}=s^{3}-b_{1}\left(s^{2}-1\right)$, which proves (9) for $m=3$.
Assume that (9) holds for some $m$ and consider $d_{k-(m+1)}$. There exist non-negative integers $a_{m-1}, b_{m-1}$ such that $d_{k-(m+1)}=a_{m-1} s+b_{m-1}, b_{m-1}<s$ and $d_{k-m}=b_{m-1} s+a_{m-1}$. Using the inductive assumption we get
$$
a_{m-1}=d_{k-m}-b_{m-1} s=s^{m}-\sum_{i=1}^{m-2} b_{i}\left(s^{m-i}-s^{m-i-2}\right)-b_{m-1} s,
$$
therefore
$$
\begin{aligned}
d_{k-(m+1)} & =a_{m-1} s+b_{m-1}=s^{m+1}-\sum_{i=1}^{m-2} b_{i}\left(s^{m-i}-s^{m-i-2}\right) s-b_{m-1} s^{2}+b_{m-1} \\
& =s^{m+1}-\sum_{i=1}^{m-1} b_{i}\left(s^{m+1-i}-s^{m-i-1}\right)
\end{aligned}
$$
which completes the proof of (9). In particular, for $m=k-1$ we get
$$
d_{1}=s^{k-1}-\sum_{i=1}^{k-3} b_{i}\left(s^{k-i-1}-s^{k-i-3}\right) .
$$
The above sum is clearly divisible by $s^{2}-1$, and it is clear that the remainder of $s^{k-1}$ when divided by $s^{2}-1$ is 1 when $k$ is odd, and $s$ when $k$ is even. It follows that the remainder when $n=d_{1}$ is divided by $s^{2}-1$ is either 1 or $s$.
To prove the other implication, assume that $n$ gives remainder 1 or $s$ when divided by $s^{2}-1$. If $n \in\left\{1, s, s^{2}\right\}$, then one of the numbers $d_{1}, d_{2}$ and $d_{3}$ is 1 . We therefore assume that $n>s^{2}$. Since the reminder when a power of $s$ is divided by $s^{2}-1$ is either 1 or $s$, there exists a positive integer $m$ such that $s^{m}-n$ is non-negative and divisible by $s^{2}-1$. By our assumption $m \geqslant 3$. We also take the smallest such $m$, so that $n>s^{m-2}$. The quotient $\frac{s^{m}-n}{s^{2}-1}$ is therefore smaller than $s^{m-2}$, so there exist $b_{1}, \ldots, b_{m-2} \in\{0,1, \ldots, s-1\}$ such that $\frac{s^{m}-n}{s^{2}-1}=\sum_{i=1}^{m-2} b_{i} s^{i-1}$. It follows that
$$
n=s^{m}-\sum_{i=1}^{m-2} b_{i}\left(s^{i+1}-s^{i-1}\right) .
$$
We now show that
$$
d_{j}=s^{m+1-j}-\sum_{i=1}^{m-1-j} b_{i}\left(s^{i+1}-s^{i-1}\right)
$$
for $j=1,2, \ldots, m-2$ by induction on $j$. For $j=1$ this follows from $d_{1}=n$. Assume now that (10) holds for some $j<m-2$. Then
$$
d_{j}=\left(s^{m-j}-\sum_{i=2}^{m-1-j} b_{i}\left(s^{i}-s^{i-2}\right)-b_{1} s\right) s+b_{1}
$$
As $d_{j}$ is positive and $b_{1} \in\{0,1, \ldots, s-1\}$, the expression $s^{m-j}-\sum_{i=2}^{m-1-j} b_{i}\left(s^{i}-s^{i-2}\right)-b_{1} s$ has to be non-negative, so we can compute the twist of $d_{j}$ as
$$
d_{j+1}=b_{1} s+s^{m-j}-\sum_{i=2}^{m-1-j} b_{i}\left(s^{i}-s^{i-2}\right)-b_{1} s=s^{m-j}-\sum_{i=1}^{m-2-j} b_{i}\left(s^{i+1}-s^{i-1}\right),
$$
which finishes the induction.
Now we use (10) for $j=m-2$ and get $d_{m-2}=s^{3}-b_{1}\left(s^{2}-1\right)=\left(s^{2}-b_{1} s\right)+b_{1}$. Then $d_{m-1}=b_{1} s+s^{2}-b_{1} s=s^{2}=s \cdot s+0, d_{m}=0 \cdot s+s=s=1 \cdot s+0$ and $d_{m+1}=0 \cdot s+1=1$.
|
{
"exam": "EGMO",
"problem_label": "5",
"problem_match": "\nProblem 5.",
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"solution_match": "\nSolution 4. ",
"tier": "T2",
"year": "2023"
}
|
Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.

Figure 6: Diagram to Solution 1
|
Part I: First we show that A lies on the radical axis of $\omega_{b}$ and $\omega_{c}$.
We first note that the line through the intersections of two circles is the radical line of the two circles. Let the tangents to $\Omega$ at $S_{b}$ and $S_{c}$ intersect at $T$. Clearly $T$ is on the radical axis of $\omega_{b}$ and $\omega_{c}$ (and in fact is the radical centre of $\omega_{b}, \omega_{c}$ and $\Omega$ ).
We next show that $A$ lies on the radical axis of $\omega_{b}$ and $\omega_{c}$. Let $P_{b}$ denote the point of tangency of $\omega_{b}$ and $A B$, and let $P_{c}$ denote the point of tangency of $\omega_{c}$ and $A C$. Furthermore, let $U$ be the intersection of the tangent to $\Omega$ at $S_{b}$ with the line $A B$, and let $V$ be the intersection of the tangent to $\Omega$ at $S_{c}$ with the line $A C$. Then $T V A U$ is parallelogram. Morover, due to equality of tangent segments we have $\left|U S_{b}\right|=\left|U P_{b}\right|,\left|V P_{c}\right|=\left|V S_{c}\right|$ and $\left|T S_{b}\right|=\left|T S_{c}\right|$. It follows that
$$
\begin{aligned}
\left|A P_{b}\right| & =\left|U P_{b}\right|-|U A|=\left|U S_{b}\right|-|T V|=\left|T S_{b}\right|-|T U|-|T V| \\
& =\left|T S_{s}\right|-|T V|-|T U|=\left|V S_{c}\right|-|A V|=\left|V P_{c}\right|-|V A|=\left|A P_{c}\right|
\end{aligned}
$$
But $\left|A P_{b}\right|,\left|A P_{c}\right|$ are exactly the square roots of powers of $A$ with respect to $\omega_{b}$ and $\omega_{c}$, hence $A$ is indeed on their radical axis.
Thus, the radical axis of $\omega_{b}, \omega_{c}$ is $A T$.
Part II: Consider the triangle $A S_{b} S_{c}$. Note that since $T$ is the intersection of the tangents at $S_{b}$ and $S_{c}$ to the circumcircle of $A S_{b} S_{c}$, it follows that $A T$ is the symmedian of $A$ in this triangle. Let $X$ denote the second intersection of the symmedian $A T$ with $\Omega$. We wish to show that $X$ is also on $I N_{a}$.
Note that $A N_{a}$ is the external angle bisector of angle $A$, and therefore it is parallel to $S_{b} S_{c}$. Let $M$ denote the midpoint of $S_{b} S_{c}$, and let $Y$ be the second intersection of $A M$ with $\Omega$. Since in $A S_{b} S_{c}, A X T$ is the symmedian and $A M Y$ is the median, it follows that $X Y$ is also parallel to $S_{b} S_{c}$. Thus, reflecting in the perpendicular bisector of $S_{b} S_{c}$ sends the line $A M Y$ to line $N_{a} M X$.
Next, consider the quadrilateral $A S_{b} I S_{c}$. From the trillium theorem we have $\left|S_{b} A\right|=\left|S_{b} I\right|$ and $\left|S_{c} A\right|=\left|S_{c} I\right|$, thus the quadrilateral is a kite, from which it follows that the reflection of the line $A M$ in $S_{b} S_{c}$ is the line $I M$. But previously we have seen that this is also the line $N_{a} M X$. Thus $M, I, N_{a}$ and $X$ are collinear, as we wanted to show.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.

Figure 6: Diagram to Solution 1
|
Part I: First we show that A lies on the radical axis of $\omega_{b}$ and $\omega_{c}$.
We first note that the line through the intersections of two circles is the radical line of the two circles. Let the tangents to $\Omega$ at $S_{b}$ and $S_{c}$ intersect at $T$. Clearly $T$ is on the radical axis of $\omega_{b}$ and $\omega_{c}$ (and in fact is the radical centre of $\omega_{b}, \omega_{c}$ and $\Omega$ ).
We next show that $A$ lies on the radical axis of $\omega_{b}$ and $\omega_{c}$. Let $P_{b}$ denote the point of tangency of $\omega_{b}$ and $A B$, and let $P_{c}$ denote the point of tangency of $\omega_{c}$ and $A C$. Furthermore, let $U$ be the intersection of the tangent to $\Omega$ at $S_{b}$ with the line $A B$, and let $V$ be the intersection of the tangent to $\Omega$ at $S_{c}$ with the line $A C$. Then $T V A U$ is parallelogram. Morover, due to equality of tangent segments we have $\left|U S_{b}\right|=\left|U P_{b}\right|,\left|V P_{c}\right|=\left|V S_{c}\right|$ and $\left|T S_{b}\right|=\left|T S_{c}\right|$. It follows that
$$
\begin{aligned}
\left|A P_{b}\right| & =\left|U P_{b}\right|-|U A|=\left|U S_{b}\right|-|T V|=\left|T S_{b}\right|-|T U|-|T V| \\
& =\left|T S_{s}\right|-|T V|-|T U|=\left|V S_{c}\right|-|A V|=\left|V P_{c}\right|-|V A|=\left|A P_{c}\right|
\end{aligned}
$$
But $\left|A P_{b}\right|,\left|A P_{c}\right|$ are exactly the square roots of powers of $A$ with respect to $\omega_{b}$ and $\omega_{c}$, hence $A$ is indeed on their radical axis.
Thus, the radical axis of $\omega_{b}, \omega_{c}$ is $A T$.
Part II: Consider the triangle $A S_{b} S_{c}$. Note that since $T$ is the intersection of the tangents at $S_{b}$ and $S_{c}$ to the circumcircle of $A S_{b} S_{c}$, it follows that $A T$ is the symmedian of $A$ in this triangle. Let $X$ denote the second intersection of the symmedian $A T$ with $\Omega$. We wish to show that $X$ is also on $I N_{a}$.
Note that $A N_{a}$ is the external angle bisector of angle $A$, and therefore it is parallel to $S_{b} S_{c}$. Let $M$ denote the midpoint of $S_{b} S_{c}$, and let $Y$ be the second intersection of $A M$ with $\Omega$. Since in $A S_{b} S_{c}, A X T$ is the symmedian and $A M Y$ is the median, it follows that $X Y$ is also parallel to $S_{b} S_{c}$. Thus, reflecting in the perpendicular bisector of $S_{b} S_{c}$ sends the line $A M Y$ to line $N_{a} M X$.
Next, consider the quadrilateral $A S_{b} I S_{c}$. From the trillium theorem we have $\left|S_{b} A\right|=\left|S_{b} I\right|$ and $\left|S_{c} A\right|=\left|S_{c} I\right|$, thus the quadrilateral is a kite, from which it follows that the reflection of the line $A M$ in $S_{b} S_{c}$ is the line $I M$. But previously we have seen that this is also the line $N_{a} M X$. Thus $M, I, N_{a}$ and $X$ are collinear, as we wanted to show.
|
{
"exam": "EGMO",
"problem_label": "6",
"problem_match": "\nProblem 6.",
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"solution_match": "\nSolution 1. ",
"tier": "T2",
"year": "2023"
}
|
Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.

Figure 6: Diagram to Solution 1
|
This is a variation of Solution 1 which avoids the theory of the symmedian point.
We begin by showing that the radical axis of $\omega_{b}, \omega_{c}$ is $A T$ as in Solution 1.
Part II: We introduce the point $S_{a}$ with the obvious meaning. Observe that the incentre $I$ of $A B C$ is the orthocentre of $S_{a} S_{b} S_{c}$ either because this is well-known, or because of an angle argument that $A$ reflects in $S_{b} S_{c}$ to $I$ (and similar results by cyclic change of letters). Therefore $A S_{a}$ is perpendicular to $S_{b} S_{c}$.
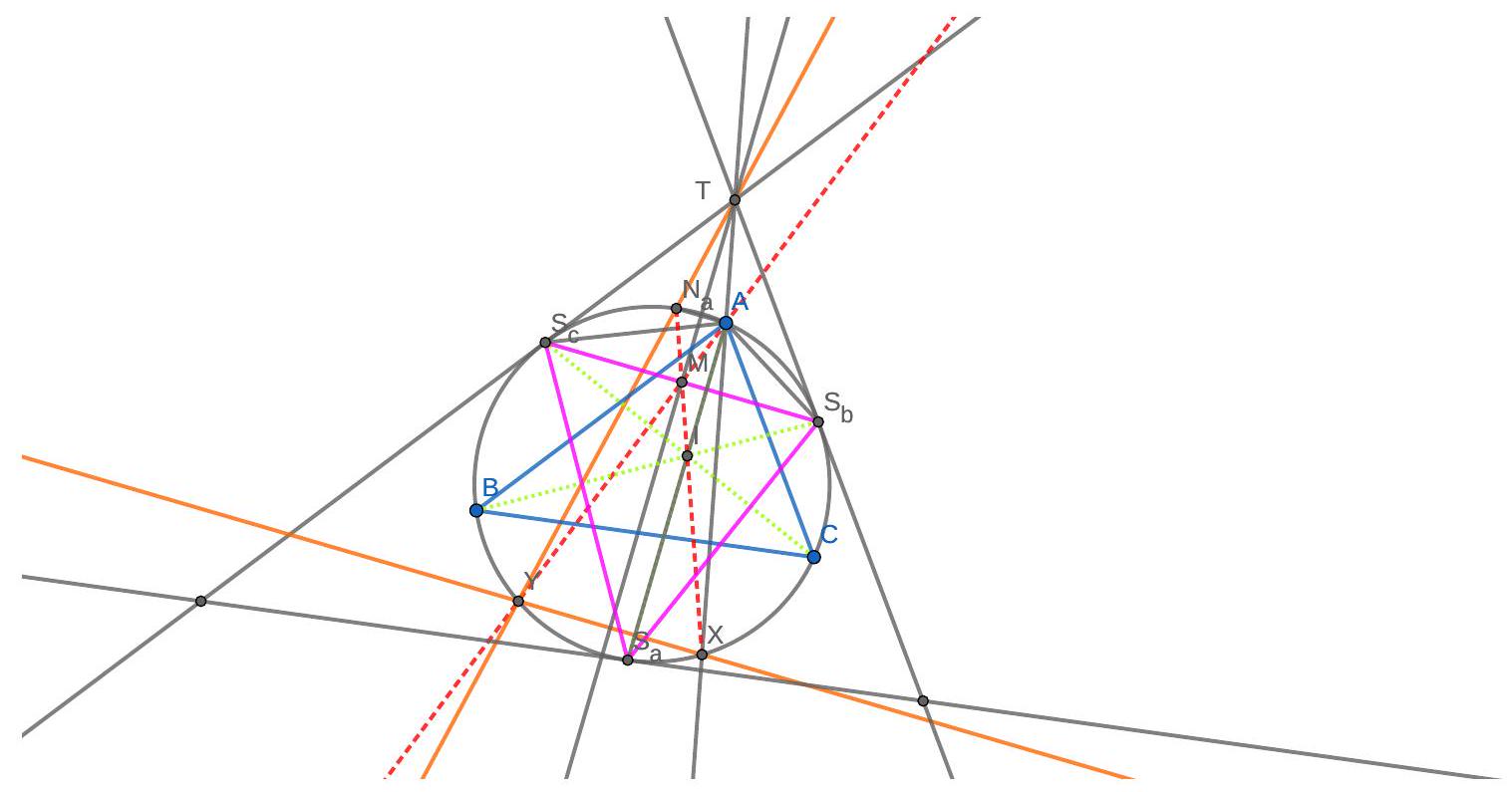
Figure 7: A reflections argument for Solution 2
Let $M$ denote the midpoint of $S_{b} S_{c}$. Then $A$ is the reflection of $S_{a}$ in the diameter parallel to $S_{b} S_{c}$, so the reflection of $A$ in the diameter perpendicular to $S_{b} S_{c}$ is $N_{a}$, the antipode
of $S_{a}$. Let the reflection of $X$ in $T M$ be $Y$, so $T Y$ passes through $N_{a}$ and is the reflection of $T X$ in $T M$.
Now $S_{b} S_{c}$ is the polar line of $T$ with respect to $\Omega$, so $A Y$ and $N_{a} X$ meet on this line, and by symmetry at its midpoint $M$. The line $N_{a} M X$ is therefore the reflection of the line $Y M A$ in $S_{b} S_{c}$, and so $N_{a} M X$ passes through $I$ (the reflection of $A$ in $S_{b} S_{c}$ ).
The triangle $A S_{c} S_{b}$ can be taken as generic, and from the argument above we can extract the fact that the symmedian point and the centroid are isogonal conjugates in that triangle.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.

Figure 6: Diagram to Solution 1
|
This is a variation of Solution 1 which avoids the theory of the symmedian point.
We begin by showing that the radical axis of $\omega_{b}, \omega_{c}$ is $A T$ as in Solution 1.
Part II: We introduce the point $S_{a}$ with the obvious meaning. Observe that the incentre $I$ of $A B C$ is the orthocentre of $S_{a} S_{b} S_{c}$ either because this is well-known, or because of an angle argument that $A$ reflects in $S_{b} S_{c}$ to $I$ (and similar results by cyclic change of letters). Therefore $A S_{a}$ is perpendicular to $S_{b} S_{c}$.

Figure 7: A reflections argument for Solution 2
Let $M$ denote the midpoint of $S_{b} S_{c}$. Then $A$ is the reflection of $S_{a}$ in the diameter parallel to $S_{b} S_{c}$, so the reflection of $A$ in the diameter perpendicular to $S_{b} S_{c}$ is $N_{a}$, the antipode
of $S_{a}$. Let the reflection of $X$ in $T M$ be $Y$, so $T Y$ passes through $N_{a}$ and is the reflection of $T X$ in $T M$.
Now $S_{b} S_{c}$ is the polar line of $T$ with respect to $\Omega$, so $A Y$ and $N_{a} X$ meet on this line, and by symmetry at its midpoint $M$. The line $N_{a} M X$ is therefore the reflection of the line $Y M A$ in $S_{b} S_{c}$, and so $N_{a} M X$ passes through $I$ (the reflection of $A$ in $S_{b} S_{c}$ ).
The triangle $A S_{c} S_{b}$ can be taken as generic, and from the argument above we can extract the fact that the symmedian point and the centroid are isogonal conjugates in that triangle.
|
{
"exam": "EGMO",
"problem_label": "6",
"problem_match": "\nProblem 6.",
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"solution_match": "\nSolution 2. ",
"tier": "T2",
"year": "2023"
}
|
Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.

Figure 6: Diagram to Solution 1
|
Assume the notation from Solution 1, part I of Solution 1, and let $O$ be the centre of $\Omega$.
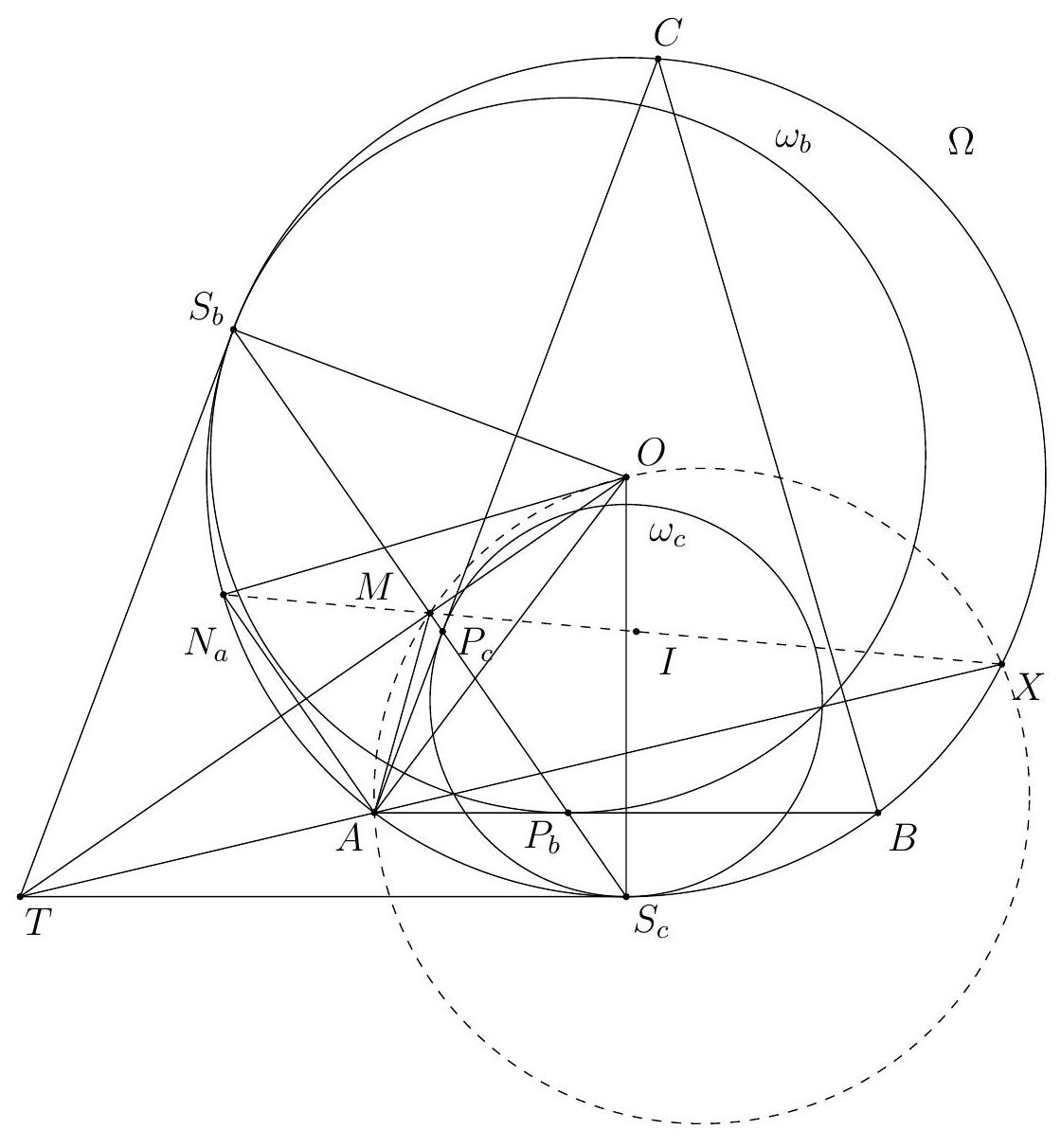
Figure 8: Diagram to Solution 3
Part II: As in Solution 1, by the trillelium theorem, $S_{c} S_{b}$ bisects $A I$, and since $N_{a} A \| S_{b} S_{c}$, then $O T$ is a bisector of $A N_{a}$. This implies $\left|M N_{a}\right|=|M A|=|M I|$, since $M$ is the midpoint of $S_{c} S_{b}$ and lies also on $O T$. Hence, $M$ is the circumcentre of triangle $I A N_{a}$. But this triangle has a right angle at $A$ (since $A I$ and $A N_{a}$ are the inner and outer angle bisector at $A$ ), hence $M$ lies on $I N_{a}$.
Again, let $X$ be the second intersection of $T A$ and $\Omega$. By the above, it suffices to prove that $X$ lies on the line $N_{a} M$. From the power of point $T$ with respect to $\Omega$ we get $|T A| \cdot|T X|=\left|T S_{c}\right|^{2}$. Since $M$ is the foot of the altitude of right triangle $T S_{c} O$, we obtain
$\left|T S_{c}\right|^{2}=|T M| \cdot|T O|$. Hence, $|T A| \cdot|T X|=|T M| \cdot|T O|$ so the points $O, M, A, X$ are concyclic. It follows that $\angle M X A=\angle M O A=\frac{1}{2} \angle N_{a} O A=\angle N_{a} X A$. Hence, $X$ lies on the line $N_{a} M$.
Remark. To show that $O M A X$ is cyclic, one can also invert the line $T A X$ in the circumcircle of the triangle $A B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.

Figure 6: Diagram to Solution 1
|
Assume the notation from Solution 1, part I of Solution 1, and let $O$ be the centre of $\Omega$.

Figure 8: Diagram to Solution 3
Part II: As in Solution 1, by the trillelium theorem, $S_{c} S_{b}$ bisects $A I$, and since $N_{a} A \| S_{b} S_{c}$, then $O T$ is a bisector of $A N_{a}$. This implies $\left|M N_{a}\right|=|M A|=|M I|$, since $M$ is the midpoint of $S_{c} S_{b}$ and lies also on $O T$. Hence, $M$ is the circumcentre of triangle $I A N_{a}$. But this triangle has a right angle at $A$ (since $A I$ and $A N_{a}$ are the inner and outer angle bisector at $A$ ), hence $M$ lies on $I N_{a}$.
Again, let $X$ be the second intersection of $T A$ and $\Omega$. By the above, it suffices to prove that $X$ lies on the line $N_{a} M$. From the power of point $T$ with respect to $\Omega$ we get $|T A| \cdot|T X|=\left|T S_{c}\right|^{2}$. Since $M$ is the foot of the altitude of right triangle $T S_{c} O$, we obtain
$\left|T S_{c}\right|^{2}=|T M| \cdot|T O|$. Hence, $|T A| \cdot|T X|=|T M| \cdot|T O|$ so the points $O, M, A, X$ are concyclic. It follows that $\angle M X A=\angle M O A=\frac{1}{2} \angle N_{a} O A=\angle N_{a} X A$. Hence, $X$ lies on the line $N_{a} M$.
Remark. To show that $O M A X$ is cyclic, one can also invert the line $T A X$ in the circumcircle of the triangle $A B C$.
|
{
"exam": "EGMO",
"problem_label": "6",
"problem_match": "\nProblem 6.",
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"solution_match": "\nSolution 3. ",
"tier": "T2",
"year": "2023"
}
|
Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.

Figure 6: Diagram to Solution 1
|
Part I is done as in solution 1.
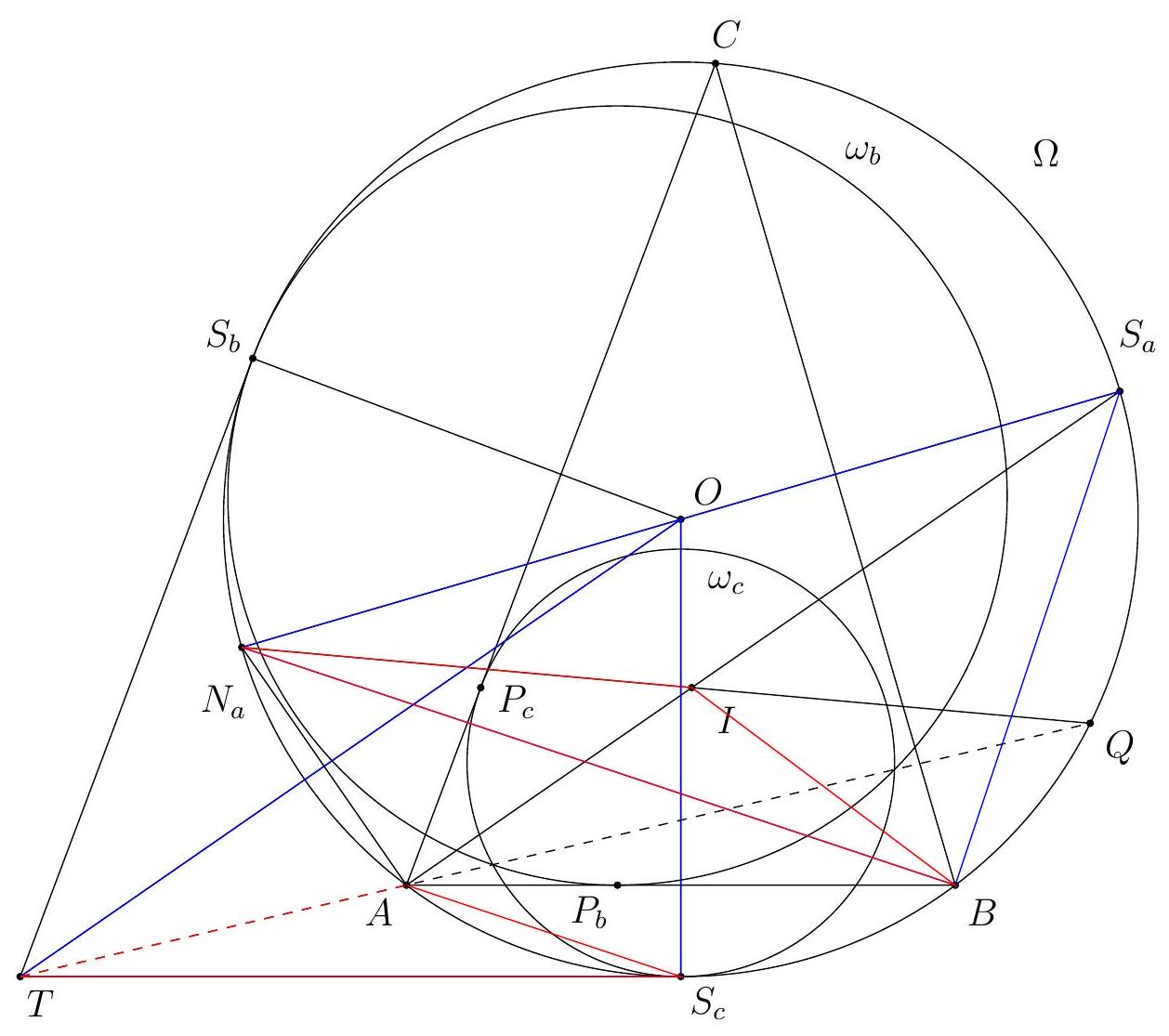
Figure 9: Diagram to Solution 4
Part II: as in Solution 1 we show that $A N_{a} \| S_{b} S_{c}$. In particular, $\angle N_{a} O T=\angle T O A$. The conclusion of the problem trivially holds if $|A B|=|A C|$, therefore we assume without loss of generality that $|A C|>|A B|$. Let $S_{a}$ be the midpoint of the arc $B C$ which does not contain $A$. Then $N_{a} S_{a}$ is a diameter, so $\angle S_{a} B N_{a}=\frac{\pi}{2}=\angle O S_{c} T$. We also compute $\angle B N_{a} S_{a}=\angle B A S_{a}=\frac{1}{2} \angle B A C=\frac{1}{2} \angle S_{c} T S_{b}=\angle S_{c} T O$. It follows that the triangles $T S_{c} O$ and $N_{a} B S_{a}$ are similar. In particular,
$$
\frac{\left|N_{a} B\right|}{\left|T S_{c}\right|}=\frac{\left|S_{a} B\right|}{\left|O S_{c}\right|}
$$
Next we compute
$$
\angle I S_{a} B=\angle N_{a} S_{a} B-\angle N_{a} S_{a} I=\angle T O S_{c}-\frac{1}{2} \angle N_{a} O A=\angle T O S_{c}-\angle T O A=\angle A O S_{c}
$$
and
$\angle I B N_{a}=\angle C B N_{a}-\angle C B I=\frac{1}{2}\left(\pi-\angle B N_{a} C\right)-\frac{1}{2} \angle C B A=\frac{1}{2} \angle A C B=\angle A C S_{c}=\angle A S_{c} T$,
hence
$$
\angle S_{a} B I=\frac{\pi}{2}-\angle I B N_{a}=\frac{\pi}{2}-\angle A S_{c} T=\angle O S_{c} A
$$
Together with (13) it follows that the triangles $I B S_{a}$ and $A S_{c} O$ are similar, so $\frac{\left|S_{a} B\right|}{\left|O S_{c}\right|}=$ $\frac{|I B|}{\left|A S_{c}\right|}$, and (12) implies $\frac{\left|N_{a} B\right|}{\left|T S_{c}\right|}=\frac{|I B|}{\left|A S_{c}\right|}$. Consequently, by (14) the triangles $T S_{c} A$ and $N_{a} B I$ are similar and therefore $\angle S_{c} T A=\angle B N_{a} I$. Now let $Q$ be the second intersection of $N_{a} I$ with $\Omega$. Then $\angle B N_{a} I=\angle B N_{a} Q=\angle B A Q$, so $\angle S_{c} T A=\angle B A Q$. Since $A B$ is parallel to $T S_{c}$, we get $A Q \| T A$, i.e. $A, T, Q$ are collinear.
Remark. After proving similarity of triangles $T S_{c} O$ and $N_{a} B S_{a}$ one can use spiral symmetry to show similarity of triangles $T S_{c} A$ and $N_{a} B I$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.

Figure 6: Diagram to Solution 1
|
Part I is done as in solution 1.

Figure 9: Diagram to Solution 4
Part II: as in Solution 1 we show that $A N_{a} \| S_{b} S_{c}$. In particular, $\angle N_{a} O T=\angle T O A$. The conclusion of the problem trivially holds if $|A B|=|A C|$, therefore we assume without loss of generality that $|A C|>|A B|$. Let $S_{a}$ be the midpoint of the arc $B C$ which does not contain $A$. Then $N_{a} S_{a}$ is a diameter, so $\angle S_{a} B N_{a}=\frac{\pi}{2}=\angle O S_{c} T$. We also compute $\angle B N_{a} S_{a}=\angle B A S_{a}=\frac{1}{2} \angle B A C=\frac{1}{2} \angle S_{c} T S_{b}=\angle S_{c} T O$. It follows that the triangles $T S_{c} O$ and $N_{a} B S_{a}$ are similar. In particular,
$$
\frac{\left|N_{a} B\right|}{\left|T S_{c}\right|}=\frac{\left|S_{a} B\right|}{\left|O S_{c}\right|}
$$
Next we compute
$$
\angle I S_{a} B=\angle N_{a} S_{a} B-\angle N_{a} S_{a} I=\angle T O S_{c}-\frac{1}{2} \angle N_{a} O A=\angle T O S_{c}-\angle T O A=\angle A O S_{c}
$$
and
$\angle I B N_{a}=\angle C B N_{a}-\angle C B I=\frac{1}{2}\left(\pi-\angle B N_{a} C\right)-\frac{1}{2} \angle C B A=\frac{1}{2} \angle A C B=\angle A C S_{c}=\angle A S_{c} T$,
hence
$$
\angle S_{a} B I=\frac{\pi}{2}-\angle I B N_{a}=\frac{\pi}{2}-\angle A S_{c} T=\angle O S_{c} A
$$
Together with (13) it follows that the triangles $I B S_{a}$ and $A S_{c} O$ are similar, so $\frac{\left|S_{a} B\right|}{\left|O S_{c}\right|}=$ $\frac{|I B|}{\left|A S_{c}\right|}$, and (12) implies $\frac{\left|N_{a} B\right|}{\left|T S_{c}\right|}=\frac{|I B|}{\left|A S_{c}\right|}$. Consequently, by (14) the triangles $T S_{c} A$ and $N_{a} B I$ are similar and therefore $\angle S_{c} T A=\angle B N_{a} I$. Now let $Q$ be the second intersection of $N_{a} I$ with $\Omega$. Then $\angle B N_{a} I=\angle B N_{a} Q=\angle B A Q$, so $\angle S_{c} T A=\angle B A Q$. Since $A B$ is parallel to $T S_{c}$, we get $A Q \| T A$, i.e. $A, T, Q$ are collinear.
Remark. After proving similarity of triangles $T S_{c} O$ and $N_{a} B S_{a}$ one can use spiral symmetry to show similarity of triangles $T S_{c} A$ and $N_{a} B I$.
|
{
"exam": "EGMO",
"problem_label": "6",
"problem_match": "\nProblem 6.",
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"solution_match": "\nSolution 4. ",
"tier": "T2",
"year": "2023"
}
|
Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.

Figure 6: Diagram to Solution 1
|
Part I: First we show that $A$ lies on the radical axis between $\omega_{b}$ and $\omega_{c}$.
Let $T$ be the radical center of the circumcircle, $\omega_{b}$ and $\omega_{c}$; then $T S_{b}$ and $T S_{c}$ are common tangents of the circles, as shown in Figure 5a. Moreover, let $P_{b}=A B \cap S_{b} S_{c}$ and $P_{c}=$ $A C \cap S_{b} S_{c}$. The triangle $T S_{c} S_{b}$ is isosceles: $A B \| T S_{c}$ and $A C \| T S_{b}$ so
$$
\angle A P_{b} P_{c}=\angle T S_{c} S_{b}=\angle S_{c} S_{b} T=\angle P_{b} P_{c} A
$$
From these angles we can see that $\omega_{b}$ passes through $P_{b}, \omega_{c}$ passes through $P_{c}$, and finally $A P_{b}$ and $A P_{c}$ are equal tangents to $\omega_{b}$ and $\omega_{c}$, so $A$ lies on the radical axis.
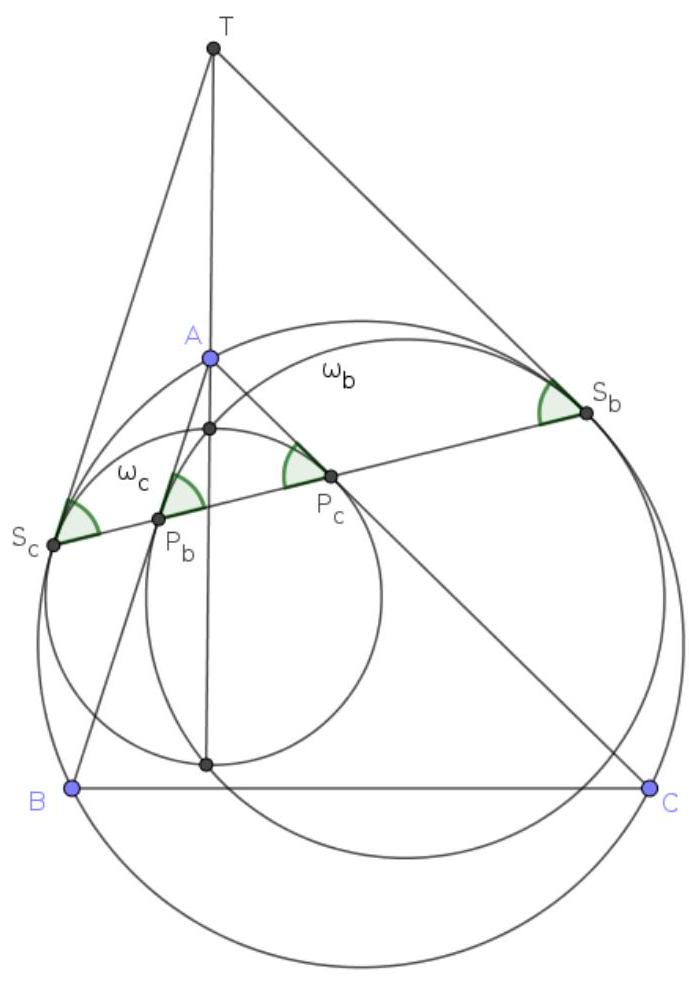
Figure 5a
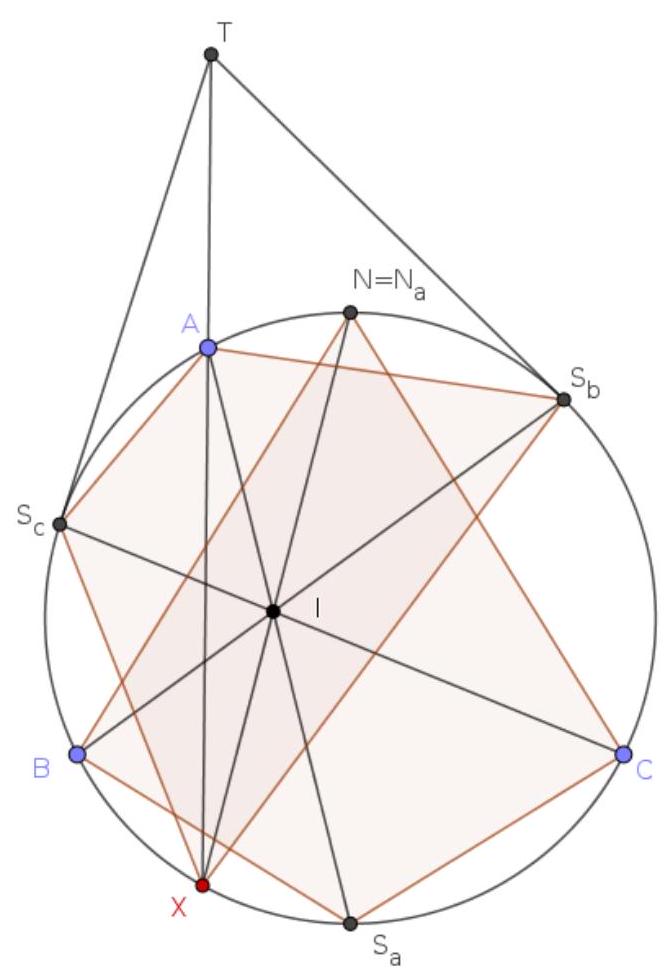
Figure 5b
Part II. Let the radical axis $T A$ meet the circumcircle again at $X$, let $S_{a}$ be the midpoint of the arc $B C$ opposite to $A$, and let $X I$ meet the circumcirlce again at $N$. (See Figure 2.) For solving the problem, we have prove that $N_{a}=N$.
The triples of points $A, I, S_{a} ; B, I, S_{b}$ and $C, I, S_{c}$ are collinear because they lie on the angle bisectors of the triangle $A B C$.
Notice that the quadrilateral $A S_{c} X S_{b}$ is harmonic, because the tangents at $S_{b}$ and $S_{c}$, and the line $A X$ are concurrent at $T$. This quadrilateral can be projected (or inverted) to the quadrilateral $S_{a} C N B$ through $I$. So, $S_{a} C N B$ also is a harmonic quadrilateral. Due to $S_{a} B=S_{a} C$, this implies $N B=N C$, so $N=N_{a}$. Done.
Remark. Instead of mentioning inversion and harmonic quadrilaterals, from the similar triangles $\triangle T S_{c} A \sim \triangle T X S_{c}$ and $\triangle T A S_{b} \sim \triangle T S_{b} X$ we can get
$$
\frac{A S_{c}}{S_{c} X}=\frac{A S_{b}}{S_{b} X}
$$
Then, we can apply the trigonometric form of Ceva's theorem to triangle $B C X$
$$
\frac{\sin \angle B X N_{a}}{\sin \angle N_{a} X C} \cdot \frac{\sin \angle C B S_{b}}{\sin \angle S_{b} B X} \cdot \frac{\sin \angle X C S_{c}}{\sin \angle S_{c} C B}=\frac{B N_{a}}{N_{a} C} \cdot \frac{-C S_{b}}{S_{b} X} \cdot \frac{X S_{c}}{-S_{c} B}=1 \cdot \frac{S_{b} A}{S_{b} N_{a}} \cdot \frac{N_{a} S_{c}}{S_{c} B}=1,
$$
so the Cevians $B S_{b}, C S_{c}$ and $X N_{a}$ are concurrent.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.

Figure 6: Diagram to Solution 1
|
Part I: First we show that $A$ lies on the radical axis between $\omega_{b}$ and $\omega_{c}$.
Let $T$ be the radical center of the circumcircle, $\omega_{b}$ and $\omega_{c}$; then $T S_{b}$ and $T S_{c}$ are common tangents of the circles, as shown in Figure 5a. Moreover, let $P_{b}=A B \cap S_{b} S_{c}$ and $P_{c}=$ $A C \cap S_{b} S_{c}$. The triangle $T S_{c} S_{b}$ is isosceles: $A B \| T S_{c}$ and $A C \| T S_{b}$ so
$$
\angle A P_{b} P_{c}=\angle T S_{c} S_{b}=\angle S_{c} S_{b} T=\angle P_{b} P_{c} A
$$
From these angles we can see that $\omega_{b}$ passes through $P_{b}, \omega_{c}$ passes through $P_{c}$, and finally $A P_{b}$ and $A P_{c}$ are equal tangents to $\omega_{b}$ and $\omega_{c}$, so $A$ lies on the radical axis.

Figure 5a

Figure 5b
Part II. Let the radical axis $T A$ meet the circumcircle again at $X$, let $S_{a}$ be the midpoint of the arc $B C$ opposite to $A$, and let $X I$ meet the circumcirlce again at $N$. (See Figure 2.) For solving the problem, we have prove that $N_{a}=N$.
The triples of points $A, I, S_{a} ; B, I, S_{b}$ and $C, I, S_{c}$ are collinear because they lie on the angle bisectors of the triangle $A B C$.
Notice that the quadrilateral $A S_{c} X S_{b}$ is harmonic, because the tangents at $S_{b}$ and $S_{c}$, and the line $A X$ are concurrent at $T$. This quadrilateral can be projected (or inverted) to the quadrilateral $S_{a} C N B$ through $I$. So, $S_{a} C N B$ also is a harmonic quadrilateral. Due to $S_{a} B=S_{a} C$, this implies $N B=N C$, so $N=N_{a}$. Done.
Remark. Instead of mentioning inversion and harmonic quadrilaterals, from the similar triangles $\triangle T S_{c} A \sim \triangle T X S_{c}$ and $\triangle T A S_{b} \sim \triangle T S_{b} X$ we can get
$$
\frac{A S_{c}}{S_{c} X}=\frac{A S_{b}}{S_{b} X}
$$
Then, we can apply the trigonometric form of Ceva's theorem to triangle $B C X$
$$
\frac{\sin \angle B X N_{a}}{\sin \angle N_{a} X C} \cdot \frac{\sin \angle C B S_{b}}{\sin \angle S_{b} B X} \cdot \frac{\sin \angle X C S_{c}}{\sin \angle S_{c} C B}=\frac{B N_{a}}{N_{a} C} \cdot \frac{-C S_{b}}{S_{b} X} \cdot \frac{X S_{c}}{-S_{c} B}=1 \cdot \frac{S_{b} A}{S_{b} N_{a}} \cdot \frac{N_{a} S_{c}}{S_{c} B}=1,
$$
so the Cevians $B S_{b}, C S_{c}$ and $X N_{a}$ are concurrent.
|
{
"exam": "EGMO",
"problem_label": "6",
"problem_match": "\nProblem 6.",
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"solution_match": "\nSolution 5. ",
"tier": "T2",
"year": "2023"
}
|
Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.

Figure 6: Diagram to Solution 1
|
Part I: First let's show that this is equivalent to proving that $T A$ and $N_{a} I$ intersect in $\Omega$.
Lemma: Let's recall that if we have two circles $\omega_{1}$ and $\omega_{2}$ which are internally tangent at point $X$ and if we have a line $A B$ tangent to $\omega_{2}$ at $Y$. Let $M$ be the midpoint of the arc $A B$ not containing $Z$. We have that $Z, Y, M$ are collinear.
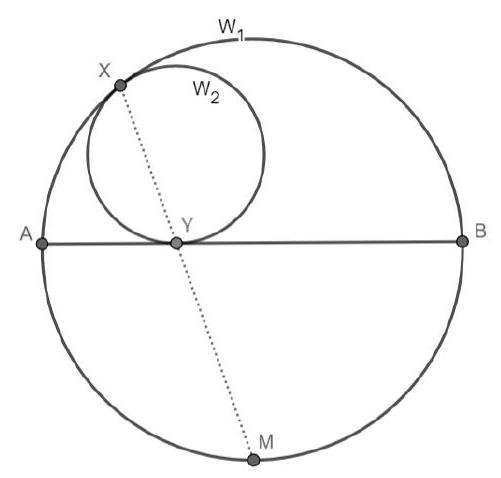
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.

Figure 6: Diagram to Solution 1
|
Part I: First let's show that this is equivalent to proving that $T A$ and $N_{a} I$ intersect in $\Omega$.
Lemma: Let's recall that if we have two circles $\omega_{1}$ and $\omega_{2}$ which are internally tangent at point $X$ and if we have a line $A B$ tangent to $\omega_{2}$ at $Y$. Let $M$ be the midpoint of the arc $A B$ not containing $Z$. We have that $Z, Y, M$ are collinear.

|
{
"exam": "EGMO",
"problem_label": "6",
"problem_match": "\nProblem 6.",
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"solution_match": "\nSolution 6. ",
"tier": "T2",
"year": "2023"
}
|
Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.

Figure 6: Diagram to Solution 1
|
Lemma
Let $P_{b}=A B \cap \omega_{b}$ and $P_{c}=A C \cap \omega_{c}$. We can notice by the lemma that $S_{b}, P_{b}$ and $S_{c}$ are collinear, and similarly $S_{c}, P_{c}$ and $S_{b}$ are also collinear. Therefore $S_{c}, P_{b}, P_{c}$, and $S_{b}$ are collinear, and since $\angle A P_{b} P_{c}=\frac{\angle A B C}{2}+\frac{\angle A C B}{2}=\angle A P_{c} P_{b}$ then $A P_{b}=A P_{c}$ so $A$ is on the radical axis of $\omega_{b}$ and $\omega_{c}$. Let $T$ be the intersection of the tangent lines of $\Omega$ through $S_{c}$ and $S_{b}$. Since $T S_{c}=T S_{b}$ then $A T$ is the radical axis between $\omega_{b}$ and $\omega_{c}$.
Part II: $T A$ and $N_{a} I$ intersect in $\Omega$.
Let $\omega_{a}$ the $A$-mixtilinear incircle (that is, the circle internally tangent to $\Omega$, and tangent to both $A B$ and $A C$ ), and let $X=\Omega \cap \omega_{a}$. It is known that $N_{a}, I, X$ are collinear.
Let $M_{c}$ and $M_{b}$ be the tangent points of $\omega_{A}$ to $A B$ and $A C$ respectively, then by the lemma $X, M_{c}, S_{c}$ are collinear and $X, M_{b}, S_{b}$ are collinear. We can see that $S_{c} T S_{b}$ and $M_{c} A M_{b}$ are homothetic with respect to $X$; therefore $T$ and $A$ are homothetic with respect to $X$, impying that $T, A, X$ are collinear.
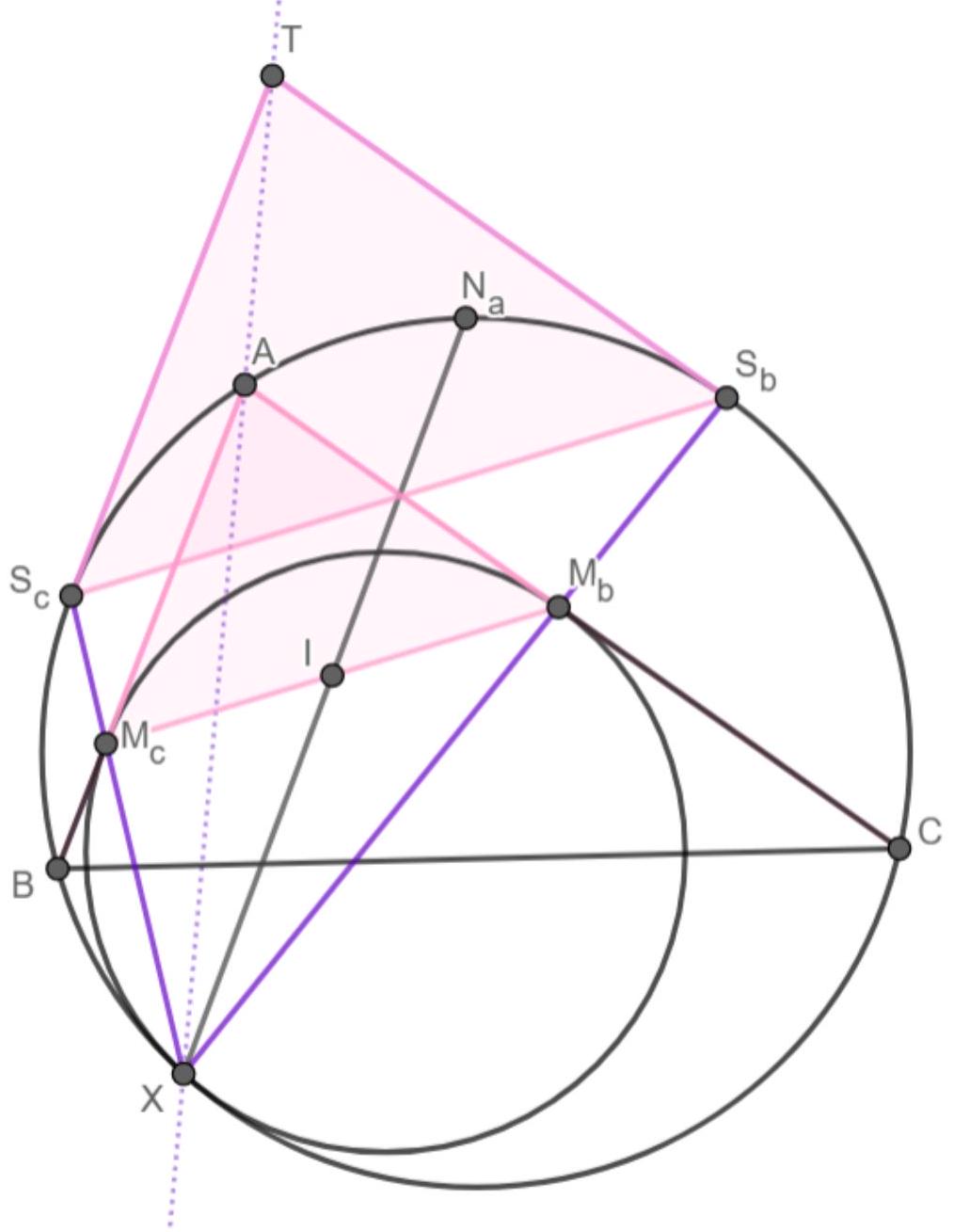
Figure 10: Diagram to Solution 6
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcircle $\Omega$. Let $S_{b}$ and $S_{c}$ respectively denote the midpoints of the arcs $A C$ and $A B$ that do not contain the third vertex. Let $N_{a}$ denote the midpoint of arc $B A C$ (the arc $B C$ containing $A$ ). Let $I$ be the incentre of $A B C$. Let $\omega_{b}$ be the circle that is tangent to $A B$ and internally tangent to $\Omega$ at $S_{b}$, and let $\omega_{c}$ be the circle that is tangent to $A C$ and internally tangent to $\Omega$ at $S_{c}$. Show that the line $I N_{a}$, and the line through the intersections of $\omega_{b}$ and $\omega_{c}$, meet on $\Omega$.
The incentre of a triangle is the centre of its incircle, the circle inside the triangle that is tangent to all three sides.

Figure 6: Diagram to Solution 1
|
Lemma
Let $P_{b}=A B \cap \omega_{b}$ and $P_{c}=A C \cap \omega_{c}$. We can notice by the lemma that $S_{b}, P_{b}$ and $S_{c}$ are collinear, and similarly $S_{c}, P_{c}$ and $S_{b}$ are also collinear. Therefore $S_{c}, P_{b}, P_{c}$, and $S_{b}$ are collinear, and since $\angle A P_{b} P_{c}=\frac{\angle A B C}{2}+\frac{\angle A C B}{2}=\angle A P_{c} P_{b}$ then $A P_{b}=A P_{c}$ so $A$ is on the radical axis of $\omega_{b}$ and $\omega_{c}$. Let $T$ be the intersection of the tangent lines of $\Omega$ through $S_{c}$ and $S_{b}$. Since $T S_{c}=T S_{b}$ then $A T$ is the radical axis between $\omega_{b}$ and $\omega_{c}$.
Part II: $T A$ and $N_{a} I$ intersect in $\Omega$.
Let $\omega_{a}$ the $A$-mixtilinear incircle (that is, the circle internally tangent to $\Omega$, and tangent to both $A B$ and $A C$ ), and let $X=\Omega \cap \omega_{a}$. It is known that $N_{a}, I, X$ are collinear.
Let $M_{c}$ and $M_{b}$ be the tangent points of $\omega_{A}$ to $A B$ and $A C$ respectively, then by the lemma $X, M_{c}, S_{c}$ are collinear and $X, M_{b}, S_{b}$ are collinear. We can see that $S_{c} T S_{b}$ and $M_{c} A M_{b}$ are homothetic with respect to $X$; therefore $T$ and $A$ are homothetic with respect to $X$, impying that $T, A, X$ are collinear.

Figure 10: Diagram to Solution 6
|
{
"exam": "EGMO",
"problem_label": "6",
"problem_match": "\nProblem 6.",
"resource_path": "EGMO/segmented/en-2023-solutions.jsonl",
"solution_match": "\nSolution 6: ",
"tier": "T2",
"year": "2023"
}
|
Problem. Two different integers $u$ and $v$ are written on a board. We perform a sequence of steps. At each step we do one of the following two operations:
(i) If $a$ and $b$ are different integers on the board, then we can write $a+b$ on the board, if it is not already there.
(ii) If $a, b$ and $c$ are three different integers on the board, and if an integer $x$ satisfies $a x^{2}+b x+c=0$, then we can write $x$ on the board, if it is not already there.
Determine all pairs of starting numbers $(u, v)$ from which any integer can eventually be written on the board after a finite sequence of steps.
|
We will show that the answer are the integer pairs $(u, v)$ such that $u \neq 0$, $v \neq 0,\{u, v\} \neq\{-1,1\}$ and $u>0$ or $v>0$.
If $u=0$ or $v=0$, then (i) will never yield a new number and we cannot use (ii) with only two numbers. Hence, if $u=0$ or $v=0$, we cannot reach every possible $y$. From now on, assume $u \neq 0$ and $v \neq 0$.
If both numbers $u, v$ were negative, we will show that there can only be negative numbers on the board. With negative numbers $a, b$, operation (i) will only yield a negative number. The same holds for operation (ii), because for a non-negative $x$ and negative $a, b, c$, we have $a x^{2}+b x+c<0$. Hence, if both $u<0$ and $v<0$, then we cannot reach every possible $y$. From now on, assume that at least one of $u, v$ is positive. Without loss of generality take $u<v$, and so $v>0$.
After one step, we can have the numbers $u, v, u+v$, which are mutually distinct due to $u, v$ being nonzero. Notice that the equation $u x^{2}+(u+v) x+v=0$ has a root -1 , and so we can have -1 on the board.
We now check two cases: case $v=1$, and case $v>1$.
If $v=1$, then $u<0$. Further split the case of $v=1$ based on whether $u=-1$ or $u<-1$.
If $v=1$ and $u=-1$, we can only additionally write number 0 on the board using operation (i); and no additional numbers using (ii) because setting $\{a, b, c\}$ to $\{-1,0,1\}$ in any order only has solutions for $x$ in $\{-1,0,1\}$. Hence, if $\{u, v\}=\{-1,1\}$, then we cannot reach every possible $y$.
If $v=1$ and $u<-1$, we can use operation (i) on numbers $u,-1$ (and then repeat choosing the obtained result and -1 ) to get any negative number smaller than $u$, and operation (i) on numbers $(u, 1)$ (and then repeat choosing the obtained result and 1 ) to get any negative number larger than $u$, as well as 0 . Then, we set $(a, b, c)=(0,1,-2)$ and apply operation (ii) to additionally get number 2. Applying (i) on $(2,1)$ (and then repeat choosing the obtained result and 1), we can get all the remaining integers too.
From now on, assume $v>1$. Recall that we can make $u+v$ and -1 .
We will now apply operation (i). First, $(v,-1)$ gives $v-1$. Next, $(v, v-1)$ gives $2 v-1$. Since $v>1$, we know $v \neq 2 v-1$, so we can apply operation (i) on $(v, 2 v-1)$ to get $3 v-1$, and then continue adding $(v, k v-1)$ to get $(k+1) v-1$ for any positive $k$. Since $v>1$, we can get an arbitrarily large integer by repeating this.
If $a$ is any positive number on the board, applying (i) to $(a,-1)$ gives $a-1$. By repeating this, we have that we can get all numbers smaller than $a$ and larger than or equal to -1 . Together with previously having found a way to get an arbitrarily large integer, we have that we can get any integer $l \geq-1$ on the board.
Now, we set $(a, b, c)=(0,1,2)$ and apply operation (ii) to additionally get number -2 . Then we can repeat operation (i) on ( $-1,-2$ ) (and afterwards on -1 and the obtained result) to get any negative number.
Therefore, if $u \neq 0, v \neq 0,\{u, v\} \neq\{-1,1\}$ and $u>0$ or $v>0$, we can write every integer on the board.
Remark. There are of course many other ways to create all integers in case of $(u, v)$ that satisfies all the requirements. Basically you will always use (i) to create arbitrarily large numbers and then (ii) to create a number in a range that you didn't have before.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Problem. Two different integers $u$ and $v$ are written on a board. We perform a sequence of steps. At each step we do one of the following two operations:
(i) If $a$ and $b$ are different integers on the board, then we can write $a+b$ on the board, if it is not already there.
(ii) If $a, b$ and $c$ are three different integers on the board, and if an integer $x$ satisfies $a x^{2}+b x+c=0$, then we can write $x$ on the board, if it is not already there.
Determine all pairs of starting numbers $(u, v)$ from which any integer can eventually be written on the board after a finite sequence of steps.
|
We will show that the answer are the integer pairs $(u, v)$ such that $u \neq 0$, $v \neq 0,\{u, v\} \neq\{-1,1\}$ and $u>0$ or $v>0$.
If $u=0$ or $v=0$, then (i) will never yield a new number and we cannot use (ii) with only two numbers. Hence, if $u=0$ or $v=0$, we cannot reach every possible $y$. From now on, assume $u \neq 0$ and $v \neq 0$.
If both numbers $u, v$ were negative, we will show that there can only be negative numbers on the board. With negative numbers $a, b$, operation (i) will only yield a negative number. The same holds for operation (ii), because for a non-negative $x$ and negative $a, b, c$, we have $a x^{2}+b x+c<0$. Hence, if both $u<0$ and $v<0$, then we cannot reach every possible $y$. From now on, assume that at least one of $u, v$ is positive. Without loss of generality take $u<v$, and so $v>0$.
After one step, we can have the numbers $u, v, u+v$, which are mutually distinct due to $u, v$ being nonzero. Notice that the equation $u x^{2}+(u+v) x+v=0$ has a root -1 , and so we can have -1 on the board.
We now check two cases: case $v=1$, and case $v>1$.
If $v=1$, then $u<0$. Further split the case of $v=1$ based on whether $u=-1$ or $u<-1$.
If $v=1$ and $u=-1$, we can only additionally write number 0 on the board using operation (i); and no additional numbers using (ii) because setting $\{a, b, c\}$ to $\{-1,0,1\}$ in any order only has solutions for $x$ in $\{-1,0,1\}$. Hence, if $\{u, v\}=\{-1,1\}$, then we cannot reach every possible $y$.
If $v=1$ and $u<-1$, we can use operation (i) on numbers $u,-1$ (and then repeat choosing the obtained result and -1 ) to get any negative number smaller than $u$, and operation (i) on numbers $(u, 1)$ (and then repeat choosing the obtained result and 1 ) to get any negative number larger than $u$, as well as 0 . Then, we set $(a, b, c)=(0,1,-2)$ and apply operation (ii) to additionally get number 2. Applying (i) on $(2,1)$ (and then repeat choosing the obtained result and 1), we can get all the remaining integers too.
From now on, assume $v>1$. Recall that we can make $u+v$ and -1 .
We will now apply operation (i). First, $(v,-1)$ gives $v-1$. Next, $(v, v-1)$ gives $2 v-1$. Since $v>1$, we know $v \neq 2 v-1$, so we can apply operation (i) on $(v, 2 v-1)$ to get $3 v-1$, and then continue adding $(v, k v-1)$ to get $(k+1) v-1$ for any positive $k$. Since $v>1$, we can get an arbitrarily large integer by repeating this.
If $a$ is any positive number on the board, applying (i) to $(a,-1)$ gives $a-1$. By repeating this, we have that we can get all numbers smaller than $a$ and larger than or equal to -1 . Together with previously having found a way to get an arbitrarily large integer, we have that we can get any integer $l \geq-1$ on the board.
Now, we set $(a, b, c)=(0,1,2)$ and apply operation (ii) to additionally get number -2 . Then we can repeat operation (i) on ( $-1,-2$ ) (and afterwards on -1 and the obtained result) to get any negative number.
Therefore, if $u \neq 0, v \neq 0,\{u, v\} \neq\{-1,1\}$ and $u>0$ or $v>0$, we can write every integer on the board.
Remark. There are of course many other ways to create all integers in case of $(u, v)$ that satisfies all the requirements. Basically you will always use (i) to create arbitrarily large numbers and then (ii) to create a number in a range that you didn't have before.
|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "# Problem 1 (SVK)\n",
"resource_path": "EGMO/segmented/en-2024-solutions.jsonl",
"solution_match": "\nSolution 1. ",
"tier": "T2",
"year": "2024"
}
|
Problem. Two different integers $u$ and $v$ are written on a board. We perform a sequence of steps. At each step we do one of the following two operations:
(i) If $a$ and $b$ are different integers on the board, then we can write $a+b$ on the board, if it is not already there.
(ii) If $a, b$ and $c$ are three different integers on the board, and if an integer $x$ satisfies $a x^{2}+b x+c=0$, then we can write $x$ on the board, if it is not already there.
Determine all pairs of starting numbers $(u, v)$ from which any integer can eventually be written on the board after a finite sequence of steps.
|
If $u=0$ or $v=0$ then we can only get $\{u, v\}$.
Proof. If $u=0$ or $v=0$, then (i) will never yield a new number and we cannot use (ii) with only two numbers.
If $\max (u, v)<0$, we cannot get non-negative numbers.
Proof. For $a, b, c<0$ :
(i) cannot generate a non-negative number as $a+b<0$.
(ii) cannot generate a non-negative number as for $x \geq 0$ : $a x^{2}+b x+c \leq c<0$.
If $u+v \neq 0, u, v \neq 0$ and $\max (u, v)>0$, we can get every number.
Proof. $u \neq v \rightarrow u+v$ can be written. $u \neq 0$, so $u+v \neq v \rightarrow u+2 v$ can be written. $v \neq 0$, so $u+2 v \neq u$, meaning that $2 u+2 v$ can be written. If for $n>1, n(u+v)$ can be written then $(n+1)(u+v)=n(u+v)+(u+v)$ can also be written, because $u+v \neq 0$, so $n(u+v) \neq(u+v)$. Therefore, by induction for all $n>0$ the number $n(u+v)$ can be written.
Taking $n=2,3, \ldots$ and $(u+v)(x+1)(x+n)=(u+v) x^{2}+(u+v)(n+1) x+(u+v) n=0$ gives $x=-1$ and $x=-n \rightarrow$ for all $n>0$ we can get $-n$ (we can get all the negative numbers). Additionally, we can get $u+(-u)=0$.
For $n \geq 1$ we can take $0 \cdot x^{2}+u x+(-u n)=0$ as $u \neq 0 \rightarrow u,-n u, 0$ are all distinct, therefore we can get $n$. Thus, we can get all the numbers.
If $u+v=0$ and $\max (u, v)>1$ we can get all the numbers.
Proof. We can get $0=u+v$ as $u \neq v$. Take $0 \cdot x^{2}+u x-u=0$ so we can get 1 written on the board. Take $\left(u^{\prime}, v^{\prime}\right)=(1, \max (u, v))$ and then use the result from claim 3. As $0<u^{\prime}=1<\max (u, v)=v^{\prime}$ and $u^{\prime}+v^{\prime}>0$ we can get all the numbers.
Remaining case: If $v=1$ and $u=-1$, we can only additionally write number 0 on the board using operation (i); and no additional numbers using (ii) because setting $\{a, b, c\}$ to $\{-1,0,1\}$ in any order only has solutions for $x$ in $\{-1,0,1\}$. Hence, if $\{u, v\}=\{-1,1\}$, then we cannot reach every possible $y$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Problem. Two different integers $u$ and $v$ are written on a board. We perform a sequence of steps. At each step we do one of the following two operations:
(i) If $a$ and $b$ are different integers on the board, then we can write $a+b$ on the board, if it is not already there.
(ii) If $a, b$ and $c$ are three different integers on the board, and if an integer $x$ satisfies $a x^{2}+b x+c=0$, then we can write $x$ on the board, if it is not already there.
Determine all pairs of starting numbers $(u, v)$ from which any integer can eventually be written on the board after a finite sequence of steps.
|
If $u=0$ or $v=0$ then we can only get $\{u, v\}$.
Proof. If $u=0$ or $v=0$, then (i) will never yield a new number and we cannot use (ii) with only two numbers.
If $\max (u, v)<0$, we cannot get non-negative numbers.
Proof. For $a, b, c<0$ :
(i) cannot generate a non-negative number as $a+b<0$.
(ii) cannot generate a non-negative number as for $x \geq 0$ : $a x^{2}+b x+c \leq c<0$.
If $u+v \neq 0, u, v \neq 0$ and $\max (u, v)>0$, we can get every number.
Proof. $u \neq v \rightarrow u+v$ can be written. $u \neq 0$, so $u+v \neq v \rightarrow u+2 v$ can be written. $v \neq 0$, so $u+2 v \neq u$, meaning that $2 u+2 v$ can be written. If for $n>1, n(u+v)$ can be written then $(n+1)(u+v)=n(u+v)+(u+v)$ can also be written, because $u+v \neq 0$, so $n(u+v) \neq(u+v)$. Therefore, by induction for all $n>0$ the number $n(u+v)$ can be written.
Taking $n=2,3, \ldots$ and $(u+v)(x+1)(x+n)=(u+v) x^{2}+(u+v)(n+1) x+(u+v) n=0$ gives $x=-1$ and $x=-n \rightarrow$ for all $n>0$ we can get $-n$ (we can get all the negative numbers). Additionally, we can get $u+(-u)=0$.
For $n \geq 1$ we can take $0 \cdot x^{2}+u x+(-u n)=0$ as $u \neq 0 \rightarrow u,-n u, 0$ are all distinct, therefore we can get $n$. Thus, we can get all the numbers.
If $u+v=0$ and $\max (u, v)>1$ we can get all the numbers.
Proof. We can get $0=u+v$ as $u \neq v$. Take $0 \cdot x^{2}+u x-u=0$ so we can get 1 written on the board. Take $\left(u^{\prime}, v^{\prime}\right)=(1, \max (u, v))$ and then use the result from claim 3. As $0<u^{\prime}=1<\max (u, v)=v^{\prime}$ and $u^{\prime}+v^{\prime}>0$ we can get all the numbers.
Remaining case: If $v=1$ and $u=-1$, we can only additionally write number 0 on the board using operation (i); and no additional numbers using (ii) because setting $\{a, b, c\}$ to $\{-1,0,1\}$ in any order only has solutions for $x$ in $\{-1,0,1\}$. Hence, if $\{u, v\}=\{-1,1\}$, then we cannot reach every possible $y$.
|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "# Problem 1 (SVK)\n",
"resource_path": "EGMO/segmented/en-2024-solutions.jsonl",
"solution_match": "\nSolution 2. ",
"tier": "T2",
"year": "2024"
}
|
Problem. Two different integers $u$ and $v$ are written on a board. We perform a sequence of steps. At each step we do one of the following two operations:
(i) If $a$ and $b$ are different integers on the board, then we can write $a+b$ on the board, if it is not already there.
(ii) If $a, b$ and $c$ are three different integers on the board, and if an integer $x$ satisfies $a x^{2}+b x+c=0$, then we can write $x$ on the board, if it is not already there.
Determine all pairs of starting numbers $(u, v)$ from which any integer can eventually be written on the board after a finite sequence of steps.
|
We show none of the initial number can be 0 , as in Solution 1. Then, we split into three cases: initial numbers having different signs, both being positive, and both being negative.
Case 1. Suppose we have two numbers $u, v$ with different signs such that $\operatorname{gcd}(u, v)=k$ for some $k \in \mathbb{Z}^{+}$. Without loss of generality assume that $u>0$ and $v<0$.
Case 1.1. $v<-k$ :
We can generate all numbers $y$ such that $k \mid y$ and $y \leq u$.
Proof. Define $u^{\prime}=\frac{u}{k}, v^{\prime}=\frac{v}{k}$. Note that by definition, $\operatorname{gcd}\left(u^{\prime}, v^{\prime}\right)=1$. If starting with numbers $u^{\prime}, v^{\prime}$, we can make a sequence of applications of only the (i) rule to write a number $y=p \cdot u^{\prime}+q \cdot v^{\prime}$ on the board, then we can apply the same sequence of moves to $u, v$ to write $k \cdot y=p \cdot u+q \cdot v$ on the board.
Therefore, we will prove instead that if $v^{\prime}<-1$, we can write all numbers $y<u^{\prime}$ on the board, which is equivalent to the lemma.
We attempt to write numbers $u^{\prime}+q \cdot v^{\prime}$ for $q \in \mathbb{Z}^{+}$on the board by repeatedly adding $v^{\prime}$ to $u^{\prime}$. This process can only ever halt if we reach a point where $u^{\prime}+q \cdot v^{\prime}=v^{\prime}$. That cannot occur, as it would imply $u^{\prime}=(1-q) \cdot v^{\prime}$. Taking into account that $u^{\prime}, v^{\prime} \neq 0$, that implies $\operatorname{gcd}\left(u^{\prime}, v^{\prime}\right)=\left|v^{\prime}\right|$. That is a contradiction, as $\left|v^{\prime}\right|>1$.
Therefore, we can write all numbers of the form $u^{\prime}+q \cdot v^{\prime}$ on the board for $q \in \mathbb{Z}^{+}$. We will use these numbers to construct an arbitrary integer $y$.
If we want to write a number $y<u^{\prime}$ on the board, and we already have a number $n<y$ on the board such that $y \equiv n\left(\bmod u^{\prime}\right)$, then we can construct $y$ by repeatedly adding $u^{\prime}$ to $n$ until we reach $y$, skipping all numbers that are already on the board. As $y<u^{\prime}$, none of the numbers we attempt to add $u^{\prime}$ to will be equal to $u^{\prime}$.
Suppose we fix any number $y<u^{\prime}$. As $\operatorname{gcd}\left(u^{\prime}, v^{\prime}\right)=1, q \cdot v^{\prime}$ takes all residues modulo $u^{\prime}$ as $q$ runs through the positive integers. Therefore, we will always be able to find a number $n$ of the form $u^{\prime}+q \cdot v^{\prime}$ such that $y \equiv n \bmod u^{\prime}$. We can generate an arbitrarily small $n^{\prime}$ by taking $n^{\prime}=n+l \cdot u^{\prime} \cdot v^{\prime}=u^{\prime}+\left(q+l \cdot u^{\prime}\right) \cdot v^{\prime}$ for large enough $l$, making both $n^{\prime}<y$ and $n^{\prime} \equiv y \bmod u^{\prime}$ true.
Therefore, we can write all numbers $y<u^{\prime}$ on the board. Thus, starting from $u$ and $v$, we can get all numbers $y \leq u$ s.t. $k \mid y$.
The numbers $k, 0$ and all negative multiples of $k$ are a subset of the integers $y \leq u$ s.t. $k \mid y$. Therefore, we have all of those numbers on the board.
We can now get an arbitrary nonzero number by applying (ii) to the polynomial $k \cdot(x-$ $n)(x+n)=k \cdot x^{2}+0 \cdot x-n^{2} \cdot k$. The coefficients of this polynomial are distinct for all integers $n \neq 0$, and they are from the set $\{k, 0\} \cup\{q \cdot k \mid q<0\}$, which we have on the board. Therefore the rule application is valid.
As this works for all integers $n \in \mathbb{Z} \backslash\{0\}$, and 0 is already on the board, we have proven that we can write all integers on the board.
Case 1.2.: $v=-k$ :
Case 1.2.1.: $k \neq 1$.
If $k \neq 1$, we can generate -1 from the polynomial $u \cdot x^{2}+(u+v) x+v$. We can now repeatedly add -1 to $v=-k$ until we reach $-2 k$ on the board. Now, we can appeal to Case 1.1.
Case 1.2.2. $k=1$.
To restate the conditions of this sub-case, $v=-k=-1$, and $u$ is an arbitrary positive number.
Case 1.2.2.1. $u=1$.
If $u=1$, we are only ever able to construct the numbers $-1,0,1$, no matter how we apply the rules.
Case 1.2.2.2. $u \neq 1$.
We can subtract 1 from $u$ until we reach 0 . This procedure also generates 1 . We now add 1 to $u$ until we get all positive numbers.
Now, we find an arbitrary polynomial with different positive coefficients that have a negative root smaller than -1 . An example is $(x+3)^{2}$.
We will now keep adding -1 to -3 to get all the negative numbers $y \leq-3$. To get -2 , we can add -3 to 1 , generating all integers.
Case 2 Suppose that both of $u, v$ are positive.
We can now use any method from the previous solutions to generate a negative number, and then appeal to Case 1.
Case 3 Suppose $u<0, v<0$.
Then there can only be negative numbers on the board. With negative numbers $a, b$, operation (i) will only yield a negative number. The same holds for operation (ii), because for a non-negative $x$ and negative $a, b, c$, we have $a x^{2}+b x+c<0$. Hence, if both $u<0$ and $v<0$, then we cannot reach every possible $y$.
|
not found
|
Yes
|
Incomplete
|
math-word-problem
|
Algebra
|
Problem. Two different integers $u$ and $v$ are written on a board. We perform a sequence of steps. At each step we do one of the following two operations:
(i) If $a$ and $b$ are different integers on the board, then we can write $a+b$ on the board, if it is not already there.
(ii) If $a, b$ and $c$ are three different integers on the board, and if an integer $x$ satisfies $a x^{2}+b x+c=0$, then we can write $x$ on the board, if it is not already there.
Determine all pairs of starting numbers $(u, v)$ from which any integer can eventually be written on the board after a finite sequence of steps.
|
We show none of the initial number can be 0 , as in Solution 1. Then, we split into three cases: initial numbers having different signs, both being positive, and both being negative.
Case 1. Suppose we have two numbers $u, v$ with different signs such that $\operatorname{gcd}(u, v)=k$ for some $k \in \mathbb{Z}^{+}$. Without loss of generality assume that $u>0$ and $v<0$.
Case 1.1. $v<-k$ :
We can generate all numbers $y$ such that $k \mid y$ and $y \leq u$.
Proof. Define $u^{\prime}=\frac{u}{k}, v^{\prime}=\frac{v}{k}$. Note that by definition, $\operatorname{gcd}\left(u^{\prime}, v^{\prime}\right)=1$. If starting with numbers $u^{\prime}, v^{\prime}$, we can make a sequence of applications of only the (i) rule to write a number $y=p \cdot u^{\prime}+q \cdot v^{\prime}$ on the board, then we can apply the same sequence of moves to $u, v$ to write $k \cdot y=p \cdot u+q \cdot v$ on the board.
Therefore, we will prove instead that if $v^{\prime}<-1$, we can write all numbers $y<u^{\prime}$ on the board, which is equivalent to the lemma.
We attempt to write numbers $u^{\prime}+q \cdot v^{\prime}$ for $q \in \mathbb{Z}^{+}$on the board by repeatedly adding $v^{\prime}$ to $u^{\prime}$. This process can only ever halt if we reach a point where $u^{\prime}+q \cdot v^{\prime}=v^{\prime}$. That cannot occur, as it would imply $u^{\prime}=(1-q) \cdot v^{\prime}$. Taking into account that $u^{\prime}, v^{\prime} \neq 0$, that implies $\operatorname{gcd}\left(u^{\prime}, v^{\prime}\right)=\left|v^{\prime}\right|$. That is a contradiction, as $\left|v^{\prime}\right|>1$.
Therefore, we can write all numbers of the form $u^{\prime}+q \cdot v^{\prime}$ on the board for $q \in \mathbb{Z}^{+}$. We will use these numbers to construct an arbitrary integer $y$.
If we want to write a number $y<u^{\prime}$ on the board, and we already have a number $n<y$ on the board such that $y \equiv n\left(\bmod u^{\prime}\right)$, then we can construct $y$ by repeatedly adding $u^{\prime}$ to $n$ until we reach $y$, skipping all numbers that are already on the board. As $y<u^{\prime}$, none of the numbers we attempt to add $u^{\prime}$ to will be equal to $u^{\prime}$.
Suppose we fix any number $y<u^{\prime}$. As $\operatorname{gcd}\left(u^{\prime}, v^{\prime}\right)=1, q \cdot v^{\prime}$ takes all residues modulo $u^{\prime}$ as $q$ runs through the positive integers. Therefore, we will always be able to find a number $n$ of the form $u^{\prime}+q \cdot v^{\prime}$ such that $y \equiv n \bmod u^{\prime}$. We can generate an arbitrarily small $n^{\prime}$ by taking $n^{\prime}=n+l \cdot u^{\prime} \cdot v^{\prime}=u^{\prime}+\left(q+l \cdot u^{\prime}\right) \cdot v^{\prime}$ for large enough $l$, making both $n^{\prime}<y$ and $n^{\prime} \equiv y \bmod u^{\prime}$ true.
Therefore, we can write all numbers $y<u^{\prime}$ on the board. Thus, starting from $u$ and $v$, we can get all numbers $y \leq u$ s.t. $k \mid y$.
The numbers $k, 0$ and all negative multiples of $k$ are a subset of the integers $y \leq u$ s.t. $k \mid y$. Therefore, we have all of those numbers on the board.
We can now get an arbitrary nonzero number by applying (ii) to the polynomial $k \cdot(x-$ $n)(x+n)=k \cdot x^{2}+0 \cdot x-n^{2} \cdot k$. The coefficients of this polynomial are distinct for all integers $n \neq 0$, and they are from the set $\{k, 0\} \cup\{q \cdot k \mid q<0\}$, which we have on the board. Therefore the rule application is valid.
As this works for all integers $n \in \mathbb{Z} \backslash\{0\}$, and 0 is already on the board, we have proven that we can write all integers on the board.
Case 1.2.: $v=-k$ :
Case 1.2.1.: $k \neq 1$.
If $k \neq 1$, we can generate -1 from the polynomial $u \cdot x^{2}+(u+v) x+v$. We can now repeatedly add -1 to $v=-k$ until we reach $-2 k$ on the board. Now, we can appeal to Case 1.1.
Case 1.2.2. $k=1$.
To restate the conditions of this sub-case, $v=-k=-1$, and $u$ is an arbitrary positive number.
Case 1.2.2.1. $u=1$.
If $u=1$, we are only ever able to construct the numbers $-1,0,1$, no matter how we apply the rules.
Case 1.2.2.2. $u \neq 1$.
We can subtract 1 from $u$ until we reach 0 . This procedure also generates 1 . We now add 1 to $u$ until we get all positive numbers.
Now, we find an arbitrary polynomial with different positive coefficients that have a negative root smaller than -1 . An example is $(x+3)^{2}$.
We will now keep adding -1 to -3 to get all the negative numbers $y \leq-3$. To get -2 , we can add -3 to 1 , generating all integers.
Case 2 Suppose that both of $u, v$ are positive.
We can now use any method from the previous solutions to generate a negative number, and then appeal to Case 1.
Case 3 Suppose $u<0, v<0$.
Then there can only be negative numbers on the board. With negative numbers $a, b$, operation (i) will only yield a negative number. The same holds for operation (ii), because for a non-negative $x$ and negative $a, b, c$, we have $a x^{2}+b x+c<0$. Hence, if both $u<0$ and $v<0$, then we cannot reach every possible $y$.
|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "# Problem 1 (SVK)\n",
"resource_path": "EGMO/segmented/en-2024-solutions.jsonl",
"solution_match": "\nSolution 3. ",
"tier": "T2",
"year": "2024"
}
|
Problem. Let $A B C$ be a triangle with $A C>A B$, and denote its circumcircle by $\Omega$ and incentre by $I$. Let its incircle meet sides $B C, C A, A B$ at $D, E, F$ respectively. Let $X$ and $Y$ be two points on minor arcs $\overparen{D F}$ and $\overparen{D E}$ of the incircle, respectively, such that $\angle B X D=\angle D Y C$. Let line $X Y$ meet line $B C$ at $K$. Let $T$ be the point on $\Omega$ such that $K T$ is tangent to $\Omega$ and $T$ is on the same side of line $B C$ as $A$. Prove that lines $T D$ and $A I$ meet on $\Omega$.
|
By the alternate segment theorem we have that:
$$
180^{\circ}=\angle D C Y+\angle C Y D+\angle Y D C=\angle D C Y+\angle D X B+\angle Y X D=\angle D C Y+\angle Y X B
$$
Therefore opposite angle of $B X Y C$ are supplementary and so $C Y X B$ cyclic.
One can apply power of a point at $K$ :
$$
K T^{2}=K B \cdot K C=K X \cdot K Y=K D^{2} \Longrightarrow K T=K D .
$$
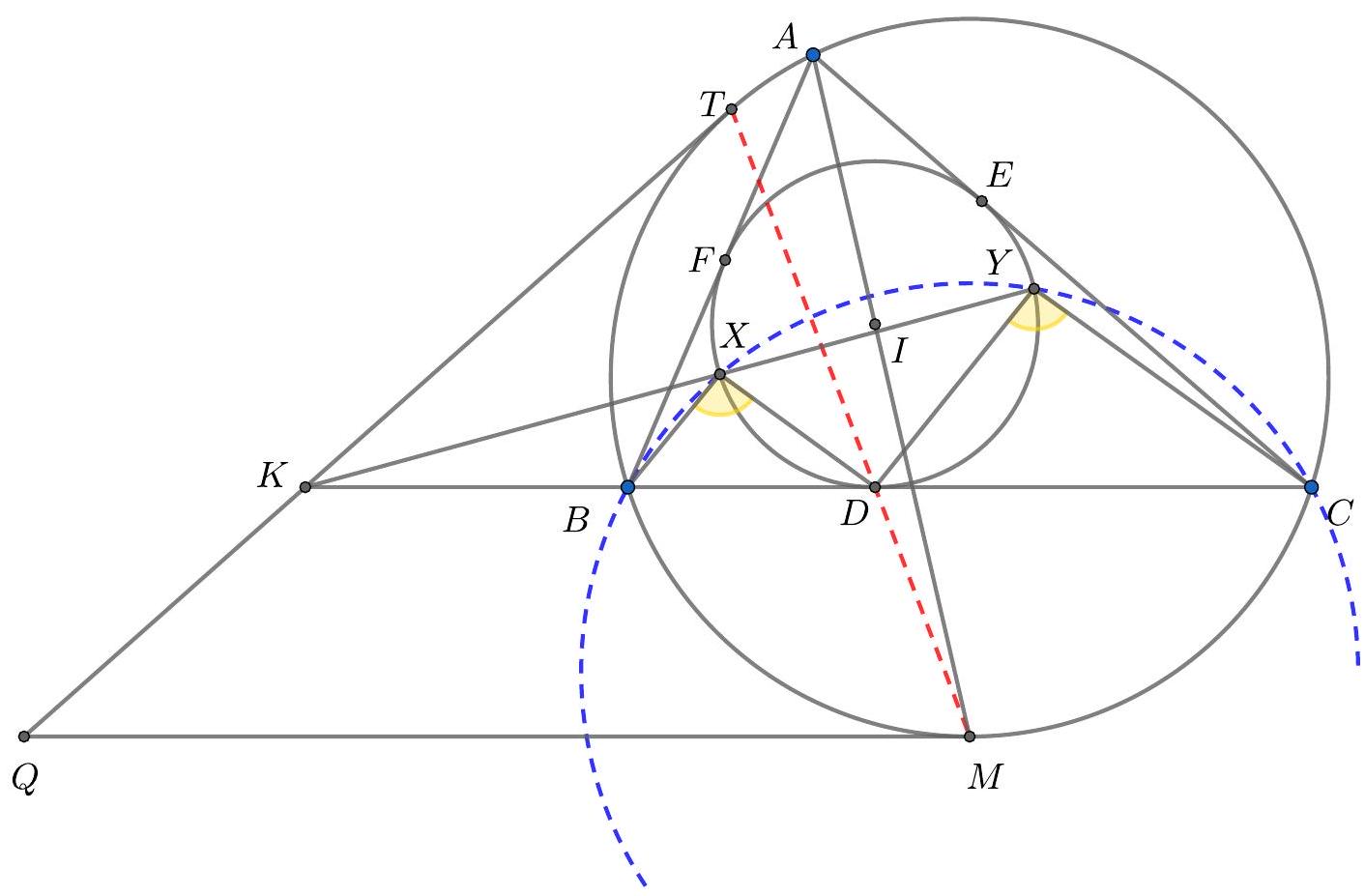
Figure 1: The proposer's solution using a new point $Q$
(Alternatively you can sidestep power of a point by observing that $K$ is the radical centre of the incircle $D E F$, the circumcircle $\Gamma$ and the circle $C Y X B$ and so $K T^{2}=K D^{2}$.)
Now let $A I$ meet $\Omega$ at $M$, the midpoint of $\widehat{B C}$ not containing $A$. Let the tangent at $M$ meet $K T$ at $Q$. Observe that $Q M \| K D$ so $\angle T K D=\angle T Q M$ and also $K T=K D$, $Q T=Q M$ hence $\triangle T K D \sim \triangle T Q M$. As $T, K, Q$ are collinear, this means that $T, D, M$ are collinear so $T D$ and $A I$ meet at $M$ which lies on $\Omega$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Problem. Let $A B C$ be a triangle with $A C>A B$, and denote its circumcircle by $\Omega$ and incentre by $I$. Let its incircle meet sides $B C, C A, A B$ at $D, E, F$ respectively. Let $X$ and $Y$ be two points on minor arcs $\overparen{D F}$ and $\overparen{D E}$ of the incircle, respectively, such that $\angle B X D=\angle D Y C$. Let line $X Y$ meet line $B C$ at $K$. Let $T$ be the point on $\Omega$ such that $K T$ is tangent to $\Omega$ and $T$ is on the same side of line $B C$ as $A$. Prove that lines $T D$ and $A I$ meet on $\Omega$.
|
By the alternate segment theorem we have that:
$$
180^{\circ}=\angle D C Y+\angle C Y D+\angle Y D C=\angle D C Y+\angle D X B+\angle Y X D=\angle D C Y+\angle Y X B
$$
Therefore opposite angle of $B X Y C$ are supplementary and so $C Y X B$ cyclic.
One can apply power of a point at $K$ :
$$
K T^{2}=K B \cdot K C=K X \cdot K Y=K D^{2} \Longrightarrow K T=K D .
$$

Figure 1: The proposer's solution using a new point $Q$
(Alternatively you can sidestep power of a point by observing that $K$ is the radical centre of the incircle $D E F$, the circumcircle $\Gamma$ and the circle $C Y X B$ and so $K T^{2}=K D^{2}$.)
Now let $A I$ meet $\Omega$ at $M$, the midpoint of $\widehat{B C}$ not containing $A$. Let the tangent at $M$ meet $K T$ at $Q$. Observe that $Q M \| K D$ so $\angle T K D=\angle T Q M$ and also $K T=K D$, $Q T=Q M$ hence $\triangle T K D \sim \triangle T Q M$. As $T, K, Q$ are collinear, this means that $T, D, M$ are collinear so $T D$ and $A I$ meet at $M$ which lies on $\Omega$.
|
{
"exam": "EGMO",
"problem_label": "2",
"problem_match": "# Problem 2 (UNK)\n",
"resource_path": "EGMO/segmented/en-2024-solutions.jsonl",
"solution_match": "\nSolution 1. ",
"tier": "T2",
"year": "2024"
}
|
Problem. Let $A B C$ be a triangle with $A C>A B$, and denote its circumcircle by $\Omega$ and incentre by $I$. Let its incircle meet sides $B C, C A, A B$ at $D, E, F$ respectively. Let $X$ and $Y$ be two points on minor arcs $\overparen{D F}$ and $\overparen{D E}$ of the incircle, respectively, such that $\angle B X D=\angle D Y C$. Let line $X Y$ meet line $B C$ at $K$. Let $T$ be the point on $\Omega$ such that $K T$ is tangent to $\Omega$ and $T$ is on the same side of line $B C$ as $A$. Prove that lines $T D$ and $A I$ meet on $\Omega$.
|
The role of $X$ and $Y$ in this problem is secondary. Draw any circle through $B$ and $C$ which meets the incircle at $X$ and $Y$ and you determine the same point $K$. This is because $K$ is the radical centre of the three circles in play. Therefore $K$ is the intersection of $B C$ with the radical axis of the circumcircle $\Omega$ and the incircle $D E F$, and so is independent of the choice of circle through $B$ and $C$ which gives rise to $X$ and $Y$. In the problem as posed, this is disguised, with angle properties of $X$ and $Y$ giving rise the the circle $B X Y C$.
You can now work with the simplified diagram shown in Figure 2.
Somehow we must use a characterization of $M$ in order to finish. In the proposer's solution, we used the tangent to the circumcircle $\Omega$ at $M$ being parallel to $B C$. In this alternative, we use the fact that the internal angle bisector of angle $\angle C T B$ meets $\Omega$ again at $M$.
Triangle $T K D$ is isosceles with apex $K$ so
$$
\angle K D T=\angle D T K=\angle D T B+\angle B T K .
$$
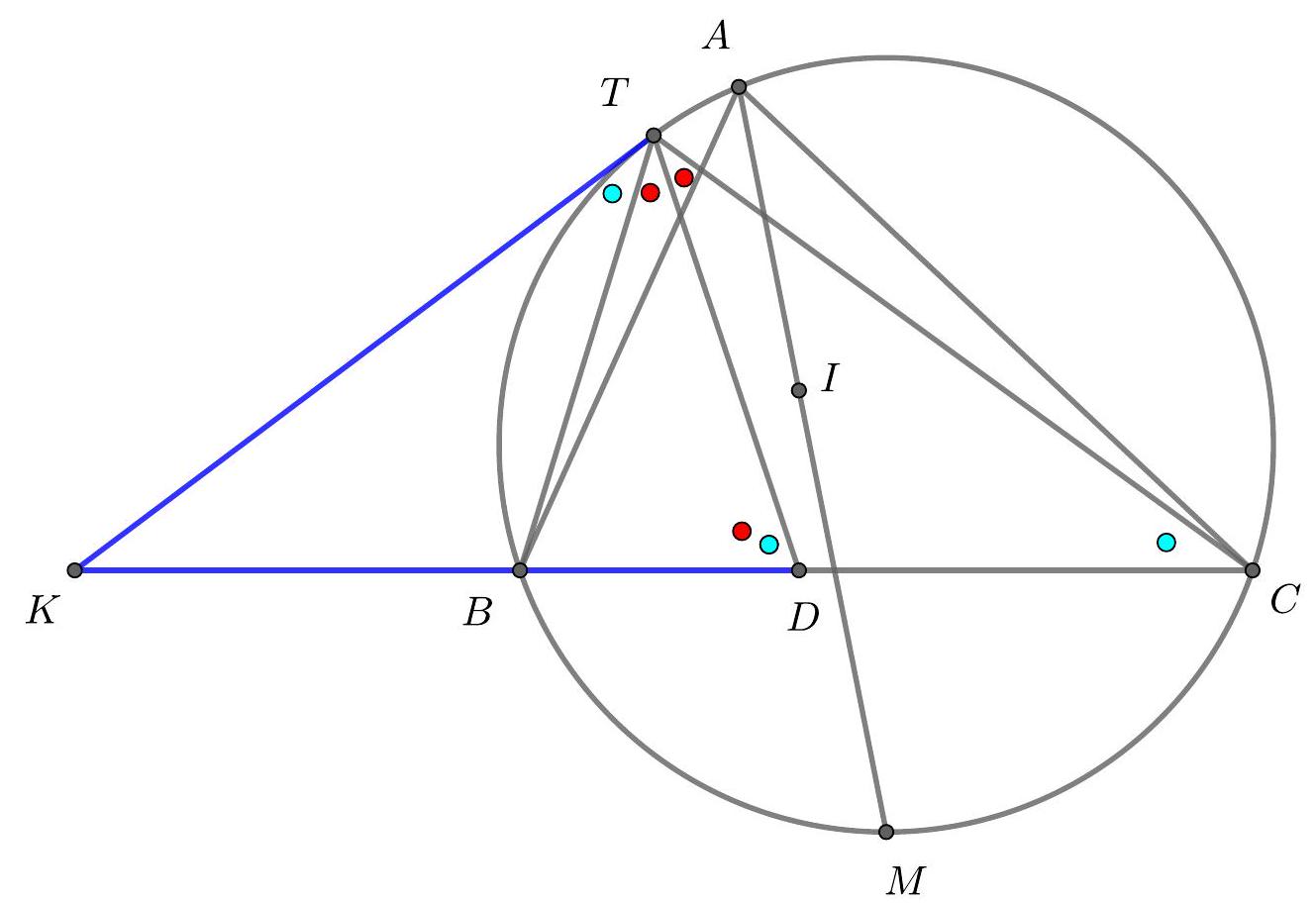
Figure 2: Illustration of an angle chase
By the alternate segment theorem, $\angle B T K=\angle B C T=\angle D C T$. Now angle $\angle K D T$ is an exterior angle of triangle $D C T$ so $\angle C T D=\angle D T B$.
Therefore the line $T D$ is the internal angle bisector of angle $\angle C T B$ and so must pass through $M$, the midpoint of the arc $\widehat{B C}$ of $\Omega$ which does not contain $T$.
Observation This affords a construction of the radical axis of the incircle and circumcircle of triangle $A B C: M$ and $D$ determine $T$ and the tangent at $T$ meets $B C$ at a point on the required radical axis. See Figure 3. Now do a cyclic change of letters of $A B C$ and find a point on $C A$ which is also on the radical axis (the dashed magenta line).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Problem. Let $A B C$ be a triangle with $A C>A B$, and denote its circumcircle by $\Omega$ and incentre by $I$. Let its incircle meet sides $B C, C A, A B$ at $D, E, F$ respectively. Let $X$ and $Y$ be two points on minor arcs $\overparen{D F}$ and $\overparen{D E}$ of the incircle, respectively, such that $\angle B X D=\angle D Y C$. Let line $X Y$ meet line $B C$ at $K$. Let $T$ be the point on $\Omega$ such that $K T$ is tangent to $\Omega$ and $T$ is on the same side of line $B C$ as $A$. Prove that lines $T D$ and $A I$ meet on $\Omega$.
|
The role of $X$ and $Y$ in this problem is secondary. Draw any circle through $B$ and $C$ which meets the incircle at $X$ and $Y$ and you determine the same point $K$. This is because $K$ is the radical centre of the three circles in play. Therefore $K$ is the intersection of $B C$ with the radical axis of the circumcircle $\Omega$ and the incircle $D E F$, and so is independent of the choice of circle through $B$ and $C$ which gives rise to $X$ and $Y$. In the problem as posed, this is disguised, with angle properties of $X$ and $Y$ giving rise the the circle $B X Y C$.
You can now work with the simplified diagram shown in Figure 2.
Somehow we must use a characterization of $M$ in order to finish. In the proposer's solution, we used the tangent to the circumcircle $\Omega$ at $M$ being parallel to $B C$. In this alternative, we use the fact that the internal angle bisector of angle $\angle C T B$ meets $\Omega$ again at $M$.
Triangle $T K D$ is isosceles with apex $K$ so
$$
\angle K D T=\angle D T K=\angle D T B+\angle B T K .
$$

Figure 2: Illustration of an angle chase
By the alternate segment theorem, $\angle B T K=\angle B C T=\angle D C T$. Now angle $\angle K D T$ is an exterior angle of triangle $D C T$ so $\angle C T D=\angle D T B$.
Therefore the line $T D$ is the internal angle bisector of angle $\angle C T B$ and so must pass through $M$, the midpoint of the arc $\widehat{B C}$ of $\Omega$ which does not contain $T$.
Observation This affords a construction of the radical axis of the incircle and circumcircle of triangle $A B C: M$ and $D$ determine $T$ and the tangent at $T$ meets $B C$ at a point on the required radical axis. See Figure 3. Now do a cyclic change of letters of $A B C$ and find a point on $C A$ which is also on the radical axis (the dashed magenta line).
|
{
"exam": "EGMO",
"problem_label": "2",
"problem_match": "# Problem 2 (UNK)\n",
"resource_path": "EGMO/segmented/en-2024-solutions.jsonl",
"solution_match": "\nSolution 2. ",
"tier": "T2",
"year": "2024"
}
|
Problem. Let $A B C$ be a triangle with $A C>A B$, and denote its circumcircle by $\Omega$ and incentre by $I$. Let its incircle meet sides $B C, C A, A B$ at $D, E, F$ respectively. Let $X$ and $Y$ be two points on minor arcs $\overparen{D F}$ and $\overparen{D E}$ of the incircle, respectively, such that $\angle B X D=\angle D Y C$. Let line $X Y$ meet line $B C$ at $K$. Let $T$ be the point on $\Omega$ such that $K T$ is tangent to $\Omega$ and $T$ is on the same side of line $B C$ as $A$. Prove that lines $T D$ and $A I$ meet on $\Omega$.
|
The centre of direct enlargement from the incircle to the circumcircle gives another way to finish the proof. This enlargement carries $D$ to $M$ since the tangent lines to their associated circles are parallel. The centre of enlargement therefore lies on the line $M D$. Let $M D$ meet the incircle again at $U$ and the circumcircle again at $V$. Draw the tangent to the incircle at $U$ to meet $B C$ at $W$ so triangle $W D U$ is isosceles with apex $W$ and has equal base angles $\angle W D U$ and $\angle D U W$. The enlargement carries the line $W U$ to the tangent line to the circumcircle at $V$ which meets $B C$ at $S$. Enlargements carry lines to parallel lines, so $\angle D V K^{\prime}=\angle D U W=\angle W D U=\angle K^{\prime} D V$. Therefore triangle $K^{\prime} D V$ is isosceles with apex $K^{\prime}$.
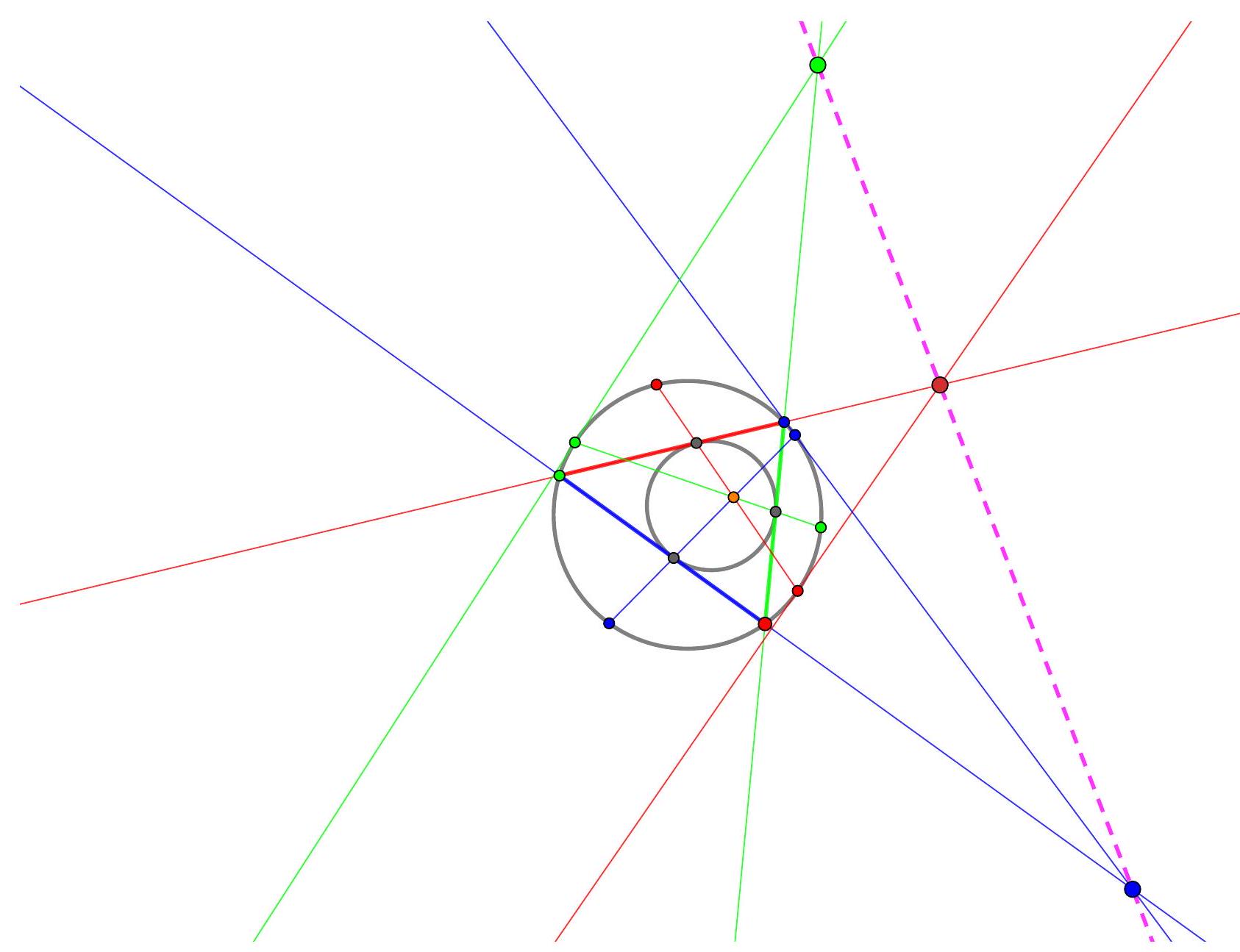
Figure 3: The three points $K$ on the radical axis.
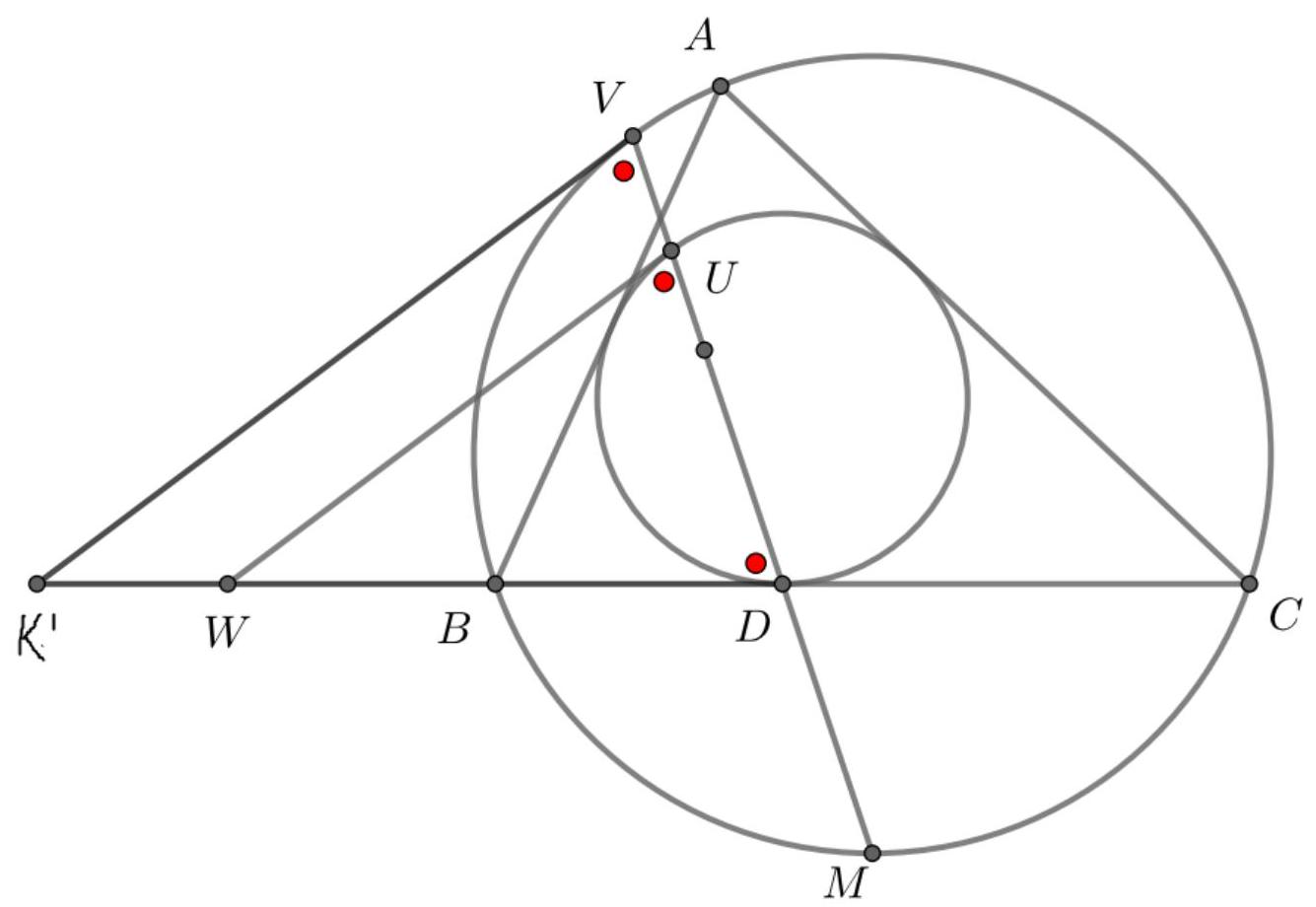
Figure 4: The enlargement of $W$ gives $K^{\prime}$.
This identifies $S$ as the intersection of the radical axis of the two circles with $B C$, so $K^{\prime}=K$ and $V=T$ and the proof is complete.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Problem. Let $A B C$ be a triangle with $A C>A B$, and denote its circumcircle by $\Omega$ and incentre by $I$. Let its incircle meet sides $B C, C A, A B$ at $D, E, F$ respectively. Let $X$ and $Y$ be two points on minor arcs $\overparen{D F}$ and $\overparen{D E}$ of the incircle, respectively, such that $\angle B X D=\angle D Y C$. Let line $X Y$ meet line $B C$ at $K$. Let $T$ be the point on $\Omega$ such that $K T$ is tangent to $\Omega$ and $T$ is on the same side of line $B C$ as $A$. Prove that lines $T D$ and $A I$ meet on $\Omega$.
|
The centre of direct enlargement from the incircle to the circumcircle gives another way to finish the proof. This enlargement carries $D$ to $M$ since the tangent lines to their associated circles are parallel. The centre of enlargement therefore lies on the line $M D$. Let $M D$ meet the incircle again at $U$ and the circumcircle again at $V$. Draw the tangent to the incircle at $U$ to meet $B C$ at $W$ so triangle $W D U$ is isosceles with apex $W$ and has equal base angles $\angle W D U$ and $\angle D U W$. The enlargement carries the line $W U$ to the tangent line to the circumcircle at $V$ which meets $B C$ at $S$. Enlargements carry lines to parallel lines, so $\angle D V K^{\prime}=\angle D U W=\angle W D U=\angle K^{\prime} D V$. Therefore triangle $K^{\prime} D V$ is isosceles with apex $K^{\prime}$.

Figure 3: The three points $K$ on the radical axis.

Figure 4: The enlargement of $W$ gives $K^{\prime}$.
This identifies $S$ as the intersection of the radical axis of the two circles with $B C$, so $K^{\prime}=K$ and $V=T$ and the proof is complete.
|
{
"exam": "EGMO",
"problem_label": "2",
"problem_match": "# Problem 2 (UNK)\n",
"resource_path": "EGMO/segmented/en-2024-solutions.jsonl",
"solution_match": "\nSolution 3. ",
"tier": "T2",
"year": "2024"
}
|
Problem. Let $A B C$ be a triangle with $A C>A B$, and denote its circumcircle by $\Omega$ and incentre by $I$. Let its incircle meet sides $B C, C A, A B$ at $D, E, F$ respectively. Let $X$ and $Y$ be two points on minor arcs $\overparen{D F}$ and $\overparen{D E}$ of the incircle, respectively, such that $\angle B X D=\angle D Y C$. Let line $X Y$ meet line $B C$ at $K$. Let $T$ be the point on $\Omega$ such that $K T$ is tangent to $\Omega$ and $T$ is on the same side of line $B C$ as $A$. Prove that lines $T D$ and $A I$ meet on $\Omega$.
|
Let $\phi$ be the inversion with center $K$ and radius $K D$. Note that this inversion maps incirlce of $A B C$ to itself and $K, X, Y$ are collinear, hence $\phi(X)=Y$. Also $\phi(D)=D$, so $\phi$ maps circle $X B D$ to cicle $Y D B^{\prime}$, where $B^{\prime}:=\phi(B)$ is the point on $B C$ different from $B$ such that $\angle B X D=\angle D Y B^{\prime}$, hence $\phi(B)=C$. From $\phi(B)=C$ we get that $K D=K T$ as $K D^{2}=K B \cdot K C=K T^{2}$ since $K D$ is the radius of inversion.
The rest of the solutions is the same as in the other solutions.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Problem. Let $A B C$ be a triangle with $A C>A B$, and denote its circumcircle by $\Omega$ and incentre by $I$. Let its incircle meet sides $B C, C A, A B$ at $D, E, F$ respectively. Let $X$ and $Y$ be two points on minor arcs $\overparen{D F}$ and $\overparen{D E}$ of the incircle, respectively, such that $\angle B X D=\angle D Y C$. Let line $X Y$ meet line $B C$ at $K$. Let $T$ be the point on $\Omega$ such that $K T$ is tangent to $\Omega$ and $T$ is on the same side of line $B C$ as $A$. Prove that lines $T D$ and $A I$ meet on $\Omega$.
|
Let $\phi$ be the inversion with center $K$ and radius $K D$. Note that this inversion maps incirlce of $A B C$ to itself and $K, X, Y$ are collinear, hence $\phi(X)=Y$. Also $\phi(D)=D$, so $\phi$ maps circle $X B D$ to cicle $Y D B^{\prime}$, where $B^{\prime}:=\phi(B)$ is the point on $B C$ different from $B$ such that $\angle B X D=\angle D Y B^{\prime}$, hence $\phi(B)=C$. From $\phi(B)=C$ we get that $K D=K T$ as $K D^{2}=K B \cdot K C=K T^{2}$ since $K D$ is the radius of inversion.
The rest of the solutions is the same as in the other solutions.
|
{
"exam": "EGMO",
"problem_label": "2",
"problem_match": "# Problem 2 (UNK)\n",
"resource_path": "EGMO/segmented/en-2024-solutions.jsonl",
"solution_match": "\nSolution 4. ",
"tier": "T2",
"year": "2024"
}
|
Problem. For a sequence $a_{1}<a_{2}<\cdots<a_{n}$ of integers, a pair $\left(a_{i}, a_{j}\right)$ with $1 \leq i<j \leq n$ is called interesting if there exists a pair $\left(a_{k}, a_{l}\right)$ of integers with $1 \leq k<l \leq n$ such that
$$
\frac{a_{l}-a_{k}}{a_{j}-a_{i}}=2
$$
For each $n \geq 3$, find the largest possible number of interesting pairs in a sequence of length $n$.
Answer. $\frac{1}{2}(n-1)(n-2)+1$.
|
Consider the numbers $a_{i}=2^{i}$ for $2 \leq i \leq n$ and $a_{1}=0$, and choose any pair $(i, j)$ with $1 \leq i<j \leq n$.
If $i=1$, the pair $(1, j)$ is interesting for all $2 \leq j \leq n-1$, as $\frac{a_{j+1}-a_{1}}{a_{j}-a_{1}}=\frac{2^{j+1}}{2^{j}}=2$.
If $i \geq 2$, the pair $(i, j)$ is also interesting for all $j$ such that $i+1 \leq j \leq n-1$, since $\frac{a_{j+1}-a_{i+1}}{a_{j}-a_{i}}=\frac{2^{j+1}-2^{i+1}}{2^{j}-2^{i}}=2$.
In addition, the pair $(n-1, n)$ is interesting, as $\frac{a_{n}-a_{0}}{a_{n}-a_{n-1}}=2$.
Hence, all pairs in which $j \leq n-1$, and additionally the pair $(n-1, n)$, are interesting, giving $\frac{1}{2}(n-1)(n-2)+1$ pairs in total.
Now, let's show that there can't be more interesting pairs. To this end we show that at least $\frac{1}{2} n(n-1)-\left(\frac{1}{2}(n-1)(n-2)+1\right)=n-2$ pairs are not interesting. Clearly, the pair $(1, n)$ is not interesting.
Let's make the following observation: if a pair $(i, j)$ is interesting and it's not $(1, n)$, then $a_{j}-a_{i}$ can't exceed $\frac{1}{2}\left(a_{n}-a_{1}\right)$. (Since, if $(i, j)$ is interesting then $a_{l}-a_{k}=2\left(a_{j}-a_{i}\right)$ for some pair $(k, l)$. If then $2\left(a_{j}-a_{i}\right)>a_{n}-a_{1}$ we would have $a_{l}-a_{k}>a_{n}-a_{1}$, which is not possible.)
Finally, for any $2 \leq i \leq n-1$ consider pairs $(1, i)$ and $(i, n)$. If both of them are interesting, then, following the observation above, the only possibility is $a_{i}-a_{1}=a_{n}-a_{i}=\frac{a_{n}-a_{1}}{2}$. Clearly, this is possible for at most one $i$, so for all other $n-3$ values of $i$, at least one of pairs $(1, i)$ and $(i, n)$ is not interesting. Combining with the pair $(1, n)$, we get at least $n-2$ not interesting pairs in total, as desired.
Comment: The originally proposed formulation considered a sequence $a_{1}<a_{2}<\cdots<$ $a_{n}$ of $n$ real numbers, rather than integers. The conclusion is however the same and the solution is identical.
|
\frac{1}{2}(n-1)(n-2)+1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Problem. For a sequence $a_{1}<a_{2}<\cdots<a_{n}$ of integers, a pair $\left(a_{i}, a_{j}\right)$ with $1 \leq i<j \leq n$ is called interesting if there exists a pair $\left(a_{k}, a_{l}\right)$ of integers with $1 \leq k<l \leq n$ such that
$$
\frac{a_{l}-a_{k}}{a_{j}-a_{i}}=2
$$
For each $n \geq 3$, find the largest possible number of interesting pairs in a sequence of length $n$.
Answer. $\frac{1}{2}(n-1)(n-2)+1$.
|
Consider the numbers $a_{i}=2^{i}$ for $2 \leq i \leq n$ and $a_{1}=0$, and choose any pair $(i, j)$ with $1 \leq i<j \leq n$.
If $i=1$, the pair $(1, j)$ is interesting for all $2 \leq j \leq n-1$, as $\frac{a_{j+1}-a_{1}}{a_{j}-a_{1}}=\frac{2^{j+1}}{2^{j}}=2$.
If $i \geq 2$, the pair $(i, j)$ is also interesting for all $j$ such that $i+1 \leq j \leq n-1$, since $\frac{a_{j+1}-a_{i+1}}{a_{j}-a_{i}}=\frac{2^{j+1}-2^{i+1}}{2^{j}-2^{i}}=2$.
In addition, the pair $(n-1, n)$ is interesting, as $\frac{a_{n}-a_{0}}{a_{n}-a_{n-1}}=2$.
Hence, all pairs in which $j \leq n-1$, and additionally the pair $(n-1, n)$, are interesting, giving $\frac{1}{2}(n-1)(n-2)+1$ pairs in total.
Now, let's show that there can't be more interesting pairs. To this end we show that at least $\frac{1}{2} n(n-1)-\left(\frac{1}{2}(n-1)(n-2)+1\right)=n-2$ pairs are not interesting. Clearly, the pair $(1, n)$ is not interesting.
Let's make the following observation: if a pair $(i, j)$ is interesting and it's not $(1, n)$, then $a_{j}-a_{i}$ can't exceed $\frac{1}{2}\left(a_{n}-a_{1}\right)$. (Since, if $(i, j)$ is interesting then $a_{l}-a_{k}=2\left(a_{j}-a_{i}\right)$ for some pair $(k, l)$. If then $2\left(a_{j}-a_{i}\right)>a_{n}-a_{1}$ we would have $a_{l}-a_{k}>a_{n}-a_{1}$, which is not possible.)
Finally, for any $2 \leq i \leq n-1$ consider pairs $(1, i)$ and $(i, n)$. If both of them are interesting, then, following the observation above, the only possibility is $a_{i}-a_{1}=a_{n}-a_{i}=\frac{a_{n}-a_{1}}{2}$. Clearly, this is possible for at most one $i$, so for all other $n-3$ values of $i$, at least one of pairs $(1, i)$ and $(i, n)$ is not interesting. Combining with the pair $(1, n)$, we get at least $n-2$ not interesting pairs in total, as desired.
Comment: The originally proposed formulation considered a sequence $a_{1}<a_{2}<\cdots<$ $a_{n}$ of $n$ real numbers, rather than integers. The conclusion is however the same and the solution is identical.
|
{
"exam": "EGMO",
"problem_label": "4",
"problem_match": "# Problem 4 (UKR)\n",
"resource_path": "EGMO/segmented/en-2024-solutions.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2024"
}
|
Problem. Let $\mathbb{N}$ denote the set of positive integers. Find all functions $f: \mathbb{N} \rightarrow \mathbb{N}$ such that the following assertions are true for every pair of positive integers $(x, y)$ :
- $x$ and $f(x)$ have the same number of positive divisors.
- If $x$ does not divide $y$ and $y$ does not divide $x$, then
$$
\operatorname{gcd}(f(x), f(y))>f(\operatorname{gcd}(x, y))
$$
Here $\operatorname{gcd}(m, n)$ is the largest positive integer that divides both $m$ and $n$.
|
Throughout this proof, when we write divisors we mean positive divisors.
Let $f$ be a function satisfying these properties. From the first one, it follows that $f(1)=1$ and for each prime number $p, f(p)=q_{p}$ for some prime number $q_{p}$. Assume $p \neq 2$, the pair $(2, p)$ in property 2 gives
$$
\operatorname{gcd}\left(q_{2}, q_{p}\right)=\operatorname{gcd}(f(2), f(p))>f(\operatorname{gcd}(2, p))=f(1)=1
$$
so $q_{p}=q_{2}$ for all $p$. Set $q=q_{2}$.
Denote by $d(n)$ the number of divisors of a positive integer $n$.
We will prove the following claim by induction on $k \geq 0$, the number of distinct prime divisors of $n$ : For a positive integer $n, f(n)$ is a power of $q$.
The claim, together with the first property, imply that $f(n)=q^{d(n)-1}$.
For $k=0$ the claim is already proved.
For $k=1$, we need to prove that $f\left(p^{m}\right)$ is a power of $q$ for all positive $m$. The case $m=1$ was already proved. Assume now the result being proved for all positive integers $\leq m$. As $d\left(p^{t}\right)=t+1$, we then know $f\left(p^{t}\right)=q^{t}$ for all $t \leq m$. Now we consider $t=m+1$.
Let $r \neq p$ be a prime. Plug the pair $\left(p^{m-1} r, p^{m}\right)$ into the second property:
$$
\operatorname{gcd}\left(f\left(p^{m-1} r\right), q^{m}\right)=\operatorname{gcd}\left(f\left(p^{m-1} r\right), f\left(p^{m}\right)\right)>f\left(p^{m-1}\right)=q^{m-1}
$$
This implies $q^{m}$ divides $f\left(p^{m-1} r\right)$. Since $f\left(p^{m-1} r\right)$ has $2 m$ divisors, and $v_{q}\left(f\left(p^{m-1} r\right)\right) \geq m$, it follows that $f\left(p^{m-1} r\right)$ does not have prime divisors other than $q$, since it would then have at least $2 \cdot\left(v_{q}\left(f\left(p^{m-1} r\right)\right)+1\right)>2 m$ divisors. Thus, $f\left(p^{m-1} r\right)$ is a power of $q$. And since it has $2 m$ divisors, we must have $f\left(p^{m-1} r\right)=q^{2 m-1}$.
Now, plug the pair $\left(p^{m+1}, p^{m-1} r\right)$ into the second property. We have
$$
\operatorname{gcd}\left(f\left(p^{m+1}\right), q^{2 m-1}\right)=\operatorname{gcd}\left(f\left(p^{m+1}\right), f\left(p^{m-1} r\right)\right)>f\left(p^{m-1}\right)=q^{m-1} .
$$
Then $f\left(p^{m+1}\right)$ is divisible by $q^{m}$. If $f\left(p^{m+1}\right)$ had a prime factor other than $q$, it would have at least $2(m+1)$ divisors, but it has $m+2$ divisors and $2(m+1)>m+2$ since $m \geq 1$. Hence, $f\left(p^{m+1}\right)$ must also be a power of $q$. By induction, the proof is finished for $k=1$.
Suppose the claim is true for all integers $n$ with at most $k$ distinct prime factors, for some $k \geq 1$. In order to prove the claim for integers with $k+1$ distinct prime factors, it suffices
to show that for every positive integer $N$ with $k$ distinct prime factors, every positive integer $m$ and every prime $p$ which does not divide $N$, the number $f\left(N p^{m}\right)$ is a power of $q$. We will prove this by induction on $m$. The case $m=0$ follows from the previous induction hypothesis. Now suppose it has already been proved for a certain $m \geq 0$.
Let $s$ be a prime divisor of $N$. Consider the numbers $\left(N p^{m+1}, N s p^{m}\right)$. By the second property,
$$
\operatorname{gcd}\left(f\left(N p^{m+1}\right), q^{d\left(N s p^{m}\right)-1}\right)=\operatorname{gcd}\left(f\left(N p^{m+1}\right), f\left(N s p^{m}\right)\right)>f\left(N p^{m}\right)=q^{d\left(N p^{m}\right)-1}
$$
Then $q^{d\left(N p^{m}\right)}$ divides $f\left(N p^{m+1}\right)$. If $f\left(N p^{m+1}\right)$ has a prime factor other than $q$, it would have at least $2\left(d\left(N p^{m}\right)+1\right)=2((m+1) d(N)+1)=(2 m+2) d(N)+2$ divisors, but it has only $(m+2) d(N)$ divisors. Hence, $f\left(N p^{m+1}\right)$ must also be a power of $q$.
Finally, let us check that the function $f(n)=q^{d(n)-1}$ does satisfy the properties of the problem for any prime number $q$. The first property obviously holds. To check the second one, note that
$$
\operatorname{gcd}(f(x), f(y))=q^{\min (d(x), d(y))}>q^{d(\operatorname{gcd}(x, y))}=f(\operatorname{gcd}(x, y))
$$
whenever $x \nmid y$ and $y \nmid x$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Problem. Let $\mathbb{N}$ denote the set of positive integers. Find all functions $f: \mathbb{N} \rightarrow \mathbb{N}$ such that the following assertions are true for every pair of positive integers $(x, y)$ :
- $x$ and $f(x)$ have the same number of positive divisors.
- If $x$ does not divide $y$ and $y$ does not divide $x$, then
$$
\operatorname{gcd}(f(x), f(y))>f(\operatorname{gcd}(x, y))
$$
Here $\operatorname{gcd}(m, n)$ is the largest positive integer that divides both $m$ and $n$.
|
Throughout this proof, when we write divisors we mean positive divisors.
Let $f$ be a function satisfying these properties. From the first one, it follows that $f(1)=1$ and for each prime number $p, f(p)=q_{p}$ for some prime number $q_{p}$. Assume $p \neq 2$, the pair $(2, p)$ in property 2 gives
$$
\operatorname{gcd}\left(q_{2}, q_{p}\right)=\operatorname{gcd}(f(2), f(p))>f(\operatorname{gcd}(2, p))=f(1)=1
$$
so $q_{p}=q_{2}$ for all $p$. Set $q=q_{2}$.
Denote by $d(n)$ the number of divisors of a positive integer $n$.
We will prove the following claim by induction on $k \geq 0$, the number of distinct prime divisors of $n$ : For a positive integer $n, f(n)$ is a power of $q$.
The claim, together with the first property, imply that $f(n)=q^{d(n)-1}$.
For $k=0$ the claim is already proved.
For $k=1$, we need to prove that $f\left(p^{m}\right)$ is a power of $q$ for all positive $m$. The case $m=1$ was already proved. Assume now the result being proved for all positive integers $\leq m$. As $d\left(p^{t}\right)=t+1$, we then know $f\left(p^{t}\right)=q^{t}$ for all $t \leq m$. Now we consider $t=m+1$.
Let $r \neq p$ be a prime. Plug the pair $\left(p^{m-1} r, p^{m}\right)$ into the second property:
$$
\operatorname{gcd}\left(f\left(p^{m-1} r\right), q^{m}\right)=\operatorname{gcd}\left(f\left(p^{m-1} r\right), f\left(p^{m}\right)\right)>f\left(p^{m-1}\right)=q^{m-1}
$$
This implies $q^{m}$ divides $f\left(p^{m-1} r\right)$. Since $f\left(p^{m-1} r\right)$ has $2 m$ divisors, and $v_{q}\left(f\left(p^{m-1} r\right)\right) \geq m$, it follows that $f\left(p^{m-1} r\right)$ does not have prime divisors other than $q$, since it would then have at least $2 \cdot\left(v_{q}\left(f\left(p^{m-1} r\right)\right)+1\right)>2 m$ divisors. Thus, $f\left(p^{m-1} r\right)$ is a power of $q$. And since it has $2 m$ divisors, we must have $f\left(p^{m-1} r\right)=q^{2 m-1}$.
Now, plug the pair $\left(p^{m+1}, p^{m-1} r\right)$ into the second property. We have
$$
\operatorname{gcd}\left(f\left(p^{m+1}\right), q^{2 m-1}\right)=\operatorname{gcd}\left(f\left(p^{m+1}\right), f\left(p^{m-1} r\right)\right)>f\left(p^{m-1}\right)=q^{m-1} .
$$
Then $f\left(p^{m+1}\right)$ is divisible by $q^{m}$. If $f\left(p^{m+1}\right)$ had a prime factor other than $q$, it would have at least $2(m+1)$ divisors, but it has $m+2$ divisors and $2(m+1)>m+2$ since $m \geq 1$. Hence, $f\left(p^{m+1}\right)$ must also be a power of $q$. By induction, the proof is finished for $k=1$.
Suppose the claim is true for all integers $n$ with at most $k$ distinct prime factors, for some $k \geq 1$. In order to prove the claim for integers with $k+1$ distinct prime factors, it suffices
to show that for every positive integer $N$ with $k$ distinct prime factors, every positive integer $m$ and every prime $p$ which does not divide $N$, the number $f\left(N p^{m}\right)$ is a power of $q$. We will prove this by induction on $m$. The case $m=0$ follows from the previous induction hypothesis. Now suppose it has already been proved for a certain $m \geq 0$.
Let $s$ be a prime divisor of $N$. Consider the numbers $\left(N p^{m+1}, N s p^{m}\right)$. By the second property,
$$
\operatorname{gcd}\left(f\left(N p^{m+1}\right), q^{d\left(N s p^{m}\right)-1}\right)=\operatorname{gcd}\left(f\left(N p^{m+1}\right), f\left(N s p^{m}\right)\right)>f\left(N p^{m}\right)=q^{d\left(N p^{m}\right)-1}
$$
Then $q^{d\left(N p^{m}\right)}$ divides $f\left(N p^{m+1}\right)$. If $f\left(N p^{m+1}\right)$ has a prime factor other than $q$, it would have at least $2\left(d\left(N p^{m}\right)+1\right)=2((m+1) d(N)+1)=(2 m+2) d(N)+2$ divisors, but it has only $(m+2) d(N)$ divisors. Hence, $f\left(N p^{m+1}\right)$ must also be a power of $q$.
Finally, let us check that the function $f(n)=q^{d(n)-1}$ does satisfy the properties of the problem for any prime number $q$. The first property obviously holds. To check the second one, note that
$$
\operatorname{gcd}(f(x), f(y))=q^{\min (d(x), d(y))}>q^{d(\operatorname{gcd}(x, y))}=f(\operatorname{gcd}(x, y))
$$
whenever $x \nmid y$ and $y \nmid x$.
|
{
"exam": "EGMO",
"problem_label": "5",
"problem_match": "# Problem 5 (HRV)\n",
"resource_path": "EGMO/segmented/en-2024-solutions.jsonl",
"solution_match": "\nSolution 1. ",
"tier": "T2",
"year": "2024"
}
|
Problem. Let $\mathbb{N}$ denote the set of positive integers. Find all functions $f: \mathbb{N} \rightarrow \mathbb{N}$ such that the following assertions are true for every pair of positive integers $(x, y)$ :
- $x$ and $f(x)$ have the same number of positive divisors.
- If $x$ does not divide $y$ and $y$ does not divide $x$, then
$$
\operatorname{gcd}(f(x), f(y))>f(\operatorname{gcd}(x, y))
$$
Here $\operatorname{gcd}(m, n)$ is the largest positive integer that divides both $m$ and $n$.
|
Firstly, one can prove that for any prime $p$ and any $m \geq 0, f\left(p^{m}\right)=q^{m}$, in the same way as in the first solution.
We will prove the claim this time by induction on $k=d(n)$. We notice again that the claim implies that $f(n)=q^{d(n)-1}$.
The cases $k=1,2,3$ are then already proved. Now suppose that for some $k \geq 3$ we have proved the claim for all positive integers $n$ with at most $k$ divisors.
Consider a positive integer $n$ with $k+1$ divisors. If $n$ is a power of a prime, then it is already proved that $f(n)$ is a power of $q$. Suppose $n$ is not a power of a prime. Consider distinct prime numbers $p_{1}$ and $p_{2}$ which divide $n$, such that $v_{p_{1}}(n) \leq v_{p_{2}}(n)$. Consider the number $\frac{n p_{2}}{p_{1}}$ : its number of divisors is $\frac{v_{p_{1}}(n)\left(v_{p_{2}}(n)+2\right)}{\left(v_{p_{1}}(n)+1\right)\left(v_{p_{2}}(n)+1\right)} d(n)$, which is strictly less than the number of divisors of $n$. Thus, by induction hypothesis, $f\left(\frac{n p_{2}}{p_{1}}\right)$ is a power of $q$.
By applying the second property to the pair $\left(n, \frac{n p_{2}}{p_{1}}\right)$, we have
$$
\operatorname{gcd}\left(f(n), q^{d\left(\frac{n p_{2}}{p_{1}}\right)-1}\right)=\operatorname{gcd}\left(f(n), f\left(\frac{n p_{2}}{p_{1}}\right)\right)>f\left(\frac{n}{p_{1}}\right)=q^{d\left(\frac{n}{p_{1}}\right)-1}
$$
This implies that $q^{d\left(\frac{n}{p_{1}}\right)}$ divides $f(n)$. Again, if other primes than $q$ divided $f(n)$, it would have at least $2\left(d\left(\frac{n}{p_{1}}\right)+1\right)$ divisors. But $2\left(d\left(\frac{n}{p_{1}}\right)+1\right)=2\left(\frac{v_{p_{1}}(n)}{v_{p_{1}}(n)+1} d(n)+1\right)>d(n)$. So $f(n)$ is a power of $q$ and the Claim is proved.
We finally check as in the first solution that $f(n)=q^{d(n)-1}$ satisfies the 2 properties for all prime $q$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Problem. Let $\mathbb{N}$ denote the set of positive integers. Find all functions $f: \mathbb{N} \rightarrow \mathbb{N}$ such that the following assertions are true for every pair of positive integers $(x, y)$ :
- $x$ and $f(x)$ have the same number of positive divisors.
- If $x$ does not divide $y$ and $y$ does not divide $x$, then
$$
\operatorname{gcd}(f(x), f(y))>f(\operatorname{gcd}(x, y))
$$
Here $\operatorname{gcd}(m, n)$ is the largest positive integer that divides both $m$ and $n$.
|
Firstly, one can prove that for any prime $p$ and any $m \geq 0, f\left(p^{m}\right)=q^{m}$, in the same way as in the first solution.
We will prove the claim this time by induction on $k=d(n)$. We notice again that the claim implies that $f(n)=q^{d(n)-1}$.
The cases $k=1,2,3$ are then already proved. Now suppose that for some $k \geq 3$ we have proved the claim for all positive integers $n$ with at most $k$ divisors.
Consider a positive integer $n$ with $k+1$ divisors. If $n$ is a power of a prime, then it is already proved that $f(n)$ is a power of $q$. Suppose $n$ is not a power of a prime. Consider distinct prime numbers $p_{1}$ and $p_{2}$ which divide $n$, such that $v_{p_{1}}(n) \leq v_{p_{2}}(n)$. Consider the number $\frac{n p_{2}}{p_{1}}$ : its number of divisors is $\frac{v_{p_{1}}(n)\left(v_{p_{2}}(n)+2\right)}{\left(v_{p_{1}}(n)+1\right)\left(v_{p_{2}}(n)+1\right)} d(n)$, which is strictly less than the number of divisors of $n$. Thus, by induction hypothesis, $f\left(\frac{n p_{2}}{p_{1}}\right)$ is a power of $q$.
By applying the second property to the pair $\left(n, \frac{n p_{2}}{p_{1}}\right)$, we have
$$
\operatorname{gcd}\left(f(n), q^{d\left(\frac{n p_{2}}{p_{1}}\right)-1}\right)=\operatorname{gcd}\left(f(n), f\left(\frac{n p_{2}}{p_{1}}\right)\right)>f\left(\frac{n}{p_{1}}\right)=q^{d\left(\frac{n}{p_{1}}\right)-1}
$$
This implies that $q^{d\left(\frac{n}{p_{1}}\right)}$ divides $f(n)$. Again, if other primes than $q$ divided $f(n)$, it would have at least $2\left(d\left(\frac{n}{p_{1}}\right)+1\right)$ divisors. But $2\left(d\left(\frac{n}{p_{1}}\right)+1\right)=2\left(\frac{v_{p_{1}}(n)}{v_{p_{1}}(n)+1} d(n)+1\right)>d(n)$. So $f(n)$ is a power of $q$ and the Claim is proved.
We finally check as in the first solution that $f(n)=q^{d(n)-1}$ satisfies the 2 properties for all prime $q$.
|
{
"exam": "EGMO",
"problem_label": "5",
"problem_match": "# Problem 5 (HRV)\n",
"resource_path": "EGMO/segmented/en-2024-solutions.jsonl",
"solution_match": "\nSolution 2. ",
"tier": "T2",
"year": "2024"
}
|
Problem. Find all positive integers $d$ for which there exists a degree $d$ polynomial $P$ with real coefficients such that there are at most $d$ different values among $P(0), P(1), \ldots, P\left(d^{2}-\right.$ d).
Remark 1 You can add a constant to a polynomial satisfying the conditions and obtain another polynomial satisfying the conditions.
Remark 2 This problem is equivalent to: Find all positive integers $d$ for which there exists a polynomial $P$ of degree $d$ that takes at most $d$ different values at members of a an arithmetic progression with $d^{2}-d+1$ (different) terms.
The answer to this EGMO problem implies a solution to this more general problem by scaling and translating, and the general result solves the EGMO problem as a special case. This means that instead of working with $0,1, \ldots, d^{2}-d$ we have the option of working with a region that is symmetric about the origin. Irrespective of the parity of $d$ we can use the $d^{2}-d+1$ integers which run from $-\left(d^{2}-d\right) / 2$ to $\left(d^{2}-d\right) / 2$ inclusive.
The advantage of using an arithmetic progression which is symmetric about the 0 is that $P(X)$ is a polynomial which works for the problem if, and only if, $P(-X)$ is a polynomial which works for the problem. This means that working at one end of the run of integers is the reflection of the activity at the other end. T Remarks dismissing the cases at the other end of the run as similar now become obviously correct rather than having to be studied separately.
|
We claim that such polynomials exist if and only if $d \leq 3$. The following examples show that such polynomials do exist for $d \leq 3$ :
$$
\left.\begin{array}{lll}
d=1: & d^{2}-d=0, & P_{1}(x)=x,
\end{array} \begin{array}{ll}
& P(0)=0 ;
\end{array}\right\}
$$
We can make more examples by adding constants.
Now we will show that there are no examples of degree greater than 3.
From now on we assume (without loss of generality) that the leading coefficient of our polynomial $P$ is positive and that all values $P(i)$ are positive (by adding a constant if necessary) for integers $i$ in the range $0 \leq i \leq d^{2}-d+1$.
Assume (for contradiction) that $P$ is a polynomial of degree $d \geq 4$ that satisfies the conditions of the problem and let $P(0), \ldots, P\left(d^{2}-d\right)$ take values among $p_{1}<\cdots<p_{d}$. For $i=1, \ldots, d$, let $n_{i} \geq 0$ be the number of appearances of $p_{i}$ among $P(0), \ldots, P\left(d^{2}-d\right)$.
By definition $n_{1}+\cdots+n_{d}=d^{2}-d+1$. Since $P$ has degree $d, n_{i} \leq d$. The key observation is now the following.
Claim 1 Make the convention that $n_{0}=n_{d+1}=0$. If $n_{i}=d$ for some $i$ in the range $1 \leq i \leq d$, then $n_{i \pm 1} \leq d-2$.
Proof. Up to scaling and hence without loss of generality, $P$ has leading coefficient +1 . $\overline{\text { Since }} n_{i}=d$, there exist non-negative integers $a_{1, i}<\cdots<a_{d, i} \leq d^{2}-d$ such that
$$
P(X)=\left(X-a_{1, i}\right) \cdots\left(X-a_{d, i}\right)+p_{i} .
$$
By construction, each of the $d-1$ intervals $I_{j}=\left[a_{j, i}, a_{j+1, i}\right]$ contains at least one local extremum of $P$, so contains exactly one such extremum because $P$, having degree $d$, has at most $d-1$ such extrema. Suppose that $i \leq d-1$ and that $P(m)=p_{i+1}>p_{i}$ for some $m \in\left\{0, \ldots, d^{2}-d\right\}$. Since $P$ has positive leading coefficient,
$$
m \in\left(a_{d, i}, \infty\right) \cup\left(a_{d-2, i}, a_{d-1, i}\right) \cup \cdots \cup\left(a_{i, 1}, a_{2, i}\right)
$$
if $d$ is odd or
$$
m \in\left(a_{d, i}, \infty\right) \cup\left(a_{d-2, i}, a_{d-1, i}\right) \cup \cdots \cup\left(-\infty, a_{1, i}\right)
$$
if $d$ is even.
Suppose that $a_{j, i}<m<a_{j+1, i}$, for some $j \in\{1, \ldots, d-1\}$. If $a_{j, i}+1<m<a_{j+1, i}-1$, then, because $I_{j}$ contains exactly one local extremum (which is a maximum),
Either $p_{i+1}=P(m)>P\left(a_{j, i}+1\right)$ or $p_{i+1}=P(m)>P\left(a_{j+1, i}-1\right)$. Since $P\left(a_{j, i}+1\right)>$ $P\left(a_{j, i}\right)=p_{i}$ and $P\left(a_{j, i}-1\right)>P\left(a_{j+1, i}\right)=p_{i}$, this contradicts the requirement that $P\left(a_{j, i}+1\right), P\left(a_{j+1, i}-1\right) \in\left\{p_{1}, \ldots, p_{d}\right\}$. Hence $m=a_{j, i}+1$ or $m=a_{j, i}-1$. Similarly, if $m>a_{d, i}$, then $m=a_{d, i}+1$, but if $m<a_{i, 1}$ (which may arise when $d$ is even), then $m=a_{i, 1}-1$. This shows that $m$ belongs to this list:
$$
a_{d, i}+1, a_{d-1, i}-1, \ldots, a_{2, i}+(-1)^{d}, a_{1, i}-(-1)^{d}
$$
This list contains at most $d$ different integers. It follows in particular that, if $n_{i+1}>d-2$, then either
$$
P\left(a_{d, i}+1\right)=p_{i+1}=P\left(a_{d-1, i}-1\right)
$$
or
$$
P\left(a_{2, i}+(-1)^{d}\right)=p_{i+1}=P\left(a_{1, i}-(-1)^{d}\right)
$$
with, additionally, $a_{2, i}+(-1)^{d} \neq a_{1, i}-(-1)^{d}$.
We have
$$
\left|P\left(a_{1, i} \pm 1\right)-p_{i}\right|=1 \cdot\left|a_{1, i} \pm 1-a_{2, i}\right| \cdot \prod_{j=3}^{d}\left|a_{1, i} \pm 1-a_{j, i}\right|
$$
and
$$
\left|P\left(a_{2, i} \mp 1\right)-p_{i}\right|=\left|a_{2, i} \mp 1-a_{1, i}\right| \cdot 1 \cdot \prod_{j=3}^{d}\left|a_{2, i} \mp 1-a_{j, i}\right| .
$$
As $a_{1, i}<a_{2, i}<a_{3, i}<\ldots<a_{d, i}$ we have $\left|a_{1, i} \pm 1-a_{j, i}\right| \geq\left|a_{2, i} \mp 1-a_{j, i}\right|$ with equality possible only if $a_{1, i}+1=a_{2, i}-1$. We also have $\left|a_{1, i} \pm 1-a_{2, i}\right|=\left|a_{2, i} \mp 1-a_{1, i}\right|$, which can be zero only if $a_{1, i}+1=a_{2, i}-1$. We conclude that $\left|P\left(a_{1, i} \pm 1\right)-p_{i}\right|>\left|P\left(a_{2, i} \mp 1\right)-p_{i}\right|$ or $a_{1, i}+1=a_{2, i}-1$.
Looking at the other end of the list of $\left(a_{j, i}\right)$ as $j$ varies, we have
$$
\left|P\left(a_{d-1, i}-1\right)-p_{i}\right|=1 \cdot\left|a_{d-1, i}-1-a_{d, i}\right| \cdot \prod_{j=1}^{d-2}\left|a_{d-1, i}-1-a_{j, i}\right|
$$
and
$$
\left|P\left(a_{d, i}+1\right)-p_{i}\right|=\left|a_{d, i}+1-a_{d-1, i}\right| \cdot 1 \cdot \prod_{j=1}^{d-2}\left|a_{d, i}+1-a_{j, i}\right|
$$
In these two formulas the shared factor outside the product is at least 2 and so is not 0 . Now look at the factors behind the product symbols. As $a_{1, i}<a_{2, i}<a_{3, i}<\ldots<a_{d, i}$, for $j \leq d-2$ we have $\left|a_{d, i}+1-a_{j, i}\right|>\left|a_{d-1, i}-1-a_{j, i}\right|$. We conclude that $\left|P\left(a_{d, i}+1\right)-p_{i}\right|>$ $\left|P\left(a_{d-1, i}-1\right)-p_{i}\right|$. Claim 1 is proved.
For each $i \in\{1, \ldots, d-1\}$, there are three possibilities:
- $n_{i}, n_{i+1} \leq d-1$
- $n_{i}=d$ and $n_{i+1} \leq d-2$
- $n_{i+1}=d$ and $n_{i} \leq d-2$.
In all three cases, $n_{i}+n_{i+1} \leq 2(d-1)$. If $n$ is even, this leads to the contradiction
$$
d^{2}-d+1=\left(n_{1}+n_{2}\right)+\cdots+\left(n_{d-1}+n_{d}\right) \leq(d / 2)[2(d-1)]=d^{2}-d
$$
This is an important staging point in the argument because we have eliminated the possibility of a polynomial of even degree $d$ satisfying the conditions of the problem if $d \geq 4$.
From now on we assume that $d \geq 5$ is odd, and
$d^{2}-d+1=\left(n_{1}+n_{2}\right)+\cdots+\left(n_{d-2}+n_{d-1}\right)+n_{d} \leq[(d-1) / 2][2(d-1)]+d=d^{2}-d+1$.
Equality must therefore hold throughout. Since the sum can also be grouped as
$$
n_{1}+\left(n_{2}+n_{3}\right)+\cdots+\left(n_{d-1}+n_{d}\right)
$$
this requires $n_{1}=n_{d}=d, n_{i}+n_{i+1}=2(d-1)$ for $i=1,2, \ldots, d-1$ i.e. $n_{i}=d$ for odd $i$ and $n_{i}=d-2$ for even $i$.
We are interested in the degree of $P$ being $d \geq 5$ and odd, and showing that no polynomial $P$ satisfying the conditions of the problem can exist. There are $d-1 \geq 4$ extremal points points which alternate between local maxima and minima (in that order) as you read from left to right (we normalize so that $P$ is monic). For any $p_{i}$ with $i$ odd, the line $y=p_{i}$ (with
$i$ odd) crosses the graph of $P$ in $d$ places with $x$-coordinates in the real closed interval $\left[0, d^{2}-d\right]$ at points $\left(z, p_{i}\right)$ so each $z$ must be an integer. Suppose that $J$ is a real interval on the $x$-axis ending at adjacent local extrema. The function defined by $P$ is monotonic on each $J$. The line $y=p_{i}$ ( $i$ odd) meets the graph at most once on $J$. Therefore it meets the graph of $P$ exactly once in the interior of each $J$ (there are $d-2$ such intervals) and at the only two possible places outside the union of these intervals.
Now consider $p_{j}$ when $j$ is even (so $n_{j}=d-2$ ). These $d-2$ intervals $J$ afford $d-2$ real values at which $P$ will take $p_{j}$ as a value where $j$ is fixed and even. The question is, are the corresponding arguments integers? The proof of Claim 1 tells us that in the middle of the run $\left\{0,1, \ldots, d^{2}-d+1\right\}$ all is well: the polynomial is assuming the value $p_{j}$ at an integer where the polynomial assumes the values $p_{j-1}$ and $p_{j+1}$ at adjacent integers in some order. The problem is at the ends of the run where $\left|P\left(a_{1, i}+1\right)-p_{i}\right|>\left|P\left(a_{2, i}-1\right)-p_{i}\right|$ and $\left|P\left(a_{d, i}+1\right)-p_{i}\right|>\left|P\left(a_{d-1, i}-1\right)-p_{i}\right|$. When $j$ is even, two of the roots of $P(x)-p_{j}$ are not integers, and we now know approximately where this trouble is happening (at the ends).
At this point we could finish if $d \geq 7$, because the run of regular behaviour in the middle is sufficiently long that we could obtain a contradiction. However we have to work a little harder to include the case $d=5$. We now show that the run of regular behaviour is slightly longer than we have currently established. We do this using Claim 2.
Claim 2. If $d$ is odd, and $n_{i}=d, n_{i \pm 1}=d-2$ for some $i$, then $P$ attains $p_{i \pm 1}$ precisely at the $d-2$ integers
$$
a_{2, i}-1, a_{3, i}+1, \cdots, a_{d-2, i}-1, a_{d-1, i}+1
$$
Proof Suppose (for contradiction) $a_{1, i}+1 \neq a_{2, i}-1$ and $P\left(a_{1, i}+1\right)=p_{i+1}$. Now $a_{1, i}<a_{2, i}$ so either $a_{1, i}+1<a_{2, i}-1$ or $a_{1, i}=a_{2, i}-1$. In the latter case, $P\left(a_{1, i}+1\right)=P\left(a_{2, i}\right)=p_{i}$, a contradiction. In the former case, the proof of Claim 1 shows that
$$
\left|P\left(a_{2, i}-1\right)-p_{i}\right|<\left|P\left(a_{1, i}+1\right)-p_{i}\right|=\left|p_{i+1}-p_{i}\right|=p_{i+1}-p_{i}
$$
so $P\left(a_{2, i}-1\right)<p_{i+1}$. The polynomial is decreasing on the interval $\left(a_{2, d}, a_{2,1}\right)$ so $p_{i}<P\left(a_{2, i}-1\right)<p_{i+1}$ which is absurd because $P\left(a_{2, i}-1\right)=p_{j}$ for some $j$. Therefore $P\left(a_{2, i}-1\right)=p_{i+1}$ for all odd $i$. A similar argument shows that $P\left(a_{d-1, i}+1\right)=p_{i+1}$ so Claim 2 is established.
Now we have n sequence of alternating falling then rising then falling etc. full runs starting at $\left(a_{2, d}, p_{d}\right)$ and ending at $\left(a_{d-1,1}, p_{1}\right)$ so the initial run of $3 d+1$ terms of this run of values is
$$
p_{d}, p_{d-1}, \cdots p_{1}, p_{1}, p_{2}, \ldots, p_{d}, p_{d}, p_{d-1}, \cdots p_{1}, p_{1}
$$
which starts at $\left(a_{2, d}, p_{d}\right)$ and ends at $\left(a_{4,1}+1, p_{1}\right)$ which is fine because $4 \leq d-1$.
There are now various ways we can finish.
(a) Consider the run of length $2 d$ consecutive values
$$
p_{d}, p_{d-1}, \cdots p_{1}, p_{1}, p_{2}, \ldots, p_{d}
$$
The first $d+1$ points determine $P(x)$. The last $d+1$ values also determine $P$ but the values are in the reverse order, so $P(X)=P(c-X)$ for some constant $c$. However, the coefficients of $X^{d}$ are have opposite signs ( $d$ is odd) so this is absurd.
(b) The idea in (a) can be expressed in terms of Lagrange interpolation to obtain essentially the same contradiction. Construct $P$ in two ways using Lagrange interpolation on both the first $d+1$ and the last $d+1$ points. The symmetry in the data forces the graph of $P$ to have a vertical axis of symmetry. This is absurd because the degree of $P$ is odd.
(c) The initial fragment length $3 d+1$ mentioned above at $(*)$ includes two identical runs of values of $P$ (in the same order) of length $d+1$. The polynomial $P$ is determined by each of them and so $P(X)=P(X+c)$ for some constant $c$ and so the polynomial defines a bounded function which is absurd.
|
d \leq 3
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Problem. Find all positive integers $d$ for which there exists a degree $d$ polynomial $P$ with real coefficients such that there are at most $d$ different values among $P(0), P(1), \ldots, P\left(d^{2}-\right.$ d).
Remark 1 You can add a constant to a polynomial satisfying the conditions and obtain another polynomial satisfying the conditions.
Remark 2 This problem is equivalent to: Find all positive integers $d$ for which there exists a polynomial $P$ of degree $d$ that takes at most $d$ different values at members of a an arithmetic progression with $d^{2}-d+1$ (different) terms.
The answer to this EGMO problem implies a solution to this more general problem by scaling and translating, and the general result solves the EGMO problem as a special case. This means that instead of working with $0,1, \ldots, d^{2}-d$ we have the option of working with a region that is symmetric about the origin. Irrespective of the parity of $d$ we can use the $d^{2}-d+1$ integers which run from $-\left(d^{2}-d\right) / 2$ to $\left(d^{2}-d\right) / 2$ inclusive.
The advantage of using an arithmetic progression which is symmetric about the 0 is that $P(X)$ is a polynomial which works for the problem if, and only if, $P(-X)$ is a polynomial which works for the problem. This means that working at one end of the run of integers is the reflection of the activity at the other end. T Remarks dismissing the cases at the other end of the run as similar now become obviously correct rather than having to be studied separately.
|
We claim that such polynomials exist if and only if $d \leq 3$. The following examples show that such polynomials do exist for $d \leq 3$ :
$$
\left.\begin{array}{lll}
d=1: & d^{2}-d=0, & P_{1}(x)=x,
\end{array} \begin{array}{ll}
& P(0)=0 ;
\end{array}\right\}
$$
We can make more examples by adding constants.
Now we will show that there are no examples of degree greater than 3.
From now on we assume (without loss of generality) that the leading coefficient of our polynomial $P$ is positive and that all values $P(i)$ are positive (by adding a constant if necessary) for integers $i$ in the range $0 \leq i \leq d^{2}-d+1$.
Assume (for contradiction) that $P$ is a polynomial of degree $d \geq 4$ that satisfies the conditions of the problem and let $P(0), \ldots, P\left(d^{2}-d\right)$ take values among $p_{1}<\cdots<p_{d}$. For $i=1, \ldots, d$, let $n_{i} \geq 0$ be the number of appearances of $p_{i}$ among $P(0), \ldots, P\left(d^{2}-d\right)$.
By definition $n_{1}+\cdots+n_{d}=d^{2}-d+1$. Since $P$ has degree $d, n_{i} \leq d$. The key observation is now the following.
Claim 1 Make the convention that $n_{0}=n_{d+1}=0$. If $n_{i}=d$ for some $i$ in the range $1 \leq i \leq d$, then $n_{i \pm 1} \leq d-2$.
Proof. Up to scaling and hence without loss of generality, $P$ has leading coefficient +1 . $\overline{\text { Since }} n_{i}=d$, there exist non-negative integers $a_{1, i}<\cdots<a_{d, i} \leq d^{2}-d$ such that
$$
P(X)=\left(X-a_{1, i}\right) \cdots\left(X-a_{d, i}\right)+p_{i} .
$$
By construction, each of the $d-1$ intervals $I_{j}=\left[a_{j, i}, a_{j+1, i}\right]$ contains at least one local extremum of $P$, so contains exactly one such extremum because $P$, having degree $d$, has at most $d-1$ such extrema. Suppose that $i \leq d-1$ and that $P(m)=p_{i+1}>p_{i}$ for some $m \in\left\{0, \ldots, d^{2}-d\right\}$. Since $P$ has positive leading coefficient,
$$
m \in\left(a_{d, i}, \infty\right) \cup\left(a_{d-2, i}, a_{d-1, i}\right) \cup \cdots \cup\left(a_{i, 1}, a_{2, i}\right)
$$
if $d$ is odd or
$$
m \in\left(a_{d, i}, \infty\right) \cup\left(a_{d-2, i}, a_{d-1, i}\right) \cup \cdots \cup\left(-\infty, a_{1, i}\right)
$$
if $d$ is even.
Suppose that $a_{j, i}<m<a_{j+1, i}$, for some $j \in\{1, \ldots, d-1\}$. If $a_{j, i}+1<m<a_{j+1, i}-1$, then, because $I_{j}$ contains exactly one local extremum (which is a maximum),
Either $p_{i+1}=P(m)>P\left(a_{j, i}+1\right)$ or $p_{i+1}=P(m)>P\left(a_{j+1, i}-1\right)$. Since $P\left(a_{j, i}+1\right)>$ $P\left(a_{j, i}\right)=p_{i}$ and $P\left(a_{j, i}-1\right)>P\left(a_{j+1, i}\right)=p_{i}$, this contradicts the requirement that $P\left(a_{j, i}+1\right), P\left(a_{j+1, i}-1\right) \in\left\{p_{1}, \ldots, p_{d}\right\}$. Hence $m=a_{j, i}+1$ or $m=a_{j, i}-1$. Similarly, if $m>a_{d, i}$, then $m=a_{d, i}+1$, but if $m<a_{i, 1}$ (which may arise when $d$ is even), then $m=a_{i, 1}-1$. This shows that $m$ belongs to this list:
$$
a_{d, i}+1, a_{d-1, i}-1, \ldots, a_{2, i}+(-1)^{d}, a_{1, i}-(-1)^{d}
$$
This list contains at most $d$ different integers. It follows in particular that, if $n_{i+1}>d-2$, then either
$$
P\left(a_{d, i}+1\right)=p_{i+1}=P\left(a_{d-1, i}-1\right)
$$
or
$$
P\left(a_{2, i}+(-1)^{d}\right)=p_{i+1}=P\left(a_{1, i}-(-1)^{d}\right)
$$
with, additionally, $a_{2, i}+(-1)^{d} \neq a_{1, i}-(-1)^{d}$.
We have
$$
\left|P\left(a_{1, i} \pm 1\right)-p_{i}\right|=1 \cdot\left|a_{1, i} \pm 1-a_{2, i}\right| \cdot \prod_{j=3}^{d}\left|a_{1, i} \pm 1-a_{j, i}\right|
$$
and
$$
\left|P\left(a_{2, i} \mp 1\right)-p_{i}\right|=\left|a_{2, i} \mp 1-a_{1, i}\right| \cdot 1 \cdot \prod_{j=3}^{d}\left|a_{2, i} \mp 1-a_{j, i}\right| .
$$
As $a_{1, i}<a_{2, i}<a_{3, i}<\ldots<a_{d, i}$ we have $\left|a_{1, i} \pm 1-a_{j, i}\right| \geq\left|a_{2, i} \mp 1-a_{j, i}\right|$ with equality possible only if $a_{1, i}+1=a_{2, i}-1$. We also have $\left|a_{1, i} \pm 1-a_{2, i}\right|=\left|a_{2, i} \mp 1-a_{1, i}\right|$, which can be zero only if $a_{1, i}+1=a_{2, i}-1$. We conclude that $\left|P\left(a_{1, i} \pm 1\right)-p_{i}\right|>\left|P\left(a_{2, i} \mp 1\right)-p_{i}\right|$ or $a_{1, i}+1=a_{2, i}-1$.
Looking at the other end of the list of $\left(a_{j, i}\right)$ as $j$ varies, we have
$$
\left|P\left(a_{d-1, i}-1\right)-p_{i}\right|=1 \cdot\left|a_{d-1, i}-1-a_{d, i}\right| \cdot \prod_{j=1}^{d-2}\left|a_{d-1, i}-1-a_{j, i}\right|
$$
and
$$
\left|P\left(a_{d, i}+1\right)-p_{i}\right|=\left|a_{d, i}+1-a_{d-1, i}\right| \cdot 1 \cdot \prod_{j=1}^{d-2}\left|a_{d, i}+1-a_{j, i}\right|
$$
In these two formulas the shared factor outside the product is at least 2 and so is not 0 . Now look at the factors behind the product symbols. As $a_{1, i}<a_{2, i}<a_{3, i}<\ldots<a_{d, i}$, for $j \leq d-2$ we have $\left|a_{d, i}+1-a_{j, i}\right|>\left|a_{d-1, i}-1-a_{j, i}\right|$. We conclude that $\left|P\left(a_{d, i}+1\right)-p_{i}\right|>$ $\left|P\left(a_{d-1, i}-1\right)-p_{i}\right|$. Claim 1 is proved.
For each $i \in\{1, \ldots, d-1\}$, there are three possibilities:
- $n_{i}, n_{i+1} \leq d-1$
- $n_{i}=d$ and $n_{i+1} \leq d-2$
- $n_{i+1}=d$ and $n_{i} \leq d-2$.
In all three cases, $n_{i}+n_{i+1} \leq 2(d-1)$. If $n$ is even, this leads to the contradiction
$$
d^{2}-d+1=\left(n_{1}+n_{2}\right)+\cdots+\left(n_{d-1}+n_{d}\right) \leq(d / 2)[2(d-1)]=d^{2}-d
$$
This is an important staging point in the argument because we have eliminated the possibility of a polynomial of even degree $d$ satisfying the conditions of the problem if $d \geq 4$.
From now on we assume that $d \geq 5$ is odd, and
$d^{2}-d+1=\left(n_{1}+n_{2}\right)+\cdots+\left(n_{d-2}+n_{d-1}\right)+n_{d} \leq[(d-1) / 2][2(d-1)]+d=d^{2}-d+1$.
Equality must therefore hold throughout. Since the sum can also be grouped as
$$
n_{1}+\left(n_{2}+n_{3}\right)+\cdots+\left(n_{d-1}+n_{d}\right)
$$
this requires $n_{1}=n_{d}=d, n_{i}+n_{i+1}=2(d-1)$ for $i=1,2, \ldots, d-1$ i.e. $n_{i}=d$ for odd $i$ and $n_{i}=d-2$ for even $i$.
We are interested in the degree of $P$ being $d \geq 5$ and odd, and showing that no polynomial $P$ satisfying the conditions of the problem can exist. There are $d-1 \geq 4$ extremal points points which alternate between local maxima and minima (in that order) as you read from left to right (we normalize so that $P$ is monic). For any $p_{i}$ with $i$ odd, the line $y=p_{i}$ (with
$i$ odd) crosses the graph of $P$ in $d$ places with $x$-coordinates in the real closed interval $\left[0, d^{2}-d\right]$ at points $\left(z, p_{i}\right)$ so each $z$ must be an integer. Suppose that $J$ is a real interval on the $x$-axis ending at adjacent local extrema. The function defined by $P$ is monotonic on each $J$. The line $y=p_{i}$ ( $i$ odd) meets the graph at most once on $J$. Therefore it meets the graph of $P$ exactly once in the interior of each $J$ (there are $d-2$ such intervals) and at the only two possible places outside the union of these intervals.
Now consider $p_{j}$ when $j$ is even (so $n_{j}=d-2$ ). These $d-2$ intervals $J$ afford $d-2$ real values at which $P$ will take $p_{j}$ as a value where $j$ is fixed and even. The question is, are the corresponding arguments integers? The proof of Claim 1 tells us that in the middle of the run $\left\{0,1, \ldots, d^{2}-d+1\right\}$ all is well: the polynomial is assuming the value $p_{j}$ at an integer where the polynomial assumes the values $p_{j-1}$ and $p_{j+1}$ at adjacent integers in some order. The problem is at the ends of the run where $\left|P\left(a_{1, i}+1\right)-p_{i}\right|>\left|P\left(a_{2, i}-1\right)-p_{i}\right|$ and $\left|P\left(a_{d, i}+1\right)-p_{i}\right|>\left|P\left(a_{d-1, i}-1\right)-p_{i}\right|$. When $j$ is even, two of the roots of $P(x)-p_{j}$ are not integers, and we now know approximately where this trouble is happening (at the ends).
At this point we could finish if $d \geq 7$, because the run of regular behaviour in the middle is sufficiently long that we could obtain a contradiction. However we have to work a little harder to include the case $d=5$. We now show that the run of regular behaviour is slightly longer than we have currently established. We do this using Claim 2.
Claim 2. If $d$ is odd, and $n_{i}=d, n_{i \pm 1}=d-2$ for some $i$, then $P$ attains $p_{i \pm 1}$ precisely at the $d-2$ integers
$$
a_{2, i}-1, a_{3, i}+1, \cdots, a_{d-2, i}-1, a_{d-1, i}+1
$$
Proof Suppose (for contradiction) $a_{1, i}+1 \neq a_{2, i}-1$ and $P\left(a_{1, i}+1\right)=p_{i+1}$. Now $a_{1, i}<a_{2, i}$ so either $a_{1, i}+1<a_{2, i}-1$ or $a_{1, i}=a_{2, i}-1$. In the latter case, $P\left(a_{1, i}+1\right)=P\left(a_{2, i}\right)=p_{i}$, a contradiction. In the former case, the proof of Claim 1 shows that
$$
\left|P\left(a_{2, i}-1\right)-p_{i}\right|<\left|P\left(a_{1, i}+1\right)-p_{i}\right|=\left|p_{i+1}-p_{i}\right|=p_{i+1}-p_{i}
$$
so $P\left(a_{2, i}-1\right)<p_{i+1}$. The polynomial is decreasing on the interval $\left(a_{2, d}, a_{2,1}\right)$ so $p_{i}<P\left(a_{2, i}-1\right)<p_{i+1}$ which is absurd because $P\left(a_{2, i}-1\right)=p_{j}$ for some $j$. Therefore $P\left(a_{2, i}-1\right)=p_{i+1}$ for all odd $i$. A similar argument shows that $P\left(a_{d-1, i}+1\right)=p_{i+1}$ so Claim 2 is established.
Now we have n sequence of alternating falling then rising then falling etc. full runs starting at $\left(a_{2, d}, p_{d}\right)$ and ending at $\left(a_{d-1,1}, p_{1}\right)$ so the initial run of $3 d+1$ terms of this run of values is
$$
p_{d}, p_{d-1}, \cdots p_{1}, p_{1}, p_{2}, \ldots, p_{d}, p_{d}, p_{d-1}, \cdots p_{1}, p_{1}
$$
which starts at $\left(a_{2, d}, p_{d}\right)$ and ends at $\left(a_{4,1}+1, p_{1}\right)$ which is fine because $4 \leq d-1$.
There are now various ways we can finish.
(a) Consider the run of length $2 d$ consecutive values
$$
p_{d}, p_{d-1}, \cdots p_{1}, p_{1}, p_{2}, \ldots, p_{d}
$$
The first $d+1$ points determine $P(x)$. The last $d+1$ values also determine $P$ but the values are in the reverse order, so $P(X)=P(c-X)$ for some constant $c$. However, the coefficients of $X^{d}$ are have opposite signs ( $d$ is odd) so this is absurd.
(b) The idea in (a) can be expressed in terms of Lagrange interpolation to obtain essentially the same contradiction. Construct $P$ in two ways using Lagrange interpolation on both the first $d+1$ and the last $d+1$ points. The symmetry in the data forces the graph of $P$ to have a vertical axis of symmetry. This is absurd because the degree of $P$ is odd.
(c) The initial fragment length $3 d+1$ mentioned above at $(*)$ includes two identical runs of values of $P$ (in the same order) of length $d+1$. The polynomial $P$ is determined by each of them and so $P(X)=P(X+c)$ for some constant $c$ and so the polynomial defines a bounded function which is absurd.
|
{
"exam": "EGMO",
"problem_label": "6",
"problem_match": "# Problem 6 (LUX+BEL)\n",
"resource_path": "EGMO/segmented/en-2024-solutions.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2024"
}
|
For a positive integer \(N\) , let \(c_{1}< c_{2}< \dots < c_{m}\) be all the positive integers smaller than \(N\) that are coprime to \(N\) . Find all \(N\geq 3\) such that
\[\gcd (N,c_{i} + c_{i + 1})\neq 1\]
for all \(1\leq i\leq m - 1\)
Here \(\gcd (a,b)\) is the largest positive integer that divides both \(a\) and \(b\) . Integers \(a\) and \(b\) are coprime if \(\gcd (a,b) = 1\) .
|
The answer is all even integers and all powers of 3. First we show that these work.
- When \(N\) is even, all \(c_{i}\) are odd, and so \(2\mid \gcd (N,c_{i} + c_{i + 1})\) for every \(i\)
- When \(N\) is a power of 3, the \(c_{i}\) are exactly the numbers in the range \(1,2,\ldots ,N - 1\) that are not divisible by 3. So, the sequence \(c_{1},\ldots ,c_{m}\) alternates between numbers congruent to 1 (mod 3) and 2 (mod 3). Thus \(3\mid \gcd (N,c_{i} + c_{i + 1})\) for every \(i\) .
Now we show that no other positive integer works. For the sake of contradiction, consider an odd candidate \(N\) that is not a power of 3, and suppose it satisfies the problem condition. Then, since \(c_{1} = 1\) and \(c_{2} = 2\) , we have \(\gcd (N,1 + 2)\neq 1\) , so \(3\mid N\) . Thus, we can write \(N\) as \(3^{k}M\) , where \(k\geq 1\) and \(\gcd (M,6) = 1\) . We have \(M\geq 5\) (as \(M\neq 1\) by assumption) and \(M + 2< N\) .
We now split into two cases based on \(M\) modulo 3.
Case 1. \(M\equiv 1\) (mod 3).
As \(3\mid M - 1\) and \(M\mid M\) , neither \(M - 1\) nor \(M\) are in the sequence \(\{c_{i}\}\) . As \(M\) is odd and \(M\equiv 1\) (mod 3), \(M - 2\) and \(M + 1\) are congruent to 1 (mod 3), are coprime to \(M\) , and are smaller than \(N\) . Thus, both \(M - 2\) and \(M + 1\) are in the sequence, and they are consecutive terms. However, this means \(\gcd (N,2M - 1)\neq 1\) . This gives a contradiction, as both 3 and \(M\) are coprime to \(2M - 1\) .
Case 2. \(M\equiv 2\) (mod 3).
This case is similar to Case 1. Neither \(M\) nor \(M + 1\) are in the sequence, but \(M - 1\) and \(M + 2\) are. We obtain a similar contradiction from \(\gcd (N,2M + 1)\neq 1\) .
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
For a positive integer \(N\) , let \(c_{1}< c_{2}< \dots < c_{m}\) be all the positive integers smaller than \(N\) that are coprime to \(N\) . Find all \(N\geq 3\) such that
\[\gcd (N,c_{i} + c_{i + 1})\neq 1\]
for all \(1\leq i\leq m - 1\)
Here \(\gcd (a,b)\) is the largest positive integer that divides both \(a\) and \(b\) . Integers \(a\) and \(b\) are coprime if \(\gcd (a,b) = 1\) .
|
The answer is all even integers and all powers of 3. First we show that these work.
- When \(N\) is even, all \(c_{i}\) are odd, and so \(2\mid \gcd (N,c_{i} + c_{i + 1})\) for every \(i\)
- When \(N\) is a power of 3, the \(c_{i}\) are exactly the numbers in the range \(1,2,\ldots ,N - 1\) that are not divisible by 3. So, the sequence \(c_{1},\ldots ,c_{m}\) alternates between numbers congruent to 1 (mod 3) and 2 (mod 3). Thus \(3\mid \gcd (N,c_{i} + c_{i + 1})\) for every \(i\) .
Now we show that no other positive integer works. For the sake of contradiction, consider an odd candidate \(N\) that is not a power of 3, and suppose it satisfies the problem condition. Then, since \(c_{1} = 1\) and \(c_{2} = 2\) , we have \(\gcd (N,1 + 2)\neq 1\) , so \(3\mid N\) . Thus, we can write \(N\) as \(3^{k}M\) , where \(k\geq 1\) and \(\gcd (M,6) = 1\) . We have \(M\geq 5\) (as \(M\neq 1\) by assumption) and \(M + 2< N\) .
We now split into two cases based on \(M\) modulo 3.
Case 1. \(M\equiv 1\) (mod 3).
As \(3\mid M - 1\) and \(M\mid M\) , neither \(M - 1\) nor \(M\) are in the sequence \(\{c_{i}\}\) . As \(M\) is odd and \(M\equiv 1\) (mod 3), \(M - 2\) and \(M + 1\) are congruent to 1 (mod 3), are coprime to \(M\) , and are smaller than \(N\) . Thus, both \(M - 2\) and \(M + 1\) are in the sequence, and they are consecutive terms. However, this means \(\gcd (N,2M - 1)\neq 1\) . This gives a contradiction, as both 3 and \(M\) are coprime to \(2M - 1\) .
Case 2. \(M\equiv 2\) (mod 3).
This case is similar to Case 1. Neither \(M\) nor \(M + 1\) are in the sequence, but \(M - 1\) and \(M + 2\) are. We obtain a similar contradiction from \(\gcd (N,2M + 1)\neq 1\) .
|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "P1.",
"resource_path": "EGMO/segmented/en-2025-solutions.jsonl",
"solution_match": "\nSolution 1. ",
"tier": "T2",
"year": "2025"
}
|
For a positive integer \(N\) , let \(c_{1}< c_{2}< \dots < c_{m}\) be all the positive integers smaller than \(N\) that are coprime to \(N\) . Find all \(N\geq 3\) such that
\[\gcd (N,c_{i} + c_{i + 1})\neq 1\]
for all \(1\leq i\leq m - 1\)
Here \(\gcd (a,b)\) is the largest positive integer that divides both \(a\) and \(b\) . Integers \(a\) and \(b\) are coprime if \(\gcd (a,b) = 1\) .
|
We give an alternative way to show that any odd \(N\) has to be the power of 3. Suppose for contradiction that \(N\) has at least 2 distinct prime factors. Choose integers \(a,b > 1\) such that
\(a b\mid N\)
- \(a\) and \(b\) are coprime;
- Every prime divisor of \(N\) divides \(a b\) .
We use the Chinese Remainder Theorem, to find an integer \(n\in [1,ab]\) such that
\[\left\{ \begin{array}{l l}{n\equiv 1\pmod {a},}\\ {n\equiv 2\pmod {b}.} \end{array} \right.\]
We claim that there is an index \(i\) such that \(c_{i} = n - 3\) and \(c_{i + 1} = n\) . Indeed, we note the following:
- \(n\) is consecutive to a multiple of \(a\) , so \(\gcd (a, n) = 1\) . In a similar way we get that \(\gcd (b, n - 3) = 1\) .
- \(n\) is 2 away from a multiple of \(b\) , therefore as \(2 \nmid b\) , \(\gcd (b, n) = 1\) . In a similar way we get that \(\gcd (a, n - 3) = 1\) .
- \(n \leq ab \leq N\) and \(n - 3 \geq (a + 1) - 3 > 0\) as \(a > 2\) .
This implies that \(n\) and \(n - 3\) coprime with \(N\) , whereas neither \(n - 2\) nor \(n - 1\) are coprime with \(N\) , which proves our claim. Finally, we claim that \(c_{i} + c_{i + 1} = (n - 3) + n = 2n - 3\) is coprime with \(N\) . Indeed we have \(2n - 3 \equiv - 1 \pmod {a}\) and \(2n - 3 \equiv 1 \pmod {b}\) . This implies that \(N\) is a prime power.
When \(N\) is odd, since \(c_{1} = 1\) and \(c_{2} = 2\) , we have \(\gcd (N, 1 + 2) \neq 1\) , so \(3 \mid N\) , which implies that \(N\) is necessarily a power of 3. This concludes our proof.
|
N \text{ is a power of 3}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
For a positive integer \(N\) , let \(c_{1}< c_{2}< \dots < c_{m}\) be all the positive integers smaller than \(N\) that are coprime to \(N\) . Find all \(N\geq 3\) such that
\[\gcd (N,c_{i} + c_{i + 1})\neq 1\]
for all \(1\leq i\leq m - 1\)
Here \(\gcd (a,b)\) is the largest positive integer that divides both \(a\) and \(b\) . Integers \(a\) and \(b\) are coprime if \(\gcd (a,b) = 1\) .
|
We give an alternative way to show that any odd \(N\) has to be the power of 3. Suppose for contradiction that \(N\) has at least 2 distinct prime factors. Choose integers \(a,b > 1\) such that
\(a b\mid N\)
- \(a\) and \(b\) are coprime;
- Every prime divisor of \(N\) divides \(a b\) .
We use the Chinese Remainder Theorem, to find an integer \(n\in [1,ab]\) such that
\[\left\{ \begin{array}{l l}{n\equiv 1\pmod {a},}\\ {n\equiv 2\pmod {b}.} \end{array} \right.\]
We claim that there is an index \(i\) such that \(c_{i} = n - 3\) and \(c_{i + 1} = n\) . Indeed, we note the following:
- \(n\) is consecutive to a multiple of \(a\) , so \(\gcd (a, n) = 1\) . In a similar way we get that \(\gcd (b, n - 3) = 1\) .
- \(n\) is 2 away from a multiple of \(b\) , therefore as \(2 \nmid b\) , \(\gcd (b, n) = 1\) . In a similar way we get that \(\gcd (a, n - 3) = 1\) .
- \(n \leq ab \leq N\) and \(n - 3 \geq (a + 1) - 3 > 0\) as \(a > 2\) .
This implies that \(n\) and \(n - 3\) coprime with \(N\) , whereas neither \(n - 2\) nor \(n - 1\) are coprime with \(N\) , which proves our claim. Finally, we claim that \(c_{i} + c_{i + 1} = (n - 3) + n = 2n - 3\) is coprime with \(N\) . Indeed we have \(2n - 3 \equiv - 1 \pmod {a}\) and \(2n - 3 \equiv 1 \pmod {b}\) . This implies that \(N\) is a prime power.
When \(N\) is odd, since \(c_{1} = 1\) and \(c_{2} = 2\) , we have \(\gcd (N, 1 + 2) \neq 1\) , so \(3 \mid N\) , which implies that \(N\) is necessarily a power of 3. This concludes our proof.
|
{
"exam": "EGMO",
"problem_label": "1",
"problem_match": "P1.",
"resource_path": "EGMO/segmented/en-2025-solutions.jsonl",
"solution_match": "\nSolution 2. ",
"tier": "T2",
"year": "2025"
}
|
An infinite increasing sequence \(a_{1}< a_{2}< a_{3}< \dots\) of positive integers is called central if for every positive integer \(n\) , the arithmetic mean of the first \(a_{n}\) terms of the sequence is equal to \(a_{n}\) .
Show that there exists an infinite sequence \(b_{1},b_{2},b_{3},\ldots\) of positive integers such that for every central sequence \(a_{1},a_{2},a_{3},\ldots\) , there are infinitely many positive integers \(n\) with \(a_{n} = b_{n}\) .
|
We claim that the sequence \(b_{1},b_{2},b_{3},\ldots\) defined by \(b_{i} = 2i - 1\) has this property.
Let \(d_{i} = a_{i} - b_{i} = a_{i} - 2i + 1\) . The condition \(a_{i}< a_{i + 1}\) now becomes \(d_{i} + 2i - 1< d_{i + 1} + 2i + 1\) , which can be rewritten as \(d_{i + 1}\geqslant d_{i} - 1\) . Thus, if \(d_{i + 1}< d_{i}\) , then \(d_{i + 1}\) must be equal to \(d_{i} - 1\) . This implies in particular that if \(d_{i_{0}}\geqslant 0\) but \(d_{i_{1}}\leqslant 0\) for some indices \(i_{1} > i_{0}\) , there must be some intermediate index \(i_{0}\leqslant i\leqslant i_{1}\) with \(d_{i} = 0\) .
Because the average of the first \(a_{n}\) terms of the sequence is equal to \(a_{n}\) , we know for all \(n\) that
\[\sum_{i = 1}^{a_{n}}d_{i} = \sum_{i = 1}^{a_{n}}(a_{i} - 2i + 1) = \sum_{i = 1}^{a_{n}}a_{i} - \sum_{i = 1}^{a_{n}}(2i - 1) = a_{n}^{2} - a_{n}^{2} = 0.\]
Because the sequence \((a_{n})\) is increasing, this implies that the sequence \((d_{i})\) contains infinitely many non- negative \((d_{i}\geqslant 0)\) and infinitely many non- positive \((d_{i}\leqslant 0)\) terms. In particular, we can find arbitrarily large indices \(i_{0}\leqslant i_{1}\) such that \(d_{i_{0}}\geqslant 0\) and \(d_{i_{1}}\leqslant 0\) . By our earlier observation, it follows that there are infinitely many \(i\) such that \(d_{i} = 0\) , as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
An infinite increasing sequence \(a_{1}< a_{2}< a_{3}< \dots\) of positive integers is called central if for every positive integer \(n\) , the arithmetic mean of the first \(a_{n}\) terms of the sequence is equal to \(a_{n}\) .
Show that there exists an infinite sequence \(b_{1},b_{2},b_{3},\ldots\) of positive integers such that for every central sequence \(a_{1},a_{2},a_{3},\ldots\) , there are infinitely many positive integers \(n\) with \(a_{n} = b_{n}\) .
|
We claim that the sequence \(b_{1},b_{2},b_{3},\ldots\) defined by \(b_{i} = 2i - 1\) has this property.
Let \(d_{i} = a_{i} - b_{i} = a_{i} - 2i + 1\) . The condition \(a_{i}< a_{i + 1}\) now becomes \(d_{i} + 2i - 1< d_{i + 1} + 2i + 1\) , which can be rewritten as \(d_{i + 1}\geqslant d_{i} - 1\) . Thus, if \(d_{i + 1}< d_{i}\) , then \(d_{i + 1}\) must be equal to \(d_{i} - 1\) . This implies in particular that if \(d_{i_{0}}\geqslant 0\) but \(d_{i_{1}}\leqslant 0\) for some indices \(i_{1} > i_{0}\) , there must be some intermediate index \(i_{0}\leqslant i\leqslant i_{1}\) with \(d_{i} = 0\) .
Because the average of the first \(a_{n}\) terms of the sequence is equal to \(a_{n}\) , we know for all \(n\) that
\[\sum_{i = 1}^{a_{n}}d_{i} = \sum_{i = 1}^{a_{n}}(a_{i} - 2i + 1) = \sum_{i = 1}^{a_{n}}a_{i} - \sum_{i = 1}^{a_{n}}(2i - 1) = a_{n}^{2} - a_{n}^{2} = 0.\]
Because the sequence \((a_{n})\) is increasing, this implies that the sequence \((d_{i})\) contains infinitely many non- negative \((d_{i}\geqslant 0)\) and infinitely many non- positive \((d_{i}\leqslant 0)\) terms. In particular, we can find arbitrarily large indices \(i_{0}\leqslant i_{1}\) such that \(d_{i_{0}}\geqslant 0\) and \(d_{i_{1}}\leqslant 0\) . By our earlier observation, it follows that there are infinitely many \(i\) such that \(d_{i} = 0\) , as desired.
|
{
"exam": "EGMO",
"problem_label": "2",
"problem_match": "P2.",
"resource_path": "EGMO/segmented/en-2025-solutions.jsonl",
"solution_match": "\nSolution 1. ",
"tier": "T2",
"year": "2025"
}
|
An infinite increasing sequence \(a_{1}< a_{2}< a_{3}< \dots\) of positive integers is called central if for every positive integer \(n\) , the arithmetic mean of the first \(a_{n}\) terms of the sequence is equal to \(a_{n}\) .
Show that there exists an infinite sequence \(b_{1},b_{2},b_{3},\ldots\) of positive integers such that for every central sequence \(a_{1},a_{2},a_{3},\ldots\) , there are infinitely many positive integers \(n\) with \(a_{n} = b_{n}\) .
|
We give an alternative proof that the sequence \(b_{i} = 2i - 1\) works. This proof is by contradiction, so we assume that there are only finitely many \(a_{i}\) such that \(a_{i} = 2i - 1\) .
Let \(S(n) = \sum_{i = 1}^{n}a_{i}\) . We have \(S(a_{n}) = a_{n}^{2}\) and \(S(a_{n + 1}) = a_{n + 1}^{2}\) . If \(a_{n + 1} = a_{n} + 1\) , then it follows that
\[S(a_{n + 1}) - S(a_{n}) = a_{n + 1}^{2} - a_{n}^{2} = a_{n + 1}^{2} - (a_{n + 1} - 1)^{2} = 2a_{n + 1} - 1.\]
On the other hand, if \(a_{n + 1} = a_{n} + 1\) , then \(S(a_{n + 1}) - S(a_{n})\) is \(a_{a_{n + 1}}\) , so it follows that \(a_{a_{n + 1}} = 2a_{n + 1} - 1\) . By assumption, this can only happen finitely many times, so for all sufficiently large \(n\) we must have \(a_{n + 1}\geqslant a_{n} + 2\) .
For large enough \(n\) , we now know that \(a_{n} > 2n - 1\) implies \(a_{n + 1} > (2n - 1) + 2 = 2(n + 1) - 1\) . This means that there are two cases possible:
(A) For all sufficiently large \(n\) (say \(n\geqslant N_{A}\) ) we have \(a_{n} > 2n - 1\)
(B) For all sufficiently large \(n\) (say \(n\geqslant N_{B}\) ) we have \(a_{n}< 2n - 1\)
In case (A), we know for \(m > N_{A}\) that
\[S(m) = S(N_{A}) + \sum_{i = N_{A} + 1}^{m}a_{i}\geqslant S(N_{A}) + \sum_{i = N_{A} + 1}^{n}2i = S(N_{A}) + m(m + 1) - N_{A}(N_{A} + 1)\] \[\qquad = m^{2} + m + S(N_{A}) - N_{A}(N_{A} + 1).\]
For \(m\) large enough (e.g. \(m > N_{A}(N_{A} + 1)\) ), this expression is always larger than \(m^{2}\) , contradicting \(S(a_{n}) = a_{n}^{2}\) for all \(n\) .
Similarly, in case (B), we similarly know for \(m > N_{B}\) that
\[S(m) = S(N_{B}) + \sum_{i = N_{B} + 1}^{m}a_{i}\leqslant S(N_{B}) + \sum_{i = N_{B} + 1}^{n}2(i - 1) = S(N_{B}) + m(m - 1) - N_{B}(N_{B} - 1)\] \[\qquad = m^{2} - m + S(N_{B}) - N_{B}(N_{B} - 1).\]
For \(m\) large enough (e.g. \(m > S(N_{B})\) ), this expression is always smaller than \(m^{2}\) , again contradicting \(S(a_{n}) = a_{n}^{2}\) for all \(n\) .
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
An infinite increasing sequence \(a_{1}< a_{2}< a_{3}< \dots\) of positive integers is called central if for every positive integer \(n\) , the arithmetic mean of the first \(a_{n}\) terms of the sequence is equal to \(a_{n}\) .
Show that there exists an infinite sequence \(b_{1},b_{2},b_{3},\ldots\) of positive integers such that for every central sequence \(a_{1},a_{2},a_{3},\ldots\) , there are infinitely many positive integers \(n\) with \(a_{n} = b_{n}\) .
|
We give an alternative proof that the sequence \(b_{i} = 2i - 1\) works. This proof is by contradiction, so we assume that there are only finitely many \(a_{i}\) such that \(a_{i} = 2i - 1\) .
Let \(S(n) = \sum_{i = 1}^{n}a_{i}\) . We have \(S(a_{n}) = a_{n}^{2}\) and \(S(a_{n + 1}) = a_{n + 1}^{2}\) . If \(a_{n + 1} = a_{n} + 1\) , then it follows that
\[S(a_{n + 1}) - S(a_{n}) = a_{n + 1}^{2} - a_{n}^{2} = a_{n + 1}^{2} - (a_{n + 1} - 1)^{2} = 2a_{n + 1} - 1.\]
On the other hand, if \(a_{n + 1} = a_{n} + 1\) , then \(S(a_{n + 1}) - S(a_{n})\) is \(a_{a_{n + 1}}\) , so it follows that \(a_{a_{n + 1}} = 2a_{n + 1} - 1\) . By assumption, this can only happen finitely many times, so for all sufficiently large \(n\) we must have \(a_{n + 1}\geqslant a_{n} + 2\) .
For large enough \(n\) , we now know that \(a_{n} > 2n - 1\) implies \(a_{n + 1} > (2n - 1) + 2 = 2(n + 1) - 1\) . This means that there are two cases possible:
(A) For all sufficiently large \(n\) (say \(n\geqslant N_{A}\) ) we have \(a_{n} > 2n - 1\)
(B) For all sufficiently large \(n\) (say \(n\geqslant N_{B}\) ) we have \(a_{n}< 2n - 1\)
In case (A), we know for \(m > N_{A}\) that
\[S(m) = S(N_{A}) + \sum_{i = N_{A} + 1}^{m}a_{i}\geqslant S(N_{A}) + \sum_{i = N_{A} + 1}^{n}2i = S(N_{A}) + m(m + 1) - N_{A}(N_{A} + 1)\] \[\qquad = m^{2} + m + S(N_{A}) - N_{A}(N_{A} + 1).\]
For \(m\) large enough (e.g. \(m > N_{A}(N_{A} + 1)\) ), this expression is always larger than \(m^{2}\) , contradicting \(S(a_{n}) = a_{n}^{2}\) for all \(n\) .
Similarly, in case (B), we similarly know for \(m > N_{B}\) that
\[S(m) = S(N_{B}) + \sum_{i = N_{B} + 1}^{m}a_{i}\leqslant S(N_{B}) + \sum_{i = N_{B} + 1}^{n}2(i - 1) = S(N_{B}) + m(m - 1) - N_{B}(N_{B} - 1)\] \[\qquad = m^{2} - m + S(N_{B}) - N_{B}(N_{B} - 1).\]
For \(m\) large enough (e.g. \(m > S(N_{B})\) ), this expression is always smaller than \(m^{2}\) , again contradicting \(S(a_{n}) = a_{n}^{2}\) for all \(n\) .
|
{
"exam": "EGMO",
"problem_label": "2",
"problem_match": "P2.",
"resource_path": "EGMO/segmented/en-2025-solutions.jsonl",
"solution_match": "\nSolution 2. ",
"tier": "T2",
"year": "2025"
}
|
An infinite increasing sequence \(a_{1}< a_{2}< a_{3}< \dots\) of positive integers is called central if for every positive integer \(n\) , the arithmetic mean of the first \(a_{n}\) terms of the sequence is equal to \(a_{n}\) .
Show that there exists an infinite sequence \(b_{1},b_{2},b_{3},\ldots\) of positive integers such that for every central sequence \(a_{1},a_{2},a_{3},\ldots\) , there are infinitely many positive integers \(n\) with \(a_{n} = b_{n}\) .
|
We claim that the sequence \(b_{1}\) , \(b_{2}\) , \(b_{3}\) , ... defined by \(b_{i} = 2i - 1\) has this property.
Lemma. If there are no terms \(a_{j}\) such that \(a_{j} - a_{j - 1} = 1\) , then \(a_{j} = a_{j - 1} + 2\) for all \(j\) .
Proof. Let \(c\) be such that \(a_{d} = c\) for some \(d\) . Now
\[a_{1} + a_{2} + \dots +a_{c} = c^{2}.\]
Equality holds for \(a_{i} = 2i - 1\) for \(1\leq i\leq c\) , so if any difference between two consecutive terms is greater, the left- hand side of the equation is greater than \(c^{2}\) , a contradiction. \(\square\)
Lemma. If both \(d\) and \(d + 1\) are terms of the sequence, i.e. \(a_{c} = d\) and \(a_{c + 1} = d + 1\) for some \(c\) , then \(a_{d + 1} = 2d + 1 = b_{d + 1}\) .
Proof. We have \(a_{1} + a_{2} + \dots +a_{d} = d^{2}\) and \(a_{1} + a_{2} + \dots +a_{d + 1} = (d + 1)^{2}\) . Hence \(a_{d + 1} = (d + 1)^{2} - d^{2} = 2d + 1\) . \(\square\)
From the observations above, we see that we are done if there are infinitely many gaps of size 1. The only remaining case is one with finitely many gaps of size 1. This will be the subject of the following lemma.
Lemma. If there are only finitely many indices \(j\) such that \(a_{j + 1} - a_{j} = 1\) , then there is an index \(n_{0}\) such that for all \(k > n_{0}\) , we have \(a_{k} = 2k - 1\) .
Proof. Let \(r\) and \(s\) be indices such that for all the \(j\) satisfying \(a_{j + 1} - a_{j} = 1\) , we have \(j < r\) , \(s\) . Furthermore, assume \(s > r\) and that there are \(i_{1}\) and \(i_{2}\) such that \(a_{i_{1}} = r\) and \(a_{i_{2}} = s\) . The first goal is to show that \(a_{s} \geq 2s - 1\) . If \(a_{r} \geq 2r - 1\) , this is clearly the case. Assume now \(a_{r} < 2r - 1\) . Now \(a_{r} \geq 2r - 1 - m\) , where \(m\) is the number of indices \(j\) with \(a_{j + 1} - a_{j} = 1\) . Denote \(a_{r + 1} = 2r + 1 - m + \theta_{1}\) , \(a_{r + 2} = 2r + 3 - m + \theta_{2}\) , etc. Remember that \(a_{r + j + 1} - a_{r + j} \geq 2\) always. Now \(0 \leq \theta_{1} \leq \theta_{2} \leq \dots\) . Furthermore, write \(s = r + h\) . Now
\[(r + h)^{2} - r^{2} = a_{r + 1} + a_{r + 2} + \dots +a_{r + h} = \sum_{j = 1}^{h}2r - 1 + 2j - m + \theta_{j}.\]
From this we deduce
\[2r h + h^{2} = 2r h - h - m h + h(h + 1) + \sum_{j = 1}^{h}\theta_{j}.\]
So we obtain \(\sum_{j = 1}^{h}\theta_{j} = m h\) . Since the sequence \(\theta_{j}\) is increasing, we have \(\theta_{h} \geq m\) . Hence, \(a_{s} = a_{r + h} \geq 2r - 1 - m + 2h + m = 2r + 2h - 1 = 2s - 1\) .
Now \(a_{s}\) is exactly the desired shape. If for any \(t > s\) , we have \(a_{t} - a_{t - 1} > 2\) , then
\[a_{s} + a_{s + 1} + \dots +a_{t} > t^{2} - s^{2},\]
again a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
An infinite increasing sequence \(a_{1}< a_{2}< a_{3}< \dots\) of positive integers is called central if for every positive integer \(n\) , the arithmetic mean of the first \(a_{n}\) terms of the sequence is equal to \(a_{n}\) .
Show that there exists an infinite sequence \(b_{1},b_{2},b_{3},\ldots\) of positive integers such that for every central sequence \(a_{1},a_{2},a_{3},\ldots\) , there are infinitely many positive integers \(n\) with \(a_{n} = b_{n}\) .
|
We claim that the sequence \(b_{1}\) , \(b_{2}\) , \(b_{3}\) , ... defined by \(b_{i} = 2i - 1\) has this property.
Lemma. If there are no terms \(a_{j}\) such that \(a_{j} - a_{j - 1} = 1\) , then \(a_{j} = a_{j - 1} + 2\) for all \(j\) .
Proof. Let \(c\) be such that \(a_{d} = c\) for some \(d\) . Now
\[a_{1} + a_{2} + \dots +a_{c} = c^{2}.\]
Equality holds for \(a_{i} = 2i - 1\) for \(1\leq i\leq c\) , so if any difference between two consecutive terms is greater, the left- hand side of the equation is greater than \(c^{2}\) , a contradiction. \(\square\)
Lemma. If both \(d\) and \(d + 1\) are terms of the sequence, i.e. \(a_{c} = d\) and \(a_{c + 1} = d + 1\) for some \(c\) , then \(a_{d + 1} = 2d + 1 = b_{d + 1}\) .
Proof. We have \(a_{1} + a_{2} + \dots +a_{d} = d^{2}\) and \(a_{1} + a_{2} + \dots +a_{d + 1} = (d + 1)^{2}\) . Hence \(a_{d + 1} = (d + 1)^{2} - d^{2} = 2d + 1\) . \(\square\)
From the observations above, we see that we are done if there are infinitely many gaps of size 1. The only remaining case is one with finitely many gaps of size 1. This will be the subject of the following lemma.
Lemma. If there are only finitely many indices \(j\) such that \(a_{j + 1} - a_{j} = 1\) , then there is an index \(n_{0}\) such that for all \(k > n_{0}\) , we have \(a_{k} = 2k - 1\) .
Proof. Let \(r\) and \(s\) be indices such that for all the \(j\) satisfying \(a_{j + 1} - a_{j} = 1\) , we have \(j < r\) , \(s\) . Furthermore, assume \(s > r\) and that there are \(i_{1}\) and \(i_{2}\) such that \(a_{i_{1}} = r\) and \(a_{i_{2}} = s\) . The first goal is to show that \(a_{s} \geq 2s - 1\) . If \(a_{r} \geq 2r - 1\) , this is clearly the case. Assume now \(a_{r} < 2r - 1\) . Now \(a_{r} \geq 2r - 1 - m\) , where \(m\) is the number of indices \(j\) with \(a_{j + 1} - a_{j} = 1\) . Denote \(a_{r + 1} = 2r + 1 - m + \theta_{1}\) , \(a_{r + 2} = 2r + 3 - m + \theta_{2}\) , etc. Remember that \(a_{r + j + 1} - a_{r + j} \geq 2\) always. Now \(0 \leq \theta_{1} \leq \theta_{2} \leq \dots\) . Furthermore, write \(s = r + h\) . Now
\[(r + h)^{2} - r^{2} = a_{r + 1} + a_{r + 2} + \dots +a_{r + h} = \sum_{j = 1}^{h}2r - 1 + 2j - m + \theta_{j}.\]
From this we deduce
\[2r h + h^{2} = 2r h - h - m h + h(h + 1) + \sum_{j = 1}^{h}\theta_{j}.\]
So we obtain \(\sum_{j = 1}^{h}\theta_{j} = m h\) . Since the sequence \(\theta_{j}\) is increasing, we have \(\theta_{h} \geq m\) . Hence, \(a_{s} = a_{r + h} \geq 2r - 1 - m + 2h + m = 2r + 2h - 1 = 2s - 1\) .
Now \(a_{s}\) is exactly the desired shape. If for any \(t > s\) , we have \(a_{t} - a_{t - 1} > 2\) , then
\[a_{s} + a_{s + 1} + \dots +a_{t} > t^{2} - s^{2},\]
again a contradiction.
|
{
"exam": "EGMO",
"problem_label": "2",
"problem_match": "P2.",
"resource_path": "EGMO/segmented/en-2025-solutions.jsonl",
"solution_match": "\nSolution 3. ",
"tier": "T2",
"year": "2025"
}
|
An infinite increasing sequence \(a_{1}< a_{2}< a_{3}< \dots\) of positive integers is called central if for every positive integer \(n\) , the arithmetic mean of the first \(a_{n}\) terms of the sequence is equal to \(a_{n}\) .
Show that there exists an infinite sequence \(b_{1},b_{2},b_{3},\ldots\) of positive integers such that for every central sequence \(a_{1},a_{2},a_{3},\ldots\) , there are infinitely many positive integers \(n\) with \(a_{n} = b_{n}\) .
|
Note that \(a_{1} = 1\) because if it is not the case, then \(a_{1}^{2} = a_{1} + \dots +a_{a_{1}} > a_{1} + a_{1} + \dots +a_{1} = a_{1}^{2}\) .
Assume by contradiction that there are only finitely many indices \(k\) such that \(a_{k} = 2k - 1\) . Set \(i\) to be the largest integer such that \(a_{i} = 2i - 1\) (which must exist as \(a_{1} = 1\) ). Assume that there exists \(j \geqslant i\) such that \(a_{j + 1} - a_{j} = 1\) . Then \(2a_{j + 1} - 1 = a_{j + 1}^{2} - a_{j}^{2} = a_{a_{j + 1}}\) and since \(a_{k} \geqslant k\) for all \(k\) , we have \(a_{j + 1} \geqslant j + 1 > i\) , which contradicts the definition of \(i\) . Thus for all \(j \geqslant i\) , we have \(a_{j + 1} \geqslant a_{j} + 2\) , which implies by induction that \(a_{j} \geqslant 2j - 1\) for \(j \geqslant i\) , and even \(a_{j} \geq 2j\) if \(j > i\) .
There are two ways to finish the solution from here.
## First way to finish the solution
For all \(n\) such that \(a_{n} \geqslant i\) , we have
\[a_{n + 1}^{2} - a_{n}^{2} = a_{a_{n + 1}} + a_{a_{n + 1} - 1} + \dots +a_{a_{n + 1}}\geqslant 2a_{n + 1} + 2(a_{n + 1} - 1) + \dots +2(a_{n} + 1)\] \[\qquad = (a_{n + 1} - a_{n})(a_{n + 1} + a_{n} + 1)\] \[\qquad >a_{n + 1}^{2} - a_{n}^{2}.\]
This gives a contradiction.
## Second way to finish the solution
For all \(n\) such that \(a_{n} \geqslant i\) , we introduce \(x_{n} = a_{n + 1} - a_{n}\) . We have
\[x_{n}^{2} + 2x_{n}a_{n} = a_{n + 1}^{2} - a_{n}^{2} = a_{a_{n + 1}} + a_{a_{n + 1} - 1} + \dots +a_{a_{n} + 1}\geqslant \sum_{j = 1}^{x_{n}}(a_{a_{n}} + 2j)\geq x_{n}a_{a_{n}} + x_{n}(x_{n} + 1).\]
By simplifying, we get \(a_{a_{n}} \leq 2a_{n} - 1\) , which gives a contradiction.
Comment. Proving that \(a_{1} = 1\) is not necessary for this solution. If there exists no \(i\) such that \(a_{i} = 2i - 1\) , then the same argument implies that there exists no \(j\) such that \(a_{j + 1} - a_{j} = 1\) , thus \(a_{j} \geqslant 2j - 1\) for \(j \geqslant 1\) .
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
An infinite increasing sequence \(a_{1}< a_{2}< a_{3}< \dots\) of positive integers is called central if for every positive integer \(n\) , the arithmetic mean of the first \(a_{n}\) terms of the sequence is equal to \(a_{n}\) .
Show that there exists an infinite sequence \(b_{1},b_{2},b_{3},\ldots\) of positive integers such that for every central sequence \(a_{1},a_{2},a_{3},\ldots\) , there are infinitely many positive integers \(n\) with \(a_{n} = b_{n}\) .
|
Note that \(a_{1} = 1\) because if it is not the case, then \(a_{1}^{2} = a_{1} + \dots +a_{a_{1}} > a_{1} + a_{1} + \dots +a_{1} = a_{1}^{2}\) .
Assume by contradiction that there are only finitely many indices \(k\) such that \(a_{k} = 2k - 1\) . Set \(i\) to be the largest integer such that \(a_{i} = 2i - 1\) (which must exist as \(a_{1} = 1\) ). Assume that there exists \(j \geqslant i\) such that \(a_{j + 1} - a_{j} = 1\) . Then \(2a_{j + 1} - 1 = a_{j + 1}^{2} - a_{j}^{2} = a_{a_{j + 1}}\) and since \(a_{k} \geqslant k\) for all \(k\) , we have \(a_{j + 1} \geqslant j + 1 > i\) , which contradicts the definition of \(i\) . Thus for all \(j \geqslant i\) , we have \(a_{j + 1} \geqslant a_{j} + 2\) , which implies by induction that \(a_{j} \geqslant 2j - 1\) for \(j \geqslant i\) , and even \(a_{j} \geq 2j\) if \(j > i\) .
There are two ways to finish the solution from here.
## First way to finish the solution
For all \(n\) such that \(a_{n} \geqslant i\) , we have
\[a_{n + 1}^{2} - a_{n}^{2} = a_{a_{n + 1}} + a_{a_{n + 1} - 1} + \dots +a_{a_{n + 1}}\geqslant 2a_{n + 1} + 2(a_{n + 1} - 1) + \dots +2(a_{n} + 1)\] \[\qquad = (a_{n + 1} - a_{n})(a_{n + 1} + a_{n} + 1)\] \[\qquad >a_{n + 1}^{2} - a_{n}^{2}.\]
This gives a contradiction.
## Second way to finish the solution
For all \(n\) such that \(a_{n} \geqslant i\) , we introduce \(x_{n} = a_{n + 1} - a_{n}\) . We have
\[x_{n}^{2} + 2x_{n}a_{n} = a_{n + 1}^{2} - a_{n}^{2} = a_{a_{n + 1}} + a_{a_{n + 1} - 1} + \dots +a_{a_{n} + 1}\geqslant \sum_{j = 1}^{x_{n}}(a_{a_{n}} + 2j)\geq x_{n}a_{a_{n}} + x_{n}(x_{n} + 1).\]
By simplifying, we get \(a_{a_{n}} \leq 2a_{n} - 1\) , which gives a contradiction.
Comment. Proving that \(a_{1} = 1\) is not necessary for this solution. If there exists no \(i\) such that \(a_{i} = 2i - 1\) , then the same argument implies that there exists no \(j\) such that \(a_{j + 1} - a_{j} = 1\) , thus \(a_{j} \geqslant 2j - 1\) for \(j \geqslant 1\) .
|
{
"exam": "EGMO",
"problem_label": "2",
"problem_match": "P2.",
"resource_path": "EGMO/segmented/en-2025-solutions.jsonl",
"solution_match": "\nSolution 4. ",
"tier": "T2",
"year": "2025"
}
|
Let \(A B C\) be an acute triangle. Points \(B\) , \(D\) , \(E\) , and \(C\) lie on a line in this order and satisfy \(B D =\) \(D E = E C\) . Let \(M\) and \(N\) be the midpoints of \(A D\) and \(A E\) , respectively. Let \(H\) be the orthocentre of triangle \(A D E\) . Let \(P\) and \(Q\) be points on lines \(B M\) and \(C N\) , respectively, such that \(D\) , \(H\) , \(M\) , and \(P\) are concyclic and \(E\) , \(H\) , \(N\) , and \(Q\) are concyclic. Prove that \(P\) , \(Q\) , \(N\) , and \(M\) are concyclic.
The orthocentre of a triangle is the point of intersection of its altitudes.
|
Denote by \(B^{\prime}\) and \(C^{\prime}\) the reflections of \(B\) and \(C\) in \(M\) and \(N\) , respectively. Points \(C^{\prime}\) , \(A\) , \(B^{\prime}\) are clearly collinear and \(D E B^{\prime}A\) is a parallelogram. Since \(E H\perp A D\) , we have \(E H\perp E B^{\prime}\) . Also \(H A\perp A B^{\prime}\) , so points \(H,E,B^{\prime},A\) are concyclic. This gives
\[\angle C^{\prime}Q H = \angle N Q H = \angle N E H = \angle A E H = \angle A B^{\prime}H = \angle C^{\prime}B^{\prime}H,\]
and so points \(C^{\prime}\) , \(B^{\prime}\) , \(Q\) , \(H\) are concyclic. Analogously points \(C^{\prime}\) , \(B^{\prime}\) , \(P\) , \(H\) are concyclic, and so all points \(B^{\prime}\) , \(C^{\prime}\) , \(P\) , \(Q\) , \(H\) are. Now we have
\[\angle N M B^{\prime} = \angle A B^{\prime}M = \angle C^{\prime}B^{\prime}P = \angle C^{\prime}Q P = \angle N Q P,\]
which proves that \(P,Q,N,M\) are also concyclic.

|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let \(A B C\) be an acute triangle. Points \(B\) , \(D\) , \(E\) , and \(C\) lie on a line in this order and satisfy \(B D =\) \(D E = E C\) . Let \(M\) and \(N\) be the midpoints of \(A D\) and \(A E\) , respectively. Let \(H\) be the orthocentre of triangle \(A D E\) . Let \(P\) and \(Q\) be points on lines \(B M\) and \(C N\) , respectively, such that \(D\) , \(H\) , \(M\) , and \(P\) are concyclic and \(E\) , \(H\) , \(N\) , and \(Q\) are concyclic. Prove that \(P\) , \(Q\) , \(N\) , and \(M\) are concyclic.
The orthocentre of a triangle is the point of intersection of its altitudes.
|
Denote by \(B^{\prime}\) and \(C^{\prime}\) the reflections of \(B\) and \(C\) in \(M\) and \(N\) , respectively. Points \(C^{\prime}\) , \(A\) , \(B^{\prime}\) are clearly collinear and \(D E B^{\prime}A\) is a parallelogram. Since \(E H\perp A D\) , we have \(E H\perp E B^{\prime}\) . Also \(H A\perp A B^{\prime}\) , so points \(H,E,B^{\prime},A\) are concyclic. This gives
\[\angle C^{\prime}Q H = \angle N Q H = \angle N E H = \angle A E H = \angle A B^{\prime}H = \angle C^{\prime}B^{\prime}H,\]
and so points \(C^{\prime}\) , \(B^{\prime}\) , \(Q\) , \(H\) are concyclic. Analogously points \(C^{\prime}\) , \(B^{\prime}\) , \(P\) , \(H\) are concyclic, and so all points \(B^{\prime}\) , \(C^{\prime}\) , \(P\) , \(Q\) , \(H\) are. Now we have
\[\angle N M B^{\prime} = \angle A B^{\prime}M = \angle C^{\prime}B^{\prime}P = \angle C^{\prime}Q P = \angle N Q P,\]
which proves that \(P,Q,N,M\) are also concyclic.

|
{
"exam": "EGMO",
"problem_label": "3",
"problem_match": "P3.",
"resource_path": "EGMO/segmented/en-2025-solutions.jsonl",
"solution_match": "\nSolution 1. ",
"tier": "T2",
"year": "2025"
}
|
Let \(A B C\) be an acute triangle. Points \(B\) , \(D\) , \(E\) , and \(C\) lie on a line in this order and satisfy \(B D =\) \(D E = E C\) . Let \(M\) and \(N\) be the midpoints of \(A D\) and \(A E\) , respectively. Let \(H\) be the orthocentre of triangle \(A D E\) . Let \(P\) and \(Q\) be points on lines \(B M\) and \(C N\) , respectively, such that \(D\) , \(H\) , \(M\) , and \(P\) are concyclic and \(E\) , \(H\) , \(N\) , and \(Q\) are concyclic. Prove that \(P\) , \(Q\) , \(N\) , and \(M\) are concyclic.
The orthocentre of a triangle is the point of intersection of its altitudes.
|
Introduce points \(B^{\prime}\) , \(C^{\prime}\) as above. Also define \(A^{\prime} = B^{\prime}E\cap C^{\prime}D\) , so that \(E A D A^{\prime}\) is a parallelogram and \(A D E\) is the medial triangle of \(A^{\prime}B^{\prime}C^{\prime}\) . It that follows that the orthocentre \(H\) of \(A D E\) is the circumcentre of \(A^{\prime}B^{\prime}C^{\prime}\) , and in particular
\[\angle C^{\prime}B^{\prime}H = 90^{\circ} - \angle B^{\prime}A^{\prime}C^{\prime} = 90^{\circ} - \angle D A E = \angle A E H = \angle N E H = \angle N Q H = \angle C^{\prime}Q H.\]
So again we have that \(C^{\prime}\) , \(B^{\prime}\) , \(Q\) , \(H\) are concyclic and conclude as in Solution 1.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let \(A B C\) be an acute triangle. Points \(B\) , \(D\) , \(E\) , and \(C\) lie on a line in this order and satisfy \(B D =\) \(D E = E C\) . Let \(M\) and \(N\) be the midpoints of \(A D\) and \(A E\) , respectively. Let \(H\) be the orthocentre of triangle \(A D E\) . Let \(P\) and \(Q\) be points on lines \(B M\) and \(C N\) , respectively, such that \(D\) , \(H\) , \(M\) , and \(P\) are concyclic and \(E\) , \(H\) , \(N\) , and \(Q\) are concyclic. Prove that \(P\) , \(Q\) , \(N\) , and \(M\) are concyclic.
The orthocentre of a triangle is the point of intersection of its altitudes.
|
Introduce points \(B^{\prime}\) , \(C^{\prime}\) as above. Also define \(A^{\prime} = B^{\prime}E\cap C^{\prime}D\) , so that \(E A D A^{\prime}\) is a parallelogram and \(A D E\) is the medial triangle of \(A^{\prime}B^{\prime}C^{\prime}\) . It that follows that the orthocentre \(H\) of \(A D E\) is the circumcentre of \(A^{\prime}B^{\prime}C^{\prime}\) , and in particular
\[\angle C^{\prime}B^{\prime}H = 90^{\circ} - \angle B^{\prime}A^{\prime}C^{\prime} = 90^{\circ} - \angle D A E = \angle A E H = \angle N E H = \angle N Q H = \angle C^{\prime}Q H.\]
So again we have that \(C^{\prime}\) , \(B^{\prime}\) , \(Q\) , \(H\) are concyclic and conclude as in Solution 1.
|
{
"exam": "EGMO",
"problem_label": "3",
"problem_match": "P3.",
"resource_path": "EGMO/segmented/en-2025-solutions.jsonl",
"solution_match": "\nSolution 1'.",
"tier": "T2",
"year": "2025"
}
|
Let \(A B C\) be an acute triangle. Points \(B\) , \(D\) , \(E\) , and \(C\) lie on a line in this order and satisfy \(B D =\) \(D E = E C\) . Let \(M\) and \(N\) be the midpoints of \(A D\) and \(A E\) , respectively. Let \(H\) be the orthocentre of triangle \(A D E\) . Let \(P\) and \(Q\) be points on lines \(B M\) and \(C N\) , respectively, such that \(D\) , \(H\) , \(M\) , and \(P\) are concyclic and \(E\) , \(H\) , \(N\) , and \(Q\) are concyclic. Prove that \(P\) , \(Q\) , \(N\) , and \(M\) are concyclic.
The orthocentre of a triangle is the point of intersection of its altitudes.
|
Let \(X\) be the second intersection of \((D H M)\) and \((E H N)\) and let \(O^{\prime}\) be the circumcentre of \((A M N)\) Note that \(\angle M X N = \angle M D H + \angle N E H = 180^{\circ} - 2\angle D A E\) and since \(\angle M O^{\prime}N = 2\angle D A E\) we have that \(X,M,O^{\prime},N\) is cyclic and since \(\angle M X H = \angle N X H\) it means that \(H X\) is the angle bisector of \(\angle M X N\) but since \(O^{\prime}M = O^{\prime}N\) it means that \(H,X,O^{\prime}\) are collinear. Let \(B M\) and \(C N\) intersect at \(T\) and let \(K\) and \(L\) be the midpoints of \(M N\) and \(B C\) . Note that \(L\) is also the midpoint of \(D E\) . Since \(M N\) is parallel to \(B C\) it means that \(T\) , \(K\) , and \(L\) are collinear, but since \(A\) , \(K\) , and \(L\) are collinear we get that \(A\) , \(T\) , \(K\) , and \(L\) are collinear. Now, \(\frac{T L}{T K} = \frac{B C}{M N} = 6\) . Since \(K L = K A\) it means that \(\frac{A T}{T K} = \frac{T L - 2T K}{T K} = 4\) so by the lemma below, \(T\) lies on \(H O^{\prime}\) . Since \(H O^{\prime}\) is the radical axis of \((D H M)\) and \((E H N)\) we finish the problem using the Radical Axes Theorem \((T M\cdot T P = T N\cdot T Q)\) .
Lemma. Let \(A^{\prime}\) be the reflection of \(A\) around the orthocentre \(H\) of \(\triangle ABC\) and \(O\) and \(M\) be the circumcentre of \(\triangle ABC\) and the midpoint of \(BC\) , respectively. Let \(T\) be the intersection of \(A^{\prime}O\) and \(AM\) . Then \(\frac{AT}{TM} = 4\) .
Proof. Since \(OM \parallel AA'\) we have \(\frac{AT}{TM} = \frac{AA'}{OM} = \frac{2AH}{OM} = \frac{4OM}{OM} = 4\) . We used here that \(AH = 2OM\) . \(\square\)

|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let \(A B C\) be an acute triangle. Points \(B\) , \(D\) , \(E\) , and \(C\) lie on a line in this order and satisfy \(B D =\) \(D E = E C\) . Let \(M\) and \(N\) be the midpoints of \(A D\) and \(A E\) , respectively. Let \(H\) be the orthocentre of triangle \(A D E\) . Let \(P\) and \(Q\) be points on lines \(B M\) and \(C N\) , respectively, such that \(D\) , \(H\) , \(M\) , and \(P\) are concyclic and \(E\) , \(H\) , \(N\) , and \(Q\) are concyclic. Prove that \(P\) , \(Q\) , \(N\) , and \(M\) are concyclic.
The orthocentre of a triangle is the point of intersection of its altitudes.
|
Let \(X\) be the second intersection of \((D H M)\) and \((E H N)\) and let \(O^{\prime}\) be the circumcentre of \((A M N)\) Note that \(\angle M X N = \angle M D H + \angle N E H = 180^{\circ} - 2\angle D A E\) and since \(\angle M O^{\prime}N = 2\angle D A E\) we have that \(X,M,O^{\prime},N\) is cyclic and since \(\angle M X H = \angle N X H\) it means that \(H X\) is the angle bisector of \(\angle M X N\) but since \(O^{\prime}M = O^{\prime}N\) it means that \(H,X,O^{\prime}\) are collinear. Let \(B M\) and \(C N\) intersect at \(T\) and let \(K\) and \(L\) be the midpoints of \(M N\) and \(B C\) . Note that \(L\) is also the midpoint of \(D E\) . Since \(M N\) is parallel to \(B C\) it means that \(T\) , \(K\) , and \(L\) are collinear, but since \(A\) , \(K\) , and \(L\) are collinear we get that \(A\) , \(T\) , \(K\) , and \(L\) are collinear. Now, \(\frac{T L}{T K} = \frac{B C}{M N} = 6\) . Since \(K L = K A\) it means that \(\frac{A T}{T K} = \frac{T L - 2T K}{T K} = 4\) so by the lemma below, \(T\) lies on \(H O^{\prime}\) . Since \(H O^{\prime}\) is the radical axis of \((D H M)\) and \((E H N)\) we finish the problem using the Radical Axes Theorem \((T M\cdot T P = T N\cdot T Q)\) .
Lemma. Let \(A^{\prime}\) be the reflection of \(A\) around the orthocentre \(H\) of \(\triangle ABC\) and \(O\) and \(M\) be the circumcentre of \(\triangle ABC\) and the midpoint of \(BC\) , respectively. Let \(T\) be the intersection of \(A^{\prime}O\) and \(AM\) . Then \(\frac{AT}{TM} = 4\) .
Proof. Since \(OM \parallel AA'\) we have \(\frac{AT}{TM} = \frac{AA'}{OM} = \frac{2AH}{OM} = \frac{4OM}{OM} = 4\) . We used here that \(AH = 2OM\) . \(\square\)

|
{
"exam": "EGMO",
"problem_label": "3",
"problem_match": "P3.",
"resource_path": "EGMO/segmented/en-2025-solutions.jsonl",
"solution_match": "\nSolution 2. ",
"tier": "T2",
"year": "2025"
}
|
Let \(A B C\) be an acute triangle. Points \(B\) , \(D\) , \(E\) , and \(C\) lie on a line in this order and satisfy \(B D =\) \(D E = E C\) . Let \(M\) and \(N\) be the midpoints of \(A D\) and \(A E\) , respectively. Let \(H\) be the orthocentre of triangle \(A D E\) . Let \(P\) and \(Q\) be points on lines \(B M\) and \(C N\) , respectively, such that \(D\) , \(H\) , \(M\) , and \(P\) are concyclic and \(E\) , \(H\) , \(N\) , and \(Q\) are concyclic. Prove that \(P\) , \(Q\) , \(N\) , and \(M\) are concyclic.
The orthocentre of a triangle is the point of intersection of its altitudes.
|
As in solution 2, we will prove that \(O'\) is both on line \(HT\) and the radical axis of the circles, hence \(T\) is on the radical axis, from which we conclude the required concyclicity. We present alternative proofs of both facts, discovered by contestants.
Let \(M_{1}\) , \(N_{1}\) be the midpoints of \(AM\) , \(AN\) , respectively, so that \(AM_{1}:M_{1}D = AN_{1}:N_{1}E = 1:3\) . It is easy to verify (e.g. by applying the theorems of Ceva or Menelaus, or by computing in barycentric coordinates as in Solution 3) that \(T\) lies on \(EM_{1}\) and \(DN_{1}\) . Note that \(M_{1}N_{1} \parallel DE\) , and also \(M_{1}O' \parallel HE\) as both are perpendicular to \(AMD\) , and similarly \(N_{1}O' \parallel HD\) . It follows that \(DEH\) and \(N_{1}M_{1}O'\) are homothetically similar triangles, and the center of their (negative) homothety is \(T = DN_{1} \cap EM_{1}\) . Therefore \(T\) also lies on \(HO'\) , as claimed. (We also have that the homothety is by factor \(\frac{M_{1}N_{1}}{ED} = -\frac{1}{4}\) .)
Now, let \(M_{2}\) , \(N_{2}\) be the second intersection points of \(O'M\) , \(O'N\) with the circumcircles of \(HMD\) , \(HNE\) , respectively. To prove that \(O'\) is on the radical axis, it suffices to show that \(O'M \cdot O'M_{2} = O'N \cdot O'N_{2}\) . But by definition of \(O'\) we have \(O'M = O'N\) , so we must show \(O'M_{2} = O'N_{2}\) , which is equivalent to \(M_{2}N_{2} \parallel MN\) . Angle chasing in circle \(MM_{2}DH\) gives
\[\angle OM_{2}H = \angle MM_{2}H = \angle MDH = \angle ADH = 90^{\circ} - \angle EAD = 90^{\circ} - \angle NAM = \angle O'M N,\]
from which it follows that \(M_{2}H \parallel MN\) . Similarly, we have \(N_{2}H \parallel MN\) , and the two facts together imply that \(M_{2}, H, N_{2}\) are collinear and the line through them is parallel to \(MN\) , as claimed. \(\square\)

|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let \(A B C\) be an acute triangle. Points \(B\) , \(D\) , \(E\) , and \(C\) lie on a line in this order and satisfy \(B D =\) \(D E = E C\) . Let \(M\) and \(N\) be the midpoints of \(A D\) and \(A E\) , respectively. Let \(H\) be the orthocentre of triangle \(A D E\) . Let \(P\) and \(Q\) be points on lines \(B M\) and \(C N\) , respectively, such that \(D\) , \(H\) , \(M\) , and \(P\) are concyclic and \(E\) , \(H\) , \(N\) , and \(Q\) are concyclic. Prove that \(P\) , \(Q\) , \(N\) , and \(M\) are concyclic.
The orthocentre of a triangle is the point of intersection of its altitudes.
|
As in solution 2, we will prove that \(O'\) is both on line \(HT\) and the radical axis of the circles, hence \(T\) is on the radical axis, from which we conclude the required concyclicity. We present alternative proofs of both facts, discovered by contestants.
Let \(M_{1}\) , \(N_{1}\) be the midpoints of \(AM\) , \(AN\) , respectively, so that \(AM_{1}:M_{1}D = AN_{1}:N_{1}E = 1:3\) . It is easy to verify (e.g. by applying the theorems of Ceva or Menelaus, or by computing in barycentric coordinates as in Solution 3) that \(T\) lies on \(EM_{1}\) and \(DN_{1}\) . Note that \(M_{1}N_{1} \parallel DE\) , and also \(M_{1}O' \parallel HE\) as both are perpendicular to \(AMD\) , and similarly \(N_{1}O' \parallel HD\) . It follows that \(DEH\) and \(N_{1}M_{1}O'\) are homothetically similar triangles, and the center of their (negative) homothety is \(T = DN_{1} \cap EM_{1}\) . Therefore \(T\) also lies on \(HO'\) , as claimed. (We also have that the homothety is by factor \(\frac{M_{1}N_{1}}{ED} = -\frac{1}{4}\) .)
Now, let \(M_{2}\) , \(N_{2}\) be the second intersection points of \(O'M\) , \(O'N\) with the circumcircles of \(HMD\) , \(HNE\) , respectively. To prove that \(O'\) is on the radical axis, it suffices to show that \(O'M \cdot O'M_{2} = O'N \cdot O'N_{2}\) . But by definition of \(O'\) we have \(O'M = O'N\) , so we must show \(O'M_{2} = O'N_{2}\) , which is equivalent to \(M_{2}N_{2} \parallel MN\) . Angle chasing in circle \(MM_{2}DH\) gives
\[\angle OM_{2}H = \angle MM_{2}H = \angle MDH = \angle ADH = 90^{\circ} - \angle EAD = 90^{\circ} - \angle NAM = \angle O'M N,\]
from which it follows that \(M_{2}H \parallel MN\) . Similarly, we have \(N_{2}H \parallel MN\) , and the two facts together imply that \(M_{2}, H, N_{2}\) are collinear and the line through them is parallel to \(MN\) , as claimed. \(\square\)

|
{
"exam": "EGMO",
"problem_label": "3",
"problem_match": "P3.",
"resource_path": "EGMO/segmented/en-2025-solutions.jsonl",
"solution_match": "\nSolution 2'.",
"tier": "T2",
"year": "2025"
}
|
Let \(A B C\) be an acute triangle. Points \(B\) , \(D\) , \(E\) , and \(C\) lie on a line in this order and satisfy \(B D =\) \(D E = E C\) . Let \(M\) and \(N\) be the midpoints of \(A D\) and \(A E\) , respectively. Let \(H\) be the orthocentre of triangle \(A D E\) . Let \(P\) and \(Q\) be points on lines \(B M\) and \(C N\) , respectively, such that \(D\) , \(H\) , \(M\) , and \(P\) are concyclic and \(E\) , \(H\) , \(N\) , and \(Q\) are concyclic. Prove that \(P\) , \(Q\) , \(N\) , and \(M\) are concyclic.
The orthocentre of a triangle is the point of intersection of its altitudes.
|
We compute using linear combinations with respect to \(A D E\) . We have \(B = 2D - E\) \(C = 2E - D\) \(M = \frac{A + D}{2}\) , and \(N = \frac{A + E}{2}\) , from which we immediately obtain that the intersection of \(T = B M\cap C N\) is \(T = \frac{3A + D + E}{5} = \frac{6M - B}{5} = \frac{6N - C}{5}\) . As in solution 2, we reduce to showing that \(T\) is on the radical axis of \(H D M\) and \(H E N\) , whence \(T M\cdot T P = T N\cdot T Q\) proves the concyclicity of \(P,Q,N,M\)
Synthetic finish, similar to Solution 2. Let \(O\) be the circumcentre of \(A D E\) and \(O^{\prime} = \frac{A + O}{2}\) be the circumcentre of \(A M N\) . As in Solution 2, we have that \(O^{\prime}\) is on the desired radical axis, so it is enough to show \(T\in O^{\prime}H\) . Let \(G = \frac{A + D + E}{3}\) be the barycentre of \(A D E\) . By properties of the Euler line, we also have \(G = \frac{H + 2O}{3}\) . Now using our known identities we find
\[T = \frac{3A + D + E}{5} = \frac{2A + 3G}{5} = \frac{2A + H + 2O}{5} = \frac{H + 4O^{\prime}}{5}\]
and in particular \(T\in H O^{\prime}\) , as we wanted to show.
Computational finish. Let \(f(T)\) be the power difference at \(T\) w.r.t. \(D H M\) and \(E H N\) . We compute \(f(A)\) and \(f(L)\) where \(L = \frac{D + E}{2}\) . Since \(T = \frac{3A + 2L}{5}\) , it is enough to show that \(3P(A) + 2P(L) = 0\) . In the following all lengths are directed. We compute trigonometrically: Let \(\alpha ,\beta ,\gamma\) be the angles of \(A D E\) and assume the diameter of its circumcircle is 1. We have
\[f(A) = \frac{A D^{2} - A E^{2}}{2} = \frac{\sin^{2}(\gamma) - \sin^{2}(\beta)}{2}.\]
To compute \(P(L)\) , let \(D^{\prime},E^{\prime}\) be the second intersection points of \(H M D,H N E\) with \(D E\) , and let \(M^{\prime},N^{\prime},F\) be the feet of the perpendiculars from \(H\) to \(A D,A E,D E\) , respectively. Note that \(D M^{\prime} =\) \(\sin \alpha \cos \beta\) , thus
\[M^{\prime}M = D M - D M^{\prime} = \frac{\sin(\alpha + \beta)}{2} - \sin \alpha \cos \beta = \frac{\sin(\beta - \alpha)}{2}.\]
We also have \(H M^{\prime} = \cos \alpha \cos \beta\) , \(H F = \cos \beta \cos \gamma\) , and \(H M^{\prime}M\sim H F D^{\prime}\) , therefore
\[F D^{\prime} = \frac{H F}{H M^{\prime}} M^{\prime}M = \frac{\cos\gamma\sin(\beta - \alpha)}{\cos\alpha}\]
and similarly
\[E^{\prime}F = \frac{\cos\beta\sin(\gamma - \alpha)}{\cos\alpha}.\]
We also have the standard \(FD = \sin \gamma \cos \beta\) and \(EF = \sin \beta \cos \gamma\) . We can finally compute
\[f(L) = LD\cdot LD^{\prime} - LE\cdot LE^{\prime} = \frac{\sin\alpha}{2} (LD^{\prime} + LE^{\prime}) = \frac{\sin\alpha}{2} (FD^{\prime} + FE^{\prime} - FD - FE)\] \[\qquad = \frac{\sin\alpha}{4\cos\alpha} (\cos \gamma \sin (\beta -\alpha) - \cos \beta \sin (\gamma -\alpha) - 2\cos \alpha (\sin \gamma \cos \beta -\sin \beta \cos \gamma))\] \[\qquad = \frac{3\sin\alpha\sin(\beta - \gamma)}{4} = \frac{3}{4} (\sin (\beta +\gamma)\sin (\beta -\gamma)) = \frac{3}{8} (\cos (2\gamma) - \cos (2\beta))\] \[\qquad = \frac{3}{4} (\sin^{2}(\beta) - \sin^{2}(\gamma)) = -\frac{3}{2} f(A).\quad \square\]

|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let \(A B C\) be an acute triangle. Points \(B\) , \(D\) , \(E\) , and \(C\) lie on a line in this order and satisfy \(B D =\) \(D E = E C\) . Let \(M\) and \(N\) be the midpoints of \(A D\) and \(A E\) , respectively. Let \(H\) be the orthocentre of triangle \(A D E\) . Let \(P\) and \(Q\) be points on lines \(B M\) and \(C N\) , respectively, such that \(D\) , \(H\) , \(M\) , and \(P\) are concyclic and \(E\) , \(H\) , \(N\) , and \(Q\) are concyclic. Prove that \(P\) , \(Q\) , \(N\) , and \(M\) are concyclic.
The orthocentre of a triangle is the point of intersection of its altitudes.
|
We compute using linear combinations with respect to \(A D E\) . We have \(B = 2D - E\) \(C = 2E - D\) \(M = \frac{A + D}{2}\) , and \(N = \frac{A + E}{2}\) , from which we immediately obtain that the intersection of \(T = B M\cap C N\) is \(T = \frac{3A + D + E}{5} = \frac{6M - B}{5} = \frac{6N - C}{5}\) . As in solution 2, we reduce to showing that \(T\) is on the radical axis of \(H D M\) and \(H E N\) , whence \(T M\cdot T P = T N\cdot T Q\) proves the concyclicity of \(P,Q,N,M\)
Synthetic finish, similar to Solution 2. Let \(O\) be the circumcentre of \(A D E\) and \(O^{\prime} = \frac{A + O}{2}\) be the circumcentre of \(A M N\) . As in Solution 2, we have that \(O^{\prime}\) is on the desired radical axis, so it is enough to show \(T\in O^{\prime}H\) . Let \(G = \frac{A + D + E}{3}\) be the barycentre of \(A D E\) . By properties of the Euler line, we also have \(G = \frac{H + 2O}{3}\) . Now using our known identities we find
\[T = \frac{3A + D + E}{5} = \frac{2A + 3G}{5} = \frac{2A + H + 2O}{5} = \frac{H + 4O^{\prime}}{5}\]
and in particular \(T\in H O^{\prime}\) , as we wanted to show.
Computational finish. Let \(f(T)\) be the power difference at \(T\) w.r.t. \(D H M\) and \(E H N\) . We compute \(f(A)\) and \(f(L)\) where \(L = \frac{D + E}{2}\) . Since \(T = \frac{3A + 2L}{5}\) , it is enough to show that \(3P(A) + 2P(L) = 0\) . In the following all lengths are directed. We compute trigonometrically: Let \(\alpha ,\beta ,\gamma\) be the angles of \(A D E\) and assume the diameter of its circumcircle is 1. We have
\[f(A) = \frac{A D^{2} - A E^{2}}{2} = \frac{\sin^{2}(\gamma) - \sin^{2}(\beta)}{2}.\]
To compute \(P(L)\) , let \(D^{\prime},E^{\prime}\) be the second intersection points of \(H M D,H N E\) with \(D E\) , and let \(M^{\prime},N^{\prime},F\) be the feet of the perpendiculars from \(H\) to \(A D,A E,D E\) , respectively. Note that \(D M^{\prime} =\) \(\sin \alpha \cos \beta\) , thus
\[M^{\prime}M = D M - D M^{\prime} = \frac{\sin(\alpha + \beta)}{2} - \sin \alpha \cos \beta = \frac{\sin(\beta - \alpha)}{2}.\]
We also have \(H M^{\prime} = \cos \alpha \cos \beta\) , \(H F = \cos \beta \cos \gamma\) , and \(H M^{\prime}M\sim H F D^{\prime}\) , therefore
\[F D^{\prime} = \frac{H F}{H M^{\prime}} M^{\prime}M = \frac{\cos\gamma\sin(\beta - \alpha)}{\cos\alpha}\]
and similarly
\[E^{\prime}F = \frac{\cos\beta\sin(\gamma - \alpha)}{\cos\alpha}.\]
We also have the standard \(FD = \sin \gamma \cos \beta\) and \(EF = \sin \beta \cos \gamma\) . We can finally compute
\[f(L) = LD\cdot LD^{\prime} - LE\cdot LE^{\prime} = \frac{\sin\alpha}{2} (LD^{\prime} + LE^{\prime}) = \frac{\sin\alpha}{2} (FD^{\prime} + FE^{\prime} - FD - FE)\] \[\qquad = \frac{\sin\alpha}{4\cos\alpha} (\cos \gamma \sin (\beta -\alpha) - \cos \beta \sin (\gamma -\alpha) - 2\cos \alpha (\sin \gamma \cos \beta -\sin \beta \cos \gamma))\] \[\qquad = \frac{3\sin\alpha\sin(\beta - \gamma)}{4} = \frac{3}{4} (\sin (\beta +\gamma)\sin (\beta -\gamma)) = \frac{3}{8} (\cos (2\gamma) - \cos (2\beta))\] \[\qquad = \frac{3}{4} (\sin^{2}(\beta) - \sin^{2}(\gamma)) = -\frac{3}{2} f(A).\quad \square\]

|
{
"exam": "EGMO",
"problem_label": "3",
"problem_match": "P3.",
"resource_path": "EGMO/segmented/en-2025-solutions.jsonl",
"solution_match": "\nSolution 3. ",
"tier": "T2",
"year": "2025"
}
|
Let \(A B C\) be an acute triangle. Points \(B\) , \(D\) , \(E\) , and \(C\) lie on a line in this order and satisfy \(B D =\) \(D E = E C\) . Let \(M\) and \(N\) be the midpoints of \(A D\) and \(A E\) , respectively. Let \(H\) be the orthocentre of triangle \(A D E\) . Let \(P\) and \(Q\) be points on lines \(B M\) and \(C N\) , respectively, such that \(D\) , \(H\) , \(M\) , and \(P\) are concyclic and \(E\) , \(H\) , \(N\) , and \(Q\) are concyclic. Prove that \(P\) , \(Q\) , \(N\) , and \(M\) are concyclic.
The orthocentre of a triangle is the point of intersection of its altitudes.
|
Let \(T = BM\cap CN\) , let \(F\) be the foot of the altitude from \(A\) to \(BC\) , let \(O\) be the circumcentre of \((ADE)\) , let \(D^{\prime}\neq D\) and \(E^{\prime}\neq E\) be the second intersections of \((DHMP)\) and \((EHNQ)\) with line \(BC\) and let \(U\) and \(V\) be the antipodes of \(D\) and \(E\) on \((DHMP)\) and \((EHNQ)\) , respectively.
We begin with a bit of barycentric coordinates. Set barycentric coordinates in \(\triangle ABC\) , set so that \(A = (1,0,0)\) , \(B = (0,1,0)\) , and \(C = (0,0,1)\) . The definitions of \(D\) and \(E\) give \(D = (0,2 / 3,1 / 3)\) and \(E = (0,1 / 3,2 / 3)\) , whence \(M = (1 / 2,1 / 3,1 / 6)\) and \(N = (1 / 2,1 / 6,1 / 3)\) . This means that line \(BM\) is given by \((1 / 2:y:1 / 6)\) while line \(CN\) is given by \((1 / 2:1 / 6:z)\) . So their intersection \(T\) is \((1 / 2:1 / 6:1 / 6) = (3:1:1)\) , giving \(T = \frac{3A + B + C}{5} = \frac{3A + D + E}{5}\) .
Our next tool is the linearity of the power of a point. Let \(f:\mathbb{R}^{2}\to \mathbb{R}\) be defined by
\[f(Z) = \mathrm{Pow}_{(DHMP)}(Z) - \mathrm{Pow}_{(EHNQ)}(Z).\]
It suffices to show that \(f(T) = 0\) ; from there, the required concyclicity will follow from \(TM\cdot TP =\) \(TN\cdot TQ\) . The key observation is that \(f\) is a linear function. In particular, \(f(T) = \frac{3f(A) + f(D) + f(E)}{5}\) So, we need only show that \(3f(A) + f(D) + f(E) = 0\) . Pick an arbitrary one- dimensional coordinate system on the line \(BC\) and let \(\tau\) be the map from a point on \(BC\) to its coordinate. We compute
\[f(A) = AM\cdot AD - AN\cdot AE = \frac{AD^2 - AE^2}{2} = \frac{FD^2 - FE^2}{2}\] \[\qquad = (\tau (E) - \tau (D))\left(\tau (F) - \tau \left(\frac{D + E}{2}\right)\right),\] \[f(D) = -DE\cdot DE^{\prime} = (\tau (E) - \tau (D))(\tau (D) - \tau (E^{\prime})),\] \[f(E) = ED\cdot ED^{\prime} = (\tau (E) - \tau (D))(\tau (E) - \tau (D^{\prime})).\]
Rearranging, it suffices to show that \(3\tau (F) = \tau (D^{\prime}) + \tau (E^{\prime}) + \tau ((D + E) / 2)\) . This can be rewritten as \(3F = D^{\prime} + E^{\prime} + (D + E) / 2\) . By projecting down to line \(BC\) , it suffices to show that the displacement vector \(H + 2A - (O + U + V)\) is perpendicular to line \(BC\) .
We do this using complex numbers. Let \((A D E)\) be the unit circle with \(A = a\) , \(D = d\) , and \(E = e\) , so that \(O = 0\) and \(H = h = a + d + e\) . Note that \(U\) satisfies \(U M\perp A D\) and \(U H\perp D H\perp A E\) . Translating these conditions into equations, we have \(u = a d\overline{{u}}\) and \(u + a e\overline{{u}} = h + a e\overline{{h}}\) . Rearranging gives
\[(d + e)u = d u + e(a d\overline{{u}}) = d(h + a e\overline{{h}}) \Rightarrow u = \frac{d h + a d e\overline{{h}}}{d + e}.\]
Computing \(v\) similarly, we get that
\[v:= H + 2A - (O + U + V) = h + 2a - \frac{(d + e)h + 2a d e\overline{{h}}}{d + e} = 2\left(a - \frac{a d e\overline{{h}}}{d + e}\right) = -\frac{2d e}{d + e}.\]
This displacement vector \(v\) satisfies \(v = d e\overline{{v}}\) and so it is orthogonal to line \(D E\) , as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let \(A B C\) be an acute triangle. Points \(B\) , \(D\) , \(E\) , and \(C\) lie on a line in this order and satisfy \(B D =\) \(D E = E C\) . Let \(M\) and \(N\) be the midpoints of \(A D\) and \(A E\) , respectively. Let \(H\) be the orthocentre of triangle \(A D E\) . Let \(P\) and \(Q\) be points on lines \(B M\) and \(C N\) , respectively, such that \(D\) , \(H\) , \(M\) , and \(P\) are concyclic and \(E\) , \(H\) , \(N\) , and \(Q\) are concyclic. Prove that \(P\) , \(Q\) , \(N\) , and \(M\) are concyclic.
The orthocentre of a triangle is the point of intersection of its altitudes.
|
Let \(T = BM\cap CN\) , let \(F\) be the foot of the altitude from \(A\) to \(BC\) , let \(O\) be the circumcentre of \((ADE)\) , let \(D^{\prime}\neq D\) and \(E^{\prime}\neq E\) be the second intersections of \((DHMP)\) and \((EHNQ)\) with line \(BC\) and let \(U\) and \(V\) be the antipodes of \(D\) and \(E\) on \((DHMP)\) and \((EHNQ)\) , respectively.
We begin with a bit of barycentric coordinates. Set barycentric coordinates in \(\triangle ABC\) , set so that \(A = (1,0,0)\) , \(B = (0,1,0)\) , and \(C = (0,0,1)\) . The definitions of \(D\) and \(E\) give \(D = (0,2 / 3,1 / 3)\) and \(E = (0,1 / 3,2 / 3)\) , whence \(M = (1 / 2,1 / 3,1 / 6)\) and \(N = (1 / 2,1 / 6,1 / 3)\) . This means that line \(BM\) is given by \((1 / 2:y:1 / 6)\) while line \(CN\) is given by \((1 / 2:1 / 6:z)\) . So their intersection \(T\) is \((1 / 2:1 / 6:1 / 6) = (3:1:1)\) , giving \(T = \frac{3A + B + C}{5} = \frac{3A + D + E}{5}\) .
Our next tool is the linearity of the power of a point. Let \(f:\mathbb{R}^{2}\to \mathbb{R}\) be defined by
\[f(Z) = \mathrm{Pow}_{(DHMP)}(Z) - \mathrm{Pow}_{(EHNQ)}(Z).\]
It suffices to show that \(f(T) = 0\) ; from there, the required concyclicity will follow from \(TM\cdot TP =\) \(TN\cdot TQ\) . The key observation is that \(f\) is a linear function. In particular, \(f(T) = \frac{3f(A) + f(D) + f(E)}{5}\) So, we need only show that \(3f(A) + f(D) + f(E) = 0\) . Pick an arbitrary one- dimensional coordinate system on the line \(BC\) and let \(\tau\) be the map from a point on \(BC\) to its coordinate. We compute
\[f(A) = AM\cdot AD - AN\cdot AE = \frac{AD^2 - AE^2}{2} = \frac{FD^2 - FE^2}{2}\] \[\qquad = (\tau (E) - \tau (D))\left(\tau (F) - \tau \left(\frac{D + E}{2}\right)\right),\] \[f(D) = -DE\cdot DE^{\prime} = (\tau (E) - \tau (D))(\tau (D) - \tau (E^{\prime})),\] \[f(E) = ED\cdot ED^{\prime} = (\tau (E) - \tau (D))(\tau (E) - \tau (D^{\prime})).\]
Rearranging, it suffices to show that \(3\tau (F) = \tau (D^{\prime}) + \tau (E^{\prime}) + \tau ((D + E) / 2)\) . This can be rewritten as \(3F = D^{\prime} + E^{\prime} + (D + E) / 2\) . By projecting down to line \(BC\) , it suffices to show that the displacement vector \(H + 2A - (O + U + V)\) is perpendicular to line \(BC\) .
We do this using complex numbers. Let \((A D E)\) be the unit circle with \(A = a\) , \(D = d\) , and \(E = e\) , so that \(O = 0\) and \(H = h = a + d + e\) . Note that \(U\) satisfies \(U M\perp A D\) and \(U H\perp D H\perp A E\) . Translating these conditions into equations, we have \(u = a d\overline{{u}}\) and \(u + a e\overline{{u}} = h + a e\overline{{h}}\) . Rearranging gives
\[(d + e)u = d u + e(a d\overline{{u}}) = d(h + a e\overline{{h}}) \Rightarrow u = \frac{d h + a d e\overline{{h}}}{d + e}.\]
Computing \(v\) similarly, we get that
\[v:= H + 2A - (O + U + V) = h + 2a - \frac{(d + e)h + 2a d e\overline{{h}}}{d + e} = 2\left(a - \frac{a d e\overline{{h}}}{d + e}\right) = -\frac{2d e}{d + e}.\]
This displacement vector \(v\) satisfies \(v = d e\overline{{v}}\) and so it is orthogonal to line \(D E\) , as desired.
|
{
"exam": "EGMO",
"problem_label": "3",
"problem_match": "P3.",
"resource_path": "EGMO/segmented/en-2025-solutions.jsonl",
"solution_match": "\nSolution 4. ",
"tier": "T2",
"year": "2025"
}
|
Let \(A B C\) be an acute triangle. Points \(B\) , \(D\) , \(E\) , and \(C\) lie on a line in this order and satisfy \(B D =\) \(D E = E C\) . Let \(M\) and \(N\) be the midpoints of \(A D\) and \(A E\) , respectively. Let \(H\) be the orthocentre of triangle \(A D E\) . Let \(P\) and \(Q\) be points on lines \(B M\) and \(C N\) , respectively, such that \(D\) , \(H\) , \(M\) , and \(P\) are concyclic and \(E\) , \(H\) , \(N\) , and \(Q\) are concyclic. Prove that \(P\) , \(Q\) , \(N\) , and \(M\) are concyclic.
The orthocentre of a triangle is the point of intersection of its altitudes.
|
This solution uses almost exclusively complex numbers. As in other solutions, we reduce to showing that \(H\) , \(S:= (D H M)\cap (E H N)\) , and \(T:= B M\cap C N\) are collinear; this is all of the synthetic information we shall use. (If one computes \(T = \frac{3A + D + E}{5}\) using means other than complex numbers, the solution becomes much shorter.)
We use complex numbers with \(A = a\) , \(D = d\) , and \(E = e\) on the unit circle. Note that \(H = a + d + e\) , \(M = \frac{a + d}{2}\) , and \(B = 2d - e\) . We will make great use of the "arbitrary line intersection formula," which says that the intersection between lines \(W X\) and \(Y Z\) can be written explicitly as
\[\frac{(\overline{{u}} x - w\overline{{x}})(y - z) - (w - x)(\overline{{y}} z - y\overline{{z}})}{(\overline{{w}} - \overline{{x}})(y - z) - (w - x)(\overline{{y}} - \overline{{z}})}.\]
We first use this to find \(T = t\) . We compute
\[b - m = (2d - e) - \frac{a + d}{2} = \frac{3d - a - 2e}{2}\] \[\overline{{b}} - m = \frac{3a e - d e - 2a d}{2a d e}\] \[\overline{{b}} m - b\overline{{m}} = \frac{2e - d}{d e}\cdot \frac{a + d}{2} -(2d - e)\cdot \frac{a + d}{2a d}\] \[\qquad = \frac{a(a + d)(2e - d) - (2d - e)(a + d)e}{2a d e} = \frac{(a + d)(2a e + e^{2} - a d - 2d e)}{2a d e}.\]
If \(\mathcal{E}\) is some expression, we use the notation \(\mathcal{E} - \{\sim \}\) to denote \(\mathcal{E}\) minus the expression formed by swapping \(d\) and \(e\) in \(\mathcal{E}\) . We now have
\[t = \frac{(\overline{{b}}m - b\overline{{m}})(c - n) - \{\sim\}}{(\overline{{b}} - \overline{{m}})(c - n) - \{\sim\}}\] \[\quad = \frac{(a + d)(2a e + e^{2} - a d - 2d e)(3e - a - 2d) - \{\sim\}}{(3a e - d e - 2a d)(3e - a - 2d) - \{\sim\}}\] \[\quad = \frac{[a^{3}(d - 2e) + a^{2}(3d^{2} - 7d e + 5e^{2}) + a(2d^{3} - d^{2}e - 3d e^{2} + 3e^{3}) + d e(4d^{2} - 8d e + 3e^{2})] - \{\sim\}}{[a^{2}(2d - 3e) + a(4d^{2} - 11d e + 9e^{2}) + d e(2d - 3e)] - \{\sim\}}\] \[\quad = \frac{a^{3}(3(d - e)) - a^{2}(2(d^{2} - e^{2})) + a(-(d^{3} - e^{3}) + 2d e(d - e)) + d e(d^{2} - e^{2})}{a^{2}(5(d - e)) - a(5(d^{2} - e^{2})) + d e(5(d - e))}\] \[\quad = \frac{3a^{3} - 2a^{2}(d + e) - a(d^{2} - d e + e^{2}) + d e(d + e)}{5(a^{2} - a(d + e) + d e)}\] \[\quad = \frac{(a - d)(a - e)(3a + d + e)}{5(a - d)(a - e)} = \frac{3a + d + e}{5}.\]
(The factorization in the last line can be motivated by noting that the expression, while cubic in \(a\) , is only quadratic in \(d\) . When written out as a polynomial in \(d\) , each coefficient is divisible by \(a - e\) ; by symmetry, the numerator is divisible by \(a - d\) as well, and the factorization follows.)
Computing \(S = s\) is slightly harder, as it is the intersection of two circles rather than of two lines. We get around this by noting that \(\{h,d,m,s\}\) are concyclic if and only if \(\{0,h - d,h - m,h - s\}\) are concyclic, which happens if and only if \(\{\frac{1}{h - d},\frac{1}{h - m},\frac{1}{h - s}\}\) are collinear. (One can see this by inversion, or just by writing out the cross- ratio in the special case when one of the points is zero.) Thus \(\frac{1}{h - s}\) is the intersection of the line through \(w:= \frac{1}{h - d}\) and \(x:= \frac{1}{h - m}\) and the line through \(y:= \frac{1}{h - e}\) and \(z:= \frac{1}{h - n}\) . We compute
\[w - x = \frac{1}{a + e} -\frac{1}{\frac{a + d}{2} + e} = -\frac{a - d}{(a + e)(a + d + 2e)}\] \[\overline{w - x} = \frac{ae^{2}(a - d)}{(a + e)(2ad + ae + de)}\] \[\overline{w} x - w\overline{x} = \frac{ae}{a + e}\cdot \frac{2}{a + d + 2e} -\frac{1}{a + e}\cdot \frac{2ade}{2ad + ae + de}\] \[\qquad = 2ae\frac{(2ad + ae + de) - d(a + d + 2e)}{(a + e)(a + d + 2e)(2ad + ae + de)}\] \[\qquad = \frac{2ae(a - d)(d + e)}{(a + e)(a + d + 2e)(2ad + ae + de)}.\]
Using the line intersection formula, we have
\[\frac{1}{h - s} = \frac{(\overline{w} x - w\overline{x})(y - z) - \{\sim\}}{(\overline{w} - \overline{x})(y - z) - \{\sim\}}\] \[= \frac{[\frac{2ae(a - d)(d + e)}{(a + e)(a + d + 2e)(2ad + ae + de)}] - \{\sim\}}{[\frac{ae^{2}(a - d)}{(a + e)(2ad + ae + de)}] - \{\sim\}}\] \[= 2(d + e)\frac{[e(ad + 2ae + de)] - \{\sim\}}{[e^{2}(a + d + 2e)(ad + 2ae + de)] - \{\sim\}}\] \[= 2(d + e)\frac{[a(de + 2e^{2}) + de^{2}] - \{\sim\}}{[a^{2}(de^{2} + 2e^{3}) + a(d^{2}e^{2} + 5de^{3} + 4e^{4}) + de(de^{2} + 2e^{3})] - \{\sim\}}\] \[= \frac{2(d + e)(a(2(e^{2} - d^{2})) + de(e - d))}{(a^{2} + de)(2(e^{3} - d^{3}) + de(e - d)) + a(4(e^{4} - d^{4}) + 5de(e^{2} - e^{2}))}\] \[= \frac{2(d + e)(2a(d + e) + de)}{(a^{2} + de)(2d^{2} + 3de + 2e^{2}) + a(d + e)(4d^{2} + 5de + 4e^{2})}.\]
Since \(h - t = \frac{2a + 4d + 4e}{5}\) , this gives us
\[\frac{h - s}{h - t} = \frac{5}{4}\cdot \frac{(a^{2} + de)(2d^{2} + 3de + 2e^{2}) + a(d + e)(4d^{2} + 5de + 4e^{2})}{(d + e)(2ad + 2ae + de)(a + 2d + 2e)}.\]
It is easy to see that this is real by using the symmetry of the expressions (both the numerator and denominator satisfy \(\mathcal{E} = a^{2}d^{3}e^{3}\overline{\mathcal{E}}\) . We conclude that \(H\) , \(S\) , and \(T\) are collinear, as desired.
|
proof
|
Yes
|
Incomplete
|
proof
|
Geometry
|
Let \(A B C\) be an acute triangle. Points \(B\) , \(D\) , \(E\) , and \(C\) lie on a line in this order and satisfy \(B D =\) \(D E = E C\) . Let \(M\) and \(N\) be the midpoints of \(A D\) and \(A E\) , respectively. Let \(H\) be the orthocentre of triangle \(A D E\) . Let \(P\) and \(Q\) be points on lines \(B M\) and \(C N\) , respectively, such that \(D\) , \(H\) , \(M\) , and \(P\) are concyclic and \(E\) , \(H\) , \(N\) , and \(Q\) are concyclic. Prove that \(P\) , \(Q\) , \(N\) , and \(M\) are concyclic.
The orthocentre of a triangle is the point of intersection of its altitudes.
|
This solution uses almost exclusively complex numbers. As in other solutions, we reduce to showing that \(H\) , \(S:= (D H M)\cap (E H N)\) , and \(T:= B M\cap C N\) are collinear; this is all of the synthetic information we shall use. (If one computes \(T = \frac{3A + D + E}{5}\) using means other than complex numbers, the solution becomes much shorter.)
We use complex numbers with \(A = a\) , \(D = d\) , and \(E = e\) on the unit circle. Note that \(H = a + d + e\) , \(M = \frac{a + d}{2}\) , and \(B = 2d - e\) . We will make great use of the "arbitrary line intersection formula," which says that the intersection between lines \(W X\) and \(Y Z\) can be written explicitly as
\[\frac{(\overline{{u}} x - w\overline{{x}})(y - z) - (w - x)(\overline{{y}} z - y\overline{{z}})}{(\overline{{w}} - \overline{{x}})(y - z) - (w - x)(\overline{{y}} - \overline{{z}})}.\]
We first use this to find \(T = t\) . We compute
\[b - m = (2d - e) - \frac{a + d}{2} = \frac{3d - a - 2e}{2}\] \[\overline{{b}} - m = \frac{3a e - d e - 2a d}{2a d e}\] \[\overline{{b}} m - b\overline{{m}} = \frac{2e - d}{d e}\cdot \frac{a + d}{2} -(2d - e)\cdot \frac{a + d}{2a d}\] \[\qquad = \frac{a(a + d)(2e - d) - (2d - e)(a + d)e}{2a d e} = \frac{(a + d)(2a e + e^{2} - a d - 2d e)}{2a d e}.\]
If \(\mathcal{E}\) is some expression, we use the notation \(\mathcal{E} - \{\sim \}\) to denote \(\mathcal{E}\) minus the expression formed by swapping \(d\) and \(e\) in \(\mathcal{E}\) . We now have
\[t = \frac{(\overline{{b}}m - b\overline{{m}})(c - n) - \{\sim\}}{(\overline{{b}} - \overline{{m}})(c - n) - \{\sim\}}\] \[\quad = \frac{(a + d)(2a e + e^{2} - a d - 2d e)(3e - a - 2d) - \{\sim\}}{(3a e - d e - 2a d)(3e - a - 2d) - \{\sim\}}\] \[\quad = \frac{[a^{3}(d - 2e) + a^{2}(3d^{2} - 7d e + 5e^{2}) + a(2d^{3} - d^{2}e - 3d e^{2} + 3e^{3}) + d e(4d^{2} - 8d e + 3e^{2})] - \{\sim\}}{[a^{2}(2d - 3e) + a(4d^{2} - 11d e + 9e^{2}) + d e(2d - 3e)] - \{\sim\}}\] \[\quad = \frac{a^{3}(3(d - e)) - a^{2}(2(d^{2} - e^{2})) + a(-(d^{3} - e^{3}) + 2d e(d - e)) + d e(d^{2} - e^{2})}{a^{2}(5(d - e)) - a(5(d^{2} - e^{2})) + d e(5(d - e))}\] \[\quad = \frac{3a^{3} - 2a^{2}(d + e) - a(d^{2} - d e + e^{2}) + d e(d + e)}{5(a^{2} - a(d + e) + d e)}\] \[\quad = \frac{(a - d)(a - e)(3a + d + e)}{5(a - d)(a - e)} = \frac{3a + d + e}{5}.\]
(The factorization in the last line can be motivated by noting that the expression, while cubic in \(a\) , is only quadratic in \(d\) . When written out as a polynomial in \(d\) , each coefficient is divisible by \(a - e\) ; by symmetry, the numerator is divisible by \(a - d\) as well, and the factorization follows.)
Computing \(S = s\) is slightly harder, as it is the intersection of two circles rather than of two lines. We get around this by noting that \(\{h,d,m,s\}\) are concyclic if and only if \(\{0,h - d,h - m,h - s\}\) are concyclic, which happens if and only if \(\{\frac{1}{h - d},\frac{1}{h - m},\frac{1}{h - s}\}\) are collinear. (One can see this by inversion, or just by writing out the cross- ratio in the special case when one of the points is zero.) Thus \(\frac{1}{h - s}\) is the intersection of the line through \(w:= \frac{1}{h - d}\) and \(x:= \frac{1}{h - m}\) and the line through \(y:= \frac{1}{h - e}\) and \(z:= \frac{1}{h - n}\) . We compute
\[w - x = \frac{1}{a + e} -\frac{1}{\frac{a + d}{2} + e} = -\frac{a - d}{(a + e)(a + d + 2e)}\] \[\overline{w - x} = \frac{ae^{2}(a - d)}{(a + e)(2ad + ae + de)}\] \[\overline{w} x - w\overline{x} = \frac{ae}{a + e}\cdot \frac{2}{a + d + 2e} -\frac{1}{a + e}\cdot \frac{2ade}{2ad + ae + de}\] \[\qquad = 2ae\frac{(2ad + ae + de) - d(a + d + 2e)}{(a + e)(a + d + 2e)(2ad + ae + de)}\] \[\qquad = \frac{2ae(a - d)(d + e)}{(a + e)(a + d + 2e)(2ad + ae + de)}.\]
Using the line intersection formula, we have
\[\frac{1}{h - s} = \frac{(\overline{w} x - w\overline{x})(y - z) - \{\sim\}}{(\overline{w} - \overline{x})(y - z) - \{\sim\}}\] \[= \frac{[\frac{2ae(a - d)(d + e)}{(a + e)(a + d + 2e)(2ad + ae + de)}] - \{\sim\}}{[\frac{ae^{2}(a - d)}{(a + e)(2ad + ae + de)}] - \{\sim\}}\] \[= 2(d + e)\frac{[e(ad + 2ae + de)] - \{\sim\}}{[e^{2}(a + d + 2e)(ad + 2ae + de)] - \{\sim\}}\] \[= 2(d + e)\frac{[a(de + 2e^{2}) + de^{2}] - \{\sim\}}{[a^{2}(de^{2} + 2e^{3}) + a(d^{2}e^{2} + 5de^{3} + 4e^{4}) + de(de^{2} + 2e^{3})] - \{\sim\}}\] \[= \frac{2(d + e)(a(2(e^{2} - d^{2})) + de(e - d))}{(a^{2} + de)(2(e^{3} - d^{3}) + de(e - d)) + a(4(e^{4} - d^{4}) + 5de(e^{2} - e^{2}))}\] \[= \frac{2(d + e)(2a(d + e) + de)}{(a^{2} + de)(2d^{2} + 3de + 2e^{2}) + a(d + e)(4d^{2} + 5de + 4e^{2})}.\]
Since \(h - t = \frac{2a + 4d + 4e}{5}\) , this gives us
\[\frac{h - s}{h - t} = \frac{5}{4}\cdot \frac{(a^{2} + de)(2d^{2} + 3de + 2e^{2}) + a(d + e)(4d^{2} + 5de + 4e^{2})}{(d + e)(2ad + 2ae + de)(a + 2d + 2e)}.\]
It is easy to see that this is real by using the symmetry of the expressions (both the numerator and denominator satisfy \(\mathcal{E} = a^{2}d^{3}e^{3}\overline{\mathcal{E}}\) . We conclude that \(H\) , \(S\) , and \(T\) are collinear, as desired.
|
{
"exam": "EGMO",
"problem_label": "3",
"problem_match": "P3.",
"resource_path": "EGMO/segmented/en-2025-solutions.jsonl",
"solution_match": "\nSolution 5. ",
"tier": "T2",
"year": "2025"
}
|
Let \(A B C\) be an acute triangle. Points \(B\) , \(D\) , \(E\) , and \(C\) lie on a line in this order and satisfy \(B D =\) \(D E = E C\) . Let \(M\) and \(N\) be the midpoints of \(A D\) and \(A E\) , respectively. Let \(H\) be the orthocentre of triangle \(A D E\) . Let \(P\) and \(Q\) be points on lines \(B M\) and \(C N\) , respectively, such that \(D\) , \(H\) , \(M\) , and \(P\) are concyclic and \(E\) , \(H\) , \(N\) , and \(Q\) are concyclic. Prove that \(P\) , \(Q\) , \(N\) , and \(M\) are concyclic.
The orthocentre of a triangle is the point of intersection of its altitudes.
|
As usual, we reduce to proving \(T = (3A + D + E) / 5\) is on the radical axis and compute; this time in Cartesian coordinates.
Let \(A(0,h)\) , \(D(b,0)\) , \(E(c,0)\) be coordinates for \(ADE\) . Then \(H(0, - \frac{b c}{h})\) , \(M(\frac{b}{2},\frac{h}{2})\) , \(N(\frac{c}{2},\frac{h}{2})\) and \(T(\frac{b + c}{5},\frac{3h}{5})\) . We compute \(O_{D}(x_{D},y_{D})\) the circumcentre of \(DMH\) and obtain \(O_{E}\) by symmetry. We then have to verify that \(O_{D}O_{E} \perp HT\) , which can be done by comparing slopes.
The centre \(O_{D}\) can be given by the intersection of perpendicular bisectors of \(DM\) and \(DH\) . This gives the following system of equations on \(x_{D},y_{D}\) :
\[h\cdot x_{D} + c\cdot y_{D} = \frac{b h}{2} -\frac{b c^{2}}{2 h}\] \[-b\cdot x_{D} + h\cdot y_{D} = -\frac{3 b^{2}}{4} +\frac{h^{2}}{4}\]
Solving the system gives
\[(h^{2} + b c)x_{D} = \frac{3 b^{2}c}{4} -\frac{b c^{2}}{2} +\frac{h^{2}b}{2} -\frac{h^{2}c}{4}\] \[(h^{2} + b c)y_{D} = -\frac{h b^{2}}{4} +\frac{h^{3}}{4} -\frac{b^{2}c^{2}}{2 h}\]
The formulas for \(x_{E}, y_{E}\) will be the same, swapping \(b \leftrightarrow c\) by symmetry; thus \(y_{D} - y_{E}\) and \(x_{D} - x_{E}\) will be antisymmetric in \(b, c\) and divisible by \(b - c\) , and explicitly:
\[(h^{2} + b c)(x_{D} - x_{E}) = \frac{b - c}{4} (5b c + 3h^{2})\] \[(h^{2} + b c)(y_{D} - y_{E}) = -\frac{b - c}{4} h(b + c)\]
So \(\frac{y_{D} - y_{E}}{x_{D} - x_{E}} = -\frac{h(b + c)}{5b c + 3h^{2}}\) .
The other slope is more immediate:
\[\frac{y_{T} - y_{H}}{x_{T} - x_{H}} = \frac{3h / 5 + b c / h}{(b + c) / 5} = \frac{5b c + 3h^{2}}{h(b + c)} = -\frac{x_{D} - x_{E}}{y_{D} - y_{E}}\]
so indeed the two slopes correspond to perpendicular lines.
## Day 2
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let \(A B C\) be an acute triangle. Points \(B\) , \(D\) , \(E\) , and \(C\) lie on a line in this order and satisfy \(B D =\) \(D E = E C\) . Let \(M\) and \(N\) be the midpoints of \(A D\) and \(A E\) , respectively. Let \(H\) be the orthocentre of triangle \(A D E\) . Let \(P\) and \(Q\) be points on lines \(B M\) and \(C N\) , respectively, such that \(D\) , \(H\) , \(M\) , and \(P\) are concyclic and \(E\) , \(H\) , \(N\) , and \(Q\) are concyclic. Prove that \(P\) , \(Q\) , \(N\) , and \(M\) are concyclic.
The orthocentre of a triangle is the point of intersection of its altitudes.
|
As usual, we reduce to proving \(T = (3A + D + E) / 5\) is on the radical axis and compute; this time in Cartesian coordinates.
Let \(A(0,h)\) , \(D(b,0)\) , \(E(c,0)\) be coordinates for \(ADE\) . Then \(H(0, - \frac{b c}{h})\) , \(M(\frac{b}{2},\frac{h}{2})\) , \(N(\frac{c}{2},\frac{h}{2})\) and \(T(\frac{b + c}{5},\frac{3h}{5})\) . We compute \(O_{D}(x_{D},y_{D})\) the circumcentre of \(DMH\) and obtain \(O_{E}\) by symmetry. We then have to verify that \(O_{D}O_{E} \perp HT\) , which can be done by comparing slopes.
The centre \(O_{D}\) can be given by the intersection of perpendicular bisectors of \(DM\) and \(DH\) . This gives the following system of equations on \(x_{D},y_{D}\) :
\[h\cdot x_{D} + c\cdot y_{D} = \frac{b h}{2} -\frac{b c^{2}}{2 h}\] \[-b\cdot x_{D} + h\cdot y_{D} = -\frac{3 b^{2}}{4} +\frac{h^{2}}{4}\]
Solving the system gives
\[(h^{2} + b c)x_{D} = \frac{3 b^{2}c}{4} -\frac{b c^{2}}{2} +\frac{h^{2}b}{2} -\frac{h^{2}c}{4}\] \[(h^{2} + b c)y_{D} = -\frac{h b^{2}}{4} +\frac{h^{3}}{4} -\frac{b^{2}c^{2}}{2 h}\]
The formulas for \(x_{E}, y_{E}\) will be the same, swapping \(b \leftrightarrow c\) by symmetry; thus \(y_{D} - y_{E}\) and \(x_{D} - x_{E}\) will be antisymmetric in \(b, c\) and divisible by \(b - c\) , and explicitly:
\[(h^{2} + b c)(x_{D} - x_{E}) = \frac{b - c}{4} (5b c + 3h^{2})\] \[(h^{2} + b c)(y_{D} - y_{E}) = -\frac{b - c}{4} h(b + c)\]
So \(\frac{y_{D} - y_{E}}{x_{D} - x_{E}} = -\frac{h(b + c)}{5b c + 3h^{2}}\) .
The other slope is more immediate:
\[\frac{y_{T} - y_{H}}{x_{T} - x_{H}} = \frac{3h / 5 + b c / h}{(b + c) / 5} = \frac{5b c + 3h^{2}}{h(b + c)} = -\frac{x_{D} - x_{E}}{y_{D} - y_{E}}\]
so indeed the two slopes correspond to perpendicular lines.
## Day 2
|
{
"exam": "EGMO",
"problem_label": "3",
"problem_match": "P3.",
"resource_path": "EGMO/segmented/en-2025-solutions.jsonl",
"solution_match": "\nSolution 6. ",
"tier": "T2",
"year": "2025"
}
|
Let \(A B C\) be an acute triangle with incentre \(I\) and \(A B \neq A C\) . Let lines \(B I\) and \(C I\) intersect the circumcircle of \(A B C\) at \(P \neq B\) and \(Q \neq C\) , respectively. Consider points \(R\) and \(S\) such that \(A Q R B\) and \(A C S P\) are parallelograms (with \(A Q \parallel R B\) , \(A B \parallel Q R\) , \(A C \parallel S P\) , and \(A P \parallel C S\) ). Let \(T\) be the point of intersection of lines \(R B\) and \(S C\) . Prove that points \(R\) , \(S\) , \(T\) , and \(I\) are concyclic.
|
We will prove that \(\triangle B I R\sim \triangle C I S\) , since the statement then follows from \(\angle T R I = \angle B R I = \angle C S I =\) \(\angle T S I\) .

Step 1. Let us prove \(\angle R B I = \angle S C I\) . We will use directed angles:
\[(B R,B I) = (B R,A B) + (A B,B I) = (A Q,A B) + (B I,B C)\] \[\qquad = (C Q,B C) + (B I,B C) = (C I,C B) + (B I,B C),\]
which is symmetric in \(B,C\) . Therefore, analogously we would obtain the same expression for \((C S,C I)\)
Step 2. Let us prove \(B R / B I = C S / C I\) . Clearly \(B R = A Q\) and \(C S = A P\) . Angle chasing gives \(\angle I C B = \angle Q C B = \angle A P Q\) , and similarly \(\angle P Q A = \angle C B I\) , and so \(\triangle I B C\sim \triangle A Q P\) , from which the desired \(A Q / B I = A P / C I\) follows. This finishes the solution.
Remark. In the alternative solutions below, the notation \((A B C)\) refers to the circle passing through points \(A\) , \(B\) , and \(C\) . \(D\) will refer to the midpoint of arc \(B C\) not containing point \(A\) , unless stated otherwise.
Let \(I_{A}\) be the \(A\) - excenter of \(\triangle A B C\) . It is well- known that points \(B\) , \(C\) , \(I\) , and \(I_{A}\) lie on a circle with diameter \(I I_{A}\) . The center of this circle is point \(D\) . It is clear that \(A\) , \(I\) and \(D\) are collinear.
In some of the solutions, some of the facts below may be used:
\(\cdot B,T,I,C\) are concyclic. Indeed, \(\angle B T C = \angle Q A P = A + \frac{B + C}{2} = 90^{\circ} + \frac{A}{2} = \angle B I C\) , so \(B,T,I,C\) are concyclic.
\(\angle Q A P = \angle B T C = \angle R T S\) . Indeed, since \(Q A\parallel B T\) and \(P A\parallel C T\) , then \(\angle Q A P = \angle B T C =\) \(\angle R T S\)
\(\cdot R Q\) and \(P S\) are tangents to \((A B C)\) . Indeed, \(\angle R Q B = \angle Q B A = \angle Q A B\) and similarly for \(P S\)
\(\cdot \triangle A Q P\sim I B C\) (see Solution 1 for the proof).
\(\cdot Q P\) is the perpendicular bisector of \(A I\) . Indeed, \(Q A = Q I\) and \(P A = P I\) so \(P Q\perp A I\) and \(P Q\) bisects \(A I\) .
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let \(A B C\) be an acute triangle with incentre \(I\) and \(A B \neq A C\) . Let lines \(B I\) and \(C I\) intersect the circumcircle of \(A B C\) at \(P \neq B\) and \(Q \neq C\) , respectively. Consider points \(R\) and \(S\) such that \(A Q R B\) and \(A C S P\) are parallelograms (with \(A Q \parallel R B\) , \(A B \parallel Q R\) , \(A C \parallel S P\) , and \(A P \parallel C S\) ). Let \(T\) be the point of intersection of lines \(R B\) and \(S C\) . Prove that points \(R\) , \(S\) , \(T\) , and \(I\) are concyclic.
|
We will prove that \(\triangle B I R\sim \triangle C I S\) , since the statement then follows from \(\angle T R I = \angle B R I = \angle C S I =\) \(\angle T S I\) .

Step 1. Let us prove \(\angle R B I = \angle S C I\) . We will use directed angles:
\[(B R,B I) = (B R,A B) + (A B,B I) = (A Q,A B) + (B I,B C)\] \[\qquad = (C Q,B C) + (B I,B C) = (C I,C B) + (B I,B C),\]
which is symmetric in \(B,C\) . Therefore, analogously we would obtain the same expression for \((C S,C I)\)
Step 2. Let us prove \(B R / B I = C S / C I\) . Clearly \(B R = A Q\) and \(C S = A P\) . Angle chasing gives \(\angle I C B = \angle Q C B = \angle A P Q\) , and similarly \(\angle P Q A = \angle C B I\) , and so \(\triangle I B C\sim \triangle A Q P\) , from which the desired \(A Q / B I = A P / C I\) follows. This finishes the solution.
Remark. In the alternative solutions below, the notation \((A B C)\) refers to the circle passing through points \(A\) , \(B\) , and \(C\) . \(D\) will refer to the midpoint of arc \(B C\) not containing point \(A\) , unless stated otherwise.
Let \(I_{A}\) be the \(A\) - excenter of \(\triangle A B C\) . It is well- known that points \(B\) , \(C\) , \(I\) , and \(I_{A}\) lie on a circle with diameter \(I I_{A}\) . The center of this circle is point \(D\) . It is clear that \(A\) , \(I\) and \(D\) are collinear.
In some of the solutions, some of the facts below may be used:
\(\cdot B,T,I,C\) are concyclic. Indeed, \(\angle B T C = \angle Q A P = A + \frac{B + C}{2} = 90^{\circ} + \frac{A}{2} = \angle B I C\) , so \(B,T,I,C\) are concyclic.
\(\angle Q A P = \angle B T C = \angle R T S\) . Indeed, since \(Q A\parallel B T\) and \(P A\parallel C T\) , then \(\angle Q A P = \angle B T C =\) \(\angle R T S\)
\(\cdot R Q\) and \(P S\) are tangents to \((A B C)\) . Indeed, \(\angle R Q B = \angle Q B A = \angle Q A B\) and similarly for \(P S\)
\(\cdot \triangle A Q P\sim I B C\) (see Solution 1 for the proof).
\(\cdot Q P\) is the perpendicular bisector of \(A I\) . Indeed, \(Q A = Q I\) and \(P A = P I\) so \(P Q\perp A I\) and \(P Q\) bisects \(A I\) .
|
{
"exam": "EGMO",
"problem_label": "4",
"problem_match": "P4.",
"resource_path": "EGMO/segmented/en-2025-solutions.jsonl",
"solution_match": "\nSolution 1. ",
"tier": "T2",
"year": "2025"
}
|
Let \(A B C\) be an acute triangle with incentre \(I\) and \(A B \neq A C\) . Let lines \(B I\) and \(C I\) intersect the circumcircle of \(A B C\) at \(P \neq B\) and \(Q \neq C\) , respectively. Consider points \(R\) and \(S\) such that \(A Q R B\) and \(A C S P\) are parallelograms (with \(A Q \parallel R B\) , \(A B \parallel Q R\) , \(A C \parallel S P\) , and \(A P \parallel C S\) ). Let \(T\) be the point of intersection of lines \(R B\) and \(S C\) . Prove that points \(R\) , \(S\) , \(T\) , and \(I\) are concyclic.
|
We use complex numbers, with \((A B C)\) as the unit circle. Set \(D = d\) , \(P = p\) , \(Q = q\) , so that \(A = a = - \frac{p q}{d}\) , \(B = b = - \frac{d q}{p}\) , and \(C = c = - \frac{d q}{q}\) . Write \(z\sim w\) if \(z / w\) is a nonzero real number. We observe that
\[\frac{R - T}{S - T}\sim \frac{R - B}{S - C} = \frac{Q - A}{P - A} = \frac{q + \frac{p q}{d}}{p + \frac{p q}{d}} = \frac{(d + p)q}{(d + q)p}.\]
So, it suffices to show that \(\frac{I - R}{I - S}\sim \frac{(d + p)q}{(d + q)p}\) . Indeed,
\[I - R = (d + p + q) - (Q + B - A) = d + p + \frac{d q}{p} - \frac{p q}{d} = (d + p)\left(1 + \frac{(d - p)q}{d p}\right) = \frac{(d + p)(d p + d q - p q)}{d p},\]
so
\[\frac{I - R}{I - S} = \frac{\frac{d + p}{d p}}{\frac{d + q}{d q}} = \frac{(d + p)q}{(d + q)p}.\]
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let \(A B C\) be an acute triangle with incentre \(I\) and \(A B \neq A C\) . Let lines \(B I\) and \(C I\) intersect the circumcircle of \(A B C\) at \(P \neq B\) and \(Q \neq C\) , respectively. Consider points \(R\) and \(S\) such that \(A Q R B\) and \(A C S P\) are parallelograms (with \(A Q \parallel R B\) , \(A B \parallel Q R\) , \(A C \parallel S P\) , and \(A P \parallel C S\) ). Let \(T\) be the point of intersection of lines \(R B\) and \(S C\) . Prove that points \(R\) , \(S\) , \(T\) , and \(I\) are concyclic.
|
We use complex numbers, with \((A B C)\) as the unit circle. Set \(D = d\) , \(P = p\) , \(Q = q\) , so that \(A = a = - \frac{p q}{d}\) , \(B = b = - \frac{d q}{p}\) , and \(C = c = - \frac{d q}{q}\) . Write \(z\sim w\) if \(z / w\) is a nonzero real number. We observe that
\[\frac{R - T}{S - T}\sim \frac{R - B}{S - C} = \frac{Q - A}{P - A} = \frac{q + \frac{p q}{d}}{p + \frac{p q}{d}} = \frac{(d + p)q}{(d + q)p}.\]
So, it suffices to show that \(\frac{I - R}{I - S}\sim \frac{(d + p)q}{(d + q)p}\) . Indeed,
\[I - R = (d + p + q) - (Q + B - A) = d + p + \frac{d q}{p} - \frac{p q}{d} = (d + p)\left(1 + \frac{(d - p)q}{d p}\right) = \frac{(d + p)(d p + d q - p q)}{d p},\]
so
\[\frac{I - R}{I - S} = \frac{\frac{d + p}{d p}}{\frac{d + q}{d q}} = \frac{(d + p)q}{(d + q)p}.\]
|
{
"exam": "EGMO",
"problem_label": "4",
"problem_match": "P4.",
"resource_path": "EGMO/segmented/en-2025-solutions.jsonl",
"solution_match": "\nSolution 2. ",
"tier": "T2",
"year": "2025"
}
|
Let \(A B C\) be an acute triangle with incentre \(I\) and \(A B \neq A C\) . Let lines \(B I\) and \(C I\) intersect the circumcircle of \(A B C\) at \(P \neq B\) and \(Q \neq C\) , respectively. Consider points \(R\) and \(S\) such that \(A Q R B\) and \(A C S P\) are parallelograms (with \(A Q \parallel R B\) , \(A B \parallel Q R\) , \(A C \parallel S P\) , and \(A P \parallel C S\) ). Let \(T\) be the point of intersection of lines \(R B\) and \(S C\) . Prove that points \(R\) , \(S\) , \(T\) , and \(I\) are concyclic.
|
In the following, all segment notations denote vectors.
As mentioned above, we find \(\triangle A Q P\sim \triangle I B C\) , and by definitions of the parallelograms we have \(B R = A Q\) and \(C S = A P\) as well as \(\angle R T S = \angle Q A P\) , so it suffices to show \(\angle R I S = \angle Q A P\) . From the similarity \(\triangle A Q P\sim \triangle I B C\) , we have a spiral map \(\lambda\) such that \(I B = \lambda A Q\) and \(I C = \lambda A P\) . It follows that \(I R = I B + B R = (\lambda +1)A Q\) and \(I S = I C + C S = (\lambda +1)A P\) . Because \(\lambda +1\) is also a spiral map, we have \(\triangle I R S\sim \triangle A Q P\) and in particular \(\angle R I S = \angle Q A P\) , as we wanted to show.
Remark. This solution is deeply related to the complex numbers solution; indeed, the vectors can be interpreted as complex numbers and the spiral map as a complex scalar multiplication. But it only relies on the additive structure of the complex numbers as a real plane and the linear map acting on them (rather than, e.g., multiplying two points together), making vectors a slightly more natural language for the claims.
Remark. The number 1 in the solution above represents the identity map.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let \(A B C\) be an acute triangle with incentre \(I\) and \(A B \neq A C\) . Let lines \(B I\) and \(C I\) intersect the circumcircle of \(A B C\) at \(P \neq B\) and \(Q \neq C\) , respectively. Consider points \(R\) and \(S\) such that \(A Q R B\) and \(A C S P\) are parallelograms (with \(A Q \parallel R B\) , \(A B \parallel Q R\) , \(A C \parallel S P\) , and \(A P \parallel C S\) ). Let \(T\) be the point of intersection of lines \(R B\) and \(S C\) . Prove that points \(R\) , \(S\) , \(T\) , and \(I\) are concyclic.
|
In the following, all segment notations denote vectors.
As mentioned above, we find \(\triangle A Q P\sim \triangle I B C\) , and by definitions of the parallelograms we have \(B R = A Q\) and \(C S = A P\) as well as \(\angle R T S = \angle Q A P\) , so it suffices to show \(\angle R I S = \angle Q A P\) . From the similarity \(\triangle A Q P\sim \triangle I B C\) , we have a spiral map \(\lambda\) such that \(I B = \lambda A Q\) and \(I C = \lambda A P\) . It follows that \(I R = I B + B R = (\lambda +1)A Q\) and \(I S = I C + C S = (\lambda +1)A P\) . Because \(\lambda +1\) is also a spiral map, we have \(\triangle I R S\sim \triangle A Q P\) and in particular \(\angle R I S = \angle Q A P\) , as we wanted to show.
Remark. This solution is deeply related to the complex numbers solution; indeed, the vectors can be interpreted as complex numbers and the spiral map as a complex scalar multiplication. But it only relies on the additive structure of the complex numbers as a real plane and the linear map acting on them (rather than, e.g., multiplying two points together), making vectors a slightly more natural language for the claims.
Remark. The number 1 in the solution above represents the identity map.
|
{
"exam": "EGMO",
"problem_label": "4",
"problem_match": "P4.",
"resource_path": "EGMO/segmented/en-2025-solutions.jsonl",
"solution_match": "\nSolution 3. ",
"tier": "T2",
"year": "2025"
}
|
Let \(A B C\) be an acute triangle with incentre \(I\) and \(A B \neq A C\) . Let lines \(B I\) and \(C I\) intersect the circumcircle of \(A B C\) at \(P \neq B\) and \(Q \neq C\) , respectively. Consider points \(R\) and \(S\) such that \(A Q R B\) and \(A C S P\) are parallelograms (with \(A Q \parallel R B\) , \(A B \parallel Q R\) , \(A C \parallel S P\) , and \(A P \parallel C S\) ). Let \(T\) be the point of intersection of lines \(R B\) and \(S C\) . Prove that points \(R\) , \(S\) , \(T\) , and \(I\) are concyclic.
|
Let \(E\) , \(F\) , \(G\) be the midpoints of \(A I\) , \(B Q\) , \(C P\) . As in Solution 1, angle chase shows that \(\triangle A Q P\sim\) \(\triangle I B C\) .
Note that by the Mean Geometry Theorem we have that \(\frac{1}{2} A Q P + \frac{1}{2} I B C = E F G\) is similar to \(\triangle I B C\) . Homothety with center \(A\) and scale- factor 2 maps \(E F G\) to \(I R S\) . Hence \(\angle R I S = \angle F E G = \angle Q A P =\) \(\angle B T C = \angle R T S\) , so \(R,T,I,S\) are concyclic.
Remark. As shown above, \(E\) lies on \(Q P\) and \(A I\perp P Q\) . One can prove that \(\angle F E G = \angle B I C\) in another way. Let \(J\) be the midpoint of \(P Q\) . Then \(\angle B I C = \angle F J G\) by midlines and \(\angle F J G = \angle F E G\) by the lemma below applied in \(B C P Q\) .
Lemma. Let \(A B C D\) is a cyclic quadrilateral and \(E\) is the intersection of its diagonals. Then the midpoints of \(A B\) , \(B C\) , \(C D\) and the foot of the perpendicular from \(E\) to \(B C\) are concyclic.

|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let \(A B C\) be an acute triangle with incentre \(I\) and \(A B \neq A C\) . Let lines \(B I\) and \(C I\) intersect the circumcircle of \(A B C\) at \(P \neq B\) and \(Q \neq C\) , respectively. Consider points \(R\) and \(S\) such that \(A Q R B\) and \(A C S P\) are parallelograms (with \(A Q \parallel R B\) , \(A B \parallel Q R\) , \(A C \parallel S P\) , and \(A P \parallel C S\) ). Let \(T\) be the point of intersection of lines \(R B\) and \(S C\) . Prove that points \(R\) , \(S\) , \(T\) , and \(I\) are concyclic.
|
Let \(E\) , \(F\) , \(G\) be the midpoints of \(A I\) , \(B Q\) , \(C P\) . As in Solution 1, angle chase shows that \(\triangle A Q P\sim\) \(\triangle I B C\) .
Note that by the Mean Geometry Theorem we have that \(\frac{1}{2} A Q P + \frac{1}{2} I B C = E F G\) is similar to \(\triangle I B C\) . Homothety with center \(A\) and scale- factor 2 maps \(E F G\) to \(I R S\) . Hence \(\angle R I S = \angle F E G = \angle Q A P =\) \(\angle B T C = \angle R T S\) , so \(R,T,I,S\) are concyclic.
Remark. As shown above, \(E\) lies on \(Q P\) and \(A I\perp P Q\) . One can prove that \(\angle F E G = \angle B I C\) in another way. Let \(J\) be the midpoint of \(P Q\) . Then \(\angle B I C = \angle F J G\) by midlines and \(\angle F J G = \angle F E G\) by the lemma below applied in \(B C P Q\) .
Lemma. Let \(A B C D\) is a cyclic quadrilateral and \(E\) is the intersection of its diagonals. Then the midpoints of \(A B\) , \(B C\) , \(C D\) and the foot of the perpendicular from \(E\) to \(B C\) are concyclic.

|
{
"exam": "EGMO",
"problem_label": "4",
"problem_match": "P4.",
"resource_path": "EGMO/segmented/en-2025-solutions.jsonl",
"solution_match": "\nSolution 4. ",
"tier": "T2",
"year": "2025"
}
|
Let \(A B C\) be an acute triangle with incentre \(I\) and \(A B \neq A C\) . Let lines \(B I\) and \(C I\) intersect the circumcircle of \(A B C\) at \(P \neq B\) and \(Q \neq C\) , respectively. Consider points \(R\) and \(S\) such that \(A Q R B\) and \(A C S P\) are parallelograms (with \(A Q \parallel R B\) , \(A B \parallel Q R\) , \(A C \parallel S P\) , and \(A P \parallel C S\) ). Let \(T\) be the point of intersection of lines \(R B\) and \(S C\) . Prove that points \(R\) , \(S\) , \(T\) , and \(I\) are concyclic.
|
Let \(O\) be the circumcenter of \((A B C)\) . Let \(M\) , \(N\) , and \(L\) be the midpoints of \(O D\) , \(P C\) , and \(Q B\) respectively.
Claim 1. \(\triangle O P Q\) and \(\triangle D C B\) are directly similar.
Proof. Clearly \(D B = D C\) and \(O Q = O P\) . Also note that \(\angle Q O P = 2\angle Q D P = 2\angle Q D A + 2\angle P D A =\) \(\angle B D A + \angle C D A = \angle B D C\) . So the two triangles are directly similar by SAS.
Claim 2. \(M L = M N\) and \(\angle L M N = 180^{\circ} - \angle B A C\)
Proof. Note that since \(\triangle O Q P\sim \triangle D B C\) by the Mean Geometry Theorem, we have that the average of the two triangles is also similar to them, therefore \(\triangle M L N\sim \triangle D B C\Rightarrow M L = M N\) and \(\angle L M N =\) \(\angle B D C = 180^{\circ} - \angle B A C\)
Let \(K\) be the reflection of \(A\) over \(M\)
Claim 3. \(K\) is the circumcenter of \(\triangle R T S\)
Proof. Note that since \(A Q R B\) and \(A P S C\) are parallelograms we have that \(A - L - R\) are collinear and that \(A - N - S\) are collinear. The homothety centered at \(A\) with scale- factor 2 maps \(\triangle L M N\) to \(\triangle R K S\) , therefore \(K R = K S\) and \(\angle R K S = \angle L M N = \angle B D C = 2(180^{\circ} - \angle R T S)\) (and \(K\) and \(T\) are in opposite sides of \(R S\) ), implying that \(K\) is the circumcenter of \(\triangle R T S\)
Claim 4. \(K T = K I\)
Proof. Note that \(A O K D\) is a parallelogram. Let \(B T\) intersect the \((A B C)\) again at point \(G\) . Since \(\angle A B G = \angle A B T = \angle Q A B = \angle Q C A\Rightarrow A Q = A G\) and also \(O Q = O G\) hence \(A O\perp Q G\) . Then by Reim's theorem we have that \(Q G\parallel T I\) and also that \(A O\parallel D K\) , so \(D K\perp T I\) . Since \(D I = D T\) , it means that \(K D\) is the perpendicular bisector of \(T I\) , therefore \(K T = K I\) .
This means that \(R T I S\) is cyclic with center \(K\) .
Remark. When \(K\) and \(T\) are on the same side of \(R S\) , it can be shown that \(\angle R K S = 2\angle R T S\) .

|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let \(A B C\) be an acute triangle with incentre \(I\) and \(A B \neq A C\) . Let lines \(B I\) and \(C I\) intersect the circumcircle of \(A B C\) at \(P \neq B\) and \(Q \neq C\) , respectively. Consider points \(R\) and \(S\) such that \(A Q R B\) and \(A C S P\) are parallelograms (with \(A Q \parallel R B\) , \(A B \parallel Q R\) , \(A C \parallel S P\) , and \(A P \parallel C S\) ). Let \(T\) be the point of intersection of lines \(R B\) and \(S C\) . Prove that points \(R\) , \(S\) , \(T\) , and \(I\) are concyclic.
|
Let \(O\) be the circumcenter of \((A B C)\) . Let \(M\) , \(N\) , and \(L\) be the midpoints of \(O D\) , \(P C\) , and \(Q B\) respectively.
Claim 1. \(\triangle O P Q\) and \(\triangle D C B\) are directly similar.
Proof. Clearly \(D B = D C\) and \(O Q = O P\) . Also note that \(\angle Q O P = 2\angle Q D P = 2\angle Q D A + 2\angle P D A =\) \(\angle B D A + \angle C D A = \angle B D C\) . So the two triangles are directly similar by SAS.
Claim 2. \(M L = M N\) and \(\angle L M N = 180^{\circ} - \angle B A C\)
Proof. Note that since \(\triangle O Q P\sim \triangle D B C\) by the Mean Geometry Theorem, we have that the average of the two triangles is also similar to them, therefore \(\triangle M L N\sim \triangle D B C\Rightarrow M L = M N\) and \(\angle L M N =\) \(\angle B D C = 180^{\circ} - \angle B A C\)
Let \(K\) be the reflection of \(A\) over \(M\)
Claim 3. \(K\) is the circumcenter of \(\triangle R T S\)
Proof. Note that since \(A Q R B\) and \(A P S C\) are parallelograms we have that \(A - L - R\) are collinear and that \(A - N - S\) are collinear. The homothety centered at \(A\) with scale- factor 2 maps \(\triangle L M N\) to \(\triangle R K S\) , therefore \(K R = K S\) and \(\angle R K S = \angle L M N = \angle B D C = 2(180^{\circ} - \angle R T S)\) (and \(K\) and \(T\) are in opposite sides of \(R S\) ), implying that \(K\) is the circumcenter of \(\triangle R T S\)
Claim 4. \(K T = K I\)
Proof. Note that \(A O K D\) is a parallelogram. Let \(B T\) intersect the \((A B C)\) again at point \(G\) . Since \(\angle A B G = \angle A B T = \angle Q A B = \angle Q C A\Rightarrow A Q = A G\) and also \(O Q = O G\) hence \(A O\perp Q G\) . Then by Reim's theorem we have that \(Q G\parallel T I\) and also that \(A O\parallel D K\) , so \(D K\perp T I\) . Since \(D I = D T\) , it means that \(K D\) is the perpendicular bisector of \(T I\) , therefore \(K T = K I\) .
This means that \(R T I S\) is cyclic with center \(K\) .
Remark. When \(K\) and \(T\) are on the same side of \(R S\) , it can be shown that \(\angle R K S = 2\angle R T S\) .

|
{
"exam": "EGMO",
"problem_label": "4",
"problem_match": "P4.",
"resource_path": "EGMO/segmented/en-2025-solutions.jsonl",
"solution_match": "\nSolution 5. ",
"tier": "T2",
"year": "2025"
}
|
Let \(A B C\) be an acute triangle with incentre \(I\) and \(A B \neq A C\) . Let lines \(B I\) and \(C I\) intersect the circumcircle of \(A B C\) at \(P \neq B\) and \(Q \neq C\) , respectively. Consider points \(R\) and \(S\) such that \(A Q R B\) and \(A C S P\) are parallelograms (with \(A Q \parallel R B\) , \(A B \parallel Q R\) , \(A C \parallel S P\) , and \(A P \parallel C S\) ). Let \(T\) be the point of intersection of lines \(R B\) and \(S C\) . Prove that points \(R\) , \(S\) , \(T\) , and \(I\) are concyclic.
|
As shown above, we have that \(BTIC\) is cyclic. Let \(D\) and \(E\) be the second intersections of \(AC\) and \(AB\) with this circle, respectively. Since the center of this circle lies on \(AI\) (by symmetry about \(AI\) ), we have that \(AB = AD\) and \(AC = AE\) , therefore \(BE = CD\) . Note that since \(C - I - Q\) and \(A - B - E\) are collinear, by Reim's theorem we have that \(AQ \parallel EI\) and since \(AQ \parallel BT\) , we have that \(BT \parallel EI\) . Similarly, we get \(CT \parallel DI\) . Let \(F\) and \(G\) be the intersections of \(ID\) and \(IE\) with \(PS\) and \(QR\) , respectively. Clearly, \(RGEB\) and \(FSCD\) are parallelograms. Since \(RGEB\) is parallelogram and \(BEIT\) is isosceles trapezoid, we have that \(RGIT\) is isosceles trapezoid. Similarly, \(SFIT\) is isosceles trapezoid. Hence, both of them are cyclic. Note also that \(QR = AB = AD = PF\) and \(QG = AE = AC = PS\) . Since \(QR\) and \(PS\) are tangents to the circumcircle of \(\triangle ABC\) we have that \(R\) and \(F\) are symmetric (reflections) about the perpendicular bisector of \(PQ\) . Similarly, \(G\) and \(S\) are symmetric about the perpendicular bisector of \(PQ\) . This gives us that \(QP \parallel RF \parallel GS\) and that \(RFSG\) is an isosceles trapezoid, hence a cyclic quadrilateral with \(\angle RGS = 180^{\circ} - \angle GQP = 180^{\circ} - \angle QAP = 180^{\circ} - \angle RTS \Rightarrow R, G, S, T\) are concyclic. Combining all the facts about the cyclic quadrilaterals we proved above, we have that \(R, G, S, F, I, T\) are concyclic. Therefore \(R, T, I, S\) lie on a circle.

|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let \(A B C\) be an acute triangle with incentre \(I\) and \(A B \neq A C\) . Let lines \(B I\) and \(C I\) intersect the circumcircle of \(A B C\) at \(P \neq B\) and \(Q \neq C\) , respectively. Consider points \(R\) and \(S\) such that \(A Q R B\) and \(A C S P\) are parallelograms (with \(A Q \parallel R B\) , \(A B \parallel Q R\) , \(A C \parallel S P\) , and \(A P \parallel C S\) ). Let \(T\) be the point of intersection of lines \(R B\) and \(S C\) . Prove that points \(R\) , \(S\) , \(T\) , and \(I\) are concyclic.
|
As shown above, we have that \(BTIC\) is cyclic. Let \(D\) and \(E\) be the second intersections of \(AC\) and \(AB\) with this circle, respectively. Since the center of this circle lies on \(AI\) (by symmetry about \(AI\) ), we have that \(AB = AD\) and \(AC = AE\) , therefore \(BE = CD\) . Note that since \(C - I - Q\) and \(A - B - E\) are collinear, by Reim's theorem we have that \(AQ \parallel EI\) and since \(AQ \parallel BT\) , we have that \(BT \parallel EI\) . Similarly, we get \(CT \parallel DI\) . Let \(F\) and \(G\) be the intersections of \(ID\) and \(IE\) with \(PS\) and \(QR\) , respectively. Clearly, \(RGEB\) and \(FSCD\) are parallelograms. Since \(RGEB\) is parallelogram and \(BEIT\) is isosceles trapezoid, we have that \(RGIT\) is isosceles trapezoid. Similarly, \(SFIT\) is isosceles trapezoid. Hence, both of them are cyclic. Note also that \(QR = AB = AD = PF\) and \(QG = AE = AC = PS\) . Since \(QR\) and \(PS\) are tangents to the circumcircle of \(\triangle ABC\) we have that \(R\) and \(F\) are symmetric (reflections) about the perpendicular bisector of \(PQ\) . Similarly, \(G\) and \(S\) are symmetric about the perpendicular bisector of \(PQ\) . This gives us that \(QP \parallel RF \parallel GS\) and that \(RFSG\) is an isosceles trapezoid, hence a cyclic quadrilateral with \(\angle RGS = 180^{\circ} - \angle GQP = 180^{\circ} - \angle QAP = 180^{\circ} - \angle RTS \Rightarrow R, G, S, T\) are concyclic. Combining all the facts about the cyclic quadrilaterals we proved above, we have that \(R, G, S, F, I, T\) are concyclic. Therefore \(R, T, I, S\) lie on a circle.

|
{
"exam": "EGMO",
"problem_label": "4",
"problem_match": "P4.",
"resource_path": "EGMO/segmented/en-2025-solutions.jsonl",
"solution_match": "\nSolution 6. ",
"tier": "T2",
"year": "2025"
}
|
Let \(A B C\) be an acute triangle with incentre \(I\) and \(A B \neq A C\) . Let lines \(B I\) and \(C I\) intersect the circumcircle of \(A B C\) at \(P \neq B\) and \(Q \neq C\) , respectively. Consider points \(R\) and \(S\) such that \(A Q R B\) and \(A C S P\) are parallelograms (with \(A Q \parallel R B\) , \(A B \parallel Q R\) , \(A C \parallel S P\) , and \(A P \parallel C S\) ). Let \(T\) be the point of intersection of lines \(R B\) and \(S C\) . Prove that points \(R\) , \(S\) , \(T\) , and \(I\) are concyclic.
|
Let \(E\) be the \(A\) - excenter of \(\triangle ABC\) . Let the midpoints of \(AQ, QB, CP, PA\) be the points \(F, G, H, J\) , respectively. Both \(PD\) and \(EC\) are perpendicular to \(CI\) , hence \(PD \parallel CE\) .
Since \(PA = PC\) we have that \(AJHC\) is an isosceles trapezoid so it is cyclic. Let \(K\) be the second intersection of \((AJHC)\) and \(AI\) . Then \(\angle ADP = \angle ACP = \angle ACH = \angle AKH \Rightarrow DP \parallel KH\) . So \(KH\) is a line passing through the midpoint of the side \(CP\) of trapezoid \(DPCE\) and parallel to the bases, hence \(K\) is the midpoint of \(DE\) . Similarly, we show that the circle \((AFGB)\) passes through the midpoint of \(DE\) . Homothety centered at \(A\) with scale- factor 2 maps \((AJH)\) to \((APS)\) , \((AFG)\) to \((AQR)\) , and line \(AI\) to line \(AI\) . This means that the circles \((AQR)\) and \((APS)\) intersect on \(AI\) , call it point \(L\) .

Now, \(\angle I L R = 180^{\circ} - \angle A Q R = \angle Q A B = \angle Q C B = 180^{\circ} - \angle I T B = 180^{\circ} - \angle I T R\) , therefore \(R,L,I,T\) are concyclic. Similarly, we get that \(S,L,T,I\) are concyclic. Combining these, it means that \(R\) and \(S\) belong to the circle \((L I T)\) . The conclusion follows.

|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let \(A B C\) be an acute triangle with incentre \(I\) and \(A B \neq A C\) . Let lines \(B I\) and \(C I\) intersect the circumcircle of \(A B C\) at \(P \neq B\) and \(Q \neq C\) , respectively. Consider points \(R\) and \(S\) such that \(A Q R B\) and \(A C S P\) are parallelograms (with \(A Q \parallel R B\) , \(A B \parallel Q R\) , \(A C \parallel S P\) , and \(A P \parallel C S\) ). Let \(T\) be the point of intersection of lines \(R B\) and \(S C\) . Prove that points \(R\) , \(S\) , \(T\) , and \(I\) are concyclic.
|
Let \(E\) be the \(A\) - excenter of \(\triangle ABC\) . Let the midpoints of \(AQ, QB, CP, PA\) be the points \(F, G, H, J\) , respectively. Both \(PD\) and \(EC\) are perpendicular to \(CI\) , hence \(PD \parallel CE\) .
Since \(PA = PC\) we have that \(AJHC\) is an isosceles trapezoid so it is cyclic. Let \(K\) be the second intersection of \((AJHC)\) and \(AI\) . Then \(\angle ADP = \angle ACP = \angle ACH = \angle AKH \Rightarrow DP \parallel KH\) . So \(KH\) is a line passing through the midpoint of the side \(CP\) of trapezoid \(DPCE\) and parallel to the bases, hence \(K\) is the midpoint of \(DE\) . Similarly, we show that the circle \((AFGB)\) passes through the midpoint of \(DE\) . Homothety centered at \(A\) with scale- factor 2 maps \((AJH)\) to \((APS)\) , \((AFG)\) to \((AQR)\) , and line \(AI\) to line \(AI\) . This means that the circles \((AQR)\) and \((APS)\) intersect on \(AI\) , call it point \(L\) .

Now, \(\angle I L R = 180^{\circ} - \angle A Q R = \angle Q A B = \angle Q C B = 180^{\circ} - \angle I T B = 180^{\circ} - \angle I T R\) , therefore \(R,L,I,T\) are concyclic. Similarly, we get that \(S,L,T,I\) are concyclic. Combining these, it means that \(R\) and \(S\) belong to the circle \((L I T)\) . The conclusion follows.

|
{
"exam": "EGMO",
"problem_label": "4",
"problem_match": "P4.",
"resource_path": "EGMO/segmented/en-2025-solutions.jsonl",
"solution_match": "\nSolution 7. ",
"tier": "T2",
"year": "2025"
}
|
Let \(n > 1\) be an integer. In a configuration of an \(n \times n\) board, each of the \(n^{2}\) cells contains an arrow, either pointing up, down, left, or right. Given a starting configuration, Turbo the snail starts in one of the cells of the board and travels from cell to cell. In each move, Turbo moves one square unit in the direction indicated by the arrow in her cell (possibly leaving the board). After each move, the arrows in all of the cells rotate \(90^{\circ}\) counterclockwise. We call a cell good if, starting from that cell, Turbo visits each cell of the board exactly once, without leaving the board, and returns to her initial cell at the end. Determine, in terms of \(n\) , the maximum number of good cells over all possible starting configurations.
|
We will show that the maximum number of good cells over all possible starting configurations is
\[\frac{n^{2}}{4} \quad \text{if} n \text{ is even and}\] \[0 \quad \text{if} n \text{ is odd.}\]
## Odd \(n\)
First, we will prove that there are no good cells if \(n\) is an odd number.
For Turbo to reach her goal, she must return to her initial cell after visiting every cell exactly once. Consider the chessboard coloring of the board. Without loss of generality, we assume that Turbo starts in a black cell. Since, at every step, Turbo moves to a cell of a different color; she will be in a white cell after \(n^{2} \equiv 1 \mod 2\) moves. Thus, it is impossible for Turbo to come back to her initial black cell on her \(n^{2}\) - th move, which is a contradiction. Thus there are no good cells.
## Lower bound for even \(n\)
We will now construct a starting configuration with \(\frac{n^{2}}{4}\) good cells for even \(n\) .
Let \((i,j)\) denote the cell in row \(i\) and column \(j\) . Consider the following cycle
\[\begin{array}{r l} & {(1,1)\rightarrow (1,2)\rightarrow (1,3)\rightarrow \ldots \rightarrow (1,n)}\\ & {\qquad \rightarrow (2,n)\rightarrow (2,n - 1)\rightarrow \ldots \rightarrow (2,2)}\\ & {\qquad \ldots}\\ & {\qquad \rightarrow (2i - 1,2)\rightarrow (2i - 1,3)\rightarrow \ldots \rightarrow (2i - 1,n)}\\ & {\qquad \rightarrow (2i,n)\rightarrow (2i,n - 1)\rightarrow \ldots \rightarrow (2i,2)}\\ & {\qquad \ldots}\\ & {\qquad \rightarrow (n,n)\rightarrow (n,n - 1)\rightarrow \ldots \rightarrow (n,2)}\\ & {\qquad \rightarrow (n,1)\rightarrow (n - 1,1)\rightarrow \ldots \rightarrow (2,1)\rightarrow (1,1).} \end{array} \quad (1,1)\]

Note that the cycle returns to the initial cell after visiting every cell exactly once. To prove that \((1,1)\) is good, we need to find a starting configuration such that Turbo traverses this cycle.
Let \(c_{i}\) be the \((i - 1)\) - th cell on the cycle: so we have \(c_{0} = (1,1)\) , \(c_{2} = (1,2)\) , ..., \(c_{n^{2} - 1} = (2,1)\) . For every \(i\) , we draw an arrow in cell \(c_{i}\) pointing towards cell \(c_{i + 1}\) (or pointing towards \(c_{0}\) if \(i = n^{2} - 1\) ) and then rotate this arrow \(i\) times \(90^{\circ}\) in the clockwise direction. After \(i\) moves, the arrow in \(c_{i}\) will have rotated \(i\) times \(90^{\circ}\) counterclockwise and be in the same direction as on the path defined above. Thus, Turbo will traverse the cycle \(c_{0}, c_{1}, c_{2}, \ldots , c_{n^{2} - 1}, c_{0}\) and \((1,1)\) is good.
Every four moves, all arrows point in the same direction as in the beginning. Moreover, the board will return to its initial configuration after traversing the full cycle, since \(n^{2}\) , the length of the cycle, is divisible by 4. Therefore Turbo can also start at any \(c_{i}\) with 4 \(| i\) and follow the same route. Hence the cells \(c_{0}, c_{4}, c_{8}, \ldots , c_{n^{2} - 4}\) are good and there are \(\frac{n^{2}}{4}\) of such cells.
## Upper bound for even \(n\)
We will prove that for even \(n\) and any start configuration there are at most \(\frac{n^{2}}{4}\) good cells.
Let \(a_{0}\) be a good cell. Let \(a_{0},a_{1},a_{2},\ldots ,a_{n^{2} - 1},a_{n^{2}} = a_{0}\) be the sequence of cells that Turbo visits when she starts at \(a_{0}\) . Now suppose there is another good cell \(b_{0}\) and let \(b_{0},b_{1},b_{2},\ldots ,b_{n^{2} - 1},b_{n^{2}} = b_{0}\) be the sequence of cells that Turbo visits when she starts at \(b_{0}\) .
Note that, since \(4\mid n^{2}\) , the arrows are back to their initial configuration after \(n^{2}\) steps. Thus, if Turbo keeps walking after returning to her initial cell, she would just traverse the same cycle over and over again.
Consider the upper left corner of the board. With standard row and column numbering, the corner cell is \((1,1)\) . This cell has only two neighbours, so both the \(a\) - route and the \(b\) - route must have cells \((2,1),(1,1),(1,2)\) in that order or \((1,2),(1,1),(2,1)\) in that order. Without loss of generality, \(a_{i - 1} =\) \((2,1)\) , \(a_{i} = (1,1)\) and \(a_{i + 1} = (1,2)\) for some \(i\) . Let \(j\) be such that \(b_{j} = (1,1)\) . If \(b_{j - 1} = (2,1) = a_{i - 1}\) then the arrow in cell \((2,1)\) must be pointed in the same direction after \(i - 1\) steps and after \(j - 1\) steps, so \(i\equiv j\) mod 4. But then the arrow in cell \(b_{j} = (1,1) = a_{i}\) must also be pointed in the same direction after \(i\) and after \(j\) steps, so Turbo moves to \(b_{j + 1} = a_{i + 1}\) in both cases, and again finds the arrow pointed in the same direction in both cases. Continuing, we find that the \(b\) - route is actually identical to \(a_{4t},a_{4t + 1},\ldots ,a_{n^{2}} = a_{0},a_{1},\ldots ,a_{4t - 1},a_{4t}\) for some \(t\) , as any other starting point would have the arrows in the wrong direction initially.
Now suppose instead that \(b_{j + 1} = (2,1) = a_{i - 1}\) . Considering the \(a\) - route, the arrows in the upper left corner after \(i - 1\) steps must be like this:

Considering the \(b\) - route instead, the arrows after \(j - 1\) steps must be like this:

From the arrows in cell \((1,1)\) we see that \(i\equiv j + 1\) mod 4. However, for the cells \((2,1)\) and \((1,2)\) this gives a contradiction.
We conclude that the only possible good cells are \(a_{4t}\) for \(t = 0,1,\ldots ,\frac{n^{2}}{4} - 1\) , which gives at most \(\frac{n^{2}}{4}\) good cells.
|
\frac{n^{2}}{4} \text{ if } n \text{ is even, and } 0 \text{ if } n \text{ is odd.}
|
Yes
|
Incomplete
|
math-word-problem
|
Combinatorics
|
Let \(n > 1\) be an integer. In a configuration of an \(n \times n\) board, each of the \(n^{2}\) cells contains an arrow, either pointing up, down, left, or right. Given a starting configuration, Turbo the snail starts in one of the cells of the board and travels from cell to cell. In each move, Turbo moves one square unit in the direction indicated by the arrow in her cell (possibly leaving the board). After each move, the arrows in all of the cells rotate \(90^{\circ}\) counterclockwise. We call a cell good if, starting from that cell, Turbo visits each cell of the board exactly once, without leaving the board, and returns to her initial cell at the end. Determine, in terms of \(n\) , the maximum number of good cells over all possible starting configurations.
|
We will show that the maximum number of good cells over all possible starting configurations is
\[\frac{n^{2}}{4} \quad \text{if} n \text{ is even and}\] \[0 \quad \text{if} n \text{ is odd.}\]
## Odd \(n\)
First, we will prove that there are no good cells if \(n\) is an odd number.
For Turbo to reach her goal, she must return to her initial cell after visiting every cell exactly once. Consider the chessboard coloring of the board. Without loss of generality, we assume that Turbo starts in a black cell. Since, at every step, Turbo moves to a cell of a different color; she will be in a white cell after \(n^{2} \equiv 1 \mod 2\) moves. Thus, it is impossible for Turbo to come back to her initial black cell on her \(n^{2}\) - th move, which is a contradiction. Thus there are no good cells.
## Lower bound for even \(n\)
We will now construct a starting configuration with \(\frac{n^{2}}{4}\) good cells for even \(n\) .
Let \((i,j)\) denote the cell in row \(i\) and column \(j\) . Consider the following cycle
\[\begin{array}{r l} & {(1,1)\rightarrow (1,2)\rightarrow (1,3)\rightarrow \ldots \rightarrow (1,n)}\\ & {\qquad \rightarrow (2,n)\rightarrow (2,n - 1)\rightarrow \ldots \rightarrow (2,2)}\\ & {\qquad \ldots}\\ & {\qquad \rightarrow (2i - 1,2)\rightarrow (2i - 1,3)\rightarrow \ldots \rightarrow (2i - 1,n)}\\ & {\qquad \rightarrow (2i,n)\rightarrow (2i,n - 1)\rightarrow \ldots \rightarrow (2i,2)}\\ & {\qquad \ldots}\\ & {\qquad \rightarrow (n,n)\rightarrow (n,n - 1)\rightarrow \ldots \rightarrow (n,2)}\\ & {\qquad \rightarrow (n,1)\rightarrow (n - 1,1)\rightarrow \ldots \rightarrow (2,1)\rightarrow (1,1).} \end{array} \quad (1,1)\]

Note that the cycle returns to the initial cell after visiting every cell exactly once. To prove that \((1,1)\) is good, we need to find a starting configuration such that Turbo traverses this cycle.
Let \(c_{i}\) be the \((i - 1)\) - th cell on the cycle: so we have \(c_{0} = (1,1)\) , \(c_{2} = (1,2)\) , ..., \(c_{n^{2} - 1} = (2,1)\) . For every \(i\) , we draw an arrow in cell \(c_{i}\) pointing towards cell \(c_{i + 1}\) (or pointing towards \(c_{0}\) if \(i = n^{2} - 1\) ) and then rotate this arrow \(i\) times \(90^{\circ}\) in the clockwise direction. After \(i\) moves, the arrow in \(c_{i}\) will have rotated \(i\) times \(90^{\circ}\) counterclockwise and be in the same direction as on the path defined above. Thus, Turbo will traverse the cycle \(c_{0}, c_{1}, c_{2}, \ldots , c_{n^{2} - 1}, c_{0}\) and \((1,1)\) is good.
Every four moves, all arrows point in the same direction as in the beginning. Moreover, the board will return to its initial configuration after traversing the full cycle, since \(n^{2}\) , the length of the cycle, is divisible by 4. Therefore Turbo can also start at any \(c_{i}\) with 4 \(| i\) and follow the same route. Hence the cells \(c_{0}, c_{4}, c_{8}, \ldots , c_{n^{2} - 4}\) are good and there are \(\frac{n^{2}}{4}\) of such cells.
## Upper bound for even \(n\)
We will prove that for even \(n\) and any start configuration there are at most \(\frac{n^{2}}{4}\) good cells.
Let \(a_{0}\) be a good cell. Let \(a_{0},a_{1},a_{2},\ldots ,a_{n^{2} - 1},a_{n^{2}} = a_{0}\) be the sequence of cells that Turbo visits when she starts at \(a_{0}\) . Now suppose there is another good cell \(b_{0}\) and let \(b_{0},b_{1},b_{2},\ldots ,b_{n^{2} - 1},b_{n^{2}} = b_{0}\) be the sequence of cells that Turbo visits when she starts at \(b_{0}\) .
Note that, since \(4\mid n^{2}\) , the arrows are back to their initial configuration after \(n^{2}\) steps. Thus, if Turbo keeps walking after returning to her initial cell, she would just traverse the same cycle over and over again.
Consider the upper left corner of the board. With standard row and column numbering, the corner cell is \((1,1)\) . This cell has only two neighbours, so both the \(a\) - route and the \(b\) - route must have cells \((2,1),(1,1),(1,2)\) in that order or \((1,2),(1,1),(2,1)\) in that order. Without loss of generality, \(a_{i - 1} =\) \((2,1)\) , \(a_{i} = (1,1)\) and \(a_{i + 1} = (1,2)\) for some \(i\) . Let \(j\) be such that \(b_{j} = (1,1)\) . If \(b_{j - 1} = (2,1) = a_{i - 1}\) then the arrow in cell \((2,1)\) must be pointed in the same direction after \(i - 1\) steps and after \(j - 1\) steps, so \(i\equiv j\) mod 4. But then the arrow in cell \(b_{j} = (1,1) = a_{i}\) must also be pointed in the same direction after \(i\) and after \(j\) steps, so Turbo moves to \(b_{j + 1} = a_{i + 1}\) in both cases, and again finds the arrow pointed in the same direction in both cases. Continuing, we find that the \(b\) - route is actually identical to \(a_{4t},a_{4t + 1},\ldots ,a_{n^{2}} = a_{0},a_{1},\ldots ,a_{4t - 1},a_{4t}\) for some \(t\) , as any other starting point would have the arrows in the wrong direction initially.
Now suppose instead that \(b_{j + 1} = (2,1) = a_{i - 1}\) . Considering the \(a\) - route, the arrows in the upper left corner after \(i - 1\) steps must be like this:

Considering the \(b\) - route instead, the arrows after \(j - 1\) steps must be like this:

From the arrows in cell \((1,1)\) we see that \(i\equiv j + 1\) mod 4. However, for the cells \((2,1)\) and \((1,2)\) this gives a contradiction.
We conclude that the only possible good cells are \(a_{4t}\) for \(t = 0,1,\ldots ,\frac{n^{2}}{4} - 1\) , which gives at most \(\frac{n^{2}}{4}\) good cells.
|
{
"exam": "EGMO",
"problem_label": "5",
"problem_match": "P5.",
"resource_path": "EGMO/segmented/en-2025-solutions.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2025"
}
|
In each cell of a \(2025 \times 2025\) board, a nonnegative real number is written in such a way that the sum of the numbers in each row is equal to 1, and the sum of the numbers in each column is equal to 1. Define \(r_{i}\) to be the largest value in row \(i\) , and let \(R = r_{1} + r_{2} + \dots + r_{2025}\) . Similarly, define \(c_{i}\) to be the largest value in column \(i\) , and let \(C = c_{1} + c_{2} + \dots + c_{2025}\) .What is the largest possible value of \(\frac{R}{C}\) ?
What is the largest possible value of \(\frac{R}{C}\) ?
|
Answer: \(\frac{2025}{89}\) .
In general, if the table is \(m^{2} \times m^{2}\) , the answer is \(\frac{m^{2}}{2m - 1}\) .
The example is as follows: label rows and columns from 1 to \(m^{2}\) , from top to bottom and left to right. For the first \(m\) columns, write \(\frac{1}{m}\) in all squares whose coordinates have the same residue modulo \(m\) and place 0 everywhere else. For the remaining \(m^{2} - m\) columns, place \(\frac{1}{m^{2}}\) everywhere. Then \(R = m^{2} \cdot \frac{1}{m} = m\) , and \(C = m \cdot \frac{1}{m} + (m^{2} - m) \cdot \frac{1}{m^{2}} = 2 - \frac{1}{m}\) . So the ratio is as claimed.
<table><tr><td>1/2</td><td>0</td><td>1/4</td><td>1/4</td></tr><tr><td>0</td><td>1/2</td><td>1/4</td><td>1/4</td></tr><tr><td>1/2</td><td>0</td><td>1/4</td><td>1/4</td></tr><tr><td>0</td><td>1/2</td><td>1/4</td><td>1/4</td></tr></table>
In particular, when \(n := m^{2} = 2025\) , we get \(\frac{2025}{89}\) . Now we need to show that \(\frac{R}{C} \leq \frac{n}{2\sqrt{n} - 1}\) .
For each row, select one cell having the largest value appearing in said row and colour it red. Then, without loss of generality, we may rearrange the columns such that the red cells appear in the first \(k\) columns from the left, and each column contains at least one red cell, for some \(k \leq n\) .
For the \(j^{\mathrm{th}}\) column, for all \(1 \leq j \leq k\) , let \(p_{j}\) and \(n_{j}\) denote the sum and number of red cells in it, respectively. We observe that \(c_{j}\) , the biggest number in the \(j^{\mathrm{th}}\) column, is at least \(\frac{p_{j}}{n_{j}}\) , for all \(1 \leq j \leq k\) . For all other columns, the largest value they contain is at least \(\frac{1}{n}\) , as their sum is 1. Thus, \(C \geq \frac{p_{1}}{n_{1}} + \frac{p_{2}}{n_{2}} + \dots + \frac{p_{k}}{n_{k}} + \frac{n - k}{n}\) .
We can also observe that \(R = p_{1} + p_{2} + \dots + p_{k}\) .
Therefore we have to show that:
\[p_{1} + p_{2} + \dots +p_{k} \leq \frac{n}{2\sqrt{n} - 1} \cdot \left(\frac{p_{1}}{n_{1}} + \frac{p_{2}}{n_{2}} + \dots + \frac{p_{k}}{n_{k}} + \frac{n - k}{n}\right). \quad (*)\]
By construction, \(n_{1} + n_{2} + \dots + n_{k} = n\) , and, as the numbers in every column are nonnegative, we see that \(p_{j} \leq 1\) for every \(j\) . Also, since each number in a red cell is at least \(\frac{1}{n}\) , we also have \(p_{j} \geq \frac{n_{j}}{n}\) .
Since our inequality is linear in each \(p_{j}\) , it suffices to prove it when each variable equals one of its two critical values. By relabeling, we may assume that \(p_{j} = \frac{n_{j}}{n}\) for \(1 \leq j \leq t\) , and \(p_{j} = 1\) for \(t + 1 \leq j \leq k\) , for an integer \(0 \leq t \leq k\) .
First, if \(t = k\) , we observe that \(p_{1} + p_{2} + \dots +p_{k} = \frac{n_{1}}{n} + \frac{n_{2}}{n} + \dots + \frac{n_{k}}{n} = 1\) , and that \(\frac{p_{1}}{n_{1}} + \frac{p_{2}}{n_{2}} + \dots + \frac{p_{k}}{n_{k}} = \frac{k}{n}\) , so the inequality becomes \(1 \leq \frac{n}{2\sqrt{n} - 1}\) , which is true.
From now on we may assume that \(t < k\) . We need to show that:
\[\frac{n_{1} + \dots + n_{t}}{n} +k - t \leq \frac{n}{2\sqrt{n} - 1} \cdot \left(\frac{t}{n} + \frac{1}{n_{t + 1}} + \dots + \frac{1}{n_{k}} + \frac{n - k}{n}\right).\]
By Cauchy- Schwarz inequality we have that:
\[\frac{1}{n_{t + 1}} + \dots + \frac{1}{n_{k}} \geq \frac{(k - t)^{2}}{n_{t + 1} + \dots + n_{k}} = \frac{(k - t)^{2}}{n - (n_{1} + \dots + n_{t})}. \quad (CS)\]
Let \(n_{1} + \dots +n_{t} = n\cdot q\) , where \(0\leq q< 1\) . Thus, it is now enough to show that:
\[q + k - t\leq \frac{n}{2\sqrt{n - 1}}\left(\frac{t}{n} +\frac{(k - t)^{2}}{n - nq} +\frac{n - k}{n}\right).\]
Let \(k - t = \ell \geq 1\) . The inequality becomes:
\[q + \ell \leq \frac{1}{2\sqrt{n} - 1}\cdot \left(n - \ell +\frac{\ell^{2}}{1 - q}\right).\]
Rearranging this we get:
\[n + q + \frac{\ell^{2}}{1 - q}\geq 2(q + \ell)\sqrt{n}.\]
If \(q = 0\) the inequality is trivially true by \(A M - G M\) . Suppose now that \(0< q< 1\) . Then, by Cauchy- Schwarz, we have:
\[q + \frac{\ell^{2}}{1 - q} = \frac{q^{2}}{q} +\frac{\ell^{2}}{1 - q}\geq (q + \ell)^{2}.\]
It is therefore enough to show that \(n + (q + \ell)^{2}\geq 2(q + \ell)\sqrt{n}\) , which is true by \(A M - G M\) , completing the proof.
Remark. Another way to show \(n + q + \frac{\ell^{2}}{1 - q}\geq 2(q + \ell)\sqrt{n}\) is to split it into two \(A M - G M\) 's, as:
\[\left(n(1 - q) + \frac{\ell^{2}}{1 - q}\right) + (nq + q)\geq 2\ell \sqrt{n} +2q\sqrt{n}.\]
|
\frac{2025}{89}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In each cell of a \(2025 \times 2025\) board, a nonnegative real number is written in such a way that the sum of the numbers in each row is equal to 1, and the sum of the numbers in each column is equal to 1. Define \(r_{i}\) to be the largest value in row \(i\) , and let \(R = r_{1} + r_{2} + \dots + r_{2025}\) . Similarly, define \(c_{i}\) to be the largest value in column \(i\) , and let \(C = c_{1} + c_{2} + \dots + c_{2025}\) .What is the largest possible value of \(\frac{R}{C}\) ?
What is the largest possible value of \(\frac{R}{C}\) ?
|
Answer: \(\frac{2025}{89}\) .
In general, if the table is \(m^{2} \times m^{2}\) , the answer is \(\frac{m^{2}}{2m - 1}\) .
The example is as follows: label rows and columns from 1 to \(m^{2}\) , from top to bottom and left to right. For the first \(m\) columns, write \(\frac{1}{m}\) in all squares whose coordinates have the same residue modulo \(m\) and place 0 everywhere else. For the remaining \(m^{2} - m\) columns, place \(\frac{1}{m^{2}}\) everywhere. Then \(R = m^{2} \cdot \frac{1}{m} = m\) , and \(C = m \cdot \frac{1}{m} + (m^{2} - m) \cdot \frac{1}{m^{2}} = 2 - \frac{1}{m}\) . So the ratio is as claimed.
<table><tr><td>1/2</td><td>0</td><td>1/4</td><td>1/4</td></tr><tr><td>0</td><td>1/2</td><td>1/4</td><td>1/4</td></tr><tr><td>1/2</td><td>0</td><td>1/4</td><td>1/4</td></tr><tr><td>0</td><td>1/2</td><td>1/4</td><td>1/4</td></tr></table>
In particular, when \(n := m^{2} = 2025\) , we get \(\frac{2025}{89}\) . Now we need to show that \(\frac{R}{C} \leq \frac{n}{2\sqrt{n} - 1}\) .
For each row, select one cell having the largest value appearing in said row and colour it red. Then, without loss of generality, we may rearrange the columns such that the red cells appear in the first \(k\) columns from the left, and each column contains at least one red cell, for some \(k \leq n\) .
For the \(j^{\mathrm{th}}\) column, for all \(1 \leq j \leq k\) , let \(p_{j}\) and \(n_{j}\) denote the sum and number of red cells in it, respectively. We observe that \(c_{j}\) , the biggest number in the \(j^{\mathrm{th}}\) column, is at least \(\frac{p_{j}}{n_{j}}\) , for all \(1 \leq j \leq k\) . For all other columns, the largest value they contain is at least \(\frac{1}{n}\) , as their sum is 1. Thus, \(C \geq \frac{p_{1}}{n_{1}} + \frac{p_{2}}{n_{2}} + \dots + \frac{p_{k}}{n_{k}} + \frac{n - k}{n}\) .
We can also observe that \(R = p_{1} + p_{2} + \dots + p_{k}\) .
Therefore we have to show that:
\[p_{1} + p_{2} + \dots +p_{k} \leq \frac{n}{2\sqrt{n} - 1} \cdot \left(\frac{p_{1}}{n_{1}} + \frac{p_{2}}{n_{2}} + \dots + \frac{p_{k}}{n_{k}} + \frac{n - k}{n}\right). \quad (*)\]
By construction, \(n_{1} + n_{2} + \dots + n_{k} = n\) , and, as the numbers in every column are nonnegative, we see that \(p_{j} \leq 1\) for every \(j\) . Also, since each number in a red cell is at least \(\frac{1}{n}\) , we also have \(p_{j} \geq \frac{n_{j}}{n}\) .
Since our inequality is linear in each \(p_{j}\) , it suffices to prove it when each variable equals one of its two critical values. By relabeling, we may assume that \(p_{j} = \frac{n_{j}}{n}\) for \(1 \leq j \leq t\) , and \(p_{j} = 1\) for \(t + 1 \leq j \leq k\) , for an integer \(0 \leq t \leq k\) .
First, if \(t = k\) , we observe that \(p_{1} + p_{2} + \dots +p_{k} = \frac{n_{1}}{n} + \frac{n_{2}}{n} + \dots + \frac{n_{k}}{n} = 1\) , and that \(\frac{p_{1}}{n_{1}} + \frac{p_{2}}{n_{2}} + \dots + \frac{p_{k}}{n_{k}} = \frac{k}{n}\) , so the inequality becomes \(1 \leq \frac{n}{2\sqrt{n} - 1}\) , which is true.
From now on we may assume that \(t < k\) . We need to show that:
\[\frac{n_{1} + \dots + n_{t}}{n} +k - t \leq \frac{n}{2\sqrt{n} - 1} \cdot \left(\frac{t}{n} + \frac{1}{n_{t + 1}} + \dots + \frac{1}{n_{k}} + \frac{n - k}{n}\right).\]
By Cauchy- Schwarz inequality we have that:
\[\frac{1}{n_{t + 1}} + \dots + \frac{1}{n_{k}} \geq \frac{(k - t)^{2}}{n_{t + 1} + \dots + n_{k}} = \frac{(k - t)^{2}}{n - (n_{1} + \dots + n_{t})}. \quad (CS)\]
Let \(n_{1} + \dots +n_{t} = n\cdot q\) , where \(0\leq q< 1\) . Thus, it is now enough to show that:
\[q + k - t\leq \frac{n}{2\sqrt{n - 1}}\left(\frac{t}{n} +\frac{(k - t)^{2}}{n - nq} +\frac{n - k}{n}\right).\]
Let \(k - t = \ell \geq 1\) . The inequality becomes:
\[q + \ell \leq \frac{1}{2\sqrt{n} - 1}\cdot \left(n - \ell +\frac{\ell^{2}}{1 - q}\right).\]
Rearranging this we get:
\[n + q + \frac{\ell^{2}}{1 - q}\geq 2(q + \ell)\sqrt{n}.\]
If \(q = 0\) the inequality is trivially true by \(A M - G M\) . Suppose now that \(0< q< 1\) . Then, by Cauchy- Schwarz, we have:
\[q + \frac{\ell^{2}}{1 - q} = \frac{q^{2}}{q} +\frac{\ell^{2}}{1 - q}\geq (q + \ell)^{2}.\]
It is therefore enough to show that \(n + (q + \ell)^{2}\geq 2(q + \ell)\sqrt{n}\) , which is true by \(A M - G M\) , completing the proof.
Remark. Another way to show \(n + q + \frac{\ell^{2}}{1 - q}\geq 2(q + \ell)\sqrt{n}\) is to split it into two \(A M - G M\) 's, as:
\[\left(n(1 - q) + \frac{\ell^{2}}{1 - q}\right) + (nq + q)\geq 2\ell \sqrt{n} +2q\sqrt{n}.\]
|
{
"exam": "EGMO",
"problem_label": "6",
"problem_match": "P6.",
"resource_path": "EGMO/segmented/en-2025-solutions.jsonl",
"solution_match": "\nSolution 1. ",
"tier": "T2",
"year": "2025"
}
|
In each cell of a \(2025 \times 2025\) board, a nonnegative real number is written in such a way that the sum of the numbers in each row is equal to 1, and the sum of the numbers in each column is equal to 1. Define \(r_{i}\) to be the largest value in row \(i\) , and let \(R = r_{1} + r_{2} + \dots + r_{2025}\) . Similarly, define \(c_{i}\) to be the largest value in column \(i\) , and let \(C = c_{1} + c_{2} + \dots + c_{2025}\) .What is the largest possible value of \(\frac{R}{C}\) ?
What is the largest possible value of \(\frac{R}{C}\) ?
|
We prove the main inequality \((\ast)\) in a slightly different manner. Instead of the strong lower bound \(p_{j}\geq \frac{n_{j}}{n}\) , we use the weaker, simpler and more immediate lower bound \(p_{j}\geq 0\) (thus proving the inequality in a larger regime).
As in Solution 1, suppose \(p_{j} = 0\) for \(1\leq j\leq t\) and \(p_{j} = 1\) for \(t + 1\leq j\leq k\) , with \(\ell = k - t\) . We also denote by \(m = n_{t + 1} + \dots +n_{k}\) and note that \(m\leq n - t\) , since \(n_{j}\geq 1\) for each \(i\leq t\) . We need to prove that:
\[\ell \leq \frac{n}{2\sqrt{n} - 1}\cdot \left(\frac{1}{n_{t + 1}} +\dots +\frac{1}{n_{k}} +\frac{n - k}{n}\right).\]
Rearranging and using the same Cauchy- Schwarz (CS) as in Solution 1, we see it suffices to show that:
\[(2\sqrt{n} -1)\ell \leq n - k + \frac{n\ell^{2}}{m},\]
or equivalently, that:
\[2\sqrt{n}\ell \leq n - t + \frac{n\ell^{2}}{m}.\]
But since \(n - t\geq m\) this immediately follows from \(2\sqrt{n}\ell \leq m + \frac{n\ell^{2}}{m}\) , which is a simple application of \(A M - G M\) .
(Note that in Solution 1 the case \(t = k\) , which is equivalent to \(m = \ell = 0\) , was dealt with separately, to avoid the appearance of \(\frac{0}{0}\) terms such as \(\frac{n\ell^{2}}{m}\) . It is easy to verify that the corresponding term should in fact be 0 and the final \(A M - G M\) replaced with \(0\leq 0\) , and all transitions are valid. Alternatively, the case can be argued directly by simply noting that \((\ast)\) evaluates to \(0\leq \frac{n - k}{2\sqrt{n} - 1}\) , which is obvious.)
|
not found
|
Yes
|
Incomplete
|
math-word-problem
|
Combinatorics
|
In each cell of a \(2025 \times 2025\) board, a nonnegative real number is written in such a way that the sum of the numbers in each row is equal to 1, and the sum of the numbers in each column is equal to 1. Define \(r_{i}\) to be the largest value in row \(i\) , and let \(R = r_{1} + r_{2} + \dots + r_{2025}\) . Similarly, define \(c_{i}\) to be the largest value in column \(i\) , and let \(C = c_{1} + c_{2} + \dots + c_{2025}\) .What is the largest possible value of \(\frac{R}{C}\) ?
What is the largest possible value of \(\frac{R}{C}\) ?
|
We prove the main inequality \((\ast)\) in a slightly different manner. Instead of the strong lower bound \(p_{j}\geq \frac{n_{j}}{n}\) , we use the weaker, simpler and more immediate lower bound \(p_{j}\geq 0\) (thus proving the inequality in a larger regime).
As in Solution 1, suppose \(p_{j} = 0\) for \(1\leq j\leq t\) and \(p_{j} = 1\) for \(t + 1\leq j\leq k\) , with \(\ell = k - t\) . We also denote by \(m = n_{t + 1} + \dots +n_{k}\) and note that \(m\leq n - t\) , since \(n_{j}\geq 1\) for each \(i\leq t\) . We need to prove that:
\[\ell \leq \frac{n}{2\sqrt{n} - 1}\cdot \left(\frac{1}{n_{t + 1}} +\dots +\frac{1}{n_{k}} +\frac{n - k}{n}\right).\]
Rearranging and using the same Cauchy- Schwarz (CS) as in Solution 1, we see it suffices to show that:
\[(2\sqrt{n} -1)\ell \leq n - k + \frac{n\ell^{2}}{m},\]
or equivalently, that:
\[2\sqrt{n}\ell \leq n - t + \frac{n\ell^{2}}{m}.\]
But since \(n - t\geq m\) this immediately follows from \(2\sqrt{n}\ell \leq m + \frac{n\ell^{2}}{m}\) , which is a simple application of \(A M - G M\) .
(Note that in Solution 1 the case \(t = k\) , which is equivalent to \(m = \ell = 0\) , was dealt with separately, to avoid the appearance of \(\frac{0}{0}\) terms such as \(\frac{n\ell^{2}}{m}\) . It is easy to verify that the corresponding term should in fact be 0 and the final \(A M - G M\) replaced with \(0\leq 0\) , and all transitions are valid. Alternatively, the case can be argued directly by simply noting that \((\ast)\) evaluates to \(0\leq \frac{n - k}{2\sqrt{n} - 1}\) , which is obvious.)
|
{
"exam": "EGMO",
"problem_label": "6",
"problem_match": "P6.",
"resource_path": "EGMO/segmented/en-2025-solutions.jsonl",
"solution_match": "\nSolution 1'.",
"tier": "T2",
"year": "2025"
}
|
In each cell of a \(2025 \times 2025\) board, a nonnegative real number is written in such a way that the sum of the numbers in each row is equal to 1, and the sum of the numbers in each column is equal to 1. Define \(r_{i}\) to be the largest value in row \(i\) , and let \(R = r_{1} + r_{2} + \dots + r_{2025}\) . Similarly, define \(c_{i}\) to be the largest value in column \(i\) , and let \(C = c_{1} + c_{2} + \dots + c_{2025}\) .What is the largest possible value of \(\frac{R}{C}\) ?
What is the largest possible value of \(\frac{R}{C}\) ?
|
1". This is an alternative way of getting the upper bound on \(\frac{R}{C}\) from
\[\frac{R}{C}\leq \frac{p_{1} + p_{2} + \ldots + p_{k}}{\frac{p_{1}}{n_{1}} + \frac{p_{2}}{n_{2}} + \ldots + \frac{p_{k}}{n_{k}} + \frac{n - k}{n}}.\]
Using the fact that \(\sum_{j = 1}^{k}n_{j} = n\) , we can rewrite the above right hand side as follows:
\[\frac{\sum_{j = 1}^{k}p_{j}}{\sum_{j = 1}^{k}\left(\frac{p_{j}}{n_{j}} +\frac{n_{j} - 1}{n}\right)}.\]
We notice that this is a quotient of affine functions in the \(p_{j}\) 's, for which the denominator does not vanish over the set defined by \(0 \leq p_{j} \leq 1\) . Therefore the maximum of this function is attained when a certain number of \(p_{j}\) 's are 1 and the others are 0. Without loss of generality we may assume that the first \(t\) are equal to 1 and the other \(k - t\) are 0 for some \(0 \leq t \leq k\) . Then one has that the previous expression is at most
\[\frac{t}{\sum_{1 \leq j \leq t} \left(\frac{1}{n_{j}} + \frac{n_{j} - 1}{n}\right) + \sum_{t < j \leq k} \frac{n_{j} - 1}{n}}.\]
We now lower bound the denominator by observing that the second sum is non negative, while each term of the first sum can be bounded by \(AM - GM\) as follows:
\[\frac{1}{n_{j}} + \frac{n_{j} - 1}{n} \geq \frac{2}{\sqrt{n}} - \frac{1}{n}.\]
We therefore have
\[\frac{R}{C} \leq \max_{1 \leq t \leq k} \frac{t}{\sum_{1 \leq j \leq t} \left(\frac{2}{\sqrt{n}} - \frac{1}{n}\right)} = \frac{n}{2\sqrt{n} - 1},\]
which finishes the proof.
|
1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In each cell of a \(2025 \times 2025\) board, a nonnegative real number is written in such a way that the sum of the numbers in each row is equal to 1, and the sum of the numbers in each column is equal to 1. Define \(r_{i}\) to be the largest value in row \(i\) , and let \(R = r_{1} + r_{2} + \dots + r_{2025}\) . Similarly, define \(c_{i}\) to be the largest value in column \(i\) , and let \(C = c_{1} + c_{2} + \dots + c_{2025}\) .What is the largest possible value of \(\frac{R}{C}\) ?
What is the largest possible value of \(\frac{R}{C}\) ?
|
1". This is an alternative way of getting the upper bound on \(\frac{R}{C}\) from
\[\frac{R}{C}\leq \frac{p_{1} + p_{2} + \ldots + p_{k}}{\frac{p_{1}}{n_{1}} + \frac{p_{2}}{n_{2}} + \ldots + \frac{p_{k}}{n_{k}} + \frac{n - k}{n}}.\]
Using the fact that \(\sum_{j = 1}^{k}n_{j} = n\) , we can rewrite the above right hand side as follows:
\[\frac{\sum_{j = 1}^{k}p_{j}}{\sum_{j = 1}^{k}\left(\frac{p_{j}}{n_{j}} +\frac{n_{j} - 1}{n}\right)}.\]
We notice that this is a quotient of affine functions in the \(p_{j}\) 's, for which the denominator does not vanish over the set defined by \(0 \leq p_{j} \leq 1\) . Therefore the maximum of this function is attained when a certain number of \(p_{j}\) 's are 1 and the others are 0. Without loss of generality we may assume that the first \(t\) are equal to 1 and the other \(k - t\) are 0 for some \(0 \leq t \leq k\) . Then one has that the previous expression is at most
\[\frac{t}{\sum_{1 \leq j \leq t} \left(\frac{1}{n_{j}} + \frac{n_{j} - 1}{n}\right) + \sum_{t < j \leq k} \frac{n_{j} - 1}{n}}.\]
We now lower bound the denominator by observing that the second sum is non negative, while each term of the first sum can be bounded by \(AM - GM\) as follows:
\[\frac{1}{n_{j}} + \frac{n_{j} - 1}{n} \geq \frac{2}{\sqrt{n}} - \frac{1}{n}.\]
We therefore have
\[\frac{R}{C} \leq \max_{1 \leq t \leq k} \frac{t}{\sum_{1 \leq j \leq t} \left(\frac{2}{\sqrt{n}} - \frac{1}{n}\right)} = \frac{n}{2\sqrt{n} - 1},\]
which finishes the proof.
|
{
"exam": "EGMO",
"problem_label": "6",
"problem_match": "P6.",
"resource_path": "EGMO/segmented/en-2025-solutions.jsonl",
"solution_match": "\nSolution ",
"tier": "T2",
"year": "2025"
}
|
In each cell of a \(2025 \times 2025\) board, a nonnegative real number is written in such a way that the sum of the numbers in each row is equal to 1, and the sum of the numbers in each column is equal to 1. Define \(r_{i}\) to be the largest value in row \(i\) , and let \(R = r_{1} + r_{2} + \dots + r_{2025}\) . Similarly, define \(c_{i}\) to be the largest value in column \(i\) , and let \(C = c_{1} + c_{2} + \dots + c_{2025}\) .What is the largest possible value of \(\frac{R}{C}\) ?
What is the largest possible value of \(\frac{R}{C}\) ?
|
\(1^{\prime \prime}\) . We follow the same notation as above. First, we apply Cauchy- Schwarz as follows :
\[\left(\sum_{i = 1}^{k} \frac{p_{i}}{n_{i}}\right) \left(\sum_{i = 1}^{k} p_{i} n_{i}\right) \geq \left(\sum_{i = 1}^{k} p_{i}\right)^{2} = R^{2}.\]
We now write \(z_{i} = 1 - p_{i}\) for all \(1 \leq i \leq k\) , and observe that all \(z_{i}\) are positive. Moreover, we have that \(\sum_{i = 1}^{k} z_{i} = k - R\) , and \(\sum_{i = 1}^{k} p_{i} n_{i} = n - \sum_{i = 1}^{k} p_{i} z_{i}\) . Thus, from our last inequality we get
\[\frac{p_{1}}{n_{1}} + \dots + \frac{p_{k}}{n_{k}} \geq \frac{R^{2}}{n - \sum_{i = 1}^{k} n_{i} z_{i}}.\]
As before we have \(C \geq \frac{p_{1}}{n_{1}} + \dots + \frac{p_{k}}{n_{k}} + \frac{n - k}{n}\) , and so
\[C \geq \frac{R^{2}}{n - \sum_{i = 1}^{k} n_{i} z_{i}} + \frac{n - k}{n} = \frac{R^{2}}{n - \sum_{i = 1}^{k} n_{i} z_{i}} + \frac{n - R - \sum_{i = 1}^{k} z_{i}}{n}.\]
Putting everything together we get
\[\frac{R}{C} \leq \frac{R}{\frac{R^{2}}{n - \sum_{i = 1}^{k} n_{i} z_{i}} + \frac{n - R - \sum_{i = 1}^{k} z_{i}}{n}} = \frac{n}{\frac{R n}{n - \sum_{i = 1}^{k} n_{i} z_{i}} + \frac{n - \sum_{i = 1}^{k} z_{i}}{R} - 1}.\]
Applying \(AM - GM\) to the denominator we get \(\frac{R}{C} \leq \frac{n}{2 \sqrt{n \frac{n - \sum_{i = 1}^{k} z_{i}}{n - \sum_{i = 1}^{k} n_{i} z_{i}} - 1}}\) , which finishes the proof by noting that \(\frac{n - \sum_{i = 1}^{k} z_{i}}{n - \sum_{i = 1}^{k} n_{i} z_{i}} \geq 1\) .
|
not found
|
Yes
|
Incomplete
|
math-word-problem
|
Combinatorics
|
In each cell of a \(2025 \times 2025\) board, a nonnegative real number is written in such a way that the sum of the numbers in each row is equal to 1, and the sum of the numbers in each column is equal to 1. Define \(r_{i}\) to be the largest value in row \(i\) , and let \(R = r_{1} + r_{2} + \dots + r_{2025}\) . Similarly, define \(c_{i}\) to be the largest value in column \(i\) , and let \(C = c_{1} + c_{2} + \dots + c_{2025}\) .What is the largest possible value of \(\frac{R}{C}\) ?
What is the largest possible value of \(\frac{R}{C}\) ?
|
\(1^{\prime \prime}\) . We follow the same notation as above. First, we apply Cauchy- Schwarz as follows :
\[\left(\sum_{i = 1}^{k} \frac{p_{i}}{n_{i}}\right) \left(\sum_{i = 1}^{k} p_{i} n_{i}\right) \geq \left(\sum_{i = 1}^{k} p_{i}\right)^{2} = R^{2}.\]
We now write \(z_{i} = 1 - p_{i}\) for all \(1 \leq i \leq k\) , and observe that all \(z_{i}\) are positive. Moreover, we have that \(\sum_{i = 1}^{k} z_{i} = k - R\) , and \(\sum_{i = 1}^{k} p_{i} n_{i} = n - \sum_{i = 1}^{k} p_{i} z_{i}\) . Thus, from our last inequality we get
\[\frac{p_{1}}{n_{1}} + \dots + \frac{p_{k}}{n_{k}} \geq \frac{R^{2}}{n - \sum_{i = 1}^{k} n_{i} z_{i}}.\]
As before we have \(C \geq \frac{p_{1}}{n_{1}} + \dots + \frac{p_{k}}{n_{k}} + \frac{n - k}{n}\) , and so
\[C \geq \frac{R^{2}}{n - \sum_{i = 1}^{k} n_{i} z_{i}} + \frac{n - k}{n} = \frac{R^{2}}{n - \sum_{i = 1}^{k} n_{i} z_{i}} + \frac{n - R - \sum_{i = 1}^{k} z_{i}}{n}.\]
Putting everything together we get
\[\frac{R}{C} \leq \frac{R}{\frac{R^{2}}{n - \sum_{i = 1}^{k} n_{i} z_{i}} + \frac{n - R - \sum_{i = 1}^{k} z_{i}}{n}} = \frac{n}{\frac{R n}{n - \sum_{i = 1}^{k} n_{i} z_{i}} + \frac{n - \sum_{i = 1}^{k} z_{i}}{R} - 1}.\]
Applying \(AM - GM\) to the denominator we get \(\frac{R}{C} \leq \frac{n}{2 \sqrt{n \frac{n - \sum_{i = 1}^{k} z_{i}}{n - \sum_{i = 1}^{k} n_{i} z_{i}} - 1}}\) , which finishes the proof by noting that \(\frac{n - \sum_{i = 1}^{k} z_{i}}{n - \sum_{i = 1}^{k} n_{i} z_{i}} \geq 1\) .
|
{
"exam": "EGMO",
"problem_label": "6",
"problem_match": "P6.",
"resource_path": "EGMO/segmented/en-2025-solutions.jsonl",
"solution_match": "\nSolution ",
"tier": "T2",
"year": "2025"
}
|
In each cell of a \(2025 \times 2025\) board, a nonnegative real number is written in such a way that the sum of the numbers in each row is equal to 1, and the sum of the numbers in each column is equal to 1. Define \(r_{i}\) to be the largest value in row \(i\) , and let \(R = r_{1} + r_{2} + \dots + r_{2025}\) . Similarly, define \(c_{i}\) to be the largest value in column \(i\) , and let \(C = c_{1} + c_{2} + \dots + c_{2025}\) .What is the largest possible value of \(\frac{R}{C}\) ?
What is the largest possible value of \(\frac{R}{C}\) ?
|
This is an alternative approach that goes via an intermediary quantity in order to establish to the upper bound on \(R / C\) .
Let \(x_{i j}\) be the entry in row \(i\) and column \(j\) . Let \(n = 2025\) . The key idea is to analyze the expression:
\[T:= \sum_{i,j}x_{i j}\max \left(x_{i j},\frac{1}{n}\right).\]
On one hand, since \(c_{j}\geq 1 / n\) , we have \(x_{i j}\max (x_{i j},\frac{1}{n})\leq x_{i j}c_{j}\) for every \((i,j)\) . So
\[T\leq \sum_{j}\sum_{i}x_{i j}c_{j} = \sum_{j}c_{j} = C.\]
On the other hand, let \(j_{i}\) be one of the indices for which \(r_{i} = x_{i j_{i}}\) . We therefore have:
\[T=\sum_{i}\left(x_{i j_{i}}\max \left(x_{i j_{i}},\frac{1}{n}\right)+\sum_{j\neq j_{i}}x_{i j}\max \left(x_{i j},\frac{1}{n}\right)\right)\] \[\geq\sum_{i}\left(r_{i}^{2}+\frac{1}{n}\sum_{j\neq j_{i}}x_{i j}\right)\] \[=\sum_{i}\left(r_{i}^{2}-\frac{1}{n}r_{i}+\frac{1}{n}\right)\geq\sum_{i}\left(\frac{2}{\sqrt{n}}r_{i}-\frac{1}{n}r_{i}\right)=\left(\frac{2}{\sqrt{n}}-\frac{1}{n}\right)R.\]
This gives the claimed result.
| null |
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
In each cell of a \(2025 \times 2025\) board, a nonnegative real number is written in such a way that the sum of the numbers in each row is equal to 1, and the sum of the numbers in each column is equal to 1. Define \(r_{i}\) to be the largest value in row \(i\) , and let \(R = r_{1} + r_{2} + \dots + r_{2025}\) . Similarly, define \(c_{i}\) to be the largest value in column \(i\) , and let \(C = c_{1} + c_{2} + \dots + c_{2025}\) .What is the largest possible value of \(\frac{R}{C}\) ?
What is the largest possible value of \(\frac{R}{C}\) ?
|
This is an alternative approach that goes via an intermediary quantity in order to establish to the upper bound on \(R / C\) .
Let \(x_{i j}\) be the entry in row \(i\) and column \(j\) . Let \(n = 2025\) . The key idea is to analyze the expression:
\[T:= \sum_{i,j}x_{i j}\max \left(x_{i j},\frac{1}{n}\right).\]
On one hand, since \(c_{j}\geq 1 / n\) , we have \(x_{i j}\max (x_{i j},\frac{1}{n})\leq x_{i j}c_{j}\) for every \((i,j)\) . So
\[T\leq \sum_{j}\sum_{i}x_{i j}c_{j} = \sum_{j}c_{j} = C.\]
On the other hand, let \(j_{i}\) be one of the indices for which \(r_{i} = x_{i j_{i}}\) . We therefore have:
\[T=\sum_{i}\left(x_{i j_{i}}\max \left(x_{i j_{i}},\frac{1}{n}\right)+\sum_{j\neq j_{i}}x_{i j}\max \left(x_{i j},\frac{1}{n}\right)\right)\] \[\geq\sum_{i}\left(r_{i}^{2}+\frac{1}{n}\sum_{j\neq j_{i}}x_{i j}\right)\] \[=\sum_{i}\left(r_{i}^{2}-\frac{1}{n}r_{i}+\frac{1}{n}\right)\geq\sum_{i}\left(\frac{2}{\sqrt{n}}r_{i}-\frac{1}{n}r_{i}\right)=\left(\frac{2}{\sqrt{n}}-\frac{1}{n}\right)R.\]
This gives the claimed result.
|
{
"exam": "EGMO",
"problem_label": "6",
"problem_match": "P6.",
"resource_path": "EGMO/segmented/en-2025-solutions.jsonl",
"solution_match": "\nSolution 2. ",
"tier": "T2",
"year": "2025"
}
|
Let $ABC$ be a triangle and $\mathrm{H}_{\mathrm{C}}$ the foot of the altitude from $C$. Let $P$ be a point on the segment $\left[\mathrm{CH}_{C}\right]$ (other than $C$), and let $E, F, G, H$ be the midpoints of $[AP],[BP],[BC],[AC]$, respectively. Show that $EFGH$ is a rectangle.
|
To prove that EFGH is a rectangle, we will show that it is a parallelogram that has a right angle.
Consider the triangle $ACP$. The points E and H are the midpoints of the sides $[AP]$ and $[AC]$, respectively. By the Midline Theorem, (HE) // (PC).
Consider the triangle BCP. The points F and G are the midpoints of the sides [BP] and [BC], respectively. By the Midline Theorem, (FG) // (PC).
We have shown that the lines (FG) and (HE) are both parallel to the line (PC). It follows that (FG) // (HE).
Consider the triangle $ABP$. The points E and F are the midpoints of the sides [AP] and [BP], respectively. By the Midline Theorem, (EF) // (AB).
Consider the triangle $ABC$. The points H and G are the midpoints of the sides [AC] and [BC], respectively. By the Midline Theorem, (HG) // (AB).
We have shown that the lines (EF) and (HG) are both parallel to the line (AB). It follows that (HG) // (EF).
Therefore, EFGH is a quadrilateral whose opposite sides are parallel. It follows that it is a parallelogram.
Furthermore, since $\left(\mathrm{CH}_{c}\right) \perp(\mathrm{AB})$ and $(EF) //(\mathrm{AB})$, we have $(EF) \perp\left(\mathrm{CH}_{c}\right)$.
Moreover, $\left(\mathrm{CH}_{\mathrm{c}}\right) //(\mathrm{EH})$. It follows that $(\mathrm{EH}) \perp(\mathrm{EF})$.
The parallelogram EFGH therefore has a right angle, which proves that EFGH is a rectangle.
Remark. Another way to prove that EFGH is a parallelogram is to use the fact that, according to the Midline Theorem, $(\mathrm{EH}) //(\mathrm{CP}) //(\mathrm{FG})$ and $\mathrm{EH}=\frac{1}{2} \mathrm{CP}=\mathrm{FG}$. Therefore, EFGH has two opposite sides that are parallel and of the same length, so it is a parallelogram.
Comment from the graders: The exercise was very well done overall. However, many students could have been faster by using the parallel and perpendicular lines in the figure without chasing angles. Additionally, several students lost points because they did not justify why they could apply Thales' theorem or why the quadrilateral EFGH had a right angle...
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $A B C$ un triangle et $\mathrm{H}_{\mathrm{C}}$ le pied de la hauteur issue de C . Soit P un point sur le segment $\left[\mathrm{CH}_{C}\right]$ (autre que $C$ ), et soient $E, F, G, H$ les milieux respectifs de $[A P],[B P],[B C],[A C]$. Montrer que EFGH est un rectangle.
|
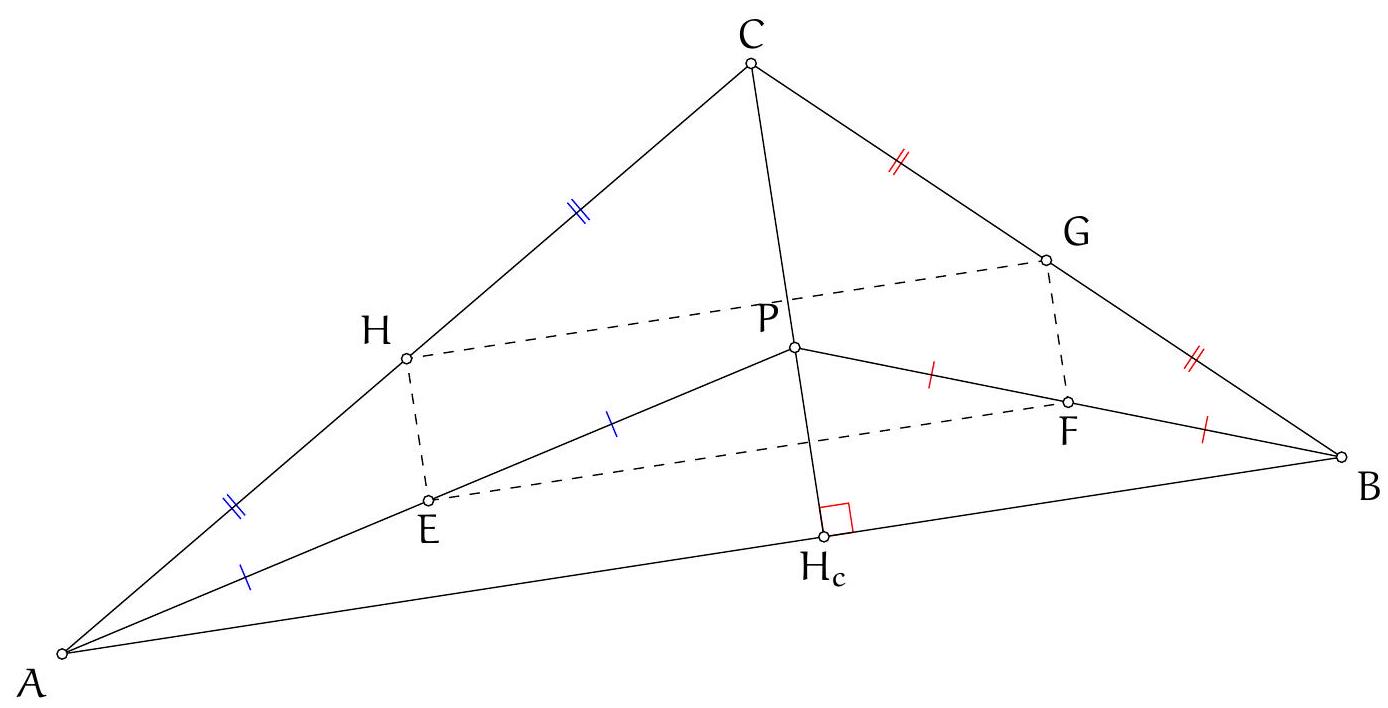
Pour démontrer que EFGH est un rectangle, nous allons montrer que c'est un parallélogramme qui possède un angle droit.
Considérons le triangle $A C P$. Les points E et H sont les milieux respectifs des côtés $[A P]$ et $[A C]$. Par le théorème de la droite des milieux, (HE) // (PC).
Considérons le triangle BCP. Les points F et G sont les milieux respectifs des côtés [BP] et [BC]. Par le théorème de la droite des milieux, (FG) // (PC).
On a montré que les droites (FG) et ( HE ) sont toutes les deux parallèles à la droite (PC). Il s'ensuit que (FG) // (HE).
Considérons le triangle $A B P$. Les points $E$ et $F$ sont les milieux respectifs des côtés [AP] et [BP]. Par le théorème de la droite des milieux, ( $E F$ ) // ( $A B$ ).
Considérons le triangle $A B C$. Les points H et G sont les milieux respectifs des côtés [AC] et [BC]. Par le théorème de la droite des milieux, (HG) // (AB).
On a montré que les droites (EF) et (HG) sont toutes les deux parallèles à la droite ( $A B$ ). Il s'ensuit que (HG) // (EF).
Par conséquent, EFGH est un quadrilatère dont les côtés opposés sont parallèles deux à deux. Il s'ensuit que c'est un parallélogramme.
Par ailleurs, comme $\left(\mathrm{CH}_{c}\right) \perp(\mathrm{AB})$ et $(E F) / /(\mathrm{AB})$, on a $(E F) \perp\left(\mathrm{CH}_{c}\right)$.
De plus, $\left(\mathrm{CH}_{\mathrm{c}}\right) / /(\mathrm{EH})$. Il s'ensuit que $(\mathrm{EH}) \perp(\mathrm{EF})$.
Le parallélogramme EFGH possède donc un angle droit, ce qui démontrer que EFGH est un rectangle.
Remarque. Une autre façon de prouver que EFGH est un parallélogramme est d'utiliser que d'après le théorème de la droite des milieux, $(\mathrm{EH}) / /(\mathrm{CP}) / /(\mathrm{FG})$ et $\mathrm{EH}=\frac{1}{2} \mathrm{CP}=\mathrm{FG}$. Donc EFGH possède deux côtés opposés parallèles et de même longueur, c'est donc un parallélogramme.
Commentaire des correcteurs: L'exercice a été très bien réussi dans l'ensemble. Cependant pas mal d'élèves pourraient aller plus vite en utilisant les droites parallèles et perpendiculaires de la figure sans faire de chasse aux angles. Deplus, plusieurs élèves ont perdu des points car ils n'ont pas justifié pourquoi ils pouvaient appliquer le théorème de Thalès ou pourquoi le quadrilatère EFGH avait un angle droit...
|
{
"exam": "French_envois",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"solution_match": "## Solution de l'exercice 1",
"tier": "T2",
"year": "2024"
}
|
Let $ABC$ be an acute triangle (all angles are acute) with $BA \neq BC$. Let $O$ be the center of its circumcircle. The line $(AB)$ intersects the circumcircle of $BOC$ a second time at $P \neq B$. Show that $PA = PC$.
|
Let's draw the figure in the case where $BC < BA$, the case $BC > BA$ being completely analogous. It is a matter of showing that $\mathrm{PA} = \mathrm{PC}$, that is, $\widehat{ACP} = \widehat{\mathrm{PAC}} (=\widehat{\mathrm{BAC}})$. Now we have:
$$
\begin{aligned}
\widehat{ACP} & = \widehat{ACO} + \widehat{OCP} \\
& = \widehat{ACO} + \widehat{OBP} \text{ by inscribed angle } \\
& = \widehat{ACO} + \widehat{OBA}
\end{aligned}
$$
Now, $AOC$ is isosceles at O, so $\widehat{ACO} = \widehat{\mathrm{OAC}} = \frac{180^{\circ} - \widehat{COA}}{2} = 90^{\circ} - \widehat{\mathrm{CBA}}$ by central angle. Similarly, $\widehat{OBA} = 90^{\circ} - \widehat{ACB}$. Finally, $\widehat{ACP} = 180^{\circ} - \widehat{ACB} - \widehat{CBA} = \widehat{BAC} = \widehat{PAC}$, hence $PA = PC$, as desired.
Comment from the graders: The exercise was very well done and widely approached, some solutions are particularly efficient in their angle chasing.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle acutangle (dont tous les angles sont aigus) avec $B A \neq B C$. Soit $O$ le centre de son cercle circonscrit. La droite $(A B)$ intersecte le cercle circonscrit à $B O C$ une deuxième fois en $P \neq B$. Montrer que $P A=P C$.
|
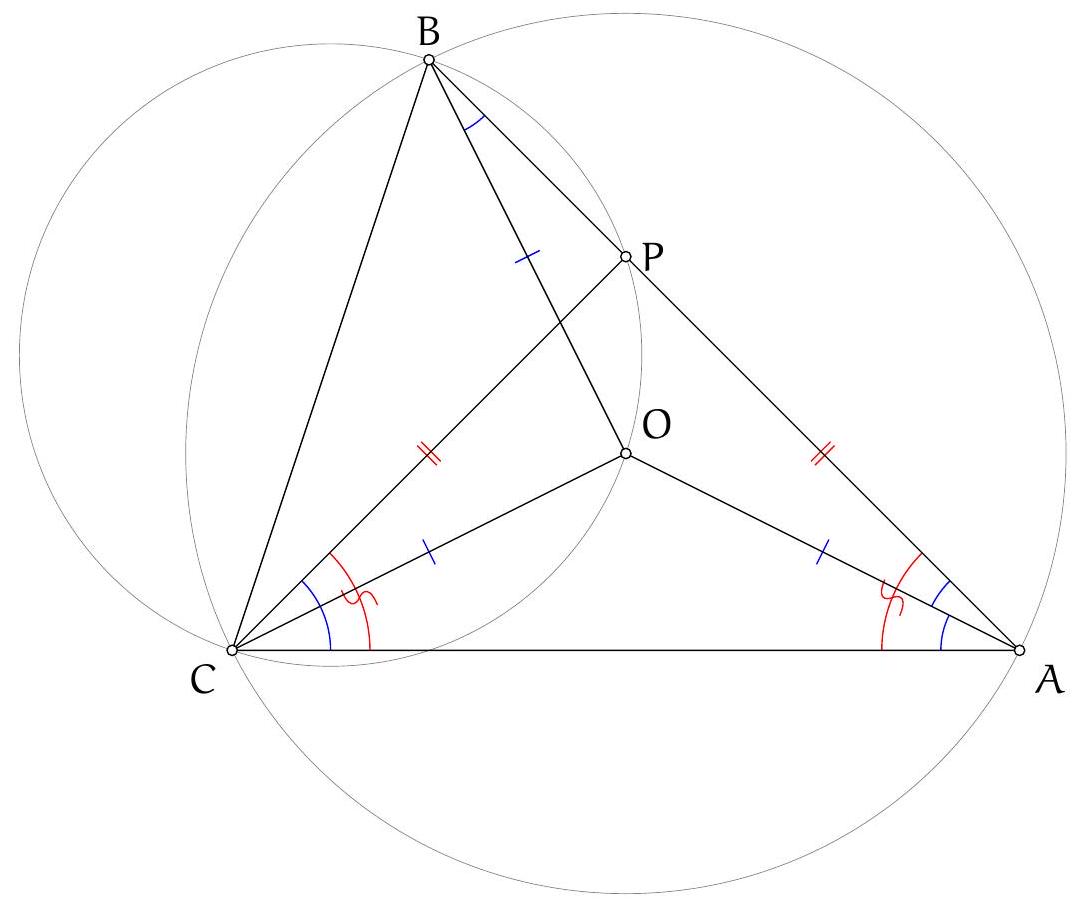
Traçons la figure dans le cas où $B C<B A$, le cas $B C>B A$ étant totalement analogue. Il s'agit de montrer que $\mathrm{PA}=\mathrm{PC}$, c'est-à-dire que $\widehat{A C P}=\widehat{\mathrm{PAC}}(=\widehat{\mathrm{BAC}})$. Or on a:
$$
\begin{aligned}
\widehat{A C P} & =\widehat{A C O}+\widehat{O C P} \\
& =\widehat{A C O}+\widehat{O B P} \text { par angle inscrit } \\
& =\widehat{A C O}+\widehat{O B A}
\end{aligned}
$$
Or, $A O C$ est isocèle en O donc $\widehat{A C O}=\widehat{\mathrm{OAC}}=\frac{180^{\circ}-\widehat{C O A}}{2}=90^{\circ}-\widehat{\mathrm{CBA}}$ par angle au centre. De même $\widehat{O B A}=90^{\circ}-\widehat{A C B}$. Finalement, $\widehat{A C P}=180^{\circ}-\widehat{A C B}-\widehat{C B A}=\widehat{B A C}=\widehat{P A C}$, d'où $P A=P C$, comme voulu.
Commentaire des correcteurs : L'exercice a été très bien réussi et beaucoup abordé, certaines solutions sont particulièrement efficaces dans leurs chasses aux angles.
|
{
"exam": "French_envois",
"problem_label": "10",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"solution_match": "## Solution de l'exercice 2",
"tier": "T2",
"year": "2024"
}
|
Let $ABC$ be a right triangle at $B$ with $BC < BA$. Let $D$ be the point on the segment $[AB]$ such that $BD = BC$. The perpendicular to $(AC)$ passing through $D$ intersects $(AC)$ at $E$. Let $B'$ be the symmetric point of $B$ with respect to $(CD)$. Show that $(EC)$ is the bisector of the angle $\widehat{\mathrm{BEB}^{\prime}}$.
|
We notice that the circle with diameter [CD] appears quite naturally. Indeed, we have right angles $\widehat{\mathrm{DB}} \widehat{ } \mathrm{C}=\widehat{\mathrm{CBD}}=\widehat{\mathrm{DEC}}=90^{\circ}$, so the points $\mathrm{B}, \mathrm{B}^{\prime}$, and $E$ lie on the circle with diameter [DC], in other words, $C, B, D, E, B^{\prime}$ are concyclic.
Then we have:
$$
\begin{aligned}
\widehat{\mathrm{BEC}} & =\widehat{\mathrm{BDC}} \text { by inscribed angle } \\
& =45^{\circ} \text { since } \mathrm{BC}=\mathrm{BD} \text { and } \widehat{\mathrm{CBD}}=90^{\circ}
\end{aligned}
$$
Furthermore:
$$
\begin{aligned}
\widehat{\mathrm{CEB}^{\prime}} & =\widehat{\mathrm{CBB}^{\prime}} \text { by inscribed angle } \\
& =45^{\circ} \text { since } \mathrm{BC}=\mathrm{BD} \text { and } \widehat{\mathrm{CBD}}=90^{\circ} .
\end{aligned}
$$
Therefore, we have $\widehat{\mathrm{BEC}}=\widehat{\mathrm{CEB}^{\prime}}$, so (EC) is the bisector of $\widehat{\mathrm{BEB}^{\prime}}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle rectangle en $B$ avec $B C<B A$. Soit $D$ le point du segment $[A B]$ tel que $B D=B C$. La perpendiculaire à $(A C)$ passant par $D$ intersecte $(A C)$ en $E$. Soit $B^{\prime}$ le symétrique de $B$ par rapport à (CD). Montrer que (EC) est la bissectrice de l'angle $\widehat{\mathrm{BEB}^{\prime}}$.
|
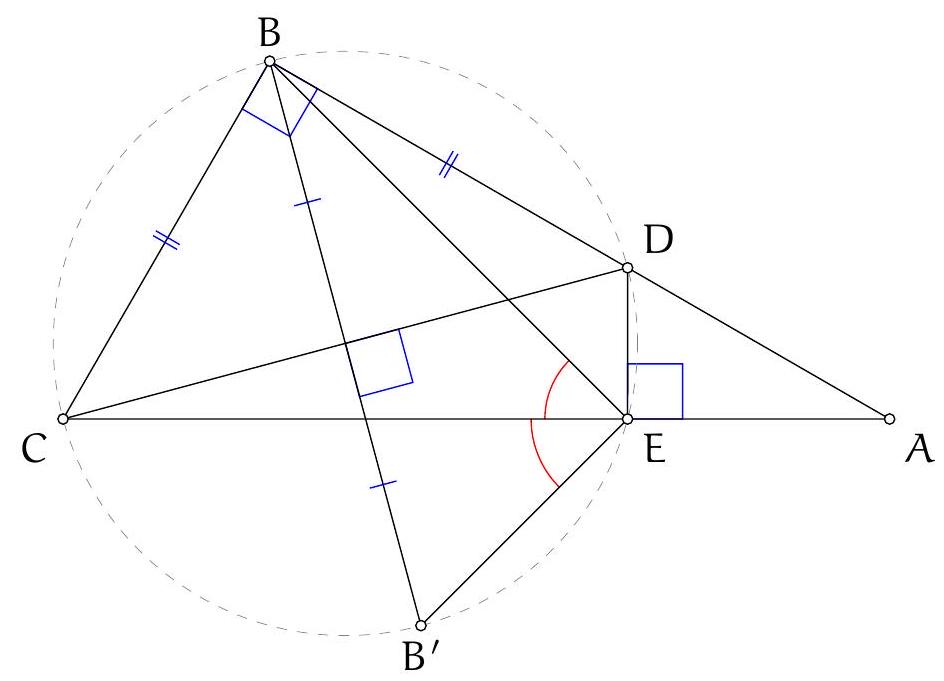
On remarque que le cercle de diamètre [CD] apparaît assez naturellement. En effet, on a des angles droits $\widehat{\mathrm{DB}} \widehat{ } \mathrm{C}=\widehat{\mathrm{CBD}}=\widehat{\mathrm{DEC}}=90^{\circ}$, les points $\mathrm{B}, \mathrm{B}^{\prime}$ et $E$ sont sur le cercle de diamètre [DC], autrement dit $C, B, D, E, B^{\prime}$ sont cocycliques.
Alors on a :
$$
\begin{aligned}
\widehat{\mathrm{BEC}} & =\widehat{\mathrm{BDC}} \text { par angle inscrit } \\
& =45^{\circ} \text { car } \mathrm{BC}=\mathrm{BD} \text { et } \widehat{\mathrm{CBD}}=90^{\circ}
\end{aligned}
$$
De plus:
$$
\begin{aligned}
\widehat{\mathrm{CEB}^{\prime}} & =\widehat{\mathrm{CBB}^{\prime}} \text { par angle inscrit } \\
& =45^{\circ} \text { car } \mathrm{BC}=\mathrm{BD} \text { et } \widehat{\mathrm{CBD}}=90^{\circ} .
\end{aligned}
$$
On a donc bien $\widehat{\mathrm{BEC}}=\widehat{\mathrm{CEB}^{\prime}}$, donc (EC) est la bissectrice de $\widehat{\mathrm{BEB}^{\prime}}$.
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"solution_match": "## Solution de l'exercice 3",
"tier": "T2",
"year": "2024"
}
|
Let $ABC$ be a right triangle at $B$ with $BC < BA$. Let $D$ be the point on the segment $[AB]$ such that $BD = BC$. The perpendicular to $(AC)$ passing through $D$ intersects $(AC)$ at $E$. Let $B'$ be the symmetric point of $B$ with respect to $(CD)$. Show that $(EC)$ is the bisector of the angle $\widehat{\mathrm{BEB}^{\prime}}$.
|
$n^{\circ} 1$
We could also show directly $\widehat{\mathrm{BEC}}=\widehat{\mathrm{CEB}^{\prime}}$ without using $\mathrm{BC}=\mathrm{BD}$. Indeed:
$$
\begin{aligned}
\widehat{\mathrm{BEC}} & =\widehat{\mathrm{BDC}} \text { by inscribed angle } \\
& =\widehat{\mathrm{CDB}^{\prime}} \text { by symmetry } \\
& =\widehat{\mathrm{CEB}} \text { by inscribed angle. }
\end{aligned}
$$
Graders' comment: The exercise was generally very well done. The most frequent error concerned the conditions for a quadrilateral to be a square.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle rectangle en $B$ avec $B C<B A$. Soit $D$ le point du segment $[A B]$ tel que $B D=B C$. La perpendiculaire à $(A C)$ passant par $D$ intersecte $(A C)$ en $E$. Soit $B^{\prime}$ le symétrique de $B$ par rapport à (CD). Montrer que (EC) est la bissectrice de l'angle $\widehat{\mathrm{BEB}^{\prime}}$.
|
$n^{\circ} 1$
On pouvait aussi montrer directement $\widehat{\mathrm{BEC}}=\widehat{\mathrm{CEB}^{\prime}}$ sans utiliser $\mathrm{BC}=\mathrm{BD}$. En effet :
$$
\begin{aligned}
\widehat{\mathrm{BEC}} & =\widehat{\mathrm{BDC}} \text { par angle inscrit } \\
& =\widehat{\mathrm{CDB}^{\prime}} \text { par symétrie } \\
& =\widehat{\mathrm{CEB}} \text { par angle inscrit. }
\end{aligned}
$$
Commentaire des correcteurs : L'exercice est globalement très bien réussi. L'erreur la plus fréquente portait sur les conditions pour qu'un quadrilatère soit un carré.
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T2",
"year": "2024"
}
|
Let $ABC$ be a triangle and $I$ the center of its inscribed circle. The perpendicular bisector of $[\mathrm{BC}]$ intersects $(A \mathrm{I})$ at $S$ and $(BI)$ at $T$. Show that $C, I, S$ and $T$ are concyclic.
|
To show that $C, I, S$, and $T$ are concyclic, we will show that $\widehat{\text{SIC}} = \widehat{\text{STC}}$.
We recall that the internal angle bisectors of a triangle $ABC$ are concurrent, and their point of intersection $I$ is the center of the inscribed circle of the triangle. Therefore, $(AI)$ is the angle bisector of $\widehat{BAC}$.
Consequently, $S$ is defined as the intersection of the perpendicular bisector of $[BC]$ and the angle bisector of $\widehat{BAC}$. The South Pole theorem ensures that $S$ lies on the circumcircle of triangle $ABC$ and that $S$ is the center of the Antarctic circle of vertex $A$, which ensures that
$$
\mathrm{SB} = \mathrm{SI}
$$
We see that triangle $SBI$ is isosceles at $S$, which ensures that $\widehat{\mathrm{SBI}} = \widehat{\mathrm{BIS}}$.
Furthermore, the points $A, B, S$, and $C$ are concyclic. Therefore,
$$
\widehat{SBC} = \widehat{SAC} = \frac{\widehat{BAC}}{2}.
$$
Now let's calculate the value of the angle $\widehat{\text{SIC}}$. We have
$$
\begin{aligned}
\widehat{SIC} & = \widehat{\mathrm{BIC}} - \widehat{\mathrm{BIS}} \\
& = \widehat{\mathrm{BIC}} - \widehat{\mathrm{SBC}} - \widehat{\mathrm{CBI}} \\
& = \widehat{\mathrm{BIC}} - \frac{\widehat{\mathrm{BAC}}}{2} - \frac{\widehat{\mathrm{CBA}}}{2}.
\end{aligned}
$$
Furthermore,
$$
\begin{aligned}
\widehat{\mathrm{BIC}} & = 180^{\circ} - \widehat{\mathrm{CBI}} - \widehat{\mathrm{ICB}} \\
& = 180^{\circ} - \frac{\widehat{\mathrm{CBA}}}{2} - \frac{\widehat{ACB}}{2} \\
& = 180^{\circ} - \frac{\widehat{\mathrm{CBA}} + \widehat{ACB}}{2} \\
& = 180^{\circ} - \frac{180^{\circ} - \widehat{\mathrm{BAC}}}{2} \\
& = 90^{\circ} + \frac{\widehat{\mathrm{BAC}}}{2}.
\end{aligned}
$$
It follows that $\widehat{\text{SIC}} = 90^{\circ} - \frac{\widehat{\mathrm{CBA}}}{2}$.
Furthermore,
$$
\begin{aligned}
\widehat{\mathrm{STC}} & = 90^{\circ} - \widehat{\mathrm{TCB}} \\
& = 90^{\circ} - \widehat{\mathrm{CBI}} \quad \text{Triangle } \mathrm{BCT} \text{ is isosceles at } \mathrm{T} \\
& = 90^{\circ} - \frac{\widehat{\mathrm{CBA}}}{2}.
\end{aligned}
$$
We have thus shown that $\widehat{\text{SIC}} = \widehat{\text{STC}}$, which ensures that the points $C, I, S$, and $T$ are concyclic by the converse of the inscribed angle theorem.
Comment from the graders: The exercise is very well done. Many students engaged in a cumbersome angle chase, while the South Pole theorem greatly simplified the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $A B C$ un triangle et I le centre de son cercle inscrit. La médiatrice de $[\mathrm{BC}]$ coupe ( $A \mathrm{I}$ ) en $S$ et (BI) et $T$. Montrer que $C, I, S$ et $T$ sont cocycliques.
|
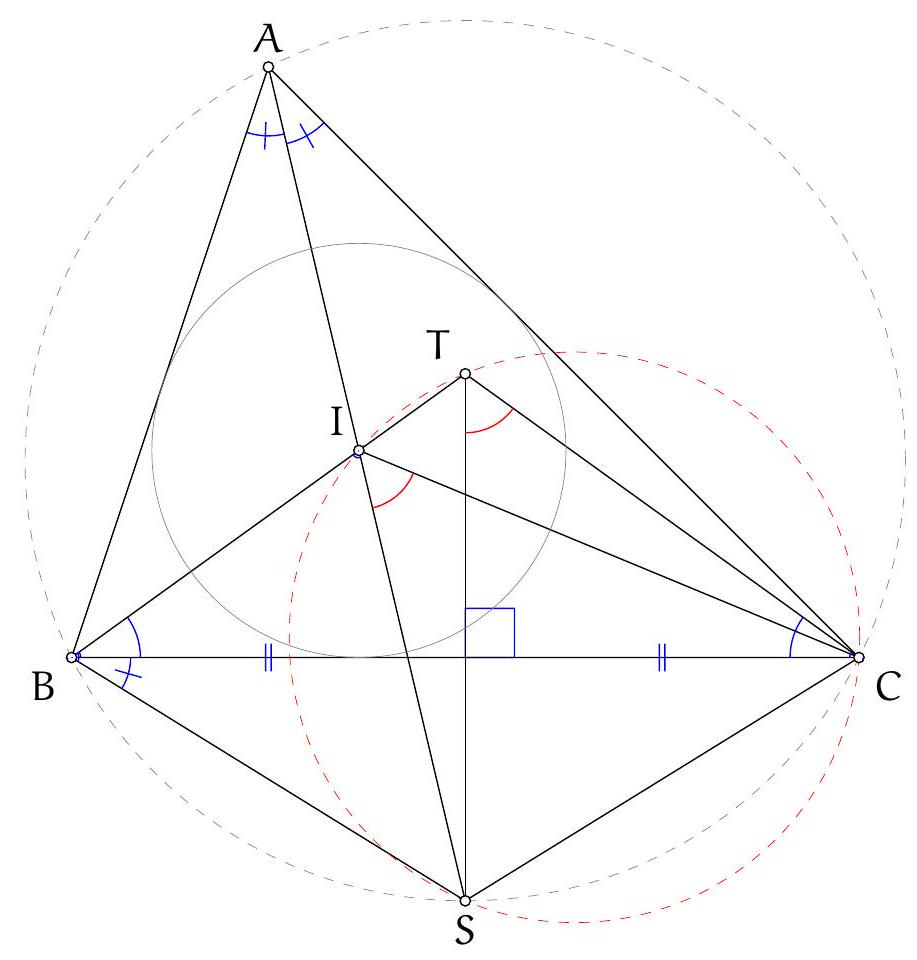
Pour montrer que $C, I, S$ et $T$ sont cocycliques, nous allons montrer que $\widehat{\text { SIC }}=\widehat{\text { STC }}$.
On rappelle que les bissectrices intérieures d'un triangle $A B C$ sont concourantes et que leur point d'intersection I est le centre du cercle inscrit dans le triangle. (AI) est donc la bissectrice de l'angle $\widehat{B A C}$.
Par conséquent, $S$ est défini comme le point d'intersection de la médiatrice de $[\mathrm{BC}]$ et de la bissectrice de l'angle $\widehat{B A C}$. Le théorème du Pôle Sud assure que $S$ appartient au cercle circonscrit au triangle $A B C$ et que $S$ est le centre du cercle antarctique du sommet $A$, ce qui assure que
$$
\mathrm{SB}=\mathrm{SI}
$$
On voit donc que triangle SBI est isocèle en S ce qui assure que $\widehat{\mathrm{SBI}}=\widehat{\mathrm{BIS}}$.
Par ailleurs les points $A, B, S$ et $C$ sont cocycliques. On a donc
$$
\widehat{S B C}=\widehat{S A C}=\frac{\widehat{B A C}}{2} .
$$
Calculons désormais la valeur de l'angle $\widehat{\text { SIC }}$. On a
$$
\begin{aligned}
\widehat{S I C} & =\widehat{\mathrm{BIC}}-\widehat{\mathrm{BIS}} \\
& =\widehat{\mathrm{BIC}}-\widehat{\mathrm{SBC}}-\widehat{\mathrm{CBI}} \\
& =\widehat{\mathrm{BIC}}-\frac{\widehat{\mathrm{BAC}}}{2}-\frac{\widehat{\mathrm{CBA}}}{2} .
\end{aligned}
$$
Par ailleurs,
$$
\begin{aligned}
\widehat{\mathrm{BIC}} & =180^{\circ}-\widehat{\mathrm{CBI}}-\widehat{\mathrm{ICB}} \\
& =180^{\circ}-\frac{\widehat{\mathrm{CBA}}}{2}-\frac{\widehat{A C B}}{2} \\
& =180^{\circ}-\frac{\widehat{\mathrm{CBA}}+\widehat{A C B}}{2} \\
& =180^{\circ}-\frac{180^{\circ}-\widehat{\mathrm{BAC}}}{2} \\
& =90^{\circ}+\frac{\widehat{\mathrm{BAC}}}{2} .
\end{aligned}
$$
Il s'ensuit que $\widehat{\text { SIC }}=90^{\circ}-\frac{\widehat{\mathrm{CBA}}}{2}$.
Par ailleurs
$$
\begin{aligned}
\widehat{\mathrm{STC}} & =90^{\circ}-\widehat{\mathrm{TCB}} \\
& =90-\widehat{\mathrm{CBI}} \quad \text { Le triangle } \mathrm{BCT} \text { est isocèle en } \mathrm{T} \\
& =90^{\circ}-\frac{\widehat{\mathrm{CBA}}}{2} .
\end{aligned}
$$
On a donc montré que $\widehat{\text { SIC }}=\widehat{\text { STC }}$ ce qui assure que les points $C, I, S$ et $T$ sont cocycliques par la réciproque du théorème de l'angle inscrit.
Commentaire des correcteurs: L'exercice est très bien réussi. Beaucoup d'élèves ont procédé à une lourde chasse aux angles alors que le théorème du Pôle Sud simplifiait grandement la résolution du problème.
|
{
"exam": "French_envois",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"solution_match": "## Solution de l'exercice 4",
"tier": "T2",
"year": "2024"
}
|
Let $A B C D E$ be a convex cyclic pentagon such that $A B=B D$. Let $P$ be the intersection point of the lines (EB) and ( $A C$ ). Let $Q$ be the intersection point of the lines ( $B C$ ) and ( $D E$ ). Show that $(\mathrm{PQ})$ and (AD) are parallel.
|
In the figure, it seems that EPCQ is a cyclic quadrilateral. We show this:
\[
\begin{aligned}
\widehat{\mathrm{QCP}} & =180^{\circ}-\widehat{\mathrm{PCB}} \\
& =180^{\circ}-\widehat{\mathrm{ACB}} \\
& =180^{\circ}-\widehat{\mathrm{ADB}} \text { by inscribed angle } \\
& =180^{\circ}-\widehat{\mathrm{BAD}} \text{ since } \mathrm{AB}=\mathrm{BD} \\
& =180^{\circ}-\widehat{\mathrm{BED}} \\
& =180^{\circ}-\widehat{\mathrm{PEQ}}.
\end{aligned}
\]
Thus, we have shown that \(\widehat{\mathrm{QCP}}+\widehat{\mathrm{PEQ}}=180^{\circ}\). Therefore, by the converse of the inscribed angle theorem, EPCQ is cyclic, which is what we wanted to prove.
Now, to show that (AD) and (PQ) are parallel, we will try to find corresponding angles. We have:
\[
\begin{aligned}
\widehat{\mathrm{EQP}} & =\widehat{\mathrm{ECP}} \text { by inscribed angle } \\
& =\widehat{\mathrm{ECA}} \\
& =\widehat{\mathrm{EDA}} \text { by inscribed angle. }
\end{aligned}
\]
Since \(\widehat{\mathrm{EQP}}=\widehat{\mathrm{EDA}}\) and \(\mathrm{Q}, \mathrm{D}, \mathrm{E}\) are collinear (in that order), by corresponding angles, the lines (PQ) and (AD) are indeed parallel.
Comment from the graders: The exercise was well handled by those who approached it. Almost all students thought to translate the equality of lengths into an equality of angles, which was the right starting point to then chase angles. Then, it was necessary to observe that the quadrilateral EPCQ is cyclic to continue, which blocked some. Some who did not see this managed to get through with a more cumbersome angle chase, while others managed to apply Thales' theorem by introducing a new point.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D E$ un pentagone cyclique convexe tel que $A B=B D$. Soit $P$ le point d'intersection des droites (EB) et ( $A C$ ). Soit $Q$ le point d'intersection des droites ( $B C$ ) et ( $D E$ ). Montrer que $(\mathrm{PQ})$ et (AD) sont parallèles.
|
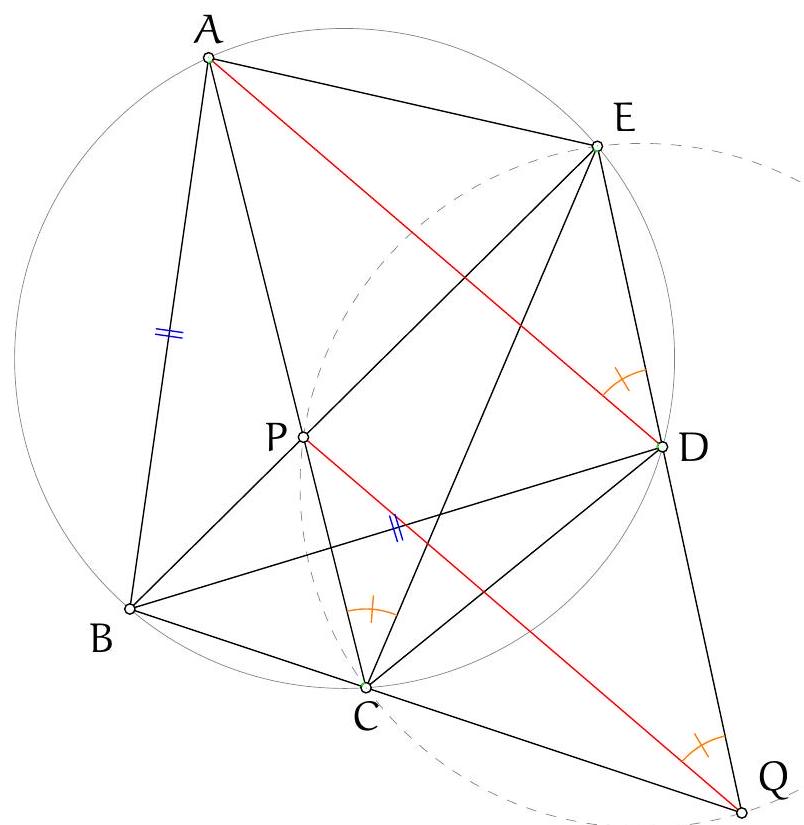
Sur la figure, il semble que EPCQ est un quadrilatère cyclique. On le montre :
$$
\begin{aligned}
\widehat{\mathrm{QCP}} & =180^{\circ}-\widehat{\mathrm{PCB}} \\
& =180^{\circ}-\widehat{\mathrm{ACB}} \\
& =180^{\circ}-\widehat{\mathrm{ADB}} \text { par angle inscrit } \\
& =180^{\circ}-\widehat{\mathrm{BAD}} \mathrm{car} \mathrm{AB}=\mathrm{BD} \\
& =180^{\circ}-\widehat{\mathrm{BED}} \\
& =180^{\circ}-\widehat{\mathrm{PEQ}} .
\end{aligned}
$$
Ainsi on a montré que $\widehat{\mathrm{QCP}}+\widehat{\mathrm{PEQ}}=180^{\circ}$. Dès lors, par réciproque de l'angle inscrit, EPCQ est cyclique, ce qu'on voulait démontrer.
Maintenant, pour montrer que ( AD ) et ( PQ ) sont parallèles, on va essayer de trouver des angles correspondants. Or on a :
$$
\begin{aligned}
\widehat{\mathrm{EQP}} & =\widehat{\mathrm{ECP}} \text { par angle inscrit } \\
& =\widehat{\mathrm{ECA}} \\
& =\widehat{\mathrm{EDA}} \text { par angle inscrit. }
\end{aligned}
$$
Comme $\widehat{\mathrm{EQP}}=\widehat{\mathrm{EDA}}$ et $\mathrm{Q}, \mathrm{D}, \mathrm{E}$ sont alignés (dans cet ordre), par angle correspondant les droites (PQ) et $(A D)$ sont bien parallèles.
Commentaire des correcteurs : L'exercice a été bien traité par les personnes qui l'ont abordé. Quasiment tous les élèves ont pensé à traduire l'égalité de longueur en égalité d'angle, ce qui était le bon point de départ pour pouvoir ensuite faire une chasse aux angles. Ensuite, il fallait observer que le quadrilatère
EPCQ est cyclique pour continuer, ce qui en a bloqué certains. Certains qui n'ont pas vu cela ont réussi à s'en sortir avec une chasse aux angles plus lourde, d'autres ont réussi à appliquer le théorème de Thalès en introduisant un nouveau point.
|
{
"exam": "French_envois",
"problem_label": "13",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"solution_match": "## Solution de l'exercice 5",
"tier": "T2",
"year": "2024"
}
|
Let $ABC$ be an isosceles triangle at $A$, $O$ the center of its circumcircle, and $I$ the center of its incircle. The parallel to ($AB$) passing through $I$ intersects ($AC$) at $D$. Show that ($CI$) and ($DO$) are perpendicular.
|
First, since $AB = AC$, $A, O, I$ are collinear, and line $(AI)$ intersects $[BC]$ at its midpoint $M$. We denote $P$ as the intersection of lines $(DO)$ and $(CI)$.
By angle chasing, we show that $I, O, D, C$ are concyclic by showing that $\widehat{\mathrm{IOC}} = \widehat{\mathrm{IDC}}$. Indeed:
\[
\begin{aligned}
\widehat{\mathrm{IOC}} & = \widehat{\mathrm{MOC}} \\
& = \frac{1}{2} \widehat{\mathrm{BOC}} \text{ because } OB = OC \\
& = \widehat{\mathrm{BAC}} \text{ by the inscribed angle theorem} \\
& = \widehat{\mathrm{IDC}} \text{ because } (BA) \parallel (ID)
\end{aligned}
\]
Therefore, by the converse of the inscribed angle theorem, $I, O, D, C$ are concyclic.
Now, let's show that $\widehat{CPD} = 90^\circ$. To do this, we will show that $\widehat{PDC} + \widehat{DCP} = 90^\circ$ (since $\widehat{\mathrm{CPD}} = 180^\circ - \widehat{\mathrm{PDC}} - \widehat{\mathrm{DCP}}$). We have:
\[
\begin{aligned}
\widehat{\mathrm{PDC}} + \widehat{\mathrm{DCP}} & = \widehat{\mathrm{ODC}} + \widehat{\mathrm{DCI}} \\
& = (180^\circ - \widehat{\mathrm{CIO}}) + \widehat{\mathrm{ICB}} \text{ by concyclicity and angle bisector} \\
& = \widehat{\mathrm{CIM}} + \widehat{\mathrm{ICM}} \\
& = 90^\circ \text{ because } (AI) \perp (BC).
\end{aligned}
\]
Thus, $\widehat{\mathrm{CPD}} = 90^\circ$, which proves that lines $(CI)$ and $(DO)$ are perpendicular.
Grader's Comment: The exercise was generally well done. Most of the submitted solutions contained a correct solution.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $A B C$ un triangle isocèle en $A$, $O$ le centre de son cercle circonscrit et $I$ le centre de son cercle inscrit. La parallèle à ( $A B$ ) passant par I coupe (AC) en D. Montrer que (CI) et (DO) sont perpendiculaires.
|
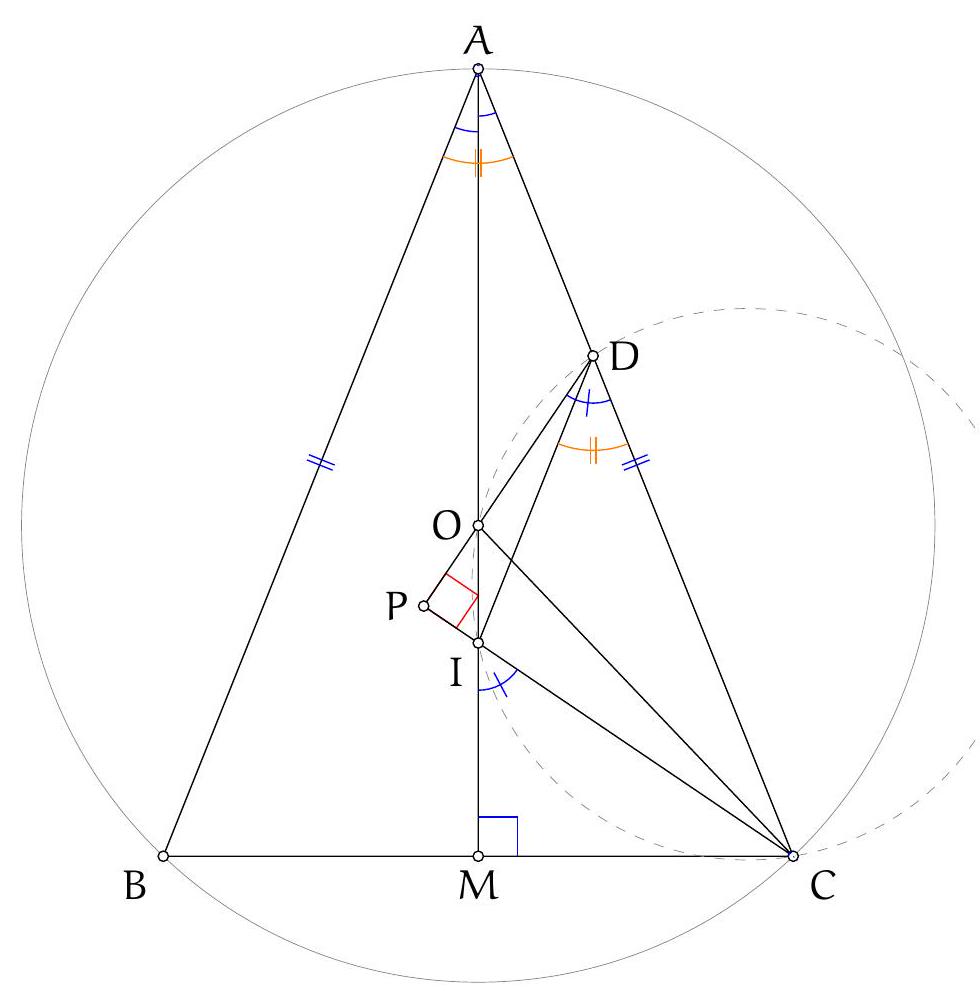
Premièrement, comme $A B=A C, A, O$, I sont alignés et la droite $(A I)$ coupe $[B C]$ en son milieu $M$. On pose P l'intersection des droites (DO) et (CI).
Par chasse aux angles, on montre que I, O, D, $C$ sont cocycliques, en montrant que $\widehat{\mathrm{IOC}}=\widehat{\mathrm{IDC}}$. En effet :
$$
\begin{aligned}
\widehat{\mathrm{IOC}} & =\widehat{\mathrm{MOC}} \\
& =\frac{1}{2} \widehat{\mathrm{BOC}} \text { car } O B=\mathrm{OC} \\
& =\widehat{\mathrm{BAC}} \text { par angle au centre } \\
& =\widehat{\mathrm{IDC}} \mathrm{car}(\mathrm{BA}) / /(\mathrm{ID})
\end{aligned}
$$
Donc par réciproque du théorème de l'angle inscrit, $\mathrm{I}, \mathrm{O}, \mathrm{D}, \mathrm{C}$ sont cocycliques.
Montrons à présent que $\widehat{C P D}=90^{\circ}$. Pour cela, on va montrer que $\widehat{P D C}+\widehat{D C P}=90^{\circ}$ (puisque $\left.\widehat{\mathrm{CPD}}=180^{\circ}-\widehat{\mathrm{PDC}}-\widehat{\mathrm{DCP}}\right)$. On a :
$$
\begin{aligned}
\widehat{\mathrm{PDC}}+\widehat{\mathrm{DCP}} & =\widehat{\mathrm{ODC}}+\widehat{\mathrm{DCI}} \\
& =\left(180^{\circ}-\widehat{\mathrm{CIO}}\right)+\widehat{\mathrm{ICB}} \text { par cocyclicité et bissectrice } \\
& =\widehat{\mathrm{CIM}}+\widehat{\mathrm{ICM}} \\
& =90^{\circ} \mathrm{car}(A \mathrm{II}) \perp(\mathrm{BC}) .
\end{aligned}
$$
Donc $\widehat{\mathrm{CPD}}=90^{\circ}$, ce qui prouve bien que les droites (CI) et (DO) sont perpendiculaires.
Commentaire des correcteurs : Exercice bien réussi dans l'ensemble. La plupart des copies rendues contenait une solution correcte.
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"solution_match": "## Solution de l'exercice 6",
"tier": "T2",
"year": "2024"
}
|
Let $ABC$ be a triangle, $D, E$ the feet of the altitudes from $A$ and $B$ respectively. The line $(DE)$ intersects the circumcircle of $ABC$ at two points $P$ and $Q$. Let $A'$ and $B'$ be the reflections of $A$ and $B$ with respect to $(BC)$ and $(AC)$ respectively. Show that $A', B', P, Q$ are concyclic.
|
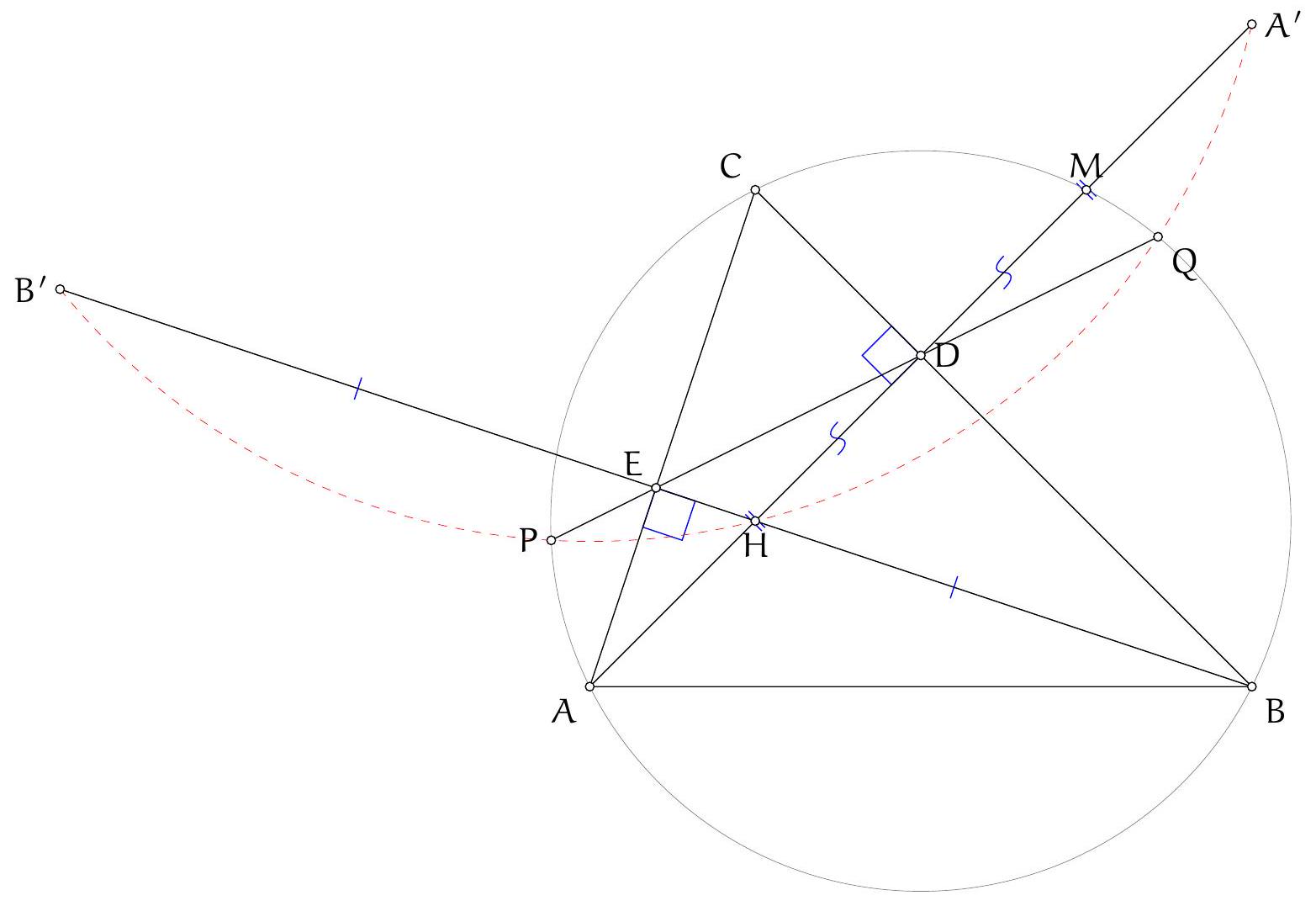
In the figure, it seems that H, the orthocenter, lies on the circle in question. Therefore, we will adopt the following strategy: we will show that \(A'\) and \(B'\) are on the circumcircle of \(P Q H\). This way, we will have \(A', B', P, Q\) being concyclic.
Let \(M\) be the symmetric point of \(H\) with respect to \((\mathrm{BC})\): then we know that \(M\) is on the circumcircle of \(\triangle ABC\). Then we have:
\[
\begin{aligned}
D A' \times D H & = D A \times D M \text{ by symmetry} \\
& = D P \times D Q \text{ by power of point } D \text{ in the circle } (A B C).
\end{aligned}
\]
Then, by the converse of the power of a point, \(P, Q, H, A'\) are concyclic. Similarly, \(P, Q, H, B'\) are also concyclic. Thus, \(A', B', P, Q\) are concyclic, on the circle \((P Q H)\).
Comment from the graders: The problem was well solved. However, many students could have gone faster by using the power of a point, rather than using similar triangles associated with 4 concyclic points and reproving the power of a point.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $A B C$ un triangle, $D, E$ les pieds des hauteurs issues de $A$ et $B$ respectivement. La droite ( $D E$ ) rencontre le cercle circonscrit à $A B C$ en deux points $P$ et $Q$. Soient $A^{\prime}$ et $B^{\prime}$ les symétriques de $A$ et $B$ par rapport à ( $B C$ ) et ( $A C$ ) respectivement. Montrer que $A^{\prime}, B^{\prime}, P, Q$ sont cocycliques.
|

Sur la figure, il semble que H l'orthocentre se situe sur le cercle en question. On va donc adopter la stratégie suivante : on va montrer que $A^{\prime}$ et $B^{\prime}$ sont sur le cercle circonscrit de $P Q H$. De cette manière on aura bien $A^{\prime}, B^{\prime}, P, Q$ cocycliques.
Soit $M$ le symétrique de H par rapport à $(\mathrm{BC})$ : alors on sait que $M$ est sur le cercle circonscrit à ABC. Alors on a :
$$
\begin{aligned}
D A^{\prime} \times D H & =D A \times D M \text { par symétrie } \\
& =D P \times D Q \text { par puissance de } D \text { dans le cercle }(A B C) .
\end{aligned}
$$
Alors par réciproque de la puissance d'un point, $P, Q, H, A^{\prime}$ sont cocycliques. De façon totalement analogue, $P, Q, H, B^{\prime}$ sont également cocycliques. Ainsi $A^{\prime}, B^{\prime}, P, Q$ sont cocycliques, sur le cercle ( $P Q H$ ).
Commentaire des correcteurs : L'exercice a été bien résolu. Cependant pas mal d'élèves pourraient aller plus vite en utilisant la puissance d'un point, plutôt que d'utiliser les triangles semblables associés à 4 points cocycliques et reprouver la puissance d'un point.
|
{
"exam": "French_envois",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"solution_match": "## Solution de l'exercice 7",
"tier": "T2",
"year": "2024"
}
|
Let $ABC$ be a triangle with circumcircle $\Gamma$, $D$ a point on $(AB)$, and $E$ a point on $(AC)$ such that $(DE)$ and $(BC)$ are parallel. The circumcircle of $ABC$ meets the circumcircle of $BDE$ again at $K$ and the circumcircle of $CDE$ again at $L$. Let $T$ be the intersection of $(BK)$ and $(CL)$. Show that $(TA)$ is tangent to the circle $\Gamma$.
|
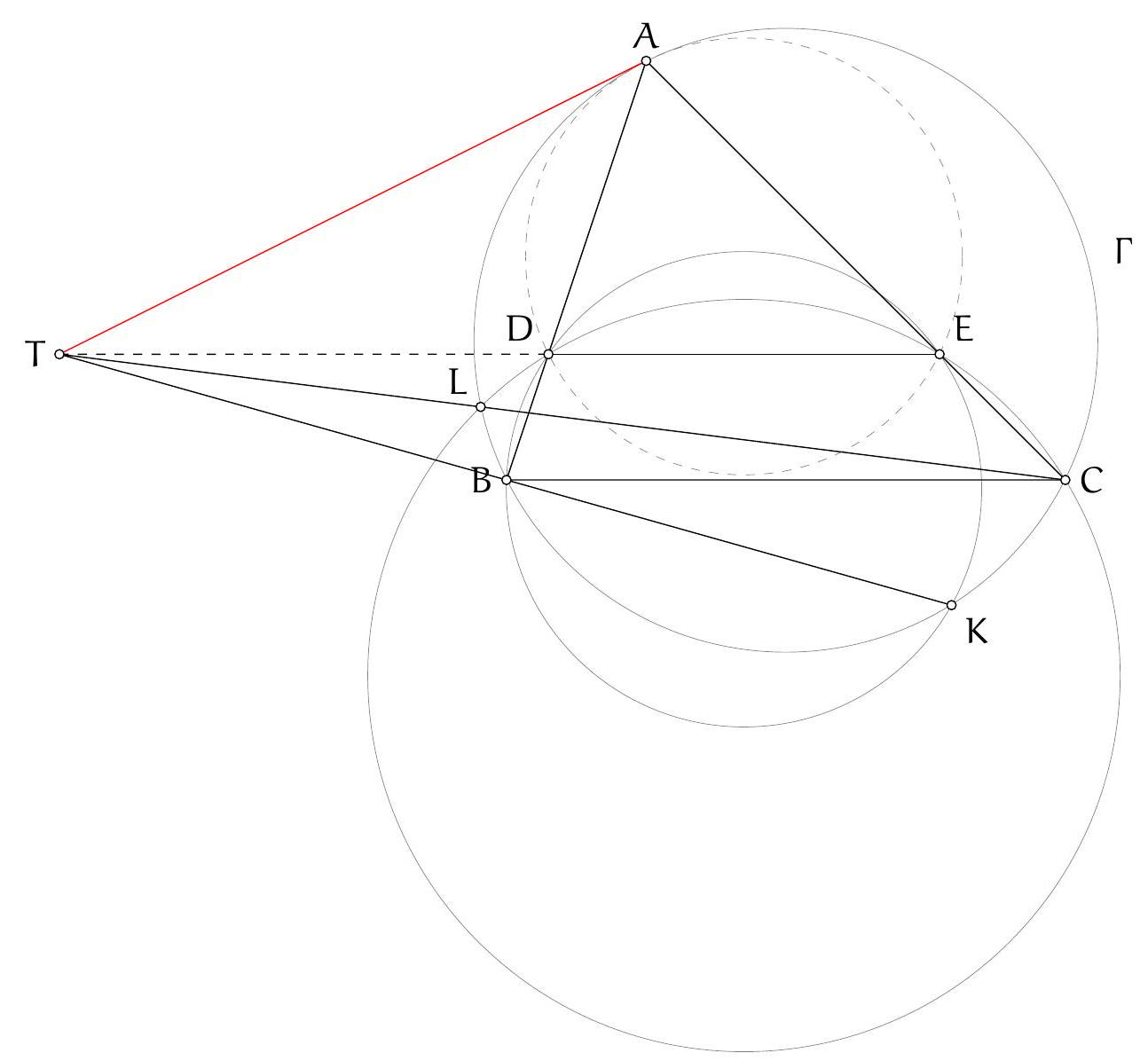
We recognize here a classic situation:
- KBDE is cyclic,
- KBLC is cyclic,
- CLDE is cyclic.
We know that in this situation, the lines (KB), (CL), (ED) are concurrent (this is the fact that the radical axes of three circles are concurrent). The lines (BK) and (CL) intersect at \( T \). It follows that \( T, D, E \) are collinear.
We then know, by expressing the power of \( T \) with respect to the three circles, that:
\[
TD \times TE = TL \times TC = TB \times TK
\]
Knowing the product \( TD \times TE \) suggests considering a circle passing through \( D, E \), and since we want a property on \( (TA) \), it is natural to introduce the circumcircle of \( ADE \).
Since \( TD \times TE = TL \times TC \), \( T \) has the same power with respect to the circumcircles of \( ABC \) and \( ADE \). Therefore, it lies on their radical axis. But since \( (DE) \) is parallel to \( (BC) \), the two circles are tangent at \( A \) with the radical axis being the common tangent to these two circles at \( A \). This can be seen simply by the tangent angle (using that \( \widehat{AED} = \widehat{ACB} \)), or by considering the homothety centered at \( A \) that maps \( D \) to \( B \): it maps \( E \) to \( C \), so it maps the circle \( (ADE) \) to \( (ABC) \), and thus these circles are indeed tangent.
We deduce that \( T \) lies on the tangent to \( \Gamma \) passing through \( A \), in other words, that \( (TA) \) is tangent to \( \Gamma \), as required.
Comment from the graders: The problem was not approached by many students, but all the students who did approach the problem had very good ideas, including those who did not reach a solution. Notably, all students recognized that the points \( T, D, E \) are collinear, which was the first idea to have to advance in the problem. It was then necessary to successfully exploit the parallelism of \( (DE) \) and \( (BC) \), and those who succeeded used essentially two different approaches: either justify that the circumcircles of \( ADE \) and \( ABC \) are tangent at \( A \) to reduce the problem to showing tangency to the circle \( (ADE) \), or by angle chasing to find other cyclic quadrilaterals on the figure.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $A B C$ un triangle de cercle circonscrit $\Gamma, D$ un point sur $(A B)$ et $E$ un point sur ( $A C)$ tel que (DE) et ( $B C$ ) sont parallèles. Le cercle circonscrit à $A B C$ rencontre le cercle circonscrit à $B D E$ une seconde fois en $K$ et le cercle circonscrit à CDE une seconde fois en $L$. Soit $T$ le point d'intersection de (BK) et (CL). Montrer que (TA) est tangente au cercle $\Gamma$.
|

On reconnait ici une situation classique :
- KBDE cyclique,
- KBLC cyclique,
- CLDE cyclique.
On sait que dans cette situation, les droites (KB), (CL), (ED) sont concourantes (il s'agit ici du fait que les axes radicaux de 3 cercles sont concourants). Or les droites (BK) et (CL) se coupent en $T$. Il suit que $\mathrm{T}, \mathrm{D}, \mathrm{E}$ sont alignés.
On sait alors, en exprimant la puissance de T par rapport aux trois cercles, que :
$$
\mathrm{TD} \times \mathrm{TE}=\mathrm{TL} \times \mathrm{TC}=\mathrm{TB} \times \mathrm{TK}
$$
Le fait de connaître le produit TD $\times$ TE incite à considérer un cercle passant par $\mathrm{D}, \mathrm{E}$, et comme on souhaite une propriété sur (TA), il est naturel d'introduire le cercle circonscrit à $A D E$.
Comme TD $\times$ TE $=T L \times T C, T$ a la même puissance par rapport aux cercles circonscrits à $A B C$ et $A D E$. Il est donc sur leur axe radical. Mais comme ( $D E$ ) est parallèles à ( BC ), les deux cercles sont tangents en $A$ d'axe radical la tangente commune à ces deux cercles en $A$. On peut le voir simplement par
angle tangentiel (en utilisant que $\widehat{A E D}=\widehat{A C B}$ ), autrement on peut le voir en considérant l'homothétie de centre $A$ envoyant $D$ sur $B$ : elle envoie $E$ sur $C$ donc elle envoie le cercle ( $A D E$ ) sur ( $A B C$ ), et donc ces cercles sont bien tangents.
On en déduit que $T$ est sur la tangente à $\Gamma$ passant par $A$, autrement dit que (TA) est tangente à $\Gamma$, comme voulu.
Commentaire des correcteurs : L'exercice n'a pas été beaucoup abordé, mais la totalité des élèves qui ont abordé l'exercice ont eu des très bonnes idées, y compris ceux qui n'ont pas abouti à une solution. Notamment, tous les élèves ont remarqué que les points $T, D, E$ sont alignés, ce qui était la première idée à avoir pour avancer dans l'exercice. Il fallait ensuite réussir à exploiter le parallélisme de (DE) et (BC), et là les élèves qui ont abouti utilisaient essentiellement deux approches différentes : soit justifier que les cercles circonscrits à $A D E$ et $A B C$ sont tangents en $A$ pour se ramener à montrer la tangence au cercle (ADE), soit par chasse aux angles en trouvant d'autres quadrilatères cycliques sur la figure.
|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "\nExercice 8.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"solution_match": "## Solution de l'exercice 8",
"tier": "T2",
"year": "2024"
}
|
Let $ABC$ be a non-isosceles triangle and $I$ the center of its inscribed circle. Let $D$ be a point on $[BC]$ (other than $B$ and $C$). The circumcircle of $DIB$ intersects $(AB)$ a second time at $E \neq B$, and the circumcircle of $DIC$ intersects $(AC)$ a second time at $F \neq C$. The circumcircle of $DEF$ meets $(AB)$ and $(AC)$ a second time at $M$ and $N$ respectively. The lines $(IB)$ and $(DE)$ intersect at $P$ and the lines $(IC)$ and $(DF)$ intersect at $Q$. Show that the lines $(EN)$, $(FM)$, and $(PQ)$ are parallel.
|
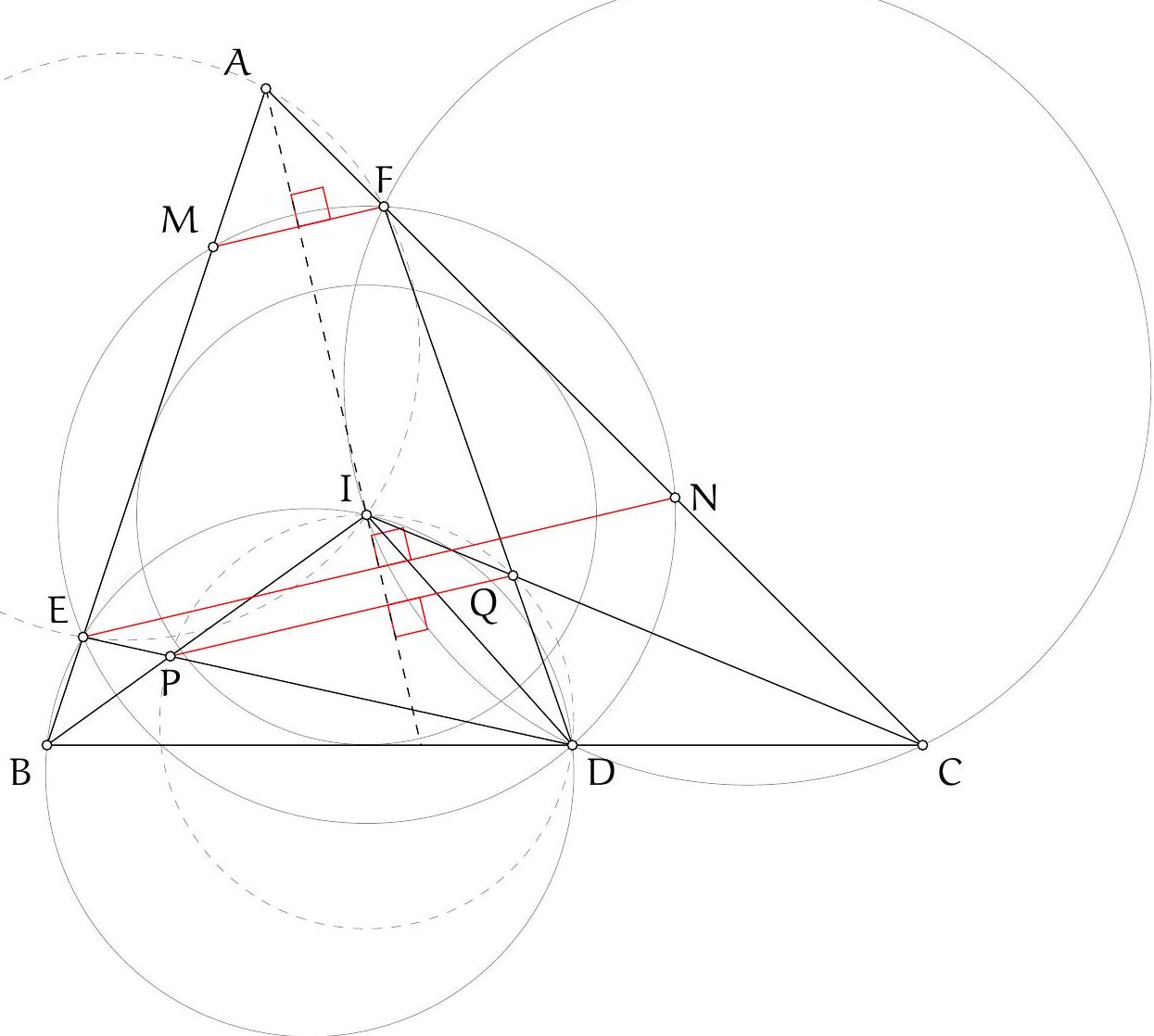
In the figure, it seems that I is the center of the circle (DEF), and that the lines (MF), (EN), (PQ) are all perpendicular to $(A I)$: this is the strategy we will use to solve the exercise.
- Lemma 1: The point I is the center of the circumcircle of DEF.
Proof: Since I is on the bisector of $\widehat{\mathrm{DBE}}$ and on the circumcircle of DBE, it is the South Pole (with respect to B) in this triangle. Therefore, ID = IE. Similarly, in FCD, we get ID = IF. Thus, $\mathrm{ID}=\mathrm{IE}=\mathrm{IF}: \mathrm{I}$ is indeed the center of the circumcircle of DEF.
- Lemma 2: The quadrilateral PQID is cyclic.
Proof: Indeed, we have:
$$
\begin{aligned}
\widehat{\mathrm{QDP}} & =\widehat{\mathrm{QDI}}+\widehat{\mathrm{IDP}} \\
& =\widehat{\mathrm{FDI}}+\widehat{\mathrm{IDE}} \\
& =\widehat{\mathrm{FCI}}+\widehat{\mathrm{IBE}} \text { by inscribed angle } \\
& =\widehat{\mathrm{ICB}}+\widehat{\mathrm{CBI}} \text { by bisectors } \\
& =180^{\circ}-\widehat{\mathrm{BIC}} \\
& =180^{\circ}-\widehat{\mathrm{PIQ}}
\end{aligned}
$$
Thus, $\widehat{\mathrm{PIQ}}+\widehat{\mathrm{QPD}}=180^{\circ}$, which means that PIDQ is cyclic.
Lemma 3: The lines (PQ) and (AI) are perpendicular.
Proof: Indeed, $\widehat{\mathrm{QPI}}=\widehat{\mathrm{QDI}}=\widehat{\mathrm{FDI}}=\widehat{\mathrm{FCI}}=\frac{1}{2} \widehat{\mathrm{ACB}}$ by inscribed angle. Furthermore:
$$
\begin{aligned}
\widehat{\mathrm{AIB}} & =180^{\circ}-\widehat{\mathrm{IBA}}-\widehat{\mathrm{BAI}} \\
& =180^{\circ}-\frac{\widehat{\mathrm{CBA}}+\widehat{\mathrm{BAC}}}{2} \\
& =180^{\circ}-\frac{180^{\circ}-\widehat{\mathrm{ACB}}}{2} \\
& =90^{\circ}+\frac{1}{2} \widehat{\mathrm{ABC}} .
\end{aligned}
$$
We conclude that (AI) and (PQ) are indeed perpendicular.
- Lemma 4: The quadrilateral AEIF is cyclic.
Proof: Indeed, BDIE and CFID are cyclic, so by Miquel's theorem, AEIF is also cyclic.
- Lemma 5: The lines (MF) and (EN) are perpendicular to (AI).
Proof: First, $\widehat{\mathrm{IEM}}=\widehat{\mathrm{IEA}}=180^{\circ}-\widehat{\mathrm{AFI}}=\widehat{\mathrm{IFN}}$ by inscribed angle. Furthermore, $\mathrm{IE}=\mathrm{IM}=\mathrm{IF}=\mathrm{IN}$ (by Lemma 1), so IEM and IFN are two isosceles triangles at I with the same base angle: hence IEM is similar to IFN. But since IE = IF: they are even congruent. We conclude that $E M=F N$. Since EMFN is cyclic, it is an isosceles trapezoid. We conclude that (MF) and (EN) are parallel, both perpendicular to (AI) (since I is the center of the circumcircle and $A$ is the intersection of the sides, so (AI) is the axis of symmetry of the isosceles trapezoid).
- Finally, (EN), (FM), (PQ) are all perpendicular to (AI), so they are parallel.
Comment from the graders: The problem was not widely attempted, but almost all students who attempted it solved it. Note that there were several possible configurations in the figure (order of points $E, M$ and $F, N$ on the lines $(A B)$ and $(A C)$), although it was not required to treat all configurations. Be careful not to get tangled up in the use of the inscribed angle theorem, especially in the case of supplementary angles.
## Senior Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $A B C$ un triangle non-isocèle et $I$ le centre de son cercle inscrit. Soit D un point sur $[B C]$ (autre que $B$ et $C$ ). Le cercle circonscrit à DIB coupe $(A B)$ une deuxième fois en $E \neq B$, et le cercle circonscrit à DIC coupe ( $A C$ ) une deuxième fois en $F \neq C$. Le cercle circonscrit à DEF rencontre ( $A B$ ) et ( $A C$ ) une deuxième fois en $M$ et $N$ respectivement. Les droites (IB) et ( $D E$ ) s'intersectent en $P$ et les droites (IC) et (DF) s'intersectent en Q. Montrer que les droites (EN), (FM) et (PQ) sont parallèles.
|

Sur la figure, il semble que I est le centre du cercle (DEF), et que les droites (MF), (EN), (PQ) sont toutes perpendiculaires à $(A I)$ : c'est donc la stratégie qu'on va utiliser pour résoudre l'exercice.
- Lemme 1: Le point I est le centre du cercle circonscrit à DEF.
Preuve : Comme I est sur la bissectrice de $\widehat{\mathrm{DBE}}$ et sur le cercle circonscrit de DBE, c'est le pôle Sud (par rapport à B) dans ce triangle. Donc ID = IE. De même dans FCD, on obtient ID = IF. Donc $\mathrm{ID}=\mathrm{IE}=\mathrm{IF}: \mathrm{I}$ est bien le centre du cercle circonscrit de DEF.
- Lemme 2: Le quadrilatère PQID est cyclique.
Preuve : En effet, on a :
$$
\begin{aligned}
\widehat{\mathrm{QDP}} & =\widehat{\mathrm{QDI}}+\widehat{\mathrm{IDP}} \\
& =\widehat{\mathrm{FDI}}+\widehat{\mathrm{IDE}} \\
& =\widehat{\mathrm{FCI}}+\widehat{\mathrm{IBE}} \text { par angle inscrit } \\
& =\widehat{\mathrm{ICB}}+\widehat{\mathrm{CBI}} \text { par bissectrices } \\
& =180^{\circ}-\widehat{\mathrm{BIC}} \\
& =180^{\circ}-\widehat{\mathrm{PIQ}}
\end{aligned}
$$
Donc $\widehat{\mathrm{PIQ}}+\widehat{\mathrm{QPD}}=180^{\circ}$, d'où le fait que PIDQ est cyclique.
Lemme 3 : Les droites (PQ) et (AI) sont perpendiculaires.
Preuve : En effet $\widehat{\mathrm{QPI}}=\widehat{\mathrm{QDI}}=\widehat{\mathrm{FDI}}=\widehat{\mathrm{FCI}}=\frac{1}{2} \widehat{\mathrm{ACB}}$ par angle inscrit. De plus :
$$
\begin{aligned}
\widehat{\mathrm{AIB}} & =180^{\circ}-\widehat{\mathrm{IBA}}-\widehat{\mathrm{BAI}} \\
& =180^{\circ}-\frac{\widehat{\mathrm{CBA}}+\widehat{\mathrm{BAC}}}{2} \\
& =180^{\circ}-\frac{180^{\circ}-\widehat{\mathrm{ACB}}}{2} \\
& =90^{\circ}+\frac{1}{2} \widehat{\mathrm{ABC}} .
\end{aligned}
$$
On en déduit que ( AI ) et (PQ) sont bien perpendiculaires.
- Lemme 4: La quadrilatère AEIF est cyclique.
Preuve : En effet BDIE et CFID sont cycliques, donc d'après le théorème de Miquel, AEIF l'est aussi.
- Lemme 5: Les droites (MF) et (EN) sont perpendiculaires à (AI).
Preuve : D'abord $\widehat{\mathrm{IEM}}=\widehat{\mathrm{IEA}}=180^{\circ}-\widehat{\mathrm{AFI}}=\widehat{\mathrm{IFN}}$ par angle inscrit. De plus $\mathrm{IE}=\mathrm{IM}=\mathrm{IF}=\mathrm{IN}$ (par le lemme 1), donc IEM et IFN sont deux triangles isocèles en I avec même angle de base : d'où IEM semblable à IFN. Mais comme IE = IF : ils sont même isométriques. On en déduit que $E M=F N$. Comme EMFN est cyclique, c'est un trapèze isocèle. On en déduit que (MF) et (EN) sont parallèles, toutes les deux perpendiculaires à (AI) (car I est le centre du cercle circonscrit et $A$ l'intersection des côtés, donc (AI) est axe de symétrie du trapèze isocèle).
- Finalement, (EN), (FM), (PQ) sont toutes les trois perpendiculaires à (AI), elle sont donc parallèles.
Commentaire des correcteurs : L'exercice n'a pas été beaucoup traité, mais la quasi totalité des élèves qui l'ont traité l'ont résolu. On notera qu'il y avait plusieurs configurations possibles dans la figure(ordre des points $E, M$ et $F, N$ sur les droites $(A B)$ et ( $A C)$. , bien qu'il ne soit pas demandé de traiter toutes les configurations. Attention à ne pas s'emmêler les pinceaux des les utilisations des théorèmes des angles inscrits, notamment dans le cas des angles supplémentaires.
## Exercices Seniors
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"solution_match": "## Solution de l'exercice 9",
"tier": "T2",
"year": "2024"
}
|
Let $ABC$ be an acute triangle (all angles are acute) with $BA \neq BC$. Let $O$ be the center of its circumcircle. The line $(AB)$ intersects the circumcircle of $BOC$ a second time at $P \neq B$. Show that $PA = PC$.
|
Let's draw the figure in the case where $BC < BA$, the case $BC > BA$ being completely analogous. It is a matter of showing that $\mathrm{PA} = \mathrm{PC}$, that is, $\widehat{ACP} = \widehat{\mathrm{PAC}} (=\widehat{\mathrm{BAC}})$. We have:
\[
\begin{aligned}
\widehat{ACP} & = \widehat{ACO} + \widehat{OCP} \\
& = \widehat{ACO} + \widehat{OBP} \text{ by inscribed angle} \\
& = \widehat{ACO} + \widehat{OBA}.
\end{aligned}
\]
Now, $AOC$ is isosceles at O, so $\widehat{ACO} = \widehat{OAC} = \frac{180^{\circ} - \widehat{COA}}{2} = 90^{\circ} - \widehat{CBA}$ by the central angle. Similarly, $\widehat{OBA} = 90^{\circ} - \widehat{ACB}$. Finally, $\widehat{ACP} = 180^{\circ} - \widehat{ACB} - \widehat{CBA} = \widehat{BAC} = \widehat{PAC}$, hence $PA = PC$, as desired.
Comment from the graders: The exercise was generally very well done!
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle acutangle (dont tous les angles sont aigus) avec $B A \neq B C$. Soit $O$ le centre de son cercle circonscrit. La droite $(A B)$ intersecte le cercle circonscrit à $B O C$ une deuxième fois en $P \neq B$. Montrer que $P A=P C$.
|
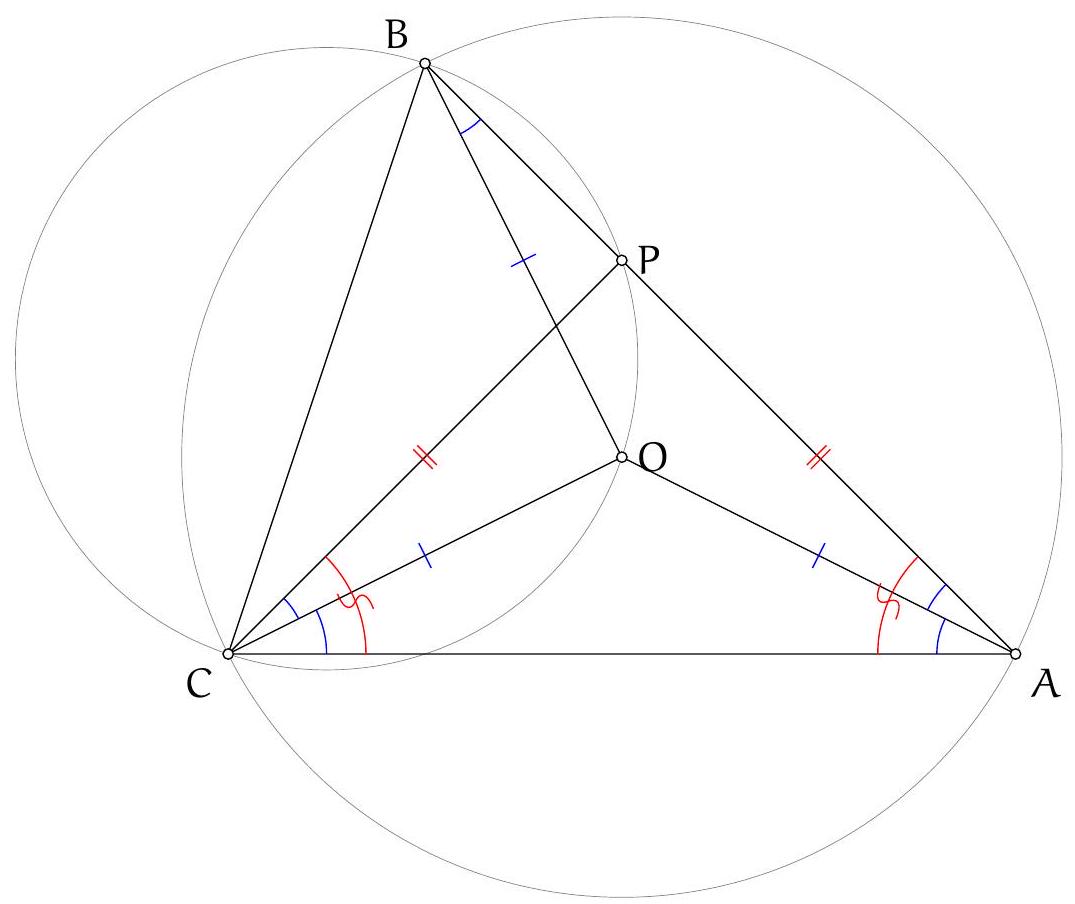
Traçons la figure dans le cas où $B C<B A$, le cas $B C>B A$ étant totalement analogue. Il s'agit de montrer que $\mathrm{PA}=\mathrm{PC}$, c'est-à-dire que $\widehat{A C P}=\widehat{\mathrm{PAC}}(=\widehat{\mathrm{BAC}})$. Or on a :
$$
\begin{aligned}
\widehat{A C P} & =\widehat{A C O}+\widehat{O C P} \\
& =\widehat{A C O}+\widehat{O B P} \text { par angle inscrit } \\
& =\widehat{A C O}+\widehat{O B A} .
\end{aligned}
$$
Or, $A O C$ est isocèle en O donc $\widehat{A C O}=\widehat{O A C}=\frac{180^{\circ}-\widehat{C O A}}{2}=90^{\circ}-\widehat{C B A}$ par angle au centre. De même $\widehat{O B A}=90^{\circ}-\widehat{A C B}$. Finalement, $\widehat{A C P}=180^{\circ}-\widehat{A C B}-\widehat{C B A}=\widehat{B A C}=\widehat{P A C}$, d'où $P A=P C$, comme voulu.
Commentaire des correcteurs : L'exercice a éte globalement tres bien reussi !
|
{
"exam": "French_envois",
"problem_label": "10",
"problem_match": "\nExercice 10.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 10",
"tier": "T2",
"year": "2024"
}
|
Let $ABC$ be a triangle, $O$ the center of its circumcircle. Suppose that $\widehat{C B A}=60^{\circ}$ and $\widehat{\mathrm{CBO}}=45^{\circ}$. Let $D$ be the point of intersection of the lines $(\mathrm{AC})$ and $(B O)$. Show that $\mathrm{AD}=\mathrm{DO}$.
|
To show that $A D=D O$ (i.e., that $A D O$ is isosceles at D), we will show that $\widehat{\mathrm{DOA}}=\widehat{\mathrm{OAD}}$. Introduce $P$ as the intersection point (other than $B$) of (BO) with the circumcircle of $A B C$.
On one hand, $\widehat{\mathrm{DOA}}=\widehat{\mathrm{POA}}=2 \widehat{\mathrm{PBA}}=2\left(60^{\circ}-45^{\circ}\right)=30^{\circ}$ according to the central angle theorem.
On the other hand, $\mathrm{OC}=\mathrm{OA}$, so $\widehat{\mathrm{OAD}}=\widehat{\mathrm{OAC}}=\widehat{\mathrm{ACO}}=\frac{180^{\circ}-\widehat{\mathrm{COA}}}{2}$. According to the central angle theorem, $\widehat{C O A}=2 \widehat{C B A}=120^{\circ}$. Therefore, $\widehat{O A D}=30^{\circ}$.
Finally, $\widehat{D O A}=30^{\circ}=\widehat{\mathrm{OAD}}$, so we have indeed shown that $\mathrm{AD}=\mathrm{DO}$.
Comment from the graders: The exercise was really very well done by all those who tackled it. However, for exercises whose solutions fit on a few lines, it is better to justify the angle chasing well, which can avoid calculation or copying errors. Additionally, many papers could have been shortened, with students taking significant detours in their calculations.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $A B C$ un triangle, $O$ le centre de son cercle circonscrit. On suppose que $\widehat{C B A}=60^{\circ}$ et $\widehat{\mathrm{CBO}}=45^{\circ}$. Soit D le point d'intersection des droites $(\mathrm{AC})$ et $(B O)$. Montrer que $\mathrm{AD}=\mathrm{DO}$.
|
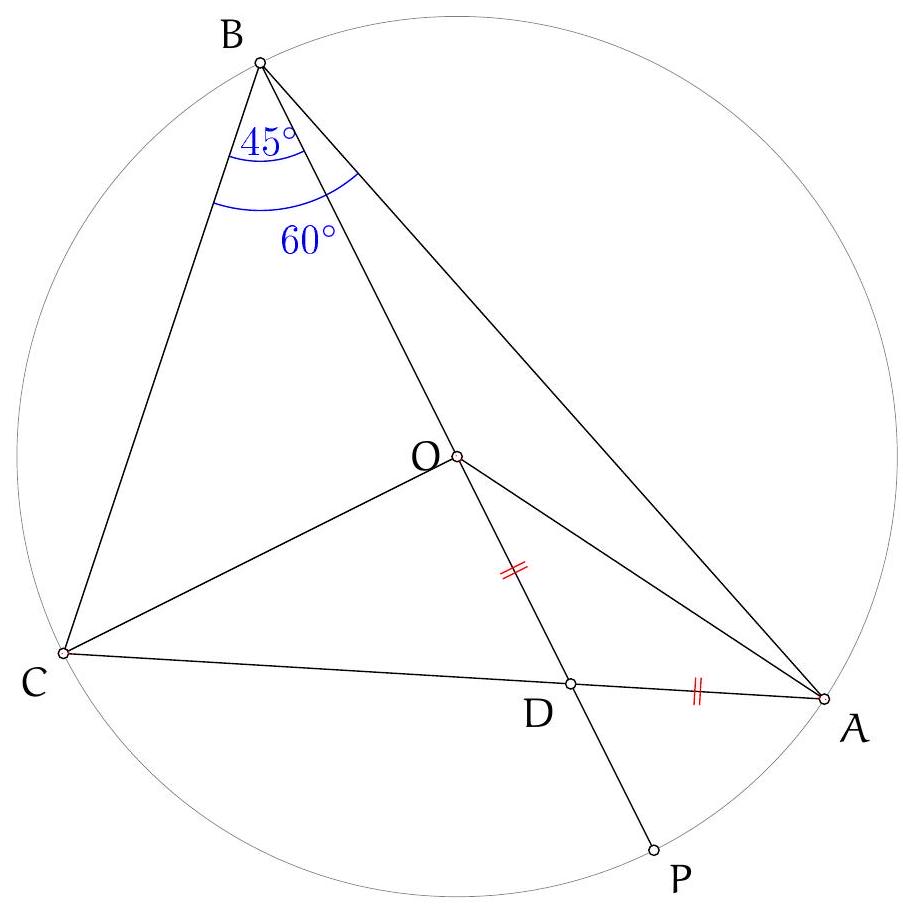
Pour montrer que $A D=D O$ (c'est-à-dire que $A D O$ est isocèle en D ), nous allons montrer que $\widehat{\mathrm{DOA}}=\widehat{\mathrm{OAD}}$. Introduisons $P$ le point d'intersection (autre que $B$ ) de (BO) avec le cercle circonscrit de $A B C$.
D'une part, $\widehat{\mathrm{DOA}}=\widehat{\mathrm{POA}}=2 \widehat{\mathrm{PBA}}=2\left(60^{\circ}-45^{\circ}\right)=30^{\circ}$ d'après le théorème de l'angle au centre.
D'autre part, $\mathrm{OC}=\mathrm{OA}$ donc $\widehat{\mathrm{OAD}}=\widehat{\mathrm{OAC}}=\widehat{\mathrm{ACO}}=\frac{180^{\circ}-\widehat{\mathrm{COA}}}{2}$. Or d'après le théorème de l'angle au centre, $\widehat{C O A}=2 \widehat{C B A}=120^{\circ}$. D'où $\widehat{O A D}=30^{\circ}$.
Finalement, $\widehat{D O A}=30^{\circ}=\widehat{\mathrm{OAD}}$, donc on a bien montré que $\mathrm{AD}=\mathrm{DO}$.
Commentaire des correcteurs: L'exercice à été vraiment très bien réussi par tous ceux qui l'ont abordé. Cependant, pour des exercices dont la solution tient sur quelques lignes, il vaut mieux bien justifier sa chasse aux angle, ce qui peut éviter des erreurs de calculs/ de recopiage. De plus, pas mal de copies auraient pu être raccourcies, les élèves faisant des détours conséquents dans leurs calculs.
|
{
"exam": "French_envois",
"problem_label": "11",
"problem_match": "\nExercice 11.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"solution_match": "## Solution de l'exercice 11",
"tier": "T2",
"year": "2024"
}
|
Let $ABC$ be a right triangle at $B$ with $BC < BA$. Let $D$ be the point on the segment $[AB]$ such that $BD = BC$. The perpendicular to $(AC)$ passing through $D$ intersects $(AC)$ at $E$. Let $B'$ be the symmetric point of $B$ with respect to $(CD)$. Show that $(EC)$ is the bisector of the angle $\widehat{\mathrm{BEB}^{\prime}}$.
|
We notice that the circle with diameter [CD] appears quite naturally. Indeed, we have right angles $\widehat{\mathrm{DB}^{\prime} \mathrm{C}}=\widehat{\mathrm{CBD}}=\widehat{\mathrm{DEC}}=90^{\circ}$, so the points $\mathrm{B}, \mathrm{B}^{\prime}$, and $E$ lie on the circle with diameter [DC], in other words, $\mathrm{C}, \mathrm{B}, \mathrm{D}, \mathrm{E}, \mathrm{B}^{\prime}$ are concyclic.
Then we have:
$$
\begin{aligned}
\widehat{\mathrm{BEC}} & =\widehat{\mathrm{BDC}} \text { by inscribed angle } \\
& =45^{\circ} \text { because } \mathrm{BC}=\mathrm{BD} \text { and } \widehat{\mathrm{CBD}}=90^{\circ} .
\end{aligned}
$$
Furthermore:
$$
\begin{aligned}
\widehat{\mathrm{CEB}^{\prime}} & =\widehat{\mathrm{CBB}^{\prime}} \text { by inscribed angle } \\
& =45^{\circ} \text { because } \mathrm{BC}=\mathrm{BD} \text { and } \widehat{\mathrm{CBD}}=90^{\circ} .
\end{aligned}
$$
Therefore, we have $\widehat{\mathrm{BEC}}=\widehat{\mathrm{CEB}^{\prime}}$, so (EC) is the bisector of $\widehat{\mathrm{BEB}^{\prime}}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle rectangle en $B$ avec $B C<B A$. Soit $D$ le point du segment $[A B]$ tel que $B D=B C$. La perpendiculaire à $(A C)$ passant par $D$ intersecte $(A C)$ en $E$. Soit $B^{\prime}$ le symétrique de B par rapport à (CD). Montrer que (EC) est la bissectrice de l'angle $\widehat{\mathrm{BEB}^{\prime}}$.
|
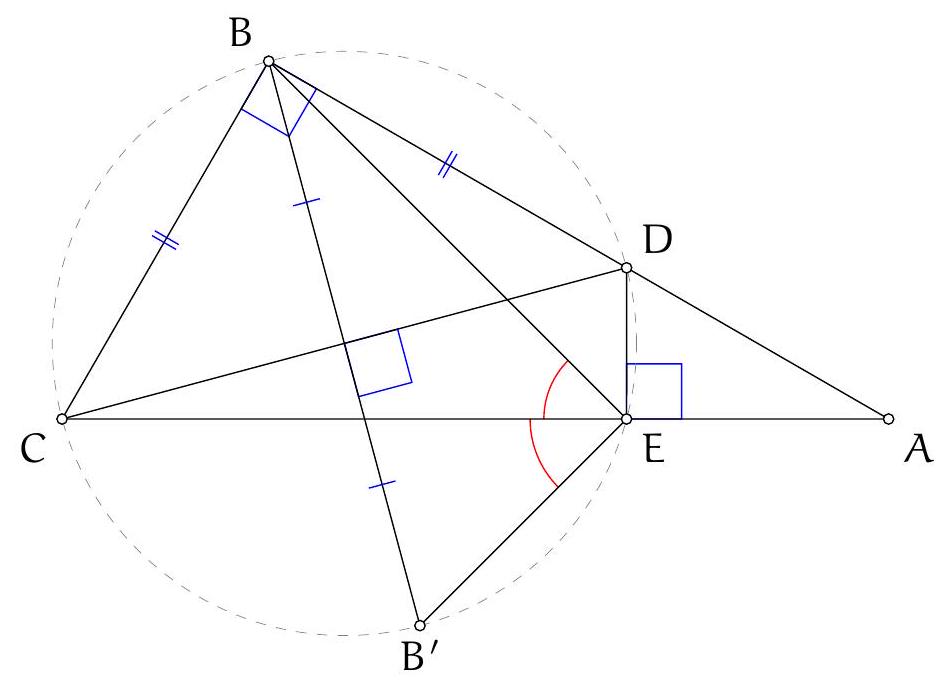
On remarque que le cercle de diamètre [CD] apparaît assez naturellement. En effet, on a des angles droits $\widehat{\mathrm{DB}^{\prime} \mathrm{C}}=\widehat{\mathrm{CBD}}=\widehat{\mathrm{DEC}}=90^{\circ}$, les points $\mathrm{B}, \mathrm{B}^{\prime}$ et $E$ sont sur le cercle de diamètre [DC], autrement dit $\mathrm{C}, \mathrm{B}, \mathrm{D}, \mathrm{E}, \mathrm{B}^{\prime}$ sont cocycliques.
Alors on a :
$$
\begin{aligned}
\widehat{\mathrm{BEC}} & =\widehat{\mathrm{BDC}} \text { par angle inscrit } \\
& =45^{\circ} \text { car } \mathrm{BC}=\mathrm{BD} \text { et } \widehat{\mathrm{CBD}}=90^{\circ} .
\end{aligned}
$$
De plus:
$$
\begin{aligned}
\widehat{\mathrm{CEB}^{\prime}} & =\widehat{\mathrm{CBB}^{\prime}} \text { par angle inscrit } \\
& =45^{\circ} \text { car } \mathrm{BC}=\mathrm{BD} \text { et } \widehat{\mathrm{CBD}}=90^{\circ} .
\end{aligned}
$$
On a donc bien $\widehat{\mathrm{BEC}}=\widehat{\mathrm{CEB}^{\prime}}$, donc (EC) est la bissectrice de $\widehat{\mathrm{BEB}^{\prime}}$.
|
{
"exam": "French_envois",
"problem_label": "12",
"problem_match": "\nExercice 12.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"solution_match": "## Solution de l'exercice 12",
"tier": "T2",
"year": "2024"
}
|
Let $ABC$ be a right triangle at $B$ with $BC < BA$. Let $D$ be the point on the segment $[AB]$ such that $BD = BC$. The perpendicular to $(AC)$ passing through $D$ intersects $(AC)$ at $E$. Let $B'$ be the symmetric point of $B$ with respect to $(CD)$. Show that $(EC)$ is the bisector of the angle $\widehat{\mathrm{BEB}^{\prime}}$.
|
$n^{\circ} 1$
We could also show directly $\widehat{\mathrm{BEC}}=\widehat{\mathrm{CEB}^{\prime}}$ without using $\mathrm{BC}=\mathrm{BD}$. Indeed:
$$
\begin{aligned}
\widehat{\mathrm{BEC}} & =\widehat{\mathrm{BDC}} \text { by inscribed angle } \\
& =\widehat{\mathrm{CDB}^{\prime}} \text { by symmetry } \\
& =\widehat{\mathrm{CEB}} \text { by inscribed angle. }
\end{aligned}
$$
Comment from the graders: The exercise was very well done, some angle chasing could have been avoided or shortened by using the cocyclicity of the points or the South Pole theorem.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle rectangle en $B$ avec $B C<B A$. Soit $D$ le point du segment $[A B]$ tel que $B D=B C$. La perpendiculaire à $(A C)$ passant par $D$ intersecte $(A C)$ en $E$. Soit $B^{\prime}$ le symétrique de B par rapport à (CD). Montrer que (EC) est la bissectrice de l'angle $\widehat{\mathrm{BEB}^{\prime}}$.
|
$n^{\circ} 1$
On pouvait aussi montrer directement $\widehat{\mathrm{BEC}}=\widehat{\mathrm{CEB}^{\prime}}$ sans utiliser $\mathrm{BC}=\mathrm{BD}$. En effet :
$$
\begin{aligned}
\widehat{\mathrm{BEC}} & =\widehat{\mathrm{BDC}} \text { par angle inscrit } \\
& =\widehat{\mathrm{CDB}^{\prime}} \text { par symétrie } \\
& =\widehat{\mathrm{CEB}} \text { par angle inscrit. }
\end{aligned}
$$
Commentaire des correcteurs : L'exercice a été très bien réussi, certaines chasses aux angles auraient pu être évitées ou raccourcies en utilisant la cocyclicité des points ou le théorème du Pôle Sud.
|
{
"exam": "French_envois",
"problem_label": "12",
"problem_match": "\nExercice 12.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T2",
"year": "2024"
}
|
Let $A B C D E$ be a convex cyclic pentagon such that $A B=B D$. Let $P$ be the intersection point of the lines (EB) and ( $A C$ ). Let $Q$ be the intersection point of the lines ( $B C$ ) and ( $D E$ ). Show that $(\mathrm{PQ})$ and (AD) are parallel.
|
In the figure, it seems that EPCQ is a cyclic quadrilateral. We show this:
\[
\begin{aligned}
\widehat{\mathrm{QCP}} & =180^{\circ}-\widehat{\mathrm{PCB}} \\
& =180^{\circ}-\widehat{\mathrm{ACB}} \\
& =180^{\circ}-\widehat{\mathrm{ADB}} \text { by inscribed angle } \\
& =180^{\circ}-\widehat{\mathrm{BAD}} \text{ since } \mathrm{AB}=\mathrm{BD} \\
& =180^{\circ}-\widehat{\mathrm{BED}} \\
& =180^{\circ}-\widehat{\mathrm{PEQ}}.
\end{aligned}
\]
Thus, we have shown that \(\widehat{Q C P}+\widehat{P E Q}=180^{\circ}\). Therefore, by the converse of the inscribed angle theorem, EPCQ is cyclic, which is what we wanted to prove.
Now, to show that (AD) and (PQ) are parallel, we will try to find corresponding angles. We have:
\[
\begin{aligned}
\widehat{\mathrm{EQP}} & =\widehat{\mathrm{ECP}} \text { by inscribed angle } \\
& =\widehat{\mathrm{ECA}} \\
& =\widehat{\mathrm{EDA}} \text { by inscribed angle. }
\end{aligned}
\]
Since \(\widehat{\mathrm{EQP}}=\widehat{\mathrm{EDA}}\) and \(\mathrm{Q}, \mathrm{D}, \mathrm{E}\) are collinear (in that order), by corresponding angles, the lines (PQ) and (AD) are indeed parallel.
Comment from the graders: The exercise was generally well handled. Most solutions that worked involved proving that EQCP is cyclic and concluding by angle chasing. Some used more advanced tools, such as some who used similarities, others applied Pascal's theorem in the degenerate hexagon \(A D E B B C\), and still others used inversions. However, it is worth noting that many students take unnecessary detours in their calculations, sometimes doing in 2 pages what can be proven in 2 lines: while having a solution that works is obviously a very good thing, it is even better to have a solution that works and is efficient. For example, it was not necessary here to introduce intermediate points, as all the necessary points were defined in the problem statement. It is also worth noting that while the vast majority of submissions include a figure, some do not: providing a clear figure is essential for illustrating reasoning in a geometry problem.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D E$ un pentagone cyclique convexe tel que $A B=B D$. Soit $P$ le point d'intersection des droites (EB) et ( $A C$ ). Soit $Q$ le point d'intersection des droites ( $B C$ ) et ( $D E$ ). Montrer que $(\mathrm{PQ})$ et (AD) sont parallèles.
|
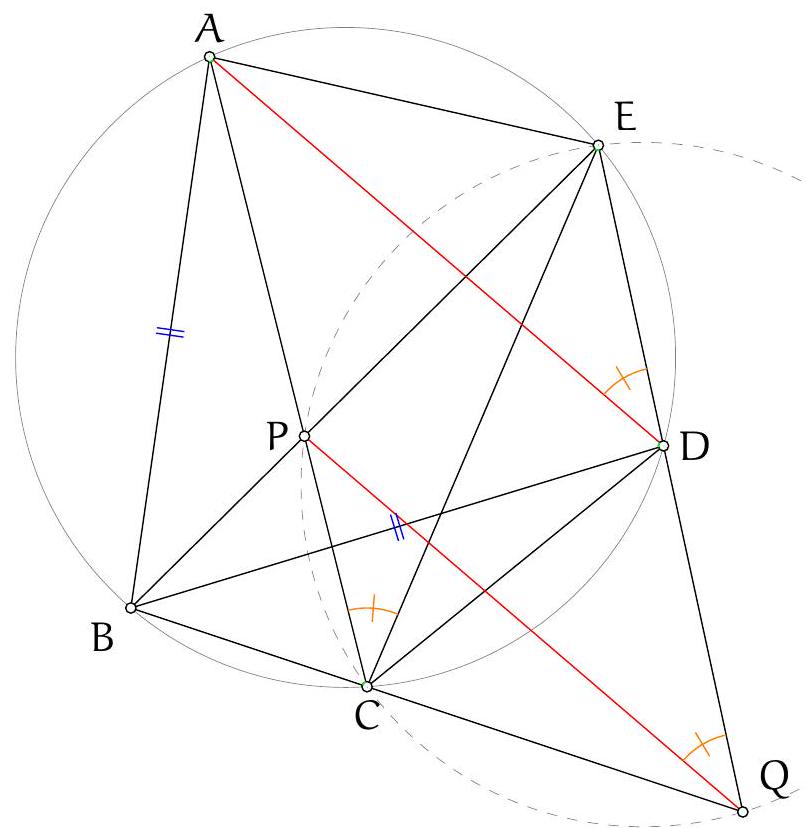
Sur la figure, il semble que EPCQ est un quadrilatère cyclique. On le montre :
$$
\begin{aligned}
\widehat{\mathrm{QCP}} & =180^{\circ}-\widehat{\mathrm{PCB}} \\
& =180^{\circ}-\widehat{\mathrm{ACB}} \\
& =180^{\circ}-\widehat{\mathrm{ADB}} \text { par angle inscrit } \\
& =180^{\circ}-\widehat{\mathrm{BAD}} \mathrm{car} \mathrm{AB}=\mathrm{BD} \\
& =180^{\circ}-\widehat{\mathrm{BED}} \\
& =180^{\circ}-\widehat{\mathrm{PEQ}} .
\end{aligned}
$$
Ainsi on a montré que $\widehat{Q C P}+\widehat{P E Q}=180^{\circ}$. Dès lors, par réciproque de l'angle inscrit, EPCQ est cyclique, ce qu'on voulait démontrer.
Maintenant, pour montrer que ( AD ) et ( PQ ) sont parallèles, on va essayer de trouver des angles correspondants. Or on a :
$$
\begin{aligned}
\widehat{\mathrm{EQP}} & =\widehat{\mathrm{ECP}} \text { par angle inscrit } \\
& =\widehat{\mathrm{ECA}} \\
& =\widehat{\mathrm{EDA}} \text { par angle inscrit. }
\end{aligned}
$$
Comme $\widehat{\mathrm{EQP}}=\widehat{\mathrm{EDA}}$ et $\mathrm{Q}, \mathrm{D}, \mathrm{E}$ sont alignés (dans cet ordre), par angle correspondant les droites (PQ) et $(A D)$ sont bien parallèles.
Commentaire des correcteurs : L'exercice a été dans l'ensemble très bien traité. La plupart des solutions qui ont abouti consistaient à prouver EQCP cyclique et à conclure par chasse aux angles. D'autres ont trouvé des solutions avec des outils plus avancés, notamment certains ont utilisé des similitudes,
d'autres ont vu qu'on pouvait appliquer le théorème de Pascal dans l'hexagone dégénéré $A D E B B C$, d'autres encore ont utilisé des inversions. Il est cependant à noter qu'un bon nombre d'élèves font beaucoup de détours peu utiles dans leurs calculs, faisant parfois en 2 pages ce qui se prouve en 2 lignes : si avoir une solution qui fonctionne est évidemment un très bonne chose, il est encore mieux d'avoir une solution qui fonctionne et qui est efficace. Il n'était par exemple pas nécessaire ici d'introduire des points intermédiaires, tous les points utiles étaient définis dans l'énoncé. On notera aussi que si la grande majorité des copies rendent une figure, certains ne le font pas : rendre une figure propre est indispensable pour illustrer son raisonnement dans un problème de géométrie.
|
{
"exam": "French_envois",
"problem_label": "13",
"problem_match": "\nExercice 13.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"solution_match": "## Solution de l'exercice 13",
"tier": "T2",
"year": "2024"
}
|
Let $ABC$ be a triangle, $D, E$ the feet of the altitudes from $A$ and $B$ respectively. The line $(DE)$ intersects the circumcircle of $ABC$ at two points $P$ and $Q$. Let $A'$ and $B'$ be the reflections of $A$ and $B$ with respect to $(BC)$ and $(AC)$ respectively. Show that $A', B', P, Q$ are concyclic.
|
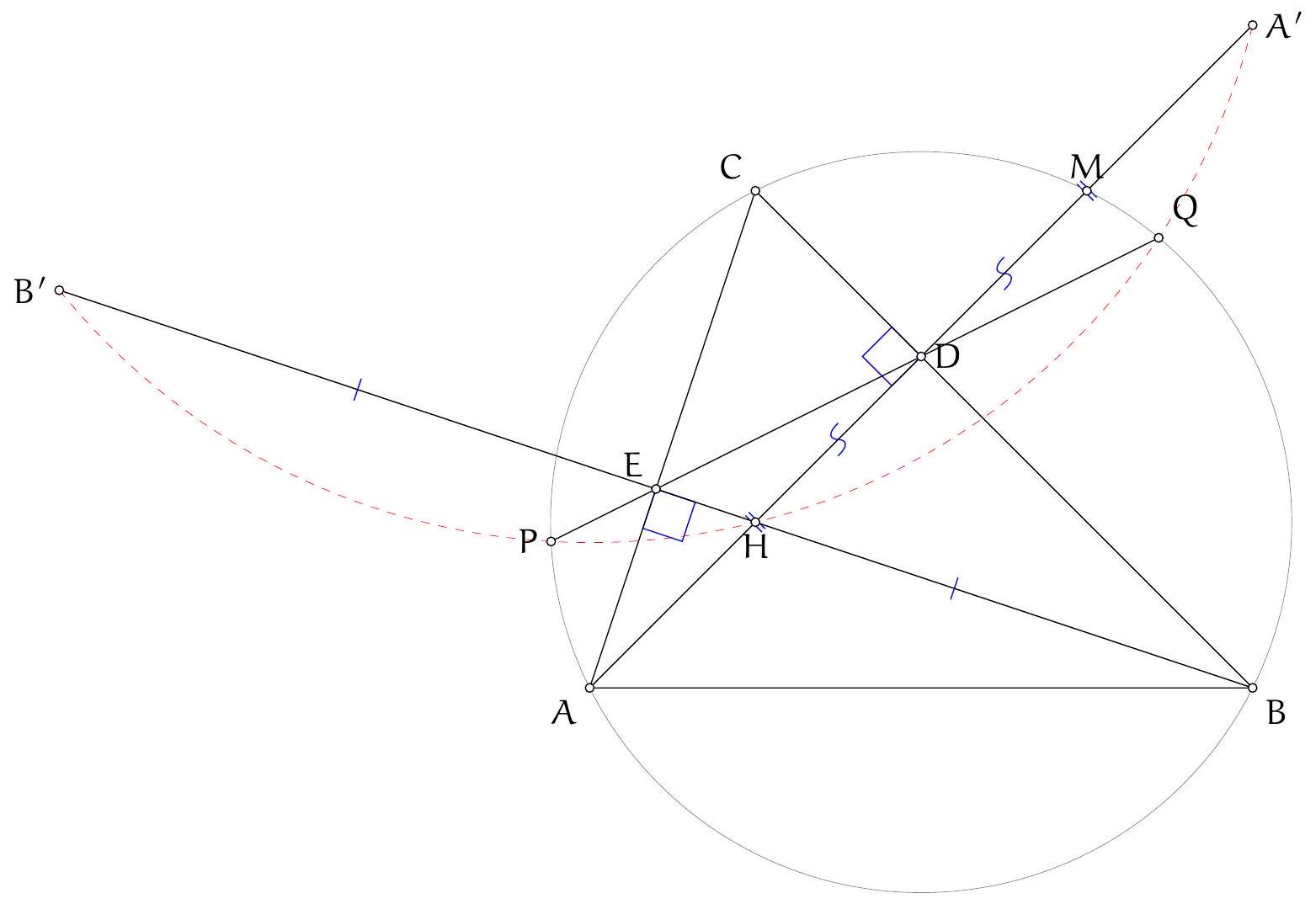
In the figure, it appears that H, the orthocenter, lies on the circle in question. Therefore, we will adopt the following strategy: we will show that \(A'\) and \(B'\) are on the circumcircle of \(P Q H\). This way, we will have \(A', B', P, Q\) being concyclic.
Let \(M\) be the symmetric point of H with respect to (BC): then we know that \(M\) is on the circumcircle of \(ABC\). Then we have:
\[
\begin{aligned}
D A' \times D H & = D A \times D M \text{ by symmetry} \\
& = D P \times D Q \text{ by power of } D \text{ in the circle } (ABC).
\end{aligned}
\]
Then, by the converse of the power of a point, \(P, Q, H, A'\) are concyclic. In a completely analogous manner, \(P, Q, H, B'\) are also concyclic. Thus, \(A', B', P, Q\) are concyclic, on the circle \((P Q H)\).
Comment from the graders: The exercise was generally well done by those who attempted it. The fact that the symmetrics of H are on the circumcircle of \(ABC\) is a useful lemma, which is good to have in mind and does not need to be reproved every time it is needed (saying "it is known that" is sufficient).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $A B C$ un triangle, $D, E$ les pieds des hauteurs issues de $A$ et $B$ respectivement. La droite ( $D E$ ) rencontre le cercle circonscrit à $A B C$ en deux points $P$ et $Q$. Soient $A^{\prime}$ et $B^{\prime}$ les symétriques de $A$ et $B$ par rapport à $(B C)$ et $(A C)$ respectivement. Montrer que $A^{\prime}, B^{\prime}, P, Q$ sont cocycliques.
|

Sur la figure, il semble que H l'orthocentre se situe sur le cercle en question. On va donc adopter la stratégie suivante : on va montrer que $A^{\prime}$ et $B^{\prime}$ sont sur le cercle circonscrit de $P Q H$. De cette manière on aura bien $A^{\prime}, B^{\prime}, P, Q$ cocycliques.
Soit $M$ le symétrique de H par rapport à ( BC ) : alors on sait que $M$ est sur le cercle circonscrit à ABC. Alors on a :
$$
\begin{aligned}
D A^{\prime} \times D H & =D A \times D M \text { par symétrie } \\
& =D P \times D Q \text { par puissance de } D \text { dans le cercle }(A B C) .
\end{aligned}
$$
Alors par réciproque de la puissance d'un point, $P, Q, H, A^{\prime}$ sont cocycliques. De façon totalement analogue, $P, Q, H, B^{\prime}$ sont également cocycliques. Ainsi $A^{\prime}, B^{\prime}, P, Q$ sont cocycliques, sur le cercle ( $P Q H$ ).
Commentaire des correcteurs : L'exercice a été globalement bien réussi par ceux qui l'ont essayé. Le fait que les symétriques de H sont sur le cercle circonscrit à $A B C$ est un lemme souvent utile, qu'il est bon d'avoir en tête, et qu'il n'y a pas besoin de reprouver à chaque fois qu'on en a besoin (dire "il est connu que" est suffisant).
|
{
"exam": "French_envois",
"problem_label": "14",
"problem_match": "\nExercice 14.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"solution_match": "## Solution de l'exercice 14",
"tier": "T2",
"year": "2024"
}
|
Let $ABCD$ be a convex cyclic quadrilateral, $M$ the midpoint of $[AC]$. The circumcircle of $CDM$ intersects $(BC)$ a second time at $N$ (other than $C$). Let $B'$ be the symmetric point of $B$ with respect to $N$. Show that $(MN)$ is tangent to the circumcircle of $B'DN$.
|
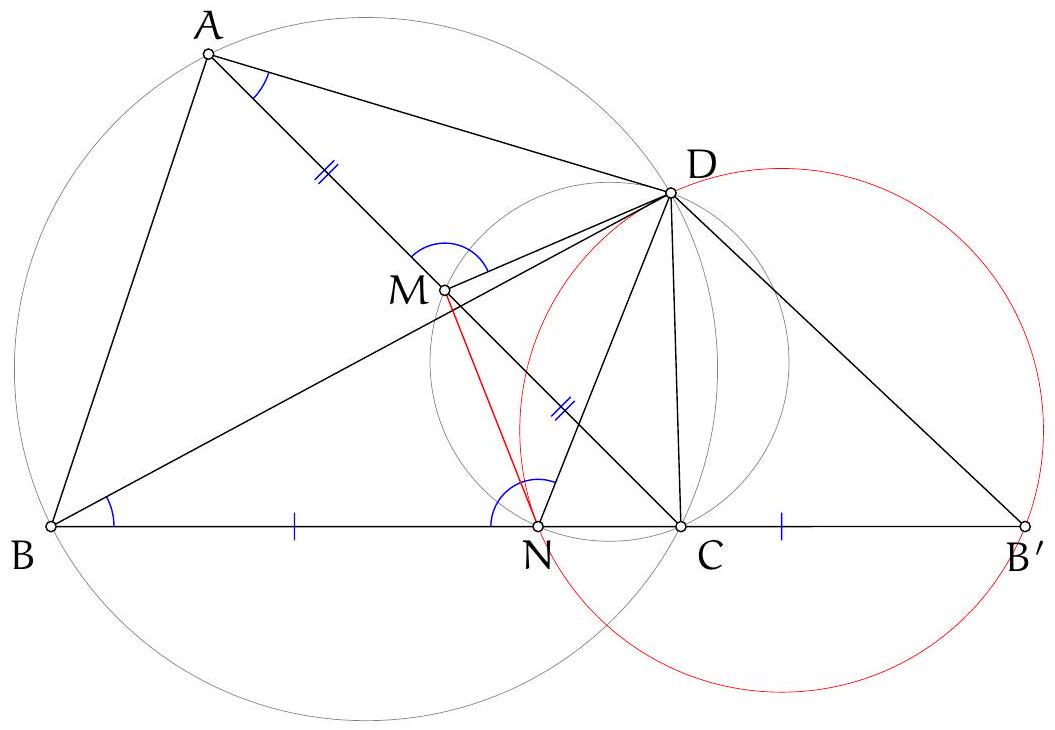
In the figure, we can identify similar triangles. Indeed, by inscribed angles, we have:
$$
\widehat{M A D}=\widehat{C A D}=\widehat{C B D}=\widehat{N B D}
$$
Again by inscribed angles, we have:
$$
\widehat{\mathrm{DMA}}=180^{\circ}-\widehat{\mathrm{CMD}}=180^{\circ}-\widehat{\mathrm{CND}}=\widehat{\mathrm{DNB}}
$$
We deduce that triangles \(A M D\) and \(B N D\) are similar. But then \(A D C\) and \(\mathrm{BDB}^{\prime}\) are similar. Indeed, we have \(\widehat{B^{\prime} B D}=\widehat{C B D}\), and \(\frac{B B^{\prime}}{A C}=\frac{2 B N}{2 A M}=\frac{B N}{A M}=\frac{B D}{A D}\), and thus \(A D C\) is similar to \(\mathrm{BDB}^{\prime}\). It follows that:
$$
\begin{aligned}
\widehat{M N D} & =\widehat{M C D} \text { by inscribed angle } \\
& =\widehat{A C D} \\
& =\widehat{\mathrm{BB}^{\prime} \mathrm{D}} \text { since } \mathrm{ADC} \sim \mathrm{BDB}^{\prime} \\
& =\widehat{\mathrm{DB}^{\prime} \mathrm{D}}
\end{aligned}
$$
Therefore, by the converse of the tangent angle, (MN) is tangent to the circumcircle of \(\mathrm{B}^{\prime} \mathrm{DN}\), which is what we wanted to show.
Comment from the graders: The problem could be solved using elementary tools (identifying similar triangles through angle equalities, deducing other pairs of similar triangles, recovering the desired angle equality), but it could also be approached by adopting the perspective of similarities, which provides several shortcuts in the steps mentioned above. This second approach was chosen by most students who responded to the problem and was very successful in the results obtained, but less successful in the consistency of the approach: introducing the similarity centered at D is superfluous if it has already been shown by angle chasing that \(\triangle \mathrm{DAM} \sim \triangle \mathrm{DBN}\).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un quadrilatère convexe cyclique, $M$ le milieu de $[A C]$. Le cercle circonscrit à $C D M$ rencontre $(B C)$ une deuxième fois en $N$ (autre que $C$ ). Soit $B^{\prime}$ le symétrique de $B$ par rapport à $N$. Montrer que (MN) est tangente au cercle circonscrit de $B^{\prime} D N$.
|

Sur la figure, on repère des triangles semblables. En effet, on a par angle inscrit :
$$
\widehat{M A D}=\widehat{C A D}=\widehat{C B D}=\widehat{N B D}
$$
Toujours par angle inscrit, on a :
$$
\widehat{\mathrm{DMA}}=180^{\circ}-\widehat{\mathrm{CMD}}=180^{\circ}-\widehat{\mathrm{CND}}=\widehat{\mathrm{DNB}}
$$
On en déduit que les triangles $A M D$ et BND sont semblables. Mais alors $A D C$ et $\mathrm{BDB}^{\prime}$ sont semblables. En effet on a $\widehat{B^{\prime} B D}=\widehat{C B D}$, et $\frac{B B^{\prime}}{A C}=\frac{2 B N}{2 A M}=\frac{B N}{A M}=\frac{B D}{A D}$, et donc ADC est semblable à $\mathrm{BDB}^{\prime}$. Il suit que :
$$
\begin{aligned}
\widehat{M N D} & =\widehat{M C D} \text { par angle inscrit } \\
& =\widehat{A C D} \\
& =\widehat{\mathrm{BB}^{\prime} \mathrm{D}} \text { car } \mathrm{ADC} \sim \mathrm{BDB}^{\prime} \\
& =\widehat{\mathrm{DB}^{\prime} \mathrm{D}}
\end{aligned}
$$
Donc par réciproque de l'angle tangentiel, (MN) est tangente au cercle circonscrit à $\mathrm{B}^{\prime} \mathrm{DN}$, ce qu'on voulait montrer.
Commentaire des correcteurs: L'exercice pouvait se résoudre avec des outils élémentaires (repérer des triangles sembables grâce aux égalités d'angles, déduire d'autres paires de triangles semblables, récupérer l'égalité d'angles voulue), mais pouvait également être raconté en adoptant le point de vue des similitudes, qui donne plusieurs raccourcis dans les étapes précédemment citées. Cette deuxième approche a été celle choisie par la plupart des élèves ayant répondu au problème, et a rencontré beaucoup de succès dans les résultats obtenus, mais un peu moins de succès dans la consistance de la démarche : introduire la similitude de centre D est superflu si on a déjà montré par chasse aux angles que $\triangle \mathrm{DAM} \sim$ $\triangle \mathrm{DBN}$.
|
{
"exam": "French_envois",
"problem_label": "15",
"problem_match": "\nExercice 15.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"solution_match": "## Solution de l'exercice 15",
"tier": "T2",
"year": "2024"
}
|
Let $ABC$ be a triangle with $\widehat{BAC}=60^{\circ}$ and let $\Gamma$ be its circumcircle. Let $H$ be the orthocenter of $ABC$ and $S$ the midpoint of the arc $\widehat{BC}$ not containing $A$. Let $P$ be the point on $\Gamma$ such that $\widehat{SPH}=90^{\circ}$. Show that there exists a circle passing through $P, S$ and which is tangent to $(AB)$ and $(AC)$.
|
According to the South Pole theorem, $S$ is the intersection point of the bisector of $\widehat{B A C}$ and the perpendicular bisector of $[B C]$. Let $O$ be the center of $\Gamma$ and $N$ the North Pole. Since $[S N]$ is a diameter of $\Gamma$, the condition $\widehat{S P H}=90^{\circ}$ can be rewritten as $P, H, N$ being collinear. We then introduce $Q$ as the intersection point of (AS) and (PN).
Notice that since $\widehat{S P Q}=90^{\circ}$, points $P, S$ lie on the circle with diameter [QS], making it a candidate for the desired circle. We want to show that it is tangent to ( $A B$ ) and ( $A C$ ). Let $M$ be the midpoint of $[Q S]$ and $R$ the orthogonal projection of $M$ onto $[A C]$. The goal is to show that $R$ lies on the circle with diameter $[Q S]$, so that we have tangency with (AC) (and by symmetry, tangency with (AB)).
Let $D$ be the midpoint of $[B C]$. We know that (HD) and $(A O)$ intersect on $\Gamma$, and that $(A H) \parallel (O M)$ (both are perpendicular to ( $B C$ )), so by the midline theorem, $A H=2 O D$. By the central angle theorem, $\widehat{S O C}=60^{\circ}$, so $\triangle SOC$ is equilateral $(\mathrm{OS}=\mathrm{OC})$, and thus $2 \mathrm{OD}=\mathrm{OS}=\mathrm{OC}=\mathrm{ON}$. Furthermore, since $(A H) \parallel (N S)$, by the theorem of Thales, $\frac{A Q}{S Q}=\frac{A H}{N S}=\frac{1}{2}$, so $Q S=2 A Q$.
In particular, $M Q=M S=\frac{Q S}{2}=A Q$. Since $\widehat{M A R}=30^{\circ}$, $M R=\frac{1}{2} A M=M Q$ (since $\sin \left(30^{\circ}\right)=\frac{1}{2}$), so $R$ is indeed on the circle with diameter [QS], making it tangent to (AC) (at $R$).
Therefore, there exists a circle passing through $P, S$ and tangent to $(A B)$ and $(A C)$: the circle with diameter [QS].
Comment from the graders: The exercise was very well done by those who submitted it. Knowledge of the Euler line or the clever use of the South Pole theorem could have shortened some proofs.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle avec $\widehat{B A C}=60^{\circ}$ et soit $\Gamma$ son cercle circonscrit. Soient H l'orthocentre de $A B C$ et $S$ le milieu de l'arc $\widehat{B C}$ ne contenant pas $A$. Soit $P$ le point de $\Gamma$ tel que $\widehat{S P H}=90^{\circ}$. Montrer qu'il existe un cercle passant par $P, S$ et qui est tangent à ( $A B$ ) et ( $A C$ ).
|
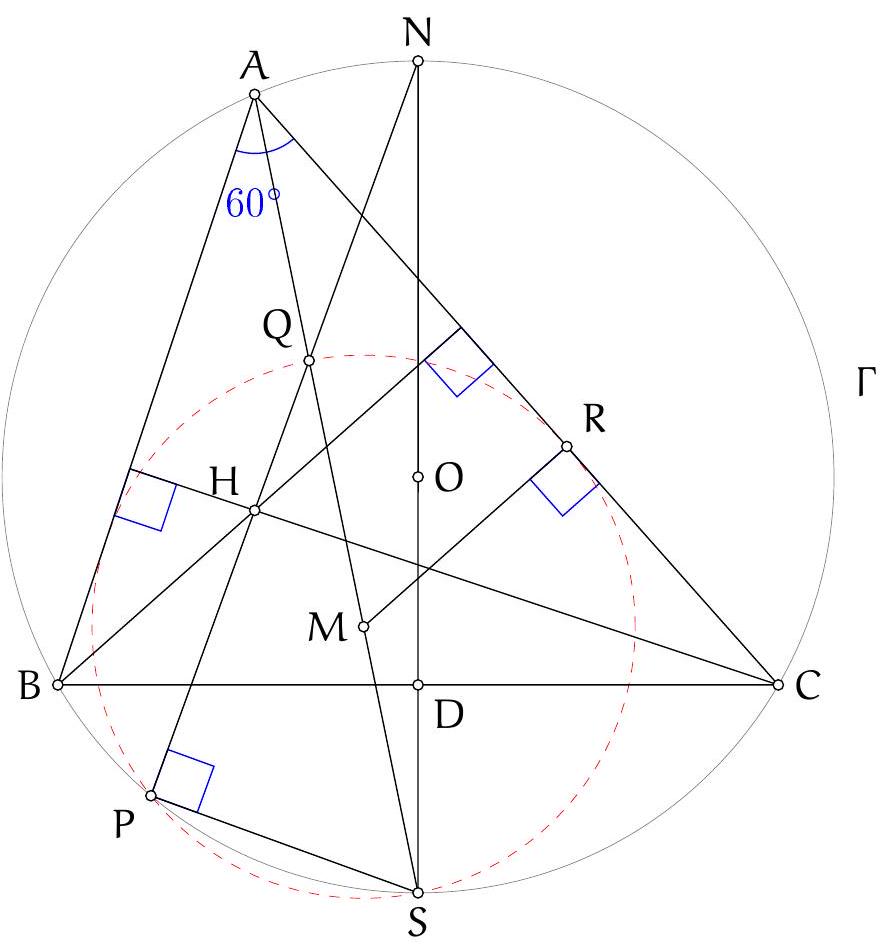
D'après le théorème du pôle Sud, $S$ est le point de concours de la bissectrice de $\widehat{B A C}$ et de la médiatrice de $[B C]$. Soit $O$ le centre de $\Gamma$ et $N$ le pôle Nord. Comme $[S N]$ est un diamètre de $\Gamma$, la condition $\widehat{S P H}=90^{\circ}$ se réécrit $P, H, N$ alignés. Introduisons alors $Q$ le point d'intersection de (AS) et (PN).
Remarquons que comme $\widehat{S P Q}=90^{\circ}, \mathrm{P}, \mathrm{S}$ se situent sur le cercle de diamètre [QS], c'est donc un candidat pour être le cercle recherché. On aimerait montrer qu'il est tangent à ( $A B$ ) et à ( $A C$ ). Posons $M$ le milieu de $[Q S]$ et $R$ le projeté orthogonal de $M$ sur $[A C]$. Le but est de montrer que $R$ est sur le cercle de diamètre $[Q S]$, de sorte à avoir la tangence avec (AC) (et pour des raisons de symétrie on aura la tangence avec (AB)).
Soit D le milieu de $[B C]$. On sait que (HD) et $(A O)$ se coupent sur $\Gamma$, et que $(A H) / /(O M)$ (les deux sont perpendiculaires à ( $B C$ ), donc par droite des milieux $A H=2 O D$. Or par angle au centre, $\widehat{S O C}=60^{\circ}$ donc SOC est équilatéral $(\mathrm{OS}=\mathrm{OC})$, et donc $2 \mathrm{OD}=\mathrm{OS}=\mathrm{OC}=\mathrm{ON}$. De plus, comme $(A H) / /(N S)$, d'après le théorème de Thalès, $\frac{A Q}{S Q}=\frac{A H}{N S}=\frac{1}{2}$ donc $Q S=2 A Q$.
En particulier $M Q=M S=\frac{Q S}{2}=A Q$. Or $\widehat{M A R}=30^{\circ}$ donc $M R=\frac{1}{2} A M=M Q$ (en effet $\sin \left(30^{\circ}\right)=\frac{1}{2}$ ), donc R est bien sur le cercle de diamètre [QS], donc ce dernier est tangent à (AC) (en R).
Donc il existe bien un cercle passant par $P, S$ et qui est tangent à $(A B)$ et $(A C)$ : le cercle de diamètre [QS].
Commentaire des correcteurs : L'exercice était très bien réussi par ceux qui l'ont rendu, la connaissance de la droite d'Euler ou l'utilisation astucieuse du théroème du pole sud pouvait raccoucir certaines
preuves.
|
{
"exam": "French_envois",
"problem_label": "16",
"problem_match": "\nExercice 16.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"solution_match": "## Solution de l'exercice 16",
"tier": "T2",
"year": "2024"
}
|
Let $ABC$ be a triangle and $O$ the center of its circumcircle. Let $d$ be the line parallel to $(BC)$ passing through $O$. Let $A'$ be the symmetric point of $A$ with respect to $(BC)$. The line parallel to $(A'B)$ passing through $C$ intersects $d$ at $C_1$, and the lines $(A'C)$ and $(BC_1)$ intersect at $C_2$. The line parallel to $(A'C)$ passing through $B$ intersects $d$ at $B_1$, and the lines $(A'B)$ and $(CB_1)$ intersect at $B_2$. Show that the points $A, A', B_2, C_2$ are concyclic.
|
Let $P$ be the intersection point of the lines $(C B_{1})$ and $(B C_{1})$, and $Q$ the intersection point of $(B B_{1})$ and $(C C_{1})$. We also set $T$ as the intersection of $(A O)$ and $(B C)$. We can then observe several properties of the figure, which we will prove.
- Lemma 1: The point $Q$ is on the circumcircle of $A B C$.
Proof: By the construction of $B_{1}, C_{1}, A^{\prime}$, $BQC$ is a parallelogram, so $\widehat{BQC} = \widehat{CA^{\prime}B}$. But by symmetry, $\widehat{CA^{\prime}B} = \widehat{BAC}$. Therefore, $\widehat{BAC} = \widehat{BQC}$: by the inscribed angle theorem, $Q$ is indeed on the circumcircle of $A B C$.
- Lemma 2: The points $P, Q, A^{\prime}$ are collinear.
Proof: The quadrilateral $BCC_{1}B_{1}$ is a trapezoid, so the line $(PQ)$ passes through the midpoints of $[B_{1}C_{1}]$ and $[BC]$. Therefore, the line $(PQ)$ passes through the midpoint of $[BC]$. Since $A^{\prime}BQC$ is a parallelogram, $(QA^{\prime})$ also passes through the midpoint of $[BC]$. We conclude that $Q, P, A^{\prime}$ are collinear.
- Lemma 3: The points $O, P, T$ are collinear.
Proof: Consider the symmetry with respect to the perpendicular bisector of $[BC]$: it fixes $O$, it swaps $B$ and $C$. It also swaps $A$ and $Q$, indeed $\widehat{Q_{CB}} = \widehat{A^{\prime}BC} = \widehat{CBA}$ by parallelism and symmetry, and $\widehat{CBQ} = \widehat{ACB}$. Now let $X$ be the intersection of $(AB)$ with $d$, and $Y$ the intersection of $(AC)$ with $d$. Since $d$ is invariant under the symmetry, the symmetry swaps $B_{1}$ and $Y$, $C_{1}$ and $X$. We deduce that $\frac{OB_{1}}{OC_{1}} = \frac{OY}{OX}$. Applying the theorem of Thales, we get $\frac{OY}{OX} = \frac{TC}{TB}$, hence $\frac{TC}{TB} = \frac{OB_{1}}{OC_{1}}$. This implies that $O, P, T$ are collinear (applying Thales in $OC_{1}PBT^{\prime}$ and in $OB_{1}BCT^{\prime}$ where $T^{\prime}$ is the intersection of $(OP)$ and $(BC)$, we get $\frac{TB}{TC} = \frac{T^{\prime}B}{T^{\prime}C}$, hence $T = T^{\prime}$). Therefore, $O, P, T$ (and thus $A, O, P, T$) are collinear.
- Lemma 4: The homothety with center $P$ and ratio $-\frac{PT}{PO}$ maps $QBC$ to $A^{\prime}C_{2}B_{2}$.
Proof: According to the theorem of Thales in $QCPB_{2}A^{\prime}$ and in $QBPC_{2}A^{\prime}$, we have $\frac{PQ}{PA^{\prime}} = \frac{PC}{PB_{2}} = \frac{PB}{PC_{2}}$, so the homothety with center $P$ that maps $Q$ to $A^{\prime}$ also maps $B$ to $C_{2}$ and $C$ to $B_{2}$. It remains to show that it maps $O$ to $T$. From the theorem of Thales in $QC_{1}PBA^{\prime}$ and then in $OC_{1}PBT$, we have $\frac{PQ}{PA^{\prime}} = \frac{PC_{1}}{PB} = \frac{PO}{PT}$, so it is indeed the homothety with ratio $-\frac{PT}{PO}$.
- We now have all the elements to conclude: the homothety of Lemma 4 maps $QBC$ to $A^{\prime}C_{2}B_{2}$ and $O$ to $T$. By Lemma 1, $O$ is the center of the circumcircle of $QBC$. Therefore, $T$ is the center of the circumcircle of $A^{\prime}C_{2}B_{2}$. Since $T$ is on $(BC)$, we have $TA = TA^{\prime}$, so $A$ is on the circle with center $T$ and radius $TA^{\prime}$. Finally, we have shown that $A, A^{\prime}, B_{2}, C_{2}$ are concyclic, and we have even found the center of the circle in question, which is $T$.
Comment from the graders: The problem is well solved by a good number of students. The solutions show a very good mastery of the concept of homothety, which allows the problem to be told in a sometimes very efficient way, revealing the roles of the different points, where other students have proposed more down-to-earth (ratio calculations) or more abstract (dynamic solution) approaches.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $A B C$ un triangle et $O$ le centre de son cercle circonscrit. Soit d la parallèle à (BC) passant par $O$. Soit $A^{\prime}$ le symétrique de $A$ par rapport à ( $B C$ ). La parallèle à ( $A^{\prime} B$ ) passant par $C$ coupe d en $C_{1}$, et les droites $\left(A^{\prime} C\right)$ et $\left(B C_{1}\right)$ s'intersectent en $C_{2}$. La parallèle à ( $A^{\prime} C$ ) passant par $B$ coupe $d$ en $B_{1}$, et les droites $\left(A^{\prime} B\right)$ et $\left(C B_{1}\right)$ s'intersectent en $B_{2}$. Montrer que les points $A, A^{\prime}, B_{2}, C_{2}$ sont cocycliques.
|
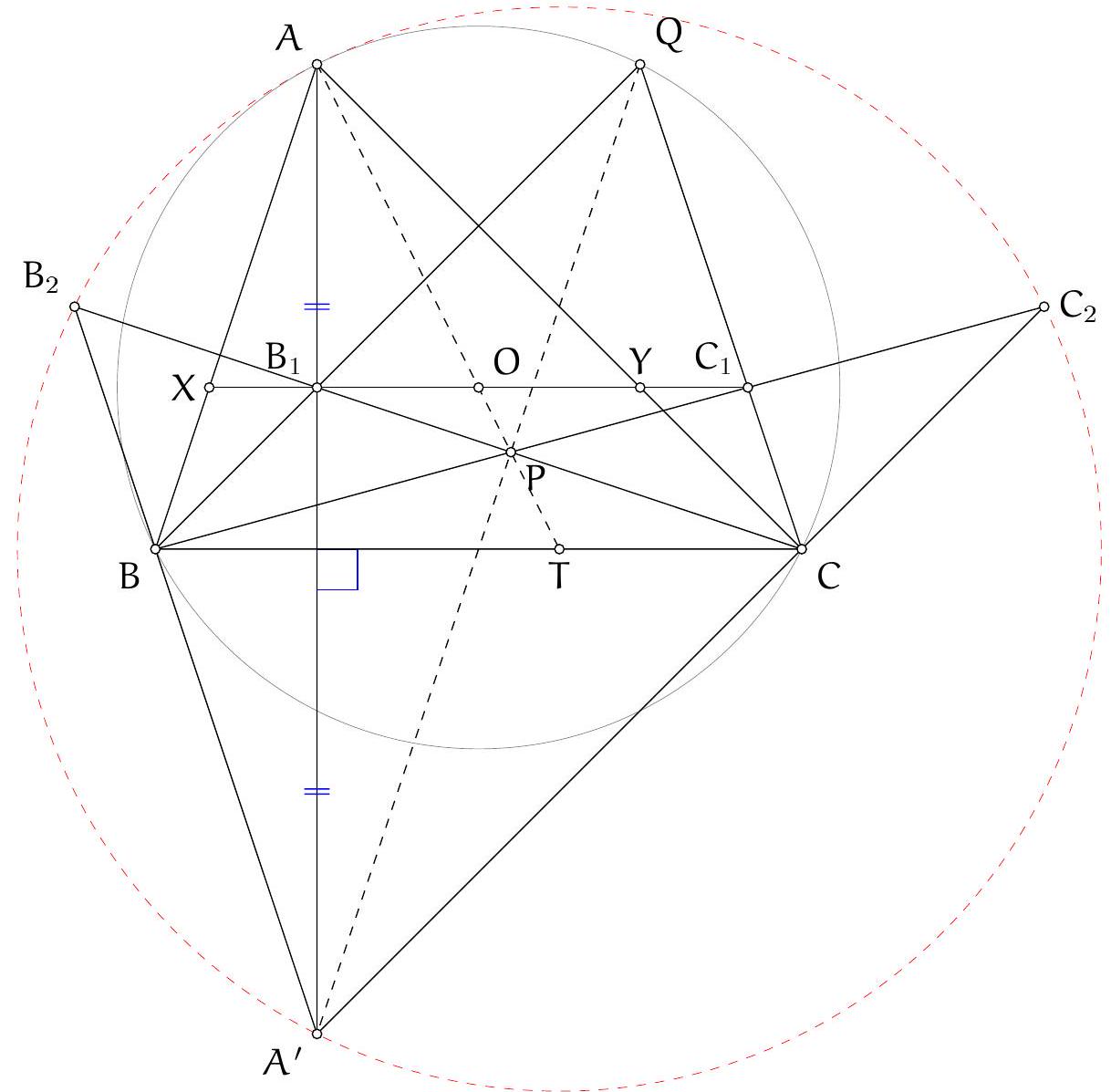
On pose $P$ le point d'intersection des droites $\left(C B_{1}\right)$ et $\left(B C_{1}\right)$, et $Q$ le point d'intersection de $\left(B B_{1}\right)$ et $\left(C C_{1}\right)$. On pose également Tl'intersection de $(A O)$ et ( $\left.B C\right)$. On peut alors remarquer plusieurs propriétés sur la figure, qu'on va montrer.
- Lemme 1: Le point $Q$ est sur le cercle circonscrit à $A B C$.
Preuve : Par construction de $\mathrm{B}_{1}, \mathrm{C}_{1}, \mathrm{~A}^{\prime} \mathrm{BQC}$ est un parallélogramme, donc $\widehat{\mathrm{BQC}}=\widehat{\mathrm{CA}^{\prime} \mathrm{B}}$. Mais par symétrie, $\widehat{C A^{\prime} B}=\widehat{B A C}$. Donc $\widehat{B A C}=\widehat{B_{Q C}}$ : par angle inscrit, $Q$ est bien sur le cercle circonscrit à $A B C$.
- Lemme 2: Les points $P, Q, A^{\prime}$ sont alignés.
Preuve : Le quadrilatère $\mathrm{BCC}_{1} \mathrm{~B}_{1}$ est un trapèze, donc la droite (PQ) passe par les milieux respectifs de $\left[B_{1} C_{1}\right]$ et $[B C]$. Donc la droite (PQ) passe par le milieu de $[B C]$. Or $A^{\prime} B Q C$ est un parallélogramme, donc $\left(Q A^{\prime}\right)$ passe également par le milieu de $[B C]$. On en déduit bien que $Q, P, A^{\prime}$ sont alignés.
- Lemme 3: Les points O, P, T sont alignés.
Preuve : Considérons la symétrie par rapport à la médiatrice de $[\mathrm{BC}]$ : elle fixe O , elle échange B et $C$. Elle échange également $A$ et $Q$, en effet $\widehat{Q_{C B}}=\widehat{A^{\prime} B C}=\widehat{C B A}$ par parallélisme et symétrie puis
$\widehat{C B Q}=\widehat{A C B}$. On pose à présent $X$ l'intersection de $(A B)$ avec $d$, et $Y$ l'intersection de $(A C)$ avec $d$. Alors comme $d$ est invariante par la symétrie, la symétrie échange $B_{1}$ et $Y, C_{1}$ et $X$. On en déduit que $\frac{\mathrm{OB}_{1}}{\mathrm{OC}_{1}}=\frac{\mathrm{OY}}{\mathrm{OX}}$. Or en appliquant le théorème de Thalès, on obtient $\frac{\mathrm{OY}}{\mathrm{OX}}=\frac{\mathrm{TC}}{\mathrm{TB}}$, d'où $\frac{\mathrm{TC}}{\mathrm{TB}}=\frac{\mathrm{OB}_{1}}{O C_{1}}$. Ceci entraîne $O, P, T$ alignés (en appliquant Thalès dans $\mathrm{OC}_{1} \mathrm{PBT}^{\prime}$ et dans $\mathrm{OB}_{1} \mathrm{BCT}^{\prime}$ où $\mathrm{T}^{\prime}$ est l'intersection de $(O P)$ et $(B C)$, on obtient $\frac{T B}{T C}=\frac{T^{\prime} B}{T^{\prime} C}$, d'où $T=T^{\prime}$ ). On a donc bien montré que $O, P, T$ (et donc $A, O, P, T)$ sont alignés.
- Lemme 4 : L'homothétie de centre P et de rapport $-\frac{\mathrm{PT}}{\mathrm{PO}}$ envoie $\mathrm{QBC} \operatorname{sur} \mathrm{A}^{\prime} \mathrm{C}_{2} \mathrm{~B}_{2}$.
Preuve: D'après le théorème de Thalès dans $\mathrm{QCPB}_{2} A^{\prime}$ et dans $\mathrm{QBPC}_{2} \mathrm{~A}^{\prime}$, on a $\frac{\mathrm{PQ}}{\mathrm{PA}^{\prime}}=\frac{\mathrm{PC}}{\mathrm{PB}_{2}}=\frac{\mathrm{PB}}{\mathrm{PC}_{2}}$, donc l'homothétie de centre $P$ qui envoie $Q$ sur $A^{\prime}$ envoie également $B$ sur $C_{2}$ et $C$ sur $B_{2}$. Il reste à montrer qu'elle envoie O sur T . Or, d'après le théorème de Thalès dans $\mathrm{QC}_{1} \mathrm{PBA}^{\prime}$ puis dans $\mathrm{OC}_{1} \mathrm{PBT}$, on a $\frac{\mathrm{PQ}}{\mathrm{PA}^{\prime}}=\frac{\mathrm{PC}_{1}}{\mathrm{~PB}}=\frac{\mathrm{PO}}{\mathrm{PT}}$, donc c'est bien l'homothétie de rapport $-\frac{\mathrm{PT}}{\mathrm{PO}}$.
- On a à présent tous les éléments pour conclure : l'homothétie du lemme 4 envoie QBC sur $A^{\prime} \mathrm{C}_{2} \mathrm{~B}_{2}$ et O sur T. Or par le lemme 1, O est le centre du cercle circonscrit de QBC. Donc T est le centre du cercle circonscrit de $A^{\prime} C_{2} B_{2}$. Mais comme $T$ est sur $(B C)$, on a $T A=T A^{\prime}$ donc $A$ est sur le cercle de centre $T$ et de rayon $T A^{\prime}$. Finalement, on a bien montré que $A, A^{\prime}, B_{2}, C_{2}$ sont cocycliques, et on a même trouvé le centre du cercle en question, qui est $T$.
Commentaire des correcteurs : Le problème est bien résolu par un bon nombre d'élèves. Les rédactions montrent une très bonne maitrise de la notion d'homothétie, qui permet de raconter l'exercice de façon parfois très efficace, avec le mérite de dévoiler les rôles des différents points, là où d'autres élèves ont proposé des approches plus terre-à-terre (des calculs de rapport) ou plus abstraites (solution en dynamique).
|
{
"exam": "French_envois",
"problem_label": "17",
"problem_match": "\nExercice 17.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"solution_match": "## Solution de l'exercice 17",
"tier": "T2",
"year": "2024"
}
|
Let $ABC$ be a triangle, with $AC > AB$, and $\Gamma$ its circumcircle. Let $T$ be the intersection point of the tangent to $\Gamma$ at $A$ with $(BC)$. Let $M$ be the midpoint of $[BC]$ and $R$ the symmetric point of $A$ with respect to $B$. Let $S$ be the point such that $SABT$ is a parallelogram. The parallel to $(AB)$ passing through $M$ intersects $(SB)$ at $P$. Suppose that $P$ is on $\Gamma$, show that $(AC)$ is tangent to the circumcircle of $SRT$.
|
Let $N$ be the intersection point of $(A T)$ and $(B S)$. We have $(P M) \parallel (A B) \parallel (S T)$, so by Thales' theorem, $\frac{B P}{B S}=\frac{B M}{B T}$. Then $\frac{B P}{B N}=\frac{B P}{\frac{B S}{2}}=2 \frac{B P}{B S}=\frac{2 B M}{B T}=\frac{B C}{B T}$, so by the converse of Thales' theorem, $(N T)$ and $(P C)$ are parallel. We then have:
\[
\begin{aligned}
\widehat{S A^{\prime} P} & =\widehat{A A^{\prime} P} \\
& =\widehat{A C P} \text{ by inscribed angle } \\
& =\widehat{A C B}+\widehat{B C P} \\
& =\widehat{\mathrm{TAB}}+\widehat{B T A} \text{ by tangent angle and alternate interior angles } \\
& =\widehat{\mathrm{CBA}} \\
& =\widehat{\mathrm{SAB}} \text{ by alternate interior angles. }
\end{aligned}
\]
Therefore, by corresponding angles, $(A B)$ and $(A^{\prime} P)$ are parallel. Since $(A B)$ and $(M P)$ are parallel, it follows that $P, M, A^{\prime}$ are collinear.
We deduce that $B T=B S, B M=B P$. Indeed:
\[
\begin{aligned}
\widehat{\mathrm{TSB}} & =\widehat{\mathrm{BPA}^{\prime}} \text{ by alternate interior angle } \\
& =\widehat{\mathrm{AA}^{\prime} \mathrm{P}} \text{ because } A A^{\prime} \mathrm{PB} \text{ is an isosceles trapezoid } \\
& =\widehat{\mathrm{CMA}^{\prime}} \text{ by alternate interior angle } \\
& =\widehat{\mathrm{BTS}^{2}} \text{ by corresponding angles. }
\end{aligned}
\]
Thus, $B T=B S$, and since $(S T) \parallel (P M)$, then $B P=B M$ as well.
Notably, STRA is an isosceles trapezoid and therefore cyclic, so $A$ is on (SRT). Moreover, $\widehat{N A B}=\widehat{A C B}$ by tangent angle, and $\widehat{A B N}=\widehat{\mathrm{BST}}=\widehat{\mathrm{STB}}=\widehat{\mathrm{CBA}}$ by alternate interior and corresponding angles. Therefore, $B A N \sim B C A$. In particular, $\widehat{B N A}=\widehat{B A C}$, so by the converse of the tangent angle, $(AC)$ is tangent to $(ANB)$.
An homothety centered at $A$ with a factor of 2 sends $N$ to $T$, $B$ to $R$, fixes $A$, and sends $(A N B)$ to the circle $(A T R)=(S R T)$, and it fixes $(A C)$. Therefore, $(S R T)$ is tangent to $(AC)$ (homotheties preserve tangency), which concludes.
Remark. The condition "We assume that $P$ is on $\Gamma^{\prime \prime}$" is difficult to draw. In fact, since $(A B)$ is parallel to $(A^{\prime} M)$ and $(A A^{\prime})$ is parallel to $(B C)$, $A A^{\prime} M B$ is a parallelogram, so $A M=A^{\prime} M=A B$. Thus, $A B M$ is isosceles at $A$. This means that the projection of $A$ onto $[B C]$ is the midpoint of $[B M]$, so the abscissa of $A$ on $[B C]$ is one quarter of the segment (starting from $B$), and conversely, such a position of $A$ implies that $P$ is on $\Gamma$. This is the condition that allows us to draw the figure.
Remark. One can show that $P$ and $M$ also lie on the circumcircle of SRT, using the fact that TSAM is an isosceles trapezoid, and then that AMPR is an isosceles trapezoid.
Comment from the graders: The problem was difficult and was solved using very different methods (barycentric, homothety, harmonic points, etc.). The solutions submitted were almost all complete.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $A B C$ un triangle, avec $A C>A B$, et $\Gamma$ son cercle circonscrit. Soit $T$ le point d'intersection de la tangente à $\Gamma$ en $A$ avec (BC). Soient $M$ le milieu de $[B C]$ et $R$ le symétrique de $A$ par rapport à $B$. Soit $S$ le point tel que $S A B T$ est un parallélogramme. La parallèle à ( $A B$ ) passant par $M$ coupe (SB) en $P$. On suppose que $P$ est sur $\Gamma$, montrer que ( $A C$ ) est tangente au cercle circonscrit à SRT.
|
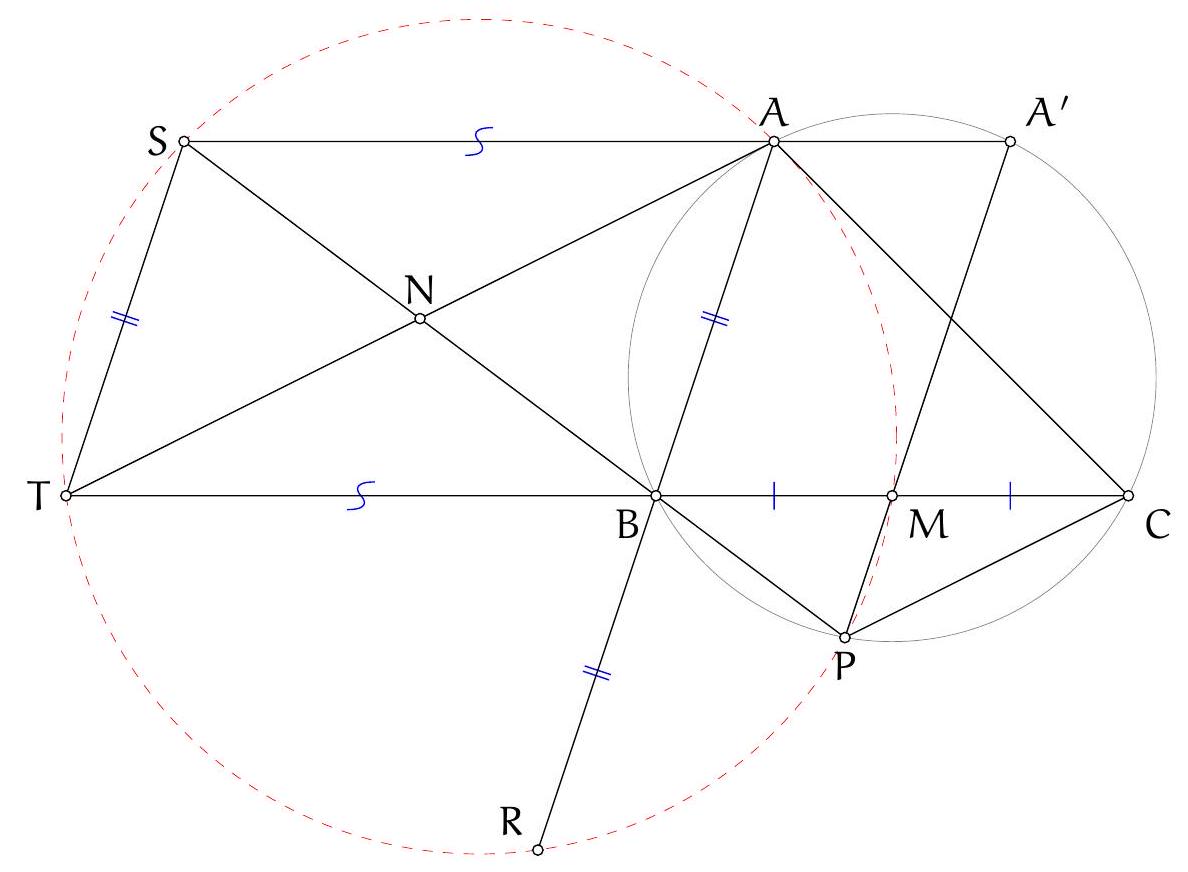
Soit $N$ le point d'intersection de $(A T)$ et ( $B S)$. On a $(P M) / /(A B) / /(S T)$ donc d'après le théorème de Thalès, $\frac{B P}{B S}=\frac{B M}{B T}$. Alors $\frac{B P}{B N}=\frac{B P}{\frac{B S}{2}}=2 \frac{B P}{B S}=\frac{2 B M}{B T}=\frac{B C}{B T}$, donc d'après la réciproque du théorème de Thalès, (NT) et (PC) sont parallèles. On a alors :
$$
\begin{aligned}
\widehat{S A^{\prime} P} & =\widehat{A A^{\prime} P} \\
& =\widehat{A C P} \text { par angle inscrit } \\
& =\widehat{A C B}+\widehat{B C P} \\
& =\widehat{\mathrm{TAB}}+\widehat{B T A} \text { par angle tangentiel et angles alternes-internes } \\
& =\widehat{\mathrm{CBA}} \\
& =\widehat{\mathrm{SAB}} \text { par angles alternes-internes. }
\end{aligned}
$$
Donc par angle correspondant, $(A B)$ et ( $A^{\prime} P$ ) sont parallèles. Or $(A B)$ et (MP) sont parallèles. Il découle que $P, M, A^{\prime}$ sont alignés.
On en déduit donc que $B T=B S, B M=B P$. En effet :
$$
\begin{aligned}
\widehat{\mathrm{TSB}} & =\widehat{\mathrm{BPA}^{\prime}} \text { par angle alterne-interne } \\
& =\widehat{\mathrm{AA}^{\prime} \mathrm{P}} \text { car } A A^{\prime} \mathrm{PB} \text { trapèze isocèle } \\
& =\widehat{\mathrm{CMA}^{\prime}} \text { par angle alterne-interne } \\
& =\widehat{\mathrm{BTS}^{2}} \text { par angle correspondants. }
\end{aligned}
$$
Donc $B T=B S$, et comme $(S T) / /(P M)$, alors $B P=B M$ de même.
Notamment STRA est un trapèze isocèle donc cyclique donc $A$ est sur (SRT). De plus, $\widehat{N A B}=\widehat{A C B}$ par angle tangentiel, et $\widehat{A B N}=\widehat{\mathrm{BST}}=\widehat{\mathrm{STB}}=\widehat{\mathrm{CBA}}$ par angle alterne-interne et correspondant. Donc $B A N \sim B C A$. En particulier $\widehat{B N A}=\widehat{B A C}$, donc par réciproque de l'angle tangentiel, (AC) est tangente à (ANB).
Or une homothétie de centre $A$ et de facteur 2 envoie N sur T , B sur R, fixe $A$ donc envoie ( $A N B$ ) sur le cercle $(A T R)=(S R T)$, et elle fixe $(A C)$. Donc $(S R T)$ est bien tangent à (AC) (les homothéties préservent les tangences), ce qui conclut.
Remarque. La condition "On suppose que $P$ est sur $\Gamma^{\prime \prime}$ est difficile à tracer. En fait, comme $(A B)$ est parallèle à $\left(A^{\prime} M\right)$ et $\left(A A^{\prime}\right)$ parallèle à $(B C), A A^{\prime} M B$ est un parallélogramme donc $A M=A^{\prime} M=A B$. Ainsi $A B M$ est isocèle en $A$. Cela signifie que le projeté de $A$ sur $[B C]$ est le milieu de $[B M]$, donc que l'abscisse de $A$ sur $[B C]$ est au quart du segment (en partant de $B$ ), et réciproquement une telle position de $A$ entraîne que $P$ est sur $\Gamma$. C'est donc la condition qui nous permet de tracer la figure.
Remarque. On peut montrer que $P$ et $M$ se situent aussi sur le cercle circonscrit à SRT, en utilisant que TSAM est un trapèze isocèle, puis que AMPR est un trapèze isocèle.
Commentaire des correcteurs : L'exercice était difficile, et a été traité avec des méthodes très différentes (barycentrique, homothétie, points harmoniques,...). Les solutions rendues étaient quasiment toutes complètes.
|
{
"exam": "French_envois",
"problem_label": "18",
"problem_match": "\nExercice 18.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-1-2023-2024.jsonl",
"solution_match": "## Solution de l'exercice 18",
"tier": "T2",
"year": "2024"
}
|
Let $ABC$ be a triangle and $\Omega$ its circumcircle. We denote $A'$ as the point diametrically opposite to $A$ on the circle $\Omega$. Let $I$ be the center of the incircle of triangle $ABC$, $E$ and $F$ the points of tangency of the incircle with the sides $AC$ and $AB$ respectively. The circumcircle of triangle $AEF$ intersects the circle $\Omega$ at point $X$. Show that the points $A'$, $I$, and $X$ are collinear.
|
Since $F$ is the point of tangency of the incircle with the side $[A C]$, the angle $\widehat{I F A}$ is a right angle and the segment $[I A]$ is a diameter of the circumcircle of triangle $A E F$. We deduce that
$$
\widehat{A X I}=90^{\circ}=\widehat{A X A^{\prime}}
$$
where we have used that $\left[A A^{\prime}\right]$ is a diameter of the circumcircle of triangle $A B C$.
We deduce that the points $A^{\prime}$, I and $X$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $\Omega$ son cercle circonscrit. On note $A^{\prime}$ le point diamétralement opposé à $\mathcal{A}$ dans le cercle $\Omega$. Soit I le centre du cercle inscrit au triangle $A B C$, $E$ et $F$ les points de contact du cercle inscrit avec les côtés $A C$ et $A B$ respectivement. le cercle circonscrit au triangle $A E F$ recoupe le cercle $\Omega$ au point $X$. Montrer que les points $A^{\prime}$, I et $X$ sont alignés.
|
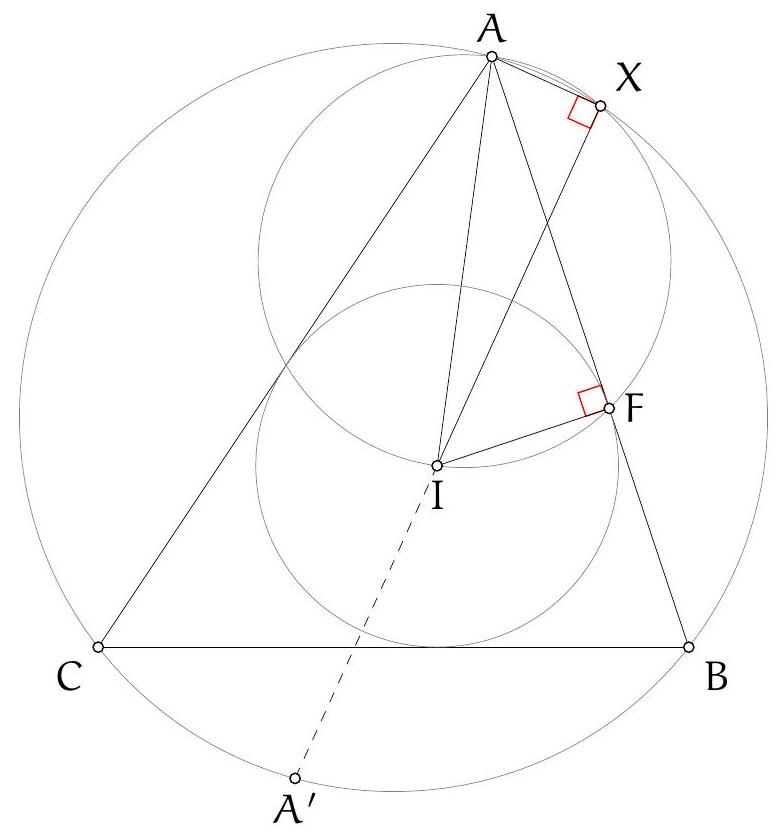
Puisque $F$ est le point de contact du cercle inscrit avec le côté $[A C$, l'angle $\widehat{I F A}$ est droit et le segment $[I A]$ est un diamètre du cercle circonscrit au triangle $A E F$. On en déduit que
$$
\widehat{A X I}=90^{\circ}=\widehat{A X A^{\prime}}
$$
où on a utilisé que $\left[A A^{\prime}\right]$ est un diamètre du cercle circonscrit au triangle $A B C$.
On déduit que les points $A^{\prime}$, I et $X$ sont alignés.
|
{
"exam": "French_envois",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"solution_match": "## Solution de l'exercice 1",
"tier": "T2",
"year": "2024"
}
|
$2 \mathrm{n}-1$ rooks are placed on a $(2 n-1) \times(2 n-1)$ chessboard so that no two rooks are ever on the same row or column. Show that every $\mathrm{n} \times \mathrm{n}$ square contains a rook.
|
Let's start by noting that there is exactly one tower per row and per column. Indeed, by hypothesis, there is at most one tower per row. And since there are $2 \mathrm{n}-1$ towers in total, there must be exactly one per row, and similarly for the columns. By slightly adapting the reasoning, we can assume that the $\mathrm{n} \times \mathrm{n}$ square is that of the cells located in the top left (i.e., the cells located in the first $n$ rows and the first $n$ columns starting from the top left corner). Suppose, for the sake of contradiction, that this square contains no towers. Then among the first $n$ rows, there must be $n$ towers. However, these $n$ towers must be in the last $\mathrm{n}-1$ columns by hypothesis. By the pigeonhole principle, there will then be two towers in the same column, which is absurd. This concludes.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
$2 \mathrm{n}-1$ tours sont placées sur échiquier de taille $(2 n-1) \times(2 n-1)$ de sorte que deux tours quelconques ne sont jamais sur la même ligne ou la même colonne. Montrer que tout carré de taille $\mathrm{n} \times \mathrm{n}$ contient une tour.
|
Commençons par remarquer qu'il y a exactement une tour par ligne et par colonne. En effet, par hypothèse il y a au plus une tour par ligne. Et puisqu'il y a $2 \mathrm{n}-1$ tours au total, il doit y en avoir exactement une par ligne, et de même pour les colonnes. Quitte à adapter légèrement le raisonnement, on peut supposer que le carré $\mathrm{n} \times \mathrm{n}$ est celui des cases situées en haut à gauche (c'est-àdire les cases situées à la fois dans les $n$ premières lignes et dans les $n$ premières colonnes en partant du coin supérieur gauche). Supposons par l'absurde que ce carré ne contienne aucune tour. Alors parmi les n premières lignes, il doit y avoir n tours. Cependant, ces n tours doivent être dans les $\mathrm{n}-1$ dernières colonnnes par hypothèse. Par principe des tiroirs, il y aura alors deux tours sur la même colonne, ce qui est absurde. Cela conclut.
|
{
"exam": "French_envois",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T2",
"year": "2024"
}
|
Determine all integers N such that $2^{\mathrm{N}}-2 \mathrm{~N}$ is a perfect square.
|
Let's show that the solutions are $\mathrm{N}=0,1$ or 2.
We already notice that $2^{0}-0=1^{2}, 2^{1}-2=0^{2}$ and $2^{2}-4=0^{2}$. Therefore, the integers 0, 1, and 2 are solutions. Suppose, for the sake of contradiction, that there exists another integer solution $\mathrm{N}$. Then there exists $x \in \mathbb{N}$ such that $2^{N}-2 \mathrm{~N}=x^{2}$. Since $2^{N}$ must be an integer, we must have $N \geqslant 0$, and thus $N \geqslant 3$. Furthermore, $x$ is divisible by 2, so $x^{2}$ is divisible by 4. Since $N \geqslant 2, 2^{N}$ is also divisible by 4, and therefore $N$ is even. We have
$$
2 N=2^{N}-x^{2}=\left(2^{\frac{N}{2}}-x\right)\left(2^{\frac{N}{2}}+x\right)
$$
Moreover, we verify that $\mathrm{N}=4, \mathrm{~N}=6$ or $\mathrm{N}=8$ are not solutions because 8, 52, and 240 are not perfect squares. Therefore, $\mathrm{N} \geqslant 10$.
Since $2 \mathrm{~N}>0$, we must have $2^{\frac{N}{2}}-x \geqslant 1$. However, we show by induction that $2^{\frac{N}{2}}>2 \mathrm{~N}$ for all even $N \geqslant 10$. Indeed, $2^{5}=32>20$ and if $2^{\frac{N}{2}}>2 N$, with $N$ even $\geqslant 10$, then
$$
2^{\frac{N+2}{2}}=2 \cdot 2^{\frac{N}{2}}>4 \mathrm{~N}>2(\mathrm{~N}+2)
$$
But then we have
$$
2^{N}-x^{2}=\left(2^{\frac{N}{2}}-x\right)\left(2^{\frac{N}{2}}+x\right) \geqslant 2^{\frac{N}{2}}+x>2 N
$$
which is absurd. This shows that there is no other solution.
Therefore, we have shown that the integer solutions are exactly 0, 1, and 2.
|
0, 1, 2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer tous les entiers N tels que $2^{\mathrm{N}}-2 \mathrm{~N}$ est un carré parfait.
|
Montrons que les solutions sont $\mathrm{N}=0,1$ ou 2.
On remarque déjà que $2^{0}-0=1^{2}, 2^{1}-2=0^{2}$ et $2^{2}-4=0^{2}$. Donc les entiers 0,1 et 2 sont solutions. Supposons par l'absurde qu'il existe N un autre entier solution. On dispose alors de $x \in \mathbb{N}$ tel que $2^{N}-2 \mathrm{~N}=x^{2}$. Puisque $2^{N}$ doit être entier, on doit avoir $N \geqslant 0$, et donc $N \geqslant 3$. En outre, $x$ est divisible par 2, donc $\chi^{2}$ est divisible par 4 . Puisque $N \geqslant 2,2^{N}$ est également divisible par 4 et donc $N$ est pair. On a
$$
2 N=2^{N}-x^{2}=\left(2^{\frac{N}{2}}-x\right)\left(2^{\frac{N}{2}}+x\right)
$$
En outre, on vérifie que $\mathrm{N}=4, \mathrm{~N}=6$ ou $\mathrm{N}=8$ ne sont pas des solutions car 8,52 et 240 ne sont pas des carrés parfaits. Donc $\mathrm{N} \geqslant 10$.
Enfin, puisque $2 \mathrm{~N}>0$, on doit avoir $2^{\frac{N}{2}}-x \geqslant 1$. Mais on montre par récurrence que $2^{\frac{N}{2}}>2 \mathrm{~N}$ pour tout $N$ pair $\geqslant 10$. En effet, $2^{5}=32>20$ et si $2^{\frac{N}{2}}>2 N$, avec $N$ pair $\geqslant 10$, alors
$$
2^{\frac{N+2}{2}}=2 \cdot 2^{\frac{N}{2}}>4 \mathrm{~N}>2(\mathrm{~N}+2)
$$
Mais alors on a
$$
2^{N}-x^{2}=\left(2^{\frac{N}{2}}-x\right)\left(2^{\frac{N}{2}}+x\right) \geqslant 2^{\frac{N}{2}}+x>2 N
$$
ce qui est absurde. Cela montre qu'il n'y a pas d'autre solution.
On a donc bien montré que les entiers solutions sont exactement 0,1 et 2 .
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T2",
"year": "2024"
}
|
Let $a, b$ and $c$ be real numbers such that $0 \leqslant a, b, c \leqslant 2$. Show that
$$
(a-b)(b-c)(a-c) \leqslant 2
$$
|
Note that there are 6 possible orders for the variables $\mathrm{a}, \mathrm{b}$ and c.
In the three cases $b \geqslant a \geqslant c, a \geqslant c \geqslant b$ and $c \geqslant b \geqslant a$, the product $(a-b)(b-c)(c-a)$ is negative, so the inequality is satisfied.
If $a \geqslant b \geqslant c$, the inequality of means applied to $a-b$ and $b-c$ and the fact that $c-a \leqslant 2$ since $a, c \in[0,2]$ gives:
$$
(a-b)(b-c)(a-c) \leqslant\left(\frac{a-b+b-c}{2}\right)^{2}(a-c)=\frac{(a-c)^{3}}{4} \leqslant \frac{2^{3}}{4}=2
$$
Similarly, if $b \geqslant c \geqslant a$, then
$$
(a-b)(b-c)(a-c)=(b-a)(b-c)(c-a) \leqslant(b-a)\left(\frac{b-c+c-a}{2}\right)^{2} \leqslant \frac{(b-a)^{3}}{4} \leqslant 2
$$
And finally, if $c \geqslant a \geqslant b$, then
$$
(a-b)(b-c)(a-c)=(c-b)(c-a)(a-b) \leqslant(c-b)\left(\frac{c-a+a-b}{2}\right)^{2} \frac{(c-b)^{3}}{4} \leqslant 2
$$
Thus, the inequality is true in all cases.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soient $a, b$ et $c$ des réels tels que $0 \leqslant a, b, c \leqslant 2$. Montrer que
$$
(a-b)(b-c)(a-c) \leqslant 2
$$
|
Notons qu'il y a 6 ordres possibles pour les variables $\mathrm{a}, \mathrm{b}$ et c .
Dans les trois cas $b \geqslant a \geqslant c, a \geqslant c \geqslant b$ et $c \geqslant b \geqslant a$, le produit $(a-b)(b-c)(c-a)$ est négatif, de sorte que l'inégalité est vérifiée.
Si $a \geqslant b \geqslant c$, l'inégalité des moyennes appliquée à $a-b$ et $b-c$ et le fait que $c-a \leqslant 2$ car $a, c \in[0,2]$ donne:
$$
(a-b)(b-c)(a-c) \leqslant\left(\frac{a-b+b-c}{2}\right)^{2}(a-c)=\frac{(a-c)^{3}}{4} \leqslant \frac{2^{3}}{4}=2
$$
De même, si $b \geqslant c \geqslant a$, alors
$$
(a-b)(b-c)(a-c)=(b-a)(b-c)(c-a) \leqslant(b-a)\left(\frac{b-c+c-a}{2}\right)^{2} \leqslant \frac{(b-a)^{3}}{4} \leqslant 2
$$
Et enfin, si $c \geqslant a \geqslant b$, alors
$$
(a-b)(b-c)(a-c)=(c-b)(c-a)(a-b) \leqslant(c-b)\left(\frac{c-a+a-b}{2}\right)^{2} \frac{(c-b)^{3}}{4} \leqslant 2
$$
Si bien que l'inégalité est vraie dans tous les cas.
|
{
"exam": "French_envois",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T2",
"year": "2024"
}
|
Determine all integers $n$ having the following property: if we set $a_{k}=\operatorname{lcm}(k, k+$ $1, \ldots, k+n-1$ ), then the sequence ( $a_{k}$ ) is increasing.
|
Let's show that the natural numbers having this property are exactly 1 and 2. First, if $n=1$, $a_{k}=k$ is an increasing sequence. And if $n=2$, since two consecutive integers are coprime, $a_{k}=k(k+1)$ is also an increasing sequence. If $n=3$, we notice that $a_{5}=210 > a_{6}=168$, so 3 does not have the desired property.
Now, let's consider $n \geqslant 4$. The idea to show that $n$ does not satisfy the property is to find a $k$ such that the $(k+i)_{0 \leqslant i \leqslant n-1}$ are coprime, while $k+1$ has a large common factor with $k+n$, to have $a_{k}>a_{k+1}$. This is why we look at $k=(n-1)!-1$.
Let $\mathrm{D}=\operatorname{lcm}(k+1, \ldots, k+n-1)$. Then we have $a_{k}=\operatorname{lcm}(k, D)=k \cdot D$. Indeed, for $1 \leqslant i \leqslant n-1$, we have $\operatorname{gcd}(k, k+i)=\operatorname{gcd}(k, i)=1$ because $i \mid k+1=(n-1)!$.
Furthermore, $a_{k+1}=\operatorname{lcm}(D, k+n)$. However, $n-1$ divides both $k+1$ (and thus $D$) and $k+n$. Therefore,
$$
a_{k+1} \leqslant D \cdot((n-2)!+1) < D \cdot((n-1)!-1) = a_{k}
$$
Indeed, for all $n \geqslant 4, (n-1)!-(n-2)!=(n-2) \cdot(n-2)! \geqslant 4 > 2$, so $(n-1)!-1 > (n-2)!+1$.
|
1 \text{ and } 2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer tous les entiers $n$ ayant la propriété suivante : si l'on pose $a_{k}=\operatorname{ppcm}(k, k+$ $1, \ldots, k+n-1$ ), alors la suite ( $a_{k}$ ) est croissante.
|
Montrons que les naturels ayant cette propriété sont exactement 1 et 2 . Déjà, si $n=1, a_{k}=k$ est une suite croissante. Et si $n=2$, puisque deux entiers consécutifs sont premiers entre eux, $a_{k}=k(k+1)$ est une suite croissante également. Si $n=3$, on remarque que $a_{5}=210>a_{6}=168$, donc 3 n'a pas la propriété désirée.
Soit maintenant $n \geqslant 4$. L'idée pour montrer que $n$ ne vérifie pas la propriété est de trouver un $k$ tel que les $(k+i)_{0 \leqslant i \leqslant n-1}$ soient premiers entre eux, tandis que $k+1$ ait un grand facteur commun avec $k+n$, pour avoir $a_{k}>a_{k+1}$. C'est pourquoi on regarde $k=(n-1)!-1$.
Posons $\mathrm{D}=\operatorname{ppcm}(k+1, \ldots, k+n-1)$. On a alors $a_{k}=\operatorname{ppcm}(k, D)=k \cdot D$. En effet, pour $1 \leqslant i \leqslant n-1$, on a $\operatorname{pgcd}(k, k+i)=\operatorname{pgcd}(k, i)=1$ car $i \mid k+1=(n-1)!$.
En outre, $a_{k+1}=\operatorname{ppcm}(D, k+n)$. Or, $n-1$ divise à la fois $k+1$ (donc $\left.D\right)$ et $k+n$. Donc
$$
a_{k+1} \leqslant D \cdot((n-2)!+1)<D \cdot((n-1)!-1)=a_{k}
$$
En effet, pour tout $n \geqslant 4,(n-1)!-(n-2)!=(n-2) \cdot(n-2)!\geqslant 4>2$, donc $(n-1)!-1>(n-2)!+1$.
|
{
"exam": "French_envois",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T2",
"year": "2024"
}
|
Prove, for all strictly positive real numbers $\mathrm{a}, \mathrm{b}, \mathrm{c}$, the following inequality:
$$
\frac{a}{9 b c+1}+\frac{b}{9 c a+1}+\frac{c}{9 a b+1} \geqslant \frac{a+b+c}{1+(a+b+c)^{2}} .
$$
|
Given the form of the inequality, one is tempted to apply the Cauchy-Schwarz inequality. However, if we apply the inequality as it is, we get:
$$
\frac{a}{9 b c+1} + \frac{b}{9 c a+1} + \frac{c}{9 a b+1} \geqslant \frac{(\sqrt{a}+\sqrt{b}+\sqrt{c})^{2}}{9(a b+b c+c a)+3}
$$
To conclude, we would then need to show that $\frac{(\sqrt{a}+\sqrt{b}+\sqrt{c})^{2}}{9(a b+b c+c a)+3} \geqslant \frac{a+b+c}{1+(a+b+c)^{2}}$, but this inequality is not always true.
To make $\mathrm{a}+\mathrm{b}+\mathrm{c}$ appear in the numerator of the right-hand side of the Cauchy-Schwarz inequality, we can, for example, multiply the numerator and the denominator by $a$ in the first fraction of the left-hand side (and similarly with $b$ and $c$ in the other two fractions). This gives, by applying the Cauchy-Schwarz inequality:
$$
\frac{a}{9 b c+1} + \frac{b}{9 c a+1} + \frac{c}{9 a b+1} = \frac{a^{2}}{9 a b c+a} + \frac{b^{2}}{9 a b c+b} + \frac{c^{2}}{9 a b c+c} \geqslant \frac{(a+b+c)^{2}}{27 a b c+a+b+c}.
$$
It then suffices to show that
$$
\frac{(a+b+c)^{2}}{27 a b c+a+b+c} \geqslant \frac{a+b+c}{1+(a+b+c)^{2}}
$$
For this, we can apply the AM-GM inequality $27 \mathrm{abc} \leqslant(\mathrm{a}+\mathrm{b}+\mathrm{c})^{3}$ to obtain:
$$
\frac{(a+b+c)^{2}}{27 a b c+a+b+c} \geqslant \frac{(a+b+c)^{2}}{(a+b+c)^{3}+(a+b+c)} = \frac{(a+b+c)}{(a+b+c)^{2}+1}
$$
as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Démontrer, pour tous réels $\mathrm{a}, \mathrm{b}, \mathrm{c}$ strictement positifs, l'inégalité suivante :
$$
\frac{a}{9 b c+1}+\frac{b}{9 c a+1}+\frac{c}{9 a b+1} \geqslant \frac{a+b+c}{1+(a+b+c)^{2}} .
$$
|
Vu la forme de l'inégalité, on est tenté d'appliquer l'inégalité des mauvais élèves. Seulement, si l'on applique l'inégalité en l'état, on trouve :
$$
\frac{a}{9 b c+1}++\frac{b}{9 c a+1}+\frac{c}{9 a b+1} \geqslant \frac{(\sqrt{a}+\sqrt{b}+\sqrt{c})^{2}}{9(a b+b c+c a)+3}
$$
Pour conclure, il faudrait alors montrer que $\frac{(\sqrt{a}+\sqrt{b}+\sqrt{c})^{2}}{9(a b+b c+c a)+3} \geqslant \frac{a+b+c}{1+(a+b+c)^{2}}$, mais cette inégalité n'est pas toujours vraie.
Pour faire apparaître $\mathrm{a}+\mathrm{b}+\mathrm{c}$ au numérateur du membre de droite de l'inégalité des mauvais élèves, on peut par exemple multiplier en haut et en bas par a dans la première fraction du membre de gauche (et de même avec b et c dans les deux autres fractions). Ceci donne, en appliquant l'inégalité des mauvais élèves:
$$
\frac{a}{9 b c+1}++\frac{b}{9 c a+1}+\frac{c}{9 a b+1}=\frac{a^{2}}{9 a b c+a}+\frac{b^{2}}{9 a b c+b} \frac{c^{2}}{9 a b c+c} \geqslant \frac{(a+b+c)^{2}}{27 a b c+a+b+c} .
$$
Il suffit alors de montrer que
$$
\frac{(a+b+c)^{2}}{27 a b c+a+b+c} \geqslant \frac{a+b+c}{1+(a+b+c)^{2}}
$$
Pour cela, on peut appliquer l'inégalité des moyennes $27 \mathrm{abc} \leqslant(\mathrm{a}+\mathrm{b}+\mathrm{c})^{3}$ pour obtenir :
$$
\frac{(a+b+c)^{2}}{27 a b c+a+b+c} \geqslant \frac{(a+b+c)^{2}}{(a+b+c)^{3}+(a+b+c)}=\frac{(a+b+c)}{(a+b+c)^{2}+1}
$$
comme voulu.
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T2",
"year": "2024"
}
|
Determine all integers $x$ such that $2^{x}+x^{2}+25$ is the cube of a prime number.
|
The exercise will use two ideas:
- Modulos to obtain information about $x$.
- Enclosures comparing $2^{x}$ and $x^{2}$ to show that the left-hand side is often strictly between two consecutive cubes (and therefore cannot be a cube of an integer).
Let $x$ be an integer such that $2^{x}+x^{2}+25$ is the cube of a prime number $p$. Since $2^{x}=p^{3}-x^{2}-25$ is an integer, $x$ is positive. Moreover, $p^{3} \geqslant 25$ so $p>2$ and $p$ is odd.
If $x=0$, then $2^{x}+x^{2}+25=26$ which is not a cube. Thus, $x \geqslant 1$. We deduce that $x^{2}+25$ has the same parity as $p^{3}$, which is odd. This forces $x$ to be even. In particular, $x \geqslant 2$ so $p^{3}>27$ and $p>3$. Let $y$ be the integer such that $x=2 y$. By looking at the equation modulo 3, we find
$$
2^{2 y}+4 y^{2}+25 \equiv 1+y^{2}+25 \equiv 2+y^{2} \quad \bmod 3
$$
If $y$ is not divisible by 3, its square is 1 modulo 3, which implies that 3 divides $p$, which is excluded. Thus, 3 divides $y$. Let $z$ be the integer such that $y=3 z$. The equation becomes
$$
2^{6 z}+36 z^{2}+25=p^{3}
$$
If $z=1$, then the left-hand side is $125=5^{3}$. Thus, $x=6 \times 1$ is a solution.
Let's show that if $z \geqslant 2$, we have $\left(2^{2 z}\right)^{3}<2^{6 z}+36 z^{2}+25<\left(2^{2 z}+1\right)^{3}$, which will show that the left-hand side cannot be the cube of an integer. The left inequality is always true since $36 z^{2}+25>0$. To show the right inequality, we need to show that $3 \times 2^{4 z}+3 \times 2^{2 z}+1>36 z^{2}+25$.
On the one hand, if $z \geqslant 2$, we have $3 \times 2^{2 z} \geqslant 3 \times 16>25$. On the other hand, we show by induction on $z$ that $2^{4 z}>12 z^{2}$.
Initialization: If $z=2$, we have $2^{4 z}=256>48=12 z^{2}$.
Induction: Suppose that $2^{4 z}>12 z^{2}$ for $z \geqslant 2$. Then
$$
2^{4(z+1)}=16 \times 2^{4 z}>16 \times 12 z^{2} \geqslant 12 \times 4 z^{2} \geqslant 12\left(z^{2}+2 z+1\right)=12(z+1)^{2}
$$
where we have used that $z^{2} \geqslant z$ and $z^{2} \geqslant 1$ for $z \geqslant 2$. Thus, the property is true for $z+1$, which completes the induction.
We therefore have $3 \times 2^{4 z}+3 \times 2^{2 z}+1>36 z^{2}+25$, which implies that the left-hand side is not the cube of an integer for $z \geqslant 2$.
The only solution is therefore $x=6$.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer tous les entiers $x$ tels que $2^{x}+x^{2}+25$ est le cube d'un nombre premier.
|
L'exercice va utiliser deux idées:
- Les modulos pour obtenir des informations sur $x$.
- Des encadrements comparant $2^{x}$ et $x^{2}$ afin de montrer que le membre de gauche est souvent strictement compris entre deux cubes consécutifs (et ne peut donc être un cube d'entier).
Soit $x$ un entier tel que $2^{x}+x^{2}+25$ est le cube d'un nombre premier $p$. Puisque $2^{x}=p^{3}-x^{2}-25$ est un entier, $x$ est positif. De plus $p^{3} \geqslant 25$ donc $p>2$ et $p$ est impair.
Si $x=0$, alors $2^{x}+x^{2}+25=26$ qui n'est pas un cube. Ainsi, $x \geqslant 1$. On déduit que $x^{2}+25$ est de la parité de $p^{3}$, c'est-à-dire impair. Ceci force $x$ à être pair. En particulier, $x \geqslant 2$ donc $p^{3}>27$ et $p>3$. Soit y l'entier tel que $x=2 y$. En regardant l'équation modulo 3 , on trouve
$$
2^{2 y}+4 y^{2}+25 \equiv 1+y^{2}+25 \equiv 2+y^{2} \quad \bmod 3
$$
Si y n'est pas divisible par 3 , son carré vaut 1 modulo 3 , ce qui implique que 3 divise $p$, ce qui est exclus. Ainsi, 3 divise $y$. Soit $z$ l'entier tel que $y=3 z$. L'équation devient
$$
2^{6 z}+36 z^{2}+25=p^{3}
$$
Si $z=1$, alors le membre de gauche vaut $125=5^{3}$. Ainsi, $x=6 \times 1$ est solution.
Montrons que si $z \geqslant 2$, on a $\left(2^{2 z}\right)^{3}<2^{6 z}+36 z^{2}+25<\left(2^{2 z}+1\right)^{3}$, ce qui montrera que le côté gauche ne peut être le cube d'un entier. L'inégalité de gauche est toujours vraie car $36 z^{2}+25>0$. Pour montrer l'inégalité de droite, il faut montrer que $3 \times 2^{4 z}+3 \times 2^{2 z}+1>36 z^{2}+25$.
D'une part, si $z \geqslant 2$, on a $3 \times 2^{2 z} \geqslant 3 \times 16>25$. D'autre part, on montre par récurrence sur $z$ que $2^{4 z}>12 z^{2}$.
Initialisation: $\operatorname{Si} z=2$, on a bien $2^{4 z}=256>48=12 z^{2}$.
Hérédité : On suppose que $2^{4 z}>12 z^{2}$ pour $z \geqslant 2$. Alors
$$
2^{4(z+1)}=16 \times 2^{4 z}>16 \times 12 z^{2} \geqslant 12 \times 4 z^{2} \geqslant 12\left(z^{2}+2 z+1\right)=12(z+1)^{2}
$$
où on a utilisé que $z^{2} \geqslant z$ et $z^{2} \geqslant 1$ pour $z \geqslant 2$. Ainsi, la propriété est vraie pour $z+1$, ce qui achève la récurrence.
On a donc bien $3 \times 2^{4 z}+3 \times 2^{2 z}+1>36 z^{2}+25$, ce qui implique que le membre de gauche $n$ 'est pas le cube d'un entier pour $z \geqslant 2$.
L'unique solution est donc $x=6$.
|
{
"exam": "French_envois",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"solution_match": "## Solution de l'exercice 7",
"tier": "T2",
"year": "2024"
}
|
Let $ABC$ be a triangle, $\omega$ its incircle, and $D, E$, and $F$ the points of tangency of $\omega$ with the sides $BC, CA$, and $AB$ respectively. The perpendicular to $(BC)$ at $C$ intersects the line $(EF)$ at $M$, and the perpendicular to $(BC)$ at $B$ intersects the line $(EF)$ at $N$. The line $(DM)$ intersects $\omega$ again at $P$ and the line $(DN)$ intersects $\omega$ again at $Q$. Show that $DP = DQ$.
|
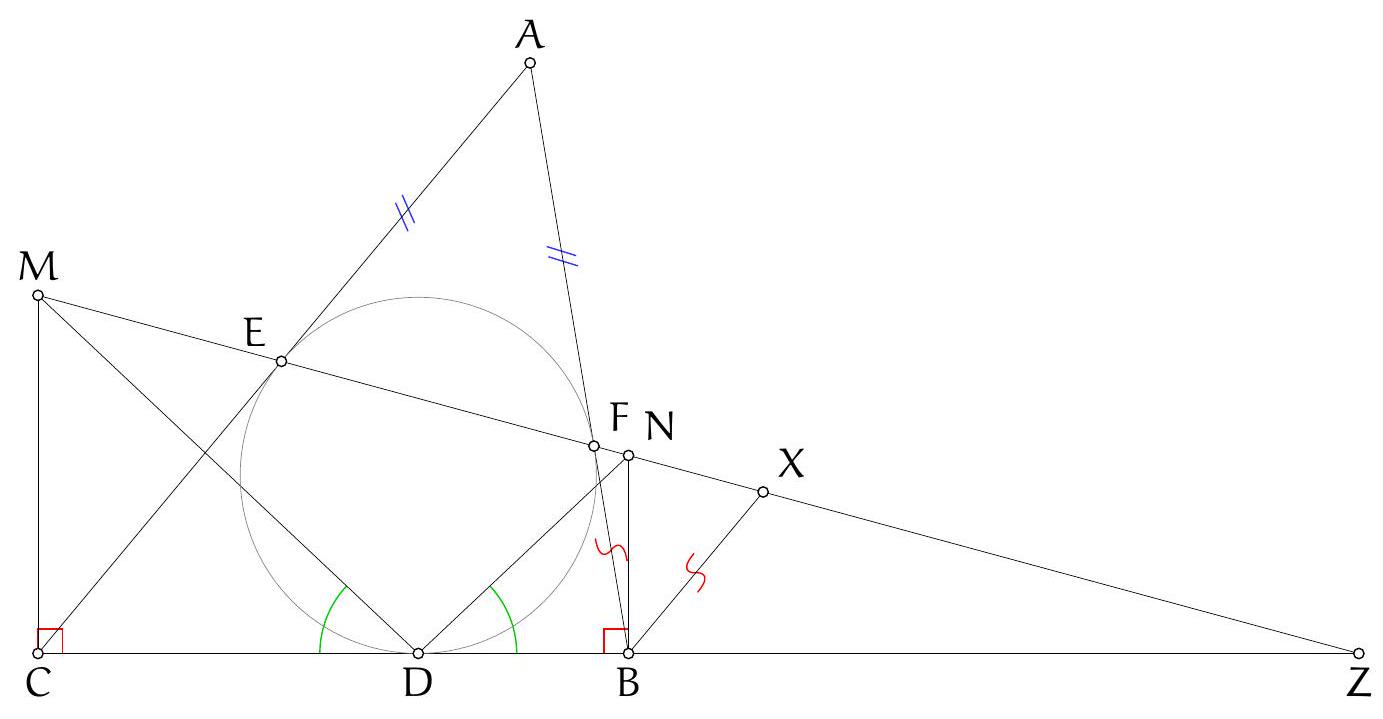
We start by "erasing" the points $P$ and $Q$ from the figure, that is, we reduce the problem to an equivalent statement that does not involve the points $P$ and $Q$.
If the statement is true, then (DI) is the perpendicular bisector of the segment [PQ], so the line (DI) is the angle bisector of $\widehat{MDN}$. Conversely, if we prove that the line (DI) is the angle bisector of $\widehat{MDN}$, the lines (DM) and (DN) will be symmetric with respect to the line (DI). Thus, since the circle $\omega$ and these lines are symmetric with respect to (DI), their intersections are also symmetric, and $P$ and $Q$ will be symmetric with respect to (DI) and $\mathrm{DP}=\mathrm{DQ}$. Therefore, it suffices to show that $\widehat{\mathrm{MDI}}=\widehat{\mathrm{NDI}}$ or, since the lines (DI) and (BC) are perpendicular, $\widehat{MDC}=\widehat{\mathrm{NDB}}$.
This equality is particularly true if the triangles MCD and NBD are similar. Since these two triangles already have a right angle in common, it suffices to show that $\frac{\mathrm{BD}}{\mathrm{CD}}=\frac{\mathrm{BN}}{\mathrm{CM}}$.
Let $Z$ be the intersection point of the lines $(BC)$ and $(EF)$ and let $X$ be the intersection point of the line parallel to (AC) passing through B with the line (EF).
The triangles $AEF$ and $FBX$ are then similar, so the triangle $FBX$ is isosceles at $B$. Therefore, using Thales' theorem for the points $E, X, Z$ and $C, B, Z$:
$$
\frac{BD}{CD}=\frac{BF}{CE}=\frac{BX}{CE}=\frac{ZB}{ZC}.
$$
By applying Thales' theorem to the points $M, N, Z$ and $C, B, Z$, we find indeed
$$
\frac{BD}{CD}=\frac{ZB}{ZC}=\frac{BN}{CM},
$$
which allows us to conclude.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle, $\omega$ son cercle inscrit et $D, E$ et $F$ les points de contact de $\omega$ avec les côtés $B C, C A$ et $A B$ respectivement. La perpendiculaire à ( $B C$ ) en $C$ coupe la droite ( $E F$ ) en $M$ et la perpendiculaire à (BC) en $B$ coupe la droite (EF) en $N$. La droite ( $D M)$ recoupe $\omega$ en $P$ et la droite $(\mathrm{DN})$ recoupe $\omega$ en Q . Montrer que $\mathrm{DP}=\mathrm{DQ}$.
|

On commence par "éffacer" les points $P$ et $Q$ de la figure, c'est-à-dire qu'on commence par se ramener à un énoncé équivalent au problème original, mais qui n'implique pas les points P et Q .
Si l'énoncé est vrai, alors (DI) est la médiatrice du segment [PQ], de sorte que la droite (DI) est la bissectrice de l'angle $\widehat{M D N}$. Réciproquement, si on prouve que la droite (DI) est la bissectrice de l'angle $\widehat{M D N}$, les droites (DM) et (DN) seront alors symétriques par rapport à la droite (DI). Ainsi, puisque le cercle $\omega$ et ces droites sont symétriques par rapport à (DI), leurs intersections le sont aussi, et $P$ et Q seront symétriques par rapport à (DI) et $\mathrm{DP}=\mathrm{DQ}$. Il suffit donc de montrer que $\widehat{\mathrm{MDI}}=\widehat{\mathrm{NDI}}$ ou encore, puisque les droites (DI) et (BC) sont perpendiculaires, $\widehat{M D C}=\widehat{\mathrm{NDB}}$.
Cette égalité est en particulier vraie si les triangles MCD et NBD sont semblables. Comme ces deux triangles ont déjà un angle droit en commun, il suffit de montrer que $\frac{\mathrm{BD}}{\mathrm{CD}}=\frac{\mathrm{BN}}{\mathrm{CM}}$.
Soit $Z$ le point d'intersection des droites $(B C)$ et $(E F)$ et soit $X$ le point d'intersection de la parallèle à (AC) passant par B avec la droite (EF).
Les triangles $A E F$ et $F B X$ sont alors semblables, ainsi le triangle $F B X$ est isocèle en $B$. On a donc, en utilisant le théorème de Thalès pour les points $E, X, Z$ et $C, B, Z$ :
$$
\frac{B D}{C D}=\frac{B F}{C E}=\frac{B X}{C E}=\frac{Z B}{Z C} .
$$
En appliquant ensuite Thalès aux points $M, N, Z$ et $C, B, Z$, on trouve bien
$$
\frac{B D}{C D}=\frac{Z B}{Z C}=\frac{B N}{C M},
$$
ce qui permet de conclure.
|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "\nExercice 8.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"solution_match": "## Solution de l'exercice 8",
"tier": "T2",
"year": "2024"
}
|
We have $\mathrm{a}+\mathrm{b}$ bowls aligned in a row. The first $a$ bowls contain an apple, while the last $b$ bowls contain a pear.
An operation consists of moving an apple from bowl $i$ to bowl $i+1$ and a pear from bowl $j$ to bowl $j-1$, where $i$ and $j$ are integers such that $i-j$ is even (A bowl can contain multiple fruits). We want to reach the final situation where the first $b$ bowls contain a pear and the last $a$ bowls contain an apple. Show that this is possible if and only if $ab$ is even.
|
Let's start by showing that it is not possible to achieve the goal when both a and b are odd. Let I be the alternating sum of the number of fruits in the bowls. In the initial and final positions described, we then have $I=0$ because $a+b$ is even. Furthermore, with each operation, I is increased by $\pm 2$ due to the condition $i-j$ being even.
Suppose, for the sake of contradiction, that it is possible to move from the initial position to the final position described. The apples must move from bowls numbered 1 to $a$ to bowls numbered $b+1$ to $a+b$, and during each operation, an apple increases its bowl number by one. Therefore, it takes
$$
\sum_{k=1}^{a}(b+k)-\sum_{k=1}^{a} k=a \cdot b
$$
operations to move from the initial position to the final position, with $ab$ being odd by hypothesis. Thus, when the final position is reached, $\mathrm{I} \equiv 2 \mathrm{ab} \equiv 2(\bmod 4)$, which is absurd because I is zero in the final position described.
Now let's show by induction that it is possible to reach the final position when a or b is even. Without loss of generality, we consider the case where b is even, the other case being directly obtained by symmetry. If $\mathrm{b}=0$, there is nothing to show. Suppose now that the property is true for $\mathrm{b}=\mathrm{n}$ even, and suppose $\mathrm{b}=\mathrm{n}+2$. By the induction hypothesis, by ignoring the last two pears, we can reach in a finite number of operations the situation where we have, in order, n bowls with a pear, then a bowls with an apple, then 2 bowls with a pear. If we perform two operations, between the bowls numbered $\mathfrak{i}=a+n$ and $\mathfrak{j}=a+n+2$, then $\mathfrak{i}=\mathfrak{j}=a+n+1$, the last three bowls now contain, in order: a pear, then a pear, then an apple. We repeat these operations that allow us to swap an apple with the two pears that follow until we reach the desired final situation.
## Senior Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
On dispose de $\mathrm{a}+\mathrm{b}$ bols alignés sur une rangée. Les a premiers bols contiennent une pomme tandis que les $b$ derniers bols contiennent une poire.
Une opération consiste à déplacer une pomme du bol $i$ au bol $i+1$ et une poire du bol $j$ au bol $j-1$, où $i$ et $j$ sont deux entiers tels que $i-j$ est pair (Un bol peut contenir plusieurs fruits). On souhaite arriver à la situation finale où les $b$ premiers bols contiennent une poire et les $a$ derniers bols contiennent une pomme. Montrer que c'est possible si et seulement si ab est pair.
|
Commençons par montrer qu'il n'est pas possible d'y arriver lorsque a et b sont impairs tous les deux. Soit I la somme alternée des nombres de fruits dans les bols. Dans les positions initiales et finales décrites, on a alors $I=0$ car $a+b$ est pair. En outre, lors de chaque opération, I est augmenté de $\pm 2$ à cause de la condition $i-j$ pair.
Supposons par l'absurde qu'il soit possible de passer de la position intiale à la position finale décrite. Les pommes doivent passer des bols de numéros 1 à $a$ vers les bols de numéros $b+1$ à $a+b$, et au cours de chaque opération, une pomme augmente de un le numéro de son bol. Il faut donc
$$
\sum_{k=1}^{a}(b+k)-\sum_{k=1}^{a} k=a \cdot b
$$
opérations pour passer de la position initiale à la position finale, avec ab impair par hypothèse. Ainsi, lorsque la position finale est atteinte, $\mathrm{I} \equiv 2 \mathrm{ab} \equiv 2(\bmod 4)$, ce qui est absurde car I est nul dans la position finale décrite.
Montrons maintenant par récurrence qu'il est possible de parvenir à la position finale lorsque a ou b est pair. Sans perte de généralité, nous traitons le cas où b est pair, l'autre cas s'obtenant directement par symétrie. Si $\mathrm{b}=0$, il n'y a rien à montrer. Supposons maintenant que la propriété soit vraie pour $\mathrm{b}=\mathrm{n}$ pair, et supposons $\mathrm{b}=\mathrm{n}+2$. Par hypothèse de récurrence, en ignorant les deux dernières poires, nous pouvons arriver en un nombre fini d'opérations à la situation où nous avons, dans l'ordre, n bols avec une poire, puis a bols avec une pomme, puis 2 bols avec une poire. Si nous faisons deux opérations, entre les bols de numéros $\mathfrak{i}=a+n$ et $\mathfrak{j}=a+n+2$, puis $\mathfrak{i}=\mathfrak{j}=a+n+1$, les trois derniers bols contiennent maintenant dans l'ordre : une poire puis une poire puis une pomme. On réitère ces opérations permettant d'échanger une pomme avec les deux poires qui suivent jusqu'à arriver à la situation finale désirée.
## Exercices Seniors
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 9",
"tier": "T2",
"year": "2024"
}
|
Let $ABC$ be a triangle and $\Omega$ its circumcircle. We denote $A^{\prime}$ as the point diametrically opposite to $A$ on the circle $\Omega$. Let $I$ be the center of the incircle of triangle $ABC$, $E$ and $F$ the points of tangency of the incircle with the sides $AC$ and $AB$ respectively. The circumcircle of triangle $AEF$ intersects the circle $\Omega$ at point $X$. Show that the points $\mathcal{A}^{\prime}$, $I$, and $X$ are collinear.
|
Since $F$ is the point of tangency of the incircle with side $[AC]$, the angle $\widehat{I F A}$ is a right angle and the segment $[I A]$ is a diameter of the circumcircle of triangle $A E F$. We deduce that
$$
\widehat{A X I}=90^{\circ}=\widehat{A X A^{\prime}}
$$
where we have used that $\left[A A^{\prime}\right]$ is a diameter of the circumcircle of triangle $A B C$.
We deduce that the points $A^{\prime}$, I, and $X$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $\Omega$ son cercle circonscrit. On note $A^{\prime}$ le point diamétralement opposé à $A$ dans le cercle $\Omega$. Soit I le centre du cercle inscrit au triangle $A B C$, $E$ et $F$ les points de contact du cercle inscrit avec les côtés $A C$ et $A B$ respectivement. le cercle circonscrit au triangle $A E F$ recoupe le cercle $\Omega$ au point $X$. Montrer que les points $\mathcal{A}^{\prime}$, I et $X$ sont alignés.
|
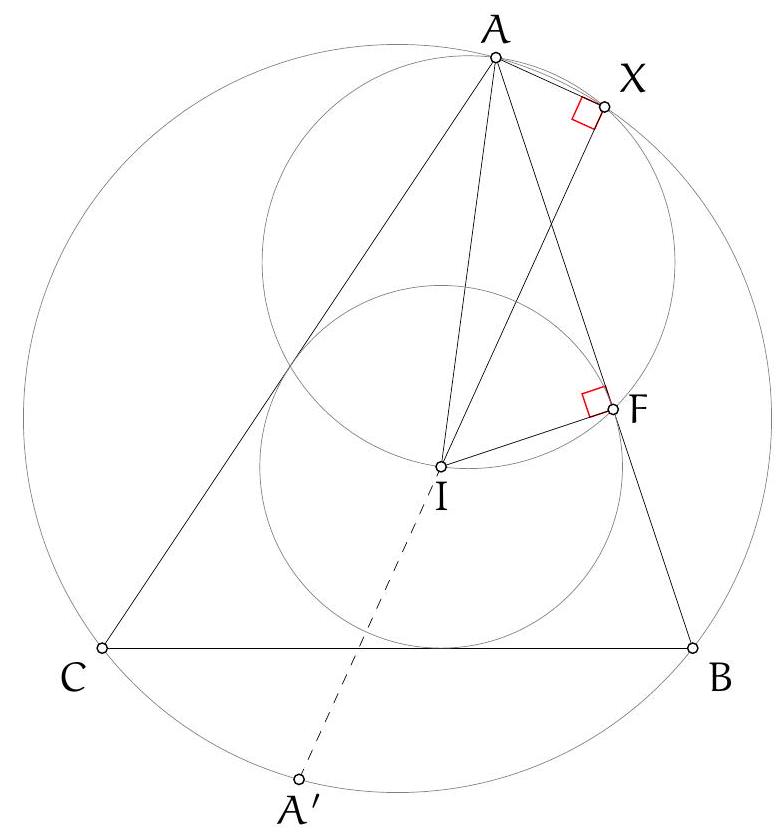
Puisque $F$ est le point de contact du cercle inscrit avec le côté [AC], l'angle $\widehat{I F A}$ est droit et le segment $[I A]$ est un diamètre du cercle circonscrit au triangle $A E F$. On en déduit que
$$
\widehat{A X I}=90^{\circ}=\widehat{A X A^{\prime}}
$$
où on a utilisé que $\left[A A^{\prime}\right]$ est un diamètre du cercle circonscrit au triangle $A B C$.
On déduit que les points $A^{\prime}$, I et $X$ sont alignés.
|
{
"exam": "French_envois",
"problem_label": "10",
"problem_match": "\nExercice 10.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 10",
"tier": "T2",
"year": "2024"
}
|
$2 \mathrm{n}-1$ rooks are placed on a $(2 \mathrm{n}-1) \times(2 \mathrm{n}-1)$ chessboard so that no two rooks are ever on the same row or column. Show that every $\mathrm{n} \times \mathrm{n}$ square contains a rook.
|
Let's start by noting that there is exactly one tower per row and per column. Indeed, by hypothesis, there is at most one tower per row. And since there are $2 \mathrm{n}-1$ towers in total, there must be exactly one per row, and similarly for the columns. By slightly adapting the reasoning, we can assume that the $\mathrm{n} \times \mathrm{n}$ square is that of the cells located in the top left (i.e., the cells located in the first $n$ rows and the first $n$ columns starting from the top left corner). Suppose, for the sake of contradiction, that this square contains no towers. Then among the $n$ first rows, there must be $n$ towers. However, these $n$ towers must be in the last $n-1$ columns by hypothesis. By the pigeonhole principle, there will then be two towers in the same column, which is absurd.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
$2 \mathrm{n}-1$ tours sont placées sur échiquier de taille $(2 \mathrm{n}-1) \times(2 \mathrm{n}-1)$ de sorte que deux tours quelconques ne sont jamais sur la même ligne ou la même colonne. Montrer que tout carré de taille $\mathrm{n} \times \mathrm{n}$ contient une tour.
|
Commençons par remarquer qu'il y a exactement une tour par ligne et par colonne. En effet, par hypothèse il y a au plus une tour par ligne. Et puisqu'il y a $2 \mathrm{n}-1$ tours au total, il doit y en avoir exactement une par ligne, et de même pour les colonnes. Quitte à adapter légèrement le raisonnement, on peut supposer que le carré $\mathrm{n} \times \mathrm{n}$ est celui des cases situées en haut à gauche (c'est-àdire les cases situées à la fois dans les $n$ premières lignes et dans les $n$ premières colonnes en partant du coin supérieur gauche). Supposons par l'absurde que ce carré ne contienne aucune tour. Alors parmi les $n$ premières lignes, il doit $y$ avoir $n$ tours. Cependant, ces $n$ tours doivent être dans les $n-1$ dernières colonnnes par hypothèse. Par principe des tiroirs, il y aura alors deux tours sur la même colonne, ce qui est absurde.
|
{
"exam": "French_envois",
"problem_label": "11",
"problem_match": "\nExercice 11.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 11",
"tier": "T2",
"year": "2024"
}
|
We define the sequence $\left(a_{n}\right)$ by $a_{0}=a_{1}=a_{2}=1$ and if $n \geqslant 3$:
$$
a_{n}=\left\lfloor\frac{n}{a_{n-1} a_{n-2} a_{n-3}}\right\rfloor
$$
Determine $\mathrm{a}_{2022}$.
|
By calculating the first terms of the sequence, we make the following conjecture, which we prove by induction on $k$:
$$
\text { If } k \geqslant 1 \text {, then } a_{4 k}=1, a_{4 k+1}=1, a_{4 k+2}=\left\lfloor\frac{4 k+2}{3}\right\rfloor \text { and } a_{4 k+3}=3 .
$$
Initialization: We have $a_{3}=3, a_{4}=1, a_{5}=1, a_{6}=2$ and $a_{7}=3$, so the property is satisfied for $\mathrm{k}=1$.
Hereditary: Suppose the property is satisfied for $k \geqslant 1$ fixed. Then we have successively:
$$
a_{4(k+1)}=\left\lfloor\frac{4(k+1)}{a_{4 k+1} a_{4 k+2} a_{4 k+3}}\right\rfloor=\left\lfloor\frac{4(k+1)}{3\lfloor(4 k+2) / 3\rfloor}\right\rfloor,
$$
and $\frac{4(\mathrm{k}+1)}{3}<2\left(\frac{4 \mathrm{k}+2}{3}-1\right)<2\left\lfloor\frac{4 \mathrm{k}+2}{3}\right\rfloor$ for $k \geqslant 2$ and $\frac{8}{3}<2\left\lfloor\frac{4 \times 1+2}{3}\right\rfloor$, so that $\mathrm{a}_{4(\mathrm{k}+1)}=1$.
$$
\mathbf{a}_{4(k+1)+1}=\left\lfloor\frac{4(k+1)+1}{a_{4 k+2} a_{4 k+3} a_{4(k+1)}}\right\rfloor=\left\lfloor\frac{4(k+1)+1}{3\lfloor(4 k+2) / 3\rfloor}\right\rfloor
$$
and here too, we have $\frac{4(k+1)}{3}<2\left\lfloor\frac{4 k+2}{3}\right\rfloor$, so $a_{4(k+1)+1}=1$.
$$
a_{4(k+1)+2}=\left\lfloor\frac{4(k+1)+2}{a_{4 k+3} a_{4(k+1)} a_{4(k+1)+1}}\right\rfloor=\left\lfloor\frac{4(k+1)+2}{3}\right\rfloor
$$
so $a_{4(k+1)+2}=\left\lfloor\frac{4(k+1)+2}{3}\right\rfloor$.
Finally,
$$
a_{4(k+1)+3}=\left\lfloor\frac{4(k+1)+3}{a_{4(k+1)} a_{4(k+1)+1} a_{4(k+1)+2}}\right\rfloor=\left\lfloor\frac{4(k+1)+3}{\lfloor(4(k+1)+2) / 3\rfloor}\right\rfloor .
$$
We have
$$
4(k+1)+3 \geqslant 3\left(\frac{4(k+1)+2}{3}\right) \geqslant 3\lfloor(4(k+1)+2) / 3\rfloor
$$
and
$$
4(k+1)+3 \leqslant 4\left(\frac{4(k+1)+2}{3}-1\right)<4\lfloor(4(k+1)+2) / 3\rfloor
$$
for $k \geqslant 1$, so $a_{4(k+1)+3}=3$. This completes the induction.
Thus $\mathrm{a}_{2022}=\mathrm{a}_{4 \times 505+2}=\left\lfloor\frac{4 \times 505+2}{3}\right\rfloor=674$.
|
674
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
On définit la suite $\left(a_{n}\right)$ par $a_{0}=a_{1}=a_{2}=1$ et si $n \geqslant 3$ :
$$
a_{n}=\left\lfloor\frac{n}{a_{n-1} a_{n-2} a_{n-3}}\right\rfloor
$$
Déterminer $\mathrm{a}_{2022}$.
|
En calculant les premiers termes de la suite, on effectue la conjecture suivante, que l'on montre par récurrence sur $k$ :
$$
\text { Si } k \geqslant 1 \text {, alors } a_{4 k}=1, a_{4 k+1}=1, a_{4 k+2}=\left\lfloor\frac{4 k+2}{3}\right\rfloor \text { et } a_{4 k+3}=3 .
$$
Initialisation : On a $a_{3}=3, a_{4}=1, a_{5}=1, a_{6}=2$ et $a_{7}=3$, de sorte que la propriété est vérifiée pour $\mathrm{k}=1$.
Hérédité : Supposons la propriété vérifiée pour $k \geqslant 1$ fixée. Alors on a successivement :
$$
a_{4(k+1)}=\left\lfloor\frac{4(k+1)}{a_{4 k+1} a_{4 k+2} a_{4 k+3}}\right\rfloor=\left\lfloor\frac{4(k+1)}{3\lfloor(4 k+2) / 3\rfloor}\right\rfloor,
$$
or $\frac{4(\mathrm{k}+1)}{3}<2\left(\frac{4 \mathrm{k}+2}{3}-1\right)<2\left\lfloor\frac{4 \mathrm{k}+2}{3}\right\rfloor$ pour $k \geqslant 2$ et $\frac{8}{3}<2\left\lfloor\frac{4 \times 1+2}{3}\right\rfloor$, de sorte que $\mathrm{a}_{4(\mathrm{k}+1)}=1$.
$$
\mathbf{a}_{4(k+1)+1}=\left\lfloor\frac{4(k+1)+1}{a_{4 k+2} a_{4 k+3} a_{4(k+1)}}\right\rfloor=\left\lfloor\frac{4(k+1)+1}{3\lfloor(4 k+2) / 3\rfloor}\right\rfloor
$$
et là aussi, on a $\frac{4(k+1)}{3}<2\left\lfloor\frac{4 k+2}{3}\right\rfloor$, de sorte que $a_{4(k+1)+1}=1$.
$$
a_{4(k+1)+2}=\left\lfloor\frac{4(k+1)+2}{a_{4 k+3} a_{4(k+1)} a_{4(k+1)+1}}\right\rfloor=\left\lfloor\frac{4(k+1)+2}{3}\right\rfloor
$$
donc $a_{4(k+1)+2}=\left\lfloor\frac{4(k+1)+2}{3}\right\rfloor$.
Enfin,
$$
a_{4(k+1)+3}=\left\lfloor\frac{4(k+1)+3}{a_{4(k+1)} a_{4(k+1)+1} a_{4(k+1)+2}}\right\rfloor=\left\lfloor\frac{4(k+1)+3}{\lfloor(4(k+1)+2) / 3\rfloor}\right\rfloor .
$$
Or on a bien
$$
4(k+1)+3 \geqslant 3\left(\frac{4(k+1)+2}{3}\right) \geqslant 3\lfloor(4(k+1)+2) / 3\rfloor
$$
et
$$
4(k+1)+3 \leqslant 4\left(\frac{4(k+1)+2}{3}-1\right)<4\lfloor(4(k+1)+2) / 3\rfloor
$$
pour $k \geqslant 1$, de sorte que $a_{4(k+1)+3}=3$. Ceci achève la récurrence.
Ainsi $\mathrm{a}_{2022}=\mathrm{a}_{4 \times 505+2}=\left\lfloor\frac{4 \times 505+2}{3}\right\rfloor=674$.
|
{
"exam": "French_envois",
"problem_label": "12",
"problem_match": "## Exercice 12.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 12",
"tier": "T2",
"year": "2024"
}
|
Determine all integers $n$ having the following property: if we set $a_{k}=\operatorname{lcm}(k, k+$ $1, \ldots, k+n-1)$, then the sequence ( $a_{k}$ ) is increasing.
|
Let's show that the natural numbers having this property are exactly 1 and 2. First, if $\mathrm{n}=1, \mathrm{a}_{\mathrm{k}}=\mathrm{k}$ is an increasing sequence. And if $\mathrm{n}=2$, since two consecutive integers are coprime, $a_{k}=k(k+1)$ is also an increasing sequence. If $n=3$, we notice that $a_{5}=210>a_{6}=168$, so 3 does not have the desired property.
Now let $n \geqslant 4$. The idea to show that $n$ does not satisfy the property is to find a $k$ such that the $(k+i)_{0 \leqslant i \leqslant n-1}$ are coprime, while $k+1$ has a large common factor with $k+n$, to have $a_{k}>a_{k+1}$. This is why we look at $k=(n-1)!-1$.
Let $\mathrm{D}=\operatorname{ppcm}(k+1, \ldots, k+n-1)$. Then we have $a_{k}=\operatorname{ppcm}(k, D)=k \cdot D$. Indeed, for $1 \leqslant \mathfrak{i} \leqslant n-1$, we have $\operatorname{pgcd}(k, k+i)=\operatorname{pgcd}(k, \mathfrak{i})=1$ because $\mathfrak{i} \mid k+1=(n-1)!$.
Furthermore, $a_{k+1}=\operatorname{ppcm}(D, k+n)$. However, $n-1$ divides both $k+1$ (and thus $D$) and $k+n$. Therefore,
$$
a_{k+1} \leqslant D \cdot((n-2)!+1)<D \cdot((n-1)!-1)=a_{k}
$$
Indeed, for all $n \geqslant 4,(n-1)!-(n-2)!=(n-2) \cdot(n-2)!\geqslant 4>2$, so $(n-1)!-1>(n-2)!+1$.
|
1 \text{ and } 2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer tous les entiers $n$ ayant la propriété suivante : si l'on pose $a_{k}=\operatorname{ppcm}(k, k+$ $1, \ldots, k+n-1)$, alors la suite ( $a_{k}$ ) est croissante.
|
Montrons que les naturels ayant cette propriété sont exactement 1 et 2 . Déjà, si $\mathrm{n}=1, \mathrm{a}_{\mathrm{k}}=\mathrm{k}$ est une suite croissante. Et si $\mathrm{n}=2$, puisque deux entiers consécutifs sont premiers entre eux, $a_{k}=k(k+1)$ est une suite croissante également. Si $n=3$, on remarque que $a_{5}=210>a_{6}=168$, donc 3 n'a pas la propriété désirée.
Soit maintenant $n \geqslant 4$. L'idée pour montrer que $n$ ne vérifie pas la propriété est de trouver un $k$ tel que les $(k+i)_{0 \leqslant i \leqslant n-1}$ soient premiers entre eux, tandis que $k+1$ ait un grand facteur commun avec $k+n$, pour avoir $a_{k}>a_{k+1}$. C'est pourquoi on regarde $k=(n-1)!-1$.
Posons $\mathrm{D}=\operatorname{ppcm}(k+1, \ldots, k+n-1)$. On a alors $a_{k}=\operatorname{ppcm}(k, D)=k \cdot D$. En effet, pour $1 \leqslant \mathfrak{i} \leqslant n-1$, on a $\operatorname{pgcd}(k, k+i)=\operatorname{pgcd}(k, \mathfrak{i})=1 \operatorname{car} \mathfrak{i} \mid k+1=(n-1)!$.
En outre, $a_{k+1}=\operatorname{ppcm}(D, k+n)$. Or, $n-1$ divise à la fois $k+1$ (donc $\left.D\right)$ et $k+n$. Donc
$$
a_{k+1} \leqslant D \cdot((n-2)!+1)<D \cdot((n-1)!-1)=a_{k}
$$
En effet, pour tout $n \geqslant 4,(n-1)!-(n-2)!=(n-2) \cdot(n-2)!\geqslant 4>2$, donc $(n-1)!-1>(n-2)!+1$.
|
{
"exam": "French_envois",
"problem_label": "13",
"problem_match": "\nExercice 13.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 13",
"tier": "T2",
"year": "2024"
}
|
Let $ABC$ be a triangle and let $J$ be the center of its $A$-excircle. Let $K$ be the symmetric point of $J$ with respect to the segment $[BC]$. Let $E$ and $F$ be the points on the lines $(BJ)$ and $(CJ)$ such that $\widehat{\mathrm{EAB}}=\widehat{\mathrm{CAF}}=90^{\circ}$. Show that $\widehat{\mathrm{FKE}}+\widehat{\mathrm{FJE}}=180^{\circ}$.
|
Since the line (BJ) is the external bisector of the angle $\widehat{A B C}$, we have $\widehat{A B J}=\widehat{C B J}=90^{\circ}-\widehat{A B C} / 2$. Since axial symmetry preserves angles, we thus have $\widehat{\mathrm{KBC}}=\widehat{\mathrm{ABE}}$.
Let $A_{1}$ be the orthogonal projection of the point $J$ onto the segment $[B C]$, so that $A_{1}$ is also the midpoint of the segment $[J K]$. The triangles $K A_{1} B$ and $B A E$ are therefore right-angled and have another angle in common, so they are similar. We thus have
$$
\frac{B K}{B E}=\frac{B A_{1}}{B A} .
$$
This equality of ratios combined with the angle equality $\widehat{\mathrm{KBE}}=\widehat{\mathrm{ABE}}+\widehat{A B K}=\widehat{\mathrm{KBA}_{1}}+\widehat{A B K}=\widehat{\mathrm{ABA}_{1}}$ implies that the triangles $K B E$ and $A_{1} B A$ are similar (this result can also be stated as the fact that $B$ is the center of the homothety sending the pair $\left(A_{1}, K\right)$ to the pair $(A, E)$ and therefore also the center of the homothety sending the pair $\left(A_{1}, \mathcal{A}\right)$ to the pair $(K, E)$ ).
We deduce that $\widehat{\mathrm{BKE}}=\widehat{\mathrm{BA}_{1} A}$. Similarly, $\widehat{\mathrm{CKF}}=\widehat{\mathrm{CA}_{1} A}$. We then have, always because symmetry preserves angles:
$$
\widehat{\mathrm{EJF}}+\widehat{\mathrm{EKF}}=\widehat{\mathrm{BJC}}+\widehat{\mathrm{EKF}}=\widehat{\mathrm{BKC}}+\widehat{\mathrm{EKF}}=360^{\circ}-\widehat{\mathrm{BKE}}-\widehat{\mathrm{CKF}}=360^{\circ}-\widehat{\mathrm{BA} A_{1} A}-\widehat{\mathrm{CA} A_{1} \mathrm{~A}}=180^{\circ} .
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et soit $J$ le centre de son cercle $A$-exinscrit. Soit K le symétrique du point $J$ par rapport au segment $[B C]$. Soient $E$ et $F$ les points sur les droites (BJ) et (CJ) tels que $\widehat{\mathrm{EAB}}=\widehat{\mathrm{CAF}}=90^{\circ}$. Montrer que $\widehat{\mathrm{FKE}}+\widehat{\mathrm{FJE}}=180^{\circ}$.
|
Puisque la droite (BJ) est la bissectrice extérieure de l'angle $\widehat{A B C}$, on a $\widehat{A B J}=\widehat{C B J}=90^{\circ}-\widehat{A B C} / 2$. Puisque la symétrie axiale préserve les angles, on a ainsi $\widehat{\mathrm{KBC}}=\widehat{\mathrm{ABE}}$.
Notons $A_{1}$ le projeté orthogonale du point $J$ sur le segment $[B C]$, de sorte que $A_{1}$ est également le milieu du segment $[J K]$. Les triangles $K A_{1} B$ et $B A E$ sont donc rectangles et ont un autre angle en commun, ils sont donc semblables. On a ainsi
$$
\frac{B K}{B E}=\frac{B A_{1}}{B A} .
$$
Cette égalité de rapport combinée avec l'égalité d'angle $\widehat{\mathrm{KBE}}=\widehat{\mathrm{ABE}}+\widehat{A B K}=\widehat{\mathrm{KBA}_{1}}+\widehat{A B K}=\widehat{\mathrm{ABA}_{1}}$ implique que les triangles $K B E$ et $A_{1} B A$ sont semblables (ce résultat peut également être formulé comme le fait que $B$ est le centre de la smilitude envoyant la paire $\left(A_{1}, K\right)$ sur la paire $(A, E)$ et donc aussi le centre de la similitude envoyant la paire $\left(A_{1}, \mathcal{A}\right)$ sur la paire $(K, E)$ ).
On déduit que $\widehat{\mathrm{BKE}}=\widehat{\mathrm{BA}_{1} A}$. De la même façon, $\widehat{\mathrm{CKF}}=\widehat{\mathrm{CA}_{1} A}$. On a alors, toujours puisque la symétrie préserve les angles:
$$
\widehat{\mathrm{EJF}}+\widehat{\mathrm{EKF}}=\widehat{\mathrm{BJC}}+\widehat{\mathrm{EKF}}=\widehat{\mathrm{BKC}}+\widehat{\mathrm{EKF}}=360^{\circ}-\widehat{\mathrm{BKE}}-\widehat{\mathrm{CKF}}=360^{\circ}-\widehat{\mathrm{BA} A_{1} A}-\widehat{\mathrm{CA} A_{1} \mathrm{~A}}=180^{\circ} .
$$
|
{
"exam": "French_envois",
"problem_label": "14",
"problem_match": "\nExercice 14.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"solution_match": "## Solution de l'exercice 14",
"tier": "T2",
"year": "2024"
}
|
Let $a, b, c>0$ such that $a^{2}<16 b c, b^{2}<16 a c$ and $c^{2}<16 a b$. Show that
$$
a^{2}+b^{2}+c^{2}<2(a b+b c+a c)
$$
|
First, note that we must have $\sqrt{a} < \sqrt{b} + \sqrt{c}$. Indeed, in the contrary case, we would have
$$
16 b c > a^{2} = \sqrt{a}^{4} \geqslant (\sqrt{b} + \sqrt{c})^{4} \geqslant 16 b c
$$
by AM-GM inequality since $\sqrt{b} + \sqrt{c} \geqslant 2 \sqrt[4]{b c}$, which is absurd. Thus, $\sqrt{a} - \sqrt{b} < \sqrt{c}$. But by symmetry, we also have $\sqrt{b} - \sqrt{a} < \sqrt{c}$, and we have $\sqrt{c} < \sqrt{a} + \sqrt{b}$. Therefore,
$$
\begin{gathered}
|\sqrt{a} - \sqrt{b}| < \sqrt{c} < \sqrt{a} + \sqrt{b} \\
\Longrightarrow a + b - 2 \sqrt{a b} < c < a + b + 2 \sqrt{a b} \\
\Longrightarrow -2 \sqrt{a b} < c - a - b < 2 \sqrt{a b} \\
\Longrightarrow (c - a - b)^{2} < 4 a b \\
\Longrightarrow a^{2} + b^{2} + c^{2} < 2(a b + b c + a c)
\end{gathered}
$$
|
a^{2} + b^{2} + c^{2} < 2(a b + b c + a c)
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $a, b, c>0$ tels que $a^{2}<16 b c, b^{2}<16 a c$ et $c^{2}<16 a b$. Montrer que
$$
a^{2}+b^{2}+c^{2}<2(a b+b c+a c)
$$
|
Remarquons tout d'abord que l'on a forcément $\sqrt{\mathrm{a}}<\sqrt{\mathrm{b}}+\sqrt{\mathrm{c}}$. En effet, dans le cas contraire, on aurait
$$
16 b c>a^{2}=\sqrt{a}^{4} \geqslant(\sqrt{b}+\sqrt{c})^{4} \geqslant 16 b c
$$
par IAG car $\sqrt{b}+\sqrt{c} \geqslant 2 \sqrt[4]{b c}$, absurde. Ainsi, $\sqrt{a}-\sqrt{b}<\sqrt{c}$. Mais par symétrie, on a aussi $\sqrt{b}-\sqrt{a}<\sqrt{c}$, et on a $\sqrt{c}<\sqrt{a}+\sqrt{b}$. Donc
$$
\begin{gathered}
|\sqrt{a}-\sqrt{b}|<\sqrt{c}<\sqrt{a}+\sqrt{b} \\
\Longrightarrow a+b-2 \sqrt{a b}<c<a+b+2 \sqrt{a b} \\
\Longrightarrow-2 \sqrt{a b}<c-a-b<2 \sqrt{a b} \\
\Longrightarrow(c-a-b)^{2}<4 a b \\
\Longrightarrow a^{2}+b^{2}+c^{2}<2(a b+b c+a c)
\end{gathered}
$$
|
{
"exam": "French_envois",
"problem_label": "15",
"problem_match": "\nExercice 15.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 15",
"tier": "T2",
"year": "2024"
}
|
Before a championship, each participating team proposes at most $t$ different colors for its jersey. A set $S$ of teams is said to be identifiable if one can assign to each team in $S$ a color appearing in its set of proposals and not appearing in any set of colors of another team. If we denote by n the total number of different colors proposed, determine the largest integer $\mathrm{g}(\mathrm{n}, \mathrm{t})$ such that one can always find an identifiable set of teams of size at least $\mathrm{g}(\mathrm{n}, \mathrm{t})$.
|
Let's show that the sought number is $g(n, t)=\left\lceil\frac{\mathrm{n}}{\mathrm{t}}\right\rceil$.
If $n$ can be written in the form $k \cdot t + r$, with $0 \leqslant r < t$, we can consider the situation where $k$ teams each request $t$ distinct colors, and then a last team requests $r$ new colors. In this situation, there are $\left\lceil\frac{\mathrm{n}}{\mathrm{t}}\right\rceil$ teams requesting at least one color, so this already shows that $g(n, t) \leqslant\left\lceil\frac{n}{t}\right\rceil$.
Now let's show with a kind of greedy algorithm that $g(n, t) \geqslant\left\lceil\frac{\mathrm{n}}{\mathrm{t}}\right\rceil$. Consider the bipartite graph where the vertices are the teams and the colors requested, and where we connect each team to all its requested colors. Thus, the degree of a team is by hypothesis less than or equal to $t$, while the degree of a color is $>0$. Let $C$ be the color with the minimal degree $\mathrm{d}>0$ and let $E$ be a team connected to $C$. We then add the team $E$ to our set $S$ under construction, and associate the color $C$ with it. Next, we delete from our graph all the teams connected to $C$ and also all the colors requested by $E$. By doing this, if we add an edge of the graph (i.e., a team and a color) to our identifiable set, it will remain identifiable because the new color will not have been requested by any previous team, and the new team will not have requested any of the previous colors. It now suffices to show that all the colors that still appear in our graph have a degree $>0$. Since at each step, we delete at most $t$ colors from the graph, this will allow us to conclude.
Suppose by contradiction that there exists a color $a$ still appearing in the graph after adding $E$ to the identifiable set, but such that its degree is zero. This means that the $\mathrm{d}^{\prime}=\operatorname{deg}(\mathrm{a})$ teams that were connected to $a$ just before adding $E$ to $S$ had all requested the color $C$. However, since $a$ is still in the graph, this means that $E$ had not requested the color $a$. This shows that in the graph before the deletion of $E$, $d=\operatorname{deg}(C) \geqslant d^{\prime}+1=\operatorname{deg}(a)+1$, which contradicts the minimality of the degree of $C$, and provides the desired contradiction.
|
\left\lceil\frac{\mathrm{n}}{\mathrm{t}}\right\rceil
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Avant un championnat, chaque équipe participante propose au plus $t$ couleurs différentes pour son maillot. Un ensemble $S$ d'équipes est dit identifiable si l'on peut assigner à chaque équipe de $S$ une couleur apparaissant dans son ensemble de propositions et n'apparaissant dans aucun ensemble de couleurs d'une autre équipe. Si l'on note n le nombre total de couleurs différentes proposées, déterminer le plus grand entier $\mathrm{g}(\mathrm{n}, \mathrm{t})$ tel que l'on puisse toujours trouver un ensemble d'équipes identifiable de taille au moins $\mathrm{g}(\mathrm{n}, \mathrm{t})$.
|
Montrons que le nombre recherché est $g(n, t)=\left\lceil\frac{\mathrm{n}}{\mathrm{t}}\right\rceil$.
Si $n$ s'écrit sous la forme $k \cdot t+r$, avec $0 \leqslant r<t$, on peut considérer la situation où $k$ équipes demandent chacunes $t$ couleurs toutes distinctes deux à deux, puis une dernière équipe demandant $r$ nouvelles couleurs. Dans cette situation, il y a $\left\lceil\frac{\mathrm{n}}{\mathrm{t}}\right\rceil$ équipes demandant au moins une couleur, donc cela montre déjà que $g(n, t) \leqslant\left\lceil\frac{n}{t}\right\rceil$.
Montrons maintenant avec une sorte d'algorithme glouton que $g(n, t) \geqslant\left\lceil\frac{\mathrm{n}}{\mathrm{t}}\right\rceil$. On considère le graphe bipartite dont les sommets sont les équipes et les couleurs demandées, et où l'on relie chaque équipe à toutes ses couleurs demandées. Ainsi, le degré d'une équipe est par hypothèse inférieur ou égal à $t$, tandis que le degré d'une couleur est $>0$. Soit C la couleur de degré minimal $\mathrm{d}>0$ et soit $E$ une équipe reliée à C . On ajoute alors l'équipe E à notre ensemble identifiable $S$ en cours de construction, et on lui associe la couleur $C$. Ensuite, on supprime dans notre graphe toutes les équipes reliées à $C$ et on supprime également toutes les couleurs demandées par E. Ce faisant, si on ajoute une arête du graphe (c'est-à-dire une équipe et une couleur) à notre ensemble identifiable, il le restera car la nouvelle couleur n'aura été demandée par aucune équipe précédente, et la nouvelle équipe n'aura demandé aucune des couleurs précédentes. Il suffit maintenant de montrer que toutes les couleurs qui apparaissent encore dans notre graphe ont un degré $>0$. Puisqu'à chaque étape, on supprime au plus $t$ couleurs du graphe, cela permettra de conclure.
Supposons par l'absurde qu'il existe une couleur a apparaissant encore dans le graphe après l'ajout de E à l'ensemble identifiable, mais telle que son degré soit nul. Cela signifie que les $\mathrm{d}^{\prime}=\operatorname{deg}(\mathrm{a})$ équipes qui étaient reliées à a juste avant l'ajout de $E$ à $S$ avaient toutes demandé la couleur $C$. Or, puisque a est encore dans le graphe, cela signifie que $E$ n'avait pas demandé la couleur a. Cela montre que dans le graphe avant la suppression de $E, d=\operatorname{deg}(C) \geqslant d^{\prime}+1=\operatorname{deg}(a)+1$, ce qui contredit la minimalité du degré de C , et nous fournit la contradiction recherchéé.
|
{
"exam": "French_envois",
"problem_label": "16",
"problem_match": "\nExercice 16.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 16",
"tier": "T2",
"year": "2024"
}
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.