problem
stringlengths 14
10.4k
| solution
stringlengths 1
24.1k
| answer
stringlengths 1
250
⌀ | problem_is_valid
stringclasses 4
values | solution_is_valid
stringclasses 3
values | question_type
stringclasses 4
values | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
10.4k
| solution_raw
stringlengths 1
24.1k
| metadata
dict |
|---|---|---|---|---|---|---|---|---|---|
Show that there are infinitely many integers $n$ such that the base 4 representation of $n^{2}$ contains only 1s and 2s.
|
We show a slightly stronger result, which is better suited for an inductive reasoning: there are infinitely many integers $n$ such that the base 4 representation of $n^{2}$ contains only 1s and 2s, and such that the first and last digit of the base 4 representation of $n^{2}$ is 1. A first example is the number $5^{2}=25=121_{4}$. Then, we show that if we have such an $n$, we can construct a new one that is strictly greater, which will prove that there are infinitely many integers with the desired property.
Let $n$ be such that the base 4 representation of $\mathrm{n}^{2}$ contains only 1s and 2s, and starts and ends with a 1. Suppose this representation contains $k$ digits. We then set $m=2^{2 k-1} \cdot n+n$. We have
$$
\mathrm{m}^{2}=4^{2 \mathrm{k}-1} \cdot \mathrm{n}^{2}+4^{\mathrm{k}} \cdot \mathrm{n}^{2}+\mathrm{n}^{2}
$$
In base 4, $m^{2}$ is thus made up of three copies of $n^{2}$, with $n^{2}$ and $4^{k} \cdot n^{2}$ being two adjacent disjoint copies, and $4^{2 \mathrm{k}-1} \cdot \mathrm{n}^{2}$ and $4^{\mathrm{k}} \cdot \mathrm{n}^{2}$ sharing exactly one power of 4 in their representation, namely $4^{2 k-1}$. But by hypothesis, the coefficients in front of 1 and in front of $4^{k-1}$ of $n^{2}$ are 1s, so the coefficient in front of $4^{2 \mathrm{k}-1}$ of $\mathrm{m}^{2}$ is a 2. Furthermore, all other coefficients in the base 4 representation of $\mathrm{m}^{2}$ appeared in that of $\mathrm{n}^{2}$, and are therefore indeed 1s or 2s. Finally, the first and last coefficients of the base 4 representation of $\mathrm{m}^{2}$, namely the coefficients in front of $4^{0}$ and $4^{3 \mathrm{k}-2}$, are indeed 1s by the inductive hypothesis.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Montrer qu'il existe une infinité d'entiers $n$ tels que l'écriture de $n^{2}$ en base 4 ne contient que des 1 et des 2 .
|
On montre un résultat un peu plus fort, qui se prête mieux à un raisonnement par récurrence : il existe une infinité d'entiers $n$ tels que l'écriture de $n^{2}$ en base 4 ne contient que des 1 et des 2 , et tels que le premier et le dernier chiffre de l'écriture en base 4 de $n^{2}$ vaut 1 . Un premier exemple est le nombre $5^{2}=25=121_{4}$. Ensuite, on montre que si l'on a un tel n , on peut en construire un nouveau qui lui est strictement supérieur, ce qui montrera bien qu'il existe une infinité d'entiers ayant la propriété recherchée.
Soit donc n tel que l'écriture de $\mathrm{n}^{2}$ en base 4 ne contient que des 1 et des 2 , et commence et se termine par un 1 . On suppose que cette écriture contient $k$ chiffres. On pose alors $m=2^{2 k-1} \cdot n+n$. On a
$$
\mathrm{m}^{2}=4^{2 \mathrm{k}-1} \cdot \mathrm{n}^{2}+4^{\mathrm{k}} \cdot \mathrm{n}^{2}+\mathrm{n}^{2}
$$
En base $4, m^{2}$ est donc constitué de trois copies de $n^{2}$, avec $n^{2}$ et $4^{k} \cdot n^{2}$ qui sont deux copies disjointes adjacentes, et $4^{2 \mathrm{k}-1} \cdot \mathrm{n}^{2}$ et $4^{\mathrm{k}} \cdot \mathrm{n}^{2}$ qui ont exactement une puissance de 4 en commun dans leur écriture, à savoir $4^{2 k-1}$. Mais par hypothèse, les coefficients devant 1 et devant $4^{k-1}$ de $n^{2}$ sont des 1 , donc le coefficient devant $4^{2 \mathrm{k}-1}$ de $\mathrm{m}^{2}$ est un 2 . En outre, tous les autres coefficients de l'écriture en base 4 de $\mathrm{m}^{2}$ apparaissaient dans celle de $\mathrm{n}^{2}$, et sont donc bien des 1 ou des 2 . Enfin, les premiers et derniers coefficients de l'écriture en base 4 de $\mathrm{m}^{2}$, à savoir les coefficients devant $4^{0}$ et $4^{3 \mathrm{k}-2}$, sont bien des 1 par hypothèse de récurrence.
|
{
"exam": "French_envois",
"problem_label": "17",
"problem_match": "\nExercice 17.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 17",
"tier": "T2",
"year": "2024"
}
|
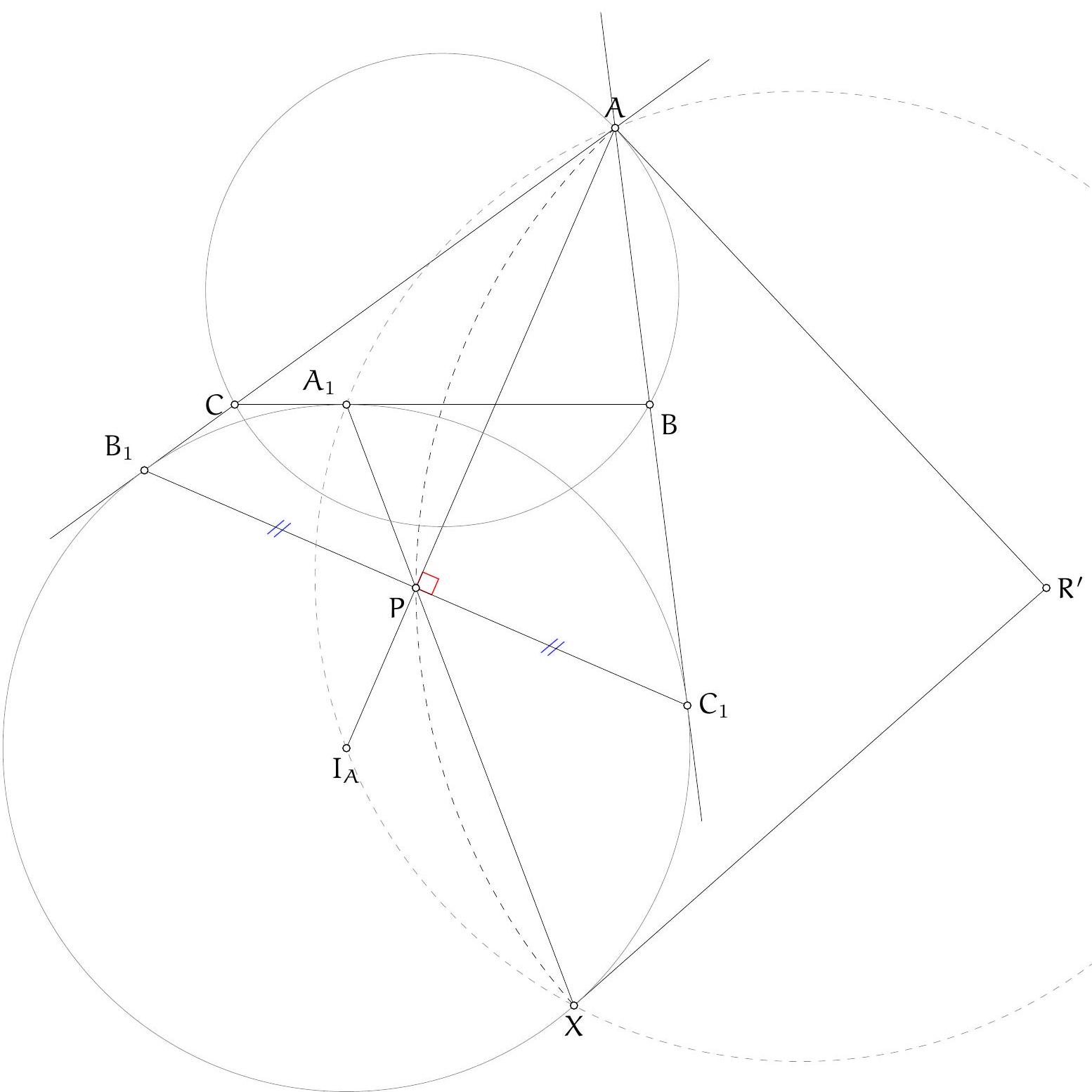
Let $ABC$ be a triangle and let $A_{1}, B_{1}$, and $C_{1}$ be the points of contact of the $A$-excircle, denoted by $\omega_{A}$, with the side $BC$ and the rays $[AC)$ and $[AB)$, respectively. Let $P$ be the midpoint of the segment $\left[B_{1} C_{1}\right]$. The line $\left(A_{1} P\right)$ intersects the circle $\omega_{A}$ again at point $X$. The tangent to the circumcircle of triangle $ABC$ at point $A$ and the tangent to the circle $\omega_{A}$ at point $X$ intersect at $R$. Show that $RX = RP$.
|
By drawing the circle centered at $R$ with radius $R A$, we notice that it also passes through $P$. Therefore, we will instead introduce $R^{\prime}$ as the center of the circumcircle of triangle $A P X$ and show that the lines $\left(A R^{\prime}\right)$ and ( $X R^{\prime}$ ) are respectively tangent to the circumcircles of triangles $A B C$ and $A_{1} B_{1} C_{1}$.
For this, note that since $P$ is the midpoint of the segment $\left[B_{1} C_{1}\right]$ and the line $\left(A I_{A}\right)$ is its perpendicular bisector, the points $A, P$ and $I_{A}$ are collinear. Moreover, since $\widehat{I_{A} B_{1} A}=90^{\circ}=180^{\circ}-\widehat{I_{A} C_{1} A}$, the points $B_{1}, I_{A}, C_{1}$ and $A$ are concyclic. By the power of a point, we have:
$$
\mathrm{PA} \times \mathrm{PI}_{\mathrm{A}}=\mathrm{PB}_{1} \times \mathrm{PC}_{1}=\mathrm{PA}_{1} \times \mathrm{PX}
$$
Thus, the points $A_{1}, I_{A}, X$ and $A$ are concyclic by the converse of the power of a point.
Now, let's show that $\left(A R^{\prime}\right)$ is tangent to the circumcircle of triangle $A B C$. On the one hand, by the inscribed angle theorem:
$$
\widehat{\mathrm{PAR}^{\prime}}=90^{\circ}-\widehat{\mathrm{PXA}}.
$$
But using the concyclicity of the points $A_{1}, I_{A}, X$ and $A$, we find
$$
\widehat{\mathrm{PAR}^{\prime}}=90^{\circ}-\widehat{\mathcal{A}_{1} X A}=90^{\circ}-\widehat{\mathcal{A}_{1} \mathrm{I}_{\mathrm{A}} A}.
$$
Let $D$ be the foot of the angle bisector of $\widehat{B A C}$ and $S$ the South pole of vertex $A$ in $A B C$. $D$ and $S$ are collinear with $A$ and $I_{A}$. Then
$$
90^{\circ}-\widehat{A_{1} I_{A} A}=\widehat{C D I_{A}}=180^{\circ}-\widehat{A B C}-\frac{1}{2} \widehat{B A C}=\widehat{A B C}+\frac{1}{2} \widehat{A C B}=\widehat{A C P}
$$
Thus, $\widehat{P_{A R}}{ }^{\prime}=\widehat{A C P}$, so the line $\left(A R^{\prime}\right)$ is tangent to the circumcircle of triangle $A B C$.
Now, let's show that the line ( $R^{\prime} X$ ) is tangent to the circumcircle of triangle $A_{1} B_{1} C_{1}$. We also have by the inscribed angle theorem:
$$
\widehat{A_{1} X R^{\prime}}=\widehat{\mathrm{PXR}^{\prime}}=90^{\circ}-\widehat{\mathrm{PAX}}=90^{\circ}-\widehat{\mathrm{I}_{A} A X}
$$
Then, by the inscribed angle in the circle passing through $A, A_{1}, I_{A}$ and $X$, and using that the triangle $I_{A} \mathcal{A}_{1} X$ is isosceles at $\mathrm{I}_{\mathrm{A}}$, we have
$$
90^{\circ}-\widehat{\mathrm{I}_{\mathrm{A}} A X}=90^{\circ}-\widehat{\mathrm{I}_{\mathrm{A}} \mathrm{~A}_{1} X}=\frac{1}{2} \widehat{\mathrm{~A}_{1} \mathrm{I}_{A} X}=\widehat{\mathrm{A}_{1} \mathrm{~B}_{1} X}
$$
where we used the inscribed angle theorem in the circle $\omega_{A}$. Thus, the line ( $\left.R^{\prime} X\right)$ is tangent to $\omega_{A}$ and $R=R^{\prime}$, which concludes.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et soient $A_{1}, B_{1}$ et $C_{1}$ les points de contact resepctifs du cercle $A$-exinscrit, noté $\omega_{A}$, avec le côté $B C$ et les demi-droites $[A C)$ et $[A B$ ). Soit $P$ le milieu du segment $\left[B_{1} C_{1}\right]$. La droite $\left(A_{1} P\right)$ recoupe le cercle $\omega_{A}$ au point $X$. La tangente au cercle circonscrit au triangle $A B C$ au point $A$ et la tangente au cercle $\omega_{A}$ au point $X$ se coupent en $R$. Montrer que $R X=R P$.
|
En traçant le cercle de centre $R$ de rayon $R A$, on s'aperçoit que celui-ci passe également par $P$. On va donc plutôt introduire $R^{\prime}$ le centre du cercle circonscrit au triangle $A P X$ et montre que les droites $\left(A R^{\prime}\right)$ et ( $X R^{\prime}$ ) sont respectivement tangentes aux cercles circonscrits au triangle $A B C$ et au triangle $A_{1} B_{1} C_{1}$.
Pour cela, notons que puisque $P$ est le milieu du segment $\left[B_{1} C_{1}\right]$ dont la droite $\left(A I_{A}\right)$ est la médiatrice, les points $A, P$ et $I_{A}$ sont alignés. De plus, puisque $\widehat{I_{A} B_{1} A}=90^{\circ}=180^{\circ}-\widehat{I_{A} C_{1} A}$, les points $B_{1}, I_{A}, C_{1}$ et $A$ sont cocycliques. Par puissance d'un point, on a :
$$
\mathrm{PA} \times \mathrm{PI}_{\mathrm{A}}=\mathrm{PB}_{1} \times \mathrm{PC}_{1}=\mathrm{PA}_{1} \times \mathrm{PX}
$$
de sorte que les points $A_{1}, I_{A}, X$ et $A$ sont cocycliques par la réciproque de la puissance d'un point.
Montrons à présent que $\left(A R^{\prime}\right)$ est tangente au cercle circonscrit au triangle $A B C$. D'une part, d'après le théorème de l'angle au centre :
$$
\widehat{\mathrm{PAR}^{\prime}}=90^{\circ}-\widehat{\mathrm{PXA}} .
$$
Mais en utilisant la cocyclicité des points $A_{1}, I_{A}, X$ et $A$, on a trouve
$$
\widehat{\mathrm{PAR}^{\prime}}=90^{\circ}-\widehat{\mathcal{A}_{1} X A}=90^{\circ}-\widehat{\mathcal{A}_{1} \mathrm{I}_{\mathrm{A}} A} .
$$
Soit alors $D$ le pied de la bissectrice de l'angle $\widehat{B A C}$ et $S$ le pôle Sud su sommet $A$ dans $A B C$. $D$ et $S$ sont alignés avec $A$ et $I_{A}$. Alors
$$
90^{\circ}-\widehat{A_{1} I_{A} A}=\widehat{C D I_{A}}=180^{\circ}-\widehat{A B C}-\frac{1}{2} \widehat{B A C}=\widehat{A B C}+\frac{1}{2} \widehat{A C B}=\widehat{A C P}
$$
Ainsi, $\widehat{P_{A R}}{ }^{\prime}=\widehat{A C P}$, donc la droite $\left(A R^{\prime}\right)$ est tangente au cercle circonscrit au triangle $A B C$.
Montrons que la droite ( $R^{\prime} X$ ) est tangente au cercle circonscrit au triangle $A_{1} B_{1} C_{1}$. On a là aussi par angle au centre :
$$
\widehat{A_{1} X R^{\prime}}=\widehat{\mathrm{PXR}^{\prime}}=90^{\circ}-\widehat{\mathrm{PAX}}=90^{\circ}-\widehat{\mathrm{I}_{A} A X}
$$
Puis, par angle inscrit dans le cercle passant par $A, A_{1}, I_{A}$ et $X$, et en utilisant que le triangle $I_{A} \mathcal{A}_{1} X$ est isocèle en $\mathrm{I}_{\mathrm{A}}$, on a
$$
90^{\circ}-\widehat{\mathrm{I}_{\mathrm{A}} A X}=90^{\circ}-\widehat{\mathrm{I}_{\mathrm{A}} \mathrm{~A}_{1} X}=\frac{1}{2} \widehat{\mathrm{~A}_{1} \mathrm{I}_{A} X}=\widehat{\mathrm{A}_{1} \mathrm{~B}_{1} X}
$$
où l'on a utilisé le théorème de l'angle au centre dans le cercle $\omega_{A}$. Ainsi, la droite ( $\left.R^{\prime} X\right)$ est tangente à $\omega_{A}$ et $R=R^{\prime}$, ce qui conclut.
|
{
"exam": "French_envois",
"problem_label": "18",
"problem_match": "\nExercice 18.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-5-2023-2024.jsonl",
"solution_match": "## Solution de l'exercice 18",
"tier": "T2",
"year": "2024"
}
|
Let $x$ and $y$ be two positive real numbers. Show that
$$
\left(x^{2}+x+1\right)\left(y^{2}+y+1\right) \geqslant 9 x y .
$$
What are the cases of equality?
|
We apply the arithmetic-geometric inequality to get
$$
\begin{gathered}
x^{2}+x+1 \geqslant 3 \sqrt[3]{x^{3}}=3 x \\
y^{2}+y+1 \geqslant 3 \sqrt[3]{y^{3}}=3 y
\end{gathered}
$$
By multiplying these two inequalities, which are positive, we obtain the inequality stated in the problem. Since $x^{2}+x+1$ and $y^{2}+y+1$ are strictly positive, we have equality when we have equality in both arithmetic-geometric inequalities. This happens when $x^{2}=x=1$ and $y^{2}=y=1$, and thus we have equality for $x=y=1$.
Comment from the graders: In general, the exercise was very well solved. Several people forget to consider the equality case.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soient $x$ et $y$ deux réels positifs. Montrer que
$$
\left(x^{2}+x+1\right)\left(y^{2}+y+1\right) \geqslant 9 x y .
$$
Quels sont les cas d'égalité?
|
On applique l'inégalité arithmético-géométrique pour avoir
$$
\begin{gathered}
x^{2}+x+1 \geqslant 3 \sqrt[3]{x^{3}}=3 x \\
y^{2}+y+1 \geqslant 3 \sqrt[3]{y^{3}}=3 y
\end{gathered}
$$
En multipliant ces deux inégalités, qui sont à termes positifs, on obtient l'inégalité de l'énoncé. Comme $x^{2}+x+1$ et $y^{2}+y+1$ sont strictement positifs, on a égalité lorsque l'on a égalité dans les deux inégalités arithmético-géométriques. Mais ceci arrive lorsque $x^{2}=x=1$ et $y^{2}=y=1$, et on a donc égalité pour $x=y=1$.
Commentaire des correcteurs: De manière générale, l'exercice a été très bien résolu. Plusieurs personnes oublient de faire le cas d'égalité.
|
{
"exam": "French_envois",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T2",
"year": "2024"
}
|
Let $a$ and $b$ be two real numbers. Suppose that $2a + a^2 = 2b + b^2$. Show that if $a$ is an integer (not necessarily positive), then $b$ is also an integer.
|
We rewrite the equality
$$
\begin{gathered}
2 a-2 b=b^{2}-a^{2} \\
2(a-b)=-(a+b)(a-b)
\end{gathered}
$$
Then either $\mathrm{b}=\mathrm{a}$, and in this case b is an integer, or
$$
2=-a-b
$$
from which
$$
\mathrm{b}=-2-\mathrm{a}
$$
and $b$ is still an integer.
Comment from the graders: The exercise was generally well handled, with a few reasoning errors. Almost all students avoided the trap $a+1=-(b+1)$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soient $a$ et $b$ deux réels. Supposons que $2 a+a^{2}=2 b+b^{2}$. Montrer que si $a$ est un entier (pas forcément positif), alors b est aussi un entier.
|
On réécrit l'égalité
$$
\begin{gathered}
2 a-2 b=b^{2}-a^{2} \\
2(a-b)=-(a+b)(a-b)
\end{gathered}
$$
Alors soit $\mathrm{b}=\mathrm{a}$, et alors b est un entier, soit
$$
2=-a-b
$$
d'où
$$
\mathrm{b}=-2-\mathrm{a}
$$
et $b$ est encore un entier.
Commentaire des correcteurs: Exercice bien traité dans l'ensemble, avec quelques erreurs de raisonnement. Presque tous les élèves ont évité le piège $a+1=-(b+1)$.
|
{
"exam": "French_envois",
"problem_label": "10",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T2",
"year": "2024"
}
|
Show that there do not exist strictly positive real numbers $x, y, z$ such that
$$
\left(2 x^{2}+y z\right)\left(2 y^{2}+x z\right)\left(2 z^{2}+x y\right)=26 x^{2} y^{2} z^{2}
$$
|
We could try to simply apply the arithmetic-geometric mean inequality to each of the factors on the left side, but this gives that the left term is greater than or equal to \(16 \sqrt{2} x^{2} y^{2} z^{2}\), which is not enough to conclude (since \(16 \sqrt{2} < 26\)). In fact, this is because we cannot have equality in all three arithmetic-geometric mean inequalities at the same time. We would like the case \(x=y=z\) to be a case of equality in the arithmetic-geometric mean inequalities we apply.
For example, take the first term \(2 x^{2} + y z\). We split it into \(x^{2} + x^{2} + y z\) (so that each of the terms is equal if \(x=y=z\)), then we can apply the arithmetic-geometric mean inequality:
\[
2 x^{2} + y z \geqslant 3 \sqrt[3]{x^{2} \cdot x^{2} \cdot y z} = 3 \sqrt[3]{x^{4} y z}
\]
By applying the arithmetic-geometric mean inequality to all the positive terms, we have
\[
\left(2 x^{2} + y z\right)\left(2 y^{2} + x z\right)\left(2 z^{2} + x y\right) \geqslant 27 \sqrt[3]{x^{4} y z \cdot y^{4} x z \cdot z^{4} y z} = 27 \sqrt[3]{x^{6} y^{6} z^{6}} = 27 x^{2} y^{2} z^{2}
\]
which is strictly greater than \(26 x^{2} y^{2} z^{2}\), so we cannot have equality.
Comment from the graders: The exercise was generally successful. Good use of the AM-GM inequality, except for a few errors in reasoning.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Montrer qu'il n'existe pas de réels $x, y, z$ strictement positifs tels que
$$
\left(2 x^{2}+y z\right)\left(2 y^{2}+x z\right)\left(2 z^{2}+x y\right)=26 x^{2} y^{2} z^{2}
$$
|
On pourrait essayer de simplement appliquer l'inégalité arithmético-géométrique sur chacun des facteurs du côté gauche, mais ceci donne que le terme de gauche est supérieur ou égal à $16 \sqrt{2} x^{2} y^{2} z^{2}$ ce qui ne suffit pas pour conclure (car $16 \sqrt{2}<26$ ). En fait, ceci vient du fait que l'on ne peut pas avoir égalité dans les trois inégalités arithmético-géométriques à la fois. On aimerait bien que le cas $x=y=z$ soit un cas d'égalité des inégalités arithmético-géométrique que l'on applique.
Prenons par exemple le premier terme $2 x^{2}+y z$. On le sépare en $x^{2}+x^{2}+y z$ (de façon à ce que chacun des termes soit égaux si $x=y=z$ ), on peut alors appliquer l'inégalité arithmético-géométrique :
$$
2 x^{2}+y z \geqslant 3 \sqrt[3]{x^{2} \cdot x^{2} \cdot y z}=3 \sqrt[3]{x^{4} y z}
$$
En appliquant l'inégalité arithmético-géométrique sur tous les termes qui sont positifs, on a
$$
\left(2 x^{2}+y z\right)\left(2 y^{2}+x z\right)\left(2 z^{2}+x y\right) \geqslant 27 \sqrt[3]{x^{4} y z \cdot y^{4} x z \cdot z^{4} y z}=27 \sqrt[3]{x^{6} y^{6} z^{6}}=27 x^{2} y^{2} z^{2}
$$
ce qui est strictement supérieur à $26 x^{2} y^{2} z^{2}$, on ne peut donc pas avoir égalité.
Commentaire des correcteurs: Exercice réussi dans l'ensemble. Bonnes utilsations de l'IAG, sauf quelques erreurs de raisonnement.
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T2",
"year": "2024"
}
|
Show that for all real numbers $x, y, z$, we have
$$
\frac{x^{2}-y^{2}}{2 x^{2}+1}+\frac{y^{2}-z^{2}}{2 y^{2}+1}+\frac{z^{2}-x^{2}}{2 z^{2}+1} \leqslant 0 .
$$
|
We rewrite the inequality as
$$
\frac{x^{2}}{2 x^{2}+1}+\frac{y^{2}}{2 y^{2}+1}+\frac{z^{2}}{2 z^{2}+1} \leqslant \frac{y^{2}}{2 x^{2}+1}+\frac{z^{2}}{2 y^{2}+1}+\frac{x^{2}}{2 z^{2}+1} .
$$
Since the inequality is not symmetric, we cannot assume without loss of generality that $x^{2} \leqslant y^{2} \leqslant z^{2}$. However, note that the sequences $\left(x^{2}, y^{2}, z^{2}\right)$ and $\left(\frac{1}{2 x^{2}+1}, \frac{1}{2 y^{2}+1}, \frac{1}{2 z^{2}+1}\right)$ are arranged in reverse order (the largest of the first sequence corresponds to the smallest of the second sequence, for example). Therefore, we can apply the rearrangement inequality, which directly implies the inequality in the statement.
Comment from the graders: Students who approached the problem generally did well. They proposed three types of solutions. Some used the rearrangement inequality (also known as the turnstile inequality), similar to the solution provided. The most common mistake was to claim that the inequality is symmetric, which is clearly not the case, and to assume an order. While this is not critical in the context of the rearrangement inequality, such imprecisions are dangerous: a few students, by illegally assuming a convenient order, dispensed with using the rearrangement inequality, and their reasoning was entirely incorrect. Others used the arithmetic-geometric mean inequality directly and effectively after slightly transforming the problem. Unfortunately, about half of the students eliminated the fractions, expanded, and then used the arithmetic-geometric mean inequality term by term. Let us recall that this strategy is risky because a single calculation error can completely invalidate the solution, and more challenging problems (such as problem 6) are difficult to solve this way.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Montrer que pour tous les réels $x, y, z$, on a
$$
\frac{x^{2}-y^{2}}{2 x^{2}+1}+\frac{y^{2}-z^{2}}{2 y^{2}+1}+\frac{z^{2}-x^{2}}{2 z^{2}+1} \leqslant 0 .
$$
|
On réécrit l'inégalité en
$$
\frac{x^{2}}{2 x^{2}+1}+\frac{y^{2}}{2 y^{2}+1}+\frac{z^{2}}{2 z^{2}+1} \leqslant \frac{y^{2}}{2 x^{2}+1}+\frac{z^{2}}{2 y^{2}+1}+\frac{x^{2}}{2 z^{2}+1} .
$$
L'inégalité n'étant pas symétrique, on ne peut pas supposer sans perte de généralité que $x^{2} \leqslant y^{2} \leqslant$ $z^{2}$. Cependant, remarquons que les suites $\left(x^{2}, y^{2}, z^{2}\right)$ et $\left(\frac{1}{2 x^{2}+1}, \frac{1}{2 y^{2}+1}, \frac{1}{2 z^{2}+1}\right)$ sont rangées dans l'ordre inverse (le plus grand de la première suite correspond au plus petit de la deuxième suite par exemple). On peut donc appliquer l'inégalité de réordonnement qui implique directement l'inégalité de l'énoncé.
Commentaire des correcteurs: Les élèves ayant abordé le problème l'ont plutôt bien réussi. Ils ont proposé trois types de solutions. Certains passent par l'inégalité de réarrangement (aussi appelée inégalité du tourniquet), à l'instar du corrigé. L'erreur la plus fréquente est alors de dire que l'inégalité est symétrique, ce qui n'est manifestement pas le cas, et de supposer un ordre. Dans le cadre de l'inégalité de réarrangement ceci n'est pas dramatique, mais ce type d'imprécisions reste dangereux : quelques élèves, en supposant illégalement un ordre commode, se sont dispensés d'utiliser l'inégalité de réarrangement, et leur raisonnement est tout à fait erroné. D'autres utilisent directement et efficacement l'inégalité arithméticogéométrique après avoir un peu transformé le problème. Une regrettable moitié enfin, se débarasse des fractions, développe, puis utilise l'IAG termes à termes. Rappelons que cette stratégie est hasardeuse car une faute de calcul rend complètement invalide la solution, et que les problèmes un peu plus durs (comme le problème 6) sont difficiles à résoudre ainsi.
|
{
"exam": "French_envois",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T2",
"year": "2024"
}
|
Let $n \geqslant 2$ and $a_{1}, \ldots, a_{n} \in[0,1]$ be real numbers. Determine the maximum value that the smallest of the numbers
$$
a_{1}-a_{1} a_{2}, a_{2}-a_{2} a_{3}, \ldots, a_{n}-a_{n} a_{1}
$$
can take.
|
Let $i$ be such that $a_{i}$ is minimal. Then we have $a_{i+1} \geqslant a_{i}$ (where $a_{n+1}=a_{1}$) and thus by the arithmetic-geometric inequality on $a_{i}$ and $1-a_{i}$, we obtain
$$
a_{i}-a_{i} a_{i+1} \leqslant a_{i}-a_{i}^{2}=a_{i}\left(1-a_{i}\right) \leqslant \frac{1}{4}\left(a_{i}+1-a_{i}\right)^{2}=\frac{1}{4}
$$
so the minimum of the numbers is at most $\frac{1}{4}$. It remains to verify that we can find $a_{i}$ such that the minimum is equal to $\frac{1}{4}$. If all the $a_{i}$ are equal to $\frac{1}{2}$, then all the $a_{i}-a_{i} a_{i+1}$ are equal to $\frac{1}{4}$ and the minimum is indeed $\frac{1}{4}$.
Comment from the graders: The problem was generally well done. It contained two steps: proving that the expression is always less than 0.25 and providing an example where this bound is achieved. Some students forget one or the other of these two steps and thus lose valuable points.
|
\frac{1}{4}
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Soit $n \geqslant 2$ et $a_{1}, \ldots, a_{n} \in[0,1]$ des réels. Déterminer la valeur maximale que peut prendre le plus petit des nombres
$$
a_{1}-a_{1} a_{2}, a_{2}-a_{2} a_{3}, \ldots, a_{n}-a_{n} a_{1}
$$
|
Soit $i$ tel que $a_{i}$ soit minimal. Alors on a $a_{i+1} \geqslant a_{i}$ (où $a_{n+1}=a_{1}$ ) et donc par inégalité arithmético-géométrique sur $a_{i}$ et $1-a_{i}$, on obtient
$$
a_{i}-a_{i} a_{i+1} \leqslant a_{i}-a_{i}^{2}=a_{i}\left(1-a_{i}\right) \leqslant \frac{1}{4}\left(a_{i}+1-a_{i}\right)^{2}=\frac{1}{4}
$$
donc le minimum des nombres vaut au plus $\frac{1}{4}$. Il reste à vérifier que l'on peut trouver des $a_{i}$ tel que le minimum soit égal à $\frac{1}{4}$. Si tous les $a_{i}$ valent $\frac{1}{2}$, alors tous les $a_{i}-a_{i} a_{i+1}$ valent $\frac{1}{4}$ et le minimum vaut bien $\frac{1}{4}$.
Commentaire des correcteurs : Le problème est bien réussi dans l'ensemble. Il contenait deux étapes: prouver que l'expresison est toujours plus petite que 0.25 et donner un exemple en lequel cette borne est atteinte. Quelques élèves oublient l'une ou l'autre de ces deux étapes et perdent alors de précieux points.
|
{
"exam": "French_envois",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T2",
"year": "2024"
}
|
Let $a, b, c$ be three strictly positive real numbers. Show that
$$
\frac{a^{4}+1}{b^{3}+b^{2}+b}+\frac{b^{4}+1}{c^{3}+c^{2}+c}+\frac{c^{4}+1}{a^{3}+a^{2}+a} \geqslant 2
$$
|
We start by applying the arithmetic-geometric inequality to the three terms in the statement:
$$
\frac{a^{4}+1}{b^{3}+b^{2}+b}+\frac{b^{4}+1}{c^{3}+c^{2}+c}+\frac{c^{4}+1}{a^{3}+a^{2}+a} \geqslant 3 \sqrt[3]{\frac{\left(a^{4}+1\right)\left(b^{4}+1\right)\left(c^{4}+1\right)}{\left(b^{3}+b^{2}+b\right)\left(c^{3}+c^{2}+c\right)\left(a^{3}+a^{2}+a\right)}}
$$
We aim to find a lower bound for the quotients $\frac{a^{4}+1}{a^{3}+a^{2}+a}$. For this, we apply arithmetic-geometric inequalities:
$$
\begin{aligned}
a^{3}+a^{2}+a & \leqslant \frac{1}{2}\left(a^{4}+a^{2}\right)+a^{2}+\frac{1}{2}\left(a^{2}+1\right)=\frac{1}{2}\left(a^{4}+1\right)+2 a^{2} \\
& \leqslant \frac{1}{2}\left(a^{4}+1\right)+\left(a^{4}+1\right)=\frac{3}{2}\left(a^{4}+1\right)
\end{aligned}
$$
and thus $\frac{a^{4}+1}{a^{3}+a^{2}+a} \geqslant \frac{2}{3}$. We have the same for $b$ and $c$, and therefore
$$
\frac{a^{4}+1}{b^{3}+b^{2}+b}+\frac{b^{4}+1}{c^{3}+c^{2}+c}+\frac{c^{4}+1}{a^{3}+a^{2}+a} \geqslant 3 \sqrt[3]{\left(\frac{2}{3}\right)^{3}}=2
$$
|
2
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soient $a, b, c$ trois réels strictement positifs. Montrer que
$$
\frac{a^{4}+1}{b^{3}+b^{2}+b}+\frac{b^{4}+1}{c^{3}+c^{2}+c}+\frac{c^{4}+1}{a^{3}+a^{2}+a} \geqslant 2
$$
|
On commence par appliquer l'inégalité arithmético-géométrique aux trois termes de l'énoncé :
$$
\frac{a^{4}+1}{b^{3}+b^{2}+b}+\frac{b^{4}+1}{c^{3}+c^{2}+c}+\frac{c^{4}+1}{a^{3}+a^{2}+a} \geqslant 3 \sqrt[3]{\frac{\left(a^{4}+1\right)\left(b^{4}+1\right)\left(c^{4}+1\right)}{\left(b^{3}+b^{2}+b\right)\left(c^{3}+c^{2}+c\right)\left(a^{3}+a^{2}+a\right)}}
$$
On cherche donc à minorer les quotients $\frac{a^{4}+1}{a^{3}+a^{2}+a}$. Pour cela, on applique des inégalités arithméticogéométriques :
$$
\begin{aligned}
a^{3}+a^{2}+a & \leqslant \frac{1}{2}\left(a^{4}+a^{2}\right)+a^{2}+\frac{1}{2}\left(a^{2}+1\right)=\frac{1}{2}\left(a^{4}+1\right)+2 a^{2} \\
& \leqslant \frac{1}{2}\left(a^{4}+1\right)+\left(a^{4}+1\right)=\frac{3}{2}\left(a^{4}+1\right)
\end{aligned}
$$
et ainsi $\frac{a^{4}+1}{a^{3}+a^{2}+a} \geqslant \frac{2}{3}$. On a de même pour $b$ et $c$, et donc
$$
\frac{\mathrm{a}^{4}+1}{\mathrm{~b}^{3}+\mathrm{b}^{2}+\mathrm{b}}+\frac{\mathrm{b}^{4}+1}{\mathrm{c}^{3}+\mathrm{c}^{2}+\mathrm{c}}+\frac{\mathrm{c}^{4}+1}{\mathrm{a}^{3}+\mathrm{a}^{2}+\mathrm{a}} \geqslant 3 \sqrt[3]{\left(\frac{2}{3}\right)^{3}}=2
$$
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "## Exercice 6.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T2",
"year": "2024"
}
|
Let $a, b, c$ be three strictly positive real numbers. Show that
$$
\frac{a^{4}+1}{b^{3}+b^{2}+b}+\frac{b^{4}+1}{c^{3}+c^{2}+c}+\frac{c^{4}+1}{a^{3}+a^{2}+a} \geqslant 2
$$
|
:
We can also think about it using the rearrangement inequality. The inequality is not symmetric, so we cannot assume without loss of generality that $a \geqslant b \geqslant c$ or something similar.
However, by strict monotonicity, $\left(a^{4}+1, b^{4}+1, c^{4}+1\right)$ is in the same order as $(a, b, c)$. Similarly, $\left(a^{3}+a^{2}+a, b^{3}+b^{2}+b, c^{3}+c^{2}+c\right)$ is also in the same order, and $\left(\frac{1}{a^{3}+a^{2}+a}, \frac{1}{b^{3}+b^{2}+b}, \frac{1}{c^{3}+c^{2}+c}\right)$ is in the reverse order. Thus, by the rearrangement inequality,
$$
\frac{a^{4}+1}{a^{3}+a^{2}+a}+\frac{b^{4}+1}{b^{3}+b^{2}+b}+\frac{c^{4}+1}{c^{3}+c^{2}+c}
$$
is the minimum value that can be taken by a sum of products of terms from $\left(a^{4}+1, b^{4}+1, c^{4}+1\right)$ with terms from $\left(\frac{1}{a^{3}+a^{2}+a}, \frac{1}{b^{3}+b^{2}+b}, \frac{1}{c^{3}+c^{2}+c}\right)$. In particular here:
$$
\frac{a^{4}+1}{b^{3}+b^{2}+b}+\frac{b^{4}+1}{c^{3}+c^{2}+c}+\frac{c^{4}+1}{a^{3}+a^{2}+a} \geqslant \frac{a^{4}+1}{a^{3}+a^{2}+a}+\frac{b^{4}+1}{b^{3}+b^{2}+b}+\frac{c^{4}+1}{c^{3}+c^{2}+c}
$$
We can now show as before that $\frac{a^{4}+1}{a^{3}+a^{2}+a} \geqslant \frac{2}{3}$ and conclude by
$$
\frac{a^{4}+1}{b^{3}+b^{2}+b}+\frac{b^{4}+1}{c^{3}+c^{2}+c}+\frac{c^{4}+1}{a^{3}+a^{2}+a} \geqslant 3 \cdot \frac{2}{3}=2
$$
Graders' comments: The problem is very well done. However, many students believe that we can assume $a \geqslant b \geqslant c$ because 'the inequality is symmetric'. However, the inequality is not symmetric: if we swap $b$ and $c$, the inequality is drastically changed. Fortunately, here by chance, the reasoning was easily rectifiable (see solution 2 in the answer key). However, the few copies that multiplied and expanded everything did not succeed, once again demonstrating that thinking before haphazardly expanding everything is always a good idea.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soient $a, b, c$ trois réels strictement positifs. Montrer que
$$
\frac{a^{4}+1}{b^{3}+b^{2}+b}+\frac{b^{4}+1}{c^{3}+c^{2}+c}+\frac{c^{4}+1}{a^{3}+a^{2}+a} \geqslant 2
$$
|
:
On peut également réfléchir avec l'inégalité de réarrangement. L'inégalité n'est pas symétrique, on ne peut donc pas supposer sans perte de généralités $a \geqslant b \geqslant c$ ou quelque chose de similaire.
Cependant, par stricte croissance, $\left(a^{4}+1, b^{4}+1, c^{4}+1\right)$ est dans le même ordre que $(a, b, c)$. De même, $\left(a^{3}+a^{2}+a, b^{3}+b^{2}+b, c^{3}+c^{2}+c\right)$ est également dans le même ordre et $\left(\frac{1}{a^{3}+a^{2}+a}, \frac{1}{b^{3}+b^{2}+b}, \frac{1}{c^{3}+c^{2}+c}\right)$ est dans le sens inverse. Ainsi, par inégalité de réarrangement,
$$
\frac{a^{4}+1}{a^{3}+a^{2}+a}+\frac{b^{4}+1}{b^{3}+b^{2}+b}+\frac{c^{4}+1}{c^{3}+c^{2}+c}
$$
est la valeur minimale que peut prendre une somme de produit de termes de $\left(a^{4}+1, b^{4}+1, c^{4}+1\right)$ avec des termes de $\left(\frac{1}{a^{3}+a^{2}+a}, \frac{1}{b^{3}+b^{2}+b}, \frac{1}{c^{3}+c^{2}+c}\right)$. En particulier ici :
$$
\frac{a^{4}+1}{b^{3}+b^{2}+b}+\frac{b^{4}+1}{c^{3}+c^{2}+c}+\frac{c^{4}+1}{a^{3}+a^{2}+a} \geqslant \frac{a^{4}+1}{a^{3}+a^{2}+a}+\frac{b^{4}+1}{b^{3}+b^{2}+b}+\frac{c^{4}+1}{c^{3}+c^{2}+c}
$$
On peut maintenant comme précédemment montrer $\frac{a^{4}+1}{a^{3}+a^{2}+a} \geqslant \frac{2}{3}$ et conclure par
$$
\frac{a^{4}+1}{b^{3}+b^{2}+b}+\frac{b^{4}+1}{c^{3}+c^{2}+c}+\frac{c^{4}+1}{a^{3}+a^{2}+a} \geqslant 3 \cdot \frac{2}{3}=2
$$
Commentaire des correcteurs : Le problème est très bien réussi. Cependant, beaucoup d'élèves croient qu'on peut supposer $a \geqslant b \geqslant c$ car 'l'inégalité est symétrique". Or l'inégalité n'est pas symétrique : si on change b et c l'inégalité est drastiquement changée. Heureusement qu'ici par chance, le raisonnement était rectifiable facilement (cf la solution 2 du corrigé). Cependant, les quelques copies qui ont tout multiplié et développé n'ont pas réussi, témoignant encore une fois du fait que réfléchir avant de tout développer hasardeusement est toujours une bonne idée.
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "## Exercice 6.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"solution_match": "## Solution alternative",
"tier": "T2",
"year": "2024"
}
|
Let $a, b, c, d$ be four real numbers such that $|a|>1,|b|>1,|c|>1$ and $|d|>1$. Suppose that $(a+1)(b+1)(c+1)(d+1)=(a-1)(b-1)(c-1)(d-1)$. Show that
$$
\frac{1}{a-1}+\frac{1}{b-1}+\frac{1}{c-1}+\frac{1}{d-1}>0
$$
|
We know from the statement that none of $\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}$ equals 1. The condition in the statement can be written as
$$
\frac{a+1}{a-1} \frac{b+1}{b-1} \frac{c+1}{c-1} \frac{d+1}{d-1}=1
$$
Notice that since $|a|>1$, we have either $a>1$ and thus $a+1>0$ and $a-1>0$, or $a<-1$ and thus $a+1<0$ and $a-1<0$. Therefore, in all cases $\frac{a+1}{a-1}$ is positive, and the same applies to $b, c, d$. We can therefore apply the arithmetic-geometric mean inequality to the product above to get
$$
\frac{\mathrm{a}+1}{\mathrm{a}-1}+\frac{\mathrm{b}+1}{\mathrm{~b}-1}+\frac{\mathrm{c}+1}{\mathrm{c}-1}+\frac{\mathrm{d}+1}{\mathrm{~d}-1} \geqslant 4 \sqrt[4]{\frac{\mathrm{a}+1}{\mathrm{a}-1} \frac{\mathrm{~b}+1}{\mathrm{~b}-1} \frac{\mathrm{c}+1}{\mathrm{c}-1} \frac{\mathrm{~d}+1}{\mathrm{~d}-1}}=4
$$
We can rewrite this as
$$
\left(1+\frac{2}{\mathrm{a}-1}\right)+\left(1+\frac{2}{\mathrm{~b}-1}\right)+\left(1+\frac{2}{\mathrm{c}-1}\right)+\left(1+\frac{2}{\mathrm{~d}-1}\right) \geqslant 4
$$
and thus
$$
\frac{1}{a-1}+\frac{1}{b-1}+\frac{1}{c-1}+\frac{1}{d-1} \geqslant 0
$$
However, the statement asks us to show that the inequality is strict. Therefore, we need to consider the case of equality in the arithmetic-geometric mean inequality. Equality holds if and only if
$$
\frac{a+1}{a-1}=\frac{b+1}{b-1}=\frac{c+1}{c-1}=\frac{d+1}{d-1}
$$
Since the product of these four terms is 1, these terms must all be 1 or all be -1. In the first case, we have $a+1=a-1$, which is impossible. In the second case, we have $a+1=1-a$ and thus $a=0$, which is also impossible because $|a|>1$. Therefore, equality cannot hold, and the inequality is indeed strict as stated.
Comment from the graders: The problem is rarely approached. Some students attempted complicated calculations, and surprisingly few managed to make it work. In inequalities, it is crucial to try to bring out the hypotheses rather than brute-forcing the calculations.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soient $a, b, c, d$ quatre réels tels que $|a|>1,|b|>1,|c|>1$ et $|d|>1$. Supposons que $(a+1)(b+1)(c+1)(d+1)=(a-1)(b-1)(c-1)(d-1)$. Montrer que
$$
\frac{1}{a-1}+\frac{1}{b-1}+\frac{1}{c-1}+\frac{1}{d-1}>0
$$
|
On sait d'après l'énoncé que aucun des $\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}$ ne vaut 1 . La condition de l'énoncé s'écrit alors
$$
\frac{a+1}{a-1} \frac{b+1}{b-1} \frac{c+1}{c-1} \frac{d+1}{d-1}=1
$$
Remarquons que comme $|a|>1$, alors on a soit $a>1$ et donc $a+1>0$ et $a-1>0$, ou alors $a<-1$ et donc $a+1<0$ et $a-1<0$. Ainsi, dans tous les cas $\frac{a+1}{a-1}$ est positif, et de même pour $b, c, d$. On peut donc appliquer l'inégalité arithmético-géométrique sur le produit précédent pour avoir
$$
\frac{\mathrm{a}+1}{\mathrm{a}-1}+\frac{\mathrm{b}+1}{\mathrm{~b}-1}+\frac{\mathrm{c}+1}{\mathrm{c}-1}+\frac{\mathrm{d}+1}{\mathrm{~d}-1} \geqslant 4 \sqrt[4]{\frac{\mathrm{a}+1}{\mathrm{a}-1} \frac{\mathrm{~b}+1}{\mathrm{~b}-1} \frac{\mathrm{c}+1}{\mathrm{c}-1} \frac{\mathrm{~d}+1}{\mathrm{~d}-1}}=4
$$
On réécrit ceci sous la forme
$$
\left(1+\frac{2}{\mathrm{a}-1}\right)+\left(1+\frac{2}{\mathrm{~b}-1}\right)+\left(1+\frac{2}{\mathrm{c}-1}\right)+\left(1+\frac{2}{\mathrm{~d}-1}\right) \geqslant 4
$$
et donc
$$
\frac{1}{a-1}+\frac{1}{b-1}+\frac{1}{c-1}+\frac{1}{d-1} \geqslant 0
$$
Mais l'énoncé nous demande de montrer que l'inégalité est stricte, on s'intéresse donc au cas d'égalité dans l'inégalité arithmético-géométrique. On a égalité si et seulement si
$$
\frac{a+1}{a-1}=\frac{b+1}{b-1}=\frac{c+1}{c-1}=\frac{d+1}{d-1}
$$
Comme le produit de ces quatre termes vaut 1 , nécessairement ces termes valent tous 1 ou tous -1 . Dans le premier cas, on a $a+1=a-1$ ce qui est impossible. Dans le deuxième cas, on a $a+1=1-a$ et donc $a=0$, ce qui est aussi impossible car $|a|>1$. Ainsi, on ne peut pas avoir égalité et l'inégalité est bien stricte comme dans l'énoncé.
Commentaire des correcteurs : Le problème est peu abordé. Certains se sont lancés dans des calculs compliqués, et étonnamment très peu ont réussi à faire fonctionner cela. En inégalité, il est crucial d'essayer de faire apparaître les hypothèses plutôt que de bourriner les calculs.
|
{
"exam": "French_envois",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 7",
"tier": "T2",
"year": "2024"
}
|
Let $\mathrm{n} \geqslant 1$ be an integer and $\mathrm{x}_{1}, \ldots, \mathrm{x}_{\mathrm{n}}$ be positive real numbers. Show that
$$
\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots+\frac{x_{n}}{n}\right)\left(1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}\right) \leqslant \frac{(n+1)^{2}}{4 n}\left(x_{1}+x_{2}+\ldots+x_{n}\right)^{2}
$$
What are the cases of equality?
|
The trick is to apply the arithmetic-geometric inequality to the left side of the inequality, but with coefficients $\sqrt{n}$ and $\frac{1}{\sqrt{n}}$:
$$
\begin{aligned}
\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots\right. & \left.+\frac{x_{n}}{n}\right)\left(1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}\right)=\sqrt{n}\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots+\frac{x_{n}}{n}\right) \frac{1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}}{\sqrt{n}} \\
& \leqslant \frac{1}{4}\left(\sqrt{n}\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots+\frac{x_{n}}{n}\right)+\frac{1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}}{\sqrt{n}}\right)^{2}
\end{aligned}
$$
For each $i$, the coefficient of $x_{i}$ is $\frac{\sqrt{n}}{i}+\frac{i}{\sqrt{n}}$. The function $t \mapsto t+\frac{1}{t}$ is decreasing for $t<1$ and increasing for $t>1$. Indeed, for example, for $1<x<y$, we have $xy>1$ and thus:
$$
y-x>\frac{y-x}{xy}=\frac{1}{x}-\frac{1}{y}
$$
Thus, the maximum coefficient is achieved at $i=1$ or $i=n$. In each case, we find a coefficient $\sqrt{n}+\frac{1}{\sqrt{n}}=\frac{n+1}{\sqrt{n}}$, and therefore
$$
\begin{aligned}
\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots+\frac{x_{n}}{n}\right)\left(1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}\right) \leqslant \frac{1}{4}\left(\frac{n+1}{\sqrt{n}}\left(x_{1}+x_{2}+\ldots+x_{n}\right)\right)^{2} \\
\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots+\frac{x_{n}}{n}\right)\left(1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}\right) \leqslant \frac{(n+1)^{2}}{4 n}\left(x_{1}+x_{2}+\ldots+x_{n}\right)^{2}
\end{aligned}
$$
We are interested in the cases of equality. For $1<i<n$, the inequality $\frac{\sqrt{n}}{i}+\frac{i}{\sqrt{n}} \leqslant \frac{n+1}{\sqrt{n}}$ is strict, so necessarily $x_{i}$ must be equal to 0. Then, we need to have equality in the arithmetic-geometric inequality, which is written as
$$
\begin{aligned}
\sqrt{n}\left(x_{1}+\frac{x_{n}}{n}\right) & =\frac{1}{\sqrt{n}}\left(x_{1}+n x_{n}\right) \\
\left(\sqrt{n}-\frac{1}{\sqrt{n}}\right) x_{1} & =\left(\sqrt{n}-\frac{1}{\sqrt{n}}\right) x_{n}
\end{aligned}
$$
If $n=1$, we always have equality (there is only one $x_{i}$), otherwise we have the condition $x_{1}=x_{n}$. Conversely, we can verify that if $x_{1}=x_{n}$ and all other $x_{i}$ are zero, we indeed have equality in the inequality of the statement.
Comment from the graders: The problem is rarely approached, and even less solved. Very few copies deal with the cases of equality, although this is part of the statement and could earn points. Be sure to know the statements of known inequalities well, as misapplying an inequality can ruin an entire proof.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $\mathrm{n} \geqslant 1$ un entier et $\mathrm{x}_{1}, \ldots, \mathrm{x}_{\mathrm{n}}$ des réels positifs. Montrer que
$$
\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots+\frac{x_{n}}{n}\right)\left(1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}\right) \leqslant \frac{(n+1)^{2}}{4 n}\left(x_{1}+x_{2}+\ldots+x_{n}\right)^{2}
$$
Quels sont les cas d'égalité?
|
L'astuce est d'appliquer une inégalité arithmético-géométrique au côté gauche de l'inégalité, mais avec des coefficients $\sqrt{n}$ et $\frac{1}{\sqrt{n}}$ :
$$
\begin{aligned}
\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots\right. & \left.+\frac{x_{n}}{n}\right)\left(1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}\right)=\sqrt{n}\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots+\frac{x_{n}}{n}\right) \frac{1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}}{\sqrt{n}} \\
& \leqslant \frac{1}{4}\left(\sqrt{n}\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots+\frac{x_{n}}{n}\right)+\frac{1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}}{\sqrt{n}}\right)^{2}
\end{aligned}
$$
Pour chaque $i$, le coefficient de $x_{i}$ est $\frac{\sqrt{n}}{i}+\frac{i}{\sqrt{n}}$. La fonction $t \mapsto t+\frac{1}{t}$ est décroissante pour $t<1$ et croissante pour $\mathrm{t}>1$. En effet, par exemple pour $1<x<y$, on a $x y>1$ et donc:
$$
y-x>\frac{y-x}{x y}=\frac{1}{x}-\frac{1}{y}
$$
Ainsi, le coefficient maximal est atteint en $i=1$ ou $i=n$. Dans chaque cas, on trouve un coefficient $\sqrt{n}+\frac{1}{\sqrt{n}}=\frac{n+1}{\sqrt{n}}$, et donc
$$
\begin{aligned}
\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots+\frac{x_{n}}{n}\right)\left(1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}\right) \leqslant \frac{1}{4}\left(\frac{n+1}{\sqrt{n}}\left(x_{1}+x_{2}+\ldots+x_{n}\right)\right)^{2} \\
\left(\frac{x_{1}}{1}+\frac{x_{2}}{2}+\ldots+\frac{x_{n}}{n}\right)\left(1 \cdot x_{1}+2 \cdot x_{2}+\ldots+n \cdot x_{n}\right) \leqslant \frac{(n+1)^{2}}{4 n}\left(x_{1}+x_{2}+\ldots+x_{n}\right)^{2}
\end{aligned}
$$
On s'intéresse aux cas d'égalité. Pour $1<i<n$, l'inégalité $\frac{\sqrt{n}}{i}+\frac{i}{\sqrt{n}} \leqslant \frac{n+1}{\sqrt{n}}$ est stricte, donc nécessairement $x_{i}$ doit être égal à 0 . Ensuite, il faut avoir égalité dans l'inégalité arithmético-géométrique, ce qui s'écrit
$$
\begin{aligned}
\sqrt{n}\left(x_{1}+\frac{x_{n}}{n}\right) & =\frac{1}{\sqrt{n}}\left(x_{1}+n x_{n}\right) \\
\left(\sqrt{n}-\frac{1}{\sqrt{n}}\right) x_{1} & =\left(\sqrt{n}-\frac{1}{\sqrt{n}}\right) x_{n}
\end{aligned}
$$
Si $n=1$, on a toujours égalité (il n'y a qu'un seul $x_{i}$ ), sinon on a la condition $x_{1}=x_{n}$. Réciproquement, on peut vérifier que si $x_{1}=x_{n}$ et tous les autres $x_{i}$ sont nuls, on a bien égalité dans l'inégalité de l'énoncé.
Commentaire des correcteurs : Le problème est peu abordé, et encore moins résolu. Très peu de copies traitent les cas d'égalité, alors que cela fait partie de l'énoncé, et pouvait faire gagner des points. Veillez à bien connaître les énoncés des inégalités connues, mal appliquer une inégalité peut fausser toute une preuve.
|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "\nExercice 8.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 8",
"tier": "T2",
"year": "2024"
}
|
Let $c$ be a non-negative integer. Find all sequences of strictly positive integers $a_{1}, a_{2}, \ldots$ such that for every strictly positive integer $n$, $a_{n}$ is equal to the number of integers $i$ satisfying $a_{i} \leqslant a_{n+1}+c$.
|
Let $\left(a_{n}\right)$ be a sequence satisfying the conditions of the statement for the constant $c$. We start by showing that the sequence is increasing. Indeed, suppose by contradiction that there exists an integer $n$ such that $a_{n}>a_{n+1}$. Then, according to the hypothesis of the statement, there are strictly more $a_{i}$ less than or equal to $a_{n+1}+c$ than $a_{i}$ less than or equal to $a_{n+2}+c$. This means that necessarily $a_{n+2}<a_{n+1}$. Continuing in this way, we find that the sequence of $a_{i}$ is strictly decreasing from rank $n$. Since it takes strictly positive integer values, this is absurd.
Now let's show that the sequence is first constant up to a certain rank, then strictly increasing. Indeed, suppose that $a_{i}=a_{j}$ with $i<j$. Then if $i>1, a_{i-1}$ and $a_{j-1}$ are both the number of $a_{k}$ less than or equal to $a_{i}+c=a_{j}+c$, and thus $a_{i-1}=a_{j-1}$. Since we have $i \leqslant j-1<j$, we have $a_{j}=a_{i} \leqslant a_{j-1} \leqslant a_{j}$ and thus $a_{i-1}=a_{j-1}=a_{j}$ and thus $a_{i-1}=a_{j}$. We continue by successively decreasing $i$ by 1 until we have $a_{j}=a_{1}$. The whole sequence cannot be equal to $a_{1}$, because by hypothesis only $a_{1}$ terms of the sequence are less than or equal to $a_{2}+c=a_{1}+c>a_{1}$. Thus, the sequence is constant and equal to $a_{1}$ up to a certain rank $N$, then increases strictly.
Let $n \geqslant N$, then we know that there are $a_{n}$ elements of the sequence less than or equal to $a_{n+1}+c$. These elements are the first $n$ $a_{i}$ (by increasing), as well as the elements $a_{n+1}, a_{n+2}, \ldots, a_{n+k}$ for some $k$. Thus, $k$ is given by the inequalities $a_{n+k} \leqslant a_{n+1}+c$ and $a_{n+k+1}>a_{n+1}+c$. Since the sequence is strictly increasing after rank $N$, necessarily
$$
a_{n+k} \geqslant a_{n+k-1}+1 \geqslant a_{n+k-2}+2 \geqslant \ldots \geqslant a_{n+1}+k-1
$$
hence $a_{n+1}+c \geqslant a_{n+k} \geqslant a_{n+1}+k-1$ and $k \leqslant c+1$. Thus, the number $a_{n}$ of elements of the sequence less than or equal to $a_{n+1}+c$ is at most
$$
a_{n}=n+k \leqslant n+c+1
$$
On the other hand, we know that $a_{n+k+1}$ is at least $a_{n+1}+c+1 \geqslant a_{n}+c+2=n+k+c+2$. We thus have $a_{n+k+1} \geqslant n+k+c+2$ which is the same upper bound as the upper bound above but for $a_{n+k+1}$. Then for all $m \geqslant n+k+1$, we have
$$
m+c+1 \geqslant a_{m} \geqslant a_{n+k+1}+(m-(n+k+1)) \geqslant n+k+c+2+m-n-k-1=m+c+1
$$
and thus $a_{m}=m+c+1$ for all $m$ sufficiently large.
Let's show that this equality is true for all $m$. If by contradiction it were false, let $M$ be maximal such that $a_{M} \neq M+c+1$. Then $a_{M}$ is the number of terms of the sequence less than or equal to $a_{M+1}+c=$ $M+2 c+2$, which are the $M$ terms $a_{1}, \ldots, a_{M}$ as well as the terms $a_{M+1}, \ldots, a_{M+c+1}=M+2 c+2$, and thus
$$
a_{M}=M+(c+1)
$$
which is absurd. Thus, for all $n, a_{n}=n+c+1$.
Let's check that this solution works well. Let $n \geqslant 1$ be an integer. Then $a_{n+1}+c=n+2 c+2$ and the integers $i$ such that $a_{i}=\mathfrak{i}+\boldsymbol{c}+1 \leqslant n+2 c+2$ are the $i$ less than or equal to $n+c+1$, there are $n+c+1=a_{n}$, as desired.
Comment from the graders: The problem is very little approached, and rarely solved. Remarks on the behavior of the sequence were worth points. Be sure to check the candidate solutions. Also, be rigorous in handling inequalities.
|
a_{n}=n+c+1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Soit c un entier positif ou nul. Trouver toutes les suites d'entiers strictement positifs $a_{1}, a_{2}, \ldots$ telles que pour tout entier strictement positif $n, a_{n}$ soit égal au nombre d'entiers $i$ vérifiant $a_{i} \leqslant a_{n+1}+c$.
|
Soit $\left(a_{n}\right)$ une suite vérifiant les conditions de l'énoncé pour la constante $c$. On commence par montrer que la suite est croissante. En effet, supposons par l'absurde qu'il existe un entier $n$ tel que $a_{n}>a_{n+1}$. Alors d'après l'hypothèse de l'énoncé, il y a strictement plus de $a_{i}$ inférieurs ou égaux à $a_{n+1}+c$ que de $a_{i}$ inférieurs ou égaux à $a_{n+2}+c$. Ceci signifie que nécessairement $a_{n+2}<a_{n+1}$. En continuant ainsi, on trouve que la suite des $a_{i}$ est strictement décroissante à partir du rang $n$. Comme elle est à valeurs entières strictement positives, c'est absurde.
Montrons maintenant que la suite est d'abord constante jusqu'à un certain rang, puis strictement croissante. Supposons en effet que $a_{i}=a_{j}$ avec $i<j$. Alors si $i>1, a_{i-1}$ et $a_{j-1}$ sont tous les deux les nombres de $a_{k}$ inférieurs ou égaux à $a_{i}+c=a_{j}+c$, et donc $a_{i-1}=a_{j-1}$. Comme on a $i \leqslant j-1<j$, on a $a_{j}=a_{i} \leqslant a_{j-1} \leqslant a_{j}$ et donc $a_{i-1}=a_{j-1}=a_{j}$ et donc $a_{i-1}=a_{j}$. On continue en diminuant successivement $i$ de 1 jusqu'à avoir $a_{j}=a_{1}$. Toute la suite ne peut pas être égale à $a_{1}$, car par hypothèse seulement $a_{1}$ termes de la suite sont inférieurs ou égaux à $a_{2}+c=a_{1}+c>a_{1}$. Ainsi, la suite est constante égale à $a_{1}$ jusqu'à un certain rang $N$, puis croît strictement.
Soit $n \geqslant N$, alors on sait qu'il y a $a_{n}$ éléments de la suite inférieurs ou égaux à $a_{n+1}+c$. Ces éléments sont les $n$ premiers $a_{i}$ (par croissance), ainsi que les éléments $a_{n+1}, a_{n+2}, \ldots, a_{n+k}$ pour un certain $k$. Ainsi, $k$ est donné par les inégalités $a_{n+k} \leqslant a_{n+1}+c$ et $a_{n+k+1}>a_{n+1}+c$. Comme la suite est strictement croissante après le rang N , nécessairement
$$
a_{n+k} \geqslant a_{n+k-1}+1 \geqslant a_{n+k-2}+2 \geqslant \ldots \geqslant a_{n+1}+k-1
$$
d'où $a_{n+1}+c \geqslant a_{n+k} \geqslant a_{n+1}+k-1$ et $k \leqslant c+1$. Ainsi, le nombre $a_{n}$ d'éléments de la suite inférieurs ou égaux à $a_{n+1}+c$ est au plus
$$
a_{n}=n+k \leqslant n+c+1
$$
D'un autre côté, on sait que $a_{n+k+1}$ vaut au moins $a_{n+1}+c+1 \geqslant a_{n}+c+2=n+k+c+2$. On a donc $a_{n+k+1} \geqslant n+k+c+2$ ce qui est la même borne que la borne supérieure ci-dessus mais pour $a_{n+k+1}$. Alors pour tout $m \geqslant n+k+1$, on a
$$
m+c+1 \geqslant a_{m} \geqslant a_{n+k+1}+(m-(n+k+1)) \geqslant n+k+c+2+m-n-k-1=m+c+1
$$
et donc $a_{m}=m+c+1$ pour tout $m$ suffisamment grand.
Montrons que cette égalité est vraie pour tout $m$. Si par l'absurde elle était fausse, soit $M$ maximal tel que $a_{M} \neq M+c+1$. Alors $a_{M}$ est le nombre de termes de la suite inférieurs ou égaux à $a_{M+1}+c=$ $M+2 c+2$, qui sont les $M$ termes $a_{1}, \ldots, a_{M}$ ainsi que les termes $a_{M+1}, \ldots, a_{M+c+1}=M+2 c+2$, et donc
$$
a_{M}=M+(c+1)
$$
ce qui est absurde. Ainsi, pour tout $\mathrm{n}, \mathrm{a}_{\mathrm{n}}=\mathrm{n}+\mathrm{c}+1$.
Vérifions que cette solution fonctionne bien. Soit $n \geqslant 1$ entier. Alors $a_{n+1}+c=n+2 c+2$ et les entiers $i$ tels que $a_{i}=\mathfrak{i}+\boldsymbol{c}+1 \leqslant n+2 c+2$ sont les $i$ inférieurs ou égaux à $n+c+1$, il y en a $n+c+1=a_{n}$, comme voulu.
Commentaire des correcteurs : Le problème est très peu abordé, et très rarement résolu. Les remarques sur le comportement de la suite valaient des points. Attention à bien vérifier les solutions candidates. Attention aussi à rester rigoureux dans la manipulation des inégalités.
## Exercices Seniors
|
{
"exam": "French_envois",
"problem_label": "15",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 9",
"tier": "T2",
"year": "2024"
}
|
Let $a$ and $b$ be two real numbers. Suppose that $2a + a^2 = 2b + b^2$. Show that if $a$ is an integer (not necessarily positive), then $b$ is also an integer.
|
We rewrite the equality
$$
\begin{gathered}
2 a-2 b=b^{2}-a^{2} \\
2(a-b)=-(a+b)(a-b)
\end{gathered}
$$
Then either $\mathrm{b}=\mathrm{a}$, and in this case, b is an integer, or
$$
2=-a-b
$$
from which
$$
\mathrm{b}=-2-\mathrm{a}
$$
and $b$ is still an integer.
Comment from the graders: The problem was successfully solved by almost everyone. Be careful of calculation errors for those who went through it a bit too quickly.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soient $a$ et $b$ deux réels. Supposons que $2 a+a^{2}=2 b+b^{2}$. Montrer que si $a$ est un entier (pas forcément positif), alors b est aussi un entier.
|
On réécrit l'égalité
$$
\begin{gathered}
2 a-2 b=b^{2}-a^{2} \\
2(a-b)=-(a+b)(a-b)
\end{gathered}
$$
Alors soit $\mathrm{b}=\mathrm{a}$, et alors b est un entier, soit
$$
2=-a-b
$$
d'où
$$
\mathrm{b}=-2-\mathrm{a}
$$
et $b$ est encore un entier.
Commentaire des correcteurs: Le problème était réussi par presque tous. Attention aux erreurs de calcul pour ceux qui sont passés un peu vite.
|
{
"exam": "French_envois",
"problem_label": "10",
"problem_match": "\nExercice 10.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 10",
"tier": "T2",
"year": "2024"
}
|
For a real number $x$, we denote $\lfloor x\rfloor$ as the greatest integer less than or equal to $x$ (for example, $\lfloor 2.7\rfloor=2$, $\lfloor\pi\rfloor=3$, and $\lfloor-1.5\rfloor=-2$). We also denote $\{x\}=x-\lfloor x\rfloor$.
Find all real numbers $x$ such that
$$
\lfloor x\rfloor\{x\}<x-1
$$
|
We rewrite $x=\lfloor x\rfloor+\{x\}$ on the right-hand side and move all terms to the left so that the inequality becomes
$$
\lfloor x\rfloor\{x\}-\lfloor x\rfloor-\{x\}+1<0
$$
or equivalently,
$$
(\lfloor x\rfloor-1)(\{x\}-1)<0
$$
Notice that for any real $x$, we have $0 \leqslant\{x\}<1$ and thus $\{x\}-1<0$. Therefore, the inequality is equivalent to
$$
\lfloor x\rfloor-1>0
$$
or $\lfloor x\rfloor>1$. This precisely means that $x \geqslant 2$. We can verify that conversely, if $x \geqslant 2$, then $x$ satisfies the inequality in the problem statement.
Comment from the graders: The exercise was initially difficult to approach because a term involving $\lfloor x\rfloor\{x\}$ is quite unusual, but it was well handled by those who tackled it. One could reason by equivalence as done in the solution. It is important in this case to maintain the reasoning by equivalence throughout (or explain that the converse is true). In particular, this is one of the cases where it is necessary to use $\Leftrightarrow$ signs between each line of mathematics. One could also better visualize the problem by considering a case disjunction, which generally used the same ideas.
|
x \geqslant 2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Pour un réel $x$, on note $\lfloor x\rfloor$ le plus grand entier relatif inférieur ou égal à $x$ (par exemple, $\lfloor 2,7\rfloor=2,\lfloor\pi\rfloor=3$ et $\lfloor-1,5\rfloor=-2$ ). On note aussi $\{x\rfloor=x-\lfloor x\rfloor$.
Trouver tous les réels $x$ tels que
$$
\lfloor x\rfloor\{x\}<x-1
$$
|
On réécrit $x=\lfloor x\rfloor+\{x\}$ dans le terme de droite et on met tous les termes à gauche pour que l'inégalité devienne
$$
\lfloor x\rfloor\{x\}-\lfloor x\rfloor-\{x\}+1<0
$$
ou encore
$$
(\lfloor x\rfloor-1)(\{x\}-1)<0
$$
Remarquons que pour tout $x$ réel, on a $0 \leqslant\{x\}<1$ et donc $\{x\}-1<0$. Alors l'inégalité est équivalente à
$$
\lfloor x\rfloor-1>0
$$
ou encore $\lfloor x\rfloor>1$. Ceci veut précisément dire que $x \geqslant 2$. On peut vérifier que réciproquement, si $x \geqslant 2$, alors $x$ vérifie bien l'inégalié de l'énoncé.
Commentaire des correcteurs : L'exercice était difficile à aborder initialement car un terme en $\lfloor x\rfloor\{x\}$ est assez inhabituel, mais plutôt bien appréhendé par ceux qui l'ont traité. On pouvait raisonner par équivalence comme cela est fait dans le corrigé. Il faut faire attention dans ce cas à bien garder le résonnement par équivalence tout du long (ou expliquer que la réciproque est vraie). En particulier c'est un des cas où il faut mettre des signes $\Leftrightarrow$ entre chaque ligne mathématique. On pouvait également pour mieux se représenter les choses faire une disjonction de cas qui utilisait en général les mêmes idées.
|
{
"exam": "French_envois",
"problem_label": "11",
"problem_match": "\nExercice 11.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 11",
"tier": "T2",
"year": "2024"
}
|
The sequence $(a_{n})$ is defined by $a_{1}=1$ and
$$
a_{n}=\frac{1}{n}+\frac{1}{a_{1} \cdot \ldots \cdot a_{n-1}}
$$
Show that for all integers $m \geqslant 3$, we have $a_{m} \leqslant 1$.
|
We set $P_{n}=\prod^{n} a_{k}$. We have
$$
\frac{P_{n}}{P_{n-1}}=\frac{1}{n}+\frac{1}{P_{n-1}}
$$
which gives
$$
n P_{n}=P_{n-1}+n
$$
We then set $M_{n}=n!P_{n}$. We deduce
$$
M_{n}=M_{n-1}+n!
$$
We deduce that $M_{n}=\sum k!$. We then deduce
$$
a_{n}=\frac{P_{n}}{P_{n-1}}=\frac{\frac{1}{n!} \sum k!}{\frac{1}{(n-1)!} \sum k!}
$$
It remains to show that
$$
\sum_{k=1}^{n} k!\leqslant \sum_{k=1}^{n-1} n \times k!
$$
which comes from using $\mathrm{n} \geqslant 3$ to have notably $\mathrm{n} \geqslant 2+1$ and
$$
\sum_{k=1}^{n} k!\leqslant 1+2+\sum_{k=3}^{n} n \times(k-1)!\leqslant n+n \sum_{k=2}^{n-1} k!
$$
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
La suite ( $a_{n}$ ) est définie par $a_{1}=1$ et
$$
a_{n}=\frac{1}{n}+\frac{1}{a_{1} \cdot \ldots \cdot a_{n-1}}
$$
Montrer que pour tout entier $m \geqslant 3$, on a $a_{m} \leqslant 1$.
|
On pose $P_{n}=\prod^{n} a_{k}$. On a
$$
\frac{P_{n}}{P_{n-1}}=\frac{1}{n}+\frac{1}{P_{n-1}}
$$
ce qui donne
$$
n P_{n}=P_{n-1}+n
$$
On pose alors $M_{n}=n!P_{n}$. On déduit
$$
M_{n}=M_{n-1}+n!
$$
On déduit que $M_{n}=\sum k!$. On déduit alors
$$
a_{n}=\frac{P_{n}}{P_{n-1}}=\frac{\frac{1}{n!} \sum k!}{\frac{1}{(n-1)!} \sum k!}
$$
Il reste à montrer que
$$
\sum_{k=1}^{n} k!\leqslant \sum_{k=1}^{n-1} n \times k!
$$
ce qui vient en utilisant $\mathrm{n} \geqslant 3$ pour avoir notamment $\mathrm{n} \geqslant 2+1$ et
$$
\sum_{k=1}^{n} k!\leqslant 1+2+\sum_{k=3}^{n} n \times(k-1)!\leqslant n+n \sum_{k=2}^{n-1} k!
$$
|
{
"exam": "French_envois",
"problem_label": "12",
"problem_match": "\nExercice 12.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 12",
"tier": "T2",
"year": "2024"
}
|
The sequence $(a_{n})$ is defined by $a_{1}=1$ and
$$
a_{n}=\frac{1}{n}+\frac{1}{a_{1} \cdot \ldots \cdot a_{n-1}}
$$
Show that for all integers $m \geqslant 3$, we have $a_{m} \leqslant 1$.
|
:
Starting from the equation on the $P_{n}$, we want to show that $a_{n} \leqslant 1$ for $n \geqslant 3$, that is, $P_{n} \leqslant P_{n-1}$. This can be rewritten as
$$
\begin{gathered}
\frac{1}{n} P_{n-1}+1 \leqslant P_{n-1} \\
P_{n-1} \geqslant \frac{n}{n-1} .
\end{gathered}
$$
We aim to prove this inequality by induction. For $n=3$, we have
$$
P_{2}=\frac{1}{2}+1=\frac{3}{2}=\frac{3}{3-1} .
$$
If the result is true at rank $n$, then at rank $n+1$,
$$
P_{n}=\frac{1}{n} P_{n-1}+1 \geqslant \frac{1}{n} \frac{n}{n-1}+1=\frac{n}{n-1} \geqslant \frac{n+1}{n}
$$
which concludes the induction.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
La suite ( $a_{n}$ ) est définie par $a_{1}=1$ et
$$
a_{n}=\frac{1}{n}+\frac{1}{a_{1} \cdot \ldots \cdot a_{n-1}}
$$
Montrer que pour tout entier $m \geqslant 3$, on a $a_{m} \leqslant 1$.
|
:
A partir de l'équation sur les $P_{n}$, on veut donc montrer que $a_{n} \leqslant 1$ pour $n \geqslant 3$, c'est-à-dire que $P_{n} \leqslant P_{n-1}$. Ceci se réécrit
$$
\begin{gathered}
\frac{1}{n} P_{n-1}+1 \leqslant P_{n-1} \\
P_{n-1} \geqslant \frac{n}{n-1} .
\end{gathered}
$$
On cherche donc à montrer cette inégalité par récurence. Pour $\mathrm{n}=3$, on a bien
$$
\mathrm{P}_{2}=\frac{1}{2}+1=\frac{3}{2}=\frac{3}{3-1} .
$$
Si le résultat est vrai au rang n , on a, au rang $\mathrm{n}+1$,
$$
P_{n}=\frac{1}{n} P_{n-1}+1 \geqslant \frac{1}{n} \frac{n}{n-1}+1=\frac{n}{n-1} \geqslant \frac{n+1}{n}
$$
ce qui conclut la récurrence.
|
{
"exam": "French_envois",
"problem_label": "12",
"problem_match": "\nExercice 12.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"solution_match": "## Solution alternative",
"tier": "T2",
"year": "2024"
}
|
The sequence $(a_{n})$ is defined by $a_{1}=1$ and
$$
a_{n}=\frac{1}{n}+\frac{1}{a_{1} \cdot \ldots \cdot a_{n-1}}
$$
Show that for all integers $m \geqslant 3$, we have $a_{m} \leqslant 1$.
|
2 :
On a $a_{n+1}-\frac{1}{n}=\frac{1}{a_{1} \ldots a_{n}}$. Thus:
$$
a_{n+1}-\frac{1}{n}=\frac{1}{a_{1} \ldots a_{n-1}} \frac{1}{a_{n}}=\left(a_{n}-\frac{1}{n-1}\right) \frac{1}{a_{n}}
$$
Therefore, $a_{n+1}=1-\frac{1}{a_{n}(n-1)}+\frac{1}{n}$. We can calculate the first few terms to find that $a_{3}=1$. We can then prove by induction on $n$ that $a_{n} \leqslant 1$.
If the result is true at rank $n$, then $a_{n+1}=1-\frac{1}{a_{n}(n-1)}+\frac{1}{n} \leqslant 1-\frac{1}{n-1}+\frac{1}{n} \leqslant 1$. This concludes the proof.
Comment from the graders: Most of those who tackled the exercise understood it well. The main task was to transform the strong recurrence relation into a simple recurrence relation and then use induction. Some students provided reasoning that required handling the first few terms manually. This should not be overlooked, especially since it can help detect a reasoning error.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
La suite ( $a_{n}$ ) est définie par $a_{1}=1$ et
$$
a_{n}=\frac{1}{n}+\frac{1}{a_{1} \cdot \ldots \cdot a_{n-1}}
$$
Montrer que pour tout entier $m \geqslant 3$, on a $a_{m} \leqslant 1$.
|
2 :
On a $a_{n+1}-\frac{1}{n}=\frac{1}{a_{1} \ldots a_{n}}$. Ainsi :
$$
a_{n+1}-\frac{1}{n}=\frac{1}{a_{1} \ldots a_{n-1}} \frac{1}{a_{n}}=\left(a_{n}-\frac{1}{n-1}\right) \frac{1}{a_{n}}
$$
Dès lors $a_{n+1}=1-\frac{1}{a_{n}(n-1)}+\frac{1}{n}$. On peut calculer les premiers termes pour avoir $a_{3}=1$. On peut ensuite prouver par récurrence sur $n$ que $a_{n} \leqslant 1$.
Si le résultat est vrai au rang $n, a_{n+1}=1-\frac{1}{a_{n}(n-1)}+\frac{1}{n} \leqslant 1-\frac{1}{n-1}+\frac{1}{n} \leqslant 1$. Ce qui conclut.
Commentaire des correcteurs : La plupart de ceux qui ont abordé l'exercice l'ont bien compris. Il s'agissait principalement de transformer la relation de récurrence forte en une relation de récurrence simple puis de faire une récurrence. Certains élèves ont donné des raisonnements qui demandaient de traiter les premiers termes à la main. Il ne faut pas oublier de le faire, surtout que cela peut permettre de déceler une erreur de raisonnement.
|
{
"exam": "French_envois",
"problem_label": "12",
"problem_match": "\nExercice 12.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T2",
"year": "2024"
}
|
Determine all functions $f$ from $\mathbb{R}$ to $\mathbb{R}$ such that for all real $x, y$:
$$
f(x) f(y) f(x-y)=x^{2} f(y)-y^{2} f(x)
$$
|
Let $f$ be a solution of the equation.
For $x=y=0$, we have:
$$
\mathbf{f}(0)^{3}=0
$$
Thus, $f(0)=0$. We exclude the function $f \equiv 0$ which is indeed a solution of the problem.
Now, consider a number $x$ such that $f(x)=0$. Then for any $y$:
$$
0=x^{2} f(y)-0
$$
Since we have excluded the case $f \equiv 0$, we can find $y$ such that $f(y) \neq 0$ and thus $x=0$. Therefore, if $f(x)=0$, we have $x=0$.
We can now observe that swapping $x$ and $y$ in the equation changes the right-hand term to its opposite, so we have:
$$
f(x) f(y) f(x-y)=x^{2} f(y)-y^{2} f(x)=-\left(y^{2} f(x)-x^{2} f(y)\right)=-f(y) f(x) f(y-x)
$$
Thus, for $x$ and $y$ non-zero, we have $f(x-y)=-f(y-x)$. By setting $y=2x$ with $x \neq 0$, we obtain that for all $x \neq 0, f(-x)=-f(x)$. Since $f(0)=0$, $f$ is odd.
We can now take $x=2y$, and the given equality with the oddness gives:
$$
f(2 y) f(y)^{2}=4 y^{2} f(y)-y^{2} f(2 y)
$$
On the other hand, with $x=-y$:
$$
f(y)^{2} f(2 y)=2 y^{2} f(y)
$$
Using these two equalities, we have:
$$
f(2 y) y^{2}=2 y^{2} f(y)
$$
If $y$ is non-zero, we have $f(y) \neq 0$, and thus the previous equality can be written as $f(2y)=2f(y)$, and equation (1) becomes:
$$
\begin{gathered}
2 f(y)^{3}=2 y^{2} f(y) \\
f(y)^{2}=y^{2}
\end{gathered}
$$
We thus find $f(y)= \pm y$. Note that, a priori, the sign could depend on $y$. Suppose, by contradiction, that $a$ and $b$ are two non-zero real numbers such that $f(a)=a$ and $f(b)=-b$. Taking $x=b$ and $y=a$, we get:
$$
-a b f(a-b)=a b(a+b)
$$
Since $a$ and $b$ are non-zero, $f(a-b)=-(a+b)$. But $f(a-b)= \pm(a-b)$, and depending on the sign, we get either $a=0$ or $b=0$, which is absurd. For $x=0$, we have both $f(x)=x$ and $f(x)=-x$, so necessarily $f$ is of the form: $f(x)=0$ for all $x$, or $f(x)=-x$ for all $x$, or $f(x)=x$ for all $x$.
These three functions are indeed solutions.
Comment from the graders: The problem was attempted by a significant number of students, often with the right ideas for substitutions. Many need to be more careful about not dividing by 0, even when the 0 is hidden in an $f(x)$ or other value. This often leads to arguments that fall back on their feet, but for the wrong reasons. Another very common mistake is that of "multigraphs": if we know that $\mathrm{f}(x)^{2}=x^{2}$ for all $x$, we cannot immediately conclude that $f$ is the identity function or its negative. Indeed, the function could arbitrarily alternate between $+x$ and $-x$.
|
f(x)=0, f(x)=x, f(x)=-x
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Déterminer toutes les fonctions f de $\mathbb{R}$ dans $\mathbb{R}$ telles que pour tous $x, y$ réels :
$$
f(x) f(y) f(x-y)=x^{2} f(y)-y^{2} f(x)
$$
|
Soit f une solution de l'équation.
Pour $x=y=0$, on $a$ :
$$
\mathbf{f}(0)^{3}=0
$$
Ainsi, $f(0)=0$. On exclut la fonction $f \equiv 0$ qui est effectivement solution du problème.
On considère maintenant, un nombre $x$ tel que $f(x)=0$. On a alors pour un $y$ quelconque :
$$
0=x^{2} f(y)-0
$$
Comme on a exclu le cas $f \equiv 0$, on peut trouver $y$ tel que $f(y) \neq 0$ et donc $x=0$. Ainsi, si $f(x)=0$, on $\mathrm{a} x=0$ 。
On peut maintenant remarquer qu'échanger $x$ et $y$ dans l'équation, change le terme de droite en son oppposé, on a donc:
$$
f(x) f(y) f(x-y)=x^{2} f(y)-y^{2} f(x)=-\left(y^{2} f(x)-x^{2} f(y)\right)=-f(y) f(x) f(y-x)
$$
Ainsi pour $x$ et $y$ non nuls, on a $f(x-y)=-f(y-x)$. En posant $y=2 x$ avec $x \neq 0$, on obtient que pour tout $x \neq 0, f(-x)=-f(x)$. Comme $f(0)=0, f$ est impaire.
On peut maintenant prendre $x=2 y$, l'égalité de l'énoncé avec l'imparité donnent :
$$
f(2 y) f(y)^{2}=4 y^{2} f(y)-y^{2} f(2 y)
$$
D'autre part, avec $x=-\mathrm{y}$ :
$$
f(y)^{2} f(2 y)=2 y^{2} f(y)
$$
En utilisant ces deux égalités, on a :
$$
f(2 y) y^{2}=2 y^{2} f(y)
$$
Si $y$ est non nul, on a $\mathrm{f}(\mathrm{y}) \neq 0$, et donc l'égalité précédente s'écrit $\mathrm{f}(2 \mathrm{y})=2 \mathrm{f}(\mathrm{y})$, et l'équation (1) s'écrit
$$
\begin{gathered}
2 f(y)^{3}=2 y^{2} f(y) \\
f(y)^{2}=y^{2}
\end{gathered}
$$
On trouve donc $f(y)= \pm y$. Attention, a priori, le signe pourrait dépendre de $y$. Soit, par l'absurde, a et $b$ deux réels non nuls tels que $f(a)=a$ et $f(b)=-b$. En prenant $x=b$ et $y=a$, on obtient:
$$
-a b f(a-b)=a b(a+b)
$$
Comme $a$ et $b$ sont non nuls, $f(a-b)=-(a+b)$. Mais $f(a-b)= \pm(a-b)$, et en fonction du signe on obtient soit $a=0$, soit $b=0$, ce qui est absurde. Pour $x=0$, on a à la fois $f(x)=x$ et $f(x)=-x$, donc nécessairement $f$ est de la forme : $f(x)=0$ pour tous $x$, ou $f(x)=-x$ pour tous $x$, ou $f(x)=x$ pour tous $x$.
Ces trois fonctions sont bien solutions.
Commentaire des correcteurs: Le problème a été tenté par un nombre important d'élèves, souvent avec les bonnes idées de substitutions. Un grand nombre doit faire plus attention à ne pas diviser par 0 , même quand ce 0 se cache dans un $f(x)$ ou autre valeur. Cela mène à des raisonnements qui souvent retombent sur leur pattes, mais pour les mauvaises raisons. Une autre erreur très fréquente est celle des "multigraphes" : si l'on sait que $\mathrm{f}(x)^{2}=x^{2}$ pour tout $x$, alors on ne peut pas immédiatement conclure que $f$ est plus ou moins la fonction identité. En effet la fonction pourrait alterner de façon arbitraire entre $+x$ et $-x$.
|
{
"exam": "French_envois",
"problem_label": "13",
"problem_match": "\nExercice 13.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 13",
"tier": "T2",
"year": "2024"
}
|
Emile has created an exercise for Benoît. He announces that he has secretly chosen a unitary polynomial $P$ of degree 2023 with integer coefficients, that is, of the form
$$
P(X)=X^{2023}+a_{2022} X^{2022}+a_{2021} X^{2021}+\ldots+a_{1} X+a_{0}
$$
where $a_{0}, a_{1}, \ldots, a_{2022}$ are integers. He gives Benoît $k$ integers $n_{1}, n_{2}, \ldots, n_{k}$, where $k$ is a positive integer, as well as the value of the product $P\left(n_{1}\right) P\left(n_{2}\right) \ldots P\left(n_{k}\right)$. From this information, Benoît must try to determine the polynomial $P$.
Find the smallest integer $k$ such that Emile can find $P$ and $n_{1}, \ldots, n_{k}$ to ensure that the only polynomial matching the information given to Benoît is $P$.
|
Let's show that the minimal $k$ is $k=2023$. Indeed, suppose first that $k<2023$ and that Émile chooses $P$ and $n_{1}, \ldots, n_{k}$. Let
$$
Q = P + (X - n_{1})(X - n_{2}) \ldots (X - n_{k})
$$
which is a polynomial with integer coefficients, always monic of degree 2023, and different from $P$. Then $P$ and $Q$ are equal at each $n_{i}$, and therefore the products $P(n_{1}) \ldots P(n_{k})$ and $Q(n_{1}) \ldots Q(n_{k})$ are equal, so Benoît cannot determine the value of the polynomial $P$.
Now suppose that $k=2023$. Émile can then choose $n_{1}=3, n_{2}=6, \ldots, n_{2023}=3 \cdot 2023$ and set
$$
P = (X-3)(X-6) \ldots (X-3 \cdot 2023) + 1
$$
Then the product $P(n_{1}) P(n_{2}) \ldots P(n_{k})$ is 1. Let $Q$ be a polynomial with integer coefficients, monic of degree 2023, such that the product $Q(n_{1}) \ldots Q(n_{k})$ is equal to 1; we need to show that necessarily $Q=P$. Since all the $Q(n_{i})$ are integers, they are all either 1 or -1. However, we can note that since the $n_{i}$ are divisible by 3, for all $i$, $Q(n_{i})$ is congruent to the constant term of $Q$. Since 1 and -1 are not congruent modulo 3, all the $Q(n_{i})$ are equal. Since 2023 is odd, they cannot all be equal to -1, so they are all 1. Then $P - Q$ is a polynomial of degree at most 2022 (since the terms of order 2023 cancel out) and is zero at each of the 2023 values of the $n_{i}$, so $Q = P$, which concludes.
Comment from the graders: The exercise was generally well understood, and many students thought to create a polynomial $P$ such that the product $P(n_{1}) P(n_{2}) \ldots P(n_{k}) = 1$, which was the right way to solve the exercise. However, be careful to better justify the arguments of polynomial division with integer coefficients; some students were a bit too quick on this step.
|
2023
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Emile a créé un exercice pour Benoît. Il lui annonce qu'il a choisi secrètement un polynôme P unitaire de degré 2023 à coefficients entiers, c'est-à-dire de la forme
$$
P(X)=X^{2023}+a_{2022} X^{2022}+a_{2021} X^{2021}+\ldots+a_{1} X+a_{0}
$$
où $a_{0}, a_{1}, \ldots, a_{2022}$ sont des entiers relatifs. Il donne à Benoît $k$ entiers $n_{1}, n_{2}, \ldots, n_{k}$, où $k$ est un entier positif, ainsi que la valeur du produit $P\left(n_{1}\right) P\left(n_{2}\right) \ldots P\left(n_{k}\right)$. A partir de ces connaissances, Benoît doit essayer de retrouver le polynôme P .
Trouver l'entier $k$ minimal tel que Emile puisse trouver $P$ et $n_{1}, \ldots, n_{k}$ afin de s'assurer que le seul polynôme coincidant avec les informations données à Benoît soit P .
|
Montrons que le $k$ minimal est $k=2023$. En effet, supposons d'abord que $k<2023$ et qu'Emile choisisse $P$ et $n_{1}, \ldots, n_{k}$. Posons
$$
\mathrm{Q}=\mathrm{P}+\left(\mathrm{X}-\mathrm{n}_{1}\right)\left(\mathrm{X}-\mathrm{n}_{2}\right) \ldots\left(\mathrm{X}-\mathrm{n}_{\mathrm{k}}\right)
$$
qui est un polynôme à coefficients entiers, toujours unitaire de degré 2023, et différent de P . Alors P et $Q$ sont égaux en chaque $n_{i}$, et donc les produits $P\left(n_{1}\right) \ldots P\left(n_{k}\right)$ et $Q\left(n_{1}\right) \ldots Q\left(n_{k}\right)$ sont égaux, donc Benoît ne peut pas retrouver la valeur du polynôme $P$.
Supposons maintenant que $k=2023$. Emile peut alors choisir $n_{1}=3, n_{2}=6, \ldots, n_{2023}=3 \cdot 2023$ et poser
$$
P=(X-3)(X-6) \ldots(X-3 \cdot 2023)+1
$$
Alors le produit $\mathrm{P}\left(\mathrm{n}_{1}\right) \mathrm{P}\left(\mathrm{n}_{2}\right) \ldots \mathrm{P}\left(\mathrm{n}_{\mathrm{k}}\right)$ vaut 1 . Soit Q un polynôme à coefficients entiers, unitaire de degré 2023 tel que le produit $Q\left(n_{1}\right) \ldots Q\left(n_{k}\right)$ soit égal à 1 , il faut montrer que nécessairement $Q=P$. Comme tous les $Q\left(n_{i}\right)$ sont entiers, ils valent tous soit 1 , soit -1 . On peut cependant remarquer que comme les $n_{i}$ sont divisibles par 3 alors pour tout $i, Q\left(n_{i}\right)$ est congru au coefficient constant de $Q$. Comme 1 et -1 ne sont pas congrus modulos 3 , tous les $Q\left(n_{i}\right)$ sont égaux. Comme 2023 est impair, ils ne peuvent pas tous être égaux à -1 , donc ils valent tous 1 . Alors $P-Q$ est un polynôme de degré au plus 2022 (car les termes d'ordre 2023 s'annulent) et est nul en chacun des 2023 valeurs des $n_{i}$, donc $\mathrm{Q}=\mathrm{P}$, ce qui conclut.
Commentaire des correcteurs : L'exercice a été plutôt bien compris et beaucoup d'élèves ont penser à créer un polynome P dont le produit $\mathrm{P}\left(\mathrm{n}_{1}\right) \mathrm{P}\left(\mathrm{n}_{2}\right) \ldots \mathrm{P}\left(\mathrm{n}_{\mathrm{k}}\right)=1$ ce qui était la bonne façon de résoudre l'exercice. Attention cepandant à mieux justifier les arguments de division euclidienne sur les polynômes à coefficients entiers, certains sont allés un peu vite sur cette étape.
|
{
"exam": "French_envois",
"problem_label": "14",
"problem_match": "\nExercice 14.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 14",
"tier": "T2",
"year": "2024"
}
|
Let $c$ be a non-negative integer. Find all sequences of strictly positive integers $a_{1}, a_{2}, \ldots$ such that for every strictly positive integer $n$, $a_{n}$ is equal to the number of integers $i$ satisfying $a_{i} \leqslant a_{n+1}+c$.
|
Let $(a_n)$ be a sequence satisfying the conditions of the statement for the constant $c$. We start by showing that the sequence is increasing. Indeed, suppose by contradiction that there exists an integer $n$ such that $a_n > a_{n+1}$. Then, according to the hypothesis of the statement, there are strictly more $a_i$ less than or equal to $a_{n+1} + c$ than $a_i$ less than or equal to $a_{n+2} + c$. This means that necessarily $a_{n+2} < a_{n+1}$. Continuing in this way, we find that the sequence of $a_i$ is strictly decreasing from rank $n$ onwards. Since it takes strictly positive integer values, this is absurd.
Now let's show that the sequence is first constant up to a certain rank, then strictly increasing. Indeed, suppose that $a_i = a_j$ with $i < j$. Then if $i > 1$, $a_{i-1}$ and $a_{j-1}$ are both the number of $a_k$ less than or equal to $a_i + c = a_j + c$, and thus $a_{i-1} = a_{j-1}$. Since $i \leq j-1 < j$, we have $a_j = a_i \leq a_{j-1} \leq a_j$ and thus $a_{i-1} = a_{j-1} = a_j$ and therefore $a_{i-1} = a_j$. We continue by successively decreasing $i$ by 1 until we have $a_j = a_1$. The entire sequence cannot be equal to $a_1$, because by hypothesis only $a_1$ terms of the sequence are less than or equal to $a_2 + c = a_1 + c > a_1$. Thus, the sequence is constant and equal to $a_1$ up to a certain rank $N$, then strictly increases.
Let $n \geq N$, then we know that there are $a_n$ elements of the sequence less than or equal to $a_{n+1} + c$. These elements are the first $n$ $a_i$ (by increasing order), as well as the elements $a_{n+1}, a_{n+2}, \ldots, a_{n+k}$ for some $k$. Since the sequence is strictly increasing after rank $N$, necessarily
$$
a_{n+k} \geq a_{n+k-1} + 1 \geq a_{n+k-2} + 2 \geq \ldots \geq a_{n+1} + k - 1
$$
hence $a_{n+1} + c \geq a_{n+1} + k - 1$ and $k \leq c + 1$. Thus, the number $a_n$ of elements of the sequence less than or equal to $a_{n+1} + c$ is at most
$$
a_n = n + k \leq n + c + 1
$$
On the other hand, we know that $a_{n+k+1}$ is at least $a_{n+1} + c + 1 \geq a_n + c + 2 = n + k + c + 2$. We have therefore $a_{n+k+1} \geq n + k + c + 2$ which is the same upper bound as the upper bound above but for $a_{n+k+1}$. Then for all $m \geq n + k + 1$, we have
$$
m + c + 1 \geq a_m \geq a_{n+k+1} + (m - (n + k + 1)) \geq n + k + c + 2 + m - n - k - 1 = m + c + 1
$$
and thus $a_m = m + c + 1$ for all $m$ sufficiently large.
Let's show that this equality is true for all $m$. If by contradiction it were false, let $M$ be maximal such that $a_M \neq M + c + 1$. Then $a_M$ is the number of terms of the sequence less than or equal to $a_{M+1} + c = M + 2c + 2$, which are the $M$ terms $a_1, \ldots, a_M$ as well as the terms $a_{M+1}, \ldots, a_{M+c+1} = M + 2c + 2$, and thus
$$
a_M = M + (c + 1)
$$
which is absurd. Thus, for all $n$, $a_n = n + c + 1$.
Let's check that this solution works well. Let $n \geq 1$ be an integer. Then $a_{n+1} + c = n + 2c + 2$ and the integers $i$ such that $a_i = i + c + 1 \leq n + 2c + 2$ are the $i$ less than or equal to $n + c + 1$, there are $n + c + 1 = a_n$, as desired.
Examiner's comment: Despite its position, the problem was not much sought after or solved. Most students who submitted an attempt understood the mechanics of the sequence and had the right reflexes: to look for the variations (increase, convexity) of the sequence before deducing that it is
arithmetic. However, many students, victims of the same bias, think they show that the sequence is strictly increasing from the beginning of the proof, while they only show that the sequence is constant and then strictly increasing from a certain rank. Finally, it is regrettable that many students forgot to check that the sequence they find at the end is indeed a solution to the problem.
|
a_n = n + c + 1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Soit c un entier positif ou nul. Trouver toutes les suites d'entiers strictement positifs $a_{1}, a_{2}, \ldots$ telles que pour tout entier strictement positif $n, a_{n}$ soit égal au nombre d'entiers $i$ vérifiant $a_{i} \leqslant a_{n+1}+c$.
|
Soit ( $a_{n}$ ) une suite vérifiant les conditions de l'énoncé pour la constante $c$. On commence par montrer que la suite est croissante. En effet, supposons par l'absurde qu'il existe un entier $n$ tel que $a_{n}>a_{n+1}$. Alors d'après l'hypothèse de l'énoncé, il y a strictement plus de $a_{i}$ inférieurs ou égaux à $a_{n+1}+c$ que de $a_{i}$ inférieurs ou égaux à $a_{n+2}+c$. Ceci signifie que nécessairement $a_{n+2}<a_{n+1}$. En continuant ainsi, on trouve que la suite des $a_{i}$ est strictement décroissante à partir du rang n . Comme elle est à valeurs entières strictement positives, c'est absurde.
Montrons maintenant que la suite est d'abord constante jusqu'à un certain rang, puis strictement croissante. Supposons en effet que $a_{i}=a_{j}$ avec $i<j$. Alors si $i>1, a_{i-1}$ et $a_{j-1}$ sont tous les deux les nombres de $a_{k}$ inférieurs ou égaux à $a_{i}+c=a_{j}+c$, et donc $a_{i-1}=a_{j-1}$. Comme on $a i \leqslant j-1<j$, on a $a_{j}=a_{i} \leqslant a_{j-1} \leqslant a_{j}$ et donc $a_{i-1}=a_{j-1}=a_{j}$ et donc $a_{i-1}=a_{j}$. On continue en diminuant successivement $i$ de 1 jusqu'à avoir $a_{j}=a_{1}$. Toute la suite ne peut pas être égale à $a_{1}$, car par hypothèse seulement $a_{1}$ termes de la suite sont inférieurs ou égaux à $a_{2}+c=a_{1}+c>a_{1}$. Ainsi, la suite est constante égale à $a_{1}$ jusqu'à un certain rang N , puis croît strictement.
Soit $n \geqslant N$, alors on sait qu'il y a $a_{n}$ éléments de la suite inférieurs ou égaux à $a_{n+1}+c$. Ces éléments sont les $n$ premiers $a_{i}$ (par croissance), ainsi que les éléments $a_{n+1}, a_{n+2}, \ldots, a_{n+k}$ pour un certain $k$. Comme la suite est strictement croissante après le rang N , nécessairement
$$
a_{n+k} \geqslant a_{n+k-1}+1 \geqslant a_{n+k-2}+2 \geqslant \ldots \geqslant a_{n+1}+k-1
$$
d'où $a_{n+1}+c \geqslant a_{n+1}+k-1$ et $k \leqslant c+1$. Ainsi, le nombre $a_{n}$ d'éléments de ls suite inférieurs ou égaux à $a_{n+1}+c$ est au plus
$$
a_{n}=n+k \leqslant n+c+1
$$
D'un autre côté, on sait que $a_{n+k+1}$ vaut au moins $a_{n+1}+c+1 \geqslant a_{n}+c+2=n+k+c+2$. On a donc $a_{n+k+1} \geqslant n+k+c+2$ ce qui est la même borne que la borne supérieure ci-dessus mais pour $a_{n+k+1}$. Alors pour tout $m \geqslant n+k+1$, on $a$
$$
m+c+1 \geqslant a_{m} \geqslant a_{n+k+1}+(m-(n+k+1)) \geqslant n+k+c+2+m-n-k-1=m+c+1
$$
et donc $a_{m}=m+c+1$ pour tout $m$ suffisamment grand.
Montrons que cette égalité est vraie pour tout $m$. Si par l'absurde elle était fausse, soit $M$ maximal tel que $a_{M} \neq M+c+1$. Alors $a_{M}$ est le nombre de termes de la suite inférieurs ou égaux à $a_{M+1}+c=$ $M+2 c+2$, qui sont les $M$ termes $a_{1}, \ldots, a_{M}$ ainsi que les termes $a_{M+1}, \ldots, a_{M+c+1}=M+2 c+2$, et donc
$$
a_{M}=M+(c+1)
$$
ce qui est absurde. Ainsi, pour tout $\mathrm{n}, \mathrm{a}_{\mathrm{n}}=\mathrm{n}+\mathrm{c}+1$.
Vérifions que cette solution fonctionne bien. Soit $n \geqslant 1$ entier. Alors $a_{n+1}+c=n+2 c+2$ et les entiers $i$ tels que $a_{i}=\mathfrak{i}+\boldsymbol{c}+1 \leqslant n+2 c+2$ sont les $i$ inférieurs ou égaux à $n+c+1$, il y en a $n+c+1=a_{n}$, comme voulu.
Commentaire des correcteurs : Le problème, malgré sa position, n'a pas été beaucoup cherché ni résolu. La plupart des élèves ayant rendu une tentative ont bien compris la mécanique de la suite et ont les bons réflexes : chercher les variations (croissance, convexité) de la suite avant d'en déduire qu'elle est
arithmétique. En revanche, beaucoup d'élèves, victimes du même tropisme, pensent montrer que la suite est strictement croissante dès le début de la preuve alors qu'ils n'ont que montré que la suite est constante puis strictement croissante à partir d'un certain rang. Enfin, on déplore que beaucoup d'élèves ont oublié de vérifier que la suite qu'ils trouvent à la fin est bien solution du problème.
|
{
"exam": "French_envois",
"problem_label": "15",
"problem_match": "\nExercice 15.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 15",
"tier": "T2",
"year": "2024"
}
|
Determine all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that for all real $x, y$, we have
$$
f\left(x^{2}+x y+f\left(y^{2}\right)\right)=x f(y)+f\left(x^{2}\right)+y^{2}
$$
|
By setting $y=0$, we find $f\left(x^{2}+f(0)\right)=x f(0)+f\left(x^{2}\right)$. By replacing $x$ with $-x$ in this equation, we find $f\left(x^{2}+f(0)\right)=-x f(0)+f\left(x^{2}\right)$, and by combining we obtain $2 x f(0)=0$ for all $x$, hence $f(0)=0$.
By setting $x=0$, we find $f\left(f\left(y^{2}\right)\right)=y^{2}+f(0)=y^{2}$. By setting $y=-x$, we find this time that $f\left(f\left(y^{2}\right)\right)=-y f(y)+y^{2}+f\left(y^{2}\right)$. We deduce that
$$
f\left(y^{2}\right)=y f(y)
$$
On the other hand, by setting $x=-f\left(y^{2}\right) / y$, we find
$$
-\frac{f(y) f\left(y^{2}\right)}{y}+y^{2}=0
$$
We deduce that if $y$ is non-zero, then $y^{3}=f(y) f\left(y^{2}\right)=y f(y)^{2}$, or equivalently $f(y)^{2}=y^{2}$. Since if $y=0$, then $f(0)=0$, we have for all real $y$ that $f(y)= \pm y$.
In the following, we assume that there exist $a$ and $b$ such that $f(a)=a$ and $f(b)=-b$. Note that then $f\left(a^{2}\right)=a^{2}$ and $f\left(b^{2}\right)=-b^{2}$, since $f\left(x^{2}\right)=x f(x)$.
By replacing $x=a$ and $y=b$ in the equation, we find
$$
\pm\left(a^{2}+a b-b^{2}\right)=-a b+b^{2}+a^{2}
$$
The case where the sign of the LHS (Left Hand Side = left-hand side of the equation) is a + gives that $b(a-b)=0$. If $b \neq 0$, then $a=b$ which gives $a=f(a)=f(b)=-b=-a$ hence $a=b=0$. In all cases, $a$ or $b$ is zero.
The case where the sign of the LHS is a - gives that $a^{2}=0$ hence $a=0$.
We deduce that the only solutions are the functions $f \equiv x$ and $f \equiv -x$.
Comment from the graders: The problem was quite popular. This functional equation required a lot of playing with the "symmetries" of the problem, particularly the fact that few terms changed if one changed the sign of a variable. Once this observation was made, one could try the substitutions $(x, y),(-x, y),(x,-y)$ and $(-x,-y)$, which gave that $f(0)=0$ and that $f$ is odd. Several options were then possible, such as playing on the involution property of $f$ or trying to cancel two terms of the equation (this is what motivates the substitution $x=-\frac{f\left(y^{2}\right)}{y}$ in the solution). The second peculiarity of the problem is that the solution led to a multigraph problem: for all $x$ we have either $f(x)=x$ or $f(x)=-x$. Note that at this stage, the identity and minus the identity are not the only functions with this property; for example, the absolute value function also satisfies this property (and there is in fact a large family of functions satisfying this). We would then like to "invert" this formula to show that we have either $f(x)=x$ for all $x$, or $f(x)=-x$ for all $x$. This subtlety was missed by several students.
Another recurring error was to deduce from $x f(x)=-x f(-x)$ that $f(x)=f(-x)$ for all non-zero $x$, and to deduce that $f$ is odd and thus that $f(0)=0$. But since the equality $f(x)=-f(-x)$ is only true for non-zero $x$, one cannot substitute $x=0$ into this equation to deduce $f(0)$.
|
f(x) = x \text{ or } f(x) = -x
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Déterminer toutes les fonctions $f: \mathbb{R} \rightarrow \mathbb{R}$ telles que pour tous $x, y$ réels, on ait
$$
f\left(x^{2}+x y+f\left(y^{2}\right)\right)=x f(y)+f\left(x^{2}\right)+y^{2}
$$
|
En posant $y=0$, on trouve $f\left(x^{2}+f(0)\right)=x f(0)+f\left(x^{2}\right)$. En remplaçant $x$ par $-x$ dans cette équation, on trouve $f\left(x^{2}+f(0)\right)=-\chi f(0)+f\left(x^{2}\right)$, et en combinant on obtient donc $2 x f(0)=0$ pour tout $x$, soit $f(0)=0$.
En posant $x=0$, on trouve $f\left(f\left(y^{2}\right)\right)=y^{2}+f(0)=y^{2}$. En posant $y=-x$, on trouve cette fois-ci que $f\left(f\left(y^{2}\right)\right)=-y f(y)+y^{2}+f\left(y^{2}\right)$. On en déduit que
$$
f\left(y^{2}\right)=y f(y)
$$
D'autre part, en posant $x=-f\left(y^{2}\right) / y$, on trouve
$$
-\frac{f(y) f\left(y^{2}\right)}{y}+y^{2}=0
$$
On déduit que si $y$ est non nul, alors $y^{3}=f(y) f\left(y^{2}\right)=y f(y)^{2}$, ou encore $f(y)^{2}=y^{2}$. Puisque si $y=0$, alors $f(0)=0$, on a donc pour tout $y$ réel que $f(y)= \pm y$.
Dans la suite, on suppose qu'il existe $a$ et $b$ tels que $f(a)=a$ et $f(b)=-b$. Notons qu'alors $f\left(a^{2}\right)=a^{2}$ et $f\left(b^{2}\right)=-b^{2}$, puisque $f\left(x^{2}\right)=x f(x)$.
En remplaçant $x=a$ et $y=b$ dans l'équation, on trouve
$$
\pm\left(a^{2}+a b-b^{2}\right)=-a b+b^{2}+a^{2}
$$
Le cas où le signe du LHS (Left Hand Side = membre de gauche de l'équation) est un + donne que $b(a-b)=0$. Si $b \neq 0$, alors $a=b$ ce qui donne $a=f(a)=f(b)=-b=-a$ donc $a=b=0$. Dans tous les cas, $a$ ou $b$ est nul.
Le cas où le signe du LHS est un - donne que $a^{2}=0$ donc $a=0$.
On déduit que les seules solutions sont les fonction $f \equiv x$ et $f \equiv-x$.
Commentaire des correcteurs : Le problème a rencontré un certain succès. Cette équation fonctionnelle nécessitait de beaucoup jouer sur les "symétries" du problème, en particulier le fait que peu de termes changeaient si l'on changeait le signe d'un variable. Une fois cette remarque effectuée, on pouvait tenter les substitutions $(x, y),(-x, y),(x,-y)$ et $(-x,-y)$, qui donnaient que $f(0)=0$ et que $f$ est impaire. Plusieurs options étaient ensuite possibles, comme jouer sur le caractère involutif de fou tenter de compenser deux termes de l'équation (c'est ce qui motive la substitution $x=-\frac{f\left(y^{2}\right)}{y}$ dans le corrigé). La deuxième spécificité du problème est que la solution aboutissait à un problème de multigraphe : on a pour tout $x$ soit $f(x)=\chi$ soit $f(x)=-\chi$. Notez qu'à ce stade, l'identité et moins l'identité ne sont pas les seules fonctions avec cette propriété, par exemple la fonction valeur absolue vérifie aussi cette propriété (et il y a en fait une large famille de fonctions vérifiant cela). On aimerait alors "inverser" cette formule pour montrer qu'on a soit $f(x)=x$ pour tout $x$, soit $f(x)=-x$ pour tout $x$. Cette subitlité a échappé à plusieurs élèves.
Une autre erreur récurrente a été de déduire de $x f(x)=-x f(-x)$ que $f(x)=f(-x)$ pour tout $x$ non nul, d'en déduire que $f$ est impaire et donc que $f(0)=0$. Mais comme l'égalité $f(x)=-f(-x)$ n'est vraie que pour les $x$ non nuls, on ne peut substituer $x=0$ dans cette équation pour déduire $f(0)$.
|
{
"exam": "French_envois",
"problem_label": "16",
"problem_match": "\nExercice 16.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 16",
"tier": "T2",
"year": "2024"
}
|
Let $n \geqslant 2$ be an integer and $C>0$ a real constant. Suppose there exists a sequence $x_{1}, x_{2}, \ldots, x_{n}$ of real numbers, not all zero, such that:
$-x_{1}+x_{2}+\ldots+x_{n}=0$.
- For every index $1 \leqslant i \leqslant n$, either $x_{i} \leqslant x_{i+1}$ or $x_{i} \leqslant x_{i+1}+C x_{i+2}$ (where we define $x_{n+1}=x_{1}$ and $x_{n+2}=x_{2}$).
1. Show that necessarily $C \geqslant 2$.
2. Suppose that $C=2$, show that $n$ is necessarily even.
|
In the entire solution, we will consider all indices modulo \( n \). Note that the condition in the statement means that for all \( i \), if \( x_{i+2} \leqslant 0 \), then \( x_{i} \leqslant x_{i+1} \) because the condition \( x_{i} \leqslant x_{i+1} + C x_{i+2} \) also implies \( x_{i} \leqslant x_{i+1} \). Similarly, in the opposite case, \( x_{i} \leqslant x_{i+1} + C x_{i+2} \) whenever \( x_{i+1} \geqslant 0 \). Therefore, we are interested in the sign of the different terms \( x_{k} \).
Let's start by showing that there are never two consecutive negative or zero terms among the \( x_{k} \). Suppose, for the sake of contradiction, that this is the case and that there exists \( i \) such that \( x_{i} \leqslant 0 \) and \( x_{i+1} \leqslant 0 \). Then we apply the property at index \( i-1 \). Since \( x_{i+1} \leqslant 0 \), we have \( x_{i-1} \leqslant x_{i} \leqslant 0 \). Reapplying this to index \( i-1 \), we find \( x_{i-2} \leqslant 0 \), and continuing this way, we find successively that all \( x_{k} \) are negative or zero. But since the sum of the \( x_{k} \) is 0, this means they are all zero, which is impossible according to the statement.
Let \( \mathfrak{i}_{1}, \ldots, \mathfrak{i}_{\mathrm{K}} \) be the indices \( i \) where \( x_{i} \) is negative or zero. Now, we can write all the inequalities we know between the \( x_{i} \): for all \( j \),
\[
\begin{gathered}
x_{\mathfrak{i}_{j}+1} \leqslant x_{\mathfrak{i}_{j}+2} + C x_{\mathfrak{i}_{\mathfrak{j}}+3}, \quad x_{\mathfrak{i}_{\mathfrak{j}}+2} \leqslant x_{\mathfrak{i}_{\mathfrak{j}}+3} + C x_{\mathfrak{i}_{\mathfrak{j}}+4}, \ldots, \quad x_{\mathfrak{i}_{j+1}-3} \leqslant x_{\mathfrak{i}_{j+1}-2} + C x_{\mathfrak{i}_{j+1}-1} \\
x_{\mathfrak{i}_{j+1}-2} \leqslant x_{\mathfrak{i}_{j+1}-1}, \quad x_{\mathfrak{i}_{j+1}-1} \leqslant x_{\mathfrak{i}_{j+1}} + C x_{\mathfrak{i}_{j+1}+1}
\end{gathered}
\]
The only interesting inequality involving the negative terms \( x_{i_{j}} \) is the last one, so for all \( j \), \( x_{i_{j}} \geqslant x_{i_{j}-1} - C x_{i_{j}+1} \). But we know that the sum of the positive terms must balance the sum of the negative terms because the sum of all \( x_{k} \) is 0, and we write
\[
-\left(x_{i_{1}} + x_{i_{2}} + \ldots + x_{i_{k}}\right) \leqslant \left(C x_{i_{1}+1} - x_{i_{1}-1}\right) + \left(C x_{i_{1}+1} - x_{i_{1}-1}\right) + \ldots + \left(C x_{i_{1}+1} - x_{i_{1}-1}\right)
\]
The left-hand side is the sum of the positive terms, and by rearranging the terms on the right, we get
\[
\begin{aligned}
\left(x_{i_{1}+1} + x_{i_{1}+2} + \ldots + x_{i_{2}-1}\right) + \left(x_{i_{2}+1} + x_{i_{2}+2} + \ldots + x_{i_{3}-1}\right) + \ldots + \left(x_{i_{k}+1} + x_{i_{k}+2} + \ldots + x_{i_{1}-1}\right) \\
& \leqslant \left(C x_{i_{1}+1} - x_{i_{2}-1}\right) + \left(C x_{i_{2}+1} - x_{i_{3}-1}\right) + \ldots + \left(C x_{\mathfrak{i}_{k}+1} - x_{i_{1}-1}\right)
\end{aligned}
\]
The reason for arranging the terms this way is as follows: the only inequalities left among the previously cited inequalities only involve the \( \chi_{k} \) for \( k \) between \( i_{j}+1 \) and the next \( \mathfrak{i}_{j+1}-1 \), i.e., in one of the sequences of consecutive strictly positive terms. We will then show that if \( C < 2 \), then for all \( \mathfrak{j} \),
\[
x_{i_{j}+1} + x_{i_{j}+2} + \ldots + x_{i_{j+1}-1} > C x_{i_{j}+1} - x_{i_{j+1}-1}
\]
We will show that for any sequence \( a_{1}, a_{2}, \ldots, a_{m} \) of strictly positive terms satisfying the inequalities
\[
a_{1} \leqslant a_{2} + C a_{3}, \quad a_{2} \leqslant a_{3} + C a_{4}, \ldots, \quad a_{m-2} \leqslant a_{m-1} + C a_{m}, \quad a_{m-1} \leqslant a_{m}
\]
then necessarily \( a_{1} + \ldots + a_{m} > C a_{1} - a_{m} \). For this, we write
\[
\begin{gathered}
C a_{1} - a_{m} = a_{1} + (C-1) a_{1} - a_{m} \leqslant a_{1} + (C-1) a_{2} + C(C-1) a_{3} - a_{m} \\
= a_{1} + (C-1) a_{2} + (C-1)^{2} a_{3} + (C-1) a_{3} - a_{m} \leqslant a_{1} + (C-1) a_{2} + (C-1)^{2} a_{3} + (C-1) a_{4} + C(C-1) a_{5} - a_{m}.
\end{gathered}
\]
We can continue this until we obtain, depending on the parity of \( m \),
\[
\leqslant \begin{cases}
a_{1} + (C-1) a_{2} + (C-1)^{2} a_{3} + \ldots + (C-1) a_{m-1} + C(C-1) a_{m} - a_{m} & \text{if } m \text{ is odd} \\
a_{1} + (C-1) a_{2} + (C-1)^{2} a_{3} + \ldots + (C-1) a_{m-2} + C(C-1) a_{m-1} - a_{m} & \text{if } m \text{ is even}
\end{cases}
\]
In the second case, we use the last inequality \( a_{m-1} \leqslant a_{m} \) to obtain
\[
\leqslant \begin{cases}
a_{1} + (C-1) a_{2} + (C-1)^{2} a_{3} + \ldots + (C-1) a_{m-1} + (C(C-1) - 1) a_{m} & \text{if } m \text{ is odd} \\
a_{1} + (C-1) a_{2} + (C-1)^{2} a_{3} + \ldots + (C-1) a_{m-2} + (C(C-1) - 1) a_{m-1} & \text{if } m \text{ is even}
\end{cases}
\]
When \( C < 2 \), all the coefficients in front of the \( a_{i} \) are strictly less than 1, and thus \( C a_{1} - a_{m} \) is strictly less than \( a_{1} + a_{2} + \ldots + a_{m} \). This concludes the first part of the exercise based on what we have seen previously.
Now, suppose \( C = 2 \). Note that in the study of the sequence \( a_{i} \), we always have the inequality \( C a_{1} - a_{m} \leqslant a_{1} + \ldots + a_{m} \), but from what we have shown previously, the inequality is always strict when \( m \) is even (since \( a_{m} \) is strictly positive). Thus, for \( C = 2 \), the sequences of consecutive positive terms must always be of odd length, which means that all \( i_{j+1} - \boldsymbol{i}_{j} \) are even (since we also count one negative term). But then, since all \( \mathfrak{i}_{j+1} - \mathfrak{i}_{\mathfrak{j}} \) are even, this means that \( n \) is necessarily even when summed over \( j \).
Comment from the graders: The exercise was very poorly done. The key point was to separate the elements of the sequence between positive and negative terms (see the video on the channel on the subject). Unfortunately, many of you thought to prove that two consecutive terms could not be strictly positive, which is quite possible (it is easy to find a counterexample for \( n = 4 \)). Often the mistake was to be too optimistic in the use of inequalities, while the statement is actually quite miraculous.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $\mathrm{n} \geqslant 2$ un entier et $\mathrm{C}>0$ une constante réelle. On suppose qu'il existe une suite $x_{1}, x_{2}, \ldots, x_{n}$ de réels non tous nuls telle que :
$-x_{1}+x_{2}+\ldots+x_{n}=0$.
- Pour tout indice $1 \leqslant i \leqslant n$, on a soit $x_{i} \leqslant x_{i+1}$, soit $x_{i} \leqslant x_{i+1}+C x_{i+2}$ (où on définit $x_{n+1}=x_{1}$ et $x_{n+2}=x_{2}$ ).
1. Montrer que nécessairement $C \geqslant 2$.
2. On suppose que $C=2$, montrer que n est nécessairement pair.
|
Dans toute la solution, on considèrera tous les indices modulo n . Remarquons que la condition de l'énoncé signifie que pour tout $i$, si $x_{i+2} \leqslant 0$, alors $x_{i} \leqslant x_{i+1}$ car la condition $x_{i} \leqslant x_{i+1}+C x_{i+2}$ implique aussi $x_{i} \leqslant x_{i+1}$, De la même façon dans le cas contraire, $x_{i} \leqslant x_{i+1}+C x_{i+2}$ dès que $x_{i+1} \geqslant 0$. On s'intéresse donc au signe des différents termes $x_{k}$.
Commençons par montrer qu'il n'existe jamais deux termes négatifs ou nuls à la suite parmi les $x_{k}$. Supposons par l'absurde que ce soit le cas et qu'il existe donc $i$ avec $x_{i} \leqslant 0$ et $x_{i+1} \leqslant 0$. Alors on applique la propriété à l'indice $i-1$. Comme $x_{i+1} \leqslant 0$, on a donc $x_{i-1} \leqslant x_{i} \leqslant 0$. En réappliquant ceci à l'indice $i-1$, on trouve $x_{i-2} \leqslant 0$, et en continuant ainsi on trouve successivement que tous les $x_{k}$ sont négatifs ou nuls. Mais comme la somme des $x_{k}$ vaut 0 , ceci veut dire qu'ils sont tous nuls, ce qui est impossible d'après l'énoncé.
Soient $\mathfrak{i}_{1}, \ldots, \mathfrak{i}_{\mathrm{K}}$ les indices $i$ où $x_{i}$ est négatif ou nul. Maintenant, on peut écrire toutes les inégalités que l'on connait entre les $x_{i}$ : pour tout $j$,
$$
\begin{gathered}
x_{\mathfrak{i}_{j}+1} \leqslant x_{\mathfrak{i}_{j}+2}+C x_{\mathfrak{i}_{\mathfrak{j}}+3}, \quad x_{\mathfrak{i}_{\mathfrak{j}}+2} \leqslant x_{\mathfrak{i}_{\mathfrak{j}}+3}+C x_{\mathfrak{i}_{\mathfrak{j}}+4}, \ldots, \quad x_{\mathfrak{i}_{j+1}-3} \leqslant x_{\mathfrak{i}_{j+1}-2}+C x_{\mathfrak{i}_{j+1}-1} \\
x_{\mathfrak{i}_{j+1}-2} \leqslant x_{\mathfrak{i}_{j+1}-1}, \quad x_{\mathfrak{i}_{j+1}-1} \leqslant x_{\mathfrak{i}_{j+1}}+C x_{\mathfrak{i}_{j+1}+1}
\end{gathered}
$$
La seule inégalité intéressante faisant apparaître les termes négatifs $x_{i_{j}}$ est cette dernière, on a donc pour tout $j, x_{i_{j}} \geqslant x_{i_{j}-1}-C x_{i_{j}+1}$. Mais on sait que la somme des termes positifs doit se compenser avec la somme des termes négatifs car la somme de tous les $x_{k}$ vaut 0 , et on écrit donc
$$
-\left(x_{i_{1}}+x_{i_{2}}+\ldots+x_{i_{k}}\right) \leqslant\left(C x_{i_{1}+1}-x_{i_{1}-1}\right)+\left(C x_{i_{1}+1}-x_{i_{1}-1}\right)+\ldots+\left(C x_{i_{1}+1}-x_{i_{1}-1}\right)
$$
Le terme de gauche vaut la somme des termes positifs, et en réordonnant les termes à droite on trouve
$$
\begin{aligned}
\left(x_{i_{1}+1}+x_{i_{1}+2}\right. & \left.+\ldots+x_{i_{2}-1}\right)+\left(x_{i_{2}+1}+x_{i_{2}+2}+\ldots+x_{i_{3}-1}\right)+\ldots+\left(x_{i_{k}+1}+x_{i_{k}+2}+\ldots+x_{i_{1}-1}\right) \\
& \leqslant\left(C x_{i_{1}+1}-x_{i_{2}-1}\right)+\left(C x_{i_{2}+1}-x_{i_{3}-1}\right)+\ldots+\left(C x_{\mathfrak{i}_{k}+1}-x_{i_{1}-1}\right)
\end{aligned}
$$
La raison pour mettre les termes de cette manière est la suivante : les seules inégalités qui nous restent parmi les inégalités citées précédemment ne prennent qu'en compte les $\chi_{k}$ pour $k$ entre un $i_{j}+1$ et le $\mathfrak{i}_{j+1}-1$ suivant, c'est-à-dire dans une des suites de termes strictement positifs successifs. On va alors montrer que si $C<2$, alors on a nécessairement pour tout $\mathfrak{j}$,
$$
x_{i_{j}+1}+x_{i_{j}+2}+\ldots+x_{i_{j+1}-1}>C x_{i_{j}+1}-x_{i_{j+1}-1}
$$
On va alors montrer que pour toute suite $a_{1}, a_{2}, \ldots, a_{m}$ de termes strictement positifs vérifiant les inégalités
$$
a_{1} \leqslant a_{2}+C a_{3}, \quad a_{2} \leqslant a_{3}+C a_{4}, \ldots, \quad a_{m-2} \leqslant a_{m-1}+C a_{m}, \quad a_{m-1} \leqslant a_{m}
$$
alors nécessairement $a_{1}+\ldots+a_{m}>\mathrm{Ca}_{1}-a_{m}$. Pour cela, on écrit
$$
\begin{gathered}
C a_{1}-a_{m}=a_{1}+(C-1) a_{1}-a_{m} \leqslant a_{1}+(C-1) a_{2}+C(C-1) a_{3}-a_{m} \\
=a_{1}+(C-1) a_{2}+(C-1)^{2} a_{3}+(C-1) a_{3}-a_{m} \leqslant a_{1}+(C-1) a_{2}+(C-1)^{2} a_{3}+(C-1) a_{4}+C(C-1) a_{5}-a_{m} .
\end{gathered}
$$
On peut continuer ainsi jusqu'à obtenir, selon la parité de m,
$$
\leqslant \begin{cases}a_{1}+(C-1) a_{2}+(C-1)^{2} a_{3}+\ldots+(C-1) a_{m-1}+C(C-1) a_{m}-a_{m} & \text { si m est impair } \\ a_{1}+(C-1) a_{2}+(C-1)^{2} a_{3}+\ldots+(C-1) a_{m-2}+C(C-1) a_{m-1}-a_{m} & \text { si m est pair }\end{cases}
$$
Dans le deuxième cas, on utilise la dernière inégalité $a_{m-1} \leqslant a_{m}$ pour obtenir
$$
\leqslant \begin{cases}a_{1}+(C-1) a_{2}+(C-1)^{2} a_{3}+\ldots+(C-1) a_{m-1}+(C(C-1)-1) a_{m} & \text { si m est impair } \\ a_{1}+(C-1) a_{2}+(C-1)^{2} a_{3}+\ldots+(C-1) a_{m-2}+(C(C-1)-1) a_{m-1} & \text { si m est pair }\end{cases}
$$
Lorsque $C<2$, tous les coefficients devant les $a_{i}$ sont strictement inférieurs à 1 et donc $C a_{1}-a_{m}$ est strictement inférieur à $a_{1}+a_{2}+\ldots+a_{m}$. Ceci conclut alors la première partie de l'exercice par ce qu'on a vu précédemment.
Maintenant, supposons que $C=2$. Remarquons que dans l'étude de la suite $a_{i}$, on a toujours l'inégalité $C a_{1}-a_{m} \leqslant a_{1}+\ldots+a_{m}$, mais par ce que l'on a montré précédemment l'inégalité est toujours stricte dans le cas où $m$ est pair (car $a_{m}$ strictement positif). Ainsi, pour que $C=2$, il faut que les suites de termes positifs consécutifs soient toujours de taille impaire., ce qui signifie que tous les $i_{j+1}-\boldsymbol{i}_{j}$ sont pairs (car on compte aussi un terme négatif). Mais alors comme tous les $\mathfrak{i}_{j+1}-\mathfrak{i}_{\mathfrak{j}}$ sont pairs, ceci signifie en sommant sur $j$ que $n$ est nécessairement pair.
Commentaire des correcteurs : L'exercie a été très peu réussi. Le point clef était de séparer les éléments de la suite entre termes positifs et négatifs (voir la vidéo sur la chaîne sur le sujet). Malheuresement, un certain nombre d'entre vous ont pensé démontrer que deux termes consécutifs ne pouvaient pas être strictement positifs, or c'est tout à fait possible (on peut facilement trouver un contre-exemple pour $\mathrm{n}=4$ ). Souvent l'erreur était d'être trop optimiste dans l'utilisation des inégalités alors que l'énoncé est en fait assez miraculeux.
|
{
"exam": "French_envois",
"problem_label": "17",
"problem_match": "\nExercice 17.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 17",
"tier": "T2",
"year": "2024"
}
|
Let $\mathbb{Z}[\mathrm{X}]$ be the set of polynomials with integer coefficients. Find all functions $f: \mathbb{Z}[X] \rightarrow \mathbb{Z}[X]$ such that for all $P, Q \in \mathbb{Z}[X]$ and $r \in \mathbb{Z}$, we have
$$
P(r)|Q(r) \Longleftrightarrow(f(P))(r)|(f(Q))(r)
$$
|
Let $f$ be a function that is a solution to the statement. First, note that if $P, Q, r$ are such that $|P(r)|=|Q(r)|$, then $f(P)(r)$ and $f(Q)(r)$ divide each other, and thus $|f(P)(r)|=|f(Q)(r)|$.
Also note that if $P$ and $Q$ are two polynomials such that for infinitely many integers $r, P(r) \mid Q(r)$, then the same is true for $f(P)$ and $f(Q)$, and thus $f(P)$ divides $f(Q)$ in $\mathbb{Q}[X]$. Indeed, we write the Euclidean division $f(Q)=R f(P)+S$ with $R, S \in \mathbb{Q}[X]$ and $\operatorname{deg}(S)<\operatorname{deg}(f(P))$. We multiply by the denominators of the coefficients of $R$ and $S$ to obtain an equality of the form $a f(Q)=R^{\prime} f(P)+S^{\prime}$ with $a$ an integer and $R^{\prime}, S^{\prime}$ two polynomials with integer coefficients. Then for infinitely many integers $r$, $a f(P)(r) \mid S^{\prime}(r)$. Since $|a f(P)(r)|$ grows faster than $\left|S^{\prime}(r)\right|$ as $|r|$ tends to infinity, we necessarily have $S^{\prime}=0$ and thus $f(P)=R f(Q)$ and $f(P)$ divides $f(Q)$ in $\mathbb{Q}[X]$. Notably, $f(Q)=0$ or $\operatorname{deg}(f(Q)) \geqslant \operatorname{deg}(f(P))$. We will often use the following consequence: if $P$ divides $Q$ in $\mathbb{Z}[X]$, then $f(P)$ divides $f(Q)$ in $\mathbb{Q}[X]$.
Let's start by finding the antecedents of the zero polynomial by $f$. Let $Q$ be such that $f(Q)=0$. Then for any polynomial $P$, we have that for all $r, f(P)(r) \mid f(Q)(r)=0$, and thus $P(r) \mid Q(r)$. By the previous remark, $Q=0$ or $\operatorname{deg}(Q) \geqslant \operatorname{deg}(P)$. Since we can take $P$ arbitrarily, we necessarily have $Q=0$. Thus, $f(P) \neq 0$ for all $P \neq 0$.
We will now focus on the image of constants by $f$. For any non-zero constant $c$, let $P(X)=c$ and $Q(X)=X$, then $P(k c) \mid Q(k c)$ for all integer $k$, and thus $f(c)$ must divide $f(Q)=f(X)$ in $\mathbb{Q}[X]$. Notably, $\operatorname{deg}(f(c)) \leqslant \operatorname{deg}(f(X))$. Since the degrees of the images of constants are bounded, there exists a constant $C \neq 0$ whose degree is maximal. Then for all integer $k, f(C)$ divides $f(k C)$ in $\mathbb{Q}[X]$, but $\operatorname{deg}(f(k C)) \leqslant \operatorname{deg}(f(C))$, and thus there exists a rational $g(k)$ such that $f(k C)=g(k) f(C)$.
Let's show that the function $g$ thus defined is, up to the sign at each point, a polynomial with rational coefficients. For this, note that for all integer $k$, we have $|k C|=|P(k C)|$ with $P(X)=X$, and thus $|f(k C)(k C)|=|f(X)(k C)|$, and thus
$$
|\boldsymbol{f}(X)(k C)|=|\boldsymbol{g}(k)||f(C)(k C)|
$$
But we already know that $f(C)$ divides $f(X)$ in $\mathbb{Q}[X]$, let $\hat{g}$ be their quotient (which is a polynomial in $\mathbb{Q}[X]$), then we have
$$
\forall k \in \mathbb{Z},|g(k)|=|\hat{g}(C k)|
$$
Now apply the property of the statement with $P(X)=k C$ and $Q(X)=X+a$ for $k$, $a$ two integers. We know that $|\mathrm{P}(\mathrm{r})|=|\mathrm{Q}(\mathrm{r})|$ at $r=k C-a$, and we have
$$
\begin{gathered}
|f(X+a)(k C-a)|=|f(k C)(k C-a)| \\
|f(X+a)(k C-a)|=|\hat{g}(k C)||f(C)(k C-a)| .
\end{gathered}
$$
However, two polynomials whose absolute values are equal at infinitely many integers are equal up to a sign. By varying $k$, we thus find the polynomial equality (up to a sign)
$$
f(X+a)(T)= \pm \hat{g}(T+a) f(C)(T)
$$
where the sign does not depend on $T$, but may depend on $a$. Now, we can calculate the values of $f$ for all constants: let $n$ be an integer, we have for all integer $a$,
$$
|f(n)(a)|=|f(X+n-a)(a)|=|\hat{g}(n) f(C)(a)|
$$
and we thus have the polynomial equality $f(n)= \pm \hat{g}(n) \cdot f(C)$. Finally, for any polynomial $P$, we can write for all integer $r$,
$$
|f(P)(r)|=|f(P(r))(r)|=|\hat{g}(P(r)) f(C)(r)|
$$
and thus $f(P)= \pm \hat{g}(P) \cdot f(C)$. It remains to find the forms of $\hat{g}$ that work. We know that if $m \mid n$ are two integers, then for all integer $r, f(m)(r) \mid f(n)(r)$, and thus $\hat{g}(m) f(C)(r) \mid \hat{g}(n) f(C)(r)$. By choosing $r$ such that $f(C)(r) \neq 0$ (possible since $f(C) \neq 0$), we get $\hat{g}(m) \mid \hat{g}(n)$. But then for all integer $k$, we know that as $n \rightarrow+\infty, \hat{g}(n k) / \hat{g}(n)$ is an integer that must tend to $k^{\text {deg }(\hat{g})}$. Thus, for $n$ large enough, $\hat{\boldsymbol{g}}(\mathrm{nk})=\mathrm{k}^{\mathrm{deg}(\hat{\boldsymbol{g}})} \hat{\boldsymbol{g}}(\mathrm{n})$, and thus the polynomials $\hat{\boldsymbol{g}}(\mathrm{kX})$ and $\mathrm{k}^{\operatorname{deg}(\hat{\boldsymbol{g}})} \hat{\boldsymbol{g}}(\mathrm{X})$ are equal. Thus, we find $\hat{g}(k)=\hat{g}(1) k^{\operatorname{deg}(\hat{g})}$ and $\hat{g}$ is thus a monomial of the form $\hat{g}(X)=a X^{n}$ for a rational $a$ and a non-negative integer $n$.
Thus, we have shown that there exists a polynomial $A=\operatorname{af}(C) \in \mathbb{Q}[X]$ and a non-negative integer $n$ such that for all $P \in \mathbb{Z}[X]$,
$$
f(P)(X)= \pm A(X) P(X)^{n}
$$
where the sign in the $\pm$ may depend on $P$, but not on $X$. With $P=1$, we get that $A$ is a polynomial with integer coefficients. Moreover, by setting $P=2, Q=3$ in the hypothesis of the statement, we get that for all integer $r$,
$$
A(r) 2^{n}\left|A(r) 3^{n} \Longleftrightarrow 2\right| 3
$$
This implies that $A(r) \neq 0$ for all $r$, and that $n \geqslant 1$.
Suppose now that $f$ is of the form above, with $A \in \mathbb{Z}[X]$ not vanishing at any integer and $n \geqslant 1$. Then we have that for all integer $r$ and $P, Q \in \mathbb{Z}[X]$,
$$
\mathrm{P}(\mathrm{r})\left|\mathrm{Q}(\mathrm{r}) \Longleftrightarrow \pm \mathrm{A}(\mathrm{r}) \mathrm{P}(\mathrm{r})^{n}\right| \pm \mathrm{A}(\mathrm{r}) \mathrm{Q}(\mathrm{r})^{\mathrm{n}}
$$
and thus $f$ satisfies the condition of the statement.
Comment from the graders: The problem was very poorly solved, but some managed to make partial progress on the problem.
|
proof
|
Yes
|
Incomplete
|
proof
|
Algebra
|
Soit $\mathbb{Z}[\mathrm{X}]$ l'ensemble des polynômes à coefficients entiers. Trouver toutes les fonctions $f: \mathbb{Z}[X] \rightarrow \mathbb{Z}[X]$ telles que pour tous $P, Q \in \mathbb{Z}[X]$ et $r \in \mathbb{Z}$, on ait
$$
P(r)|Q(r) \Longleftrightarrow(f(P))(r)|(f(Q))(r)
$$
|
Soit f une fonction solution de l'énoncé. Commençons par remarquer que si $P, Q, r$ sont tels que $|P(r)|=|Q(r)|$, alors $f(P)(r)$ et $f(Q)(r)$ se divisent mutuellement, et donc $|f(P)(r)|=|f(Q)(r)|$.
Remarquons aussi que si $P$ et $Q$ sont deux polynômes tels que pour une infinité d'entiers $r, P(r) \mid Q(r)$, alors c'est aussi le cas pour $f(P)$ et $f(Q)$, et donc $f(P)$ divise $f(Q)$ dans $\mathbb{Q}[X]$. En effet, on écrit la division euclidienne $f(Q)=R f(P)+S$ avec $R, S \in \mathbb{Q}[X]$ et $\operatorname{deg}(S)<\operatorname{deg}(f(P))$. On multiplie par les dénominateurs des coefficients de $R$ et $S$ pour obtenir une égalité de la forme $a f(Q)=R^{\prime} f(P)+S^{\prime}$ avec a entier et $R^{\prime}, S^{\prime}$ deux polynômes à coefficients entiers. Alors pour une infinité de $r$ entiers, $a f(P)(r) \mid$ $S^{\prime}(r)$. Comme $|a f(P)(r)|$ croît plus rapidement que $\left|S^{\prime}(r)\right|$ lorsque $|r|$ tend vers l'infini, on obtient que nécessairement $S^{\prime}=0$ et donc que $f(P)=\operatorname{Rf}(Q)$ et $f(P)$ divise $f(Q)$ dans $\mathbb{Q}[X]$. Notamment, $f(Q)=0$ ou $\operatorname{deg}(f(Q)) \geqslant \operatorname{deg}(f(P))$. On utilisera souvent la conséquence suivante : si $P$ divise $Q$ dans $\mathbb{Z}[X]$, alors $f(P)$ divise $f(Q)$ dans $\mathbb{Q}[X]$.
Commençons par trouver les antécédents du polynôme nul par $f$. Soit $Q$ tel que $f(Q)=0$. Alors pour tout polynôme $P$, on a que pour tout $r, f(P)(r) \mid f(Q)(r)=0$, et alors $P(r) \mid Q(r)$. Par la remarque précédente, $Q=0$ ou $\operatorname{deg}(Q) \geqslant \operatorname{deg}(P)$. Comme on peut prendre $P$ quelconque, on a nécessairement $\mathrm{Q}=0$. Ainsi, $f(P) \neq 0$ pour tout $P \neq 0$.
On va s'intéresser à l'image des constantes par $f$. Pour toute constante $c$ non nulle, posons $P(X)=c$ et $Q(X)=X$, alors $P(k c) \mid Q(k c)$ pour tout entier $k$, et donc $f(c)$ doit diviser $f(Q)=f(X)$ dans $\mathbb{Q}[X]$. Notamment, $\operatorname{deg}(f(c)) \leqslant \operatorname{deg}(f(X))$. Comme les degrés des images des constantes sont bornés, il existe donc une constante $C \neq 0$ dont le degré est maximal. Alors pour tout entier $k, f(C)$ divise $f(k C)$ dans $\mathbb{Q}[X]$, mais $\operatorname{deg}(f(k C)) \leqslant \operatorname{deg}(f(C))$, et donc il existe un rationnel $g(k)$ tel que $f(k C)=g(k) f(C)$.
Montrons que la fonction $g$ ainsi définie est, au signe en chaque point près, un polynôme à coefficients rationnels. Pour cela, remarquons que pour tout entier $k$, on a $|k C|=|P(k C)|$ avec $P(X)=X$, et donc $|f(k C)(k C)|=|f(X)(k C)|$, et donc
$$
|\boldsymbol{f}(X)(k C)|=|\boldsymbol{g}(k)||f(C)(k C)|
$$
Mais on sait déjà que $f(C)$ divise $f(X)$ dans $\mathbb{Q}[X]$, soit $\hat{g}$ leur quotient (qui est un polynôme dans $\mathbb{Q}[X]$ ), alors on a
$$
\forall k \in \mathbb{Z},|g(k)|=|\hat{g}(C k)|
$$
Appliquons maintenant la propriété de l'énoncé avec $P(X)=k C$ et $Q(X)=X+a$ pour $k$, $a$ deux entiers. On sait que $|\mathrm{P}(\mathrm{r})|=|\mathrm{Q}(\mathrm{r})|$ en $r=k C-a$, et on a donc
$$
\begin{gathered}
|f(X+a)(k C-a)|=|f(k C)(k C-a)| \\
|f(X+a)(k C-a)|=|\hat{g}(k C)||f(C)(k C-a)| .
\end{gathered}
$$
Or, deux polynômes dont les valeurs absolues sont égales en une infinité d'entiers sont égaux au signe près. En faisant varier $k$, on trouve donc l'égalité polynomiale (au signe près)
$$
f(X+a)(T)= \pm \hat{g}(T+a) f(C)(T)
$$
où le signe ne dépend pas de $T$, mais peut dépendre de $a$. A présent, on peut calculer les valeurs de $f$ en toutes les constantes : soit $n$ un entier, on a pour tout a entier,
$$
|f(n)(a)|=|f(X+n-a)(a)|=|\hat{g}(n) f(C)(a)|
$$
et on a donc l'égalité polynomiale $f(n)= \pm \hat{g}(n) \cdot f(C)$. Enfin, pour un polynôme $P$ quelconque, on peut écrire pour tout $r$ entier,
$$
|f(P)(r)|=|f(P(r))(r)|=|\hat{g}(P(r)) f(C)(r)|
$$
et donc $f(P)= \pm \hat{g}(P) \cdot f(C)$. Il reste à trouver les formes de $\hat{g}$ qui conviennent. On sait que si $m \mid n$ sont deux entiers, alors pour tout entier $r, f(m)(r) \mid f(n)(r)$, et donc $\hat{g}(m) f(C)(r) \mid \hat{g}(n) f(C)(r)$. En choisissant $r$ tel que $f(C)(r) \neq 0$ (possible car $f(C) \neq 0$ ), on obtient $\hat{g}(m) \mid \hat{g}(n)$. Mais alors pour tout entier $k$, on sait que lorsque $n \rightarrow+\infty, \hat{g}(n k) / \hat{g}(n)$ est un entier qui doit tendre vers $k^{\text {deg }(\hat{g})}$. Ainsi, pour $n$ assez grand, $\hat{\boldsymbol{g}}(\mathrm{nk})=\mathrm{k}^{\mathrm{deg}(\hat{\boldsymbol{g}})} \hat{\boldsymbol{g}}(\mathrm{n})$, et donc les polynômes $\hat{\boldsymbol{g}}(\mathrm{kX})$ et $\mathrm{k}^{\operatorname{deg}(\hat{\boldsymbol{g}})} \hat{\boldsymbol{g}}(\mathrm{X})$ sont égaux. Ainsi, on trouve $\hat{g}(k)=\hat{g}(1) k^{\operatorname{deg}(\hat{g})}$ et $\hat{g}$ est donc un monôme de la forme $\hat{g}(X)=a X^{n}$ pour un rationnel a et un entier positif $n$.
Ainsi, on a montré qu'il existait un polynôme $A=\operatorname{af}(C) \in \mathbb{Q}[X]$ et un entier $n$ positif ou nul tel que pour tout $P \in \mathbb{Z}[X]$,
$$
f(P)(X)= \pm A(X) P(X)^{n}
$$
où le signe dans le $\pm$ peut dépendre de $P$, mais pas de $X$. Avec $P=1$, on obtient que $A$ est un polynôme à coefficients entiers. De plus, en posant $P=2, Q=3$ dans l'hypothèse de l'énoncé, on obtient que pour tout entier $r$,
$$
A(r) 2^{n}\left|A(r) 3^{n} \Longleftrightarrow 2\right| 3
$$
Ceci implique que $A(r) \neq 0$ pour tout $r$, et que $n \geqslant 1$.
Supposons maintenant que f soit de la forme ci-dessus, avec $A \in \mathbb{Z}[X]$ ne s'annulant en aucun entier et $n \geqslant 1$. Alors on a bien que pour tout $r$ entier et $P, Q \in \mathbb{Z}[X]$,
$$
\mathrm{P}(\mathrm{r})\left|\mathrm{Q}(\mathrm{r}) \Longleftrightarrow \pm \mathrm{A}(\mathrm{r}) \mathrm{P}(\mathrm{r})^{n}\right| \pm \mathrm{A}(\mathrm{r}) \mathrm{Q}(\mathrm{r})^{\mathrm{n}}
$$
et donc f vérifie la condition de l'énoncé.
Commentaire des correcteurs : L'exercice a été très peu réussi, mais certains ont réussi à avoir des avancées partielles sur le problème.
|
{
"exam": "French_envois",
"problem_label": "18",
"problem_match": "\nExercice 18.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-algebre-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 18",
"tier": "T2",
"year": "2024"
}
|
Let $a, b$ be two integers. Show that, if neither $a$ nor $b$ is a multiple of 3, then $a^{4}-b^{2}$ is a multiple of 3.
|
Let's recall that if $k$ is not a multiple of 3, then $k$ is 1 or 2 modulo 3. Thus $\mathrm{k}^{2}$ is $1^{2}=1$ or $2^{2} \equiv 4 \equiv 1(\bmod 3):$ the square of any number not divisible by 4 is 1 modulo 3.
Thus $a^{4}-b^{2} \equiv\left(a^{2}\right)^{2}-b^{2} \equiv 1^{2}-1 \equiv 0(\bmod 3)$, so $a^{4}-b^{2}$ is a multiple of 3.
Comment from the graders: The exercise was generally very well done, however, many students could have gone faster by using modulos instead of explicit division algorithms, which would have simplified the calculations.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soient $a, b$ deux entiers relatifs. Montrer que, si ni $a$, ni $b$ n'est multiple de 3 , alors $a^{4}-b^{2}$ est multiple de 3.
|
Rappelons que si $k$ n'est pas un multiple de 3 , alors $k$ vaut 1 ou 2 modulo 3. Ainsi $\mathrm{k}^{2}$ vaut $1^{2}=1$ ou $2^{2} \equiv 4 \equiv 1(\bmod 3):$ tout carré d'un nombre non divisible par 4 vaut 1 modulo 3.
Ainsi $a^{4}-b^{2} \equiv\left(a^{2}\right)^{2}-b^{2} \equiv 1^{2}-1 \equiv 0(\bmod 3)$, donc $a^{4}-b^{2}$ est un multiple de 3 .
Commentaire des correcteurs : L'exercice a été très bien réussi dans l'ensemble, cependant pas mal d'élèves pourraient aller plus vite en utilisant des modulos plutôt que les écritures explicites des divisions euclidiennes, les calculs seraient de fait allégés.
|
{
"exam": "French_envois",
"problem_label": "10",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T2",
"year": "2024"
}
|
Let $n$ be an integer such that $n \geqslant 2$. We denote $d$ as the greatest divisor of $n$ different from $n$. We assume that $\mathrm{d}>1$. Prove that $\mathrm{n}+\mathrm{d}$ is not a power of 2.
|
Suppose by contradiction that $n+d$ is a power of 2. Note that $d$ divides $n$, so $d$ divides $n+d$, so $d$ divides a power of 2. Thus $d$ is a power of 2: we set $d=2^{k}$ for some $k \in \mathbb{N}$. We have $k \geqslant 1$ since $d \neq 1$. Let $n=d a=2^{k} a$ with $a \in \mathbb{N}^{*}$. Since $d$ is different from $n$, we have $a \geqslant 2$. Thus $2^{k-1} a$ is a divisor of $n$, greater than or equal to $2^{k}=d$, and different from $n$. By hypothesis $d=2^{k-1} a$, so $a=2$. Thus $n=2^{k+1}$.
We then find $\mathrm{n}+\mathrm{d}=2^{\mathrm{k}}(2+1)=3 \times 2^{\mathrm{k}}$ which is not a power of 2, which is a contradiction. Thus $n+d$ is not a power of 2.
Grader's comment: The exercise was very well done, but several papers forgot that 1 is an odd divisor of a power of 2.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $n$ un entier vérifiant $n \geqslant 2$. On note $d$ le plus grand diviseur de $n$ différent de $n$. On suppose que $\mathrm{d}>1$. Démontrer que $\mathrm{n}+\mathrm{d}$ n'est pas une puissance de 2 .
|
Supposons par l'absurde que $n+d$ est une puissance de 2 . Notons que $d$ divise $n$, donc $d$ divise $n+d$, donc $d$ divise une puissance de 2 . Ainsi $d$ est une puissance de $2:$ on pose $d=2^{k}$ pour un certain $k \in \mathbb{N}$. On a $k \geqslant 1$ car $d \neq 1$. Posons $n=d a=2^{k} a$ avec $a \in \mathbb{N}^{*}$. Comme $d$ est différent de $n$, on a $a \geqslant 2$. Ainsi $2^{k-1} a$ est un diviseur de $n$, supérieur ou égal à $2^{k}=d$, et différent de $n$. Par hypothèse $d=2^{k-1} a$, donc $a=2$. Ainsi $n=2^{k+1}$.
On trouve alors $\mathrm{n}+\mathrm{d}=2^{\mathrm{k}}(2+1)=3 \times 2^{\mathrm{k}}$ qui n'est pas une puissance de 2 , ce qui est une contradiction. Ainsi $n+d$ n'est pas une puissance de 2 .
Commentaire des correcteurs : L'exercice a été très bien réussi, mais plusieurs copies ont oublié que 1 est un diviseur impair d'une puissance de 2.
|
{
"exam": "French_envois",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T2",
"year": "2024"
}
|
Determine all integers $n \geqslant 0$ such that $2023+n$ ! is a perfect square.
|
Let $n \geqslant 0$ such that $2023+n$ ! is a perfect square. If $n \geqslant 4$, then 4 divides $n$ !, so $2023+\mathrm{n}!\equiv 2023 \equiv 3(\bmod 4)$. But 3 is not a square modulo 4 (the squares modulo 4 are 0 and 1), so we have a contradiction. Thus $n \leqslant 3$.
Note that $44^{2}=1936<2023+0!=2023+1!=2024<2023+2!=2025=45^{2}<2023+3!+2029=$ $2116=46^{2}$. Thus for $\mathrm{n}=0,1,3,2023+\mathrm{n}$ ! is not a square, but for $\mathrm{n}=2$ it is a square. Thus $2023+\mathrm{n}$ ! is a square if and only if $n=2$.
Graders' comment: The exercise was very well done. A few papers forgot the case $\mathrm{n}=$ 0.
|
n=2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer tous les entiers $n \geqslant 0$ tels que $2023+n$ ! est un carré parfait.
|
Soit $n \geqslant 0$ tel que $2023+n$ ! est un carré parfait. Si $n \geqslant 4$, alors 4 divise $n$ !, donc $2023+\mathrm{n}!\equiv 2023 \equiv 3(\bmod 4)$. Or 3 n'est pas un carré modulo 4 (les carrés modulo 4 sont 0 et 1 ), donc on a une contradiction. Ainsi $n \leqslant 3$.
Notons que $44^{2}=1936<2023+0!=2023+1!=2024<2023+2!=2025=45^{2}<2023+3!+2029<$ $2116=46^{2}$. Ainsi pour $\mathrm{n}=0,1,3,2023+\mathrm{n}$ ! n'est pas un carré, mais pour $\mathrm{n}=2$ c'est un carré. Ainsi $2023+\mathrm{n}$ ! est un carré si et seulement si $n=2$.
Commentaire des correcteurs : L'exercice a été très bien réussi. Quelques copies ont oublié le cas $\mathrm{n}=$ 0 .
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T2",
"year": "2024"
}
|
Determine all triplets $(p, q, r)$ of prime numbers such that $p+q^{2}=r^{4}$.
|
Note that the equation can be rewritten as $p=\left(r^{2}\right)^{2}-q^{2}=\left(r^{2}-q\right)\left(r^{2}+q\right)$. Since $r^{2}+q$ is strictly positive, and $p$ is also positive, $r^{2}-q$ must be positive as well. In particular, from the previous equation, we have that $r^{2}-q=1$ and $r^{2}+q=p$. If $r$ and $q$ are both odd, then $r^{2}-q$ is even, which is a contradiction. Therefore, one of $r$ and $q$ must be even, and thus must be 2 since $q$ and $r$ are primes.
If $r=2$, then $r^{2}-q=1$, so $q=4-1=3$. Additionally, $p=q+r^{2}=7$, so $(p, q, r)=(7,3,2)$ is a potential solution.
If $q=2$, then $r^{2}=q+1=3$ which is impossible.
Conversely, for $(\mathfrak{p}, \mathbf{q}, \mathrm{r})=(7,3,2), \mathfrak{p}+\mathrm{q}^{2}=7+9=16=2^{4}$.
Graders' comment: The exercise is very well solved. Many different approaches from the one proposed in the solution were possible, and the students always handled them well.
|
(7,3,2)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer tous les triplets $(p, q, r)$ de nombres premiers tels que $p+q^{2}=r^{4}$.
|
Notons que l'équation se réécrit $p=\left(r^{2}\right)^{2}-q^{2}=\left(r^{2}-q\right)\left(r^{2}+q\right)$. Come $r^{2}+q$ est strictement positif, et $p$ aussi, $r^{2}-q$ aussi. En particulier, d'après l'équation précédente, on a que $r^{2}-q=1$ et $r^{2}+q=p$. Si $r$ et $q$ sont impairs, alors $r^{2}-q$ est pair, ce qui est contradictoire. Ainsi parmi $r$ et $q$, un est pair, donc vaut 2 car $q$ et $r$ sont premiers.
Si $r=2$, alors $r^{2}-q=1$, donc $q=4-1=3$. De plus $p=q+r^{2}=7$, donc $(p, q, r)=(7,3,2)$ est une éventuelle solution.
Si $q=2$, alors $r^{2}=q+1=3$ ce qui est impossible.
Réciproquement, pour $(\mathfrak{p}, \mathbf{q}, \mathrm{r})=(7,3,2), \mathfrak{p}+\mathrm{q}^{2}=7+9=16=2^{4}$.
Commentaire des correcteurs : L'exercice est très bien résolu. Beaucoup d'approches différentes de celle proposée dans le corrigé étaient envisageables, et les élèves les ont toujours bien mises en oeuvre.
|
{
"exam": "French_envois",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T2",
"year": "2024"
}
|
Determine all quadruplets $(a, b, c, d)$ of positive integers with $a, b, c$ strictly positive such that
\[
\begin{aligned}
& \operatorname{LCM}(b, c)=a+d \\
& \operatorname{LCM}(c, a)=b+d \\
& \operatorname{LCM}(a, b)=c+d
\end{aligned}
\]
|
Given the system is symmetric, we assume that \( c \) is the maximum of \( a, b, \) and \( c \). Since \( c \) divides \( \operatorname{LCM}(b, c) \), \( c \) divides \( a + d \). Since \( c \) divides \( \operatorname{LCM}(c, a) \), \( c \) divides \( b + d \), so \( c \) divides \( a + d - (b + d) = a - b \). Since \( -c < a - b < c \), we have \( a = b \). The last line then gives \( a = \operatorname{LCM}(a, b) = c + d \geq c \). To have equality, we must have \( d = 0 \) and \( a = c \).
Conversely, if \( a = b = c \) and \( d = 0 \), each equation is equivalent to \( a = a + 0 \), which is true. The solution quadruplets are therefore \( (a, a, a, 0) \) for \( a \in \mathbb{N}^{*} \).
Graders' comments: The exercise was generally well done. However, many students forget that \( A \) divides \( B \) does not imply \( A \leq B \): this only works if \( A \) is positive and \( B \) is strictly positive. If \( B \) is only positive, it can be zero. Many students reason by implication but forget to verify the solutions at the end: in competitions, this systematically costs a point.
|
(a, a, a, 0)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer tous les quadruplets ( $a, b, c, d$ d'entiers positifs avec $a, b, c$ strictement positifs tels que
$$
\begin{aligned}
& \operatorname{PPCM}(b, c)=a+d \\
& \operatorname{PPCM}(c, a)=b+d \\
& \operatorname{PPCM}(a, b)=c+d
\end{aligned}
$$
|
Le système étant symétrique, on suppose que c est le maximum de $\mathrm{a}, \mathrm{b}$ et c . Comme c divise $\operatorname{PPCM}(\mathrm{b}, \mathrm{c}), \mathrm{c}$ divise $\mathrm{a}+\mathrm{d}$. Comme c divise $\operatorname{PPCM}(\mathrm{c}, \mathrm{a}), \mathrm{c}$ divise $\mathrm{b}+\mathrm{d}$, donc c divise $a+d-(b+d)=a-b$. Or $-c<a-b<c$ donc $a=b$. La dernière ligne donne alors $a=\operatorname{PPCM}(a, b)=c+d \geqslant c$. Pour avoir égalité, on a donc $d=0$ et $a=c$.
Réciproquement, si $\mathrm{a}=\mathrm{b}=\mathrm{c}$ et $\mathrm{d}=0$, chaque équation équivaut à $\mathrm{a}=\mathrm{a}+0$, qui est vrai. Les quadruplets solution sont donc les ( $\mathbf{a}, \mathrm{a}, \mathrm{a}, 0$ ) pour $a \in \mathbb{N}^{*}$.
Commentaire des correcteurs: L'exercice a été bien réussi dans l'ensemble. Cependant beaucoup d'élèves oublient que $A$ divise $B$ n'implique pas $A \leqslant B$ : cela ne marche que si $A$ est positif et $B$ strictement positif. Si B est uniquement positif, il peut être nul. Et beaucoup d'élèves raisonnent par implication, mais oublient de vérifier les solutions à la fin : en compétition cela coûte systématiquement un point.
|
{
"exam": "French_envois",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T2",
"year": "2024"
}
|
An integer $n \geqslant 2$ is written on the board. Each day, someone chooses $p$, a prime divisor of the integer $n$ written on the board, erases it, and writes $n+\frac{n}{p}$ in its place. Show that $p=3$ is chosen infinitely many times.
|
Let's fix $N \in \mathbb{N}$. Denote by $2^{a_{k}} 3^{b_{k}} c_{k}$ the integer written on the board on day $k$, with $c_{k}$ being the product of prime numbers different from 2 and 3. Suppose, for the sake of contradiction, that we can never choose $p=3$ from day $N$ onwards.
If on the $k$-th day we choose $p \neq 2,3$, then the number written on the board becomes $2^{a_{k}} 3^{b_{k}} \frac{c_{k}}{p}(p+1)$. Let $p+1=2^{b} 3^{c} d$ with $b, c$, and $d$ being positive integers and $d$ being coprime with 2 and 3. Since $p$ is a prime and different from 2, it is odd, so $b \geqslant 1$, and thus $d \leqslant \frac{p+1}{2}$. Therefore, as the number written on the board is $2^{a_{k}+b} 3^{b_{k}+c} \frac{c_{k}}{p} d$, we have $a_{k+1}=a_{k}+b$, $b_{k+1}=b_{k}+c$, and $c_{k+1}=\frac{c_{k}}{p} d \leqslant c_{k} \frac{p+1}{2 p} < c_{k}$.
If on the $k$-th day we choose $p=2$, the number written on the board becomes $\frac{3}{2} 2^{a_{k}} 3^{b_{k}} c_{k}=2^{a_{k}-1} 3^{b_{k}+1} c_{k}$. In particular, the sequence $\left(c_{k}\right)_{k \geqslant N}$ is decreasing and strictly positive. It cannot therefore decrease strictly infinitely often, otherwise it would become negative. Therefore, from a certain day $k>N$, we no longer choose $p \neq 2,3$, so $p=2$ is chosen every day from the $k$-th day onwards.
If from day $k>N$ we only choose $p=2$, then $a_{j+1}=a_{j}-1$ for all $j \geqslant k$. Therefore, the sequence of integers $\left(a_{j}\right)_{j \geqslant k}$ strictly decreases, and it must therefore become strictly negative, which is absurd.
Thus, we are forced to choose $p=3$ at least once after the $N$-th day.
Suppose that $p=3$ is not chosen infinitely often. From a certain day, denoted $N$, $p=3$ is no longer chosen. This contradicts what we have just proven: $p=3$ must therefore be chosen infinitely often.
Comment from the graders: The idea behind the reasoning in the exercise was generally understood, but the solutions were quite poorly written overall, preferring informal descriptions to precise and carefully demonstrated statements. Writing such proofs in middle school is certainly not an easy task, but it is still necessary to avoid some pitfalls. If these were minor and relatively easy to overcome in this problem (provided they were seen, which was rare), this is not always the case and "intuitively true" conclusions can turn out to be completely false because crucial steps of reasoning had not been considered. Some students did not understand the question: it was not a matter of showing that one could choose $p=3$ infinitely often with a judicious choice of operations. It was necessary to show that whatever the sequence of operations chosen from any integer (and even if one tried to avoid doing so), one must choose $p=3$ infinitely often. Most other students understood that the prime factors of $n$ became smaller and smaller, since a factor $p>2$ was replaced by the even number $p+1$, whose prime factors were all strictly less than $p$. This intuition is correct, but should not appear as such in a copy, because this statement is not clear: in what sense did the prime factors become smaller and smaller? Their maximum? Their number? Some kind of combination of both, one might say intuitively, but it still needs to be described! The whole problem with using this informal intuition as a step in reasoning is that it seems natural to deduce from it that after a certain time, the integer written on the board has only 2 and 3 as prime factors. This is not true, since one can, for example, multiply a valid sequence by 5. This may seem a trivial counterexample, but it shows that there are counterexamples, and therefore that there may be more subtle counterexamples than this one. The solution allows finding one of the ways to formalize this intuition, by explicitly identifying an integer quantity that can only decrease (a "mono-variant") and which must therefore be constant from a certain point onwards. Some students took another approach, essentially reasoning by strong induction based on the following observation: if $\mathrm{n}=\mathrm{ab}$, then one can also consider that each day two numbers $a$ and $b$ are written on two different boards, and that each day the operation is performed on one of the two boards. As a result, one or the other of the integers is modified according to the operation infinitely often and we have therefore used $\mathrm{p}=3$ infinitely often by the induction hypothesis.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Un entier $n \geqslant 2$ est écrit au tableau. Chaque jour, quelqu' un choisit $p$ un diviseur premier de l'entier écrit $n$ au tableau, efface celui-ci et écrit $n+\frac{n}{p}$ à la place. Montrer que $p=3$ est choisi une infinité de fois.
|
Fixons $N \in \mathbb{N}$. Notons $2^{a_{k}} 3^{b_{k}} c_{k}$ l'entier écrit au tableau le jour $k$, avec $c_{k}$ produit de nombres premiers distincts de 2 et 3 . Supposons par l'absurde qu'on peut ne jamais choisir $p=3$ à partir du jour $N$.
Si le $k$-ième jour on choisit $p \neq 2,3$, alors le nombre écrit au tableau devient $2^{a_{k}} 3^{b_{k}} \frac{c_{k}}{p}(p+1)$. Posons $p+1=2^{b} 3^{c} d$ avec $b, c$, $d$ des entiers positifs et d premier avec 2 et 3 . Comme $p$ est premier et différent de 2 , il est pair, donc $a \geqslant 1$, donc $d \leqslant \frac{p+1}{2}$. Ainsi comme le nombre écrit au tableau est $2^{a_{k}+a} 3^{b_{k}+b} \frac{c_{k}}{p} d$, donc $a_{k+1}=a_{k}+a, b_{k+1}=b_{k}+b$ et $c_{k+1}=\frac{c_{k}}{p} d \leqslant c_{k} \frac{p+1}{2 p}<c_{k}$.
Si le $k$-ième jour on choisit $p=2$, le nombre écrit au tableau devient $\frac{3}{2} 2^{a_{k}} 3^{b_{k}} c_{k}=2^{a_{k}-1} 3^{b_{k}+1} c_{k}$. En particulier, la suite $\left(c_{k}\right)_{k} \geqslant \mathrm{~N}$ décroît et est strictement positive. Elle ne peut donc décroître strictement infiniment souvent, sinon elle deviendrait négative. Donc à partir d'un certain jour $k>N$, on ne choisit plus $p \neq 2,3$, donc $p=2$ est choisit chaque jour à partir du k-ième jour.
Or si à partir du jour $k>N$ on ne choisit que $p=2$, alors $a_{j+1}=a_{j}-1$ pour tout $j \geqslant k$. Donc la suite d'entiers $\left(a_{j}\right)_{j \geqslant k}$ décroît strictement, elle doit donc devenir strictement négative ce qui est absurde.
Ainsi, on est obligé de choisir au moins une fois $p=3$ après le N -ième jour.
Supposons que $p=3$ n'est pas choisi une infinité de fois. A partir d'un certain jour, noté $N, p=3$ n'est plus jamais choisi. Cela contredit ce qu'on vient de prouver : $p=3$ est donc choisi une infinité de fois.
Commentaire des correcteurs: L'idée du raisonnement derrière l'exercice a généralement été comprise, mais les solutions ont été assez mal rédigées dans leur ensemble, préférant des descriptions informelles à des énoncés précis et soigneusement démontrés. Rédiger de telles démonstrations au collège n'est certainement pas chose facile, mais est tout de même nécessaire pour éviter quelques écueils. Si ceux-ci étaient mineurs et relativement faciles à contourner dans ce problème (pour peu qu'on les vît, ce qui était rare), ce n'est pas toujours le cas et des conclusions 'intuitivement vraies" peuvent s'avérer complètement fausses parce que des étapes cruciales de raisonnement n'auraient pas été envisagées. Quelques élèves n'ont pas compris la question : il ne s'agissait pas ici de montrer que l'on pouvait choisir $p=3$ une infinité de fois avec un choix judicieux d'opérations. Il fallait montrer que quelle que soit la suite d'opérations choisie à partir de n'importe quel entier (et même si on essayait d'éviter de le faire), on doit choisir $p=3$ une infinité de fois. Les autres élèves ont, pour la plupart, compris que les facteurs premiers de $n$ devenaient de plus en plus petits, puisqu'un facteur $p>2$ était remplacé par le nombre pair $p+1$, dont tous les facteurs premiers étaient strictement inférieurs à $p$. Cette intuition est correcte, mais ne doit pas figurer telle quelle dans une copie, parce que cet énoncé n'est pas clair : en quel sens les facteurs premiers devenaient-ils de plus en plus petits? Leur maximum? Leur nombre? Une espèce de combinaison des deux, dirait-on intuitivement, mais encore faut-il la décrire! Tout le problème d'employer cette intuition informelle comme une étape de raisonnement est qu'il semble naturel d'en déduire qu'au bout d'un certain moment, l'entier écrit au tableau n'a plus que des 2 et des 3 comme facteurs premiers. Ceci n'est pas vrai, puisqu'on peut par exemple multiplier une suite valide par 5 . Cela peut paraître un contre-exemple trivial, mais cela montre qu'il existe des contre-exemples, et donc qu'il peut exister des contre-exemples plus subtils que celui-ci. Le corrigé permet de trouver une des façons de formaliser cette intuition, en explicitant une quantité entière qui ne peut que décroître (un "mono-variant") et qui doit donc être constante à partir d'un certain moment. Quelques élèves ont pris une autre approche, consistant essentiellement à raisonner par récurrence (forte) en se reposant sur l'observation suivante : si $\mathrm{n}=\mathrm{ab}$, alors on peut aussi considérer qu'on a chaque jour deux nombres $a$ et $b$ écrits sur deux tableaux différents, et qu'on effectue chaque jour l'opération sur l'un des deux tableaux. Partant, l'un ou l'autre des entiers est modifié selon l'opération une infinité de fois et on a donc par hypothèse de récurrence
utilisé $\mathrm{p}=3$ une infinité de fois.
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T2",
"year": "2024"
}
|
Let $k$ be an integer coprime with $n$ satisfying $1 \leqslant k < n$. Augustin colors the integers of $\{1,2, \ldots, n-1\}$ with as many colors as he wishes. However, if $\mathbf{j}$ is an integer satisfying $1 \leqslant j \leqslant n-1$, the integers $j$ and $n-j$ are of the same color. Additionally, if $i$ is an integer satisfying $1 \leqslant i \leqslant n$ and $i \neq k$, the integers $i$ and $|i-k|$ are of the same color.
Prove that Augustin has colored all the integers the same color.
|
For $k=1$, we see that $n$ has the same color as $n-1$, then that $n-2$ has the same color as $n-1$, etc., and all integers have the same color.
For $k=2$, $n$ is odd and we see that $n, n-2, \ldots, 1$ have the same color, then that $n-1$ has the same color as 1, and that $n-1, n-3, \ldots, 2$ have the same color.
By doing the same for small values of $k$, we realize that we always manage to show successively that $n-k, \ldots, n-(n-1)k$ taken modulo $n$ are all of the same color. Let's try to formalize this.
Let $c$ be the color of $n$. We prove by induction the following property for all $\boldsymbol{j} \in \{1, \ldots, \boldsymbol{n}-1\}$: $\mathcal{P}(\mathfrak{j})$: "The remainder of the Euclidean division of $n-jk$ is not congruent to 0 modulo $n$, and is colored with the color $c$."
Initialization: for $j=1$, since $1 \leqslant n-k \leqslant n-1$, the remainder of the Euclidean division of $n-k$ is $n-k$, is not congruent to 0 modulo $n$, and is colored with the color $c$.
Induction: Let $j \in \{0, \ldots, n-2\}$, suppose that $P(j)$ is true and let's show $P(j+1)$. Let $r$ be the remainder of the Euclidean division of $n-jk$ by $n$.
First case: if $r > k$, then $n > r \geqslant r-k > 0$. Now $r-k \equiv n-jk-k \equiv n-(j+1)k \pmod{n}$. Therefore, the remainder of the Euclidean division of $n-jk$ by $n$ is $r-k$, is non-zero, and is of the same color as $r$, hence of color $c$, which concludes.
Second case: if $r = k$, then $n-jk \equiv k \pmod{n}$, i.e., $(j+1)k \equiv 0 \pmod{n}$. Since $n$ is coprime with $k$, and divides $(\mathfrak{j}+1)k$, $n$ divides $\mathfrak{j}+1$, but since $\mathfrak{j}+1 \in \{1, \ldots, n-1\}$, this case is impossible.
Third case: if $k > r$, then $k-r$ is of the same color as $r$, hence of color $c$. Moreover, we have $1 \leqslant k-r \leqslant k \leqslant n-1$, so $n-(k-r)$ satisfies $1 \leqslant n-(k-r) \leqslant n-1$ and is of color $c$. Now $n-(k-r) \equiv r-k \equiv n-(j+1)k \pmod{n}$, so $n-(k-r)$ is the remainder of the Euclidean division of $n-(j+1)k$ by $n$, is non-zero, and of color $c$, which concludes.
This concludes the induction.
Now let $\boldsymbol{j} \in \{1, \ldots, \boldsymbol{n}-1\}$. There exists $\ell \in \{0, \ldots, \boldsymbol{n}-1\}$ such that $\boldsymbol{j} \equiv \boldsymbol{n}-\ell k \pmod{\boldsymbol{n}}$: indeed, this is equivalent to $\ell k \equiv n-j \pmod{n}$, or to $\ell \equiv (n-\mathfrak{j})k^{-1} \pmod{n}$ (where $k^{-1}$ is the inverse of $k$ modulo $n$, which exists since $k$ is coprime with $n$), and admits a solution in $\{0, \ldots, n-1\}$. In particular, $j$ is the remainder of the division of $n-\ell j$ by $n$, so it is of color $c$. Thus all integers from 1 to $n-1$ have the same color as $n$, so all integers are colored the same color.
Comment from the graders: The exercise is relatively poorly solved: many provided proofs are incomplete, as they forget certain constraints (e.g., $i \neq k$ to say that $|i-k|$ and $i$ have the same color, forgetting that $i$ and $i+k$ do not have the same color if $i > n-k$, etc).
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit k un entier premier avec n vérifiant $1 \leqslant \mathrm{k}<\mathrm{n}$. Augustin colorie les entiers de $\{1,2, \ldots, \mathfrak{n}-1\}$ avec autant de couleur qu'il le souhaite. Cependant, si $\boldsymbol{j}$ est un entier vérifiant $1 \leqslant \mathfrak{j} \leqslant$ $n-1$, les entiers $j$ et $n-j$ sont de la même couleur. De plus, si $i$ est un entier vérifiant $1 \leqslant i \leqslant n$ et $i \neq k$, les entiers $i$ et $|i-k|$ sont de la même couleur.
Démontrer que Augustin a colorié tous les entiers de la même couleur.
|
Pour $k=1$, on voit que $n$ a la même couleur que $n-1$, puis que $n-2$ à la même couleur que $n-1$, etc et tous les entiers ont la même couleur.
Pour $k=2$, $n$ est impair et on voit que $n, n-2, \ldots, 1$ ont la même couleur, puis que $n-1$ a la même couleur que 1 , et que $n-1, n-3, \ldots, 2$ ont la même couleur.
En faisant la même chose pour des petites valeurs de $k$, on se rend compte qu'on arrive à chaque fois à montrer successivement que $n-k, \ldots, n-(n-1) k$ pris modulo $n$ sont tous de la même couleur. Essayons de formaliser cela.
Notons c la couleur de n . On montre par récurrence la propriété suivante pour tout $\boldsymbol{j} \in\{1, \ldots, \boldsymbol{n}-1\}$ : $\mathcal{P}(\mathfrak{j})$ : "Le reste de la division euclidienne de $n-j k n$ 'est pas congru à 0 modulo $n$, et est colorié avec la couleur c.
Initialisation : pour $j=1$, comme $1 \leqslant n-k \leqslant n-1$, le reste de la division euclidienne de $n-k$ vaut $n-k$, n'est pas congru à 0 modulo $n$, et est colorié avec la couleur $c$.
Hérédité : Soit $j \in\{0, \ldots, n-2\}$, supposons que $P(j)$ est vraie et montrons $P(j+1)$. Notons $r$ le reste de la division euclidienne de $n-j k$ par $n$.
Premier cas : si $r>k$, alors $n>r \geqslant r-k>0$. Or $r-k \equiv n-j k-k \equiv n-(j+1) k(\bmod n)$. Donc le reste de la division euclidienne de $n-j k$ par $n$ vaut $r-k$, est non nul et est de la même couleur que $r$, donc de la couleur c ce qui conclut.
Second cas, si $r=k$, alors $n-j k \equiv k(\bmod n)$, i.e. $(j+1) k \equiv 0(\bmod n)$. Comme $n$ est premier avec $k$, et divise $(\mathfrak{j}+1) \mathrm{k}, \mathrm{n}$ divise $\boldsymbol{j}+1$, mais comme $\boldsymbol{j}+1 \in\{1 \ldots, n-1\}$, ce cas est impossible.
Troisième cas : si $k>r$, alors $k-r$ est de la couleur de de $r$, donc de la couleur $c$. De plus on a $1 \leqslant k-r \leqslant k \leqslant n-1$, donc $n-(k-r)$ vérifie $1 \leqslant n-(k-r) \leqslant n-1$ et est de la couleur $c$. Or $n-(k-r) \equiv r-k \equiv n-(j+1) k(\bmod n)$, donc $n-(k-r)$ est le reste de la division euclidienne de $\mathrm{n}-(\mathrm{j}+1) \mathrm{k}$ par n , est non nul et de couleur c , ce qui conclut.
Ceci conclut l'hérédité.
Maintenant donnons nous $\boldsymbol{j} \in\{1, \ldots, \boldsymbol{n}-1\}$. Il existe $\ell \in\{0 \ldots, \boldsymbol{n}-1\}$ tel que $\boldsymbol{j} \equiv \boldsymbol{n}-\ell k(\bmod \boldsymbol{n}):$ en effet, ceci est équivalent à $\ell k \equiv n-j(\bmod n)$, soit à $\ell \equiv(n-\mathfrak{j}) k^{-1}(\bmod n)\left(\right.$ où $k^{-1}$ est l'inverse de k modulo n , qui existe car k est premier avec n ), et admet une solution dans $\{0 \ldots, \mathrm{n}-1\}$. En particulier, $j$ est le reste de la divison euclidienne de $n-\ell j$ par $n$, donc de couleur $c$. Ainsi tous les entiers de 1 à $n-1$ ont la même couleur que $n$, donc tous les entiers sont coloriés de la même couleur.
Commentaire des correcteurs : L'exercice est relativement mal résolu : beaucoup de preuves fournies s'avèrent incomplètes, car elles oublient certaines contraintes ( $i \neq k$ pour dire que $|i-k|$ et $i$ ont la même couleur, oubli que $i$ et $i+k$ n'ont pas la même couleur si $i>n-k$, etc).
|
{
"exam": "French_envois",
"problem_label": "14",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 7",
"tier": "T2",
"year": "2024"
}
|
Determine all pairs ( $a, p$ ) of strictly positive integers, with $p$ prime, such that for any pair ( $m, n$ ) of strictly positive integers, the remainder of the Euclidean division of $a^{2^{n}}$ by $p^{n}$ is non-zero, and is the same as that of $a^{2^{m}}$ by $p^{m}$.
|
By taking $\mathrm{n}=1$ in the statement, we obtain that for any positive integer $m$, the remainder of $a^{2^{m}}$ modulo $p^{m}$ is the same as that of $a^{2}$ modulo $p$, and thus is constant. Let $r$ be this remainder: we have $r \neq 0$ and thus $r \in \{1, \ldots, p-1\}$. We have $a^{2} \equiv r \pmod{p}$ and $a^{4} \equiv r \pmod{p^{2}}$, so $a^{4} \equiv r \pmod{p}$, and thus $r^{2} \equiv r \pmod{p}$. Since $r$ is coprime with $p$, $r$ is invertible $\bmod p$, so $r \equiv 1 \pmod{p}$. Therefore, $a^{2^{m}} \equiv 1 \pmod{p^{m}}$ for all $m$. In particular, $a^{2} \equiv 1 \pmod{p}$.
Now
$$
a^{2^{m}}-1=\left(a^{2^{m-1}}-1\right)\left(a^{2^{m-1}}+1\right)=\cdots=\left(a^{2}-1\right)\left(a^{2}+1\right)\left(a^{4}+1\right) \ldots\left(a^{2^{m-1}}+1\right)
$$
If $p \geq 3$, for all $k \geq 1, a^{2^{k}}+1 \equiv 1^{2^{k-1}}+1 \equiv 2 \not\equiv 0 \pmod{p}$, so if $a \neq 1, V_{p}\left(a^{2^{m}}-1\right)=$ $V_{p}\left(a^{2}-1\right)$. Since for all $m, p^{m}$ divides $a^{2^{m}}-1$, we have $m \leq V_{p}\left(a^{2^{m}}-1\right)=V_{p}\left(a^{2}-1\right)$, which is absurd because $V_{p}\left(a^{2}-1\right)$ is finite. Thus $a=1$. Conversely, for any prime $p$, $a=1$ is a solution because the remainder of $1^{2^{m}}$ modulo $p^{m}$ is always 1 and is non-zero.
If $p=2$ and $a \neq 1, a^{2} \equiv 1 \pmod{2}$, so $a$ is odd. Conversely, if $a$ is odd, recall that
$$
a^{2^{m}}-1=\left(a^{2^{m-1}}-1\right)\left(a^{2^{m-1}}+1\right)=\cdots=\left(a^{2}-1\right)\left(a^{2}+1\right)\left(a^{4}+1\right) \ldots\left(a^{2^{m-1}}+1\right)
$$
The product on the right contains $m$ terms, all of which are even, so it is divisible by $2^{m}$. Thus for all $n$, the remainder of $a^{2^{n}}$ modulo $2^{n}$ is 1 and is non-zero, so all pairs of the form $(a, 2)$ with $a$ odd are solutions.
Thus, the pairs of solutions are those of the form $(1, p)$ for $p \geq 3$ and $(a, 2)$ for $a$ odd.
|
(1, p) \text{ for } p \geq 3 \text{ and } (a, 2) \text{ for } a \text{ odd}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer tous les couples ( $a, p$ ) d'entiers strictement positifs, avec $p$ premier, tels que pour tout couple ( $m, n$ ) d'entiers strictement positifs, le reste de la division euclidienne de $a^{2^{n}}$ par $p^{n}$ est non nul, et est le même que celui de $a^{2^{m}}$ par $p^{m}$.
|
En prenant $\mathrm{n}=1$ dans l'énoncé, on obtient que pour tout entier m strictement positif, le reste de $a^{2^{m}}$ modulo $p^{m}$ vaut celui de $a^{2}$ modulo $p$, donc est constant. Notons $r$ ce reste : on a donc $r \neq 0$ ainsi $r \in\{1, \ldots, p-1\}$. On a $a^{2} \equiv r(\bmod p)$ et $a^{4} \equiv r\left(\bmod p^{2}\right)$, donc $a^{4} \equiv r(\bmod p)$, donc $r^{2} \equiv r(\bmod p)$. Ainsi comme $r$ est premier avec $p, r$ est inversible $\bmod p$, donc $r \equiv 1(\bmod p)$. On a donc $a^{2^{m}} \equiv 1\left(\bmod p^{m}\right)$ pour tout $m$. En particulier $a^{2} \equiv 1(\bmod p)$
Or
$$
a^{2^{m}}-1=\left(a^{2^{m-1}}-1\right)\left(a^{2^{m-1}}+1\right)=\cdots=\left(a^{2}-1\right)\left(a^{2}+1\right)\left(a^{4}+1\right) \ldots\left(a^{2^{m-1}}+1\right)
$$
Si $p \geqslant 3$, pour tout $k \geqslant 1, a^{2^{k}}+1 \equiv 1^{2^{k-1}}+1 \equiv 2 \not \equiv 0(\bmod p)$, donc si $a \neq 1 V_{p}\left(a^{2^{m}}-1\right)=$ $V_{p}\left(a^{2}-1\right)$. Or pour tout $m, p^{m}$ divise $a^{2^{m}}-1$, donc $m \leqslant V_{p}\left(a^{2^{m}}-1\right)=V_{p}\left(a^{2}-1\right)$ ce qui est absurde car $V_{p}\left(a^{2}-1\right)$ est fini. Ainsi $a=1$. Réciproquement pour tout $p$ premier, $a=1$ est solution car le reste de $1^{2^{m}}$ modulo $p^{m}$ vaut toujours 1 et est non nul.
Si $p=2$ et $a \neq 1, a^{2} \equiv 1(\bmod 2)$, donc $a$ est impair. Réciproquement si a est impair, rappelons que
$$
a^{2^{m}}-1=\left(a^{2^{m-1}}-1\right)\left(a^{2^{m-1}}+1\right)=\cdots=\left(a^{2}-1\right)\left(a^{2}+1\right)\left(a^{4}+1\right) \ldots\left(a^{2^{m-1}}+1\right)
$$
Le produit de droite contient $m$ termes tous pairs, donc est divisible par $2^{m}$. Ainsi pour tout $n$, le reste de $a^{2^{n}}$ modulo $2^{n}$ vaut 1 et est non nul, donc tous les couples de la forme ( $a, 2$ ) avec a impair sont solutions.
Ainsi les couples solutions sont ceux de la forme ( $1, \mathfrak{p}$ ) pour $p \geqslant 3$ et $(a, 2)$ pour a impair.
|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "\nExercice 8.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 8",
"tier": "T2",
"year": "2024"
}
|
Determine all pairs ( $a, p$ ) of strictly positive integers, with $p$ prime, such that for any pair ( $m, n$ ) of strictly positive integers, the remainder of the Euclidean division of $a^{2^{n}}$ by $p^{n}$ is non-zero, and is the same as that of $a^{2^{m}}$ by $p^{m}$.
|
Starting from the fact that $a^{2^{m}} \equiv 1\left(\bmod p^{m}\right)$ for all $m$, since $p$ divides $a^{2}-1$, by LTE if $p \geqslant 3$ that if $a>1, V_{p}\left(a^{2^{m}}-1\right)=V_{p}\left(a^{2}-1\right)+V_{p}\left(2^{m-1}\right)=V_{p}\left(a^{2}-1\right)$. In particular, since $V_{p}\left(a^{2^{m}}-1\right) \geqslant m$ for all $m \geqslant 1, V_{p}\left(a^{2}-1\right) \geqslant m$ for all $m$ which is absurd, so $a=1$. Conversely, $a=1$ and $p \geqslant 3$ works as in the previous solution.
For the case $p=2$, similarly as before we have $p$ odd, so 4 divides $p^{2}-1=(p-1)(p+1)$, so by LTE, since 4 divides $a^{4}-1$, if $a>1 V_{2}\left(a^{2^{m}}-1\right)=V_{2}\left(a^{2}-1\right)+V_{2}\left(2^{m-1}\right) \geqslant 2+m-1=m+1$, thus $a^{2^{m}}-1$ is divisible by $2^{m}$ for all $m$, and we conclude in the same way as before.
Comment from the graders: The exercise is solved in an uneven manner by those who have attempted it. Indeed, some miss certain solutions (either the case $p=2$ or the case $a=1$: small values should allow them to spot these solutions. Also, be careful with the use of LTE: the LTE theorem has assumptions, they must be verified under penalty of writing false statements.
|
a=1, p \geqslant 3 \text{ or } p=2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer tous les couples ( $a, p$ ) d'entiers strictement positifs, avec $p$ premier, tels que pour tout couple ( $m, n$ ) d'entiers strictement positifs, le reste de la division euclidienne de $a^{2^{n}}$ par $p^{n}$ est non nul, et est le même que celui de $a^{2^{m}}$ par $p^{m}$.
|
$A$ partir du fait que $a^{2^{m}} \equiv 1\left(\bmod p^{m}\right)$ pour tout $m$, on a comme $p$ divise $a^{2}-1$, par LTE si $p \geqslant 3$ que si $a>1, V_{p}\left(a^{2^{m}}-1\right)=V_{p}\left(a^{2}-1\right)+V_{p}\left(2^{m-1}\right)=V_{p}\left(a^{2}-1\right)$. En particulier, comme $V_{p}\left(a^{2^{m}}-1\right) \geqslant m$ pour tout $m \geqslant 1, V_{p}\left(a^{2}-1\right) \geqslant m$ pour tout $m$ ce qui est absurde donc $a=1$. Réciproquement, $a=1$ et $p \geqslant 3$ convient comme dans la solution précédente.
Pour le cas $p=2$, de même que précédemment on a $p$ impair, donc 4 divise $p^{2}-1=(p-1)(p+1)$, donc par LTE, comme 4 divise $a^{4}-1$, si $a>1 V_{2}\left(a^{2^{m}}-1\right)=V_{2}\left(a^{2}-1\right)+V_{2}\left(2^{m-1}\right) \geqslant 2+m-1=m+1$, ainsi $a^{2^{m}}-1$ est divisible par $2^{m}$ pour tout m , et on conclut de la même façon que précédemment.
Commentaire des correcteurs : L'exercice est résolu de manière inégale par ceux qui s'y sont essayés. En effet, certains loupent certaines solutions (soit le cas $p=2$ soit le cas $a=1$ : les petites valeurs devraient pourtant permettre de repérer ces solutions. Attention aussi aux utilisations du LTE : le théorème LTE a des hypothèses, il faut les vérifier sous peine d'écrire des choses fausses.
|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "\nExercice 8.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T2",
"year": "2024"
}
|
Determine all quadruplets $(x, y, z, t)$ of strictly positive integers such that $2^{x} 3^{y} + 5^{z} = 7^{\mathrm{t}}$.
|
Suppose $x \geqslant 2$, by looking modulo $4, 1 \equiv 2^{x} 3^{y} + 5^{z} \equiv 7^{\mathrm{t}} \equiv (-1)^{\mathrm{t}} \pmod{4}$, so $t$ is even.
The equation taken modulo 3 becomes $0 + (-1)^{z} \equiv 1 \pmod{3}$, so $z$ is even. In particular, let $z = 2 \mathrm{~b}, \mathrm{t} = 2 \mathrm{c}$, then we have $2^{\mathrm{x}} 3^{\mathrm{y}} = (7^{\mathrm{b}} - 5^{\mathrm{c}})(7^{\mathrm{b}} + 5^{\mathrm{c}})$. The gcd of $7^{\mathrm{b}} + 5^{\mathrm{c}}$ and $7^{\mathrm{b}} - 5^{\mathrm{c}}$ divides their sum and product, so it divides $2^{x} 3^{y}$ and $2 \times 7^{\text{b}}$, thus it divides 2. Since $7^{\mathrm{b}} + 5^{\mathrm{c}}$ and $7^{\mathrm{b}} - 5^{\mathrm{c}}$ are equal modulo 2, they have the same parity, and their product is even, so each is even, their gcd is 2. As
- In the first case, if $\mathrm{c} \geqslant 2$, modulo $25, 7^{\mathfrak{b}} \equiv 2 \pmod{25}$. However, the powers of 7 are $1, 7, -1, -7$ modulo 25, but never 2. Since $\mathrm{c} \neq 0$ because $z \neq 0$, we have $\mathrm{c} = 1$, so $7^{\mathrm{b}} = 5 + 2 = 7$, thus $b = 1$. We then have $12 = 2^{x-1} 3^{y}$, so $(x, y, z, t) = (3, 1, 2, 2)$, which is indeed a solution because $2^{3} \times 3 + 5^{2} = 24 + 25 = 49 = 7^{2}$.
- In the second case, $(7^{\text{b}} - 5^{\mathrm{c}}, 7^{\text{b}} + 5^{\mathrm{c}}) = (2^{\mathrm{x}-1}, 2 \times 3^{y})$. By parity, we have $x \geqslant 2$, and since the case where $x = 2$ is already covered by the previous case, we can assume $x \geqslant 3$. Let $x' = x - 1$, then we have $7^{\mathrm{b}} = 5^{\mathrm{c}} + 2^{\mathrm{x}'}$ with $x' \geqslant 2$. Looking modulo $4, (-1)^{\mathrm{b}} \equiv 1 \pmod{4}$, so $b$ is even. Looking modulo $5, 2^{\mathrm{b}} \equiv 2^{\mathrm{x}'} \pmod{5}$. The powers of 2 alternate between 1, 2, 4, 3 modulo 5, so two powers of 2 have the same value modulo 5 if and only if their exponents are equal modulo 4, so $b$ and $x'$ have the same parity. Looking modulo $3, 1 \equiv (-1)^{\mathfrak{c}} + (-1)^{x'} \pmod{3}$, so $c$ and $x'$ are odd (since $3^{2} \equiv 1 \pmod{8}$). This contradicts the fact that $b$ and $x'$ have the same parity.
Before treating the last case, solve the equation in the case $x = 1$: we have $2 \times 3^{y} + 5^{z} = 7^{\mathrm{t}}$. Modulo 3, we get as before that $z$ is even, so $5^{z} \equiv 25^{z / 2} \equiv 1 \pmod{8}$. In particular, modulo 8, $(-1)^{\mathrm{t}} \equiv 1 + 2 \times 3^{y}$. The right-hand side is 3 if $y$ is even, -1 otherwise, so $t$ is odd and $y$ is odd (since $3^{2} \equiv 1 \pmod{8}$). Then, looking modulo 5, since the powers of 7 are $1, 2, 4, 3, 1$ and the powers of 3 are $1, 3, 4, 2, 1$, we have $7^{\mathrm{t}} \equiv 2$ or 3 because $t$ is odd, and 7 has order 4 (which is even) modulo 5. Since $y$ is odd, we have $2 \times 3^{y} \equiv 1$ or 4 modulo 5 because the order of 3 modulo 5 is even. The equation modulo 5 gives $2 \times 3^{y} \equiv 7^{\mathrm{t}}$, which is impossible. Therefore, there is no solution with $x = 1$. For the third case, $(7^{\mathfrak{b}} - 5^{\mathfrak{c}}, 7^{\mathfrak{b}} + 5^{\mathrm{c}}) = (2 \times 3^{y}, 2^{\mathrm{x}-1})$, we have $7^{\mathrm{b}} - 5^{\mathrm{c}} = 2 \times 3^{y}$. Since $\mathrm{c} > 0$, we are reduced to the previous case, and there is no solution.
Thus, the only solution is $(x, y, z, t) = (3, 1, 2, 2)$.
Comment from the graders: The problem was very difficult and was rarely approached. It is regrettable that the few copies that manage to find the factorization rarely think to consider the gcd of $7^{\mathrm{b}} + 5^{\mathrm{c}}$ and $7^{\mathrm{b}} - 5^{\mathrm{c}}$ (or even simply the parity of these two numbers!) and plunge headlong into large case disjunctions or abusive uses of Zsigmondy's theorem, which many could have avoided (only one student used this theorem effectively).
|
(3, 1, 2, 2)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer tous les quadruplets $(x, y, z, t)$ d'entiers strictement positifs tels que $2^{x} 3^{y}+$ $5^{z}=7^{\mathrm{t}}$ 。
|
Supposons $x \geqslant 2$, en regardant modulo $4,1 \equiv 2^{x} 3^{y}+5^{z} \equiv 7^{\mathrm{t}} \equiv(-1)^{\mathrm{t}}$ $(\bmod 4)$, donc $t$ est pair.
L'équation prise modulo 3 devient $0+(-1)^{z} \equiv 1(\bmod 3)$ donc $z$ est pair. En particulier, posons $z=$ $2 \mathrm{~b}, \mathrm{t}=2 \mathrm{c}$, on a alors $2^{\mathrm{x}} 3^{\mathrm{y}}=\left(7^{\mathrm{b}}-5^{\mathrm{c}}\right)\left(7^{\mathrm{b}}+5^{\mathrm{c}}\right)$. Le pgcd de $7^{\mathrm{b}}+5^{\mathrm{c}}$ et $7^{\mathrm{b}}-5^{\mathrm{c}}$ divise leur somme et leur produit, donc il divise $2^{x} 3^{y}$ et $2 \times 7^{\text {b }}$, ainsi il divise 2 . Or $7^{b}+5^{c}$ et $7^{b}-5^{c}$ sont égaux mod 2 donc ils ont la même parité, et leur produit est pair, donc chacune est pair, leur pgcd vaut 2 . Comme
- Dans le premier cas, si $\mathrm{c} \geqslant 2$, modulo $25,7^{\mathfrak{b}} \equiv 2(\bmod 25)$. Or les puissances de 7 valent $1,7,-1,-7$ modulo 25 , mais jamais 2 . Comme $\mathrm{c} \neq 0$ car $z \neq 0$, on a donc $\mathrm{c}=1$, donc $7^{\mathrm{b}}=$ $5+2=7$, donc $b=1$. On a donc $12=2^{x-1} 3^{y}$ donc $(x, y, z, t)=(3,1,2,2)$, qui réciproquement est solution car $2^{3} \times 3+5^{2}=24+25=49=7^{2}$.
- Dans le second cas $\left(7^{\text {b }}-5^{\mathrm{c}}, 7^{\text {b }}+5^{\mathrm{c}}\right)=\left(2^{\mathrm{x}-1}, 2 \times 3^{y}\right)$. Par parité, on a $x \geqslant 2$, et comme le cas où $x=2$ est déjà couvert par le cas précédent, on peut supposer $x \geqslant 3$. On pose $x^{\prime}=x-1$, on a alors $7^{\mathrm{b}}=5^{\mathrm{c}}+2^{\mathrm{x}^{\prime}}$ avec $x^{\prime} \geqslant 2$. En regardant modulo $4,(-1)^{\mathrm{b}} \equiv 1(\bmod 4)$, donc b est pair. En regardant modulo $5,2^{\mathrm{b}} \equiv 2^{\mathrm{x}^{\prime}}(\bmod 5)$. Or les puissances de 2 alternent entre 1, 2, 4, $3 \bmod 5$, donc deux puissances de 2 ont même valeur modulo 5 si et seulement si leur exposant sont égaux modulo 4 , donc b et $x^{\prime}$ ont même parité. En regardant modulo $3,1 \equiv(-1)^{\mathfrak{c}}+(-1)^{x^{\prime}}(\bmod 3)$ donc c et $x^{\prime}$ sont impairs. Ceci contredit le fait que b et $x^{\prime}$ ont même parité.
Avant de traiter le dernier cas, résolvons l'équation dans le cas $x=1$ : on a $2 \times 3^{y}+5^{z}=7^{\mathrm{t}}$. Modulo 3 , on obtient comme avant que $z$ est pair, donc $5^{z} \equiv 25^{z / 2} \equiv 1(\bmod 8)$. En particulier modulo 8 , $(-1)^{\mathrm{t}} \equiv 1+2 \times 3^{y}$. Le terme de droite vaut 3 si $y$ est pair, -1 sinon, donc $t$ est impair et $y$ est impair $\left(\operatorname{car} 3^{2} \equiv 1(\bmod 8)\right)$. On a alors en regardant modulo 5 , comme les puissances de 7 valent $1,2,4,3,1$ et les puissances de 3 valent $1,3,4,2,1$, on a $7^{\mathrm{t}} \equiv 2$ ou 3 car t est impair, et 7 d'ordre 4 (qui est pair) modulo 5 . Comme y est impair, on a $2 \times 3^{y} \equiv 1$ ou 4 modulo 5 car l'ordre de 3 modulo 5 est pair. Or l'équation modulo 5 donne $2 \times 3^{y} \equiv 7^{\mathrm{t}}$ ce qui est impossible. Il n'y a donc pas de solution avec $x=1$. Pour le troisième cas $\left(7^{\mathfrak{b}}-5^{\mathfrak{c}}, 7^{\mathfrak{b}}+5^{\mathrm{c}}\right)=\left(2 \times 3^{y}, 2^{\mathrm{x}-1}\right)$, on a $7^{\mathrm{b}}-5^{\boldsymbol{c}}=2 \times 3^{y}$. Comme $\mathrm{c}>0$, on est ramené au cas précédent il n'y a pas de solution.
Ainsi la seule solution est $(x, y, z, t)=(3,1,2,2)$.
Commentaire des correcteurs : L'exercice était très difficile et a été très peu abordé. Il est tout de même regrettable que les quelques copies qui réussissent à trouver la factorisation ne pensent que rarement à considérer le pgcd de $7^{z}+5^{\mathrm{t}}$ et $7^{z}-5^{\mathrm{t}}$ (ou même simplement la parité de ces deux nombres!) et se lancent tête baissée dans de grandes disjonctions de cas ou dans des utilisations abusives du théorème de Zsigmondy, que beaucoup auraient pu s'épargner (un seul élève a su utiliser ce théorème vraiment efficacement).
## Exercices Seniors
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 9",
"tier": "T2",
"year": "2024"
}
|
Let $a, b$ be two integers. Show that, if neither $a$ nor $b$ is a multiple of 3, then $a^{4}-b^{2}$ is a multiple of 3.
|
Let's recall that if $k$ is not a multiple of 3, then $k$ is 1 or 2 modulo 3. Thus $\mathrm{k}^{2}$ is $1^{2}=1$ or $2^{2} \equiv 4 \equiv 1(\bmod 3)$: the square of any number not divisible by 4 is 1 modulo 3.
Thus $a^{4}-b^{2} \equiv\left(a^{2}\right)^{2}-b^{2} \equiv 1^{2}-1 \equiv 0(\bmod 3)$, so $a^{4}-b^{2}$ is a multiple of 3.
Examiner's comment: Very well done exercise.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soient $a, b$ deux entiers relatifs. Montrer que, si ni $a$, ni $b$ n'est multiple de 3 , alors $a^{4}-b^{2}$ est multiple de 3.
|
Rappelons que si $k$ n'est pas un multiple de 3 , alors $k$ vaut 1 ou 2 modulo 3. Ainsi $\mathrm{k}^{2}$ vaut $1^{2}=1$ ou $2^{2} \equiv 4 \equiv 1(\bmod 3)$ : tout carré d'un nombre non divisible par 4 vaut 1 modulo 3.
Ainsi $a^{4}-b^{2} \equiv\left(a^{2}\right)^{2}-b^{2} \equiv 1^{2}-1 \equiv 0(\bmod 3)$, donc $a^{4}-b^{2}$ est un multiple de 3 .
Commentaire des correcteurs: Exercice très bien réussi.
|
{
"exam": "French_envois",
"problem_label": "10",
"problem_match": "\nExercice 10.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 10",
"tier": "T2",
"year": "2024"
}
|
Let n be an integer such that $\mathrm{n} \geqslant 2$. We denote d as the greatest divisor of n different from n. We assume that $\mathrm{d}>1$. Prove that $\mathrm{n}+\mathrm{d}$ is not a power of 2.
|
Suppose by contradiction that $n+d$ is a power of 2. Note that $d$ divides $n$, so $d$ divides $n+d$, so $d$ divides a power of 2. Thus $d$ is a power of 2: we set $d=2^{k}$ for some $k \in \mathbb{N}$. We have $k \geqslant 1$ because $d \neq 1$. Let $n=d a=2^{k} a$ with $a \in \mathbb{N}^{*}$. Since $d$ is different from $n$, we have $a \geqslant 2$. Thus $2^{k-1} a$ is a divisor of $n$, greater than or equal to $2^{k}=d$, and different from $n$. By hypothesis $d=2^{k-1} a$, so $a=2$. Thus $n=2^{k+1}$.
We then find $\boldsymbol{n}+\mathrm{d}=2^{\mathrm{k}}(2+1)=3 \times 2^{\mathrm{k}}$ which is not a power of 2, leading to a contradiction. Thus $\mathrm{n}+\mathrm{d}$ is not a power of 2.
Graders' comment: Well-executed exercise, however, some students go too fast and forget steps, essential to arrive at contradictions, then unjustified.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit n un entier vérifiant $\mathrm{n} \geqslant 2$. On note d le plus grand diviseur de n différent de n . On suppose que $\mathrm{d}>1$. Démontrer que $\mathrm{n}+\mathrm{d}$ n'est pas une puissance de 2 .
|
Supposons par l'absurde que $n+d$ est une puissance de 2 . Notons que divise $n$, donc $d$ divise $n+d$, donc $d$ divise une puissance de 2 . Ainsi $d$ est une puissance de 2 : on pose $d=2^{k}$ pour un certain $k \in \mathbb{N}$. On a $k \geqslant 1$ car $d \neq 1$. Posons $n=d a=2^{k} a$ avec $a \in \mathbb{N}^{*}$. Comme dest différent de $n$, on a $a \geqslant 2$. Ainsi $2^{k-1} a$ est un diviseur de $n$, supérieur ou égal à $2^{k}=d$, et différent de $n$. Par hypothèse $d=2^{k-1} a$, donc $a=2$. Ainsi $n=2^{k+1}$.
On trouve alors $\boldsymbol{n}+\mathrm{d}=2^{\mathrm{k}}(2+1)=3 \times 2^{\mathrm{k}}$ qui n'est pas une puissance de 2 , ce qui est une contradiction. Ainsi $\mathrm{n}+\mathrm{d}$ n'est pas une puissance de 2 .
Commentaire des correcteurs: Exercice bien réussi, cependant quelques élèves vont un peu trop vite et oublient des étapes, essentielles pour aboutir à des contradictions, alors injustifiées.
|
{
"exam": "French_envois",
"problem_label": "11",
"problem_match": "\nExercice 11.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 11",
"tier": "T2",
"year": "2024"
}
|
Determine all quadruplets $(a, b, c, d)$ of positive integers with $a, b, c$ strictly positive such that
\[
\begin{aligned}
& \operatorname{LCM}(b, c)=a+d \\
& \operatorname{LCM}(c, a)=b+d \\
& \operatorname{LCM}(a, b)=c+d
\end{aligned}
\]
|
Given the system is symmetric, we assume that $c$ is the maximum of $\mathrm{a}, \mathrm{b}$, and $c$. Since $c$ divides $\operatorname{LCM}(\mathrm{b}, \mathrm{c})$, $c$ divides $a+d$. Since $c$ divides $\operatorname{LCM}(\mathrm{c}, \mathrm{a})$, $c$ divides $b+d$, so $c$ divides $a+d-(b+d)=a-b$. Since $-c<a-b<c$, we have $a=b$. The last line then gives $a=\operatorname{LCM}(a, b)=c+d \geqslant c$. To have equality, we must have $d=0$ and $a=c$.
Conversely, if $\mathrm{a}=\mathrm{b}=\mathrm{c}$ and $\mathrm{d}=0$, each equation is equivalent to $\mathrm{a}=\mathrm{a}+0$, which is true. The quadruplets that are solutions are therefore the $(a, a, a, 0)$ for $a \in \mathbb{N}^{*}$.
Graders' comments: The exercise is very well done, however, some students forgot to verify that the solutions found were solutions to the system, which penalized them.
|
(a, a, a, 0)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer tous les quadruplets ( $a, b, c, d$ ) d'entiers positifs avec $a, b, c$ strictement positifs tels que
$$
\begin{aligned}
& \operatorname{PPCM}(b, c)=a+d \\
& \operatorname{PPCM}(c, a)=b+d \\
& \operatorname{PPCM}(a, b)=c+d
\end{aligned}
$$
|
Le système étant symétrique, on suppose que c est le maximum de $\mathrm{a}, \mathrm{b}$ et c . Comme c divise $\operatorname{PPCM}(\mathrm{b}, \mathrm{c})$, c divise $a+d$. Comme c divise $\operatorname{PPCM}(\mathrm{c}, \mathrm{a})$, c divise $b+\mathrm{d}$, donc c divise $a+d-(b+d)=a-b$. Or $-c<a-b<c$ donc $a=b$. La dernière ligne donne alors $a=\operatorname{PPCM}(a, b)=c+d \geqslant c$. Pour avoir égalité, on a donc $d=0$ et $a=c$.
Réciproquement, si $\mathrm{a}=\mathrm{b}=\mathrm{c}$ et $\mathrm{d}=0$, chaque équation équivaut à $\mathrm{a}=\mathrm{a}+0$, qui est vrai. Les quadruplets solution sont donc les $(a, a, a, 0)$ pour $a \in \mathbb{N}^{*}$.
Commentaire des correcteurs: L'exercice est très bien réussi, cependant quelques élèves ont oublié de vérifier que les solutions trouvées étaient solutions du système ce qui les a pénalisés.
|
{
"exam": "French_envois",
"problem_label": "12",
"problem_match": "\nExercice 12.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 12",
"tier": "T2",
"year": "2024"
}
|
An integer $n \geqslant 2$ is written on the board. Each day, someone chooses $p$, a prime divisor of the integer $n$ written on the board, erases it, and writes $n+\frac{n}{p}$ in its place. Show that $p=3$ is chosen infinitely many times.
|
Let's fix $N \in \mathbb{N}$. Denote $2^{a_{k}} 3^{b_{k}} \mathbf{c}_{k}$ as the integer written on the board on day $k$, where $c_{k}$ is the product of primes distinct from 2 and 3. Suppose, for the sake of contradiction, that we can never choose $p=3$ from day $N$ onwards.
If on the $k$-th day we choose $p \neq 2,3$, then the number written on the board becomes $2^{a_{k}} 3^{b_{k}} \frac{c_{k}}{p}(p+1)$. Let $p+1=2^{b} 3^{c} d$ where $b, c$, and $d$ are positive integers and $d$ is coprime with 2 and 3. Since $p$ is a prime and different from 2, it is odd, so $b \geqslant 1$, thus $d \leqslant \frac{p+1}{2}$. Therefore, as the number written on the board is $2^{a_{k}+b} 3^{b_{k}+c} \frac{c_{k}}{p} d$, we have $a_{k+1}=a_{k}+b, b_{k+1}=b_{k}+c$, and $c_{k+1}=\frac{c_{k}}{p} d \leqslant c_{k} \frac{p+1}{2 p}<c_{k}$.
If on the $k$-th day we choose $p=2$, the number written on the board becomes $\frac{3}{2} 2^{a_{k}} 3^{b_{k}} c_{k}=2^{a_{k}-1} 3^{b_{k}+1} c_{k}$. In particular, the sequence $\left(c_{k}\right)_{k \geqslant N}$ is decreasing and strictly positive. It cannot therefore decrease strictly infinitely often, otherwise it would become negative. Therefore, from a certain day $k>N$, we no longer choose $p \neq 2,3$, so $p=2$ is chosen every day from the $k$-th day onwards.
If from day $k>N$ we only choose $p=2$, then $a_{j+1}=a_{j}-1$ for all $j \geqslant k$. Therefore, the sequence of integers $\left(a_{j}\right)_{j \geqslant k}$ strictly decreases, and it must therefore become strictly negative, which is absurd.
Thus, we are forced to choose $p=3$ at least once after the $N$-th day.
Suppose that $p=3$ is not chosen infinitely often. From a certain day, denoted $N$, $p=3$ is no longer chosen. This contradicts what we have just proven: $p=3$ is therefore chosen infinitely often.
Comment from the graders: Some students misunderstood the problem: it was to prove that one is forced to choose $p=3$ infinitely often regardless of the choices made, not that one could arrange for it to be the case. The problem is generally well approached by those who correctly interpreted it, but many students lack rigor. The challenge was to find a rigorous argument (thus a priori a monovariant, whether it be the one proposed in the solution, the reverse lexicographic order of the exponents, or many other possibilities) to clarify the phrase read in too many copies: "the prime factors decrease." This phrase, devoid of mathematical meaning, does not constitute a valid argument, and one must clarify the intuition behind it. This is a common pitfall in combinatorics: it is sometimes delicate to move from intuition to a rigorous argument, and often a significant part of the difficulty of the problem lies precisely in this step.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Un entier $n \geqslant 2$ est écrit au tableau. Chaque jour, quelqu'un choisit $p$ un diviseur premier de l'entier écrit $n$ au tableau, efface celui-ci et écrit $n+\frac{n}{p}$ à la place. Montrer que $p=3$ est choisi une infinité de fois.
|
Fixons $N \in \mathbb{N}$. Notons $2^{a_{k}} 3^{b_{k}} \mathbf{c}_{k}$ l'entier écrit au tableau le jour $k$, avec $c_{k}$ produit de nombres premiers distincts de 2 et 3 . Supposons par l'absurde qu'on peut ne jamais choisir $p=3$ à partir du jour $N$.
Si le $k$-ième jour on choisit $p \neq 2,3$, alors le nombre écrit au tableau devient $2^{a_{k}} 3^{b_{k}} \frac{c_{k}}{p}(p+1)$. Posons $p+1=2^{b} 3^{c} d$ avec $b, c$, d des entiers positifs et d premier avec 2 et 3 . Comme $p$ est premier et différent de 2 , il est pair, donc $a \geqslant 1$, donc $d \leqslant \frac{p+1}{2}$. Ainsi comme le nombre écrit au tableau est $2^{a_{k}+a} 3^{b_{k}+b} \frac{c_{k}}{p} d$, donc $a_{k+1}=a_{k}+a, b_{k+1}=b_{k}+b$ et $c_{k+1}=\frac{c_{k}}{p} d \leqslant c_{k} \frac{p+1}{2 p}<c_{k}$.
Si le $k$-ième jour on choisit $p=2$, le nombre écrit au tableau devient $\frac{3}{2} 2^{a_{k}} 3^{b_{k}} c_{k}=2^{a_{k}-1} 3^{b_{k}+1} c_{k}$. En particulier, la suite $\left(c_{k}\right)_{k} \geqslant \mathrm{~N}$ décroît et est strictement positive. Elle ne peut donc décroître strictement infiniment souvent, sinon elle deviendrait négative. Donc à partir d'un certain jour $k>N$, on ne choisit plus $p \neq 2,3$, donc $p=2$ est choisit chaque jour à partir du k-ième jour.
Or si à partir du jour $k>N$ on ne choisit que $p=2$, alors $a_{j+1}=a_{j}-1$ pour tout $j \geqslant k$. Donc la suite d'entiers $\left(a_{j}\right)_{j \geqslant k}$ décroît strictement, elle doit donc devenir strictement négative ce qui est absurde.
Ainsi, on est obligé de choisir au moins une fois $p=3$ après le N -ième jour.
Supposons que $p=3$ n'est pas choisi une infinité de fois. A partir d'un certain jour, noté $N, p=3$ n'est plus jamais choisi. Cela contredit ce qu'on vient de prouver : $p=3$ est donc choisi une infinité de fois.
Commentaire des correcteurs : Certains élèves ont mal compris l'énoncé : il s'agissait de prouver que l'on était obligé de choisir $p=3$ une infinité de fois quels que soient les choix effectués, pas que l'on pouvait s'arranger pour que ce soit le cas. L'exercice est généralement bien abordé par ceux qui l'ont correctement interprété, mais de trop nombreux élèves manquent de rigueur. L'enjeu était de trouver un argument rigoureux (donc a priori un monovariant, que ce soit celui proposé par le corrigé, l'ordre lexicographique inversé des exposants ou beaucoup d'autres possibilités) pour clarifier la phrase lue dans de trop nombreuses copies : "les facteurs premiers décroissent". Cette phrase dénuée de sens mathématique ne constitue en aucun cas un argument recevable, il faut clarifier l'intuition qui se cache derrière. C'est un écueil que l'on croise souvent en combinatoire : il est parfois délicat de passer de l'intuition à l'argument rigoureux, et souvent une partie de la difficulté de l'exercice réside justement dans cette étape.
|
{
"exam": "French_envois",
"problem_label": "13",
"problem_match": "\nExercice 13.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 13",
"tier": "T2",
"year": "2024"
}
|
Let $k$ be an integer coprime with $n$ satisfying $1 \leqslant k < n$. Augustin colors the integers of $\{1,2, \ldots, n-1\}$ with as many colors as he wishes. However, if $\mathbf{j}$ is an integer satisfying $1 \leqslant j \leqslant n-1$, the integers $j$ and $n-j$ are of the same color. Additionally, if $i$ is an integer satisfying $1 \leqslant i \leqslant n$ and $i \neq k$, the integers $i$ and $|i-k|$ are of the same color.
Prove that Augustin has colored all the integers the same color.
|
For $k=1$, we see that $n$ has the same color as $n-1$, then that $n-2$ has the same color as $n-1$, etc., and all integers have the same color.
For $k=2$, $n$ is odd and we see that $n, n-2, \ldots, 1$ have the same color, then that $n-1$ has the same color as 1, and that $n-1, n-3, \ldots, 2$ have the same color.
By doing the same for small values of $k$, we realize that we always manage to show successively that $n-k, \ldots, n-(n-1)k$ taken modulo $n$ are all the same color. Let's try to formalize this.
Let $c$ be the color of $\boldsymbol{n}$. We prove by induction the following property for all $\boldsymbol{j} \in\{1, \ldots, \mathfrak{n}-1\}$: $\mathcal{P}(\mathfrak{j})$: "The remainder of the Euclidean division of $n-j k$ is not congruent to 0 modulo $n$, and is colored with the color $c$."
Initialization: for $j=1$, since $1 \leqslant n-k \leqslant n-1$, the remainder of the Euclidean division of $n-k$ is $n-k$, is not congruent to 0 modulo $n$, and is colored with the color $c$.
Induction: Let $j \in\{0, \ldots, n-2\}$, suppose that $P(j)$ is true and let's show $P(j+1)$. Let $r$ be the remainder of the Euclidean division of $n-j k$ by $n$.
First case: if $r>k$, then $n>r \geqslant r-k>0$. Now $r-k \equiv n-j k-k \equiv n-(j+1) k(\bmod n)$. Therefore, the remainder of the Euclidean division of $n-j k$ by $n$ is $r-k$, is non-zero, and is the same color as $r$, hence color $c$, which concludes.
Second case: if $r=k$, then $n-j k \equiv k(\bmod n)$, i.e., $(j+1) k \equiv 0(\bmod n)$. Since $n$ is coprime with $k$, and divides $(\mathfrak{j}+1) \mathrm{k}, \mathrm{n}$ divides $\boldsymbol{j}+1$, but since $\boldsymbol{j}+1 \in\{1 \ldots, n-1\}$, this case is impossible.
Third case: if $k>r$, then $k-r$ is the same color as $r$, hence color $c$. Moreover, we have $1 \leqslant k-r \leqslant k \leqslant n-1$, so $n-(k-r)$ satisfies $1 \leqslant n-(k-r) \leqslant n-1$ and is color $c$. Now $n-(k-r) \equiv r-k \equiv n-(j+1) k(\bmod n)$, so $n-(k-r)$ is the remainder of the Euclidean division of $\mathrm{n}-(\mathrm{j}+1) \mathrm{k}$ by $n$, is non-zero, and is color $c$, which concludes.
This concludes the induction.
Now let $\boldsymbol{j} \in\{1, \ldots, \mathfrak{n}-1\}$. There exists $\ell \in\{0 \ldots, \mathfrak{n}-1\}$ such that $\boldsymbol{j} \equiv \boldsymbol{n}-\ell k(\bmod \boldsymbol{n})$: indeed, this is equivalent to $\ell k \equiv n-j(\bmod n)$, or to $\ell \equiv(n-\mathfrak{j}) k^{-1}(\bmod n)$ (where $k^{-1}$ is the inverse of $k$ modulo $n$, which exists because $k$ is coprime with $n$), and admits a solution in $\{0 \ldots, \mathrm{n}-1\}$. In particular, $j$ is the remainder of the division of $n-\ell j$ by $n$, so it is color $c$. Thus all integers from 1 to $n-1$ have the same color as $n$, so all integers are colored the same color.
Comment from the graders: The exercise is relatively poorly solved: many provided proofs are incomplete, as they forget certain constraints ($i \neq k$ to say that $|i-k|$ and $i$ have the same color, forgetting that $i$ and $i+k$ do not have the same color if $i>n-k$, etc.). It is crucial that students re-read their work with a fresh mind: some copies make no sense when re-read with a fresh mind, and several students could have avoided a setback by re-reading their work with a clear head.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit k un entier premier avec n vérifiant $1 \leqslant \mathrm{k}<\mathrm{n}$. Augustin colorie les entiers de $\{1,2, \ldots, \mathfrak{n}-1\}$ avec autant de couleur qu'il le souhaite. Cependant, si $\boldsymbol{j}$ est un entier vérifiant $1 \leqslant \mathfrak{j} \leqslant$ $n-1$, les entiers $j$ et $n-j$ sont de la même couleur. De plus, si $i$ est un entier vérifiant $1 \leqslant i \leqslant n$ et $i \neq k$, les entiers $i$ et $|i-k|$ sont de la même couleur.
Démontrer que Augustin a colorié tous les entiers de la même couleur.
|
Pour $k=1$, on voit que $n$ a la même couleur que $n-1$, puis que $n-2$ à la même couleur que $n-1$, etc et tous les entiers ont la même couleur.
Pour $k=2$, $n$ est impair et on voit que $n, n-2, \ldots, 1$ ont la même couleur, puis que $n-1$ a la même couleur que 1 , et que $n-1, n-3, \ldots, 2$ ont la même couleur.
En faisant la même chose pour des petites valeurs de $k$, on se rend compte qu'on arrive à chaque fois à montrer successivement que $n-k, \ldots, n-(n-1) k$ pris modulo $n$ sont tous de la même couleur. Essayons de formaliser cela.
Notons c la couleur de $\boldsymbol{n}$. On montre par récurrence la propriété suivante pour tout $\boldsymbol{j} \in\{1, \ldots, \mathfrak{n}-1\}$ : $\mathcal{P}(\mathfrak{j})$ : "Le reste de la division euclidienne de $n-j k n$ 'est pas congru à 0 modulo $n$, et est colorié avec la couleur c.
Initialisation : pour $j=1$, comme $1 \leqslant n-k \leqslant n-1$, le reste de la division euclidienne de $n-k$ vaut $n-k$, n'est pas congru à 0 modulo $n$, et est colorié avec la couleur $c$.
Hérédité : Soit $j \in\{0, \ldots, n-2\}$, supposons que $P(j)$ est vraie et montrons $P(j+1)$. Notons $r$ le reste de la division euclidienne de $n-j k$ par $n$.
Premier cas : si $r>k$, alors $n>r \geqslant r-k>0$. Or $r-k \equiv n-j k-k \equiv n-(j+1) k(\bmod n)$. Donc le reste de la division euclidienne de $n-j k$ par $n$ vaut $r-k$, est non nul et est de la même couleur que $r$, donc de la couleur $c$ ce qui conclut.
Second cas, si $r=k$, alors $n-j k \equiv k(\bmod n)$, i.e. $(j+1) k \equiv 0(\bmod n)$. Comme $n$ est premier avec $k$, et divise $(\mathfrak{j}+1) \mathrm{k}, \mathrm{n}$ divise $\boldsymbol{j}+1$, mais comme $\boldsymbol{j}+1 \in\{1 \ldots, n-1\}$, ce cas est impossible.
Troisième cas : si $k>r$, alors $k-r$ est de la couleur de de $r$, donc de la couleur $c$. De plus on a $1 \leqslant k-r \leqslant k \leqslant n-1$, donc $n-(k-r)$ vérifie $1 \leqslant n-(k-r) \leqslant n-1$ et est de la couleur $c$. Or $n-(k-r) \equiv r-k \equiv n-(j+1) k(\bmod n)$, donc $n-(k-r)$ est le reste de la division euclidienne de $\mathrm{n}-(\mathrm{j}+1) \mathrm{k}$ par n , est non nul et de couleur c , ce qui conclut.
Ceci conclut l'hérédité.
Maintenant donnons nous $\boldsymbol{j} \in\{1, \ldots, \mathfrak{n}-1\}$. Il existe $\ell \in\{0 \ldots, \mathfrak{n}-1\}$ tel que $\boldsymbol{j} \equiv \boldsymbol{n}-\ell k(\bmod \boldsymbol{n}):$ en effet, ceci est équivalent à $\ell k \equiv n-j(\bmod n)$, soit à $\ell \equiv(n-\mathfrak{j}) k^{-1}(\bmod n)\left(\right.$ où $k^{-1}$ est l'inverse de k modulo n , qui existe car k est premier avec n ), et admet une solution dans $\{0 \ldots, \mathrm{n}-1\}$. En particulier, $j$ est le reste de la divison euclidienne de $n-\ell j$ par $n$, donc de couleur $c$. Ainsi tous les entiers de 1 à $n-1$ ont la même couleur que $n$, donc tous les entiers sont coloriés de la même couleur.
Commentaire des correcteurs : L'exercice est relativement mal résolu : beaucoup de preuves fournies s'avèrent incomplètes, car elles oublient certaines contraintes ( $i \neq k$ pour dire que $|i-k|$ et $i$ ont la même couleur, oubli que $i$ et $i+k$ n'ont pas la même couleur si $i>n-k$, etc). Il est crucial que les élèves se relisent à froid : certaines copies n'ont vraiment pas de sens en les relisant à froid, et plusieurs élèves auraient évité une déconvenue en relisant leur production à tête reposée.
|
{
"exam": "French_envois",
"problem_label": "14",
"problem_match": "\nExercice 14.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 14",
"tier": "T2",
"year": "2024"
}
|
Let $\left(P_{n}\right)_{n \in \mathbb{N}}$ be a sequence of polynomials with integer coefficients. Suppose there exists a monic polynomial $Q$ with integer coefficients such that $P_{n+1}-P_{n}=Q$ for all $n \geqslant 0$. Furthermore, suppose that for all $\mathrm{n} \geqslant 0, \mathrm{P}_{\mathrm{n}}$ has an integer root. Show that we are in one of the following two cases:
- $P_{0}$ and $Q$ have a common integer root
- There exists a polynomial with integer coefficients $R$ such that $\mathrm{P}_{0}=R Q$ and the degree of $R$ is 1.
|
Suppose that $P_{0}$ and $Q$ have no common integer roots. Note that by immediate induction $P_{n}=P_{0}+n Q$ for all $n \geqslant 0$. Let $x_{n}$ be an integer root of $P_{n}$ for all $n \geqslant 0$, we have that $n Q\left(x_{n}\right)=-P_{0}\left(x_{n}\right)$, so $Q\left(x_{n}\right)$ divides $P_{0}\left(x_{n}\right)$.
Note that if $x_{k}=x_{j}$ with $k \neq j$, then $P_{0}\left(x_{k}\right)+k Q\left(x_{k}\right)=0=P_{0}\left(x_{j}\right)+j Q\left(x_{j}\right)$, so $(k-j) Q\left(x_{k}\right)=0$, thus $Q\left(x_{k}\right)=0$. Therefore, $P_{0}\left(x_{k}\right)=0$, so $P_{0}$ and $Q$ have a common integer root, which is contradictory. Thus the sequence $\left(x_{k}\right)_{k \geqslant 0}$ is injective and therefore takes arbitrarily large values.
Perform the Euclidean division of $P_{0}$ by $Q$. Since $Q$ is monic with integer coefficients (and $P_{0}$ has integer coefficients), there exist polynomials $R$ and $S$ with integer coefficients such that $P_{0}=Q R+S$ with $S$ of degree less than or equal to $Q$.
Evaluating at $x_{n}, P_{0}\left(x_{n}\right)=Q\left(x_{n}\right) R\left(x_{n}\right)+S\left(x_{n}\right)$, so since $Q\left(x_{n}\right)$ divides $P_{0}\left(x_{n}\right), Q\left(x_{n}\right)$ divides $S\left(x_{n}\right)=P_{0}\left(x_{n}\right)-Q\left(x_{n}\right) R\left(x_{n}\right)$. For any integer $k$ with $|k|$ sufficiently large, since the degree of $S$ is strictly less than that of $Q,|S(k)|<|Q(k)|$. Since the sequence $(x_{n})$ takes arbitrarily large values, there are infinitely many $n$ such that $|S\left(x_{n}\right)|<|Q\left(x_{n}\right)|$. Since $Q\left(x_{n}\right)$ divides $S\left(x_{n}\right)$, we deduce that there are infinitely many $n$ such that $S\left(x_{n}\right)=0$. Since the sequence is injective, $S$ has infinitely many roots, so $S=0$. Thus $P_{0}=Q R$.
Furthermore, evaluating at $x_{n}$, we have $-n Q\left(x_{n}\right)=P_{0}\left(x_{n}\right)=Q\left(x_{n}\right) R\left(x_{n}\right)$. If $Q\left(x_{n}\right)=0$, then $P_{0}\left(x_{n}\right)=0$ and $P_{0}$ and $Q$ have a common root, contradiction. Thus $Q\left(x_{n}\right) \neq 0$, so $R\left(x_{n}\right)=-n$. Thus for any integer $N \geqslant 0$, there are at least $N$ integers $y$ such that $R(y) \in[-N, N]$.
If the degree of $R$, denoted $d$, is at least 2, for a sufficiently large $M$ and for a $C>0$, we have for all $x$ such that $|x| \geqslant M,|R(x)| \geqslant C|x|^{d}$. Thus for sufficiently large $N$, the number of integers such that $|R(x)| \leqslant N$ is less than $2 M+1$ (the number of integers in $[-M, M]$), plus the number of integers $|x| \geqslant M$ such that $|P(x)| \leqslant N$. For these $x$, we have $C|x|^{d} \leqslant N$ so $|x| \leqslant(N / C)^{1 / d}$. Thus there are at most $2 M+1+2(N / C)^{1 / d}+1$ integers such that $P(y) \in[-N, N]$, which is strictly less than $N$ for sufficiently large $N$, which is contradictory.
Thus the degree of $R$ is at most 1. Since we have $R\left(x_{n}\right)=-n$ for all $n$, the degree of $R$ is 1.
Alternatively, to prove that the degree of $R$ is 1, we could note that for all $n, x_{n+1}-x_{n}$ divides $R\left(x_{n+1}\right)-R\left(x_{n}\right)=-1$. In particular, $x_{n+1}-x_{n}= \pm 1$ for all $n$. Since the sequence $\left(x_{n}\right)$ is injective, we cannot have $x_{n+1}-x_{n}=1$ and $x_{n+2}-x_{n+1}=-1$, or have $x_{n+1}-x_{n}=-1$ and $x_{n+2}-x_{n+1}=1$ otherwise $x_{n}=x_{n+2}$. Thus, by easy induction, either for all $n$, $x_{n+1}-x_{n}=1$, and thus $x_{n}=x_{0}+n\left(x_{1}-x_{0}\right)$, or $x_{n+1}-x_{n}=-1$, and thus $x_{n}=x_{0}-n\left(x_{1}-x_{0}\right)$.
In the first case, by setting $S(X)=R\left(x_{0}+X\left(x_{1}-x_{0}\right)\right)-X$, we see that $Q(n)=0$ for all $n$. Since $S$ is a polynomial, it is the zero polynomial, so for all real $x$, $R\left(x_{0}+x\left(x_{1}-x_{0}\right)\right)=x$. Thus by setting $x=\frac{y-x_{0}}{x_{1}-x_{0}}$ (which is well-defined since $x_{1} \neq x_{0}$), we have that $R(y)=\frac{y-x_{0}}{x_{1}-x_{0}}$ for all $y$, so by identification $R(X)=\frac{X-x_{0}}{x_{1}-x_{0}}: R$ is of degree 1.
In the second case, by setting $S(X)=R\left(x_{0}-X\left(x_{1}-x_{0}\right)\right)-X$, we see that $Q(n)=0$ for all $n$. Since $S$ is a polynomial, it is the zero polynomial, so for all real $x$, $R\left(x_{0}-x\left(x_{1}-x_{0}\right)\right)=x$. Thus by setting $x=\frac{x_{0}-y}{x_{1}-x_{0}}$ (which is well-defined since $x_{1} \neq x_{0}$), we have that $R(y)=\frac{x_{0}-y}{x_{1}-x_{0}}$ for all $y$, so by identification $R(X)=\frac{X-x_{0}}{x_{1}-x_{0}}: R$ is of degree 1.
Comment from the graders: The exercise was very well handled by the students who approached it. Almost all of them correctly saw that an $R$ of degree at least 2 would "grow and shrink too quickly" to hit all negative integers, but some did not rigorously formalize this true idea. Additionally, it is important to keep in mind that we can consider the Euclidean division of $P_{0}$ by $Q$ in $\mathbb{Z}[X]$ only because $Q$ is monic. Finally, never forget the trivial cases: it is a shame to see students lose a point for not specifying that $R$ cannot be constant.
|
proof
|
Yes
|
Incomplete
|
proof
|
Algebra
|
Soit $\left(P_{n}\right)_{n \in \mathbb{N}}$ une suite de polynômes à coefficients entiers. On suppose qu'il existe un polynôme $Q$ unitaire à coefficient entier tel que $P_{n+1}-P_{n}=Q$ pour tout $n \geqslant 0$. On suppose de plus que pour tout $\mathrm{n} \geqslant 0, \mathrm{P}_{\mathrm{n}}$ a une racine entière. Montrer qu'on est dans un des deux cas suivants :
- $P_{0}$ et $Q$ ont une racine entière en commun
- Il existe un polynôme à coefficients entiers R tel que $\mathrm{P}_{0}=R Q$ et le degré de R est 1 .
|
Supposons que $\mathrm{P}_{0}$ et Q n'ont pas de racines entière en commun. Notons que par récurrence immédiate $P_{n}=P_{0}+n Q$ pour tout $n \geqslant 0$. Notons $x_{n}$ une racine entière de $P_{n}$ pour tout $n \geqslant 0$, on a que $n Q\left(x_{n}\right)=-P_{0}\left(x_{n}\right)$, donc $Q\left(x_{n}\right)$ divise $P_{0}\left(x_{n}\right)$.
Notons que si $x_{k}=x_{j}$ avec $k \neq j$, alors $P_{0}\left(x_{k}\right)+k Q\left(x_{k}\right)=0=P_{0}\left(x_{j}\right)+j Q\left(x_{j}\right)$, donc $(k-j) Q\left(x_{k}\right)=$ 0 , donc $Q\left(x_{k}\right)=0$. Ainsi $P_{0}\left(x_{k}\right)=0$, donc $P_{0}$ et $Q$ ont une racine entière en commun, ce qui est contradictoire. Ainsi la suite $\left(x_{k}\right)_{k \geqslant 0}$ est injective donc prend des valeurs arbitrairement grandes.
Faisons la division euclidienne de $\mathrm{P}_{0}$ par Q . Comme Q est unitaire à coefficient entier (et $\mathrm{P}_{0}$ à coefficients entiers), il existe des polynômes $R$ et $S$ à coefficients entiers tels que $P_{0}=Q R+S$ avec $S$ de degré inférieur ou égal à Q.
En évaluant en $x_{n}, P_{0}\left(x_{n}\right)=Q\left(x_{n}\right) R\left(x_{n}\right)+S\left(x_{n}\right)$, donc comme $Q\left(x_{n}\right)$ divise $P_{0}\left(x_{n}\right), Q\left(x_{n}\right)$ divise $S\left(x_{n}\right)=P_{0}\left(x_{n}\right)-Q\left(x_{n}\right) R\left(x_{n}\right)$. Or pour tout entier $k$ avec $|k|$ assez grand, comme le degré de $S$ est strictement inférieur à celui de $\mathrm{Q},|S(k)|<|\mathrm{Q}(\mathrm{k})|$. Comme la suite ( $\mathrm{x}_{\mathrm{n}}$ ) prend des valeurs arbitrairement grande, il existe une infinité de $n$ tels que $\left|S\left(x_{n}\right)\right|<\left|Q\left(x_{n}\right)\right|$. Comme $Q\left(x_{n}\right)$ divise $S\left(x_{n}\right)$, on en déduit qu'il existe une infinité de $n$ tels que $S\left(x_{n}\right)=0$. Comme la suite est injective, $S$ a une infinité de racine, donc $S=0$. Ainsi $P_{0}=Q R$.
De plus, en évaluant en $x_{n}$, on a $-n Q\left(x_{n}\right)=P_{0}\left(x_{n}\right)=Q\left(x_{n}\right) R\left(x_{n}\right)$. Si $Q\left(x_{n}\right)=0$, alors $P_{0}\left(x_{n}\right)=0$ et $P_{0}$ et $Q$ ont une racine en commun, contradiction. Ainsi $Q\left(x_{n}\right) \neq 0$, donc $R\left(x_{n}\right)=-n$. Ainsi pour tout entier $N \geqslant 0$, il existe au moins $N$ entiers $y$ tels que $R(y) \in[-N, N]$.
Or si le degré de $R$ noté $d$ vaut au moins 2 , pour un $M$ assez grand et pour un $C>0$, on a pour tout $x$ vérifiant $|x| \geqslant M,|R(x)| \geqslant C|x|^{d}$. Ainsi pour $N$ assez grand, le nombre d'entier tel que $|R(x)| \leqslant N$ est plus petit que $2 M+1$ (le nombre d'entiers dans $[-M, M]$ ), auquel on ajoute le nombre d'entiers $|x| \geqslant M$ tel que $|P(x)| \leqslant N$. Pour ces $x$, on a $C|x|^{d} \leqslant N$ donc $|x| \leqslant(N / C)^{1 / d}$. Ainsi on a au plus $2 M+1+2(N / c)^{1 / d}+1$ entiers tels que $P(y) \in[-n, n]$, ce qui est strictement inférieurs à $N$ pour $N$ assez grand, ce qui est contradictoire.
Ainsi le degré de $R$ est au plus 1 . Comme on a $R\left(x_{n}\right)=-n$ pour tout $n$, le degré de $R$ vaut 1 .
Alternativement, pour prouver que le degré de $R$ valait $n$, on pouvait remarquer que pour tout $n, x_{n+1}-x_{n}$ divise $R\left(x_{n+1}\right)-R\left(x_{n}\right)=-1$. En particulier $x_{n+1}-x_{n}= \pm 1$ pour tout $n$. Comme la suite $\left(x_{n}\right)$ est injective, on ne peut avoir $x_{n+1}-x_{n}=1$ et $x_{n+2}-x_{n+1}=-1$, ou avoir $x_{n+1}-x_{n}=-1$ et $x_{n+2}-x_{n+1}=1$ sinon $x_{n}=x_{n+2}$. Ainsi on a facilement par récurrence que soit pour tout $n$, $x_{n+1}-x_{n}=1$, et donc $x_{n}=x_{0}+n\left(x_{1}-x_{0}\right)$, soit $x_{n+1}-x_{n}=-1$, et donc $x_{n}=x_{0}-n\left(x_{1}-x_{0}\right)$.
Dans le premier cas, en posant $S(X)=R\left(x_{0}+X\left(x_{1}-x_{0}\right)\right)-X$, on voit que $Q(n)=0$ pour tout $n$. Comme $S$ est un polynôme, c'est le polynôme nul, donc pour tout $x$ réel, $R\left(x_{0}+x\left(x_{1}-x_{0}\right)\right)=x$. Ainsi en posant $x=\frac{y-x_{0}}{x_{1}-x_{0}}$ (qui est bien défini car $x_{1} \neq x_{0}$ ), on a que $R(y)=\frac{y-x_{0}}{x_{1}-x_{0}}$ pour tout $y$, donc par identification $R(X)=\frac{X-x_{0}}{x_{1}-x_{0}}: R$ est de degré 1 .
Dans le second cas, en posant $S(X)=R\left(x_{0}-X\left(x_{1}-x_{0}\right)\right)-X$, on voit que $Q(n)=0$ pour tout $n$. Comme $S$ est un polynôme, c'est le polynôme nul, donc pour tout $x$ réel, $R\left(x_{0}-x\left(x_{1}-x_{0}\right)\right)=x$. Ainsi en posant $x=\frac{x_{0}-y}{x_{1}-x_{0}}$ (qui est bien défini car $x_{1} \neq x_{0}$ ), on a que $R(y)=\frac{x_{0}-y}{x_{1}-x_{0}}$ pour tout $y$, donc par identification $R(X)=\frac{X-x_{0}}{x_{1}-x_{0}}: R$ est de degré 1 .
Commentaire des correcteurs: L'exercice a été très bien traité par les élèves qui l'ont abordé. Presque tous ont bien vu qu'un R de degré au moins 2 " croirait et décroirait trop vite" pour attendre tous les entiers négatifs, mais certains n'ont pas rendu cette idée, certes vraie, rigoureuse. De plus, il faut garder
en tête qu'on peut considérer la divison euclidienne de $P_{0}$ par $Q$ dans $Z[X]$ seulement parce que $Q$ est unitaire. Enfin, ne jamais oublier les cas triviaux : il est dommage de voir des élèves perdre un point pour ne pas avoir préciser que $R$ ne pouvait être constant.
|
{
"exam": "French_envois",
"problem_label": "15",
"problem_match": "\nExercice 15.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 15",
"tier": "T2",
"year": "2024"
}
|
Let $p$ be a prime number and $n$ an integer satisfying $n \geqslant 2$.
- Under what condition do there exist $n+1$ integers (not necessarily distinct) such that, for any choice of $n$ integers among the $n+1$, their sum is a power of $p$?
- Under what condition do there exist $n+1$ strictly positive integers (not necessarily distinct) such that, for any choice of $n$ integers among the $n+1$, their sum is a power of $p$?
|
Let's try to analyze the statement. Let $x_{1}, \ldots, x_{n+1}$ be the integers such that for any choice of $n$ integers among the $n+1$ integers, their sum is a power of $p$. There exist $\alpha_{1}, \ldots, \alpha_{n+1}$ positive integers such that $x_{2}+\cdots+x_{n+1}=p^{\alpha_{1}}, x_{1}+x_{3}+\cdots+x_{n+1}=p^{\alpha_{2}}, \ldots, x_{1}+ \cdots+x_{n}=p^{\alpha_{n+1}}$.
In particular, note that $p^{\alpha_{i}}=x_{1}+\cdots+x_{n+1}-x_{i}$ for all $i \in\{1, \ldots, n+1\}$ and that $p^{\alpha_{1}}+ \cdots+p^{\alpha_{n+1}}=\mathfrak{n}\left(x_{1}+\cdots+x_{n+1}\right)$, so for all $i \in\{1, \ldots, n+1\}, x_{i}=\frac{p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}}}{n^{2}}-p^{\alpha_{i}}$.
Conversely, if we are given $\alpha_{1}, \ldots, \alpha_{n+1}$ positive integers such that $x_{i}=\frac{p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}}}{n}-p^{\alpha_{i}}$ for all $i \in\{1, \ldots, n+1\}$, then we see that $x_{1}+\cdots+x_{i-1}+x_{i+1}+\cdots+x_{n+1}=p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}}- p^{\alpha_{1}}-\cdots-p^{\alpha_{i-1}}-p^{\alpha_{i+1}}-\cdots-p^{\alpha_{n+1}}=p^{\alpha_{i}}$.
The question then reduces to the following: do there exist positive integers $\alpha_{1}, \ldots, \alpha_{n+1}$ such that $n$ divides $p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}}$ for the first question, and for the second question such that $\frac{p^{\alpha_{1}+\cdots+p^{\alpha_{n+1}}}}{n}-p^{\alpha_{i}}>0$, i.e., $p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}}>n p^{\alpha_{i}}$ for all $i$.
Let's first try to answer the first part of the question: under what condition on $n$ do there exist $\alpha_{1}, \ldots, \alpha_{n+1}$ such that $n$ divides $p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}}$? Already, modulo $p-1$, we have $p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}} \equiv n+1 \pmod{p-1}$. Let $d$ be the gcd of $p-1$ and $n$, then if $n$ divides $p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}}$, since $d$ divides $p-1$, $d$ also divides $n+1$. Since $d$ divides $n$, we get that $d$ divides $n+1-n=1$, so $d=1$. Thus, it is necessary that $n$ and $p-1$ are coprime.
Conversely, if $n$ and $p-1$ are coprime, let $x \in\{1, \ldots, n+1\}$, we take $\alpha_{1}=\cdots=\alpha_{x}=0$ and $\alpha_{x+1}=\cdots=\alpha_{n+1}=1$. We are looking for a certain $x$ such that $n$ divides $x+(n+1-x) p$, i.e., $x$ such that $x+p-x p \equiv 0 \pmod{n}$, or $x \equiv p(p-1)^{-1} \pmod{n}$ (which exists because $p-1$ and $n$ are coprime). We can take such an $x$ in $\{1, \ldots, n\}$ such that the previous congruence is true. Thus, the condition for the first question is exactly that $n$ and $p-1$ are coprime.
For the second question, we are looking for more to have $p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}}>n p^{\alpha_{i}}$ for all $i$. Up to reordering the $\alpha_{i}$, we can assume $\alpha_{1} \leqslant \alpha_{2} \leqslant \cdots \leqslant \alpha_{n+1}$, the condition is equivalent to $p^{\alpha_{1}}+\cdots+ p^{\alpha_{n+1}}>n p^{\alpha_{n+1}}$. If $\alpha_{2}<\alpha_{n+1}$, we have:
$$
p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}} \leqslant 2 p^{\alpha_{2}}+(n-1) p^{\alpha_{n+1}} \leqslant p^{\alpha_{2}+1}+(n-1) p^{\alpha_{n+1}} \leqslant n p^{\alpha_{n+1}}
$$
Thus, we have $\alpha_{2} \geqslant \alpha_{n+1}$, so $\alpha_{2}=\cdots=\alpha_{n+1}$. In this case, it is clear that $p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}}>n p^{\alpha_{n+1}}$ is satisfied. It remains to find under what condition on $n$ there exist $\alpha_{1} \leqslant \alpha_{2}$ two positive integers such that $n$ divides $p^{\alpha_{1}}+n p^{\alpha_{2}}$ and thus under what condition $n$ divides $p^{\alpha_{1}}$. It is then clear that the solutions are the powers of $p$. Thus, the condition for the second question is that $n$ is a power of $p$.
Comment from the graders: Each part of this exercise was generally well done by the students who tackled it. However, several students, after successfully solving one of the two parts, believed that the other was just a simple corollary, which was not true; they therefore poorly treated it, leading to incorrect results. It's a pity!
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Soit $p$ un nombre premier et $n$ un entier vérifiant $n \geqslant 2$.
- A quelle condition existe-t-il $n+1$ entiers (pas forcément distincts) tels que, pour tout choix de $n$ entiers parmi les $\mathrm{n}+1$, leur somme est une puissance de p ?
- A quelle condition existe-t-il $n+1$ entiers strictement positifs (pas forcément distincts) tels que, pour tout choix de $n$ entiers parmi les $n+1$, leur somme est une puissance de $p$ ?
|
Essayons d'analyser l'énoncé. Posons $x_{1}, \ldots, x_{n+1}$ les entiers tels que pour tout choix de $n$ entiers parmi les $n+1$ entiers, alors leur somme est une puissance de $p$. Il existe donc $\alpha_{1}, \ldots, \alpha_{n+1}$ des entiers positifs tels que $x_{2}+\cdots+x_{n+1}=p^{\alpha_{1}}, x_{1}+x_{3}+\cdots+x_{n+1}=p^{\alpha_{2}}, \ldots, x_{1}+$ $\cdots+x_{n}=p^{\alpha_{n+1}}$.
En particulier, notons déjà que $p^{\alpha_{i}}=x_{1}+\cdots+x_{n+1}-x_{i}$ pour tout $i \in\{1, \ldots, n+1\}$ et que $p^{\alpha_{1}}+$ $\cdots+p^{\alpha_{n+1}}=\mathfrak{n}\left(x_{1}+\cdots+x_{n+1}\right)$, donc pour tout $i \in\{1, \ldots, n+1\}, x_{i}=\frac{p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}}}{n^{2}}-p^{\alpha_{i}}$.
Réciproquement, si on se donne $\alpha_{1}, \ldots, \alpha_{n+1}$ des entiers positifs tels que $x_{i}=\frac{p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}}}{n}-p^{\alpha_{i}}$ pour tout $i \in\{1, \ldots, n+1\}$, alors on voit que $x_{1}+\cdots+x_{i-1}+x_{i+1}+\cdots+x_{n+1}=p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}}-$ $p^{\alpha_{1}}-\cdots-p^{\alpha_{i-1}}-p^{\alpha_{i+1}}-\cdots-p^{\alpha_{n+1}}=p^{\alpha_{i}}$.
La question revient donc à la suivant : existe-t-il des entiers positifs $\alpha_{1}, \ldots, \alpha_{n+1}$ tels que $n$ divise $p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}}$ pour la première question, et pour la seconde question tels que $\frac{\mathrm{p}^{\alpha_{1}+\cdots+p^{\alpha_{n+1}}}}{n}-\mathrm{p}^{\alpha_{i}}>0$, i.e. $p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}}>n p^{\alpha_{i}}$ pour tout $i$.
Essayons de répondre d'abord à la première partie de la question : à quelle condition sur n existe-t-il $\alpha_{1}, \ldots, \alpha_{n+1}$ tels que $n$ divise $p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}}$ ? Déjà, modulo $p-1$, on a $p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}} \equiv n+1$ $(\bmod p-1)$. Notons $d$ le pgcd de $p-1$ et $n$, alors si $n$ divise $p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}}$, comme $d$ divise $p-1$, d divise aussi $n+1$. Comme divise $n$, on obtient que $d$ divise $n+1-n=1$, donc $d=1$. Ainsi il faut que $n$ et $p-1$ sont premiers entre eux.
Réciproquement si $n$ et $p-1$ sont premiers entre eux, soit $x \in\{1, \ldots, n+1\}$ on prend $\alpha_{1}=\cdots=\alpha_{x}=0$ et $\alpha_{x+1}=\cdots=\alpha_{n+1}=1$. On cherche donc un certain $x$ tel que $x$ tel que $n$ divise $x+(n+1-x) p$, i.e. $x$ tel que $x+p-x p \equiv 0\left(\bmod \mathfrak{n}\right.$ ), soit $x \equiv p(p-1)^{-1}(\bmod \mathfrak{n})$ (qui existe car $p-1$ et $n$ sont premiers entre eux). On peut prendre un tel $x$ dans $\{1, \ldots, n\}$ tel que la précédente congruence est vraie. Ainsi la condition pour la première question est exactement $n$ et $p-1$ sont premiers entre eux.
Pour la seconde question, on cherche de plus à avoir $p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}}>n p^{\alpha_{i}}$ pour tout $i$. Quitte à réordonner les $\alpha_{i}$, on peut supposer $\alpha_{1} \leqslant \alpha_{2} \leqslant \cdots \leqslant \alpha_{n+1}$, la condition est équivalente à $p^{\alpha_{1}}+\cdots+$ $p^{\alpha_{n+1}}>n p^{\alpha_{n+1}}$. Si $\alpha_{2}<\alpha_{n+1}$, on a:
$$
p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}} \leqslant 2 p^{\alpha_{2}}+(n-1) p^{\alpha_{n+1}} \leqslant p^{\alpha_{2}+1}+(n-1) p^{\alpha_{n+1}} \leqslant n p^{\alpha_{n+1}}
$$
Ainsi on a $\alpha_{2} \geqslant \alpha_{n+1}$, donc $\alpha_{2}=\cdots=\alpha_{n+1}$. Dans ce cas, il est clair que $p^{\alpha_{1}}+\cdots+p^{\alpha_{n+1}}>n p^{\alpha_{n+1}}$ est vérifié. Il reste donc à chercher à quelle condition sur $n$ existe-t-il $\alpha_{1} \leqslant \alpha_{2}$ deux entiers positifs tels que $n$ divise $p^{\alpha_{1}}+n p^{\alpha_{2}}$ donc à quelle condition $n$ divise $p^{\alpha_{1}}$. Il est alors clair que les solutions sont les puissances de $p$. Ainsi la condition pour la seconde question est que $n$ soit une puissance de $p$.
Commentaire des correcteurs : Chacune des parties de cet exercice a été globalement réussie par les élèves qui l'ont abordée. Néanmoins, plusieurs élèves, après avoir réussi l'une des deux parties, ont cru que l'autre n'en était qu'un simple corollaire, ce qui n'était pas vrai ; ils l'ont donc mal traitée, aboutissant à des résultats incorrects. C'est dommage!
|
{
"exam": "French_envois",
"problem_label": "16",
"problem_match": "\nExercice 16.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 16",
"tier": "T2",
"year": "2024"
}
|
Let $a, b$ be integers such that $\mathrm{pgcd}(\mathrm{a}, \mathrm{b})$ has at least two distinct prime factors. Let $S=\{x \in \mathbb{N} \mid x \equiv a[b]\}$. An element of $S$ is said to be irreducible if it cannot be written as a product of at least two elements of $S$ (not necessarily distinct).
Show that there exists $\mathrm{N}>0$ such that every element of $S$ can be written as a product of at most N irreducible elements of $S$ (not necessarily distinct).
|
Let $d=\operatorname{gcd}(a, b)$, and write $a=d a^{\prime}, b=d b^{\prime}$. Let's start by treating the case where $\operatorname{gcd}\left(d, b^{\prime}\right)>1$. If this is the case, then we have $\operatorname{gcd}\left(a^{2}, b\right)=d \operatorname{gcd}\left(d a^{\prime 2}, b^{\prime}\right)>d$. Therefore, for all $k \geqslant 2$, we have $a^{k} \not \equiv a[b]$. In particular, every element of $S$ is irreducible, and thus $N=1$ is suitable.
Now suppose that $d$ and $b^{\prime}$ are coprime. Then $a$ and $b^{\prime}$ are coprime; let $\omega$ be the order of $a$ modulo $b^{\prime}$. We then have that $a^{\omega+1} \equiv a[b]$. Therefore, any product of $\omega+1$ elements of $S$ is still an element of $S$. This means in particular that any non-irreducible element of $S$ can be written as a product of $k$ elements of $S$ for some $k \in \llbracket 2, \omega \rrbracket$.
Let $p$ and $q$ be two prime divisors of $d$, and let $x \in S$. If $x$ is irreducible, it's fine; otherwise, write $x=\mathfrak{u}_{1} \mathfrak{u}_{2} \ldots \mathfrak{u}_{k}$ with $\mathfrak{u}_{1}, \ldots, \mathfrak{u}_{k} \in S$, for some $k \in \llbracket 2, \omega \rrbracket$. First, let's show that we can assume $v_{\mathfrak{p}}\left(\mathfrak{u}_{\mathfrak{j}}\right)<\varphi\left(b^{\prime}\right)+v_{\mathfrak{p}}(d)$ for all $\boldsymbol{j}<\mathrm{k}$. For this, we note that if $v_{\mathfrak{p}}\left(\mathfrak{u}_{\mathfrak{j}}\right) \geqslant \varphi\left(b^{\prime}\right)+v_{\mathfrak{p}}(d)$, then we can replace $\mathfrak{u}_{j}$ by $\frac{\mathfrak{u}_{j}}{p^{\varphi\left(b^{\prime}\right)}}$ and $\mathfrak{u}_{k}$ by $p^{\varphi\left(b^{\prime}\right)} \mathfrak{u}_{k}$. We have $p^{\varphi\left(b^{\prime}\right)} \equiv 1\left[b^{\prime}\right]$, so $p^{\varphi\left(b^{\prime}\right)} \mathfrak{u}_{k} \equiv \mathfrak{u}_{k} \equiv a\left[b^{\prime}\right]$. On the other hand, $d \mid \mathfrak{u}_{k}$, so $p^{\varphi\left(b^{\prime}\right)} \mathfrak{u}_{k} \equiv 0 \equiv a[d]$. Therefore, by the Chinese Remainder Theorem, we have $p^{\varphi\left(b^{\prime}\right)} \mathfrak{u}_{k} \equiv a[b]$. On the other hand, we also have $\frac{u_{j}}{p^{\varphi\left(b^{\prime}\right)}} \equiv a\left[b^{\prime}\right]$, and we also have (since $v_{\mathfrak{p}}\left(u_{j}\right) \geqslant \varphi\left(b^{\prime}\right)+v_{p}(d)$) that $d \left\lvert\, \frac{u_{j}}{p^{\varphi\left(b^{\prime}\right)}}\right.$. Therefore, $\frac{u_{j}}{p^{\varphi\left(b^{\prime}\right)}} \equiv a[b]$.
We now have $v_{\mathfrak{p}}\left(\mathfrak{u}_{\mathfrak{j}}\right)<\varphi\left(b^{\prime}\right)+v_{\mathfrak{p}}(d)$ for $\boldsymbol{j}<\mathrm{k}$. Similarly, we can assume that $v_{\boldsymbol{q}}\left(\mathfrak{u}_{\mathrm{k}}\right)<\varphi\left(b^{\prime}\right)+v_{q}(d)$. Any writing of $\boldsymbol{u}_{j}(j<k)$ as a product of irreducibles only involves multiples of $d$, and thus of $p$, and therefore includes at most $v_{p}\left(u_{j}\right)$ factors. Similarly for $q$ with $\mathfrak{u}_{k}$. Finally, we have managed to write $x$ as a product of at most $(\omega-1)\left(\varphi\left(b^{\prime}\right)+v_{p}(d)-1\right)+\varphi\left(b^{\prime}\right)+v_{q}(d)-1$ irreducible factors, as desired.
Comment from the graders: The exercise is successfully completed by a handful of students. It seems that the notion of irreducibility posed comprehension problems, showing that any number in $S$ can be written as a finite number of irreducible elements did not answer the question. Finally, it is regrettable that for some, the copies returned for this submission problem are almost illegible.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soient $a, b$ deux entiers tels que $\mathrm{pgcd}(\mathrm{a}, \mathrm{b}) \mathrm{a}$ au moins deux facteurs premiers distincts. Soit $S=\{x \in \mathbb{N} \mid x \equiv a[b]\}$. Un élément de $S$ est dit irréductible s'il ne peut pas s'écrire comme un produit d'au moins deux éléments de $S$ (pas forcément distincts).
Montrer qu'il existe $\mathrm{N}>0$ tel que tout élément de $S$ s'écrit comme produit d'au plus N éléments irréductibles de $S$ (pas forcément distincts).
|
Soit $d=\operatorname{pgcd}(a, b)$, et écrivons $a=d a^{\prime}, b=d b^{\prime}$. Commençons par traiter le cas où $\operatorname{pgcd}\left(\mathrm{d}, \mathrm{b}^{\prime}\right)>1$. Si c'est le cas, alors on a $\operatorname{pgcd}\left(\mathrm{a}^{2}, \mathrm{~b}\right)=\operatorname{dpgcd}\left(\mathrm{da}^{\prime 2}, \mathrm{~b}^{\prime}\right)>\mathrm{d}$. Donc, pour tout $k \geqslant 2$, on a $a^{k} \not \equiv a[b]$. En particulier, tout élément de $S$ est irréductible, et donc $N=1$ convient.
Supposons à présent que $d$ et $b^{\prime}$ sont premiers entre eux. On a alors $a$ et $b^{\prime}$ premiers entre eux; soit $\omega$ l'ordre de a modulo $b^{\prime}$. On a alors que $\mathrm{a}^{\omega+1} \equiv \mathrm{a}[\mathrm{b}]$. Donc tout produit de $\omega+1$ éléments de $S$ est encore un élément de $S$. Ceci signifie en particulier que tout élément non irréductible de $S$ peut s'écrire comme un produit de $k$ éléments de $S$ pour un certain $k \in \llbracket 2, \omega \rrbracket$.
Soient $p$ et $q$ deux diviseurs premiers de d, et soit $x \in S$. Si $x$ est irréductible, c'est bon; sinon, écrivons $x=\mathfrak{u}_{1} \mathfrak{u}_{2} \ldots \mathfrak{u}_{k}$ avec $\mathfrak{u}_{1}, \ldots, \mathfrak{u}_{k} \in S$, pour un $k \in \llbracket 2, \omega \rrbracket$. Montrons d'abord qu'on peut supposer $v_{\mathfrak{p}}\left(\mathfrak{u}_{\mathfrak{j}}\right)<\varphi\left(\mathfrak{b}^{\prime}\right)+v_{\mathfrak{p}}(\mathrm{d})$ pour tout $\boldsymbol{j}<\mathrm{k}$. Pour cela, on remarque que, si $v_{\mathfrak{p}}\left(\mathfrak{u}_{\mathfrak{j}}\right) \geqslant \varphi\left(\mathrm{b}^{\prime}\right)+v_{\mathfrak{p}}(\mathrm{d})$, alors on peut remplacer $\mathfrak{u}_{j}$ par $\frac{\mathfrak{u}_{j}}{p^{\varphi\left(b^{\prime}\right)}}$ et $\mathfrak{u}_{k}$ par $p^{\varphi\left(b^{\prime}\right)} \mathfrak{u}_{k}$. On a $p^{\varphi\left(b^{\prime}\right)} \equiv 1\left[b^{\prime}\right]$, donc $p^{\varphi\left(b^{\prime}\right)} \mathfrak{u}_{k} \equiv \mathfrak{u}_{k} \equiv a\left[b^{\prime}\right]$. D'autre part, $\mathrm{d} \mid \mathfrak{u}_{k}$ donc $\mathrm{p}^{\varphi\left(\mathrm{b}^{\prime}\right)} \mathfrak{u}_{\mathrm{k}} \equiv 0 \equiv \mathrm{a}[\mathrm{d}]$. Donc, d'après le théorème des restes chinois, on a $p^{\varphi\left(b^{\prime}\right)} \mathfrak{u}_{k} \equiv a[b]$. D'autre part, on a aussi $\frac{u_{j}}{p^{\varphi\left(b^{\prime}\right)}} \equiv a\left[b^{\prime}\right]$, et on a également (puisque $v_{\mathfrak{p}}\left(u_{j}\right) \geqslant$ $\left.\varphi\left(b^{\prime}\right)+v_{p}(d)\right)$ que $d \left\lvert\, \frac{u_{j}}{p^{\varphi\left(b^{\prime}\right)}}\right.$. Donc $\frac{u_{j}}{p^{\varphi\left(b^{\prime}\right)}} \equiv a[b]$.
On a à présent $v_{\mathfrak{p}}\left(\mathfrak{u}_{\mathfrak{j}}\right)<\varphi\left(\mathrm{b}^{\prime}\right)+v_{\mathfrak{p}}(\mathrm{d})$ pour $\boldsymbol{j}<\mathrm{k}$. De même, on peut supposer que $v_{\boldsymbol{q}}\left(\mathfrak{u}_{\mathrm{k}}\right)<$ $\varphi\left(b^{\prime}\right)+v_{q}(d)$. Toute écriture de $\boldsymbol{u}_{j}(j<k)$ sous forme de produit d'irréductibles fait apparaître seulement des multiples de $d$, donc de $p$, et comprend donc au plus $v_{p}\left(u_{j}\right)$ facteurs. De même pour $q$ avec $\mathfrak{u}_{k}$. Finalement, on a réussi à écrire $x$ sous la forme d'un produit d'au plus $(\omega-1)\left(\varphi\left(b^{\prime}\right)+v_{p}(d)-1\right)+$ $\varphi\left(\mathrm{b}^{\prime}\right)+v_{\mathrm{q}}(\mathrm{d})-1$ facteurs irréductibles, comme souhaité.
Commentaire des correcteurs : L'exercice est réussi par une poignée d'élèves. Il semble que la notion d'irréductibilité a posé des problèmes de compréhension, montrer que tout nombre de $S$ peut s'écrire comme un nombre fini d'éléments irréductibles ne répondait pas à l'énoncé. Enfin, il est regrettable que pour certains, les copies rendues pour ce problème d'envoi soient pratiquement illisibles.
|
{
"exam": "French_envois",
"problem_label": "17",
"problem_match": "\nExercice 17.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 17",
"tier": "T2",
"year": "2024"
}
|
For every integer $k \geqslant 1$, we denote $p(k)$ as the smallest prime number that does not divide $k$. Let $\left(a_{n}\right)_{n \in \mathbb{N}}$ be a sequence such that $a_{0} \in \mathbb{N}^{*}$ and for all $n \geqslant 0, a_{n+1}$ is the smallest positive integer different from $a_{0}, \ldots, a_{n}$ such that $a_{n}^{a_{n+1}}-1$ is divisible by $p\left(a_{n}\right)$. Prove that every positive integer appears exactly once in the sequence $\left(a_{n}\right)_{n \in \mathbb{N}}$.
|
Let's first note that the sequence is well-defined: if $a_{1}, \ldots, a_{n}$ are constructed, since $a_{n}$ is coprime with $p(a_{n})$, there exists an infinite number of integers $k$ such that $a_{n}^{k} \equiv 1 \pmod{p(a_{n})}$, which are all multiples of the order of $a_{n}$ modulo $p(a_{n})$. In particular, there is at least one of these integers $n$ not appearing among $a_{1}, \ldots, a_{n}$, so $a_{n+1}$ is well-defined.
Note that each integer appears at most once in the sequence by construction. We need to show that all integers appear at least once. Suppose there exists an integer $N$ that does not appear in the sequence $(x_{n})$, and take $N$ to be minimal. Let $N_{0}$ be an integer such that if $n \geqslant N_{0}, a_{n} > N$.
We show that for every prime $q$, there are a finite number of $n$ such that $p(a_{n}) = q$. Suppose this is not the case, and fix $q$ a prime such that $p(a_{n}) = q$ for an infinite number of $n$. We then define $\phi: \mathbb{N} \rightarrow \mathbb{N}$ strictly increasing such that $p(a_{\phi(n)}) = q$. Note that every multiple of $q-1$ appears: indeed, if we fix $M$ a multiple of $q-1$, then since the $p(a_{\phi(n)+1})$ are pairwise distinct, there exists $n$ such that $a_{\phi(n)+1} > M$. Since $q-1$ divides $M$, by Fermat's Little Theorem, $a_{\phi(n)}^{M} \equiv 1 \pmod{q-1}$, which contradicts the definition of $a_{\phi(n)+1}$.
Thus, all multiples of $q-1$ appear. Let $p_{1} < \cdots < p_{k}$ be the primes strictly less than $q$. We know that for all $j \geqslant 1, (p_{1} \ldots p_{k})^{j(q-1)}$ is congruent to 1 modulo $q$, divisible by $q-1$ for $j$ large enough (since all factors of $q-1$ are among $p_{1}, \ldots, p_{k}$), so it appears in the sequence, and satisfies $p((p_{1} \ldots p_{k})^{j(q-1)}) = q$. Since there are infinitely many such terms, there exists $N_{1} > N_{0}$ such that $a_{N_{1}} = (p_{1} \ldots p_{k})^{j(q-1)}$ for $j$ large enough. Thus, $a_{N_{1}}^{N} \equiv 1 \pmod{q}$, which contradicts the fact that $a_{N_{1}+1} > N$.
Thus, we have shown that for every prime $q$, there are a finite number of $n$ such that $p(a_{n}) = q$. In particular, for all $M \in \mathbb{N}$, since the sequence $(p(a_{n}))$ takes each value between 1 and $M$ a finite number of times, from a certain rank $p(a_{n}) > M$, so $(p(a_{n}))$ tends to $+\infty$. In particular, for all $k$, from a certain rank, $p_{1} \ldots p_{k}$ divides $a_{n}$.
Let $k$ and $m$ be such that $p_{1} \ldots p_{k}$ divides $a_{m}$, $p_{k+1}$ does not divide $a_{m}$, and $p_{1} \ldots p_{k+1}$ divides $a_{n}$ for all $n \geqslant m+1$. Then $p(a_{m}) = p_{k+1}$, and $a_{n}^{p_{1} \ldots p_{k} p_{k+1}} \equiv 1 \pmod{p_{k+1}}$. By Fermat's Little Theorem, $a_{n}^{p_{1} \ldots p_{k} p_{k+1}} \equiv a^{p_{1} \ldots p_{k}} \pmod{p_{k+1}}$, so for all $i$ such that $1 \leqslant i \leqslant p_{k}-1$, $a^{i p_{1} \ldots p_{k}} \equiv 1 \pmod{p_{k+1}}$. Thus, for all $i$ such that $1 \leqslant i \leqslant p_{k}-1$, $i p_{1} \ldots p_{k}$ appears in the sequence $(a_{n})$. Taking $i$ an inverse of $p_{1} \ldots p_{k}$ modulo $p_{k+1}-1$ in $\{1, \ldots, p_{k+1}-1\}$, we then have that $(i p_{1} \ldots p_{k})^{N} \equiv N \pmod{p_{k+1}}$, so if $a_{n} = i p_{1} \ldots p_{k}$, then $a_{n+1} < N$, so $n \leqslant N_{0}$. Thus, if such $k$, $m$ exist, then $p_{k}$ divides $a_{1} \ldots a_{n+1}$, so $k$ is bounded.
However, for all $K \in \mathbb{N}$, we can find $k \geqslant K$ and $m$ such that $p_{1} \ldots p_{k}$ divides $a_{m}$, $p_{k+1}$ does not divide $a_{m}$, and $p_{1} \ldots p_{k+1}$ divides $a_{n}$ for all $n \geqslant m+1$. Indeed, for all $k \geqslant 1$, let $r_{k}$ be the first rank from which $p_{1} \ldots p_{k}$ divides $a_{n}$. The sequence $(r_{j})$ is increasing and cannot be stationary, otherwise some $a_{n}$ would be divisible by all primes. Therefore, it tends to $+\infty$, so for all $K$, there exists $k \geqslant K$ such that $r_{k+1} > r_{k}$. Thus, $a_{r_{k+1}-1}$ is divisible by $p_{1} \ldots p_{k}$ since $r_{k+1}-1 \geqslant r_{k}$, and not by $p_{k+1}$. But all terms after $r_{k+1}$ are divisible by $p_{1} \ldots p_{k+1}$, so $m = r_{k+1}-1$ works. We have thus obtained that for all $K \in \mathbb{N}$, we can find $k \geqslant K$ and $m$ such that $p_{1} \ldots p_{k}$ divides $a_{m}$, $p_{k+1}$ does not divide $a_{m}$, and $p_{1} \ldots p_{k+1}$ divides $a_{n}$ for all $n \geqslant m+1$, leading to a contradiction.
Thus, each integer appears exactly once in the sequence.
Comment from the graders: The exercise is successfully solved by a handful of students. Some used less elementary results than the solution, for example Bertrand's postulate.
|
proof
|
Yes
|
Incomplete
|
proof
|
Number Theory
|
Pour tout entier $k \geqslant 1$, on note $p(k)$ le plus petit nombre premier ne divisant pas $k$. Soit $\left(a_{n}\right)_{n \in \mathbb{N}}$ une suite telle que $a_{0} \in \mathbb{N}^{*}$ et pour tout $n \geqslant 0, a_{n+1}$ est le plus petit entier strictement positif différent de $a_{0}, \ldots, a_{n}$ tel que $a_{n}^{a_{n+1}}-1$ est divisible par $p\left(a_{n}\right)$. Démontrer que tout entier strictement positif apparaît une unique fois dans la suite $\left(a_{n}\right)_{n \in \mathbb{N}}$.
|
Déjà notons que la suite est bien définie: si $a_{1}, \ldots, a_{n}$ sont construits, comme $a_{n}$ est premier avec $p\left(a_{n}\right)$, il existe une infinité d'entiers $k$ tels que $a_{n}^{k} \equiv 1\left(\bmod p\left(a_{n}\right)\right)$ qui sont tous les multiples de l'ordre de $a_{n}$ modulo $p\left(a_{n}\right)$. En particulier, il existe au moins un de ces entiers $n$ 'apparaissant pas parmi $a_{1}, \ldots, a_{n}$, donc $a_{n+1}$ existe bien.
Notons que chaque entier apparaît au plus une fois dans la suite par construction. Il faut donc montrer que tous apparaissent au moins une fois. Supposons qu'il existe un entier $N$ qui n'apparaît pas dans la suite $\left(x_{n}\right)$, on prend alors $N$ minimal. On note $N_{0}$ un entier tel que si $n \geqslant N_{0}, a_{n}>N$.
Montrons que pour tout premier $q$, il existe un nombre fini de $n$ tels que $p\left(a_{n}\right)=q$. Supposons que ce n'est pas le cas, et fixons $q$ un nombre premier tel que $p\left(a_{n}\right)=q$ pour une infinité de $n$. On se donne alors $\phi: \mathbb{N} \rightarrow \mathbb{N}$ strictement croissante telle que $p\left(a_{\phi(n)}\right)=q$. Notons alors que tout multiple de $q-1$ apparaît : en effet si on fixe $M$ un multiple de $q-1$, alors comme les $p\left(a_{\phi(n)+1}\right)$ sont deux à deux distincts, il existe $n$ tel que $a_{\phi(n)+1}>M$. Or comme $q-1$ divise $M, a_{\phi(n)}^{M} \equiv 1(\bmod q-1)$ par petit Fermat, ce qui contredit la définition de $a_{\phi(n)+1}$.
Ainsi tous les multiples de $\mathrm{q}-1$ apparaissent. on note $\mathrm{p}_{1}<\cdots<\mathrm{p}_{\mathrm{k}}$ les nombres premiers strictement inférieurs à $q$. On sait que pour tout $j \geqslant 1,\left(p_{1} \ldots p_{k}\right)^{j(q-1)}$ est congru à 1 modulo $q$, divisible par $q-1$ pour $j$ assez grand (car tous les facteurs de $q-1$ sont parmi $p_{1}, \ldots, p_{k}$ ) donc apparaît dans la suite, et vérifie $p\left(\left(p_{1} \ldots p_{k}\right)^{j(q-1)}\right)=q$. Comme il y a une infinité de tels termes, il existe $\mathrm{N}_{1}>\mathrm{N}_{0}$ tel que $a_{N_{1}}=\left(p_{1} \ldots p_{k}\right)^{j(q-1)}$ pour $j$ assez grand. Ainsi $a_{N_{1}}^{N} \equiv 1(\bmod q)$, ce qui contredit le fait que $a_{N_{1}+1}>N$.
Ainsi on a bien prouvé que pour tout premier $\mathbf{q}$, il existe un nombre fini de $n$ tels que $p\left(a_{n}\right)=q$. En particulier, pour tout $M \in \mathbb{N}$, comme la suite $\left(p\left(a_{n}\right)\right)$ prend un nombre fini de fois chaque valeurs entre 1 et $M$, à partir d'un certain rang $p\left(a_{n}\right)>M$, donc $\left(p\left(a_{n}\right)\right)$ tend vers $+\infty$. En particulier, pour tout $k$, à partir d'un certain rang, $p_{1} \ldots, p_{k}$ divise $a_{n}$.
Soit $k$ et $m$ tels que $p_{1} \ldots p_{k}$ divise $a_{m}, p_{k+1}$ ne divise pas $a_{m}$, et $p_{1} \ldots p_{k+1}$ divise $a_{n}$ pour tout $n \geqslant$ $m+1$. On a alors $p\left(a_{m}\right)=p_{k+1}$, et $a_{n}^{p_{1} \ldots p_{k} p_{k+1}} \equiv 1\left(\bmod p_{k+1}\right)$. Or par Petit Fermat, $a_{n}^{p_{1} \ldots p_{k} p_{k+1}} \equiv$ $a^{p_{1} \ldots p_{k}}\left(\bmod p_{k+1}\right)$, donc pour tout $i$ vérifiant $1 \leqslant i \leqslant p_{k}-1$, $a^{i p_{1} \ldots p_{k}} \equiv 1\left(\bmod p_{k+1}\right)$. Ainsi pour tout $i$ vérifiant $1 \leqslant i \leqslant p_{k}-1$, $i p_{1} \ldots p_{k}$ apparaît dans la suite $\left(a_{n}\right)$. En prenant $i$ un inverse de $p_{1} \ldots p_{\mathrm{k}}$ modulo $p_{\mathrm{k}+1}-1$ dans $\left\{1, \ldots, p_{\mathrm{k}+1}-1\right\}$, on a alors que $\left(i p_{1} \ldots \mathrm{p}_{\mathrm{k}}\right)^{\mathrm{N}} \equiv \mathrm{N}\left(\bmod \mathrm{p}_{\mathrm{k}+1}\right)$, donc si $a_{n}=i p_{1} \ldots p_{k}$, alors $a_{n+1}<N$, donc $n \leqslant N_{0}$. Ainsi si de tels $k$, $m$ existent, alors $p_{k}$ divise $a_{1} \ldots a_{n+1}$, donc $k$ est borné.
Or pour tout $K \in \mathbb{N}$, on peut trouver $k \geqslant K$ et $m$ tels que $p_{1} \ldots p_{k}$ divise $a_{m}, p_{k+1}$ ne divise pas $a_{m}$, et $p_{1} \ldots p_{k+1}$ divise $a_{n}$ pour tout $n \geqslant m+1$. En effet, notons pour tout $k \geqslant 1 r_{k}$ le premier rang à partir duquel $p_{1} \ldots p_{k}$ divise $a_{n}$. La suite $\left(r_{j}\right)$ est croissante, et ne peut être stationnaire sinon un $a_{n}$ serait divisible par tous les nombres premiers. Donc elle tend vers $+\infty$, pour tout $K$, il existe $k \geqslant \mathrm{~K}$ tel que $r_{k+1}>r_{k}$. Ainsi $a_{r_{k+1}-1}$ est divisible par $p_{1} \ldots p_{k}$ car $r_{k+1}-1 \geqslant r_{k}$, et pas par $p_{k+1}$. Mais tous les termes après $r_{k+1}$ sont divisibles par $p_{1} \ldots p_{k+1}$, donc $m=r_{k+1}-1$ convient. On a donc bien obtenu que pour tout $K \in \mathbb{N}$, on peut trouver $k \geqslant K$ et $m$ tels que $p_{1} \ldots p_{k}$ divise $a_{m}, p_{k+1}$ ne divise pas $a_{m}$, et $p_{1} \ldots p_{k+1}$ divise $a_{n}$ pour tout $n \geqslant m+1$, donc on a abouti à une contradiction.
Ainsi chaque entier apparaît une unique fois dans la suite.
Commentaire des correcteurs : L'exercice est réussi par une poignée d'élèves. Certains ont utilisé des résultats moins élémentaires que le corrigé par exemple le postulat de Bertrand.
|
{
"exam": "French_envois",
"problem_label": "18",
"problem_match": "\nExercice 18.",
"resource_path": "French/segmented/envois/fr-Corrige-envoi-arithmetique-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 18",
"tier": "T2",
"year": "2024"
}
|
At the beginning, the 9 squares of a $3 \times 3$ chessboard each contain a 0. At each step, Pedro chooses two squares that share a side, and adds either 1 to both squares or -1 to both squares. Show that it is impossible to reach in a finite number of moves the situation where all squares are filled with a 2.
|
The idea here is to introduce an invariant I.
Let's naturally color the chessboard in black and white so that there are 4 black squares and 5 white ones. Let I be the sum of the black squares minus the sum of the white squares. At the beginning, $\mathrm{I}=0$, and in a hypothetical situation where all the squares are filled with a $2, \mathrm{I}=-2$.
However, I does not change; indeed, at each step, we choose two adjacent squares, which are of different colors, and add the same number to them. As a result, I is not modified during the execution of a step, hence the result.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Au début, les 9 cases d'un échiquier $3 \times 3$ contiennent chacune un 0 . A chaque étape, Pedro choisit deux cases partageant un côté, et ajoute soit 1 aux deux cases, soit -1 aux deux cases. Montrer qu'il est impossible d'atteindre en un nombre fini de coups la situation où toutes les cases sont remplies par un 2.
|
L'idée ici est de faire apparaître un invariant I.
Colorions l'échiquier naturellement en noir et blanc de telle sorte qu'il y a 4 cases noires et 5 blanches. Soit donc I la somme des cases noires moins la somme des cases blanches. Au début, $\mathrm{I}=0$, et dans une hypothétique situation où toutes les cases sont remplies par un $2, \mathrm{I}=-2$.
Or I ne varie pas; en effet, à chaque étape on choisit deux cases partageant un côté commun, donc de couleur différente, et on leur ajoute le même nombre. Il en résulte que I n'est modifié lors de l'accomplissement d'une étape, d'où le résultat.
|
{
"exam": "French_envois",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/envois/fr-Corrigé-Envoi-5-2019.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T2",
"year": "2019"
}
|
Let $m, n, k$ be three positive integers such that $m^{2}+n=k^{2}+k$. Show that $m \leqslant n$.
|
We write $(2 k+1)^{2}=4\left(k^{2}+k\right)+1=4\left(m^{2}+n\right)+1=(2 m)^{2}+4 n+1$.
If $n < m$, we can write
$$
(2 m)^{2}<(2 m)^{2}+4 n+1<4 m^{2}+4 m+1=(2 m+1)^{2}
$$
which is impossible since $(2 k+1)^{2}=(2 m)^{2}+4 n+1$ is a square and cannot be between two consecutive squares. Therefore, $n \geqslant m$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soient $m, n, k$ trois entiers positifs tels que $m^{2}+n=k^{2}+k$. Montrer que $m \leqslant n$.
|
On écrit $(2 k+1)^{2}=4\left(k^{2}+k\right)+1=4\left(m^{2}+n\right)+1=(2 m)^{2}+4 \mathfrak{n}+1$.
Or si $\mathrm{n}<\mathrm{m}$, on peut écrire
$$
(2 \mathfrak{m})^{2}<(2 \mathfrak{m})^{2}+4 \mathfrak{n}+1<4 \mathfrak{m}^{2}+4 \mathfrak{m}+1=(2 \mathrm{~m}+1)^{2}
$$
ce qui est impossible puisque $(2 \mathrm{k}+1)^{2}=(2 \mathrm{~m})^{2}+4 \mathfrak{n}+1$ est un carré et ne peut donc pas être entre deux carrés consécutifs. D'où $n \geqslant m$.
|
{
"exam": "French_envois",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/envois/fr-Corrigé-Envoi-5-2019.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T2",
"year": "2019"
}
|
Let $ABC$ be a triangle with all three angles acute, with $AB > AC$, and let $\Omega$ be its circumcircle. We denote $M$ as the midpoint of [BC]. The tangents to $\Omega$ at $B$ and $C$ intersect at $P$, and the lines $(AP)$ and $(BC)$ intersect at $S$. We denote $D$ as the foot of the altitude from $B$ in $ABP$, and $\omega$ as the circumcircle of $CSD$. Finally, we denote $K$ as the second intersection point (after $C$) of $\omega$ and $\Omega$.
Show that $\widehat{\mathrm{CKM}}=90^{\circ}$.
|
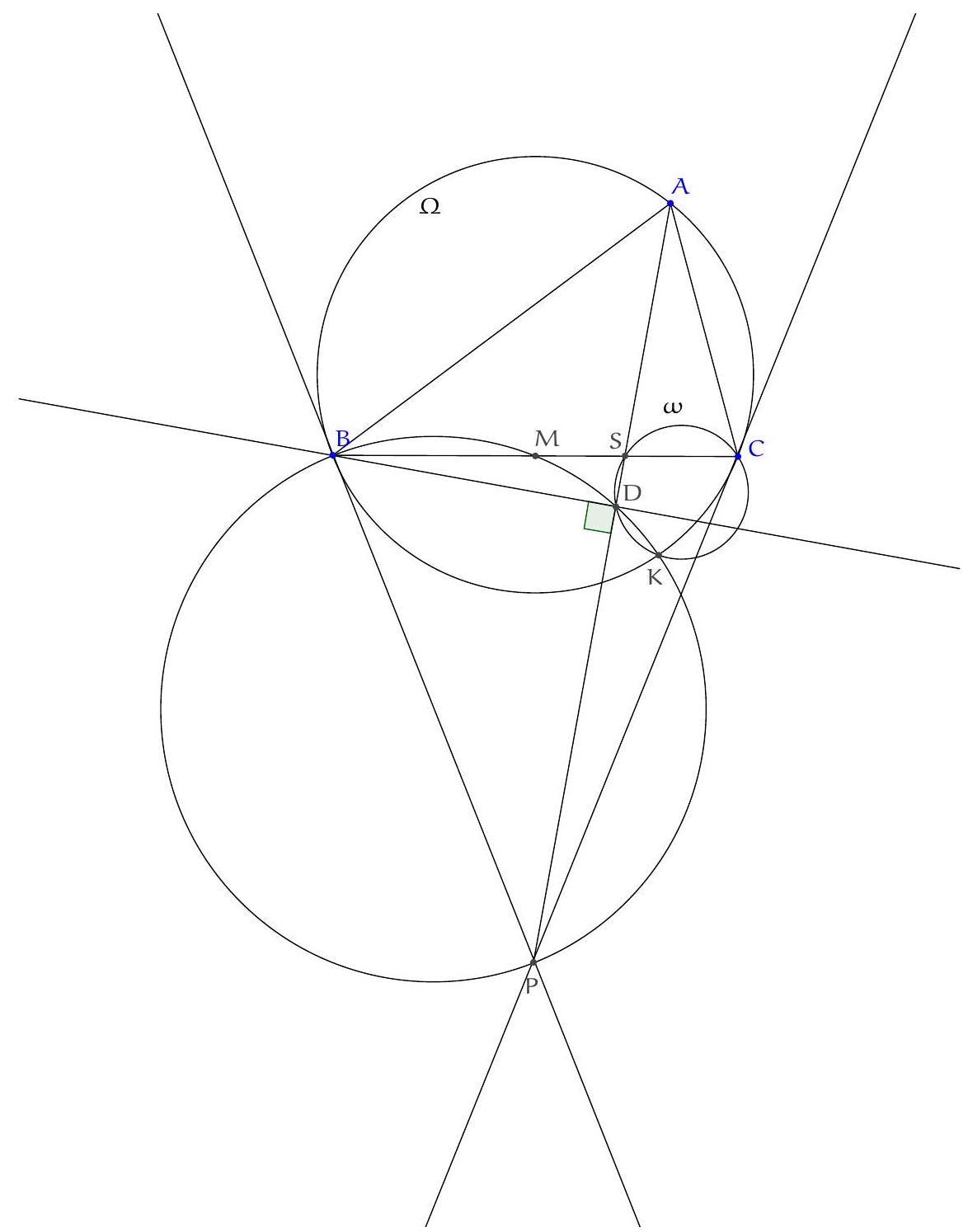
The idea is to realize that the figure contains many cyclic points. To start, we have $\mathrm{PB}=\mathrm{PC}$, so (MP) is the perpendicular bisector of $[\mathrm{BC}]$, and in particular, the angle $\widehat{\mathrm{BMP}}$ is right. Since $\widehat{B D P}$ is also right, the points $B, D, M$ and $P$ are cyclic on the circle $\Gamma$ with diameter [BP]. If we draw this circle on our figure, it appears that $\Gamma$ also passes through K. Indeed, we will verify by angle chasing that $B, D, K$ and $P$ are cyclic. On one hand, using the inscribed angle theorem, we have
$$
\widehat{\mathrm{KDP}}=180^{\circ}-\widehat{\mathrm{KDS}}=\widehat{\mathrm{KCS}}=\widehat{\mathrm{KCB}}.
$$
On the other hand, using the limiting case of the inscribed angle theorem, we have
$$
\widehat{\mathrm{KBP}}=\widehat{\mathrm{KCB}}
$$
so the five points $B, D, K, M$ and $P$ are cyclic. We can now conclude by decomposing the angle $\widehat{\mathrm{CKM}}$ at D to use as many circles as possible:
$$
\widehat{\mathrm{CKM}}=\widehat{\mathrm{CKD}}+\widehat{\mathrm{DKM}}=180^{\circ}-\widehat{\mathrm{CSD}}+\widehat{\mathrm{DBM}}=\widehat{\mathrm{BSD}}+\widehat{\mathrm{DBS}}=180^{\circ}-\widehat{\mathrm{BDS}}=90^{\circ}
$$
## Common Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle dont les trois angles sont aigus, avec $A B>A C$, et soit $\Omega$ son cercle circonscrit. On note $M$ le milieu de [BC]. Les tangentes à $\Omega$ en $B$ et $C$ s'intersectent en $P$, et les droites $(A P)$ et $(B C)$ se coupent en $S$. On note $D$ le pied de la hauteur issue de $B$ dans $A B P$, et $\omega$ le cercle circonscrit à CSD. Enfin, on note K le second point d'intersection (après C ) de $\omega$ et $\Omega$.
Montrer que $\widehat{\mathrm{CKM}}=90^{\circ}$.
|

L'idée est de se rendre compte que la figure contient de nombreux points cocycliques. Pour commencer, on a $\mathrm{PB}=\mathrm{PC}$ donc (MP) est la médiatrice de $[\mathrm{BC}]$, et en particulier l'angle $\widehat{\mathrm{BMP}}$ est droit. Comme $\widehat{B D P}$ l'est aussi, les points $B, D, M$ et $P$ sont cocycliques sur le cercle $\Gamma$ de diamètre [BP]. Si on trace ce cercle sur notre figure, il semble que $\Gamma$ passe aussi par K . En effet, on va vérifier par chasse aux angles que $B, D, K$ et $P$ sont cocycliques. D'une part, en utilisant le théorème de l'angle inscrit, on a
$$
\widehat{\mathrm{KDP}}=180^{\circ}-\widehat{\mathrm{KDS}}=\widehat{\mathrm{KCS}}=\widehat{\mathrm{KCB}} .
$$
D'autre part, en utilisant le cas limite du théorème de l'angle inscrit, on a
$$
\widehat{\mathrm{KBP}}=\widehat{\mathrm{KCB}}
$$
donc les cinq points $B, D, K, M$ et $P$ sont cocycliques. On peut maintenant conclure en décomposant l'angle $\widehat{\mathrm{CKM}}$ en D pour pouvoir utiliser un maximum de cercles :
$$
\widehat{\mathrm{CKM}}=\widehat{\mathrm{CKD}}+\widehat{\mathrm{DKM}}=180^{\circ}-\widehat{\mathrm{CSD}}+\widehat{\mathrm{DBM}}=\widehat{\mathrm{BSD}}+\widehat{\mathrm{DBS}}=180^{\circ}-\widehat{\mathrm{BDS}}=90^{\circ}
$$
## Exercices Communs
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-Corrigé-Envoi-5-2019.jsonl",
"solution_match": "## Solution de l'exercice 3",
"tier": "T2",
"year": "2019"
}
|
Let $ABC$ be an isosceles triangle at $A$ but not a right triangle. Let $D$ be the point on $(BC)$ such that $(AD)$ is perpendicular to $(AB)$, and let $E$ be the orthogonal projection of $D$ onto $(AC)$. Finally, let $H$ be the midpoint of $[BC]$.
Show that $AHE$ is isosceles at $H$.
|
Let's start by noting that points $A, D, E$ and $H$ are concyclic on the circle with diameter [AD]. From this, we deduce by angle chasing:
$$
\widehat{\mathrm{HEA}}=\widehat{\mathrm{HDA}}=90^{\circ}-\widehat{\mathrm{DBA}}=90^{\circ}-\widehat{\mathrm{BCA}}=\widehat{\mathrm{HAE}},
$$
thus triangle AHE is isosceles at H.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle isocèle en $A$ mais pas rectangle. Soit $D$ le point de ( $B C$ ) tel que $(A D)$ soit perpendiculaire à $(A B)$, et soit $E$ le projeté orthogonal de $D$ sur $(A C)$. Soit enfin $H$ le milieu de [BC].
Montrer que $A H E$ est isocèle en H .
|
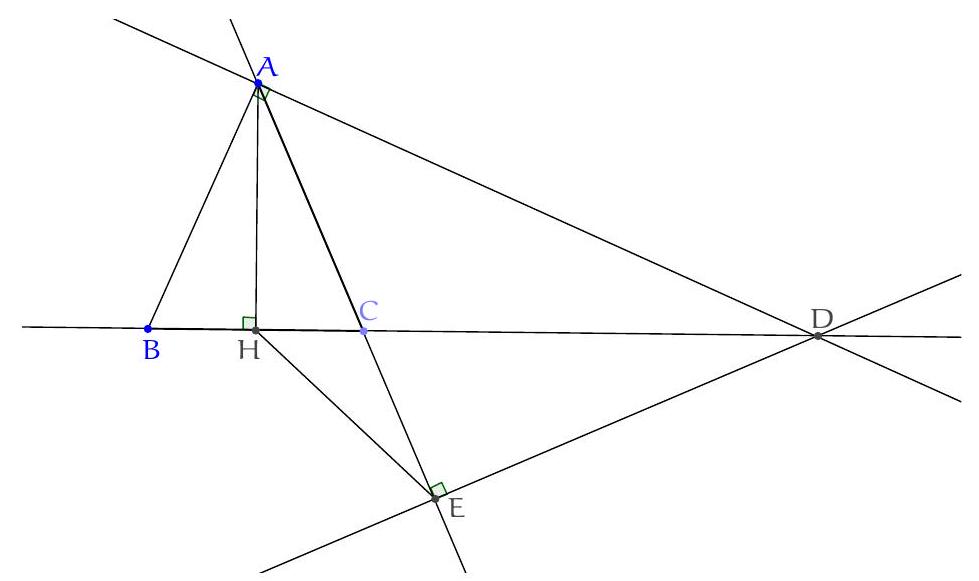
Commençons par remarquer que les points $A, D, E$ et $H$ sont cocycliques sur le cercle de diamètre [AD]. On en déduit par chasse au angles :
$$
\widehat{\mathrm{HEA}}=\widehat{\mathrm{HDA}}=90^{\circ}-\widehat{\mathrm{DBA}}=90^{\circ}-\widehat{\mathrm{BCA}}=\widehat{\mathrm{HAE}},
$$
donc le triangle AHE est isocèle en H .
|
{
"exam": "French_envois",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/envois/fr-Corrigé-Envoi-5-2019.jsonl",
"solution_match": "## Solution de l'exercice 4",
"tier": "T2",
"year": "2019"
}
|
Let $n \geqslant 2$ and let $x_{1}, x_{2}, \ldots, x_{n}$ be real numbers such that $x_{1}+x_{2}+\cdots+x_{n}=0$ and $x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}=1$.
Show that there exists $i$ such that $x_{i} \geqslant \frac{1}{\sqrt{n(n-1)}}$.
|
We denote $\mathrm{N}^{+}$ the number of indices $i$ such that $x_{i}>0$ and $N^{-}$ the number of indices $i$ such that $x_{i} \leqslant 0$, so that $\mathrm{N}^{+}+\mathrm{N}^{-}=\mathrm{n}$. We also denote
$$
S_{1}^{+}=\sum_{i \text { such that } x_{i}>0} x_{i} \quad \text { and } \quad S_{1}^{-}=\sum_{i \text { such that } x_{i} \leqslant 0}\left(-x_{i}\right)
$$
as well as
$$
S_{2}^{+}=\sum_{i \text { such that } x_{i}>0} x_{i}^{2} \quad \text { and } \quad S_{2}^{-}=\sum_{i \text { such that } x_{i} \leqslant 0} x_{i}^{2} .
$$
The interest of these quantities is that they allow us to both restate the hypotheses and use well-known inequalities such as Cauchy-Schwarz. The hypotheses of the statement can be rewritten as $S_{1}^{+}=$ $S_{1}^{-}$ and $S_{2}^{+}+S_{2}^{-}=1$. To make the square root appear in the result, we will use $S_{2}^{+}$. More precisely, we will show that $S_{2}^{+} \geqslant \frac{1}{n}$. Since the sum $S_{2}^{+}$ contains at most $n-1$ terms (the numbers cannot all be $>0$), one of these terms is greater than $\frac{1}{n(n-1)}$, i.e., $x_{i}^{2} \geqslant \frac{1}{\sqrt{n(n-1)}}$ for some $i$ with $x_{i}>0$, which allows us to conclude.
To show this, we write:
$$
1-S_{2}^{+}=S_{2}^{-} \leqslant\left(S_{1}^{-}\right)^{2}=\left(S_{1}^{+}\right)^{2} \leqslant N^{+} S_{2}^{+} \leqslant(n-1) S_{2}^{+} .
$$
The first inequality is obtained by expanding $\left(S_{1}^{-}\right)^{2}$ and keeping only the terms $\chi_{i}^{2}$. The second is the Cauchy-Schwarz inequality, and the third is the fact that the $x_{i}$ are not all strictly positive. We deduce that $S_{2}^{+} \geqslant \frac{1}{n}$, which allows us to conclude.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $n \geqslant 2$ et soient $x_{1}, x_{2}, \ldots, x_{n}$ des nombres réels tels que $x_{1}+x_{2}+\cdots+x_{n}=0$ et $x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}=1$.
Montrer qu'il existe $i$ tel que $x_{i} \geqslant \frac{1}{\sqrt{n(n-1)}}$.
|
On note $\mathrm{N}^{+}$le nombre d'indices $i$ tels que $x_{i}>0$ et $N^{-}$le nombre d'indices $i$ tels que $x_{i} \leqslant 0$, de sorte que $\mathrm{N}^{+}+\mathrm{N}^{-}=\mathrm{n}$. On note également
$$
S_{1}^{+}=\sum_{i \text { tel que } x_{i}>0} x_{i} \quad \text { et } \quad S_{1}^{-}=\sum_{i \text { tel que } x_{i} \leqslant 0}\left(-x_{i}\right)
$$
ainsi que
$$
S_{2}^{+}=\sum_{i \text { tel que } x_{i}>0} x_{i}^{2} \quad \text { et } \quad S_{2}^{-}=\sum_{i \text { tel que } x_{i} \leqslant 0} x_{i}^{2} .
$$
L'intérêt de ces quantités est qu'elles permettent à la fois de reformuler les hypothèses et d'utiliser des inégalités bien connues comme celle de Cauchy-Schwarz. Les hypothèses de l'énoncé se réécrivent $S_{1}^{+}=$ $S_{1}^{-}$et $S_{2}^{+}+S_{2}^{-}=1$. Pour faire apparaître la racine dans le résultat, on va utiliser $S_{2}^{+}$. Plus précisément, on va montrer que $S_{2}^{+} \geqslant \frac{1}{n}$. Comme la somme $S_{2}^{+}$contient au maximum $n-1$ termes (les nombres ne peuvent pas être tous $>0)$, un de ces termes est plus grand que $\frac{1}{n(n-1)}$, soit $x_{i}^{2} \geqslant \frac{1}{\sqrt{n(n-1)}}$ pour un certain $i$ avec $x_{i}>0$, ce qui permet de conclure.
Pour montrer cela, on écrit :
$$
1-S_{2}^{+}=S_{2}^{-} \leqslant\left(S_{1}^{-}\right)^{2}=\left(S_{1}^{+}\right)^{2} \leqslant N^{+} S_{2}^{+} \leqslant(n-1) S_{2}^{+} .
$$
La première inégalité s'obtient en développant $\left(S_{1}^{-}\right)^{2}$ et en ne gardant que les termes $\chi_{i}^{2}$. La seconde est l'inégalité de Cauchy-Schwarz, et la troisième est le fait que les $x_{i}$ ne sont pas tous strictement positifs. On en déduit $S_{2}^{+} \geqslant \frac{1}{n}$, ce qui permet de conclure.
|
{
"exam": "French_envois",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/envois/fr-Corrigé-Envoi-5-2019.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T2",
"year": "2019"
}
|
Find all triplets $(a, b, c)$ of strictly positive integers such that
$$
3^{a}-5^{b}=c^{2}
$$
|
Since $3^{a}$ and $5^{b}$ are both odd, we have $c$ even, so $c^{2} \equiv 0[4]$. Since $5^{b} \equiv 1[4]$, we must have $3^{a} \equiv 1[4]$, so $a$ is even. We write $a=2 a^{\prime}$, and the equation becomes
$$
5^{b}=3^{2 a^{\prime}}-c^{2}=\left(3^{a^{\prime}}-c\right)\left(3^{a^{\prime}}+c\right) .
$$
Note that the sum of the two factors is $2 \times 3^{a^{\prime}}$, so it is not divisible by 5, and one of the two factors is not divisible by 5 and must be 1. It must be the smaller one, so we have
$$
3^{a^{\prime}}-c=1 \quad \text{and} \quad 3^{a^{\prime}}+c=5^{b}
$$
or, by adding the last two equations, $2 \times 3^{a^{\prime}}=5^{b}+1$.
We can now observe that $a^{\prime}=1$ is a solution, but there do not seem to be any more. A natural way to separate the case $a^{\prime}=1$ from the rest is to look modulo 9. Indeed, in this case, as soon as $a^{\prime} \geqslant 2$, both sides must be divisible by 9, i.e., $5^{b} \equiv -1[9]$. This implies that $b$ must be divisible by 3. Moreover, looking modulo 3, we get that $b$ must be odd. The equation then becomes
$$
2 \times 3^{a^{\prime}}=5^{3 b^{\prime}}+1=125^{b^{\prime}}+1
$$
with $\mathbf{b}^{\prime}$ odd. But then, the right-hand side factors by $125+1=126=2 \times 7 \times 9$. In particular, it is divisible by 7, which is not the case for the left-hand side. It is therefore impossible to have $a^{\prime} \geqslant 2$. We must therefore have $\boldsymbol{a}^{\prime}=1$, which leads to the solution $(\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c})=(2,1,2)$ in the original equation.
|
(2,1,2)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Trouver tous les triplets ( $a, b, c$ ) d'entiers strictement positifs tels que
$$
3^{a}-5^{b}=c^{2}
$$
|
Comme $3^{a}$ et $5^{b}$ sont tous deux impairs, on a c pair donc $c^{2} \equiv 0[4]$. Comme $5^{b} \equiv 1[4]$, on doit avoir $3^{a} \equiv 1[4]$, donc a est pair. On écrit $a=2 a^{\prime}$, et l'équation devient
$$
5^{b}=3^{2 a^{\prime}}-c^{2}=\left(3^{a^{\prime}}-c\right)\left(3^{a^{\prime}}+c\right) .
$$
Notons que la somme des deux facteurs vaut $2 \times 3^{a^{\prime}}$, donc elle n'est pas divisible par 5 , donc un des deux facteurs n'est pas divisible par 5 et ne peut valoir que 1 . C'est nécessairement le plus petit, donc on a
$$
3^{a^{\prime}}-c=1 \quad \text { et } 3^{a^{\prime}}+c=5^{b}
$$
ou encore (en sommant les deux dernières égalités) $2 \times 3^{a^{\prime}}=5^{b}+1$.
On peut maintenant remarquer que $a^{\prime}=1$ est solution, mais qu'il ne semble plus y en avoir ensuite. Une manière naturelle de séparer le cas $a^{\prime}=1$ du reste est de regarder modulo 9 . En effet, dans ce cas, dès que $a^{\prime} \geqslant 2$, les deux membres doivent être divisibles par 9 , i.e. $5^{b} \equiv-1[9]$. Ceci implique que $b$ doit être divisible par 3. De plus, en regardant modulo 3, on obtient que b doit être impair. L'équation se réécrit donc
$$
2 \times 3^{a^{\prime}}=5^{3 b^{\prime}}+1=125^{b^{\prime}}+1
$$
avec $\mathbf{b}^{\prime}$ impair. Mais alors, le membre de droite se factorise par $125+1=126=2 \times 7 \times 9$. En particulier, il est divisible par 7 , ce qui n'est pas le cas du membre de gauche. Il est donc impossible d'avoir $a^{\prime} \geqslant 2$. On doit donc avoir $\boldsymbol{a}^{\prime}=1$, ce qui conduit à la solution $(\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c})=(2,1,2)$ dans l'équation de départ.
## Exercices Seniors
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/envois/fr-Corrigé-Envoi-5-2019.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T2",
"year": "2019"
}
|
Let $\left(a_{n}\right)_{n \geqslant 0}$ be a sequence of real numbers. Suppose that $a_{n}=\left|a_{n+1}-a_{n+2}\right|$ for all natural numbers $n$. Furthermore, $a_{0}$ and $a_{1}$ are strictly positive and distinct. Show that the sequence $\left(a_{n}\right)_{n \geqslant 0}$ is not bounded.
|
It is clear that the sequence $(a_{n})$ has positive terms.
Let $i$ be such that $a_{i}<a_{j}$ for $j<i$. Suppose by contradiction that $i \geqslant 4$. Then $a_{i-2}=\left|a_{i}-a_{i-1}\right|=$ $a_{i-1}-a_{i}<a_{i-1}$, so $a_{i-3}=\left|a_{i-2}-a_{i-1}\right|=a_{i-1}-a_{i-2}=a_{i}$, which contradicts the hypothesis on $i$.
Thus, if $m=\min \left\{a_{1}, a_{2}, a_{3}\right\}$, then for all $i$, $a_{i} \geqslant m$. Indeed, if there exists $i$ with $a_{i}<m$, choose $i$ minimal, then $a_{i}$ is smaller than all previous terms, so $i \leqslant 3$ which contradicts the definition of $m$.
Moreover, $m>0$ because $a_{3} \geqslant 0$ and $a_{3}=0 \rightarrow a_{1}=a_{2}$.
From then on, we write $a_{i}=\left|a_{i+1}-a_{i+2}\right|$ for all $i$, so
- If $a_{i+1}>a_{i+2}$, then $a_{i+1}=a_{i}+a_{i+2} \geqslant a_{i}+m$
- Otherwise, $a_{i+2}=a_{i+1}+a_{i} \geqslant a_{i}+m$
In all cases, there exists a term in the sequence $\geqslant a_{i}+m$. We can therefore prove by a very simple induction on $k$ the existence of $i$ such that $a_{i} \geqslant m k$, so the sequence $(a_{i})$ is not bounded.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $\left(a_{n}\right)_{n \geqslant 0}$ une suite de réels. On suppose que $a_{n}=\left|a_{n+1}-a_{n+2}\right|$ pour tout entier naturel $n$. De plus, $a_{0}$ et $a_{1}$ sont strictement positifs et distincts. Montrer que la suite $\left(a_{n}\right)_{n \geqslant 0} n$ 'est pas bornée.
|
Il est clair que la suite ( $a_{n}$ ) est à termes positifs.
Soit $i$ tel que $a_{i}<a_{j}$ pour $j<i$. Supposons par l'absurde que $i \geqslant 4$. Alors $a_{i-2}=\left|a_{i}-a_{i-1}\right|=$ $a_{i-1}-a_{i}<a_{i-1}$ donc $a_{i-3}=\left|a_{i-2}-a_{i-1}\right|=a_{i-1}-a_{i-2}=a_{i}$, ce qui contredit l'hypothèse sur $i$.
Ainsi, si $m=\min \left\{a_{1}, a_{2}, a_{3}\right\}$, alors pour tout $i, a_{i} \geqslant m$. En effet, s'il existe $i$ avec $a_{i}<m$, choisissons $i$ minimal, alors $a_{i}$ est plus petit que tous les termes précédents, donc $i \leqslant 3$ ce qui contredit la définition de $m$.
De plus, $m>0$ car $a_{3} \geqslant 0$ et $a_{3}=0 \rightarrow a_{1}=a_{2}$.
Dès lors, on écrit $a_{i}=\left|a_{i+1}-a_{i+2}\right|$ pour tout $i$, donc
- Si $a_{i+1}>a_{i+2}$, d'où $a_{i+1}=a_{i}+a_{i+2} \geqslant a_{i}+m$
- Sinon, $a_{i+2}=a_{i+1}+a_{i} \geqslant a_{i}+m$
Dans tous les cas, il existe un terme de la suite $\geqslant a_{i}+m$. On peut donc prouver par une très simple récurrence sur $k$ l'existence de $i$ tel que $a_{i} \geqslant m k$, donc la suite ( $a_{i}$ ) n'est pas bornée.
|
{
"exam": "French_envois",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/envois/fr-Corrigé-Envoi-5-2019.jsonl",
"solution_match": "\nSolution de l'exercice 7",
"tier": "T2",
"year": "2019"
}
|
Let $ABCD$ be a trapezoid with $(AB)$ parallel to $(CD)$. Suppose there are two circles $\omega_{1}$ and $\omega_{2}$ inside the trapezoid such that $\omega_{1}$ is tangent to the sides $[DA]$, $[AB]$, and $[BC]$, and $\omega_{2}$ is tangent to the sides $[BC]$, $[CD]$, and $[DA]$. Let $\left(d_{1}\right)$ be the second tangent (after $(AD)$) to $\omega_{2}$ passing through $A$, and let $\left(d_{2}\right)$ be the second tangent (after $(BC)$) to $\omega_{1}$ passing through $C$.
Show that $\left(d_{1}\right)$ and $\left(d_{2}\right)$ are parallel.
|
Let $X$ be the intersection point of $(AD)$ and $(BC)$. We denote $E$ and $F$ as the centers of $\omega_{1}$ and $\omega_{2}$, respectively. Note that $\omega_{1}$ is the incircle of $\triangle XAB$ and $\omega_{2}$ is the $X$-excircle of $\triangle XCD$. Finally, let $G$ be the center of the $X$-excircle of $\triangle XAB$.
We verify that triangles $XAG$ and $XEB$ are similar. Indeed, we have $\widehat{AXG} = \widehat{EXB} = \frac{1}{2} \widehat{AXB}$. Furthermore, we have $\widehat{GAX} = 90^\circ + \frac{1}{2} \widehat{BAX}$ and $\widehat{BEX} = 180^\circ - \frac{1}{2} \widehat{AXB} - \widehat{ABX} = 90^\circ + \frac{1}{2} \widehat{BAX}$, so $XAG$ and $XEB$ are indeed similar. Let $s$ be the direct similarity that maps $X$ to $X$, $A$ to $E$, and $G$ to $B$. According to the described homothety, we have $\frac{XC}{XB} = \frac{XF}{XG}$, so $s(F) = C$.
By similarity, we deduce that $\widehat{XAF} = \widehat{XEC}$. The rest of the exercise is now a simple angle chase, which can be carried out in many different ways. For example, let $Y$ be the intersection of $(d_2)$ with $(AD)$. Showing that $(d_1)$ and $(d_2)$ are parallel amounts to showing that $\widehat{XYC} = \widehat{XAd}$. We have
\[
\widehat{XYC} = 180^\circ - \widehat{AXB} - \widehat{XCY} = \widehat{BCY} - \widehat{AXB} = 2 \widehat{BCE} - \widehat{AXB}.
\]
Moreover, we can write
\[
\widehat{BCE} = 180^\circ - \widehat{XCE} = \frac{1}{2} \widehat{AXB} + \widehat{XEC} = \frac{1}{2} \widehat{AXB} + \widehat{XAF}
\]
which gives $\widehat{XYC} = 2 \widehat{XAF} = \widehat{XAd_1}$, hence the result.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un trapèze avec $(A B)$ parallèle à $(C D)$. On suppose qu'il y a deux cercles $\omega_{1}$ et $\omega_{2}$ à l'intérieur du trapèze tels que $\omega_{1}$ est tangent aux côtés [DA], $\left.A B\right]$ et $[B C]$ et $\omega_{2}$ est tangent aux côtés $[B C],[C D]$ et $[D A]$. Soit $\left(d_{1}\right)$ la seconde tangente (après $\left.(A D)\right)$ à $\omega_{2}$ passant par $A$, et soit $\left(d_{2}\right)$ la seconde tangente (après $(B C)$ ) à $\omega_{1}$ passant par $C$.
Montrer que $\left(\mathrm{d}_{1}\right)$ et $\left(\mathrm{d}_{2}\right)$ sont parallèles.
|
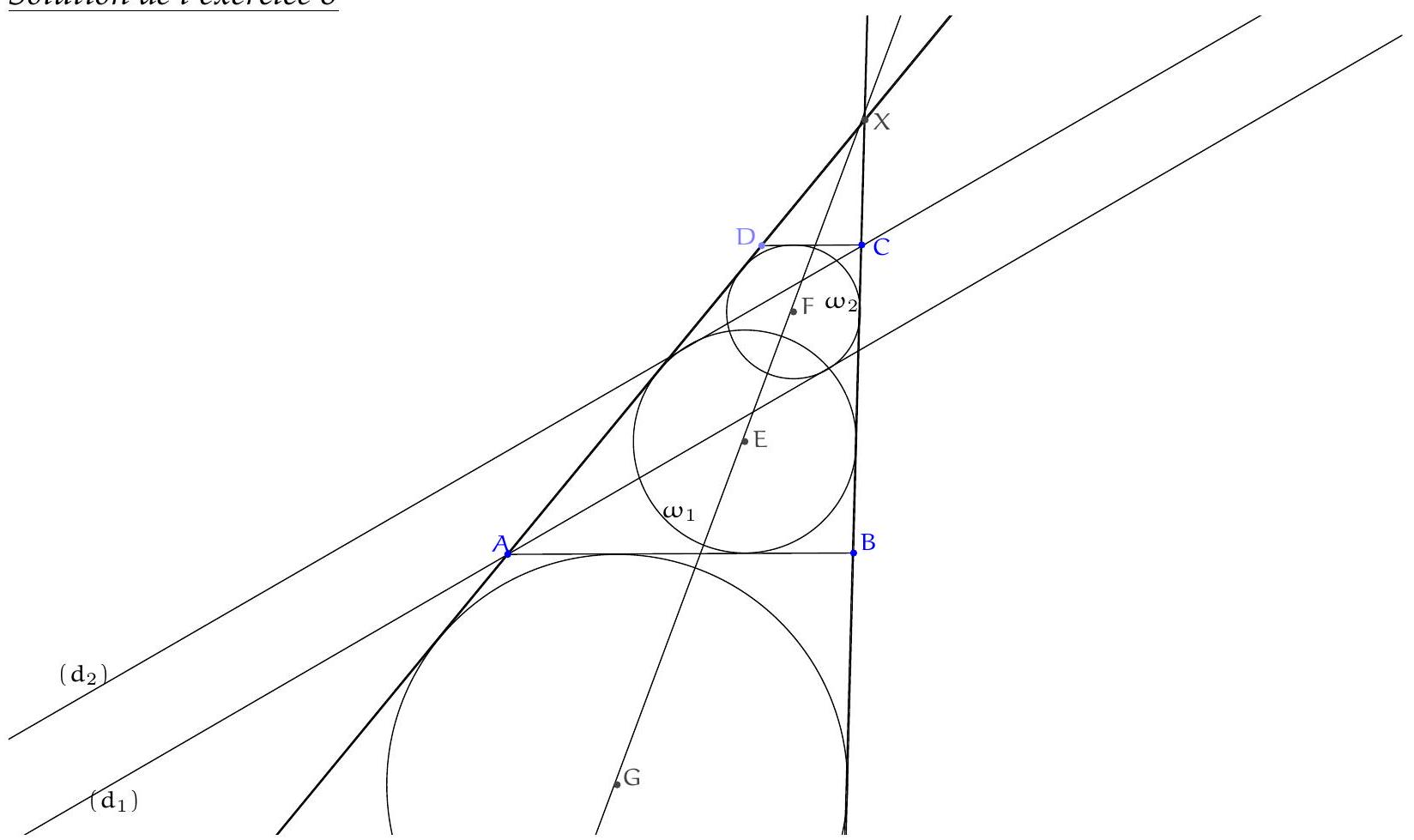
On note $X$ le point d'intersection de ( $A D$ ) et ( $B C$ ). On note respectivement $E$ et $F$ les centres de $\omega_{1}$ et $\omega_{2}$. Notons que $\omega_{1}$ est le cercle inscrit à $X A B$ et que $\omega_{2}$ est le cercle $X$-exinscrit à XCD. Enfin, on note $G$ le centre du cercle $X$-exinscrit à $X A B$.
On vérifie que les triangles XAG et $X E B$ sont semblables. En effet, on a $\widehat{A X G}=\widehat{E X B}=\frac{1}{2} \widehat{A X B}$. De plus, on a $\widehat{G A X}=90^{\circ}+\frac{1}{2} \widehat{B A X}$ et $\widehat{B E X}=180^{\circ}-\frac{1}{2} \widehat{A X B}-\widehat{A B X}=90^{\circ}+\frac{1}{2} \widehat{B A X}$, donc XAG et XEB sont bien semblables. Soit $s$ la similitude (directe) qui envoie $X$ sur $X, A$ sur $E$ et $G$ sur $B$. D'après l'homothétie décrite précédemment, on a $\frac{X C}{X B}=\frac{X F}{X G}$, donc $s(F)=C$.
Par similitude, on en déduit $\widehat{X A F}=\widehat{\mathrm{XEC}}$. La fin de l'exercice est maintenant une simple chasse aux angles, qui peut être menée de nombreuses manières différentes. Notons par exemple Y l'intersection de $\left(\mathrm{d}_{2}\right)$ avec $(A D)$. Montrer que $\left(\mathrm{d}_{1}\right)$ et $\left(\mathrm{d}_{2}\right)$ sont parallèles revient à montrer $\widehat{X Y C}=\widehat{X_{A d}}$. Or, on a
$$
\widehat{X Y C}=180^{\circ}-\widehat{A X B}-\widehat{X C Y}=\widehat{B C Y}-\widehat{A X B}=2 \widehat{B C E}-\widehat{A X B} .
$$
De plus, on peut écrire
$$
\widehat{\mathrm{BCE}}=180^{\circ}-\widehat{\mathrm{XCE}}=\frac{1}{2} \widehat{\mathrm{AXB}}+\widehat{\mathrm{XEC}}=\frac{1}{2} \widehat{A X B}+\widehat{\mathrm{XAF}}
$$
ce qui donne $\widehat{X Y C}=2 \widehat{X A F}=\widehat{\mathrm{XAd}_{1}}$, d'où finalement le résultat.
|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "\nExercice 8.",
"resource_path": "French/segmented/envois/fr-Corrigé-Envoi-5-2019.jsonl",
"solution_match": "## Solution de l'exercice 8",
"tier": "T2",
"year": "2019"
}
|
Let $S=\{1, \ldots, n\}$, with $n \geqslant 3$ an integer, and let $k$ be a strictly positive integer. We denote $S^{k}$ as the set of $k$-tuples of elements of $S$. Let $f: S^{k} \rightarrow S$ be such that, if $x=\left(x_{1}, \ldots, x_{k}\right) \in S^{k}$ and $y=\left(y_{1}, \ldots, y_{k}\right) \in S^{k}$ with $x_{i} \neq y_{i}$ for all $1 \leqslant i \leqslant k$, then $f(x) \neq f(y)$.
Show that there exists $\ell$ with $1 \leqslant \ell \leqslant k$ and a function $g: S \rightarrow S$ satisfying, for all $x_{1}, \ldots, x_{k} \in S$, $f\left(x_{1}, \ldots, x_{k}\right)=g\left(x_{\ell}\right)$.
|
We will show the result by induction on $k$. The case $k=1$ is trivial, so let's assume the result is true for $k-1 \geq 1$ and show it for $k$.
Suppose there exist $k-1$ elements $a_{2}, \ldots, a_{k}$ of $S$ such that the function $\phi: a \in S \mapsto f\left(a, a_{2}, \ldots, a_{k}\right) \in S$ is injective. By equality of cardinality, it is also bijective.
Therefore, if $b_{2}, \ldots, b_{k}$ are elements of $S$ with $b_{i} \neq a_{i}$ for all $i \in\{2, \ldots, k\}$, and $b \in S$, then $\phi(a) \neq f\left(b, b_{2}, \ldots, b_{k}\right)$ for $S \ni a \neq b$. By surjectivity of $\phi, \phi(b)=f\left(b, b_{2}, \ldots, b_{k}\right)$.
Let $c_{2}, \ldots, c_{k}$ be elements of $S$; since $n \geq 3$, there exist $b_{2}, \ldots, b_{k}$ such that $a_{i} \neq b_{i} \neq c_{i}$ for all $i \in\{2, \ldots, k\}$. Therefore, the previous reasoning shows that, if $b \in S, \phi(b)=f\left(b, b_{2}, \ldots, b_{k}\right) = f\left(b, c_{2}, \ldots, c_{k}\right)$, and thus $\ell=1$, and $g=\phi$ are suitable.
We assume therefore that there exist two functions $\alpha, \beta: S^{k-1} \rightarrow S$ such that, for all $a_{2}, \ldots, a_{k}$ in $S$, $\alpha=\alpha\left(a_{2}, \ldots, a_{k}\right) \neq \beta\left(a_{2}, \ldots, a_{n}\right)=\beta$, and $f\left(\alpha, a_{2}, \ldots, a_{k}\right)=f\left(\beta, a_{2}, \ldots, a_{k}\right)$.
Let's show that $f^{\prime}:\left(a_{2}, \ldots, a_{k}\right) \in S^{k-1} \mapsto f\left(\alpha, a_{2}, \ldots, a_{k}\right)=f\left(\beta, a_{2}, \ldots, a_{k}\right)$ satisfies the conditions of the problem. Indeed, if $\left(a_{2}, \ldots, a_{k}\right)$ and $\left(b_{2}, \ldots, b_{k}\right)$ are two $(k-1)$-tuples whose coordinates are all different, then either $\alpha=\alpha\left(a_{2}, \ldots, a_{k}\right) \neq \alpha\left(b_{2}, \ldots, b_{k}\right)=\alpha^{\prime}$, in which case $g\left(a_{2}, \ldots, a_{k}\right) = f\left(\alpha, a_{2}, \ldots, a_{k}\right) \neq f\left(\alpha^{\prime}, b_{2}, \ldots, b_{k}\right) g\left(b_{2}, \ldots, b_{k}\right)$ by hypothesis, or $\alpha \neq \beta\left(b_{2}, \ldots, b_{k}\right)$, in which case we have $g\left(a_{2}, \ldots, a_{k}\right) \neq g\left(b_{2}, \ldots, b_{k}\right)$.
Therefore, by the induction hypothesis, and without loss of generality, we can assume the existence of $h: S \rightarrow S$ such that $g\left(a_{2}, \ldots, a_{k}\right)=h\left(a_{2}\right)$ for $a_{2}, \ldots, a_{k}$ in $S$. $h$ must be injective because $h(a) = g(a, a, \ldots, a) \neq g(b, \ldots, b)=h(b)$ if $a \neq b$ are elements of $S$. By equality of cardinality, $h$ is surjective.
Let's show that $f\left(a_{1}, \ldots, a_{k}\right)=h\left(a_{2}\right)$ for all $a_{1}, \ldots, a_{k} \in S$, which will conclude the proof. Suppose, for the sake of contradiction, the existence of a $k$-tuple $a=\left(a_{1}, \ldots, a_{k}\right) \in S^{k}$ such that $f(a) \neq h\left(a_{2}\right)$. By surjectivity, there exists $b_{2} \in S$ with $h\left(b_{2}\right)=f(a)$ and $b_{2} \neq a_{2}$. Let $b_{i} \neq a_{i}$ be elements of $S$, for $3 \leqslant i \leqslant k$. We have $\alpha = \alpha\left(b_{2}, \ldots, b_{k}\right)$ and $\beta=\beta\left(b_{2}, \ldots, b_{k}\right)$ two elements of $S$ such that $f\left(\alpha, b_{2}, \ldots, b_{k}\right)=f\left(\beta, b_{2}, \ldots, b_{k}\right) = h\left(b_{2}\right)=f(a)$. The hypothesis made on $f$ ensures therefore $\alpha=a_{1}=\beta$, which is a contradiction according to the definition of $\alpha$ and $\beta$.
[^0]: Animath, French Olympiad Preparation, 11-13 rue Pierre et Marie Curie, 75005 Paris.
copies.ofm@gmail.com
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soit $S=\{1, \ldots, n\}$, avec $n \geqslant 3$ un entier, et soit $k$ un entier strictement positif. On note $S^{k}$ l'ensemble des $k$-uplets d'éléments de $S$. Soit $f: S^{k} \rightarrow S$ telle que, si $x=\left(x_{1}, \ldots, \chi_{k}\right) \in S^{k}$ et $y=\left(y_{1}, \ldots, y_{k}\right) \in S^{k}$ avec $x_{i} \neq y_{i}$ pour tout $1 \leqslant i \leqslant k$, alors $f(x) \neq f(y)$.
Montrer qu'il existe $\ell$ avec $1 \leqslant \ell \leqslant k$ et une fonction $g: S \rightarrow S$ vérifiant, pour tous $x_{1}, \ldots, x_{k} \in S$, $f\left(x_{1}, \ldots, x_{k}\right)=g\left(x_{\ell}\right)$.
|
Nous montrerons le résultat par récurrence sur k. Le cas $k=1$ est trivial, supposons donc le résultat vrai pour $\mathrm{k}-1 \geqslant 1$ et montrons le pour k .
Supposons l'existence de $k-1$ éléments $a_{2}, \ldots, a_{k}$ de $S$ tels que la fonction $\phi: a \in S \mapsto f\left(a, a_{2}, \ldots, a_{k}\right) \in$ $S$ est injective. Par égalité de cardinal, elle est aussi bijective.
Dès lors, si $b_{2}, \ldots, b_{k}$ sont des éléments de $S$ avec $b_{i} \neq a_{i}$ pour tout $i \in\{2, \ldots, k\}$, et $b \in S$, alors $\phi(a) \neq f\left(b, b_{2}, \ldots, b_{k}\right)$ pour $S \ni a \neq b$. Par surjectivité de $\phi, \phi(b)=f\left(b, b_{2}, \ldots, b_{k}\right)$.
Soient $c_{2}, \ldots, c_{k}$ des éléments de $S$; puisque $n \geqslant 3$, il existe $b_{2}, \ldots, b_{k}$ tels que $a_{i} \neq b_{i} \neq c_{i}$ pour tout $i \in\{2, \ldots, k\}$. Dès lors le raisonnement précédent montre que, si $b \in S, \phi(b)=f\left(b, b_{2}, \ldots, b_{k}\right)=$ $\mathrm{f}\left(\mathrm{b}, \mathrm{c}_{2}, \ldots, \mathrm{c}_{\mathrm{k}}\right)$, et ainsi $\ell=1$, et $\mathrm{g}=\phi$ conviennent.
Nous supposons donc qu'il existe deux fonctions $\alpha, \beta: S^{k-1} \rightarrow S$ avec, pour tous $a_{2}, \ldots, a_{k}$ dans $S$, $\alpha=\alpha\left(a_{2}, \ldots, a_{k}\right) \neq \beta\left(a_{2}, \ldots, a_{n}\right)=\beta$, et $f\left(\alpha, a_{2}, \ldots, a_{k}\right)=f\left(\beta, a_{2}, \ldots, a_{k}\right)$.
Montrons que $f^{\prime}:\left(a_{2}, \ldots, a_{k}\right) \in S^{k-1} \mapsto f\left(\alpha, a_{2}, \ldots, a_{k}\right)=f\left(\beta, a_{2}, \ldots, a_{k}\right)$ satisfait les conditions du problème. En effet, si $\left(a_{2}, \ldots, a_{k}\right)$ et $\left(b_{2}, \ldots, b_{k}\right)$ sont deux $(k-1)$-uplets dont les coordonnées sont toutes différentes, alors soit $\alpha=\alpha\left(a_{2}, \ldots, a_{k}\right) \neq \alpha\left(b_{2}, \ldots, b_{k}\right)=\alpha^{\prime}$, auquel cas $g\left(a_{2}, \ldots, a_{k}\right)=$ $f\left(\alpha, a_{2}, \ldots, a_{k}\right) \neq f\left(\alpha^{\prime}, b_{2}, \ldots, b_{k}\right) g\left(b_{2}, \ldots, b_{k}\right)$ par hypothèse, soit $\alpha \neq \beta\left(b_{2}, \ldots, b_{k}\right)$ auquel cas on a de même $g\left(a_{2}, \ldots, a_{k}\right) \neq g\left(b_{2}, \ldots, b_{k}\right)$.
Dès lors par hypothèse de récurrence, et sans perte de généralité, on peut supposer l'existence de $h$ : $S \rightarrow S$ telle que $g\left(a_{2}, \ldots, a_{k}\right)=h\left(a_{2}\right)$ pour $a_{2}, \ldots, a_{k}$ dans S. $h$ doit être injective car $h(a)=$ $g(a, a, \ldots, a) \neq g(b, \ldots, b)=h(b)$ si $a \neq b$ sont des éléments de S. Par égalité de cardinal, $h$ est surjective.
Montrons que $f\left(a_{1}, \ldots, a_{k}\right)=h\left(a_{2}\right)$ pour tous $a_{1}, \ldots, a_{k} \in S$, ce qui conclura. Supposons par l'absurde l'existence d'un $k$-uplet $a=\left(a_{1}, \ldots, a_{k}\right) \in S^{k}$ tel que $f(a) \neq h\left(a_{2}\right)$. Par surjectivité, il existe $b_{2} \in S$ avec $h\left(b_{2}\right)=f(a)$ avec $b_{2} \neq a_{2}$ donc. Soient $b_{i} \neq a_{i}$ des éléments de $S$, pour $3 \leqslant i \leqslant k$. On a $\alpha=$ $\alpha\left(b_{2}, \ldots, b_{k}\right)$ et $\beta=\beta\left(b_{2}, \ldots, b_{k}\right)$ deux éléments de $S$ tels que $f\left(\alpha, b_{2}, \ldots, b_{k}\right)=f\left(\beta, b_{2}, \ldots, b_{k}\right)=$ $h\left(b_{2}\right)=f(a)$. L'hypothèse faite sur $f$ assure donc $\alpha=a_{1}=\beta$, ce qui est une contradiction d'après la définition de $\alpha$ et $\beta$.
[^0]: Animath, Préparation Olympique Française de Mathématiques, 11-13 rue Pierre et Marie Curie, 75005 Paris.
copies.ofm@gmail.com
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-Corrigé-Envoi-5-2019.jsonl",
"solution_match": "\nSolution de l'exercice 9",
"tier": "T2",
"year": "2019"
}
|
Let $A B C D$ be an isosceles trapezoid with (AD)//(BC).
(a) Show that $A B C D$ has a circumcircle.
(b) Let O be the center of the circumcircle of $A B C D$ and E the intersection of the diagonals. Show that O is on the circumcircle of AEB.
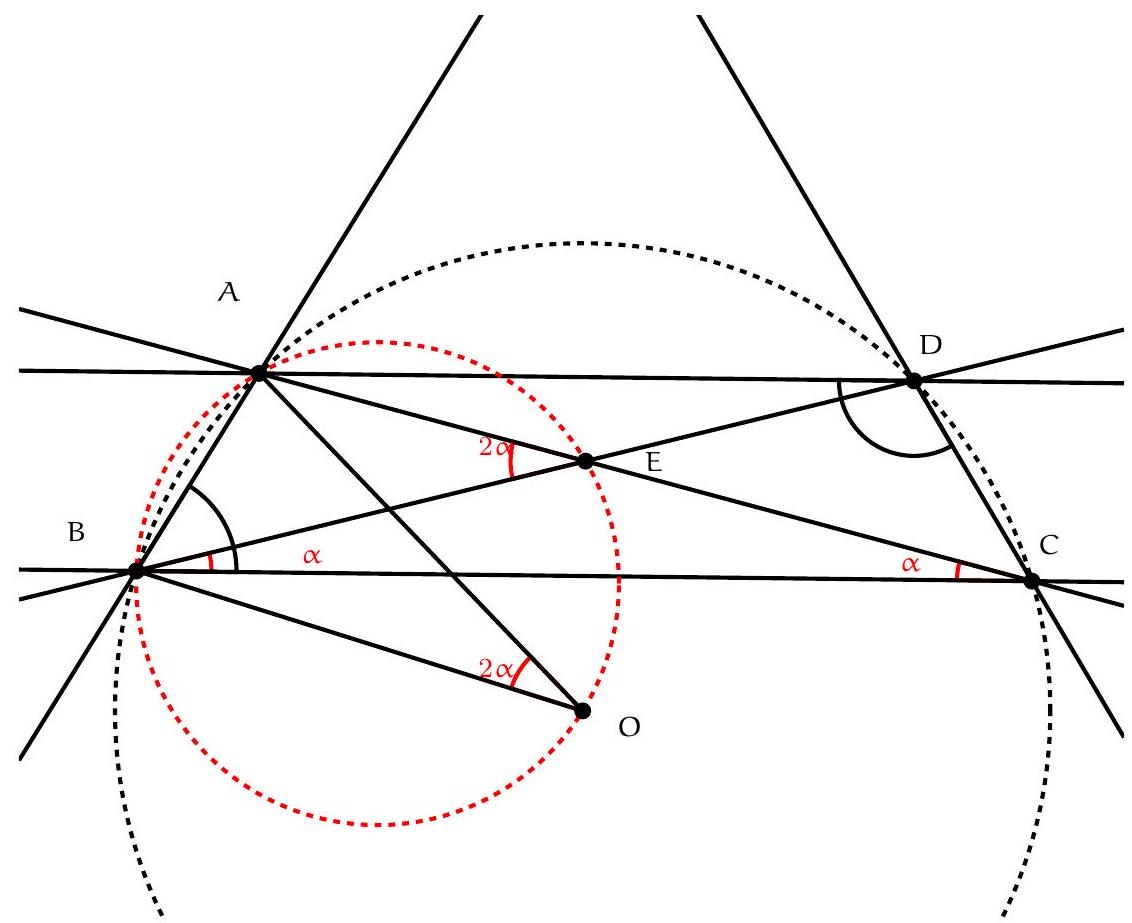
|
a) $A B C D$ is an isosceles trapezoid, so $\widehat{A B C}=\widehat{D C B}$. We also know that $(A D) / /(C B)$, thus $\widehat{D C B}=180-\widehat{C D A}$. With these two equalities, we find that $\widehat{A B C}+\widehat{C D A}=180$, which shows that points $A, B, C$ and $D$ are on the same circle.
b) We will denote $\alpha$ as the angle $\widehat{A C B}$ and try to calculate different angles to reach the required conclusion. By symmetry, we find that $\widehat{D B C}=\alpha$ as well. Thus, in triangle EBC, knowing that the sum of the angles is 180, we find $\widehat{\mathrm{AEB}}=180-\widehat{\mathrm{BEC}}=\widehat{\mathrm{EBC}}+\widehat{\mathrm{ECB}}=2 \alpha$. Using the inscribed angle theorem, knowing that the inscribed angle $\widehat{A C B}=\alpha$, we have $\widehat{A O B}=2 \alpha$. But then, $\widehat{A O B}=2 \alpha=\widehat{A E B}$, which shows that points $A, E, O$ and $B$ are concyclic.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un trapèze isocèle avec (AD)//(BC).
(a) Montrer que $A B C D$ admet un cercle circonscrit.
(b) On note O le centre du cercle circonscrit de $A B C D$ et E l'intersection des diagonales. Montrer que O est sur le cercle circonscrit de AEB.

|
a) $A B C D$ est un trapèze isocèle, ainsi $\widehat{A B C}=\widehat{D C B}$. On sait également que $(A D) / /(C B)$, donc $\widehat{D C B}=180-\widehat{C D A}$. Avec ces deux égalités on trouve que $\widehat{A B C}+\widehat{C D A}=180$, ce qui montre bien que les points $A, B, C$ et $D$ sont sur le même cercle.
b) On va noter $\alpha$ l'angle $\widehat{A C B}$ et on va essayer de calculer différents angles afin d'arriver à la conclusion demandée. On trouve par symétrie que $\widehat{D B C}=\alpha$ également. Ainsi, dans le triangle EBC , sachant que la somme des angles vaut 180 , on trouve $\widehat{\mathrm{AEB}}=180-\widehat{\mathrm{BEC}}=\widehat{\mathrm{EBC}}+\widehat{\mathrm{ECB}}=2 \alpha$. Avec le théorème de l'angle au centre, sachant que l'angle inscrit $\widehat{A C B}=\alpha$, on a $\widehat{A O B}=2 \alpha$. Mais alors, $\widehat{A O B}=2 \alpha=\widehat{A E B}$ ce qui montre bien que les points $A, E, O$ et $B$ sont cocycliques.
|
{
"exam": "French_envois",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"solution_match": "\nDémonstration.",
"tier": "T2",
"year": null
}
|
Let $\omega_{1}$ and $\omega_{2}$ be two circles with centers $\mathrm{O}_{1}$ and $\mathrm{O}_{2}$, respectively, and suppose they intersect at points $A$ and $B$. The circle passing through the points $O_{1}, O_{2}$, and $B$ intersects the circle $\omega_{1}$ at $C$. Show that the points $C$, $A$, and $O_{2}$ are collinear.
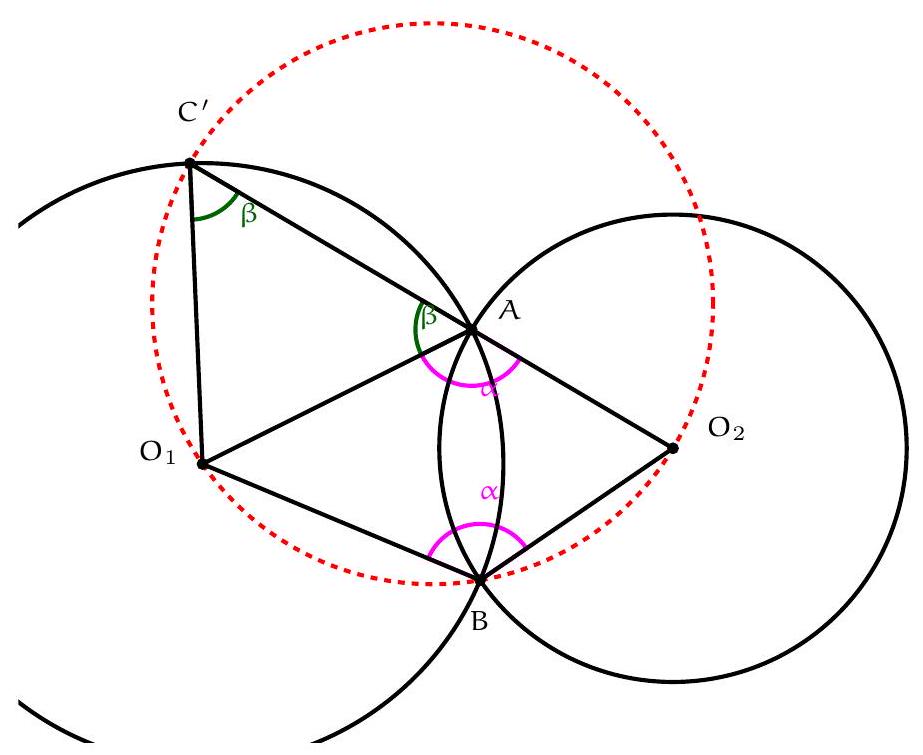
|
To solve this exercise, we will first introduce $\mathrm{C}^{\prime}$ as the second intersection of the line $\left(A O_{2}\right)$ with the circle $\omega_{1}$, then we will show that $\mathrm{C}=\mathrm{C}^{\prime}$.
We can decompose the straight angle $\widehat{\mathrm{O}_{2} \mathrm{AC}^{\prime}}$ into two angles: $\widehat{\mathrm{C}^{\prime} \mathrm{AO}_{1}}$ and $\widehat{\mathrm{O}_{1} \mathrm{AO}_{2}}$, whose sum is therefore 180 degrees. On the one hand, by performing an axial symmetry with axis $\left(\mathrm{O}_{1} \mathrm{O}_{2}\right)$, the points $A$ and $B$ are exchanged, but then the angle $\widehat{\mathrm{O}_{1} \mathrm{AO}_{2}}$ equals the angle $\widehat{\mathrm{O}_{1} \mathrm{BO}_{2}}$. On the other hand, $\mathrm{O}_{1} \mathrm{~A}=\mathrm{O}_{1} \mathrm{C}^{\prime}$ since $O_{1}$ is the center of the circle $\omega_{1}$, thus the triangle $O_{1} A C^{\prime}$ is isosceles at $O_{1}$, and we find that ${\widehat{O_{2} \mathrm{C}^{\prime} O_{1}}}_{1}=\widehat{\mathrm{AC}^{\prime} \mathrm{O}_{1}}={\widehat{\mathrm{C}^{\prime} \mathrm{AO}_{1}}}_{1}=180-{\widehat{\mathrm{O}_{1} \mathrm{AO}_{2}}}_{2}=180-{\widehat{\mathrm{O}_{1} \mathrm{BO}_{2}}}_{2}$, so in particular, $\widehat{\mathrm{O}_{2} \mathrm{C}^{\prime} \mathrm{O}_{1}}=$ $180-{\widehat{\mathrm{O}_{2}} \mathrm{BO}_{1}}$, which proves that the points $\mathrm{O}_{1}, \mathrm{~B}, \mathrm{O}_{2}$ and $\mathrm{C}^{\prime}$ are concyclic. Thus, if we take the definition of the point C, we get that $\mathrm{O}_{1}, \mathrm{O}_{2}, \mathrm{~B}$ and C are concyclic and that $\mathrm{C}^{\prime}$ is on $\omega_{1}$, so that $C^{\prime}=C$, but since the points $A, O_{2}$ and $C^{\prime}=C$ are collinear, we have in particular that $A, O_{2}$ and $C$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $\omega_{1}$ et $\omega_{2}$ deux cercles de centre $\mathrm{O}_{1}$ et $\mathrm{O}_{2}$, on suppose qu'ils se coupent en $A$ et $B$. Le cercle passant par les points $O_{1}, O_{2}$ et $B$ coupe le cercle $\omega_{1}$ en $C$. Montrer que les points $C$, $A$ et $O_{2}$ sont alignés.

|
Pour résoudre cet exercice, on va plutôt introduire dans un premier temps $\mathrm{C}^{\prime}$ la deuxième intersection de la droite $\left(A O_{2}\right)$ avec le cercle $\omega_{1}$ puis on va montrer que $\mathrm{C}=\mathrm{C}^{\prime}$.
On peut décomposer l'angle plat $\widehat{\mathrm{O}_{2} \mathrm{AC}^{\prime}}$ en deux angles : $\widehat{\mathrm{C}^{\prime} \mathrm{AO}_{1}}$ et $\widehat{\mathrm{O}_{1} \mathrm{AO}_{2}}$ dont la somme vaut donc 180 degrés. D'une part, en faisant une symétrie axiale d'axe $\left(\mathrm{O}_{1} \mathrm{O}_{2}\right)$, alors les points $A$ et $B$ sont échangés, mais alors l'angle $\widehat{\mathrm{O}_{1} \mathrm{AO}_{2}}$ vaut l'angle $\widehat{\mathrm{O}_{1} \mathrm{BO}_{2}}$. D'autre part, $\mathrm{O}_{1} \mathrm{~A}=\mathrm{O}_{1} \mathrm{C}^{\prime}$ comme $O_{1}$ est le centre du cercle $\omega_{1}$, ainsi le triangle $O_{1} A C^{\prime}$ est isocèle en $O_{1}$, et on trouve que ${\widehat{O_{2} \mathrm{C}^{\prime} O_{1}}}_{1}=\widehat{\mathrm{AC}^{\prime} \mathrm{O}_{1}}={\widehat{\mathrm{C}^{\prime} \mathrm{AO}_{1}}}_{1}=180-{\widehat{\mathrm{O}_{1} \mathrm{AO}_{2}}}_{2}=180-{\widehat{\mathrm{O}_{1} \mathrm{BO}_{2}}}_{2}$, donc en particulier, $\widehat{\mathrm{O}_{2} \mathrm{C}^{\prime} \mathrm{O}_{1}}=$ $180-{\widehat{\mathrm{O}_{2}} \mathrm{BO}_{1}}$, ce qui démontre bien que les points $\mathrm{O}_{1}, \mathrm{~B}, \mathrm{O}_{2}$ et $\mathrm{C}^{\prime}$ sont cocycliques. Ainsi, si on reprend la définition du point C , on obtient que $\mathrm{O}_{1}, \mathrm{O}_{2}, \mathrm{~B}$ et C sont cocycliques et que $\mathrm{C}^{\prime}$ est sur $\omega_{1}$, donc que $C^{\prime}=C$, mais comme les points $A, O_{2}$ et $C^{\prime}=C$ sont alignés on a entre autre que $A, O_{2}$ et $C$ sont alignés.
|
{
"exam": "French_envois",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"solution_match": "\nDémonstration.",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle and $H$ its orthocenter. The circumcircle of $ABH$, with center $O$, intersects the line $(BC)$ at $D$, and the line $(DH)$ intersects the line $(AC)$ at $P$. Show that the center of the circumcircle of $APD$ is on the circumcircle of $ODB$.
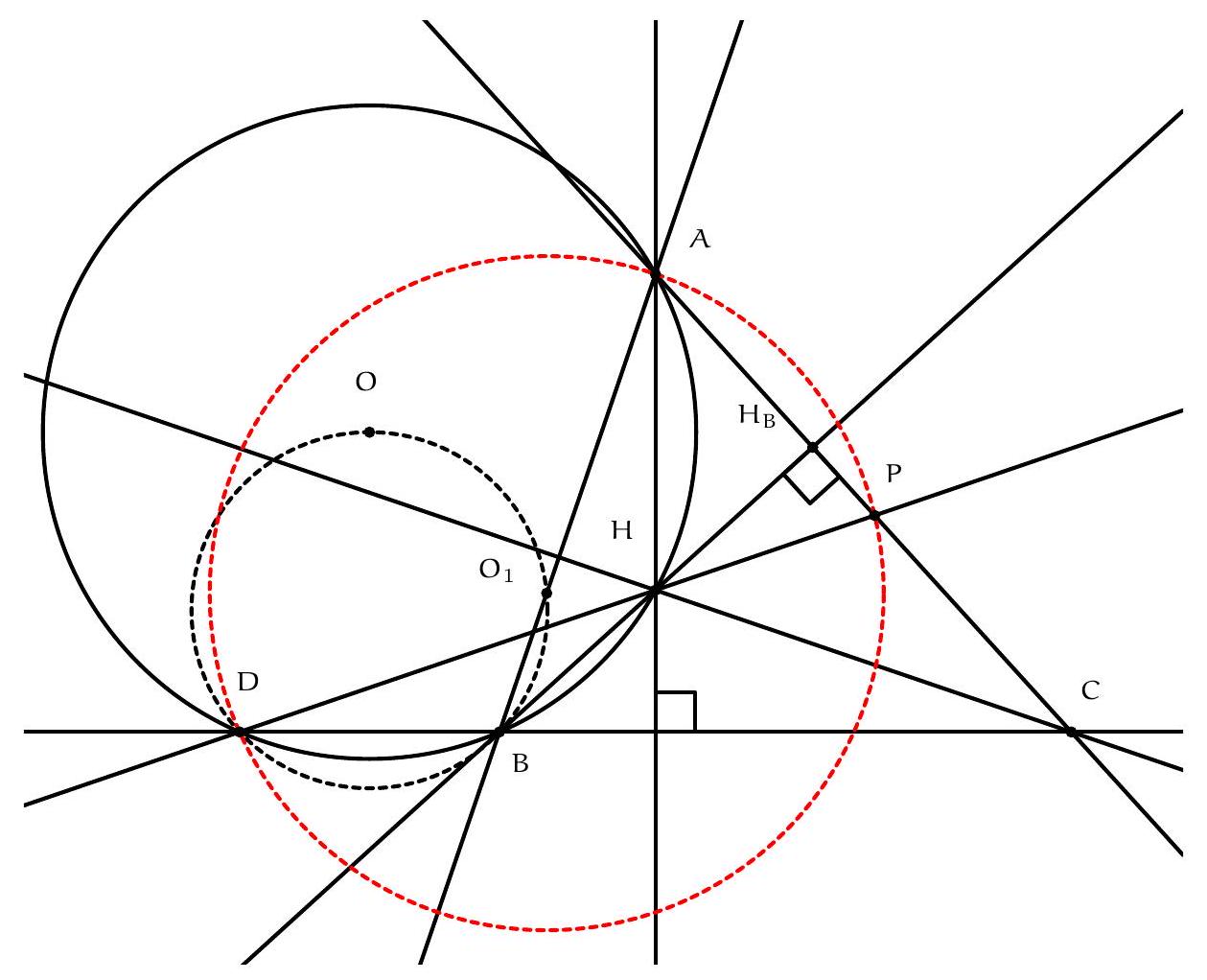
|
A careful construction allows us to conjecture that the center of the circle APD is also on the line $(A B)$, so it is quite natural to introduce $\mathrm{O}_{1}$, the point on the line $(A B)$ that is equidistant from $A$ and $D$. $c^{\prime}$ is then a good candidate to be the center of the circle APD.
Step 1. $\mathrm{O}_{1}$ is the center of the circle APD.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $H$ son orthocentre. Le cercle circonscrit de $A B H$, de centre $O$, recoupe la droite (BC) en $D$, la droite ( DH ) intersecte la droite ( $A C$ ) en $P$. Montrer que le centre du cercle circonscrit de APD est sur le cercle circonscrit de ODB.

|
Une construction soigneuse nous permet de conjecturer que le centre du cercle APD est également sur la droite ( $A B$ ), c'est donc tout naturellement que l'on introduit $\mathrm{O}_{1}$, le point de la droite $(A B)$ qui est à égale distance de $A$ et de $D, c^{\prime}$ est alors un bon candidat pour être le centre du cercle APD.
Étape 1. $\mathrm{O}_{1}$ est le centre du cercle de APD.
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"solution_match": "\nDémonstration.",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle and $H$ its orthocenter. The circumcircle of $ABH$, with center $O$, intersects the line $(BC)$ at $D$, and the line $(DH)$ intersects the line $(AC)$ at $P$. Show that the center of the circumcircle of $APD$ is on the circumcircle of $ODB$.

|
We introduce $\mathrm{H}_{\mathrm{B}}$ as the foot of the altitude from B in triangle ABC, and we set $x=\widehat{\mathrm{H}_{\mathrm{B}} \mathrm{PH}}$. Since triangle $\mathrm{HH}_{\mathrm{B}} \mathrm{P}$ is right-angled at $\mathrm{H}_{\mathrm{B}}$, we have $\widehat{\mathrm{H}_{\mathrm{B}} \mathrm{HP}}=90-\widehat{\mathrm{H}_{\mathrm{B}} \mathrm{PH}}=90-x$. On the other hand, $x=\widehat{\mathrm{H}_{\mathrm{B}} \mathrm{BP}}=\widehat{\mathrm{DHB}}$, and this angle equals $\widehat{\mathrm{DAB}}=x$ by the cocyclicity of points $A, H, B$ and D.
We denote $M$ as the midpoint of segment [AD], then $M$ and $\mathrm{O}_{1}$ lie on the perpendicular bisector of segment [AD], so $\left(\mathrm{MO}_{1}\right) \perp(\mathrm{AD})$, and thus $\widehat{M O_{1} \mathrm{~A}}=90-\widehat{\mathrm{MAO}_{1}}$.
Since $O_{1} A=O D$, we have $\widehat{A O_{1} D}=2 x=2 \widehat{A P D}$. On one hand, $\widehat{A O_{1} D}=2 \widehat{A P D}$, and on the other hand, $O A=O_{1} \mathrm{D}$, we want to deduce that $\mathrm{O}_{1}$ is indeed the center of the circumcircle of APD. But by the central angle theorem, this is indeed the case.
Step 2. $\mathrm{O}_{1}$ lies on the circle ODB.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $H$ son orthocentre. Le cercle circonscrit de $A B H$, de centre $O$, recoupe la droite (BC) en $D$, la droite ( DH ) intersecte la droite ( $A C$ ) en $P$. Montrer que le centre du cercle circonscrit de APD est sur le cercle circonscrit de ODB.

|
On introduit $\mathrm{H}_{\mathrm{B}}$ le pied de la hauteur issue de B dans le triangle ABC , on pose alors $x=\widehat{\mathrm{H}_{\mathrm{B}} \mathrm{PH}}$. Comme le triangle $\mathrm{HH}_{\mathrm{B}} \mathrm{P}$ est droit en $\mathrm{H}_{\mathrm{B}}$, on a $\widehat{\mathrm{H}_{\mathrm{B}} \mathrm{HP}}=90-\widehat{\mathrm{H}_{\mathrm{B}} \mathrm{PH}}=90-x$. Mais d'autre part, $x=\widehat{\mathrm{H}_{\mathrm{B}} \mathrm{BP}}=\widehat{\mathrm{DHB}}$, ce dernier angle vaut l'angle $\widehat{\mathrm{DAB}}=x$ par cocyclicité des points $A, H, B$ et D.
On note $M$ le milieu du segment [AD], alors $M$ et $\mathrm{O}_{1}$ sont sur la médiatrice du segment [AD], donc $\left(\mathrm{MO}_{1}\right) \perp(\mathrm{AD})$, et ainsi $\widehat{M O_{1} \mathrm{~A}}=90-\widehat{\mathrm{MAO}_{1}}$.
Or $O_{1} A=O D$, donc $\widehat{A O_{1} D}=2 x=2 \widehat{A P D}$. On a maintenant d'une part que $\widehat{A O_{1} D}=2 \widehat{A P D}$ mais d'autre part que $O A=O_{1} \mathrm{D}$, on voudrait en déduire que $\mathrm{O}_{1}$ est bien le centre du cercle circonscrit de APD. Mais par angle au centre c'est bien le cas.
Étape 2. $\mathrm{O}_{1}$ est sur le cercle ODB.
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"solution_match": "\nDémonstration.",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle and $H$ its orthocenter. The circumcircle of $ABH$, with center $O$, intersects the line $(BC)$ at $D$, and the line $(DH)$ intersects the line $(AC)$ at $P$. Show that the center of the circumcircle of $APD$ is on the circumcircle of $ODB$.

|
We notice that points $\mathrm{O}, \mathrm{M}$, and $\mathrm{O}_{1}$ are on the (same) perpendicular bisector of [AC], so they are collinear. We thus find the angle $\widehat{\mathrm{OO}_{1} \mathrm{D}}=x$. On the other hand, $\widehat{\mathrm{DOB}}=2 \widehat{\mathrm{DAB}}=$ $2(90-x)$. Since triangle ODB is isosceles at O, we can calculate the angle $\widehat{\mathrm{OBD}}$, which is thus $x$. Therefore, $\widehat{\mathrm{OO}_{1} \mathrm{D}}=x=\widehat{\mathrm{OBD}}$, which concludes step 2.
We know that $\mathrm{O}_{1}$ is the center of the circle APD and lies on the circle ODB, so the center of the circle APD is indeed on the circle ODB, which concludes.
## Common Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $H$ son orthocentre. Le cercle circonscrit de $A B H$, de centre $O$, recoupe la droite (BC) en $D$, la droite ( DH ) intersecte la droite ( $A C$ ) en $P$. Montrer que le centre du cercle circonscrit de APD est sur le cercle circonscrit de ODB.

|
On remarque que les points $\mathrm{O}, \mathrm{M}$ et $\mathrm{O}_{1}$ sont sur la (même) médiatrice de [AC], ils sont donc alignés. On trouve ainsi l'angle $\widehat{\mathrm{OO}_{1} \mathrm{D}}=x$. Mais d'autre part, $\widehat{\mathrm{DOB}}=2 \widehat{\mathrm{DAB}}=$ $2(90-x)$. Comme le triangle ODB est isocèle en O , on peut calculer l'angle $\widehat{\mathrm{OBD}}$ qui vaut ainsi $x$. Mais alors, $\widehat{\mathrm{OO}_{1} \mathrm{D}}=x=\widehat{\mathrm{OBD}}$, ce qui conclut l'étape 2 .
On sait que $\mathrm{O}_{1}$ est le centre du cercle APD et sur le cercle ODB, donc le centre du cercle de APD est bien sur le cercle ODB ce qui conclut.
## Exercices Communs
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"solution_match": "\nDémonstration.",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle, $H$ the foot of the altitude from $A$, $L$ the foot of the bisector from $B$, and $M$ the midpoint of $[AB]$. We assume that in triangle $HLM$, the two properties hold: $(AH)$ is an altitude and $(BL)$ is a bisector. Show that $(CM)$ is a median.
|
We take the triangle $ABC$, we will prove that it is equilateral, using the two properties, the third will follow.
We have $(AH) \perp(ML)$ and $(AH) \perp(BC)$, so $(BC) \parallel (ML)$. We thus find that $L$ is the midpoint of $[AC]$. However, $\frac{AL}{LC}=\frac{AB}{BC}$ which shows that $AB=BC$, and $(BL)$ is a bisector, an altitude, and a median.
It is now necessary that $(BL)$ bisects $\widehat{MLH}$, or again $(AC)$ as an external bisector, so by angle chasing $\beta=\widehat{\mathrm{HLC}}=\widehat{MLA}=\alpha$. Therefore, $\alpha=\beta$ and $ABC$ is equilateral, so in particular $(CM)$ is the median in MHL.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle, $H$ le pied de la hauteur issue de $A$, $L$ le pied de la bissectrice issue de $B$ et $M$ le milieu de $[A B]$. On suppose que dans le triangle HLM on a les deux propriétés: $(A H)$ est une hauteur et ( BL ) est une bissectrice. Montrer que ( CM ) est une médiane.
|
On prend le triangle $A B C$, on va démontrer qu'il est équilatéral, en utilisant les deux propriétés, la troisième découlera.
On a $(A H) \perp(M L)$ et $(A H) \perp(B C)$, donc $(B C) / /(M L)$. On trouve ainsi que $L$ est le milieu de $[A C]$. Cependant, $\frac{A L}{L C}=\frac{A B}{B C}$ ce qui montre que $A B=B C$, et (BL) est une bissectrice, une hauteur et une médiane.
Il faut maintenant que (BL) bissecte $\widehat{M L H}$, ou encore (AC) comme bissectrice extérieure, donc par chasse aux angles $\beta=\widehat{\mathrm{HLC}}=\widehat{M L A}=\alpha$. Donc $\alpha=\beta$ et $A B C$ est équilatéral, donc en particulier (CM) est la médiane dans MHL.
|
{
"exam": "French_envois",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"solution_match": "\nDémonstration.",
"tier": "T2",
"year": null
}
|
Let $\omega_{1}$ and $\omega_{2}$ be two circles that intersect at $P$ and $Q$. Suppose that the common tangent to $\omega_{1}$ and $\omega_{2}$, the one closest to $P$, touches the circles $\omega_{1}$ and $\omega_{2}$ at $A$ and $B$ respectively. The tangents at $P$ to the circles $\omega_{1}$ and $\omega_{2}$ intersect $\omega_{2}$ and $\omega_{1}$ at $D$ and $C$ respectively. Let $H$ and $K$ be points on the segments $[A C]$ and $[B D]$ such that $A H=A P$ and $B K=B P$. Show that the points $A, B, K, Q$ and $H$ lie on the same circle.
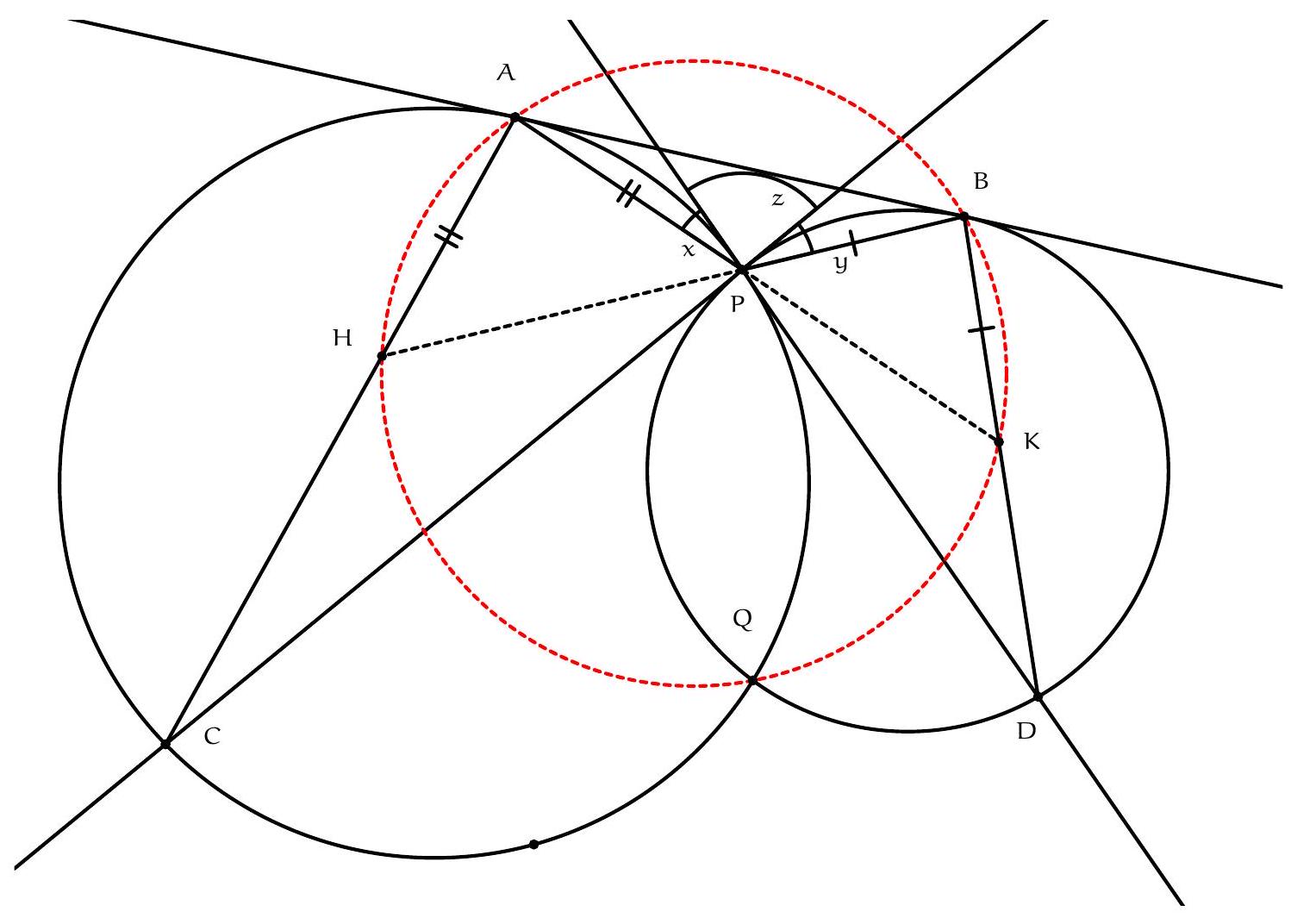
|
We conjecture on a good figure that the points $\mathrm{H}, \mathrm{P}$ and B are collinear, as well as the points $K, P$ and $A$.
Lemma. The points $\mathrm{H}, \mathrm{P}$ and B are collinear, as well as the points $\mathrm{K}, \mathrm{P}$ and A.
We denote $x=\widehat{\mathrm{PAB}}, y=\widehat{\mathrm{ABP}}$ and $z=\widehat{\mathrm{CPD}}$. Since the line (PC) is tangent to $\omega_{2}$, we know that the angle that the tangent forms with the line (PB) is also $x$, and similarly, the angle between (PC) and (AP) is $y$ (it is a matter of choosing the correct orientations). $z$ is the angle between the two tangents. In this case, $\widehat{APB}=x+y+z$ and in total, the angles of the triangle $ABP$ are $x, y$ and $x+y+z$, which shows that $2x+2y+z=180$.
By the angle at the tangent, the angle $\widehat{CAP}=z$, but $AH=AP$ so the triangle $AHP$ is isosceles at $A$, and $\widehat{AHP}=\widehat{APH}=\frac{180-z}{2}=\frac{2x+2y}{2}=x+y$, then the angle $\widehat{HPB}=\widehat{HPA}+\widehat{APB}=x+y+x+z+y=2x+2y+z=180$, which shows that the points $H, P$ and $B$ are collinear. The symmetric reasoning shows that $K, P$ and $A$ are collinear.
We found in the proof of the lemma that $\widehat{AHB}=\widehat{AHP}=x+y$, but then by symmetry $\widehat{BKA}=\widehat{BKP}=x+y$, and by the angle at the tangent, $\widehat{PQA}=x$ and $\widehat{PQB}=y$, so $\widehat{AQB}=x+y$, we thus have $\widehat{AHB}=\widehat{BKA}=\widehat{BQA}$ which shows that the points $A, H, Q, K$ and $P$ are concyclic.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $\omega_{1}$ et $\omega_{2}$ deux cercles qui se coupent en $P$ et $Q$. On suppose que la tangente commune à $\omega_{1}$ et $\omega_{2}$, la plus proche de P , touche les cercles $\omega_{1}$ et $\omega_{2}$ en $A$ et $B$ respectivement. Les tangentes en $P$ aux cercles $\omega_{1}$ et $\omega_{2}$ recoupe $\omega_{2}$ et $\omega_{1}$ en $D$ et $C$ respectivement. On pose $H$ et $K$ sur les segments $[A C]$ et $[B D]$ de tel sorte que $A H=A P$ et $B K=B P$. Montrer que les points $A, B, K, Q$ et $H$ sont sur le même cercle.

|
On conjecture sur une bonne figure que les points $\mathrm{H}, \mathrm{P}$ et B sont alignés, de même pour les points $K, P$ et $A$.
Lemme. Les points $\mathrm{H}, \mathrm{P}$ et B sont alignés, ainsi que les points $\mathrm{K}, \mathrm{P}$ et A .
On note $x=\widehat{\mathrm{PAB}}, y=\widehat{\mathrm{ABP}}$ et $z=\widehat{\mathrm{CPD}}$. Comme la droite ( PC$)$ est tangente à $\omega_{2}$ on sait que l'angle que la tangente forme avec la droite ( PB ) est également $x$, de la même manière l'angle entre (PC) et (AP) est y (il s'agit de choisir les bonnes orientations). $z$ est l'angle entre les deux tangentes. Dans ce cas $\widehat{A P B}=x+y+z$ et au total les angles du triangle $A B P$ sont $x, y$ et $x+y+z$, cela montre que $2 x+2 y+z=180$.
Par angle à la tangente l'angle $\widehat{C A P}=z$, mais $A H=A P$ donc les triangle $A H P$ est isocèle en $A$, et $\widehat{A H P}=\widehat{A P H}=\frac{180-z}{2}=\frac{2 x+2 y}{2}=x+y$, alors l'angle $\widehat{\mathrm{HPB}}=\widehat{\mathrm{HPA}}+\widehat{\mathrm{APB}}=x+y+x+z+y=$ $2 x+2 y+z=180$, ce qui montre bien que les points $H, P$ et $B$ sont alignés. Le raisonnement symétrique montre que $K, P$ et $A$ sont alignés.
On a trouvé dans la preuve du lemme que $\widehat{A H B}=\widehat{A H P}=x+y$, mais alors par symétrie $\widehat{B K A}=\widehat{B K P}=x+y$, et par angle à la tangente, $\widehat{P Q A}=x$ et $\widehat{P Q B}=y$, donc $\widehat{A Q B}=x+y$, on a ainsi $\widehat{A H B}=\widehat{B K A}=\widehat{B Q A}$ ce qui montre bien que les points $A, H, Q, K$ et $P$ sont cocycliques.
|
{
"exam": "French_envois",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"solution_match": "\nDémonstration.",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle, $D$ is the midpoint of the arc $BC$ of the circle $ABC$ not containing $A$, and $Z$ is the unique point on the external bisector of $\widehat{BAC}$ such that $ZA = ZC$. Show that the circle $ADZ$ passes through the midpoint of the side $[AB]$.
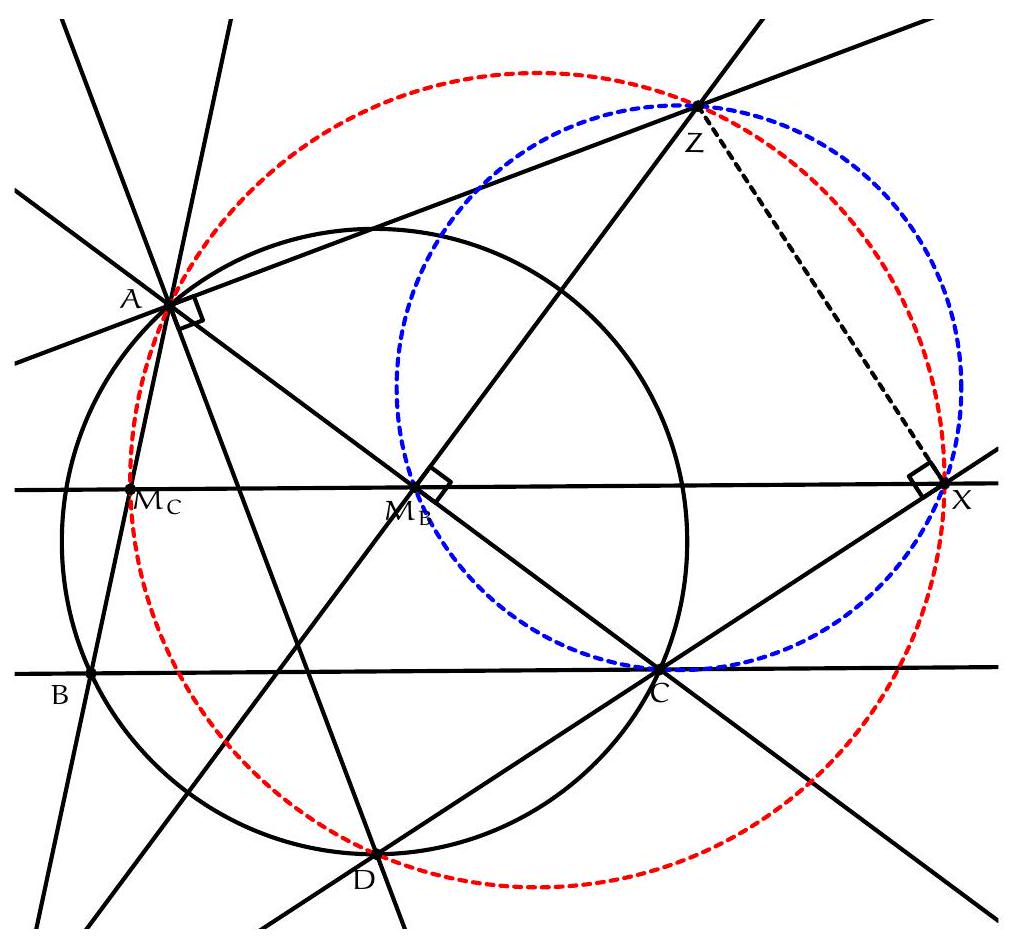
|
Proof 1:
Let $\alpha=\widehat{B A C}$, and let $M_{B}$ be the midpoint of $[A B]$ and $M_{C}$ the midpoint of $[A C]$. We denote $X$ as the intersection of the lines $\left(M_{B} M_{C}\right)$ and (DC).
Since $\left(M_{B} M_{C}\right) / /(B C)$, we find $\widehat{M_{B} X C}=\widehat{B C D}=\widehat{B A D}=\frac{\alpha}{2}$, the penultimate equality follows from the fact that the points $A, B, C$ and $D$ are concyclic and that $D$ is the south pole of $A$ in the triangle $A B C$. We now calculate that $\widehat{C A Z}=90-\frac{\alpha}{2}, Z$ and $M_{B}$ are on the perpendicular bisector of $[A C]$ so $\left(Z M_{B}\right) \perp(A C)$, and we find then $\widehat{A Z M_{B}}=\widehat{C_{Z M}}=\frac{\alpha}{2}$, but then $\widehat{C_{Z M}}=\widehat{C_{B M}}$, which shows that the points $Z, M_{B}, C$ and $X$ are concyclic.
Since $Z, M_{B}, C$ and $X$ are concyclic and $\widehat{Z M_{B} C}=90$ we must have $\widehat{Z C X}=90$. We also have $\widehat{D A Z}=90$, which shows that the points $A, Z, X$ and $D$ are concyclic.
We also have, $\widehat{M_{B} A D}=\frac{\alpha}{2}=\widehat{M_{B} X D}$ which shows that the points $A, M_{B}, D$ and $X$ are concyclic. But in this case: $A, M_{B}, D, X$ and $Z$ are concyclic. Therefore, in particular, the circle $A D Z$ passes through the midpoint of the segment $[A B]$.
## Proof 2:
Here we will present a slightly more general method than the previous one, which involves composing three similarities and finding certain properties.
Let $S_{Z, \mu, r}$ be the direct similarity with center $Z$, angle $\mu$ (oriented), and ratio $r$.
Then, $S_{M_{B}, 180,1}$ fixes $M_{B}$, swaps $A$ and $B$, and also swaps $D$ with a point called $D^{\prime}$.
We find by immediate angle chasing that $\widehat{A Z C}=\alpha$.
$S_{Z, \alpha, 1}$ fixes $Z$, then sends $A$ to $C$.
We find by angle chasing that $\widehat{C D B}=180-\alpha$. Therefore, $S_{D, 180-\alpha, 1}$ fixes $D$ and sends $C$ to $B$.
We then perform $T=S_{M_{B}, 180,1}+S_{Z, \alpha, 1}+S_{D, 180-\alpha,}$, this transformation is also a direct similarity with ratio $1 \times 1 \times 1$ and angle $180+180-\alpha+\alpha=360$, the result is thus a translation, but $T$ sends $B$ to $B$, a translation that has a fixed point is the identity, so $T$ is in fact the identity. But the transformation $T$ sends $D$ to $\mathrm{D}^{\prime}$, then $\mathrm{D}^{\prime}$ to $\mathrm{D}^{\prime \prime}$, and $\mathrm{D}^{\prime \prime}$ to $\mathrm{D}^{\prime \prime \prime}=\mathrm{D}$, $\mathrm{D}^{\prime \prime}$ is sent to $\mathrm{D}^{\prime \prime \prime}=\mathrm{D}$ by the similarity centered at $D$ so $\mathrm{D}^{\prime \prime}=\mathrm{D}^{\prime \prime \prime}=\mathrm{D}$, thus the similarity centered at $Z$ sends $D^{\prime}$ to $D$, so in particular $Z D^{\prime}=Z D$ and $\widehat{D^{\prime} Z D}=\alpha$. In the triangle $A^{\prime} D Z$, the point $M_{B}$ is the foot of the altitude, bisector, etc., so in particular, $\widehat{M_{B} Z C}=\frac{\alpha}{2}=\widehat{M_{B} A D}$, which concludes.
This second approach may seem long, but it is much more general and can be applied to other configurations than the particular case we have just seen.
## Senior Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle, $D$ est le milieu de l'arc $B C$ du cercle $A B C$ ne contenant pas $A, Z$ est l'unique point sur la bissectrice extérieure de $\widehat{B A C}$ tel que $Z A=Z C$. Montrer que le cercle $A D Z$ passe par le milieu du côté de $[A B]$.

|
Preuve 1:
On note $\alpha=\widehat{B A C}$, on pose $M_{B}$ le milieu de $[A B]$ et $M_{C}$ le milieu de $[A C]$. On note $X$ l'intersection des droites $\left(M_{B} M_{C}\right)$ et (DC).
Alors comme $\left(M_{B} M_{C}\right) / /(B C)$, on trouve $\widehat{M_{B} X C}=\widehat{B C D}=\widehat{B A D}=\frac{\alpha}{2}$, l'avant-dernière égalité découle du fait que les points $A, B, C$ et $D$ sont cocycliques et que $D$ est le pôle sud de $A$ dans le triangle $A B C$. On calcule maintenant que $\widehat{C A Z}=90-\frac{\alpha}{2}, Z$ et $M_{B}$ sont sur la médiatrice de $[A C]$ donc $\left(Z M_{B}\right) \perp(A C)$, et on trouve alors $\widehat{A Z M_{B}}=\widehat{C_{Z M}}=\frac{\alpha}{2}$, mais alors $\widehat{C_{Z M}}=\widehat{C_{B M}}$, ce qui montre que les points $Z, M_{B}, C$ et $X$ sont cocycliques.
Comme $Z, M_{B}, C$ et $X$ sont cocycliques et $\widehat{Z M_{B} C}=90$ on doit avoir $\widehat{Z C X}=90$. On a de plus, $\widehat{D A Z}=90$, ce qui montre que les points $A, Z, X$ et $D$ sont cocycliques.
On a également, $\widehat{M_{B} A D}=\frac{\alpha}{2}=\widehat{M_{B} X D}$ ce qui montre que les points $A, M_{B}, D$ et $X$ sont cocycliques. Mais dans ce cas : $A, M_{B}, D, X$ et $Z$ sont cocycliques. Donc en particulier, le cercle $A D Z$ passe par le milieu du segment $[A B]$.
## Preuve 2:
On va présenter ici une méthode un peu plus générale que la méthode précédente, il s'agit de composer trois similitudes et d'en trouver certaines propriétés.
On pose $S_{Z, \mu, r}$ la similitude directe de centre $Z, d^{\prime}$ angle $\mu$ (orienté) et de rapport r .
Alors, $S_{M_{B}, 180,1}$ fixe $M_{B}$ échange $A$ et $B$ elle échange également $D$ avec une point appelé $D^{\prime}$.
On trouve par chasse aux angles immédiate que $\widehat{A Z C}=\alpha$.
$S_{Z, \alpha, 1}$ fixe $Z$, envoie alors $A$ sur $C$.
On trouve par chasse aux angles que $\widehat{C D B}=180-\alpha$. Donc $S_{D, 180-\alpha, 1}$ fixe $D$ et envoie $C$ sur $B$.
On effectue alors $T=S_{M_{B}, 180,1}+S_{Z, \alpha, 1}+S_{D, 180-\alpha,}$, cette transformation est également une similitude directe de rapport $1 \times 1 \times 1$ et d'angle $180+180-\alpha+\alpha=360$, le résultat est donc une translation, mais $T$ envoie $B$ sur $B$, une translation qui a un point fixe est l'identité donc $T$ est en fait l'identité. Mais la transformation $T$ envoie $D$ sur $\mathrm{D}^{\prime}$ puis $\mathrm{D}^{\prime}$ sur $\mathrm{D}^{\prime \prime}$ et $\mathrm{D}^{\prime \prime}$ sur $\mathrm{D}^{\prime \prime \prime}=\mathrm{D}, \mathrm{D}^{\prime \prime}$ est envoyé sur $\mathrm{D}^{\prime \prime \prime}=\mathrm{D}$ par la similitude de centre D donc $\mathrm{D}^{\prime \prime}=\mathrm{D}^{\prime \prime \prime}=\mathrm{D}$, ainsi la similitude de centre $Z$ envoie $D^{\prime}$ sur $D$, donc en particulier $Z D^{\prime}=Z D$ et $\widehat{D^{\prime} Z D}=\alpha$. Dans le triangle $A^{\prime} D Z$, le point $M_{B}$ est le pied de la hauteur, bissectrice, etc..., donc en particulier, $\widehat{M_{B} Z C}=\frac{\alpha}{2}=\widehat{M_{B} A D}$, ce qui conclut.
Cette deuxième approche peut sembler longue mais elle est beaucoup plus général et peut s'appliquer à d'autre configurations que le cas particulier que l'on vient de voir.
## Exercices Seniors
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"solution_match": "## Démonstration.",
"tier": "T2",
"year": null
}
|
Let $ABC$ be an isosceles triangle at $A$, $\Gamma$ is a circle tangent to $(AC)$ at $C$ outside the triangle $ABC$. We denote $\omega$ as the circle passing through $A$ and $B$ and internally tangent to $\Gamma$ at $D$. $E$ is the second intersection of $(AD)$ and $\Gamma$, show that $(BE)$ is tangent to $\Gamma$.
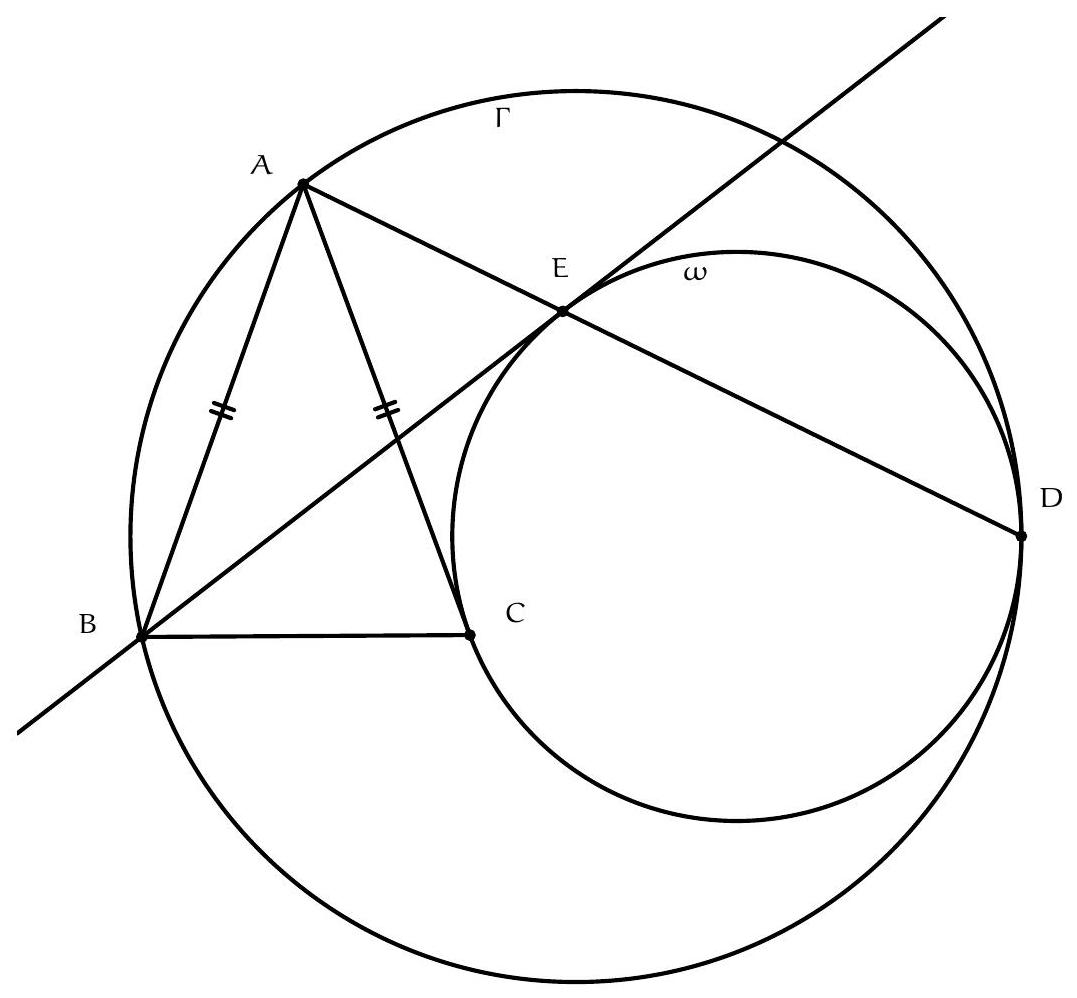
|
Proof 1:
Let $I_{A}$ denote the inversion with center $A$ and radius $r=AB=AC$, thus, $B$ and $C$ are fixed by $I_{A}$. The power of $A$ with respect to the circle $\omega$ is exactly the square of the radius, so the circle $\omega$ is fixed by the inversion. This shows that $D$ and $E$ are exchanged by $I_{A}$. Therefore, the circle $\Gamma$ passing through $A, B$, and $D$ will be mapped to a line passing through $B$ and $E$ and tangent to the circle $\omega$, which concludes the proof.
## Proof 2:
We construct $B^{\prime}$, the second intersection point of $\Gamma$, such that $AB=AB^{\prime}=AC$. Then, we want to show that $E^{\prime}$, the intersection of the lines $(BB^{\prime})$ and $(AD)$, lies on $\omega$.
We have $\widehat{BDA}=x$ and $\widehat{ABB^{\prime}}=x$. By the isosceles property of $ABB^{\prime}$ at $A$, we find $\widehat{AB^{\prime}B}=x$. Therefore, the triangles $ABD$ and $AEB$ are similar, and we get $AB^{2}=AE \times AD$. Thus, $E^{\prime}$ lies on $\omega$, which shows that $E^{\prime}=E$. The homothety centered at $D$ that maps the circle $\omega$ to the circle $\Gamma$ sends the point $E$ to the point $A$ and thus the tangent at $E$ to $\omega$ to the tangent at $A$ to $\Gamma$. It turns out that since $AB=AB^{\prime}$, the tangent at $A$ to $\Gamma$ is parallel to the line $(B^{\prime})$, but the tangent at $E$ to $\omega$ must be parallel to the tangent at $A$ to $\Gamma$. This shows that the tangent at $E$ to $\omega$ and $(BB^{\prime})$ are in fact the same line, which concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle isocèle en $A, \Gamma$ est un cercle tangent à ( $A C$ ) en $C$ à l'extérieur du triangle $A B C$. On note $\omega$ le cercle passant par $A$ et $B$ et tangent intérieurement à $\Gamma$ en $D$. E est la seconde intersection de (AD) et de $\Gamma$, montrer que (BE) est tangente à $\Gamma$.

|
Preuve 1:
On note $I_{A}$ l'inversion de centre $A$ et de rayon $r=A B=A C$, ainsi, $B$ et $C$ sont fixe par $I_{A}$, la puissance de $A$ par rapport au cercle $\omega$ est exactement le rayon au carré donc les cercle $\omega$ est fixe par inversion. Cela montre que $D$ et $E$ sont échangés dans $I_{A}$. Mais alors le cercle $\Gamma$ passant par $A, B$ et $D$ va être envoyé sur une droite passant par $B$ et $E$ et tangente au cercle $\omega$, cela conclut.
## Preuve 2:
On construit $B^{\prime}$, le deuxième point de $\Gamma$, tel que $A B=A B^{\prime}=A C$. Alors, on veut démontrer que $l^{\prime}$ intersection, $E^{\prime}$ des droites $\left(B B^{\prime}\right)$ et ( $\left.A D\right)$ est sur $\omega$.
On a $\widehat{B D A}=x$ et $\widehat{A B B^{\prime}}=x$. Par isocélité de $A B B^{\prime}$ en $A$, on trouve $\widehat{A B^{\prime} B}=x$. Donc les triangles $A B D$ et $A E B$ sont semblables, on trouve alors $A B^{2}=A E \times A D$. Donc $E^{\prime}$ est sur $\omega$, ce qui montre que $E^{\prime}=E$. L'homothetie de centre $D$ qui envoie le cercle $\omega$ sur le cercle $\Gamma$ envoie ainsi le point $E$ sur le point $A$ et donc la tangente en $E$ à $\omega$ sur la tangente en $A$ à $\Gamma$ ?. Il se trouve que comme $A B=A B^{\prime}$, la tangente en $A$ à $\Gamma$ est parallèle à la droite $\left(B^{\prime}\right)$, mais la tangente en $E$ à $\omega$ doit être parallèle à la tangente en $A$ à $\Gamma$. Cela montre que la tangente en $E$ à $\omega$ et ( $\left.\mathrm{BB}^{\prime}\right)$ ne sont en fait qu'une seule et même droite et cela conclut.
|
{
"exam": "French_envois",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"solution_match": "## Démonstration.",
"tier": "T2",
"year": null
}
|
Let ADE be an isosceles triangle at $A$. Let the circle $\omega$ be tangent to the lines (AD) and (AE) at $D$ and $E$. Let $B$ and $C$ be two points beyond $D$ and $E$ on the lines ( $A D$ ) and ( $A E$ ). Suppose that $B C > B D + C E$. Finally, let $F$ and $G$ be two points on the segment $[B C]$ such that $B D = B F$ and $C G = C E$, the lines $(D G)$ and $(F E)$ intersect at $K$, the tangent to $\omega$ parallel to ( $B C$ ) and between $A$ and ( $B C$ ) touches $\omega$ at $L$. Show that the center of the inscribed circle of ABC is on (KL).
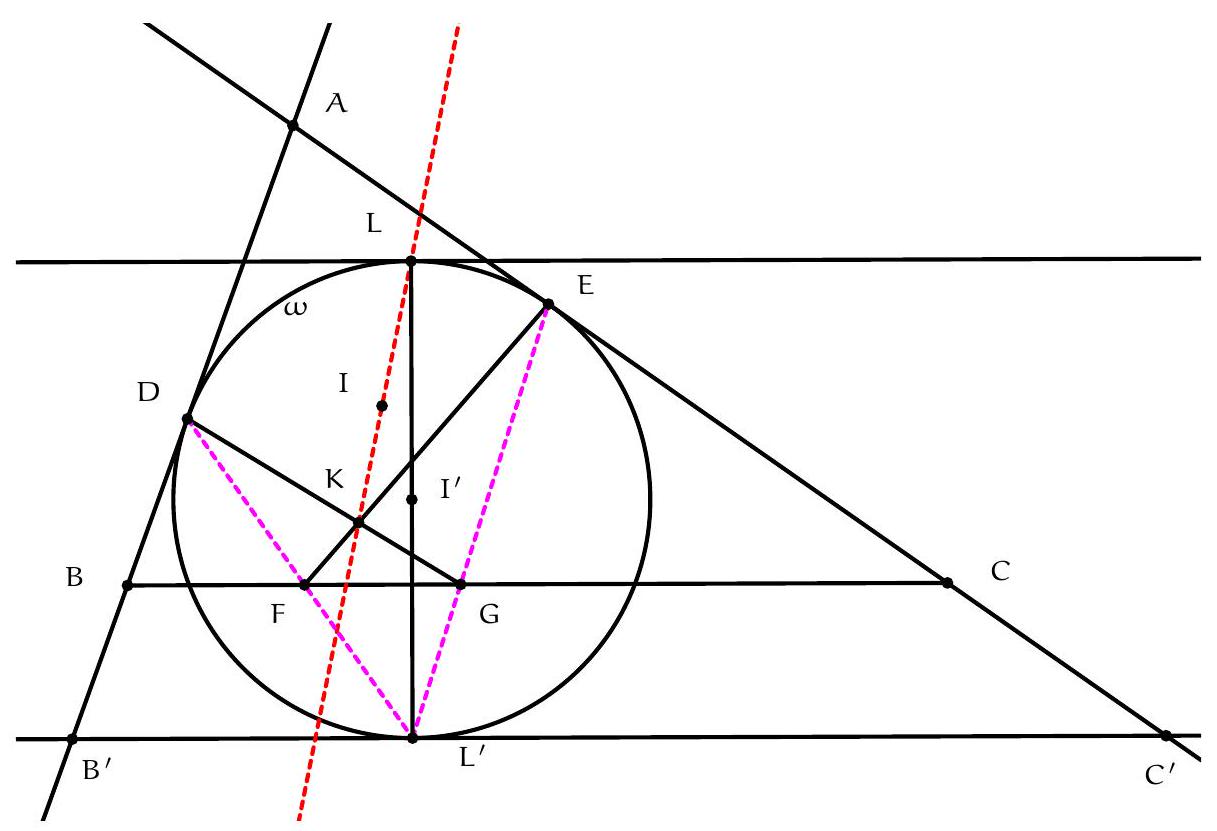
|
Let $B^{\prime}$ and $C^{\prime}$ be two points on the rays $[A D]$ and $[A C]$ beyond $D$ and $E$ such that $\left(B^{\prime} C^{\prime}\right) \parallel (B C)$ and that $\left(B^{\prime} C^{\prime}\right)$ is tangent to $\omega$ at $L^{\prime}$.
Lemma. $D, F$ and $L^{\prime}$ are collinear, as are $E, G$ and $L^{\prime}$.
We have $(B F) \parallel \left(B^{\prime} L^{\prime}\right)$ and $D B = B F$, as well as $\mathrm{DB}^{\prime} = \mathrm{B}^{\prime} \mathrm{L}^{\prime}$, so $\mathrm{DBF} \sim \mathrm{DB}^{\prime} \mathrm{L}^{\prime}$, by Thales. We obtain that $D, F$ and $L^{\prime}$ are collinear, and the symmetric reasoning shows that $E, G$ and $L^{\prime}$ are collinear.
We note that $\omega$ is the incircle of $A B^{\prime} C^{\prime}$. The tangent at $L$ and the tangent at $L^{\prime}$ are two parallel lines, so the segment $[LL']$ is a diameter of $\omega$, thus $\widehat{\mathrm{L}^{\prime} \mathrm{EL}} = 90^\circ$ and $\widehat{\mathrm{L}^{\prime} \mathrm{DL}} = 90^\circ$.
Since $I$ is the incenter of $A B C$, $I$ is the intersection of the angle bisectors of $\widehat{A B C}$, $\widehat{B C A}$, and $\widehat{C A B}$, or by the isosceles triangles $D B F$, $G C E$, and $EAD$, $I$ is the intersection of the perpendicular bisectors of $[DF]$, $[GE]$, and $[ED]$. The fact that these perpendicular bisectors are concurrent leads us to say that the quadrilateral DEFG is cyclic with the circumcenter $I$.
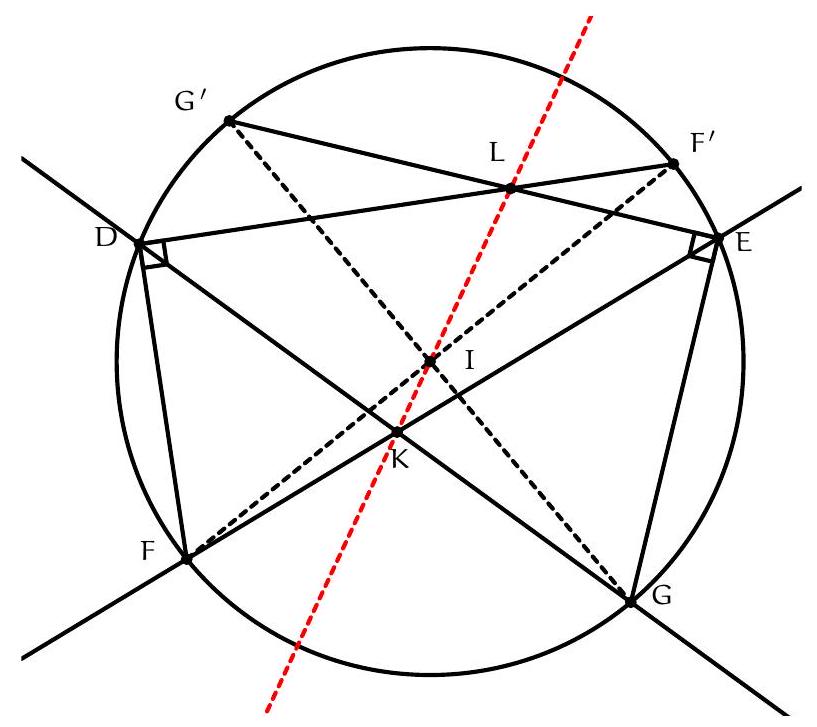
Now we isolate the circle DEFG, the point $I$, the point $K$, and the point $L$, knowing that $I$ is the center of the circle DEFG, that $K$ is the intersection of the diagonals, and that $L$ is such that $\widehat{\mathrm{L}^{\prime} \mathrm{EL}} = 90^\circ$ and $\widehat{\mathrm{L}^{\prime} \mathrm{DL}} = 90^\circ$.
We now intersect the line $(EL)$ with the circle EDFG at $\mathrm{G}^{\prime}$, and the line $(DL)$ with the circle EDG at $\mathrm{F}^{\prime}$. Knowing that $\widehat{L^{\prime} E L} = 90^\circ$ and $\widehat{L^{\prime} D L} = 90^\circ$, we find that $\mathrm{G}^{\prime}$ (resp. $\mathrm{D}^{\prime}$) is the point diametrically opposite to $G$ (resp. $D$) in the circle EDFG, so $I$ is the intersection of the lines $\mathrm{GG}^{\prime}$ and $\mathrm{DD}^{\prime}$. We number the points $\mathrm{G}^{\prime}, \mathrm{G}, \mathrm{D}, \mathrm{F}^{\prime}, \mathrm{F}$, and $E$ as 1, 2, 3, 4, 5, and 6 and apply Pascal since the 6 points are on the same circle, then $\left(G^{\prime} G\right) \cap \left(F^{\prime} F\right), (G D) \cap (F E)$, and $\left(\mathrm{DF}^{\prime}\right) \cap \left(E G^{\prime}\right) ((12) \cap (45), (23) \cap (56)$, and $(34) \cap (61))$ are collinear, which proves that the points $K$, $I$, and $L$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit ADE un triangle isocèle en $A$. Soit le cercle $\omega$, tangent aux droites (AD) et (AE) en $D$ et $E$. Soit $B$ et $C$ deux points au delà de $D$ et $E$ sur les droites ( $A D$ ) et ( $A E$ ). On suppose que $B C>B D+C E$. Finalement, soit $F$ et $G$ deux points sur le segment $[B C]$ de tel sorte que $B D=B F$ et $C G=C E$, les droites $(D G)$ et $(F E)$ se coupent en $K$, la tangente à $\omega$ parallèle à ( $B C$ ) et entre $A$ et ( $B C$ ) touche $\omega$ en L. Montrer que le centre du cercle inscrit de ABC est sur (KL).

|
Soit $B^{\prime}$ et $C^{\prime}$ deux points sur les demi-droites $[A D]$ et $[A C]$ au delà de $D$ et $E$ de tel sorte que $\left(B^{\prime} C^{\prime}\right) / /(B C)$ et que $\left(B^{\prime} C^{\prime}\right)$ soit tangente à $\omega$ en $L^{\prime}$.
Lemme. $D, F$ et $L^{\prime}$ sont alignés de même pour $E, G$ et $L^{\prime}$.
On a $(B F) / /\left(B^{\prime} L^{\prime}\right)$ et $D B=B F$, ainsi que $\mathrm{DB}^{\prime}=\mathrm{B}^{\prime} \mathrm{L}^{\prime}$, donc $\mathrm{DBF} \sim \mathrm{DB}^{\prime} \mathrm{L}^{\prime}$, par Thalès. On obtient que $D, F$ et $L^{\prime}$ sont alignés, le raisonnement symétrique montre que $E, G$ et $L^{\prime}$ sont alignés.
On remarque que $\omega$ est le cercle inscrit de $A B^{\prime} C^{\prime}$. La tangente en $L$ et la tangente en $L^{\prime}$ sont deux droites parallèles, donc le segment [LL'] est un diamètre de $\omega$, ainsi $\widehat{\mathrm{L}^{\prime} \mathrm{EL}}=90$ et $\widehat{\mathrm{L}^{\prime} \mathrm{DL}}=90$.
Comme I est le centre du cercle inscrit de $A B C$, I est l'intersection des bissectrices des angles $\widehat{A B C}, \widehat{B C A}$ et $\widehat{C A B}$ ou encore par isocélité des triangles $D B F, G C E$ et EAD que I est l'intersection des médiatrices de [DF], [GE] et [ED], le fait que ces médiatrices soient concourantes nous amène à dire que le quadrilatère DEFG est cyclique et de centre du cercle circonscrit I.

On va isoler maintenant le cercle DEFG, le point $I$, le point $L$ et le point $K$, en sachant que $I$ est le centre du cercle DEFG, que K est l'intersection des diagonales et que L est tel que $\widehat{\mathrm{L}^{\prime} \mathrm{EL}}=90$ et $\widehat{\mathrm{L}^{\prime} \mathrm{DL}}=90$.
On intersecte maintenant la droite ( EL ) avec le cercle EDFG en $\mathrm{G}^{\prime}$, et la droite ( DL ) également avec le cercle EDG et en $F^{\prime}$. En sachant que $\widehat{L^{\prime} E L}=90$ et $\widehat{L^{\prime} D L}=90$ on trouve que $\mathrm{G}^{\prime}$ (resp. $\mathrm{D}^{\prime}$ ) est le point diamétralement opposé à G (resp. D) dans le cercle EDFG, donc I est l'intersection des droites $\mathrm{GG}^{\prime}$ et $\mathrm{DD}^{\prime}$. On numérote les points $\mathrm{G}^{\prime}, \mathrm{G}, \mathrm{D}, \mathrm{F}^{\prime}, \mathrm{F}$ et $E$ comme 1, 2, 3, 4,5 et 6 et appliquer Pascal comme les 6 points sont sur le même cercle, alors $\left(G^{\prime} G\right) \cap\left(F^{\prime} F\right),(G D) \cap(F E)$ et $\left(\mathrm{DF}^{\prime}\right) \cap\left(E G^{\prime}\right)((12) \cap(45),(23) \cap(56)$ et $(34) \cap(61))$ sont alignés ce qui démontre bien que les points K, I et L sont alignés.
|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "\nExercice 8.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"solution_match": "\nDémonstration.",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle and $O$ the center of its circumcircle. We denote by $A_B$ and $A_C$ the other intersections of the circle $BOC$ with $(AB)$ and $(AC)$, and $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$. We define $B_C$, $B_A$, $C_A$, and $C_B$ in the same manner, as well as $\left(\ell_{2}\right)$ and $\left(\ell_{3}\right)$. We denote by $A^{*} B^{*} C^{*}$ the triangle formed by the lines $\left(\ell_{1}\right),\left(\ell_{2}\right)$, and $\left(\ell_{3}\right)$. Show that the circumcircles of triangles $ABC$ and $A^{*} B^{*} C^{*}$ are tangent.

|
In this exercise, we will first provide a proof by angle chasing before making a connection to the Feuerbach point. The proof we will give also demonstrates several properties of the Feuerbach point, which we will state at the end.
We denote $A^{\prime}$ as the intersection of the lines $(B C)$ and $\left(A_{B} A_{C}\right)$, and we define the points $B^{\prime}$ and $C^{\prime}$ in the same manner.
We denote $T$ as the intersection of the circumcircles of $A B_{A} B^{\prime}$ and $A B C$, and we want to ultimately prove that $T$ is the point of tangency of the circles $A^{*} B^{*} C^{*}$ and $A B C$.
Lemma 1. $T$ is also on the circumcircle of $B^{\prime} B_{C} C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $O$ le centre de son cercle circonscrit. On note $A_{B}$ et $A_{C}$ les autres intersections du cercle $B O C$ avec $(A B)$ et $(A C)$ et $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$, on définit de la même manière $B_{C}$, $B_{A}, C_{A}$ et $C_{B}$ ainsi que $\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. On note $A^{*} B^{*} C^{*}$ le triangle formé par les droites $\left(\ell_{1}\right),\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. Montrer que les cercles circonscrits des triangle $A B C$ et $A^{*} B^{*} C^{*}$ sont tangents.

|
Dans cet exercice nous allons d'abord donner une preuve en chasse aux angles uniquement avant de faire un lien avec le point de Feuerbach. La preuve que nous allons don-
ner démontre en outre plusieurs propriétés du point de Feuerbach que nous énoncerons à la fin.
On note $A^{\prime}$, l'intersection des droites $(B C)$ et $\left(A_{B} A_{C}\right)$, on df́init de la même manière les points $B^{\prime}$ et $C^{\prime}$.
On note $T$ l'intersection des cercles circonscrits de $A B_{A} B^{\prime}$ et $A B C$, on veut démontrer au final que $T$ est le point de tangence des cercles $A^{*} B^{*} C^{*}$ et $A B C$.
Lemme 1. T est également sur le cercle circonscrit de $B^{\prime} B_{C} C$.
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"solution_match": "\nDémonstration.",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle and $O$ the center of its circumcircle. We denote by $A_B$ and $A_C$ the other intersections of the circle $BOC$ with $(AB)$ and $(AC)$, and $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$. We define $B_C$, $B_A$, $C_A$, and $C_B$ in the same manner, as well as $\left(\ell_{2}\right)$ and $\left(\ell_{3}\right)$. We denote by $A^{*} B^{*} C^{*}$ the triangle formed by the lines $\left(\ell_{1}\right),\left(\ell_{2}\right)$, and $\left(\ell_{3}\right)$. Show that the circumcircles of triangles $ABC$ and $A^{*} B^{*} C^{*}$ are tangent.

|
Angle chasing: $\left(B^{\prime} T, T C\right)=\left(B^{\prime} T, A T\right)+(A T, T C)$ according to the Chasles relation, using the cocyclicity of points $T, A, B_{A}$ and $B^{\prime}$ as well as that of points $T, A, B$ and $C$, we find $\left(B^{\prime} T, A T\right)+(A T, T C)=\left(B^{\prime} B_{A}, A B_{A}\right)+(A B, B C)=\left(B^{\prime} B_{A}, A B\right)+(A B, B C)=$ $\left(B^{\prime} B_{A}, B C\right)=\left(B^{\prime} B_{C}, B_{C} C\right)$, thus $\left(B^{\prime} T, T C\right)=\left(B^{\prime} B_{C}, B_{C} C\right)$, so the points $T, B^{\prime}, B_{C}$ and $C$ are cocyclic, which concludes the proof of the lemma.
Lemma 2. The points $B^{\prime}$, $B$ and $T$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $O$ le centre de son cercle circonscrit. On note $A_{B}$ et $A_{C}$ les autres intersections du cercle $B O C$ avec $(A B)$ et $(A C)$ et $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$, on définit de la même manière $B_{C}$, $B_{A}, C_{A}$ et $C_{B}$ ainsi que $\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. On note $A^{*} B^{*} C^{*}$ le triangle formé par les droites $\left(\ell_{1}\right),\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. Montrer que les cercles circonscrits des triangle $A B C$ et $A^{*} B^{*} C^{*}$ sont tangents.

|
En chasse aux angles : $\left(B^{\prime} T, T C\right)=\left(B^{\prime} T, A T\right)+(A T, T C)$ d'après le relation de Chasles, en utilisant la cocyclicité des points $T, A, B_{A}$ et $B^{\prime}$ ainsi que celle des points $T, A, B$ et $C$, on trouve $\left(B^{\prime} T, A T\right)+(A T, T C)=\left(B^{\prime} B_{A}, A B_{A}\right)+(A B, B C)=\left(B^{\prime} B_{A}, A B\right)+(A B, B C)=$ $\left(B^{\prime} B_{A}, B C\right)=\left(B^{\prime} B_{C}, B_{C} C\right)$, ainsi $\left(B^{\prime} T, T C\right)=\left(B^{\prime} B_{C}, B_{C} C\right)$, donc les points $T, B^{\prime}, B_{C}$ et $C$ sont cocycliques, ce qui conclut la preuve du lemme.
Lemme 2. les points $B^{\prime}$, $B$ et $T$ sont alignés.
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"solution_match": "\nDémonstration.",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle and $O$ the center of its circumcircle. We denote by $A_B$ and $A_C$ the other intersections of the circle $BOC$ with $(AB)$ and $(AC)$, and $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$. We define $B_C$, $B_A$, $C_A$, and $C_B$ in the same manner, as well as $\left(\ell_{2}\right)$ and $\left(\ell_{3}\right)$. We denote by $A^{*} B^{*} C^{*}$ the triangle formed by the lines $\left(\ell_{1}\right),\left(\ell_{2}\right)$, and $\left(\ell_{3}\right)$. Show that the circumcircles of triangles $ABC$ and $A^{*} B^{*} C^{*}$ are tangent.

|
We look at the circles $B^{\prime} T C B_{C}, A B^{\prime} T B_{A}$ and $A C B_{A} B_{C}$ (all these points are concyclic according to the previous lemma), their radical axes are ( $B^{\prime} T$ ), ( $B_{A} A$ ) and ( $B_{C} C$ ), which shows by the concurrency of the radical axes that the points $B, B^{\prime}$ and $T$ are collinear.
Lemma 3. $\left(A A^{*}\right)$ is tangent to the circumcircle of $A B C$.
|
proof
|
Yes
|
Incomplete
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $O$ le centre de son cercle circonscrit. On note $A_{B}$ et $A_{C}$ les autres intersections du cercle $B O C$ avec $(A B)$ et $(A C)$ et $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$, on définit de la même manière $B_{C}$, $B_{A}, C_{A}$ et $C_{B}$ ainsi que $\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. On note $A^{*} B^{*} C^{*}$ le triangle formé par les droites $\left(\ell_{1}\right),\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. Montrer que les cercles circonscrits des triangle $A B C$ et $A^{*} B^{*} C^{*}$ sont tangents.

|
On regarde les cercles $B^{\prime} T C B_{C}, A B^{\prime} T B_{A}$ et $A C B_{A} B_{C}$ (tous ces points sont cocycliques d'après le lemme précédent), leurs axes radicaux sont ( $B^{\prime} T$ ), ( $B_{A} A$ ) et ( $B_{C} C$ ), ce qui montre par concourance des axes radicaux que les points $B, B^{\prime}$ et $T$ sont alignés.
Lemme 3. $\left(A A^{*}\right)$ est tangente au cercle circonscrit de $A B C$.
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"solution_match": "\nDémonstration.",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle and $O$ the center of its circumcircle. We denote by $A_B$ and $A_C$ the other intersections of the circle $BOC$ with $(AB)$ and $(AC)$, and $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$. We define $B_C$, $B_A$, $C_A$, and $C_B$ in the same manner, as well as $\left(\ell_{2}\right)$ and $\left(\ell_{3}\right)$. We denote by $A^{*} B^{*} C^{*}$ the triangle formed by the lines $\left(\ell_{1}\right),\left(\ell_{2}\right)$, and $\left(\ell_{3}\right)$. Show that the circumcircles of triangles $ABC$ and $A^{*} B^{*} C^{*}$ are tangent.

|
Lemme 3.1. $O, C_{A}$ and $B_{A}$ are aligned.
|
proof
|
Yes
|
Incomplete
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $O$ le centre de son cercle circonscrit. On note $A_{B}$ et $A_{C}$ les autres intersections du cercle $B O C$ avec $(A B)$ et $(A C)$ et $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$, on définit de la même manière $B_{C}$, $B_{A}, C_{A}$ et $C_{B}$ ainsi que $\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. On note $A^{*} B^{*} C^{*}$ le triangle formé par les droites $\left(\ell_{1}\right),\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. Montrer que les cercles circonscrits des triangle $A B C$ et $A^{*} B^{*} C^{*}$ sont tangents.

|
Lemme 3.1. $O, C_{A}$ et $B_{A}$ sont alignés.
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"solution_match": "## Démonstration.",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle and $O$ the center of its circumcircle. We denote by $A_B$ and $A_C$ the other intersections of the circle $BOC$ with $(AB)$ and $(AC)$, and $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$. We define $B_C$, $B_A$, $C_A$, and $C_B$ in the same manner, as well as $\left(\ell_{2}\right)$ and $\left(\ell_{3}\right)$. We denote by $A^{*} B^{*} C^{*}$ the triangle formed by the lines $\left(\ell_{1}\right),\left(\ell_{2}\right)$, and $\left(\ell_{3}\right)$. Show that the circumcircles of triangles $ABC$ and $A^{*} B^{*} C^{*}$ are tangent.

|
We will show that $C_{A}$ is on the perpendicular bisector of $[B C]$.
We have $\left(C_{A} O, B C\right)=\left(C_{A} O, A C\right)+(A C, B C)=\left(C_{A} O, A C_{A}\right)+(A C, B C)=(A B, A O)+(A C, B C)=$ 90 (since the altitude from a vertex of a triangle and the line connecting this vertex with the circumcenter are isogonal conjugates), which shows that ( $C_{A} O$ ) and ( $B C$ ) are perpendicular, but O is on the perpendicular bisector of $[\mathrm{BC}]$ so $\mathrm{C}_{A}$ is also.
Symmetrically, $B_{A}$ is on the perpendicular bisector of $[B C]$ and thus $O, B_{A}$ and $C_{A}$ are collinear.
Lemma 3.2. The triangle $A^{*} C_{A} B_{A}$ is isosceles at $A^{*}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $O$ le centre de son cercle circonscrit. On note $A_{B}$ et $A_{C}$ les autres intersections du cercle $B O C$ avec $(A B)$ et $(A C)$ et $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$, on définit de la même manière $B_{C}$, $B_{A}, C_{A}$ et $C_{B}$ ainsi que $\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. On note $A^{*} B^{*} C^{*}$ le triangle formé par les droites $\left(\ell_{1}\right),\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. Montrer que les cercles circonscrits des triangle $A B C$ et $A^{*} B^{*} C^{*}$ sont tangents.

|
On va démontrer que $C_{A}$ est sur la médiatrice de $[B C]$.
On a $\left(C_{A} O, B C\right)=\left(C_{A} O, A C\right)+(A C, B C)=\left(C_{A} O, A C_{A}\right)+(A C, B C)=(A B, A O)+(A C, B C)=$ 90 (car la hauteur issue d'un sommet d'un triangle et la droite reliant ce somet avec le centre du cercle circonscrit sont conjugués isogonales), ce qui montre que ( $C_{A} O$ ) et ( $B C$ ) sont perpendiculaires, mais O est sur le médiatrice de $[\mathrm{BC}]$ donc $\mathrm{C}_{A}$ également.
De manière symétrique, $B_{A}$ est sur la médiatrice de $[B C]$ et ainsi $O, B_{A}$ et $C_{A}$ sont alignés.
Lemme 3.2. Le triangle $A^{*} C_{A} B_{A}$ est isocèle en $A^{*}$.
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"solution_match": "\nDémonstration.",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle and $O$ the center of its circumcircle. We denote by $A_B$ and $A_C$ the other intersections of the circle $BOC$ with $(AB)$ and $(AC)$, and $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$. We define $B_C$, $B_A$, $C_A$, and $C_B$ in the same manner, as well as $\left(\ell_{2}\right)$ and $\left(\ell_{3}\right)$. We denote by $A^{*} B^{*} C^{*}$ the triangle formed by the lines $\left(\ell_{1}\right),\left(\ell_{2}\right)$, and $\left(\ell_{3}\right)$. Show that the circumcircles of triangles $ABC$ and $A^{*} B^{*} C^{*}$ are tangent.

|
\left(A^{*} C_{A}, C_{A} B_{A}\right)=\left(C_{B} C_{A}, C_{A} O\right)=\left(C_{B} B, B O\right)=(C B, B O)=(O C, B C)=
\left(\mathrm{OB}_{A}, \mathrm{~B}_{\mathrm{C}} \mathrm{B}_{\mathrm{A}}\right)=\left(\mathrm{CB}_{\mathrm{A}}, \mathrm{B}_{\mathrm{A}} \mathrm{A}^{*}\right)
Thus, $A^{*} B_{A} C_{A}$ is isosceles at $A^{*}$.
Moreover, the angles at $B_{A}$ and $B$ in the triangles $A^{*} B_{A} C_{A}$ and $B C O$ are equal, which shows that $A^{*} B_{A} C_{A} \sim O B C$.
Therefore, $\left(C_{A} A^{*}, A^{*} B_{A}\right)=2\left(C_{A} A, A B_{A}\right)$ and $A^{*}$ is the circumcenter of $A B_{A} C_{A}$. But in this case $\left(A^{*} A, A C\right)=\left(A A^{*}, A C_{A}\right)=90-\left(C_{A} B_{A}, B_{A} A\right)=90-\left(B_{A}, B_{A} A\right)=90-$ $(O C, C A)=(A B, B C)$ (we always use the fact that the altitude from a vertex of a triangle and the line connecting this vertex with the circumcenter are isogonal conjugates).
Thus, $\left(A A^{*}\right)$ is indeed a tangent to $A B C$.
Lemma 4. The points $C_{B}, B_{C}, T, A$ and $A^{*}$ are concyclic.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $O$ le centre de son cercle circonscrit. On note $A_{B}$ et $A_{C}$ les autres intersections du cercle $B O C$ avec $(A B)$ et $(A C)$ et $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$, on définit de la même manière $B_{C}$, $B_{A}, C_{A}$ et $C_{B}$ ainsi que $\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. On note $A^{*} B^{*} C^{*}$ le triangle formé par les droites $\left(\ell_{1}\right),\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. Montrer que les cercles circonscrits des triangle $A B C$ et $A^{*} B^{*} C^{*}$ sont tangents.

|
$\left(A^{*} C_{A}, C_{A} B_{A}\right)=\left(C_{B} C_{A}, C_{A} O\right)=\left(C_{B} B, B O\right)=(C B, B O)=(O C, B C)=$ $\left(\mathrm{OB}_{A}, \mathrm{~B}_{\mathrm{C}} \mathrm{B}_{\mathrm{A}}\right)=\left(\mathrm{CB}_{\mathrm{A}}, \mathrm{B}_{\mathrm{A}} \mathrm{A}^{*}\right)$
Donc $A^{*} B_{A} C_{A}$ est isocèle en $A^{*}$.
De plus, les angles en $B_{A}$ et $B$ des triangles $A^{*} B_{A} C_{A}$ et $B C O$ sont égaux, ce qui montre en fait que $A^{*} B_{A} C_{A} \sim O B C$.
Ainsi, $\left(C_{A} A^{*}, A^{*} B_{A}\right)=2\left(C_{A} A, A B_{A}\right)$ et $A^{*}$ est le centre du cercle circonscrit de $A B_{A} C_{A}$. Mais dans ce cas $\left(A^{*} A, A C\right)=\left(A A^{*}, A C_{A}\right)=90-\left(C_{A} B_{A}, B_{A} A\right)=90-\left(B_{A}, B_{A} A\right)=90-$ $(O C, C A)=(A B, B C)$ (on utilise toujours le fait que la hauteur issue d'un sommet d'un triangle et la droite reliant ce somet avec le centre du cercle circonscrit sont conjugués isogonales)
Donc $\left(A A^{*}\right)$ est bien une tangente de $A B C$.
Lemme 4. Les points $C_{B}, B_{C}, T, A$ et $A^{*}$ sont cocycliques.
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"solution_match": "\nDémonstration.",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle and $O$ the center of its circumcircle. We denote by $A_B$ and $A_C$ the other intersections of the circle $BOC$ with $(AB)$ and $(AC)$, and $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$. We define $B_C$, $B_A$, $C_A$, and $C_B$ in the same manner, as well as $\left(\ell_{2}\right)$ and $\left(\ell_{3}\right)$. We denote by $A^{*} B^{*} C^{*}$ the triangle formed by the lines $\left(\ell_{1}\right),\left(\ell_{2}\right)$, and $\left(\ell_{3}\right)$. Show that the circumcircles of triangles $ABC$ and $A^{*} B^{*} C^{*}$ are tangent.

|
Step 1. $C_{B}, B_{C}, A$ and $A^{*}$ are concyclic.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $O$ le centre de son cercle circonscrit. On note $A_{B}$ et $A_{C}$ les autres intersections du cercle $B O C$ avec $(A B)$ et $(A C)$ et $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$, on définit de la même manière $B_{C}$, $B_{A}, C_{A}$ et $C_{B}$ ainsi que $\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. On note $A^{*} B^{*} C^{*}$ le triangle formé par les droites $\left(\ell_{1}\right),\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. Montrer que les cercles circonscrits des triangle $A B C$ et $A^{*} B^{*} C^{*}$ sont tangents.

|
Étape 1. $C_{B}, B_{C}, A$ et $A^{*}$ sont cocycliques.
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"solution_match": "\nDémonstration.",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle and $O$ the center of its circumcircle. We denote by $A_B$ and $A_C$ the other intersections of the circle $BOC$ with $(AB)$ and $(AC)$, and $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$. We define $B_C$, $B_A$, $C_A$, and $C_B$ in the same manner, as well as $\left(\ell_{2}\right)$ and $\left(\ell_{3}\right)$. We denote by $A^{*} B^{*} C^{*}$ the triangle formed by the lines $\left(\ell_{1}\right),\left(\ell_{2}\right)$, and $\left(\ell_{3}\right)$. Show that the circumcircles of triangles $ABC$ and $A^{*} B^{*} C^{*}$ are tangent.

|
We calculate the angle $\left(C_{B} A, B_{C} A\right)$:
$\left(C_{B} A, A B_{C}\right)=\left(C_{B} A, A O\right)+\left(A O, A B_{C}\right)=\left(C_{B} B, B O\right)+\left(C O, C B_{C}\right)$ by cocyclicity of points $\mathrm{C}_{\mathrm{B}} \mathrm{BAO}$ and $\mathrm{AOB}_{\mathrm{C}} \mathrm{C},\left(\mathrm{C}_{\mathrm{B}} \mathrm{B}, \mathrm{BO}\right)+\left(\mathrm{CO}, \mathrm{CB}_{\mathrm{C}}\right)=(\mathrm{CB}, \mathrm{BO})+(\mathrm{CO}, \mathrm{CB})=(\mathrm{CO}, \mathrm{BO})=2(\mathrm{CA}, \mathrm{AB})$, so $\left(C_{B} A, A B_{C}\right)=2(C A, A B)$. We also find that $\left(C_{B} A^{*}, A^{*} B_{C}\right)=2(C A, A B)$ according to Lemma 3.2, thus $\left(C_{B} A, A B_{C}\right)=\left(C_{B} A^{*}, A^{*} B_{C}\right)$, hence the points $C_{B}, B_{C}, A$ and $A^{*}$ are cocyclic.
Step 2. T is on the circumcircle of $C_{B}, B_{C}, A$ and $A^{*}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $O$ le centre de son cercle circonscrit. On note $A_{B}$ et $A_{C}$ les autres intersections du cercle $B O C$ avec $(A B)$ et $(A C)$ et $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$, on définit de la même manière $B_{C}$, $B_{A}, C_{A}$ et $C_{B}$ ainsi que $\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. On note $A^{*} B^{*} C^{*}$ le triangle formé par les droites $\left(\ell_{1}\right),\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. Montrer que les cercles circonscrits des triangle $A B C$ et $A^{*} B^{*} C^{*}$ sont tangents.

|
On calcule l'angle $\left(C_{B} A, B_{C} A\right)$ :
$\left(C_{B} A, A B_{C}\right)=\left(C_{B} A, A O\right)+\left(A O, A B_{C}\right)=\left(C_{B} B, B O\right)+\left(C O, C B_{C}\right)$ par cocyclicité des points $\mathrm{C}_{\mathrm{B}} \mathrm{BAO}$ et $\mathrm{AOB}_{\mathrm{C}} \mathrm{C},\left(\mathrm{C}_{\mathrm{B}} \mathrm{B}, \mathrm{BO}\right)+\left(\mathrm{CO}, \mathrm{CB}_{\mathrm{C}}\right)=(\mathrm{CB}, \mathrm{BO})+(\mathrm{CO}, \mathrm{CB})=(\mathrm{CO}, \mathrm{BO})=2(\mathrm{CA}, \mathrm{AB})$, donc $\left(C_{B} A, A B_{C}\right)=2(C A, A B)$, on trouve également que $\left(C_{B} A^{*}, A^{*} B_{C}\right)=2(C A, A B)$ d'après le lemme 3.2, ainsi $\left(C_{B} A, A B_{C}\right)=\left(C_{B} A^{*}, A^{*} B_{C}\right)$, ainsi les points $C_{B}, B_{C}, A$ et $A^{*}$ sont cocycliques.
Étape 2. T est sur le cercle circonscrit de $C_{B}, B_{C}, A$ et $A^{*}$.
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"solution_match": "\nDémonstration.",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle and $O$ the center of its circumcircle. We denote by $A_B$ and $A_C$ the other intersections of the circle $BOC$ with $(AB)$ and $(AC)$, and $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$. We define $B_C$, $B_A$, $C_A$, and $C_B$ in the same manner, as well as $\left(\ell_{2}\right)$ and $\left(\ell_{3}\right)$. We denote by $A^{*} B^{*} C^{*}$ the triangle formed by the lines $\left(\ell_{1}\right),\left(\ell_{2}\right)$, and $\left(\ell_{3}\right)$. Show that the circumcircles of triangles $ABC$ and $A^{*} B^{*} C^{*}$ are tangent.

|
\(\left(A^{*} B_{C}, B_{C} T\right)=\left(B^{\prime} B_{C}, B_{C} T\right)=\left(B^{\prime} C, C T\right)=\left(B^{\prime} C, C T\right)=(A C, C T)=(A A, A T)=\) \(\left(A A^{*}, A T\right)\), where the line \((A A)\) denotes here the tangent at \(A\) to the circle \(A B C\), according to lemmas 1 and 3, then the points \(A^{*}, B_{C}, T\) and \(A\) are concyclic.
In conclusion, the points \(C_{B}, B_{C}, T, A\) and \(A^{*}\) are concyclic.
Symmetrically, \(C^{*}, A_{B}, B_{A}, T\) and \(C\).
Since \(T\) is on the circle \(C_{B} B_{C} T A A^{*}\), we can exchange the roles of \(B\) and \(C\), and similarly, we can exchange the roles of \(A\) and \(B\) knowing that the points \(C^{*} A_{B} B_{A} T C\) are cyclic. We can find the concyclicity of the following quadrilaterals: \(A B^{\prime} \mathrm{TB}_{A}, \mathrm{BC}^{\prime} \mathrm{TC}_{A}, \mathrm{CA}^{\prime} \mathrm{TA}_{\mathrm{C}}, \mathrm{BA}^{\prime} \mathrm{TA}_{\mathrm{B}}\), \(A C^{\prime} \mathrm{TC}_{A}, C B^{\prime} \mathrm{TB}_{C}\), and the concyclicity of the following pentagons: \(A A^{*} \mathrm{TC}_{A} B_{A}, C C^{*} \mathrm{~TB}_{C} A_{C}\) and \(B B^{*} T A_{B} C_{B}\), but also \(B, B^{\prime}\) and \(T\) are collinear, \(A A^{\prime} T\) and \(C C^{\prime} T\) are collinear, as well as \(O C_{A} B_{C}\), \(O B_{C} A_{C}\) and \(O C_{B} A_{B}\). After understanding the exercise and the various properties of the figure a bit better, we can conclude.
First, we recall Miquel's theorem, whose proof by angle chasing is left to the reader:
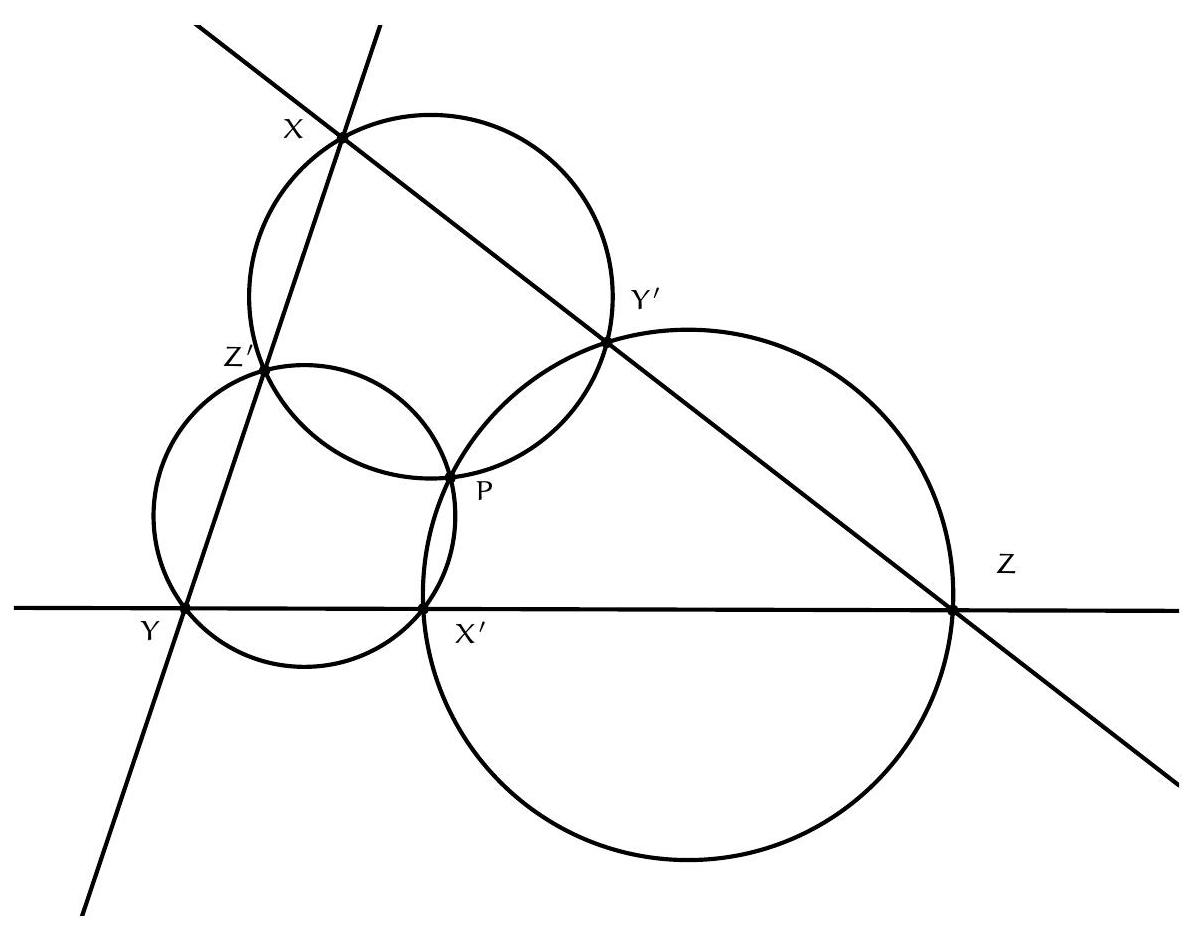
Let \(X Y Z\) be a triangle, and \(X^{\prime}, Y^{\prime}\) and \(Z^{\prime}\) be points on the sides \(Y Z, X Y\) and \(Z X\), then the circumcircles of \(Y X^{\prime} Z^{\prime}\), \(X Y^{\prime} Z^{\prime}\) and \(X^{\prime} Y^{\prime} Z\) are concurrent at \(P\).
First, we set: \(X, Y, Z = A_{C}, B^{\prime}, C^{*}\) and \(X^{\prime}, Y^{\prime}, Z^{\prime} = B_{C}, A^{\prime}, C\). Then the circumcircles of \(C A_{C} A^{\prime}\), \(B^{\prime} B_{C} C\) and \(B_{C} C^{*} A^{\prime}\) intersect at \(T\), because \(T\) is on the circumcircles of \(C A_{C} A^{\prime}\) and \(B^{\prime} B_{C} C\). Thus, \(T, B_{C}, C^{*}\) and \(A^{\prime}\) are concyclic.
By setting \(X, Y, Z = A^{\prime}, C_{B}, B^{*}\) and \(X^{\prime}, Y^{\prime}, Z^{\prime} = A^{*}, C^{*}, B_{C}\). Then \(B_{C} C^{*} A^{\prime}\), \(C_{B} B_{C} A^{*}\) and \(A^{*} B^{*} C^{*}\) are concurrent at \(T\) as well (since \(T\) is already on the circumcircles of \(B_{C} C^{*} A^{\prime}\) and \(C_{B} B_{C} A^{*}\)). This proves that the point \(T\) is on the circumcircle of \(A^{*} B^{*} C^{*} T\).
We will now prove that the circumcircles of \(A B C\) and \(A^{*} B^{*} C^{*}\) are tangent at \(T\). We introduce \((t)\) the tangent at \(T\) to the circle \(A B C\), and we will prove that \((t)\) is also tangent to the circle \(A^{*} B^{*} C^{*}\).
We have \(\left(C^{*} T, t\right) = \left(C^{*} T, T C\right) + (T C, t) = \left(C^{*} A_{B}, A_{B} C\right) + (T B, B C)\) (by concyclicity and tangent angle). Now, \(\left(C^{*} A_{B}, A_{B} C\right) = (B A, A C) + (A B, B C)\) by direct angle chasing, but \(\left(B C^{\prime}, C^{\prime} C_{B}\right) = (B A, A C) + (A B, B C)\) as well. Thus, \(\left(C^{*} T, t\right) = \left(B C^{\prime}, C^{\prime} C_{B}\right) + (T B, B C) = \left(B T, T C_{B}\right) + (T B, B C) = \left(B C, T C_{B}\right) = \left(T B^{*}, B^{*} C^{*}\right)\).
This concludes the proof of the exercise.
Remark. It is also possible to prove, with more advanced tools, that the lines \((A B), (B C), (C A), (A^{*} B^{*}), (B^{*} C^{*})\) and \((C^{*} A^{*})\) are tangent to the same parabola \(\mathcal{P}\) with focus \(T\) and directrix the line connecting \(O\) and the center of the circumcircle of \(A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}\).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $O$ le centre de son cercle circonscrit. On note $A_{B}$ et $A_{C}$ les autres intersections du cercle $B O C$ avec $(A B)$ et $(A C)$ et $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$, on définit de la même manière $B_{C}$, $B_{A}, C_{A}$ et $C_{B}$ ainsi que $\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. On note $A^{*} B^{*} C^{*}$ le triangle formé par les droites $\left(\ell_{1}\right),\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. Montrer que les cercles circonscrits des triangle $A B C$ et $A^{*} B^{*} C^{*}$ sont tangents.

|
$\left(A^{*} B_{C}, B_{C} T\right)=\left(B^{\prime} B_{C}, B_{C} T\right)=\left(B^{\prime} C, C T\right)=\left(B^{\prime} C, C T\right)=(A C, C T)=(A A, A T)=$ $\left(A A^{*}, A T\right)$, où la droite $(A A)$ désigne ici la tangente en $A$ au cercle $A B C$, d'après les lemmes 1 et 3 , alors les points $A^{*}, B_{C}, T$ et $A$ sont cocycliques.
En conclusion, les points $C_{B}, B_{C}, T, A$ et $A^{*}$ sont cocycliques.
On a de manière symétrique $C^{*}, A_{B}, B_{A}, T$ et $C$.
Comme $T$ est sur le cercle $C_{B} B_{C} T A A^{*}$ on peut échanger les rôles de $B$ et $C$, de la même manière on peut échanger les rôles de $A$ et $B$ en sachant que les points $C^{*} A_{B} B_{A} T C$ sont cycliques. On peut trouver la cocyclicité des quadrilatères suivants : $A B^{\prime} \mathrm{TB}_{A}, \mathrm{BC}^{\prime} \mathrm{TC}_{A}, \mathrm{CA}^{\prime} \mathrm{TA}_{\mathrm{C}}, \mathrm{BA}^{\prime} \mathrm{TA}_{\mathrm{B}}$, $A C^{\prime} \mathrm{TC}_{A}, C B^{\prime} \mathrm{TB}_{C}$, on trouve la cyclicité des pentagones suivants: $A A^{*} \mathrm{TC}_{A} B_{A}, C C^{*} \mathrm{~TB}_{C} A_{C}$ et $B B^{*} T A_{B} C_{B}$, mais également $B, B^{\prime}$ et $T$ sont alignés, $A A^{\prime} T$ et $C C^{\prime} T$ alignés, ainsi que $O C_{A} B_{C}$, $O B_{C} A_{C}$ et $O C_{B} A_{B}$. Après avoir compris un peu mieux l'exercice et les différentes propriétés de la figure on peut conclure.
On rappelle avant tout le théorème de Miquel dont la démonstration en chasse aux angles est laissée au lecteur:

Soit $X Y Z$ un triangle, $X^{\prime}, Y^{\prime}$ et $Z^{\prime}$ des points sur les côtés $Y Z, X Y$ et $Z X$, alors les cercles $Y X^{\prime} Z^{\prime}$, $X Y^{\prime} Z^{\prime}$ et $X^{\prime} Y^{\prime} Z$ sont concourants en $P$.
On pose dans un premier temps: $X, Y, Z=A_{C}, B^{\prime}, C^{*}$ et $X^{\prime}, Y^{\prime}, Z^{\prime}=B_{C}, A^{\prime}, C$. Alors les cercles circonscrits de $C A_{C} A^{\prime}, B^{\prime} B_{C} C$ et $B_{C} C^{*} A^{\prime}$ se coupent en $T$, car $T$ est sur les cercles circonscrits $\operatorname{de} C A_{C} A^{\prime}$ et $B^{\prime} B_{C} C$. Ainsi, $T, B_{C}, C^{*}$ et $A^{\prime}$ sont cocycliques.
En posant $X, Y, Z=A^{\prime}, C_{B}, B^{*}$ et $X^{\prime}, Y^{\prime}, Z^{\prime}=A^{*}, C^{*}, B_{C}$. Alors $B_{C} C^{*} A^{\prime}, C_{B} B_{C} A^{*}$ et $A^{*} B^{*} C^{*}$ sont concourantes en $T$ également (car $T$ est déjà sur les cercles circonscrits de $B_{C} C^{*} A^{\prime}$ et $C_{B} B_{C} A^{*}$ ). Cela démontre ainsi que le point $T$ est sur le cercle circonscrit de $A^{*} B^{*} C^{*} T$.
On va maintenant démontrer que les cercles circonscrits de $A B C$ et $A^{*} B^{*} C^{*}$ sont tangents en $T$. On introduit ( t ) la tangente en $T$ au cercle $A B C$, on va démontrer que ( $t$ ) est également tangente au cercle $A^{*} B^{*} C^{*}$.
On a $\left(C^{*} T, t\right)=\left(C^{*} T, T C\right)+(T C, t)=\left(C^{*} A_{B}, A_{B} C\right)+(T B, B C)$ (par cocyclicité et angle tangent). Or, $\left(C^{*} A_{B}, A_{B} C\right)=(B A, A C)+(A B, B C)$ par chasse au angle direct, mais $\left(B C^{\prime}, C^{\prime} C_{B}\right)=(B A, A C)+$ $(A B, B C)$ également. Ainsi, $\left(C^{*} \mathrm{~T}, \mathrm{t}\right)=\left(\mathrm{BC}^{\prime}, \mathrm{C}^{\prime} \mathrm{C}_{\mathrm{B}}\right)+(\mathrm{TB}, \mathrm{BC})=\left(\mathrm{BT}, \mathrm{TC}_{\mathrm{B}}\right)+(\mathrm{TB}, \mathrm{BC})=$ $\left(\mathrm{BC}, \mathrm{TC}_{\mathrm{B}}\right)=\left(\mathrm{TB}^{*}, \mathrm{~B}^{*} \mathrm{C}^{*}\right)$.
Ce qui conclut la preuve de l'exo.
Remarque. Il est également possible de démontrer, avec des outiles plus ava, cés, que les droites $(A B),(B C),(C A),\left(A^{*} B^{*}\right),\left(B^{*} C^{*}\right)$ et $\left(C^{*} A^{*}\right)$ sont tangentes à une même parabole $\mathcal{P}$ de foyer $T$ et de directrice la droite qui relie $O$ et le centre du cercle circonscrit de $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$.
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"solution_match": "\nDémonstration.",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle and $O$ the center of its circumcircle. We denote by $A_B$ and $A_C$ the other intersections of the circle $BOC$ with $(AB)$ and $(AC)$, and $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$. We define $B_C$, $B_A$, $C_A$, and $C_B$ in the same manner, as well as $\left(\ell_{2}\right)$ and $\left(\ell_{3}\right)$. We denote by $A^{*} B^{*} C^{*}$ the triangle formed by the lines $\left(\ell_{1}\right),\left(\ell_{2}\right)$, and $\left(\ell_{3}\right)$. Show that the circumcircles of triangles $ABC$ and $A^{*} B^{*} C^{*}$ are tangent.

|
We will start with some lemmas on parabolas.
Lemma. For any parabola, there exists a focus and a directrix such that for any point $P$ on the parabola, the distance from $P$ to the focus and to the line is the same.
|
proof
|
Yes
|
Incomplete
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $O$ le centre de son cercle circonscrit. On note $A_{B}$ et $A_{C}$ les autres intersections du cercle $B O C$ avec $(A B)$ et $(A C)$ et $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$, on définit de la même manière $B_{C}$, $B_{A}, C_{A}$ et $C_{B}$ ainsi que $\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. On note $A^{*} B^{*} C^{*}$ le triangle formé par les droites $\left(\ell_{1}\right),\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. Montrer que les cercles circonscrits des triangle $A B C$ et $A^{*} B^{*} C^{*}$ sont tangents.

|
On va commencer par quelques lemmes sur les paraboles
Lemme. pour toute parabole il existe un foyer et une directrice tel que pour tout point P de la parabole, la distance de $P$ au foyer et à la droite soit la même.
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"solution_match": "\nDémonstration.",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle and $O$ the center of its circumcircle. We denote by $A_B$ and $A_C$ the other intersections of the circle $BOC$ with $(AB)$ and $(AC)$, and $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$. We define $B_C$, $B_A$, $C_A$, and $C_B$ in the same manner, as well as $\left(\ell_{2}\right)$ and $\left(\ell_{3}\right)$. We denote by $A^{*} B^{*} C^{*}$ the triangle formed by the lines $\left(\ell_{1}\right),\left(\ell_{2}\right)$, and $\left(\ell_{3}\right)$. Show that the circumcircles of triangles $ABC$ and $A^{*} B^{*} C^{*}$ are tangent.

|
We will demonstrate the following result on ellipses: every ellipse has two foci, called $F_{1}$ and $F_{2}$, such that for each point $E$ on the ellipse, $F_{1} E + F_{2} E$ is constant.
We recall that a conic section is a section of a cone, that is, the intersection of a cone with a plane, and we look at the points of intersection of the plane and the conic in the plane in question.

We can take the two spheres tangent to both the cone and the plane, the lower sphere touches the plane at a point $F_{1}$ and the upper sphere touches the plane at a point $F_{2}$. For a point $E$ on the ellipse (in red in the drawing), the line $F_{1} E$ is a tangent to the lower sphere, and the line $\mathrm{E}_{1} \mathrm{E}$ is also a tangent because it belongs to the cone and the sphere is tangent to the cone. Thus, $\mathrm{EF}_{1} = E \mathrm{E}_{1}$, and similarly, $\mathrm{EF}_{2} = \mathrm{EE}_{2}$. Therefore, $\mathrm{EF}_{1} + \mathrm{EF}_{2} = \mathrm{E}_{1} \mathrm{E}_{2}$, and $\mathrm{E}_{1} \mathrm{E}_{2}$ is clearly a constant for all points $E$. Hence, $\mathrm{EF}_{1} + \mathrm{EF}_{2}$ is constant, which concludes the proof.
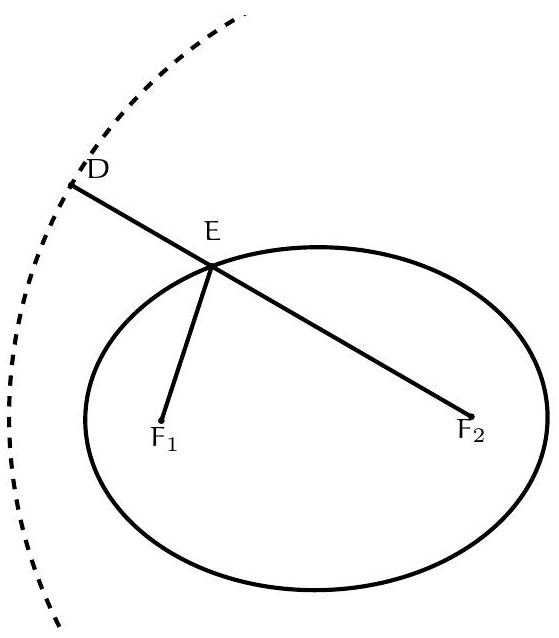
We now construct the point $D$ such that $E \mathrm{~F}_{1} = E D$ and that the points $\mathrm{D}, E$, and $\mathrm{F}_{2}$ are collinear. Then for any $E$ on the ellipse, we find that $F_{2} D = F_{1} E + F_{2} E$ is a constant, so as $E$ moves along the ellipse, the point $D$ moves on a circle centered at $F_{2}$.
We now seek to construct an ellipse. The intersection of the plane and the conic section is parallel to one of the "sides" of the cone, in this case, the point $\mathrm{F}_{2}$ is sent to infinity. Let's see what happens to our point $D$ from before; it moves on a circle centered at a point at infinity, which is a line. To construct the point $E$, we now take the point on a ray of the circle (i.e., a line perpendicular to the locus of points $D$ in our case) and take the point on this line that is the same distance from $D$ and $F_{1}$. In other words, there exists a point $F_{1}$ and a line (d) such that for every point on the parabola, the distance to the line (called the directrix) and to the point is the same.
Lemma. Let $\mathcal{P}$ be a parabola and $(t)$ a tangent to $\mathcal{P}$ at $E$, then the reflection of $F$ with respect to $(t)$ is on the directrix of the parabola.
|
proof
|
Yes
|
Incomplete
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $O$ le centre de son cercle circonscrit. On note $A_{B}$ et $A_{C}$ les autres intersections du cercle $B O C$ avec $(A B)$ et $(A C)$ et $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$, on définit de la même manière $B_{C}$, $B_{A}, C_{A}$ et $C_{B}$ ainsi que $\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. On note $A^{*} B^{*} C^{*}$ le triangle formé par les droites $\left(\ell_{1}\right),\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. Montrer que les cercles circonscrits des triangle $A B C$ et $A^{*} B^{*} C^{*}$ sont tangents.

|
On va démontrer le résultat suivant sur les ellipses : chaque ellipse admet deux foyers, appelés $F_{1}$ et $F_{2}$ tel que pour chaque point $E$ de l'ellipse $F_{1} E+F_{2} E$ est constante.
on rappelle qu'une conique est une section conique c'est-à-dire que l'on coupe un cône avec un plan quelconque et que l'on regarde les points d'intersection du plan et de la conique dans le plan du plan en question.

On peut prendre les deux sphères tangentes au cône et au plan à la fois, la sphère du bas touche le plan en un point $F_{1}$ et la sphère du haut touche le plan en un point $F_{2}$, alors pour un point $E$ sur l'ellipse (en rouge sur le dessin), la droite $F_{1} E$ est une tangente à la sphère du bas, la droite $\mathrm{E}_{1} \mathrm{E}$ également car elle appartient au cône et que la phère est tangente au cône. Ainsi, $\mathrm{EF}_{1}=E \mathrm{E}_{1}$, de la même manière $\mathrm{EF}_{2}=\mathrm{EE}_{2}$, ainsi $\mathrm{EF}_{1}+\mathrm{EF}_{2}=\mathrm{E}_{1} \mathrm{E}_{2}$ et $\mathrm{E}_{1} \mathrm{E}_{2}$ est clairement une constante pour tout les points E . Donc $\mathrm{EF}_{1}+\mathrm{EF}_{2}$ est constant, ce qui conclut.

On contruit maintenant le point D tel que $E \mathrm{~F}_{1}=E D$ et que les points $\mathrm{D}, E$ te $\mathrm{F}_{2}$ soient alignés. Alors pour tout $E$ sur l'ellipse on trouve que $F_{2} D=F_{1} E+F_{2} E$ est une constante, donc quand $E$ bouge sur l'ellipse, le point D bouge sur une cercle de centre $F_{2}$.
On cherche maintenant à contruire une ellipse, pour construire une ellipse l'intersection du plan et de la conique ce fait de manière parallèle à un des "côtés" du cône, dans ce cas le point $\mathrm{F}_{2}$ est envoyé à l'infini. Regardons ce qu'il advient de notre point D précédent, il bouge sur un cercle de centre un point à l'infini donc une droite, pour construire le point $E$, il s'agit maintenant de prendre le point sur un rayon du cercle (c'est-à-dire une droite perpendiculaire au lieu des points D dans notre cas) et de prendre le point sur cette droite qui à la même distance à D et à $F_{1}$, autrement dit il existe un point $F_{1}$ et une droite ( d ) tel que pour tout point de la parabole la distance à la droite (appelée directrice) et au point soit la même.
Lemme. Soit $\mathcal{P}$ une parabole et $(t)$ une tangente à $\mathcal{P}$ en $E$, alors le symétrique de $F$ par rapport à $(t)$ est sur la directrice de la parabole.
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"solution_match": "\nDémonstration.",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle and $O$ the center of its circumcircle. We denote by $A_B$ and $A_C$ the other intersections of the circle $BOC$ with $(AB)$ and $(AC)$, and $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$. We define $B_C$, $B_A$, $C_A$, and $C_B$ in the same manner, as well as $\left(\ell_{2}\right)$ and $\left(\ell_{3}\right)$. We denote by $A^{*} B^{*} C^{*}$ the triangle formed by the lines $\left(\ell_{1}\right),\left(\ell_{2}\right)$, and $\left(\ell_{3}\right)$. Show that the circumcircles of triangles $ABC$ and $A^{*} B^{*} C^{*}$ are tangent.

|
Let $\mathrm{E}_{1}$ be the orthogonal projection of E onto the directrix, then $\mathrm{FE}=\mathrm{EE}_{1}$. We denote $\mathrm{E}^{\prime}$ as the symmetric point of F with respect to (t), then $\mathrm{EE}^{\prime}=\mathrm{EF}=\mathrm{EE} \mathrm{E}_{1}$. Since $\mathrm{EE}_{1}$ is the distance from E to the parabola's directrix, the point $E^{\prime}$ is on the same side of the directrix as the parabola. Now, we take G as the point on the parabola such that ( $\mathrm{GE}^{\prime}$ ) is perpendicular to the directrix. Then, denoting $\mathrm{G}_{1}$ as the orthogonal projection of G onto the directrix, we have on one hand: $\mathrm{FG}=\mathrm{GG}_{1}=\mathrm{GE}^{\prime}$, so $E^{\prime}=G_{1}$ and $E^{\prime}$ is on the directrix. This concludes the proof.
Lemma. Let $\left(t_{1}\right),\left(t_{2}\right)$, and $\left(t_{3}\right)$ be three tangents to a parabola $\mathcal{P}$ with focus $F$, then the circumcircle of the triangle formed by $\left(t_{1}\right),\left(t_{2}\right)$, and $\left(t_{3}\right)$ also passes through $F$.
|
proof
|
Yes
|
Incomplete
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $O$ le centre de son cercle circonscrit. On note $A_{B}$ et $A_{C}$ les autres intersections du cercle $B O C$ avec $(A B)$ et $(A C)$ et $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$, on définit de la même manière $B_{C}$, $B_{A}, C_{A}$ et $C_{B}$ ainsi que $\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. On note $A^{*} B^{*} C^{*}$ le triangle formé par les droites $\left(\ell_{1}\right),\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. Montrer que les cercles circonscrits des triangle $A B C$ et $A^{*} B^{*} C^{*}$ sont tangents.

|
Soit $\mathrm{E}_{1}$ la projection orthogonale de E sur la directrice, alors $\mathrm{FE}=\mathrm{EE}_{1}$, on note $\mathrm{E}^{\prime}$ le symétrique de F par rapport à ( t ), on a alors $\mathrm{EE}^{\prime}=\mathrm{EF}=\mathrm{EE} \mathrm{E}_{1}$, comme $\mathrm{EE}_{1}$ est la distance de E à la parabole la droite, le point $E^{\prime}$ est du même côté de la directrice que la parabole. On prend maintenant G le point de la parabole tel que ( $\mathrm{GE}^{\prime}$ ) est perpendiculaire à la directrice, alors en notant $\mathrm{G}_{1}$ la projection orthogonale de G sur la directrice, on a d'une part : $\mathrm{FG}=\mathrm{GG}_{1}=\mathrm{GE}^{\prime}$ donc $E^{\prime}=G_{1}$ est $E^{\prime}$ est sur la directrice. Ce qui conclut.
Lemme. Soit $\left(t_{1}\right),\left(t_{2}\right)$ et $\left(t_{3}\right)$ trois tangentes à une parabole $\mathcal{P}$ de foyer $F$, alors le cercle circonscrit du triangle formé par $\left(t_{1}\right),\left(t_{2}\right)$ et $\left(t_{3}\right)$ passe par $F$ également.
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"solution_match": "\nDémonstration.",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle and $O$ the center of its circumcircle. We denote by $A_B$ and $A_C$ the other intersections of the circle $BOC$ with $(AB)$ and $(AC)$, and $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$. We define $B_C$, $B_A$, $C_A$, and $C_B$ in the same manner, as well as $\left(\ell_{2}\right)$ and $\left(\ell_{3}\right)$. We denote by $A^{*} B^{*} C^{*}$ the triangle formed by the lines $\left(\ell_{1}\right),\left(\ell_{2}\right)$, and $\left(\ell_{3}\right)$. Show that the circumcircles of triangles $ABC$ and $A^{*} B^{*} C^{*}$ are tangent.

|
The three symmetrical points of F with respect to the three lines are on the directrix, hence aligned, which shows according to Steiner that the point $F$ is on the circumcircle of the triangle induced by the three tangents, and furthermore that the orthocenter of this triangle is on the directrix.
There exists a unique conic tangent to five lines. By taking the conics tangent to the lines $(A B),(B C),(C A)$ and $\left(B_{A} B_{C}\right)$ and the line at infinity, we find a parabola tangent to the first four lines. According to the previous lemma, the focus is on the circumcircles of $B^{\prime} B_{C} C$ and $B^{\prime} A B_{A}$, which is therefore $F$ (since $B^{\prime}$ is on the tangents and cannot be the focus of the parabola). In the same way, we can prove that the six lines $(A B)$, $(B C),(C A),\left(A^{*} B^{*}\right),\left(B^{*} C^{*}\right)$ and $\left(C^{*} A^{*}\right)$ are tangent to the same parabola $\mathcal{P}$ with focus $T$ and directrix the line connecting $O$ and the center of the circumcircle of $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$.
## Link with the Feuerbach Point
We define the intersection of the tangents at $B$ and $C$ as $A^{\prime \prime}$. We define $B^{\prime \prime}$ and $C^{\prime \prime}$ in the same way, then the circle $A B C$ is the incircle of $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$. We will show that the circle $A^{*} B^{*} C^{*}$ is the nine-point circle of the triangle $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$. Here, we will show that the points $A^{*}, B^{*}$ and $C^{*}$ are the midpoints of the sides of $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$. We already know that the lines $\left(A A^{*}\right),\left(B B^{*}\right)$ and $\left(C C^{*}\right)$ are tangents to the circumcircle of $A B C$, which shows that the points $A^{*}, B^{*}$ and $C^{*}$ are on the sides of the triangle $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$. It remains to prove that they are the midpoints of the sides.
To conclude, we will prove the following two lemmas.
Lemma 1. Let $A B C$ be a triangle, $D, E$ and $F$ the points of tangency of the incircle on the sides $B C, C A$ and $A B$. We also denote the point $X$ as the orthogonal projection of $C$ onto the angle bisector from $B$, then the points $X, E$ and $F$ are collinear.
|
proof
|
Yes
|
Incomplete
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $O$ le centre de son cercle circonscrit. On note $A_{B}$ et $A_{C}$ les autres intersections du cercle $B O C$ avec $(A B)$ et $(A C)$ et $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$, on définit de la même manière $B_{C}$, $B_{A}, C_{A}$ et $C_{B}$ ainsi que $\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. On note $A^{*} B^{*} C^{*}$ le triangle formé par les droites $\left(\ell_{1}\right),\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. Montrer que les cercles circonscrits des triangle $A B C$ et $A^{*} B^{*} C^{*}$ sont tangents.

|
Les trois symétriques de F par rapport aux trois droites sont sur la directrice, donc alignés, ce qui montre d'après Steiner que le point $F$ est sur le cercle circonscrit du triangle induit par les trois tangentes et de plus que l'orthocentre de ce triangle est sur la directrice.
Il existe une unique conique tangente à cinq droites, en prenant la coniques tangentes aux droites $(A B),(B C),(C A)$ et $\left(B_{A} B_{C}\right)$ et la droite à l'infini on trouve une parabole tangente aux quatres premiers droites, d'après le lemme précédent le foyer est sur les cercles circonscrits de $B^{\prime} B_{C} C$ et $B^{\prime} A B_{A}$, il s'agit donc de $F\left(B^{\prime}\right.$ est sur les tangentes donc ne peut pas être le foyer de la parabole). De la même manière on arrive à démontrer que finalement les 6 droites $(A B)$, $(B C),(C A),\left(A^{*} B^{*}\right),\left(B^{*} C^{*}\right)$ et $\left(C^{*} A^{*}\right)$ sont tangentes à une même parabole $\mathcal{P}$ de foyer $T$ et de directrice la droite qui relie $O$ et le centre du cercle circonscrit de $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$.
## Lien avec le point de Feuerbach
On pose que l'intersection des tangentes en $B$ et $C$ sont $A^{\prime \prime}$. On définit de la même manière $B^{\prime \prime}$ et $C^{\prime \prime}$, alors le cercle $A B C$ est le cercle inscrit de $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$, on va montrer que le cercle $A^{*} B^{*} C^{*}$ est le cercle d'Euler du triangle $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$, on va ici montrer que les points $A^{*}, B^{*}$ et $C^{*}$ sont les milieux des côtés de $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$. On sait déjà que les droites $\left(A A^{*}\right),\left(B B^{*}\right)$ et $\left(C C^{*}\right)$ sont des tangentes au cercle circonscrit de $A B C$, ce qui montre que les points $A^{*}, B^{*}$ et $C^{*}$ sont sur les côtés du triangles $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$, il faut maintenant démontrer qu'ils sont les milieux des côtés.
Pour conclure on va démontrer les deux lemmes suivants.
Lemme 1. Soit $A B C$ un triangle, $D, E$ et $F$ les points de tangence du cercle inscrit sur les côtés, $B C, C A$ et $A B$. On note également les points $X$ la projection orthogonale de $C$ sur la bissectrice issue de $B$, alors les points $X, E$ et $F$ sont alignés.
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"solution_match": "\nDémonstration.",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle and $O$ the center of its circumcircle. We denote by $A_B$ and $A_C$ the other intersections of the circle $BOC$ with $(AB)$ and $(AC)$, and $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$. We define $B_C$, $B_A$, $C_A$, and $C_B$ in the same manner, as well as $\left(\ell_{2}\right)$ and $\left(\ell_{3}\right)$. We denote by $A^{*} B^{*} C^{*}$ the triangle formed by the lines $\left(\ell_{1}\right),\left(\ell_{2}\right)$, and $\left(\ell_{3}\right)$. Show that the circumcircles of triangles $ABC$ and $A^{*} B^{*} C^{*}$ are tangent.

|
There is an orthogonal projection, so we can think of the Simson line. We then denote $Y$ as the intersection point of the lines $(C X)$ and $(A B)$. We know that the circle passing through $A$, $C$, and $I$ is the antarctic circle, and thus the symmetric point of $C$ with respect to the bisector from $B$ is also on this circle by axial symmetry along the bisector, which passes through the center. Therefore, the points $A, Y, C$, and $I$ are concyclic. According to the Simson line, the orthogonal projections of $I$ onto the three sides of the triangle are collinear, which are the points $E, F$, and $X$, thus proving the lemma.
Lemma 2. We still denote $D$ as the tangency point of the incircle of $A B C$ on $B C$ and $D^{\prime}$ as the tangency point of the $A$-excircle (with center $I_{A}$) of $A B C$ on $B C$. We then denote $X$ and $Y$ as the projections of $B$ and $C$ onto $(A I)$, respectively. Then the points $D, D^{\prime}, X$, and $Y$ are concyclic with diameter $\left[\mathrm{DD}^{\prime}\right]$.
|
proof
|
Yes
|
Incomplete
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $O$ le centre de son cercle circonscrit. On note $A_{B}$ et $A_{C}$ les autres intersections du cercle $B O C$ avec $(A B)$ et $(A C)$ et $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$, on définit de la même manière $B_{C}$, $B_{A}, C_{A}$ et $C_{B}$ ainsi que $\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. On note $A^{*} B^{*} C^{*}$ le triangle formé par les droites $\left(\ell_{1}\right),\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. Montrer que les cercles circonscrits des triangle $A B C$ et $A^{*} B^{*} C^{*}$ sont tangents.

|
Il y a une projection orthogonale donc on peut penser à la droite de Simson. On note alors $Y$ le point d'intersection des droites $(C X)$ et $(A B)$, on sait que le cercle passant par $A$, $C$ et I est le cercle antarctique et ainsi le symétrique de $C$ par rapport à la bissectrice issue de $B$ est également sur ce cercle par symétrie axiale le long de la bissectrice, qui passe par le centre, alors les points $A, Y, C$ et I sont cocycliques, donc d'après la droite de Simson, les projections orthogonales de I sur les trois côtés du triangle sont alignés, il s'agit alors des points $E, F$ et $X$ ce qui montre le lemme.
Lemme 2. On note toujours $D$ le point de tangence du cercle inscrit de $A B C$ sur $B C$ et $D^{\prime}$ le point de tangence du cercle $A$-exinscrit (de centre $I_{A}$ ) de $A B C$ sur $B C$, on note alors $X$ et $Y$ les projections respectives de $B$ et $C$ sur ( $A I$ ), alors les points $D, D^{\prime}, X$ et $Y$ sont cocycliques de diamètre $\left[\mathrm{DD}^{\prime}\right]$.
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"solution_match": "\nDémonstration.",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle and $O$ the center of its circumcircle. We denote by $A_B$ and $A_C$ the other intersections of the circle $BOC$ with $(AB)$ and $(AC)$, and $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$. We define $B_C$, $B_A$, $C_A$, and $C_B$ in the same manner, as well as $\left(\ell_{2}\right)$ and $\left(\ell_{3}\right)$. We denote by $A^{*} B^{*} C^{*}$ the triangle formed by the lines $\left(\ell_{1}\right),\left(\ell_{2}\right)$, and $\left(\ell_{3}\right)$. Show that the circumcircles of triangles $ABC$ and $A^{*} B^{*} C^{*}$ are tangent.

|
We will thus show that $\widehat{\mathrm{DXD}^{\prime}}=90$, by taking (AI) and (BC) as reference lines, we find by cocyclicity of points $D^{\prime}, B, X$ and $I_{A}$, thanks to the right angles, that $\left(X D^{\prime}\right) \backslash \backslash\left(B I_{A}\right)$, in the same way $(X D) \backslash \backslash(B I)$, by passing to the antiparallel $\left(X D^{\prime}, X D\right)=$ $\left(\mathrm{BI}_{\mathrm{A}}, \mathrm{BI}\right)=90$ which indeed shows that $X$ is on the circle with diameter [ $\mathrm{DD}^{\prime}$ ], in the same way $Y$ is on the circle with diameter $\left[D^{\prime}\right]$, which proves Lemma 2. We note here that the midpoint of side $[B C]$ is also the midpoint of [DD'], and thus the center of the circle passing through $D^{\prime}$, D, X, and Y.
We can now conclude and show that this exercise is equivalent to the Feuerbach point. Indeed, according to Lemma 1, the point $A_{C}$ is the orthogonal projection of $A^{\prime \prime}$ on ( $C^{\prime \prime} \mathrm{O}$ ), similarly $\mathrm{B}_{\mathrm{C}}$ is the orthogonal projection of $\mathrm{B}^{\prime \prime}$ on $\left(\mathrm{C}^{\prime \prime} \mathrm{O}\right)$, this shows, according to Lemma 2, that the center of the circumcircle of $B_{C} A_{C} C$ is the midpoint of $A^{\prime \prime} B^{\prime \prime}$, and according to the previous proof, the center of the circle $B_{C} A_{C} C$ is $C^{*}$ which is thus the midpoint of $A^{\prime \prime} B^{\prime \prime}$. Therefore, the circle $A^{*} B^{*} C^{*}$ is the nine-point circle and ABC is the incircle. The exercise then shows that the nine-point circle and the incircle are tangent, the point of tangency is called the Feuerbach point.
## Properties of the Feuerbach Point
We can then find the following properties of the Feuerbach point: Let $A B C$ be a triangle, D, E, and $G$ the points of tangency of the incircle with the sides $B C, C A$, and $A B$. We denote $M_{A}, M_{B}$, and $M_{C}$ the midpoints of the sides $B C, C A$, and $A B$. Then, setting $F$ as the Feuerbach point, we find that the lines (DF), (EG), and $M_{B} M_{C}$ are concurrent. We also find the following property: the circle passing through the points $D, F$, and $M_{A}$ also passes through $X$ and $Y$, the intersections of (BI) and (CI) with the line (EG). The last remark means that the Feuerbach point is the focus of a conic tangent to the lines $\mathrm{DE}, \mathrm{EG}, \mathrm{GD}, \mathrm{M}_{\mathrm{A}} M_{B}, M_{B} M_{C}$, and $M_{C} M_{A}$, we have also seen that the directrix of this conic is the line passing through the orthocenter of the triangle $M_{A} M_{B} M_{C}$, (let $O$ be the circumcenter) of $A B C$ and the orthocenter of DEG. It is possible to prove that this line is in fact the line (OI) (exercise left to the reader).
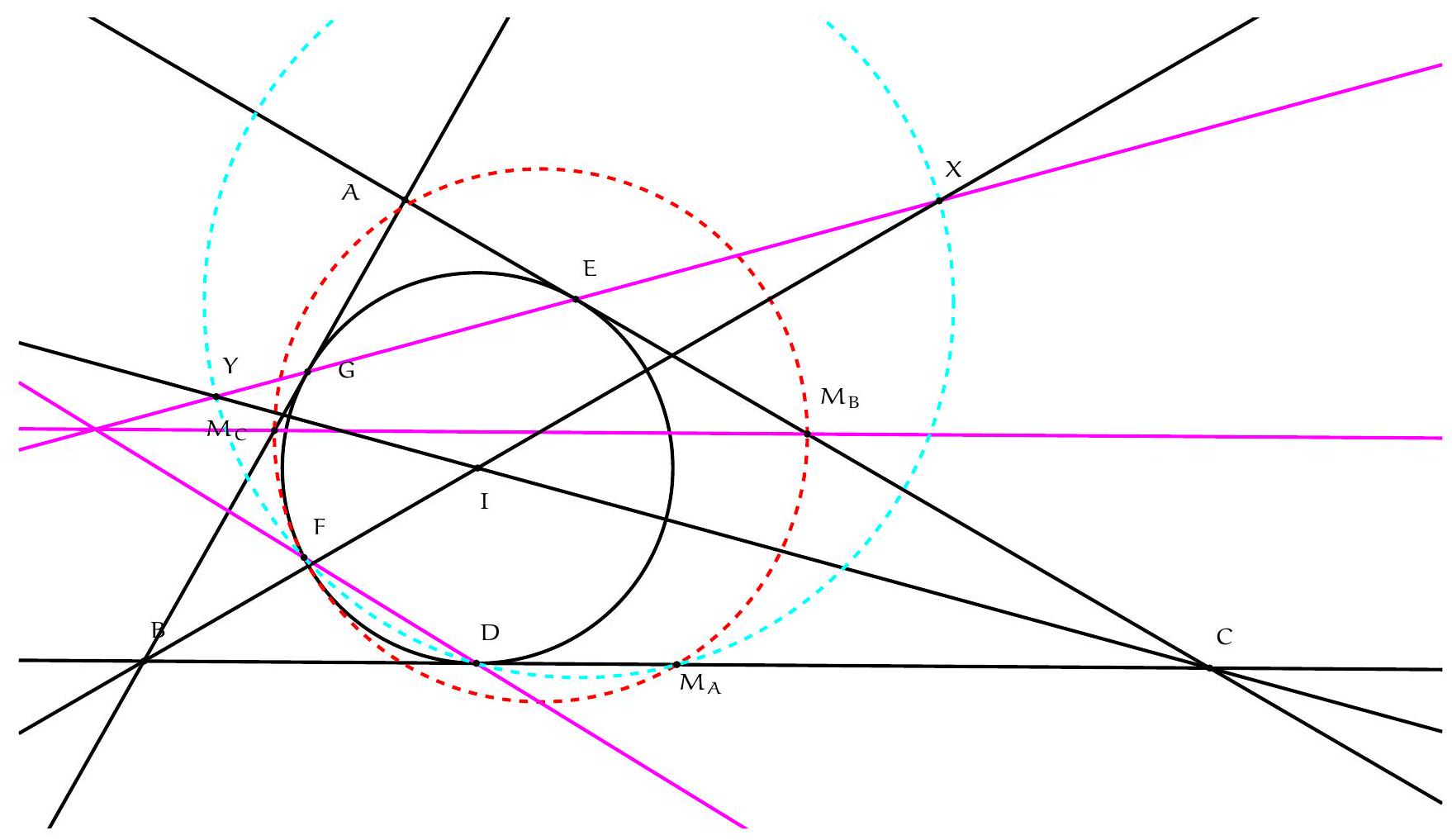
|
proof
|
Yes
|
Incomplete
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $O$ le centre de son cercle circonscrit. On note $A_{B}$ et $A_{C}$ les autres intersections du cercle $B O C$ avec $(A B)$ et $(A C)$ et $\left(\ell_{1}\right)=\left(A_{B} A_{C}\right)$, on définit de la même manière $B_{C}$, $B_{A}, C_{A}$ et $C_{B}$ ainsi que $\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. On note $A^{*} B^{*} C^{*}$ le triangle formé par les droites $\left(\ell_{1}\right),\left(\ell_{2}\right)$ et $\left(\ell_{3}\right)$. Montrer que les cercles circonscrits des triangle $A B C$ et $A^{*} B^{*} C^{*}$ sont tangents.

|
On va de ce fait montrer que $\widehat{\mathrm{DXD}^{\prime}}=90$, en prenant (AI) et (BC) comme droites de référence, on trouve par cocyclicité des points $D^{\prime}, B, X$ et $I_{A}$, grâce aux angles droits, que $\left(X D^{\prime}\right) \backslash \backslash\left(B I_{A}\right)$, de la même manière $(X D) \backslash \backslash(B I)$, par passage aux antiparallèle $\left(X D^{\prime}, X D\right)=$ $\left(\mathrm{BI}_{\mathrm{A}}, \mathrm{BI}\right)=90$ ce qui démontre bien que $X$ est sur le cercle de diamètre [ $\mathrm{DD}^{\prime}$ ], de la même manière $Y$ est sur le cercle de diamètre $\left[D^{\prime}\right]$, ce qui montre le lemme 2 . On remarque ici que le milieu du côté $[B C]$ est également le milieu de [DD'], et ainsi le centre du cercle passant par $D^{\prime}$, D, X et Y .
Nous pouvons maintenant conclure et montrer que cet exercice est équivalent au point de Feuerbach. En effet, d'après le lemme 1 , le point $A_{C}$ est la projection orthogonale de $A^{\prime \prime}$ sur ( $C^{\prime \prime} \mathrm{O}$ ), de la même manière $\mathrm{B}_{\mathrm{C}}$ est la projection orthogonale de $\mathrm{B}^{\prime \prime}$ sur $\left(\mathrm{C}^{\prime \prime} \mathrm{O}\right)$, cela montre, d'après le lemme 2 que le centre du cercle circonscrit de $B_{C} A_{C} C$ est le milieu de $A^{\prime \prime} B^{\prime \prime}$, or d'après la preuve précédente le centre du cercle $B_{C} A_{C} C$ est $C^{*}$ qui est ainsi le milieu de $A^{\prime \prime} B^{\prime \prime}$. Ainsi le cercle $A^{*} B^{*} C^{*}$ est le cercle d'Euler et ABC le cercle inscrit. L'exercice montre alors que le cercle d'Euler et le cercle inscrit sont tangents, le point de tangence est appelé point de Feuerbach.
## Propriétés du point de Feuerbach
On peut alors trouver les propriétés suivantes sur le point de Feuerbach : Soit $A B C$ un triangle, D, E et $G$ les points de tangence du cercle inscrit avec les côtés $B C, C A$ et $A B$. On note $M_{A}, M_{B}$ et $M_{C}$ les milieux des côtés $B C, C A$ et $A B$. Alors en posant $F$ le point de Feuerbach, on trouve que les droites (DF), (EG) et $M_{B} M_{C}$ sont concourantes. On trouve également la propriété suivante : le cercle passant par les points $D, F$ et $M_{A}$ passe également par $X$ et $Y$ intersections de (BI) et (CI) avec la droite (EG). La dernière remarque revient à dire que le point de Feuerbach est le foyer d'une conique tangente aux droites $\mathrm{DE}, \mathrm{EG}, \mathrm{GD}, \mathrm{M}_{\mathrm{A}} M_{B}, M_{B} M_{C}$ et $M_{C} M_{A}$, on a aussi vu que la directrice de cette conique est la droite passant par l'orthocentre du triangle $M_{A} M_{B} M_{C}$, (soit $O$ le centre du cercle circonscrit) de $A B C$ et l'orthocentre de DEG. Il est possible de démontrer que cette droite est en fait la droite (OI) (exercice laissé au lecteur).

|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-1.jsonl",
"solution_match": "\nDémonstration.",
"tier": "T2",
"year": null
}
|
Find the number of solutions of $n^{2} m^{6}=180 t+2$ for $n, m$ and $t$ positive integers.
|
We consider the expression modulo 4. The left side is a square and is therefore congruent to 0 or 1. 180 is congruent to 0 modulo 4, so $180 t+2$ is congruent to $0 * t+2=2$. The equation has no solutions modulo 4, so it has no solutions in $\mathbb{N}$
|
0
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Trouver le nombre de solutions de $n^{2} m^{6}=180 t+2$ pour $n, m$ et $t$ des entiers positifs.
|
On considère l'expression modulo 4. La gauche est un carré et est donc congru à 0 ou 1.180 est congru à 0 modulo 4 donc $180 t+2$ est congru à $0 * t+2=2$. L'équation n'a pas de solutions modulo 4 , elle n'en a donc pas non plus dans $\mathbb{N}$
|
{
"exam": "French_envois",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-2.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T2",
"year": null
}
|
Find the sum of all $n$ such that $n^{2}+8 n+44$ is a perfect square.
|
Let $f$ be the function under study. An idea in this type of exercise is to trap $f(n)$ between two consecutive integer squares $k^{2}<f(n)<(k+1)^{2}$ and to say by contradiction that if $f(n)=\mathfrak{i}^{2}$ then $k<i<k+1$ which is impossible since we are dealing with integers.
Here, the calculations can be shortened by noting that $f$ has the same parity as $n+4$, so if $(n+4)^{2}=n^{2}+8 n+16<f(n)<n^{2}+12 n+36=(n+6)^{2}$ which is true as soon as $n>2, f(n)$ is not a square. For the small cases, 2 is a solution and 1 is not.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Trouver la somme des $n$ tels que $n^{2}+8 n+44$ soit un carré parfait.
|
Soit f la fonction étudiée, une idée dans ce genre d'exercice est de coincer $f(n)$ entre 2 carrés d'entiers consécutifs $k^{2}<f(n)<(k+1)^{2}$ et de dire par l'absurde que si $f(n)=\mathfrak{i}^{2}$ alors $k<i<k+1$ ce qui est impossible car on a des entiers.
Ici les calculs peuvent s'abréger en remarquant que f a même parité que $n+4$, ainsi si $(n+4)^{2}=n^{2}+8 n+16<f(n)<n^{2}+12 n+36=(n+6)^{2}$ ce qui est vrai dès que $n>2, f(n)$ n'est pas un carré. Pour les petits cas 2 est solution et 1 non.
|
{
"exam": "French_envois",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-2.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T2",
"year": null
}
|
An integer $n$ is perfect if the sum of its divisors is $2n$. Let $n$ be a perfect integer and $p$ its smallest prime divisor. Show that the exponent of $p$ in the prime factorization of $n$ is even.
|
Let $n=p_{1}^{a_{1}} \cdots p_{k}^{a_{k}}$ with the $p_{i}$ distinct primes. The sum of the divisors of $n$ is $\sigma(n)=\prod_{i=1}^{k}\left(1+\cdots+p_{i}^{a_{i}}\right)$ (cf. page 14 of the complete arithmetic course available at maths-olympiques.fr).
Suppose by contradiction that $a_{1}$ is odd, then $1+\cdots+p_{1}^{a_{1}}=\left(1+p_{1}\right)+p_{1}^{2}\left(1+p_{1}\right)+\cdots+$ $p_{1}^{a_{1}-1}\left(1+p_{1}\right)$. Then $p_{1}+1$ divides $1+\cdots+p_{1}^{a_{1}}$, and thus also $2 n=\prod_{i=1}^{k}\left(1+\cdots+p_{i}^{a_{i}}\right)$. If $p_{1}+1$ is not prime: it has a largest prime divisor $q < p_{1}$ which satisfies $q \mid 2 n$; then since $q$ is coprime with $n$, $q=2$; but then $q^2 \mid p_{1}+1 \mid 2 n$ and thus $q \mid n$, contradiction.
Therefore, $p_{1}+1$ is prime and then necessarily $p_{1}=2$ and $p_{1}+1=p_{2}=3$. Then $n, \frac{n}{2}, \frac{n}{3}$ and $\frac{n}{6}$ are integers and divide $n$. Since $n>6$, they are different from 1. Thus $2 n=\sigma(n) \geqslant$ $n+\frac{n}{2}+\frac{n}{3}+\frac{n}{6}+1=2 n+1$, contradiction. Therefore, $a_{1}$ is even.
## Common Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Un entier $n$ est parfait si la somme de ses diviseurs est 2 n . Soit n un entier parfait et $p$ son plus petit diviseur premier. Montrer que l'exposant de $p$ dans la décomposition en produit de puissances de nombres premiers de n est pair.
|
Soit $n=p_{1}^{a_{1}} \cdots p_{k}^{a_{k}}$ avec les $p_{i}$ premiers distincts. La somme des diviseurs de $n$ est $\sigma(n)=\prod_{i=1}^{k}\left(1+\cdots+p_{i}^{a_{i}}\right)$ (cf. la page 14 du cours d'arithmétique complet disponible sur maths-olympiques.fr).
Supposons par l'absurde que $a_{1}$ soit impair, alors $1+\cdots+p_{1}^{a_{1}}=\left(1+p_{1}\right)+p_{1}^{2}\left(1+p_{1}\right)+\cdots+$ $p_{1}^{a_{1}-1}\left(1+p_{1}\right)$. Alors $p_{1}+1$ divise $1+\cdots+p_{1}^{a_{1}}$, donc aussi $2 n=\prod_{i=1}^{k}\left(1+\cdots+p_{i}^{a_{i}}\right)$. Si $p_{1}+1$ $\mathrm{n}^{\prime}$ est pas premier: il a un plus grand diviseur premier $\mathrm{q}<\mathrm{p}_{1}$ qui vérifie $\mathrm{q} \mid 2 \mathrm{n}$; alors comme q est premier avec $\mathrm{n}, \mathrm{q}=2$; mais alors $\mathrm{q}^{2}\left|\mathrm{p}_{1}+1\right| 2 \mathrm{n}$ et donc $\mathrm{q} \mid \mathrm{n}$, contradiction.
Donc $p_{1}+1$ est premier et alors nécessairement $p_{1}=2$ et $p_{1}+1=p_{2}=3$. Alors $n, \frac{n}{2}, \frac{n}{3}$ et $\frac{n}{6}$ sont entiers et divisent de $n$. Comme $n>6$, ils sont différents de 1 . Ainsi $2 n=\sigma(n) \geqslant$ $n+\frac{n}{2}+\frac{n}{3}+\frac{n}{6}+1=2 n+1$, contradiction. Donc $a_{1}$ est pair.
## Exercices Communs
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-2.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T2",
"year": null
}
|
Let $n$ be a strictly positive integer. Show that there exist $n$ pairwise distinct integers $r_{1}, \ldots, r_{n}$ such that each $r_{i}$ divides $r_{1}+\cdots+r_{n}$.
|
The solution is inspired by Egyptian fractions, which are n-tuples of distinct integers $a_{1}, \ldots, a_{n}$ satisfying $1 / a_{1}+\cdots+1 / a_{n}=1$, for example
$1 / 2+1 / 3+1 / 6=1$.
Then, by setting $r_{i}:=\prod_{j \neq i} a_{j}=\frac{a_{1} \cdots a_{n}}{a_{i}} \in \mathbb{Z}$, they will be distinct and their sum will be $a_{1} \cdots a_{n}$, which each $r_{i}$ divides.
We prove by induction that an Egyptian fraction exists for each $n \geqslant 3$. The example serves as the base case.
Induction step: assume proven for $n$, prove for $n+1$. We write the coefficients in increasing order, then we write $a_{n}^{\prime}=1+a_{n}$ and $a_{n+1}^{\prime}=a_{n}\left(1+a_{n}\right)$. We notice $1 / a_{n}^{\prime}+1 / a_{n+1}^{\prime}=1 / a_{n}$. By setting $a_{i}^{\prime}=a_{i}$ for $i \in\{1, \ldots, n-1\}$, we have an Egyptian fraction of length $n+1$, which concludes the induction (from the example we have $1 / 7+1 / 42=1 / 6$ and this gives: $1 / 2+1 / 3+1 / 7+1 / 42=1$).
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $n$ un entier strictement positif. Montrer qu'il existe $n$ entiers 2 à 2 distincts $r_{1}, \ldots, r_{n}$ tels que chaque $r_{i}$ divise $r_{1}+\cdots+r_{n}$.
|
La solution s'inspire des fractions égyptiennes, une fraction égyptienne est uplet d'entiers distincts $a_{1}, \ldots, a_{n}$ vérifiant $1 / a_{1}+\cdots+1 / a_{n}=1$, par exemple
$1 / 2+1 / 3+1 / 6=1$.
Alors en posant $r_{i}:=\prod_{j \neq i} a_{j}=\frac{a_{1} \cdots a_{n}}{a_{i}} \in \mathbb{Z}$, ils seront distinct et leur somme fera $a_{1} \cdots a_{n}$, que chaque $r_{i}$ divise.
On montre par récurrence qu'une fraction égyptienne existe pour chaque $\mathrm{n} \geqslant 3$. L'exemple fait l'initialisation.
Hérédité : supposons prouvé pour n prouvons pour $\mathrm{n}+1$, on écrit les coefficients triés dans l'ordre croissant, puis on écrit $a_{n}^{\prime}=1+a_{n}$ et $a_{n+1}^{\prime}=a_{n}\left(1+a_{n}\right)$ On remarque $1 / a_{n}^{\prime}+1 / a_{n+1}^{\prime}=1 / a_{n}$. En posant $a_{i}^{\prime}=a_{i}$ pour $i \in\{1, \ldots, n-1\}$, on dispose d'une fraction égyptienne de longueur $n+1$, ce qui conclut la récurrence (depuis l'exemple on a $1 / 7+1 / 42=1 / 6$ et cela donne : $1 / 2+1 / 3+1 / 7+1 / 42=1)$.
|
{
"exam": "French_envois",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-2.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T2",
"year": null
}
|
Let $n$ be a positive integer. Show that there exists a positive integer $m$ such that $n!=$ $\varphi(\mathrm{m})$, where $\varphi$ is the Euler's totient function. (We recall that if $m=p_{1}^{\alpha_{1}} \cdots p_{k}^{\alpha_{k}}$ with $p_{1}, \ldots, p_{\mathrm{k}}$ distinct prime numbers, $\left.\varphi(m)=m\left(\left(1-\frac{1}{\mathfrak{p}_{1}}\right) \cdots\left(1-\frac{1}{\mathfrak{p}_{\mathrm{k}}}\right)\right)\right)$
|
We proceed by construction starting from the largest prime numbers to the smallest.
The idea is to constrain the value of $\phi(m)$. The construction may seem a bit cumbersome, but one should not be intimidated and understand the idea behind it.
Let $p_{1}, p_{2}, \ldots$ be the prime numbers $p_{k} \leqslant n < p_{k+1}$
We show by downward induction that for all $i$ there exists $m_{i}$ such that
- $m_{i}$ is a product of $p_{j}$ with $k \geqslant j \geqslant i$
- For all $j \geqslant i, p_{j}$ has the same exponent in $m_{i}$ and $n$!
- $\phi\left(m_{i}\right) \mid n!$
The initialization is done for $i=k+1$ with $m_{k+1}=1$.
For the induction step, we multiply $m_{i+1}$ by $p_{i}$ until we have as many $p_{i}$ in $\phi\left(m_{i}\right)$ as in $n!$ to obtain $m_{i}$, thus respecting the first two hypotheses on $m_{i}$.
Let's verify that the last one is also satisfied. For $j \geqslant i$, we know there is no problem, the risk is an excessive valuation for a $p_{l}$ where $l$ is small, but given the construction, if $p_{l}^{\alpha} \mid \phi\left(m_{i}\right)$, then $p_{l}^{\alpha} \mid \left(p_{i}-1\right)\left(p_{i+1}-1\right) \cdots \left(p_{k}-1\right) \mid n!$; thus, we are assured that the induction works. With $m=m_{1}$, we obtain a solution to the exercise.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $n$ un entier positif. Montrer qu'il existe un entier positif $m$ tel que $n!=$ $\varphi(\mathrm{m})$, où $\varphi$ est la fonction indicatrice $d^{\prime}$ Euler. (On rappelle que si $m=p_{1}^{\alpha_{1}} \cdots p_{k}^{\alpha_{k}}$ avec $p_{1}, \ldots, p_{\mathrm{k}}$ des nombres premiers 2 à 2 distincts, $\left.\varphi(m)=m\left(\left(1-\frac{1}{\mathfrak{p}_{1}}\right) \cdots\left(1-\frac{1}{\mathfrak{p}_{\mathrm{k}}}\right)\right)\right)$
|
On procède par construction en partant des plus grands nombres premiers au plus petit.
L'idée est de contraindre la valeur de $\phi(m)$. La construction peut paraître un peu lourde mais il ne faut pas se laisser et impressionner et comprendre l'idée qui est derrière.
Soit $p_{1}, p_{2} \ldots$ les nombres premiers $p_{k} \leqslant n<p_{k+1}$
On montre par récurrence descendante que pour tout $i$ il existe $m_{i}$ tel que
- $m_{i}$ est un produit de $p_{j}$ avec $k \geqslant j \geqslant i$
- Pour tout $j \geqslant i, p_{j}$ a le même exposant dans $m_{i}$ et $n$ !
- $\phi\left(m_{i}\right) \mid n!$
L'initialisation se fait pour $\mathrm{i}=\mathrm{k}+1$ avec $\mathrm{m}_{\mathrm{k}+1}=1$.
Pour l'hérédité on multiplie $m_{i+1}$ par $p_{i}$ jusqu'à avoir autant de $p_{i}$ dans $\phi\left(m_{i}\right)$ que dans $n$ ! pour obtenir $m_{i}$ on respecte ainsi les 2 premières hypothèses sur $m_{i}$.
Vérifions que la dernière est aussi vérifiée, pour $j \geqslant i$ on sait que l'on n'a pas de problème, le risque est une trop grosse valuation pour un $p_{l}$ où $l$ petit or vu la construction si $p_{l}^{\alpha} \mid \phi\left(m_{i}\right)$, $p_{l}^{\alpha}\left|\left(p_{i}-1\right)\left(p_{i+1}-1\right) \cdots\left(p_{k}-1\right)\right| n!$ on est donc assuré que la récurrence marche. Avec $m=m_{1}$, on obtient une solution à l'exercice.
|
{
"exam": "French_envois",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-2.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T2",
"year": null
}
|
Let $n \geqslant 3$ be an integer, show that there exist two integers $x$ and $y$ such that $7 x^{2}+y^{2}=2^{n}$.
|
Another solution by induction! Initialization: $x_{3}=y_{3}=1$.
Hereditary: We assume by induction for $n, \left(X=\left(x_{n}+y_{n}\right) / 2, Y=\left|7 x_{n}-y_{n}\right| / 2\right)$ $\left(X=\left|x_{n}-y_{n}\right| / 2, Y=\left(7 x_{n}+y_{n}\right) / 2\right)$ the two pairs satisfy $7 X^{2}+Y^{2}=2^{n+1}$. The first pair is a solution if $x_{n}$ and $y_{n}$ have the same congruence modulo 4 ( $X$ and $Y$ are odd) otherwise the second pair works, which concludes.
## Exercises Seniors
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $n \geqslant 3$ un entier, montrer qu'il existe deux entier $x$ et $y$ tels que $7 x^{2}+y^{2}=2^{n}$.
|
Encore une solution par récurrence! Initialisation: $x_{3}=y_{3}=1$.
Hérédité : On suppose prouvé par récurrence pour $n,\left(X=\left(x_{n}+y_{n}\right) / 2, Y=\left|7 x_{n}-y_{n}\right| / 2\right)$ $\left(X=\left|x_{n}-y_{n}\right| / 2, Y=\left(7 x_{n}+y_{n}\right) / 2\right)$ les 2 couples vérifient $7 X^{2}+Y^{2}=2^{n+1}$. Le premier couple est solution si $x_{n}$ et $y_{n}$ on même congruence modulo 4 ( $X$ et $Y$ impairs) sinon le second convient, ce qui conclut.
## Exercices Seniors
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-2.jsonl",
"solution_match": "## Solution de l'exercice 6",
"tier": "T2",
"year": null
}
|
Let $p \geqslant 5$ be a prime number. Show that there exists an integer $n$ such that for all $x \in\{n-1, n, n+1\}, p^{2} \nmid x^{p-1}-1$ and $p \nmid x$.
|
Lemme: between 0 and $p^{2}$ there are exactly $p-1$ elements whose $(p-1)$-th power is congruent to 1 modulo $p^{2}$.
Proof: We take $\omega$ a primitive root modulo $p^{2}$ (recall that $\omega$ is a primitive root modulo m means that the powers of $\omega$ correspond to all the invertible elements modulo m, which exists as long as $m$ is $1,2,4$ or a power of an odd prime or twice a power of an odd prime, refer to the course notes for more details), the elements of order dividing $p-1$ are then those whose discrete logarithm (log satisfies that $\log (x)<\phi(m)$ and $\omega^{(\log (x))}=$ $x(\bmod m))$ is divisible by $p$, which gives exactly $p-1$ possibilities.
We use a pigeonhole principle: the socks are the $x$ between 0 and $p^{2}$ of order dividing $p-1$, there are $p-1$ of them by the lemma, the $p$ drawers are the intervals $k p+1 ;(k+1) p$, so there is an empty drawer from which we can draw the desired $n$ by taking for example $\mathrm{kp}+2$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $p \geqslant 5$ un nombre premier. Montrer qu'il existe un entier $n$ tel que pour tout $x \in\{n-1, n, n+1\}, p^{2} \nmid x^{p-1}-1$ et $p \nmid x$.
|
Lemme : entre 0 et $p^{2}$ il y a exactement $p-1$ éléments dont la puissance $(p-1)$-ième est congrue à 1 modulo $p^{2}$.
preuve: On prend $\omega$ une racine primitive modulo $p^{2}$ (pour rappel $\omega$ une racine primitive modulo m signifie que les puissances de $\omega$ correspondent à tout les inversibles modulo m , ce qui existe dès que $m$ est $1,2,4$ ou une puissance de premier impair ou 2 fois une puissance de premier impair, lire les polycopiés pour plus de détail), les éléments d'ordre divisant
$p-1$, sont alors ce dont le logarithme discret (log vérifie que $\log (x)<\phi(m)$ et $\omega^{(\log (x))}=$ $x(\bmod m))$ est divisible par $p$, ce qui donne bien $p-1$ possibilités.
On utilise un principe des tiroirs : les chaussettes sont les $x$ entre 0 et $p^{2}$ d'ordre divisant $p-1$, il y en a $p-1$ par le lemme, les $p$ tiroirs sont les intervalles $k p+1 ;(k+1) p$, il y donc un tiroir vide d'où l'on peut tirer le n voulu en prenant par exemple $\mathrm{kp}+2$.
|
{
"exam": "French_envois",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-2.jsonl",
"solution_match": "\nSolution de l'exercice 7",
"tier": "T2",
"year": null
}
|
Let $P$ be a polynomial with rational coefficients of degree greater than or equal to 2, and $\left(q_{n}\right)_{n \in \mathbb{N}}$ a sequence of rationals such that for all $n \geqslant 0, q_{n}=P\left(q_{n+1}\right)$. Show that the sequence $q_{n}$ is periodic from a certain rank.
|
Let $u$ be an integer such that $u_{1}$ is an integer. Let $\tilde{P}(X)=u P\left(\frac{1}{u} X\right)$. Let $v$ be an integer such that $v \tilde{P}$ has integer coefficients. Let $a$ be the leading coefficient of $v \tilde{P}$. We define $Q(X) = a \tilde{P}\left(\frac{1}{a} X\right)$, $m = a^{\operatorname{deg}(P)-2} v$, and for all $n \in \mathbb{N}$, $r_{n} = u a q_{n}$.
We have $m Q(X)$ is a monic polynomial with integer coefficients, and for all $n$, $r_{n} = Q\left(r_{n+1}\right)$. $r_{0}$ is an integer, and since for all $n$, $r_{n+1}$ is a rational root of the monic polynomial $m Q(X) - m r_{n}$ with integer coefficients, by induction, $r_{n}$ is an integer for all $n$.
Since $\operatorname{deg}(Q) > 1$, $\left|Q(x) / x\right|$ tends to $+\infty$ as $|x|$ tends to $+\infty$. Therefore, there exists $M > \left|r_{0}\right|$ such that for all $x$, $\left|Q(x)\right| \leqslant M \Rightarrow |x| \leqslant M$. By immediate induction, $\left|r_{n}\right| \leqslant M$ for all $n$. Thus, the sequence $r$ takes values in a finite set. Let $p$ be minimal such that $\left\{r_{0}, \ldots, r_{p-1}\right\} = \left\{r_{0}, r_{1}, \ldots\right\}$. We will show by induction on $n$ that $r_{n+p} = r_{n}$ for all $n$. By hypothesis, $r_{n+p} \in \left\{r_{n}, \ldots, r_{n+p-1}\right\} = \left\{r_{0}, \ldots, r_{p-1}\right\}$. Therefore, $r_{n+p} = r_{n+k}$ with $k \in \{0, \ldots, p-1\}$. Then if $k > 0$, $r_{p-1} = Q^{\circ(n+1)}\left(r_{n+p}\right) = Q^{\circ(n+1)}\left(r_{n+k}\right) = r_{k-1}$, and there is a contradiction with the minimality of $p$. Therefore, $k = 0$ and $r_{n} = r_{n+p}$. This concludes the induction.
We have just shown that the sequence is periodic with period $p$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit P un polynôme à coefficients rationnels de degré supérieur ou égal à 2 , et $\left(q_{n}\right)_{n \in \mathbb{N}}$ une suite de rationnels tels que pour tout $n \geqslant 0, q_{n}=P\left(q_{n+1}\right)$. Montrer que la suite $q_{n}$ est périodique à partir d'un certain rang.
|
Soit $u$ entier tel que $u_{1}$ soit entier. Soit $\tilde{P}(X)=u P\left(\frac{1}{u} X\right)$. Soit $v$ entier tel que $v \tilde{P}$ soit à coefficients entiers. Soit a le coefficient dominant de $v \tilde{P}$. On pose $Q(X)=$ $a \tilde{P}\left(\frac{1}{a} X\right), m=a^{\operatorname{deg}(P)-2} v$ et pour tout $n \in \mathbb{N}, r_{n}=u a q_{n}$.
Nous avons $m Q(X)$ unitaire à coefficients entiers et pour tout $n, r_{n}=Q\left(r_{n+1}\right) . r_{0}$ est entier, or comme pour tout $n, r_{n+1}$ est racine rationnelle du polynôme $m Q(X)-m r_{n}$ unitaire à coefficients entiers, par récurrence, $r_{n}$ est entier pour tout $n$.
Comme $\operatorname{deg}(Q)>1,|Q(x) / x|$ tend vers $+\infty$ quand $|x|$ tend vers $+\infty$. Donc il existe $M>\left|r_{0}\right|$ tel que pour tout $x,|Q(x)| \leqslant M \Rightarrow|x| \leqslant M$. Par récurrence immédiate, $\left|r_{n}\right| \leqslant M$ pour tout n . La suite r prend donc ses valeurs dans un ensemble fini. Soit $p$ minimal tel que $\left\{r_{0}, \ldots, r_{p-1}\right\}=\left\{r_{0}, r_{1}, \ldots\right\}$. Montrons par récurrence sur $n$ que $r_{n+p}=r_{n}$ pour tout $n$. Par hypothèse, $r_{n+p} \in\left\{r_{n}, \ldots, r_{n+p-1}\right\}=\left\{r_{0}, \ldots, r_{p-1}\right\}$. Donc $r_{n+p}=r_{n+k}$ avec $k \in\{0, \ldots, p-1\}$. Alors si $k>0, r_{p-1}=Q^{\circ(n+1)}\left(r_{n+p}\right)=Q^{\circ(n+1)}\left(r_{n+k}\right)=r_{k-1}$ et il y a contradiction avec la minimalité de $p$. Donc $k=0$ et $r_{n}=r_{n+p}$. Ce qui conclut la récurrence.
Nous venons de montrer que la suite est périodique de période $p$.
|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "\nExercice 8.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-2.jsonl",
"solution_match": "\nSolution de l'exercice 8",
"tier": "T2",
"year": null
}
|
For a positive integer $m$, we denote $d(m)$ as the number of positive divisors of $m$ (including 1 and $m$). Let $k$ be a strictly positive integer. Show that there are infinitely many positive integers $n$ such that $n$ has exactly $k$ distinct prime divisors and for all positive integers $a, b$ with $n=a+b$, $d(n)$ does not divide $d\left(a^{2}+b^{2}\right)$
|
Let's prove that every integer of the form $n = m 2^{p-1}$ with $p$ an odd prime, having $k-1$ prime factors strictly greater than 3 and satisfying $\left(\frac{5}{4}\right)^{(p-1)/2} > m$ is a solution.
If $a + b = n$ and $d(n) \mid d(a^2 + b^2)$, then $p \mid d(a^2 + b^2)$. Therefore, there exists a prime $q$ such that $q$ has an exponent $cp-1$ in $a^2 + b^2$. If $q \geq 5$, then $a^2 + b^2 \geq 5^{q-1} > n^2$, but $a^2 + b^2 = n^2 - 2ab \leq n^2$. Therefore, $q = 2$ or $3$.
If $q = 3$, by looking at $a^2 + b^2$ modulo 3, 3 divides $a$ and $b$ and thus $n$, which contradicts the hypothesis.
If $q = 2$, if $a$ and $b$ have distinct 2-adic valuations, the smallest one is $p-1$, and the valuation of the sum of squares is $2p-2$, which is absurd.
If they have the same 2-adic valuation, $a = 2^t a_0$ and $b = 2^t b_0$ with $a_0$ and $b_0$ odd, then $a_0^2 + b_0^2 = x 2^{cp-1-2t}$. The left side is 1 modulo 4, so $cp-1-2t = 1$. Since $t < p-1$, the only solution is $c = 1$, which leads to a parity contradiction, thus concluding the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Pour $m$ entier positif, on note $d(m)$ le nombre de diviseurs positifs de $m$ (1 et m compris). Soit k un entier strictement positif. Montrer qu'il existe une infinité d'entiers positifs $n$ tels que $n$ ait exactement $k$ diviseurs premiers distincts et tel que pour tout $a, b$ entiers strictement positifs avec $n=a+b, d(n)$ ne divise pas $d\left(a^{2}+b^{2}\right)$
|
Prouvons que chaque entier de la forme $n=m 2^{p-1}$ avec $p$ premier impair, possédant $k-1$ facteurs premiers strictement plus grand que 3 et vérifiant $(5 / 4)^{(p-1) / 2}>$ m est solution.
Si $a+b=n$ et $d(n) \mid d\left(a^{2}+b^{2}\right)$ alors $p \mid d\left(a^{2}+b^{2}\right)$. Donc il existe $q$ premier tel que $q$ ait un exposant $c p-1$ dans $a^{2}+b^{2}$. Si $q \geqslant 5, a^{2}+b^{2} \geqslant 5^{q-1}>n^{2}$, or $a^{2}+b^{2}=n^{2}-2 a b \leqslant n^{2}$. Donc $\mathrm{q}=2 \mathrm{ou} 3$.
Si $q=3$ en regardant $a^{2}+b^{2}$ modulo 3,3 divise $a$ et $b$ donc $n$, contradiction avec l'hypothèse.
Si $q=2$, si $a$ et $b$ ont des valuations 2 -adiques distinctes la plus petite est $p-1$ celle de la somme des carrés $2 p-2$, absurde.
S'ils ont même valuation 2-adique $a=2^{\mathrm{t}} a_{0} b=2^{\mathrm{t}} b_{0}$ avec $a_{0}$ et $b_{0}$ impaire $a_{0}^{2}+b_{0}^{2}=$ $x 2^{\text {cp-1-2t }}$ la gauche fait 1 modulo 4 , donc $\mathrm{cp}-1-2 \mathrm{t}=1$ or $\mathrm{t}<\mathrm{p}-1$, donc $\mathrm{c}=1$ est la seule solution, on a un problème de parité absurde, ce qui conclut.
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-2.jsonl",
"solution_match": "\nSolution de l'exercice 9",
"tier": "T2",
"year": null
}
|
Antoine proposes to Baptiste to play "crazy alphabet": They start by agreeing on a letter. Then, taking turns, each can choose to say 1 to 2 following letters in the alphabet starting from A. The one who says the chosen letter wins. If Antoine starts, for which starting letters does he have a strategy to win the game for sure?
Here is an example of a game: the initially chosen letter is E. Antoine says "A", Baptiste says "BC", Antoine says "CD", and Baptiste says "E". In this case, Baptiste has won.
|
Let's show that Antoine has a winning strategy if, and only if, the rank of the chosen letter in the alphabet is not a multiple of 3. Let's color the letters of the alphabet in blue-white-red order. If the arrival letter is red (i.e., its rank in the alphabet is a multiple of 3), Baptiste has the following strategy: every time Antoine chooses to say a letter, Baptiste says two, and every time Antoine decides to say two letters, he says only one. According to this strategy, regardless of his past choices, Antoine can only choose between a blue letter or a blue and white letter at each turn and will not say the final red letter. On the other hand, if the chosen letter is white or blue, Antoine has a winning strategy: he just needs to take A if the final letter is blue or A and B if it is white, and then apply the strategy that was Baptiste's in the red case.
Comment from the correctors: The exercise is understood in most of the copies. Some students lose points by forgetting to show that they have found all the letters for which Antoine has a winning strategy. Specifically, it was necessary to explain why Antoine does not have a winning strategy for letters whose rank is a multiple of 3. Apart from this pitfall, many answers are laborious or imprecise: this was not penalized when the reasoning was clearly understood. Writing a combinatorial exercise is often a source of difficulty, but it is a quick improvement path and it is therefore strongly recommended to read the corrected exercises in order to be able to draw inspiration from clear and effective writing in the future.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
Antoine propose à Baptiste de jouer à l'"alphabet en folie" : Ils commencent par se mettre d'accord sur une lettre. Puis, à tour de rôle, chacun peut choisir de prononcer entre 1 et 2 lettres suivantes dans l'alphabet en partant de A. Celui qui prononce la lettre choisie a gagné. Si Antoine commence, pour quelles lettres de départ dispose-t-il d'une stratégie lui permettant de gagner la partie à coup sûr?
Voici un exemple de partie : la lettre choisie initialement est E. Antoine dit "A", Baptiste "BC", Antoine "CD" et Baptiste dit "E". Dans ce cas, Baptiste a gagné.
|
Montrons que Antoine a une stratégie gagnante si, et seulement si, le rang de la lettre choisie dans l'alphabet n'est pas un multiple de 3 . Colorons les lettres de l'alphabet en bleu-blanc-rouge dans l'ordre. Si la lettre d'arrivée est rouge (c'est à dire que son rang dans l'alphabet est un multiple de 3), Baptiste possède la stratégie suivante : à chaque fois qu'Antoine choisit de dire une lettre, Baptiste en dit deux et à chaque fois qu'Antoine décide de dire deux lettres il n'en dit qu'une. Selon cette stratégie, quels que soient ses choix passés, Antoine n'a le choix à chaque tour qu'entre une lettre bleue ou une lettre bleue et une blanche et ne dira pas la lettre finale rouge. En revanche, si la lettre choisie est blanche ou bleue, Antoine possède une stratégie gagnante : il lui suffit de prendre A si la lettre finale est bleue ou A et B si elle est blanche, puis d'appliquer la stratégie qui était celle de Baptiste dans le cas rouge.
Commentaire des correcteurs: L'exercice est compris dans l'ensemble des copies. Certains élèves perdent des points en oubliant de montrer qu'ils trouvent bien toutes les lettres pour lesquelles Antoine a une stratégie gagnante. Précisément, il était nécessaire d'expliquer pourquoi Antoine n'a pas de stratégie gagnante pour les lettres dont le rang est un multiple de 3. Outre cet écueil, beaucoup de rédactions sont laborieuses ou peu précises : cela n'a pas été pénalisé lorsque le raisonnement était manifestement compris. La rédaction d'un exercice de combinatoire est souvent source de difficulté, il s'agit toutefois d'une piste d'amélioration rapide et il est donc vivement conseillé de lire les corrigés des exercices afin de pouvoir s'inspirer de rédactions claires et efficaces à l'avenir.
|
{
"exam": "French_envois",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-4-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T2",
"year": "2024"
}
|
Aurélien cuts a sheet of paper into 7 pieces. A step then consists of choosing a piece and cutting it into 4, 7, or 10 pieces. Can Aurélien thus obtain 2021 pieces?
|
The exercise describes a sequence of operations and asks whether it is possible to go from an initial state to a final state, so it is legitimate to look for an invariant of the system.
Here, we will show that the number of pieces Aurélien has is always of the form $3k+1$, where $k$ is a natural number.
This is the case in the initial situation, as Aurélien has $7=3 \times 2+1$ pieces. Then, if this is the case at a certain step and Aurélien has $3k+1$ pieces with $k$ a natural number, Aurélien replaces one piece with $3 \times 1+1$ pieces, $3 \times 2+1$ pieces, or $3 \times 3+1$ pieces, so that at the end of the operation, he has $3(k+1)+1$, $3(k+2)+1$, or $3(k+3)+1$ pieces. Step by step, we have the announced result. Since $2021=3 \times 673+2$ is not of the indicated form, it is impossible to obtain 2021 pieces by the described process.
Comment from the graders: The exercise was very well done by those who tackled it. Some lack a bit of practice to properly justify, which can be detrimental in more complicated cases. I advise you to look at the solution for something perfectly clear.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Aurélien découpe une feuille de papier en 7 morceaux. Une étape consiste ensuite à choisir un morceau et à le découper en 4,7 ou 10 morceaux. Aurélien peut-il obtenir ainsi 2021 morceaux ?
|
L'exercice décrit une suite d'opérations et demande s'il est possible de passer d'un état initial à un état final, on peut donc légitimement chercher un invariant du système.
Ici, nous allons montrer que le nombre de morceausx d'Aurélien est toujours de la forme $3 k+1$, avec $k$ un entier naturel.
C'est le cas dans la situation initiale, puisqu'Aurélien dispose de $7=3 \times 2+1$ morceaux. Puis, si c'est le cas lors d'une étape et qu'Aurélien dispose de $3 k+1$ morceaux avec $k$ un entier naturel, Aurélien remplace un morceau par $3 \times 1+1$ morceaux, par $3 \times 2+1$ morceaux ou par $3 \times 3+1$ morceaux, de sorte qu'il lui reste, à la fin de l'opération, $3(k+1)+1,3(k+2)+1$ ou $3(k+3)+1$ morceaux. De proche en proche, on a bien le résultat annoncé. Comme $2021=3 \times 673+2$ n'est pas de la forme indiquée, on ne peut jamais obtenir 2021 morceaux par le processus décrit.
Commentaire des correcteurs : Exercice très bien réussi par ceux qui l'ont abordé. Certains manquent un peu d'habitude pour bien justifier proprement, ce qui peut être dommageable dans des cas plus compliqués. Je vous conseille de regarder le corrigé pour quelque chose de parfaitement clair.
|
{
"exam": "French_envois",
"problem_label": "10",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-4-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T2",
"year": "2024"
}
|
We have five colors and a $99 \times 99$ grid. We color some squares of the grid with one of the five colors such that
- Each color appears the same number of times in the grid.
- No row and no column contains squares of different colors.
What is the maximum number of squares that can be colored while following these rules?
|
Answer: $\mathrm{N}=5 \times 19 \times 20=1900$.
Since each row or column can only contain one color, let's think about it starting from the rows. We say that a row or column is of a certain color (say red) when the only color that the cells in this row or column can have is red. If a row or column has no color, we arbitrarily assign it a color. Thus, a red cell must be at the intersection of a red row and a red column. Consequently, the number of red cells can be bounded by the product of the number of red rows and the number of red columns. Now, let's introduce some notation. We number the available colors from 1 to 5 and denote $x_{i}$ as the number of rows colored with the i-th color, and $y_{i}$ as the number of columns colored with this color. Let's also denote $N$ as the number of cells colored by each color. We want to maximize the total number of colored cells, $5N$. The arguments mentioned above show that $\forall i: N \leqslant x_{i} y_{i}$. We obviously also have $x_{1}+x_{2}+\ldots+x_{5}=y_{1}+y_{2}+\ldots y_{5}=99$. Studying small cases shows that to maximize $N$, the $x_{i}$ and $y_{i}$ should all be roughly equal, each being $\frac{99}{5}$ rounded either up or down. A more in-depth study of small cases where 99 is replaced by a small number congruent to $4 \bmod 5$, like 99, allows us to conjecture that the following construction is optimal:
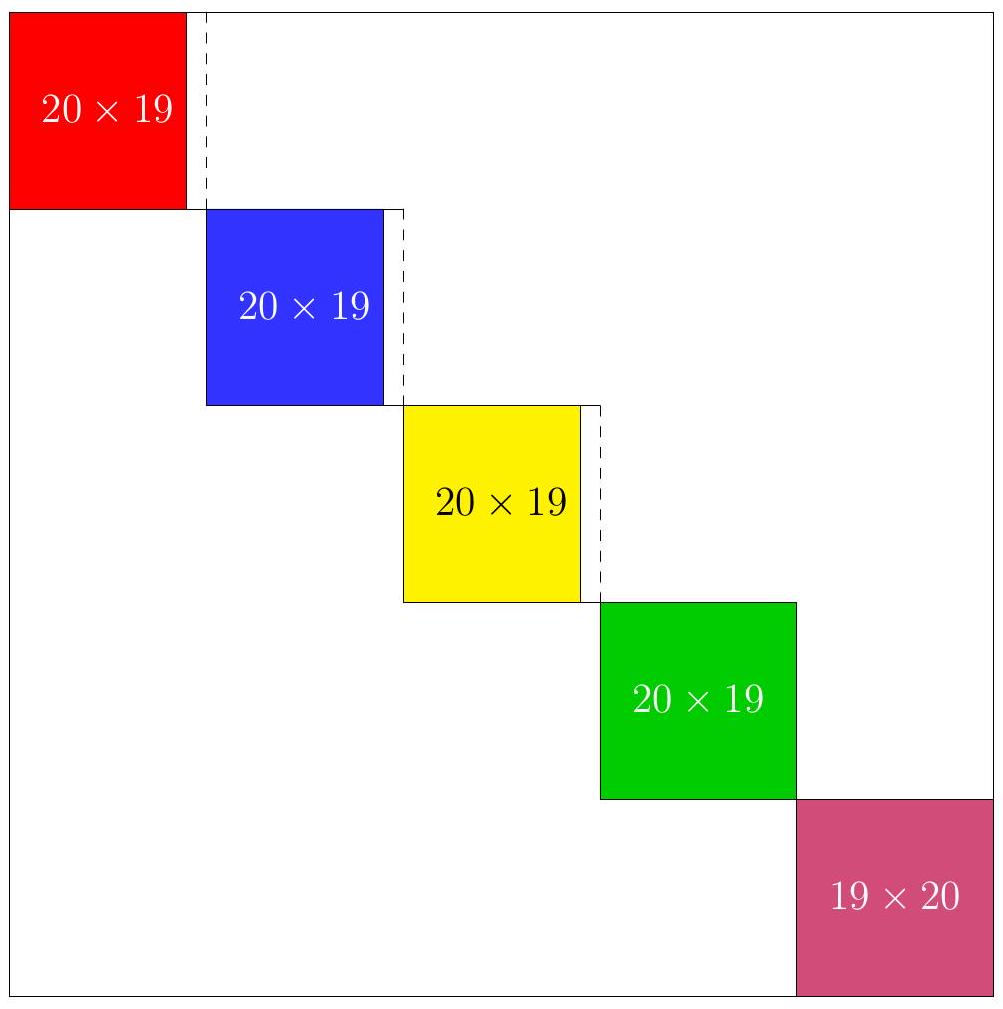
Here, we have $N=19 \cdot 20$.
Let's now prove the optimality. Suppose, for the sake of contradiction, that we have a valid configuration where $\mathrm{N}>19 \times 20$, so $\forall i: x_{i} y_{i}>19 \times 20$. We then note that $x_{i}+y_{i}>39$. Indeed,
$$
x_{i} y_{i}=\frac{1}{4}\left(\left(x_{i}+y_{i}\right)^{2}-\left(x_{i}-y_{i}\right)^{2}\right)
$$
Thus,
$$
38^{2}<4 \cdot 19 \cdot 20=39^{2}-1<\left(x_{i}+y_{i}\right)^{2}-\left(x_{i}-y_{i}\right)^{2}<\left(x_{i}+y_{i}\right)^{2}
$$
So $38<x_{i}+y_{i}$. Moreover, if $x_{i}+y_{i}=39$, then $\left(x_{i}-y_{i}\right)^{2}<1$ So $x_{i}=y_{i}$, which is impossible because 39 is odd. Therefore, $x_{i}+y_{i} \geqslant 40$.
The final count $2 \cdot 99=\left(x_{1}+y_{1}\right)+\left(x_{2}+y_{2}\right)+\ldots+\left(x_{5}+y_{5}\right) \geqslant 5 \times 40=200$ is a contradiction and completes the proof.
Graders' Comments: The problem was not solved by many students who attempted it. Overall, a good number of students found a configuration that worked for $\mathrm{N}=1900$, which was indeed the maximum answer. However, few of them showed that it was not possible to do better, with many content to say that from the configuration they provided, no more cells could be colored: but this does not mean that another configuration, completely different (and not starting from the configuration at $\mathrm{N}=1900$), could not have more colored cells. Furthermore, a number of students assumed that there must be the same number of rows and columns for each color, leading to 1805: but the constraint was to have the same number of cells for each color in total, with no condition on the number of rows and columns per color, and indeed the optimal configurations do not have the same number of rows and columns per color. Finally, some students had the right reasoning but forgot to answer the question in the statement, which was "what is the maximum number of cells that can be colored in the grid": it is emphasized the importance of reading over and being sure that the question has been answered before submitting a copy.
|
1900
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On dispose de cinq couleurs et d'une grille $99 \times 99$. On colorie certains carrés de la grille avec l'une des cinq couleurs de sorte que
- Chaque couleur apparaît le même nombre de fois dans la grille.
- Aucune ligne et aucune colonne ne contient des cases de couleur différente.
Quelle est le plus grand nombre possible de cases que l'on peut colorier en suivant ces règles?
|
Réponse : $\mathrm{N}=5 \times 19 \times 20=1900$.
Comme chaque ligne ou colonne ne peut contenir qu'une couleur, on va réfléchir en partant des lignes. On dit qu'une ligne ou colonne est d'une couleur (disons rouge) quand la seule couleur que peuvent avoir des cases de cette ligne ou colonne est le rouge. Si une ligne ou colonne n'a pas de couleur, on lui assigne arbitrairement une couleur. Ainsi, une case rouge se trouve forcément à l'intersection d'une ligne rouge et d'une colonne rouge. Par conséquent, on peut majorer le nombre de case rouge par le produit du nombre de ligne rouges par le nombre de colonnes rouges. Introduisons maintenant des notations. On numérotes les couleurs disponibles de 1 à 5 et on note $x_{i}$ le nombre de lignes colorées de la i-ième couleur, et $y_{i}$ le nombre de colonnes colorées de cette couleur. Notons enfin N le nombre de cases coloriées par couleur. On veut maximiser le nombre total de cases coloriées, 5 N . Les arguments précédemment cités montrent que $\forall i: N \leqslant x_{i} y_{i}$. ON a évidemment aussi, $x_{1}+x_{2}+\ldots+x_{5}=y_{1}+y_{2}+\ldots y_{5}=99$. L'étude des petits cas nous montre que pour maximiser $N$ il faut que les $x_{i}$ et les $y_{i}$ soient tous environs égaux, valant tous $\frac{99}{5}$ arrondi soit par excès ou par défaut. Une étude plus approfondie des petits cas où on remplace 99 par un petit nombre congru à $4 \bmod 5$, comme 99 , nous permet de conjecturer que la construction suivante est optimale :

Ici, on a $N=19 \cdot 20$.
Prouvons maintenant l'optimalité. Supposons par l'absurde disposer d'une configuration valide où $\mathrm{N}>$ $19 \times 20$, donc $\forall i: x_{i} y_{i}>19 \times 20$. On remarque ensuite que $x_{i}+y_{i}>39$. En effet,
$$
x_{i} y_{i}=\frac{1}{4}\left(\left(x_{i}+y_{i}\right)^{2}-\left(x_{i}-y_{i}\right)^{2}\right)
$$
Donc
$$
38^{2}<4 \cdot 19 \cdot 20=39^{2}-1<\left(x_{i}+y_{i}\right)^{2}-\left(x_{i}-y_{i}\right)^{2}<\left(x_{i}+y_{i}\right)^{2}
$$
Donc $38<x_{i}+y_{i}$. De plus, si $x_{i}+y_{i}=39$, alors $\left(x_{i}-y_{i}\right)^{2}<1$ Donc $x_{i}=y_{i}$, ce qui est impossible car 39 est impair. Donc $x_{i}+y_{i} \geqslant 40$.
Le compte final $2 \cdot 99=\left(x_{1}+y_{1}\right)+\left(x_{2}+y_{2}\right)+\ldots+\left(x_{5}+y_{5}\right) \geqslant 5 \times 40=200$ est une contradiction et termine la preuve.
Commentaire des correcteurs : Le problème n'a pas été beaucoup résolu par les élèves qui l'ont abordé. Dans l'ensemble, une bonne partie des élèves ont trouvé une configuration qui marchait pour $\mathrm{N}=1900$, qui était bien la réponse maximale. Mais peu d'entre eux ont montré qu'on ne pouvait pas faire mieux, beaucoup se sont contentés de dire qu'en partant de la configuration qu'ils avaient donnés, on ne pouvait pas colorier plus de cases : mais ceci ne veut pas dire qu'on ne peut pas trouver une autre configuration, complètement différente (et qui ne part pas de la configuration à $\mathrm{N}=1900$ ), avec plus de cases coloriées. Enfin, un certain nombre d'élèves sont partis du principe qu'il devait forcément y avoir le même nombre de ligne et de colonne par couleur, et ont abouti à 1805 : mais la contrainte était d'avoir le même nombre de cases par couleur au total, aucune condition ne portait sur le nombre de lignes et de colonnes par couleur, et d'ailleurs les configurations optimales n'ont pas le même nombre de lignes et de colonnes par couleur. Enfin, certains élèves avaient le bon raisonnement, mais ont oublié de répondre à la question de l'énoncé, qui était "quel est le plus grand nombre de cases possibles à colorier dans la grille" : on souligne l'importance de bien se relire et d'être sûr qu'on a bien répondu à la question posée avant de rendre une copie.
|
{
"exam": "French_envois",
"problem_label": "11",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-4-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T2",
"year": "2024"
}
|
The game is played on an $\mathrm{n} \times \mathrm{n}$ chessboard. At the beginning, there are 99 stones on each square. Taking turns, Aimeric and Benoit choose a row or a column and remove one stone from each square of the chosen row or column. They can only choose a row or a column if it contains at least one stone on each square. The first player who cannot make a move loses the game. Aimeric plays the first turn. Determine all $n$ for which Benoit has a winning strategy.
|
Answer: The even n.
In the following, we number the columns from left to right and the rows from top to bottom.
We will show that there are exactly 99n turns of the game, so if n is even, Benoit will have had the last turn (and therefore will have won), otherwise it is Aimeric.
Consider the cells of one of the main diagonals of the grid. Since each row and each column contains exactly one of these cells, at each step, the sum of the number of stones on these cells decreases by exactly 1. If all the cells of the main diagonal are empty, it is no longer possible to perform any action. Conversely, let's show that if one of the cells of the main diagonal contains at least one pebble, it is still possible to play.
Suppose this cell is at the intersection of row $i$ and column $i$. If row $i$ or column $i$ does not contain an empty cell, then it is still possible to play on this column or this row. Therefore, we can assume that row $i$ contains an empty cell, say in column $a$, and that column $i$ contains an empty cell, say in row $b$. Let $r_{i}$ be the number of times played on row $i$, $r_{b}$ the number of times played on row $b$, $c_{i}$ the number of times played on column $i$, and finally $c_{a}$ the number of times played on column $a$.
Since the cell at the intersection of row $i$ and column $a$ is empty, we have $c_{a} + r_{i} = 99$. Similarly, we have $r_{b} + c_{i} = 99$. But since $r_{i} + c_{i} < 99$ (because the cell at the intersection of row $i$ and column $i$ is not empty), we have $r_{b} + c_{a} > 99$, which is absurd because the cell at the intersection of row $b$ and column $a$ has lost more than 99 pebbles.
We deduce that the game ends if and only if each cell of the main diagonal is empty, therefore after exactly 99n steps, which allows us to conclude as announced.
Comment from the graders: Many students understood the importance of the parity of the number of turns, but some of them assume that all cells must be empty when no more moves are possible, without proving it. Many papers treat the case of even n with a mirror strategy, but this strategy is not directly adaptable to the case of odd n without additional argument. Drawings, unfortunately too rare, were appreciated and facilitated the understanding of combinatorial arguments.
|
The even n
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Une partie se joue sur un échiquier de taille $\mathrm{n} \times \mathrm{n}$. Au début, il y a 99 pierres sur chaque case. Tour à tour, Aimeric et Benoit choisissent une ligne ou une colonne et retirent une pierre de chaque case de la ligne ou de la colonne choisie. Ils ne peuvent choisir une ligne ou une colonne que si elle comporte au moins une pierre sur chaque case. Le premier joueur qui ne peut pas se déplacer perd la partie. Aimeric joue le premier tour. Déterminer tous les $n$ pour lesquels Benoit a une stratégie gagnante.
|
Réponse : Les n pairs.
Dans la suite, on numérote les colonnes de gauche à droite et les lignes de haut en bas.
Nous allons montrer qu'il y a exactement 99 n tours de jeu, de sorte que si n est pair, Benoit aura eu le dernier tour de jeu (donc aura gagné), sinon c'est Aimeric.
Considérons les cases de l'une des grandes diagonales de la grille. Comme chaque ligne et chaque colonne contient exactement une de ces cases, à chaque étape, la somme du nombre de pierres sur ces cases diminue d'exactement 1 . Si toutes les cases de la grande diagonale sont vides, il n'est plus possible d'effectuer aucune action. Montrons que réciproquement, si l'une des cases de la grande diagonale contient au moins un caillou, il est encore possible de jouer.
Supposons que cette case soit à l'intersection de la ligne $i$ et de la colonne $i$. Si la ligne $i$ et ou la colonne i ne contiennent pas de case vide, alors il est encore possible de jouer sur cette colonne ou cette ligne. On peut donc supposer que la ligne $i$ contient une case vide, disons sur la colonne $a$, et que la colonne $i$ contient une case vide, disons sur la ligne $b$. Notons $r_{i}$ le nombre de fois que l'on a joué sur la ligne $i$, $r_{b}$ le nombre de fois que l'on a joué sur la ligne $b, c_{i}$ le nombre de fois que l'on a joué sur la colonne $i$ et enfin $c_{a}$ le nombre de fois que l'on a joué sur la colonne $a$.
Puisque la case à l'intersection de la ligne $i$ et de la colonne a est vie, on a $c_{a}+r_{i}=99$. De même, on a $r_{b}+c_{i}=99$. Mais puisque $r_{i}+c_{i}<99$ (car la case à l'intersection de la ligne et de la colonne $i$ est non vide), on a $\mathrm{r}_{\mathrm{b}}+\mathrm{c}_{\mathrm{a}}>99$, ce qui est absurde car la case à l'intersection de la ligne b et de la colonne a a perdu alors strictement plus que 99 caillous.
On déduit que la partie finit si et seulement si chaque case de la grande diagonale est vide, donc au bout d'exactement 99 n étapes, ce qui permet de conclure comme annoncé.
Commentaire des correcteurs: Beaucoup d'élèves ont compris l'importance de la parité du nombre de tours de jeu, mais certains d'entre eux supposent que toutes les cases doivent être vides lorsque plus aucun coup n'est jouable, sans le démontrer. Beaucoup de copies traitent le cas n pair avec une stratégie miroir, mais celle-ci n'est pas directement adaptable au cas n impair sans argument supplémentaire. Les dessins, malheureusement trop rares, ont été appréciés et ont facilité la compréhension des arguments combinatoires.
|
{
"exam": "French_envois",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-4-2023-2024.jsonl",
"solution_match": "## Solution de l'exercice 4",
"tier": "T2",
"year": "2024"
}
|
Let $n$ be a natural number. Joseph can shoot $2 n+1$ arrows. Each of his shots is either a failure or a success. A shot is said to be "balanced" if the number of failures before this shot added to the number of successes after this shot is equal to $n$. Determine whether the number of balanced shots is even or odd.
|
Let's show that the number of balanced shots is odd.
First remark: consider a sequence of two shots such that the first is successful and the next is missed. Then there are as many missed shots before both and as many successful shots after, so either both shots are balanced, or neither of them is. Similarly, if the first is missed and the next is successful, by noting e as the number of failures before these two shots and r as the number of successes after, the first shot is balanced if and only if $e+(1+r)=n$ and the second is balanced if and only if $(e+1)+r=n$. We notice that these two conditions are equal. Thus, since this does not change the balance of the previous and subsequent shots, assuming that for a sequence of 2 shots where one is successful and the other is missed, it is the first that is missed does not change the parity of the number of balanced shots. We can therefore reduce to the case where Joseph starts with a sequence of failures, followed by successes. In the order of the shots, the number of upcoming successes added to the number of past failures starts at the total number of successes R, strictly increases with each failure until it reaches the value 2n, then decreases with each success until it reaches the total number of failures E. Since $\mathrm{E}+\mathrm{R}=2 * \mathrm{n}+1$, exactly one of these two values E and R is smaller than n and the other is strictly greater. The value n is therefore reached for only one shot in this configuration, and it is therefore odd in the general case.
Comment from the graders: The exercise was difficult and was only attempted by a relatively small number of students. The solution was mostly intuited, but rarely convincingly justified.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Soit $n$ un entier naturel. Joseph peut tirer $2 n+1$ flèches. Chacun de ses tirs est un échec ou une réussite. Un tir est dit "équilibré" si le nombre d'échecs avant ce tir additionné au nombre de réussites après ce tir est égal à $n$. Déterminer si le nombre de tirs équilibrés est pair ou impair.
|
Montrons que le nombre de tirs équilibrés est impair.
Première remarque : considérons une succession de deux tirs telle que le premier est réussi et le suivant raté. Alors il y a autant de tirs ratés avant pour les deux et autant de tirs réussis après donc soit les deux tirs sont équilibrés, soit aucun des deux ne l'est. De même, si le premier est raté et le suivant réussi, en notant e le nombre d'échecs avant ces deux tirs et r le nombre de réussites après, le premier tir est équilibré si et seulement si $e+(1+r)=n$ et le deuxième est équilibré si et seulement si $(e+1)+r=n$. On remarque que ces deux conditions sont égales. Ainsi, puisque cela ne modifie pas l'équilibre des tirs précédents et suivants, supposer que pour une succession de 2 tirs dont l'un est réussi et l'autre est raté, c'est le premier qui est raté ne modifie pas la parité du nombre de tirs équilibrés. On peut donc se ramener au cas où Joseph commence par une succession d'échecs, puis de réussites. Dans l'ordre des tirs, le nombre de succès à venir additionné au nombre d'échecs passés débute au nombre de réussites total R , augmente strictement à chaque échec jusqu'à atteindre la valeur 2 n puis diminue à chaque réussite jusqu'à atteindre le nombre d'échec total E . Or $\mathrm{E}+\mathrm{R}=2 * \mathrm{n}+1$ donc exactement une de ces deux valeurs E et R est plus petite que n et l'autre est strictement plus grande. La valeur n n'est donc atteinte que pour un seul tir dans cette configuration, et elle est donc impair dans le cas général.
Commentaire des correcteurs : L'exercice était difficile et n'a été abordé que par un nombre assez faible d'étudiants. La solution a été intuitée la plupart du temps, mais rarement justifié de manière convaincante.
|
{
"exam": "French_envois",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-4-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T2",
"year": "2024"
}
|
In a school, there are n courses and n students. The students are enrolled in multiple courses such that no two different students have exactly the same courses. Prove that one course can be removed so that no pair of students ends up with exactly the same courses.
|
We will show by strong induction on $n$ the following stronger property:
$\mathcal{P}_{n}$: For all $m \geqslant n$, in a class with $n$ students and $m$ courses such that no two students have exactly the same courses, it is possible to remove a course so that the students do not have exactly the same courses among the remaining courses.
Initialization: If $n=1$, there is nothing to prove.
Hereditary: Let $n \geqslant 2$. Suppose that $\mathcal{P}_{k}$ is true for all $1 \leqslant k \leqslant n-1$. Let $m \geqslant n$. Consider then a class of $n$ students who take $m$ courses denoted $C_{1}, \ldots, C_{m}$. If no two students have exactly the same courses among the courses $C_{1}, \ldots, C_{m-1}$, then we have proven what we needed to. Otherwise, there exist $k$ pairs of students $\left(A_{1}, B_{1}\right), \ldots,\left(A_{k}, B_{k}\right)$ with $k \geqslant 1$, such that the students $A_{i}$ and $B_{i}$ take the same courses among $C_{1}, \ldots, C_{m-1}$ (and then exactly one of them, say $A_{i}$, takes the course $C_{m}$). Let $E_{1}, \ldots, E_{n-2 k}$ be the set of remaining students. Consider the subset of $n-k$ students $\left\{A_{1}, \ldots, A_{k}, E_{1}, \ldots, E_{n-2 k}\right\}$ and the set of courses $\left\{C_{1}, \ldots, C_{m-1}\right\}$. By the induction hypothesis, since $n-k \leqslant m-1$, we have a course, say $C_{m-1}$, which, if removed, ensures that no pair of two students among the considered students have the same courses among $C_{1}, \ldots, C_{m-2}$. Then, among these $n-k$ considered students, there is no pair of students having exactly the same courses among $C_{1}, \ldots, C_{m-2}, C_{m}$. But then a student $B_{i}$ does not have exactly the same courses as $A_{i}$ (due to the course $C_{m}$ or another student (since $A_{i}$ does not have the same courses as another student among $C_{1}, \ldots, C_{m-2}$)). This completes the induction.
The property $\mathcal{P}_{n}$ is therefore true for all $n$, in particular, the statement is true for $m=n$ courses and $n$ students.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Dans une école il y a n cours et n élèves. Les élèves sont inscrits dans plusieurs cours de sorte que deux élèves différents n'ont jamais exactement les même cours. Prouver qu'on peut supprimer un cours de sorte qu'aucune paire d'élèves ne se retrouve avec exactement les mêmes cours.
|
On va montrer par récurrence forte sur n la propriété plus forte suivante :
$\mathcal{P}_{n}$ :Pour tout $m \geqslant n$, dans une classe à $n$ élèves et $m$ cours telle que deux élèves n'ont jamais exactement les mêmes cours, alors il est possible de retirer un cours de sorte que les élèves ne suivent pas exactement les mêmes cours parmi les cours restants.
Initialisation: $\mathrm{Si} \mathrm{n}=1$, il n'y a rien à démontrer.
Hérédité : Soit $n \geqslant 2$. Supposons que $\mathcal{P}_{k}$ est vraie pour tout $1 \leqslant k \geqslant n-1$. Soit $m \geqslant n$. Considérons alors une classe de $n$ élèves qui suivent $m$ cours notés $C_{1}, \ldots, C_{m}$. Si deux élèves ne suivent jamais les mêmes cours parmi les cours $C_{1}, \ldots, C_{m-1}$, alors on a démontré ce qu'il fallait. Sinon, il existe $k$ paires d'élèves $\left(A_{1}, B_{1}\right), \ldots,\left(A_{k}, B_{k}\right)$ avec $k \geqslant 1$, telles que les élèves $A_{i}$ et $B_{i}$ suivent les mêmes cours parmi $C_{1}, \ldots, C_{m-1}$ (et alors exactement l'un d'eux, disons $A_{i}$, suit le cours $C_{m}$ ). Notons $E_{1}, \ldots, E_{n-2 k}$ l'ensemble des élèves restant. Considérons le sous-ensemble de $n-k$ élèves $\left\{A_{1}, \ldots, A_{k}, E_{1}, \ldots, E_{n-2 k}\right\}$ et l'ensemble de cours $\left\{C_{1}, \ldots, C_{m-1}\right\}$. D'après l'hypothèse de récurrence, puisque $n-k \leqslant m-1$, on dispose d'un cours, disons $C_{m-1}$ qui, si on le retire, vérifie qu'aucune paire de deux élèves parmi les élèves considérés ne suivent les mêmes cours parmi $C_{1}, \ldots, C_{m-2}$. Alors, parmi ces $n-k$ élèves considérés, il n'y a pas de paire d'élèves ayant exactement les mêmes cours parmi $C_{1}, \ldots, C_{m-2}, C_{m}$. Mais alors un élève $B_{i}$ ne suit pas exactement les mêmes cours que $A_{i}$ (à cause du cours $C_{m}$ ou qu'un autre élève (car $A_{i}$ ne suit pas les mêmes cours qu'un autre élève parmi $C_{1}, \ldots, C_{m-2}$ ). Ceci achève la récurrence.
La propriété $\mathcal{P}_{n}$ est donc vraie pour tout n , en particulier, l'énoncé est vrai pour $\mathrm{m}=\mathrm{n}$ cours et n élèves.
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-4-2023-2024.jsonl",
"solution_match": "## Solution de l'exercice 6",
"tier": "T2",
"year": "2024"
}
|
In a school, there are n courses and n students. The students are enrolled in multiple courses such that no two different students have exactly the same courses. Prove that one course can be removed so that no pair of students ends up with exactly the same courses.
|
Let $E_{1}, \ldots, E_{n}$ be the $n$ students and $C_{1}, \ldots, C_{n}$ be the $n$ courses.
We proceed by contradiction and assume the opposite: for any course $C_{i}$ that we remove, there exist two students $E_{i_{1}}$ and $E_{i_{2}}$ who have exactly the same courses except for the course $C_{i}$. If multiple such pairs exist for the same course $C_{i}$, we keep only one. Since these two students do not follow exactly the same courses, one follows the course $C_{i}$ and the other does not. Therefore, their courses do not coincide if we remove another course $C_{j}$.
Consider then the graph where the vertices are the students and two students are connected by an edge if there exists an $i$ (which is then unique according to the previous paragraph) such that, if we remove $C_{i}$, the two students have the same courses. Since each course $C_{i}$ induces a pair of students connected by an edge, the obtained graph has at least one cycle, which we denote as $E_{i_{1}} \ldots E_{i_{k}} E_{i_{1}}$, with $k \leqslant n$. Let $j_{\ell}$ be the number of the course that induces the edge $E_{i_{\ell}} E_{i_{\ell+1}}$. The students $E_{i_{1}}$ and $E_{i_{k}}$ then follow the same courses among those that are not $C_{j_{1}}, \ldots, C_{j_{k-1}}$. In particular, either they both follow the course $C_{j_{k}}$, or they both do not follow it, which contradicts the fact that the edge $E_{i_{k}} E_{i 1}$ belongs to the graph. We have the desired contradiction.
Comment from the graders: The problem was very little addressed and very little solved. Several students manage to model the problem with a graph, which is excellent.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Dans une école il y a n cours et n élèves. Les élèves sont inscrits dans plusieurs cours de sorte que deux élèves différents n'ont jamais exactement les même cours. Prouver qu'on peut supprimer un cours de sorte qu'aucune paire d'élèves ne se retrouve avec exactement les mêmes cours.
|
:
Notons $E_{1}, \ldots, E_{n}$ les $n$ élèves et $C_{1}, \ldots, C_{n}$ les $n$ cours.
On procède par l'absurde et l'on suppose l'inverse : quelque soit le cours $C_{i}$ que l'on supprime, il existe deux élèves $E_{i_{1}}$ et $E_{i_{2}}$ ayant exactement les mêmes cours en dehors du cours $C_{i}$. Si deux telles paires ou plus existent pour un même cours $C_{i}$, on n'en garde qu'une seule. Comme ces deux élèves ne suivent pas exactement les mêmes cours, l'un suit le cours $C_{i}$ et l'autre ne le suit pas. Leurs cours ne coïncident donc pas si l'on supprime un autre cours $C_{j}$.
Considérons alors le graphe dont les sommets sont les élèves et deux élèves sont reliés par une arêtes s'il existe un $i$ (qui est alors unique d'après le paragraphe précédent) tel que, si l'on supprime $C_{i}$, les deux élèves ont les mêmes cours. Comme chaque cours $C_{i}$ induit une paire d'élèves reliés par une arête, le graphe obtenu admet au moins un cycle, que l'on note $E_{i_{1}} \ldots E_{i_{k}} E_{i_{1}}$, avec $k \leqslant n$. Notons $j_{\ell}$ le numéro du cours qui induit l'arête $E_{i_{\ell}} E_{i_{\ell+1}}$. Les élèves $E_{i_{1}}$ et $E_{i_{k}}$ suivent alors les mêmes cours parmi ceux qui ne sont pas $C_{j_{1}}, \ldots, C_{j_{k-1}}$. En particulier, soient ils suivent tous les deux le cours $C_{j_{k}}$, soient ils ne le suivent pas tous les deux, ce qui contredit le fait que l'arête $E_{i_{k}} E_{i 1}$ appartient au graphe. On a la contradiction désirée.
Commentaire des correcteurs: Le problème a été très peu abordé et très peu résolu. Plusieurs élèves parviennent à modéliser le problème par un graphe, ce qui est excellent.
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-4-2023-2024.jsonl",
"solution_match": "## Solution alternative",
"tier": "T2",
"year": "2024"
}
|
Determine the largest even integer $n$ with the following property: no matter how an $n \times n$ grid is tiled with dominoes, there exists a row that cuts the grid into two non-empty parts and does not intersect any domino.
|
Answer: $\mathrm{n}=6$
Let's start by mentioning that the answer can be guessed by trying the exercise for small values of n.
The problem asks to find the largest integer n satisfying a certain property, so it necessarily has two parts. We will first show that 6 satisfies the property, then we will show that if $n \geqslant 8$, there exists a domino configuration that does not respect the property.
Case $\mathrm{n}=\mathbf{6}$: Suppose, to the contrary, that there exists a domino configuration such that every line cutting the board into two non-empty parts cuts at least one domino. We will only consider horizontal lines separating two rows and vertical lines separating two columns of the board, and we call these lines separators, and the two non-empty parts of the board obtained with a separator sections.
On the one hand, a domino can only be intersected by at most one separator (and this separator cuts the domino into two equal squares). On the other hand, a separator intersects an even number of dominos. Indeed, each section obtained contains an even number of cells (the sections are rectangles with one side of length 6). Since each domino sectioned covers exactly one cell of the section and the other cells are covered by dominos contained in the section and are therefore in even numbers, we can deduce that a separator intersects an even number of dominos.
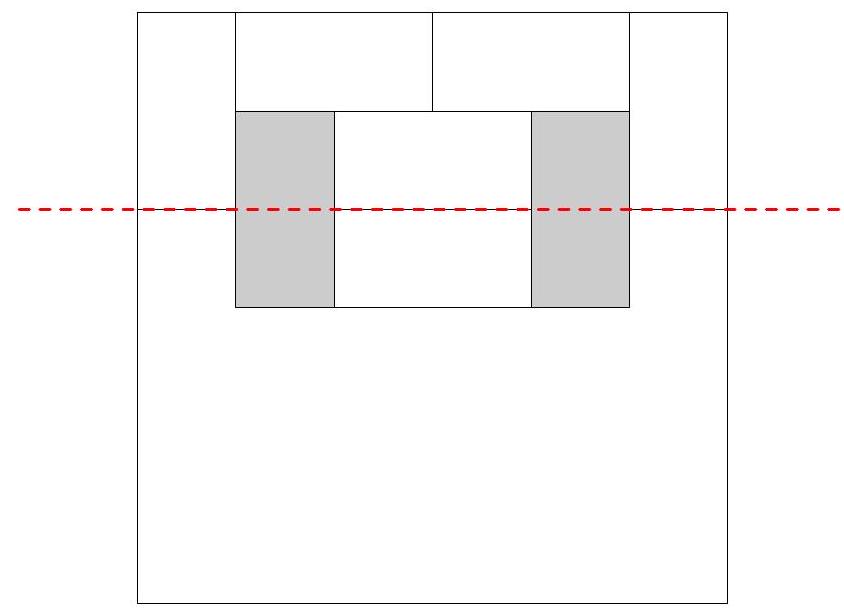
By hypothesis, each separator intersects at least one domino, so it intersects at least 2. There are 10 separators, so at least 20 dominos of the tiling are intersected by a separator. However, the tiling of a $6 \times 6$ square contains exactly 18 dominos. We have reached a contradiction.
Case $n \geqslant 8$: We will provide for every integer $n \geqslant 8$ a tiling of the $n \times n$ grid such that every line cutting the board into two non-empty parts intersects at least one domino.
Consider the following pattern:
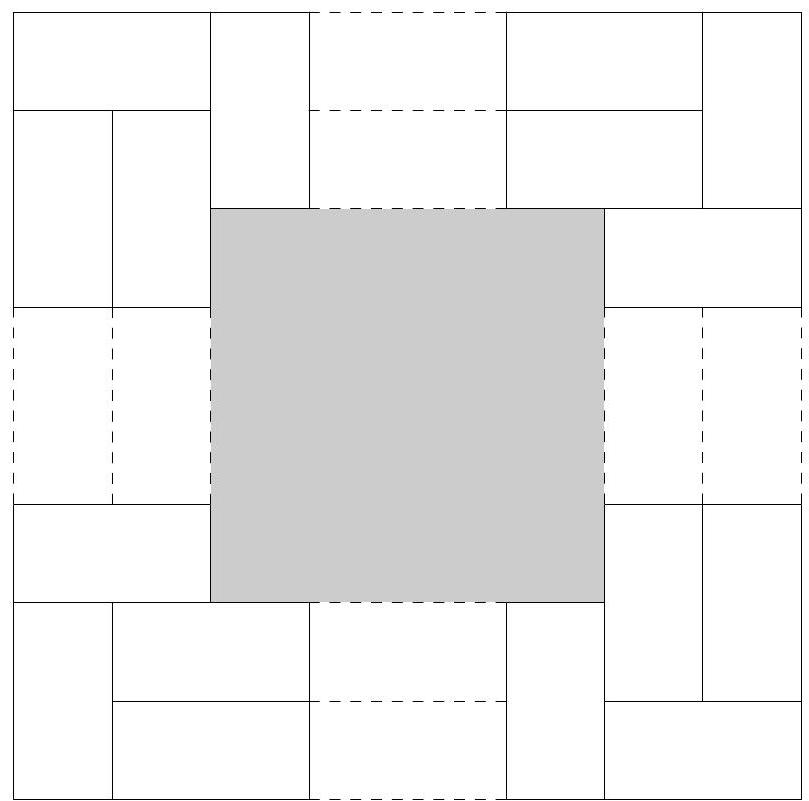
We then tile the inside of the gray square with the following pattern:
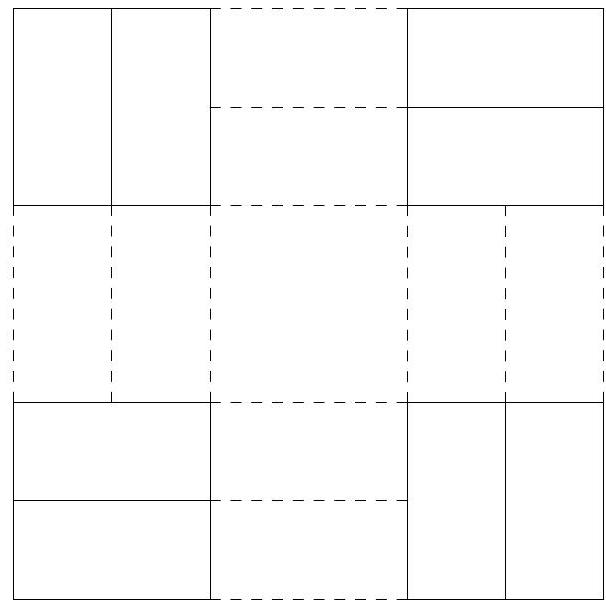
In this way, we obtain a tiling that satisfies the property stated in the problem.
Comment from the graders: The problem was very little addressed and, in sum, very little solved. Students who submitted an attempt provided good arguments to show that $\mathrm{n} \leqslant 6$ by proposing constructions by induction.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Déterminer le plus grand entier $n$ pair ayant la propriété suivante : quelle que soit la façon de paver une grille $\mathrm{n} \times \mathrm{n}$ avec des dominos, il existe une ligne coupant le tableau en deux parties non vides et n'intersectant aucun domino.
|
Réponse: $\mathrm{n}=6$
Mentionnons pour commencer que la réponse peut se deviner en essayant l'exercice pour des petites valeurs de n.
Le problème demande de trouver le plus grand entier n vérifiant une certaine propriété, il comporte donc nécessairement deux parties. Nous allons montrer d'abord que 6 vérifie la propriété, puis nous allons montrer que si $n \geqslant 8$, il existe une configuration de dominos ne respectant pas la propriété.
Cas $\mathrm{n}=\mathbf{6}$ : Supposons au contraire qu'il existe une configuration de dominos telle que chaque ligne coupant le tableau en deux parties non vides coupe au moins un domino. On ne va considérer que les lignes horizontales séparant deux rangées et les lignes verticales séparant deux colonnes du tableau, on appelle ces lignes des séparatrices, et les deux parties non vides du tableau obtenues avec une séparatrice des sections.
D'une part, un domino ne peut être intersecté que par au plus une séparatrice (et cette séparatrice coupe le domino en deux carrés égaux). D'autre part, une séparatrice intersecte un nombre pair de dominos, En effet, chaque section obtenue contient un nombre pair de cases (les sections sont des rectangles dont l'un des côtés est de longueur 6). Comme chaque domino sectionné recouvre exactement une case de la section et que les autres cases sont recouvertes par des dominos inclus dans la section et sont donc en nombre pair, on déduit bien qu'une séparatrice intersecte un nombre pari de dominos.

Par hypothèse, chaque séparatrice intersecte au moins un domino, donc elle en intersecte au moins 2 . Il y a 10 séparatrices, donc au moins 20 dominos du pavage sont intersectés par une séparatrice. Or, le pavage d'un carré $6 \times 6$ contient exactement 18 dominos. On a abouti à une contradiction.
Cas $n \geqslant 8$ : Nous allons donner pour tout entier $n \geqslant 8$ un pavage de la grille $n \times n$ tel que toute ligne coupant le tableau en deux parties non vides intersecte au moins un domino.
On considère le motif suivant:

On pave ensuite l'intérieur du carré grisé avec le motif suivant :

On obtient bien de cette façon un pavage qui vérifie la propriété de l'énoncé.
Commentaire des correcteurs : Le problème a été très peu abordé et en somme très peu résolu. Les élèves ayant rendu une tentative ont donné de bons arguments pour montrer que $\mathrm{n} \leqslant 6$ en proposant des constructions par récurrence.
|
{
"exam": "French_envois",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-4-2023-2024.jsonl",
"solution_match": "## Solution de l'exercice 7",
"tier": "T2",
"year": "2024"
}
|
Aline and Elsa are playing the following game. They have 100 stones which they divide into two piles (not necessarily of the same size) at the beginning of the game. Then, each in turn, starting with Aline, they perform the following move: they choose a pile, then a positive integer less than or equal to half the size of the chosen pile, and remove that number of stones from the pile. The first player who cannot make a move loses.
Determine all the initial configurations for which Elsa has a winning strategy.
|
In the following, we denote by $(x, y)$ the configuration where the first pile is of size $x$ and the second pile is of size $y$.
We observe in the case of a single pile, starting from the end, that the losing configurations for Aline are the piles with $2^{n}-1$ stones.
Returning to the case of a generic initial configuration $(\boldsymbol{a}, \boldsymbol{b})$. By definition, the position $(1,1)$ is losing. $(a, b)$ is losing for the player who must play if $\frac{a+1}{b+1}$ is a power (positive or negative) of 2. Indeed, if $\frac{a+1}{b+1}=2^{n}$, if one draws from $a$, the quotient decreases but strictly by less than a factor of 2. Conversely, if one draws from pile $b$, it increases but strictly by less than a factor of 2, which maintains a winning position for the next player.
Conversely, if $2^{\mathrm{n}}(b+1)<\mathrm{a}+1<2^{\mathrm{n}+1}(b+1)$ with $\mathrm{n} \geqslant 0$ then one takes the necessary number of stones from pile $a$ so that exactly $2^{n}(b+1)-1$ remain. This is possible because $a < 2^{n+1}(b+1)-1$ hence $a \leqslant 2^{n+1}(b+1)-2$ from which $\frac{a}{2} \leqslant 2^{n}(b+1)-1$ which means that more than half are left.
Comment from the graders: The exercise was difficult and was only submitted by one student.
|
not found
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Aline et Elsa jouent au jeu suivant. Elles disposent de 100 pierres qu'elles séparent en deux piles (pas forcément de même taille) au début du jeu. Puis chacune à leur tour, en commençant par Aline, elles effectuent le mouvement suivant : elles choisissent une pile, puis un entier strictement positif inférieur ou égal à la moitié de la taille de la pile choisie et retirent ce nombre de pierres de la pile. La première joueuse qui ne peut plus effectuer de mouvement perd.
Déterminer toutes les configurations initiales pour lesquelles Elsa a une stratégie gagnante.
|
Dans la suite, on désigne par $(x, y)$ la configuration où la première pile est de taille $x$ et la deuxième pile est de taille $y$.
On observe sur le cas à une seule pile en commençant par la fin que les solutions perdantes pour Aline sont les piles à $2^{n}-1$ pierres.
Revenons au cas d'une configuration intiale générique $(\boldsymbol{a}, \boldsymbol{b}$ ). Par définition, la position $(1,1)$ est perdante. $(a, b)$ est perdante pour la personne qui doit jouer si $\frac{a+1}{b+1}$ est une puissance (positive ou négative) de 2. En effet, si $\frac{a+1}{b+1}=2^{n}$, si on pioche dans $a$, on diminue le quotient mais strictement de moins qu'un facteur 2. À l'inverse, si on pioche dans la pile $b$ on l'augmente mais strictement moins que d'un facteur 2 ce qui conserve bien une position gagnante pour la joueuse suivante.
Réciproquement, si $2^{\mathrm{n}}(b+1)<\mathrm{a}+1<2^{\mathrm{n}+1}(b+1)$ avec $\mathrm{n} \geqslant 0$ alors on prend le nombre nécessaire de pierres de la pile a de sorte qu'il en reste précisément $2^{n}(b+1)-1$. Cela est possible car $a<$ $2^{n+1}(b+1)-1$ donc $a \leqslant 2^{n+1}(b+1)-2$ d'où $\frac{a}{2} \leqslant 2^{n}(b+1)-1$ ce qui signifie qu'on en a laissé plus que la moitié.
Commentaire des correcteurs : L'exercice était difficile et n'a été rendu que par un élève.
|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "\nExercice 8.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-4-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 8",
"tier": "T2",
"year": "2024"
}
|
Let $N$ be a strictly positive integer. Suppose there exist four subsets $A_{1}, A_{2}, A_{3}$ and $\boldsymbol{A}_{4}$ of $\{1, \ldots, \boldsymbol{N}\}$, each of cardinality 500, and suppose that for all $x, y$ in $\{1, \ldots, N\}$, there exists an index $i$ such that $x$ and $y$ are in $A_{i}$. Determine the largest possible value of $N$.
|
Answer: 833.
We will approach this problem using graph theory. The problem's modeling leads us to consider a graph where the vertices are the elements of $S$, and they are connected by an edge of color $i$ if the two vertices belong to the set $A_i$.
In the following, we will also say that a graph $G_1$ covers a graph $G_2$ if every edge of $G_2$ is an edge of $G_1$.
We denote $K_m$ as the graph consisting of $m$ vertices where all vertices are connected. Such a graph is called complete.
We denote $K_{m, m}$ as the graph consisting of two sets of vertices $S_1$ and $S_2$, both of cardinality $m$, and in which each vertex of $S_1$ is connected to all vertices of $S_2$. Such a graph is commonly called a complete bipartite graph, and we will call $S_1$ and $S_2$ the teams of $K_{m, m}$.
Lemma: Let $K_{m, m}$ be a complete bipartite graph and $S_1$ and $S_2$ its teams. Suppose it is possible to cover $K_{m, m}$ with complete graphs $K_k$ and $K_\ell$ of sizes $k, \ell < 2m$. Then $m < \frac{k + \ell}{3}$.
Proof of the lemma: Let's start by showing that $K_k$ and $K_\ell$ each contain either $S_1$ or $S_2$. Indeed, let $v \in S_1$ not belonging to $K_\ell$. For any vertex $w$ of $S_2$, the edge $vw$ therefore belongs to $K_k$, but then $w$ belongs to $K_k$, so $K_k$ contains all the vertices of $S_2$. But then, by reasoning on a vertex of $S_1$ not belonging to $K_k$, we obtain that $K_\ell$ also contains all the elements of $S_2$. Thus, each vertex of $S_2$ belongs to $K_k$ and $K_\ell$ and each vertex of $S_1$ belongs to $K_k$ or $K_\ell$, so that $k + \ell \geq |S_1| + 2|S_2| = 3m$.
Let's return to the problem. Suppose, for the sake of contradiction, that $N \geq 834$. Note that if we could have $N$ even larger, we could reduce to the case $N = 834$ by arbitrarily adding elements of $\{1, \ldots, 834\}$ that were not yet in the sets.
We partition our set of points as follows:
- $Z$ the set of points in $A_1$ and $A_2$.
- $X$ the set of points in $A_1$ but not in $A_2$.
- $Y$ the set of points in $A_2$ but not in $A_1$.
- $W$ the rest (neither in $A_1$ nor in $A_2$).
We then have $|X| + |Y| + |Z| + |W| = 834$ and $|X| + |Z| = |Y| + |Z| = 500$, which gives us $|W| - |Z| = -166$.
Case 1: $|W| = 0$. It follows that $|Z| = 166$, $|X| = |Y| = 334$. This contradicts our lemma because it implies that we can cover $K_{334, 334}$ with two cliques of size 500.
Case 2: $|W| > 0$. Then $Z \subset K_2 \cap K_3$ (i.e., each of its elements is in $A_3$ or $A_4$) so that each of its vertices is connected to the elements of $|W|$, thus $|K_3 \cap Z| + |K_4 \cap Z| \geq |Z|$. Thus, we can see that if $|W| > 0$: (Using that $W \subset K_3 \cap K_4$)
$$
|K_3 \cap (X \cup Y)| + |K_4 \cap (X \cup Y)| \leq 1000 - 2|W| - |Z|
$$
Then, we must cover $K_{500 - |Z|, 500 - |Z|}$ (the graph formed using the sets $X$ and $Y$) with two cliques of sizes $|K_3 \cap (X \cup Y)|$ and $|K_4 \cap (X \cup Y)|$. By our lemma, $3(500 - |Z|) \leq 1000 - 2|W| - |Z|$, and since $|Z| = |W| + 166$, we obtain a contradiction!
Moreover, for $N = 833$, we have an explicit construction: Using our notations $X, Y, Z$. With $|Z| = 167$ and $|X| = |Y| = 333$. We place all the elements of $X$ in $A_3$ and $A_4$ and one element of $Y$ in both, half of the remaining elements of $Y$ in $A_3$ and the other half in $A_4$.
Comment from the graders: The problem was little addressed and solved by only one student.
## Senior Exercises
|
833
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Soit $N$ un entier strictement positif. On suppose qu'il existe quatre sous-ensembles $A_{1}, A_{2}, A_{3}$ et $\boldsymbol{A}_{4}$ de $\{1, \ldots, \boldsymbol{N}\}$, chacun de cardinal 500 et on suppose que, pour tous $x, y$ dans $\{1, \ldots, N\}$, il existe un indice $i$ tel que $x$ et $y$ sont dans $A_{i}$. Déterminer la plus grande valeur de $N$ possible.
|
Réponse : 833.
Nous allons traiter ce problème avec le langage des graphes. La modélisation du problème pousse à considérer le graphe dont les sommets sont les éléments de $S$, qui sont reliés par une arête de couleur $i$ si les deux sommets apprtiennent à l'ensemble $A_{i}$.
Dans la suite, on dira également qu'un graphe $G_{1}$ recouvre un graphe $G_{2}$ si toute arête de $G_{2}$ est une arête de $\mathrm{G}_{1}$.
On note $\mathrm{K}_{\mathrm{m}}$ le graphe constitué de m sommets et dont tous les sommets sont réliés. Un tel graphe est dit complet.
On note $\mathrm{K}_{\mathrm{m}, \mathrm{m}}$ le graphe constitué de 2 ensembles de sommets $S_{1}$ et $S_{2}$, tous les deux de cardinal m et dans lequel chaque sommet de $S_{1}$ est relié à tous les sommets de $S_{2}$. Un tel graphe est communément appelé bipartite complet, et on appellera $\mathrm{S}_{1}$ et $\mathrm{S}_{2}$ les équipes de $\mathrm{K}_{\mathrm{m}, \mathrm{m}}$.
Lemme : Soit $\mathrm{K}_{\mathrm{m}, \mathrm{m}}$ un graphe bipartite complet et $S_{1}$ et $S_{2}$ ses équipes. Supposons qu'il est possible de recouvrir $K_{m, m}$ avec de graphes complets $K_{k}$ et $K_{\ell}$ de taille respective $k, \ell<2 \mathrm{~m}$. Alors $\mathrm{m}<\frac{\mathrm{k}+\ell}{3}$.
Preuve du lemme: Commençons par montrer que $\mathrm{K}_{\mathrm{k}}$ et $\mathrm{K}_{\ell}$ contiennent chacun soit $S_{1}$ soit $S_{2}$. En effet, soit $v \in S_{1}$ n' appartenant pas à $K_{\ell}$. Pour tout sommet $w$ de $S_{2}$, l'arête $v w$ appartient donc à $K_{k}$, mais alors $w$ appartient à $K_{k}$, donc $K_{k}$ contient tous les sommets de $S_{2}$. Mais alors, en raisonnant sur un sommet de $S_{1}$ n'appartenant pas à $K_{k}$, on obtient que $K_{\ell}$ contient aussi tous les éléments de $S_{2}$. Ainsi, chaque sommet de $S_{2}$ appartient à $K_{k}$ et à $K_{\ell}$ et chaque sommet de $S_{1}$ appartient à $K_{k}$ ou à $K_{\ell}$, de sorte que $k+\ell \geqslant\left|S_{1}\right|+2\left|S_{2}\right|=3 \mathrm{~m}$
Revenons au problème. On suppose par l'absurde que $\mathrm{N} \geqslant 834$. Remarquons que si on pouvait avoir N encore plus grand, on pourrait se ramener au cas $\mathrm{N}=834$ en ajoutant arbitrairement des éléments de $\{1, . .834\}$ qui n'y étaient pas encore aux ensembles.
Nous partitionnons notre ensemble de points comme suit:
- Z l'ensemble des points dans $A_{1}$ et $A_{2}$.
- Xl'ensemble des points dans $A_{1}$ mais pas $A_{2}$.
- Yl'ensemble des points dans $A_{2}$ mais pas $A_{1}$.
- $W$ le reste (ni dans $A_{1}$, ni dans $A_{2}$ ).
On a alors $|\mathrm{X}|+|\mathrm{Y}|+|\mathrm{Z}|+|\mathrm{W}|=834$ et $|\mathrm{X}|+|\mathrm{Z}|=|\mathrm{Y}|+|\mathrm{Z}|=500$ ce qui nous donne $|\mathrm{W}|-|\mathrm{Z}|=-166$.
Cas 1: $|W|=0$. Il vient $|Z|=166,|X|=|Y|=334$. Ceci contredit notre lemme car cela implique que nous pouvons couvrir $\mathrm{K}_{334,334}$ avec deux cliques de taille 500 .
Cas 2: $|W|>O$. Alors $Z \subset K_{2} \cap K_{3}$ (c'est-à-dire que chacun de ses éléments est dans $A_{3}$ ou $A_{4}$ ) pour que chacun de ses sommets soit connecté aux éléments de $|W|$ donc $\left|K_{3} \cap Z\right|+\left|K_{4} \cap Z\right| \geqslant|Z|$. Ainsi, nous pouvons voir que si $|W|>0$ : (En utilisant que $W \subset K_{3} \cap K_{4}$ )
$$
\left|K_{3} \cap(X \cup Y)\right|+\left|K_{4} \cap(X \cup Y)\right| \leqslant 1000-2|W|-|Z|
$$
Alors, nous devons couvrir $K_{500-|Z|, 500-|Z|}$ (graphe formé à l'aide des ensembles $X$ et $Y$ ) avec deux cliques de tailles $\left|K_{3} \cap(X \cup Y)\right|, \mid K_{4} \cap(X \cup Y)$. Par notre lemme, $3(500-|Z|) \leqslant 1000-2|W|-|Z|$ or comme $|Z|=|W|+166$, on obtient une contradiction!
Par ailleurs, pour $\mathrm{N}=833$, on dispose d'une construction explicite : En reprenant nos notations $\mathrm{X}, \mathrm{Y}, \mathrm{Z}$. Avec $|Z|=167$ et $|\mathrm{X}|=|\mathrm{Y}|=333$. On place tous les éléments de X dans $A_{3}$ et $A_{4}$ et un élément de $|\mathrm{Y}|$ dans les deux, la moitié des éléments de Y qu'il reste dans $A_{3}$ et l'autre dans $A_{4}$.
Commentaire des correcteurs : L'exercice a été peu traité, et résolu par un seul élève.
## Exercices Seniors
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-4-2023-2024.jsonl",
"solution_match": "## Solution de l'exercice 9",
"tier": "T2",
"year": "2024"
}
|
Aurélien cuts a sheet of paper into 7 pieces. A step then consists of choosing a piece and cutting it into 4, 7, or 10 pieces. Can Aurélien thus obtain 2021 pieces?
|
The exercise describes a sequence of operations and asks whether it is possible to go from an initial state to a final state, so it is legitimate to look for an invariant of the system.
Here, we will show that the number of pieces Aurélien has is always of the form $3k+1$, with $k$ a natural number.
This is the case in the initial situation, since Aurélien has $7=3 \times 2+1$ pieces. Then, if this is the case at a certain step and Aurélien has $3k+1$ pieces with $k$ a natural number, Aurélien replaces one piece with $3 \times 1+1$ pieces, $3 \times 2+1$ pieces, or $3 \times 3+1$ pieces, so that he ends up with $3(k+1)+1$, $3(k+2)+1$, or $3(k+3)+1$ pieces at the end of the operation.
Step by step, we indeed get the announced result. Since $2021=3 \times 673+2$ is not of the indicated form, it is impossible to obtain 2021 pieces by the described process.
Comment from the graders: The exercise was very well done. Note, however, a reduction criterion $\bmod 3$ that allows avoiding Euclidean division to calculate $2021=2 \bmod 3$: a number is congruent to the sum of its digits $\bmod 9$ and therefore $\bmod 3$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Aurélien découpe une feuille de papier en 7 morceaux. Une étape consiste ensuite à choisir un morceau et à le découper en 4,7 ou 10 morceaux. Aurélien peut-il obtenir ainsi 2021 morceaux ?
|
L'exercice décrit une suite d'opérations et demande s'il est possible de passer d'un état initial à un état final, on peut donc légitimement chercher un invariant du système.
Ici, nous allons montrer que le nombre de morceausx d'Aurélien est toujours de la forme $3 k+1$, avec $k$ un entier naturel.
C'est le cas dans la situation initiale, puisqu'Aurélien dispose de $7=3 \times 2+1$ morceaux. Puis, si c'est le cas lors d'une étape et qu'Aurélien dispose de $3 k+1$ morceaux avec $k$ un entier naturel, Aurélien remplace un morceau par $3 \times 1+1$ morceaux, par $3 \times 2+1$ morceaux ou par $3 \times 3+1$ morceaux, de sorte qu'il lui reste, à la fin de l'opération, $3(k+1)+1,3(k+2)+1$ ou $3(k+3)+1$ morceaux.
De proche en proche, on a bien le résultat annoncé. Comme $2021=3 \times 673+2$ n'est pas de la forme indiquée, on ne peut jamais obtenir 2021 morceaux par le processus décrit.
Commentaire des correcteurs : Exercice très bien réussi. Notons tout de même un critère de réduction $\bmod 3$ permettant de ne pas faire de division euclidienne pour calculer $2021=2 \bmod 3$ : un nombre est congru à la somme de ces chiffres $\bmod 9$ et donc $\bmod 3$.
|
{
"exam": "French_envois",
"problem_label": "10",
"problem_match": "\nExercice 10.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-4-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 10",
"tier": "T2",
"year": "2024"
}
|
We have five colors and a $99 \times 99$ grid. We color some squares of the grid with one of the five colors such that
- Each color appears the same number of times in the grid.
- No row and no column contains squares of different colors.
What is the maximum number of squares that can be colored while following these rules?
|
Answer: N = 5 $\times 19 \times 20=1900$.
Since each row or column can only contain one color, let's think about it starting from the rows. We say that a row or column is of a certain color (say red) when the only color that the cells in this row or column can have is red. If a row or column has no color, we arbitrarily assign it a color. Thus, a red cell must be at the intersection of a red row and a red column. Consequently, the number of red cells can be bounded by the product of the number of red rows and the number of red columns. Now, let's introduce some notation. We number the available colors from 1 to 5 and denote $x_{i}$ as the number of rows colored with the i-th color, and $y_{i}$ as the number of columns colored with this color. Let N be the number of cells colored by each color. We want to maximize the total number of colored cells, 5 N. The arguments mentioned above show that $\forall i: N \leqslant x_{i} y_{i}$. We obviously also have $x_{1}+x_{2}+\ldots+x_{5}=y_{1}+y_{2}+\ldots y_{5}=99$. Studying small cases shows that to maximize N, the $x_{i}$ and the $y_{i}$ should all be roughly equal, each being $\frac{99}{5}$ rounded either up or down. A more in-depth study of small cases where 99 is replaced by a small number congruent to $4 \bmod 5$, like 99, allows us to conjecture that the following construction is optimal:
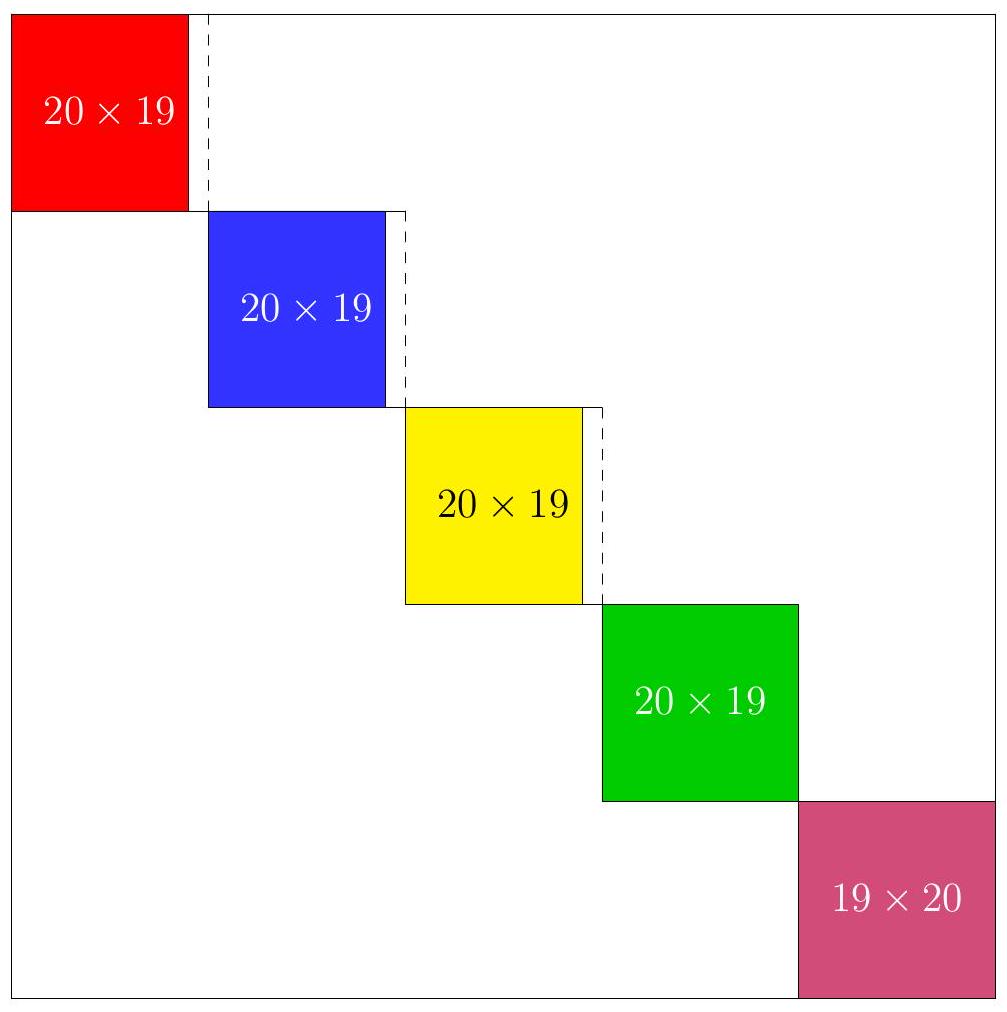
Here, we have $N=19 \cdot 20$.
Let's now prove the optimality. Suppose, for the sake of contradiction, that we have a valid configuration where $\mathrm{N}>$ $19 \times 20$, so $\forall i: x_{i} y_{i}>19 \times 20$. We then note that $x_{i}+y_{i}>39$. Indeed,
$$
x_{i} y_{i}=\frac{1}{4}\left(\left(x_{i}+y_{i}\right)^{2}-\left(x_{i}-y_{i}\right)^{2}\right)
$$
Thus,
$$
38^{2}<4 \cdot 19 \cdot 20=39^{2}-1<\left(x_{i}+y_{i}\right)^{2}-\left(x_{i}-y_{i}\right)^{2}<\left(x_{i}+y_{i}\right)^{2}
$$
So $38<x_{i}+y_{i}$. Moreover, if $x_{i}+y_{i}=39$, then $\left(x_{i}-y_{i}\right)^{2}<1$. Therefore, $x_{i}=y_{i}$, which is impossible because 39 is odd. Thus, $x_{i}+y_{i} \geqslant 40$.
The final count $2 \cdot 99=\left(x_{1}+y_{1}\right)+\left(x_{2}+y_{2}\right)+\ldots+\left(x_{5}+y_{5}\right) \geqslant 5 \times 40=200$ is a contradiction and completes the proof.
Comment from the graders: The problem was solved relatively well by the students. Two common errors should be noted: arriving at a result of $\mathrm{N}=1805$ and having the correct result but only providing intuitive arguments to prove its optimality. Students should read their work more carefully and take advantage of submissions to improve their rigor, especially in combinatorics.
|
1900
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On dispose de cinq couleurs et d'une grille $99 \times 99$. On colorie certains carrés de la grille avec l'une des cinq couleurs de sorte que
- Chaque couleur apparaît le même nombre de fois dans la grille.
- Aucune ligne et aucune colonne ne contient des cases de couleur différente.
Quelle est le plus grand nombre possible de cases que l'on peut colorier en suivant ces règles?
|
Réponse : N = 5 $\times 19 \times 20=1900$.
Comme chaque ligne ou colonne ne peut contenir qu'une couleur, on va réfléchir en partant des lignes. On dit qu'une ligne ou colonne est d'une couleur (disons rouge) quand la seule couleur que peuvent avoir des cases de cette ligne ou colonne est le rouge. Si une ligne ou colonne n'a pas de couleur, on lui assigne arbitrairement une couleur. Ainsi, une case rouge se trouve forcément à l'intersection d'une ligne rouge et d'une colonne rouge. Par conséquent, on peut majorer le nombre de case rouge par le produit du nombre de ligne rouges par le nombre de colonnes rouges. Introduisons maintenant des notations. On numérotes les couleurs disponibles de 1 à 5 et on note $x_{i}$ le nombre de lignes colorées de la i-ième couleur, et $y_{i}$ le nombre de colonnes colorées de cette couleur. Notons enfin N le nombre de cases coloriées par couleur. On veut maximiser le nombre total de cases coloriées, 5 N . Les arguments précédemment cités montrent que $\forall i: N \leqslant x_{i} y_{i}$. ON a évidemment aussi, $x_{1}+x_{2}+\ldots+x_{5}=y_{1}+y_{2}+\ldots y_{5}=99$. L'étude des petits cas nous montre que pour maximiser N il faut que les $x_{i}$ et les $y_{i}$ soient tous environs égaux, valant tous $\frac{99}{5}$ arrondi soit par excès ou par défaut. Une étude plus approfondie des petits cas où on remplace 99 par un petit nombre congru à $4 \bmod 5$, comme 99 , nous permet de conjecturer que la construction suivante est optimale :

Ici, on a $N=19 \cdot 20$.
Prouvons maintenant l'optimalité. Supposons par l'absurde disposer d'une configuration valide où $\mathrm{N}>$ $19 \times 20$, donc $\forall i: x_{i} y_{i}>19 \times 20$. On remarque ensuite que $x_{i}+y_{i}>39$. En effet,
$$
x_{i} y_{i}=\frac{1}{4}\left(\left(x_{i}+y_{i}\right)^{2}-\left(x_{i}-y_{i}\right)^{2}\right)
$$
Donc
$$
38^{2}<4 \cdot 19 \cdot 20=39^{2}-1<\left(x_{i}+y_{i}\right)^{2}-\left(x_{i}-y_{i}\right)^{2}<\left(x_{i}+y_{i}\right)^{2}
$$
Donc $38<x_{i}+y_{i}$. De plus, si $x_{i}+y_{i}=39$, alors $\left(x_{i}-y_{i}{ }^{2}<1\right.$ Donc $x_{i}=y_{i}$, ce qui est impossible car 39 est impair. Donc $x_{i}+y_{i} \geqslant 40$.
Le compte final $2 \cdot 99=\left(x_{1}+y_{1}\right)+\left(x_{2}+y_{2}\right)+\ldots+\left(x_{5}+y_{5}\right) \geqslant 5 \times 40=200$ est une contradiction et termine la preuve.
Commentaire des correcteurs : Le problème a été plutôt bien résolu par les élèves. On soulignera 2 erreurs courantes : aboutir à un résultat de $\mathrm{N}=1805$ et avoir le bon résultat mais ne donner que des arguments intuitifs pour démontrer qu'il est optimal. Les élèves devraient mieux se relire et profiter des envois pour travailler leur rigueur, surtout en combinatoire
|
{
"exam": "French_envois",
"problem_label": "11",
"problem_match": "\nExercice 11.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-4-2023-2024.jsonl",
"solution_match": "## Solution de l'exercice 11",
"tier": "T2",
"year": "2024"
}
|
Let $k$ be a strictly positive integer and $P$ a point in the plane. Determine the smallest integer $n$ having the following property: one can draw $n$ lines not passing through $P$ such that every ray originating from the point $P$ intersects at least $k$ lines.
|
Answer: $\mathrm{n}=2 \mathrm{k}+1$
The statement asks to determine the smallest integer $n$ possessing a certain property, it necessarily contains two parts. On the one hand, we show that if $n$ is less than $2 k$, it does not satisfy the property, on the other hand we show that $2 \mathrm{k}+1$ satisfies the property.
Let $n$ be an integer less than or equal to $2 k$. Consider a set of $n$ lines not passing through $P$. Take $d$ a line passing through $P$ and parallel to one of the $n$ lines. The line $d$ intersects at most $n-1 \leqslant 2 k-1$ of the other lines. We can distribute these points of intersection into two groups of points, such that the points of each group are located on the same side of $d$ relative to $P$. One of the groups is of size less than $k-1$, so there exists a ray emanating from $P$ that intersects at most $k-1$ lines.
Construction for $n=2 k+1$: Consider a regular polygon $A_{1} \ldots, A_{2 k+1}$ with $2 k+1$ sides and whose circumcircle is centered at $P$ and whose sides are extended. We obtain a set of $2 k+1$ lines. Consider a ray emanating from the vertex $P$, and say it intersects the segment $\left[A_{1} A_{2}\right]$ (possibly at one of its endpoints) by forming an angle of $\theta \leqslant \frac{360}{2 \mathrm{n}}$ with its perpendicular bisector, and such that the intersection point between $d$ and $\left[A_{1} A_{2}\right]$ is closer to $A_{2}$ than to $A_{1}$. Then the ray intersects the line $\left(A_{r} \mathcal{A}_{r+1}\right)$ if and only if it forms an angle less than $\pi / 2$ with the perpendicular bisector of the segment $\left[A_{r} A_{r+1}\right]$. This condition induces the following inequality on $r$
$$
\frac{r}{n} 360^{\circ}-\theta \leqslant 90^{\circ} .
$$
This inequality is valid for the $r \leqslant\left\lfloor\frac{k+1}{2}\right\rfloor$.
Similarly, the ray $d$ intersects the line $\left(A_{2 k+2-r} A_{2 k+1-r}\right)$ for the $r$ satisfying $r \leqslant\left\lfloor\frac{k}{2}\right\rfloor-1$. It follows that the line $d$ intersects the segment $\left[A 1 A_{2}\right]$ and at least $\left.\left\lfloor\frac{k+1}{2}\right\rfloor+\frac{k}{2}\right\rfloor-1=k-1$ lines, which is at least $k$ lines.
Comment from the graders: A rather mixed review for this problem. Most students find the correct bound of $2 \mathrm{k}+1$ and the proof that it cannot be less, but many have difficulty finding a construction or proving its proper functioning. The main point here was to understand under what condition a given line intersects our ray emanating from $P$.
|
2k+1
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Soit $k$ un entier strictement positif et $P$ un point du plan. Déterminer le plus petit entier $n$ ayant la propriété suivante : on peut tracer $n$ droites ne passant pas par $P$ de sorte que toute demi-droite d'origine le point $P$ coupe au moins $k$ droites.
|
Réponse : $\mathrm{n}=2 \mathrm{k}+1$
L'énoncé demande de déterminer le plus petit entier n possédant une certaine propriété, il contient nécessairement deux parties. D'une part, on montre que si $n$ est inférieur à $2 k$, il ne vérifie pas la propriété, d'autre part on montre que $2 \mathrm{k}+1$ vérifie la propriété.
Soit $n$ un entier inférieur ou égal à $2 k$. Considérons un ensemble de $n$ droites ne passant pas par $P$. Prenons $d$ une droite passant par $P$ et parallèle à l'une des $n$ droites. La droite $d$ coupe au plus $n-1 \leqslant 2 k-1$ des autres droites. On peut répartir ces points d'intersection en deux groupes de points, de sorte que les points de chaque groupe sont situés du même côté sur d par rapport à $P$. L'un des groupes est de taille inférieure à $k-1$, de sorte qu'il existe une demi-droite issue de P coupent au plus $k-1$ droites.
Construction pour $n=2 k+1$ : Considérons un polygone régulier $A_{1} \ldots, A_{2 k+1}$ à $2 k+1$ côtés et dont le cercle circonscrit est de centre $P$ et dont on prolonge les côtés. On obtient un ensemble de $2 k+1$ droites. Considérons une demi-droite dissue du sommet $P$, et disons qu'elle intersecte le segment $\left[A_{1} A_{2}\right]$ (éventuellement en l'une de ses extrémités) en effectuant un angle de $\theta \leqslant \frac{360}{2 \mathrm{n}}$ avec sa médiatrice, et de sorte que le point d'intersection entre d et $\left[A_{1} A_{2}\right]$ soit plus proche de $A_{2}$ que de $A_{1}$. Alors la demi-droit coupe la droite $\left(A_{r} \mathcal{A}_{r+1}\right)$ si et seulement si elle forme un angle inférieur à $\pi / 2$ avec la médiatrice du segment $\left[A_{r} A_{r+1}\right]$. Cette condition induit l'inégalité suivante sur $r$
$$
\frac{r}{n} 360^{\circ}-\theta \leqslant 90^{\circ} .
$$
Cette inégalité est valable pour les $r \leqslant\left\lfloor\frac{k+1}{2}\right\rfloor$.
De la même façon, la demi-droite d coupe la droite $\left(A_{2 k+2-r} A_{2 k+1-r}\right)$ pour les $r$ satisfaisant $r \leqslant\left\lfloor\frac{k}{2}\right\rfloor-1$. Il vient que la droite $d$ coupe le segment $\left[A 1 A_{2}\right]$ et au moins $\left.\left\lfloor\frac{k+1}{2}\right\rfloor+\frac{k}{2}\right\rfloor-1=k-1$ droites, soit au moins $k$ droites.
Commentaire des correcteurs : Un bilan assez mitigé pour cet exercice. La plupart des élèves trouvent la bonne borne de $2 \mathrm{k}+1$ et la preuve qu'on ne peut pas faire moins, mais beaucoup ont du mal à trouver une construction ou bien à donner preuve de son bon fonctionnement. Il s'agissait ici surtout de bien comprendre sous quelle condition une droite donnée intersecte notre demi-droite partant de P .
|
{
"exam": "French_envois",
"problem_label": "12",
"problem_match": "\nExercice 12.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-4-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 12",
"tier": "T2",
"year": "2024"
}
|
Let $k \geqslant 1$ be an integer.
Consider 4 k tokens, of which 2 k are red and 2 k are blue. A sequence of these 4 k tokens can be transformed into another sequence by a move, which consists of interchanging a certain number (possibly just one) of consecutive red tokens with an equal number of consecutive blue tokens. For example, a move allows us to go from rbbbrrrb to rrrbrbbb where $r$ denotes a red token and $b$ denotes a blue token.
Determine the smallest number $n$ (as a function of $k$) such that, starting from any initial sequence of the 4 k tokens, it takes at most n moves to reach the state where the first 2 k tokens are red.
|
Answer: $n=k$.
The problem asks to determine the smallest $n$ satisfying a certain property, so it necessarily has two parts. Here, first, we show that given an initial configuration of tokens, it is always possible to reach the described final configuration in at most $k$ steps. In the second part, we provide an initial configuration from which it takes at least $k$ steps to reach the final situation.
We can always reach the final situation in at most $k$ operations: Consider an initial configuration of 4 $k$ tokens. We call the first half the set of the 2 $k$ tokens on the left and the second half the set of the 2 $k$ tokens on the right. Among the 2 $k$ tokens in the first half, there are at least $k$ red tokens or at least $k+1$ blue tokens.
If there are at least $k$ red tokens, then we can exchange each of the blue tokens in the first half with a red token in the second half. Since at each step, we remove at least one blue token from the first half to place it in the second half, it takes at most $k$ steps to exchange all the blue tokens.
If there are at least $k+1$ blue tokens in the first half, then we can, in at most $k-1$ operations, exchange all the red tokens in the first half with blue tokens in the second half. After these steps, the 2 $k$ blue tokens are in the first half and the 2 $k$ red tokens are in the second half. By then exchanging the two groups of 2 $k$ consecutive tokens, we have reached the desired final situation in at most $k-1+1$ operations.
There exists an initial configuration for which it takes at least $k$ operations: Consider the configuration brbr...br (which consists of 2 $k$ blocks of the form br). Note that with each operation, the number of consecutive red token blocks decreases by at most 2. Since there are 2 $k$ blocks of consecutive red tokens in the initial situation and only one block of consecutive red tokens in the desired final situation, it is impossible to go from one to the other in $k-1$ operations or fewer. Therefore, it takes at least $k$ operations.
Graders' comments: The problem was generally well solved. A large majority of students manage to show that the goal can always be reached in $k$ moves. However, half of these students botch the proof that the alternating token configuration requires at least $k$ moves. Often the arguments are not quantified, or only take the initial configuration into account. For example, a common mistake is to think that a move displaces at most one token, which is false after several moves. Some students then try to justify that the number of moves used to create a large block compensates for the number of tokens then moved, but such arguments are not quantified and are not rigorous.
|
n=k
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Soit $k \geqslant 1$ un nombre entier.
Considérons 4 k jetons, dont 2 k sont rouges et 2 k sont bleus. Une suite de ces 4 k jetons peut être transformée en une autre suite par un mouvement, consistant à interchanger un certain nombre (éventuellement un seul) de jetons rouges consécutifs avec un nombre égal de jetons bleus consécutifs. Par exemple, un mouvement permet de passer de rbbbrrrb à rrrbrbbb où $r$ désigne un jeton rouge et b désigne un jeton bleu.
Déterminer le plus petit nombre $n$ (comme fonction de $k$ ) tel que, partant de n'importe quelle suite initiale des 4 k jetons, il faut au plus n mouvements pour atteindre l'état dans lequel les 2 k premiers jetons sont rouges.
|
Réponse : $\mathrm{n}=\mathrm{k}$.
Le problème demande de déterminer le plus petit n vérifiant une certaine propriété, il contient donc nécessairement deux parties. Ici, dans un premier temps, on montre qu'étant donnée une configuration initiale de jetons, il est toujours possible d'arriver à la configuration finale décrite en au plus k étapes. Dans un second temps, on donne une configuration initiale à partir de laquelle il faut au moins $k$ étapes pour arriver à la situation finale.
On peut toujours atteindre la situation finale en au plus $k$ opérations: Considérons une configuration initiale de 4 k jetons. On appelle première moitié l'ensemble des 2 k jetons les plus à gauche et deuxième moitié l'ensemble des 2 k jetons les plus à droite. Parmi les 2 k jetons de la première moitié, il y a au moins $k$ jetons rouges ou au moins $k+1$ jetons bleus.
S'il y a au moins $k$ jetons rouges, alors on peut échanger chacun des jetons bleus de la première moitié avec un jeton rouge de la deuxième moitié. Comme à chaque étape, on enlève au moins un jeton bleu de la première moitié pour le placer dans la deuxième moitié, il faut au plus $k$ étapes pour échanger tous les jetons bleus.
S'il y au moins $k+1$ jetons bleus dans la première moitié, alors on peut, en au plus $k-1$ opérations, échanger tous les jetons rouges de la première moitié avec des jetons bleus de la deuxième moitié. A l'issue de ces étapes, les $2 k$ jetons bleus sont dans la première moitié et les $2 k$ jetons rouges sont la deuxième moitié. En échangeant alors les deux groupes de $2 k$ jetons consécutifs, on a atteint la situation finale voulue en au plus $k-1+1$ opérations.
Il existe une configuration initiale pour laquelle il faut au moins $k$ opérations : Considérons la configuration brbr...br (qui consiste en 2 k blocs de la forme br). Notons qu'à chaque opération, le nombre de blocs de jetons rouges consécutifs diminue d'au plus 2 . Comme il y a 2 k blocs de jetons rouges consécutifs dans la situation initiale et un seul bloc de jetons rouges consécutifs dans la situation finale voulue, on ne peut passer de l'une à l'autre en $k-1$ opérations ou moins. Il faut donc au moins $k$ opérations.
Commentaire des correcteurs : Le problème a été bien résolu dans l'ensemble. Une large majorité d'élèves parvient à montrer que l'on peut toujours atteindre l'objectif en $k$ mouvements. Mais Une moitié de ces élèves bacle la preuve que la configuration des jetons alternés nécessite au moins $k$ mouvements. Souvent les arguments ne sont pas quantifiés, ou alors ne prennent en compte que la configuration initiale. Par exemple, une erreur commune est de penser qu'un mouvement déplace au plus un jeton, ce qui est faux après plusieurs mouvements. Des élèves tentent alors de justifier que le nombre de mouvements utilisés pour créer un gros bloc compense le nombre de jetons alors déplacé, mais de tels arguments ne sont pas quantifiés et ne sont pas rigoureux.
|
{
"exam": "French_envois",
"problem_label": "13",
"problem_match": "\nExercice 13.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-4-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 13",
"tier": "T2",
"year": "2024"
}
|
Aline and Elsa are playing the following game. They have 100 stones which they divide into two piles (not necessarily of the same size) at the beginning of the game. Then, each in turn, they perform the following move: they choose a pile, then a positive integer less than or equal to half the size of the chosen pile, and remove that number of stones from the pile. The first player who cannot make a move loses.
Determine all the initial configurations for which Elsa has a winning strategy.
|
In the following, we denote by $(x, y)$ the configuration where the first pile is of size $x$ and the second pile is of size $y$.
We observe in the case of a single pile, starting from the end, that the losing configurations for Aline are the piles with $2^{n}-1$ stones.
Let's return to the case of a generic initial configuration $(\boldsymbol{a}, \boldsymbol{b})$. By definition, the position $(1,1)$ is losing. $(a, b)$ is losing for the player who must play if $\frac{a+1}{b+1}$ is a power (positive or negative) of 2. Indeed, if $\frac{a+1}{b+1}=2^{n}$, if one draws from $a$, the quotient decreases but strictly by less than a factor of 2. Conversely, if one draws from pile $b$, the quotient increases but strictly by less than a factor of 2, which maintains a winning position for the next player.
Conversely, if $2^{n}(b+1)<a+1<2^{n+1}(b+1)$ with $n \geqslant 0$, then one takes the necessary number of stones from pile $a$ so that exactly $2^{n}(b+1)-1$ remain. This is possible because $a < 2^{n+1}(b+1)-1$ and thus $a \leqslant 2^{n+1}(b+1)-2$, from which $\frac{a}{2} \leqslant 2^{n}(b+1)-1$, meaning that more than half are left.
Comment from the graders: The problem was quite discriminatory. Among the small number of students who proposed solutions, they were either entirely correct and quite efficient, or rather confused, trying too much to adapt the strategy for a single pile to the case of two piles.
|
not found
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Aline et Elsa jouent au jeu suivant. Elles disposent de 100 pierres qu'elles séparent en deux piles (pas forcément de même taille) au début du jeu. Puis chacune à leur tour, elles effectuent le mouvement suivant : elles choisissent une pile, puis un entier strictement positif inférieur ou égal à la moitié de la taille de la pile choisie et retirent ce nombre de pierres de la pile. La première joueuse qui ne peut plus effectuer de mouvement perd.
Déterminer toutes les configurations initiales pour lesquelles Elsa a une stratégie gagnante.
|
Dans la suite, on désigne par $(x, y)$ la configuration où la première pile est de taille $x$ et la deuxième pile est de taille $y$.
On observe sur le cas à une seule pile en commençant par la fin que les solutions perdantes pour Aline sont les piles à $2^{n}-1$ pierres.
Revenons au cas d'une configuration intiale générique $(\boldsymbol{a}, \boldsymbol{b}$ ). Par définition, la position $(1,1)$ est perdante. $(a, b)$ est perdante pour la personne qui doit jouer si $\frac{a+1}{b+1}$ est une puissance (positive ou négative) de 2. En effet, si $\frac{a+1}{b+1}=2^{n}$, si on pioche dans $a$, on diminue le quotient mais strictement de moins qu'un facteur 2. À l'inverse, si on pioche dans la pile $b$ on l'augmente mais strictement moins que d'un facteur 2 ce qui conserve bien une position gagnante pour la joueuse suivante.
Réciproquement, si $2^{n}(b+1)<a+1<2^{n+1}(b+1)$ avec $n \geqslant 0$ alors on prend le nombre nécessaire de pierres de la pile a de sorte qu'il en reste précisément $2^{n}(b+1)-1$. Cela est possible car $a<$ $2^{n+1}(b+1)-1$ donc $a \leqslant 2^{n+1}(b+1)-2$ d'où $\frac{a}{2} \leqslant 2^{n}(b+1)-1$ ce qui signifie qu'on en a laissé plus que la moitié.
Commentaire des correcteurs : Le problème a été assez discriminant. Parmi le petit nombre d'élèves ayant proposé des solutions, celles-ci étaient soit entièrement juste et assez efficace, soit plutôt confuses, essayant trop d'adapter la stratégie pour une seule pile au cas des deux piles.
|
{
"exam": "French_envois",
"problem_label": "14",
"problem_match": "\nExercice 14.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-4-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 14",
"tier": "T2",
"year": "2024"
}
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.