problem
stringlengths 14
10.4k
| solution
stringlengths 1
24.1k
| answer
stringlengths 1
250
⌀ | problem_is_valid
stringclasses 4
values | solution_is_valid
stringclasses 3
values | question_type
stringclasses 4
values | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
10.4k
| solution_raw
stringlengths 1
24.1k
| metadata
dict |
|---|---|---|---|---|---|---|---|---|---|
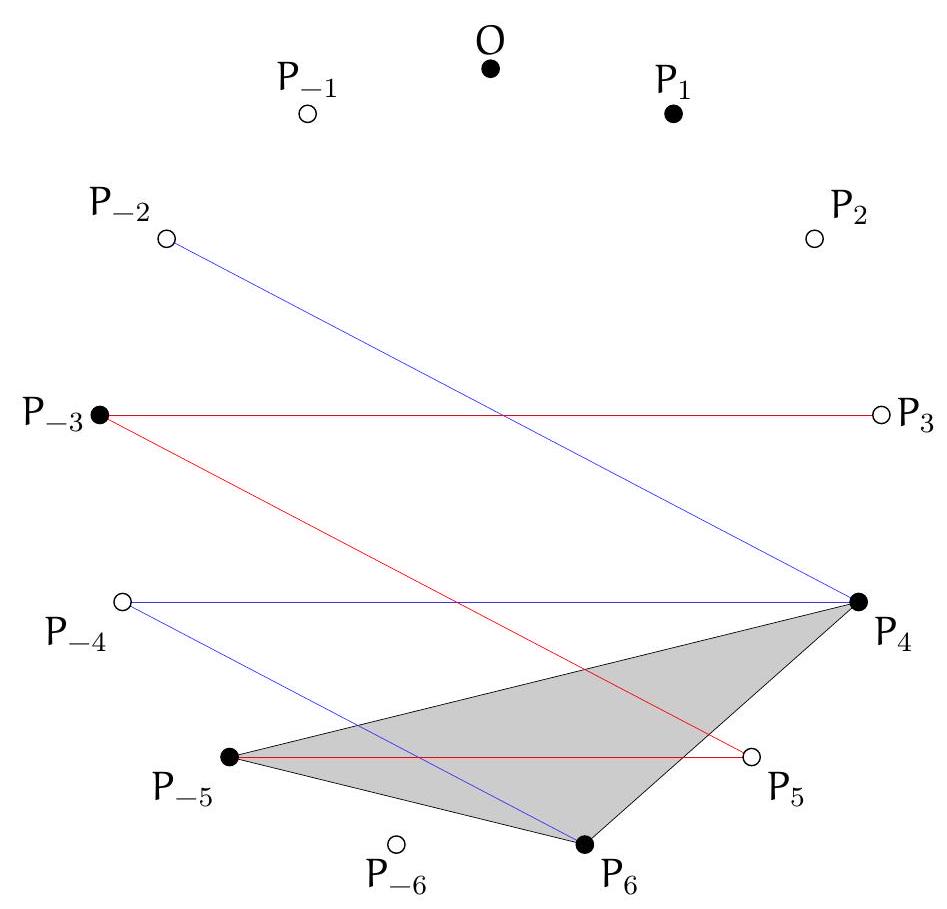
Let $n \geqslant 3$ be an integer. We color 2 n vertices of a $4 \mathrm{n}+1$-gon. Show that there exist three colored vertices that form an isosceles triangle.
|
We proceed by contradiction, assuming that no triplet of colored vertices forms an isosceles triangle.
First, fix a colored vertex \( O \) and denote \( \mathrm{OP}_{1} \ldots \mathrm{P}_{2 n} \mathrm{P}_{-2 n} \ldots \mathrm{P}_{-1} \) as the rest of the polygon. Since the triangle \( O P_{i} P_{-i} \) is isosceles for \( 1 \leqslant i \leqslant 2 n \), at most one of the two vertices \( P_{i} \) and \( P_{-i} \) is colored.
Suppose that two consecutive vertices are never both colored. In particular, \( \mathrm{P}_{1} \) and \( \mathrm{P}_{-1} \) are not colored because they are adjacent to \( O \) which is colored. But then each of the \( 2 \mathrm{n}-1 \) pairs \( ( \mathrm{P}_{i}, \mathrm{P}_{-i} ) \) of remaining vertices contains at most one colored vertex, and at least \( 2 \mathrm{n}-1 \) vertices among the \( P_{i} \) are colored. We conclude that each pair \( \left(P_{i}, P_{-i}\right) \) with \( i \geqslant 2 \) contains exactly one colored vertex. Thus, either \( P_{i} \) or \( P_{-i} \) is colored for \( i \geqslant 2 \).
Suppose that \( \mathrm{P}_{2 n} \) is colored. Then \( \mathrm{P}_{2 n-1} \) is not colored, so \( \mathrm{P}_{-2 n+1} \) is colored. But then \( \mathrm{P}_{-2 n+2} \) is not colored, so \( P_{2 n-2} \) is colored. The triangle \( P_{2 n-2}, P_{2 n}, P_{-2 n+1} \) being isosceles and colored, we find a contradiction.
We have shown that there exist two consecutive colored vertices, say \( O \) and \( P_{1} \). The vertices \( P_{-1} \) and \( P_{2} \) are then not colored, under penalty of creating an isosceles triangle with \( O \) and \( P_{1} \). Similarly, the triangle \( \mathrm{OP}_{1} \mathrm{P}_{-2 n} \) is isosceles at \( \mathrm{P}_{-2 n} \) which is not colored.
Consider then the following sequence of vertices, of length \( 2(n-1): P_{3}, P_{-3}, \ldots, P_{2 i-1}, P_{-2 i+1}, \ldots, P_{2 n-1}, P_{-2 n+1} \)
Two consecutive vertices of this sequence form an isosceles triangle with \( O \) or with \( P_{1} \), and cannot both be colored.
The same applies to the sequence \( P_{-2}, P_{4}, \ldots, P_{-2 i} P_{2 i+2}, \ldots, P_{-2 n+2}, P_{2 n} \).
These two sequences therefore contain at most half of the colored vertices each. But since they contain together exactly \( 2 \mathrm{n}-2 \) colored vertices, the previous inequalities are saturated and in each sequence, exactly one vertex out of two is colored.
If \( P_{3} \) is colored, then \( \mathrm{P}_{5} \) is colored and the triangle \( \mathrm{P}_{1} \mathrm{P}_{3} \mathrm{P}_{5} \) is isosceles and colored. Similarly, if \( \mathrm{P}_{-2} \) is colored, then \( \mathrm{P}_{-4} \) is colored and the triangle \( \mathrm{OP}_{-2} \mathrm{P}_{-4} \) is isosceles and colored. We deduce that \( \mathrm{P}_{-2 n+1}, \mathrm{P}_{2 n} \) and \( \mathrm{P}_{2 n-2} \) are colored and form an isosceles triangle, which concludes.
Comment from the graders: The problem admitted many solutions and was, overall, well solved by those who attempted it.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soit $n \geqslant 3$ un entier. On colorie 2 n sommets d'un $4 \mathrm{n}+1$-gone régulier. Montrer qu'il existe trois sommets coloriés qui forment un triangle isocèle.
|
On porcède par l'absurde en supposant qu'aucun triplet de sommets coloriés ne forme de triangle isocèle.
Dans un premier temps, fixons un sommet colorié O et notons $\mathrm{OP}_{1} \ldots \mathrm{P}_{2 n} \mathrm{P}_{-2 n} \ldots \mathrm{P}_{-1}$ le reste du polygone. Puisque le triangle $O P_{i} P_{-i}$ est isocèle pour $1 \leqslant i \leqslant 2 n$, au plus l'un des deux sommets $P_{i}$ et $P_{-i}$ est colorié.
Supposons que deux sommets consécutifs ne sont jamais tous les deux coloriés. En particulier, $\mathrm{P}_{1}$ et $\mathrm{P}_{-1}$ ne sont pas coloriés car ils sont adjacents à O qui est colorié. Mais alors chacune des $2 \mathrm{n}-1$ paires ( $\mathrm{P}_{i}, \mathrm{P}_{-i}$ ) de sommets restants contient au plus un point colorié, et au moins $2 \mathrm{n}-1$ sommets parmis les $P_{i}$ sont coloriés. On conclut que chaque paire $\left(P_{i}, P_{-i}\right)$ avec $i \geqslant 2$ contient exactement un sommet colorié. Ainsi, soit $P_{i}$ soit $P_{-i}$ est colorié pour $i \geqslant 2$.
Supposons que $\mathrm{P}_{2 n}$ est colorié. Alors $\mathrm{P}_{2 n-1}$ n'est pas colorié, donc $\mathrm{P}_{-2 n+1}$ est colorié. Mais alors $\mathrm{P}_{-2 n+2}$ n'est pas colorié, donc $P_{2 n-2}$ est colorié. Le triangle $P_{2 n-2}, P_{2 n}, P_{-2 n+1}$ étant isocèle et colorié, on trouve une contradiction.
On a montré qu'il existe deux sommets consécutifs coloriés, disons 0 et $P_{1}$. Les sommets $P_{-1}$ et $P_{2}$ ne sont alors pas coloriés, sous peine de créer un triangle isocèle avec $O$ et $P_{1}$. De même, le triangle $\mathrm{OP}_{1} \mathrm{P}_{-2 n}$ est isocèle en $\mathrm{P}_{-2 n}$ dont $\mathrm{P}_{-2 n} \mathrm{n}$ 'est pas colorié.
Considérons alors la suite de sommets suivante, de longueur $2(n-1): P_{3}, P_{-3}, \ldots, P_{2 i-1}, P_{-2 i+1}, \ldots, P_{2 n-1}, P_{-2 n+1}$
Deux sommets consécutifs de cette suite forment un triangle isocèle avec $O$ ou avec $P_{1}$, et ne peuvent pas être tous les deux coloriés.
Il en va de même pour la suite $P_{-2}, P_{4}, \ldots, P_{-2 i} P_{2 i+2}, \ldots, P_{-2 n+2}, P_{2 n}$.
Ces deux suites contiennent donc chacune au plus une moitié de sommets coloriés. Mais comme elles contiennent ensemble exactement $2 \mathrm{n}-2$ sommets coloriés, les inégalités précédents sont saturées et dans chaque suite, exactement un sommet sur deux est colorié.
Si $P_{3}$ est colorié, alors $\mathrm{P}_{5}$ est colorié et le triangle $\mathrm{P}_{1} \mathrm{P}_{3} \mathrm{P}_{5}$ est isocèle colorié. De même, si $\mathrm{P}_{-2}$ est colorié, alors $\mathrm{P}_{-4}$ est colorié et le triangle $\mathrm{OP}_{-2} \mathrm{P}_{-4}$ est isocèle colorié. On déduit que $\mathrm{P}_{-2 n+1}, \mathrm{P}_{2 n}$ et $\mathrm{P}_{2 n-2}$ sont coloriés et forment un triangle isocèle, ce qui conclut.

Commentaire des correcteurs : Le problème admettait de nombreuses solutions et a été, dans l'ensemble, bien résolu par ceux qui l'ont cherché.
|
{
"exam": "French_envois",
"problem_label": "15",
"problem_match": "\nExercice 15.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-4-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 15",
"tier": "T2",
"year": "2024"
}
|
Consider a regular 2022-gon with side length 1. The points are numbered $A_{1}, \ldots, A_{2022}$ in a certain order. Initially, Elie starts from point $A_{1}$, then jumps from point to point to $A_{2}$, then from $A_{2}$ to $A_{3}$, and so on, each time taking the shortest arc. When he reaches $A_{2022}$, he finally returns to $A_{1}$. Determine the maximum value of the sum of the lengths of the arcs that Elie has traveled, among all possible numberings of the points.
|
Response: $\mathrm{If} N=1011$, The maximum value is $2\left(\mathrm{~N}^{2}-\mathrm{N}+1\right)$.
The problem asks to find the maximum value of a sum of lengths, which necessarily involves two parts. First, we show that the path traveled by Elie is necessarily of length less than $2\left(\mathrm{~N}^{2}-\mathrm{N}+1\right)$, this part is called the analysis. Second, we provide an example of a numbering for which the path traveled is exactly of length $2\left(N^{2}-N+1\right)$, this step is called the construction.
Analysis: In the following, we keep the notation $N=1011$. We also denote $\underline{P Q}$ as the length of the shortest arc connecting P and Q, and $\overline{\mathrm{PQ}}$ as the length of the longest arc. Consider a numbering $A_{1}, \ldots, A_{2 N}$ in any order. We also set $A_{2 N+1}=A_{1}$.
Since estimating each segment $A_{i} A_{i+1}$ by its minimum length is too rough, we will instead lower-bound the sum $A_{1} \overline{A_{2}+\ldots}+A_{2 N} A_{1}$ by upper-bounding groups of terms. More precisely, we will look at the path traveled between two consecutive odd vertices.
Let $1 \leqslant i \leqslant N$. We want to show that $\underline{A_{2 i-1} A_{2 i}}+\underline{A_{2 i} A_{2 i+1}} \leqslant \overline{A_{2 i-1} A_{2 i+1}}$, in other words, that passing through $A_{2 i}$ is less costly than taking the large arc $A_{2 i-1} \mathcal{A}_{2 i+1}$. The desire to prove such an inequality can come from attempts on small cases.
If $A_{2 i}$ is on the small arc $A_{2 i-1} A_{2 i+1}$, then $\underline{A_{2 i-1} A_{2 i}}+\underline{A_{2 i} A_{2 i+1}}=\underline{A_{2 i-1} A_{2 i+1}} \leqslant \overline{A_{2 i-1} A_{2 i+1}}$. Suppose now that $A_{2 i}$ is on the large arc $A_{2 i-1} A_{2 i+1}$. If the small arc $A_{2 i} A_{2 i+1}$ does not contain $A_{2 i-1}$ or if the small arc $A_{2 i-1} A_{2 i}$ does not contain $A_{2 i+1}$, then $\underline{A_{2 i-1} A_{2 i}}+\underline{A_{2 i} A_{2 i+1}}=\overline{A_{2 i-1} A_{2 i+1}}$. If now $A_{2 i-1}$ is on the small arc $A_{2 i} A_{2 i+1}$, then $A_{2 i+1}$ is on the large arc $A_{2 i-1} A_{2 i}$ and $A_{2 i-1} A_{2 i}+$ $\underline{A_{2 i} A_{2 i+1}} \leqslant \underline{A_{2 i-1} A_{2 i}}+\overline{A_{2 i} A_{2 i+1}}=\overline{A_{2 i-1} A_{2 i+1}}$. The case where $A_{2 i-1}$ is on the small arc $A_{2 i} A_{2 i+1}$ is treated similarly.
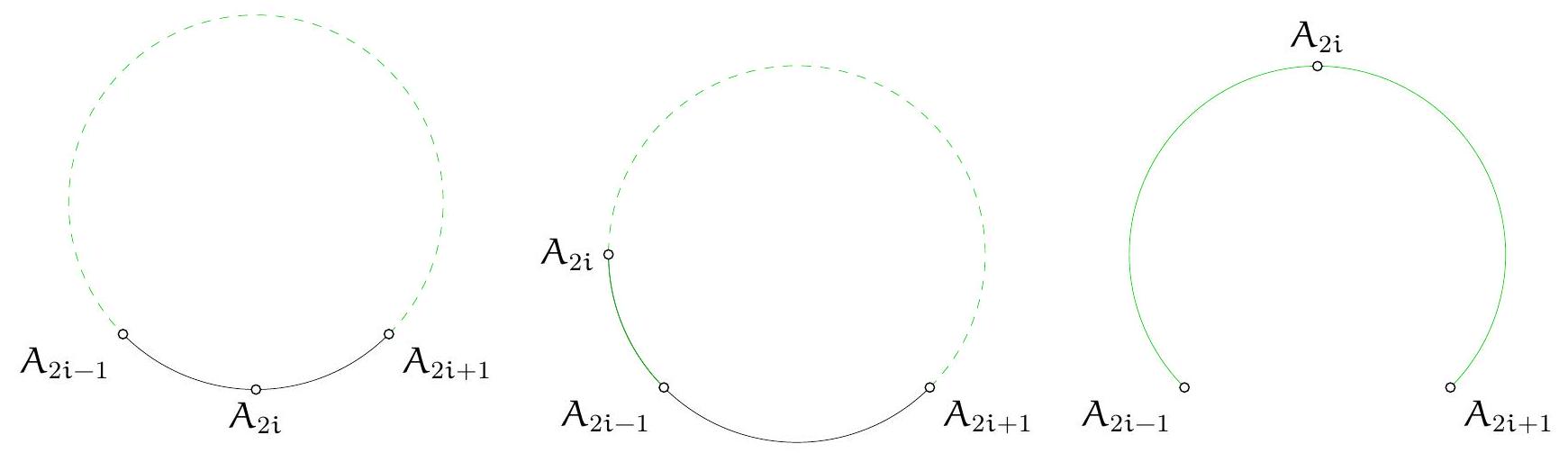
We therefore have
$$
\begin{aligned}
\underline{A_{1} A_{2}}+\ldots+\underline{A_{2 N} A_{1}} & \leqslant \overline{A_{1} A_{3}}+\ldots+\overline{A_{2 N-1} A_{1}} \\
& =\left(2 \mathrm{~N}-\underline{A_{1} A_{3}}\right)+\ldots+\left(2 N-\underline{A_{2 N-1} A_{1}}\right) \\
& \left.=2 N^{2}-\underline{\left(A_{1} A_{3}\right.}+\ldots+\underline{A_{2 N-1}} \overline{A_{1}}\right) .
\end{aligned}
$$
It is therefore sufficient to minimize the sum $\underline{A_{1} A_{3}}+\ldots+\underline{A_{2 N-1} A_{1}}$. For this, note that there exist two odd-numbered vertices $A$ and B at a distance of at least $\mathrm{N}-1$ (since there are N odd vertices). As the sum is cyclic, we can assume that $A=A_{1}$ (by renumbering the vertices if necessary). But then the path $A_{1} \ldots A_{2 N-1} A_{1}$ requires traveling an arc $\underline{A_{1} B}$ to go from $A_{1}$ to $B$ and then an arc $B A_{1}$ to go from $B$ to $A_{1}$. Such a path is therefore at least twice the length of the small arc $A B$, which is $2(N-1)$.
It follows that
$$
\underline{A_{1} A_{2}}+\ldots+\underline{A_{2 N} A_{1}} \leqslant \overline{A_{1} A_{3}}+\ldots+\overline{A_{2 N-1} A_{1}} \geqslant 2 N^{2}-2(N-1)=2\left(N^{2}-N+1\right)
$$
Construction: Conversely, number the vertices in the order $A_{1} A_{3} \ldots A_{2 N-1} A_{2} \ldots A_{2 N}$. The path of Elie is then of length
$$
\underline{A_{1} A_{2}}+\ldots+\underline{A_{2 N} A_{1}} \leqslant \overline{A_{1} A_{3}}+\ldots+\overline{A_{2 N-1} A_{1}}=\underbrace{N+N-1+\ldots+N+N-1}_{N-1 \text { times }}+N+1=2 N^{2}-2 N+2
$$
Graders' Comments: The problem was not solved by many students. Many students found a construction that achieves the correct bound, but among those who attempted the problem, too many students still try to justify that one cannot do better by one of the two arguments:
- Either by saying that at each step, the point $A_{k}$ is placed in the "optimal" position. But performing the "best" operation at each step is not a guarantee of arriving at the best configuration. Here, placing the point $A_{k}$ diametrically opposite to the point $A_{k+1}$ forces, at the end, to have $A_{2022}$ and $A_{1}$ adjacent. Who says that not systematically placing the points $A_{k}$ and $A_{k+1}$ as far apart as possible does not allow increasing the distance between $A_{1}$ and $A_{2022}$ to have a greater total distance?
- Or by saying that if points are swapped on the found configuration, the distance is not increased. This reasoning also does not prove that the configuration is a global maximum, but only proves that the configuration is a local maximum.
We hope that upon reading this comment, students will no longer make these two common reasoning errors.
|
2(N^2 - N + 1)
|
Yes
|
Incomplete
|
math-word-problem
|
Geometry
|
On considère un 2022-gone régulier de côté 1 . Les points sont numérotés $A_{1}, \ldots, A_{2022}$ dans un certain ordre. Au départ, Elie part du point $A_{1}$, puis saute de point en point vers le point $A_{2}$, puis de $A_{2}$ vers $A_{3}$ etc... chaque fois en prenant l'arc le plus court. Lorsqu'il atteint $A_{2022}$, il rejoint finalement $A_{1}$. Déterminer la valeur maximale de la somme des longueurs des arcs qu'a parcouru Elie, parmi toutes les numérotations de points possibles.
|
Réponse: $\mathrm{Si} N=1011$, La valeur maximale est $2\left(\mathrm{~N}^{2}-\mathrm{N}+1\right)$.
Le problème demande de trouver la valeur maximale d'une somme de longueurs, il contient nécessairement deux parties. Dans un premier temps, on montre que le chemin parcouru par Elie est forcément de longueur inférieure à $2\left(\mathrm{~N}^{2}-\mathrm{N}+1\right)$, cette partie s'appelle l'analyse. Dans un second temps, on donne l'exemple d'une numérotation pour laquelle le chemin parcouru est exactement de longueur $2\left(N^{2}-N+1\right)$, cette étape s'appelle la construction.
Analyse : Dans la suite, on garde la notation $N=1011$. On note également $\underline{P Q}$ la longueur de l'arc le plus court reliant P et Q et $\overline{\mathrm{PQ}}$ la longueur de l'arc le plus long. Considérons une numérotation $A_{1}, \ldots, A_{2 N}$ dans un ordre quelconque. On pose aussi $A_{2 N+1}=A_{1}$.
Puisque majorer chaque portion $A_{i} A_{i+1}$ par sa longueur minimale est une estimation trop grossière, on va plutôt minorer la somme $A_{1} \overline{A_{2}+\ldots}+A_{2 N} A_{1}$ en majorant des paquets de terme. Plus précisément, nous allons regarder le chemin parcouru entre deux sommets impairs consécutifs.
Soit $1 \leqslant i \leqslant N$. On désire montrer que $\underline{A_{2 i-1} A_{2 i}}+\underline{A_{2 i} A_{2 i+1}} \leqslant \overline{A_{2 i-1} A_{2 i+1}}$, autrement dit, que passer par $A_{2 i}$ est moins coûteux que prendre le grand arc $A_{2 i-1} \mathcal{A}_{2 i+1}$. La volonté de démontrer une telle inégalité peut venir de tentatives sur des petits cas.
Si $A_{2 i}$ est sur le petit arc $A_{2 i-1} A_{2 i+1}$, alors $\underline{A_{2 i-1} A_{2 i}}+\underline{A_{2 i} A_{2 i+1}}=\underline{A_{2 i-1} A_{2 i+1}} \leqslant \overline{A_{2 i-1} A_{2 i+1}}$. Supposons désormais que $A_{2 i}$ est sur le grand arc $A_{2 i-1} A_{2 i+1}$. Si le petit arc $A_{2 i} A_{2 i+1}$ ne contient pas $A_{2 i-1}$ ou si le petit arc $A_{2 i-1} A_{2 i}$ ne contient pas $A_{2 i+1}$, alors $\underline{A_{2 i-1} A_{2 i}}+\underline{A_{2 i} A_{2 i+1}}=\overline{A_{2 i-1} A_{2 i+1}}$. Si maintenant $A_{2 i-1}$ est sur le petit arc $A_{2 i} A_{2 i+1}$, alors $A_{2 i+1}$ est sur le grand arc $A_{2 i-1} A_{2 i}$ et $A_{2 i-1} A_{2 i}+$ $\underline{A_{2 i} A_{2 i+1}} \leqslant \underline{A_{2 i-1} A_{2 i}}+\overline{A_{2 i} A_{2 i+1}}=\overline{A_{2 i-1} A_{2 i+1}}$. Le cas où $A_{2 i-1}$ est sur le petit arc $A_{2 i} A_{2 i+1}$ se traite de façon similaire.

On a donc
$$
\begin{aligned}
\underline{A_{1} A_{2}}+\ldots+\underline{A_{2 N} A_{1}} & \leqslant \overline{A_{1} A_{3}}+\ldots+\overline{A_{2 N-1} A_{1}} \\
& =\left(2 \mathrm{~N}-\underline{A_{1} A_{3}}\right)+\ldots+\left(2 N-\underline{A_{2 N-1} A_{1}}\right) \\
& \left.=2 N^{2}-\underline{\left(A_{1} A_{3}\right.}+\ldots+\underline{A_{2 N-1}} \overline{A_{1}}\right) .
\end{aligned}
$$
Il suffit donc de minimiser la somme $\underline{A_{1} A_{3}}+\ldots+\underline{A_{2 N-1} A_{1}}$. Pour cela, notons qu'il existe deux sommets $A$ et B de numéro impair à distance au moins $\mathrm{N}-1$ (car il y a N sommets impairs). Comme la somme
est cyclique, on peut supposer que $A=A_{1}$ (quitte à renuméroter les sommets). Mais alors le chemin $A_{1} \ldots A_{2 N-1} A_{1}$ nécessite de parcourir un arc $\underline{A_{1} B}$ pour aller de $A_{1}$ vers $B$ puis un arc $B A_{1}$ pour aller de $B$ vers $A_{1}$. Un tel chemin est donc de longueur au moins le double du petit arc $A B$, soit $2(N-1)$.
Il vient
$$
\underline{A_{1} A_{2}}+\ldots+\underline{A_{2 N} A_{1}} \leqslant \overline{A_{1} A_{3}}+\ldots+\overline{A_{2 N-1} A_{1}} \geqslant 2 N^{2}-2(N-1)=2\left(N^{2}-N+1\right)
$$
Construction : Réciproquement, numérotons les sommets dans l'ordre $A_{1} A_{3} \ldots A_{2 N-1} A_{2} \ldots A_{2 N}$. Le chemin d'Elie est alors de longueur
$$
\underline{A_{1} A_{2}}+\ldots+\underline{A_{2 N} A_{1}} \leqslant \overline{A_{1} A_{3}}+\ldots+\overline{A_{2 N-1} A_{1}}=\underbrace{N+N-1+\ldots+N+N-1}_{N-1 \text { fois }}+N+1=2 N^{2}-2 N+2
$$
Commentaire des correcteurs : Le problème n'a pas été beaucoup résolu. Beaucoup d'élèves ont trouvé une construction réalisant la bonne borne, mais parmi ceux qui ont cherché l'exercice, trop d'élèves encore tentent de justifier qu'on ne peut pas faire mieux par l'un des deux arguments :
- Soit en disant qu'à chaque étape on place le point $A_{k}$ à l'endroit "optimal". Mais effectuer la "meilleure" opération à chaque fois n'est pas gage d'arriver à la meilleure configuration. Ici, placer le point $A_{k}$ diamétralement opposé au point $A_{k+1}$ impose à la fin d'avoir $A_{2022}$ et $A_{1}$ adjacents. Qui nous dit que ne pas systématiquement placer les points $A_{k}$ et $A_{k+1}$ le plus éloigné possible ne permet pas d'augmenter la distance entre $A_{1}$ et $A_{2022}$ pour avoir une plus grande distance totale?
- Soit en disant que si l'on échange des points sur la configuration trouvée, on n'augmente pas la distance. Là aussi, ce raisonnement ne permet pas de prouver que la configuration est un maximum global, mais seulement de prouver que la configuration est un maximum local.
Nous espérons qu'à la lecture de ce commentaire, les élèves ne commettront plus ces deux erreurs communes de raisonnement.
|
{
"exam": "French_envois",
"problem_label": "16",
"problem_match": "\nExercice 16.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-4-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 16",
"tier": "T2",
"year": "2024"
}
|
Consider 51 strictly positive integers with a sum of 100 on a line. Show that for any integer $1 \leqslant k<100$, there exist consecutive integers with a sum of $k$ or $100-k$.
|
We slightly rephrase the statement to make it more visual: imagine a circle with a circumference of 100, graduated from 0 to 99. On this circle, 51 graduations are marked in black and the other 49 are marked with dotted lines. Without loss of generality, we mark the graduation 0 in black. Our positive integers correspond to the lengths between the black graduations. It is easy to verify that this is a bijective representation of the problem. For any $k$, by the pigeonhole principle, since the function that maps $j$ to $j+k$ is injective (modulo 100), there exists a black graduation $j$ such that its image $j+k$ is also black. Two cases arise. Either the segment $[j, j+k]$ does not cross 0, and then we have the desired integers. Or it crosses 0, and then $[j+k, j]$ does not cross 0 and is of length $n-k$. In both cases, we have found consecutive integers with a sum of $k$ or $n-k$.
Graders' comment: The exercise is well handled.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
On considère 51 entiers strictement positifs de somme 100 sur une ligne. Montrer que pour tout entier $1 \leqslant k<100$, il existe des entiers consécutifs de somme $k$ ou $100-k$.
|
On reformule légèrement l'énoncé pour le rendre plus visuel : on se représente un cercle de périmètre 100 gradué (de 0 à 99 par exemple) sur-lequel on a marqué en noir 51 graduations et en pointillés les 49 autres. Sans perte de généralité on marque en noir la graduation 0. Nos entiers positifs correspondent aux longueurs entre les graduations noires. On vérifie facilement qu'il s'agit d'une représentation bijective du problème. Pour tout $k$, par principe des tiroirs, comme l'application qui à $j$ associe $j+k$ est injective (modulo 100), il existe une graduation marquée en noir $j$ telle que son image $j+k$ l'est aussi. Deux cas se présentent alors. Soit le segment $[j, j+k]$ ne coupe pas 0 et alors on a bien les entiers souhaités. Soit il coupe 0 et alors $[j+k, j]$ ne coupe pas 0 et est de longueur $n-k$. Dans les deux cas, on a trouvé des entiers consécutifs de somme $k$ ou $n-k$.
Commentaire des correcteurs: L'exercice est plutôt bien traité.
|
{
"exam": "French_envois",
"problem_label": "17",
"problem_match": "\nExercice 17.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-4-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 17",
"tier": "T2",
"year": "2024"
}
|
Let $\mathrm{C}_{1}, \mathrm{C}_{2}, \ldots \mathrm{C}_{\mathrm{n}}$ be circles of the same radius arranged in the plane such that they are never tangent to each other and there always exists a path passing through the circles to go from a point on one of them to another (in other words, the circles are connected). Denoting $S$ as the set of intersection points of the circles, show that $|S| \geqslant n$.
|
First, we rephrase the problem in terms of graphs. We denote by \( C \) the set of centers of the circles and \( S \) the set of intersection points which form the vertices of a graph \( G \). We connect by an edge every pair \( (c, s) \in C \times S \) if \( s \) belongs to the circle centered at \( c \). Notice then that for every edge \( (c, s) \), \( \operatorname{deg}(c) \geqslant \operatorname{deg}(s) \). Indeed, according to the statement, for every point \( c_{i} \) connected to \( s \) other than \( c \), we can associate another intersection point of \( c_{i} \) with \( c \) since the circles are not tangent. Given \( c_{i} \) and \( c_{j} \) distinct, these second points \( s_{i} \) and \( s_{j} \) cannot be the same since all circles have the same radius. Now that the problem is reformulated, we can reason solely on the graph: \( G \) is a bipartite graph between \( C \) and \( S \) such that for every edge \( (c, s) \), \( \operatorname{deg}(c) \geqslant \operatorname{deg}(s) \). It easily follows that \( |C| \leqslant |S| \). Indeed, denoting \( A \) the set of edges and \( a = (c_{a}, s_{a}) \) these edges: \( |C| = \sum_{a \in \mathcal{A}} \frac{1}{\operatorname{deg}(c_{a})} \leqslant \sum_{a \in \mathcal{A}} \frac{1}{\operatorname{deg}(s_{a})} = S \), which concludes.
Graders' comments: The problem was attempted by few students and solved by only one. Attempting a proof by induction was doomed to fail: indeed, one can add a circle without necessarily adding an intersection point to the figure formed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $\mathrm{C}_{1}, \mathrm{C}_{2}, \ldots \mathrm{C}_{\mathrm{n}}$ des cercles de même rayon disposés dans le plan de sorte qu'ils ne soient jamais tangents 2 à 2 et qu'il existe toujours un chemin passant par les cercles pour aller d'un point de l'un d'entre eux à un autre (autrement dit, les cercles sont connectés). En notant S l'ensemble des points d'intersection des cercles, montrer que $|S| \geqslant n$.
|
Dans un premier temps, on reformule le problème en termes de graphes. On note C l'ensemble des centres des cercles et S l'ensemble des points d'intersections qui constituent les sommets d'un graphe $G$. On relie par une arête tout couple ( $c, s) \in C \times S$ si $s$ appartient au cercle de centre $c$. Remarquons alors que pour toute arête $(c, s), \operatorname{deg}(c) \geqslant \operatorname{deg}(s)$. En effet, d'après l'énoncé, à tout point $c_{i}$ relié à $s$ autre que c on peut associer un autre point d'intersection de $\mathrm{c}_{\mathrm{i}}$ avec c car les cercles ne sont pas tangents. Étant donnés $\boldsymbol{c}_{\boldsymbol{i}}$ et $\boldsymbol{c}_{\boldsymbol{j}}$ distincts, ces deuxièmes points $s_{i}$ et $s_{j}$ ne peuvent pas être confondus puisque tous les cercles sont de même rayons. Maintenant que le problème est reformulé, on peut raisonner uniquement sur le graphe : $G$ est un graphe bipartite entre $C$ et $S$ tel que pour toute arête $(c, s), \operatorname{deg}(c) \geqslant \operatorname{deg}(s)$. Il vient aisément que $|C| \leqslant|S|$ En effet, en notant A l'ensemble des arêtes et $a=\left(c_{a}, s_{a}\right)$ ces arêtes $:|C|=\sum_{a \in \mathcal{A}} \frac{1}{\operatorname{deg}\left(c_{a}\right)} \leqslant \sum_{a \in \mathcal{A}} \frac{1}{\operatorname{deg}\left(s_{a}\right)}=S$ ce qui conclut.
Commentaire des correcteurs : Le problème a été peu tenté, et résolu par un seul élève. Faire une récurrence était voué à l'échec : en effet, on peut rajouter un cercle, sans pour autant rajouter de point d'intersection à la figure formée.
|
{
"exam": "French_envois",
"problem_label": "18",
"problem_match": "\nExercice 18.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-4-2023-2024.jsonl",
"solution_match": "\nSolution de l'exercice 18",
"tier": "T2",
"year": "2024"
}
|
Find all triplets of positive integers $(x, y, z)$ satisfying the equation
$$
x! + 2^y = z!
$$
|
Let $(x, y, z)$ be a solution triplet.
First, we aim to reduce the number of values that $x$ can take. Note that $x! < z!$ so $x < z$. In particular, $x!$ divides $z!$ and $x!$, so $x!$ divides $z! - x! = 2^y$. Suppose, for the sake of contradiction, that $x \geq 3$, in this case 3 divides $x!$ but does not divide $2^y$, which makes it impossible for $x!$ to divide $2^y$. Thus, $x = 0, 1$ or 2.
We now perform a case disjunction between $x! = 1$ so $x = 0$ or 1, or $x! = 2$ so $x = 2$.
- Case $x = 0$ or 1: the equation becomes $1 + 2^y = z!$. We then perform a second case disjunction:
- Case $y = 0$: we find $z = 2$. Conversely, $(0,0,2)$ and $(1,0,2)$ are indeed solutions.
- Case $y \geq 1$: thus $1 + 2^y \geq 3$ and $1 + 2^y$ is odd. However, $z!$ is even if $z \geq 2$, and equals 0 or 1 if $z = 1$, neither of which can satisfy our equation. Thus, if we assume $y \geq 1$, there are no solutions.
- Case $x = 2$: We distinguish according to the values of $y$:
- Case $y = 0$: we get $3 = z!$ which has no solutions (since $2! < 3 < 3!$).
- Case $y = 1$: we get $4 = z!$ which has no solutions (since $2! < 3 < 3!$).
- Case $y \geq 2$: we get that 2 divides $2^y + 2$, but 4 does not divide $2^y + 2$. Thus, 2 divides $z!$ but 4 does not divide $z!$, so $z = 2$ or 3. Since $2^y + 2 \geq 4 + 2 = 6$, we get $z = 3$, so $2 + 2^y = 6$, thus $2^y = 4$ and $y = 2$. Conversely, $(2,2,3)$ is indeed a solution since $2 + 4 = 6$.
Thus, the solutions are the triplets $(0,0,2), (1,0,2)$, and $(2,2,3)$.
Comment from the graders: The exercise, rather simple, was approached by a large number of students. Most managed to find the correct set of solutions and thought to use moduli or divisibility, which is very good. However, many errors were made, consisting in neglecting to properly handle the small cases. For example, many papers hastily claimed that a power of 2 is even, which is false for $2^0 = 1$. Attention must be paid to such details. It is also recalled that 0 is a positive integer.
|
(0,0,2), (1,0,2), (2,2,3)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Trouver toutes les triplets d'entiers positifs $(x, y, z)$ satisfaisant l'équation
$$
x!+2^{y}=z!
$$
|
Soit ( $x, y, z$ ) un triplet solution.
On cherche dans un premier temps à réduire le nombre de valeurs que $x$ peut prendre. Pour ce faire notons que $x$ ! < $<$ ! donc $x<z$. En particulier, $x$ ! divise $z$ ! et $x$ !, donc $x$ ! divise $z$ ! $-x!=2^{y}$. Supposons par l'absurde que $x \geqslant 3$, dans ce cas 3 divise $x$ ! mais ne divise pas $2^{y}$, ce qui rend impossible le fait que $x$ ! divise $2^{y}$. Ainsi $x=0,1$ ou 2 .
On effectue maintenant une disjonction de cas entre $x!=1$ donc $x=0$ ou 1 , ou bien $x!=2$ donc $x=2$.
- Cas $x=0$ ou 1 : l'équation devient $1+2^{y}=z$ !. On effectue alors une deuxième disjonction de cas
- Cas $y=0$ : on trouve $z=2$. Réciproquement, $(0,0,2)$ et $(1,0,2)$ sont bien solution.
- Cas $y \geqslant 1$ : ainsi $1+2^{y} \geqslant 3$ et $1+2^{y}$ est impair. Or $z$ ! est pair si $z \geqslant 2$, et vaut 0 ou 1 si $z=1$, aucun des deux cas ne peut donc satisfaire notre équation. Ainsi, si on suppose que $y \geqslant 1$, il n'y a pas de solution.
- Cas $x=2$ : On distingue encore selon les valeurs de $y$ :
- Cas $\mathrm{y}=0$ : on obtient $3=z$ ! qui n'a pas de solutions (car $2!<3<3$ !).
- Cas $\mathrm{y}=1$ : on obtient $4=z$ ! qui n'a pas de solutions (car $2!<3<3$ !).
- Cas $y \geqslant 2$ : on obtient que 2 divise $2^{y}+2$, mais que 4 ne divise pas $2^{y}+2$. Ainsi 2 divise $z$ ! mais 4 ne divise pas $z$ !, donc $z=2$ ou 3 . Comme de plus $2^{y}+2 \geqslant 4+2=6$, on obtient $z=3$, donc $2+2^{y}=6$, donc $2^{y}=4$ donc $y=2$. Réciproquement, $(2,2,3)$ est bien solution $\mathrm{car} 2+4=6$.
Ainsi les solutions sont les triplets $(0,0,2),(1,0,2)$ et $(2,2,3)$.
Commentaire des correcteurs : L'exercice, plutôt simple, a été abordé par un grand nombre d'élèves. La plupart ont réussi à trouver le bon ensemble de solutions, et ont bien pensé à utiliser les modulos ou la divisibilité, ce qui est très bien. Cependant, de nombreuses erreurs ont été commises, consistant à négliger de traiter proprement les petits cas. Par exemple, de nombreuses copies affirmaient hâtivement qu'une puissance de 2 est paire, ce qui est faux pour $2^{0}=1$. Il faut faire attention à ce genre de détails. On rappelle également que 0 est un entier positif.
|
{
"exam": "French_envois",
"problem_label": "10",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-5.jsonl",
"solution_match": "## Solution de l'exercice 1",
"tier": "T2",
"year": null
}
|
Let $ABC$ be an equilateral triangle and $P$ a point on the circumcircle of this triangle but distinct from $A$, $B$, and $C$. The lines passing through $P$ and parallel to $(BC)$, $(CA)$, and $(AB)$ intersect the lines $(CA)$, $(AB)$, and $(BC)$ at $M$, $N$, and $Q$ respectively. Show that the points $M$, $N$, and $Q$ are collinear.
|
Consider the following figure:
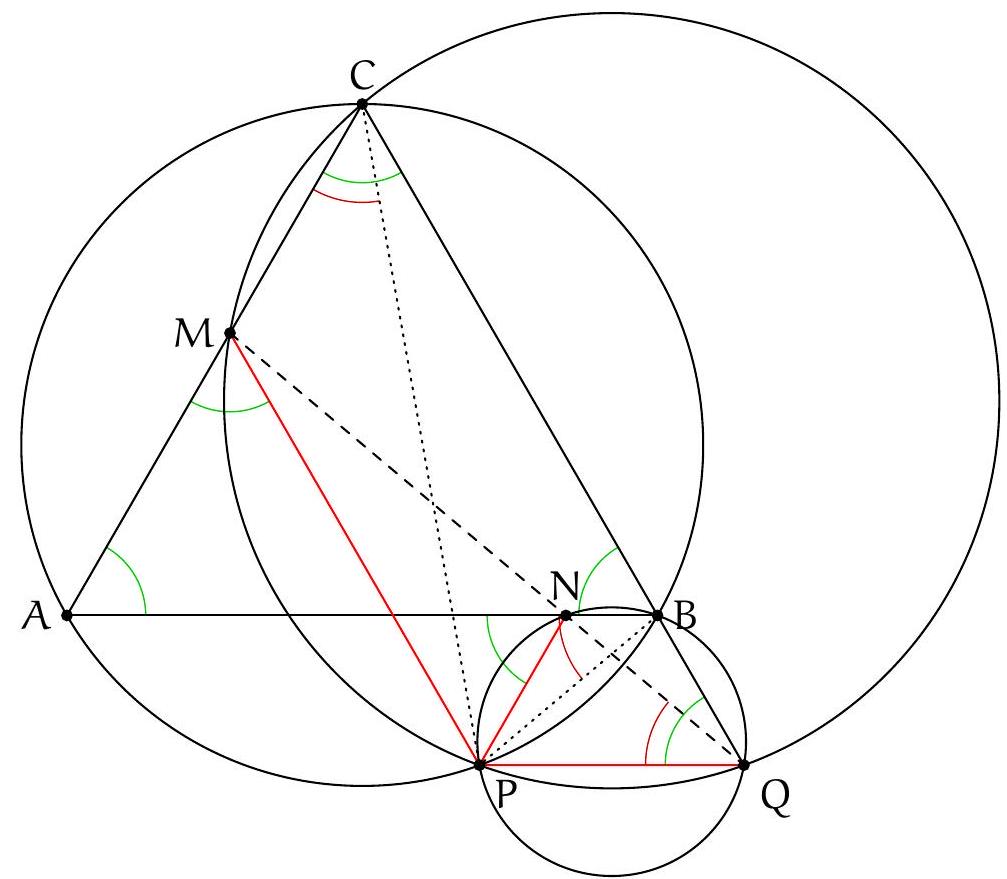
Let's show that \(P, N, B, Q\) are concyclic. Since \((PN)\) is parallel to \((AC)\), and \((NB)\) is parallel to \((AB)\), \(\widehat{ANP} = \widehat{CAB} = 60^\circ\). Since \((PQ)\) is parallel to \((AB)\), \(\widehat{PQB} = \widehat{ABC} = 60^\circ\). Thus, \(P, N, B, Q\) are concyclic. Therefore, \(\widehat{PQN} = \widehat{PBN} = \widehat{PBA}\).
Let's show that \(P, M, C, Q\) are concyclic. Since \((PM)\) is parallel to \((BC)\), \(\widehat{AMP} = \widehat{ACB} = 60^\circ\). Since \(\widehat{PQC} = \widehat{PQB} = 60^\circ\), \(P, M, C, Q\) are concyclic. Therefore, \(\widehat{PQM} = \widehat{PCM} = \widehat{PCA}\). By the concyclicity of \(A, P, B, C\), \(\widehat{PQM} = \widehat{PCA} = \widehat{PBA} = \widehat{PQN}\), so \(Q, N, M\) are collinear.
Graders' comments: Well solved overall. Many proofs are a bit too long. Some reasoning errors (alignment of points cannot be used to prove they are actually aligned).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle equilatéral et P un point sur le cercle circonscrit de ce triangle mais distincs de $A$, $B$ et $C$. Les droites passant par $P$ et parallèles à $(B C),(C A)$ et $(A B)$ intersectent les droites (CA), (AB) et (BC) en $M$, $N$ et $Q$ respectivement. Montrer que les points $M, N$ et $Q$ sont alignés.
|
On se place dans le cas de la figure suivante :

Montrons que $P, N, B, Q$ sont cocycliques. Comme $(P N)$ est parallèle à $(A C)$, et $(N B)$ est parallèle à $(\mathrm{AB}), \widehat{A N P}=\widehat{C A B}=60$. Comme $(\mathrm{PQ})$ est parallèle à $(\mathrm{AB}), \widehat{\mathrm{PQB}}=\widehat{A B C}=60$. Ainsi $\mathrm{P}, \mathrm{N}, \mathrm{B}, \mathrm{Q}$ sont cocycliques. Ainsi $\widehat{\mathrm{PQN}}=\widehat{\mathrm{PBN}}=\widehat{\mathrm{PBA}}$.
Montrons que $P, M, C, Q$ sont cocycliques. Comme $(P M)$ est parallèle à $(B C), \widehat{A M P}=\widehat{A C B}=60$. Or $\widehat{\mathrm{PQC}}=\widehat{\mathrm{PQB}}=60$. Ainsi $\mathrm{P}, \mathrm{M}, \mathrm{C}, \mathrm{Q}$ sont cocycliques. Ainsi $\widehat{\mathrm{PQM}}=\widehat{\mathrm{PCM}}=\widehat{\mathrm{PCA}}$. Par cocyclité de $A, P, B, C, \widehat{P Q M}=\widehat{P C A}=\widehat{P B A}=\widehat{P Q N}$ donc $Q, N, M$ sont alignés.
Commentaire des correcteurs : Bien résolu dans l'ensemble. Beaucoup de preuves qui sont un peu trop longues. Quelques erreurs de raisonnement (on ne peut pas utiliser que les points sont alignés pour montrer qu'ils le sont effectivement).
|
{
"exam": "French_envois",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-5.jsonl",
"solution_match": "## Solution de l'exercice 2",
"tier": "T2",
"year": null
}
|
Let $x, y, z$ be three positive real numbers, such that $x \leqslant 1$. Prove that:
$$
x y + y + 2 z \geqslant 4 \sqrt{x y z}
$$
|
Note that since $x \leqslant 1, x y+y \geqslant x y+x y=2 x y$. In particular, by the arithmetic-geometric mean inequality,
$$
x y+y+2 z \geqslant 2 x y+2 z=2(x y+z) \geqslant 4 \sqrt{x y z}
$$
which gives the desired inequality.
Comment from the graders: The exercise was quite simple and was approached by many students, and almost all of them succeeded. However, I encourage students to carefully proofread their work before submitting, to ensure that inequalities are written correctly and that no cases have been overlooked (for example, by simplifying an equation by $y z$ when $y z$ could be zero).
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $x, y, z$ trois réels positifs, tel que $x \leqslant 1$. Démontrer que:
$$
x y+y+2 z \geqslant 4 \sqrt{x y z}
$$
|
Notons que comme $x \leqslant 1, x y+y \geqslant x y+x y=2 x y$. En particulier par inégalité arithmético-géométrique
$$
x y+y+2 z \geqslant 2 x y+2 z=2(x y+z) \geqslant 4 \sqrt{x y z}
$$
ce qui donne l'inégalité voulue.
Commentaire des correcteurs : L'exercice était assez simple et a été abordé par de nombreux élèves, et réussi par presque chacun d'entre eux. J'invite toutefois les élèves à bien se relire lorsqu'ils soumettent une copie, afin de vérifier que les inégalités sont écrites correctement et que des cas n'ont pas été oubliés (par exemple en simplifiant une équation par $y z$ alors que $y z$ peut être nul).
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-5.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T2",
"year": null
}
|
2024 students, all of different heights, need to line up in a single file. However, each student does not want to have both a shorter student in front of them and a shorter student behind them. How many ways are there to form such a line?
|
Let's look at the tallest student: if they are not placed at the very beginning or the very end of the line, they are between two students who are shorter than them. Thus, the tallest student must be placed at the end or at the beginning.
By this reasoning, and by looking at small cases, we can conjecture that if we need to place $n \geqslant 1$ students all of different heights with the constraint given in the statement, there are $2^{\text {n-1 }}$ possibilities. Let's prove this by induction on $n$.
Initialization: for $\mathrm{n}=1$ student, there is only one possible line and $1=2^{\mathrm{n}-1}$.
Hereditary: suppose the hypothesis is true at rank $n$ for a $n \geqslant 1$, let's show that it is true at rank $n+1$. The tallest student is necessarily placed either at the very beginning or at the very end. If we remove this student from the line, the line of $n$ people still satisfies the statement: there are therefore potentially $2^{n-1}$ possibilities for the line without the tallest person. If we add the tallest person at the front or the back of the line, the line still satisfies the statement (since the person next to the tallest will not be between two people who are shorter), as there are two choices for placing the tallest person, there are $2^{\mathfrak{n}}=2^{\mathfrak{n + 1 - 1}}$ possibilities to form the line, which concludes the induction.
Thus, by applying the property for $\mathrm{n}=2024$, there are $2^{2023}$ possibilities.
Comment from the graders: The exercise was very well done overall, with few errors. Two main methods of proof were used: the first is similar to what the statement suggests, and involves seeing how to place the students, one by one. The second involves understanding what the "shape" of the distribution of students will be, in a V shape, and counting these configurations using various arguments.
|
2^{2023}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
2024 élèves, tous de taille différente, doivent se placer en file indienne. Cependant, chaque élève ne souhaite pas avoir à la fois devant lui et derrière lui un élève plus petit que lui. Combien y a-t-il de façons de former une telle file indienne?
|
Regardons l'élève de plus grande taille : s'il n'est pas placé au tout début ou à la toute fin de la file, il est entre deux élèves plus petits que lui. Ainsi l'élève le plus grand doit être placé à la fin ou au début.
Via ce raisonnement, et en regardant les petits cas on peut conjecturer que si on doit placer $n \geqslant 1$ élèves tous de taille différente avec la contrainte de l'énoncé, il y a $2^{\text {n-1 }}$ possibilités. Montrons cela par récurrence sur n .
Initialisation : pour $\mathrm{n}=1$ élèves, il n'y a qu'une file possible et $1=2^{\mathrm{n}-1}$.
Hérédité : supposons l'hypothèse vraie au rang $n$ pour un $n \geqslant 1$, montrons qu'elle l'est au rang $n+1$. L'élève le plus grand est frocément placé soit au tout début, soit à la toute fin. Si on l'enlève de la file, la file de $n$ personnes vérifie toujours l'énoncé : il y a donc potentiellement $2^{n-1}$ possibilité pour la file sans la personne la plus grande. Si on rajoute la personne la plus grande devant ou derrière la file vérifie toujours l'énoncé (car la personne à côté du plus grand ne sera pas entre deux personnes plus petites), comme il y a deux choix de placements du plus grand, il y a $2^{\mathfrak{n}}=2^{\mathfrak{n + 1 - 1}}$ possibilités pour former la file, ce qui conclut la récurrence.
Ainsi en appliquant la propriété pour $\mathrm{n}=2024$, il y a $2^{2023}$ possibilités.
Commentaire des correcteurs: Exercice très bien réussi dans l'ensemble, avec peu d'erreurs. Deux méthodes de preuve principales ont été employées : la première est semblable à ce que fait l'énoncé, et consiste à voir comment placer les élèves, un par un. La seconde consiste à comprendre quelle va être la "forme" de la répartition des élèves, en V , et à compter ces configurations par divers arguments.
|
{
"exam": "French_envois",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-5.jsonl",
"solution_match": "## Solution de l'exercice 4",
"tier": "T2",
"year": null
}
|
Let $A, B, C, D$ and $E$ be five points in this order on a circle such that $A E=D E$. Let $P$ be the point of intersection of $(A C)$ and $(B D)$. Let $Q$ be the point on the ray $[B A)$ such that $A Q=D P$. Let $R$ be the point on the ray $[C D)$ such that $D R=A P$. Show that the lines $(P E)$ and $(Q R)$ are perpendicular.
|
In the case of the following figure:
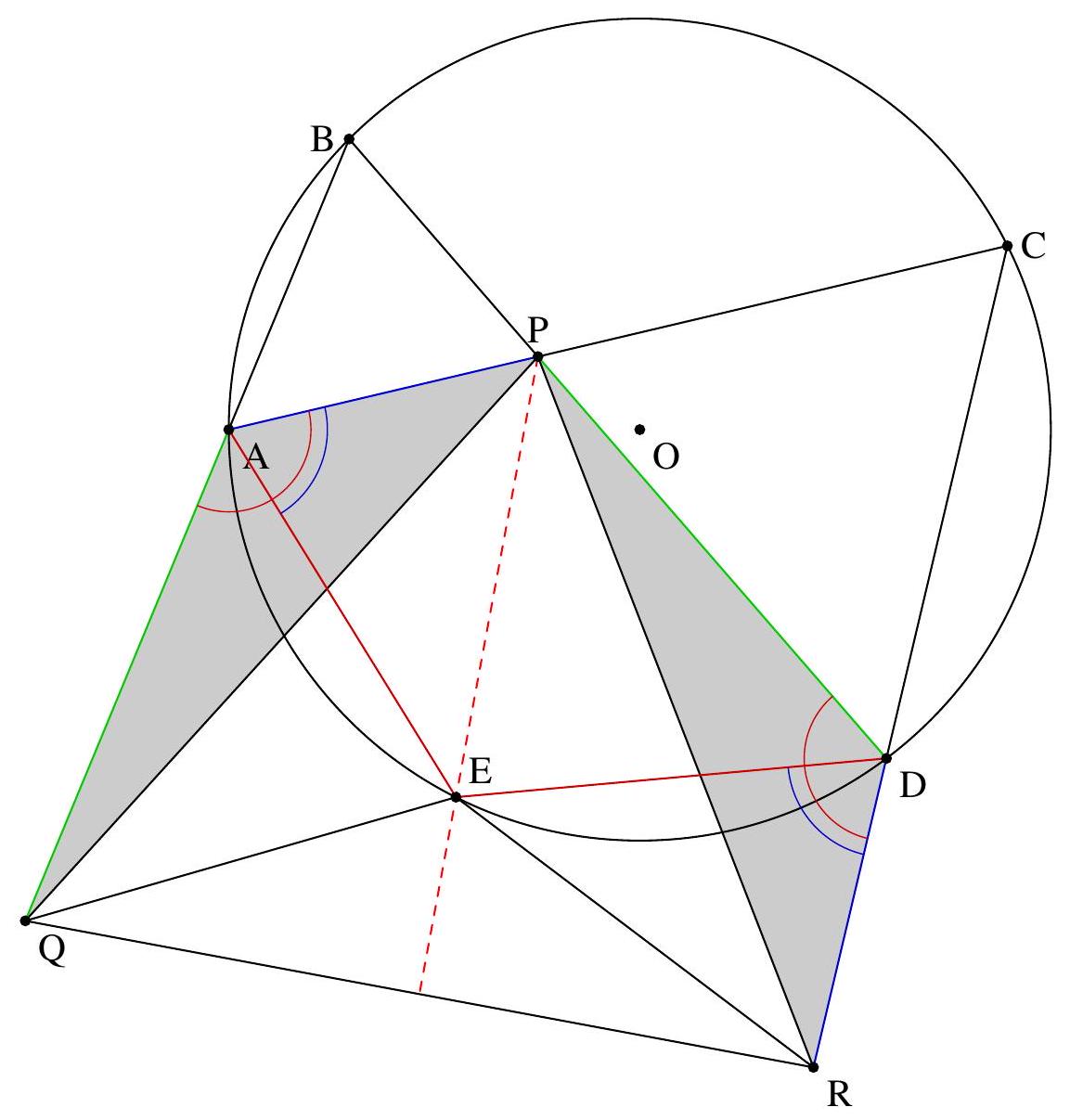
In this statement, we have many equal lengths $(A Q=D P, D R=A P, A E=D E)$. As shown in the figure, it is helpful to color the equal lengths to identify potential congruent triangles and make progress in the problem.
The triangles DRP and AQP appear to be congruent: let's prove it. First, note that $\mathrm{DR}=A \mathrm{~A}$ and $\mathrm{DP}=\mathrm{AR}$ by hypothesis. Additionally, $\widehat{\mathrm{RDP}}=180-\widehat{\mathrm{CDP}}=180-\widehat{\mathrm{CDB}}=180-\widehat{\mathrm{CAB}}=180-\widehat{\mathrm{PAB}}=\widehat{\mathrm{PAQ}}$. Thus, the triangles DRP and AQP are congruent.
In particular, $P Q=P R$, so $P$ lies on the perpendicular bisector of $(Q R)$.
The triangles $D E R$ and $A E P$ appear to be congruent: let's prove it. We have $D E=A E$ and $D R=A P$. Additionally, $\widehat{\mathrm{EDR}}=180-\widehat{\mathrm{EDC}}=\widehat{\mathrm{CAE}}=\widehat{\mathrm{PAE}}$. Thus, the triangles DER and AEP are congruent, and $E P=E R$.
Similarly, the triangles $A E Q$ and $D E P$ are congruent (since $A, Q$ play a symmetric role to $D, R$), so $E P=E Q$, and thus $E R=E Q: E$ lies on the perpendicular bisector of $(Q R)$.
Therefore, the perpendicular bisector of $(Q R)$ is $(E P)$, so $(E P)$ and $(Q R)$ are perpendicular.
Comment from the graders: The exercise is very well done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $A, B, C, D$ et $E$ cinq points dans cet ordre sur un cercle tels que $A E=D E$. Soit $P$ le point d'intersection de $(A C)$ et $(B D)$. Soit $Q$ le point de la demi-droite $[B A)$ tel que $A Q=D P$. Soit $R$ le point de la demi-droite $[C D)$ tel que $D R=A P$. Montrer que les droites $(P E)$ et $(Q R)$ sont perpendiculaires.
|
On se place dans le cas de la figure suivante:

Dans cet énoncé on a de nombreuses égalités de longueur $(A Q=D P, D R=A P, A E=D E$. Comme sur la figure, il ne faut pas hésiter à colorier les longueurs égales pour voir des potentiels triangles isométriques, et avancer dans le problème).
Les triangles DRP et AQP ont l'air d'être isométriques : prouvons-le. Notons déjà que $\mathrm{DR}=A \mathrm{~A}$ et $\mathrm{DP}=\mathrm{AR}$ par hypothèse. De plus $\widehat{\mathrm{RDP}}=180-\widehat{\mathrm{CDP}}=180-\widehat{\mathrm{CDB}}=180-\widehat{\mathrm{CAB}}=180-\widehat{\mathrm{PAB}}=$ $\widehat{\mathrm{PAQ}}$. Ainsi les triangles DRP et AQP sont isométriques.
En particulier $P Q=P R$, donc $P$ est sur la médiatrice de $(Q R)$.
Les triangles $D E R$ et $A E P$ ont l'air d'être isométriques : prouvons-le. On a $D E=A E$ et $D R=A P$. De plus $\widehat{\mathrm{EDR}}=180-\widehat{\mathrm{EDC}}=\widehat{\mathrm{CAE}}=\widehat{\mathrm{PAE}}$. Ainsi les triangles DER et AEP sont isométriques et $E P=E R$.
De même les triangles $A E Q$ et $D E P$ sont isométriques ( $\operatorname{car} A, Q$ jouent un rôle symétrique à $D, R$ ), ainsi $E P=E Q$, donc $E R=E Q: E$ est sur la médiatrice de $(Q R)$.
Ainsi la médiatrice de ( $Q R$ ) est ( $E P$ ), donc ( $E P$ ) et $(Q R)$ sont perpendiculaires.
Commentaire des correcteurs : L'exercice est très bien réussi.
|
{
"exam": "French_envois",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-5.jsonl",
"solution_match": "## Solution de l'exercice 5",
"tier": "T2",
"year": null
}
|
Is it possible to find a block of 1000 consecutive positive integers that contains exactly 5 prime numbers?
|
At first glance, it seems difficult to guarantee exactly 5 prime numbers in a block of 1000 consecutive integers: no elementary arithmetic theorem allows ensuring closely spaced prime numbers without other primes between them. Therefore, we can try to determine how many prime numbers can be found in a block of 1000 consecutive numbers.
First, it is relatively well-known that one can find 1000 consecutive numbers, none of which are prime. Indeed, $1001!+2, \ldots, 1001!+1001$ are not prime: if $2 \leqslant i \leqslant 1001, 1001!+i$ is divisible by $i$ and strictly greater than $i$, so it is not prime.
We can also note that between 1 and 1000 there are many prime numbers: at least more than 5, since $2,3,5,7,11,13$ are prime.
Let $\mathrm{P}(\mathrm{n})$ be the number of prime numbers in the set $\{n, \ldots, n+999\}$. The natural next step after our two previous remarks is to wonder how to evaluate the number $P(n)$ as $n$ ranges over $\mathbb{N}^{*}$. To go from $\{n, \ldots, n+999\}$ to $\{n+1, \ldots, n+1+999\}$, we add $n+1000$ and remove $n$. Thus, we add at most one prime number and remove at most one prime number: we have
$$
\mathrm{P}(\mathrm{n}+1)-\mathrm{P}(\mathrm{n}) \in\{-1,0,1\}
$$
Thus $P$ varies by at most 1, and we know that $P(1)>5>P(1001!+2)$. It seems quite intuitive that this implies there exists an integer $k$ such that $\mathrm{P}(\mathrm{k})=5$, we will prove this.
Let $k$ be the smallest integer such that $\mathrm{P}(\mathrm{k}) \leqslant 5$. We know that $\mathrm{k}>1$, so $\mathrm{P}(\mathrm{k}-1)>5$ by minimality. Thus, we must have $P(k)=P(k-1)-1$ (to have $P(k) \leqslant 5$), so $P(k)>4$. Thus $P(k) \geqslant 5$, and by definition $P(k) \leqslant 5$, so $P(k)=5$.
Thus the answer to the statement is yes: there does exist a block of 1000 consecutive integers with exactly five prime numbers.
Comment from the graders: The exercise was generally well handled, but few students managed to properly formulate the fact that there exist 1000 consecutive composite numbers.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Est-il possible de trouver un bloc de 1000 nombres entiers strictement positifs consécutifs qui contient exactement 5 nombres premiers?
|
A première vue, il semble difficile de garantir exactement 5 nombre premier dans un bloc de 1000 entiers consécutifs : aucun théorème d'arithmétique élémentaire permet de s'assurer d'avoir des nombres premiers rapprochés, mais pas d'autres nombres premier entre eux. On peut donc essayer de se demander combien de nombres premiers on peut trouver dans un bloc de 1000 nombres consécutifs.
Déjà, il est relativement connu qu'on peut trouver 1000 nombres consécutifs dont aucun n'est premier. En effet, $1001!+2, \ldots, 1001!+1001$ ne sont pas premiers : si $2 \leqslant i \leqslant 1001,1001!+i$ est divisible par $i$ et strictement plus grand que $i$, donc il n'est pas premier.
On peut aussi remarquer qu'entre 1 et 1000 il y a beaucoup de nombres premiers : en tout cas strictement plus que 5 , vu que $2,3,5,7,11,13$ sont premiers.
Notons $\mathrm{P}(\mathrm{n})$ le nombre de nombres premiers dans l'ensemble $\{n, \ldots, n+999\}$. L'étape naturelle après nos deux remarques précédentes est de se demander comment évalue le nombre $P(n)$ lorsque $n$ parcourt $\mathbb{N}^{*}$. Pour passer de $\{n, \ldots, n+999\}$ à $\{n+1, \ldots, n+1+999\}$, on rajoute $n+1000$ et on enlève $n$. Ainsi on ajoute au plus un nombre premier, et on enlève au plus un nombre premier : on a donc
$$
\mathrm{P}(\mathrm{n}+1)-\mathrm{P}(\mathrm{n}) \in\{-1,0,1\}
$$
Ainsi $P$ ne varie que de 1 en 1 , et on sait que $P(1)>5>P(1001!+2)$. Il semble assez intuitif que cela implique qu'il existe un entier k tel que $\mathrm{P}(\mathrm{k})=5$, nous allons prouver cela.
Soit $k$ le premier entier tel que $\mathrm{P}(\mathrm{k}) \leqslant 5$. On sait que $\mathrm{k}>1$, donc $\mathrm{P}(\mathrm{k}-1)>5$ par minimalité. Ainsi, on a forcément $P(k)=P(k-1)-1$ (pour avoir $P(k) \leqslant 5$ ), donc $P(k)>4$. Ainsi $P(k) \geqslant 5$, or par définition $P(k) \leqslant 5$, donc $P(k)=5$.
Ainsi la réponse à l'énoncé est oui : il existe bien un bloc de 1000 entiers consécutifs avec exactement cinq entiers premiers.
Commentaire des correcteurs : L'exercice a globalement été bien traité, mais peu d'élèves ont réussi à bien formuler le fait qu'il existe 1000 nombres composés consécutifs.
|
{
"exam": "French_envois",
"problem_label": "14",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-5.jsonl",
"solution_match": "## Solution de l'exercice 6",
"tier": "T2",
"year": null
}
|
It is said that an integer $k>1$ is superb if there exist $\mathrm{m}, \mathrm{n}, \mathrm{a}$ three strictly positive integers such that
$$
5^{\mathrm{m}}+63 \mathrm{n}+49=\mathrm{a}^{\mathrm{k}}
$$
Determine the smallest superb integer.
|
Suppose $k=2$ is superb: there exist three strictly positive integers $\mathrm{m}, \mathrm{n}, \mathrm{a}$ such that $5^{\mathrm{m}}+63 \mathrm{n}+49=a^{2}$. By looking modulo 3, $5^{\mathrm{m}}+1 \equiv 2^{\mathrm{m}}+1 \equiv \mathrm{a}^{2}(\bmod 3)$. The powers of 2 modulo 9 alternate between 2 if m is odd, and 1 if m is even, so $2^{\mathrm{m}}+1$ is either 2 or 0 modulo 3. Since squares modulo 3 are 0 and 1, we deduce that $2^{\mathrm{m}}+1$ is 0 modulo 3, hence $m$ is odd. By looking modulo 7, we get $5^{\mathrm{m}} \equiv \boldsymbol{a}^{2}(\bmod 7)$. The squares modulo 7 are $0,1,2,4$, and the powers of 5 alternate between $1,5,4,6,2,3$. Thus $5^{\mathrm{m}}$ is 0, 1, 2, or 4 if and only if $m$ is 0, 2, or 4 modulo 6, which is impossible since $m$ is odd. Thus $k \neq 2$.
Suppose $k=3$ is superb: there exist three strictly positive integers $\mathrm{m}, \mathrm{n}$, a such that $5^{\mathrm{m}}+63 \mathrm{n}+49=a^{3}$. By looking modulo 7, $5^{\mathrm{m}} \equiv \mathrm{a}^{3}$. The cubes modulo 7 are $0,1,6$. The powers of 5 modulo 7 alternate between $1,5,4,6,2,3$. Thus we get that $m \equiv 0(\bmod 6)$ or $m \equiv 3(\bmod 6)$: in all cases, 3 divides m. We then look modulo 9: we have $5^{\mathrm{m}}+4 \equiv \mathrm{a}^{3}$. Since m is divisible by 3, $5^{m}$ and $a^{3}$ are cubes. The cubes modulo 9 are $0,1,8$. Thus $5^{m}-a^{3}$ can be 0, 1, 2, 7, 8 modulo 9, but not 4, which is contradictory. Thus $k \neq 3$.
Suppose $k=3$ is superb: there exist three strictly positive integers $\mathbf{m}, \mathrm{n}$, a such that $5^{\mathrm{m}}+63 \mathrm{n}+49=a^{4}=\left(a^{2}\right)^{2}$. In particular, 2 is superb, which is contradictory.
Note that 5 is superb: by taking $\mathbf{a}=3$, we have $\mathbf{a}^{\mathrm{k}}=3^{5}=243=5^{1}+63 \times 3+49$ so 5 is superb. Thus 5 is the smallest superb integer.
Comment from the graders: The problem was solved by few students, who did it well.
|
5
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
On dit qu'un entier $k>1$ est superbe s'il existe $\mathrm{m}, \mathrm{n}, \mathrm{a}$ trois entiers strictement positifs tels que
$$
5^{\mathrm{m}}+63 \mathrm{n}+49=\mathrm{a}^{\mathrm{k}}
$$
Déterminer le plus petit entier superbe.
|
Supposons que $k=2$ est superbe : il existe trois entiers strictement positifs $\mathrm{m}, \mathrm{n}, \mathrm{a}$ tels que $5^{\mathrm{m}}+63 \mathrm{n}+$ $49=a^{2}$. En regardant modulo $3,5^{\mathrm{m}}+1 \equiv 2^{\mathrm{m}}+1 \equiv \mathrm{a}^{2}(\bmod 3)$. Or les puissances de 2 modulo 9 valent alternativement 2 si m est impair, puis 1 si m est pair, donc $2^{\mathrm{m}}+1$ vaut soit 2 soit 0 modulo 3 . Comme les carrés modulo 3 sont 0 et 1 , on en déduit que $2^{\mathrm{m}}+1$ vaut 0 modulo 3 , donc que $m$ est impair. En regardant modulo 7 , on obtient que $5^{\mathrm{m}} \equiv \boldsymbol{a}^{2}(\bmod 7)$. Or les carrés modulo 7 sont $0,1,2,4$, et les puissances de 5 alternent entre $1,5,4,6,2,3$. Ainsi $5^{\mathrm{m}}$ vaut $0,1,2$ ou 4 si et seulement si $m$ vaut 0,2 ou 4 modulo 6 , ce qui est impossible car $m$ est pair. Ainsi $k \neq 2$.
Supposons que $\mathrm{k}=3$ est superbe : il existe trois entiers strictement positifs $\mathrm{m}, \mathrm{n}$, a tels que $5^{\mathrm{m}}+63 \mathrm{n}+$ $49=a^{3}$. En regardant modulo $7,5^{\mathrm{m}} \equiv \mathrm{a}^{3}$. Or les cubes modulo 7 sont $0,1,6$. Et les puissances de 5 modulo 7 alternent entre $1,5,4,6,2,3$. Ainsi on obtient que $m \equiv 0(\bmod 6)$ ou $m \equiv 3(\bmod 6)$ : dans tous les cas 3 divise m . On regarde alors modulo 9 : on a $5^{\mathrm{m}}+4 \equiv \mathrm{a}^{3}$. Or comme m est divisible par 3 , $5^{m}$ et $a^{3}$ sont des cubes. Les cubes modulo 9 sont $0,1,8$. Ainsi $5^{m}-a^{3}$ peut valoir $0,1,2,7,8$ modulo 9 , mais pas 4 ce qui est contradictoire. Ainsi $k \neq 3$.
Supposons que $k=3$ est superbe : il existe trois entiers strictement positifs $\mathbf{m}, \mathrm{n}$, a tels que $5^{\mathrm{m}}+63 \mathrm{n}+$ $49=a^{4}=\left(a^{2}\right)^{2}$. En particulier, 2 est superbe ce qui est contradictoire.
Notons que 5 est superbe : en prenant $\mathbf{a}=3$, on a $\mathbf{a}^{\mathrm{k}}=3^{5}=243=5^{1}+63 \times 3+49$ donc 5 est superbe. Ainsi 5 est le plus petit entier superbe.
Commentaire des correcteurs : L'exercice a été traité par peu d'élèves, qui l'ont bien résolu.
|
{
"exam": "French_envois",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-5.jsonl",
"solution_match": "## Solution de l'exercice 7",
"tier": "T2",
"year": null
}
|
Let $x, y, z$ be three real numbers satisfying $x+y+z=2$ and $xy+yz+zx=1$. Determine the maximum value that $x-y$ can take.
|
Let $(x, y, z)$ be a triplet satisfying the statement. By swapping $x$ and the maximum of the triplet, and then $z$ and the minimum of the triplet, we can assume $x \geqslant z \geqslant y$, while increasing $x-y$.
Since $x+y+z=2$, we have $4=(x+y+z)^{2}=x^{2}+y^{2}+z^{2}+2(x y+y z+x z)=x^{2}+y^{2}+z^{2}+2$, thus $x^{2}+y^{2}+z^{2}=2$.
In particular, $(x-y)^{2}+(y-z)^{2}+(x-z)^{2}=2\left(x^{2}+y^{2}+z^{2}\right)-2(x y+y z+x z)=2$. By the arithmetic-quadratic inequality, $(x-z)^{2}+(z-y)^{2} \geqslant \frac{(x-z+z-y)^{2}}{2}=\frac{(x-y)^{2}}{2}$, so $2 \geqslant(x-y)^{2}+\frac{(x-y)^{2}}{2}=\frac{3(x-y)^{2}}{2}$, thus $(x-y) \leqslant \frac{2}{\sqrt{3}}$.
Let's try to show that this value is attainable. If we have $x-y=\frac{2}{\sqrt{3}}$, then we have equality in the arithmetic-quadratic inequality: thus $x-z=z-y$, so since their sum is $x-y$, $x-z=z-y=\frac{1}{\sqrt{3}}$. In particular, since $x+y+z=3 z+(z-x)+(z-y)=3 z$, we have $z=\frac{2}{3}, x=\frac{2}{3}+\frac{1}{\sqrt{3}}$ and $y=\frac{2}{3}-\frac{1}{\sqrt{3}}$. Conversely, for these values of $x, y, z$, we indeed have:
$-x+y+z=3 \times \frac{2}{3}=2$
$-x y+y z+z x=x y+(x+y) z=\left(\frac{2}{3}+\frac{1}{\sqrt{3}}\right)\left(\frac{2}{3}-\frac{1}{\sqrt{3}}+\frac{4}{3} \times \frac{2}{3}=\frac{4}{9}-\frac{1}{3}+\frac{8}{9}=\frac{9}{9}=1\right)$
$-x-y=2 \times \frac{1}{\sqrt{3}}=\frac{2}{\sqrt{3}}$
Thus $(x, y, z)$ satisfies the conditions of the statement, and $x-y=\frac{2}{\sqrt{3}}$, so the maximum value that $x-y$ can take is $\frac{2}{\sqrt{3}}$.
Graders' comment: The exercise was not approached much. The main mistake is forgetting to find $x, y, z$ for which equality holds.
|
\frac{2}{\sqrt{3}}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Soit $x, y, z$ trois nombres réels vérifiant $x+y+z=2$ et $x y+y z+z x=1$. Déterminer la valeur maximale que peut prendre $x-y$.
|
Soit ( $x, y, z$ ) un triplet vérifiant l'énoncé. Quitte à échanger $x$ et le maximum du triplet, puis $z$ et le minimum du triplet, on peut supposer $x \geqslant z \geqslant y$, tout en augmentant $x-y$.
Comme $x+y+z=2$, on a $4=(x+y+z)^{2}=x^{2}+y^{2}+z^{2}+2(x y+y z+x z)=x^{2}+y^{2}+z^{2}+2$, donc $x^{2}+y^{2}+z^{2}=2$.
En particulier $(x-y)^{2}+(y-z)^{2}+(x-z)^{2}=2\left(x^{2}+y^{2}+z^{2}\right)-2(x y+y z+x z)=2$. Or par inégalité arithmético quadratique, $(x-z)^{2}+(z-y)^{2} \geqslant \frac{(x-z+z-y)^{2}}{2}=\frac{(x-y)^{2}}{2}$, donc $2 \geqslant(x-y)^{2}+\frac{(x-y)^{2}}{2}=$ $\frac{3(x-y)^{2}}{2}$, donc $(x-y) \leqslant \frac{2}{\sqrt{3}}$.
Essayons de montrer que cette valeur est atteignable. Si on a $x-y=\frac{2}{\sqrt{3}}$, alors on a égalité dans l'inégalité arithmético quadratique : ainsi $x-z=z-y$, donc comme leur somme vaut $x-y, x-z=z-y=\frac{1}{\sqrt{3}}$. En particulier, comme $x+y+z=3 z+(z-x)+(z-y)=3 z$, on a $z=\frac{2}{3}, x=\frac{2}{3}+\frac{1}{\sqrt{3}}$ et $y=\frac{2}{3}-\frac{1}{\sqrt{3}}$. Réciproquement, pour ces valeurs de $x, y, z$, on a bien :
$-x+y+z=3 \times \frac{2}{3}=2$
$-x y+y z+z x=x y+(x+y) z=\left(\frac{2}{3}+\frac{1}{\sqrt{3}}\right)\left(\frac{2}{3}-\frac{1}{\sqrt{3}}+\frac{4}{3} \times \frac{2}{3}=\frac{4}{9}-\frac{1}{3}+\frac{8}{9}=\frac{9}{9}=1\right.$
$-x-y=2 \times \frac{1}{\sqrt{3}}=\frac{2}{\sqrt{3}}$
Ainsi $(x, y, z)$ vérifie les conditions de l'énoncé, et $x-y=\frac{2}{\sqrt{3}}$, donc la valeur maximale que peut prendre $x-y$ est $\frac{2}{\sqrt{3}}$.
Commentaire des correcteurs : L'exercice a été assez peu abordé. La principale erreur est d'oublier de trouver des $x, y, z$ pour lesquels on a égalité.
|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "\nExercice 8.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-5.jsonl",
"solution_match": "\nSolution de l'exercice 8",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle and $I$ the center of the inscribed circle. We denote $D$ and $E$ as the feet of the angle bisectors from $B$ and $C$. Let $X$ be the intersection of the reflections of $(AB)$ and $(AC)$ with respect to $(CE)$ and $(BD)$. Show that the lines $(XI)$ and $(BC)$ are perpendicular.
|
Let $Y$ and $Z$ be the intersections of $(DX)$ and $(EX)$ with the line $(BC)$. We will show that the triangle $ZXY$ is isosceles at $X$ and that $I$ is the center of its inscribed circle. If we manage to prove these properties, the conclusion of the exercise will follow. Indeed, the line $(XI)$ is then the bisector of the isosceles triangle $XYZ$ at $X$, and therefore it is also the altitude.
Let $\omega$ be the inscribed circle of triangle $ABC$. We know that the line $(AB)$ is tangent to $\omega$. Since the line $(CI)$ is an axis of symmetry of $\omega$, it follows that the line $(XE)$ is also tangent to $\omega$. Similarly, the line $(DX)$ is tangent to $\omega$. By definition, the line $(YZ)$ is the line $(BC)$ and is therefore also tangent to $\omega$. This shows that $\omega$ is the inscribed circle of triangle $XYZ$. In particular, the line $(XI)$ is the bisector from $X$.
We complete the proof of the exercise by showing that $\widehat{XZY} = \widehat{XYZ}$. Let $\alpha$ be the angle at $A$ in triangle $ABC$. We then have,
\[
\begin{aligned}
\widehat{\mathrm{XZY}} & = \widehat{\mathrm{EZC}} \\
& = \widehat{\mathrm{XEC}} - \widehat{\mathrm{ECZ}} \\
& = \widehat{\mathrm{AEC}} - \widehat{\mathrm{ECA}} \\
& = \widehat{\mathrm{EAC}} = \alpha.
\end{aligned}
\]
Similarly, $\widehat{XYZ} = \alpha$, which shows that triangle $ZYX$ is isosceles at $X$ and concludes the proof of the exercise.
Comment from the graders: This geometry problem was approached by very few students. Most of them succeeded well, using various methods. The simplest methods of resolution in this problem were those that made the most use of symmetry arguments. One can only recommend, when faced with a figure that presents such symmetries, to try to exploit them.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $I$ le centre du cercle inscrit. On note $D$ et $E$ les pieds des bissectrices issues de $B$ et $C$. Soit $X$ l'intersection des symétriques de $(A B)$ et $(A C)$ par rapport à $(C E)$ et $(B D)$. Montrer que les droites (XI) et (BC) sont perpendiculaires.
|
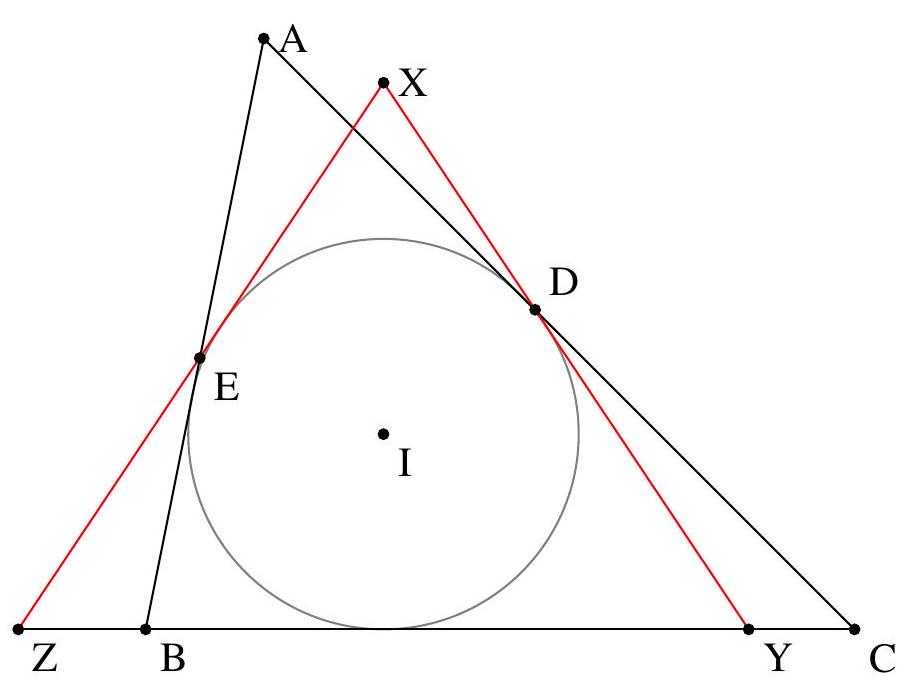
Notons $Y$ et $Z$ les intersections respectives de (DX) et (EX) avec la droite (BC). On va montrer que le triangle ZXY est isocèle en $X$ et que I est le centre de son cercle inscrit. Si on arrive à montrer ces propriétés, la conclusion de l'exercice suivrait. En effet, la droite (XI) est alors la bissectrice du triangle $X Y Z$ isocèle en $X$, donc en également la hauteur.
Soit $\omega$ le cercle inscrit du triangle $A B C$, on sait donc que la droite $(A B)$ est tangente à $\omega$, comme la droite $(\mathrm{CI})$ est un axe de symétrie de $\omega$ il suit que la droite (XE) est également tangente à $\omega$. De la même manière, la droite (DX) est tangente à $\omega$. Par définition la droite (YZ) est la droite (BC) donc également tangente à $\omega$. Cela montre que $\omega$ est le cercle inscrit du triangle XYZ. En particulier, la droite (XI) est la bissetrice issue de $X$.
On finit la preuve de l'exercice en montrant que $\widehat{X Z Y}=\widehat{X Y Z}$. On note $\alpha$ l'angle en $A$ dans le triangle ABC. On a alors,
$$
\begin{aligned}
\widehat{\mathrm{XZY}} & =\widehat{\mathrm{EZC}} \\
& =\widehat{\mathrm{XEC}}-\widehat{\mathrm{ECZ}} \\
& =\widehat{\mathrm{AEC}}-\widehat{\mathrm{ECA}} \\
& =\widehat{\mathrm{EAC}}=\alpha .
\end{aligned}
$$
De la même manière $\widehat{X Y Z}=\alpha$ ce qui montre bien que le triangle ZYX est isocèle en $X$ et conclut la preuve de l'exercice.
Commentaire des correcteurs : Cet exercice de géométrie a été abordé par très peu d'élèves. La plupart d'entre eux l'ont bien réussi, par diverses méthodes. Les méthodes de résolution les plus simples, dans cet exercice, étaient celles qui faisaient le plus appel aux arguments de symétrie. On ne peut que conseiller, face à une figure qui présente de telles symétries, de chercher à les exploiter.
## Exercices Seniors
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-5.jsonl",
"solution_match": "\nSolution de l'exercice 9",
"tier": "T2",
"year": null
}
|
Find all triplets of positive integers $(x, y, z)$ satisfying the equation
$$
x! + 2^y = z!
$$
|
Let $(x, y, z)$ be a solution triplet.
First, we aim to reduce the number of values that $x$ can take. Note that $x! < z!$ so $x < z$. In particular, $x!$ divides $z!$ and $x!$, so $x!$ divides $z! - x! = 2^y$. Suppose, for the sake of contradiction, that $x \geq 3$, in this case 3 divides $x!$ but does not divide $2^y$, which makes it impossible for $x!$ to divide $2^y$. Thus, $x = 0, 1$ or 2.
We now perform a case disjunction between $x! = 1$ so $x = 0$ or 1, or $x! = 2$ so $x = 2$.
- Case $x = 0$ or 1: the equation becomes $1 + 2^y = z!$. We then perform a second case disjunction:
- Case $y = 0$: we find $z = 2$. Conversely, $(0,0,2)$ and $(1,0,2)$ are indeed solutions.
- Case $y \geq 1$: thus $1 + 2^y \geq 3$ and $1 + 2^y$ is odd. However, $z!$ is even if $z \geq 2$, and equals 0 or 1 if $z = 1$, neither of which can satisfy our equation. Thus, if we assume $y \geq 1$, there are no solutions.
- **Case** $x = 2$: We distinguish further according to the values of $y$:
- Case $y = 0$: we get $3 = z!$ which has no solutions (since $2! < 3 < 3!$).
- Case $y = 1$: we get $4 = z!$ which has no solutions (since $2! < 3 < 3!$).
- Case $y \geq 2$: we get that 2 divides $2^y + 2$, but 4 does not divide $2^y + 2$. Thus, 2 divides $z!$ but 4 does not divide $z!$, so $z = 2$ or 3. Since $2^y + 2 \geq 4 + 2 = 6$, we get $z = 3$, so $2 + 2^y = 6$, thus $2^y = 4$ and $y = 2$. Conversely, $(2,2,3)$ is indeed a solution because $2 + 4 = 6$.
Thus, the solutions are the triplets $(0,0,2)$, $(1,0,2)$, and $(2,2,3)$.
Comment from the graders: Almost all students who attempted the problem understood it well. However, solving the equation without errors was more challenging: many students forgot some cases (typically the case $x = 0$; it is also worth noting that $0! = 1$), made hasty generalizations (for example, that $1 + 2^{y-1}$ is always odd - which is true only if $y \geq 2$, and the case $y \leq 1$ must be treated), or forgot to verify that the triplets they found were solutions (a common mistake; it is always necessary to do so, even if it only involves saying "we verify conversely that [...] are indeed solutions"). Some students did not justify certain more general arguments ("the only factorials with a difference of 1 are 2 and 1", or "the only factorials that are powers of 2 are 2 and 1"), or did so very vaguely (by talking about "rate of growth", which is not applicable here). Such statements must always be justified (especially since the argument can be made in one or two sentences). Finally, a surprisingly large number of papers contain minor inconsistencies or oversights, generally not penalized: we invite candidates to carefully proofread their papers before submitting them.
|
(0,0,2), (1,0,2), (2,2,3)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Trouver toutes les triplets d'entiers positifs $(x, y, z)$ satisfaisant l'équation
$$
x!+2^{y}=z!
$$
|
Soit ( $x, y, z$ ) un triplet solution.
On cherche dans un premier temps à réduire le nombre de valeurs que $x$ peut prendre. Pour ce faire notons que $x!<z$ ! donc $x<z$. En particulier, $x$ ! divise $z$ ! et $x$ !, donc $x$ ! divise $z$ ! $-x!=2^{y}$. Supposons par l'absurde que $x \geqslant 3$, dans ce cas 3 divise $x$ ! mais ne divise pas $2^{y}$, ce qui rend impossible le fait que $x$ ! divise $2^{y}$. Ainsi $x=0,1$ ou 2 .
On effectue maintenant une disjonction de cas entre $x!=1$ donc $x=0$ ou 1 , ou bien $x!=2$ donc $x=2$.
- Cas $x=0$ ou 1 : l'équation devient $1+2^{y}=z$ !. On effectue alors une deuxième disjonction de cas
- Cas $y=0$ : on trouve $z=2$. Réciproquement, $(0,0,2)$ et $(1,0,2)$ sont bien solution.
- Cas $y \geqslant 1$ : ainsi $1+2^{y} \geqslant 3$ et $1+2^{y}$ est impair. Or $z$ ! est pair si $z \geqslant 2$, et vaut 0 ou 1 si $z=1$, aucun des deux cas ne peut donc satisfaire notre équation. Ainsi, si on suppose que $y \geqslant 1$, il n'y a pas de solution.
- $\boldsymbol{C a s} x=2$ : On distingue encore selon les valeurs de $y$ :
- Cas $y=0$ : on obtient $3=z$ ! qui n'a pas de solutions (car $2!<3<3$ !).
- Cas $y=1$ : on obtient $4=z$ ! qui n'a pas de solutions (car $2!<3<3$ !).
- Cas $y \geqslant 2$ : on obtient que 2 divise $2^{y}+2$, mais que 4 ne divise pas $2^{y}+2$. Ainsi 2 divise $z$ ! mais 4 ne divise pas $z$ !, donc $z=2$ ou 3 . Comme de plus $2^{y}+2 \geqslant 4+2=6$, on obtient $z=3$, donc $2+2^{y}=6$, donc $2^{y}=4$ donc $y=2$. Réciproquement, $(2,2,3)$ est bien solution car $2+4=6$.
Ainsi les solutions sont les triplets $(0,0,2),(1,0,2)$ et $(2,2,3)$.
Commentaire des correcteurs : La quasi-totalité des élèves ayant traité l'exercice l'ont bien compris. Mais résoudre l'équation sans faute était plus compliqué : bien des élèves ont oublié des cas (typiquement, le cas $x=0$; on rappelle d'ailleurs que $0!=1$ ), fait des généralisations hâtives (par exemple que $1+2^{y-1}$ était toujours impair - ce qui n'est vrai que si $y \geqslant 2$, et il faut traiter le cas $y \leqslant 1$ ), ou oublié de vérifier que les triplets qu'ils ont trouvés étaient des solutions (faute assez répandue; il faut toujours le faire, même s'il ne s'agit que de dire "on vérifie réciproquement que [...] sont bien des solutions"). Quelques élèves n'ont pas justifié certains arguments plus généraux ("les seules factorielles de différence 1 sont 2 et 1 ", ou "les seules factorielles qui sont des puissances de 2 sont 2 et 1 "), ou l'ont fait très vaguement (en parlant de "vitesse de croissance", qui n'est pas un concept applicable ici). Ce genre d'affirmation doit toujours être justifié (surtout dans la mesure où l'argument tient en une ou deux phrases). Enfin, un nombre surprenant de copies contient de légères incohérences ou des étourderies, en général non sanctionnées : nous invitons les candidats à bien se relire avant d'envoyer les copies.
|
{
"exam": "French_envois",
"problem_label": "10",
"problem_match": "\nExercice 10.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-5.jsonl",
"solution_match": "## Solution de l'exercice 10",
"tier": "T2",
"year": null
}
|
Félix wants to color the integers from 1 to 2023 such that if $a, b$ are two distinct integers between 1 and 2023 and $a$ divides $\mathbf{b}$, then $a$ and $b$ are of different colors. What is the minimum number of colors Félix needs?
|
We can try to color the numbers greedily: 1 can be colored with a color we denote as $a$, 2 and 3 with the same color $b$ (but not color $a$), then 4 and 6 with color $c$ (we can also color 5 and 7 with color $c$), etc. It seems that an efficient coloring is to color all numbers $n$ such that $2^{k} \leqslant n<2^{k+1}$ with color $k+1$, as long as $n \leqslant 2023$. Thus, we color $[1,2[$ with color $1$, $[2,4[$ with color $2$, ..., $[1024,2023]$ with color $11$. If $a \neq b$ are of the same color $k \in \{1, \ldots, 11\}$, then $0<\frac{a}{b}<\frac{2^{k+1}}{2^{k}}=2$, so if $b$ divides $a$, then $\frac{a}{b}$ is an integer and must be 1. Thus, $a=b$, which is a contradiction. Therefore, our coloring satisfies the condition of the problem and requires 11 colors.
Conversely, if a coloring satisfies the problem statement, the numbers $2^{0}=1, 2^{1}, \ldots, 2^{10}$ are between 1 and 2023, and if we take $a \neq b$ among these 11 numbers, either $a$ divides $b$ or $b$ divides $a$. Thus, these 11 numbers must be of different colors. Therefore, at least 11 colors are needed.
Thus, the minimum number of colors required is 11.
Comment from the graders: The exercise is very well done. As in any problem where we need to find the minimum number such that, it is important to split the proof into two parts: why $n=11$ colors are sufficient, and why if $n \leqslant 10$, $n$ colors are not sufficient.
|
11
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Félix souhaite colorier les entiers de 1 à 2023 tels que si $a, b$ sont deux entiers distincts entre 1 et 2023 et a divise $\mathbf{b}$, alors a et $b$ sont de couleur différentes. Quel est le nombre minimal de couleur dont Félix a besoin?
|
On peut essayer de colorier de manière gloutonne les nombres : 1 peut être colorié d'une couleur qu'on note $a$, 2 et 3 de la même couleur $b$ (mais pas de la couleur $a$ ), puis 4,6 de la couleur $c$ (on peut aussi colorier 5 et 7 de la couleur c), etc. Il semble donc qu'une coloriation performante soit pour tout $k$ de colorier les nombres $n$ vérifiant $2^{k} \leqslant n<2^{k+1}$ de la couleur $k+1$, tant que $n \leqslant 2023$. Ainsi on colorie $[1,2[$ de couleur $1,[2,4[$ de couleur $2, \ldots,[1024,2023]$ de couleur 11 . Si $a \neq b$ sont de la même couleur $\mathrm{k} \in\{1, \ldots, 11\}$ alors $0<\frac{\mathrm{a}}{\mathrm{b}}<\frac{2^{k+1}}{2^{k}}=2$, donc si b divise a , alors $\frac{\mathrm{a}}{\mathrm{b}}$ est entier donc vaut 1 . On a alors $\mathrm{a}=\mathrm{b}$ ce qui est contradictoire. Ainsi notre coloriage vérifie bien la condition de l'énoncé, et nécessite 11 couleurs.
Réciproquement si un coloriage vérifie l'énoncé, les nombres $2^{0}=1,2^{1}, \ldots, 2^{10}$ sont entre 1 et 2023 , et si on prend $a \neq b$ parmi ces 11 nombres, soit $a$ divise $b$, soit $b$ divise $a$. Ainsi ces 11 nombres sont de couleurs différentes. Il faut donc au moins 11 couleurs.
Ainsi le nombre minimal de couleurs requises est 11.
Commentaire des correcteurs : L'exercice est très bien réussi. Comme dans tout exercice où on demande de trouver le nombre minimal tel que, il est important de découper la preuve en deux parties : pourquoi $n=11$ couleurs suffisent, et pourquoi si $n \leqslant 10, n$ couleurs ne suffisent pas.
|
{
"exam": "French_envois",
"problem_label": "11",
"problem_match": "\nExercice 11.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-5.jsonl",
"solution_match": "## Solution de l'exercice 11",
"tier": "T2",
"year": null
}
|
Let $A, B, C, D$ and $E$ be five points in this order on a circle such that $A E=D E$. Let $P$ be the point of intersection of $(A C)$ and $(B D)$. Let $Q$ be the point on the ray $[B A)$ such that $A Q=D P$. Let $R$ be the point on the ray $[C D)$ such that $D R=A P$. Show that the lines $(P E)$ and $(Q R)$ are perpendicular.
|
In the case of the following figure:
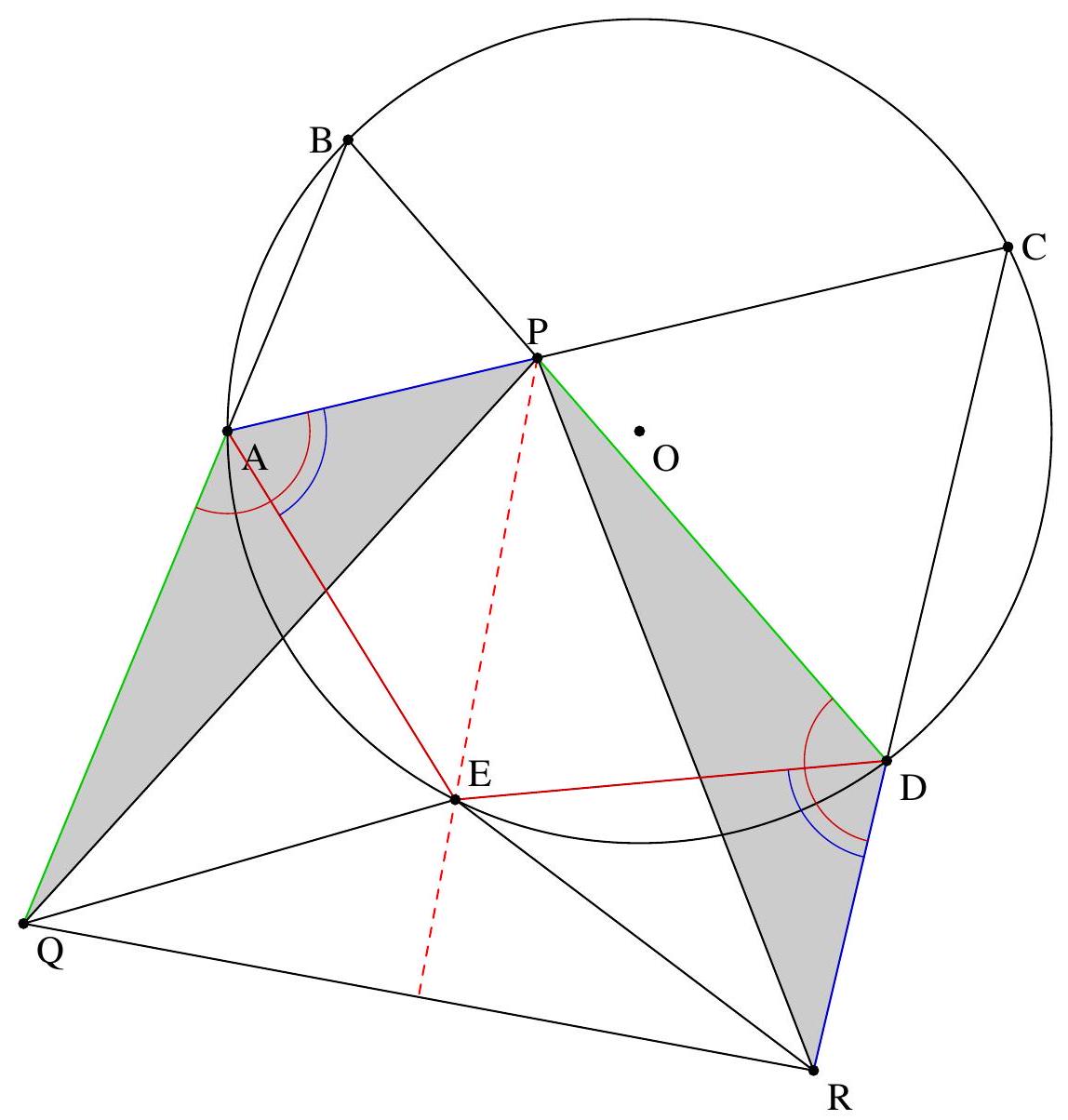
In this statement, we have many equal lengths ($A Q = D P$, $D R = A P$, $A E = D E$). As shown in the figure, it is helpful to color the equal lengths to identify potential congruent triangles and make progress in the problem.
The triangles DRP and AQP appear to be congruent: let's prove it. First, note that $\mathrm{DR} = A Q$ and $\mathrm{DP} = A R$ by hypothesis. Additionally, $\widehat{\mathrm{RDP}} = 180 - \widehat{\mathrm{CDP}} = 180 - \widehat{\mathrm{CDB}} = 180 - \widehat{\mathrm{CAB}} = 180 - \widehat{\mathrm{PAB}} = \widehat{\mathrm{PAQ}}$. Thus, the triangles DRP and AQP are congruent.
In particular, $P Q = P R$, so $P$ lies on the perpendicular bisector of $(Q R)$.
The triangles DER and AEP also appear to be congruent: let's prove it. We have $D E = A E$ and $D R = A P$. Additionally, $\widehat{\mathrm{EDR}} = 180 - \widehat{\mathrm{EDC}} = \widehat{\mathrm{CAE}} = \widehat{\mathrm{PAE}}$. Thus, the triangles DER and AEP are congruent, and $E P = E R$.
Similarly, the triangles AEQ and DEP are congruent (since $A, Q$ play a symmetric role to $D, R$), so $E P = E Q$, and thus $E R = E Q$: $E$ lies on the perpendicular bisector of $(Q R)$.
Therefore, the perpendicular bisector of $(QR)$ is $(EP)$, so $(EP)$ and $(QR)$ are perpendicular.
Comment from the graders: This problem was successfully solved by a large majority of students who attempted it. The main issue was imprecision in vocabulary: two triangles with all equal lengths are called congruent rather than equal or identical. The concept of similar triangles is weaker than the previous one and only indicates the equality of angles (and thus also the ratios of lengths, but not the lengths themselves).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $A, B, C, D$ et $E$ cinq points dans cet ordre sur un cercle tels que $A E=D E$. Soit $P$ le point d'intersection de ( $A C)$ et $(B D)$. Soit $Q$ le point de la demi-droite $[B A)$ tel que $A Q=D P$. Soit $R$ le point de la demi-droite [CD) tel que $D R=A P$. Montrer que les droites $(P E)$ et $(Q R)$ sont perpendiculaires.
|
On se place dans le cas de la figure suivante :

Dans cet énoncé on a de nombreuses égalités de longueur ( $A Q=D P, D R=A P, A E=D E$. Comme sur la figure, il ne faut pas hésiter à colorier les longueurs égales pour voir des potentiels triangles isométriques, et avancer dans le problème).
Les triangles DRP et $A Q P$ ont l'air d'être isométriques : prouvons-le. Notons déjà que $\mathrm{DR}=A Q$ et $\mathrm{DP}=A R$ par hypothèse. De plus $\widehat{\mathrm{RDP}}=180-\widehat{\mathrm{CDP}}=180-\widehat{\mathrm{CDB}}=180-\widehat{\mathrm{CAB}}=180-\widehat{\mathrm{PAB}}=$ $\widehat{P A Q}$. Ainsi les triangles DRP et AQP sont isométriques.
En particulier $P Q=P R$, donc $P$ est sur la médiatrice de $(Q R)$.
Les triangles DER et $A E P$ ont l'air d'être isométriques : prouvons-le. On a $D E=A E$ et $D R=A P$. De plus $\widehat{\mathrm{EDR}}=180-\widehat{\mathrm{EDC}}=\widehat{\mathrm{CAE}}=\widehat{\mathrm{PAE}}$. Ainsi les triangles DER et AEP sont isométriques et $E P=E R$.
De même les triangles $A E Q$ et $D E P$ sont isométriques (car $A, Q$ jouent un rôle symétrique à $D, R$ ), ainsi $E P=E Q$, donc $E R=E Q: E$ est sur la médiatrice de $(Q R)$.
Ains i la médiatrice de (QR) est (EP), donc (EP) et $(Q R)$ sont perpendiculaires.
Commentaire des correcteurs : Cet exercice a été réussi par une large majorité des élèves l'ayant traité. Le principal problème était une imprécision dans le vocabulaire : deux triangles dont toutes les longueurs
sont égales sont dits isométriques plutôt qu'égaux ou identiques. Quant à la notion de triangles semblables, elle est plus faible que la précédente, et traduit simplement l'égalité des angles (et donc aussi des rapports de longueurs, mais pas des longueurs elles-mêmes).
|
{
"exam": "French_envois",
"problem_label": "12",
"problem_match": "\nExercice 12.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-5.jsonl",
"solution_match": "## Solution de l'exercice 12",
"tier": "T2",
"year": null
}
|
It is said that a polynomial $P$ is fantastic if there exist real numbers $\mathrm{a}_{0}, \ldots, \mathrm{a}_{2022}$ such that
$$
P(X)=X^{2023}+a_{2022} X^{2022}+\cdots+a_{1} X+a_{0}
$$
if it has 2023 roots $r_{1}, \ldots, r_{2023}$ (not necessarily distinct) in $[0,1]$, and if $P(0)+P(1)=0$. Determine the maximum value that $\mathrm{r}_{1} \cdot \mathrm{r}_{2} \cdots \mathrm{r}_{2023}$ can take for a fantastic polynomial.
|
The answer is $2^{-2023}$, we will show this in two steps: first, we will show that we cannot find a polynomial with a larger value, and second, we will exhibit a polynomial that satisfies the conditions of the problem and whose product of roots is indeed equal to $2^{-2023}$.
By hypothesis, we can rewrite $P(X)=\prod_{k=1}^{2023}\left(X-r_{k}\right)$. In particular, $P(0)=-\prod_{k=1}^{2023} r_{k}$ and $P(1)=\prod_{k=1}^{2023}\left(1-r_{k}\right)$. The hypothesis $P(0)+P(1)=0$ becomes:
$$
\prod_{k=1}^{2023}\left(1-r_{k}\right)=\prod_{k=1}^{2023} r_{k}=r_{1} \cdot r_{2} \cdots r_{2023}
$$
Thus, since for all $k, r_{k} \geqslant 0$ and $1-r_{k} \geqslant 0$, by the arithmetic-geometric mean inequality,
$$
\left(r_{1} \cdot r_{2} \cdots r_{2023}\right)^{2}=\prod_{k=1}^{2023}\left(1-r_{k}\right) r_{k} \leqslant \prod_{k=1}^{2023}\left(\frac{\left(1-r_{k}\right)+r_{k}}{2}\right)^{2}=\frac{1}{4^{2023}}
$$
Thus, $r_{1} \cdot r_{2} \cdots r_{2023} \leqslant 2^{-2023}$.
Furthermore, if $P(X)=\left(X-\frac{1}{2}\right)^{2023}$, then $P$ is a monic polynomial of degree 2023, has 2023 roots in $[0,1]$, and satisfies $P(0)+P(1)=\left(-\frac{1}{2}\right)^{2023}+\left(\frac{1}{2}\right)^{2023}=0$, so $P$ is fantastic. The product of its roots is $2^{-2023}$. Therefore, the maximum value that $r_{1} \cdot r_{2} \cdots r_{2023}$ can take for a fantastic polynomial is $2^{-2023}$.
Graders' comments: The exercise required finding the maximum value that the product of roots could take for a particular class of polynomials. Almost all students found the case achieving the maximum (and thus its value), and a satisfactory proportion of these students completed the proof, generally by applying the AM-GM inequality. Vieta's formulas seem to be well mastered but were absolutely not necessary for solving the problem. A key takeaway: the AM-GM inequality is often a judicious inequality to show that a product of positive reals is maximal when all its terms are equal.
|
2^{-2023}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
On dit qu'un polynôme $P$ est fantabuleux s'il existe des réels $\mathrm{a}_{0}, \ldots, \mathrm{a}_{2022}$ tel que
$$
P(X)=X^{2023}+a_{2022} X^{2022}+\cdots+a_{1} X+a_{0}
$$
s'il a 2023 racines $r_{1}, \ldots, r_{2023}$ (non nécessairement distinctes) dans $[0,1]$, et si $P(0)+P(1)=0$. Déterminer la valeur maximale que peut prendre $\mathrm{r}_{1} \cdot \mathrm{r}_{2} \cdots \mathrm{r}_{2023}$ pour un polynôme fantabuleux.
|
La réponse est $2^{-2023}$, on va montrer cela en deux temps, dans un premier temps on va montrer que l'on ne peut pas trouver de polynôme avec une valeur plus grand et dans un second temps exhiber un polynôme qui vérifie les conditions de l'énoncé et dont le produit de racine est bien égal à $2^{-2023}$.
Notons que par hypothèse, on peut réécrire $P(X)=\prod_{k=1}^{2023}\left(X-r_{k}\right)$. En particulier, $P(0)=-\prod_{k=1}^{2023} r_{k}$ et $\mathrm{P}(1)=\prod_{\mathrm{k}=1}^{2023}\left(1-\mathrm{r}_{\mathrm{k}}\right)$. L'hypothèse $\mathrm{P}(0)+\mathrm{P}(1)=0$ devient :
$$
\prod_{k=1}^{2023}\left(1-r_{k}\right)=\prod_{k=1}^{2023} r_{k}=r_{1} \cdot r_{2} \cdots r_{2023}
$$
Ainsi comme pour tout $k, r_{k} \geqslant 0$ et $1-\mathrm{r}_{\mathrm{k}} \geqslant 0$, par inégalité arithmético-géométrique,
$$
\left(r_{1} \cdot r_{2} \cdots r_{2023}\right)^{2}=\prod_{k=1}^{2023}\left(1-r_{k}\right) r_{k} \leqslant \prod_{k=1}^{2023}\left(\frac{\left(1-r_{k}\right)+r_{k}}{2}\right)^{2}=\frac{1}{4^{2023}}
$$
Ainsi $r_{1} \cdot r_{2} \cdots r_{2023} \leqslant 2^{-2023}$.
Notons de plus que si $\mathrm{P}(\mathrm{X})=\left(\mathrm{X}-\frac{1}{2}\right)^{2023}$, P est bien unitaire de degré 2023, a 2023 racines dans $[0,1]$, vérifie $\mathrm{P}(0)+\mathrm{P}(1)=\left(-\frac{1}{2}\right)^{2023}+\left(\frac{1}{2}\right)^{2023}=0$ donc P est fantabuleux. Le produit de ses racines vaut $2^{-2023}$. Ainsi la valeur maximale que peut prendre $r_{1} \cdot r_{2} \cdots r_{2023}$ pour un polynôme fantabuleux est $2^{-2023}$.
Commentaire des correcteurs: L'exercice demandait de trouver la valeur maximale que pouvait prendre un produit de racines pour une classe de polynômes particuliers. Presque tous les élèves ont trouvé le cas réalisant le maximum (et donc sa valeur), et une proportion satisfaisante de ces élèves ont mené la preuve jusqu'au bout, généralement en appliquant l'IAG. Les relations de Viète semblent bien maitrisées mais n'étaient absolument pas nécessaires à la résolution du problème. Une idée à retenir : l'IAG est souvent une inégalité judicieuse pour montrer qu'un produit de réels positifs est maximal lorsque tous ses termes sont égaux.
|
{
"exam": "French_envois",
"problem_label": "13",
"problem_match": "\nExercice 13.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-5.jsonl",
"solution_match": "## Solution de l'exercice 13",
"tier": "T2",
"year": null
}
|
Is it possible to find a block of 1000 consecutive positive integers that contains exactly 5 prime numbers?
|
At first glance, it seems difficult to guarantee exactly 5 prime numbers in a block of 1000 consecutive integers: no elementary arithmetic theorem allows ensuring closely spaced prime numbers without other prime numbers between them. Therefore, we can try to determine how many prime numbers can be found in a block of 1000 consecutive numbers.
First, it is relatively well-known that one can find 1000 consecutive numbers, none of which are prime. Indeed, $1001!+2, \ldots, 1001!+1001$ are not prime: if $2 \leqslant i \leqslant 1001, 1001!+i$ is divisible by $i$ and strictly greater than $i$, so it is not prime.
We can also note that between 1 and 1000 there are many prime numbers: at least more than 5, since $2, 3, 5, 7, 11, 13$ are prime.
Let $\mathrm{P}(\mathrm{n})$ be the number of prime numbers in the set $\{\mathrm{n}, \ldots, n+999\}$. The natural next step after our two previous remarks is to wonder how to evaluate the number $P(n)$ as $n$ ranges over $\mathbb{N}^{*}$. To go from $\{n, \ldots, n+999\}$ to $\{n+1, \ldots, n+1+999\}$, we add $n+1000$ and remove $n$. Thus, we add at most one prime number and remove at most one prime number: we have
$$
\mathrm{P}(\mathrm{n}+1)-\mathrm{P}(\mathrm{n}) \in\{-1,0,1\} .
$$
Thus $P$ varies by at most 1, and we know that $P(1)>5>P(1001!+2)$. It seems quite intuitive that this implies there exists an integer $k$ such that $\mathrm{P}(\mathrm{k})=5$, we will prove this.
Let $k$ be the smallest integer such that $\mathrm{P}(\mathrm{k}) \leqslant 5$. We know that $\mathrm{k}>1$, so $\mathrm{P}(\mathrm{k}-1)>5$ by minimality. Thus, we must have $P(k)=P(k-1)-1$ (to have $P(k) \leqslant 5$), so $P(k)>4$. Thus $P(k) \geqslant 5$, and by definition $P(k) \leqslant 5$, so $P(k)=5$.
Thus the answer to the statement is yes: there does exist a block of 1000 consecutive integers with exactly five prime numbers.
Comment from the graders: The exercise was very well done by the students who attempted it. A common error I found is in the proof of the existence of 1000 consecutive non-prime numbers. Some students write that $1000!, 1000!+1, \ldots, 1000!+999$ are not prime, although there is no a priori way to see that $1000!+1$ is not prime. Moreover, other students tried to use the prime number theorem, which was not necessarily a good idea, as it involves concepts of sequence equivalents that are not well mastered. Even if this reasoning can be justified, I did not consider it sufficient to say that since the density of prime numbers is zero, there exist 1000 consecutive non-prime numbers.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Est-il possible de trouver un bloc de 1000 nombres entiers strictement positifs consécutifs qui contient exactement 5 nombres premiers?
|
A première vue, il semble difficile de garantir exactement 5 nombre premier dans un bloc de 1000 entiers consécutifs : aucun théorème d'arithmétique élémentaire permet de s'assurer d'avoir des nombres premiers rapprochés, mais pas d'autres nombres premier entre eux. On peut donc essayer de se demander combien de nombres premiers on peut trouver dans un bloc de 1000 nombres consécutifs.
Déjà, il est relativement connu qu'on peut trouver 1000 nombres consécutifs dont aucun n'est premier. En effet, $1001!+2, \ldots, 1001!+1001$ ne sont pas premiers : si $2 \leqslant i \leqslant 1001,1001!+i$ est divisible par $i$ et strictement plus grand que $i$, donc il n'est pas premier.
On peut aussi remarquer qu'entre 1 et 1000 il y a beaucoup de nombres premiers : en tout cas strictement plus que 5 , vu que $2,3,5,7,11,13$ sont premiers.
Notons $\mathrm{P}(\mathrm{n})$ le nombre de nombre premier dans l'ensemble $\{\mathrm{n}, \ldots, n+999\}$. L'étape naturelle après nos deux remarques précédentes est de se demander comment évalue le nombre $P(n)$ lorsque $n$ parcourt $\mathbb{N}^{*}$. Pour passer de $\{n, \ldots, n+999\}$ à $\{n+1, \ldots, n+1+999\}$, on rajoute $n+1000$ et on enlève $n$. Ainsi on ajoute au plus un nombre premier, et on enlève au plus un nombre premier : on a donc
$$
\mathrm{P}(\mathrm{n}+1)-\mathrm{P}(\mathrm{n}) \in\{-1,0,1\} .
$$
Ainsi $P$ ne varie que de 1 en 1 , et on sait que $P(1)>5>P(1001!+2)$. Il semble assez intuitif que cela implique qu'il existe un entier $k$ tel que $\mathrm{P}(\mathrm{k})=5$, nous allons prouver cela.
Soit $k$ le premier entier tel que $\mathrm{P}(\mathrm{k}) \leqslant 5$. On sait que $\mathrm{k}>1$, donc $\mathrm{P}(\mathrm{k}-1)>5$ par minimalité. Ainsi, on a forcément $P(k)=P(k-1)-1$ (pour avoir $P(k) \leqslant 5$ ), donc $P(k)>4$. Ainsi $P(k) \geqslant 5$, or par définition $P(k) \leqslant 5$, donc $P(k)=5$.
Ainsi la réponse à l'énoncé est oui : il existe bien un bloc de 1000 entiers consécutifs avec exactement cinq entiers premiers.
Commentaire des correcteurs : L'exercice a été très réussi par les élèves qui l'ont cherché. Une erreur que j'ai retrouvée souvent est au niveau de la preuve de l'existence de 1000 entiers consécutifs non premiers. Certains écrivent que $1000!, 1000!+1, \ldots, 1000!+999$ ne sont pas premiers, alors que rien ne permet de voir a priori que $1000!+1$ n'est pas premier. Par ailleurs, d'autres élèves ont voulu utilisé le théorème des nombres premiers, ce qui n'était pas forcément une bonne idée, car mettant en jeu des concepts d'équivalents de suite qui ne sont pas bien maîtrisés. Même si ce raisonnement peut être justifié, je n'ai pas jugé suffisant de dire que la densité des nombres premiers étant nulle, il existe 1000 entiers consécutifs tous non premiers.
|
{
"exam": "French_envois",
"problem_label": "14",
"problem_match": "\nExercice 14.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-5.jsonl",
"solution_match": "## Solution de l'exercice 14",
"tier": "T2",
"year": null
}
|
It is said that a strictly positive rational number q is magnificent if there exist four strictly positive integers $a, b, c, d$ such that
$$
\mathrm{q}=\frac{\mathrm{a}^{2021}+\mathrm{b}^{2023}}{\mathrm{c}^{2022}+\mathrm{d}^{2024}}
$$
Does there exist a strictly positive rational number that is not magnificent?
|
The question posed is quite puzzling: it seems difficult to decide whether or not a number can be written in this form. Therefore, we can try to fix a positive rational number of the form \( \frac{r}{s} \) with \( r, s \) being strictly positive integers, and look for suitable \( a, b, c, d \) to have
$$
\frac{r}{s}=\frac{a^{2021}+b^{2023}}{c^{2022}+d^{2024}}
$$
This will at least help us understand whether all rationals are beautiful, or to find a set of rationals that might be non-beautiful. Here, the choice of \( a, b, c, d \) is not clear. The most natural approach is to take \( a = r^{r_a} s^{s_a}, b = r^{r_b} s^{s_b}, c = r^{r_c} s^{s_c} \) and \( d = r^{r_d} s^{s_d} \) with the \( r_i \) and \( s_i \) being positive integers. We then obtain:
$$
\frac{r}{s}=\frac{r^{2021 r_a} s^{2021 s_a} + r^{2023 r_b} s^{2023 s_b}}{r^{2022 r_c} s^{2022 s_c} + r^{2024 r_d} s^{2024 s_d}}
$$
To hope to factorize and simplify this term, the simplest is to have \( 2021 r_a = 2023 r_b \), i.e., to set \( r_b = 2021 r_1 \) and \( r_a = 2023 r_1 \) for some positive integer \( r_1 \). Similarly, we set \( r_c = 2024 r_2 \) and \( r_d = 2022 r_2 \) for some positive integer \( r_2 \), \( s_a = 2023 s_1 \) and \( s_b = 2021 s_1 \) for some positive integer \( s_1 \), and \( s_c = 2024 s_2 \) and \( s_d = 2022 s_2 \) for some positive integer \( r_2 \).
We then have
$$
\frac{r}{s}=\frac{r^{2021 \times 2023 r_1} s^{2021 \times 2023 s_1}}{r^{2022 \times 2024 r_2} s^{2022 \times 2024 s_2}}=r^{2021 \times 2023 r_1 - 2022 \times 2024 r_2} s^{2021 \times 2023 s_1 - 2022 \times 2024 s_2}
$$
Thus, it suffices to find \( r_1, r_2, s_1, s_2 \) positive integers such that \( 2021 \times 2023 r_1 - 2022 \times 2024 r_2 = 1 \) and \( -2021 \times 2023 s_1 + 2022 \times 2024 s_2 = 1 \). For this, it suffices to use Bézout's theorem. Indeed, \( 2021 \times 2023 \) and \( 2022 \times 2024 \) are coprime: if we reason by contradiction by considering \( p \) a prime factor of these two numbers, \( p \) divides two numbers between 2021 and 2024, so it divides their difference, so \( p = 2 \) or 3. But \( 2021 \times 2023 \) is odd and not divisible by 3, so we have a contradiction. Thus, there exist two integers \( e, f \) such that \( 2021 \times 2023 e - 2022 \times 2024 f = 1 \). By adding \( 2022 \times 2024 \) several times to \( e \), and \( 2021 \times 2023 \) the same number of times to \( f \), we can assume \( e, f \) are positive. Similarly, there exist two positive integers \( g \) and \( h \) such that \( -2021 \times 2023 g + 2022 \times 2024 h = 1 \). Setting \( s_1 = g, s_2 = h, r_1 = e, r_2 = f \) gives that \( r / s \) is beautiful: thus, every positive rational number is beautiful.
Comment from the graders: The exercise was very well done by the students who attempted it.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
On dit qu'un nombre rationnel strictement positif q est magnifique s'il existe quatre entiers strictement positifs $a, b, c, d$ tels que
$$
\mathrm{q}=\frac{\mathrm{a}^{2021}+\mathrm{b}^{2023}}{\mathrm{c}^{2022}+\mathrm{d}^{2024}}
$$
Existe-t-il un rationnel strictement positif qui n'est pas magnifique?
|
La question posée est assez déroutante : il a l'air d'être dur de décider ou non si un nombre peut s'écrire de cette forme. On peut donc essayer de se fixe un rationnel strictement positif de la forme $r / s$ avec $r, s$ des entiers strictement positif, et chercher des bons $a, b, c, d$ pour avoir
$$
\frac{r}{s}=\frac{a^{2021}+b^{2023}}{c^{2022}+d^{2024}}
$$
Cela permettra au moins de comprendre si tous les rationnels sont magnifique, ou de trouver un ensemble de rationnels qui pourraient être non magnifique. Ici le choix de $a, b, c, d$ n'est pas clair. Le plus naturel est de prendre $a=r^{r_{a}} \boldsymbol{s}^{s_{a}}, b=r^{r_{b}} s^{s_{b}}, c=r^{r_{c}} \boldsymbol{s}^{s_{c}}$ et $d=r^{r_{d}} \boldsymbol{s}^{s_{d}}$ avec les $r_{i}$ et $s_{i}$ des entiers positifs. On obtient alors :
$$
\frac{\mathrm{r}}{\mathrm{~s}}=\frac{\mathrm{r}^{2021 \mathrm{r}_{\mathrm{a}}} \mathrm{~s}^{2021 \mathrm{~s}_{\mathrm{a}}}+\mathrm{r}^{2023 r_{\mathrm{b}}} \mathrm{~s}^{2023 s_{\mathrm{b}}}}{\mathrm{r}^{2022 r_{\mathrm{c}}} \mathrm{~s}^{2022 s_{\mathrm{c}}}+\mathrm{r}^{2024 \mathrm{r}_{\mathrm{d}}} \mathrm{~s}^{2024 \mathrm{~s}_{\mathrm{d}}}}
$$
Pour espérer factoriser et simplifier ce terme, le plus simple est d'avoir $2021 r_{a}=2023 r_{b}$, i.e. de poser $r_{b}=2021 r_{1}$ et $r_{a}=2023 r_{1}$ pour un certain entier positif $r_{1}$. De même on pose $r_{c}=2024 r_{2}$ et $r_{d}=2022 r_{2}$ pour un certain entier positif $r_{2}, s_{a}=2023 s_{1}$ et $s_{b}=2021 s_{1}$ pour un certain entier positif $s_{1}$, et $s_{c}=2024 s_{2}$ et $s_{d}=2022 s_{2}$ pour un certain entier positif $r_{2}$.
On a alors
$$
\frac{r}{\mathrm{~s}}=\frac{\mathrm{r}^{2021 \times 2023 r_{1}} s^{2021 \times 2023 s_{1}}}{\mathrm{r}^{2022 \times 2024 \mathrm{r}_{2}} \mathrm{~s}^{2022 \times 2024 \mathrm{~s}_{2}}}=\mathrm{r}^{2021 \times 2023 \mathrm{r}_{1}-2022 \times 2024 \mathrm{r}_{2}} \mathrm{~s}^{2021 \times 2023 \mathrm{~s}_{1}-2022 \times 2024 \mathrm{~s}_{2}}
$$
Ainsi il suffit de trouver $r_{1}, r_{2}, s_{1}, s_{2}$ des entiers positifs tels que $2021 \times 2023 r_{1}-2022 \times 2024 r_{2}=1$ et $-2021 \times 2023 \mathrm{~s}_{1}+2022 \times 2024 \mathrm{~s}_{2}=1$. Pour cela, il suffit d'utiliser le théorème de Bézout. En effet, $2021 \times 2023$ et $2022 \times 2024$ sont premiers entre eux : si on raisonne par l'absurde en considérant $p$ un facteur premier de ces deux nombres, $p$ divise deux nombres entre 2021 et 2024, donc divise leur différence, donc $p=2$ ou 3 . Or $2021 \times 2023$ est impair, et non divisible par 3 , donc on a une contradiction. Ainsi il existe deux entiers $e, f$ tels que $2021 \times 2023 e-2022 \times 2024 f=1$. Quitte à rajouter $2022 \times 2024$ plusieurs fois à $e$, et $2021 \times 2023$ le même nombre de fois à $f$, on peut supposer $e, f$ positifs. De même il existe deux entiers positifs $g$ et $h$ tels que $-2021 \times 2023 g+2022 \times 2024 h=1$. Poser $s_{1}=g, s_{2}=h, r_{1}=$ $e, r_{2}=\mathrm{f}$ donne bien que $\mathrm{r} / \mathrm{s}$ est magnifique : ainsi tout rationnel strictement positif est magnifique.
Commentaire des correcteurs : L'exercice a été très réussi par les élèves qui l'ont cherché.
|
{
"exam": "French_envois",
"problem_label": "15",
"problem_match": "\nExercice 15.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-5.jsonl",
"solution_match": "## Solution de l'exercice 15",
"tier": "T2",
"year": null
}
|
Let \( p \) be a prime number. Martin the frog is located at position 0 on the real line. Each second, Martin makes a move: he can stay at his position, jump 1 to the right, or jump 1 to the left. Martin wants to be back at his initial position after \( p-1 \) moves; he then notes \( s_{p} \) as the number of sequences of \( p-1 \) moves that allow him to return to his initial position. What is the remainder of \( s_{p} \) modulo \( p \)?
For example, for \( p=3, s_{p}=3 \) since Martin can choose to stay at his position twice, make a jump to the right and then to the left, or make a jump to the left and then to the right.
|
We propose two solutions: a first solution that is very elementary and purely combinatorial, and a second solution using ideas from analytic combinatorics, coupled with number theory.
## First Solution:
Let $a_{n}(k)$ denote the number of sequences of $n$ moves such that if Martin was initially at position 0, he ends up at position $k$ (for example, for $n=2, a_{2}(0)=2$ and $a_{2}(2)=a_{2}(-2)=1$). This amounts to counting the number of $n$-tuples with values in $\{-1,0,1\}$ whose sum is $k$. We will try to understand $\left(a_{p}(k)\right)_{k}$ modulo $p$, and find a recurrence relation on the $\left(a_{n}(k)\right)$ to determine the remainder of $a_{p-1}(0)$ modulo $p$.
We will prove the following lemma:
Lemma 1. $a_{p}(k)$ is 0 modulo $p$, except if $k=p, 0$ or $-p$: in these cases, $a_{p}(k)$ is 1 modulo $p$.
|
not found
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Soit p un nombre premier. Martin la grenouille est situé en position 0 sur la droite réelle. A chaque seconde, Martin effectue un mouvement : il peut rester à sa position, faire un saut de 1 sur la droite, ou faire un saut de 1 sur la gauche. Martin souhaite être revenu au bout de $p-1$ mouvements à sa position initiale : il note alors $s_{p}$ le nombre de séquences de $p-1$ mouvements lui permettant de revenir à sa position initiale. Quel est le reste de $s_{p}$ modulo $p$ ?
Par exemple, pour $p=3, s_{p}=3$ puisque Martin peut choisit de rester à sa position deux fois, de faire un saut sur la droite puis sur la gauche, ou faire un saut sur la gauche puis sur la droite.
|
On propose deux solutions : une première solution très élémentaire et uniquement combinatoire, et une seconde solution utilisant des idées de combinatoire analytique, couplées à de la théorie des nombres.
## Première solution :
Notons $a_{n}(k)$ le nombre de suites de $n$ mouvements tel que si Martin était initialement à la position 0 , il se retrouve à la position $k$ (par exemple, pour $n=2, a_{2}(0)=2$ et $a_{2}(2)=a_{2}(-2)=1$. Cela revient donc à compter le nombre de n uplets à valeurs dans $\{-1,0,1\}$ de somme $k$. On va essayer de comprendre $\left(a_{p}(k)\right)_{k}$ modulo $p$, et de trouver une relation de récurrence sur les $\left(a_{n}(k)\right)$ pour trouver le reste de $a_{p-1}(0)$ modulo $p$.
On va montrer le lemme suivant :
Lemme 1. $a_{p}(k)$ vaut 0 modulo $p$, sauf si $k=p, 0$ ou $-p$ : dans ce cas $a_{p}(k)$ vaut 1 modulo $p$.
|
{
"exam": "French_envois",
"problem_label": "16",
"problem_match": "\nExercice 16.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-5.jsonl",
"solution_match": "## Solution de l'exercice 16",
"tier": "T2",
"year": null
}
|
Let \( p \) be a prime number. Martin the frog is located at position 0 on the real line. Each second, Martin makes a move: he can stay at his position, jump 1 to the right, or jump 1 to the left. Martin wants to be back at his initial position after \( p-1 \) moves; he then notes \( s_{p} \) as the number of sequences of \( p-1 \) moves that allow him to return to his initial position. What is the remainder of \( s_{p} \) modulo \( p \)?
For example, for \( p=3, s_{p}=3 \) since Martin can choose to stay at his position twice, make a jump to the right and then to the left, or make a jump to the left and then to the right.
|
We fix $k$ an integer different from $\pm p$ (if $k= \pm p$, we see that $a_{p}(k)=1$), and we denote $A$ the set of $p$-tuples with sum $k$. We define $T: A \mapsto A$ the following application: if $\left(a_{1}, \ldots, a_{p}\right)$ is in $A, T\left(a_{1}, \ldots, a_{p}\right)=\left(a_{2}, \ldots, a_{p}, a_{1}\right)$. It is clear that $T\left(a_{1}, \ldots, a_{p}\right)$ is well in $A$, and that applying $T$ $p$ times to an element of $A$ yields the same element of $A$. Note that $T$ is clearly injective, and thus bijective because $A$ is finite. For each $y$, we define $\Omega_{y}:=\left\{T^{k}(y) \mid k \geqslant 0\right.$ where $T^{k}$ is the composition $k$ times of $T$.
Let $x, y$ be two elements of $A$ such that $\Omega_{y} \cap \Omega_{x}$ is non-empty. There exist $h, \ell$ positive such that $T^{h}(x)=$ $T^{\ell}(y)$. In particular, by applying $\ell(p-1)$ times $T, T^{h+\ell(p-1)}(x)=T^{\ell p}(y)=y$, so for any positive integer $j$, $\mathrm{T}^{\mathrm{j}}(\mathrm{y})=\mathrm{T}^{\mathrm{h}+\ell(p-1)+\mathrm{j}}(\mathrm{x}) \in \Omega_{x}$: thus $\Omega_{y} \subset \Omega_{x}$. Similarly, we have the reverse inclusion, so $\Omega_{x}=\Omega_{y}$. Thus the $\left(\Omega_{x}\right)$ partition the set $A$.
Let $x$ be in $A$, let's show that $\Omega_{x}$ has cardinality $p$, except if $x=(0, \ldots, 0)$. First, since $T$ applied $p$ times gives the identity, we know that $\Omega_{x}=\left\{T^{k}(x) \mid k \in\{0, \ldots, p-1\}\right.$ and thus has at most cardinality $p$. Suppose there exist $i \neq j$ two elements of $\{0, \ldots, p-1\}$ such that $T^{i}(x)=T^{j}(x)$. By symmetry, we can assume $i<j$, so we have $T^{p-j+i}(x)=T^{p-j+j}(x)=x$, thus $x=T^{k}(x)$ with $h=p-j+i \in\{1, \ldots, p-1\}$. Let $x=\left(x_{1}, \ldots, x_{n}\right)$, the equation $x=T^{h}(x)$ translates to $x_{j}=x_{j+h}$ for all integer $j$ (taking indices modulo $p$). In particular, for all integer $\ell \geqslant 0, x_{j+h \ell}=x_{j}$. Taking $\ell$ an inverse of $h$ modulo $p$, we have that for all $j, x_{j}=x_{j+1}$. Thus $x$ is of the form $(1, \ldots, 1),(0, \ldots, 0)$ or $(-1, \ldots,-1)$ which is contradictory with the fact that $k \neq \pm p$ unless $x=(0, \ldots, 0)$. Thus $\Omega_{x}=\left\{T^{k}(x) \mid k \in\{0, \ldots, p-1\}\right.$ has cardinality $p$ except if $x=(0, \ldots, 0)$.
Since $A$ is partitioned into sets of cardinality $p$, its size is divisible by $p$ if $k \neq 0$. If $k=0, A$ minus $(0, \ldots, 0)$ is partitioned into sets of cardinality $p$, so the size of $A$ is 1 modulo $p$.
Now, note that for any integer $k$, and any $n \geqslant 2, s_{n}(k)=s_{n-1}(k-1)+s_{n-1}(k)+s_{n-1}(k+1)$. Indeed, an $n$-tuple with sum $k$ and values in $\{-1,0,1\}$ can either start with 1 and end with an $n-1$-tuple with sum $k-1$, or start with -1 and end with an $n-1$-tuple with sum $k+1$, or start with 0 and end with an $n-1$-tuple with sum $k$. Therefore, there are as many $n$-tuples with sum $k$ as there are $n-1$-tuples with sum $k-1, k$, or $k+1$.
Now, from these observations, let's try to conclude. For $p=3, s_{p}=3$, so the remainder of $s_{p}$ modulo $p$ is 0. Using the previous formula,
\[
\begin{aligned}
s_{\mathfrak{p}-1}(k)-s_{\mathfrak{p}-1}(k+3) & =s_{\mathfrak{p}-1}(k)+s_{\mathfrak{p}-1}(k+1)+s_{\mathfrak{p}-1}(k+2)-\left(s_{\mathfrak{p}-1}(k+1)+s_{\mathfrak{p}-1}(k+2)-s_{\mathfrak{p}-1}(k+3)\right) \\
& =s_{\mathfrak{p}}(k+1)-s_{\mathfrak{p}}(k+2)
\end{aligned}
\]
Summing the previous formula for $k$ a multiple of 3 between 0 and $3(p-1)$, we get that:
\[
s_{\mathfrak{p}-1}(0)-s_{\mathfrak{p}-1}(3 p)=\sum_{k=0}^{p-1} s_{p}(3 k+1)-s_{p}(3 k+2)
\]
We have $s_{\mathfrak{p}}(n)=0$ except for $n= \pm p$ or 0. And we clearly have $s_{p-1}(3 p)=0$, since $3 p>p-1$, so a $p-1$-tuple in $\{-1,0,1\}$ cannot have sum $3 p$. Thus the previous formula gives that $s_{p-1}$ is 1 modulo $p$ and $p$ is of the form $3 k+1, p-1$ if $p$ is of the form $3 k+2$.
## Second Solution:
The statement can be reformulated as follows: $s_{p}$ is the number of $p-1$-tuples in $\{-1,0,1\}$ with sum zero. In particular, by adding 1 to each step, $s_{p}$ is the number of $p-1$-tuples in $\{0,1,2\}$ with sum $p-1$. This is also the coefficient of degree $p-1$ of $\left(1+X+X^{2}\right)^{p-1}$ according to the theory of generating functions: indeed, each term of the product $\left(1+X+X^{2}\right) \ldots\left(1+X+X^{2}\right)$ corresponds to $p-1$ choices of 0, 1, or 2, and the sum of the different steps corresponds to the power of $X$ in the overall product.
Thus we seek to understand what the remainder of the $p-1$-th coefficient of $Q(X):=\left(1+X+X^{2}\right)^{p-1}$ is modulo $p$. We can try to understand the values of $Q$ modulo $p$: if $a$ is an integer, and $p$ does not divide $1+a+a^{2}, Q(a) \equiv 1(\bmod p)$ by Fermat's little theorem. Otherwise $Q(a) \equiv 0(\bmod p)$.
In particular $\sum_{a=0}^{p-1} Q(a) \equiv-n_{p}$ where $n$ is the number of distinct roots of $X^{2}+X+1$ modulo $p$. For $p=3$, there is only one root: 1. For $p \neq 3, 1$ is not a root, so these are the roots of $X^{3}-1$ different from 1. There exists an element of order 3 modulo $p$ if and only if 3 divides $p-1$: indeed, if there exists an element of order 3 modulo $p$, by Fermat's little theorem, 3 divides $p-1$. If 3 divides $p-1$, let $y$ be a primitive root modulo $p, y^{(p-1) / 3}$ is an element of order 3.
Thus $n_{3}=1$, if $p \neq 3$ and 3 does not divide $p-1, n_{p}=0$ and if $p \neq 3$ and 3 divides $p-1, X^{2}+X+1$ has a root. As it is a polynomial of degree 2, it has 2 roots. Moreover, these roots are distinct: otherwise their discriminant would be 0 modulo $p$, but it is -3. Thus if 3 divides $p-1, n=2$.
Now $Q$ is unitary of degree $2(p-1)$. Write $Q$ in the form $\sum_{k=0}^{2(p-1)} a_{k} X^{k}$ with $a_{2(p-1)}=1$ and $a_{p-1}=s_{p}$. We have:
\[
\sum_{a=0}^{p-1} Q(a) \equiv \sum_{k=0}^{2(p-1)} a_{k} \sum_{a=0}^{p-1} a^{k} \quad(\bmod p)
\]
For $k=0, \sum_{a=0}^{p-1} a^{k} \equiv 0(\bmod p)$. For $k>0,0^{k}=0$, so if we take $y$ a primitive root modulo $p$,
\[
\sum_{a=0}^{p-1} a^{k} \equiv \sum_{a=1}^{p-1} a^{k} \equiv \sum_{n=0}^{p-2}\left(y^{n}\right)^{k} \equiv \sum_{n=0}^{p-2}\left(y^{k}\right)^{n} \quad(\bmod p)
\]
If $y^{k} \not \equiv 1(\bmod n)$ (which is the case if $p-1$ does not divide $k$), then $\sum_{n=0}^{p-2}\left(y^{k}\right)^{n} \equiv \frac{y^{(p-1) k}-1}{y^{k}-1} \equiv 0(\bmod p)$ because $y^{p-1} \equiv 1(\bmod p)$. If $p-1$ divides $k, \sum_{n=0}^{p-2}\left(y^{k}\right)^{n} \equiv p-1(\bmod p)$. Thus, we obtain
\[
\sum_{a=0}^{p-1} Q(a) \equiv \sum_{k=0}^{2(p-1)} a_{k} \sum_{a=0}^{p-1} a^{k} \quad(\bmod p) \equiv-a_{p-1}-a_{2(p-1)}=-a_{p-1}-1
\]
So $\mathrm{a}_{\mathrm{p}-1} \equiv \mathrm{n}-1(\bmod \mathrm{p})$
Thus:
- If $p=3$, the remainder of $s_{p}$ modulo $p$ is 0,
- if $p \neq 3$ and 3 does not divide $p-1$ (i.e., if $p \equiv 2(\bmod 3)$), the remainder of $s_{p}$ modulo $p$ is $p-1$,
- if 3 divides $p-1$, the remainder of $s_{p}$ modulo $p$ is 1.
Comment from the graders: The exercise was very poorly done. Those who succeeded followed the first solution. Many tried to calculate a sum, then quickly got stuck by the binomial coefficients, which were difficult to look at $\bmod p$.
$\mathcal{E}_{x e r c i c e}$ 17. Determine all injective functions $f$ from $\mathbb{N}$ to $\mathbb{N}$ such that any polynomial $\sum_{i=0}^{n} a_{i} x^{i}$ has a real root if and only if the polynomial $\sum_{i=0}^{n} a_{i
|
not found
|
Yes
|
Incomplete
|
math-word-problem
|
Combinatorics
|
Soit p un nombre premier. Martin la grenouille est situé en position 0 sur la droite réelle. A chaque seconde, Martin effectue un mouvement : il peut rester à sa position, faire un saut de 1 sur la droite, ou faire un saut de 1 sur la gauche. Martin souhaite être revenu au bout de $p-1$ mouvements à sa position initiale : il note alors $s_{p}$ le nombre de séquences de $p-1$ mouvements lui permettant de revenir à sa position initiale. Quel est le reste de $s_{p}$ modulo $p$ ?
Par exemple, pour $p=3, s_{p}=3$ puisque Martin peut choisit de rester à sa position deux fois, de faire un saut sur la droite puis sur la gauche, ou faire un saut sur la gauche puis sur la droite.
|
On se fixe $k$ un entier différent de $\pm p$ (si $k= \pm p$, on voit bien que $a_{p}(k)=1$ ), on note $A$ l'ensemble des $p$ uplets de somme $k$. On définit $T: A \mapsto A$ l'application suivante : si $\left(a_{1}, \ldots, a_{p}\right)$ est dans $A, T\left(a_{1}, \ldots, a_{p}\right)=\left(a_{2}, \ldots, a_{p}, a_{1}\right)$. Il est clair que $T\left(a_{1}, \ldots, a_{p}\right)$ est bien dans $A$, et qu'en appliquant $p$ fois $T$ à un élément de $A$, on obtient le même élément de $A$. Notons que $T$ est clairement injective, donc bijective car $A$ est fini. Pour chaque $y$, on définit $\Omega_{y}:=\left\{T^{k}(y) \mid k \geqslant 0\right.$ où $T^{k}$ est la composée $k$ fois de $T$.
Soit $x, y$ deux éléments de $A$ tels que $\Omega_{y} \cap \Omega_{x}$ est non vide. Il existe $h, \ell$ positif tels que $T^{h}(x)=$ $T^{\ell}(y)$. En particulier en appliquant $\ell(p-1)$ fois $T, T^{h+\ell(p-1)}(x)=T^{\ell p}(y)=y$, donc pour tout entier j positif, $\mathrm{T}^{\mathrm{j}}(\mathrm{y})=\mathrm{T}^{\mathrm{h}+\ell(p-1)+\mathrm{j}}(\mathrm{x}) \in \Omega_{x}$ : on a donc $\Omega_{y} \subset \Omega_{x}$. De même on a l'inclusion réciproque, donc $\Omega_{x}=\Omega_{y}$. Ainsi les $\left(\Omega_{x}\right)$ partitionnent l'ensemble $A$.
Soit $x$ dans $A$, montrons que $\Omega_{x}$ est de cardinal $p$, sauf si $x=(0, \ldots, 0)$. Déjà, comme $T$ appliqué $p$ fois donne l'identité, on sait que $\Omega_{x}=\left\{T^{k}(x) \mid k \in\{0, \ldots, p-1\}\right.$ donc est au plus de cardinal $p$. Supposons qu'il existe $i \neq j$ deux éléments de $\{0, \ldots, p-1\}$ tels que $T^{i}(x)=T^{j}(x)$. Par symétrie, on peut supposer $i<j$, on a donc $T^{p-j+i}(x)=T^{p-j+j}(x)=x$, donc $x=T^{k}(x)$ avec $h=p-j+i \in\{1, \ldots, p-1\}$. Posons $x=\left(x_{1}, \ldots, x_{n}\right)$, l'équation $x=T^{h}(x)$ se retraduit par $x_{j}=x_{j+h}$ pour tout entier $j$ (en prenant les indices modulo $p$. En particulier, pour tout entier $\ell \geqslant 0, x_{j+h \ell}=x_{j}$. En prenant $\ell$ un inverse de $h$ modulo $p$, on a que pour tout $j, x_{j}=x_{j+1}$. Ainsi $x$ est de la forme $(1, \ldots, 1),(0, \ldots, 0)$ ou $(-1, \ldots,-1)$ ce qui est contradictoire avec le fait que $k \neq \pm p$ sauf si $x=(0, \ldots, 0)$. Ainsi $\Omega_{x}=\left\{T^{k}(x) \mid k \in\{0, \ldots, p-1\}\right.$ est bien de cardinal $p$ sauf si $x=(0, \ldots, 0)$.
Comme $A$ est partitionné en ensembles de cardinal $p$, sa taille est divisible par $p$ si $k \neq 0$. Si $k=0, A$ privé de $(0, \ldots, 0)$ est partitionné en ensembles de cardinal $p$, donc la taille de $A$ vaut 1 modulo p .
Maintenant, notons que pour tout entier $k$, et tout $n \geqslant 2, s_{n}(k)=s_{n-1}(k-1)+s_{n-1}(k)+s_{n-1}(k+1)$. En effet, un $n$-uplet de somme $k$ à valeurs dans $\{-1,0,1\}$ peut soit commencer par 1 et finir par un $n-1$-uplet de somme $k-1$, soit commencer par -1 et finir par un $n-1$-uplet de somme $k+1$, soit commencer par 0 et finir par un $n-1$-uplet de somme $k$. Donc il y a autant de $n$-uplets de somme $k$ que de $\mathrm{n}-1$-uplets de somme $k-1, k$ ou $k+1$.
Maintenant, à partir de ces observations essayons de conclure. Pour $p=3, s_{p}=3$, donc le reste de $s_{p}$ modulo $p$ est 0 . Via la formule précédente,
$$
\begin{aligned}
s_{\mathfrak{p}-1}(k)-s_{\mathfrak{p}-1}(k+3) & =s_{\mathfrak{p}-1}(k)+s_{\mathfrak{p}-1}(k+1)+s_{\mathfrak{p}-1}(k+2)-\left(s_{\mathfrak{p}-1}(k+1)+s_{\mathfrak{p}-1}(k+2)-s_{\mathfrak{p}-1}(k+3)\right) \\
& =s_{\mathfrak{p}}(k+1)-s_{\mathfrak{p}}(k+2)
\end{aligned}
$$
En sommant la formule précédente pour $k$ multiple de 3 entre 0 et $3(p-1)$, on obtient que :
$$
s_{\mathfrak{p}-1}(0)-s_{\mathfrak{p}-1}(3 p)=\sum_{k=0}^{p-1} s_{p}(3 k+1)-s_{p}(3 k+2)
$$
Or on a $s_{\mathfrak{p}}(n)=0$ sauf pour $n= \pm p$ ou 0 . Et on a clairement $s_{p-1}(3 p)=0$, car $3 p>p-1$, donc un $p-1$-uplet de $\{-1,0,1\}$ ne peut pas avoir somme $3 p$. Ainsi la formule précédente donne que $s_{p-1}$ vaut 1 modulo $p$ et $p$ est de la forme $3 k+1, p-1$ si $p$ est de la forme $3 k+2$.
## Seconde solution :
L'énoncé peut être reformulé de la façon suivante : $s_{p}$ est le nombre de $p-1$ uplets dans $\{-1,0,1\}$ de somme nulle. En particulier, en ajoutant 1 à chaque pas, $s_{p}$ est le nombre de $p-1$ uplets dans $\{0,1,2\}$ de somme $p-1$. C'est donc également le coefficient de degré $p-1$ de $\left(1+X+X^{2}\right)^{p-1}$ d'après la théorie des séries génératrices : en effet, chaque terme du produit $\left(1+X+X^{2}\right) \ldots\left(1+X+X^{2}\right)$ correspond à $p-1$ choix de 0,1 ou 2 , et la somme des différents pas correspond à la puissance de $X$ dans le produit global.
Ainsi on cherche à comprendre ce que vaut le reste du $p-1$-ième coefficient de $Q(X):=\left(1+X+X^{2}\right)^{p-1}$ modulo $p$. On peut essayer de comprendre les valeurs de $Q$ modulo $p$ : si a est un entier, et $p$ ne divise pas $1+a+a^{2}, Q(a) \equiv 1(\bmod p)$ par le théorème de petit Fermat. Sinon $Q(a) \equiv 0(\bmod p)$.
En particulier $\sum_{a=0}^{p-1} Q(a) \equiv-n_{p}$ où $n$ est le nombre de solution de racines distinctes de $X^{2}+X+1$ modulo $p$. Pour $p=3$, il n'y a qu'une seule racine : 1 . Pour $p \neq 3,1$ n'est pas racine, donc ce sont les racines de $X^{3}-1$ différentes de 1 . Or il existe un élément d'ordre 3 modulo $p$ si et seulement si 3 divise $p-1$ : en effet, s'il existe un élément d'ordre 3 modulo $p$, par petit Fermat, 3 divise $p-1$. Si 3 divise $p-1$, soit $y$ une racine primitive modulo $p, y^{(p-1) / 3}$ est un élement d'ordre 3.
Ainsi $n_{3}=1$, si $p \neq 3$ et 3 ne divise pas $p-1, n_{p}=0$ et si $p \neq 3$ et 3 divise $p-1, X^{2}+X+1$ a une racine. Comme c'est un polynôme de degré 2 il a 2 racines. De plus celles-ci sont distinctes : sinon sont discrminant vaudrait 0 modulo $p$, or celui-ci vaut -3 . Ainsi si 3 divise $p-1, n=2$.
Or $Q$ est unitaire de degré $2(p-1)$. Ecrivons $Q$ sous la forme $\sum_{k=0}^{2(p-1)} a_{k} X^{k}$ avec $a_{2(p-1)}=1$ et $a_{p-1}=s_{p}$. Ona:
$$
\sum_{a=0}^{p-1} Q(a) \equiv \sum_{k=0}^{2(p-1)} a_{k} \sum_{a=0}^{p-1} a^{k} \quad(\bmod p)
$$
Pour $k=0, \sum_{a=0}^{p-1} a^{k} \equiv 0(\bmod p)$. Pour $k>0,0^{k}=0$, donc si on se donne $y$ une racine primitive modulo p ,
$$
\sum_{a=0}^{p-1} a^{k} \equiv \sum_{a=1}^{p-1} a^{k} \equiv \sum_{n=0}^{p-2}\left(y^{n}\right)^{k} \equiv \sum_{n=0}^{p-2}\left(y^{k}\right)^{n} \quad(\bmod p)
$$
Si $y^{k} \not \equiv 1(\bmod n)($ ce qui est le cas si $p-1$ ne divise pas $k)$, alors $\sum_{n=0}^{p-2}\left(y^{k}\right)^{n} \equiv \frac{y^{(p-1) k}-1}{y^{k}-1} \equiv 0(\bmod p)$ $\operatorname{car} y^{p-1} \equiv 1(\bmod p)$. Si $p-1$ divise $k, \sum_{n=0}^{p-2}\left(y^{k}\right)^{n} \equiv p-1(\bmod p)$. Ainsi, on obtient
$$
\sum_{a=0}^{p-1} Q(a) \equiv \sum_{k=0}^{2(p-1)} a_{k} \sum_{a=0}^{p-1} a^{k} \quad(\bmod p) \equiv-a_{p-1}-a_{2(p-1)}=-a_{p-1}-1
$$
Donc $\mathrm{a}_{\mathrm{p}-1} \equiv \mathrm{n}-1(\bmod \mathrm{p})$
Ainsi :
- Si $p=3$, le reste de $s_{p}$ modulo $p$ vaut 0 ,
- si $p \neq 3$ et 3 ne divise pas $p-1$ (i.e. si $p \equiv 2(\bmod 3)$ ), le reste de $s_{p}$ modulo $p$ vaut $p-1$,
- si 3 divise $p-1$, le reste de $s_{p}$ modulo $p$ vaut 1 .
Commentaire des correcteurs: L'exercice a été très peu réussi. Les élèves l'ayant réussi ont suivi la première solution. Beaucoup ont essayé de calculer une somme, puis se sont retrouvés très vite bloqués par les coefficients binomiaux, qu'il était difficile de regarder $\bmod p$.
$\mathcal{E}_{x e r c i c e}$ 17. Déterminer toutes les fonctions f injective de $\mathbb{N}$ dans $\mathbb{N}$ telles que tout polynôme $\sum_{i=0}^{n} a_{i} x^{i}$, celui-ci a une racine réelle si et seulement si le polynôme $\sum_{i=0}^{n} a_{i} x^{f(i)}$ a une racine réelle.
|
{
"exam": "French_envois",
"problem_label": "16",
"problem_match": "\nExercice 16.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-5.jsonl",
"solution_match": "\nDémonstration.",
"tier": "T2",
"year": null
}
|
Let \( p \) be a prime number. Martin the frog is located at position 0 on the real line. Each second, Martin makes a move: he can stay at his position, jump 1 to the right, or jump 1 to the left. Martin wants to be back at his initial position after \( p-1 \) moves; he then notes \( s_{p} \) as the number of sequences of \( p-1 \) moves that allow him to return to his initial position. What is the remainder of \( s_{p} \) modulo \( p \)?
For example, for \( p=3, s_{p}=3 \) since Martin can choose to stay at his position twice, make a jump to the right and then to the left, or make a jump to the left and then to the right.
|
It turns out that the injectivity condition was unnecessary: we will prove the result without the injectivity of \( f \). Note that the polynomial 1 has no real roots; the condition in the statement tells us that \( \chi^{f(0)} \) has no real roots either: the only possibility for \( f(0) \) is therefore \( f(0)=0 \). Similarly, \( f(n) \neq 0 \) if \( n \neq 0 \) because \( X^{n} \) has a real root, and 1 does not.
Let's show that \( f(n) \) has the same parity as \( n \) for all integers \( n \). Note that if \( n \) is even, \( X^{n} + 1 \) has no real roots, so \( X^{f(n)} + 1 \) does not either. This implies that \( f(n) \) is even (otherwise, -1 would be a real root). Similarly, if \( n \) is odd, \( f(n) \) is odd. Let \( \alpha = f(1) \), so \( \alpha \) is odd.
Let \( t \) be a real number. For the following, we need to understand, for any real \( b \) such that \( b > 1 \), whether the equation \( x^{b} - x = t \) has a solution on \( \mathbb{R}^{+} \). For all \( t > 0 \), we define \( f_{b}: \mathbb{R}^{+} \rightarrow \mathbb{R} \) which maps \( x \) to \( x^{b} - x \).
Lemma 2. The equation \( x^{b} - x = t \) has a solution if and only if \( t \geqslant f_{b}\left(x_{b}\right) \) where \( x_{b} = \left(\frac{1}{b}\right)^{\frac{1}{b-1}} \).
|
not found
|
Yes
|
Problem not solved
|
math-word-problem
|
Combinatorics
|
Soit p un nombre premier. Martin la grenouille est situé en position 0 sur la droite réelle. A chaque seconde, Martin effectue un mouvement : il peut rester à sa position, faire un saut de 1 sur la droite, ou faire un saut de 1 sur la gauche. Martin souhaite être revenu au bout de $p-1$ mouvements à sa position initiale : il note alors $s_{p}$ le nombre de séquences de $p-1$ mouvements lui permettant de revenir à sa position initiale. Quel est le reste de $s_{p}$ modulo $p$ ?
Par exemple, pour $p=3, s_{p}=3$ puisque Martin peut choisit de rester à sa position deux fois, de faire un saut sur la droite puis sur la gauche, ou faire un saut sur la gauche puis sur la droite.
|
Il s'avère que la condition d'injectivité était inutile : nous allons prouver le résultat sans l'injectivité de f. Notons que le polynôme 1 n'a pas de racine réelle, la condition de l'énoncé nous apprend que $\chi^{f(0)}$ n'en a pas non plus: la seule possibilité pour $f(0)$ est donc $f(0)=0$. De même, $f(n) \neq 0$ si $n \neq 0$ car $X^{n}$ a une racine réelle, et 1 n'en a pas.
Montrons que $f(n)$ a la même parité que $n$ pour tout entier $n$. Notons que si $n$ est pair, $X^{n}+1 n$ 'a pas de racine réelle donc $X^{f(n)}+1$ non plus. Ceci implique que $f(n)$ est pair (sinon -1 serait une racine réelle ). De même si $n$ est impair, $f(n)$ est impair. Posons $\alpha=f(1), \alpha$ est donc impair.
Soit $t$ un réel. Pour la suite, nous aurons besoin de comprendre, pour tout $b$ réel vérifiant $b>1$, si l'équation $x^{b}-x=t$ sur $\mathbb{R}^{+}$. Pour tout $t>0$, on pose $f_{b}: \mathbb{R}^{+} \rightarrow \mathbb{R}$ qui à $x$ associe $x^{b}-x$.
Lemme 2. L'équation $x^{b}-x=t$ a une solution si et seulement si $t \geqslant f_{b}\left(x_{b}\right)$ où $x_{b}=\left(\frac{1}{b}\right)^{\frac{1}{b-1}}$.
|
{
"exam": "French_envois",
"problem_label": "16",
"problem_match": "\nExercice 16.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-5.jsonl",
"solution_match": "## Solution de l'exercice 17",
"tier": "T2",
"year": null
}
|
Let \( p \) be a prime number. Martin the frog is located at position 0 on the real line. Each second, Martin makes a move: he can stay at his position, jump 1 to the right, or jump 1 to the left. Martin wants to be back at his initial position after \( p-1 \) moves; he then notes \( s_{p} \) as the number of sequences of \( p-1 \) moves that allow him to return to his initial position. What is the remainder of \( s_{p} \) modulo \( p \)?
For example, for \( p=3, s_{p}=3 \) since Martin can choose to stay at his position twice, make a jump to the right and then to the left, or make a jump to the left and then to the right.
|
The function $\mathrm{f}_{\mathrm{b}}$ is continuous and differentiable on $\mathbb{R}^{+}$. The derivative of $\mathrm{f}_{\mathrm{b}}$ is $\mathrm{b} x^{\mathrm{b}-1}-1$, which is negative up to $x_{b}$ and then positive. Thus, $f$ decreases and then increases. Since $f$ has a limit of $+\infty$ as $x \to +\infty$, the values taken by $f$ on $\mathbb{R}^{+}$ are exactly $\left[f\left(x_{b}\right),+\infty[\right.$ by continuity, which gives the desired result.
We will also need the following lemma:
Lemma 3. Let $b>a$ be two strictly positive integers, with $b$ even. If the equation $x^{b}-x^{a}=t a$ has a solution, then this equation has a positive solution.
|
not found
|
Yes
|
Problem not solved
|
math-word-problem
|
Combinatorics
|
Soit p un nombre premier. Martin la grenouille est situé en position 0 sur la droite réelle. A chaque seconde, Martin effectue un mouvement : il peut rester à sa position, faire un saut de 1 sur la droite, ou faire un saut de 1 sur la gauche. Martin souhaite être revenu au bout de $p-1$ mouvements à sa position initiale : il note alors $s_{p}$ le nombre de séquences de $p-1$ mouvements lui permettant de revenir à sa position initiale. Quel est le reste de $s_{p}$ modulo $p$ ?
Par exemple, pour $p=3, s_{p}=3$ puisque Martin peut choisit de rester à sa position deux fois, de faire un saut sur la droite puis sur la gauche, ou faire un saut sur la gauche puis sur la droite.
|
La fonction $\mathrm{f}_{\mathrm{b}}$ est continue et dérivable sur $\mathbb{R}^{+}$. Lla dérivée de $\mathrm{f}_{\mathrm{b}}$ est $\mathrm{b} x^{\mathrm{b}-1}-1$, qui est négative jusqu'en $x_{b}$ puis positive. Ainsi f décroît puis croît. Comme f a pour limite $+\infty$ en $+\infty$, les valeurs prises par $f$ sur $\mathbb{R}^{+}$sont exactement $\left[f\left(x_{b}\right),+\infty[\right.$ par continuité, ce qui donne le résultat voulu.
On aura aussi besoin du lemme suivant :
Lemme 3. Soit $b>a$ deux entiers strictement positifs, avec $b$ pair. Si l'équation $x^{b}-x^{a}=t a$ une solution, alors cette équation a une solution positive.
|
{
"exam": "French_envois",
"problem_label": "16",
"problem_match": "\nExercice 16.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-5.jsonl",
"solution_match": "\nDémonstration.",
"tier": "T2",
"year": null
}
|
Let \( p \) be a prime number. Martin the frog is located at position 0 on the real line. Each second, Martin makes a move: he can stay at his position, jump 1 to the right, or jump 1 to the left. Martin wants to be back at his initial position after \( p-1 \) moves; he then notes \( s_{p} \) as the number of sequences of \( p-1 \) moves that allow him to return to his initial position. What is the remainder of \( s_{p} \) modulo \( p \)?
For example, for \( p=3, s_{p}=3 \) since Martin can choose to stay at his position twice, make a jump to the right and then to the left, or make a jump to the left and then to the right.
|
Let $x$ be a solution of the equation. As a best pair, $|x|^{b}-|x|^{a} \leqslant x^{b}-x^{a}=t$. The function that maps $y$ to $y^{b}-y^{a}$ is continuous and tends to $+\infty$ as $y \to +\infty$, so the equation $y^{b}-y^{a}=t$ has a solution in $[|x|,+\infty[$, and thus a positive solution.
Now apply the hypothesis of the statement to the polynomial $X^{2 n}-X-t$. This polynomial has a real root if and only if $t \geqslant f_{2 n}\left(x_{2 n}\right)$. In particular, the polynomial $X^{f(2 n)}-X^{\alpha}-t$ has a real root if and only if $t \geqslant f_{2 n}\left(x_{2 n}\right)$.
- If $f(2 n) < \alpha$, then the function that maps $x$ to $x^{f(2 n)}-x^{\alpha}$ tends to $-\infty$ and $+\infty$, and $+\infty$ as $x \to -\infty$ because $\alpha$ is odd. Thus, by continuity, the equation $x^{f(2 n)}-x^{\alpha}=t$ always has a solution, so $X^{f(2 n)}-X^{\alpha}-t$ always has a root, which is absurd.
- If $f(2 n) = \alpha$, then the polynomial has a root only for $t=0$, which is absurd.
Thus, $f(2 n) > \alpha$. In particular, by the previous lemma, the polynomial $X^{f(2 n)}-X^{\alpha}-t$ has a real root if and only if it has a positive real root, i.e., if and only if the equation $x^{f(2 n)}-x^{\alpha}=t$ has a positive solution. Since $x \mapsto x^{\alpha}$ is bijective from $\mathbb{R}^{+}$ to $\mathbb{R}^{+}$, the polynomial $X^{f(2 n)}-X^{\alpha}-t$ has a real root if and only if the equation $x^{f(2 n) / \alpha}-x=t$ has a positive root, and thus if and only if $t \geqslant f_{f(2 n) / \alpha}\left(x_{f(2 n) / \alpha}\right)$. Let $u=f(2 n) / \alpha > 1$, then we have $f_{u}\left(x_{u}\right)=f_{2 n}\left(x_{2 n}\right)$.
- If $2 n > u$, since $x_{u} < 1$, $f_{u}\left(x_{u}\right) > f_{2 n}\left(x_{u}\right) \geqslant f_{2 n}\left(x_{2 n}\right) = f_{u}\left(x_{u}\right)$ (via the variations of $f_{2 n}$), which is absurd.
- If $2 n < u$, since $x_{2 n} < 1$, $f_{2 n}\left(x_{2 n}\right) > f_{u}\left(x_{2 n}\right) \geqslant f_{u}\left(x_{u}\right) = f_{2 n}\left(x_{2 n}\right)$ (via the variations of $f_{u}$), which is absurd.
Thus, $u = 2 n$, so $f(2 n) = 2 n \alpha$.
It remains to show that if $n$ is odd, $f(n) = \alpha n$. For this, we proceed similarly to the previous argument: we consider the polynomial $X^{2 n}-X^{n}-t$, and show that it has a real root if and only if $t \geqslant f_{2 n / n}\left(x_{2 n / n}\right) = f_{2}\left(x_{2}\right)$. Then we show that $X^{f(2 n)}-X^{f(n)}-t$ has a root if and only if $t \geqslant f_{2}\left(x_{2}\right)$. Since $f(n)$ is odd and $f(2 n)$ is even, we deduce that $f(2 n) > f(n)$, and then that $f_{2}\left(x_{2}\right) = f_{f(2 n) / f(n)}\left(x_{f(2 n) / f(n)}\right)$. Similarly, we prove that $f(2 n) / f(n) = 2$, so $f(2 n) = 2 f(n)$. Since $f(2 n) = 2 n \alpha$, we have $f(n) = n \alpha$. Thus, if $f$ is a solution, $f$ is of the form $f: n \mapsto an$ for some odd $a$.
Conversely, if there exists an odd $a$ such that $f(n) = an$ for all positive integers $n$, then if the polynomial $\sum_{k=0}^{n} a_{k} X^{k}$ has a real root $x_{0}$, the polynomial $\sum_{k=0}^{n} a_{k} X^{f(k)} = \sum_{k=0}^{n} a_{k} X^{a k}$ has the root $x_{0}^{1 / a}$. Conversely, if $\sum_{k=0}^{n} a_{k} X^{a k}$ has a real root $y_{0}$, then $y_{0}^{a}$ is a root of $\sum_{k=0}^{n} a_{k} X^{k}$. Thus, $f$ satisfies the statement.
The functions that satisfy the statement are those for which there exists an odd $a$ such that $f(n) = an$ for all positive integers $n$.
Comment from the graders: The exercise was rarely attempted, but students who did attempt it generally succeeded with various proofs. Be very cautious with expressions of the form $x^{q}$ where $q$ is rational and $x$ is negative: this does not always have a clear meaning.
|
not found
|
Yes
|
Incomplete
|
math-word-problem
|
Combinatorics
|
Soit p un nombre premier. Martin la grenouille est situé en position 0 sur la droite réelle. A chaque seconde, Martin effectue un mouvement : il peut rester à sa position, faire un saut de 1 sur la droite, ou faire un saut de 1 sur la gauche. Martin souhaite être revenu au bout de $p-1$ mouvements à sa position initiale : il note alors $s_{p}$ le nombre de séquences de $p-1$ mouvements lui permettant de revenir à sa position initiale. Quel est le reste de $s_{p}$ modulo $p$ ?
Par exemple, pour $p=3, s_{p}=3$ puisque Martin peut choisit de rester à sa position deux fois, de faire un saut sur la droite puis sur la gauche, ou faire un saut sur la gauche puis sur la droite.
|
Soit $x$ une solution de l'équation. Comme best pair, $|x|^{b}-|x|^{a} \leqslant x^{b}-x^{a}=t$. Or l'application qui à $y$ associe $y^{b}-y^{a}$ est continue, et tend vers $+\infty$ en $+\infty$, donc l'équation $y^{b}-y^{a}=t$ a une solution dans $[|x|,+\infty[$, donc une solution positive.
Maintenant appliquons l'hypothèse de l'énoncé au polynôme $X^{2 n}-X-t$. Celui-ci a une racine réelle si et seulement si $t \geqslant f_{2 n}\left(x_{2 n}\right)$. En particulier, le polynôme $X^{f(2 n)}-X^{\alpha}-t$ a une racine réelle si et seulement si $t \geqslant f_{2 n}\left(x_{2 n}\right)$.
- $\operatorname{Si} \mathrm{f}(2 \mathrm{n})<\alpha$, alors la fonction qui à $x$ associe $\chi^{f(2 n)}-\chi^{\alpha}$ tend vers $-\infty$ et $+\infty$, et $+\infty$ en $-\infty$ car $\alpha$ est impair. Ainsi par continuité, l'équation $x^{f(2 n)}-x^{\alpha}=\mathrm{t}$ a toujours une solution donc $X^{f(2 n)}-X^{\alpha}-t$ a toujours une racine ce qui est absurde.
$-\operatorname{Si} f(2 \mathrm{n})=\alpha$, alors le polynôme n'a une racine que pour $\mathrm{t}=0$ ce qui est absurde.
Ainsi $f(2 \mathfrak{n})>\alpha$. En particulier , par le lemme précédent le polynôme $X^{f(2 \mathfrak{n})}-X^{\alpha}-t$ a une racine réelle si et seulement s'il a une racine réelle positive, c'est-à-dire si et seulement si l'équation $\chi^{\mathrm{f}(2 \mathfrak{n})}-\chi^{\alpha}=\mathrm{t}$ a une solution positive. Comme $x \mapsto \chi^{\alpha}$ est bijectif de $\mathbb{R}^{+}$dans $\mathbb{R}^{+}$, le polynôme $X^{f(2 n)}-X^{\alpha}-t$ a une racine réelle si et seulement si l'équation $\chi^{f(2 n) / \alpha}-\chi=t$ a une racine positive, donc si et seulement si $t \geqslant f_{f(2 n) / \alpha}\left(x_{f(2 n) / \alpha}\right)$. Posons $u=f(2 n) / \alpha>1$, on a donc $f_{u}\left(x_{\mathfrak{u}}\right)=f_{2 n}\left(x_{2 n}\right)$.
- Si $2 n>u$, Comme $x_{u}<1, f_{u}\left(x_{u}\right)>f_{2 n}\left(x_{u}\right) \geqslant f_{2 n}\left(x_{2 n}\right)=f_{u}\left(x_{u}\right)$ (via les variations de $f_{2 n}$ ) ce qui est absurde.
- Si $2 n<u$, Comme $x_{2 n}<1, f_{2 n}\left(x_{2 n}\right)>f_{u}\left(x_{2 n}\right) \geqslant f_{u}\left(x_{u}\right)=f_{2 n}\left(x_{2 n}\right)$ (via les variations de $f_{u}$ ) ce qui est absurde.
Ainsi $u=2 \mathfrak{n}$, donc $\mathbf{f}(2 \mathfrak{n})=2 \mathfrak{n} \boldsymbol{\alpha}$.
Il reste alors à montrer que si n est impair, $\mathrm{f}(\mathrm{n})=\alpha \mathrm{n}$. Pour cela on fait de même que dans l'argument précédent : on regarde le polynôme $X^{2 n}-X^{n}-t$, on montre qu'il a une racine réelle si et seulement si
$t \geqslant f_{2 n / n}\left(x_{2 n / n}\right)=f_{2}\left(x_{2}\right)$. Ensuite on obtient que $X^{f(2 n)}-X^{f(n)}-t$ a une racine si et seulement si $t \geqslant f_{2}\left(x_{2}\right)$. Comme $f(n)$ est impair, et $f(2 n)$ pair, on en déduit que $f(2 n)>f(n)$, puis que $f_{2}\left(x_{2}\right)=$ $f_{f(2 n) / f(n)}\left(x_{f(2 n) / f(n)}\right)$. De même on prouve que $f(2 n) / f(n)=2$, donc $f(2 n)=2 f(n)$. Or $f(2 n)=$ $2 \mathrm{n} \alpha$, donc $\mathrm{f}(\mathrm{n})=\mathrm{n} \alpha$. Ainsi si f est solution, f est de la forme $\mathrm{f}: \mathrm{n} \mapsto$ an pour un certain a impair.
Réciproquement s'il existe a impair tel que $f(n)=$ an pour tout entier positif $n$, alors si le polynôme $\sum_{k=0}^{n} a_{k} X^{k}$ a une racine réelle $x_{0}$, le polynôme $\sum_{k=0}^{n} a_{k} X^{f(k)}=\sum_{k=0}^{n} a_{k} X^{a k}$ a pour racine $x_{0}^{1 / a}$. Réciproquement si $\sum_{k=0}^{n} a_{k} X^{a k}$ a une racine réelle $y_{0}, y_{0}^{a}$ est racine de $\sum_{k=0}^{n} a_{k} X^{k}$. Ainsi $f$ vérifie bien l'énoncé.
Les fonctions vérifiant l'énoncé sont les fonctions telles qu'il existe a impair tel que $f(n)=$ an pour tout entier positif n .
Commentaire des correcteurs : L'exercice a été très peu abordé, mais les élèves l'ayant abordé ont majoritairement réussi l'exercice avec des preuves variées. Attention aux expressions de la forme $\chi^{q}$ avec $q$ rationnel et $x$ négatif : cela n'a pas forcément un sens clair. Il faut être très précautionneux.
|
{
"exam": "French_envois",
"problem_label": "16",
"problem_match": "\nExercice 16.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-5.jsonl",
"solution_match": "\nDémonstration.",
"tier": "T2",
"year": null
}
|
A convex quadrilateral $ABCD$ admits an inscribed circle with center $I$. Let $I_a, I_b, I_c$, and $I_d$ be the centers of the inscribed circles of triangles $DAB, ABC, BCD$, and $CDA$ respectively. Suppose that the common tangents to the circumcircles of $AI_bI_d$ and $CI_bI_d$ meet at $X$, and that the common external tangents to the circumcircles of $BI_aI_c$ and $DI_aI_c$ meet at $Y$. Show that $\widehat{XIY}=90$.
|
We denote $\omega_{i}$ as the incircle with center $I_{i}$ and radius $r_{i}$ for $i \in \{A, B, C, D\}$. We also denote $O_{A}, O_{B}, O_{C}$, and $O_{D}$ as the centers of the circles $A I_{b} I_{d}, B I_{a} I_{c}, C I_{b} I_{d}$, and $D I_{a} I_{c}$. We start by proving the following lemma:
Lemma 4. The circles $\omega_{a}$ and $\omega_{c}$ are tangent to each other at the same point on (AC).
Proof: (We also refer to Lemma 36 from the 2022 Geometry D course at Valbonne).
Let $X_{a}$ be the tangency point of $\omega_{a}$ on (BD) and $X_{c}$ be the tangency point of $\omega_{c}$ on (BD). We know that $ABCD$ is circumscribed, which implies that $AB - AD = BC - CD$. We can calculate the distance $BX_{a}$, which is
$$
BX_{a} = \frac{AB - AD + BD}{2} = \frac{BC - CD + BD}{2} = BX_{c},
$$
which shows that $X_{a} = X_{c}$. We rename this tangency point as $T$. Then the points $I_{a}, T$, and $I_{c}$ are collinear and $(I_{a} I_{c}) \perp (BD)$. We denote $\widehat{ABT} = 2\varphi$ and $\widehat{TBC} = 2\mu$, then $\widehat{ABI} = \varphi + \mu$ and $\widehat{ABI_{a}} = \varphi$, which shows that $\widehat{I_{a}BI} = \mu$ and thus that the lines (BT) and (BI) are isogonal conjugates in the triangle $BI_{a}I_{c}$. Since (BT) is the altitude in this same triangle, by a classical lemma, we know that the line (BI) also passes through the circumcenter of the triangle $BI_{a}I_{c}$. Therefore, $O_{B}$ is on the line (BI). Similarly, $O_{D}$ is on the line (DI). We also know that $(O_{B} O_{D}) \perp (I_{a} I_{c})$, so $(DB) \parallel (O_{B} O_{D})$. We will now prove that the line (IY) bisects the angle $\widehat{BID}$. $X$ is on the line $O_{B} O_{D}$ such that $\frac{XO_{B}}{XO_{D}} = \frac{r_{b}}{r_{d}}$. By the Angle Bisector Theorem, we want to show that $\frac{IO_{B}}{IO} = \frac{r_{b}}{r_{d}}$. Since $(DB) \parallel (O_{B} O_{D})$, we have $\frac{IO_{B}}{IO} = \frac{IB}{ID}$. We now calculate
$$
X := r_{b} \cdot \frac{1}{r_{d}} = \frac{\sin (\widehat{IAB}) \cdot AI}{\sin (\widehat{ABI})} \frac{\sin (\widehat{ADI})}{\sin (\widehat{IAD}) \cdot AI}
$$
from the Law of Sines in triangles IAB and IAD, we have $X = \frac{\sin (\widehat{ADI})}{\sin (\widehat{ABI})}$. On the other hand,
$$
X' := r_{b} \cdot \frac{1}{r_{d}} = \frac{2 I_{a} I_{c}}{\sin (\widehat{I_{a} D I_{c}})} \cdot \frac{\sin (\widehat{I_{a} B I_{c}})}{2 I_{a} I_{c}} = \frac{\sin (\widehat{I_{a} D I_{c}})}{\sin (\widehat{I_{a} I_{c}})},
$$
and since $\widehat{ADI} = \widehat{ADC} / 2 = \widehat{I_{a} D I_{c}}$ and also $\widehat{ABI} = \widehat{I_{a} B I_{c}}$, this shows that $X = X'$ and thus that the line (IY) is the external bisector of the angle $\widehat{BID}$. We show similarly that the line (XI) is the external bisector of the angle $\widehat{AIC}$. To prove that $\widehat{X I Y} = 90$, we need to show that the angles $\widehat{AIC}$ and $\widehat{BID}$ have the same bisector. If the following proposition is true, then, (DI, IC) = (AI, IB). Or, $(CI, ID) + (AI, IB) \equiv 0 \pmod{180}$. We will prove this last relation. We call $E$ the intersection point of the lines (AD) and (BC). Then (AI, IB) = 90 + $\frac{(BE, EA)}{2}$ and $(CI, ID) = 90 - \frac{(BE, EA)}{2}$, so $(AI, IB) + (BE, EA) = 180 \equiv 0 \pmod{180}$, which concludes the proof.
Graders' Comment: Well solved by the few students who submitted a solution.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Un quadrilatère convexe $A B C D$ admet un cercle inscrit de centre $I$. Soit $\mathrm{I}_{\mathrm{a}}, \mathrm{I}_{\mathrm{b}}, \mathrm{I}_{\mathrm{c}}$ et $\mathrm{I}_{\mathrm{d}}$ les centres des cercles inscrits de triangles $\mathrm{DAB}, \mathrm{ABC}, \mathrm{BCD}$ et $C D A$ respectivement. On suppose que les tangentes communes aux cercle circonscrits de $\mathrm{AI}_{\mathrm{b}} \mathrm{I}_{\mathrm{d}}$ et $\mathrm{Cl}_{\mathrm{b}} \mathrm{I}_{\mathrm{d}}$ se rencontrent en $X$ et que les tangentes commune extérieures des cercles circonscrits de $\mathrm{BI}_{\mathrm{a}} \mathrm{I}_{\mathrm{c}}$ et $\mathrm{DI}_{\mathrm{a}} \mathrm{I}_{\mathrm{c}}$ se rencontrent en $Y$. Montrer que $\widehat{\mathrm{XIY}}=90$.
|
On note $\omega_{i}$ le cercle inscrit de centre $I_{i}$ et de rayon $r_{i}$ pour $i \in\{A, B, C, D\}$, on note également $O_{A}, O_{B}$, $O_{C}$ et $O_{D}$ les centres des cercles $A I_{b} I_{d}, B I_{a} I_{c}, C I_{b} I_{d}$ et $D I_{a} I_{c}$. On commence par démontrer le lemme suivant:
Lemme 4. Les cercles $\omega_{a}$ et $\omega_{c}$ sont tangents tous les deux en le même point sur (AC).
Preuve : (On référe également au Lemme 36 du cours de Géométrie D de Valbonne 2022).

Soit $X_{a}$ le point de tangence de $\omega_{a}$ sur (BD) et $X_{c}$ le point de tangence de $\omega_{c}$ sur (BD). On sait que $A B C D$ est circonscriptible, cela implique que $A B-A D=B C-C D$. On Peut calculer la distance $B X_{a}$ elle vaut
$$
B X_{a}=\frac{A B-A D+B D}{2}=\frac{B C-C D+B D}{2}=B X_{c},
$$
ce qui montre que $X_{a}=X_{c}$.
On renomme $T$ le point de tangence. Alors les points $\mathrm{I}_{a}, T$ et $\mathrm{I}_{c}$ sont alignés et $\left(I_{a} I_{c}\right) \perp(B D)$. On note $\widehat{A B T}=2 \varphi$ et $\widehat{T B C}=2 \mu$, alors $\widehat{A B I}=\varphi+\mu$ et $\widehat{\mathrm{ABI}_{a}}=\varphi$, ce qui montre que $\widehat{I_{a} B I}=\mu$ et ainsi que les droites (BT) et (BI) sont conjuguées isogonales dans le triangle $\mathrm{BI}_{\mathrm{a}} \mathrm{I}_{\mathrm{c}}$, or (BT) est la hauteur dans ce même triangle et par un lemme classique on sait alors que la droite (BI) passe également par le centre du cercle circonscrit au triangle $\mathrm{BI}_{\mathrm{a}} \mathrm{I}_{\mathrm{c}}$. Donc $\mathrm{O}_{B}$ est sur la droite (BI). De la même manière $\mathrm{O}_{\mathrm{D}}$ se trouve sur la droite (DI). On sait aussi que $\left(O_{B} O_{D}\right) \perp\left(I_{a} I_{c}\right)$ donc $(D B) / /\left(O_{B} O_{D}\right)$. On va maintenant démontrer que la droite (IY) bissecte l'angle $\widehat{\text { BID. }}$. $X$ se trouve sur la droite $\mathrm{O}_{B} \mathrm{O}_{D}$ de telle sorte que $\frac{X O_{B}}{\mathrm{XO}_{\mathrm{D}}}=\frac{\mathrm{r}_{\mathrm{b}}}{\mathrm{r}_{\mathrm{d}}}$, par le lemme de la bissectrice on veut montrer que $\frac{\mathrm{IO}_{B}}{\mathrm{IO}}=\frac{\mathrm{r}_{\mathrm{b}}}{r_{d}}$, or comme $(\mathrm{DB}) / /\left(\mathrm{O}_{B} \mathrm{O}_{\mathrm{D}}\right)$
on a $\frac{\mathrm{IO}_{\mathrm{B}}}{\mathrm{IO}}=\frac{\mathrm{IB}}{\mathrm{ID}}$. On calcule maintenant
$$
X:=r_{b} \cdot \frac{1}{r_{d}}=\frac{\sin (\widehat{\mathrm{IAB}}) \cdot A \mathrm{II}}{\sin (\widehat{\mathrm{ABI}})} \frac{\sin (\widehat{\mathrm{ADI}})}{\sin (\widehat{\mathrm{IAD}}) \cdot \mathrm{AI}}
$$
d'après la loi des sinus dans les triangles IAB et IAD, on a d'une part $X=\frac{\sin (\widehat{A D I})}{\sin (\widehat{A B I})}$. On trouve d'autre part,
$$
X^{\prime}:=r_{b} \cdot \frac{1}{r_{d}}=\frac{2 I_{a} I_{c}}{\sin \left(\widehat{I_{a} D I_{c}}\right)} \cdot \frac{\sin \left(\widehat{I_{a} B I_{c}}\right)}{2 \mathrm{I}_{\mathrm{a}} \mathrm{I}_{c}}=\frac{\sin \left(\widehat{\mathrm{I}_{\mathrm{a}} \mathrm{DI}_{\mathrm{c}}}\right)}{\sin \left(\widehat{\mathrm{I}_{\mathrm{a}} \mathrm{I}_{\mathrm{c}}}\right)},
$$
or, $\widehat{A D I}=\widehat{A D C} / 2=\widehat{\mathrm{I}_{\mathrm{a}} \mathrm{DI}_{\mathrm{c}}}$ et également $\widehat{A B I}=\widehat{\mathrm{I}_{\mathrm{a}} \mathrm{BI}_{\mathrm{c}}}$ ce qui montre que $X=\mathrm{X}^{\prime}$ et ainsi que la droite (IY) est la bissectrice extérieure de l'angle $\widehat{\text { BID }}$. On montre de la même manière que la droite (XI) est la bissectrice extérieure de l'angle $\widehat{A I C}$. Dans le but de démontrer que $\widehat{X I Y}=90$ il faut démontrer que les angles $\widehat{A I C}$ et $\widehat{\text { BID }}$ ont les même bissectrice. Si la proposition suivante est vraie alors, (DI, IC) $=$ $(A I, I B)$. Ou encore $(C I, I D)+(A I, I B) \equiv 0(\bmod 180)$. On va démontrer cette dernière relation, on appelle $E$ le point d'intersection des droites (AD) et (BC), Alors (AI, IB) $=90+\frac{(B E, E A)}{2}$ et $(C I, I D)=90-\frac{(B E, E A)}{2}, \operatorname{donc}(A I, I B)+(B E, E A)=180 \equiv 0(\bmod 180)$, ce qui conclut.
Commentaire des correcteurs: Bien résolu pour les quelques élèves qui ont rendu une copie.
|
{
"exam": "French_envois",
"problem_label": "18",
"problem_match": "\nExercice 18.",
"resource_path": "French/segmented/envois/fr-corrige-envoi-5.jsonl",
"solution_match": "## Solution de l'exercice 18",
"tier": "T2",
"year": null
}
|
Let $x, y$ be strictly positive real numbers. Show that:
$$
x+\frac{y^{2}}{x} \geqslant 2 y
$$
and find the cases of equality.
|
The inequality of the mean gives
$$
x+\frac{y^{2}}{x} \geqslant 2 \sqrt{x \cdot \frac{y^{2}}{x}}=2 y
$$
Suppose we have equality, then $x=\frac{y^{2}}{x}$ so $x^{2}=y^{2}$ so $x=y$. Conversely, if $x=y, x+\frac{y^{2}}{x}=$ $y+\frac{y^{2}}{y}=2 y$ we indeed have equality.
Comment from the graders: The problem is very well done! Be sure to justify that the announced cases of equality are indeed the only possible cases of equality.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soient $x, y$ des réels strictement positifs. Montrer que:
$$
x+\frac{y^{2}}{x} \geqslant 2 y
$$
et trouver les cas d'égalité.
|
L'inégalité de la moyenne donne
$$
x+\frac{y^{2}}{x} \geqslant 2 \sqrt{x \cdot \frac{y^{2}}{x}}=2 y
$$
Supposons qu'on a égalité, alors $x=\frac{y^{2}}{x}$ donc $x^{2}=y^{2}$ donc $x=y$. Réciproquement si $x=y, x+\frac{y^{2}}{x}=$ $y+\frac{y^{2}}{y}=2 y$ on a bien égalité.
Commentaire des correcteurs Le problème est très bien réussi! Attention à bien justifier que les cas d'égalités annoncés sont bien les seuls cas d'égalité possibles.
|
{
"exam": "French_envois",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-2.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T2",
"year": null
}
|
Let $x \geqslant 0$ be a real number. Show that:
$$
1+x^{2}+x^{6}+x^{8} \geqslant 4 x^{4}
$$
and find the cases of equality.
|
We use the arithmetic-geometric inequality in the case $\mathrm{n}=4$. We obtain $1+x^{2}+x^{6}+x^{8} \geqslant 4 x^{\frac{2+6+8}{4}}=4 x^{4}$.
Suppose we have equality. According to the equality case $\chi^{2}=1$, so $x=1$. Conversely, if $x=1$, we have $1+x^{2}+x^{6}+x^{8}=4=4 x^{4}$.
Comment from the graders: The problem was very well done! Some students approached this problem with polynomials rather than inequalities.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $x \geqslant 0$ un réel. Montrer que :
$$
1+x^{2}+x^{6}+x^{8} \geqslant 4 x^{4}
$$
et trouver les cas d'égalité.
|
On utilise l'inégalité arithmético-géométrique, dans le cas $\mathrm{n}=4$. On obtient $1+x^{2}+x^{6}+x^{8} \geqslant 4 x^{\frac{2+6+8}{4}}=4 x^{4}$.
Supposons qu'on a égalité. D'après le cas d'égalité $\chi^{2}=1$, donc $x=1$. Réciproquement si $x=1$, on a $1+x^{2}+x^{6}+x^{8}=4=4 x^{4}$.
Commentaire des correcteurs Le problème très bien réussi! Certains élèves ont approché ce problème avec des polynômes plutôt qu'avec des inégalités.
|
{
"exam": "French_envois",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-2.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T2",
"year": null
}
|
Let $a, b, c$ be real numbers. Show that:
$$
2 a^{2}+20 b^{2}+5 c^{2}+8 a b-4 b c-4 a c \geqslant 0
$$
and find the cases of equality.
|
The inequality is equivalent to $4bc + 4ac - 8ab \leqslant 2a^2 + 20b^2 + 5c^2$. We know that $4ac = 2 \times a \times (2c) \leqslant a^2 + (2c)^2 = a^2 + 4c^2$ and that $4bc = 2 \times c(2b) \leqslant 4b^2 + c^2$. We also have $-8ab = 2 \times (-a) \times (4b) \leqslant a^2 + 16b^2$. By summing all these inequalities, we obtain $4bc + 4ac - 8ab \leqslant 2a^2 + 20b^2 + 5c^2$.
Suppose we have equality, in this case we have equality in the three inequalities used: we thus have $a = 2c$, $c = 2b$ so $a = 4b$ and $-a = 4b$. In particular, $-a = a$ so $a = 0$ and therefore $b$ and $c$ are also zero. Conversely, if $a = b = c = 0$, we indeed have equality.
We could have also noticed that $2a^2 + 20b^2 + 5c^2 + 8ab - 4bc - 4ac = (a + 4b)^2 + (a - 2c)^2 + (2b - c)^2 \geqslant 0$ and found the equality case in the same way.
Comment from the graders: The problem was very well done, and all students found the factorization. Be careful, the equality case was a bit elaborate in this exercise.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $a, b, c$ des nombres réels. Montrer que:
$$
2 a^{2}+20 b^{2}+5 c^{2}+8 a b-4 b c-4 a c \geqslant 0
$$
et trouver les cas d'égalité.
|
L'inégalité est équivalente à $4 b c+4 a c-8 a b \leqslant 2 a^{2}+20 b^{2}+5 c^{2}$. Or on sait que $4 a c=2 \times a \times(2 c) \leqslant a^{2}+(2 c)^{2}=a^{2}+4 c^{2}$ et que $4 b c=2 \times c(2 b) \leqslant 4 b^{2}+c^{2}$. On a également $-8 \mathfrak{a b}=2 \times(-\mathfrak{a}) \times(4 b) \leqslant \mathfrak{a}^{2}+16 b^{2}$. En sommant toutes ces inégalités, on obtient $4 b c+4 a c-8 a b \leqslant 2 a^{2}+20 b^{2}+5 c^{2}$.
Supposons qu'on a égalité, dans ce cas on a égalité dans les trois inégalités utilisées : on a donc $\mathrm{a}=2 \mathrm{c}$, $c=2 b$ donc $a=4 b$ et $-a=4 b$. En particulier $-a=a$ donc $a=0$ donc $b$ et $c$ sont également nuls. Réciproquement, si $\mathrm{a}=\mathrm{b}=\mathrm{c}=0$, on a bien égalité.
On aurait pu également remarquer que $2 a^{2}+20 b^{2}+5 c^{2}+8 a b-4 b c-4 a c=(a+4 b)^{2}+(a-2 c)^{2}+$ $(2 b-c)^{2} \geqslant 0$ et trouver de la même façon le cas d'égalité.
Commentaire des correcteurs Le problème est très bien réussi et tous les élèves ont trouvé la factorisation. Attention, le cas d'égalité était un peu élaboré dans cet exercice.
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-2.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T2",
"year": null
}
|
Find all functions $f$ from $\mathbb{R}$ to $\mathbb{R}$ such that for all real numbers $x, y$,
$$
f(x) f(y)=f(x y)+x+y
$$
|
By evaluating at $y=0$ we obtain $f(x) f(0)=f(0)+x$ for all real $x$. For $x=1$, we get that $f(0) \neq 0$, otherwise we would have $1=0$. By evaluating at $x=0$ we obtain $f(0)^{2}=f(0)$, so $f(0)=1$ and thus $f(x)=1+x$ for all real $x$.
Conversely, let $f$ be the function such that $f(x)=1+x$ for all real $x$ and let $(x, y) \in \mathbb{R}^{2}$, then $\mathrm{f}(\mathrm{x}) \mathrm{f}(\mathrm{y})=(1+x)(1+y)=1+x y+x+y=f(x y)+x+y$ so $f$ does indeed satisfy the equation. The unique solution to the equation is therefore the function $f$ such that $f(x)=1+x$ for all real $x$.
Comment from the graders: The exercise is generally well done. However, it is important to distinguish between two parts in a functional equation:
- The analysis, which involves choosing a function $f$ that satisfies the equation and determining the properties satisfied by $f$. Here, it is established that if $f$ is a solution to the equation, then for all real $x$, $f(x)=x+1$.
- The synthesis, which involves verifying that conversely, the function $f$ that maps $x$ to $x+1$ is indeed a solution to the equation.
Some students forgot the second part and were penalized.
|
f(x)=1+x
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Trouver toutes les fonctions $f$ de $\mathbb{R}$ dans $\mathbb{R}$ telles que pour tous réels $x, y$,
$$
f(x) f(y)=f(x y)+x+y
$$
|
En évaluant en $y=0$ on obtient $f(x) f(0)=f(0)+x$ pour tout réel $x$. Pour $x=1$, on obtient que $f(0) \neq 0$, sinon on aurait $1=0$. En évaluant en $x=0$ on obtient $f(0)^{2}=f(0)$ donc $f(0)=1$ donc $f(x)=1+x$ pour tout $x$ réel.
Réciproquement soit $f$ la fonction telle que $f(x)=1+x$ pour tout $x$ réel et soit $(x, y) \in \mathbb{R}^{2}$, alors $\mathrm{f}(\mathrm{x}) \mathrm{f}(\mathrm{y})=(1+x)(1+y)=1+x y+x+y=f(x y)+x+y$ donc $f$ vérifie bien l'équation. L'unique solution de l'équation est donc la fonction $f$ telle que $f(x)=1+x$ pour tout $x$ réel.
Commentaire des correcteurs L'exercice est globalement bien réussi. Cependant, il faut bien distinguer deux parties dans une équation fonctionnelle :
- L'analyse qui consiste à choisir une fonction f vérifiant l'équation et déterminer les propriétés vérifiée par f . Ici, on établit que si f est une solution de l'équation, alors pour tout réel $\mathrm{x}, \mathrm{f}(\mathrm{x})=$ $x+1$.
- La synthèse qui consiste à vérifier que réciproquement, la fonction f qui à $x$ associe $x+1$ est bien solution de l'équation.
Certains élèves ont oublié la deuxième partie et ont été pénalisés.
|
{
"exam": "French_envois",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-2.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T2",
"year": null
}
|
Find all triplets of real numbers ( $\mathrm{a}, \mathrm{b}, \mathrm{c}$ ) satisfying the system of equalities:
$$
\left\{\begin{array}{l}
a\left(b^{2}+c\right)=c(c+a b) \\
b\left(c^{2}+a\right)=a(a+b c) \\
c\left(a^{2}+b\right)=b(b+a c)
\end{array}\right.
$$
|
The equalities are rewritten as $a b(b-c)=c(c-a)$, $b c(c-a)=a(a-b)$, and $\mathrm{ca}(\mathrm{a}-\mathrm{b})=\mathrm{b}(\mathrm{b}-\mathrm{c})$. By multiplying these three equalities, we obtain $(\mathrm{abc})^{2}(\mathrm{c}-\mathrm{a})(\mathrm{b}-\mathrm{c})(\mathrm{a}-\mathrm{b})=$ $\mathrm{abc}(\mathrm{c}-\mathrm{a})(\mathrm{b}-\mathrm{c})(\mathrm{a}-\mathrm{b})$. In particular, two cases arise:
- Either $\mathrm{abc}=0$. Since the equalities are cyclic, assume $\mathrm{a}=0$. By the first equality $\mathbf{c}^{2}=0$ hence $\mathbf{c}=0$. By the third equality $\boldsymbol{b}^{2}=0$ hence $\mathrm{b}=0$
- Or two of the elements among $a, b, c$ are equal, assume $a=b$. In this case $b c(c-a)=0$. If $\mathrm{b}=0$ or $\mathrm{c}=0$ we fall back to the previous case, otherwise $\mathrm{a}=\mathrm{b}=\mathrm{c}$.
- Or $a b c=1$, in this case $a, b, c$ are non-zero. The equalities are rewritten as: $b-c=c^{2}(c-a)$, $c-a=a^{2}(a-b)$, and $a-b=b^{2}(b-c)$. In particular, $a-b, b-c$, and $c-a$ have the same sign, but their sum is zero, and we necessarily have $\mathrm{a}-\mathrm{b}=\mathrm{b}-\mathrm{c}=\mathrm{c}-\mathrm{a}=0$ i.e., $\mathrm{a}=\mathrm{b}=\mathrm{c}$.
Comment from the graders: Many students submitted a solution to this problem, but few received full marks. Indeed, there were several recurring errors:
- If $a \geqslant b$ and $c \geqslant d$, it is not necessarily true that $a c \geqslant b d$. This is true for positive real numbers, but not for negative real numbers: for example, $2 \geqslant-1,0 \geqslant-1$ but $0 \times 2=0<(-1) \times(-1)=1$.
- Several students assumed $a \geqslant b \geqslant c$. However, such an assumption cannot be made since the system is not symmetric: swapping a and b completely changes the system. On the other hand, the system is cyclic: replacing a with $b$, b with $c$, and $c$ with a does not change it. Therefore, we can assume that a is the largest, but we cannot assume any additional inequality on b and c.
- Some students forgot to verify that $\mathrm{a}=\mathrm{b}=\mathrm{c}$ is a solution: it must be done.
|
a=b=c
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Trouver tous les triplets de réels ( $\mathrm{a}, \mathrm{b}, \mathrm{c}$ ) vérifiant le système d'égalités :
$$
\left\{\begin{array}{l}
a\left(b^{2}+c\right)=c(c+a b) \\
b\left(c^{2}+a\right)=a(a+b c) \\
c\left(a^{2}+b\right)=b(b+a c)
\end{array}\right.
$$
|
Les égalités se réécrivent $a b(b-c)=c(c-a), b c(c-a)=a(a-b)$ et $\mathrm{ca}(\mathrm{a}-\mathrm{b})=\mathrm{b}(\mathrm{b}-\mathrm{c})$. En multipliant ces trois égalités, on obtient $(\mathrm{abc})^{2}(\mathrm{c}-\mathrm{a})(\mathrm{b}-\mathrm{c})(\mathrm{a}-\mathrm{b})=$ $\mathrm{abc}(\mathrm{c}-\mathrm{a})(\mathrm{b}-\mathrm{c})(\mathrm{a}-\mathrm{b})$. En particulier deux cas se présentent :
- Soit $\mathrm{abc}=0$. Les égalités étant cycliques, supposons $\mathrm{a}=0$. Par la première égalité $\mathbf{c}^{2}=0$ donc $\mathbf{c}=0$. Par la troisième égalité $\boldsymbol{b}^{2}=0$ donc $\mathrm{b}=0$
- Soit deux des éléments parmi $a, b, c$ sont égaux, on suppose $a=b$. Dans ce cas $b c(c-a)=0$. Si $\mathrm{b}=0$ ou $\mathrm{c}=0$ on retombe dans le cas précédent, sinon $\mathrm{a}=\mathrm{b}=\mathrm{c}$.
- Soit $a b c=1$, dans ce cas $a, b, c$. sont non nuls Les égalités se réécrivent $: b-c=c^{2}(c-a)$, $c-a=a^{2}(a-b)$ et $a-b=b^{2}(b-c)$. En particulier $a-b, b-c$ et $c-a$ sont de même signe, mais de somme nulle et on a donc nécessairement $\mathrm{a}-\mathrm{b}=\mathrm{b}-\mathrm{c}=\mathrm{c}-\mathrm{a}=0$ i.e; $\mathrm{a}=\mathrm{b}=\mathrm{c}$.
Commentaire des correcteurs Beaucoup d'élèves ont rendu une copie à ce problème mais rares sont ceux qui ont eu la totalité des points. En effet il y a eu plusieurs d'erreurs récurrentes :
- Si $a \geqslant b$ et $c \geqslant d$, on n'a pas nécessairement $a c \geqslant b d$. Cela est vrai pour des nombres réels positifs, mais pas pour des nombres réels négatifs : par exemple $2 \geqslant-1,0 \geqslant-1$ mais $0 \times 2=0<(-1) \times(-1)=1$.
- Plusieurs élèves ont supposé $a \geqslant b \geqslant c$. Pourtant on ne peut pas faire une telle supposition puisque le système n'est pas symétrique : échanger a et b change totalement le système. En revanche, le système est cyclique : remplacer a par $b, b$ par $c$ et $c$ par a ne le change pas. On peut donc supposer que a est le plus grand, mais on ne peut pas supposer d'inégalité supplémentaire sur bet c.
- Certains oublient de vérifier que $\mathrm{a}=\mathrm{b}=\mathrm{c}$ est une solution : il faut le faire.
|
{
"exam": "French_envois",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-2.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T2",
"year": null
}
|
Let $a, b, c > 0$ such that: $a + b + c = 1$. Show that:
$$
\frac{a}{b} + \frac{a}{c} + \frac{b}{a} + \frac{b}{c} + \frac{c}{a} + \frac{c}{b} + 6 \geqslant 2 \sqrt{2} \left( \sqrt{\frac{1-a}{a}} + \sqrt{\frac{1-c}{c}} + \sqrt{\frac{1-b}{b}} \right)
$$
and determine the cases of equality.
|
The right-hand side of the inequality is $2 \sqrt{2}\left(\sqrt{\frac{b+c}{a}}+\sqrt{\frac{a+b}{c}}+\sqrt{\frac{a+c}{b}}\right)$. We use the arithmetic-geometric mean inequality: $2 \sqrt{2 \frac{b+c}{a}} \leqslant 2+\frac{b+c}{a}$. Similarly, $2 \sqrt{\frac{b+a}{c}} \leqslant 2+\frac{b+a}{c}$ and $2 \sqrt{\frac{a+c}{b}} \leqslant 2+\frac{a+c}{b}$. By summing these three inequalities, we obtain
$$
\frac{a}{b}+\frac{a}{c}+\frac{b}{a}+\frac{b}{c}+\frac{c}{a}+\frac{c}{b}+6 \geqslant 2 \sqrt{2}\left(\sqrt{\frac{1-a}{a}}+\sqrt{\frac{1-c}{c}}+\sqrt{\frac{1-b}{b}}\right)
$$
Suppose we have equality, then by looking at the first case of equality, we have $\frac{b+c}{a}=2$ so $1-a=2a$ so $a=\frac{1}{3}$. By looking at the other two cases of equality, we get $a=b=c=\frac{1}{3}$. Conversely, if $a=b=c=\frac{1}{3}$, then $\frac{a}{b}+\frac{a}{c}+\frac{b}{a}+\frac{b}{c}+\frac{c}{a}+\frac{c}{b}+6=12$ and $2 \sqrt{2}\left(\sqrt{\frac{1-a}{a}}+\sqrt{\frac{1-c}{c}}+\sqrt{\frac{1-b}{b}}\right)=2 \sqrt{2}(3 \times \sqrt{2})=12$; we indeed have equality.
Comment from the graders: The problem is generally well done. A minority of students used inequalities in the wrong direction or performed unnecessary manipulations. Be careful not to forget the case of equality!
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soient $a, b, c>0$ tels que : $a+b+c=1$. Montrer que :
$$
\frac{a}{b}+\frac{a}{c}+\frac{b}{a}+\frac{b}{c}+\frac{c}{a}+\frac{c}{b}+6 \geqslant 2 \sqrt{2}\left(\sqrt{\frac{1-a}{a}}+\sqrt{\frac{1-c}{c}}+\sqrt{\frac{1-b}{b}}\right)
$$
et déterminer les cas d'égalité.
|
Le terme de droite de l'inégalité vaut $2 \sqrt{2}\left(\sqrt{\frac{b+c}{a}}+\sqrt{\frac{a+b}{c}}+\sqrt{\frac{a+c}{b}}\right)$. On utilise l'inégalité arithmético-géométrique : $2 \sqrt{2 \frac{b+c}{a}} \leqslant 2+\frac{b+c}{a}$. De même $2 \sqrt{\frac{b+a}{c}} \leqslant 2+\frac{b+a}{c}$ et $2 \sqrt{\frac{a+c}{b}} \leqslant 2+\frac{a+c}{b}$. En sommant ces trois inégalités, on obtient
$$
\frac{a}{b}+\frac{a}{c}+\frac{b}{a}+\frac{b}{c}+\frac{c}{a}+\frac{c}{b}+6 \geqslant 2 \sqrt{2}\left(\sqrt{\frac{1-a}{a}}+\sqrt{\frac{1-c}{c}}+\sqrt{\frac{1-b}{b}}\right)
$$
Supposons qu'on a égalité, alors en regardant le premier cas d'égalité, on a $\frac{b+c}{a}=2$ donc $1-a=2 a$ donc $\mathrm{a}=\frac{1}{3}$. En regardant les deux autres cas d'égalité on obtient $\mathrm{a}=\mathrm{b}=\mathrm{c}=\frac{1}{3}$. Réciproquement si $\mathrm{a}=\mathrm{b}=\mathrm{c}=\frac{1}{3}, \frac{\mathrm{a}}{\mathrm{b}}+\frac{\mathrm{a}}{\mathrm{c}}+\frac{\mathrm{b}}{\mathrm{a}}+\frac{\mathrm{b}}{\mathrm{c}}+\frac{\mathrm{c}}{\mathrm{a}}+\frac{\mathrm{c}}{\mathrm{b}}+6=12$ et $2 \sqrt{2}\left(\sqrt{\frac{1-\mathrm{a}}{\mathrm{a}}}+\sqrt{\frac{1-\mathrm{c}}{\mathrm{c}}}+\sqrt{\frac{1-\mathrm{b}}{\mathrm{b}}}\right)=2 \sqrt{2}(3 \times \sqrt{2})=12 ;$ on a bien égalité.
Commentaire des correcteurs Le problème est globalement bien réussi. Une minorité d'élèves ont employé des inégalités dans le mauvais sens ou effectué des manipulations superflues. Attention à ne pas oublier le cas d'égalité!
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-2.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T2",
"year": null
}
|
Let $a, b, c$ be strictly positive real numbers such that: $a b+b c+c a=a b c$. Show that:
$$
\frac{1}{a^{2}+b^{2}}+\frac{1}{b^{2}+c^{2}}+\frac{1}{c^{2}+a^{2}} \leqslant \frac{1}{6},
$$
and find the cases of equality.
|
Let $u=\frac{1}{a}, v=\frac{1}{b}, w=\frac{1}{c}$. By dividing by $abc$, the condition rewrites as $u+v+w=1$. The desired inequality rewrites as $\frac{u^{2} v^{2}}{u^{2}+w^{2}}+\frac{u^{2} w^{2}}{u^{2}+w^{2}}+\frac{v^{2} w^{2}}{v^{2}+w^{2}} \leqslant \frac{1}{6}$. We use the arithmetic-geometric inequality on the denominators: $u^{2}+v^{2} \geqslant 2 u v$ and similarly for the other two. We obtain $\frac{u^{2} v^{2}}{u^{2}+w^{2}}+\frac{u^{2} w^{2}}{u^{2}+w^{2}}+\frac{v^{2} w^{2}}{v^{2}+w^{2}} \leqslant \frac{1}{2}(u v+v w+u w)$. Now $1=(u+v+w)^{2}=u^{2}+v^{2}+w^{2}+2(u v+$ $v w+w u) \geqslant 3(u v+v w+u w)$ by the cyclic lemma. In particular $u v+v w+u w \leqslant \frac{1}{3}$, so $\frac{u^{2} v^{2}}{u^{2}+w^{2}}+\frac{u^{2} w^{2}}{u^{2}+w^{2}}+\frac{v^{2} w^{2}}{v^{2}+w^{2}} \leqslant \frac{1}{6}$.
For the equality cases, we have equality in the cyclic lemma, so $u=v=w$ and thus $a=b=c$. By plugging into the condition, $3a^2=a^3$ so $a=b=c=3$. Conversely, if $a=b=c=3$, we have $\frac{1}{a^{2}+b^{2}}+\frac{1}{b^{2}+c^{2}}+\frac{1}{c^{2}+a^{2}}=\frac{3}{2 \times 9}=\frac{1}{6}$, so we indeed have equality.
Comment from the graders: The problem is well solved by the copies that have treated it. However, be careful with the equality cases: you need to specify in which inequality you are looking at the equality case, calculate each variable (which is done with the condition imposed on the variables), and do not forget to verify that you have equality! You also need to state the inequalities you use. Be careful of the bad students' inequality: some got the inequality sign wrong, others used it for negative numbers and ended up with false results.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $a, b, c$ des réels strictement positifs tels que : $a b+b c+c a=a b c$. Montrer que :
$$
\frac{1}{a^{2}+b^{2}}+\frac{1}{b^{2}+c^{2}}+\frac{1}{c^{2}+a^{2}} \leqslant \frac{1}{6},
$$
et trouver les cas d'égalité.
|
Posons $u=\frac{1}{a}, v=\frac{1}{b}, w=\frac{1}{c}$. En divisant par abc, la condition se réécrit $u+v+w=1$. L'inégalité voulue se réécrit $\frac{u^{2} v^{2}}{\mathfrak{u}^{2}+w^{2}}+\frac{\mathfrak{u}^{2} w^{2}}{\mathfrak{u}^{2}+w^{2}}+\frac{v^{2} w^{2}}{v^{2}+w^{2}} \leqslant \frac{1}{6}$. On utilise l'inégalité arithmético-géométrique sur les dénominateurs: $\mathfrak{u}^{2}+v^{2} \geqslant 2 u v$ et similairement sur les deux autres. On obtient $\frac{u^{2} v^{2}}{u^{2}+w^{2}}+\frac{u^{2} w^{2}}{u^{2}+w^{2}}+\frac{v^{2} w^{2}}{v^{2}+w^{2}} \leqslant \frac{1}{2}(u v+v w+u w)$. Or $1=(u+v+w)^{2}=u^{2}+v^{2}+w^{2}+2(u v+$ $v w+w u) \geqslant 3(u v+v w+u w)$ par lemme du tourniquet. En particulier $u v+v w+u w \leqslant \frac{1}{3}$ donc $\frac{\mathcal{u}^{2} v^{2}}{\mathfrak{u}^{2}+w^{2}}+\frac{\mathfrak{u}^{2} w^{2}}{\mathfrak{u}^{2}+w^{2}}+\frac{v^{2} w^{2}}{v^{2}+w^{2}} \leqslant \frac{1}{6}$.
Pour les cas d'égalité, on a égalité dans le lemme du tourniquet, donc $u=v=w$ donc $\mathrm{a}=\mathrm{b}=\mathrm{c}$. En réinjectant dans la condition, $3 \mathrm{a}^{2}=\mathrm{a}^{3}$ donc $\mathrm{a}=\mathrm{b}=\mathrm{c}=3$. Réciproquement si $\mathrm{a}=\mathrm{b}=\mathrm{c}=3$, on a $\frac{1}{\mathrm{a}^{2}+\mathrm{b}^{2}}+\frac{1}{\mathrm{~b}^{2}+\mathrm{c}^{2}}+\frac{1}{\mathrm{c}^{2}+\mathrm{a}^{2}}=\frac{3}{2 \times 9}=\frac{1}{6}$ on a bien égalité.
Commentaire des correcteurs Le problème est bien réussi par les copies qui l'ont traité. Attention toutefois aux cas d'égalités : il faut préciser dans quelle inégalité utilisée vous regardez le cas d'égalité, calculer chaque variable (ce qui se fait avec la condition imposée sur les variables) et ne pas oublier alors de vérifier qu'on a égalité! Il faut également penser à énoncer les inégalités qu'on utilise. Attention à l'inégalité des mauvais élèves : certains se sont trompés de sens d'inégalité, d'autres l'ont utilisé pour des nombres négatifs et aboutissent à des résultats faux.
|
{
"exam": "French_envois",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-2.jsonl",
"solution_match": "\nSolution de l'exercice 7",
"tier": "T2",
"year": null
}
|
Let $a_{1}, \ldots, a_{2019}$ be positive integers. Show that the following are equivalent:
(i) there exists a real number $x$ such that for all $i \in\{1, \ldots, 2019\}$, we have: $a_{i}=\lfloor i x\rfloor$
(ii) for all $\boldsymbol{i}, \mathfrak{j} \in\{1, \ldots, 2019\}$ satisfying $i+j \leqslant 2019$, we have: $a: a_{i}+a_{j} \leqslant a_{i+j} \leqslant a_{i}+a_{j}+1$.
|
First, let's prove the direct sense: if there exists a real number \( x \) such that for all \( i \) between 1 and 2019, \( a_{i} = \lfloor i x \rfloor \), and if we are given \( i, j \) between 1 and 2019 such that \( i + j \leq 2019 \), then \((i + j)x = ix + jx \geq \lfloor ix \rfloor + \lfloor jx \rfloor = a_{i} + a_{j} \) and \((i + j)x = ix + jx < \lfloor ix \rfloor + 1 + \lfloor jx \rfloor + 1 = a_{i} + a_{j} + 2\), so \( a_{i} + a_{j} \leq a_{i+j} < a_{i} + a_{j} + 2 \). Since the \( a_{i} \) are integers, we have \( a_{i} + a_{j} \leq a_{i+j} \leq a_{i} + a_{j} + 1 \).
Conversely, suppose that for all \( i, j \) between 1 and 2019 such that \( i + j \leq 2019 \), \( a_{i} + a_{j} \leq a_{i+j} \leq a_{i} + a_{j} + 1 \). Finding \( x \) such that for all \( i \) between 1 and 2019, \( a_{i} = \lfloor i x \rfloor \) amounts to finding \( x \) such that for all \( i \) between 1 and 2019, \( a_{i} \leq i x < a_{i} + 1 \), that is, such that for all \( i \), \( \frac{a_{i}}{i} \leq x < \frac{a_{i} + 1}{i} \). It is therefore sufficient to show that the maximum of the \( \frac{a_{i}}{i} \) for \( i \) between 1 and 2019 is strictly less than the minimum of the \( \frac{a_{j} + 1}{j} \) for \( j \) between 1 and 2019, or more simply that \( \frac{a_{i}}{i} \leq \frac{a_{i} + 1}{j} \) for all \( i, j \) between 1 and 2019.
Let's prove this by strong induction on \( m = \max(i, j) \). If \( m = 1 \), \( i = j = 1 \) so the inequality is obvious. For the induction step, suppose the inequality is true for all \( i, j \) between 1 and \( m \). We want to show the inequality \( \frac{a_{i}}{i} < \frac{a_{j} + 1}{j} \), where \( 1 \leq i, j \leq m + 1 \). There are three cases to consider:
- If \( i = j \), the inequality is obvious.
- If \( i < j \), applying the induction hypothesis to \( (i, j - i) \): \( a_{j} \geq a_{i} + a_{j-i} > a_{i} + (j - i) \frac{a_{i}}{i} - 1 = a_{i} \times \frac{j}{i} - 1 \) so \( \frac{a_{j} + 1}{j} > \frac{a_{i}}{i} \).
- If \( i > j \), applying the induction hypothesis to \( (i - j, j) \): \( a_{i} \leq a_{j} + a_{i-j} + 1 < a_{j} + \frac{(i - j)(a_{j} + 1)}{j} = a_{j} \frac{i}{j} + \frac{i - j}{j} < (a_{j} + 1) \frac{i}{j} \) so \( \frac{a_{i}}{i} < \frac{a_{j} + 1}{j} \).
Comment from the examiners: The exercise was difficult and only a very small number of students managed to prove the second implication. The first implication was generally well addressed.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soient $a_{1}, \ldots, a_{2019}$ des entiers positifs. Montrer qu'il y a équivalence entre:
(i) il existe un réel $x$ tel que pour tout $i \in\{1, \ldots, 2019\}$, on a : $a_{i}=\lfloor i x\rfloor$
(ii) pour tous $\boldsymbol{i}, \mathfrak{j} \in\{1, \ldots, 2019\}$ vérifiant $i+j \leqslant 2019$, on $a: a_{i}+a_{j} \leqslant a_{i+j} \leqslant a_{i}+a_{j}+1$.
|
Prouvons tout d'abord le sens direct : s'il existe $x$ réel tel que pour tout $i$ entre 1 et $2019, a_{i}=\lfloor i x\rfloor$, et si on se donne $\boldsymbol{i}, \boldsymbol{j}$ entre 1 et 2019 tels que $\boldsymbol{i}+\mathfrak{j} \leqslant 2019$, alors $(\mathfrak{i}+\mathfrak{j}) \mathbf{x}=$ $i x+j x \geqslant\lfloor i x\rfloor+\lfloor j x\rfloor=a_{i}+a_{j}$ et $(i+j) x=i x+j x<\lfloor i x\rfloor+1+\lfloor j x\rfloor+1=a_{i}+a_{j}+2$, donc $a_{i}+a_{j} \leqslant a_{i+j}<a_{i}+a_{j}+2$. Comme les $a_{i}$ sont entiers, on a donc $a_{i}+a_{j} \leqslant a_{i+j} \leqslant a_{i}+a_{j}+1$.
Réciproquement supposons que pour tout $i, j$ entre 1 et 2019 tels que $i+j \leqslant 2019, a_{i}+a_{j} \leqslant a_{i+j} \leqslant$ $a_{i}+a_{j}+1$. Trouver $x$ tel que pour tout $i$ entre 1 et 2019, $a_{i}=\lfloor i x\rfloor$ revient à trouver $x$ tel que pour tout $i$ entre 1 et 2019, $a_{i} \leqslant i x<a_{i}+1$, c'est-à-dire tel que pour tout $i, \frac{a_{i}}{i} \leqslant x<\frac{a_{i}+1}{i}$. Il suffit donc de montrer que le maximum des $\frac{a_{i}}{i}$ pour $i$ entre 1 et 2019 est strictement inférieur au minimum des $\frac{a_{j}+1}{j}$ pour $j$ entre 1 et 2019 , ou plus simplement que $\frac{a_{i}}{i} \leqslant \frac{a_{i}+1}{j}$ pour tout $i, j$ entre 1 et 2019.
Montrons cela par récurrence forte sur $\mathfrak{m}=\max (\mathfrak{i}, \mathfrak{j})$. Si $\mathfrak{m}=1, \mathfrak{i}=\mathfrak{j}=1$ donc l'inégalité est évidente. Pour l'hérédité, supposons l'inégalité vraie pour tout $i, j$ entre 1 et m . On veut montrer l'inégalité $\frac{\mathrm{a}_{i}}{\mathrm{i}}<$ $\frac{a_{j}+1}{j}$, où $1 \leqslant \mathfrak{i}, \mathfrak{j} \leqslant \mathfrak{m}+1$. Il y a trois cas à traiter :
- Si $i=$ j l'inégalité est évidente.
- Si $i<j$, en appliquant l'hypothèse de récurrence à $(i, j-i): a_{j} \geqslant a_{i}+a_{j-i}>a_{i}+(j-i) \frac{a_{i}}{i}-1=$ $a_{i} \times \frac{j}{i}-1$ donc $\frac{a_{j}+1}{j}>\frac{a_{i}}{i}$
- Si $\boldsymbol{i}>\mathfrak{j}$, en appliquant l'hypothèse de récurrence à $(\mathfrak{i}-\mathfrak{j}, \mathfrak{j}): a_{i} \leqslant a_{j}+a_{i-j}+1<a_{j}+$ $\frac{(i-j)\left(a_{j}+1\right)}{j}=a_{j} \frac{i}{j}+\frac{i-j}{j}<\left(a_{j}+1\right) \frac{i}{j}$ donc $\frac{a_{i}}{i}<\frac{a_{j}+1}{j}$
Commentaire des correcteurs L'exercice était difficile et seulement un nombre très réduit d'élèves sont parvenus à montrer la seconde implication. La première implication est dans l'ensemble bien abordée.
|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "\nExercice 8.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-2.jsonl",
"solution_match": "\nSolution de l'exercice 8",
"tier": "T2",
"year": null
}
|
Let $a, b, c, d$ be strictly positive real numbers such that: $a+b+c+d=1$. Show that:
$$
\frac{a^{4}}{a^{3}+a^{2} b+a b^{2}+b^{3}}+\frac{b^{4}}{b^{3}+b^{2} c+b c^{2}+c^{3}}+\frac{c^{4}}{c^{3}+c^{2} d+c d^{2}+d^{3}}+\frac{d^{4}}{d^{3}+d^{2} a+d a^{2}+a^{3}} \geqslant \frac{1}{4}
$$
and determine the cases of equality.
|
In this solution, we will use the inequality $2\left(x^{2}+y^{2}\right) \geqslant (x+y)^{2} (*)$, valid for all real numbers $x, y$ with equality if and only if $x=y$. First, note that $a^{3} + a^{2}b + ab^{2} + b^{3} = (a^{2} + b^{2})(a + b)$. In particular, the inequality can be rewritten as $\sum_{\text{cyc}} \frac{a^{4}}{(a^{2} + b^{2})(a + b)} \geqslant \frac{1}{4}$. Let $S$ be the sum on the left side of the inequality. Each denominator of the terms in $S$ is symmetric in the two variables it contains, so we seek a relationship between $S$ and $\sum_{\text{cyc}} \frac{b^{4}}{(a^{2} + b^{2})(a + b)}$. Let's calculate the difference of the two terms:
$$
S - \sum_{\text{cyc}} \frac{b^{4}}{(a^{2} + b^{2})(a + b)} = \sum_{\text{cyc}} \frac{a^{4} - b^{4}}{(a^{2} + b^{2})(a + b)} = \sum_{\text{cyc}} \frac{a^{2} - b^{2}}{(a + b)} = \sum_{\text{cyc}} a - b = 0
$$
In particular, $S = \sum_{\text{cyc}} \frac{b^{4}}{(a^{2} + b^{2})(a + b)}$, so $2S = \sum_{\text{cyc}} \frac{a^{4} + b^{4}}{(a^{2} + b^{2})(a + b)}$. By (*), $a^{4} + b^{4} \geqslant \frac{(a^{2} + b^{2})^{2}}{2}$, so by summing, $2S \geqslant \sum_{\text{cyc}} \frac{a^{2} + b^{2}}{2(a + b)}$. (*) gives again $a^{2} + b^{2} \geqslant \frac{(a + b)^{2}}{2}$, so by summing, $2S \geqslant \sum_{\text{cyc}} \frac{a + b}{4} = \frac{2(a + b + c + d)}{4} = \frac{1}{2}$, hence $S \geqslant \frac{1}{4}$.
Suppose we have equality. In this case, we have the cyclic equalities $a = b$, so $a = b = c = d$. By the condition on the sum, $4a = 1$ so $a = \frac{1}{4}$.
Conversely, if $a = b = c = d = \frac{1}{4}$, then $a + b + c + d = 1$ and $S = \sum_{\text{cyc}} \frac{a^{4}}{a^{3} + a^{2}b + b^{2} + b^{3}} = \sum_{\text{cyc}} \frac{a^{4}}{4a^{3}} = \sum_{\text{cyc}} \frac{a}{4} = 4 \frac{a}{4} = \frac{1}{4}$, so we indeed have equality.
Comment from the graders: The problem was difficult and few managed to have a complete solution. It was possible to use Jensen's inequality applied to the function that maps $x$ to $\frac{1}{1 + x + x^{2} + x^{3}}$, but the cases of equality were more delicate: for the cases of equality, if its second derivative $f''$ is strictly positive over the set of values that the variables can take on which we want to use the inequality, then the variables are equal (if $f''$ is strictly positive except at a finite number of points, the reasoning still holds). However, the strict convexity of the function in question was not clear, so a justification was expected. Be careful with the addition of fractions.
## Senior Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $a, b, c, d$ des réels strictement positifs tels que : $a+b+c+d=1$. Montrer que :
$$
\frac{a^{4}}{a^{3}+a^{2} b+a b^{2}+b^{3}}+\frac{b^{4}}{b^{3}+b^{2} c+b c^{2}+c^{3}}+\frac{c^{4}}{c^{3}+c^{2} d+c d^{2}+d^{3}}+\frac{d^{4}}{d^{3}+d^{2} a+d a^{2}+a^{3}} \geqslant \frac{1}{4}
$$
et déterminer les cas d'égalité.
|
Dans cette solution, on va utiliser à plusieurs reprises l'inégalité $2\left(x^{2}+y^{2}\right) \geqslant$ $(x+y)^{2}(*)$, valable pour tous réels $x, y$ avec égalité si et seulement si $x=y$. Déjà notons que $a^{3}+$ $a^{2} b+a b^{2}+b^{3}=\left(a^{2}+b^{2}\right)(a+b)$. En particulier l'inégalité se réécrit $\sum_{\text {cycl. }} \frac{a^{4}}{\left(a^{2}+b^{2}\right)(a+b)} \geqslant \frac{1}{4}$. Notons $S$ la somme de gauche dans l'inégalité précédente. Chaque dénominateur des termes de $S$ est symétrique en les deux variables qu'il contient, on cherche donc une relation entre $S$ et $\sum_{c y c l} \frac{b^{4}}{\left(a^{2}+b^{2}\right)(a+b)}$. Calculons la différence des deux termes:
$$
S-\sum_{c y c l .} \frac{b^{4}}{\left(a^{2}+b^{2}\right)(a+b)}=\sum_{c y c l .} \frac{a^{4}-b^{4}}{\left(a^{2}+b^{2}\right)(a+b)}=\sum_{c y c l .} \frac{a^{2}-b^{2}}{(a+b)}=\sum_{c y c l .} a-b=0
$$
En particulier $S=\sum_{\text {cycl. }} \frac{b^{4}}{\left(a^{2}+b^{2}\right)(a+b)}$ donc $2 S=\sum_{\text {cycl. }} \frac{a^{4}+b^{4}}{\left(a^{2}+b^{2}\right)(a+b)} . \operatorname{Par}(*), a^{4}+b^{4} \geqslant \frac{\left(a^{2}+b^{2}\right)^{2}}{2}$ donc en sommant $2 S \geqslant \sum_{\text {cycl. }} \frac{a^{2}+b^{2}}{2(a+b)} .(*)$ donne de nouveau $a^{2}+b^{2} \geqslant \frac{(a+b)^{2}}{2}$ donc en sommant $2 S \geqslant \sum_{\text {cycl. }} \frac{a+b}{4}=$ $\frac{2(\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{d})}{4}=\frac{1}{2}$ donc $S \geqslant \frac{1}{4}$.
Supposons qu'on a égalité. Dans ce cas on a les égalités cycliques $\mathrm{a}=\mathrm{b}$, soit $\mathrm{a}=\mathrm{b}=\mathrm{c}=\mathrm{d}$. Par la condition sur la somme $4 a=1$ donc $a=\frac{1}{4}$.
Réciproquement si $a=b=c=d=\frac{1}{4}$, alors $a+b+c+d=1$ et $S=\sum_{\text {cycl. }} \frac{a^{4}}{a^{3}+a^{2} b+b^{2}+b^{3}}=\sum_{\text {cycl. }} \frac{a^{4}}{4 a^{3}}=$ $\sum_{\text {cycl. }} \frac{\mathrm{a}}{4}=4 \frac{\mathrm{a}}{4}=\frac{1}{4}$ on a bien égalité.
Commentaire des correcteurs Le problème était difficile et peu sont ceux qui ont réussi à avoir une solution complète. Il était possible d'utiliser l'inégalité de Jensen appliquée à la fonction qui à $x$ associe $\frac{1}{1+x+x^{2}+x^{3}}$, mais les cas d'égalité étaient eux plus délicats : pour les cas d'égalité, si sa dérivée seconde $f^{\prime \prime}$ est strictement positive sur l'ensemble des valeurs que prennent les variables sur lesquelles on veut utiliser l'inégalité, alors on a égalité des variables (si $f^{\prime \prime}$ est strictement positive sauf sur un nombre fini de points le raisonnement se tient). Néanmoins la convexité stricte de la fonction en quesion n'était pas claire, on attendait donc une justification. Attention aux additions de fractions.
## Exercices Seniors
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-2.jsonl",
"solution_match": "\nSolution de l'exercice 9",
"tier": "T2",
"year": null
}
|
Find all functions $f$ from $\mathbb{R}$ to $\mathbb{R}$ such that for all real numbers $x, y$,
$$
f(x) f(y)=f(x y)+x+y
$$
|
By evaluating at $y=0$ we obtain $\boldsymbol{f}(\mathrm{x}) \boldsymbol{f}(0)=\boldsymbol{f}(0)+x$ for all real $x$. For $x=1$, we get that $f(0) \neq 0$, otherwise we would have $1=0$. By evaluating at $x=0$ we get $f(0)^{2}=f(0)$, so $f(0)=1$ and thus $f(x)=1+x$ for all real $x$.
Conversely, let $f$ be the function such that $f(x)=1+x$ for all real $x$ and let $(x, y) \in \mathbb{R}^{2}$, then $\mathbf{f}(\mathrm{x}) \mathrm{f}(\mathrm{y})=(1+x)(1+y)=1+x y+x+y=f(x y)+x+y$ so $f$ does indeed satisfy the equation. The unique solution to the equation is therefore the function $f$ such that $f(x)=1+x$ for all real $x$.
Grader's Comment: The exercise is generally well done. Be careful when dividing by a number to ensure that the number is non-zero. Also, do not forget to verify that the solutions found do indeed satisfy the functional equation.
|
f(x)=1+x
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Trouver toutes les fonctions f de $\mathbb{R}$ dans $\mathbb{R}$ telles que pour tous réels $x, y$,
$$
f(x) f(y)=f(x y)+x+y
$$
|
En évaluant en $y=0$ on obtient $\boldsymbol{f}(\mathrm{x}) \boldsymbol{f}(0)=\boldsymbol{f}(0)+x$ pour tout réel $x$. Pour $x=1$, on obtient que $f(0) \neq 0$, sinon on aurait $1=0$. En évaluant en $x=0$ on obtient $f(0)^{2}=f(0)$ donc $f(0)=1$ donc $f(x)=1+x$ pour tout $x$ réel.
Réciproquement soit $f$ la fonction telle que $f(x)=1+x$ pour tout $x$ réel et soit $(x, y) \in \mathbb{R}^{2}$, alors $\mathbf{f}(\mathrm{x}) \mathrm{f}(\mathrm{y})=(1+x)(1+y)=1+x y+x+y=f(x y)+x+y$ donc $f$ vérifie bien l'équation. L'unique solution de l'équation est donc la fonction $f$ telle que $f(x)=1+x$ pour tout $x$ réel.
Commentaire des correcteurs L'exercice est globalement bien réussi. Attention, lorsque l'on divise par un nombre, à bien vérifier que ce nombre est non nul. Il ne faut pas non plus oublier de contrôler que les solutions trouvées vérifient bien l'équation fonctionnelle.
|
{
"exam": "French_envois",
"problem_label": "10",
"problem_match": "\nExercice 10.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-2.jsonl",
"solution_match": "\nSolution de l'exercice 10",
"tier": "T2",
"year": null
}
|
Let $x, y$ be real numbers. Show that:
$$
|x|+|y| \leqslant|x-y|+|x+y| .
$$
|
If $x$ and $y$ are positive, $|x|+|y|=x+y=|x+y|$. If $x$ and $y$ are negative, $|x|+|y|=-x-y=|x+y|$. If $x$ is positive and $y$ is negative, $|x|+|y|=x-y=|x-y|$. If $x$ is negative and $y$ is positive, $|x|+|y|=y-x=|x-y|$. In all cases, by the positivity of the absolute value, $|x|+|y| \leqslant|x-y|+|x+y|$.
Comment from the graders: The number of cases considered in the disjunctions was often very high (often 8), whereas this number could easily be reduced to 2. Proofs using the triangle inequality are perfect and elegant. Proofs squaring the inequality were cumbersome and not always correct.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $x, y$ des réels. Montrer que:
$$
|x|+|y| \leqslant|x-y|+|x+y| .
$$
|
Si $x$ et $y$ sont positifs, $|x|+|y|=x+y=|x+y|$. Si $x$ et $y$ sont négatifs $|x|+|y|=-x-y=|x+y|$. Si $x$ est positif et $y$ négatif $|x|+|y|=x-y=|x-y|$. Si $x$ est négatif et $y$ positif $|x|+|y|=y-x=|x-y|$. Dans tous les cas par positivité de la valeur absolue $|x|+|y| \leqslant|x-y|+|x+y|$.
Commentaire des correcteurs Le nombre de cas traités dans les disjonctions de cas était très important (souvent 8), alors que ce nombre pouvait aisément être ramené à 2. Les preuves utilisant l'inégalité triangulaires sont parfaites et élégantes. Les preuves passant l'inégalité au carré étaient lourdes et n'étaient pas toujours justes.
|
{
"exam": "French_envois",
"problem_label": "11",
"problem_match": "\nExercice 11.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-2.jsonl",
"solution_match": "\nSolution de l'exercice 11",
"tier": "T2",
"year": null
}
|
Find all polynomials $P$ with real coefficients such that for all real $x, y$,
$$
x P(x)+y P(y) \geqslant 2 P(x y)
$$
|
If $P(X)=c X$ with $c \geqslant 0, x P(x)+y P(y)=c\left(x^{2}+y^{2}\right) \geqslant 2 c x y=2 P(x y)$ by the mean inequality, polynomials of the form $cX$ with $c \geqslant 0$ are suitable. Let's show that these are the only ones. Suppose $P$ is not constant. By evaluating the inequality at $(x, 0)$, we get $xP(x) \geqslant 2P(0)$. By looking at the limit as $x \to +\infty$, we get that the leading coefficient of $P$ must be strictly positive (since $P$ cannot tend to $-\infty$). By evaluating at $(x, x)$, we get $x P(x) \geqslant P\left(x^{2}\right)$. The polynomial $X P(X)$ is of degree $\operatorname{deg}(P)+1$, and $P\left(X^{2}\right)$ is of degree $2 \operatorname{deg}(P)$. If $2 \operatorname{deg}(P)>\operatorname{deg}(P)+1$, then $P\left(X^{2}\right)-X P(X)$ is a polynomial of degree $2 \operatorname{deg}(P)$ with a strictly positive leading coefficient, so it is strictly positive for large $x$, a contradiction. In particular, $2 \operatorname{deg}(P) \leqslant \operatorname{deg}(P)+1$ so $P$ is a polynomial of degree at most 1 with a strictly positive leading coefficient.
Now let $P(X)=aX+b$ with $a \geqslant 0$. By evaluating the inequality at $(x, x)$, we get $a x^{2}+b x \geqslant a x^{2}+b$ so $b x \geqslant b$. For $x=2$, we get $b \geqslant 0$, and for $x=0$ we get $b \leqslant 0$ so $b=0$. Thus $P(X)=a X$ with $a \geqslant 0$ which concludes the proof.
Comment from the graders: Students often assumed that the leading coefficient was positive, but it needs to be verified at the beginning. Similarly, the degree of the polynomial must be justified. Finally, it should not be forgotten to check that the polynomials found satisfy the statement.
|
P(X)=aX \text{ with } a \geqslant 0
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Trouver tous les polynômes $P$ à coefficients réels tels que pour tous réels $x, y$,
$$
x P(x)+y P(y) \geqslant 2 P(x y)
$$
|
Si $P(X)=c X$ avec $c \geqslant 0, x P(x)+y P(y)=c\left(x^{2}+y^{2}\right) \geqslant 2 c x y=2 P(x y)$ par inégalité de la moyenne, les polynômes de la forme cX avec $\mathrm{c} \geqslant 0$ conviennent, montrons que ce sont les seuls. Supposons P non constant. En évaluant en ( $x, 0$ ) l'inégalité, on obtient $\mathrm{xP}(x) \geqslant 2 \mathrm{P}(0)$. En regardant la limite en $+\infty$, on obtient que le coefficient dominant de $P$ est forcément strictement positif (car $P$ ne peut tendre vers $-\infty)$. En évaluant en $(x, x)$, on obtient $x P(x) \geqslant P\left(x^{2}\right)$. Le polynôme $X P(X)$ est de degré $\operatorname{deg}(P)+1, P\left(X^{2}\right)$ est de degré $2 \operatorname{deg}(P)$. Si $2 \operatorname{deg}(P)>\operatorname{deg}(P)+1$, alors $P\left(X^{2}\right)-X P(X)$ est un polynôme de degré $2 \operatorname{deg}(P)$ de coefficient dominant strictement positif, donc il est strictement positif pour $x$ assez grand, contradiction. En particulier $2 \operatorname{deg}(\mathrm{P}) \leqslant \operatorname{deg}(\mathrm{P})+1$ donc P est un polynôme de degré au plus 1 et de coefficient dominant strictement positif.
Maintenant posons $\mathrm{P}(X)=\mathrm{aX}+\mathrm{b}$ avec $\mathrm{a} \geqslant 0$. En évaluant l'inégalité en $(x, x)$ on obtient $a x^{2}+b x \geqslant$ $\mathrm{a} x^{2}+\mathrm{b}$ donc $\mathrm{b} x \geqslant \mathrm{~b}$. Pour $x=2$, on obtient $\mathrm{b} \geqslant 0$, pour $x=0$ on obtient $\mathrm{b} \leqslant 0$ donc $\mathrm{b}=0$. Ainsi $P(X)=a X$ avec $a \geqslant 0$ ce qui conclut.
Commentaire des correcteurs Les élèves partaient souvent du principe que le coefficient dominant était positif, cependant il faut le vérifier au début. De même, il fallait justifier le calcul du degré du polynôme. Enfin, il ne faut pas oublier de vérifier que les polynômes trouvés satisfont bien l'énoncé.
|
{
"exam": "French_envois",
"problem_label": "12",
"problem_match": "\nExercice 12.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-2.jsonl",
"solution_match": "\nSolution de l'exercice 12",
"tier": "T2",
"year": null
}
|
Find all periodic sequences $\left(x_{n}\right)_{n \in \mathbb{N}^{*}}$ of strictly positive real numbers, such that for all $\mathrm{n} \geqslant 1$,
$$
x_{n+2}=\frac{1}{2}\left(\frac{1}{x_{n+1}}+x_{n}\right) .
$$
|
Let $n \geqslant 1$. By multiplying the recurrence relation by $x_{n+1}$, we obtain that $x_{n+2} x_{n+1}=\frac{1}{2}\left(1+x_{n+1} x_{n}\right)$. Thus $\left(x_{n+2} x_{n+1}-1\right)=\frac{1}{2}\left(x_{n+1} x_{n}-1\right)$. In particular, $x_{n+1} x_{n}-1= \frac{1}{2^{n-1}}\left(x_{2} x_{1}-1\right)$. If the sequence $\left(x_{n}\right)$ is periodic, the sequence $x_{n+1} x_{n}-1$ is also periodic with the same period, which according to the previous equation is only possible if $x_{2} x_{1}-1=0$. In this case, for all $n \geqslant 1$, $x_{n+1} x_{n}-1=0$, so $x_{n+1}=\frac{1}{x_{n}}$. By substituting this back into the recurrence relation, we obtain that for all $n \geqslant 1$, $x_{n+2}=\frac{1}{2}\left(x_{n+2}+x_{n}\right)$, hence $\frac{1}{2} x_{n+2}=\frac{1}{2} x_{n}$, which means $x_{n+2}=x_{n}$. In particular, $(x_{n})$ is 2-periodic and satisfies $x_{2}=\frac{1}{x_{1}}$. Therefore, $x_{n}=x_{1}$ if $n$ is odd, and $x_{n}=\frac{1}{x_{1}}$ if $n$ is even.
Conversely, let $a \in \mathbb{R}^{+*}$ and $\left(x_{n}\right)_{n \in \mathbb{N}^{*}}$ such that $x_{n}=a$ if $n$ is odd, and $x_{n}=\frac{1}{a}$ if $n$ is even. Since $\frac{1}{x_{n+1}}=x_{n}$, we have $\frac{1}{2}\left(\frac{1}{x_{n+1}}+x_{n}\right)=x_{n}=x_{n+2}$ for all $n \geqslant 1$. The sequence $\left(x_{n}\right)$ is therefore 2-periodic and satisfies the given recurrence relation.
The sequences satisfying the statement are the sequences $\left(x_{n}\right)_{n \in \mathbb{N}^{*}}$ such that $x_{n}=a$ if $n$ is odd, and $x_{n}=\frac{1}{a}$ if $n$ is even for $a>0$.
Comment from the graders: There were several possible solutions. Several errors were made with quantifiers, notably some confusion between $\forall$ and $\exists$. It is important not to forget to verify that the sequences found satisfy the statement!
|
x_{n}=a \text{ if } n \text{ is odd, and } x_{n}=\frac{1}{a} \text{ if } n \text{ is even for } a>0
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Trouver toutes les suites périodiques $\left(x_{n}\right)_{n \in \mathbb{N}^{*}}$ de réels strictement positifs, et telles que pour tout $\mathrm{n} \geqslant 1$,
$$
x_{n+2}=\frac{1}{2}\left(\frac{1}{x_{n+1}}+x_{n}\right) .
$$
|
Soit $n \geqslant 1$. En multipliant la relation de récurrence par $x_{n+1}$, on obtient que $x_{n+2} x_{n+1}=\frac{1}{2}\left(1+x_{n+1} x_{n}\right)$. Ainsi $\left(x_{n+2} x_{n+1}-1\right)=\frac{1}{2}\left(x_{n+1} x_{n}-1\right)$. En particulier $x_{n+1} x_{n}-1=$ $\frac{1}{2^{n-1}}\left(x_{2} x_{1}-1\right)$. Si la suite $\left(x_{n}\right)$ est périodique, la suite $x_{n+1} x_{n}-1$ l'est aussi de même période, ce qui n'est possible d'après l'équation précédente que si $x_{2} x_{1}-1=0$. Dans ce cas pour tout $\mathrm{n} \geqslant 1$, $x_{n+1} x_{n}-1=0$, donc $x_{n+1}=\frac{1}{x_{n}}$. En réinjectant cela dans l'équation de récurrence, on obtient que pour tout $n \geqslant 1, x_{n+2}=\frac{1}{2}\left(x_{n+2}+x_{n}\right)$ donc $\frac{1}{2} x_{n+2}=\frac{1}{2} x_{n}$ soit $x_{n+2}=x_{n}$. En particulier ( $x_{n}$ ) est 2 -périodique et vérifie $x_{2}=\frac{1}{x_{1}}$. On a donc $x_{n}=x_{1}$ si $n$ est impair, $x_{n}=\frac{1}{x_{1}}$ si $n$ est pair.
Réciproquement soit $a \in \mathbb{R}^{+*}$ et $\left(x_{n}\right)_{n \in \mathbb{N}^{*}}$ telle que $x_{n}=a$ si $n$ est impair, $x_{n}=\frac{1}{a}$ si $n$ est pair. Comme $\frac{1}{x_{n+1}}=x_{n}$, on a $\frac{1}{2}\left(\frac{1}{x_{n+1}}+x_{n}\right)=x_{n}=x_{n+2}$ pour tout $n \geqslant 1$. La suite $\left(x_{n}\right)$ est donc 2 -périodique et vérifie la relation de récurrence donnée.
Les suites vérifiant l'énoncé sont les suites $\left(x_{n}\right)_{n \in \mathbb{N}^{*}}$ avec $\left(x_{n}\right)_{n \in \mathbb{N}^{*}}$ telle que $x_{n}=a$ si $n$ est impair, $x_{n}=\frac{1}{a}$ si $n$ est pair pour $a>0$.
Commentaire des correcteurs Il y avait plusieurs solutions possibles. Plusieurs erreurs ont été faites avec les quantificateurs, notemment quelques confusion entre le $\forall$ et $\exists$. Il ne faut pas oublier de vérifier que les suites trouvées satisfont l'énoncé !
|
{
"exam": "French_envois",
"problem_label": "13",
"problem_match": "\nExercice 13.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-2.jsonl",
"solution_match": "\nSolution de l'exercice 13",
"tier": "T2",
"year": null
}
|
Find all functions $f$ from $\mathbb{R}$ to $\mathbb{R}$ such that for all real numbers $x, y$,
$$
f(x f(x)+f(y))=f(x)^{2}+y
$$
|
Evaluating the equality at $(0, \mathrm{y}), \mathbf{f}(\mathrm{f}(\mathrm{y}))=\mathrm{f}(0)^{2}+\mathrm{y}$. In particular, $\mathrm{f} \circ \mathrm{f}$ is bijective, so $f$ is injective and surjective, hence bijective. Let $a$ be such that $f(a)=0$. Evaluating at $(a, a)$, we get $f(0)=f(a f(a)+f(a))=f(a)^{2}+a=a$, so $f(0)=a$. In particular, we obtain that $f(f(0))=0$. Since for all $y, f(f(y))=f(0)^{2}+y$, evaluating at $y=0$, we get $f(0)^{2}=0$ so $f(0)=0$. In particular, for all $y, f(f(y))=y$.
Now evaluate the equality at $(x, 0)$, we get $f(x f(x))=f(x)^{2}$. Evaluating the previous equality at $f(x)$, we get $f(f(x) f(f(x)))=f(f(x))^{2}$, so $f(x f(x))=x^{2}$. In particular, $x^{2}=f(x)^{2}$ for all real $x$, so for all real $x, f(x)= \pm x$.
Now let's show that for all $x, f(x)=x$ or for all $x, f(x)=-x$. Suppose there exist $a$ and $b$ non-zero such that $f(a)=a$ and $f(b)=-b$. Evaluating the initial equality at $(a, b)$, we get that $f\left(a^{2}-b\right)=a^{2}+b$, so $a^{2}+b$ is either $a^{2}-b$ or $b-a^{2}$, thus $a=0$ or $b=0$, which is absurd. We therefore deduce that for all $x, f(x)=x$ or for all $x, f(x)=-x$.
Conversely, if $f(x)=x$ for all real $x, f(x f(x)+f(y))=f\left(x^{2}+y\right)=x^{2}+y=f(x)^{2}+y$ so $f$ is a solution. If $f(x)=-x$ for all real $x, f(x f(x)+f(y))=f\left(-x^{2}-y\right)=x^{2}+y=f(x)^{2}+y$ so $f$ is a solution. The solutions are therefore the identity function and its opposite.
Comment from the correctors: The most frequent mistake was to confuse " $\forall x, f(x)=x$ or $f(x)=-x$ " and " $f(x)=x \forall x$ or $f(x)=-x \forall x$ ".
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Trouver toutes les fonctions $f$ de $\mathbb{R}$ dans $\mathbb{R}$ telles que pour tous réels $x, y$,
$$
f(x f(x)+f(y))=f(x)^{2}+y
$$
|
En évaluant l'égalité en $(0, \mathrm{y}), \mathbf{f}(\mathrm{f}(\mathrm{y}))=\mathrm{f}(0)^{2}+\mathrm{y}$. En particulier $\mathrm{f} \circ \mathrm{f}$ est bijective, donc $f$ est injective et surjective donc bijective. Soit a tel que $f(a)=0$. En évaluant en (a, a), $f(0)=f(a f(a)+f(a))=f(a)^{2}+a=a$ donc $f(0)=a$. En particulier on obtient que $f(f(0))=0$. Comme pour tout $y, f(f(y))=f(0)^{2}+y$, en évaluant en $y=0$, on obtient $f(0)^{2}=0$ donc $f(0)=0$. En particulier, pour tout $y, f(f(y))=y$.
Evaluons désormais l'égalité en $(x, 0)$, on obtient $f(x f(x))=f(x)^{2}$. En évaluant l'égalité précédente en $f(x)$ on obtient $f(f(x) f(f(x)))=f(f(x))^{2}$ donc $f(x f(x))=x^{2}$. En particulier $x^{2}=f(x)^{2}$ pour tout $x$ réel, donc pour tout réel $x, f(x)= \pm x$.
Montrons désormais que pour tout $x, f(x)=x$ ou pour tout $x, f(x)=-x$. Supposons qu'il existe $a$ et $b$ non nuls tels que $f(a)=a$ et $f(b)=-b$. En évaluant l'égalité initiale en $(a, b)$, on obtient que $f\left(a^{2}-b\right)=a^{2}+b$, donc $a^{2}+b$ vaut $a^{2}-b$ ou $b-a^{2}$, ainsi $a=0$ ou $b=0$ ce qui est absurde. On en déduit donc que pour tout $x, f(x)=x$ ou pour tout $x, f(x)=-x$.
Réciproquement si $f(x)=x$ pour tout réel $x, f(x f(x)+f(y))=f\left(x^{2}+y\right)=x^{2}+y=f(x)^{2}+y$ donc $f$ est solution. Si $f(x)=-x$ pour tout réel $x, f(x f(x)+f(y))=f\left(-x^{2}-y\right)=x^{2}+y=f(x)^{2}+y$ donc $f$ est solution. Les solutions sont donc la fonction identité et son opposé.
Commentaire des correcteurs L'erreur la plus fréquente à été de confondre " $\forall x, f(x)=x$ ou $f(x)=-\chi$ " et " $f(x)=x \forall x$ ou $f(x)=-x \forall x$ ".
|
{
"exam": "French_envois",
"problem_label": "14",
"problem_match": "\nExercice 14.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-2.jsonl",
"solution_match": "\nSolution de l'exercice 14",
"tier": "T2",
"year": null
}
|
Let $a_{1}, \ldots, a_{2019}$ be positive integers. Show that the following are equivalent:
(i) there exists a real number $x$ such that for all $i \in\{1, \ldots, 2019\}$, we have: $a_{i}=\lfloor i x\rfloor$
(ii) for all $i, j \in\{1, \ldots, 2019\}$ satisfying $i+j \leqslant 2019$, we have: $a_{i}+a_{j} \leqslant a_{i+j} \leqslant a_{i}+a_{j}+1$.
|
First, let's prove the direct sense: if there exists a real number \( x \) such that for all \( i \) between 1 and 2019, \( a_{i} = \lfloor i x \rfloor \), and if we are given \( i, j \) between 1 and 2019 such that \( i + j \leq 2019 \), then \((i + j)x = ix + jx \geq \lfloor ix \rfloor + \lfloor jx \rfloor = a_{i} + a_{j} \) and \((i + j)x = ix + jx < \lfloor ix \rfloor + 1 + \lfloor jx \rfloor + 1 = a_{i} + a_{j} + 2\), so \( a_{i} + a_{j} \leq a_{i+j} < a_{i} + a_{j} + 2 \). Since the \( a_{i} \) are integers, we have \( a_{i} + a_{j} \leq a_{i+j} \leq a_{i} + a_{j} + 1 \).
Conversely, suppose that for all \( i, j \) between 1 and 2019 such that \( i + j \leq 2019 \), \( a_{i} + a_{j} \leq a_{i+j} \leq a_{i} + a_{j} + 1 \). Finding \( x \) such that for all \( i \) between 1 and 2019, \( a_{i} = \lfloor i x \rfloor \) amounts to finding \( x \) such that for all \( i \) between 1 and 2019, \( a_{i} \leq i x < a_{i} + 1 \), that is, such that for all \( i \), \( \frac{a_{i}}{i} \leq x < \frac{a_{i} + 1}{i} \). It is therefore sufficient to show that the maximum of \( \frac{a_{i}}{i} \) for \( i \) between 1 and 2019 is strictly less than the minimum of \( \frac{a_{j} + 1}{j} \) for \( j \) between 1 and 2019, or more simply that \( \frac{a_{i}}{i} < \frac{a_{i} + 1}{j} \) for all \( i, j \) between 1 and 2019.
Let's prove this by strong induction on \( m = \max(i, j) \). If \( m = 1 \), \( i = j = 1 \) so the inequality is obvious. For the induction step, suppose the inequality is true for all \( i, j \) between 1 and \( m \). We want to show the inequality \( \frac{a_{i}}{i} < \frac{a_{i} + 1}{j} \), where \( 1 \leq i, j \leq m + 1 \). There are three cases to consider:
- If \( i = j \), the inequality is obvious.
- If \( i < j \), applying the induction hypothesis to \( (i, j - i) \): \( a_{j} \geq a_{i} + a_{j - i} > a_{i} + (j - i) \frac{a_{i}}{i} - 1 = a_{i} \times \frac{j}{i} - 1 \) so \( \frac{a_{j} + 1}{j} > \frac{a_{i}}{i} \).
- If \( i > j \), applying the induction hypothesis to \( (i - j, j) \): \( a_{i} \leq a_{j} + a_{i - j} + 1 < a_{j} + \frac{(i - j)(a_{j} + 1)}{j} = a_{j} \frac{i}{j} + \frac{i - j}{j} < (a_{j} + 1) \frac{i}{j} \) so \( \frac{a_{i}}{i} < \frac{a_{j} + 1}{j} \).
Comment from the graders: Several students made the task more complicated by looking for a more complex solution, which was difficult to write and ultimately led to an error. To avoid this, they should have tried to reformulate the problem to simplify it.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soient $a_{1}, \ldots, a_{2019}$ des entiers positifs. Montrer qu'il y a équivalence entre :
(i) il existe un réel $x$ tel que pour tout $i \in\{1, \ldots, 2019\}$, on a : $a_{i}=\lfloor i x\rfloor$
(ii) pour tous $i, j \in\{1, \ldots, 2019\}$ vérifiant $i+j \leqslant 2019$, on $a: a_{i}+a_{j} \leqslant a_{i+j} \leqslant a_{i}+a_{j}+1$.
|
Prouvons tout d'abord le sens direct: s'il existe x réel tel que pour tout $i$ entre 1 et $2019, a_{i}=\lfloor i x\rfloor$, et si on se donne $\boldsymbol{i}, \boldsymbol{j}$ entre 1 et 2019 tels que $\boldsymbol{i}+\mathfrak{j} \leqslant 2019$, alors $(\mathfrak{i}+\mathfrak{j}) \mathbf{x}=$ $i x+j x \geqslant\lfloor i x\rfloor+\lfloor j x\rfloor=a_{i}+a_{j}$ et $(i+j) x=i x+j x<\lfloor i x\rfloor+1+\lfloor j x\rfloor+1=a_{i}+a_{j}+2$, donc $a_{i}+a_{j} \leqslant a_{i+j}<a_{i}+a_{j}+2$. Comme les $a_{i}$ sont entiers, on a donc $a_{i}+a_{j} \leqslant a_{i+j} \leqslant a_{i}+a_{j}+1$.
Réciproquement supposons que pour tout $i, j$ entre 1 et 2019 tels que $i+j \leqslant 2019, a_{i}+a_{j} \leqslant a_{i+j} \leqslant$ $a_{i}+a_{j}+1$. Trouver $x$ tel que pour tout $i$ entre 1 et 2019, $a_{i}=\lfloor i x\rfloor$ revient à trouver $x$ tel que pour tout $i$ entre 1 et 2019, $a_{i} \leqslant i x<a_{i}+1$, c'est-à-dire tel que pour tout $i, \frac{a_{i}}{i} \leqslant x<\frac{a_{i}+1}{i}$. Il suffit donc de montrer que le maximum des $\frac{a_{i}}{i}$ pour $i$ entre 1 et 2019 est strictement inférieur au minimum des $\frac{a_{j}+1}{j}$ pour $j$ entre 1 et 2019 , ou plus simplement que $\frac{a_{i}}{i}<\frac{a_{i}+1}{j}$ pour tout $i, j$ entre 1 et 2019.
Montrons cela par récurrence forte sur $\mathfrak{m}=\max (\mathfrak{i}, \mathfrak{j})$. Si $\mathfrak{m}=1, \mathfrak{i}=\mathfrak{j}=1$ donc l'inégalité est évidente. Pour l'hérédité, supposons l'inégalité vraie pour tout $i, j$ entre 1 et m . On veut montrer l'inégalité $\frac{\mathrm{a}_{i}}{\mathrm{i}}<$ $\frac{a_{i}+1}{j}$, où $1 \leqslant i, j \leqslant \mathfrak{m}+1$. Il y a trois cas à traiter :
- Si $i=$ j l'inégalité est évidente.
- Si $i<j$, en appliquant l'hypothèse de récurrence à $(i, j-i): a_{j} \geqslant a_{i}+a_{j-i}>a_{i}+(j-i) \frac{a_{i}}{i}-1=$ $a_{i} \times \frac{j}{i}-1$ donc $\frac{a_{j}+1}{j}>\frac{a_{i}}{i}$
- Si $\boldsymbol{i}>\mathfrak{j}$, en appliquant l'hypothèse de récurrence à $(\mathfrak{i}-\mathfrak{j}, \mathfrak{j}): a_{i} \leqslant \mathfrak{a}_{\mathfrak{j}}+\mathfrak{a}_{i-j}+1<\mathfrak{a}_{j}+$ $\frac{(i-j)\left(a_{j}+1\right)}{j}=a_{j} \frac{i}{j}+\frac{i-j}{j}<\left(a_{j}+1\right) \frac{i}{j}$ donc $\frac{a_{i}}{i}<\frac{a_{j}+1}{j}$
Commentaire des correcteurs Plusieurs élèves se sont compliqués la tâche en cherchant une solution trop compliquée, difficile à rédiger et ont donc fini par faire une erreur. Pour éviter cela, il aurait fallu chercher à reformuler le problème pour le simplifier.
|
{
"exam": "French_envois",
"problem_label": "15",
"problem_match": "\nExercice 15.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-2.jsonl",
"solution_match": "\nSolution de l'exercice 15",
"tier": "T2",
"year": null
}
|
Let $1<t<2$ be a real number. Show that for any sufficiently large integer $d$, there exists a polynomial $P(X)=\sum_{k=0}^{d} a_{k} X^{k}$, with $a_{d}=1$ and $a_{0}, \ldots, a_{d-1} \in\{1,-1\}$, such that:
$$
|P(t)-2019| \leqslant 1
$$
|
Let $d \geqslant 2019$ be an integer and $a_{1}<\ldots<a_{k}$ the $d$-tuples of the form $\left( \pm 1, \ldots, \pm 1\right.$ ), ordered lexicographically (starting from the right!, i.e., $a_{i}>a_{j}$ if and only if the first non-zero term of $a_{i}-a_{j}$ from the right is $>0$ ), with $k=2^{d}$.
To go from $a_{i}$ to $a_{i+1}$, we look at the first -1 from the right in $a_{i}$, change it to a 1, and replace all 1s to its right with -1s. For example, if $\mathrm{d}=3$, the triplets are in the order $a_{1}=(-1,-1,-1), a_{2}=(-1,-1,1), a_{3}=(-1,1,-1), a_{4}=(-1,1,1) a_{5}=(1,-1,-1), a_{6}=$ $(1,-1,1), a_{7}=(1,1,-1)$ and $a_{8}=(1,1,1)$.
We associate with $a_{i}=\left(a_{i 1}, \ldots, a_{i d}\right)$ the polynomial $P_{i}(X)=\sum_{j=1}^{d} a_{i j} X^{j-1}$, so that $M:=-P_{1}(t)=$ $P_{k}(t)=1+\ldots+t^{d-1}>d$.
Now, $\left|P_{i+1}(t)-P_{i}(t)\right|=2\left|t^{\mathrm{l}}-\left(1+\ldots+t^{\mathrm{l}-1}\right)\right|$ for some $l \geqslant 0$ (which depends on $i$ ) for all $i$.
Let's show $t^{\mathrm{l}}-\left(1+\ldots+\mathrm{t}^{\mathrm{l}-1}\right) \leqslant 1$ : this is equivalent to $\mathrm{t}^{\mathrm{l}+1}-\mathrm{t}^{\mathrm{l}}-\left(\mathrm{t}^{\mathrm{l}}-1\right) \leqslant \mathrm{t}-1$ after multiplying by $t-1$, or after rearrangement $t^{l}(2-t)+t \geqslant 2$, which is true since $t^{l} \geqslant 1$.
Thus, $P_{i+1}(t)$ is greater than $P_{i}(t)$ by at most 2, which shows that, since $2019-t^{d} \in[-M ; M]$, there exists $i$ such that $\left|P_{i}(t)-\left(2019-t^{d}\right)\right| \leqslant 1$, which concludes by setting $P=X^{d}+P_{i}$.
Comment from the graders: The received solutions were generally good. However, most students forgot important elements of the proof. A few students proposed an alternative algorithmic proof, which was very elegant.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $1<t<2$ un nombre réel. Montrer que pour tout entier $d$ suffisamment grand, il existe un polynôme $P(X)=\sum_{k=0}^{d} a_{k} X^{k}$, avec $a_{d}=1$ et $a_{0}, \ldots, a_{d-1} \in\{1,-1\}$, tel que :
$$
|\mathrm{P}(\mathrm{t})-2019| \leqslant 1
$$
|
Soient $d \geqslant 2019$ un entier et $a_{1}<\ldots<a_{k}$ les $d$-uplets de la forme $\left( \pm 1, \ldots, \pm 1\right.$ ), ordonnés par ordre lexicographique (en partant de la droite!, c'est-à-dire que $a_{i}>a_{j}$ si et seulement si le premier terme non nul de $a_{i}-a_{j}$ en partant de la droite est $>0$ ), avec $k=2^{d}$.
Pour passer de $a_{i}$ à $a_{i+1}$, on regarde le premier -1 en partant de la droite dans $a_{i}$, on le change par un 1 , et on remplace tous les 1 à sa droite par des -1 . Par exemple si $\mathrm{d}=3$, les triplets sont dans l'ordre $a_{1}=(-1,-1,-1), a_{2}=(-1,-1,1), a_{3}=(-1,1,-1), a_{4}=(-1,1,1) a_{5}=(1,-1,-1), a_{6}=$ $(1,-1,1), a_{7}=(1,1,-1)$ et $a_{8}=(1,1,1)$.
On associe à $a_{i}=\left(a_{i 1}, \ldots, a_{i d}\right)$ le polynôme $P_{i}(X)=\sum_{j=1}^{d} a_{i j} X^{j-1}$, de telle sorte que $M:=-P_{1}(t)=$ $P_{k}(t)=1+\ldots+t^{d-1}>d$.
Or $\left|P_{i+1}(t)-P_{i}(t)\right|=2\left|t^{\mathrm{l}}-\left(1+\ldots+t^{\mathrm{l}-1}\right)\right|$ pour un certain $l \geqslant 0$ (qui dépend de $i$ ) pour tout $i$.
Montrons $t^{\mathrm{l}}-\left(1+\ldots+\mathrm{t}^{\mathrm{l}-1}\right) \leqslant 1$ : cela équivaut à $\mathrm{t}^{\mathrm{l}+1}-\mathrm{t}^{\mathrm{l}}-\left(\mathrm{t}^{\mathrm{l}}-1\right) \leqslant \mathrm{t}-1$ après multiplication par $t-1$, soit après réarrangement $t^{l}(2-t)+t \geqslant 2$, ce qui est vrai car $t^{l} \geqslant 1$.
Dès lors, $P_{i+1}(t)$ est plus grand que $P_{i}(t)$ d'au plus 2 , ce qui montre que, puisque $2019-t^{d} \in[-M ; M]$, il existe $i$ tel que $\left|P_{i}(t)-\left(2019-t^{d}\right)\right| \leqslant 1$, ce qui conclut en posant $P=X^{d}+P_{i}$
Commentaire des correcteurs Les copies reçues étaient globalement bonnes. Cependant, la plupart des élèves oublient des éléments de rédactions importants. Quelques élèves ont proposé une preuve algorithmique alternative très jolie.
|
{
"exam": "French_envois",
"problem_label": "16",
"problem_match": "\nExercice 16.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-2.jsonl",
"solution_match": "\nSolution de l'exercice 16",
"tier": "T2",
"year": null
}
|
Find all functions $\mathrm{f}: \mathbb{R} \rightarrow \mathbb{R}$ such that for all real numbers $x, y$,
$$
(f(x)+y)(f(x-y)+1)=f(f(x f(x+1))-y f(y-1))
$$
|
Clearly, $f(x)=x$ is a solution; we will show that it is the only one. In the following, we set $a=f(0)$.
With $y=0$ we have $\mathbf{f}(\mathbf{f}(\boldsymbol{x}(\mathrm{x}+1)))=\mathbf{f}(\mathrm{x})(\mathbf{f}(\mathrm{x})+1)(*)$ for all $x$.
If we take $y=-f(x)$ we see that the function $f$ has zeros.
Therefore, to exploit $(*)$ it is interesting to choose $y$ such that $f(f(x f(x+1))-y f(y-1))=f(f(x f(x+$ $1))$), which is possible by taking $y=z+1$ with $f(z)=0$. We then have $(f(x)+z+1)(f(x-z)+1)=$ $f(x)(f(x)+1)$, which simplifies with $x=z:(z+1)(f(-1)+1)=0$.
If $z=-1$, we have $f(-1)=0$, so with $x=0, y=1$, we have $a+1=a$, an obvious contradiction.
We have thus shown $f(-1)=-1$. We take $x=0, y=1$ again to get $f(0)=0$. Therefore, with $y=1$ in the equation, we see that $(f(x)+1)(f(x-1)+1)=f(x)(f(x)+1)$ (1) according to $(*)$.
$x=0$ and then $x=-1$ in the original equation give $y(f(-y)+1)=(y-1)(f(-y-1)+1)$ (2). Thus, if we had $\left(1^{\prime}\right): f(x)=f(x-1)+1$, we could deduce from (2) $y(f(-y)+1)=(y-1) f(-y)$, and then $f(-y)=-y$, which would show that $f$ is the identity.
To show $\left(1^{\prime}\right)$, let's start by proving that $f(x)=0 \Longleftrightarrow x=0$.
Let $t$ be such that $f(t)=0$; according to (1), we have $f(t-1)=-1$. (2) then gives, with $y=-t, t=0$, as desired.
Let's now show $f(x)=-1 \Longleftrightarrow x=-1$.
If $f(t)=-1, (*)$ gives $f(f(t f(t+1)))=0$ so $t f(t+1)=0$. But $t \neq 0$ since $f(0) \neq-1$, so $f(t+1)=0$ and thus $t=-1$ as desired.
To show ( $1^{\prime}$ ) according to (1), it is therefore enough to see that $f(-2)=f(-1)-1=-2$. But $\boldsymbol{f}(2)=2$ using (1) so $(*)$ with $x=-2$ gives $2=f(-2)+f(-2)^{2}$ and thus $f(-2) \in\{-2,1\}$. But if $f(-2)=1$, (1) gives $f(-3)=0$, which is impossible according to what we have shown. This concludes the proof of ( $1^{\prime}$ ) and thus the solution.
Comment from the graders The problem was quite challenging. A few brave students made substantial progress on the problem, or even solved it completely. Several students were content to verify that the identity function was a solution, but this did not earn any points. However, students who showed that if $f$ is a solution then $f$ is the identity but forgot to mention that conversely the identity is a solution lost a point, in line with the practice in competitions.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Trouver toutes les fonctions $\mathrm{f}: \mathbb{R} \rightarrow \mathbb{R}$ telles que pour tous réels $x, y$,
$$
(f(x)+y)(f(x-y)+1)=f(f(x f(x+1))-y f(y-1))
$$
|
Clairement, $f(x)=x$ est une solution; on va montrer que c'est la seule. On pose dans la suite $a=f(0)$.
Avec $y=0$ on a $\mathbf{f}(\mathbf{f}(\boldsymbol{x}(\mathrm{x}+1)))=\mathbf{f}(\mathrm{x})(\mathbf{f}(\mathrm{x})+1)(*)$ pour tout x .
Si on prend $y=-f(x)$ on voit que la fonction $f$ admet des zéros.
Dès lors pour exploiter $(*)$ il est intéressant de choisir y tel que $f(f(x f(x+1))-y f(y-1))=f(f(x f(x+$ $1))$ ), ce qui est possible en prenant $y=z+1$ avec $f(z)=0$. On a alors $(f(x)+z+1)(f(x-z)+1)=$ $f(x)(f(x)+1)$, ce qui se simplifie avec $x=z:(z+1)(f(-1)+1)=0$.
Si $z=-1$, on a $f(-1)=0$, donc avec $x=0, y=1$, on a $a+1=a$, une évidente contradiction.
On a donc montré $f(-1)=-1$. On reprend $x=0, y=1$ pour avoir $f(0)=0$. Dès lors $y=1$ dans l'équation montre que $(f(x)+1)(f(x-1)+1)=f(x)(f(x)+1)$ (1) d'après $(*)$.
$x=0$ puis $x=-1$ dans l'équation originelle donne $y(f(-y)+1)=(y-1)(f(-y-1)+1)$ (2). Ainsi, si on avait $\left(1^{\prime}\right): f(x)=f(x-1)+1$, on pourrait déduire de (2) $y(f(-y)+1)=(y-1) f(-y)$, puis $f(-y)=-y$, ce qui montrerait que $f$ est l'identité.
Pour montrer $\left(1^{\prime}\right)$, commençons par prouver que $f(x)=0 \Longleftrightarrow x=0$.
Soit $t$ tel que $f(t)=0$; d'après (1), on a $f(t-1)=-1$. (2) donne alors, avec $y=-t, t=0$, comme voulu.
Montrons à présent $f(x)=-1 \Longleftrightarrow x=-1$.
Si $f(t)=-1,(*)$ donne $f(f(t f(t+1)))=0$ donc $t f(t+1)=0$. Or $t \neq 0$ car $f(0) \neq-1$, donc $f(t+1)=0$ et ainsi $t=-1$ comme voulu.
Pour montrer ( $1^{\prime}$ ) d'après (1), il suffit donc de voir que $f(-2)=f(-1)-1=-2$. Or $\boldsymbol{f}(2)=2$ en utilisant (1) donc $(*)$ avec $x=-2$ donne $2=f(-2)+f(-2)^{2}$ et donc $f(-2) \in\{-2,1\}$. Mais si $f(-2)=1$, (1) donne $f(-3)=0$, impossible d'après ce qu'on a montré. Cela conclut la preuve de ( $1^{\prime}$ ) et donc la solution.
Commentaire des correcteurs L'exercice était assez délicat. Quelques élèves courageux ont avancé de façon substantielle dans le problème, voire même l'ont résolu complètement. Plusieurs élèves se sont contentés de vérifier que la fonction identité était solution, mais cela ne rapportait aucun point. En revanche, des élèves ont montré que si f est solution alors f est l'identité mais ont oublié de signaler que réciproquement l'identité était solution. Ces élèves ont alors perdu un point, conformément à l'usage en compétition.
|
{
"exam": "French_envois",
"problem_label": "17",
"problem_match": "\nExercice 17.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-2.jsonl",
"solution_match": "\nSolution de l'exercice 17",
"tier": "T2",
"year": null
}
|
Let $\mathrm{P}, \mathrm{Q}$ be two non-constant polynomials with real coefficients and coprime. Show that there are at most three real numbers $\lambda$ such that:
$$
P+\lambda Q=R^{2}
$$
where $R \in \mathbb{R}[X]$.
|
We proceed by contradiction, assuming the existence of four distinct reals $\lambda_{1}, \ldots, \lambda_{4}$ and four polynomials $R_{1}, \ldots, R_{4}$ such that $P+\lambda_{i} Q=R_{i}^{2}$ for $i=1,2,3,4$.
We have $P^{\prime}+\lambda_{i} Q^{\prime}=2 R_{i} R_{i}^{\prime}$ and thus $R_{i} \mid Q^{\prime}\left(P+\lambda_{i} Q\right)-Q\left(P^{\prime}+\lambda_{i} Q^{\prime}\right)=P Q^{\prime}-Q^{\prime}$.
Notice that if $T \mid R_{i}, R_{j}$ then $T \mid R_{i}^{2}-R_{j}^{2}=\left(\lambda_{i}-\lambda_{j}\right) Q$ and then $T \mid R_{i}^{2}-\lambda_{i} Q=P$ and thus $T$ is constant, since $P, Q$ are coprime.
Therefore, the $R_{i}$ are pairwise coprime and thus $R_{1} R_{2} R_{3} R_{4} \mid P Q^{\prime}-P^{\prime} Q$.
Let $A, B$ be non-zero polynomials; the degree of $A+\lambda B$, if $\lambda \in \mathbb{R}$, is equal to $\max \{\operatorname{deg}(A), \operatorname{deg}(B)\}$, unless $\operatorname{deg}(A)=\operatorname{deg}(B)$ and $\lambda=-\frac{a}{b}$ where $a, b$ are the leading coefficients of $A$ and $B$ respectively, in which case it is smaller.
If $A=P$ and $B=Q$, this shows that either $\operatorname{deg} R_{i}=\frac{1}{2} \max \{\operatorname{deg}(P), \operatorname{deg}(Q)\}$ for all $i$, and thus $\operatorname{deg}\left(R_{1} R_{2} R_{3} R_{4}\right)=2 \max \operatorname{deg}\{P, Q\}>\operatorname{deg}(P)+\operatorname{deg}(Q)-1 \geqslant \operatorname{deg}\left(P Q^{\prime}-P^{\prime} Q\right)$, or there is an $R_{i}$ such that $\operatorname{deg}\left(R_{i}\right)<\operatorname{deg}\left(R_{j}\right)$ for $j \neq i$; then for $A=P+\lambda_{i} Q=: P_{1}$ and $B=Q$ we see that $\operatorname{deg}\left(R_{i}\right)=\frac{1}{2} \operatorname{deg}\left(P_{1}\right)$ and $\operatorname{deg} R_{j}=\frac{1}{2} \max \left\{\operatorname{deg}\left(P_{1}\right), \operatorname{deg}(Q)\right\}$ and thus $\operatorname{deg}\left(R_{1} R_{2} R_{3} R_{4}\right)=\frac{3}{2} \max \left\{\operatorname{deg}\left(P_{1}\right), \operatorname{deg}(Q)\right\}+\frac{1}{2} \operatorname{deg}\left(P_{1}\right)>$ $\operatorname{deg}(\mathrm{Q})+\operatorname{deg}\left(\mathrm{P}_{1}\right)-1 \geqslant \operatorname{deg}\left(\mathrm{P}_{1} \mathrm{Q}^{\prime}-\mathrm{P}_{1}^{\prime} \mathrm{Q}\right)=\operatorname{deg}\left(\mathrm{PQ}^{\prime}-\mathrm{P}^{\prime} \mathrm{Q}\right)$.
By an argument on degrees, we therefore necessarily have $P Q^{\prime}-P^{\prime} Q=0$ and thus $P \mid P^{\prime} Q$. Since $P$ and $Q$ are coprime, we have $P \mid P^{\prime}$, which is an obvious contradiction to $P$ being non-constant.
Comment from the graders: The received solutions were of very high quality (apart from a few minor errors). Given the supposed great difficulty of the exercise, it was a pleasant surprise!
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soient $\mathrm{P}, \mathrm{Q}$ deux polynômes à coefficients réels, non constants et premiers entre eux. Montrer qu'il existe au plus trois réels $\lambda$ tels que:
$$
P+\lambda Q=R^{2}
$$
où $R \in \mathbb{R}[X]$.
|
On procède par l'absurde en supposant l'existence de quatre réels distincts $\lambda_{1}, \ldots, \lambda_{4}$ et quatre polynômes $R_{1}, \ldots, R_{4}$ tels que $P+\lambda_{i} Q=R_{i}^{2}$ pour $i=1,2,3,4$.
On a $P^{\prime}+\lambda_{i} Q^{\prime}=2 R_{i} R_{i}^{\prime}$ et donc $R_{i} \mid Q^{\prime}\left(P+\lambda_{i} Q\right)-Q\left(P^{\prime}+\lambda_{i} Q^{\prime}\right)=P Q^{\prime}-Q^{\prime}$.
Remarquons que si $T \mid R_{i}, R_{j}$ alors $T \mid R_{i}^{2}-R_{j}^{2}=\left(\lambda_{i}-\lambda_{j}\right) Q$ puis $T \mid R_{i}^{2}-\lambda_{i} Q=P$ et donc $T$ est constant, car $\mathrm{P}, \mathrm{Q}$ sont premiers entre eux.
Dès lors les $R_{i}$ sont deux à deux premiers entre eux et ainsi $R_{1} R_{2} R_{3} R_{4} \mid P Q^{\prime}-P^{\prime} Q$.
Soient $A, B$ des polynômes non nuls ; le degré de $A+\lambda B$, si $\lambda \in \mathbb{R}$, est égal à $\max \{\operatorname{deg}(A), \operatorname{deg}(B)\}$, sauf si $\operatorname{deg}(A)=\operatorname{deg}(B)$ et $\lambda=-\frac{a}{b}$ où $a, b$ sont les coefficients dominants de $A$ et $B$ respectivement, auquel cas il est plus petit.
Si $A=P$ et $B=Q$, cela montre que, soit $\operatorname{deg} R_{i}=\frac{1}{2} \max \{\operatorname{deg}(P), \operatorname{deg}(Q)\}$ pour tout $i$, et donc que $\operatorname{deg}\left(R_{1} R_{2} R_{3} R_{4}\right)=2 \max \operatorname{deg}\{P, Q\}>\operatorname{deg}(P)+\operatorname{deg}(Q)-1 \geqslant \operatorname{deg}\left(P Q^{\prime}-P^{\prime} Q\right)$, soit il y a un $R_{i}$, tel que $\operatorname{deg}\left(R_{i}\right)<\operatorname{deg}\left(R_{j}\right)$ pour $j \neq i ;$ alors pour $A=P+\lambda_{i} Q=: P_{1}$ et $B=Q$ on voit que $\operatorname{deg}\left(R_{i}\right)=\frac{1}{2} \operatorname{deg}\left(P_{1}\right)$ et $\operatorname{deg} R_{j}=\frac{1}{2} \max \left\{\operatorname{deg}\left(P_{1}\right), \operatorname{deg}(Q)\right\}$ et $\operatorname{donc} \operatorname{deg}\left(R_{1} R_{2} R_{3} R_{4}\right)=\frac{3}{2} \max \left\{\operatorname{deg}\left(P_{1}\right), \operatorname{deg}(Q)\right\}+\frac{1}{2} \operatorname{deg}\left(P_{1}\right)>$ $\operatorname{deg}(\mathrm{Q})+\operatorname{deg}\left(\mathrm{P}_{1}\right)-1 \geqslant \operatorname{deg}\left(\mathrm{P}_{1} \mathrm{Q}^{\prime}-\mathrm{P}_{1}^{\prime} \mathrm{Q}\right)=\operatorname{deg}\left(\mathrm{PQ}^{\prime}-\mathrm{P}^{\prime} \mathrm{Q}\right)$.
Par un argument sur les degrés, on a donc nécessairement $P Q^{\prime}-P^{\prime} Q=0$ et ainsi $P \mid P^{\prime} Q$. Or $P$ et $Q$ sont premiers entre eux donc $P \mid P^{\prime}$, ce qui est une évidente contradiction à $P$ non constant.
Commentaire des correcteurs Les copies reçues étaient d'un très bon niveau (à part quelques petites erreurs). Etant donné la grande difficulté supposée de l'exercice, c'était une agréable surprise!
|
{
"exam": "French_envois",
"problem_label": "18",
"problem_match": "\nExercice 18.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-2.jsonl",
"solution_match": "\nSolution de l'exercice 18",
"tier": "T2",
"year": null
}
|
Let $ABCD$ be a quadrilateral and $M, N, P, Q$ the midpoints of $[AB], [BC], [CD]$, [DA].
Show that the quadrilateral MNPQ is a parallelogram.
|
Since points $M$ and $N$ are the midpoints of sides $[A B]$ and $[B C]$, respectively, the lines $(MN)$ and $(AC)$ are parallel. Since points $P$ and $Q$ are the midpoints of sides $[C D]$ and $[D A]$, respectively, the lines $(PQ)$ and $(AC)$ are parallel. Therefore, the lines $(PQ)$ and $(MN)$ are parallel. In the same way, we find that the lines $(NP)$ and $(MQ)$ are parallel. Thus, the opposite sides of quadrilateral MNPQ are parallel, making it a parallelogram.
Comment from the graders The exercise is well handled.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un quadrilatère et $M, N, P, Q$ les milieux respectifs de $[A B],[B C],[C D]$, [DA].
Montrer que le quadrilatère MNPQ est un parallélogramme.

|
Puisque les points $M$ et $N$ sont les milieux respectifs des côtés $[A B]$ et $[B C]$, les droites (MN) et ( $A C$ ) sont parallèles. Puisque les points $P$ et $Q$ sont les milieux respectifs des côtés $[C D]$ et $[D A]$, les droites $(P Q)$ et ( $A C$ ) sont parallèles. Donc les droites ( $P Q)$ et $(M N)$ sont parallèles. On obtient de la même façon que les droites (NP) et (MQ) sont parallèles. Donc les côtés opposés deux à deux du quadrilatère MNPQ sont parallèles, ce qui en fait un parallélogramme.
Commentaire des correcteurs L'exercice est bien traité.
|
{
"exam": "French_envois",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/envois/fr-corrigé-commentaire-envoi-1.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a right triangle at $B$. Let $M$ be the intersection point of the median from $B$ with the line $(AC)$, and $(d)$ the perpendicular to the line $(BC)$ passing through the point $M$. Let $U$ be the midpoint of the segment $[AB]$, $V$ the midpoint of the segment $[AM]$, $I$ the intersection point of the line $(UV)$ with the line $(d)$, and $J$ the intersection point of the line $(UV)$ with the line $(BC)$.
Show that $AC=IJ$.
|
The lines d and (AB) are perpendicular to the line (BC), so they are parallel. By Thales' theorem, we get $\frac{V I}{V U}=\frac{A V}{V M}=1$, so $V$ is the midpoint of the segment [UI]. The quadrilateral $A I M U$ has its diagonals intersecting at their midpoint, so it is a parallelogram. The points $U$ and $M$ are the midpoints of the segments $[A B]$ and $[A C]$, respectively, so the lines (UM) and (BC) are parallel. Therefore, the line (UM) is perpendicular to the segment $[A B]$, and the quadrilateral AIMU is a rectangle.
Let l be the line perpendicular to the segment [BC] passing through V. This line is the perpendicular bisector of the segment $[\mathrm{UM}]$ and the segment $[\mathrm{AI}]$, so the point $U$ is the reflection of the point $M$ with respect to the line $l$ and the point $A$ is the reflection of the point I with respect to the line $l$, so the line $(A M)$ is the reflection of the line (UI) with respect to the line $l$. Since the line $(B C)$ is its own reflection with respect to the line $l$, the intersection point of the line (BC) with the line (UI) is the reflection of the intersection point of the line $(A M)$ with the line $B C$, so the points C and J are symmetric with respect to the line l. Symmetry preserves lengths, so $A C=I J$.
Comment from the graders Even if the argument seemed easy for some, a proper justification was expected, for example using Thales' theorem. Be careful of some confusions: a line is the bisector of an angle or the perpendicular bisector of a segment, not for example the bisector of a segment.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle rectangle en $B$. Soit $M$ le point d'intersection de la médiane issue de $B$ avec la droite (AC), et (d) la perpendiculaire à la droite (BC) passant par le point $M$. Soit $U$ le milieu du segment $[A B]$, V le milieu du segment [AM], I le point d'intersection de la droite (UV) avec la droite (d), et J le point d'instersection de la droite (UV) avec la droite (BC).
Montrer que $A C=I J$.

|
Les droites d et ( AB ) sont perpendiculaires à la droite ( BC ) donc elles sont parallèles. On obtient par le théorème de Thalès que $\frac{V I}{V U}=\frac{A V}{V M}=1$ donc $V$ est le milieu du segment [UI]. Le quadrilatère $A I M U$ a ses diagonales qui se coupent en leur milieu, c'est donc un parallélogramme. Les points $U$ et $M$ sont les milieux respectifs des segments $[A B]$ et $[A C]$ donc les droites (UM) et (BC) sont parallèles. Donc la droite (UM) est perpendiculaire au segment $[A B]$ et le quadrilatère AIMU est un rectangle.
Soit l la droite perpendiculaire au segment [BC] passant par V. Cette droite est la médiatrice du segment $[\mathrm{UM}]$ et du segment $[\mathrm{AI}]$ donc le point $U$ est le symétrique du point $M$ par rapport à la droite $l$ et le point $A$ est le symétrique du point I par rapport à la droite $l$ donc la droite $(A M)$ est la symétrique de la droite (UI) par rapport à la droite $l$. Puisque la droite $(B C)$ est sa propre symétrique par rapport à la droite $l$, le point d'intersection de la droite (BC) avec la droite (UI) est le symétrique du point d'intersection de la droite $(A M)$ avec la droite $B C$ donc les points C et J sont symétriques par rapport à la droite l . La symétrie conserve les longueurs, donc $A C=I J$.
Commentaire des correcteurs Même si l'argument semblait facile pour certains, on attendait une vraie justification, avec par exemple le théorème de Thalès. Attention à quelques confusions : une droite est bien la bissectrice d'un angle ou la médiatrice d'un segment, et non par exemple la bissectrice d'un segment.
|
{
"exam": "French_envois",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/envois/fr-corrigé-commentaire-envoi-1.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T2",
"year": null
}
|
Let $d_{1}, d_{2}, d_{3}$ be concurrent lines and $A, A^{\prime}$ points on the line $d_{1}, B, B^{\prime}$ points on the line $d_{2}, C, C^{\prime}$ points on the line $d_{3}$ such that the lines $(A B)$ and $\left(A^{\prime} B^{\prime}\right)$ are parallel and the lines $(BC)$ and $(B^{\prime}C^{\prime})$ are parallel.
Show that the lines $(A C)$ and $\left(A^{\prime} C^{\prime}\right)$ are parallel.
|
Let $S$ be the point of concurrency of the three lines. Since the lines $(A B)$ and $\left(A^{\prime} B^{\prime}\right)$ are parallel, by Thales' theorem,
$$
\frac{A S}{A^{\prime} S}=\frac{B S}{B^{\prime} S}
$$
Similarly, we find
$$
\frac{B S}{B^{\prime} S}=\frac{C S}{C^{\prime} S}
$$
We deduce that
$$
\frac{A S}{A^{\prime} S}=\frac{C S}{C^{\prime} S}
$$
which means, by Thales' theorem, that the lines $(A C)$ and $\left(A^{\prime} C^{\prime}\right)$ are parallel. Comment from the graders The exercise is well done, most students noticed the use of Thales' theorem. Pay attention to consider all configurations, notably the possible orders for the vertices $A, B$ and $C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $d_{1}, d_{2}, d_{3}$ des droites concourantes et $A, A^{\prime}$ des points sur la droite $d_{1}, B, B^{\prime}$ des points sur la droite $d_{2}, C, C^{\prime}$ des points sur la droite $d_{3}$ tels que les droites $(A B)$ et $\left(A^{\prime} B^{\prime}\right)$ sont parallèles et les droites ( BC ) et ( $\mathrm{B}^{\prime} \mathrm{C}^{\prime}$ ) sont parallèles.
Montrer que les droites $(A C)$ et $\left(A^{\prime} C^{\prime}\right)$ sont parallèles.

|
Soit $S$ le point de concours des trois droites. Puisque les droites $(A B)$ et $\left(A^{\prime} B^{\prime}\right)$ sont parallèles, d'après le théorème de Thalès,
$$
\frac{A S}{A^{\prime} S}=\frac{B S}{B^{\prime} S}
$$
De même on trouve
$$
\frac{B S}{B^{\prime} S}=\frac{C S}{C^{\prime} S}
$$
On déduit que
$$
\frac{A S}{A^{\prime} S}=\frac{C S}{C^{\prime} S}
$$
ce qui signifie, d'après le théorème de Thalès, que les droites $(A C)$ et $\left(A^{\prime} C^{\prime}\right)$ sont parallèles. Commentaire des correcteurs L'exercice est bien réussi, la plupart des élèves ont remarqué l'utilisation du théorème de Thalès. attention à prendre en compte toutes les configurations, notemment les ordres possibles pour les sommets $A, B$ et $C$.
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-corrigé-commentaire-envoi-1.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T2",
"year": null
}
|
Let $ABC$ be an isosceles and obtuse triangle at $A$. Let $\Gamma$ be the circle centered at $B$ passing through $A$, and $\Omega$ the circle centered at $C$ passing through $A$. Let $D$ be the intersection point of the circle $\Gamma$ with the segment $[BC]$, $E$ the second intersection point of the line $(AD)$ with the circle $\Omega$, and $F$ the intersection point of the line $(BC)$ with the circle $\Omega$ that is not on the segment $[BC]$.
Show that the triangle $DFE$ is isosceles at $F$.
|
Let $X$ be the intersection point of the circle $\Omega$ with the segment [BC]. The points $B$ and $C$ are symmetric with respect to the perpendicular bisector of the segment $[\mathrm{BC}]$, so the circles $\Gamma$ and $\Omega$ are also symmetric. It follows that $D$ and $X$ are symmetric with respect to the perpendicular bisector of the segment $[\mathrm{BC}]$. Therefore, triangle DAX is isosceles at $A$ and $\widehat{A D X}=\widehat{A X D}$.
The points $F, E, X$, and $A$ are concyclic, so $\widehat{F E A}=\widehat{F X A}$. We deduce
$$
\widehat{\mathrm{FED}}=\widehat{\mathrm{FEA}}=\widehat{\mathrm{FXA}}=\widehat{\mathrm{DXA}}=\widehat{\mathrm{XDA}}=\widehat{\mathrm{FDE}}
$$
This shows that triangle FDE is isosceles at F.
Comment from the graders: Some students noted symmetries in the figure, but it was important to justify them rigorously.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle isocèle et obtus en $A$. Soit $\Gamma$ le cercle de centre $B$ passant par $A$, et $\Omega$ le cercle de centre $C$ passant par $A$. Soit $D$ le point d'intersection du cercle $\Gamma$ avec le segment $[B C]$, E le deuxième point d'intersection de la droite (AD) avec le cercle $\Omega$, et $F$ le point d'intersection de la droite (BC) avec le cercle $\Omega$ qui n'est pas sur le segment $[B C]$.
Montrer que le triangle DFE est isocèle en $F$.

|
Soit $X$ le point d'intersection du cercle $\Omega$ avec le segment [BC]. Les points $B$ et C sont symétriques par rapport à la médiatrice du segment $[\mathrm{BC}]$ donc les cercles $\Gamma$ et $\Omega$ le sont aussi. Il vient que D et $X$ sont symétriques par rapport à la médiatrice du segment $[\mathrm{BC}]$. Le triangle DAX est donc isocèle en $A$ et $\widehat{A D X}=\widehat{A X D}$.
Les points $F, E, X$ et $A$ sont cocycliques donc $\widehat{F E A}=\widehat{F X A}$. On déduit
$$
\widehat{\mathrm{FED}}=\widehat{\mathrm{FEA}}=\widehat{\mathrm{FXA}}=\widehat{\mathrm{DXA}}=\widehat{\mathrm{XDA}}=\widehat{\mathrm{FDE}}
$$
Ce qui donne bien que le triangle FDE est isocèle en F .
Commentaire des correcteurs Certains élèves ont noté des symétries dans la figure, mais il fallait veiller à la justifier de façon rigoureuse.
|
{
"exam": "French_envois",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/envois/fr-corrigé-commentaire-envoi-1.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T2",
"year": null
}
|
Let $\Gamma$ be a circle, $P$ a point outside the circle. The tangents to the circle $\Gamma$ passing through the point $P$ are tangent to the circle $\Gamma$ at $A$ and $B$. Let $M$ be the midpoint of the segment [BP] and $C$ the intersection point of the line ( $A M$ ) and the circle $\Gamma$. Let D be the second intersection of the line ( PC ) and the circle $\Gamma$.
Show that the lines $(A D)$ and $(B P)$ are parallel.
|
Using the power of point $M$ with respect to the circle $\Gamma, \mathrm{MB}^{2}=M C \cdot M A$. Since $M$ is the midpoint of the segment $[B P], M P^{2}=M B^{2}$, thus $M P^{2}=M C \cdot M A$. From the converse of the power of a point with respect to a circle, we deduce that the line (PM) is tangent to the circumcircle of triangle PAC. We obtain from the tangent angle theorem that $\widehat{M P C}=\widehat{P A C}$. Since the line $(\mathrm{PA})$ is tangent to the circle $\Gamma$, again by the tangent angle theorem, $\widehat{\mathrm{PAC}}=\widehat{\mathrm{ADC}}$. In summary:
$$
\widehat{\mathrm{BPD}}=\widehat{M P C}=\widehat{\mathrm{PAC}}=\widehat{A D C}=\widehat{A D P}
$$
thus the lines $(A D)$ and (BP) are parallel.
Comment from the graders Some of the proposed proofs were incorrect. A good way to check that your proof is correct is to verify that you have used all the hypotheses. Several students do not use at any point that the point $M$ is the midpoint of the segment [PB], which is a crucial hypothesis. Be careful to proofread to avoid typographical errors such as writing one angle or triangle in place of another.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $\Gamma$ un cercle, $P$ un point à l'extérieur du cercle. Les tangentes au cercle $\Gamma$ passant par le point $P$ sont tangentes au cercle $\Gamma$ en $A$ et $B$. Soit $M$ est le milieu du segment [BP] et $C$ le point d'intersection de la droite ( $A M$ ) et du cercle $\Gamma$. Soit D la deuxième intersection de la droite ( PC ) et du cercle $\Gamma$.
Montrer que les droites $(A D)$ et $(B P)$ sont parallèles.

|
En utilisant la puissance du point $M$ par rapport au cercle $\Gamma, \mathrm{MB}^{2}=M C \cdot M A$. Puisque $M$ est le milieu du segment $[B P], M P^{2}=M B^{2}$ donc $M P^{2}=M C \cdot M A$. On déduit de la réciproque de la puissance d'un point par rapport à un cercle que la droite ( PM ) est tangente au cercle circonscrit au triangle PAC. On obtient du théorème de l'angle tangent que $\widehat{M P C}=\widehat{P A C}$. Or la droite $(\mathrm{PA})$ est tangente au cercle $\Gamma$ donc à nouveau par le théorème de l'angle tangent, $\widehat{\mathrm{PAC}}=\widehat{\mathrm{ADC}}$. En résumé :
$$
\widehat{\mathrm{BPD}}=\widehat{M P C}=\widehat{\mathrm{PAC}}=\widehat{A D C}=\widehat{A D P}
$$
donc les droites $(A D)$ et (BP) sont parallèles.
Commentaire des correcteurs Quelques démonstrations proposées étaient fausses. Une bonne façon de vérifier que sa démonstration est correcte est de vérifier qu'on a utilisé toutes les hypothèses. Plusieurs élèves n'utilisent à aucun moment que le point $M$ est le milieu du segment [PB], ce qui est pourtant une hypothèse cruciale. Attention à se relire pour éviter des erreurs typographiques comme écrire un angle ou un triangle à la place d'un autre.
|
{
"exam": "French_envois",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/envois/fr-corrigé-commentaire-envoi-1.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T2",
"year": null
}
|
Let $A, B, C$ and $D$ be four points on a circle in that order. Let $U$ be the intersection point of the lines $(A B)$ and $(CD)$, and $V$ the intersection point of the lines $(BC)$ and $(D A)$. Let $K$ be the intersection point of the angle bisector from $U$ in triangle $AUC$ and the angle bisector from $V$ in triangle $A V C$. Let $L$ be the intersection point of the perpendicular bisector of segment $[KU]$ and the perpendicular bisector of segment $[KV]$.
Show that the points $U, V$ and $L$ are collinear.
|
Point L is the center of the circumcircle of triangle UKV. To show that points U, L, and V are collinear, it suffices to show that $\widehat{U L V}=180^{\circ}$. By the central angle theorem, $\widehat{U K V}=\frac{1}{2} \widehat{U L V}$. Therefore, it suffices to show that $\widehat{U K V}=90^{\circ}$.
The sum of the angles of triangle UKV is $180^{\circ}$, so it suffices to show that $\widehat{\mathrm{KUV}}+\widehat{\mathrm{KVU}}=90^{\circ}$. On one hand, $\widehat{K U V}=\widehat{C U V}-\widehat{K U C}=\widehat{C U V}-\frac{1}{2} \widehat{B U C}$. But $\widehat{B U C}=180^{\circ}-\widehat{U B C}-\widehat{B C U}=\widehat{A D C}-\widehat{U C B}$. We deduce
$$
\widehat{\mathrm{KUV}}=\widehat{\mathrm{CUV}}-\frac{1}{2} \widehat{\mathrm{ADC}}+\frac{1}{2} \widehat{\mathrm{UCB}}
$$
Similarly, we obtain
$$
\widehat{\mathrm{KVU}}=\widehat{\mathrm{CVU}}-\frac{1}{2} \widehat{\mathrm{CBA}}+\frac{1}{2} \widehat{\mathrm{VCD}}
$$
But $\widehat{C B A}+\widehat{A D C}=180^{\circ}$ and
$$
\widehat{U C B}=\widehat{V C D}=\widehat{U C V}=180^{\circ}-\widehat{C U V}-\widehat{C V U}
$$
Finally
$$
\begin{aligned}
& \widehat{\mathrm{KUV}}+\widehat{\mathrm{KVU}}=\widehat{\mathrm{CUV}}-\frac{1}{2} \widehat{\mathrm{ADC}}+\frac{1}{2} \widehat{\mathrm{UCB}}+\widehat{\mathrm{CVU}}-\frac{1}{2} \widehat{\mathrm{CBA}}+\frac{1}{2} \widehat{\mathrm{VCD}} \\
& =\widehat{\mathrm{CUV}}+\widehat{\mathrm{CVU}}-\frac{1}{2} \cdot 180^{\circ}+2 \cdot \frac{1}{2} \cdot\left(180^{\circ}-\widehat{\mathrm{CUV}}-\widehat{\mathrm{CVU}}\right)=90^{\circ}
\end{aligned}
$$
which gives the desired result.
Comment from the graders: The exercise was generally well solved. Be sure to ensure that everything you assert is justified. Some false statements were noted. For example, contrary to what some students claimed, a quadrilateral with two opposite right angles is not necessarily a rectangle.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A, B, C$ et $D$ quatre points sur un cercle dans cet ordre. Soit $U$ le point d'intersection des droites $(A B)$ et (CD), et $V$ le point d'intersection des droites (BC) et ( $D A$ ). Soit $K$ le point d'intersection de la bissectrice issue de U dans le triangle AUC et de la bissectrice issue de V dans le triangle $A V C$. Soit L le point d'intersection de la médiatrice du segment $[\mathrm{KU}]$ et de la médiatrice du segment [KV].
Montrer que les points $\mathrm{U}, \mathrm{V}$ et L sont alignés.

|
Le point L est le centre du cercle circonscrit au triangle UKV. Pour montrer que les points U, L et V sont alignés, il suffit de montrer que $\widehat{U L V}=180^{\circ}$. Par le théorème de l'angle au centre, $\widehat{U K V}=\frac{1}{2} \widehat{U L V}$. Il suffit donc de montrer que $\widehat{U K V}=90^{\circ}$.
La somme des angles du triangle UKV vaut $180^{\circ}$, donc il suffit de montrer que $\widehat{\mathrm{KUV}}+\widehat{\mathrm{KVU}}=90^{\circ}$. D'une part $\widehat{K U V}=\widehat{C U V}-\widehat{K U C}=\widehat{C U V}-\frac{1}{2} \widehat{B U C}$. Or $\widehat{B U C}=180^{\circ}-\widehat{U B C}-\widehat{B C U}=\widehat{A D C}-\widehat{U C B}$. On déduit
$$
\widehat{\mathrm{KUV}}=\widehat{\mathrm{CUV}}-\frac{1}{2} \widehat{\mathrm{ADC}}+\frac{1}{2} \widehat{\mathrm{UCB}}
$$
De la même manière, on obtient
$$
\widehat{\mathrm{KVU}}=\widehat{\mathrm{CVU}}-\frac{1}{2} \widehat{\mathrm{CBA}}+\frac{1}{2} \widehat{\mathrm{VCD}}
$$
Or $\widehat{C B A}+\widehat{A D C}=180^{\circ}$ et
$$
\widehat{U C B}=\widehat{V C D}=\widehat{U C V}=180^{\circ}-\widehat{C U V}-\widehat{C V U}
$$
Finalement
$$
\begin{aligned}
& \widehat{\mathrm{KUV}}+\widehat{\mathrm{KVU}}=\widehat{\mathrm{CUV}}-\frac{1}{2} \widehat{\mathrm{ADC}}+\frac{1}{2} \widehat{\mathrm{UCB}}+\widehat{\mathrm{CVU}}-\frac{1}{2} \widehat{\mathrm{CBA}}+\frac{1}{2} \widehat{\mathrm{VCD}} \\
& =\widehat{\mathrm{CUV}}+\widehat{\mathrm{CVU}}-\frac{1}{2} \cdot 180^{\circ}+2 \cdot \frac{1}{2} \cdot\left(180^{\circ}-\widehat{\mathrm{CUV}}-\widehat{\mathrm{CVU}}\right)=90^{\circ}
\end{aligned}
$$
ce qui donne le résultat voulu.
Commentaire des correcteurs L'exercice a été plutôt bien résolu. Attention à bien s'assurer que tout ce que l'on affirme est justifié. On a pu noté certaines affirmations fausses. Par exemple, contrairement à ce que certains élèves ont affirmé, un quadrilatère dont les deux angles opposés sont droits n'est pas forcément un rectangle.
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/envois/fr-corrigé-commentaire-envoi-1.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T2",
"year": null
}
|
Two circles with centers B and C and different radii are externally tangent at a point $A$. Let $t$ be a common tangent to the two circles that does not contain the point $A$. The perpendicular to the line $t$ passing through the point $A$ intersects the perpendicular bisector of the segment $[B C]$ at a point $F$. Show that $B C=2 A F$.
|
Let $X$ and $Y$ be the points of tangency of $t$ with the circles centered at $B$ and $C$ respectively. Let $O$ be the point of intersection of the line $t$ with the common tangent to the two circles at $A$. The points $X$ and $A$ are symmetric with respect to the line $(OB)$, and the points $Y$ and $A$ are symmetric with respect to the line $(OC)$. We deduce that $\widehat{BOA} = \frac{1}{2} \widehat{XOA}$ and $\widehat{COA} = \frac{1}{2} \widehat{YOA}$. Therefore,
$$
\widehat{BOC} = \widehat{BOA} + \widehat{AOC} = \frac{1}{2} \widehat{XOA} + \frac{1}{2} \widehat{AOY} = \frac{1}{2} \widehat{XOY} = 90^{\circ}
$$
Let $M$ be the midpoint of $[BC]$. The triangle $BOC$ is right-angled at $O$, so $M$ is the center of the circumcircle of this triangle. This gives $MO = MB = \frac{1}{2} BC$. Since the lines $(OA)$ and $(MF)$ are perpendicular to the line $(BC)$, they are therefore parallel. Finally,
$$
\widehat{MOY} = \widehat{MOC} + \widehat{COY} = \widehat{MCO} + \widehat{AOC} = 90^{\circ}
$$
so the lines $(OM)$ and $(AF)$ are perpendicular to the line $t$ and are therefore parallel. Thus, the quadrilateral $OMFA$ is a parallelogram and $BC = 2OM = 2AF$.
Comment from the graders: We observed several interesting solutions. The exercise required several initiatives, and thus many solutions were incomplete. Some students attempted a computational solution. The calculations were often too laborious and burdened with somewhat heavy notation.
|
BC = 2AF
|
Yes
|
Yes
|
proof
|
Geometry
|
Deux cercles de centres respectifs B et C et de rayons différents sont tangents extérieurement en un point $A$. Soit $t$ une tangente commune aux deux cercles ne contenant pas le point $A$. La perpendiculaire à la droite $t$ passant par le point $A$ coupe la médiatrice du segment $[B C]$ en un point $F$. Montrer que $B C=2 A F$.

|
Soient $X$ et $Y$ les points de tangences de $t$ avec les cercles de centre B et $C$ respectivement. Soit $O$ le point d'intersection la droite $t$ avec la tangente commune au deux cercles en $A$. Les points $X$ et $A$ sont symétriques para rapport à la droite $(O B)$ et les points $Y$ et $A$ sont symétriques par rapport à la droite $(\mathrm{OC})$. On déduit $\widehat{\mathrm{BOA}}=\frac{1}{2} \widehat{\mathrm{XOA}}$ et $\widehat{\mathrm{COA}}=\frac{1}{2} \widehat{\mathrm{YOA}}$. On en déduit :
$$
\widehat{\mathrm{BOC}}=\widehat{\mathrm{BOA}}+\widehat{\mathrm{AOC}}=\frac{1}{2} \widehat{\mathrm{XOA}}+\frac{1}{2} \widehat{\mathrm{AOY}}=\frac{1}{2} \widehat{\mathrm{XOY}}=90^{\circ}
$$
Soit $M$ le milieu de $[B C]$. Le triangle $B O C$ est rectangle $O$ donc $M$ est le centre du cercle circonscrit à ce triangle. Ceci donne $M O=M B=\frac{1}{2} B C$. Comme les droites $(O A)$ et ( $M F$ ) sont perpendiculaires à la droite (BC), elles sont donc parallèles. Enfin,
$$
\widehat{M O Y}=\widehat{M O C}+\widehat{C O Y}=\widehat{M C O}+\widehat{A O C}=90^{\circ}
$$
donc les droites $(\mathrm{OM})$ et ( AF ) sont perpendiculaires à la droite $t$ donc elles sont parallèles. Donc le quadrilatère OMFA est un parallélogramme et $\mathrm{BC}=2 \mathrm{OM}=2 A \mathrm{~F}$.
Commentaire des correcteurs On a pu constaté plusieurs solutions intéressantes. L'exercice nécessitait plusieurs initiatives, ainsi plusieurs solutions étaient incomplètes. Quelques élèves ont tenté une solution calculatoire. Les calculs étaient alors souvent trop laborieux et chargés de notations un peu lourdes.
|
{
"exam": "French_envois",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/envois/fr-corrigé-commentaire-envoi-1.jsonl",
"solution_match": "\nSolution de l'exercice 7",
"tier": "T2",
"year": null
}
|
Let $A B C$ be an acute non-isosceles triangle at $A$. Let $M$ be the midpoint of the segment $[B C]$, $H$ the orthocenter of the triangle $A B C$, $O_{1}$ the midpoint of the segment $[A H]$, and $O_{2}$ the center of the circumcircle of the triangle $CBH$. Show that the quadrilateral $\mathrm{O}_{1} \mathrm{AMO}_{2}$ is a parallelogram.
|
Let $\mathrm{H}_{\mathrm{A}}$ be the foot of the altitude from vertex $A$, $\mathrm{H}_{\mathrm{B}}$ the foot of the altitude from vertex $B$, and $O$ the center of the circumcircle of triangle $ABC$.
We notice that $\mathrm{O}_{2}$ is on the perpendicular bisector of $[\mathrm{BC}]$, so the lines $\left(\mathrm{MO}_{2}\right)$ and $(\mathrm{AH})$ are parallel because they are perpendicular to $(\mathrm{BC})$. Therefore, it suffices to show that $\mathrm{MO}_{2}=A \mathrm{O}_{1}$.
Let $X$ be the symmetric point of $H$ with respect to point $M$. Then $M$ is the midpoint of $[BC]$ and $[\mathrm{XH}]$, so $BHCX$ is a parallelogram and $\widehat{\mathrm{XBA}}=\widehat{\mathrm{XBC}}+\widehat{\mathrm{CBA}}=\widehat{\mathrm{HCB}}+\widehat{\mathrm{CBA}}=90^{\circ}$ (since triangle $\mathrm{BCH}_{\mathrm{C}}$ is right-angled at $\mathrm{H}_{\mathrm{C}}$) and similarly $\widehat{\mathrm{XCA}}=90^{\circ}$, so $X$ is the point diametrically opposite to $A$ on the circumcircle of $ABC$.
The symmetry with center $M$ sends $B$ to $C$, $C$ to $B$, and $H$ to $X$, so it sends the circumcircle of $BCH$ to the circumcircle of $BCX$, and thus it sends $\mathrm{O}_{2}$ to $O$. In particular, $\mathrm{MO}_{2}=\mathrm{MO}$.
Since points $O$ and $M$ are the midpoints of segments $[X A]$ and $[X H]$, respectively, by Thales' theorem,
$$
\frac{\mathrm{OM}}{\mathrm{AH}}=\frac{\mathrm{XM}}{\mathrm{XH}}=\frac{1}{2}
$$
so $\mathrm{AH}=2 \mathrm{OM}$, hence
$$
\mathrm{MO}_{2}=\mathrm{MO}=\frac{1}{2} A \mathrm{H}=A \mathrm{O}_{1}
$$
which concludes the proof.
Comment from the graders: This problem required knowledge of several properties of the orthocenter, particularly the fact that the symmetric point of the orthocenter $H$ with respect to the midpoint of side $[BC]$ lies on the circumcircle of triangle $ABC$ and is also the symmetric point of vertex $A$ with respect to the center $O$. Many students noticed the first step of the problem, which is that the lines $\left(\mathrm{MO}_{2}\right)$ and $(\mathrm{AH})$ are parallel. This shows a real effort in solving a difficult problem, which is encouraging.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle acutangle non isocèle en $A$. Soit $M$ le milieu du segment $[B C], H$ l'orthocentre du triangle $A B C, O_{1}$ le milieu du segment $[A H]$ et $O_{2}$ le centre du cercle circonscrit au triangle CBH . Montrer que le quadrilatère $\mathrm{O}_{1} \mathrm{AMO}_{2}$ est un parallélogramme.

|
Soit $\mathrm{H}_{\mathrm{A}}$ le pied de la hauteur issue du sommet $A, \mathrm{H}_{\mathrm{B}}$ le pied de la hauteur issue du sommet B et O le centre du cercle circonscrit au triangle ABC .
On remarque déjà que $\mathrm{O}_{2}$ est sur la médiatrice de $[\mathrm{BC}]$ donc les droites $\left(\mathrm{MO}_{2}\right)$ et $(\mathrm{AH})$ sont parallèles car elles sont perpendiculaires à ( BC ). Il suffit donc de montrer que $\mathrm{MO}_{2}=A \mathrm{O}_{1}$.
Soit $X$ le symétrique du point $H$ par rapport au point $M$. Alors $M$ est le milieu de [BC] et $[\mathrm{XH}]$ donc BHCX est un parallélogramme et $\widehat{\mathrm{XBA}}=\widehat{\mathrm{XBC}}+\widehat{\mathrm{CBA}}=\widehat{\mathrm{HCB}}+\widehat{\mathrm{CBA}}=90^{\circ}$ (car le triangle $\mathrm{BCH}_{\mathrm{C}}$ est rectangle en $\mathrm{H}_{\mathrm{C}}$ ) et de même $\widehat{\mathrm{XCA}}=90^{\circ}$ donc $X$ est le point diamétralement opposé à $A$ sur le cercle circonscrit à $A B C$.
La symétrie de centre $M$ envoie $B$ sur $C, C$ sur $B$ et H sur $X$ donc elle envoie le cercle circonscrit à $B C H$ sur le cercle circonscrit à BCX donc elle envoie $\mathrm{O}_{2}$ sur O . En particulier, $\mathrm{MO}_{2}=\mathrm{MO}$.
Comme les points $O$ et $M$ sont les milieux respectifs des segments $[X A]$ et $[X H]$, d'après le théorème de Thalès,
$$
\frac{\mathrm{OM}}{\mathrm{AH}}=\frac{\mathrm{XM}}{\mathrm{XH}}=\frac{1}{2}
$$
donc $\mathrm{AH}=2 \mathrm{OM}$ donc
$$
\mathrm{MO}_{2}=\mathrm{MO}=\frac{1}{2} A \mathrm{H}=A \mathrm{O}_{1}
$$
ce qui conclut.
Commentaire des correcteurs Cet exercice demandait de connaître plusieurs propriétés de l'orthocentre, en particulier le fait que le symétrique de l'orthocentre H par rapport au milieu du côté [BC] appartient au cercle circonscrit au triangle $A B C$ et est également le symétrique du sommet $A$ par rapport au centre O. Plusieurs élèves ont remarqué la première étape du problème qui est que les droites $\left(\mathrm{MO}_{2}\right)$ et ( AH ) sont parallèles. Ceci montre un réel effort de recherche sur un problème difficile de la part des élèves, ce qui est encourageant.
|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "\nExercice 8.",
"resource_path": "French/segmented/envois/fr-corrigé-commentaire-envoi-1.jsonl",
"solution_match": "\nSolution de l'exercice 8",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle, $\Gamma$ the circumcircle, and $\omega$ the circle with the same center as $\Gamma$ and tangent to the line $(BC)$. The tangents to the circle $\omega$ passing through $A$ intersect $(BC)$ at a point $X$ on the side of $B$ and at a point $Y$ on the side of $C$. The tangent to the circle $\Gamma$ at $B$ and the line parallel to $(AC)$ passing through $X$ intersect at a point $S$, and the tangent to the circle $\Gamma$ at $C$ and the line parallel to $(AB)$ passing through $Y$ intersect at a point $T$.
Show that the line $(ST)$ is tangent to the circle $\Gamma$.
|
To avoid having to separate the different cases based on the position of point $Y$ relative to the segment $[B C]$, we will use oriented angles: ( $A B, C D$ ) denotes the angle (relative) by which the line ( $A B$ ) must be rotated to be parallel to the line ( $C D$ ).
We will show that the line (TA) is tangent to the circumcircle of triangle $A B C$, and similarly for the line (SA), which will establish that the line (ST) is tangent to this circle.
To show that the line $(A T)$ is tangent to the circle $\Gamma$, it suffices to show that $(A C, A T)=(B C, B A)$. The lines $(T Y)$ and $(A B)$ are parallel, so $(B C, B A)=(B C, Y T)=(Y C, Y T)$, thus we are reduced to showing that $(A C, A T)=(Y C, Y T)$, in other words, that the points $T, A, Y$, and $C$ are concyclic.
For this, we can show that $(Y T, Y A)=(C T, C A)$. Indeed, $(Y T, Y A)=(A B, A Y)$ (by the parallelism of $(A B)$ and $(Y T))$ and $(C T, C A)=(B C, B A)$, so it remains to show that $(A B, A Y)=(B C, B A)$, in other words, that the triangle $A Y B$ is isosceles at $Y$.
Let $O$ be the center of the circle $\Gamma$, which is also the center of the circle $\omega$, and let $M$ and $N$ be the points of contact of the circle $\omega$ with the segments [YA] and [YB], respectively. Then the triangles OMA and ONB are right triangles, $\mathrm{OA}=\mathrm{OB}$, and $\mathrm{OM}=\mathrm{ON}$, so $\mathrm{MA}=\sqrt{\mathrm{OA}^{2}-\mathrm{OM}^{2}}=\sqrt{\mathrm{OB}^{2}-\mathrm{ON}}{ }^{2}=\mathrm{NB}$, and since $\mathrm{YM}=\mathrm{YN}$, we deduce $Y A=Y B$ and the triangle $Y A B$ is isosceles at $Y$ as desired.
Comment from the graders: Unfortunately, there was an imprecision in the statement, as the triangle $A B C$ needed to have acute angles. This oversight on our part caused some confusion for some students who drew a figure with an obtuse angle at $A$ and therefore thought the statement was false. The exercise remained rather difficult. Some students tried to conclude using similarities, but the hypotheses were never strong enough.
## Senior Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle, $\Gamma$ sont cercle circonscrit et $\omega$ le cercle de même centre que $\Gamma$ et tangent à la droite ( BC ). Les tangentes au cercle $\omega$ passant par $A$ coupent ( BC ) en un point $X$ du côté de $B$ et en un point $Y$ du côté de $C$. La tangente au cercle $\Gamma$ en $B$ et la parallèle à la droite $(A C)$ passant par $X$ se coupent en un point $S$ et la tangente au cercle $\Gamma$ en $C$ et la parallèle à la droite $(A B)$ passant par $Y$ se coupent en un point $T$.
Montrer que la droite (ST) est tangente au cercle $\Gamma$.

|
Afin d'éviter d'avoir à séparer les différents cas, en fonction de la position du point $Y$ par rapport au segment $[B C]$, nous allons utiliser les angles de droite orientés : ( $A B, C D$ ) désigne l'angle (relatif) dont il faut tourner la droite ( $A B$ ) pour qu'elle soit parallèle à la droite ( $C D$ ).
Nous allons montrer que la droite (TA) est tangente au cercle circonscrit au triangle $A B C$ et de même pour la droite (SA), ce qui donnera bien que la droite (ST) est tangente à ce cercle.
Pour montrer que la droite $(A T)$ est tangente au cercle $\Gamma$, il suffit de montrer que $(A C, A T)=(B C, B A)$. Les droites $(T Y)$ et $(A B)$ sont parallèles donc $(B C, B A)=(B C, Y T)=(Y C, Y T)$, donc on est ramené à montrer que $(A C, A T)=(Y C, Y T)$, autrement dit que les points $T, A, Y$ et $C$ sont cocycliques.
Pour cela, on peut montrer que $(Y T, Y A)=(C T, C A)$. En effet, $(Y T, Y A)=(A B, A Y)$ (par parallélisme de $(A B)$ et $(Y T))$ et $(C T, C A)=(B C, B A)$ donc il ne reste plus qu'à montrer que $(A B, A Y)=$ ( $B C, B A$ ), autrement dit que le triangle $A Y B$ est isocèle en $Y$.
Soit $O$ le centre du cercle $\Gamma$, qui est aussi le centre du cercle $\omega$, et soit $M$ et $N$ les points de contact respectifs du cercle $\omega$ avec les segments [YA] et [YB]. Alors les triangles OMA et ONB sont rectangles, $\mathrm{OA}=\mathrm{OB}$ et $\mathrm{OM}=\mathrm{ON}$ donc $\mathrm{MA}=\sqrt{\mathrm{OA}^{2}-\mathrm{OM}^{2}}=\sqrt{\mathrm{OB}^{2}-\mathrm{ON}}{ }^{2}=\mathrm{NB}$ et puisque $\mathrm{YM}=\mathrm{YN}$, on déduit $Y A=Y B$ et le triangle $Y A B$ est isocèle en $Y$ comme voulu.
Commentaire des correcteurs Il y avait malhreusement une imprécision dans l'énoncé puisqu'il fallait que le triangle $A B C$ ait des angles aigus. Cet oubli de notre part a provoqué quelques confusions pour certains élèves qui ont tracé une figure avec un angle obtu en $A$ et ont donc pensé que l'énoncé était faux. L'exercice restait plutôt difficile. Quelques élèves ont essayé de conclure avec les similitudes, mais les hypothèses n'étaient jamais assez fortes.
## Exercices Seniors
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-corrigé-commentaire-envoi-1.jsonl",
"solution_match": "\nSolution de l'exercice 9",
"tier": "T2",
"year": null
}
|
Let $d_{1}, d_{2}, d_{3}$ be concurrent lines and $A, A^{\prime}$ be points on the line $d_{1}, B, B^{\prime}$ be points on the line $d_{2}, C, C^{\prime}$ be points on the line $d_{3}$ such that the lines ( $A B$ ) and ( $A^{\prime} B^{\prime}$ ) are parallel and the lines $(B C)$ and ( $B^{\prime} \mathrm{C}^{\prime}$ ) are parallel.
Show that the lines ( $A C$ ) and ( $A^{\prime} C^{\prime}$ ) are parallel.
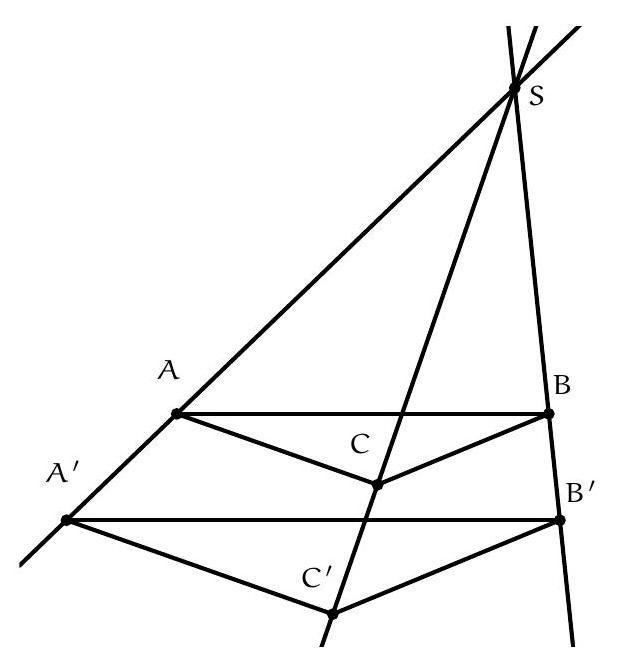
|
Let $S$ be the point of concurrency of the three lines. Since the lines ( $A B$ ) and ( $A^{\prime} B^{\prime}$ ) are parallel, by Thales' theorem,
$$
\frac{A S}{A^{\prime} S}=\frac{B S}{B^{\prime} S}
$$
Similarly, we find
$$
\frac{B S}{B^{\prime} S}=\frac{C S}{C^{\prime} S}
$$
We deduce that
$$
\frac{A S}{A^{\prime} S}=\frac{C S}{C^{\prime} S}
$$
which means, by Thales' theorem, that the lines ( $A C$ ) and ( $A^{\prime} \mathrm{C}^{\prime}$ ) are parallel.
Comment from the graders The exercise is well done, most students noticed the use of Thales' theorem. Pay attention to consider all configurations, notably the possible orders for the vertices $A, B$ and $C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $d_{1}, d_{2}, d_{3}$ des droites concourantes et $A, A^{\prime}$ des points sur la droite $d_{1}, B, B^{\prime}$ des points sur la droite $d_{2}, C, C^{\prime}$ des points sur la droite $d_{3}$ tels que les droites ( $A B$ ) et ( $A^{\prime} B^{\prime}$ ) sont parallèles et les droites $(B C)$ et ( $B^{\prime} \mathrm{C}^{\prime}$ ) sont parallèles.
Montrer que les droites ( $A C$ ) et ( $A^{\prime} C^{\prime}$ ) sont parallèles.

|
Soit $S$ le point de concours des trois droites. Puisque les droites ( $A B$ ) et ( $A^{\prime} B^{\prime}$ ) sont parallèles, d'après le théorème de Thalès,
$$
\frac{A S}{A^{\prime} S}=\frac{B S}{B^{\prime} S}
$$
De même on trouve
$$
\frac{B S}{B^{\prime} S}=\frac{C S}{C^{\prime} S}
$$
On déduit que
$$
\frac{A S}{A^{\prime} S}=\frac{C S}{C^{\prime} S}
$$
ce qui signifie, d'après le théorème de Thalès, que les droites ( $A C$ ) et ( $A^{\prime} \mathrm{C}^{\prime}$ ) sont parallèles.
Commentaire des correcteurs L'exercice est bien réussi, la plupart des élèves ont remarqué l'utilisation du théorème de Thalès. attention à prendre en compte toutes les configurations, notemment les ordres possibles pour les sommets $A, B$ et $C$.
|
{
"exam": "French_envois",
"problem_label": "10",
"problem_match": "\nExercice 10.",
"resource_path": "French/segmented/envois/fr-corrigé-commentaire-envoi-1.jsonl",
"solution_match": "\nSolution de l'exercice 10",
"tier": "T2",
"year": null
}
|
Let $ABC$ be an isosceles and obtuse triangle at $A$. Let $\Gamma$ be the circle centered at $B$ passing through $A$, and $\Omega$ the circle centered at $C$ passing through $A$. Let $D$ be the intersection point of the circle $\Gamma$ with the segment $[BC]$, $E$ the second intersection point of the line $(AD)$ with the circle $\Omega$, and $F$ the intersection point of the line $(BC)$ with the circle $\Omega$ that is not on the segment $[BC]$.
Show that the triangle $DFE$ is isosceles at $F$.
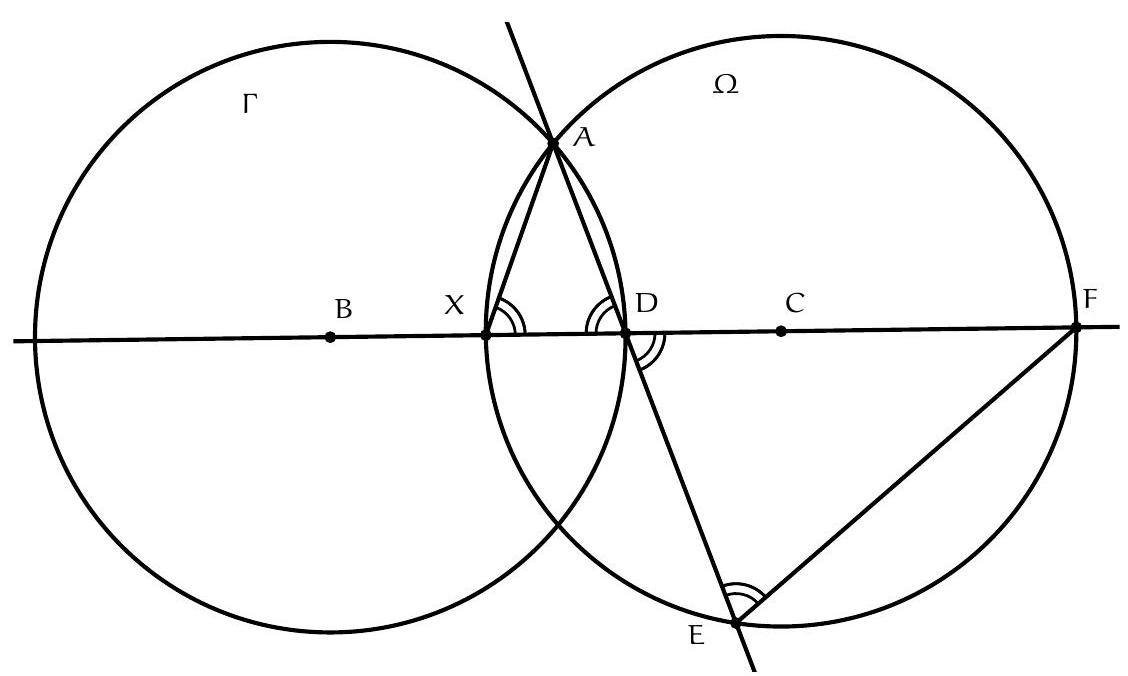
|
Let $X$ be the intersection point of the circle $\Omega$ with the segment [BC]. The points B and C are symmetric with respect to the perpendicular bisector of the segment $[\mathrm{BC}]$, so the circles $\Gamma$ and $\Omega$ are also symmetric. It follows that D and $X$ are symmetric with respect to the perpendicular bisector of the segment $[\mathrm{BC}]$. Therefore, triangle DAX is isosceles at $A$ and $\widehat{A D X}=\widehat{A X D}$.
The points $F, E, X$ and $A$ are concyclic, so $\widehat{F E A}=\widehat{F X A}$. We deduce
$$
\widehat{\mathrm{FED}}=\widehat{\mathrm{FEA}}=\widehat{\mathrm{FXA}}=\widehat{\mathrm{DXA}}=\widehat{\mathrm{XDA}}=\widehat{\mathrm{FDE}}
$$
This shows that triangle FDE is isosceles at F.
Comment from the graders: We have observed that almost all proofs were complete, even if some were very long and computational.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle isocèle et obtus en $A$. Soit $\Gamma$ le cercle de centre $B$ passant par $A$, et $\Omega$ le cercle de centre $C$ passant par $A$. Soit $D$ le point d'intersection du cercle $\Gamma$ avec le segment $[B C]$, E le deuxième point d'intersection de la droite (AD) avec le cercle $\Omega$, et $F$ le point d'intersection de la droite (BC) avec le cercle $\Omega$ qui n'est pas sur le segment $[B C]$.
Montrer que le triangle DFE est isocèle en $F$.

|
Soit $X$ le point d'intersection du cercle $\Omega$ avec le segment [BC]. Les points B et C sont symétriques par rapport à la médiatrice du segment $[\mathrm{BC}]$ donc les cercles $\Gamma$ et $\Omega$ le sont aussi. Il vient que D et $X$ sont symétriques par rapport à la médiatrice du segment $[\mathrm{BC}]$. Le triangle DAX est donc isocèle en $A$ et $\widehat{A D X}=\widehat{A X D}$.
Les points $F, E, X$ et $A$ sont cocycliques donc $\widehat{F E A}=\widehat{F X A}$. On déduit
$$
\widehat{\mathrm{FED}}=\widehat{\mathrm{FEA}}=\widehat{\mathrm{FXA}}=\widehat{\mathrm{DXA}}=\widehat{\mathrm{XDA}}=\widehat{\mathrm{FDE}}
$$
Ce qui donne bien que le triangle FDE est isocèle en F .
Commentaire des correcteurs On a observé pratiquement que des preuves complètes, même si certaines étaient très longues et calculatoires.
|
{
"exam": "French_envois",
"problem_label": "11",
"problem_match": "\nExercice 11.",
"resource_path": "French/segmented/envois/fr-corrigé-commentaire-envoi-1.jsonl",
"solution_match": "\nSolution de l'exercice 11",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle, $\Gamma$ its circumcircle, and $\Omega$ another circle passing through the points $A$ and $B$. The line $(AC)$ intersects the circle $\Omega$ at a point $D$ and the tangent to the circle $\Gamma$ at $B$ intersects $\Omega$ at a point $E$.
Show that the lines $(BC)$ and $(DE)$ are parallel.

|
The line (BE) is tangent to the circle $\Omega$ at B, so by the tangent angle theorem, $\widehat{\mathrm{EBA}}=\widehat{\mathrm{BCA}}$. The points D, A, B, and E are concyclic, so $\widehat{\mathrm{EDA}}=180^{\circ}-\widehat{\mathrm{EBA}}$. We deduce that $\widehat{\mathrm{EDA}}=180^{\circ}-\widehat{\mathrm{BCD}}$, which shows that the lines (BC) and (ED) are parallel.
Comment from the markers: The vast majority of the submitted solutions provided complete proofs. However, many students engaged in angle chasing that is only valid in their specific case. Some students considered all possible cases, which was rewarded.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle, $\Gamma$ son cercle circonscrit et $\Omega$ un autre cercle passant par les points $A$ et $B$. La droite (AC) coupe le cercle $\Omega$ en un point $D$ et la tangente à cercle $\Gamma$ en B coupe $\Omega$ en un point E .
Montrer que les droites $(B C)$ et ( $D E$ ) sont parallèles.

|
La droite ( BE ) est tangente au cercle $\Omega$ en $B$ donc par le théorème de l'angle tangent, $\widehat{\mathrm{EBA}}=\widehat{\mathrm{BCA}}$. Les points $\mathrm{D}, \mathrm{A}, \mathrm{B}$ et E sont cocycliques donc $\widehat{\mathrm{EDA}}=180^{\circ}-\widehat{\mathrm{EBA}}$. On déduit que $\widehat{\mathrm{EDA}}=180^{\circ}-\widehat{\mathrm{BCD}}$ ce qui donne bien que les droites ( BC ) et (ED) sont parallèles.
Commentaire des correcteurs La grande majorité des copies reçues ont fourni des preuves complètes. Cependant, beaucoup d'élèves font des chasses aux angles qui ne sont valides que dans leur cas de figure. Certains élèves ont traité tous les cas, ce qui a été récompensé.
|
{
"exam": "French_envois",
"problem_label": "12",
"problem_match": "\nExercice 12.",
"resource_path": "French/segmented/envois/fr-corrigé-commentaire-envoi-1.jsonl",
"solution_match": "\nSolution de l'exercice 12",
"tier": "T2",
"year": null
}
|
Let $A, B, C$ and $D$ be four points on a circle in that order. Let $U$ be the intersection point of the lines $(A B)$ and $(C D)$, and $V$ the intersection point of the lines $(BC)$ and $(D A)$. Let $K$ be the intersection point of the angle bisector from $U$ in triangle $AUC$ and the angle bisector from $V$ in triangle $AVC$. Let $L$ be the intersection point of the perpendicular bisector of segment $[KU]$ and the perpendicular bisector of segment $[KV]$.
Show that the points $U, V$ and $L$ are collinear.
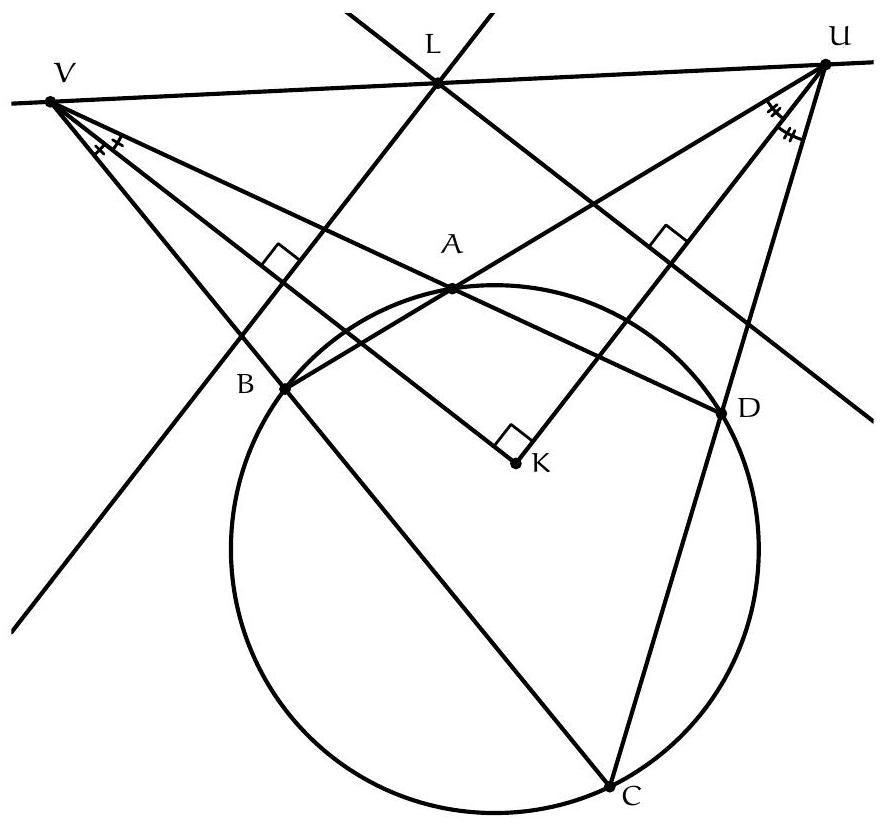
|
Point L is the center of the circumcircle of triangle UKV. To show that points U, L, and V are collinear, it suffices to show that $\widehat{\mathrm{ULV}}=180^{\circ}$. By the central angle theorem, $\widehat{U K V}=\frac{1}{2} \widehat{U L V}$. Therefore, it suffices to show that $\widehat{U K V}=90^{\circ}$.
The sum of the angles of triangle UKV is $180^{\circ}$, so it suffices to show that $\widehat{\mathrm{KUV}}+\widehat{\mathrm{KVU}}=90^{\circ}$. On one hand, $\widehat{K U V}=\widehat{C U V}-\widehat{K U C}=\widehat{C U V}-\frac{1}{2} \widehat{B U C}$. But $\widehat{B U C}=180^{\circ}-\widehat{U B C}-\widehat{B C U}=\widehat{A D C}-\widehat{U C B}$. We deduce
$$
\widehat{\mathrm{KUV}}=\widehat{\mathrm{CUV}}-\frac{1}{2} \widehat{\mathrm{ADC}}+\frac{1}{2} \widehat{\mathrm{UCB}}
$$
Similarly, we obtain
$$
\widehat{\mathrm{KVU}}=\widehat{\mathrm{CVU}}-\frac{1}{2} \widehat{\mathrm{CBA}}+\frac{1}{2} \widehat{\mathrm{VCD}}
$$
But $\widehat{C B A}+\widehat{A D C}=180^{\circ}$ and
$$
\widehat{U C B}=\widehat{V C D}=\widehat{U C V}=180^{\circ}-\widehat{C U V}-\widehat{C V U}
$$
Finally
$$
\begin{aligned}
& \widehat{\mathrm{KUV}}+\widehat{\mathrm{KVU}}=\widehat{\mathrm{CUV}}-\frac{1}{2} \widehat{\mathrm{ADC}}+\frac{1}{2} \widehat{\mathrm{UCB}}+\widehat{\mathrm{CVU}}-\frac{1}{2} \widehat{\mathrm{CBA}}+\frac{1}{2} \widehat{\mathrm{VCD}} \\
& =\widehat{\mathrm{CUV}}+\widehat{\mathrm{CVU}}-\frac{1}{2} \cdot 180^{\circ}+2 \cdot \frac{1}{2} \cdot\left(180^{\circ}-\widehat{\mathrm{CUV}}-\widehat{\mathrm{CVU}}\right)=90^{\circ}
\end{aligned}
$$
which gives the desired result.
Comment from the graders: The exercise was generally well solved. Be sure to justify all assertions. Some false statements were noted. For example, contrary to what some students claimed, a quadrilateral with two opposite right angles is not necessarily a rectangle. Also, be careful not to use the statement to prove the statement.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A, B, C$ et $D$ quatre points sur un cercle dans cet ordre. Soit $U$ le point d'intersection des droites $(A B$ ) et ( $C D$ ), et V le point d'intersection des droites (BC) et ( $D A$ ). Soit K le point d'intersection de la bissectrice issue de U dans le triangle AUC et de la bissectrice issue de V dans le triangle $A V C$. Soit L le point d'intersection de la médiatrice du segment $[\mathrm{KU}]$ et de la médiatrice du segment [KV].
Montrer que les points $\mathrm{U}, \mathrm{V}$ et L sont alignés.

|
Le point L est le centre du cercle circonscrit au triangle UKV. Pour montrer que les points U , L et V sont alignés, il suffit de montrer que $\widehat{\mathrm{ULV}}=180^{\circ}$. Par le théorème de l'angle au centre, $\widehat{U K V}=\frac{1}{2} \widehat{U L V}$. Il suffit donc de montrer que $\widehat{U K V}=90^{\circ}$.
La somme des angles du triangle UKV vaut $180^{\circ}$, donc il suffit de montrer que $\widehat{\mathrm{KUV}}+\widehat{\mathrm{KVU}}=90^{\circ}$. D'une part $\widehat{K U V}=\widehat{C U V}-\widehat{K U C}=\widehat{C U V}-\frac{1}{2} \widehat{B U C}$. Or $\widehat{B U C}=180^{\circ}-\widehat{U B C}-\widehat{B C U}=\widehat{A D C}-\widehat{U C B}$. On déduit
$$
\widehat{\mathrm{KUV}}=\widehat{\mathrm{CUV}}-\frac{1}{2} \widehat{\mathrm{ADC}}+\frac{1}{2} \widehat{\mathrm{UCB}}
$$
De la même manière, on obtient
$$
\widehat{\mathrm{KVU}}=\widehat{\mathrm{CVU}}-\frac{1}{2} \widehat{\mathrm{CBA}}+\frac{1}{2} \widehat{\mathrm{VCD}}
$$
Or $\widehat{C B A}+\widehat{A D C}=180^{\circ}$ et
$$
\widehat{U C B}=\widehat{V C D}=\widehat{U C V}=180^{\circ}-\widehat{C U V}-\widehat{C V U}
$$
Finalement
$$
\begin{aligned}
& \widehat{\mathrm{KUV}}+\widehat{\mathrm{KVU}}=\widehat{\mathrm{CUV}}-\frac{1}{2} \widehat{\mathrm{ADC}}+\frac{1}{2} \widehat{\mathrm{UCB}}+\widehat{\mathrm{CVU}}-\frac{1}{2} \widehat{\mathrm{CBA}}+\frac{1}{2} \widehat{\mathrm{VCD}} \\
& =\widehat{\mathrm{CUV}}+\widehat{\mathrm{CVU}}-\frac{1}{2} \cdot 180^{\circ}+2 \cdot \frac{1}{2} \cdot\left(180^{\circ}-\widehat{\mathrm{CUV}}-\widehat{\mathrm{CVU}}\right)=90^{\circ}
\end{aligned}
$$
ce qui donne le résultat voulu.
Commentaire des correcteurs L'exercice a été plutôt bien résolu. Attention à bien s'assurer que tout ce que l'on affirme est justifié. On a pu noté certaines affirmations fausses. Par exemple, contrairement à ce que certains élèves ont affirmé, un quadrilatère dont les deux angles opposés sont droits n'est pas forcément un rectangle. Attention également à ne pas utiliser l'énoncé pour démontrer l'énoncé.
|
{
"exam": "French_envois",
"problem_label": "13",
"problem_match": "\nExercice 13.",
"resource_path": "French/segmented/envois/fr-corrigé-commentaire-envoi-1.jsonl",
"solution_match": "\nSolution de l'exercice 13",
"tier": "T2",
"year": null
}
|
Let BCDE be a square and O its center. Let $A$ be a point located outside the square $B C D E$ such that the triangle $A B C$ is a right triangle at $A$. Show that the point $O$ lies on the bisector of the angle $\widehat{B A C}$.
|
The diagonals of the square BCDE intersect perpendicularly at O, so $\widehat{\mathrm{BOC}}=90^{\circ}=\widehat{\mathrm{BAC}}$, hence the points $\mathrm{A}, \mathrm{B}, \mathrm{O}$, and C are concyclic. Since O lies on the perpendicular bisector of the segment $[B C]$, O is the South Pole of $A$ in the triangle $A B C$, so O lies on the bisector of the angle $\widehat{B A C}$. Comment from the markers The exercise is rather well done, the proposed solutions are interesting but some are computational.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit BCDE un carré et soit O son centre. Soit $A$ un point situé à l'extérieur du carré $B C D E$ tel que le triangle $A B C$ est rectangle en $A$. Montrer que le point $O$ appartiant à la bissectrice de l'angle $\widehat{B A C}$.

|
Les diagonales du carré BCDE se coupent perpendiculairement en O donc $\widehat{\mathrm{BOC}}=90^{\circ}=\widehat{\mathrm{BAC}}$ donc les points $\mathrm{A}, \mathrm{B}, \mathrm{O}$ et C sont cocycliques. Comme O est sur la médiatrice du segment $[B C]$, $O$ est le pôle Sud de $A$ dans le triangle $A B C$ donc $O$ est sur la bissectrice de l'angle $\widehat{B A C}$. Commentaire des correcteurs L'exercice est plutôt bien réussi, les solutions proposées sont intéressantes mais calculatoires pour certaines.
|
{
"exam": "French_envois",
"problem_label": "14",
"problem_match": "\nExercice 14.",
"resource_path": "French/segmented/envois/fr-corrigé-commentaire-envoi-1.jsonl",
"solution_match": "\nSolution de l'exercice 14",
"tier": "T2",
"year": null
}
|
Let $\Omega$ and $\Gamma$ be two intersecting circles. We denote $A$ as one of their intersections. Let $d$ be any line passing through the point $A$. We denote $P$ and $Q$ as the intersections of the line $d$ with the circles $\Omega$ and $\Gamma$ respectively, different from $A$.
Show that there exists a point independent of the line $d$ chosen and which always lies on the perpendicular bisector of the segment $[\mathrm{PQ}]$.
|
By symmetry, we can assume that the radius of circle $\Omega$ is greater than the radius of circle $\Gamma$.
Let $\mathrm{O}_{1}$ be the center of circle $\Omega$ and $\mathrm{O}_{2}$ be the center of circle $\Gamma$. Let B be the point such that the quadrilateral $\mathrm{AO}_{1} \mathrm{BO}_{2}$ is a parallelogram. We will show that point B lies on the perpendicular bisector of the segment $[\mathrm{PQ}]$. Since point B is independent of the choice of line d, this will show that the perpendicular bisectors of the segment $[\mathrm{PQ}]$ pass through a fixed point as the line $d$ varies.
To show that $B P=B Q$, we will show that triangles $\mathrm{PO}_{1} B$ and $\mathrm{BO}_{2} \mathrm{Q}$ are isometric. We already know that $\mathrm{O}_{1} \mathrm{P}=\mathrm{O}_{1} \mathrm{~A}=\mathrm{O}_{2} \mathrm{~B}$ and $\mathrm{O}_{1} \mathrm{~B}=\mathrm{O}_{2} \mathrm{~A}=\mathrm{O}_{2} \mathrm{Q}$. It remains to show that $\widehat{\mathrm{BO}_{1} \mathrm{P}}=\widehat{\mathrm{BO}_{2} \mathrm{Q}}$.
On the one hand
$$
\widehat{\mathrm{PO}_{1} \mathrm{~B}}=360^{\circ}-\widehat{\mathrm{PO}_{1} \mathrm{~A}}-\widehat{\mathrm{AO} O_{1} \mathrm{~B}}=360^{\circ}-\left(180^{\circ}-2 \widehat{\mathrm{O}_{1} \mathrm{AP}}\right)-\widehat{\mathrm{AO} O_{1} B}=180^{\circ}+2 \widehat{\mathrm{O}_{1} \mathrm{AP}}-\widehat{\mathrm{AO} \mathrm{O}_{1} \mathrm{~B}}
$$
On the other hand
$$
\widehat{\mathrm{BO}_{2} \mathrm{Q}}=\widehat{\mathrm{BO}_{2} \mathrm{~A}}+\widehat{\mathrm{AO}_{2} \mathrm{Q}}=\widehat{\mathrm{BO}_{2} \mathrm{~A}}+\left(180^{\circ}-2 \widehat{\mathrm{O}_{2} \mathrm{AQ}}\right)=180^{\circ}+\widehat{\mathrm{BO}_{2} \mathrm{~A}}-2 \widehat{2 \mathrm{O}_{2} \mathrm{AQ}}
$$
But $\widehat{O_{1} \mathrm{AP}}+\widehat{\mathrm{O}_{1} \mathrm{AO}_{2}}+\widehat{\mathrm{O}_{2} \mathrm{AQ}}=180^{\circ}$, so $2 \widehat{\mathrm{O}_{1} \mathrm{AP}}+2 \widehat{\mathrm{O}_{1} \mathrm{AO}_{2}}+2 \widehat{\mathrm{O}_{2} \mathrm{AQ}}=360$ and $\widehat{\mathrm{O}_{1} \mathrm{AO}_{2}}=$ $180^{\circ}-\widehat{\mathrm{AO}_{1} \mathrm{~B}}=180^{\circ}-\widehat{\mathrm{BO}_{2} \mathrm{~A}}$ so
$$
2 \widehat{\mathrm{O}_{1} \mathrm{AP}}+180^{\circ}-\widehat{\mathrm{AO} O_{1} \mathrm{~B}}+180^{\circ}-\widehat{\mathrm{BO}_{2} \mathrm{~A}}+2 \widehat{\mathrm{O}_{2} \mathrm{AQ}}=360^{\circ}
$$
so
$$
2 \widehat{\mathrm{O}_{1} \mathrm{AP}}-\widehat{\mathrm{AO}_{1} \mathrm{~B}}=\widehat{\mathrm{BO}_{2} \mathrm{~A}}-2 \widehat{\mathrm{O}_{2} \mathrm{AQ}}
$$
We find that $\widehat{\mathrm{PO}_{1} \mathrm{~B}}=\widehat{\mathrm{BO}_{2} \mathrm{Q}}$ and point B is indeed on the perpendicular bisector of $[\mathrm{PQ}]$.
Comment from the graders: The exercise is well solved by those who have tackled it, and several different solutions have been observed. Many students engage in angle chasing with non-oriented angles, but they have not been penalized.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $\Omega$ et $\Gamma$ deux cercles sécants. On note $A$ une de leurs intersections. Soit d une droite quelconque passant par le point $A$. On note $P$ et $Q$ les intersections respectives de la droite $d$ avec les cercles $\Omega$ et $\Gamma$ différentes de $A$.
Montrer qu'il existe un point indépendant de la droite d choisie et qui appartient toujours à la médiatrie du segment $[\mathrm{PQ}]$.

|
Par symétrie, on peut supposer que le rayon du cercle $\Omega$ est supérieur au rayon du cercle $\Gamma$.
Soit $\mathrm{O}_{1}$ le centre du cercle $\Omega$ et $\mathrm{O}_{2}$ le centre du cercle $\Gamma$. Soit B le point tel que le quadrilatère $\mathrm{AO}_{1} \mathrm{BO}_{2}$ soit un parallélogramme. On va montrer que le point B appartient à la médiatrice du segment $[\mathrm{PQ}]$. Comme le point B est indépendant du choix de la droite d, ceci montrera bien que les médiatrices des semgent $[\mathrm{PQ}]$ passent par un point fixe lorsque la droite $d$ varie.
Pour montrer que $B P=B Q$, on va montrer que les triangles $\mathrm{PO}_{1} B$ et $\mathrm{BO}_{2} \mathrm{Q}$ sont isométriques. On sait déjà que $\mathrm{O}_{1} \mathrm{P}=\mathrm{O}_{1} \mathrm{~A}=\mathrm{O}_{2} \mathrm{~B}$ et $\mathrm{O}_{1} \mathrm{~B}=\mathrm{O}_{2} \mathrm{~A}=\mathrm{O}_{2} \mathrm{Q}$. Il reste donc à montrer que $\widehat{\mathrm{BO}_{1} \mathrm{P}}=\widehat{\mathrm{BO}_{2} \mathrm{Q}}$.
D'une part
$$
\widehat{\mathrm{PO}_{1} \mathrm{~B}}=360^{\circ}-\widehat{\mathrm{PO}_{1} \mathrm{~A}}-\widehat{\mathrm{AO} O_{1} \mathrm{~B}}=360^{\circ}-\left(180^{\circ}-2 \widehat{\mathrm{O}_{1} \mathrm{AP}}\right)-\widehat{\mathrm{AO} O_{1} B}=180^{\circ}+2 \widehat{\mathrm{O}_{1} \mathrm{AP}}-\widehat{\mathrm{AO} \mathrm{O}_{1} \mathrm{~B}}
$$
D'autre part
$$
\widehat{\mathrm{BO}_{2} \mathrm{Q}}=\widehat{\mathrm{BO}_{2} \mathrm{~A}}+\widehat{\mathrm{AO}_{2} \mathrm{Q}}=\widehat{\mathrm{BO}_{2} \mathrm{~A}}+\left(180^{\circ}-2 \widehat{\mathrm{O}_{2} \mathrm{AQ}}\right)=180^{\circ}+\widehat{\mathrm{BO}_{2} \mathrm{~A}}-2 \widehat{2 \mathrm{O}_{2} \mathrm{AQ}}
$$
Mais $\widehat{O_{1} \mathrm{AP}}+\widehat{\mathrm{O}_{1} \mathrm{AO}_{2}}+\widehat{\mathrm{O}_{2} \mathrm{AQ}}=180^{\circ}$ donc $2 \widehat{\mathrm{O}_{1} \mathrm{AP}}+2 \widehat{\mathrm{O}_{1} \mathrm{AO}_{2}}+2 \widehat{\mathrm{O}_{2} \mathrm{AQ}}=360$ et $\widehat{\mathrm{O}_{1} \mathrm{AO}_{2}}=$ $180^{\circ}-\widehat{\mathrm{AO}_{1} \mathrm{~B}}=180^{\circ}-\widehat{\mathrm{BO}_{2} \mathrm{~A}}$ donc
$$
2 \widehat{\mathrm{O}_{1} \mathrm{AP}}+180^{\circ}-\widehat{\mathrm{AO} O_{1} \mathrm{~B}}+180^{\circ}-\widehat{\mathrm{BO}_{2} \mathrm{~A}}+2 \widehat{\mathrm{O}_{2} \mathrm{AQ}}=360^{\circ}
$$
donc
$$
2 \widehat{\mathrm{O}_{1} \mathrm{AP}}-\widehat{\mathrm{AO}_{1} \mathrm{~B}}=\widehat{\mathrm{BO}_{2} \mathrm{~A}}-2 \widehat{\mathrm{O}_{2} \mathrm{AQ}}
$$
On trouve bien $\widehat{\mathrm{PO}_{1} \mathrm{~B}}=\widehat{\mathrm{BO}_{2} \mathrm{Q}}$ et le point B est bien sur la médiatrice de $[\mathrm{PQ}]$.
Commentaire des correcteurs L'exercice est bien résolu par ceux qui l'ont traité et on a pu observé plusieurs solutions différentes. Beaucoup d'élèves font des chasses aux angles non orientés mais ils n'ont pas été pénalisés.
|
{
"exam": "French_envois",
"problem_label": "15",
"problem_match": "\nExercice 15.",
"resource_path": "French/segmented/envois/fr-corrigé-commentaire-envoi-1.jsonl",
"solution_match": "\nSolution de l'exercice 15",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle, $H$ its orthocenter, and $M$ the midpoint of the segment $[BC]$. Let $d$ be a line passing through the point $M$. Suppose that $d$ intersects the circle with diameter $[AH]$ at $P$ and $Q$. Show that the orthocenter of the triangle $APQ$ is on the circumcircle of the triangle $ABC$.
|
Let N be the midpoint of $[\mathrm{PQ}]$ and K the orthocenter of triangle APQ. If we call $\mathrm{K}^{\prime}$ the symmetric of K with respect to the midpoint $N$ of segment $[P Q]$, then $[P Q]$ and $\left[K K^{\prime}\right]$ have the same midpoint $N$ so $\mathrm{PKQK}^{\prime}$ is a parallelogram, thus $\widehat{\mathrm{K}^{\prime} \mathrm{PA}}=\widehat{\mathrm{K}^{\prime} \mathrm{PQ}}+\widehat{\mathrm{QPA}^{\prime}}=\widehat{\mathrm{PQK}}+\widehat{\mathrm{QPA}^{\prime}}=90^{\circ}(\mathrm{since}(\mathrm{PA})$ and (QK) are perpendicular). Similarly, $\widehat{K^{\prime} Q A}=90^{\circ}$, so $K^{\prime}$ is the point diametrically opposite to $A$ on the circumcircle of $A P Q$, in other words $K^{\prime}=\mathrm{H}$: the symmetric of K with respect to the midpoint N of segment $[\mathrm{PQ}]$ is H.
Let X be the symmetric of H with respect to M and Y the second intersection of the line ( MH ) with the circumcircle of triangle $A B C$. By a similar reasoning to the one previously conducted, we know that $X$ is the point diametrically opposite to $A$ on the circumcircle of $A B C$ so $\widehat{H Y A}=\widehat{X Y A}=90^{\circ}$, thus $Y$ is on the circle with diameter $[\mathrm{AH}]$. Since $X$ is the point diametrically opposite to $A$ on the circumcircle of $A B C$, it suffices to show that $\widehat{X K A}=90^{\circ}$ to complete the exercise.
We decompose the angle into three parts: $\widehat{\mathrm{XKA}}=360^{\circ}-\widehat{\mathrm{XKH}}-\widehat{\mathrm{HKQ}}-\widehat{\mathrm{QKA}}$
The points $M$ and $N$ are the midpoints of segments $[H X]$ and $[H K]$, respectively, so the lines (MN) and (KX) are parallel. We deduce $\widehat{\mathrm{XKH}}=\widehat{\mathrm{MNH}}=\widehat{\mathrm{PNH}}$.
The segments $[\mathrm{PQ}]$ and $[\mathrm{KH}]$ intersect at their midpoints, so the quadrilateral PHQK is a parallelogram. $\mathrm{D}^{\prime}$ where $\widehat{\mathrm{HKQ}}=\widehat{\mathrm{KHP}}=\widehat{\mathrm{NHP}}$.
The point Q is the orthocenter of triangle KPA, so $\widehat{\mathrm{QKA}}=180^{\circ}-\widehat{\mathrm{QPA}}$.
We deduce
$\widehat{\mathrm{XKA}}=360^{\circ}-\widehat{\mathrm{PNH}}-\widehat{\mathrm{NHP}}-\left(180^{\circ}-\widehat{\mathrm{QPA}}\right)=180^{\circ}-\widehat{\mathrm{PNH}}-\widehat{\mathrm{NHP}}+\widehat{\mathrm{QPA}}=\widehat{\mathrm{NPH}}+\widehat{\mathrm{QPA}}=\widehat{\mathrm{APH}}=90^{\circ}$
since $P$ is on the circle with diameter $[\mathrm{AH}]$. Thus, $\widehat{X K A}=90^{\circ}$, so K is indeed on the circumcircle of ABC.
Comment from the graders: This problem required a bit of knowledge. Most students who attempted the problem identified the interest of the nine-point circle and the symmetrics of the orthocenter with respect to the midpoints of the sides.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle, $H$ son orthocentre et $M$ le milieu du segment $[B C]$. Soit $d$ une droite passant par le point $M$. On suppose que $d$ coupe le cercle de diamètre $[A H]$ en $P$ et $Q$. Montrer que l'orthocentre du triangle $A P Q$ est sur le cercle circonscrit du triangle $A B C$.

|
Soit N le milieu de $[\mathrm{PQ}]$ et K l'orthocentre du triangle APQ . Si on appelle $\mathrm{K}^{\prime}$ le symétrique de K par rapport au milieu $N$ du segment $[P Q]$, alors $[P Q]$ et $\left[K K^{\prime}\right]$ ont le même milieu $N$ donc $\mathrm{PKQK}^{\prime}$ est un parallélogramme donc $\widehat{\mathrm{K}^{\prime} \mathrm{PA}}=\widehat{\mathrm{K}^{\prime} \mathrm{PQ}}+\widehat{\mathrm{QPA}^{\prime}}=\widehat{\mathrm{PQK}}+\widehat{\mathrm{QPA}^{\prime}}=90^{\circ}(\mathrm{car}(\mathrm{PA})$ et (QK) sont perpendiculaires). De même, $\widehat{K^{\prime} Q A}=90^{\circ}$ donc $K^{\prime}$ est le point diamétralement opposé à $A$ sur le cercle circonscrit à $A P Q$, autrement dit $K^{\prime}=\mathrm{H}$ : le symétrique de K par rapport au milieu N du segment $[\mathrm{PQ}]$ est H .
Soit X le symétrique de H par rapport à M et Y la seconde intersection de la droite ( MH ) avec le cercle circonscrit au triangle $A B C$. Par un raisonnement analogue à celui mené précédemment, on sait que $X$ est le point diamétralement opposé à $A$ sur le cercle circonscrit à $A B C$ donc $\widehat{H Y A}=\widehat{X Y A}=90^{\circ}$ donc $Y$ est sur le cercle de diamètre $[\mathrm{AH}]$. Puisque $X$ est le point diamétralement opposé à $A$ sur le cercle circonscrit à $A B C$, il suffit de montrer que $\widehat{X K A}=90^{\circ}$ pour finir l'exercice.
On décompose l'angle en trois morceaux : $\widehat{\mathrm{XKA}}=360^{\circ}-\widehat{\mathrm{XKH}}-\widehat{\mathrm{HKQ}}-\widehat{\mathrm{QKA}}$
Les points $M$ et $N$ sont la milieux respectifs des segments $[H X]$ et $[H K]$ donc les droites (MN) et (KX) sont parallèles. On déduit $\widehat{\mathrm{XKH}}=\widehat{\mathrm{MNH}}=\widehat{\mathrm{PNH}}$.
Les segments $[\mathrm{PQ}]$ et $[\mathrm{KH}]$ se coupent en leur milieu donc le quadrilatère PHQK est un parallèlogramme. $\mathrm{D}^{\prime}$ où $\widehat{\mathrm{HKQ}}=\widehat{\mathrm{KHP}}=\widehat{\mathrm{NHP}}$.
Le point Q est l'orthocentre du triangle KPA donc $\widehat{\mathrm{QKA}}=180^{\circ}-\widehat{\mathrm{QPA}}$.
On déduit
$\widehat{\mathrm{XKA}}=360^{\circ}-\widehat{\mathrm{PNH}}-\widehat{\mathrm{NHP}}-\left(180^{\circ}-\widehat{\mathrm{QPA}}\right)=180^{\circ}-\widehat{\mathrm{PNH}}-\widehat{\mathrm{NHP}}+\widehat{\mathrm{QPA}}=\widehat{\mathrm{NPH}}+\widehat{\mathrm{QPA}}=\widehat{\mathrm{APH}}=90^{\circ}$
car $P$ est sur le cercle de diamètre $[\mathrm{AH}]$. Ainsi, $\widehat{X K A}=90^{\circ}$ donc K est bien sur le cercle circonscrit à ABC.
Commentaire des correcteurs Ce problème nécessitait un peu de culture. La plupart des élèves ayant essayé le problème ont identifié l'intérêt du cercle d'Euler et des symétriques de l'orthocentre par rapport au milieu des côtés.
|
{
"exam": "French_envois",
"problem_label": "16",
"problem_match": "\nExercice 16.",
"resource_path": "French/segmented/envois/fr-corrigé-commentaire-envoi-1.jsonl",
"solution_match": "\nSolution de l'exercice 16",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle and $I$ the center of its inscribed circle. The perpendicular to the line $(AI)$ passing through the point $I$ intersects the line $(AB)$ at a point $D$ and the line $(AC)$ at a point $E$. Suppose there exist two points $F$ and $G$ on the segment $[BC]$ such that $BA = BF$ and $CA = CG$. Let $T$ be the intersection point of the circumcircles of triangles $ADF$ and $AEG$.
Show that the center of the circumcircle of triangle $AIT$ lies on the line $(BC)$.
|
Let $M$ and $N$ be the midpoints of the segments [AD] and [AE] respectively, and let $X$ be the intersection point of the line (MN) (which is also the perpendicular bisector of the segment [AI]) with the line (BC). Let $\mathrm{O}_{1}$ and $\mathrm{O}_{2}$ be the centers of the circumcircles of triangles ADF and AEG respectively. We wish to show that the point $X$ is the center of the circumcircle of AIT, meaning it lies on the perpendicular bisector of the segment [AT], i.e., on the line $\left(\mathrm{O}_{1} \mathrm{O}_{2}\right)$.
Let $P, Q$, and $R$ be the points of tangency of the incircle of triangle $ABC$ with the sides $[BC]$, $[AC]$, and $[AB]$ respectively. The point $\mathrm{O}_{1}$ lies on the perpendicular bisector of the segment $[AD]$, so the line $\left(\mathrm{O}_{1} M\right)$ is perpendicular to the line (AB). Therefore, the lines $\left(\mathrm{O}_{1} M\right)$ and (IR) are parallel. By Thales' theorem, we deduce that $\frac{\mathrm{O}_{1} \mathrm{I}}{\mathrm{O}_{1} \mathrm{~B}}=\frac{\mathrm{MR}}{\mathrm{MB}}$. Similarly, $\frac{\mathrm{O}_{2} \mathrm{C}}{\mathrm{O}_{2} \mathrm{I}}=\frac{\mathrm{NC}}{\mathrm{NQ}}$. Moreover, triangle ABF is isosceles at B, so the perpendicular bisector of $[AF]$ is the angle bisector of $\widehat{ABF}$, hence $\mathrm{O}_{1}$ lies on (BI), and similarly, $\mathrm{O}_{2}$ lies on (CI).
By Menelaus' theorem applied to the points $\mathrm{M}, \mathrm{N}, \mathrm{X}$ in triangle $ABC$:
$$
\frac{X B}{X C} \cdot \frac{N C}{N A} \cdot \frac{M A}{M B}=1
$$
and applying it to triangle BIC, the collinearity of points $\mathrm{O}_{1}, \mathrm{O}_{2}$, and $X$ is equivalent to $\frac{\mathrm{O}_{1} \mathrm{I}}{\mathrm{O}_{1} \mathrm{~B}} \cdot \frac{\mathrm{XB}}{X \mathrm{C}} \cdot \frac{\mathrm{O}_{2} \mathrm{C}}{\mathrm{O}_{2} \mathrm{I}}=1$. We wish to show this equality.
We already know $\frac{\mathrm{XB}}{\mathrm{XC}}=\frac{\mathrm{NA}}{\mathrm{NC}} \cdot \frac{\mathrm{MB}}{\mathrm{MA}}, \frac{\mathrm{O}_{1} \mathrm{I}}{\mathrm{O}_{1} \mathrm{~B}}=\frac{\mathrm{MR}}{\mathrm{MB}}, \frac{\mathrm{O}_{2} \mathrm{C}}{\mathrm{O}_{2} \mathrm{I}}=\frac{\mathrm{NC}}{\mathrm{NQ}}$ so
$$
\frac{\mathrm{O}_{1} \mathrm{I}}{\mathrm{O}_{1} \mathrm{~B}} \cdot \frac{\mathrm{XB}}{\mathrm{XC}} \cdot \frac{\mathrm{O}_{2} \mathrm{C}}{\mathrm{O}_{2} \mathrm{I}}=\frac{\mathrm{MR}}{\mathrm{MB}} \cdot \frac{\mathrm{NA}}{\mathrm{NC}} \cdot \frac{\mathrm{MB}}{\mathrm{MA}} \cdot \frac{\mathrm{NC}}{\mathrm{NQ}}=\frac{\mathrm{MR} \cdot \mathrm{NA}}{\mathrm{MA} \cdot \mathrm{NQ}}=1
$$
since $M A=\frac{1}{2} D A=\frac{1}{2} E A=N A$ and $A R=A Q$ so $M R=N Q$. Thus, $\mathrm{O}_{1}, \mathrm{O}_{2}, X$ are collinear.
Comment from the examiners: The problem was difficult and was therefore rarely attempted. A few students provided an interesting reformulation of the problem. Those who delved deeper into the problem showed creativity: some used Desargues' theorem, others used an inversion.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $I$ le centre de son cercle inscrit. La perpendiculaire à la droite ( $A \mathrm{I}$ ) passant par le point I coupe la droite ( AB ) en un point D et la droite ( AC ) en un point E . On suppose qu'il existe deux points $F$ et $G$ sur le segment $[B C]$ tels que $B A=B F$ et $C A=C G$. Soit $T$ le point d'intersection des cercles circonscrits aux triangles ADF et AEG.
Montrer que le centre du cercle circonscrit au triangle AIT se trouve sur la droite (BC).

|
Soient $M$ et $N$ les milieux respectifs des segments [AD] et [AE] et soit $X$ le point d'intersection de la droite (MN) (qui est aussi la médiatrice du segment [AI]) avec la droite (BC). Soient $\mathrm{O}_{1}$ et $\mathrm{O}_{2}$ les centres respectifs des cercles circonscrits aus triangles ADF et AEG. On souhaite montrer que le point $X$ est le centre du cercle circonscrit à AIT donc qu'il appartient à la médiatrice du segment [AT], c'est-à-dire à la droite $\left(\mathrm{O}_{1} \mathrm{O}_{2}\right)$.
Soient $P, Q$ et $R$ les points de contact respectifs du cercle inscrit au triangle $A B C$ avec les côtés $[B C],[A C]$ et $[A B]$. Le point $O_{1}$ est sur la médiatrice du segment $[A D]$ donc la droite $\left(O_{1} M\right.$ ) est perpendiculaire à la droite ( $A B$ ). Les droites $\left(O_{1} M\right.$ ) et (IR) sont donc parallèles. D'après le théorème de Thalès, on déduit que $\frac{\mathrm{O}_{1} \mathrm{I}}{\mathrm{O}_{1} \mathrm{~B}}=\frac{\mathrm{MR}}{\mathrm{MB}}$. On a de même $\frac{\mathrm{O}_{2} \mathrm{C}}{\mathrm{O}_{2} \mathrm{I}}=\frac{\mathrm{NC}}{\mathrm{NQ}}$. De plus, le triangles ABF est isocèle en B donc la médiatrice de $[A F]$ est la bissectrice de $\widehat{A B F}$ donc $\mathrm{O}_{1}$ est sur (BI) et de même $\mathrm{O}_{2}$ est sur (CI).
D'après le théorème de Ménélaus appliquée aux points $\mathrm{M}, \mathrm{N}, \mathrm{X}$ dans le triangle $A B C$ :
$$
\frac{X B}{X C} \cdot \frac{N C}{N A} \cdot \frac{M A}{M B}=1
$$
et en l'appliquant au triangle BIC, l'alignement des points $\mathrm{O}_{1}, \mathrm{O}_{2}$ et $X$ équivaut à $\frac{O_{1} \mathrm{I}}{\mathrm{O}_{1} \mathrm{~B}} \cdot \frac{\mathrm{XB}}{X \mathrm{C}} \cdot \frac{\mathrm{O}_{2} \mathrm{C}}{\mathrm{O}_{2} \mathrm{I}}=1$. On souhaite donc montrer cette égalité.
On sait déjà $\frac{\mathrm{XB}}{\mathrm{XC}}=\frac{\mathrm{NA}}{\mathrm{NC}} \cdot \frac{\mathrm{MB}}{\mathrm{MA}}, \frac{\mathrm{O}_{1} \mathrm{I}}{\mathrm{O}_{1} \mathrm{~B}}=\frac{\mathrm{MR}}{\mathrm{MB}}, \frac{\mathrm{O}_{2} \mathrm{C}}{\mathrm{O}_{2} \mathrm{I}}=\frac{\mathrm{NC}}{\mathrm{NQ}}$ donc
$$
\frac{\mathrm{O}_{1} \mathrm{I}}{\mathrm{O}_{1} \mathrm{~B}} \cdot \frac{\mathrm{XB}}{\mathrm{XC}} \cdot \frac{\mathrm{O}_{2} \mathrm{C}}{\mathrm{O}_{2} \mathrm{I}}=\frac{\mathrm{MR}}{\mathrm{MB}} \cdot \frac{\mathrm{NA}}{\mathrm{NC}} \cdot \frac{\mathrm{MB}}{\mathrm{MA}} \cdot \frac{\mathrm{NC}}{\mathrm{NQ}}=\frac{\mathrm{MR} \cdot \mathrm{NA}}{\mathrm{MA} \cdot \mathrm{NQ}}=1
$$
car $M A=\frac{1}{2} D A=\frac{1}{2} E A=N A$ et $A R=A Q$ donc $M R=N Q$. Ainsi, $O_{1}, O_{2}, X$ sont alignés.
Commentaire des correcteurs L'exercice était difficile et a donc été très peu abordé. Quelques élèves ont donné une reformulation intéressante de l'énoncé. Les élèves qui ont cherché l'exercice plus en profondeur ont fait preuve d'inventivité : certains ont utilise le théorème de Desargues, d'autres une inversion.
|
{
"exam": "French_envois",
"problem_label": "17",
"problem_match": "\nExercice 17.",
"resource_path": "French/segmented/envois/fr-corrigé-commentaire-envoi-1.jsonl",
"solution_match": "\nSolution de l'exercice 17",
"tier": "T2",
"year": null
}
|
Let ABC be a triangle, and let O be the center of its circumcircle. Let I be the center of the incircle of triangle $ABC$ and D the point of tangency of this circle with the segment [AC]. The lines (OI) and $(AB)$ intersect at a point $P$. Let $M$ be the midpoint of the arc $AC$ not containing $B$ and $N$ be the midpoint of the arc $BC$ containing $A$.
Show that the lines (MD) and (NP) intersect on the circumcircle of $ABC$.
|
Let $X$ be the intersection point of the line (MD) with the circumcircle of triangle $ABC$, and let $P'$ be the intersection point of the line $(XN)$ with the segment $[AB]$. Let $S$ be the intersection point of the angle bisector of $\widehat{BAC}$ with the circumcircle of triangle $ABC$. We know that the points $N$, $O$, and $S$ are collinear.
Let $E$ and $F$ be the points of tangency of the incircle of triangle $ABC$ with the segments $[AB]$ and $[BC]$, respectively. The point $M$ is the midpoint of the arc $CA$, so it lies on the angle bisector of $\widehat{AXC}$. The point $D$ is the foot of this bisector. According to the Angle Bisector Theorem, $\frac{AX}{XC} = \frac{DA}{DC} = \frac{AE}{CF}$. Since $\widehat{EAX} = \widehat{BAX} = \widehat{BCX} = \widehat{FCX}$, it follows that triangles $AEX$ and $CFX$ are similar, so point $X$ is the center of the similarity that maps points $E$ and $F$ to points $A$ and $C$, respectively. Therefore, $X$ is the intersection point of the circumcircles of triangles $ABC$ and $EFB$. Since $[BI]$ is a diameter of the circumcircle of triangle $EFB$, we deduce that $\widehat{IXB} = 90^\circ$. Let $Y$ be the point diametrically opposite to point $B$ in the circumcircle of triangle $ABC$. Then $\widehat{YXB} = 90^\circ = \widehat{IXB}$. Therefore, points $X$, $I$, and $Y$ are collinear.
According to Pascal's Theorem applied to the hexagon $SABYXN$, the points $O = (BY) \cap (SN)$, $I = (YX) \cap (AS)$, and $P' = (AB) \cap (XN)$ are collinear. Therefore, point $P'$ is the intersection of lines $(OI)$ and $(AB)$, so $P = P'$, which means that lines $(MD)$ and $(NP)$ intersect on the circumcircle of triangle $ABC$.
Comment from the graders: Various solutions were proposed: using an inversion centered at $M$ that fixes points $A$, $I$, and $C$ to show that points $X$, $I$, and $Y$ are collinear, using $Z$ as the center of the positive homothety that maps the incircle to the circumcircle and considering the mixtilinear circle, or using barycentric coordinates.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit ABC un triangle, soit O le centre de son cercle circonscrit. Soit I le centre du cercle inscrit au triangle $A B C$ et D le point de tangence de ce cercle avec le segment [AC]. Les droites (OI) et $(A B)$ se coupent en un point $P$. Soit $M$ le milieu de l'arc $A C$ ne contenant pas $B$ et $N$ le milieu de l'arc $B C$ contenant $A$.
Montrer que les droites (MD) et (NP) se coupent sur le cercle circonscrit à ABC.

|
Soit $X$ le point d'intersection de la droite (MD) avec le cercle circonscrit au triangle $A B C$ et soit $P^{\prime}$ le point d'intersection de la droite $(X N)$ avec le segment $[A B]$. Soit $S$ le point d'intersection de la bissectrice de l'angle $\widehat{B A C}$ avec le cercle circonscrit au triangle $A B C$. On sait que les points $\mathrm{N}, \mathrm{O}$ et S sont alignés.
Soit $E$ et $F$ les points de contact respectifs du cercle inscrit au triangles $A B C$ avec les segment $[A B]$ et [BC].
Le point $M$ est le milieu de l'arc $C A$, il est donc sur la bissectrice de l'angle $\widehat{A X C}$. Le point $D$ est le pied de cette bissectrice. D' après le théorème de la bissectrice, $\frac{A X}{X C}=\frac{D A}{D C}=\frac{A E}{C F}$. Puisque $\widehat{E A X}=\widehat{B A X}=$ $\widehat{B C X}=\widehat{F C X}$, il vient que les triangles $A E X$ et $C F X$ sont semblables donc le point $X$ est le centre de la similitude qui envoie les points $E$ et $F$ sur les points $A$ et $C$, il est donc le point d'intersection des cercles circonscrits aux triangles $A B C$ et EFB. Puisque [BI] est un diamètre du cercle circonscrit au triangle EBF , on déduit $\widehat{\mathrm{IXB}}=90^{\circ}$. Soit $Y$ le point diamétralement opposé au point B dans le cercle circonscrit au triangle ABC . Alors $\widehat{\mathrm{YXB}}=90=\widehat{\mathrm{IXB}}$. Les points $X$, I et $Y$ sont donc alignés.
D'après le théorème de Pascal appliqué à l'hexagone SABYXN , les points $\mathrm{O}=(\mathrm{BY}) \cap(\mathrm{SN}), \mathrm{I}=$ $(Y X) \cap(A S)$ et $P^{\prime}=(A B) \cap(X N)$ sont alignés. Le point $P^{\prime}$ correspond donc au point d'intersection des droites (OI) et ( $A B$ ) donc $P=P^{\prime}$ ce qui donne bien que les droites (MD) et (NP) se coupent sur le cercle circonscrit au triangle $A B C$.
Commentaire des correcteurs Des solutions variées ont été proposées : utiliser une inversion de centre $M$ fixant les points $A$, I et $C$ pour montrer que les points $X$, I et $Y$ sont alignés, utiliser $Z$ le centre de l'homotétie positive envoyant le cercle inscrit sur le cercle circonscrit et considérer le cercle mixti-linéaire ou enocre utiliser les coordonnées barycentriques.
|
{
"exam": "French_envois",
"problem_label": "18",
"problem_match": "\nExercice 18.",
"resource_path": "French/segmented/envois/fr-corrigé-commentaire-envoi-1.jsonl",
"solution_match": "\nSolution de l'exercice 18",
"tier": "T2",
"year": null
}
|
Find all integers $p$ such that $p, p+2$ and $p+4$ are all three prime?
A prime number is an integer $\geqslant 2$ that is divisible only by 1 and itself.
|
First, we can expect there to be very few. We wish to obtain information about these prime numbers.
Note that a prime number divisible by 3 is a fortiori equal to 3. We consider 3 cases based on the remainder of the division of $p$ by 3 (modulo 3):
$-p=3k: p$ is divisible by 3, so $p=3$. $\{3,5,7\}$ is indeed a triplet of prime numbers.
$-p=3k+1: p+2$ is divisible by 3 and prime, so $p=1$ (impossible).
$-p=3k+2: p+4$ is divisible by 3 and prime, so $p=-1$ (impossible).
Hence $\mathrm{p}=3$.
Comment from the markers The exercise is generally very well handled, apart from some attempts modulo 10, the argument modulo 3 was well understood. Be careful not to forget the case $\mathrm{p}=2$.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Trouver tous les entiers $p$ tels que $p, p+2$ et $p+4$ soient tous les 3 premiers?
Un nombre premier est un entier $\geqslant 2$ qui n'est divisible que par 1 et lui-même.
|
Tout d'abord, on peut s'attendre à ce qu'il n'y en ait que très peu. On souhaite obtenir des informations sur ces nombres premiers.
Notons qu'un nombre premier divisible par 3 est a fortiori égal à 3 . On considère 3 cas en fonction du reste de la division de $p$ par 3 (modulo 3 ):
$-p=3 k: p$ est divisible par 3 donc $p=3 .\{3,5,7\}$ est bien un triplet de nombres premiers.
$-p=3 k+1: p+2$ est divisible par 3 et premier donc $p=1$ (impossible).
$-p=3 k+2: p+4$ est divisible par 3 et premier donc $p=-1$ (impossible).
D'où $\mathrm{p}=3$.
Commentaire des correcteurs L'exercice est globalement très bien traité, à part quelques tentatives modulo 10 , l'argument modulo 3 a bien été compris. Attention à ne pas oublier le cas $\mathrm{p}=2$.
|
{
"exam": "French_envois",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T2",
"year": null
}
|
Determine all pairs of positive integers $(n, p)$ where $p$ is a prime number and such that $n+p$ is a power of $n$.
A power of $n$ is of the form $n^{k}$ for $k$ a natural number.
|
Let $(\mathfrak{p}, \mathfrak{n})$ be a potential solution pair. We have a natural number $k$ such that
$$
\mathrm{n}+\mathrm{p}=\mathrm{n}^{\mathrm{k}}
$$
First, if $k=0$, then $n+p=1$. Since $p$ is prime, $p>1$ and $n \geqslant 0$, so $n+p=1<p \leqslant p+n$, which is absurd. Therefore, $k \geqslant 1$.
We can then rewrite the equation as follows:
$$
p=n\left(n^{k-1}-1\right)
$$
We obtain that $n$ divides $p$. Since $p$ is prime, it must be that $n=1$ or $n=p$.
If $n=1$, then $1+p=1$, which is absurd since $p \neq 0$.
Therefore, $\mathrm{n}=\mathrm{p}$. Then $2 \mathrm{p}=\mathrm{p}^{\mathrm{k}}$ so 2 divides $p$. Thus, $\mathrm{p}=2$ and the equation becomes $2+2=2^{k}$, so $k=2$. Conversely, the pair $(2,2)$ satisfies $2+2=2^{2}$, and thus $2+2$ is a power of 2.
The only solution pair is therefore (2,2).
Comment from the graders: The exercise is well done. Several approaches could have worked. However, it was quite easy to forget some special cases.
|
(2,2)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer tous les couples d'entiers $(n, p)$ strictement positifs où $p$ est un nombre premier et tels que $n+p$ soit une puissance de $n$.
Une puissance de $n$ est de la forme $\mathrm{n}^{\mathrm{k}}$ pour k entier naturel.
|
Soit $(\mathfrak{p}, \mathfrak{n}$ ) un éventuel couple solution. On dispose d'un entier naturel $k$ tel que
$$
\mathrm{n}+\mathrm{p}=\mathrm{n}^{\mathrm{k}}
$$
Tout d'abord, si $k=0$, alors $n+p=1$. Or $p$ étant premier, $p>1$ et $n \geqslant 0$ donc $n+p=1<p \leqslant p+n$ ce qui est absurde. On a donc $k \geqslant 1$.
On peut alors réécrire l'équation comme ceci :
$$
p=n\left(n^{k-1}-1\right)
$$
On obtient que $n$ divise $p$. Comme $p$ est premier, il faut donc que $n=1$ ou $n=p$.
Si $n=1$, alors $1+p=1$ ce qui est absurde puisque $p \neq 0$.
On a donc $\mathrm{n}=\mathrm{p}$. Alors $2 \mathrm{p}=\mathrm{p}^{\mathrm{k}}$ donc 2 divise p . Ainsi, $\mathrm{p}=2$ et l'équation devient $2+2=2^{k}$ donc $k=2$. Réciproquement, le couple $(2,2)$ vérifie bien que $2+2=2^{2}$ et donc que $2+2$ est une puissance de 2 .
Le seul couple solution est donc (2,2).
Commentaire des correcteurs L'exercice est bien réussi. Plusieurs approches pouvaient fonctionner. Il était cependant assez facile d'oublier des cas particuliers.
|
{
"exam": "French_envois",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T2",
"year": null
}
|
We place 23 matches on a table and 2 players play a game: each, on their turn, removes between 1 and 4 matches (inclusive). The one who takes the last match wins. Is there a winning strategy for one of the two?
A winning strategy is a way of playing that allows one of the two to win regardless of how their opponent plays.
|
Player 1 has a winning strategy. Here it is:
1. P1 takes 3 matches: a multiple of 5 remains
2. P2 removes $\mathrm{r} \in\{1,2,3,4\}$
3. P1 removes $5-\mathrm{r}$: a multiple of 5 remains
And so on. Therefore, every time P2 plays, there is a number of matches divisible by 5. Each time P1 plays, however, there is a number of matches that is not divisible by 5 and therefore, in particular, not zero! This ensures P1's victory.
Comment from the graders The exercise is very well done, but it is necessary to think about detailing the writing, which is sometimes a bit too succinct.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
On pose 23 allumettes sur une table et 2 joueurs jouent à un jeu : chacun, à son tour, retire entre 1 et 4 allumettes (inclus). Celui qui prend la dernière gagne. Existe-t-il une stratégie gagnante pour l'un des deux?
Une stratégie gagnante est une manière de jouer qui permet à l'un des deux de gagner peu importe comment son adversaire joue.
|
Le $1^{\text {er }}$ joueur possède une stratégie gagnante. La voici :
1. J1 prend 3 allumettes : il en reste un multiple de 5
2. J2 en retire $\mathrm{r} \in\{1,2,3,4\}$
3. J1 en enlève $5-\mathrm{r}$ : il en reste un multiple de 5
Et ainsi de suite. Donc à chaque fois que J 2 joue, il y a un nombre d'allumettes divisible par 5. A chaque fois que J1 joue, en revanche, il y en a un nombre non-divisible par 5 et donc en particulier non nul! Ce qui assure à J 1 de gagner.
Commentaire des correcteurs L'exercice est très bien réussi, il faut cependant penser à bien détailler la rédaction parfois un peu trop succincte.
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T2",
"year": null
}
|
Determine all triplets of positive integers ( $a, b, \mathfrak{n}$ ) satisfying:
$$
a!+b!=2^{n}
$$
|
Factorials having many odd factors in common, one immediately thinks that obtaining a power of 2 will be very constraining.
Assume that $\mathrm{a}, \mathrm{b} \geqslant 3$, then 3 divides the sum of the factorials and thus $2^{\mathrm{n}}$: $\mathrm{c}^{\prime}$ is absurd.
This means that one of the two is in $\{1,2\}$. By symmetry, we only need to consider two cases:
1. $a=1$: there are two small cases:
- $b=1: n=1$
- $b \geqslant 2$: the two sides do not have the same parity, which is impossible
2. $a=2: b \geqslant 2$ (as seen above), a few cases:
- $\mathrm{b}=2,3: \mathrm{n}=2,3$
- $\mathrm{b} \geqslant 4$: there is a problem modulo 4, which is impossible
Thus: the only solutions are in $\{(1,1,1),(2,2,2),(2,3,3),(3,2,3)\}$.
Comment from the graders:
The exercise was well done. It is important not to forget to specify that we can assume $a \geqslant b$ before using this inequality in the reasoning.
|
(1,1,1),(2,2,2),(2,3,3),(3,2,3)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer tous les triplets d'entiers ( $a, b, \mathfrak{n}$ ) strictement positifs vérifiant:
$$
a!+b!=2^{n}
$$
|
Les factorielles ayant beaucoup de facteurs impairs en commun, on se dit directement qu'obtenir une puissance de 2 va être très contraignant.
Supposons que $\mathrm{a}, \mathrm{b} \geqslant 3$, 3 divise donc la somme des factorielles et donc $2^{\mathrm{n}}$ : $\mathrm{c}^{\prime}$ est absurde.
C'est à dire que l'un des deux est dans $\{1,2\}$. Par symétrie, on ne traite que deux cas :
1. $a=1$ : encore deux petits cas de figure:
$-b=1: n=1$
- $b \geqslant 2$ : les deux membres n'ont pas la même parité, c'est impossible
2. $a=2: b \geqslant 2$ (comme vu au-dessus), quelques cas :
$-\mathrm{b}=2,3: \mathrm{n}=2,3$
- $\mathrm{b} \geqslant 4$ : il y a un problème modulo 4 , impossible
D'où : les seules solutions sont dans $\{(1,1,1),(2,2,2),(2,3,3),(3,2,3)\}$.
Commentaire des correcteurs
L'exercice plutôt bien réussi. Il ne faut pas oublier de bien préciser que l'on peut supposer $a \geqslant b$ avant d'utiliser cette inégalité dans son raisonnement.
|
{
"exam": "French_envois",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T2",
"year": null
}
|
Find all pairs of prime numbers ( $p, q$ ) such that:
$$
\mathrm{p}^{2}\left(\mathrm{p}^{3}-1\right)=\mathrm{q}(\mathrm{q}+1)
$$
|
If $p=q$, then $p^{4}-p=p+1$. But $p^{4}=p \cdot p^{3} \geqslant 8 p>2 p+1$ for any prime number $p$ since $p \geqslant 2$. Therefore, $p \neq q$ and thus $p$ and $q$ are coprime.
$p^{2}$ is coprime with $q$, so by Gauss's lemma, $p^{2} \mid q+1$. Therefore, there exists $k \in \mathbb{N}^{*}$ such that $q+1=kp^{2}$.
Since $q$ is coprime with $p^{2}$, $q \mid p^{3}-1=(p-1)(p^{2}+p+1)$. Thus, $q \mid p-1$ or $q \mid p^{2}+p+1$.
If $q \mid p-1$, then
$$
p<kp p^{2}-1=q \leqslant p-1
$$
which is absurd.
Therefore, $q \mid p^{2}+p+1$ so $kp^{2}-1=q \leqslant p^{2}+p+1$ which gives $(k-1)p^{2} \leqslant p+2$. If $k=1$, then $q=p^{2}-1=(p-1)(p+1)$ which is prime only if $p=2$.
In this case, $q=3$ but $2^{2}(2^{3}-1)=28 \neq 12=3(3+1)$.
We conclude that $k \geqslant 2$ and $p>2$, so $p+2<p^{2} \leqslant(k-1)p^{2} \leqslant p+2$ which is also absurd.
Finally, there is no solution.
Comment from the graders
Few students fully solved the problem. Many divisibility errors were observed, and often the case $p=q$ was not considered.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Trouver tous les couples de nombres premiers ( $p, q$ ) tels que :
$$
\mathrm{p}^{2}\left(\mathrm{p}^{3}-1\right)=\mathrm{q}(\mathrm{q}+1)
$$
|
Si $p=q$, alors $p^{4}-p=p+1$. Or $p^{4}=p \cdot p^{3} \geqslant 8 p>2 p+1$ pour tout nombre premier $p$ car $p \geqslant 2$. On a donc $p \neq q$ et donc $p$ et $q$ sont premiers entre eux.
$p^{2}$ est premier avec $q$ donc d'après le lemme de Gauss, $p^{2} \mid q+1$. On dispose donc de $k \in \mathbb{N}^{*}$ tel que $\mathrm{q}+1=\mathrm{kp}^{2}$.
Comme q est premier avec $\mathrm{p}^{2}, \mathrm{q} \mid \mathrm{p}^{3}-1=(\mathrm{p}-1)\left(\mathrm{p}^{2}+\mathrm{p}+1\right)$. Donc $\mathrm{q} \mid \mathrm{p}-1$ ou $\mathrm{q} \mid \mathrm{p}^{2}+\mathrm{p}+1$.
Si $q \mid p-1$, alors
$$
\mathrm{p}<\mathrm{kp} \mathrm{p}^{2}-1=\mathrm{q} \leqslant \mathrm{p}-1
$$
ce qui est absurde.
On a donc $\mathrm{q} \mid \mathrm{p}^{2}+\mathrm{p}+1$ donc $\mathrm{kp}^{2}-1=\mathrm{q} \leqslant \mathrm{p}^{2}+\mathrm{p}+1$ soit $(\mathrm{k}-1) \mathrm{p}^{2} \leqslant \mathrm{p}+2$. Si $k=1$, alors $\mathrm{q}=\mathrm{p}^{2}-1=(p-1)(p+1)$ qui n'est premier que si $p=2$.
On a alors $q=3$ mais $2^{2}\left(2^{3}-1\right)=28 \neq 12=3(3+1)$.
On en déduit que $k \geqslant 2$ et $p>2$, donc $p+2<p^{2} \leqslant(k-1) p^{2} \leqslant p+2$ ce qui est également absurde.
Finalement il n'y a pas de solution.
Commentaire des correcteurs
Peu d'élèves ont entièrement réussi le problème. On a pu voir beaucoup d'erreurs de divisibilité et bien souvent, le cas $\mathrm{p}=\mathrm{q}$ n'a pas été considéré.
|
{
"exam": "French_envois",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T2",
"year": null
}
|
Find all pairs of strictly positive integers ( $\mathrm{m}, \mathfrak{n}$ ) for which:
$$
1+2^{n}+3^{n}+4^{n}=10^{m}
$$
|
This equation is valid for all $n$, $m$, so it is also valid when taken modulo an integer $k$, that is, by only considering the remainders of the division by $k$.
We start by looking at it modulo 3:
$$
1+(-1)^{n}+0+1^{n} \equiv 1^{\mathrm{m}}(\bmod 3) \text{ so } (-1)^{n} \equiv -1
$$
So $n$ is odd: let $\mathrm{k} \in \mathbb{N}$ such that $\mathrm{n}=2 \mathrm{k}+1$.
Now suppose that $\mathrm{n}, \mathrm{m} \geqslant 3$ and look at it modulo 8:
$$
1+0+3 \cdot 3^{2 k}+0 \equiv 0(\bmod 8) \text{ i.e. } 1+3 \cdot 1 \equiv 0
$$
Which is absurd.
We deduce that one of the two is in $\{1,2\}$.
It then suffices to consider the cases $n=1, n=2, m=1$ and $\mathrm{m}=2$.
For $\boldsymbol{n}=1$ we find $1+2+3+4=10$, so $(1,1)$ is a solution. For $n=2, 1+4+9+16=30$ is not a power of 10 (since 30 is divisible by 3). Since the function that maps $n$ to $1+2^{n}+3^{n}+4^{n}$ is strictly increasing for a fixed $m$, there is at most one solution. Since $(1,1)$ and $(3,2)$ are solutions (because $1+2^{3}+3^{3}+4^{3}=1+8+27+64=100=10^{2}$), these are the only solutions with $\mathrm{m}=1$ or 2. The set of solutions is therefore $\{(1,1),(2,3)\}$.
## Comment from the Examiners
Even though many students almost succeeded in the problem, few achieved the maximum score: indeed, several did not justify why, for $\mathrm{m}=2$, only $\mathrm{n}=3$ was a solution (which could have been done by bounding or using a growth argument). Writing is not a race; it is better to write a page and have all the arguments well explained than to compact everything into 9 lines and end up with a poorly clear and often incomplete paper (moreover, often the compact papers are much more difficult to read than papers that are a bit longer but well detailed). Do not forget to check that the pairs obtained do indeed satisfy the equation.
|
(1,1),(2,3)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Trouver tous les couples d'entiers strictement positifs ( $\mathrm{m}, \mathfrak{n}$ ) pour lesquels:
$$
1+2^{n}+3^{n}+4^{n}=10^{m}
$$
|
Cette équation est valable pour tous $n$, $m$, elle est donc valable en la passant modulo un entier $k$, c'est-à-dire en ne considérant que les restes de la division par rapport à $k$.
On commence par la regarder modulo 3 :
$$
1+(-1)^{n}+0+1^{n} \equiv 1^{\mathrm{m}}(\bmod 3) \operatorname{donc}(-1)^{n} \equiv-1
$$
Donc n est impair : soit $\mathrm{k} \in \mathbb{N}$ tel que $\mathrm{n}=2 \mathrm{k}+1$.
On suppose à présent que $\mathrm{n}, \mathrm{m} \geqslant 3$ et on regarde modulo 8 :
$$
1+0+3 \cdot 3^{2 k}+0 \equiv 0(\bmod 8) \text { ie } 1+3 \cdot 1 \equiv 0
$$
Ce qui est absurde.
On en déduit que l'un des deux est dans $\{1,2\}$.
Il suffit alors de traiter les cas $n=1, n=2, m=1$ et $\mathrm{m}=2$.
Pour $\boldsymbol{n}=1$ on trouve $1+2+3+4=10,(1,1)$ est solution. Pour $n=2,1+4+9+16=30$ n'est pas une puissance de 10 (car 30 est divisible par 3). Comme l'application qui à $n$ associe $1+2^{n}+3^{n}+4^{n}$ est strictement croissante à $m$ fixé on a au plus une solution. Comme $(1,1)$ et $(3,2)$ sont solutions (car $1+2^{3}+3^{3}+4^{3}=1++27+64=100=10^{2}$ ), ce sont donc les seules solutions avec $\mathrm{m}=1$ ou 2 . L'ensemble des solutions est donc $\{(1,1),(2,3)\}$.
## Commentaire des correcteurs
Même si beaucoup d'élèves ont quasiment réussi l'exercice, peu se retrouvent avec la note maximale : en effet, plusieurs n'ont pas justifié pourquoi, pour $\mathrm{m}=2$, seul $\mathrm{n}=3$ était solution (ce qui pouvait se faire par encadrement ou en utilisant un argument de croissance). La rédaction n'est pas une course, il vaut mieux écrire une page et avoir tous les arguments bien expliqués que de compacter tout en 9 lignes et se retrouver avec une copie peu claire pour le correcteur et souvent incomplète (de plus, souvent les copies compactes sont bien plus compliquées à lire que des copies un peu longues mais bien détaillées). Il ne faut pas oublier de vérifier que les couples obtenus vérifient bien l'équation.
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T2",
"year": null
}
|
Let $p \geqslant 3$ be a prime number. For $k \in \mathbb{N}$ satisfying $1 \leqslant k \leqslant p-1$, the number of divisors of $\mathrm{kp}+1$ that are strictly between $k$ and $p$ is denoted by $a_{k}$.
What is the value of $a_{1}+a_{2}+\ldots+a_{p-1}$?
|
The answer is $p-2$.
We will show that each of $\{2, \ldots, \boldsymbol{p}-1\}$ contributes exactly once to the count represented by $a_{1}+a_{2}+\ldots+a_{p-1}$.
Let $2 \leqslant \mathrm{~m} \leqslant \mathrm{p}-1$ be an integer, we aim to show two things:
1. $m$ is counted at most once
2. $m$ is indeed counted
$m$ is counted at most once:
By contradiction, suppose there exist $1 \leqslant i<j \leqslant p-1$ two integers satisfying:
- $m \mid i p+1$ and $m>i$
- $m \mid j p+1$ and $m>j$
We then have $m \mid p(j-i)$, but $\operatorname{gcd}(m, p)=1$, so $m \mid j-i$. However, this is impossible because $0<j-i<$ $j<m$: $m$ is counted at most once.
$m$ is indeed counted:
Consider the $m-1$ integers $\{p+1,2 p+1, \ldots,(m-1) p+1\}$.
Just as before, we see that they are distinct modulo $m$. Moreover, none of them is $\equiv 1(\bmod m)$ because if we remove the +1, no integer is divisible by $m$.
Thus, $m$ is counted exactly once, and this concludes the proof.
Comment from the graders
The approach was generally understood, but the formalization of this reasoning was not always rigorous.
|
p-2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Soit $p \geqslant 3$ un nombre premier. Pour $k \in \mathbb{N}$ vérifiant $1 \leqslant k \leqslant p-1$, le nombre de diviseurs de $\mathrm{kp}+1$ qui sont compris strictement entre $k$ et $p$ est noté $a_{k}$.
Que vaut $a_{1}+a_{2}+\ldots+a_{p-1}$ ?
|
La réponse est $p-2$.
Nous allons montrer que chacun de $\{2, \ldots, \boldsymbol{p}-1\}$ contribue exactement une fois au comptage représenté $\operatorname{par} a_{1}+a_{2}+\ldots+a_{p-1}$.
Soit $2 \leqslant \mathrm{~m} \leqslant \mathrm{p}-1$ un entier, on se propose de montrer deux choses :
1. $m$ est compté au plus une fois
2. m est bien compté
m est compté au plus une fois :
Par l'absurde, on suppose qu'il existe $1 \leqslant i<j \leqslant p-1$ deux entiers vérifiant:
- $m \mid i p+1$ et $m>i$
- $m \mid j p+1$ et $m>j$
On a donc $m \mid p(j-i)$ or $\operatorname{pgcd}(m, p)=1$ donc $m \mid j-i$. Cependant, c'est impossible car $0<j-i<$ $j<m$ : m est compté au plus une fois
m est bien compté :
On considère les $m-1$ entiers $\{p+1,2 p+1, \ldots,(m-1) p+1\}$.
Exactement comme précédemment, on voit qu'ils sont 2 à 2 distincts modulo m. De plus, aucun d'entre eux n'est $\equiv 1(\bmod m)$ car si on retire les +1 aucun entier n'est divisible par $m$.
D'où $m$ est compté une et une fois et cela conclut.
Commentaire des correcteurs
Le chemin à suivre a été globalement compris, mais la formalisation de ce raisonnement n'était pas toujours rigoureuse.
|
{
"exam": "French_envois",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 7",
"tier": "T2",
"year": null
}
|
Determine all integers $n \geqslant 1$ such that there exists a permutation $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ of $(1,2, \ldots, \mathbf{n})$ satisfying the following condition:
$$
\mathrm{k} \mid \mathrm{a}_{1}+\mathrm{a}_{2}+\ldots+\mathrm{a}_{\mathrm{k}}
$$
for all $k \in\{1,2, \ldots, n\}$.
|
We start by looking at what happens for $\mathrm{n}=1,2,3: \mathfrak{n}=1,3$ are solutions but $\mathrm{n}=2$ is not. Let $\mathrm{n}>3$ satisfy the property stated in the problem.
We have $n \left\lvert\, a_{1}+a_{2}+\ldots+a_{n}=1+2+\ldots+n=\frac{n(n+1)}{2}\right.$ and thus $\frac{n+1}{2} \in \mathbb{Z}: n$ is odd.
Next, $n-1 \left\lvert\, a_{1}+a_{2}+\ldots+a_{n-1}=\frac{n(n+1)}{2}-a_{n}\right.$.
And $n-1 \left\lvert\, \frac{(n-1)(n+1)}{2}\right.$ so $n-1 \left\lvert\, \frac{n+1}{2}-a_{n}\right.$.
However, there is a "size issue": $-(n-1)<\frac{n+1}{2}-a_{n}<n-1$
which is not absurd, but implies that $a_{n}=\frac{n+1}{2}$.
We continue (no problem, $\mathrm{n}>3$ ):
$n-2 \left\lvert\, \frac{n(n+1)}{2}-\frac{n+1}{2}-a_{n-1}=\frac{(n-1)(n+1)}{2}-a_{n-1}\right.$.
And $n-2 \left\lvert\, \frac{(n-2)(n+1)}{2}\right.$ so $n-2 \left\lvert\, \frac{n+1}{2}-a_{n-1}\right.$.
As before, $-(n-2)<\frac{n+1}{2}-a_{n-1}<n-2$ and thus $a_{n}=a_{n-1}=\frac{n+1}{2}$: this is absurd.
The only solutions are therefore indeed 1 and 3.
Comment from the graders
Few students fully succeeded in the problem. The solutions are quite diverse overall, even if they revolve around the same idea.
|
1, 3
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer tous les entiers $n \geqslant 1$ tels qu'il existe une permutation $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ de $(1,2, \ldots, \mathbf{n})$ vérifiant la condition suivante :
$$
\mathrm{k} \mid \mathrm{a}_{1}+\mathrm{a}_{2}+\ldots+\mathrm{a}_{\mathrm{k}}
$$
pour tout $k \in\{1,2, \ldots, n\}$.
|
On commence par regarder ce qu'il se passe pour $\mathrm{n}=1,2,3: \mathfrak{n}=1,3$ sont solutions mais $\mathrm{n}=2$ ne l'est pas. Soit $\mathrm{n}>3$ vérifiant la propriété de l'énoncé.
On a $n \left\lvert\, a_{1}+a_{2}+\ldots+a_{n}=1+2+\ldots+n=\frac{n(n+1)}{2}\right.$ et donc $\frac{n+1}{2} \in \mathbb{Z}: n$ est impair.
Ensuite $n-1 \left\lvert\, a_{1}+a_{2}+\ldots+a_{n-1}=\frac{n(n+1)}{2}-a_{n}\right.$.
$\operatorname{Et} n-1 \left\lvert\, \frac{(n-1)(n+1)}{2}\right.$ donc $n-1 \left\lvert\, \frac{n+1}{2}-a_{n}\right.$.
Cependant, il y a un "problème de taille" : $-(n-1)<\frac{n+1}{2}-a_{n}<n-1$
ce qui $n$ 'est pas absurde, mais implique que $a_{n}=\frac{n+1}{2}$.
On poursuit (pas de souci, $\mathrm{n}>3$ ) :
$n-2 \left\lvert\, \frac{n(n+1)}{2}-\frac{n+1}{2}-a_{n-1}=\frac{(n-1)(n+1)}{2}-a_{n-1}\right.$.
Et $n-2 \left\lvert\, \frac{(n-2)(n+1)}{2}\right.$ donc $n-2 \left\lvert\, \frac{n+1}{2}-a_{n-1}\right.$.
Comme précédemment, $-(n-2)<\frac{n+1}{2}-a_{n-1}<n-2$ et donc $a_{n}=a_{n-1}=\frac{n+1}{2}$ : c'est absurde.
Les seules solutions sont donc bien 1 et 3 .
Commentaire des correcteurs
Peu d'élèves ont entièrement réussi le problème. Les solutions sont assez diverses dans l'ensemble même si elles tournent autour de la même idée.
|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "\nExercice 8.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 8",
"tier": "T2",
"year": null
}
|
Do there exist integers $\mathbf{a}$ and $b$ for which: $\mathbf{a}^{5} \mathbf{b}+3$ and $\mathbf{a b}^{5}+3$ are both perfect cubes?
A perfect cube is an integer $n$ for which there exists $m \in \mathbb{Z}$ such that: $n=m^{3}$.
|
We will show that there are no integers \(a\) and \(b\) satisfying the conditions of the problem.
Let \(a\) and \(b\) be integers such that \(a^{5} b + 3\) and \(a b^{5} + 3\) are perfect cubes. Let \(m\) and \(n\) be integers such that \(a^{5} b + 3 = m^{3}\) and \(a b^{5} + 3 = n^{3}\). Suppose that \(3 \mid n\). Then \(27 \mid n\). Moreover, \(3 \mid a b^{5}\) so \(3 \mid a\) or \(3 \mid b^{5}\). If \(3 \mid a\), then \(3^{5} \mid a^{5}\) and thus \(3 \mid a^{5} b + 3 = m^{3}\). But then \(27 \mid m^{3}\) and \(27 \mid a^{5}\) so \(27 \mid m^{3} - a^{5} b = 3\), which is absurd. If \(3 \mid b\), then \(3^{5} \mid b^{5}\) and in particular \(27 \mid n^{3} - a b^{5} = 3\), which is also absurd. We deduce that 3 does not divide \(n\) and similarly 3 does not divide \(m\). If \(3 \mid a\), then \(3 \mid m\), \(n\), which is excluded. We deduce that 3 does not divide \(a\) and \(b\) either. Note that
\[
m^{3} - n^{3} = a^{5} b - a b^{5} = a b (a - b) (a + b) \left(a^{2} + b^{2}\right)
\]
Since \(a\) and \(b\) are not divisible by 3, \(a^{2} \equiv b^{2} \equiv 1 \bmod 3\) so \(3 \mid a^{2} - b^{2} = (a - b)(a + b)\) and thus \(3 \mid m^{3} - n^{3}\). According to Fermat's theorem, \(m^{3} \equiv m \bmod 3\) and \(n^{3} \equiv n \bmod 3\). We deduce that \(m \equiv m^{3} \equiv n^{3} \equiv n \bmod 3\). It follows that
\[
m^{2} + m n + n^{2} \equiv 3 m^{2} = 0 \quad \bmod 3
\]
We deduce that 3 divides \(m - n\) and 3 divides \(m^{2} + m n + n^{2}\) so \(9 \mid (m - n)(m^{2} + m n + n^{2}) = m^{3} - n^{3}\). It follows that \(9 \mid a b (a - b)(a + b)\left(a^{2} + b^{2}\right)\). But 3 does not divide \(a\), \(b\), and \(a^{2} + b^{2} \equiv 2 \bmod 3\) so 3 does not divide \(a^{2} + b^{2}\) and thus 9 does not divide \(a^{2} + b^{2}\). We deduce that \(9 \mid a^{2} - b^{2}\), i.e., \(a^{2} \equiv b^{2} \bmod 9\). Thus
\[
m^{3} = a^{5} b + 3 \equiv a^{3} \cdot a^{2} \cdot b + 3 \equiv a^{3} b^{2} \cdot b + 3 \equiv (a b)^{3} + 3 \quad \bmod 9
\]
However, cubes modulo 9 take only the values \(-1, 0\), and \(1\). We cannot have \(m^{3} - (a b)^{3} \equiv 3 \bmod 9\). The condition of the problem cannot therefore be satisfied, as announced.
## Comment from the Examiners
Several students were content to test all cases, others provided good proofs by contradiction. Overall, the problem was well handled by those who tackled it.
## Exercises for Seniors
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Existe-t-il des entiers $\mathbf{a}$ et $b$ pour lesquels : $\mathbf{a}^{5} \mathbf{b}+3$ et $\mathbf{a b}^{5}+3$ sont tous deux des cubes parfaits?
Un cube parfait est un entier $n$ pour lequel il existe $m \in \mathbb{Z}$ tel que : $n=m^{3}$.
|
Nous allons montrer qu'il n'y a pas d'entiers a et b satisfaisant les conditions du problème.
Soient $a$ et $b$ des entiers tels que $a^{5} b+3$ et $a b^{5}+3$ sont des cubes parfaits. Soit $m$ et $n$ des entiers tels que $a^{5} b+3=m^{3}$ et $a b^{5}+3=n^{3}$. Supposons que $3 \mid n$. Alors $27 \mid n$. De plus $3 \mid a b^{5}$ donc $3 \mid a$ ou $3 \mid b^{5}$. Si $3 \mid a$, alors $3^{5} \mid a^{5}$ donc $3 \mid a^{5} b+3=m^{3}$. Mais alors $27 \mid m^{3}$ et $27 \mid a^{5}$ donc $27 \mid m^{3}-a^{5} b=3$ ce qui est absurde. Si $3 \mid b$, alors $3^{5} \mid b^{5}$ et en particulier $27 \mid n^{3}-a b^{5}=3$ ce qui est aussi absurde. On déduit que 3 ne divise pas n et de même 3 ne divise pas m . Si $3 \mid \mathrm{a}$, alors $3 \mid \mathrm{m}$, n ce qui est exclut. On déduit donc que 3 ne divise pas non plus a et b. Notons que
$$
m^{3}-n^{3}=a^{5} b-a b^{5}=a b(a-b)(a+b)\left(a^{2}+b^{2}\right)
$$
Comme $a$ et $b$ ne sont pas divisibles par $3, a^{2} \equiv b^{2} \equiv 1 \bmod 3$ donc $3 \mid a^{2}-b^{2}=(a-b)(a+b)$ et donc $3 \mid m^{3}-n^{3}$. D'après le théorème de Fermat, $m^{3} \equiv m \bmod 3$ et $n^{3} \equiv n \bmod 3$. On déduit que $\mathrm{m} \equiv \mathrm{m}^{3} \equiv \mathrm{n}^{3} \equiv \mathrm{n} \bmod 3$. Il vient que
$$
m^{2}+m n+n^{2} \equiv 3 m^{2}=0 \quad \bmod 3
$$
On déduit que 3 divise $m-n$ et 3 divise $m^{2}+m n+n^{2}$ donc $9 \mid(m-n)\left(m^{2}+m n+n^{2}\right)=m^{3}-n^{3}$. Il vient que $9 \mid a b(a-b)(a+b)\left(a^{2}+b^{2}\right)$. Mais 3 ne divise pas $a, b$ et $a^{2}+b^{2} \equiv 2 \bmod 3$ donc 3 ne divise pas non plus $a^{2}+b^{2}$ et donc 9 non plus. On déduit que $9 \mid a^{2}-b^{2}$, soit $a^{2} \equiv b^{2} \bmod 9$. Ainsi
$$
\mathrm{m}^{3}=\mathrm{a}^{5} \mathrm{~b}+3 \equiv \mathrm{a}^{3} \cdot \mathrm{a}^{2} \cdot \mathrm{~b}+3 \equiv \mathrm{a}^{3} \mathrm{~b}^{2} \cdot \mathrm{~b}+3 \equiv(\mathrm{ab})^{3}+3 \quad \bmod 9
$$
Or les cubes modulo 9 prennent uniquement les valeurs $-1,0$ et 1 . On ne peut donc avoir $\mathrm{m}^{3}-(a b)^{3} \equiv 3$ mod 9. La condition de l'énoncé ne peut donc pas être satisfaite, comme annoncé.
## Commentaire des correcteurs
Plusieurs élèves se sont contentés de tester tous les cas, d'autres ont fourni de bons raisonnements par l'absurde. Globalement le problème est bien réussi par ceux qui l'ont abordé.
## Exercices Seniors
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 9",
"tier": "T2",
"year": null
}
|
Find all triplets ( $\mathbf{p , q , r}$ ) of prime numbers such that the 3 differences
$$
|p-q|,|q-r|,|r-p|
$$
are also prime numbers.
|
Note that the three numbers must be pairwise distinct since 0 is not a prime number. Therefore, we can assume, without loss of generality, that $p>q>r$. A prime number is odd or equal to 2.
Suppose that $p, q$, and $r$ are all odd. Then $p-q, q-r$, and $r-p$ are even. Since their absolute values are prime, these numbers must all be 2. Thus the integers $p, p+2$, and $p+4$ are prime. If $p$ is divisible by 3, then $p=3$ and $q=5$ and $r=7$.
However, the triplet $(3,5,7)$ is not a solution to the problem: $7-3=4$ is not prime.
If $p$ is not divisible by 3, then $p$ is of the form $3k+1$ or $3k+2$. The first case implies that $p+2$ is divisible by 3, so $p+2=3$ but $p=1$ is not a prime number. The second case implies that $p+4$ is divisible by 3, but $p+4=3$ does not yield a positive solution.
Suppose that $r=2$. Then $p$ and $q$ are odd and $p-q$ is even and prime, so it must be 2. It follows that $q+2$, $q$, and $q-2$ are all prime. From the previous case, this implies that $q-2=3$ so $p=7$. Conversely, the triplet $(p, q, r)=(2,5,7)$ and its permutations are indeed solutions to the problem.
The only triplets that are solutions are therefore $(2,5,7)$ and its permutations.
Graders' Comments
Many students had the main ideas, but lost points for poor writing. It is always necessary to check that the solutions obtained satisfy the statement. Some claimed without any justification that if $p, p+2$, and $p+4$ are prime, then $p=3$. Similarly, some said that we cannot have $|p-q|=|q-r|=|r-p|=2$ without justifying it, which was quite clear (we can assume $p>q>r$ for example). It is better to detail the important points a bit more to avoid losing points.
|
(2,5,7) \text{ and its permutations}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Trouver tous les triplets ( $\mathbf{p , q , r}$ ) de nombres premiers tels que les 3 différences
$$
|p-q|,|q-r|,|r-p|
$$
soient également des nombres premiers.
|
Notons que les trois nombres doivent être deux à deux distincts puisque 0 n'est pas un nombre premier. On peut donc supposer, quitte à échanger l'ordre des variables, que $p>q>r$. Un nombre premier est impair ou égal à 2 .
On suppose que $p, q$ et $r$ sont tous impairs. Alors $p-q, q-r$ et $r-p$ sont pairs. Comme leur valeur absolue est première, ces nombres valent tous 2 . Ainsi les entiers $p, p+2$ et $p+4$ sont premiers. Si $p$ est divisible par 3 , alors $\mathrm{p}=3$ et $\mathrm{q}=5$ et $\mathrm{r}=7$.
Cependant, le triplet $(3,5,7)$ n'est pas solution du problème : $7-3=4$ n'est pas premier.
Si $p$ n'est pas divisible par 3 , alors $p$ est de la forme $3 k+1$ ou $3 k+2$. Le premier cas implique que $p+2$ soit divisible par 3 donc $p+2=3$ mais $p=1$ n'est pas un nombre premier. Le deuxième cas implique que $p+4$ soit divisible par 3 , mais $p+4=3$ ne donne pas de solution strictement positive.
On suppose que $r=2$. Alors $p$ et $q$ sont impaires et $p-q$ est pair et premier donc égal à 2 . Il vient que $q+2$, $q$ et $q-2$ sont tous les trois des nombres premiers. D'après le cas précédent, cela implique que $\boldsymbol{q}-2=3$ donc $p=7$. Réciproquement, le triplet $(p, q, r)=(2,5,7)$ et ses permutations sont donc bien solutions au problème.
Les seuls triplets solutions sont donc $(2,5,7)$ ainsi que ses permutations.
Commentaire des correcteurs
Beaucoup d'élèves ont les idées majeures, mais perdent bêtement des points pour la rédaction. Il faut toujours vérifier que les solutions obtenues satisfont bien l'énoncé. Certains ont affirmé sans aucune justification que si $p, p+2$ et $p+4$ sont premiers alors $p=3$. De même certains ont dit qu'on ne peut pas avoir $|\mathrm{p}-\mathrm{q}|=|\mathrm{q}-\mathrm{r}|=|\mathrm{r}-\mathrm{p}|=2$ sans le justifier, ce qui était assez clair (on peut supposer $p>q>r$ par exemple). Il vaut mieux un peu plus détailler les points importants pour ne pas perdre de points.
|
{
"exam": "French_envois",
"problem_label": "10",
"problem_match": "\nExercice 10.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 10",
"tier": "T2",
"year": null
}
|
Find all integers $z \in \mathbb{Z}$ such that
$$
2^{z}+2=r^{2}
$$
where $r \in \mathbb{Q}$ is a rational number.
A rational number is a number that can be written in the form $\frac{\mathrm{a}}{\mathrm{b}}$ with $\mathrm{a}, \mathrm{b}$ integers and $\mathrm{b} \neq 0$.
|
Note that if $(z, r)$ is a solution pair, $(z, -r)$ is also a solution pair. Therefore, we can assume for the rest that $r \geqslant 0$. Since $2^{z} + z > 0$, we even have $r > 0$. We set $r = \frac{a}{b}$, with $a$ and $b$ being strictly positive integers and coprime.
If $z \geqslant 0$, then $2^{z} + 2$ is an integer, so $r$ is an integer and $b = 1$. We must now solve the equation $2^{z} + 2 = a^{2}$ in the positive integers. If $z \geqslant 2$, then the equation viewed modulo 4 gives $a^{2} \equiv 2 \bmod 4$ which has no solution since a square is always congruent to 0 or 1 modulo 4. We deduce that $z = 0$ or $z = 1$. In the first case, we get $3 = a^{2}$ which has no integer solution. In the second case, we find $4 = a^{2}$, so $a = 2$. Conversely, the pairs $(1, -2)$ and $(1, 2)$ do indeed satisfy the equation.
If $z < 0$, then we set $z' = -z$, with $z' > 0$. The equation becomes $\frac{1}{2^{z'}} + 2 = \frac{a^{2}}{b^{2}}$. By eliminating the denominators, we get
$$
b^{2}\left(1 + 2^{z' + 1}\right) = a^{2} \cdot 2^{z'}
$$
Since $1 + 2^{z' + 1}$ is coprime with $2^{z'}$, by the lemma of Gauss, we get that $2^{z' + 1} + 1$ divides $a^{2}$. Since $a$ and $b$ are coprime, by the lemma of Gauss, we also get that $a^{2}$ divides $1 + 2^{z' + 1}$. We deduce that $a^{2} = 2^{z' + 1} + 1$, which we rewrite as $2^{z' + 1} = (a - 1)(a + 1)$. We deduce that $a + 1$ and $a - 1$ are both powers of 2 whose difference is 2. We therefore deduce that $a + 1 = 4$ and $a - 1 = 2$, so $a = 3$ and $z' = 2$. Thus, $b = 2$. Conversely, the pairs $\left(-2, -\frac{3}{2}\right)$ and $\left(-2, \frac{3}{2}\right)$ are indeed solutions to the equation. The solutions are therefore $\left\{\left(-2, -\frac{3}{2}\right), \left(-2, \frac{3}{2}\right), (1, -2), (1, 2)\right\}$.
Comment from the graders
One third of the students wrote that $x^{2} = 4$ implies $x = 2$ and thus forgot the solution $x = -2$. Some students did not see that we were working in $\mathbb{Z}$ and $\mathbb{Q}$ and only looked at the equation over the positive integers. Apart from that, the exercise was quite well done.
|
\left\{\left(-2, -\frac{3}{2}\right), \left(-2, \frac{3}{2}\right), (1, -2), (1, 2)\right\}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Trouver tous les nombres entiers $z \in \mathbb{Z}$ tels que
$$
2^{z}+2=r^{2}
$$
où $r \in \mathbb{Q}$ est un nombre rationnel.
Un nombre rationnel est un nombre qui s'écrit sous la forme $\frac{\mathrm{a}}{\mathrm{b}}$ avec $\mathrm{a}, \mathrm{b}$ des entiers et $\mathrm{b} \neq 0$.
|
Notons que si $(z, r)$ est un couple solution, $(z,-r)$ est également un couple solution. On peut donc supposer pour la suite que $r \geqslant 0$. Etant donné que $2^{z}+z>0$, on a même $r>0$. On pose $r=\frac{a}{b}$, avec $a$ et $b$ des entiers strictement positifs et premiers entre eux.
Si $z \geqslant 0$, alors $2^{z}+2$ est entier donc r est entier et $\mathrm{b}=1$. On doit désormais résoudre l'équation $2^{z}+2=a^{2}$ dans les entiers positifs. Si $z \geqslant 2$, alors l'équation vue modulo 4 donne $a^{2} \equiv 2 \bmod 4$ ce qui n'a pas de solution puisqu'un carré est toujours congru à 0 ou à 1 modulo 4 . On déduit que $z=0$ ou $z=1$. Dans le premier cas, on obtient $3=\mathfrak{a}^{2}$ qui n'admet pas de solution entière. Dans le deuxième cas on trouve $4=a^{2}$ soit $a=2$. Réciproquement, les couples $(1,-2)$ et $(1,2)$ satisfont bien l'équation.
$\mathrm{Si} z<0$, alors on pose $z^{\prime}=-z$, avec $z^{\prime}>0$. L'équation dévient $\frac{1}{2^{z^{\prime}}}+2=\frac{a^{2}}{b^{2}}$. En supprimant les dénominateurs on obtient
$$
b^{2}\left(1+2^{z^{\prime}+1}\right)=a^{2} \cdot 2^{z^{\prime}}
$$
Puisque $1+2^{z^{\prime}+1}$ est premier avec $2^{z^{\prime}}$, par le lemme de Gauss on obtient que $2^{z^{\prime}+1}+1$ divise $a^{2}$. Comme $a$ et $b$ sont premiers entre eux, par le lemme de Gauss on obtient aussi que $a^{2}$ divise $1+2^{z^{\prime}+1}$. On déduit que $a^{2}=2^{z^{\prime}+1}+1$, que l'on réécrit $2^{z^{\prime}+1}=(a-1)(a+1)$. On déduit que $a+1$ et $a-1$ sont tous les deux des puissances de 2 dont la différence vaut 2 . On déduit donc que $a+1=4$ et $a-1=2$ soit $\mathrm{a}=3$ et $z^{\prime}=2$. Ainsi $\mathrm{b}=2$. Réciproquement, les couples $\left(-2,-\frac{3}{2}\right)$ et $\left(-2, \frac{3}{2}\right)$ sont bien solutions de l'équation. Les solutions sont donc $\left\{\left(-2,-\frac{3}{2}\right),\left(-2, \frac{3}{2}\right),(1,-2),(1,2)\right\}$.
Commentaire des correcteurs
Un tiers des élèves a écrit que $x^{2}=4$ implique que $x=2$ et oublie donc la solution $x=-2$. Quelques élèves n'ont pas vu que l'on se plaçait dans $\mathbb{Z}$ et $\mathbb{Q}$ et ont juste regardé l'équation sur les entiers positifs. Mis à part cela, l'exercice est assez bien réussi.
|
{
"exam": "French_envois",
"problem_label": "11",
"problem_match": "\nExercice 11.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 11",
"tier": "T2",
"year": null
}
|
Determine all triplets of positive integers $(\mathfrak{a}, \mathfrak{b}, \mathfrak{n})$ satisfying:
$$
a! + b! = 2^n
$$
|
Factorials have many odd factors in common, so we immediately think that obtaining a power of 2 will be very constraining.
Suppose $\mathrm{a}, \mathrm{b} \geqslant 3, 3$ divides the sum of the factorials and thus $2^{\mathrm{n}}$: $\mathbf{c}^{\text {'s absurd. }}$ This means that one of the two must be in $\{1,2\}$. By symmetry, we only need to consider two cases:
1. $a=1$: there are two small cases:
$-\mathrm{b}=1: \mathrm{n}=1$
$-\mathrm{b} \geqslant 2$: the two sides do not have the same parity, which is impossible
2. $a=2: b \geqslant 2$ (as seen above), a few cases:
$-\mathrm{b}=2,3: \mathbf{n}=2,3$
$-\mathrm{b} \geqslant 4$: there is a problem modulo 4, which is impossible
Thus, the only solutions are in $\{(1,1,1),(2,2,2),(2,3,3),(3,2,3)\}$.
Grader's Comment
There were quite a few logical errors. It is not because one cannot have $\mathbf{a} \geqslant 3$ and $\mathbf{b} \geqslant 3$ at the same time that we must have $\mathrm{a}<3$ and $\mathrm{b}<3$ (we rather have $\mathrm{a}<3$ or $\mathrm{b}<3$). 1 is a power of 2 that should not be forgotten, and 0 is not in $\mathbb{N}^{*}$, and 1 is an odd divisor of 2 that should not be forgotten either. Do not forget to mention the symmetric solutions if we assume $a \geqslant b$.
|
(1,1,1),(2,2,2),(2,3,3),(3,2,3)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer tous les triplets d'entiers $(\mathfrak{a}, \mathfrak{b}, \mathfrak{n}$ ) strictement positifs vérifiant:
$$
a!+b!=2^{n}
$$
|
Les factorielles ayant beaucoup de facteurs impairs en commun, on se dit directement qu'obtenir une puissance de 2 va être très contraignant.
Supposons que $\mathrm{a}, \mathrm{b} \geqslant 3,3$ divise donc la somme des factorielles et donc $2^{\mathrm{n}}$ : $\mathbf{c}^{\text {'est absurde. }}$ C'est à dire que l'un des deux est dans $\{1,2\}$. Par symétrie, on ne traite que deux cas :
1. $a=1$ : encore deux petits cas de figure :
$-\mathrm{b}=1: \mathrm{n}=1$
$-\mathrm{b} \geqslant 2$ : les deux membres n'ont pas la même parité, c 'est impossible
2. $a=2: b \geqslant 2$ (comme vu au-dessus), quelques cas :
$-\mathrm{b}=2,3: \mathbf{n}=2,3$
$-\mathrm{b} \geqslant 4$ : il y a un problème modulo 4 , impossible
D'où : les seules solutions sont dans $\{(1,1,1),(2,2,2),(2,3,3),(3,2,3)\}$.
Commentaire des correcteurs
Il y a eu pas mal d'erreurs de logique. Ce n'est pas parce que l'on ne peut pas avoir $\mathbf{a} \geqslant 3$ et $\mathbf{b} \geqslant 3$ en même temps qu'on a forcément $\mathrm{a}<3$ et $\mathrm{b}<3$ (on a plutôt $\mathrm{a}<3$ ou $\mathrm{b}<3$ ). 1 est une puissance de 2 qu'il ne faut pas oublier et 0 n'est pas dans $\mathbb{N}^{*}$ et 1 est un diviseur impair de 2 qu'il ne faut pas oublier non plus. Ne pas oublier de rappeller les solutions symétriques si on suppose $a \geqslant b$.
|
{
"exam": "French_envois",
"problem_label": "12",
"problem_match": "\nExercice 12.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 12",
"tier": "T2",
"year": null
}
|
Determine all triplets of integers $(x, y, z)$ satisfying the following property:
$$
\operatorname{gcd}(x, y, z) < \operatorname{gcd}(x+y, y+z, z+x)
$$
|
Note that since $\operatorname{gcd}(x, y, z)$ divides each of $x, y, z$, it also divides $\operatorname{gcd}(x+y, y+z, z+x)$.
We observe that if the triplet $(x, y, z)$ is a solution, then the triplets $(k x, k y, k z)$ are solutions for all $k \in \mathbb{N}^{*}$. Therefore, we can assume, by dividing each variable by $\operatorname{gcd}(x, y, z)$, that the integers $x, y, z$ are coprime. In particular, they are not all even.
Let $d=\operatorname{gcd}(x+y, y+z, z+x)$. Then $d$ divides $(x+y)+(x+z)-(y+z)=2 x$ and similarly $d$ divides $2 y$ and $2 z$. Therefore, $d$ divides $\operatorname{gcd}(2 x, 2 y, 2 z)=2 \operatorname{gcd}(x, y, z)=2$. We deduce that $d=1$ or $d=2$. But since $d>1, d=2$ so the integers $x, y, z$ are all of the same parity. Since they are not all even, they are all odd.
Conversely, if $x, y$ and $z$ are all odd, given that $\operatorname{gcd}(x, y, z)$ and 2 are coprime and divide $\operatorname{gcd}(x+y, y+z, z+x)$, we have indeed
$$
\operatorname{gcd}(x, y, z)<2 \operatorname{gcd}(x, y, z) \leqslant \operatorname{gcd}(x+y, y+z, z+x)
$$
The solution triplets are therefore the triplets $\left\{(k x, k y, k z), k \in \mathbb{N}^{*}, x, y, z\right.$ odd $\}$. Comment from the graders
The graders were very satisfied with the different approaches of the students. A few errors are to be noted: it is not because $2 n \equiv k \mod a$ that $k$ is even and it is not because $\operatorname{gcd}(x, y, z)=\operatorname{gcd}(x+ y, y+z, z+x)$ that $(x, y, z)=(x+y, y+z, z+x)$.
|
(k x, k y, k z), k \in \mathbb{N}^{*}, x, y, z \text{ odd}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer tous les triplets d'entiers $(x, y, z)$ vérifiant la propriété suivante :
$$
\operatorname{pgcd}(x, y, z)<\operatorname{pgcd}(x+y, y+z, z+x)
$$
|
Notons que puisque $\operatorname{pgcd}(x, y, z)$ divise chacun des $x, y, z$, il divise également $\operatorname{pgcd}(x+y, y+z, z+x)$.
On remarque que si le triplet $(x, y, z)$ est solution, alors les triplets $(k x, k y, k z)$ sont solutions pour tout $k \in \mathbb{N}^{*}$. On peut donc supposer, quitte à diviser chaque variable par $\operatorname{pgcd}(x, y, z)$, que les entiers $x, y, z$ sont premiers entre eux dans leur ensemble. En particulier ils ne sont pas tous pairs.
Soit $d=\operatorname{pgcd}(x+y, y+z, z+x)$. Alors d divise $(x+y)+(x+z)-(y+z)=2 x$ et de même $d$ divise $2 y$ et $2 z$. Donc $d$ divise $\operatorname{pgcd}(2 x, 2 y, 2 z)=2 \operatorname{pgcd}(x, y, z)=2$. On déduit que $d=1$ ou $d=2$. Mais comme $\mathrm{d}>1, \mathrm{~d}=2$ donc les entiers $x, y, z$ sont tous de même parité. Comme ils ne sont pas tous paires, ils sont tous impaires.
Réciproquement, si $x, y$ et $z$ sont tous les trois impaires, étant donné que $\operatorname{pgcd}(x, y, z)$ et 2 sont premiers entre eux et divisent $\operatorname{pgcd}(x+y, y+z, z+x)$, on a bien
$$
\operatorname{pgcd}(x, y, z)<2 \operatorname{pgcd}(x, y, z) \leqslant \operatorname{pgcd}(x+y, y+z, z+x)
$$
Les triplets solutions sont donc les triplets $\left\{(k x, k y, k z), k \in \mathbb{N}^{*}, x, y, z\right.$ impaires $\}$. Commentaire des correcteurs
Les correcteurs étaient très satisfait des différentes approches des élèves. Quelques erreurs sont à noter : ce n'est pas parce que $2 \mathrm{n} \equiv k$ mod a que $k$ est pair et ce $n$ 'est pas parce que $\operatorname{pgcd}(x, y, z)=\operatorname{pgcd}(x+$ $y, y+z, z+x)$ que $(x, y, z)=(x+y, y+z, z+x)$.
|
{
"exam": "French_envois",
"problem_label": "13",
"problem_match": "\nExercice 13.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 13",
"tier": "T2",
"year": null
}
|
Do there exist integers $a$ and $b$ for which: $\mathbf{a}^{5} \mathbf{b}+3$ and $a^{5}+3$ are both perfect cubes?
A perfect cube is an integer $n$ for which there exists $m \in \mathbb{Z}$ such that: $\mathfrak{n}=\mathrm{m}^{3}$.
|
We will show that there are no integers $a$ and $b$ satisfying the conditions of the problem.
Let $a$ and $b$ be integers such that $a^{5} b+3$ and $a b^{5}+3$ are perfect cubes. Let $m$ and $n$ be integers such that $a^{5} b+3=m^{3}$ and $a b^{5}+3=n^{3}$. Suppose that $3 \mid n$. Then $27 \mid n$. Moreover, $3 \mid a b^{5}$, so $3 \mid a$ or $3 \mid b^{5}$. If $3 \mid a$, then $3^{5} \mid a^{5}$, so $3 \mid a^{5} b+3=m^{3}$. But then $27 \mid m^{3}$ and $27 \mid a^{5}$, so $27 \mid m^{3}-a^{5} b=3$, which is absurd. If $3 \mid b$, then $3^{5} \mid b^{5}$, and in particular $27 \mid n^{3}-a b^{5}=3$, which is also absurd. We deduce that 3 does not divide $n$ and similarly 3 does not divide $m$. If $3 \mid a$, then $3 \mid m$, $n$, which is excluded. We deduce that 3 does not divide $a$ and $b$ either. Note that
$$
m^{3}-n^{3}=a^{5} b-a b^{5}=a b(a-b)(a+b)\left(a^{2}+b^{2}\right)
$$
Since $a$ and $b$ are not divisible by 3, $a^{2} \equiv b^{2} \equiv 1 \bmod 3$ so $3 \mid a^{2}-b^{2}=(a-b)(a+b)$ and thus $3 \mid m^{3}-n^{3}$. According to Fermat's theorem, $m^{3} \equiv m \bmod 3$ and $n^{3} \equiv n \bmod 3$. We deduce that $m \equiv m^{3} \equiv n^{3} \equiv n \bmod 3$. It follows that
$$
m^{2}+m n+n^{2} \equiv 3 m^{2}=0 \quad \bmod 3
$$
We deduce that 3 divides $m-n$ and 3 divides $m^{2}+m n+n^{2}$, so $9 \mid (m-n)\left(m^{2}+m n+n^{2}\right)=m^{3}-n^{3}$. It follows that $9 \mid a b(a-b)(a+b)\left(a^{2}+b^{2}\right)$. But 3 does not divide $a, b$ and $a^{2}+b^{2} \equiv 2 \bmod 3$, so 3 does not divide $a^{2}+b^{2}$ and thus 9 does not divide it either. We deduce that $9 \mid a^{2}-b^{2}$, i.e., $a^{2} \equiv b^{2} \bmod 9$. Thus
$$
m^{3}=a^{5} b+3 \equiv a^{3} \cdot a^{2} \cdot b+3 \equiv a^{3} b^{2} \cdot b+3 \equiv (a b)^{3}+3 \quad \bmod 9
$$
However, cubes modulo 9 take only the values $-1, 0$, and $1$. We cannot therefore have $m^{3}-(a b)^{3} \equiv 3 \bmod 9$. The condition of the problem cannot therefore be satisfied, as announced.
Comment from the graders
Many students have a brute-force solution that involves looking at the pairs $(a b^{5}, b a^{5})$ modulo 9 in some way or another, which is not necessarily a bad thing, but it is more subtle to use Fermat's little theorem in competition to save time (and because often the studies are not exhaustive). Most students have a slightly different solution from the corrected one, which consists in noticing that $a^{5} b+3$ and $b^{5} a+3$ cannot be congruent to cubes at the same time $\bmod 9$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Existe-t-il des entiers $a$ et $b$ pour lesquels : $\mathbf{a}^{5} \mathbf{b}+3$ et $a^{5}+3$ sont tous deux des cubes parfaits?
Un cube parfait est un entier $n$ pour lequel il existe $m \in \mathbb{Z}$ tel que : $\mathfrak{n}=\mathrm{m}^{3}$.
|
Nous allons montrer qu'il n'y a pas d'entiers a et b satisfaisant les conditions du problème.
Soient $a$ et $b$ des entiers tels que $a^{5} b+3$ et $a b^{5}+3$ sont des cubes parfaits. Soit $m$ et $n$ des entiers tels que $a^{5} b+3=m^{3}$ et $a b^{5}+3=n^{3}$. Supposons que $3 \mid n$. Alors $27 \mid n$. De plus $3 \mid a b^{5}$ donc $3 \mid a$ ou $3 \mid b^{5}$. Si $3 \mid a$, alors $3^{5} \mid a^{5}$ donc $3 \mid a^{5} b+3=m^{3}$. Mais alors $27 \mid m^{3}$ et $27 \mid a^{5}$ donc $27 \mid m^{3}-a^{5} b=3$ ce qui est absurde. Si $3 \mid b$, alors $3^{5} \mid b^{5}$ et en particulier $27 \mid n^{3}-a b^{5}=3$ ce qui est aussi absurde. On déduit que 3 ne divise pas $n$ et de même 3 ne divise pas $m$. Si $3 \mid a$, alors $3 \mid \mathrm{m}$, n ce qui est exclut. On déduit donc que 3 ne divise pas non plus $a$ et $b$. Notons que
$$
m^{3}-n^{3}=a^{5} b-a b^{5}=a b(a-b)(a+b)\left(a^{2}+b^{2}\right)
$$
Comme $a$ et $b$ ne sont pas divisibles par $3, a^{2} \equiv b^{2} \equiv 1 \bmod 3$ donc $3 \mid a^{2}-b^{2}=(a-b)(a+b)$ et donc $3 \mid \mathrm{m}^{3}-\mathrm{n}^{3}$. D'après le théorème de Fermat, $\mathrm{m}^{3} \equiv \mathrm{~m} \bmod 3$ et $\mathrm{n}^{3} \equiv \mathrm{n} \bmod 3$. On déduit que $\mathrm{m} \equiv \mathrm{m}^{3} \equiv \mathrm{n}^{3} \equiv \mathrm{n} \bmod 3$. Il vient que
$$
m^{2}+m n+n^{2} \equiv 3 m^{2}=0 \quad \bmod 3
$$
On déduit que 3 divise $m-n$ et 3 divise $m^{2}+m n+n^{2}$ donc $9 \mid(m-n)\left(m^{2}+m n+n^{2}\right)=m^{3}-n^{3}$. Il vient que $9 \mid a b(a-b)(a+b)\left(a^{2}+b^{2}\right)$. Mais 3 ne divise pas $a, b$ et $a^{2}+b^{2} \equiv 2 \bmod 3$ donc 3 ne divise pas non plus $a^{2}+b^{2}$ et donc 9 non plus. On déduit que $9 \mid a^{2}-b^{2}$, soit $a^{2} \equiv b^{2} \bmod 9$. Ainsi
$$
\mathrm{m}^{3}=\mathrm{a}^{5} \mathrm{~b}+3 \equiv \mathrm{a}^{3} \cdot \mathrm{a}^{2} \cdot \mathrm{~b}+3 \equiv \mathrm{a}^{3} \mathrm{~b}^{2} \cdot \mathrm{~b}+3 \equiv(\mathrm{ab})^{3}+3 \quad \bmod 9
$$
Or les cubes modulo 9 prennent uniquement les valeurs $-1,0$ et 1 . On ne peut donc avoir $\mathrm{m}^{3}-(a b)^{3} \equiv 3$ mod 9. La condition de l'énoncé ne peut donc pas être satisfaite, comme annoncé.
Commentaire des correcteurs
Beaucoup d'élèves ont une solution brutale qui consiste à regarder les paires $\left(\mathrm{ab}^{5}, \mathrm{ba}^{5}\right)$ modulo 9 d 'une façon ou d'une autre, ce n'est pas forcément une mauvaise chose mais il est plus subtil d'utiliser le petit théorème de Fermat en compétition pour ne pas perdre de temps (et parce que souvent les études ne sont pas exhaustives). La plupart des élèves ont une solution légèrement différente du corrigé qui consiste à remarquer que $a^{5} b+3$ et $b^{5} a+3$ ne peuvent pas être congrus à des cubes en même temps $\bmod 9$.
|
{
"exam": "French_envois",
"problem_label": "14",
"problem_match": "\nExercice 14.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 14",
"tier": "T2",
"year": null
}
|
Let $p$ be an odd prime, $h<p$ an integer, $e \in\{1,2\}$.
We set $n=h \cdot p^{e}+1$ and assume that:
$$
\left\{\begin{array}{r}
n \mid 2^{n-1}-1 \\
n \nmid 2^{h}-1
\end{array}\right.
$$
Show that $n$ is prime.
|
Let $\omega$ be the order of 2 modulo $n$. By hypothesis, $\omega$ divides $n-1$ but $\omega$ does not divide $h=\frac{n-1}{p^{e}}$, so $p$ divides $\omega$.
$\omega$ divides $\phi(n)$ by Euler's theorem, so $p$ divides $\phi(n)$. Clearly, $p$ does not divide $n$, so there exists a prime $q$ that divides $n$ with $q=1(\bmod p)$ (according to the formula for $\phi$).
We write $n=q^{a}N$ where $N$ is coprime with $q$. Modulo $p$ we have $1=1^{a} * N$ so $N=1(\bmod p)$. We will show that $n=q$.
Therefore, if $n \neq q$, either $a \geqslant 2$ or $N \geqslant p+1$ and thus $n \geqslant(p+1)^{2}>p^{2}+1>ph+1$ so $e=2$ and the reasoning shows that either $a=1$ or $N=1$ and in all cases $a \leqslant 2$ and $N<p^{2}$.
We will consider two cases:
- If $a=2, n \equiv q^{2} \equiv(1+pk)^{2} \equiv 1+2kp(\bmod p)$ where $q=1+kp$. But $n \equiv 1\left(\bmod p^{2}\right)$ so $p$ divides $2k$; $p$ divides $k$ and thus $q \geqslant p^{2}+1$ and $n=q^{2}>p^{3}+1>p^{2}h+1=n$, contradiction.
- If $a=1, q=1+kp, N=1+lp$ with $k, l>0$ (since $q \equiv N \equiv 1(\bmod p))$. We must have $k, l<p$ otherwise $n=qN \geqslant(1+p^{2})(1+p)>p^{3}+1>p^{2}h+1=n$. Moreover, $1+(k+l)p \equiv n \equiv 1$ $\left(\bmod p^{2}\right)$ so $k+l=p$. One of $k$ and $l$ is therefore odd, which forces $q$ or $N$ to be even, so in all cases $n$ is even, which contradicts $n \mid 2^{n-1}-1$.
In all cases $n=q$ is prime.
Comment from the graders
The graders noted many errors of inattention and poor use of the order of an element modulo $n$. Some students were caught trying to cheat the graders, which is unnecessary and will surely not earn points in a competition.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $p$ un nombre premier impair, $h<p$ un entier, $e \in\{1,2\}$.
On pose $n=h \cdot p^{e}+1$ et on suppose que:
$$
\left\{\begin{array}{r}
n \mid 2^{n-1}-1 \\
n \nmid 2^{h}-1
\end{array}\right.
$$
Montrer que n est premier.
|
Soit $\omega$ l'ordre de 2 modulo $n$. Par hypothèse, $\omega$ divise $n-1$ mais $\omega$ ne divise pas $h=\frac{n-1}{p^{e}}$, donc $p$ divise $\omega$.
$\omega$ divise $\phi(n)$ par le théorème d'Euler donc $p$ divise $\phi(n)$. Evidemment, $p$ ne divise pas $n$ donc il existe q premier qui divise n avec $\mathrm{q}=1(\bmod \mathrm{p})$ (d'après la formule donnant $\phi)$
On écrit $\mathrm{n}=\mathrm{q}^{\mathrm{a}} \mathrm{N}$ où N est premier avec q . Modulo p on a $1=1^{\mathrm{a}} * \mathrm{~N}$ donc $\mathrm{N}=1(\bmod \mathrm{p})$. On va montrer que $\mathrm{n}=\mathrm{q}$.
Dès lors, si $n \neq q$, soit $a \geqslant 2$ soit $N \geqslant p+1$ et donc $n \geqslant(p+1)^{2}>p^{2}+1>p h+1$ donc $e=2$ et le raisonnement montre que soit $a=1$, soit $N=1$ et dans tous les cas $a \leqslant 2$ et $N<p^{2}$.
Traitons deux cas :
- Si $a=2, n \equiv q^{2} \equiv(1+p k)^{2} \equiv 1+2 k p(\bmod p)$ où $q=1+k p$. Or $n \equiv 1\left(\bmod p^{2}\right)$ donc $p$ divise $2 k ; p$ divise $k$ et donc $q \geqslant p^{2}+1$ et $n=q^{2}>p^{3}+1>p^{2} h+1=n$, contradiction
- Si $a=1, q=1+k p, N=1+l p$ avec $k, l>0(\operatorname{car} q \equiv N \equiv 1(\bmod p))$. On a obligatoirement $k, l<p$ car sinon $n=q N \geqslant\left(1+p^{2}\right)(1+p)>p^{3}+1>p^{2} h+1=n$. De plus $1+(k+l) p \equiv n \equiv 1$ $\left(\bmod p^{2}\right)$ donc $k+l=p$. Un parmi $k$ et $l$ est donc impair, ce qui oblige $q$ ou $N$ pair, donc dans tous les cas $n$ est pair, ce qui contredit $n \mid 2^{n-1}-1$.
Dans tous les cas $\mathrm{n}=\mathrm{q}$ est premier.
Commentaire des correcteurs
Les correcteurs ont noté beaucoup d'erreurs d'inattention et de mauvaises utilisations de l'ordre d'un élément modulo $n$. Certains élèves ont été surpris en train d'essayer d'arnaquer les correcteurs, ce qui est inutile et ne permettra sûrement pas de gagner des points en compétition.
|
{
"exam": "French_envois",
"problem_label": "15",
"problem_match": "\nExercice 15.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 15",
"tier": "T2",
"year": null
}
|
Let $m, n \geqslant 2$ be integers satisfying the following property:
$$
a^{n} \equiv 1 \quad(\bmod m) \quad a=1, \ldots, n
$$
Prove that $m$ is a prime number and that $\mathrm{n}=\mathrm{m}-1$.
|
Let's start by assuming that $m=p$ is a prime number. We must therefore show that $n=p-1$. If $n \geqslant p$, we have $p^{n} \equiv 1(\bmod p)$, an obvious contradiction. Therefore, $n<p$.
Consider $T=X^{n}-1$ the polynomial in $\mathbb{Z} / p \mathbb{Z}[X]$. By hypothesis, its roots are $1, \ldots, n$, which are $n$ in number and distinct, and since $\mathbb{Z} / p \mathbb{Z}$ is an integral domain, and $T$ is of degree $n$, these are the only roots. Thus, $T=(X-1) \cdot \ldots \cdot(X-n)$. By looking at the coefficient of $X^{n-1}$ in $T$, we see that $0 \equiv 1+\ldots+n(\bmod p)$ by Vieta's formulas. Therefore, $p \left\lvert\, \frac{n(n+1)}{2}\right.$, and since $n<p$, we necessarily have $n=p-1$.
Let's return to the general case. Let $p$ be a prime divisor of $m$. We have $n=p-1$ since the hypothesis of the statement remains true for $m=p$. Thus, if $q$ is another prime divisor of $m$, $q-1=n=p-1$ and $q=p$. It remains to see that $m$ cannot be a power of $p$ other than $p$. It is clearly sufficient to see this for $m=p^{2}$. Now, $(p-1)^{p-1} \equiv(-1)^{p-1}+p \times(-1)^{p-2}\left(p^{p}\right)\left(\bmod p^{2}\right)$ by the binomial theorem. Since $p-1$ is even, and $p^{2} \nmid -p(p-1)$, we have $(p-1)^{p-1} \not \equiv 1\left(\bmod p^{2}\right)$. This completes the proof.
Comment from the graders
There were quite a few good papers but plenty of small errors, so the grades were mostly between 4 and 7.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $m, n \geqslant 2$ des entiers vérifiant la propriété suivante:
$$
a^{n} \equiv 1 \quad(\bmod m) \quad a=1, \ldots, n
$$
Prouver que $m$ est un nombre premier et que $\mathrm{n}=\mathrm{m}-1$.
|
Commençons par supposer que $m=p$ est un nombre premier. On doit donc montrer $n=p-1$. Si $n \geqslant p$, on a $p^{n} \equiv 1(\bmod p)$, une évidente contradiction. Donc $n<p$.
Considérons $T=X^{n}-1$ le polynôme de $\mathbb{Z} / p \mathbb{Z}[X]$. Il a pour racines par hypothèse $1, \ldots, n$, qui sont au nombre de $n$ et distinctes, et, puisque $\mathbb{Z} / p \mathbb{Z}$ est intègre, et que $T$ est de degré $n$, ce sont les seules. Donc $T=(X-1) \cdot \ldots \cdot(X-n)$. En regardant le coefficient en $X^{n-1}$ de $T$, on voit que $0 \equiv 1+\ldots+n(\bmod p)$ par les formules de Viète. Ainsi, $p \left\lvert\, \frac{n(n+1)}{2}\right.$, donc (puisque $n<p$ ) on a nécessairement $n=p-1$.
Revenons au cas général. Soit $p$ un diviseur premier de $m$. On a $n=p-1$ puisque l'hypothèse de l'énoncé reste vraie pour $m=p$. Dès lors, si $q$ est un autre diviseur premier de $m, q-1=n=p-1$ et $q=p$. Il reste à voir que $m$ ne peut pas être une puissance de $p$ autre que $p$. Il suffit clairement de le voir pour $\mathrm{m}=\mathrm{p}^{2}$. Or $(p-1)^{\mathrm{p}-1} \equiv(-1)^{\mathrm{p}-1}+\mathrm{p} \times(-1)^{\mathfrak{p}-2}\left(\mathrm{p}^{\mathrm{p}}\right)\left(\bmod \mathrm{p}^{2}\right)$ par le binôme de Newton. Puisque $p-1$ est pair, et que $p^{2} \nmid-p(p-1)$, on a bien $(p-1)^{p-1} \not \equiv 1\left(\bmod p^{2}\right)$. Ceci achève la démonstration.
Commentaire des correcteurs
Il y avait pas mal de bonnes copies mais plein de petites erreurs donc les notes se trouvent majoritairement entre 4 et 7 .
|
{
"exam": "French_envois",
"problem_label": "16",
"problem_match": "\nExercice 16.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 16",
"tier": "T2",
"year": null
}
|
Let $S$ be a non-empty set of strictly positive integers satisfying the following property: For all integers $a, b \in S$, the integer $a b + 1$ also belongs to $S$.
Show that the set of prime numbers that do not divide any of the elements of $S$ is finite.
|
Let $p$ be a prime number and let $a_{1}, a_{2}, \ldots a_{k}$ be the possible remainders of the elements of $S$ modulo $p$. We assume that 0 does not belong to $R=\left\{a_{1}, \ldots, a_{k}\right\}$, that is, $p$ does not divide any element of $S$.
We know that for all $i, j, a_{i} a_{j}+1 \in R$. Note that if $j$ and $l$ are distinct, then $a_{i} a_{j}+1$ and $a_{i} a_{l}+1$ are distinct. Indeed
$$
a_{i} a_{j}+1-\left(a_{i} a_{l}+1\right) \equiv a_{i}\left(a_{j}-a_{l}\right) \neq 0 \quad \bmod p
$$
Thus for a fixed $i$, $R=\left\{a_{1}, \ldots, a_{k}\right\}=\left\{a_{i} a_{1}+1, \ldots, a_{i} a_{k}+1\right\}$. It follows that
$$
a_{1}+\ldots+a_{k} \equiv a_{i} a_{1}+1+\ldots+a_{i} a_{k}+1 \equiv a_{i}\left(a_{1}+\ldots+a_{k}\right)+k \bmod p
$$
If $a_{1}+\ldots+a_{k} \equiv 0 \bmod p$, then $k \equiv 0 \bmod p$ so $k=p$ and $0 \in R$ which contradicts the hypothesis. We deduce that $a_{1}+\ldots+a_{k}$ is invertible modulo $p$ and
$$
a_{i} \equiv \frac{k}{a_{1}+\ldots+a_{k}} \bmod p
$$
This term does not depend on $i$. Therefore, the $a_{i}$ are equal and $R$ is a singleton denoted $\{a\}$. Thus $a^{2}+1 \equiv a$ $\bmod p$ so $p \mid a^{2}+1-a$ and $p \leqslant n^{2}-n+1$ for all $n$ in $S$. If $n_{0}$ is the smallest element of $S$, then in particular $p \leqslant n_{0}^{2}-n_{0}+1$.
In conclusion, if $p$ does not divide any element of $S$, $p$ is bounded by $n_{0}^{2}-n_{0}+1$. Thus the set of prime numbers not dividing any element of $S$ is finite.
Comment from the graders
The problem was well solved by the few students who tackled it.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $S$ un ensemble non vide d'entiers strictement positifs vérifiant la propriété suivante : Pour tous entiers $a, b \in S$, l'entier $a b+1$ appartient aussi à $S$.
Montrer que l'ensemble des nombres premiers ne divisant aucun des éléments de $S$ est fini.
|
Soit $p$ un nombre premier et soit $a_{1}, a_{2}, \ldots a_{k}$ les restes possibles des éléments de $S$ modulo $p$. On suppose que 0 n'appartient pas à $R=\left\{a_{1}, \ldots, a_{k}\right\}$, c'est-à-dire que $p$ ne divise aucun élément de $S$.
On sait que pour tout $i, j, a_{i} a_{j}+1 \in R$. Notons que si $j$ et $l$ sont distincts, alors $a_{i} a_{j}+1$ et $a_{i} a_{l}+1$ sont distincts. En effet
$$
a_{i} a_{j}+1-\left(a_{i} a_{l}+1-\equiv a_{i}\left(a_{j}-a_{l}\right) \neq 0 \quad \bmod p\right.
$$
Ainsi pour $i$ fixé, $R=\left\{a_{1}, \ldots, a_{k}\right\}=\left\{a_{i} a_{1}+1, \ldots, a_{i} a_{k}+1\right\}$. Il vient que
$$
a_{1}+\ldots+a_{k} \equiv a_{i} a_{1}+1+\ldots+a_{i} a_{k}+1 \equiv a_{i}\left(a_{1}+\ldots+a_{k}\right)+k \bmod p
$$
Si $a_{1}+\ldots+a_{k} \equiv 0 \bmod p$, alors $k \equiv 0 \bmod p$ donc $k=p$ et $0 \in R$ ce qui est contraire à l'hypothèse. On déduit que $a_{1}+\ldots+a_{k}$ est inversible modulo $p$ et
$$
a_{i} \equiv \frac{k}{a_{1}+\ldots+a_{k}} \bmod p
$$
Ce terme ne dépend pas de $i$. Donc les $a_{i}$ sont égaux et $R$ est un singleton noté $\{a\}$. Ainsi $a^{2}+1 \equiv a$ $\bmod p$ donc $p \mid a^{2}+1-a$ et $p \leqslant n^{2}-n+1$ pour tout $n$ dans $S$. Si $n_{0}$ est le plus petit élément de $S$, alors en particulier $p \leqslant \mathfrak{n}_{0}^{2}-\mathfrak{n}_{0}+1$.
En conclusion, si $p$ ne divise aucun élément de $S$, $p$ est borné par $n_{0}^{2}-n_{0}+1$. Ainsi l'ensemble des nombres premiers ne divisant aucun élément de $S$ est fini.
Commentaire des correcteurs
L'exercice a été bien résolu par les quelques élèves qui l'ont traité.
|
{
"exam": "French_envois",
"problem_label": "17",
"problem_match": "\nExercice 17.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 17",
"tier": "T2",
"year": null
}
|
Find all integers $n \geqslant 1$ for which the function:
$$
x \longmapsto x^{x}
$$
takes all possible values modulo $n$ as $x$ runs through $\llbracket 0, n-1 \rrbracket$.
We say that it is a surjection in $\mathbb{Z} / n \mathbb{Z}$.
|
Let's already note that if $n$ satisfies the property, then any divisor $d$ of $n$ also satisfies it. Let $f$ be the function that maps $x$ in $\mathbb{N}^{*}$ to $\mathbb{Z} / \mathfrak{Z} \mathbb{Z}$.
For $n=p^{2}$ with $p$ prime, note that $p$ is not in the image of $f$. Indeed, if $f(x) \equiv p\left(\bmod p^{2}\right)$, $p$ divides $x^{x}$, so $p$ divides $x$. In particular, since $x \geqslant p \geqslant 2$, $p^{2}$ divides $x^{x}=f(x)$, a contradiction. In particular, if $n$ satisfies the property, in its prime factorization, all the $p$-adic valuations are at most 1.
For $n=p$ prime, let us take $y \in \mathbb{N}$. We seek $x$ a positive integer such that $x^{x} \equiv y(\bmod p)$. For this, we use Fermat's little theorem: if $p-1$ divides $x-1$, then $x^{x} \equiv x^{x-1} \times x \equiv x(\bmod p)$. In particular, it suffices to take $x$ strictly positive such that $x \equiv 1(\bmod p-1)$ and $x \equiv y(\bmod p)$. This is possible by the Chinese remainder theorem, since $p$ and $p-1$ are coprime, so $f$ is surjective.
It remains to treat the case where $n$ is a product of distinct prime factors: suppose $n=p_{1} \ldots p_{k}$ with the $(p_{i})$ primes and pairwise distinct. We can try to use the previous argument again: let $y \in \mathbb{N}$, we seek $x$ a strictly positive integer such that $x^{x}=y(\bmod \boldsymbol{n})$, this is equivalent by the Chinese remainder theorem to $x^{x}=y\left(\bmod p_{i}\right)$ for all $i$ between 1 and $k$. It suffices to take $x$ such that $x \equiv 1\left(\bmod p_{i}-1\right)$ and $x \equiv y\left(\bmod p_{i}\right)$ for all $i$, that is, $x \equiv 1\left(\bmod \prod_{i=1}^{k}\left(p_{i}-1\right)\right)$ and $x \equiv y$ $\left(\bmod p_{i}\right)$ for all $i$. Note that the $(p_{i})$ are pairwise coprime, but a priori we cannot assert that $p_{i}$ is coprime with $\prod_{i=1}^{k}\left(p_{i}-1\right)$ for all $i$.
If for all $(i, j)$ between 1 and $k$, $p_{i}$ does not divide $p_{j}-1$, in this case $p_{i}$ is coprime with $\prod_{i=1}^{k}\left(p_{i}-1\right)$ for all $i$, so by the Chinese remainder theorem we can find $x$ such that $x \equiv 1\left(\bmod \prod_{i=1}^{k}\left(p_{i}-1\right)\right)$ and $x \equiv y$ $\left(\bmod p_{i}\right)$ for all $i$, thus $x^{x} \equiv y(\bmod \boldsymbol{n})$.
Suppose there exists $(i, j)$ such that $p_{i}$ divides $p_{j}-1$. Since $i \neq j$, it suffices in this case to verify that $f$ is not surjective modulo $m$ with $m=p_{i} p_{j}$, suppose that $f$ is surjective modulo $m$. Let $a \in \mathbb{N}, y$ such that $y \equiv 0\left(\bmod p_{i}\right)$ and $y \equiv a\left(\bmod p_{j}\right)$ by the Chinese remainder theorem. Suppose there exists $x$ such that $x^{x} \equiv y\left(\bmod p_{i} p_{j}\right)$. In this case, $x^{x} \equiv 0\left(\bmod p_{i}\right)$, so $p_{i}$ divides $x$, let then $x=k p_{i}$. In this case, $x^{x} \equiv\left(x^{k}\right)^{p_{i}} \equiv a\left(\bmod p_{j}\right)$. We obtain, by raising to the power $\frac{p_{j}-1}{p_{i}}, a^{\frac{p_{j}-1}{p_{i}}}=\left(x^{k}\right)^{p_{j}-1}=1$ $\left(\bmod p_{j}\right)$. In particular, if $a$ is a primitive root modulo $p_{j}$, since $a$ has order exactly $p_{j}-1$, we obtain a contradiction, the function $f$ is not surjective.
Thus the function is surjective if and only if $n=p_{1} \ldots p_{k}$ with the $(p_{i})$ primes and pairwise distinct and for all $(i, j)$ between 1 and $k$, $p_{i}$ does not divide $p_{j}-1$.
Comment from the graders
The submissions received on this problem are of very good quality. The problem was relatively difficult, but many made good progress. Some submissions tried to use the Chinese remainder theorem, which could be useful, but it could cause many errors: notably, just because the function is surjective modulo $p$ for all prime numbers $p$, it does not mean it is surjective for all "squarefree" numbers, that is, without any prime factor with multiplicity greater than or equal to 2. Also, be careful with the use of Euler's theorem $\left(a^{\phi(n)}=1(\bmod n)\right)$: to use it, the number must be coprime with $n$.
|
proof
|
Yes
|
Incomplete
|
math-word-problem
|
Number Theory
|
Trouver tous les entiers $n \geqslant 1$ pour lesquels la fonction:
$$
x \longmapsto x^{x}
$$
prenne toutes les valeurs possibles modulo $n$ lorsque $x$ parcourt $\llbracket 0, n-1 \rrbracket$.
On dit que c'est une surjection dans $\mathbb{Z} / n \mathbb{Z}$.
|
Notons déjà que si $n$ vérifie la propriété, alors tout diviseur d de n la vérifie également. Posons f l'application qui à $x$ dans $\mathbb{N}^{*}$ dans $\mathbb{Z} / \mathfrak{Z} \mathbb{Z}$.
Pour $n=p^{2}$ avec $p$ premier, notons que $p$ n'est pas dans l'image de $f$. En effet, si $f(x) \equiv p\left(\bmod p^{2}\right)$, $p$ divise $x^{x}$ donc $p$ divise $x$. En particulier, comme $x \geqslant p \geqslant 2, p^{2}$ divise $x^{x}=f(x)$ contradiction. En particulier, si $n$ vérifie la propriété, dans sa décomposition en facteurs premiers toutes les valuations $p$ adiques valent au plus 1.
Pour $n=p$ premier, donnons nous $y \in \mathbb{N}$. On cherche $x$ entier positif tel que $x^{x} \equiv y(\bmod p)$. Pour cela, on utilise le petit théorème de Fermat: si $p-1$ divise $x-1, x^{x} \equiv x^{x-1} \times x \equiv x(\bmod p)$. En particulier, il suffit de prendre $x$ strictement positif tel que $x \equiv 1(\bmod p-1)$ et $x \equiv y(\bmod p)$. Ceci est possible par le théorème des restes chinois, car $p$ et $p-1$ sont premiers entre eux, donc $f$ est surjective.
Il reste à traiter le cas où $n$ est un produit de facteurs premiers deux à deux distincts : supposons $n=p_{1} \ldots p_{k}$ avec les ( $p_{i}$ ) premiers et deux à deux distincts. On peut réessayer d'utiliser l'argument précédent : soit $y \in \mathbb{N}$, on cherche $x$ entier strictement positif tel que $x^{x}=y(\bmod \boldsymbol{n})$, ceci est équivalent par théorème des restes chinois à $x^{x}=y\left(\bmod p_{i}\right)$ pour tout $i$ entre 1 et $k$. Il suffit de prendre $x$ tel que $x \equiv 1\left(\bmod p_{i}-1\right)$ et $x \equiv y\left(\bmod p_{i}\right)$ pour tout $i$, c'est à dire $x \equiv 1\left(\bmod \prod_{i=1}^{k}\left(p_{i}-1\right)\right)$ et $x \equiv y$ $\left(\bmod p_{i}\right)$ pour tout $i$. Notons que les $\left(p_{i}\right)$ sont deux à deux premiers entre eux, mais à priori on ne peut pas affirmer que $p_{i}$ est premier $\prod_{i=1}^{k}\left(p_{i}-1\right)$ pour tout $i$.
Si pour tout $(\boldsymbol{i}, \mathfrak{j})$ entre 1 et $k, p_{i}$ ne divise pas $\mathfrak{p}_{\mathfrak{j}}-1$, dans ce cas $\mathfrak{p}_{\boldsymbol{i}}$ est premier $\prod_{i=1}^{k}\left(\mathfrak{p}_{\boldsymbol{i}}-1\right)$ pour tout $\boldsymbol{i}$, donc par théorème des restes chinois on peut trouver $x$ tel que $x \equiv 1\left(\bmod \prod_{i=1}^{k}\left(p_{i}-1\right)\right)$ et $x \equiv y$ $\left(\bmod p_{i}\right)$ pour tout i , ainsi $x^{x} \equiv y(\bmod \boldsymbol{n})$.
Supposons qu'il existe $(i, j)$ tel que $p_{i}$ divise $p_{j}-1$. Comme $i \neq j$, il suffit dans ce cas de vérifier que $f$ n'est pas surjective modulo $m$ avec $m=p_{i} p_{j}$, supposons que $f$ est surjective modulo $m$. Soit $a \in \mathbb{N}, y$ tel que $y \equiv 0\left(\bmod p_{i}\right)$ et $y \equiv a\left(\bmod p_{j}\right)$ par théorème des restes chinois. Supposons qu'il existe $x$ tel que $x^{x} \equiv y\left(\bmod p_{i} p_{j}\right)$. Dans ce cas $x^{x} \equiv 0\left(\bmod p_{i}\right)$ donc $p_{i}$ divise $x$, posons alors $x=k p_{i}$. Dans ce cas, $x^{x} \equiv\left(x^{k}\right)^{\mathfrak{p}_{i}} \equiv a\left(\bmod \mathfrak{p}_{j}\right)$. On obtient, en élevant à la puissance $\frac{\mathfrak{p}_{j}-1}{\mathfrak{p}_{i}}, a^{\frac{p_{j}-1}{p_{i}}}=\left(x^{k}\right)^{\mathfrak{p}_{j}-1}=1$ $\left(\bmod \mathfrak{p}_{\mathfrak{j}}\right)$. En particulier, si a est une racine primitive modulo $\mathfrak{p}_{\mathfrak{j}}$, comme a est d'ordre exactement $\mathfrak{p}_{\mathfrak{j}}-1$, on obtient une contradiction, l'application f n'est pas surjective.
Ainsi l'application est surjective si et seulement si $\mathrm{n}=\mathrm{p}_{1} \ldots \mathrm{p}_{\mathrm{k}}$ avec les $\left(\boldsymbol{p}_{\boldsymbol{i}}\right)$ premiers et deux à deux distincts et pour tout $(\boldsymbol{i}, \mathfrak{j})$ entre 1 et $k, p_{i}$ ne divise pas $\mathfrak{p}_{\mathfrak{j}}-1$.
Commentaire des correcteurs
Les copies reçues sur ce problème sont de très bon niveau. Le problème était relativement difficile, mais nombreux sont ceux qui ont trouvé de bonnes avancées. Certaines copies ont voulu utiliser le lemme chinois, certes il pouvait être utile, mais il pouvait causer beaucoup d'erreurs : notamment ce n'est pas
parce que l'application est surjective modulo $p$ pour tout nombre $p$ premier qu'elle l'est pour tout nombre "squarefree" c'est-à-dire sans facteur premier avec multiplicité supérieure ou égale à 2 . Attention aussi à l'utilisation du théorème d'Euler $\left(a^{\phi(n)}=1(\bmod n)\right)$ : pour pouvoir l'utiliser, il faut que le nombre soit premier avec n .
|
{
"exam": "French_envois",
"problem_label": "18",
"problem_match": "\nExercice 18.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 18",
"tier": "T2",
"year": null
}
|
In how many ways can 7 rooks be placed on a $7 \times 7$ chessboard such that no rook can attack another?
A rook can attack another rook if it is on the same row or the same column.
|
If we place 7 towers so that no two towers are in the same column, knowing that there are 7 columns, then there will be exactly one tower on each column (and the same for each row).
There are 7 possible positions to place a tower in the first column. There are then 6 possible positions to place a tower in the second column without it being in the same row as the first tower. And so on, on the $k$-th column there are $8-k$ ways to place a tower without it being in the same row as a tower already placed.
Thus, there are 7! $=7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1=5040$ ways to arrange the towers in this manner.
If we denote $\sigma(i)$ as the row number of the tower present on the i-th column in one of the configurations satisfying the statement, then $\sigma$ is what is called a permutation.
Comment from the graders
The problem was very well done.
|
5040
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
De combien de façons peut-on placer 7 tours sur un échiquier $7 \times 7$ telle qu'aucune tour ne puisse en attaquer une autre?
Une tour peut attaquer une autre tour si elle se situe sur la même ligne ou la même colonne.
|
Si on place 7 tours de sorte que deux tours ne soient pas sur la même colonne, sachant qu'il y a 7 colonne, alors il y aura exactement une tour sur chaque colonne (et de même sur chaque ligne).
Il y a 7 positions possibles pour placer une tour sur la première colonne. Il y a ensuite 6 positions possibles pour placer une tour sur la seconde colonne sans qu'elle soit sur la même ligne que la première tour. Ainsi de suite, sur la $k$-ième colonne il y a $8-k$ manières de placer une tour sans qu'elle soit sur la même ligne qu'une tour déjà placée.
Ainsi il y a 7 ! $=7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1=5040$ manières de disposer les tours de cette manière.
Si on note $\sigma(i)$ le numéro de ligne de la tour présente sur la i-ième colonne dans une des configurations satisfaisant l'énoncé, alors $\sigma$ est ce que l'on appelle une permutation.
Commentaire des correcteurs
Le problème a été très bien réussi.
|
{
"exam": "French_envois",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-4.jsonl",
"solution_match": "## Solution de l'exercice 1",
"tier": "T2",
"year": null
}
|
The integers from 1 to 2020 are written on the board. Jacques has the right to erase two of them and write their difference or their sum in their place, and to repeat this until only one integer remains. Is it possible for the integer obtained at the end to be 321?
|
The statement presents a finite sequence of operations, and the problem asks whether it is possible to go from the initial situation to a certain final situation. A first idea to try in this case is to look for an invariant.
A second idea is to test the problem with smaller values. For example, one can test the statement for integers written from 1 to 4 and see what values can be reached at the end of the process described in the statement. It is observed that starting from a fixed value \( n \), all possible results have the same parity, that of the sum of the numbers from 1 to \( n \). After testing this conjecture for integers written from 1 to 5, one then tries to show that the parity of the sum of the integers written on the board is invariant under the described operation.
If at a given moment, the sum of the integers written on the board is \( S \) and Jacques chooses the integers \( x \) and \( y \), then these integers will be replaced by \( x+y \) or by \( x-y \), and then \( S \) will be replaced by \((S-x-y)+y-x = S-2x\) or by \((S-y-x)+(x-y) = S-2y\). These two integers have the same parity, so the sum of the integers written on the board retains the same parity throughout the process. Since in the initial situation, the sum of the integers written on the board is
\[
1+2+3+\cdots+2020 = \frac{2020 \cdot 2021}{2} = 1010 \cdot 2021
\]
and is even, the number written on the board in the final situation will also be even and it cannot therefore be the number 321.
Comment from the graders
It was necessary in this problem to invoke the notion of invariant. Explanations from students who did not explicitly mention the parity invariant were not always very convincing. Be careful not to give a reasoning that is too "hands-on."
|
321
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Les entiers de 1 à 2020 sont écris au tableau. Jacques a le droit d'en effacer deux et d'écrire à la place leur différence ou leur somme, et de recommencer jusqu'à ce qu'il ne reste plus qu'un entier. Est-il possible que l'entier obtenu à la fin soit 321 ?
|
L'énoncé présente une suite finie d'opérations et le problème demande s'il est possible de partir de la situation initiale pour arriver à une certaine situation finale. Une première idée à essayer dans ce cas est de chercher un invariant.
Une seconde idée est de tester le problème avec des plus petites valeurs. Par exemple, on peut tester l'énoncé pour les entiers écrits de 1 à 4 et regarder à quelles valeurs ont peut aboutir à la fin du processus décrit dans l'énoncé. On remarque que partant d'une valeur fixée n , les résultats possibles ont tous la même parité, celle de la somme des nombres de 1 à $n$. Après avoir testé cette conjecture pour les entiers écrits de 1 à 5 , on essaye donc de montrer que la parité de la somme des entiers écrits au tableau est invariante sous l'opération décrite.
Si un instant donné, la somme des entiers écrits au tableau vaut $S$ et que Jacques choisit les entiers $x$ et $y$, alors ces entiers seront remplacés par $x+y$ ou par $x-y$ et alors $S$ sera remplacé par $(S-x-y)+y-x=$ $S-2 x$ ou par $(S-y-x)+(x-y)=S-2 y$. Ces deux entiers ont la même parité, donc la somme des entiers écrits au tableau garde la même parité tout au long du processus. Puisque dans la situation initiale, la somme des entiers écrits au tableau est
$$
1+2+3+\cdots+2020=\frac{2020 \cdot 2021}{2}=1010 \cdot 2021
$$
et est paire, le nombre écrit au tableau dans la situation finale sera également pair et il ne peut donc pas s'agir du nombre 321.
Commentaire des correcteurs
Il était nécessaire dans ce problème d'évoquer la notion d'invariant. Les explications des élèves qui n'évoquaient pas explicitement l'invariant de parité n'étaient pas toujours très convaincantes. Attention à ne pas faire un raisonnement qui soit trop "avec les mains".
|
{
"exam": "French_envois",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T2",
"year": null
}
|
Andréa, Baptiste, and Camille are playing soccer with three people. One player is in goal, the other two are on the field trying to score. The player who scores then becomes the goalkeeper for the next shot.
During the afternoon, Andréa was on the field 12 times, Baptiste was on the field 21 times, and Camille was in goal 8 times. Their teacher knows who scored the 6th goal. Who was it?
|
If we denote n as the number of games played, then in total there have been n times a goalkeeper. We now use the assumptions given in the statement. If Andrea has been on the field 12 times, he has therefore been $\mathrm{n}-12$ times in goal. If Baptiste has been on the field 21 times, he has been $\mathrm{n}-21$ times in goal. Thus $\mathrm{n}-12+\mathrm{n}-21+8=\mathrm{n}$, which gives us that $n=25$. This also means that Andrea was in goal 13 times. But it is impossible to be in goal twice in a row. Thus, we know that Andrea was in goal at the beginning, and he was exactly once every two times. In particular, he was in goal in the seventh game, and therefore Andrea scored the 6th goal.
## Comment from the graders
The exercise was largely successful. Some proofs and writing are particularly efficient.
|
Andrea
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
Andréa, Baptiste et Camille jouent au foot à trois. Un des joueur est aux cages, les deux autres sont sur le terrain et essaient de marquer. Le joueur qui marque devient ensuite gardien pour le tir suivant.
Durant l'après-midi, Andréa a été sur le terrain 12 fois, Baptiste l'a été 21 fois et Camille a été aux cages 8 fois. Leur professeur sait qui a marqué le 6 -ième but. Qui était-ce?
|
Si on note n le nombre de parties jouées, alors au total il y a eu n fois un gardien. On utilise à présent les hypothèses données par l'énoncé. Si Andréa a été 12 fois sur le terrain, il a donc été $\mathrm{n}-12$ fois aux cages. Si Baptiste a été 21 fois sur le terrain, il a été $\mathrm{n}-21$ fois aux cages. Ainsi $\mathrm{n}-12+\mathrm{n}-21+8=\mathrm{n}$, ce qui nous donne que $n=25$. Cela veut également dire que Andréa a été aux cages 13 fois. Mais il est impossible d'être aux cages deux fois d'affilée. Ainsi, on sait que Andréa était aux cages au début, et l'a été exactement une fois sur deux. En particulier, il a été aux cages à la septième partie et donc Andréa a marqué le 6-ième but.
## Commentaire des correcteurs
L'exercice a été largement réussi. Certaines preuves et rédaction sont particulièrement efficaces.
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-4.jsonl",
"solution_match": "## Solution de l'exercice 3",
"tier": "T2",
"year": null
}
|
We choose 5 positive divisors of $10^{2020}$. Show that there are two of them whose product is a square.
|
We start by looking at the form that a potential divisor of $10^{2020}$ can take. The divisors of $10^{2020}$ are of the form $2^{\mathrm{a}} 5^{\mathrm{b}}$. The product of two divisors is therefore also a number of the form $2^{a} 5^{b}$ and it is a perfect square if and only if $a$ and $b$ are both even. We are thus reduced to proving the following result: if we have 5 pairs of integers $\left(a_{i}, b_{i}\right)$ with $1 \leqslant i \leqslant 5$ and the $a_{i}$ and $b_{i}$ are all less than or equal to 2020, then we can find two indices $j$ and $k$ such that $\left(a_{i}+a_{j}, b_{i}+b_{j}\right)$ is a pair of two even integers. We quickly check if this result is true for a few pairs of integers and now seek to prove this result. We are led to consider the parity of the integers in question. There are 4 possibilities for a pair $(\mathrm{a}, \mathrm{b})$: either $a$ and $b$ are even, or $a$ and $b$ are odd, or $a$ is even and $b$ is odd, or $a$ is odd and $b$ is even. Thus, by the pigeonhole principle, if we choose 5 pairs of integers $\left(a_{i}, b_{i}\right)$ with $1 \leqslant i \leqslant 5$, there are two pairs $\left(a_{j}, b_{j}\right)$ and $\left(a_{k}, b_{k}\right)$ having the same characteristic, that is, such that $a_{j}$ and $a_{k}$ are of the same parity and $b_{j}$ and $b_{k}$ are of the same parity. Then $a_{j}+a_{k}$ and $b_{j}+b_{k}$ are both even. Thus, by choosing 5 divisors of $10^{2020}$, we can find 2 such that their product is a square.
Comment from the graders:
The exercise was generally very well done. Some considered that every divisor of $10^{2020}$ is of the form $2^{x}$, $5^{y}$, or $10^{z}$, which is not true (for example, 20 is a divisor of $10^{2020}$ and has none of the forms mentioned). Some said that if we have two divisors of the form $2^{b} 5^{c}$ and $2^{\mathrm{d}} 5^{f}$ with $b$ and $d$ of the same parity, and $c$ and $f$ of the same parity, then their product is a square; this needed to be justified by saying that two numbers of different parity have an even sum. Attention to the verb "must": many said that for the product of $2^{\mathrm{b}} 5^{\mathrm{c}}$ and $2^{\mathrm{d}} 5^{\mathrm{f}}$ to be a square, it must have $\mathrm{b}+\mathrm{d}$ even and $\mathrm{c}+\mathrm{f}$ even, which is true. However, they then used the fact that if $\mathrm{b}+\mathrm{d}$ is even and $\mathrm{c}+\mathrm{f}$ is even, then the product of $2^{\mathrm{b}} 5^{\mathrm{c}}$ and $2^{\mathrm{d}} 5^{\mathrm{f}}$ is a square, which is not the same as what was stated. When one says "for A it must have B," one asserts that A implies B, that is, if one has A then one has B. To say that B implies A, one must say "for A it suffices to have B." "It must be that" and "it suffices that" have different meanings.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
On choisit 5 diviseurs positifs de $10^{2020}$. Montrer qu'il y en a deux dont le produit est un carré.
|
On commence par regarder la forme que peut prendre un éventuel diviseur de $10^{2020}$. Les diviseurs de $10^{2020}$ sont de la forme $2^{\mathrm{a}} 5^{\mathrm{b}}$. Le produit de deux diviseurs est donc également un nombre de la forme $2^{a} 5^{b}$ et c'est un carré parfait si et seulement si $a$ et $b$ sont tous les deux pairs. On est donc ramené à montrer le résultat suivant : si on a 5 paires d'entiers $\left(a_{i}, b_{i}\right)$ avec $1 \leqslant i \leqslant 5$ et les $a_{i}$ et $b_{i}$ tous les deux inférieurs ou égaux à 2020, alors on peut trouver deux indices $j$ et $k$ tels que $\left(a_{i}+a_{j}, b_{i}+b_{j}\right)$ est un couple de deux nombres entiers pairs. On s'empresse de regarder si ce résultat est vrai pour quelques paires d'entiers et on cherche désormais à démontrer ce résultat. On est amené à regarder la parité des entiers considérés. Il y a 4 possibilités pour un couple ( $\mathrm{a}, \mathrm{b}$ ) : soit a et b sont pairs, soit $a$ et $b$ sont impairs, soit $a$ est pair et $b$ est pair, soit $a$ est impair et $b$ est pair. Ainsi par le principe des tiroirs, si on choisit 5 paires d'entiers $\left(a_{i}, b_{i}\right)$ avec $1 \leqslant i \leqslant 5$, il y a deux couples $\left(a_{j}, b_{j}\right)$ et $\left(a_{k}, b_{k}\right)$ possédant la même caractéristique, c'est-à-dire tels que $a_{j}$ et $a_{k}$ soient de le même parité et $b_{j}$ et $b_{k}$ soient de même parité. Alors $a_{j}+a_{k}$ et $b_{j}+b_{k}$ sont tous les deux paires. Ainsi, en choisissant 5 diviseurs de $10^{2020}$, on peut en trouver 2 tels que leur produit soit un carré.
Commentaire des correcteurs
Exercice globalement très bien réussi. Certains ont considéré que tout diviseur de $10^{2} 020$ était sous la forme $2^{x}, 5^{y}$ ou $10^{z}$ ce qui n'est pas vrai (par exemple 20 est un diviseur de $10^{2020}$ et n'a aucune des formes citées). Certains ont dit que si on avait deux diviseurs sous la forme $2^{b} 5^{c}$ et $2^{\mathrm{d}} 5^{f}$ avec b et d de même parité, c et f de même parité alors leur produit est un carré, il fallait justifier cela en disant que deux nombres de parité différente ont une somme paire. Attention au verbe falloir : beaucoup ont dit que pour que le produit de $2^{\mathrm{b}} 5^{\mathrm{c}}$ et $2^{\mathrm{d}} 5^{\mathrm{f}}$ soit un carré il fallait avoir $\mathrm{b}+\mathrm{d}$ pair et $\mathrm{c}+\mathrm{f}$ pair, ce qui est vrai. Néanmoins ils ont utilisé après que si on a $\mathrm{b}+\mathrm{d}$ pair et $\mathrm{c}+\mathrm{f}$ pair alors le produit de $2^{\mathrm{b}} 5^{\mathrm{c}}$ et $2^{\mathrm{d}} 5^{\mathrm{f}}$ est un carré, ce qui n'est pas la même chose que ce qui était dit. Quand on affirme "pour A il faut avoir B", on affirme que A implique B , c'est-à-dire que si on a A alors on a B . Pour dire que B implique A , on doit dire "pour A il suffit d'avoir B". "Il faut que" et "il suffit que" ont des sens différents.
|
{
"exam": "French_envois",
"problem_label": "4",
"problem_match": "## Exercice 4.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T2",
"year": null
}
|
Martin is trying to fill each cell of a rectangular grid with 8 rows and n columns with one of the four letters $\mathrm{P}, \mathrm{O}, \mathrm{F}$, and M such that for any pair of distinct rows, there is at most one column where the intersections of the two rows are cells with the same letter. What is the largest integer n for which this is possible?
|
In this problem, we are looking for the largest integer satisfying a certain property. Suppose we want to show that the largest integer sought is the integer c. To show that $c$ is indeed the largest integer, we will on the one hand show that if an integer $n$ satisfies the property, then $n \leqslant \mathrm{c}$, and on the other hand, we will show that we can find a table with exactly c columns. The statement provides an assumption about the rows and columns of a table.
We start by looking at the information we have about the rows of this table. There are 8 rows, so there are $\binom{8}{2}=28$ pairs of rows.
We then look at the information we have about the columns of the table. Since the statement's hypothesis mentions identical letters within the same column, we will count how many pairs of identical letters belong to the same column. We fix a column of the table and see how many pairs of identical letters we can form at a minimum. After several trials on a column of size 8, we conjecture that there are always at least 4 pairs of identical letters within the same column. Indeed, in a column, there are 8 letters, so a letter appears at least 2 times.
- If each letter appears at most 2 times, then each letter appears exactly 2 times since there are 8 cells in the column and 4 possible letters. We thus have 4 pairs of identical letters in the column.
- If a letter appears exactly 3 times, say the letter $P$, then we can form 3 pairs of letters $P$. Among the 5 remaining letters, at least one of the letters $O, F$, and $M$ appears twice according to the pigeonhole principle, which gives us a fourth pair of identical letters.
- If a letter appears at least 4 times in the column, say the letter $P$, we can form 4 pairs of letters P.
Thus, in a column, we can always find 4 pairs of identical letters. Therefore, for each column, there are at least 4 pairs of rows such that the intersections with the column have the same letter. But according to the statement's hypothesis, a pair of rows can be associated with at most one column such that its intersections with the two rows are two cells containing the same letter. We deduce that there are at most $4 \times n$ pairs of rows. So $4 \mathrm{n} \leqslant 28$ and $n \leqslant 7$.
Conversely, there exists a configuration with the following 7 columns:
| $P$ | $P$ | $P$ | $P$ | $P$ | $P$ | $P$ |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| $O$ | $O$ | $O$ | $O$ | $O$ | $P$ | $O$ |
| $F$ | $F$ | $F$ | $F$ | $O$ | $O$ | $P$ |
| $M$ | $M$ | $M$ | $M$ | $P$ | $O$ | $O$ |
| $P$ | $M$ | $F$ | $O$ | $F$ | $F$ | $F$ |
| $O$ | $F$ | $M$ | $P$ | $M$ | $F$ | $M$ |
| $F$ | $P$ | $P$ | $M$ | $M$ | $M$ | $F$ |
| $M$ | $O$ | $O$ | $F$ | $F$ | $M$ | $M$ |
The largest integer n of columns is therefore $\mathrm{n}=7$.
Graders' Comments
The exercise is generally well done; students have understood that the constraint is that each column adds 4 pairs of identical letters, but few have provided a fully rigorous proof of this fact. Some have given a set of 7 columns and justified that 7 is optimal because it was not possible to add a column to what they had done. However, this justification is not sufficient. Indeed, just because the construction cannot be enlarged does not mean that its size is maximal: one can imagine a larger, very different construction from the one given.
|
7
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Martin cherche à remplir chaque case d'une grille rectangulaire ayant 8 lignes et n colonnes avec l'une des quatre lettres $\mathrm{P}, \mathrm{O}, \mathrm{F}$ et M de sorte que pour toute paire de lignes distinctes, il existe au plus une colonne telle que ses intersections avec les deux lignes sont des cases ayant la même lettre. Quel est le plus grand entier n tel que cela est possible?
|
Dans ce problème, on cherche le plus grand entier satisfaisant une certaine propriété. Supposons que l'on veuille montrer que le plus grand entier recherché est l'entier c. Pour montrer que $c$ est bien le plus grand entier, on va d'une part montrer que si un entier $n$ satisfait la propriété, alors $n \leqslant \mathrm{c}$ et d'autre part on va montrer que l'on peut trouver un tableau possédant exactement c colonnes. L'énoncé présente une hypothèse portant les lignes et les colonnes d'un tableau.
On commence par regarder les informations que l'on possède sur les lignes de ce tableau. Il y a 8 lignes donc il y a $\binom{8}{2}=28$ paires de lignes.
On regarde ensuite les informations dont on dispose sur les colonnes du tableau. Puisque l'hypothèse de l'énoncé évoque les lettres identiques au sein d'une même colonne, nous allons compter combien de paires de lettres identiques appartiennent à une même colonne. On fixe donc une colonne du tableau et on regarde combien de paires de lettres indetiques on peut réaliser au minimum. Après plusieurs essais sur une colonne de taille 8 , on conjecture qu'il y a toujours au moins 4 paires de lettres identiques au sein d'une même colonne. En effet, dans une colonne il y a 8 lettres donc une lettre apparaît au moins 2 fois.
- Si chaque lettre apparaît au plus 2 fois, alors chaque lettre apparaît exactement 2 fois puisqu'il y a 8 cases dans la colonne et 4 lettres possibles. On a donc 4 paires de lettres identiques dans la colonne.
- Si une lettre apparait exactement 3 fois, disons la lettre $P$, alors on peut former 3 paires de lettres $P$. Parmi les 5 lettres restantes, on a au moins une lettre parmi les lettres $O, F$ et $M$ qui apparaît deux fois d'après le principe des tiroirs, ce qui nous fournit une quatrième paire de lettres identiques.
- Si une lettre apparaît au moins 4 fois dans la colonne, disons la lettre $P$, on peut former 4 paires de lettres P .
Ainsi, dans une colonne, on peut toujours trouver 4 paires de lettres identiques. Donc pour chaque colonne, il y a au moins 4 paires de lignes telles que les intersections avec la colonne ont la même lettre. Mais d'après l'hypothèse de l'énoncé, une paire de lignes ne peut être associée qu'à au plus une colonne telle que ses intersections avec les deux lignes sont deux cases possédant la même lettre. On déduit qu'il y a au plus $4 \times n$ paires de lignes. Donc $4 \mathrm{n} \leqslant 28$ et $n \leqslant 7$.
Réciproquement, il existe une configuration avec les 7 colonnes suivantes :
| $P$ | $P$ | $P$ | $P$ | $P$ | $P$ | $P$ |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| $O$ | $O$ | $O$ | $O$ | $O$ | $P$ | $O$ |
| $F$ | $F$ | $F$ | $F$ | $O$ | $O$ | $P$ |
| $M$ | $M$ | $M$ | $M$ | $P$ | $O$ | $O$ |
| $P$ | $M$ | $F$ | $O$ | $F$ | $F$ | $F$ |
| $O$ | $F$ | $M$ | $P$ | $M$ | $F$ | $M$ |
| $F$ | $P$ | $P$ | $M$ | $M$ | $M$ | $F$ |
| $M$ | $O$ | $O$ | $F$ | $F$ | $M$ | $M$ |
Le plus grand entier n de colonnes est donc $\mathrm{n}=7$.
Commentaire des correcteurs
L'exercice est globalement bien réussi, les élèves ont bien compris que la contrainte était que chaque colonne rajoutait 4 paires de lettres identiques, mais peu ont fait une preuve totalement rigoureuse de ce fait. Certains ont donné un ensemble de 7 colonnes et justifié le fait que 7 était optimal car il n'était pas possible de rajouter une colonne à ce qu'ils avaient faits. Mais cette justification n'est pas suffisante. En
effet, ce n'est pas parce que la construction ne peut être agrandie que pour autant sa taille est maximale : on peut imaginer qu'il existe une construction plus grande très différente de celle donnée.
|
{
"exam": "French_envois",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T2",
"year": null
}
|
In 5 boxes, there are respectively 402, 403, 404, 405, and 406 stones. The only allowed operation is to take 4 stones from a pile that has at least 4 stones and put one stone in each of the other piles. What is the maximum number of stones that can be in a single pile?
|
The statement presents a sequence of operations and describes a certain initial situation. A first idea to try in this case is to look for an invariant.
A second idea is to test the statement for smaller values, for example, for piles of size $0,1,2,3$ and 4. After several trials, one notices that the piles always have, up to permutation, the sizes $0,1,2,3$ and 4. After testing on piles of size $1,2,3,4$ and 5, one realizes that the piles always have distinct values modulo 5. One hastens to prove this conjecture.
Removing 4 stones from a pile is equivalent, modulo 5, to adding 1. Since one adds one to each of the other piles, the values of the piles all increase by 1 modulo 5. Thus, if before the operation these values were distinct modulo 5, after the operation they will remain distinct modulo 5. We have thus determined our invariant.
Thus, the sum of the sizes of any 4 piles will never exceed $0+1+2+3=6$, and therefore no pile will ever contain more than $2020-6=2014$ stones.
Conversely, we must now prove that it is always possible to ensure that a pile contains 2014 stones after a finite number of operations. For this, it suffices to never touch the pile containing 404 stones, and to perform the operation on the other piles until it is no longer possible to perform a single operation. Thus, the remaining piles will have $0,1,2,3$ stones at the end of the process, so there will indeed be $2020-(0+1+2+3)=2014$ stones in the same pile.
## Comment from the Examiners
Many students are content with constructing the bound without showing that it is indeed optimal. In rarer cases, some students prove only the minimality without the attainability. Most proofs of optimality are based on work modulo 5, but some more original proofs avoid this, with work on the last operations (rarely perfectly executed).
|
2014
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
Dans 5 boites se trouvent respectivement 402,403, 404, 405 et 406 pierres. La seule opération autorisée est de prendre 4 pierres dans un tas ayant au moins 4 pierres et d'en mettre une dans chacun des autres tas. Quel est le plus grand nombre de pierre qu'il est possible d'avoir dans un seul tas?
|
L'énoncé présente une suite d'opérations et décrit une certaine situation initiale. Une première idée à essayer dans ce cas est de chercher un invariant.
Une deuxième idée est de tester l'énoncé pour des valeurs plus petites, par exemple pour des tas de taille $0,1,2,3$ et 4 . Après plusieurs essais, on remarque que les tas ont toujours, à permutation près, les tailles $0,1,2,3$ et 4 . Après avoir testé sur des tas de taille $1,2,3,4$ et 5 , on s'aperçoit que les tas ont toujours des valeurs distinctes deux à deux modulo 5 . On s'empresse de démontrer cette conjecture.
Enlever 4 pierres d'un tas revient, modulo 5, à en ajouter 1. Comme on en ajoute une dans chacun des autres tas, les valeurs des tas augmentent toutes de 1 modulo 5 . Ainsi, si avant l'opération ces valeurs étaient distinctes deux à deux modulo 5 , après l'opération elles resteront distinctes deux à deux modulo 5 . On a donc déterminé notre invariant.
Ainsi la somme des tailles de 4 tas quelconques ne pourra jamais dépasser $0+1+2+3=6$ et donc un tas quelconque ne pourra jamais contenir plus que $2020-6=2014$ pierres.
Réciproquement, nous devons désormais démontrer que l'on peut toujours faire en sorte qu'un tas contienne 2014 pierres au bout d'un nombre fini d'opérations. Pour cela, il suffit de ne jamais toucher au tas contenant 404 pierres, et de faire l'opération sur les autres tas jusqu'à ce que ce ne soit plus possible de faire une seule opération. Ainsi les tas restants auront $0,1,2,3$ pierres à la fin du procédé, donc il y aura bien $2020-(0+1+2+3)=2014$ pierres sur le même tas.
## Commentaire des correcteurs
Un grand nombre d'élèves se contente de la construction de la borne sans montrer qu'elle est effectivement optimale. Dans de plus rares cas, certains élèves ne prouvent que la minimalité sans l'atteignabilité. La majorité des preuves d'optimalité se basent sur un travail modulo 5 , mais certaines preuves plus originales s'en passent, avec un travail sur les dernières opérations (travail rarement parfaitement exécuté).
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T2",
"year": null
}
|
A bad wizard has imprisoned $n$ mathematicians. He has $n$ colors. The wizard places a hat of one of the $n$ colors on each mathematician's head; two hats can have the same color. Each mathematician can see the color of the hat of each of their colleagues but not their own. The mathematicians must then all at the same time announce the color of their hat. If at least one of the mathematicians guesses correctly, all the mathematicians are free. They can, of course, consult on a strategy before knowing the color of the other mathematicians' hats.
Propose a strategy that ensures the mathematicians will be freed.
|
First, we will encode the different pieces of information. For example, we number the colors from 1 to $n$ and also number the mathematicians from 1 to $n$. We denote $i_{1}, \ldots i_{n}$ as the colors of the mathematicians' hats.
Since a mathematician cannot see his own hat but only the hats of the others, he will have to declare a number that depends on the hats he observes. We can, for example, look for an expression that depends symmetrically on each of the hats.
An important piece of information that depends symmetrically on each of the hats is, for example, the sum of the numbers of all the hats, namely $i_{1}+i_{2}+\ldots i_{n}$. This sum has a certain remainder $s$ modulo $n$. Therefore, we have $i_{l} \equiv s-\sum_{j \neq l} i_{j} \bmod n$. We need to ensure that there exists an index $l$ such that mathematician $l$ declares the number $s-\sum_{j \neq l} i_{j} \bmod n$. We recognize in $\sum_{j \neq l} i_{j}$ the sum of the numbers of the hats seen by mathematician $l$.
Thus, if each mathematician numbered $k$ declares the number between 1 and $n$ congruent to $k-\sum_{j \neq k} i_{j} \bmod n$, then the mathematician whose number is congruent to $s$ modulo $n$ will declare the number $s-\sum_{j \neq s} i_{j}=i_{s} \bmod n$ which is the color of his hat. All the mathematicians are therefore freed!
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
Un mauvais sorcier a enfermé $n$ mathématiciens. Il dispose de $n$ couleurs. Le sorcier place sur la tête de chaque mathématicien un chapeau d'une des $n$ couleurs; deux chapeaux peuvent avoir la même couleur. Chaque mathématicien peut voir la couleur du chapeau de chacun de ses collègues mais pas la sienne. Les mathématiciens doivent alors tous en même en temps annoncer la couleur de leur chapeau. Si au moins un des mathématiciens devine correctement, tous les mathématiciens sont libres. Ils peuvent bien sûr se concerter sur une stratégie avant de connaître la couleur des chapeaux des autres mathématiciens.
Proposez une stratégie qui assure que les mathématiciens soient libérés.
|
Tout d'abord, nous allons coder les différentes informations. Par exemple, on numérote les couleurs de 1 à $n$ et on numérote les mathématiciens de 1 à $n$ également. On note $i_{1}, \ldots i_{n}$ les couleurs des chapeaux des mathématiciens.
Puisqu'un mathématicien ne peut pas voir son propre chapeau mais uniquement les chapeaux des autres, il va devoir déclarer un nombre qui dépend des chapeaux qu'il observe. On peut par exemple chercher une expression qui va dépendre de façon symétrique de chacun des chapeaux.
Une information importante et qui dépend de façon symétrique de chacun des chapeaux est par exemple la somme des numéros de tous les chapeaux, à savoir $i_{1}+i_{2}+\ldots i_{n}$. Cette somme admet un certain reste $s$ modulo $n$. On a donc $i_{l} \equiv s-\sum_{j \neq l} i_{j} \bmod n$. On doit donc s'assurer qu'il existe un indice $l$ tel que le mathématicien $l$ déclare le numéro $s-\sum_{j \neq l} i_{j} \bmod n$. On reconnaît dans $\sum_{j \neq l} i_{j}$ la somme des numéros des chapeaux vus par le mathématicien $l$.
Ainsi, si chaque mathématicien de numéro $k$ déclare le nombre entre 1 et $n$ congru à $k-\sum_{j \neq k} \dot{i}_{j} \bmod n$, alors le mathématicien dont le numéro est congru à $s$ modulo $n$ déclarera le numéro $s-\sum_{j \neq s} \mathfrak{i}_{j}=i_{s}$ $\bmod n$ qui est la couleur de son chapeau. Tous les mathématiciens sont donc libérés !
|
{
"exam": "French_envois",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 7",
"tier": "T2",
"year": null
}
|
A coloring of the integers $\{1,2, \cdots, 2020\}$ in blue and red is said to be pleasant if there do not exist two distinct integers in $\{1,2, \cdots, 2020\}$ of the same color whose sum is a power of 2. How many such colorings exist?
|
A first idea is to test the statement for smaller values, for example for a coloring of the integers from 1 to 7.
Let's color the numbers in order: to color 1, there is no apparent constraint, the same for coloring 2. However, since $3+1=4$, the color of 3 is imposed. To color 4, there is no apparent constraint because $4+3=7$, $4+2=6$, and $4+1=5$ are not powers of two. However, since $5+3=6+2=7+1=8$, the color of 5, 6, and 7 is imposed. By testing all possible colorings, we see that regardless of the colors chosen to color 1, 2, and 4, the resulting coloring is pleasant. We can therefore assume that a pleasant coloring is fixed once the colors of the powers of 2 are chosen and that any coloring of the powers of 2 can be extended to a pleasant coloring.
We will show that for any coloring of the powers of 2 between 1 and 2020, there exists a unique way to color the other numbers to obtain a pleasant coloring.
To do this, we will proceed by induction. Let's show that if we color the powers of 2 from 1 to N, then there is a unique pleasant way to color the other integers from 1 to N.
The result is clear for $N=1$.
Let N be such that the result is true for $N-1$. We color the powers of 2 from 1 to N. By the induction hypothesis, there is a unique pleasant way to color the other integers from 1 to $N-1$.
If $N=2^k$ for some integer k, then N is already colored and the coloring is pleasant: indeed, if $1 \leq \ell < 2^k$, then $2^k + \ell$ is not a power of 2 because $2^k < 2^k + \ell < 2^{k+1}$. Thus, in this case, there is a unique way to complete the coloring.
If N is not a power of 2, then $N=2^k + n$ with $1 \leq n < 2^k$ and k an integer. Then N cannot be colored the same color as $2^k - n$ because $N + 2^k - n = 2^{k+1}$. We therefore color N with the other color, and this is indeed the unique way to complete the coloring in a pleasant manner. The resulting coloring is pleasant: indeed, let t be an integer such that $1 \leq t < N$ and $t + N$ is a power of 2, we have $2^k < N \leq t + N < 2N = 2^{k+1} + 2n < 2^{k+1} + 2^{k+1} = 2^{k+2}$, so $t + N = 2^{k+1}$. Therefore, $t = 2^{k+1} - 2^k - n = 2^k - n$. Since we have colored N and $2^k - n$ with different colors, the coloring is pleasant.
There are 11 powers of 2 between 1 and 2020, which are $1=2^0, 2=2^1, \cdots, 1024=2^{10}$, and there are $2^{11}$ ways to color them in blue and red. Thus, there are $2^{11}$ pleasant colorings.
Comment from the graders
Most students recognized the importance of the powers of 2. Some proposed alternatively to look at elements congruent to $2^n$ modulo $2^{n+1}$, which also worked. Many proved that there were at most 2048 colorings, but very few verified that the colorings thus produced were suitable, which was, however, an important part of the exercise. It is important to detail the arguments used: for example, making an induction is a good idea when you want to generalize something.
|
2^{11}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Un coloriage des entiers $\{1,2, \cdots, 2020\}$ en bleu et rouge est dit agréable s'il n'existe pas deux entiers distincts dans $\{1,2, \cdots, 2020\}$ de même couleur dont la somme est une puissance de 2 . Combien de tels coloriage existent-ils?
|
Une première idée est de tester l'énoncé pour des valeurs plus petites, par exemple pour un coloriage des entiers de 1 à 7 .
Colorions dans l'ordre les nombres : pour colorier 1, on n'a pas de contrainte apparente, idem pour colorier 2 . Par contre comme $3+1=4$, la couleur de 3 est imposée. Pour colorier 4 , il n'y a pas de contrainte apparente car $4+3=7,4+2=6$ et $4+1=5$ ne sont pas des puissances de deux. Par contre comme $5+3=6+2=7+1=8$, la couleur de 5,6 et 7 est imposée. En testant tous les coloriages possibles, on voit que peu importe les couleurs choisies pour colorier 1, 2 et 4 , le coloriage obtenu est agréable. On peut donc supposer qu'un coloriage agréable est fixé une fois la couleur des puissances de 2 est choisie et que tout coloriage des puissances de 2 peut être prolonger en un coloriage agréable.
Nous allons montrer que pour tout coloriage des puissances de 2 entre 1 et 2020, il existe une unique manière de colorier les autres nombres de sorte à obtenir un coloriage agréable.
Pour cela nous allons procéder par récurrence. Montrons que si on colorie les puissances de 2 de 1 à N , alors il existe une unique manière agréable de colorier les autres entiers de 1 à N .
Le résultat est clair pour $N=1$.
Soit N tel que le résultat soit vrai pour $\mathrm{N}-1$. On colorie les puissances de 2 de 1 à N . Par hypothèse de récurrence, il existe une unique manière agréable de colorier les autres entiers de 1 à $\mathrm{N}-1$.
Si $\mathrm{N}=2^{\mathrm{k}}$ pour un certain entier k , alors N est déjà colorié et le coloriage est agréable : en effet si $1 \leqslant \ell<2^{k}$, alors $2^{k}+\ell$ n'est pas une puissance de 2 car $2^{k}<2^{k}+\ell<2^{k+1}$. Ainsi dans ce cas il y a une unique manière de compléter le coloriage.
Si $N$ n'est pas une puissance de 2 , alors $N=2^{k}+n$ avec $1 \leqslant n<2^{k}$ et $k$ un entier. Alors $N$ ne peut pas être colorié de la même couleur que $2^{k}-n$ car $N+2^{k}-n=2^{k+1}$. On colorie donc N de l'autre couleur, et c'est bien l'unique manière de compléter le coloriage de manière agréable. Le coloriage obtenu est agréable : en effet soit $t$ entier tel que $1 \leqslant t<N$ et $t+N$ est une puissance de 2 , on a $2^{k}<\mathrm{N} \leqslant \mathrm{t}+\mathrm{N}<2 \mathrm{~N}=2^{\mathrm{k}+1}+2 \mathrm{n}<2^{\mathrm{k}+1}+2^{\mathrm{k}+1}=2^{\mathrm{k}+2}$, donc $\mathrm{t}+\mathrm{N}=2^{\mathrm{k}+1}$. On a donc $\mathrm{t}=2^{\mathrm{k}+1}-2^{k}-\mathrm{n}=2^{k}-\mathrm{n}$. Comme on a colorié N et $2^{k}-\mathrm{n}$ de deux couleurs différentes, le coloriage est agréable.
Il y a 11 puissances de 2 entre 1 et 2020 qui sont $1=2^{0}, 2=2^{2}, \cdots, 1024=2^{10}$, et il y a $2^{11}$ manières de les colorier en bleu et rouge. Ainsi il y a $2^{11}$ coloriages agréables.
Commentaire des correcteurs
La majorité des élèves a vu l'importance des puissances de 2 . Certains ont proposé alternativement de regarder les éléments congrus à $2^{n}$ modulo $2^{n+1}$ ce qui fonctionnait aussi. Nombreux sont ceux qui ont prouvé qu'il y avait au plus 2048 coloriages, mais très peu ont vérifié que les coloriages ainsi produit convenaient, alors que c'était pourtant une partie importante de l'exercice. Il faut penser à détailler les arguments utilisés : par exemple faire une récurrence est une bonne idée quand on veut généraliser quelque chose.
|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "\nExercice 8.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 8",
"tier": "T2",
"year": null
}
|
Let n be an integer. We have n colors, and each point on a circle is colored with one of these colors. Show that there exist two parallel lines that intersect the circle at 4 distinct points of the same color.
|
The statement asks us to prove an existence, and we can try to show this existence using the pigeonhole principle. Keeping this information in mind, we try to translate the required result.
Consider two parallel lines cutting the circle at 4 distinct points. These 4 points delimit a quadrilateral with two parallel sides, and the perpendicular bisectors of these two segments are coincident: indeed, they are perpendicular to two parallel sides, so they are parallel, and they pass through the center of the circle, so they are indeed coincident. The quadrilateral is therefore an isosceles trapezoid. It therefore has two equal sides and two diagonals of the same length.
Conversely, if 4 points $A, B, C$ and $D$ are in this order on a circle with center $O$ and delimit a quadrilateral such that $A B = C D$, then the perpendicular bisector of the segment $[\mathrm{BC}]$ is the axis of symmetry mapping $B$ to $C$. This axis of symmetry contains $O$ and thus the symmetry preserves the circle. Since $A B = C D$, this symmetry maps $A$ to $D$ and therefore the perpendicular bisector of the segment $[B C]$ is also that of the segment $[A D]$, and the quadrilateral $A B C D$ is an isosceles trapezoid.

Now suppose that $A C = B D$. Then the triangles $A O C$ and $D O B$ are isometric because one is obtained by applying a rotation to the other triangle. We deduce that $\mathrm{BC} = A D$ and that the quadrilateral $A B C D$ is an isosceles trapezoid again.
We now seek to show that there exist two pairs of points $(A, B)$ and $(C, D)$, all of the same color, such that $A B = C D$. According to the previous discussion, these points would then be the vertices of an isosceles trapezoid.
For such an exercise, known as combinatorial geometry, it is good to always think of regular objects, for example, circles or regular polygons. Here, thinking of such objects is relevant since regular polygons are inscribed in a circle.
To combine this idea with the pigeonhole principle, we will consider $(\mathrm{n}+1)$-gons. An $(n+1)$-gon on the circle, by the pigeonhole principle, has two vertices of the same color. We have thus obtained a pair of vertices of the same color.
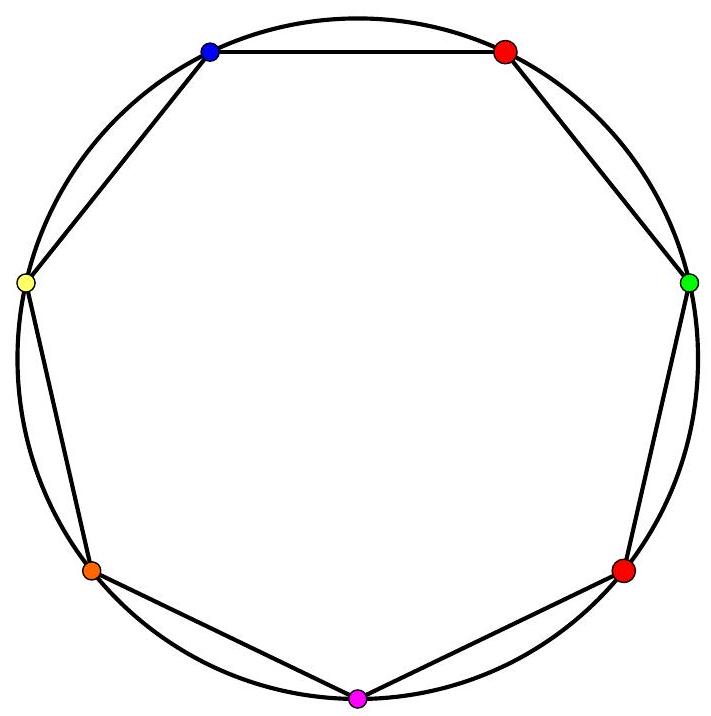
We will call the color of the pair the common color of the two vertices and the distance of the pair the distance between its two vertices. We will create more such pairs. Do not forget that we would like the distances of the different pairs we create to be the same. In an $(\mathrm{n}+1)$-gon, there are $\left\lfloor\frac{\mathfrak{n}+1}{2}\right\rfloor$ distinct possible distances between any two vertices. To obtain two pairs of the same distance, we therefore need $\left\lfloor\frac{\mathrm{n}+1}{2}\right\rfloor+1$ regular polygons.
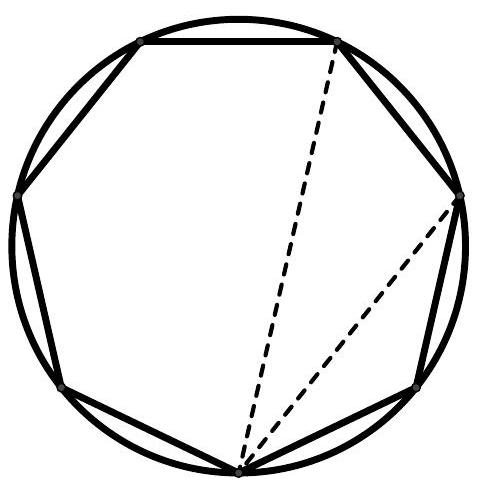
Do not forget that we also want the colors of the pairs to be identical. Thus, we take $\mathrm{n} \cdot\left\lfloor\frac{\mathrm{n}+1}{2}\right\rfloor+1(\mathrm{n}+1)$-gons that are disjoint and inscribed in the circle. We then obtain $n \cdot\left\lfloor\frac{\mathrm{n}+1}{2}\right\rfloor+1$ pairs of distinct vertices, and the vertices of the same pair are of the same color and their distance belongs to a set of size $\left\lfloor\frac{n+1}{2}\right\rfloor$. According to the pigeonhole principle, there are therefore $n+1$ pairs of vertices of the same distance among these pairs. Since there are $n$ colors, again by the pigeonhole principle, among these $n+1$ pairs of the same distance, there are at least 2 of the same color. We have thus obtained two pairs of the same distance and the same color, so we have 4 points $A, B, C$ and $D$ of the same color such that $A B = C D$. Thus, we have two parallel lines cutting the circle at 4 points of the same color.
Comment from the graders
The exercise, clearly too difficult, was not solved by anyone. Only one student thought to use an $(\mathrm{n}+1)$-gon to apply the pigeonhole principle, but it was necessary to continue and correctly count the different distances between any two vertices of an $(n+1)$-gon and then think about considering several $(\mathrm{n}+1)$-gons. A few students thought to reduce the parallelism condition to a condition on arc lengths.
## Senior Exercises
|
proof
|
Yes
|
Incomplete
|
proof
|
Combinatorics
|
Soit n un entier. On dispose de n couleurs, et chaque point d'un cercle est colorié de l'une de ces couleurs. Montrer qu'il existe deux droites parallèles qui intersectent le cercle en 4 points distincts de même couleur
|
L'énoncé nous demande de démontrer une existence, on peut essayer de montrer cette existence à l'aide du principe des tiroirs. Gardant cette information en tête, on essaye de traduire le résultat demandé.
Considérons deux droites parallèles coupant le cercle en 4 points distincts. Ces 4 points délimitent un quadrilatère dont deux côtés sont parallèles et les médiatrices de ces deux segments sont confondues : en effet, elles sont perpendiculaires à deux côtés parallèles donc elles sont parallèles et elles passent par le centre du cercle donc elles sont bien confondues. Le quadrilatère est donc un trapèze isocèle. il possède donc deux côtés égaux et deux diagonales de même longueur.
Réciproquement, si 4 points $A, B, C$ et $D$ sont dans cet ordre sur un cercle de centre $O$ et délimitent un quadrilatère tels que $A B=C D$, alors la médiatrice du segment $[\mathrm{BC}]$ est l'axe de la symétrie envoyant $B$ sur $C$. Cet axe de symétrie contient $O$ donc la symétrie conserve le cercle. Puisque $A B=C D$, cette symétrie envoye $A$ sur $D$ et donc la médiatrice du segment $[B C]$ est aussi celle du segment $[A D]$ et le quadrilatère $A B C D$ est un trapèze isocèle.

On suppose désormais que $A C=B D$. Alors les triangles $A O C$ et $D O B$ sont isométriques car l'un est obtenu en appliquant une rotation sur l'autre triangle. On déduit que $\mathrm{BC}=A D$ et que la quadrilatère $A B C D$ est un trapèze isocèle à nouveau.
On cherche donc désormais à montrer qu'il existe deux paires de points $(A, B)$ et $(C, D)$, tous de même couleur, telles que $A B=C D$. D'après la discussion précédente, ces points seraient alors les sommets d'un trapèze isocèle.
Pour un tel exercice, dit de géométrie combinatoire, il est bon de penser toujours à des objets réguliers, par exemple à des cercles ou des polygones réguliers. Ici, penser à de tels objets est pertinent puisque les polygones réguliers sont inscriptibles dans un cercle.
Pour combiner cette idée avec celle du principe des tiroirs, nous allons considérer des $\mathrm{n}+1$-gones réguliers. Un $(n+1)$-gone régulier sur le cercle, d'après le principe des tiroirs, possède deux sommets de même couleur. On a donc obtenu une paire de sommets de même couleur.

On appellera couleur de la paire la couleur commune des deux sommets et distance de la paire la distance entre ses deux sommets. On va créer plus de telles paires. N'oublions pas que nous aimerions que la distance des différentes paires que nous créons soit la même. Or, dans un $\mathrm{n}+1$-gone régulier, il y a $\left\lfloor\frac{\mathfrak{n}+1}{2}\right\rfloor$ distances distinctes possibles entre deux sommets quelconques. Pour obtenir deux paires de même distance, il faut donc $\left\lfloor\frac{\mathrm{n}+1}{2}\right\rfloor+1$ polygones réguliers.

N'oublions pas que nous désirons également que les couleurs des paires soient identiques. Ainsi, on prend $\mathrm{n} \cdot\left\lfloor\frac{\mathrm{n}+1}{2}\right\rfloor+1(\mathrm{n}+1)$-gones réguliers disjoints inscrits dans le cercle. On obtient alors $n \cdot\left\lfloor\frac{\mathrm{n}+1}{2}\right\rfloor+1$ paires de sommets tous distincts et les sommets d'une même paire sont de même couleur et leur distance appartient à un ensemble de taille $\left\lfloor\frac{n+1}{2}\right\rfloor$. D'après le principe des tiroirs, il y a donc parmi ces paires $n+1$ paires de sommets de même distance. Comme il y a $n$ couleurs, à nouveau d'après le principe des tiroirs, parmi ces $n+1$ paires de même distance, il y en a au moins 2 de même couleur. On a donc obtenu deux paires de même distance et de même couleur, on a donc 4 points $A, B, C$ et $D$ de même couleur tels que $A B=C D$. Ainsi, on a bien deux droites parallèles coupant le cercle en 4 points de même couleur.
Commentaire des correcteurs
L'exercice, manifestement trop difficile, n'a été résolu par personne. Un seul élève a pensé à utiliser un $\mathrm{n}+1$-gone régulier pour appliquer le principe des tiroirs, mais il fallait poursuivre et compter correctement les différentes distances entre deux sommets quelconques d'un $n+1$-gone puis penser à considérer plusieurs $\mathrm{n}+1$-gones. Quelques élèves ont pensé à ramener la condition de parallélisme à une condition sur les longueurs d'arc.
## Exercices Seniors
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-4.jsonl",
"solution_match": "## Solution de l'exercice 9",
"tier": "T2",
"year": null
}
|
We choose 5 divisors of $10^{2020}$. Show that there are two of them whose product is a square.
翻译结果如上,保留了原文的换行和格式。
|
We start by looking at the form an eventual divisor of $10^{2020}$ can take. The divisors of $10^{2020}$ are of the form $2^{\mathrm{a}} 5^{\mathrm{b}}$. The product of two divisors is therefore also a number of the form $2^{a} 5^{b}$ and it is a perfect square if and only if $a$ and $b$ are both even. We are thus reduced to proving the following result: if we have 5 pairs of integers $\left(a_{i}, b_{i}\right)$ with $1 \leqslant i \leqslant 5$ and the $a_{i}$ and $b_{i}$ all being less than or equal to 2020, then we can find two indices $j$ and $k$ such that $\left(a_{i}+a_{j}, b_{i}+b_{j}\right)$ is a pair of two even integers. We quickly check if this result is true for a few pairs of integers and now seek to prove this result. We are led to consider the parity of the integers in question. There are 4 possibilities for a pair $(a, b):$ either $a$ and $b$ are even, or $a$ and $b$ are odd, or $a$ is even and $b$ is odd, or $a$ is odd and $b$ is even. Thus, by the pigeonhole principle, if we choose 5 pairs of integers $(a_{i}, b_{i})$ with $1 \leqslant i \leqslant 5$, there are two pairs $(a_{j}, b_{j})$ and $\left(a_{k}, b_{k}\right)$ having the same characteristic, that is, such that $a_{j}$ and $a_{k}$ are of the same parity and $b_{j}$ and $b_{k}$ are of the same parity. Then $a_{j}+a_{k}$ and $b_{j}+b_{k}$ are both even. Thus, by choosing 5 divisors of $10^{2020}$, we can find 2 such that their product is a square.
Comment from the graders
The exercise is very well done. A recurring mistake is to misidentify the divisors of $10^{2020}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
On choisit 5 diviseurs de $10^{2020}$. Montrer qu'il y en a deux dont le produit est un carré.
|
On commence par regarder la forme que peut prendre un éventuel diviseur de $10^{2020}$. Les diviseurs de $10^{2020}$ sont de la forme $2^{\mathrm{a}} 5^{\mathrm{b}}$. Le produit de deux diviseurs est donc également un nombre de la forme $2^{a} 5^{b}$ et c'est un carré parfait si et seulement si $a$ et $b$ sont tous les deux pairs. On est donc ramené à montrer le résultat suivant : si on a 5 paires d'entiers $\left(a_{i}, b_{i}\right)$ avec $1 \leqslant i \leqslant 5$ et les $a_{i}$ et $b_{i}$ tous les deux inférieurs ou égaux à 2020, alors on peut trouver deux indices $j$ et $k$ tels que $\left(a_{i}+a_{j}, b_{i}+b_{j}\right)$ est un couple de deux nombres entiers pairs. On s'empresse de regarder si ce résultat est vrai pour quelques paires d'entiers et on cherche désormais à démontrer ce résultat. On est amené à regarder la parité des entiers considérés. Il y a 4 possibilités pour un couple $(a, b):$ soit $a$ et b sont pairs, soit $a$ et $b$ sont impairs, soit $a$ est pair et $b$ est pair, soit $a$ est impair et $b$ est pair. Ainsi par le principe des tiroirs, si on choisit 5 paires d'entiers ( $a_{i}, b_{i}$ ) avec $1 \leqslant i \leqslant 5$, il y a deux couples ( $a_{j}, b_{j}$ ) et $\left(a_{k}, b_{k}\right)$ possédant la même caractéristique, c'est-à-dire tels que $a_{j}$ et $a_{k}$ soient de le même parité et $b_{j}$ et $b_{k}$ soient de même parité. Alors $a_{j}+a_{k}$ et $b_{j}+b_{k}$ sont tous les deux paires. Ainsi, en choisissant 5 diviseurs de $10^{2020}$, on peut en trouver 2 tels que leur produit soit un carré.
Commentaire des correcteurs
L'exercice est très bien réussi. Une erreur récurrente est de mal identifier les diviseurs de $10^{2020}$.
|
{
"exam": "French_envois",
"problem_label": "10",
"problem_match": "## Exercice 10.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 10",
"tier": "T2",
"year": null
}
|
At a party, 2019 people sit around a round table, distributing themselves evenly. After sitting down, they notice that a card indicating a name is placed at each seat, and no one is sitting at the seat where their name is written. Show that the table can be rotated so that two people end up sitting in front of their name.
|
We start by testing the statement with smaller values, for example, for a party of 5 people.
Then, we try to encode the information. We call a rotation a configuration obtained after rotating the table from its original position. For a rotation $r$, we associate $n(r)$ the number of people sitting opposite their name after the rotation.
Since for every person there is a unique rotation that makes them sit opposite their name, $\sum_{r=0}^{2018} n(r)=$ 2019. There are 2019 rotations, and the null rotation satisfies $n(r)=0$. Therefore, since 2018 positive integers have a sum of 2019, one of them must be at least 2 by the pigeonhole principle, which means that a rotation indeed brings two names opposite the correct people.
Comment from the graders
The problem is very well executed. When applying the pigeonhole principle, it is not necessary to specify which are the socks and which are the drawers when the situation is sufficiently clear.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Lors d'une fête, 2019 personnes s'assoient autour d'une table ronde, en se répartissant de façon régulière. Après s'être assises, elles constatent qu'un carton indiquant un nom est posé à chacune des places et que personne n'est assis à la place où figure son nom. Montrer qu'on peut tourner la table de telle sorte que deux personnes se retrouvent assises en face de leur nom.
|
On commence par tester l'énoncé sur des valeurs plus petites, par exemple pour une fête de 5 personnes.
Ensuite, on essaye de coder l'information. On appelle rotation une configuration obtenue après avoir tourné la table depuis sa position d'origine. À une rotation $r$, on associe $n(r)$ le nombre de personnes assises face à leur nom après la rotation.
Comme pour toute personne il existe une unique rotation qui la rend assise face à son nom, $\sum_{r=0}^{2018} n(r)=$ 2019. Or il y a 2019 rotations et la rotation nulle vérifie $n(r)=0$. Donc comme 2018 entiers positifs ont pour somme 2019, l'un d'eux vaut donc au moins 2 par principe des tiroirs, ce qui signifie bien qu'une rotation amène deux noms en face des bonnes personnes.
Commentaire des correcteurs
Le problème est très bien réussi. Lorsque l'on applique le principe des tiroirs, il n'est pas nécessaire de préciser qui sont les chaussettes et qui sont les tiroirs lorsque la situation est suffisamment claire.
|
{
"exam": "French_envois",
"problem_label": "11",
"problem_match": "\nExercice 11.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 11",
"tier": "T2",
"year": null
}
|
Martin is trying to fill each cell of a rectangular grid with 8 rows and $n$ columns with one of the four letters $\mathrm{P}, \mathrm{O}, \mathrm{F}$, and M such that for any pair of distinct rows, there is at most one column where the intersections of the two rows are cells with the same letter. What is the largest integer $n$ for which this is possible?
|
In this problem, we are looking for the largest integer satisfying a certain property. Suppose we want to show that the largest integer sought is the integer c. To show that c is indeed the largest integer, we will on the one hand show that if an integer n satisfies the property, then $n \leqslant c$, and on the other hand, we will show that we can find a table with exactly c columns.
The statement presents a hypothesis about the rows and columns of a table.
We start by looking at the information we have about the rows of this table. There are 8 rows, so there are $\binom{8}{2}=28$ pairs of rows.
We then look at the information we have about the columns of the table. Since the hypothesis in the statement mentions identical letters within the same column, we will count how many pairs of identical letters belong to the same column. We fix a column of the table and see how many pairs of identical letters we can form at a minimum. After several trials on a column of size 8, we conjecture that there are always at least 4 pairs of identical letters within the same column. Indeed, in a column, there are 8 letters, so a letter appears at least 2 times.
- If each letter appears at most 2 times, then each letter appears exactly 2 times since there are 8 cells in the column and 4 possible letters. We therefore have 4 pairs of identical letters in the column.
- If a letter appears exactly 3 times, say the letter $P$, then we can form 3 pairs of letters $P$. Among the 5 remaining letters, at least one of the letters $O, F$, and $M$ appears twice according to the pigeonhole principle, which gives us a fourth pair of identical letters.
- If a letter appears at least 4 times in the column, say the letter $P$, we can form 4 pairs of letters P.
Thus, in a column, we can always find 4 pairs of identical letters. Therefore, for each column, there are at least 4 pairs of rows such that the intersections with the column have the same letter. But according to the hypothesis of the statement, a pair of rows can be associated with at most one column such that its intersections with the two rows are two cells containing the same letter. We deduce that there are at most $4 \times n$ pairs of rows. So $4 \mathrm{n} \leqslant 28$ and $\mathrm{n} \leqslant 7$.
Conversely, there exists a configuration with the following 7 columns:
| $P$ | $P$ | $P$ | $P$ | $P$ | $P$ | $P$ |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| $O$ | $O$ | $O$ | $O$ | $O$ | $P$ | $O$ |
| $F$ | $F$ | $F$ | $F$ | $O$ | $O$ | $P$ |
| $M$ | $M$ | $M$ | $M$ | $P$ | $O$ | $O$ |
| $P$ | $M$ | $F$ | $O$ | $F$ | $F$ | $F$ |
| $O$ | $F$ | $M$ | $P$ | $M$ | $F$ | $M$ |
| $F$ | $P$ | $P$ | $M$ | $M$ | $M$ | $F$ |
| $M$ | $O$ | $O$ | $F$ | $F$ | $M$ | $M$ |
The largest integer n of columns is therefore $\mathrm{n}=7$.
Examiner's Comment
Many students managed to find the answer $\mathrm{n}=7$ and provided an example. Most propose a correct argument to show that it is optimal, but sometimes this reasoning is written in a somewhat unclear manner.
|
7
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Martin cherche à remplir chaque case d'une grille rectangulaire ayant 8 lignes et $n$ colonnes avec l'une des quatre lettres $\mathrm{P}, \mathrm{O}, \mathrm{F}$ et M de sorte que pour toute paire de lignes distinctes, il existe au plus une colonne telle que ses intersections avec les deux lignes sont des cases ayant la même lettre. Quel est le plus grand entier n tel que cela est possible?
|
Dans ce problème, on cherche le plus grand entier satisfaisant une certaine propriété. Supposons que l'on veuille montrer que le plus grand entier recherché est l'entier c. Pour montrer que c est bien le plus grand entier, on va d'une part montrer que si un entier n satisfait la propriété, alors $n \leqslant c$ et d'autre part on va montrer que l'on peut trouver un tableau possédant exactement c colonnes.
L'énoncé présente une hypothèse portant les lignes et les colonnes d'un tableau.
On commence par regarder les informations que l'on possède sur les lignes de ce tableau. Il y a 8 lignes donc il y a $\binom{8}{2}=28$ paires de lignes.
On regarde ensuite les informations dont on dispose sur les colonnes du tableau. Puisque l'hypothèse de l'énoncé évoque les lettres identiques au sein d'une même colonne, nous allons compter combien de paires de lettres identiques appartiennent à une même colonne. On fixe donc une colonne du tableau et on regarde combien de paires de lettres indetiques on peut réaliser au minimum. Après plusieurs essais sur une colonne de taille 8 , on conjecture qu'il y a toujours au moins 4 paires de lettres identiques au sein d'une même colonne. En effet, dans une colonne il y a 8 lettres donc une lettre apparaît au moins 2 fois.
- Si chaque lettre apparait au plus 2 fois, alors chaque lettre apparaît exactement 2 fois puisqu'il y a 8 cases dans la colonne et 4 lettres possibles. On a donc 4 paires de lettres identiques dans la colonne.
- Si une lettre apparaît exactement 3 fois, disons la lettre $P$, alors on peut former 3 paires de lettres $P$. Parmi les 5 lettres restantes, on a au moins une lettre parmi les lettres $O, F$ et $M$ qui apparaît deux fois d'après le principe des tiroirs, ce qui nous fournit une quatrième paire de lettres identiques.
- Si une lettre apparaît au moins 4 fois dans la colonne, disons la lettre $P$, on peut former 4 paires de lettres P .
Ainsi, dans une colonne, on peut toujours trouver 4 paires de lettres identiques. Donc pour chaque colonne, il y a au moins 4 paires de lignes telles que les intersections avec la colonne ont la même lettre. Mais d'après l'hypothèse de l'énoncé, une paire de lignes ne peut être associée qu'à au plus une colonne telle que ses intersections avec les deux lignes sont deux cases possédant la même lettre. On déduit qu'il y a au plus $4 \times n$ paires de lignes. Donc $4 \mathrm{n} \leqslant 28$ et $\mathrm{n} \leqslant 7$.
Réciproquement, il existe une configuration avec les 7 colonnes suivantes :
| $P$ | $P$ | $P$ | $P$ | $P$ | $P$ | $P$ |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| $O$ | $O$ | $O$ | $O$ | $O$ | $P$ | $O$ |
| $F$ | $F$ | $F$ | $F$ | $O$ | $O$ | $P$ |
| $M$ | $M$ | $M$ | $M$ | $P$ | $O$ | $O$ |
| $P$ | $M$ | $F$ | $O$ | $F$ | $F$ | $F$ |
| $O$ | $F$ | $M$ | $P$ | $M$ | $F$ | $M$ |
| $F$ | $P$ | $P$ | $M$ | $M$ | $M$ | $F$ |
| $M$ | $O$ | $O$ | $F$ | $F$ | $M$ | $M$ |
Le plus grand entier n de colonnes est donc $\mathrm{n}=7$.
Commentaire des correcteurs
De nombreux élèves ont réussi à trouver la réponse $\mathrm{n}=7$ et ont exhibé un exemple. La plupart proposent un argument correct pour montrer que c'est optimal, mais parfois ce raisonnement est rédigé de façon peu claire.
|
{
"exam": "French_envois",
"problem_label": "12",
"problem_match": "\nExercice 12.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 12",
"tier": "T2",
"year": null
}
|
Let $\mathrm{N}>1$. Alice and Bob play the following game. 2 N cards numbered from 1 to 2 N are shuffled and then arranged in a line, with the numbered faces visible. Taking turns, Alice and Bob choose a card, either the one all the way to the right or the one all the way to the left of the line, and keep it for themselves, until all the cards have been taken. Alice starts. At the end of the game, each player calculates the sum of the numbers on the cards they have taken. The player with the highest sum wins. Does either player have a way to ensure they do not lose?
|
We start by testing the game for small values, for example, for a game consisting of $2 \cdot 3$ cards. After several trials, we notice, for example, that the strategy of always taking the largest card among the card at the far left and the card at the far right does not always work, for either player.
Let's test the case $\mathrm{N}=2$. Each of the two players will only take two cards. In this type of problem, a first idea is to try to find a strategy that allows a player to play as they wish, regardless of the opponent's moves. So let's look at the cards Alice and Bob can ensure they obtain. We denote XYZW the cards laid out in a row in this order. Suppose Alice takes the card $X$. If Bob chooses the card Y, Alice has the choice between the cards Z and W. If Bob chooses the card $W$, Alice has the choice between the cards $Z$ and $Y$. Thus, by choosing the card X, Alice ensures she can take the card $Z$ if she wishes. However, before Alice's first move, Bob cannot guarantee taking any of the four cards.
We now want to generalize this process. Let's look at the case $N=3$. The cards are XYZWUV. We notice that if Alice takes the card $X$ on the first turn, she ensures she can take the cards $Z$ and $U$ if she wants. These observations are sufficient to think that Alice has a winning strategy by taking the cards $X, Z, U$ if $X+Z+U>Y+W+V$ and taking the cards $Y, W, V$ otherwise. We now prove that this strategy works in the general case.
Alice colors every other card black (the card all the way to the right is white, the one all the way to the left is black). She calculates the sum of the numbers on the white cards and the sum of the numbers on the black cards.
If the sum of the white cards is greater, she chooses the white card all the way to the right. Bob will necessarily take a black card next. At each turn, Alice can choose between a white or black card, and by taking the white one, she leaves Bob no choice but to take a black card.
Thus, at the end, Alice will have all the white cards and Bob will have all the black cards. Therefore, she will have a score greater than or equal to Bob's. She proceeds similarly if the sum of the black cards is greater.
Comment from the graders
Most students were able to find the correct strategy. Among those who did not, many proposed a "turn-by-turn" strategy without justifying that it would prevent losing. Such an approach cannot solve the problem.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Soit $\mathrm{N}>1$. Alice et Bob jouent au jeu suivant. 2 N cartes numérotées de 1 à 2 N sont mélangées puis disposées dans une ligne, de manière à ce que les faces numérotées soient visibles. Chacun à leur tour, Alice et Bob choisissent une carte, soit celle tout à droite soit celle soit à gauche de la ligne, et la garde pour eux, jusqu'à ce que toutes les cartes aient été prises. Alice commence. A la fin du jeu, chaque joueur calcule la somme des numéros des cartes qu'il a prises. Le joueur ayant la plus grande somme gagne. Un joueur dispose-t-il d'une façon de ne pas perdre?
|
On commence par tester le jeu pour des petites valeurs, par exemple pour un jeu composé de $2 \cdot 3$ cartes. Après plusieurs essais, on s'aperçoit par exemple que la stratégie qui consiste à prendre toujours la plus grande carte parmi la carte située la plus à gauche et la carte située la plus à droite ne fonctionne pas toujours, pour aucun des deux joueurs.
Testons le cas $\mathrm{N}=2$. Chacun des deux joueurs ne pourra prendre que deux cartes. Dans ce type de problème, une première idée est d'essayer de chercher une stratégie qui permet à un joueur de jouer comme il le souhaite, quelque soit les coups de l'adversaire. Regardons donc les cartes qu'Alice et Bob peuvent s'assurer d'obtenir. On note XYZW les cartes étalées sur la rangée dans cet ordre. Supposons qu'Alice prenne la carte $X$. Si Bob choisit la carte Y, Alice a le choix entre les cartes Z et W. Si Bob choisit la carte $W$, Alice a le choix entre les cartes $Z$ et $Y$. Ainsi, en choisissant la carte X, Alice s'assure de pouvoir prendre la carte $Z$ si elle le souhaite. En revanche, avant le premier coup d'Alice, Bob ne peut pas garantir de prendre une des quatre cartes.
On désire désormais généraliser ce processus. On regarde alors le cas $N=3$. Les cartes sont XYZWUV. On s'aperçoit alors que si Alice prend la carte $X$ au premier tour, elle s'assure de pouvoir prendre les cartes $Z$ et $U$ si elle le veut. Ces remarques sont suffisantes pour penser qu' Alice dispose d'une stratégie gagnante en récupérant les cartes $X, Z, U$ si $X+Z+U>Y+W+V$ et en récupérant les cartes $Y, W, V$ dans le cas contraire. On prouve à présent que cette stratégie fonctionne dans le cas général.
Alice colorie une carte sur deux en noir (la carte toute à droite est blanche, celle toute à gauche est noire). Elle calcule la somme des numéros des cartes blanches et celle de numéros des cartes noires.
Si la somme des blanches est plus grande, elle choisit la carte blanche tout à droite. Bob prendra obligatoirement une carte noire ensuite. A chaque tour Alice peut choisir entre une carte blanche ou noire et en prenant la blanche, elle ne laisse pas la choix à Bob, qui prendra forcément une carte noire.
Ainsi à la fin Alice aura toutes les cartes blanches et Bob toutes les cartes noires. Donc elle aura un score supérieur ou égal à celui de Bob. Elle procède de même si la somme des cartes noires est plus grande.
Commentaire des correcteurs
La majorité des élèves a su trouver la bonne stratégie. Parmi ceux qui ne l'ont pas trouvée, beaucoup ont proposé une stratégie "au tour par tour", sans justifier qu'elle permettait de ne pas perdre. Une telle approche ne peut pas permettre de résoudre l'exercice.
|
{
"exam": "French_envois",
"problem_label": "13",
"problem_match": "\nExercice 13.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 13",
"tier": "T2",
"year": null
}
|
Consider a grid of size $2019 \times 2019$. On this grid, pebbles are placed. A configuration is said to be beautiful if there does not exist a parallelogram formed by four pebbles $A B C D$, such that $A, B, C$, and $D$ are not all aligned.
What is the maximum number of pebbles that can be placed on the grid?
|
In this problem, we are looking for the largest integer satisfying a certain property. Suppose we want to show that the largest integer sought is the integer c. To show that c is indeed the largest integer, we will first show that if an integer n satisfies the property, then $\mathrm{n} \leqslant \mathrm{c}$, and secondly, we will show that we can find a grid with exactly c pebbles satisfying the property.
We quickly test the statement for smaller values, for example, for a grid of size $3 \times 3$, $4 \times 4$, or even $5 \times 5$, in order to guess the value. We find in these small cases that the largest integers are 5, 7, and 9, respectively. We can conjecture that the value sought will therefore be $2 \times 2019-1=4037$. By testing these small values, we have noticed that the presence of pebbles in a column forces certain positions to be empty. We will therefore try to formalize this reasoning.
We consider pairs of pebbles that are in the same column. If there are two such pairs whose pebbles are at the same distance on different columns, then we obtain a parallelogram, which we want to avoid.
Let $n_{i}$ be the number of pebbles in the $i$-th column. Consequently, there are at least $n_{i}-1$ pairs with distinct distances on column $i$. Since for two fixed columns, the distance between any two pebbles in the first column must be different from the distance between any two pebbles in the second column, all the distances between pairs of pebbles in the same column must be distinct. This gives a total of $\left(n_{1}-1\right)+\left(n_{2}-1\right)+\cdots+\left(n_{2019}-1\right)=n-2019$ distinct distances with n being the total number of pebbles. However, there are at most 2018 possible distances, since there are 2019 positions for a pebble in a column. This shows that $\mathrm{n} \leqslant 2018+2019=4037$.
Conversely, if we fill each cell in the first row with a pebble and each cell in the first column with a pebble and leave the other cells empty, we then place $2 \times 2019-1=4037$ pebbles without creating any parallelograms.
The largest integer sought is therefore 4037.
Grader's Comments
Many students had the right idea to solve the problem, but many had difficulty formalizing the result correctly. If one attempts to solve this problem by induction, one must explicitly state the grids being manipulated and be careful that a sub-grid of a "maximal" grid is not necessarily maximal.
|
4037
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On considère une grille de taille $2019 \times 2019$. Sur cette grille sont posés des cailloux. Une configuration est dite belle s'il n'existe pas de parallélogramme formé par quatre cailloux $A B C D$, tels que $A, B, C$, et $D$ ne soient pas tous alignés.
Quel est le plus grand nombre de cailloux qu'il est possible de mettre dans une grille?
|
Dans ce problème, on cherche le plus grand entier satisfaisant une certaine propriété. Supposons que l'on veuille montrer que le plus grand entier recherché est l'entier c. Pour montrer que c est bien le plus grand entier, on va d'une part montrer que si un entier n satisfait la propriété, alors $\mathrm{n} \leqslant \mathrm{c}$ et d'autre part on va montrer que l'on peut trouver une grille possédant exactement c cailloux satisfaisant la propriété.
On s'empresse de tester l'énoncé pour des valeurs plus petites, par exemple pour une grille de taille $3 \times 3$, $4 \times 4$ ou même $5 \times 5$, afin de deviner la valeur. On trouve dans ces petits cas que les plus grands entiers sont respectivement 5, 7 et 9 . On peut conjecturer que la valeur recherchée sera donc $2 \times 2019-1=4037$. En testant ces petites valeurs, on a pu remarquer que la présence de cailloux sur une colonne forçait que certains emplacements soient vides. Nous allons donc essayer de formaliser ce raisonnement.
On considère les paires de cailloux qui sont sur la même colonne. S'il y a deux telles paires dont les cailloux sont à même distance sur des colonnes différentes alors on obtient un parallélogramme, ce que l'on veut éviter.
Soit $n_{i}$ le nombre de cailloux dans la $i$-ième colonne. Sur la colonne $i$ il y a par conséquent au moins $n_{i}-1$ paires à distances distinctes. Puisque pour deux colonnes fixées, la distance entre deux quelconques cailloux de la première colonne doit être différente de la distance entre deux quelconques cailloux de la deuxième colonne, toutes les distances entre deux paires de cailloux appartenant à la même colonne doivent être distinctes. Cela fait en tout $\left(n_{1}-1\right)+\left(n_{2}-1\right)+\cdots+\left(n_{2019}-1\right)=n-2019$ distances distinctes avec n le nombre total de cailloux. Or il y a au plus 2018 distances possibles, puisqu'il y a 2019 emplacements pour un cailloux dans une colonne. Ceci montre que $\mathrm{n} \leqslant 2018+2019=4037$.
Réciproquement, si on remplit chaque case de la première ligne par un caillou et chaque case de la première colonne par un caillou et on laisse les autres cases vides, on a alors placé $2 \times 2019-1=4037$ cailloux sans créer de parallélogrammes.
Le plus grand entier recherché est donc 4037.
Commentaire des correcteurs
Une grande partie des élèves a eu la bonne idée pour résoudre l'exercice, mais beaucoup ont eu du mal à formaliser le résultat correctement. Si on tente de résoudre cet exercice par récurrence, il faut expliciter les grilles que l'on manipule et faire attention au fait qu'une sous-grille d'une grille "maximale" n'est pas forcément maximale.
|
{
"exam": "French_envois",
"problem_label": "14",
"problem_match": "\nExercice 14.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 14",
"tier": "T2",
"year": null
}
|
A high school has an odd number of classes, and in each class, there is an odd number of students. One student is chosen from each class to be part of the student committee. If the number of classes with more boys than girls is odd, show that the number of ways to form a student committee containing an odd number of boys exceeds the number of ways to form a student committee containing an odd number of girls.
|
In the absence of ideas in the face of the problem, we can try to prove the result by induction. To see if this could work, we can look at what happens to the result when moving from a high school with 3 students to one with 4 students. We also check that the assumptions of the statement are suitable for induction. We realize that we will have to distinguish several cases, depending on the distribution of boys and girls in the different classes. We start the induction.
We will show the result by strong induction on the total number of students. If there are no students, then the result is true, as well as if there is only one student in the high school.
Suppose there are \( n \) students in total in classes satisfying the statement. Suppose the statement of the exercise is true whenever there are strictly fewer than \( n \) students. There are two cases to consider:
- If there is no class with a girl and a boy, then there is an odd number of classes with only boys and the other classes have only girls, so the committee will necessarily have an odd number of boys, and the statement is verified.
- If there is a class with a girl and a boy, let's call them Alice and Bob, respectively. If we remove Alice and Bob from the class, then there are more ways to choose the committee with an odd number of boys. If we consider only the committees with either Alice or Bob, then there are as many committees with an odd number of boys as with an odd number of girls: indeed, swapping Alice and Bob changes the parity of the number of boys and girls. Thus, the statement is verified.
By strong induction, the statement is verified regardless of the total number of students.
A slightly more clever solution is to proceed differently: let \( n \) be the number of classes, and let \( f_i \) and \( g_i \) be the number of girls and boys in class \( i \) for \( 1 \leq i \leq n \). Then the following quantity, when expanded, counts the number of ways to form a committee with an odd number of boys minus the number of ways to form a committee with an odd number of girls:
\[
\prod_{i=1}^{n}\left(g_{i}-f_{i}\right)
\]
But this product is positive if there is an odd number of classes with more boys than girls, which gives the desired result.
Comment from the graders:
Most students proceeded by induction on the number of classes, using the rearrangement inequality. Most did so correctly, but some wrote strict inequalities without justifying why the equality case does not occur (which requires citing one of the assumptions of the statement: the odd number of students per class).
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Un lycée comporte un nombre impair de classes, et, dans chaque classe, un nombre impair d'élèves. Un élève est choisi dans chaque classe pour faire parti du comité des élèves. Si le nombre de classes avec le plus de garçons que de filles est impair, montrer que le nombre de façons de former un comité des élèves contenant un nombre impair de garçons excède le nombre de façons de former un comité d'élèves contenant un nombre impair de filles.
|
En l'absence d'idées face au problème, on peut essayer de démontrer le résultat par récurrence. Pour regarder si cela pourrait fonctionner, on peut regarder ce qu'il advient du résultat si l'on passe d'un lycée avec 3 élèves à un lycée avec 4 élèves. On vérifie également que les hypothèses de l'énoncé sont adaptées à une récurrence. On s'aperçoit que nous allons devoir distinguer plusieurs cas, selon la répartition garçon/filles dans les différentes classes. On démarre donc la récurrence.
Nous allons montrer le résultat par récurrence forte sur le nombre d'élèves au total. S'il n'y a aucun élève, alors le résultat est vrai, de même s'il n'y a qu'un élève dans le lycée.
Supposons qu'il y ait n élèves en tout dans des classes satisfaisant l'énoncé. Supposons que l'énoncé de l'exercice est vrai dès lors qu'il y a strictement moins que n élèves. Il y a deux cas à étudier :
- S'il n'y a de classe avec une fille et un garçon, alors il y a un nombre impair de classe avec que des garçons et les autres classes n'ont que des filles, donc le comité aura nécessairement un nombre impair de garçons, l'énoncé est vérifié.
- S'il existe une classe avec une fille et un garçon, appelons-les respectivement Alice et Bob. Si on enlève Alice et Bob de la classe alors il y a plus de manières de choisir le comité avec un nombre impair de garçons. Si on considère uniquement les comités avec soit Alice soit Bob, alors on a autant de comité avec un nombre impair de garçons qu'avec un nombre impair de filles : en effet, échanger Alice et Bob change la parité du nombre de garçons et de filles. Ainsi l'énoncé est vérifié.
Par récurrence forte, l'énoncé est vérifié quelque soit le nombre total d'élèves.
Une solution un peu plus astucieuse consiste à procéder différemment : soit $n$ le nombre de classes, et soient $f_{i}$ et $g_{i}$ les nombres de filles et garçons dans la classe $i$ pour $1 \leqslant i \leqslant n$. Alors la quantité suivante, lorsqu'on la développ,e compte le nombre de façons de faire un comité avec un nombre impair de garçons moins celui de faire un comité avec un nombre impair de filles :
$$
\prod_{i=1}^{n}\left(g_{i}-f_{i}\right)
$$
Mais ce produit est positif s'il y a un nombre impair de classes avec plus de garçons que de filles, ce qui donne bien le résultat voulu.
Commentaire des correcteurs
Les élèves ont pour la plupart procédé par récurrence sur le nombre de classes, en utilisant l'inégalité de réordonnement. La plupart ont procédé de manière correcte, mais certains ont écrit des inégalités strictes sans justifier pourquoi le cas d'égalité ne se présente pas (qui demande de citer une des hypothèses de l'énoncé : le nombre impair d'élèves par classe).
|
{
"exam": "French_envois",
"problem_label": "15",
"problem_match": "\nExercice 15.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 15",
"tier": "T2",
"year": null
}
|
Consider a $2019 \times 2019$ grid. We denote by $C_{i, j}$ the cell in the i-th column and the j-th row for $1 \leqslant \mathfrak{i}, \mathfrak{j} \leqslant 2019$. A coloring of the grid is wonderful if there do not exist $1 \leqslant \mathfrak{i}<\ell \leqslant 2019$ and $1 \leqslant j<k \leqslant 2019$ such that the cells $C_{i, j}, C_{i, k}$ and $C_{\ell, j}$ are of the same color. What is the smallest integer N such that there exists a wonderful coloring with N colors?
|
In this problem, we are looking for the smallest integer satisfying a certain property. Suppose we want to show that the smallest integer sought is the integer c. To show that c is indeed the smallest integer sought, we will, on the one hand, show that if an integer $n$ satisfies the property, then $n \geqslant c$, and on the other hand, we will show that we can find a coloring with exactly c colors satisfying the property.
We quickly test the statement on smaller values, for example, for grids of size $3 \times 3$, $4 \times 4$, or even $5 \times 5$, to guess the minimal value in the general case, as well as a possible construction. We notice that for a $3 \times 3$ grid, we need at least 2 colors for a wonderful coloring. For a $5 \times 5$ grid, we observe that we need at least 3 colors. We conjecture that for N odd, we need at least $\frac{\mathrm{N}+1}{2}$.
The difficulty of the exercise lies in the fact that we first need to try to guess the minimal value before making the proof. In the absence of an idea for a direct proof that we need at least $\frac{\mathrm{N}+1}{2}$ colors, we can try to show by contradiction that a coloring with $\frac{\mathrm{N}-1}{2}$ colors will not be wonderful.
For this, we note that the data of two cells $C_{i, j} C_{l, j}$ (with $i<l$) of red color on a column $j$ prevents the cells of row $i$ and on a column $k \geqslant j$ from being red. We can say that these two cells generate a prohibition on row $i$. We can try to count these prohibitions. This count depends on the number of colors we use, which encourages us to reason by contradiction to show that a coloring with $\frac{\mathrm{N}-1}{2}$ colors will generate too many prohibitions.
Where to look for prohibitions? We can start by proceeding manually: we look at the minimum number of prohibitions generated by column 1, then the prohibitions generated by row 2, etc. This manual operation is performed again on small cases, such as a $5 \times 5$ or $7 \times 7$ grid. We notice at the end of these operations on small cases that the contradiction is obtained by looking at column N, on which there are always too many prohibitions. We will therefore formalize this reasoning by looking at the number of prohibitions.
We assume that we have a wonderful coloring of the grid with 1009 colors (even if some colors are not used for the coloring in question).
In the following, we will say that the pair $\left(C_{i, j}, C_{l, j}\right)$ generates a prohibition for the cell $C_{i, k}$ for color $c$ if the cells $C_{i, j}$ and $C_{l, j}$ are of color $c$, which prevents the cell $C_{i, k}$ from being of color c by hypothesis.
Let $j \leqslant 2018$ be a fixed column and let $k_{j}$ be the number of colors appearing on at least two cells of column $j$. For a color of number c, we denote $n_{c}$ the number of cells of column $j$ colored with color c. Up to renumbering the colors, we can assume that these are the colors $1, \ldots, \mathrm{k}_{\mathrm{j}}$ that appear at least 2 times and that the colors $k_{j+1}, \ldots, 1009$ appear at most once in the column.
Given a color $\mathrm{c} \leqslant \mathrm{k}_{\mathrm{j}}$, there are at least $\mathrm{n}_{\mathrm{c}}-1$ pairs of cells of color c in column j. Indeed, the cell of color c located at the bottom of the column forms a pair with each of the $n_{c}-1$ other cells of the column. Each of these pairs generates a prohibition for one of the cells of column 2019: the pair of cells $\left(C_{i, j}, C_{l, j}\right)(i<l)$ generates a prohibition for the cell $C_{i, 2019}$. Thus, the cells of column $j$ generate $\sum_{c=1}^{k_{j}}\left(n_{c}-1\right)$ prohibitions in the last column. Since the colors $k_{j+1}, \ldots, 1009$ occupy at most one cell in column $j$, we have at least
$$
\sum_{c=1}^{k_{j}}\left(n_{c}-1\right)=\sum_{c=1}^{k_{j}} n_{c}-k_{j} \geqslant 2019-\left(1009-k_{j}\right)-k_{j}=1010
$$
prohibitions generated in column 2019.
Thus, each column of number $k \leqslant 2018$ generates at least 1010 prohibitions for the cells of column 2019, which gives a total of at least 2018 - 1010 prohibitions for column 2019.
Now, we note that if the cell of row $i$ of column 2019 receives 2 prohibitions for the same color $c$, this means that there exist cells $C_{i, j}, C_{l, j}, C_{i, j^{\prime}}, C_{l^{\prime}, j^{\prime}}$ with $j<j^{\prime}$, all of color $c$, whose pairs $\left(C_{i, j}, C_{l, j}\right),\left(C_{i, j^{\prime}}, C_{l^{\prime}, j^{\prime}}\right)$ generate the same prohibition for the cell $C_{i, 2019}$ for color $c$. But the fact that the cells $C_{i, j}, C_{l, j}, C_{i, j^{\prime}}$ is forbidden by hypothesis. Thus, if a cell has $m$ prohibitions, these prohibitions concern m different colors.
Finally, these prohibitions cannot concern the cell $\mathrm{C}_{2019,2019}$. Thus, by the pigeonhole principle, since there are 2018 - 1010 prohibitions on column 2019 at least, there is a cell among the cells $\mathrm{C}_{1,2019}, \ldots, \mathrm{C}_{2018,2019}$ that has at least 1010 prohibitions, it is therefore forbidden for at least 1010 different colors, which is absurd since we can only use 1009 different colors. In conclusion, a wonderful coloring has at least 1010 different colors. Conversely, if we have 1010 colors, we can construct a wonderful coloring, inspired by the following configuration for $\mathrm{N}=7$.

## Comment from the Examiners
Very few students submitted a solution for this problem. Some students who attempted the problem misunderstood the statement and provided unclear explanations. The construction was found by many students who worked on the problem.
|
1010
|
Yes
|
Incomplete
|
math-word-problem
|
Combinatorics
|
On considère une grille $2019 \times 2019$. On note $C_{i, j}$ la case sur la i-ième colonne et la j-ième ligne pour $1 \leqslant \mathfrak{i}, \mathfrak{j} \leqslant 2019$. Un coloriage de la grille est formidable s'il n'existe pas $1 \leqslant \mathfrak{i}<\ell \leqslant 2019$ et $1 \leqslant j<k \leqslant 2019$ tels que les cases $C_{i, j}, C_{i, k}$ et $C_{\ell, j}$ soient de la même couleur. Quel est le plus petit entier N tel qu'il existe un coloriage formidable avec N couleurs?
|
Dans ce problème, on cherche le plus petit entier satisfaisant une certaine propriété. Supposons que l'on veuille montrer que le plus petit entier recherché est l'entier c. Pour montrer que c est bien le plus petit entier recherché, on va d'une part montrer que si un entier $n$ satisfait la propriété, alors $n \geqslant c$ et d'autre part on va montrer que l'on peut trouver un coloriage avec exactement c couleurs satisfaisant la propriété.
On s'empresse de tester l'énoncé sur des plus petites valeurs, par exemple pour des grilles de taille $3 \times 3$, $4 \times 4$ ou même $5 \times 5$, afin de deviner la valeur minimale dans le cas général, ainsi qu'une éventuelle construction. On s'aperçoit que pour une grille $3 \times 3$, on a besoin d'au moins 2 couleurs pour une coloriage formidable. Pour une grille $5 \times 5$, on remarque que l'on a besoin de 3 couleurs au moins. On conjecture donc que pour N impair, on a besoin d'au moins $\frac{\mathrm{N}+1}{2}$.
La difficulté de l'exercice repose dans le fait qu'il faut d'abord essayer de deviner la valeur minimale avant de faire la preuve. En l'absence d'idée d'une preuve directe qu'il faut bien au moins $\frac{\mathrm{N}+1}{2}$ couleurs, on peut essayer de montrer par l'absurde qu'un coloriage possédant $\frac{\mathrm{N}-1}{2}$ ne sera pas formidable.
Pour cela, on remarque que la donnée de deux cases $C_{i, j} C_{l, j}$ (avec $i<l$ ) de couleur rouge sur une colonne $j$ empêche les cases de ligne $i$ et sur une colonne $k \geqslant j$ d'être de la couleur rouges. On peut dire que ces deux cases génèrent une interdiction sur la ligne $i$. On peut essayer de compter ces interdictions. Ce comptage dépend du nombre de couleurs que l'on utilise, ce qui nous encourage bien à résonner par l'absurde pour montrer qu'un coloriage avec $\frac{\mathrm{N}-1}{2}$ couleurs générera trop d'interdictions.
Où chercher les interdictions? On peut commencer par procéder manuellement : on regarde le nombre minimal d'interdictions générées par la colonne 1, puis les interdictions générées par la ligne 2 etc... Cette opération manuelle s'effectue à nouveau sur des petits cas, comme une grille $5 \times 5$ ou $7 \times 7$. On s'aperçoit au terme de ces opérations sur des petits cas que la contradiction s'obtient en regardant la colonne N , sur laquelle se trouvent toujours trop d'interdictions. Nous allons donc formaliser ce raisonnement en regardant le nombre d'interdictions.
On suppose donc que l'on dispose d'un coloriage formidable de la grille possédant 1009 couleurs (quitte à avoir des couleurs qui ne sont pas utilisées pour le coloriage en question).
Dans la suite, on dira que la paire $\left(C_{i, j}, C_{l, j}\right)$ génère une interdiction pour la case $C_{i, k}$ pour la couleur $c$ si les cases $C_{i, j}$ et $C_{l, j}$ sont de la couleur $c$, ce qui empêche la case $C_{i, k}$ d'être de la couleur c par hypothèse.
Soit $j \leqslant 2018$ une colonne fixée et soit $k_{j}$ le nombre de couleurs apparaissant sur au moins deux cases de la colonnes $j$. Pour une couleur de numéro c , on note $n_{c}$ le nombre de cases de la colonne $j$ coloriées avec la couleur c . Quitte à renuméroter les couleurs, on peut supposer que ce sont les couleurs $1, \ldots, \mathrm{k}_{\mathrm{j}}$ qui apparaissent au moins 2 fois et que les couleurs $k_{j+1}, \ldots, 1009$ apparaissent au plus une fois dans la colonne.
Etant donnée une couleur $\mathrm{c} \leqslant \mathrm{k}_{\mathrm{j}}$, il y a au moins $\mathrm{n}_{\mathrm{c}}-1$ paires de cases de la couleur c dans la colonne j. En effet, la case de la couleur c située la plus basse dans la colonne forme une paire avec chacune des $n_{c}-1$ autres cases de la colonne. Chacune de ces paires génère une interdiction pour l'une des cases de la colonne 2019 : la paire de cases $\left(C_{i, j}, C_{l, j}\right)(i<l)$ génère une interdiction pour la case $C_{i, 2019}$. Ainsi, les cases de la colonne $j$ génère $\sum_{c=1}^{k_{j}}\left(n_{c}-1\right)$ interdictions dans la dernière colonne. Or, puisque les couleurs $k_{j+1}, \ldots, 1009$ occupent au plus une case dans la colonne $j$, on a au moins
$$
\sum_{c=1}^{k_{j}}\left(n_{c}-1\right)=\sum_{c=1}^{k_{j}} n_{c}-k_{j} \geqslant 2019-\left(1009-k_{j}\right)-k_{j}=1010
$$
interdictions générées dans la colonne 2019.
Ainsi, chaque colonne de numéro $k \leqslant 2018$ génère au moins 1010 interdictions pour les cases de la colonne 2019, ce qui donne au total au moins 2018 - 1010 interdictions pour la colonne 2019.
A présent, on note que si la case de ligne $i$ de la colonne 2019 reçoit 2 interdictions pour la même couleur $c$, cela signifie qu'il existe des cases $C_{i, j}, C_{l, j}, C_{i, j^{\prime}}, C_{l^{\prime}, j^{\prime}}$ avec $j<j^{\prime}$, toutes de couleurs $c$, dont les paires $\left(C_{i, j}, C_{l, j}\right),\left(C_{i, j^{\prime}}, C_{l^{\prime}, j^{\prime}}\right)$ génèrent la même interdiction pour la case $C_{i, 2019}$ pour la couleur $c$. Mais le fait que les cases $C_{i, j}, C_{l, j}, C_{i, j^{\prime}}$ est interdit par hypothèses. Ainsi, si une case possède $m$ interdictions, ces interdictions concernent m couleurs différentes.
Enfin, ces interdictions ne peuvent pas concerner la case $\mathrm{C}_{2019,2019}$. Ainsi, d'après le principe des tiroirs, puisqu'il y a 2018 - 1010 interdictions sur la colonne 2019 au moins, il y a une case parmi les cases $\mathrm{C}_{1,2019}, \ldots, \mathrm{C}_{2018,2019}$ qui possède au moins 1010 interdictions, elle est donc interdite pour au moins 1010 couleurs différentes, ce qui est absurde puisque l'on ne peut utiliser que 1009 couleurs différentes. En conclusion, un coloriage formidable possède au moins 1010 couleurs différentes. Réciproquement, si l'on dispose de 1010 couleurs, on peut construire un coloriage formidable, en s'inspirant de la configuration suivante pour $\mathrm{N}=7$.

## Commentaire des correcteurs
Très peu d'élèves ont rendu une copie pour cet exercice. Quelques élèves ayant traité l'exercice ont mal compris l'énoncé et ont donné des explications peu claires. La construction a été assez largement trouvée parmi les élèves qui ont cherché l'exercice.
|
{
"exam": "French_envois",
"problem_label": "16",
"problem_match": "\nExercice 16.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 16",
"tier": "T2",
"year": null
}
|
A super-domino is a rectangular tile in a three-dimensional grid of one of the three following forms: $1 \times 1 \times 2, 1 \times 2 \times 1$, and $2 \times 1 \times 1$. What are the integers $a, b, c>1$ such that it is possible to tile a rectangular prism of dimensions $\mathrm{a} \times \mathrm{b} \times \mathrm{c}$ in a three-dimensional grid with super-dominos so that there are as many super-dominos of each of the 3 types?
|
In this problem, we are looking for all integers \(a, b, c\) that satisfy certain properties. We will therefore establish that if \(a, b,\) and \(c\) satisfy the property, then \(a, b,\) and \(c\) are of a certain form, and on the other hand, show that if \(a, b,\) and \(c\) are of the found form, then they indeed satisfy the property.
We can also note that this is a tiling problem, so we can expect to need to use a clever coloring of the rectangular prism. If we do not have any initial idea about the form of the integers \(a, b,\) and \(c\), we can start by making some observations.
If we can tile a rectangular prism \(a \times b \times c\) with \(N\) super-dominoes of each of the three types, then necessarily there will be \(2N + 2N + 2N = abc\) tiles covered, so 6 divides \(abc\). Thus, one coordinate is even. Without loss of generality, assume \(a\) is even.
For simplicity, we assume that the prism is composed of \(abc\) tiles with coordinates \((i, j, k)\), where \(i\) is the x-coordinate, \(j\) is the y-coordinate, and \(k\) is the depth.
We now seek a coloring of our prism. First, the objects being manipulated are dominoes, each composed of 2 cubes; we will therefore look for a 2-color coloring, like a checkerboard. Let's start by focusing on a face, for example, the tiles of depth 1. A domino \(1 \times 1 \times 2\) occupies at most one tile on this face, while the other two types of dominoes occupy 0 or 2 tiles on this face. We can therefore try to adapt our coloring to this observation by applying the same coloring to each slice (by slice, we mean here the set of tiles with the same depth), i.e., a coloring where the color of a tile \((i, j, k)\) depends on \(i\) and \(j\) but not on \(k\). The advantage will be that the two cubes of any domino \(1 \times 1 \times 2\) will be the same color. From this observation, we can try to ensure that the 2 cubes of dominoes \(1 \times 2 \times 1\) and \(2 \times 1 \times 1\) are of different colors. This leads us to think of a checkerboard coloring, which we apply uniformly to each slice. Let's formalize this coloring and see what information it provides.
We color white the tiles \((i, j, k)\) such that \(i + j\) is even, and black the others. Thus, the cubes of a super-domino \(1 \times 1 \times 2\) are the same color, either white or black, while a super-domino \(1 \times 2 \times 1\) contains exactly one white cube and one black cube, the same for a super-domino \(2 \times 1 \times 1\). We deduce that when we tile our rectangular prism with the same number of super-dominoes of each type, the total number of white tiles covered is even: indeed, a super-domino \(1 \times 1 \times 2\) covers 2 or 0, and a super-domino of one of the other two types covers 1. Thus, to be able to tile the rectangular prism \(a \times b \times c\) with the same number of super-dominoes of each type, there must be an even number of white tiles. The slice consisting of the tiles of depth 1 contains exactly \(\frac{ab}{2}\) white tiles, and all slices are colored the same way, and there are \(c\) slices. There are therefore \(\frac{ab}{2} \times c\) white tiles, and this number must be even. We deduce that 4 divides \(abc\). Since 6 and 4 divide \(abc\), we have that 12 divides \(abc\) if a prism \(a \times b \times c\) satisfies the statement.
We now tackle the converse by showing that we can tile a prism \(a \times b \times c\) correctly if 12 divides \(abc\). To find such a tiling, we always start by looking at prisms of small dimensions, for example, a prism \(2 \times 2 \times 3\). These trials are more useful than one might think. Indeed, if we manage to tile this prism, we can tile larger prisms by cutting these large prisms into smaller prisms of dimension \(2 \times 2 \times 3\), for example. We notice that with two dominoes of each type, we can tile a prism \(2 \times 2 \times 3\) and \(3 \times 4 \times 3\) (see the figure, the tiling on the right is split into two parts for better readability). Moreover, this allows us to tile a prism \(2 \times 4 \times 3\) by joining two prisms \(2 \times 2 \times 3\) along the width or two prisms \(3 \times 2 \times 3\) along the width. Since any integer \(a > 1\) can be written as a sum of 2 and 3, by joining the right number of prisms of the form \(2 \times 4 \times 3\) and \(3 \times 4 \times 3\), we can tile any prism \(a \times 4 \times 3\) for \(a > 1\). Similarly, we can tile prisms of the form \(a \times 2 \times 6\), with \(a > 1\). If 12 divides \(abc\), then there are two possibilities:
- One dimension of the rectangular prism is divisible by 6 and another dimension is even. In this case, we know how to tile this rectangular prism using prisms \(a \times 2 \times 6\), \(a > 1\).
- One dimension of the rectangular prism is divisible by 4 and another dimension is divisible by 3. In this case, we know how to tile this rectangular prism using prisms \(a \times 4 \times 3\), \(a > 1\).
- Two dimensions of the prism are even, and the third is divisible by 3. In this case, we know how to tile this rectangular prism using prisms \(2 \times 2 \times 3\).
- One dimension of the rectangular prism is divisible by 12 and the others are odd, not divisible by 3, and greater than or equal to 5. Then we decompose the rectangular prism \(12a \times b \times c\) into a prism \(12a \times 3 \times c\) and \(12a \times (b-3) \times c\), and tile each as previously if \(b-3\) is even.
This completes the construction and shows that the rectangular prisms that can be tiled in this way are those such that 12 divides \(abc\).
## Comment from the Examiners
The problem was difficult and was solved by a small number of students, but a certain number of students managed to make progress on the problem, by showing that certain prisms could be tiled.
|
12 \text{ divides } abc
|
Yes
|
Incomplete
|
math-word-problem
|
Combinatorics
|
Un super-domino est un pavé droit dans une grille en trois dimensions de l'une des trois formes suivantes : $1 \times 1 \times 2,1 \times 2 \times 1$ et $2 \times 1 \times 1$. Quels sont les entiers $a, b, c>1$ tels qu'il est possible de paver un pavé droit de dimensions $\mathrm{a} \times \mathrm{b} \times \mathrm{c}$ dans un grille en trois dimensions avec des super-dominos de sorte qu'il y ait autant de super-dominos de chacun des 3 types?
|
Dans ce problème, on cherche tous les entiers $a, b, c$ satisfaisant certaines propriétés. Nous allons donc établir que si $\mathrm{a}, \mathrm{b}$ et c satisfont la propriété alors $\mathrm{a}, \mathrm{b}$ et c sont d'une certaine forme, et d'autre part montrer que si $a, b$ et $c$ sont de la forme trouvée, alors ils satisfont bien la propriété.
On peut également noter qu'il s'agit d'un problème de pavage, nous pouvons donc nous attendre à devoir utiliser un coloriage adroit du pavé droit. Si l'on n'a à priori pas d'idée sur la forme des entiers $a, b$ et $c$, on peut commencer par effectuer quelques remarques.
Si on parvient à paver un pavé droit $\mathrm{a} \times \mathrm{b} \times \mathrm{c}$ avec N super-dominos de chacun des trois types, alors nécessairement il y aura $2 \mathrm{~N}+2 \mathrm{~N}+2 \mathrm{~N}=\mathrm{abc}$ cases pavées, donc 6 divise $a b c$. Ainsi une coordonnée est paire. Supposons donc sans perte de généralité que a est pair.
Pour simplifier, on supposera que le pavé est composé de abc cases de coordonnées $(i, j, k)$, où $i$ est l'abscisse, $j$ l'ordonnée de la case et $k$ la profondeur.
On cherche désormais un coloriage de notre pavé. Tout d'abord, les objets manipulés sont des dominos, composés de 2 cubes; On va donc chercher un coloriage à 2 couleurs, du type damier. Regardons les caractéristiques d'un éventuel coloriage. On peut commencer par se concentrer sur une face, par exemple sur les cases de profondeur 1 . Un domino $1 \times 1 \times 2$ occupe au maximum une case sur cette face tandis que les deux autres types de dominos occupent 0 ou 2 cases de cette face. On peut donc essayer d'adapter notre coloriage à cette remarque en appliquant le même coloriage à chacune des tranches (par tranche, on entend ici l'ensemble des cases possédant la même profondeur), c'est-à-dire un coloriage où la couleur d'une case ( $i, j, k$ ) dépend de $i$ et de $j$ mais pas de $k$. L'avantage sera que les deux cubes d'un quelconque domino $1 \times 1 \times 2$ seront de la même couleur. De ce constat, on peut chercher à faire en sorte que les 2 cubes des dominos $1 \times 2 \times 1$ et $2 \times 1 \times 1$ soient de couleur différentes. Ceci nous fait penser à un coloriage en damier, que l'on applique uniformément à chacune des tranches. Formalisons donc ce coloriage et voyons l'information qu'il nous apporte.
On colorie en blanc les cases $(i, j, k)$ telles que $i+j$ est paire, et en noir les autres. Ainsi, les cubes d'un super-domino $1 \times 1 \times 2$ sont de la même couleur, noir ou blanc, tandis qu'un super-domino $1 \times 2 \times 1$ contient exactement un cube blanc et un cube noir, de même pour un super-domino $2 \times 1 \times 1$. On déduit que lorsque l'on pave notre pavé droit avec le même nombre de super-domino de chaque type, le nombre total de cases blanches recouvertes est pair : en effet un super-domino $1 \times 1 \times 2$ en recouvre 2 ou 0 , et un super-domino d'un des deux autres type en recouvre 1 . Ainsi pour pouvoir paver le pavé droit $a \times b \times c$ avec autant de super-dominos de chaque type, il faut qu'il y ait un nombre pair de cases blanches. Or, la tranche constituée des cases de profondeur 1 contient exactement $\frac{\mathrm{ab}}{2}$ cases blanches et toutes les tranches sont coloriées de la même façon et il y a c tranches. Il y a donc $\frac{\mathrm{ab}}{2} \times \mathrm{c}$ cases blanches et ce nombre doit être pair. On déduit que 4 divise abc. Comme 6 et 4 divisent abc , on a que 12 divise abc si un pavé $a \times b \times c$ satisfait l'énoncé.
On s'attaque désormais à la réciproque en montrant que l'on peut paver correctement un pavé $\mathrm{a} \times \mathrm{b} \times \mathrm{c}$ si 12 divise abc. Pour trouver un tel pavage, on commence toujours par regarder les pavés de petites dimensions, par exemple un pavé $2 \times 2 \times 3$. Ces essais sont plus utiles qu'on ne le croit. En effet, si l'on parvient à paver ce pavé, on pourra paver correctement des pavés plus gros en découpant ces gros pavés en petits pavés de dimension $2 \times 2 \times 3$ par exemple. Or, on remarque qu'avec deux dominos de chaque type, on peut paver un pavé $2 \times 2 \times 3$ et $3 \times 4 \times 3$ (voir la figure, le pavage de droite est découpé en deux parties pour être plus lisible). De plus, cela permet de paver un pavé $2 \times 4 \times 3$ en recollant selon
la largeur deux pavés $2 \times 2 \times 3$ en recollant deux $3 \times 2 \times 3$ selon la largeur. Puisque tout entier $a>1$ s'écrit comme somme de 2 et de 3 , en recollant le bon nombre de pavés de la forme $2 \times 4 \times 3$ et $3 \times 4 \times 3$, on peut paver n'importe quel pavé $a \times 4 \times 3$ pour $a>1$. De même, on peut paver les pavés de la forme $a \times 2 \times 6$, avec $a>1$. Or si 12 divise $a b c$ alors il y a deux possibilités:
- Une dimension du pavé droit est divisible par 6 et une autre dimension est paire. Dans ce cas on sait comment paver ce pavé droit à l'aide des pavés $a \times 2 \times 6, a>1$.
- Une dimension du pavé droit est divisible par 4 et une autre dimension est divisible par 3. Dans ce cas on sait comment paver ce pavé droit à l'aide des pavés $\mathbf{a} \times 4 \times 3$, $\boldsymbol{a}>1$.
- Deux dimensions du pavé sont paires, et la dernière est divisible par 3. Dans ce cas on sait comment paver ce pavé droit à l'aide des pavés $2 \times 2 \times 3$.
- Une dimension du pavé droit est divisible par 12 et les autres sont impaires, non divisibles par 3, supérieures ou égales à 5 . Alors on décompose le pavé droit $12 \mathrm{a} \times \mathrm{b} \times \mathrm{c}$ en un pavé $12 \mathrm{a} \times 3 \times \mathrm{c}$ et $12 a \times(b-3) \times c$, et on pave chacun comme précédemment cas $b-3$ est pair.
Ceci achève la construction et montre que les pavé droits qui peuvent être ainsi pavés sont ceux tels que 12 divise abc.

## Commentaire des correcteurs
L'exercice était difficile et a été résolu par un faible nombre d'élèves, mais un certain nombre d'élèves a réussi à avancer sur le problème, en montrant que certains pavés étaient pavables.
|
{
"exam": "French_envois",
"problem_label": "17",
"problem_match": "## Exercice 17.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 17",
"tier": "T2",
"year": null
}
|
2019 students participate in a competition and each answers 6 questions. At the end of the competition, it is noted that, among the correct answers given by any group of 3 students, there is at least one correct answer to at least 5 of the 6 questions of the competition. What is the minimum value of the total number of correct answers to the questions of the competition?
|
In this problem, we are looking for the smallest integer satisfying a certain property. Suppose we want to show that the smallest integer sought is the integer c. To show that c is indeed the smallest integer sought, we will on the one hand show that if an integer n satisfies the property, then $n \geqslant c$, and on the other hand, we will show that we can find a configuration with exactly c correct answers given.
We can start by arranging the data in a $2019 \times 6$ table, where the 2019 rows represent the 2019 students and the 6 columns represent the 6 problems. In the cell ( $\boldsymbol{i}, \mathfrak{j}$ ), we write a 1 if student $\boldsymbol{i}$ answered question $j$ correctly and we write a 0 otherwise. The problem invites us to perform a double-counting, this presentation in the form of a table allows us to see which double-counting is interesting. The assumptions concerning the triplets of students invite us to attempt a double-counting. But first, we make some simple observations. We can note that if three students all answered incorrectly to questions 5 and 6, then we have a triplet of students whose answers are not correct for at least 5 exercises. Thus, if $q_{1}$ and $\mathrm{q}_{2}$ are two questions from the contest, there are at most 2 students who answered incorrectly to these questions. Since there are $\binom{6}{2}=15$ ways to choose a pair of questions $\left\{\mathbf{q}_{1}, \mathbf{q}_{2}\right\}$, and for each pair there are at most two students who answered incorrectly to these two questions, so there are at most $2 \cdot 15=30$ pairs $\left(\left\{q_{1}, q_{2}\right\}, e\right)$ such that student $e$ answered incorrectly to questions $q_{1}$ and $q_{2}$. In the table, this translates to the fact that there are at most 30 pairs of 0s such that the two 0s belong to the same row. This upper bound on the number of pairs of 0s belonging to the same row allows us to guess the double-counting we will perform: we will count in two different ways the number N of pairs of 0s such that the two 0s belong to the same row. Such a pair will be called bad in the following. We have already counted "by columns," which gave us $\mathrm{N} \leqslant 30$. We will now seek to count "by rows."
We denote by E the set of students who answered at most 4 questions. To each of the students in E, we can associate at least one pair of incorrect answers, so $|E| \leqslant N \leqslant 30$.
For a student $e \in E$ we denote $\mathrm{n}(e)$ the number of questions to which he answered incorrectly. Then $\mathrm{N}=$ $\sum_{e \in E}\binom{\mathfrak{n}(e)}{2}$, since the only bad pairs belong to rows associated with elements of E and if there are $n(e) 0$ in a row, there are $\binom{n(e)}{2}$ ways to create pairs of 0s from this row. We now use the convexity of the function $x \mapsto \frac{x(x-1)}{2}=\binom{x}{2}$ to apply Jensen's inequality and obtain a lower bound for N:
$$
N=\sum_{e \in \mathrm{E}}\binom{\mathfrak{n}(e)}{2} \geqslant|\mathrm{E}|\binom{\frac{\sum_{e \in \mid} n(e)}{|E|}}{2}
$$
We denote f the total number of incorrect answers given by the students in E, and $v$ the total number of correct answers, such that $\mathrm{f}+v=6|\mathrm{E}|$. We therefore have $\sum_{e \in \mathrm{E}} \mathfrak{n}(e)=\mathrm{f}$. Thus:
$$
\begin{aligned}
& 30 \geqslant N \geqslant \frac{f(f-|E|)}{2|E|} \\
& \mathbf{f}^{2}-\mathbf{f}|\mathrm{E}|-60|\mathrm{E}| \leqslant 0
\end{aligned}
$$
This last equation provides that $f \leqslant \frac{|E|+\sqrt{|E|^{2}+240|E|}}{2}$.
Let $V$ be the total number of correct answers given by all the students, then $V$ is the sum of the number of correct answers from the students in E and the sum of the correct answers from the students who are not
in E. By definition, the students who are not in E answered correctly to at least 5 questions. So
$$
\mathrm{V} \geqslant v+(2019-|\mathrm{E}|) 5=2019 \times 5-5|\mathrm{E}|+v=2019 \times 5-5|\mathrm{E}|+6|\mathrm{E}|-\mathrm{f}=5 \times 2019+|\mathrm{E}|-\mathrm{f}
$$
But using the inequality obtained in f above we get
$$
\mathrm{V} \geqslant 2019 \times 5+\frac{|\mathrm{E}|-\sqrt{|\mathrm{E}|^{2}+240|\mathrm{E}|}}{2}
$$
The right side is decreasing in $|E|$ and since $|E| \leqslant 30$, so $V \geqslant 2019 \times 5+\frac{30-\sqrt{30^{2}+240 \times 30}}{2}=10065$. Therefore V $\geqslant 10065$.
Conversely, it is possible that 2019 - 30 students answered 5 problems, and that 30 students answered 4 problems: it is sufficient that for each of the 15 sets of 4 questions among the 6 there are two students who answered exactly those. This configuration satisfies the statement, and is such that the number of correct answers is exactly 10065.
## Comment from the Examiners
The exercise, difficult, was solved by very few students. However, it is commendable to see that several students provided some elements of answers even if they did not have a complete proof. Some errors to avoid:
1. Just because we have a configuration with 10065 correct answers and we cannot remove a correct answer from this configuration, it does not necessarily mean that this is the optimal configuration and that 10065 is the optimal value.
2. Just because we have a minimum number of correct answers among students who answered correctly to at most 4 questions AND a minimum number of correct answers among students who answered correctly to at least 5 questions, it does not mean that the global minimum for the number of correct answers is the sum of these two minimums. In other words, the global minimum is not necessarily the sum of the two local minimums, especially when the two groups of students and their sizes are not independent.
|
10065
|
Yes
|
Incomplete
|
math-word-problem
|
Combinatorics
|
2019 élèves participent à un concours et répondent chacun à 6 questions. A la fin du concours, on remarque que, parmi les bonnes réponses données par un quelconque groupe de 3 élèves, il y a au moins une réponse correcte à au moins 5 des 6 questions du concours. Quelle est la valeur minimale du nombre total de réponses correctes aux questions du concours?
|
Dans ce problème, on cherche le plus petit entier satisfaisant une certaine propriété. Supposons que l'on veuille montrer que le plus petit entier recherché est l'entier c. Pour montrer que c est bien le plus petit entier recherché, on va d'une part montrer que si un entier n satisfait la propriété, alors $n \geqslant c$ et d'autre part on va montrer que l'on peut trouver une configuration avec exactement c réponses correctes données.
On peut commencer par ranger les données dans un tableau $2019 \times 6$, où les 2019 lignes représentent les 2019 élèves et les 6 colonnes les 6 problèmes. Dans la case ( $\boldsymbol{i}, \mathfrak{j}$ ), on inscrit un 1 si l'élève $\boldsymbol{i}$ a répondu correctement à la question $j$ et on inscrit un 0 sinon. Le problème nous invite à effectuer un doublecomptage, cette présentation sous forme de tableau permet de voir quel double-comptage est intéressant. Les hypothèses concernant les triplets d'élèves invitent à tenter d'effectuer un double comptage. Mais d'abord, on effectue quelques remarques simples. On peut noter que si trois élèves ont répondu tous les trois faux aux questions 5 et 6 , alors on a un triplet d'élèves dont les réponses ne sont pas correctes pour au moins 5 exercices. Ainsi, si $q_{1}$ et $\mathrm{q}_{2}$ sont deux questions du concours, il y a au plus 2 élèves qui ont répondu faux à ces questions. Comme il y a $\binom{6}{2}=15$ façons de choisir une paire de questions $\left\{\mathbf{q}_{1}, \mathbf{q}_{2}\right\}$, et pour chaque paire il y a au plus deux élèves qui ont mal répondu à ces deux questions donc il y a au plus $2 \cdot 15=30$ paires $\left(\left\{q_{1}, q_{2}\right\}, e\right)$ telles que l'élève $e$ a mal répondu aux questions $q_{1}$ et $q_{2}$. Dans le tableau, cela se traduit par le fait qu'il y a au plus 30 paires de 0 tels que les deux 0 appartiennent à la même ligne. Cette majoration du nombre de paires de 0 appartenant à la même ligne nous permet de deviner le double comptage que nous allons effectuer : nous allons compter de deux façons différentes le nombre N de paires de 0 tels que les deux 0 appartiennent à la même ligne. Une telle paire sera dite mauvaise dans la suite. On a déjà compté "selon les colonnes", ce qui nous a donné $\mathrm{N} \leqslant 30$. On va chercher à présent à compter "selon les lignes".
On note El 'ensemble des élèves qui ont répondu à au plus 4 questions. A chacun des élèves de E , on peut associer au moins un couple de réponses fausses donc $|E| \leqslant N \leqslant 30$
Pour un élève $e \in E$ on note $\mathrm{n}(e)$ le nombre de questions auxquelles il a répondu faux. Alors $\mathrm{N}=$ $\sum_{e \in E}\binom{\mathfrak{n}(e)}{2}$, puisque les seuls mauvaises paires appartiennent à des lignes associées à des éléments de E et que s'il y a $n(e) 0$ dans une lignes, il y a $\binom{n(e)}{2}$ façons de créer des paires de 0 de cette lignes. On utilise à présent la convexité de la fonction $x \mapsto \frac{x(x-1)}{2}=\binom{x}{2}$ pour appliquer l'inégalité de Jensen et obtenir une minoration de N :
$$
N=\sum_{e \in \mathrm{E}}\binom{\mathfrak{n}(e)}{2} \geqslant|\mathrm{E}|\binom{\frac{\sum_{e \in \mid} n(e)}{|E|}}{2}
$$
On note f le nombre total de réponses fausses proposées par les élèves de E , et $v$ le nombre total de réponses justes, de telles sorte que $\mathrm{f}+v=6|\mathrm{E}|$. On a donc $\sum_{e \in \mathrm{E}} \mathfrak{n}(e)=\mathrm{f}$. Ainsi :
$$
\begin{aligned}
& 30 \geqslant N \geqslant \frac{f(f-|E|)}{2|E|} \\
& \mathbf{f}^{2}-\mathbf{f}|\mathrm{E}|-60|\mathrm{E}| \leqslant 0
\end{aligned}
$$
Cette dernière équation fournit que $f \leqslant \frac{|E|+\sqrt{|E|^{2}+240|E|}}{2}$.
Soit $V$ le nombre total de réponses justes données par l'ensembe des élèves, alors $V$ est la somme du nombre de bonnes réponses des élèves de E et la somme des bonnes réponses des élèves qui ne sont pas
dans E. Par définition, les élèves qui ne sont pas dans E ont répondu correctement à au moins 5 questions. Donc
$$
\mathrm{V} \geqslant v+(2019-|\mathrm{E}|) 5=2019 \times 5-5|\mathrm{E}|+v=2019 \times 5-5|\mathrm{E}|+6|\mathrm{E}|-\mathrm{f}=5 \times 2019+|\mathrm{E}|-\mathrm{f}
$$
Mais en utilisant l'inégalité obtenue en f plus haut on obtient
$$
\mathrm{V} \geqslant 2019 \times 5+\frac{|\mathrm{E}|-\sqrt{|\mathrm{E}|^{2}+240|\mathrm{E}|}}{2}
$$
Le côté droit est décroissant en $|E|$ et puisque $|E| \leqslant 30$, donc $V \geqslant 2019 \times 5+\frac{30-\sqrt{30^{2}+240 \times 30}}{2}=10065$. Donc V $\geqslant 10065$.
Réciproquement, il est possible que 2019 - 30 élèves aient répondu à 5 problèmes, et que 30 élèves aient répondu à 4 problèmes : il suffit que pour chacun des 15 ensembles de 4 questions parmi les 6 il y ait deux élèves qui ont répondu exactement à celles là. Cette configuration satisfait l'énoncé, et est telle que le nombre de bonnes réponses est exactement 10065.
## Commentaire des correcteurs
L'exercice, difficile, n'a été résolu que par très peu d'élèves. Cependant, il est appréciable de voir que plusieurs élèves ont rendu quelques éléments de réponses même s'ils ne disposaient pas d'une preuve complète. Quelques erreurs à éviter :
1. Ce n'est pas parce qu'on dispose d'une configuration à 10065 bonnes réponses et qu'on ne peut pas enlever de bonne réponse dans cette configuration que c'est forcément la configuration optimale et que 10065 est la valeur optimale.
2. Ce n'est pas parce qu'on a un minimum de bonnes réponses sur les élèves qui ont répondu correctement à au plus 4 questions ET qu'on a un minimum de bonnes réponses sur les élèves ayant répondu correctement à au moins 5 questions que le minimum pour le nombre global d'élèves est la somme de ces deux minimums. Autrement dit, le minimum global n'est pas forcément la somme des deux minimums locaux, surtout lorsque les deux groupes d'élèves et leur taille ne sont pas indépendants.
|
{
"exam": "French_envois",
"problem_label": "18",
"problem_match": "\nExercice 18.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 18",
"tier": "T2",
"year": null
}
|
Martin and Théo are playing a game: Martin writes an integer on the board. Théo then has the right to erase the number and add 2, or to erase the number and subtract 3, as many times as he wants. Théo wins if he manages to get 2020 after a finite number of steps, otherwise Martin wins. Which player has a winning strategy?
|
We start by testing the statement for integers close to 2020. For example, we notice that if Martin writes the integers 2018, 2016, ... Theo can write 2020 on the board by adding a sufficiently large number of 2s to the number written by Martin. We also notice that if Martin writes 2019, Theo can also win by replacing 2019 with 2021, then 2023, and finally 2023 with 2020.
This observation allows us to conjecture, on the one hand, that Theo can always win regardless of the number written by Martin, and on the other hand, that if a number \( k \) is written on the board, Theo can write the numbers \( k+1 \) or \( k-1 \) after a finite number of operations.
We will therefore show that Theo can always win regardless of the number written by Martin. Suppose that at a given moment, the number \( k \) is written on the board. Then, by replacing \( k \) with \( k+2 \) by adding 2, \( k+2 \) with \( k+4 \) by adding 2, and finally \( k+4 \) with \( k+1 \) by subtracting 3, Theo has replaced the number \( k \) with the number \( k+1 \) in a finite number of operations. We will call this transformation operation A. On the other hand, if the integer \( k \) is written on the board at a given moment, by replacing \( k \) with \( k+2 \) and \( k+2 \) with \( k-1 \), Theo has replaced the integer \( k \) with the integer \( k-1 \). We will call this transformation operation B.
Now suppose that Martin has written the number \( k_{0} \) on the board. If \( k_{0} = 2020 \), Theo has already won. If \( k_{0} < 2020 \), then by performing \( 2020 - k_{0} \) times operation A, Theo can replace the integer \( k_{0} \) with 2020 and win. If \( k_{0} > 2020 \), by performing \( k_{0} - 2020 \) times operation B, Theo can again replace the integer \( k_{0} \) with 2020. In all cases, Theo wins!
Comment from the graders: The exercise was successfully solved by all students who attempted it.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Martin et Théo jouent à un jeu : Martin écrit un nombre entier au tableau. Théo a ensuite le droit d'effacer le nombre et de lui ajouter 2 , ou d'effacer le nombre et de lui enlever 3 , ceci autant de fois qu'il veut. Théo gagne s'il arrive à obtenir 2020 après un nombre fini d'étapes, sinon Martin gagne. Quel joueur a une stratégie gagnante ?
|
On commence par tester l'énoncé pour des entiers proches de 2020. Par exemple, on remarque que si Martin écrit les entiers 2018, 2016, ... Théo peut écrire 2020 au tableau en rajoutant au nombre écrit par Martin un nombre suffisamment grand de 2 . On remarque aussi que si Martin écrit 2019, Théo peut aussi gagner en remplaçant 2019 par 2021 puis 2023 puis 2023 par 2020.
Cette remarque nous permet de conjecturer d'une part que Théo peut toujours gagner quelque soit le nombre écrit par Martin, d'autre part que si un nombre k est écrit au tableau, Théo peut écrire les nombres $k+1$ ou $k-1$ au bout d'un nombre fini d'opérations.
Nous montrons donc que Théo peut toujours gagner quelque soit le nombre écrit par Martin. Supposons qu'à un instant donné, le nombre $k$ est écrit au tableau. Alors en remplaçant $k$ par $k+2$ en ajoutant 2 , $k+2$ par $k+4$ en ajoutant 2 et enfin $k+4$ par $k+1$ en retranchant 3 , Théo a remplacé le nombre $k$ par le nombre $k+1$ en un nombre fini d'opération. Nous appellerons cette transformation l'opération A. D'autre part, toujours si l'entier $k$ est écrit au tableau à un instant donné, en remplaçant $k$ par $k+2$ et $k+2$ par $k-1$, Théo a remplacé l'entier $k$ par l'entier $k-1$. Nous appellerons cette transformation l'opération B.
Supposons désormais que Martin a écrit le nombre $k_{0}$ au tableau. Si $k_{0}=2020$, Théo a déjà gagné. Si $\mathrm{k}_{0}<2020$, alors en effectuant $2020-\mathrm{k}_{0}$ fois l'opération $A$, Théo peut remplacer l'entier $k_{0}$ par 2020 et gagner. Si $k_{0}>2020$, en effectuant $k_{0}-2020$ fois l'opération $B$, Théo peut remplacer à nouveau l'entier $k_{0}$ par 2020. Dans tous les cas, Théo gagne!
Commentaire des correcteurs : L'exercice a été résolu avec succès par tous les élèves qui l'ont abordé.
|
{
"exam": "French_envois",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-5.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle such that $\widehat{BAC}=60^{\circ}$. Let $O$ be the center of the circumcircle of triangle $ABC$, $H$ its orthocenter, and $I$ the point of intersection of the angle bisectors. Show that the points $B$, $O$, $I$, $H$, and $C$ are concyclic.
|
We handle the case where the angles of the triangle are acute.
Before embarking on an angle chase, we consider which angle equalities we need to determine to show that the 5 points lie on the same circle. For this, we note that we have, a priori, easier access to the angles of triangles BOC, BHC, and BIC than to the angles of triangle BOH, for example. This motivates us to show that $\widehat{\mathrm{BOC}}=\widehat{\mathrm{BHC}}=\widehat{\mathrm{BIC}}$.
First, according to the inscribed angle theorem, $\widehat{B O C}=2 \cdot \widehat{B A C}=120^{\circ}$. We know, therefore, that we need to show successively that $\widehat{\mathrm{BHC}}=120^{\circ}$ and $\widehat{\mathrm{BIC}}=120^{\circ}$.
To calculate $\widehat{\mathrm{BHC}}$, we use the definition of point H as the intersection of the altitudes of triangle $A B C$. We introduce $D, E$, and $F$ as the feet of the altitudes from vertices $A, B$, and $C$, respectively. We then use the fact (which is classical) that $\widehat{\mathrm{HEA}}=180^{\circ}-\widehat{\mathrm{HFA}}=90^{\circ}$ to obtain that points $A, E, H$, and $F$ are concyclic. Thus, $\widehat{\mathrm{FHE}}=180^{\circ}-\widehat{\mathrm{EAF}}=120^{\circ}$, so $\widehat{\mathrm{BHC}}=\widehat{\mathrm{EHF}}=120^{\circ}$.
Finally, to show that $\widehat{\mathrm{BIC}}=120^{\circ}$, we use the fact that point I is the intersection of the angle bisectors of the triangle. This definition gives us access to the angles $\widehat{\mathrm{BCI}}$ and $\widehat{\mathrm{BCI}}$ in terms of the angles of the triangle. Therefore, we have:
$\widehat{\mathrm{BIC}}=180^{\circ}-\widehat{\mathrm{IBC}}-\widehat{\mathrm{ICB}}=180^{\circ}-\frac{1}{2} \widehat{\mathrm{ABC}}-\frac{1}{2} \widehat{\mathrm{ACB}}=180^{\circ}-\frac{1}{2}\left(180^{\circ}-\widehat{\mathrm{BAC}}\right)=180^{\circ}-60^{\circ}=120^{\circ}$
In conclusion, $\widehat{\mathrm{BOC}}=\widehat{\mathrm{BHC}}=\widehat{\mathrm{BIC}}=120^{\circ}$, so the 5 points $\mathrm{B}, \mathrm{O}, \mathrm{H}, \mathrm{I}$, and C are concyclic.
We can handle the case where one of the angles of triangle $A B C$ is obtuse in a similar manner.
Comment from the graders: The exercise is mostly well done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle tel que $\widehat{B A C}=60^{\circ}$. Soit $O$ le centre du cercle circonscrit au triangle $A B C, H$ son orthocentre et $I$ le point d'intersection des bissectrices. Montrer que les points B, O, I, H et C sont cocycliques.
|
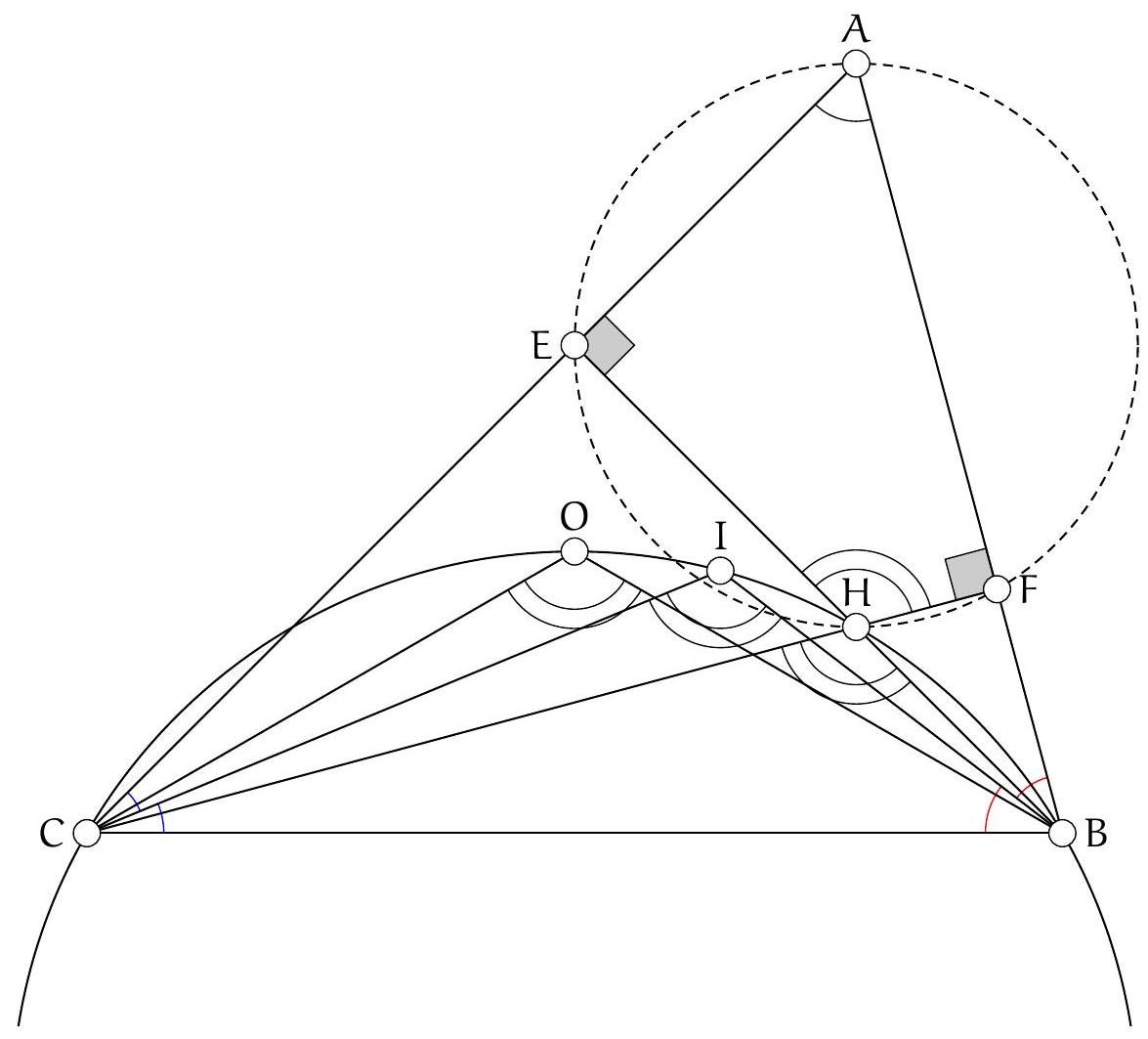
On traite le cas où les angles du triangle sont aigus.
Avant de se lancer dans une chasse aux angles, on se demande quelles égalités d'angles nous allons déterminer pour montrer que les 5 points sont sur un même cercle. Pour cela, on note qu'on a, à priori, plus facilement accès aux angles des triangles BOC, BHC et BIC qu'aux angles du triangle BOH par exemple. Ceci nous motive à montrer que $\widehat{\mathrm{BOC}}=\widehat{\mathrm{BHC}}=\widehat{\mathrm{BIC}}$.
Tout d'abord, d'après le théorème de l'angle inscrit, $\widehat{B O C}=2 \cdot \widehat{B A C}=120^{\circ}$. On sait donc que nous allons devoir montrer successivement $\widehat{\mathrm{BHC}}=120^{\circ}$ et $\widehat{\mathrm{BIC}}=120^{\circ}$.
Pour calculer $\widehat{\mathrm{BHC}}$, on utilise la définition du point H comme le point d'intersection des hauteurs du triangle $A B C$. On introduit donc $D, E$ et $F$ les pieds des hauteurs respectivement issues des sommets $A, B$ et $C$. On utilise alors le fait (classique) que $\widehat{\mathrm{HEA}}=180^{\circ}-\widehat{\mathrm{HFA}}=90^{\circ}$ pour obtenir que les points $A, E, H$ et $F$ sont cocycliques. Ainsi $\widehat{\mathrm{FHE}}=180^{\circ}-\widehat{\mathrm{EAF}}=120^{\circ}$ donc $\widehat{\mathrm{BHC}}=\widehat{\mathrm{EHF}}=120^{\circ}$
Enfin, pour montrer que $\widehat{\mathrm{BIC}}=120^{\circ}$, on se sert du fait que le point I est le point d'intersection des bissectrices du triangle. Cette définition nous donne en effet accès aux angles $\widehat{\mathrm{BCI}}$ et $\widehat{\mathrm{BCI}}$ en fonction des angles du triangle. On a donc:
$\widehat{\mathrm{BIC}}=180^{\circ}-\widehat{\mathrm{IBC}}-\widehat{\mathrm{ICB}}=180^{\circ}-\frac{1}{2} \widehat{\mathrm{ABC}}-\frac{1}{2} \widehat{\mathrm{ACB}}=180^{\circ}-\frac{1}{2}\left(180^{\circ}-\widehat{\mathrm{BAC}}\right)=180^{\circ}-60^{\circ}=120^{\circ}$
En conclusion, $\widehat{\mathrm{BOC}}=\widehat{\mathrm{BHC}}=\widehat{\mathrm{BIC}}=120^{\circ}$ donc les 5 points $\mathrm{B}, \mathrm{O}, \mathrm{H}, \mathrm{I}$ et C sont cocycliques.
On peut traiter de façon similaire le cas où un des angles du triangle $A B C$ est obtus.
Commentaire des correcteurs: L'exercice est majoritairement bien réussi.
|
{
"exam": "French_envois",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-5.jsonl",
"solution_match": "## \nSolution de l'exercice 2",
"tier": "T2",
"year": null
}
|
1. Do there exist numbers $a_{0}, \ldots, a_{2020}$, each being -1 or 1, such that $a_{0} \times a_{1} + a_{1} \times a_{2} + \cdots + a_{2019} \times a_{2020} + a_{2020} \times a_{0} = 1010$?
2. Do there exist numbers $a_{1}, \ldots, a_{2020}$, each being -1 or 1, such that $a_{1} \times a_{2} + a_{2} \times a_{3} + \cdots + a_{2019} \times a_{2020} + a_{2020} \times a_{1} = 1010$?
|
Let's look at the statement: we want to know if we can find numbers $\left(a_{i}\right)_{1 \leqslant i \leqslant n}$ equal to +1 or -1 such that $a_{1} a_{2}+\cdots+a_{n} a_{1}$ equals 1010, with in the first question $n=2021$, and in the second $n=2020$. For this, we can test with small $n$ values to see which numbers can be written in the form $a_{1} a_{2}+\cdots+a_{n} a_{1}$. For $n=3$, we find 3 (if we only take 1s) and -1 (if we take $a_{1}=a_{2}=1, a_{3}=-1$). For $n=4$, we find $4,0,-4$ (to get 4 we only take 1s, to get 0 it suffices to take three $a_{i}$ equal to 1 and one equal to -1, to get -4, it suffices to alternate the $a_{i}$ equal to 1 and those equal to -1). We can continue to test values for small $n$. We can note that the numbers we can obtain seem to be regularly spaced by 4, they are even congruent to $n$ modulo 4.
We also note that if $a= \pm 1$ and $b= \pm 1$, then $a b \pm 1$ and that $a b=1$ if $a=b$ and $a b=-1$ if $a=-b$.
1. Here we are in the case where $n=2021$ and we want to obtain a sum of 1010. This seems impossible due to parity, so we will look at the parity of the sum. Let $a_{0}, \ldots, a_{2020}$ be numbers equal to -1 or 1. For simplicity, we set $a_{2021}=a_{0}$. Since we always have $a_{i} a_{i+1}= \pm 1, a_{0} \times$ $a_{1}+a_{1} \times a_{2}+\cdots+a_{2019} \times a_{2020}+a_{2020} \times a_{0}$ is a sum of 2021 odd numbers, hence odd. It cannot therefore be equal to 1010 which is even. There do not exist numbers $a_{0}, \ldots, a_{2020}$ equal to -1 or 1 such that $a_{0} \times a_{1}+a_{1} \times a_{2}+\cdots+a_{2019} \times a_{2020}+a_{2020} \times a_{0}=1010$.
2. In this case $\mathrm{n}=2020$ is divisible by 4. A priori, given the tests performed for small values, we expect the number obtained to be divisible by 4, but $1010=2 \times 505$ is not divisible by 4. We could try to reuse the previous parity argument, but since 2020 is even, it would prove that the sum is even, which 1010 is also. It will therefore be necessary to more precisely count the moments where $a_{i} a_{i+1}=-1$ and those where $a_{i} a_{i+1}=1$. We know that $a_{i} a_{i+1}=-1$ if and only if $a_{i}=-a_{i+1}$, so it suffices to count the number of sign changes in the sequence $a_{i}$!
Let $a_{1}, \ldots, a_{2020}$ be numbers equal to -1 or 1 such that $a_{1} \times a_{2}+a_{2} \times a_{3}+\cdots+a_{2019} \times a_{2020}+$ $a_{2020} \times a_{1}=1010$. Set $a_{2021}=a_{1}$. We denote $N$ the number of $i$ such that $1 \leqslant i \leqslant 2020$ such that $a_{i}=-a_{i+1}$. In particular, in the sum $a_{1} \times a_{2}+a_{2} \times a_{3}+\cdots+a_{2019} \times a_{2020}+a_{2020} \times a_{1}$ there are N values -1 and $(2020-\mathrm{N})$ values 1. The sum is therefore $2020-\mathrm{N}-\mathrm{N}=2020-2 \mathrm{~N}$, so we have $2020-2 \mathrm{~N}=1010$ or $2 \mathrm{~N}=1010$ hence $\mathrm{N}=505$. But N is even. Indeed, N is the number of sign changes in the sequence $\left(a_{1}, \ldots, a_{2020}, a_{1}\right)$ and this sequence starts with $a_{1}$ and ends with $a_{1}$, so it necessarily has an even number of sign changes since $a_{1}$ is of the same sign as itself. We cannot therefore have $N=505$, which provides a contradiction. There do not exist numbers $a_{1}, \ldots, a_{2020}$ equal to -1 or 1 such that $a_{1} \times a_{2}+\cdots+a_{2019} \times a_{2020}+a_{2020} \times a_{1}=1010$.
Comment from the graders: The exercise was well handled: the first question was almost always successful, for the second question, the majority of the copies mention that an odd number of products equal to -1 is possible but few find a rigorous argument to prove it: one could verify that changing $a_{i}$ to $-a_{i}$ does not change the parity of the number of products equal to -1 and say that in the situation where all the $a_{i}$ are equal to 1, the number of products equal to -1 is even, it could therefore not be odd at the end. One could also interpret the products -1 as the changes in parity of the sequence ( $a_{i}$ ) composed of $a_{1}, \ldots, a_{2019}, a_{1}$. Since it starts at $a_{1}$ and ends at $a_{1}$, the number of sign changes is necessarily even.
|
proof
|
More than one problem
|
Incomplete
|
math-word-problem
|
Combinatorics
|
1. Existe-t-il des nombres $a_{0}, \ldots, a_{2020}$ valant -1 ou 1 tels que $a_{0} \times a_{1}+a_{1} \times a_{2}+\cdots+a_{2019} \times$ $a_{2020}+a_{2020} \times a_{0}=1010 ?$
2. Existe-t-il des nombres $a_{1}, \ldots, a_{2020}$ valant -1 ou 1 tels que $a_{1} \times a_{2}+a_{2} \times a_{3}+\cdots+a_{2019} \times$ $a_{2020}+a_{2020} \times a_{1}=1010 ?$
|
Déjà regardons l'énoncé : on veut savoir si on peut trouver des nombres $\left(a_{i}\right)_{1 \leqslant i \leqslant n}$ valant +1 ou -1 tels que $a_{1} a_{2}+\cdots+a_{n} a_{1}$ vaut 1010 avec dans la première question $n=2021$, dans la seconde $n=2020$. Pour cela on peut tester avec des $n$ petits quels sont les nombres qu'on peut écrire sous la forme $a_{1} a_{2}+\cdots+a_{n} a_{1}$. Pour $n=3$, on trouve 3 (si on ne prend que des 1 ) et -1 (si on prend $a_{1}=a_{2}=1, a_{3}=-1$ ). Pour $n=4$, on trouve $4,0,-4$ (pour avoir 4 on ne prend que des 1 , pour avoir 0 il suffit de prendre trois $a_{i}$ valant 1 et un valant -1 , pour avoir -4 , il suffit d'altener les $a_{i}$ valant 1 et ceux valant -1 . On peut continuer à tester les valeurs pour des $n$ petits. On peut remarquer que déjà les nombres qu'on peut obtenir ont l'air d'être régulièrement écartés de 4 , ils sont même congrus à $n$ modulo 4.
Notons également que si $a= \pm 1$ et $b= \pm 1$, alors $a b \pm 1$ et que $a b=1$ si $a=b$ et $a b=-1$ si $a=-b$ 。
1. Ici on est dans le cas où $n=2021$ et on veut obtenir une somme de 1010. Cela semble impossible à cause de la parité, on va donc regarder la parité de la somme. Soient $a_{0}, \ldots, a_{2020}$ des nombres valant -1 ou 1 . Pour simplifier on pose $a_{2021}=a_{0}$. Comme on a toujours $a_{i} a_{i+1}= \pm 1, a_{0} \times$ $a_{1}+a_{1} \times a_{2}+\cdots+a_{2019} \times a_{2020}+a_{2020} \times a_{0}$ est une somme de 2021 nombres impairs, donc impaire. Elle ne peut donc pas valoir 1010 qui est pair. Il n'existe pas de nombres $a_{0}, \ldots, a_{2020}$ valant -1 ou 1 tels que $a_{0} \times a_{1}+a_{1} \times a_{2}+\cdots+a_{2019} \times a_{2020}+a_{2020} \times a_{0}=1010$.
2. Dans ce cas $\mathrm{n}=2020$ est divisible par 4 . A priori vu les tests effectués pour des petites valeurs, on s'attend à ce que le nombre obtenu soit divisible par 4 , or $1010=2 \times 505$ n'est pas divisible par 4. On pourrait essayer de réutiliser l'argument de parité précédent, mais comme 2020 est pair, il prouverait que la somme est paire, or 1010 l'est aussi. Il va donc falloir plus précisément compter les moments où $a_{i} a_{i+1}=-1$ et ceux où $a_{i} a_{i+1}=1$. Or on sait que $a_{i} a_{i+1}=-1$ si et seulement si $a_{i}=-a_{i+1}$, il suffit donc de compter le nombre de changement de signes de la suite $a_{i}$ !
Soient $a_{1}, \ldots, a_{2020}$ des nombres valant -1 ou 1 tels que $a_{1} \times a_{2}+a_{2} \times a_{3}+\cdots+a_{2019} \times a_{2020}+$ $a_{2020} \times a_{1}=1010$. Posons $a_{2021}=a_{1}$. On note $N$ le nombre de $i$ tels que $1 \leqslant i \leqslant 2020$ tels que $a_{i}=-a_{i+1}$. En particulier dans la somme $a_{1} \times a_{2}+a_{2} \times a_{3}+\cdots+a_{2019} \times a_{2020}+a_{2020} \times a_{1}$ il y a N valeurs -1 et $(2020-\mathrm{N})$ valeurs 1 . La somme vaut donc $2020-\mathrm{N}-\mathrm{N}=2020-2 \mathrm{~N}$, on a donc $2020-2 \mathrm{~N}=1010$ soit $2 \mathrm{~N}=1010$ donc $\mathrm{N}=505$. Or N est pair. En effet N est le nombre de changement de signs dans la suite $\left(a_{1}, \ldots, a_{2020}, a_{1}\right)$ et cette suite commence par $a_{1}$ et termine $a_{1}$ donc elle a nécessairement un nombre pair de changements de signe puisque $a_{1}$ est du même signe que lui-même. On ne peut donc pas avoir $N=505$, ce qui fournit une contradiction. Il n'existe pas de nombres $a_{1}, \ldots, a_{2020}$ valant -1 ou 1 tels que $a_{1} \times a_{2}+\cdots+a_{2019} \times a_{2020}+a_{2020} \times a_{1}=1010$.
Commentaire des correcteurs: L'exercice a été bien traité : la première question a été quasiment toujours réussie, pour la seconde question, la majorité des copies mentionne qu'un nombre impair de produits valant -1 est possible mais peu trouvent un argument rigoureux pour le prouver : on pouvait vérifier que changer $a_{i}$ en $-a_{i}$ ne changeait pas la parité du nombre de produits valant -1 et dire que dans la situation où tous les $a_{i}$ valent 1 , le nombre de produits valant -1 est pair, il ne pouvait donc être impair à la fin. On pouvait également interpréter les produits -1 comme les changements de parité de la suite ( $a_{i}$ ) composée de $a_{1}, \ldots, a_{2019}, a_{1}$. Comme elle commence à $a_{1}$ et termine à $a_{1}$, le nombre de changements de signe est forcément pair.
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "## Exercice 3.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-5.jsonl",
"solution_match": "## Solution de l'exercice 3",
"tier": "T2",
"year": null
}
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.