problem
stringlengths 14
10.4k
| solution
stringlengths 1
24.1k
| answer
stringlengths 1
250
⌀ | problem_is_valid
stringclasses 4
values | solution_is_valid
stringclasses 3
values | question_type
stringclasses 4
values | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
10.4k
| solution_raw
stringlengths 1
24.1k
| metadata
dict |
|---|---|---|---|---|---|---|---|---|---|
Let $ABC$ be a triangle with acute angles. The altitude from $A$ intersects the circumcircle of triangle $ABC$ at a point $D$. The altitude from $B$ intersects the circumcircle of triangle $ABC$ at a point $E$. The line $(ED)$ intersects the sides $[AC]$ and $[BC]$ at points $P$ and $Q$ respectively. Show that the points $P, Q, B$ and $A$ are concyclic.
|
Let's determine which angles seem easy to access. For example, it seems complicated to obtain the angle $\widehat{\mathrm{PBQ}}$ or the angle $\widehat{\mathrm{PBA}}$. On the other hand, we already know the angle $\widehat{\mathrm{QBA}}$, so it seems reasonable to try to show that $\widehat{\mathrm{QPA}}=180^{\circ}-\widehat{\mathrm{QBA}}$.
Now, $180^{\circ}-\widehat{\mathrm{QPA}}=\widehat{\mathrm{EPA}}$, so we try to show that $\widehat{\mathrm{EPA}}=\widehat{\mathrm{QBA}}$. Two right angles are given: if we let $H_{B}$ be the foot of the altitude from vertex $B$ and $H_{A}$ be the foot of the altitude from vertex $A$, then the angles $\widehat{A H_{A} B}$ and $\widehat{B H_{B} A}$ are right angles.
We have not yet used the hypothesis that points $E$ and $D$ are on the circumcircle of triangle $A B C$. This hypothesis translates into an angle equality using the inscribed angle theorem. This gives notably $\widehat{\mathrm{DEB}}=\widehat{\mathrm{DAB}}$.
By reporting these angle equalities on the figure, we find that $\widehat{\mathrm{PEH}_{B}}=\widehat{\mathrm{H}_{\mathrm{A}} \mathrm{AB}}$ and $\widehat{\mathrm{PH}_{B} \mathrm{E}}=\widehat{\mathrm{BH}_{\mathrm{A}} \mathrm{A}}$. The triangles $\mathrm{PEH}_{B}$ and $\mathrm{BAH}_{\mathrm{A}}$ are therefore similar (there are two pairs of equal angles). Thus, $\widehat{\mathrm{EPH}_{\mathrm{B}}}=\widehat{\mathrm{ABH}_{\mathrm{A}}}$, which is the equality we wanted to prove.
Comment from the graders: The exercise is very well done, and the students have shown several effective ways of looking at the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle dont les angles sont aigus. La hauteur issue de $A$ recoupe le cercle circonscrit au triangle $A B C$ en un point $D$. La hauteur issue de $B$ recoupe le cercle circonscrit au triangle $A B C$ en un point $E$. La droite (ED) coupe les côtés $[A C]$ et $[B C]$ respectivement en les points $P$ et $Q$. Montrer que les points $P, Q, B$ et $A$ sont cocycliques.
|
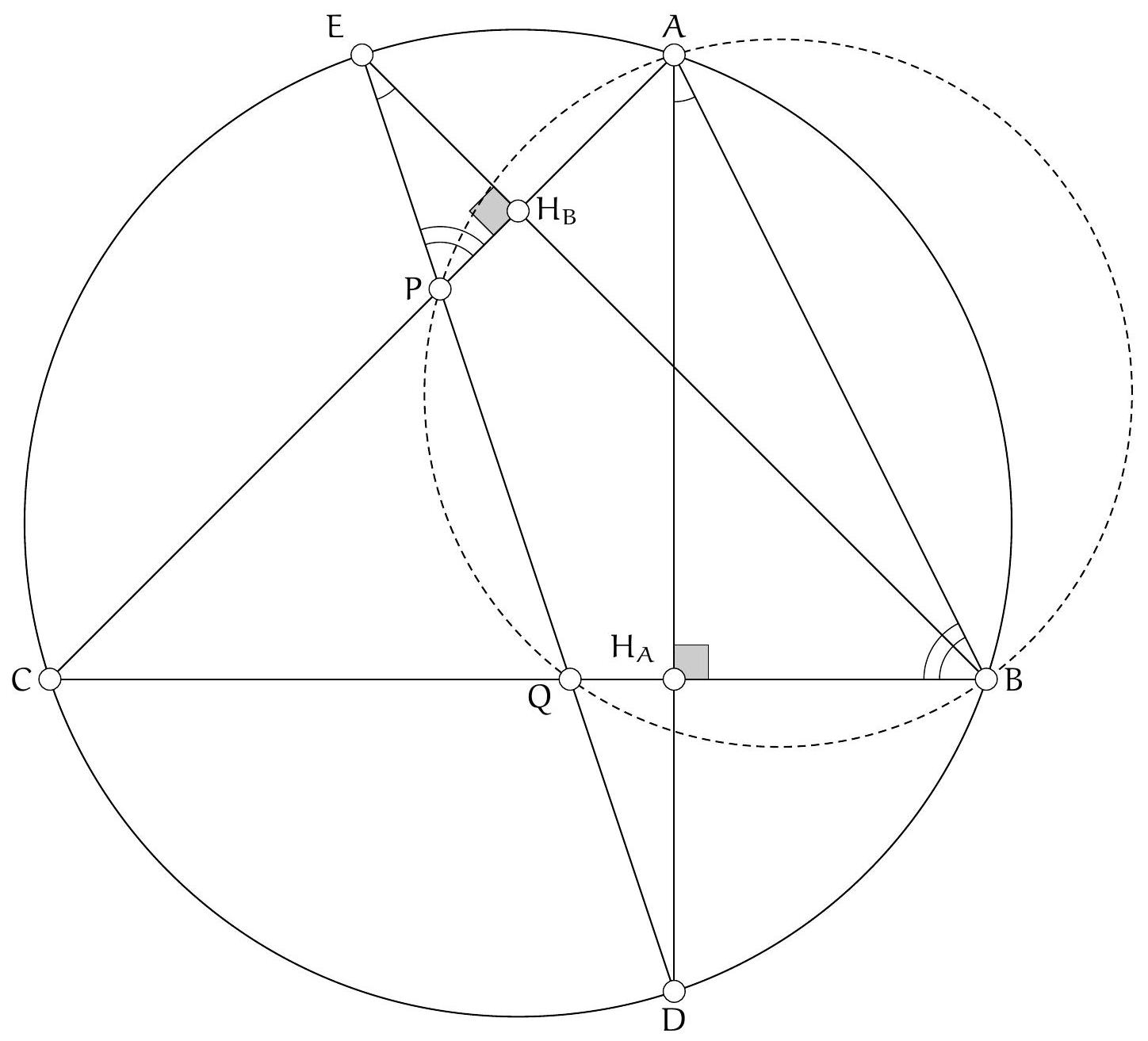
Déterminons quels sont les angles qui semblent faciles d'accès. Par exemple, il semble compliqué de pouvoir obtenir l'angle $\widehat{\mathrm{PBQ}}$ ou l'angle $\widehat{\mathrm{PBA}}$. En revanche, on connait déjà l'angle $\widehat{\mathrm{QBA}}$ donc il semble raisonnable d'essayer de montrer que $\widehat{\mathrm{QPA}}=180^{\circ}-\widehat{\mathrm{QBA}}$.
Or, $180^{\circ}-\widehat{\mathrm{QPA}}=\widehat{\mathrm{EPA}}$, on essaye donc de montrer que $\widehat{\mathrm{EPA}}=\widehat{\mathrm{QBA}}$. Deux angles droits nous sont donnés : si on pose $H_{B}$ le pied de la hauteur issue du sommet $B$ et $H_{A}$ le pied de la hauteur issue du sommet $A$, alors les angles $\widehat{A H_{A} B}$ et $\widehat{B H_{B} A}$ sont droits.
On n'a pas encore utilisé l'hypothèse que les points $E$ et $D$ étaient sur le cercle circonscrit au triangle $A B C$. Cette hypothèse se traduit par une égalité d'angle à l'aide du théorème de l'angle inscrit. Ceci donne notemment $\widehat{\mathrm{DEB}}=\widehat{\mathrm{DAB}}$.
En reportant ces différentes égalités d'angles sur la figure, on trouve donc que $\widehat{\mathrm{PEH}_{B}}=\widehat{\mathrm{H}_{\mathrm{A}} \mathrm{AB}}$ et $\widehat{\mathrm{PH}_{B} \mathrm{E}}=\widehat{\mathrm{BH}_{\mathrm{A}} \mathrm{A}}$. Les triangles $\mathrm{PEH}_{B}$ et $\mathrm{BAH}_{\mathrm{A}}$ sont donc sembables (il y a deux paires d'angles égaux deux à deux). Ainsi, $\widehat{\mathrm{EPH}_{\mathrm{B}}}=\widehat{\mathrm{ABH}_{\mathrm{A}}}$ qui est l'égalité que l'on souhaitait démontrer.
Commentaire des correcteurs: L'exercice est très bien réussi et les élèves ont montré plusieurs façons efficaces de voir les choses.
|
{
"exam": "French_envois",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-5.jsonl",
"solution_match": "## Solution de l'exercice 4",
"tier": "T2",
"year": null
}
|
The cells of an $8 \times 8$ chessboard are white. A move consists of swapping the colors of the cells of a $3 \times 1$ or $1 \times 3$ rectangle (white cells become black and black cells become white). Is it possible to achieve the configuration where all cells of the chessboard are black in a finite number of moves?
|
The statement presents a finite sequence of operations, and the problem asks whether it is possible to go from the initial situation to a certain final situation. A first idea in this case is to look for an invariant.
One can possibly try by hand to see if it is possible to end up with a configuration where all the squares are black. After several attempts, one realizes that one cannot achieve the desired configuration, and one can therefore conjecture that the answer to the exercise is negative.
Here, the support of the statement is a chessboard, so we will look for a coloring invariant, that is, we will look for a clever coloring of the chessboard that highlights the invariant. What are the characteristics of a good coloring? First of all, since the considered rectangles have 3 squares, one can look for a coloring that has at most 3 colors. Also, one can look for a coloring such that each rectangle $3 \times 1$ or $1 \times 3$ has one square of each color. We therefore adopt the following coloring (where we have replaced the colors with numbers, given that the exercise already talks about the colors of the squares).
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 |
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 |
| 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 |
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 |
| 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
What does this coloring tell us? Each rectangle $3 \times 1$ or $1 \times 3$ has exactly one square of each number. Therefore, when one changes the colors of a rectangle, exactly one square of each number changes color. Since the numbers of squares of number 1, 2, and 3 are not the same, this encourages us to count at each step the number of white squares of each number.
Let $\mathrm{N}_{1}$ be the number of white squares containing the number 1, called type 1, $\mathrm{~N}_{2}$ the number of white squares of type 2, and $\mathrm{N}_{3}$ the number of white squares of type 3. In the initial situation, $\mathrm{N}_{1}=\mathrm{N}_{3}=21$ and $\mathrm{N}_{2}=22$, these numbers are not all equal. We will therefore be interested in the evolution of the difference between the numbers $N_{1}$ and $N_{2}$. Changing the color of the squares of a rectangle $3 \times 1$ or $1 \times 3$ simultaneously decreases or increases each of the numbers $N_{1}, N_{2}$, and $N_{3}$. In particular, the difference $N_{1}-N_{2}$, at each step, increases by $2, 0$, or $-2$. In particular, its parity does not change. Now $\mathrm{N}_{1}-\mathrm{N}_{2}$ is odd at the start. In the final situation required, $N_{1}-N_{2}=0.0$ is even, so the number $N_{1}-N_{2}$ cannot be zero after a finite number of steps. Therefore, it is not possible to end up with a completely black chessboard. Comment from the examiners: The exercise was not approached by many students. The exercise is, however, a very instructive exercise on invariants by coloring.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Les cases d'un échiquier $8 \times 8$ sont blanches. Un coup consiste à échanger les couleurs des cases d'un rectangle $3 \times 1$ ou $1 \times 3$ (les cases blanches deviennent noires et les cases noires deviennent blanches). Est-il possible d'aboutir en un nombre fini de coups à la configuration où toutes les cases de l'échiquier sont noires?
|
L'énoncé présente une suite finie d'opérations et le problème demande s'il est possible de partir de la situation initiale pour arriver à une certaine situation finale. Une première idée dans ce cas est de chercher un invariant.
On peut éventuellement essayer à la main de voir s'il est possible d'aboutir à une configuration où toutes les cases sont noires. Après plusieurs essais, on se rend compte qu' on n'arrive pas à aboutir la configuration désirée et on peut donc conjecturer que la réponse à l'exercice est négative.
Ici, le support de l'énoncé est un échiquier, on va donc chercher un invariant de coloriage, c'est-à-dire que nous allons chercher un coloriage astucieux de l'échiquier qui mette en évidence l'invariant. Quelles sont les caractéristiques d'un bon coloriage ? Tout d'abord, puisque les rectangles considérés possèdent 3 cases, on peut chercher un coloriage qui possède au plus 3 couleurs. Aussi, on peut chercher un coloriage tel que chaque rectangle $3 \times 1$ ou $1 \times 3$ possède une case de chaque couleur. On adopte donc le coloriage suivant (où on a remplacé les couleurs par des numéros, étant donné que l'exercice parle déjà de couleurs de cases).
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 |
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 |
| 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
| 3 | 1 | 2 | 3 | 1 | 2 | 3 | 1 |
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 |
| 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 |
Que nous apprend ce coloriage ? Chaque rectangle $3 \times 1$ ou $1 \times 3$ possède exactement une case de chaque numéro. Donc lorsque l'on change les couleurs d'un rectangle, exactement une case de chaque numéro change de couleur. Puisque les nombres de cases de numéro 1,2 et 3 ne sont pas identiques, ceci nous encourage à compter à chaque étape le nombre de cases blanches de chaque numéro.
Soit $\mathrm{N}_{1}$ le nombre de cases blanches contenant le numéro 1, dites de type $1, \mathrm{~N}_{2}$ le nombre de cases blanches de types 2 et $\mathrm{N}_{3}$ le nombre de cases blanches de type 3. Dans la situation initiale, $\mathrm{N}_{1}=\mathrm{N}_{3}=21$ et $\mathrm{N}_{2}=22$, ces nombres ne sont pas tous égaux. On va donc s'intéresser à l'évolution de la différence entre les nombres $N_{1}$ et $N_{2}$. Changer la couleur des cases d'un rectangle $3 \times 1$ ou $1 \times 3$ fait en même temps diminuer ou augmenter chacun des nombres $N_{1}, N_{2}$ et $N_{3}$. En particulier, la différence $N_{1}-N_{2}$, à chaque étape, augmente de $2,0 \mathrm{ou}-2$. En particulier, sa parité ne change pas. Or $\mathrm{N}_{1}-\mathrm{N}_{2}$ est impair au départ. Dans la situation finale demandée, $N_{1}-N_{2}=0.0$ est pair, donc le nombre $N_{1}-N_{2}$ ne peut être nul au bout d'un nombre fini d'étape. On ne peut donc pas arriver à un échiquier entièrement noir. Commentaire des correcteurs: L'exercice n'a pas été abordé par beaucoup d'élèves. L'exercice est cela dit un exercice d'invariant par coloriage très instructif.
|
{
"exam": "French_envois",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-5.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T2",
"year": null
}
|
Determine all triplets $(x, y, z)$ of natural numbers satisfying the equation:
$$
2^{x}+3^{y}=z^{2}
$$
|
First, let's analyze the problem: we have a Diophantine equation with a power of 2, a power of 3, and a square. We quickly test small values of \( z \) to find solutions. We can observe that \( 2^{0} + 3^{1} = 2^{2} \), \( 2^{3} + 3^{0} = 3^{2} \), and \( 2^{4} + 3^{2} = 5^{2} \). Since we have a few solutions, we won't find immediate contradictions by simply looking modulo something.
However, we have a square, so it is natural to look modulo 4 or modulo 3 to try to get information about \( x \) and \( y \). Ideally, we would like to show that either \( x \) or \( y \) is even, as this would give us another square in the equation, allowing us to factorize. We will look modulo 4, and first consider the case where 4 divides \( 2^{x} \), i.e., the case \( x \geq 2 \).
Suppose \( x \geq 2 \). Since a square is congruent to 0 or 1 modulo 4, \( z^{2} \) is congruent to 0 or 1 modulo 4, and thus \( 3^{y} \) is also congruent to 0 or 1 modulo 4. Since \( 3^{y} \) is not divisible by 4, we must have \( 3^{y} \equiv 1 \pmod{4} \). Since \( 3^{2} \equiv 9 \equiv 1 \pmod{4} \), we must have \( y \) even (if \( y = 2k + 1 \), then \( 3^{y} \equiv 9^{k} \times 3 \equiv 3 \pmod{4} \)). Let \( y = 2k \) where \( k \) is an integer. We get \( 2^{x} = z^{2} - (3^{k})^{2} = (z - 3^{k})(z + 3^{k}) \). Note that \( z + 3^{k} \) is strictly positive, so
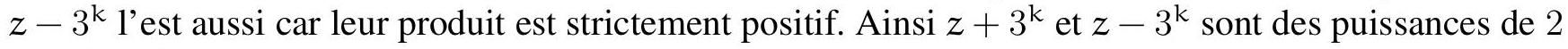 because they divide \( 2^{x} \).
Here we have two terms whose product is \( 2^{x} \). We want to show that one of them cannot be very large. To do this, we will consider the gcd of \( z + 3^{k} \) and \( z - 3^{k} \) and compute it using the fact that it divides their sum, difference, and product.
Let \( d \) be the gcd of \( (z - 3^{k}) \) and \( (z + 3^{k}) \). Then \( d \) divides \( (z + 3^{k}) - (z - 3^{k}) = 2 \times 3^{k} \), but \( d \) also divides \( 2^{x} \), so \( d \) divides 2. Since \( z + 3^{k} \equiv z - 3^{k} \pmod{2} \), if \( d = 1 \), then \( (z - 3^{k}) \) and \( (z + 3^{k}) \) are odd, so \( 2^{x} \) is also odd, which contradicts the fact that \( x \geq 2 \). Therefore, \( d = 2 \).
In particular, since \( (z - 3^{k}) \) and \( (z + 3^{k}) \) are powers of 2 with gcd 2, the smaller of the two is 2. Since \( z + 3^{k} > z - 3^{k} \), we have \( z = 3^{k} + 2 \). Considering the gcd here is not necessary; we could have directly arrived at this by setting \( z + 3^{k} = 2^{a} \) and \( z - 3^{k} = 2^{b} \), observing that \( a > b \), and writing \( 2 \times 3^{k} = 2^{a} - 2^{b} = 2^{b}(2^{a-b} - 1) \), but it is a good reflex when we have a product to look at the gcd of the factors.
From this, we deduce that \( z + 3^{k} = 2^{x-1} \) and \( z - 3^{k} = 2 \), so by taking the difference \( 2 \times 3^{k} + 2 = 2^{x-1} \) and thus \( 3^{k} + 1 = 2^{x-2} \). This equation is quite well-known, but if we don't know it, since we have powers of 2 and 3, it is relevant to look modulo 2, 4, 8, or 3, 9. Since \( 3 + 1 = 2^{2} \), looking modulo 4 and 3 won't conclude immediately, so we look modulo 8.
If \( x \geq 5 \), 8 divides \( 2^{x-2} \), so 8 divides \( 3^{k} + 1 \). However, the powers of 3 modulo 8 are 1 or 3, so \( 3^{k} + 1 \) is 2 or 4 modulo 8 and is not divisible by 8, which gives a contradiction. Therefore, we must have \( x = 2, 3, \) or 4.
For \( x = 2 \), \( 1 = 1 + 3^{k} \) so \( 3^{k} = 0 \), which is impossible. For \( x = 3 \), \( 1 + 3^{k} = 2 \) so \( 3^{k} = 1 \) and \( k = 0 \), thus \( y = 0 \). For \( x = 4 \), \( 1 + 3^{k} = 4 \) so \( 3^{k} = 3 \), thus \( k = 1 \) and \( y = 2 \).
Conversely, if \( (x, y) = (3, 0) \), then \( z^{2} = 2^{x} + 3^{y} = 9 = 3^{2} \) so \( z = \pm 3 \) and the triplet \( (3, 0, 3) \) is a solution. If \( (x, y) = (4, 2) \), then \( z^{2} = 2^{x} + 3^{y} = 25 = 5^{2} \) so \( z = 5 \) and the triplet \( (4, 2, 5) \) is a solution.
It remains to treat the case where \( x = 0 \) and the case where \( x = 1 \). For the case where \( x = 0 \), we have \( 2^{x} = 1 \), which is a square, so we will factorize and reuse the gcd technique. If \( x = 0 \), the equation becomes \( 3^{y} = z^{2} - 1 = (z - 1)(z + 1) \). The gcd of \( z - 1 \) and \( z + 1 \) divides \( 3^{y} \) and divides \( z + 1 - (z - 1) = 2 \), so it must be 1. Since \( 3^{y} = (z - 1)(z + 1) \), \( z - 1 \) and \( z + 1 \) are positive powers of 3 (since \( z + 1 > 0 \) and thus \( z - 1 > 0 \), their product is strictly positive), the smallest of the two must be 1, so \( z - 1 = 1 \) and \( z = 2 \). We get \( 3^{y} = z^{2} - 1 = 3 \) so \( y = 1 \). Conversely, \( (0, 1, 2) \) is a solution because \( 1 + 3 = 2^{2} \).
For the case \( x = 1 \), we don't see any solutions, so we need to find a relevant modulo to evaluate the equation. Since there is a power of 3 and a square, we can look modulo 3. If \( x = 1 \), the equation becomes \( 2 + 3^{y} = z^{2} \). If \( y = 0 \), the equation becomes \( z^{2} = 3 \), which has no integer solutions. Therefore, \( y > 0 \) and \( z^{2} \equiv 2 \pmod{3} \). However, a square modulo 3 is congruent to 0 or 1, so there are no solutions for \( x = 1 \). The solutions are therefore \( (0, 1, 2) \), \( (3, 0, 3) \), and \( (4, 2, 5) \).
Comment from the graders: The exercise was generally well done. However, it is necessary to verify the solutions obtained and justify everything that is stated: for example, it is necessary to justify that if two powers of 2 are 2 units apart, they must be 2 and 4 (this can be easily done by looking modulo 4).
|
(0, 1, 2), (3, 0, 3), (4, 2, 5)
|
Yes
|
Incomplete
|
math-word-problem
|
Number Theory
|
Déterminer tous les triplets $(x, y, z)$ d'entiers naturels satisfaisant l'équation:
$$
2^{x}+3^{y}=z^{2}
$$
|
Tout d'abord, analysons le problème : on a une équation diophantienne avec une puissance 2 , une puissance de 3 et un carré. On s'empresse donc de tester les petites valeurs de $z$ et de trouver la solution. On peut remarquer que $2^{0}+3^{1}=2^{2}, 2^{3}+3^{0}=3^{2}$ et $2^{4}+3^{2}=5^{2}$. A priori comme on a quelques solutions, on ne va pas trouver de contradictions immédiates simplement en regardant modulo quelque chose.
Néanmoins on a un carré, donc il est naturel de regarder modulo 4 ou modulo 3 et d'essayer d'obtenir des informations sur $x$ et $y$. Idéalement, on aimerait obtenir que soit $x$ soit $y$ est pair, comme ça on aurait un autre carré dans l'équation ce qui nous permettrait de factoriser. On va donc regarder modulo 4, pour cela on a envie de traitrer en premier le cas où 4 divise $2^{\mathrm{x}}$, i.e. le cas $x \geqslant 2$.
Supposons $x \geqslant 2$. Comme un carré est congru à 0 ou 1 modulo $4, z^{2}$ est congru à 0 ou 1 modulo 4 , donc $3^{y}$ aussi. Comme il n'est pas divisible par 4 , on a forcément $3^{y} \equiv 1(\bmod 4)$. Comme $3^{2} \equiv 9 \equiv 1$ $(\bmod 4)$, on a nécessairement $y$ pair $\left(\right.$ si $\left.y=2 k+1,3^{y} \equiv 9^{k} \times 3 \equiv 3(\bmod 4)\right)$. Posons $y=2 k$ avec $k$ entier, on obtient $2^{\mathrm{x}}=z^{2}-\left(3^{k}\right)^{2}=\left(z-3^{k}\right)\left(z+3^{k}\right)$. Notons que $z+3^{k}$ est strictement positif, donc
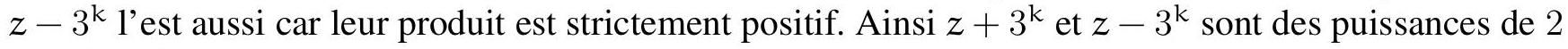 car elles divisent $2^{x}$.
Ici on a deux termes dont le produit vaut $2^{x}$, on aimerait montrer que l'un d'entre eux ne peut pas être très grand. Pour cela on va considérer le pgcd de $z+3^{k}$ et $z-3^{k}$ et le calculer en utilisant qu'il divise leur somme, différence et produit.
Soit d le pgcd de $\left(z-3^{k}\right)$ et $\left(z+3^{k}\right)$, alors $d$ divise $\left(z+3^{k}\right)-\left(z-3^{k}\right)=2 \times 3^{k}$, mais $d$ divise aussi $2^{\mathrm{x}}$ donc $d$ divise 2 . Comme $z+3^{k} \equiv z-3^{k}(\bmod 2)$, si d vaut $1,\left(z-3^{k}\right)$ et $\left(z+3^{k}\right)$ sont impairs donc $2^{\mathrm{x}}$ aussi, ce qui contredit le fait que $x \geqslant 2$. On a donc $\mathrm{d}=2$
En particulier comme $\left(z-3^{k}\right)$ et $\left(z+3^{k}\right)$ sont des puissances de 2 de pgcd 2 , le plus petit des deux vaut 2 donc comme $z+3^{k}>z-3^{k}, z=3^{k}+2$. Considérer le pgcd ici n'est pas nécessaire, on aurait pu directement aboutir à cela en posant $z+3^{\mathrm{k}}=2^{\mathrm{a}}, z-3^{\mathrm{k}}=2^{\mathrm{b}}$, observé que $\mathrm{a}>\mathrm{b}$ et écrit $2 \times 3^{\mathrm{k}}=2^{\mathrm{a}}-2^{\mathrm{b}}=2^{\mathrm{b}}\left(2^{\mathrm{a}-\mathrm{b}}-1\right)$, mais un bon réflexe quand on a un produit est de regarder le pgcd des facteurs.
De ceci, on déduit que $z+3^{k}=2^{x-1}$ et $z-3^{k}=2$, donc en faisant la différence $2 \times 3^{k}+2=2^{x-1}$ donc $3^{\mathrm{k}}+1=2^{\mathrm{x}-2}$. Cette équation est assez connue, mais si on ne la connait pas, comme on a des puissances de 2 et de 3 , il est pertinent de regarder modulo $2,4,8$ ou 3,9 . Comme $3+1=2^{2}$, regarder modulo 4 et 3 ne conclura pas tout de suite, on regarde donc modulo 8 .
Si $x \geqslant 5,8$ divise $2^{x-2}$ donc 8 divise $3^{x}+1$. Or les puissances de 3 modulo 8 valent 1 ou 3 donc $3^{x}-1$ vaut 2 ou 4 modulo 8 et n'est pas divisible par 8 , ce qui donne une contradiction. On a donc forcément $x=2,3$ ou 4 .
Pour $x=2,1=1+3^{k}$ donc $3^{k}=0$ ce qui est impossible. Pour $x=3,1+3^{k}=2$ donc $3^{k}=1$ donc $k=0$ et $y=0$. Pour $x=4,1+3^{k}=4$ donc $3^{k}=3$, on a donc $k=1$ soit $y=2$.
Réciproquement, si $(x, y)=(3,0), z^{2}=2^{x}+3^{y}=9=3^{2}$ donc $z= \pm 3$ et le triplet $(3,0,3)$ convient. Si $(x, y)=(4,2), z^{2}=2^{x}+3^{y}=25=5^{2}$ donc $z=5$ et le triplet $(4,2,5)$ convient.
Il reste donc à traiter le cas où $x=0$ et celui où $x=1$. Pour le cas où $x=0$, on a $2^{x}=1$ qui est un carré, on va donc factoriser et réutiliser la technique du pgcd. Si $x=0$, l'équation se réécrit $3^{y}=z^{2}-1=(z-1)(z+1)$. Le pgcd de $z-1$ et $z+1$ divise $3^{y}$ et divise $z+1-(z-1)=2$ donc il vaut nécessairement 1 . Comme $3^{y}=(z-1)(z+1), z-1$ et $z+1$ sont des puissances de 3 positives (car $z+1>0$ donc $z-1>0$ leur produit étant strictement positif) de pgcd 1 , le plus petit des deux
vaut nécessairement 1 donc $z-1=1, z=2$. On obtient $3^{y}=z^{2}-1=3$ donc $y=1$. Réciproquement $(0,1,2)$ est solution car $1+3=2^{2}$.
Pour le cas $x=1$, on ne voit pas de solution, il faut donc trouver un modulo pertinent pour évaluer l'équation, comme il y a une puissance de 3 et un carré, on peut regarder modulo 3 . $\mathrm{Si} x=1$ l'équation devient $2+3^{y}=z^{2}$. Si $y=0$ l'équation devient $z^{2}=3$ qui n'a pas de solution entière. On a donc $y>0$ donc $z^{2} \equiv 2(\bmod 3)$. Or un carré modulo 3 est congru à 0 ou 1 , il n'y a donc pas de solution pour $x=1$. Les solutions sont donc $(0,1,2),(3,0,3)$ et $(4,2,5)$.
Commentaire des correcteurs: Exercice globalement bien réussi. Il faut néanmoins penser à vérifier les solutions obtenues et justifier tout ce qui est affirmé : par exemple il faut justifier que si deux puissances de 2 sont distance de 2 ce sont forcément 2 et 4 (on peut le faire facilement en regardant modulo 4).
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-5.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T2",
"year": null
}
|
A grid of size $\mathrm{n} \times \mathrm{n}$ contains $\mathrm{n}^{2}$ cells. Each cell contains a natural number between 1 and $\boldsymbol{n}$, such that each integer in the set $\{1, \ldots, n\}$ appears exactly $n$ times in the grid. Show that there exists a column or a row of the grid containing at least $\sqrt{n}$ different numbers.
|
Let's first look at what happens in what seems to be the 'worst case': if each row/column does not contain many numbers, each number will be present a lot. In particular, for any $i$, the number of $i$ seems to be written in few rows and columns. But a priori, if the number $i$ appears too much in a row, it will appear in many columns and vice versa. A priori, the worst case seems to be the one where each number appears in as many columns as rows, and since each number appears $n$ times, the square must be of dimension $\sqrt{n}$, so $i$ appears in at least $2 \sqrt{n}$ rows and columns.
Of course, this analysis is by no means a proof, but we see two important ideas: first, the number of distinct numbers in each row/column seems to be related to the number of rows/columns in which each number appears. Second, for any $i$ between 1 and $n$, the number $i$ appears at least on $2 \sqrt{n}$ rows and columns. We will therefore try to formalize this.
Let $a_{c, i}$ for $c$ a column or a row and $i$ an integer between 1 and $n$ be the number of times $i$ appears in $c$, let $c_{i}$ (resp. $l_{i}$) be the number of columns (resp. rows) to which $i$ belongs. Let $C$ be the set of columns and $L$ the set of rows.
Note that the hypothesis that $i$ appears $n$ times translates as $c_{i} \times l_{i} \geqslant n$ because $i$ appears in at most $c_{i} l_{i}$ cells.
Note that for any $i$, $l_{i}+c_{i}$ being the number of rows or columns where $i$ appears, it is $\sum_{c \in C \cup L} a_{c, i}$. The number of distinct elements in column $c$ is, in turn, $\sum_{i=1}^{n} a_{c, i}$. In particular, we see that the $a_{c, i}$ play an important role in the problem.
Now it remains to relate the number of appearances of $i$ in the different rows/columns to the number of numbers in each row. For this, we will look at the sum of the $a_{c, i}$ (we sum over $i$ from 1 to $n$ and over $c$ columns and rows) and use the two previous interpretations.
We thus obtain $\sum_{i=1}^{n} \sum_{c \in C \cup L} a_{c, i}=\sum_{i=1}^{n} c_{i}+l_{i} \geqslant \sum_{i=1}^{n} 2 \sqrt{c_{i} l_{i}} \geqslant 2 n \sqrt{n}$.
We deduce that $\sum_{c \in C \cup L} \sum_{i=1}^{n} a_{c, i} \geqslant \sum_{i=1}^{n} 2 \sqrt{c_{i} l_{i}}=2 n \sqrt{n}$.
In particular, since there are $2 n$ rows or columns, there exists $c$ rows or columns such that $\sum_{i=1}^{n} a_{c, i} \geqslant \sqrt{n}$ i.e., $c$ contains at least $\sqrt{n}$ different numbers.
Comment from the graders: The exercise was very difficult and only one student succeeded. It was necessary to try to relate the number of numbers per row to the number of columns/rows where a number appears, and few students had this idea.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Une grille de taille $\mathrm{n} \times \mathrm{n}$ contient $\mathrm{n}^{2}$ cases. Chaque case contient un entier naturel compris entre 1 et $\boldsymbol{n}$, de telle sorte que chaque entier de l'ensemble $\{1, \ldots, n\}$ apparaît exactement $n$ fois dans la grille. Montrer qu'il existe une colonne ou une ligne de la grille contenant au moins $\sqrt{n}$ nombres différents.
|
Essayons d'abord de regarder ce qui se passe dans ce qui semble être 'le pire cas" : si chaque ligne/colonne ne contient pas beaucoup de numéros, chaque numéro va y être beaucoup présent. En particulier, pour tout $i$, le nombre de $i$ semble être écrit dans peu de lignes et de colonnes. Mais à priori si le numéro $i$ apparait trop dans une ligne, il apparaitra dans beaucoup de colonnes et inversement. A priori, le pire cas semble être celui où chaque numéro apparaît dans autant de colonnes que de lignes et comme chaque numéro apparaît $n$ fois, le carré doit être de dimension $\sqrt{n}$, donc $i$ apparait dans au moins $2 \sqrt{n}$ lignes et colonnes.
Bien sûr, cette analyse ne constitue en rien une preuve, mais on voit deux idées importantes : premièrement, le nombre de numéros distincts dans chaque ligne/colonne semble avoir un lien avec le nombre de lignes/colonnes où chaque numéro apparaît. Deuxièmement, pour tout $i$ entre 1 et $n$, le nombre $i$ apparait au moins sur $2 \sqrt{n}$ lignes et colonnes. On va donc essayer de formaliser ça.
Notons $a_{c, i}$ pour $c$ une colonne ou une ligne et $i$ un entier entre 1 et $n$ le nombre de fois qu'apparait $i$ dans $c$, notons $c_{i}$ (resp. $l_{i}$ ) le nombre de colonnes (resp. lignes) à laquelle $i$ appartient. On note C l'ensemble des colonnes $L$ celui des lignes.
Notons que l'hypothèse du fait que $i$ apparait $n$ fois se traduit comme $c_{i} \times l_{i} \geqslant n$ car $i$ apparait dans au plus $c_{i} l_{i}$ cases.
Notons que pour tout $i$, $l_{i}+c_{i}$ étant le nombre de ligne ou de colonne où apparait $i$, il vaut $\sum_{c \in C \cup L} a_{c, i}$. Le nombre d'éléments distincts dans la colonne $c$ vaut, quant à lui, $\sum_{i=1}^{n} a_{c, i}$. En particulier, on voit bien que les $a_{c, i}$ jouent un rôle important dans le problème.
Maintenant il reste à relier le nombre d'apparitions de i dans les différentes lignes/colonnes au nombre de numéros dans chaque ligne. Pour cela on va regarder la somme des $a_{c, i}$ (on somme sur $i$ entre 1 et $n$ et sur c colonne et ligne) et utiliser les deux interprétations précédentes.
On obtient ainsi $\sum_{i=1}^{n} \sum_{c \in C \cup L} a_{c, i}=\sum_{i=1}^{n} c_{i}+l_{i} \geqslant \sum_{i=1}^{n} 2 \sqrt{c_{i} l_{i}} \geqslant 2 n \sqrt{n}$.
On en déduit que $\sum_{c \in C \cup L} \sum_{i=1}^{n} a_{c, i} \geqslant \sum_{i=1}^{n} 2 \sqrt{c_{i} l_{i}}=2 n \sqrt{n}$.
En particulier, comme il y a $2 n$ lignes ou colonnes, il existe $c$ colonnes ou lignes telles que $\sum_{i=1}^{n} a_{c, i} \geqslant \sqrt{n}$ i.e. c contient au moins $\sqrt{\mathrm{n}}$ numéros différents.
Commentaire des correcteurs: L'exercice était très dur et seul un élève l'a réussi. Il fallait essayer de relier le nombre de numéros par ligne aux nombres de colonnes/lignes où apparait un numéro et rares sont ceux qui ont eu l'idée.
|
{
"exam": "French_envois",
"problem_label": "14",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-5.jsonl",
"solution_match": "\nSolution de l'exercice 7",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a non-isosceles triangle at $B$. Let $D$ be the foot of the angle bisector of $\angle ABC$. Let $M$ be the midpoint of the arc $\widehat{AC}$ containing $B$ on the circumcircle of triangle $ABC$. The circumcircle of triangle $BDM$ intersects the segment $[AB]$ at a point $K$ distinct from $B$. Let $J$ be the symmetric point of $A$ with respect to point $K$. The line $(DJ)$ intersects the line $(AM)$ at a point $O$. Show that the points $J, B, M$, and $O$ are concyclic.
|
First, we recognize in the figure some known points: point $M$ is the midpoint of the arc $A C$ containing $B$, which is the North Pole of point $B$ in triangle $A B C$, meaning it is the intersection of the external bisector of angle $\widehat{A B C}$, the perpendicular bisector of segment $[A C]$, and the circumcircle of triangle $A B C$. Therefore, the angle $\widehat{D B M}$ is a right angle (by definition of the external bisector). The fact that $M$ lies on the perpendicular bisector of segment $[A C]$ also invites us to consider this bisector. Let $N$ be the midpoint of segment $[A C]$. Then $\widehat{\mathrm{DNM}}=90^{\circ}$. We deduce that points $B, M, N$, and $D$ are concyclic, and $D$ lies on the circle passing through points $B, K$, and $D$.
New concyclic points provide two pieces of information: one about angles using the inscribed angle theorem and one about lengths using the power of a point. Since most points lie on two lines intersecting at vertex $A$, we will use the power of point $A$ with respect to various circles.
Notably, by the power of a point, $A K \cdot A B=A D \cdot A N$. Therefore,
$$
A J \cdot A B=2 A K \cdot A B=2 A D \cdot A N=A D \cdot A C
$$
Thus, points $\mathrm{D}, \mathrm{C}, \mathrm{B}$, and $J$ are concyclic by the converse of the power of a point. To conclude, we will use directed angles to avoid having to handle different possible configurations separately.
We now have all the tools to perform an angle chase. The angles that are difficult to access are $\widehat{\mathrm{OMJ}}, \widehat{\mathrm{OBJ}}, \widehat{M J B} \ldots$ On the other hand, angles $\widehat{\mathrm{DJB}}$ and $\widehat{\mathrm{OMB}}$ seem easier to obtain using the circles present in the figure.
Since points D, C, B, and O are concyclic, we find
$$
(J B, J O)=(J B, J D)=(C B, C D)=(C B, C A)=(M B, M A)=(M B, M O)
$$
Thus, quadrilateral JBMO is indeed cyclic.
Comment from the graders: The problem was not approached by many students and was solved by two students. Some students noted that point $M$ is the North Pole of point $B$, which is a very good reflex.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle non isocèle en $B$. Soit $D$ le pied de la bissectrice de l'angle $\widehat{A B C}$. Soit $M$ le milieu de l'arc $\widehat{A C}$ contenant $B$ sur le cercle circonscrit au triangle $A B C$. Le cercle circonscrit au triangle $B D M$ coupe la segment $[A B]$ en un point $K$ distinct de $B$. Soit $J$ le symétrique du point $A$ par rapport au point K . La droite (DJ) intersecte la droite ( $A M$ ) en un point O . Montrer que les points $\mathrm{J}, \mathrm{B}, \mathrm{M}$ et O sont cocycliques.
|
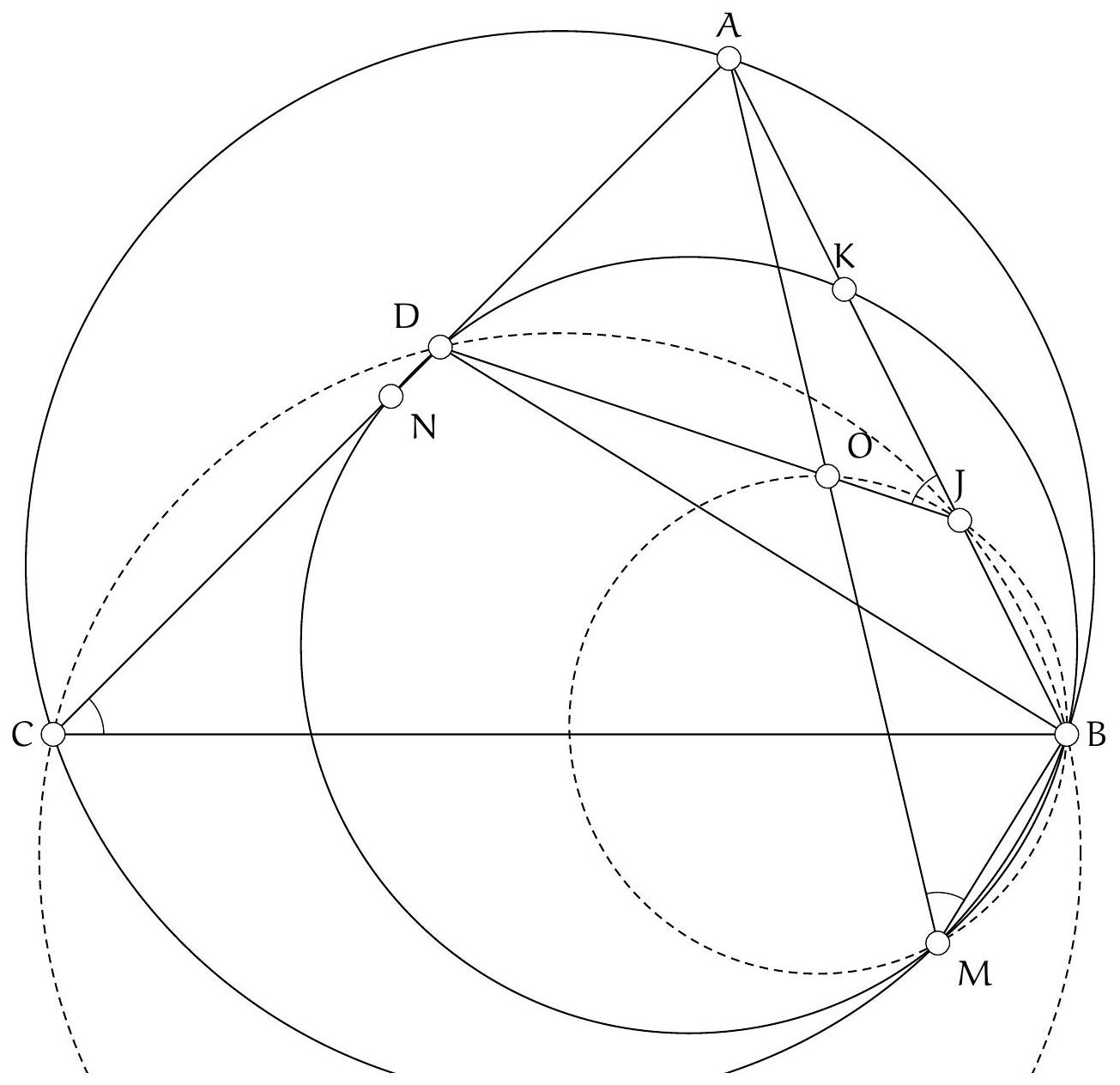
Tout d'abord, on reconnaît dans la figure quelques points connus : le point $M$ est le milieu de l'arc $A C$ contenant $B$, il s'agit donc du pôle Nord du point $B$ dans le triangle $A B C$, c'est-à-dire qu'il est le point d'intersection de la bissectrice extérieure de l'angle $\widehat{A B C}$, de la médiatrice du segment $[A C]$ et du cercle circonscrit au triangle $A B C$. On obtient donc que l'angle $\widehat{D B M}$ est droit (par définition de la bissectrice extérieure). Le fait que $M$ appartient à la médiatrice du segment $[A C]$ nous invite également à considérer cette médiatrice. Soit N le milieu du segment $[A C]$. Alors $\widehat{\mathrm{DNM}}=90^{\circ}$. On déduit donc que les points $B, M, N$ et $D$ sont cocycliques et $D$ appartient au cercle passant par les pointe $B, K$ et $D$.
De nouveaux points cocycliques apportent deux informations : une information sur les angles grâce au théorème de l'angle inscrit et une information sur les longueurs grâce à la puissance d'un point. Puisque la majorité des points se trouve sur deux droites se coupant en le sommet $A$, nous allons utiliser la puissance du point $A$ par rapport à divers cercles.
Notamment, par puissance d'un point $A K \cdot A B=A D \cdot A N$. Donc
$$
A J \cdot A B=2 A K \cdot A B=2 A D \cdot A N=A D \cdot A C
$$
donc les points $\mathrm{D}, \mathrm{C}, \mathrm{B}$ et J sont cocycliques d'après la réciproque de la puissance d'un point. Pour conclure, nous allons utiliser les angles orientés, pour éviter d'avoir à traiter séparément les différentes configurations possibles.
Nous avons à présent tous les outils pour effectuer une chasse aux angles. Des angles difficiles d'accès sont les angles $\widehat{\mathrm{OMJ}}, \widehat{\mathrm{OBJ}}, \widehat{M J B} \ldots$ En revanche, les angles $\widehat{\mathrm{DJB}}$ et $\widehat{\mathrm{OMB}}$ semblent plus faciles à obtenir à l'aide des cercles présents sur la figure.
Puisque les points D, C, B et O sont cocycliques, on trouve
$$
(J B, J O)=(J B, J D)=(C B, C D)=(C B, C A)=(M B, M A)=(M B, M O)
$$
donc le quadrilatère JBMO est bien cyclique.
Commentaire des correcteurs : L'exercice n'a pas été abordé par beaucoup d'élèves et il a été résolu par deux élèves. Quelques élèves ont noté que le point $M$ est le pôle Nord du point $B$, ce qui est un très bon réflexe.
|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "\nExercice 8.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-5.jsonl",
"solution_match": "## Solution de l'exercice 8",
"tier": "T2",
"year": null
}
|
Determine the smallest integer $\mathrm{n} \geqslant 2$ such that there exist strictly positive integers $a_{1}, \ldots, a_{n}$ such that
$$
a_{1}^{2}+\ldots+a_{n}^{2} \mid\left(a_{1}+\ldots+a_{n}\right)^{2}-1
$$
|
Let's analyze the problem. In this problem, we are looking for the smallest integer \( n \) satisfying a certain property. Suppose we want to show that the smallest integer sought is the integer \( c \). To show that \( c \) is indeed the smallest integer, we must on the one hand show that if an integer \( n \) satisfies the property, then \( n \geqslant c \), and on the other hand, we must show that we can find \( c \) integers satisfying the divisibility relation.
Since there is a divisibility relation, we can expect to use various ideas:
- If \( a \mid b \) then \( a \) divides the linear combinations of \( a \) and \( b \)
- If \( a \mid b \) and \( a \) and \( b \) are strictly positive, then \( a \mid b \)
- If \( a \mid b \), the divisors of \( a \) also divide \( b \)
Once this initial analysis is done, we can start by looking for integers \( a_{i} \) satisfying the property for small values of \( n \), for example, for \( n=2,3 \) or even 4 if we are brave, before realizing that this method will not allow us to determine \( n \).
However, having searched for \( a_{i} \) for small values of \( n \) allows us to find potential properties that the \( a_{i} \) must satisfy. For example, we may have noticed that the integers \( a_{i} \) cannot all be even, since in that case the sum of the \( a_{i}^{2} \) would be even but \( \left(a_{1}+\ldots+a_{n}\right)^{2}-1 \) is odd. We then realize that what matters in this argument is not the parity of the \( a_{i} \) but the parity of the sum.
We obtain that \( a_{1}+a_{2}+\ldots+a_{n} \) is odd. Otherwise, since \( a_{1}^{2}+a_{2}^{2}+\ldots+a_{n}^{2} \equiv a_{1}+a_{2}+\ldots+a_{n} \bmod 2 \), \( a_{1}+\ldots+a_{n} \) is also even, but then \( a_{1}^{2}+\ldots+a_{n}^{2} \) is even and divides \( \left(a_{1}+a_{2}+\ldots+a_{n}\right)^{2}-1 \) which is odd, which is absurd.
We deduce that \( \left(a_{1}+\ldots+a_{n}\right)^{2}-1 \) is even. The previous parity argument invites us to refine this study. We will therefore look to see if \( \left(a_{1}+\ldots+a_{n}\right)^{2}-1 \) is divisible by 4, 8, etc. The presence of multiple squares invites us to look at each term with well-chosen moduli.
For example, modulo 4, \( \left(a_{1}+\ldots+a_{n}\right)^{2} \equiv 1 \) so 4 divides \( \left(a_{1}+\ldots+a_{n}\right)^{2}-1 \). Let's not stop here; we also know that the squares of odd numbers can only be 1 modulo 8. Thus, \( \left(a_{1}+\ldots+a_{n}\right)^{2}-1 \) is divisible by 8. Since 8 is coprime with \( a_{1}^{2}+\ldots+a_{n}^{2} \) which is odd, we deduce that
\[
8\left(a_{1}^{2}+\ldots+a_{n}^{2}\right) \mid \left(a_{1}+\ldots+a_{n}\right)^{2}-1
\]
Another remark that we can make about the statement is that it involves the sum of squares of numbers on one side and the square of the sum of numbers on the other side. This suggests the Cauchy-Schwarz inequality or the inequality of arithmetic and quadratic means. We can therefore try to compare the quantities \( 8\left(a_{1}^{2}+\ldots+a_{n}^{2}\right) \) and \( \left(a_{1}+\ldots+a_{n}\right)^{2}-1 \).
This idea of comparing the terms is consistent with what we are trying to show. The divisibility obtained gives that \( 8\left(a_{1}^{2}+\ldots+a_{n}^{2}\right) \leqslant \left(a_{1}+\ldots+a_{n}\right)^{2}-1 \). In the inequality of arithmetic and quadratic means, the square of the sum is smaller than the sum of the squares of the elements multiplied by the number of variables. We suspect that the inequality obtained will be false for \( n \) too small, which will provide the desired bound. More precisely,
\[
8\left(a_{1}^{2}+\ldots+a_{n}^{2}\right) \leqslant \left(a_{1}+\ldots+a_{n}\right)^{2}-1 \leqslant n\left(a_{1}^{2}+\ldots+a_{n}^{2}\right)-1 < n\left(a_{1}^{2}+\ldots+a_{n}^{2}\right)
\]
where the middle inequality corresponds to the inequality of arithmetic and quadratic means. We finally obtain that \( n > 8 \) so \( n \geqslant 9 \).
Conversely, we seek 9 integers satisfying the property. We can expect that small integers will work. We can therefore look for \( a_{i} \) equal to 1 or 2. Finally, we find that by taking \( a_{1}=\cdots=a_{7}=1 \) and \( a_{8}=a_{9}=2 \), we have 15 which divides \( 11^{2}-1=120=15 \times 8 \).
The expected answer is therefore \( n=9 \).
Comment from the graders: The problem was solved by only one student. This is an instructive and very complete exercise, involving both arithmetic arguments and inequalities.
|
9
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer le plus petit entier $\mathrm{n} \geqslant 2$ tel qu'il existe des entiers strictement positifs $a_{1}, \ldots, a_{n}$ tels que
$$
a_{1}^{2}+\ldots+a_{n}^{2} \mid\left(a_{1}+\ldots+a_{n}\right)^{2}-1
$$
|
Analysons le problème. Dans ce problème, on cherche le plus petit entier n satisfaisant une certaine propriété. Supposons que l'on veuille montrer que le plus petit entier recherché est l'entier c. Pour montrer que c'est bien le plus petit entier, on doit d'une part montrer que si un entier n satisfait la propriété, alors $n \geqslant c$ et on doit montrer d'autre part que l'on peut trouver $c$ entiers satisfaisant la relation de divisibilité.
Pusiqu'il y a une relation de divisibilité, on peut s'attendre à utiliser divers idées :
- Si $a \mid b$ alors $a$ divise les combinaisons linéaires de $a$ et $b$
- Si $a \mid b$ et que $a$ et $b$ sont strictement positifs, alors $a \mid b$
- Si $a \mid b$, les diviseurs de $a$ divisent également $b$
Une fois cette première analyse effectuée, on peut commencer par regarder si on trouve des entiers $a_{i}$ satisfaisant la propriété pour des petites valeurs de $n$, par exemple pour $n=2,3$ ou même 4 si on est courageux, avant de se convaincre que cette méthode ne permettra pas de déterminer n .
Néanmoins, avoir cherché des $a_{i}$ pour des petites valeurs de $n$ nous permet de trouver d'éventuelles propriétés que doivent satisfaire les $a_{i}$. Par exemple, on a pu remarquer que les entiers $a_{i}$ ne peuvent pas tous être pairs, puisque dans ce cas la somme des $a_{i}^{2}$ serait paire mais $\left(a_{1}+\ldots+a_{n}\right)^{2}-1$ est impair. On se rend alors compte que ce qui importe dans cet argument, ce n'est pas la parité des $a_{i}$ qui entre en jeu mais la parité de la somme.
On obtient que $a_{1}+a_{2}+\ldots+a_{n}$ est impair. Dans le cas contraire, puisque $a_{1}^{2}+a_{2}^{2}+\ldots+a_{n}^{2} \equiv$ $a_{1}+a_{2}+\ldots+a_{n} \bmod 2, a_{1}+\ldots+a_{n}$ est pair également mais alors $a_{1}^{2}+\ldots+a_{n}^{2}$ est pair et divise $\left(a_{1}+a_{2}+\ldots+a_{n}\right)^{2}-1$ qui est impair, ce qui est absurde.
On déduit que $\left(a_{1}+\ldots+a_{n}\right)^{2}-1$ est pair. L'argument de parité précédent nous invite à préciser cette étude. On va donc chercher si $\left(a_{1}+\ldots+a_{n}\right)^{2}-1$ est divisible par $4,8 \ldots$. La présence des multiples carré nous invite à regarder chaque terme avec des modulos bien choisis.
Par exemple, modulo $4,\left(a_{1}+\ldots+a_{n}\right)^{2} \equiv 1$ donc 4 divise $\left(a_{1}+\ldots+a_{n}\right)^{2}-1$. Ne nous arrêtons pas en si bon chemin, nous savons également que les carrés des nombres impairs ne peuvent que valoir 1 modulo 8. Ainsi, $\left(a_{1}+\ldots+a_{n}\right)^{2}-1$ est divisible par 8 . Or 8 est premier avec $a_{1}^{2}+\ldots+a_{n}^{2}$ qui est impair. On déduit de tout cela que
$$
8\left(a_{1}^{2}+\ldots+a_{n}^{2}\right) \mid\left(a_{1}+\ldots+a_{n}\right)^{2}-1
$$
Enfin, une autre remarque que l'on peut formuler sur l'énoncé est qu'il implique la somme des carrés de nombres d'un côté et le carré de la somme des nombres de l'autre côté. Ceci fait penser à l'inégalité de Cauchy-Schwarz, ou à l'inégalité des moyennes arithmétiques et quadratiques. On peut donc essayer de comparer les quantités $8\left(a_{1}^{2}+\ldots+a_{n}^{2}\right)$ et $\left(a_{1}+\ldots+a_{n}\right)^{2}-1$.
Cette idée de comparer les termes est cohérente avec ce que l'on cherche à montrer. La divisibilité obtenue donne que $8\left(a_{1}^{2}+\ldots+a_{n}^{2}\right) \leqslant\left(a_{1}+\ldots+a_{n}\right)^{2}-1$. Or, dans l'inégalité des moyennes arithmétique et quadratique, le carré de la somme est plus petit que la somme des carrés des éléments multipliée par le
nombre de variables. On se doute donc que l'inégalité obtenue va être fausse pour n trop petit, ce qui va nous fournir la borne souhaitée. Plus précisement,
$$
8\left(a_{1}^{2}+\ldots+a_{n}^{2}\right) \leqslant\left(a_{1}+\ldots+a_{n}\right)^{2}-1 \leqslant n\left(a_{1}^{2}+\ldots+a_{n}^{2}\right)-1<n\left(a_{1}^{2}+\ldots+a_{n}^{2}\right)
$$
où l'inégalité au milieu correspond à l'inégalité des moyennes arithmétiques et quadratiques. On obtient finalement que $\mathrm{n}>8$ donc $\mathrm{n} \geqslant 9$.
Réciproquement, on cherche 9 entiers satisfaisant la propriété. On peut s'attendre à ce que de petits entiers fonctionnent. On peut donc chercher des $a_{i}$ valant 1 ou 2 . Finalement, on trouve qu'en prenant $a_{1}=\cdots=a_{7}=1$ et $a_{8}=a_{9}=2$, on a bien 15 qui divise $11^{2}-1=120=15 \times 8$.
La réponse attendue est donc $\mathrm{n}=9$.
Commentaire des correcteurs: L'exercice n'a été résolu que par un élève. C'est un exercice instructif et très complet, faisant appel à des arguments arithmétiques et des inégalités.
## Exercices Seniors
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-5.jsonl",
"solution_match": "\nSolution de l'exercice 9",
"tier": "T2",
"year": null
}
|
Let $\left(x_{n}\right)_{n \in \mathbb{N}}$ be a real sequence such that $x_{0}=0$ and $x_{1}=1$ and for all $n \geqslant 0, x_{n+2}=$ $3 x_{n+1}-2 x_{n}$. We also set $y_{n}=x_{n}^{2}+2^{n+2}$ for all natural numbers $n$. Show that for all integers $n>0, y_{n}$ is the square of an odd integer.
|
We start by testing the statement for small values of \( n \). We therefore calculate the first values of the sequences \(\left(x_{n}\right)\) and \(\left(y_{n}\right)\). For example, we find \( x_{2}=3 \), \( x_{4}=7 \), \( x_{5}=15 \ldots \) We can therefore conjecture that \( x_{n}=2^{n}-1 \). We promptly set out to prove this by induction.
The result is already true for ranks 0 and 1. If we assume \( x_{n}=2^{n}-1 \) and \( x_{n+1}=2^{n+1}-1 \), we have \( x_{n+2} = 3 x_{n+1} - 2 x_{n} = 3 \times 2^{n+1} - 3 - 2 \times 2^{n} + 2 = (3-1) \times 2^{n+1} - 1 = 2^{n+2} - 1 \), which completes the induction. We then substitute this expression for \( x_{n} \) into the expression for \( y_{n} \). All that remains is to manipulate this new expression algebraically:
\[
y_{n} = \left(2^{n}-1\right)^{2} + 2^{n+2} = 2^{2 n} - 2^{n+1} + 1 + 2^{n+2} = 2^{2 n} - 2^{n+1} + 1 + 2 \times 2^{n+1} = 2^{2 n} + 2^{n+1} + 1 = \left(2^{n} + 1\right)^{2}
\]
This shows that \( y_{n} \) is the square of an odd integer.
Comment from the graders: The exercise was solved by all the students who tackled it!
|
y_{n} = \left(2^{n} + 1\right)^{2}
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $\left(x_{n}\right)_{n \in \mathbb{N}}$ une suite réelle telle que $x_{0}=0$ et $x_{1}=1$ et pour tout $n \geqslant 0, x_{n+2}=$ $3 x_{n+1}-2 x_{n}$. On pose également $y_{n}=x_{n}^{2}+2^{n+2}$ pour tout entier naturel $n$. Montrer que pour tout entier $n>0, y_{n}$ est le carré d'un entier impair.
|
On commence par tester l'énoncé pour des petites valeurs de n . On calcule donc les premières valeurs des suites $\left(x_{n}\right)$ et $\left(y_{n}\right)$. On trouve par exemple $x_{2}=3, x_{4}=7$, $x_{5}=15 \ldots$ On peut donc conjecturer que $x_{n}=2^{n}-1$. On s'empresse de le démontrer par récurrence.
Le résultat est déjà au rang 0 et 1 . Si on suppose $x_{n}=2^{n}-1$ et $x_{n+1}=2^{n+1}-1$, on a $x_{n+2}=$ $3 x_{n+1}-2 x_{n}=3 \times 2^{n+1}-3-2 \times 2^{n}+2=(3-1) \times 2^{n+1}-1=2^{n+2}-1$ ce qui achève la récurrence. On injecte alors cette expression de $x_{n}$ dans l'expression de $y_{n}$. Il ne nous reste plus qu'à manipuler algébriquement cette nouvelle expression :
$$
y_{n}=\left(2^{n}-1\right)^{2}+2^{n+2}=2^{2 n}-2^{n+1}+1+2^{n+2}=2^{2 n}-2^{n+1}+1+2 \times 2^{n+1}=2^{2 n}+2^{n+1}+1=\left(2^{n}+1\right)^{2}
$$
Ceci montre bien que $y_{n}$ est le carré d'un entier impair.
Commentaire des correcteurs: L'exercice a été résolu par tous les élèves qui l'ont abordé !
|
{
"exam": "French_envois",
"problem_label": "10",
"problem_match": "\nExercice 10.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-5.jsonl",
"solution_match": "\nSolution de l'exercice 10",
"tier": "T2",
"year": null
}
|
Find all functions $f$ from $\mathbb{R}$ to $\mathbb{R}$ such that for every pair $(x, y)$ of real numbers:
$$
f(f(x)) + f(f(y)) = 2y + f(x - y)
$$
|
Let's analyze the problem: here we are dealing with a functional equation with two variables. The first thing to do is to try some classic substitutions: $x=y=0$, $x=0, y=0, x=y$. Since we have a $f(x-y)$, it is very tempting to see what it gives for $x=y$. Let's set $C=f(0)$, for $x=y$, we get $2 f(f(x))=2 x+C$ which simplifies to $f(f(x))=x+\frac{C}{2}$.
Now that we have a more manageable expression for $f(f(x))$, we can substitute it back into the original equation and see what it gives.
Substituting back into the original equation, we have $x+y+C=2 y+f(x-y)$, which simplifies to $f(x-y)=x-y+C$. For $y=0$, we get $f(x)=x+C$ for all real $x$. Now, we need to determine $C$ before performing the verification, so we try to see what constraint the equation $f(f(x))=x+\frac{C}{2}$ imposes on $C$.
In particular, $f(f(x))=f(x+C)=x+2 C$, so $2 C=\frac{C}{2}$, which gives $4 C=C$, and thus $3 C=0$, so $C=0$. Therefore, we have $f(x)=x$ for all real $x$. Now we must not forget to verify that the function we found is indeed a solution! Conversely, the identity function works because in this case, $f(f(x))+f(f(y))=f(x)+f(y)=x+y=2 y+x-y=2 y+f(x-y)$ for all real $x, y$.
Comment from the graders: The exercise was very well done. Be careful not to conclude that $f$ is the identity when you find $f(X)=X$ with $X$ depending on $x$ and $y$ (you need to verify that $X$ can take all real values).
|
f(x)=x
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Trouver toutes les fonctions $f$ de $\mathbb{R}$ dans $\mathbb{R}$ telles que pour tout couple $(x, y)$ de réels :
$$
f(f(x))+f(f(y))=2 y+f(x-y)
$$
|
Analysons le problème : ici on est face à une équation fonctionnelle, avec deux variables. La première chose à faire est d'essayer les quelques substitutions classiques : $x=y=0$, $x=0, y=0, x=y$. Ici comme on a un $f(x-y)$, il est très tentant de regarder ce que ça donne pour $x=y$. Posons donc $C=f(0)$, pour $x=y$, on obtient $2 f(f(x))=2 x+C$ soit $f(f(x))=x+\frac{C}{2}$.
Maintenant qu'on a une expression plus maniable de $f(f(x))$, on peut la réinjecter dans l'équation et regarder ce que ça donne.
En réinjectant dans l'équation initiale, on a donc $x+y+C=2 y+f(x-y)$ soit $f(x-y)=x-y+C$, pour $y=0$ on a donc $f(x)=x+C$ pour tout réel $x$. Maintenant, il faudrait déterminer $C$ avant d'effectuer la vérification, on essaie donc de voir quelle contrainte l'équation $f(f(x))=x+\frac{C}{2}$ donne sur $C$.
En particulier $f(f(x))=f(x+C)=x+2 C$ donc $2 C=\frac{C}{2}$ donc $4 C=C, 3 C=0$ donc $C=0$, on a donc $f(x)=x$ pour tout réel $x$. Maintenant on n'oublie pas de vérifier que la fonction trouvée est bien solution ! Réciproquement la fonction identité convient car dans ce cas, $f(f(x))+f(f(y))=f(x)+f(y)=$ $x+y=2 y+x-y=2 y+f(x-y)$ pour tout $x, y$ réels.
Commentaire des correcteurs: L'exercice a été très bien réussi. Il faut faire attention à ne pas conclure que $f$ est l'identité lorsque l'on trouve $f(X)=X$ avec $X$ dépendant de $x$ et $y$ (il faut vérifier que $X$ peut prendre toutes les valeurs réelles).
|
{
"exam": "French_envois",
"problem_label": "11",
"problem_match": "\nExercice 11.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-5.jsonl",
"solution_match": "\nSolution de l'exercice 11",
"tier": "T2",
"year": null
}
|
Let $ABC$ be an acute-angled triangle. Let $D$ be the foot of the angle bisector of $\widehat{BAC}$. The perpendicular to the line $(AD)$ passing through the point $B$ intersects the circumcircle of triangle $ADB$ at a point $E$. Let $O$ be the center of the circumcircle of triangle $ABC$. Show that the points $A$, $O$, and $E$ are collinear.
|
Let's examine the angles we can easily obtain. Since points $A, E, D$, and $B$ are on the same circle, we should be able to use the inscribed angle theorem to get an equality involving $\widehat{\mathrm{EAD}}$. Since the line $(\mathrm{BE})$ is perpendicular to the line $(\mathrm{AD})$, we should be able to calculate the angle $\widehat{\mathrm{EBA}}$. Of course, we also know the angle $\widehat{O A B}$. It seems reasonable to show the collinearity of points $A, O$, and $E$ by showing that $\widehat{O A B}=\widehat{\mathrm{EAB}}$. We calculate these two angles separately in terms of the angles of triangle $A B C$.
On the one hand, according to the central angle theorem and since triangle $A O B$ is isosceles at $O$, we have
$$
\widehat{\mathrm{OAB}}=\frac{1}{2}\left(180^{\circ}-\widehat{\mathrm{AOB}}\right)=90^{\circ}-\widehat{\mathrm{ACB}}
$$
On the other hand, $\widehat{E A B}=\widehat{\mathrm{EAD}}+\widehat{\mathrm{DAB}}$. Using the inscribed angle theorem and the fact that $\widehat{\mathrm{DAB}}=\frac{1}{2} \widehat{\mathrm{BAC}}$, we get:
$$
\widehat{\mathrm{EAD}}+\widehat{\mathrm{DAB}}=\widehat{\mathrm{EBD}}+\frac{1}{2} \widehat{\mathrm{BAC}}=90^{\circ}-\widehat{\mathrm{BDA}}+\frac{1}{2} \widehat{\mathrm{BAC}}
$$
Since the sum of the angles in triangle $ADC$ is $180^{\circ}$, we have $\widehat{\mathrm{BDA}}=\widehat{\mathrm{DCA}}+\widehat{\mathrm{DAC}}=\widehat{\mathrm{ACB}}+\frac{1}{2} \widehat{\mathrm{BAC}}$. Thus,
$$
90^{\circ}-\widehat{\mathrm{BDA}}+\frac{1}{2} \widehat{\mathrm{BAC}}=90^{\circ}-\left(\widehat{\mathrm{ACB}}+\frac{1}{2} \widehat{\mathrm{BAC}}\right)+\frac{1}{2} \widehat{\mathrm{BAC}}=90^{\circ}-\widehat{\mathrm{ACB}}
$$
and we find that $\widehat{O A B}=90^{\circ}-\widehat{A C B}=\widehat{E A B}$, so points $A, O$, and $E$ are collinear. Comment from the graders: The exercise is well done. However, many students submitted a very complicated proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle aux angles aigus. Soit $D$ le pied de la bissectrice de l'angle $\widehat{B A C}$. La perpendiculaire à la droite $(A D)$ passant par le point $B$ recoupe le cercle circonscrit au triangle $A D B$ en un point $E$. Soit $O$ le centre du cercle circonscrit au triangle $A B C$. Montrer que les points $A, O$ et $E$ sont alignés.
|
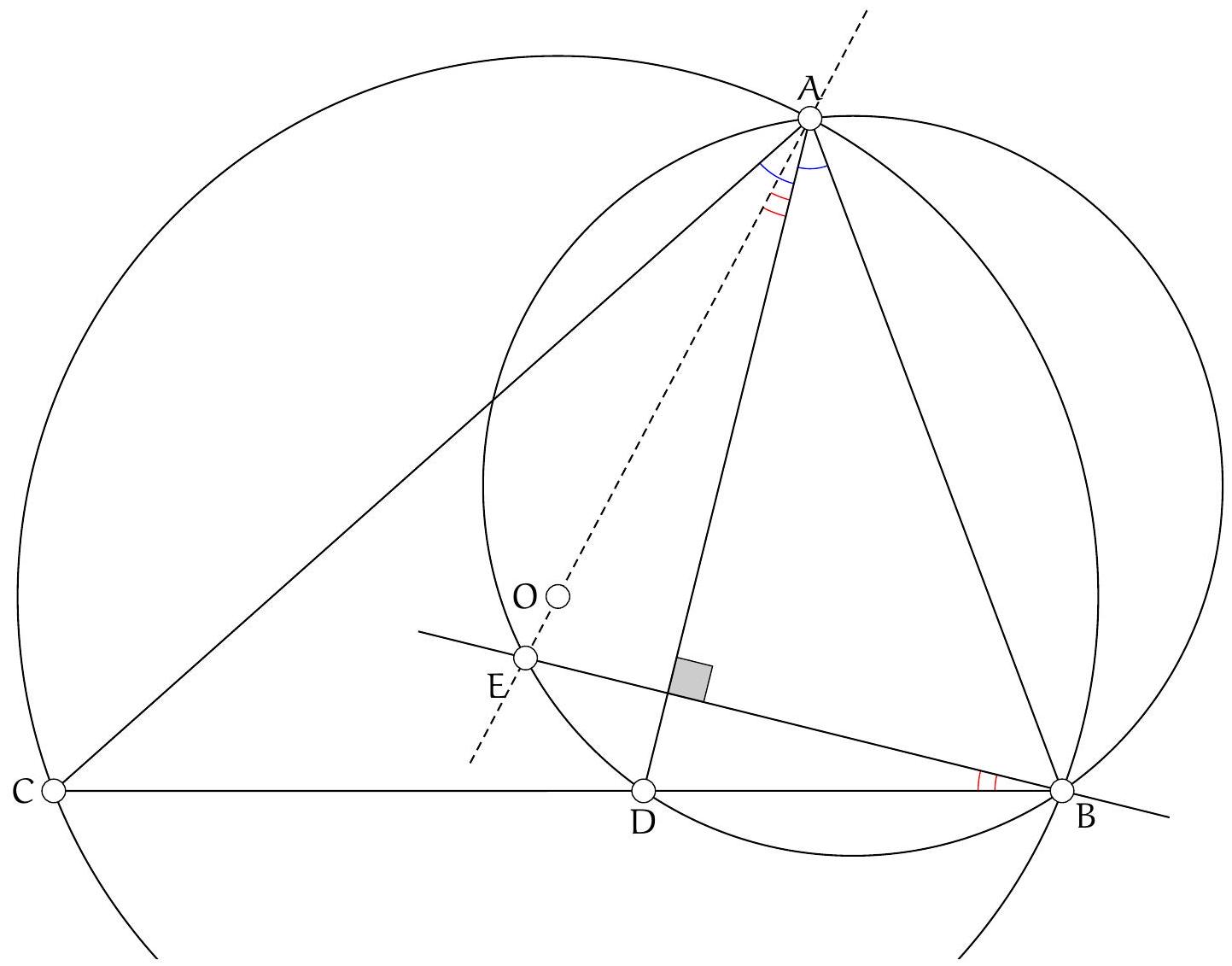
Examinons les angles que nous pouvons obtenir facilement. Puisque les points $A, E, D$ et $B$ sont sur un même cercle, on doit pouvoir utilise le théorème de l'angle inscrit pour avoir une égalité portant sur $\widehat{\mathrm{EAD}}$. Puisque la droite $(\mathrm{BE})$ est perpendiculaire à la droite $(\mathrm{AD})$, on doit pouvoir calculer l'angle $\widehat{\mathrm{EBA}}$. Enfin, on connaît bien sûr l'angle $\widehat{O A B}$. Il semble donc raisonnable de montrer l'alignement des points $A, O$ et $E$ en montrant que $\widehat{O A B}=\widehat{\mathrm{EAB}}$. On calcule séparément ces deux angles en fonction des angles du triangle $A B C$.
D'une part, d'après le théorème de l'angle au centre et puisque le triangle $A O B$ est isocèle en O , on a
$$
\widehat{\mathrm{OAB}}=\frac{1}{2}\left(180^{\circ}-\widehat{\mathrm{AOB}}\right)=90^{\circ}-\widehat{\mathrm{ACB}}
$$
D'autre part, $\widehat{E A B}=\widehat{\mathrm{EAD}}+\widehat{\mathrm{DAB}}$. On utilise alors le théorème de l'angle inscrit et le fait que $\widehat{\mathrm{DAB}}=$ $\frac{1}{2} \widehat{\mathrm{BAC}}$, on obtient :
$$
\widehat{\mathrm{EAD}}+\widehat{\mathrm{DAB}}=\widehat{\mathrm{EBD}}+\frac{1}{2} \widehat{\mathrm{BAC}}=90^{\circ}-\widehat{\mathrm{BDA}}+\frac{1}{2} \widehat{\mathrm{BAC}}
$$
Or la somme des angles du triangle ADC fait $180^{\circ}$ donc $\widehat{\mathrm{BDA}}=\widehat{\mathrm{DCA}}+\widehat{\mathrm{DAC}}=\widehat{\mathrm{ACB}}+\frac{1}{2} \widehat{\mathrm{BAC}}$. Ainsi
$$
90^{\circ}-\widehat{\mathrm{BDA}}+\frac{1}{2} \widehat{\mathrm{BAC}}=90^{\circ}-\left(\widehat{\mathrm{ACB}}+\frac{1}{2} \widehat{\mathrm{BAC}}\right)+\frac{1}{2} \widehat{\mathrm{BAC}}=90^{\circ}-\widehat{\mathrm{ACB}}
$$
et on trouve bien que $\widehat{O A B}=90^{\circ}-\widehat{A C B}=\widehat{E A B}$ donc les points $A, O$ et $E$ sont alignés. Commentaire des correcteurs: L'exercice est bien réussi. Cependant, plusieurs élèves ont rendu un preuve très compliquée.
|
{
"exam": "French_envois",
"problem_label": "13",
"problem_match": "\nExercice 13.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-5.jsonl",
"solution_match": "## Solution de l'exercice 13",
"tier": "T2",
"year": null
}
|
A grid of size $\mathrm{n} \times \mathrm{n}$ contains $\mathrm{n}^{2}$ cells. Each cell contains a natural number between 1 and $\boldsymbol{n}$, such that each integer in the set $\{1, \ldots, n\}$ appears exactly $n$ times in the grid. Show that there exists a column or a row of the grid containing at least $\sqrt{n}$ different numbers.
|
Let's first look at what happens in what seems to be the 'worst case': if each row/column does not contain many numbers, each number will be present a lot. In particular, for any $i$, the number of $i$ seems to be written in few rows and columns. But a priori, if the number $i$ appears too much in a row, it will appear in many columns and vice versa. A priori, the worst case seems to be the one where each number appears in as many columns as rows, and since each number appears $n$ times, the square must be of dimension $\sqrt{n}$, so $i$ appears in at least $2 \sqrt{n}$ rows and columns.
Of course, this analysis is by no means a proof, but we see two important ideas: first, the number of distinct numbers in each row/column seems to be linked to the number of rows/columns in which each number appears. Second, for any $i$ between 1 and $n$, the number $i$ appears at least on $2 \sqrt{n}$ rows and columns. We will therefore try to formalize this.
Let $a_{c, i}$ for $c$ a column or a row and $i$ an integer between 1 and $n$ be the number of times $i$ appears in $c$, let $c_{i}$ (resp. $l_{i}$) be the number of columns (resp. rows) to which $i$ belongs. Let $C$ be the set of columns and $L$ the set of rows.
Note that the hypothesis that $i$ appears $n$ times translates as $c_{i} \times l_{i} \geqslant n$ because $i$ appears in at most $c_{i} l_{i}$ cells.
Note that for any $i$, $l_{i}+c_{i}$ being the number of rows or columns where $i$ appears, it is $\sum_{c \in C \cup L} a_{c, i}$. The number of distinct elements in column $c$ is, in turn, $\sum_{i=1}^{n} a_{c, i}$. In particular, we see that the $a_{c, i}$ play an important role in the problem.
Now it remains to relate the number of appearances of $i$ in the different rows/columns to the number of numbers in each row. For this, we will look at the sum of the $a_{c, i}$ (we sum over $i$ from 1 to $n$ and over $c$ columns and rows) and use the two previous interpretations.
We thus obtain $\sum_{i=1}^{n} \sum_{c \in C \cup L} a_{c, i}=\sum_{i=1}^{n} c_{i}+l_{i} \geqslant \sum_{i=1}^{n} 2 \sqrt{c_{i} l_{i}} \geqslant 2 n \sqrt{n}$.
We deduce that $\sum_{c \in C \cup L} \sum_{i=1}^{n} a_{c, i} \geqslant \sum_{i=1}^{n} 2 \sqrt{c_{i} l_{i}}=2 n \sqrt{n}$.
In particular, since there are $2 n$ rows or columns, there exists $c$ rows or columns such that $\sum_{i=1}^{n} a_{c, i} \geqslant \sqrt{n}$ i.e., $c$ contains at least $\sqrt{n}$ different numbers.
Graders' comments: The exercise was generally well done by those who tackled it, but it is important to be clear in explanations and precise in the definitions of the different objects introduced.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Une grille de taille $\mathrm{n} \times \mathrm{n}$ contient $\mathrm{n}^{2}$ cases. Chaque case contient un entier naturel compris entre 1 et $\boldsymbol{n}$, de telle sorte que chaque entier de l'ensemble $\{1, \ldots, n\}$ apparaît exactement $n$ fois dans la grille. Montrer qu'il existe une colonne ou une ligne de la grille contenant au moins $\sqrt{n}$ nombres différents.
|
Essayons d'abord de regarder ce qui se passe dans ce qui semble être 'le pire cas" : si chaque ligne/colonne ne contient pas beaucoup de numéros, chaque numéro va y être beaucoup présent. En particulier, pour tout $i$, le nombre de $i$ semble être écrit dans peu de lignes et de colonnes. Mais à priori si le numéro $i$ apparait trop dans une ligne, il apparaitra dans beaucoup de colonnes et inversement. A priori, le pire cas semble être celui où chaque numéro apparaît dans autant de colonnes que de lignes et comme chaque numéro apparaît $n$ fois, le carré doit être de dimension $\sqrt{n}$, donc $i$ apparait dans au moins $2 \sqrt{n}$ lignes et colonnes.
Bien sûr, cette analyse ne constitue en rien une preuve, mais on voit deux idées importantes : premièrement, le nombre de numéros distincts dans chaque ligne/colonne semble avoir un lien avec le nombre de lignes/colonnes où chaque numéro apparaît. Deuxièmement, pour tout $i$ entre 1 et $n$, le nombre $i$ apparait au moins sur $2 \sqrt{n}$ lignes et colonnes. On va donc essayer de formaliser ça.
Notons $a_{c, i}$ pour $c$ une colonne ou une ligne et $i$ un entier entre 1 et $n$ le nombre de fois qu'apparait $i$ dans $c$, notons $c_{i}$ (resp. $l_{i}$ ) le nombre de colonnes (resp. lignes) à laquelle $i$ appartient. On note C l'ensemble des colonnes $L$ celui des lignes.
Notons que l'hypothèse du fait que $i$ apparait $n$ fois se traduit comme $c_{i} \times l_{i} \geqslant n$ car $i$ apparait dans au plus $c_{i} l_{i}$ cases.
Notons que pour tout $i$, $l_{i}+c_{i}$ étant le nombre de ligne ou de colonne où apparait $i$, il vaut $\sum_{c \in C \cup L} a_{c, i}$. Le nombre d'éléments distincts dans la colonne $c$ vaut, quant à lui, $\sum_{i=1}^{n} a_{c, i}$. En particulier, on voit bien que les $a_{c, i}$ jouent un rôle important dans le problème.
Maintenant il reste à relier le nombre d'apparitions de $i$ dans les différentes lignes/colonnes au nombre de numéros dans chaque ligne. Pour cela on va regarder la somme des $a_{c, i}$ (on somme sur $i$ entre 1 et $n$ et sur c colonne et ligne) et utiliser les deux interprétations précédentes.
On obtient ainsi $\sum_{i=1}^{n} \sum_{c \in C \cup L} a_{c, i}=\sum_{i=1}^{n} c_{i}+l_{i} \geqslant \sum_{i=1}^{n} 2 \sqrt{c_{i} l_{i}} \geqslant 2 n \sqrt{n}$.
On en déduit que $\sum_{c \in C \cup L} \sum_{i=1}^{n} a_{c, i} \geqslant \sum_{i=1}^{n} 2 \sqrt{c_{i} l_{i}}=2 n \sqrt{n}$.
En particulier, comme il y a $2 n$ lignes ou colonnes, il existe $c$ colonnes ou lignes telles que $\sum_{i=1}^{n} a_{c, i} \geqslant \sqrt{n}$ i.e. c contient au moins $\sqrt{\mathrm{n}}$ numéros différents.
Commentaire des correcteurs: L'exercice a été globalement bien réussi par ceux qui l'ont traité, mais il faut faire attention à être clair dans ses explications et être précis dans les définitions des différents objets introduits.
|
{
"exam": "French_envois",
"problem_label": "14",
"problem_match": "\nExercice 14.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-5.jsonl",
"solution_match": "\nSolution de l'exercice 14",
"tier": "T2",
"year": null
}
|
Find all integers $n \geqslant 1$ such that for every prime $p<n, n-\left\lfloor\frac{n}{p}\right\rfloor p n$ is not divisible by a square different from 1.
|
Let's analyze the problem: we are looking for integers \( n \) that satisfy a certain property. We can start by finding the small values of \( n \) that work: by testing integers \( n \) between 1 and 20, we find \(\{1, 2, 3, 5, 7, 13\}\).
One of the first things to do when facing this problem is to understand the meaning of \( n - \left\lfloor \frac{n}{p} \right\rfloor p \). Since \(\frac{n}{p}\) is the division of \( n \) by \( p \), we can try to see if this quantity can be interpreted from the Euclidean division.
Note that \( n - \left\lfloor \frac{n}{p} \right\rfloor p \) is the remainder of the Euclidean division of \( n \) by \( p \). Indeed, if \( n = pq + r \) with \( q \) an integer and \( 0 \leq r \leq p-1 \), we have \(\left\lfloor \frac{n}{p} \right\rfloor = \left\lfloor q + \frac{r}{p} \right\rfloor = q\), so \( n - \left\lfloor \frac{n}{p} \right\rfloor p = r \).
Next, we observe that all the solutions found except 1 are prime numbers: we will try to show that an integer \( n \) satisfying the property must be prime, for example, by taking \( p \) as one of its divisors.
Let \( n > 1 \) be an integer satisfying the property. We deduce from this that if \( n \) is not prime, and if \( p < n \) is a prime divisor of \( n \), then \( n - \left\lfloor \frac{n}{p} \right\rfloor p = 0 \) is divisible by 4, which is a perfect square, leading to a contradiction.
Now, what can we do to advance: let's analyze what the property can give us. If \( n \geq 12 \), for \( p = 2 \) the remainder of the Euclidean division is 1, for \( p = 3 \) it is 1 or 2, so this does not help. For \( p = 5 \), we get that the remainder cannot be 4, for \( p = 7 \), the remainder cannot be 4, for \( p = 8 \) the remainder cannot be 4, 8, or 9. A priori, continuing like this indefinitely seems complicated, as we will just have a very large system, which will probably have solutions (since there are infinitely many numbers congruent to 1 modulo \( p_1 \times \ldots \times p_k \), looking at the remainders by the first \( k \) prime numbers seems less useful). However, 4 seems to play an important role: 4 cannot be a remainder of the division of \( n \) by \( p \). In particular, if \( p \geq 5 \), \( p \) cannot divide \( n - 4 \)! It seems interesting to look at what \( n - 4 \) can be, and similarly what \( n - 8 \) and \( n - 9 \) can be, as these cannot have prime factors greater than 10. To avoid cases where these quantities are negative, we assume \( n \geq 11 \).
Let \( n \) be a prime number greater than or equal to 11 satisfying the statement. Let \( p \) divide \( n - 4 \), we have \( p < n \). If \( p \geq 5 \), the remainder of the Euclidean division of \( p \) by 5 is 4 and it is divisible by 4, which is a square different from 1, leading to a contradiction. Moreover, \( p \) cannot be 2 because otherwise 2 divides \( n - 4 \) and thus 2 divides \( n \), which means \( n \) is not prime. Therefore, \( n - 4 = 3^x \) with \( x \) a positive integer because \( n - 4 > 1 \).
By making the same reasoning for \( n - 8 \) and \( n - 9 \), they cannot be divisible by \( p \) if \( p \geq 10 \).
Now let's analyze the prime factors of \( n - 8 \) and \( n - 9 \): they can be divisible by 2, 3, 5, 7. For the factor 3, since 3 divides \( n - 4 \), \( n \equiv 1 \pmod{3} \), so \( n - 8 \equiv 2 \pmod{3} \) and \( n - 9 \equiv 1 \pmod{3} \), these are not divisible by 3.
Moreover, \( n - 8 \) is not divisible by 2 because \( n \) is not. Since \( n - 8 \) and \( n - 9 \) are coprime, three cases present themselves to us: either \( n - 8 \) is a power of 5, or it is a power of 7, or \( n - 8 \) is divisible by 5 and 7, in which case \( n - 9 \) is a power of 2.
- If \( n - 8 = 5^y \) with \( y \) a positive integer, we have \( n - 4 = 5^y + 4 = 3^x \).
Here, since 4 is a square, we would like to show that \( 3^x \) is a square to factorize the equation. For this, we look modulo 4 because we have squares and \( 5 \equiv 1 \pmod{4} \).
Looking modulo 4, we have \( 3^x \equiv 1^y \equiv 1 \pmod{4} \). Otherwise, since the order of 3 modulo 4 is 2, 2 divides \( x \) so \( x \) is even. Let \( x = 2k \), we have \( (3^k - 2)(3^k + 2) = 5^y \) so \( 3^k - 2 \) is positive and \( 3^k - 2 \) and \( 3^k + 2 \) are powers of 5. Here we have a product of terms equal to a power of 2, so we try to compute their gcd to hope to bound one of the terms. In particular, the gcd of \( 3^k + 2 \) and \( 3^k - 2 \) divides \( (3^k + 2) - (3^k - 2) = 4 \) which is not divisible by 5, and it divides their product, i.e., \( 5^y \), so it is 1. Since \( 3^k - 2 \) and \( 3^k + 2 \) are powers of 2 with gcd 1, the smallest one is 1, so we have \( 3^k - 2 = 1 \) which gives \( k = 1 \) so \( x = 2 \). We get \( n = 3^x + 4 = 9 + 4 = 13 \).
- If \( n - 8 = 7^y \) with \( y \) a positive integer, we have \( n - 4 = 7^y + 4 = 3^x \).
Since 4 is a square, we would like to show that \( x \) is even to factorize. For this, we look modulo 7. Note that if \( y = 0 \), there is no solution to this equation. Otherwise, we have \( 3^x \equiv 4 \pmod{7} \), and the powers of 3 modulo 7 are \( 1, 3, 2, 6, 4, 5, 1 \), so the order of 3 is 6 and we have \( x \equiv 4 \pmod{6} \) so \( x \) is even. Let \( x = 2k \), we have \( (3^k - 2)(3^k + 2) = 7^y \) so \( 3^k - 2 \) is positive and \( 3^k - 2 \) and \( 3^k + 2 \) are powers of 7.
In particular, the gcd of \( 3^k + 2 \) and \( 3^k - 2 \) divides \( (3^k + 2) - (3^k - 2) = 4 \) which is not divisible by 7, and it divides \( 7^y \) so it is 1. Since \( 3^k - 2 \) and \( 3^k + 2 \) are powers of 2 with gcd 1, the smallest one is 1, so we have \( 3^k - 2 = 1 \) so \( k = 1 \) so \( x = 2 \), we get \( 7^y = 3^x - 4 = 5 \) which is impossible.
- Otherwise, \( n - 9 = 2^y \) with \( y \) a positive integer, we have \( n - 4 = 2^y + 5 = 3^x \). Note that since \( n - 4 \geq 7 \), we have \( x \geq 1 \) and \( y \geq 1 \).
Here we do not have a square a priori, but we can try to get information about the parity of \( x \) and \( y \). Since we have powers of 2 and 3, we will look modulo 3 and 4. Note that if \( y = 1 \), the equation becomes \( 3^x = 7 \), there is no solution. Since \( x \geq 1 \) and looking modulo 3, we have \( 2^y \equiv -5 \equiv 1 \pmod{3} \) and the order of 2 modulo 3 is 2, so \( y \) is even. Since \( y \geq 2 \), we have \( 3^x \equiv 1 \pmod{4} \) and since the order of 3 modulo 4 is 2, \( x \) is even. We write \( x = 2b \), \( y = 2c \), we have \( 5 = (3^b - 2^c)(3^b + 2^c) \) so \( 3^b - 2^c \) is positive and since \( 3^b - 2^c < 3^b + 2^c \), \( 3^b - 2^c \) and \( 3^b + 2^c \) are 1 and 5 respectively. We deduce that \( 3^b \times 2 = (3^b + 2^c) + (3^b - 2^c) = 6 \) so \( b = 1 \) so \( x = 2 \), we fall back into the previous case \( n = 13 \).
In particular, we have obtained that \( n = 13 \) or \( n < 11 \) and \( n \) is prime, i.e., \( n \) is \( 2, 3, 5, 7 \) or 13. Let's verify that these are solutions:
- There is no prime number strictly less than 1 and 2, so 1 and 2 are solutions.
- The remainder of the division of 3 by 2 is 1, which has no square factors, so 3 is a solution.
- The remainders of the Euclidean divisions of 5 by 2 and 3 are 1 and 2, which have no square factors, so 5 is a solution.
- The remainders of the Euclidean divisions of 7 by 2, 3, and 5 are 1, 1, and 2, which have no square factors, so 7 is a solution.
- The remainders of the Euclidean divisions of 13 by 2, 3, 5, 7, and 11 are 1, 1, 3, 6, and 2, which have no square factors, so 13 is a solution.
The set of solutions is therefore \(\{1, 2, 3, 5, 7, 13\}\).
Comment from the graders: This arithmetic problem was solved by few students, all of whom showed that they are extremely comfortable. The other students who approached the problem simply noted that if \( n \geq 2 \) is a solution, then it is prime, which was a good start, but there were still many steps missing before reaching the solution.
|
\{1, 2, 3, 5, 7, 13\}
|
Incomplete
|
Incomplete
|
math-word-problem
|
Number Theory
|
Trouver tous les entiers $n \geqslant 1$ tel que pour tout nombre premier $p<n, n-\left\lfloor\frac{n}{p}\right\rfloor p n$ 'est pas divisible par un carré différent de 1.
|
Analysons le problème : on cherche les entiers $n$ vérifiant une certaine propriété. On peut déjà commencer par chercher les petites valeurs de n qui conviennent : en testant les entiers $n$ entre 1 et 20 on trouve $\{1,2,3,5,7,13\}$.
Une des premières choses à faire devant ce problème est de réussir à donner un sens à $n-\left\lfloor\frac{n}{p}\right\rfloor p$. $\frac{n}{p}$ étant la division de $n$ par $p$ on peut essayer de regarder si cette quantité ne s'interprète pas à partir de la division euclidienne.
Notons que $n-\left\lfloor\frac{n}{p}\right\rfloor p$ est le reste de la division euclidienne de $n$ par $p$. En effet si $n=p q+r$ avec $q$ entier et $0 \leqslant r \leqslant p-1$, on a $\left\lfloor\frac{n}{p}\right\rfloor=\left\lfloor q+\frac{r}{p}\right\rfloor=q$ donc $n-\left\lfloor\frac{n}{p}\right\rfloor p=r$.
Ensuite, on note que toutes les solutions trouvées sauf 1 sont des nombres premiers : on va donc essayer de montrer qu'un entier $n$ vérifiant la propriété est forcément premier, par exemple en prenant $p$ un de ses diviseurs.
Soit $n>1$ un entier vérifiant la propriété. On déduit de ceci que si $n$ n'est pas premier, si $p<n$ est un diviseur premier de $n$, alors $n-\left\lfloor\frac{n}{p}\right\rfloor p=0$ est divisible par 4 qui est un carré parfait, contradiction.
Maintenant que peut-on faire pour avancer : analysons ce que la propriété peut nous donner. Si $\boldsymbol{n} \geqslant 12$, pour $p=2$ le reste de la division euclidienne vaut 1 , pour $p=3$ il vaut 1 ou 2 , donc cela n'apporte rien. Pour $p=5$, on obtient que le reste ne peut valoir 4 , pour $p=7$, le reste ne peut valoir 4 , pour $p=8$ le reste ne peut valoir ni 4 ni 8 ni 9 . A priori, continuer comme ça indéfiniment semble compliqué, vu qu'on aura juste un très gros système, qui admettra probablement des solutions (comme il y a une infinité de nombre congru à 1 modulo $p_{1} \times \ldots p_{k}$, le fait de regarder les restes par les $k$ premiers nombre premiers semble peu utile). Par contre, 4 semble jouer un rôle important : 4 ne peut pas être un reste de la divison de $n$ par $p$. En particulier si $p \geqslant 5, p$ ne peut diviser $n-4$ ! Il semble donc intéressant de regarder ce que peut valoir $n-4$, et de même ce que peuvent valoir $n-8$ et $n-9$ car ceux-ci ne peuvent pas avoir de facteur premier plus grand que 10 . Pour éviter les cas où ces quantités sont négatives, on supposer $n \geqslant 11$.
Soit n premier supérieur ou égal à 11 vérifiant l'énoncé. Soit p divisant $\boldsymbol{n}-4$, on a $\mathrm{p}<\mathrm{n}$. Si $\mathrm{p} \geqslant 5$, le reste de la division euclidienne de p par 5 vaut 4 et il est divisible par 4 qui est un carré différent de 1, ce qui donne une contradiction. De plus, $p$ ne peut valoir 2 car sinon 2 divise $n-4$ donc 2 divise $n, n$ 'est dans ce cas pas premier. Ainsi $\mathrm{n}-4=3^{x}$ avec $x$ un entier strictement positif car $\mathrm{n}-4>1$.
En faisant le même raisonnement $\mathrm{n}-8$ et $\mathrm{n}-9$ ne sont pas divisibles par $p$ si $p \geqslant 10$.
Maintenant analysons les facteurs premiers de $\boldsymbol{n}-8$ et $\mathrm{n}-9$ : ils peuvent être divisibles par 2, 3, 5, 7. Pour le facteur 3 , comme 3 divise $n-4, n \equiv 1(\bmod 3)$, donc $n-8 \equiv 2(\bmod 3)$ et $n-9 \equiv 1$ $(\bmod 3)$, ceux-ci ne sont pas divisibles par 3.
De plus $n-8$ n'est pas divisible par 2 car $n$ ne l'est pas. Comme $n-8$ et $n-9$ sont premiers entre eux, trois cas se présentent à nous : soit $\mathrm{n}-8$ est une puissance de 5 , soit c'est une puissance de 7 , soit $\mathrm{n}-8$ est divisible par 5 et 7 , dans ce cas $n-9$ est une puissance de 2 .
- $\operatorname{Sin}-8=5^{y}$ avec $y$ entier positif, on a $n-4=5^{y}+4=3^{x}$.
Ici 4 étant un carré, on aimerait montrer que $3^{x}$ est un carré pour factoriser l'équation. Pour cela, on regarde modulo 4 car on a des carrés et $5 \equiv 1(\bmod 4)$.
Regardons modulo 4 , on a $3^{x} \equiv 1^{y} \equiv(\bmod 4)$. Sinon comme l'ordre de 3 modulo 4 est 2 , 2 divise $x$ donc $x$ est pair. Posons $x=2 k$, on a $\left(3^{k}-2\right)\left(3^{k}+2\right)=5^{y}$ donc $3^{k}-2$ est positif et $3^{k}-2$ et $3^{k}+2$ sont des puissances de 5 . Ici on a un produit de terme valant une puissance de 2 , on essaie donc de calculer leur pgcd pour espérer borner un des termes. En particulier, le pgcd de $3^{\mathrm{k}}+2$ et $3^{\mathrm{k}}-2$ divise $\left(3^{\mathrm{k}}+2\right)-\left(3^{\mathrm{k}}-2\right)=4$ qui n'est pas divisible par 5 , et il divise leur produit c'est-à-dire $5^{y}$, il vaut donc 1 . Comme $3^{k}-2$ et $3^{k}+2$ sont des puissances de 2 de pgcd 1 , la plus petite vaut 1 , on a donc $3^{\mathrm{k}}-2=1$ soit $\mathrm{k}=1$ soit $\chi=2$. On obtient $\mathrm{n}=3^{\mathrm{x}}+4=9+4=13$.
- $\operatorname{Sin}-8=7^{y}$ avec $y$ entier positif, on a $\mathrm{n}-4=7^{y}+4=3^{x}$.
Comme 4 est un carré, on aimerait réussir à montrer que $x$ est pair pour factoriser, pour cela on regarde modulo 7 . Notons que si $y=0$, il n'y a pas de solution à cette équation. Sinon on a $3^{\mathrm{x}} \equiv 4(\bmod 7)$, or les puissances de 3 modulo 7 valent $1,3,2,6,4,5,1$, l'ordre de 3 vaut donc 6 et on a forcément $x \equiv 4(\bmod 6)$ donc $x$ est pair. Posons $x=2 k$, on a $\left(3^{k}-2\right)\left(3^{k}+2\right)=7^{y}$ donc $3^{k}-2$ est positif et $3^{k}-2$ et $3^{k}+2$ sont des puissances de 7 .
En particulier, le pgcd de $3^{l}+2$ et $3^{k}-2$ divise $\left(3^{k}+2\right)-\left(3^{k}-2\right)=4$ qui n'est pas divisible par 7 , il divise aussi $7^{y}$ et vaut donc 1 . Comme $3^{k}-2$ et $3^{k}+2$ sont des puissances de 2 de pgcd 1 , la plus petite vaut 1 , on a donc $3^{k}-2=1$ donc $k=1$ donc $x=2$, on a donc $7^{y}=3^{x}-4=5$ ce qui est impossible.
- Sinon $\boldsymbol{n}-9=2^{y}$ avec $y$ entier positif, on a $\boldsymbol{n}-4=2^{y}+5=3^{x}$. Notons que comme $\mathrm{n}-4 \geqslant 7$, on a $x \geqslant 1$ et $y \geqslant 1$
Ici on n'a pas de carré à priori, mais on peut essayer d'obtenir des informations sur la parité de $x$ et $y$. Vu qu'on a des puissances de 2 et 3 on va donc regarder modulo 3 et 4 . Notons que si $y=1$, l'équation devient $3^{x}=7$, il n'y a pas de solution. Comme $x \geqslant 1$ en regardant modulo 3 , on a $2^{y} \equiv-5 \equiv 1(\bmod 3)$ et l'ordre de 2 modulo 3 est 2 , on obtient que $y$ est pair. Comme $y \geqslant 2$, on a $3^{x} \equiv 1(\bmod 4)$ et comme l'ordre de 3 modulo 4 est 2 , $x$ est pair. On écrit donc $x=2 b$, $\mathrm{y}=2 \mathrm{c}$, on a $5=\left(3^{\mathrm{b}}-2^{\mathrm{c}}\right)\left(3^{\mathrm{b}}+2^{\mathrm{c}}\right)$ donc $3^{\mathrm{b}}-2^{\mathrm{c}}$ est positif et comme $3^{\mathrm{b}}-2^{\mathrm{c}}<3^{\mathrm{b}}+2^{\mathrm{c}}, 3^{\mathrm{b}}-2^{\mathrm{c}}$ et $3^{b}+2^{c}$ valent respectivement 1 et 5 . On en déduit que $3^{b} \times 2=\left(3^{b}+2^{c}\right)+\left(3^{b}-2^{c}\right)=6$ donc $\mathrm{b}=1$ donc $x=2$, on retombe dans le cas précédent $\mathrm{n}=13$.
En particulier, on a obtenu que $\mathrm{n}=13$ ou $\mathrm{n}<11$ et n premier, i.e. n vaut $2,3,5,7$ ou 13 . Vérifions que ce sont des solutions :
- Il n'y a pas de nombre premier strictement inférieur à 1 et 2 donc 1 et 2 sont solutions.
- Le reste de la division de 3 par 2 est 1 qui n'a pas de facteurs carrés, donc 3 est solution.
- Les restes des divisions euclidiennes de 5 par 2 et 3 sont 1 et 2 qui sont sans facteurs carrés donc 5 est solution.
- Les restes des divisions euclidiennes de 7 par 2, 3 et 5 sont 1,1 et 2 qui sont sans facteurs carrés donc 7 est solution.
- Les restes des divisions euclidiennes de 13 par 2, 3, 5, 7 et 11 sont 1, 1, 3, 6 et 2 qui sont sans facteurs carrés donc 13 est solution.
L'ensemble des solutions est donc $\{1,2,3,5,7,13\}$.
Commentaire des correcteurs: Cet exercice d'arithmétique a été résolu par peu d'élèves, qui ont tous montré qu'ils sont extrêmement à l'aise. Les autres élèves qui ont abordé le problème ont simplement remarqué que si $n \geqslant 2$ était solution alors il était premier, ce qui était un bon début, mais il manquait encore de nombreuses étapes avant d'arriver à la solution.
|
{
"exam": "French_envois",
"problem_label": "15",
"problem_match": "\nExercice 15.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-5.jsonl",
"solution_match": "\nSolution de l'exercice 15",
"tier": "T2",
"year": null
}
|
Let $\mathrm{P}, \mathrm{Q}$ be polynomials with real coefficients such that $\mathrm{P} \circ \mathrm{Q}=\mathrm{P}^{2019}$. Suppose that all the roots of P are real. Show that they are all equal.
|
When faced with a polynomial problem, a first reflex might be to look at the different degrees. Here, we see that $Q$ is a polynomial of degree 2019 because $2019\deg (P)=\deg\left(P^{2019}\right) \deg(P \circ Q)=\deg(P) \deg(Q)$.
Now, we need to use the hypothesis that the roots of $P$ are real. We write $P(X)=\prod_{i=1}^{k}(X- x_{i})^{a_{i}}$ where the roots $x_{1}, \ldots, x_{k}$ are pairwise distinct.
Rewrite the equation as: $\prod_{i=1}^{l}\left(Q(X)-x_{i}\right)^{a_{i}}=\prod_{i=1}^{k}\left(X-x_{i}\right)^{2019 a_{i}}$.
A priori, we know that the right-hand term will be zero if evaluated at $x_{j}$, so we look at what this implies for the left-hand term. Let $X=\{x_{1}, \ldots, x_{k}\}$, then we necessarily have $Q(x_{j}) \in \{x_{1}, \ldots, x_{k}\}=X$ for all $1 \leqslant j \leqslant k$.
Moreover, since the right-hand side of the equation is a real split polynomial, for every $\mathfrak{j}$, the polynomial $Q(X)-x_{j}$, which divides a split polynomial, is also split and of degree 2019, thus it has 2019 real roots in $X$.
Furthermore, if $i \neq j$, $Q-x_{i}$ and $Q-x_{j}$ must have disjoint roots: indeed, we cannot have $Q(x)=x_{i}$ and $Q(x)=x_{j}$. Thus, the polynomials $Q-x_{i}$ are $|X|=k$ distinct split polynomials whose roots are in $X$ and have no common roots. Necessarily, each of these polynomials has only one root: thus for every $i$ there exists $j(i)$ such that $Q(X)-x_{i}=c(X-x_{j(i)})^{2019}$ with $c$ being the leading coefficient of $Q$. Moreover, the mapping from $\{1, \ldots, k\}$ to $\{1, \ldots, k\}$ that maps $i$ to $j(i)$ is bijective.
Now we have a very precise expression for the $Q-x_{i}$, recall that we want to show that there is only one $x_{i}$. To do this, we can try to look at the coefficients of $Q-x_{i}$ which are almost those of $Q$. The coefficient of $X^{2018}$ in $Q$ is therefore the same as that of $Q-x_{i}$, which is $-2019 x_{j(i)} c$ for all $i$. Since $\mathfrak{i} \mapsto \mathfrak{j}(\mathfrak{i})$ is a bijection of $\{1, \ldots, k\}$, we have $x_{j}=x_{1}$ for all $1 \leqslant \mathfrak{j} \leqslant k$, and thus by the hypothesis on the $x_{i}$, $k=1$. This is exactly what we wanted to prove.
Comment from the graders: This problem concerning polynomials was not widely attempted. Few achieved the full score of 7, however, some had understood the idea but omitted some details in their answers.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soient $\mathrm{P}, \mathrm{Q}$ des polynômes à coefficients réels tels que $\mathrm{P} \circ \mathrm{Q}=\mathrm{P}^{2019}$. On suppose que toutes les racines de P sont réelles. Montrer qu'elles sont toutes égales.
|
Face à un problème de polynôme, un premier réflexe peut être de regarder les différents degrés. Ici, on voit que $Q$ est un polynôme de degré 2019 car 2019deg $(P)=\operatorname{deg}\left(P^{2019}\right) \operatorname{deg}(\mathrm{P} \circ$ $Q)=\operatorname{deg}(P) \operatorname{deg}(Q)$.
Maintenant, il faut utiliser l'hypothèse du fait que les racines de $P$ sont réelles. On écrit $P(X)=\prod_{i=1}^{k}(X-$ $\left.x_{i}\right)^{a_{i}}$ où les racines $x_{1}, \ldots, x_{k}$ sont deux à deux distinctes.
Réécrivons ainsi l'équation: $\prod_{i=1}^{l}\left(Q(X)-x_{i}\right)^{a_{i}}=\prod_{i=1}^{k}\left(X-x_{i}\right)^{2019 a_{i}}$.
A priori, on sait que le terme de droite va être nul si on l'évalue en $x_{j}$, on regarde donc ce qu'on en déduit pour le terme de gauche. Posons $X=\left\{x_{1}, \ldots, x_{k}\right\}$, on a alors nécessairement $Q\left(x_{j}\right) \in\left\{x_{1}, \ldots, x_{k}\right\}=X$ pour tout $1 \leqslant j \leqslant k$.
De plus comme le terme de droite de l'égalité est un polynôme scindé réel, forcément pour tout $\mathfrak{j}$, comme le polynôme $\mathrm{Q}(\mathrm{X})-\mathrm{x}_{\mathrm{j}}$ divise un polynôme scindé, lui aussi est scindé et de degré 2019 donc admet 2019 racines réelles dans $X$.
Notons de plus que si $i \neq j, Q-x_{i}$ et $Q-x_{j}$ ont nécessairement des racines disjointes : en effet on ne peut avoir $Q(x)=x_{i}$ et $Q(x)=x_{j}$. Ainsi les polynômes $Q-x_{i}$ sont $|X|=k$ polynômes distincts scindés dont les racines sont dans $X$ et qui n'ont aucune racine en commun. Nécessairement, chacun de ces polynômes n'a qu'une racine : ainsi pour tout $i$ il existe $j(i)$ tel que $Q(X)-x_{i}=c\left(X-x_{j(i)}\right)^{2019}$ avec c le coefficient dominant de Q . De plus, l'application de $\{1, \ldots, \mathrm{k}\}$ dans $\{1, \ldots, \mathrm{k}\}$ quià $i$ associe $j(i)$ est bijective.
Maintenant on a une expression très précise des $\mathrm{Q}-x_{i}$, rappelons que l'on veut montrer qu'il n'y a qu'un seul $x_{i}$. Pour cela, on peut essayer de regarder les coefficients de $Q-x_{i}$ qui sont quasiment ceux de $Q$. Le coefficient de $X^{2018}$ dans $Q$ vaut donc celui de $Q-x_{i}$, c'est-à-dire $-2019 x_{j(i)} c$ pour tout i. Puisque $\mathfrak{i} \mapsto \mathfrak{j}(\mathfrak{i})$ est une bijection de $\{1, \ldots, k\}$, on a $x_{j}=x_{1}$ pour tout $1 \leqslant \mathfrak{j} \leqslant k$, et donc par hypothèse sur les $x_{i}, k=1$. C'est exactement ce que l'on voulait prouver.
Commentaire des correcteurs: Ce problème concernant des polynômes a été cherché peu cherché. Rares sont ceux qui ont eu la note de 7 , cependant certains avaient bien compris l'idée mais ont omis quelques détails dans leur copie.
|
{
"exam": "French_envois",
"problem_label": "16",
"problem_match": "\nExercice 16.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-5.jsonl",
"solution_match": "\nSolution de l'exercice 16",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle, $\Omega$ its circumcircle, and $O$ the center of $\Omega$. Let $S$ be the center of the circle tangent to the sides $AB$ and $AC$ and internally tangent to the circle $\Omega$ at a point $K$. The circle with diameter $[AS]$ intersects the circle $\Omega$ at a point $T$. Let $M$ be the midpoint of the segment $[BC]$. Show that the points $K$, $T$, $M$, and $O$ are concyclic.
|
In this problem, we will use various results around the circle tangent to sides $AB$ and $AC$ of the circle $\Omega$. This circle is called the $A$-mixtilinear circle, and we will denote it by $\omega$. We denote $U$ as the point of tangency of this circle with side $AB$ and $V$ as the point of tangency with side $AC$. We also denote $I$ as the center of the inscribed circle of triangle $ABC$.
Result $n^{\circ} 1$: The line $(KU)$ is the bisector of the angle $\widehat{AKB}$.
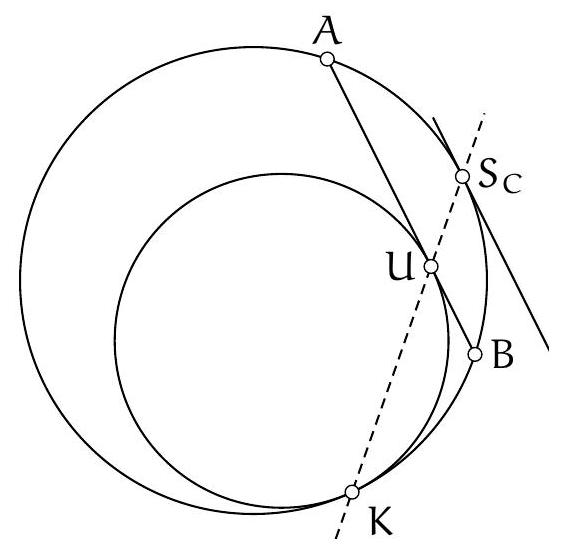
To prove this result, we can consider the homothety $h$ centered at $K$ that maps $\omega$ to $\Omega$. Let $S_C$ be the image of $U$ under $h$. Then $h((AB))$ is the tangent line to the circle $\Omega$ at point $S_C$, and this line is parallel to the line $(AB)$. This means that the triangle $AS_C B$ is isosceles, so $S_C$ is the south pole of $K$ in the triangle $ABK$, and thus the line $(UK)$ is indeed the bisector of the angle $\widehat{AKB}$.
Similarly, the line $(VK)$ is the bisector of the angle $\widehat{AKC}$ and it intersects the circle $\Omega$ at a point denoted by $S_B$.
Result $n^{\circ} 2$: The point $I$ is the midpoint of the segment $[UV]$.
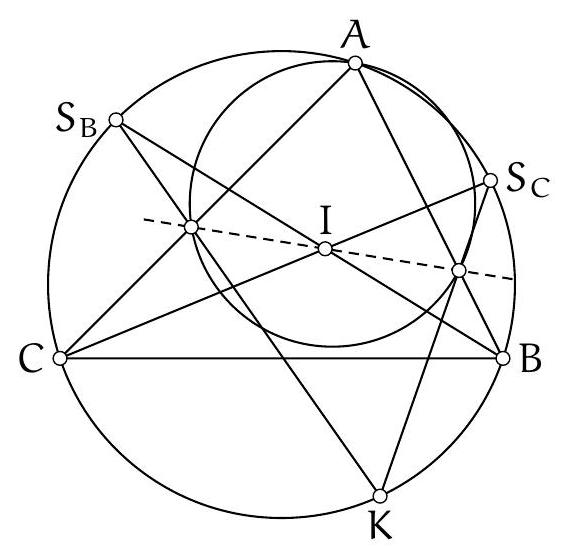
Note that the triangle $UAV$ is isosceles, so the line $(AI)$ is the perpendicular bisector of the segment $[UV]$. Therefore, it suffices to show that the point $I$ lies on the segment $[UV]$.
To do this, we apply Pascal's theorem to the hexagon $A C S_C K S_B B$. This theorem tells us that the points $U = (AB) \cap (K S_C)$, $V = (AC) \cap (K S_B)$, and $I = (BS_B) \cap (C S_C)$ are collinear, as we wanted. (Here we have used result $n^{\circ} 1$ to have the collinearity of the points $K, U$, and $S_C$ and $K, V$, and $S_B$.)
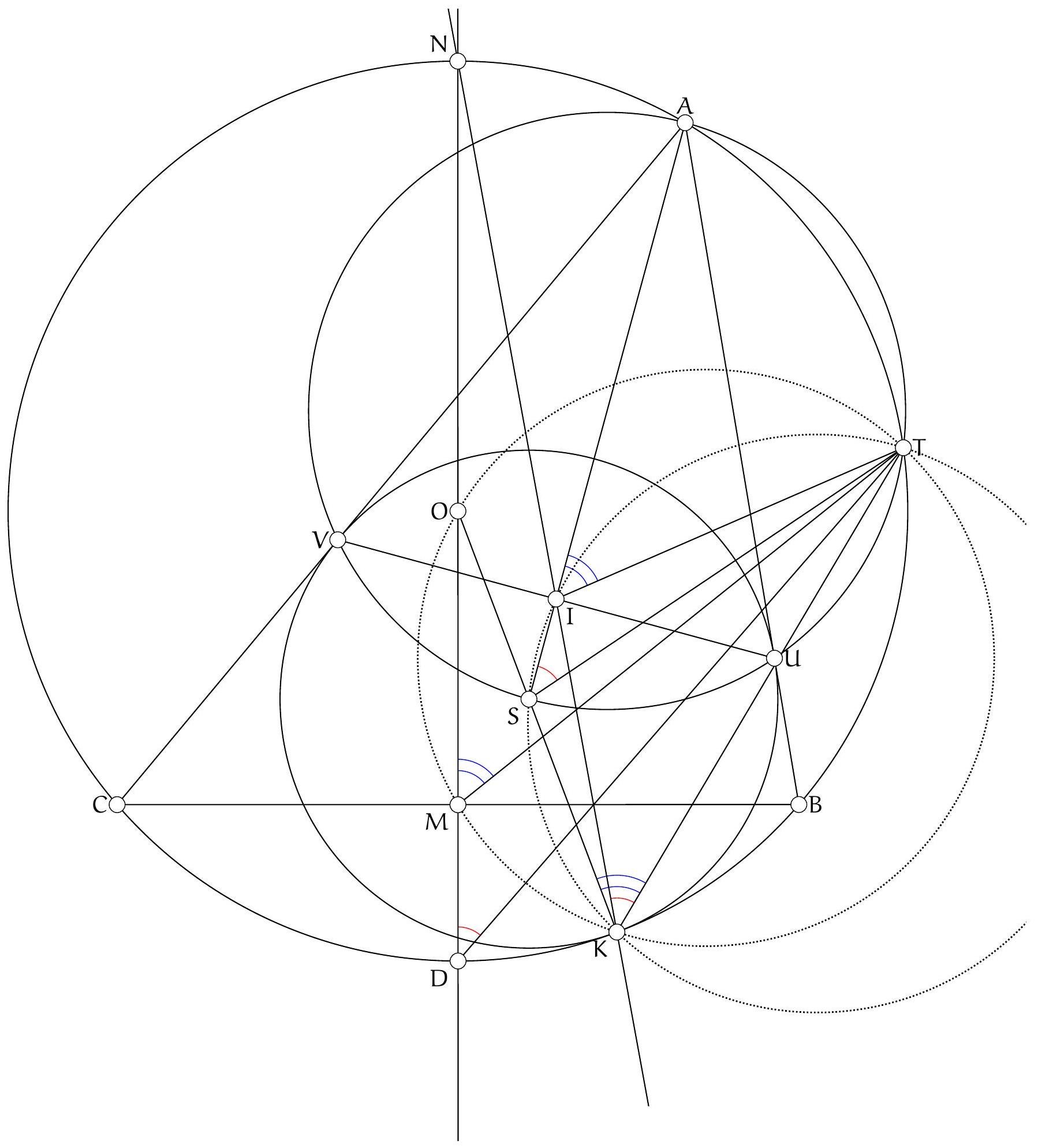
We can now proceed to the solution of the exercise, now that these reminders are done.
First, by drawing the figure, we notice that the points $U$ and $V$ belong to the circle with diameter $[AS]$. We quickly prove this result. Since the line $(AB)$ is tangent to the circle $\omega$ with center $S$ at point $U$, we have $\widehat{SUA} = 90^\circ$. Similarly, $\widehat{SVA} = 90^\circ$, so the points $A, U, S$, and $V$ are indeed on the same circle with $[AS]$ as a diameter.
The next idea that comes to mind is to use the definition of point $T$ as the second intersection of the circumcircles of triangles $ABC$ and $AUV$. Indeed, this definition indicates that $T$ is the center of the similarity that maps point $U$ to point $B$ and point $V$ to point $C$. Let's see what happens to the other points after this similarity. The point $I$ is the midpoint of the segment $[UV]$, so it is mapped to the midpoint of the segment $[BC]$, which is $M$. The point $S$ is the midpoint of the arc $UV$ of the circle $\omega$, so it is mapped to the midpoint of the arc $BC$ of the circle $\Omega$, which is the south pole of point $A$ in the triangle $ABC$, denoted by $D$.
The point $A$ becomes the north pole of point $T$ in the triangle $TVU$. It is therefore mapped to the north pole of point $T$ in the triangle $TBC$, which we will denote by $N$.
Considering this similarity has thus naturally introduced new points that will likely be useful in solving the problem. We also note that if $s$ is this similarity and $X$ and $Y$ are any two points, then the triangles $\mathrm{TXs}(\mathrm{X})$ and $\mathrm{TYs}(\mathrm{Y})$ are similar. We have thus obtained many similar triangles and therefore many angle equalities.
We have introduced the point $N$. It seems to be collinear with the points $K$ and $I$, so we will try to prove this result. The most reasonable way to do this is to proceed by angle chasing. For example, we can try to prove that $\widehat{\mathrm{VKI}} = \widehat{\mathrm{VKN}}$. This idea makes sense because the points $\mathrm{S}_{\mathrm{B}}, \mathrm{V}$, and $K$ are collinear, and this collinearity would allow us to pass from an angle calculation in the triangle $UKV$ to an angle calculation in the triangle $ABC$, which we know well.
How do we calculate the angle $\widehat{\mathrm{VKI}}$? Since $I$ is the midpoint of the segment $[UV]$ and we already have the tangents to the circle $\omega$ at $U$ and $V$, we are strongly invited to use the symmedian from vertex $K$, which is none other than the line $(AK)$. Thus, $\widehat{\mathrm{VKI}} = \widehat{\mathrm{UKA}}$. The points $\mathrm{K}, \mathrm{U}, \mathrm{S}_{\mathrm{C}}$ are collinear, so
$$
\widehat{U K A} = \widehat{S_{C} K A} = \widehat{A B S_{C}} = \frac{1}{2} \widehat{A C B}
$$
We have thus gotten rid of the points $\mathrm{U}, \mathrm{V}$, and $K$, which is encouraging. It remains to show that $\frac{1}{2} \widehat{A C B} = \widehat{S_{B} K N} = \widehat{S_{B} B N}$, which results from the following angle chasing:
$$
\widehat{S_{B} B N} = \widehat{C B N} - \widehat{S_{B} B C} = 90^\circ - \frac{1}{2} \widehat{B A C} - \frac{1}{2} \widehat{A B C} = \frac{1}{2} \widehat{B C A}
$$
In summary, $\widehat{\mathrm{VKI}} = \frac{1}{2} \widehat{\mathrm{ACB}} = \widehat{\mathrm{S}_{\mathrm{B}} \mathrm{BN}} = \widehat{\mathrm{S}_{\mathrm{B}} \mathrm{KN}} = \widehat{\mathrm{VKN}}$, so the points $K$, $I$, and $N$ are collinear.
Let's use what we have just found. From this collinearity: $\widehat{\mathrm{IKT}} = \widehat{\mathrm{NKT}} = \widehat{\mathrm{NDT}}$. The triangles NDT and IST are similar, so $\widehat{\mathrm{NDT}} = \widehat{\mathrm{IST}}$. We have obtained $\widehat{\mathrm{IKT}} = \widehat{\mathrm{IST}}$, so the points $\mathrm{T}, \mathrm{I}, \mathrm{S}$, and $K$ are concyclic.
Another collinearity that we have not yet used is that of the points $O, S$, and $K$, which is true because the homothety centered at $K$ that maps the circle $\omega$ to $\Omega$ maps the point $S$ to the point $O$. This collinearity, along with the fact that the points $T, I, S$, and $K$ are concyclic, gives us
$$
\widehat{\mathrm{OKT}} = \widehat{\mathrm{SKT}} = 180^\circ - \widehat{\mathrm{SIT}} = \widehat{\mathrm{AIT}}
$$
But the triangles AIT and NMT are similar. Thus:
$$
\widehat{\mathrm{OKT}} = \widehat{\mathrm{AIT}} = \widehat{\mathrm{NMT}} = \widehat{\mathrm{OMT}}
$$
and the points $\mathrm{O}, \mathrm{M}, \mathrm{K}$, and $T$ are indeed concyclic.
Comment from the graders: The exercise was quite challenging. The few students who solved it demonstrated a good mastery of various tools such as inversion, manipulation of cross-ratios, and the theorems of Menelaus and Ceva... and a good knowledge of the properties of the mixtilinear circle. Some students, even if they did not solve the problem, still submitted their progress in the problem, which was very appreciated.
|
proof
|
Yes
|
Incomplete
|
proof
|
Geometry
|
Soit $A B C$ un triangle, $\Omega$ son cercle circonscrit et $O$ le centre de $\Omega$. Soit $S$ le centre du cercle tangent aux côtés $A B$ et $A C$ et tangent intérieurement au cercle $\Omega$ en un point K . Le cercle de diamètre $[A S]$ recoupe le cercle $\Omega$ en un point $T$. Soit $M$ le milieu du segment [BC]. Montrer que les points K, T, M et O sont cocycliques.
|
Dans ce problème, nous allons utiliser divers résultats autour du cercle tangent aux côtés $A B$ et $A C$ au cercle $\Omega$. Ce cercle est appelé le cercle $A$-mixtilinéaire, on le notera $\omega$. On note U le point de contact de ce cercle avec le côté $A B$ et V le point de contact avec le côté $A C$. On note également I le centre du cercle inscrit du triangle $A B C$.
Résultat $n^{\circ} 1$ : La droite (KU) est la bissectrice de l'angle $\widehat{A K B}$.

Pour montrer ce résultat, on peut par exemple considérer l'homothétie $h$ de centre K qui envoie $\omega$ sur $\Omega$. Soit $S_{C}$ l'image de $U$ par $h$. Alors $h((A B))$ est la droite tangente au cercle $\Omega$ en le point $S_{C}$, et cette droite est parallèle à la droite $(A B)$. Ceci signifie que le triangle $A S_{C} B$ est isocèle donc $S_{C}$ est le pôle sud de $K$ dans le triangle $A B K$ donc la droite (UK) est bien la bissectrice de l'angle $\widehat{A K B}$.
De même la droite ( VK ) est la bissectrice de l'angle $A K C$ et elle coupe le cercle $\Omega$ en un point noté $S_{B}$.
Résultat $n^{\circ} 2$ : Le point I est le milieu du segment [UV].

Notons que le triangle UAV est isocèle donc la droite (AI) est la médiatrice du segment [UV]. Dès lors, il suffit de démontrer que le point I appartient au segment [UV].
Pour cela, on applique le théorème de Pascal à l'hexagone $A C S_{C} K S_{B} B$. Ce théorème nous dit que les points $U=(A B) \cap\left(K S_{C}\right), V=(A C) \cap\left(K S_{B}\right)$ et $I=\left(B S_{B}\right) \cap\left(C S_{C}\right)$ sont alignés, comme nous le voulions. (On a ici utilisé le résultat $n^{\circ} 1$ pour avoir l'alignement des points $K, U$ et $S_{C}$ et $K, V$ et $S_{B}$.)

Nous pouvons désormais passer à la résolution de l'exercice, maintenant que ces rappels sont faits.
Tout d'abord, en traçant la figure on s'aperçoit que les points U et V appartiennent au cercle de diamètre [AS]. On s'empresse de démontrer ce résultat. Puisque la droite $(A B)$ au cercle $\omega$ de centre $S$ en le point U , on a $\widehat{S U A}=90^{\circ}$. De même $\widehat{S V A}=90^{\circ}$, les points $A, U, S$ et $V$ sont donc bien sur un même cercle dont $[A S]$ est un diamètre.
Une première idée qui nous vient ensuite à l'esprit est d'utiliser la définition du point T comme second point d'intersection des cercles circonscrits aux triangles $A B C$ et $A U V$. En effet, cette définition nous
indique que $T$ est le centre de la similitude qui envoie le point $U$ sur le point $B$ et le point $V$ sur le point $C$. Regardons ce qui deviennent les autres points après cette similitude. Le point I est le milieu du segment [UV], il est donc envoyé sur le milieu du segment [BC], à savoir $M$. Le point $S$ est le milieu de l'arc UV du cercle $\omega$, il est donc envoyé sur le milieu de l'arc BC du cercle $\Omega$, à savoir le pôle Sud du point $A$ dans le triangle $A B C$, que l'on notera $D$.
Le point $A$ devient le pôle Nord du point T dans le triangle TVU. Il est donc envoyé sur le pôle Nord du point T dans le triangle TBC, on notera N ce point.
Considérer cette similitude a donc permis d'introduire naturellement de nouveaux points qui seront sans doute utiles à la résolution du problème. On note de plus que si $s$ est cette similitude et $X$ et $Y$ deux points quelconques, alors les triangles $\mathrm{TXs}(\mathrm{X})$ et $\mathrm{TYs}(\mathrm{Y})$ sont semblables. On a donc obtenu de nombreux triangles semblables et donc de nombreuses égalités d'angles.
On a introduit le point N . Il semble aligné avec les points K et I , nous allons donc tenter de démontrer ce résultat. La façon la plus raisonnable de le faire est de procéder par chasse aux angles. Par exemple on peut essayer de démontrer que $\widehat{\mathrm{VKI}}=\widehat{\mathrm{VKN}}$. Cette idée a du sens puisque les points $\mathrm{S}_{\mathrm{B}}, \mathrm{V}$ et K sont alignés et cet alignement permettrait de passer d'un calcul d'angle dans le triangle UKV à un calcul d'angle dans le triangle $A B C$, que l'on connaît bien.
Comment calculer l'angle $\widehat{\mathrm{VKI}}$ ? Comme I est le milieu du segment [UV] et que l'on a déjà les tangentes au cercle $\omega$ en $U$ et $V$, on est fortement invités à utiliser la symédiane issue du sommet K , qui n'est autre que la droite $(A K)$. Ainsi, $\widehat{\mathrm{VKI}}=\widehat{\mathrm{UKA}}$. Les points $\mathrm{K}, \mathrm{U}, \mathrm{S}_{\mathrm{C}}$ sont alignés donc
$$
\widehat{U K A}=\widehat{S_{C} K A}=\widehat{A B S_{C}}=\frac{1}{2} \widehat{A C B}
$$
On s'est donc débarrassé des points $\mathrm{U}, \mathrm{V}$ et K ce qui est encourageant. Il nous reste à montrer que $\frac{1}{2} \widehat{A C B}=\widehat{S_{B} K N}=\widehat{S_{B} B N}$, ce qui résulte de la chasse aux angles suivante :
$$
\widehat{S_{B} B N}=\widehat{C B N}-\widehat{S_{B} B C}=90^{\circ}-\frac{1}{2} \widehat{B A C}-\frac{1}{2} \widehat{A B C}=\frac{1}{2} \widehat{B C A}
$$
En résumé, $\widehat{\mathrm{VKI}}=\frac{1}{2} \widehat{\mathrm{ACB}}=\widehat{\mathrm{S}_{\mathrm{B}} \mathrm{BN}}=\widehat{\mathrm{S}_{\mathrm{B}} \mathrm{KN}}=\widehat{\mathrm{VKN}}$ donc les points K , I et N sont alignés.
Utilisons ce que nous venons de trouver. D'après cet alignement : $\widehat{\mathrm{IKT}}=\widehat{\mathrm{NKT}}=\widehat{\mathrm{NDT}}$. Or les triangles NDT et IST sont semblables, donc $\widehat{\mathrm{NDT}}=\widehat{\mathrm{IST}}$. On a obtenu $\widehat{\mathrm{IKT}}=\widehat{\mathrm{IST}}$ donc les points $\mathrm{T}, \mathrm{I}, \mathrm{S}$ et K sont cocycliques.
Un autre alignement que nous n'avons pas encore utilisé est celui des points $O, S$ et $K$, qui est vrai car l'homothétie de centre K envoyant le cercle $\omega$ sur $\Omega$ envoie le point $S$ sur le point O . Cet alignement ainsi que le fait que les points $T, I, S$ et $K$ sont cocycliques nous donne
$$
\widehat{\mathrm{OKT}}=\widehat{\mathrm{SKT}}=180^{\circ}-\widehat{\mathrm{SIT}}=\widehat{\mathrm{AIT}}
$$
Mais les triangles AIT et NMT sont semblables. Ainsi :
$$
\widehat{\mathrm{OKT}}=\widehat{\mathrm{AIT}}=\widehat{\mathrm{NMT}}=\widehat{\mathrm{OMT}}
$$
et les points $\mathrm{O}, \mathrm{M}, \mathrm{K}$ et T sont bien cocycliques.
Commentaire des correcteurs : L'exercice était plutôt corsé. Les quelques élèves l'ayant résolu ont montré une belle maitrise de divers outils comme l'inversion, la manipulation de birapports, les théorèmes de Ménélaüs et Céva... et une bonne culture des propriétés du cercle mixti-linéaire. Quelques élèves, même s'ils n'ont pas résolu le problème, ont tout de même renvoyé leurs avancées dans le problème et cela a été très apprécié.
|
{
"exam": "French_envois",
"problem_label": "17",
"problem_match": "\nExercice 17.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-5.jsonl",
"solution_match": "\nSolution de l'exercice 17",
"tier": "T2",
"year": null
}
|
Let $G$ be a finite undirected graph, $\mathrm{n} \in \mathbb{N}^{*}, \mathrm{~d} \in \mathbb{N}^{*}$ such that the degree of every vertex in $G$ is bounded by $d$, and $x$ a vertex of $G$. We denote $a(n, x)$ as the number of induced connected subgraphs of $G$ containing $n$ vertices including the vertex $x$ (an induced subgraph $U$ is a graph whose vertices are vertices of $G$ and if $x$ and $y$ are vertices of $U$, $x$ is connected by an edge to $y$ in $U$ if and only if $x$ is connected by an edge to $y$ in $G$).
1. Show that $a(n, x) \leqslant 2^{n d}$.
2. Show that $a(n, x) \leqslant\left(\frac{(d+1)^{d+1}}{d^{d}}\right)^{n}$.
|
Here, we are faced with a graph problem, more specifically counting the induced subgraphs containing $n$ elements, one of which is fixed. We would like to bound this. While the first question seems potentially doable by counting, the second one does not appear very interpretable: $\frac{(\mathrm{d}+1)^{\mathrm{d}+1}}{\mathrm{~d}^{\mathrm{d}}}$ does not correspond to anything special. A priori, there is no clear combinatorial argument to make this quantity appear.
Since a priori we do not have good ideas to see how to proceed, we can try to do this randomly! We will therefore try to construct a connected induced subgraph of G randomly. We could take vertices at random, but this behaves very poorly with connectivity; it is difficult to obtain easy information about the connected components of such a graph. Rather than choosing vertices, we will choose edges! Here it will be easier to see which points are connected. The goal will be to study the connected component of $\times$ in the graph formed by the chosen edges.
We color each edge of G white independently with probability $p \in[0,1]$. Let X be the set of vertices connected to $x$ in the graph whose edges are the white ones, i.e., the connected component of $x$ in the random graph. Let $A_{n}(x)$ be the set of connected induced subgraphs of $G$ containing $n$ vertices, one of which is the vertex $x$ (we can see an induced subgraph as a set of vertices). Note that since the events $X=H$ for $H$ in $A_{n}(x)$ are disjoint, $1 \geqslant \sum_{H \in A_{n}(x)} P(X=H)$.
A priori, it is therefore sufficient to estimate $P(X=G)$ to have a bound on $a(n, x)$, so we will try to understand how we can have $\mathrm{X}=\mathrm{H}$. A simple solution is that all the edges of H are well colored white, and the edges going from H to its complement are not. It will therefore be necessary to evaluate the probability of this event, by counting the number of edges of each category.
Let H be in $A_{n}(x)$, we have $P(X=H) \geqslant \mathbb{P}\left(A_{H}\right)$ where $A_{H}$ is the event "all the internal edges of $H$ are colored, and the edges connecting H to the outside are not colored". By independence, if we denote $l$ the number of internal edges of $H$ and $k$ the number of edges connecting $G$ to the outside, $\mathbb{P}\left(A_{H}\right)=p^{l}(1-p)^{k}$. Since $G$ is of size $n$ and the degree of each vertex is bounded by $d, l+k \leqslant n d$.
Here, for the first bound, it is quite natural to take $p=\frac{1}{2}$ since we want a bound by a power of 2.
For $p=\frac{1}{2}$, we therefore get $\mathbb{P}\left(A_{G}\right)=2^{-(l+k)} \geqslant \frac{1}{2^{n d}}$. Thus, we have $1 \geqslant \sum_{G \in A_{n}(x)} \frac{1}{2^{n d}}=a(n, x) \frac{1}{2^{n d}}$, so $a(n, x) \leqslant 2^{\text {nd }}$.
Here the reasoning holds if we replace induced subgraph by subgraph because the probability of having the connected component as the subgraph H is the probability that the edges of H are white, and the edges that are not in H are not, we have at most nd edges concerned, so $\mathbb{P}\left(A_{H}\right) \geqslant 2^{-\mathrm{nd}}$ and we get the same result.
For the second inequality, we would like to have a better lower bound of $\mathbb{P}(\mathrm{X}=\mathrm{H})$. A priori, what we did in the first part was quite symmetric, we put as much probability for a white edge and a non-white edge. We would like to unbalance this, for example, by putting a low probability for the white edges. Thus, we would like to have few white edges to color to obtain H. A priori, with the number of vertices fixed, the graph with the minimum number of edges is a tree: it is therefore natural to consider a spanning subtree.
For this, we will use the fact that H contains a subtree $T$ with the same number of vertices (and $\mathrm{n}-1$ edges). In particular, $P(X=H) \geqslant P\left(B_{H}\right)$ with $B_{G}$ the event: the edges of $T$ are colored, the others are not. Since there are at most dn edges with an endpoint in $H$, we therefore have $P\left(B_{H}\right) \geqslant p^{n-1}(1-p)^{d n} \geqslant p^{n}(1-p)^{d n}$.
Now we would like to obtain the desired inequality, for this it is natural to try to optimize the previous quantity in $p$. If we define $f:[0,1] \mapsto \mathbb{R}$ which associates $p$ with $p^{n}(1-p)^{\text {dn }}$, $f$ is $C^{1}$ and has derivative $n p^{n-1}(1-$ $p)^{\mathrm{dn}}-\mathrm{dnp}^{\mathrm{n}}(1-p)^{\mathrm{d} n-1}=n^{\mathrm{n}-1}(1-p)^{\mathrm{dn}-1}(1-p-d p)$ which $\mathrm{s}^{\prime}$ cancels and admits a minimum for $1-p-d p=0$ that is $p=\frac{1}{d+1}$.
Let's take $p=\frac{1}{d+1}$, we have $P\left(A_{H}\right) \geqslant(d+1)^{-n}\left(\frac{d}{d+1}\right)^{d n}=\left(\frac{d^{d}}{(d+1)^{d+1}}\right)^{n}$. We get
$$
1 \geqslant \sum_{G \in A_{n}(x)} P\left(B_{G}\right) \geqslant a(n, x) \times\left(\frac{d^{d}}{(d+1)^{d+1}}\right)^{n}
$$
So $a(n, x) \leqslant\left(\frac{(\mathrm{d}+1)^{\mathrm{d}+1}}{\mathrm{~d}^{\mathrm{d}}}\right)^{n}$.
Note that for a fixed $d$, the second bound is bounded by $(e(\mathrm{~d}+1))^{n}$, so much better for large $d$.
Comment from the graders: The exercise was difficult, only 2 students managed the second question. A non-probabilistic approach was possible by reducing to counting the subtrees of the complete d-ary tree.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soit G un graphe fini non orienté, $\mathrm{n} \in \mathbb{N}^{*}, \mathrm{~d} \in \mathbb{N}^{*}$ tel que le degré de tout sommet de G est borné par $d, x$ un sommet de $G$. On note $a(n, x)$ le nombre de sous-graphes induits connexes de G contenant n sommets dont le sommet $x$ (un sous-graphe induit $U$ est un graphe dont les sommets sont des sommets de $G$ et si $x$ et $y$ sont des sommets de $U$, $x$ est relié par une arête à $y$ dans $U$ si et seulement si $x$ est relié par une arête à $y$ dans $G$ ).
1. Montrer que $a(n, x) \leqslant 2^{n d}$.
2. Montrer que $a(n, x) \leqslant\left(\frac{(d+1)^{d+1}}{d^{d}}\right)^{n}$
|
Ici, on est face à un problème de graphe, plus précisément on compter les sousgraphes induits contenant $n$ éléments dont un fixé. On aimerait majorer cela, autant la première question semble pouvoir se faire potentiellement en comptant, autant la seconde n'a pas l'air très interprétable : $\frac{(\mathrm{d}+1)^{\mathrm{d}+1}}{\mathrm{~d}^{\mathrm{d}}}$ ne correspond à rien de spécial. A priori, il n'y a pas d'argument combinatoire clair pour faire apparaître cette quantité.
Comme à priori, on n'a pas de bonnes idées pour voir commencer avancer, on peut tenter de faire cela au hasard! On va donc essayer d'introduire des probabilités. On aimerait construire aléatoirement un sousgraphe induit connexe de G. On pourrait prendre des sommets au hasard mais ça se comporte très mal avec la connexité, il est difficile d'obtenir des informations faciles sur les composantes connexes d'un tel graphe. Plutôt que de choisir des sommets on va donc choisir des arêtes! Ici il sera plus facile de voir quels points sont reliés. L'objectif sera donc d'étudier la composante connexe de $\times$ dans le graphe formé des arêtes choisies.
On colorie chaque arête en blanc de G indépendamment avec probabilité $p \in[0,1]$. On note X l'ensemble des sommets reliés à $x$ dans le graphe dont les arêtes sont les blanches, i.e. la composante connexe de $x$ dans le graphe aléatoire. Posons $A_{n}(x)$ l'ensemble des sous-graphes induits connexes de $G$ contenant $n$ sommets dont le sommet $x$ (on peut voir un sous-graphe induit comme un ensemble de sommets). Notons que comme les évènements $X=H$ pour $H$ dans $A_{n}(x)$ sont disjoints $1 \geqslant \sum_{H \in A_{n}(x)} P(X=H)$.
A priori, il suffit donc d'estimer $P(X=G)$ pour avoir une borne sur $a(n, x)$, on va donc essayer de comprendre comment on peut avoir $\mathrm{X}=\mathrm{H}$. Une solution simple est que toutes les arêtes de H soient bien blanches, et les arêtes allant de H à son complémentaire ne le soient pas. Il va donc falloir évaluer la probabilité de cet évènement, en dénombrant le nombre d'arête de chaque catégorie
Soit H dans $A_{n}(x)$, on a $P(X=H) \geqslant \mathbb{P}\left(A_{H}\right)$ où $A_{H}$ est l'évènement "toutes les arêtes internes à $H$ sont coloriées, et les arêtes reliant H à l'extérieur ne sont pas coloriées". Par indépendance, si on note $l$ le nombre d'arêtes internes à $H$ et $k$ le nombre d'arêtes reliant $G$ à l'extérieur, $\mathbb{P}\left(A_{H}\right)=p^{l}(1-p)^{k}$. Or comme $G$ est de taille $n$ et le degré de chaque sommet est borné par $d, l+k \leqslant n d$.
Ici pour la première borne, il est assez naturel de prendre $p=\frac{1}{2}$ vu qu'on veut une borne par une puissance de 2.
Pour $p=\frac{1}{2}$, on obtient donc $\mathbb{P}\left(A_{G}\right)=2^{-(l+k)} \geqslant \frac{1}{2^{n d}}$. Ainsi, on a $1 \geqslant \sum_{G \in A_{n}(x)} \frac{1}{2^{n d}}=a(n, x) \frac{1}{2^{n d}}$, donc $a(n, x) \leqslant 2^{\text {nd }}$.
Ici le raisonnement effectué tient si on change sous-graphe induit par sous-graphe car la probabilité d'avoir comme composante connexe le sous-graphe H est la probabilité que les arêtes de H soient blanches, et les arêtes qui ne sont pas dans H ne le soient pas, on a au plus nd arêtes concernées, donc $\mathbb{P}\left(A_{H}\right) \geqslant 2^{-\mathrm{nd}}$ et on obtient le même résultat.
Pour la seconde inégalité, on aimerait avoir une meilleure minoration de $\mathbb{P}(\mathrm{X}=\mathrm{H})$. A priori, ce qu'on a fait dans la première partie était assez symétrique, on mettait autant de probabilité pour une arête blanche et une arête non blanche. On aimerait bien déséquilibrer cela, par exemple mettre une faible probabilité pour les arêtes blanches. Ainsi, on a envie d'avoir peu d'arêtes blanches à colorier pour obtenir H. A priori, à nombre de sommets fixé, le graphe ayant le minimum d'arête est un arbre : il est donc naturel de considérer un sous-arbre couvrant.
Pour cela, on va utiliser le fait que H contient un sous-arbre $T$ avec le même nombre de sommet (et $\mathrm{n}-1$ arêtes). En particulier, $P(X=H) \geqslant P\left(B_{H}\right)$ avec $B_{G}$ l'évènement: les arêtes de $T$ sont coloriées, les autres ne le sont pas. Comme il y a au plus dn arêtes avec une extrémité dans $H$, on a donc $P\left(B_{H}\right) \geqslant$ $p^{n-1}(1-p)^{d n} \geqslant p^{n}(1-p)^{d n}$.
Maintenant on aimerait obtenir l'inégalité voulue, pour cela il est naturel d'essayer d'optimiser la quantité précédente en $p$. Si on pose $f:[0,1] \mapsto \mathbb{R}$ qui à $p$ associe $p^{n}(1-p)^{\text {dn }}$, $f$ est $C^{1}$ et de dérivée $n p^{n-1}(1-$ $p)^{\mathrm{dn}}-\mathrm{dnp}^{\mathrm{n}}(1-p)^{\mathrm{d} n-1}=n^{\mathrm{n}-1}(1-p)^{\mathrm{dn}-1}(1-p-d p)$ qui $\mathrm{s}^{\prime}$ annule et admet un minimum pour $1-p-d p=0$ c'est-à-dire $p=\frac{1}{d+1}$.
Prenons donc $p=\frac{1}{d+1}$, on a $P\left(A_{H}\right) \geqslant(d+1)^{-n}\left(\frac{d}{d+1}\right)^{d n}=\left(\frac{d^{d}}{(d+1)^{d+1}}\right)^{n}$. On obtient
$$
1 \geqslant \sum_{G \in A_{n}(x)} P\left(B_{G}\right) \geqslant a(n, x) \times\left(\frac{d^{d}}{(d+1)^{d+1}}\right)^{n}
$$
Donc $a(n, x) \leqslant\left(\frac{(\mathrm{d}+1)^{\mathrm{d}+1}}{\mathrm{~d}^{\mathrm{d}}}\right)^{n}$.
Notons que à d fixé, la seconde borne est bornée par $(e(\mathrm{~d}+1))^{n}$ donc bien meilleure pour d grand.
Commentaire des correcteurs: L'exercice était difficile, seuls 2 élèves ont réussi la deuxième question. Une approche non probabiliste était possible en se ramenant à compter les sous-abres de l'arbre d-aire complet.
|
{
"exam": "French_envois",
"problem_label": "18",
"problem_match": "\nExercice 18.",
"resource_path": "French/segmented/envois/fr-corrigé-commenté-envoi-5.jsonl",
"solution_match": "\nSolution de l'exercice 18",
"tier": "T2",
"year": null
}
|
Let $\omega$ and $\Omega$ be two concentric circles (i.e., they have the same center) such that the circle $\omega$ is inside the circle $\Omega$. Let $X$ and $Y$ be two points on the circle $\omega$. We denote by $P$ and $Q$ the points of intersection of the circle $\Omega$ with the tangents at $X$ and $Y$ to $\omega$, such that $P$ and $Q$ are on the same side with respect to the line $(\mathrm{XY})$. Show that the points $X, Y, P$ and $Q$ are concyclic.
|
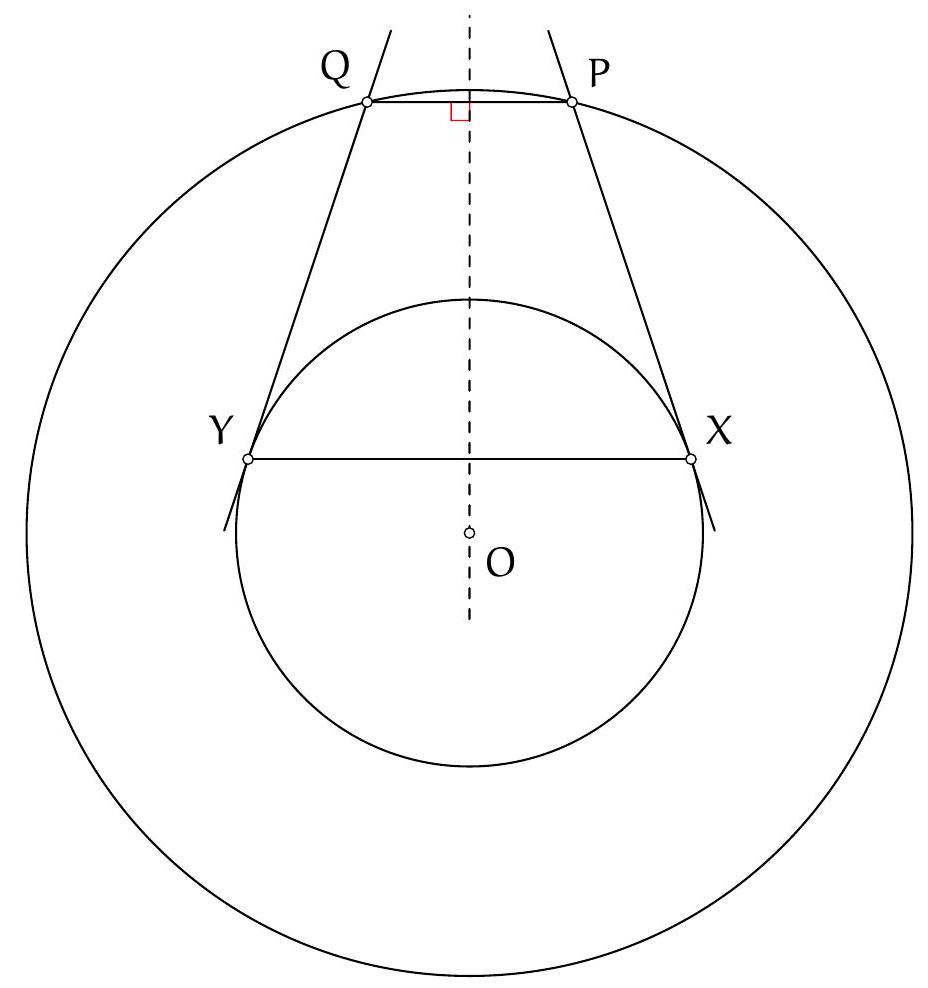
The quadrilateral $X Y Q P$ appears to be an isosceles trapezoid in the figure. We start by proving this.
Let $d$ be the perpendicular bisector of $[\mathrm{XY}]$. Since $O$ is the center of the circle $\omega$, $O$ lies on $d$. Thus, the circles centered at $O$, including $\omega$ and $\Omega$, are mapped to themselves by the reflection across $d$. We denote this reflection by $s$.
We have $s(X)=\mathrm{Y}$, $s(\omega)=\omega$, and $s(\Omega)=\Omega$, so $s$ maps the tangent to $\omega$ at $X$ to the tangent to $s(\omega)=\omega$ at $s(X)=Y$. The point of intersection $P$ of $\Omega$ with the tangent to $\omega$ at $X$ is mapped to the point of intersection of $s(\Omega)$ with the tangent to $s(\omega)$ at $s(X)$.
This is the point of intersection of $\Omega$ with the tangent to $\omega$ at $Y$, which is the point $Q$. In other words, $P$ and $Q$ are symmetric with respect to the perpendicular bisector of $[\mathrm{XY}]$. The segments $[\mathrm{XY}]$ and $[\mathrm{PQ}]$ are perpendicular to $d$ and thus parallel to each other, and the segments $[\mathrm{PX}]$ and $[\mathrm{QY}]$ are symmetric with respect to $d$. This is sufficient to conclude that the quadrilateral $PQYX$ is an isosceles trapezoid.
We conclude that it is a cyclic quadrilateral. By corresponding angles, $\widehat{\mathrm{QPX}}=180^{\circ}-\widehat{\mathrm{PXY}}$ and since $s$ preserves angles, $\widehat{\mathrm{YQP}}=\widehat{\mathrm{QPX}}$. We deduce that
$$
\widehat{Y Q P}=\widehat{Q P X}=180^{\circ}-\widehat{P X Y}
$$
thus the points $P, Q, Y$, and $X$ are indeed concyclic by the converse of the inscribed angle theorem.
Comment from the graders: The problem was generally well done, but there were three recurring issues:
- Several students freely use the fact that two triangles with two sides of the same length and one common angle are congruent. Unfortunately, this fact is false: here, it could be resolved by noting that the triangles were right (in which case the criterion is true by the Pythagorean theorem). But in a general case, it is completely false: the sides must be adjacent to the angle. Thus, it is necessary to clearly specify that the triangles are right.
- Many students assume that (QY) and (PX) intersect. This is the case except when the lines are parallel: it was therefore necessary to also consider this case. In olympiads, introducing a point that does not exist in a particular case often costs 1 point to some candidates: it is therefore important to be cautious and handle the special case separately.
- Some students talk about symmetry without a rigorous argument. It is important to specify why the objects are mapped to each other by symmetry.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $\omega$ et $\Omega$ deux cercles concentriques (c'est-à-dire qu'ils ont le même centre) de sorte que le cercle $\omega$ soit à l'intérieur du cercle $\Omega$. Soient $X$ et $Y$ deux points sur le cercle $\omega$. On note $P$ et $Q$ les points d'intersection respectifs du cercle $\Omega$ avec les tangentes en $X$ et $Y$ à $\omega$, de telle sorte que $P$ et $Q$ soient du même côté par rapport à la droite $(\mathrm{XY})$. Montrer que les points $X, Y, P$ et $Q$ sont cocycliques.
|

Le quadrilatère $X Y Q P$ semble être un trapèze isocèle sur la figure. On commence par le démontrer.
Soit d la médiatrice de $[\mathrm{XY}]$. Puisque O est le centre du cercle $\omega, \mathrm{O}$ appartient à d . Ainsi, les cercles centrés en $O$, et en particulier $\omega$ et $\Omega$, sont envoyés sur eux-mêmes par la symétrie d'axe $d$. On note $s$ cette symétrie.
On a $s(X)=\mathrm{Y}, \mathrm{s}(\omega)=\omega$ et $s(\Omega)=\Omega$, donc $s$ envoie la tangente à $\omega$ en $X$ sur la tangente à $s(\omega)=\omega$ en $s(X)=Y$. Le point d'intersection P de $\Omega$ avec la tangente à $\omega$ en $X$ est envoyé sur le point d'intersection de $s(\Omega)$ avec la tangente à $s(\omega)$ en $s(X)$.
Il s'agit du point d'intersection de $\Omega$ avec la tangente à $\omega$ en $Y$, à savoir le point $Q$. Autrement dit, $P$ et Q sont symétriques par rapport à la médiatrice de $[\mathrm{XY}]$. Les segments $[\mathrm{XY}]$ et $[\mathrm{PQ}]$ sont perpendiculaires à $d$ donc parallèles entre eux et les segments $[\mathrm{PX}]$ et $[\mathrm{QY}]$ sont symétriques par rapport à d . Ceci suffit à conclure que le quadrilatère PQYX est un trapèze isocèle.
Concluons qu'il s'agit d'un quadrilatère cyclique. Par angles correspondants, $\widehat{\mathrm{QPX}}=180^{\circ}-\widehat{\mathrm{PXY}}$ et puisque $s$ conserve les angles, $\widehat{\mathrm{YQP}}=\widehat{\mathrm{QPX}}$. On déduit que
$$
\widehat{Y Q P}=\widehat{Q P X}=180^{\circ}-\widehat{P X Y}
$$
donc les points $P, Q, Y$ et $X$ sont bien cocycliques d'après la réciproque du théorème de l'angle inscrit.
Commentaire des correcteurs : Le problème a été plutôt bien réussi, mais il y a eu trois problèmes récurrents :
- Plusieurs élèves utilisent allègrement que deux triangles avec deux côtés de même longueur et un angle en commun sont isométriques. Malheureusement ce fait est faux : ici on pouvait s'en sortir en utilisant que les triangles étaient rectangles (dans ce cas le critère est vrai par Pythagore). Mais dans un cas général c'est totalement faux : il faut que les côtés soient adjacents à l'angle. Ainsi il est nécessaire de bien préciser rectangle.
- Beaucoup d'élèves supposent que (QY) et (PX) s'intersectent. C'est le cas sauf quand les droites sont parallèles : il fallait donc aussi traiter ce cas. En olympiade, introduire un point qui n'existe pas dans un cas particulier coûte régulièrement 1 point à certains candidats : il faut donc être prudent et traiter le cas particulier à côté.
- Certains élèves parlent de symétrie sans vraiment d'argument rigoureux. Il est important de préciser pourquoi les objets sont envoyés l'un sur l'autre par symétrie.
|
{
"exam": "French_envois",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-1.jsonl",
"solution_match": "## Solution de l'exercice 1",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle with $\widehat{BAC}=60^{\circ}$. Let $D$ and $E$ be the feet of the angle bisectors from vertices $B$ and $C$, respectively. Let $I$ be the intersection point of the lines $(BD)$ and $(CE)$. Show that the points $A$, $I$, $D$, and $E$ are concyclic.
|
We are going to do an angle hunt to prove that $\widehat{I D A}+\widehat{I E A}=180^{\circ}$. Let $x=\widehat{A C E}=\widehat{E C B}$ and $y=\widehat{A B D}=\widehat{\mathrm{DBC}}$. Since the sum of the angles in a triangle is $180^{\circ}$, we have
$$
\begin{aligned}
180^{\circ} & =\widehat{\mathrm{BAC}}+\widehat{\mathrm{ABC}}+\widehat{\mathrm{ACB}} \\
& =60^{\circ}+2 y+2 x
\end{aligned}
$$
This implies that $x+y=60^{\circ}$. We can therefore express all the angles in the figure in terms of $x$ and in particular the two angles of interest, $\widehat{I D A}$ and $\widehat{I E A}$. We have $\widehat{I D A}=\widehat{B D A}=180^{\circ}-60^{\circ}-y$ and $\widehat{I E A}=\widehat{C E A}=180^{\circ}-60^{\circ}-x$. Therefore, the sum is
$$
\widehat{\mathrm{IDA}}+\widehat{\mathrm{IEA}}=180^{\circ}-60^{\circ}-\mathrm{y}+180^{\circ}-60^{\circ}-x=180^{\circ}+60^{\circ}-x-y=180^{\circ}
$$
This is the desired equality.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle avec $\widehat{B A C}=60^{\circ}$. Soient $D$ et $E$ les pieds des bissectrices issues respectivement des sommets $B$ et $C$. Soit I le point d'intersection des droites (BD) et (CE). Montrer que les points $A$, I, $D$ et $E$ sont cocycliques.
|

On va faire une chasse aux angles pour démontrer que $\widehat{I D A}+\widehat{I E A}=180^{\circ}$. Notons $x=\widehat{A C E}=\widehat{E C B}$ ainsi que $y=\widehat{A B D}=\widehat{\mathrm{DBC}}$. Comme la somme des angles d'un triangle vaut $180^{\circ}$ on a ainsi
$$
\begin{aligned}
180^{\circ} & =\widehat{\mathrm{BAC}}+\widehat{\mathrm{ABC}}+\widehat{\mathrm{ACB}} \\
& =60^{\circ}+2 y+2 x
\end{aligned}
$$
Ce qui implique que $x+y=60^{\circ}$. On peut donc exprimer tous les angles de la figure en fonction de $x$ et en particulier les deux angles qui nous intéressent, $\widehat{I D A}$ et $\widehat{I E A}$. On a $\widehat{I D A}=\widehat{B D A}=180^{\circ}-60^{\circ}-y$ ainsi que $\widehat{I E A}=\widehat{C E A}=180^{\circ}-60^{\circ}-x$. Donc la somme vaut
$$
\widehat{\mathrm{IDA}}+\widehat{\mathrm{IEA}}=180^{\circ}-60^{\circ}-\mathrm{y}+180^{\circ}-60^{\circ}-x=180^{\circ}+60^{\circ}-x-y=180^{\circ}
$$
Ce qui est l'égalité voulue.
|
{
"exam": "French_envois",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-1.jsonl",
"solution_match": "## \nSolution de l'exercice 2",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle with $\widehat{BAC}=60^{\circ}$. Let $D$ and $E$ be the feet of the angle bisectors from vertices $B$ and $C$, respectively. Let $I$ be the intersection point of the lines $(BD)$ and $(CE)$. Show that the points $A$, $I$, $D$, and $E$ are concyclic.
|
For exercise 2
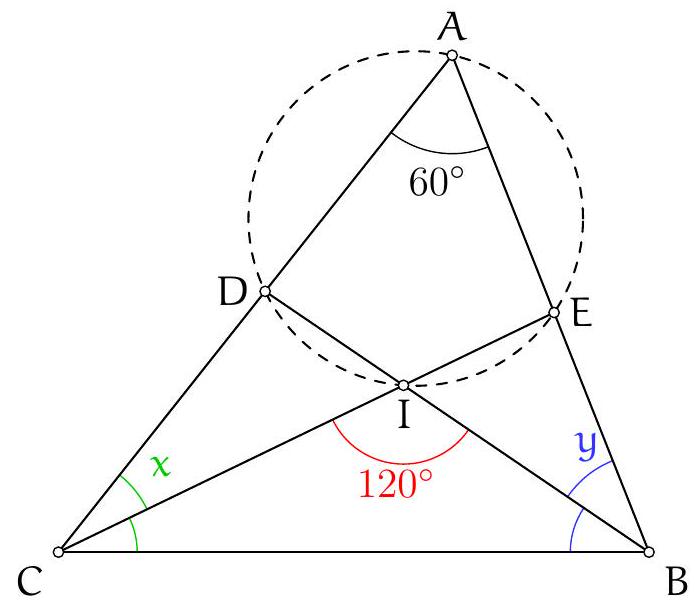
Once we have obtained that $x+y=60^{\circ}$, we can conclude in another way, by demonstrating that $\widehat{\mathrm{DAE}}+\widehat{\mathrm{DIE}}=180^{\circ}$. Indeed, in triangle BCI, we have $\widehat{\mathrm{BIC}}=180^{\circ}-x-y=120^{\circ}$, so that $\widehat{\mathrm{DIE}}+\widehat{\mathrm{DAE}}=\widehat{\mathrm{BIC}}+\widehat{\mathrm{BAC}}=120^{\circ}+60^{\circ}=180^{\circ}$.
Graders' comment: The exercise was very well done overall. Even though the exercise was relatively quick, it is important to make a neat and clear figure and to clearly specify the steps of reasoning.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle avec $\widehat{B A C}=60^{\circ}$. Soient $D$ et $E$ les pieds des bissectrices issues respectivement des sommets $B$ et $C$. Soit I le point d'intersection des droites (BD) et (CE). Montrer que les points $A$, I, $D$ et $E$ sont cocycliques.
|
de l'exercice 2

Une fois que l'on a obtenu que $x+y=60^{\circ}$, on peut conclure d'une autre façon, en démontrant que $\widehat{\mathrm{DAE}}+\widehat{\mathrm{DIE}}=180^{\circ}$. En effet, dans le triangle BCI, on a $\widehat{\mathrm{BIC}}=180^{\circ}-\mathrm{x}-\mathrm{y}=120^{\circ}$, de sorte que $\widehat{\mathrm{DIE}}+\widehat{\mathrm{DAE}}=\widehat{\mathrm{BIC}}+\widehat{\mathrm{BAC}}=120^{\circ}+60^{\circ}=180^{\circ}$.
Commentaire des correcteurs: Exercice très bien réussi dans l'ensemble. Même si l'exercice était relativement rapide, il faut bien penser à faire une belle figure propre et bien préciser les étapes de raisonnement.
|
{
"exam": "French_envois",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-1.jsonl",
"solution_match": "## Solution alternative",
"tier": "T2",
"year": null
}
|
Let ABC be a triangle with O as the center of the circumscribed circle. Let $\ell$ be a line perpendicular to the line $(A O)$. The line $(\ell)$ intersects the sides $(A B)$ and $(A C)$ at points $D$ and $E$. Show that the points $B, C, E$ and $D$ are concyclic.
|
Let $X$ and $Y$ be the orthogonal projections of $O$ onto $(AC)$ and $(DE)$, respectively. Note that $X$ is the midpoint of the segment $[AC]$ and also the foot of the angle bisector of $\angle COA$ in the isosceles triangle $AOC$ at $O$.
Since $\angle EXO = 90^\circ = \angle EYO$, we deduce that $E, X, O$, and $Y$ are concyclic by the inscribed angle theorem. By the central angle theorem, we then have:
$$
\angle CBA = \angle COA / 2 = \angle XOA = 180^\circ - \angle YEX = 180^\circ - \angle CED
$$
From this, we deduce the concyclicity of points $B, C, D$, and $E$.
Comment from the graders: The exercise is very well done, however, many proofs get lost in numerous calculations when it is possible to do much simpler.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit ABC un triangle dont O est le centre du cercle circonscrit. On note $\ell$ une droite perpendiculaire à la droite $(A O)$. La droite $(\ell)$ intersecte les côtés $(A B)$ et $(A C)$ en les points $D$ et $E$. Montrer que les points $B, C, E$ et $D$ sont cocycliques.
|
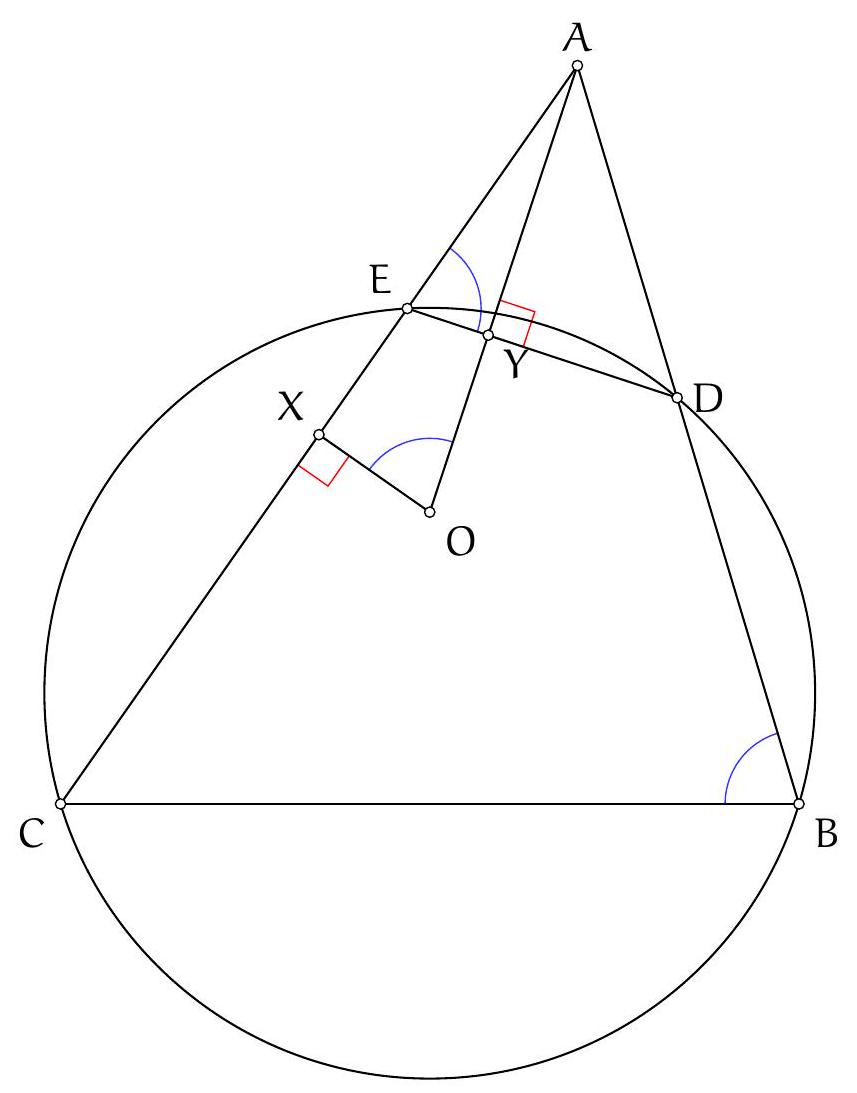
Posons $X$ et $Y$ les projetés orthogonaux de $O$ sur ( $A C$ ) et (DE) respectivement. Notons que $X$ est le milieu du segment $[A C]$ et aussi le pied de la bissectrice de l'angle $\widehat{\mathrm{COA}}$ dans le triangle $A O C$ isocèle en O.
Comme $\widehat{\mathrm{EXO}}=90^{\circ}=\widehat{\mathrm{EYO}}$, on en déduit que $\mathrm{E}, \mathrm{X}, \mathrm{O}$ et Y sont cocycliques par le théorème de l'angle inscrit. Par le théorème de l'angle au centre, on a alors :
$$
\widehat{\mathrm{CBA}}=\widehat{\mathrm{COA}} / 2=\widehat{\mathrm{XOA}}=180^{\circ}-\widehat{\mathrm{YEX}}=180^{\circ}-\widehat{\mathrm{CED}}
$$
On en déduit la cocyclicité des points $\mathrm{B}, \mathrm{C}, \mathrm{D}$ et E .
Commentaire des correcteurs: L'exercice est très bien réussi, néanmoins beaucoup de preuves se perdent dans de nombreux calculs quand il est possible de faire bien plus simple.
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-1.jsonl",
"solution_match": "## Solution de l'exercice 3",
"tier": "T2",
"year": null
}
|
Let $\omega_{1}$ and $\omega_{2}$ be two disjoint circles. An external common tangent to these two circles intersects $\omega_{1}$ at $A$ and $\omega_{2}$ at $B$. The second external common tangent to these two circles intersects $\omega_{1}$ at $D$ and $\omega_{2}$ at $C$. The line (BD) intersects $\omega_{1}$ at the point $P$ other than $D$ and $\omega_{2}$ at the point $Q$ other than B. Show that BQ = DP.
|
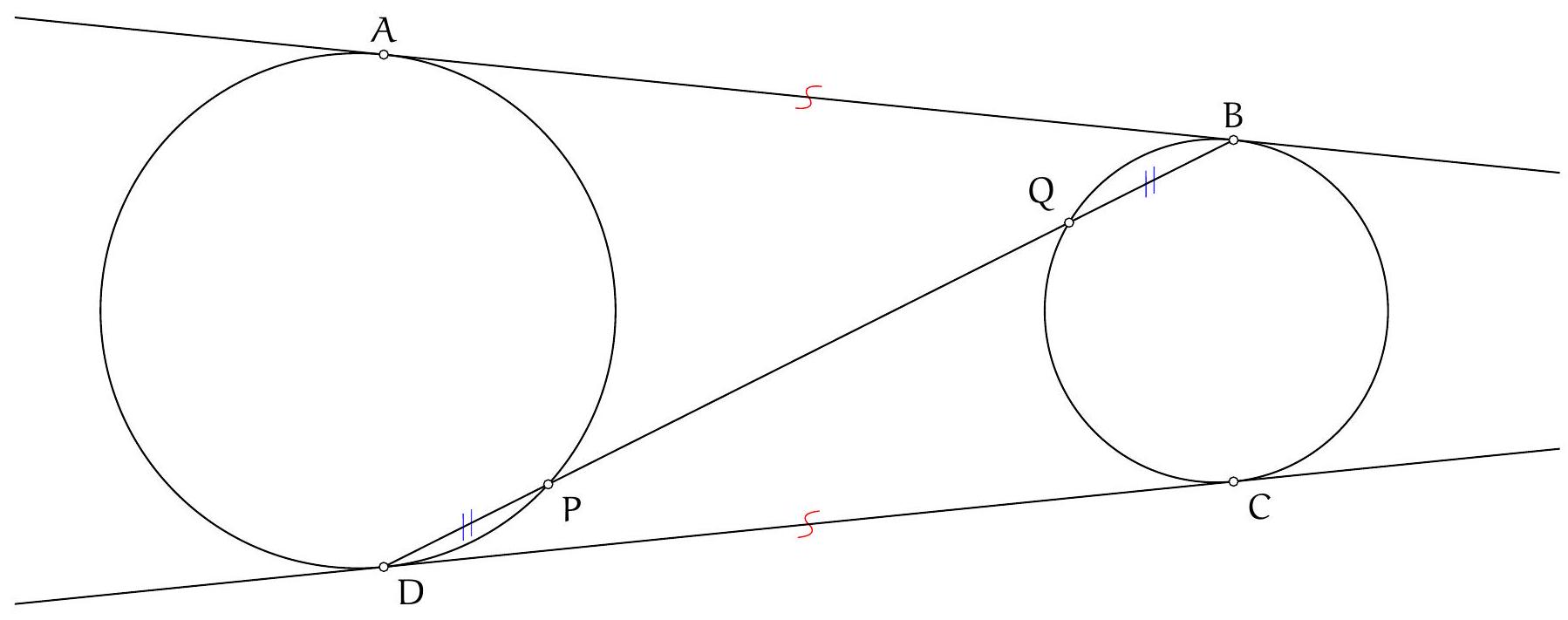
A symmetry with respect to the line joining the centers of the two circles exchanges $A$ and $D$ as well as $B$ and $C$. Therefore, $A B = D C$. We then think of applying the power of a point, which gives us:
$$
\mathrm{DQ} \cdot \mathrm{DB} = \mathrm{DC}^2 = \mathrm{AB}^2 = \mathrm{BP} \cdot \mathrm{BD}
$$
where the first equality comes from the power of the point from $D$ with respect to $\omega_{2}$ and the third equality comes from the power of the point from $B$ with respect to the circle $\omega_{1}$. We can rewrite this identity as follows:
$$
(B P - D Q) B D = 0
$$
This implies that $\mathrm{BP} = \mathrm{DQ}$ and therefore that $\mathrm{DP} = \mathrm{BQ}$, leading to the conclusion.
Comment from the graders: The exercise was generally very well done. Using the power of a point simplified the problem: some solutions managed to solve it without, but it may be useful to study the solution with this concept to see how it simplified the resolution of the problem. Note that very few solutions considered the case where the circles have the same radius, in which case the tangents do not intersect. This case must be treated separately. Finally, while the need to make a clear and large diagram is understood by most students, there are still some solutions that do not follow this instruction.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $\omega_{1}$ et $\omega_{2}$ deux cercles disjoints. Une tangente commune extérieure à ces deux cercles coupe $\omega_{1}$ en $A$ et $\omega_{2}$ en $B$. La deuxième tangente commune extérieure à ces deux cercles coupe $\omega_{1}$ en $D$ et $\omega_{2}$ en $C$. La droite (BD) coupe $\omega_{1}$ en le point $P$ autre que $D$ et $\omega_{2}$ en le point $Q$ autre que B. Montrer que BQ = DP.
|

Une symétrie axiale par rapport à la droite joignant les centres des deux cercles échange $A$ et $D$ ainsi que $B$ et $C$. Donc, $A B=D C$. On pense alors à appliquer la puissance d'un point, on a alors :
$$
\mathrm{DQ} \cdot \mathrm{DB}=\mathrm{DC}^{2}=\mathrm{AB}^{2}=\mathrm{BP} \cdot \mathrm{BD}
$$
où la première égalité vient de la puissance du point depuis D par rapport à $\omega_{2}$ et la troisième égalité vient de la puissance du point depuis B par rapport au cercle $\omega_{1}$. On peut réécrire cette identité de la manière suivante :
$$
(B P-D Q) B D=0
$$
Cela implique que $\mathrm{BP}=\mathrm{DQ}$ et donc que $\mathrm{DP}=\mathrm{BQ}$, d'où la conclusion.
Commentaire des correcteurs: L'exercice a globalement été très bien réussi. Utiliser des puissances de points simplifiait l'exercice : certaines copies ont réussi à faire sans, mais il peut être bon d'ètudier la solution avec cette notion afin de voir comment elle simplifiait la résolution du problème. Signalons que très peu de copies ont pensé au fait que lorsque les cercles ont même rayon, alors les tangentes ne se coupent pas. Il faut donc traiter ce cas à part. Enfin si la nècessitè de faire une figure propre et grande est acquise pour la plupart des élèves, il y a encore quelques copies qui ne respectent pas cette consigne.
|
{
"exam": "French_envois",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-1.jsonl",
"solution_match": "## Solution de l'exercice 4",
"tier": "T2",
"year": null
}
|
Let $ABC$ be an acute triangle with $AB < AC < BC$ and let $\Omega$ be its circumcircle. Let $D$ and $E$ be the points diametrically opposite to points $B$ and $C$ respectively in the circle $\Omega$. The circle centered at $A$ with radius $AE$ intersects $[AC]$ at $K$. The circle centered at $A$ with radius $AD$ intersects $(BA)$ at $L$ (such that $A$ lies between $B$ and $L$). Show that the lines $(EK)$ and $(DL)$ intersect on the circle $\Omega$.
|
Let $X$ be the second intersection point of the line (EK) with the circle $\Omega$. The first thing to understand is that points K and L are of little importance and are only there to create isosceles right triangles.
Thus, we know that $[CE]$ is a diameter of the circle $\Omega$ and we obtain that $\widehat{\mathrm{EAK}}=90^{\circ}$. The triangle EAK is isosceles at $A$ because $AK = AE$ according to the problem statement. Combining this with the information that $\widehat{\mathrm{EAK}}=90^{\circ}$ shows that $\widehat{\mathrm{KEA}}=45^{\circ}$. Similarly, the triangle DAL is a right isosceles triangle at $A$ and thus
$$
\widehat{\mathrm{XDA}}=180^{\circ}-\widehat{\mathrm{AEX}}=180^{\circ}-45^{\circ}=180^{\circ}-\widehat{\mathrm{LDA}}
$$
This shows that the points $X, D$, and $L$ are collinear.
Comment from the graders: The problem is well handled. However, a significant number of students engaged in a lengthy angle chase when a direct solution was possible.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle acutangle avec $A B<A C<B C$ et soit $\Omega$ son cercle circonscrit. Soient D et E les points diamètralement opposés respectivement aux points B et C dans le cercle $\Omega$. Le cercle de centre $A$ et de rayon $A E$ intersecte $[A C]$ en $K$. Le cercle de centre $A$ et de rayon $A D$ coupe $(B A)$ en $L$ (de telle sorte $A$ se trouve entre B et $L$ ). Montrer que les droites (EK) et (DL) se coupent sur le cercle $\Omega$.
|
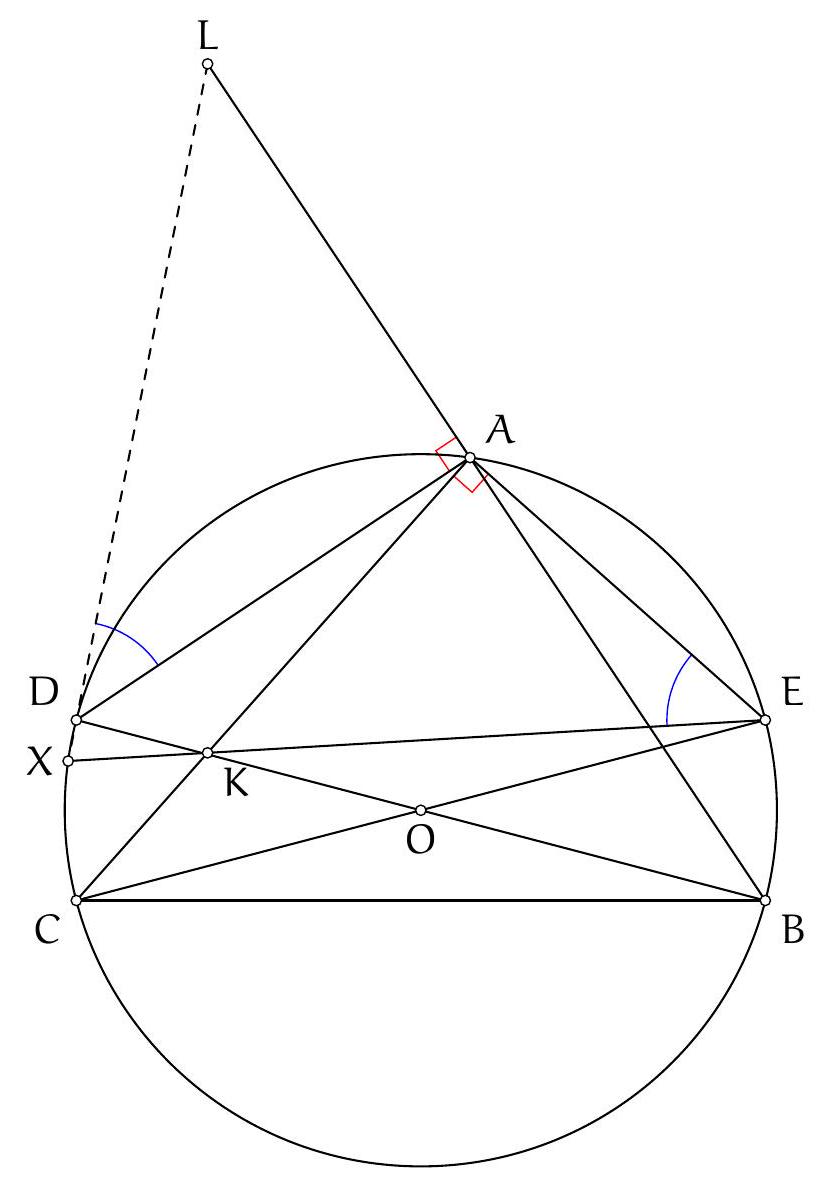
Notons $X$ le second point d'intersection de la droite (EK) avec le cercle $\Omega$. La première chose à comprendre est que les points K et L sont très peu importants et qu'ils ne sont là que pour créer des triangles rectangles isocèles.
Ainsi, on sait que $[C E]$ est un diamètre du cercle $\Omega$ et on obtient donc que $\widehat{\mathrm{EAK}}=90^{\circ}$. Le triangle EAK est isocèle en $A$ car $A K=A E$ d'après les hypothèses de l'énoncé, en combinant cela avec l'information que $\widehat{\mathrm{EAK}}=90^{\circ}$ cela montre que $\widehat{\mathrm{KEA}}=45^{\circ}$. De la même manière le triangle DAL est rectangle isocèle en $A$ et donc
$$
\widehat{\mathrm{XDA}}=180^{\circ}-\widehat{\mathrm{AEX}}=180^{\circ}-45^{\circ}=180^{\circ}-\widehat{\mathrm{LDA}}
$$
Ce qui montre bien que les points $X, D$ et $L$ sont alignés.
Commentaire des correcteurs : L'exercice est bien traité. En revanche, une quantité significative d'élèves a déployé une longue chasse aux angles quand il était possible d'avoir une solution directe.
|
{
"exam": "French_envois",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-1.jsonl",
"solution_match": "## Solution de l'exercice 5",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle with $\widehat{ABC}=\widehat{ACB}=40^{\circ}$. The bisector from vertex $B$ intersects the line $(AC)$ at point $D$. Show that $BD + DA = BC$.
|
To solve this kind of exercise, a good idea is often to try to transfer the lengths we are interested in to places where the calculations will be easier to perform. This is why we introduce $X$ as the point on the segment $[B C]$ such that $B D = B X$. We then want to show that $X C = A D$ to conclude.
A quick angle chase shows in the first place that $\widehat{\mathrm{BXD}} = 80^{\circ}$. Indeed, by the construction of point $X$, triangle BDX is isosceles at B, so we can calculate $\widehat{\mathrm{BXD}} = (180^{\circ} - 20^{\circ}) / 2 = 80^{\circ}$. This gives that $\widehat{\mathrm{CDX}} = \widehat{\mathrm{DXB}} - \widehat{\mathrm{DCX}} = 80^{\circ} - 40^{\circ} = 40^{\circ} = \widehat{\mathrm{DCX}}$, and thus that triangle DXC is isosceles at X. This shows that $\mathrm{DX} = \mathrm{XC}$. Solving the exercise therefore comes down to showing that $A D = D X$.
By closely examining the quadrilateral BADX, we notice that line (BD) is the angle bisector of $\widehat{A B X}$, and since we want to show that $A D = D X$, we naturally think of the South Pole theorem. It is therefore sufficient to show that points $B, A, D$, and $X$ are concyclic to conclude. This then involves a second small angle chase.
Indeed, $\widehat{\mathrm{BAD}} + \widehat{\mathrm{BXD}} = 100^{\circ} + 80^{\circ} = 180^{\circ}$, which clearly shows that quadrilateral ADXB is cyclic. Then, according to the South Pole theorem in triangle $B A X$, $A D = D X$. This thus concludes the proof of the exercise.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle avec $\widehat{A B C}=\widehat{A C B}=40^{\circ}$. La bissectrice issue du sommet $B$ coupe la droite ( $A C$ ) au point $D$. Montrer que $B D+D A=B C$.
|
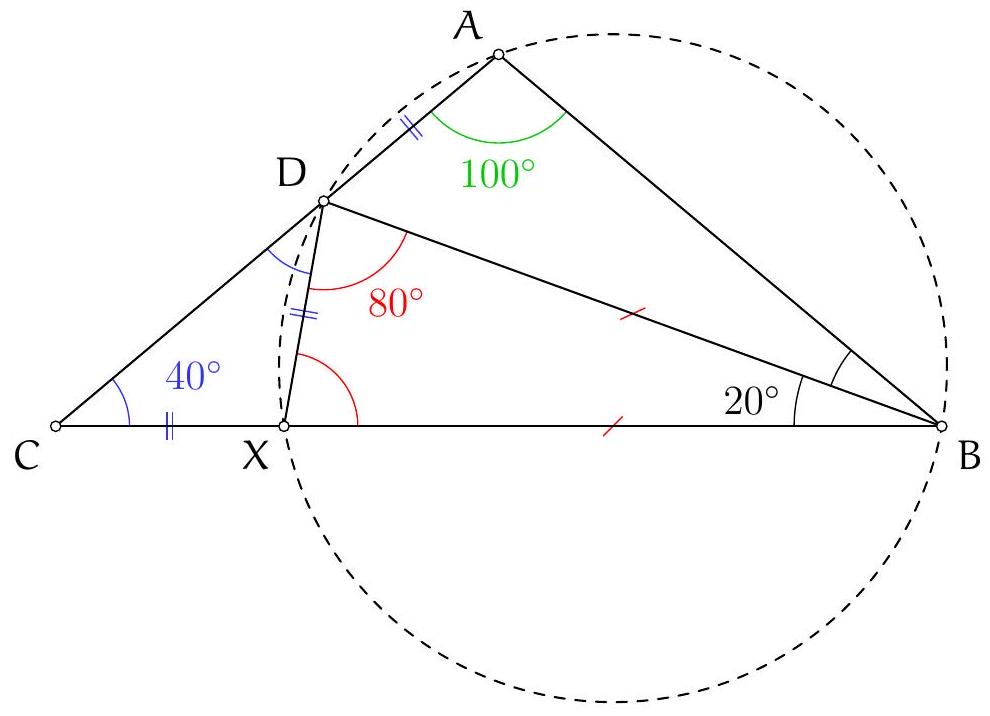
Pour résoudre ce genre d'exercice, une bonne idée est souvent d'essayer de reporter les longueurs qui nous intéressent à des endroits où les calculs seront plus faciles à faire. C'est pour cela que l'on introduit $X$ le point du segment $[B C]$ de telle sorte que $B D=B X$. On veut alors démontrer que $X C=A D$ pour conclure.
Une chasse aux angles rapide montre dans un premier temps que $\widehat{\mathrm{BXD}}=80^{\circ}$. En effet, on sait par construction du point $X$ que le triangle BDX est isocèle en B , on peut donc calculer $\widehat{\mathrm{BXD}}=\left(180^{\circ}-\right.$ $\left.20^{\circ}\right) / 2=80^{\circ}$. Cela donne ensuite que $\widehat{\mathrm{CDX}}=\widehat{\mathrm{DXB}}-\widehat{\mathrm{DCX}}=80^{\circ}-40^{\circ}=40^{\circ}=\widehat{\mathrm{DCX}}$ et donc que le triangle DXC est isocèle en X . Cela montre que $\mathrm{DX}=\mathrm{XC}$. Résoudre l'exercice revient donc à montrer que $A D=D X$.
En regardant très fort le quadrilatère BADX on remarque que la droite ( BD ) est la bissectrice de l'angle $\widehat{A B X}$ et comme on veut démontrer que $A D=D X$ on pense naturellement au théorème du pôle sud. Il suffit donc de démontrer que les points $B, A, D$ et $X$ sont cocycliques pour conclure, il s'agit alors d'une deuxième petite chasse aux angles.
En effet, $\widehat{\mathrm{BAD}}+\widehat{\mathrm{BXD}}=100^{\circ}+80^{\circ}=180^{\circ}$ ce qui montre bien que le quadriltère ADXB est cyclique, puis d'après le théorème du pôle Sud dans le triangle $B A X$ que $A D=D X$. Cela conclut ainsi la preuve de l'exercice.
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-1.jsonl",
"solution_match": "## Solution de l'exercice 6",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle with $\widehat{ABC}=\widehat{ACB}=40^{\circ}$. The bisector from vertex $B$ intersects the line $(AC)$ at point $D$. Show that $BD + DA = BC$.
|
Exercise 6
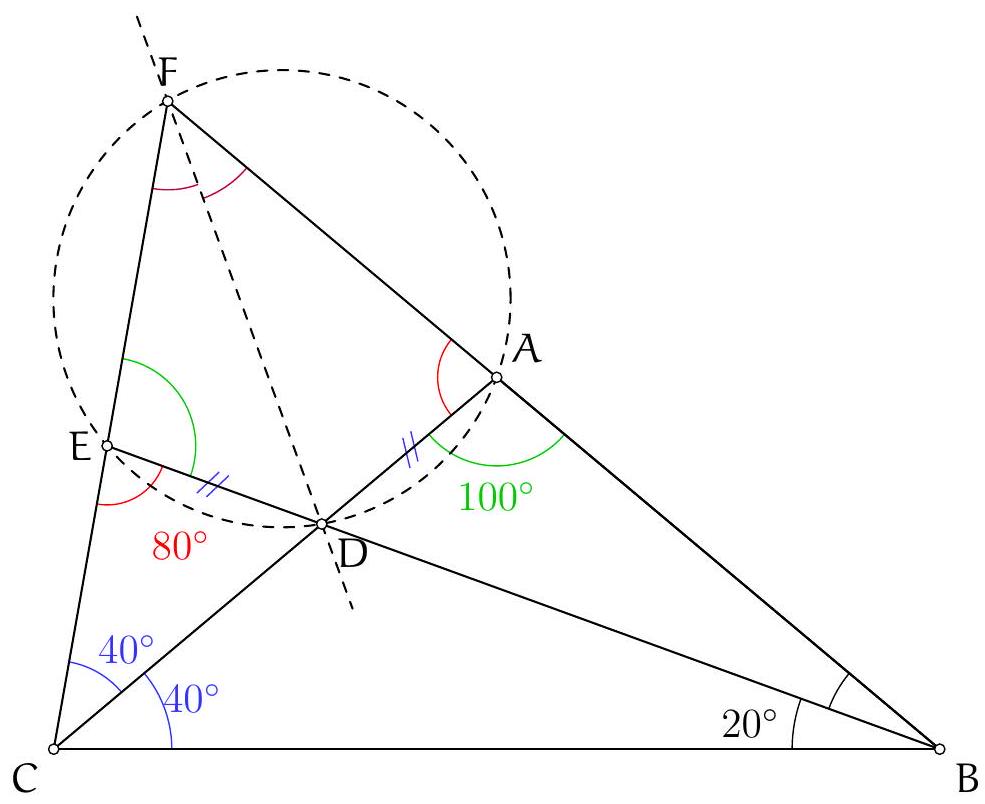
A second solution is presented, corresponding to a second way of transferring the lengths to be studied.
Let $E$ be the point on the ray $[B D)$ such that $B E = B C$. We aim to show that $E D = D A$, so that $B D + D A = B D + D E = B E = B C$. The triangle $E B C$ is isosceles at $B$, so $180^{\circ} = \widehat{\mathrm{EBC}} + \widehat{\mathrm{ECB}} + \widehat{\mathrm{CEB}} = 20^{\circ} + 2 \widehat{\mathrm{CEB}}$. Thus, $\widehat{\mathrm{CEB}} = 80^{\circ}$ and $\widehat{\mathrm{ECD}} = \widehat{\mathrm{ECB}} - \widehat{\mathrm{DCB}} = 80^{\circ} - 40^{\circ} = 40^{\circ}$. Therefore, point $D$ is the foot of the angle bisector from vertex $C$ in triangle $E C B$.
Now let $F$ be the intersection point of the lines $(E C)$ and $(A B)$. The idea behind introducing this point is that we already know two angle bisectors of this triangle: the line $(BD)$ is the angle bisector of $\widehat{A B C}$ and the line $(CD)$ is the angle bisector of $\widehat{F C B}$. Thus, point $D$ is the incenter of triangle $F C B$. Therefore, it lies on the angle bisector of $\widehat{\mathrm{BFC}}$.
We have $\widehat{D E F} = 180^{\circ} - \widehat{D E C} = 100^{\circ}$ and $\widehat{D A F} = 180^{\circ} - \widehat{D A B} = 80^{\circ}$, so $\widehat{D E F} + \widehat{D A F} = 180^{\circ}$ and points $F, E, D$, and $A$ are concyclic. Therefore, point $D$ lies on the circumcircle of triangle $F E A$ and on the angle bisector of $\widehat{E F A}$, making it the South Pole of point $F$. As such, $D$ lies on the perpendicular bisector of segment $[A E]$ and $D E = D A$ as announced.
Comment from the graders: The exercise was generally well done by the students who attempted it: some even found very different (but often more laborious) approaches than those in the solution. Some students tried to calculate all the lengths, hoping that the trigonometric expressions would simplify nicely at the end. While this was possible (the simplest way being via the Law of Sines), be careful, in competitions, trying to calculate many lengths without achieving anything usually earns very few points. Therefore, it is important to avoid overly complicated calculations.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle avec $\widehat{A B C}=\widehat{A C B}=40^{\circ}$. La bissectrice issue du sommet $B$ coupe la droite ( $A C$ ) au point $D$. Montrer que $B D+D A=B C$.
|
de l'exercice 6

On présente une deuxième solution, correspondant à une deuxième façon de reporter les longueurs à étudier.
Soit $E$ le point de la demi-droite $[B D)$ tel que $B E=B C$. On cherche à montrer que $E D=D A$, de sorte que $B D+D A=B D+D E=B E=B C$. Le triangle $E B C$ est isocèle en $B$, de sorte que $180^{\circ}=\widehat{\mathrm{EBC}}+\widehat{\mathrm{ECB}}+\widehat{\mathrm{CEB}}=20^{\circ}+2 \widehat{\mathrm{CEB}}$. Ainsi, $\widehat{\mathrm{CEB}}=80^{\circ}$ et $\widehat{\mathrm{ECD}}=\widehat{\mathrm{ECB}}-\widehat{\mathrm{DCB}}=80^{\circ}-40^{\circ}=40^{\circ}$. Le point D est donc le pied de la bissectrice issue du sommet C dans le triangle ECB .
Soit désormais $F$ le point d'intersection des droites ( $E C$ ) et ( $A B$ ). L'idée derrière l'introduction de ce point est que l'on connait déjà deux bissectrices de ce triangle : la droite (BD) est la bissectrice de l'angle $\widehat{A B C}$ et la droite (CD) est la bissectrice de l'angle $\widehat{F C B}$. Ainsi, le point $D$ est le centre du cercle inscrit au triangle FCB. Il est donc sur la bissectrice de l'angle $\widehat{\mathrm{BFC}}$.
Or on a $\widehat{D E F}=180^{\circ}-\widehat{D E C}=100^{\circ}$ et $\widehat{D A F}=180^{\circ}-\widehat{D A B}=80^{\circ}$, de sorte que $\widehat{D E F}+\widehat{D A F}=180^{\circ}$ et les points $F, E, D$ et $A$ sont cocycliques. Le point $D$ est donc sur le cercle circonscrit au triangle $F E A$ et sur la bissectrice de l'angle $\widehat{E F A}$, il s'agit donc du pôle Sud du point F . A ce titre, D est sur la médiatrice du segment $[A E]$ et $D E=D A$ comme annoncé.
Commentaire des correcteurs: L'exercice est globalement bien réussi par les élèves l'ayant tenté : certains ont même trouvé des approches très différentes (mais souvent un peu plus laborieuses) que celles du corrigé. Un certain nombre d'élève ont essayé de calculer toutes les longueurs, en espérant que les expressions trigonométriques se simplifieraient bien à la fin. Il était possible de faire ainsi (le plus simple étant via la loi des sinus), mais attention, en compétition, essayer de calculer pleins de longueurs sans aboutir à rien rapporte habituellement très peu de points. Il faut donc éviter d'aboutir à des calculs trop compliqués.
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-1.jsonl",
"solution_match": "## Solution alternative",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle. We denote $D$ and $E$ as the midpoints of sides $AB$ and $AC$, respectively. Let $O$ be the center of the circumcircle of triangle $ABC$. We denote $K$ as the intersection point of lines $(OE)$ and $(BC)$. We denote $L$ as the second intersection point of line $(OD)$ with the circumcircle of triangle $OKB$. We denote $F$ as the orthogonal projection of $A$ onto line $(KL)$. Show that points $D$, $E$, and $F$ are collinear.
|
By drawing the figure, we notice that point $A$ also belongs to the circle passing through $O, K$, and $B$. We start by proving this fact.
On the one hand, according to Thales' theorem, the lines $(DE)$ and $(BC)$ are parallel, so we have the equality of alternate interior angles:
$$
\widehat{\mathrm{OKB}} = \widehat{\mathrm{OED}}.
$$
On the other hand, since $\widehat{\mathrm{ODA}} = 90^{\circ} = 180^{\circ} - \widehat{\mathrm{OEA}}$, the points $\mathrm{O}, \mathrm{E}, \mathrm{A}$, and $D$ are concyclic, so with the inscribed angle theorem we obtain
$$
\widehat{OAB} = \widehat{OAD} = \widehat{OED} = \widehat{OKB}.
$$
This proves that point $\mathcal{A}$ belongs to the circle passing through $\mathrm{O}, \mathrm{K}$, and $B$. Note that $O$ is the midpoint of the arc $AB$ in the circumcircle of triangle $AKB$. Therefore, point $O$ is the South pole of point $K$ in triangle $ABK$. In particular, $\widehat{OKB} = \widehat{AKO}$.
Since $\widehat{AFK} = 90^{\circ} = 180^{\circ} - \widehat{AEK}$, the points $A, F, K$, and $E$ are concyclic. Therefore, with the inscribed angle theorem:
$$
\widehat{AFE} = \widehat{AKE} = \widehat{AKO}.
$$
On the other hand, since $\widehat{AFL} = 90^{\circ} = \widehat{ADL}$, the points $A, D, F$, and $L$ are concyclic. Therefore, with the inscribed angle theorem in the circle passing through $A, D, F$, and $L$ and then in the circle passing through $A, L, K$, and $O$:
$$
\widehat{AFD} = \widehat{ALD} = \widehat{ALO} = \widehat{AKO}
$$
We deduce that $\widehat{AFD} = \widehat{AKO} = \widehat{AFE}$. Therefore, points $F, D$, and $E$ are collinear, as desired.
Remark 1. Once we have shown that point $A$ is on the circle passing through $\mathrm{O}, \mathrm{K}$, and $B$, we can conclude directly by noting that points $\mathrm{E}, \mathrm{D}$, and $F$ are the orthogonal projections of point $A$ onto the sides of triangle $OKL$. The Simson line property indicates that these points are collinear. The Simson line property is a classic in triangle geometry, which can be found in the beginner geometry workbook of the POFM (Exercise 3.10). The end of the proof given above essentially re-proves this property.
Comment from the graders: The exercise, although difficult, is well handled. Very few students, however, thought of the Simson line to conclude.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle. On note $D$ et $E$ les milieux respectifs des côtés $A B$ et $A C$. Soit $O$ le centre du cercle circonscrit du triangle $A B C$. On note K le point d'intersection des droites (OE) et (BC). On note L le deuxième point d'intersection de la droite (OD) avec le cercle circonscrit au triangle OKB. On note $F$ la projection orthogonale de $A$ sur le droite (KL). Montrer que les points D, $E$ et $F$ sont alignés.
|
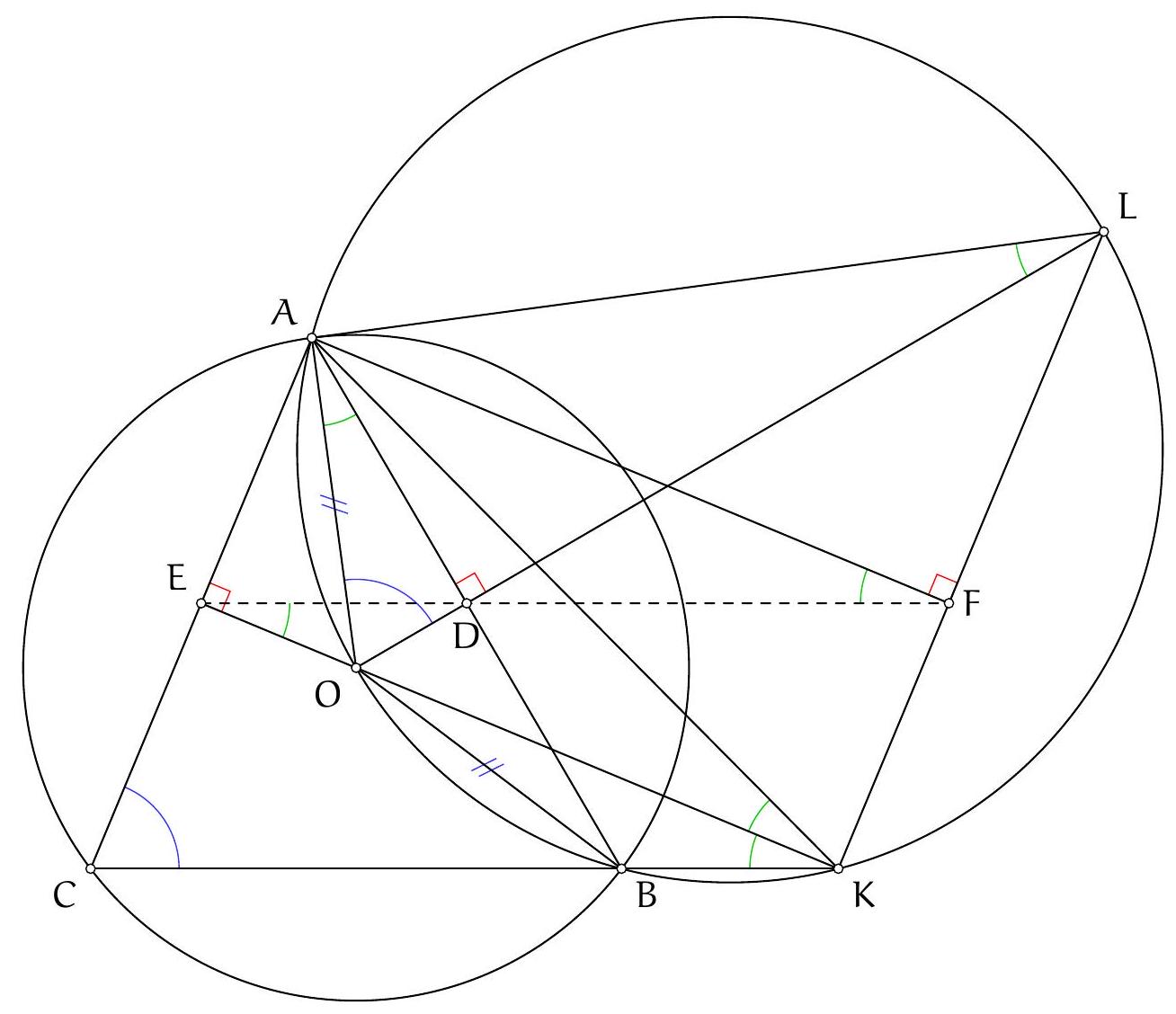
En traçant la figure, on s'aperçoit que le point $A$ appartient également au cercle passant $O, K$ et $B$. On commence par démontrer ce fait.
D'une part, d'après le théorème de Thalès les droites ( DE ) et ( BC ) sont parallèles, on a l'égalité des angles alternes-internes :
$$
\widehat{\mathrm{OKB}}=\widehat{\mathrm{OED}} .
$$
D'autre part, puisque $\widehat{\mathrm{ODA}}=90^{\circ}=180^{\circ}-\widehat{\mathrm{OEA}}$, les points $\mathrm{O}, \mathrm{E}, \mathrm{A}$ et D sont cocycliques, de sorte qu'avec le théorème de l'angle inscrit on obtient
$$
\widehat{O A B}=\widehat{O A D}=\widehat{O E D}=\widehat{O K B} .
$$
Ce qui prouve bien que le point $\mathcal{A}$ appartient au cercle passant par $\mathrm{O}, \mathrm{K}$ et B . Notons que O est le milieu de l'arc $A B$ dans le cercle circonscrit au triangle $A K B$. Le point $O$ est donc le pôle Sud du point $K$ dans le triangle $A B K$. En particulier, $\widehat{O K B}=\widehat{A K O}$.
Puisque $\widehat{A F K}=90^{\circ}=180^{\circ}-\widehat{A E K}$, les points $A, F, K$ et $E$ sont cocycliques. On a donc avec le théorème de l'angle inscrit:
$$
\widehat{A F E}=\widehat{A K E}=\widehat{A K O} .
$$
D'autre part, puisque $\widehat{A F L}=90^{\circ}=\widehat{A D L}$, les points $A, D, F$ et $L$ sont cocycliques. On a alors avec le théorème de l'angle inscrit dans le cercle passant par $A, D, F$ et $L$ puis dans celui passant par $A, L, K$ et O :
$$
\widehat{A F D}=\widehat{A L D}=\widehat{A L O}=\widehat{A K O}
$$
On déduit que $\widehat{A F D}=\widehat{A K O}=\widehat{A F E}$. Les points $F, D$ et $E$ sont donc alignés, comme voulu.
Remarque 1. Une fois que l'on a montré que le point A est sur le cercle passant par $\mathrm{O}, \mathrm{K}$ et B , on peut conclure directement en remarquant que les points $\mathrm{E}, \mathrm{D}$ et F sont les projetés orthogonaux du point A sur les côtés du triangle OKL. La propriété de la droite de Simson nous indique que ces points sont alignés. La propriété de la droite de Simson est un classique de la géométrie du triangle, que l'on pourra retrouver dans le polycopié de géométrie pour débutants de la POFM (Exercice 3.10). La fin de la preuve donnée ci-dessus redémontre en substance cette propriété.
Commentaire des correcteurs: L'exercice, pourtant difficile, est bien traité. Très peu d'élèves ont cependant penser à la droite de Simson pour conclure.
|
{
"exam": "French_envois",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-1.jsonl",
"solution_match": "## Solution de l'exercice 7",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle with acute angles, $\omega$ its circumcircle, and $O$ the center of $\omega$. The perpendicular from $A$ to $(BC)$ intersects $(BC)$ at $D$ and $\omega$ at $E$. Let $F$ be a point on the segment $[AE]$ such that $2 \cdot FD = AE$. Let $\ell$ be the perpendicular to $(OF)$ passing through $F$. Show that the line $\ell$, the line $(BC)$, and the tangent to $\omega$ at $E$ are concurrent.
|
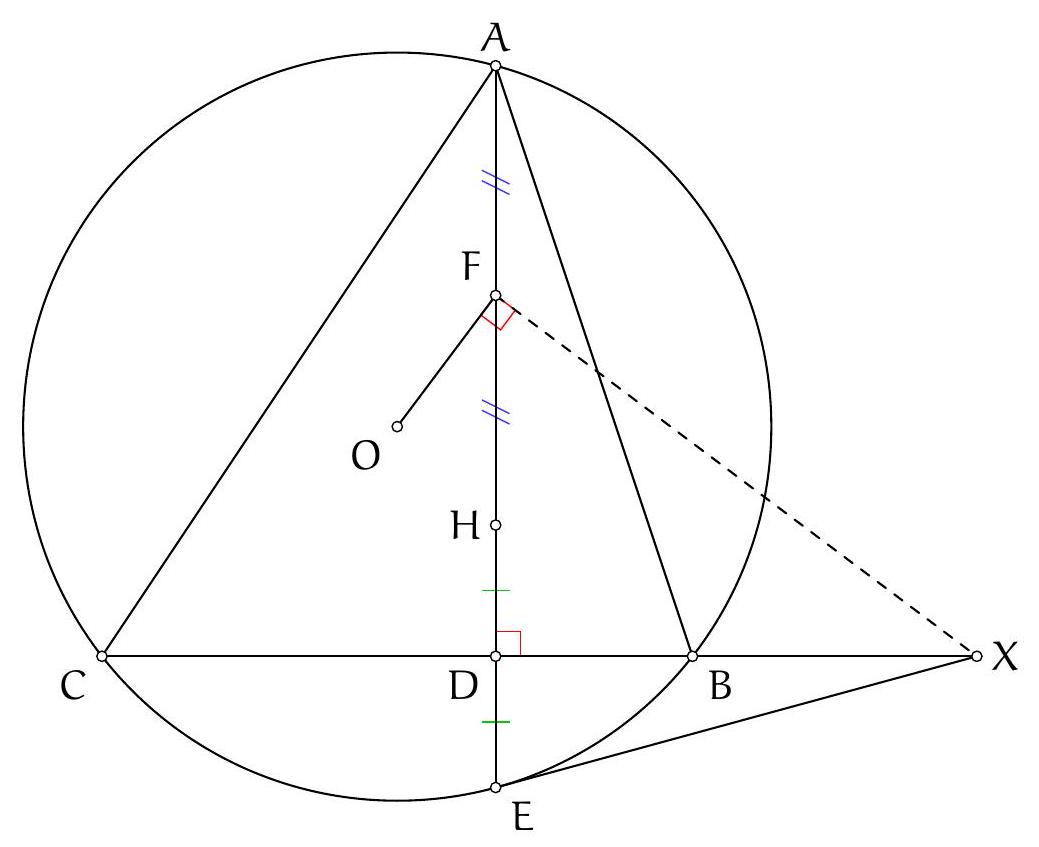
We want to show that three lines are concurrent. One strategy would be to consider the intersection point of two of these lines and show that this point lies on the third line, which is the strategy we will adopt here.
In the case of our exercise, it was possible to choose any pair of lines among the lines $(\ell)$, $(BC)$, and the tangent to $\omega$ at $E$ and arrive at the same conclusion.
Let $X$ be the intersection point of the tangent to $\omega$ at $E$ with the line $(BC)$. We will show that $X$ lies on $\ell$ by showing that the lines $(FX)$ and $(FO)$ are perpendicular. To show that they are indeed perpendicular, we will use the converse of the Pythagorean theorem by showing that $XO^2 = OF^2 + FX^2$. We will denote the radius of $\omega$ as $R$ in the following.
On the one hand, since $(XE)$ is tangent to the circle $\omega$, we have $XO^2 = XE^2 + OE^2 = XE^2 + R^2$. According to the Pythagorean theorem in the right triangle $XDE$ at $D$, $XE^2 = XD^2 + DE^2$. We deduce that
$$
XO^2 = XD^2 + DE^2 + R^2
$$
On the other hand, according to the Pythagorean theorem in the right triangle $FDX$ at $D$, $XF^2 = XD^2 + FD^2$. To calculate $OF^2$, we use the power of point $F$ with respect to the circle $\omega$. Indeed, this formula tells us that the power of point $F$ with respect to the circle $\omega$ is $OF^2 - R^2$. Since it is also equal to $-FA \times FE$, we deduce that $OF^2 = R^2 - FA \times FE$. We then have,
$$
XF^2 + OF^2 = (XD^2 + FD^2) + (R^2 - FA \times FE)
$$
To show that $XO^2 = XF^2 + OF^2$, it suffices to show that $DE^2 = FD^2 - FA \times FE$, or equivalently $D^2 + FA \times FE$. It then remains to introduce the length hypothesis on point $F$.
Let $H$ be the orthocenter of triangle $ABC$. We know that the points $H$ and $E$ are symmetric with respect to the line $(BC)$ (a classic result in triangle geometry that can be found in the beginner's geometry workbook of the POFM, exercise 4.8). We deduce that $DE = DH$. But then,
$$
FH = FD - DH = \frac{1}{2}(AE - HE) = \frac{1}{2}AH.
$$
In particular, $F$ is the midpoint of the segment $[AH]$. It remains to calculate $DE^2 + FA \times FE$ in the following way
$$
\begin{aligned}
DE^2 + FA \times FE & = DE^2 + FA \times (FH + \underbrace{DH + DE}_{=2DE}) \\
& = DE^2 + FA^2 + 2DE \times FA \\
& = (FA + DE)^2 \\
& = (FH + DH)^2 = FD^2.
\end{aligned}
$$
This concludes that $XO^2 = XF^2 + OF^2$ and completes the proof of the problem.
Comment from the graders: The exercise was very difficult, and few students managed to make good progress. The most elementary approach was to introduce the midpoint of $[BC]$, then notice an isosceles trapezoid (or a parallelogram), to start a chase of angles.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit ABC un triangle dont les angles sont aigus, $\omega$ son cercle circonscrit et O le centre de $\omega$. La perpendiculaire issue de $A$ par rapport à $(B C)$ intersecte $(B C)$ en $D$ et $\omega$ en $E$. Soit $F$ un point sur le segment $[A E]$ tel que $2 \cdot F D=A E$. Soit $\ell$ la perpendiculaire à $(O F)$ passant par $F$. Montrer que la droite $\ell$, la droite $(B C)$ et la tangente à $\omega$ en $E$ sont concourantes.
|

On désire montrer que trois droites sont concourantes. Une stratégie serait donc de considérer le point d'intersection de deux de ces droites et de montrer que ce point appartient à la troisième droite, c'est la stratégie que nous allons adopter ici.
Dans le cas de notre exercice, il était possible de choisir n'importe quelle paire de droites parmi les droites $(\ell),(B C)$ et la tangente à $\omega$ en $E$ et aboutir.
Soit $X$ le point d'intersection de la tangente à $\omega$ en $E$ avec la droite (BC). Nous allons montrer que $X$ est sur $\ell$ en montrant que les droites (FX) et (FO) sont perpendiculaires. Et pour montrer qu'elles sont bien perpendiculaires, on va utiliser la réciproque du théorème de Pythagore en montrant que $\mathrm{XO}^{2}=$ $\mathrm{OF}^{2}+\mathrm{FX}$. On notera dans la suite R le rayon de $\omega$.
D'une part, puisque ( $X E$ ) est tangente au cercle $\omega$, on a $X O^{2}=X E^{2}+O E^{2}=X E^{2}+R^{2}$. D'après le théorème de Pythagore dans le triangle $X D E$ rectangle en $D, X E^{2}=X D^{2}+D E^{2}$. On en déduit que
$$
X O^{2}=X D^{2}+D E^{2}+R^{2}
$$
D'autre part, d'après le théorème de Pythagore dans le triangle FDX rectangle en $\mathrm{D}, \mathrm{XF}^{2}=\mathrm{XD}^{2}+\mathrm{FD}^{2}$. Pour calculer $\mathrm{OF}^{2}$, on utilise la formule de la puissance du point F par rapport au cercle $\omega$. En effet, cette formule nous dit que la puissance du point $F$ par rapport au cercle $\omega$ vaut $\mathrm{OF}^{2}-R^{2}$. Comme d'autre part elle vaut $-F A \times F E$, on déduit que $\mathrm{OF}^{2}=R^{2}-F A \times F E$. On a alors,
$$
X F^{2}+O F^{2}=\left(X D^{2}+F D^{2}\right)+\left(R^{2}-F A \times F E\right)
$$
Pour montrer que $X O^{2}=X F^{2}+\mathrm{FO}^{2}$, il suffit donc de montrer que $\mathrm{DE}^{2}=\mathrm{FD}^{2}-\mathrm{FA} \times \mathrm{FE}$, ou encore $D^{2}+F A \times F E$. Il s'agit alors de faire apparaître l'hypothèse de longueur sur le point $F$.
Notons H l'orthocentre du triangle $A B C$. On sait que les points H et E sont symétriques par rapport à la droite $(\mathrm{BC})$ (résultat classique de géométrie du triangle que l'on pourra retrouver dans le polycopié
de géométrie pour débutant de la POFM, exercice 4.8). On déduit que $\mathrm{DE}=\mathrm{DH}$. Mais alors,
$$
\mathrm{FH}=\mathrm{FD}-\mathrm{DH}=\frac{1}{2}(A E-\mathrm{HE})=\frac{1}{2} A H .
$$
En particulier, F est le milieu du segment $[\mathrm{AH}]$. Il ne reste plus qu'à calculer $\mathrm{DE}^{2}+\mathrm{FA} \times \mathrm{FE}$ de la manière suivante
$$
\begin{aligned}
\mathrm{DE}^{2}+\mathrm{FA} \times \mathrm{FE} & =\mathrm{DE}^{2}+\mathrm{FA} \times(\mathrm{FH}+\underbrace{\mathrm{DH}+\mathrm{DE}}_{=2 \mathrm{DE}}) \\
& =\mathrm{DE}^{2}+\mathrm{FA}^{2}+2 \mathrm{DE} \times \mathrm{FA} \\
& =(\mathrm{FA}+\mathrm{DE})^{2} \\
& =(\mathrm{FH}+\mathrm{DH})^{2}=\mathrm{FD}^{2} .
\end{aligned}
$$
Ce qui conclut bien que $\mathrm{XO}^{2}=\mathrm{XF}^{2}+\mathrm{FO}^{2}$ et termine la preuve du problème.
Commentaire des correcteurs: L'exercice était très difficile, et peu d'élèves ont réussi à avoir de bonnes avancées. L'approche la plus élémentaire était d'introduire le milieu de [BC], puis de remarquer un trapèze isocèle (ou un parallélogramme), pour pouvoir entamer une chasse aux angles.
|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "\nExercice 8.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-1.jsonl",
"solution_match": "## Solution de l'exercice 8",
"tier": "T2",
"year": null
}
|
Let $ABC$ be an equilateral triangle. Let $X$ be a point on the line $(BC)$ different from $B$ and $C$. Let $Y$ and $Z$ be two points on the lines $(AB)$ and $(AC)$ such that the lines $(BZ)$ and $(CY)$ are parallel to the line $(AX)$. The line $(XY)$ intersects the line $(AC)$ at $M$ and the line $(XZ)$ intersects the line $(AB)$ at $N$. Show that the line $(MN)$ is tangent to the incircle of $ABC$.
|
We start by stating two lemmas that will be useful in the following. The usefulness of the first lemma will be obvious to the reader, while the interest of the second lemma may seem less clear.
Lemma 1. Let $ABC$ be a triangle and $\omega$ the $A$-excircle of this triangle. We denote by $J$ the center of $\omega$ and $\alpha$ the angle at $A$. Then, $\widehat{\mathrm{BJC}}=90-\alpha / 2$, and there is a form of uniqueness. Let $X$ be a point on the line $(AB)$. If we rotate the line $(JX)$ around $J$ by an angle of $90-\alpha / 2$ and denote by $Y$ the intersection of this line with the line $(AB)$, then the line $(YX)$ is tangent to $\omega$.
Remark 2. The attentive reader will notice that the rotation by an angle of $90-\alpha / 2$ from $J$ is not unique; one must pay attention to the direction in which the rotation is performed (in fact, one must work with oriented angles).
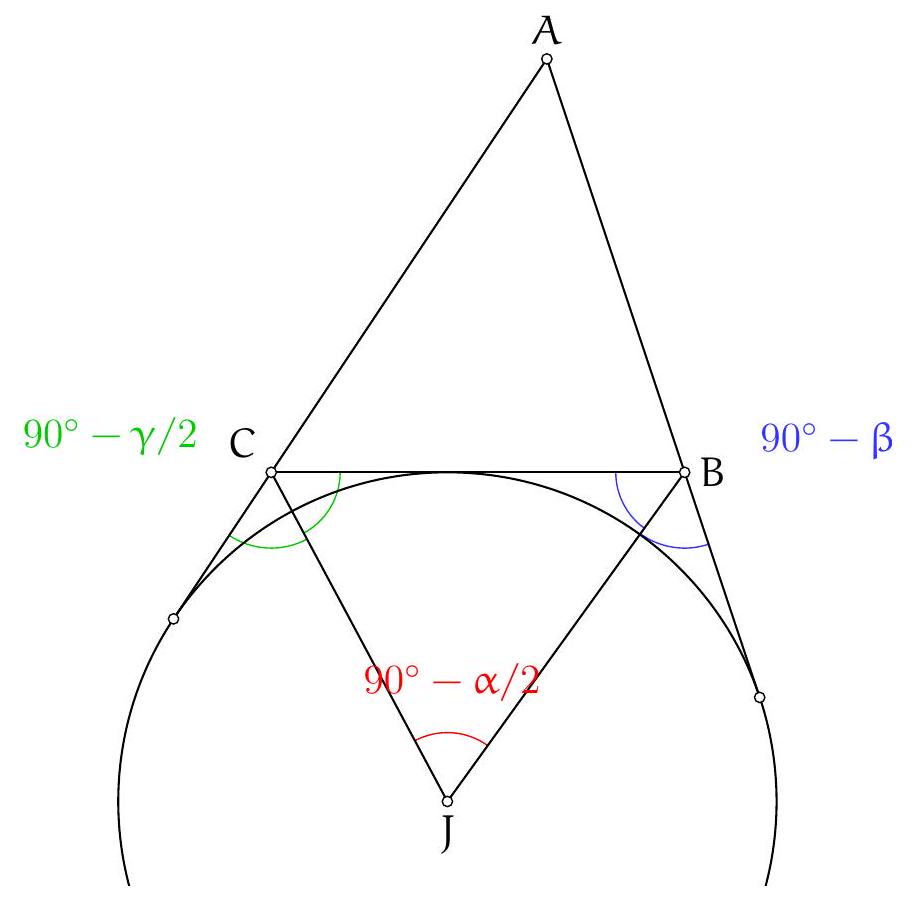
|
proof
|
Yes
|
Incomplete
|
proof
|
Geometry
|
Soit $A B C$ un triangle équilatéral. Soit $X$ un point de la droite ( $B C$ ) différent de $B$ et $C$. Soient $Y$ et $Z$ deux points sur les droites $(A B)$ et $(A C)$ de telle sorte que les deux droites ( $B Z$ ) et ( $C Y$ ) sont parallèles à la droite $(A X)$. La droite $(X Y)$ intersecte la droite ( $A C)$ en $M$ et la droite ( $X Z$ ) intersecte la droite $(A B)$ en $N$. Montrer que la droite ( $M N$ ) est tangente au cercle inscrit de $A B C$.
|
On commence par énoncer deux lemmes qui vont être utiles dans la suite. Si l'utilité du premier lemme sautera aux yeux du lecteur l'intérêt du deuxième lemme paraîtra sans doute moins clair.
Lemme 1. Soit $A B C$ un triangle et $\omega$ le cercle $A$-exinscrit de ce triangle, on note J le centre de $\omega$ et $\alpha$ l'angle en A . Alors, $\widehat{\mathrm{BJC}}=90-\alpha / 2$, de plus il existe une forme d'unicité. Soit X un point de la droite (AB), si on effectue une rotation de la droite (JX) autour de J par un angle $90-\alpha / 2$ et que l'on note par Y l'intersection de cette droite avec la droite ( AB ), alors la droite ( YX ) est tangente à $\omega$.
Remarque 2. Le lecteur attentif remarquera que la rotation d'angle $90-\alpha / 2$ depuis J n'est pas unique, il faut faire attention au sens dans lequel on effectue la rotation (en fait il faut travailler avec des angles orientés).

|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-1.jsonl",
"solution_match": "\nSolution de l'exercice 9",
"tier": "T2",
"year": null
}
|
Let $ABC$ be an equilateral triangle. Let $X$ be a point on the line $(BC)$ different from $B$ and $C$. Let $Y$ and $Z$ be two points on the lines $(AB)$ and $(AC)$ such that the lines $(BZ)$ and $(CY)$ are parallel to the line $(AX)$. The line $(XY)$ intersects the line $(AC)$ at $M$ and the line $(XZ)$ intersects the line $(AB)$ at $N$. Show that the line $(MN)$ is tangent to the incircle of $ABC$.
|
First, we notice that the uniqueness follows from the first part of the lemma. Indeed, the point $Y$ is uniquely defined and satisfies the condition $\widehat{\mathrm{XJY}}=90-\alpha / 2$. All that remains is to prove the first part of the lemma. We denote $\beta$ and $\gamma$ as the angles at $B$ and $C$. Then, ( $B J$ ) and (CJ) are external bisectors, so
$$
\widehat{\mathrm{JBC}}=(180-\beta) / 2=90-\beta / 2
$$
and
$$
\widehat{\mathrm{JCB}}=90-\gamma / 2
$$
Since the angles in triangle BCJ sum to 180, it follows that $\widehat{\mathrm{BJC}}=90-\alpha / 2$ as claimed.
Lemma 2. Let ABCD be an isosceles trapezoid with $(\mathrm{AB})$ parallel to $(\mathrm{CD})$. We denote X as the intersection point of the diagonals (AC) and (BD), and Y as the intersection point of the lines (AD) and (BC). The line (XY) intersects the line (CD) at point Z. The point Z is then the midpoint of the segment [DC].
Remark 3. It is possible that the lines (AD) and (BC) are parallel in this case. We consider the point Y "at infinity" (this is a well-defined notion, but we do not formalize it here) in the same direction as the line (AD) and thus of the line (BC) by hypothesis. In this case, a line passing through Y is simply a line parallel to (AD) (and thus to (BC)). Morally, passing through a point at infinity forces a direction.
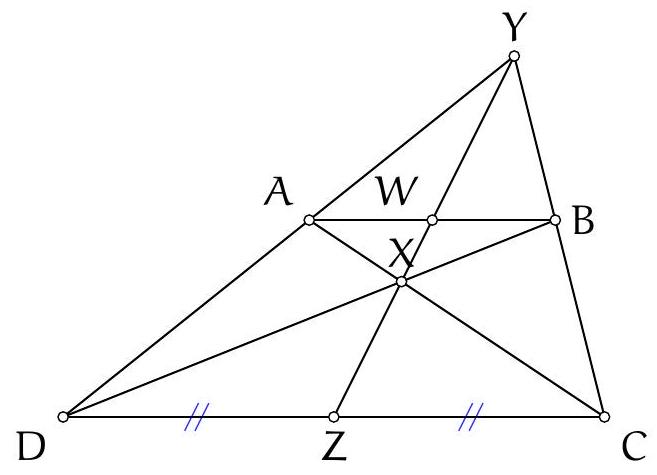
|
proof
|
Yes
|
Incomplete
|
proof
|
Geometry
|
Soit $A B C$ un triangle équilatéral. Soit $X$ un point de la droite ( $B C$ ) différent de $B$ et $C$. Soient $Y$ et $Z$ deux points sur les droites $(A B)$ et $(A C)$ de telle sorte que les deux droites ( $B Z$ ) et ( $C Y$ ) sont parallèles à la droite $(A X)$. La droite $(X Y)$ intersecte la droite ( $A C)$ en $M$ et la droite ( $X Z$ ) intersecte la droite $(A B)$ en $N$. Montrer que la droite ( $M N$ ) est tangente au cercle inscrit de $A B C$.
|
On remarque dans un premier temps que l'unicité découle de la première partie du lemme. En effet, le point $Y$ est défini de manière unique et vérifie alors bien la condition $\widehat{\mathrm{XJY}}=90-\alpha / 2$. Il ne nous reste plus qu'à démontrer la première partie du lemme. On note $\beta$ et $\gamma$ les angles en $B$ et $C$. Alors, ( $B J$ ) et (CJ) sont des bissectrices extérieures donc
$$
\widehat{\mathrm{JBC}}=(180-\beta) / 2=90-\beta / 2
$$
et
$$
\widehat{\mathrm{JCB}}=90-\gamma / 2
$$
Comme les angles dans le triangle BCJ ont pour somme 180 il faut donc que $\widehat{\mathrm{BJC}}=90-\alpha / 2$ comme annoncé.
Lemme 2. Soit ABCD un trapèze isocèle avec $(\mathrm{AB})$ parallèle à $(\mathrm{CD})$. On note X le point d'intersection des diagonales (AC) et (BD) ainsi que Y le point d'intersection des droites (AD) et (BC). La droite (XY) intersecte la droite (CD) au point Z. Le point Z est alors le milieu du segment [DC].
Remarque 3. Il est possible que les droites (AD) et (BC) soient parallèles dans ce cas on considère le point Y "à l'infini" (c'est en principe une notion bien définie mais on ne le fait pas proprement ici) dans la même direction que la droite (AD) et donc de la droite (BC) par hypothèses. Dans ce cas une droite qui passe par Y est juste une droite qui est parallèles à (AD) (et donc à (BC)). Moralement, passer par un point à l'infini c'est forcer une direction.

|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-1.jsonl",
"solution_match": "## Démonstration.",
"tier": "T2",
"year": null
}
|
Let $ABC$ be an equilateral triangle. Let $X$ be a point on the line $(BC)$ different from $B$ and $C$. Let $Y$ and $Z$ be two points on the lines $(AB)$ and $(AC)$ such that the lines $(BZ)$ and $(CY)$ are parallel to the line $(AX)$. The line $(XY)$ intersects the line $(AC)$ at $M$ and the line $(XZ)$ intersects the line $(AB)$ at $N$. Show that the line $(MN)$ is tangent to the incircle of $ABC$.
|
There is a natural proof of this lemma using tools from projective geometry, but we will give an elementary proof here. Let $W$ be the intersection of the line $(XY)$ with the line $(AB)$. We can then write the following identities, which follow from Thales' theorem.
Since the three lines $(AC)$, $(BD)$, and $(WZ)$ intersect at $Y$ and the lines $(AB)$ and $(CD)$ are parallel, we have the equality
$$
\frac{AW}{WB} = \frac{CZ}{ZD}
$$
where we have taken care of the orientations of the lengths (here both sides of the equation are negative). Similarly, since the three lines $(AD)$, $(BC)$, and $(WZ)$ intersect at $Z$ and the lines $(AB)$ and $(CD)$ are parallel, we have the equality
$$
\frac{BW}{WA} = \frac{CZ}{ZD}
$$
By combining these two equalities, we obtain
$$
\left(\frac{CZ}{ZD}\right)^2 = 1
$$
And thus, taking care of the signs,
$$
\frac{CZ}{ZD} = -1
$$
This concludes the proof of the lemma.
Let's now return to the problem.
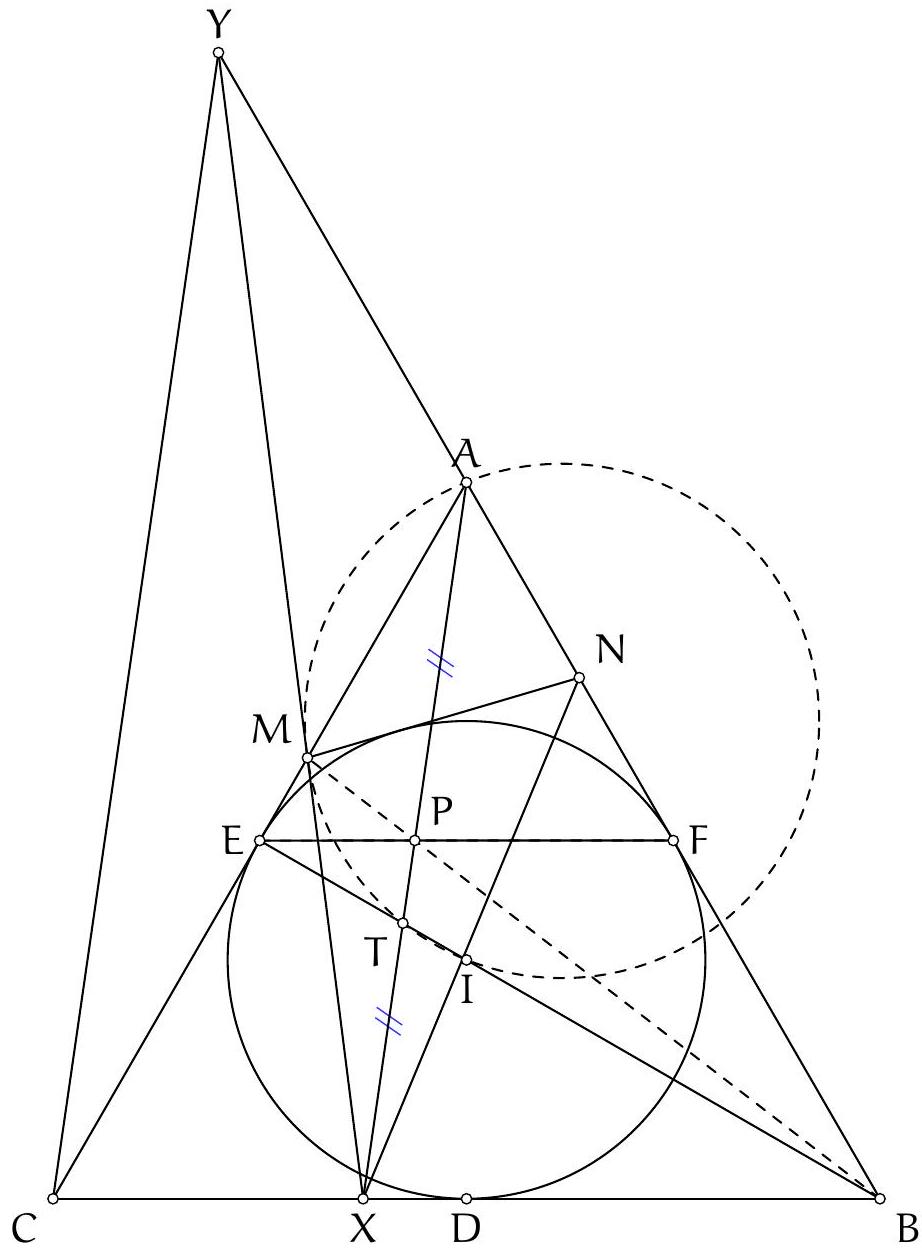
Let $D$, $E$, and $F$ be the points of tangency of the incircle in the triangle $ABC$. We will prove a stronger result. If we denote $x = \widehat{\mathrm{CAX}}$, we will show that $\widehat{MIE} = x$. This would conclude the proof because by symmetry we would have $\widehat{MIF} = \widehat{BAX} = 60 - x$ and thus $\widehat{MIN} = 120 - (60 - x) - x = 60$, which concludes the proof according to Lemma 1.
Let $T$ be the intersection of the lines $(AX)$ and $(BE)$. The equality $\widehat{MIE} = \widehat{EAT}$ is equivalent to the property that the points $A$, $M$, $I$, and $T$ are concyclic. A quick angle chase shows that this property is also equivalent to the lines $(MT)$ and $(AB)$ being parallel (for example, we can use parallels/antiparallels with respect to the lines $(EB)$ and $(EA)$). We also denote $P$ as the intersection of the lines $(MB)$ and $(AX)$.
We then apply Lemma 2 to the trapezoid $AXCY$ to show that the point $P$ is the midpoint of the segment $[AX]$. Thus, by the midline theorem, we have $F$, $P$, and $E$ collinear. We then observe that in the quadrilateral $AMTB$ with $P$ being the intersection of the lines $(AT)$ and $(MB)$ and $E$ being the intersection of the lines $(AM)$ and $(BT)$, the line $(EP)$ passes through the midpoint of the segment $[AB]$. It follows that we can then apply the converse of Lemma 2 (uniqueness is left to the reader) to show that the quadrilateral $AMTB$ is indeed a trapezoid with $(AB) \parallel (MT)$, which concludes the proof.
Comment from the graders: The exercise was very difficult. A handful of students managed to solve it using essentially computational techniques (and sometimes advanced ones) that were largely different from the solution provided in the answer key.
## Senior Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle équilatéral. Soit $X$ un point de la droite ( $B C$ ) différent de $B$ et $C$. Soient $Y$ et $Z$ deux points sur les droites $(A B)$ et $(A C)$ de telle sorte que les deux droites ( $B Z$ ) et ( $C Y$ ) sont parallèles à la droite $(A X)$. La droite $(X Y)$ intersecte la droite ( $A C)$ en $M$ et la droite ( $X Z$ ) intersecte la droite $(A B)$ en $N$. Montrer que la droite ( $M N$ ) est tangente au cercle inscrit de $A B C$.
|
Il existe une preuve naturelle de ce lemme en utilisant des outils de la géométrie projective mais on va donner ici une preuve élémentaire. Soit $W$ l'intersection de la droite ( $X Y$ ) avec la droite ( $A B$ ), on peut alors écrire les identités suivantes qui découlent du théorème de Thalès.
Comme les trois droites $(A C),(B D)$ et $(W Z)$ sont concourantes en $Y$ et les droites $(A B)$ et (CD) sont parallèles, on a l'égalité
$$
\frac{A W}{W B}=\frac{C Z}{Z D}
$$
où l'on a pris soin des orientations de longueurs (ici les deux côtés de l'équation sont négatifs). De la même manière les trois droites ( $A D$ ), ( $B C$ ) et ( $W Z$ ) sont concourantes en $Z$ et que les droites $(A B)$ et $(C D)$ sont parallèles, on a donc l'égalité
$$
\frac{B W}{W A}=\frac{C Z}{Z D}
$$
En combinant ces deux égalités on obtient
$$
\left(\frac{C Z}{Z D}\right)^{2}=1
$$
Et donc, en prenant soin des signes
$$
\frac{C Z}{Z D}=-1
$$
Ce qui conclut la preuve du lemme.
Revenons désormais au problème.

On note $D$, $E$ et $F$ les points de tangences du cercle inscrit dans le triangle $A B C$. On va montrer un résultat a priori plus fort. Si on note $x=\widehat{\mathrm{CAX}}$ on va démontrer que $\widehat{M I E}=x$. Cela conclurait alors car par symétrie on aurait $\widehat{M I F}=\widehat{B A X}=60-x$ et donc $\widehat{M I N}=120-(60-x)-x=60$ ce qui conclurait d'après le Lemme 1.
Soit $T$ le point d'intersection des droites $(A X)$ et $(B E)$, l'égalité $\widehat{M I E}=\widehat{E A T}$ est équivalente à la propriété que les points $A, M$, I et $T$ sont cocycliques. Une chasse aux angles immédiate montre que cette propriété est encore équivalente à ce que les droites $(M T)$ et $(A B)$ soient parallèles (par exemple on peut utiliser des parallèles/antiparallèles par rapport aux droites (EB) et (EA)). On note de plus $P$ l'intersection des droites (MB) et ( $A X$ ).
On applique alors le Lemme 2 dans un premier temps au trapèze $A X C Y$ pour montrer que le point $P$ et le milieu du segment $[A X]$. Ainsi, d'après la droite des milieux on a $F, P$ et $E$ alignés. On remarque alors que dans le quadrilatère $A M T B$ avec $P$ l'intersection des droites $(A T)$ et ( $M B$ ) ainsi que E l'intersection des droites ( $A M$ ) et (BT), la droite (EP) passe par le milieu du segment $[A B]$, il suit que l'on peut alors appliquer la réciproque du Lemme 2 (il y a une unicité laissée au lecteur) pour montrer que le quadrilatère AMTB est bien un trapèze avec $(A B) / /(M T)$ ce qui conclut.
Commentaire des correcteurs : L'exercice était très difficile. Une poignée d'élèves en est venue à bout, à l'aide de techniques essentiellement calculatoires (et parfois avancées) largement différentes de la solution proposée par le corrigé.
## Exercices Seniors
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-1.jsonl",
"solution_match": "## Démonstration.",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle with $\widehat{BAC}=60^{\circ}$. Let $D$ and $E$ be the feet of the angle bisectors from vertices $B$ and $C$, respectively. Let $I$ be the intersection point of the lines $(BD)$ and $(CE)$. Show that the points $A$, $I$, $D$, and $E$ are concyclic.
|
We are going to do an angle hunt to prove that $\widehat{\mathrm{IDA}}+\widehat{\mathrm{IEA}}=180^{\circ}$. Let $x=\widehat{\mathrm{ACE}}=\widehat{\mathrm{ECB}}$ and $y=\widehat{A B D}=\widehat{\mathrm{DBC}}$. Since the sum of the angles in a triangle is $180^{\circ}$, we have
$$
\begin{aligned}
180^{\circ} & =\widehat{\mathrm{BAC}}+\widehat{A B C}+\widehat{A C B} \\
& =60^{\circ}+2 y+2 x .
\end{aligned}
$$
This implies that $x+y=60^{\circ}$. We can therefore express all the angles in the figure in terms of $x$ and in particular the two angles of interest, $\widehat{\text { IDA }}$ and $\widehat{I E A}$. We have $\widehat{I D A}=\widehat{\mathrm{BDA}}=180^{\circ}-60^{\circ}-y$ and $\widehat{I E A}=\widehat{C E A}=180^{\circ}-60^{\circ}-x$. Therefore, the sum is
$$
\widehat{\mathrm{IDA}}+\widehat{\mathrm{IEA}}=180^{\circ}-60^{\circ}-\mathrm{y}+180^{\circ}-60^{\circ}-x=180^{\circ}+60^{\circ}-x-y=180^{\circ}
$$
This is the desired equality.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle avec $\widehat{B A C}=60^{\circ}$. Soient $D$ et $E$ les pieds des bissectrices issues respectivement des sommets $B$ et $C$. Soit I le point d'intersection des droites (BD) et (CE). Montrer que les points $A$, I, D et $E$ sont cocycliques.
|
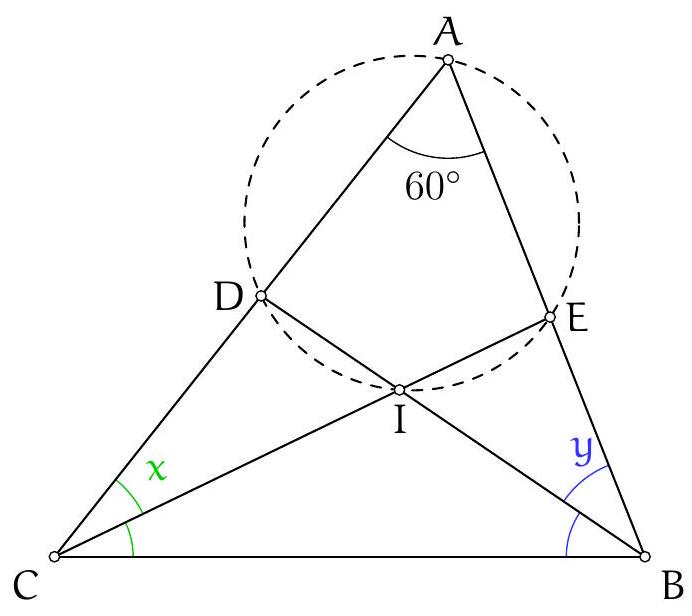
On va faire une chasse aux angles pour démontrer que $\widehat{\mathrm{IDA}}+\widehat{\mathrm{IEA}}=180^{\circ}$. Notons $x=\widehat{\mathrm{ACE}}=\widehat{\mathrm{ECB}}$ ainsi que $y=\widehat{A B D}=\widehat{\mathrm{DBC}}$. Comme la somme des angles d'un triangle vaut $180^{\circ}$ on a ainsi
$$
\begin{aligned}
180^{\circ} & =\widehat{\mathrm{BAC}}+\widehat{A B C}+\widehat{A C B} \\
& =60^{\circ}+2 y+2 x .
\end{aligned}
$$
Ce qui implique que $x+y=60^{\circ}$. On peut donc exprimer tous les angles de la figure en fonction de $x$ et en particulier les deux angles qui nous intéressent, $\widehat{\text { IDA }}$ et $\widehat{I E A}$. On a $\widehat{I D A}=\widehat{\mathrm{BDA}}=180^{\circ}-60^{\circ}-y$ ainsi que $\widehat{I E A}=\widehat{C E A}=180^{\circ}-60^{\circ}-\chi$. Donc la somme vaut
$$
\widehat{\mathrm{IDA}}+\widehat{\mathrm{IEA}}=180^{\circ}-60^{\circ}-\mathrm{y}+180^{\circ}-60^{\circ}-x=180^{\circ}+60^{\circ}-x-y=180^{\circ}
$$
Ce qui est l'égalité voulue.
|
{
"exam": "French_envois",
"problem_label": "10",
"problem_match": "\nExercice 10.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-1.jsonl",
"solution_match": "## Solution de l'exercice 10",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle with $\widehat{BAC}=60^{\circ}$. Let $D$ and $E$ be the feet of the angle bisectors from vertices $B$ and $C$, respectively. Let $I$ be the intersection point of the lines $(BD)$ and $(CE)$. Show that the points $A$, $I$, $D$, and $E$ are concyclic.
|
Exercise 10
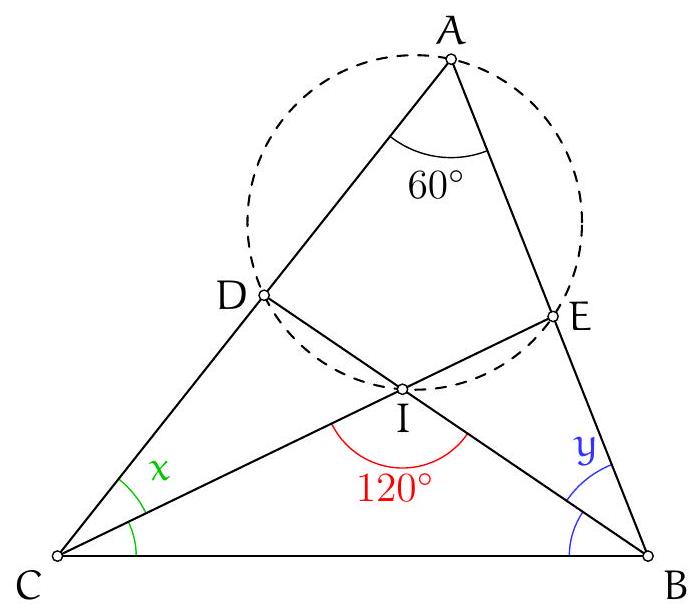
Once we have obtained that \(x + y = 60^{\circ}\), we can conclude in another way by demonstrating that \(\widehat{\mathrm{DAE}} + \widehat{\mathrm{DIE}} = 180^{\circ}\). Indeed, in triangle BCI, we have \(\widehat{\mathrm{BIC}} = 180^{\circ} - x - y = 120^{\circ}\), so that \(\widehat{\mathrm{DIE}} + \widehat{\mathrm{DAE}} = \widehat{\mathrm{BIC}} + \widehat{\mathrm{BAC}} = 120^{\circ} + 60^{\circ} = 180^{\circ}\).
Graders' Comment: Very well done exercise. It is important to make a neat diagram and to detail your reasoning thoroughly.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle avec $\widehat{B A C}=60^{\circ}$. Soient $D$ et $E$ les pieds des bissectrices issues respectivement des sommets $B$ et $C$. Soit I le point d'intersection des droites (BD) et (CE). Montrer que les points $A$, I, D et $E$ sont cocycliques.
|
de l'exercice 10

Une fois que l'on a obtenu que $x+y=60^{\circ}$, on peut conclure d'une autre façon, en démontrant que $\widehat{\mathrm{DAE}}+\widehat{\mathrm{DIE}}=180^{\circ}$. En effet, dans le triangle BCI, on a $\widehat{\mathrm{BIC}}=180^{\circ}-\mathrm{x}-\mathrm{y}=120^{\circ}$, de sorte que $\widehat{\mathrm{DIE}}+\widehat{\mathrm{DAE}}=\widehat{\mathrm{BIC}}+\widehat{\mathrm{BAC}}=120^{\circ}+60^{\circ}=180^{\circ}$.
Commentaire des correcteurs : Exercice très bien réussi. Il faut bien penser à faire une figure propre et à bien détailler son raisonnement.
|
{
"exam": "French_envois",
"problem_label": "10",
"problem_match": "\nExercice 10.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-1.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle, $L, M$ and $N$ the midpoints of the sides $[BC], [CA]$, and $[AB]$. Suppose that $\widehat{ANC}=\widehat{ALB}$. Show that $\widehat{CAL}=\widehat{ABM}$.
|
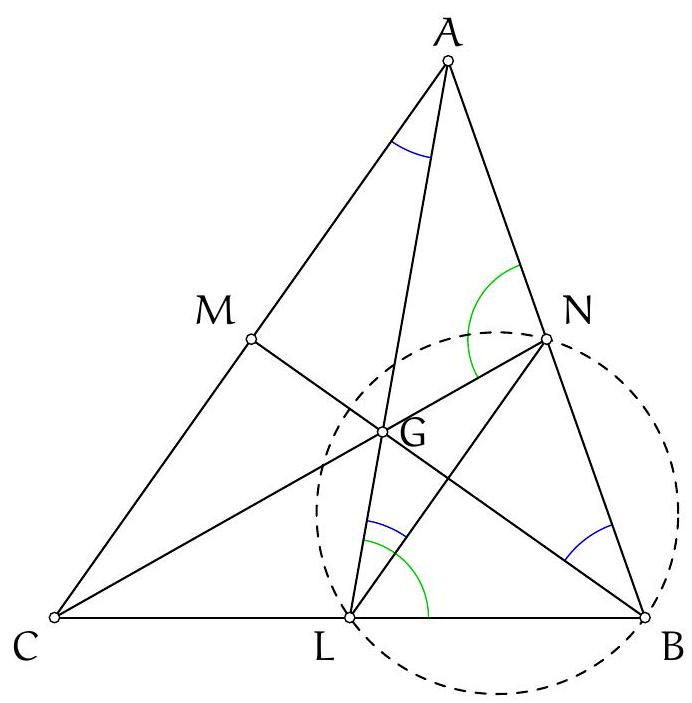
First, we try to interpret the condition given in the problem, $\widehat{A N C} = \widehat{A L B}$. To do this, we introduce \( G \) as the centroid of triangle \( ABC \) (recall that it is also the intersection of the three medians \( (AL), (BM) \), and \( (CN) \)). The condition in the problem implies that the quadrilateral \( NGBL \) is cyclic.
Thus, we have \(\widehat{C A L} = \widehat{A L N}\) by alternate interior angles. Since the quadrilateral \( NGBL \) is cyclic, we have \(\widehat{C A L} = \widehat{A L N} = \widehat{G L N} = \widehat{G B N} = \widehat{A B M}\), which concludes the proof.
Comment from the graders: The problem is well solved. A handful of students believed that the statement necessarily implied that the triangle was isosceles or even equilateral, but this is not the case.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle, $L, M$ et $N$ les milieux respectifs des côtés $[B C],[C A]$ et $[A B]$. On suppose que $\widehat{A N C}=\widehat{A L B}$. Montrer que $\widehat{C A L}=\widehat{A B M}$.
|

On essaie dans un premier temps d'interpréter la condition de l'énoncé $\widehat{A N C}=\widehat{A L B}$. Pour cela on commence par introduire G le centre de gravité du triangle $A B C$ (on rappelle que c'est aussi l'intersection des trois médianes ( $A L),(B M)$ et ( $C N)$ ). La condition de l'énoncé revient à dire que le quadrilatère NGBL est cyclique.
On a ainsi $\widehat{C A L}=\widehat{A L N}$ par angles alternes-internes. Puis comme le quadrilatère NGBL est cyclique on a $\widehat{C A L}=\widehat{A L N}=\widehat{G L N}=\widehat{G B N}=\widehat{A B M}$, ce qui conclut.
Commentaire des correcteurs : L'exercice est bien résolu. Une poignée d'élèves a cru que l'énoncé impliquait forcément que le triangle était isocèle voire même équilatéral, mais il n'en est rien.
|
{
"exam": "French_envois",
"problem_label": "11",
"problem_match": "\nExercice 11.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-1.jsonl",
"solution_match": "## Solution de l'exercice 11",
"tier": "T2",
"year": null
}
|
Let $ABC$ be an acute triangle. Let $P$ and $Q$ be two points on the segment [BC]. We denote by $\mathrm{O}_{1}, \mathrm{O}_{2}, \mathrm{O}_{3}$ and $\mathrm{O}_{4}$ the centers of the circumcircles of triangles ABP, ABQ, ACP and ACQ, respectively. Show that the points $\mathrm{O}_{1}, \mathrm{O}_{2}, \mathrm{O}_{3}$ and $\mathrm{O}_{4}$ are concyclic if and only if $\widehat{\mathrm{BAP}}=\widehat{\mathrm{QAC}}$.
|
The figure contains many objects, so we will try to simplify it a bit. We notice that there are many radical axes (the lines $(AB)$, $(AP)$, $(AQ)$, and $(AC)$ in the figure) and thus many right angles with the centers of the circles. We have the following perpendicularities:
$$
\left(\mathrm{O}_{1} \mathrm{O}_{2}\right) \perp (A B), \left(\mathrm{O}_{1} \mathrm{O}_{3}\right) \perp (A P), \left(\mathrm{O}_{2} \mathrm{O}_{4}\right) \perp (A Q), \left(\mathrm{O}_{3} \mathrm{O}_{4}\right) \perp (A C)
$$
In particular, we want to prove a cocyclicity relation, and for that, we need to focus on angles between lines (and we don't need more information). Specifically:
$$
\left(\mathrm{O}_{1} \mathrm{O}_{3}, \mathrm{O}_{1} \mathrm{O}_{2}\right) = \left(\mathrm{O}_{1} \mathrm{O}_{3}, A \mathrm{P}\right) + (A \mathrm{P}, \mathrm{AB}) + \left(\mathrm{AB}, \mathrm{O}_{1} \mathrm{O}_{2}\right) = -\frac{\pi}{2} + (A \mathrm{P}, \mathrm{AB}) + \frac{\pi}{2} = (A \mathrm{P}, \mathrm{AB})
$$
Similarly,
$$
\left(\mathrm{O}_{4} \mathrm{O}_{3}, \mathrm{O}_{4} \mathrm{O}_{2}\right) = (\mathrm{AC}, \mathrm{AQ})
$$
Thus,
$$
\begin{array}{cl}
\left(\mathrm{O}_{1} \mathrm{O}_{2}, \mathrm{O}_{1} \mathrm{O}_{3}\right) = \left(\mathrm{O}_{2} \mathrm{O}_{4}, \mathrm{O}_{3} \mathrm{O}_{4}\right) & \left(\mathrm{O}_{1} \mathrm{O}_{2} \mathrm{O}_{3} \mathrm{O}_{4} \text{ cyclic }\right) \\
\mathbb{\Downarrow} & \\
(\mathrm{AB}, \mathrm{AP}) = (\mathrm{AQ}, \mathrm{AC}), & (\widehat{\mathrm{BAP}} = \widehat{\mathrm{QAC}})
\end{array}
$$
This concludes the proof.
Comment from the graders: The exercise was generally well solved by the students who attempted it. There are more direct approaches than others. The solution above from the POFM provides a good example of how one could arrive at the result with minimal effort and angle chasing.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle acutangle. Soient $P$ et $Q$ deux points sur le segment [BC]. On note respectivement $\mathrm{O}_{1}, \mathrm{O}_{2}, \mathrm{O}_{3}$ et $\mathrm{O}_{4}$ les centres des cercles circonscrits des triangles ABP, ABQ, ACP et ACQ . Montrer que les points $\mathrm{O}_{1}, \mathrm{O}_{2}, \mathrm{O}_{3}$ et $\mathrm{O}_{4}$ sont cocycliques si et seulement si $\widehat{\mathrm{BAP}}=\widehat{\mathrm{QAC}}$.
|
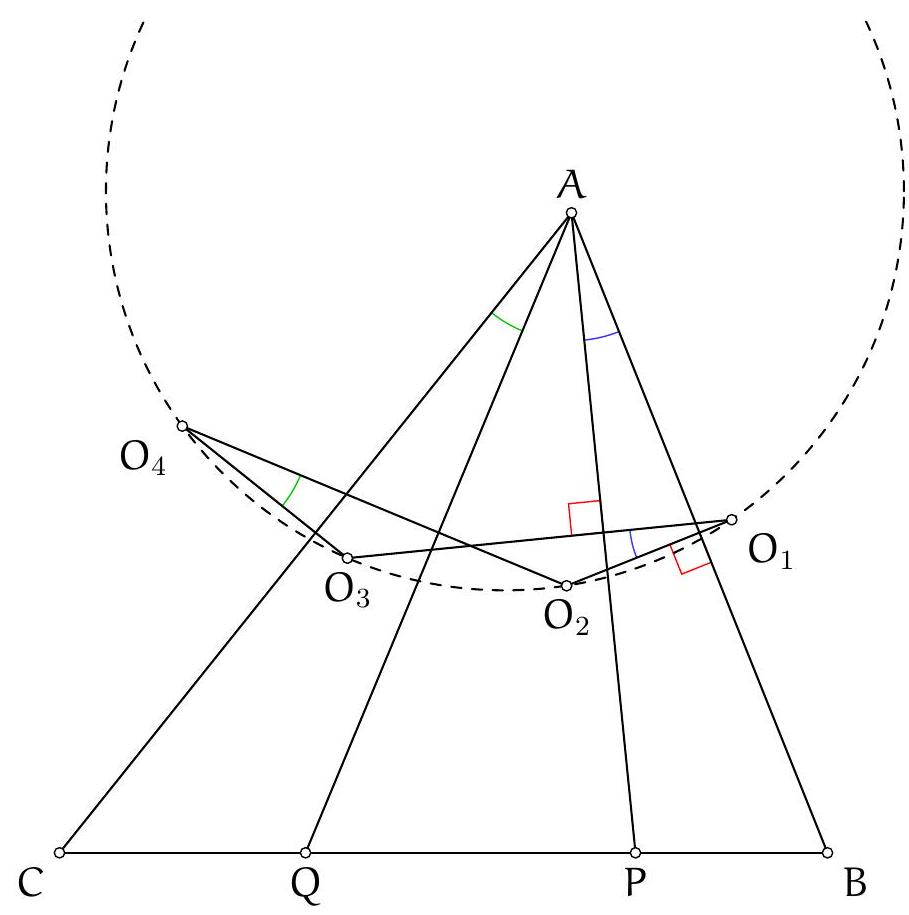
La figure comporte beaucoup d'objets on va donc essayer de la simplifier un peu. On remarque donc dans un premier temps qu'il y a beaucoup d'axes radicaux (les droites ( $A B$ ), ( $A P$ ), ( $A Q$ ) et ( $A C$ ) sur la figure et donc beaucoup d'angles droits avec les centres des cercles. On a les perpendicularités suivantes :
$$
\left(\mathrm{O}_{1} \mathrm{O}_{2}\right) \perp(A B),\left(\mathrm{O}_{1} \mathrm{O}_{3}\right) \perp(A P),\left(\mathrm{O}_{2} \mathrm{O}_{4}\right) \perp(A Q),\left(\mathrm{O}_{3} \mathrm{O}_{4}\right) \perp(A C)
$$
En particulier, on veut démontrer une relation de cocyclicité et il faut pour cela se préoccuper d'angles entre droites (et on n'a pas besoin de plus d'informations). En particulier :
$$
\left(\mathrm{O}_{1} \mathrm{O}_{3}, \mathrm{O}_{1} \mathrm{O}_{2}\right)=\left(\mathrm{O}_{1} \mathrm{O}_{3}, A \mathrm{AP}\right)+(A \mathrm{P}, \mathrm{AB})+\left(\mathrm{AB}, \mathrm{O}_{1} \mathrm{O}_{2}\right)=-\frac{\pi}{2}+(A P, A B)+\frac{\pi}{2}=(A P, A B)
$$
De la même manière,
$$
\left(\mathrm{O}_{4} \mathrm{O}_{3}, \mathrm{O}_{4} \mathrm{O}_{2}\right)=(\mathrm{AC}, \mathrm{AQ})
$$
Ainsi,
$$
\begin{array}{cl}
\left(\mathrm{O}_{1} \mathrm{O}_{2}, \mathrm{O}_{1} \mathrm{O}_{3}\right)=\left(\mathrm{O}_{2} \mathrm{O}_{4}, \mathrm{O}_{3} \mathrm{O}_{4}\right) & \left(\mathrm{O}_{1} \mathrm{O}_{2} \mathrm{O}_{3} \mathrm{O}_{4} \text { cyclique }\right) \\
\mathbb{\Downarrow} & \\
(\mathrm{AB}, \mathrm{AP})=(\mathrm{AQ}, \mathrm{AC}), & (\widehat{\mathrm{BAP}}=\widehat{\mathrm{QAC}})
\end{array}
$$
Ce qui conclut.
Commentaire des correcteurs: L'exercice a été en général bien résolu par les élèves qui l'ont tenté. Il y a des approches plus directes que d'autres. Le corrigé ci-dessus de la POFM donne un bon exemple de comment on pouvait arriver au résultat avec un minimum d'effort et chasse aux angles.
|
{
"exam": "French_envois",
"problem_label": "12",
"problem_match": "\nExercice 12.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-1.jsonl",
"solution_match": "## Solution de l'exercice 12",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle. Let $t$ be the tangent at $A$ to the circumcircle of triangle $ABC$. We denote $A'$ as the point on $t$ such that the line $(BC)$ intersects the segment $[AA']$ at its midpoint. We denote $C'$ as the reflection of $C$ with respect to $t$. Show that the points $B, A, C'$, and $A'$ are concyclic.
|
Let $X$ be the intersection point of the lines ($A A^{\prime}$) and ($B C$). Furthermore, let $C^{*}$ be the symmetric point of $C$ with respect to point $X$. We will show that the points $B, A, C^{\prime}$, and $A^{\prime}$ are concyclic on a circle that also contains the point $C^{\star}$. We start by using the lengths and the power of the point from $X$.
\[
\begin{aligned}
X A \cdot X A^{\prime} & = -X A^{2} \\
& = -X B \cdot X C \\
& = X B \cdot X C^{\star}.
\end{aligned}
\]
This shows that the points $B, A, C^{*}$, and $A^{\prime}$ are concyclic. It remains to place the point $C^{\prime}$ on the circle. For this, we note that $\widehat{A C^{\prime} A^{\prime}} = \widehat{A C A^{\prime}}$ by symmetry, and that $\widehat{A C^{*} A^{\prime}} = \widehat{A C A^{\prime}}$ because the quadrilateral $A C A^{\prime} C^{\star}$ is a parallelogram. This concludes that $\widehat{A C^{\prime} A^{\prime}} = \widehat{A C^{\star} A^{\prime}}$. Finally, the points $B, A, C^{\star}, C^{\prime}$, and $A^{\prime}$ are concyclic.
Comment from the graders: The exercise is generally well done. A direct angle chase was not sufficient. Generally, any additional idea allowed for a solution with a bit of ingenuity, which explains the great variety of solutions (similar triangles, power of a point, introduction of a new point, and even some solutions using inversion or analytic methods). Some students misread the problem statement.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle. Soit $t$ la tangente en $A$ au cercle circonscrit du triangle $A B C$. On note $A^{\prime}$ le point de $t$ de telle sorte que la droite ( $B C$ ) coupe le segment $\left[A A^{\prime}\right]$ en son milieu. On note $C^{\prime}$ le symétrique de C par rapport à $t$. Montrer que les points $B, A, C^{\prime}$ et $A^{\prime}$ sont cocycliques.
|

On note $X$ le point d'intersection des droites ( $A A^{\prime}$ ) et ( $B C$ ). On note de plus $C^{*}$ le symétrique de C par rapport au point $X$. On va montrer que les points $B, A, C^{\prime}$ et $A^{\prime}$ sont cocycliques sur un cercle qui contient de plus le point $\mathrm{C}^{\star}$. On commence par utiliser les longueurs et la puissance du point depuis X .
$$
\begin{aligned}
X A \cdot X A^{\prime} & =-X A^{2} \\
& =-X B \cdot X C \\
& =X B \cdot X C^{\star} .
\end{aligned}
$$
Ce qui montre bien que les points $B, A, C^{*}$ et $A^{\prime}$ sont cocycliques. Il ne reste plus qu'à placer le point $C^{\prime}$ sur le cercle. Pour cela on remarque que $\widehat{A C^{\prime} A^{\prime}}=\widehat{A C A^{\prime}}$ par symétrie puis que $\widehat{A C^{*} A^{\prime}}=\widehat{A C A^{\prime}}$ comme le quadrilatère $A C A^{\prime} C^{\star}$ est une parallèlogramme. Cela conclut donc que $\widehat{A C^{\prime} A^{\prime}}=\widehat{A C^{\star} A^{\prime}}$. Et enfin que les points $B, A, C^{\star}, C^{\prime}$ et $A^{\prime}$ sont cocycliques.
Commentaire des correcteurs : L'exercice est bien réussi en général. Une chasse aux angles frontale ne suffisait pas. En général n'importe quelle autre idée supplémentaire permettait d'aboutir avec un peu d'astuce, ce qui explique la grande variété de solutions (triangles semblables, puissance d'un point, introduction d'un nouveau point, et même quelques solutions à partir d'inversions ou en analytique). Certains élèves se sont trompés en lisant l'énoncé.
|
{
"exam": "French_envois",
"problem_label": "13",
"problem_match": "\nExercice 13.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-1.jsonl",
"solution_match": "## Solution de l'exercice 13",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a non-isosceles triangle at $A$ and $I$ the center of its inscribed circle. We denote $D$ as the point on the line $(BC)$ such that $\widehat{\mathrm{DIA}}=90^{\circ}$. We denote $E$ as the foot of the perpendicular from $I$ to the line $AD$ in the triangle $ADI$. Show that the point $E$ lies on the circumcircle of triangle $ABC$.
|

We introduce \(\Omega\) as the circumcircle of triangle \(ABC\) and \(\omega\) as the antipodal circle centered at \(S\), the midpoint of the arc \(BC\) not containing \(A\). \(\omega\) passes through \(B\), \(C\), and \(I\). We also denote \(\gamma\) as the circle with diameter \([AI]\), which intersects \(\Omega\) at \(A\) and \(H\).
Let's consider the radical axes of the circles \(\omega\), \(\Omega\), and \(\gamma\). Since the circles \(\gamma\) and \(\Omega\) are tangent (their centers lie on the angle bisector from \(A\) in triangle \(ABC\)), their radical axis is the line perpendicular to \((AC)\) passing through \(I\), which is the line \((DI)\). The other two radical axes are \((BC)\) and \((AH)\). Since the radical axes are concurrent, the line \((AH)\) passes through \(D\), so the points \(A\), \(H\), and \(D\) are collinear. The circle \(\gamma\) has diameter \([AI]\), so \(\widehat{AHI} = 90^\circ\), which shows that \(H\) is the foot of the perpendicular from \(I\) to \(DA\) in triangle \(DAI\), i.e., \(H = E\). By definition, \(H\) is on \(\Omega\), which concludes the proof.
Comment from the graders: The problem was widely discussed and generally well solved, but very few students saw the direct solution using the perspective that \(D\) is the radical center of three circles (or even simply that it lies on the common tangent of two circles).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle non isocèle en $A$ et $I$ le centre de son cercle inscrit. On note D le point de la droite (BC) tel que $\widehat{\mathrm{DIA}}=90^{\circ}$. On note E le pied de la hauteur issue de I dans le triangle ADI. Montrer que le point $E$ est sur le cercle circonscrit du triangle $A B C$.
|

On introduit $\Omega$ le cercle circonscrit du triangle $A B C$ ainsi que $\omega$ le cercle antarctique de centre $S$, le milieu de l'arc BC ne contenant pas $A$. $\omega$ passe ainsi par B, C et I. On note de plus $\gamma$ le cercle de diamètre $[A I]$, ce cercle recoupe $\Omega$ en $A$ et $H$.
Regardons les axes radicaux des cercles $\omega, \Omega$ et $\gamma$. Comme les cercles $\gamma$ et $\Omega$ sont tangents (leurs centres se trouvent sur la bissectrice depuis $A$ dans le triangles $A B C$ ) leur axe radical est la droite perpendiculaire à (AC) passant par I soit la droite (DI). Les deux autres axes radicaux sont $(B C)$ et $(A H)$. Comme les axes radicaux sont concourants, on a que la droite $(A H)$ passe par $D$, donc les points $A, H$ et D sont alignés. Le cercle $\gamma$ a pour diamètre $[A I]$ donc on a $\widehat{A H I}=90^{\circ}$, ce qui montre que H est le pied de la hauteur issue de I dans le triangle DAI , soit $\mathrm{H}=\mathrm{E}$. Mais par définition H est sur $\Omega$, ce qui conclut.
Commentaire des correcteurs: Le problème a été beaucoup traité et en général bien résolu, mais très peu d'élèves ont vu la solution directe adoptant le point de vue que D est le centre radical de trois cercles (ou même simplement qu'il est sur la tangente commune de deux cercles).
|
{
"exam": "French_envois",
"problem_label": "14",
"problem_match": "\nExercice 14.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-1.jsonl",
"solution_match": "## Solution de l'exercice 14",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle and $\Omega$ its circumcircle. Let $X$ be the point of intersection of the tangents to $\Omega$ at $B$ and $C$. Let $\varphi$ be the angle $\widehat{B A X}$ and $\mu$ be the angle $\widehat{X A C}$. Let $Y$ be the point on the line $(A X)$ such that $\widehat{A C Y}=\varphi$. Show that $\widehat{A B Y}=\mu$.
|
We redefine the points of the statement in a way that suits us. We denote $\omega_{1}$ (resp. $\omega_{2}$) as the circle passing through $A, B$ (resp. $A$ and $C$) and tangent to $(AC)$ (resp. $(AB)$) at $A$. We denote $Y'$ as the intersection of the circles $\omega_{1}$ and $\omega_{2}$ other than $A$. To conclude, it suffices to show that the points $Y', A$, and $X$ are collinear. Indeed, by the tangent angle theorem, we have $\widehat{\mathrm{BAY}} = \widehat{A C Y'}$ and $\widehat{C A Y'} = \widehat{A B Y'}$.
Now, consider $\mathfrak{J}$, the inversion centered at $A$ composed with a reflection over the bisector of the angle $\widehat{B A C}$ which exchanges $B$ and $C$ (this is what is called a projective involution). The circles $\omega_{1}$ and $\omega_{2}$ are then mapped to the lines parallel to $(AB)$ and $(AC)$ passing through $C$ and $B$, respectively. The point $Y'$ is thus mapped to the point $A'$, the symmetric point of $A$ with respect to the midpoint of $[BC]$ by the involution $\mathcal{J}$. The line $(A Y')$ is exchanged with the median $(A A')$ in the triangle $ABC$. Since the line $(A X)$ is the symmedian, we have that the line $(A Y')$ and the line $(A X)$ are the same line, which concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit ABC un triangle et $\Omega$ son cercle circonscrit. On note X le point d'intersection des tangentes à $\Omega$ en $B$ et $C$. On note $\varphi$ l'angle $\widehat{B A X}$ et $\mu$ l'angle $\widehat{X A C}$. On note $Y$ le point de la droite ( $A X$ ) tel que $\widehat{A C Y}=\varphi$. Montrer que $\widehat{A B Y}=\mu$.
|
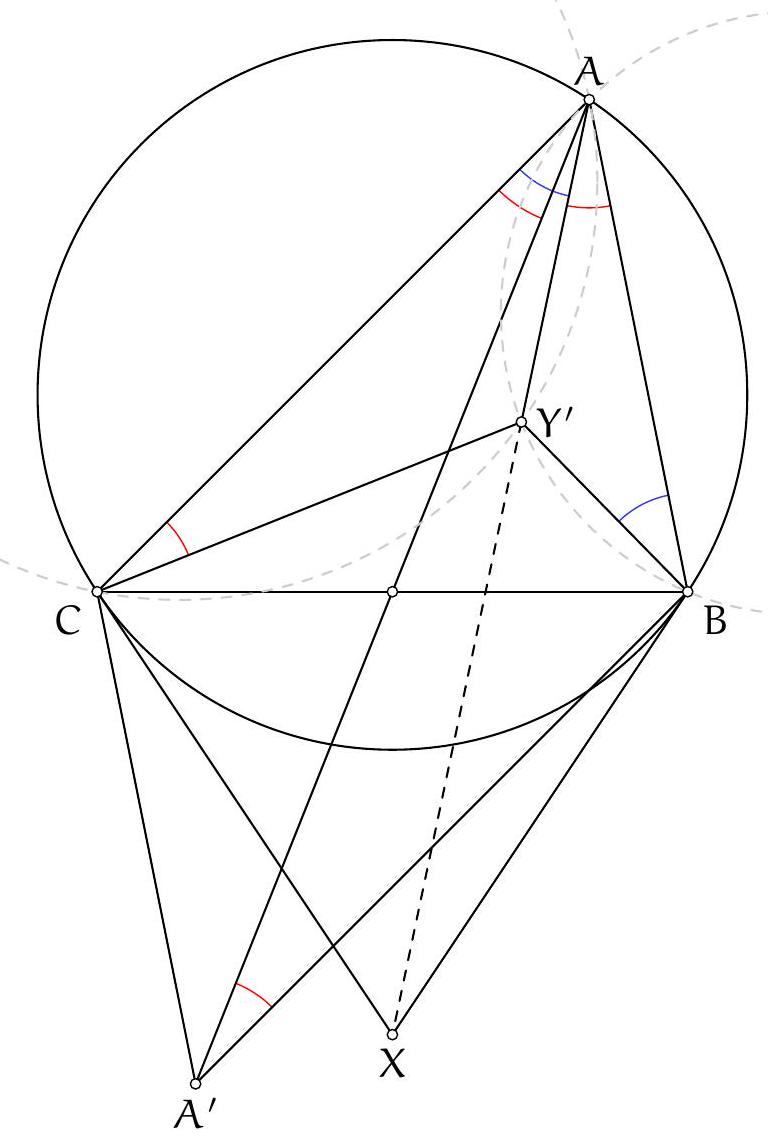
On redéfinit les points de l'énoncé de la manière qui nous arrange. On note $\omega_{1}$ (resp. $\omega_{2}$ ) le cercle passant par $A, B$ (resp. $A$ et $C$ ) et tangent en $A$ à ( $A C)$ (resp. ( $A B$ )). On note $Y^{\prime} l^{\prime}$ 'intersection des cercles $\omega_{1}$ et $\omega_{2}$ autre que $A$. Pour conclure il suffit de montrer que les points $Y^{\prime}, A$ et $X$ sont alignés. En effet, on a par théorème de l'angle tangent que $\widehat{\mathrm{BAY}}=\widehat{A C Y^{\prime}}$ ainsi que $\widehat{C A Y^{\prime}}=\widehat{A B Y^{\prime}}$.
Regardons maintenant $\mathfrak{J}$, l'inversion de centre $A$ composée avec une symétrie d'axe la bissectrice de l'angle $\widehat{B A C}$ qui échange $B$ et $C$ (il s'agit de ce que l'on appelle une involution projective). Les cercles $\omega_{1}$ et $\omega_{2}$ sont alors envoyés respectivement sur les droites parallèles à ( $A B$ ) et ( $A C$ ) passant par C et B. Le point $Y^{\prime}$ est donc envoyé sur le point $A^{\prime}$, le symétrique de $A$ par rapport au milieu de $[B C]$ par $l^{\prime}$ 'involution $\mathcal{J}$, la droite $\left(A Y^{\prime}\right)$ est échangée avec la médiane ( $A A^{\prime}$ ) dans le triangle $A B C$. Comme la droite $\left(A X\right.$ ) est la symédiane on a donc que la droite ( $A Y^{\prime}$ ) et la droite $(A X)$ sont la même droite ce qui conclut.
|
{
"exam": "French_envois",
"problem_label": "15",
"problem_match": "\nExercice 15.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-1.jsonl",
"solution_match": "## Solution de l'exercice 15",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle and $\Omega$ its circumcircle. Let $X$ be the point of intersection of the tangents to $\Omega$ at $B$ and $C$. Let $\varphi$ be the angle $\widehat{B A X}$ and $\mu$ be the angle $\widehat{X A C}$. Let $Y$ be the point on the line $(A X)$ such that $\widehat{A C Y}=\varphi$. Show that $\widehat{A B Y}=\mu$.
|
For Exercise 15
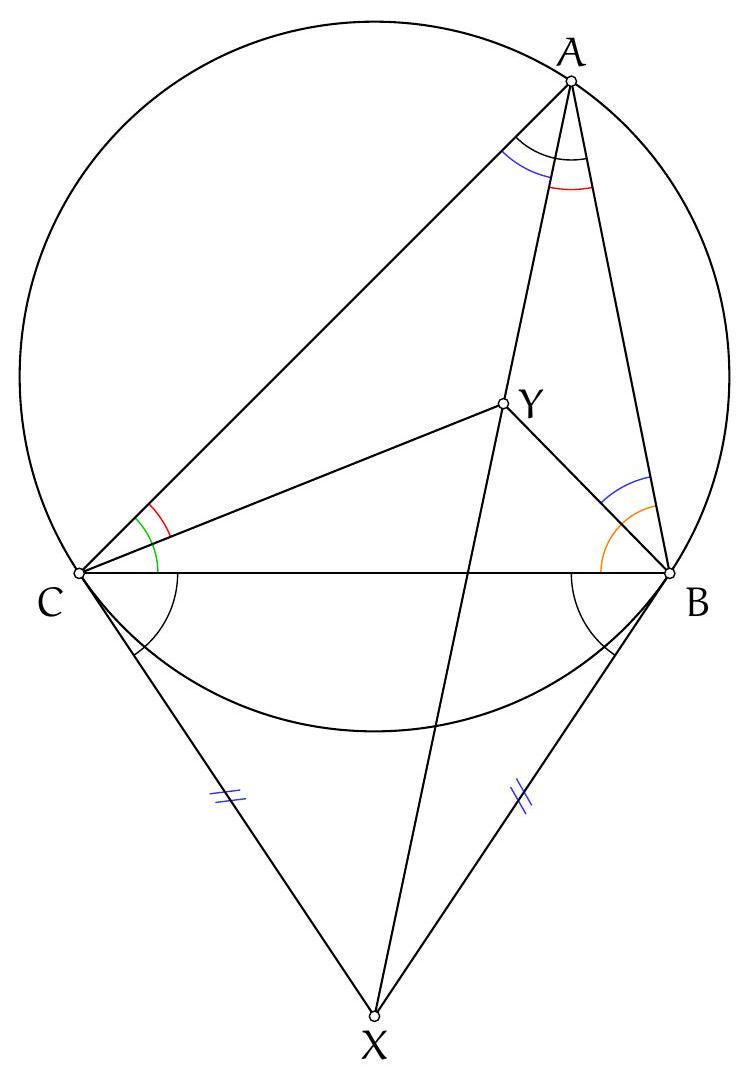
Let $\alpha=\widehat{B A C}$, $\beta=\widehat{A B C}$, and $\gamma=\widehat{B C A}$. We will use a classic tool when dealing with symmedians, the angle chasing with sines. First, we note that according to the tangent angle theorem:
$$
\widehat{B C X}=\widehat{C B X}=\widehat{B A C}=\alpha
$$
Triangle $B C X$ is therefore isosceles at $X$. We also have $\widehat{A B X}=\alpha+\beta=180^{\circ}-\gamma$. Similarly, we have $\widehat{A C X}=180^{\circ}-\beta$. By applying the law of sines in triangle $A B X$, and then in triangle $A C X$, we find
$$
\frac{\sin (\gamma)}{\sin (\varphi)}=\frac{\sin \left(180^{\circ}-\gamma\right)}{\sin (\varphi)}=\frac{A X}{B X}=\frac{A X}{C X}=\frac{\sin (\beta)}{\sin (\mu)}
$$
By applying the law of sines this time in triangle $A B Y$ and then in triangle $A B C$, we have
$$
\frac{Y C}{Y A}=\frac{\sin (\mu)}{\sin (\varphi)}=\frac{\sin (\beta)}{\sin (\gamma)}=\frac{A C}{B C}
$$
This shows that triangles $BYA$ and $AYC$ are similar. Indeed, they share an angle $\varphi$ and a common ratio
$$
\frac{B A}{Y A}=\frac{A C}{C Y}
$$
This similarity implies that $\widehat{A B Y}=\widehat{Y A C}$, which concludes the proof.
Comment from the graders: The exercise is well solved. It actually admitted an elementary solution by angle chasing, which escaped the vigilance of the problem designers as well as several students who developed the arsenal of known properties around the symmedian, falling victim to the same bias as the problem designers.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit ABC un triangle et $\Omega$ son cercle circonscrit. On note X le point d'intersection des tangentes à $\Omega$ en $B$ et $C$. On note $\varphi$ l'angle $\widehat{B A X}$ et $\mu$ l'angle $\widehat{X A C}$. On note $Y$ le point de la droite ( $A X$ ) tel que $\widehat{A C Y}=\varphi$. Montrer que $\widehat{A B Y}=\mu$.
|
de l'exercice 15

On pose $\alpha=\widehat{B A C}, \beta=\widehat{A B C}$ et $\gamma=\widehat{B C A}$. On va utiliser un autre outil classique lorsque qu'il y a des symédianes en jeu, la chasse aux sinus. On remarque dans un premier temps que d'après le théorème de l'angle tangent :
$$
\widehat{B C X}=\widehat{C B X}=\widehat{B A C}=\alpha
$$
Le triangle $B C X$ est donc isocèle en $X$. On a de plus $\widehat{A B X}=\alpha+\beta=180^{\circ}-\gamma$. De même, on a $\widehat{A C X}=180^{\circ}-\beta$. En appliquant la loi des sinus dans le triangle $A B X$, puis dans le triangle $A C X$, on trouve
$$
\frac{\sin (\gamma)}{\sin (\varphi)}=\frac{\sin \left(180^{\circ}-\gamma\right)}{\sin (\varphi)}=\frac{A X}{B X}=\frac{A X}{C X}=\frac{\sin (\beta)}{\sin (\mu)}
$$
En appliquant la loi des sinus cette fois-ci dans le triangle $A B Y$ puis dans le triangle $A B C$, on a
$$
\frac{Y C}{Y A}=\frac{\sin (\mu)}{\sin (\varphi)}=\frac{\sin (\beta)}{\sin (\gamma)}=\frac{A C}{B C}
$$
Cela montre que les triangles BYA et $A Y C$ sont semblables. En effet, ils ont un angle $\varphi$ en commun et un rapport en commun
$$
\frac{B A}{Y A}=\frac{A C}{C Y}
$$
Cette relation de similitude implique que $\widehat{A B Y}=\widehat{Y A C}$, ce qui conclut.
Commentaire des correcteurs: L'exercice est bien résolu. Il admettait en fait une solution élémentaire en chasse aux angles, qui a échappé à la vigilance des concepteurs du sujet mais aussi à plusieurs élèves qui ont développé l'arsenal de propriétés connues autour de la symédiane, victimes de la même déformation que les concepteurs du sujet.
|
{
"exam": "French_envois",
"problem_label": "15",
"problem_match": "\nExercice 15.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-1.jsonl",
"solution_match": "## Solution alternative",
"tier": "T2",
"year": null
}
|
Let $ABCD$ be a convex quadrilateral such that $AC = BD$ and such that the sides $AB$ and $CD$ are not parallel. Let $P$ be the intersection point of the diagonals $(AC)$ and $(BD)$. Let $E$ and $F$ be points on the segments $[BP]$ and $[AP]$ respectively such that $\mathrm{PC} = \mathrm{PE}$ and $\mathrm{PD} = \mathrm{PF}$. Show that the circumcircle of the triangle formed by the lines $(AB)$, $(CD)$, and $(EF)$ is tangent to the circumcircle of the triangle $ABP$.
|
First, we denote X as the intersection of lines (CD) and (FE), Y as the intersection of lines (AB) and (CD), and Z as the intersection of lines (AB) and (FE).
The first idea in this exercise is to consider a Miquel point (for what a Miquel point is, we refer to T. Budzinski's course notes, Geometric Transformations, Theorem 4.14), which we will denote as \( M \) and which naturally appears in the configuration. Indeed, the flat triangles AFC and BED are isometric. Thus, if we consider the direct similarity that maps segment [AF] to segment [EB], it is a rotation (since \( \frac{AF}{EB} = 1 \)), and this rotation also maps point C to point D. As announced, we denote \( M \) as the center of the rotation (the Miquel point). \( M \) is therefore the Miquel point of the following complete quadrilaterals: \( ABFE \), \( ABCD \), and \( FEDC \). In principle, the order of the points matters, as there are 3 classes of order for 4 same points that give 3 different Miquel points. To distinguish them, we adopt the notations from Theorem 4.14 cited above.
The point \( M \) is therefore on the circumcircles of many triangles, particularly the circumcircles of \( ABP \), \( ZAF \), and \( BDY \). Thus, it is a good candidate to be our point of tangency. In the following, we will show that \( M \) is also on the circumcircle of triangle \( XYZ \) and that it is the point of tangency between the circumcircles of triangles \( XYZ \) and \( ABP \).
We now observe that quadrilateral DCEF is an isosceles trapezoid with (CE) // (DF). Since \( M \) is the intersection of the circumcircles of \( PFE \) and \( PCD \) other than \( P \), we deduce that \( M \) is on the axis of symmetry of trapezoid FDCE. \( M \) is therefore on the external bisector from \( P \) in triangles \( PFE \) and \( PCD \), in particular, \( M \) is the North Pole of these triangles. By the classical properties of the Miquel point, \( M \) is also the center of the direct similarity that maps \( F \) to \( A \) and \( E \) to \( B \). Therefore, \( \triangle MFE \sim \triangle MAB \), in particular, \( MA = MB \) and \( M \) is then the North Pole in triangle \( ABP \).
To conclude, it suffices to show that \( M \) is the North Pole in triangle \( XYZ \). We first show that this assertion implies the end of the exercise.
If \( M \) is the North Pole of triangle \( XYZ \), then it is indeed on the circumcircle of this triangle. Let \( t \) (resp. \( t' \)) be the tangent to the circumcircle of \( ABP \) (resp. \( XYZ \)) at \( M \). We want to show that \( t \) and \( t' \) are the same line. Since \( M \) is the North Pole, we have \( t \parallel (AB) \). But similarly, \( t' \parallel (ZY) \). This shows that \( t \parallel t' \) and thus that they are the same line.
To conclude, we will show that \( M \) is on the perpendicular bisector of segment [ZY]. Since \( M \) is on the external bisector from \( X \) (because \( M \) is on the common perpendicular bisector of (DF) and (EC) and lines (EF) and (DC) intersect at \( X \)), this would conclude well. It suffices to show that \( (MZ, MA) = (MB, MY) \). However, we have many cyclic properties that appear with the Miquel point and the trapezoid DFEC.
\[
\begin{aligned}
(MZ, MA) & = (FZ, FA) \\
& = (FE, FC) \\
& = (DE, DC) \\
& = (MB, MY)
\end{aligned}
\]
(ZAFM cyclic)
(opposite angles)
(FECD cyclic)
(MBYD cyclic).
This concludes the proof.
Comment from the graders: The problem is well solved by the students who approached it. Most students used the properties of the Miquel point of one or the other of the various quadrilaterals (all Miquel points were coincident here). Relatively few students supplemented this concept with the concept of the North Pole, which helped simplify the reasoning here (many students in fact redemonstrated one or the other of the properties by hand through more or less complicated angle chasing).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un quadrilatère convexe tel que $A C=B D$ et tel que les côtés $A B$ et $C D$ ne sont pas parallèles. Soit $P$ le point d'intersection des diagonales (AC) et (BD). Soient $E$ et $F$ des points respectivement sur les segments $[B P]$ et $[A P]$ tels que $\mathrm{PC}=\mathrm{PE}$ et $\mathrm{PD}=\mathrm{PF}$. Montrer que le cercle circonscrit au triangle formé par les droites (AB), (CD) et (EF) est tangent au cercle circonscrit au triangle ABP.
|

On note dans un premier temps X l'intersection des droites (CD) et ( $F E$ ), Y l'intersection des droites $(A B)$ et (CD) ainsi que Zl'intersection des droites ( $A B$ ) et (FE).
La première idée de cet exercice est de considérer un point de Miquel (pour savoir ce qu'est un point de Miquel on fait référence au polycopié de T. Budzinski, Transformations Géométriques, Théorème 4.14), que l'on notera $M$ et qui intervient naturellement dans la configuration. En effet, les triangles plats AFC et BED sont isométriques. Ainsi si on considère la similitude directe qui envoie le segment [AF] sur le segment $[E B]$ il s'agit d'une rotation (comme $A F / E B=1$ ) et cette rotation envoie donc également le point C sur le point D . Comme annoncé, on note $M$ le centre de la rotation (le point de Miquel). $M$ est donc le point de Miquel des quadrilatères complets suivants : $A B F E, A B C D$ et $F E C D$. En principe l'ordre des points importe comme il y a 3 classes d'ordre pour 4 mêmes points qui donnent 3 points de Miquel différents pour les distinguer on adopte ici les notations du Théorème 4.14 cité précédemment.
Le point $M$ est donc sur les cercles circonscrits de plein de triangles et en particulier sur le cercle circonscrit des ABP, ZAF et BDY, c'est donc un bon candidat pour être notre point de tangence. Dans la suite on va donc montrer que $M$ est également sur le cercle circonscrit au triangle $X Y Z$ et que c'est le point de tangence entre les cercles circonscrits des triangles XYZ et $A B P$.
On remarque maintenant que le quadrilatère DCEF est un trapèze isocèle avec (CE)//(DF). $M$ étant le point d'intersection des cercles circonscrits à PFE et PCD autre que $P$, on en déduit que $M$ est sur l'axe de symétrie du trapèze FDCE. $M$ est donc sur la bissectrice extérieure issue de $P$ dans les triangles PFE et PCD, en particulier $M$ est le pôle Nord de ces triangles. Par les propriétés classique du point de Miquel, $M$ est également le centre de la similitude directe qui envoie $F$ sur $A$ et $E$ sur $B$. Donc MFE $\sim M A B$, en particulier $M A=M B$ et $M$ est alors le pôle Nord dans le triangle ABP.
Pour conclure il suffit de montrer que $M$ est le pôle Nord dans le triangle $X Y Z$. On montre dans un premier temps que cet assertion implique bien la fin de l'exercice.
Si $M$ est le pôle Nord du triangle $X Y Z$, alors il est bien sur le cercle circonscrit de ce triangle. Soit $t$ (resp. $t^{\prime}$ ) la tangente au cercle circonscrit de $A B P$ (resp. $X Y Z$ ) en $M$. On voudrait montrer que $t$ et $t^{\prime}$ sont la même droite. Comme $M$ est le pôle Nord, on a $t / /(A B)$. Mais de la même manière $t^{\prime} / /(Z Y)$. Ce qui montre bien que $t / / t^{\prime}$ et donc qu'il s'agit de la même droite.
Pour conclure on va montrer que $M$ est sur la médiatrice du segment [ZY]. Comme $M$ est sur la bissectrice extérieure issue de $X$ (car $M$ est sur la md́atrice commune de (DF) et (EC) et les droites (EF) et ( DC ) se coupent en $X$ ), cela conclurait bien. Il suffit donc de montrer que ( $M Z, M A$ ) $=(M B, M Y$ ). Or on a plein de cocyclicités qui apparaissent avec le point de Miquel et le trapèze DFEC.
$$
\begin{aligned}
(M Z, M A) & =(F Z, F A) \\
& =(F E, F C) \\
& =(D E, D C) \\
& =(M B, M Y)
\end{aligned}
$$
(ZAFM cyclique)
(angles opposés)
(FECD cyclique)
(MBYD cyclique).
Ce qui conclut.
Commentaire des correcteurs: Le problème est bien résolu par les élèves qui l'ont abordé. Les élèves ont pour la plupart utilisé les propriétés du point de Miquel de l'un ou l'autre des divers quadrilatères (tous les points de Miquel étaient confondus ici). Relativement peu d'élèves ont complété cette notion avec la notion de pôle Nord, qui aidait ici à simplifier les raisonnements (beaucoup d'élèves ont en fait redémontré l'une ou l'autre des propriétés à la main via des chasses aux angles plus ou moins compliquées).
|
{
"exam": "French_envois",
"problem_label": "16",
"problem_match": "\nExercice 16.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-1.jsonl",
"solution_match": "## Solution de l'exercice 16",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle and $H$ its orthocenter. We denote by $\ell_{1}$ and $\ell_{2}$ two lines passing through $H$ and perpendicular to each other. We denote $X_{1}, Y_{1}$ and $Z_{1}$ the points of intersection of $\ell_{1}$ with the lines $(BC)$, $(CA)$, and $(AB)$ respectively. We also denote $X_{2}, Y_{2}$ and $Z_{2}$ the points of intersection of $\ell_{2}$ with the lines $(BC)$, $(CA)$, and $(AB)$ respectively. Show that the midpoints of the segments $\left[X_{1} X_{2}\right]$, $\left[Y_{1} Y_{2}\right]$, and $\left[Z_{1} Z_{2}\right]$ are collinear.
|
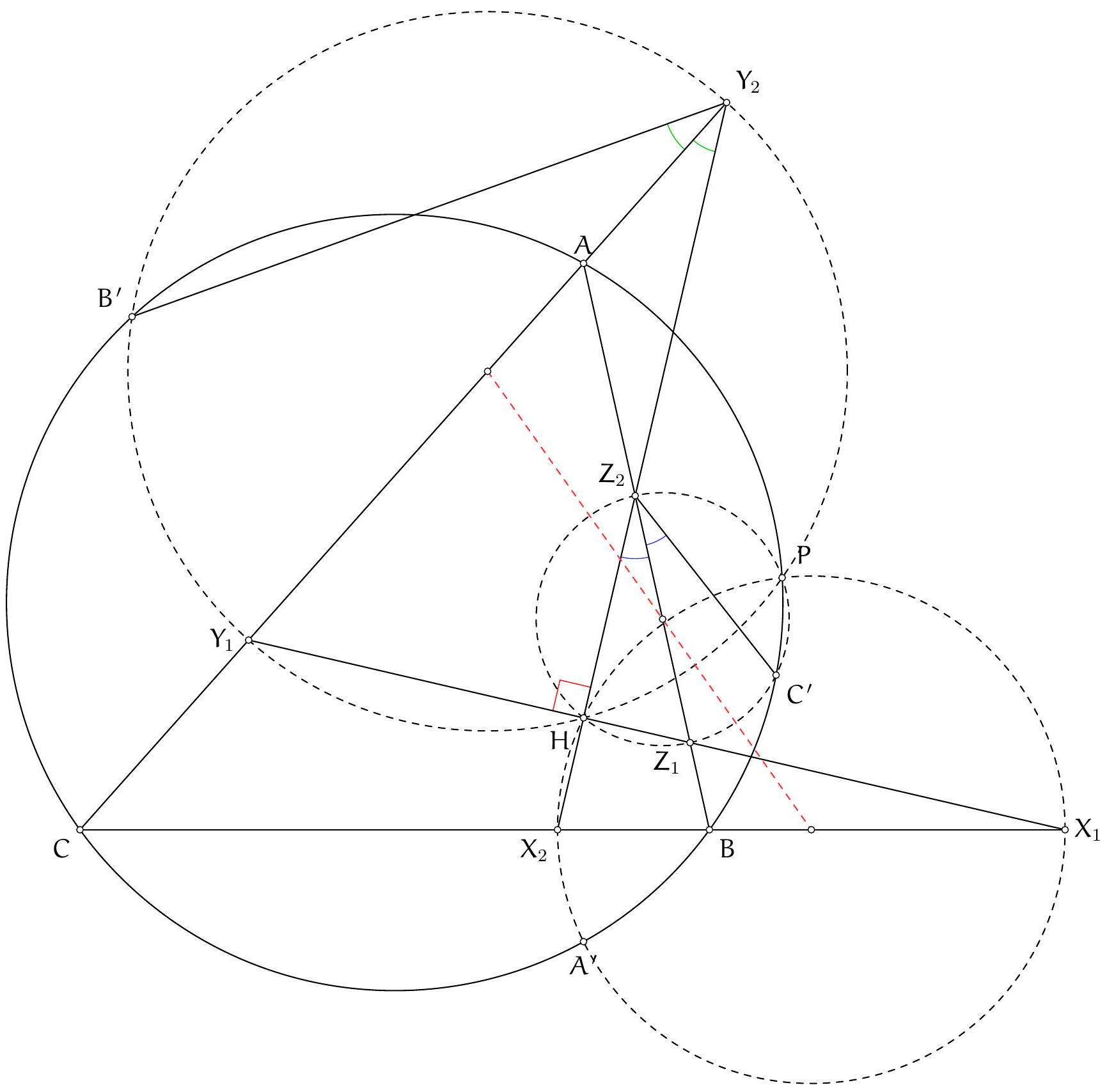
The approach presented in this solution is lengthy, but purely elementary, and all the numerous steps should appear natural.
First step: Midpoints. Introducing a midpoint in an exercise is always a thorn in our side because this condition is difficult to use with our favorite tool: angle chasing. We can therefore wonder how to remove this thorn; here, a solution should seem reasonable. Due to the right angle \(\widehat{\mathrm{X}_{1} \mathrm{HX}_{2}}\), the midpoint of \([\mathrm{X}_{1} \mathrm{X}_{2}]\) is naturally the midpoint of the diameter of the circumcircle of triangle \(\mathrm{HX}_{1} \mathrm{X}_{2}\), hence the center of this circle, which will now be named \(\Gamma_{\mathrm{A}}\).
On our figure, we therefore draw three circles \(\Gamma_{A}, \Gamma_{B}\), and \(\Gamma_{C}\), where \(\Gamma_{B}\) and \(\Gamma_{C}\) are defined similarly. We can thus stop thinking about midpoints as midpoints and think of them as centers of circles.
Second step: Erasing the centers. Manipulating centers of circles is often more pleasant than manipulating midpoints of segments, but it is not yet entirely satisfactory. By drawing our three new circles, we observe that they appear to intersect again at another point besides H. In the face of such an observation, a first question is to wonder what such information would imply by symmetry. For example, on my figure, perhaps B seems to lie on \(\Gamma_{A}\), but if this were always the case, by symmetry, C should also lie on \(\Gamma_{\mathrm{A}}\), and on my figure, this is not the case at all, so my conjecture must be eliminated.
Here, no such argument, the concurrency of the three circles implies nothing by symmetry. Better yet, let's now consider what would follow from the concurrency of these three circles at a point P. The three centers would be on the perpendicular bisector of \([\mathrm{HP}]\), a common chord of the three circles, which would conclude! In the other direction, if the three centers are collinear, then the reflection of H with respect to the line of the three centers is on each circle, so they do intersect. Instead of the collinearity of the three centers, we can show the concurrency of the three circles, a property that is a priori much more pleasant!
Interlude: How do we know if we are going in the right direction? This is generally a difficult question, but here we can answer affirmatively because we can erase pieces of the figure (here the three midpoints) and simplify it. We have drawn the triangle, the two lines, and the 6 points of intersection, do we prefer to draw three midpoints and show their collinearity or three circles and show their concurrency? The second option.
Even if the two options seem similar in complexity (which is not the difficulty), a geometry Olympiad problem maximizes its difficulty relative to its complexity, so an equivalent statement of comparable complexity will almost always be easier, otherwise, this statement would have been posed instead. We are now convinced that we are going in the right direction, and we will not be afraid to move even further away from the base problem. This is often a good thing, as long as we keep the equivalence with the base problem, of course.
Third step: Properties of point P. After a naive angle chase that was unfruitful, we look for properties of the circles \(\Gamma\) or the point P. Two possibilities: we observe that P is on the circumcircle of \(\mathrm{ABC}, \Omega\), because we have drawn this circle. Indeed, in an exercise centered on a triangle ABC, we always draw its circumcircle on at least one figure, if not on all. Another way to make this conjecture presupposes a certain familiarity with the Miquel point. The intersection point of \(\Gamma_{\mathrm{B}}\) and \(\Gamma_{\mathrm{C}}\) is the Miquel point of \(\ell_{1}, \ell_{2}, (AB), (AC)\). Saying that it is on \(\Gamma_{\mathrm{A}}\) is equivalent to saying that it is a Miquel point of the pentagon \(\ell_{1}, \ell_{2}, (AB), (AC), (BC)\) (any circumcircle of a trilateral formed by 3 of these lines passes through P).
A good way to visualize the Miquel points of a pentagon (which do not exist for any pentagon) is to remember the Simson (or Steiner) line. A point is on the circumcircle of a trilateral (or triangle) if and only if its projections (orthogonal) on the three sides are collinear, so a point is the Miquel point of 4 lines if and only if its 4 projections are collinear, and of 5 if and only if its 5 projections are collinear. With this vision of things, assuming P is on the three circles \(\Gamma\), the projections of P on the sides are all on the line connecting the two projections of P on \(\ell_{1}\) and on \(\ell_{2}\), so they are collinear and P is on \(\Omega\).
Why choose \(\Omega\) when P is on 10 circles, literally? It is the only one that involves only already introduced points and especially that preserves the symmetry between A, B, and C. To show the concurrency of \(\Gamma_{\mathrm{A}}, \Gamma_{\mathrm{B}}\), and \(\Gamma_{\mathrm{C}}\), we can show that \(\Gamma_{\mathrm{B}}\) and \(\Gamma_{\mathrm{C}}\) intersect on \(\Omega\), at a point which will then also be on \(\Gamma_{\mathrm{A}}\).
Interlude: Are we going in the right direction? Which do we prefer, showing the concurrency of \(\Gamma_{\mathrm{A}}, \Gamma_{\mathrm{B}}\), and \(\Gamma_{\mathrm{C}}\), or that of \(\Gamma_{\mathrm{B}}, \Gamma_{\mathrm{C}}\), and \(\Omega\)? Advantage of the first: it preserves the symmetry. Advantage of the second: it is further from the statement without being more complex. The second wins.
Fourth step: We have one hypothesis left: \(\ell_{1}\) and \(\ell_{2}\) intersect at the orthocenter. I had forgotten. Let's correct that. How to use the orthocenter hypothesis? We certainly do not want to draw heights that do not pass through anything here. However, the circumcircle is already drawn and important, and we know that many reflections of H are on it. Which to choose? With respect to the sides or the midpoints of the sides? This time, it is enough to ask the question to have the answer: the reflections with respect to the sides are also on the circles \(\Gamma\), as these are stable under axial symmetry! They are therefore much more interesting: this is clearly the right way to use the midpoint hypothesis. Let's name them \(A', B',\) and \(C'\).
Conclusion: We have reformulated all the elements of the statement into equivalent elements (H is indeed the only point whose three reflections are on the circumcircle of triangle \(ABC\)) and usable for an angle chase. We have preserved the symmetry between B and C, let's try to preserve it a little more for the angle chase (it is not always possible). We define P as the intersection point other than H of \(\Gamma_{\mathrm{B}}\) and \(\Gamma_{\mathrm{C}}\). We want to show that it lies on \(\Omega\). Rather than showing that it is cyclic with \(A, B, C\), let's show that it is cyclic with \(A, B', C'\). Indeed, we know nothing about the direction of the line PB or PC, while \(PB'\) and \(PC'\) are chords of \(\Gamma_{\mathrm{B}}\) and \(\Gamma_{\mathrm{C}}\). Moreover, the angle \(\widehat{B'AC'}\) is known (i.e., it can be expressed with simple operations in terms of the angles of triangle \(ABC\)).
We want to find the known value of \(\widehat{B'PC'}\). To exploit the definition of P, we break this angle into \(\widehat{B'PH}\) and \(\widehat{HPC'}\). We are therefore looking for a simple relationship between these two angles. These are inscribed angles, which intercept an arc twice the length of \(HY_1\) on one side and \(HZ_1\) on the other. We are therefore looking for a relationship between the angles \(\widehat{HY_2Y_1}\) and \(\widehat{Z_1Z_2H}\), but these two angles are between the same line \(\ell_2\) and the sides of the triangle. We therefore have a relationship, which, when traced back, gives a simple relationship between \(\widehat{B'AC'}\) and \(\widehat{B'PC'}\), which can only be the sum of the two being \(180^\circ\), which would conclude. We are now convinced that this small angle chase will finish the problem, it only remains to write it to complete the proof of the exercise.
Comment from the graders: The students very well understood how to rephrase the statement to reduce it to the concurrency of three circles. Subsequently, the methods used are varied and mainly involve the Miquel point. A handful of students were more than delighted to apply results invoking parabolas.
If such technology could apparently annihilate the exercise, it only provides a rephrasing of the reasoning around the Miquel point common to the different quadrilaterals of the figure, more elementary and, to the taste of the graders, much more instructive for the students.
|
proof
|
Yes
|
Incomplete
|
proof
|
Geometry
|
Soit $A B C$ un triangle et H son orthocentre. On note $\ell_{1}$ et $\ell_{2}$ deux droites passant par H et perpendiculaire entre elles. On note $X_{1}, Y_{1}$ et $Z_{1}$ les points d'intersection de $\ell_{1}$ avec les droites ( $B C$ ), $(C A)$ et $(A B)$ respectivement. On note également $X_{2}, Y_{2}$ et $Z_{2}$ les points d'intersection de $\ell_{2}$ avec les droites $(B C),(C A)$ et $(A B)$ respectivement. Montrer que les milieux des segments $\left[X_{1} X_{2}\right],\left[Y_{1} Y_{2}\right]$ et $\left[Z_{1} Z_{2}\right]$ sont alignés.
|

L'approche présentée dans ce corrigé est longue, mais purement élémentaire et les nombreuses étapes doivent toutes paraître naturelles.
Première étape : les milieux. L'introduction d'un milieu dans un exercice est toujours une épine dans notre pied car cette condition est difficile à utiliser avec notre outil favori : la chasse aux angles. On peut donc se demander comment retirer cette épine ; ici, une solution doit paraître raisonnable. Du fait de
l'angle droit $\widehat{\mathrm{X}_{1} \mathrm{HX}_{2}}$, le milieu de $\left[\mathrm{X}_{1} \mathrm{X}_{2}\right]$ est naturellement le milieu du diamètre du cercle circonscrit au triangle $\mathrm{HX}_{1} \mathrm{X}_{2}$, donc le centre de ce cercle, qui sera maintenant nommé $\Gamma_{\mathrm{A}}$.
Sur notre figure, on trace donc trois cercles $\Gamma_{A}, \Gamma_{B}$ et $\Gamma_{C}$, où $\Gamma_{B}$ et $\Gamma_{C}$ sont définis de manière similaire. On peut ainsi arrêter de penser aux milieux comme des milieux et on y pense comme des centres de cercles.
Deuxième étape : Effacer les centres. Manipuler des centres de cercles est souvent plus agréable que manipuler des milieux de segments, mais ce n'est pas encore tout à fait satisfaisant. En traçant nos trois nouveaux cercles, on constate qu'ils ont l'air de se couper à nouveau en un autre point que H. Devant une telle observation, une première interrogation est de se demander ce qu' une telle information impliquerait par symétrie. Par exemple, sur ma figure, peut-être que $B$ semble se trouver sur $\Gamma_{A}$, mais si c'était toujours le cas, par symétrie, C devrait aussi se situer sur $\Gamma_{\mathrm{A}}$, et sur ma figure ce n'est pas du tout le cas, ma conjecture est donc à éliminer.
Ici pas de tel argument, la concourance des trois cercles n'entraîne rien par symétrie. Mieux, regardons maintenant ce qui découlerait de la concourance de ces trois cercles en un point P . Les trois centres seraient sur la médiatrice de $[\mathrm{HP}]$, corde commune aux trois cercles, ce qui conclurait! Dans l'autre sens, si les trois centres sont alignés, alors le symétrique de H par rapport à la droite des trois centres est sur chaque cercle, ils se recoupent donc bien. A la place de l'alignement des trois centres, on peut montrer la concourance des trois cercles, une propriété a priori bien plus agréable!
Interlude : Comment savoir si on est allé dans la bonne direction? C'est généralement une question difficile mais ici on peut répondre par l'affirmative car on peut effacer des morceaux de la figure (ici les trois milieux) et la simplifier. On a tracé le triangle, les deux droites et les 6 points d'intersection, préfère-t-on tracer trois milieux et montrer leur alignement ou trois cercles et montrer leur concourance? La deuxième option.
Même si les deux options semblent similaires en complexité (ce qui n'est pas la difficulté), un problème de géométrie olympique maximise sa difficulté par rapport à sa complexité donc un énoncé équivalent et de complexité comparable sera presque toujours plus facile, sinon cet énoncé aurait été posé à la place. On est maintenant convaincu d'aller dans la bonne direction, et on aura pas peur de s'éloigner encore plus de problème de base. C'est souvent une bonne chose, tant qu'on garde l'équivalence avec le problème de base bien sûr.
Troisième étape : Les propriétés du point P . Après une chasse aux angles naïve infructueuse, on cherche des propriétés des cercles $\Gamma$ ou du point $P$. Deux possibilités : on constate que $P$ est sur le cercle circonscrit à $\mathrm{ABC}, \Omega$, parce qu'on a tracé ce cercle. En effet, dans un tel exercice centré sur un triangle ABC , on trace toujours son cercle circonscrit sur au moins une figure, si ce n'est sur toutes. Une autre manière d'effectuer cette conjecture présuppose une certaine habitude avec le point de Miquel. Le point d'intersection de $\Gamma_{\mathrm{B}}$ et de $\Gamma_{\mathrm{C}}$ est le point de Miquel de $\ell_{1}, \ell_{2},(A B),(A C)$. Dire qu'il est sur $\Gamma_{\mathrm{A}}$ revient à dire que c'est un point de Miquel du pentalatère $\ell_{1}, \ell_{2},(A B),(A C),(B C)$ (tout cercle circonscrit au trilatère formé par 3 de ces droites passe par P ).
Une bonne manière de se représenter les points de Miquel de pentalatère (qui n'existent pas pour n'importe quel pentalatère) est de se rappeler de la droite de Simson (ou Steiner). Un point est sur le cercle circonscrit à un trilatère (ou triangle) si et seulement si ses projetés (orthogonaux) sur les trois côtés sont alignés, donc un point est le point de Miquel de 4 droites si et seulement ses 4 projetés sont alignés, et de 5 si et seulement si ses 5 projetés sont alignés. Avec cette vision des choses, en supposant $P$ sur les trois cercles $\Gamma$, les projetés de $P$ sur les côtés sont tous sur la droite reliant les deux projetés de P sur $\ell_{1}$ et sur $\ell_{2}$, ils sont donc alignés et $P$ est sur $\Omega$.
Pourquoi avoir choisi $\Omega$ alors que P est sur 10 cercles, littéralement? C'est le seul qui ne fait intervenir que des points déjà introduits et surtout qui conserve la symétrie entre $A, B$ et $C$. Pour montrer la concourance de $\Gamma_{\mathrm{A}}, \Gamma_{\mathrm{B}}$ et $\Gamma_{\mathrm{C}}$, on peut montrer que $\Gamma_{\mathrm{B}}$ et $\Gamma_{\mathrm{C}}$ se coupent sur $\Omega$, en un point qui sera alors
aussi sur $\Gamma_{\mathrm{A}}$.
Interlude : va-t-on dans la bonne direction? Que préfère-t-on, montrer la concourrance de $\Gamma_{\mathrm{A}}, \Gamma_{\mathrm{B}}$ et $\Gamma_{\mathrm{C}}$, ou bien celle de $\Gamma_{\mathrm{B}}, \Gamma_{\mathrm{C}}$ et $\Omega$ ? Avantage du premier : cela conserve la symétrie. Avantage du deuxième : c'est plus loin de l'énoncé sans être plus complexe. Le deuxième gagne.
Quatrième étape : Il nous reste une hypothèse : $\ell_{1}$ et $\ell_{2}$ se coupent en l'orthocentre. J'avais oublié. Corrigeons ça. Comment utiliser l'hypothèse d'orthocentre? On ne souhaite surtout pas tracer des hauteurs qui ne passent par rien ici. Par contre, le cercle circonscrit est déjà tracé et important, et on sait que de nombreux symétriques de H s'y trouvent. Lesquels choisir? Par rapport aux côtés ou aux milieux des côtés? Cette fois, il suffit de se poser la question pour avoir la réponse : les symétriques par rapport aux côtés sont aussi sur les cercles $\Gamma$, car ceci sont stables par la symétrie axiale! Ils sont donc beaucoup plus intéressants : c'est clairement la bonne manière d'utiliser l'hypothèse de milieu. Nommons les $A^{\prime}, B^{\prime}$ et $C^{\prime}$ 。
Conclusion: On a reformulé tous les éléments de l'énoncé en des éléments équivalents ( H est bien le seul point dont les trois symétriques sont sur le cercle circonscrit du triangle $A B C$ ) et utilisables pour faire une chasse aux angles. On a conservé la symétrie entre B et C , essayons de la conserver encore pour la chasse aux angles (ce n'est pas toujours possible). On définit $P$ comme le point d'intersection autre que H de $\Gamma_{\mathrm{B}}$ et $\Gamma_{\mathrm{C}}$. On veut montrer qu'il se trouve sur $\Omega$. Plutôt que de montrer qu'il est cocyclique avec $A, B, C$, montrons qu'il est cocyclique avec $A B^{\prime} C^{\prime}$. En effet, on ne sait rien de la direction de la droite PB ou PC , alors que $\mathrm{PB}^{\prime}$ et $\mathrm{PC}^{\prime}$ sont des cordes de $\Gamma_{\mathrm{B}}$ et $\Gamma_{\mathrm{C}}$. De plus, l'angle $\widehat{\mathrm{B}^{\prime} \mathrm{AC}}$ ' est connu (c'est-à-dire qu'on peut l'exprimer avec des opérations simples en fonction des angles du triangle $A B C$ ).
On veut donc trouver la valeur connue de $\widehat{\mathrm{B}^{\prime} \mathrm{PC}^{\prime}}$. Pour exploiter la définition de P , on éclate cet angle en $\widehat{\mathrm{B}^{\prime} \mathrm{PH}}$ et $\widehat{\mathrm{HPC}^{\prime}}$. On cherche donc une relation simple entre ces deux angles. Ce sont des angles inscrits, qui interceptent un arc de deux fois la longueur de $\mathrm{HY}_{1}$ d'un côté de $\mathrm{HZ}_{1}$ de l'autre. On cherche donc une relation entre l'angle $\widehat{\mathrm{HY}_{2} \mathrm{Y}_{1}}$ et $\widehat{\mathrm{Z}_{1} \mathrm{Z}_{2} \mathrm{H}}$, mais ces deux angles sont entre la même droite $\ell_{2}$ et les côtés du triangle. On a donc une relation, qui, en remontant tout, donne une relation simple entre $\widehat{B^{\prime} A C^{\prime}}$ et $\widehat{\mathrm{B}^{\prime} \mathrm{PC}^{\prime}}$, qui ne peut être que la somme des deux valant $180^{\circ}$, ce qui terminerait. On est maintenant convaincu que cette petite chasse aux angles va terminer ce problème, il suffit de l'écrire pour finir la preuve de l'exercice.
Commentaire des correcteurs : Les élèves ont très bien vu comment réécrire l'énoncé pour se ramener à la concourance de trois cercles. Ensuite, les méthodes employées sont variées et utilisent principalement le point de Miquel. Une poignée d'élèves ont été plus que ravis d'appliquer des résultats invoquant des paraboles.
Si une telle technologie permettait en apparence d'annihiler l'exercice, elle ne donne ici qu'une réécriture des raisonnements autour du point de Miquel commun aux différents quadrilatères de la figure, des raisonnements plus élémentaires et, au goût des correcteurs, bien plus instructifs pour les élèves.
|
{
"exam": "French_envois",
"problem_label": "17",
"problem_match": "\nExercice 17.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-1.jsonl",
"solution_match": "## Solution de l'exercice 17",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle and $\omega$ its incircle, with the points of tangency on $[BC]$, $[CA]$, and $[AB]$ being $D$, $E$, and $F$ respectively. Let $\Omega$ be the circle tangent to $\omega$ and passing through $B$ and $C$, and let $T$ be the point of tangency of these two circles. Let $X$ and $Y$ be the midpoints of segments $[DE]$ and $[DF]$. Let $U$ and $V$ be the second points of intersection of lines $(TX)$ and $(TY)$ with $\Omega$. Also, let $Z$ and $W$ be the second points of intersection of lines $(AB)$ and $(AC)$ with $\Omega$. Show that $(ZU)$, $(WV)$, $(XY)$, and the angle bisector of $\widehat{BAC}$ are concurrent.
|
Throughout the proof, we will use the results of the following lemma. We start with a notation.
Let ABC be a triangle, we denote $\Omega$ as the circumcircle of $ABC$, and also denote $\omega$ as the circle tangent to $(AB)$, $(AC)$, and internally to $\Omega$. We say that this circle is the mixtilinear (internal) circle of triangle $ABC$ from $A$.
Lemma 3. Let ABC be a triangle, we denote $I$ as the center of its incircle, and also denote $\Omega$ as the circumcircle of $ABC$ and $\omega$ as the mixtilinear circle from $A$. We denote $T$ (resp. $D$ and $F$) as the point of tangency of $\omega$ with $\Omega$ (resp. $(AC)$ and $(AB)$), and $N$ as the north pole (the midpoint of the arc $BC$ that contains $A$). Under these assumptions and notations, we know that $I$ is the midpoint of the segment $[DF]$ and that the points $T$, $I$, and $N$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $\omega$ son cercle inscrit dont les points de tangence sur [BC], [CA] et $[A B]$ sont respectivement $D$, $E$ et $F$. On note $\Omega$ le cercle tangent à $\omega$ et passant par $B$ et $C$ et $T$ le point de tangence de ces deux cercles. On note $X$ et $Y$ les milieux des segments [DE] et [DF]. On note $U$ et $V$ les seconds points d'intersection des droites (TX) et (TY) avec $\Omega$. On note également $Z$ et $W$ les seconds points d'intersection des droites (AB) et (AC) avec $\Omega$. Montrer que (ZU), (WV), (XY) et la bissectrice de l'angle $\widehat{B A C}$ sont concourantes.
|
Pendant toute la preuve on va utiliser les résultats du lemme qui suit. On commence d'abord par une notation.
Soit ABC un triangle, on note $\Omega$ le cercle circonscrit à $A B C$, on note également $\omega$ le cercle tangent à (AB), (AC) et intérieurement à $\Omega$, on dit que ce cercle est le cercle mixtilinéaire (intérieur) du triangle $A B C$ depuis $A$.
Lemme 3. Soit ABC un triangle, on note I le centre de son cercle inscrit, on note de de plus, $\Omega$ le cercle circonscrit à ABC ainsi que $\omega$ le cercle mixtilinéaire depuis A . On note T (resp. D et F) le point de tangence de $\omega$ avec $\Omega$ (resp. (AC) et (AB)) ainsi que N le pôle nord (le milieu de l'arc BC qui contient A). Sous ces hypothèses et notation on sait alors que I est le milieu du segment [DF] et que les points T, I et N sont alignés.
|
{
"exam": "French_envois",
"problem_label": "18",
"problem_match": "\nExercice 18.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-1.jsonl",
"solution_match": "## Solution de l'exercice 18",
"tier": "T2",
"year": null
}
|
Let $ABC$ be a triangle and $\omega$ its incircle, with the points of tangency on $[BC]$, $[CA]$, and $[AB]$ being $D$, $E$, and $F$ respectively. Let $\Omega$ be the circle tangent to $\omega$ and passing through $B$ and $C$, and let $T$ be the point of tangency of these two circles. Let $X$ and $Y$ be the midpoints of segments $[DE]$ and $[DF]$. Let $U$ and $V$ be the second points of intersection of lines $(TX)$ and $(TY)$ with $\Omega$. Also, let $Z$ and $W$ be the second points of intersection of lines $(AB)$ and $(AC)$ with $\Omega$. Show that $(ZU)$, $(WV)$, $(XY)$, and the angle bisector of $\widehat{BAC}$ are concurrent.
|
Let $E$ and $W$ be the midpoints of the arcs $AC$ and $AB$, respectively. According to the "bocal lemma," we know that the points $W$, $D$, and $T$ are collinear, as well as the points $T$, $F$, and $E$. Furthermore, according to the "South Pole theorem," the points $B$, $I$, and $E$ are collinear, as well as the points $C$, $I$, and $W$. We can then apply Pascal's theorem to the hexagon $BETWCA$ to conclude that the points $D$, $I$, and $F$ are collinear. Since the axis $(AI)$ is an axis of symmetry that exchanges $(AB)$ with $(AC)$ and $\omega$ with itself, we can deduce that the point $I$ is indeed the midpoint of the segment $[EF]$.
For the second part of the lemma, let $\beta$ and $\gamma$ be the angles at $B$ and $C$, respectively, in the triangle $ABC$. In the triangle $TDF$, we observe that the line $(TI)$ is a median according to the first part of the lemma. Moreover, by classical properties of the construction of the symmedian (see, for example, Alexander Semenov's course at the Valbonne 2022 workshop or Thomas Budzinski's course at Montpellier 2016), the line $(TA)$ is the symmedian. Thus, $\widehat{\mathrm{ITC}} = \widehat{\mathrm{ITF}} + \widehat{\mathrm{FTC}} = \widehat{\mathrm{ATD}} + \widehat{\mathrm{FTC}} = \gamma / 2 + \beta / 2 = \widehat{\mathrm{BTI}}$, where the last equality follows by symmetry. This concludes the second part of the lemma.
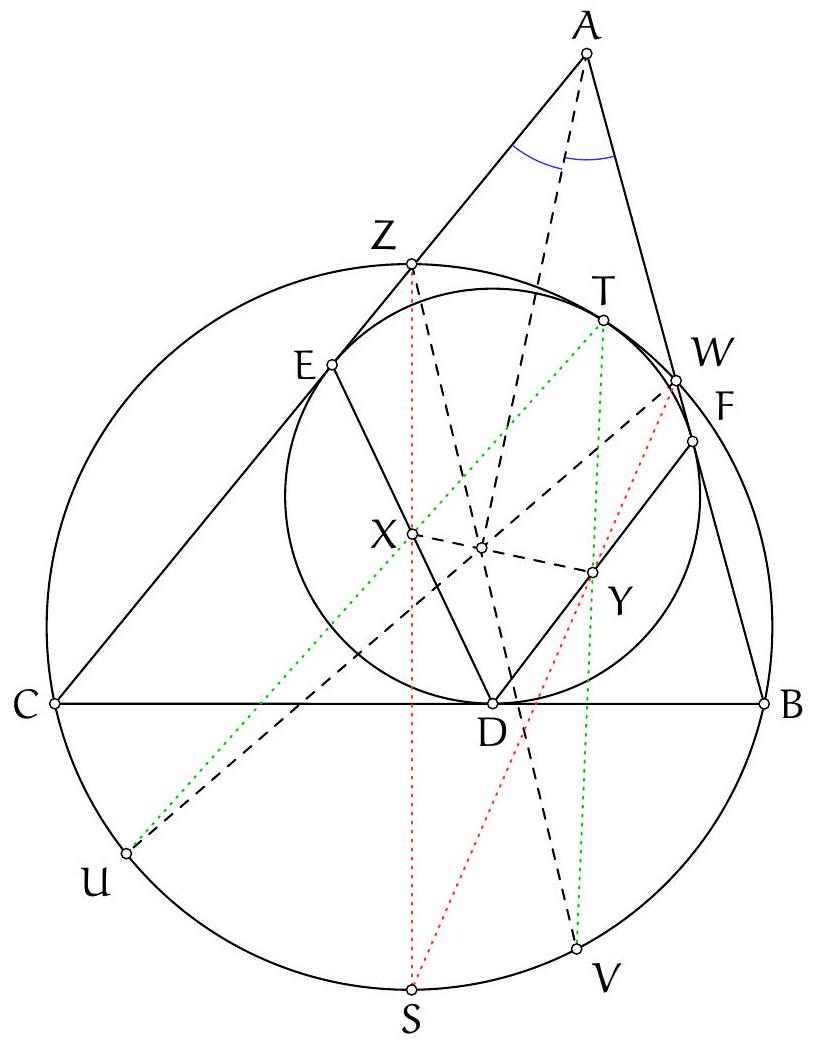
We can now proceed to the proof of the exercise.
Considering the triangle $ZBC$, we note that $\omega$ is the mixtilinear incircle from $B$. Thus, according to Lemma 3, the point $Y$ is the incenter of this triangle, and the line $(TY)$ passes through the North Pole from $B$ in $ZBC$, which is the point $V$ in the statement. Similarly, the point $X$ is the incenter of the triangle $WBC$, and $U$ is the midpoint of the arc $BW$ that contains $C$. This shows, in particular, that the line $(WW)$ bisects the exterior angle $\widehat{AWZ}$, and similarly, the line $(ZU)$ is the exterior bisector of the angle $\widehat{WZA}$. Thus, it is now clear that in the triangle $AWZ$, the lines $(WV)$, $(ZU)$, and the angle bisector from $A$ are concurrent at a point $P$.
We also want to show that the line $(YZ)$ passes through this point $P$. To do this, we want to apply Pascal's theorem to the hexagon $TUZSWV$, where $S$ denotes the midpoint of the arc $BC$ on the circle $\Omega$. But the line $(ZY)$ is indeed the angle bisector of $\widehat{\mathrm{BZC}}$ since $Y$ is the incenter of the triangle $ZBC$. Similarly, the line $(WX)$ passes through the point $S$. We can then conclude by applying Pascal's theorem.
Comment from the graders: Students who approached the problem almost all solved it. Those who noticed the mixtilinear circle in the figure came up with a much shorter proof. It is recommended to state the properties of the mixtilinear circle used in the proof to make the solution more pleasant to read.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $\omega$ son cercle inscrit dont les points de tangence sur [BC], [CA] et $[A B]$ sont respectivement $D$, $E$ et $F$. On note $\Omega$ le cercle tangent à $\omega$ et passant par $B$ et $C$ et $T$ le point de tangence de ces deux cercles. On note $X$ et $Y$ les milieux des segments [DE] et [DF]. On note $U$ et $V$ les seconds points d'intersection des droites (TX) et (TY) avec $\Omega$. On note également $Z$ et $W$ les seconds points d'intersection des droites (AB) et (AC) avec $\Omega$. Montrer que (ZU), (WV), (XY) et la bissectrice de l'angle $\widehat{B A C}$ sont concourantes.
|
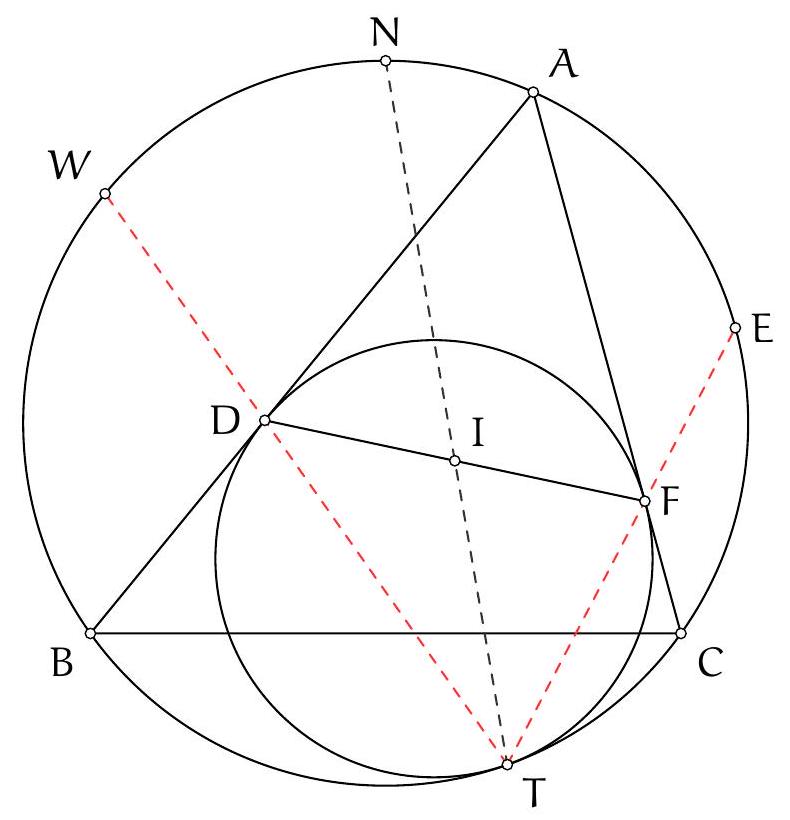
Notons E et $W$ les milieux respectifs des arcs $A C$ et $A B$. D'après le lemme du bocal on sait que les points $W$, D et T sont alignés ainsi que les points $\mathrm{T}, \mathrm{F}$ et E . On sait de plus d'après le théorème du pôle sud que les points $B$, I et $E$ sont alignés ainsi que les points $C$, $I$ et $W$. On peut alors appliquer le théorème de Pascal à l'hexagone BETWCA pour conclure que les points $D$, I et $F$ sont alignés. Comme l'axe (AI) est un axe de symétrie qui échange $(A B)$ avec $(A C)$ et $\omega$ avec lui-même on peut en déduire que le point I est bien le milieu du segment [EF].
Pour la deuxième partie du lemme, on note $\beta$ et $\gamma$ les angles en $B$ et $C$ respectivement dans le triangle $A B C$. Dans le triangle TDF on remarque que la droite (TI) est une médiane d'après la première partie du lemme. De plus, par des propriétés classique de la construction de la symédiane (voir par exemple le cours d'Alexander Semenov au stage de Valbonne 2022 ou bien celui de Thomas Budzinski à Montpellier
2016) la droite (TA) est la symédiane. Ainsi, $\widehat{\mathrm{ITC}}=\widehat{\mathrm{ITF}}+\widehat{\mathrm{FTC}}=\widehat{\mathrm{ATD}}+\widehat{\mathrm{FTC}}=\gamma / 2+\beta / 2=\widehat{\mathrm{BTI}}$ où la dernière égalité découle par symétrie. Cela conclut la deuxième partie du lemme.

On peut maintenant passer à la preuve de l'exercice.
En se plaçant dans le triangle $Z B C$ on remarque que $\omega$ est le cercle mixtiliniéaire depuis B. Ainsi, d'après le Lemme 3, le point $Y$ est le centre du cercle inscrit de ce triangle et de plus, la droite (TY) passe par le pôle Nord issu de $B$ dans $Z B C$, ce point est le point $V$ de l'énoncé. De la même manière le point $X$ est le centre du cercle inscrit du triangle WBC et $U$ est le milieu de l'arc BW qui contient $C$. Cela montre en particulier que la droite ( $W \mathrm{~W}$ ) bissecte extérieurement l'angle $\widehat{A W Z}$, de la même manière la droite (ZU) est la bissectrice extérieure de l'angle $\widehat{W Z A}$. Ainsi il est maintenant clair que dans le triangle $A W Z$ les droites (WV), (ZU) et la bissectrice issue de $A$ sont concourantes en un point $P$.
On veut également démontrer que la droite ( $Y Z$ ) passe par ce point $P$. On veut pour cela appliquer le théorème de Pascal à l'hexagone TUZSWV, où $S$ dénote le milieu de l'arc $B C$ sur le cercle $\Omega$. Mais la droite (ZY) est bien la bissectrice de l'angle $\widehat{\mathrm{BZC}}$ comme $Y$ est le centre du cercle inscrit au triangle ZBC. De la même manière la droite $(W X)$ passe bien par le point $S$, on peut alors conclure en appliquant le théorème de Pascal.
Commentaire des correcteurs: Les élèves ayant abordé le problème ont presque tous résolu le problème. Ceux qui ont remarqué le cercle mixtilinéaires de la figure s'en sont sortis avec une preuve beaucoup plus courte. Il est conseillé d'énoncer les propriétés du cercle mixtilinéaires utilisées lors de la preuve pour rendre une copie plus agréable à lire.
|
{
"exam": "French_envois",
"problem_label": "18",
"problem_match": "\nExercice 18.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-1.jsonl",
"solution_match": "## Démonstration.",
"tier": "T2",
"year": null
}
|
Let x, y be strictly positive real numbers. Show that
$$
\left(x+\frac{2}{y}\right)\left(\frac{y}{x}+2\right) \geqslant 8
$$
When do we have equality?
|
In this exercise, we are dealing with strictly positive terms whose product $x \cdot \frac{2}{y} \cdot \frac{y}{x} \cdot 2=4$ is known. We think of using the arithmetic-geometric mean inequality, which gives us both
$$
x+\frac{2}{y} \geqslant 2 \sqrt{\frac{2 x}{y}}
$$
and
$$
\frac{y}{x}+2 \geqslant 2 \sqrt{\frac{2 y}{x}}
$$
The two inequalities only involve positive terms, so we can combine them to get
$$
\left(x+\frac{2}{y}\right)\left(\frac{y}{x}+2\right) \geqslant 2 \sqrt{\frac{2 x}{y}}\left(\frac{y}{x}+2\right) \geqslant 4 \sqrt{\frac{2 x \cdot 2 y}{y x}}=8 .
$$
Let's find the cases of equality. For this, we need equality in both of the previous inequalities. Since $\frac{y}{x}+2>0$, we have equality in the first inequality if and only if we have equality in the first application of the arithmetic-geometric mean inequality, i.e., if $x=\frac{2}{y}$, or $x y=2$.
Similarly, to have equality in the second inequality, we need $\frac{y}{x}=2$. By multiplying the two equations together, we find $y^{2}=4$, so $y=2$ since $y$ is positive. Then, we get $x=1$. Conversely, $x=1$ and $y=2$ is a case of equality, and it is the only one.
Graders' comments: While the problem was generally well solved, here are some areas for improvement:
- Many students do not know the AM-GM inequality and reprove it.
- The case of equality is often forgotten.
- Many students expand the expression before applying the AM-GM inequality, rather than applying it directly to the terms in parentheses.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soient x, y deux réels strictement positifs. Montrer que
$$
\left(x+\frac{2}{y}\right)\left(\frac{y}{x}+2\right) \geqslant 8
$$
Quand a-t-on égalité?
|
Dans cet exercice, on a affaire à des termes strictement positifs dont le produit $x \cdot \frac{2}{y} \cdot \frac{y}{x} \cdot 2=4$ est connu. On pense donc à utiliser l'inégalité arithmético-géométrique qui donne à la fois
$$
x+\frac{2}{y} \geqslant 2 \sqrt{\frac{2 x}{y}}
$$
et
$$
\frac{y}{x}+2 \geqslant 2 \sqrt{\frac{2 y}{x}}
$$
Les deux inégalités ne font intervenir que des termes positifs donc on peut les combiner pour avoir
$$
\left(x+\frac{2}{y}\right)\left(\frac{y}{x}+2\right) \geqslant 2 \sqrt{\frac{2 x}{y}}\left(\frac{y}{x}+2\right) \geqslant 4 \sqrt{\frac{2 x \cdot 2 y}{y x}}=8 .
$$
Cherchons les cas d'égalité. Pour ceci, il faut avoir égalité dans les deux inégalités précédentes. Comme $\frac{y}{x}+2>0$, on a égalité dans la première égalité si et seulement si on a égalité dans la première application de l'inégalité arithmético-géométrique, c'est-à-dire si $x=\frac{2}{y}$, soit $x y=2$.
De même, pour avoir égalité dans la deuxième inégalité, il faut que $\frac{y}{x}=2$. En multipliant les deux équations ensemble, on trouve $y^{2}=4$, donc $y=2$ car $y$ est positif. Ensuite, on obtient $x=1$. Réciproquement, $x=1$ et $y=2$ est un cas d'égalité, c'est le seul.
Commentaire des correcteurs : Si nle problème a été bien réussi dans l'ensemble, voilà quelques pistes de progression :
- Beaucoup d'élèves ne connaissent pas l'IAG et la redémontrent.
- Le cas d'égalité a souvent été oublié.
- Beaucoup d'élèves développent l'expression avant d'y appliquer l'IAG, plutôt que de l'appliquer directement dans les parenthèses.
|
{
"exam": "French_envois",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-2.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T2",
"year": null
}
|
Find all real numbers $x, y$ such that
$$
x(x-2 y)+y(2 y-4)+4=0
$$
|
Let's develop the equation to obtain
$$
x^{2}-2 x y+2 y^{2}-4 y+4=0 .
$$
The terms $x^{2}-2 x y$ remind us of the remarkable identity $x^{2}-2 x y+y^{2}=(x-y)^{2}$. We then separate the $2 y^{2}$ into $y^{2}+y^{2}$ to write
$$
(x-y)^{2}+y^{2}-4 y+4=0
$$
But we then recognize a second remarkable identity $y^{2}-4 y+4=(y-2)^{2}$. By factoring, this gives
$$
(x-y)^{2}+(y-2)^{2}=0
$$
However, the sum of squares of real numbers is necessarily positive, and can only be zero if both squares are zero. Thus, if $x$ and $y$ are solutions to the equation, we have both
$$
x-y=0 \quad \text { and } \quad y-2=0
$$
Therefore, the only possible solution to the equation is $x=y=2$. We can verify reciprocally that this is indeed a solution, so it is the only one.
Comment from the graders: Students generally found the solution using the method presented in the solution. Unfortunately, most forget to verify that the solution they found is indeed a solution to the problem. Indeed, it is sufficient that at one step, the equivalence is not justified for the verification to be necessary. Some considered the expression as a polynomial in $x$, whose roots need to be found, which only exist for certain values of $y$.
|
x=y=2
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Trouver tous les réels $x, y$ tels que
$$
x(x-2 y)+y(2 y-4)+4=0
$$
|
Développons l'équation pour obtenir
$$
x^{2}-2 x y+2 y^{2}-4 y+4=0 .
$$
Les termes $x^{2}-2 x y$ nous font penser à l'identité remarquable $x^{2}-2 x y+y^{2}=(x-y)^{2}$. On sépare alors le $2 y^{2}$ en $y^{2}+y^{2}$ pour écrire
$$
(x-y)^{2}+y^{2}-4 y+4=0
$$
Mais on reconnait alors une deuxième identité remarquable $y^{2}-4 y+4=(y-2)^{2}$. En factorisant, ceci donne
$$
(x-y)^{2}+(y-2)^{2}=0
$$
Or, une somme de carrés de nombre réels est forcément positive, et ne peut être nulle que si les deux carrés sont tous les deux nuls. Ainsi, si $x$ et $y$ sont solution de l'équation, on a à la fois
$$
x-y=0 \quad \text { et } \quad y-2=0
$$
Ainsi, l'unique solution possible de l'équation est $x=y=2$. On peut vérifier réciproquement que ceci est bien une solution, c'est donc la seule.
Commentaire des correcteurs : Les élèves ont en général trouvé la solution avec la méthode présentée dans le corrigé. Malheureusement, la plupart oublient de vérifier que la solution qu'ils ont trouvé est bien solution du problème. Il suffit en effet qu'à une seule étape, l'équivalence ne soit pas justifiée pour que la vérification soit nécessaire. Certains ont considéré l'expression comme un polynôme en $x$, dont il s'agit de trouver les racines, celles-ci n'existant que pour certianes valeurs de y .
|
{
"exam": "French_envois",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-2.jsonl",
"solution_match": "## Solution de l'exercice 2",
"tier": "T2",
"year": null
}
|
For a real number $x$, we denote $\lfloor x\rfloor$ as the greatest integer less than or equal to $x$ (for example, $\lfloor 2.7\rfloor=2, \lfloor\pi\rfloor=3$ and $\lfloor-1.5\rfloor=-2$).
Let $a, b$ be two real numbers such that
$$
a+\lfloor a\rfloor=b+\lfloor b\rfloor .
$$
Show that $a=b$.
|
Suppose by contradiction $a \neq b$. By symmetry (i.e., $a$ and $b$ play the same role), we can assume $a < b$. We then have
$$
\lfloor a\rfloor \leqslant a < b
$$
so $\lfloor a\rfloor$ is an integer less than or equal to $b$, and thus by definition we have $\lfloor a\rfloor \leqslant \lfloor b\rfloor$. Adding $a < b$, we get
$$
a + \lfloor a\rfloor < b + \lfloor b\rfloor
$$
which is absurd. Therefore, we must have $a = b$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Pour un réel $x$, on note $\lfloor x\rfloor$ le plus grand entier relatif inférieur ou égal à $x$ (par exemple, $\lfloor 2,7\rfloor=2,\lfloor\pi\rfloor=3$ et $\lfloor-1,5\rfloor=-2)$.
Soient $a, b$ deux réels tels que
$$
a+\lfloor a\rfloor=b+\lfloor b\rfloor .
$$
Montrer que $a=b$.
|
Supposons par l'absurde $a \neq b$. Par symétrie (c'est-à-dire que $a$ et $b$ jouent le même rôle), on peut supposer $a<b$. On a alors
$$
\lfloor a\rfloor \leqslant a<b
$$
donc $\lfloor a\rfloor$ est un entier relatif inférieur ou égal à $b$, et donc par définition on a $\lfloor a\rfloor \leqslant\lfloor b\rfloor$. En ajoutant $a<b$, on obtient alors
$$
a+\lfloor a\rfloor<b+\lfloor b\rfloor
$$
ce est absurde. On a donc bien $a=b$.
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-2.jsonl",
"solution_match": "## Solution de l'exercice 3",
"tier": "T2",
"year": null
}
|
For a real number $x$, we denote $\lfloor x\rfloor$ as the greatest integer less than or equal to $x$ (for example, $\lfloor 2.7\rfloor=2, \lfloor\pi\rfloor=3$ and $\lfloor-1.5\rfloor=-2$).
Let $a, b$ be two real numbers such that
$$
a+\lfloor a\rfloor=b+\lfloor b\rfloor .
$$
Show that $a=b$.
|
For a real number $x$, let $\{x\}$ denote the fractional part of $x$ given by $\{x\}=x-\lfloor x\rfloor$. This is a real number between 0 inclusive and 1 exclusive.
We then rewrite the equation by setting $a=\lfloor a\rfloor+\{a\}$ and $b=\lfloor b\rfloor+\{b\}$ to get
$$
2\lfloor a\rfloor+\{a\}=2\lfloor b\rfloor+\{b\}.
$$
Rearranging the terms, we obtain
$$
2\lfloor a\rfloor-2\lfloor\mathbf{b}\rfloor=\{\mathbf{b}\}-\{\mathbf{a}\}
$$
But we have
$$
\{b\}-\{a\} \leqslant\{b\}<1
$$
and
$$
\{b\}-\{a\} \geqslant-\{a\}>-1
$$
However, according to the equation above, $\{b\}-\{a\}$ is an integer, and it must therefore be zero. Thus, we have $\{b\}-\{a\}=0$, which then gives $2\lfloor a\rfloor-2\lfloor b\rfloor=0$.
Hence, we have
$$
\lfloor a\rfloor=\lfloor b\rfloor \text { and } \quad\{a\}=\{b\}
$$
so
$$
a=\lfloor a\rfloor+\{a\}=\lfloor b\rfloor+\{b\}=b
$$
Graders' comments: The exercise was very well done, with some diversity in approaches. A few points are lost due to carelessness. Some students seem confused about how the floor function works with negatives.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Pour un réel $x$, on note $\lfloor x\rfloor$ le plus grand entier relatif inférieur ou égal à $x$ (par exemple, $\lfloor 2,7\rfloor=2,\lfloor\pi\rfloor=3$ et $\lfloor-1,5\rfloor=-2)$.
Soient $a, b$ deux réels tels que
$$
a+\lfloor a\rfloor=b+\lfloor b\rfloor .
$$
Montrer que $a=b$.
|
Pour un réel $x$, posons $\{x\}$ la partie fractionnaire de $x$ donnée par $\{x\}=x-\lfloor x\rfloor$. C'est un nombre réel compris entre 0 inclus et 1 exclus.
On réécrit alors l'équation en posant $a=\lfloor a\rfloor+\{a\}$ et $b=\lfloor b\rfloor+\{b\}$ pour avoir
$$
2\lfloor a\rfloor+\{a\}=2\lfloor b\rfloor+\{b\} .
$$
En réarrangeant les termes, on obtient
$$
2\lfloor a\rfloor-2\lfloor\mathbf{b}\rfloor=\{\mathbf{b}\}-\{\mathbf{a}\}
$$
Mais on a
$$
\{b\}-\{a\} \leqslant\{b\}<1
$$
et
$$
\{b\}-\{a\} \geqslant-\{a\}>-1
$$
Mais d'après l'égalité au-dessus, $\{b\}-\{a\}$ est un entier, et il est donc nul. On a donc $\{b\}-\{a\}=0$, ce qui donne ensuite $2\lfloor a\rfloor-2\lfloor b\rfloor=0$.
Ainsi, on a
$$
\lfloor a\rfloor=\lfloor b\rfloor \text { et } \quad\{a\}=\{b\}
$$
donc
$$
a=\lfloor a\rfloor+\{a\}=\lfloor b\rfloor+\{b\}=b
$$
Commentaire des correcteurs : Exercice très bien réussi, avec une certaine diversité dans les approches. Quelques rares points sont perdus par étourderie. Certains élèves semblent confus sur le fonctionnement de la partie entière dans les négatifs.
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-2.jsonl",
"solution_match": "## Solution alternative",
"tier": "T2",
"year": null
}
|
Let $\boldsymbol{n}$ be a strictly positive integer and $x \geqslant \mathrm{n}$ a real number. Show that $x+\frac{\mathfrak{n}}{\boldsymbol{x}} \geqslant \mathrm{n}+1$ and provide the cases of equality.
|
The real $x$ is strictly positive, so we can multiply the equation by $x$ to get that the equation is equivalent to
$$
x^{2}+n \geqslant(n+1) x
$$
which gives, by rearranging the terms,
$$
x^{2}-(n+1) x+n \geqslant 0
$$
We then recognize a factorization
$$
(x-n)(x-1) \geqslant 0
$$
But this is true because $x \geqslant n$ and $x \geqslant 1$. Equality holds when $x=n$ or $x=1$. But if $x=1$, then $n=1$ and $x=n$. Thus, in all cases, the only case of equality is $x=n$.
|
x=n
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $\boldsymbol{n}$ un entier strictement positif et $x \geqslant \mathrm{n}$ un réel. Montrer que $x+\frac{\mathfrak{n}}{\boldsymbol{x}} \geqslant \mathrm{n}+1$ et donner les cas d'égalité.
|
Le réel $x$ est strictement positif donc on peut multiplier l'équation par $x$ pour avoir que l'équation est équivalente à
$$
x^{2}+n \geqslant(n+1) x
$$
ce qui donne, en réarrangeant les termes,
$$
x^{2}-(n+1) x+n \geqslant 0
$$
On reconnait alors une factorisation
$$
(x-n)(x-1) \geqslant 0
$$
Mais ceci est vrai car $x \geqslant \mathrm{n}$ et $x \geqslant 1$.
On a égalité lorsque $x=n$ ou $x=1$. Mais si $x=1$, alors $n=1$ et $x=n$. Ainsi, dans tous les cas, le seul cas d'égalité est $x=n$.
|
{
"exam": "French_envois",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-2.jsonl",
"solution_match": "## Solution de l'exercice 4",
"tier": "T2",
"year": null
}
|
Let $\boldsymbol{n}$ be a strictly positive integer and $x \geqslant \mathrm{n}$ a real number. Show that $x+\frac{\mathfrak{n}}{\boldsymbol{x}} \geqslant \mathrm{n}+1$ and provide the cases of equality.
|
From exercise 4
We start from the expanded equation $x^{2}-(n+1) x+n \geqslant 0$.
The condition $x \geqslant n$ is quite unnatural, so we prefer conditions of the type $t \geqslant 0$. We set $x=n+t$ with $t \geqslant 0$. The equation then rewrites as
$$
n^{2}+2 n t+t^{2}-(n+1)(n+t)+n \geqslant 0
$$
or equivalently
$$
t^{2}+(n-1) t \geqslant 0
$$
But this new equation is clearly true since $t \geqslant 0$ and $n \geqslant 1$. Moreover, we have equality if and only if $t=0$, or equivalently $x=n$.
Comment from the graders: The problem was well handled by the students, almost all the solutions submitted were complete and followed the same pattern as the corrected solutions. However, most of the papers were penalized for lack of justification, particularly in justifying signs. It is important to remember that when multiplying or dividing an inequality by a quantity, one must ensure the sign of that quantity: if it is strictly positive, it preserves the direction of the inequality; if it is strictly negative, it reverses the direction of the inequality; and if one multiplies by a zero quantity, there is no equivalence. This is a detail of utmost importance. Regarding the case of equality, several students forgot to address it, and others forgot the condition $x \geqslant n$, so they considered that for any $n \in \mathbb{N}^{*}, x=1$ was a case of equality. This was true only for $n=1$, and thus it was already counted in the case $x=n$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $\boldsymbol{n}$ un entier strictement positif et $x \geqslant \mathrm{n}$ un réel. Montrer que $x+\frac{\mathfrak{n}}{\boldsymbol{x}} \geqslant \mathrm{n}+1$ et donner les cas d'égalité.
|
de l'exercice 4
On repart de l'équation développée $x^{2}-(n+1) x+n \geqslant 0$.
La condition $x \geqslant n$ est très peu naturelle, on préfère des conditions de type $t \geqslant 0$. On pose donc $x=n+t$ $\operatorname{avec} t \geqslant 0$. L'équation se réécrit alors
$$
n^{2}+2 n t+t^{2}-(n+1)(n+t)+n \geqslant 0
$$
ou encore
$$
t^{2}+(n-1) t \geqslant 0
$$
Mais cette nouvelle équation est clairement vraie car $t \geqslant 0$ et $n \geqslant 1$. De plus, on a égalité si et seulement si $t=0$, ou encore $x=n$.
Commentaire des correcteurs : Le problème a été bien réussi par les élèves, les solutions rendues étaient presque toutes abouties et suivaient le même schéma que les solutions du corrigé. En revanche, la plupart de ses copies ont été pénalisées pour des manques de justifications, notamment des justifications de signes. On rappelle que lorsqu'on multiplie ou divise une inégalité par une quantité, il faut s'assurer du signe de cette quantité : si elle est strictement positive, ça conserve le sens de l'inégalité, si elle est strictement négative, ça change le sens de l'inégalité, et si on multiplie par une quantité nulle, on n'a pas équivalence. C'est donc un détail qui a toute son importance. En ce qui concerne le cas d'égalité, plusieurs élèves ont oublié de le traiter, et d'autres ont oublié la condition $x \geqslant \mathrm{n}$, de sorte qu'ils considéraient que pour tout $\mathrm{n} \in \mathbb{N}^{*}, x=1$ était un cas d'égalité. Ce n'était vrai que pour $\mathrm{n}=1$, et donc c'était déjà compté dans le cas $x=\mathrm{n}$.
|
{
"exam": "French_envois",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-2.jsonl",
"solution_match": "## Solution alternative",
"tier": "T2",
"year": null
}
|
Find all triplets of non-negative real numbers $(\mathrm{a}, \mathrm{b}, \mathrm{c})$ such that
$$
\left\{\begin{array}{l}
a^{2}+a b=c \\
b^{2}+b c=a \\
c^{2}+c a=b
\end{array}\right.
$$
|
First, assume one of the reals is zero, without loss of generality $a=0$. Then the first equation gives $\mathrm{c}=0$ and the last equation gives $\mathrm{b}=0$. Conversely, the triplet $\mathrm{a}=\mathrm{b}=\mathrm{c}=0$ is indeed a solution. Now assume that the three reals are all non-zero.
Suppose now that two of the reals are equal, without loss of generality $\mathrm{a}=\mathrm{b}$. We can then subtract the second and third equations to get $b^{2}-c^{2}=0$. Since $b$ and $c$ are both positive, we have $a=b=c$. In the first equation, we then have $2 a^{2}=a$. But $a$ is non-zero, so we can divide by $2 a$ to get $a=\frac{1}{2}$. Conversely, the triplet $a=b=c=\frac{1}{2}$ is indeed a solution. We now assume that the three reals are pairwise distinct.
Multiply the equations to obtain
$$
a(a+b) b(b+c) c(c+a)=a b c
$$
We have assumed previously that the reals are all non-zero, so we can divide by $abc$ to get
$$
(a+b)(b+c)(c+a)=1
$$
By subtracting the first two equations, we get $a^{2}-b^{2}+b a-b c=c-a$ which factors to
$$
(a-b)(a+b)=(c-a)(b+1)
$$
Similarly, by subtracting the second and third equations, and the third and first equations, we get
$$
\left\{\begin{array}{l}
(b-c)(b+c)=(a-b)(c+1) \\
(c-a)(c+a)=(b-c)(a+1)
\end{array}\right.
$$
By multiplying these three equations and dividing by $(a-b)(b-c)(c-a)$ on both sides (which is non-zero since we assumed $a, b, c$ are pairwise distinct), we get
$$
(1+a)(1+b)(1+c)=(a+b)(b+c)(c+a)
$$
But we have previously shown that the second term equals 1, which is absurd because
$$
(1+a)(1+b)(1+c)>1 \cdot 1 \cdot 1=1
$$
Thus, the only solutions are those found at the beginning of the solution, namely $\mathrm{a}=\mathrm{b}=\mathrm{c}=0$ and $\mathrm{a}=\mathrm{b}=\mathrm{c}=\frac{1}{2}$.
Graders' comments: The problem was approached and fairly well executed. However, several recurring errors are noted:
- Some obtain the two solution triplets but do not verify that they are solutions. When reasoning with implications, it is not at all certain that the found triplets are solutions.
- Many assume, for example, $a>b>c$. Two issues: it is forgotten that multiple variables can be equal. But more importantly, to do this, the system must be symmetric, meaning that if two variables, for example $a$ and $b$, are swapped, the system does not change. This is not the case at all: the system is completely altered.
|
a=b=c=0 \text{ or } a=b=c=\frac{1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Trouver tous les triplets de réels positifs ou nuls ( $\mathrm{a}, \mathrm{b}, \mathrm{c})$ tels que
$$
\left\{\begin{array}{l}
a^{2}+a b=c \\
b^{2}+b c=a \\
c^{2}+c a=b
\end{array}\right.
$$
|
Supposons d'abord qu'un des réels est nul, sans perte de généralité $a=0$. Alors la première équation donne $\mathrm{c}=0$ et la dernière équation donne $\mathrm{b}=0$. Réciproquement, le triplet $\mathrm{a}=\mathrm{b}=\mathrm{c}=0$ est bien solution, on suppose à présent que les trois réels sont non nuls.
Supposons maintenant que deux des réels soient égaux, sans perte de généralité $\mathrm{a}=\mathrm{b}$. On peut alors soustraire les deuxième et troisième équations pour avoir $b^{2}-c^{2}=0$. Comme $b$ et $c$ sont tous les deux positifs, on a donc $a=b=c$. Dans la première équation, on a alors $2 a^{2}=a$. Mais $a$ est non nul donc on peut diviser par $2 a$ pour avoir $a=\frac{1}{2}$. Réciproquement, le triplet $a=b=c=\frac{1}{2}$ est bien solution. On suppose désormais que les trois réels sont deux à deux distincts.
Faisons le produit des équations pour obtenir
$$
a(a+b) b(b+c) c(c+a)=a b c
$$
On a supposé précédememnt que les réels étaient tous non nuls donc on peut diviser par abc pour avoir
$$
(a+b)(b+c)(c+a)=1
$$
En faisant la différence des deux premières équations, on obtient $a^{2}-b^{2}+b a-b c=c-a$ ce qui se factorise en
$$
(a-b)(a+b)=(c-a)(b+1)
$$
En faisant de même avec les deuxième et troisième lignes puis avec les troisième et première lignes, on obtient en plus
$$
\left\{\begin{array}{l}
(b-c)(b+c)=(a-b)(c+1) \\
(c-a)(c+a)=(b-c)(a+1)
\end{array}\right.
$$
En faisant le produit de ces trois équations et en divisant par $(a-b)(b-c)(c-a)$ des deux côtés (qui est non nul car on a supposé $a, b, c$ deux à deux distincts), on obtient
$$
(1+a)(1+b)(1+c)=(a+b)(b+c)(c+a)
$$
Mais on a montré précédemment que ce deuxième terme vaut 1 , ce qui est absurde car
$$
(1+a)(1+b)(1+c)>1 \cdot 1 \cdot 1=1
$$
Ainsi, les seules solutions sont celles trouvées au début de la solution, c'est-à-dire $\mathrm{a}=\mathrm{b}=\mathrm{c}=0$ et $\mathrm{a}=\mathrm{b}=\mathrm{c}=\frac{1}{2}$.
Commentaire des correcteurs : Le problème a été abordé et plutôt bien réussi. Néanmoins, plusieurs erreurs sont récurrentes :
- Certains obtiennent les deux triplets solutions, mais ne vérifient pas qu'ils sont solution. Quand on raisonne à coup d'implication, il n'est pas du tout sûr que les triplets trouvés soient solution.
- Beaucoup supposent par exemple $a>b>c$. Deux problèmes : on oublie que plusieurs variables peuvent être égales. Mais surtout pour faire cela, il faut que le système soit symétrique : c'est-àdire que si on inverse deux variables, par exemple $a$ et $b$, alors le système ne change pas. Ce n'est pas du tout le cas : le système est complètement changé.
|
{
"exam": "French_envois",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-2.jsonl",
"solution_match": "## Solution de l'exercice 5",
"tier": "T2",
"year": null
}
|
Show that for all strictly positive real numbers $\mathrm{a}, \mathrm{b}, \mathrm{c}$:
$$
\frac{b c}{a^{2}+2 b c}+\frac{c a}{b^{2}+2 c a}+\frac{a b}{c^{2}+2 a b} \leqslant 1 \leqslant \frac{a^{2}}{a^{2}+2 b c}+\frac{b^{2}}{b^{2}+2 c a}+\frac{c^{2}}{c^{2}+2 a b}
$$
|
Let's start by solving one of the inequalities. In this problem, the simplest inequality to study is the one on the right. We apply the arithmetic-geometric inequality to the denominators to get $2 \mathrm{bc} \leqslant \mathrm{b}^{2}+\mathrm{c}^{2}$ for example, which gives
$$
\frac{a^{2}}{a^{2}+2 b c}+\frac{b^{2}}{b^{2}+2 c a}+\frac{c^{2}}{c^{2}+2 a b} \geqslant \frac{a^{2}}{a^{2}+b^{2}+c^{2}}+\frac{b^{2}}{a^{2}+b^{2}+c^{2}}+\frac{c^{2}}{a^{2}+b^{2}+c^{2}}=1 .
$$
For the left side, we notice that it looks a lot like the right side. Let's call $G$ and $D$ the left and right sides of the equation, respectively. We then have
$$
\begin{gathered}
\mathrm{G}+2 \cdot \mathrm{D}=\frac{\mathrm{a}^{2}}{\mathrm{a}^{2}+2 \mathrm{bc}}+\frac{\mathrm{b}^{2}}{\mathrm{~b}^{2}+2 \mathrm{ca}}+\frac{\mathrm{c}^{2}}{\mathrm{c}^{2}+2 \mathrm{ab}}+\frac{2 \mathrm{bc}}{\mathrm{a}^{2}+2 \mathrm{bc}}+\frac{2 c a}{\mathrm{~b}^{2}+2 \mathrm{ca}}+\frac{2 a b}{\mathrm{c}^{2}+2 a b} . \\
\frac{\mathrm{a}^{2}+2 \mathrm{bc}}{\mathrm{a}^{2}+2 b c}+\frac{b^{2}+2 c a}{b^{2}+2 c a}+\frac{c^{2}+2 a b}{c^{2}+2 a b}=3 .
\end{gathered}
$$
We therefore have
$$
\mathrm{G}=\frac{1}{2}(3-\mathrm{D}) \leqslant \frac{1}{2}(3-1)=1
$$
by the right inequality that we have shown previously.
Comment from the graders: The exercise was well done. A number of students found only one of the two inequalities: it is important to submit everything that has been found, even if only half of the exercise has been solved. A number of students simply put everything over a common denominator and then proved the inequality, which was not very elegant but worked well.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Montrer que pour tous réels $\mathrm{a}, \mathrm{b}, \mathrm{c}$ strictement positifs:
$$
\frac{b c}{a^{2}+2 b c}+\frac{c a}{b^{2}+2 c a}+\frac{a b}{c^{2}+2 a b} \leqslant 1 \leqslant \frac{a^{2}}{a^{2}+2 b c}+\frac{b^{2}}{b^{2}+2 c a}+\frac{c^{2}}{c^{2}+2 a b}
$$
|
Commençons par résoudre une des inégalités. Dans ce problème, l'inégalité la plus simple à étudier est celle de droite. On applique l'inégalité arithmético-géométrique sur les dénominateurs pour avoir $2 \mathrm{bc} \leqslant \mathrm{b}^{2}+\mathrm{c}^{2}$ par exemple, ce qui donne
$$
\frac{a^{2}}{a^{2}+2 b c}+\frac{b^{2}}{b^{2}+2 c a}+\frac{c^{2}}{c^{2}+2 a b} \geqslant \frac{a^{2}}{a^{2}+b^{2}+c^{2}}+\frac{b^{2}}{a^{2}+b^{2}+c^{2}}+\frac{c^{2}}{a^{2}+b^{2}+c^{2}}=1 .
$$
Pour le côté gauche, on remarque que celui-ci ressemble beaucoup au côté droit. Appelons $G$ et $D$ les côtés gauche et droit de l'équation respectivement. On a alors
$$
\begin{gathered}
\mathrm{G}+2 \cdot \mathrm{D}=\frac{\mathrm{a}^{2}}{\mathrm{a}^{2}+2 \mathrm{bc}}+\frac{\mathrm{b}^{2}}{\mathrm{~b}^{2}+2 \mathrm{ca}}+\frac{\mathrm{c}^{2}}{\mathrm{c}^{2}+2 \mathrm{ab}}+\frac{2 \mathrm{bc}}{\mathrm{a}^{2}+2 \mathrm{bc}}+\frac{2 c a}{\mathrm{~b}^{2}+2 \mathrm{ca}}+\frac{2 a b}{\mathrm{c}^{2}+2 a b} . \\
\frac{\mathrm{a}^{2}+2 \mathrm{bc}}{\mathrm{a}^{2}+2 b c}+\frac{b^{2}+2 c a}{b^{2}+2 c a}+\frac{c^{2}+2 a b}{c^{2}+2 a b}=3 .
\end{gathered}
$$
On a donc
$$
\mathrm{G}=\frac{1}{2}(3-\mathrm{D}) \leqslant \frac{1}{2}(3-1)=1
$$
par l'inégalité de droite que l'on a montré précédemment.
Commentaire des correcteurs : L'exercice a été bien réussi. Un certain nombre d'élève n'a trouvé qu'une seule des deux inégalités : il est important d'envoyer tout ce qui a été trouvé sur l'envoi, même si on n'a trouvé que la moitié de l'exercice. Un certain nombre d'élèves ont juste tout mis au même dénominateur, et ensuite prouvé l'inégalité, ce qui n'était pas très élégant mais fonctionnait bien.
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-2.jsonl",
"solution_match": "## Solution de l'exercice 6",
"tier": "T2",
"year": null
}
|
Let $x, y, z$ be strictly positive real numbers such that $x y + y z + z x = 1$. Show that
$$
2\left(x^{2}+y^{2}+z^{2}\right)+\frac{4}{3}\left(\frac{1}{x^{2}+1}+\frac{1}{y^{2}+1}+\frac{1}{z^{2}+1}\right) \geqslant 5
$$
|
In this exercise, we would like to apply the arithmetic-geometric inequality to obtain a lower bound of the form $\left(x^{2}+1\right)+\frac{1}{x^{2}+1} \geqslant 2$. However, if we approach it poorly, we cannot conclude. Indeed, we might have suspected this by studying the equality case of the equation. Given the condition $x y+y z+z x=1$, we suspect that equality will occur for $x=y=z=\frac{1}{\sqrt{3}}$. By substituting these values into the equation, we find that equality holds, but this is not an equality case of the earlier arithmetic-geometric inequality.
In the equality case $x=y=z=\frac{1}{\sqrt{3}}$, we have $x^{2}+1=\frac{4}{3}$ and $\frac{1}{x^{2}+1}=\frac{3}{4}$. We therefore apply the arithmetic-geometric inequality with appropriate coefficients to have the equality of the two terms in this case:
$$
\frac{3}{4}\left(x^{2}+1\right)+\frac{4}{3}\left(\frac{1}{x^{2}+1}\right) \geqslant 2
$$
By summing these three equations, we have
$$
\frac{3}{4}\left(x^{2}+y^{2}+z^{2}+3\right)+\frac{4}{3}\left(\frac{1}{x^{2}+1}+\frac{1}{y^{2}+1}+\frac{1}{z^{2}+1}\right) \geqslant 6
$$
which gives
$$
\frac{3}{4}\left(x^{2}+y^{2}+z^{2}\right)+\frac{4}{3}\left(\frac{1}{x^{2}+1}+\frac{1}{y^{2}+1}+\frac{1}{z^{2}+1}\right) \geqslant \frac{15}{4}
$$
Compared to the inequality in the statement, we still need to bound the term $\frac{5}{4}\left(x^{2}+y^{2}+z^{2}\right)$. But we have, by the arithmetic-geometric inequality,
$$
\frac{5}{4}\left(x^{2}+y^{2}+z^{2}\right) \geqslant \frac{5}{4}(x y+y z+z x)=\frac{5}{4}
$$
By adding this inequality to the inequality obtained previously, we get
$$
2\left(x^{2}+y^{2}+z^{2}\right)+\frac{4}{3}\left(\frac{1}{x^{2}+1}+\frac{1}{y^{2}+1}+\frac{1}{z^{2}+1}\right) \geqslant \frac{15}{4}+\frac{5}{4}=5
$$
|
5
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soient $x, y, z$ des réels strictement positifs tels que $x y+y z+z x=1$. Montrer que
$$
2\left(x^{2}+y^{2}+z^{2}\right)+\frac{4}{3}\left(\frac{1}{x^{2}+1}+\frac{1}{y^{2}+1}+\frac{1}{z^{2}+1}\right) \geqslant 5
$$
|
Dans cet exercice, on aimerait bien appliquer l'inégalité arithmético-géométrique de façon à obtenir une minoration du type $\left(x^{2}+1\right)+\frac{1}{x^{2}+1} \geqslant 2$. Mais si on s'y prend mal, on n'arrive pas à conclure. En effet, on aurait pu s'en douter en étudiant le cas d'égalité de l'équation. Au vu de la condition $x y+y z+z x=1$, on se doute que l'égalité va se produire pour $x=y=z=\frac{1}{\sqrt{3}}$. En introduisant ces valeurs dans l'équation, on trouve bien que l'on a égalité, mais ceci n'est pas un cas d'égalité de l'inégalité arithméticogéométrique plus tôt.
Dans le cas d'égalité $x=y=z=\frac{1}{\sqrt{3}}$, on a $x^{2}+1=\frac{4}{3}$ et $\frac{1}{x^{2}+1}=\frac{3}{4}$. On applique donc l'inégalité arithmético-géométrique avec des coefficients appropriés pour avoir l'égalité des deux termes dans ce cas :
$$
\frac{3}{4}\left(x^{2}+1\right)+\frac{4}{3}\left(\frac{1}{x^{2}+1}\right) \geqslant 2
$$
En sommant ces trois équations, on a
$$
\frac{3}{4}\left(x^{2}+y^{2}+z^{2}+3\right)+\frac{4}{3}\left(\frac{1}{x^{2}+1}+\frac{1}{y^{2}+1}+\frac{1}{z^{2}+1}\right) \geqslant 6
$$
qui donne
$$
\frac{3}{4}\left(x^{2}+y^{2}+z^{2}\right)+\frac{4}{3}\left(\frac{1}{x^{2}+1}+\frac{1}{y^{2}+1}+\frac{1}{z^{2}+1}\right) \geqslant \frac{15}{4}
$$
Par rapport à l'inégalité de l'énoncé, il nous reste un terme $\frac{5}{4}\left(x^{2}+y^{2}+z^{2}\right)$ à minorer. Mais on a, par l'inégalité arithmético-géométrique,
$$
\frac{5}{4}\left(x^{2}+y^{2}+z^{2}\right) \geqslant \frac{5}{4}(x y+y z+z x)=\frac{5}{4}
$$
En ajoutant cette inégalité à l'inégalité obtenue précédemment, on obtient bien
$$
2\left(x^{2}+y^{2}+z^{2}\right)+\frac{4}{3}\left(\frac{1}{x^{2}+1}+\frac{1}{y^{2}+1}+\frac{1}{z^{2}+1}\right) \geqslant \frac{15}{4}+\frac{5}{4}=5
$$
|
{
"exam": "French_envois",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-2.jsonl",
"solution_match": "## Solution de l'exercice 7",
"tier": "T2",
"year": null
}
|
Let $x, y, z$ be strictly positive real numbers such that $x y + y z + z x = 1$. Show that
$$
2\left(x^{2}+y^{2}+z^{2}\right)+\frac{4}{3}\left(\frac{1}{x^{2}+1}+\frac{1}{y^{2}+1}+\frac{1}{z^{2}+1}\right) \geqslant 5
$$
|
Exercise 7
Let $s=x^{2}+y^{2}+z^{2}$. Note that by the poor student's inequality,
$$
\frac{4}{3}\left(\frac{1}{x^{2}+1}+\frac{1}{y^{2}+1}+\frac{1}{z^{2}+1}\right) \geqslant \frac{4}{3} \frac{(1+1+1)^{2}}{x^{2}+y^{2}+z^{2}+3}=\frac{12}{s+3}
$$
Thus, it suffices to show that $2 s+\frac{12}{s+3} \geqslant 5$. By multiplying both sides by $s+3$, which is positive, it suffices to show that $2 s(s+3)+12 \geqslant 5(s+3)$. This is equivalent to $2 s^{2}+6 s+12 \geqslant 5 s+15$ and thus to $2 s^{2}+s \geqslant 3$. By the turnstile lemma, $s \geqslant x y+y z+x z=1$, so $2 s^{2}+s \geqslant 3$. We have the desired result.
Graders' Comment: The exercise was well solved by the students who attempted it. Be careful not to get tangled up in the inequalities. Here, one could directly use the poor student's inequality: setting $s=x^{2}+y^{2}+z^{2}$ allowed concluding by multiplying by $s+3$. Note that it is not necessary to reprove $x^{2}+y^{2}+z^{2} \geqslant x y+y z+x z$ each time to use it: this is the turnstile lemma, which is covered in the POFM course.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soient $x, y, z$ des réels strictement positifs tels que $x y+y z+z x=1$. Montrer que
$$
2\left(x^{2}+y^{2}+z^{2}\right)+\frac{4}{3}\left(\frac{1}{x^{2}+1}+\frac{1}{y^{2}+1}+\frac{1}{z^{2}+1}\right) \geqslant 5
$$
|
de l'exercice 7
Posons $s=x^{2}+y^{2}+z^{2}$. Notons que par l'inégalité des mauvais élèves,
$$
\frac{4}{3}\left(\frac{1}{x^{2}+1}+\frac{1}{y^{2}+1}+\frac{1}{z^{2}+1}\right) \geqslant \frac{4}{3} \frac{(1+1+1)^{2}}{x^{2}+y^{2}+z^{2}+3}=\frac{12}{s+3}
$$
Ainsi il suffit de montrer que $2 s+\frac{12}{s+3} \geqslant 5$. En multipliant des deux côtés par $s+3$ qui est positif, il suffit de montrer que $2 s(s+3)+12 \geqslant 5(s+3)$. Ceci est équivalent à $2 s^{2}+6 s+12 \geqslant 5 s+15$ et donc à $2 s^{2}+s \geqslant 3$. Or par le lemme du tourniquet, $s \geqslant x y+y z+x z=1$, donc $2 s^{2}+s \geqslant 3$. On a bien le résultat voulu.
Commentaire des correcteurs : L'exercice a été bien résolu par les élèves l'ayant cherché. Attention à ne pas s'emmêler dans les inégalités. Ici on pouvait directement utiliser l'inégalité des mauvais élèves : poser $s=x^{2}+y^{2}+z^{2}$ permettait de conclure en multipliant par $s+3$. Notons qu'il n'est pas nécessaire de reprouver à chaque fois $x^{2}+y^{2}+z^{2} \geqslant x y+y z+x z$ pour l'utiliser : c'est le lemme du tourniquet, qui est présent dans le cours de la POFM.
|
{
"exam": "French_envois",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-2.jsonl",
"solution_match": "## Solution alternative",
"tier": "T2",
"year": null
}
|
Let $a$ and $b$ be two real numbers. We define the sequences $\left(a_{n}\right)$ and $\left(b_{n}\right)$ by $a_{0}=a, b_{0}=b$ and for all $n$ a natural number, $a_{n+1}=a_{n}+b_{n}$ and $b_{n+1}=a_{n} b_{n}$. Determine all pairs $(a, b)$ such that $\mathrm{a}_{2022}=\mathrm{a}_{0}$ and $\mathrm{b}_{2022}=\mathrm{b}_{0}$.
|
Suppose that $(a, b)$ is a solution to the statement. We calculate
$$
\sum_{i=1}^{2022} a_{i}=\sum_{i=1}^{2022}\left(a_{i-1}+b_{i-1}\right)=\sum_{i=0}^{2021} a_{i}+\sum_{i=0}^{2021} b_{i}
$$
But we have
$$
\sum_{i=0}^{2021} a_{i}=a_{0}+\sum_{i=1}^{2021} a_{i}=a_{2022}+\sum_{i=1}^{2021} a_{i}=\sum_{i=1}^{2022} a_{i}
$$
so we can rewrite the previous equation as
$$
\sum_{i=0}^{2021} b_{i}=0
$$
Similarly, we have
$$
0=\sum_{i=1}^{2022} b_{i}=\sum_{i=1}^{2022} a_{i-1} b_{i-1}=\sum_{i=0}^{2021} a_{i} b_{i}
$$
To make the products $a_{i} b_{i}$ appear, we square the equation $a_{i+1}=a_{i}+b_{i}$ to get $a_{i+1}^{2}=$ $a_{i}^{2}+b_{i}^{2}+2 a_{i} b_{i}$. We sum this from $i=0$ to 2021 to get
$$
\sum_{i=1}^{2022} a_{i}^{2}=\sum_{i=0}^{2021} a_{i}^{2}+\sum_{i=0}^{2021} b_{i}^{2}+2 \sum_{i=0}^{2021} a_{i} b_{i}
$$
But again,
$$
\sum_{i=1}^{2022} a_{i}^{2}=\sum_{i=0}^{2021} a_{i}^{2}
$$
so
$$
\sum_{i=0}^{2021} b_{i}^{2}=0
$$
A sum of squares of real numbers is necessarily non-negative, and can only be zero if all the $b_{i}$ are zero. This implies in particular that $b=0$. Conversely, if $a$ is a real number, the pair $(a, 0)$ works because we can show by induction that for all $n$, $a_{n}=a$ and $b_{n}=0$, and then $a_{2022}=a=a_{0}$.
Comment from the graders: The exercise was very difficult, was rarely attempted, and even less often successfully completed. However, several students manage to obtain that $b_{0}+\cdots+b_{2021}=0$, which is a good start.
|
(a, 0)
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Soient $a$ et $b$ deux réels. On définit les suites $\left(a_{n}\right)$ et $\left(b_{n}\right)$ par $a_{0}=a, b_{0}=b$ et pour tout $n$ entier naturel, $a_{n+1}=a_{n}+b_{n}$ et $b_{n+1}=a_{n} b_{n}$. Déterminer toutes les paires $(a, b)$ telles que $\mathrm{a}_{2022}=\mathrm{a}_{0}$ et $\mathrm{b}_{2022}=\mathrm{b}_{0}$.
|
Supposons que $(a, b)$ soit une solution de l'énoncé. On calcule
$$
\sum_{i=1}^{2022} a_{i}=\sum_{i=1}^{2022}\left(a_{i-1}+b_{i-1}\right)=\sum_{i=0}^{2021} a_{i}+\sum_{i=0}^{2021} b_{i}
$$
Mais on a
$$
\sum_{i=0}^{2021} a_{i}=a_{0}+\sum_{i=1}^{2021} a_{i}=a_{2022}+\sum_{i=1}^{2021} a_{i}=\sum_{i=1}^{2022} a_{i}
$$
donc on peut réécrire l'équation précédente comme
$$
\sum_{i=0}^{2021} b_{i}=0
$$
De la même manière, on a
$$
0=\sum_{i=1}^{2022} b_{i}=\sum_{i=1}^{2022} a_{i-1} b_{i-1}=\sum_{i=0}^{2021} a_{i} b_{i}
$$
Pour faire apparaître les produits $a_{i} b_{i}$, on élève l'équation $a_{i+1}=a_{i}+b_{i}$ au carré pour avoir $a_{i+1}^{2}=$ $a_{i}^{2}+b_{i}^{2}+2 a_{i} b_{i}$. On somme ceci entre $i=0$ et 2021 pour avoir
$$
\sum_{i=1}^{2022} a_{i}^{2}=\sum_{i=0}^{2021} a_{i}^{2}+\sum_{i=0}^{2021} b_{i}^{2}+2 \sum_{i=0}^{2021} a_{i} b_{i}
$$
Mais encore une fois,
$$
\sum_{i=1}^{2022} a_{i}^{2}=\sum_{i=0}^{2021} a_{i}^{2}
$$
donc
$$
\sum_{i=0}^{2021} b_{i}^{2}=0
$$
Une somme de carrés de nombres réels est nécessairement positive, et ne peut être nulle que si tous les $b_{i}$ sont nuls. Ceci implique notamment $b=0$. Réciproquement, si a est un réel, le couple ( $a, 0$ ) fonctionne car on montre par récurrence que pour tout $n, a_{n}=a$ et $b_{n}=0$, et alors $a_{2022}=a=a_{0}$.
Commentaire des correcteurs : L'exercice était très difficile, a été peu abordé, et encore moins réussi. Plusieurs élèves arrivent cependant à obtenir que $b_{0}+\cdots+b_{2021}=0$ ce qui est un bon début.
|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "\nExercice 8.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-2.jsonl",
"solution_match": "## Solution de l'exercice 8",
"tier": "T2",
"year": null
}
|
Let $b_{1}, \ldots, b_{n}$ be non-negative real numbers such that $b_{1}+b_{2}+\ldots+b_{n}=2$. Let $a_{0}, a_{1}, \ldots, a_{n}$ be real numbers such that $a_{0}=a_{n}=0$. Suppose that for all $i$ between 1 and $n$ inclusive,
$$
\left|a_{i}-a_{i-1}\right| \leqslant b_{i}
$$
Show that we have
$$
\left(a_{0}+a_{1}\right) b_{1}+\left(a_{1}+a_{2}\right) b_{2}+\ldots+\left(a_{n-1}+a_{n}\right) b_{n} \leqslant 2
$$
|
For any index $i$, we have two upper bounds for $a_{i}$. Indeed, we can write
$$
\begin{aligned}
a_{i}=a_{i}-a_{0}= & \left(a_{i}-a_{i-1}\right)+\left(a_{i-1}-a_{i-2}\right)+\ldots+\left(a_{1}-a_{0}\right) \\
& \leqslant b_{i}+b_{i-1}+\ldots+b_{1}=\sum_{j=1}^{i} b_{j}
\end{aligned}
$$
and
$$
\begin{aligned}
a_{i}=a_{i}-a_{n} & =\left(a_{i}-a_{i+1}\right)-\left(a_{i+1}-a_{i+2}\right)+\ldots+\left(a_{n-1}-a_{n}\right) \\
& \leqslant b_{i+1}+b_{i+2}+\ldots+b_{n}=\sum_{j=i+1}^{n} b_{j}
\end{aligned}
$$
To effectively upper bound $a_{i}$, we want to find the smallest of these two terms. But the sum of the two is 2, so we simply need to determine whether $\sum_{j=1}^{i} b_{j}$ is less than or greater than 1.
Let $m$ be the smallest integer such that $\sum_{j=1}^{m} b_{j}>1$. We then write
$$
\sum_{i=1}^{n}\left(a_{i-1}+a_{i}\right) b_{i}=\sum_{i=1}^{m-1}\left(a_{i-1}+a_{i}\right) b_{i}+\left(a_{m-1}+a_{m}\right) b_{m}+\sum_{i=m+1}^{n}\left(a_{i-1}+a_{i}\right) b_{i}
$$
For $i<m$, we upper bound $a_{i}$ by $\sum_{j=1}^{i} b_{j}$, and for $i \geqslant m$, we upper bound $a_{i}$ by $\sum_{j=i+1}^{n} b_{j}$ to obtain $\sum_{i=1}^{n}\left(a_{i-1}+a_{i}\right) b_{i} \leqslant \sum_{i=1}^{m-1}\left(b_{i}+2 \sum_{j=1}^{i-1} b_{j}\right) b_{i}+\left(\sum_{j=1}^{m-1} b_{j}+\sum_{j=m+1}^{n} b_{j}\right) b_{m}+\sum_{i=1}^{m}\left(b_{i}+2 \sum_{j=i+1}^{n} b_{j}\right) b_{i}$.
Let $x=\sum_{j=1}^{m-1} b_{j}$ and $y=\sum_{j=m+1}^{n} b_{j}$. By definition of $m$, we have $x \leqslant 1$ and $y \leqslant 1$. Consider the first sum in the previous term. In this sum, we have a term $b_{i}^{2}$ for all $i \leqslant m-1$ and a term $2 b_{i} b_{j}$ for all $j<i \leqslant m-1$. Thus, this sum is nothing other than $x^{2}$. Similarly, the right sum is nothing other than $y^{2}$. We can therefore write, since $x+b_{m}+y=2$,
$$
\begin{aligned}
\sum_{i=1}^{n}\left(a_{i-1}+a_{i}\right) b_{i} & \leqslant x^{2}+(x+y)(2-x-y)+y^{2} \\
= & 2(x+y)-2 x y
\end{aligned}
$$
It remains to show that $2(x+y)-2 x y \leqslant 2$ to conclude, or equivalently $x+y-x y \leqslant 1$. But this can be rewritten, by moving all terms to the right side of the inequality,
$$
(1-x)(1-y) \geqslant 0
$$
which is satisfied since we have seen that $x \leqslant 1$ and $y \leqslant 1$.
Comment from the graders: The exercise was very difficult, was rarely approached, and solved by no one. It is a pity to see that few students wrote down their lines of reasoning: typically, given $\left(b_{i}\right)$ fixed, to find the $\left(a_{i}\right)$ maximizing the sum.
## Senior Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soient $b_{1}, \ldots, b_{n}$ des réels positifs ou nuls tels que $b_{1}+b_{2}+\ldots+b_{n}=2$. Soient $a_{0}, a_{1}, \ldots, a_{n}$ des nombres réels tels que $a_{0}=a_{n}=0$. Supposons que pour tout $i$ compris entre 1 et $n$ inclus,
$$
\left|a_{i}-a_{i-1}\right| \leqslant b_{i}
$$
Montrer que l'on a
$$
\left(a_{0}+a_{1}\right) b_{1}+\left(a_{1}+a_{2}\right) b_{2}+\ldots+\left(a_{n-1}+a_{n}\right) b_{n} \leqslant 2
$$
|
Pour tout indice $i$, on a deux majorations de $a_{i}$. En effet, on peut écrire
$$
\begin{aligned}
a_{i}=a_{i}-a_{0}= & \left(a_{i}-a_{i-1}\right)+\left(a_{i-1}-a_{i-2}\right)+\ldots+\left(a_{1}-a_{0}\right) \\
& \leqslant b_{i}+b_{i-1}+\ldots+b_{1}=\sum_{j=1}^{i} b_{j}
\end{aligned}
$$
et
$$
\begin{aligned}
a_{i}=a_{i}-a_{n} & =\left(a_{i}-a_{i+1}\right)-\left(a_{i+1}-a_{i+2}\right)+\ldots+\left(a_{n-1}-a_{n}\right) \\
& \leqslant b_{i+1}+b_{i+2}+\ldots+b_{n}=\sum_{j=i+1}^{n} b_{j}
\end{aligned}
$$
Afin de majorer efficacement $a_{i}$, on voudrait trouver le plus petit de ces deux termes. Mais la somme des deux vaut 2 , donc il faut simplement déterminer si $\sum_{j=1}^{i} b_{j}$ est inférieur ou supérieur à 1 .
Soit $m$ l'entier minimal tel que $\sum_{j=1}^{m} b_{j}>1$. On écrit alors
$$
\sum_{i=1}^{n}\left(a_{i-1}+a_{i}\right) b_{i}=\sum_{i=1}^{m-1}\left(a_{i-1}+a_{i}\right) b_{i}+\left(a_{m-1}+a_{m}\right) b_{m}+\sum_{i=m+1}^{n}\left(a_{i-1}+a_{i}\right) b_{i}
$$
Pour $i<m$, on majore $a_{i}$ par $\sum_{j=1}^{i} b_{j}$, et pour $i \geqslant m$, on majore $a_{i}$ par $\sum_{j=i+1}^{n} b_{j}$ pour obtenir $\sum_{i=1}^{n}\left(a_{i-1}+a_{i}\right) b_{i} \leqslant \sum_{i=1}^{m-1}\left(b_{i}+2 \sum_{j=1}^{i-1} b_{j}\right) b_{i}+\left(\sum_{j=1}^{m-1} b_{j}+\sum_{j=m+1}^{n} b_{j}\right) b_{m}+\sum_{i=1}^{m}\left(b_{i}+2 \sum_{j=i+1}^{n} b_{j}\right) b_{i}$.
Posons $x=\sum_{j=1}^{m-1} b_{j}$ et $y=\sum_{j=m+1}^{n} b_{j}$. Par définition de $m$, on a $x \leqslant 1$ et $y \leqslant 1$. Considérons la première somme dans le terme précédent. Dans celle-ci, on a un terme $b_{i}^{2}$ pour tout $i \leqslant m-1$ et un terme $2 b_{i} b_{j}$ pour tous $j<i \leqslant m-1$. Ainsi, cette somme n'est rien d'autre que $x^{2}$. De même, la somme de droite n'est rien d'autre que $y^{2}$. On peut donc écrire, comme $x+b_{m}+y=2$,
$$
\begin{aligned}
\sum_{i=1}^{n}\left(a_{i-1}+a_{i}\right) b_{i} & \leqslant x^{2}+(x+y)(2-x-y)+y^{2} \\
= & 2(x+y)-2 x y
\end{aligned}
$$
Il nous reste enfin à voir que $2(x+y)-2 x y \leqslant 2$ pour conclure, ou encore $x+y-x y \leqslant 1$. Mais ceci se réécrit, en passant tous les termes à droite de l'inégalité,
$$
(1-x)(1-y) \geqslant 0
$$
ce qui est vérifié car on a vu que $x \leqslant 1$ et $y \leqslant 1$.
Commentaire des correcteurs : L'exercice était très difficile, a été très peu abordé et résolu par personne. Il est dommage de voir que peu d'élèves ont écrit leur piste de recherche : typiquement à $\left(b_{i}\right)$ fixé de trouver les $\left(a_{i}\right)$ maximisant la somme.
## Exercices Seniors
|
{
"exam": "French_envois",
"problem_label": "16",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-2.jsonl",
"solution_match": "## Solution de l'exercice 9",
"tier": "T2",
"year": null
}
|
Let $\left(u_{n}\right)_{n \in \mathbb{N}}$ be a periodic sequence with period 2022 and period 5. Show that $\left(u_{n}\right)$ is constant.
A sequence $\left(u_{n}\right)$ is said to be periodic with period $t$ if, for all natural numbers $n, u_{n+t}=u_{n}$.
|
Let's start by noting that if a sequence $\left(u_{n}\right)$ is $t$-periodic, then for all $n$, we have $u_{n}=u_{n+t}=u_{n+2t}$, for example. Thus, we can show by induction that for all natural numbers $k$ and $n$, $u_{n+kt}=u_{n}$: the sequence is $kt$-periodic for all $k$.
Let $n$ be a natural number. Then, since the sequence is 2022-periodic,
$$
u_{n+1}=u_{n+1+2 \times 2022}=u_{n+4045}=u_{n+5 \times 809}
$$
But the sequence is 5-periodic, so this also equals $u_{n}$. Thus, for all natural numbers $n$, we have $u_{n+1}=u_{n}$. We deduce by induction that for all $n$, $u_{n}=u_{0}$, and therefore the sequence $(u_{n})$ is constant.
Grader's Comment: The exercise was successfully completed by almost everyone who attempted it, using three main methods:
- Show that $u_{0}=u_{1}=u_{2}=u_{3}=u_{4}$.
- Show that $u_{n}=u_{n+1}$.
- Use Bézout's theorem to show $u_{0}=u_{n}$.
The few students who did not get 7 points mostly used somewhat strong properties without justifying them (even a quick justification would have sufficed).
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $\left(u_{n}\right)_{n \in \mathbb{N}}$ une suite périodique de période 2022 et de période 5 . Montrer que $\left(u_{n}\right)$ est constante.
Une suite $\left(u_{n}\right)$ est dite périodique de période $t$ si, pour tout entier naturel $n, u_{n+t}=u_{n}$.
|
Commençons par remarquer que si une suite $\left(u_{n}\right)$ est $t$-périodique, alors on a pour tout $n, u_{n}=u_{n+t}=$ $u_{n+2 t}$ par exemple. Ainsi, on peut montrer par récurrence que pour tous les entiers naturels $k$ et $n$, $u_{n+k t}=u_{n}$ : la suite est kt-périodique pour tout $k$.
Soit $n$ un entier naturel. On a alors, comme la suite est 2022-périodique,
$$
u_{n+1}=u_{n+1+2 \times 2022}=u_{n+4045}=u_{n+5 \times 809}
$$
Mais la suite est 5 -périodique donc ceci vaut aussi $u_{n}$. Ainsi, pour tout entier naturel $n$, on a $u_{n+1}=u_{n}$. On en déduit par récurrence que pour tout $n, u_{n}=u_{0}$ et donc la suite ( $u_{n}$ ) est constante.
Commentaire des correcteurs : L'exo a été réussi par qusiment toutes les personnes l'ayant abordé, avec 3 méthodes principales :
- Montrer que $u_{0}=u_{1}=u_{2}=u_{3}=u_{4}$.
- Montrer que $u_{n}=u_{n+1}$.
- Utiliser le théorème de Bezout pour montrer $u_{0}=u_{n}$.
Les quelques élèves qui n'ont pas eu 7 points ont la plupart du temps utilisé des propriétés un peu fortes sans les justifier (même rapidement, cela aurait suffit).
|
{
"exam": "French_envois",
"problem_label": "10",
"problem_match": "\nExercice 10.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-2.jsonl",
"solution_match": "\nSolution de l'exercice 10",
"tier": "T2",
"year": null
}
|
Let $n$ be a strictly positive integer and $x \geqslant n$ a real number. Show that $x+\frac{n}{x} \geqslant n+1$ and provide the cases of equality.
|
The real $x$ is strictly positive, so we can multiply the equation by $x$ to get that the equation is equivalent to
$$
x^{2}+n \geqslant(n+1) x
$$
which gives, by rearranging the terms,
$$
x^{2}-(n+1) x+n \geqslant 0
$$
We can look for the roots of this quadratic polynomial or recognize the factorization
$$
(x-n)(x-1) \geqslant 0
$$
But this is true because $x \geqslant n$ and $x \geqslant 1$. Equality holds when $x=\mathfrak{n}$ or $x=1$. But if $x=1$, then $\mathfrak{n}=1$ and $x=n$. Thus, in all cases, the only case of equality is $x=\mathrm{n}$.
|
x=n
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $n$ un entier strictement positif et $x \geqslant n$ un réel. Montrer que $x+\frac{n}{x} \geqslant n+1$ et donner les cas d'égalité.
|
Le réel $x$ est strictement positif donc on peut multiplier l'équation par $x$ pour avoir que l'équation est équivalente à
$$
x^{2}+n \geqslant(n+1) x
$$
ce qui donne, en réarrangeant les termes,
$$
x^{2}-(n+1) x+n \geqslant 0
$$
On peut chercher les racines de ce polynôme de degré 2 ou alors reconnaitre la factorisation
$$
(x-n)(x-1) \geqslant 0
$$
Mais ceci est vrai car $x \geqslant n$ et $x \geqslant 1$.
On a égalité lorsque $x=\mathfrak{n}$ ou $x=1$. Mais si $x=1$, alors $\mathfrak{n}=1$ et $x=n$. Ainsi, dans tous les cas, le seul cas d'égalité est $x=\mathrm{n}$.
|
{
"exam": "French_envois",
"problem_label": "11",
"problem_match": "\nExercice 11.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-2.jsonl",
"solution_match": "## Solution de l'exercice 11",
"tier": "T2",
"year": null
}
|
Let $n$ be a strictly positive integer and $x \geqslant n$ a real number. Show that $x+\frac{n}{x} \geqslant n+1$ and provide the cases of equality.
|
From Exercise 11
We start from the expanded equation $x^{2}-(n+1) x+n \geqslant 0$.
The condition $x \geqslant n$ is quite unnatural, so we prefer conditions of the type $t \geqslant 0$. We set $x=n+t$ with $t \geqslant 0$. The equation then rewrites as
$$
n^{2}+2 n t+t^{2}-(n+1)(n+t)+n \geqslant 0
$$
or equivalently
$$
t^{2}+(n-1) t \geqslant 0
$$
But this new equation is clearly true since $t \geqslant 0$ and $n \geqslant 1$. Moreover, equality holds if and only if $t=0$, or equivalently $x=n$.
Graders' Comment: The problem was well handled by the students, almost all the solutions submitted were complete. The solutions were quite varied, some went through the study of a quadratic, others by a derivative calculation, or even by the arithmetic-geometric inequality. However, a number of papers were penalized for lack of justification, particularly for sign justifications. It is important to remember that when multiplying or dividing an inequality by a quantity, one must ensure the sign of that quantity: if it is strictly positive, it preserves the direction of the inequality, if it is strictly negative, it changes the direction of the inequality, and if one multiplies by a zero quantity, there is no equivalence. This is a detail of great importance. Regarding the case of equality, several papers forgot to address it, and others forgot the condition $x \geqslant n$, so they considered that for all $n \in \mathbb{N}^{*}, x=1$ was a case of equality. This was true only for $n=1$, and thus was already counted in the case $x=n$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $n$ un entier strictement positif et $x \geqslant n$ un réel. Montrer que $x+\frac{n}{x} \geqslant n+1$ et donner les cas d'égalité.
|
de l'exercice 11
On repart de l'équation développée $x^{2}-(n+1) x+n \geqslant 0$.
La condition $x \geqslant n$ est très peu naturelle, on préfère des conditions de type $t \geqslant 0$. On pose donc $x=n+t$ $\operatorname{avec} t \geqslant 0$. L'équation se réécrit alors
$$
\mathrm{n}^{2}+2 n t+\mathrm{t}^{2}-(n+1)(n+t)+n \geqslant 0
$$
ou encore
$$
\mathrm{t}^{2}+(n-1) \mathrm{t} \geqslant 0
$$
Mais cette nouvelle équation est clairement vraie car $\mathrm{t} \geqslant 0$ et $\mathrm{n} \geqslant 1$. De plus, on a égalité si et seulement si $t=0$, ou encore $x=n$.
Commentaire des correcteurs : Le problème a été bien réussi par les élèves, les solutions rendues étaient presque toutes abouties. Les solutions étaient assez variées, certaines passaient par l'étude d'un trinôme, d'autres par un calcul de dérivée, ou encore par l'inégalité arithmético-géométrique. Néanmoins, un certain nombre de copies ont été pénalisées pour des manques de justifications, notamment des justifications de signes. On rappelle que lorsqu'on multiplie ou divise une inégalité par une quantité, il faut s'assurer du signe de cette quantité : si elle est strictement positive, ça conserve le sens de l'inégalité, si elle est strictement négative, ça change le sens de l'inégalité, et si on multiplie par une quantité nulle, on n'a pas équivalence. C'est donc un détail qui a toute son importance. En ce qui concerne le cas d'égalité, plusieurs copies ont oublié de le traiter, et d'autres ont oublié la condition $x \geqslant n$, de sorte qu'elles considérées que pour tout $\mathrm{n} \in \mathbb{N}^{*}, x=1$ était un cas d'égalité. Ce n'était vrai que pour $\mathrm{n}=1$, et donc c'était déjà compté dans le cas $x=n$.
|
{
"exam": "French_envois",
"problem_label": "11",
"problem_match": "\nExercice 11.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-2.jsonl",
"solution_match": "## Solution alternative",
"tier": "T2",
"year": null
}
|
Let $(a_n)$ be a sequence of real numbers. Suppose that $a_0 = 1$ and for all $n \geqslant 1, a_n$ is the smallest positive solution of
$$
\left(a_n - a_{n-1}\right)\left(a_n + a_{n-1} - 2 \sqrt{n}\right) = 2.
$$
Find the smallest integer $n$ such that $a_n \geqslant 2022$.
|
To get an idea of the problem, we calculate the first values of $a_{n}$: for $a_{1}$, the equation is
$$
\left(a_{1}-1\right)\left(a_{1}-1\right)=2
$$
so $a_{1}-1=\sqrt{2}$ or $-\sqrt{2}$. Only the first case gives a positive solution $a_{1}=1+\sqrt{2}$. Now let's calculate $a_{2}$: the equation becomes
$$
\left(a_{2}-1-\sqrt{2}\right)\left(a_{2}+1-\sqrt{2}\right)=2
$$
which can be expanded to
$$
\left(a_{2}-\sqrt{2}\right)^{2}-1^{2}=2
$$
or $a_{2}-\sqrt{2}= \pm \sqrt{3}$. Only one sign gives a positive solution $a_{2}=\sqrt{2}+\sqrt{3}$.
From these first values, we hypothesize that the sequence $a_{n}$ is given by $a_{n}=\sqrt{n}+\sqrt{n+1}$ and we prove this by induction. It is true for $n=0$. Suppose it is true for $n-1$ and show it for $n$: the equation giving $a_{n}$ is
$$
\left(a_{n}-\sqrt{n-1}-\sqrt{n}\right)\left(a_{n}+\sqrt{n-1}-\sqrt{n}\right)=2
$$
which can be expanded to
$$
\left(a_{n}-\sqrt{n}\right)^{2}-(\sqrt{n-1})^{2}=2
$$
and thus
$$
\left(a_{n}-\sqrt{n}\right)^{2}=n+1
$$
so $a_{n}-\sqrt{n}= \pm \sqrt{n+1}$. Only the positive sign gives a positive solution, so we have $a_{n}=\sqrt{n}+$ $\sqrt{n+1}$, which concludes the induction.
We immediately notice that the sequence $(a_{n})$ is increasing, and consequently, if we find an $n$ such that $a_{n-1}<2022 \leqslant a_{n}$, it is the $n$ we are looking for. Indeed, if we have $0 \leqslant m<n$, then $m \leqslant n-1$ and thus $a_{m} \leqslant a_{n-1}<2022$ as required: $n$ is indeed the smallest index such that $a_{n} \geqslant 2022$.
But now we have
$$
\mathrm{a}_{1011^{2}-1}=\sqrt{1011^{2}-1}+1011<2 \cdot 1011=2022<1011+\sqrt{1011^{2}+1}=a_{1011^{2}}
$$
so the sought $n$ is $\mathrm{n}=1011^{2}$.
Comment from the graders: The problem was well solved by the students who submitted a paper. A vast majority perfectly conjectured $a_{n}=\sqrt{n}+\sqrt{n+1}$ and then proved it by induction. It is worth noting that calculating the first terms to guess an expression is a very good initiative to take in the rough draft as it can be the first step in solving a problem (as was the case here). From there, one could quickly conclude, but it was important to avoid calculation errors and to justify properly (arguments of increasing were relevant). These points were missing in some papers. It is also worth noting that in a test or competition, there is no calculator, so one must get used to looking for efficient calculations by hand.
|
1011^2
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Soit ( $a_{n}$ ) une suite de réels. On suppose que $a_{0}=1$ et que pour tout $n \geqslant 1, a_{n}$ est la plus petite solution strictement positive de
$$
\left(a_{n}-a_{n-1}\right)\left(a_{n}+a_{n-1}-2 \sqrt{n}\right)=2 .
$$
Trouver le plus petit entier $n$ tel que $a_{n} \geqslant 2022$.
|
Pour se donner une idée du problème, on calcule les premières valeurs de $a_{n}$ : pour $a_{1}$, l'équation s'écrit
$$
\left(a_{1}-1\right)\left(a_{1}-1\right)=2
$$
donc $a_{1}-1=\sqrt{2}$ ou $-\sqrt{2}$. Seul le premier cas donne une solution positive $a_{1}=1+\sqrt{2}$. Cherchons maintenant à calculer $a_{2}: 1$ 'équation devient
$$
\left(a_{2}-1-\sqrt{2}\right)\left(a_{2}+1-\sqrt{2}\right)=2
$$
ce que l'on peut développer en
$$
\left(a_{2}-\sqrt{2}\right)^{2}-1^{2}=2
$$
ou encore $a_{2}-\sqrt{2}= \pm \sqrt{3}$. Un seul signe donne une solution positive $a_{2}=\sqrt{2}+\sqrt{3}$.
A partir de ces premières valeurs, on fait l'hypothèse que la suite $a_{n}$ est donnée par $a_{n}=\sqrt{n}+\sqrt{n+1}$ et on montre ceci par récurrence. C'est vrai pour $n=0$. Supposons que ceci soit vrai pour $n-1$ et montrons le au rang $n$ : l'équation donnant $a_{n}$ est
$$
\left(a_{n}-\sqrt{n-1}-\sqrt{n}\right)\left(a_{n}+\sqrt{n-1}-\sqrt{n}\right)=2
$$
ce que l'on développe en
$$
\left(a_{n}-\sqrt{n}\right)^{2}-(\sqrt{n-1})^{2}=2
$$
et donc
$$
\left(a_{n}-\sqrt{n}\right)^{2}=n+1
$$
donc $a_{n}-\sqrt{n}= \pm \sqrt{n+1}$. Seul le signe + donne une solution positive, donc on a bien $a_{n}=\sqrt{n}+$ $\sqrt{n+1}$ ce qui conclut la récurrence.
On remarque immédiatement que la suite ( $a_{n}$ ) est croissante, et par conséquent si on trouve un $n$ tel que $a_{n-1}<2022 \leqslant a_{n}$, il s'agit du $n$ cherché. En effet, si on a $0 \leqslant m<n$, on a alors $m \leqslant n-1$ donc $a_{m} \leqslant a_{n-1}<2022$ comme voulu : $n$ est bien le plus petit indice tel que $a_{n} \geqslant 2022$.
Mais maintenant on a
$$
\mathrm{a}_{1011^{2}-1}=\sqrt{1011^{2}-1}+1011<2 \cdot 1011=2022<1011+\sqrt{1011^{2}+1}=a_{1011^{2}}
$$
donc le n cherché est $\mathrm{n}=1011^{2}$.
Commentaire des correcteurs : Le problème a été bien réussi par les élèves qui ont rendu une copie. Une très grande majorité a parfaitement conjecturé $a_{n}=\sqrt{n}+\sqrt{n+1}$ puis l'a montré par récurrence. On rappelle que calculer les premiers termes pour deviner une expression est une très bonne initiative à prendre au brouillon car ça peut être la première étape dans la résolution d'un problème (comme c'était le cas ici). À partir de là on pouvait rapidement conclure, mais il fallait faire attention à ne pas faire d'erreurs de calculs, et à bien justifier (notamment des arguments de croissance étaient pertinents). Ces points là manquaient dans certaines copies. On notera aussi qu'en test ou en compétition, il n'y a pas de calculatrice, il faut donc prendre l'habitude de chercher à faire des calculs efficaces à la main.
|
{
"exam": "French_envois",
"problem_label": "12",
"problem_match": "\nExercice 12.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-2.jsonl",
"solution_match": "\nSolution de l'exercice 12",
"tier": "T2",
"year": null
}
|
Let $n \geqslant 3$ and let $x_{1}, \ldots, x_{n}$ be real numbers. Show that
$$
2\left(x_{1}+\cdots+x_{n}\right)^{2} \leqslant n\left(x_{1}^{2}+\cdots+x_{n}^{2}+x_{1} x_{2}+x_{2} x_{3}+\cdots+x_{n-1} x_{n}+x_{n} x_{1}\right)
$$
|
The difficulty of the exercise lies in the fact that the statement is not symmetric. Given the statement, we want to make the products $x_{i} x_{i+1}$ appear; for this, we can think of using the expansion of $\left(x_{i}+x_{i+1}\right)^{2}$. We have
$$
\begin{gathered}
\left(x_{1}+x_{2}\right)^{2}+\cdots+\left(x_{n-1}+x_{n}\right)^{2}+\left(x_{n}+x_{1}\right)^{2}=\left(x_{1}^{2}+2 x_{1} x_{2}+x_{2}^{2}\right)+\cdots+\left(x_{n-1}^{2}+2 x_{n-1} x_{n}+x_{n}^{2}\right)+\left(x_{n}^{2}+2 x_{n} x_{1}+x_{1}^{2}\right) \\
=2\left(x_{1}^{2}+\ldots x_{n}^{2}+x_{1} x_{2}+x_{2} x_{3}+\cdots+x_{n-1} x_{n}+x_{n} x_{1}\right)
\end{gathered}
$$
and we recognize the right-hand side of the statement, with a coefficient 2 instead of $n$. The inequality in the statement can then be rewritten as
$$
4\left(x_{1}+\ldots+x_{n}\right)^{2} \leqslant \mathfrak{n}\left(\left(x_{1}+x_{2}\right)^{2}+\left(x_{2}+x_{3}\right)^{3}+\ldots+\left(x_{n-1}+x_{n}\right)^{2}+\left(x_{n}+x_{1}\right)^{2}\right)
$$
But this is then an application of the Cauchy-Schwarz inequality. Indeed, we have
$$
\begin{gathered}
\mathfrak{n}\left(\left(x_{1}+x_{2}\right)^{2}+\left(x_{2}+x_{3}\right)^{3}+\ldots+\left(x_{n-1}+x_{n}\right)^{2}+\left(x_{n}+x_{1}\right)^{2}\right)=\left(1^{2}+\ldots+1^{2}\right)\left(\left(x_{1}+x_{2}\right)^{2}+\ldots+\left(x_{n}+x_{1}\right)^{2}\right) \\
\geqslant\left(1 \cdot\left(x_{1}+x_{2}\right)+1 \cdot\left(x_{2}+x_{3}\right)+\ldots+1 \cdot\left(x_{n}+x_{1}\right)\right)^{2} \\
=\left(2 x_{1}+2 x_{2}+\ldots+2 x_{n}\right)^{2}=4\left(x_{1}+\ldots+x_{n}\right)^{2} .
\end{gathered}
$$
Examiner's comment: The exercise was very well done by those who attempted it. The most frequent mistake was to use the Chebyshev inequality, forgetting the hypothesis on the order of the terms. Students who thought to rewrite the right-hand term as a sum of $\left(x_{i}+x_{i+1}\right)^{2}$ succeeded in concluding with Cauchy-Schwarz, AM-QM, Chebyshev, Jensen, or the less successful students.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $n \geqslant 3$ et soient $x_{1}, \ldots, x_{n}$ des réels. Montrer que
$$
2\left(x_{1}+\cdots+x_{n}\right)^{2} \leqslant n\left(x_{1}^{2}+\cdots+x_{n}^{2}+x_{1} x_{2}+x_{2} x_{3}+\cdots+x_{n-1} x_{n}+x_{n} x_{1}\right)
$$
|
La difficulté de l'exercice est le fait que l'énoncé n'est pas symétrique. Au vu de celui-ci, on veut faire apparaître les produits $x_{i} x_{i+1}$; pour cela, on peut penser à utiliser le développement de $\left(x_{i}+x_{i+1}\right)^{2}$. On a
$$
\begin{gathered}
\left(x_{1}+x_{2}\right)^{2}+\cdots+\left(x_{n-1}+x_{n}\right)^{2}+\left(x_{n}+x_{1}\right)^{2}=\left(x_{1}^{2}+2 x_{1} x_{2}+x_{2}^{2}\right)+\cdots+\left(x_{n-1}^{2}+2 x_{n-1} x_{n}+x_{n}^{2}\right)+\left(x_{n}^{2}+2 x_{n} x_{1}+x_{1}^{2}\right) \\
=2\left(x_{1}^{2}+\ldots x_{n}^{2}+x_{1} x_{2}+x_{2} x_{3}+\cdots+x_{n-1} x_{n}+x_{n} x_{1}\right)
\end{gathered}
$$
et on reconnaît le membre de droite de l'énoncé, avec un coefficient 2 au lieu de $n$. L'inégalité de l'énoncé se réécrit alors
$$
4\left(x_{1}+\ldots+x_{n}\right)^{2} \leqslant \mathfrak{n}\left(\left(x_{1}+x_{2}\right)^{2}+\left(x_{2}+x_{3}\right)^{3}+\ldots+\left(x_{n-1}+x_{n}\right)^{2}+\left(x_{n}+x_{1}\right)^{2}\right)
$$
Mais ceci est alors une application de l'inégalité de Cauchy-Schwarz. En effet, on a
$$
\begin{gathered}
\mathfrak{n}\left(\left(x_{1}+x_{2}\right)^{2}+\left(x_{2}+x_{3}\right)^{3}+\ldots+\left(x_{n-1}+x_{n}\right)^{2}+\left(x_{n}+x_{1}\right)^{2}\right)=\left(1^{2}+\ldots+1^{2}\right)\left(\left(x_{1}+x_{2}\right)^{2}+\ldots+\left(x_{n}+x_{1}\right)^{2}\right) \\
\geqslant\left(1 \cdot\left(x_{1}+x_{2}\right)+1 \cdot\left(x_{2}+x_{3}\right)+\ldots+1 \cdot\left(x_{n}+x_{1}\right)\right)^{2} \\
=\left(2 x_{1}+2 x_{2}+\ldots+2 x_{n}\right)^{2}=4\left(x_{1}+\ldots+x_{n}\right)^{2} .
\end{gathered}
$$
Commentaire des correcteurs : Exercice très bien réussi par ceux qui l'ont tenté. L'erreur la plus fréquente était d'utiliser l'inégalité de Tchebychev en oubliant l'hypothèse sur l'ordre des termes. Les élèves ayant pensé à réécrire le terme de droite comme somme de $\left(x_{i}+x_{i+1}\right)^{2}$ ont réussi à conclure avec CauchySchwarz, AM-QM, Tchebychev, Jensen ou les mauvais élèves.
|
{
"exam": "French_envois",
"problem_label": "13",
"problem_match": "\nExercice 13.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-2.jsonl",
"solution_match": "## Solution de l'exercice 13",
"tier": "T2",
"year": null
}
|
Let $a, b, c, x, y, z>0$ such that $a+b+c=x+y+z$ and $a b c=x y z$. Furthermore, assume $a \leqslant x<y<z \leqslant c$ and $a<b<c$. Show that $a=x, b=y, c=z$.
|
The terms $a+b+c$ and $a b c$ remind us of Viète's formulas, which link the coefficients of a polynomial to its roots. This invites us to consider the polynomials $P(X)=(X-a)(X-b)(X-c)$ and $Q(X)=(X-x)(X-y)(X-z)$. In expanded form, we have
$P(X)=X^{3}-(a+b+c) X^{2}+(a b+b c+c a) X-a b c, \quad Q(X)=X^{3}-(x+y+z) X^{2}+(x y+y z+z x) X-x y z$
and the statement assures us that the coefficients of degrees 0 and 2 are identical for both polynomials. But we can consider the difference $P(X)-Q(X)$, which is then a monomial of the form $\alpha X$, for some real $\alpha$.
Given the statement, we need to show that $P(X)=Q(X)$, or equivalently that $\alpha=0$. To do this, we simply evaluate $P(X)-Q(X)$ at $X=a$ and $X=c$. At these two points, we have $P(X)=0$, and then
$$
\alpha a=-Q(a)=-(a-x)(a-y)(a-z) \geqslant 0
$$
since $a$ is less than $x, y$, and $z$. Since $a>0$, we deduce $\alpha \geqslant 0$. But we also have
$$
\alpha c=-Q(c)=-(c-x)(c-y)(c-z) \leqslant 0
$$
since $c$ is greater than $x, y$, and $z$. Since $c>0$, we deduce $\alpha \leqslant 0$. Thus, we have $\alpha=0$ as desired, that is, $P(X)=Q(X)$.
But then the two polynomials must have the same roots, which are $a<b<c$ for $P(X)$ and $x<y<z$ for $Q(X)$. Therefore, we have
$$
\mathrm{a}=\mathrm{x}, \mathrm{~b}=\mathrm{y}, \mathrm{c}=z
$$
Comment from the graders: The problem was not attempted by many, but those who did generally did very well. The most common solution was to use polynomials of degree 3 as in the solution. Other solutions were found, such as using polynomials of degree 2, case distinctions based on signs, or even using the rearrangement inequality. Note that several solutions invoked the intermediate value theorem: when using it, all assumptions must be stated, including the continuity assumption, even if it is obvious to verify. Another common mistake was the direction of inequalities: when using an inequality, one must ensure it is used in the correct direction. Sometimes using an inequality in the wrong direction (and thus false) can give the impression of leading to a solution, but since the initial inequality used is false, the solution is also false.
|
a=x, b=y, c=z
|
Yes
|
Yes
|
proof
|
Algebra
|
Soient $a, b, c, x, y, z>0$ tels que $a+b+c=x+y+z$ et $a b c=x y z$. On suppose de plus $a \leqslant x<y<z \leqslant c$ et $a<b<c$. Montrer que $a=x, b=y, c=z$.
|
Les termes $a+b+c$ et $a b c$ nous rappellent les formules de Viète qui lient les coefficients d'un polynôme à ses racines. Ceci nous invite à considérer les polynômes $P(X)=(X-a)(X-b)(X-c)$ et $Q(X)=$ $(X-x)(X-y)(X-z)$. Sous forme développée, on a
$P(X)=X^{3}-(a+b+c) X^{2}+(a b+b c+c a) X-a b c, \quad Q(X)=X^{3}-(x+y+z) X^{2}+(x y+y z+z x) X-x y z$
et l'énoncé nous assure que les coefficients de degrés 0 et 2 sont identiques pour les deux polynômes. Mais on peut considérer la différence $P(X)-Q(X)$ qui est alors un monôme de la forme $\alpha X$, pour un certain $\alpha$ réel.
Au vu de l'énoncé, il faut montrer que $P(X)=Q(X)$, ou encore que $\alpha=0$. Mais pour ceci, on évalue simplement $P(X)-Q(X)$ en $X=a$ et $X=c$. En ces deux points, on a $P(X)=0$, et alors
$$
\alpha a=-Q(a)=-(a-x)(a-y)(a-z) \geqslant 0
$$
car $a$ est inférieur à $x, y$ et $z$. Comme $a>0$, on en déduit $\alpha \geqslant 0$. Mais on a aussi
$$
\alpha c=-Q(c)=-(c-x)(c-y)(c-z) \leqslant 0
$$
car $c$ est supérieur à $x, y$ et $z$. Comme $c>0$, on en déduit $\alpha \leqslant 0$. Ainsi, on a $\alpha=0$ comme voulu, c'est-à-dire que $P(X)=Q(X)$.
Mais alors les deux polynômes doivent avoir les mêmes racines qui sont $a<b<c$ pour $P(X)$ et $x<y<z$ pour $Q(X)$. On a donc bien
$$
\mathrm{a}=\mathrm{x}, \mathrm{~b}=\mathrm{y}, \mathrm{c}=z
$$
Commentaire des correcteurs : L'exercice n'a pas été beaucoup abordé mais il a été dans l'ensemble très bien réussi par ceux qui l'ont tenté. La solution la plus courante était de passer par des polynômes de degré 3 comme dans le corrigé. D'autres solutions ont été trouvées, comme passer par des polynômes de degré 2 , faire des disjonctions de cas sur les signes ou encore utiliser l'inégalité de réarrangement. Notons que plusieurs copies ont évoqué le théorème des valeurs intermédiaires : lors de son utilisation il faut rappeler toutes les hypothèses, notamment l'hypothèse de continuité doit être écrite même si elle est évidente à vérifier. Une autre erreur faite plusieurs fois est celle du sens des inégalités : lorsqu'on utilise une inégalité, il faut vérifier qu'on l'utilise dans le bon sens. Parfois utiliser une inégalité dans le mauvais sens (donc fausse) peut donner l'impression d'aboutir, mais vu que l'inégalité utilisée initialement est fausse, la solution l'est aussi.
|
{
"exam": "French_envois",
"problem_label": "14",
"problem_match": "\nExercice 14.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-2.jsonl",
"solution_match": "## Solution de l'exercice 14",
"tier": "T2",
"year": null
}
|
For a function $f$ and $n$ a strictly positive integer, we denote $f^{n}$ the $n$-th composition of $f$ defined by $\mathrm{f}^{\mathrm{n}}=\mathrm{f} \circ \mathrm{f} \circ \ldots \circ \mathrm{f}$ where f appears n times on the right-hand side.
Find all functions $\mathrm{f}: \mathbb{N}^{*} \rightarrow \mathbb{N}^{*}$ such that
$$
f^{f(n)}(m)+m n=f(m) f(n)
$$
for all $\mathrm{m}, \mathrm{n} \in \mathbb{N}^{*}$.
|
When $m=n$, we find that $f(m)^{2}=f^{f(m)}(m)+m^{2}>m^{2}$, which gives $f(m)>m$ since $f(m)$ is positive, and thus as $f(m)$ is an integer, $f(m) \geqslant m+1$. By a simple induction, we find that for all positive integers $k$, $m$, $f^{k}(m) \geqslant m+k$.
But we notice that apart from the first term in the statement, the rest is symmetric in $m$ and $n$, and we can write that for all $m, n>0$,
$$
f^{f(n)}(m)+m n=f(m) f(n)=f^{f(m)}(n)+n m
$$
and thus $f^{f(n)}(m)=f^{f(m)}(n)$. We now want to use the fact that we are dealing with a composition, and we set $n=f(a)$ so that $f^{f(m)}(n)=f^{f(m)+1}(a)$. By evaluating the previous equation with $a=m$, we have
$$
f^{f(m)+1}(m)=f^{f(f(m))}(m)
$$
But this implies that $f(f(m))=f(m)+1$. Indeed, otherwise, let $\alpha=\min (f(f(m)), f(m)+1)$ and $k=\max (f(f(m)), f(m)+1)-\alpha>0$ so that the equation reads $f^{k}\left(f^{\alpha}(m)\right)=f^{\alpha}(m)$. But this is absurd since $f^{k}\left(f^{\alpha}(m)\right) \geqslant f^{\alpha}(m)+k>f^{\alpha}(m)$.
We deduce that for all $m \in \mathbb{N}^{*} f(f(m))=f(m)+1$. By a simple induction, for all $k \geqslant 1$, $f^{k}(m)=f(m)+k-1$. Thus the equation in the statement gives for all $m, n \in \mathbb{N}^{*}$,
$$
\mathbf{f}(\mathrm{m})+\mathrm{f}(\mathrm{n})-1+\mathrm{mn}=\mathbf{f}(\mathrm{m}) \mathbf{f}(\mathfrak{n})
$$
If $n=m$, we obtain an equation simply linking $f(n)$ and $n$ :
$$
2 \mathrm{f}(\mathrm{n})+\mathrm{n}^{2}-1=\mathrm{f}(\mathrm{n})^{2}
$$
This is a quadratic equation that can be factored, for example, as $(f(n)-1)^{2}=n^{2}$, so $\mathrm{f}(\mathrm{n})=\mathrm{n}+1$ since $\mathrm{f}(\mathrm{n})$ is strictly positive.
Conversely, if $f(n)=n+1$ for all $n$, then we can write for all $m, n$ :
$$
f^{f(n)}(m)+m n=m+f(n)+m n=m n+m+n+1=(m+1)(n+1)=f(m) f(n)
$$
and this function is indeed a solution to the equation in the statement.
Comment from the graders: Students who solved the problem all have a solution studying the predecessors of the smallest element in the image of f. It is excellent to have been able to adapt this kind of argument to a functional equation. This was indeed where the difficulty lay, and some subtleties of the argument escaped the vigilance of some students. Moreover, several students did not hesitate to propose their proof of elementary properties of f, which is very good to practice: the injectivity of f, the fact that 1 is not reached, the symmetry of the functional equation in $m$ and $n$...
|
f(n) = n + 1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Pour une fonction $f$ et $n$ un entier strictement positif, on note $f^{n}$ la composée $n$-ième de f définie par $\mathrm{f}^{\mathrm{n}}=\mathrm{f} \circ \mathrm{f} \circ \ldots \circ \mathrm{f}$ pù f apparaît n fois dans le membre de droite.
Trouver toutes les fonctions $\mathrm{f}: \mathbb{N}^{*} \rightarrow \mathbb{N}^{*}$ telles que
$$
f^{f(n)}(m)+m n=f(m) f(n)
$$
pour tous $\mathrm{m}, \mathrm{n} \in \mathbb{N}^{*}$.
|
En $m=n$, on trouve que $f(m)^{2}=f^{f(m)}(m)+m^{2}>m^{2}$, ce qui donne $f(m)>m$ car $f(m)$ est positif, et donc comme $f(m)$ est entier, $f(m) \geqslant m+1$. Par une récurrence simple, on trouve que pour tous les entiers $k$, $m$ strictement positifs, $f^{k}(m) \geqslant m+k$.
Mais on remarque qu'à part le premier terme de l'énoncé, le reste est symétrique en $m$ et $n$, et on peut écrire que pour tous $m, n>0$,
$$
f^{f(n)}(m)+m n=f(m) f(n)=f^{f(m)}(n)+n m
$$
et donc $f^{f(n)}(m)=f^{f(m)}(n)$. On veut maintenant utiliser le fait que l'on a affaire à une composée, et on pose donc $n=f(a)$ afin que $f^{f(m)}(n)=f^{f(m)+1}(a)$. En évaluant l'équation précédente avec $a=m$, on a
$$
f^{f(\mathfrak{m})+1}(\mathfrak{m})=f^{f(f(\mathfrak{m}))}(\mathfrak{m})
$$
Mais ceci implique alors que $f(f(m))=f(m)+1$. En effet, sinon, soit $\alpha=\min (f(f(m)), f(m)+1)$ et $k=\max (f(f(m)), f(m)+1)-\alpha>0$ afin que l'équation s'écrive $f^{k}\left(f^{\alpha}(m)\right)=f^{\alpha}(m)$. Mais c'est absurde car $f^{k}\left(f^{\alpha}(m)\right) \geqslant f^{\alpha}(m)+k>f^{\alpha}(m)$.
On déduit que pour tout $m \in \mathbb{N}^{*} f(f(m))=f(m)+1$. Par une récurrence simple, pour tout $k \geqslant 1$, $f^{k}(m)=f(m)+k-1$. Ainsi l'équation de l'énoncé donne pour tous $m, n \in \mathbb{N}^{*}$,
$$
\mathbf{f}(\mathrm{m})+\mathrm{f}(\mathrm{n})-1+\mathrm{mn}=\mathbf{f}(\mathrm{m}) \mathbf{f}(\mathfrak{n})
$$
Si $n=m$, on obtient une équation liant simplement $f(n)$ et $n$ :
$$
2 \mathrm{f}(\mathrm{n})+\mathrm{n}^{2}-1=\mathrm{f}(\mathrm{n})^{2}
$$
C'est une équation du second degré que l'on peut par exemple factoriser en $(f(n)-1)^{2}=n^{2}$, donc $\mathrm{f}(\mathrm{n})=\mathrm{n}+1$ car $\mathrm{f}(\mathrm{n})$ est strictement positif.
Réciproquement, si $f(n)=n+1$ pour tout $n$, alors on peut écrire pour tous $m, n$ :
$$
f^{f(n)}(m)+m n=m+f(n)+m n=m n+m+n+1=(m+1)(n+1)=f(m) f(n)
$$
et cette fonction est bien solution de l'équation de l'énoncé.
Commentaire des correcteurs: Les élèves ayant résolu le problème on tous une solution étudiant les antécédents du plus petit élément de l'image de f. Il est excellent d'avoir su adapter ce genre d'argument à une équation fonctionnelle. C'était d'ailleurs là que résidait la difficulté, et quelques subtilités de l'argument ont échappé à la vigilance de quelques élèves. Par ailleurs, plusieurs élèves n'ont pas hésité à proposer leur preuve de propriétés élémentaires de f, ce sur quoi il est très bon de s'entraîner : l'injectivité de f , le fait que 1 n 'est pas atteint, la symétrie de l'équation fonctionnelle en $m$ et $n$...
|
{
"exam": "French_envois",
"problem_label": "15",
"problem_match": "\nExercice 15.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-2.jsonl",
"solution_match": "## Solution de l'exercice 15",
"tier": "T2",
"year": null
}
|
Let $b_{1}, \ldots, b_{n}$ be non-negative real numbers such that $b_{1}+b_{2}+\ldots+b_{n}=2$. Let $a_{0}, a_{1}, \ldots, a_{n}$ be real numbers such that $a_{0}=a_{n}=0$. Suppose that for all $i$ between 1 and $n$ inclusive,
$$
\left|a_{i}-a_{i-1}\right| \leqslant b_{i}
$$
Show that we have
$$
\left(a_{0}+a_{1}\right) b_{1}+\left(a_{1}+a_{2}\right) b_{2}+\ldots+\left(a_{n-1}+a_{n}\right) b_{n} \leqslant 2
$$
|
For any index $i$, we have two upper bounds for $a_{i}$. Indeed, we can write
$$
\begin{aligned}
a_{i}=a_{i}-a_{0}= & \left(a_{i}-a_{i-1}\right)+\left(a_{i-1}-a_{i-2}\right)+\ldots+\left(a_{1}-a_{0}\right) \\
& \leqslant b_{i}+b_{i-1}+\ldots+b_{1}=\sum_{j=1}^{i} b_{j}
\end{aligned}
$$
and
$$
\begin{aligned}
a_{i}=a_{i}-a_{n} & =\left(a_{i}-a_{i+1}\right)-\left(a_{i+1}-a_{i+2}\right)+\ldots+\left(a_{n-1}-a_{n}\right) \\
& \leqslant b_{i+1}+b_{i+2}+\ldots+b_{n}=\sum_{j=i+1}^{n} b_{j} .
\end{aligned}
$$
To effectively upper bound $a_{i}$, we want to find the smallest of these two terms. But the sum of the two is 2, so we just need to determine whether $\sum_{j=1}^{i} b_{j}$ is less than or greater than 1.
Let $m$ be the smallest integer such that $\sum_{j=1}^{m} b_{j}>1$. We then write
$$
\sum_{i=1}^{n}\left(a_{i-1}+a_{i}\right) b_{i}=\sum_{i=1}^{m-1}\left(a_{i-1}+a_{i}\right) b_{i}+\left(a_{m-1}+a_{m}\right) b_{m}+\sum_{i=m+1}^{n}\left(a_{i-1}+a_{i}\right) b_{i}
$$
For $i<m$, we upper bound $a_{i}$ by $\sum_{j=1}^{i} b_{j}$, and for $i \geqslant m$, we upper bound $a_{i}$ by $\sum_{j=i+1}^{n} b_{j}$ to obtain
$$
\sum_{i=1}^{n}\left(a_{i-1}+a_{i}\right) b_{i} \leqslant \sum_{i=1}^{m-1}\left(b_{i}+2 \sum_{j=1}^{i-1} b_{j}\right) b_{i}+\left(\sum_{j=1}^{m-1} b_{j}+\sum_{j=m+1}^{n} b_{j}\right) b_{m}+\sum_{i=1}^{m}\left(b_{i}+2 \sum_{j=i+1}^{n} b_{j}\right) b_{i}
$$
Let $x=\sum_{j=1}^{m-1} b_{j}$ and $y=\sum_{j=m+1}^{n} b_{j}$. By definition of $m$, we have $x \leqslant 1$ and $y \leqslant 1$. Consider the first sum in the previous term. In this sum, we have a term $b_{i}^{2}$ for all $i \leqslant m-1$ and a term $2 b_{i} b_{j}$ for all $j<i \leqslant m-1$. Thus, this sum is nothing other than $x^{2}$. Similarly, the right sum is nothing other than $y^{2}$. We can therefore write, since $x+b_{m}+y=2$,
$$
\begin{aligned}
\sum_{i=1}^{n}\left(a_{i-1}+a_{i}\right) b_{i} & \leqslant x^{2}+(x+y)(2-x-y)+y^{2} \\
= & 2(x+y)-2 x y
\end{aligned}
$$
It remains to show that $2(x+y)-2 x y \leqslant 2$ to conclude, or equivalently $x+y-x y \leqslant 1$. But this can be rewritten, by moving all terms to the right side of the inequality,
$$
(1-x)(1-y) \geqslant 0
$$
which is true since we have seen that $x \leqslant 1$ and $y \leqslant 1$.
Comment from the graders: The problem was rarely attempted, and it is particularly unfortunate because it was a good prototype of a problem that could appear in international olympiads, so it is a shame not to at least provide some hints on how each one could have progressed on the problem. This problem illustrates recurring errors made by students in such problems:
- Often students claim that if the sequence $\left(a_{i}\right)$ satisfies a certain property, it can be changed to increase the sum in the problem, and then conclude directly that we can reduce to the case where the sequence does not satisfy this property. Be careful: this is not necessarily true. Indeed, if we say that a certain property is a problem, and count the number of problems in the sequence, there is no reason for this number to decrease. One must provide a procedure to remove the problems one by one, without creating new ones: often a good technique is to introduce a variant (either the number of problems or something else). Another option for this is to show that there is a maximizer, but this is often complicated. Here it could have been shown, but goes beyond the scope of mathematical olympiad theorems.
- Some, under the pretext that the problem is difficult, do not prove their assertions. Surprisingly, what is not proven often turns out to be false, difficult, or incomplete: just because the problem is difficult does not mean one can allow less detail.
- Many students tried to show directly that one can assume the sequence is first increasing and then decreasing. This was difficult to prove properly, and especially it was not the first reflex to have. Here, using a graphical representation was useful: in fact, we always have $a_{k} \leqslant b_{1}+\cdots+b_{k}$ and $a_{k} \leqslant b_{k+1}+\cdots+b_{n}$. We can therefore graphically represent the points $\left(k, b_{1}+\cdots+b_{k}\right)$ and $\left(k, b_{k+1}+\cdots+b_{n}\right)$ and connect the two types of points to obtain a curve. It is natural to then look at the minimum of these two curves and set $a_{k}$ to be the sequence corresponding to this curve. This is exactly what is done in the solution, and it is recurrent that students forget to graphically represent the constraints to try to understand what is happening and see what is really the right way to approach the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soient $b_{1}, \ldots, b_{n}$ des réels positifs ou nuls tels que $b_{1}+b_{2}+\ldots+b_{n}=2$. Soient $a_{0}, a_{1}, \ldots, a_{n}$ des nombres réels tels que $a_{0}=a_{n}=0$. Supposons que pour tout $i$ compris entre 1 et $n$ inclus,
$$
\left|a_{i}-a_{i-1}\right| \leqslant b_{i}
$$
Montrer que l'on a
$$
\left(a_{0}+a_{1}\right) b_{1}+\left(a_{1}+a_{2}\right) b_{2}+\ldots+\left(a_{n-1}+a_{n}\right) b_{n} \leqslant 2
$$
|
Pour tout indice $i$, on a deux majorations de $a_{i}$. En effet, on peut écrire
$$
\begin{aligned}
a_{i}=a_{i}-a_{0}= & \left(a_{i}-a_{i-1}\right)+\left(a_{i-1}-a_{i-2}\right)+\ldots+\left(a_{1}-a_{0}\right) \\
& \leqslant b_{i}+b_{i-1}+\ldots+b_{1}=\sum_{j=1}^{i} b_{j}
\end{aligned}
$$
et
$$
\begin{aligned}
a_{i}=a_{i}-a_{n} & =\left(a_{i}-a_{i+1}\right)-\left(a_{i+1}-a_{i+2}\right)+\ldots+\left(a_{n-1}-a_{n}\right) \\
& \leqslant b_{i+1}+b_{i+2}+\ldots+b_{n}=\sum_{j=i+1}^{n} b_{j} .
\end{aligned}
$$
Afin de majorer efficacement $a_{i}$, on voudrait trouver le plus petit de ces deux termes. Mais la somme des deux vaut 2 , donc il faut simplement déterminer si $\sum_{j=1}^{i} b_{j}$ est inférieur ou supérieur à 1 .
Soit $m$ l'entier minimal tel que $\sum_{j=1}^{m} b_{j}>1$. On écrit alors
$$
\sum_{i=1}^{n}\left(a_{i-1}+a_{i}\right) b_{i}=\sum_{i=1}^{m-1}\left(a_{i-1}+a_{i}\right) b_{i}+\left(a_{m-1}+a_{m}\right) b_{m}+\sum_{i=m+1}^{n}\left(a_{i-1}+a_{i}\right) b_{i}
$$
Pour $i<m$, on majore $a_{i}$ par $\sum_{j=1}^{i} b_{j}$, et pour $i \geqslant m$, on majore $a_{i}$ par $\sum_{j=i+1}^{n} b_{j}$ pour obtenir
$$
\sum_{i=1}^{n}\left(a_{i-1}+a_{i}\right) b_{i} \leqslant \sum_{i=1}^{m-1}\left(b_{i}+2 \sum_{j=1}^{i-1} b_{j}\right) b_{i}+\left(\sum_{j=1}^{m-1} b_{j}+\sum_{j=m+1}^{n} b_{j}\right) b_{m}+\sum_{i=1}^{m}\left(b_{i}+2 \sum_{j=i+1}^{n} b_{j}\right) b_{i}
$$
Posons $x=\sum_{j=1}^{m-1} b_{j}$ et $y=\sum_{j=m+1}^{n} b_{j}$. Par définition de $m$, on a $x \leqslant 1$ et $y \leqslant 1$. Considérons la première somme dans le terme précédent. Dans celle-ci, on a un terme $b_{i}^{2}$ pour tout $i \leqslant m-1$ et un terme $2 b_{i} b_{j}$ pour tous $j<i \leqslant m-1$. Ainsi, cette somme n'est rien d'autre que $x^{2}$. De même, la somme de droite n'est rien d'autre que $y^{2}$. On peut donc écrire, comme $x+b_{m}+y=2$,
$$
\begin{aligned}
\sum_{i=1}^{n}\left(a_{i-1}+a_{i}\right) b_{i} & \leqslant x^{2}+(x+y)(2-x-y)+y^{2} \\
= & 2(x+y)-2 x y
\end{aligned}
$$
Il nous reste enfin à voir que $2(x+y)-2 x y \leqslant 2$ pour conclure, ou encore $x+y-x y \leqslant 1$. Mais ceci se réécrit, en passant tous les termes à droite de l'inégalité,
$$
(1-x)(1-y) \geqslant 0
$$
ce qui est vérifié car on a vu que $x \leqslant 1$ et $y \leqslant 1$.
Commentaire des correcteurs : L'exercice a été très peu abordé, et c'est particulièrement dommage car c'était un bon prototype d'exercice pouvant tomber à des olympiades internationales, donc il est dommage de ne pas laisser au moins des pistes pour voir comment en test chacun aurait pu avancer sur le problème. Celui-ci témoigne d'erreurs récurrentes commises par les élèves dans de tels problèmes :
- Souvent des élèves affirment que si la suite $\left(a_{i}\right)$ vérifie telle propriété, on peut la changer pour agumenter la somme de l'énoncé, puis conclut directement qu'on se ramène au cas où la suite ne vérifie pas ça. Attention : cela n'est pas forcément vrai. En effet, si on dit que telle propriété est un problème, et qu'on compte le nombre de problèmes de la suite, celui-ci n'a aucune raison de décroître. Il faut donner un procédé permettant d'enlever les problèmes 1 par 1 , sans en créer de nouveau : souvent une bonne technique est d'introduire un variant (soit le nombre de problème, soit autre chose). Une autre option pour cela est de montrer qu'il y a un maximisant, mais cela est souvent compliqué. Ici cela pouvait se montrer, mais dépasse le cadre des théorèmes de mathématique olympique.
- Certains, sous prétexte que l'exercice est dur, ne prouvent pas leurs affirmations. Etonnamment, souvent ce qui n'est pas prouvé se révèle être faux, difficile ou incomplet : ce n'est pas parce que l'exercice est dur, qu'il faut se permettre moins de détail.
- Beaucoup d'élèves ont essayé de montrer directement qu'on pouvait supposer la suite croissante puis décroissante. C'était difficile à prouver proprement, et surtout ce n'était pas le premier réflexe à avoir. Ici utiliser une représentation graphique était utile : en fait on a forcément $a_{k} \leqslant b_{1}+\cdots+$ $b_{k}$ et $a_{k} \leqslant b_{k+1}+\cdots+b_{n}$. on peut donc représenter graphiquement les points $\left(k, b_{1}+\cdots+b_{k}\right)$ et $\left(k, b_{k+1}+\cdots+b_{n}\right)$ et relier les deux types de points pour obtenir une courbe. Il est naturel d'ensuite regarder le minimum de ces deux courbes et de poser $a_{k}$ la suite correspondant à cette courbe. C'est exactement ce qui est fait dans le corrigé, et il est récurrent que les élèves oublient de représenter graphiquement les contraintes pour essayer de comprendre ce qui se passe, et voir quel est vraiment la bonne façon d'aborder l'énoncé.
|
{
"exam": "French_envois",
"problem_label": "16",
"problem_match": "\nExercice 16.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-2.jsonl",
"solution_match": "## Solution de l'exercice 16",
"tier": "T2",
"year": null
}
|
Let $\alpha \neq 0$. Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that for all real numbers $x, y$,
$$
f\left(x^{2}+y+f(y)\right)=f(x)^{2}+\alpha y
$$
|
Let $x=0$. Then the equation becomes $f(y+f(y))=f(0)^{2}+\alpha y$ for all $y$. Since $\alpha$ is non-zero, the right-hand side describes all real numbers as $y$ varies, and thus $f$ is surjective.
Let $y=0$. Then we can write for all real $x$,
$$
\mathbf{f}(\mathrm{x})^{2}=\mathbf{f}\left(\mathrm{x}^{2}+\mathrm{f}(0)\right)=\mathbf{f}\left((-\mathrm{x})^{2}+\mathbf{f}(0)\right)=\mathrm{f}(-\mathrm{x})^{2}
$$
We know that $f$ is surjective, so let $c$ be a preimage of 0. The equation in the statement with $x=0$ and $\mathrm{y}=\mathrm{c}$ gives
$$
\alpha \mathrm{c}+\mathrm{f}(0)^{2}=\mathrm{f}(0+\mathrm{c}+\mathrm{f}(\mathrm{c}))=\mathrm{f}(\mathrm{c})=0
$$
But we know that $\mathrm{f}(-\mathrm{c})^{2}=\mathrm{f}(\mathrm{c})^{2}=0$ so $-c$ is also a preimage of 0. By the equation above applied to $c$ and $-c$, we have $\alpha \mathrm{c}+\mathrm{f}(0)^{2}=0=-\alpha \mathrm{c}+\mathrm{f}(0)^{2}$. Since $\alpha \neq 0$, we deduce that necessarily $\mathrm{c}=0$.
Now that we know 0 is the only preimage of 0, we set the right-hand term in the initial equation to zero by choosing $y=-\frac{f(x)^{2}}{\alpha}$, then $f\left(x^{2}+y+f(y)\right)=0$, which means $x^{2}+y+f(y)=0$ or
$$
\begin{gathered}
x^{2}-\frac{f(x)^{2}}{\alpha}+f\left(-\frac{f(x)^{2}}{\alpha}\right)=0 \\
x^{2}=\frac{f(x)^{2}}{\alpha}-f\left(-\frac{f(x)^{2}}{\alpha}\right)
\end{gathered}
$$
for all real $x$. Therefore, if $f(x)= \pm f\left(x^{\prime}\right)$, the above equation gives $x^{2}=x^{\prime 2}$, so $x= \pm x^{\prime}$.
Let $x \neq 0$ be a real number. Consider the equation $f\left(x^{\prime}\right)= \pm f(x)$. We have seen that this equation has exactly two solutions, which are $x$ and $-x$ (which are distinct since $x \neq 0$). But there is a solution to $f\left(x^{\prime}\right)=-f(x)$ by the surjectivity of $f$. Since $f(x) \neq 0$, it cannot be $x^{\prime}=x$, so it must be $x^{\prime}=-x$. Thus, $f(-x)=-f(x)$, and the only solution to $f\left(x^{\prime}\right)=f(x)$ is $x^{\prime}=x$. Since 0 is the unique preimage of 0, $f$ is both odd and injective.
The initial equation with $y=0$ gives for all real $x$, $f\left(x^{2}\right)=f(x)^{2}$. Thus, the equation in the statement can be rewritten as
$$
\forall x, y \in \mathbb{R}, \quad f\left(x^{2}+y+f(y)\right)=f\left(x^{2}\right)+\alpha y
$$
so with $z=x^{2}$,
$$
\forall y \in \mathbb{R}, z \geqslant 0, \quad \mathrm{f}(z+y+f(y))=f(z)+\alpha y
$$
If now $z \leqslant 0$, we calculate for all $y$, by the oddness of $f$,
$$
\begin{aligned}
f(z+y+f(y)) & =-f(-z-y-f(y))=-f((-z)+(-y)+f(-y)) \\
& =-(f(-z)+\alpha(-y))=f(z)+\alpha y
\end{aligned}
$$
This is the same equation as for $z \geqslant 0$, hence
$$
\forall y, z \in \mathbb{R}, \quad \mathrm{f}(z+y+f(y))=f(z)+\alpha y
$$
With $z=0$, we have in particular for all $y$, $f(y+f(y))=\alpha y$. Let $z=x+f(x)$ in the above equation to get for all $x, y \in \mathbb{R}$,
$$
f(x+f(x)+y+f(y))=f(x+f(x))+\alpha y=\alpha x+\alpha y=\alpha(x+y)=f(x+y+f(x+y))
$$
and thus, by injectivity, $f(x+y)=f(x)+f(y)$. Therefore, $f$ is a solution to Cauchy's equation. But $f$ is increasing because if $x>y$, we have
$$
f(x)=f(y)+f(x-y)=f(y)+f\left((\sqrt{x-y})^{2}\right)=f(y)+f(\sqrt{x-y})^{2} \geqslant f(y)
$$
so $f$ is linear on $\mathbb{R}$. From the equation $f\left(x^{2}\right)=f(x)^{2}$, its leading coefficient satisfies $a^{2}=a$ so $a=0$ or $a=1$, meaning that $f$ is either zero or the identity on $\mathbb{R}$. Since $f$ is surjective, it must be the identity: for all $x$, $f(x)=x$.
Substituting back into the equation, we get
$$
\forall x, y \in \mathbb{R}, \quad x^{2}+2 y=x^{2}+\alpha y
$$
so with $x=0, y=1$, we have $\alpha=2$ necessarily. Conversely, if $\alpha=2$, the identity is indeed a solution by the previous calculation. Thus, if $\alpha \neq 2$, there is no solution, and if $\alpha=2$, the identity is a solution.
Comment from the graders: The problem was rarely attempted, a handful of students solved it perfectly. Some tried quite natural initial steps, showing in particular that $f$ is surjective and that $f(0)=0$, but did not go further. Be careful to note for which values the equalities obtained are indeed true: when substituting one variable in terms of another, we lose generality. For example, after setting $y=f\left(-x^{2}\right)$, the resulting equality is not true for all $x$ and $y$.
|
f(x) = x \text{ if } \alpha = 2; \text{ no solution otherwise}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Soit $\alpha \neq 0$. Trouver toutes les fonctions $f: \mathbb{R} \rightarrow \mathbb{R}$ telles que pour tous réels $x, y$,
$$
f\left(x^{2}+y+f(y)\right)=f(x)^{2}+\alpha y
$$
|
Posons $x=0$. Alors l'équation devient $f(y+f(y))=f(0)^{2}+\alpha y$ pour tout $y$. Comme $\alpha$ est non nul, le côté droit décrit tous les réels lorsque $y$ varie, et ainsi $f$ est surjective.
Posons $y=0$. Alors on peut écrire pour tout réel $x$,
$$
\mathbf{f}(\mathrm{x})^{2}=\mathbf{f}\left(\mathrm{x}^{2}+\mathrm{f}(0)\right)=\mathbf{f}\left((-\mathrm{x})^{2}+\mathbf{f}(0)\right)=\mathrm{f}(-\mathrm{x})^{2}
$$
On sait que f est surjective, soit donc c un antécédent de 0 . L'équation de l'énoncé $\operatorname{avec} x=0$ et $\mathrm{y}=\mathrm{c}$ donne
$$
\alpha \mathrm{c}+\mathrm{f}(0)^{2}=\mathrm{f}(0+\mathrm{c}+\mathrm{f}(\mathrm{c}))=\mathrm{f}(\mathrm{c})=0
$$
Mais on sait que $\mathrm{f}(-\mathrm{c})^{2}=\mathrm{f}(\mathrm{c})^{2}=0$ donc -c est aussi un antécédent de 0 . Par l'équation ci-dessus appliquée à c et à -c , on a donc $\alpha \mathrm{c}+\mathrm{f}(0)^{2}=0=-\alpha \mathrm{c}+\mathrm{f}(0)^{2}$. Comme $\alpha \neq 0$, on en déduit que nécessairement $\mathrm{c}=0$.
Maintenant que l'on sait que 0 est le seul antécédent de 0 , on annule le terme de droite dans l'équation de départ en choisissant $y=-\frac{f(x)^{2}}{\alpha}$, alors $f\left(x^{2}+y+f(y)\right)=0$, soit $x^{2}+y+f(y)=0$ ou encore
$$
\begin{gathered}
x^{2}-\frac{f(x)^{2}}{\alpha}+f\left(-\frac{f(x)^{2}}{\alpha}\right)=0 \\
x^{2}=\frac{f(x)^{2}}{\alpha}-f\left(-\frac{f(x)^{2}}{\alpha}\right)
\end{gathered}
$$
pour tout réel $x$. Dès lors, si $f(x)= \pm f\left(x^{\prime}\right)$, l'équation précédente donne $x^{2}=x^{\prime 2}$ donc $x= \pm x^{\prime}$.
Soit $x \neq 0$ un réel. Etudions l'équation $f\left(x^{\prime}\right)= \pm f(x)$. On a vu que celle ci avait exactement deux solutions, qui sont $x$ et $-x$ (qui sont distincts car $x \neq 0$ ). Mais il existe une solution à $f\left(x^{\prime}\right)=-f(x)$ par surjectivité de f. Comme $f(x) \neq 0$, cela ne peut pas être $x^{\prime}=x$, c'est donc $x^{\prime}=-x$. Ainsi, $f(-x)=-f(x)$, et la seule solution à $f\left(x^{\prime}\right)=f(x)$ est $x^{\prime}=x$. Comme en plus 0 est l'unique antécédent de 0 , f est à la fois impaire et injective.
L'équation initiale avec $y=0$ donne pour tout $x$ réel, $f\left(x^{2}\right)=f(x)^{2}$. Ainsi, l'équation de l'énoncé se réécrit
$$
\forall x, y \in \mathbb{R}, \quad f\left(x^{2}+y+f(y)\right)=f\left(x^{2}\right)+\alpha y
$$
donc $\operatorname{avec} z=x^{2}$,
$$
\forall y \in \mathbb{R}, z \geqslant 0, \quad \mathrm{f}(z+y+f(y))=f(z)+\alpha y
$$
Si maintenant $z \leqslant 0$, on calcule pour tout $y$, par imparité de f ,
$$
\begin{aligned}
f(z+y+f(y)) & =-f(-z-y-f(y))=-f((-z)+(-y)+f(-y)) \\
& =-(f(-z)+\alpha(-y))=f(z)+\alpha y
\end{aligned}
$$
C'est la même équation que pour $z \geqslant 0$, d'où
$$
\forall y, z \in \mathbb{R}, \quad \mathrm{f}(z+y+f(y))=f(z)+\alpha y
$$
Avec $z=0$, on a notamment pour tout $y, f(y+f(y))=\alpha y$. Posons $z=x+f(x)$ dans l'équation ci-dessus pour avoir pour tous $x, y \in \mathbb{R}$,
$$
f(x+f(x)+y+f(y))=f(x+f(x))+\alpha y=\alpha x+\alpha y=\alpha(x+y)=f(x+y+f(x+y))
$$
et donc, par injectivité, $f(x+y)=f(x)+f(y)$. Ainsi, $f$ est solution de l'équation de Cauchy. Mais $f$ est croissante car si $x>y$, on a
$$
f(x)=f(y)+f(x-y)=f(y)+f\left((\sqrt{x-y})^{2}\right)=f(y)+f(\sqrt{x-y})^{2} \geqslant f(y)
$$
donc $f$ est linéaire sur $\mathbb{R}$. D'après l'équation $f\left(x^{2}\right)=f(x)^{2}$, son coefficient dominant a vérifie $a^{2}=$ a donc $\mathrm{a}=0$ ou $\mathrm{a}=1$, c'est-à-dire que f est soit nulle, soit l'identité sur $\mathbb{R}$. f étant surjective, nécessairement, c'est l'identité : pour tout $x, f(x)=x$.
En réinjectant dans l'équation, on obtient
$$
\forall x, y \in \mathbb{R}, \quad x^{2}+2 y=x^{2}+\alpha y
$$
donc avec $x=0, y=1$, on a $\alpha=2$ nécessairement. Réciproquement, si $\alpha=2$, l'identité est bien solution par le calcul précédent. Ainsi, si $\alpha \neq 2$, il n'y a aucune solution, et si $\alpha=2$, l'identité est solution.
Commentaire des correcteurs : L'exercice a été très peu abordé, une poignée d'élèves l'ont résolu parfaitement. Certains ont tenté des débuts de solution assez naturels, en montrant notamment que f était surjective et que $f(0)=0$, mais ne sont pas allés plus loin. Attention à bien noter pour quelles valeurs les égalités obtenues sont effectivement vraies : lorsqu'on fait une substitution d'une variable en fonction d'une autre on perd de la généralité. Par exemple après avoir posé $y=f\left(-x^{2}\right)$, l'égalité qui en résute n'est pas vraie pour tout $x$ et pour tout $y$.
|
{
"exam": "French_envois",
"problem_label": "17",
"problem_match": "\nExercice 17.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-2.jsonl",
"solution_match": "## Solution de l'exercice 17",
"tier": "T2",
"year": null
}
|
Let $\mathrm{P}(\mathrm{X})$ be a unitary polynomial with real coefficients of degree 2022. Emile plays the following game: he writes the polynomial $P(X)$ on the board and at each step, if the polynomial $f(X)$ is written on the board, Emile can replace it with:
- The polynomial $f(X)+c$, for $c$ a real number of his choice, or
- the polynomial $\mathrm{P}(\mathrm{f}(\mathrm{X})$ ).
Find all non-negative integers $n$ such that, regardless of the initial polynomial $P$, Emile can find a sequence of operations such that the resulting polynomial has exactly $n$ distinct real roots.
|
It is said that an integer n works if, for any initial polynomial P, Emile can find a sequence of operations such that the obtained polynomial has exactly n distinct real roots.
Let's start with the simple remark that at each step, whatever Emile chooses, the polynomial written on the board will be monic, of even degree, and non-constant.
We show the following points:
1. $\underline{S i n}$ works, then $\mathrm{n}+2$ also works:
Let $P(X)$ be a polynomial as described. Suppose Emile can find a sequence of operations that allows him to obtain a polynomial $f(X)$ with $n$ distinct real roots written on the board.
We will look for two constants $a$ and $b$ such that the polynomial $g(X)=P(f(X)+a)+b$ has exactly $n+2$ distinct real roots. Then Emile can simply add $a$, compose with $P$, and then add $b$ to the obtained polynomial to get the desired polynomial.
We wish to use the fact that $f(X)$ has exactly $n$ roots by ensuring that a root of $f$ is a root of $g(X)=P(f(X)+a)+b$, which imposes $b=-P(a)$. The roots of $g(X)$ are then the reals $x$ such that $f(x)+a$ is a preimage of $P(a)$. To have the fewest possible cases to handle, we choose $|a|$ to be very large so that the equation $P(X)=P(a)$ has exactly two real solutions: this is possible because for $c$ large enough, the equation $P(X)=c$ has exactly two real solutions.
Let $a, a'$ be the two solutions of $P(X)=P(a)$. Thus, the roots of $g(X)$ are the roots of $f(X)$ and the solutions of $f(x)+a=a'$, i.e., the preimages of $a'-a$ by $f$. Again, we want the fewest possible preimages (without having none), so we want $a'-a$ to be very large. Since $f$ is monic of even degree, if $a'-a$ is large enough, $a'-a$ has exactly 2 preimages by $f$, which gives that $g(X)$ has exactly $n+2$ roots.
Let's verify that we can indeed choose $a$ as desired. Take $a$ negative such that $|a|$ is very large. As $a$ tends to $-\infty$, $P(a)$ tends to $+\infty$ and $a'$ is the largest solution of $P(X)=P(a)$ which tends to $+\infty$. If $|a|$ is large enough, $a'-a$ can become arbitrarily large, as desired.
2. $\underline{n}=0$ and $\mathrm{n}=2021$ work:
Let $P(X)$ be a polynomial as described.
The case of $\mathrm{n}=0$ is simple. Indeed, $P(X)$ is monic of even degree, so it has a minimum on $\mathbb{R}$. If $c$ is strictly greater than the opposite of this minimum, $P(x)+c=0$ has no solution on $\mathbb{R}$. Thus, if Emile replaces $P(X)$ with $P(X)+c$ on the first turn, he obtains a polynomial with no real roots as desired.
For $\mathfrak{n}=2021$, it is a bit more subtle. Since $x \mapsto P(x)$ is decreasing for $x$ sufficiently small and increasing for $x$ sufficiently large, $P$ has an odd number of local extrema. Thus there exists $c$ such that an odd number of these extrema are solutions of $P(x)=c$. Indeed, suppose the values taken at these extrema are $c_{1}, \ldots, c_{k}$, and say that $c_{i}$ is the value of $P$ at $n_{i}$ distinct extrema. Then the number of extrema of $P$ is $n_{1}+\cdots+n_{k}$ and is odd, so there exists $i$ such that $n_{i}$ is odd, which is what we wanted.
Suppose now that Emile replaces the initial polynomial $P(X)$ with $P(X)-c$. This polynomial is positive at $-\infty$ and $+\infty$ and thus changes sign an even number of times. But by definition of $c$, it also has an odd number of zeros which are local extrema (i.e., where it does not change sign), and thus $P(X)-c$ has an odd number of distinct real roots. This number is necessarily less than 2022, so less than 2021 because it is odd. By the previous part of the proof, by adding 2 several times to the number of distinct roots, Emile can always obtain, after a certain number of steps, a polynomial with exactly 2021 distinct real roots.
By combining the first two parts of the proof, we obtain that all even $n$ and all odd $n$ greater than or equal to 2021 work. It remains to see that the others do not work.
3. $\mathrm{n} \leqslant 2019$ odd does not work:
Let $n \leqslant 2019$ be odd. In this part of the proof, we need to exhibit a polynomial $P(X)$ that prevents Emile from obtaining $n$ distinct real roots in a finite number of steps. From the proof of the previous part, we need to find a polynomial $P(X)$ such that if an odd number of local extrema of $P$ satisfy $P(x)=c$, then $P(X)-c$ has strictly more than 2019 distinct roots.
Consider the polynomial $P(X)=X^{2}(X^{2}-1) \ldots (X^{2}-1010)$. It is even, so all its local extrema come in pairs, except for the one at 0 which is zero. But the polynomial $P(X)$ has 2021 distinct roots, and it seems to be a good candidate for this part. Since $P(X)$ is even, for all $c \neq 0$, the equation $P(x)=c$ has an even number of solutions, and the equation $P(x)=0$ has an odd number of solutions (precisely 2021).
Suppose by contradiction that after a certain number of steps, Emile manages to obtain a polynomial with $n$ distinct real roots, this polynomial will then be of the form $f(P(X))$, with $f(X)$ monic and non-constant. Let $r_{1}, \ldots, r_{k}$ be the roots of $f(X)$. The roots of $f(P(X))$ are exactly the reals that are solutions to an equation of the form $P(x)=r_{i}$. Let $n_{i}$ be the number of solutions to $P(x)=r_{i}$. We have $n_{1}+n_{2}+\ldots+n_{k}=n$. Since $n$ is odd, one of the $n_{i}$ must be odd. But the only real $r_{i}$ that has an odd number of preimages by $P$ is 0, which has 2021. Thus, $r_{i}=0$ and $n_{i}=2021$, which gives $n \geqslant 2021$, a contradiction.
To conclude, the integers $n$ that work are the even integers and the odd integers greater than or equal to 2021.
Comment from the graders: The problem was only tackled by one submission which solved it perfectly. The problem was very difficult, however, it is a pity that there were not more submissions proposing at least some research directions. It is not necessary to have fully solved a problem to submit something, and here there were several intermediate steps that could have earned points even if the solution was not complete.
|
the even integers and the odd integers greater than or equal to 2021
|
Yes
|
Incomplete
|
math-word-problem
|
Algebra
|
Soit $\mathrm{P}(\mathrm{X})$ un polynôme à coefficients réels unitaire de degré 2022. Emile joue au jeu suivant : il écrit le polynôme $P(X)$ au tableau et à chaque étape, si le polynôme $f(X)$ est écrit au tableau, Emile peut le remplacer par :
- Le polynôme $f(X)+c$, pour $c$ un réel de son choix, ou
- le polynôme $\mathrm{P}(\mathrm{f}(\mathrm{X})$ ).
Trouver tous les entiers positifs ou nuls $n$ tels que, quelque soit le polynôme $P$ initial, Emile peut trouver une suite d'opérations telles que le polynôme obtenu ait exactement n racines réelles distinctes.
|
On dit qu'un entier n fonctionne si quelque soit le polynôme P initial, Emile peut trouver une suite d'opérations telles que le polynôme obtenu ait exactement n racines réelles distinctes.
Commençons par faire la remarque simple qu'à chaque étape, quoique choisisse Emile, le polynôme écrit au tableau sera unitaire, de degré pair, et non constant.
On montre les points suivants :
1. $\underline{S i n}$ fonctionne, alors $\mathrm{n}+2$ aussi :
Soit $P(X)$ un polynôme comme dans l'énoncé. Supposons qu'Emile peut trouver une suite d'opérations qui lui permet d'obtenir un polynôme $f(X)$ avec $n$ racines réelles distinctes écrit au tableau.
On va chercher à trouver deux constantes $a$ et $b$ telles que le polynôme $g(X)=P(f(X)+a)+b$ ait exactement $n+2$ racines réelles distinctes. Alors Emile pourra simplement ajouter $a$, composer par P , puis ajouter b au polynôme obtenu pour avoir le polynôme voulu.
On souhaite utiliser le fait que $f(X)$ ait exactement $n$ racines en faisant en sorte qu'une racine de $f$ soit une racine de $g(X)=P(f(X)+a)+b$, ce qui impose $b=-P(a)$. Les racines de $g(X)$ sont alors les réels $x$ tels que $f(x)+a$ soit un antécédent de $P(a)$. Pour avoir le moins de cas possibles à traiter, on choisit |a| très grand pour que l'équation $P(X)=P(a)$ ait exactement deux solutions réelles : c'est possible car pour c assez grand, l'équation $\mathrm{P}(\mathrm{X})=\mathrm{c}$ a exactement deux solutions réelles.
Soient $a, a^{\prime}$ les deux solutions de $P(X)=P(a)$. Ainsi, les racines de $g(X)$ sont les racines de $f(X)$ et les solutions de $f(x)+a=a^{\prime}$, c'est-à-dire les antécédents par $f$ de $a^{\prime}-a$. Encore une fois, on veut le moins d'antécédents possibles (sans pour autant en avoir aucun), donc on voudrait que $a^{\prime}-a$ soit très grand. $f$ étant unitaire de degré pair, si $a^{\prime}-a$ est assez grand, $a^{\prime}-a$ exactement 2 antécédents par f , ce qui donne bien que $g(X)$ a exactement $n+2$ racines.
Vérifions que l'on peut bien choisir a comme voulu. Prenons a négatif tel que $|a|$ soit très grand. Lorsque $a$ tend vers $-\infty, P(a)$ tend vers $+\infty$ et $a^{\prime}$ est la solution la plus grande de $P(X)=P(a)$ qui tend vers $+\infty . S \mathrm{Si}|a|$ est assez grand, $a^{\prime}-a$ peut devenir arbitrairement grand, comme voulu.
2. $\underline{n}=0$ et $\mathrm{n}=2021$ fonctionnent:
Soit $P(X)$ un polynôme comme dans l'énoncé.
Le cas de $\mathrm{n}=0$ est simple. En effet, $\mathrm{P}(\mathrm{X})$ est unitaire de degré pair, donc il admet un minimum $\operatorname{sur} \mathbb{R}$. Si c est strictement supérieur à l'opposé de ce minimum, $\mathrm{P}(\mathrm{x})+\mathrm{c}=0 \mathrm{n}$ 'a aucune solution sur $\mathbb{R}$. Ainsi, si Emile remplace $P(X)$ par $P(X)+c$ au premier tour, il obtient un polynôme sans racines réelles comme voulu.
Pour $\mathfrak{n}=2021$, c'est un peu plus subtil. Comme $x \mapsto P(x)$ est décroissant pour $x$ assez petit et croissant pour x assez grand, P a un nombre impair d'extrema locaux. Ainsi il existe c tel qu'un nombre impair de ces extrema soient en des solutions de $\mathrm{P}(\mathrm{x})=\mathrm{c}$. En effet, supposons que les valeurs prises en ces extrema soient $c_{1}, \ldots, c_{k}$, et disons que $c_{i}$ est la valeur de $P$ en $n_{i}$ extrema distincts. Alors le nombre d'extrema de $P$ est $n_{1}+\cdots+n_{k}$ et est impair, donc il existe $i$ tel que $n_{i}$ soit impair, et c'est ce qu'on voulait.
Supposons maintenant qu'Emile remplace le polynôme $P(X)$ initial par $P(X)-c$. Celui-ci est positif en $-\infty$ et $+\infty$ donc change de signe un nombre pair de fois. Mais par définition de $c$, il a aussi un nombre impair de zéros qui sont des extrema locaux (c'est-à-dire où il ne change pas de signe), et donc $\mathrm{P}(\mathrm{X})-\mathrm{c}$ a un nombre impair de racines réelles distinctes. Ce nombre est nécessairement inférieur à 2022, donc à 2021 car il est impair. Par la partie précédente de la démonstration, en ajoutant 2 à plusieures reprises au nombre de racines distinctes, Emile peut toujours obtenir, après un certain nombre d'étapes, un polynôme avec exactement 2021 racines réelles distinctes.
En combinant les deux premières parties de la démonstration, on obtient que tous les n pairs et les n impairs supérieurs ou égaux à 2021 fonctionnent. Il reste à voir que les autres ne fonctionnent pas.
3. $\mathrm{n} \leqslant 2019$ impair ne fonctionne pas :
Soit $n \leqslant 2019$ impair. Dans cette partie de la démonstration, il faut exhiber un polynôme $P(X)$ qui empêche Emile d'obtenir $n$ racines réelles distinctes en un nombre fini d'étapes. D'après la preuve de la partie précédente, il faut trouver un polynôme $P(X)$ tel que si un nombre impair d'extrema locaux de $P$ vérifient $P(x)=c$, alors $P(X)-c$ a strictement plus de 2019 racines distinctes.
Considérons le polynôme $P(X)=X^{2}\left(X^{2}-1\right) \ldots\left(X^{2}-1010\right)$. Il est pair donc tous ses extrema locaux vont par paires, sauf celui en 0 qui est nul. Mais le polynôme $P(X)$ a 2021 racines distinctes, et il semble donc être un bon candidat pour cette partie. Comme $P(X)$ est pair, pour tout $\mathrm{c} \neq 0$, l'équation $\mathrm{P}(\mathrm{x})=\mathrm{c}$ a un nombre pair de solutions, et l'équation $\mathrm{P}(\mathrm{x})=0$ a un nombre impair de solutions (précisément 2021).
Supposons par l'absurde qu'au bout d'un certain nombre d'étapes, Emile arrive à obtenir un polynôme avec $n$ racines réelles distinctes, ce polynôme sera alors de la forme $f(P(X))$, avec $f(X)$ unitaire non constant. Soient $r_{1}, \ldots, r_{k}$ les racines de $f(X)$. Les racines de $f(P(X))$ sont exactement les réels solutions d'une équation de la forme $P(x)=r_{i}$. Soit $n_{i}$ le nombre de solutions à $P(x)=r_{i}$. On a $n_{1}+n_{2}+\ldots+n_{k}=n$. Comme $n$ est impair, un des $n_{i}$ est forcément impair. Mais le seul réel $r_{i}$ ayant un nombre impair d'antécédents par $P$ est 0 , qui en a 2021. Ainsi, $r_{i}=0$ et $n_{i}=2021$, ce qui donne $n \geqslant 2021$, absurde.
Pour conclure, les entiers n qui fonctionnent sont les entiers pairs et les entiers impairs supérieurs ou égaux à 2021.
Commentaire des correcteurs : L'exercice n'a été abordé que par une copie qui l'a réussi parfaitement. L'exercice était très difficile, néanmoins il est dommage qu'il n'y ait pas eu plus de copies proposant au moins des pistes de recherche. Il n'est pas nécessaire d'avoir résolu entièrement un problème pour rendre quelque chose, et ici il y avait plusieurs étapes intermédiaires importantes qui pouvaient rapporter des points même si la solution n'était pas aboutie.
|
{
"exam": "French_envois",
"problem_label": "18",
"problem_match": "\nExercice 18.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-2.jsonl",
"solution_match": "## Solution de l'exercice 18",
"tier": "T2",
"year": null
}
|
Show that for any integer n, the number $\mathrm{n}^{3}-7 \mathrm{n}$ is divisible by 6.
|
A first approach is to look at the expression modulo 6:
$$
\mathrm{n}^{3}-7 n \equiv \mathrm{n}^{3}-\mathrm{n} \equiv(\mathrm{n}-1) \mathrm{n}(\mathrm{n}+1) \quad \bmod 6
$$
so it suffices to show that 6 divides $(n-1) \mathfrak{n}(n+1)$. Among three consecutive numbers, at least one is divisible by 2 and at least one is divisible by 3. Since 2 and 3 are coprime, $6 \mid n^{3}-n$ and thus 6 divides $n^{3}-7 n$.
A second approach that also works here is to look at the expression $n^{3}-7 n$ and to show by hand that it is always zero by considering the cases for the values that $n$ can take modulo 6.
| n | $\mathrm{n}^{3}-7 \mathrm{n}$ |
| :---: | :---: |
| 0 | $0^{3}-7 \cdot 0 \equiv 0+0 \equiv 0$ |
| 1 | $1^{3}-7 \cdot 1 \equiv 1-1 \equiv 0$ |
| 2 | $2^{3}-7 \cdot 2 \equiv 8-2 \equiv 0$ |
| 3 | $3^{3}-7 \cdot 3 \equiv 3-3 \equiv 0$ |
| $4 \equiv-2$ | $(-2)^{3}-7 \cdot(-2) \equiv-2+2 \equiv 0$ |
| $5 \equiv-1$ | $(-1)^{3}-7 \cdot(-1) \equiv-1+1 \equiv 0$ |
Thus, regardless of the value of $n$ modulo 6, $\mathrm{n}^{3}-7 \mathrm{n} \equiv 0$.
Grader's comment: The exercise is very well solved.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Montrer que pour tout entier n , le nombre $\mathrm{n}^{3}-7 \mathrm{n}$ est divisible par 6 .
|
Une première approche est de regarder l'expression modulo 6 :
$$
\mathrm{n}^{3}-7 n \equiv \mathrm{n}^{3}-\mathrm{n} \equiv(\mathrm{n}-1) \mathrm{n}(\mathrm{n}+1) \quad \bmod 6
$$
donc il suffit de montrer que 6 divise $(n-1) \mathfrak{n}(n+1)$. Or parmi trois nombres consécutifs, au moins un est divisible par 2 et au moins un est divisible par 3 . Ainsi comme 2 et 3 sont premiers entre eux, $6 \mid n^{3}-n$ et donc 6 divise $n^{3}-7 n$.
Une deuxième approche qui fonctionne aussi ici consiste aussi à regarder l'expression $n^{3}-7 n$ et de montrer à la main que celle-ci est toujours nulle en faisant une disjonction de cas sur les valeurs que peut prendre n modulo 6 .
| n | $\mathrm{n}^{3}-7 \mathrm{n}$ |
| :---: | :---: |
| 0 | $0^{3}-7 \cdot 0 \equiv 0+0 \equiv 0$ |
| 1 | $1^{3}-7 \cdot 1 \equiv 1-1 \equiv 0$ |
| 2 | $2^{3}-7 \cdot 2 \equiv 8-2 \equiv 0$ |
| 3 | $3^{3}-7 \cdot 3 \equiv 3-3 \equiv 0$ |
| $4 \equiv-2$ | $(-2)^{3}-7 \cdot(-2) \equiv-2+2 \equiv 0$ |
| $5 \equiv-1$ | $(-1)^{3}-7 \cdot(-1) \equiv-1+1 \equiv 0$ |
Ainsi, quelle que soit la valeur de n modulo $6, \mathrm{n}^{3}-7 \mathrm{n} \equiv 0$.
Commentaire des correcteurs: L'exercice est très bien résolu.
|
{
"exam": "French_envois",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T2",
"year": null
}
|
Let $\mathrm{a}, \mathrm{b}, \mathrm{c} \geqslant 1$ be integers such that $\mathrm{a}^{\mathrm{b}} \mid \mathrm{b}^{\mathrm{c}}$ and $\mathrm{a}^{\mathrm{c}} \mid \mathrm{c}^{\mathrm{b}}$. Show that $\mathrm{a}^{2} \mid \mathrm{bc}$.
|
We will look at the $p$-adic valuations of each of the prime numbers $a, b$, and $c$. Indeed, it suffices to show that for any prime number $p$, we have $2 v_{\mathfrak{p}}(\mathfrak{a})=v_{\mathfrak{p}}\left(\mathrm{a}^{2}\right) \leqslant v_{\mathfrak{p}}(\mathrm{bc})=v_{\mathfrak{p}}(b)+v_{\mathfrak{p}}(\mathfrak{c})$.
Let $p$ be a prime number. The hypothesis that $\mathrm{a}^{\mathrm{b}} \mid \mathrm{b}^{\mathrm{c}}$ translates in terms of $p$-adic valuation to $b v_{p}(a) \leqslant c v_{p}(b)$, or equivalently $v_{p}(a) \leqslant \frac{c}{b} v_{p}(b)$. Similarly, we obtain that $v_{p}(a) \leqslant \frac{b}{c} v_{p}(c)$.
By multiplying the two relations, we find that $v_{\mathfrak{p}}(\mathfrak{a})^{2} \leqslant v_{\mathfrak{p}}(\mathrm{b}) v_{\mathfrak{p}}(\mathfrak{c})$. Therefore, according to the inequality of means:
$$
v_{p}(a) \leqslant \sqrt{v_{p}(b) v_{p}(c)} \leqslant \frac{v_{p}(b)+v_{p}(c)}{2}
$$
which gives us $2 v_{\mathfrak{p}}(\mathrm{a}) \leqslant v_{\mathfrak{p}}(\mathrm{b})+v_{\mathfrak{p}}(\mathrm{c})$ as desired. Since this is true for any prime $p$, we indeed have $\mathrm{a}^{2} \mid \mathrm{bc}$.
Grader's Comment: The exercise is very well solved.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $\mathrm{a}, \mathrm{b}, \mathrm{c} \geqslant 1$ des entiers tels que $\mathrm{a}^{\mathrm{b}} \mid \mathrm{b}^{\mathrm{c}}$ et $\mathrm{a}^{\mathrm{c}} \mid \mathrm{c}^{\mathrm{b}}$. Montrer que $\mathrm{a}^{2} \mid \mathrm{bc}$.
|
Nous allons regarder les valuations $p$-adiques de chacun des nombres premiers $a, b$ et $c$. En effet, il suffit de montrer que pour tout nombre premier $p$, on a $2 v_{\mathfrak{p}}(\mathfrak{a})=v_{\mathfrak{p}}\left(\mathrm{a}^{2}\right) \leqslant v_{\mathfrak{p}}(\mathrm{bc})=v_{\mathfrak{p}}(b)+v_{\mathfrak{p}}(\mathfrak{c})$.
Soit $p$ un nombre premier. Lhypothèse que $\mathrm{a}^{\mathrm{b}} \mid \mathrm{b}^{\mathrm{c}}$ se traduit en terme de valuation p -adique par $b v_{p}(a) \leqslant c v_{p}(b)$, ou encore $v_{p}(a) \leqslant \frac{c}{b} v_{p}(b)$. De même, on obtient que $v_{p}(a) \leqslant \frac{b}{c} v_{p}(c)$.
En multipliant les deux relations, on trouve que $v_{\mathfrak{p}}(\mathfrak{a})^{2} \leqslant v_{\mathfrak{p}}(\mathrm{b}) v_{\mathfrak{p}}(\mathfrak{c})$. On a donc, d'après l'inégalité des moyennes:
$$
v_{p}(a) \leqslant \sqrt{v_{p}(b) v_{p}(c)} \leqslant \frac{v_{p}(b)+v_{p}(c)}{2}
$$
ce qui donne bien $2 v_{\mathfrak{p}}(\mathrm{a}) \leqslant v_{\mathfrak{p}}(\mathrm{b})+v_{\mathfrak{p}}(\mathrm{c})$ comme voulu. Ceci étant vrai pour tout premier $p$, on a bien $\mathrm{a}^{2} \mid \mathrm{bc}$.
Commentaire des correcteurs: L'exercice est très bien résolu.
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"solution_match": "## Solution de l'exercice 3",
"tier": "T2",
"year": null
}
|
Find all pairs of non-zero natural numbers $(x, n)$ such that
$$
3 \cdot 2^{x}+4=n^{2}
$$
|
For $x=0$, the equation becomes $n^{2}=7$ which has no solution. Suppose $x>0$, we factorize: $3 \cdot 2^{x}=(n-2)(n+2)$. The left-hand side is even, so the right-hand side is even. The two factors on the right-hand side are of the same parity, so they are both even, and we have two cases:
- Case 1: $3 \cdot 2^{\mathrm{a}}=\mathrm{n}-2$ and $2^{\mathrm{b}}=\mathrm{n}+2$, with $\mathrm{a}+\mathrm{b}=\mathrm{x}$. We can combine these two equations to find $2^{b}=3 \cdot 2^{a}+4$. Note that $n+2$ and $n-2$ have a difference of 4, so they cannot both be divisible by 8. Therefore, we have $a \leqslant 2$ or $b \leqslant 2$. Since $2^{b}>4$, we have $b>2$ and we deduce that $a \leqslant 2$. If $a=0,2^{b}=3+4=7$ which is not possible. If $a=1,2^{b}=6+4=10$ which is not possible either. If $\mathbf{a}=2$, then $2^{b}=12+4=16$ so $b=4$. We get $x=6$ and $n=14$. Conversely, we verify that $3 \cdot 2^{6}+4=196=14^{2}$ and the pair $(6,14)$ is indeed a solution.
- Case 2: $3 \cdot 2^{\mathrm{a}}=\mathrm{n}+2$ and $2^{\mathrm{b}}=\mathrm{n}-2$, with $\mathrm{a}+\mathrm{b}=\mathrm{x}$. The two equations combined give $2^{\mathrm{b}}+4=3 \cdot 2^{\mathrm{a}}$. Similarly, we have $\mathrm{a} \leqslant 2$ or $\mathrm{b} \leqslant 2$.
1. If $b \leqslant 2$, then $b=0,1$ or 2. If $b=0$, then $5=3 \cdot 2^{a}$ which is not possible. If $b=1$, $6=3 \cdot 2^{\mathrm{a}}$ and $\mathrm{a}=1$, so $x=2$ and $\mathrm{n}=4$ and we verify that $3 \cdot 2^{2}+4=16=4^{2}$ and $(2,4)$ is indeed a solution. If $b=2$, then $8=3 \cdot 2^{a}$ which is not possible.
2. If $a \leqslant 2$, then $a=0,1$ or 2. If $a=0,2^{b}+4=3<4$ which is not possible. If $a=1$, we fall back to the case where $b=1$ and the pair $(2,4)$. If $a=2,2^{b}+4=12$ so $b=3$. This gives $x=5$ and $\mathfrak{n}=10$. Conversely, we verify that $3 \cdot 2^{5}+4=100=10^{2}$ and $(5,10)$ is indeed a solution.
Thus, the set of pairs $(\boldsymbol{x}, \mathrm{n})$ solutions is $\{(2,4),(5,10),(6,14)\}$.
Comment from the graders: The exercise is generally well solved, but many students forget some cases, or simply forget to verify the solutions found, which is crucial in a Diophantine equation.
|
(2,4),(5,10),(6,14)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Trouver tous les couples d'entiers naturels non nuls $(x, n)$ tels que
$$
3 \cdot 2^{x}+4=\mathrm{n}^{2}
$$
|
Pour $x=0$, l'équation devient $n^{2}=7$ qui n'a pas de solution. Supposons $x>0$, on factorise : $3 \cdot 2^{x}=(n-2)(n+2)$. Le membre de gauche est pair donc le membre de droite est paire. Les deux facteurs du membre de droite sont de même parité donc ils sont tous les deux pairs et on a deux cas :
- Cas 1: $3 \cdot 2^{\mathrm{a}}=\mathrm{n}-2$ et $2^{\mathrm{b}}=\mathrm{n}+2$, avec $\mathrm{a}+\mathrm{b}=\mathrm{x}$. On peut combiner ces deux équations pour trouver $2^{b}=3 \cdot 2^{a}+4$. Notons que $n+2$ et $n-2$ ont pour différence 4 donc ils ne peuvent pas être tous les deux divisibles par 8 . On a donc $a \leqslant 2$ ou $b \leqslant 2$. Or $2^{b}>4$, donc $b>2$ et on déduit que $a \leqslant 2$. Si $a=0,2^{b}=3+4=7$ ce qui n'est pas possible. Si $a=1,2^{b}=6+4=10$ ce qui n'est pas possible non plus. Si $\mathbf{a}=2$, alors $2^{b}=12+4=16$ donc $b=4$. On obtient $x=6$ et $n=14$. réciproquement, on vérifie que $3 \cdot 2^{6}+4=196=14^{2}$ et le couple $(6,14)$ est bien solution.
- Cas 2: $3 \cdot 2^{\mathrm{a}}=\mathrm{n}+2$ et $2^{\mathrm{b}}=\mathrm{n}-2$, avec $\mathrm{a}+\mathrm{b}=\mathrm{x}$. Les deux équations combinées donnent $2^{\mathrm{b}}+4=3 \cdot 2^{\mathrm{a}}$. De même que précédemment, on a $\mathrm{a} \leqslant 2$ ou $\mathrm{b} \leqslant 2$.
1. Si $b \leqslant 2$, alors $b=0,1$ ou 2 . Si $b=0$, alors $5=3 \cdot 2^{a}$ ce qui $n$ 'est pas possible. Si $b=1$, $6=3 \cdot 2^{\mathrm{a}}$ et $\mathrm{a}=1$, soit $x=2$ et $\mathrm{n}=4$ et on vérifie que $3 \cdot 2^{2}+4=16=4^{2}$ et $(2,4)$ est bien solution. Si $b=2$, alors $8=3 \cdot 2^{a}$ ce qui n'est pas possible.
2. Si $a \leqslant 2$, alors $a=0,1$ ou 2 . Si $a=0,2^{b}+4=3<4$ ce qui $n$ 'est pas possible. Si $a=1$, on retombe sur le cas où $b=1$ et sur le couple $(2,4)$. Si $a=2,2^{b}+4=12$ donc $b=3$. Ceci donne $x=5$ et $\mathfrak{n}=10$. Réciproquement, on vérifie que $3 \cdot 2^{5}+4=100=10^{2}$ et $(5,10)$ est bien solution.
Ainsi l'ensemble des couples ( $\boldsymbol{x}, \mathrm{n}$ ) solutions est $\{(2,4),(5,10),(6,14)\}$
Commentaire des correcteurs: L'exercice est globalement bien résolu, mais de nombreux élèves oublient des cas, ou oublient tout simplement de vérifier les solutions trouvées, chose pourtant cruciale dans une équation diophantienne.
|
{
"exam": "French_envois",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T2",
"year": null
}
|
A set $E$ of strictly positive integers is said to be interesting if for all $\mathrm{n} \geqslant 1$ and for all $x_{1}, \ldots, x_{n}$ elements of $E$ that are pairwise distinct, their arithmetic mean $\frac{1}{n}\left(x_{1}+\ldots+x_{n}\right)$ and their geometric mean $\left(x_{1} \cdot \ldots \cdot x_{n}\right)^{\frac{1}{n}}$ are integers.
1. Does there exist an interesting set $E$ containing exactly 2022 elements?
2. Does there exist an interesting set $E$ that is infinite?
|
1) To start, we can observe that if $n \geq 1$, then as soon as $x_{1}, \ldots, x_{n} \geq 1$ are integers all multiples of $n$, each of the numbers $\frac{x_{k}}{n}$ is an integer, so their sum $\frac{1}{n}\left(x_{1}+\ldots+x_{n}\right)$ is an integer. Similarly, if $n \geq 1$, then as soon as $x_{1}, \ldots, x_{n} \geq 1$ are integers all perfect $n$-th powers, each of the numbers $x_{k}^{1 / n}$ is an integer, so their product $\left(x_{1} \times \ldots \times x_{n}\right)^{\frac{1}{n}}$ is an integer. To find an interesting set $E$ containing exactly 2022 elements, it is sufficient that for all $1 \leqslant n \leqslant 2022$, all elements of $E$ are both multiples of $n$ and perfect $n$-th powers. For this, it is sufficient that all elements of $E$ are both multiples of 2022!, and perfect 2022!-th powers. Thus, $E=\left\{(2022!)^{k 2022!}, 1 \leqslant k \leqslant 2022\right\}$ works.
2) We will show that there does not exist an infinite interesting set. In fact, we will show that there does not even exist an infinite set of strictly positive integers satisfying the hypothesis on arithmetic means. Indeed, suppose by contradiction that such an infinite set $E$ exists, that is, for all $n \geq 1$ and $x_{1}, \ldots, x_{n} \in E$ pairwise distinct, the arithmetic mean $\frac{1}{n}\left(x_{1}+\ldots+x_{n}\right)$ is an integer. Let $a<b$ be any two elements of $E$ and $n \geq 2$. Choose $x_{1}<\ldots<x_{n-1}$ distinct elements of $E$, and distinct from $a$ and $b$. The hypothesis applied successively to the $n$-tuples $\left(x_{1}, \ldots, x_{n-1}, a\right)$ and $\left(x_{1}, \ldots, x_{n-1}, b\right)$ ensures that $n$ divides both $x_{1}+\ldots+x_{n-1}+a$ and $x_{1}+\ldots+x_{n-1}+b$. Thus, $n$ divides the difference of these two numbers, which is $a-b$. Since this is true for all $n \geq 2$, the integer $a-b$ has an infinite number of divisors. It is therefore zero, that is, $a=b$. This is in contradiction with our initial hypothesis, so such a set $E$ does not exist.
Graders' comments: The first question of the exercise is more often addressed than the second. Be careful, several students construct a set whose arithmetic and geometric means of all the elements of the set are integers, but not the means of the elements of any subset.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Un ensemble E d'entiers strictement positifs est dit intéressant si pour tout $\mathrm{n} \geqslant 1$ et pour tous $x_{1}, \ldots, x_{n}$ des éléments de $E$ deux à deux distincts, leur moyenne arithmétique $\frac{1}{n}\left(x_{1}+\ldots+x_{n}\right)$ et leur moyenne géométrique $\left(x_{1} \cdot \ldots \cdot x_{n}\right)^{\frac{1}{n}}$ sont des entiers.
1. Existe-t-il un ensemble E intéressant contenant exactement 2022 éléments?
2. Existe-t-il un ensemble E intéressant infini?
|
1) Pour commencer, on peut remarquer que si $n \geqslant 1$, alors dès que $x_{1}, \ldots, x_{n} \geqslant 1$ sont des entiers tous multiples de $n$, chacun des nombres $\frac{x_{k}}{n}$ est un entier, de sorte que leur somme $\frac{1}{n}\left(x_{1}+\ldots+x_{n}\right)$ est un entier. De même, si $n \geqslant 1$, alors dès que $x_{1}, \ldots, x_{n} \geqslant 1$ sont des entiers tous puissances $n$-ièmes parfaites, chacun des nombres $x_{k}^{1 / n}$ est entier, de sorte que leur produit $\left(x_{1} \times \ldots \times x_{n}\right)^{\frac{1}{n}}$ est un entier. Pour trouver un ensemble E intéressant contenant exactement 2022 éléments, il suffit donc que pour tout $1 \leqslant n \leqslant 2022$, tous les éléments de $E$ soient à la fois des multiples de $n$ et des puissances $n$-ièmes parfaites. Pour cela, il suffit que tous les éléments de E soient à la fois des multiples de 2022!, et des puissances 2022!-ièmes parfaites. Ainsi, $E=\left\{(2022!)^{k 2022!}, 1 \leqslant k \leqslant 2022\right\}$ convient.
2) Nous allons montrer qu'il n'existe pas d'ensemble intéressant infini. En fait, on va montrer qu'il n'existe même pas d'ensemble infini d'entiers strictement positifs vérifiant l'hypothèse sur les moyennes arithmétiques. En effet, supposons par l'absurde qu'un tel ensemble infini E existe, c'est-à-dire que pour tout $n \geqslant 1$ et $x_{1}, \ldots, x_{n} \in E$ deux à deux distincts, la moyenne arithmétique $\frac{1}{n}\left(x_{1}+\ldots+x_{n}\right)$ est un entier. Soit $a<b$ deux éléments quelconques de $E$ et $n \geqslant 2$. Choisissons $x_{1}<\ldots<x_{n-1}$ des éléments deux à deux distincts de $E$, et distincts de plus de a et $b$. L'hypothèse appliquée successivement aux $n$-uplets $\left(x_{1}, \ldots, x_{n-1}, a\right)$ et $\left(x_{1}, \ldots, x_{n-1}, b\right)$ assure que $n$ divise à la fois $x_{1}+\ldots+x_{n-1}+a$ et $x_{1}+\ldots+x_{n-1}+b$. Ainsi, $n$ divise la différence de ces deux nombres qui vaut $a-b$. Ceci étant vrai pour tout $\mathrm{n} \geqslant 2$, l'entier $\mathrm{a}-\mathrm{b}$ admet un nombre infini de diviseurs. Il est donc nul, c'est-à-dire que $\mathrm{a}=\mathrm{b}$. Ceci est en contradiction avec notre hypothèse de départ, un tel ensemble $E$ n'existe donc pas.
Commentaire des correcteurs : La première question de l'exercice est plus souvent traitée que la deuxième. Attention, plusieurs élèves y construisent un ensemble dont les moyennes arithmétique et géométrique de tous les éléments de l'ensemble sont entièress, mais pas les moyennes des éléments de n'importe quel sous-ensemble.
|
{
"exam": "French_envois",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"solution_match": "## Solution de l'exercice 5",
"tier": "T2",
"year": null
}
|
Let $p$ be a prime number. Show that there exists a permutation $\left(a_{1}, \ldots, a_{p}\right)$ of $(1, \ldots, p)$ such that the integers $a_{1}, a_{1} \cdot a_{2}, \ldots, a_{1} \cdot a_{2} \cdot \ldots \cdot a_{p}$ give $p$ pairwise distinct remainders when performing their Euclidean division by $p$.
|
We can be very optimistic about this exercise and want $a_{1} a_{2} \cdots a_{k} \equiv k$ $\bmod p$ for all $k$ between 1 and $p$. Therefore, it is necessary that $a_{1}=1$ and for all $k \neq 1$:
$$
a_{k} \equiv \frac{a_{1} \cdots a_{k}}{a_{1} \cdots a_{k-1}} \equiv \frac{k}{k-1} \quad \bmod p
$$
where we denote $\frac{a}{b}$ as any integer whose remainder $c$ by the Euclidean division by $p$ satisfies $cb \equiv a \bmod p$, which always exists as long as $b$ is non-zero. Thus, for $k \neq 1$, we can set $a_{k}$ as the element of $\{1, \ldots, p\}$ satisfying $(k-1) a_{k} \equiv k \bmod p$.
It remains to verify that all the numbers $a_{k}$ we have formed are indeed distinct from each other, and thus that $\left\{a_{1}, \ldots, a_{p}\right\}$ is indeed a permutation of $\{1, \ldots, p\}$. Suppose there exist $i<j$ such that $a_{i} \equiv a_{j}$. If $i=1$, for all $j \geqslant 2, \frac{j}{j-1} \neq 1 \bmod p$. Otherwise $\frac{i}{i-1} \equiv \frac{j}{j-1}$ implies that $i-j \equiv i-i$, which is $i \equiv j$ $\bmod p$, contradicting our initial assumption.
Thus all the $a_{k}$ are different modulo $p$. Given that there are $p$ terms in the sequence and $p$ elements in $\{1,2, \cdots, p\},\left(a_{1}, a_{2}, \cdots, a_{p}\right)$ is a permutation of $(1,2, \cdots p)$.
Comment from the graders: The exercise was poorly addressed. The main idea of the problem was to create a permutation such that $a_{1} a_{2} \ldots a_{i} \equiv i \bmod p$. To implement this, a good understanding of the concept of inverse modulo $p$ was required, which was the case for most students who submitted a solution.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $p$ un nombre premier. Montrer qu'il existe une permutation $\left(a_{1}, \ldots, a_{p}\right)$ de $(1, \ldots, p)$ telle que les entiers $a_{1}, a_{1} \cdot a_{2}, \ldots, a_{1} \cdot a_{2} \cdot \ldots \cdot a_{p}$ donnent $p$ restes deux à deux distincts lorsque qu'on réalise leur divison euclidienne par $p$.
|
On peut être très optimiste sur cet exercice et vouloir que $a_{1} a_{2} \cdots a_{k} \equiv k$ $\bmod p$ pour tout $k$ compris entre 1 et $p$. Il faut donc que $a_{1}=1$ et pour tout $k \neq 1$ :
$$
a_{k} \equiv \frac{a_{1} \cdots a_{k}}{a_{1} \cdots a_{k-1}} \equiv \frac{k}{k-1} \quad \bmod p
$$
où l'on note $\frac{\mathrm{a}}{\mathrm{b}}$ tout nombre entier dont le reste c par la division euclidienne par $p$ vérifie $\mathrm{cb} \equiv \mathrm{a} \bmod p$, qui existe toujours dès que $b$ est non nul. Ainsi, pour $k \neq 1$, on peut poser $a_{k}$ l'élément de $\{1, \ldots, p\}$ vérifiant $(k-1) a_{k} \equiv k \bmod p$.
Il reste juste à vérifier que tous les nombres $a_{k}$ que l'on a formés sont bien deux à deux distincts, et ainsi que $\left\{a_{1}, \ldots, a_{p}\right\}$ est bien une permutation de $\{1, \ldots, p\}$. Supposons qu'il existe $i<j$ tels que $a_{i} \equiv a_{j}$. Si $\mathfrak{i}=1$, pour tout $\mathfrak{j} \geqslant 2, \frac{\mathfrak{j}}{\mathfrak{j}-1} \neq 1 \bmod \boldsymbol{p}$. Sinon $\frac{i}{i-1} \equiv \frac{\mathfrak{j}}{\mathfrak{j}-1}$ implique que $\mathfrak{i}-\mathfrak{j} \equiv \mathfrak{i}-\mathfrak{i}$, soit $\mathfrak{i} \equiv \mathfrak{j}$ $\bmod p$, ce qui est en contradiction avec notre hypothèse de départ.
Ainsi tous les $a_{k}$ sont différents modulo $p$. Etant donné qu'il y a $p$ termes dans la suite et $p$ éléments dans $\{1,2, \cdots, p\},\left(a_{1}, a_{2}, \cdots, a_{p}\right)$ est une permutation de $(1,2, \cdots p)$.
Commentaire des correcteurs: L'exercice a été peu traité. Avoir l'idée de créer une permutation telle que $a_{1} a_{2} \ldots a_{i} \equiv i \bmod p$ était l'idée principale du problème. Pour la mettre en oeuvre, il fallait une bonne compréhension de la notion d'inverse modulo $p$, et c'était le cas de la plupart des élèves qui ont rendu une solution.
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T2",
"year": null
}
|
Let $n \geqslant 1$ be an integer. Find all divisors $d \geqslant 1$ of $3 n^{2}$ such that $n^{2}+d$ is a perfect square.
|
Let $d \geqslant 1$ be a divisor of $3 n^{2}$ such that $n^{2}+d$ is a perfect square. Since $n^{2}<n^{2}+d \leq n^{2}+3 n^{2}=(2 n)^{2}$, there exists $k \in \llbracket 1, n \rrbracket$ such that $n^{2}+d=(n+k)^{2}$. Simplifying, we get $d=2 k n+k^{2}$, so that $k(k+2 n) \mid 3 n^{2}$.
Let $\alpha=\operatorname{gcd}(k, n) \geqslant 1$. There exist integers $\ell, m \geqslant 1$ that are coprime such that $k=\alpha l$, $n=\alpha m$. The divisibility relation then becomes, after simplification, $\ell(\ell+2 m) \mid 3 m^{2}$. Since $\operatorname{gcd}(\ell+2 m, m)=\operatorname{gcd}(\ell+2 m-2 m, m)=\operatorname{gcd}(\ell, m)=1$, that is, $\ell+2 m$ is coprime with $m$, and thus with $m^{2}$. Since $\ell+2 m \mid 3 m^{2}$, by Gauss's lemma, $\ell+2 m \mid 3$, that is, $\ell+2 m \in\{1,3\}$. But $\ell, m \geqslant 1$ so $\ell+2 m \geqslant 3$. In other words, $\ell+2 m=3$ and thus necessarily, $\ell=m=1$. Then $k=n=\alpha$, and $d=k(k+2 n)=3 n^{2}$.
Conversely, $d=3 n^{2}$ works since it is a divisor of $3 n^{2}$ and $n^{2}+3 n^{2}=(2 n)^{2}$.
Graders' comments: The exercise is poorly addressed. All copies have the correct intuition of the unique solution. Other proofs than the one in the solution have been proposed by students (they notably pass through the parity of $p$-adic valuations for $p$ prime and by finding the $m$ such that $\frac{m+3}{m}$ is a square of a rational number).
|
d=3n^2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Soit $n \geqslant 1$ un entier. Trouver tous les diviseurs $d \geqslant 1$ de $3 n^{2}$ tels que $n^{2}+d$ soit un carré parfait.
|
Soit $d \geqslant 1$ un diviseur de $3 n^{2}$ tel que $n^{2}+d$ soit un carré parfait. Puisque $n^{2}<n^{2}+d<=n^{2}+3 n^{2}=(2 n)^{2}$, il existe $k \in \llbracket 1, n \rrbracket$ tel que $n^{2}+d=(n+k)^{2}$. En simplifiant, on obtient $d=2 k n+k^{2}$, de sorte que $k(k+2 n) \mid 3 n^{2}$.
Notons $\alpha=\operatorname{gcd}(k, n) \geqslant 1$. On dispose d'entiers $\ell, m \geqslant 1$ premiers entre eux tels que avec $k=\alpha l$, $\mathrm{n}=\alpha \mathrm{m}$. La relation de divisibilité précédente s'écrit alors, après simplification, $\ell(\ell+2 \mathrm{~m}) \mid 3 \mathrm{~m}^{2}$. Or on $\operatorname{agcd}(\ell+2 \mathrm{~m}, \mathrm{~m})=\operatorname{gcd}(\ell+2 \mathrm{~m}-2 \mathrm{~m}, \mathrm{~m})=\operatorname{gcd}(\ell, \mathrm{m})=1$, c'est-à-dire $\ell+2 \mathrm{~m}$ premier avec m , donc avec $\mathrm{m}^{2}$. Comme $\ell+2 \mathrm{~m} \mid 3 \mathrm{~m}^{2}$, on a par le lemme de Gauss $\ell+2 \mathrm{~m} \mid 3$, c'est-à-dire $\ell+2 \mathrm{~m} \in\{1,3\}$. Mais $\ell, \mathrm{m} \geqslant 1$ donc $\ell+2 \mathrm{~m} \geqslant 3$. Autrement dit, $\ell+2 \mathrm{~m}=3$ et donc nécessairement, $\ell=\mathrm{m}=1$. Alors $k=n=\alpha$, et $d=k(k+2 n)=3 n^{2}$.
Réciproquement, $d=3 n^{2}$ convient puisque c'est un diviseur de $3 n^{2}$ et que $n^{2}+3 n^{2}=(2 n)^{2}$.
Commentaire des correcteurs: L'exercice est peu traité. Toutes les copies ont la bonne intuition de l'unique solution. D'autres démonstrations que celle du corrigé ont été proposées par des élèves (elles passent notamment par la parité des valuations $p$-adiques pour $p$ premier et en trouvant les $m$ tels que $\frac{\mathrm{m}+3}{\mathrm{~m}}$ est un carré de rationnel).
|
{
"exam": "French_envois",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 7",
"tier": "T2",
"year": null
}
|
A set $A$ of integers is said to be admissible if it satisfies the following property: for all $x, y \in A$ (not necessarily distinct), and for all $k \in \mathbb{Z}$, we have $x^{2}+k x y+y^{2} \in A$.
Determine all pairs of non-zero integers ( $\mathrm{m}, \mathrm{n}$ ) such that the only admissible set containing both $m$ and $n$ is $\mathbb{Z}$.
|
Note that if $\mathrm{d}=\operatorname{gcd}(\mathrm{m}, \mathfrak{n})>1$ then the set $A$ of multiples of $d$ is an admissible set containing $n$ and $m$ but $n$ not being equal to $\mathbb{Z}$. Indeed, if $x$ and $y$ are multiples of $d$, then for any integer $k, x^{2}+k x y+y^{2}$ is well divisible by $d$ and is in $A$. We deduce that the pairs $(m, n)$ sought must satisfy $\operatorname{gcd}(m, n)=1$.
Conversely, let $m$ and $n$ be integers such that $\operatorname{gcd}(m, n)=1$. Let us show that any admissible set containing $m$ and $n$ is $\mathbb{Z}$. Let $A$ be an admissible set containing $m$ and $n$. Note that if $x \in A$, then the hypothesis gives us that for any integer $k$, the integer $x^{2}+k x \cdot x+x^{2}=(k+2) x^{2}$ is in $A$. We deduce that any multiple of $x^{2}$ is in $A$ if $x$ is in $A$.
Note that if $\operatorname{gcd}(m, n)=1$, then we also have $\operatorname{gcd}\left(m^{2}, n^{2}\right)=1$. According to Bézout's theorem, we therefore have integers $u, v \in \mathbb{Z}$ such that $u^{2}+v n^{2}=1$. Since $u m^{2}$ and $v n^{2}$ are in $A$, applying the hypothesis to $x=u m^{2}, y=v n^{2}$ and $k=2$, we have
$$
\left(u m^{2}\right)^{2}+2 u m^{2} v n^{2}+\left(v n^{2}\right)^{2}=\left(u m^{2}+v n^{2}\right)^{2}=1^{2}=1 \in A
$$
Consequently, $\forall k \in \mathbb{Z}, k \cdot 1^{2} \in A$. Thus $A=\mathbb{Z}$ and the only admissible set containing $m$ and $n$ is $\mathbb{Z}$.
The sought pairs are therefore the pairs of integers $(m, n)$ that are coprime.
Graders' comments: Among the students who submitted an attempt, many provided complete solutions. Among the incomplete solutions, most students guessed the nature of the solution pairs and managed to show that if 1 is in $A$, then $A=\mathbb{Z}$. Getting this far in such a difficult problem is already very good!
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Un ensemble $A$ d'entiers est dit admissible s'il vérifie la propriété suivante : pour tous $x, y \in A$ (non nécessairement distincts), et pour tout $k \in \mathbb{Z}$, on a $x^{2}+k x y+y^{2} \in A$.
Déterminer tous les couples d'entiers non nuls ( $\mathrm{m}, \mathrm{n}$ ) tels que le seul ensemble admissible contenant à la fois $m$ et $n$ soit $\mathbb{Z}$.
|
Remarquons que si $\mathrm{d}=\operatorname{gcd}(\mathrm{m}, \mathfrak{n})>1$ alors l'ensemble $A$ des multiples de d est un ensemble admissible contenant $n$ et $m$ mais $n$ 'étant pas égal à $\mathbb{Z}$. En effet, si $x$ et $y$ sont multiples de $d$, alors pour tout entier $k, x^{2}+k x y+y^{2}$ est bien divisible par $d$ et est dans $A$. On déduit que les couples $(m, n)$ recherchés doivent vérifier $\operatorname{gcd}(m, n)=1$.
Réciproquement, soient $m$ et $n$ des entiers tels que $\operatorname{gcd}(m, n)=1$. Montrons que tout ensemble admissible contenant $m$ et $n$ est $\mathbb{Z}$. Soit $A$ un ensemble admissible contenant $m$ et $n$. Remarquons que si $x \in A$, alors l'hypothèse nous donne que pour tout entier $k$, l'entier $x^{2}+k x \cdot x+x^{2}=(k+2) x^{2}$ est dans $A$. On déduit que tout multiple de $x^{2}$ est dans $A$ si $x$ est dans $A$.
Notons que si $\operatorname{gcd}(m, n)=1$, alors on a aussi $\operatorname{gcd}\left(m^{2}, n^{2}\right)=1$. D'après le théorème de Bezout, on dispose donc d'entiers $u, v \in \mathbb{Z}$ tels que $u^{2}+v n^{2}=1$. Comme $u m^{2}$ et $v n^{2}$ sont dans $A$, en appliquant l'hypothèse à $x=u m^{2}, y=v n^{2}$ et $k=2$, on a
$$
\left(u m^{2}\right)^{2}+2 u m^{2} v n^{2}+\left(v n^{2}\right)^{2}=\left(u m^{2}+v n^{2}\right)^{2}=1^{2}=1 \in A
$$
Par conséquent, $\forall k \in \mathbb{Z}, k \cdot 1^{2} \in A$. Ainsi $A=\mathbb{Z}$ et le seul ensemble admissible contenant $m$ et $n$ est $\mathbb{Z}$.
Les couples recherchés sont donc les couples d'entiers ( $m, n$ ) premiers entre eux.
Commentaire des correcteurs : Parmi les élèves ayant rendu une tentatives, on trouve beaucoup de solutions complètes. Parmi les solutions non complètes, la plupart des élèves ont deviné la nature des couples solutions et ont réussi à montrer que si 1 est dans $A$, alors $A=\mathbb{Z}$. Avoir été si loin dans ce problème difficile est déjà très bien!
|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "\nExercice 8.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 8",
"tier": "T2",
"year": null
}
|
Determine all triplets of natural numbers $(a, b, c)$ such that
$$
\mathrm{a}! + 5^{\mathrm{b}} = 7^{\mathrm{c}}
$$
|
A first reflex to have is to look at the small values of $\mathrm{a}, \mathrm{b}$, and $\mathrm{c}$ that one can find in a solution $(a, b, c)$.
First, if $a=0$ or $a=1$, then $a!=1$, so $0 \equiv a!+5^{b} \equiv 7^{c} \equiv 1(\bmod 2)$, which is impossible. We deduce that $a \geqslant 2$.
Then, if $a \geqslant 7$, then $5^{b} \equiv a!+5^{b} \equiv 7^{c}(\bmod 5)$ and $5^{b} \equiv a!+5^{b} \equiv 7^{c}(\bmod 7)$, so $b=c=0$. But then $\mathrm{a}!+5^{\mathrm{b}}=\mathrm{a}!+1 \neq 1=7^{\mathrm{c}}$, which is impossible. We deduce that $2 \leqslant \mathrm{a} \leqslant 6$.
Now suppose that $\mathrm{b} \leqslant 1$. Then
$$
7^{\mathfrak{c}}=\mathrm{a}!+5^{\mathrm{b}} \in\{2,6,24,120,720\}+\{1,5\}=\{3,7,11,25,29,121,125,721,725\}
$$
In this last set, only 7 itself is a power of 7. We deduce the two solution triplets $(\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c})=(2,1,1)$ and $(3,0,1)$, which are the only two solutions for $b \leqslant 1$.
We finally consider the cases where $b \geqslant 2$. Then $a!\equiv a!+5^{b} \equiv 7^{\mathrm{c}}(\bmod 25)$. Since $7^{2} \equiv-1$ $(\bmod 25)$, we know that $7^{\mathrm{c}} \equiv 1,7,-1$ or $-7(\bmod 25)$ (depending on whether $\mathrm{c} \equiv 0,1,2$ or $3(\bmod 4))$ and that $\mathrm{a}!\equiv 2,6,-1,-5$ or $-5(\bmod 25)$ (depending on whether $a$ is $2,3,4,5$ or 6). This means that $a=4$ and $\mathrm{c} \equiv 2(\bmod 4)$.
But then $(-3)^{\mathrm{b}} \equiv \mathrm{a}!+5^{\mathrm{b}} \equiv(-1)^{\mathrm{c}} \equiv 1(\bmod 8)$, which means that $b$ is even. We then set $\beta=\mathrm{b} / 2$ and $\gamma=\mathrm{c} / 2$, so that
$$
24=\mathrm{a}!=7^{\mathrm{c}}-5^{\mathrm{b}}=\left(7^{\gamma}+5^{\beta}\right)\left(7^{\gamma}-5^{\beta}\right) .
$$
We deduce in particular that $7^{\gamma}+5^{\beta} \leqslant 24$, so that $\gamma \leqslant 1$ and $\mathrm{c} \leqslant 2$. Since $\mathrm{c} \equiv 2(\bmod 4)$, this means that $\mathrm{c}=2$, so that $5^{\mathrm{b}}=7^{\mathrm{c}}-\mathrm{a}!=49-24=25=5^{2}$.
The solutions sought are therefore the triplets $(\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c})=(2,1,1),(3,0,1)$ and $(4,2,2)$.
Comment from the graders: Generally well handled by those who wrote it, the main issue with this problem was to properly reduce to $a<7$, and to work modulo the right power of a prime number, here 25, which was rather well found. One must pay close attention to the edge cases $(\mathrm{b}=0, \mathrm{c}=0)$.
## Senior Exercises
|
(2,1,1),(3,0,1),(4,2,2)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer tous les triplets d'entiers naturels $(a, b, c)$ tels que
$$
\mathrm{a}!+5^{\mathrm{b}}=7^{\mathrm{c}}
$$
|
Un premier réflexe à avoir est de regarder les petites valeurs de $\mathrm{a}, \mathrm{b}$ et c que l'on peut trouver dans une solution ( $a, b, c$ ).
Tout d'abord, si $a=0$ ou $a=1$, alors $a!=1$, donc $0 \equiv a!+5^{b} \equiv 7^{c} \equiv 1(\bmod 2)$, ce qui est impossible. On en déduit que $a \geqslant 2$.
Puis, si $a \geqslant 7$, alors $5^{b} \equiv a!+5^{b} \equiv 7^{c}(\bmod 5)$ et $5^{b} \equiv a!+5^{b} \equiv 7^{c}(\bmod 7)$, donc $b=c=0$. Mais alors $\mathrm{a}!+5^{\mathrm{b}}=\mathrm{a}!+1 \neq 1=7^{\mathrm{c}}$, ce qui est impossible. On en déduit que $2 \leqslant \mathrm{a} \leqslant 6$.
Supposons maintenant que $\mathrm{b} \leqslant 1$. Alors
$$
7^{\mathfrak{c}}=\mathrm{a}!+5^{\mathrm{b}} \in\{2,6,24,120,720\}+\{1,5\}=\{3,7,11,25,29,121,125,721,725\}
$$
Dans ce dernier ensemble, seul 7 lui-même est une puissance de 7 . On en déduit les deux triplets solutions $(\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c})=(2,1,1)$ et $(3,0,1)$, qui sont les deux seules solutions pour $b \leqslant 1$.
On s'intéresse enfin aux cas où $b \geqslant 2$. Alors $a!\equiv a!+5^{b} \equiv 7^{\mathrm{c}}(\bmod 25)$. Or, comme $7^{2} \equiv-1$ $(\bmod 25)$, on sait que $7^{\mathrm{c}} \equiv 1,7,-1$ ou $-7(\bmod 25)($ selon que $\mathrm{c} \equiv 0,1,2$ ou $3(\bmod 4))$ et que $\mathrm{a}!\equiv 2,6,-1,-5$ ou $-5(\bmod 25)($ selon que $a$ vaut $2,3,4,5$ ou 6$)$. Cela signifie donc que $a=4$ et $\mathrm{c} \equiv 2(\bmod 4)$.
Mais alors $(-3)^{\mathrm{b}} \equiv \mathrm{a}!+5^{\mathrm{b}} \equiv(-1)^{\mathrm{c}} \equiv 1(\bmod 8)$, ce qui signifie que b est pair. On pose alors $\beta=\mathrm{b} / 2$ et $\gamma=\mathrm{c} / 2$, de sorte que
$$
24=\mathrm{a}!=7^{\mathrm{c}}-5^{\mathrm{b}}=\left(7^{\gamma}+5^{\beta}\right)\left(7^{\gamma}-5^{\beta}\right) .
$$
On en déduit notamment que $7^{\gamma}+5^{\beta} \leqslant 24$, donc que $\gamma \leqslant 1$ et $\mathrm{c} \leqslant 2$. Comme $\mathrm{c} \equiv 2(\bmod 4)$, cela signifie que $\mathrm{c}=2$, donc que $5^{\mathrm{b}}=7^{\mathrm{c}}-\mathrm{a}!=49-24=25=5^{2}$.
Les solutions recherchées sont donc les triplets $(\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c})=(2,1,1),(3,0,1)$ et $(4,2,2)$.
Commentaire des correcteurs: Globalement bien traité pour ceux qui l'ont rédigé, le principal souci de cet exercice consistait à bien se ramener à $a<7$, et à travailler modulo la bonne puissance de nombre premier, ici 25 , ce qui a été plutôt bien trouvé. Il faut bien faire attention aux cas limites $(\mathrm{b}=0, \mathrm{c}=0)$.
## Exercices Seniors
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 9",
"tier": "T2",
"year": null
}
|
Let $a, b, c \geqslant 1$ be integers such that $a^{b} \mid b^{c}$ and $a^{c} \mid c^{b}$. Show that $a^{2} \mid b c$.
|
We will look at the $p$-adic valuations of each of the prime numbers $\mathrm{a}$, $\mathrm{b}$, and $\mathrm{c}$. Indeed, it suffices to show that for any prime number $p$, we have $2 v_{p}(a) = v_{p}(a^2) \leq v_{p}(bc) = v_{p}(b) + v_{p}(c)$.
Let $p$ be a prime number. The hypothesis that $a^b \mid b^c$ translates in terms of $p$-adic valuation to $\mathrm{b} v_{\mathfrak{p}}(\mathrm{a}) \leq \mathrm{c} v_{p}(\mathrm{b})$, or equivalently $v_{p}(\mathrm{a}) \leq \frac{\mathrm{c}}{\mathrm{b}} \nu_{p}(\mathrm{b})$. Similarly, we obtain that $v_{p}(\mathrm{a}) \leq \frac{\mathrm{b}}{\mathrm{c}} \nu_{p}(\mathrm{c})$.
By multiplying the two relations, we find that $v_{\mathfrak{p}}(\mathrm{a})^2 \leq \nu_{p}(b) v_{p}(c)$. Therefore, according to the inequality of means:
$$
v_{p}(a) \leq \sqrt{v_{p}(b) v_{p}(c)} \leq \frac{v_{p}(b) + v_{p}(c)}{2}
$$
which gives us $2 v_{p}(a) \leq v_{p}(b) + v_{p}(c)$ as desired. Since this is true for any prime $p$, we have $a^2 \mid bc$.
Grader's Comment: The problem is generally well done. A handful of students made the mistake of claiming that if $a$ divides $b^c$, then $a$ divides $b$. This claim can be refuted by considering $\mathrm{a}=25$, $\mathrm{b}=10$, and $\mathrm{c}=2$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $a, b, c \geqslant 1$ des entiers tels que $a^{b} \mid b^{c}$ et $a^{c} \mid c^{b}$. Montrer que $a^{2} \mid b c$.
|
Nous allons regarder les valuations $p$-adiques de chacun des nombres premiers $\mathrm{a}, \mathrm{b}$ et c . En effet, il suffit de montrer que pour tout nombre premier $p$, on a $2 v_{p}(a)=v_{p}\left(a^{2}\right) \leqslant$ $v_{p}(b c)=v_{p}(b)+v_{p}(c)$.
Soit $p$ un nombre premier. L'hypothèse que $a^{b} \mid b^{c}$ se traduit en terme de valuation $p$-adique par $\mathrm{b} v_{\mathfrak{p}}(\mathrm{a}) \leqslant \mathrm{c} v_{p}(\mathrm{~b})$, ou encore $v_{p}(\mathrm{a}) \leqslant \frac{\mathrm{c}}{\mathrm{b}} \nu_{p}(\mathrm{~b})$. De même, on obtient que $v_{p}(\mathrm{a}) \leqslant \frac{\mathrm{b}}{\mathrm{c}} \nu_{p}(\mathrm{c})$.
En multipliant les deux relations, on trouve que $v_{\mathfrak{p}}(\mathrm{a})^{2} \leqslant \nu_{p}(b) v_{p}(c)$. On a donc, d'après l'inégalité des moyennes:
$$
v_{p}(a) \leqslant \sqrt{v_{p}(b) v_{p}(c)} \leqslant \frac{v_{p}(b)+v_{p}(c)}{2}
$$
ce qui donne bien $2 v_{p}(a) \leqslant v_{p}(b)+v_{p}(c)$ comme voulu. Ceci étant vrai pour tout premier $p$, on a bien $a^{2} \mid b c$.
Commentaire des correcteurs : Le problème est globalement bien réussi. Une poignée d'élèves s'est trompée en affirmant que si $a$ divise $b^{c}$, alors $a$ divise $b$. Cette affirmation peut être réfutée en regardant $\mathrm{a}=25, \mathrm{~b}=10$ et $\mathrm{c}=2$.
|
{
"exam": "French_envois",
"problem_label": "10",
"problem_match": "\nExercice 10.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 10",
"tier": "T2",
"year": null
}
|
Find all integers $n \geqslant 1$ such that
$$
6^{n}-1 \mid 7^{n}-1
$$
|
Let $n$ be a potential integer satisfying $6^{n}-1 \mid 7^{n}-1$.
We have $5=6-1 \mid 6^{n}-1^{n}$, so $5 \mid 7^{n}-1$. We then calculate the powers of 7 modulo 5:
| | $n$ | 0 | 1 | 2 | 3 | 4 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $7^{\mathrm{n}}(\bmod 5)$ | 1 | 2 | 4 | 3 | 1 | |
Thus, if we denote $n=4 q+r$ as the Euclidean division of $n$ by 4, we have $7^{n} \equiv\left(7^{4}\right)^{q} \times 7^{r} \equiv 1^{q} 7^{r} \equiv 7^{r}$ $(\bmod 5)$. Therefore, for $5 \mid 7^{n}-1$, it is necessary that $r=0$, in other words, $n$ is a multiple of 4.
By then looking modulo 7, we get $6^{n} \equiv(-1)^{4 \mathrm{q}} \equiv 1(\bmod 7)$, so $7\left|6^{n}-1\right| 7^{n}-1$, which is not possible.
Therefore, there is no $n$ satisfying $6^{n}-1 \mid 7^{n}-1$.
Comment from the graders: The exercise is very well solved and was handled by many students.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Trouver tous les entiers $n \geqslant 1$ tels que
$$
6^{n}-1 \mid 7^{n}-1
$$
|
Soit $n$ un éventuel entier vérifiant $6^{n}-1 \mid 7^{n}-1$.
On a $5=6-1 \mid 6^{n}-1^{n}$, donc $5 \mid 7^{n}-1$. On calcule donc les puissances de 7 modulo 5 :
| | $n$ | 0 | 1 | 2 | 3 | 4 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| $7^{\mathrm{n}}(\bmod 5)$ | 1 | 2 | 4 | 3 | 1 | |
Ainsi, si on note $n=4 q+r$ la division euclidienne de $n$ par 4 , on a $7^{n} \equiv\left(7^{4}\right)^{q} \times 7^{r} \equiv 1^{q} 7^{r} \equiv 7^{r}$ $(\bmod 5)$. Donc pour que $5 \mid 7^{n}-1$, il faut que $r=0$, autrement dit $n$ est multiple de 4 .
En regardant alors modulo 7 , on obtient $6^{n} \equiv(-1)^{4 \mathrm{q}} \equiv 1(\bmod 7)$, donc $7\left|6^{n}-1\right| 7^{n}-1$, ce qui n'est pas possible.
Il n'y a donc aucun $n$ vérifiant $6^{n}-1 \mid 7^{n}-1$.
Commentaire des correcteurs: L'exercice est très bien résolu et a été traité par de nombreux élèves.
|
{
"exam": "French_envois",
"problem_label": "11",
"problem_match": "\nExercice 11.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 11",
"tier": "T2",
"year": null
}
|
Determine all pairs of strictly positive integers ( $\mathfrak{m}, \mathfrak{n}$ ) such that
$$
m n-1 \mid n^{3}-1
$$
|
Notice that the pairs $(1, \mathfrak{n})$ and $(\mathfrak{m}, 1)$ are solutions for all strictly positive integers $m$ and $n$. We assume from now on that $m, n \geqslant 2$.
Note that the numbers $m n-1, n^{3}-1$ are strictly positive. The divisibility condition therefore implies that $\mathrm{mn}-1 \leqslant \mathrm{n}^{3}-1$, so $\mathrm{m} \leqslant \mathrm{n}^{2}$.
We start by bringing a bit of symmetry to the problem by noting that $\mathrm{mn}-1$ divides $(\mathrm{mn})^{3}-1^{3}$, so $\mathfrak{m n}-1$ divides $(\mathfrak{m n})^{3}-1-\mathfrak{m}^{3}\left(\mathfrak{n}^{3}-1\right)=\mathfrak{m}^{3}-1$.
Now that the problem is completely symmetric in $m$ and $n$, we can assume without loss of generality that $m \geqslant n . m \geqslant n$. Since $m n-1$ divides $n^{3}-1$ and $m n-1$, it also divides $n^{3}-1-$ $(m n-1)=n\left(n^{2}-\mathfrak{m}\right)$. Since $m n-1$ and $n$ are coprime, by Gauss's lemma, $m n-1$ divides $n^{2}-m$. But then, if $n^{2}-m$ is non-zero, since $m \geqslant n$ and $m \geqslant 1$,
$$
0<\mathfrak{n}^{2}-\mathfrak{m}<\mathrm{mn}-1 \leqslant \mathfrak{n}^{2}-\mathrm{m}
$$
which is impossible. Therefore, we have $n^{2}=m$. Conversely, the pair $(\left.n^{2}, n\right)$ is indeed a solution $\left(n^{2}, n\right)$.
Thus, the pairs of solutions are $\left\{(1, \mathfrak{n}),(\mathfrak{n}, 1),\left(\mathfrak{n}^{2}, \mathfrak{n}\right),\left(\mathfrak{n}, \mathfrak{n}^{2}\right)\right\}$.
|
\left\{(1, \mathfrak{n}),(\mathfrak{n}, 1),\left(\mathfrak{n}^{2}, \mathfrak{n}\right),\left(\mathfrak{n}, \mathfrak{n}^{2}\right)\right\}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer tous les couples d'entiers strictement positifs ( $\mathfrak{m}, \mathfrak{n}$ ) tels que
$$
m n-1 \mid n^{3}-1
$$
|
Remarquons que les couples $(1, \mathfrak{n})$ et $(\mathfrak{m}, 1)$ sont solutions pour tous les entiers strictement positifs $m$ et $n$. On suppose dans la suite que $m, n \geqslant 2$.
Notons que les nombres $m n-1, n^{3}-1$ sont strictement positifs. La condition de divisibilité implique donc que $\mathrm{mn}-1 \leqslant \mathrm{n}^{3}-1$, donc $\mathrm{m} \leqslant \mathrm{n}^{2}$.
On commence par ramener un peu de symétrie au problème en remarquant que $\mathrm{mn}-1$ divise $(\mathrm{mn})^{3}-1^{3}$, de sorte que $\mathfrak{m n}-1$ divise $(\mathfrak{m n})^{3}-1-\mathfrak{m}^{3}\left(\mathfrak{n}^{3}-1\right)=\mathfrak{m}^{3}-1$.
Maintenant que le problème est complètement symétrique en $m$ et $n$, on peut supposer sans perte de généralité que $m \geqslant n . m \geqslant n$. Puisque $m n-1$ divise $n^{3}-1$ et $m n-1$, il divise également $n^{3}-1-$ $(m n-1)=n\left(n^{2}-\mathfrak{m}\right)$. Comme $m n-1$ et $n$ sont premiers entre eux, on a par le lemme de Gauss que $m n-1$ divise $n^{2}-m$. Mais alors, si $n^{2}-m$ est non nul, puisque $m \geqslant n$ et $m \geqslant 1$,
$$
0<\mathfrak{n}^{2}-\mathfrak{m}<\mathrm{mn}-1 \leqslant \mathfrak{n}^{2}-\mathrm{m}
$$
ce qui est impossible. On a donc $n^{2}=m$. Réciproquement, le couple ( $\left.n^{2}, n\right)$ est bien solution $\left(n^{2}, n\right)$.
Ainsi, les couples solutions sont $\left\{(1, \mathfrak{n}),(\mathfrak{n}, 1),\left(\mathfrak{n}^{2}, \mathfrak{n}\right),\left(\mathfrak{n}, \mathfrak{n}^{2}\right)\right\}$.
|
{
"exam": "French_envois",
"problem_label": "12",
"problem_match": "\nExercice 12.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 12",
"tier": "T2",
"year": null
}
|
Determine all pairs of strictly positive integers ( $\mathfrak{m}, \mathfrak{n}$ ) such that
$$
m n-1 \mid n^{3}-1
$$
|
:
Similarly as before, we reduce to the case where $n \geqslant 2$.
Let $(m, n)$ be a solution. Therefore, there exists an integer $a$ such that $n^{3}-1=a(m n-1)$. Passing modulo $n$, we get $-1 \equiv -a \pmod{n}$, which simplifies to $a \equiv 1 \pmod{n}$. Let's write $a = k n + 1$.
Substituting back, we get $n^{3}-1=(k n+1)(m n-1)=k m n^{2}+(m-k) n-1$, which simplifies to $n^{2}=k m n + m - k$.
Passing modulo $n$ again, we get $m \equiv k \pmod{n}$. If $m = n p + r$ and $k = n q + r'$ are the Euclidean divisions of $m$ and $k$ by $n$, then $r = r'$. We can rewrite the equation as $n^{2} = (n p + r)(n q + r) n + n p + r - (n q + r)$, which can be further simplified to:
$$
n = p - q + n^{2} p q + n r (p + q) + r^{2}
$$
If $p \geqslant 1$, then $n = p - q + n^{2} p q + n r (p + q) + r^{2} \geqslant n^{2} q - q = q(n^{2} - 1)$. Thus, if $q \geqslant 1$, it must be that $n \geqslant n^{2} - 1$, which is impossible since $n \geqslant 2$.
We have just shown that at least one of $p$ and $q$ must be zero.
If $p = 0$ and $q \geqslant 1$, we have $n = q(n r - 1) + r^{2}$. Since $r = m \geqslant 1$, $n r - 1 \geqslant 1$ so $q(n r - 1) \geqslant n r - 1$ and thus $n = q(n r - 1) + r^{2} \geqslant (n r - 1) + 1 = n r \geqslant n$. All these inequalities are therefore equalities, which implies $q = r = 1$. We thus get $m = 1$.
If $q = 0$ and $p \geqslant 1$, we have $n = p(n r + 1) + r^{2}$. Thus, if $r \geqslant 1$, we have $n \geqslant n + 2$, so $r = 0$, then $n = r$ and finally $m = n^{2}$.
If $p = q = 0$, we have $n = r^{2}$ and $m = r$.
Thus, the solutions are the pairs $(1, n)$ and $\left(n^{2}, n\right)$ for all $n \geqslant 1$, as well as the pairs $\left(r, r^{2}\right)$ with $r \geqslant 1$. We verify reciprocally that all these pairs are solutions, and that $n = 1$ gives the same solutions (since a priori these are only the solutions with $n \geqslant 2$).
Comment from the graders: The exercise is generally well done. Many students forget to handle the special cases of their reasoning, but in such a problem it is precisely the special/degenerate cases that provide the solutions.
|
(1, n), (n^2, n), (r, r^2)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer tous les couples d'entiers strictement positifs ( $\mathfrak{m}, \mathfrak{n}$ ) tels que
$$
m n-1 \mid n^{3}-1
$$
|
:
De même que précédemment, on se ramène au cas où $n \geqslant 2$.
Soit $(m, n)$ une solution. On a donc un entier a tel que $n^{3}-1=a(m n-1)$. En passant modulo $n$, on obtient $-1 \equiv-a(\bmod \mathfrak{n})$, soit $a \equiv 1(\bmod \mathfrak{n})$. Écrivons donc $a=k n+1$.
En réinjectant, on obtient $n^{3}-1=(k n+1)(m n-1)=k m n^{2}+(m-k) n-1$, ce qui se simplifie en $\mathrm{n}^{2}=\mathrm{kmn}+\mathrm{m}-\mathrm{k}$.
Repasser modulo $n$ nous donne $m \equiv k(\bmod n)$, donc si $m=n p+r$ et $k=n q+r^{\prime}$ sont les divisions euclidiennes de $m$ et $k$ par $n$, on a $r=r^{\prime}$. On réécrit donc l'égalité sous la forme $n^{2}=$ $(n p+r)(n q+r) n+n p+r-(n q+r)$, qu'on peut encore une fois simplifier:
$$
n=p-q+n^{2} p q+n r(p+q)+r^{2}
$$
Si $p \geqslant 1$, alors $n=p-q+n^{2} p q+n r(p+q)+r^{2} \geqslant n^{2} q-q=q\left(n^{2}-1\right)$. Ainsi si $q \geqslant 1$, il faut $n \geqslant n^{2}-1$, impossible car $n \geqslant 2$.
On vient de montrer qu'au moins un nombre parmi $p$ et $q$ doit être nul.
Si $p=0$ et $q \geqslant 1$, on a $n=q(n r-1)+r^{2}$. Comme $r=m \geqslant 1, \mathfrak{n r}-1 \geqslant 1$ donc $\mathbf{q}(\mathfrak{n r}-1) \geqslant \mathfrak{n r}-1$ donc $n=q(n r-1)+r^{2} \geqslant(\mathfrak{n r}-1)+1=n r \geqslant n$. Toutes ces inégalités sont donc des égalités, ce qui impose $\mathrm{q}=\mathrm{r}=1$. On obtient donc $\mathrm{m}=1$.
Si $q=0$ et $p \geqslant 1$, on a $n=p(n r+1)+r^{2}$. Ainsi, si $r \geqslant 1$, on a $n \geqslant n+2$, donc $r=0$, puis $n=r$ et finalement $m=n^{2}$.
Si $p=q=0$, on a $n=r^{2}$ et $m=r$.
Ainsi les solutions sont les couples $(1, n)$ et $\left(n^{2}, n\right)$ pour tout $n \geqslant 1$, ainsi que les couples $\left(r, r^{2}\right)$ avec $r \geqslant 1$. On vérifie réciproquement que tous ces couples sont solutions, et que $n=1$ donne bien les mêmes solutions (puisqu'a priori ce ne sont que les solutions avec $n \geqslant 2$ ).
Commentaire des correcteurs: L'exercice est globalement bien réussi. Pas mal d'élèves oublient de traiter les cas particuliers de leur raisonnement, alors que dans un tel problème c'est justement les cas particuliers/dégénérés qui donnent les solutions.
|
{
"exam": "French_envois",
"problem_label": "12",
"problem_match": "\nExercice 12.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"solution_match": "## Solution alternative",
"tier": "T2",
"year": null
}
|
Let $\mathrm{f}: \mathbb{N}^{\star} \rightarrow \mathbb{N}^{\star}$ be a function such that for any integer $\mathrm{n} \geqslant 1, \mathrm{f}(\mathrm{f}(\mathrm{n}))$ is equal to the number of positive divisors of $n$. Show that if $p$ is a prime number, then $f(p)$ is also a prime number.
|
In the following, we denote $d(n)$ as the number of positive divisors of $n$. If $p$ is prime, we have $f(f(p))=2$ by definition. Applying $f$ to both sides of the equality, we see that $f(2)=d(f(p))$. We want to show that $f(2)=2$, which will prove that $f(p)$ has exactly two divisors and is therefore prime. Moreover, we have $f(2)=d(f(2))$. For an integer $\boldsymbol{n} \geqslant 2$ to be equal to its number of divisors, all numbers less than $n$ must divide $n$, including $n-1$ which is always coprime with $n$, so $n-1=1$ and $n=2$. We deduce that $f(2) \in\{1,2\}$. If $f(2)=1$, then $d(f(p))=1$ for all prime $p$, so $f(p)=1$ for prime $p$, since 1 is the only integer with a single divisor. But then
$$
1=\mathbf{f}(3)=\mathbf{f}\left(\mathrm{d}\left(2^{2}\right)\right)=\mathbf{f}\left(\mathbf{f}\left(\mathbf{f}\left(2^{2}\right)\right)\right)=\mathrm{d}\left(\mathbf{f}\left(2^{2}\right)\right)
$$
and we deduce that $f(4)=1$. But then
$$
\mathbf{f}(\mathbf{f}(4))=\mathbf{f}(1)=\mathbf{f}(\mathbf{f}(2))=\mathrm{d}(2)=2 \neq \mathrm{d}(4)
$$
which provides the desired contradiction. Therefore, we have $\boldsymbol{f}(2)=2$, which concludes the proof.
Comment from the graders: Many students solved the problem, but many others went too fast. Indeed, from the equality $f(f(f(p)))=f(p)$, it is tempting to immediately conclude that $\boldsymbol{f}(\mathfrak{p})=2$. However, another possible case is the case where $f(2)=1$, since 1 also satisfies $d(n)=n$. Handling this case was the main difficulty of the problem. It is therefore a pity to have missed it.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $\mathrm{f}: \mathbb{N}^{\star} \rightarrow \mathbb{N}^{\star}$ une fonction telle que pour tout entier $\mathrm{n} \geqslant 1, \mathrm{f}(\mathrm{f}(\mathrm{n}))$ soit égal au nombre de diviseurs positifs de $n$. Montrer que si $p$ est un nombre premier, alors $f(p)$ est aussi un nombre premier.
|
Dans la suite, on note $d(n)$ le nombre de diviseurs positifs de $n$. Si $p$ est premier, on a $f(f(p))=2$ par définition. En appliquant f des deux côtés de l'égalité, on voit que $f(2)=d(f(p))$. On veut donc montrer que $f(2)=2$, ce qui prouvera que $f(p)$ a exactement deux diviseurs et est donc premier. Or, on a aussi $f(2)=d(f(2))$. Or, pour qu'un entier $\boldsymbol{n} \geqslant 2$ soit égal à son nombre de diviseurs, tous les nombres inférieurs à $n$ doivent diviser $n$, y compris $n-1$ qui est toujours premier avec $n$, donc $n-1=1$ et $n=2$. On déduit que $f(2) \in\{1,2\}$. Si $f(2)=1$, alors $d(f(p))=1$ pour tout $p$ premier, donc $f(p)=1$ pour $p$ premier, puisque 1 est le seul entier à admettre un seul diviseur. Mais alors
$$
1=\mathbf{f}(3)=\mathbf{f}\left(\mathrm{d}\left(2^{2}\right)\right)=\mathbf{f}\left(\mathbf{f}\left(\mathbf{f}\left(2^{2}\right)\right)\right)=\mathrm{d}\left(\mathbf{f}\left(2^{2}\right)\right)
$$
et l'on déduit que $f(4)=1$. Mais alors
$$
\mathbf{f}(\mathbf{f}(4))=\mathbf{f}(1)=\mathbf{f}(\mathbf{f}(2))=\mathrm{d}(2)=2 \neq \mathrm{d}(4)
$$
ce qui fournit la contradiction désirée. On a donc bien $\boldsymbol{f}(2)=2$, ce qui conclut.
Commentaire des correcteurs : Une bonne partie des élèves ont résolu le problème, mais beaucoup d'autres sont allés bien trop vite. En effet, à partir de l'égalité $f(f(f(p)))=f(p)$, il est tentant de conclure immédiatemment que $\boldsymbol{f}(\mathfrak{p})=2$. Mais un autre cas possible est le cas où $f(2)=1$, puisque 1 vérifie aussi que $d(n)=n$. C'est traiter ce cas qui constituait la principale difficulté du problème. Il est donc dommage d'être passé à côté.
|
{
"exam": "French_envois",
"problem_label": "13",
"problem_match": "\nExercice 13.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"solution_match": "## Solution de l'exercice 13",
"tier": "T2",
"year": null
}
|
It is said that two integers $a, b \in \mathbb{N}^{\star}$ are connected if there exists a prime number $p$ such that $\mathrm{a}=\mathrm{pb}$ or $\mathrm{b}=\mathrm{pa}$.
Find all integers $n \geqslant 1$ having the following property: one can write all the positive divisors of $n$ (including 1 and $n$) exactly once on a circle in such a way that each divisor is connected to each of its two neighbors?
|
First, let's consider the case where $n$ has only one prime factor, so $\mathrm{n}=\mathrm{p}^{\alpha}$. If $\alpha \leqslant 1$, any configuration works. However, if $\alpha \geqslant 2$, 1 must be placed next to two different numbers, and is only connected to one other divisor of $p^{\alpha}$ (which is $p$), so this is not possible.
Notice that the parity of the number of prime factors counted with multiplicity must change between a number and a number that is connected to it. Thus, if $n$ has an odd number of divisors, the existence of such a configuration would imply that 1 has both an even and an odd number of prime factors, which is not possible. The numbers with an odd number of divisors are perfect squares, so these do not satisfy the property in the statement.
Now, let's try to solve the case where we have two prime factors, say $n=p^{a} q^{b}$ with one of the numbers $a$ or $b$ being odd, and without loss of generality, assume it is $a$.
The following arrangement works:
$$
1, q, q^{2}, \ldots, q^{b}, p q^{b}, p q^{b-1}, \ldots, p q, p^{2} q, \ldots, p^{a-1} q^{b}, p^{a} q^{b}, p^{a} q^{b-1}, \ldots, p^{a} q, p^{a}, p^{a-1}, \ldots, p, 1
$$
We use the fact that $a$ is odd to say that we have indeed written $p^{a-1} q^{b}$ just before $p^{a} q^{b}$.
We proceed by induction on the number of prime divisors: suppose we have shown for some $k \geqslant 2$ that all numbers of the form $\prod_{i=1}^{k} p_{i}^{\alpha_{i}}$ with at least one of the $\alpha_{i}$ odd satisfy the property in the statement, and let $n=\prod_{i=1}^{k+1} p_{i}^{\alpha_{i}}$ with at least one of the $\alpha_{i}$ odd, say $\alpha_{1}$. Then the induction hypothesis tells us that we can order the divisors of $n^{\prime}=\prod_{i=1}^{k} p_{i}^{\alpha_{i}}$ as $d_{1}, \ldots d_{m}$ such that $d_{i}$ and $d_{i+1}$ are all connected, as well as $d_{m}$ and $d_{1}$. Then the following arrangement works for $m$ (since $m$ is even):
$$
d_{1}, p_{k+1} d_{1}, \ldots, p_{k+1}^{\alpha_{k+1}} d_{1}, p_{k+1}^{\alpha_{k+1}} d_{2}, \ldots p_{k+1} d_{2}, d_{2}, d_{3}, \ldots, p_{k+1}^{\alpha_{k+1}} d_{m}, \ldots p_{k+1} d_{m}, d_{m}, d_{1}
$$
Thus, the numbers that do not satisfy this property are the squares (different from 1) and the powers (greater than 2) of prime numbers.
Comment from the graders: The exercise, which is somewhat combinatorial, is relatively less treated but generally well succeeded by the students who approached it. Most students who have the intuition of the construction to be carried out for composite numbers have difficulty formulating it rigorously (by induction).
|
not found
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
On dit que deux entiers $a, b \in \mathbb{N}^{\star}$ sont reliés s'il existe un nombre premier $p$ tel que $\mathrm{a}=\mathrm{pb}$ ou $\mathrm{b}=\mathrm{pa}$.
Trouver tous les entiers $n \geqslant 1$ ayant la propriété suivante : on peut écrire tous les diviseurs positifs de $n$ (1 et n compris) exactement une fois sur un cercle de sorte que tout diviseur soit relié avec chacun de ses deux voisins?
|
Traitons d'abord le cas où $n$ n'a qu'un seul facteur premier, donc $\mathrm{n}=\mathrm{p}^{\alpha}$. Si $\alpha \leqslant 1$, n'importe quelle configuration marche. En revanche, si $\alpha \geqslant 2,1$ doit être placé à côté de deux nombres différents, et n'est relié qu'à un seul autre diviseur de $p^{\alpha}$ (celui-ci étant $p$ ), ce n'est donc pas possible.
Remarquons que la parité du nombre de diviseurs premiers comptés avec multiplicité change forcément entre un nombre et un nombre qui lui est relié. Ainsi, si $n$ a un nombre impair de diviseurs, l'existence d'une telle configuration impliquerait que 1 a à la fois un nombre pair et un nombre impair de diviseurs premiers, ce qui n'est pas possible. Les nombres ayant un nombre impair de diviseurs étant les carrés parfaits, ceux-ci ne vérifient pas non plus la propriété de l'énoncé.
Maintenant, essayons de résoudre le cas où on a deux facteurs premiers, mettons $n=p^{a} q^{b}$ avec l'un des nombres $a$ ou b étant impair, et l'on suppose sans perte de généralité qu'il s'agit de $a$.
L'arrangement suivant fonctionne :
$$
1, q, q^{2}, \ldots, q^{b}, p q^{b}, p q^{b-1}, \ldots, p q, p^{2} q, \ldots, p^{a-1} q^{b}, p^{a} q^{b}, p^{a} q^{b-1}, \ldots, p^{a} q, p^{a}, p^{a-1}, \ldots, p, 1
$$
On utilise le fait que a est impair pour dire qu'on a effectivement écrit $p^{a-1} q^{b}$ juste avant $p^{a} q^{b}$.
On procède maintenant par récurrence sur le nombre de diviseurs premiers : supposons avoir montré pour un $k \geqslant 2$ que tous les nombres de la forme $\prod_{i=1}^{k} p_{i}^{\alpha_{i}}$ avec au moins l'un des $\alpha_{i}$ impair vérifient la propriété de l'énoncé, et soit $n=\prod_{i=1}^{k+1} p_{i}^{\alpha_{i}}$ avec au moins l'un des $\alpha_{i}$ impairs, disons $\alpha_{1}$. Alors l'hypothèse de récurrence nous dit qu'on peut ordonner les diviseurs de $n^{\prime}=\prod_{i=1}^{k} p_{i}^{\alpha_{i}}$ de la forme $d_{1}, \ldots d_{m}$ de sorte que $d_{i}$ et $d_{i+1}$ soient tous reliés, de même que $d_{m}$ et $d_{1}$. Alors l'arrangement suivant fonctionne pour $m$ (car mest pair) :
$$
d_{1}, p_{k+1} d_{1}, \ldots, p_{k+1}^{\alpha_{k+1}} d_{1}, p_{k+1}^{\alpha_{k+1}} d_{2}, \ldots p_{k+1} d_{2}, d_{2}, d_{3}, \ldots, p_{k+1}^{\alpha_{k+1}} d_{m}, \ldots p_{k+1} d_{m}, d_{m}, d_{1}
$$
Ainsi les nombres qui ne vérifient pas cette propriété sont les carrés (différents de 1 ) et le puissances (plus grandes que 2) de nombres premiers.
Commentaire des correcteurs: L'exercice, un peu combinatoire, est relativement peu traité mais globalement bien réussi par les élèves qui l'ont abordé. La plupart des élèves qui ont l'intuition de la construction à réaliser pour des nombres composés ont des difficultés à la formuler rigoureusement (par une récurrence).
|
{
"exam": "French_envois",
"problem_label": "14",
"problem_match": "\nExercice 14.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 14",
"tier": "T2",
"year": null
}
|
Let $m, n \geqslant 2$ be integers such that $\operatorname{PGCD}(m, n)=\operatorname{PGCD}(m, n-1)=1$. We define the sequence $\left(n_{k}\right)_{k \in \mathbb{N}}$ by $n_{0}=m$ and $n_{k+1}=n \cdot n_{k}+1$ for $k \in \mathbb{N}$. Show that the integers $n_{1}, \ldots, n_{m-1}$ cannot all be prime numbers.
|
First, the sequence $(\mathrm{n}_{\mathrm{k}})$ is an arithmetico-geometric sequence. Therefore, we can establish a closed formula for its general term, namely $n_{k}=n^{k} m+\frac{n^{k+1}-1}{n-1}$, which can also be obtained by induction from the calculation of the first few terms. From this expression, we deduce in particular that $n_{k}>m$ for all $k>0$. We will now show that one of the numbers $n_{1}, \ldots, n_{m-1}$ is divisible by $m$, which will make this number a composite number.
By passing modulo $m$, we deduce $n_{k} \equiv \frac{\mathfrak{n}^{k+1}-1}{n-1} \bmod m$ by induction, where we have used that $n-1$ is invertible modulo $m$ because $n-1$ is coprime with $m$.
Let $\omega$ be the order of $n \bmod m$ (which exists because $m$ and $n$ are coprime). We have $\omega \leqslant \varphi(m) \leqslant m-1$ according to Euler's theorem. We deduce that $m \mid n^{\omega}-1$, which implies that $m$ divides $n_{\omega-1}-1$ as desired. Thus, the $n_{k}$ are not all prime.
Graders' comments: The exercise is very well solved. Almost all students thought to justify that $m<n_{k}$, which is necessary to conclude that $n_{k}$ is composite if it is divisible by $m$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $m, n \geqslant 2$ des entiers tels que $\operatorname{PGCD}(m, n)=\operatorname{PGCD}(m, n-1)=1$. On définit la suite $\left(n_{k}\right)_{k \in \mathbb{N}}$ par $n_{0}=m$ et $n_{k+1}=n \cdot n_{k}+1$ pour $k \in \mathbb{N}$. Montrer que les entiers $n_{1}, \ldots, n_{m-1}$ ne peuvent pas tous être des nombres premiers.
|
Tout d'abord, la suite ( $\mathrm{n}_{\mathrm{k}}$ ) est une suite arithmético-géométrique. On peut donc établir une formule close pour son terme général, à savoir $n_{k}=n^{k} m+\frac{n^{k+1}-1}{n-1}$, que l'on peut aussi obtenir par récurrence à partir du calcul des premiers termes. De cette expression on déduit en particulier que $n_{k}>m$ pour tout $k>0$. On va désormais montrer que l'un des nombres $n_{1}, \ldots, n_{m-1}$ est divisible par $m$, ce qui fera de ce nombre un nombre composé.
En passant modulo $m$, on déduit $n_{k} \equiv \frac{\mathfrak{n}^{k+1}-1}{n-1} \bmod m$ par récurrence, où l'on a utilisé que $n-1$ est inversible modulo $m$ car $n-1$ est premier avec $m$.
Soit $\omega$ l'ordre de $n \bmod m$ (celui-ci existe car $m$ et $n$ premiers entre eux). On a $\omega \leqslant \varphi(m) \leqslant m-1$ d'après le théorème d'Euler. On déduit que $m \mid n^{\omega}-1$, ce qui implique que $m$ divise $n_{\omega-1}-1$ comme voulu. Ainsi, les $n_{k}$ ne sont pas tous premiers.
Commentaire des correcteurs: L'exercice est très bien résolu. Les élèves ont pratiquement tous pensé à justifier le fait que $m<n_{k}$, ce qui est nécessaire pour conclure que $n_{k}$ est composé s'il est divisible par m.
|
{
"exam": "French_envois",
"problem_label": "15",
"problem_match": "\nExercice 15.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 15",
"tier": "T2",
"year": null
}
|
Let $p$ be an odd prime and $x_{1}, \ldots, x_{p}$ be integers.
We assume that for all $k \geqslant 1$ integer, we have
$$
\mathrm{p} \mid \mathrm{x}_{1}^{\mathrm{k}}+\cdots+\mathrm{x}_{\mathrm{p}}^{\mathrm{k}}
$$
Show that the integers $x_{1}, \ldots, x_{p}$ are all congruent modulo $p$.
|
Note that the relation is also true for $k=0$ because $\underbrace{1+\ldots+1}_{\mathrm{p} \text { times }} \equiv 0$ $\bmod p$
Let $\mathrm{Q}(\mathrm{X})=\sum_{\mathrm{k}=0}^{n} \mathrm{a}_{\mathrm{k}} X^{\mathrm{k}}$ be a polynomial with integer coefficients. We have
$$
\mathrm{Q}\left(\mathrm{x}_{1}\right)+\ldots+\mathrm{Q}\left(\mathrm{x}_{\mathrm{p}}\right)=\sum_{\ell=1}^{p} \sum_{k=0}^{n} \mathrm{a}_{\mathrm{k}} x_{\ell}^{k}=\sum_{\mathrm{k}=0}^{n} \mathrm{a}_{\mathrm{k}} \underbrace{\sum_{\ell=1}^{p} x_{\ell}^{k}}_{\equiv 0 \bmod p} \equiv 0 \bmod p
$$
Suppose, for the sake of contradiction, that the $x_{i}$ do not all give the same remainder modulo $p$. Let $\left\{y_{1}, \ldots, y_{r}\right\}$ be the set of remainders modulo $p$ generated by the set $\left\{x_{1}, \ldots, x_{p}\right\}$, with $y_{1} \equiv x_{1}$. Let $a_{1}$ be the number of elements in the set $\left\{x_{1}, \ldots, x_{p}\right\}$ that have the remainder $y_{1}$. Let $P(X)=\left(X-y_{2}\right) \ldots\left(X-y_{r}\right)$. $P$ is zero at each of the $y_{i}$ for $i \neq 0$. Note that since $y_{1} \neq y_{i} \bmod p, P\left(y_{1}\right) \neq 0 \bmod p$. The relation established earlier then gives us $a_{1} P\left(y_{1}\right) \equiv 0 \bmod p$, which implies that $a_{1}=0 \bmod p$, i.e., $a_{1}=p$. This is in contradiction with our initial assumption, so the $x_{i}$ are all equal.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soient $p$ un nombre premier impair et $x_{1}, \ldots, x_{p}$ des entiers relatifs.
On suppose que pour tout $k \geqslant 1$ entier, on a
$$
\mathrm{p} \mid \mathrm{x}_{1}^{\mathrm{k}}+\cdots+\mathrm{x}_{\mathrm{p}}^{\mathrm{k}}
$$
Montrer que les entiers $x_{1}, \ldots, x_{p}$ sont tous congrus modulo $p$.
|
Notons que la relation est également vrai pour $k=0$ car $\underbrace{1+\ldots+1}_{\mathrm{p} \text { fois }} \equiv 0$ $\bmod p$
Soit $\mathrm{Q}(\mathrm{X})=\sum_{\mathrm{k}=0}^{n} \mathrm{a}_{\mathrm{k}} X^{\mathrm{k}}$ un polynôme à coefficients entiers. On a
$$
\mathrm{Q}\left(\mathrm{x}_{1}\right)+\ldots+\mathrm{Q}\left(\mathrm{x}_{\mathrm{p}}\right)=\sum_{\ell=1}^{p} \sum_{k=0}^{n} \mathrm{a}_{\mathrm{k}} x_{\ell}^{k}=\sum_{\mathrm{k}=0}^{n} \mathrm{a}_{\mathrm{k}} \underbrace{\sum_{\ell=1}^{p} x_{\ell}^{k}}_{\equiv 0 \bmod p} \equiv 0 \bmod p
$$
On suppose par l'absurde que les $x_{i}$ ne donnent pas tous le même reste modulo $p$. Soit $\left\{y_{1}, \ldots, y_{r}\right\}$ l'ensemble des restes modulo $p$ généré par l'ensemble $\left\{x_{1}, \ldots, x_{p}\right\}$, avec $y_{1} \equiv x_{1}$. On note $a_{1}$ le nombre d'éléments de l'ensemble $\left\{x_{1}, \ldots, x_{p}\right\}$ qui ont pour reste $y_{1}$. Soit $P(X)=\left(X-y_{2}\right) \ldots\left(X-y_{r}\right)$. P est nul en chacun des $y_{i}$ pour $i \neq 0$. Notons que comme $y_{1} \neq y_{i} \bmod p, P\left(y_{1}\right) \neq 0 \bmod p$. La relation établie plus haut nous donne alors $a_{1} P\left(y_{1}\right) \equiv 0 \bmod p$, ce qui implique que $a_{1}=0 \bmod p$, c'est-à-dire que $a_{1}=p$. Cela est en contradiction avec notre supposition de départ, donc les $x_{i}$ sont tous égaux.
|
{
"exam": "French_envois",
"problem_label": "16",
"problem_match": "\nExercice 16.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 16",
"tier": "T2",
"year": null
}
|
Let $p$ be an odd prime and $x_{1}, \ldots, x_{p}$ be integers.
We assume that for all $k \geqslant 1$ integer, we have
$$
\mathrm{p} \mid \mathrm{x}_{1}^{\mathrm{k}}+\cdots+\mathrm{x}_{\mathrm{p}}^{\mathrm{k}}
$$
Show that the integers $x_{1}, \ldots, x_{p}$ are all congruent modulo $p$.
|
: We present a somewhat more conceptual solution that relies on the structure of the field $\mathbb{Z} / p \mathbb{Z}$ and on the fact that the Newton sums of the roots of a polynomial determine its coefficients.
Let $P(X)=\left(X-x_{1}\right) \ldots\left(X-x_{p}\right)$ be the monic polynomial with integer coefficients whose roots are the $x_{\ell}$. The hypothesis of the statement indicates that the Newton sums of the $x_{\ell}$ are zero modulo $p$.
It is possible to relate the coefficients of the polynomial $P$ to the Newton sums of the polynomial $P$ via the following formulas: if $a_{k}$ is the coefficient of $X^{k}$ in the expression of $P$, then for all $0 \leqslant k \leqslant p$:
$$
k a_{p-k}=(-1)^{k-1} \sum_{\ell=1}^{k-1} a_{p-\ell}\left(x_{1}^{\ell}+\ldots+x_{p}^{\ell}\right)
$$
These formulas can be derived by induction using Vieta's formulas.
We then observe that if $k \neq 0, p, k a_{p-k} \equiv 0 \bmod p$ because each of the $x_{1}^{\ell}+\ldots+x_{p}^{\ell}$ is divisible by $p$. Thus, in $\mathbb{Z} / p \mathbb{Z}[X]$, the polynomial $P$ is of the form $P(X)=X^{p}-a=X^{p}-a^{p}=(X-a)^{p}$, where we have used that $a^{p} \equiv a(\bmod p)$ by Fermat's little theorem and that in the formula $(X-a)^{p}=$ $\sum_{k=0}^{p}\binom{p}{k} a^{p-k} X^{k}$, only the coefficients $\binom{p}{0}$ and $\binom{p}{p}$ are non-zero modulo $p$. This implies that the $x_{i}$ are all equal (to $a$) modulo $p$ as desired.
Grader's Comment: The exercise is very well done. This exercise required knowledge of polynomials modulo $p$, and the students presented various proofs to solve it.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soient $p$ un nombre premier impair et $x_{1}, \ldots, x_{p}$ des entiers relatifs.
On suppose que pour tout $k \geqslant 1$ entier, on a
$$
\mathrm{p} \mid \mathrm{x}_{1}^{\mathrm{k}}+\cdots+\mathrm{x}_{\mathrm{p}}^{\mathrm{k}}
$$
Montrer que les entiers $x_{1}, \ldots, x_{p}$ sont tous congrus modulo $p$.
|
: On présente une solution un peu plus conceptuelle qui s'appuie sur la structure de corps de $\mathbb{Z} / p \mathbb{Z}$ et sur le fait que les sommes de Newton des racines d'un polynôme déterminent ses coefficients.
Soit $P(X)=\left(X-x_{1}\right) \ldots\left(X-x_{p}\right)$ le polynôme unitaire à coefficients entiers dont les racines sont les $x_{\ell}$. L'hypothèse de l'énoncé nous indique que les sommes de Newton des $x_{\ell}$ sont nulles modulo $p$.
Or il est possible de relier les coefficients du polynômes P aux sommes de Newton du polynôme P , via les formules suivantes: si $a_{k}$ est le coefficient devant $X^{k}$ dans l'écriture de $P$, alors pour tout $0 \leqslant k \leqslant p$ :
$$
k a_{p-k}=(-1)^{k-1} \sum_{\ell=1}^{k-1} a_{p-\ell}\left(x_{1}^{\ell}+\ldots+x_{p}^{\ell}\right)
$$
On peut retrouver ces formules par récurrence à l'aide des relations de Viète.
On remarque alors que si $k \neq 0, p, k a_{p-k} \equiv 0 \bmod p$ car chacune des $x_{1}^{\ell}+\ldots+x_{p}^{\ell}$ est divisible par $p$. Ainsi, dans $\mathbb{Z} / p \mathbb{Z}[X]$, le polynôme $P$ est de la forme $P(X)=X^{p}-a=X^{p}-a^{p}=(X-a)^{p}$, où l'on a utilisé que $a^{p} \equiv a(\bmod p)$ par le petit théorème de Fermat et que dans la formule $(X-a)^{p}=$ $\sum_{k=0}^{p}\binom{p}{k} a^{p-k} X^{k}$, seuls les coefficients $\binom{p}{0}$ et $\binom{p}{p}$ sont non nuls modulo $p$. Cela implique que les $x_{i}$ sont tous égaux (à $a$ ) modulo $p$ comme voulu.
Commentaire des correcteurs : L'exercice est très bien réussi. Cet exercice demandait de la culture sur les polynômes modulo $p$, et les élèves ont présenté diverses preuves pour s'en sortir.
|
{
"exam": "French_envois",
"problem_label": "16",
"problem_match": "\nExercice 16.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T2",
"year": null
}
|
Let $n$ be a strictly positive integer and let $a, a_{1}, \ldots, a_{n}$ be strictly positive integers. Suppose that for any integer $k$ for which the integer $a k+1$ is a perfect square, at least one of the integers $a_{1} k+1, \ldots, a_{n} k+1$ is also a perfect square.
Show that there exists an index $1 \leqslant i \leqslant n$ such that $a=a_{i}$.
|
Let's start with two lemmas on quadratic residues.
Lemma 1: If $x$ is a quadratic residue modulo $p$ with $p$ an odd prime, it is also a quadratic residue modulo $p^{2}$ (and even $\mathrm{p}^{\mathrm{m}}$, but we don't need this here).
|
proof
|
Yes
|
Incomplete
|
proof
|
Number Theory
|
Soit $n$ un entier strictement positif et soient $a, a_{1}, \ldots, a_{n}$ des entiers strictement positifs. On suppose que pour tout entier $k$ pour lequel l'entier $a k+1$ est un carré parfait, au moins l'un des entiers $a_{1} k+1, \ldots, a_{n} k+1$ est également un carré parfait.
Montrer qu'il existe un indice $1 \leqslant i \leqslant n$ tel que $a=a_{i}$.
|
Commençons par deux lemmes sur les résidus quadratiques.
Lemme 1 : Si $x$ est résidu quadratique modulo $p$ avec $p$ premier impair, il l'est aussi modulo $p^{2}$ (et même $\mathrm{p}^{\mathrm{m}}$, mais on n'en a pas besoin ici).
|
{
"exam": "French_envois",
"problem_label": "17",
"problem_match": "\nExercice 17.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 17",
"tier": "T2",
"year": null
}
|
Let $n$ be a strictly positive integer and let $a, a_{1}, \ldots, a_{n}$ be strictly positive integers. Suppose that for any integer $k$ for which the integer $a k+1$ is a perfect square, at least one of the integers $a_{1} k+1, \ldots, a_{n} k+1$ is also a perfect square.
Show that there exists an index $1 \leqslant i \leqslant n$ such that $a=a_{i}$.
|
Indeed, let $a$ be such that $a^{2} \equiv x(\bmod p)$, which we rewrite as $a^{2}-x=k p$. But then we get $\left(a-2^{-1} k p\right)^{2} \equiv a^{2}-k p \equiv x\left(\bmod p^{2}\right)$, and 2 is invertible modulo $p^{2}$ since $p$ is odd. Thus, $x$ is indeed a quadratic residue modulo $p^{2}$.
Lemma 2: If $t$ is a non-zero integer and $p$ is a prime such that $p \equiv 1(\bmod 8 t)$, then $\left(\frac{t}{p}\right)=1$.
Proof: Indeed, let $q$ be a prime divisor of $t$ and $\alpha=\nu_{q}(t)$. If $q=2,\left(\frac{2}{p}\right)=1$ because $p \equiv 1(\bmod 8)$. So $q$ is a quadratic residue modulo $p$. Note now that $\alpha$ is even, then $q^{\alpha}$ is automatically a square modulo $p$, and if $\alpha$ is odd, $q^{\alpha}$ is the product of $q$ (which is a square) with $q^{\alpha-1}$ which is a square, so $q^{\alpha}$ is a square modulo $p$. If $q \geqslant 3$, since $p \equiv 1(\bmod 4)$, the law of quadratic reciprocity gives us $\left(\frac{q}{p}\right)=\left(\frac{p}{q}\right)=\left(\frac{1}{q}\right)=1$, Similarly, we deduce that $\left(\frac{q^{\alpha}}{p}\right)=1$. The multiplicativity of the Legendre symbols allows us to conclude that $\left(\frac{t}{p}\right)=1$.
We also recall a particular case of Dirichlet's theorem on arithmetic progressions: for any integer $t$, there are infinitely many primes $p$ such that $p \equiv 1 \bmod 8 t$.
Let's return to the exercise. Suppose by contradiction that all the $a_{i}$ are different from $a$.
Let $M=\max \left\{a, a_{1}, \ldots, a_{n}\right\} \geqslant 2$. We then construct a sequence of primes $p_{1}, \ldots p_{n}$ by induction as follows: by Dirichlet's theorem on arithmetic progressions, there is at least one prime $p_{1} \equiv 1\left(\bmod 8 a_{1}\left(a_{1}-a\right)\right)$ with $p_{1}>M$. (We use here the fact that $\left.a_{1}-a \neq 0\right)$.
For $2 \leqslant i \leqslant n$, we then take $p_{i}$ such that $p_{i} \equiv 1\left(\bmod 8 a_{i}\left(a_{i}-a\right)\right.$ ) with $p_{i}>p_{i-1}$ (which exists for the same reasons as $p_{1}$ ).
In particular, the $p_{i}$ are pairwise distinct, and $p_{i} \equiv 1 \bmod 8 a_{i}$ and $p_{i} \equiv 1 \bmod 8\left(a_{i}-a\right)$, so by the second lemma, for all $i,\left(\frac{a_{i}}{p_{i}}\right)=\left(\frac{a_{i}-a}{p_{i}}\right)=1$.
By definition, for all $i$ there exists $n_{i}$ such that $n_{i}^{2} \equiv a_{i}-a\left(\bmod p_{i}\right)$, and by replacing $n_{i}$ with $n_{i}+p_{i}$, we can assume $p_{i}^{2} \nmid n_{i}^{2}-\left(a_{i}-a\right)\left(p_{i} \neq 2\right)$. Thus, we can write $n_{i}^{2} \equiv a c_{i} p_{i}+\left(a_{i}-a\right)\left(\bmod p_{i}^{2}\right)$ with $p_{i} \nmid c_{i}$ since $a$ and $p_{i}$ are coprime $\left(a<p_{i}\right)$.
Next, since $a_{i}$ is invertible modulo $p_{i}$ for all $i$, the Chinese remainder theorem indicates that we can find an integer $k$ such that for all $i, k \equiv\left(c_{i} p_{i}-1\right) a_{i}^{-1} \bmod p_{i}^{2}$, or $a_{i} k+1 \equiv c_{i} p_{i}$ $\left(\bmod p_{i}^{2}\right)$.
Notice that, by construction,
$$
a k+1 \equiv a \frac{c_{i} p_{i}-1}{a_{i}}+1 \equiv \frac{a c_{i} p_{i}-a+a_{i}}{a_{i}} \equiv \frac{n_{i}^{2}}{a_{i}} \equiv a_{i}\left(\frac{n_{i}}{a_{i}}\right)^{2} \quad\left(\bmod p_{i}^{2}\right)
$$
Since $\left(\frac{a_{i}}{p_{i}}\right)=1$, $a_{i}$ is also a quadratic residue modulo $p_{i}^{2}$ by the first lemma, so there is an integer, say $\mathrm{N}_{i}$, such that $a k+1 \equiv \mathrm{~N}_{i}^{2}\left(\bmod p_{i}^{2}\right)$.
Then the Chinese remainder theorem gives us an integer $x$ such that $x \equiv N_{i}\left(\bmod p_{i}^{2}\right)$ for all $i$ and $x \equiv 1(\bmod a)\left(\text{since } a\right.$ is coprime with the $\left.p_{i}\right)$. But then $x^{2} \equiv N_{i}^{2} \equiv a k+1\left(\bmod p_{i}^{2}\right)$ for all $i$, and $x^{2} \equiv 1^{2} \equiv a k+1(\bmod a)$, so $x^{2} \equiv a k+1\left(\bmod a P^{2}\right)$, where we have set $P=\prod_{i=1}^{n} p_{i}$.
We now rewrite the congruence as $x^{2}=a k+1+m a P^{2}=a\left(P^{2} m+k\right)+1$. We finally use the hypothesis of the statement: there exists an index $j$ such that $a_{j}\left(P^{2} m+k\right)+1$ is a perfect square. But then $a_{j}\left(P^{2} m+k\right)+1 \equiv a_{j} k+1 \equiv c_{j} p_{j}\left(\bmod p_{j}^{2}\right)$, and since $p_{j} \nmid c_{j}, v_{p_{j}}\left(a_{j}\left(P^{2} m+k\right)+1\right)=1$, which is in contradiction with the fact that it is a perfect square. Our initial statement was therefore false, and one of the $a_{i}-a$ is non-zero.
Comment from the graders: The exercise is generally well done by the few students who tackled it, and who present very different solutions from the corrected one.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $n$ un entier strictement positif et soient $a, a_{1}, \ldots, a_{n}$ des entiers strictement positifs. On suppose que pour tout entier $k$ pour lequel l'entier $a k+1$ est un carré parfait, au moins l'un des entiers $a_{1} k+1, \ldots, a_{n} k+1$ est également un carré parfait.
Montrer qu'il existe un indice $1 \leqslant i \leqslant n$ tel que $a=a_{i}$.
|
En effet, soit a tel que $a^{2} \equiv x(\bmod p)$, ce qu'on réécrit sous la forme $a^{2}-x=k p$. Mais alors on obtient $\left(a-2^{-1} k p\right)^{2} \equiv a^{2}-k p \equiv x\left(\bmod p^{2}\right)$, et 2 est inversible modulo $p^{2}$ car $p$ est impair. Ainsi, $x$ est bien un résidu quadratique modulo $p^{2}$.
Lemme 2: Sii $t$ est un entier non nul et $p$ est un nombre premier tel que $p \equiv 1(\bmod 8 \mathrm{t})$, alors $\left(\frac{\mathrm{t}}{\mathrm{p}}\right)=1$.
Démonstration : En effet, soit $q$ un diviseur premier de $t$ et $\alpha=\nu_{q}(t)$. Si $q=2,\left(\frac{2}{p}\right)=1$ car $p \equiv 1(\bmod 8)$. donc $q$ est résidu quadratique modulo $p$. Notons maintenant que $\alpha$ est pair, alors $q^{\alpha}$ est automatiquement un carré modulo $p$, et si $\alpha$ est impair, $q^{\alpha}$ est le produit de $q$ (qui est un carré) avec $q^{\alpha-1}$ qui est un carré, donc $q^{\alpha}$ est un carré modulo $p$. Si $q \geqslant 3$, comme $p \equiv 1(\bmod 4)$, la loi de réciprocité quadratique nous donne $\left(\frac{q}{p}\right)=\left(\frac{p}{q}\right)=\left(\frac{1}{q}\right)=1$, De même que précédemment, on déduit que $\left(\frac{q^{\alpha}}{p}\right)=1$. La multiplicativité des symboles de Legendre permet de conclure que $\left(\frac{t}{p}\right)=1$.
On rappelle également un cas particulier du théorème de la progression arithmétique de Dirichlet : pour tout $t$ entier, il existe une infinité de nombres premiers $p$ tels que $p \equiv 1 \bmod 8 t$.
Revenons à l'exercice. Supposons par l'absurde que tous les $a_{i}$ sont différents de $a$.
Posons $M=\max \left\{a, a_{1}, \ldots, a_{n}\right\} \geqslant 2$. On construit alors une suite de nombres premiers $p_{1}, \ldots p_{n}$ par récurrence comme suit : par le théorème de la progression arithmétique de Dirichlet, il existe au moins un nombre premier $p_{1} \equiv 1\left(\bmod 8 a_{1}\left(a_{1}-a\right)\right)$ avec $p_{1}>M$. (On utilise ici le fait que $\left.a_{1}-a \neq 0\right)$.
Pour $2 \leqslant i \leqslant n$, on prend ensuite $p_{i}$ tel que $p_{i} \equiv 1\left(\bmod 8 a_{i}\left(a_{i}-a\right)\right.$ ) avec $p_{i}>p_{i-1}$ (qui existe pour les mêmes raisons que $p_{1}$ ).
En particulier les $p_{i}$ sont deux-à-deux distincts, et $p_{i} \equiv 1 \bmod 8 a_{i}$ et $p_{i} \equiv 1 \bmod 8\left(a_{i}-a\right)$, de sorte que d'après le deuxième lemme, pour tout $i,\left(\frac{a_{i}}{p_{i}}\right)=\left(\frac{a_{i}-a}{p_{i}}\right)=1$.
Par définition, pour tout $i$ il existe $n_{i}$ tel que $n_{i}^{2} \equiv a_{i}-a\left(\bmod p_{i}\right)$, et quitte à remplacer $n_{i}$ par $n_{i}+p_{i}$, on peut supposer $p_{i}^{2} \nmid n_{i}^{2}-\left(a_{i}-a\right)\left(p_{i} \neq 2\right)$. Ainsi, on peut écrire $n_{i}^{2} \equiv a c_{i} p_{i}+\left(a_{i}-a\right)\left(\bmod p_{i}^{2}\right)$ avec $p_{i} \nmid c_{i}$ puisque a et $p_{i}$ sont premiers entre eux $\left(a<p_{i}\right)$.
Ensuite, comme $a_{i}$ est inversible modulo $p_{i}$ pour tout $i$, le théorème des restes chinois indique que l'on peut trouver un entier $k$ vérifiant que pour tout $i, k \equiv\left(c_{i} p_{i}-1\right) a_{i}^{-1} \bmod p_{i}^{2}$, ou encore $a_{i} k+1 \equiv c_{i} p_{i}$ $\left(\bmod p_{i}^{2}\right)$.
Remarquons que, par construction,
$$
a k+1 \equiv a \frac{c_{i} p_{i}-1}{a_{i}}+1 \equiv \frac{a c_{i} p_{i}-a+a_{i}}{a_{i}} \equiv \frac{n_{i}^{2}}{a_{i}} \equiv a_{i}\left(\frac{n_{i}}{a_{i}}\right)^{2} \quad\left(\bmod p_{i}^{2}\right)
$$
Or $\left(\frac{a_{i}}{p_{i}}\right)=1$, donc $a_{i}$ est également un résidu quadratique modulo $p_{i}^{2}$ par le premier lemme, donc on a un entier, mettons $\mathrm{N}_{i}$, tel que $a k+1 \equiv \mathrm{~N}_{i}^{2}\left(\bmod p_{i}^{2}\right)$.
Alors le théorème des restes chinois nous donne un entier $x$ tel que $x \equiv N_{i}\left(\bmod p_{i}^{2}\right)$ pour tout $i$ et $x \equiv 1(\bmod a)\left(\operatorname{car} a\right.$ est premier avec les $\left.p_{i}\right)$. Mais alors $x^{2} \equiv N_{i}^{2} \equiv a k+1\left(\bmod p_{i}^{2}\right)$ pour tout $i$, et $x^{2} \equiv 1^{2} \equiv a k+1(\bmod a)$, donc $x^{2} \equiv a k+1\left(\bmod a P^{2}\right)$, où on a posé $P=\prod_{i=1}^{n} p_{i}$.
On réécrit maintenant la congruence sous la forme $x^{2}=a k+1+m a P^{2}=a\left(P^{2} m+k\right)+1$. On utilise enfin l'hypothèse de l'énoncé : il existe un indice $j$ tel que $a_{j}\left(P^{2} m+k\right)+1$ soit un carré parfait. Mais alors $a_{j}\left(P^{2} m+k\right)+1 \equiv a_{j} k+1 \equiv c_{j} p_{j}\left(\bmod p_{j}^{2}\right)$, et comme $p_{j} \nmid c_{j}, v_{p_{j}}\left(a_{j}\left(P^{2} m+k\right)+1\right)=1$, ce qui est en contradiction avec le fait que c'est un carré parfait. Notre affirmation de départ était donc fausse, et l'un des $a_{i}-a$ est non nul.
Commentaire des correcteurs : L'exercice est globalement bien réussi par les quelques élèves qui l'ont traité, et qui présentent des solutions très différentes de celle du corrigé.
|
{
"exam": "French_envois",
"problem_label": "17",
"problem_match": "\nExercice 17.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"solution_match": "\nDémonstration:",
"tier": "T2",
"year": null
}
|
Determine all polynomials $\mathrm{P} \in \mathbb{Z}[\mathrm{X}]$ such that:
(i) $\mathrm{P}(\mathrm{n}) \geqslant 1$ for all $n \geqslant 1$
(ii) $\mathrm{P}(\mathrm{mn})$ and $\mathrm{P}(\mathrm{m}) \mathrm{P}(\mathrm{n})$ have the same number of prime divisors for all $\mathrm{m}, \mathrm{n} \geqslant 1$.
|
For all integers $\mathfrak{n} \in \mathbb{N}^{*}$, we denote $\mathcal{D}(n)$ the set of prime divisors of $n$, and $\delta(n)=|\mathcal{D}(n)|$. Let $P \in \mathbb{Z}[X]$ be a polynomial satisfying the two conditions.
We start by proving the following result:
Lemma: Let $\mathrm{n} \geqslant 1$. For all $k \in \mathbb{N}^{*}, \mathcal{D}\left(\mathrm{P}\left(\mathrm{n}^{\mathrm{k}}\right)\right)=\mathcal{D}(\mathrm{P}(\mathrm{n}))$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Déterminer tous les polynômes $\mathrm{P} \in \mathbb{Z}[\mathrm{X}]$ tels que :
(i) $\mathrm{P}(\mathrm{n}) \geqslant 1$ pour tout $n \geqslant 1$
(ii) $\mathrm{P}(\mathrm{mn})$ et $\mathrm{P}(\mathrm{m}) \mathrm{P}(\mathrm{n})$ ont le même nombre de diviseurs premiers pour tous $\mathrm{m}, \mathrm{n} \geqslant 1$.
|
Dans la suite, pour tout entier $\mathfrak{n} \in \mathbb{N}^{*}$, on note $\mathcal{D}(n)$ l'ensemble des diviseurs premiers de $n$, et $\delta(n)=|\mathcal{D}(n)|$. Soit $P \in \mathbb{Z}[X]$ un polynôme vérifiant les deux conditions.
On commence par montrer le résultat suivant :
Lemme : Soit $\mathrm{n} \geqslant 1$. Pour tout $k \in \mathbb{N}^{*}, \mathcal{D}\left(\mathrm{P}\left(\mathrm{n}^{\mathrm{k}}\right)\right)=\mathcal{D}(\mathrm{P}(\mathrm{n}))$.
|
{
"exam": "French_envois",
"problem_label": "18",
"problem_match": "\nExercice 18.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"solution_match": "\nSolution de l'exercice 18",
"tier": "T2",
"year": null
}
|
Determine all polynomials $\mathrm{P} \in \mathbb{Z}[\mathrm{X}]$ such that:
(i) $\mathrm{P}(\mathrm{n}) \geqslant 1$ for all $n \geqslant 1$
(ii) $\mathrm{P}(\mathrm{mn})$ and $\mathrm{P}(\mathrm{m}) \mathrm{P}(\mathrm{n})$ have the same number of prime divisors for all $\mathrm{m}, \mathrm{n} \geqslant 1$.
|
First, we show the result for small values of $k$.
By hypothesis, $\delta\left(\mathrm{P}\left(\mathrm{n}^{2}\right)\right)=\delta\left(\mathrm{P}(\mathrm{n})^{2}\right)=\delta(\mathrm{P}(\mathrm{n}))$. Similarly, $\delta\left(\mathrm{P}\left(\mathrm{n}^{4}\right)\right)=\delta\left(\mathrm{P}\left(\mathrm{n}^{2}\right)\right)=\delta(\mathrm{P}(\mathrm{n}))$. But $\delta\left(\mathrm{P}\left(\mathrm{n}^{4}\right)\right)=\delta\left(\mathrm{P}\left(\mathrm{n}^{3}\right) \mathrm{P}(\mathrm{n})\right)$. Since $\mathrm{P}\left(\mathrm{n}^{4}\right)$ has the same number of prime divisors as $\mathrm{P}(\mathrm{n})$, the last equality ensures that $\mathcal{D}\left(\mathrm{P}\left(\mathrm{n}^{3}\right)\right) \subset \mathcal{D}(\mathrm{P}(\mathrm{n}))$. Furthermore, $\delta\left(\mathrm{P}\left(\mathrm{n}^{3}\right)\right)=\delta\left(\mathrm{P}\left(\mathrm{n}^{2}\right) \mathrm{P}(\mathrm{n})\right) \geqslant \delta(\mathrm{P}(\mathrm{n}))$. Consequently, the previous inclusion is saturated by cardinality, and $\mathcal{D}\left(\mathrm{P}\left(\mathrm{n}^{3}\right)\right)=\mathcal{D}(\mathrm{P}(\mathrm{n}))$. Then $\delta(\mathrm{P}(\mathrm{n}))=\delta\left(\mathrm{P}\left(\mathrm{n}^{3}\right)\right)=\delta\left(\mathrm{P}\left(\mathrm{n}^{2}\right) \mathrm{P}(\mathrm{n})\right)$, so necessarily $\mathcal{D}\left(\mathrm{P}\left(\mathrm{n}^{2}\right)\right) \subset \mathcal{D}(\mathrm{P}(\mathrm{n}))$. By equality of cardinals, $\mathcal{D}(\mathrm{P}(\mathrm{n}))=\mathcal{D}\left(\mathrm{P}\left(\mathrm{n}^{2}\right)\right)=\mathcal{D}\left(\mathrm{P}\left(\mathrm{n}^{3}\right)\right)$.
Now let $k \geqslant 3$. We show the equality $\mathcal{D}\left(\mathrm{P}\left(\mathrm{n}^{\mathrm{k}}\right)\right)=\mathcal{D}(\mathrm{P}(\mathrm{n}))$ by induction. Suppose that $\mathcal{D}(\mathrm{P}(\mathrm{n}))=\mathcal{D}\left(\mathrm{P}\left(\mathrm{n}^{2}\right)\right)=\ldots=\mathcal{D}\left(\mathrm{P}\left(\mathrm{n}^{\mathrm{k}}\right)\right)$. Then $\delta\left(\mathrm{P}\left(\mathrm{n}^{\mathrm{k}+1}\right)\right)=\delta\left(\mathrm{P}\left(\mathrm{n}^{\mathrm{k}}\right) \mathrm{P}(\mathrm{n})\right)$, where by the induction hypothesis, $\mathrm{P}\left(\mathrm{n}^{\mathrm{k}}\right)$ and $\mathrm{P}(\mathrm{n})$ have exactly the same prime divisors, so $\delta\left(\mathrm{P}\left(\mathrm{n}^{\mathrm{k}}\right) \mathrm{P}(\mathrm{n})\right)=\delta(\mathrm{P}(\mathrm{n}))$, and $\delta\left(\mathrm{P}\left(\mathrm{n}^{\mathrm{k}+1}\right)\right)=\delta(\mathrm{P}(\mathrm{n}))$. Then on the one hand, $\delta\left(\mathrm{P}\left(\mathrm{n}^{\mathrm{k}+2}\right)\right)=\delta\left(\mathrm{P}\left(\mathrm{n}^{\mathrm{k}}\right) \mathrm{P}\left(\mathrm{n}^{2}\right)\right)=\delta\left(\mathrm{P}\left(\mathrm{n}^{2}\right)\right)$ since $\mathcal{D}\left(\mathrm{P}\left(\mathrm{n}^{\mathrm{k}}\right)\right)=\mathcal{D}(\mathrm{P}(\mathrm{n}))$ (since $\mathrm{k} \geqslant 3$), so $\delta\left(\mathrm{P}\left(\mathrm{n}^{\mathrm{k}+2}\right)\right)=\delta(\mathrm{P}(\mathrm{n}))$. But on the other hand, with the equality $\delta\left(\mathrm{P}\left(\mathrm{n}^{\mathrm{k}+2}\right)\right)=\delta\left(\mathrm{P}\left(\mathrm{n}^{\mathrm{k}+1}\right) \mathrm{P}(\mathrm{n})\right)$, we see that necessarily, $\mathcal{D}\left(\mathrm{P}\left(\mathrm{n}^{\mathrm{k}+1}\right)\right) \subset \mathcal{D}(\mathrm{P}(\mathrm{n}))$. By equality of cardinals, we have $\mathcal{D}\left(\mathrm{P}\left(\mathrm{n}^{\mathrm{k}+1}\right)\right)=\mathcal{D}(\mathrm{P}(\mathrm{n}))$, which completes the induction step.
We now use the equality $\mathcal{D}\left(\mathrm{P}\left(\mathrm{n}^{\mathrm{k}}\right)\right)=\mathcal{D}(\mathrm{P}(\mathrm{n}))$ to conclude the exercise. We write $\mathrm{P}=\mathrm{X}^{\mathrm{d}} \mathrm{Q}$, where $d \in \mathbb{N}$ and $Q \in \mathbb{Z}[X]$ satisfies $Q(0) \neq 0$. Clearly, $Q(n) \geqslant 1$ if $n \geqslant 1$. Fix a prime $p$ that does not divide $Q(0)$. For $k \geqslant 1, p \nmid Q\left(p^{k}\right)$, so $\mathcal{D}\left(Q\left(p^{k}\right)\right)=\mathcal{D}(Q(p))$ from the previous point. Indeed, if $d=0$ this corresponds to the equality proved earlier, and if $d \geqslant 1, \{p\} \cup \mathcal{D}\left(Q\left(p^{k}\right)\right)=\mathcal{D}\left(P\left(p^{k}\right)\right)=\mathcal{D}(P(p))=\{p\} \cup \mathcal{D}(Q(p))$ where $p \nmid Q\left(p^{k}\right)$ and $p \nmid Q(p)$.
Suppose by contradiction that $Q$ is non-constant. $Q$ therefore tends to $+\infty$ at infinity. Then $\delta(Q(p)) \geqslant 1$ because otherwise $Q\left(p^{k}\right)$ would be equal to 1 for all $k \geqslant 1$, so $Q(X)-1$ would have an infinite number of roots and would therefore be constant. Let $\mathcal{D}(Q(p))=\left\{q_{1}, \ldots, q_{s}\right\}$ where $s \geqslant 1$ and $q_{1}<\ldots<q_{s}$ are prime numbers. Let $\alpha=\max _{r \text { prime }} \nu_{r}(Q(1)) \geqslant 0$. There exists $k_{0} \geqslant 1$ such that for all $k \geqslant k_{0}$, there exists $i(k) \in \llbracket 1, s \rrbracket$ with $v_{q_{i(k)}}\left(Q\left(p^{k}\right)\right) \geqslant \alpha+1$. Indeed, since $Q$ tends to $+\infty$ at $\infty$, for $k$ large enough, $Q\left(p^{k}\right)$ is strictly greater than $\left.\left(q_{1} \ldots q_{s}\right)^{\alpha}\right)$. Let $\beta=\varphi\left(\left(q_{1} \ldots q_{s}\right)^{\alpha+1}\right) \geqslant 1$, and $N \geqslant 1$ such that $N \beta \geqslant k_{0}$. Then $q_{i(N \beta)}^{\alpha+1} \mid Q\left(p^{N \beta}\right)$, but $p^{N \beta} \equiv 1\left(\bmod \left(q_{1} \ldots q_{s}\right)^{\alpha+1}\right)$ since $p \notin\left\{q_{1}, \ldots, q_{s}\right\}$. In particular, $Q\left(p^{N \beta}\right) \equiv Q(1)\left(\bmod q_{i(N \beta)}^{\alpha+1}\right)$, and thus $q_{i(N \beta)}^{\alpha+1} \mid Q(1)$. This contradicts the maximality of $\alpha$. Therefore, $Q$ is constant and equal to $a \in \mathbb{N}^{*}$, and $P=a X^{d}$ with $d \in \mathbb{N}$.
We verify conversely that polynomials of the form $a X^{d}$ with $d \in \mathbb{N}$ and $a \in \mathbb{N}^{*}$ are solutions.
Comment from the graders: Only five students attempted this problem. It was very pleasant to read the different (excellent) ideas of the students, whether they led to a complete solution or not. Almost all students invoked a result (attributed to Schür) that the set of prime numbers dividing one of the $\mathrm{P}(\mathrm{n})$ is infinite if P is non-constant with integer coefficients. This result, quite powerful and whose proof would constitute an exercise in itself, was of great help here.
|
P=a X^{d}
|
Yes
|
Incomplete
|
proof
|
Number Theory
|
Déterminer tous les polynômes $\mathrm{P} \in \mathbb{Z}[\mathrm{X}]$ tels que :
(i) $\mathrm{P}(\mathrm{n}) \geqslant 1$ pour tout $n \geqslant 1$
(ii) $\mathrm{P}(\mathrm{mn})$ et $\mathrm{P}(\mathrm{m}) \mathrm{P}(\mathrm{n})$ ont le même nombre de diviseurs premiers pour tous $\mathrm{m}, \mathrm{n} \geqslant 1$.
|
On montre d'abord le résultat pour des petites valeurs de k .
Tout d'abord, par hypothèse, $\delta\left(\mathrm{P}\left(\mathrm{n}^{2}\right)\right)=\delta\left(\mathrm{P}(\mathrm{n})^{2}\right)=\delta(\mathrm{P}(\mathrm{n}))$. De même, $\delta\left(\mathrm{P}\left(\mathrm{n}^{4}\right)\right)=\delta\left(\mathrm{P}\left(\mathrm{n}^{2}\right)\right)=$ $\delta(P(n))$. Mais $\delta\left(P\left(n^{4}\right)\right)=\delta\left(P\left(n^{3}\right) P(n)\right)$. $P\left(n^{4}\right)$ ayant le même nombre de diviseurs premiers que $P(n)$, cette dernière égalité assure que $\mathcal{D}\left(P\left(n^{3}\right)\right) \subset \mathcal{D}(P(n))$. Par ailleurs $\delta\left(P\left(n^{3}\right)\right)=\delta\left(P\left(n^{2}\right) P(n)\right) \geqslant$ $\delta(P(n))$. Par conséquent, l'inclusion précédente est saturée par cardinalité, et $\mathcal{D}\left(P\left(n^{3}\right)\right)=\mathcal{D}(P(n))$. Alors $\delta(P(n))=\delta\left(P\left(n^{3}\right)\right)=\delta\left(P\left(n^{2}\right) P(n)\right)$, donc nécessairement $\mathcal{D}\left(P\left(n^{2}\right)\right) \subset \mathcal{D}(P(n))$. Par égalité des cardinaux, $\mathcal{D}(\mathrm{P}(\mathrm{n}))=\mathcal{D}\left(\mathrm{P}\left(\mathrm{n}^{2}\right)\right)=\mathcal{D}\left(\mathrm{P}\left(\mathrm{n}^{3}\right)\right)$.
Soit maintenant $k \geqslant 3$. On montre l'égalité $\mathcal{D}\left(\mathrm{P}\left(\mathrm{n}^{\mathrm{k}}\right)\right)=\mathcal{D}(\mathrm{P}(\mathrm{n}))$ par récurrence. Supposons que $\mathcal{D}(P(n))=\mathcal{D}\left(P\left(n^{2}\right)\right)=\ldots=\mathcal{D}\left(P\left(n^{k}\right)\right)$. Alors $\delta\left(P\left(n^{k+1}\right)\right)=\delta\left(P\left(n^{k}\right) P(n)\right)$, où par hypothèse de récurrence, $P\left(n^{k}\right)$ et $P(n)$ ont exactement les mêmes diviseurs premiers, donc $\delta\left(P\left(n^{k}\right) P(n)\right)=\delta(P(n))$, et $\delta\left(P\left(n^{k+1}\right)\right)=\delta(P(n))$. Alors d'une part, $\delta\left(P\left(n^{k+2}\right)\right)=\delta\left(P\left(n^{k}\right) P\left(n^{2}\right)\right)=\delta\left(P\left(n^{2}\right)\right)$ puisque $\mathcal{D}\left(\mathrm{P}\left(\mathrm{n}^{\mathrm{k}}\right)\right)=\mathcal{D}(\mathrm{P}(\mathrm{n}))$ (vu que $\mathrm{k} \geqslant 3$ ) d'où $\delta\left(P\left(\mathrm{n}^{\mathrm{k}+2}\right)\right)=\delta(\mathrm{P}(\mathrm{n}))$. Mais d'autre part, avec l'égalité $\delta\left(P\left(n^{k+2}\right)\right)=\delta\left(P\left(n^{k+1}\right) P(n)\right)$, on voit que nécessairement, $\mathcal{D}\left(P\left(n^{k+1}\right)\right) \subset \mathcal{D}(P(n))$. Par égalité des cardinaux, on a bien $\mathcal{D}\left(\mathrm{P}\left(\mathrm{n}^{\mathrm{k+1}}\right)\right)=\mathcal{D}(\mathrm{P}(\mathrm{n}))$, ce qui achève l'hérédité.
On utilise désormais l'égalité $\mathcal{D}\left(\mathrm{P}\left(\mathrm{n}^{\mathrm{k}}\right)\right)=\mathcal{D}(\mathrm{P}(\mathrm{n}))$ pour conclure l'exercice. On écrit $\mathrm{P}=\mathrm{X}^{\mathrm{d}} \mathrm{Q}$, où $d \in \mathbb{N}$ et $Q \in \mathbb{Z}[X]$ vérifie $Q(0) \neq 0$. Clairement $Q(n) \geqslant 1$ si $n \geqslant 1$. Fixons $p$ premier ne divisant pas $Q(0)$. Pour $k \geqslant 1, p \nmid Q\left(p^{k}\right)$ donc $\mathcal{D}\left(Q\left(p^{k}\right)\right)=\mathcal{D}(Q(p)) d$ 'après le point précédent. En effet, si $d=0$ cela correspond à l'égalité démontrée plus haut, et si $d \geqslant 1,\{p\} \cup \mathcal{D}\left(Q\left(p^{k}\right)\right)=\mathcal{D}\left(P\left(p^{k}\right)\right)=\mathcal{D}(P(p))=$ $\{p\} \cup \mathcal{D}(Q(p))$ où $p \nmid Q\left(p^{k}\right)$ et $p \nmid Q(p)$.
Supposons par l'absurde que $Q$ est non constant. $Q$ tend donc vers $+\infty$ à l'infini. Alors $\delta(Q(p)) \geqslant 1$ car dans le cas contraire $Q\left(p^{k}\right)$ serait égal à 1 pour tout $k \geqslant 1$, donc $Q(X)-1$ admettrait une infinité de racines et serait donc constant. Notons $\mathcal{D}(Q(p))=\left\{q_{1}, \ldots, q_{s}\right\}$ où $s \geqslant 1$ et $q_{1}<\ldots<q_{s}$ des nombres premiers. Soit $\alpha=\max _{r \text { premier }} \nu_{r}(Q(1)) \geqslant 0$. Il existe $k_{0} \geqslant 1$ tel que pour tout $k \geqslant k_{0}$, il existe $i(k) \in \llbracket 1, s \rrbracket$ avec $v_{q_{i(k)}}\left(Q\left(p^{k}\right)\right) \geqslant \alpha+1$ En effet, comme $Q$ tend vers $+\infty$ en $\infty$, pour $k$ assez grand, $Q\left(p^{k}\right)$ est strictement supérieur à $\left.\left(q_{1} \ldots q_{s}\right)^{\alpha}\right)$. Soit $\beta=\varphi\left(\left(q_{1} \ldots q_{s}\right)^{\alpha+1}\right) \geqslant 1$, et $N \geqslant 1$ tel que $N \beta \geqslant k_{0}$. Alors $q_{i(N \beta)}^{\alpha+1} \mid Q\left(p^{N \beta}\right)$, mais $p^{N \beta} \equiv 1\left(\bmod \left(q_{1} \ldots q_{s}\right)^{\alpha+1}\right)$ puisque $p \notin\left\{q_{1}, \ldots, q_{s}\right\}$. En particulier, $Q\left(p^{N \beta}\right) \equiv Q(1)\left(\bmod q_{i(N \beta)}^{\alpha+1}\right)$, et donc $q_{i(N \beta)}^{\alpha+1} \mid Q(1)$. Cela est en contradiction avec la maximalité de $\alpha$. Ainsi, $Q$ est constant égal à $a \in \mathbb{N}^{*}$, et $P=a X^{d}$ avec $d \in \mathbb{N}$.
On vérifie réciproquement que les polynômes de la forme $a X^{d}$ avec $d \in \mathbb{N}$ et $a \in \mathbb{N}^{*}$ sont solutions.
Commentaire des correcteurs: Seuls cinq élèves ont rendu une tentative sur cet exercice. Il était très agréable de lire les différentes (excellentes) idées des élèves, qu'elles aient mené à une solution complète ou pas. Les élèves ont pratiquement tous invoqué un résultat (attribué à Schür) sur le fait que l'ensemble des nombres premiers divisant l'un des $\mathrm{P}(\mathrm{n})$ est infini si P est non constant à coefficients entiers. Ce résultat, assez puissant et dont la preuve constituerait un exercice en soi, était d'une grande aide ici.
|
{
"exam": "French_envois",
"problem_label": "18",
"problem_match": "\nExercice 18.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-3.jsonl",
"solution_match": "\nDémonstration:",
"tier": "T2",
"year": null
}
|
Six baskets of fruit contain pears, peaches, and apples. The number of peaches in each basket is equal to the total number of apples in the other baskets. The number of apples in each basket is equal to the total number of pears in the other baskets. Show that the total number of fruits is a multiple of 31.
|
Let $p_{1}, p_{2}, \ldots, p_{6}$ be the number of pears in each basket, and $q_{1}, q_{2}, \ldots, q_{6}$ be the number of apples in each basket. Let $P$ also denote the total number of pears. We have:
$$
\begin{aligned}
& \mathrm{q}_{1}=\mathrm{p}_{2}+\mathrm{p}_{3}+\mathrm{p}_{4}+\mathrm{p}_{5}+\mathrm{p}_{6}=\mathrm{P}-\mathrm{p}_{1} \\
& \mathrm{q}_{2}=\mathrm{p}_{1}+\mathrm{p}_{3}+\mathrm{p}_{4}+\mathrm{p}_{5}+\mathrm{p}_{6}=\mathrm{P}-\mathrm{p}_{2} \\
& \\
& \mathrm{q}_{6}=\mathrm{p}_{1}+\mathrm{p}_{2}+\mathrm{p}_{3}+\mathrm{p}_{4}+\mathrm{p}_{5}=\mathrm{P}-\mathrm{p}_{3}
\end{aligned}
$$
Therefore: $q_{1}+q_{2}+\cdots+q_{6}=\left(P-p_{1}\right)+\left(P-p_{2}\right)+\cdots+\left(P-p_{6}\right)=6 P-\left(p_{1}+p_{2}+\cdots+p_{6}\right)=5 P$ The total number of apples is equal to 5 times the total number of pears. Similarly, the total number of peaches is equal to 5 times the total number of apples, hence 25 times the total number of pears. The total number of fruits is therefore equal to $31=25+5+1$ times the total number of pears, and is thus a multiple of 31.
Examiner's comment: Very well done exercise.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Six paniers à fruits contiennent des poires, des pêches et des pommes. Le nombre de pêches dans chaque panier est égal au nombre total de pommes dans les autres paniers. Le nombre de pommes dans chaque panier est égal au nombre total de poires dans les autres paniers. Montrez que le nombre total de fruits est un multiple de 31.
|
Notons $p_{1}, p_{2}, \ldots, p_{6}$ le nombre de poires dans chaque panier, et $q_{1}, q_{2}, \ldots, q_{6}$ le nombre de pommes dans chaque panier. Notons également $P$ le nombre total de poires. On a:
$$
\begin{aligned}
& \mathrm{q}_{1}=\mathrm{p}_{2}+\mathrm{p}_{3}+\mathrm{p}_{4}+\mathrm{p}_{5}+\mathrm{p}_{6}=\mathrm{P}-\mathrm{p}_{1} \\
& \mathrm{q}_{2}=\mathrm{p}_{1}+\mathrm{p}_{3}+\mathrm{p}_{4}+\mathrm{p}_{5}+\mathrm{p}_{6}=\mathrm{P}-\mathrm{p}_{2} \\
& \\
& \mathrm{q}_{6}=\mathrm{p}_{1}+\mathrm{p}_{2}+\mathrm{p}_{3}+\mathrm{p}_{4}+\mathrm{p}_{5}=\mathrm{P}-\mathrm{p}_{3}
\end{aligned}
$$
D'où: $q_{1}+q_{2}+\cdots+q_{6}=\left(P-p_{1}\right)+\left(P-p_{2}\right)+\cdots+\left(P-p_{6}\right)=6 P-\left(p_{1}+p_{2}+\cdots+p_{6}\right)=5 P$ Le nombre total de pommes est égal à 5 fois le nombre total de poires. De même, le nombre total de pêches est égal à 5 fois le nombre total de pommes, donc à 25 fois le nombre total de poires. Le nombre total de fruits est donc égal à $31=25+5+1$ fois le nombre total de poires, et est donc multiple de 31.
Commentaire des correcteurs : Exercice très bien réussi.
|
{
"exam": "French_envois",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T2",
"year": null
}
|
A East-West maritime line sees 10 ships departing every morning at distinct times, 5 ships depart from the West side and 5 from the East side. We assume that they all sail at the same speed and that as soon as two ships meet, they turn around and head back in the direction they came from, always at the same speed. What is the possible number of encounters between ships?
|
The number of crossings does not change if we say that the boats continue straight ahead instead of turning around when they meet. Each boat that leaves from one side crosses all the other boats that leave from the other side. Therefore, there are $5 \times 5=25$ encounters.
Comment from the graders: The poorly worded statement of this exercise clearly confused the students, perhaps because it was not precise enough. Indeed, it was considered that all the boats were already in the water and had set off before the first encounter. It was then necessary to determine how many encounters there could be between the boats (not just the maximum number, but all possible numbers of encounters).
While many students gave the correct number (there are always 25), very few seemed to understand (or at least explain) that it did not actually depend on the gaps between the boats. Some students recognized that the changes in direction of the boats followed certain "phases" (the first two boats meet, head off in opposite directions, "transmit" this to the outermost boats, which head off in the opposite direction and "retransmit" the correct direction to the central boats, one by one) and tried to use this to arrive at 25. But none justified the existence of these phases, nor why they could be treated separately, even though they do not really occur successively! To convince oneself of this, one can consider the case where the three boats coming from the west and the five boats coming from the east are very close to each other, but the last two boats coming from the west are much farther away. Other approaches were attempted, with generally insufficient justifications. It is recalled that assertions, in an olympic exercise, are insufficient: they must be demonstrated. If one does not know how to demonstrate them, it is an even surer sign that a proof is necessary. A better approach (which a few rare papers found, in various forms) was to note, as in the solution, that from the point of view of the number of encounters, the statement produces the same results as if the two boats continued on their way after a crossing. In this case, a crossing must involve two boats heading in opposite directions, each boat coming from the west must cross each boat coming from the east, hence $5 \cdot 5=25$ crossings.
|
25
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Une ligne maritime Est-Ouest voit partir chaque matin 10 bateaux à des moments tous distincts, 5 bateaux partent du côté Ouest et 5 du côté Est. On suppose qu'ils naviguent tous à la même vitesse et que dès que deux bateaux se rencontrent ils se retournent et repartent chacun de leur côté, toujours à la même vitesse. Quel est le nombre possible de rencontres entre bateaux?
|
Le nombre de croisements ne change pas si on dit que les bateaux continuent tout droit au lieu de faire demi-tour lors d'une rencontre. Chaque bateau qui part d'un côté croise tous les autres bateaux qui partent de l'autre côté. Il y a donc $5 \times 5=25$ rencontres.
Commentaire des correcteurs: L'énoncé de cet exercice mal réussi a manifestement troublé les élèves, peut-être parce qu'il n'était pas assez précis. On considérait en effet que tous les bateaux étaient déjà à l'eau et partis avant la première rencontre. Il fallait alors déterminer combien il pouvait y avoir de rencontres entre bateaux (pas simplement le nombre maximal, mais bien tous les nombres de rencontres possibles).
Si beaucoup d'élèves ont donné le nombre correct (il y en a toujours 25), très peu semblent avoir compris (ou du moins expliqué) que cela ne dépendait effectivement pas des écarts entre les bateaux. Un certain nombre d'élèves ont reconnu que les changements de sens des bateaux suivaient des sortes de "phases", (les deux premiers bateaux se rencontrent, repartent dans des directions opposés, "transmettent" cela vers les bateaux extrêmes, qui repartent en sens opposé et "retransmettent" de proche en proche vers les bateaux centraux la bonne direction) et ont tenté de s'en servir pour aboutir au 25. Mais aucun n'a justifié l'existence de ces phases, ni pourquoi on pouvait les traiter séparément, alors que celles-ci ne se déroulent pas vraiment successivement! Pour s'en convaincre, on pourra considérer le cas où les trois bateaux venant de l'ouest et les cinq bateaux venant de l'est sont très proches les uns des autres, mais les deux derniers bateaux venant de l'ouest sont bien plus lointains. D'autres approches ont été tentées, avec des justifications en général insuffisantes. On rappelle que les affirmations, dans un exercice olympique, sont insuffisantes : celles-ci doivent être démontrées. Si l'on ne sait pas les démontrer, c'est un signe d'autant plus sûr qu'une preuve est nécessaire. Une meilleure approche (que quelques rares copies ont trouvée, sous diverses formes) consistait à remarquer, comme dans le corrigé, que du point de vue du nombre de rencontres, l'énoncé produit les mêmes résultats que si les deux bateaux poursuivaient leur chemin après un croisement. Dans ce cas, un croisement doit impliquer deux bateaux de directions opposées, chaque bateau venant de l'ouest doit croiser chaque bateau venant de l'est, d'où $5 \cdot 5=25$ croisements.
|
{
"exam": "French_envois",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T2",
"year": null
}
|
Let $n \geqslant 6$. Prove that every square can be cut into exactly n squares (not necessarily of the same size).
|
We can show this by induction. If we have a partition of the square into $n$ squares, we can obtain a partition into $\mathrm{n}+3$ squares by subdividing one of the squares into 4. Therefore, it is sufficient to show that we can partition a square into 6, 7, and 8 squares. For 6, we subdivide the square into a $3 \times 3$ grid and merge the 4 squares in the top-left. For 7, we subdivide the square into 4, then subdivide one of the resulting squares into 4. For 8, we subdivide the square into a $4 \times 4$ grid and merge the 9 squares in the top-left.
Comment from the graders: The exercise was very well done. Two methods appeared, either with induction, or a cut according to the parity, but they were well explained overall.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $n \geqslant 6$. Prouvez que chaque carré peut être découpé en exactement n carrés (pas nécessairement de même taille).
|
On peut le montrer par récurrence. Si on a un découpage du carré en $n$ carrés, on peut obtenir un découpage en $\mathrm{n}+3$ carrés en subdivisant l'un des carrés en 4 . Il suffit donc de montrer que l'on peut découper un carré en 6,7 et 8 carrés. Pour 6 , on subdivise le carré en une grille $3 \times 3$ et on fusionne les 4 carrés en haut-gauche. Pour 7 , on subdivise le carré en 4 , puis on subdivise l'un des carrés obtenus en 4 . Pour 8 , on subdivise le carré en une grille $4 \times 4$ et on fusionne les 9 carrés en haut-gauche.
Commentaire des correcteurs : Exercice très bien réussi. Deux méthodes sont apparues, soit avec une récurrence, soit une découpe selon la parité, mais elles étaient bien expliquées dans l'ensemble.
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T2",
"year": null
}
|
A certain number of diagonals divide a convex polygon into triangles. These segments can only intersect at a vertex of the polygon. On each vertex of the polygon, the number of triangles that touch this vertex is written. Is it possible to reconstruct the diagonals knowing only the numbers on the vertices?
|
It is always possible to reconstruct the diagonals using this procedure:
- Consider a "visible" vertex $v$ that touches only one triangle.
- Draw the diagonal connecting the two vertices $x$ and $y$ adjacent to $v$.
- "Hide" $v$ and subtract 1 from the number of triangles adjacent to $x, y$.
- Continue until only 3 vertices remain.
This uses the fact that in any triangulation of a convex polygon, there exists a vertex adjacent to only one triangle. To show this, consider the diagonal $d$ that "skips" the fewest vertices: if $v$ is a skipped vertex, it is not connected to any diagonal, otherwise it would be shorter than $d$ (since they cannot intersect). Therefore, it is adjacent to only one triangle.
Comment from the graders: Well done on the exercise. Be sure to justify the existence of the vertex with a 1, which is not absolutely obvious.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Un certain nombre de diagonales divisent un polygone convexe en triangles. Ces segments ne peuvent s'intersecter que sur un sommet du polygone. Sur chaque sommet du polygone on écrit le nombre de triangles qui touchent ce sommet. Est-il possible de reconstruire les diagonales en connaissant seulement les nombres sur les sommets?
|
Il est toujours possible de reconstruire les diagonales en utilisant ce procédé :
- On considère un sommet "visible" $v$ qui ne touche qu'un seul triangle.
- On trace la diagonale qui relie les deux sommets $x$ et $y$ adjacents à $v$.
- On "cache" $v$ et on retire 1 au nombre de triangles adjacents de $x, y$.
- On continue jusqu'à ce qu'il ne reste plus que 3 sommets.
On utilise pour cela le fait que dans toute triangulation d'un polygone convexe, il existe un sommet adjacent à un seul triangle. Pour le montrer, on considère la diagonale d qui "saute" le moins de sommets : si $v$ est un sommet sauté, il n'est relié à aucune diagonale sinon elle serait plus courte que d (car elles ne peuvent pas s'intersecter). Il est donc adjacent à un unique triangle.
Commentaire des correcteurs : Exercice bien réussi. Attention, il fallait bien justifier l'existence du sommet avec un 1 qui n'est pas absolument évidente.
|
{
"exam": "French_envois",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T2",
"year": null
}
|
Nimatha and Thanima are playing a game on an $8 \times 8$ chessboard. Taking turns, starting with Nimatha, each player chooses a cell that has not yet been chosen and colors it in their color (red for Nimatha, blue for Thanima). Show that Thanima can always ensure that Nimatha cannot color any $2 \times 2$ square entirely in red.
|
Consider the following coloring:
| 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 5 | 6 | 6 | 7 | 7 | 8 | 8 | 5 |
| 9 | 9 | 10 | 10 | 11 | 11 | 12 | 12 |
| 13 | 14 | 14 | 15 | 15 | 16 | 16 | 13 |
| 17 | 17 | 18 | 18 | 19 | 19 | 20 | 20 |
| 21 | 22 | 22 | 23 | 23 | 24 | 24 | 21 |
| 25 | 25 | 26 | 26 | 27 | 27 | 28 | 28 |
| 29 | 30 | 30 | 31 | 31 | 32 | 32 | 29 |
When Nimatha plays on a number \( X \), Thanima responds by playing on the second occurrence of the number \( X \). Each \( 2 \times 2 \) square contains two identical numbers: if one is colored red, the other is colored blue. Thus, it is impossible for Nimatha to create a \( 2 \times 2 \) square entirely red if Thanima follows this strategy.
Comment from the graders: The exercise is generally well done. However, all students who tried to propose a strategy without tiling did not succeed: indeed, it is often difficult to construct a strategy that works in all cases when there are 64 possible moves at the beginning.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Nimatha et Thanima jouent à un jeu sur un échiquier $8 \times 8$. Tour par tour en commençant par Nimatha, chaque joueur choisit une case qui n'a pas encore été choisie et la colorie dans sa couleur (rouge pour Nimatha, bleu pour Thanima). Montrez que Thanima peut toujours faire que Nimatha ne puisse colorier aucun carré $2 \times 2$ entièrement en rouge.
|
On considère le coloriage suivant :
| 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 5 | 6 | 6 | 7 | 7 | 8 | 8 | 5 |
| 9 | 9 | 10 | 10 | 11 | 11 | 12 | 12 |
| 13 | 14 | 14 | 15 | 15 | 16 | 16 | 13 |
| 17 | 17 | 18 | 18 | 19 | 19 | 20 | 20 |
| 21 | 22 | 22 | 23 | 23 | 24 | 24 | 21 |
| 25 | 25 | 26 | 26 | 27 | 27 | 28 | 28 |
| 29 | 30 | 30 | 31 | 31 | 32 | 32 | 29 |
Lorsque Nimatha joue sur un nombre $X$, Thanima réagit en jouant sur la seconde occurrence du nombre $X$. Tout carré $2 \times 2$ contient deux nombres identiques : si l'un est coloré en rouge, l'autre est coloré en bleu. Ainsi, il est impossible pour Nimatha de créer un carré $2 \times 2$ entièrement rouge si Thanima suit cette stratégie.
Commentaire des correcteurs: L'exercice est globalement bien réussi. Mais tous les élèves ayant voulu proposer une stratégie sans pavage n'ont pas réussi : en effet, souvent il est difficile de construire une stratégie marchant dasn tous les cas quand il y a 64 coups possibles au tout début.
|
{
"exam": "French_envois",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T2",
"year": null
}
|
At least $\mathrm{n}\left(\sqrt{\mathrm{n}}+\frac{1}{2}\right)$ squares of an $\mathrm{n} \times \mathrm{n}$ chessboard have been marked. Show that there exist four marked squares which form the corners of a rectangle.
|
We are trying to use the pigeonhole principle. If there are two cells marked at coordinates $(i, j)$ and $(i, k)$, we put a sock in the drawer labeled $(\mathfrak{j}, k)$. There are $\frac{n(n-1)}{2}$ possible drawers. If $S^{\prime}$ there are two socks in the same drawer $(\mathfrak{j}, k)$, it means there exist $i, i^{\prime}$ such that $(i, j),(i, k),\left(i^{\prime}, j\right),\left(i^{\prime}, k\right)$ are all marked, and we have found four marked cells that form the corners of a rectangle. It only remains to show that there are strictly more socks than drawers. We denote $d_{i}$ as the number of marked cells in the i-th column. We have:
$$
\sum_{i=1}^{n} d_{i} \geqslant n\left(\sqrt{n}+\frac{1}{2}\right)
$$
The number of socks is:
$$
\sum_{i=1}^{n} \frac{d_{i}^{2}-d_{i}}{2}
$$
Using Cauchy-Schwarz, we have:
$$
\begin{aligned}
\sum_{i=1}^{n} \frac{d_{i}^{2}-d_{i}}{2} & \geqslant \frac{1}{2}\left(\frac{\left(\sum_{i=1}^{n} d_{i}\right)^{2}}{n}-\sum_{i=1}^{n} d_{i}\right) \\
& \geqslant \frac{1}{2 n}\left(n\left(\sqrt{n}+\frac{1}{2}\right)\right)\left(n\left(\sqrt{n}+\frac{1}{2}\right)-n\right) \\
& =\frac{1}{2} n\left(\sqrt{n}+\frac{1}{2}\right)\left(\sqrt{n}-\frac{1}{2}\right) \\
& =\frac{1}{2} n\left(n-\frac{1}{4}\right)
\end{aligned}
$$
Which is indeed strictly greater than the number of drawers.
Grader's comment: Very few copies solved the problem. Here it was natural to try to look at pairs of points by column: this was the key idea of the problem, and it allowed writing inequalities as in the solution.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Au moins $\mathrm{n}\left(\sqrt{\mathrm{n}}+\frac{1}{2}\right)$ carrés d'un échiquier $\mathrm{n} \times \mathrm{n}$ ont été marqués. Montrer qu'il existe quatre cases marquées qui forment les coins d'un rectangle.
|
On essaye d'utiliser le principe des tiroirs. S'il y a deux cases marquées aux coordonnées $(i, j)$ et $(i, k)$, on met une chaussette dans le tiroir étiqueté $(\mathfrak{j}, k)$. Il y a $\frac{n(n-1)}{2}$ tiroirs possibles. $S^{\prime}$ il y a deux chaussettes dans le même tiroir $(\mathfrak{j}, k)$, c'est qu'il existe $i, i^{\prime}$ tels que $(i, j),(i, k),\left(i^{\prime}, j\right),\left(i^{\prime}, k\right)$ sont toutes marquées, et on a bien trouvé quatre cases marquées qui forment les coins d'un rectangle. Il ne reste plus qu'à montrer qu'il y a strictement plus de chaussettes de tiroirs. On note $d_{i}$ le nombre de cases marquées dans la i-ème colonne. On a :
$$
\sum_{i=1}^{n} d_{i} \geqslant n\left(\sqrt{n}+\frac{1}{2}\right)
$$
Le nombre de chaussettes vaut :
$$
\sum_{i=1}^{n} \frac{d_{i}^{2}-d_{i}}{2}
$$
En utilisant Cauchy-Schwarz, on a :
$$
\begin{aligned}
\sum_{i=1}^{n} \frac{d_{i}^{2}-d_{i}}{2} & \geqslant \frac{1}{2}\left(\frac{\left(\sum_{i=1}^{n} d_{i}\right)^{2}}{n}-\sum_{i=1}^{n} d_{i}\right) \\
& \geqslant \frac{1}{2 n}\left(n\left(\sqrt{n}+\frac{1}{2}\right)\right)\left(n\left(\sqrt{n}+\frac{1}{2}\right)-n\right) \\
& =\frac{1}{2} n\left(\sqrt{n}+\frac{1}{2}\right)\left(\sqrt{n}-\frac{1}{2}\right) \\
& =\frac{1}{2} n\left(n-\frac{1}{4}\right)
\end{aligned}
$$
Ce qui est effectivement strictement plus grand que le nombre de tiroirs.
Commentaire des correcteurs : Très peu de copies ont rendu l'exercice. Ici il était naturel d'essayer de regarder les paires de points par colonne : c'était l'idée clé du problème, et elle permettait ensuite d'écrire des inégalités comme dans le corrigé.
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T2",
"year": null
}
|
Let $n \geqslant 3$ be an integer. Each row of an $(n-2) \times n$ table contains the numbers from 1 to $n$ once each, and we assume that in each column all the numbers are different. Show that the table can be completed to an $n \times n$ table such that in each row and in each column there are all the numbers from 1 to $n$.
|
Let $a_{i}, b_{i}$ be the two numbers missing in column $i$. Each of the numbers from 1 to $n$ appears in two copies among the $a_{i}, b_{i}$. Construct a multigraph where the vertices are the numbers from 1 to $n$, and for each $i=1, \ldots, n$, we add an edge between $a_{i}$ and $b_{i}$. Each vertex in this graph has a degree of 2, so it consists of a set of disjoint cycles. We can therefore orient the edges of each cycle in an arbitrary direction. We then obtain a directed multigraph where each vertex has an in-degree of 1 and an out-degree of 1. If the edge in the i-th column points from $u$ to $v$, then we write $u$ at coordinates $(i, n-1)$ and $v$ at coordinates $(i, n)$. The property of the degrees ensures that each number appears exactly once in each row.
Graders' comments: Overall, it is good, and all students have the construction. However, few provide a complete justification for it.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soit $n \geqslant 3$ un entier. Chaque ligne d'un tableau $(n-2) \times n$ contient les nombres de 1 à $n$ en un exemplaire chacun, on suppose de plus que dans chaque colonne tous les nombres sont différents. Montrer que l'on peut compléter le tableau en un tableau $\mathrm{n} \times \mathrm{n}$ de telle sorte que dans chaque ligne et dans chaque colonne il y ait tous les nombres de 1 à $n$.
|
Notons $a_{i}, b_{i}$ les deux nombres qu'il manque dans la colonne $i$. Chacun des nombres de 1 à $n$ apparaît en deux exemplaires parmi les $a_{i}, b_{i}$. Construisons un multigraphe dont les sommets sont les nombres de 1 à $n$, et pour chaque $i=1, \ldots, n$, on ajoute une arête entre $a_{i}$ et $b_{i}$. Chaque sommet de ce graphe est de degré 2 , il s'agit donc d'un ensemble de cycles disjoints. On peut donc orienter les arêtes de chaque cycle dans un sens arbitraire. On obtient alors un multigraphe orienté dont chaque sommet à un degré entrant de 1 et un degré sortant de 1 . Imaginons que l'arête de la i-ème colonne pointe de $u$ vers $v$, alors on écrit $u$ aux coordonnées $(i, n-1)$ et $v$ aux coordonnées ( $i, n$ ). La propriété des degrés donne que chaque nombre apparaît exactement une fois sur chaque ligne.
Commentaire des correcteurs : Bien dans l'ensemble, tous les élèves ont la construction. Néanmoins, peu proposent une justification complète de celle-ci.
|
{
"exam": "French_envois",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 7",
"tier": "T2",
"year": null
}
|
In a tournament organized between 6 teams, each team plays against each other team exactly once. When a team wins, it gets 3 points, and the losing team receives 0 points. If the game is a draw, both teams receive 1 point. Determine the values of \( a \) for which it is possible that the final scores of the teams can be the six consecutive numbers \( a, a+1, \ldots, a+5 \)?
|
In each match, between two and three points are awarded in total. Given that there are 15 matches in total, there must have been between 30 and 45 points distributed among the teams. Therefore, we must have:
$$
\begin{aligned}
& 30 \leqslant a+(a+1)+(a+2)+\cdots+(a+5) \leqslant 45 \\
& 30 \leqslant 6 a+15 \leqslant 45
\end{aligned}
$$
This means that $a$ can only be 3, 4, or 5.
If $a=5$, no match could have ended in a draw, so all scores are multiples of 3. It is therefore not possible to have 6 consecutive numbers for the scores, and this case is not possible.
If $a=3$, the scores are $3,4,5,6,7,8$. The teams with 6 and 7 points have each won at least one match, and the team with 8 points has won at least 2 matches, so at least 4 matches did not end in a draw. Thus, the total number of points distributed among the teams is at least 34, but $3+4+5+6+7+8=33$, so this case is not possible.
The case $a=4$ is possible. The scores are $4,5,6,7,8,9$. Here is a table that works:
| X | 3 | 1 | 0 | 0 | 0 |
| :---: | :---: | :---: | :---: | :---: | :---: |
| 0 | X | 1 | 0 | 3 | 1 |
| 1 | 1 | X | 3 | 0 | 1 |
| 3 | 3 | 0 | X | 1 | 0 |
| 3 | 0 | 3 | 1 | X | 1 |
| 3 | 1 | 1 | 3 | 1 | X |
The number written in the j-th column of the i-th row is the score obtained by team i in its match against team $j$.
Comment from the graders: The exercise was very well done by the students who attempted it.
|
4
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Dans un tournoi organisé entre 6 équipes, chaque équipe joue contre chaque autre équipe exactement une fois. Lorsqu'une équipe gagne, elle obtient 3 points, et l'équipe perdante reçoit 0 point. Si la partie est nulle, les deux équipes reçoivent un point. Déterminez les a pour lesquels il est possible que les scores finaux des équipes puissent être les six nombres consécutifs $a, a+1, \ldots, a+5$ ?
|
Lors de chaque match, entre deux et trois points sont attribués au total. Étant donné qu'il y a 15 matchs au total, il y a donc eu entre 30 et 45 points de répartis entre les équipes. On doit donc avoir:
$$
\begin{aligned}
& 30 \leqslant a+(a+1)+(a+2)+\cdots+(a+5) \leqslant 45 \\
& 30 \leqslant 6 a+15 \leqslant 45
\end{aligned}
$$
Ce qui signifie que a peut seulement être 3,4 ou 5 .
Si $a=5$, aucun match n'a pu être nul donc tous les scores sont des multiples de 3. Il n'est donc pas possible d'avoir 6 nombres consécutifs pour les scores, et ce cas n'est pas possible.
Si $a=3$, les scores sont $3,4,5,6,7,8$. Les équipes qui ont 6 et 7 points ont chacune gagné au moins un match, et l'équipe qui a 8 points a gagné au moins 2 matchs, donc au moins 4 matchs n'ont pas fini par une partie nulle. Ainsi, le nombre total de points répartis entre les équipe vaut au moins 34 , or $3+4+5+6+7+8=33$, ce cas n'est donc pas possible.
Le cas $a=4$ est possible. Les scores sont $4,5,6,7,8,9$. Voici un tableau qui fonctionne :
| X | 3 | 1 | 0 | 0 | 0 |
| :---: | :---: | :---: | :---: | :---: | :---: |
| 0 | X | 1 | 0 | 3 | 1 |
| 1 | 1 | X | 3 | 0 | 1 |
| 3 | 3 | 0 | X | 1 | 0 |
| 3 | 0 | 3 | 1 | X | 1 |
| 3 | 1 | 1 | 3 | 1 | X |
Le nombre écrit sur la j-ème colonne de la i-ème ligne est le score obtenu par l'équipe i lors de son match contre l'équipe $j$.
Commentaire des correcteurs: L'exercice est très bien réussi par les élèves l'ayant traité.
|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "\nExercice 8.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 8",
"tier": "T2",
"year": null
}
|
Several numbers are written in a line. Thanima has the right to choose two adjacent numbers such that the number on the left is strictly greater than the number on the right, she then swaps these two numbers and multiplies them by 2. Show that Thanima can only perform a finite number of such operations.
|
We start by placing a token on the minimum (if there is a tie, on the leftmost number). We move the token by the number on which it is placed. We will show that the token always moves to the left.
To do this, suppose by contradiction that at some point, the token moved to the right. Let \( x \) be the position of the token before the swap, \( i \) the initial position of the token, and \( j \) the initial position of the number with which the token is swapped. If \( i < j \), then since the token has never moved to the right before, the other number must have moved at least as many times as the token; it has therefore been doubled at least as many times. Since the token was placed on the minimum, the number on the token is smaller (or equal) to the number at position \( x+1 \). The move to the right was therefore not possible. If \( j < i \), then the token and the number initially at \( j \) have already been swapped once; immediately after this swap, the number with the token was smaller than the number initially at \( j \). The same argument as in the previous case applies: if the number initially at \( j \) is again immediately to the right of the token, it must have been doubled at least as many times; it has therefore remained larger and cannot be swapped again. Thus, the token always moves to the left.
Now, we prove the result by induction on the number \( n \) of numbers written on the line. Since the token always moves to the left, after a certain number of moves, it no longer moves. We then notice that the numbers to the left and right of the token form two separate instances of the initial problem, and we can perform only a finite number of operations on each instance by the induction hypothesis. Therefore, we can perform only a finite number of operations on the entire instance. The base case for \( n=0 \) is obvious.
Comment from the graders: Very few (4) solutions were submitted for this difficult exercise. Two of them only touch on the exercise, and the other two use a solution not included in the official solution, which consists of showing that two numbers can be swapped at most once. However, none manage to develop the arguments convincingly.
## Senior Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Plusieurs nombres sont écrits sur une ligne. Thanima a le droit de choisir deux nombres adjacents de telle sorte que le nombre de gauche soit strictement plus grand que le nombre de droite, elle échange alors ces deux nombres et les multiplie par 2. Montrer que Thanima ne peut effectuer qu'un nombre fini de telles opérations.
|
On commence par poser un jeton sur le minimum (si égalité, sur le nombre le plus à gauche). On bouge le jeton avec le nombre sur lequel il est posé. On va montrer que le jeton se déplace toujours vers la gauche.
Pour cela, supposons par l'absurde qu'à un moment, le jeton s'est déplacé vers la droite. Alors soit x la position du jeton avant l'échange, $i$ la position initiale du jeton, et $j$ la position initiale du nombre avec qui le jeton est échangé. $\mathrm{Si} i<j$, alors comme le jeton n'est jamais allé vers la droite avant, l'autre nombre a dû faire au moins autant de déplacements que le jeton; il a donc été multiplié par deux au moins autant de fois. Comme le jeton avait été posé sur le minimum, le nombre du jeton est plus petit (ou égal) au nombre à la position $x+1$. Le déplacement vers la droite n'était donc pas possible. $\mathrm{Si} j<i$, alors le jeton et le nombre qui était initialement sur $j$ ont déjà été échangés une fois; juste après cet échange, le nombre avec le jeton était plus petit que le nombre qui était initialement en j. Le même argument que le cas précédent s'applique : si le nombre initialement en $j$ est à nouveau juste à droite du jeton, il a du être doublé au moins autant de fois; il est donc resté plus grand et ne peut pas être échangé à nouveau. Ainsi, le jeton se déplace toujours vers la gauche.
Maintenant, on démontre le résultat par récurrence sur le nombre n de nombres écrits sur la ligne. Comme le jeton se déplace toujours vers la gauche, à partir d'un certain nombre de mouvements, il ne bouge plus. On remarque alors que les nombres à gauche et à droite du jeton forment deux instances séparées du problème initial, et on ne peut effectuer qu'un nombre fini d'opérations sur chaque instance par hypothèse de récurrence. On ne peut donc effectuer qu'un nombre fini d'opérations sur l'instance entière. L'initialisation en $n=0$ est évidente.
Commentaire des correcteurs: Très peu (4) de solutions rendues pour cet exercice difficile. Deux ne font qu'effleurer l'exercice, et les deux autres utilisent une solution ne figurant pas dans la correction, consistant à montrer que deux nombres ne peuvent être échangés qu'au plus une fois. Cependant, aucun ne parvient à développer les arguments de façon convaincante.
## Exercices Seniors
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 9",
"tier": "T2",
"year": null
}
|
Count the number of rearrangements $\boldsymbol{a}_{1}, \boldsymbol{a}_{2}, \ldots, \boldsymbol{a}_{2023}$ of the sequence $1,2, \ldots, 2023$ such that $\mathrm{a}_{\mathrm{k}}>\mathrm{k}$ for exactly one value of $k$.
|
To a valid rearrangement, one can associate a subset of 1, ..., 2023 of cardinality at least 2: the set of $k$ such that $a_{k} \neq k$.
It can be shown that to a subset of cardinality at least 2 of $1, \ldots, 2023$, one can associate a unique valid rearrangement that corresponds to it. If the set is $\mathrm{E}=\left\{e_{1}, \ldots, e_{n}\right\}$ with $e_{1}<e_{2}<\cdots<e_{n}$, the unique rearrangement that has $E$ as its associated set satisfies: $a_{e_{1}}=e_{n}, a_{e_{2}}=e_{1}, a_{e_{3}}=e_{2}, \ldots, a_{e_{n}}=e_{n-1}$ and for all $k \notin E, a_{k}=k$.
Thus, the number of valid rearrangements is equal to the number of subsets of $1, \ldots, 2023$ of cardinality at least 2. The answer is therefore:
$$
2^{2023}-2024
$$
Graders' comments: Most of the submitted solutions are correct. Only two reasoned as in the solution. The others either reasoned by induction by replacing 2023 with n, or proceeded by summation (two submissions presented the correct sum but did not know how to compute it: perhaps they do not know the sum of a geometric series)
|
2^{2023}-2024
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Comptez le nombre de réarrangements $\boldsymbol{a}_{1}, \boldsymbol{a}_{2}, \ldots, \boldsymbol{a}_{2023}$ de la séquence $1,2, \ldots, 2023$ telle que $\mathrm{a}_{\mathrm{k}}>\mathrm{k}$ pour exactement une valeur de $k$.
|
À un réarrangement valide, on peut lui associer un sous-ensemble de 1, ..., 2023 de cardinal au moins $2: l$ 'ensemble des $k$ tels que $a_{k} \neq k$.
On peut montrer qu'à un sous-ensemble de cardinal au moins 2 de $1, \ldots, 2023$, on peut associer un unique réarrangement valide qui lui correspond. Si l'ensemble est $\mathrm{E}=\left\{e_{1}, \ldots, e_{n}\right\}$ avec $e_{1}<e_{2}<\cdots<e_{n}$, l'unique réarrangement qui a pour ensemble associé $E$ vérifie : $a_{e_{1}}=e_{n}, a_{e_{2}}=e_{1}, a_{e_{3}}=e_{2}, \ldots, a_{e_{n}}=$ $e_{n-1}$ et pour tout $k \notin E, a_{k}=k$.
Ainsi, le nombre de réarrangements valides est égal au nombre de sous-ensembles de $1, \ldots, 2023$ de cardinal au moins 2 . La réponse est donc :
$$
2^{2023}-2024
$$
Commentaire des correcteurs: La plupart des copies rendues donnent une solution correcte. Seulement deux ont raisonné comme dans le corrigé. Les autres ont soit raisonné par récurrence en remplaçant 2023 par n, soit omt procédé par sommation (deux copies ont présenté la somme correcte mais n'ont pas su la calculer : peut-être qu'il ne connaissent pas la somme d'une suite géométrique)
|
{
"exam": "French_envois",
"problem_label": "10",
"problem_match": "\nExercice 10.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 10",
"tier": "T2",
"year": null
}
|
A terrible group of bandits is preparing to share a loot. Each bandit aims at two other bandits with their pistols. The bandits are called in a certain order. When a bandit is called, if they are still alive, they shoot at the bandits they were aiming at. After all the bandits have been called, there have been 28 victims. Show that no matter the order in which the bandits were called, there would have been at least 10 victims.
|
Suppose by contradiction that there exists an order causing 9 or fewer victims. There are then three categories of bandits:
- Those who died before firing
- Those who managed to fire and then died
- Those who are still alive at the end
The bandits of the first and second categories total at most 9, as there are at most 9 victims. The bandits of the second and third categories only aim at bandits of the first or second categories (if they fired, their targets are dead). They therefore aim at a subset of at most 9 bandits. Moreover, the bandits of the first category aim at no more than \(2 \times 9 = 18\) bandits: there are at most 9 bandits in this category, and each aims at no more than 2 bandits. There are finally at most \(18 + 9 = 27\) bandits targeted: there exists a bandit who is not targeted by anyone. This bandit survives regardless of the order of calls, which contradicts the statement.
Comment from the graders: The principle was generally understood, but it was difficult for several papers to rigorously justify the intuition. In particular, some consider optimal cases but without justifying that they are optimal (they may also not be achievable).
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Un terrible groupe de bandits se prépare à se partager un butin. Chaque bandit vise deux autres bandits avec ses pistolets. Les bandits sont appelés dans un certain ordre. Lorsqu'un bandit est appelé, s'il est encore en vie, il tire sur les bandits qu'il visait. Après que tous les bandits ont été appelés, il y a eu 28 victimes. Montrez que quelque soit l'ordre dans lequel on avait appelé les bandits, il y aurait eu au moins 10 victimes.
|
Supposons par l'absurde qu'il existe un ordre qui cause 9 victimes ou moins. Il y a alors trois catégories de bandits :
- Ceux qui sont morts avant de tirer
- Ceux qui ont pu tirer puis sont morts
- Ceux qui sont encore en vie à la fin
Les bandits de 1ère et 2ème catégorie sont au total au plus 9 , car il y a au plus 9 victimes. Les bandits de 2ème et 3ème catégorie ne visent que des bandits de lère ou 2ème catégorie (s'ils ont tiré, leurs cibles sont mortes). Ils visent donc un sous-ensemble d'au plus 9 bandits. De plus, les bandits de 1ère catégorie ne visent qu'au plus $2 \times 9=18$ bandits : il y a au plus 9 bandits de cette catégorie et chacun vise au plus 2 bandits. Il y a finalement au plus $18+9=27$ bandits visés : il existe un bandit qui n'est visé par personne. Ce bandit survit quelque soit l'ordre d'appel, ce qui contredit l'énoncé.
Commentaire des correcteurs: Le principe était généralement compris mais il a été difficile pour plusieurs copies de justifier rigoureusement l'intuition. En particulier, certains considèrent les cas optimaux mais sans justifier qu'ils sont optimaux (ils peuvent par ailleurs ne pas être atteignables).
|
{
"exam": "French_envois",
"problem_label": "11",
"problem_match": "\nExercice 11.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 11",
"tier": "T2",
"year": null
}
|
The numbers $0,1, \ldots, n$ are written on a board. At any time, Thanima can erase a number if it is the arithmetic mean of two numbers still present on the board. Thanima's goal is to erase as many numbers as possible, and she plays optimally. Depending on n, how many numbers are left on the board at the end?
|
If $n \leqslant 2$, the answer is $n$.
Otherwise, at the end of the process, there are always at least two numbers: we cannot erase 0 or n.
If $n=2^{k}$ is a power of 2, it is possible to have only two numbers left on the board at the end: we start by erasing all numbers congruent to 1 modulo 2, then all numbers congruent to 2 modulo $4, \ldots$, then all numbers congruent to $2^{i}$ modulo $2^{i+1}, \ldots$, and finally $2^{k-1}$. Then only 0 and $2^{k}$ remain.
If n is not a power of 2, we can always end up with 3 numbers: we write $\mathrm{n}=2^{\mathrm{k}}+\mathrm{a}$ with $0<\mathrm{a}<2^{\mathrm{k}}$. We erase in order $\boldsymbol{n}-1, \boldsymbol{n}-2, \ldots, 2^{\mathrm{k}}+1$, then we erase the numbers between 1 and $2^{\mathrm{k}}-1$ using the same technique used for $n=2^{k}$. In the end, only $0,2^{k}$, and $n$ remain.
Now let's show that when $\mathrm{n}>2$ is not a power of 2, we cannot end up with only 0 and n. Suppose, for the sake of contradiction, that there exists a sequence of deletions that allows us to end up with only 0 and $n$. Taking the sequence of deletions in reverse, we get a sequence of insertions where we start from 0 and $n$, and if $x$ and $y$ are present, we can add $\frac{x+y}{2}$ if it is an integer. By induction, we then prove that all numbers obtained are divisible by $p$, in particular, we cannot obtain 1, which is the desired contradiction.
Grader's comment: The exercise was generally very well done by those who tackled it; some imprecisions, notably solutions that do not specify the order in which to remove the integers between $2^{k}$ and n, although this order is important.
|
not found
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Les nombres $0,1, \ldots, n$ sont écrits sur un tableau. À tout moment, Thanima peut effacer un nombre s'il est la moyenne arithmétique de deux nombres encore présents sur le tableau. L'objectif de Thanima est d'effacer le plus de nombre possible, et elle joue de façon optimale. En fonction de n, combien de nombres reste t-il à la fin sur le tableau?
|
Si $n \leqslant 2$, la réponse est $n$.
Sinon, à la fin du procédé, il existe toujours au moins deux nombres : on ne peut effacer ni 0 ni n .
Si $n=2^{k}$ est une puissance de 2 , il est possible de n'avoir que deux nombres sur le tableau à la fin : on commence par effacer tous les nombres congrus à 1 modulo 2 , puis tous les nombres congrus à 2 modulo $4, \ldots$, puis tous les nombres congrus à $2^{i}$ modulo $2^{i+1}, \ldots$, puis $2^{k-1}$. Il ne reste alors plus que 0 et $2^{k}$.
Si n n'est pas une puissance de 2 , on peut toujours obtenir 3 nombres : on écrit $\mathrm{n}=2^{\mathrm{k}}+\mathrm{a}$ avec $0<\mathrm{a}<2^{\mathrm{k}}$. On efface dans l'ordre $\boldsymbol{n}-1, \boldsymbol{n}-2, \ldots, 2^{\mathrm{k}}+1$, puis on efface les nombres entre 1 et $2^{\mathrm{k}}-1$ en utilisant la même technique qui est utilisée pour $n=2^{k}$. À la fin, il reste $0,2^{k}$ et $n$.
Montrons maintenant que lorsque $\mathrm{n}>2$ n'est pas une puissance de 2 , on ne peut pas finir avec seulement 0 et n . Supposons par l'absurde qu'il existe une séquence de suppressions qui permet de ne finir qu'avec 0 et $n$. Soit $p$ un nombre premier impair qui divise $n$. En prenant la séquence des suppressions à l'envers, on obtient une séquence d'insertions où l'on part de 0 et $n$, et si $x$ et $y$ sont présents, on peut ajouter $\frac{x+y}{2}$ si c'est un nombre entier. Par récurrence, on démontre alors que tous les nombres obtenus sont divisibles par $p$, en particulier, on ne peut pas obtenir 1, ce qui est la contradiction recherchée.
Commentaire des correcteurs : Exercice globalement très réussi par ceux l'ayant traité ; quelques imprécisions, notamment des solutions qui ne précisent pas dans quel ordre enlever les entiers entre $2^{k}$ et n , alors que celui-ci est important.
|
{
"exam": "French_envois",
"problem_label": "12",
"problem_match": "\nExercice 12.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"solution_match": "## Solution de l'exercice 12",
"tier": "T2",
"year": null
}
|
A rectangle is divided into dominoes $1 \times 2$ and $2 \times 1$. In each domino, a diagonal is drawn. No two diagonals share an endpoint. Show that exactly two corners of the rectangle are endpoints of these diagonals.
|
Let's note that this pattern (as well as all its rotations and symmetries) is impossible:
Indeed, the only way to complete the bottom-left square is to add this domino:
Similarly, the only way to complete the bottom-right square is to add this domino:
We cannot continue indefinitely, as we eventually reach the edge of the rectangle.
This pattern is also impossible (as well as all its rotations and symmetries):
because the only way to complete the square in the corner is by adding this domino:
which results in the previously forbidden pattern. Through a detailed analysis, these two cases demonstrate that it is actually not possible for two dominos that share an edge to have their diagonals in different directions (ascending or descending). If we form the graph \( G \) where the vertices are the dominos and there is an edge between two dominos if they share a common edge, \( G \) is connected. Thus, all dominos have their diagonals in the same direction; from this, the required property easily follows.
Comment from the graders: The exercise was rarely addressed. Those who submitted a solution generally understood the problem well and treated all cases and saw the pattern in the solution. Some have a different argument by looking at a path between opposite diagonals, and others use a graph theory reasoning.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Un rectangle est divisé en dominos $1 \times 2$ et $2 \times 1$. Dans chaque domino, une diagonale est tracée. Deux diagonales n'ont jamais d'extrémité commune. Montrez que exactement deux coins du rectangle sont des extrémités de ces diagonales.
|
Remarquons que ce motif (ainsi que toutes ses rotations et symétries) est impossible :

En effet, le seul moyen de compléter le carré bas-gauche est d'ajouter ce domino :

De même, le seul moyen de compléter le carré bas-droite est d'ajouter ce domino :

On ne peut pas continuer pour toujours, car on finit par atteindre le bord du rectangle.
Ce motif aussi est impossible (ainsi que toutes ses rotations et symétries) :

car le seul moyen de compléter le carré dans le coin est en ajoutant ce domino :

ce qui fait apparaître le motif interdit précédent. Grâce à une analyse minutieuse, ces deux cas démontrent qu'il n'est en fait pas possible que deux dominos qui partagent un bord aient leurs diagonales dans des sens différents (montantes ou descendantes). Si on forme le graphe G dont les sommets sont les dominos et où il y a une arête entre deux dominos s'ils partagent un bord en commun, $G$ est connexe. Ainsi, tous les dominos ont leur diagonale dans le même sens; on en déduit facilement la propriété demandée.
Commentaire des correcteurs: L'exercice a été peu traité. Ceux qui ont rendu une copie ont en général bien compris l'exercice et bien traité tous les cas et vu le motif du corrigé. Certains ont une argumentation différente en regardant un chemin entre les diagonales opposées, et d'autres utilisent un raisonnement de théorie des graphes.
|
{
"exam": "French_envois",
"problem_label": "13",
"problem_match": "\nExercice 13.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 13",
"tier": "T2",
"year": null
}
|
Let $G$ be a graph with $n$ vertices. An edge $e$ of $G$ is a dead-end if it is possible to partition $G$ into two sets $A$ and $B$ such that:
- There are at most 2023 edges of $G$ having one endpoint in $A$ and one endpoint in $B$.
- The edge $e$ has one of its endpoints in $A$ and the other in $B$.
Show that there are at most 2023($\mathrm{n}-1$) dead-ends.
|
We prove this by strong induction on $n$. The case $\mathrm{n}=1$ is immediate. If there is no dead end in $G$, the property is trivial. Otherwise, let $e$ be a dead end of $G$. We obtain a partition of the vertices of $G$ into two sets $A$, $B$ such that there are at most 2023 edges between $A$ and $B$. By the induction hypothesis, there are at most $2023(|A|-1)$ dead ends when considering only the vertices of $A$ and the edges connecting these vertices. Similarly, there are at most $2023(|B|-1)$ dead ends when considering only the vertices of $B$ and the edges connecting them. We note that if an edge $e$ is not a dead end in the subgraph restricted to $A$ (the same for $B$), then it is not a dead end in $G$ either. Therefore, there are at most:
$$
2023 + 2023(|A|-1) + 2023(|B|-1) = 2023(|\mathrm{G}|-1)
$$
dead ends in $G$, which completes the induction step.
Grader's Comment: The exercise is generally well done. Several students forget to check and even mention that a dead end of a graph $G$ belonging to a subgraph $A$ of $G$ is a dead end for $A$, which is unfortunate because it is an important argument in the proof. Indeed, being a dead end in two different graphs is not a priori related.
|
2023(|\mathrm{G}|-1)
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soit $G$ un graphe à $n$ sommets. Une arête e de $G$ est un cul-de-sac s'il est possible de partitionner $G$ en deux ensembles $A$ et $B$ tels que :
- Il y a au plus 2023 arêtes de G ayant une extrémité dans A et une extrémité dans B.
- L'arête e a l'une de ses extrémités dans $A$ et l'autre dans B.
Montrez qu'il y a au plus 2023( $\mathrm{n}-1$ ) culs-de-sac.
|
On le démontre par récurrence forte sur n . Le cas $\mathrm{n}=1$ est immédiat. S'il n'existe aucun cul-de-sac dans G, la propriété est triviale. Sinon, soit e un cul-de-sac de G. On obtient une partition des sommets de $G$ en deux ensembles $A$, $B$ telle qu'il y a au plus 2023 arêtes entre $A$ et $B$. D'après l'hypothèse de récurrence, il y a au plus $2023(|A|-1)$ culs-de-sacs lorsque l'on ne considère que les sommets de $A$ et les arêtes qui relient ces sommets. De même, il y a au plus 2023(|B|-1) culs-de-sacs lorsque l'on ne considère que les sommets de $B$ et les arêtes qui les relient. On remarque que si une arête e n'est pas un cul-de-sac dans le graphe restreint à $A$ (de même pour $B$ ), alors elle n'est pas non plus un cul-de-sac dans G. Il y a donc au plus :
$$
2023+2023(|A|-1)+2023(|B|-1)=2023(|\mathrm{G}|-1)
$$
culs-de-sacs dans G, ce qui termine l'hérédité.
Commentaire des correcteurs : L'exercice est globalement bien réussi. Plusieurs élèves oublient de vérifier et même de mentionner qu'un cul-de-sac d'un graphe G appartenant à un sous-graphe $A$ de $G$ est un cul-de-sac pour $A$, c'est dommage car c'est un argument important de la preuve. En effet, être un cul-de-sac dans deux graphes différents n'est à priori pas lié.
|
{
"exam": "French_envois",
"problem_label": "14",
"problem_match": "\nExercice 14.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 14",
"tier": "T2",
"year": null
}
|
We place a certain number of open segments in the plane, none of which are parallel to the $x$ and $y$ axes. These segments are disjoint. Thanima starts moving from $(0,0)$ parallel to the $x$-axis. Each time she encounters a wall, she turns 90 degrees and continues moving without crossing the wall.
Prove that it is impossible for Thanima to visit both sides of all the walls.
|
We start by proving that there exists a wall that is lower than all the others (i.e., the set of points below this segment does not intersect any segment). Suppose, for the sake of contradiction, that this is not the case. We can then construct a cycle $A_{1}, B_{1}, A_{2}, B_{2}, \ldots, A_{k}, B_{k}$ that does not intersect itself, where $A_{i}$ and $B_{i}$ are on the same wall, and $\left[B_{i}, A_{i+1}\right]$ is a vertical segment where $B_{i}$ is above $A_{i+1}$ (considering the indices modulo $k$). We consider $l$, $r$ such that $\left[B_{l}, A_{l+1}\right]$ is the leftmost and $\left[B_{r}, A_{r+1}\right]$ is the rightmost. The cycle gives a broken line between $B_{l}$ and $A_{r+1}$, and another between $B_{r}$ and $A_{l+1}$. However, the broken lines do not pass to the left of $\left[B_{l}, A_{l+1}\right]$ or to the right of $\left[B_{r}, A_{r+1}\right]$, and their endpoints are "crossed," so they must intersect. This is a contradiction with the fact that the cycle does not intersect itself.
Similarly, there exists a wall higher than all the others. If Thanima passes by the upper side of the highest wall, she continues to walk to infinity in the positive y direction. If Thanima passes by the lower side of the lowest wall, she continues to walk to infinity in the negative y direction. These two cases cannot happen simultaneously, so she passes through only one of these two sides. In particular, she cannot pass through all sides of all walls.
Comment from the graders: The problem was rarely addressed. Most solutions were correct and close to the proposed solution; however, they presented a number of imprecisions, which must be particularly attentive to when it comes to something as visual as combinatorial geometry.
|
proof
|
Yes
|
Yes
|
proof
|
Logic and Puzzles
|
On place un certain nombre de segments ouverts dans le plan, aucun d'entre eux n'est parallèle aux axes $x$ et $y$. Ces segments sont disjoints. Thanima commence à se déplacer depuis $(0,0)$ parallèlement à l'axe $x$. À chaque fois qu'elle rencontre un mur, elle tourne de 90 degrés, et continue à se déplacer sans traverser le mur.
Démontrez qu'il est impossible que Thanima visite les deux côtés de tous les murs.
|
On commence par démontrer qu'il existe un mur qui est plus bas que tous les autres (c'est à dire que l'ensemble des points sous ce segment n'intersecte aucun segment). Supposons par l'absurde que ce $n$ 'est pas le cas. On peut alors construire un cycle $A_{1}, B_{1}, A_{2}, B_{2}, \ldots, A_{k}, B_{k}$ qui ne s'intersecte pas lui-même, où $A_{i}$ et $B_{i}$ sont sur le même mur, et $\left[B_{i}, A_{i+1}\right]$ est un segment vertical où $B_{i}$ est au dessus de $A_{i+1}$ (on considère les indices modulo $k$ ). On considère $l$, $r$ tel que $\left[B_{l}, A_{l+1}\right]$ soit le plus à gauche et $\left[B_{r}, A_{r+1}\right]$ soit le plus à droite. Le cycle donne une ligne brisée entre $B_{l}$ et $A_{r+1}$, et une autre entre $B_{r}$ et $A_{l+1}$. Cependant, les lignes brisées ne passent ni à gauche de $\left[B_{l}, A_{l+1}\right]$ ni à droite de $\left[B_{r}, A_{r+1}\right]$, et leurs extrémités sont "croisées", elles doivent donc s'intersecter. C'est une contradiction avec le fait que le cycle ne s'intersecte pas lui-même.
Similairement, il existe un mur plus haut que tous les autres. Si Thanima passe par le côté haut du mur le plus haut, elle continue à marcher vers l'infini en direction des y positifs. Si Thanima passe par le côté bas du mur le plus bas, elle continue à marcher vers l'infini en direction des y négatifs. Ces deux cas ne peuvent pas arriver simultanément, elle ne passe donc que par un seul de ces deux côtés. En particulier, elle ne peux pas passer par tous les côtés de tous les murs.
Commentaire des correcteurs: L'exercice a été peu traité. La plupart des solutions sont justes et proches de celle proposées dans le corrigé; néanmoins, elles présentaient un certain nombre d'imprécisions, auxquelles il faut être particulièrement attentif quand il s'agit de quelque chose d'aussi visuel que la géométrie combinatoire.
|
{
"exam": "French_envois",
"problem_label": "15",
"problem_match": "\nExercice 15.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 15",
"tier": "T2",
"year": null
}
|
Let $k \geqslant 1$ be an integer. What is the smallest integer $n$ such that, no matter how $n$ points are placed in the plane, it is possible to choose a subset $S$ consisting of $k$ of these points that satisfies "for every pair $P, Q$ of points in $S$, the distance between $P$ and $Q$ is less than or equal to 2" or "for every pair $P, Q$ of points in $S$, the distance between $P$ and $Q$ is strictly greater than 1."
|
Let's start by showing that $\mathrm{n}=(k-1)^{2}+1$ is possible. For this, consider the disk of radius 1 centered at a point $P_{1}$ of the set. If there are at least $k$ points in this disk, we can take for $S$ these $k$ points (the distances between them are less than or equal to 2). Therefore, we can assume that there are at most $(k-1)$ points in the disk.
Now consider a disk of radius 1 centered at a $P_{2}$ of the set that is not in the previous disk. By the same argument, we can assume that there are at most $(k-1)$ points in this disk.
Continuing to choose points outside the previous disks, and since we exclude at most $(k-1)$ points at each step, we can construct $S=\left\{P_{1}, \ldots, P_{k}\right\}$ such that the distances between these points are all strictly greater than 1.
To show that $\mathrm{n}=(\mathrm{k}-1)^{2}$ is not possible, we place at a very large distance from each other $k-1$ groups, where each group consists of $\mathrm{k}-1$ points at a very small distance from each other.
Comment from the graders: This exercise was very well done by those who tackled it, with very varied methods: some used the same technique as the solution, others resorted to graph theory, for example.
|
(k-1)^2 + 1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Soit $k \geqslant 1$ un entier. Quel est le plus petit entier $n$ tel que, quelque soit la manière de placer n points dans le plan, il est possible de choisir un sous-ensemble $S$ constitué de $k$ de ces points qui vérifie "pour toute paire $P, Q$ de points de $S$, la distance entre $P$ et $Q$ est inférieure ou égale à 2 " ou "pour toute paire $P, Q$ de points de $S$, la distance entre $P$ et $Q$ est strictement plus grande que 1."
|
Commençons par montrer que $\mathrm{n}=(k-1)^{2}+1$ est possible. Pour cela, considérons le disque de rayon 1 centré sur un point $P_{1}$ de l'ensemble. S'il y a au moins $k$ points dans ce disque, on peut prendre pour $S$ ces $k$ points (les distances entre eux sont inférieures ou égales à 2 ). On peut donc supposer qu'il y a au plus $(k-1)$ points dans le disque.
Considérons alors un disque de rayon 1 centré sur un $P_{2}$ de l'ensemble qui n'est pas dans le disque précédent. Par le même argument, on peut supposer qu'il y a au plus $(k-1)$ points dans ce disque.
En continuant à choisir des points en dehors des disques précédents, et comme on exclut au plus ( $k-1)$ points à chaque étape, on arrive à construire $S=\left\{P_{1}, \ldots, P_{k}\right\}$ de telle manière à ce que les distances entre ces points soient toutes strictement supérieures à 1 .
Pour montrer que $\mathrm{n}=(\mathrm{k}-1)^{2}$ n'est pas possible, on place à distance très grande les uns des autres $k-1$ groupes, ou chaque groupe est constitué de $\mathrm{k}-1$ points à distance très petite.
Commentaire des correcteurs : Exercice très bien réussi par ceux qui l'ont traité, avec des méthodes très variées : certains ont utilisé la même technique que la correction, d'autres ont recouru à la théorie des graphes par exemples.
|
{
"exam": "French_envois",
"problem_label": "16",
"problem_match": "\nExercice 16.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 16",
"tier": "T2",
"year": null
}
|
Let $k, n \geqslant 1$ be two fixed integers. Thanima had 2 n candies of each color. She gave two candies of different colors to each of the children in her family. Knowing that no matter how $k+1$ children are chosen, there are two among them who received a candy of the same color, find the maximum possible number of children.
|
We can model the problem with a graph: each vertex of this graph is a color. If Thanima gave a candy of color $\mathrm{c}_{1}$ and a candy of color $\mathrm{c}_{2}$ to a child in her family, we add an edge between $\mathrm{c}_{1}$ and $\mathrm{c}_{2}$.
Since Thanima has only 2 n candies of each color, the maximum degree of each vertex is 2 n. We also know that it is impossible to choose $k+1$ disjoint edges. We are looking for the maximum number of edges.
We see that it is possible to obtain 3 kn edges. For this, we create a graph in which we put $k$ times the following structure: we create three vertices, and between each pair of these three vertices, we add n edges. Let's show that it is not possible to do more than 3 kn. For this, we consider a set C of disjoint edges of maximum cardinality. According to the statement, we have $|\mathrm{C}| \leqslant \mathrm{k}$. Thus, each edge of the graph must intersect one of the edges of C, otherwise it would contradict the maximality of C. Let $\mathrm{V}_{\mathrm{C}}$ be the set of vertices that appear in one of the edges of C. The number of edges in the graph is:
$$
\sum_{v \in \mathrm{~V}_{\mathrm{C}}} \mathrm{~d}_{\text {ext }}(v)+\frac{\mathrm{d}_{\mathrm{int}}(v)}{2}
$$
where $\mathrm{d}_{\text {ext }}(v)$ is the number of edges that connect $v$ to vertices that are not in $V_{C}$, and $\mathrm{d}_{\text {int }}(v)$ is the number of edges that connect $v$ to vertices of $\mathrm{V}_{\mathrm{C}}$. Let $(\mathrm{a}, \mathrm{b})$ be an edge of C, and let $x, y$ be two different vertices that are not in $\mathrm{V}_{\mathrm{C}}$, we cannot have both edges between a and $x$ and between $b$ and $y$, otherwise replacing $(a, b)$ with $(a, x)$ and $(b, y)$ in $C$ would give a larger set of disjoint edges. Two cases can occur:
- Both $a$ and $b$ have edges to the complement of $\mathrm{V}_{\mathrm{C}}$, in this case, all these edges go to the same vertex, and the degree bound on this vertex gives $d_{\text {ext }}(a)+d_{\text {ext }}(b) \leqslant 2 n$.
- Or there is at most one vertex among $a$ and $b$ that has edges to the complement of $\mathrm{V}_{\mathrm{C}}$, in this case we also have $\mathrm{d}_{\text {ext }}(a)+\mathrm{d}_{\text {ext }}(b) \leqslant 2 \mathrm{n}$.
Since $\mathrm{d}_{\mathrm{int}}(v) \leqslant 2 \mathrm{n}-\mathrm{d}_{\text {ext }}(v)$ for all vertices $v$, we have:
$$
\begin{aligned}
\mathrm{d}_{e x t}(a)+d_{e x t}(b)+\frac{d_{i n t}(a)+d_{i n t}(b)}{2} & \leqslant d_{e x t}(a)+d_{e x t}(b)+\frac{4 n-d_{e x t}(a)+d_{e x t}(b)}{2} \\
& =2 n+\frac{d_{e x t}(a)+d_{e x t}(b)}{2} \\
& \leqslant 3 n
\end{aligned}
$$
Thus, by grouping the terms two by two, we obtain that the number of edges in the graph is:
$$
\sum_{v \in \mathrm{~V}_{\mathrm{C}}} \mathrm{~d}_{\text {ext }}(v)+\frac{\mathrm{d}_{\mathrm{int}}(v)}{2} \leqslant 3 \mathrm{kn}
$$
Comment from the graders: The exercise was very little addressed.
|
3kn
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Soit $k, n \geqslant 1$ deux entiers fixés. Thanima possédait 2 n bonbons de chaque couleur. Elle a donné deux bonbons de couleurs différentes à chacun des enfants de sa famille. Sachant que quelque soit la manière de choisir $k+1$ enfants, il y en a deux parmi eux qui ont reçu une couleur de bonbon en commun, trouvez le nombre maximum possible d'enfants.
|
On peut modéliser le problème par un graphe : chaque sommet de ce graphe est une couleur. Si Thanima a donné un bonbon d'une couleur $\mathrm{c}_{1}$ et un bonbon d'une couleur $\mathrm{c}_{2}$ à un enfant de sa famille, on ajoute une arête entre $\mathrm{c}_{1}$ et $\mathrm{c}_{2}$.
Comme Thanima n'a que 2 n bonbons de chaque couleur, le degré maximal de chaque sommet est 2 n . On sait de plus qu'il est impossible de choisir $k+1$ arêtes disjointes. On cherche le nombre maximal d'arêtes.
On voit qu'il est possible d'obtenir 3 kn arêtes. Pour cela, on crée un graphe dans lequel on met $k$ fois la structure suivante : on crée trois sommets, et entre chaque paire de ces trois sommets, on ajoute n arêtes. Montrons qu'il n'est pas possible de faire plus que 3 kn . Pour cela, on considère un ensemble C d'arêtes disjointes de plus grand cardinal. D'après l'énoncé, on a $|\mathrm{C}| \leqslant \mathrm{k}$. Ainsi, chaque arête du graphe doit intersecter l'une des arêtes de C , sinon cela contredirait la maximalité de C . Notons $\mathrm{V}_{\mathrm{C}}$ l'ensemble des sommets qui apparaissent dans l'une des arêtes de C. Le nombre d'arêtes du graphe vaut :
$$
\sum_{v \in \mathrm{~V}_{\mathrm{C}}} \mathrm{~d}_{\text {ext }}(v)+\frac{\mathrm{d}_{\mathrm{int}}(v)}{2}
$$
où $\mathrm{d}_{\text {ext }}(v)$ est le nombre d'arêtes qui relient $v$ à des sommets qui ne sont pas dans $V_{C}$, et $\mathrm{d}_{\text {int }}(v)$ est le nombre d'arêtes qui relient $v$ à des sommets de $\mathrm{V}_{\mathrm{C}}$. Soit $(\mathrm{a}, \mathrm{b}$ ) une arête de C , et soient $x, y$ deux sommets différents qui ne sont pas dans $\mathrm{V}_{\mathrm{C}}$, on ne peut pas à la fois avoir d'arêtes entre a et $x$ et entre $b$ et $y$, sinon remplacer $(a, b)$ par $(a, x)$ et $(b, y)$ dans $C$ donnerait un ensemble d'arêtes disjointes plus grand. Deux cas peuvent arriver :
- À la fois $a$ et $b$ ont des arêtes vers le complémentaire de $\mathrm{V}_{\mathrm{C}}$, dans ce cas, toutes ces arêtes vont vers le même sommet, et la borne de degré sur ce sommet donnent $d_{\text {ext }}(a)+d_{\text {ext }}(b) \leqslant 2 n$.
- Soit il y a au plus un sommet parmi $a$ et $b$ qui a des arêtes vers le complémentaire de $\mathrm{V}_{\mathrm{C}}$, dans ce cas on a aussi $\mathrm{d}_{\text {ext }}(a)+\mathrm{d}_{\text {ext }}(b) \leqslant 2 \mathrm{n}$.
Comme $\mathrm{d}_{\mathrm{int}}(v) \leqslant 2 \mathrm{n}-\mathrm{d}_{\text {ext }}(v)$ pour tout sommet $v$, on a :
$$
\begin{aligned}
\mathrm{d}_{e x t}(a)+d_{e x t}(b)+\frac{d_{i n t}(a)+d_{i n t}(b)}{2} & \leqslant d_{e x t}(a)+d_{e x t}(b)+\frac{4 n-d_{e x t}(a)+d_{e x t}(b)}{2} \\
& =2 n+\frac{d_{e x t}(a)+d_{e x t}(b)}{2} \\
& \leqslant 3 n
\end{aligned}
$$
Ainsi, en groupant les termes deux à deux, on obtient que le nombre d'arête dans le graphe est :
$$
\sum_{v \in \mathrm{~V}_{\mathrm{C}}} \mathrm{~d}_{\text {ext }}(v)+\frac{\mathrm{d}_{\mathrm{int}}(v)}{2} \leqslant 3 \mathrm{kn}
$$
Commentaire des correcteurs : L'exercice a été très peu abordé.
|
{
"exam": "French_envois",
"problem_label": "17",
"problem_match": "\nExercice 17.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 17",
"tier": "T2",
"year": null
}
|
Thanima owns a magnificent necklace made of rubies, emeralds, and sapphires, represented by a sequence of R, E, and S. With one magical operation, she can perform one of the following actions:
- Replace a pattern RR in the necklace with a pattern ES (or ES with RR).
- Replace a pattern EEE with a pattern SR (or SR with EEE).
- Remove a pattern SS, or add a pattern SS anywhere.
- Remove a pattern RES, or add a pattern RES anywhere.
It is not possible to cyclically shift the letters due to the clasp. She also cannot flip the necklace.
Is it possible to transform a necklace containing only one sapphire into a necklace containing only one emerald using magical operations?
|
Suppose Thanima has three objects numbered 1, 2, and 3 on three stands numbered 1, 2, and 3. At the beginning, each object is on the stand with the same number. Thanima can read the letters of the necklace one by one from left to right and perform the following operations:
- If she sees an E, she swaps the objects on stands 1 and 2.
- If she sees an S, she swaps the objects on stands 2 and 3.
- If she sees an R, she moves the object on stand 1 to stand 2, the object on stand 2 to stand 3, and the object on stand 3 to stand 1.
We notice that:
- When adding the pattern SS somewhere, the objects on stands 2 and 3 are swapped twice in a row, which does not change their final positions.
- When adding the pattern RES somewhere, the object that was on stand 1 at that moment is moved to stand 2 by R, then to stand 1 by E. The object that was on stand 2 is moved to stand 3 by R, then to stand 2 by S. The object on stand 3 is moved to stand 1 by R, then to stand 2 by E, and back to stand 3 by S. Therefore, it does not change the final positions of the objects.
- When applying RR, the object on stand 1 is moved to stand 3, the object on stand 2 is moved to stand 1, and the object on stand 3 is moved to stand 2. When applying ES, the object on stand 1 is moved to stand 3, the object on stand 2 is moved to stand 1, and the object on stand 3 is moved to stand 2. Therefore, it does not change the final positions of the objects by replacing the pattern RR with the pattern RES.
- When applying EEE, it is equivalent to swapping the objects on stands 1 and 2. When applying SR, the object on stand 1 is sent to stand 2, the object on stand 2 is sent to stand 1, and the object on stand 3 remains on stand 3. Therefore, it does not change the final positions of the objects by replacing the pattern EEE with the pattern SR.
We conclude that no magical operation can change the final positions of the objects. Since the necklaces "S" and "E" do not result in the same final positions of the objects, it is impossible to transform one into the other using magical operations.
Comment from the graders: Very few (3) solutions were submitted for this very difficult exercise; none were conclusive, but the students had good ideas, which is very encouraging. The idea was indeed to find an invariant, which in this case involved interpreting the letters R, E, and S as operations on a set. Once this idea was in mind, a reasonable strategy was to look for simplifications that produced words that could be identified with the identity operation.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
Thanima possède un magnifique collier constitué de rubis, d'émeraudes et de saphirs, que l'on représente par une suite de $\mathrm{R}, \mathrm{E}$ et S . En une opération magique, elle peut faire l'une des actions suivantes :
- Remplacer un motif RR dans le collier par un motif ES (ou ES par RR).
- Remplacer un motif EEE par un motif SR (ou SR par EEE).
- Supprimer un motif SS, ou ajouter un motif SS n'importe où.
- Supprimer un motif RES, ou ajouter un motif RES n'importe où.
Il n'est pas possible de déplacer les lettres cycliquement à cause du fermoir. Elle ne peut pas non plus retourner le collier.
Est-il possible de passer d'un collier contenant uniquement un saphir à un collier contenant uniquement une émeraude avec des opérations magiques?
|
Supposons que Thanima dispose de trois objets numérotés 1,2 et 3 sur trois supports numérotés 1,2 et 3 . Au début, chaque objet se trouve sur le support qui porte le même numéro. Thanima peut lire les lettres du collier une par une de gauche à droite et faire les opérations suivantes :
- Si elle voit un E, elle échange les objets qui se trouvent sur les supports 1 et 2.
- Si elle voit un $S$, elle échange les objets qui se trouvent sur les supports 2 et 3.
- Si elle voit un R, elle déplace l'objet sur le support 1 sur le support 2, l'objet sur le support 2 sur le support 3 , et l'objet sur le support 3 sur le support 1 .
On remarque que :
- Lorsque l'on ajoute un motif SS quelque part, on échange deux fois de suite les objets sur les supports 2 et 3 , ce qui ne change pas la position finale des objets.
- Lorsque l'on ajoute un motif RES quelque part, l'objet qui était sur le support 1 à ce moment est déplacé sur le support 2 par $R$, puis sur le support 1 par $E$. L'objet qui était sur le support 2 est déplacé sur le support 3 par $R$, puis sur le support 2 par $S$. L'objet sur le support 3 est déplacé sur le support 1 par R, puis sur le support 2 par E puis à nouveau sur le support 3 par S . On ne change donc pas la position finale des objets.
- Lorsque l'on applique RR, l'objet sur le support 1 est déplacé sur le support 3 , l'objet sur le support 2 est déplacé sur le support 1, et l'objet sur le support 3 est déplacé sur le support 2 . Lorsque l'on applique ES, l'objet sur le support 1 est déplacé sur le support 3, l'objet sur le support 2 est déplacé sur le support 1, et l'objet sur le support 3 est déplacé sur le support 2 . On ne change donc pas la position finale des objets en remplaçant un motif RR par un motif RES.
- Lorsque l'on applique EEE, cela revient à échanger les objets sur les supports 1 et 2 . Lorsque l'on applique $S R$, l'objet sur le support 1 est envoyé sur le support 2 , l'objet 2 est envoyé sur le support 1 et l'objet sur le support 3 reste sur le support 3 . On ne change donc pas la position finale des objets en remplaçant un motif EEE par un motif SR.
On conclut qu'aucune opération magique ne permet de changer la position finale des objets. Or les colliers "S" et "E" ne donnent pas les mêmes positions finales des objets, il est donc impossible de passer de l'un à l'autre par des opérations magiques.
Commentaire des correcteurs : Très peu (3) de solutions rendues pour cet exercice très difficile; aucune n'a été concluante, mais les élèves ont eu de bonnes idées, ce qui est très encourageant. L'idée était effectivement de trouver un invariant, qui consistait ici en une interprétation des lettres R, E et S en tant qu'opérations sur un ensemble. Une fois cette idée en tête, une stratégie raisonnable consistait alors à chercher des simplifications produisant des mots que l'on pouvait identifier à l'opération identité.
|
{
"exam": "French_envois",
"problem_label": "18",
"problem_match": "\nExercice 18.",
"resource_path": "French/segmented/envois/fr-corrigé-envoi-4.jsonl",
"solution_match": "\nSolution de l'exercice 18",
"tier": "T2",
"year": null
}
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.