problem
stringlengths 14
10.4k
| solution
stringlengths 1
24.1k
| answer
stringlengths 1
250
⌀ | problem_is_valid
stringclasses 4
values | solution_is_valid
stringclasses 3
values | question_type
stringclasses 4
values | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
10.4k
| solution_raw
stringlengths 1
24.1k
| metadata
dict |
|---|---|---|---|---|---|---|---|---|---|
Determine all polynomials P and Q with integer coefficients such that, if the sequence $\left(x_{n}\right)$ is defined by $x_{0}=2015, x_{2 n+1}=P\left(x_{2 n}\right)$ and $x_{2 n+2}=\mathrm{Q}\left(x_{2 n+1}\right)$ for all $n \geqslant 0$, then every positive integer $\mathrm{m}>0$ divides at least one non-zero term of the sequence.
|
Let P and Q be two such polynomials.
We will say that a sequence $\left(\mathrm{y}_{\mathrm{n}}\right)$ of integers has property D if every integer $\mathrm{m}>0$ divides at least one non-zero term of this sequence. We will say that a polynomial T with integer coefficients has property D if there exists an integer a such that the sequence $\left(x_{n}\right)$ defined by $x_{0}=a$ and $x_{n+1}=T\left(x_{n}\right)$ has property D.
We now begin with three lemmas.
Lemma 1. Let $(x_{n})$ be a sequence of integers and let $k$ be a non-zero natural number. Then $(x_{n})$ has property D if and only if one of the $k$ sequences $\left(x_{k n}\right),\left(x_{k n+1}\right), \ldots,\left(x_{k n+k-1}\right)$ has property D.
Proof of Lemma 1. Suppose first that none of the $k$ sequences $\left(x_{k n}\right),\left(x_{k n+1}\right), \ldots,\left(x_{k n+k-1}\right)$ has property D. Then, for each integer $\ell \in\{0,1, \ldots, k-1\}$, there exists an integer $M_{\ell}$ that does not divide any non-zero term of the sequence $(x_{k n+\ell})$. In particular, the integer $\prod_{\ell=0}^{k-1} M_{\ell}$ cannot divide any non-zero term of the sequence $\left(x_{n}\right)$, which therefore cannot have property D either.
Conversely, if a sequence $\left(x_{k n+\ell}\right)$ has property D, then clearly $\left(x_{n}\right)$ also has property D.
Lemma 2. Let T be a polynomial with integer coefficients, of degree d and leading coefficient $\rho$. If T has property D, then $\mathrm{d}=1$ and $|\rho|<4$.
Proof of Lemma 2. If T is constant, the sequence $(x_{n})$ takes only a finite number of distinct values, which prevents it from having property D. We now proceed by contradiction, and assume that $d \geqslant 2$ or that $d=1$ and $|\rho| \geqslant 4$. Then there exists a real number $c>0$ such that
$$
|\mathrm{T}(\mathrm{x})|>3|x| \text { for all } x \text { such that }|x|>c \text {. (1) }
$$
Note that there are only a finite number of integers in [-c; c] and that each of them can only be reached a finite number of times by T. Thus, there exists an integer $N \geqslant 0$ such that $\left|x_{N}\right|>c$. An immediate induction using (1) shows that then $\left|x_{i}\right|>c$ for all $i \geqslant N$.
Moreover, without loss of generality, we can choose $N$ to be minimal with this property. We then have
$$
\left|x_{i}\right| \leqslant c \text { for all } i<N, \text { and }\left|x_{i}\right|>c \text { for all } i \geqslant N \text {. (2) }
$$
In particular, from (1) and (2), we deduce that $\left|x_{N+1}\right|>\max \left(c,\left|x_{0}\right|, \cdots,\left|x_{N}\right|\right)$.
Let $m=\left|x_{N+1}-x_{N}\right|$, which is a strictly positive integer. Then:
$m \geqslant\left|x_{N+1}\right|-\left|x_{N}\right|>2\left|x_{N}\right|>\max \left(\left|x_{0}\right|, \cdots,\left|x_{N}\right|\right)$, which ensures that $m$ does not divide any non-zero $x_{i}$ when $i \leqslant N$. But then $m$ does not divide $x_{N+1}$ either.
On the other hand, since T has integer coefficients, $x_{n+1}-x_{n}=T\left(x_{n}\right)-T\left(x_{n-1}\right)$ is divisible by $x_{n}-x_{n-1}$ for all $n \geqslant 1$. In particular, for all $n \geqslant N$, $x_{n+1}-x_{n}$ is divisible by $m$, and thus
$$
x_{n+1}-x_{N+1}=\left(x_{n+1}-x_{n}\right)+\left(x_{n}-x_{n-1}\right)+\cdots+\left(x_{N+2}-x_{N+1}\right)
$$
is also divisible by $m$. But, since $m$ does not divide $x_{N+1}$, it does not divide $x_{n}$ for all $n \geqslant N+1$ either. Finally, $m$ does not divide any non-zero term of the sequence, in contradiction with the hypothesis that $\left(x_{n}\right)$ has property D.
Lemma 3. Let $T(X)=\rho X+\theta$ be a polynomial with integer coefficients. If T has property D, then $\rho=1$.
Proof of Lemma 3. If T has property D, let $x_{0}$ be an integer such that the sequence $(x_{n})$ defined by $x_{n+1}=T\left(x_{n}\right)$ has property D. According to Lemma 1, one of the sequences $\left(x_{2 n}\right)$ and $\left(x_{2 n+1}\right)$ has property D, and satisfies $x_{n+2}=T\left(T\left(x_{n}\right)\right)$. The polynomial $T(T(X))$ therefore also has property D.
Now, $T(T(X))$ has leading coefficient $\rho^{2}$. Lemma 2 then shows that $\rho^{2}<4$, so $\rho \in\{-1,0,1\}$. Since $\rho$ is the leading coefficient of T, we necessarily have $\rho \neq 0$. Moreover, if $\rho=-1$, then $T(T(X))=X$ does not have property D. It follows that $\rho=1$.
Let's return to the exercise.
We set $H(X)=P(Q(X))$ and $K(X)=Q(P(X))$.
According to Lemma 1, one of the two sequences $(x_{2 k})$ and $(x_{2 k+1})$ has property D, so one of the polynomials H and K has property D, since $x_{2 k+2}=H(x_{2 k})$ and $x_{2 k+3}=K(x_{2 k+1})$.
Since $\operatorname{deg} H=(\operatorname{deg} P) \cdot(\operatorname{deg} Q)=\operatorname{deg} K$, Lemma 2 indicates that $\operatorname{deg} H=\operatorname{deg} P=\operatorname{deg} Q=\operatorname{deg} K=1$. Let us then write $P(X)=a X+b$ and $Q(X)=c X+d$. We then have $H(X)=a c X+a d+b$ and $K(X)=a c X+b c+d$, so Lemma 3 indicates that $a=c= \pm 1$.
Finally, note that $x_{2 n}=2015+(a d+b) n$ and that $x_{2 n+1}=(a 2015+d)+(b c+d) n$. Now, an arithmetic sequence $\left(y_{n}\right)$ with common difference $r$ has property D if and only if $r$ divides $y_{0}$:
- if $y_{0}=q r$, and if $m \in \mathbb{N}^{*}$, then $q^{2} m-q \geqslant 0$ and $m$ divides $y_{q^{2} m-q}=q^{2} m r$;
- if $r$ does not divide $y_{0}$, then $r$ does not divide any integer $y_{n}$.
Now, Lemma 1 indicates that $\left(x_{n}\right)$ has property D if and only if $\left(x_{2 n}\right)$ or $\left(x_{2 n+1}\right)$ has property D. In the first case, this means that $a d+b$ divides $x_{0}=2005$. In the second case, this means that $b c+d$ divides $x_{1}=2005 c+d$. Note that $|a d+b|=|b c+d|$.
The pairs of polynomials $(P(X), Q(X))$ we are looking for are therefore the pairs $(P(X), Q(X))=(\varepsilon X+b, \varepsilon X+d)$ such that $\varepsilon= \pm 1$ and $b+\varepsilon d$ divides 2005 or $2005+\varepsilon d$.
|
not found
|
Yes
|
Incomplete
|
proof
|
Number Theory
|
Déterminer tous les polynômes P et Q à coefficients entiers tels que, si l'on définit la suite $\left(x_{n}\right)$ par $x_{0}=2015, x_{2 n+1}=P\left(x_{2 n}\right)$ et $x_{2 n+2}=\mathrm{Q}\left(x_{2 n+1}\right)$ pour tout $n \geqslant 0$, alors tout entier $\mathrm{m}>0$ divise au moins un terme non nul de la suite.
|
Soit P et Q deux tels polynômes.
On dira qu'une suite $\left(\mathrm{y}_{\mathrm{n}}\right)$ d'entiers possède la propriété D si tout entier $\mathrm{m}>0$ divise au moins un terme non nul de cette suite. On dira qu'un polynôme T à coefficients entiers possède la propriété D s'il existe un entier a tel que la suite $\left(x_{n}\right)$ définie par $x_{0}=a$ et $x_{n+1}=T\left(x_{n}\right)$ possède la propriété D.
Nous débutons maintenant par trois lemmes.
Lemme 1. Soit ( $x_{n}$ ) une suite d'entiers et soit $k$ un entier naturel non nul. Alors ( $x_{n}$ ) possède la propriété D si et seulement si l'une des $k$ suites $\left(x_{k n}\right),\left(x_{k n+1}\right), \ldots,\left(x_{k n+k-1}\right)$ possède la propriété D.
Preuve du lemme 1. Supposons d'abord qu'aucune des $k$ suites $\left(x_{k n}\right),\left(x_{k n+1}\right), \ldots,\left(x_{k n+k-1}\right)$ ne possède la propriété $D$. Alors, pour chaque entier $\ell \in\{0,1, \ldots, k-1\}$, il existe un entier $M_{\ell}$ qui ne divise aucun terme non nul de la suite ( $x_{k n+\ell}$ ). En particulier, l'entier $\prod_{\ell=0}^{k-1} M_{\ell}$ ne peut donc diviser aucun terme non nul de la suite $\left(x_{n}\right)$, qui ne peut posséder la propriété D non plus.
Réciproquement, si une suite $\left(x_{k n+\ell}\right)$ a la propriété $D$, alors clairement $\left(x_{n}\right)$ a la propriété $D$ aussi.
Lemme 2. Soit T un polynôme à coefficients entiers, de degré d et de coefficient dominant $\rho$. Si R possède la propriété D , alors $\mathrm{d}=1$ et $|\rho|<4$.
Preuve du lemme 2. Si T est constant, la suite ( $x_{n}$ ) ne prend qu'un nombre fini de valeurs distinctes, ce qui lui interdit d'avoir la propriété D. Procédons maintenant par l'absurde, et supposons que $d \geqslant 2$ ou que $d=1$ et $|\rho| \geqslant 4$. Il existe alors un réel $c>0$ tel que
$$
|\mathrm{T}(\mathrm{x})|>3|x| \text { pour tout } x \text { tel que }|x|>c \text {. (1) }
$$
On note qu'il n'existe qu'un nombre fini d'entiers dans [-c; c] et que chacun d'eux ne peut être atteint qu'un nombre fini de fois par $T$. Ainsi, il existe un entier $N \geqslant 0$ tel que $\left|x_{N}\right|>c$. Une récurrence immédiate à l'aide de (1) montre qu'alors $\left|x_{i}\right|>c$ pour tout $i \geqslant N$.
De plus, sans perte de généralité, on peut choisir $N$ minimal ayant cette propriété. On a donc
$$
\left|x_{i}\right| \leqslant c \text { pour tout } i<N, \text { et }\left|x_{i}\right|>c \text { pour tout } i \geqslant N \text {. (2) }
$$
En particulier, de (1) et (2), on déduit que $\left|x_{N+1}\right|>\max \left(c,\left|x_{0}\right|, \cdots,\left|x_{N}\right|\right)$.
Posons $m=\left|x_{N+1}-x_{N}\right|$, qui est bien un entier strictement positif. Alors:
$m \geqslant\left|x_{N+1}\right|-\left|x_{N}\right|>2\left|x_{N}\right|>\max \left(\left|x_{0}\right|, \cdots,\left|x_{N}\right|\right)$, ce qui assure $m$ ne divise aucun $x_{i}$ non nul lorsque $i \leqslant N$. Mais alors $m$ ne divise pas $x_{N+1}$ non plus.
D'autre part, puisque $T$ est à coefficients entiers, $x_{n+1}-x_{n}=T\left(x_{n}\right)-T\left(x_{n-1}\right)$ est divisible par $x_{n}-x_{n-1}$ pour tout $n \geqslant 1$. En particulier, pour tout $n \geqslant N$, on a $x_{n+1}-x_{n}$ divisible par $m$, et donc
$$
x_{n+1}-x_{N+1}=\left(x_{n+1}-x_{n}\right)+\left(x_{n}-x_{n-1}\right)+\cdots+\left(x_{N+2}-x_{N+1}\right)
$$
est lui aussi divisible par $m$. Mais, $m$ ne divisant pas $x_{N+1}$, il ne divise donc pas non plus $x_{n}$ pour tout $n \geqslant N+1$. Finalement, $m$ ne divise aucun terme non nul de la suite, en contradiction avec l'hypothèse que $\left(x_{n}\right)$ possède la propriété $D$.
Lemme 3. Soit $T(X)=\rho X+\theta$ un polynôme à coefficients entiers. Si $T$ possède la propriété $D$, alors $\rho=1$.
Preuve du lemme 3. Si T possède la propriété D , soit $x_{0}$ un entier tel que la suite ( $x_{n}$ ) définie par $x_{n+1}=T\left(x_{n}\right)$ ait la propriété $D$. D'après le lemme 1, l'une des suites $\left(x_{2 n}\right)$ et $\left(x_{2 n+1}\right)$ a la propriété $D$, et satisfait bien $x_{n+2}=T\left(T\left(x_{n}\right)\right)$. Le polynôme $T(T(X))$ a donc également la propriété D .
Or, $T(T(X))$ est de coefficient dominant $\rho^{2}$. Le lemme 2 montre donc que $\rho^{2}<4$, donc que $\rho \in\{-1,0,1\}$. Puisque $\rho$ est un coefficient dominant de $T$, on a nécessairement $\rho \neq 0$. De plus, si $\rho=-1$, alors $T(T(X))=X$ n'a pas la propriété $D$. Il s'ensuit que $\rho=1$.
Revenons maintenant à l'exercice.
On pose $H(X)=P(Q(X))$ et $K(X)=Q(P(X))$.
D'après le lemme 1, l'une des deux suites ( $\mathrm{x}_{2 \mathrm{k}}$ ) et $\left(\mathrm{x}_{2 \mathrm{k}+1}\right)$ possède la propriété D , donc l'un des polynômes H et K possède la propriété D , car $\mathrm{x}_{2 \mathrm{k}+2}=\mathrm{H}\left(\mathrm{x}_{2 \mathrm{k}}\right)$ et $\mathrm{x}_{2 \mathrm{k}+3}=\mathrm{K}\left(\mathrm{x}_{2 \mathrm{k}+1}\right)$.
Puisque $\operatorname{deg} H=(\operatorname{deg} P) \cdot(\operatorname{deg} Q)=\operatorname{deg} K$, le lemme 2 indique que $\operatorname{deg} H=\operatorname{deg} P=\operatorname{deg} \mathbf{Q}=$ $\operatorname{deg} K=1$. Notons alors $P(X)=a X+b$ et $Q(X)=c X+d$. On a alors $H(X)=a c X+a d+b$ et $K(X)=a c X+b c+d$, donc le lemme 3 indique que $a=c= \pm 1$.
Finalement, notons que $x_{2 n}=2015+(a d+b) n$ et que $x_{2 n+1}=(a 2015+d)+(b c+d) n$. Or, une suite arithmétique $\left(y_{n}\right)$ de raison $r$ a la propriété $D$ si et seulement si $r$ divise $y_{0}$ :
- si $y_{0}=q r$, et si $m \in \mathbb{N}^{*}$, alors $q^{2} m-q \geqslant 0$ et $m$ divise $y_{q^{2} m-q}=q^{2} m r$;
- si $r$ ne divise pas $y_{0}$, alors $r$ ne divise aucun entier $y_{n}$.
Or, le lemme 1 inidique que $\left(x_{n}\right)$ a la propriété $D$ si et seulement si $\left(x_{2 n}\right)$ ou $\left(x_{2 n+1}\right)$ a la propriété $D$. Dans le premier cas, cela signifie que $a d+b$ divise $x_{0}=2005$. Dans le second cas, cela signifie que $b c+d$ divise $x_{1}=2005 c+d$. Or, notons que $|a d+b|=|b c+d|$.
Les paires des polynômes $(P(X), Q(X))$ recherchées sont donc les paires $(P(X), Q(X))=$ $(\varepsilon X+b, \varepsilon X+d)$ telles que $\varepsilon= \pm 1$ et $b+\varepsilon$ d divise 2005 ou $2005+\varepsilon d$.
|
{
"exam": "French_tests",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/tests/fr-2014-2015-ofm-2014-2015-test-fevrier-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T1",
"year": "2014"
}
|
Determine all real numbers $x, y, z$ satisfying the following system of equations: $x=\sqrt{2 y+3}, y=\sqrt{2 z+3}, z=\sqrt{2 x+3}$.
|
It is clear that the numbers $x, y, z$ must be strictly positive. The first two equations give $x^{2}=2 y+3$ and $y^{2}=2 z+3$. By subtracting them, we obtain $x^{2}-y^{2}=2(y-z)$. From this, we deduce that if $x \leqslant y$ then $y \leqslant z$, and similarly if $y \leqslant z$ then $z \leqslant x$. Therefore, if $x \leqslant y$, we have $x \leqslant y \leqslant z \leqslant x$, which implies that $x=y=z$.
We can similarly show that if $x \geqslant y$ then $x=y=z$. Therefore, in all cases, $x, y, z$ are equal, and their common value satisfies the equation $x^{2}=2 x+3$, which can also be written as $(x-3)(x+1)=0$. Since $x$ is strictly positive, it must be that $x=y=z=3$. Conversely, it is immediately verified that $x=y=z=3$ is indeed a solution to the system.
|
x=y=z=3
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Déterminer tous les nombres réels $x, y, z$ satisfaisant le système d'équations suivant : $x=\sqrt{2 y+3}, y=\sqrt{2 z+3}, z=\sqrt{2 x+3}$.
|
Il est évident que les nombres $x, y, z$ doivent être strictement positifs. Les deux premières équations donnent $x^{2}=2 y+3$ et $y^{2}=2 z+3$. En les soustrayant, on obtient $x^{2}-y^{2}=2(y-z)$. On en déduit que si $x \leqslant y$ alors $y \leqslant z$, et de même si $y \leqslant z$ alors $z \leqslant x$. Donc si $x \leqslant y$, on a $x \leqslant y \leqslant z \leqslant x$, ce qui impose que $x=y=z$.
On montre de même que si $x \geqslant y$ alors $x=y=z$. Donc dans tous les cas, $x, y, z$ sont égaux, et leur valeur commune satisfait l'équation $x^{2}=2 x+3$, qui s'écrit encore $(x-3)(x+1)=0$. Or, $x$ est strictement positif, donc nécessairement $x=y=z=3$. Réciproquement, on vérifie immédiatement que $x=y=z=3$ est bien solution du système.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2014-2015-ofm-2014-2015-test-fevrier-junior-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T1",
"year": "2014"
}
|
Let $n$ and $k$ be strictly positive integers. There are $n k$ objects (of the same size) and $k$ boxes that can each hold $n$ objects. Each object is colored in one of $k$ possible colors. Show that it is possible to arrange the objects in the boxes so that each box contains objects of at most 2 different colors.
|
We show this by induction on $k$. If $k=1$, the statement is obvious. Suppose the property holds for all integers $<k$.
If one of the colors $c$ is taken exactly $n$ times, we place all objects of color $c$ in the last box. The induction hypothesis allows us to place the remaining $n(k-1)$ objects in the first $k-1$ boxes such that each box contains objects of at most 2 different colors.
Suppose, therefore, that no color is taken exactly $n$ times. If all colors are taken $\leqslant n-1$ times, then there are at most $(n-1) k$ objects in total, which contradicts the hypothesis. Therefore, one of the colors $c_{1}$ is taken $\geqslant n+1$ times. Similarly, one of the colors $c_{2}$ is taken $\leqslant n-1$ times.
We then place all objects of color $c_{2}$ in the last box. We complete this box with objects of color $c_{1}$. The induction hypothesis allows us to place the remaining $n(k-1)$ objects in the first $k-1$ boxes such that each box contains objects of at most 2 different colors.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soient $n$ et $k$ des entiers strictement positifs. Il y a $n k$ objets (de même taille) et $k$ boîtes qui peuvent contenir chacune $n$ objets. Chaque objet est colorié en une couleur parmi $k$ couleurs possibles. Montrer qu'il est possible de ranger les objets dans les boîtes de sorte que chaque boîte contienne des objets d'au plus 2 couleurs différentes.
|
On le montre par récurrence sur $k$. Si $k=1 c^{\prime}$ est évident. Supposons la propriété vraie pour tous les entiers $<k$.
Si l'une des couleurs $c$ est prise exactement $n$ fois, on range tous les objets dont la couleur est $c$ dans la dernière boîte. L'hypothèse de récurrence permet de ranger les $n(k-1)$ objets restants dans les $k-1$ premières boîtes de sorte que chaque boîte contienne des objets d'au plus 2 couleurs différentes.
Supposons donc qu'aucune couleur ne soit prise exactement $n$ fois. Si toutes les couleurs sont prises $\leqslant n-1$ fois, alors il y a au plus $(n-1) k$ objets au total, ce qui contredit l'hypothèse. Donc l'une des couleurs $c_{1}$ est prise $\geqslant n+1$ fois. De même, l'une des couleurs $c_{2}$ est prise $\leqslant n-1$ fois.
On place alors tous les objets de couleur $c_{2}$ dans la dernière boîte. On complète cette boîte avec des objets de couleur $c_{1}$. L'hypothèse de récurrence permet de ranger les $n(k-1)$ objets restants dans les $k-1$ premières boîtes de sorte que chaque boîte contienne des objets d'au plus 2 couleurs différentes.
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2014-2015-ofm-2014-2015-test-fevrier-junior-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T1",
"year": "2014"
}
|
It is said that a strictly positive integer $n$ is amusing if for every strictly positive divisor $d$ of $n$, the integer $d+2$ is prime. Determine all the amusing integers that have the maximum number of divisors.
|
Let $n$ be an amusing integer and $p$ a prime divisor of $n$. Then $p$ is odd, since $p+2$ is prime.
Suppose that $p \geqslant 5$. Then $p+2$ is prime, and $p+2>3$, so $p+2$ is not divisible by 3. We deduce that $p$ is not congruent to 1 modulo 3. It is clear that $p$ is not congruent to 0 modulo 3, so $p \equiv 2(\bmod 3)$. Suppose that $p^{2} \mid n$. Then $p^{2} \equiv 1(\bmod 3)$, so $p^{2}+2 \equiv 0$ $(\bmod 3)$. Furthermore, $p^{2}+2$ is prime, so $p^{2}+2=3$, which is impossible.
We deduce from the above that if $p \geqslant 5$ is a prime divisor of $n$, then $p^{2}$ does not divide $n$.
Similarly, if $p_{1}$ and $p_{2}$ are distinct prime divisors $\geqslant 5$ of $n$, then $p_{1} p_{2}$ divides $n$, so $p_{1} p_{2}+2$ is divisible by 3, which is impossible.
Therefore, every amusing integer $n$ is of the form $n=3^{k}$ or $3^{k} p$ where $p$ is prime.
We check that $3+2, 3^{2}+2, 3^{3}+2$, and $3^{4}+2$ are prime, but $3^{5}+2$ is not, so $k \leqslant 4$. The amusing integers of the form $3^{k}$ therefore have at most 5 divisors.
If $n=3^{4} \times 5=405$, then $n+2$ is not prime, so $n$ is not amusing.
If $n=3^{k} p$ with $p \geqslant 7$ prime, and $k \geqslant 3$, then the numbers $p, 3 p, 9 p, 27 p$ are divisors of $n$ congruent to $p, 3 p, 4 p, 2 p$ modulo 5. None is congruent to 0 modulo 5, and the congruences of these four numbers modulo 5 are distinct, so in some order they are $1, 2, 3, 4$. We deduce that there is a divisor $d \geqslant 7$ of $n$ such that $d \equiv 3(\bmod 5)$. We have $d+2>5$ and $5 \mid d$, which implies that $d$ is not prime.
We deduce from the above that the amusing integers of the form $3^{k} p$ satisfy $k \leqslant 2$ or $(k \leqslant 3$ and $p=5$), so have at most 8 divisors, with equality only when $k=3$ and $p=5$. Conversely, we check that $3^{3} \times 5$ is amusing, so the unique amusing integer having a maximum number of divisors is $3^{3} \times 5=135$.
|
135
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
On dit qu'un entier strictement positif $n$ est amusant si pour tout diviseur strictement positif $d$ de $n$, l'entier $d+2$ est premier. Déterminer tous les entiers amusants dont le nombre de diviseurs est maximum.
|
Soit $n$ un entier amusant et $p$ un diviseur premier de $n$. Alors $p$ est impair, puisque $p+2$ est premier.
Supposons que $p \geqslant 5$. Alors $p+2$ est premier, et $p+2>3$, donc $p+2$ n'est pas divisible par 3. On en déduit que $p$ n'est pas congru à 1 modulo 3 . Il est clair que $p \mathrm{n}^{\prime}$ est pas congru à 0 modulo 3 , donc $p \equiv 2(\bmod 3)$. Supposons que $p^{2} \mid n$. Alors $p^{2} \equiv 1(\bmod 3)$, donc $p^{2}+2 \equiv 0$ $(\bmod 3)$. De plus, $p^{2}+2$ est premier, donc $p^{2}+2=3$, ce qui est impossible.
On déduit de ce qui précède que si $p \geqslant 5$ est un diviseur premier de $n$, alors $p^{2}$ ne divise pas $n$.
De même, si $p_{1}$ et $p_{2}$ sont des diviseurs premiers distincts $\geqslant 5$ de $n$, alors $p_{1} p_{2}$ divise $n$, donc $p_{1} p_{2}+2$ est divisible par 3 , ce qui est impossible.
Par conséquent, tout entier amusant $n$ est de la forme $n=3^{k}$ ou bien $3^{k} p$ où $p$ est premier.
On vérifie que $3+2,3^{2}+2,3^{3}+2$ et $3^{4}+2$ sont premiers mais $3^{5}+2$ ne l'est pas, donc $k \leqslant 4$. Les entiers amusants de la forme $3^{k}$ ont donc au plus 5 diviseurs.
Si $n=3^{4} \times 5=405$, alors $n+2$ n'est pas premier donc $n$ n'est pas amusant.
Si $n=3^{k} p$ avec $p \geqslant 7$ premier, et $k \geqslant 3$, alors les nombres $p, 3 p, 9 p, 27 p$ sont des diviseurs de $n$ congrus à $p, 3 p, 4 p, 2 p$ modulo 5 . Aucun n'est congru à 0 modulo 5 , et les congruences de ces quatre nombres modulo 5 sont deux à deux distinctes, donc à l'ordre près valent $1,2,3,4$. On en déduit qu'il existe un diviseur $d \geqslant 7$ de $n$ tel que $d \equiv 3(\bmod 5)$. On a donc $d+2>5$ et $5 \mid d$, ce qui entraîne que $d$ n'est pas premier.
On déduit de ce qui précède que les entiers amusants de la forme $3^{k} p$ vérifient $k \leqslant 2$ ou bien $(k \leqslant 3$ et $p=5$ ), donc ont au plus 8 diviseurs, avec égalité seulement lorsque $k=3$ et $p=5$. Réciproquement, on vérifie que $3^{3} \times 5$ est amusant, donc l'unique entier ammusant ayant un nombre maximal de diviseurs est $3^{3} \times 5=135$.
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2014-2015-ofm-2014-2015-test-fevrier-junior-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T1",
"year": "2014"
}
|
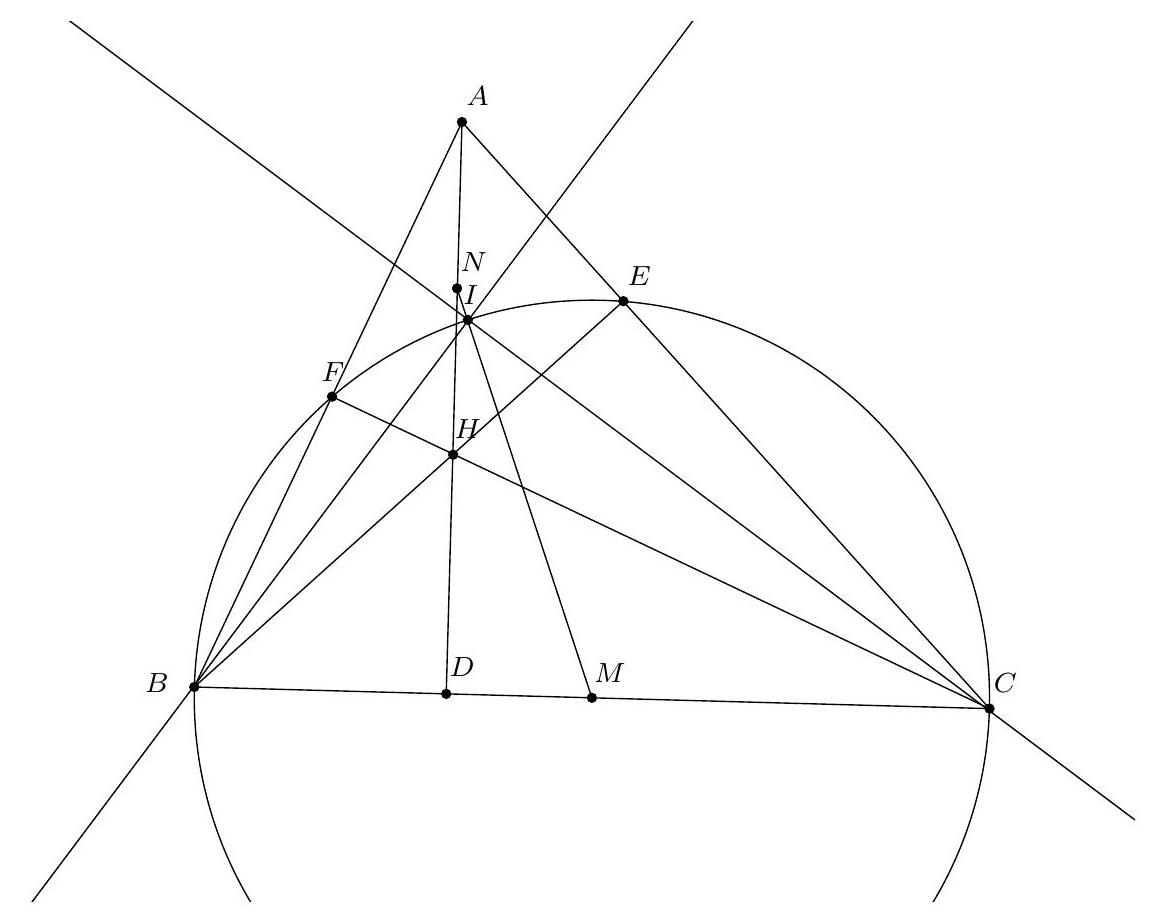
Let $ABC$ be a non-isosceles triangle. Let $\omega$ be the incircle and $I$ its center. We denote $M, N, P$ as the points of tangency of $\omega$ with the sides $[BC], [CA], [AB]$. Let $J$ be the intersection point between $(MN)$ and $(IC)$. The line $(PJ)$ intersects $\omega$ again at $K$. Show that
a) $CKIP$ is cyclic;
b) $(CI)$ is the bisector of $\widehat{PC K}$.
|
a) Since $(I N) \perp(N C)$ and $(I M) \perp(M C)$, the points $M$ and $N$ are located on the circle with diameter [IC], so $I, M, C, N$ are concyclic.
From the power of a point with respect to this circle, we have $J I \cdot J C = J M \cdot J N$. On the other hand, using the power with respect to the inscribed circle, we have $J M \cdot J N = J K \cdot J P$, so finally $J I \cdot J C = J K \cdot J P$, which implies that $P, I, K, C$ are concyclic.
b) From part a), we have $\widehat{I C P} = \widehat{I K P}$ and $\widehat{K C I} = \widehat{K P I}$. Since $I P K$ is isosceles at $I$, we have $\widehat{I K P} = \widehat{K P I}$, which implies that $\widehat{I C P} = \widehat{K C I}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle non isocèle. Soit $\omega$ le cercle inscrit et $I$ son centre. On note $M, N, P$ les points de contact de $\omega$ avec les côtés $[B C],[C A],[A B]$. Soit $J$ le point d'intersection entre $(M N)$ et $(I C)$. La droite $(P J)$ recoupe $\omega$ en $K$. Montrer que
a) $C K I P$ est cyclique;
b) $(C I)$ est la bissectrice de $\widehat{P C K}$.
|
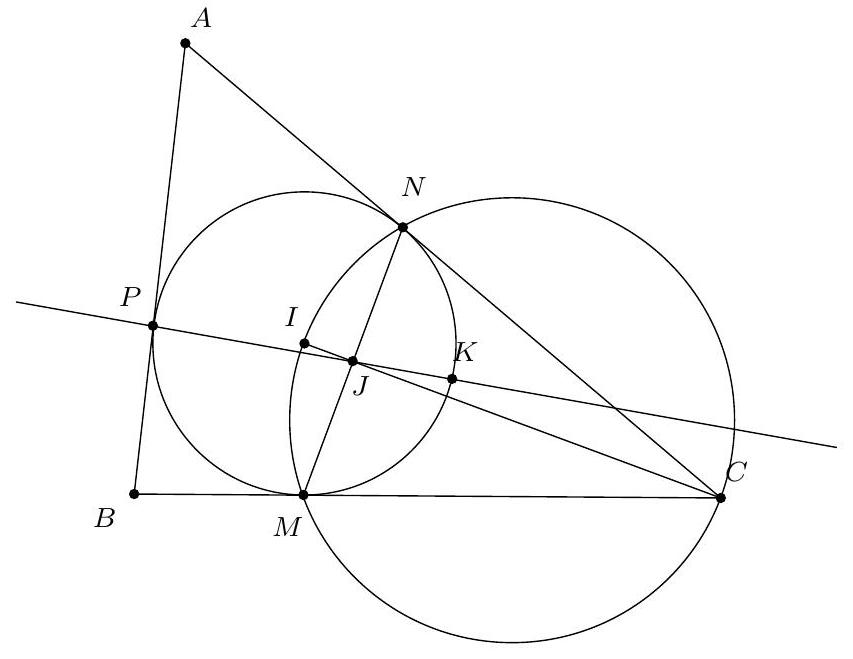
a) Comme $(I N) \perp(N C)$ et $(I M) \perp(M C)$, les points $M$ et $N$ sont situés sur le cercle de diamètre [IC], donc $I, M, C, N$ sont cocycliques.
D'après la puissance d'un point par rapport à ce cercle, on a $J I \cdot J C=J M \cdot J N$. D'autre part, en utilisant la puissance par rapport au cercle inscrit, on a $J M \cdot J N=J K \cdot J P$, donc finalement $J I \cdot J C=J K \cdot J P$, ce qui entraîne que $P, I, K, C$ sont cocycliques.
b) D'après la question a), on a $\widehat{I C P}=\widehat{I K P}$ et $\widehat{K C I}=\widehat{K P I}$. Or, $I P K$ est isocèle en $I$, donc $\widehat{I K P}=\widehat{K P I}$, ce qui entraîne que $\widehat{I C P}=\widehat{K C I}$.
|
{
"exam": "French_tests",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/tests/fr-2014-2015-ofm-2014-2015-test-fevrier-junior-corrige.jsonl",
"solution_match": "## Solution de l'exercice 4",
"tier": "T1",
"year": "2014"
}
|
a) Prove that for all strictly positive real numbers $a, b, k$ such that $a < b$, we have
$$
\frac{a}{b} < \frac{a+k}{b+k}
$$
b) Prove that
$$
\frac{1}{100} + \frac{4}{101} + \frac{7}{102} + \frac{10}{103} + \cdots + \frac{148}{149} > 25
$$
|
a) Since $a k < b k$, then $a b + a k < a b + b k$. This can be written as $a(b+k) < b(a+k)$, or equivalently $\frac{a}{b} < \frac{a+k}{b+k}$.
b) Let $A = \frac{1}{100} + \frac{4}{101} + \frac{7}{102} + \frac{10}{103} + \cdots + \frac{148}{149}$. By applying the above, we deduce
$$
A > \frac{1}{100} + \frac{3}{100} + \frac{5}{100} + \frac{7}{100} + \cdots + \frac{99}{100} = \frac{50 + 2(0 + 1 + 2 + 3 + \cdots + 49)}{100}
$$
It is sufficient to verify that the latter term equals 25, either by manually calculating the numerator or by using the formula
$$
1 + 2 + 3 + \cdots + n = \frac{n(n+1)}{2}
$$
which gives
$$
\frac{50 + 2(0 + 1 + 2 + 3 + \cdots + 49)}{100} = \frac{50 + 49 \times 50}{100} = 25
$$
|
25
|
Yes
|
Yes
|
proof
|
Inequalities
|
a) Prouver que, pour tous réels strictement positifs $a, b, k$ tels que $a<b$, on a
$$
\frac{a}{b}<\frac{a+k}{b+k}
$$
b) Prouver que
$$
\frac{1}{100}+\frac{4}{101}+\frac{7}{102}+\frac{10}{103}+\cdots+\frac{148}{149}>25
$$
|
a) On a $a k<b k$, donc $a b+a k<a b+b k$. Ceci s'écrit $a(b+k)<b(a+k)$, ou encore $\frac{a}{b}<\frac{a+k}{b+k}$.
b) Soit $A=\frac{1}{100}+\frac{4}{101}+\frac{7}{102}+\frac{10}{103}+\cdots+\frac{148}{149}$. En appliquant ce qui précède, on en déduit
$$
A>\frac{1}{100}+\frac{3}{100}+\frac{5}{100}+\frac{7}{100}+\cdots+\frac{99}{100}=\frac{50+2(0+1+2+3+\cdots+49)}{100}
$$
Il suffit donc de vérifier que ce dernier terme vaut 25 , soit en calculant à la main le numérateur, soit en utilisant la formule
$$
1+2+3+\cdots+n=\frac{n(n+1)}{2}
$$
qui donne
$$
\frac{50+2(0+1+2+3+\cdots+49)}{100}=\frac{50+49 \times 50}{100}=25
$$
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2014-2015-ofm-2014-2015-test-janvier-corrige.jsonl",
"solution_match": "## Solution de l'exercice 1",
"tier": "T1",
"year": "2014"
}
|
Let $ABC$ be an acute triangle such that $AC > AB$, $D$ on $(BC)$ such that $AD = AB$ and $D$ different from $B$. Let $\Gamma$ be the circumcircle of $ABC$, $\Delta$ the tangent to $\Gamma$ at $C$, and $E$ the intersection of $(AD)$ and $\Delta$.
Show that $CD^2 = AD \cdot DE - BD \cdot DC$.
|
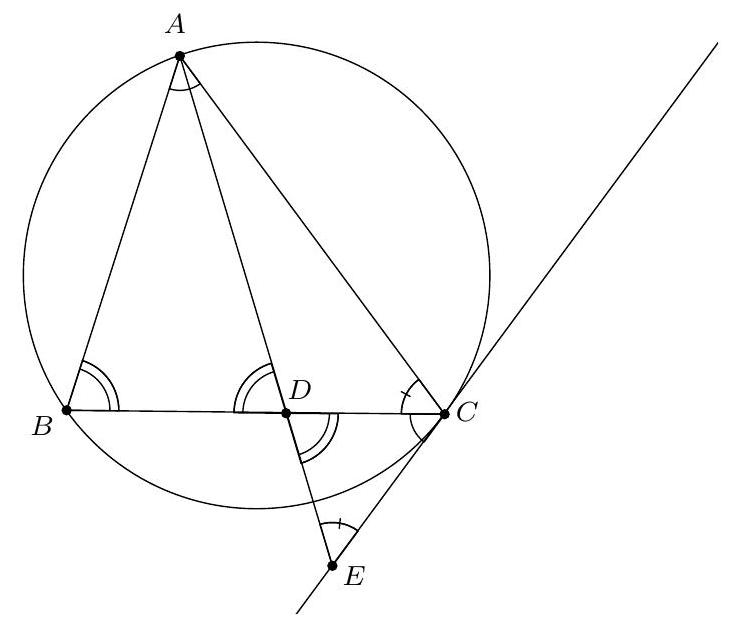
Given that $\widehat{E D C}=\widehat{A D B}=\widehat{C B A}$ and $\widehat{D C E}=\widehat{B A C}$, triangles $A B C$ and $C D E$ are similar. Therefore, we have $\frac{A B}{C D}=\frac{B C}{D E}$, so
$$
A D \cdot D E - B D \cdot D C = A B \cdot D E - B D \cdot D C = B C \cdot C D - B D \cdot C D = (B C - B D) C D = C D^{2} .
$$
|
CD^2 = AD \cdot DE - BD \cdot DC
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle acutangle tel que $A C>A B, D \operatorname{sur}(B C)$ tel que $A D=A B$ et $D$ différent de $B$. Soit $\Gamma$ le cercle circonscrit à $A B C, \Delta$ la tangente à $\Gamma$ en $C, E$ l'intersection de $(A D)$ et $\Delta$.
Montrer que $C D^{2}=A D \cdot D E-B D \cdot D C$.
|

On a $\widehat{E D C}=\widehat{A D B}=\widehat{C B A}$ et $\widehat{D C E}=\widehat{B A C}$ donc $A B C$ et $C D E$ sont semblables. On en déduit que $\frac{A B}{C D}=\frac{B C}{D E}$, donc
$$
A D \cdot D E-B D \cdot D C=A B \cdot D E-B D \cdot D C=B C \cdot C D-B D \cdot C D=(B C-B D) C D=C D^{2} .
$$
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2014-2015-ofm-2014-2015-test-janvier-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T1",
"year": "2014"
}
|
Let $n$ be a strictly positive integer such that $n(n+2015)$ is the square of an integer.
a) Prove that $n$ is not a prime number.
b) Give an example of such an integer $n$.
|
a) Suppose that $n$ is prime and there exists an integer $m$ satisfying $n(n+2015)=m^{2}$. Then $n$ divides $m^{2}$, so $n$ divides $m$. We can therefore write $m=n r$. It follows that $n(n+2015)=n^{2} r^{2}$, and then $n+2015=n r^{2}$. Consequently, $2015=n r^{2}-n=n\left(r^{2}-1\right)$ is divisible by $n$.
Since $2015=5 \times 13 \times 31$, $n$ must be one of the integers 5, 13, 31.
If $n=5$ then $r^{2}-1=13 \times 31=403$, which is impossible because 404 is not a perfect square. Similarly, $5 \times 31+1=156$ and $5 \times 13+1=66$ are not perfect squares, which rules out the cases $n=13$ and $n=31$.
b) We seek integers $n$ and $m$ such that
$$
(2 m)^{2}=4 n(n+2015)=(2 n)^{2}+2 \times(2 n) \times 2015=(2 n+2015)^{2}-2015^{2}
$$
This is equivalent to $2015^{2}=(2 n+2015)^{2}-(2 m)^{2}=(2 n+2015+2 m)(2 n+2015-2 m)$.
Let $a=2015 \times 5$ and $b=\frac{2015}{5}$. It suffices that
$$
2 n+2015+2 m=a \text { and } 2 n+2015-2 m=b
$$
By adding these equations, we find that $4 n+4030=a+b=403 \times 25+403$, so $\underline{n=1612}$, and by subtracting we get $4 m=a-b=403 \times 24$ so $m=403 \times 6$.
|
1612
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $n$ un entier strictement positif tel que $n(n+2015)$ est le carré d'un entier.
a) Prouver que $n$ n'est pas un nombre premier.
b) Donner un exemple d'un tel entier $n$.
|
a) Supposons que $n$ est premier et qu'il existe un entier $m$ vérifiant $n(n+2015)=m^{2}$. Alors $n$ divise $m^{2}$, donc $n$ divise $m$. On peut donc écrire $m=n r$. Il vient $n(n+2015)=n^{2} r^{2}$, puis $n+2015=n r^{2}$. Par conséquent, $2015=n r^{2}-n=n\left(r^{2}-1\right)$ est divisible par $n$.
Or, $2015=5 \times 13 \times 31$, donc $n$ est l'un des entiers 5, 13, 31 .
Si $n=5$ alors $r^{2}-1=13 \times 31=403$, ce qui est impossible car 404 n'est pas un carré parfait. De même, $5 \times 31+1=156$ et $5 \times 13+1=66$ ne sont pas des carrés parfaits, ce qui exclut les cas $n=13$ et $n=31$.
b) On cherche $n$ et $m$ entiers tels que
$$
(2 m)^{2}=4 n(n+2015)=(2 n)^{2}+2 \times(2 n) \times 2015=(2 n+2015)^{2}-2015^{2}
$$
Ceci équivaut à $2015^{2}=(2 n+2015)^{2}-(2 m)^{2}=(2 n+2015+2 m)(2 n+2015-2 m)$.
Soient $a=2015 \times 5$ et $b=\frac{2015}{5}$. Il suffit donc que
$$
2 n+2015+2 m=a \text { et } 2 n+2015-2 m=b
$$
En additionnant ces égalités, on trouve que $4 n+4030=a+b=403 \times 25+403$, donc $\underline{n=1612}$, et en soustrayant on obtient $4 m=a-b=403 \times 24$ donc $m=403 \times 6$.
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2014-2015-ofm-2014-2015-test-janvier-corrige.jsonl",
"solution_match": "## Solution de l'exercice 3",
"tier": "T1",
"year": "2014"
}
|
We want to color the three-element parts of $\{1,2,3,4,5,6,7\}$, such that if two of these parts have no element in common, then they must be of different colors. What is the minimum number of colors needed to achieve this goal?
|
Consider the sequence of sets $\{1,2,3\},\{4,5,6\},\{1,2,7\},\{3,4,6\},\{1,5,7\},\{2,3,6\},\{4,5,7\}$, $\{1,2,3\}$.
Each set must have a different color from the next, so there must be at least two colors. If there were exactly two colors, then the colors would have to alternate, which is impossible because the last set is the same as the first and should be of the opposite color.
Conversely, let's show that three colors suffice:
- We color blue the sets that contain at least two elements among 1, 2, 3.
- We color green the sets not colored blue and that contain at least two elements among 4, 5, 6.
- We color red the sets not colored blue or green.
It is clear that two blue sets have an element in common among 1, 2, 3; similarly, two green sets have an element in common among 4, 5, 6. Finally, any red set contains three elements, which necessarily includes the element 7: two red sets therefore also have an element in common.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On veut colorier les parties à trois éléments de $\{1,2,3,4,5,6,7\}$, de sorte que si deux de ces parties n'ont pas d'élément en commun alors elles soient de couleurs différentes. Quel est le nombre minimum de couleurs pour réaliser cet objectif?
|
Considérons la suite de parties $\{1,2,3\},\{4,5,6\},\{1,2,7\},\{3,4,6\},\{1,5,7\},\{2,3,6\},\{4,5,7\}$, $\{1,2,3\}$.
Chaque partie doit avoir une couleur différente de la suivante, donc déjà il y a au moins deux couleurs. S'il n'y avait qu'exactement deux couleurs, alors les couleurs devraient alterner, ce qui est impossible car la dernière partie est la même que la première et devrait être de couleur opposée.
Réciproquement, montrons que trois couleurs suffisent:
- On colorie en bleu les parties qui contiennent au moins deux éléments parmi 1, 2, 3.
- On colorie en vert les parties non coloriées en bleu et qui contiennent au moins deux éléments parmi 4, 5, 6 .
- On colorie en rouge les parties non coloriées en bleu ou en vert.
Il est évident que deux parties bleues ont un élément en commun parmi 1, 2, 3 ; de même, deux parties vertes ont un élément en commun parmi $4,5,6$. Enfin, toute partie rouge contient trois éléments, dont contient nécessairement l'élément 7 : deux parties rouges ont donc également un élément en commun.
|
{
"exam": "French_tests",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/tests/fr-2014-2015-ofm-2014-2015-test-janvier-corrige.jsonl",
"solution_match": "## Solution de l'exercice 4",
"tier": "T1",
"year": "2014"
}
|
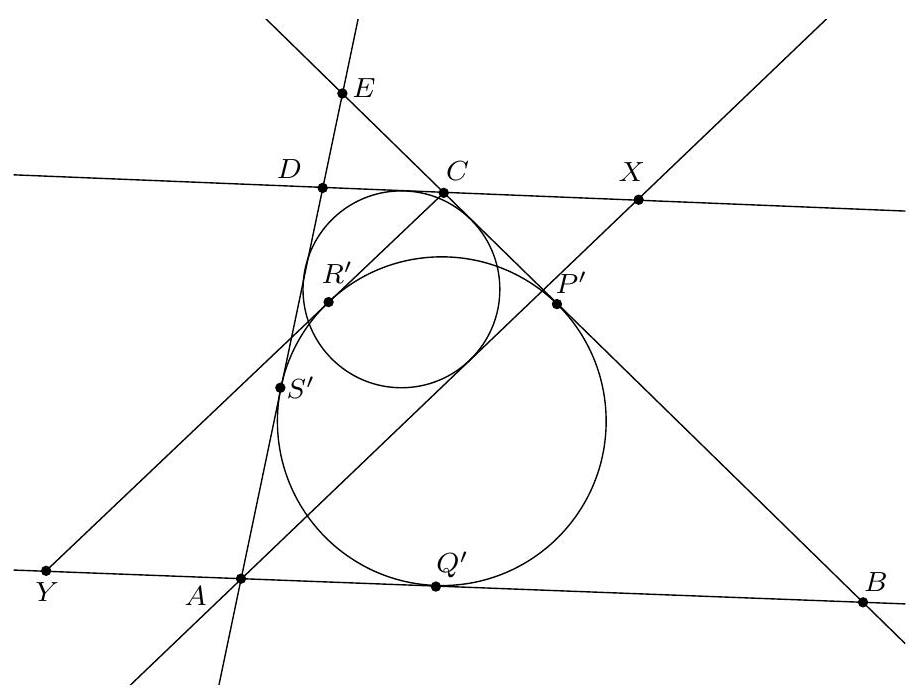
Let $ABCD$ be a trapezoid such that $(AB) / /(CD)$. Two circles $\omega_{1}$ and $\omega_{2}$ are located inside the trapezoid such that $\omega_{1}$ is tangent to $(DA)$, $(AB)$, $(BC)$ and $\omega_{2}$ is tangent to $(BC)$, $(CD)$, $(DA)$. Let $d_{1}$ be a line passing through $A$, other than $(AD)$, tangent to $\omega_{2}$. Let $d_{2}$ be a line passing through $C$, other than $(CB)$, tangent to $\omega_{1}$. Show that $d_{1} / / d_{2}$.
|
By continuity, we can assume that $A B \neq C D$. Furthermore, by swapping $A$ and $B$ with $C$ and $D$, as well as $\omega_{1}$ and $\omega_{2}$, we can assume $A B > C D$.
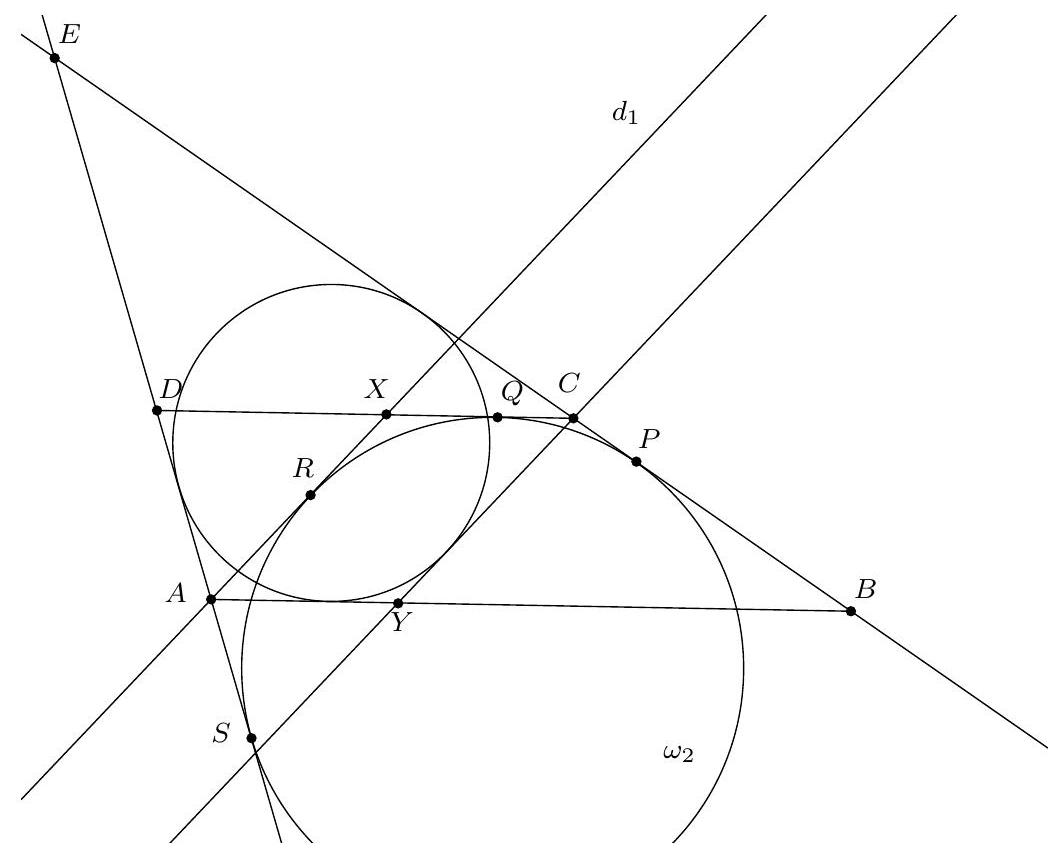
Let $E$ be the intersection of $(A D)$ and $(B C)$. Suppose that $(C D)$ intersects $\omega_{1}$.
We denote $P, Q, R, S$ as the points of tangency of $\omega_{2}$ with $(B C), (C D), d_{1}, (D A)$. Let $X$ be the intersection of $(C D)$ with $d_{1}$. Let $d_{2}^{\prime}$ be the line parallel to $d_{1}$ passing through $C$ and $Y = (A B) \cap d_{2}^{\prime}$. We orient the lines such that the algebraic measures $\overline{E A}, \overrightarrow{A B}, \overline{B C}, \overline{D C}, \overline{A X}, \overline{Y C}$ are positive.
\[
\begin{aligned}
(E A + Y C) - (C E + A Y) & = (\overline{E A} + \overline{Y C}) - (\overline{C E} + \overline{A Y}) \\
& = \overline{E S} + \overline{S A} + \overline{A X} - \overline{C P} - \overline{P E} - \overline{X C} \\
& = \overline{S A} + \overline{A X} - \overline{C P} - \overline{X C} \text{ since } \overline{E S} = \overline{P E} \\
& = \overline{R A} + \overline{A X} - \overline{X Q} = \overline{R X} - \overline{X Q} = 0
\end{aligned}
\]
Thus, $E A Y C$ is circumscribed. It follows that $d_{2}^{\prime} = (C Y) = d_{2}$, so $d_{1} \parallel d_{2}$.
If now $(C D)$ does not intersect $\omega_{1}$, we define this time $d_{1}^{\prime}$ as the line parallel to $d_{2}$ passing through $A$, $X = (C D) \cap d_{1}^{\prime}$, and $Y = (A B) \cap d_{2}$. We show as above that $E A X C$ is circumscribed (the proof is left to the reader).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un trapèze tel que $(A B) / /(C D)$. Deux cercles $\omega_{1}$ et $\omega_{2}$ sont situés à l'intérieur du trapèze de sorte que $\omega_{1}$ est tangent à $(D A),(A B),(B C)$ et $\omega_{2}$ est tangent à $(B C),(C D),(D A)$. Soit $d_{1}$ une droite passant par $A$, autre que $(A D)$, tangente à $\omega_{2}$. Soit $d_{2}$ une droite passant par $C$, autre que $(C B)$, tangente à $\omega_{1}$. Montrer que $d_{1} / / d_{2}$.
|
Par continuité, on peut supposer que $A B \neq C D$. De plus, quitte à échanger $A$ et $B$ avec $C$ et $D$, ainsi que $\omega_{1}$ et $\omega_{2}$, on peut supposer $A B>C D$.

Soit $E$ l'intersection de $(A D)$ et $(B C)$. Supposons que $(C D)$ coupe $\omega_{1}$.
On note $P, Q, R, S$ les points de contact de $\omega_{2}$ avec $(B C),(C D), d_{1},(D A)$. Soit $X$ l'intersection de $(C D)$ avec $d_{1}$. Soit $d_{2}^{\prime}$ la parallèle à $d_{1}$ passant par $C$ et $Y=(A B) \cap d_{2}^{\prime}$. On oriente les droites de sorte que les mesures algébriques $\overline{E A}, \overrightarrow{A B}, \overline{B C}, \overline{D C}, \overline{A X}, \overline{Y C}$ soient positives.
$$
\begin{aligned}
(E A+Y C)-(C E+A Y) & =(\overline{E A}+\overline{Y C})-(\overline{C E}+\overline{A Y}) \\
& =\overline{E S}+\overline{S A}+\overline{A X}-\overline{C P}-\overline{P E}-\overline{X C} \\
& =\overline{S A}+\overline{A X}-\overline{C P}-\overline{X C} \operatorname{car} \overline{E S}=\overline{P E} \\
& =\overline{R A}+\overline{A X}-\overline{X Q}=\overline{R X}-\overline{X Q}=0
\end{aligned}
$$
donc $E A Y C$ est circonscriptible. Il vient $d_{2}^{\prime}=(C Y)=d_{2}$, donc $d_{1} / / d_{2}$.
Si maintenant $(C D)$ ne coupe pas $\omega_{1}$, on définit cette fois $d_{1}^{\prime}$ la parallèle à $d_{2}$ passant par $A$, $X=(C D) \cap d_{1}^{\prime}$ et $Y=(A B) \cap d_{2}$. On montre comme ci-dessus que EAXC est circonscriptible (la preuve est laissée au lecteur).

|
{
"exam": "French_tests",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/tests/fr-2014-2015-ofm-2014-2015-test-janvier-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T1",
"year": "2014"
}
|
Let $a_{1}, a_{2}, \ldots, a_{n}$ be strictly positive integers. For all $k=1,2, \ldots, n$, we denote
$$
m_{k}=\max _{1 \leq \ell \leq k} \frac{a_{k-\ell+1}+a_{k-\ell+2}+\cdots+a_{k}}{\ell} .
$$
Show that for any $\alpha>0$, the number of integers $k$ such that $m_{k}>\alpha$ is strictly less than $\frac{a_{1}+a_{2}+\cdots+a_{n}}{\alpha}$.
|
Let $k_{1}$ be the largest integer $k$ such that $m_{k}>\alpha$. There exists $\ell_{1}$ such that $a_{k_{1}-\ell_{1}+1}+\cdots+a_{k_{1}}>\ell_{1} \alpha$.
Let $k_{2}$ be the largest integer $\leqslant k_{1}-\ell_{1}$ such that $m_{k}>\alpha$. There exists $\ell_{2}$ such that $a_{k_{2}-\ell_{2}+1}+\cdots+a_{k_{2}}>\ell_{2} \alpha$. ...
We thus construct a finite sequence $k_{1}>k_{2}>\cdots>k_{r}$ such that any integer $k$ satisfying $m_{k}>\alpha$ is found in one of the intervals $I_{j}=\llbracket k_{j}-\ell_{j}+1, k_{j} \rrbracket$. Moreover, these intervals are pairwise disjoint.
Consequently, the number of integers $k$ such that $m_{k}>\alpha$ is less than or equal to the sum of the lengths of the intervals, namely $\ell_{1}+\cdots+\ell_{r}$.
Now, $\sum_{j=1}^{r} \ell_{j}<\frac{1}{\alpha} \sum_{j}\left(a_{k_{j}-\ell_{j}+1}+\cdots+a_{k_{j}}\right) \leqslant \frac{1}{\alpha}\left(a_{1}+\cdots+a_{n}\right)$. QED.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $a_{1}, a_{2}, \ldots, a_{n}$ des entiers strictement positifs. Pour tout $k=1,2, \ldots, n$, on note
$$
m_{k}=\max _{1 \leq \ell \leq k} \frac{a_{k-\ell+1}+a_{k-\ell+2}+\cdots+a_{k}}{\ell} .
$$
Montrer que pour tout $\alpha>0$, le nombre d'entiers $k$ tel que $m_{k}>\alpha$ est strictement plus petit que $\frac{a_{1}+a_{2}+\cdots+a_{n}}{\alpha}$.
|
Soit $k_{1}$ le plus grand entier $k$ tel que $m_{k}>\alpha$. Il existe $\ell_{1}$ tel que $a_{k_{1}-\ell_{1}+1}+\cdots+a_{k_{1}}>\ell_{1} \alpha$.
Soit $k_{2}$ le plus grand entier $\leqslant k_{1}-\ell_{1}$ tel que $m_{k}>\alpha$. Il existe $\ell_{2}$ tel que $a_{k_{2}-\ell_{2}+1}+\cdots+a_{k_{2}}>\ell_{2} \alpha$. ...
On construit ainsi une suite finie $k_{1}>k_{2}>\cdots>k_{r}$ telle que tout entier $k$ vérifiant $m_{k}>\alpha$ se trouve dans l'un des intervalles $I_{j}=\llbracket k_{j}-\ell_{j}+1, k_{j} \rrbracket$. De plus, ces intervalles sont deux à deux disjoints.
Par conséquent, le nombre d'entiers $k$ tels que $m_{k}>\alpha$ est inférieur ou égal à la somme des longueurs des intervalles, à savoir $\ell_{1}+\cdots+\ell_{r}$.
Or, $\sum_{j=1}^{r} \ell_{j}<\frac{1}{\alpha} \sum_{j}\left(a_{k_{j}-\ell_{j}+1}+\cdots+a_{k_{j}}\right) \leqslant \frac{1}{\alpha}\left(a_{1}+\cdots+a_{n}\right)$. CQFD.
|
{
"exam": "French_tests",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/tests/fr-2014-2015-ofm-2014-2015-test-janvier-corrige.jsonl",
"solution_match": "## Solution de l'exercice 6",
"tier": "T1",
"year": "2014"
}
|
Let $a, b, c, n$ be integers, with $n \geq 2$. Let $p$ be a prime number that divides $a^{2}+a b+b^{2}$ and $a^{n}+b^{n}+c^{n}$, but does not divide $a+b+c$.
Prove that $n$ and $p-1$ are not coprime.
|
If $p$ divides $a$ and $b$, then $p$ divides $c^{n}$, hence $p$ divides $c$, which contradicts the last assertion. Therefore, by possibly swapping $a$ and $b$, we assume that $p$ does not divide $b$. By possibly multiplying $a, b, c$ by an inverse of $b$ modulo $p$, we can assume that $b=1$ and thus
$$
p \mid a^{2}+a+1, \quad p \mid a^{n}+1+c^{n}, \quad p \nmid a+1+c.
$$
Since $a^{2}+a+1$ is odd, $p$ is also odd.
Since $p$ divides $\left(a^{2}+a+1\right)(a-1)=a^{3}-1$, the order of $a$ modulo $p$ is 1 or 3.
First case: $a \equiv 1 \pmod{p}$. Then $p=3$, so $c^{n} \equiv -1 - a^{n} \equiv 1 \pmod{3}$.
In particular, $c$ is invertible modulo 3, so $c \equiv \pm 1 \pmod{3}$. Since $p \nmid a+1+c$, we must have $c \equiv -1 \pmod{3}$. Finally, since $c^{n} \equiv 1 \pmod{3}$, the integer $n$ is even, hence not coprime with $p-1$.
Second case: the order of $a$ modulo $p$ is 3. Since the order of $a$ modulo $p$ also divides $p-1$ by Fermat's little theorem, we have $3 \mid p-1$.
Suppose that $n$ is coprime with $p-1$. Then $x \mapsto x^{n}$ is a bijection from $\mathbb{Z} / p \mathbb{Z}$ to itself:
- if $n \equiv 1 \pmod{3}$ then $c^{n} \equiv -a^{n} - 1 \equiv -a - 1 \equiv a^{2} \equiv (a^{2})^{n} \pmod{p}$, so by the bijectivity of $x \mapsto x^{n}$ in $\mathbb{Z} / p \mathbb{Z}$ we have $c \equiv a^{2} \equiv -a - 1 \pmod{p}$: contradiction!
- if $n \equiv 2 \pmod{3}$ then $c^{n} \equiv -a^{n} - 1 \equiv -a^{2} - 1 \equiv a \equiv (a^{2})^{n} \pmod{p}$, so by the bijectivity of $x \mapsto x^{n}$ in $\mathbb{Z} / p \mathbb{Z}$ we have $c \equiv a^{2} \equiv -a - 1 \pmod{p}$: contradiction!
We conclude that $n \equiv 0 \pmod{3}$, so 3 is a common divisor of $n$ and $p-1$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $a, b, c, n$ des entiers, avec $n \geq 2$. Soit $p$ un nombre premier qui divise $a^{2}+a b+b^{2}$ et $a^{n}+b^{n}+c^{n}$, mais qui ne divise pas $a+b+c$.
Prouver que $n$ et $p-1$ ne sont pas premiers entre eux.
|
Si $p$ divise $a$ et $b$, alors $p$ divise $c^{n}$ donc $p$ divise $c$, ce qui contredit la dernière assertion. Donc, quitte à échanger $a$ et $b$, on suppose que $p$ ne divise pas $b$. Quitte à multiplier $a, b, c$ par un inverse de $b$ modulo $p$, on peut supposer que $b=1$ et donc
$$
p\left|a^{2}+a+1, \quad p\right| a^{n}+1+c^{n}, \quad p \nmid a+1+c .
$$
Comme $a^{2}+a+1$ est impair, $p$ l'est aussi.
Comme $p$ divise $\left(a^{2}+a+1\right)(a-1)=a^{3}-1$, l'ordre de $a$ modulo $p$ est 1 ou 3 .
Premier cas: $a \equiv 1(\bmod p)$. Alors $p=3$, donc $c^{n} \equiv-1-a^{n} \equiv 1(\bmod 3)$.
En particulier, $c$ est inversible modulo 3 , donc $c \equiv \pm 1(\bmod 3)$. Comme $p \nmid a+1+c$, on a nécessairement $c \equiv-1(\bmod 3)$. Enfin, comme $c^{n} \equiv 1(\bmod 3)$, l'entier $n$ est pair donc n'est pas premier avec $p-1$.
Deuxième cas: l'ordre de $a$ modulo $p$ est 3 . Comme par ailleurs l'ordre de $a$ modulo $p$ divise $p-1$ en vertu du petit théorème de Fermat, on a $3 \mid p-1$.
Supposons que $n$ est premier avec $p-1$. Alors $x \mapsto x^{n}$ est une bijection de $\mathbb{Z} / p \mathbb{Z}$ sur lui-même :
- si $n \equiv 1(\bmod 3)$ alors $c^{n} \equiv-a^{n}-1 \equiv-a-1 \equiv a^{2} \equiv\left(a^{2}\right)^{n}(\bmod p)$ donc par bijectivité de $x \mapsto x^{n}$ dans $\mathbb{Z} / p \mathbb{Z}$ on a $c \equiv a^{2} \equiv-a-1(\bmod p):$ contradiction!
- si $n \equiv 2(\bmod 3)$ alors $c^{n} \equiv-a^{n}-1 \equiv-a^{2}-1 \equiv a \equiv\left(a^{2}\right)^{n}(\bmod p)$ donc par bijectivité de $x \mapsto x^{n}$ dans $\mathbb{Z} / p \mathbb{Z}$ on a $c \equiv a^{2} \equiv-a-1(\bmod p):$ contradiction!
On en déduit que $n \equiv 0(\bmod 3)$, donc 3 est un diviseur commun de $n$ et de $p-1$.
|
{
"exam": "French_tests",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/tests/fr-2014-2015-ofm-2014-2015-test-janvier-corrige.jsonl",
"solution_match": "## Solution de l'exercice 7",
"tier": "T1",
"year": "2014"
}
|
Let $a_{1}, a_{2}, \ldots, a_{2 n}$ be real numbers such that $a_{1}+a_{2}+\cdots+a_{2 n}=0$.
Prove that there exist at least $2 n-1$ pairs $\left(a_{i}, a_{j}\right)$ with $i<j$ such that $a_{i}+a_{j} \geqslant 0$.
|
Without loss of generality, we can assume that $a_{1} \leq a_{2} \leq \cdots \leq a_{2 n}$. We distinguish two cases:
- If $a_{n}+a_{2 n-1} \geq 0$ then we have $a_{i}+a_{2 n-1} \geq 0$ for $i=n, \cdots, 2 n-2$, and $a_{i}+a_{2 n} \geq 0$ for $i=n \cdots, 2 n-1$. This provides at least $2 n-1$ non-negative sums.
- If $a_{n}+a_{2 n-1}<0$ then
$$
a_{1}+\cdots+a_{n-1}+a_{n+1}+\cdots a_{2 n-2}+a_{2 n}>0
$$
On the other hand, we have $0>a_{n}+a_{2 n-1} \geq a_{n-1}+a_{2 n-2} \geq \cdots \geq a_{2}+a_{n+1}$, so
$$
a_{2}+a_{3}+\cdots+a_{n-1}+a_{n+1}+\cdots+a_{2 n-2}<0
$$
From (1) and (2), we deduce that $a_{1}+a_{2 n} \geq 0$, which ensures that $a_{i}+a_{2 n} \geq 0$ for $i=1, \cdots 2 n-1$.
Another solution. Let $b_{1} \leqslant b_{2} \leqslant \cdots \leqslant b_{\ell}$ be the non-negative integers among $a_{1}, \ldots, a_{2 n}$. First case: $\ell>n$. Then there are at least $\frac{\ell(\ell-1)}{2} \geq \frac{n(n+1)}{2}$ pairs $\left(a_{i}, a_{j}\right)$ with $i<j, a_{i} \geqslant 0$ and $a_{j} \geqslant 0$. Now, $\frac{n(n+1)}{2}-(2 n-1)=\frac{n^{2}-3 n+2}{2}=\frac{(n-1)(n-2)}{2} \geqslant 0$, so there are at least $2 n-1$ pairs $\left(a_{i}, a_{j}\right)$ with $i<j$ such that $a_{i}+a_{j} \geqslant 0$.
Second case: $\ell \leqslant n$. Let $c_{1} \leqslant \cdots \leqslant c_{\ell}$ be the smallest integers among $a_{1}, \ldots, a_{2 n}$. Since $\ell \leqslant n$, we have $c_{\ell}<0$. Moreover, $\sum_{i=1}^{2 n} a_{i}$ is equal to the sum of $\sum_{i=1}^{\ell}\left(b_{i}+c_{i}\right)$ and negative terms, so $\sum_{i=1}^{\ell}\left(b_{i}+c_{i}\right) \geqslant 0$. Now, $b_{\ell}+c_{\ell} \geqslant b_{i}+c_{i}$ for all $i$, so $b_{\ell}+c_{\ell} \geqslant 0$.
We thus form $2 n-\ell$ pairs $\left(a_{i}, a_{j}\right)$ by taking $a_{j}=b_{\ell}$ and $a_{i}$ other than $c_{1}, \ldots, c_{\ell-1}, b_{\ell}$.
Furthermore, for all $k=1, \ldots, \ell-1$, we have $\sum_{i=1}^{\ell}\left(b_{i}+c_{i+k}\right) \geqslant 0$ (where by convention $c_{\ell+1}=c_{1}$, $c_{\ell+2}=c_{2}$, etc.), so for all $k$ there exists $i$ such that $b_{i}+c_{i+k} \geqslant 0$. This provides $\ell-1$ additional pairs.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $a_{1}, a_{2}, \ldots, a_{2 n}$ des réels tels que $a_{1}+a_{2}+\cdots+a_{2 n}=0$.
Prouver qu'il existe au moins $2 n-1$ couples $\left(a_{i}, a_{j}\right)$ avec $i<j$ tels que $a_{i}+a_{j} \geqslant 0$.
|
Sans perte de généralité, on peut supposer que $a_{1} \leq a_{2} \leq \cdots \leq a_{2 n}$. On distingue deux cas :
- Si $a_{n}+a_{2 n-1} \geq 0$ alors on a $a_{i}+a_{2 n-1} \geq 0$ pour $i=n, \cdots, 2 n-2$, et $a_{i}+a_{2 n} \geq 0$ pour $i=n \cdots, 2 n-1$. Cela fournit bien $2 n-1$ sommes positives ou nulles.
- Si $a_{n}+a_{2 n-1}<0$ alors
$$
a_{1}+\cdots+a_{n-1}+a_{n+1}+\cdots a_{2 n-2}+a_{2 n}>0
$$
D'autre part, on a $0>a_{n}+a_{2 n-1} \geq a_{n-1}+a_{2 n-2} \geq \cdots \geq a_{2}+a_{n+1}$, donc
$$
a_{2}+a_{3}+\cdots+a_{n-1}+a_{n+1}+\cdots+a_{2 n-2}<0
$$
De (1) et (2), on déduit que $a_{1}+a_{2 n} \geq 0$, ce qui assure que $a_{i}+a_{2 n} \geq 0$ pour $i=1, \cdots 2 n-1$.
Autre solution. Notons $b_{1} \leqslant b_{2} \leqslant \cdots \leqslant b_{\ell}$ les entiers positifs ou nuls parmi $a_{1}, \ldots, a_{2 n}$. Premier cas: $\ell>n$. Alors il y a au moins $\frac{\ell(\ell-1)}{2} \geq \frac{n(n+1)}{2}$ couples $\left(a_{i}, a_{j}\right)$ avec $i<j, a_{i} \geqslant 0$ et $a_{j} \geqslant 0$. Or, $\frac{n(n+1)}{2}-(2 n-1)=\frac{n^{2}-3 n+2}{2}=\frac{(n-1)(n-2)}{2} \geqslant 0$, donc il y a au moins $2 n-1$ couples $\left(a_{i}, a_{j}\right)$ avec $i<j$ tels que $a_{i}+a_{j} \geqslant 0$.
Deuxième cas : $\ell \leqslant n$. Notons $c_{1} \leqslant \cdots \leqslant c_{\ell}$ les plus petits entiers parmi $a_{1}, \ldots, a_{2 n}$. Comme $\ell \leqslant n$, on a $c_{\ell}<0$. De plus, $\sum_{i=1}^{2 n} a_{i}$ est égal à la somme de $\sum_{i=1}^{\ell}\left(b_{i}+c_{i}\right)$ et de termes négatifs, donc $\sum_{i=1}^{\ell}\left(b_{i}+c_{i}\right) \geqslant 0$. Or, $b_{\ell}+c_{\ell} \geqslant b_{i}+c_{i}$ pour tout $i$, donc $b_{\ell}+c_{\ell} \geqslant 0$.
On forme ainsi déjà $2 n-\ell$ couples $\left(a_{i}, a_{j}\right)$ en prenant $a_{j}=b_{\ell}$ et $a_{i}$ autre que $c_{1}, \ldots, c_{\ell-1}, b_{\ell}$.
De plus, pour tout $k=1, \ldots, \ell-1$, on a $\sum_{i=1}^{\ell}\left(b_{i}+c_{i+k}\right) \geqslant 0$ (où par convention $c_{\ell+1}=c_{1}$, $c_{\ell+2}=c_{2}$, etc.), donc pour tout $k$ il existe $i$ tel que $b_{i}+c_{i+k} \geqslant 0$. Ceci fournit encore $\ell-1$ couples supplémentaires.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2015-2016-ofm-2015-2016-test-decembre-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T1",
"year": "2015"
}
|
Let $ABC$ be a triangle with all angles acute, and $H$ its orthocenter. The bisectors of $\widehat{ABH}$ and $\widehat{ACH}$ intersect at a point $I$. Show that $I$ is collinear with the midpoints of $[BC]$ and $[AH]$.
|
Let $D, E, F$ be the feet of the altitudes, $O$ the center of the circumcircle, $M$ the midpoint of $[B C]$, and $N$ the midpoint of $[A H]$. We have $2 \overrightarrow{M N}=2 \overrightarrow{O N}-2 \overrightarrow{O M}=\overrightarrow{O A}+\overrightarrow{O H}-\overrightarrow{O B}-\overrightarrow{O C}$.
Since $\overrightarrow{O H}=\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}$, it follows that $\overrightarrow{M N}=\overrightarrow{O A}$. Therefore, it suffices to show that $(M I)$ is parallel to $(O A)$.
Since $B C F$ is a right triangle at $F$, the point $F$ lies on the circle centered at $M$ passing through $B$ and $C$. The same applies to point $E$. The angle bisector of $\widehat{A B H}$ passes through the midpoint of the arc $E F$, and similarly for the angle bisector of $\widehat{A C H}$, so $I$ is the midpoint of the arc $E F$. Denoting $C^{\prime}$ as the midpoint of $[A B]$, we deduce the angle equalities $(M I, M B)=2(C I, C B)=$ $(C E, C B)+(C F, C B)=(C A, C B)+(C F, A B)+(A B, C B)$.
On the other hand, $(O A, M B)=\left(O A, O C^{\prime}\right)+\left(O C^{\prime}, A B\right)+(A B, M B)=(C A, C B)+(C F, A B)+$ $(A B, C B)$ because $\left(O C^{\prime}\right)$ and $(C F)$ are parallel.
Therefore, $(O A, M B)=(M I, M B)$, which proves that $(O A)$ and $(M I)$ are parallel.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle dont tous les angles sont aigus, et $H$ son orthocentre. Les bissectrices de $\widehat{A B H}$ et $\widehat{A C H}$ se coupent en un point $I$. Montrer que $I$ est aligné avec les milieux de $[B C]$ et de $[A H]$.
|
Notons $D, E, F$ les pieds des hauteurs, $O$ le centre du cercle circonscrit, $M$ le milieu de $[B C]$ et $N$ le milieu de $[A H]$. On a $2 \overrightarrow{M N}=2 \overrightarrow{O N}-2 \overrightarrow{O M}=\overrightarrow{O A}+\overrightarrow{O H}-\overrightarrow{O B}-\overrightarrow{O C}$.
Or, $\overrightarrow{O H}=\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}$ donc $\overrightarrow{M N}=\overrightarrow{O A}$. Par conséquent, il suffit de montrer que ( $M I$ ) est parallèle à $(O A)$.
Comme $B C F$ est un triangle rectangle en $F$, le point $F$ est situé sur le cercle de centre $M$ passant par $B$ et $C$. Il en va de même pour le point $E$. La bissectrice de $\widehat{A B H}$ passe par le milieu de l'arc $E F$, et de même pour la bissectrice de $\widehat{A C H}$, donc $I$ est le milieu de l'arc $E F$. En notant $C^{\prime}$ le milieu de $[A B]$, on en déduit les égalités d'angles de droites $(M I, M B)=2(C I, C B)=$ $(C E, C B)+(C F, C B)=(C A, C B)+(C F, A B)+(A B, C B)$.
D'autre part, $(O A, M B)=\left(O A, O C^{\prime}\right)+\left(O C^{\prime}, A B\right)+(A B, M B)=(C A, C B)+(C F, A B)+$ $(A B, C B)$ car $\left(O C^{\prime}\right)$ et $(C F)$ sont parallèles.
Par conséquent, $(O A, M B)=(M I, M B)$, ce qui prouve que $(O A)$ et $(M I)$ sont parallèles.
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2015-2016-ofm-2015-2016-test-decembre-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T1",
"year": "2015"
}
|
For any integer $n \in \mathbb{N}^{*}$, we denote $v_{3}(n)$ as the 3-adic valuation of $n$, which is the greatest integer $k$ such that $n$ is divisible by $3^{k}$. We set $u_{1}=2$ and $u_{n}=4 v_{3}(n)+2-\frac{2}{u_{n-1}}$ for all $n \geqslant 2$ (provided that $u_{n-1}$ is defined and non-zero).
Show that, for any positive rational number $q$, there exists a unique integer $n \geqslant 1$ such that $u_{n}=q$.
|
First, note that $u_{1}=2, u_{2}=1, u_{3}=3, u_{4}=\frac{3}{2}, u_{5}=\frac{2}{3}$ and $u_{6}=3$. We prove by induction that, for all integers $n \geq 2$, we have $0<u_{n}$ and
$$
0<u_{3 n-1}<1<u_{3 n-2}<2<u_{3 n}=2+u_{n}:
$$
this is already true for $n=2$.
Since $u_{3 n}=u_{n}+2$, we show successively that $u_{3 n+1}, u_{3 n+2}$ and $u_{3 n+3}$ are well defined, with
$$
\begin{aligned}
& u_{3 n+1}=2-\frac{2}{u_{3 n}}=1+\frac{u_{n}}{2+u_{n}}, \text { so } 1<u_{3 n+1}<2 ; \\
& u_{3 n+2}=2-\frac{2}{u_{3 n+1}}=1+\frac{u_{n}}{1+u_{n}}, \text { so } 0<u_{3 n+2}<1 ; \\
& u_{3 n+3}=4 v_{3}(3(n+1))+2-\frac{2}{u_{3 n+2}}=4 v_{3}(n)+4-\frac{2}{u_{n}}=2+u_{n+1} .
\end{aligned}
$$
This concludes the induction.
Now, consider the function $\varphi:\{x \in \mathbb{Q}: 0<x$ and $x \notin\{1,2\}\} \mapsto\{x \in \mathbb{Q}: 0<x\}$ such that
$$
\begin{aligned}
\varphi: & x \mapsto \frac{x}{1-x} \text { if } 0<x<1 ; \\
& x \mapsto 2 \frac{x-1}{2-x} \text { if } 1<x<2 ; \\
& x \mapsto x-2 \text { if } 2<x
\end{aligned}
$$
Furthermore, for any irreducible fraction $\frac{p}{q}$, with $p \geq 0$ and $q>0$, we set $\left\|\frac{p}{q}\right\|=p+q$. Then:
- $\left\|\varphi\left(\frac{p}{q}\right)\right\|=\left\|\frac{p}{q-p}\right\|=p<p+q=\left\|\frac{p}{q}\right\|$ if $0<p<q$;
- $\left\|\varphi\left(1+\frac{p}{q}\right)\right\|=\left\|2 \frac{p}{q-p}\right\| \leq 2 q<(p+q)+q=\left\|1+\frac{p}{q}\right\|$ if $0<p<q$;
- $\left\|\varphi\left(2+\frac{p}{q}\right)\right\|=\left\|\frac{p}{q}\right\|=p+q<(p+2 q)+q=\left\|2+\frac{p}{q}\right\|$ if $0<p$ and $0<q$.
In all cases, if $x$ is a positive rational number such that $x \notin\{1,2\}$, we have $\|\varphi(x)\|<\|x\|$. Now, for any positive rational number $x$ and for all integers $n \geq 1$:
- if $0<x<1$, then $u_{n}=\varphi(x) \Leftrightarrow u_{3 n+2}=x$;
- if $1<x<2$, then $u_{n}=\varphi(x) \Leftrightarrow u_{3 n+1}=x$;
- if $2<x$, then $u_{n}=\varphi(x) \Leftrightarrow u_{3 n}=x$.
An induction on $\|x\|$ immediately shows that, for any positive rational number $x$, there exists a unique integer $n \geq 1$ such that $u_{n}=x$, which concludes the exercise.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Pour tout entier $n \in \mathbb{N}^{*}$, on note $v_{3}(n)$ la valuation 3 -adique de $n$, c'est-à-dire le plus grand entier $k$ tel que $n$ est divisible par $3^{k}$. On pose $u_{1}=2$ et $u_{n}=4 v_{3}(n)+2-\frac{2}{u_{n-1}}$ pour tout $n \geqslant 2$ (si tant est que $u_{n-1}$ soit défini et non nul).
Montrer que, pour tout nombre rationnel strictement positif $q$, il existe un et un seul entier $n \geqslant 1$ tel que $u_{n}=q$.
|
Tout d'abord, notons que $u_{1}=2, u_{2}=1, u_{3}=3, u_{4}=\frac{3}{2}, u_{5}=\frac{2}{3}$ et $u_{6}=3$. On prouve par récurrence que, pour tout entier $n \geq 2$, on a $0<u_{n}$ et
$$
0<u_{3 n-1}<1<u_{3 n-2}<2<u_{3 n}=2+u_{n}:
$$
c'est déjà vrai pour $n=2$.
Puisque $u_{3 n}=u_{n}+2$, on montre successivement que $u_{3 n+1}, u_{3 n+2}$ et $u_{3 n+3}$ sont bien définis, avec
$$
\begin{aligned}
& u_{3 n+1}=2-\frac{2}{u_{3 n}}=1+\frac{u_{n}}{2+u_{n}}, \text { donc } 1<u_{3 n+1}<2 ; \\
& u_{3 n+2}=2-\frac{2}{u_{3 n+1}}=1+\frac{u_{n}}{1+u_{n}}, \text { donc } 0<u_{3 n+2}<1 ; \\
& u_{3 n+3}=4 v_{3}(3(n+1))+2-\frac{2}{u_{3 n+2}}=4 v_{3}(n)+4-\frac{2}{u_{n}}=2+u_{n+1} .
\end{aligned}
$$
Ceci conclut la récurrence.
Maintenant, considérons la fonction $\varphi:\{x \in \mathbb{Q}: 0<x$ et $x \notin\{1,2\}\} \mapsto\{x \in \mathbb{Q}: 0<x\}$ telle que
$$
\begin{aligned}
\varphi: & x \mapsto \frac{x}{1-x} \text { si } 0<x<1 ; \\
& x \mapsto 2 \frac{x-1}{2-x} \text { si } 1<x<2 ; \\
& x \mapsto x-2 \text { si } 2<x
\end{aligned}
$$
En outre, pour toute fraction irréductible $\frac{p}{q}$, avec $p \geq 0$ et $q>0$, on pose $\left\|\frac{p}{q}\right\|=p+q$. Alors :
- $\left\|\varphi\left(\frac{p}{q}\right)\right\|=\left\|\frac{p}{q-p}\right\|=p<p+q=\left\|\frac{p}{q}\right\|$ si $0<p<q$ ;
- $\left\|\varphi\left(1+\frac{p}{q}\right)\right\|=\left\|2 \frac{p}{q-p}\right\| \leq 2 q<(p+q)+q=\left\|1+\frac{p}{q}\right\|$ si $0<p<q$ ;
- $\left\|\varphi\left(2+\frac{p}{q}\right)\right\|=\left\|\frac{p}{q}\right\|=p+q<(p+2 q)+q=\left\|2+\frac{p}{q}\right\|$ si $0<p$ et $0<q$.
Dans tous les cas, si $x$ est un rationnel strictement positif tel que $x \notin\{1,2\}$, on a $\|\varphi(x)\|<\|x\|$. Or, pour tout rationnel strictement positif $x$ et pour tout entier $n \geq 1$ :
- si $0<x<1$, alors $u_{n}=\varphi(x) \Leftrightarrow u_{3 n+2}=x ;$
- si $1<x<2$, alors $u_{n}=\varphi(x) \Leftrightarrow u_{3 n+1}=x$;
- si $2<x$, alors $u_{n}=\varphi(x) \Leftrightarrow u_{3 n}=x$.
Une récurrence sur $\|x\|$ montre donc immédiatement que, pour tout rationnel strictement positif $x$, il existe un entier unique entier $n \geq 1$ tel que $u_{n}=x$, ce qui conclut l'exercice.
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2015-2016-ofm-2015-2016-test-decembre-corrige.jsonl",
"solution_match": "## Solution de l'exercice 3",
"tier": "T1",
"year": "2015"
}
|
Prove that for all integers $n \geq 2$, we have: $\sum_{k=2}^{n} \frac{1}{\sqrt[k]{(2 k)!}} \geq \frac{n-1}{2 n+2}$.
N.B. If $a>0$, we denote $\sqrt[k]{a}$ the unique positive real number $b$ such that $b^{k}=a$.
|
We reason by induction on $n \geq 2$.
For $n=2$, we have $\frac{1}{\sqrt{24}} > \frac{1}{6}$.
Suppose the desired inequality holds for the value $n-1 \geq 2$. For the value $n$, the right-hand side increases by $\frac{n-1}{2 n+2} - \frac{n-2}{2 n} = \frac{1}{n(n+1)}$.
According to the induction hypothesis, it suffices to prove that $\frac{1}{\sqrt[n]{(2 n)!}} \geq \frac{1}{n(n+1)}$.
For $k=1,2, \cdots, n$, we have $(n-k)(n-k+1) \geq 0$, so $0 \leq k(2 n-k+1) \leq n(n+1)$.
By multiplying these inequalities term by term, we get $(2 n)! \leq (n(n+1))^{n}$, from which the conclusion follows.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prouver que, pour tout entier $n \geq 2$, on a : $\sum_{k=2}^{n} \frac{1}{\sqrt[k]{(2 k)!}} \geq \frac{n-1}{2 n+2}$.
N.B. Si $a>0$, on note $\sqrt[k]{a}$ l'unique nombre réel $b>0$ tel que $b^{k}=a$.
|
On raisonne par récurrence sur $n \geq 2$.
Pour $n=2$, on a bien $\frac{1}{\sqrt{24}}>\frac{1}{6}$.
Supposons que l'inégalité désirée soit vraie pour la valeur $n-1 \geq 2$. Pour la valeur $n$, le membre de droite augmente de $\frac{n-1}{2 n+2}-\frac{n-2}{2 n}=\frac{1}{n(n+1)}$.
D'après l'hypothèse de récurrence, il suffit donc de prouver que $\frac{1}{\sqrt[n]{(2 n)!}} \geq \frac{1}{n(n+1)}$.
Or, pour $k=1,2, \cdots, n$, on a $(n-k)(n-k+1) \geq 0$, donc $0 \leq k(2 n-k+1) \leq n(n+1)$.
En multipliant ces inégalités membre à membre, il vient $(2 n)!\leq(n(n+1))^{n}$, $\mathrm{d}^{\prime}$ où la conclusion.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2015-2016-ofm-2015-2016-test-fevrier-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T1",
"year": "2015"
}
|
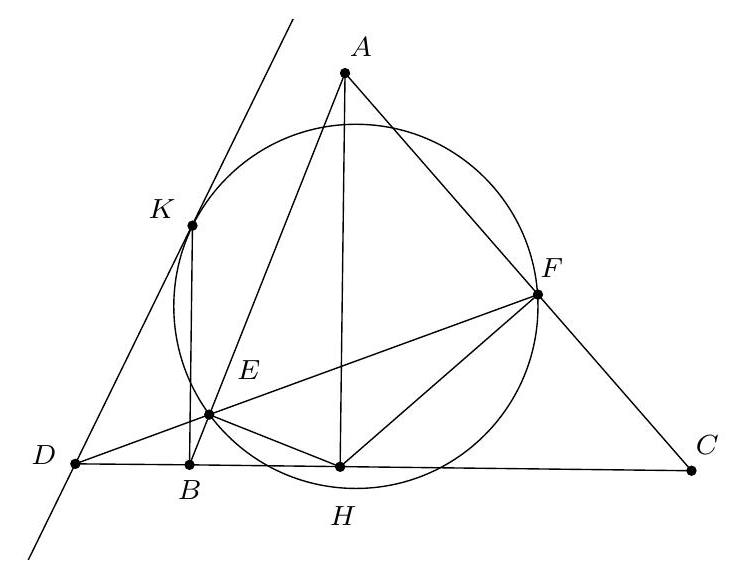
Let $ABC$ be a non-right triangle such that $AB < AC$. We denote $H$ as the projection of $A$ onto $(BC)$, and $E, F$ as the projections of $H$ onto $(AB)$ and $(AC)$, respectively. The line $(EF)$ intersects $(BC)$ at point $D$. Consider the semicircle with diameter $[CD]$ located in the same half-plane delimited by $(CD)$ as $A$. Let $K$ be the point on this semicircle that projects onto $B$. Show that $(DK)$ is tangent to the circle $KEF$.
|
As $A E H F$ are concyclic (on the circle with diameter $[A H]$), we have $(E F, E A)=(H F, H A)=$ $(H F, C A)+(C A, C B)+(C B, H A)=(C A, C B)=(C F, C B)$, so $(E F, E B)=(C F, C B)$. Therefore, $B, E, F, C$ are concyclic. From the power of a point with respect to a circle, we have $D E \cdot D F=D B \cdot D C$. On the other hand, since $D K C$ is a right triangle at $K$, the triangles $D K B$ and $D C K$ are similar, which implies $\frac{D K}{D B}=\frac{D C}{D K}$, or equivalently $D K^{2}=D B \cdot D C$.
Thus, $D K^{2}=D E \cdot D F$, and therefore, from the power of $D$ with respect to the circle $K E F$, we conclude that $(D K)$ is tangent to the circle $K E F$ at $K$.
Remark: The choice of the semicircle is not important.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle non rectangle tel que $A B<A C$. On note $H$ le projeté de $A$ sur $(B C)$, et $E, F$ les projetés respectifs de $H$ sur $(A B)$ et $(A C)$. La droite $(E F)$ coupe $(B C)$ au point $D$. On considère le demi-cercle de diamètre $[C D]$ situé dans le même demi-plan délimité par $(C D)$ que $A$. Soit $K$ le point de ce demi-cercle qui se projette sur $B$. Montrer que $(D K)$ est tangente au cercle $K E F$.
|
Comme $A E H F$ sont cocycliques (sur le cercle de diamètre $[A H]$ ), on a $(E F, E A)=(H F, H A)=$ $(H F, C A)+(C A, C B)+(C B, H A)=(C A, C B)=(C F, C B)$, donc $(E F, E B)=(C F, C B)$. Par conséquent, $B, E, F, C$ sont cocycliques. D'après la puissance d'un point par rapport à un cercle, on a $D E \cdot D F=D B \cdot D C$. D'autre part, comme $D K C$ est rectangle en $K$, les triangles $D K B$ et $D C K$ sont semblables, ce qui implique $\frac{D K}{D B}=\frac{D C}{D K}$, ou encore $D K^{2}=D B \cdot D C$.
Il vient $D K^{2}=D E \cdot D F$, et donc d'après la puissance de $D$ par rapport au cercle $K E F$, on en déduit que $(D K)$ est tangente en $K$ au cercle $K E F$.
Remarque : le choix du demi-cercle n'a pas d'importance.
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2015-2016-ofm-2015-2016-test-fevrier-corrige.jsonl",
"solution_match": "## Solution de l'exercice 2",
"tier": "T1",
"year": "2015"
}
|
Let $n \geq 1$ be an integer. A group of $2 n$ people meet. Each of these people has at least $n$ friends in this group (in particular, if $A$ is a friend of $B$ then $B$ is a friend of $A$, and one is not a friend with oneself). Prove that it is possible to arrange these $2 n$ people around a round table so that each person is between two of their friends.
|
Consider an arbitrary arrangement of guests:
AB.... $A$.
where $A, B$ denote different people, but the two $A$s represent the same person (we are around a round table).
In what follows, we will consider the arrangement as a sequence of people, ordered from left to right.
If two neighbors are not friends, we will say that it is a tension.
If there is no tension, it is over.
If there is a tension, by circular symmetry, we can always assume that $A$ and $B$ are not friends.
Since $B$ has at least $n$ friends, plus himself, we deduce that $B$ has at most $n-1$ "enemies".
Suppose that in the arrangement above and after $B$, we never find two neighbors $A'$ and $B'$ (in this order) who are friends respectively of $A$ and $B$.
Then, since such an arrangement does not occur before $B$ either, we deduce that it never appears, and therefore to the right of each friend of $A$ must be an enemy of $B$. Thus, the number of enemies of $B$ is at least equal to the number of friends of $A$, which implies $n-1 \geq n$. Contradiction.
Therefore, we can find two neighbors $A'$ and $B'$ (in this order) who are friends respectively of $A$ and $B$.
The arrangement is then of the form:
$$
A B \ldots A' B' \ldots A
$$
Under these conditions, we can eliminate the tension between $A$ and $B$ by reversing the order of the people between $B$ and $A'$:
$$
A\left(B \ldots A'\right) B' \ldots A \rightarrow A\left(A' \ldots B\right) B' \ldots A
$$
This provides a new arrangement but with at least one less tension than in the previous one, since clearly the modification does not create any new tension (however, it can eliminate a potential tension between $A'$ and $B'$).
By repeating this procedure as many times as necessary (a finite number of times in any case, since the initial number of tensions is finite), we eliminate all tensions, and the goal is achieved.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soit $n \geq 1$ un entier. Un groupe de $2 n$ personnes se réunit. Chacune de ces personnes possède au moins $n$ amies dans ce groupe (en particulier, si $A$ est amie avec $B$ alors $B$ est amie avec $A$, et on n'est pas ami avec soi-même). Prouver que l'on peut disposer ces $2 n$ personnes autour d'une table ronde de sorte que chacune soit entre deux de ses amies.
|
Considérons une disposition arbitraire des invités :
AB.... $A$.
où $A, B$ désignent des personnes différentes, mais les deux $A$ représentent la même personne (on est autour d'une table ronde).
Dans ce qui suit, on considérera la disposition comme une suite de personnes, ordonnée de gauche à droite.
Si deux voisins ne sont pas amis, on dira que c'est une tension.
S'il n'y a aucune tension, c'est fini.
S'il existe une tension, par symétrie circulaire, on peut toujours supposer que $A$ et $B$ ne sont pas amis.
Comme $B$ a au moins $n$ amis, plus lui-même, on en déduit que $B$ a au plus $n-1$ "ennemis".
Supposons que dans la disposition ci-dessus et après $B$, on ne trouve jamais deux voisins $A^{\prime}$ et $B^{\prime}$ (dans cet ordre) qui sont amies respectivement de $A$ et de $B$.
Alors, comme une telle disposition n'arrive pas non plus avant $B$, on en déduit qu'elle n'apparaît jamais, et donc qu'à droite de chaque ami de $A$ doit se trouver un ennemi de $B$. Donc, le nombre d'ennemis de $B$ est au moins égal au nombre d'amis de $A$, ce qui implique $n-1 \geq n$. Contradiction.
Par suite, on peut trouver deux voisins $A^{\prime}$ et $B^{\prime}$ (dans cet ordre) qui sont amies respectivement de $A$ et de $B$.
La disposition est alors de la forme :
$$
A B \ldots A^{\prime} B^{\prime} \ldots A
$$
Dans ces conditions, on peut éliminer la tension entre $A$ et $B$ en renversant l'ordre des personnes entre $B$ et $A^{\prime}$ :
$$
A\left(B \ldots A^{\prime}\right) B^{\prime} \ldots A \rightarrow A\left(A^{\prime} \ldots B\right) B^{\prime} \ldots A
$$
Cela fournit une nouvelle disposition mais avec au moins une tension de moins que dans la précédente, puisque clairement la modification ne crée pas de nouvelle tension (par contre, elle peut éliminer une tension éventuelle entre $A^{\prime}$ et $B^{\prime}$ ).
En répétant cette procédure autant que nécessaire (un nombre fini de fois en tout cas, puisque le nombre initial de tensions est fini), on fait disparaître toutes les tensions, et l'objectif est atteint.
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2015-2016-ofm-2015-2016-test-fevrier-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T1",
"year": "2015"
}
|
The cells of a 10 by 10 grid are colored in white and black. A coloring of these cells is said to be homogeneous if it contains a $3 \times 3$ monochromatic square, and inhomogeneous otherwise. Show that there are more inhomogeneous colorings than homogeneous colorings.
|
There are $2^{100}$ possible colorings. If $c$ is a $3 \times 3$ square, the number of colorings such that $c$ is monochrome is equal to $2 \times 2^{91}=2^{92}$. There are 64 $3 \times 3$ squares, so there are at most $64 \times 2^{92}=2^{98}$ homogeneous colorings.
|
2^{98}
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Les cases d'une grille à 10 lignes et 10 colonnes sont coloriées en blanc et en noir. Un coloriage de ces cases est dit homogène s'il contient un carré $3 \times 3$ monochrome, et inhomogène sinon. Montrer qu'il existe plus de coloriages inhomogènes que de coloriages homogènes.
|
Il y a $2^{100}$ coloriages possibles. Si $c$ est un carré $3 \times 3$, le nombre de coloriages tels que $c$ soit monochrome est égal à $2 \times 2^{91}=2^{92}$. Or, il y a 64 carrés $3 \times 3$, donc il y a au plus $64 \times 2^{92}=2^{98}$ coloriages homogènes.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2015-2016-ofm-2015-2016-test-fevrier-junior-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T1",
"year": "2015"
}
|
Show that if $a, b, c$ are positive real numbers satisfying $a+b+c=1$ then
$$
\frac{7+2 b}{1+a}+\frac{7+2 c}{1+b}+\frac{7+2 a}{1+c} \geqslant \frac{69}{4}
$$
|
Given $7+2 b=5+2(1+b)$, we write the left-hand side in the form
$$
5\left(\frac{1}{1+a}+\frac{1}{1+b}+\frac{1}{1+c}\right)+2\left(\frac{1+b}{1+a}+\frac{1+c}{1+b}+\frac{1+a}{1+c}\right)
$$
Using the inequality $\frac{1}{x}+\frac{1}{y}+\frac{1}{z} \geqslant \frac{9}{x+y+z}$, we bound the first term from below by $\frac{45}{4}$.
Using the inequality $x+y+z \geqslant 3 \sqrt[3]{x y z}$, we bound the second term from below by 6. The assertion to be proved follows.
|
\frac{69}{4}
|
Yes
|
Yes
|
proof
|
Inequalities
|
Montrer que si $a, b, c$ sont des nombres réels positifs vérifiant $a+b+c=1$ alors
$$
\frac{7+2 b}{1+a}+\frac{7+2 c}{1+b}+\frac{7+2 a}{1+c} \geqslant \frac{69}{4}
$$
|
Comme $7+2 b=5+2(1+b)$, on écrit le membre de gauche sous la forme
$$
5\left(\frac{1}{1+a}+\frac{1}{1+b}+\frac{1}{1+c}\right)+2\left(\frac{1+b}{1+a}+\frac{1+c}{1+b}+\frac{1+a}{1+c}\right)
$$
En utilisant l'inégalité $\frac{1}{x}+\frac{1}{y}+\frac{1}{z} \geqslant \frac{9}{x+y+z}$, on minore le premier terme par $\frac{45}{4}$.
En utilisant l'inégalité $x+y+z \geqslant 3 \sqrt[3]{x y z}$, on minore le second terme par 6 . L'assertion à démontrer en découle.
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2015-2016-ofm-2015-2016-test-fevrier-junior-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T1",
"year": "2015"
}
|
Let $ABC$ be a triangle, and $M$ the midpoint of $[BC]$. We denote $I_{b}$ and $I_{c}$ as the centers of the incircles of $AMB$ and $AMC$. Show that the second point of intersection of the circumcircles of triangles $ABI_{b}$ and $ACI_{c}$ lies on the line $(AM)$.
|
Let $T$ be the intersection between the circle with diameter $[B C]$ and the ray $\left[M A\right)$. It suffices to show that $T$ lies on the circle $A B I_{b}$ (by symmetry of the roles of $B$ and $C$, this will show that it also lies on the circle $A C I_{c}$).
Since $\widehat{B T C}$ is a right angle, we have $\widehat{A T B}=90^{\circ}+\frac{1}{2} \widehat{A M B}=\widehat{A I_{b} B}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle, et $M$ le milieu de $[B C]$. On note $I_{b}$ et $I_{c}$ les centres des cercles inscrits à $A M B$ et $A M C$. Montrer que le second point d'intersection des cercles circonscrits aux triangles $A B I_{b}$ et $A C I_{c}$ se situe sur la droite $(A M)$.
|
Soit $T$ l'intersection entre le cercle de diamètre $[B C]$ et la demi-droite $\left[M A\right.$ ). Il suffit de montrer que $T$ appartient au cercle $A B I_{b}$ (par symétrie des rôles de $B$ et $C$, ceci montrera qu'il appartient également au cercle $A C I_{c}$ ).
Comme $\widehat{B T C}$ est droit, on a $\widehat{A T B}=90^{\circ}+\frac{1}{2} \widehat{A M B}=\widehat{A I_{b} B}$.
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2015-2016-ofm-2015-2016-test-fevrier-junior-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T1",
"year": "2015"
}
|
Let $n \geqslant 1$ be an integer. Suppose there exist exactly 2005 pairs $(x, y)$ of natural numbers such that $\frac{1}{x}+\frac{1}{y}=\frac{1}{n}$. Show that $n$ is the square of an integer.
N.B. If $x \neq y$ then $(x, y) \neq(y, x)$.
|
We notice that $x>n$ and $y>n$.
The equation can be written as $xy=n(x+y)$, or equivalently $n^2=(x-n)(y-n)$. From this, we deduce that there are exactly 2005 pairs of natural numbers $(u, v)$ such that $n^2=uv$.
If $n^2=uv$ then $u$ is a divisor of $n^2$. Conversely, if $u$ is a divisor of $n^2$ then the equation $n^2=uv$ uniquely determines $v$. We deduce that $n^2$ has exactly 2005 divisors.
Let's write $n=p_1^{\alpha_1} \cdots p_r^{\alpha_r}$ with $p_i$ distinct primes and $\alpha_i$ integers. Therefore, $n^2=p_1^{2\alpha_1} \cdots p_r^{2\alpha_r}$. We know that the number of divisors of $n^2$ is equal to $(2\alpha_1+1) \cdots (2\alpha_r+1)$. The prime factorization of 2005 is $5 \times 401$, so either $r=1$ and $2\alpha_1+1=2005$, or $r=2$ and $2\alpha_1+1=5$, $2\alpha_2+1=401$. In all cases, the $\alpha_i$ are even, so $n$ is a perfect square.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $n \geqslant 1$ un entier. On suppose qu'il existe exactement 2005 couples $(x, y)$ d'entiers naturels tels que $\frac{1}{x}+\frac{1}{y}=\frac{1}{n}$. Montrer que $n$ est le carré d'un entier.
N.B. Si $x \neq y$ alors $(x, y) \neq(y, x)$.
|
On remarque que $x>n$ et $y>n$.
L'équation s'écrit $x y=n(x+y)$, ou encore $n^{2}=(x-n)(y-n)$. On en déduit qu'il y a exactement 2005 couples d'entiers naturels $(u, v)$ tels que $n^{2}=u v$.
Si $n^{2}=u v$ alors $u$ est un diviseur de $n^{2}$. Réciproquement, si $u$ est un diviseur de $n^{2}$ alors l'équation $n^{2}=u v$ détermine uniquement $v$. On en déduit que $n^{2}$ admet exactement 2005 diviseurs.
Ecrivons $n=p_{1}^{\alpha_{1}} \cdots p_{r}^{\alpha_{r}}$ avec $p_{i}$ premiers distincts et $\alpha_{i}$ entiers. On a donc $n^{2}=p_{1}^{2 \alpha_{1}} \cdots p_{r}^{2 \alpha_{r}}$. On sait que le nombre de diviseurs de $n^{2}$ est égal à $\left(2 \alpha_{1}+1\right) \cdots\left(2 \alpha_{r}+1\right)$. Or, la décomposition en facteurs premiers de 2005 est $5 \times 401$, donc soit $r=1$ et $2 \alpha_{1}+1=2005$, soit $r=2$ et $2 \alpha_{1}+1=5$, $2 \alpha_{2}+1=401$. Dans tous les cas, les $\alpha_{i}$ sont pairs donc $n$ est un carré parfait.
|
{
"exam": "French_tests",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/tests/fr-2015-2016-ofm-2015-2016-test-fevrier-junior-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T1",
"year": "2015"
}
|
Let $ABC$ be an isosceles triangle at $A$, where the angle at $A$ is not a right angle. Let $D$ be the point on $(BC)$ such that $(AD) \perp (AB)$. Let $E$ be the orthogonal projection of $D$ onto $(AC)$. Finally, let $H$ be the midpoint of $[BC]$. Show that $AH = HE$.
|
First, since the angles $\widehat{A H D}$ and $\widehat{A E D}$ are right angles, the points $A, H, E, D$ lie on the circle with diameter $[A D]$.
Let $\theta=\widehat{C B A}=\widehat{A C B}$. Since $A H C$ is a right triangle at $H$, $\widehat{H A C}=90^{\circ}-\theta$. Since $B A D$ is a right triangle at $A$, $\widehat{A D B}=90^{\circ}-\theta$, and thus $\widehat{A D H}=\widehat{H A E}$.
By the cocyclicity of $A, H, E, D$, the angles $\widehat{A D H}$ and $\widehat{A E H}$ are equal or supplementary, so $\widehat{H A E}=\widehat{A E H}$ or $\widehat{H A E}+\widehat{A E H}=180^{\circ}$.
The second case cannot occur because the sum of the angles in triangle $A E H$ is $180^{\circ}$, so we have $\widehat{H A E}=\widehat{A E H}$. This implies that $H A E$ is isosceles at $H$, hence $H A=H E$.
Another approach using angles between lines. We know that if $T$ is a tangent at a point $A$ to a circle $(C)$ and if $B$ and $M$ are two other points on $(C)$, then $(T, A B)=(M A, M B)$.
In the problem, since $(A B)$ is perpendicular to the diameter $(A D)$, it is tangent to the circle. Therefore, from the above, we have $(A B, A H)=(E A, E H)$. Since $A B C$ is isosceles, we have $(A B, A H)=(A H, A C)$, so $(A H, A E)=(A H, A C)=(A B, A H)=(E A, E H)$. We conclude that $H A E$ is isosceles at $H$, hence $H A=H E$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle isocèle en $A$, dont l'angle en $A$ n'est pas droit. Soit $D$ le point de $(B C)$ tel que $(A D) \perp(A B)$. Soit $E$ le projeté orthogonal de $D$ sur $(A C)$. Soit enfin $H$ le milieu de $[B C]$. Montrer que $A H=H E$.
|
Tout d'abord, comme les angles $\widehat{A H D}$ et $\widehat{A E D}$ sont droits, les points $A, H, E, D$ sont sur le cercle de diamètre $[A D]$.
Notons $\theta=\widehat{C B A}=\widehat{A C B}$. Comme $A H C$ est rectangle en $H, \widehat{H A C}=90^{\circ}-\theta$. Comme $B A D$ est rectangle en $A, \widehat{A D B}=90^{\circ}-\theta$, et donc $\widehat{A D H}=\widehat{H A E}$.
Par cocyclicité de $A, H, E, D$, les angles $\widehat{A D H}$ et $\widehat{A E H}$ sont égaux ou supplémentaires, donc $\widehat{H A E}=\widehat{A E H}$ ou $\widehat{H A E}+\widehat{A E H}=180^{\circ}$.
Le deuxième cas ne peut pas se produire car la somme des angles du triangle $A E H$ vaut $180^{\circ}$, donc on a $\widehat{H A E}=\widehat{A E H}$. On en déduit que $H A E$ est isocèle en $H$, d'où $H A=H E$.
Autre approche avec les angles de droites. On sait que si $T$ est une tangente en un point $A$ à un cercle $(C)$ et si $B$ et $M$ sont deux autres points de $(C)$, alors $(T, A B)=(M A, M B)$.
Dans l'exercice, comme $(A B)$ est perpendiculaire au diamètre $(A D)$, elle est tangente au cercle donc d'après ce qui précède on a $(A B, A H)=(E A, E H)$. Or, comme $A B C$ est isocèle on a $(A B, A H)=(A H, A C)$ donc $(A H, A E)=(A H, A C)=(A B, A H)=(E A, E H)$. On en conclut que $H A E$ est isocèle en $H$, d'où $H A=H E$.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2015-2016-ofm-2015-2016-test-janvier-corrige.jsonl",
"solution_match": "## Solution de l'exercice 1",
"tier": "T1",
"year": "2015"
}
|
Find all integers $m \geqslant 1$ and $n \geqslant 1$ such that $\frac{5^{m}+2^{n+1}}{5^{m}-2^{n+1}}$ is the square of an integer.
|
The following demonstration is valid for $m, n \in \mathbb{N}$.
First, $5^{m}-2^{n+1}$ must divide $5^{m}+2^{n+1}$, so it divides $5^{m}+2^{n+1}-(5^{m}-2^{n+1})=2^{n+2}$, therefore it is a power of 2. However, $5^{m}-2^{n+1}$ is odd, so $5^{m}-2^{n+1}=1$.
Let's write $5^{m}+2^{n+1}=a^{2}$. We then have $(a-1)(a+1)=a^{2}-1=5^{m}+2^{n+1}-5^{m}+2^{n+1}=2^{n+2}$, so $a-1$ and $a+1$ are powers of 2.
Let's write $a-1=2^{c}$ and $a+1=2^{d}$ with $c+d=n+2$. Then $c<d$ so $a-1=2^{c}$ divides $2^{d}-2^{c}=(a+1)-(a-1)=2$, thus $a-1=1$ or $a-1=2$.
If $a=2$ then $2^{d}=a+1=3$, which is impossible.
We deduce that $a=3, c=1, d=2$ and $n+2=3$, which gives $n=1$ and $5^{m}=1+2^{n+1}=5$, then $m=1$.
Finally, $m=n=1$.
|
m=n=1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Trouver tous les entiers $m \geqslant 1$ et $n \geqslant 1$ tels que $\frac{5^{m}+2^{n+1}}{5^{m}-2^{n+1}}$ soit le carré d'un entier.
|
La démonstration qui suit est valable pour $m, n \in \mathbb{N}$.
Déjà, $5^{m}-2^{n+1}$ doit diviser $5^{m}+2^{n+1}$, donc divise $5^{m}+2^{n+1}-\left(5^{m}-2^{n+1}\right)=2^{n+2}$, par conséquent c'est une puissance de 2 . Or, $5^{m}-2^{n+1}$ est impair, donc $5^{m}-2^{n+1}=1$.
Ecrivons $5^{m}+2^{n+1}=a^{2}$. On a donc $(a-1)(a+1)=a^{2}-1=5^{m}+2^{n+1}-5^{m}+2^{n+1}=2^{n+2}$, donc $a-1$ et $a+1$ sont des puissances de 2 .
Ecrivons $a-1=2^{c}$ et $a+1=2^{d}$ avec $c+d=n+2$. Alors $c<d$ donc $a-1=2^{c}$ divise $2^{d}-2^{c}=(a+1)-(a-1)=2$, donc $a-1=1$ ou $a-1=2$.
Si $a=2$ alors $2^{d}=a+1=3$, ce qui est impossible.
On en déduit que $a=3, c=1, d=2$ et $n+2=3$, ce qui donne $n=1$ et $5^{m}=1+2^{n+1}=5$, puis $m=1$.
Finalement, $m=n=1$.
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2015-2016-ofm-2015-2016-test-janvier-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T1",
"year": "2015"
}
|
Consider 7 islands $A_{1}, \ldots, A_{7}$. We are allowed to build bridges, either between an island $A_{i}$ and the next island $A_{i+1}$ (for $i \in\{1,2, \ldots, 6\}$), or between an island $A_{i}$ and the last one $A_{7}$ (for $i \in\{1,2, \ldots, 6\}$). In how many ways can these constructions be carried out with the minimum number of bridges so that one can travel from any island to any other?
Example for 3 islands instead of 7: the three possible constructions using two bridges are
1) a bridge between $A_{1}$ and $A_{2}$, and a bridge between $A_{1}$ and $A_{3}$
2) a bridge between $A_{1}$ and $A_{2}$, and a bridge between $A_{2}$ and $A_{3}$
3) a bridge between $A_{1}$ and $A_{3}$, and a bridge between $A_{2}$ and $A_{3}$.
|
A configuration will be considered good if it satisfies the conditions of the statement.
Let $a_{n}$ be the number of good configurations with $n$ islands. We have $a_{1}=a_{2}=1$ and $a_{3}=3$.
Starting from a good configuration with $n$ islands such that $A_{n-1}$ and $A_{n}$ are not connected, then $A_{n-1}$ and $A_{n-2}$ are necessarily connected, so if we remove the island $A_{n-1}$, we obtain a good configuration with $n-1$ islands. Conversely, any good configuration with $n-1$ islands comes from one and only one good configuration with $n$ islands where the last two are not connected: it is indeed sufficient to interpose an island between the last two and to place a bridge between it and the $n$ - 2-nd.
We deduce that there are $a_{n-1}$ good configurations with $n$ islands such that $A_{n-1}$ and $A_{n}$ are not connected.
On the other hand, starting from a good configuration with bridges between $A_{n}$ and $A_{n-1}, A_{n-1}$ and $A_{n-2}, \ldots$, $A_{n-k+1}$ and $A_{n-k}(k \geqslant 1)$ but not between $A_{n-k}$ and $A_{n_{k}-1}$, if we remove the islands $A_{n-1}, \ldots, A_{n-k}$, then we obtain a good configuration with $n-k$ islands. We deduce as above that there are $a_{n-1}+a_{n-2}+\cdots+a_{1}$ good configurations with a bridge between $A_{n}$ and $A_{n-1}$.
We see, therefore, that $a_{n}=2 a_{n-1}+a_{n-2}+\cdots+a_{1}$.
We deduce step by step that $a_{4}=8, a_{5}=21, a_{6}=55$ and $a_{7}=144$.
|
144
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On considère 7 îles $A_{1}, \ldots, A_{7}$. On est autorisé à construire des ponts, soit entre une île $A_{i}$ et l'île suivante $A_{i+1}$ (pour $i \in\{1,2, \ldots, 6\}$ ), soit entre une île $A_{i}$ et la dernière $A_{7}$ (pour $i \in\{1,2, \ldots, 6\}$ ). De combien de manières peut-on réaliser ces constructions avec le moins de ponts possibles de sorte que l'on puisse se rendre d'une île vers n'importe quelle autre ?
Exemple pour 3 îles au lieu de 7 : les trois constructions possibles utilisant deux ponts sont 1) un pont entre $A_{1}$ et $A_{2}$, et un pont entre $A_{1}$ et $A_{3}$
2) un pont entre $A_{1}$ et $A_{2}$, et un pont entre $A_{2}$ et $A_{3}$
3) un pont entre $A_{1}$ et $A_{3}$, et un pont entre $A_{2}$ et $A_{3}$.
|
On dira qu'une configuration est bonne si elle satisfait les conditions de l'énoncé.
Notons $a_{n}$ le nombre de bonnes configurations avec $n$ îles. On a $a_{1}=a_{2}=1$ et $a_{3}=3$.
Partant d'une bonne configuration avec $n$ îles telle que $A_{n-1}$ et $A_{n}$ ne soient pas reliées, alors $A_{n-1}$ et $A_{n-2}$ sont nécessairement reliées, donc si on supprime l'île $A_{n-1}$ on obtient une bonne configuration avec $n-1$ îles. Réciproquement, toute bonne configuration avec $n-1$ îles provient d'une et une seule bonne configuration avec $n$ îles dont les deux dernières ne sont pas reliées : il suffit en effet d'intercaler une île entre les deux dernières et de mettre un pont entre celle-ci et la $n$ - 2-ième.
On en déduit qu'il y a $a_{n-1}$ bonnes configurations avec $n$ îles telles que $A_{n-1}$ et $A_{n}$ ne soient pas reliées.
D'autre part, partant d'une bonne configuration avec des ponts entre $A_{n}$ et $A_{n-1}, A_{n-1}$ et $A_{n-2}, \ldots$, $A_{n-k+1}$ et $A_{n-k}(k \geqslant 1)$ mais pas entre $A_{n-k}$ et $A_{n_{k}-1}$, si on supprime les îles $A_{n-1}, \ldots, A_{n-k}$ alors on obtient une bonne configuration avec $n-k$ îles. On en déduit comme ci-dessus qu'il y a $a_{n-1}+a_{n-2}+\cdots+a_{1}$ bonnes configurations comportant un pont entre $A_{n}$ et $A_{n-1}$.
On voit donc que $a_{n}=2 a_{n-1}+a_{n-2}+\cdots+a_{1}$.
On en déduit de proche en proche que $a_{4}=8, a_{5}=21, a_{6}=55$ et $a_{7}=144$.
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2015-2016-ofm-2015-2016-test-janvier-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T1",
"year": "2015"
}
|
Determine all functions $f$ from $\mathbb{R}$ to $\mathbb{R}$ such that, for all real $x$ and $y$, the following equality holds:
$$
f(x+y)=f(x-y)+f(f(1-x y))
$$
|
For $y=0$ we find that $f(x)=f(x)+f(f(1))$ so $f(f(1))=0$. For $x=0$ we find $f(y)=f(-y)+f(f(1))$ so $f(y)=f(-y)$ for all $y$.
For $y=1$ we get $f(x+1)=f(x-1)+f(f(1-x))$. By replacing $x$ with $-x+2$, we get $f(-x+3)=f(-x+1)+f(f(x-1))$.
Since $f(x-1)=f(1-x)$, then $f(f(1-x))=f(f(x-1))$. Consequently, $f(x+1)=f(x-1)+f(-x+3)-f(-x+1)=f(x-3)$ because $f(-t)=f(t)$ for all $t$.
We deduce, by replacing $x$ with $x+1$, that $f(x+2)=f(x-2)$ for all $x$.
Take $y=2$ in the functional equation. We have $f(x+2)=f(x-2)+f(f(1-2x))$, so $f(f(1-2x))=0$ for all $x$. By replacing $x$ with $(1-t)/2$, we find that $f(f(t))=0$ for all $t$.
We return to the functional equation: $f(x+y)=f(x-y)+f(f(1-xy))$, so $f(x+y)=f(x-y)$ for all $x$ and $y$. We take $x=y=t/2$: we get $f(t)=f(0)$, so $f$ is constant. Since $f(f(1))=0$, this constant is zero, and finally $f(x)=0$ for all $x$.
|
f(x)=0
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Déterminer toutes les fonctions $f$ de $\mathbb{R}$ dans $\mathbb{R}$ telles que, pour tous $x$ et $y$ réels, on ait l'égalité
$$
f(x+y)=f(x-y)+f(f(1-x y))
$$
|
Pour $y=0$ on trouve que $f(x)=f(x)+f(f(1))$ donc $f(f(1))=0$. Pour $x=0$ on trouve $f(y)=f(-y)+f(f(1))$ donc $f(y)=f(-y)$ pour tout $y$.
Pour $y=1$ on obtient $f(x+1)=f(x-1)+f(f(1-x))$. En remplaçant $x$ par $-x+2$, il vient $f(-x+3)=f(-x+1)+f(f(x-1))$.
Or, $f(x-1)=f(1-x)$ donc $f(f(1-x))=f(f(x-1))$. Par conséquent, $f(x+1)=f(x-1)+$ $f(-x+3)-f(-x+1)=f(x-3)$ puisque $f(-t)=f(t)$ pour tout $t$.
On en déduit, en remplaçant $x$ par $x+1$, que $f(x+2)=f(x-2)$ pour tout $x$.
Prenons $y=2$ dans l'équation fonctionnelle. On a $f(x+2)=f(x-2)+f(f(1-2 x))$, donc $f(f(1-2 x))=0$ pour tout $x$. En remplaçant $x$ par $(1-t) / 2$, on trouve que $f(f(t))=0$ pour tout $r$.
On revient à l'équation fonctionnelle : $f(x+y)=f(x-y)+f(f(1-x y))$, donc $f(x+y)=f(x-y)$ pour tous $x$ et $y$. On prend $x=y=t / 2$ : il vient $f(t)=f(0)$, donc $f$ est constante. Comme $f(f(1))=0$, cette constante est nulle, et finalement $f(x)=0$ pour tout $x$.
|
{
"exam": "French_tests",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/tests/fr-2015-2016-ofm-2015-2016-test-janvier-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T1",
"year": "2015"
}
|
a) Find all integers $m \geqslant 1$ and $n \geqslant 1$ such that $\frac{5^{m}+2^{n+1}}{5^{m}-2^{n+1}}$ is the square of an integer.
b) More generally, find all integers $m \geqslant 1$ and $n \geqslant 1$, as well as the prime numbers $p$, such that $\frac{5^{m}+2^{n} p}{5^{m}-2^{n} p}$ is the square of an integer.
|
a) See exercise 2 above.
b) Suppose $p=5$. Then $\frac{5^{m-1}+2^{n}}{5^{m-1}-2^{n}}$ is the square of an integer. From part a) (which also works for integers $\geqslant 0$), we have $m=n=2$.
Suppose finally $p \neq 2$ and $p \neq 5$. Let $d$ be the GCD of $5^{m}+2^{n} p$ and $5^{m}-2^{n} p$. Then $d$ divides $5^{m}+2^{n} p+5^{m}-2^{n} p=2 \times 5^{m}$. Since $d$ is the GCD of two odd numbers, it is odd, so it divides $5^{m}$.
Moreover, $d$ divides $5^{m}+2^{n} p-\left(5^{m}-2^{n} p\right)=2^{n+1} p$ and it is odd, so it divides $p$. Since $p$ and 5 are coprime, we deduce that $d=1$ and that $5^{m}-2^{n} p=1$; furthermore, $5^{m}+2^{n} p=a^{2}$ for some integer $a$.
We thus have $(a-1)(a+1)=a^{2}-1=2^{n+1} p$.
The GCD of $a-1$ and $a+1$ divides $(a+1)-(a-1)=2$, so it is 1 or 2. Moreover, $a-1$ and $a+1$ are of the same parity, and their product is even, so their GCD is 2. We deduce that $\left(a-1=2, a+1=2^{n} p\right)$ or $\left(a-1=2 p, a+1=2^{n}\right)$ or $\left(a-1=2^{n}, a+1=2 p\right)$.
In the first case, we would have $a=3$, so $4=a+1=2^{n} p$, which is impossible.
In the second case, we have $p=2^{n-1}-1$. Since $p$ is prime, $n=1$ and $n=2$ do not work, so $n \geqslant 3$. Consequently, $5^{m}=2^{n} p+1 \equiv 1[8]$. Since $5^{2 \ell+1}=5 \times 25^{\ell} \equiv 5 \times 1^{\ell}=5$ [8], the integer $m$ is necessarily even. Let $m=2 \ell$, then $\left(5^{\ell}-1\right)\left(5^{\ell}+1\right)=2^{n} p$. One of the factors is equal to $2 p$ and the other to $2^{n-1}$. Since their difference is 2, we have $\pm 2=2 p-2^{n-1}=2 p-(p+1)=p-1$, so $p=3, n=3$ and $m=2$.
In the third case, we have $p=2^{n-1}+1$. We cannot have $n=1$, otherwise $p=2$. If $n=2$ then $p=3$ and $5^{m}=1+2^{n} p=13$. Impossible. Therefore, $n \geqslant 3$. The same reasoning as above leads to $m=2 \ell$ with $\pm 2=2 p-2^{n-1}=2 p-(p-1)=p+1$, which contradicts $p \geqslant 3$.
|
m=2, n=2 \text{ for } p=5; m=2, n=3, p=3
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
a) Trouver tous les entiers $m \geqslant 1$ et $n \geqslant 1$ tels que $\frac{5^{m}+2^{n+1}}{5^{m}-2^{n+1}}$ soit le carré d'un entier.
b) Plus généralement, trouver tous les entiers $m \geqslant 1$ et $n \geqslant 1$, ainsi que les nombres premiers $p$, tels que $\frac{5^{m}+2^{n} p}{5^{m}-2^{n} p}$ soit le carré d'un entier.
|
a) Voir exercice 2 ci-dessus.
b) Supposons que $p=5$. Alors $\frac{5^{m-1}+2^{n}}{5^{m-1}-2^{n}}$ est le carré d'un entier. D'après la partie a) (qui marchait aussi dans le cas d'entiers $\geqslant 0$, on a $m=n=2$.
Supposons enfin $p \neq 2$ et $p \neq 5$. Soit $d$ le PGCD de $5^{m}+2^{n} p$ et de $5^{m}-2^{n} p$. Alors $d$ divise $5^{m}+2^{n} p+5^{m}-2^{n} p=2 \times 5^{m}$. Comme $d$ est le PGCD de deux nombres impairs, il est impair, doncil divise $5^{m}$.
De plus, $d$ divise $5^{m}+2^{n} p-\left(5^{m}-2^{n} p\right)=2^{n+1} p$ et il est impair, donc il divise $p$. Comme $p$ et 5 sont premiers entre eux, en en déduit que $d=1$ et que $5^{m}-2^{n} p=1$; de plus, $5^{m}+2^{n} p=a^{2}$ pour un certain entier $a$.
On a donc $(a-1)(a+1)=a^{2}-1=2^{n+1} p$.
Le PGCD de $a-1$ et de $a+1$ divise $(a+1)-(a-1)=2$, donc il vaut 1 ou 2 . De plus, $a-1$ et $a+1$ sont de même parité, et leur produit est pair, donc leur PGCD vaut 2 . On en déduit que $\left(a-1=2, a+1=2^{n} p\right)$ ou $\left(a-1=2 p, a+1=2^{n}\right)$ ou $\left(a-1=2^{n}, a+1=2 p\right)$.
Dans le premier cas on aurait $a=3$, donc $4=a+1=2^{n} p$, ce qui est impossible.
Dans le deuxième cas, on a $p=2^{n-1}-1$. Comme $p$ est premier, $n=1$ et $n=2$ ne conviennent pas donc $n \geqslant 3$. Par conséquent, $5^{m}=2^{n} p+1 \equiv 1[8]$. Comme $5^{2 \ell+1}=5 \times 25^{\ell} \equiv 5 \times 1^{\ell}=5$ [8], l'entier $m$ est nécessairement pair. Posons $m=2 \ell$, alors $\left(5^{\ell}-1\right)\left(5^{\ell}+1\right)=2^{n} p$. L'un des facteurs est égal à $2 p$ et l'autre à $2^{n-1}$. Comme leur différence est égale 2 , on a $\pm 2=2 p-2^{n-1}=2 p-(p+1)=p-1$, donc $p=3, n=3$ et $m=2$.
Dans le troisième cas, on a $p=2^{n-1}+1$. On ne peut pas avoir $n=1$, $\operatorname{sinon} p=2$. Si $n=2$ alors $p=3$ et $5^{m}=1+2^{n} p=13$. Impossible. Donc $n \geqslant 3$. Le même raisonnement que plus haut conduit à $m=2 \ell$ avec $\pm 2=2 p-2^{n-1}=2 p-(p-1)=p+1$, ce qui contredit $p \geqslant 3$.
|
{
"exam": "French_tests",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/tests/fr-2015-2016-ofm-2015-2016-test-janvier-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T1",
"year": "2015"
}
|
Let $I$ be the center of the incircle of a triangle $ABC$. Let $D$ be the point diametrically opposite to $A$ on the circumcircle. Suppose that the point $E$ on the ray $[BA)$ and the point $F$ on the ray $[CA)$ satisfy the condition
$$
BE=CF=\frac{AB+BC+CA}{2}.
$$
Show that $(EF) \perp (DI)$.
|
Let $a, b, c$ be the lengths of the sides, $r$ the radius of the inscribed circle, and $p = (a + b + c) / 2$. Since $[AD]$ is a diameter, the angles $\widehat{ABD}$ and $\widehat{ACD}$ are right angles, so
\[
\begin{aligned}
DE^2 - DF^2 & = (DB^2 + BE^2) - (DC^2 + CF^2) = DB^2 - DC^2 \\
& = (AD^2 - DC^2) - (AD^2 - DB^2) = AC^2 - AB^2 \\
& = b^2 - c^2.
\end{aligned}
\]
On the other hand, if $C'$ is the point of tangency of the inscribed circle with $[AB]$, we know that $BC' = p - b$, so $C'E = BE - BC' = b$. It follows that $IE^2 = (IC')^2 + (C'E)^2 = r^2 + b^2$, and similarly $IF^2 = r^2 - c^2$, so
\[
DE^2 - DF^2 = IE^2 - IF^2.
\]
This means that the points $D$ and $I$ have the same difference in powers with respect to $E$ and $F$ (considered as circles of zero radius), so $(DI) \perp (EF)$.
Clarification: Let's explain why if $C$ and $C'$ are two circles with centers $O$ and $O'$, and if $P_C(A) - P_{C'}(A) = P_C(B) - P_{C'}(B)$, then $(AB) \perp (OO')$. Let $R$ and $R'$ be the radii of the circles, and $C, D$ the projections of $A$ and $B$ on $(OO')$.
We have $P_C(A) - P_{C'}(A) = OA^2 - O'A^2 - (R^2 - (R')^2) = OC^2 - O'C^2 - (R^2 - (R')^2)$, so $OC^2 - O'C^2 = OD^2 - O'D^2$. This can be written as $(\overline{OC} - \overline{O'C})(\overline{OC} + \overline{O'C}) = (\overline{OD} - \overline{O'D})(\overline{OD} + \overline{O'D})$, or $2 \overline{O'O} \cdot \overline{MC} = 2 \overline{O'O} \cdot \overline{MD}$ where $M$ is the midpoint of $[O'O]$. Consequently, $C = D$, and thus $(AB) = (AC) \perp (OO')$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $I$ le centre du cercle inscrit à un triangle $A B C$. Soit $D$ le point diamétralement opposé à $A$ sur le cercle circonscrit. On suppose que le point $E$ de la demi-droite $[B A)$ et le point $F$ de la demi-droite $[C A)$ satisfont la condition
$$
B E=C F=\frac{A B+B C+C A}{2} .
$$
Montrer que $(E F) \perp(D I)$.
|
Notons $a, b, c$ les longueurs des côtés, $r$ le rayon du cercle inscrit et $p=(a+b+c) / 2$. Comme $[A D]$ est un diamètre, les angles $\widehat{A B D}$ et $\widehat{A C D}$ sont droits donc
$$
\begin{aligned}
D E^{2}-D F^{2} & =\left(D B^{2}+B E^{2}\right)-\left(D C^{2}+C F^{2}\right)=D B^{2}-D C^{2} \\
& =\left(A D^{2}-D C^{2}\right)-\left(A D^{2}-D B^{2}\right)=A C^{2}-A B^{2} \\
& =b^{2}-c^{2} .
\end{aligned}
$$
D'autre part, si $C^{\prime}$ est le point de contact du cercle inscrit avec $[A B]$, on sait que $B C^{\prime}=p-b$, donc $C^{\prime} E=B E-B C^{\prime}=b$. Il vient $I E^{2}=\left(I C^{\prime}\right)^{2}+\left(C^{\prime} E\right)^{2}=r^{2}+b^{2}$, et de même $I F^{2}=r^{2}-c^{2}$, donc
$$
D E^{2}-D F^{2}=I E^{2}-I F^{2}
$$
Ceci signifie que les points $D$ et $I$ ont la même différence de puissances par rapport à $E$ et $F$ (considérés comme des cercles de rayon nul), donc $(D I) \perp(E F)$.
Précision : expliquons pourquoi si $C$ et $C^{\prime}$ sont deux cercles de centres $O$ et $O^{\prime}$, et si $P_{C}(A)$ -$P_{C^{\prime}}(A)=P_{C}(B)-P_{C^{\prime}}(B)$ alors $(A B) \perp\left(O O^{\prime}\right)$. Notons $R$ et $R^{\prime}$ les rayons des cercles et $C, D$ les projetés respectifs de $A$ et $B$ sur $\left(O O^{\prime}\right)$.
On a $P_{C}(A)-P_{C^{\prime}}(A)=O A^{2}-O^{\prime} A^{2}-\left(R^{2}-\left(R^{\prime}\right)^{2}\right)=O C^{2}-O^{\prime} C^{2}-\left(R^{2}-\left(R^{\prime}\right)^{2}\right)$, donc $O C^{2}-$ $O^{\prime} C^{2}=O D^{2}-O^{\prime} D^{2}$. Ceci s'écrit encore $\left(\overline{O C}-\overline{O^{\prime} C}\right)\left(\overline{O C}+\overline{O^{\prime} C}\right)=\left(\overline{O D}-\overline{O^{\prime} D}\right)\left(\overline{O D}+\overline{O^{\prime} D}\right)$, ou encore $2 \overline{O^{\prime} O} \cdot \overline{M C}=2 \overline{O^{\prime} O} \cdot \overline{M D}$ où $M$ est le milieu de $\left[O^{\prime} O\right]$. Par conséquent, $C=D$, et donc $(A B)=(A C) \perp\left(O O^{\prime}\right)$.
|
{
"exam": "French_tests",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/tests/fr-2015-2016-ofm-2015-2016-test-janvier-corrige.jsonl",
"solution_match": "## Solution de l'exercice 6",
"tier": "T1",
"year": "2015"
}
|
Solve in real numbers the system of equations
$$
\begin{gathered}
x_{1}\left(x_{1}-1\right)=x_{2}-1 \\
x_{2}\left(x_{2}-1\right)=x_{3}-1 \\
\cdots \\
x_{2016}\left(x_{2016}-1\right)=x_{2017}-1 \\
x_{2017}\left(x_{2017}-1\right)=x_{1}-1 .
\end{gathered}
$$
|
Let us conventionally set $x_{2018}=x_{1}$. For all $i=1, \ldots, 2017$, we have $x_{i+1}-$ $x_{i}=x_{i}\left(x_{i}-1\right)+1-x_{i}=\left(x_{i}-1\right)^{2} \geqslant 0$, so $x_{1}=x_{2018} \geqslant x_{2017} \geqslant \cdots \geqslant x_{1}$. We deduce that the $x_{i}$ are all equal, hence $0=x_{i+1}-x_{i}=\left(x_{i}-1\right)^{2}=0$. Therefore, $x_{i}=1$ for all $i$. Conversely, it is clear that $x_{i}=1$ is a solution.
|
x_{i}=1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Résoudre en nombres réels le système d'équations
$$
\begin{gathered}
x_{1}\left(x_{1}-1\right)=x_{2}-1 \\
x_{2}\left(x_{2}-1\right)=x_{3}-1 \\
\cdots \\
x_{2016}\left(x_{2016}-1\right)=x_{2017}-1 \\
x_{2017}\left(x_{2017}-1\right)=x_{1}-1 .
\end{gathered}
$$
|
Posons par convention $x_{2018}=x_{1}$. Pour tout $i=1, \ldots, 2017$, on a $x_{i+1}-$ $x_{i}=x_{i}\left(x_{i}-1\right)+1-x_{i}=\left(x_{i}-1\right)^{2} \geqslant 0$, donc $x_{1}=x_{2018} \geqslant x_{2017} \geqslant \cdots \geqslant x_{1}$. On en déduit que les $x_{i}$ sont tous égaux, donc $0=x_{i+1}-x_{i}=\left(x_{i}-1\right)^{2}=0$. Par conséquent, $x_{i}=1$ pour tout $i$. Réciproquement, il est clair que $x_{i}=1$ est solution.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2016-2017-ofm-2016-2017-test-fevrier-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T1",
"year": "2016"
}
|
Let $a$ and $b$ be strictly positive integers. Prove that if
$$
a+\frac{b}{a}-\frac{1}{b}
$$
is an integer, then it is a square.
|
By multiplying by $a$, we obtain that $a^{2}+b-\frac{a}{b}$ is an integer, so $k=\frac{a}{b}$ is an integer.
Similarly, by multiplying by $b$ we see that $\frac{b^{2}}{a}$ is an integer. Since $\frac{b^{2}}{a}=\frac{b}{k}$, we have $b=k c$ where $c$ is an integer.
Since $\frac{b}{a}-\frac{1}{b}=\frac{1}{k}-\frac{1}{k c}$ is an integer, by multiplying by $k$ we see that $\frac{1}{c}$ is an integer, so $c=1$, $b=k$ and $a=k^{2}$. Finally, $a+\frac{b}{a}-\frac{1}{b}=k^{2}$ is a square.
|
k^{2}
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $a$ et $b$ des entiers strictement positifs. Prouver que si
$$
a+\frac{b}{a}-\frac{1}{b}
$$
est un entier alors c'est un carré.
|
En multipliant par $a$, on obtient que $a^{2}+b-\frac{a}{b}$ est un entier, donc $k=\frac{a}{b}$ est un entier.
De même, en multipliant par $b$ on voit que $\frac{b^{2}}{a}$ est un entier. Comme $\frac{b^{2}}{a}=\frac{b}{k}$, on a $b=k c$ où $c$ est un entier.
Comme $\frac{b}{a}-\frac{1}{b}=\frac{1}{k}-\frac{1}{k c}$ est un entier, en multipliant par $k$ on voit que $\frac{1}{c}$ est un entier, donc $c=1$, $b=k$ et $a=k^{2}$. Finalement, $a+\frac{b}{a}-\frac{1}{b}=k^{2}$ est un carré.
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2016-2017-ofm-2016-2017-test-fevrier-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T1",
"year": "2016"
}
|
Consider 2017 lines in the plane, which intersect pairwise at distinct points. Let $E$ be the set of these intersection points.
We want to assign a color to each point in $E$ such that any two points on the same line, whose segment connecting them contains no other point of $E$, are of different colors.
What is the minimum number of colors needed to achieve such a coloring?
|
The sought minimum $m$ is $m=3$, and with what follows, it will be quite evident that the result remains true for $n \geq 3$ lines.
First, we note that, in the obtained configuration, there is at least one non-subdivided region that is a triangle. Indeed, three non-concurrent lines and two never parallel lines form a triangle. Now, any line that crosses a triangle divides it into two polygons, at least one of which is a triangle. Therefore, starting from three of the given lines and "adding" the other 2014 one by one, we are assured of the existence of such a triangular region in the final configuration. The three vertices of such a triangle must be of different colors, which implies that $m \geq 3$.
To conclude, we will construct an appropriate three-coloring. We start by noting that, since there are only a finite number of intersection points, we can choose an orthogonal coordinate system in which these points have distinct x-coordinates. We then number the points $M_{1}, M_{2}, \ldots, M_{k}$ according to increasing x-coordinates (where $k=\frac{2017 \times 2016}{2}$). For any $i$, the point $M_{i}$ has at most four neighbors, and if it belongs to a segment joining two of its neighbors, only one of these two neighbors has an x-coordinate less than that of $M_{i}$. This ensures that, for any $i \leq k$, among the neighbors of $M_{i}$, at most two have indices less than $i$. We can then color the $M_{i}$ in the order of the numbering according to the following procedure: we color $M_{1}$ green and $M_{2}$ red. And, for any $i$ such that $2 \leq i \leq k-1$, if we assume that the points $M_{1}, M_{2}, \ldots, M_{i}$ have been colored either green, red, or blue so that no two adjacent points are (yet) the same color, then, according to the previous remark, at most two neighbors of $M_{i+1}$ have already been colored, leaving one color free for $M_{i+1}$.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On considère 2017 droites du plan, qui se rencontrent deux à deux en des points distincts. On appelle $E$ l'ensemble de ces points d'intersection.
On veut attribuer une couleur à chacun des points de $E$ de sorte que deux quelconques de ces points qui appartiennent à une même droite et dont le segment qui les relient ne contient aucun autre point de $E$, soient de couleurs différentes.
Combien faut-il au minimum de couleurs pour pouvoir réaliser une telle coloration?
|
Le minimum $m$ cherché est $m=3$ et, avec ce qui suit, il sera assez évident que le résultat reste vrai pour $n \geq 3$ droites.
Tout d'abord, on note que, dans la configuration obtenue, il y a au moins une région non subdivisée qui est un triangle. En effet, trois droites non concourantes et deux jamais parallèles forment un triangle. Or, toute droite qui traverse un triangle, le partage en deux polygones dont
au moins un est un triangle et donc, en partant de trois des droites données et en "ajoutant" une par une les 2014 autres, on est assuré de l'existence d'une telle région triangulaire dans la configuration finale. Les trois sommets d'un tel triangle doivent être de couleurs distinctes, ce qui implique que $m \geq 3$.
Pour conclure, nous allons construire une coloration adéquate à trois couleurs. On commence par remarquer que, puisqu'il n'y a qu'un nombre fini de points d'intersection, on peut choisir un repère orthogonal dans lequel ces points ont des abscisses deux à deux distinctes. On numérote alors les points $M_{1}, M_{2} \ldots, M_{k}$ selon les abscisses croissantes (et où $k=\frac{2017 \times 2016}{2}$ ). Pour tout $i$, le point $M_{i}$ possède au plus quatre voisins et, s'il appartient à un segment qui joint deux de ses voisins, un seul de ces deux voisins a une abscisse inférieure à celle de $M_{i}$. Cela assure que, pour tout $i \leq k$, parmi les voisins de $M_{i}$, il y en a au plus deux qui ont des indices inférieurs à $i$. On peut alors colorier les $M_{i}$ dans l'ordre de la numérotation selon la procédure suivante : on colorie $M_{1}$ en vert et $M_{2}$ en rouge. Et, pour tout $i$ tel que $2 \leq i \leq k-1$, si l'on suppose que les points $M_{1}, M_{2} \ldots, M_{i}$ ont été colorés chacun soit en vert, soit en rouge, soit en bleu de sorte que deux points voisins ne soient pas (encore) de la même couleur alors, d'après la remarque précédente, au plus deux voisins de $M_{i+1}$ ont déjà été colorés, ce qui laisse une couleur libre pour $M_{i+1}$.
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2016-2017-ofm-2016-2017-test-fevrier-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T1",
"year": "2016"
}
|
Let $ABC$ be a triangle with all angles acute.
The altitudes $\left[A A_{1}\right],\left[B B_{1}\right]$, and $\left[C C_{1}\right]$ intersect at point $H$. Let $A_{2}$ be the symmetric point of $A$ with respect to $\left(B_{1} C_{1}\right)$, and let $O$ be the center of the circumcircle of $ABC$.
a) Prove that the points $O, A_{2}, B_{1}, C$ are concyclic.
b) Prove that $O, H, A_{1}, A_{2}$ are concyclic.
|
a) $A, H, B_{1}, C_{1}$ are concyclic on the circle with diameter $[A H]$, so $\widehat{A B_{1} C_{1}}=\widehat{A H C_{1}}=90^{\circ}-$ $\widehat{C_{1} A H}$. Since, $\left(A A_{2}\right) \perp\left(B_{1} C_{1}\right)$, we have $\widehat{A_{2} A B_{1}}=\widehat{C_{1} A H}$, i.e., the rays $[A H)$ and $\left[A A_{2}\right)$ are symmetric with respect to the bisector of $\widehat{B A C}$. We deduce that $A_{2} \in[A O)$. Since $A O = C O$, we have $\widehat{A C O}=\widehat{O A C}=\widehat{A A_{2} B_{1}}$, so $O, A_{2}, B_{1}, C$ are concyclic.
b) Using the power of $A$ with respect to the circles $O, A_{2}, B_{1}, C$ and $H, A_{1}, C, B_{1}$, we have $A B_{1} \cdot A C = A O \cdot A A_{2}$ and $A B_{1} \cdot A C = A H \cdot A A_{1}$. Consequently, $A O \cdot A A_{2} = A H \cdot A A_{1}$. According to the power of a point with respect to a circle, we deduce that $O A_{2}, H, A_{1}$ are concyclic.
Remark. The assumption that $A B C$ is acute is superfluous.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle dont tous les angles sont aigus.
Les hauteurs $\left[A A_{1}\right],\left[B B_{1}\right]$ et $\left[C C_{1}\right]$ se coupent au point $H$. Soit $A_{2}$ le symétrique de $A$ par rapport à $\left(B_{1} C_{1}\right)$, et soit $O$ le centre du cercle circonscrit à $A B C$.
a) Prouver que les points $O, A_{2}, B_{1}, C$ sont cocycliques.
b) Prouver que $O, H, A_{1}, A_{2}$ sont cocycliques.
|
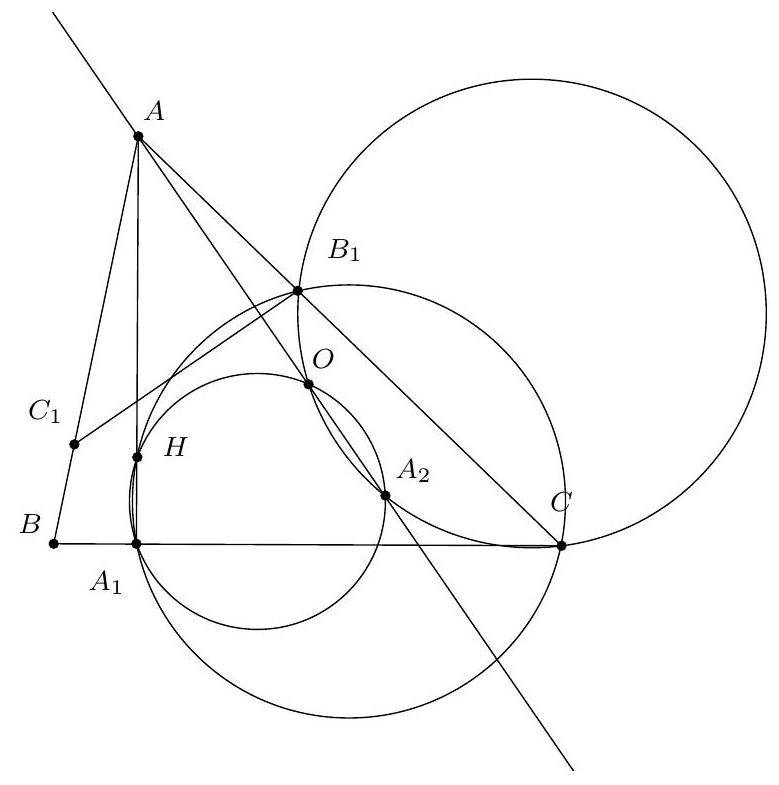
a) $A, H, B_{1}, C_{1}$ sont cocycliques sur le cercle de diamètre $[A H]$, donc $\widehat{A B_{1} C_{1}}=\widehat{A H C_{1}}=90^{\circ}-$ $\widehat{C_{1} A H}$. Or, $\left(A A_{2}\right) \perp\left(B_{1} C_{1}\right)$ donc $\widehat{A_{2} A B_{1}}=\widehat{C_{1} A H}$, i.e. les demi-droites $[A H)$ et $\left[A A_{2}\right)$ sont symétriques par rapport à la bissectrice de $\widehat{B A C}$. On en déduit que $A_{2} \in[A O)$. Comme $A O=$ $C O$, on a $\widehat{A C O}=\widehat{O A C}=\widehat{A A_{2} B_{1}}$, donc $O, A_{2}, B_{1}, C$ sont cocycliques.
b) En utilisant la puissance de $A$ par rapport aux cercles $O, A_{2}, B_{1}, C$ et $H, A_{1}, C, B_{1}$, on a $A B_{1}$. $A C=A O \cdot A A_{2}$ et $A B_{1} \cdot A C=A H \cdot A A_{1}$. Par conséquent, $A O \cdot A A_{2}=A H \cdot A A_{1}$. D'après la puissance d'un point par rapport à un cercle, on en déduit que $O A_{2}, H, A_{1}$ sont cocycliques.
Remarque. L'hypothèse que $A B C$ est acutangle est superflue.
|
{
"exam": "French_tests",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/tests/fr-2016-2017-ofm-2016-2017-test-fevrier-corrige.jsonl",
"solution_match": "## Solution de l'exercice 4",
"tier": "T1",
"year": "2016"
}
|
Let $a_{0}, a_{1}, \ldots, a_{99}, b_{0}, b_{1}, \ldots, b_{99}$ be strictly positive real numbers.
For $k=0,1, \ldots, 198$, we set $S_{k}=\sum_{i=0}^{198} a_{i} b_{k-i}$, with $a_{j}=0$ and $b_{j}=0$ if $j<0$ or $j>99$.
Is it possible that the numbers $S_{0}, S_{1}, \ldots, S_{198}$ are all equal?
|
No. Let's reason by contradiction. Indeed, since $a_{0} b_{0}=a_{0} b_{99}+\cdots+a_{99} b_{0}$ where the $\cdots$ represent strictly positive terms, we have $a_{0} b_{0}>a_{0} b_{99}$, hence $b_{0}>b_{99}$, and similarly $a_{0}>a_{99}$. Consequently, $S_{0}=a_{0} b_{0}>a_{99} b_{99}=S_{198}$, which is contradictory.
Another proof that does not require the positivity assumption (but only the fact that $a_{99} \neq 0$ and $b_{99} \neq 0$):
Suppose that $S_{0}=S_{1}=\ldots=S_{198}=\alpha$.
Note that $\alpha \neq 0$.
Let $P(x)=a_{0}+a_{1} x+\ldots+a_{99} x^{99}$ and $Q(x)=b_{0}+b_{1} x+\ldots+b_{99} x^{99}$. Since $P(x) Q(x)=S_{0}+S_{1} x+\ldots+S_{198} x^{198}=\alpha\left(1+x+\ldots+x^{198}\right)$
$=\alpha \frac{1-x^{199}}{1-x}$ for $x \neq 1$, we observe that $P(x) Q(x) \neq 0$ for all $x \neq 1$. On the other hand, since $\alpha \neq 0$ because $P$ and $Q$ are non-zero polynomials, we have $P(1) Q(1)=199 \alpha \neq 0$.
Therefore, $P(x) Q(x) \neq 0$ for all real $x$, and thus $P$ does not have any real roots. This contradicts the fact that $P$ is of odd degree.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $a_{0}, a_{1}, . ., a_{99}, b_{0}, b_{1}, \ldots, b_{99}$ des réels strictement positifs.
Pour $k=0,1, \ldots, 198$, on pose $S_{k}=\sum_{i=0}^{198} a_{i} b_{k-i}$, avec $a_{j}=0$ et $b_{j}=0$ si $j<0$ ou $j>99$.
Est-il possible que les nombres $S_{0}, S_{1}, \ldots, S_{198}$ soient tous égaux?
|
Non. Raisonnons par l'absurde. En effet, comme $a_{0} b_{0}=a_{0} b_{99}+\cdots+a_{99} b_{0}$ où les $\cdots$ représentent des termes strictement positifs, on a $a_{0} b_{0}>a_{0} b_{99}$ donc $b_{0}>b_{99}$, et de même $a_{0}>a_{99}$. Par conséquent, $S_{0}=a_{0} b_{0}>a_{99} b_{99}=S_{198}$, ce qui est contradictoire.
Autre démonstration qui ne nécessite pas l'hypothèse de positivité (mais seulement le fait que $a_{99} \neq 0$ et $b_{99} \neq 0$ :
supposons que $S_{0}=S_{1}=\ldots=S_{198}=\alpha$.
Notons que $\alpha \neq 0$.
On pose $P(x)=a_{0}+a_{1} x+\ldots+a_{99} x^{99}$ et $Q(x)=b_{0}+b_{1} x+\ldots+b_{99} x^{99}$. Comme $P(x) Q(x)=S_{0}+S_{1} x+\ldots+S_{198} x^{198}=\alpha\left(1+x+\ldots+x^{198}\right)$
$=\alpha \frac{1-x^{199}}{1-x}$ pour $x \neq 1$, on constate que $P(x) Q(x) \neq 0$ pour tout $x \neq 1$. D'autre
part, on a $\alpha \neq 0$ puisque $P$ et $Q$ sont des polynômes non nuls, donc $P(1) Q(1)=199 \alpha \neq 0$.
Par conséquent, $P(x) Q(x) \neq 0$ pour tout réel $x$, et donc $P$ n'admet pas de racine réelle. Ceci contredit le fait que $P$ est de degré impair.
|
{
"exam": "French_tests",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/tests/fr-2016-2017-ofm-2016-2017-test-fevrier-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T1",
"year": "2016"
}
|
1) Pierre distributes the integers $1,2, \ldots, 2012$ into two disjoint groups such that the sums of the elements in each group are equal.
Without even looking at the distribution chosen by Pierre, Clara claims that it is possible to eliminate two numbers from each group so that, in each group, the sums of the remaining elements are still equal.
Prove that Clara is right.
2) Pierre distributes the integers $1,2, \ldots, 20$ into two disjoint groups such that the sums of the elements in each group are equal.
Without even looking at the distribution chosen by Pierre, Clara claims that it is possible to eliminate two numbers from each group so that, in each group, the sums of the remaining elements are still equal.
Prove that, this time, Clara might have been better off looking before speaking.
|
We color the elements of group $G_{1}$ in red, and those of $G_{2}$ in blue. Without loss of generality, we can assume that 1 is red. When two consecutive integers are not in the same group, we say that we have an alternation.
- If we have at least four alternations, we can find the configuration ...rb...br...rb...br..., where the dots indicate that we remain on the same color, except possibly for the last segment. In the described situation, the conclusion is assured by eliminating the integers responsible for the first and fourth alternations (we cannot use the first two alternations because $c^{\prime}$ might be the same blue number involved).
- If we have exactly three alternations ...rb...br...rb... with at least two consecutive blues in the first blue segment, we can erase the numbers involved in the first two alternations. Similarly, if there are at least two consecutive reds in the second red segment, we can erase the numbers involved in the second and third alternations.
If we are not in one of these two cases, it means we have ...rbrb...., where the first group of dots represents only reds, and the second group of dots represents only blues. Let $k$ be the number of reds in this first segment. The sum of the red numbers is then $\frac{k(k+1)}{2}+(k+2)$, while the sum of all integers from 1 to 2012 is $2012 \times 2013 / 2$. Since the sum of the numbers in each group is the same, we must have $\frac{k(k+1)}{2}+(k+2) = 2012 \times 2012 / 4$, or equivalently, $k(k+3)+4 = 2012 \times 2013 / 2$. However, this equation has no solution modulo 3, which ensures that this configuration is ultimately not possible.
- If we have exactly two alternations, we must be in the configuration ....rb...br...., where the dots indicate that there are no color changes. If there are at least two blues, we can erase the numbers involved in the two alternations. Otherwise, there is only one blue, but then it must be equal to 1012539, which is impossible.
- If there is only one alternation, we are in the configuration ....rb... If, as above, we denote $k$ as the number of reds, we must have $\frac{k(k+1)}{2} = 1012539$, or $k(k+1) = 2025078$, which also has no integer solution (we can see this modulo 10).
Finally, in all cases, we can eliminate two numbers from each group so that, in each group, the respective sums of the remaining elements are equal.
2) For example, for $n=20$, we color the integers from 1 to 14 in red, and the others in blue. The sums of the two groups are equal, but if we eliminate two reds, the sum of the reds will decrease by at most $14+13=27$, while if we eliminate two blues, the sum of the blues will decrease by at least $15+16=31$. It is then impossible that after elimination, the two groups still have equal sums.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
1) Pierre répartit les entiers $1,2, \ldots, 2012$ en deux groupes disjoints dont les sommes respectives des éléments sont égales.
Sans même regarder la répartion choisie par Pierre, Clara affirme alors que l'on peut éliminer deux nombres de chaque groupe de sorte que, dans chaque groupe, les sommes respectives des éléments restants soient égales.
Prouver que Clara a raison.
2) Pierre répartit les entiers $1,2, \ldots, 20$ en deux groupes disjoints dont les sommes respectives des éléments sont égales.
Sans même regarder la répartion choisie par Pierre, Clara affirme alors que l'on peut éliminer deux nombres de chaque groupe de sorte que, dans chaque groupe, les sommes respectives des éléments restants soient égales.
Prouver que, cette fois, Clara aurait peut-être mieux fait de regarder avant de parler.
|
On colorie les éléments du groupe $G_{1}$ en rouge, et ceux de $G_{2}$ en bleu. Sans perte de généralité, on peut supposer que 1 est rouge. Lorsque deux entiers consécutifs ne sont pas dans le même groupe, on dit que l'on a une alternance.
- Si l'on a au moins quatre alternances, on peut trouver la configuration ...rb...br...rb...br..., où les pointillés indiquent toujours que l'on reste sur la même couleur, sauf peut-être pour le dernier paquet. Dans la situation décrite, la conclusion est assurée en éliminant les entiers responsables des première et quatrième alternances (on ne peut utiliser les deux premières alternances car $c^{\prime}$ est peut-être le même nombre bleu qui est concerné).
- Si l'on a exactement trois alternances ...rb...br...rb... avec au moins deux bleus successifs dans le premier paquet de bleus, on peut effacer les nombres impliqués dans les deux premières alternances. De même, s'il y a au moins deux rouges successifs dans le second paquet de rouges, on peut effacer les nombres impliqués dans les seconde et troisième alternances.
Si l'on n'est pas dans un de ces deux cas, c'est que l'on a ...rbrb...., où le premier groupe de pointillés ne désigne que des rouges, et le second groupe de pointillés ne désigne que des bleus. On appelle $k$ le nombre de rouges dans ce premier paquet. La somme des nombres rouges est alors $\frac{k(k+1)}{2}+(k+2)$, alors que la somme de tous les entiers de 1 à 2012 vaut $2012 \times 2013 / 2$. Puisque la somme des nombres dans chaque groupe est la même, on doit avoir $\frac{k(k+1)}{2}+(k+2)=$ $2012 \times 2012 / 4$, autrement dit, $k(k+3)+4=2012 \times 2013 / 2$. Or, cette équation n'a pas de solution modulo 3, ce qui assure que cette configuration n'est finalement pas possible.
- Si l'on a exactement deux alternances, on est forcément dans la configuration ....rb...br...., où les pointillés indiquent qu'il n'y a pas de changements de couleurs. S'il y a au moins deux bleus, on peut effacer les nombres impliqués dans les deux alternances. Sinon, c'est qu'il n'y a qu'un bleu, mais alors il doit être égal à 1012539, ce qui est impossible.
- S'il n'y a qu'une alternance, c'est que l'on est dans la configuration ....rb... Si, comme ci-dessus, on note $k$ le nombre de rouges, on doit avoir $\frac{k(k+1)}{2}=1012539$, soit $k(k+1)=2025078$ qui n'a pas non plus de solution entière (on peut le voir modulo 10).
Finalement, dans tous les cas, on peut éliminer deux nombres de chaque groupe de sorte que, dans chaque groupe, les sommes respectives des éléments restants soient égales.
2) Par exemple, pour $n=20$, on colorie en rouge les entiers de 1 à 14 , et les autres en bleu. Les sommes des deux groupes sont égales, mais si l'on élimine deux rouges, la somme des rouges diminuera d'au plus $14+13=27$, alors que si on élimine deux bleus, la somme des bleus diminuera d'au moins $15+16=31$. Il est alors impossible qu'après élimination, les deux groupes aient encore des sommes égales.
|
{
"exam": "French_tests",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/tests/fr-2016-2017-ofm-2016-2017-test-fevrier-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T1",
"year": "2016"
}
|
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
f\left(a^{2}\right)-f\left(b^{2}\right) \leqslant(f(a)+b)(a-f(b)), \quad \text { for all } a, b \in \mathbb{R}
$$
|
By taking $(a, b)=(0,0)$, we obtain $f(0)^{2} \leqslant 0$ hence $f(0)=0$. By taking $(a, b)=(x, 0)$ and then $(a, b)=(0, x)$, we find that $f\left(x^{2}\right)=x f(x)$. By substituting into the initial equation, we deduce that $a f(a)-b f(b) \leqslant(f(a)+b)(a-f(b)$, thus $f(a) f(b) \leqslant a b$ for all $a, b$. On the other hand, $f\left(x^{2}\right)=x f(x)$ implies that $x f(x)=-x f(-x)$, so $f$ is odd. By replacing $b$ with $-b$ in $f(a) f(b) \leqslant a b$, we deduce that $f(a) f(b)=a b$ for all $a$ and $b$. In particular, $f(1)^{2}=1$ so $f(1)=1$ or $f(1)=-1$. Since $f(a) f(1)=a$ for all $a$, we conclude that $f(x)=x$ or $f(x)=-x$ for all $x$.
Conversely, it is easily verified that the functions $f(x)=x$ and $f(x)=-x$ are solutions to the functional equation.
|
f(x)=x \text{ or } f(x)=-x
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Trouver toutes les fonctions $f: \mathbb{R} \rightarrow \mathbb{R}$ telles que
$$
f\left(a^{2}\right)-f\left(b^{2}\right) \leqslant(f(a)+b)(a-f(b)), \quad \text { pour tous } a, b \in \mathbb{R}
$$
|
En prenant $(a, b)=(0,0)$, on obtient $f(0)^{2} \leqslant 0$ donc $f(0)=0$. En prenant $(a, b)=(x, 0)$ puis $(a, b)=(0, x)$, on trouve que $f\left(x^{2}\right)=x f(x)$. En remplaçant dans l'équation initiale, on en déduit que $a f(a)-b f(b) \leqslant(f(a)+b)(a-f(b)$, donc $f(a) f(b) \leqslant a b$ pour tous $a, b$. D'autre part, $f\left(x^{2}\right)=x f(x)$ entraîne que $x f(x)=-x f(-x)$, donc $f$ est impaire. En remplaçant $b$ par $-b$ dans $f(a) f(b) \leqslant a b$, on en déduit que $f(a) f(b)=a b$ pour tous $a$ et $b$. En particulier, $f(1)^{2}=1$ donc $f(1)=1$ ou $f(1)=-1$. Comme $f(a) f(1)=a$ pour tout $a$, on en déduit que $f(x)=x$ ou $f(x)=-x$ pour tout $x$.
Réciproquement, on vérifie facilement que les fonctions $f(x)=x$ et $f(x)=-x$ sont solutions de l'équation fonctionnelle.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2016-2017-ofm-2016-2017-test-janvier-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T1",
"year": "2016"
}
|
Let $S$ be the set of two-digit numbers that do not contain the digit 0. Two numbers in $S$ are called friends if their largest digits are equal, and if the difference between their smallest digits is equal to 1. For example, 68 and 85 are friends, 78 and 88 are friends, but 58 and 75 are not friends.
Determine the largest integer $m$ such that there exists a subset $T$ of $S$ with $m$ elements, such that any two elements of $T$ are not friends.
|
Answer: 45. We can take for $T$ the set of numbers whose smallest digit is odd.
Conversely, if $x=\overline{a b}$ with $1 \leqslant b<a \leqslant 9$ then $x$ and $x+1$ are friends. If $x=\overline{a b}$ with $2 \leqslant a<b \leqslant 9$ and $a$ even, then $x$ and $x+10$ are friends. We have thus found 36 disjoint pairs of friends. Consequently, among the 72 numbers $\geqslant 21, T$ can contain at most 36 numbers, so $|T| \leqslant 9+36=45$.
|
45
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Soit $S$ l'ensemble des nombres à deux chiffres qui ne contiennent pas le chiffre 0. Deux nombres de $S$ sont dits amis si leurs plus grands chiffres sont égaux, et si la différence entre leurs plus petits chiffres est égale à 1 . Par exemple, 68 et 85 sont amis, 78 et 88 sont amis, mais 58 et 75 ne sont pas amis.
Déterminer le plus grand entier $m$ tel qu'il existe une partie $T$ de $S$ possédant $m$ éléments, telle que deux éléments quelconques de $T$ ne soient pas amis.
|
Réponse : 45 . On peut prendre pour $T$ l'ensemble des nombres dont le plus petit chiffre est impair.
Réciproquement, si $x=\overline{a b}$ avec $1 \leqslant b<a \leqslant 9$ alors $x$ et $x+1$ sont amis. Si $x=\overline{a b}$ avec $2 \leqslant a<b \leqslant 9$ et $a$ pair, alors $x$ et $x+10$ sont amis. On a ainsi trouvé 36 paires d'amis disjointes. Par conséquent, parmi les 72 nombres $\geqslant 21, T$ ne peut contenir qu'au plus 36 nombres, donc $|T| \leqslant 9+36=45$.
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2016-2017-ofm-2016-2017-test-janvier-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T1",
"year": "2016"
}
|
Let $P(x)=x^{4}-x^{3}-3 x^{2}-x+1$. Show that there are infinitely many integers $n$ such that $P\left(3^{n}\right)$ is not prime.
|
We observe that $3^{2} \equiv-1(\bmod 5)$ and $3^{4} \equiv 1(\bmod 5)$. Let $n \geqslant 1$. Let $x=3^{4 n+1}$, then $x=\left(3^{4}\right)^{n} \times 3 \equiv 3(\bmod 5)$, so $P(x) \equiv 3^{4}-3^{3}-3^{3}-3+1 \equiv 1+3+3-3+1 \equiv 0$ $(\bmod 5)$.
On the other hand, $P(x)>x^{4}-x^{3}-3 x^{3}-x^{3}=x^{3}(x-5)>x-5>3^{4 n}-5>5$, so $P\left(3^{4 n+1}\right)$ is not prime.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $P(x)=x^{4}-x^{3}-3 x^{2}-x+1$. Montrer qu'il existe une infinité d'entiers $n$ tels que $P\left(3^{n}\right)$ ne soit pas premier.
|
On observe que $3^{2} \equiv-1(\bmod 5)$ et $3^{4} \equiv 1(\bmod 5)$. Soit $n \geqslant 1$. Soit $x=3^{4 n+1}$, alors $x=\left(3^{4}\right)^{n} \times 3 \equiv 3(\bmod 5)$, donc $P(x) \equiv 3^{4}-3^{3}-3^{3}-3+1 \equiv 1+3+3-3+1 \equiv 0$ $(\bmod 5)$.
D'autre part, $P(x)>x^{4}-x^{3}-3 x^{3}-x^{3}=x^{3}(x-5)>x-5>3^{4 n}-5>5$, donc $P\left(3^{4 n+1}\right)$ n'est $^{\prime}$ pas premier.
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2016-2017-ofm-2016-2017-test-janvier-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T1",
"year": "2016"
}
|
Let $ABC$ be a right triangle at $C$. Let $D$ be the foot of the altitude from $C$, and $Z$ the point on $[AB]$ such that $AC = AZ$. The bisector of $\widehat{BAC}$ intersects $(CB)$ and $(CZ)$ at $X$ and $Y$ respectively. Show that the four points $B, X, Y, D$ lie on the same circle.
|
$C A Z$ is isosceles at $A$ so $(A Y)$, which is the bisector of $\widehat{C A Z}$, is perpendicular to $(C Z)$. Therefore, $A D Y C$ is cyclic.
We then have $\widehat{D Y X}=180^{\circ}-\widehat{A Y D}=180^{\circ}-\widehat{A C D}=180^{\circ}-\widehat{X B D}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle rectangle en $C$. Soient $D$ le pied de la hauteur issue de $C$, et $Z$ le point de $[A B]$ tel que $A C=A Z$. La bissectrice de $\widehat{B A C}$ coupe $(C B)$ et $(C Z)$ en $X$ et $Y$ respectivement. Montrer que les quatre points $B, X, Y, D$ sont sur un même cercle.
|
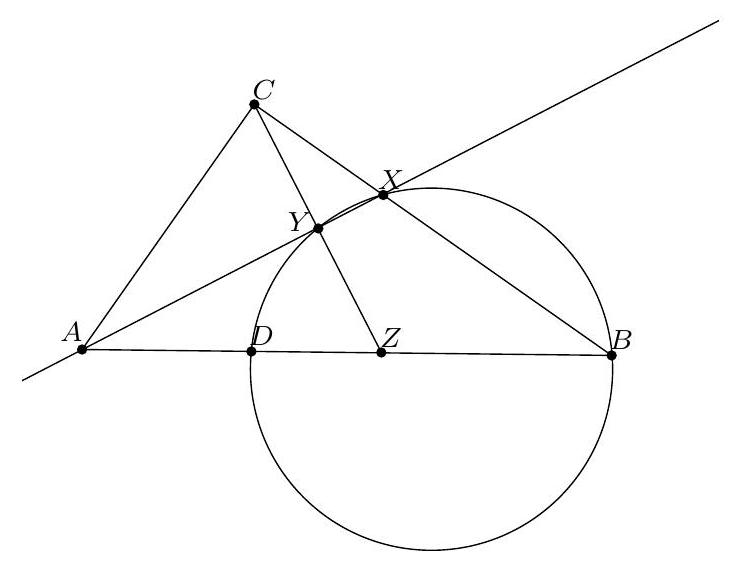
$C A Z$ est isocèle en $A$ donc $(A Y)$, qui est la bissectrice de $\widehat{C A Z}$, est perpendiculaire à $(C Z)$. Donc $A D Y C$ est cyclique.
On a alors $\widehat{D Y X}=180^{\circ}-\widehat{A Y D}=180^{\circ}-\widehat{A C D}=180^{\circ}-\widehat{X B D}$.
|
{
"exam": "French_tests",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/tests/fr-2016-2017-ofm-2016-2017-test-janvier-corrige.jsonl",
"solution_match": "## Solution de l'exercice 4",
"tier": "T1",
"year": "2016"
}
|
Let $a \in [0 ; 1]$. We define the sequence $\left(x_{n}\right)$ by
$x_{0}=a$ and $x_{n+1}=1-\left|1-2 x_{n}\right|$, for all $n \geq 0$.
Prove that the sequence $\left(x_{n}\right)$ is periodic from a certain rank if and only if $a$ is a rational number.
(Note: we say that $\left(x_{n}\right)$ is periodic from a certain rank if there exist integers $T>0$ and $n \geqslant 0$ such that $x_{k+T}=x_{k}$ for all $k \geqslant n$.)
|
First, note that if $x_{n} \in [0 ; 1]$, then $-1 \leq 1 - 2x_{n} \leq 1$, hence $0 \leq x_{n+1} \leq 1$. Since $x_{0} \in [0 ; 1]$, we deduce by induction that $x_{n} \in [0 ; 1]$ for all $n \geq 0$.
- Suppose that $a$ is a rational number. An immediate induction ensures that, for all $n \geq 0$, $x_{n}$ is a rational number.
For all $n \geq 0$, let $x_{n} = \frac{p_{n}}{q_{n}}$, where $p_{n}$ and $q_{n}$ are positive integers and coprime. Then $x_{n+1} = \frac{q_{n} - |q_{n} - 2p_{n}|}{q_{n}}$, hence $q_{n+1} \leq q_{n}$.
The sequence $(q_{n})$, a decreasing sequence of natural numbers, is then stationary from a certain rank. Therefore, there exist integers $q > 0$ and $N \geq 0$ such that $q_{n} = q$ for all $n \geq N$.
For all $n \geq N$, the number $x_{n}$ is thus a rational number in $[0 ; 1]$ with denominator $q$. However, there are only finitely many such rationals, and there exist $n_{0} \geq N$ and $k > 0$ such that $x_{n_{0}+k} = x_{n_{0}}$. The recursive definition of $(x_{n})$ then ensures that $(x_{n})_{n \geq n_{0}}$ is periodic with period $k$.
- Now suppose that there exist integers $k > 0$ and $N \geq 0$ such that $x_{n+k} = x_{n}$ for all $n \geq N$.
For $n \geq 0$, we have $x_{n+1} = 2x_{n}$ or $x_{n+1} = 2 - 2x_{n}$ depending on whether $1 - 2x_{n}$ is positive or negative. We can thus write $x_{n+1} = a + 2b x_{n}$, where $a$ is an integer and $b = \pm 1$. It is then easy to prove by induction that, for all $i \geq 0$, there exists an integer $a_{i}$ such that $x_{N+i} = a_{i} + 2^{i} b_{i} x_{N}$ with $b_{i} = \pm 1$.
In particular, we have $x_{N} = x_{N+k} = a_{k} + 2^{k} b_{k} x_{N}$. Since $2^{k} b_{k} = \pm 2^{k} \neq 1$, this linear equation in $x_{N}$ has a unique solution $x_{N} = \frac{a_{k}}{1 - 2^{k} b_{k}}$. Thus, $x_{N}$ is a rational number. It is easy to verify that, for $m \geq 0$, if $x_{m+1}$ is rational, then $x_{m}$ is rational. Therefore, by downward induction, we deduce that $a = x_{0}$ is rational.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $a \in[0 ; 1]$. On définit la suite $\left(x_{n}\right)$ par
$x_{0}=a$ et $x_{n+1}=1-\left|1-2 x_{n}\right|$, pour tout $n \geq 0$.
Prouver que la suite $\left(x_{n}\right)$ est périodique à partir d'un certain rang si et seulement si $a$ est un nombre rationnel.
(Note: on dit que $\left(x_{n}\right)$ est périodique à partir d'un certain rang s'il existe des entiers $T>0$ et $n \geqslant 0$ tels que $x_{k+T}=x_{k}$ pour tout $k \geqslant n$.)
|
On note tout d'abord que si $x_{n} \in[0 ; 1]$ alors $-1 \leq 1-2 x_{n} \leq 1$, d'où $0 \leq x_{n+1} \leq 1$. Puisque $x_{0} \in[0 ; 1]$, on déduit ainsi par récurrence que $x_{n} \in[0 ; 1]$ pour tout $n \geq 0$.
- Supposons que $a$ soit un nombre rationnel. Une récurrence immédiate assure alors que, pour tout $\mathrm{n} \geq 0, x_{n}$ est un nombre rationnel.
Pour tout $n \geq 0$, on pose $x_{n}=\frac{p_{n}}{q_{n}}$, avec $p_{n}$ et $q_{n}$ entiers positifs et premiers entre eux. Alors $x_{n+1}=\frac{q_{n}-\left|q_{n}-2 p_{n}\right|}{q_{n}}$, d'où $q_{n+1} \leq q_{n}$.
La suite $\left(q_{n}\right)$, suite décroissante d'entiers naturels, est alors stationnaire à partir d'un certain rang. Il existe donc des entiers $q>0$ et $N \geq 0$ tels que $q_{n}=q$ pour tout $n \geq N$.
Pour tout $n \geq N$, le nombre $x_{n}$ est donc un nombre rationnel de $[0 ; 1]$ dont le dénominateur vaut $q$. Or, il n'y a qu'un nombre fini de tels rationnels et il existe donc $n_{0} \geq N$ et $k>0$ tels que $x_{n_{0}+k}=x_{n_{0}}$. La définition par récurrence de $\left(x_{n}\right)$ assure alors que $\left(x_{n}\right)_{n \geq n_{0}}$ est périodique de période $k$.
- Supposons maintenant qu'il existe des entiers $k>0$ et $N \geq 0$ tels que $x_{n+k}=x_{n}$ pour tout $n \geq N$.
Pour $n \geq 0$, on a $x_{n+1}=2 x_{n}$ ou $x_{n+1}=2-2 x_{n}$ selon que $1-2 x_{n}$ est positif ou négatif. On peut donc poser $x_{n+1}=a+2 b x_{n}$, où $a$ est un entier et $b= \pm 1$. On prouve alors facilement par récurrence que, pour tout $i \geq 0$, il existe un entier $a_{i}$ tel que $x_{N+i}=a_{i}+2^{i} b_{i} x_{N}$ avec $b_{i}= \pm 1$.
En particulier, on a $x_{N}=x_{N+k}=a_{k}+2^{k} b_{k} x_{N}$. Puisque $2^{k} b_{k}= \pm 2^{k} \neq 1$, cette équation du premier degré en $x_{N}$ admet une unique solution $x_{N}=\frac{a_{k}}{1-2^{k} b_{k}}$. Ainsi, $x_{N}$ est un nombre rationnel. Or, il est facile de vérifier que, pour $m \geq 0$, si $x_{m+1}$ et rationnel alors $x_{m}$ est rationnel donc, par récurrence descendante, on déduit que $a=x_{0}$ est rationnel.
|
{
"exam": "French_tests",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/tests/fr-2016-2017-ofm-2016-2017-test-janvier-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T1",
"year": "2016"
}
|
Prove that there exists an integer $n>0$ such that among the 2016 rightmost digits in the decimal representation of $2^{n}$, there are at least 1008 digits 9.
|
One can legitimately wonder when to find 9s to the right of the decimal representation of $2^{n}$. One might think it's when the power of 2 is slightly less than a power of 10. We will therefore look for numbers of the form $2^{n}+1$ that are divisible by 5 to a high power. For such a number, by multiplying by the appropriate power of 2, we will obtain a number of the form $2^{k}\left(2^{n}+1\right)=2^{n+k}+2^{k}$ divisible by a large power of 10, and it will suffice to subtract the $2^{k}$ in question to obtain the desired power of 2.
Lemma. For any integer $k \geq 1$, the number $a_{k}=2^{2 \cdot 5^{k-1}}+1$ is divisible by $5^{k}$.
Proof of the lemma. We proceed by induction on $k$:
- For $k=1$, we have $a_{1}=5$ which is indeed divisible by 5.
- Suppose the result is established for some $k \geq 1$.
Let $a=4^{5^{k-1}}=a_{k}-1$. We note that then $a=-1 \bmod 5$.
We have $a_{k+1}=4^{5^{k}}+1=a^{5}+1=(a+1)\left(a^{4}-a^{3}+a^{2}-a+1\right)$.
By the induction hypothesis, we have $a+1=0 \bmod 5^{k-1}$.
On the other hand, since $a=-1 \bmod 5$, we have $a^{4}-a^{3}+a^{2}-a+1=0 \bmod 5$.
Thus, $a_{k+1}$ is divisible by $5^{k}$, which completes the induction.
As expected, we deduce that, for all $k \geq 1$, the number $2^{2 k}\left(2^{2 \cdot 5^{2 k-1}}+1\right)=2^{2 k+2 \cdot 5^{2 k-1}}+2^{2 k}$ is divisible by $10^{2 k}$. Its decimal representation therefore ends with at least $2 k$ zeros.
Now, for $k \geq 1$, we have $2^{2 k}<10^{k}$. Thus, the decimal representation of $2^{2 k} n^{\prime}$ uses no more than $k$ digits. Consequently, among the $2 k$ rightmost digits of the decimal representation of $2^{2 k+2 \cdot 5^{2 k-1}}$, there are at least $k$ digits 9.
The desired result corresponds to $k=1008$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prouver qu'il existe un entier $n>0$ tel que parmi les 2016 chiffres de droite dans $l^{\prime}$ écriture décimale de $2^{n}$, il y a au moins 1008 chiffres 9.
|
On peut légitimement se demander quand trouver des 9 à la droite de l'écriture décimale de $2^{n}$. On peut penser que c'est quand la puissance de 2 est légèrement inférieure à une puissance de 10 . On va donc chercher des nombres de la forme $2^{n}+1$ qui sont divisibles par 5 selon une puissance élevée. Pour un tel nombre, en multipliant par la puissance de 2 adéquate, on obtiendra un nombre de la forme $2^{k}\left(2^{n}+1\right)=2^{n+k}+2^{k}$ divisible par une grande puissance de 10 , et il suffira de retrancher le $2^{k}$ en question pour obtenir le type de puissance de 2 cherché.
Lemme. Pour tout entier $k \geq 1$, le nombre $a_{k}=2^{2 \cdot 5^{k-1}}+1$ est divisible par $5^{k}$.
Preuve du lemme. On raisonne par récurrence sur $k$ :
- Pour $k=1$, on a $a_{1}=5$ qui est bien divisible par 5.
- Supposons le résultat établi pour un certain $k \geq 1$.
Posons $a=4^{5^{k-1}}=a_{k}-1$. On note qu'alors $a=-1 \bmod 5$.
On a alors $a_{k+1}=4^{5^{k}}+1=a^{5}+1=(a+1)\left(a^{4}-a^{3}+a^{2}-a+1\right)$.
D'après l'hypothèse de récurrence, on a $a+1=0 \bmod 5^{k-1}$.
D'autre part, puisque $a=-1 \bmod 5$, on a $a^{4}-a^{3}+a^{2}-a+1=0 \bmod 5$.
Ainsi, $a_{k+1}$ est divisible par $5^{k}$, ce qui achève la récurrence.
Comme prévu, on en déduit que, pour tout $k \geq 1$, le nombre $2^{2 k}\left(2^{2 \cdot 5^{2 k-1}}+1\right)=2^{2 k+2 \cdot 5^{2 k-1}}+2^{2 k}$ est divisible par $10^{2 k}$. Son écriture décimale se termine donc par au moins $2 k$ chiffres 0 .
Or, pour $k \geq 1$, on a $2^{2 k}<10^{k}$. Ainsi, l'écriture décimale de $2^{2 k} n^{\prime}$ utilise pas plus de $k$ chiffres. Par suite, parmi les $2 k$ chiffres de droite de l'écriture décimale de $2^{2 k+2 \cdot 5^{2 k-1}}$, il y a au moins $k$ chiffres 9.
Le résultat demandé correspond à $k=1008$.
|
{
"exam": "French_tests",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/tests/fr-2016-2017-ofm-2016-2017-test-janvier-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T1",
"year": "2016"
}
|
Let $n \geq 5$ be an integer, and $E_{1}, E_{2}, \ldots, E_{2 n-1}$ be distinct two-element subsets of $\{1,2, \ldots, n\}$.
Prove that among the $2 n-1$ subsets $E_{i}$, one can choose $n$ such that the union of these $n$ subsets contains no more than $\frac{2}{3} n+1$ elements.
|
We will prove by induction on $k \leq \frac{2 n-1}{3}$ that we can always eliminate $3 k$ of the $2 n-1$ parts so that the union of the remaining $2 n-1-3 k$ does not contain more than $n-k$ elements.
The case $k=0$ is immediate.
Now let $1 \leq k \leq \frac{2 n-1}{3}$. Suppose we have eliminated $3(k-1)$ of the $E_{i}$ so that the union $U_{k-1}$ of the remaining $2 n-1-3(k-1)$ does not contain more than $n-k+1$ elements.
Each of the $E_{i}$ contains two elements. From $2(2 n-1-3(k-1)) < 4(n-k+1)$, we deduce that there exists an element $x$ in $U_{k-1}$ that belongs to at most three of the $E_{i}$ that form $U_{k-1}$. Thus, by eliminating three more of the $E_{i}$ not already eliminated, including all those that contain $x$, this ensures that the union of the remaining $n-3 k$ does not contain more than $n-k$ elements.
This completes the induction.
For $k=\left\lfloor\frac{n-1}{3}\right\rfloor$, we have $n-\left\lfloor\frac{n-1}{3}\right\rfloor \leq n-\frac{n-1}{3}=\frac{2}{3} n+1$, which concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soit $n \geq 5$ un entier, et $E_{1}, E_{2}, \ldots, E_{2 n-1}$ des parties distinctes à deux éléments de $\{1,2, \ldots, n\}$.
Prouver que, parmi les $2 n-1$ parties $E_{i}$, on peut en choisir $n$ de sorte que la réunion de ces $n$ parties ne contienne pas plus de $\frac{2}{3} n+1$ éléments.
|
On va prouver par récurrence sur $k \leq \frac{2 n-1}{3}$ que l'on peut toujours éliminer $3 k$ des $2 n-1$ parties de sorte que la réunion des $2 n-1-3 k$ restantes ne contienne pas plus de $n-k$ éléments.
Le cas $k=0$ est immédiat.
Soit maintenant $1 \leq k \leq \frac{2 n-1}{3}$. On suppose que l'on a éliminé $3(k-1)$ des $E_{i}$ de sorte que la réunion $U_{k-1}$ des $2 n-1-3(k-1)$ autres ne contienne pas plus de $n-k+1$ éléments.
Chacun des $E_{i}$ contient deux éléments. De $2(2 n-1-3(k-1))<4(n-k+1)$, on déduit alors qu'il existe un élément $x$ de $U_{k-1}$ qui n'appartient qu'à au plus trois de $E_{i}$ qui forment $U_{k-1}$. Ainsi, en éliminant encore trois des $E_{i}$ non déà éliminés, dont tous ceux qui contiennent $x$, cela assure que la réunion des $n-3 k$ restants ne contient pas plus de $n-k$ éléments.
Cela achève la récurrence.
Pour $k=\left\lfloor\frac{n-1}{3}\right\rfloor$, on a $n-\left\lfloor\frac{n-1}{3}\right\rfloor \leq n-\frac{n-1}{3}=\frac{2}{3} n+1$, ce qui conclut.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2016-2017-ofm-2016-2017-test-novembre-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T1",
"year": "2016"
}
|
Let $ABC$ be a triangle. We denote $P$ as the symmetric point of $B$ with respect to $(AC)$ and $Q$ as the symmetric point of $C$ with respect to $(AB)$.
Let $T$ be the intersection between $(PQ)$ and the tangent at $A$ to the circumcircle of $(APQ)$.
Show that the symmetric point of $T$ with respect to $A$ lies on $(BC)$.
|
Let $B'$ and $C'$ be the symmetrical points of $B$ and $C$ with respect to $A$. Since triangle $A B' P$ is isosceles at $A$, we have $\widehat{A B' P} = \frac{1}{2} \left(180^{\circ} - \widehat{B' A P}\right) = \frac{1}{2} \widehat{P A B} = \widehat{B A C}$, so $\left(B' P\right) \parallel (A C)$.
Similarly, $\left(C' Q\right) \parallel (A B)$, so the lines $\left(B' P\right)$ and $\left(C' Q\right)$ intersect. Let $A'$ be their point of intersection.
Triangles $A' B' C'$ and $A C B$ are similar because their sides are pairwise parallel.
Moreover, $A B' P$ and $A C' Q$ are similar because $\widehat{A B' P} = \widehat{A C' Q}$ and because these two triangles are isosceles at $A$.
Now let's prove the required assertion. By symmetry with respect to $A$, it is equivalent to showing that $T, B', C'$ are collinear. Applying Menelaus' theorem in $A' P Q$, this is equivalent to
$$
\frac{B' P}{B' A'} \times \frac{C' A'}{C' Q} \times \frac{T Q}{T P} = 1 \quad (E)
$$
Since $T A Q$ and $T P A$ are similar, we have $\frac{T A}{T P} = \frac{T Q}{T A} = \frac{A Q}{A P}$, so $\frac{T Q}{T P} = \frac{A Q^2}{A P^2} = \frac{A C^2}{A B^2}$.
Since $A' B' C'$ and $A C B$ are similar, we have $\frac{C' A'}{B' A'} = \frac{A B}{A C}$.
Since $A B' P$ and $A C' Q$ are similar, we have $\frac{B' P}{C' Q} = \frac{A P}{A Q} = \frac{A B}{A C}$.
We deduce that $(E)$ is true.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle. On note $P$ le symétrique de $B$ par rapport à $(A C)$ et $Q$ le symétrique de $C$ par rapport à $(A B)$.
Soit $T$ l'intersection entre $(P Q)$ et la tangente en $A$ au cercle circonscrit à $(A P Q)$.
Montrer que le symétrique de $T$ par rapport à $A$ appartient à $(B C)$.
|
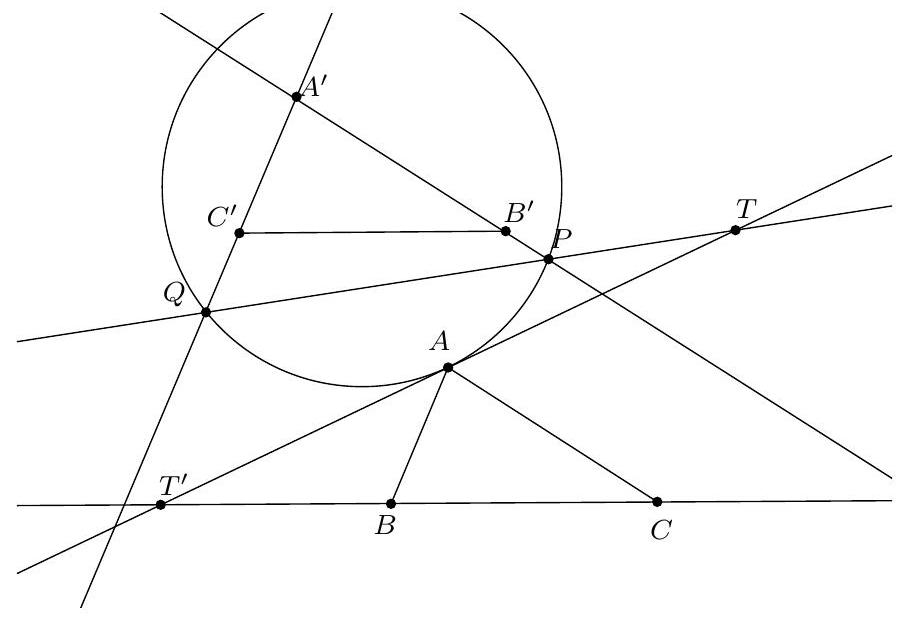
Soient $B^{\prime}$ et $C^{\prime}$ les symétriques de $B$ et $C$ par rapport à $A$. Comme le triangle $A B^{\prime} P$ est isocèle en $A$, on a $\widehat{A B^{\prime} P}=\frac{1}{2}\left(180^{\circ}-\widehat{B^{\prime} A P}\right)=\frac{1}{2} \widehat{P A B}=\widehat{B A C}$, donc $\left(B^{\prime} P\right) \|(A C)$.
De même, $\left(C^{\prime} Q\right) \|(A B)$, donc les droites $\left(B^{\prime} P\right)$ et $\left(C^{\prime} Q\right)$ sont sécantes. Notons $A^{\prime}$ leur point d'intersection.
Les triangles $A^{\prime} B^{\prime} C^{\prime}$ et $A C B$ sont semblables car leurs côtés sont deux à deux parallèles.
De plus, $A B^{\prime} P$ et $A C^{\prime} Q$ sont semblables car $\widehat{A B^{\prime} P}=\widehat{A C^{\prime} Q}$ et car ces deux triangles sont isocèles en $A$.
Montrons maintenant l'assertion demandée. Par symétrie par rapport à $A$, il revient au même de montrer que $T, B^{\prime}, C^{\prime}$ sont alignés. En appliquant le théorème de Ménélaüs dans $A^{\prime} P Q$, cela équivaut à
$$
\frac{B^{\prime} P}{B^{\prime} A^{\prime}} \times \frac{C^{\prime} A^{\prime}}{C^{\prime} Q} \times \frac{T Q}{T P}=1 \quad(E)
$$
Comme $T A Q$ et $T P A$ sont semblables, on a $\frac{T A}{T P}=\frac{T Q}{T A}=\frac{A Q}{A P}$, donc $\frac{T Q}{T P}=\frac{A Q^{2}}{A P^{2}}=\frac{A C^{2}}{A B^{2}}$.
Comme $A^{\prime} B^{\prime} C^{\prime}$ et $A C B$ sont semblables, on a $\frac{C^{\prime} A^{\prime}}{B^{\prime} A^{\prime}}=\frac{A B}{A C}$.
Comme $A B^{\prime} P$ et $A C^{\prime} Q$ sont semblables, on a $\frac{B^{\prime} P}{C^{\prime} Q}=\frac{A P}{A Q}=\frac{A B}{A C}$.
On en déduit que $(E)$ est vraie.
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2016-2017-ofm-2016-2017-test-novembre-corrige.jsonl",
"solution_match": "## Solution de l'exercice 2",
"tier": "T1",
"year": "2016"
}
|
Determine all integers $a>0$ for which there exist strictly positive integers $n, s, m_{1}, \cdots, m_{n}, k_{1}, \cdots, k_{s}$ such that
$$
\left(a^{m_{1}}-1\right) \cdots\left(a^{m_{n}}-1\right)=\left(a^{k_{1}}+1\right) \cdots\left(a^{k_{s}}+1\right)
$$
|
We will prove that the integers $a$ sought are $a=2$ and $a=3$.
First, we observe that $2^{2}-1=2+1$ and that $(3-1)(3-1)=3+1$, which ensures that $a=2$ and $a=3$ are indeed solutions to the problem.
Conversely, let $a, n, s, m_{1}, \cdots, m_{n}, k_{1}, \cdots, k_{s}$ be strictly positive integers such that
$$
\left(a^{m_{1}}-1\right) \cdots\left(a^{m_{n}}-1\right)=\left(a^{k_{1}}+1\right) \cdots\left(a^{k_{s}}+1\right)
$$
Clearly, we have $a \neq 1$, since if $a=1$ the right-hand side is 0 but not the left-hand side.
By contradiction: suppose that $a>3$.
We set $A=\left(a^{m_{1}}-1\right) \cdots\left(a^{m_{n}}-1\right)=\left(a^{k_{1}}+1\right) \cdots\left(a^{k_{s}}+1\right)$.
Lemma 1. Each of the numbers $m_{1}, \cdots, m_{n}$ and $a-1$ is a power of 2.
Proof of Lemma 1. Let $i \in\{1, \cdots, n\}$ and $\gamma$ be an odd divisor of $m_{i}$ (possibly $\gamma=1$), say $m_{i}=\gamma \times b$. Let $p$ be a prime divisor of $a^{\gamma}-1$.
Since $a^{\gamma} \equiv 1(\bmod p)$, we have $a^{m_{i}} \equiv\left(a^{\gamma}\right)^{b} \equiv 1(\bmod p)$.
Thus $A$ is divisible by $p$, which ensures that there exists $j$ such that $a^{k_{j}}+1$ is divisible by $p$. As above, we then have $\left(a^{\gamma}\right)^{k_{j}}-1 \equiv 0(\bmod p)$ and, since $\gamma$ is odd, we also have $\left(a^{k_{j}}\right)^{\gamma} \equiv-1$ $(\bmod p)$.
Hence $p$ divides $\left(\left(a^{k_{j}}\right)^{\gamma}+1\right)-\left(\left(a^{\gamma}\right)^{k_{j}}-1\right)=2$, so $p=2$.
Thus, the only prime divisor of $a^{\gamma}-1$ is $p=2$, which proves that $a^{\gamma}-1$ is a power of 2. There exists an integer $c$ such that
$$
2^{c}=a^{\gamma}-1=(a-1)\left(a^{\gamma-1}+\cdots+a+1\right) .
$$
In particular, $a-1$ is therefore a power of 2 and $a$ is odd. But, since $\gamma$ is odd, $a^{\gamma-1}+\cdots+a+1$ is odd and must also be a power of 2. This implies that $\gamma=1$ and thus that the only odd divisor of $m_{i}$ is 1, which concludes the proof of Lemma 1.
From the lemma, we have $a-1=2^{c}$ and $a-1>2$, so $a-1$ is divisible by 4. For any integer $k \geq 0$, we then have $a^{k}+1 \equiv 2(\bmod 4)$.
For each $i$, we set $a_{i}=\frac{1}{2}\left(a^{2^{i}}+1\right)$. We know that $a_{i}$ is an odd integer.
We easily verify by induction that, for any integer $d \geq 0$ :
$$
a^{2^{d}}-1=(a-1)(a+1)\left(a^{2}+1\right) \cdots\left(a^{2^{d-1}}+1\right)=2^{c} \cdot 2^{d} \cdot a_{0} a_{1} \cdots a_{d-1}
$$
Lemma 2. The numbers $a_{0}, a_{1}, a_{2}, \cdots$ are pairwise coprime.
Proof of Lemma 2. Let $0 \leq i<j$. Note that $a_{i}$ and $a_{j}$ are odd, so their gcd $d$ is odd. From (1), the number $a^{2^{j}}-1$ is divisible by $a_{i}$. Since $a^{2^{j}}+1=2 a_{j}$, we deduce that any common divisor of $a_{i}$ and $a_{j}$ also divides $\left(a^{2^{j}}+1\right)-\left(a^{2^{j}}-1\right)=2$. Thus $d$ is odd and divides 2, so $d=1$. Therefore, $a_{i}$ and $a_{j}$ are coprime, and this completes the proof of Lemma 2.
From Lemma 1, we know that each $m_{i}$ is a power of 2. Using (1) for each $m_{i}$, we deduce that $A$ can be written in the form
$$
A=2^{N}\left(a_{0}\right)^{N_{0}} \cdots\left(a_{q}\right)^{N_{q}}(2),
$$
with $N>N_{0}+\cdots N_{q}$. Since each $a^{k_{j}}+1$ is congruent to 2 modulo 4, we must therefore have $s=N$. For each $j$, if we set $k_{j}=2^{r} t$ with $t$ odd, then $a^{k_{j}}+1=\left(a^{2^{r}}\right)^{t}+1 \equiv(-1)^{t}+1 \equiv 0$ $(\bmod 2)^{r}+1$. Thus $a^{k_{j}}+1$ is divisible by $a_{r}$.
Thus, each of the numbers $a^{k_{j}}+1$ is divisible by one of the $a_{i}$. Since $s>N_{0}+\cdots N_{q}$, there exists $i$ for which $a_{i}$ divides more than $N_{i}$ of the $a^{k_{j}}+1$. Therefore, $A$ is divisible by $\left(a_{i}\right)^{N_{i}+1}$, which is impossible according to (2), since $a_{i}$ is odd and coprime with each of the other $a_{j}$ according to Lemma 2.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer tous les entiers $a>0$ pour lesquels il existe des entiers strictement positifs $n, s, m_{1}, \cdots, m_{n}, k_{1}, \cdots, k_{s}$ tels que
$$
\left(a^{m_{1}}-1\right) \cdots\left(a^{m_{n}}-1\right)=\left(a^{k_{1}}+1\right) \cdots\left(a^{k_{s}}+1\right)
$$
|
On va prouver que les entiers $a$ cherchés sont $a=2$ et $a=3$.
Tout d'abord, on constate que $2^{2}-1=2+1$ et que $(3-1)(3-1)=3+1$, ce qui assure que $a=2$ et $a=3$ sont effectivement des solutions du problème.
Réciproquement, soit $a, n, s, m_{1}, \cdots, m_{n}, k_{1}, \cdots, k_{s}$ des entiers strictement positifs tels que
$$
\left(a^{m_{1}}-1\right) \cdots\left(a^{m_{n}}-1\right)=\left(a^{k_{1}}+1\right) \cdots\left(a^{k_{s}}+1\right)
$$
Clairement, on a $a \neq 1$, puisque si $a=1$ le membre de droite vaut 0 mais pas celui de gauche.
Par l'absurde: supposons que $a>3$.
On pose $A=\left(a^{m_{1}}-1\right) \cdots\left(a^{m_{n}}-1\right)=\left(a^{k_{1}}+1\right) \cdots\left(a^{k_{s}}+1\right)$.
Lemme 1. Chacun des nombres $m_{1}, \cdots, m_{n}$ et $a-1$ est une puissance de 2.
Preuve du lemme 1. Soit $i \in\{1, \cdots, n\}$ et $\gamma$ un diviseur impair de $m_{i}$ (éventuellement $\gamma=1$ ), disons $m_{i}=\gamma \times b$. Soit $p$ un diviseur premier de $a^{\gamma}-1$.
Puisque $a^{\gamma} \equiv 1(\bmod p)$, on a $a^{m_{i}} \equiv\left(a^{\gamma}\right)^{b} \equiv 1(\bmod p)$.
Ainsi $A$ est divisible par $p$, ce qui assure qu'il existe $j$ tel que $a^{k_{j}}+1$ soit divisible par $p$. Comme ci-dessus, on a alors $\left(a^{\gamma}\right)^{k_{j}}-1 \equiv 0(\bmod p)$ et, puisque $\gamma$ est impair, on a aussi $\left(a^{k_{j}}\right)^{\gamma} \equiv-1$ $(\bmod p)$.
Par suite $p$ divise $\left(\left(a^{k_{j}}\right)^{\gamma}+1\right)-\left(\left(a^{\gamma}\right)^{k_{j}}-1\right)=2$, d'où $p=2$.
Ainsi, le seul diviseur premier de $a^{\gamma}-1$ est $p=2$, ce qui prouve que $a^{\gamma}-1$ est une puissance de 2. Il existe donc un entier $c$ tel que
$$
2^{c}=a^{\gamma}-1=(a-1)\left(a^{\gamma-1}+\cdots+a+1\right) .
$$
En particulier, $a-1$ est donc une puissance de 2 et $a$ est impair. Mais, puisque $\gamma$ est impair, $a^{\gamma-1}+\cdots+a+1$ est impair et doit aussi être une puissance de 2 . Cela implique que $\gamma=1$ et donc que le seul diviseur impair de $m_{i}$ est 1 , ce qui conclut la preuve du lemme 1.
D'après le lemme, on a $a-1=2^{c}$ et $a-1>2$, donc $a-1$ est divisible par 4. Pour tout entier $k \geq 0$, on a alors $a^{k}+1 \equiv 2(\bmod 4)$.
Pour tout $i$, on pose $a_{i}=\frac{1}{2}\left(a^{2^{i}}+1\right)$. On sait donc que $a_{i}$ est un entier impair.
On vérifie facilement par récurrence que, pour tout entier $d \geq 0$ :
$$
a^{2^{d}}-1=(a-1)(a+1)\left(a^{2}+1\right) \cdots\left(a^{2^{d-1}}+1\right)=2^{c} \cdot 2^{d} \cdot a_{0} a_{1} \cdots a_{d-1}
$$
Lemme 2. Les nombres $a_{0}, a_{1}, a_{2}, \cdots$ sont deux à deux premiers entre eux.
Preuve du lemme 2. Soit $0 \leq i<j$. On note que $a_{i}$ et $a_{j}$ sont impairs donc leur pgcd $d$ est impair. D'après (1), le nombre $a^{2^{j}}-1$ est divisible par $a_{i}$. Puisque $a^{2^{j}}+1=2 a_{j}$, on en déduit que tout diviseur commun à $a_{i}$ et $a_{j}$ divise aussi $\left(a^{2^{j}}+1\right)-\left(a^{2^{j}}-1\right)=2$. Ainsi $d$ est impair et divise 2, donc $d=1$. On a donc $a_{i}$ et $a_{j}$ premiers entre eux, et cela achève la preuve du lemme 2.
D'après le lemme 1, on sait que chaque $m_{i}$ est une puissance de 2 . En utilisant (1) pour chaque $m_{i}$, on déduit que $A$ peut s'écrire sous la forme
$$
A=2^{N}\left(a_{0}\right)^{N_{0}} \cdots\left(a_{q}\right)^{N_{q}}(2),
$$
avec $N>N_{0}+\cdots N_{q}$. Puisque chaque $a^{k_{j}}+1$ est congru à 2 modulo 4 , on doit donc avoir $s=N$. Or, pour tout $j$, si l'on pose $k_{j}=2^{r} t$ avec $t$ impair, alors $a^{k_{j}}+1=\left(a^{2^{r}}\right)^{t}+1 \equiv(-1)^{t}+1 \equiv 0$ $(\bmod 2)^{r}+1$. Ainsi $a^{k_{j}}+1$ est divisible par $a_{r}$.
Ainsi, chacun des nombres $a^{k_{j}}+1$ est divisible par un des $a_{i}$. Puisque $s>N_{0}+\cdots N_{q}$, il existe $i$ pour lequel $a_{i}$ divise plus de $N_{i}$ des $a^{k_{j}}+1$. Par suite, $A$ est divisible par $\left(a_{i}\right)^{N_{i}+1}$, ce qui est impossible d'après (2), puisque $a_{i}$ est impair et premier avec chacun des autres $a_{j}$ d'après le lemme 2.
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2016-2017-ofm-2016-2017-test-novembre-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T1",
"year": "2016"
}
|
The integers $1,2, \ldots, 2018$ are written on the board. Then 2017 operations are performed as follows: choose two numbers $a$ and $b$, erase them, and write $a+b+2 a b$ in their place. At the end, only one integer remains on the board.
What are the possible values that its units digit can take?
|
Since there are 1009 odd numbers between 1 and 2018, we know that the sum of the integers initially written on the board is odd. Furthermore, one of these integers is congruent to $2(\bmod 5)$. An immediate induction then shows that, after each operation, the sum of the integers written on the board remains odd, and one of these integers is congruent to 2 $(\bmod 5)$. Consequently, the last integer written on the board is congruent to $1(\bmod 2)$ and to 2 $(\bmod 5)$, that is, to $7(\bmod 10)$.
|
7
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Les entiers $1,2, \ldots, 2018$ sont écrits au tableau. On effectue alors 2017 opérations comme suit : choisir deux nombres $a$ et $b$, les effacer, et écrire $a+b+2 a b$ à la place. À la fin, il ne reste qu'un seul entier sur le tableau.
Quelles sont les valeurs que son chiffre des unités peut prendre?
|
Puisqu'il y a 1009 nombres impairs entre 1 et 2018, on sait que la somme des entiers initialement inscrits au tableau est impaire. En outre, l'un de ces entiers est congru à $2(\bmod 5)$. Une récurrence immédiate permet alors de montrer que, après chaque opération, la somme des entiers écrits sur le tableau reste impaire, et l'un de ces entiers est congru à 2 $(\bmod 5)$. Par conséquent, le dernier entier écrit sur le tableau est congru à $1(\bmod 2)$ et à 2 $(\bmod 5)$, c'est-à-dire à $7(\bmod 10)$.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2017-2018-Corrige-03-2018.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T1",
"year": "2017"
}
|
Let $ABC$ be an isosceles triangle at $A$, such that $\widehat{BAC}=100^{\circ}$. Let $D$ be the intersection point of $(AC)$ and the bisector of $\widehat{ABC}$.
Show that $BC = AD + BD$.
|
According to the law of sines, note that $\mathrm{BD} \leqslant \mathrm{BC}$ if and only if $\sin (\widehat{\mathrm{BCD}}) \leqslant$ $\sin (\widehat{\mathrm{BDC}})$. Since $\widehat{\mathrm{BDC}}=130^{\circ}$ and $\widehat{\mathrm{BCD}}=40^{\circ}$, we have $\mathrm{BD} \geqslant \mathrm{BC}$. Let $E$ be the point on $[\mathrm{BC}]$ such that $B D=B E$, and let $A^{\prime}$ be the symmetric point of $A$ with respect to ( $A D$ ).
The law of sines then indicates that
$$
\mathrm{CE}=\frac{\sin (\widehat{\mathrm{CDE}})}{\sin (\widehat{\mathrm{ECD}})} \mathrm{DE}=\frac{\sin (\widehat{\mathrm{CDE}})}{\sin (\widehat{\mathrm{ECD}})} \times \frac{\sin (\widehat{\mathrm{EAD}})}{\sin \left(\widehat{\mathrm{A}^{\prime} \mathrm{ED}}\right)} A^{\prime} \mathrm{D}=\frac{\sin \left(40^{\circ}\right) \sin \left(80^{\circ}\right)}{\sin \left(40^{\circ}\right) \sin \left(80^{\circ}\right)} A D=A D .
$$
We deduce that $B C=C E+B E=A D+B D$.
|
BC = AD + BD
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle isocèle en $A$, tel que $\widehat{B A C}=100^{\circ}$. Soit $D$ le point d'intersection de (AC) et de la bissectrice de $\widehat{A B C}$.
Montrer que BC $=A D+B D$.
|
D'après la loi des sinus, notons que $\mathrm{BD} \leqslant \mathrm{BC}$ si et seulement $\operatorname{si} \sin (\widehat{\mathrm{BCD}}) \leqslant$ $\sin (\widehat{\mathrm{BDC}})$. Puisque $\widehat{\mathrm{BDC}}=130^{\circ}$ et $\widehat{\mathrm{BCD}}=40^{\circ}$, on a bien $\mathrm{BD} \geqslant \mathrm{BC}$. Soit E le point de $[\mathrm{BC}]$ tel que $B D=B E$, et soit $A^{\prime}$ le symétrique de $A$ par rapport à ( $A D$ ).
La loi des sinus indique alors que
$$
\mathrm{CE}=\frac{\sin (\widehat{\mathrm{CDE}})}{\sin (\widehat{\mathrm{ECD}})} \mathrm{DE}=\frac{\sin (\widehat{\mathrm{CDE}})}{\sin (\widehat{\mathrm{ECD}})} \times \frac{\sin (\widehat{\mathrm{EA}} \widehat{\mathrm{D}})}{\sin \left(\widehat{\mathrm{A}^{\prime} \mathrm{ED}}\right)} A^{\prime} \mathrm{D}=\frac{\sin \left(40^{\circ}\right) \sin \left(80^{\circ}\right)}{\sin \left(40^{\circ}\right) \sin \left(80^{\circ}\right)} A D=A D .
$$
On en déduit que $B C=C E+B E=A D+B D$.
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2017-2018-Corrige-03-2018.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T1",
"year": "2017"
}
|
Find all non-zero natural numbers $k, \ell$ such that $2^{k}+3^{\ell}$ is a perfect square.
|
A first idea is to consider the equation from the statement modulo $n$, where $n$ is not too large such that $\mathbb{Z} / \mathrm{n} \mathbb{Z}$ does not contain too many quadratic residues. Under these conditions, $n=3$ and $n=8$ seem to be good candidates, as the squares modulo 3 are 0 and 1, while the squares modulo 8 are 0, 1, and 4.
Since $k \geqslant 1$ and $\ell \geqslant 1$, we have $2^{k} \equiv 1(\bmod 3)$ and $3^{\ell} \equiv 1(\bmod 8)$, which means that $k$ and $\ell$ are even. By setting $\mathrm{a}=\mathrm{k} / 2, \mathrm{~b}=\ell / 2$ and $\mathrm{c}=\sqrt{2^{k}+3^{\ell}}$, we notice that $\left(\mathrm{c}-2^{\mathrm{a}}\right)\left(\mathrm{c}+2^{\mathrm{a}}\right)=$ $c^{2}-2^{k}=3^{\ell}$ is a power of 3.
 must necessarily be $3^{\ell}$, while the other is 1. The factor $c+2^{a}$ is the larger of the two, which shows that $c-2^{a}=1$ and $\mathrm{c}+2^{a}=3^{\ell}$, hence $2^{a+1}=3^{\ell}-1=9^{b}-1=\left(3^{b}-1\right)\left(3^{b}+1\right)$. Similarly, since $3^{\mathrm{b}}-1$ and $3^{\mathrm{b}}+1$ are even and $\operatorname{PGCD}\left(2,3^{\mathrm{b}}-1,3^{\mathrm{b}}+1\right)$ divides 2, one of the factors $3^{b}-1$ and $3^{b}+1$ must necessarily be $2^{a}$, while the other is 2. Therefore, $3^{\mathrm{b}}-1=2$ and $3^{\mathrm{b}}+1=2^{\mathrm{a}}$, which shows that $\mathrm{a}=2$ and $\mathrm{b}=1$, or $\mathrm{k}=4$ and $\ell=2$.
Conversely, if $(k, \ell)=(4,2)$, we have $2^{k}+3^{\ell}=2^{4}+3^{2}=16+9=25=5^{2}$. This shows that the pair $(k, \ell)=(4,2)$ is the only solution to the problem.
|
(k, \ell) = (4, 2)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Trouver tous les entiers naturels non nuls $k, \ell$ tels que $2^{k}+3^{\ell}$ soit un carré parfait.
|
Une première idée est de consiérer l'équation de l'énoncé modulo $n$, où n est un nombre pas trop grand tel que $\mathbb{Z} / \mathrm{n} \mathbb{Z}$ ne contienne pas trop de résidus quadratiques. Dans ces conditions, $n=3$ et $n=8$ semblent de bons candidats, car les carrés modulo 3 sont 0 et 1 , alors que les carrés modulo 8 sont 0,1 et 4 .
Puisque $k \geqslant 1$ et $\ell \geqslant 1$, on a donc $2^{k} \equiv 1(\bmod 3)$ et $3^{\ell} \equiv 1(\bmod 8)$, ce qui signifie que $k$ et $\ell$ sont pairs. En posant $\mathrm{a}=\mathrm{k} / 2, \mathrm{~b}=\ell / 2$ et $\mathrm{c}=\sqrt{2^{k}+3^{\ell}}$, on remarque alors que $\left(\mathrm{c}-2^{\mathrm{a}}\right)\left(\mathrm{c}+2^{\mathrm{a}}\right)=$ $c^{2}-2^{k}=3^{\ell}$ est une puissance de 3 .
 vaut nécessairement $3^{\ell}$, tandis que l'autre vaut 1 . Le facteur $c+2^{a}$ est le plus grand des deux, ce qui montre que $c-2^{a}=1$ et $\mathrm{c}+2^{a}=3^{\ell}$, donc que $2^{a+1}=3^{\ell}-1=9^{b}-1=\left(3^{b}-1\right)\left(3^{b}+1\right)$. De même, puisque $3^{\mathrm{b}}-1$ et $3^{\mathrm{b}}+1$ sont pairs et que $\operatorname{PGCD}\left(2,3^{\mathrm{b}}-1,3^{\mathrm{b}}+1\right)$ divise 2 , l'un des facteurs $3^{b}-1$ et $3^{b}+1$ vaut nécessairement $2^{a}$, tandis que l'autre vaut 2 . Par conséquent, $3^{\mathrm{b}}-1=2$ et $3^{\mathrm{b}}+1=2^{\mathrm{a}}$, ce qui montre que $\mathrm{a}=2$ et $\mathrm{b}=1$, ou encore $\mathrm{k}=4$ et $\ell=2$.
Réciproquement, si $(k, \ell)=(4,2)$, on a bien $2^{k}+3^{\ell}=2^{4}+3^{2}=16+9=25=5^{2}$. Ceci montre que la paire $(k, \ell)=(4,2)$ est la seule solution du problème.
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2017-2018-Corrige-03-2018.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T1",
"year": "2017"
}
|
Let $a, b, c, d$ be real numbers such that $0 \leqslant a \leqslant b \leqslant c \leqslant d$. Show that
$$
a b^{3}+b c^{3}+c d^{3}+d a^{3} \geqslant a^{2} b^{2}+b^{2} c^{2}+c^{2} d^{2}+d^{2} a^{2}
$$
|
A first idea is to consider the "symmetric sums $\gg$ each other $S_{1}=a b^{3}+b^{3}+c d^{3}+d a^{3}$ and $S_{2}=a^{3} b+b^{3} c+c^{3} d+d^{3} a$. We then observe that
$S_{1}-S_{2}=\left(d^{3}-b^{3}\right)(c-a)+\left(c^{3}-a^{3}\right)(b-d)=(d-b)(c-a)\left(d^{2}+bd+d^{2}-c^{2}-ac-a^{2}\right) \geqslant 0$.
The Cauchy-Schwarz inequality then indicates that $S_{1}^{2} \geqslant S_{1} S_{2} \geqslant\left(a^{2} b^{2}+b^{2} c^{2}+c^{2} d^{2}+d^{2} a^{2}\right)^{2}$, which concludes.
## Exercises of Group A - Statements and Solutions
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $a, b, c, d$ des réels tels que $0 \leqslant a \leqslant b \leqslant c \leqslant d$. Montrer que
$$
a b^{3}+b c^{3}+c d^{3}+d a^{3} \geqslant a^{2} b^{2}+b^{2} c^{2}+c^{2} d^{2}+d^{2} a^{2}
$$
|
Une première idée est de considérer les sommes «symétriques $\gg$ l'une de l'autre $S_{1}=a b^{3}+b^{3}+c d^{3}+d a^{3}$ et $S_{2}=a^{3} b+b^{3} c+c^{3} d+d^{3} a$. On constate alors que
$S_{1}-S_{2}=\left(d^{3}-b^{3}\right)(c-a)+\left(c^{3}-a^{3}\right)(b-d)=(d-b)(c-a)\left(d^{2}+b d+d^{2}-c^{2}-a c-a^{2}\right) \geqslant 0$.
L'inégalité de Cauchy-Schwarz indique alors que $S_{1}^{2} \geqslant S_{1} S_{2} \geqslant\left(a^{2} b^{2}+b^{2} c^{2}+c^{2} d^{2}+d^{2} a^{2}\right)^{2}$, ce qui conclut.
## Exercices du groupe A - Énoncés et solutions
|
{
"exam": "French_tests",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/tests/fr-2017-2018-Corrige-03-2018.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T1",
"year": "2017"
}
|
Let $n$ be an odd natural number, and let $a_{1}, \ldots, a_{n}$ be non-zero natural numbers. We denote $A$ as the product of the integers $a_{i}$, and $d$ as their greatest common divisor.
Show that
$$
\operatorname{GCD}\left(a_{1}^{n}+A, a_{2}^{n}+A, \ldots, a_{n}^{n}+A\right) \leqslant 2 d^{n}
$$
|
For all $i$, we set $b_{i}=a_{i} / d$, so that $\operatorname{PGCD}\left(b_{1}, \ldots, b_{n}\right)=1$, and we also set $B=b_{1} \times \ldots \times b_{n}$ and $\Delta=\operatorname{PGCD}\left(b_{1}^{n}+B, b_{2}^{n}+B, \ldots, b_{n}^{n}+B\right)$. Then $\operatorname{PGCD}\left(a_{1}^{n}+A, a_{2}^{n}+A, \ldots, a_{n}^{n}+A\right)=d^{n} \times \Delta$, and it remains to prove that $\Delta \leqslant 2$.
We then consider a potential prime factor $p$ of $\Delta$. If $p$ divides one of the integers $b_{i}$, then it also divides $B$, so it divides each integer $b_{j}$, which is absurd. Therefore, $p$ does not divide any of the integers $b_{i}$, and does not divide $B$ either. This shows that $\Delta$ is coprime with $B$. Since $b_{1}^{n} \equiv b_{2}^{n} \equiv \ldots \equiv b_{n}^{n}=-B(\bmod \Delta)$, then $B^{n} \equiv b_{1}^{n} \times \ldots \times b_{n}^{n} \equiv(-1)^{n} B^{n} \equiv-B^{n}$ $(\bmod \Delta)$. Therefore, $\Delta$ divides $2 B^{n}$. We conclude that $\Delta$ divides 2, which completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $n$ un entier naturel impair, et soit $a_{1}, \ldots, a_{n}$ des entiers naturels non nuls. On note $A$ le produit des entiers $a_{i}$, et $d$ leur plus grand diviseur commun.
Montrer que
$$
\operatorname{PGCD}\left(a_{1}^{n}+A, a_{2}^{n}+A, \ldots, a_{n}^{n}+A\right) \leqslant 2 d^{n}
$$
|
Pour tout $i$, on pose $b_{i}=a_{i} / d$, de sorte que $\operatorname{PGCD}\left(b_{1}, \ldots, b_{n}\right)=1$, et on pose également $B=b_{1} \times \ldots \times b_{n}$ et $\Delta=\operatorname{PGCD}\left(b_{1}^{n}+B, b_{2}^{n}+B, \ldots, b_{n}^{n}+B\right)$. Alors $\operatorname{PGCD}\left(a_{1}^{n}+A, a_{2}^{n}+A, \ldots, a_{n}^{n}+A\right)=d^{n} \times \Delta$, et il reste à démontrer que $\Delta \leqslant 2$.
On considère alors un éventuel facteur premier $p$ de $\Delta$. Si $p$ divise un des entiers $b_{i}$, alors il divise $B$ également, donc il divise chaque entier $b_{j}$, ce qui est absurde. Par conséquent, $p$ ne divise aucun des entiers $b_{i}$, et ne divise pas $B$ non plus. Cela montre que $\Delta$ est premier avec $B$. Or, puisque $b_{1}^{n} \equiv b_{2}^{n} \equiv \ldots \equiv b_{n}^{n}=-B(\bmod \Delta)$, alors $B^{n} \equiv b_{1}^{n} \times \ldots \times b_{n}^{n} \equiv(-1)^{n} B^{n} \equiv-B^{n}$ $(\bmod \Delta)$. Par conséquent, $\Delta$ divise $2 \mathrm{~B}^{n}$. On en déduit que $\Delta$ divise 2 , ce qui conclut.
|
{
"exam": "French_tests",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/tests/fr-2017-2018-Corrige-03-2018.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T1",
"year": "2017"
}
|
Let $q$ be a real number. Margaret wrote 10 distinct real numbers in a line. Then she adds three more lines as follows:
$\triangleright$ on the $2^{\text {nd }}$ line, she writes all numbers of the form $a-b$, where $a$ and $b$ are real numbers (not necessarily distinct) from the $1^{\text {st }}$ line;
$\triangleright$ on the $3^{\text {rd }}$ line, she writes all numbers of the form $q a b$, where $a$ and $b$ are real numbers (not necessarily distinct) from the $2^{\text {nd }}$ line;
$\triangleright$ on the $4^{\text {th }}$ line, she writes all numbers of the form $a^{2}+b^{2}-c^{2}-d^{2}$, where $a, b, c$ and $d$ are real numbers (not necessarily distinct) from the $2^{\text {nd }}$ line.
Find all real numbers $q$ such that, regardless of the 10 numbers written on the $1^{\text {st }}$ line, every number on the $3^{\text {rd }}$ line is also on the $4^{\text {th }}$ line.
|
We will say that a real number $q$ is good if it has the property required in the statement. First of all, it is clear that if $q$ is good, then $-q$ is also good, and vice versa. On the other hand, $q=0$ is obviously good. We are therefore looking for good real numbers $q>0$, if there are any.
Let $\lambda$ be a large real number and let $\varepsilon=1 / \lambda$. Suppose Margaret has written ten numbers $x_{1}, \ldots, x_{10}$ such that $0 \leqslant x_{1}<\ldots<x_{8} \leqslant \varepsilon, x_{9}=1$ and $x_{10}=\lambda$. Then the 2nd line contains the numbers $\pm \lambda, \pm(\lambda-1)$ and $\pm 1$, as well as elements of the set $\Omega_{2}=[0,1] \cup[\lambda-\varepsilon, \lambda]$ and their opposites. In particular, Margaret therefore writes the reals $q \lambda^{2}$ and $q \lambda$ on the 3rd line.
We then consider a number from the 4th line, of the form $z=a^{2}+b^{2}-c^{2}-d^{2}$, and such that $z \geqslant 0$. Each of the reals $a^{2}, b^{2}, c^{2}, d^{2}$ belongs to the set $\left\{0, \lambda^{2}\right\}+\{-2 \lambda, 0\}+[0,2]$, so $z$ belongs to the set $\Omega_{4}=\left\{0, \lambda^{2}, 2 \lambda^{2}\right\}+\{-4 \lambda,-2 \lambda, 0,2 \lambda, 4 \lambda\}+[-4,4]$.
If $q$ is good, then $q \lambda^{2}$ and $q \lambda$ belong to $\Omega_{4}$, so by letting $\lambda$ tend to $+\infty$ we deduce respectively that $q \in\{1,2\}$ and that $q \in\{2,4\}$. This shows that only $q=2$ is likely to be good.
Conversely, if $q=2$, every number on the 3rd line is of the form $2(a-b)(c-d)$ with $a, b, c, d$ reals from the 1st line. Since $2(a-b)(c-d)=(a-d)^{2}+(b-c)^{2}-(a-c)^{2}-(b-d)^{2}$, this number also appears on the 4th line. Therefore, the good reals are $-2, 0$, and $2$.
|
-2, 0, 2
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Soit q un nombre réel. Margaret a écrit 10 nombres réels, deux à deux distincts, sur une ligne. Puis elle ajoute trois lignes comme suit :
$\triangleright$ sur la $2^{\text {nde }}$ ligne, elle écrit tous les nombres de la forme $a-b$, où $a$ et $b$ sont deux réels (non nécessairement distincts) de la $1{ }^{\text {ère }}$ ligne;
$\triangleright$ sur la $3^{\text {ème }}$ ligne, elle écrit tous les nombres de la forme $q a b$, où $a$ et $b$ sont deux réels (non nécessairement distincts) de la $2^{\text {nde }}$ ligne;
$\triangleright$ sur la $4^{\text {ème }}$ ligne, elle écrit tous les nombres de la forme $a^{2}+b^{2}-c^{2}-d^{2}$, où $a, b, c$ et $d$ sont des réels (non nécessairement distincts) de la $2^{\text {nde }}$ ligne.
Trouver tous les réels q tels que, quels que soient les 10 nombres écrits sur la $1{ }^{\text {ère }}$ ligne, chaque nombre de la $3^{\text {ème }}$ ligne soit également sur la $4^{\text {ème }}$ ligne.
|
On va dire qu'un réel q est bon s'il a la propriété demandée dans l'énoncé. Tout d'abord, il est clair que, si q est bon, alors - q l'est aussi, et réciproquement. D'autre part, $q=0$ est manifestement bon. On cherche donc les bons réels $q>0$, s'il y en a.
Soit $\lambda$ un grand nombre réel et soit $\varepsilon=1 / \lambda$. On suppose que Margaret a écrit dix nombres $x_{1}, \ldots, x_{10}$ tels que $0 \leqslant x_{1}<\ldots<x_{8} \leqslant \varepsilon, x_{9}=1$ et $x_{10}=\lambda$. Alors la $2^{\text {nde }}$ ligne contient les nombres $\pm \lambda, \pm(\lambda-1)$ et $\pm 1$, ainsi que des éléments de l'ensemble $\Omega_{2}=[0,1] \cup[\lambda-\varepsilon, \lambda]$ et leurs opposés. En particulier, Margaret écrit donc les réels $q \lambda^{2}$ et $q \lambda$ sur la $3^{\text {ème }}$ ligne.
On considère alors un nombre de la $4^{\text {ème }}$ ligne, de la forme $z=a^{2}+b^{2}-c^{2}-d^{2}$, et tel que $z \geqslant 0$. Chacun des réels $\mathrm{a}^{2}, \mathrm{~b}^{2}, \mathrm{c}^{2}, \mathrm{~d}^{2}$ appartient à l'ensemble $\left\{0, \lambda^{2}\right\}+\{-2 \lambda, 0\}+[0,2]$, donc $z$ appartient à l'ensemble $\Omega_{4}=\left\{0, \lambda^{2}, 2 \lambda^{2}\right\}+\{-4 \lambda,-2 \lambda, 0,2 \lambda, 4 \lambda\}+[-4,4]$.
Si q est bon, alors $q \lambda^{2}$ et $\mathrm{q} \lambda$ appartiennent à $\Omega_{4}$, donc en faisant tendre $\lambda$ vers $+\infty$ on en déduit respectivement que $q \in\{1,2\}$ et que $q \in\{2,4\}$. Cela montre que seul $q=2$ est susceptible d'être bon.
Réciproquement, si $q=2$, tout nombre de la $3^{\text {ème }}$ est de la forme $2(a-b)(c-d)$ avec $a, b, c, d$ des réels de la $1^{\text {ère }}$ ligne. Puisque $2(a-b)(c-d)=(a-d)^{2}+(b-c)^{2}-(a-c)^{2}-(b-d)^{2}$, ce nombre est figure également sur la $4^{\text {ème }}$ ligne. Par conséquent, les bons réels sont $-2,0$ et 2 .
|
{
"exam": "French_tests",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/tests/fr-2017-2018-Corrige-03-2018.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T1",
"year": "2017"
}
|
Let $ABC$ be a non-isosceles acute triangle. Let $O$ be the center of the circumcircle of $ABC$ and $H$ the orthocenter of $ABC$. Let $P$ and $Q$ be the points of intersection of $(AO)$ with $(BH)$ and $(CH)$, respectively.
Show that the center of the circumcircle of $P Q H$ lies on a median of the triangle $A B C$.
|
Let $\Omega$ be the circumcircle of $ABC$, $\omega$ the circumcircle of $PQH$, and $X$ the center of $\omega$. Since $B$ and $C$ play symmetric roles, we will show that $X$ lies on the median from $A$. Let $M$ be the intersection of the lines $(AX)$ and $(BC)$: we will show that $M$ is the midpoint of $[BC]$, that is, $\widehat{CMO}=90^{\circ}$.
First, a simple angle chasing shows that $\widehat{QHP}=\widehat{CAB}$, $\widehat{HPQ}=\widehat{ABC}$, and $\widehat{PQH}=\widehat{PHA}=\widehat{BCA}$. The triangles $ABC$ and $HPQ$ are therefore similar, and there exists a similarity $s$ such that $s(A)=H$, $s(B)=P$, $s(C)=Q$, and $s(O)=X$.
Furthermore, since $\widehat{PQH}=\widehat{PHA}$, we know that $(AH)$ is tangent to $\omega$ at $H$. Consequently, if we set $S=s^{-1}(\mathcal{A})$, then we know that $S$ is the intersection of $(BC)$ and the tangent to $\Omega$ at $A$. Since $s$ maps $BSO$ to $PAX$, we deduce that $\widehat{MSO}=\widehat{BSO}=\widehat{XAP}=\widehat{MAO}$, so the points $M, S, O$, and $A$ are concyclic. Now, $\widehat{SAO}=90^{\circ}$. It follows that $\widehat{SMO}=90^{\circ}$ as well, which concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle acutangle non isocèle. Soit O le centre du cercle circonscrit à $A B C$ et $H$ l'orthocentre de $A B C$. Soit $P$ et $Q$ les points d'intersection respectifs de ( $A O)$ avec (BH) et (CH).
Montrer que le centre du cercle circonscrit à $P Q H$ se situe sur une médiane du triangle $A B C$.
|
Soit $\Omega$ le cercle circonscrit à $A B C, \omega$ le cercle circonscrit à PQH , et $X$ le centre de $\omega$. Puisque $B$ et $C$ jouent des rôles symétriques, on va montrer que $X$ se trouve sur la médiane issue de $A$. Soit alors $M$ le point d'intersection des droites $(A X)$ et (BC) : montrons que $M$ est le milieu de $[B C]$, c'est-à-dire que $\widehat{C M O}=90^{\circ}$.
Tout d'abord, une simple chasse aux angles montre que $\widehat{\mathrm{QHP}}=\widehat{\mathrm{CAB}}, \widehat{\mathrm{HPQ}}=\widehat{\mathrm{ABC}}$ et $\widehat{\mathrm{PQH}}=$ $\widehat{P H A}=\widehat{B C A}$. Les triangles $A B C$ et $H P Q$ sont donc semblables, et il existe une similitude $s$ telle que $s(A)=H, s(B)=P, s(C)=Q$ et $s(O)=X$.
$D^{\prime}$ autre part, puisque $\widehat{P Q H}=\widehat{P H A}$ on sait que $(A H)$ est tangente à $\omega$ en $H$. Par conséquent, si on pose $S=s^{-1}(\mathcal{A})$, alors on sait que $S$ est le point d'intersection de (BC) et de la tangente à $\Omega$ en $A$. Puisque s envoie $B S O$ sur $P A X$, on en déduit que $\widehat{M S O}=\widehat{B S O}=\widehat{\mathrm{XAP}}=\widehat{\mathrm{MAO}}$, donc que les points $M, S, O$ et $A$ sont cocycliques. Or, $\widehat{S A O}=90^{\circ}$. Il s'ensuit que $\widehat{S M O}=90^{\circ}$ également, ce qui conclut.
|
{
"exam": "French_tests",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/tests/fr-2017-2018-Corrige-03-2018.jsonl",
"solution_match": "\nSolution de l'exercice 7",
"tier": "T1",
"year": "2017"
}
|
Let $n \geq 3$ be an integer and consider $n$ lines in general position (i.e., no three lines are concurrent and no two lines are parallel). How many triangles are formed by these lines?
N.B. For example, in the figure below, there are 4 triangles.
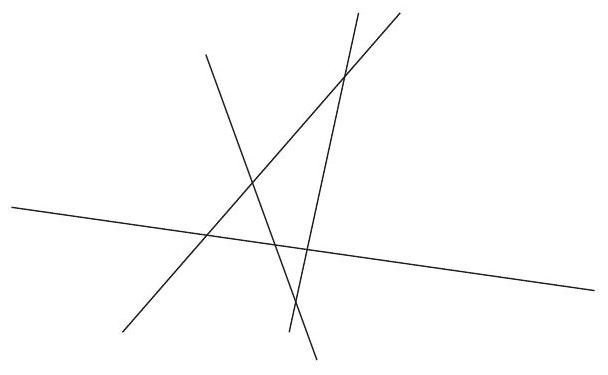
|
If we number the $n$ lines from 1 to $n$, we notice that each triangle is encoded by a subset of $\{1,2, \ldots, n\}$ with three elements. Therefore, there are $\binom{n}{3}=$ $\frac{n(n-1)(n-2)}{6}$ triangles.
|
\frac{n(n-1)(n-2)}{6}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Soit $n \geq 3$ un entier et considérons $n$ droites en position générale (c'est-à-dire que trois droites ne sont jamais concourantes et deux droites jamais parallèles). Combien de triangles sont formés par ces droites?
N.B. Par exemple, dans la figure ci-dessous, il y a 4 triangles.

|
Si on numérote de 1 à $n$ les $n$ droites, on remarque que chaque triangle est codé par la donnée d'un sous-ensemble de $\{1,2, \ldots, n\}$ à trois éléments. Il y a donc $\binom{n}{3}=$ $\frac{n(n-1)(n-2)}{6}$ triangles.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-fevrier-junior-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T1",
"year": "2017"
}
|
Let $ABC$ be a triangle. We denote $L, M, N$ as the midpoints of $[BC], [CA]$, and $[AB]$. Let $(d)$ be the tangent at $A$ to the circumcircle of $ABC$. The line $(LM)$ intersects $(d)$ at $P$, and the line $(LN)$ intersects $(d)$ at $Q$. Show that $(CP)$ and $(BQ)$ are parallel.
|
Since $(A Q, A B) = (C A, C B) = (L Q, L B)$, points $A, Q, B, L$ are concyclic, and similarly, points $A, P, C, M$ are concyclic. Therefore, $(C P, B C) = (C P, C L) = (A P, A L) = (A Q, A L) = (B Q, B L) = (B Q, B C)$, so lines $(C P)$ and $(B Q)$ are parallel.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle. On note $L, M, N$ les milieux de $[B C],[C A]$ et $[A B]$. Notons $(d)$ la tangente en $A$ au cercle circonscrit à $A B C$. La droite $(L M)$ coupe $(d)$ en $P$, et la droite $(L N)$ coupe $(d)$ en $Q$. Montrer que $(C P)$ et $(B Q)$ sont parallèles.
|

On a $(A Q, A B)=(C A, C B)=(L Q, L B)$ donc $A, Q, B, L$ sont cocycliques, et de même $A, P, C, M$ sont cocycliques. On a donc $(C P, B C)=(C P, C L)=(A P, A L)=(A Q, A L)=(B Q, B L)=$ $(B Q, B C)$, donc $(C P)$ et $(B Q)$ sont parallèles.
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-fevrier-junior-corrige.jsonl",
"solution_match": "## Solution de l'exercice 2",
"tier": "T1",
"year": "2017"
}
|
Let $p$ and $n$ be strictly positive integers, with $p$ prime, and $n \geqslant p$. Suppose that $1+n p$ is a perfect square. Show that $n+1$ is a sum of $p$ non-zero perfect squares (not necessarily distinct).
|
Let $k$ be such that $1+n p=k^{2}$, then $n p=(k-1)(k+1)$.
First case: $p$ divides $k-1$. Then we can write $k-1=p \ell$, so $k=p \ell+1$. By substituting into the equation, we get that $n+1=p \ell^{2}+2 \ell+1=(p-1) \ell^{2}+(\ell+1)^{2}$.
Second case: $p$ divides $k+1$. Using the same method, we get $n+1=p \ell^{2}-2 \ell+1=(p-1) \ell^{2}+(\ell-1)^{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soient $p$ et $n$ des entiers strictement positifs, avec $p$ premier, et $n \geqslant p$. On suppose que $1+n p$ est un carré parfait. Montrer que $n+1$ est une somme de $p$ carrés parfaits non nuls (non nécessairement distincts).
|
Soit $k$ tel que $1+n p=k^{2}$, alors $n p=(k-1)(k+1)$.
Premier cas : $p$ divise $k-1$. Alors on peut écrire $k-1=p \ell$, donc $k=p \ell+1$. En reportant dans l'égalité, on obtient que $n+1=p \ell^{2}+2 \ell+1=(p-1) \ell^{2}+(\ell+1)^{2}$.
Deuxième cas : $p$ divise $k+1$. On obtient avec la même méthode $n+1=p \ell^{2}-2 \ell+1=$ $(p-1) \ell^{2}+(\ell-1)^{2}$.
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-fevrier-junior-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T1",
"year": "2017"
}
|
Let $n \geqslant 1$ be an integer. For any non-empty subset $A$ of $\{1,2, \ldots, n\}$, we denote $P(A)$ as the product of all elements of $A$. For example, for $A=\{2,4,7\}$, we have $P(A)=$ 56. Determine the sum of $\frac{1}{P(A)}$ as $A$ ranges over all non-empty subsets of $\{1,2, \ldots, n\}$.
|
We have the identity $\left(1+x_{1}\right)\left(1+x_{2}\right) \cdots\left(1+x_{n}\right)=1+\sum x_{i}+\sum_{i<j} x_{i} x_{j}+\cdots$. By taking $x_{i}=\frac{1}{a_{i}}$, we obtain
$$
\sum_{k \geqslant 0} \sum_{a_{1}<\cdots<a_{k}} \frac{1}{a_{1} a_{2} \cdots a_{k}}=\left(1+\frac{1}{1}\right) \cdots\left(1+\frac{1}{n}\right)=\frac{2}{1} \times \frac{3}{2} \times \frac{4}{3} \cdots \times \frac{n+1}{n}=n+1
$$
Thus, $1+\sum_{A} \frac{1}{P(A)}=n+1$ and therefore $\sum_{A} \frac{1}{P(A)}=n$.
|
n
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Soit $n \geqslant 1$ un entier. Pour tout sous-ensemble non vide $A$ de $\{1,2, \ldots, n\}$, on note $P(A)$ le produit de tous les éléments de $A$. Par exemple, pour $A=\{2,4,7\}$, on a $P(A)=$ 56. Déterminer la somme des $\frac{1}{P(A)}$ lorsque $A$ parcourt tous les sous-ensembles non vides de $\{1,2, \ldots, n\}$.
|
On a l'identité $\left(1+x_{1}\right)\left(1+x_{2}\right) \cdots\left(1+x_{n}\right)=1+\sum x_{i}+\sum_{i<j} x_{i} x_{j}+\cdots$. En prenant $x_{i}=\frac{1}{a_{i}}$, on obtient
$$
\sum_{k \geqslant 0} \sum_{a_{1}<\cdots<a_{k}} \frac{1}{a_{1} a_{2} \cdots a_{k}}=\left(1+\frac{1}{1}\right) \cdots\left(1+\frac{1}{n}\right)=\frac{2}{1} \times \frac{3}{2} \times \frac{4}{3} \cdots \times \frac{n+1}{n}=n+1
$$
On a donc $1+\sum_{A} \frac{1}{P(A)}=n+1$ donc $\sum_{A} \frac{1}{P(A)}=n$.
|
{
"exam": "French_tests",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-fevrier-junior-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T1",
"year": "2017"
}
|
Determine the maximum value of $\sqrt{x}+\sqrt{2 y+2}+\sqrt{3 z+6}$ when $x, y, z$ are strictly positive real numbers satisfying $x+y+z=3$.
|
According to the Cauchy-Schwarz inequality, we have
$$
\sqrt{x} \sqrt{1}+\sqrt{y+1} \sqrt{2}+\sqrt{z+2} \sqrt{3} \leqslant \sqrt{x+y+1+z+2} \sqrt{1+2+3}=6
$$
Equality is achieved when $x=y=z=1$. Therefore, the maximum value is 6.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Déterminer la valeur maximale de $\sqrt{x}+\sqrt{2 y+2}+\sqrt{3 z+6}$ lorsque $x, y, z$ sont des nombres réels strictement positifs vérifiant $x+y+z=3$.
|
D'après l'inégalité de Cauchy-Schwarz, on a
$$
\sqrt{x} \sqrt{1}+\sqrt{y+1} \sqrt{2}+\sqrt{z+2} \sqrt{3} \leqslant \sqrt{x+y+1+z+2} \sqrt{1+2+3}=6
$$
L'égalité est atteinte lorsque $x=y=z=1$. Donc la valeur maximale est 6 .
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-fevrier-senior-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T1",
"year": "2017"
}
|
Let $ABC$ be an acute triangle, and let $P$ be a point located inside the triangle $ABC$. Let $D$ be the midpoint of the segment $[PC]$, $E$ the intersection point of the lines $(AP)$ and $(BC)$, and $Q$ the intersection point of the lines $(BP)$ and $(DE)$. Show that, if the angles $\widehat{PAC}$ and $\widehat{PCB}$ are equal, then $\sin (\widehat{BCQ})=\sin (\widehat{BAP})$.
|
Let $R$ be the intersection point of the lines $(C Q)$ and $(A P)$. It suffices to prove the equality of the angles $(C B, C Q)=(A B, A R)$. To do this, it suffices to prove that the points $B, C, A, R$ are concyclic, that is, $(B R, B C)=(A R, R C)$. Since $(A R, A C) = (C P, C B)$, it suffices to prove that $(B R, B C)=(C P, C B)$, hence that the lines $(B R)$ and $(P C)$ are parallel.
For this last point, one can use that if $X=(C P) \cap(B R)$ then $(X, D, P, C)$ is a harmonic division. One can also do without projective geometry as follows:
We use Ceva's theorem in the triangle $P C E$, since the lines $(P B)$, $(D E)$, and $(R C)$ are concurrent at $Q$, with $R \in(P E)$ and $B \in(C E)$. We deduce that
$$
1=\frac{C B}{E B} \cdot \frac{P D}{C D} \cdot \frac{R E}{R P}=\frac{C B}{E B} \cdot \frac{R E}{R P}
$$
that is,
$$
\frac{R E}{E B}=\frac{R P}{C B}
$$
By applying the converse of Thales' theorem to the triangles $B R E$ and $C P E$, we deduce from this last equality that the lines $(B R)$ and $(P C)$ are indeed parallel, which concludes.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle acutangle, et soit $P$ un point situé à l'intérieur du triangle $A B C$. Soit $D$ le milieu du segment $[P C], E$ le point d'intersection des droites $(A P)$ et $(B C)$, et $Q$ le point d'intersection des droites $(B P)$ et $(D E)$. Montrer que, si les angles $\widehat{P A C}$ et $\widehat{P C B}$ sont égaux, alors $\sin (\widehat{B C Q})=\sin (\widehat{B A P})$.
|
Soit $R$ le point d'intersection des droites $(C Q)$ et $(A P)$. Il suffit de prouver l'égalité des angles de droites $(C B, C Q)=(A B, A R)$. Pour ce faire, il suffit de prouver que les points $B, C, A, R$ sont cocycliques, c'est-à-dire que $(B R, B C)=(A R, R C)$. Comme $(A R, A C)=$ $(C P, C B)$, il suffit de prouver que $(B R, B C)=(C P, C B)$, donc que les droites $(B R)$ et $(P C)$ sont parallèles.
Pour ce dernier point, on peut utiliser que si $X=(C P) \cap(B R)$ alors $(X, D, P, C)$ est une division harmonique. On peut également se passer de géométrie projective comme suit :
On utilise le théorème de Ceva dans le triangle $P C E$, puisque les droites $(P B),(D E)$ et $(R C)$ sont concourantes en $Q$, avec $R \in(P E)$ et $B \in(C E)$. On en déduit que
$$
1=\frac{C B}{E B} \cdot \frac{P D}{C D} \cdot \frac{R E}{R P}=\frac{C B}{E B} \cdot \frac{R E}{R P}
$$
c'est-à-dire
$$
\frac{R E}{E B}=\frac{R P}{C B}
$$
En appliquant la réciproque du théorème de Thalès aux triangles $B R E$ et $C P E$, on déduit de cette dernière égalité que les droites $(B R)$ et $(P C)$ sont bien parallèles, ce qui conclut.

|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-fevrier-senior-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T1",
"year": "2017"
}
|
Find all possible values for $f(2018)$ where $f$ is a function from $\mathbb{Q}$ to $\mathbb{R}_{+}$ satisfying the following three conditions:
- $f(2)=1 / 2$;
- for any rational $x$, if $f(x) \leqslant 1$, then $f(x+1) \leqslant 1$;
- $f(x y)=f(x) f(y)$ for all rational $x$ and $y$.
|
First, the equality $1 / 2=f(2)=f(1 \times 2)=f(1) f(2)=f(1) / 2$ shows that $f(1)=1$, and thus that $f(n) \leqslant 1$ for any non-zero natural number $n$.
Furthermore, for all $x, y$ with $y \neq 0$ we have $f(y) \neq 0$, and $f(x / y)=f(x) / f(y)$ since $f(x / y) f(y)=f((x / y) y)=f(x)$. In particular, $f(1 / 2)=2$. Finally, for any rational $x$, we have $f(x)^{2}=f\left(x^{2}\right)=f(-x)^{2}$, so $f$ is even.
Let then $k$ be an odd natural number, of the form $k=2 n+1$: we necessarily have $f(k) \leqslant 1$. We also know that $f(-k / 2)>1$, since $1 / 2=-k / 2+(n+1)$, so $f(-2 / k)=1 / f(-k / 2) \leqslant 1$, which implies that $f\left(\frac{k-2}{k}\right)=f\left(-\frac{2}{k}+1\right) \leqslant 1$, consequently $f(k-2) \leqslant f(k)$.
This allows us to show by induction that for any $k \geqslant 1$ odd we have $f(k) \geqslant 1$, and thus $f(k)=1$.
We deduce from all this that $f(2018)=f(2) f(1009)=1 / 2$.
Conversely, it remains to verify that a function $f$ as described in the statement does indeed exist. It suffices for this to observe that the function $f$ defined by
$$
f: p / q \mapsto \begin{cases}0 & \text { if } p=0 \\ 2^{v_{2}(q)-v_{2}(p)} & \text { if } p \neq 0\end{cases}
$$
where $v_{2}(n)$ denotes the 2-adic valuation of the integer $n$, satisfies the conditions of the statement.
|
\frac{1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Trouver toutes les valeurs possibles pour $f(2018)$ où $f$ est une fonction de $\mathbb{Q}$ dans $\mathbb{R}_{+}$vérifiant les trois conditions suivantes:
- $f(2)=1 / 2$ ;
- pour tout rationnel $x$, si $f(x) \leqslant 1$, alors $f(x+1) \leqslant 1$;
- $f(x y)=f(x) f(y)$ pour tous rationnels $x$ et $y$.
|
Tout d'abord, l'égalité $1 / 2=f(2)=f(1 \times 2)=f(1) f(2)=f(1) / 2$ montre que $f(1)=1$, et donc que $f(n) \leqslant 1$ pour tout entier naturel non nul $n$.
Notons de plus que pour tous $x, y$ avec $y \neq 0$ on a $f(y) \neq 0$, et $f(x / y)=f(x) / f(y)$ puisque $f(x / y) f(y)=f((x / y) y)=f(x)$. En particulier, $f(1 / 2)=2$. Enfin, pour tout rationnel $x$, on a $f(x)^{2}=f\left(x^{2}\right)=f(-x)^{2}$, donc $f$ est paire.
Soit alors $k$ un entier naturel impair, de la forme $k=2 n+1$ : on a nécessairement $f(k) \leqslant 1$. On sait également que $f(-k / 2)>1$, puisque $1 / 2=-k / 2+(n+1)$, donc $f(-2 / k)=1 / f(-k / 2) \leqslant 1$, ce qui implique que $f\left(\frac{k-2}{k}\right)=f\left(-\frac{2}{k}+1\right) \leqslant 1$, par conséquent $f(k-2) \leqslant f(k)$.
Ceci permet de montrer par récurrence que pour tout $k \geqslant 1$ impair on a $f(k) \geqslant 1$, et donc $f(k)=1$.
On déduit de tout ceci que $f(2018)=f(2) f(1009)=1 / 2$.
Réciproquement, il reste à vérifier qu'une fonction $f$ telle que décrite dans l'énoncé existe bien. Il suffit pour ce faire de constater que la fonction $f$ définie par
$$
f: p / q \mapsto \begin{cases}0 & \text { si } p=0 \\ 2^{v_{2}(q)-v_{2}(p)} & \text { si } p \neq 0\end{cases}
$$
où $v_{2}(n)$ désigne la valuation 2-adique de l'entier $n$, satisfait bien les conditions de l'énoncé.
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-fevrier-senior-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T1",
"year": "2017"
}
|
For any natural number $n$, we denote $S(n)$ as the sum of the digits of the decimal representation of $n$. We say that a natural number $n$ is pretty if $S(n)=S\left(n^{2}\right)$. Determine all possible values of $S(n)$ for the pretty numbers $n$.
|
Modulo 9, $S(n)$ satisfies the equation $x^{2}=x$. By testing $x=$ $0,1, \ldots, 8$, we find that the only solutions (modulo 9) are 0 and 1, so $S(n)$ is necessarily congruent to 0 or 1 modulo 9. Conversely, we verify that if $n=10^{k}-1=99 \cdots 9$ ( $k$ times) then $n^{2}=99 \cdots 9800 \cdots 01$ (with $k-1$ digits 9 and $k-1$ digits 0), so $S(n)=S\left(n^{2}\right)=9 k$. Similarly, if $n=2 \times 10^{k}-1=199 \cdots 9$ then $n^{2}=399 \cdots 9600 \cdots 01$ so $S(n)=S\left(n^{2}\right)=9 k+1$.
We conclude that the possible values of $S(n)$ are the natural numbers congruent to 0 or 1 modulo 9.
|
the natural numbers congruent to 0 or 1 modulo 9
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Pour tout entier naturel $n$, on note $S(n)$ la somme des chiffres de l'écriture décimale de $n$. On dit qu'un entier naturel $n$ est joli si $S(n)=S\left(n^{2}\right)$. Déterminer toutes les valeurs possibles de $S(n)$ pour les entiers jolis $n$.
|
Modulo 9, $S(n)$ vérifie l'équation $x^{2}=x$. On vérifie en testant $x=$ $0,1, \ldots, 8$ que les seules solutions (modulo 9) sont 0 et 1 , donc $S(n)$ est nécessairement congru à 0 ou 1 modulo 9 . Réciproquement, on vérifie que si $n=10^{k}-1=99 \cdots 9$ ( $k$ fois) alors $n^{2}=99 \cdots 9800 \cdots 01$ (avec $k-1$ chiffres 9 et $k-1$ chiffres 0 ), donc $S(n)=S\left(n^{2}\right)=9 k$. De même, si $n=2 \times 10^{k}-1=199 \cdots 9$ alors $n^{2}=399 \cdots 9600 \cdots 01$ donc $S(n)=S\left(n^{2}\right)=9 k+1$.
On en conclut que les valeurs possibles de $S(n)$ sont les entiers naturels congrus à 0 ou à 1 modulo 9.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-janvier-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T1",
"year": "2017"
}
|
We fix a natural number $n \geqslant 2$. Determine all real numbers $x \geqslant-1$ such that for all real numbers $a_{1}, \ldots, a_{n} \geqslant 1$ we have
$$
\frac{a_{1}+x}{2} \times \cdots \times \frac{a_{n}+x}{2} \leqslant \frac{a_{1} a_{2} \cdots a_{n}+x}{2} .
$$
|
By setting $a_{i}=1$ for all $i$, we obtain the condition $\left(\frac{1+x}{2}\right)^{n} \leqslant \frac{1+x}{2}$. Let $y=\frac{1+x}{2}$. By hypothesis, $y \geqslant 0$. Since $y^{n} \leqslant y$, we have $y^{n-1} \leqslant 1$ and thus $y \leqslant 1$, which implies $x \leqslant 1$.
Conversely, let's show that any $x \in[-1,1]$ works. We proceed by induction on $n$. For $n=1$ the inequality is obvious. Suppose it is true at rank $n-1$. The left-hand side of the inequality is then less than or equal to $\frac{a+x}{2} \times \frac{b+x}{2}$, where $a=a_{1} a_{2} \cdots a_{n-1}$ and $b=a_{n}$. It then suffices to show that $\left(\frac{a+x}{2}\right)\left(\frac{b+x}{2}\right) \leqslant\left(\frac{a b+x}{2}\right)$. By expanding, the inequality becomes $(a+b-2) x+x^{2} \leqslant a b$. Since $a+b-2 \geqslant 0$, and since $x \leqslant 1$ and $x^{2} \leqslant 1$, the left-hand side of the inequality is bounded by $(a+b-2)+1$, so it suffices to show that $(a+b-2)+1 \leqslant a b$, or equivalently that $0 \leqslant a b-a-b+1$. Now, we have $a b-a-b+1=(a-1)(b-1)$. Since $a \geqslant 1$ and $b \geqslant 1$, the inequality $(a-1)(b-1) \geqslant 0$ is indeed satisfied.
|
x \in [-1, 1]
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
On fixe un entier naturel $n \geqslant 2$. Déterminer tous les nombres réels $x \geqslant-1$ tels que pour tous nombres réels $a_{1}, \ldots, a_{n} \geqslant 1$ on ait
$$
\frac{a_{1}+x}{2} \times \cdots \times \frac{a_{n}+x}{2} \leqslant \frac{a_{1} a_{2} \cdots a_{n}+x}{2} .
$$
|
En prenant $a_{i}=1$ pour tout $i$, on obtient la condition $\left(\frac{1+x}{2}\right)^{n} \leqslant \frac{1+x}{2}$. Notons $y=\frac{1+x}{2}$. Par hypothèse, $y \geqslant 0$. Comme $y^{n} \leqslant y$, on a $y^{n-1} \leqslant 1$ donc $y \leqslant 1$, ce qui implique $x \leqslant 1$.
Réciproquement, montrons que tout $x \in[-1,1]$ convient. On raisonne par récurrence sur $n$. Pour $n=1$ l'inégalité est évidente. Supposons qu'elle soit vraie au rang $n-1$. Le membre de gauche de l'inégalité est alors inférieur ou égal à $\frac{a+x}{2} \times \frac{b+x}{2}$, où $a=a_{1} a_{2} \cdots a_{n-1}$ et $b=a_{n}$. Il suffit alors de montrer que $\left(\frac{a+x}{2}\right)\left(\frac{b+x}{2}\right) \leqslant\left(\frac{a b+x}{2}\right)$. En développant, l'inégalité devient $(a+b-2) x+x^{2} \leqslant a b$. Comme $a+b-2 \geqslant 0$, et comme $x \leqslant 1$ et $x^{2} \leqslant 1$, le membre de gauche de l'inégalité est majoré par $(a+b-2)+1$, donc suffit de montrer que $(a+b-2)+1 \leqslant a b$, ou encore que $0 \leqslant a b-a-b+1$. Or, on a $a b-a-b+1=(a-1)(b-1)$. Comme $a \geqslant 1$ et $b \geqslant 1$, l'inégalité $(a-1)(b-1) \geqslant 0$ est bien vérifiée.
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-janvier-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T1",
"year": "2017"
}
|
Let $n \geqslant 2$ be a natural number. We are given $2n$ balls. On each of these balls, a number is written. We assume that whenever the balls are grouped into $n$ pairs, two of these pairs have the same sum.
(a) Show that four of these balls bear the same number.
(b) Show that the number of distinct values written on the balls is $\leqslant n-1$.
|
(a) We denote $a_{1} \geqslant a_{2} \geqslant \cdots \geqslant a_{2 n}$ the values taken by the $2 n$ balls in descending order. We pair them as follows: $\left(a_{1}, a_{2}\right),\left(a_{3}, a_{4}\right), \ldots$ Since there exist $i<j$ odd such that $a_{i}+a_{i+1}=a_{j}+a_{j+1}$, and since $a_{i} \geqslant a_{i+1} \geqslant a_{j} \geqslant a_{j+1}$, we have $a_{i}=a_{i+1}=a_{j}=a_{j+1}$.
(b) Suppose there are at least $n$ distinct values, which we order in descending order $b_{1}>b_{2}>\cdots>b_{n}$. We order the other balls in descending order $c_{1} \geqslant \cdots \geqslant c_{n}$. We form the $n$ pairs $\left(b_{i}, c_{i}\right)$, and we observe that if $i<j$ then $b_{i}+c_{i}>b_{j}+c_{j}$, which contradicts the fact that two of these sums must be equal.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soit $n \geqslant 2$ un entier naturel. On se donne $2 n$ boules. Sur chacune de ces boules est écrit un nombre. On suppose que, à chaque fois que l'on regroupe les boules en $n$ paires, deux de ces paires ont la même somme.
(a) Montrer que quatre de ces boules comportent le même nombre.
(b) Montrer que le nombre de valeurs distinctes inscrites sur les boules est $\leqslant n-1$.
|
(a) On note $a_{1} \geqslant a_{2} \geqslant \cdots \geqslant a_{2 n}$ les valeurs prises par les $2 n$ boules dans l'ordre décroissant. On les apparie ainsi : $\left(a_{1}, a_{2}\right),\left(a_{3}, a_{4}\right), \ldots$ Comme il existe $i<j$ impairs tels que $a_{i}+a_{i+1}=a_{j}+a_{j+1}$, et comme $a_{i} \geqslant a_{i+1} \geqslant a_{j} \geqslant a_{j+1}$, on a $a_{i}=a_{i+1}=a_{j}=a_{j+1}$.
(b) Supposons qu'il y ait au moins $n$ valeurs distinctes, que l'on ordonne par ordre décroissant $b_{1}>b_{2}>\cdots>b_{n}$. On ordonne les autres boules dans l'ordre décroissant $c_{1} \geqslant \cdots \geqslant c_{n}$. On forme les $n$ paires $\left(b_{i}, c_{i}\right)$, et on constate que si $i<j$ alors $b_{i}+c_{i}>b_{j}+c_{j}$, ce qui contredit le fait que deux de ces sommes doivent être égales.
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-janvier-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T1",
"year": "2017"
}
|
Let $A B C D$ be a convex quadrilateral with area $S$. We denote $a=A B, b=B C, c=C D$ and $d=D A$. For any permutation $x, y, z, t$ of $a, b, c, d$, show that
$$
S \leqslant \frac{1}{2}(x y+z t)
$$
|
If $x$ and $y$ are adjacent, without loss of generality, we need to show that $S \leqslant \frac{1}{2}(a b+c d)$. This follows from $S_{A B C}=\frac{1}{2} A B \cdot B C \cdot \sin \widehat{A B C} \leqslant \frac{1}{2} a b$, and similarly $S_{C D A} \leqslant \frac{1}{2} c d$. If $x$ and $y$ are opposite sides, we need to show that $S \leqslant \frac{1}{2}(a c+b d)$. Let $A^{\prime}$ be the symmetric point of $A$ with respect to the perpendicular bisector of $[B D]$. Then $B A^{\prime} D$ is isometric to $D A B$. We apply the above to $A^{\prime} B C D$, which gives $S=S_{B A D}+S_{B C D}=S_{B A^{\prime} D}+S_{B C D}=S_{A^{\prime} B C D} \leqslant \frac{1}{2}\left(A^{\prime} B \cdot B C+\right.$ $\left.C D \cdot D A^{\prime}\right)=\frac{1}{2}(a c+b d)$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $A B C D$ un quadrilatère convexe d'aire $S$. On note $a=A B, b=B C, c=C D$ et $d=D A$. Pour toute permutation $x, y, z, t$ de $a, b, c, d$, montrer que
$$
S \leqslant \frac{1}{2}(x y+z t)
$$
|
Si $x$ et $y$ sont adjacents, sans perte de généralité on se ramène à montrer que $S \leqslant \frac{1}{2}(a b+c d)$. Cela découle de $S_{A B C}=\frac{1}{2} A B \cdot B C \cdot \sin \widehat{A B C} \leqslant \frac{1}{2} a b$, et de même $S_{C D A} \leqslant \frac{1}{2} c d$. Si $x$ et $y$ sont des côtés opposés, on doit montrer que $S \leqslant \frac{1}{2}(a c+b d)$. Soit $A^{\prime}$ le symétrique de $A$ par rapport à la médiatrice de $[B D]$. Alors $B A^{\prime} D$ est isométrique à $D A B$. On applique ce qui précède à $A^{\prime} B C D$, ce qui donne $S=S_{B A D}+S_{B C D}=S_{B A^{\prime} D}+S_{B C D}=S_{A^{\prime} B C D} \leqslant \frac{1}{2}\left(A^{\prime} B \cdot B C+\right.$ $\left.C D \cdot D A^{\prime}\right)=\frac{1}{2}(a c+b d)$.
|
{
"exam": "French_tests",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-janvier-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T1",
"year": "2017"
}
|
Determine all real numbers $a$ such that there exists an infinite sequence of strictly positive real numbers $x_{0}, x_{1}, x_{2}, x_{3}, \ldots$ satisfying for all $n$ the equality
$$
x_{n+2}=\sqrt{a x_{n+1}-x_{n}} .
$$
|
If $a>1$, we can take the constant sequence equal to $a-1$. Suppose $a \leqslant 1$. Since the square root is well defined, we necessarily have $a x_{n+1}-x_{n}>0$, so already $a \geqslant 0$, and furthermore $x_{n+1} \geqslant a x_{n+1}>x_{n}$. Consequently, the sequence is strictly increasing.
Since $x_{n+1} \leqslant x_{n+2} \leqslant \sqrt{x_{n+1}-x_{n}}<\sqrt{x_{n+1}}$, we deduce that $x_{n}<1$ for all $n$. Moreover, $x_{n+1}^{2} \leqslant x_{n+1}-x_{n}$, so $x_{n+1} \geqslant x_{n+1}^{2}+x_{n} \geqslant x_{n} x_{0}+x_{n}=\left(1+x_{0}\right) x_{n}$, which shows that $x_{n} \geqslant \left(1+x_{0}\right)^{n} x_{0}$ for all $n$. This contradicts that $x_{n} \leqslant 1$.
|
a > 1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Déterminer tous les nombres réels $a$ tels qu'il existe une suite infinie de nombres réels strictement positifs $x_{0}, x_{1}, x_{2}, x_{3}, \ldots$ vérifiant pour tout $n$ l'égalité
$$
x_{n+2}=\sqrt{a x_{n+1}-x_{n}} .
$$
|
Si $a>1$, on peut prendre la suite constante égale à $a-1$. Supposons $a \leqslant 1$. Comme la racine carré est bien définie, on a nécessairement $a x_{n+1}-x_{n}>0$, donc déjà $a \geqslant 0$, et de plus $x_{n+1} \geqslant a x_{n+1}>x_{n}$. Par conséquent, la suite est strictement croissante.
Comme $x_{n+1} \leqslant x_{n+2} \leqslant \sqrt{x_{n+1}-x_{n}}<\sqrt{x_{n+1}}$, on en déduit que $x_{n}<1$ pour tout $n$. De plus, $x_{n+1}^{2} \leqslant x_{n+1}-x_{n}$ donc $x_{n+1} \geqslant x_{n+1}^{2}+x_{n} \geqslant x_{n} x_{0}+x_{n}=\left(1+x_{0}\right) x_{n}$, ce qui montre que $x_{n} \geqslant$ $\left(1+x_{0}\right)^{n} x_{0}$ pour tout $n$. Ceci contredit que $x_{n} \leqslant 1$.
|
{
"exam": "French_tests",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-janvier-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T1",
"year": "2017"
}
|
In a country, there are 64 cities. There are roads connecting certain pairs of cities, but Bob does not know which ones (the roads do not cross each other but can potentially pass over each other; furthermore, the roads can be traveled in both directions). Alice, on the other hand, knows the network perfectly. Bob can choose any pair of cities and ask Alice if they are directly connected by a road. Bob's goal is to determine whether it is possible to travel from any city to any other (by potentially taking several successive roads). Show that there is no algorithm (i.e., no strategy based on Alice's successive answers) that allows him to be sure in fewer than 2016 questions.
|
We notice that $2016=64 \times 63 / 2=\binom{64}{2}$, so there are exactly 2016 pairs of cities. The road network is an undirected graph with 64 vertices. Each pair of cities corresponds to a question, and we want to know if Bob can determine whether the graph is connected in fewer than 2016 questions. Suppose, for the sake of contradiction, that Bob has an algorithm that requires fewer than 2016 questions: consequently, for any graph with 64 vertices, if Bob follows his algorithm by asking a sequence of questions $Q_{1}, Q_{2}, \ldots$ and stops at a question $Q_{n}$ as soon as he can conclude with certainty whether the graph is connected or not, then $n \leqslant 2015$ (the integer $n$ depends on the graph). Note that the answer to $Q_{n}$ must be "yes" if the graph is connected and "no" if the graph is not connected, otherwise Bob could have already concluded at question $Q_{n-1}$.
We start with the graph $G_{0}$ having no edges. Bob, using his algorithm, asks a sequence of questions $Q_{1}, Q_{2}, \ldots, Q_{n_{0}}$ to Alice.
The question $Q_{n_{0}}$ corresponds to a pair of cities. Let $G_{1}$ be the graph obtained by adding an edge between these two cities. Following his algorithm, Bob asks the questions $Q_{1}, \ldots, Q_{n_{0}}$ again, and additional questions $Q_{n_{0}+1}, \ldots, Q_{n_{1}}$. We have $n_{1}>n_{0}$ because, for the graph $G_{1}$, the answer to $Q_{n_{0}}$ is "yes", and the answer to $Q_{n_{1}}$ is "no" since the graph $G_{1}$ is not connected.
We continue this procedure and construct a sequence of graphs $G_{0}, G_{1}, G_{2}, \ldots$, each graph being constructed from the previous one by adding an edge, until we obtain a connected graph $G_{k}$. Since $n_{k-1}>n_{k-1}>\cdots>n_{0} \geqslant 1$, we have $n_{k-1} \geqslant k$ and thus $k \leqslant 2015$.
However, $G_{k}$ has $k$ edges, so there exists a pair of cities $X$ and $Y$ that are not directly connected. On the other hand, since $G_{k}$ is connected, we can go from $X$ to $Y$ by following a path consisting of edges in $G_{k}$. Let $j$ be the largest index such that one of the edges $A$ of this path belongs to $G_{j}$ but not to $G_{j-1}$. Let $G^{\prime}$ be the graph obtained by removing the edge $A$ from $G_{k}$ and adding the edge $X Y$, then the answers to the questions $Q_{1}, \ldots, Q_{n_{j-1}}$ are the same for $G^{\prime}$ as for $G_{j-1}$. However, Bob was able to conclude with certainty that $G_{j-1}$ is not connected, so $G^{\prime}$ is not connected either.
But this is contradictory because, since $G_{k}$ is connected, $G^{\prime}$ is also connected.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Dans un pays se trouvent 64 villes. Il existe des routes qui relient certaines paires de villes, mais Bob ne sait pas lesquelles (les routes ne se croisent pas mais peuvent éventuellement passer les unes au-dessus des autres ; de plus, les routes peuvent être parcourues dans les deux sens). Alice, elle, connaît parfaitement le réseau. Bob peut choisir n'importe quelle paire de villes et demander à Alice si elles sont reliées directement par une route. Le but de Bob est de déterminer s'il est possible de voyager de n'importe quelle ville à n'importe quelle autre (en empruntant éventuellement plusieurs routes successives). Montrer qu'il n'existe aucun algorithme (c'est-à-dire aucune stratégie en fonction des réponses successives d'Alice) lui permettant de le savoir à coup sûr en moins de 2016 questions.
|
On remarque que $2016=64 \times 63 / 2=\binom{64}{2}$, donc il y a exactement 2016 paires de villes. Le réseau routier est un graphe non orienté ayant 64 sommets. Chaque paire de villes correspond à une
question, et on veut savoir si en moins de 2016 questions Bob peut déterminer si le graphe est connexe. Supposons par l'absurde que Bob possède un algorithme en moins de 2016 questions : par conséquent, pour tout graphe ayant 64 sommets, si Bob suit son algorithme en posant une suite de questions $Q_{1}, Q_{2}, \ldots$ et s'arrête à une question $Q_{n}$ dès qu'il peut conclure à coup sûr si le graphe est connexe ou non, alors $n \leqslant 2015$ (l'entier $n$ dépend du graphe). Remarquons que la réponse à $Q_{n}$ est nécessairement "oui" si le graphe est connexe et "non" si le graphe est non connexe, sinon Bob aurait déjà pu conclure à la question $Q_{n-1}$.
On part du graphe $G_{0}$ ne possédant aucune arête. Bob, en utilisant son algorithme, pose une suite de questions $Q_{1}, Q_{2}, \ldots, Q_{n_{0}}$ à Alice.
La question $Q_{n_{0}}$ correspond à une paire de villes. Soit $G_{1}$ le graphe consistant à rajouter une arête entre ces deux villes. En suivant son algorithme, Bob pose à nouveau les questions $Q_{1}, \ldots, Q_{n_{0}}$, et d'autres questions $Q_{n_{0}+1}, \ldots, Q_{n_{1}}$. On a bien $n_{1}>n_{0}$ car, pour le graphe $G_{1}$, la réponse à $Q_{n_{0}}$ est "oui", et la réponse à $Q_{n_{1}}$ est "non" puisque le graphe $G_{1}$ n'est pas connexe.
On continue la procédure, et on construit ainsi une suite de graphes $G_{0}, G_{1}, G_{2}, \ldots$, chaque graphe étant construit à partir du précédent en rajoutant une arête, jusqu'à obtenir un graphe connexe $G_{k}$. Comme $n_{k-1}>n_{k-1}>\cdots>n_{0} \geqslant 1$, on a $n_{k-1} \geqslant k$ donc $k \leqslant 2015$.
Or, $G_{k}$ possède $k$ arêtes, donc il existe une paire de villes $X$ et $Y$ qui ne sont pas reliées directement. En revanche, comme $G_{k}$ est connexe on peut aller de $X$ vers $Y$ en suivant un chemin consistant en des arêtes de $G_{k}$. Soit $j$ le plus grand indice tel que l'une des arêtes $A$ de ce chemin appartient à $G_{j}$ mais pas à $G_{j-1}$. Soit $G^{\prime}$ le graphe obtenu en enlevant l'arête $A$ au graphe $G_{k}$ et en ajoutant l'arête $X Y$, alors la réponse aux questions $Q_{1}, \ldots, Q_{n_{j-1}}$ est la même pour $G^{\prime}$ que pour $G_{j-1}$. Or, Bob a pu conclure à coup sûr que $G_{j-1}{\text { n'est pas connexe, donc } G^{\prime}}^{\prime}$ ne l'est pas non plus.
Mais ceci est contradictoire car, $G_{k}$ étant connexe, $G^{\prime}$ l'est aussi.
|
{
"exam": "French_tests",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-janvier-corrige.jsonl",
"solution_match": "## Solution de l'exercice 6",
"tier": "T1",
"year": "2017"
}
|
Find all triplets $(a, b, c)$ of strictly positive real numbers such that
\[
\left\{\begin{array}{l}
a \sqrt{b}-c=a \\
b \sqrt{c}-a=b \\
c \sqrt{a}-b=c
\end{array}\right.
\]
|
We notice that $\mathrm{a}=\mathrm{b}=\mathrm{c}=4$ is a solution. We will show that this is in fact the only one.
If two of the three numbers are equal to 4 (say a and b), it is easily verified that the third one is also 4, because $4 \sqrt{4}-\mathrm{c}=4$, so $\mathrm{c}=4$. If one of the three numbers is 4 (say a), then $c \sqrt{a}-b=c$ becomes $2 \mathrm{c}-\mathrm{b}=\mathrm{c}$, so $\mathrm{b}=\mathrm{c}$. Moreover, $\mathrm{a} \sqrt{\mathrm{b}}-\mathrm{b}=4$, which can be rewritten as $(\sqrt{\mathrm{b}}-2)^{2}=0$, so $\mathrm{b}=4$ and $\mathrm{c}=4$. It remains to show that it is impossible for the three numbers to all be different from 4.
If this is the case, then either at least two of the numbers are strictly greater than 4, or at least two are strictly less than 4. We treat these two cases separately.
If at least two of the numbers are $>4$, let's say that c is the smallest of the three numbers. Then $a, b>4$, so $a=a \sqrt{b}-c>2 a-c$, so $c>a>4$, which contradicts the minimality of $c$. Similarly, if at least two of the numbers are $<4$, suppose that $c$ is the largest. Then $a, b<4$, so $a=a \sqrt{b}-c<2 a-c$, so $c<a$, which contradicts the maximality of $c$. The only solution is therefore indeed $(4,4,4)$.
|
(4,4,4)
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Trouver tous les triplets ( $a, b, c$ ) de réels strictement positifs tels que
$$
\left\{\begin{array}{l}
a \sqrt{b}-c=a \\
b \sqrt{c}-a=b \\
c \sqrt{a}-b=c
\end{array}\right.
$$
|
On remarque que $\mathrm{a}=\mathrm{b}=\mathrm{c}=4$ est solution. On va montrer que c'est en fait la seule.
Si deux des trois nombres sont égaux à 4 (disons a et b), on vérifie facilement que le troisième aussi, car $4 \sqrt{4}-\mathrm{c}=4$, donc $\mathrm{c}=4$. Si un des trois nombres vaut 4 (disons a), alors $c \sqrt{a}-b=c$ devient $2 \mathrm{c}-\mathrm{b}=\mathrm{c}$, donc $\mathrm{b}=\mathrm{c}$. De plus, on $\mathrm{a} \sqrt{\mathrm{b}}-\mathrm{b}=4$, qui se réécrit $(\sqrt{\mathrm{b}}-2)^{2}=0$, donc $\mathrm{b}=4$ et $\mathrm{c}=4$. Il reste à montrer qu'il est impossible que les trois nombres soient différents de 4.
Si c'est le cas, alors soit au moins deux des nombres sont strictement supérieurs à 4 , soit au moins deux sont strictement inférieurs à 4 . On traite les deux cas séparément.
Si au moins deux des nombres sont $>4$, mettons que c soit le plus petit des trois nombres. Alors $a, b>4$, donc $a=a \sqrt{b}-c>2 a-c$, donc $c>a>4$, ce qui contredit la minimalité de $c$. De même, si au moins deux des nombres sont $<4$, supposons que $c$ est le plus grand. Alors $a, b<4$, donc $a=a \sqrt{b}-c<2 a-c$, donc $c<a$, ce qui contredit la maximalité de $c$. La seule solution est donc bien $(4,4,4)$.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-mai-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T1",
"year": "2017"
}
|
Find all pairs $(m,n)$ of strictly positive integers such that
$$
\mathrm{m}!+\mathrm{n}!=\mathrm{m}^{\mathrm{n}}
$$
Note. For any integer $n$, recall that $n!$ denotes the integer $1 \times 2 \times 3 \times \cdots \times n$.
|
We easily check that the pairs $(2,2)$ and $(2,3)$ are solutions. We will show that these are the only ones.
We start by dealing with the case where $m$ or $n$ is 1 or 2. If $m=1$, then $m^n=1$ but $m!+n!\geqslant 2$, so there is no solution. If $m=2$, the equation becomes $2+n!=2^{n-1}$. If $n \geqslant 4$, then the left-hand side is congruent to 2 modulo 4, and the right-hand side to 0, so $n$ must be 1, 2, or 3, and $n=1$ does not work. If $n=1$, the equation becomes $m!+1=m$, but $m$ divides $m!$ and $m$, so $m$ divides 1 and $m=1$, but $(1,1)$ is not a solution. Finally, if $n=2$, we get $m!+2=m^2$. But $m$ divides $m!$ and $m^2$ so $m$ divides 2, so $m$ is 1 or 2 and we fall back on cases already treated.
We now deal with the case $2<m \leqslant n$. In this case, $m!$ divides $n!$ so $m!$ divides $m^n$. In particular, $m-1$ divides $m!$ and thus also $m^n$, but $m-1$ is coprime with $m$, and thus also with $m^n$. Therefore, $m-1$ can only be 1, so $m=2$, a contradiction.
Finally, we deal with the case $2<n<m$. In this case, $n!$ divides $m!$, so we can write $n!\left(1+\frac{m!}{n!}\right)=m^n$. In particular, $1+\frac{m!}{n!}$ divides $m^n$. But $\frac{m!}{n!}=(n+1)(n+2) \ldots m$ is divisible by $m$, so $1+\frac{m!}{n!}$ is coprime with $m$, and thus with $m^n$. We therefore have $1+\frac{n!}{m!}=1$, which is impossible.
|
(2,2) \text{ and } (2,3)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Trouver toutes les paires (m,n) d'entiers strictement positifs telles que
$$
\mathrm{m}!+\mathrm{n}!=\mathrm{m}^{\mathrm{n}}
$$
Remarque. Pour tout entier $n$, on rappelle que $n$ ! désigne l'entier $1 \times 2 \times 3 \times \cdots \times n$.
|
On vérifie facilement que les paires $(2,2)$ et $(2,3)$ sont solutions. On va montrer que ce sont les seules.
On commence par traiter le cas où $m$ ou $n$ vaut 1 ou 2 . Si $m=1$, alors $m^{n}=1$ mais $m!+n!\geqslant 2$, donc il n'y a pas de solution. Si $m=2$, l'équation devient $2+n!=2^{n-1}$. Si $n \geqslant 4$, alors le membre de gauche est congru à 2 modulo 4 , et le membre de droite à 0 , donc $n$ vaut 1,2 ou 3 , et $n=1$ ne marche pas. Si $n=1$, l'équation devient $m!+1=m$, mais $m$ divise $m$ ! et $m$, donc $m$ divise 1 et $m=1$, mais $(1,1) n^{\prime}$ est pas solution. Enfin, si $n=2$, on obtient $m!+2=m^{2}$. Mais $m$ divise $m$ ! et $m^{2}$ donc $m$ divise 2 , donc $m$ vaut 1 ou 2 et on retombe sur des cas déjà traités.
On traite maintenant le cas $2<\mathrm{m} \leqslant \mathrm{n}$. Dans ce cas m ! divise $n$ ! donc m ! divise $\mathrm{m}^{\mathrm{n}}$. En particulier, $m-1$ divise $m$ ! donc aussi $m^{n}$, mais $m-1$ est premier avec $m$, donc aussi avec $m^{n}$. Par conséquent, $\mathrm{m}-1$ ne peut valoir que 1 donc $\mathrm{m}=2$, contradiction.
Enfin, on traite le cas $2<n<m$. Dans ce cas $n$ ! divise $m$ !, donc on peut écrire $n!\left(1+\frac{m!}{n!}\right)=m^{n}$. En particulier, $1+\frac{m!}{n!}$ divise $m^{n}$. Mais $\frac{m!}{n!}=(n+1)(n+2) \ldots$ m est divisible par $m$, donc $1+\frac{m!}{n!}$ est premier avec $m$, donc avec $m^{n}$. On a donc $1+\frac{n!}{m!}=1$, ce qui est impossible.
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-mai-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T1",
"year": "2017"
}
|
Let $ABCD$ be a trapezoid such that $(AB)$ and $(CD)$ are parallel. Suppose that $AD < CD$ and that $ABCD$ is inscribed in a circle $\Gamma$. Let $P$ be a point on $\Gamma$ such that $(DP)$ is parallel to $(AC)$. The tangent to $\Gamma$ at $D$ intersects $(AB)$ at $E$, and the chords $[BP]$ and $[CD]$ intersect at $Q$. Show that $EQ = AC$.
|
We know that $(CQ)$ is parallel to $(\mathrm{AE})$, so the statement reduces to showing that $A C Q E$ is a parallelogram, hence it suffices to show that (EQ) and (AC) are parallel. The quadrilateral BQDE is a trapezoid, with $(B E)$ and (DQ) parallel. We will first show that it is an isosceles trapezoid. Indeed, we have
$$
\widehat{\mathrm{EDQ}}=\widehat{\mathrm{EDC}}=180^{\circ}-\widehat{\mathrm{DAC}}
$$
according to the limiting case of the inscribed angle theorem. On the other hand, we have
$$
\widehat{\mathrm{DQB}}=180^{\circ}-\widehat{\mathrm{BDC}}-\widehat{\mathrm{DBP}}=180^{\circ}-\widehat{\mathrm{BAC}}-\widehat{\mathrm{DAP}}
$$
Now, the quadrilaterals $A B C D$ and $A C P D$ are inscribed trapezoids, hence isosceles, so $P C=$ $A D=B C$, thus $C$ is the midpoint of the arc between $B$ and $P$. Therefore, $\widehat{B A C}=\widehat{C A P}$, so
$$
\widehat{\mathrm{DQB}}=180^{\circ}-\widehat{\mathrm{CAP}}-\widehat{\mathrm{DAP}}=180^{\circ}-\widehat{\mathrm{DAC}}=\widehat{\mathrm{EDQ}}
$$
thus the trapezoid EBQD is indeed isosceles and has an axis of symmetry. We deduce
$$
\widehat{\mathrm{DQE}}=\widehat{\mathrm{QDB}}=\widehat{\mathrm{CDB}}=\widehat{\mathrm{DCA}},
$$
using at the end the fact that $A B C D$ has an axis of symmetry. This shows that (QE) and (AC) are parallel, which concludes the proof.
## Exercise common to groups A and B - Statement and solution
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un trapèze tel que $(A B)$ et $(C D)$ sont parallèles. On suppose que $A D<$ $C D$ et que $A B C D$ est inscrit dans un cercle $\Gamma$. Soit $P$ sur $\Gamma$ tel que (DP) est parallèle à ( $A C$ ). La tangente à $\Gamma$ en $D$ recoupe $(A B)$ en $E$, et les cordes $[B P]$ et $[C D]$ s'intersectent en $Q$. Montrer que $E Q=A C$.
|
On sait que (CQ) est parallèle à $(\mathrm{AE})$, donc l'énoncé revient à montrer que $A C Q E$ est un parallélogramme, donc il suffit de montrer que (EQ) et (AC) sont parallèles. Le quadrilatère BQDE est un trapèze, avec $(B E)$ et (DQ) parallèles. On va d'abord montrer que c'est un trapèze isocèle. En effet, on a
$$
\widehat{\mathrm{EDQ}}=\widehat{\mathrm{EDC}}=180^{\circ}-\widehat{\mathrm{DAC}}
$$
d'après le cas limite du théorème de l'angle inscrit. D'autre part, on a
$$
\widehat{\mathrm{DQB}}=180^{\circ}-\widehat{\mathrm{BDC}}-\widehat{\mathrm{DBP}}=180^{\circ}-\widehat{\mathrm{BAC}}-\widehat{\mathrm{DAP}}
$$
Or, les quadrilatères $A B C D$ et $A C P D$ sont des trapèzes inscriptibles, donc isocèles, donc $P C=$ $A D=B C$, donc $C$ est le milieu de l'arc entre $B$ et $P$. On a donc $\widehat{B A C}=\widehat{C A P}$, donc
$$
\widehat{\mathrm{DQB}}=180^{\circ}-\widehat{\mathrm{CAP}}-\widehat{\mathrm{DAP}}=180^{\circ}-\widehat{\mathrm{DAC}}=\widehat{\mathrm{EDQ}}
$$
donc le trapèze EBQD est bien isocèle, et a un axe de symétrie. On en déduit
$$
\widehat{\mathrm{DQE}}=\widehat{\mathrm{QDB}}=\widehat{\mathrm{CDB}}=\widehat{\mathrm{DCA}},
$$
en utilisant à la fin le fait que $A B C D$ a un axe de symétrie. Cela montre que ( QE ) et ( $A C$ ) sont parallèles, ce qui conclut.
## Exercice commun aux groupes A et B - Énoncé et solution
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-mai-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T1",
"year": "2017"
}
|
A large square with side $n$ is cut into $n^{2}$ small squares with side 1. We want to color each of the $(n+1)^{2}$ vertices of the small squares in red or blue such that each of the small squares has exactly 2 red vertices. How many possible colorings are there?
|
The answer is $2^{\mathrm{n}+2}-2$. To show this, we start by coloring the $n+1$ highest vertices. There are $2^{n+1}$ ways to do this.
If there exist two consecutive vertices of the same color on the top row ($2^{n+1}-2$ colorings of the top row), then they fix the colors on the row just below, and so on, which gives $2^{n+1}-2$ colorings.
If the colors on the top row are alternating (2 colorings of the top row), then we are forced to alternate the colors on the row below, and on the following rows... However, at each row, we can choose the color with which we start, which gives $2 \times 2^{n}$ colorings, hence $2^{n+2}-2$ in total.
## Exercises of Group A - Statements and Solutions
|
2^{\mathrm{n}+2}-2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Un grand carré de côté $n$ est découpé en $n^{2}$ petits carrés de côté 1 . On veut colorier en rouge ou bleu chacun des $(n+1)^{2}$ sommets des petits carrés de telle manière que chacun des petits carrés a exactement 2 sommets rouges. Combien y a-t-il de coloriages possibles?
|
La réponse est $2^{\mathrm{n}+2}-2$. Pour le montrer, on commence par colorier les $n+1$ sommets les plus hauts. Il y a $2^{n+1}$ manières de le faire.
Si il existe deux sommets consécutifs de même couleur sur la rangée supérieure ( $2^{n+1}-2$ coloriages de la rangée supérieure), alors ils fixent les couleurs sur la rangée juste en-dessous, et ainsi de suite, ce qui donne $2^{n+1}-2$ coloriages.
Si les couleurs sur la rangée supérieure sont alternées ( 2 coloriages de la rangée supérieure), alors on est obligé d'alterner les couleurs sur la rangée d'en-dessous, et sur les suivantes... On peut cependant, à chaque ligne, choisir la couleur par laquelle on commence, ce qui donne $2 \times 2^{n}$ coloriages, donc $2^{n+2}-2$ au total.
## Exercices du groupe A - Énoncés et solutions
|
{
"exam": "French_tests",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-mai-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T1",
"year": "2017"
}
|
Determine all integers $n \geqslant 2$ satisfying the following property: for all integers $a_{1}, a_{2}, \ldots, a_{n}$ whose sum is not divisible by $n$, there exists an index $i$ such that none of the numbers
$$
a_{i}, a_{i}+a_{i+1}, \ldots, a_{i}+\cdots+a_{i+n-1}
$$
is divisible by $n$ (for $i>n$, we set $a_{i}=a_{i-n}$ ).
|
These are exactly the prime numbers!
Indeed, if $n=ab$, we can take $a_{1}=0$ and $a_{2}=\cdots=a_{n}=a$. The sum of the $a_{i}$ is $a(n-1)$, which is not divisible by $n$. However, for any $1 \leqslant i \leqslant n$, if $i+b-1 \leqslant n$, then the number $a_{i}+\cdots+a_{i+b-1}=ab=n$ is divisible by $n$. If $i+b-1>n$, then the number $a_{i}+\cdots+a_{i+b}=ab=n$ is divisible by $n$.
Conversely, suppose $n$ is prime, and let $a_{1}, \ldots, a_{n}$ be integers whose sum is not divisible by $n$. If $n$ does not satisfy the property, then for any index $i$, there exists $j(i)$ with $i+1 \leqslant j(i) \leqslant i+n$ such that
$$
a_{i}+a_{i+1}+\cdots+a_{j(i)-1}
$$
is divisible by $n$. Furthermore, since the sum of the $a_{i}$ is not divisible by $n$, we cannot have $j(i)=i+n$, so $i+1 \leqslant j(i) \leqslant i+n-1$. We then define by induction a sequence of indices $\left(i_{n}\right)$ by $i_{1}=1$ and $i_{n+1}=j\left(i_{n}\right)$. We know that for all $k$, the integer
$$
a_{i_{k}}+\cdots+a_{i_{k+1}-1}
$$
is divisible by $n$; therefore, by summing, for all indices $k<\ell$, the integer
$$
a_{i_{k}}+\cdots+a_{i_{\ell}-1}
$$
is divisible by $n$. By the pigeonhole principle, there exist $1 \leqslant k<\ell \leqslant n+1$ such that $i_{k} \equiv i_{\ell}(\bmod n)$. The number of terms in the sum (1) is then $i_{\ell}-i_{k}$, which is divisible by $n$, so each of the $a_{i}$ appears exactly $\frac{i_{\ell}-i_{k}}{n}$ times. Moreover, we know that $i_{j+1}-i_{j} \leqslant n-1$ for all $j$ and that $\ell-k \leqslant n$, so $i_{\ell}-i_{k} \leqslant n(n-1)$. The sum (1) is therefore
$$
\frac{i_{\ell}-i_{k}}{n} \times \sum_{i=1}^{n} a_{i} .
$$
But $\frac{i_{\ell}-i_{k}}{n} \leqslant n-1$ and cannot be divisible by $n$, and the sum of the $a_{i}$ is not divisible by $n$ either. Since $n$ is prime, the sum (1) is not divisible by $n$, leading to a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Déterminer tous les entiers $n \geqslant 2$ vérifiant la propriété suivante : pour tous entiers $a_{1}, a_{2}, \ldots, a_{n}$ dont la somme n'est pas divisible par $n$, $i l$ existe un indice $i$ tel qu'aucun des nombres
$$
a_{i}, a_{i}+a_{i+1}, \ldots, a_{i}+\cdots+a_{i+n-1}
$$
n'est divisible par $n$ (pour $i>n$, on pose $a_{i}=a_{i-n}$ ).
|
Ce sont exactement les nombres premiers!
En effet, si $n=a b$, on peut prendre $a_{1}=0$ et $a_{2}=\cdots=a_{n}=a$. La somme des $a_{i}$ vaut $a(n-1)$ donc n'est pas divisible par $n$. Cependant, soit $1 \leqslant i \leqslant n$. Si $i+b-1 \leqslant n$, alors le nombre $a_{i}+\cdots+a_{i+b-1}=a b=n$ est divisible par $n$. Si $i+b-1>n$, alors le nombre $a_{i}+\cdots+a_{i+b}=a b=n$ est divisible par $n$.
Réciproquement, supposons $n$ premier, et soient $a_{1}, \ldots, a_{n}$ des entiers dont la somme n'est pas divisible par $n$. Si $n$ ne vérifie pas la propriété, alors pour tout indice $i$, il existe $j(i)$ avec $\mathfrak{i}+1 \leqslant \mathfrak{j}(\mathfrak{i}) \leqslant \mathfrak{i}+\boldsymbol{n}$ tel que
$$
a_{i}+a_{i+1}+\cdots+a_{j(i)-1}
$$
est divisible par $n$. De plus, comme la somme des $a_{i} n^{\prime}$ est pas divisible par $n$, on ne peut pas avoir $\mathfrak{j}(\mathfrak{i})=\mathfrak{i}+\mathfrak{n}$, donc $\mathfrak{i}+1 \leqslant \mathfrak{j}(\mathfrak{i}) \leqslant \mathfrak{i}+\mathfrak{n}-1$. On définit alors par récurrence une suite $d^{\prime}$ 'indices $\left(i_{n}\right)$ par $i_{1}=1$ et $i_{n+1}=j\left(i_{n}\right)$. On sait que pour tout $k$, l'entier
$$
a_{i_{k}}+\cdots+a_{i_{k+1}-1}
$$
est divisible par n donc, en sommant, pour tous indices $k<\ell$, l'entier
$$
a_{i_{k}}+\cdots+a_{i_{\ell}-1}
$$
est divisible par $n$. Par le principe des tiroirs, il existe $1 \leqslant k<\ell \leqslant n+1$ tels que $\mathfrak{i}_{k} \equiv \mathfrak{i}_{\ell}(\bmod n)$. Le nombre de termes de la somme (1) vaut alors $\mathfrak{i}_{\ell}-\mathfrak{i}_{k}$ donc est divisible par $n$, donc chacun des $a_{i} y$ apparaît exactement $\frac{\boldsymbol{i}_{\ell}-\mathfrak{i}_{k}}{n}$ fois. De plus, on sait que $\mathfrak{i}_{j+1}-\mathfrak{i}_{j} \leqslant n-1$ pour tout $j$ et que $\ell-k \leqslant n$, donc $\mathfrak{i}_{\ell}-\mathfrak{i}_{k} \leqslant n(n-1)$. La somme (1) vaut donc
$$
\frac{\mathfrak{i}_{\ell}-\mathfrak{i}_{k}}{n} \times \sum_{i=1}^{n} a_{i} .
$$
Mais $\frac{i_{\ell}-i_{k}}{n} \leqslant n-1$ donc ne peut pas être divisible par $n$, et la somme des $a_{i}$ ne l'est pas non plus. Comme n est premier, la somme (1) n'est pas divisible par n , d'où la contradiction.
|
{
"exam": "French_tests",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-mai-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T1",
"year": "2017"
}
|
Let $ABC$ be a triangle with $AB \neq AC$, and let $\omega$ be the $A$-excircle of $ABC$. We denote by $D, E$ and $F$ the points of tangency of $\omega$ with $[BC]$, $[AC)$, and $[AB)$. The circumcircle of $AEF$ intersects $(BC)$ at $P$ and $Q$. We denote by $M$ the midpoint of $[AD]$. Show that the circumcircle of $MPQ$ is tangent to $\omega$.
Note. We recall that the $A$-excircle of $ABC$ is the unique circle tangent to the segment $[BC]$, to the ray $[AB)$ beyond $B$, and to the ray $[AC)$ beyond $C$.
|
Let $\Gamma$ be the circle passing through $A, E, F, P$ and $Q$. Let $T$ be the second intersection point of (AD) with $\omega$. We will show that $\omega$ and the circumcircle of MPQ are tangent at $T$. To do this, we first show that $M, P, Q$ and $T$ are concyclic.
Let $J$ be the center of $\omega$, and $N$ the midpoint of [DT]. Then the angles $\widehat{A E J}$ and $\widehat{A F J}$ are right angles, so $E$ and $F$ lie on the circle with diameter $[A J]$, hence $\Gamma$ is the circle with diameter $[A J]$. Moreover, the line (JN) is the perpendicular bisector of [DT], so the angle $\widehat{A N J}$ is also a right angle and $N \in \Gamma$. The power of $D$ with respect to $\Gamma$ then gives
$$
\mathrm{DP} \times \mathrm{DQ}=\mathrm{DA} \times \mathrm{DN}=\mathrm{DA} \times \frac{1}{2} \mathrm{DT}=\frac{1}{2} \mathrm{DA} \times \mathrm{DT}=\mathrm{DM} \times \mathrm{DT}
$$
so $M, T, P$ and $Q$ are indeed concyclic.
We now draw the tangent at $T$ to $\omega$, which intersects ( $B C$ ) at $X$. We have $X D=X T$, so the points $X$, J and $N$ are collinear on the perpendicular bisector of [DT]. The triangles XND and XDJ are then
right-angled at $N$ and $D$ and share the angle $\widehat{D R J}$, so they are similar, so $\frac{X N}{X D}=\frac{X D}{X J}$, so $\mathrm{XD}^{2}=\mathrm{XN} \times \mathrm{XJ}$. We also know that $\mathrm{XT}=\mathrm{XD}$, and the power of $X$ with respect to $\Gamma$ gives $\mathrm{XN} \times X \mathrm{~J}=\mathrm{XP} \times \mathrm{XQ}$. We then obtain
$$
X T^{2}=X P \times X Q
$$
so $(X T)$ is tangent to the circumcircle of PQT, which concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle avec $A B \neq A C$, et soit $\omega$ le cercle $A$-exinscrit à $A B C$. On note $D, E$ et $F$ les points de tangence de $\omega$ avec $[B C],[A C)$ et $[A B)$. Le cercle circonscrit à $A E F$ recoupe ( $B C$ ) en $P$ et $Q$. On note $M$ le milieu de $[A D]$. Montrer que le cercle circonscrit à MPQ est tangent à $\omega$.
Remarque. On rappelle que le cercle $A$-exinscrit à $A B C$ est l'unique cercle tangent au segment $[B C]$, à la demi-droite $[A B)$ au-delà de $B$ et à la demi-droite $[A C)$ au-delà de $C$.
|
On note $\Gamma$ le cercle passant par $A, E, F, P$ et $Q$. Soit $T$ le second point d'intersection de (AD) avec $\omega$. On va montrer que $\omega$ et le cercle circonscrit à MPQ sont tangents en $T$. On commence pour cela par montrer que $M, P, Q$ et $T$ sont cocycliques.
Soient $J$ le centre de $\omega$, et $N$ le milieu de [DT]. Alors les angles $\widehat{A E J}$ et $\widehat{A F J}$ sont droits, donc $E$ et $F$ sont sur le cercle de diamètre $[A J]$, donc $\Gamma$ est le cercle de diamètre $[A J]$. De plus, la droite (JN) est la médiatrice de [DT], donc l'angle $\widehat{A N J}$ est aussi droit et $N \in \Gamma$. La puissance de $D$ par rapport à $\Gamma$ donne alors
$$
\mathrm{DP} \times \mathrm{DQ}=\mathrm{DA} \times \mathrm{DN}=\mathrm{DA} \times \frac{1}{2} \mathrm{DT}=\frac{1}{2} \mathrm{DA} \times \mathrm{DT}=\mathrm{DM} \times \mathrm{DT}
$$
donc $M, T, P$ et Q sont bien cocycliques.
On trace maintenant la tangente en $T$ à $\omega$, qui recoupe ( $B C$ ) en $X$. On a $X D=X T$, donc les points $X$, J et $N$ sont alignés sur la médiatrice de [DT]. Les triangles XND et XDJ sont alors
rectangles en $N$ et $D$ et partagent l'angle $\widehat{D R J}$, donc ils sont semblables, donc $\frac{X N}{X D}=\frac{X D}{X J}$, donc $\mathrm{XD}^{2}=\mathrm{XN} \times \mathrm{XJ}$. On sait aussi que $\mathrm{XT}=\mathrm{XD}$, et la puissance de $X$ par rapport à $\Gamma$ donne $\mathrm{XN} \times X \mathrm{~J}=\mathrm{XP} \times \mathrm{XQ}$. On obtient donc
$$
X T^{2}=X P \times X Q
$$
donc $(X T)$ est tangente au cercle circonscrit à PQT, ce qui conclut.
|
{
"exam": "French_tests",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-mai-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T1",
"year": "2017"
}
|
Find all quadruplets ( $\mathfrak{p}, \mathrm{q}, \mathrm{r}, \mathfrak{n}$ ) of strictly positive integers satisfying the following three conditions:
- $p$ and $q$ are prime,
- $p+q$ is not divisible by 3,
- $p+q=r(p-q)^{n}$.
|
First, suppose that $p \neq 3$ and $q \neq 3$, and consider $p$ and $q$ modulo 3. Since $p+q \not \equiv 0 \pmod{3}$, we do not have $p \equiv 1 \pmod{3}$ and $q \equiv 2 \pmod{3}$, nor $p \equiv 2 \pmod{3}$ and $q \equiv 1 \pmod{3}$. Therefore, we are assured that $p \equiv q \equiv 1 \pmod{3}$ or $p \equiv q \equiv 2 \pmod{3}$. In both cases, 3 divides $p-q$ and thus divides $p+q = r(p-q)^n$ since $n \geq 1$. This is absurd and invalidates our assumption, showing that $p=3$ or $q=3$.
On the other hand, since $n \geq 0$, we know that $p-q$ divides $p+q$, so $p \neq q$, meaning that $p$ and $q$ are coprime. Since $p-q$ divides $(p+q)+(p-q)=2p$ and $(p+q)-(p-q)=2q$, we know that $p-q$ divides $\gcd(2p, 2q) = 2\gcd(p, q) = 2$. It follows that $p-q \in \{-2, -1, 1, 2\}$. Therefore, $(p, q) \in \{(2,3), (3,2), (3,5), (5,3)\}$; we treat these four cases one by one:
- if $(p, q) = (2,3)$, the equation becomes $5 = (-1)^n r$; its solutions are $r=5$ and $n \in 2\mathbb{N}^*$;
- if $(p, q) = (3,2)$, the equation becomes $5 = 1^n r$; its solutions are $r=5$ and $n \in \mathbb{N}^*$;
- if $(p, q) = (3,5)$, the equation becomes $8 = (-2)^n r$; its solutions are $(r, n) = (2,2)$;
- if $(p, q) = (5,3)$, the equation becomes $8 = 2^n r$; its solutions are $(r, n) = (1,3), (2,2)$, and $(4,1)$.
In conclusion, the solutions are: $(2,3,5,2n)_{n \in \mathbb{N}^*}, (3,2,5,n)_{n \in \mathbb{N}^*}, (3,5,2,2), (5,3,1,3), (5,3,2,2)$, and $(5,3,4,1)$.
|
(2,3,5,2n)_{n \in \mathbb{N}^*}, (3,2,5,n)_{n \in \mathbb{N}^*}, (3,5,2,2), (5,3,1,3), (5,3,2,2), (5,3,4,1)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Trouver tous les quadruplets ( $\mathfrak{p}, \mathrm{q}, \mathrm{r}, \mathfrak{n}$ ) d'entiers strictement positifs vérifiant les trois conditions suivantes:
- $p$ et $q$ sont premiers,
- $p+q$ n'est $^{\text {pas divisible par 3, }}$
$-p+q=r(p-q)^{n}$.
|
On suppose d'abord que $\mathrm{p} \neq 3$ et $\mathrm{q} \neq 3$, et on considère p et q modulo 3. Puisque $p+q \not \equiv 0[3]$, on n'a pas $p \equiv 1[3]$ et $q \equiv 2[3]$, ni $p \equiv 2[3]$ et $q \equiv 1[3]$. On est donc assuré que $p \equiv q \equiv 1[3]$ ou bien que $p \equiv q \equiv 2$ [3]. Dans ces deux cas, 3 divise $p-q$ et donc divise $\mathrm{p}+\mathrm{q}=\mathrm{r}(\mathrm{p}-\mathrm{q})^{\mathrm{n}}$ puisque $\mathrm{n} \geqslant 1$. Ceci est absurde et invalide donc notre supposition, ce qui montre que $p=3$ ou $q=3$.
D'autre part, puisque $n \geqslant 0$, on sait que $p-q$ divise $p+q$, donc $p \neq q$, de sorte que $p$ et $q$ sont premiers entre eux. Puisque $p-q$ divise $(p+q)+(p-q)=2 p$ et $(p+q)-(p-q)=2 q$, on sait donc que $p-q$ divise $\operatorname{PGCD}(2 \mathfrak{p}, 2 \mathrm{q})=2 \operatorname{PGCD}(p, q)=2$. Il s'ensuit que $p-q \in\{-2,-1,1,2\}$. On en déduit donc que $(p, q) \in\{(2,3),(3,2),(3,5),(5,3)\}$; on traite ces quatre cas un à un :
- si $(p, q)=(2,3)$, l'équation devient $5=(-1)^{\mathrm{n}} r$; ses solutions sont $\mathrm{r}=5$ et $n \in 2 \mathbb{N}^{*}$;
- si $(p, q)=(3,2), l^{\prime}$ 'equation devient $5=1^{n} r$; ses solutions sont $r=5$ et $n \in \mathbb{N}^{*}$;
- si $(p, q)=(3,5)$, l'équation devient $8=(-2)^{\mathrm{n}} \mathrm{r}$; ses solutions sont $(\mathrm{r}, \mathfrak{n})=(2,2)$;
- si $(p, q)=(5,3)$, l'équation devient $8=2^{\mathfrak{n}} r$; ses solutions sont $(r, n)=(1,3),(2,2)$ et $(4,1)$.
En conclusion, les solutions sont : $(2,3,5,2 \mathfrak{n})_{\mathfrak{n} \in \mathbb{N}^{*}},(3,2,5, \mathfrak{n})_{\mathfrak{n} \in \mathbb{N}^{*}},(3,5,2,2),(5,3,1,3),(5,3,2,2)$ et $(5,3,4,1)$.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-novembre-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T1",
"year": "2017"
}
|
Let $\omega_{1}, \omega_{2}$ be two circles tangent to each other at a point $T$, such that $\omega_{1}$ is inside $\omega_{2}$. Let $M$ and $N$ be two distinct points on $\omega_{1}$, different from $T$. Let [AB] and [CD] be two chords of the circle $\omega_{2}$ passing through $M$ and $N$ respectively. Suppose that the segments [BD], $[A C]$, and $[M N]$ intersect at a point $K$.
Show that (TK) is the bisector of the angle $\widehat{M T N}$.
|
Let $E$ and $F$ be the points of intersection of $(TM)$ and $(TN)$ with $\omega_{2}$, other than $T$. Since $\omega_{1}$ and $\omega_{2}$ are tangent at $T$, the homothety centered at $T$ that maps $\omega_{1}$ to $\omega_{2}$ also maps $M$ to $E$ and $N$ to $F$. This implies that
$$
\frac{\mathrm{TM}}{\mathrm{TN}}=\frac{\mathrm{ME}}{\mathrm{NF}}
$$
Furthermore, the power of points $M$ and $N$ with respect to $\omega_{2}$ is respectively $A M \cdot M B=T M \cdot M E$ and $C N \cdot N D=T N \cdot N F$. This shows that
$$
\frac{\mathrm{TM}^{2}}{\mathrm{TN}^{2}}=\frac{\mathrm{TM} \cdot \mathrm{ME}}{\mathrm{TN} \cdot \mathrm{NF}}=\frac{\mathrm{AM} \cdot \mathrm{MB}}{\mathrm{CN} \cdot \mathrm{ND}}
$$
On the other hand, in triangles $A M K$ and $D N K$, the law of sines indicates that
$$
A M \cdot \sin (\widehat{M A K})=M K \cdot \sin (\widehat{A K M}) \text { and that DN } \cdot \sin (\widehat{N D K})=N K \cdot \sin (\widehat{D K N}) .
$$
Since $A, B, C$ and $D$ are concyclic, we also have $\sin (\widehat{B A C})=\sin (\widehat{B D C})$, so that
$$
\sin (\widehat{M A K})=\sin (\widehat{B A C})=\sin (\widehat{B D C})=\sin (\widehat{K D N})
$$
It follows that $\frac{A M}{D N}=\frac{M K \cdot \sin (\widehat{A K M})}{N K \cdot \sin (\widehat{D K N})}$ and, similarly, that $\frac{B M}{C N}=\frac{M K \cdot \sin (\widehat{B K M})}{N K \cdot \sin (\widehat{C K N})}$. Since the angles $\widehat{B K M}$ and $\widehat{D K N}$ on one hand, and $\widehat{A K M}$ and $\widehat{C K M}$ on the other, are vertically opposite, hence equal, we deduce that
$$
\frac{A M \cdot M B}{D N \cdot N C}=\frac{M K^{2}}{N K^{2}}
$$
We conclude that TM $\cdot N K=T N \cdot M K$.
The law of sines in triangles TKM and TKN also indicates that
$$
\mathrm{TM} \cdot \sin (\widehat{\mathrm{KTM}})=\mathrm{KM} \cdot \sin (\widehat{\mathrm{MKT}}) \text { and that } \mathrm{TN} \cdot \sin (\widehat{\mathrm{KTN}})=\mathrm{KN} \cdot \sin (\widehat{\mathrm{NKT}})
$$
Since $\widehat{M K T}$ and $\widehat{N K T}$ are supplementary, they have the same sine, so that
$$
\frac{\sin (\widehat{K T M})}{\sin (\widehat{\mathrm{KTN}})}=\frac{\mathrm{KM} \cdot \sin (\widehat{\mathrm{MKT}}) \cdot \mathrm{TN}}{\mathrm{TM} \cdot \mathrm{KN} \cdot \sin (\widehat{\mathrm{NKT}})}=1
$$
which proves that (TK) is the angle bisector of $\widehat{M T N}$.
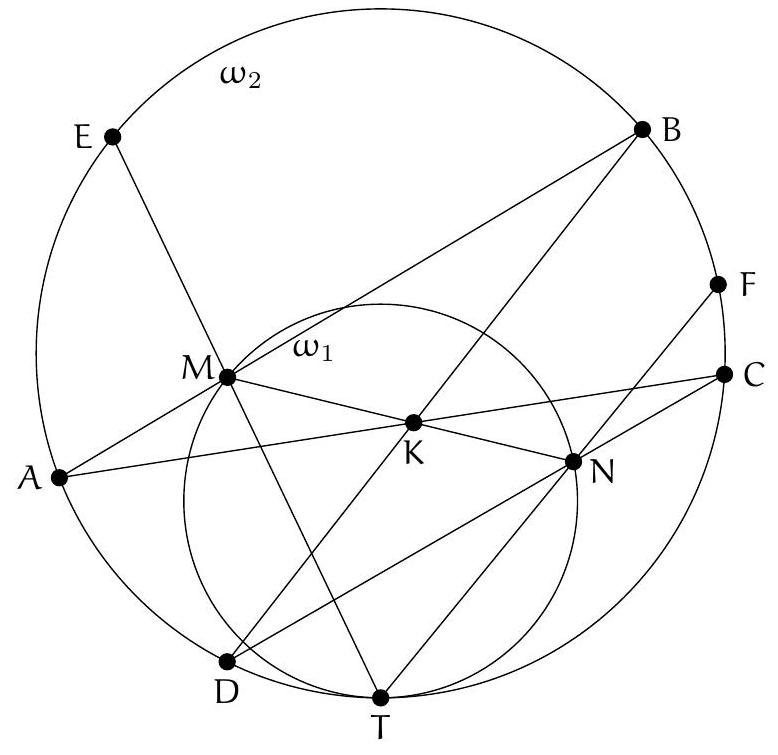
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient deux cercles $\omega_{1}, \omega_{2}$ tangents l'un à l'autre en un point $T$, tels que $\omega_{1}$ soit à l'intérieur de $\omega_{2}$. Soient $M$ et $N$ deux points distincts sur $\omega_{1}$, différents de $T$. Soient [AB] et [CD] deux cordes du cercle $\omega_{2}$ passant respectivement par $M$ et $N$. On suppose que les segments [BD], $[A C]$, et $[M N]$ s'intersectent en un point $K$.
Montrer que (TK) est la bissectrice de l'angle $\widehat{M T N}$.
|
Soit $E$ et $F$ les points d'intersection respectifs de (TM) et (TN) avec $\omega_{2}$, autres que $T$. Puisque $\omega_{1}$ et $\omega_{2}$ sont tangents en $T$, l'homothétie de centre T et qui envoie $\omega_{1}$ sur $\omega_{2}$ envoie également $M$ sur $E$ et $N$ sur $F$. On en déduit que
$$
\frac{\mathrm{TM}}{\mathrm{TN}}=\frac{\mathrm{ME}}{\mathrm{NF}}
$$
En outre, la puissance des points $M$ et $N$ par rapport à $\omega_{2}$ vaut respectivement $A M \cdot M B=T M \cdot M E$ et $C N \cdot N D=T N \cdot N F$. Cela montre que
$$
\frac{\mathrm{TM}^{2}}{\mathrm{TN}^{2}}=\frac{\mathrm{TM} \cdot \mathrm{ME}}{\mathrm{TN} \cdot \mathrm{NF}}=\frac{\mathrm{AM} \cdot \mathrm{MB}}{\mathrm{CN} \cdot \mathrm{ND}}
$$
D'autre part, dans les triangles $A M K$ et $D N K$, la loi des sinus indique que
$$
A M \cdot \sin (\widehat{M A K})=M K \cdot \sin (\widehat{A K M}) \text { et que DN } \cdot \sin (\widehat{N D K})=N K \cdot \sin (\widehat{D K N}) .
$$
Puisque $A, B, C$ et $D$ sont cocycliques, on a également $\sin (\widehat{B A C})=\sin (\widehat{B D C})$, de sorte que
$$
\sin (\widehat{M A K})=\sin (\widehat{B A C})=\sin (\widehat{B D C})=\sin (\widehat{K D N})
$$
Il s'ensuit que $\frac{A M}{D N}=\frac{M K \cdot \sin (\widehat{A K M})}{N K \cdot \sin (\widehat{D K N})}$ et, de même, que $\frac{B M}{C N}=\frac{M K \cdot \sin (\widehat{B K M})}{N K \cdot \sin (\widehat{C K N})}$. Puisque les angles $\widehat{B K M}$ et $\widehat{D K N}$ d'une part, et $\widehat{A K M}$ et $\widehat{C K M}$ d'autre part, sont opposés par le sommet, donc sont égaux deux à deux, on en déduit que
$$
\frac{A M \cdot M B}{D N \cdot N C}=\frac{M K^{2}}{N K^{2}}
$$
On en conclut que TM $\cdot N K=T N \cdot M K$.
La loi des sinus dans les triangles TKM et TKN indique en outre que
$$
\mathrm{TM} \cdot \sin (\widehat{\mathrm{KTM}})=\mathrm{KM} \cdot \sin (\widehat{\mathrm{MKT}}) \text { et que } \mathrm{TN} \cdot \sin (\widehat{\mathrm{KTN}})=\mathrm{KN} \cdot \sin (\widehat{\mathrm{NKT}})
$$
Puisque $\widehat{M K T}$ et $\widehat{N K T}$ sont supplémentaires, ils ont même sinus, de sorte que
$$
\frac{\sin (\widehat{K T M})}{\sin (\widehat{\mathrm{KTN}})}=\frac{\mathrm{KM} \cdot \sin (\widehat{\mathrm{MKT}}) \cdot \mathrm{TN}}{\mathrm{TM} \cdot \mathrm{KN} \cdot \sin (\widehat{\mathrm{NKT}})}=1
$$
ce qui prouve que (TK) est la bissectrice de $\widehat{M T N}$.

|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-novembre-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T1",
"year": "2017"
}
|
In the cells of a rectangular table with $n$ rows and $m$ columns, real numbers are written. We assume that for any row or column, the sum of the numbers written in that row or column is an integer. Show that it is possible to replace each real number $x$ by the integer $\lfloor x\rfloor$ or $\lceil x\rceil$ so that the sums of each column and each row remain unchanged.
Note: We recall that if $x$ is a real number, $\lfloor x\rfloor$ is the unique integer such that $\lfloor x\rfloor \leqslant x<\lfloor x\rfloor+1$, and $\lceil x\rceil$ is the unique integer such that $\lceil x\rceil-1<x \leqslant\lceil x\rceil$.
|
By subtracting the integer part from each entry in the array, we can assume that each number is between 0 and 1. We say that a cell is "fractional" if its number is not an integer. Note that, if C is a fractional cell, then there must necessarily be another fractional cell on the same row as C, and there must also be another fractional cell on the same column as C.
Let's choose a fractional cell $C_{0}$, and for all $n \in \mathbb{N}$:
- if $n$ is even, we choose a fractional cell $C_{n+1}$ on the same row as $C_{n}$;
- if $n$ is odd, we choose a fractional cell $C_{n+1}$ on the same column as $C_{n}$.
By the pigeonhole principle, there exist two integers $k<\ell$ such that $C_{k}=C_{\ell}$. Without loss of generality, we assume that $\ell$ is as small as possible, among all choices of cells $C_{0}, C_{1}, \ldots$ and integers $k<\ell$ that we might make.
Thus, we have $k=0$, and we have a "cycle" $C_{0}, \ldots, C_{\ell-1}, C_{\ell}$ of distinct fractional cells (except $C_{0}$ and $C_{\ell}$) such that the segments $\left[C_{i}, C_{i+1}\right]$ are alternately horizontal and vertical. Since this cycle is of minimal length $\ell$, we know that each row and each column contains either 0 or 2 cells of the cycle, and these cells are consecutive in the cycle.
For all $i<\ell-1$, we denote by $x_{i}$ the number written on the cell $C_{i}$, and we set $y_{i}=x_{i}$ if $i$ is even, and $y_{i}=1-x_{i}$ if $i$ is odd. Then we replace $x_{i}$ with the real number
$$
x_{i}^{\prime}=x_{i}+(-1)^{i} \varepsilon
$$
where $\varepsilon=\min \left\{y_{i} \mid i<\ell\right\}$. By construction of $\varepsilon$, we have $0 \leqslant x_{i}^{\prime} \leqslant 1$ for all $i<\ell$, with $x_{i}^{\prime}=0$ or $x_{i}^{\prime}=1$ for at least one integer $i$.
This process has not modified the sum of any row or column, and has reduced the number of fractional cells, while assigning to each modified cell a value $x_{i}^{\prime}$ such that
$$
\left\{\left\lfloor x_{i}^{\prime}\right\rfloor,\left\lceil x_{i}^{\prime}\right\rceil\right\} \subseteq\{0,1\}=\left\{\left\lfloor x_{i}\right\rfloor,\left\lceil x_{i}\right\rceil\right\}.
$$
We can therefore repeat this process until all fractional cells are eliminated, which concludes the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Dans les cases d'un tableau rectangulaire à $n$ lignes et $m$ colonnes sont écrits des nombres réels. On suppose que pour toute ligne ou colonne, la somme des nombres écrits sur cette ligne ou colonne est un entier. Montrer qu'il est possible de remplacer chaque réel $x$ par l'entier $\lfloor x\rfloor$ ou $\lceil x\rceil$ de sorte que les sommes de chaque colonne et de chaque ligne demeurent inchangées.
Remarque : On rappelle que si $x$ est un nombre réel, $\lfloor x\rfloor$ est l'unique entier tel que $\lfloor x\rfloor \leqslant x<\lfloor x\rfloor+1$, et $\lceil x\rceil$ est l'unique entier tel que $\lceil x\rceil-1<x \leqslant\lceil x\rceil$.
|
Quitte à soustraire sa partie entière à chaque entrée du tableau, on peut supposer que chaque nombre est compris entre 0 et 1 . On dit qu'une case est « fractionnaire $\gg$ si son nombre n'est pas entier. Remarquons que, si C est une case fractionnaire, alors il existe nécessairement une autre case fractionnaire sur la même ligne que C , et il existe aussi une autre case fractionnaire sur la même colonne que C .
Choisissons donc une case $C_{0}$ fractionnaire, puis, pour tout $n \in \mathbb{N}$ :
- si $n$ est pair, on choisit une case $C_{n+1}$ fractionnaire sur la même ligne que $C_{n}$;
- si $n$ est impair, on choisit une case $C_{n+1}$ fractionnaire sur la même colonne que $C_{n}$.
Par principe des tiroirs, il existe deux entiers $k<\ell$ tels que $C_{k}=C_{\ell}$. Sans perte de généralité, on suppose que $\ell$ est aussi petit que possible, parmi tous les choix de cases $C_{0}, C_{1}, \ldots$ et d'entiers $k<\ell$ que l'on aura pu faire.
On a donc $k=0$, et l'on dispose ainsi d'un $«$ cycle $\gg C_{0}, \ldots, C_{\ell-1}, C_{\ell}$ de cases fractionnaires deux à deux distinctes (sauf $C_{0}$ et $C_{\ell}$ ) et telles que les segments $\left[C_{i}, C_{i+1}\right]$ sont alternativement horizontaux et verticaux. Ce cycle étant de longueur $\ell$ minimale, on sait que chaque ligne et chaque colonne contient soit 0 , soit 2 cases du cycle, et que ces cases sont consécutives dans le cycle.
Pour tout $i<\ell-1$, on note $x_{i}$ le nombre écrit sur la case $C_{i}$, et l'on pose $y_{i}=x_{i}$ si $i$ est pair, et $y_{i}=1-x_{i}$ si $i$ est impair. Puis l'on remplace $x_{i}$ par le réel
$$
x_{i}^{\prime}=x_{i}+(-1)^{i} \varepsilon
$$
où $\varepsilon=\min \left\{y_{i} \mid i<\ell\right\}$. Par construction de $\varepsilon$, on a donc $0 \leqslant x_{i}^{\prime} \leqslant 1$ pour tout $i<\ell$, avec $x_{i}^{\prime}=0$ ou $x_{i}^{\prime}=1$ pour au moins un entier $i$.
Ce procédé n'a modifié la somme d'aucune ligne ni colonne, et a permis de réduire le nombre de cases fractionnaires, tout en affectant à chaque case modifiée une valeur $x_{i}^{\prime}$ telle que
$$
\left\{\left\lfloor x_{i}^{\prime}\right\rfloor,\left\lceil x_{i}^{\prime}\right\rceil\right\} \subseteq\{0,1\}=\left\{\left\lfloor x_{i}\right\rfloor,\left\lceil x_{i}\right\rceil\right\} .
$$
On peut donc réitérer ce procédé jusqu'à éliminer toutes les cases fractionnaires, ce qui conclut le problème.
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2017-2018-pofm-2017-2018-test-novembre-corrige.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T1",
"year": "2017"
}
|
Let $x$ and $y$ be two integers such that $5x + 6y$ and $6x + 5y$ are perfect squares. Show that $x$ and $y$ are both divisible by 11.
Note: an integer $n$ is a perfect square if it is the square of an integer.
|
Let $a$ and $b$ be integers such that $5 x + 6 y = a^2$ and $6 x + 5 y = b^2$. We note that $a^2 + b^2 = 11(x + y)$ is divisible by 11. Now, modulo 11, the squares are $0, 1, 3, 4, 5$, and 9: thus, the sum of two squares is zero (mod. 11) if and only if the two squares in question are zero (mod. 11) as well.
In our case, this means that $a$ and $b$ are divisible by 11. Therefore, there exist integers $A$ and $B$ such that $a = 11 A$ and $b = 11 B$. But then
$$
11 x = (6 \times 6 - 5 \times 5) x = 6(b^2 - 5 y) - 5(a^2 - 6 y) = 6 b^2 - 5 a^2 = 11^2 (6 B^2 - 5 A^2)
$$
so that $x = 11(6 B^2 - 5 A^2)$ is indeed divisible by 11. Similarly, we show that $y = 11(6 A^2 - 5 B^2)$ is also divisible by 11.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $x$ et $y$ deux entiers tels que $5 x+6 y$ et $6 x+5 y$ soient des carrés parfaits. Montrer que $x$ et $y$ sont tous deux divisibles par 11.
Note : on dit qu'un entier $n$ est un carré parfait si c'est le carré d'un entier.
|
Soit $a$ et $b$ deux entiers tels que $5 x+6 y=a^{2}$ et $6 x+5 y=b^{2}$. On note que $a^{2}+b^{2}=11(x+y)$ est divisible par 11 . Or, modulo 11 , les carrés sont $0,1,3,4,5$ et 9 : ainsi, la somme de deux carrés est nulle (mod. 11) si et seulement si les deux carrés en question sont nuls (mod. 11) eux aussi.
Dans notre cas, cela signifie que $a$ et $b$ sont divisibles par 11. Il existe donc des entiers $A$ et $B$ tels que $a=11 A$ et $b=11 \mathrm{~B}$. Mais alors
$$
11 x=(6 \times 6-5 \times 5) x=6\left(b^{2}-5 y^{2}\right)-5\left(a^{2}-6 y\right)=6 b^{2}-5 a^{2}=11^{2}\left(6 B^{2}-5 A^{2}\right)
$$
de sorte que $x=11\left(6 B^{2}-5 A^{2}\right)$ est bien divisible par 11. De même, on montre que $y=$ $11\left(6 A^{2}-5 B^{2}\right)$ est lui aussi divisible par 11.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2018-2019-Test-09-01-Corrigé.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T1",
"year": "2018"
}
|
Let $\Gamma$ be a circle with center $O$ and radius $r$, and $\ell$ be a line that does not intersect $\Gamma$. We denote $E$ as the point of intersection between $\ell$ and the line perpendicular to $\ell$ passing through $O$.
Let $M$ be a point on $\ell$ different from $E$. The tangents to the circle $\Gamma$ passing through $M$ touch $\Gamma$ at $A$ and $B$. Finally, let $H$ be the point of intersection of the lines $(AB)$ and $(OE)$.
Show that $\mathrm{OH}=\mathrm{r}^{2} / \mathrm{OE}$.
|
First, the triangles OAM, OBM, and OEM are respectively right-angled at $A, B$, and $E$, so the points $A, O, B, E, M$ all belong to the same circle with diameter [OM].
According to the law of sines in triangles OBH and OEA, we know that
$$
\frac{\mathrm{OH} \times \mathrm{OE}}{\mathrm{r}^{2}}=\frac{\mathrm{OH}}{\mathrm{OB}} \times \frac{\mathrm{OE}}{\mathrm{OA}}=\frac{\sin (\widehat{\mathrm{OBA}})}{\sin (\widehat{\mathrm{OHB}})} \times \frac{\sin (\widehat{\mathrm{OAE}})}{\sin (\widehat{\mathrm{OEA}})}
$$
Since the points $O, B, E$, and $A$ are concyclic, we know that $\widehat{O B A}=\widehat{O E A}$. On the other hand, since the lines $(\mathrm{AH})$ and $(\mathrm{HO})$ are respectively perpendicular to $(\mathrm{OM})$ and $(\mathrm{ME})$, we also know that
$$
\widehat{\mathrm{OHB}}=180^{\circ}-\widehat{\mathrm{AHO}}=180^{\circ}-\widehat{\mathrm{OME}}=180^{\circ}-\widehat{\mathrm{OAE}}
$$
This shows that $\sin (\widehat{O B A})=\sin (\widehat{O E A})$ and that $\sin (\widehat{O H B})=\sin (\widehat{O A E})$, which concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $\Gamma$ un cercle de centre $O$ et de rayon $r$ et $\ell$ une droite qui ne coupe pas $\Gamma$. On note $E$ le point d'intersection entre $\ell$ et la droite perpendiculaire à $\ell$ passant par $O$.
Soit $M$ un point de $\ell$ différent de $E$. Les tangentes au cercle $\Gamma$ et passant par $M$ touchent $\Gamma$ en $A$ et $B$. Enfin, soit $H$ le point d'intersection des droites ( $A B$ ) et ( $O E$ ).
Montrer que $\mathrm{OH}=\mathrm{r}^{2} / \mathrm{OE}$.
|
Tout d'abord, les triangles OAM, OBM et OEM sont respectivement rectangles en $A, B$ et $E$, de sorte que les points $A, O, B, E, M$ appartiennent tous à un même cercle de diamètre [OM].
Or, d'après la loi des sinus dans les triangles OBH et OEA, on sait que
$$
\frac{\mathrm{OH} \times \mathrm{OE}}{\mathrm{r}^{2}}=\frac{\mathrm{OH}}{\mathrm{OB}} \times \frac{\mathrm{OE}}{\mathrm{OA}}=\frac{\sin (\widehat{\mathrm{OBA}})}{\sin (\widehat{\mathrm{OHB}})} \times \frac{\sin (\widehat{\mathrm{OAE}})}{\sin (\widehat{\mathrm{OEA}})}
$$
Les points $O, B, E$ et $A$ étant cocycliques, on sait que $\widehat{O B A}=\widehat{O E A}$. D'autre part, puisque les droites $(\mathrm{AH})$ et $(\mathrm{HO})$ sont respectivement perpendiculaires à $(\mathrm{OM})$ et $(\mathrm{ME})$, on sait également que
$$
\widehat{\mathrm{OHB}}=180^{\circ}-\widehat{\mathrm{AHO}}=180^{\circ}-\widehat{\mathrm{OME}}=180^{\circ}-\widehat{\mathrm{OAE}}
$$
Cela montre que $\sin (\widehat{O B A})=\sin (\widehat{O E A})$ et que $\sin (\widehat{O H B})=\sin (\widehat{O A E})$, ce qui conclut.

|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2018-2019-Test-09-01-Corrigé.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T1",
"year": "2018"
}
|
Let $n$ be a natural number. A staircase of size $n$ is made up of small $1 \times 1$ squares, with 1 square for the first step, 2 squares for the second step, and so on, up to $n$ squares for the $n^{\text{th}}$ step.
We have square stones (with integer side lengths) of all sizes to build this staircase, and we denote $f(n)$ as the minimum number of stones needed to build a staircase of size $n$. For example, $f(2)=3$ and $f(4)=7$, as illustrated below.

1. Find all integers $n \geqslant 0$ such that $f(n)=n$.
2. Find all integers $n \geqslant 0$ such that $f(n)=n+1$.
|
Let's start with some definitions and general observations. In the following, we denote by $(i, j)$ the $1 \times 1$ small square located at the $j$-th level of the $i$-th step. We will call the upper square each small square $(k, k)$, i.e., each square located at the very top of a step.
We consider the construction of a staircase of size $n$ using $f(n)$ square stones. Two distinct upper squares cannot belong to the same stone. Since there are exactly $n$ upper squares in a staircase of size $n$, we deduce that $f(n) \geqslant n$ for all $n \geqslant 0$. We now address questions 1 and 2.
1. First, it is clear that $f(0)=0$. Now let $n \geqslant 1$ be an integer such that $f(n)=n$.
From the above observation, each stone contains a unique upper square. This is particularly the case for the stone containing the square $(n, 1)$. But then this stone divides the staircase into two symmetric parts. Thus, each part forms a staircase of size $(n-1) / 2$, such that $f((n-1) / 2)=(n-1) / 2$. Consequently, an immediate induction shows that there exists an integer $k \geqslant 0$ such that $n=2^{k}-1$.
Conversely, and following this construction in the other direction, an immediate induction shows that $f\left(2^{k}-1\right)=2^{k}-1$ for all integers $k \geqslant 0$.
The integers $n$ sought are therefore the integers of the form $n=2^{k}-1$ with $k \geqslant 0$.
2. This time, we know that $n \geqslant 2$. Furthermore, the stone containing the square $(n, 1)$ cannot contain an upper square; indeed, if it did, it would cut the staircase into two symmetric parts, each forming a staircase of size $(n-1) / 2$, so $f(n)-n$ would have to be even.
It is therefore the only stone that does not contain an upper square. Let $\ell \times \ell$ be the dimensions of this stone. Once $\ell$ and $n$ are fixed, each other stone must contain an upper square, and the dimensions of the stones are therefore prescribed. In particular, an immediate induction on $n+i-j$ shows that the stones containing the squares $(i, j)$ and $(n+1-j, n+1-i)$ actually occupy symmetric positions.
In order to reduce the problem to treating only staircases where each stone contains an upper square, we specifically focus on the stones containing the squares $(n, 1)$, $(n-\ell, 1)$, $(n, \ell+1)$, and $(n-\ell, \ell+1)$; the latter stone exists only if $n \neq 2 \ell$.
We first assume that $n \neq 2 \ell$. In this case, our four stones are pairwise disjoint, with respective sizes $\ell \times \ell$, $(n+1-\ell) / 2$, $(n+1-\ell) / 2$, and $(n+1-2 \ell) / 2$, and they cut the staircase into four small staircases: two staircases of size $(n-1-\ell) / 2$ and two staircases of size $(n-1-2 \ell) / 2$. Given the results of the first question, there therefore exist two non-zero natural numbers $k$ and $k'$ such that $n=2^{k}+\ell-1=2^{k'}+2 \ell-1$.
This means that $\ell=2^{k}-2^{k'}$, so $k \geqslant k'$ and $n=2^{k+1}-2^{k'}-1$. Conversely, if there exist integers $k \geqslant k' \geqslant 1$ such that $n=2^{k+1}-2^{k'}-1$, it is indeed sufficient to choose $\ell=2^{k}-2^{k'}$ for our construction to work.
Similarly, if $n=2 \ell$, we actually have three stones, which cut the staircase into four small staircases of size $(n-1-\ell) / 2=(\ell-1) / 2$, so there exists a non-zero natural number $k$ such that $\ell=2^{k}-1$ and $n=2^{k+1}-2$. Conversely, if there exists an integer $k \geqslant 1$ such that $n=2^{k+1}-2$, it is indeed sufficient to choose $\ell=n / 2$ for our construction to work. The integers $n$ sought are therefore the integers of the form $n=2^{k+1}-2^{k'}-1$ with $k \geqslant k' \geqslant 0$.
## Exercise for both Junior and Senior groups
|
n=2^{k}-1 \text{ for } k \geqslant 0 \text{ and } n=2^{k+1}-2^{k'}-1 \text{ for } k \geqslant k' \geqslant 0
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Soit $n$ un entier naturel. Un escalier de taille $n$ est constitué de petits carrés $1 \times 1$, avec 1 carré pour la première marche, 2 carrés pour la deuxième marche, et ainsi de suite, jusqu'à $n$ carrés pour la $n^{\text {ème }}$ marche.
On dispose de pierres carrées (de coté entier) de toutes les tailles pour construire cet escalier et on note $f(n)$ le nombre minimum de pierres que l'on doit utiliser pour un escalier de taille $n$. Par exemple, $f(2)=3$ et $f(4)=7$, comme illustré ci-dessous.

1. Trouver tous les entiers $n \geqslant 0$ tels que $f(n)=n$.
2. Trouver tous les entiers $n \geqslant 0$ tels que $f(n)=n+1$
|
Commençons par quelques définitions et observations générales. Dans la suite, on note $(i, j)$ le petit carré $1 \times 1$ situé au jème étage de la $i^{\text {ème }}$ marche. On appellera carré supérieur chaque petit carré ( $k, k$ ), c'est-à-dire chaque carré situé tout en haut d'une marche.
On considère une construction de l'escalier de taille $n$ à partir de $f(n)$ pierres carrées. Deux carrés supérieurs distincts ne peuvent appartenir à la même pierre. Puisqu'il y a exactement $n$ carrés supérieurs dans un escalier de taille $n$, on en déduit que $f(n) \geqslant n$ pour tout $n \geqslant 0$. On traite maintenant les questions 1 et 2.
1. Tout d'abord, il est clair que $f(0)=0$. Soit maintenant $n \geqslant 1$ un entier tel que $f(n)=n$.
Au vu de l'observation ci-dessus, chaque pierre contient un unique carré supérieur. C'est en particulier le cas de la pierre contenant le carré ( $n, 1$ ). Mais alors cette pierre sépare l'escalier en 2 parties symétriques. Ainsi, chaque partie forme un escalier de taille $(n-1) / 2$, tel que $f((n-1) / 2)=(n-1) / 2$. Par conséquent, une récurrence immédiate montre qu'il existe un entier $k \geqslant 0$ tel que $n=2^{k}-1$.
Réciproquement, et en suivant cette construction dans l'autre sens, une récurrence immédiate montre que $f\left(2^{k}-1\right)=2^{k}-1$ pour tout entier $k \geqslant 0$.
Les entiers $n$ recherchés sont donc bien les entiers de la forme $n=2^{k}-1$ avec $k \geqslant 0$.
2. Cette fois-ci, on sait que $n \geqslant 2$. D'autre part, la pierre contenant le carré ( $n, 1$ ) ne saurait contenir de carré supérieur; en effet, si c'était le cas, elle couperait l'escalier en 2 parties symétriques, formant chacune un escalier de taille ( $n-1$ )/2, de sorte que $f(n)-n$ devrait être pair.
Il s'agit donc de la seule la seule pierre qui ne contient pas de carré supérieur. Soit $\ell \times \ell$ les dimensions de cette pierre. Une fois $\ell$ et $n$ fixés, chaque autre pierre doit contenir un carré supérieur, et les dimensions des pierres sont donc prescrites. En particulier, une récurrence immédiate sur $n+i-j$ montre que les pierres contenant les carrés ( $i, j$ ) et $(\mathfrak{n}+1-\mathfrak{j}, \mathfrak{n}+1-\mathfrak{i})$ occupent en fait des positions symétriques.
Afin de se ramener à ne traiter que des escaliers où chaque pierre contient un carré supérieur, on s'intéresse donc spécifiquement aux pierres contenant les carrés ( $\mathrm{n}, 1$ ), $(n-\ell, 1),(n, \ell+1)$ et $(n-\ell, \ell+1)$; cette dernière pierre n'existe que si $n \neq 2 \ell$.
On suppose tout d'abord que $n \neq 2 \ell$. Dans ce cas, nos quatre pierres sont deux à deux disjointes, de tailles respectives $\ell \times \ell,(n+1-\ell) / 2,(n+1-\ell) / 2$ et $(n+1-2 \ell) / 2$, et elles coupent l'escalier en quatre petits escaliers : deux escaliers de taille ( $n-1-\ell$ ) /2 et deux escaliers de taille $(n-1-2 \ell) / 2$. Au vu des résultats de la première question, il existe donc deux entiers naturels non nuls $k$ et $k^{\prime}$ tels que $n=2^{\mathrm{k}}+\ell-1=2^{\mathrm{k}^{\prime}}+2 \ell-1$.
Cela signifie que $\ell=2^{k}-2^{k^{\prime}}$, donc que $k \geqslant k^{\prime}$ et que $n=2^{k+1}-2^{k^{\prime}}-1$. Réciproquement, s'il existe des entiers $k \geqslant k^{\prime} \geqslant 1$ tels que $n=2^{k+1}-2^{k^{\prime}}-1$, il suffit en effet de choisir $\ell=2^{k}-2^{k^{\prime}}$ pour que notre construction fonctionne.
De même, si $n=2 \ell$, on a en fait trois pierres, qui coupent l'escalier en quatre petits escaliers de taille $(n-1-\ell) / 2=(\ell-1) / 2$, donc il existe un entier naturel non nul $k$ tel que $\ell=2^{k}-1$ et $n=2^{k+1}-2$. Réciproquement, s'il existe un entier $k \geqslant 1$ tel que $\mathrm{n}=2^{\mathrm{k}+1}-2$, il suffit en effet de choisir $\ell=\mathrm{n} / 2$ pour que notre construction fonctionne. Les entiers $n$ recherchés sont donc bien les entiers de la forme $n=2^{k+1}-2^{k^{\prime}}-1$ avec $k \geqslant k^{\prime} \geqslant 0$.
## Exercice commun aux groupes Junior et Senior
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2018-2019-Test-09-01-Corrigé.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T1",
"year": "2018"
}
|
Find all functions $\mathrm{f}: \mathbb{N} \rightarrow \mathbb{N}$ such that
$$
x f(y)+y f(x)=(x+y) f\left(x^{2}+y^{2}\right)
$$
for all natural numbers $x$ and $y$.
Note: recall that $\mathbb{N}$ denotes the set of natural numbers, i.e., $\mathbb{N}=\{0,1,2, \ldots\}$.
|
In the following, we will denote $\mathbf{E}_{x, y}$ as the equation from the statement.
First, the equation $E_{x, 0}$ indicates that $x f(0)=x f\left(x^{2}\right)$, which shows that $f\left(x^{2}\right)=f(0)$ for all integers $x \geqslant 1$. Consequently, for all integers $y \geqslant 1$, the equation $\mathbf{E}_{x, y^{2}}$ indicates that $x+y^{2}$ divides $x(f(0)-f(x))$. This divisibility relation being valid even when $y$ is arbitrarily large, we deduce that $f(x)=f(0)$ for any $x$.
Conversely, we easily verify that constant functions are indeed solutions to the equation.
## Exercises of the Senior Group
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Trouver toutes les fonctions $\mathrm{f}: \mathbb{N} \rightarrow \mathbb{N}$ telles que
$$
x f(y)+y f(x)=(x+y) f\left(x^{2}+y^{2}\right)
$$
pour tous les entiers naturels $x$ et $y$.
Note : on rappelle que $\mathbb{N}$ désigne l'ensemble des entiers naturels, c'est-à-dire $\mathbb{N}=\{0,1,2, \ldots\}$.
|
Dans la suite, on notera $\mathbf{E}_{x, y}$ l'équation de l'énoncé.
Tout d'abord, l'équation $E_{x, 0}$ indique que $x f(0)=x f\left(x^{2}\right)$, ce qui montre que $f\left(x^{2}\right)=f(0)$ pour tout entier $x \geqslant 1$. Par conséquent, pour tout entier $y \geqslant 1$, l'équation $\mathbf{E}_{x, y^{2}}$ indique que $x+y^{2}$ divise $x(f(0)-f(x))$. Cette relation de divisibilité étant valide même quand $y$ est arbitrairement grand, on en déduit que $f(x)=f(0)$ quel que soit $x$.
Réciproquement, on vérifie aisément que les fonctions constantes sont bien des solutions de l'équation.
## Exercices du groupe Senior
|
{
"exam": "French_tests",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/tests/fr-2018-2019-Test-09-01-Corrigé.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T1",
"year": "2018"
}
|
Let $n$ be an odd integer, and let $S$ be a set of $n$ points in the plane with integer coordinates. Consider a permutation $\mathrm{f}: \mathrm{S} \rightarrow \mathrm{S}$ that satisfies the following property:
For any pair of points $A$ and $B$ belonging to $S$, the distance between $f(A)$ and $f(B)$ is greater than or equal to the distance between $A$ and $B$.
Show that there exists a point $X$, belonging to $S$, such that $f(X)=X$.
|
Since $S$ has odd cardinality, $f$ admits an orbit of odd cardinality. Without loss of generality, we can therefore assume that $S$ is equal to this orbit, and even that $S=\left\{P_{1}, \ldots, P_{n}\right\}$ with $f\left(P_{i}\right)=P_{i+1}$ for all $i \leqslant n$, setting $P_{1}=n+1$.
If $f$ has no fixed point, it follows that $n \geqslant 3$. Let's show that this case is actually impossible.
Indeed, under these conditions, the statement shows that $P_{1} P_{2} \leqslant P_{2} P_{3} \leqslant \ldots \leqslant P_{n} P_{1}$, so that all these inequalities are in fact equalities. Furthermore, without loss of generality, by considering a point $P_{i}$ rather than $P_{1}$ and by performing integer translations and dividing all our coordinates by 2, we can assume that the coordinates of the vector $\overrightarrow{\mathrm{P}_{1} \mathrm{P}_{2}}$ are not both even. Now, we will denote $x_{i}$ and $y_{i}$ the coordinates of the point $P_{i}$.
Since the squares modulo 4 are 0 and 1, we deduce that $P_{i} P_{i+1}^{2}=P_{1} P_{2}^{2}=\left(x_{i}-x_{i+1}\right)^{2}+$ $\left(y_{i}-y_{i+1}\right)^{2}$ is congruent to 1 or 2 modulo 4.
In the first case, it follows that the sum $\Delta_{i}=x_{i}+y_{i}+x_{i+1}+y_{i+1} \equiv 1(\bmod 2)$. We deduce that
$$
n \equiv \sum_{i=1}^{n} \Delta_{i} \equiv 2 \sum_{i=1}^{n}\left(x_{i}+y_{i}\right) \equiv 0 \quad(\bmod 2)
$$
In the second case, we have directly $\Delta_{i}^{x}=x_{i}+x_{i+1} \equiv 1(\bmod 2)$ and $\Delta_{i}^{y}=y_{i}+y_{i+1} \equiv 1$ $(\bmod 2)$, so that
$$
n \equiv \sum_{i=1}^{n} \Delta_{i}^{x} \equiv 2 \sum_{i=1}^{n} x_{i} \equiv 0 \quad(\bmod 2)
$$
Since $n$ is odd, neither of these two cases is possible, which concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soit $n$ un entier impair, et soit $S$ un ensemble de $n$ points du plan à coordonnées entières. On considère une permutation $\mathrm{f}: \mathrm{S} \rightarrow \mathrm{S}$ qui satisfait la propriété suivante :
Pour toute paire de points $A$ et $B$ appartenant à $S$, la distance entre $f(A)$ et $f(B)$ est supérieure ou égale à la distance entre $A$ et $B$.
Montrer qu'il existe un point $X$, appartenant à $S$, tel que $f(X)=X$.
|
Puisque $S$ est de cardinal impair, f admet une orbite de cardinal impair. Sans perte de généralité, on peut donc supposer que $S$ est égal à cette orbite, et même que $S=\left\{P_{1}, \ldots, P_{n}\right\}$ avec $f\left(P_{i}\right)=P_{i+1}$ pour tout $i \leqslant n$, en posant $P_{1}=n+1$.
Si f n'a aucun point fixe, $\mathrm{c}^{\prime}$ est donc que $n \geqslant 3$. Montrons que ce cas est en fait impossible.
En effet, dans ces conditions, l'énoncé montre que $P_{1} P_{2} \leqslant P_{2} P_{3} \leqslant \ldots \leqslant P_{n} P_{1}$, de sorte que toutes ces inégalités sont en fait des égalités. En outre, toujours sans perte de généralité, quitte à considérer un point $P_{i}$ plutôt que $P_{1}$ et quitte à effectuer des translations à coordonnées entières et à diviser toutes nos coordonnées par 2, on peut supposer que les coordonnées du vecteur $\overrightarrow{\mathrm{P}_{1} \mathrm{P}_{2}}$ ne sont pas toutes les deux paires. Maintenant, on va noter $x_{i}$ et $y_{i}$ les coordonnées du point $P_{i}$.
Puisque les carrés modulo 4 sont 0 et 1 , on en déduit que $P_{i} P_{i+1}^{2}=P_{1} P_{2}^{2}=\left(x_{i}-x_{i+1}\right)^{2}+$ $\left(y_{i}-y_{i+1}\right)^{2}$ est congru à 1 ou 2 modulo 4 .
Dans le premier cas, $c^{\prime}$ est donc que la somme $\Delta_{i}=x_{i}+y_{i}+x_{i+1}+y_{i+1} \equiv 1(\bmod 2)$. On en déduit que
$$
n \equiv \sum_{i=1}^{n} \Delta_{i} \equiv 2 \sum_{i=1}^{n}\left(x_{i}+y_{i}\right) \equiv 0 \quad(\bmod 2)
$$
Dans le deuxième cas, on a directement $\Delta_{i}^{x}=x_{i}+x_{i+1} \equiv 1(\bmod 2)$ et $\Delta_{i}^{y}=y_{i}+y_{i+1} \equiv 1$ $(\bmod 2)$, de sorte que
$$
n \equiv \sum_{i=1}^{n} \Delta_{i}^{x} \equiv 2 \sum_{i=1}^{n} x_{i} \equiv 0 \quad(\bmod 2)
$$
Puisque n est impair, aucun de ces deux cas n'est possible, ce qui conclut.
|
{
"exam": "French_tests",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/tests/fr-2018-2019-Test-09-01-Corrigé.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T1",
"year": "2018"
}
|
Let $ABC$ be a triangle, and let $E$ and $F$ be two points lying on the lines $(AB)$ and $(AC)$ respectively, distinct from $A, B$, and $C$. Let $\Omega$ be the circumcircle of $ABC$, $O$ the center of $\Omega$, and $\Gamma$ the circumcircle of $AEF$. Let $P$ be the intersection point of $\Gamma$ and $\Omega$ other than $A$, and let $Q$ be the reflection of $P$ over the line $(EF)$.
Show that $Q$ lies on the line $(BC)$ if and only if $O$ lies on the circle $\Gamma$.
|
Since (BC) and (EF) are two lines of notable interest, we denote 7 as their point of intersection, possibly at infinity. Then Q belongs to the line (BC) if and only if, in terms of angles between lines, we have (BT, ET) = (ET, PT).
Moreover, always in terms of angles between lines, we already know that
\[
\begin{aligned}
(\mathrm{PB}, \mathrm{PE}) & =(\mathrm{PB}, \mathrm{PA})+(\mathrm{PA}, \mathrm{PE})=(\mathrm{CB}, \mathrm{CA})+(\mathrm{FA}, \mathrm{FE}) \\
& =(\mathrm{CT}, \mathrm{CF})+(\mathrm{CF}, \mathrm{FT})=(\mathrm{CT}, \mathrm{FT})=(\mathrm{TB}, \mathrm{TE}),
\end{aligned}
\]
which means that the points \(\mathrm{P}, \mathrm{E}, \mathrm{B}\) and T are concyclic. Consequently, we know that \((B T, E T)=(B P, E P)\) and \((E T, P T)=(E B, P B)=(A B, P B)\).
We also know that \(2(B A, B P)=(O A, O P)\) and that \((E A, E P)=(B A, B P)+(B P, E P)\). Thus,
\[
\begin{aligned}
\text{Q belongs to the line }(\mathrm{BC}) & \Leftrightarrow(\mathrm{BP}, \mathrm{EP})=(\mathrm{AB}, \mathrm{~PB}) \\
& \Leftrightarrow(\mathrm{EA}, \mathrm{EP})=2(\mathrm{BA}, \mathrm{BP})=(\mathrm{OA}, \mathrm{OP}) \\
& \Leftrightarrow \mathrm{O} \text{ belongs to the circle } \Gamma.
\end{aligned}
\]
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle, et soit $E$ et $F$ deux points appartenant respectivement aux droites $(A B)$ et $(A C)$, distincts de $A, B$ et $C$. Soit également $\Omega$ le cercle circoncscrit à $A B C$, soit $O$ le centre de $\Omega$, et soit $\Gamma$ le cercle circonscrit à $A E F$. Enfin, soit $P$ le point d'intersection $\operatorname{de} \Gamma$ et $\Omega$ autre que $A$, et soit $Q$ le symétrique de $P$ par rapport à la droite (EF).
Montrer que Q appartient à la droite ( BC ) si et seulement si O appartient au cercle $\Gamma$.
|
Puisque (BC) et (EF) sont deux droites d'intérêt notoire, on note 7 leur point d'intersection, éventuellement rejeté à l'infini. Alors Q appartient à la droite ( BC ) si et seulement si, en angles de droites, on a (BT, ET) $=(\mathrm{ET}, \mathrm{PT})$.
Or, toujours en angles de droites, on sait déjà que
$$
\begin{aligned}
(\mathrm{PB}, \mathrm{PE}) & =(\mathrm{PB}, \mathrm{PA})+(\mathrm{PA}, \mathrm{PE})=(\mathrm{CB}, \mathrm{CA})+(\mathrm{FA}, \mathrm{FE}) \\
& =(\mathrm{CT}, \mathrm{CF})+(\mathrm{CF}, \mathrm{FT})=(\mathrm{CT}, \mathrm{FT})=(\mathrm{TB}, \mathrm{TE}),
\end{aligned}
$$
ce qui signifie que les points $\mathrm{P}, \mathrm{E}, \mathrm{B}$ et T sont cocycliques. Par conséquent, on sait que $(B T, E T)=(B P, E P)$ et $(E T, P T)=(E B, P B)=(A B, P B)$.
On sait aussi que $2(B A, B P)=(O A, O P)$ et que $(E A, E P)=(B A, B P)+(B P, E P)$. Ainsi,
$$
\begin{aligned}
\text { Q appartient à la droite }(\mathrm{BC}) & \Leftrightarrow(\mathrm{BP}, \mathrm{EP})=(\mathrm{AB}, \mathrm{~PB}) \\
& \Leftrightarrow(\mathrm{EA}, \mathrm{EP})=2(\mathrm{BA}, \mathrm{BP})=(\mathrm{OA}, \mathrm{OP}) \\
& \Leftrightarrow \mathrm{O} \text { appartient au cercle } \Gamma .
\end{aligned}
$$

|
{
"exam": "French_tests",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/tests/fr-2018-2019-Test-09-01-Corrigé.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T1",
"year": "2018"
}
|
Let $S$ be a set of integers. We say that $S$ is non-summable if, for all integers $x$ and $y$ belonging to $S$, the sum $x+y$ does not belong to $S$. For any integer $n \geqslant 1$, we denote by $s_{n}$ the number of subsets of $\{1,2, \ldots, 2 n\}$ that are non-summable.
Prove that $s_{n} \geqslant 2^{n}$.
|
Let $S$ be a subset of $\{n+1, \ldots, 2 n\}$. Such a subset is non-summable, since for all integers $x, y$ and $z$ belonging to $S$, we have $x+y \geqslant 2(n+1)>2 n \geqslant z$. Now, there are $2^{n}$ subsets of $\{n+1, \ldots, 2 n\}$. We can thus conclude that $s_{n} \geqslant 2^{n}$.
Note: In fact, we can prove that $2^{\mathfrak{n}+4} \geqslant s_{n} \geqslant 2^{\mathfrak{n}+1}$ for all $n \geqslant 3$. The inequality $s_{n} \geqslant 2^{\mathrm{n}+1}$ can be obtained, for example, as follows.
For any integer $k \in\{1, \ldots, 2 \mathfrak{n}\}$, let $E_{k}$ be the set of subsets of $\{\lfloor k / 2\rfloor+1, \ldots, k\}$ to which $k$ belongs. If a set $S$ belongs to $E_{k}$, then for all $x$ and $y$ belonging to $S$, we have $x+y \geqslant 2\lfloor k / 2\rfloor+2>k=\max S$, so $S$ is non-summable.
Now, $E_{k}$ contains exactly $2^{k-\lfloor k / 2\rfloor-1}$ sets, and $k$ is the maximum element of any set $S$ belonging to $E_{k}$, so the sets $E_{k}$ are pairwise disjoint. If we set $k=2 \ell-\varepsilon$, with $\varepsilon=0$ or $\varepsilon=1$, we then have $k-\lfloor k / 2\rfloor-1=2 \ell-\varepsilon-(\ell-\varepsilon)-1=\ell-1$, so $\left|E_{k}\right|=2^{\ell-1}$.
Finally, since $\boldsymbol{n} \geqslant 3$, the sets $\{1,2 \mathfrak{n}\}$ and $\{2,2 \mathfrak{n}\}$ are both non-summable, and do not belong to $E_{2 n}$. We can thus conclude that
$$
s_{2 n} \geqslant 2+\sum_{k=1}^{2 n}\left|E_{k}\right|=2+\sum_{\ell=1}^{n}\left|E_{2 \ell-1}\right|+\left|E_{2 \ell}\right|=2+2 \sum_{\ell=1}^{n} 2^{\ell-1}=2+2^{n+1}-2=2^{n+1} .
$$
|
2^{n+1}
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soit $S$ un ensemble d'entiers. On dit que $S$ est insommable si, pour tous les entiers $x$ et $y$ appartenant à $S$, la somme $x+y$ n'appartient pas à $S$. Pour tout entier $n \geqslant 1$, on note $s_{n}$ le nombre de sous-ensembles de $\{1,2, \ldots, 2 n\}$ qui sont insommables.
Démontrer que $s_{n} \geqslant 2^{n}$.
|
Soit $S$ une partie de $\{n+1, \ldots, 2 n\}$. Une telle partie est insommable, puisque, pour tous les entiers $x, y$ et $z$ appartenant à $S$, on a $x+y \geqslant 2(n+1)>2 n \geqslant z$. Or, il existe $2^{n}$ parties de $\{n+1, \ldots, 2 n\}$. On en déduit bien que $s_{n} \geqslant 2^{n}$.
Note : On peut en fait démontrer que $2^{\mathfrak{n}+4} \geqslant s_{n} \geqslant 2^{\mathfrak{n}+1}$ pour tout $n \geqslant 3$. L'inégalité $s_{n} \geqslant$ $2^{\mathrm{n}+1}$ s'obtient, par exemple, comme suit.
Pour tout entier $k \in\{1, \ldots, 2 \mathfrak{n}\}$, on note $E_{k}$ l'ensemble des parties de $\{\lfloor k / 2\rfloor+1, \ldots, k\}$ auxquelles appartient $k$. $S i$ un ensemble $S$ appartient à $E_{k}$, alors pour tous $x$ et $y$ appartenant à $S$, on a bien $x+y \geqslant 2\lfloor k / 2\rfloor+2>k=\max S$, donc $S$ est insommable.
Or, $E_{k}$ contient exactement $2^{k-\lfloor k / 2\rfloor-1}$ ensembles, et $k$ est l'élément maximum de tout ensemble $S$ appartenant à $E_{k}$, donc les ensembles $E_{k}$ sont deux à deux disjoints. Si on pose $k=2 \ell-\varepsilon$, avec $\varepsilon=0$ ou $\varepsilon=1$, on a alors $k-\lfloor k / 2\rfloor-1=2 \ell-\varepsilon-(\ell-\varepsilon)-1=\ell-1$, donc $\left|E_{k}\right|=2^{\ell-1}$.
Enfin, puisque $\boldsymbol{n} \geqslant 3$, les ensembles $\{1,2 \mathfrak{n}\}$ et $\{2,2 \mathfrak{n}\}$ sont tous deux insommables, et n'appartiennent pas à $E_{2 n}$. On en déduit que
$$
s_{2 n} \geqslant 2+\sum_{k=1}^{2 n}\left|E_{k}\right|=2+\sum_{\ell=1}^{n}\left|E_{2 \ell-1}\right|+\left|E_{2 \ell}\right|=2+2 \sum_{\ell=1}^{n} 2^{\ell-1}=2+2^{n+1}-2=2^{n+1} .
$$
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2018-2019-Test-15-05-Corrigé.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T1",
"year": "2018"
}
|
Let $m$ and $n$ be two natural numbers. Prove that $n!\neq m^{2}+2019$.
|
Let's proceed by contradiction and assume that we have two natural integers $m$ and $n$ such that $n!=m^{2}+2019$. First, we know that $n!\geqslant 2019>6!=720$, so $n \geqslant 7$. Consequently, $n!$ is divisible by $7!=2^{4} \times 3^{2} \times 5 \times 7$, and we have $0 \equiv m^{2}+2019$ $(\bmod 7!)$.
By virtue of the prime factorization stated above and the Chinese Remainder Theorem, this means that -2019 is a square modulo $k$ for any integer $k$, among $2^{4}$, $3^{2}$, 5, and 7.
We could show that this does not constitute a contradiction for $k=5$ and $k=7$. However, -2019 is not a square modulo 9 (nor modulo 16). Indeed, if $m^{2} \equiv -2019 \equiv -3$ $(\bmod 9)$, then 3 divides $m$, so 9 divides $m^{2}$, which should therefore be congruent to both 0 and -3 modulo 9.
Thus, as soon as $n \geqslant 7$, we actually have $n!\equiv 0 \not \equiv m^{2}-3 \equiv m^{2}+2019(\bmod 9)$, which shows that no pair of natural integers $(m, n)$ can satisfy the equation $n!=m^{2}+2019$.
Note: We also have $-2019 \equiv 5(\bmod 8)$, while $n^{2} \equiv 1(\bmod 8)$ for any odd integer $n$. Thus, as expected, -2019 is not a square modulo 8, and therefore not modulo $2^{4}$ either.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $m$ et $n$ deux entiers naturels. Démontrer que $n!\neq m^{2}+2019$.
|
Procédons par l'absurde, et supposons que l'on dispose de deux entiers naturels $m$ et $n$ tels que $n!=m^{2}+2019$. Tout d'abord, on sait que $n!\geqslant 2019>6!=720$, donc que $n \geqslant 7$. Par conséquent, $n!$ est divisible par $7!=2^{4} \times 3^{2} \times 5 \times 7$, et l'on a $0 \equiv m^{2}+2019$ $(\bmod 7!)$.
En vertu de la décomposition en produit de facteurs premiers énoncée ci-dessus et du théorème Chinois, cela signifie que -2019 est un carré modulo $k$ pour tout entier $k$, parmi $2^{4}, 3^{2}$, 5 et 7 .
On pourrait démontrer que cela ne constitue pas une contradiction pour $k=5$ et $k=7$. En revanche, -2019 n'est pas un carré modulo 9 (ni modulo 16). En effet, si m² $\equiv-2019 \equiv-3$ $(\bmod 9)$, alors 3 divise $m$, donc 9 divise $m^{2}$, qui devrait donc être congru à la fois à 0 et à -3 modulo 9.
Ainsi, dès lors que $n \geqslant 7$, on a en fait $n!\equiv 0 \not \equiv m^{2}-3 \equiv m^{2}+2019(\bmod 9)$, ce qui montre bien que nulle paire d'entiers naturels ( $m, n$ ) ne peut satisfaire l'équation $n!=m^{2}+2019$.
Note : On a également $-2019 \equiv 5(\bmod 8)$, alors que $n^{2} \equiv 1(\bmod 8)$ pour tout entier $n$ impair. Ainsi, comme prévu, -2019 n'est pas un carré modulo 8 , donc modulo $2^{4}$ non plus.
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2018-2019-Test-15-05-Corrigé.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T1",
"year": "2018"
}
|
Let $ABC$ be a triangle, and let $M$ be the foot of the median from $A$. Let $\ell_{\mathrm{b}}$ be the bisector of $\widehat{A M B}$ and $\ell_{c}$ be the bisector of $\widehat{A M C}$. Furthermore, let $B^{\prime}$ be the orthogonal projection of $B$ onto $\ell_{b}$, let $C^{\prime}$ be the orthogonal projection of $C$ onto $\ell_{c}$, and let $A^{\prime}$ be the point of intersection of the lines $(A M)$ and $(B^{\prime} C^{\prime})$.
Prove that $A^{\prime} B^{\prime}=A^{\prime} C^{\prime}$.
|
Let $\beta$ be the angle $\widehat{A M B^{\prime}}$ and $\gamma$ be the angle $\widehat{A M C^{\prime}}$. By construction, we know that $2(\beta+\gamma)=180^{\circ}$, so $\widehat{\mathrm{B}^{\prime} \mathrm{MC}^{\prime}}=\beta+\gamma=90^{\circ}$. Thus, the line $\ell_{\mathrm{b}}=\left(\mathrm{MB}^{\prime}\right)$ is perpendicular to the lines $\left(\mathrm{BB}^{\prime}\right)$ and $\ell_{c}=\left(M C^{\prime}\right)$, and the line $\ell_{c}=\left(M C^{\prime}\right)$ is perpendicular to the lines $\left(C C^{\prime}\right)$ and $\ell_{b}=\left(M B^{\prime}\right)$.
Furthermore, we notice that $\widehat{\mathrm{B}^{\prime} \mathrm{BM}}=180^{\circ}-\widehat{\mathrm{BB}^{\prime} M}-\widehat{\mathrm{BMB}^{\prime}}=180^{\circ}-90^{\circ}-\beta=\gamma$ and that, similarly, $\widehat{C^{\prime} C M}=\beta$. Thus, the two triangles $B B^{\prime} M$ and $M C^{\prime} C$ are similar. Moreover, since $M$ is the foot of the median of $A B C$ from $A$, $c^{\prime}$ is actually the midpoint of [BC], so $B M=M C$. The two triangles $B B^{\prime} M$ and $M C C^{\prime}$ are therefore isometric.
In particular, we deduce that $B B^{\prime}=M C^{\prime}$ and that $C C^{\prime}=M B^{\prime}$. But then, since the triangle $M B^{\prime} C^{\prime}$ is right-angled at $M$, it has an angle and two sides of the same measures as the triangle $B^{\prime} M B$, and it is therefore isometric with $B^{\prime} M B$ and with $C^{\prime} C M$.
We thus deduce in particular that
$$
\widehat{A^{\prime} C^{\prime} M}=\widehat{B^{\prime} C^{\prime} M}=\widehat{M B B^{\prime}}=\gamma=\widehat{A M C^{\prime}}=\widehat{A^{\prime} M C^{\prime}}
$$
so that the triangle $A^{\prime} C^{\prime} M$ is isosceles at $A^{\prime}$. Similarly, the triangle $A^{\prime} B^{\prime} M$ is isosceles at $A^{\prime}$, and we conclude as expected that $A^{\prime} B^{\prime}=A^{\prime} M=A^{\prime} C^{\prime}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle, et soit $M$ le pied de la médiane issue de $A$. Soit également $\ell_{\mathrm{b}}$ la bissectrice de $\widehat{A M B}$ et $\ell_{c}$ la bissectrice de $\widehat{A M C}$. Enfin, soit $B^{\prime}$ le projeté orthogonal de $B$ sur $\ell_{b}$, soit $C^{\prime}$ le projeté orthogonal de $C$ sur $\ell_{c}$, et soit $A^{\prime}$ le point $d^{\prime}$ intersection des droites $(A M)$ et ( $B^{\prime} C^{\prime}$ ).
Démontrer que $A^{\prime} B^{\prime}=A^{\prime} C^{\prime}$.
|
Soit $\beta$ l'angle $\widehat{A M B^{\prime}}$ et $\gamma$ l'angle $\widehat{A M C^{\prime}}$. Par construction, on sait que $2(\beta+\gamma)=180^{\circ}$, donc que $\widehat{\mathrm{B}^{\prime} \mathrm{MC}^{\prime}}=\beta+\gamma=90^{\circ}$. Ainsi, la droite $\ell_{\mathrm{b}}=\left(\mathrm{MB}^{\prime}\right)$ est perpendiculaire aux droites $\left(\mathrm{BB}^{\prime}\right)$ et $\ell_{c}=\left(M C^{\prime}\right)$, et la droite $\ell_{c}=\left(M C^{\prime}\right)$ est perpendiculaire aux droites $\left(C C^{\prime}\right)$ et $\ell_{b}=\left(M B^{\prime}\right)$.
$D^{\prime}$ autre part, on remarque que $\widehat{\mathrm{B}^{\prime} \mathrm{BM}}=180^{\circ}-\widehat{\mathrm{BB}^{\prime} M}-\widehat{\mathrm{BMB}^{\prime}}=180^{\circ}-90^{\circ}-\beta=\gamma$ et que, de même, $\widehat{C^{\prime} C M}=\beta$. Ainsi, les deux triangles $B B^{\prime} M$ et $M C^{\prime} C$ sont semblables. En outre, puisque $M$ est le pied de la médiane de $A B C$ issue de $A$, $c^{\prime}$ est en fait le milieu de [BC], donc $B M=M C$. Les deux triangles $B B^{\prime} M$ et $M C C^{\prime}$ sont donc isométriques.
En particulier, on en déduit que $B B^{\prime}=M C^{\prime}$ et que $C C^{\prime}=M B^{\prime}$. Mais alors, puisque le triangle $M B^{\prime} C^{\prime}$ est rectangle en $M$, il a un angle et deux côtés de mêmes mesures que le triangle $B^{\prime} M B$, et il est donc isométrique avec $B^{\prime} M B$ et avec $C^{\prime} C M$.
On en déduit notamment que
$$
\widehat{A^{\prime} C^{\prime} M}=\widehat{B^{\prime} C^{\prime} M}=\widehat{M B B^{\prime}}=\gamma=\widehat{A M C^{\prime}}=\widehat{A^{\prime} M C^{\prime}}
$$
donc que le triangle $A^{\prime} C^{\prime} M$ est isocèle en $A^{\prime}$. De même, le triangle $A^{\prime} B^{\prime} M$ est isocèle en $A^{\prime}$, et on en conclut comme prévu que $A^{\prime} B^{\prime}=A^{\prime} M=A^{\prime} C^{\prime}$.

|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2018-2019-Test-15-05-Corrigé.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T1",
"year": "2018"
}
|
Let $\mathrm{f}: \mathbb{Z} \mapsto \mathbb{R}$ be a function such that
$$
\mathbf{f}(\mathrm{n}+2)=(f(n+1)+\mathbf{f}(\mathrm{n})) / 2
$$
for all integers $n$. Suppose that $f$ is bounded, that is, there exists a real number $\mathbf{F}$ such that $-F \leqslant f(n) \leqslant F$ for all $n$.
Prove that $f$ is a constant function.
|
Suppose that $f$ is not constant. There exists an integer $n$ and a real number $\varepsilon \neq 0$ such that $f(n+1) - f(n) = \varepsilon$.
For any integer $k$, let $\Delta_k = f(k+1) - f(k)$. Then
$$
\Delta_{k+1} = f(k+2) - f(k+1) = (f(k+1) + f(k)) / 2 - f(k+1) = -\Delta_k / 2
$$
and, conversely, $\Delta_{k-1} = -2 \Delta_k$. An immediate induction then shows that $\Delta_{n-k} = (-2)^k \varepsilon$ for all $k \geq 0$.
However, for any integer $k$, we know that $|\Delta_k| \leq |f(k+1)| + |f(k)| \leq 2F$. But this is incompatible with the fact that $|\Delta_{n-k}| = 2^k |\varepsilon|$ for all $k \geq 0$. Our initial assumption was therefore absurd, and $f$ is indeed constant.
## Exercises for the Senior Group
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $\mathrm{f}: \mathbb{Z} \mapsto \mathbb{R}$ une fonction telle que
$$
\mathbf{f}(\mathrm{n}+2)=(f(n+1)+\mathbf{f}(\mathrm{n})) / 2
$$
pour tout entier $n$. On suppose que f est bornée, c'est-à-dire qu'il existe un réel $\mathbf{F}$ tel que $-F \leqslant f(n) \leqslant F$ pour tout $n$.
Démontrer que $f$ est une fonction constante.
|
Supposons que f n'est pas constante. Il existe donc un entier n et un réel $\varepsilon \neq 0$ tels que $f(n+1)-f(n)=\varepsilon$.
Pour tout entier $k$, posons $\Delta_{k}=f(k+1)-f(k)$. Alors
$$
\Delta_{k+1}=f(k+2)-f(k+1)=(f(k+1)+f(k)) / 2-f(k+1)=-\Delta_{k} / 2
$$
et, réciproquement, $\Delta_{\mathrm{k}-1}=-2 \Delta_{\mathrm{k}}$. Une récurrence immédiate indique alors que $\Delta_{\mathrm{n}-\mathrm{k}}=$ $(-2)^{k} \varepsilon$ pour tout $k \geqslant 0$.
Or, pour tout entier $k$, on sait que $\left|\Delta_{k}\right| \leqslant|\mathbf{f}(k+1)|+|f(k)| \leqslant 2 \mathbf{F}$. Mais ceci est incompatible avec le fait que $\left|\Delta_{n-k}\right|=2^{k}|\varepsilon|$ pout tout $k \geqslant 0$. Notre supposition initiale était donc absurde, et $f$ est bien constante.
## Exercices du groupe Senior
|
{
"exam": "French_tests",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/tests/fr-2018-2019-Test-15-05-Corrigé.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T1",
"year": "2018"
}
|
Let $A, B, C$ and $P$ be four points in the plane such that $ABC$ is an equilateral triangle and $AP < BP < CP$. We assume that the only given lengths $AP, BP$, and $CP$ allow us to uniquely determine the length $AB$.
Prove that $P$ lies on the circumcircle of $ABC$.
|
Let $\Gamma_{\mathrm{a}}, \Gamma_{\mathrm{b}}$ and $\Gamma_{\mathrm{c}}$ be the circles centered at $P$ and passing through $A$, $B$, and $C$ respectively. Let $C^{\bullet}$ be the symmetric point of $C$ with respect to $(AP)$. Note that $C^{\bullet}$ is the only point on $\Gamma_{\mathrm{c}}$, other than $C$ itself, such that $A C = A C^{\bullet}$.
Now, let $r$ be the rotation centered at $\mathcal{A}$ with an angle of $60^{\circ}$ in the clockwise direction. Without loss of generality, we assume that $C = r(B)$.
Then, for any point $B^{\prime}$ on $\Gamma_{b}$, we associate the point $C^{\prime} = r(B^{\prime})$. The triangle $A B^{\prime} C^{\prime}$ is equilateral, and the hypothesis of the problem states that for any $B^{\prime}$, the point $C^{\prime}$ can only belong to $\Gamma_{c}$ if it is equal to $C$ or $C^{\bullet}$.
As $B^{\prime}$ describes $\Gamma_{b}$, the point $C^{\prime}$ describes the circle $r(\Gamma_{b})$, centered at $r(P)$ and with radius $PB$. This circle cannot contain both points $C$ and $C^{\bullet}$, since then its center would lie on the perpendicular bisector $(AP)$ of $[C^{\bullet}]$, which is not the case for $r(P)$.
Since $r(\Gamma_{b})$ already contains $C$, it cannot contain any other point of $\Gamma_{c}$. Given that $r(P)A = PA < PB$, we know that $A$ is located inside $r(\Gamma_{b})$, which is therefore internally tangent to $\Gamma_{c}$ at the point $C$.
Since $PB = r(P)C < PC$, it follows that the points $C, r(P)$, and $P$ are collinear in that order. This implies that $PC = r(P)C + r(P)P = PB + PA$, or equivalently, $CP \cdot AB = BP \cdot AC + AP \cdot BC$. The Ptolemy's theorem then indicates that the points $A, B, C$, and $P$ are concyclic, which concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A, B, C$ et $P$ quatre points du plan tels que $A B C$ soit un triangle équilatéral et que $A P<B P<C P$. On suppose que la seule donnée des longueurs $A P, B P$ et $C P$ nous permet de déterminer, de manière unique, la longueur $A B$.
Démontrer que P appartient au cercle circonscrit à $A B C$.
|
Soit $\Gamma_{\mathrm{a}}, \Gamma_{\mathrm{b}}$ et $\Gamma_{\mathrm{c}}$ les cercles de centre P et passant respectivement par $A$, $B$ et $C$. Soit également $C^{\bullet}$ le symétrique de $C$ par rapport à ( $A P$ ). Notons que $C^{\bullet}$ est le seul point de $\Gamma_{\mathrm{c}}$, autre que C lui-même, tel que $A C=A C^{\bullet}$.
On note maintenant r la rotation de centre $\mathcal{A}$ et d'angle $60^{\circ}$ dans le sens horaire. Quitte à faire subir une symétrie à la figure de répart, on suppose que $C=r(B)$.
Puis, à tout point $B^{\prime}$ de $\Gamma_{b}$, on associe le point $C^{\prime}=r\left(B^{\prime}\right)$. Le triangle $A B^{\prime} C^{\prime}$ est équilatéral, et l'hypothèse de l'énoncé stipule donc que, pour tout $B^{\prime}$, le point $C^{\prime}$ ne peut appartenir à $\Gamma_{c}$ que s'il est égal à $C$ ou à $C^{\bullet}$.
Or, quand $B^{\prime}$ décrit $\Gamma_{b}$, le point $C^{\prime}$ décrit le cercle $r\left(\Gamma_{b}\right)$, de centre $r(P)$ et de rayon $P B$. Ce cercle ne peut contenir à la fois les points $C$ et $C^{\bullet}$, puisque alors son centre se trouverait sur la médiatrice (AP) de $\left[C^{\bullet}\right]$, ce qui n'est pas le cas de $r(P)$.
Comme $\mathrm{r}\left(\Gamma_{\mathrm{b}}\right)$ contient déjà C , il ne peut donc pas contenir d'autre point de $\Gamma_{\mathrm{c}}$, et puisque $\mathrm{r}(\mathrm{P}) A=\mathrm{PA}<\mathrm{PB}$, on sait que $A$ est situé à l'intérieur $\operatorname{de} \mathrm{r}\left(\Gamma_{\mathrm{b}}\right)$, qui est donc tangent intérieurement, en le point $C$, à $\Gamma_{\mathrm{c}}$.
Comme $P B=r(P) C<P C, c^{\prime}$ est en fait que les points $C, r(P)$ et $P$ sont alignés dans cet ordre. On en déduit que $P C=r(P) C+r(P) P=P B+P A$, ou encore que $C P \cdot A B=B P \cdot A C+A P$. $B C$. L'égalité de Ptolémée indique donc que les points $A, B, C$ et $P$ sont cocycliques, ce qui conclut.

|
{
"exam": "French_tests",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/tests/fr-2018-2019-Test-15-05-Corrigé.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T1",
"year": "2018"
}
|
Let $a_{0}, a_{1}, \ldots, a_{d}$ be integers such that $\operatorname{GCD}\left(a_{0}, a_{1}\right)=1$. For any integer $n \geqslant 1$, we define
$$
u_{n}=\sum_{k=0}^{d} a_{k} \varphi(n+k)
$$
Prove that 1 is the only natural number that divides all integers $u_{n}$.
We recall that $\varphi(n+k)$ is the number of natural numbers $\ell<n+k$ such that $\operatorname{GCD}(\ell, n+k)=1$.
|
Let us proceed by contradiction and assume that there exists a prime number $p$ that divides all integers $u_{n}$.
First, since $\varphi(1)=\varphi(2)=1$ and $\varphi(\mathfrak{n})$ is even for all $\mathfrak{n} \geqslant 2$, we note that $u_{1} \equiv a_{0}+a_{1}(\bmod 2)$ and that $u_{2} \equiv a_{0}(\bmod 2)$. Since $a_{0}$ and $a_{1}$ are coprime, the integers $\mathfrak{u}_{1}$ and $\mathfrak{u}_{2}$ cannot both be even, so $p \geqslant 3$.
Let $\delta$ then be the largest integer such that $p$ does not divide $a_{\delta}$. For any integer $n \geqslant 1$, we denote by $T_{n}$ the $\delta$-tuple $(\varphi(n), \varphi(n+1), \ldots, \varphi(n+\delta-1))$, considered modulo $p$. Since $u_{n} \equiv 0(\bmod p)$, it follows that
$$
\varphi(n+\delta) \equiv-a_{\delta}^{-1} \sum_{k=0}^{\delta-1} a_{k} \varphi(n+k) \quad(\bmod p)
$$
Thus, if we denote by $\lambda:(\mathbb{Z} / \mathrm{p} \mathbb{Z})^{\delta} \mapsto(\mathbb{Z} / \mathrm{p} \mathbb{Z})^{\delta}$ the function defined by
$$
\lambda:\left(x_{0}, x_{1}, \ldots, x_{\delta-1}\right) \mapsto\left(x_{1}, x_{2}, \ldots, x_{\delta-1},-a_{\delta}^{-1} \sum_{k=0}^{\delta-1} a_{k} x_{k}\right)
$$
we have $\mathbf{T}_{\mathfrak{n}+1}=\lambda\left(\mathbf{T}_{\mathfrak{n}}\right)$. By the pigeonhole principle, there exist two integers $k, \ell \geqslant 1$ such that $\mathbf{T}_{\mathrm{k}}=\mathbf{T}_{\mathrm{k}+\ell}$. We then have $\mathbf{T}_{\mathbf{n}}=\mathbf{T}_{\mathrm{n}+\ell}$ and $\varphi(\mathrm{n}) \equiv \varphi(\mathrm{n}+\ell)(\bmod p)$ for all $n \geqslant k$.
We then prove the following lemma: for all integers $a \geqslant 1$ and $b \geqslant 3$, there exists a prime number $q>a$ such that $q \not \equiv 1(\bmod b)$. Indeed, the integer $m=\max \{a, b\}!-1$ is congruent to -1 $(\bmod b)$, so it must have a prime factor $q \not \equiv 1(\bmod b)$, and $q$ cannot divide $\mathrm{m}+1=\max \{\mathrm{a}, \mathrm{b}\}!$, so $\mathrm{q}>\mathrm{a}$.
By applying this lemma twice, we deduce that there exist two prime numbers $q$ and $r$ such that $q, r \not \equiv 1(\bmod p)$ and $q>r>k+\ell$. But then $q$ is coprime with $\ell$, so $q^{\varphi(\ell)} \equiv 1(\bmod \ell)$, and $\varphi\left(q^{\varphi(\ell)} n\right) \equiv \varphi(n)(\bmod p)$ for all $n \geqslant k$.
Since $q>r \geqslant k$, we deduce that
$$
\begin{array}{rlr}
(q-1) q^{\varphi(\ell)} & \equiv \varphi\left(q^{\varphi(\ell)+1}\right) \equiv \varphi(q) & \equiv q-1 \quad(\bmod p) \\
(r-1)(q-1) q^{\varphi(\ell)-1} & \equiv \varphi\left(r q^{\varphi(\ell)}\right) & \equiv \varphi(r)
\end{array}
$$
Since $q, r \not \equiv 1(\bmod p)$, it follows that $q^{\varphi(\ell)} \equiv(q-1) q^{\varphi(\ell)-1} \equiv 1(\bmod p)$, so $q^{\varphi(\ell)-1} \equiv 0$ $(\bmod p)$, which is impossible. We have thus obtained the desired contradiction, which concludes the proof.
Note: We can also appeal to Dirichlet's theorem, which states that for all integers $a$ and $b$ that are coprime, there are infinitely many prime numbers $q \equiv a(\bmod b)$. There then exist prime numbers $q_{0}>q_{1}>\ldots>q_{d}>p+d$ congruent to $1(\bmod p)$. Then, if we choose $k \in\{0,1\}$ such that $p$ does not divide $a_{k}$, there also exists a prime number $r$ such that $r \equiv 2(\bmod p)$ and $r \equiv k-i\left(\bmod q_{i}\right)$ for all $i \neq k$. Then $p$ does not divide $u_{r-k}$.
Exercise 7. Let $n \geqslant 2$ be an integer. Clara has a board of size $3 n \times 3 n$, similar to a chessboard. She has just invented a new piece, the leopard, which she can move as follows: by moving it one square up, one square to the right, or one square diagonally, down and to the left. Clara placed her leopard on one of the squares of the board, then moved it so that it never passes through the same square twice, until it returns to its starting square.
What is the maximum number of moves Clara could have made in this way?
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $a_{0}, a_{1}, \ldots, a_{d}$ des entiers tels que $\operatorname{PGCD}\left(a_{0}, a_{1}\right)=1$. Pour tout entier $n \geqslant 1$, on pose
$$
u_{n}=\sum_{k=0}^{d} a_{k} \varphi(n+k)
$$
Démontrer que 1 est le seul entier naturel divisant tous les entiers $u_{n}$.
On rappelle que $\varphi(n+k)$ est le nombre d'entiers naturels $\ell<n+k$ tels que $\operatorname{PGCD}(\ell, n+k)=1$.
|
Procédons par l'absurde, et supposons qu'il existe un nombre premier $p$ qui divise tous les entiers $u_{n}$.
Tout d'abord, puisque $\varphi(1)=\varphi(2)=1$ et que $\varphi(\mathfrak{n})$ est pair pour tout $\mathfrak{n} \geqslant 2$, on remarque que $u_{1} \equiv a_{0}+a_{1}(\bmod 2)$ et que $u_{2} \equiv a_{0}(\bmod 2)$. Comme $a_{0}$ et $a_{1}$ sont premiers entre eux, les entiers $\mathfrak{u}_{1}$ et $\mathfrak{u}_{2}$ ne peuvent donc pas être pairs tous les deux, de sorte que $p \geqslant 3$.
Soit alors $\delta$ le plus grand entier tel que $p$ ne divise pas $a_{\delta}$. Pour tout entier $n \geqslant 1$, on note $T_{n}$ le $\delta$-uplet $(\varphi(n), \varphi(n+1), \ldots, \varphi(n+\delta-1))$, considéré modulo $p$. Puisque $u_{n} \equiv 0(\bmod p)$, $c^{\prime}$ est que
$$
\varphi(n+\delta) \equiv-a_{\delta}^{-1} \sum_{k=0}^{\delta-1} a_{k} \varphi(n+k) \quad(\bmod p)
$$
Ainsi, si l'on note $\lambda:(\mathbb{Z} / \mathrm{p} \mathbb{Z})^{\delta} \mapsto(\mathbb{Z} / \mathrm{p} \mathbb{Z})^{\delta}$ la fonction définie par
$$
\lambda:\left(x_{0}, x_{1}, \ldots, x_{\delta-1}\right) \mapsto\left(x_{1}, x_{2}, \ldots, x_{\delta-1},-a_{\delta}^{-1} \sum_{k=0}^{\delta-1} a_{k} x_{k}\right)
$$
on a $\mathbf{T}_{\mathfrak{n}+1}=\lambda\left(\mathbf{T}_{\mathfrak{n}}\right)$. Or, d'après le principe des tiroirs, il existe deux entiers $k, \ell \geqslant 1$ tels que $\mathbf{T}_{\mathrm{k}}=\mathbf{T}_{\mathrm{k}+\ell}$. On a alors $\mathbf{T}_{\mathbf{n}}=\mathbf{T}_{\mathrm{n}+\ell}$ et $\varphi(\mathrm{n}) \equiv \varphi(\mathrm{n}+\ell)(\bmod p)$ pour tout $n \geqslant k$.
On montre alors le lemme suivant : pour tous les entiers $a \geqslant 1$ et $b \geqslant 3$, il existe un nombre premier $q>a$ tel que $q \not \equiv 1(\bmod b)$. En effet, l'entier $m=\max \{a, b\}!-1$ est congru à -1 $(\bmod b)$, donc il admet nécessairement un facteur premier $q \not \equiv 1(\bmod b)$, et $q$ ne peut pas diviser $\mathrm{m}+1=\max \{\mathrm{a}, \mathrm{b}\}!$, donc $\mathrm{q}>\mathrm{a}$.
En appliquant ce lemme deux fois de suite, on en déduit qu'il existe deux nombres premiers $q$ et $r$ tels que $q, r \not \equiv 1(\bmod p)$ et $q>r>k+\ell$. Mais alors $q$ est premier avec $\ell$, donc $q^{\varphi(\ell)} \equiv 1(\bmod \ell)$, et $\varphi\left(q^{\varphi(\ell)} n\right) \equiv \varphi(n)(\bmod p)$ pour tout $n \geqslant k$.
Puisque $q>r \geqslant k$, on en déduit que
$$
\begin{array}{rlr}
(q-1) q^{\varphi(\ell)} & \equiv \varphi\left(q^{\varphi(\ell)+1}\right) \equiv \varphi(q) & \equiv q-1 \quad(\bmod p) \\
(r-1)(q-1) q^{\varphi(\ell)-1} & \equiv \varphi\left(r q^{\varphi(\ell)}\right) & \equiv \varphi(r)
\end{array}
$$
Comme $q, r \not \equiv 1(\bmod p), c^{\prime}$ est que $q^{\varphi(\ell)} \equiv(q-1) q^{\varphi(\ell)-1} \equiv 1(\bmod p)$, donc que $q^{\varphi(\ell)-1} \equiv 0$ $(\bmod p)$, ce qui est impossible. On a ainsi obtenu la contradiction souhaitée, ce qui conclut.
Note : On peut aussi faire appel au théorème de Dirichlet, qui affirme que, pour tous les entiers $a$ et $b$ premiers entre eux, il existe une infinité de nombres premiers $q \equiv a(\bmod b)$. Il existe alors des nombres premiers $q_{0}>q_{1}>\ldots>q_{d}>p+d$ congrus à $1(\bmod p)$. Puis, si on choisit $k \in\{0,1\}$ tel que $p$ ne divise pas $a_{k}$, il existe aussi un nombre premier $r$ tel que $r \equiv 2(\bmod p)$ et $r \equiv k-i\left(\bmod q_{i}\right)$ pour tout $i \neq k$. Alors $p$ ne divise pas $u_{r-k}$.
Exercice 7 . Soit $n \geqslant 2$ un entier. Clara dispose d'un plateau de taille $3 n \times 3 n$, semblable à un échiquier. Elle vient d'inventer une nouvelle pièce, le léopard, qu'elle peut mouvoir comme suit : en le déplaçant d'une case vers le haut, d'une case vers la droite, ou bien d'une case en diagonale, vers le bas et la gauche. Clara a posé son léopard sur une des cases du plateau, puis elle l'a déplacé, de sorte qu'il ne passe jamais deux fois par la même case, jusqu'à ce qu'il revienne à sa case de départ.
Quelle est le plus grand nombre possible de déplacements que Clara a pu effectuer en procédant de la sorte?
|
{
"exam": "French_tests",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/tests/fr-2018-2019-Test-15-05-Corrigé.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T1",
"year": "2018"
}
|
Let $a_{0}, a_{1}, \ldots, a_{d}$ be integers such that $\operatorname{GCD}\left(a_{0}, a_{1}\right)=1$. For any integer $n \geqslant 1$, we define
$$
u_{n}=\sum_{k=0}^{d} a_{k} \varphi(n+k)
$$
Prove that 1 is the only natural number that divides all integers $u_{n}$.
We recall that $\varphi(n+k)$ is the number of natural numbers $\ell<n+k$ such that $\operatorname{GCD}(\ell, n+k)=1$.
|
First, Clara can perform $9 \mathfrak{n}^{2}-3$ as illustrated below in the case where $\mathrm{n}=3$.
Now, let's show that she cannot do better. First, we identify each cell in row $i$ (from the bottom) and column $j$ (from the left) with the pair $(i, j)$, where $1 \leqslant i, j \leqslant 3 n$. Then we color the cells of the board with three colors $C_{0}, C_{1}$, and $C_{2}$, assigning the color $C_{i+j \mod 3}$ to the cell $(i, j)$. Each move of the leopard consists of moving by a vector $(0,1), (1,0)$, or $(-1,-1)$. Consequently, it always moves from a cell of color $C_{k}$ to a cell of color $C_{k+1 \mod 3}$. Therefore, it has made a number of moves divisible by 3, and it suffices to show that it has not passed through all the cells.
To this end, note that its path describes a planar graph consisting of a single cycle, which therefore contains an internal face (finite) and an external face. If the leopard has passed through the cell $(1, 3 \mathfrak{n})$, it must have used the edge $(1, 3 \mathfrak{n}) \rightarrow (2, 3 \mathfrak{n})$, thus circling its internal face clockwise. But similarly, if it has passed through the cell $(3 n, 1)$, it must have used the edge $(3 n, 1) \rightarrow (3 n, 2)$, thus circling its internal face counterclockwise. Therefore, it could not have passed through both of these cells during the same path, which concludes the proof.
[^0]: Animath,
French Mathematical Olympiad Preparation, 11-13 rue Pierre et Marie Curie, 75005 Paris.
|
proof
|
Yes
|
Incomplete
|
proof
|
Number Theory
|
Soit $a_{0}, a_{1}, \ldots, a_{d}$ des entiers tels que $\operatorname{PGCD}\left(a_{0}, a_{1}\right)=1$. Pour tout entier $n \geqslant 1$, on pose
$$
u_{n}=\sum_{k=0}^{d} a_{k} \varphi(n+k)
$$
Démontrer que 1 est le seul entier naturel divisant tous les entiers $u_{n}$.
On rappelle que $\varphi(n+k)$ est le nombre d'entiers naturels $\ell<n+k$ tels que $\operatorname{PGCD}(\ell, n+k)=1$.
|
Tout d'abord, Clara peut effectuer $9 \mathfrak{n}^{2}-3$ en procédant comme illustré ci-dessous dans le cas où $\mathrm{n}=3$.

Montrons maintenant qu'elle ne peut pas mieux faire. Tout d'abord, on identifie chaque case en ligne $i$ (en partant du bas) et en colonne $j$ (en partant de la gauche) à la paire ( $i, j$ ), où $1 \leqslant i, j \leqslant 3 n$. Puis on colorie les cases du plateau de trois couleurs $C_{0}, C_{1}$ et $C_{2}$, en affectant à la case $(\mathfrak{i}, \mathfrak{j})$ la couleur $\mathrm{C}_{\boldsymbol{i}+\boldsymbol{j}}(\bmod 3)$. Chaque mouvement du léopard consiste à se mouvoir d'un vecteur $(0,1),(1,0)$ ou $(-1,-1)$. Par conséquent, il passe systématiquement d'une case de couleur $C_{k}$ à une case de couleur $C_{k+1}(\bmod 3)$. Il a donc effectué un nombre de déplacements divisible par 3, et il suffit de démontrer qu'il n'a pas pu passer par toutes les cases.
À cette fin, remarquons que son parcours décrit un graphe planaire formé d'un seul cycle, qui contient donc une face interne (finie) et une face externe. Or, si le léopard est passé par la case $(1,3 \mathfrak{n})$, il a dû utiliser l'arête $(1,3 \mathfrak{n}) \rightarrow(2,3 \mathfrak{n})$, donc contourner sa face interne dans le sens horaire. Mais, de même, s'il est passé par la case ( $3 n, 1$ ), il a dû utiliser l'arête $(3 n, 1) \rightarrow(3 n, 2)$, donc contourner sa face interne dans le sens anti-horaire. Il n'a donc pas pu passer par ces deux cases lors du même trajet, ce qui conclut.
[^0]: Animath,
Préparation Olympique Française de Mathématiques, 11-13 rue Pierre et Marie Curie, 75005 Paris.
|
{
"exam": "French_tests",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/tests/fr-2018-2019-Test-15-05-Corrigé.jsonl",
"solution_match": "\nSolution de l'exercice 7",
"tier": "T1",
"year": "2018"
}
|
Let $A B C D$ be a trapezoid such that $(A B)$ is parallel to $(C D)$. Let $P$ be a point on $[A C]$ and $Q$ be a point on $[B D]$ such that $\widehat{A P D}=\widehat{\mathrm{BQC}}$.
Prove that $\widehat{A Q D}=\widehat{\mathrm{BPC}}$.
|
The statement gives us several angle equalities: let's exploit them! First, we notice that
$$
\widehat{\mathrm{DPC}}=180^{\circ}-\widehat{\mathrm{APD}}=180^{\circ}-\widehat{\mathrm{CQB}}=\widehat{\mathrm{DQC}},
$$
which means that the points $C, D, P$ and $Q$ are concyclic.
From this, we deduce that
$$
\widehat{\mathrm{BQP}}=180^{\circ}-\widehat{\mathrm{PQD}}=180^{\circ}-\widehat{\mathrm{PCD}}=180^{\circ}-\widehat{\mathrm{PAB}}
$$
which again means that the points $A, B, P$ and $Q$ are concyclic.
We conclude that
$$
\begin{aligned}
\widehat{\mathrm{AQD}} & =\widehat{\mathrm{AQP}}+\widehat{\mathrm{PQD}}=\widehat{\mathrm{ABP}}+\widehat{\mathrm{PCD}}=(\widehat{\mathrm{ABC}}-\widehat{\mathrm{PBC}})+(\widehat{\mathrm{BCD}}-\widehat{\mathrm{BCP}}) \\
& =(\widehat{\mathrm{ABC}}+\widehat{\mathrm{BCD}})-(\widehat{\mathrm{PBC}}+\widehat{\mathrm{BCP}})=180^{\circ}-\left(180^{\circ}-\widehat{\mathrm{CPB}}\right)=\widehat{\mathrm{CPB}}
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un trapèze tel que $(A B)$ soit parallèle à $(C D)$. Soit $P$ un point de $[A C]$ et $Q$ un point de $[B D]$ tels que $\widehat{A P D}=\widehat{\mathrm{BQC}}$.
Démontrer que $\widehat{A Q D}=\widehat{\mathrm{BPC}}$.
|
L'énoncé nous donne plein d'égalités d'angles : exploitons-les! Tout d'abord, on remarque que
$$
\widehat{\mathrm{DPC}}=180^{\circ}-\widehat{\mathrm{APD}}=180^{\circ}-\widehat{\mathrm{CQB}}=\widehat{\mathrm{DQC}},
$$
ce qui signifie que les points $C, D, P$ et $Q$ sont cocycliques.
On en déduit que
$$
\widehat{\mathrm{BQP}}=180^{\circ}-\widehat{\mathrm{PQD}}=180^{\circ}-\widehat{\mathrm{PCD}}=180^{\circ}-\widehat{\mathrm{PAB}}
$$
ce qui signifie là encore que les points $A, B, P$ et $Q$ sont cocycliques.
On en conclut que
$$
\begin{aligned}
\widehat{\mathrm{AQD}} & =\widehat{\mathrm{AQP}}+\widehat{\mathrm{PQD}}=\widehat{\mathrm{ABP}}+\widehat{\mathrm{PCD}}=(\widehat{\mathrm{ABC}}-\widehat{\mathrm{PBC}})+(\widehat{\mathrm{BCD}}-\widehat{\mathrm{BCP}}) \\
& =(\widehat{\mathrm{ABC}}+\widehat{\mathrm{BCD}})-(\widehat{\mathrm{PBC}}+\widehat{\mathrm{BCP}})=180^{\circ}-\left(180^{\circ}-\widehat{\mathrm{CPB}}\right)=\widehat{\mathrm{CPB}}
\end{aligned}
$$

|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2018-2019-Test-20-03-Corrigé-web.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T1",
"year": "2018"
}
|
Let $a, b, c$ be non-negative real numbers such that $a+b+c=1$.
Prove that
$$
\frac{5+2 b+c^{2}}{1+a}+\frac{5+2 c+a^{2}}{1+b}+\frac{5+2 a+b^{2}}{1+c} \geqslant 13
$$
|
Let $S$ be the sum
$$
\frac{5+2 b+c^{2}}{1+a}+\frac{5+2 c+a^{2}}{1+b}+\frac{5+2 a+b^{2}}{1+c}
$$
Let $x_{i}$ be the $i^{\text {th }}$ smallest element of the set $\{a, b, c\}$. The rearrangement inequality indicates that
$$
\begin{aligned}
& \frac{b}{1+a}+\frac{c}{1+b}+\frac{a}{1+c} \geqslant \frac{x_{1}}{1+x_{1}}+\frac{x_{2}}{1+x_{2}}+\frac{x_{3}}{1+x_{3}} \text { and } \\
& \frac{c^{2}}{1+a}+\frac{a^{2}}{1+b}+\frac{b^{2}}{1+c} \geqslant \frac{x_{1}^{2}}{1+x_{1}}+\frac{x_{2}^{2}}{1+x_{2}}+\frac{x_{3}^{2}}{1+x_{3}},
\end{aligned}
$$
so that
$$
\begin{aligned}
S & \geqslant \frac{5+2 x_{1}+x_{1}^{2}}{1+x_{1}}+\frac{5+2 x_{2}+x_{2}^{2}}{1+x_{2}}+\frac{5+2 x_{3}+x_{3}^{2}}{1+x_{3}} \\
& \geqslant 4\left(\frac{1}{1+x_{1}}+\frac{1}{1+x_{2}}+\frac{1}{1+x_{3}}\right)+\left(1+x_{1}\right)+\left(1+x_{2}\right)+\left(1+x_{3}\right) \\
& \geqslant 4+4\left(\frac{1}{1+x_{1}}+\frac{1}{1+x_{2}}+\frac{1}{1+x_{3}}\right)
\end{aligned}
$$
The function $\mathrm{f}: \mathrm{x} \mapsto 1 /(1+x)$ being convex, we also know that
$$
\frac{1}{1+x_{1}}+\frac{1}{1+x_{2}}+\frac{1}{1+x_{3}}=f\left(x_{1}\right)+\mathbf{f}\left(x_{2}\right)+\mathbf{f}\left(x_{3}\right) \geqslant 3 \mathbf{f}\left(\frac{x_{1}+x_{2}+x_{3}}{3}\right)=3 \mathbf{f}(1 / 3)=9 / 4
$$
We deduce that $S \geqslant 4+9=13$.
|
13
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $a, b, c$ des nombres réels positifs ou nuls tels que $a+b+c=1$.
Démontrer que
$$
\frac{5+2 b+c^{2}}{1+a}+\frac{5+2 c+a^{2}}{1+b}+\frac{5+2 a+b^{2}}{1+c} \geqslant 13
$$
|
Soit $S$ la somme
$$
\frac{5+2 b+c^{2}}{1+a}+\frac{5+2 c+a^{2}}{1+b}+\frac{5+2 a+b^{2}}{1+c}
$$
Notons également $x_{i}$ le $i^{\text {ème }}$ plus petit élément de l'ensemble $\{a, b, c\}$. L'inégalité du réordonnement indique que
$$
\begin{aligned}
& \frac{b}{1+a}+\frac{c}{1+b}+\frac{a}{1+c} \geqslant \frac{x_{1}}{1+x_{1}}+\frac{x_{2}}{1+x_{2}}+\frac{x_{3}}{1+x_{3}} \text { et } \\
& \frac{c^{2}}{1+a}+\frac{a^{2}}{1+b}+\frac{b^{2}}{1+c} \geqslant \frac{x_{1}^{2}}{1+x_{1}}+\frac{x_{2}^{2}}{1+x_{2}}+\frac{x_{3}^{2}}{1+x_{3}},
\end{aligned}
$$
de sorte que
$$
\begin{aligned}
S & \geqslant \frac{5+2 x_{1}+x_{1}^{2}}{1+x_{1}}+\frac{5+2 x_{2}+x_{2}^{2}}{1+x_{2}}+\frac{5+2 x_{3}+x_{3}^{2}}{1+x_{3}} \\
& \geqslant 4\left(\frac{1}{1+x_{1}}+\frac{1}{1+x_{2}}+\frac{1}{1+x_{3}}\right)+\left(1+x_{1}\right)+\left(1+x_{2}\right)+\left(1+x_{3}\right) \\
& \geqslant 4+4\left(\frac{1}{1+x_{1}}+\frac{1}{1+x_{2}}+\frac{1}{1+x_{3}}\right)
\end{aligned}
$$
La fonction $\mathrm{f}: \mathrm{x} \mapsto 1 /(1+x)$ étant convexe, on sait en outre que
$$
\frac{1}{1+x_{1}}+\frac{1}{1+x_{2}}+\frac{1}{1+x_{3}}=f\left(x_{1}\right)+\mathbf{f}\left(x_{2}\right)+\mathbf{f}\left(x_{3}\right) \geqslant 3 \mathbf{f}\left(\frac{x_{1}+x_{2}+x_{3}}{3}\right)=3 \mathbf{f}(1 / 3)=9 / 4
$$
On en déduit que $S \geqslant 4+9=13$.
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2018-2019-Test-20-03-Corrigé-web.jsonl",
"solution_match": "## Solution de l'exercice 2",
"tier": "T1",
"year": "2018"
}
|
It is said that a pair of integers ( $\mathbf{a}, \mathrm{b}$ ) is Cypriot if $\mathrm{a} \geqslant \mathrm{b} \geqslant 2$, if a and b are coprime, and if $a+b$ divides $a^{b}+b^{a}$.
Prove that there are infinitely many distinct Cypriot pairs.
|
Let $k=a-b$. Since $a$ and $b$ are coprime, we know that $a \neq b$, so $k \geqslant 1$. Thus,
$$
a^{b}+b^{a} \equiv a^{b}+(-a)^{a} \equiv a^{b}\left(1+(-1)^{a} a^{k}\right) \quad(\bmod a+b)
$$
Since $a$ is coprime with $b$, it is also coprime with $a+b$.
According to Gauss's theorem, we want $a+b=2a-k$ to divide $1+(-1)^{a} a^{k}$, or equivalently $a^{\mathrm{k}}+(-1)^{\mathrm{a}}$.
For lack of a better approach, let's examine the small values of $k$. Choosing $k=1$ would mean that $a+b$ divides $a \pm 1$, which is impossible since $a+b > a+1 > a-1$. So we look at $k=2$.
In this case, we want $2a-2=2(a-1)$ to divide $a^{2}+(-1)^{a}$. Note that $a^{2}+(-1)^{a} \equiv 1+(-1)^{\mathrm{a}} \pmod{a-1}$. Consequently, and since $a \geqslant 2$, we must necessarily choose $a$ to be odd. In this case, it remains to ensure that $2(a-1)$ divides $a^{2}-1=(a-1)(a+1)$, which means that 2 must divide $a-1$. But this is indeed the case, since $a$ is odd.
In conclusion, we have shown that all pairs $(2k+1, 2k-1)$, where $k \geqslant 2$, are Cypriot.
Note: There are other Cypriot pairs. We leave it to the reader to verify that the integers $\mathrm{a}=(2\ell)^{4\ell}+2\ell-1$ and $\mathrm{b}=(2\ell)^{4\ell}-2\ell-1$ also form a Cypriot pair for any integer $\ell \geqslant 1$.
## Exercise for both Junior and Senior groups
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
On dit qu'une paire d'entiers ( $\mathbf{a}, \mathrm{b}$ ) est chypriote si $\mathrm{a} \geqslant \mathrm{b} \geqslant 2$, si a et b sont premiers entre eux, et si $a+b$ divise $a^{b}+b^{a}$.
Démontrer qu'il existe une infinité de paires chypriotes distinctes.
|
Posons $k=a-b$. Puisque $a$ et $b$ sont premiers entre eux, on sait que $a \neq b$, donc que $k \geqslant 1$. Ainsi,
$$
a^{b}+b^{a} \equiv a^{b}+(-a)^{a} \equiv a^{b}\left(1+(-1)^{a} a^{k}\right) \quad(\bmod a+b)
$$
Or, $a$ est premier avec $b$ donc avec $a+b$ aussi.
D'après le théorème de Gauss, on souhaite donc que $a+b=2 a-k$ divise $1+(-1)^{a} a^{k}$, ou encore $a^{\mathrm{k}}+(-1)^{\mathrm{a}}$.
Faute de mieux, étudions maintenant les petites valeurs de k. Choisir $k=1$ reviendrait à souhaiter que $a+b$ divise $a \pm 1$, ce qui est impossible puisque $a+b>a+1>a-1$. On regarde donc $k=2$.
Dans ce cas, on souhaite que $2 a-2=2(a-1)$ divise $a^{2}+(-1)^{a}$. Or, notons que $a^{2}+(-1)^{a} \equiv$ $1+(-1)^{\mathrm{a}}(\bmod a-1)$. Par conséquent, et puisque $a \geqslant 2$, il nous faut nécessairement choisir $a$ impair. Dans ce cas, il reste à faire en sorte que $2(a-1)$ divise $a^{2}-1=(a-1)(a+1)$, c'est-à-dire que 2 divise $a-1$. Mais c'est justement le cas, puisque a est impair.
En conclusion, on a bien montré que toutes les paires $(2 k+1,2 k-1)$, où $k \geqslant 2$, étaient chypriotes.
Note : Il existe d'autres paires chypriotes. On laisse ainsi au lecteur le plaisir de vérifier que les entiers $\mathrm{a}=(2 \ell)^{4 \ell}+2 \ell-1$ et $\mathrm{b}=(2 \ell)^{4 \ell}-2 \ell-1$ forment également une paire chypriote pour tout entier $\ell \geqslant 1$.
## Exercice commun aux groupes Junior et Senior
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2018-2019-Test-20-03-Corrigé-web.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T1",
"year": "2018"
}
|
Let $\mathcal{C}$ be a circle of radius 1, and let $T$ be a real number. We say that a set of triangles is $T$-meric if it satisfies the following three conditions:
$\triangleright$ the vertices of each triangle belong to $\mathcal{C}$;
$\triangleright$ the triangles have pairwise disjoint interiors (but two triangles may share a side or a vertex);
$\triangleright$ each triangle has a perimeter strictly greater than $\mathbf{T}$.
Find all real numbers $\mathbf{T}$ such that, for any integer $\mathrm{n} \geqslant 1$, there exists a $T$-meric set containing exactly $n$ triangles.
|
We will demonstrate that the sought real numbers are exactly the reals $\mathbf{T} \leqslant 4$. To do this, let us fix a real $\mathbf{T} \leqslant 4$. We start by showing that there exist T-merary sets of any size, thanks to the following construction. Let $[A B]$ be a diameter of $\mathcal{C}$, and let $P$ be any point on $\mathcal{C}$, other than $A$ and $B$. The triangle inequality indicates that $A B P$ has a perimeter $A B + B P + P A > 2 A B = 4 \geqslant T$.
Armed with this observation, we show by induction on $n$ that there exist $n$ points $P_{1}, \ldots, P_{n}$, placed in this order on one of the two semicircles $\overline{A B}$ (with $P_{1}$ close to $A$ and $P_{n}$ close to $B$), and such that the set formed by the triangles $A P_{i} P_{i+1}$ (for $i \leqslant n-1$) and $A B P_{n}$ is T-merary. For $n=1$, we have just seen that it suffices to place $P_{1}$ anywhere on $\overline{A B}$.
Then, once the existence of the points $P_{1}, \ldots, P_{n}$ is established, we construct the point $P_{n+1}$. For this, we consider the real $\varepsilon = A B + B P_{n} + P_{n} A - T$, which is strictly positive by hypothesis. We then place $P_{n+1}$ anywhere on the arc $\overline{B P_{n}}$, such that $B P_{n+1} < \varepsilon / 2$. Indeed, under these conditions, our $n+1$ triangles are well of pairwise disjoint interiors, and it suffices to verify that $A B P_{n+1}$ and $A P_{n} P_{n+1}$ have a perimeter strictly greater than $T$.
The first case is a particular case of our initial observation, and the second case follows again from the triangle inequality, since $A P_{n} P_{n+1}$ has a perimeter
$$
A P_{n} + P_{n} P_{n+1} + P_{n+1} A \geqslant A P_{n} + (P_{n} B - B P_{n+1}) + (A B - B P_{n+1}) = T + \varepsilon - 2 B P_{n+1} > T
$$
This concludes our induction, and thus the fact that we indeed have T-merary sets of any size.
Conversely, consider a real $\mathbf{T} > 4$, and set $\varepsilon = (\mathbf{T} - 4) / 2 > 0$. Let $A B C$ be a triangle whose vertices belong to $\mathcal{C}$ and whose perimeter is strictly greater than $T$. Denoting $a, b$, and $c$ the lengths $B C, C A$, and $A B$, and $p = (a + b + c) / 2 > T / 2$ the semi-perimeter of $A B C$, Heron's formula indicates that $A B C$ has an area
$$
\mathcal{S} = \sqrt{p(p-a)(p-b)(p-c)}
$$
Since $p - a \geqslant p - 2 \geqslant T / 2 - 2 = \varepsilon$ and similarly, $p - b \geqslant \varepsilon$ and $p - c \geqslant \varepsilon$, we deduce that $\mathcal{S} \geqslant \sqrt{p \varepsilon^3} \geqslant \sqrt{2 \varepsilon^3}$.
Consequently, if a T-merary set contains $n$ triangles, those being of pairwise disjoint interiors, they cover, in total, an area of at least $n \sqrt{2 \varepsilon^3}$. This area cannot exceed $\pi$, which is the area of the disk contained inside $\mathcal{C}$, so we deduce that $n \leqslant \pi / \sqrt{2 \varepsilon^3}$, which concludes the problem.
Note: By invoking other arguments and without using Heron's formula, we could also show that $n \leqslant \pi / \varepsilon$, which provides a better approximation as soon as $T$ is close to 4.
## Exercises for the Senior Group
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Soit $\mathcal{C}$ un cercle de rayon 1 , et soit $T$ un nombre réel. On dit qu'un ensemble de triangles est T-méraire s'il satisfait les trois conditions suivantes:
$\triangleright$ les sommets de chaque triangle appartiennent à $\mathcal{C}$;
$\triangleright$ les triangles sont d'intérieurs deux à deux disjoints (mais deux triangles peuvent partager un côté ou un sommet);
$\triangleright$ chaque triangle est de périmètre strictement plus grand que $\mathbf{T}$.
Trouver tous les réels $\mathbf{T}$ tels que, pour tout entier $\mathrm{n} \geqslant 1$, il existe un ensemble T-méraire contenant exactement n triangles.
|
Nous allons démontrer que les réels recherchés sont exactement les réels $\mathbf{T} \leqslant 4$. Pour ce faire, fixons on réel $\mathbf{T} \leqslant 4$. On commence par montrer qu'il existe des ensembles T-méraires de n'importe quelle taille, grâce à la construction suivante. Soit $[A B]$ un diamètre de $\mathcal{C}$, et soit $P$ un point quelconque de $\mathcal{C}$, autre que $A$ et $B$. L'inégalité triangulaire indique que $A B P$ est de périmètre $A B+B P+P A>2 A B=4 \geqslant T$.
Forts de cette remarque, on montre par récurrence sur $n$ qu'il existe $n$ points $P_{1}, \ldots, P_{n}$, placés dans cet ordre sur l'un des deux demi-cercles $\overline{A B}$ (avec $P_{1}$ proche de $A$ et $P_{n}$ proche de B), et tel que l'ensemble formé des triangles $A P_{i} P_{i+1}$ (pour $i \leqslant n-1$ ) et $A B P_{n}$ soit $T$ méraire. Pour $n=1$, on vient de voir qu'il suffit de placer $P_{1} n$ 'importe où sur $\overline{A B}$.
Puis, une fois acquise l'existence des points $P_{1}, \ldots, P_{n}$, construisons le point $P_{n+1}$. Pour ce faire, on considère le réel $\varepsilon=A B+B P_{n}+P_{n} A-T$, qui est strictement positif par hypothèse. On place alors $\mathrm{P}_{n+1}$ n'importe où sur l'arc $\overline{B P_{n}}$, de sorte que $B P_{n+1}<\varepsilon / 2$. En effet, dans ces conditions, nos $n+1$ triangles sont bien d'intérieurs deux à deux disjoints, et il suffit de vérifier que $A B P_{n+1}$ et $A P_{n} P_{n+1}$ sont de périmètre strictement plus grand que $T$.
Le premier cas est un cas particulier de notre remarque initiale, et le deuxième cas découle encore une fois de l'inégalité triangulaire, puisque $A P_{n} P_{n+1}$ est de périmètre
$$
A P_{n}+P_{n} P_{n+1}+P_{n+1} A \geqslant A P_{n}+\left(P_{n} B-B P_{n+1}\right)+\left(A B-B P_{n+1}\right)=T+\varepsilon-2 B P_{n+1}>T
$$
Ceci conclut notre récurrence, et donc le fait que l'on a bien des ensembles T-méraires de n'importe quelle taille.
Réciproquement, considérons un réel $\mathbf{T}>4$, et posons $\varepsilon=(\mathbf{T}-4) / 2>0$. Soit également $A B C$ un triangle dont les sommets appartiennent à $\mathcal{C}$ et dont le périmètre est strictement plus grand que T. En notant $a, b$ et $c$ les longueurs $B C, C A$ et $A B$, et $p=(a+b+c) / 2>T / 2$ le demi-périmètre de $A B C$, la formule de Héron indique que $A B C$ est d'aire
$$
\mathcal{S}=\sqrt{p(p-a)(p-b)(p-c)}
$$
Puisque $p-a \geqslant p-2 \geqslant T / 2-2=\varepsilon$ et que, de même, $p-b \geqslant \varepsilon$ et $p-c \geqslant \varepsilon$ on en déduit que $\mathcal{S} \geqslant \sqrt{\mathrm{p} \mathrm{\varepsilon}^{3}} \geqslant \sqrt{2 \varepsilon^{3}}$.
Par conséquent, si un ensemble T-méraire contient $n$ triangles, ceux-ci étant d'intérieurs deux à deux disjoints, ils couvrent, dans leur ensemble, une surface égale à $n \sqrt{2 \varepsilon^{3}}$ au moins. Cette surface ne pouvant pas dépasser $\pi$, qui est la surface du disque contenu à l'intérieur $\mathcal{C}$, on en déduit que $n \leqslant \pi / \sqrt{2 \mathcal{\varepsilon}^{3}}$, ce qui conclut le problème.
Note : En invoquant d'autres arguments, et sans faire appel à la formule de Héron, on pourrait également montrer que $n \leqslant \pi / \varepsilon$, ce qui nous fournit une meilleure approximation dès lors que T est proche de 4.
## Exercices du groupe Senior
|
{
"exam": "French_tests",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/tests/fr-2018-2019-Test-20-03-Corrigé-web.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T1",
"year": "2018"
}
|
Let \( u \) be a non-zero natural number.
Prove that there are only a finite number of triplets of natural numbers \( (a, b, n) \) such that \( n! = u^a - u^b \).
Note: recall that \( 0! = 1! = 1 \).
|
Let $p$ be an odd prime that does not divide $u$, and let $k$ be an integer such that $p^{k}>u^{p-1}-1$. Set $q=p^{k-1}$. We first show that $u$ is not a $q^{\text{th}}$ power $\left(\bmod p^{k}\right)$. Indeed, if $u$ were a $q^{\text{th}}$ power $\left(\bmod p^{k}\right)$, then there would exist an integer $v$ such that $u \equiv v^{q}\left(\bmod p^{k}\right)$, and then we would have $1 \equiv v^{\varphi\left(p^{k}\right)} \equiv v^{q(p-1)} \equiv u^{p-1} \left(\bmod p^{k}\right)$, which is not the case.
Consequently, we also know, for any integer $\ell \geqslant k$, that $u$ is not a $q^{\text{th}}$ power $\left(\bmod p^{\ell}\right)$. We deduce that $p^{\ell-k}$ divides $\omega_{p^{\ell}}(u)$, where $\omega_{p^{\ell}}(u)$ denotes the order of $u\left(\bmod p^{\ell}\right)$. Indeed, let $g$ be a primitive root $\left(\bmod p^{\ell}\right)$, and let $x$ be an integer such that $u \equiv g^{x} \left(\bmod p^{\ell}\right)$. Then $1 \equiv u^{\omega_{p^{\ell}}(u)} \equiv g^{x \omega_{p^{\ell}}(u)} \left(\bmod p^{\ell}\right)$, which means that $\varphi\left(p^{\ell}\right)=(p-1)p^{\ell-1}$ divides $x \omega_{p^{\ell}}(u)$. Since $q=p^{k-1}$ does not divide $x$, it follows that $p^{\ell-k}$ divides $\omega_{p^{\ell}}(u)$.
Suppose finally that there exists a triplet $(a, b, n)$ of integers such that $u^{a}-u^{b}=n!$ and $n \geqslant kp$. Set also $d=a-b$ and $\ell=\lfloor n / p\rfloor$. Then $p^{\ell}$ divides $n!=u^{b}(u^{d}-1)$ and, since $p$ does not divide $u$, it follows that $u^{d} \equiv 1 \left(\bmod p^{\ell}\right)$. We deduce that $\omega_{p^{\ell}}(u)$ divides $d$, and therefore that $p^{\ell-k}$ divides $d$ as well. This means in particular that $d \geqslant p^{\ell-k}$, and thus
$$
2^{n(n+1)} \geqslant n^{n+1} \geqslant n!+1 \geqslant u^{d} \geqslant u^{p^{\ell-k}} \geqslant u^{p^{p / p-k}},
$$
or equivalently that $p^{k} n(n+1) \geqslant p^{n / p} \log _{2}(u)$.
Once the integers $u, p$ and $k$ are fixed, the right-hand side grows much faster than the left-hand side. Therefore, there exists an integer $\mathbf{N}$, which depends only on $u$, $p$ and $k$, such that $n \leqslant N$.
Thus, only a finite number of integers $n$ belong to a triplet $(a, b, n)$ such that $n!=u^{a}-u^{b}$. Once such an integer $n$ is fixed, we know that $u^{a}>u^{b}$, so $a \geqslant b+1$, and thus $n! \geqslant u^{a}-u^{a-1}=(u-1)u^{a-1}$, which shows that $a$ and $b$ are themselves bounded. This concludes our solution.
Note: It was not necessary to directly invoke the existence of a primitive root $\left(\bmod p^{\ell}\right)$, for example by proceeding as follows. Let $s$ be the order of $u \left(\bmod p\right)$, and let $k$ be the $p$-adic valuation of $u^{s}-1$. Then, for all $\ell \geqslant k$, one can in fact show that $u$ has order $\omega=p^{\ell-k}s \left(\bmod p^{\ell}\right)$.
To do this, we will first show by induction, for all $m \geqslant 1$, that the $p^{\text{th}}$ roots of unity $\left(\bmod p^{m}\right)$ are the integers congruent to $1 \left(\bmod p^{m-1}\right)$. Indeed, the result is immediate for $m=1$. Then, if $m \geqslant 2$ and if $x^{p} \equiv 1 \left(\bmod p^{m}\right)$, then $x^{p} \equiv 1 \left(\bmod p^{m-1}\right)$, so we can write $x=1+y^{m-2}$, and by expanding a binomial of Newton we deduce that $1 \equiv x^{p} \equiv 1+y^{m-1} \left(\bmod p^{m}\right)$, which concludes the induction.
Using the above induction, we note that $u^{s}$ has order $\varpi=p^{\ell-k} \left(\bmod p^{\ell}\right)$. Since $s$ divides $\omega$, we know in addition that $\omega=s \varpi$, which concludes.
In general, this reasoning plays a crucial role in the proof of the existence of a primitive root $\left(\bmod p^{\ell}\right)$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit u un entier naturel non nul.
Démontrer qu'il n'existe qu'un nombre fini de triplets d'entiers naturels ( $a, b, n$ ) tels que $\mathrm{n}!=\mathrm{u}^{\mathrm{a}}-\mathrm{u}^{\mathrm{b}}$.
Note : on rappelle que $0!=1!=1$.
|
Soit $p$ un nombre premier impair qui ne divise pas $u$, et soit $k$ un entier tel que $p^{k}>u^{p-1}-1$. Posons $q=p^{k-1}$. On montre tout d'abord que $u$ n'est $^{\text {pres }}$ une puissance $q^{\text {ème }}\left(\bmod p^{k}\right)$. En effet, si $u$ était une puissance $q^{\text {ème }}\left(\bmod p^{k}\right)$, alors il existerait un entier $v$ tel que $u \equiv v^{q}\left(\bmod p^{k}\right)$, et alors on aurait $1 \equiv v^{\varphi\left(p^{k}\right)} \equiv v^{q(p-1)} \equiv \mathfrak{u}^{p-1}$ $\left(\bmod p^{k}\right)$, ce qui $n^{\prime}$ est pas le cas.
Par conséquent, on sait également, pour tout entier $\ell \geqslant k$, que $u$ n'est pas non plus une puissance $q^{\text {ème }}\left(\bmod p^{\ell}\right)$. On en déduit que $p^{\ell-k}$ divise $\omega_{p^{\ell}}(u)$, où $\omega_{p^{\ell}}(u)$ désigne l'ordre de $u\left(\bmod p^{\ell}\right)$. En effet, soit $g$ une racine primitive $\left(\bmod p^{\ell}\right)$, et soit $x$ un entier tel que $u \equiv g^{x}$ $\left(\bmod \mathfrak{p}^{\ell}\right)$. Alors $1 \equiv u^{\omega_{p^{\ell}}(\mathfrak{u})} \equiv \mathrm{g}^{x \omega_{p^{\ell}}(\mathfrak{u})}\left(\bmod \mathrm{p}^{\ell}\right)$, ce qui signifie que $\varphi\left(\mathrm{p}^{\ell}\right)=(p-1) \mathrm{p}^{\ell-1}$ divise $x \omega_{p^{\ell}}(u)$. Puisque $q=p^{k-1}$ ne divise pas $x$, $c^{\prime}$ est donc que $p^{\ell-k}$ divise $\omega_{p^{\ell}}(u)$.
Supposons enfin qu'il existe un triplet ( $a, b, n$ ) d'entiers tels que $u^{a}-u^{b}=n$ ! et $n \geqslant k p$. Posons également $d=a-b$ et $\ell=\lfloor n / p\rfloor$. Alors $p^{\ell}$ divise $n!=u^{b}\left(u^{d}-1\right)$ et, puisque $p$ ne divise pas $u$, $c^{\prime}$ est donc que $a^{d} \equiv 1\left(\bmod p^{\ell}\right)$. On en déduit que $\omega_{p^{\ell}}(u)$ divise $d$, donc que $p^{\ell-k}$ divise $d$ également. Cela signifie en particulier que $d \geqslant p^{\ell-k}$, donc que
$$
2^{\mathfrak{n}(\mathfrak{n}+1)} \geqslant \mathfrak{n}^{n+1} \geqslant n!+1 \geqslant \mathfrak{u}^{d} \geqslant \mathfrak{u}^{p^{\ell-k}} \geqslant \mathfrak{u}^{p^{p / p-k}},
$$
ou encore que $p^{k} n(n+1) \geqslant p^{n / p} \log _{2}(u)$.
Une fois les entiers $u, p$ et $k$ fixés, le membre de droite croît beaucoup plus vite que le membre de gauche. Il existe donc un entier $\mathbf{N}$, qui ne dépend que de $u$, $p$ et $k$, et tel que $n \leqslant N$.
Ainsi, seul un nombre fini d'entiers $n$ appartient à un triplet ( $a, b, n$ ) tel que $n!=u^{a}-u^{b}$. Or, une fois un tel entier $n$ fixé, on sait que $u^{a}>u^{b}$, donc que $a \geqslant b+1$, et donc que $n!\geqslant \mathfrak{u}^{\mathrm{a}}-\mathfrak{u}^{\mathrm{a}-1}=(\mathfrak{u}-1) \mathfrak{u}^{\mathrm{a}-1}$, ce qui montre que $a$ et $b$ sont eux-mêmes bornés. Ceci conlut notre solution.
Note : Il n'était pas nécessaire de recourir directement à l'existence d'une racine primitive $\left(\bmod p^{\ell}\right)$, par exemple en procédant comme suit. Soit $s$ l'ordre de $_{u}(\bmod p)$, et soit $k$ la valuation $p$-adique de $u^{s}-1$. Alors, pour tout $\ell \geqslant k$, on peut en fait montrer que $u$ est $d^{\prime}$ ordre $\omega=p^{\ell-\mathrm{k}} s\left(\bmod p^{\ell}\right)$.
Pour ce faire, on va d'abord montrer par récurrence, pour tout $m \geqslant 1$, les racines $p^{\text {èmes }}$ de l'unité $^{\left(\bmod p^{\mathrm{m}}\right)}$ sont les entiers congrus à $1\left(\bmod p^{\mathrm{m}-1}\right)$. En effet, le résultat est immédiat pour $m=1$. Puis, si $m \geqslant 2$ et si $x^{p} \equiv 1\left(\bmod p^{\mathfrak{m}}\right)$, alors $x^{p} \equiv 1\left(\bmod p^{m-1}\right)$, donc on peut écrire $x=1+y^{\mathrm{m}-2}$, et en développant un binôme de Newton on en déduit que $1 \equiv x^{\mathfrak{p}} \equiv 1+y^{\mathfrak{m}-1}\left(\bmod \mathfrak{p}^{\mathfrak{m}}\right)$, ce qui conclut la récurrence.
À l'aide de la récurrence ci-dessus, on remarque donc que $u^{s}$ est d'ordre $\varpi=p^{\ell-k}$ $\left(\bmod p^{\ell}\right)$. Puisque $s$ divise $\omega$, on sait en outre que $\omega=s \varpi$, ce qui conclut.
De manière générale, ce raisonnement joue en fait un rôle crucial dans la preuve de l'existence $d^{\prime}$ une racine primitive $\left(\bmod p^{\ell}\right)$.
|
{
"exam": "French_tests",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/tests/fr-2018-2019-Test-20-03-Corrigé-web.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T1",
"year": "2018"
}
|
Let $ABC$ be a triangle, and let $I$ be the center of the inscribed circle in $ABC$. Let $A', B'$, and $C'$ be three points respectively located on $(AI)$, $(BI)$, and $(CI)$. Assume that $A', B'$, and $C'$ are distinct from $A, B, C$, and $I$, and that they are collinear. Finally, let $P_A$ be the point of intersection of the perpendicular bisectors of $[BB']$ and $[CC']$. Similarly, let $P_B$ be the point of intersection of the perpendicular bisectors of $[CC']$ and $[AA']$, and let $P_C$ be the point of intersection of the perpendicular bisectors of $[AA']$ and $[BB']$.
Prove that the circumcircles of triangles $ABC$ and $P_A P_B P_C$ are tangent to each other.
|
We start by drawing a figure as shown below, without forgetting the line $\ell$ passing through $A^{\prime}, B^{\prime}$, and $C^{\prime}$, as well as the circles $\Omega$ and $\Gamma$, which are respectively circumscribed around $A B C$ and $\mathrm{P}_{\mathrm{A}} \mathrm{P}_{\mathrm{B}} \mathrm{P}_{\mathrm{C}}$.
Given the problem statement, a reasonable approach is to find a suitable characterization of the potential tangency point, which we will denote as $T$, between $\Omega$ and $\Gamma$. Such a characterization is as follows: $T$ is the center of one of the two homotheties mapping $\Gamma$ to $\Omega$. Let $h$ be this homothety: it is the homothety with a positive ratio if one of the two circles is contained within the other, and the homothety with a negative ratio otherwise.
Given the definitions of $\Gamma$ and $\Omega$, it is tempting to study the image of $\mathrm{P}_{\mathrm{A}} \mathrm{P}_{\mathrm{B}} \mathrm{P}_{\mathrm{C}}$ under $h$, or the image of $A B C$ under $\mathrm{h}^{-1}$. On the figure, we observe two things:
$\triangleright$ The points $h\left(P_{A}\right), h\left(P_{B}\right)$, and $h\left(P_{C}\right)$ seem to be the points of intersection of (AI), (BI), and (CI) with $\Omega$;
$\triangleright$ The lines $(A T), (B T)$, and $(C T)$ seem to intersect the line $\ell$ at points on $\left(P_{B} P_{C}\right)$, $\left(\mathrm{P}_{C} \mathrm{P}_{\mathrm{A}}\right)$, and $\left(\mathrm{P}_{\mathrm{A}} \mathrm{P}_{\mathrm{B}}\right)$, respectively.
Let's explore these ideas!
First, we denote $A^{\prime \prime}, B^{\prime \prime}$, and $C^{\prime \prime}$ as these points of intersection. The point $A^{\prime \prime}$ is the south pole of $A B C$ with respect to the vertex $A$. We know that $A^{\prime \prime} B = A^{\prime \prime} C = A^{\prime \prime} I$. Similarly, we have $B^{\prime \prime} C = B^{\prime \prime} A = B^{\prime \prime} I$ and $C^{\prime \prime} A = C^{\prime \prime} B = C^{\prime \prime} I$. Thus, the lines $\left(A^{\prime \prime} B^{\prime \prime}\right)$ and $\left(P_{A} P_{B}\right)$ are the perpendicular bisectors of [CI] and $\left[C^{\prime}\right]$, respectively, which shows in particular that they are parallel. Similarly, $\left(B^{\prime \prime} C^{\prime \prime}\right)$ is parallel to $\left(P_{B} P_{C}\right)$ and $\left(C^{\prime \prime} A^{\prime \prime}\right)$ is parallel to $\left(P_{A} P_{B}\right)$. This shows that the triangles $P_{A} P_{B} P_{C}$ and $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$ are homothetic to each other.
In particular, there exists a unique homothety that maps $P_{A} P_{B} P_{C}$ to $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$. We can indeed denote this homothety as $h$, and denote its center as $T$, so that $h$ maps $\Omega$ to $\Gamma$. Here, the point $T$ is the intersection of the lines $\left(A^{\prime \prime} P_{A}\right), \left(B^{\prime \prime} P_{B}\right)$, and $\left(C^{\prime \prime} P_{C}\right)$, and it remains to show that $T$ lies on $\Omega$.
On the other hand, since $(P_{A} P_{B})$ is the perpendicular bisector of $\left[C C^{\prime}\right]$, and if $(TC)$ intersects $(P_{A} P_{B})$ at a point $X$ which also lies on $\ell$, then the lines $\ell$ and $(T C) = (C X)$ are symmetric with respect to $(P_{A} P_{B})$. Conversely, we denote $\ell_{a}, \ell_{b}$, and $\ell_{c}$ as the reflections of $\ell$ with respect to $\left(P_{B} P_{C}\right), \left(P_{C} P_{A}\right)$, and $\left(P_{A} P_{B}\right)$, respectively.
We can then seek to show that the lines $\ell_{a}, \ell_{b}$, and $\ell_{c}$ are concurrent at a point $\hat{T}$ which belongs to $\Omega$, and then that the points $\hat{T}, P_{A}$, and $A^{\prime \prime}$ are collinear: we will deduce that $T = \hat{T}$, which will conclude the problem. Let $T_{c}$ be the intersection of $\ell_{a}$ and $\ell_{b}$. We note that
\[
\begin{aligned}
\left(T_{c} A, T_{c} B\right) & = \left(\ell_{a}, \ell_{b}\right) = \left(\ell_{a}, \ell\right) + \left(\ell, \ell_{b}\right) = 2\left(P_{B} P_{C}, \ell\right) + 2\left(\ell, P_{C} P_{A}\right) = 2\left(P_{B} P_{C}, P_{A} P_{C}\right) \\
& = 2\left(B^{\prime \prime} C^{\prime \prime}, A^{\prime \prime} C^{\prime \prime}\right) = 2\left(B^{\prime \prime} C^{\prime \prime}, C C^{\prime \prime}\right) + 2\left(C C^{\prime \prime}, A^{\prime \prime} C^{\prime \prime}\right) \\
& = \left(A C^{\prime \prime}, C C^{\prime \prime}\right) + \left(C C^{\prime \prime}, B C^{\prime \prime}\right) = \left(A C^{\prime \prime}, B C^{\prime \prime}\right) = (A C, B C).
\end{aligned}
\]
This shows that the points $T_{c}, A, B$, and $C^{\prime \prime}$ are concyclic, so $T_{c}$ indeed lies on $\Omega$. If $T_{c} = A$, then $\ell_{b} = (A B)$, so $(A C, B C) = \left(\ell_{a}, \ell_{b}\right) = \left(\ell_{a}, B A\right)$, so $\ell_{a}$ is the tangent to $\Omega$ at $A$, and $T_{c}$ is necessarily the intersection of $\ell_{a}, \ell_{b}$, and $\ell_{c}$. Similarly, we introduce the points $T_{a}$ and $T_{b}$. If one of these three points is $A, B$, or $C$, then it constitutes the desired point $\hat{T}$. Otherwise, $T_{c}$ is the intersection of $\ell_{a}$ with $\Omega$ other than $A$, but also the intersection of $\ell_{b}$ with $\Omega$ other than $B$, and by reasoning similarly on $T_{a}$ and $T_{b}$ we see that $T_{a} = T_{b} = T_{c}$ lies on $\Omega$.
Moreover, since we obtained the lines $\ell_{a}, \ell_{b}$, and $\ell_{c}$ by applying axial symmetries to $\ell$, it is important to apply these symmetries to other points, particularly the points $A^{\prime}, B^{\prime}$, and $C^{\prime}$ on $\ell$. Thus, we denote $A_{b}^{\prime}$ and $A_{c}^{\prime}$ as the reflections of $A^{\prime}$ with respect to $\left(P_{A} P_{C}\right)$ and $\left(P_{A} P_{B}\right)$: they lie on $\ell_{b}$ and $\ell_{c}$.
In these conditions,
\[
\begin{aligned}
\left(P_{A} A_{b}^{\prime}, P_{A} A_{c}^{\prime}\right) & = \left(P_{A} A_{b}^{\prime}, P_{A} A^{\prime}\right) + \left(P_{A} A^{\prime}, P_{A} A_{c}^{\prime}\right) = 2\left(P_{A} P_{C}, P_{A} A^{\prime}\right) + 2\left(P_{A} A^{\prime}, P_{A} P_{B}\right) \\
& = 2\left(P_{A} P_{C}, P_{A} P_{B}\right) = \left(\ell_{b}, \ell_{c}\right) = \left(\hat{T} A_{b}^{\prime}, \hat{T} A_{c}^{\prime}\right).
\end{aligned}
\]
This means that the points $P_{A}, A_{b}^{\prime}, \hat{T}$, and $A_{c}^{\prime}$ are concyclic.
On the other hand, since $P_{A} A_{b}^{\prime} = P_{A} A^{\prime} = P_{A} A_{c}^{\prime}$, we know that the triangle $P_{A} A_{b}^{\prime} A_{c}^{\prime}$ is isosceles at $P_{A}$. We deduce that
\[
\begin{aligned}
& \left(\ell_{b}, P_{A} \hat{T}\right) = \left(A_{b}^{\prime} \hat{T}, P_{A} \hat{T}\right) = \left(A_{b}^{\prime} A_{c}^{\prime}, P_{A} A_{c}^{\prime}\right) \\
& = 90^{\circ} - \left(A_{b}^{\prime} P_{A}, A_{c}^{\prime} P_{A}\right) / 2 = 90^{\circ} - \left(P_{C} P_{A}, P_{B} P_{A}\right) \\
& = 90^{\circ} + (BI, IC) = (BA, AI) = (BA, AA^{\prime \prime}) = (B \hat{T}, \hat{T} A^{\prime \prime}) = (\ell_{b}, \hat{T} A^{\prime \prime}).
\end{aligned}
\]
This means that $\hat{T}$ is indeed collinear with $P_{A}$ and $A^{\prime \prime}$. We show similarly that $\hat{T}$ is collinear with $P_{B}$ and $B^{\prime \prime}$, as well as with $P_{C}$ and $C^{\prime \prime}$. Consequently, we have $T = \hat{T}$, which concludes the proof.
|
proof
|
Yes
|
Incomplete
|
proof
|
Geometry
|
Soit $A B C$ un triangle, soit I le centre du cercle inscrit dans $A B C$. Soit $A^{\prime}, B^{\prime}$ et $C^{\prime}$ trois points respectivement situés sur (AI), (BI) et (CI). On suppose que $A^{\prime}, B^{\prime}$ et $C^{\prime}$ sont distincts de $A, B, C$ et $I$, et qu'ils sont alignés. Enfin, soit $P_{A}$ le point d'intersection des médiatrices de $\left[\mathrm{BB}^{\prime}\right]$ et $\left[\mathrm{CC}^{\prime}\right]$. De même, soit $\mathrm{P}_{\mathrm{B}}$ le point d'intersection des médiatrices de $\left[C C^{\prime}\right]$ et $\left[A A^{\prime}\right]$, et soit $P_{C}$ le point d'intersection des médiatrices de $\left[A A^{\prime}\right]$ et $\left[B B^{\prime}\right]$.
Démontrer que les cercles circonscrits aux triangles $A B C$ et $P_{A} P_{B} P_{C}$ sont tangents l'un à l'autre.
|
On commence par tracer une figure comme ci-dessous, sans oublier la droite $\ell$ qui passe par $A^{\prime}, B^{\prime}$ et $C^{\prime}$ ni les cercles $\Omega$ et $\Gamma$, respectivement circonscrits à $A B C$ et à $\mathrm{P}_{\mathrm{A}} \mathrm{P}_{\mathrm{B}} \mathrm{P}_{\mathrm{C}}$.

Au vu de l'énoncé, une approche raisonnable est de trouver une caractérisation adaptée du point de tangence éventuel, que l'on notera $T$, entre $\Omega$ et $\Gamma$. Une telle caractérisation est la suivante : T est le centre d'une des deux homothéties envoyant $\Gamma$ sur $\Omega$. Soit h cette homothétie : il s'agit de l'homothétie de rapport positif si l'un des deux cercles est inclus à l'intérieur de l'autre, et de l'homothétie de rapport négatif sinon.
Au vu de la définition de $\Gamma$ et $\Omega$, il est tentant d'étudier l'image de $\mathrm{P}_{\mathrm{A}} \mathrm{P}_{\mathrm{B}} \mathrm{P}_{\mathrm{C}}$ par $h$, ou bien celle de $A B C$ par $\mathrm{h}^{-1}$. Or, sur la figure, on constate deux choses:
$\triangleright$ les points $h\left(P_{A}\right), h\left(P_{B}\right)$ et $h\left(P_{C}\right)$ semblent être les points d'intersection respectifs de (AI), (BI) et (CI) avec $\Omega$;
$\triangleright$ les droites $(A T),(B T)$ et $(C T)$ semblent recouper la droite $\ell$ en des points de $\left(P_{B} P_{C}\right)$, $\left(\mathrm{P}_{C} \mathrm{P}_{\mathrm{A}}\right)$ et $\left(\mathrm{P}_{\mathrm{A}} \mathrm{P}_{\mathrm{B}}\right)$ respectivement.
Exploitons ces idées!
Tout d'abord, on note donc $A^{\prime \prime}, B^{\prime \prime}$ et $C^{\prime \prime}$ ces points d'intersection. Le point $A^{\prime \prime} n^{\prime}$ est autre que le pôle sud de $A B C$ par rapport au sommet $A$. On sait donc que $A^{\prime \prime} B=A^{\prime \prime} C=A^{\prime \prime} \mathrm{I}$. De même, on a $B^{\prime \prime} C=B^{\prime \prime} A=B^{\prime \prime} I$ et $C^{\prime \prime} A=C^{\prime \prime} B=C^{\prime \prime}$. Ainsi, les droites $\left(A^{\prime \prime} B^{\prime \prime}\right)$ et $\left(P_{A} P_{B}\right)$ sont les médiatrices respectives de [CI] et de $\left[C^{\prime}\right]$, ce qui montre en particulier qu'elles sont parallèles. De même, $\left(B^{\prime \prime} C^{\prime \prime}\right)$ est parallèle à $\left(P_{B} P_{C}\right)$ et $\left(C^{\prime \prime} A^{\prime \prime}\right)$ est parallèle à $\left(P_{A}, P_{B}\right)$. Cela montre que les triangles $P_{A} P_{B} P_{C}$ et $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$ sont homothétiques l'un de l'autre.
En particulier, il existe une unique homothétie qui envoie $P_{A} P_{B} P_{C}$ sur $A^{\prime \prime} B^{\prime \prime} C^{\prime \prime}$. On peut effectivement la noter $h$, et noter $T$ son centre, de sorte que $h$ envoie $\Omega$ sur $\Gamma$. Ici, le point T n'est autre que le point de concours des droites $\left(A^{\prime \prime} P_{A}\right),\left(B^{\prime \prime} P_{B}\right)$ et $\left(C^{\prime \prime} P_{C}\right)$, et il reste à montrer que $T$ appartient à $\Omega$.
D'autre part, puisque ( $\mathrm{P}_{A} \mathrm{P}_{B}$ ) est a médiatrice de $\left[C C^{\prime}\right]$, et si (TC) recoupe ( $\mathrm{P}_{A} \mathrm{P}_{B}$ ) en un point $X$ qui appartient aussi à $\ell$, alors les droites $\ell$ et $(T C)=(C X)$ sont symétriques l'une de l'autre par rapport à ( $\mathrm{P}_{\mathrm{A}} \mathrm{P}_{\mathrm{B}}$ ). Réciproquement, on note $\ell_{\mathrm{a}}, \ell_{b}$ et $\ell_{c}$ les symétriques respectifs de $\ell$ par rapport à $\left(P_{B} P_{C}\right),\left(P_{C} P_{A}\right)$ et $\left(P_{A} P_{B}\right)$.
On peut alors chercher à montrer que les droites $\ell_{a}, \ell_{b}$ et $\ell_{c}$ sont concourantes en un point $\hat{T}$ qui appartiendra à $\Omega$, puis que les points $\hat{T}, \mathrm{P}_{A}$ et $A^{\prime \prime}$ sont alignés: on en déduira que $T=\hat{T}$, ce qui conclura le problème. Soit alors $T_{c}$ le point d'intersection de $\ell_{a}$ et $\ell_{b}$. On remarque que
$$
\begin{aligned}
\left(\mathrm{T}_{\mathrm{c}} A, \mathrm{~T}_{\mathrm{c}} \mathrm{~B}\right) & =\left(\ell_{\mathrm{a}}, \ell_{\mathrm{b}}\right)=\left(\ell_{\mathrm{a}}, \ell\right)+\left(\ell, \ell_{\mathrm{b}}\right)=2\left(\mathrm{P}_{\mathrm{B}} \mathrm{P}_{\mathrm{C}}, \ell\right)+2\left(\ell, \mathrm{P}_{\mathrm{C}} \mathrm{P}_{\mathrm{A}}\right)=2\left(\mathrm{P}_{\mathrm{B}} \mathrm{P}_{\mathrm{C}}, \mathrm{P}_{\mathrm{A}} \mathrm{P}_{\mathrm{C}}\right) \\
& =2\left(\mathrm{~B}^{\prime \prime} \mathrm{C}^{\prime \prime}, \mathrm{A}^{\prime \prime} \mathrm{C}^{\prime \prime}\right)=2\left(\mathrm{~B}^{\prime \prime} \mathrm{C}^{\prime \prime}, C C^{\prime \prime}\right)+2\left(C C^{\prime \prime}, A^{\prime \prime} \mathrm{C}^{\prime \prime}\right) \\
& =\left(A C^{\prime \prime}, C C^{\prime \prime}\right)+\left(C C^{\prime \prime}, B C^{\prime \prime}\right)=\left(A C^{\prime \prime}, B C^{\prime \prime}\right)=(A C, B C) .
\end{aligned}
$$
Ceci montre que les points $T_{c}, A, B$ et $C^{\prime \prime}$ sont cocycliques, donc que $T_{c}$ appartient bien à $\Omega$. Or, si $T_{c}=A$, alors $\ell_{b}=(A B)$, donc $(A C, B C)=\left(\ell_{a}, \ell_{b}\right)=\left(\ell_{a}, B A\right)$, donc $\ell_{a}$ est la tangente à $\Omega$ en $A$, et $T_{c}$ est nécessairement le point d'intersection de $\ell_{a}, \ell_{b}$ et $\ell_{c}$. De même, on introduit les points $T_{a}$ et $T_{b}$. Si l'un de ces trois points est $A, B$ ou $C$, alors il constitue bien le point $\hat{T}$ désiré. Sinon, $T_{c}$ est le point d'intersection de $\ell_{a}$ avec $\Omega$ autre que $A$, mais également le point d'intersection de $\ell_{b}$ avec $\Omega$ autre que $B$, et en raisonnant de manière analogue sur $T_{a}$ et $T_{b}$ on constate bien que $T_{a}=T_{b}=T_{c}$ appartient à $\Omega$.
Par ailleurs, et puisque l'on a obtenu les droites $\ell_{a}, \ell_{b}$ et $\ell_{c}$ en appliquant à $\ell$ des symétries axiales, il est important d'appliquer ces symétries à d'autres points en particulier, notamment les points $A^{\prime}, B^{\prime}$ et $C^{\prime}$ présents sur $\ell$. Ainsi, on note $A_{b}^{\prime}$ et $A_{c}^{\prime}$ les symétriques de $A^{\prime}$ par rapport à $\left(\mathrm{P}_{\mathrm{A}} \mathrm{P}_{\mathrm{C}}\right)$ et à $\left(\mathrm{P}_{\mathrm{A}} \mathrm{P}_{\mathrm{B}}\right)$ : ils se trouvent sur $\ell_{\mathrm{b}}$ et $\ell_{\mathrm{c}}$.
Dans ces conditions,
$$
\begin{aligned}
\left(P_{A} A_{b}^{\prime}, P_{A} A_{c}^{\prime}\right) & =\left(P_{A} A_{b}^{\prime}, P_{A} A^{\prime}\right)+\left(P_{A} A^{\prime}, P_{A} A_{c}^{\prime}\right)=2\left(P_{A} P_{C}, P_{A} A^{\prime}\right)+2\left(P_{A} A^{\prime}, P_{A} P_{B}\right) \\
& =2\left(P_{A} P_{C}, P_{A} P_{B}\right)=\left(\ell_{b}, \ell_{c}\right)=\left(\hat{T} A_{b}^{\prime}, \hat{T} A_{c}^{\prime}\right) .
\end{aligned}
$$
Cela signifie que les points $\mathrm{P}_{\mathrm{A}}, \mathrm{A}_{\mathrm{b}}^{\prime}, \hat{T}$ et $A_{c}^{\prime}$ sont cocycliques.
D'autre part, puisque $P_{A} A_{b}^{\prime}=P_{A} A^{\prime}=P_{A} A_{c}^{\prime}$, on sait que le triangle $P_{A} A_{b}^{\prime} A_{c}^{\prime}$ est isocèle en $P_{A}$. On en déduit que
$$
\begin{aligned}
& \left(\ell_{b}, P_{A} \hat{T}\right)=\left(A_{b}^{\prime} \hat{T}, P_{A} \hat{T}\right)=\left(A_{b}^{\prime} A_{c}^{\prime}, P_{A} A_{c}^{\prime}\right) \\
& =90^{\circ}-\left(A_{b}^{\prime} \mathrm{P}_{\mathrm{A}}, \mathcal{A}_{\mathrm{c}}^{\prime} \mathrm{P}_{\mathrm{A}}\right) / 2=90^{\circ}-\left(\mathrm{P}_{\mathrm{C}} \mathrm{P}_{\mathrm{A}}, \mathrm{P}_{\mathrm{B}} \mathrm{P}_{\mathrm{A}}\right) \\
& =90^{\circ}+(\mathrm{BI}, \mathrm{IC})=(\mathrm{BA}, \mathrm{AI})=\left(\mathrm{BA}, \mathrm{AA}^{\prime \prime}\right)=\left(\mathrm{B} \hat{\mathrm{~T}}, \hat{\mathrm{~T}} \mathrm{~A}^{\prime \prime}\right)=\left(\ell_{\mathrm{b}}, \hat{\mathrm{~T}} \mathrm{~A}^{\prime \prime}\right) .
\end{aligned}
$$
Cela signifie que $\hat{\top}$ est bien aligné avec $P_{A}$ et $A^{\prime \prime}$. On montre de même que $\hat{T}$ est aligné avec $P_{B}$ et $B^{\prime \prime}$, ainsi qu'avec $P_{C}$ et $C^{\prime \prime}$. Par conséquent, on a bien $T=\hat{T}$, ce qui conclut.
|
{
"exam": "French_tests",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/tests/fr-2018-2019-Test-20-03-Corrigé-web.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T1",
"year": "2018"
}
|
Let $a$ and $b$ be real numbers such that $a b \geqslant a^{3}+b^{3}$.
Prove that $a+b \leqslant 1$.
|
Since $(a+b)^{2}=(a-b)^{2}+4 a b \geqslant 4 a b$, we deduce that
$$
(a+b)^{3}=a^{3}+b^{3}+3(a+b) a b \leqslant(3 a+3 b+1) a b \leqslant(3 a+3 b+1)(a+b)^{2} / 4
$$
If $a+b>1$, we can divide our inequality by $(a+b)^{2} / 4$, which means that $4(a+b) \leqslant$ $3 a+3 b+1$, so that $a+b \leqslant 1$ anyway.
|
a+b \leqslant 1
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $a$ et $b$ deux réels tels que $a b \geqslant a^{3}+b^{3}$.
Démontrer que $a+b \leqslant 1$.
|
Puisque $(a+b)^{2}=(a-b)^{2}+4 a b \geqslant 4 a b$, on en déduit que
$$
(a+b)^{3}=a^{3}+b^{3}+3(a+b) a b \leqslant(3 a+3 b+1) a b \leqslant(3 a+3 b+1)(a+b)^{2} / 4
$$
Si $a+b>1$, on peut diviser notre inégalité par $(a+b)^{2} / 4$, ce qui signifie que $4(a+b) \leqslant$ $3 a+3 b+1$, donc que $a+b \leqslant 1$ tout de même.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2018-2019-Test-26-02-Corrige.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T1",
"year": "2018"
}
|
A coloring of $\mathbb{Q}$ consists of coloring every rational number either red or blue. We say that a coloring of $\mathbb{Q}$ is harmonious if, for all rational numbers $x$ and $y$ of the same color, the rational number $x+y$ is still of the same color.
Find all harmonious colorings of $\mathbb{Q}$.
|
We will show that the sought colorings are as follows:
$\triangleright$ we color all rationals with the same color;
$\triangleright$ we color all non-negative rationals with one color, and all strictly negative rationals with the other color;
$\triangleright$ we color all strictly positive rationals with one color, and all non-positive rationals with the other color.
First, it is clear that each of these colorings is harmonious. Let's show that these are the only ones.
In the following, we assume that we have a fixed harmonious coloring. We denote by B the set of rationals colored blue and R the set of rationals colored red.
With these notations, if $x$ is any rational number belonging to a set $E \in \{B, R\}$, we will first show that for any positive rational number $p / q$, $p x / q$ also belongs to $E$. Indeed, if $x / q \notin E$, then an immediate induction shows that $x = q x / q \notin E$, which is not possible. We deduce that $x / q \in E$, and then that $p x / q \in E$, again by immediate induction.
Thus, all strictly positive rationals are the same color as 1, and all strictly negative rationals are the same color as -1. Given our goal, it remains to show that if 1 and -1 are the same color, then 0 is also of that color: this follows precisely from the fact that $0 = 1 + (-1)$ and the harmonious nature of our coloring.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Un coloriage de $\mathbb{Q}$ consiste à colorier tout nombre rationnel soit en rouge, soit en bleu. On dit qu'un coloriage de $\mathbb{Q}$ est harmonieux si, pour tous les rationnels $x$ et $y$ d'une même couleur, le rationnel $x+y$ est encore de la même couleur.
Trouver tous les coloriages de $\mathbb{Q}$ qui sont harmonieux.
|
On va montrer que les coloriages recherchés sont les suivants :
$\triangleright$ on colorie tous les rationnels avec la même couleur;
$\triangleright$ on colorie tous les rationnels positifs ou nuls avec une même couleur, et tous les rationnels strictement négatifs avec l'autre couleur;
$\triangleright$ on colorie tous les rationnels strictement positifs avec une même couleur, et tous les rationnels négatifs ou nuls avec l'autre couleur.
Tout d'abord, il est clair que chacun de ces coloriages est harmonieux. Montrons que ce sont les seuls.
Dans la suite, on supposera que l'on dispose d'un coloriage harmonieux fixé. On note B l'ensemble des rationnels coloriés en bleu et R l'ensemble des rationnels coloriés en rouge.
Avec ces notations, si $x$ est un rationnel quelconque appartenant à un ensemble $E \in\{B, R\}$, on va d'abord montrer que pour tout nombre rationnel $p / q$ strictement positif, $p x / q$ appartient aussi à $E$. En effet, si $x / q \notin E$, alors une récurrence immédiate montre que $x=q x / q \notin E$, ce qui $n^{\prime}$ est pas possible. On en déduit que $x / q \in E$, puis que $p x / q \in E$, toujours par récurrence immédiate.
Ainsi, tous les rationnels strictement positifs sont de la même couleur que 1, et tous les rationnels strictement négatifs sont de la même couleur que -1 . Vu notre objectif, il reste à montrer que, si 1 et -1 sont de la même couleur, alors 0 est de cette couleur là également : ceci découle précisément du fait que $0=1+(-1)$ est du caractère harmonieux de notre coloriage.
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2018-2019-Test-26-02-Corrige.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T1",
"year": "2018"
}
|
Let $ABC$ be an isosceles triangle at $A$, and let $D$ be a point on ($AC$) such that $A$ is located between $C$ and $D$, but is not the midpoint of [CD].
We denote $d_{1}$ and $d_{2}$ as the internal and external bisectors of the angle $\widehat{BAC}$, and $\Delta$ as the perpendicular bisector of [BD]. Finally, let $E$ and $F$ be the points of intersection of $\Delta$ with the lines $d_{1}$ and $d_{2}$, respectively.
Prove that the points $A, D, E$, and $F$ are concyclic.
|
A pretty figure suggests that points $A, B, D, E$, and $F$ are concyclic: this is what we will show.
Let $\Gamma$ be the circumcircle of $A B D$, and let $G_{1}$ and $G_{2}$ be the points of intersection of lines $d_{1}$ and $d_{2}$ with $\Gamma$, and other than $D$ itself. It suffices to show that $E=G_{1}$ and that $\mathrm{F}=\mathrm{G}_{2}$.
Since $\mathrm{d}_{2}$ is the external bisector of $\widehat{B A C}$, it is the internal bisector of $\widehat{B A D}$, and the South Pole theorem indicates that $\mathrm{G}_{2}$ is equidistant from B and D. Similarly, $\mathrm{d}_{1}$ is the internal bisector of $\widehat{B A C}$, hence the external bisector of $\widehat{B A D}$, and the North Pole theorem indicates that $\mathrm{G}_{1}$ is equidistant from B and D.
But then $\left(G_{1} G_{2}\right)$ is indeed the perpendicular bisector of $[B D]$, so $G_{1}=E$ and $G_{2}=F$, which concludes.
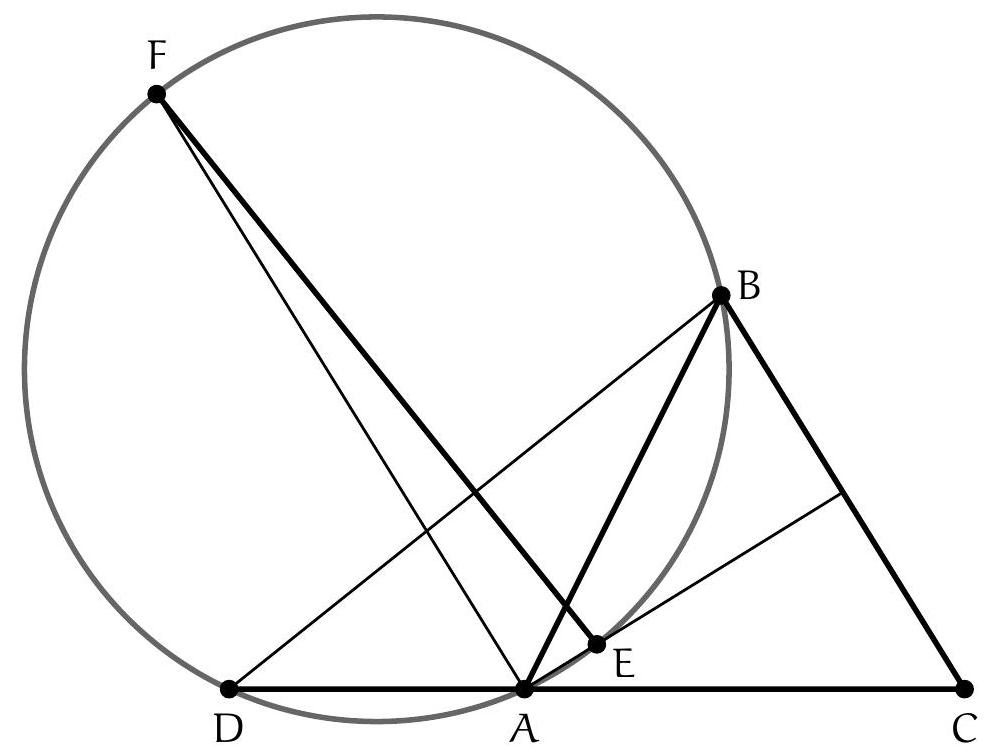
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle isocèle en $A$, et soit $D$ un point sur ( $A C$ ) tel que $A$ soit situé entre C et D , mais ne soit pas le milieu de [CD].
On note $d_{1}$ et $d_{2}$ les bissectrices intérieure et extérieure de l'angle $\widehat{B A C}$, et $\Delta$ la médiatrice de [BD]. Enfin, soit $E$ et $F$ les points d'intersection respectifs de $\Delta$ avec les droites $d_{1}$ et $d_{2}$.
Démontrer que les points $A, D, E$ et $F$ sont cocycliques.
|
Une jolie figure suggère même que les points $A, B, D, E$ et $F$ sont cocycliques : c'est ce que nous allons montrer.
Soit $\Gamma$ le cercle circonscrit à $A B D$, et soit $G_{1}$ et $G_{2}$ les points d'intersection respectifs des droites $d_{1}$ et $d_{2}$ avec $\Gamma$, et autres que $D$ lui-même. Il nous suffit de montrer que $E=G_{1}$ et que $\mathrm{F}=\mathrm{G}_{2}$.
Puisque $\mathrm{d}_{2}$ est la bissectrice extérieure de $\widehat{B A C}$, donc la bissectrice intérieure de $\widehat{B A D}$, le théorème du pôle Sud indique que $\mathrm{G}_{2}$ est équidistant de B et D . De même, $\mathrm{d}_{1}$ est la bissectrice intérieure de $\widehat{B A C}$, donc la bissectrice extérieure de $\widehat{B A D}$, et le théorème du pôle Nord indique que $\mathrm{G}_{1}$ est équidistant de B et D .
Mais alors $\left(G_{1} G_{2}\right)$ est bien la médiatrice de $[B D]$, donc $G_{1}=E$ et $G_{2}=F$, ce qui conclut.

|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2018-2019-Test-26-02-Corrige.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T1",
"year": "2018"
}
|
In a tournament with $n$ players, numbered from 1 to $n$, each pair of players meets exactly once. This meeting ends with one player winning and the other losing. We denote $v_{\mathrm{k}}$ as the number of victories of player $k$ during the tournament, and $d_{k}$ as their number of defeats.
Prove that $\sum_{k=1}^{n} v_{k}^{2}=\sum_{k=1}^{n} d_{k}^{2}$.
|
Since each player has played $n-1$ games and the total number of wins among all players is $n(n-1) / 2$, we know that
$$
\sum_{k=1}^{n} v_{k}=n(n-1) / 2
$$
and that $v_{k}+d_{k}=n-1$ for all $k \leqslant n$. We deduce that
$$
\sum_{k=1}^{n} d_{k}^{2}=\sum_{k=1}^{n}\left(n-1-v_{k}\right)^{2}=n(n-1)^{2}-2(n-1) \sum_{k=1}^{n} v_{k}+\sum_{k=1}^{n} v_{k}^{2}=\sum_{k=1}^{n} v_{k}^{2}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Dans un tournoi auxquels participent $n$ joueurs, numérotés de 1 à $n$, chaque paire de joueurs se rencontre exactement une fois. Cette rencontre se termine par la victoire d'un des deux joueurs et la défaite de l'autre joueur. On note $v_{\mathrm{k}}$ le nombre de victoires du joueur $k$ au cours du tournoi, et $d_{k}$ son nombre de défaites.
Démontrer que $\sum_{k=1}^{n} v_{k}^{2}=\sum_{k=1}^{n} d_{k}^{2}$.
|
Puisque chaque joueur a disputé $n-1$ parties et que l'ensemble des joueurs a totalisé $n(n-1) / 2$ victoires, on sait que
$$
\sum_{k=1}^{n} v_{k}=n(n-1) / 2
$$
et que $v_{k}+d_{k}=n-1$ pour tout $k \leqslant n$. On en déduit que
$$
\sum_{k=1}^{n} d_{k}^{2}=\sum_{k=1}^{n}\left(n-1-v_{k}\right)^{2}=n(n-1)^{2}-2(n-1) \sum_{k=1}^{n} v_{k}+\sum_{k=1}^{n} v_{k}^{2}=\sum_{k=1}^{n} v_{k}^{2}
$$
|
{
"exam": "French_tests",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/tests/fr-2018-2019-Test-26-02-Corrige.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T1",
"year": "2018"
}
|
Carine and Cyril are playing the following game. First, Cyril chooses an integer $\mathrm{n} \geqslant 1$. Then, in each cell of a $3 \times 3$ grid (similar to a tic-tac-toe board), he writes an integer.
Next, it's Carine's turn. She can, as many times as she wishes, perform the following operation: she chooses a cell $\mathbf{c}$, then increases by 1 the value of $\mathbf{c}$ and its neighbors (i.e., the cells that share a side with it). Carine wins the game if she manages to make all 9 integers equal modulo $n$.
Which player has a winning strategy?
|
We will show that Carine has a winning strategy. First, let's adopt some notations. We denote the cell located in row $\boldsymbol{i}$ and column $\mathfrak{j}$ as $(\mathfrak{i}, \mathfrak{j})$, and we denote the integer written on this cell as $k_{i, j}$. Without loss of generality, we assume that our integers are written modulo $n$.
We will also denote $a_{i, j}$ as an action by Carine consisting of choosing the cell $(i, j)$, thus increasing the integers $k_{\hat{i}, \hat{j}}$ such that $|\mathfrak{i}-\hat{\mathfrak{i}}|+|\mathfrak{j}-\hat{j}| \leqslant 1$. Given the winning condition for Carine, we also assume she has an operation $a_{\infty}$ which consists of subtracting 1 from all cells.
Then, by performing the actions $a_{1,1}, a_{3,1}, a_{2,3}$, and $a_{\infty}$, Carine manages to increase the integer $k_{2,1}$ by 1 without changing the others. Similarly, she can increase each of the integers $k_{2,3}, k_{1,2}$, and $k_{3,2}$ individually. We call $b_{2,1,2,3}, b_{1,2}$, and $b_{3,2}$ the corresponding "actions".
Then, by performing the action $a_{1,1}$ and performing the actions $b_{2,1}$ and $b_{1,2}$ $n-1$ times, Carine has increased the integer $k_{1,1}$ without changing the others. Similarly, she can increase the integers $k_{1,3}, k_{3,1}$, and $k_{3,3}$ individually.
Therefore, it is sufficient for her to modify the values of each of the cells other than $(2,2)$ so that all integers become equal, and then she will have won.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
Carine et Cyril jouent au jeu suivant. Tout d'abord, Cyril choisit un entier $\mathrm{n} \geqslant 1$. Puis, dans chacune des cases d'une grille $3 \times 3$ (apparentée à un jeu de morpion), il écrit un entier.
Vient ensuite le tour de Carine. Elle peut, autant de fois qu'elle le souhaite, effectuer l'opération suivante : elle choisit une case $\mathbf{c}$, puis augmente de 1 la valeur de $\mathbf{c}$ et de ses voisines (c'est-à-dire des cases qui partagent un côté avec c). Carine gagne la partie si elle réussit à faire en sorte que les 9 entiers soient tous égaux modulo $n$.
Quel est le joueur qui dispose d'une stratégie gagnante?
|
On va montrer que Carine a une stratégie gagnante. Tout d'abord, adoptons quelques notations. On note ( $\mathfrak{i}, \mathfrak{j}$ ) la case située en ligne $\boldsymbol{i}$ et en colonne $\mathfrak{j}$, et on note $k_{i, j}$ l'entier écrit sur cette case. Sans perte de généralité, on suppose que nos entiers sont écrits modulo $n$.
On va également noter $a_{i, j}$ une action de Carine consistant à choisir la case $(i, j)$, donc à augmenter de 1 les entiers $k_{\hat{i}, \hat{j}}$ tels que $|\mathfrak{i}-\hat{\mathfrak{i}}|+|\mathfrak{j}-\hat{j}| \leqslant 1$. Au vu de la condition de victoire de Carine, on suppose aussi qu'elle dispose d'une opération $a_{\infty}$ qui consiste à ôter 1 à toutes les cases.
Alors, en effectuant les actions $a_{1,1}, a_{3,1}, a_{2,3}$ et $a_{\infty}$, Carine se débrouille pour augmenter $l^{\prime}$ entier $k_{2,1}$ de 1 sans changer les autres. De même, elle peut augmenter isolément chacun des entiers $k_{2,3}, k_{1,2}$ et $k_{3,2}$. On appelle $b_{2,1,2,3}, b_{1,2}$ et $b_{3,2}$ les "actions" correspondantes.
Puis, en réalisant l'action $a_{1,1}$ et en réalisant $n-1$ fois les actions $b_{2,1}$ et $b_{1,2}$, Carine a augmenté l'entier $k_{1,1}$ sans changer les autres. De même, elle peut augmenter isolément les entiers $k_{1,3}, k_{3,1}$ et $k_{3,3}$.
Il lui suffit donc de modifier les valeurs de chacune des cases autres que $(2,2)$ pour que tous les entiers deviennent égaux, et alors elle aura gagné.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2018-2019-Test-27-02-Corrige.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T1",
"year": "2018"
}
|
Find the functions $f: \mathbb{R} \mapsto \mathbb{R}$ such that, for all real numbers $x$ and $y$, we have:
$$
f\left(x^{2}+x+f(y)\right)=y+f(x)+f(x)^{2}
$$
|
First, it is clear that the function $\mathrm{f}: x \mapsto x$ is a solution. We will show that it is the only one.
In the following, we will denote by $E_{x, y}$ the equation $f\left(x^{2}+x+f(y)\right)=y+f(x)+f(x)^{2}$. First, $E_{0, y}$ indicates that $f(f(y))=y+f(0)+f(0)^{2}$, which shows that $f$ is both injective and surjective, hence bijective.
On the other hand, for all real numbers $x$ and $t$, note that $x^{2}+x=t^{2}+t$ if and only if $0=$ $x^{2}-t^{2}+x-t=(x-t)(x+t+1)$, that is, if $x=t$ or $t=-1-x$. In particular, by setting $t=-1-x$, then $E_{x, y}$ and $E_{t, y}$ indicate that $f(x)+(x)^{2}=f(t)+(t)^{2}$. Consequently, if $x \neq-1 / 2$, and since we then have $t \neq x$ and $f$ is injective, we also have $f(t)=-1-f(x)$ and $f(x) \neq-1 / 2$. We deduce in particular that $f(-1 / 2)=-1 / 2$.
We have just shown that $-1 / 2$ is a fixed point of $f$. Now, if $y$ and $x$ are fixed points of $f$, the equation $\mathbf{E}_{x, y}$ shows that $x^{2}+x+y$ is also a fixed point. Similarly, if $x$ and $x^{2}+x+y$ are fixed points of $f$, and since $f$ is bijective, then $y$ is also a fixed point. Here, by choosing $x=-1 / 2$, we observe that as soon as $y$ is a fixed point of $f, y-1 / 4$ and $y+1 / 4$ are also fixed points. In particular, 0 and $1 / 4$ are fixed points.
Under these conditions, $E_{x, 0}$ and $E_{0, y}$ show respectively that $f\left(x^{2}+x\right)=f(x)+f(x)^{2}$ and that $f(f(y))=y$. Then, if $t$ is a positive real number, let $x$ be a real number such that $x^{2}+x=t-1 / 4$. Then $\mathbf{E}_{x, 1 / 4}$ indicates that
$$
\mathbf{f}(\mathbf{t})=\mathbf{f}\left(\mathrm{x}^{2}+x+\mathbf{f}(1 / 4)\right)=1 / 4+\boldsymbol{f}(\mathrm{x})+\mathrm{f}(\mathrm{x})^{2} \geqslant 0
$$
Furthermore, if $z$ is a real number such that $z^{2}+z=\mathrm{t}$, then $\mathbf{E}_{z, \mathrm{f}(\mathrm{y})}$ indicates that
$$
f(t+y)=f(y)+f(z)+f(z)^{2}=f(y)+f\left(z^{2}+z\right)=f(y)+f(t)
$$
We deduce both that $f$ is increasing and that $f$ is in fact additive.
The function $f$ is therefore linear, that is, of the form $f: x \mapsto \lambda x$. We conclude by observing that, since $-1 / 2$ is a fixed point of $f$, it follows that $\lambda=1$, hence that $f$ is indeed the identity function.
|
f(x) = x
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Trouver les fonctions $f: \mathbb{R} \mapsto \mathbb{R}$ telles que, pour tous les réels $x$ et $y$, on ait:
$$
f\left(x^{2}+x+f(y)\right)=y+f(x)+f(x)^{2}
$$
|
Tout d'abord, il est clair que la fonction $\mathrm{f}: x \mapsto x$ est une solution. On va montrer que c'est la seule.
Dans la suite, on notera $E_{x, y}$ l'équation $f\left(x^{2}+x+f(y)\right)=y+f(x)+f(x)^{2}$. En premier lieu, $E_{0, y}$ indique que $f(f(y))=y+f(0)+f(0)^{2}$, ce qui montre que $f$ est à la fois injective et surjective, donc bijective.
D'autre part, pour tous les réels $x$ et $t$, notons que $x^{2}+x=t^{2}+t$ si et seulement si $0=$ $x^{2}-t^{2}+x-t=(x-t)(x+t+1)$, c'est-à-dire si $x=t$ ou $t=-1-x$. En particulier, en posant $t=-1-x$, alors $E_{x, y}$ et $E_{t, y}$ indiquent que $f(x)+(x)^{2}=f(t)+(t)^{2}$. Par conséquent, si $x \neq-1 / 2$, et puisque l'on a alors $t \neq x$ et que $f$ est injective, on a également $f(t)=-1-f(x)$ et $f(x) \neq-1 / 2$. On en déduit notamment que $f(-1 / 2)=-1 / 2$.
On vient de montrer que $-1 / 2$ est un point fixe de $f$. Or, si $y$ et $x$ sont des points fixes de $f$, l'équation $\mathbf{E}_{x, y}$ montre que $x^{2}+x+y$ en est un également. De même, si $x$ et $x^{2}+x+y$ sont des points fixes de $f$, et puisque $f$ est bijective, alors $y$ en est un également. Ici, en choisissant $x=-1 / 2$, on constate donc que, dès lors que $y$ est un point fixe de $f, y-1 / 4$ et $y+1 / 4$ en sont aussi. En particulier, 0 et $1 / 4$ sont des points fixes.
Dans ces conditions, $E_{x, 0}$ et $E_{0, y}$ montrent respectivement que $f\left(x^{2}+x\right)=f(x)+f(x)^{2}$ et que $f(f(y))=y$. Puis, si $t$ est un réel positif, soit $x$ un réel tel que $x^{2}+x=t-1 / 4$. Alors $\mathbf{E}_{x, 1 / 4}$ indique que
$$
\mathbf{f}(\mathbf{t})=\mathbf{f}\left(\left(\mathrm{x}^{2}+x+\mathbf{f}(1 / 4)\right)=1 / 4+\boldsymbol{f}(\mathrm{x})+\mathrm{f}(\mathrm{x})^{2} \geqslant 0\right.
$$
Par ailleurs, si $z$ est un réel tel que $z^{2}+z=\mathrm{t}$, alors $\mathbf{E}_{z, \mathrm{f}(\mathrm{y})}$ indique que
$$
f(t+y)=f(y)+f(z)+f(z)^{2}=f(y)+f\left(z^{2}+z\right)=f(y)+f(t)
$$
On en déduit à la fois que $f$ est croissante et que $f$ est en fait additive.
La fonction $f$ est donc linéaire, c'est-à-dire de la forme $f: x \mapsto \lambda x$. On conclut en observant que, puisque $-1 / 2$ est un point fixe de f , $\mathrm{c}^{\prime}$ est que $\lambda=1$, donc que f est bien la fonction identité.
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2018-2019-Test-27-02-Corrige.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T1",
"year": "2018"
}
|
Let $p$ be a prime number.
Prove that there exists a prime $q$ such that $\mathfrak{n}^{p} \not\equiv p$ for all $n \in \mathbb{Z}$.
|
First, if $p$ does not divide $q-1$, then $x \mapsto x^{p}$ is a bijection of $\mathbb{Z} / q \mathbb{Z}$ onto itself, so $q$ cannot work. We are thus led to seek $q \equiv 1(\bmod p)$ such that for all $n \not \equiv 0(\bmod q), n$ has order $\omega_{q}(n) \neq p \omega_{q}(p)$ modulo $q$, where $\omega_{q}(p)$ is the order of $p$ modulo $q$.
Since the possible orders are exactly the divisors of $q-1$, this means that $q-1$ must be divisible by $p$ and by $\omega_{q}(p)$ but not by $p \omega_{q}(p)$. Consequently, $p$ must necessarily divide $\omega_{q}(p)$, and a first idea would be to check if we can have $\omega_{q}(p)=p$.
In this direction, $q$ must divide $p^{p}-1$ but not $p-1$. Thus, $q$ must divide the integer
$$
\mathbf{N}=\frac{p^{p}-1}{p-1}=1+p+p^{2}+\ldots+p^{p-1}
$$
Under these conditions, if $q$ still divides $p-1$, then $\mathbf{N} \equiv p(\bmod q)$, which is impossible. Thus, we are assured here that $q$ does not divide $p-1$, and therefore that $\omega_{q}(p)=p$.
It remains to ensure that we can choose $q$ so that $q \not \equiv 1\left(\bmod p^{2}\right)$. If such a $q$ did not exist, then $N$ itself would be congruent to $1\left(\bmod p^{2}\right)$. We conclude the problem by noting that $\mathbf{N} \equiv 1+p \not \equiv 1\left(\bmod p^{2}\right)$.
|
proof
|
Incomplete
|
Yes
|
proof
|
Number Theory
|
Soit p un nombre premier.
Démontrer qu'il existe un nombre premier $q$ tel que $\mathfrak{n}^{p} \not \equiv p$ pour tout $n \in \mathbb{Z}$.
|
Tout d'abord, si $p$ ne divise pas $q-1$, alors $x \mapsto x^{p}$ est une bijection de $\mathbb{Z} / q \mathbb{Z}$ dans lui-même, donc $q$ ne peut pas convenir. On en vient à chercher $q \equiv 1(\bmod p)$ tel que, pour tout $n \not \equiv 0(\bmod q), n$ soit d'ordre $\omega_{q}(n) \neq p \omega_{q}(p)$ modulo $q$, où $\omega_{q}(p)$ est l'ordre de $p$ modulo $q$.
Puisque les ordres possibles sont exactement les diviseurs de $q-1$, cela signifie que $q-1$ doit être divisible par $p$ et par $\omega_{q}(p)$ mais pas $p \omega_{q}(p)$. Par conséquent, $p$ doit nécessairement diviser $\omega_{q}(p)$, et une première idée serait de vérifier si on ne peut pas justement avoir $\omega_{q}(p)=p$.
Dans cette optique, $q$ doit diviser $p^{p}-1$ mais pas $p-1$. Ainsi, $q$ doit diviser l'entier
$$
\mathbf{N}=\frac{p^{p}-1}{p-1}=1+p+p^{2}+\ldots+p^{p-1}
$$
Dans ces conditions, si $q$ divise quand même $p-1$, alors $\mathbf{N} \equiv p(\bmod q)$, ce qui est impossible. Ainsi, on est ici assuré que $q$ ne divise pas $p-1$, donc que $\omega_{q}(p)=p$.
Il reste donc à s'assurer que l'on peut choisir $q$ de sorte que $q \not \equiv 1\left(\bmod p^{2}\right)$. Si un tel $q$ $n^{\prime}$ existait pas, alors $N$ lui même serait congru à $1\left(\bmod p^{2}\right)$. On conclut donc le problème en remarquant que $\mathbf{N} \equiv 1+p \not \equiv 1\left(\bmod p^{2}\right)$.
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2018-2019-Test-27-02-Corrige.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T1",
"year": "2018"
}
|
A country comprises $2018 n+1$ cities, where $n$ is a non-zero natural number. Some pairs of cities are connected by direct railway lines, such that there is at most one line between any two cities; each line is bidirectional. The distance between two cities $A$ and $B$ is then the minimum number of lines to take to go from $A$ to $B$.
Find the set of integers $n$ for which it is possible to construct a railway network that meets the following criterion:
For any city $C$ and for any $i \in\{1,2, \ldots, 2018\}$, there are exactly $n$ cities at distance $i$ from $C$.
|
In what follows, we will of course reinterpret the statement in terms of graphs, and we will show that the integers $n$ sought are the even integers.
Suppose first that we have an integer $n$ and a graph satisfying the criterion of the statement. Then every vertex has degree $n$. The sum of the degrees of the vertices of the graph is therefore $(2018 n+1) n$. Now, this sum is always even. We deduce that
$$
n \equiv (2018 n+1) n \equiv 0 \quad(\bmod 2)
$$
that is, $n$ is even.
Conversely, if $n$ is even, we first form a cycle of $2018 n+1$ vertices. Then we add auxiliary edges between two vertices $u$ and $v$ whenever the distance between $u$ and $v$ (in our cycle without auxiliary edges) is between 2 and $n / 2$. It is then easy to verify that this graph (with auxiliary edges) satisfies the criterion of the statement.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Un pays comprend $2018 n+1$ villes, où $n$ est un entier naturel non nul. Certaines paires de villes sont reliées par des lignes directes de chemin de fer, de sorte qu'il y ait au plus une ligne entre deux villes ; chaque ligne va dans les deux sens. La distance entre deux villes $A$ et $B$ est alors le nombre minimal de lignes à prendre pour aller de $A$ à $B$.
Trouver l'ensemble des entiers $n$ pour lesquels il possible de construire un réseau ferré respectant le critère suivant:
Pour toute ville C et pour tout $i \in\{1,2, \ldots, 2018\}$, il y a exactement $n$ villes à distance $i$ de $C$.
|
Dans toute la suite, on va bien sûr réinterpréter l'énoncé en termes de graphes, et on va montrer que les entiers n recherchés sont les entiers pairs.
Supposons d'abord que l'on dispose d'un entier $n$ et d'un graphe respectant le critère de l'énoncé. Alors tout sommet est de degré $n$. La somme des degrés des sommets du graphe vaut donc $(2018 n+1) n$. Or, cette somme est toujours paire. On en déduit que
$$
n \equiv(2018 n+1) n \equiv 0 \quad(\bmod 2)
$$
c'est-à-dire que $n$ est pair.
Réciproquement, si $n$ est pair, on forme d'abord un cycle de $2018 n+1$ sommets. Puis on rajoute des arêtes auxiliaires entre deux sommets $u$ et $v$ dès lors que la distance entre $u$ et $v$ (dans notre cycle sans arêtes auxiliaires) est comprise entre 2 et $n / 2$. Il est alors aisé de vérifier que ce graphe (avec arêtes auxiliaires) respecte le critère de l'énoncé.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2018-2019-Test_RMM_28_novembre_corrige.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T1",
"year": "2018"
}
|
We have, in the plane, 16 distinct points, which we denote by $A_{i, j}$ for $i, j \in\{1,2,3,4\}$. These points satisfy the following alignment and cocyclicity relations:
$\triangleright$ for all $i \in\{1,2,3,4\}$, the points $A_{i, 1}, A_{i, 2}, A_{i, 3}$, and $A_{i, 4}$ are collinear;
$\triangleright$ for all $j \in\{1,2,3,4\}$, the points $A_{1, j}, A_{2, j}, A_{3, j}$, and $A_{4, j}$ are collinear;
$\triangleright$ the quadrilaterals $A_{1,1} A_{1,2} A_{2,2} A_{2,1}, A_{2,1} A_{2,2} A_{3,2} A_{3,1}, A_{3,1} A_{3,2} A_{4,2} A_{4,1}, A_{1,2} A_{1,3} A_{2,3} A_{2,2}$, $A_{1,3} A_{1,4} A_{2,4} A_{2,3}, A_{1,1} A_{2,2} A_{2,3} A_{1,4}$, and $A_{1,1} A_{2,2} A_{3,2} A_{4,1}$ are cyclic.
Show that the quadrilateral $A_{4,1} A_{3,2} A_{3,3} A_{4,4}$ is also cyclic.
Note: a quadrilateral is said to be cyclic if its four vertices lie on the same circle.
|
Below, we will denote $\Delta_{i}$ as the line $\left(A_{i, 1} A_{i, 2}\right)$ and $\Delta^{j}$ as the line $\left(A_{1, j} A_{2, j}\right)$. A figure and angle chasing show that the lines $\Delta_{1}$ and $\Delta_{3}$ are parallel, since ( $\Delta_{1}, \Delta^{1}$ ) $\equiv$ $\left(\Delta^{2}, \Delta_{2}\right) \equiv\left(\Delta_{3}, \Delta^{1}\right)\left(\bmod 180^{\circ}\right)$. Similarly, we know that $\Delta_{2} / / \Delta_{4}$, that $\Delta^{1} / / \Delta^{3}$ and that $\Delta^{2} / / \Delta^{4}$.
Thus, and provided that the quadrilateral $A_{1,1} A_{1,2} A_{2,2} A_{2,1}$ formed by the lines $\Delta_{1}, \Delta^{1}$, $\Delta_{2}$ and $\Delta^{2}$ is cyclic, it suffices to define the point $A_{i, j}$ as the intersection of $\Delta_{i}$ and $\Delta^{j}$ to ensure our alignment relations and to be certain that our first five quadrilaterals are cyclic. In particular, by angle chasing, each quadrilateral $A_{i, j} A_{i+1, j} A_{i+1, j+1} A_{i, j+1}$ is then cyclic.
In the following, we will assume these alignment and cocyclicity relations are established, and we now focus on the quadrilateral $A_{1,1} A_{2,2} A_{2,3} A_{1,4}$. Given the symmetric role it seems to play with the quadrilaterals $A_{1,1} A_{2,2} A_{3,2} A_{4,1}$ on one hand and $A_{1,1} A_{2,2} A_{3,2} A_{4,1}$ on the other, it would be good to find a simple criterion that is equivalent to its cyclic nature.
This criterion only involves the lines $\Delta_{1}$ and $\Delta_{2}$ on one hand, and the four lines $\Delta^{j}$ on the other, with the pairs $\left(\Delta^{1}, \Delta^{2}\right)$ and $\left(\Delta^{3}, \Delta^{4}\right)$ playing symmetric roles. This leads us to consider the intersection points $X=\Delta_{1} \cap \Delta_{2}, Y=\Delta^{1} \cap \Delta^{2}$ and $Z=\Delta^{3} \cap \Delta^{4}$, which the figure seems to show are collinear. This suggests the following lemma.
Lemma: The quadrilateral $A_{1,1} A_{2,2} A_{2,3} A_{1,4}$ is cyclic if and only if $X$, $Y$ and $Z$ are collinear. Proof: Suppose first that $\mathrm{X}, \mathrm{Y}$, and $Z$ are collinear. Thales' theorem then indicates that the quadrilaterals $A_{1,1} A_{1,2} A_{2,2} A_{2,1}$ and $A_{1,3} A_{2,3} A_{2,4} A_{3,4}$ are homothetic to each other, so $\left(A_{2,1} A_{1,2}\right) / /\left(A_{2,3} A_{1,4}\right)$. We deduce that ( $\left.A_{1,1} A_{1,4}, A_{1,1} A_{2,2}\right) \equiv\left(A_{1,1} A_{1,2}, A_{1,1} A_{2,2}\right) \equiv$ $\left(A_{2,1} A_{1,2}, A_{2,1} A_{2,2}\right) \equiv\left(A_{2,3} A_{1,4}, A_{2,3} A_{2,2}\right)\left(\bmod 180^{\circ}\right)$, which means that $A_{1,1} A_{1,4} A_{2,3} A_{2,2}$ is indeed cyclic.
Conversely, once the lines $\Delta_{1}, \Delta_{2}, \Delta^{1}, \Delta^{2}$ and $\Delta^{3}$ are fixed, the point $A_{4,1}$ and then the line $\Delta^{4}$ are uniquely defined, so $Z$ must necessarily be collinear with $X$ and $Y$.
We also take $T=\Delta_{3} \cap \Delta_{4}$. Here, since $A_{1,1} A_{2,2} A_{2,3} A_{1,4}$ and $A_{1,1} A_{2,2} A_{3,2} A_{4,1}$ are cyclic, the lemma shows the collinearity of the points $X, Y$ and $Z$, and $X, Y$ and $T$ respectively. Thus, the points $T, Y$ and $Z$ are collinear, and the lemma shows this time that the quadrilateral $A_{4,1} A_{3,2} A_{3,3} A_{4,4}$ is cyclic.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
On dispose, dans le plan, 16 points deux à deux distincts, que l'on note $A_{i, j}$ pour $i, j \in\{1,2,3,4\}$. Ces points vérifient les relations d'alignement et de cocyclicité suivantes :
$\triangleright$ pour tout $i \in\{1,2,3,4\}$, les points $A_{i, 1}, A_{i, 2}, A_{i, 3}$ et $A_{i, 4}$ sont alignés;
$\triangleright$ pour tout $j \in\{1,2,3,4\}$, les points $A_{1, j}, A_{2, j}, A_{3, j}$ et $A_{4, j}$ sont alignés;
$\triangleright$ les quadrilatères $A_{1,1} A_{1,2} A_{2,2} A_{2,1}, A_{2,1} A_{2,2} A_{3,2} A_{3,1}, A_{3,1} A_{3,2} A_{4,2} A_{4,1}, A_{1,2} A_{1,3} A_{2,3} A_{2,2}$, $A_{1,3} A_{1,4} A_{2,4} A_{2,3}, A_{1,1} A_{2,2} A_{2,3} A_{1,4}$ et $A_{1,1} A_{2,2} A_{3,2} A_{4,1}$ sont cycliques.
Montrer que le quadrilatère $A_{4,1} A_{3,2} A_{3,3} A_{4,4}$ est lui aussi cyclique.
Note: on dit qu'un quadrilatère est cyclique si ses quatre sommets sont sur un même cercle.
|
Ci-dessous, on notera $\Delta_{i}$ la droite $\left(A_{i, 1} A_{i, 2}\right)$ et $\Delta^{j}$ la droite $\left(A_{1, j} A_{2, j}\right)$. Une figure et une chasse aux angles nous montrent que les droites $\Delta_{1}$ et $\Delta_{3}$ sont parallèles, puisque ( $\Delta_{1}, \Delta^{1}$ ) $\equiv$ $\left(\Delta^{2}, \Delta_{2}\right) \equiv\left(\Delta_{3}, \Delta^{1}\right)\left(\bmod 180^{\circ}\right)$. De même, on sait que $\Delta_{2} / / \Delta_{4}$, que $\Delta^{1} / / \Delta^{3}$ et que $\Delta^{2} / / \Delta^{4}$.
Ce faisant, et sous réserve que le quadrilatère $A_{1,1} A_{1,2} A_{2,2} A_{2,1}$ formé par les droites $\Delta_{1}, \Delta^{1}$, $\Delta_{2}$ et $\Delta^{2}$ soit cyclique, il suffit de définir le point $A_{i, j}$ comme le point d'intersection de $\Delta_{i}$ et $\Delta^{j}$ pour être assuré de nos relations d'alginement, et pour être certain que nos cinq premiers quadrilatères sont cycliques. En particulier, toujours par chasse aux angles, chaque quadrilatère $A_{i, j} A_{i+1, j} A_{i+1, j+1} A_{i, j+1}$ est alors cyclique.
Dans toute la suite, on supposera ces relations d'alignement et de cocyclicité acquises, et on s'intéresse maintenant au quadrilatère $A_{1,1} A_{2,2} A_{2,3} A_{1,4}$. Vu le rôle symétrique qu'il semble jouer avec les quadrilatères $A_{1,1} A_{2,2} A_{3,2} A_{4,1}$ d'une part et $A_{1,1} A_{2,2} A_{3,2} A_{4,1}$ d'autre part, il serait bon de trouver un critère simple qui soit équivalent avec son caractère cyclique.
Or, il ne met en jeu que les droites $\Delta_{1}$ et $\Delta_{2}$ d'une part, et les quatre droites $\Delta^{j}$ d'autre part, les paires $\left(\Delta^{1}, \Delta^{2}\right)$ et $\left(\Delta^{3}, \Delta^{4}\right)$ jouant des rôles symétriques. On en vient alors à considérer les points d'intersection $X=\Delta_{1} \cap \Delta_{2}, Y=\Delta^{1} \cap \Delta^{2}$ et $Z=\Delta^{3} \cap \Delta^{4}$, dont la figure semble montrer qu'ils sont alignés. Cela suggère le lemme suivant.
Lemme: Le quadrilatère $A_{1,1} A_{2,2} A_{2,3} A_{1,4}$ est cyclique si et seulement si $X$, $Y$ et $Z$ sont alignés. Démonstration : Supposons d'abord $\mathrm{X}, \mathrm{Y}$ et Z alignés. Le théorème de Thalès indique alors que les quadrilatères $A_{1,1} A_{1,2} A_{2,2} A_{2,1}$ et $A_{1,3} A_{2,3} A_{2,4} A_{3,4}$ sont homothétiques l'un de l'autre, doncque $\left(A_{2,1} A_{1,2}\right) / /\left(A_{2,3} A_{1,4}\right)$. On en déduit que ( $\left.A_{1,1} A_{1,4}, A_{1,1} A_{2,2}\right) \equiv\left(A_{1,1} A_{1,2}, A_{1,1} A_{2,2}\right) \equiv$ $\left(A_{2,1} A_{1,2}, A_{2,1} A_{2,2}\right) \equiv\left(A_{2,3} A_{1,4}, A_{2,3} A_{2,2}\right)\left(\bmod 180^{\circ}\right)$, ce qui signifie que $A_{1,1} A_{1,4} A_{2,3} A_{2,2}$ est bien cyclique.
Réciproquement, une fois fixées les droites $\Delta_{1}, \Delta_{2}, \Delta^{1}, \Delta^{2}$ et $\Delta^{3}$, le point $A_{4,1}$ puis la droite $\Delta^{4}$ sont définis de manière unique, donc $Z$ se retrouve nécessairement aligné avec $X$ et $Y$.
On en profite aussi pour poser $T=\Delta_{3} \cap \Delta_{4}$. Ici, puisque $A_{1,1} A_{2,2} A_{2,3} A_{1,4}$ et $A_{1,1} A_{2,2} A_{3,2} A_{4,1}$ sont cycliques, le lemme montre l'alignement des points $X, Y$ et $Z$, et $X, Y$ et $T$ d'autre part. Ainsi, les points $T, Y$ et $Z$ sont alignés, et le lemme montre cette fois-ci que le quadrilatère $A_{4,1} A_{3,2} A_{3,3} A_{4,4}$ est cyclique.
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2018-2019-Test_RMM_28_novembre_corrige.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T1",
"year": "2018"
}
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.