problem
stringlengths 14
10.4k
| solution
stringlengths 1
24.1k
| answer
stringlengths 1
250
⌀ | problem_is_valid
stringclasses 4
values | solution_is_valid
stringclasses 3
values | question_type
stringclasses 4
values | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
10.4k
| solution_raw
stringlengths 1
24.1k
| metadata
dict |
|---|---|---|---|---|---|---|---|---|---|
It is said that an integer $k$ is olympic if there exist four integers $a, b, c$ and $d$, all coprime with $k$, such that $k$ divides $a^{4}+b^{4}+c^{4}+d^{4}$. Let $n$ be any integer.
Show that $n^{2}-2$ is olympic.
|
Let $p_{1}^{\alpha_{1}} \cdots p_{\ell}^{\alpha_{\ell}}$ be the prime factorization of $n^{2}-2$. Thanks to the Chinese Remainder Theorem, it suffices to show that each of the integers $p_{i}^{\alpha_{i}}$ is Olympic.
Suppose first that $p_{i}=2$. Since $n^{2}-2 \equiv\{2,3\}(\bmod 4)$, we know that $\alpha_{i} \leqslant 1$. Clearly, 2 is Olympic, since $1+1+1+1 \equiv 0(\bmod 2)$.
Now consider an odd prime divisor $p$ of $n^{2}-2$. Since 2 is not a square modulo 3 or 5, we know that $p \geqslant 7$. Furthermore, if $p^{\alpha}$ is Olympic, then $p$ is clearly so as well. Conversely, if $p$ is Olympic (and odd), Hensel's lemma shows that the fourth powers modulo $p^{k}$ are exactly the integers whose residues (modulo $p$) are fourth powers modulo $p$, and it follows that $p^{\alpha}$ is also Olympic.
We are thus reduced to showing that every prime $p \geqslant 7$ such that 2 is a square modulo $p$ is Olympic. We will proceed by case analysis, depending on the value of $p$ modulo 4 or 8. However, we first recall Fermat's little theorem, which states that the order $\omega_{p}(x)$ of an invertible element modulo $p$ must divide $p-1$. We also recall that $\mathbb{Z} / p \mathbb{Z}$ contains an element of order $p-1$, as indicated by Theorem 17 of the POFM Arithmetic course on the properties of $\mathbb{Z} / \mathrm{n} \mathbb{Z}$. We deduce the following lemma.
Lemma: The $k$-th powers are the elements $x$ whose order $\omega_{p}(x)$ divides $(p-1) / \delta$, where $\delta=\operatorname{GCD}(k, p-1)$.
Proof: Let $z$ be an element of order $p-1$. The $k$-th powers are the elements of the form $z^{a k+b(p-1)}$, with $a$ and $b$ integers, i.e., the elements of the form $z^{\mathrm{c} \delta}$ with $c$ an integer. The order of these elements modulo $p$ clearly divides $(p-1) / \delta$.
Conversely, $\omega_{p}(x)$ divides $(p-1) / \delta$ if and only if $x$ is one of the roots of the polynomial $P(X)=1-X^{(\mathfrak{p}-1) / \delta}$. However, the elements of the form $z^{\mathfrak{c} \delta}$ already constitute $(p-1) / \delta$ roots of $P(X)$. Therefore, the $k$-th powers are exactly the roots of $P(X)$, which concludes the proof of the lemma.
We finally proceed with the case analysis announced above.
1. If $p \equiv 1(\bmod 8)$, and since -1 is of order 2, it is a fourth power. Since $0 \equiv 1+1+(-1)+(-1)(\bmod p)$, the integer $p$ is Olympic.
2. If $p \equiv 5(\bmod 8)$, then -1 is a square. Let $i$ and $-i$ be its square roots. They are of order 4, so they are not squares. However, $(1+i)^{2} \equiv 2 i(\bmod p)$. Since the set of squares is closed under product and inverse (and thus division), 2 is not a square, which actually means that $p$ does not divide $n^{2}-2$. This case is therefore impossible.
3. If $p \equiv 3(\bmod 4)$, then being a fourth power is in fact the same as being a square. It suffices to show that 0 is a sum of four non-zero squares modulo $p$.
We will first show that it is a sum of $\ell$ non-zero squares, with $2 \leqslant \ell \leqslant 4$. Indeed, let $Q$ be the set of squares. Note that $|Q|=(p+1) / 2$, since every non-zero square has exactly two square roots modulo $p$. Thus, for any $k \in \mathbb{Z} / p \mathbb{Z}$, and by the pigeonhole principle, the set $(k-Q) \cap Q$ is non-empty, which means that $k$ is a sum of two squares. If $k \neq 0$, one of these squares is even non-zero. But then, by writing $0 \equiv k+(-k)(\bmod p)$, we can indeed write 0 as a sum of four squares, at least two of which are non-zero.
Furthermore, by the identity $k^{2} \equiv(3 k / 5)^{2}+(4 k / 5)^{2}(\bmod p)$, every non-zero square is in fact a sum of two non-zero squares. Consequently, 0 is indeed a sum of four non-zero squares, which means that $p$ is Olympic.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
On dit qu'un entier $k$ est olympique s'il existe quatre entiers $a, b, c$ et $d$, tous premiers avec $k$, tels que $k$ divise $a^{4}+b^{4}+c^{4}+d^{4}$. Soit $n$ un entier quelconque.
Montrer que $n^{2}-2$ est olympique.
|
Soit $p_{1}^{\alpha_{1}} \cdots p_{\ell}^{\alpha_{\ell}}$ la décomposition de $n^{2}-2$ en produits de facteurs premiers. Grâce au théorème Chinois, il nous suffit en fait de montrer que chacun des entiers $p_{i}^{\alpha_{i}}$ est olympique.
Supposons tout d'abord que $p_{i}=2$. Puisque $n^{2}-2 \equiv\{2,3\}(\bmod 4)$, on sait que $\alpha_{i} \leqslant 1$. Or, il est clair que 2 est olympique, puisque $1+1+1+1 \equiv 0(\bmod 2)$.
On considère maintenant un diviseur premier $p$ impair de $n^{2}-2$. Puisque 2 n'est pas carré modulo 3 ou 5 , on sait en fait que $p \geqslant 7$. Par ailleurs, si $p^{\alpha}$ est olympique, alors $p$ l'est clairement lui aussi. Réciproquement, si $p$ est olympique (et impair), le lemme de Hensel montre que les puissances $4{ }^{\text {èmes }}$ modulo $p^{k}$ sont exactement les entiers dont les résidus (modulo $p$ ) sont des puissances $4^{\text {èmes }}$ modulo $p$, et il s'ensuit que $p^{\alpha}$ est également olympique.
On se ramène donc à montrer que tout nombre premier $p \geqslant 7$ tel que 2 soit un carré modulo $p$ est olympique. On va procéder par disjonction de cas, selon la valeur de $p$ modulo 4 ou 8 . Cependant, on rappelle d'abord le petit théorème de Fermat, qui stipule que l'ordre $\omega_{p}(x)$ d'un élément inversible modulo $p$ doit diviser $p-1$. On rappelle également que $\mathbb{Z} / p \mathbb{Z}$
contient un élément d'ordre $p-1$, comme l'indique le Théorème 17 du cours d'Arithmétique de la POFM sur les propriétés de $\mathbb{Z} / \mathrm{n} \mathbb{Z}$. On en déduit le lemme suivant.
Lemme : Les puissances $k^{\text {èmes }}$ sont les éléments $x$ dont l'ordre $\omega_{p}(x)$ divise $(p-1) / \delta$, où $\delta=\operatorname{PGCD}(k, p-1)$.
Démonstration : Soit $z$ un élément d'ordre $p-1$. Les puissances $k^{\text {èmes }}$ sont les éléments de la forme $z^{a k+b(p-1)}$, avec a et b entiers, c'est-à-dire les éléments de la forme $z^{\mathrm{c} \mathrm{\delta}}$ avec c entier. L'ordre de ces éléments modulo $p$ divise clairement $(p-1) / \delta$.
Réciproquement, $\omega_{p}(x)$ divise $(p-1) / \delta$ si et seulement si $x$ est une des racines du polynôme $P(X)=1-X^{(\mathfrak{p}-1) / \delta}$. Or, les éléments de la forme $z^{\mathfrak{c} \delta}$ constituent déjà $(p-1) / \delta$ racines de $P(X)$. Par conséquent, les puissances ${ }^{k e \text { èmes }}$ sont exactement les racines de $P(X)$, ce qui conclut la preuve du lemme.
On procède enfin à la disjonction de cas annoncée ci-dessus.
1. Si $p \equiv 1(\bmod 8)$, et puisque -1 est d'ordre 2 , c'est une puissance $4^{\text {ème }}$. Comme $0 \equiv$ $1+1+(-1)+(-1)(\bmod p)$, l'entier $p$ est olympique.
2. Si $p \equiv 5(\bmod 8)$, alors -1 est un carré. Soit $i$ et $-i$ ses racines carrées. Elles sont d'ordre 4 , donc ce ne sont pas des carrés. Or, $(1+i)^{2} \equiv 2 i(\bmod p)$. Puisque l'ensemble des carrés est clos par produit et par inverse (donc par division), 2 n'est donc pas un carré, ce qui signifiait en fait que $p$ ne divisait pas $n^{2}-2$. Ce cas s'avère donc impossible.
3. Si $p \equiv 3(\bmod 4)$, alors être une puissance $4{ }^{\text {ème }}$ revient en fait à être un carré. Il suffit donc de montrer que 0 est somme de quatre carrés non nuls modulo $p$.
On va d'abord montrer que c'est une somme de $\ell$ carrés non nuls, avec $2 \leqslant \ell \leqslant 4$. En effet, soit Q l'ensemble des carrés. Notons que $|Q|=(p+1) / 2$, puisque tout carré non nul a exactement deux racines carrés modulo $p$. Ainsi, pour tout $k \in \mathbb{Z} / p \mathbb{Z}$, et par principe des tiroirs, $l^{\prime}$ ensemble $(k-Q) \cap Q$ est non vide, ce qui signifie que $k$ est somme de deux carrés. Si $k \neq 0$, l'un de ces carrés est même non nul. Mais alors, en écrivant $0 \equiv k+(-k)(\bmod p)$, on peut bien écrire 0 comme une somme de quatre carrés dont au moins deux sont non nuls.
Puis, en vertu de l'identité $k^{2} \equiv(3 k / 5)^{2}+(4 k / 5)^{2}(\bmod p)$, tout carré non nul est en fait somme de deux carrés non nuls. Par conséquent, 0 est bien somme de quatre carrés non nuls, ce qui signifie que $p$ est olympique.
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2018-2019-Test_RMM_28_novembre_corrige.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T1",
"year": "2018"
}
|
Let $x$ and $y$ be two real numbers. We define
$$
M=\max \{x y+1, x y-x-y+3,-2 x y+x+y+2\} .
$$
Prove that $M \geqslant 2$, and determine the cases of equality.
|
Among the three numbers $x y+1, x y-x-y+3$ and $-2 x y+x+y+2$, we denote $K$ as the smallest, $L$ as the second smallest, and $M$ as the largest. Therefore, $K \leqslant L \leqslant M$ and
$$
3 M \geqslant K+L+M=(x y+1)+(x y-x-y+3)+(-2 x y+x+y+2)=6,
$$
which means that $M \geqslant 2$.
Furthermore, if $M=2$, the inequalities $K \leqslant L \leqslant M$ are in fact equalities, which means that
$$
x y+1=x y-x-y+3=-2 x y+x+y+2=2
$$
Let $p$ be the product $x y$ and $s$ be the sum $x+y$. The equalities in equation (1) are satisfied if and only if $p=1$ and $s=2$.
The arithmetic-geometric mean inequality generally indicates that
$$
\frac{s^{2}}{4}=\left(\frac{x+y}{2}\right)^{2} \geqslant x y=p
$$
with equality if and only if $x=y$. This result can also be seen if we note that
$$
\left(\frac{x+y}{2}\right)^{2}=\left(\frac{x-y}{2}\right)^{2}+x y
$$
Here, since we want to have $s^{2} / 4=1=p$, we must also have $x=y$, so that $x=y=1$.
Finally, conversely, if $x=y=1$, we can easily verify that
$$
x y+1=x y-x-y+3=-2 x y+x+y+2=2
$$
so that $M=2$ as well.
|
M=2
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $x$ et $y$ deux nombres réels. On pose
$$
M=\max \{x y+1, x y-x-y+3,-2 x y+x+y+2\} .
$$
Démontrer que $M \geqslant 2$, et déterminer les cas d'égalité.
|
Parmi les trois nombres $x y+1, x y-x-y+3$ et $-2 x y+x+y+2$, on note $K$ le plus petit, $L$ le deuxième plus petit et $M$ le plus grand. Alors $K \leqslant L \leqslant M$ donc
$$
3 M \geqslant K+L+M=(x y+1)+(x y-x-y+3)+(-2 x y+x+y+2)=6,
$$
ce qui signifie que $M \geqslant 2$.
En outre, si $M=2$, les inégalités $K \leqslant L \leqslant M$ sont en fait des égalités, ce qui signifie que
$$
x y+1=x y-x-y+3=-2 x y+x+y+2=2
$$
En notant $p$ le produit $x y$ et $s$ la somme $x+y$, les égalités de l'équation (1) sont vérifiées si et seulement si $p=1$ et $s=2$.
Or, l'inégalité arithmético-géométrique indique, de manière générale, que
$$
\frac{s^{2}}{4}=\left(\frac{x+y}{2}\right)^{2} \geqslant x y=p
$$
avec égalité si et seulement si $x=y$. Ce résultat se retrouve bien si l'on remarque que
$$
\left(\frac{x+y}{2}\right)^{2}=\left(\frac{x-y}{2}\right)^{2}+x y
$$
Ici, puisque l'on souhaite avoir $s^{2} / 4=1=p$, il nous faut donc également avoir $x=y$, de sorte que $x=y=1$.
Enfin, réciproquement, on vérifie aisément, si $x=y=1$, que
$$
x y+1=x y-x-y+3=-2 x y+x+y+2=2
$$
de sorte que $M=2$ également.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web-05-2020.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T1",
"year": "2019"
}
|
Let $x$ and $y$ be two real numbers. We define
$$
M=\max \{x y+1, x y-x-y+3,-2 x y+x+y+2\} .
$$
Prove that $M \geqslant 2$, and determine the cases of equality.
|
$n^{\circ} 1$ Here is another way to prove that the equalities of equation (1) are satisfied if and only if $x=y=1$. First, if $x=y=1$, these equalities are clearly satisfied.
Conversely, if they are satisfied, then the equality $x y-x-y+3=2$ can be rewritten as $0=x y-x-y+1=(x-1)(y-1)$. Since $x$ and $y$ play symmetric roles, we can assume, without loss of generality, that $x=1$. For the equality $x y+1=2$ to be satisfied, it is then necessary that $y=1$, which concludes the proof here.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $x$ et $y$ deux nombres réels. On pose
$$
M=\max \{x y+1, x y-x-y+3,-2 x y+x+y+2\} .
$$
Démontrer que $M \geqslant 2$, et déterminer les cas d'égalité.
|
$n^{\circ} 1$ Voici une autre manière de démontrer que les égalités de l'équation (1) sont vérifiées si et seulement si $x=y=1$. Tout d'abord, si $x=y=1$, ces égalités sont clairement vérifiées.
Réciproquement, si elles sont vérifiées, alors on peut réécrire l'égalité $x y-x-y+3=2$ comme $0=x y-x-y+1=(x-1)(y-1)$. Puisque $x$ et $y$ jouent des rôles symétriques, on peut supposer, sans perte de généralité, que $x=1$. Pour que l'égalité $x y+1=2$ soit vérifiée, il est alors nécessaire que $y=1$, ce qui conclut ici.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web-05-2020.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2019"
}
|
Let $x$ and $y$ be two real numbers. We define
$$
M=\max \{x y+1, x y-x-y+3,-2 x y+x+y+2\} .
$$
Prove that $M \geqslant 2$, and determine the cases of equality.
|
$n^{\circ} 2$ The idea of introducing the variables $p$ and $s$, as in the first solution, or directly using the equality $x y - x - y + 3 = 2$ to obtain a factorization, as in the second solution, might seem miraculous. Of course, this is not the case, and these approaches actually stem from what are known as Viète's formulas.
These formulas state that $x$ and $y$ are the two roots, possibly identical, of the polynomial
$$
P(X) = (X - x)(X - y) = X^2 - (x + y)X + xy = X^2 - sX + p.
$$
Since the equalities in equation (1) are symmetric in $x$ and $y$, a general result (which holds even if we had three unknowns $x, y$, and $z$, or even any number of unknowns) allows us to express them directly in terms of the values taken by the polynomial $P$.
For example, the equalities $p + 1 = 2$, $p - s + 3 = 2$, and $-2p + s + 2 = 2$ can be rewritten as $P(0) = 1$, $P(1) = 0$, and $P(1/2) = 1/4$. Here, the equality $P(1) = 0$ means precisely that $(x - 1)(y - 1) = 0$, which is the factorization used in our second solution.
We could also proceed more systematically. Indeed, since $P(1) = 0$, we know that the polynomial $P(X)$ is divisible by $X - 1$. We can therefore write it in the form $P(X) = (X - 1)(X - a)$, and then verify that $P(0) = a$, and thus that $P(X) = (X - 1)^2$.
If we had been less lucky and had not identified a root of our polynomial $P$, it would still have been possible to write $P$ as a Lagrange interpolation polynomial. Here, this method allows us to write
$$
\begin{aligned}
P(X) & = \frac{X - 1}{0 - 1} \frac{X - 1/2}{0 - 1/2} P(0) + \frac{X - 1}{1/2 - 1} \frac{X - 0}{1/2 - 0} P(1/2) + \frac{X - 1/2}{1 - 1/2} \frac{X - 0}{1 - 0} P(1) \\
& = 2(X - 1)(X - 1/2) - X(X - 1) = X^2 - 2X + 1 = (X - 1)^2
\end{aligned}
$$
from which it follows that the two roots of $P$ are $x = y = 1$.
Comment from the graders: The exercise was generally well solved. Few students noticed that the first inequality was a simple consequence of the fact that the maximum is greater than the arithmetic mean.
Be careful with handling inequalities: some students wrote that $xy < 1$ and $x + y \geq xy$ to conclude that $x + y \geq 1$, which is not true. Other students proved the required inequality but forgot to consider the equality cases, which was an important part of the exercise: unlike equality cases in classical inequalities, this one was harder to find, and asserting without proof that $x = y = 1$ was not sufficient.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $x$ et $y$ deux nombres réels. On pose
$$
M=\max \{x y+1, x y-x-y+3,-2 x y+x+y+2\} .
$$
Démontrer que $M \geqslant 2$, et déterminer les cas d'égalité.
|
$n^{\circ} 2$ Avoir pensé à introduire les variables $p$ et $s$, comme dans la première solution, ou bien à utiliser directement l'égalité $x y-x-y+3=2$ pour obtenir une factorisation, comme dans la deuxième solution, pourrait passer pour miraculeux. Il n'en est bien sûr rien, et ces approchent découlent en fait de ce que l'on appelle les relations de Viète.
Ces relations consistent à dire que $x$ et $y$ sont les deux racines, éventuellement confondues, du polynôme
$$
P(X)=(X-x)(X-y)=X^{2}-(x+y) X+x y=X^{2}-s X+p .
$$
Puisque les égalités de l'équation (1) sont symétriques en $x$ et en $y$, un résultat général (valable même si on avait eu trois inconnues $x, y$ et $z$, ou même un nombre quelconque d'inconnues) permet en fait de démontrer qu'elles peuvent s'exprimer directement à partir des valeurs que prend le polynôme $P$.
Par exemple, les égalités $p+1=2, p-s+3=2$ et $-2 p+s+2=2$ peuvent se réécrire comme $P(0)=1, P(1)=0$ et $P(1 / 2)=1 / 4$. Ici, l'égalité $P(1)=0$ signifie précisément que $(x-1)(y-1)=0$, ce qui est la factorisation utilisée dans notre deuxième solution.
On pourrait également procéder de manière plus systématique. En effet, puisque $P(1)=0$, on sait que le polynôme $P(X)$ est divisible par $X-1$. On peut donc l'écrire sous la forme $P(X)=(X-1)(X-a)$, puis vérifier que $P(0)=a$, et donc que $P(X)=(X-1)^{2}$.
Si l'on avait été moins chanceux, et que l'on n'avait pas identifié de racine de notre polynôme $P$, il aurait toujours été possible d'écrire $P$ comme un polynôme d'interpolation de Lagrange. Ici, cette méthode nous permet d'écrire que
$$
\begin{aligned}
P(X) & =\frac{X-1}{0-1} \frac{X-1 / 2}{0-1 / 2} P(0)+\frac{X-1}{1 / 2-1} \frac{X-0}{1 / 2-0} P(1 / 2)+\frac{X-1 / 2}{1-1 / 2} \frac{X-0}{1-0} P(1) \\
& =2(X-1)(X-1 / 2)-X(X-1)=X^{2}-2 X+1=(X-1)^{2}
\end{aligned}
$$
d'où le fait que les deux racines de $P$ soient $x=y=1$.
Commentaire des correcteurs L'exercice a été plutôt bien résolu. Peu d'élèves ont vu que la première inégalité était une conséquence simple du fait que le maximum est plus grand que la moyenne arithmétique.
Attention au maniement des inégalités : certains élèves ont écrit que $x y<1$ et $x+y \geqslant x y$ pour en conclure que $x+y \geqslant 1$, ce qui n'est pas vrai. D'autres élèves ont démontré l'inégalité demandée mais oublié de regarder les cas d'égalité alors que c'était une partie importante de l'exercice : contrairement à des cas d'égalité dans des inégalités classiques, celui-là était plus dur à trouver, et affirmer sans preuve que $x=y=1$ ne suffisait pas.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web-05-2020.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2019"
}
|
In the train, as they return from EGMOnd aan Zee, Clara and Edwige play the following game. Initially, the integer $n=1 \times 2 \times \cdots \times 20$ is written on a piece of paper. Then, each in turn, starting with Clara, the players replace the integer $n$ by one of the numbers $k n / 10$, where $k$ is an integer between 1 and 9 inclusive. The first player to write a number that is not an integer loses, and her opponent wins.
Clara and Edwige are formidable players and play optimally. Which of the two will win?
|
Let's consider the number $n$ written on the piece of paper when player X is about to play, and before the game ends. We partially factorize $n$ as a product of prime numbers: $n=2^{x} \times 5^{y} \times m$, where $x$ and $y$ are natural numbers and $m$ is a non-zero natural number that is coprime with 2 and 5.
We will then prove the property $\mathcal{P}_{n}$ by induction on $n$: player X will lose if $x$ and $y$ are both even, and will win otherwise. First, $\mathcal{P}_{1}$ is obvious, since X will have to replace the number $n=1$ with a number between $1 / 10$ and $9 / 10$.
Let then $n \geqslant 1$ be any integer. Suppose $\mathcal{P}_{1}, \ldots, \mathcal{P}_{n}$, and we will prove $\mathcal{P}_{n+1}$.
$\triangleright$ If $x$ and/or $y$ is odd, we denote $r$ and $s$ as the remainders of $x$ and $y$ modulo 2. Then player X replaces the integer $n$ with the integer $n^{\prime}=n /\left(2^{r} \times 5^{s}\right)$. Since $n^{\prime}=2^{x-r} \times 5^{y-s} \times m$, the property $\mathcal{P}_{n^{\prime}}$ ensures that X's opponent will lose.
$\triangleright$ If $x$ and $y$ are both even, we still assume that X replaces $n$ with an integer $n^{\prime}$ (which is only possible if $x \geqslant 1$ or $y \geqslant 1$). If X replaces $n$ with the number $n^{\prime}=n / 2=2^{x-1} \times 5^{y} \times m$, then $\mathcal{P}_{n^{\prime}}$ ensures that X's opponent will win. Otherwise, we can write $n^{\prime}$ in the form $n^{\prime}=2^{x^{\prime}} \times 5^{y-1} \times m^{\prime}$ (with $m^{\prime}$ coprime with 2 and 5): regardless of the values of $x^{\prime}$ and $m^{\prime}$, the property $\mathcal{P}_{n^{\prime}}$ still ensures that X's opponent will lose.
We thus have the property $\mathcal{P}_{20!}$, where we have set $20!=1 \times 2 \times \cdots \times 20$. In particular, we easily observe that $20!=2^{18} \times 5^{4} \times m$, where we have set $m=3^{8} \times 7^{2} \times 11 \times 13 \times 17 \times 19$. Since Clara, who plays first, $c^{\prime}$ is therefore Edwige who will win.
|
Edwige
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Dans le train, alors qu'elles rentrent de EGMOnd an Zee, Clara et Edwige jouent au jeu suivant. Initialement, l'entier $n=1 \times 2 \times \cdots \times 20$ est écrit sur une feuille de papier. Puis, chacune à son tour, et en commençant par Clara, les joueuses remplacent l'entier $n$ par un des nombres $k n / 10$, où $k$ est un entier compris entre 1 et 9 inclus. La première joueuse à écrire un nombre qui n'est pas entier perd, et son adversaire gagne.
Clara et Edwige sont deux joueuses redoutables, et jouent donc de manière optimale. Laquelle des deux va-t-elle gagner?
|
Intéressons-nous au nombre $n$ écrit sur la feuille de papier au moment où la joueuse X s'apprête à jouer, et avant que la partie ne se termine. On factorise partiellement $n$ comme produit de nombres premiers : $n=2^{x} \times 5^{y} \times m$, où $x$ et $y$ sont des entiers naturels et $m$ est un entier naturel non nul premier avec 2 et 5 .
On va alors démontrer la propriété $\mathcal{P}_{n}$ par récurrence sur $n$ : la joueuse X perdra si $x$ et $y$ sont tous deux pairs, et gagnera dans le cas contraire. Tout d'abord, $\mathcal{P}_{1}$ est évidente, puisque X devra remplacer le nombre $n=1$ par un nombre compris entre $1 / 10$ et $9 / 10$.
Soit alors $n \geqslant 1$ un entier quelconque. On suppose $\mathcal{P}_{1}, \ldots, \mathcal{P}_{n}$, et on va démontrer $\mathcal{P}_{n+1}$.
$\triangleright$ Si $x$ et/ou $y$ est impair, on note $r$ et $s$ les restes de $x$ et $y$ modulo 2. Alors la joueuse X remplace l'entier $n$ par l'entier $n^{\prime}=n /\left(2^{r} \times 5^{s}\right)$. Puisque $n^{\prime}=2^{x-r} \times 5^{y-s} \times m$, la propriété $\mathcal{P}_{n^{\prime}}$ assure alors que l'adversaire de X perdra.
$\triangleright$ Si $x$ et $y$ sont pairs, on suppose tout de même que X remplace $n$ par un entier $n^{\prime}$ (ce qui n'est possible que si $x \geqslant 1$ ou $y \geqslant 1$ ). Si X remplace $n$ par le nombre $n^{\prime}=n / 2=$ $2^{x-1} \times 5^{y} \times m$, alors $\mathcal{P}_{n^{\prime}}$ assure que l'aversaire de $X$ gagnera. Sinon, on peut écrire $n^{\prime}$ sous la forme $n^{\prime}=2^{x^{\prime}} \times 5^{y-1} \times m^{\prime}$ (avec $m^{\prime}$ premier avec et 2 et 5 ): quelles que soient les valeurs de $x^{\prime}$ et de $m^{\prime}$, la propriété $\mathcal{P}_{n^{\prime}}$ assure quand même que l'adversaire de X perdra.
On dispose donc de la propriété $\mathcal{P}_{20!}$, où l'on a posé $20!=1 \times 2 \times \cdots \times 20$. En particulier, on constate aisément que $20!=2^{18} \times 5^{4} \times m$, où l'on a posé $m=3^{8} \times 7^{2} \times 11 \times 13 \times 17 \times 19$. Puisque Clara qui joue la première, $c^{\prime}$ est donc Edwige qui gagnera.
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web-05-2020.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T1",
"year": "2019"
}
|
In the train, as they return from EGMOnd aan Zee, Clara and Edwige play the following game. Initially, the integer $n=1 \times 2 \times \cdots \times 20$ is written on a piece of paper. Then, each in turn, starting with Clara, the players replace the integer $n$ by one of the numbers $k n / 10$, where $k$ is an integer between 1 and 9 inclusive. The first player to write a number that is not an integer loses, and her opponent wins.
Clara and Edwige are formidable players and play optimally. Which of the two will win?
|
$n^{\circ} 1$ We will once again provide a winning strategy for Edwige, which slightly differs from the previous one. This strategy is very simple (even if proving that it works is less so): if Clara has just transformed her number $n$ into a new number $n^{\prime}=k n / 10$, then Edwige will transform $n^{\prime}$ back into $n^{\prime \prime}=k n^{\prime} / 10$.
To show that this strategy will allow Edwige to win, and since the game will last at most $20!=1 \times 2 \times \cdots \times 20$ moves, it suffices to prove that $n^{\prime \prime}$ will necessarily be an integer. Thus, Edwige cannot lose, and she will therefore win.
First, we observe that the integer $20!$ is equal to $u^{2} \times v$, where we have set $u=2^{9} \times 2^{4} \times 5^{2} \times 7$ and $v=11 \times 13 \times 17 \times 19$. We will now prove that, if Edwige applies the strategy above, then each of the integers $n$ she leaves to Clara will be of the form $n=\hat{u}^{2} v$, with $\hat{u}$ an integer and $v=11 \times 13 \times 17 \times 19$.
This is already the case at the beginning of the game. Then, if Clara transforms an integer $n=\hat{u}^{2} v$ into another integer $n^{\prime}=k n / 10$, Edwige will transform $n^{\prime}$ into the number $n^{\prime \prime}=k n^{\prime} / 10=(k \hat{u} / 10)^{2} v$. It is therefore necessary to prove that $k \hat{u} / 10$ is an integer, that is, that 2 and 5 both divide $k \hat{u}$.
Since $n^{\prime}$ is an integer, and since $10 n^{\prime}=k n=k \hat{u}^{2} v$, we know that 2 and 5 both divide $k \hat{u}^{2} v$. However, 2 does not divide $v$, and therefore divides $k$ or $\hat{u}$: it therefore also divides $k \hat{u}$. Similarly, 5 does not divide $v$, and therefore divides $k$ or $\hat{u}$: it therefore also divides $k \hat{u}$. This concludes our proof.
Examiner's Comment Many students had good ideas about the problem, but few managed to obtain a real proof that Edwige has a winning strategy. Indeed, a number of students immediately gave Clara an "optimal strategy" from the start: to prove that Edwige wins, one must give a strategy to Edwige and verify that no matter what Clara does, Edwige will win. In particular, Clara has no reason to follow a strategy that seems to be the best at first glance (and which, quite often, is not).
Some students quickly considered that the only important values of $k$ were $k=1, k=2$, and $k=5$, as divisors of 10. However, $k=4$ and $k=8$ were just as important, allowing for 2-adic valuations that were otherwise inaccessible.
Moreover, several students understood that Edwige had an interest in leaving Clara at each step with an integer of the form $2^{x} 5^{y} m$, with $m$ an integer coprime with 10 and $x$ and $y$ even, but did not prove that Edwige could indeed leave Clara in such a state at each step; and especially that Edwige could play the move in question!
Finally, it would have been good to prove that the game ends in all cases, without which Edwige of course does not win.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Dans le train, alors qu'elles rentrent de EGMOnd an Zee, Clara et Edwige jouent au jeu suivant. Initialement, l'entier $n=1 \times 2 \times \cdots \times 20$ est écrit sur une feuille de papier. Puis, chacune à son tour, et en commençant par Clara, les joueuses remplacent l'entier $n$ par un des nombres $k n / 10$, où $k$ est un entier compris entre 1 et 9 inclus. La première joueuse à écrire un nombre qui n'est pas entier perd, et son adversaire gagne.
Clara et Edwige sont deux joueuses redoutables, et jouent donc de manière optimale. Laquelle des deux va-t-elle gagner?
|
$n^{\circ} 1$ Nous allons de nouveau fournir une stratégie gagnante pour Edwige, qui diffère légèrement de la stratégie précédente. Cette stratégie est toute simple (même si montrer qu'elle convient l'est moins) : si Clara vient de transformer son nombre $n$ en un nouveau nombre $n^{\prime}=k n / 10$, alors Edwige transforme de nouveau $n^{\prime}$ en $n^{\prime \prime}=k n^{\prime} / 10$.
Pour montrer que cette stratégie permettra à Edwige de gagner, et puisque la partie durera au plus $20!=1 \times 2 \times \cdots \times 20$ coups, il suffit de démontrer que $n^{\prime \prime}$ sera nécessairement un entier. Ainsi, Edwige ne pourra pas perdre, et elle gagnera donc.
Tout d'abord, on constate que l'entier 20! est égal à $u^{2} \times v$, où l'on a posé $u=2^{9} \times 2^{4} \times 5^{2} \times 7$ et $v=11 \times 13 \times 17 \times 19$. On va maintenant démontrer que, si Edwige applique la stratégie ci-dessus, alors chacun des entiers $n$ qu'elle laissera à Clara sera de la forme $n=\hat{u}^{2} v$, avec $\hat{u}$ entier et $v=11 \times 13 \times 17 \times 19$.
C'est déjà le cas au début du jeu. Puis, si Clara transforme un entier $n=\hat{u}^{2} v$ en un autre entier $n^{\prime}=k n / 10$, Edwige transformera $n^{\prime}$ en le nombre $n^{\prime \prime}=k n^{\prime} / 10=(k \hat{u} / 10)^{2} v$. Il s'agit donc de démontrer que $k \hat{u} / 10$ est un entier, c'est-à-dire que 2 et 5 divisent tous deux $k \hat{u}$.
Puisque $n^{\prime}$ est un entier, et comme $10 n^{\prime}=k n=k \hat{u}^{2} v$, on sait que 2 et 5 divisent tous deux $k \hat{u}^{2} v$. Or, 2 ne divise pas $v$, et divise donc $k$ ou $\hat{u}$ : il divise donc aussi $k \hat{u}$. De même, 5 ne divise pas $v$, et divise donc $k$ ou $\hat{u}$ : il divise donc aussi $k \hat{u}$. Cela conclut notre démonstration.
Commentaire des correcteurs Beaucoup d'élèves ont eu des bonnes idées sur le problème, mais peu ont réussi à obtenir une vraie preuve du fait qu'Edwige a une stratégie gagnante. En effet, un certain nombre d'élèves donne dès le départ une «stratégie optimale »à Clara : pour démontrer qu'Edwige gagne, il faut donner une stratégie à Edwige et vérifier quen peu importe ce que Clara faitn Edwige gagnera. En particulier, Clara n'a aucune raison de suivre une stratégie qui semble être la meilleure à vue d'œil (et qui, assez souvent, ne l'est pas).
Certains élèves ont rapidement considéré que seuls les seules valeurs de $k$ importantes étaient $k=1, k=2$ et $k=5$, en tant que diviseurs de 10 . Cependant, $k=4$ et $k=8$ étaient tout aussi importants, permettant d'obtenir des valuations 2-adiques inaccessibles autrement.
Par ailleurs, plusieurs élèves ont bien compris que Edwige avait intérêt à laisser Clara à chaque étape avec un entier de la forme $2^{x} 5^{y} m$, avec $m$ entier premier avec 10 et $x$ et $y$ pairs, mais n'ont pas prouvé que Edwige pouvait bien laisser Clara à chaque fois dans un tel état; et surtout qu'Edwige pouvait jouer le coup en question!
Enfin, il aurait été bien de prouver que la partie termine dans tous les cas, ce sans quoi Edwige ne gagne bien sûr pas.
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web-05-2020.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2019"
}
|
Determine all natural numbers $x, y$ and $z$ such that
$$
45^{x}-6^{y}=2019^{z}
$$
|
We start by decomposing each term into a product of prime factors. The equation then becomes
$$
3^{2 x} \cdot 5^{x}-3^{y} \cdot 2^{y}=3^{z} \cdot 673^{z}
$$
We will now handle different cases:
$\triangleright$ If $y>2 x$, then $3^{z} \cdot 673^{z}=3^{2 x}\left(5^{x}-3^{y-2 x} \times 2^{y}\right)$. Gauss's theorem then indicates that $3^{z}$ divides $3^{2 x}$ (since $5^{x}-3^{y-2 x} \times 2^{y}$ is not divisible by 3, and is thus coprime with $3^{z}$) and that $3^{2 x}$ divides $3^{z}$ (since $673^{z}$ is not divisible by 3, and is thus coprime with $3^{2 x}$). We deduce that $z=2 x$, and the equation becomes
$$
673^{2 x}=5^{x}-3^{y-2 x} \cdot 2^{y}
$$
However, since $673^{2 x} \geqslant 5^{x}$, this equation has no solution, and this case is therefore impossible.
$\triangleright$ If $y=2 x$, then $3^{z} \cdot 673^{z}=3^{2 x}\left(5^{x}-2^{y}\right)$. As before, Gauss's theorem indicates that $3^{2 x}$ divides $3^{z}$. We deduce that $2 x \leqslant z$, and the equation becomes
$$
3^{z-2 x} \cdot 673^{z}=5^{x}-2^{y}
$$
However, since $673^{z} \geqslant 5^{z} \geqslant 5^{x}$, this equation has no solution either, and this case is therefore impossible.
$\triangleright$ If $y<2 x$, then $3^{z} \cdot 673^{z}=3^{y}\left(3^{2 x-y} \cdot 5^{x}-2^{y}\right)$. Once again, since neither $673^{z}$ nor $3^{2 x-y} \cdot 5^{x}-2^{y}$ are divisible by 3, Gauss's theorem indicates that $3^{z}$ and $3^{y}$ divide each other. We deduce that $z=y$, and the equation becomes
$$
673^{y}=3^{2 x-y} \cdot 5^{x}-2^{y}
$$
We then distinguish several sub-cases:
$\triangleright$ If $y=0$, the equation becomes $2=3^{2 x} \cdot 5^{x}$, and of course has no solution.
$\triangleright$ If $y=1$, the equation becomes $675=3^{2 x-1} \cdot 5^{x}$. Since $675=3^{3} \times 5^{2}$, we deduce the existence of the solution $(x, y, z)=(2,1,1)$.
$\triangleright$ If $y \geqslant 2$, consider the equation modulo 4: it becomes $1 \equiv 3^{y}(\bmod 4)$, which means that $y$ is even.
Then, since we necessarily have $x \geqslant 1$, and if we consider the equation modulo 5, it becomes $(-2)^{y} \equiv-2^{y}(\bmod 5)$, which means that $y$ is odd. The equation therefore has no solution in this sub-case.
The unique solution to the equation is thus the triplet $(2,1,1)$.
|
(2,1,1)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer tous les entiers naturels $x, y$ et $z$ tels que
$$
45^{x}-6^{y}=2019^{z}
$$
|
On commence par décomposer chaque terme en produit de facteurs premiers. L'équation devient alors
$$
3^{2 x} \cdot 5^{x}-3^{y} \cdot 2^{y}=3^{z} \cdot 673^{z}
$$
Nous allons maintenant traiter différents cas :
$\triangleright$ Si $y>2 x$, alors $3^{z} \cdot 673^{z}=3^{2 x}\left(5^{x}-3^{y-2 x} \times 2^{y}\right)$. Le théorème de Gauss indique alors que $3^{z}$ divise $3^{2 x}$ (car $5^{x}-3^{y-2 x} \times 2^{y}$ n'est pas divisible par 3, doncest premier avec $3^{z}$ ) et que $3^{2 x}$ divise $3^{z}$ (car $673^{z}$ n'est pas divisible par 3 , donc est premier avec $3^{2 x}$. On en déduit que $z=2 x$, et l'équation devient
$$
673^{2 x}=5^{x}-3^{y-2 x} \cdot 2^{y}
$$
Mais, puisque $673^{2 x} \geqslant 5^{x}$, cette équation n'a en fait pas de solution, et ce cas est donc impossible.
$\triangleright$ Si $y=2 x$, alors $3^{z} \cdot 673^{z}=3^{2 x}\left(5^{x}-2^{y}\right)$. Comme précédemment, le théorème de Gauss indique que $3^{2 x}$ divise $3^{z}$. On en déduit que $2 x \leqslant z$, et l'équation devient
$$
3^{z-2 x} \cdot 673^{z}=5^{x}-2^{y}
$$
Mais, puisque $673^{z} \geqslant 5^{z} \geqslant 5^{x}$, cette équation n'a pas de solution elle non plus, et ce cas est donc impossible.
$\triangleright$ Si $y<2 x$, alors $3^{z} \cdot 673^{z}=3^{y}\left(3^{2 x-y} \cdot 5^{x}-2^{y}\right)$. Une fois encore, puisque ni $673^{z} \mathrm{ni}$ $3^{2 x-y} \cdot 5^{x}-2^{y}$ ne sont divisibles par 3 , le théorème de Gauss indique que $3^{z}$ et $3^{y}$ se divisent mutuellement. On en déduit que $z=y$, et l'équation devient
$$
673^{y}=3^{2 x-y} \cdot 5^{x}-2^{y}
$$
On distingue alors plusieurs sous-cas :
$\triangleright$ Si $y=0$, l'équation devient $2=3^{2 x} \cdot 5^{x}$, et n'a bien sûr aucune solution.
$\triangleright$ Si $y=1$, l'équation devient $675=3^{2 x-1} \cdot 5^{x}$. Puisque $675=3^{3} \times 5^{2}$, on en déduit l'existence de la solution $(x, y, z)=(2,1,1)$.
$\triangleright$ Si $y \geqslant 2$, considérons notre équation modulo 4 : elle devient $1 \equiv 3^{y}(\bmod 4)$, ce qui signifie que $y$ est pair.
Puis, comme on a nécessairement $x \geqslant 1$, et si on considère l'équation modulo 5 , celle-ci devient $(-2)^{y} \equiv-2^{y}(\bmod 5)$, ce qui signifie que $y$ est impair. L'équation n'admet donc aucune solution dans ce sous-cas.
L'unique solution de l'équation est donc le triplet $(2,1,1)$.
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web-05-2020.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T1",
"year": "2019"
}
|
Determine all natural numbers $x, y$ and $z$ such that
$$
45^{x}-6^{y}=2019^{z}
$$
|
$n^{\circ} 1$ We can directly treat the cases $y>2 x$ and $y=2 x$ at the same time, by presenting the arguments mentioned above in a slightly different order. First, since $2019^{z}<45^{x} \leqslant 2019^{x}$, we deduce that $z<x$. Furthermore, if one of the three integers $2 x, y$, and $z$ (we will call it $t$) is strictly smaller than the other two, then the integer $3^{2 x} \cdot 5^{x}-3^{y} \cdot 2^{y}-3^{z} \cdot 673^{z}$ is not divisible by $3^{t+1}$, which is impossible since it is supposed to be zero. Since we already know that $z<x \leqslant 2 x$, we deduce that $y=z$, and thus that $y=z<x$.
|
not found
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer tous les entiers naturels $x, y$ et $z$ tels que
$$
45^{x}-6^{y}=2019^{z}
$$
|
$n^{\circ} 1$ On peut traiter directement les cas $y>2 x$ et $y=2 x$ en une seule fois, en reprentant les arguments mentionnés ci-dessus dans un ordre légèrement différent. Tout d'abord, puisque $2019^{z}<45^{x} \leqslant 2019^{x}$, on en déduit que $z<x$. En outre, si l'un des trois entiers $2 x, y$ et $z$ (on l'appellera $t$ ) est strictement plus petit que les deux autres, alors l'entier $3^{2 x} \cdot 5^{x}-3^{y} \cdot 2^{y}-3^{z} \cdot 673^{z}$ n'est pas divisible par $3^{t+1}$, ce qui est impossible puisqu'il est censé être nul. Puisque l'on sait déjà que $z<x \leqslant 2 x$, on en déduit que $y=z$, et donc que $y=z<x$.
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web-05-2020.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2019"
}
|
Determine all natural numbers $x, y$ and $z$ such that
$$
45^{x}-6^{y}=2019^{z}
$$
|
$n^{\circ} 2$ We work directly from the equation
$$
45^{x}-6^{y}=2019^{z}
$$
First, since $45^{x}>2019^{z}$, we know that $x \geqslant 1$. Considering the equation modulo 5, it rewrites as
$$
-1 \equiv-1^{y} \equiv(-1)^{z} \quad(\bmod 5)
$$
This means that $z$ is an odd integer.
Then, considering the equation modulo 4, and since $z$ is odd, it rewrites as
$$
1-2^{y} \equiv 45^{x}-6^{y} \equiv 2019^{z} \equiv(-1)^{z} \equiv-1 \quad(\bmod 4)
$$
This means that $y=1$.
Finally, since $x \geqslant 1$, considering the equation modulo 9, it rewrites as
$$
3 \equiv 45^{x}-6^{y} \equiv 3^{z} \quad(\bmod 9)
$$
This means that $z=1$.
The equation then becomes $45^{x}=6^{y}+2019^{z}=2025=45^{2}$, and the triplet $(x, y, z)=(2,1,1)$ appears as a solution to the equation in the statement.
In conclusion, the unique solution sought is the triplet $(2,1,1)$.
Comment from the graders The exercise was well solved. In particular, many students began by writing the small powers of 45, 6, and 2019, which allowed them to see remarkable relationships modulo 10, and then realize that looking at the equation modulo small numbers could be useful. Others correctly recognized that 45, 6, and 2019 are multiples of 3, which led them to use the concept of 3-adic valuation. In both cases, these are excellent reflexes that did not fail to bear fruit. However, it is regrettable that several students implicitly assumed $x, y$, and $z$ were non-zero, although nothing guaranteed this a priori: one must be careful to read the statement well to avoid losing points that are not easy to obtain otherwise!
|
(2,1,1)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer tous les entiers naturels $x, y$ et $z$ tels que
$$
45^{x}-6^{y}=2019^{z}
$$
|
$n^{\circ} 2$ On travaille directement à partir de l'équation
$$
45^{x}-6^{y}=2019^{z}
$$
Tout d'abord, puisque $45^{x}>2019^{z}$, on sait que $x \geqslant 1$. Considérée modulo 5 , l'équation se réécrit
$$
-1 \equiv-1^{y} \equiv(-1)^{z} \quad(\bmod 5)
$$
Cela signifie que $z$ est un entier impair.
Puis, en considérant l'équation modulo 4, et puisque $z$ est impair, celle-ci se réécrit
$$
1-2^{y} \equiv 45^{x}-6^{y} \equiv 2019^{z} \equiv(-1)^{z} \equiv-1 \quad(\bmod 4)
$$
Cela signifie que $y=1$.
Enfin, puisque $x \geqslant 1$, en considérant l'équation modulo 9 , celle-ci se réécrit
$$
3 \equiv 45^{x}-6^{y} \equiv 3^{z} \quad(\bmod 9)
$$
Cela signifie que $z=1$.
L'équation devient alors $45^{x}=6^{y}+2019^{z}=2025=45^{2}$, et le triplet $(x, y, z)=(2,1,1)$ apparaît alors manifestement comme une solution de l'équation de l'énoncé.
En conclusion, l'unique solution recherchée est le triplet $(2,1,1)$.
Commentaire des correcteurs L'exercice a été bien résolu. En particulier, de nombreux élèves ont commencé par écrire les petites puissances de 45, 6 et 2019, ce qui leur a permis de voir des relations remarquables modulo 10 , puis de prendre conscience que regarder l'équation modulo de petits nombres pouvait être utile. D'autres ont reconnu, à juste titre, que 45, 6 et 2019 étaient des multiples de 3, ce qui les a poussés à utiliser la notion de valuation 3-adique. Dans les deux cas, il s'agit d'excellents réflexes, qui n'ont pas manqué de porter leurs fruits. On peut néanmoins regretter que plusieurs élèves aient implicitement supposé $x, y$ et $z$ non nuls, alors que rien ne venait le garantir a priori : il faut faire attention de bien lire l'énoncé pour éviter de perdre ainsi, par naïveté, des points pas faciles à obtenir par ailleurs!
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web-05-2020.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2019"
}
|
Let $ABC$ be a triangle and $\Gamma$ a circle passing through $A$. Suppose that $\Gamma$ intersects the segments $[AB]$ and $[AC]$ at two points, which we call $D$ and $E$ respectively, and that it intersects the segment $[BC]$ at two points, which we call $F$ and $G$, such that $F$ lies between $B$ and $G$. Let $T$ be the point of intersection between the tangent at $F$ to the circumcircle of $BDF$ and the tangent at $G$ to the circumcircle of $CEG$.
Prove that, if the points $A$ and $T$ are distinct, then $(AT)$ and $(BC)$ are parallel.
|
Let's start by drawing a figure.
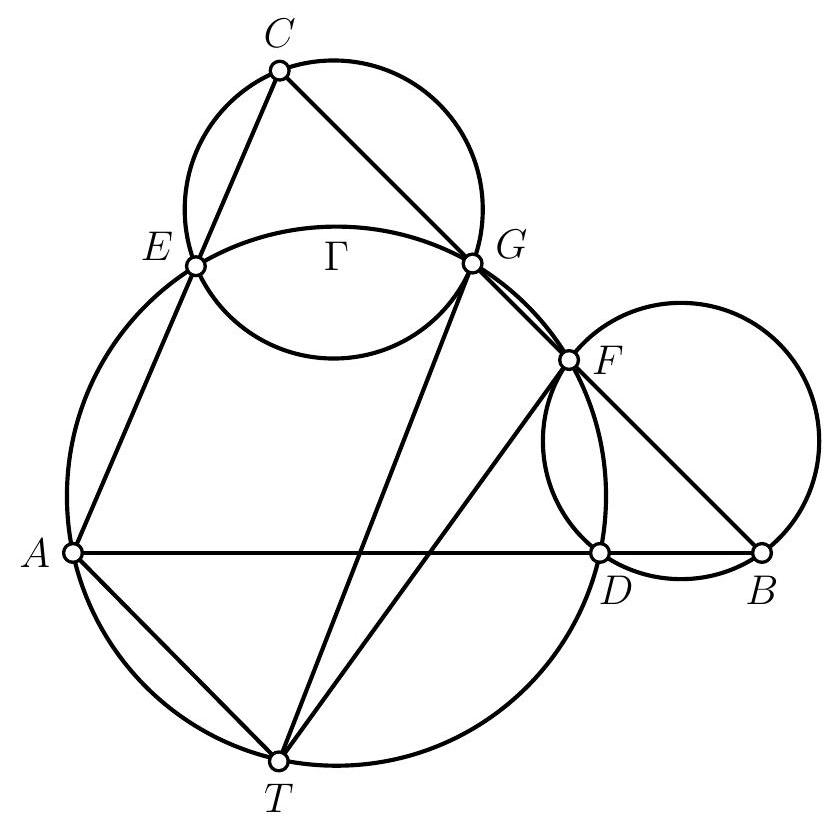
A striking first observation is that $T$ appears to lie on the circle $\Gamma$. After verifying this on a second figure, we promptly set out to prove this first result. To do so, we embark on an angle chase using the properties of cyclic points and the limiting case of the inscribed angle theorem:
$$
\begin{aligned}
(T G, T F) & =(T G, B C)+(B C, T F)=(T G, C G)+(B F, T F)=(E G, E C)+(D B, D F) \\
& =(E G, A E)+(A D, D F)=(D G, A D)+(A D, D F)=(A D, D F)
\end{aligned}
$$
The points $A, F, G$, and $T$ are therefore concyclic, and $T$ lies on $\Gamma$. But then
$$
\begin{aligned}
(A T, B C) & =(A T, A F)+(A F, B C)=(G T, G F)+(A F, G F) \\
& =(G T, G C)+(A E, G E)=(E G, E C)+(C E, G E)=0^{\circ},
\end{aligned}
$$
which means precisely that the lines $(A T)$ and $(B C)$ are parallel.
Comment from the graders: The problem was correctly solved by 7 students. Some students, even if they did not completely solve the problem, used their figure to conjecture that the point $T$ lies on the circle $\Gamma$ and concluded by assuming this result. This approach was highly appreciated as it is the right attitude when facing a geometry problem.
## Senior Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $\Gamma$ un cercle passant par $A$. On suppose que $\Gamma$ recoupe les segments $[A B]$ et $[A C]$ en deux points, que l'on appelle respectivement $D$ et $E$, et qu'il coupe le segment $[B C]$ en deux points, que l'on appelle $F$ et $G$, de sorte que $F$ se trouve entre $B$ et $G$. Soit $T$ le point d'intersection entre la tangente en $F$ au cercle circonscrit à $B D F$ et la tangente en $G$ au cercle circonscrit à $C E G$.
Démontrer que, si les points $A$ et $T$ sont distincts, alors $(A T)$ et $(B C)$ sont parallèles.
|
Commençons par tracer une figure.

Une première remarque frappante est que $T$ semble être situé sur le cercle $\Gamma$. Après avoir vérifié qu'il l'était bien sur une deuxième figure, on s'empresse donc de démontrer ce premier résultat. Pour ce faire, on entame donc une chasse aux angles de droites, en utilisant les relations de cocyclicité et le cas limite du théorème de l'angle au centre :
$$
\begin{aligned}
(T G, T F) & =(T G, B C)+(B C, T F)=(T G, C G)+(B F, T F)=(E G, E C)+(D B, D F) \\
& =(E G, A E)+(A D, D F)=(D G, A D)+(A D, D F)=(A D, D F)
\end{aligned}
$$
Les points $A, F, G$ et $T$ sont donc cocycliques, et $T$ appartient à bien $\Gamma$. Mais alors
$$
\begin{aligned}
(A T, B C) & =(A T, A F)+(A F, B C)=(G T, G F)+(A F, G F) \\
& =(G T, G C)+(A E, G E)=(E G, E C)+(C E, G E)=0^{\circ},
\end{aligned}
$$
ce qui signifie précisément que les droites $(A T)$ et $(B C)$ sont parallèles.
Commentaire des correcteurs L'exercice a été correctement résolu par 7 élèves. Quelques élèves, même s'ils n'ont pas complètement résolu le problème, ont utilisé leur figure pour conjecturer que le point $T$ appartenait au cercle $\Gamma$ et ont conclu en admettant ce résultat. Ce procédé a été grandement apprécié car c'est la bonne attitude face à un problème de géometrie.
## Exercices Senior
|
{
"exam": "French_tests",
"problem_label": "5",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web-05-2020.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T1",
"year": "2019"
}
|
Let $ABC$ be a triangle and $\Gamma$ a circle passing through $A$. Suppose that $\Gamma$ intersects the segments $[AB]$ and $[AC]$ at two points, which we call $D$ and $E$ respectively, and that it intersects the segment $[BC]$ at two points, which we call $F$ and $G$, such that $F$ lies between $B$ and $G$. Let $T$ be the point of intersection between the tangent at $F$ to the circumcircle of $BDF$ and the tangent at $G$ to the circumcircle of $CEG$.
Prove that, if the points $A$ and $T$ are distinct, then $(AT)$ and $(BC)$ are parallel.
|
Let's start by drawing a figure.
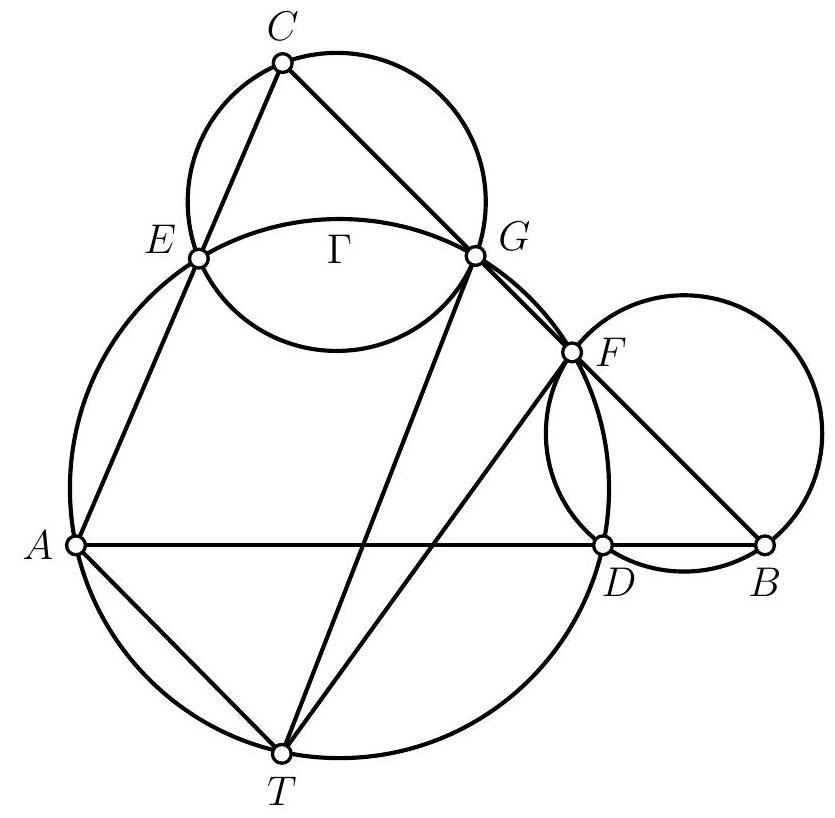
A striking first observation is that $T$ appears to lie on the circle $\Gamma$. After verifying this on a second figure, we promptly set out to prove this first result. To do so, we embark on an angle chase using the properties of cyclic points and the limiting case of the inscribed angle theorem:
$$
\begin{aligned}
(T G, T F) & =(T G, B C)+(B C, T F)=(T G, C G)+(B F, T F)=(E G, E C)+(D B, D F) \\
& =(E G, A E)+(A D, D F)=(D G, A D)+(A D, D F)=(A D, D F) .
\end{aligned}
$$
The points $A, F, G$, and $T$ are therefore concyclic, and $T$ lies on $\Gamma$. But then
$$
\begin{aligned}
(A T, B C) & =(A T, A F)+(A F, B C)=(G T, G F)+(A F, G F) \\
& =(G T, G C)+(A E, G E)=(E G, E C)+(C E, G E)=0^{\circ},
\end{aligned}
$$
which precisely means that the lines $(A T)$ and $(B C)$ are parallel.
Comment from the graders: The exercise was very well done! The most efficient students noted that it was sufficient to show that the point $T'$, the intersection of the line parallel to the line $(B C)$ passing through the point $A$ with the circle $\Gamma$, lies on both tangents. It is a pity to note that several students submitted a very neat figure but did not attempt to make conjectures from this figure, even though the point $T$ clearly lies on the circle $\Gamma$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $\Gamma$ un cercle passant par $A$. On suppose que $\Gamma$ recoupe les segments $[A B]$ et $[A C]$ en deux points, que l'on appelle respectivement $D$ et $E$, et qu'il coupe le segment $[B C]$ en deux points, que l'on appelle $F$ et $G$, de sorte que $F$ se trouve entre $B$ et $G$. Soit $T$ le point d'intersection entre la tangente en $F$ au cercle circonscrit à $B D F$ et la tangente en $G$ au cercle circonscrit à $C E G$.
Démontrer que, si les points $A$ et $T$ sont distincts, alors $(A T)$ et $(B C)$ sont parallèles.
|
Commençons par tracer une figure.

Une première remarque frappante est que $T$ semble être situé sur le cercle $\Gamma$. Après avoir vérifié qu'il l'était bien sur une deuxième figure, on s'empresse donc de démontrer ce premier résultat. Pour ce faire, on entame donc une chasse aux angles de droites, en utilisant les relations de cocyclicité et le cas limite du théorème de l'angle au centre :
$$
\begin{aligned}
(T G, T F) & =(T G, B C)+(B C, T F)=(T G, C G)+(B F, T F)=(E G, E C)+(D B, D F) \\
& =(E G, A E)+(A D, D F)=(D G, A D)+(A D, D F)=(A D, D F) .
\end{aligned}
$$
Les points $A, F, G$ et $T$ sont donc cocycliques, et $T$ appartient à bien $\Gamma$. Mais alors
$$
\begin{aligned}
(A T, B C) & =(A T, A F)+(A F, B C)=(G T, G F)+(A F, G F) \\
& =(G T, G C)+(A E, G E)=(E G, E C)+(C E, G E)=0^{\circ},
\end{aligned}
$$
ce qui signifie précisément que les droites $(A T)$ et $(B C)$ sont parallèles.
Commentaire des correcteurs L'exercice a été très bien réussi! Les élèves les plus efficaces ont noté qu'il suffisait de montrer que le point $T^{\prime} \mathrm{d}^{\prime}$ intersection de la droite parallèle à la droite $(B C)$ passant par le point $A$ avec le cercle $\Gamma$ appartenait aux deux tangentes. Il est dommage de constater que plusieurs élèves ont rendu une figure très propre mais n'ont pas cherché à effectuer de conjectures à partir de cette figure, alors même que le point $T$ appartient visiblement au cercle $\Gamma$.
|
{
"exam": "French_tests",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web-05-2020.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T1",
"year": "2019"
}
|
Let $S$ be a set of integers. We say that $S$ is beautiful if it contains all integers of the form $2^{a}-2^{b}$, where $a$ and $b$ are non-zero natural numbers. We also say that $S$ is strong if, for any non-constant polynomial $P(X)$ with coefficients in $S$, the integer roots of $P(X)$ also belong to $S$.
Find all sets that are both beautiful and strong.
|
The set $\mathbb{Z}$ is clearly beautiful and strong. We will prove that it is the only one. To do this, consider a set $S$ that is beautiful and strong: we will actually prove, by strong induction on $n$, that the integers $n$ and $-n$ necessarily belong to $S$.
First, since $S$ is beautiful, it contains the integers $2^{1}-2^{1}=0, 2^{2}-2^{1}=2$, and $2^{1}-2^{2}=-2$. It also contains the integers 1 and -1, which are roots of the polynomials $2-2X$ and $2+2X$, respectively.
We now consider an integer $n \geqslant 3$ such that $-n-1, \ldots, n-1$ all belong to $S$. Let $\alpha$ be the 2-adic valuation of $n$, and $m$ be the odd integer such that $n=2^{\alpha} m$. By noting $\varphi(m)$ as the Euler's totient function of $m$, we observe that the integer $k=2^{\alpha+\varphi(m)+1}-2^{\alpha+1}$, which clearly belongs to $S$, is also a multiple of $2^{\alpha}$ and $m$, and thus of $n$.
Let $\overline{a_{\ell} a_{\ell-1} \ldots a_{0}}$ be the base-$n$ representation of $k / n$. All the integers $\pm a_{0}, \ldots, \pm a_{\ell}$ are between $1-n$ and $n-1$, and thus belong to $S$. By construction, $n$ is an integer root of the polynomial $P(X)=k-\sum_{i=0}^{\ell} a_{i} X^{i+1}$, whose coefficients are all in $S$, so $n$ is in $S$ as well. Similarly, $-n$ is an integer root of the polynomial $Q(X)=k-\sum_{i=0}^{\ell} a_{i}(-X)^{i+1}$, so $-n \in S$, which concludes the induction and the proof.
Remark: Given the statement, one could suspect that using polynomials of degree $d \geqslant 2$ might be useful, otherwise the creators of the statement would have directly chosen to define strong sets as sets stable under division. The remark below is mainly intended to illustrate the fact that if one seeks to drastically simplify a hypothesis in a mathematical statement, here with the goal of showing that $\mathbb{Z}$ would be the only beautiful set stable under division, it is very important to look for simple constructions that could invalidate this simplification.
We will in fact prove that there exists a set $S$ that is beautiful and stable under division, but different from $\mathbb{Z}$: this demonstrates that using polynomials of degree $d \geqslant 2$ was actually necessary to solve this problem. To construct this set, we need Zsygmondy's theorem and the known property that there exist Fermat numbers (i.e., integers of the form $2^{p}-1$) that are not prime, even if $p$ is large enough (below, we will need the inequality $p \geqslant 7$). For example, when $p=11$, $2^{11}-1=23 \times 89$. Indeed, write $2^{p}-1$ as the product $2^{p}-1=q \times r \times m$, where $q$ and $r$ are two primes, and $m$ is any integer. We then consider the set $S$ consisting of 0 and integers of the form
$$
\pm 2^{a} \prod_{k \geqslant 2}\left(2^{k}-1\right)^{\alpha_{k}}
$$
where the $\alpha_{k}$ are integers, only finitely many of which are non-zero. The set $S$ is clearly beautiful and stable under division.
Suppose now that $q \in S$: we then write $q$ as
$$
q=\prod_{k \geqslant 2}\left(2^{k}-1\right)^{\alpha_{k}}
$$
and let $\ell$ be the maximal index such that $\alpha_{\ell} \neq 0$. Since the order of 2 modulo $q$ and $r$ divides $p$, it is equal to $p$, so $\ell \geqslant p \geqslant 7$.
Zsygmondy's theorem then indicates that there exists a prime $s$ that divides $2^{\ell}-1$ and no integer $2^{k}-1$ for $1 \leqslant k \leqslant \ell-1$. We then note that
$$
v_{s}(q)=\sum_{k \geqslant 2} \alpha_{k} v_{s}\left(2^{k}-1\right)=\alpha_{\ell} v_{s}\left(2^{\ell}-1\right) \neq 0 .
$$
We deduce that $s=q$, so $\ell=p$, and that $v_{q}\left(2^{\ell}-1\right)=1$. This means in particular that $r \neq q$. But then, even for $\ell=p$, and instead of choosing $s=q$, we could have satisfied Zsygmondy's theorem by choosing $s=r$, leading to a contradiction. We therefore conclude that $q \notin S$, and thus that $S \neq \mathbb{Z}$.
Comment from the graders: This number theory problem was quite difficult as it required a trick: the simplest solution involved the base-$b$ decomposition of an integer. Only five students thought of this and they all received the maximum score. The grading scale valued this trick, making it impossible to score more than 3 if this base decomposition was not mentioned.
Almost all students realized that the only beautiful and strong set would be $\mathbb{Z}$, without necessarily knowing how to prove it.
Many students tried to show that every integer (sometimes restricted to odd or prime integers) has a multiple in $S$, which was essential for the subsequent steps. Many also showed that $S$ is symmetric with respect to 0 (i.e., if $n \in S$, then $-n \in S$), which allows avoiding dealing with negative integers in the subsequent steps.
Let's finally address some common errors:
$\triangleright$ Managing negative integers sometimes led to a significant error, especially when students attempted to prove by induction that $\llbracket 1, n \rrbracket \subseteq S$ for all $n \geqslant 1$. Some students introduced an integer $k \geqslant 1$ such that $n k \in S$, and they claimed that $n-k$ belonged to $S$ by induction hypothesis as an integer strictly less than $n$. However, these students did not rule out the case where $k \geqslant 2 n$, so it was possible to have $n-k \leqslant -n$, thus undermining their entire reasoning.
$\triangleright$ Some students noted that it sufficed for all primes to be in $S$ to conclude. This is true, but no known solution immediately proves this result. In this case, several students thought they had solved the problem by showing this result. They based their reasoning on the belief (erroneous, as indicated in the remark above) that if $n$ and $m$ are two distinct odd natural numbers, then the order of 2 modulo $n$ is different from the order of 2 modulo $m$. This error is equivalent to the misconception of Zsigmondy's theorem, which states that for $n \notin\{1,6\}$, $2^{n}-1$ has exactly one primitive prime divisor.
$\triangleright$ Finally, vague arguments like "we construct more and more integers by taking the integer roots of polynomials with coefficients in an increasingly large set" can help form an idea, but obviously do not earn any points.
It is worth noting that in a problem like this, explicitly verifying that small values of $n$ (e.g., $n=0, n=1$, and $n=2$) are in $S$ always earns a point, yet some students did not have this reflex.
Finally, many students proved that if $a b \in S$ and $a \in S$ is non-zero, then $b \in S$. This result, while correct, is misleading because it invites the use of only the degree 1 polynomials in the statement, which are clearly insufficient to conclude, as indicated in the remark above.
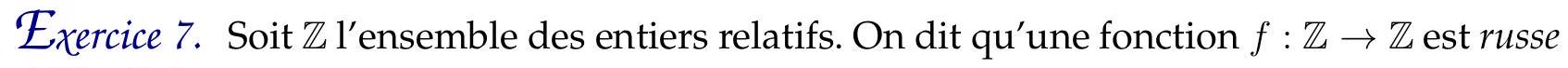 if the equality
$$
f(f(x+y)+y)=f(f(x)+y)
$$
is satisfied for all integers $x$ and $y$. An integer $v$ is said to be $f$-rare if the set of integers $x$ such that $f(x)=v$ is a finite and non-empty set.
a) Prove that there exists a Russian function $f$ for which there exists an $f$-rare integer.
b) Prove that for any Russian function $f$, there is at most one $f$-rare integer.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Soit $S$ un ensemble d'entiers relatifs. On dit que $S$ est beau s'il contient tous les entiers de la forme $2^{a}-2^{b}$, où $a$ et $b$ sont des entiers naturels non nuls. On dit également que $S$ est fort si, pour tout polynôme $P(X)$ non constant et à coefficients dans $S$, les racines entières de $P(X)$ appartiennent également à $S$.
Trouver tous les ensembles qui sont à la fois beaux et forts.
|
L'ensemble $\mathbb{Z}$ est clairement beau et fort. Nous allons démontrer que c'est le seul. Pour ce faire, considérons un ensemble $S$ beau et fort : nous allons en fait prouver, par récurrence forte sur $n$, que les entiers $n$ et $-n$ appartiennent nécessairement à $S$.
Tout d'abord, puisque $S$ est beau, il contient les entiers $2^{1}-2^{1}=0,2^{2}-2^{1}=2$ et $2^{1}-2^{2}=-2$. Il contient donc aussi les entiers 1 et -1 , qui sont des racines respectives des polynômes $2-2 X$ et $2+2 X$.
On considère désormais un entier $n \geqslant 3$ tel que $-n-1, \ldots, n-1$ appartiennent tous à $S$. Soit $\alpha$ la valuation 2 -adique de $n$, et $m$ l'entier impair tel que $n=2^{\alpha} m$. En notant $\varphi(m)$ l'indicatrice d'Euler de $m$, on constate alors que l'entier $k=2^{\alpha+\varphi(m)+1}-2^{\alpha+1}$, qui appartient manifestement à $S$, est également un multiple de $2^{\alpha}$ et de $m$, donc de $n$.
Soit $\overline{a_{\ell} a_{\ell-1} \ldots a_{0}}$ l'écriture de $k / n$ en base $n$. Tous les entiers $\pm a_{0}, \ldots, \pm a_{\ell}$ sont compris entre $1-n$ et $n-1$, donc appartiennent à $S$. Par construction, $n$ est une racine entière du polynôme $P(X)=k-\sum_{i=0}^{\ell} a_{i} X^{i+1}$, dont tous les coefficients sont dans $S$, donc $n$ est dans $S$ lui aussi. De même, $-n$ est une racine entière du polynôme $Q(X)=k-\sum_{i=0}^{\ell} a_{i}(-X)^{i+1}$, donc $-n \in S$, ce qui conclut la récurrence et la démonstration.
Remarque: Au vu de l'énoncé, on pouvait se douter qu'utiliser des polynomes de degré $d \geqslant 2$ pourrait être utile, ce sans quoi les créateurs de l'énoncé auraient directement choisi de définir, tout simplement, les ensembles forts comme les ensembles stables par division. La remarque ci-dessous a pour but principal d'illustrer le fait que, si l'on cherche à simplifier drastiquement une hypothèse d'un énoncé mathématique, ici avec pour objectif de montrer que $\mathbb{Z}$ serait le seul ensemble beau stable par division, il est très important de chercher des constructions simples qui permettraient d'invalider cette simplification.
On va en fait démontrer qu'il existe un ensemble $S$ beau et stable par division, mais différent de $\mathbb{Z}$ : cela démontre qu'utiliser des polynomes de degré $d \geqslant 2$ était en fait nécessaire pour résoudre cet exercice. Pour construire cet ensemble, on a besoin du théorème de Zsygmondy ainsi que de la propriété connue suivante : il existe des nombres de Fermat (c'est-à-dire les entiers de la forme $2^{p}-1$ ) qui ne sont pas premiers, même si $p$ est assez grand (ci-dessous, on aura besoin de l'inégalité $p \geqslant 7$ ). C'est le cas, par exemple, quand $p=11$, car $2^{11}-1=23 \times 89$. En effet, écrivons $2^{p}-1$ comme le produit $2^{p}-1=q \times r \times m$, où $q$ et $r$ sont deux nombres premiers, et $m$ est un entier quelconque. On considère alors l'ensemble $S$ formé de 0 ainsi que des entiers de la forme
$$
\pm 2^{a} \prod_{k \geqslant 2}\left(2^{k}-1\right)^{\alpha_{k}}
$$
où les $\alpha_{k}$ sont des entiers relatifs dont seul un nombre fini est non nul. L'ensemble $S$ est manifestement beau et stable par division.
Supposons maintenant que $q \in S$ : on écrit alors $q$ sous la forme
$$
q=\prod_{k \geqslant 2}\left(2^{k}-1\right)^{\alpha_{k}}
$$
et on note $\ell$ l'indice maximal tel que $\alpha_{\ell} \neq 0$. Puisque l'ordre de 2 modulo $q$ et $r$ divise $p$, il est égal à $p$, de sorte que $\ell \geqslant p \geqslant 7$.
Le théorème de Zsygmondy indique alors qu'il existe un nombre premier $s$ qui divise $2^{\ell}-1$ et aucun entier $2^{k}-1$ pour $1 \leqslant k \leqslant \ell-1$. On remarque alors que
$$
v_{s}(q)=\sum_{k \geqslant 2} \alpha_{k} v_{s}\left(2^{k}-1\right)=\alpha_{\ell} v_{s}\left(2^{\ell}-1\right) \neq 0 .
$$
On en déduit que $s=q$, donc que $\ell=p$, et que $v_{q}\left(2^{\ell}-1\right)=1$. Cela signifie en particulier que $r \neq q$. Mais alors, même pour $\ell=p$, et au lieu de choisir $s=q$, on aurait pu satisfaire le théorème de Zsygmondy en choisissant $s=r$, obtenant ainsi une contradiction. On en conclut donc bien que $q \notin S$, et donc que $S \neq \mathbb{Z}$.
Commentaire des correcteurs Ce problème de théorie des nombres était assez difficile car nécessitait une astuce : la solution la plus simple faisait appel à la décomposition d'un entier en base $b$. Seuls cinq élèves y ont pensé et ils ont tous obtenu la note maximale. Le barème valorisait cette astuce, si bien qu'il était impossible d'avoir une note strictement supérieure à 3 si cet élément de décomposition en base n'était pas évoqué.
Quasiment tous les élèves se sont rendus compte que le seul ensemble beau et fort serait $\mathbb{Z}$, sans forcément savoir le prouver.
Beaucoup d'élèves ont pensé à montrer que tout entier (parfois en ne se restreignant qu'aux entiers impairs ou premiers) possédait un multiple dans $S$, ce qui était essentiel dans la suite. Beaucoup ont également montré que $S$ était symétrique par rapport à 0 (c'est-à-dire que, $n \in S$, alors $-n \in S$ ), ce qui permet d'éviter de se préoccuper des entiers négatifs dans la suite.
Revenons enfin sur quelques erreurs régulièrement rencontrées:
$\triangleright$ La gestion des entiers négatifs a parfois été source d'une erreur importante, notamment quand les élèves ont entrepris de démontrer par récurrence que $\llbracket 1, n \rrbracket \subseteq S$ pour tout $n \geqslant 1$. Certains élèves ont en effet introduit un entier $k \geqslant 1$ tel que $n k \in S$, et ils ont affirmé que $n-k$ appartenait par hypothèse de récurrence à $S$ en tant qu'entier strictement inférieur à $n$. Cependant, ces élèves n'ont pas écarté le cas où $k \geqslant 2 n$, de sorte que l'on pouvait avoir $n-k \leqslant-n$, remettant ainsi en cause tout leur raisonnement.
$\triangleright$ Quelques élèves ont remarqué qu'il suffisait que tous les nombres premiers soient dans $S$ pour conclure. C'est vrai, mais aucune solution connue ne prouve immédiatement ce résultat. En l'occurence, plusieurs élèves pensaient avoir résolu l'exercice en montrant ce résultat. Ils se fondaient sur la croyance (erronnée, comme indiqué dans la remarque ci-dessus) que, si $n$ et $m$ sont deux entiers naturels impairs distincts, alors l'ordre de 2 modulo $n$ est différent de celui de 2 modulo $m$. Cette erreur est équivalente à la méconnaissance du théorème de Zsigmondy consistant à croire que pour $n \notin\{1,6\}$, $2^{n}-1$ a exactement un diviseur premier primitif.
$\triangleright$ Enfin, les raisonnements vagues du style « on construit de plus en plus d'entiers en prenant les racines entières de polynômes à coefficients dans un ensemble de plus en plus grand » peuvent aider à se faire une idée, mais ne rapportent évidemment aucun point
Soulignons le fait que, dans un exercice comme celui-ci, vérifier explicitement que les petites valeurs de $n$ (par exemple $n=0, n=1$ et $n=2$ ) sont dans $S$ rapporte forcément un point, et pourtant quelques élèves n'ont pas eu ce réflexe.
Enfin, beaucoup d'élèves prouvent que si $a b \in S$ et $a \in S$ non nul, alors $b \in S$. Ce résultat certes correct est en fait trompeur, car il invite à n'utiliser que les polynômes de degré 1 de l'énoncé, qui ne suffisent manifestement pas à conclure, comme indiqué dans la remarque ci-dessus.
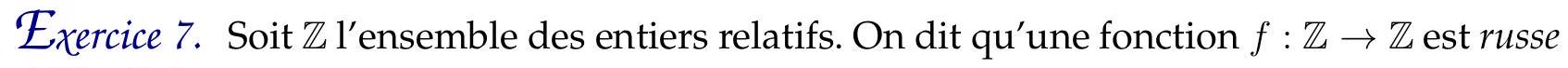 si l'égalité
$$
f(f(x+y)+y)=f(f(x)+y)
$$
est vérifiée pour tous les entiers $x$ et $y$. On dit également qu'un entier $v$ est $f$-rare si l'ensemble des entiers $x$ tels que $f(x)=v$ est un ensemble fini et non vide.
a) Démontrer qu'il existe une fonction $f$ russe pour laquelle il existe un entier $f$-rare.
b) Démontrer que, pour toute fonction $f$ russe, il existe au plus un entier $f$-rare.
|
{
"exam": "French_tests",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web-05-2020.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T1",
"year": "2019"
}
|
Let $S$ be a set of integers. We say that $S$ is beautiful if it contains all integers of the form $2^{a}-2^{b}$, where $a$ and $b$ are non-zero natural numbers. We also say that $S$ is strong if, for any non-constant polynomial $P(X)$ with coefficients in $S$, the integer roots of $P(X)$ also belong to $S$.
Find all sets that are both beautiful and strong.
|
a) Let $f$ be the function defined by $f(0)=0$ and $f(n)=2^{v_{2}(n)+1}$, where $v_{2}(n)$ is the 2-adic valuation of $n$. First, it is clear that 0 is $f$-rare, since its only preimage under $f$ is 0 itself.
Furthermore, let $x$ and $y$ be two integers: by setting $v_{2}(0)=\infty$ and $\infty+1=\infty$, it appears that $v_{2}(f(x))=v_{2}(x)+1$, that $v_{2}(x+y)=\min \left\{v_{2}(x), v_{2}(y)\right\}$ if $v_{2}(x) \neq v_{2}(y)$, and that $v_{2}(x+y) \geqslant \min \left\{v_{2}(x), v_{2}(y)\right\}+1$ otherwise.
Finally, we have $f(x)=f(y)$ if and only if $v_{2}(x)=v_{2}(y)$. Consequently, $\triangleright$ if $v_{2}(x) \geqslant v_{2}(y)$, then
$$
v_{2}(f(x+y))=v_{2}(x+y)+1 \geqslant v_{2}(y)+1
$$
so $v_{2}(f(x+y)+y)=v_{2}(y)=v_{2}(f(x)+y)$ and $f(f(x+y)+y)=f(f(x)+y)$;
$\triangleright$ if $v_{2}(x)<v_{2}(y)$, then
$$
v_{2}(f(x+y))=v_{2}(x+y)+1=v_{2}(x)+1=v_{2}(f(x))
$$
so $f(x+y)=f(x)$ and $f(f(x+y)+y)=f(f(x)+y)$.
Thus, $f$ is a Russian function, which answers the question.
b) Let $v$ be a potential $f$-rare integer. We set $X_{v}=\{x \in \mathbb{Z}: f(x)=v\}$, then $a=\min \left(X_{v}\right)$ and $b=\max \left(X_{v}\right)$.
First, an immediate induction on $k$ shows that $f(f(x)+y)=f(f(x+k y)+y)$ for all integers $x, y$ and $k$. Therefore, if we set $y=a-f(x)$, then
$$
f(f(x+k y)+y)=f(f(x)+y)=f(a)=v
$$
so $f(x+k y)+y \in X_{v}$, which means that $f(x+k y) \geqslant a-y=f(x)$ for all $k \in \mathbb{Z}$. Similarly, if we set $z=b-f(x)$, then $f(x+\ell z)+z \in X_{v}$, which means that $f(x+\ell z) \leqslant b-z=f(x)$ for all $\ell \in \mathbb{Z}$.
The set $X_{f(x)}$ therefore contains the integer $x+m y z$ for all $m \in \mathbb{Z}$. Consequently, if the integer $r=f(x)$ is $f$-rare, it must be that $y z=0$, and thus that $r=f(x) \in\{a, b\} \subseteq X_{v}$. Thus, only the elements of $X_{v}$ can be $f$-rare.
But then, for any integer $w$ that would be $f$-rare, we know that $v$ belongs to both $X_{v}$ and $X_{w}$, which proves that $v=w$, as expected.
Comment from the graders This very difficult problem was substantially solved by three students. In doing so, they exceeded the expectations that the graders had formulated in view of the difficulty of the problem.
Moreover, several students proposed Russian functions that were in fact not: it is important to be meticulous when verifying that a function satisfies the conditions of a problem, especially if this verification is not obvious, as was the case here, and if it is supposed to provide a ready-made answer to a question in the problem.
|
not found
|
Yes
|
Incomplete
|
math-word-problem
|
Number Theory
|
Soit $S$ un ensemble d'entiers relatifs. On dit que $S$ est beau s'il contient tous les entiers de la forme $2^{a}-2^{b}$, où $a$ et $b$ sont des entiers naturels non nuls. On dit également que $S$ est fort si, pour tout polynôme $P(X)$ non constant et à coefficients dans $S$, les racines entières de $P(X)$ appartiennent également à $S$.
Trouver tous les ensembles qui sont à la fois beaux et forts.
|
a) Soit $f$ la fonction définie par $f(0)=0$ et $f(n)=2^{v_{2}(n)+1}$, où $v_{2}(n)$ est la valuation 2 adique de $n$. Tout d'abord, il est clair que 0 est $f$-rare, puisque son seul antécédent par $f$ est 0 lui-même.
D'autre part, soit $x$ et $y$ deux entiers relatifs : en posant $v_{2}(0)=\infty$ et $\infty+1=\infty$, il apparaît que $v_{2}(f(x))=v_{2}(x)+1$, que $v_{2}(x+y)=\min \left\{v_{2}(x), v_{2}(y)\right\}$ si $v_{2}(x) \neq v_{2}(y)$, et que $v_{2}(x+y) \geqslant \min \left\{v_{2}(x), v_{2}(y)\right\}+1$ sinon.
Enfin, on a $f(x)=f(y)$ si et seulement si $v_{2}(x)=v_{2}(y)$. Par conséquent, $\triangleright \operatorname{si} v_{2}(x) \geqslant v_{2}(y)$, alors
$$
v_{2}(f(x+y))=v_{2}(x+y)+1 \geqslant v_{2}(y)+1
$$
donc $v_{2}(f(x+y)+y)=v_{2}(y)=v_{2}(f(x)+y)$ et $f(f(x+y)+y)=f(f(x)+y)$;
$\triangleright \operatorname{si} v_{2}(x)<v_{2}(y)$, alors
$$
v_{2}(f(x+y))=v_{2}(x+y)+1=v_{2}(x)+1=v_{2}(f(x))
$$
donc $f(x+y)=f(x)$ et $f(f(x+y)+y)=f(f(x)+y)$.
Ainsi, $f$ est une fonction russe, ce qui répond à la question.
b) Soit $v$ un éventuel entier $f$-rare. On pose $X_{v}=\{x \in \mathbb{Z}: f(x)=v\}$, puis $a=\min \left(X_{v}\right)$ et $b=\max \left(X_{v}\right)$.
Tout d'abord, une récurrence immédiate sur $k$ montre que $f(f(x)+y)=f(f(x+k y)+y)$ pour tous les entiers relatifs $x, y$ et $k$. Par conséquent, si on pose $y=a-f(x)$, alors
$$
f(f(x+k y)+y)=f(f(x)+y)=f(a)=v
$$
donc $f(x+k y)+y \in X_{v}$, de sorte que $f(x+k y) \geqslant a-y=f(x)$ pour tout $k \in \mathbb{Z}$. De même, si on pose $z=b-f(x)$, alors $f(x+\ell z)+z \in X_{v}$, de sorte que $f(x+\ell z) \leqslant b-z=f(x)$ pour tout $\ell \in \mathbb{Z}$.
L'ensemble $X_{f(x)}$ contient donc l'entier $x+m y z$ pour tout $m \in \mathbb{Z}$. Par conséquent, si l'entier $r=f(x)$ est $f$-rare, c'est que $y z=0$, et donc que $r=f(x) \in\{a, b\} \subseteq X_{v}$. Ainsi, seuls les éléments de $X_{v}$ sont susceptibles d'être $f$-rares.
Mais alors, pour tout entier $w$ qui serait $f$-rare, on sait que $v$ appartient à la fois à $X_{v}$ et à $X_{w}$, ce qui démontre que $v=w$, comme attendu.
Commentaire des correcteurs Ce problème très difficile a été substantiellement résolu par trois élèves. Ceux-ci ont, ce faisant, dépassé les attentes que les correcteurs avaient formulées au vu de la difficulté du problème.
Par ailleurs, plusieurs élèves ont proposé des fonctions russes qui n'en étaient en fait pas : il est important d'être méticuleux quand on vérifie qu'une fonction satisfait les conditions d'un énoncé, d'autant plus si cette vérification n'a rien d'évident, comme c'était le cas ici, et qu'elle est censée fournir une réponse toute faite à une question de l'énoncé.
|
{
"exam": "French_tests",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web-05-2020.jsonl",
"solution_match": "## Solution de l'exercice 7",
"tier": "T1",
"year": "2019"
}
|
Let $a_{1}, a_{2}, \ldots$ be the sequence of integers such that $a_{1}=1$ and, for all integers $n \geqslant 1$,
$$
a_{n+1}=a_{n}^{2}+a_{n}+1
$$
Prove, for all integers $n \geqslant 1$, that $a_{n}^{2}+1$ divides $a_{n+1}^{2}+1$.
|
For all integers $n \geqslant 1$, let $b_{n}=a_{n}^{2}+1$. We conclude by directly observing that
$$
b_{n+1} \equiv\left(a_{n}^{2}+a_{n}+1\right)^{2}+1 \equiv\left(b_{n}+a_{n}\right)^{2}+1 \equiv a_{n}^{2}+1 \equiv b_{n} \equiv 0 \quad\left(\bmod b_{n}\right)
$$
$\underline{\text { Alternative Solution } n^{\circ} 1}$ It suffices to observe, for all integers $n \geqslant 1$, that
$$
\begin{aligned}
a_{n+1}^{2}+1 & =\left(a_{n}^{2}+a_{n}+1\right)^{2}+1 \\
& =a_{n}^{4}+2 a_{n}^{3}+3 a_{n}^{2}+2 a_{n}+2 \\
& =a_{n}^{2}\left(a_{n}^{2}+1\right)+2 a_{n}^{3}+2 a_{n}^{2}+2 a_{n}+2 \\
& =a_{n}^{2}\left(a_{n}^{2}+1\right)+2 a_{n}\left(a_{n}^{2}+1\right)+2 a_{n}^{2}+2 \\
& =a_{n}^{2}\left(a_{n}^{2}+1\right)+2 a_{n}\left(a_{n}^{2}+1\right)+2\left(a_{n}^{2}+1\right) \\
& =\left(a_{n}^{2}+2 a_{n}+2\right)\left(a_{n}^{2}+1\right)
\end{aligned}
$$
is indeed a multiple of $a_{n}^{2}+1$.
Comment from the graders The exercise was well solved. Some attempted induction, with little success, as it was difficult to obtain the result by induction. Few papers worked modulo $a_{n}^{2}+1$, which greatly simplified the calculations.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $a_{1}, a_{2}, \ldots$ la suite d'entiers telle que $a_{1}=1$ et, pour tout entier $n \geqslant 1$,
$$
a_{n+1}=a_{n}^{2}+a_{n}+1
$$
Démontrer, pour tout entier $n \geqslant 1$, que $a_{n}^{2}+1$ divise $a_{n+1}^{2}+1$.
|
Pour tout entier $n \geqslant 1$, posons $b_{n}=a_{n}^{2}+1$. On conclut en constatant directement que
$$
b_{n+1} \equiv\left(a_{n}^{2}+a_{n}+1\right)^{2}+1 \equiv\left(b_{n}+a_{n}\right)^{2}+1 \equiv a_{n}^{2}+1 \equiv b_{n} \equiv 0 \quad\left(\bmod b_{n}\right)
$$
$\underline{\text { Solution alternative } n^{\circ} 1}$ Il suffit de constater, pour tout entier $n \geqslant 1$, que
$$
\begin{aligned}
a_{n+1}^{2}+1 & =\left(a_{n}^{2}+a_{n}+1\right)^{2}+1 \\
& =a_{n}^{4}+2 a_{n}^{3}+3 a_{n}^{2}+2 a_{n}+2 \\
& =a_{n}^{2}\left(a_{n}^{2}+1\right)+2 a_{n}^{3}+2 a_{n}^{2}+2 a_{n}+2 \\
& =a_{n}^{2}\left(a_{n}^{2}+1\right)+2 a_{n}\left(a_{n}^{2}+1\right)+2 a_{n}^{2}+2 \\
& =a_{n}^{2}\left(a_{n}^{2}+1\right)+2 a_{n}\left(a_{n}^{2}+1\right)+2\left(a_{n}^{2}+1\right) \\
& =\left(a_{n}^{2}+2 a_{n}+2\right)\left(a_{n}^{2}+1\right)
\end{aligned}
$$
est effectivement un multiple de $a_{n}^{2}+1$.
Commentaire des correcteurs L'exercice a été bien résolu. Certains ont tenté une récurrence, sans grand succès, car il était difficile d'obtenir le résultat par récurrence. Peu de copies ont travaillé modulo $a_{n}^{2}+1$, ce qui simplifiait pourtant grandement les calculs.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T1",
"year": "2019"
}
|
We distribute the integers $1, 2, \ldots, 8$ into two sets $A$ and $B$, then we denote $P_{A}$ as the product of all elements in $A$ and $P_{B}$ as the product of all elements in $B$.
What are the minimum and maximum values that the sum $P_{A} + P_{B}$ can take?
Note: if a set $E$ is empty, we consider the product of its elements to be equal to 1.
|
Let $A$ and $B$ be two disjoint sets whose union is equal to the set $E=\{1, \ldots, 8\}$.
First, let's maximize the sum $P_{A}+P_{B}$. Without loss of generality, we can assume that $P_{A} \leqslant P_{B}$. Then, if $A$ contains an integer $k \geqslant 2$, we set $A^{\prime}=A \backslash\{k\}$ and $B^{\prime}=$ $B \cup\{k\}$. Then
$$
P_{A^{\prime}}+P_{B^{\prime}} \geqslant P_{B^{\prime}}=k P_{B} \geqslant 2 P_{B} \geqslant P_{A}+P_{B} .
$$
Thus, when the sum $P_{A}+P_{B}$ reaches its maximum value, we know that $A \subseteq\{1\}$, so $P_{A}=1$ and $P_{B}=8!$, hence $P_{A}+P_{B}=8!+1=40321$.
Now, let's minimize the sum $P_{A}+P_{B}$. The arithmetic-geometric mean inequality indicates that $P_{A}+P_{B} \geqslant 2 c$, where we have set $c=\sqrt{P_{A} P_{B}}=\sqrt{8!}$. Since $401^{2}=160801 < 161280=4 c^{2}$, we know that $2 c>401$, and therefore $P_{A}+P_{B} \geqslant\lceil 2 c\rceil \geqslant 402$.
A first instinct is to find two sets $A$ and $B$ such that $P_{A}+P_{B}=402$. We then make some preliminary remarks for this search. First, knowing which set contains the integer 1 makes no difference. Then we prove that one of the two sets contains the integer 6 and the other contains the integers 2 and 3. Indeed, let $X$ be the set that contains 6 and $Y$ the one that does not contain 6:
$\triangleright$ since $P_{Y} \equiv 402-P_{X} \equiv 0(\bmod 6)$, it follows that $Y$ contains the integer 3 and an even integer;
$\triangleright$ if it is $X$ that contains the integer 2, then $P_{Y} \equiv 402-P_{X} \equiv 2(\bmod 4)$, so $X$ contains an even integer but not divisible by 4, which is impossible.
By removing the integers $1,2,3$ and 6 from the sets $A$ and $B$, we are thus reduced to finding a partition of the set $\hat{E}=\{4,5,7,8\}$ into two subsets $\hat{A}$ and $\hat{B}$ such that $P_{\hat{A}}+P_{\hat{B}}=402 / 6=67$. Suppose, without loss of generality, that $\hat{A}$ contains the integer 4. Then $P_{\hat{B}} \equiv 67-P_{\hat{A}} \equiv 1(\bmod 2)$, so $\hat{A}$ also contains the integer 8. Furthermore, if $\hat{A}$ also contains one of the two integers 5 or 7, then $P_{\hat{A}}+P_{\hat{B}} \geqslant P_{\hat{A}} \geqslant 4 \times 5 \times 8 \geqslant 160>67$. Therefore, we must necessarily have $\hat{A}=\{4,8\}$ and $\hat{B}=\{5,7\}$, and we are happy to verify that, in this case, we indeed have $P_{\hat{A}}+P_{\hat{B}}=32+35=67$.
In conclusion, the maximum value of $P_{A}+P_{B}$ is equal to $P_{\emptyset}+P_{E}=8!+1=40321$, and the minimum value of $P_{A}+P_{B}$ is equal to $P_{\{2,3,5,7\}}+P_{\{1,4,6,8\}}=402$.
|
40321 \text{ and } 402
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On répartit les entiers de $1,2, \ldots, 8$ en deux ensembles $A$ et $B$, puis on note $P_{A}$ le produit de tous les éléments de $A$ et $P_{B}$ le produit de tous les éléments de $B$.
Quelles sont les valeurs minimale et maximale que peut prendre la somme $P_{A}+P_{B}$ ?
Note : si un ensemble $E$ est vide, on considérera que le produit de ses éléments est égal à 1.
|
Soit $A$ et $B$ deux ensembles disjoints dont la réunion est égale à l'ensemble $E=\{1, \ldots, 8\}$.
Tâchons tout d'abord de maximiser la somme $P_{A}+P_{B}$. Sans perte de généralité, on peut supposer que $P_{A} \leqslant P_{B}$. Puis, si $A$ contient un entier $k \geqslant 2$, on pose $A^{\prime}=A \backslash\{k\}$ et $B^{\prime}=$ $B \cup\{k\}$. Alors
$$
P_{A^{\prime}}+P_{B^{\prime}} \geqslant P_{B^{\prime}}=k P_{B} \geqslant 2 P_{B} \geqslant P_{A}+P_{B} .
$$
Ainsi, lorsque la somme $P_{A}+P_{B}$ atteint sa valeur maximale, on sait que $A \subseteq\{1\}$, donc que $P_{A}=1$ et que $P_{B}=8!$, de sorte que $P_{A}+P_{B}=8!+1=40321$.
Tâchons maintenant de minimiser la somme $P_{A}+P_{B}$. L'inégalité arithmético-géométrique indique que $P_{A}+P_{B} \geqslant 2 c$, où l'on a posé $c=\sqrt{P_{A} P_{B}}=\sqrt{8!}$. Comme $401^{2}=160801<$ $161280=4 c^{2}$, on sait que $2 c>401$, et donc que $P_{A}+P_{B} \geqslant\lceil 2 c\rceil \geqslant 402$.
Un premier réflexe est donc de rechercher deux ensembles $A$ et $B$ tels que $P_{A}+P_{B}=402$. On formule alors quelques remarques préliminaires à cette recherche. Tout d'abord, savoir quel ensemble contient l'entier 1 ne change rien. Puis on démontre que l'un des deux ensembles contient l'entier 6 et que l'autre contient les entiers 2 et 3 . En effet, soit $X$ l'ensemble qui contient 6 et $Y$ celui qui ne contient pas 6 :
$\triangleright$ puisque $P_{Y} \equiv 402-P_{X} \equiv 0(\bmod 6)$, c'est que $Y$ contient l'entier 3 ainsi qu'un entier pair;
$\triangleright$ si c'est $X$ qui contient l'entier 2, alors $P_{Y} \equiv 402-P_{X} \equiv 2(\bmod 4)$, donc $X$ contient un entier pair mais pas divisible par 4 , ce qui est impossible.
Quitte à supprimer les entiers $1,2,3$ et 6 des ensembles $A$ et $B$, on se ramène donc à trouver une partition de l'ensemble $\hat{E}=\{4,5,7,8\}$ en deux sous-ensembles $\hat{A}$ et $\hat{B}$ tels que $P_{\hat{A}}+$ $P_{\hat{B}}=402 / 6=67$. Supposons, sans perte de généralité, que $\hat{A}$ contient l'entier 4. Alors $P_{\hat{B}} \equiv 67-P_{\hat{A}} \equiv 1(\bmod 2)$, donc $\hat{A}$ contient aussi l'entier 8 . En outre, si $\hat{A}$ contient également l'un des deux entiers 5 ou 7 , alors $P_{\hat{A}}+P_{\hat{B}} \geqslant P_{\hat{A}} \geqslant 4 \times 5 \times 8 \geqslant 160>67$. On a donc nécessairement $\hat{A}=\{4,8\}$ et $\hat{B}=\{5,7\}$, et on est tout heureux de vérifier que, dans ce cas, on a effectivement $P_{\hat{A}}+P_{\hat{B}}=32+35=67$.
En conclusion, la valeur maximale de $P_{A}+P_{B}$ est égale à $P_{\emptyset}+P_{E}=8!+1=40321$, et la valeur minimale de $P_{A}+P_{B}$ est égale à $P_{\{2,3,5,7\}}+P_{\{1,4,6,8\}}=402$.
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T1",
"year": "2019"
}
|
We distribute the integers $1, 2, \ldots, 8$ into two sets $A$ and $B$, then we denote $P_{A}$ as the product of all elements in $A$ and $P_{B}$ as the product of all elements in $B$.
What are the minimum and maximum values that the sum $P_{A} + P_{B}$ can take?
Note: if a set $E$ is empty, we consider the product of its elements to be equal to 1.
|
$n^{\circ} 1$ Let $A$ and $B$ be two disjoint sets whose union is equal to the set $E=\{1, \ldots, 8\}$, and let $c=\sqrt{8!}$. Without loss of generality, we can assume that $P_{A} \leqslant P_{B}$; since $P_{A} \times P_{B}=P_{E}=c^{2}$, this means that $P_{A} \leqslant c$.
But then $P_{A}+P_{B}=f\left(P_{A}\right)$, where we have set $f(x)=x+c^{2} / x$, and it remains for us to find the minimum and maximum values that $f\left(P_{A}\right)$ can take. We therefore study the variation of $f$: if $x \leqslant y \leqslant c$, then
$$
f(y)-f(x)=\frac{y^{2}+c^{2}}{y}-\frac{x^{2}+c^{2}}{x}=\frac{\left(c^{2}-x y\right)(x-y)}{x y} \leqslant 0 .
$$
The function $f$ is therefore decreasing on the interval $(0, c]$ and, consequently:
$\triangleright$ to maximize $f\left(P_{A}\right)$, it suffices to minimize $P_{A}$, that is, to choose $A$ empty, or again $P_{A}=1$;
$\triangleright$ to minimize $f\left(P_{A}\right)$, it suffices to maximize $P_{A}$, knowing that $P_{A}$ is a product of elements of $E$ and that $P_{A} \leqslant c$.
We therefore need to calculate the value of the integer $\lfloor c\rfloor$. Since $c^{2}=8!=40320$ and
$$
200^{2}=40000<40320<40401=201^{2}
$$
$c$ is therefore that $\lfloor c\rfloor=200$. We therefore study the integers $200,199,198, \ldots$ until we find an integer $n$ that can be written as a product of elements of $E$. Instead of proceeding brutally, we can make two preliminary remarks:
$\triangleright$ generally, $n$ must divide $8!=2^{7} \times 3^{2} \times 5 \times 7$;
$\triangleright$ moreover, if $n$ is odd, then $n$ even divides $3 \times 5 \times 7=105$, so $n \leqslant 105$.
We deduce from the first remark that $n$ cannot take any of the values
$$
200=2^{3} \times 5^{2}, 198=11 \times 18,196=4 \times 7^{2}, 194=2 \times 97
$$
so that $n=192=4 \times 6 \times 8$ is in fact the integer sought.
Consequently, the maximum value of $P_{A}+P_{B}$ is equal to $f(1)=8!+1=40321$, and the minimum value of $P_{A}+P_{B}$ is equal to $f(192)=192+210=402$.
Comment from the correctors The exercise was solved in a very heterogeneous way. Many students found the value of the maximum, but few provided a good justification for its maximality: for example, one could use the rearrangement inequality, or assert that if $P_{A}<8!$, then $P_{A} \leqslant 8!/ 2$.
For the minimum, it was already more difficult to find how to obtain the minimum value of 402, and few students saw how to use an arithmetic-geometric inequality to show that this was optimal. However, some used more atypical approaches and found results, notably through the study of functions or through clever comparisons. Many said that one had to obtain the terms as close as possible to have equality: the idea is interesting, but it needed to be formalized to obtain rigorous results.
|
40321 \text{ and } 402
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On répartit les entiers de $1,2, \ldots, 8$ en deux ensembles $A$ et $B$, puis on note $P_{A}$ le produit de tous les éléments de $A$ et $P_{B}$ le produit de tous les éléments de $B$.
Quelles sont les valeurs minimale et maximale que peut prendre la somme $P_{A}+P_{B}$ ?
Note : si un ensemble $E$ est vide, on considérera que le produit de ses éléments est égal à 1.
|
$n^{\circ} 1$ Soit $A$ et $B$ deux ensembles disjoints dont la réunion est égale à l'ensemble $E=\{1, \ldots, 8\}$, et soit $c=\sqrt{8}$ !. Sans perte de généralité, on peut supposer que $P_{A} \leqslant P_{B} ;$ puisque $P_{A} \times P_{B}=P_{E}=c^{2}$, cela signifie que $P_{A} \leqslant c$.
Mais alors $P_{A}+P_{B}=f\left(P_{A}\right)$, où l'on a posé $f(x)=x+c^{2} / x$, et il nous reste donc à trouver les valeurs minimale et maximale que peut prendre $f\left(P_{A}\right)$. On étudie donc le sens de variation de $f$ : si $x \leqslant y \leqslant c$, alors
$$
f(y)-f(x)=\frac{y^{2}+c^{2}}{y}-\frac{x^{2}+c^{2}}{x}=\frac{\left(c^{2}-x y\right)(x-y)}{x y} \leqslant 0 .
$$
La fonction $f$ est donc décroissante sur l'intervalle $(0, c]$ et, par conséquent :
$\triangleright$ afin de maximiser $f\left(P_{A}\right)$, il suffit de minimiser $P_{A}$, c'est-à-dire de choisir $A$ vide, ou encore $P_{A}=1$;
$\triangleright$ afin de minimiser $f\left(P_{A}\right)$, il suffit de maximiser $P_{A}$, sachant que $P_{A}$ est un produit d'éléments de $E$ et que $P_{A} \leqslant c$.
Il nous faut donc calculer la valeur de l'entier $\lfloor c\rfloor$. Puisque $c^{2}=8!=40320$ et que
$$
200^{2}=40000<40320<40401=201^{2}
$$
$c^{\prime}$ est donc que $\lfloor c\rfloor=200$. On étudie donc les entiers $200,199,198, \ldots$ jusqu'à tomber sur un entier $n$ que l'on pourra écrire comme un produit d'éléments de $E$. Au lieu de procéder brutalement, on peut formuler deux remarques préalables:
$\triangleright$ de manière générale, $n$ doit diviser $8!=2^{7} \times 3^{2} \times 5 \times 7$;
$\triangleright$ en outre, si $n$ est impair, alors $n$ divise même $3 \times 5 \times 7=105$, donc $n \leqslant 105$.
On déduit de la première remarque que $n$ ne peut prendre aucune des valeurs
$$
200=2^{3} \times 5^{2}, 198=11 \times 18,196=4 \times 7^{2}, 194=2 \times 97
$$
de sorte que $n=192=4 \times 6 \times 8$ est en fait l'entier recherché.
Par conséquent, la valeur maximale de $P_{A}+P_{B}$ est égale à $f(1)=8!+1=40321$, et la valeur minimale de $P_{A}+P_{B}$ est égale à $f(192)=192+210=402$.
Commentaire des correcteurs L'exercice a été résolu de façon très hétérogène. Beaucoup d'élèves ont trouvé la valeur du maximum, mais peu ont fourni une bonne justification de sa maximalité : on pouvait par exemple utiliser l'inégalité du réordonnement, ou bien affirmer que si $P_{A}<8$ !, on a forcément $P_{a} \leqslant 8!/ 2$.
Pour le minimum, il était déjà plus difficile de trouver comment obtenir la valeur minimale de 402, et peu d'élèves ont vu comment utiliser une inégalité arithmético-géométrique permettait de montrer que celle-ci était optimale. Néanmoins, certains ont utilisé des approches plus atypiques et trouvé des résultats, notamment via l'étude de fonctions ou via des comparaisons astucieuses. Nombreux ont dit qu'il fallait obtenir les termes les plus proches possible pour avoir égalité : l'idée est intéressante, mais il fallait formaliser pour obtenir des résultats rigoureux.
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2019"
}
|
Let $ABC$ be a triangle and let $\omega$ be its circumcircle. Let $\ell_{B}$ and $\ell_{C}$ be two parallel lines passing through points $B$ and $C$, respectively. We denote by $D$ the intersection point, other than $B$, between $\omega$ and the line $\ell_{B}$. Similarly, we denote by $E$ the intersection point, other than $C$, between $\omega$ and the line $\ell_{C}$.
We assume that the lines $\ell_{C}$ and $(A D)$ intersect at a point $F$, and that the lines $\ell_{B}$ and $(A E)$ intersect at a point $G$. We then denote by $O, O_{1}$, and $O_{2}$ the centers of the circumcircles of triangles $ABC$, $ADG$, and $AEF$, respectively. Finally, we denote by $P$ the center of the circumcircle of triangle $OO_{1}O_{2}$.
Prove that the line $(OP)$ is parallel to both lines $\ell_{B}$ and $\ell_{C}$.
|
Let's start by drawing a figure, taking care to highlight the triangle $O O_{1} O_{2}$, since $P$ is the center of the circumcircle of this triangle. We also note $\omega_{1}, \omega_{2}$, and $\omega^{\prime}$ as the circumcircles of $A D G$, $A E F$, and $O O_{1} O_{2}$, respectively.
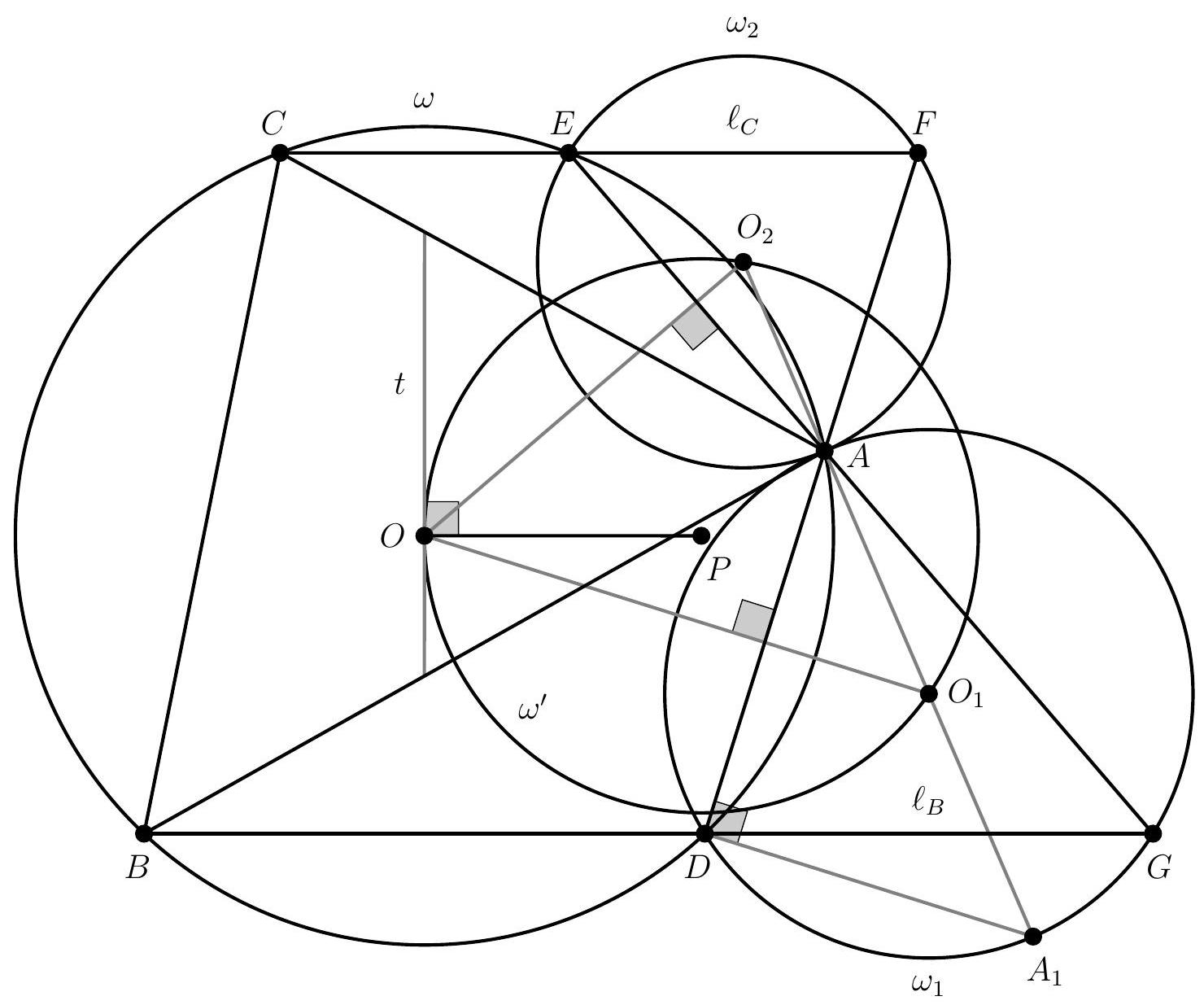
We immediately notice that the points $A, O_{1}$, and $O_{2}$ seem to be collinear, so we quickly set out to prove this. Indeed, the lines $(D G)$ and $(E F)$ are parallel to each other. Thales' theorem then indicates that there is a homothety $h$, centered at $A$, which maps the triangle $A D G$ to the triangle $A F E$. We deduce that $O_{2}=h\left(O_{1}\right)$, and therefore that the points $A$, $O_{1}$, and $O_{2}$ are indeed collinear.
To prove that $(O P)$ is parallel to $\ell_{B}$ and $\ell_{C}$, we will now calculate the angle between the lines $\left(O P, \ell_{B}\right)$. To do this, we start by getting rid of the point $P$ by invoking the tangent at $O$ to $\omega^{\prime}$: if we denote this tangent by $t$, then
\[
\begin{aligned}
\left(O P, \ell_{B}\right) & =(O P, t)+\left(t, O O_{2}\right)+\left(O O_{2}, \ell_{B}\right) \\
& =90^{\circ}+\left(O_{1} O, O_{1} O_{2}\right)+\left(O O_{2}, \ell_{B}\right) \\
& =90^{\circ}+\left(O_{1} O, O_{1} A\right)+\left(O O_{2}, \ell_{B}\right) .
\end{aligned}
\]
Since $(A D)$ is the radical axis of the circles $\omega_{1}$ and $\omega^{\prime}$, the lines $(A D)$ and $\left(O O_{1}\right)$ are perpendicular to each other. Similarly, $(A E)$ and $\left(O O_{2}\right)$ are perpendicular. We deduce that
\[
\begin{aligned}
\left(O P, \ell_{B}\right) & =90^{\circ}+\left(O_{1} O, O_{1} A\right)+\left(O O_{2}, \ell_{B}\right) \\
& =90^{\circ}+\left(O_{1} O, A D\right)+\left(A D, O_{1} A\right)+\left(O O_{2}, A E\right)+\left(A E, \ell_{B}\right) \\
& =90^{\circ}+90^{\circ}+\left(A D, O_{1} A\right)+90^{\circ}+\left(A E, \ell_{B}\right) \\
& =90^{\circ}+\left(A D, O_{1} A\right)+\left(A E, \ell_{B}\right)
\end{aligned}
\]
By doing so, we have already eliminated the points $P, O$, and $O_{2}$, suggesting that we are on the right track. Our next victim will be the point $O_{1}$. Indeed, if we denote by $A_{1}$ the symmetric point of $A$ with respect to $O_{1}$, then $\left[A A_{1}\right]$ is a diameter of $\omega_{1}$, so
\[
\left(A D, O_{1} A\right)=\left(A D, A A_{1}\right)=\left(A D, D A_{1}\right)+\left(D A_{1}, A A_{1}\right)=90^{\circ}+(D G, A G)=90^{\circ}+(B D, A E)
\]
But then we have already won, since
\[
\left(O P, \ell_{B}\right)=90^{\circ}+\left(A D, O_{1} A\right)+\left(A E, \ell_{B}\right)=90^{\circ}+90^{\circ}+(B D, A E)+\left(A E, \ell_{B}\right)=\left(B D, \ell_{B}\right),
\]
which concludes the proof.
$\underline{\text { Alternative Solution } n^{\circ} 1}$ We reuse the names of the points and circles introduced in the previous solution.
Since the lines $\ell_{B}$ and $\ell_{C}$ are parallel, and since $A, B, C, D$, and $E$ are concyclic, we know that $(G A, G D)=(E A, E F)$ and, similarly, $(F E, F A)=(D G, D A)$. The triangles $A E F$ and $A G D$ are therefore similar. Consequently, the triangles $F O_{2} A$ and $D O_{1} A$ are also similar, so $\left(A F, A O_{2}\right)=\left(A D, A O_{1}\right)$, and therefore the points $O_{1}$, $A$, and $O_{2}$ are collinear.
Next, since the line $(A D)$ is the radical axis of the circles $\omega$ and $\omega_{1}$, it is perpendicular to $\left(O O_{1}\right)$. We deduce, from the theorem of the angle at the center, and by denoting $A_{1}$ the symmetric point of $A$ with respect to $O_{1}$, that
\[
\begin{aligned}
\left(O_{1} O_{2}, O_{1} O\right) & =\left(A A_{1}, A D\right)+\left(A D, O O_{1}\right)=\left(A A_{1}, D A_{1}\right)+\left(D A_{1}, A D\right)+90^{\circ} \\
& =(A G, D G)+90^{\circ}+90^{\circ}=(G A, G D) .
\end{aligned}
\]
We show similarly that $\left(O_{2} O, O_{2} O_{1}\right)=(F E, F A)=(D G, D A)$. The triangles $O O_{1} O_{2}$ and $A G D$ are therefore indirectly similar.
But then the triangles $O O_{1} P$ and $A G O_{1}$ are also indirectly similar. We conclude that
\[
\left(O P, O_{1} O_{2}\right)=\left(G D, A O_{1}\right)=\left(G D, O_{1} O_{2}\right),
\]
which means that $(O P)$ is parallel to the line $(G D)=\ell_{B}$, and therefore to $\ell_{C}$ as well.
Remark: If one decides to use directed angles, it is important to never divide angles by two, for example, to use the theorem of the angle at the center or when encountering an isosceles triangle or an angle bisector. Indeed, here is an example of a horror that could result if one does not take this precaution:
«Since the line $\left(O O_{1}\right)$ is the angle bisector of $\widehat{A O_{1} D}$, we know that $\left(O_{1} O, O_{1} A\right)=\left(O_{1} D, O_{1} A\right) / 2$. Since $A O_{1} D$ is isosceles at $O_{1}$, we deduce that
\[
\left(A D, A O_{1}\right)=\left(\left(D O_{1}, D A\right)+\left(A D, A O_{1}\right)\right) / 2=\left(D O_{1}, A O_{1}\right) / 2=\left(O_{1} O, O_{1} A\right)
\]
But this equality is of course completely false, since we actually have $\left(A D, A O_{1}\right)=\left(O_{1} O, O_{1} A\right)+90^{\circ}$. Oops!»
The reason why the above reasoning is false is that directed angles are angles modulo $180^{\circ}$. Consequently, if we divide a directed angle by two, we get a relation that is only valid modulo $90^{\circ}$. We will therefore avoid, at all costs, if we decide to use directed angles, dividing angles by two.
Comment from the graders: The problem was solved by a small number of people. However, many students managed to make significant progress in the problem, trying to prove what they could conjecture from their figure, which is an excellent approach. Simple observations, such as the fact that the lines $\left(O O_{1}\right)$ and $(A D)$ are perpendicular, were actually valuable for solving the problem and were thus rewarded. Do not hesitate to write down all your ideas, even seemingly trivial observations.
|
proof
|
Yes
|
Incomplete
|
proof
|
Geometry
|
Soit $A B C$ un triangle et soit $\omega$ son cercle circonscrit. Soit $\ell_{B}$ et $\ell_{C}$ deux droites parallèles l'une à l'autre, passant respectivement par les points $B$ et $C$. On note $D$ le point d'intersection, autre que $B$, entre $\omega$ et la droite $\ell_{B}$. De même, on note $E$ le point d'intersection, autre que $C$, entre $\omega$ et la droite $\ell_{C}$.
On suppose que les droites $\ell_{C}$ et $(A D)$ se coupent en un point $F$, et que les droites $\ell_{B}$ et $(A E)$ se coupent en un point $G$. On note alors $O, O_{1}$ et $O_{2}$ le centres respectifs des cercles circonscrits aux triangles $A B C, A D G$ et $A E F$. Enfin, on note $P$ le centre du cercle circonscrit au triangle $O O_{1} O_{2}$.
Démontrer que la droite $(O P)$ est parallèle aux deux droites $\ell_{B}$ et $\ell_{C}$.
|
Commençons par tracer une figure, en prenant soin de faire apparaître le triangle $O O_{1} O_{2}$, puisque $P$ en est le centre du cercle circonscrit. On en profite pour noter $\omega_{1}, \omega_{2}$ et $\omega^{\prime}$ les cercles circonscrits à $A D G$, à $A E F$ et à $O O_{1} O_{2}$.

On remarque tout de suite que les points $A, O_{1}$ et $O_{2}$ semblent alignés, et on s'empresse donc de le démontrer. En effet, les droites $(D G)$ et $(E F)$ sont parallèles l'une à l'autre. Le théorème de Thalès indique alors qu'il existe une homothétie $h$, de centre $A$, qui envoie le triangle $A D G$ sur le triangle $A F E$. On en déduit que $O_{2}=h\left(O_{1}\right)$, et donc que les points $A$, $O_{1}$ et $O_{2}$ sont bien alignés.
Afin de démontrer que $(O P)$ est parallèle à $\ell_{B}$ et à $\ell_{C}$, on va maintenant calculer l'angle de droites $\left(O P, \ell_{B}\right)$. Pour ce faire, on commence par se débarrasser du point $P$, en invoquant la
tangente en $O$ à $\omega^{\prime}$ : si l'on note $t$ cette tangente, alors
$$
\begin{aligned}
\left(O P, \ell_{B}\right) & =(O P, t)+\left(t, O O_{2}\right)+\left(O O_{2}, \ell_{B}\right) \\
& =90^{\circ}+\left(O_{1} O, O_{1} O_{2}\right)+\left(O O_{2}, \ell_{B}\right) \\
& =90^{\circ}+\left(O_{1} O, O_{1} A\right)+\left(O O_{2}, \ell_{B}\right) .
\end{aligned}
$$
Puis, comme $(A D)$ est l'axe radical des cercles $\omega_{1}$ et $\omega^{\prime}$, les droites $(A D)$ et $\left(O O_{1}\right)$ sont perpendiculaires l'une à l'autre. De même, $(\mathrm{AE})$ et $\left(\mathrm{OO}_{2}\right)$ sont perpendiculaires. On en déduit que
$$
\begin{aligned}
\left(O P, \ell_{B}\right) & =90^{\circ}+\left(O_{1} O, O_{1} A\right)+\left(O O_{2}, \ell_{B}\right) \\
& =90^{\circ}+\left(O_{1} O, A D\right)+\left(A D, O_{1} A\right)+\left(O O_{2}, A E\right)+\left(A E, \ell_{B}\right) \\
& =90^{\circ}+90^{\circ}+\left(A D, O_{1} A\right)+90^{\circ}+\left(A E, \ell_{B}\right) \\
& =90^{\circ}+\left(A D, O_{1} A\right)+\left(A E, \ell_{B}\right)
\end{aligned}
$$
Ce faisant, on s'est déjà débarrassés des points $P, O$ et $O_{2}$, ce qui suggère que l'on est sur la bonne voie. Notre prochaine victime sera donc le point $O_{1}$. En effet, si l'on note $A_{1}$ le symétrique de $A$ par rapport à $O_{1}$, alors $\left[A A_{1}\right]$ est un diamètre de $\omega_{1}$, de sorte que
$$
\left(A D, O_{1} A\right)=\left(A D, A A_{1}\right)=\left(A D, D A_{1}\right)+\left(D A_{1}, A A_{1}\right)=90^{\circ}+(D G, A G)=90^{\circ}+(B D, A E)
$$
Mais alors on a déjà gagné, puisque
$$
\left(O P, \ell_{B}\right)=90^{\circ}+\left(A D, O_{1} A\right)+\left(A E, \ell_{B}\right)=90^{\circ}+90^{\circ}+(B D, A E)+\left(A E, \ell_{B}\right)=\left(B D, \ell_{B}\right),
$$
ce qui conclut.
$\underline{\text { Solution alternative } n^{\circ} 1}$ On réutilise, ci-dessous, les noms des points et cercles introduits dans la solution précédente.
Puisque les droites $\ell_{B}$ et $\ell_{C}$ sont parallèles, et comme $A, B, C, D$ et $E$ sont cocycliques, on sait tout d'abord que $(G A, G D)=(E A, E F)$ et que, de même, $(F E, F A)=(D G, D A)$. Les triangles $A E F$ et $A G D$ sont donc semblables. Par conséquent, les triangles $F O_{2} A$ et $D O_{1} A$ sont également semblables, de sorte que $\left(A F, A O_{2}\right)=\left(A D, A O_{1}\right)$, et donc que les points $O_{1}$, $A$ et $O_{2}$ sont alignés.
Ensuite, puisque la droite $(A D)$ est l'axe radical des cercles $\omega$ et $\omega_{1}$, elle est perpendiculaire à $\left(O O_{1}\right)$. On en déduit, d'après le théorème de l'angle au centre, et en notant $A_{1}$ le symétrique de $A$ par rapport à $O_{1}$, que
$$
\begin{aligned}
\left(O_{1} O_{2}, O_{1} O\right) & =\left(A A_{1}, A D\right)+\left(A D, O O_{1}\right)=\left(A A_{1}, D A_{1}\right)+\left(D A_{1}, A D\right)+90^{\circ} \\
& =(A G, D G)+90^{\circ}+90^{\circ}=(G A, G D) .
\end{aligned}
$$
On montre de même que $\left(O_{2} O, O_{2} O_{1}\right)=(F E, F A)=(D G, D A)$. Les triangles $O O_{1} O_{2}$ et $A G D$ sont donc indirectement semblables.
Mais alors les triangles $O O_{1} P$ et $A G O_{1}$ sont, aux aussi, indirectement semblables. On en conclut que
$$
\left(O P, O_{1} O_{2}\right)=\left(G D, A O_{1}\right)=\left(G D, O_{1} O_{2}\right),
$$
ce qui signifie bien que $(O P)$ est parallèle à la droite $(G D)=\ell_{B}$, donc à $\ell_{C}$ également.
Remarque: Si l'on entreprend d'utiliser des angles de droites, il est important de ne jamais diviser brutalement les angles par deux, par exemple pour utiliser le théorème de l'angle au centre ou bien quand on rencontre un triangle isocèle ou une bissectrice. En effet, voici un exemple d'horreur à laquelle on pourrait aboutir si on ne prend pas cette peine :
«Puisque la droite $\left(O O_{1}\right)$ est la bissectrice de l'angle $\widehat{A O_{1} D}$, on sait que $\left(O_{1} O, O_{1} A\right)=\left(O_{1} D, O_{1} A\right) / 2$. Puisque $A O_{1} D$ est isocèle en $O_{1}$, on en déduit que
$$
\left(A D, A O_{1}\right)=\left(\left(D O_{1}, D A\right)+\left(A D, A O_{1}\right)\right) / 2=\left(D O_{1}, A O_{1}\right) / 2=\left(O_{1} O, O_{1} A\right)
$$
Mais cette égalité est bien sûr complètement fausse, puisque l'on a en fait $\left(A D, A O_{1}\right)=\left(O_{1} O, O_{1} A\right)+90^{\circ}$. Oups!»
La raison pour laquelle le raisonnement ci-dessus est faux est que les angles de droites sont des angles modulo $180^{\circ}$. Par conséquent, si on divise un angle de droite par deux, on récupère une relation qui n'est valide que modulo $90^{\circ}$. On s'abstiendra donc à tout prix, si on décide d'utiliser des angles de droites, de diviser des angles par deux.
Commentaire des correcteurs L'exercice a été résolu par un faible nombre de personnes. Cependant, de nombreux élèves ont réussi à avancer significativement dans le problème, en essayant de démontrer ce qu'ils pouvaient conjecturer à partir de leur figure, ce qui est une excellente démarche. Des remarques simples, comme le fait que les droites $\left(O O_{1}\right)$ et $(A D)$ sont perpendiculaires, étaient en fait précieuses pour la résolution du problème et étaient alors récompensées. N'hésitez pas à écrire toutes vos idées, même les remarques qui pourraient sembler anodines.
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T1",
"year": "2019"
}
|
In the land of wonders, there are $n$ cities. Each pair of cities is connected by a one-way road, which starts from one of the two cities and arrives at the other. To find her way, Alice questions the King of Hearts: with each question, Alice chooses a pair of cities, and the King of Hearts tells her which is the starting city of the road connecting these two cities.
Prove that, in $5 n$ questions or fewer, Alice can determine whether there exists a city from which at most one road starts.
|
We will describe a strategy that Alice can implement to achieve her goal in $5 n$ questions or fewer. At any time, we will say that a city $v$ is bad if Alice has already found two roads that leave from $v$, and that $v$ is good otherwise. Similarly, we will say that a pair of cities $\{v, w\}$ is explored if Alice has already asked the Queen of Hearts about this pair, and unexplored otherwise.
In addition, in parallel with these questions, Alice has drawn a map on which the $n$ cities are represented by $n$ vertices, and she adds an edge on this map, between the cities $v$ and $w$ for each question she asks about the pair $\{v, w\}$. In the following, we will identify Wonderland with the graph that Alice is building.
First, Alice clearly has no interest in asking the Queen of Hearts about a pair of cities that would both be bad, or about a pair of cities already explored. Alice's strategy therefore begins as follows. As long as there is an unexplored pair $\{v, w\}$ formed by two good cities, Alice chooses such a pair and asks the Queen of Hearts about this pair. At the end of this first step, no vertex in our graph has strictly more than two outgoing edges. Alice has therefore asked at most $2 n$ questions.
Furthermore, let $X$ be the set of cities that are still good at the end of this step, and let $x$ be the cardinality of $X$, so that there are $x(x-1) / 2$ roads between cities in $X$. Every pair $\{v, w\}$ formed by two cities in $X$ is clearly explored; and every city in $X$, since it is good, is therefore the origin of at most one road going to another city in $X$. There are therefore at most $x$ roads between cities in $X$, which means that $x \leqslant 3$.
Alice therefore only has to ask the Queen of Hearts about all pairs $\{v, x\}$ where $x \in X$: this will make $n x \leqslant 3 n$ additional questions, at the end of which Alice will know exactly how many roads leave from each of the cities in $X$. If, at this stage of the algorithm, there is a good city $v$, it is because there was indeed no more than one road that left from $v$.
Comment from the Examiners Due to its difficulty, this problem was solved by a small number of students. Many noticed that for $n \leqslant 11$, Alice could simply ask the direction of all the roads; unfortunately, this did not advance the problem. The key was to realize that, in general, it was necessary to avoid asking a question about a city from which two roads left.
Some students proposed strategies that did not work in $5 n$ questions, but in $6 n$ questions or more (for example, 10n questions), and this was valued. Some students also scored points by showing that at most 3 cities could have fewer than 2 outgoing roads.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Au pays des merveilles se trouvent $n$ villes. Chaque paire de villes est reliée par une route à sens unique, qui part d'une des deux villes et arrive à l'autre. Afin de s'y retrouver, Alice interroge le roi de cœur : à chaque question, Alice choisit une paire de villes, et le roi de cœur lui dit quelle est la ville de départ de la route qui relie ces deux villes.
Démontrer que, en $5 n$ questions ou moins, Alice peut arriver à savoir s'il existe une ville d'où part au plus une route.
|
Nous allons décrire une stratégie qu'Alice peut mettre en place pour aboutir à ses fins en $5 n$ questions ou moins. À tout moment, on dira qu'une ville $v$ est mauvaise si Alice a déjà trouvé deux routes qui partent de $v$, et que $v$ est bonne sinon. De même, on dira qu'une paire de villes $\{v, w\}$ est explorée si Alice a déjà interrogé le roi de cœur sur cette paire-là, et inexplorée sinon.
Enfin, en parallèle de ces questions, Alice a dessiné une carte sur laquelle les $n$ villes sont représentées par $n$ sommets, et elle ajoute une arête sur cette carte, entre les villes $v$ et $w$ à chaque question qu'elle pose sur la paire $\{v, w\}$. Dans la suite, nous allons identifier le pays des merveilles au graphe qu'Alice est en train de construire.
Tout d'abord, Alice n'a manifestement jamais intérêt à interroger le roi de cœur sur une paire de villes qui seraient toutes deux mauvaises, ou sur une paire de villes déjà explorée. La stratégie d'Alice débute donc comme suit. Tant qu'il existe une paire inexplorée $\{v, w\}$ formée de deux bonnes villes, Alice choisit une telle paire et interroge le roi de cœur sur cette paire. À la fin de cette première étape, nul sommet de notre graphe n'a strictement plus de deux arêtes sortantes. Alice a donc posé au plus $2 n$ questions.
En outre, soit $X$ l'ensemble des villes toujours bonnes à l'issue de cette étape, et soit $x$ le cardinal de $X$, de sorte qu'il y a $x(x-1) / 2$ routes entre villes de $X$. Toute paire $\{v, w\}$ formée de deux villes de $X$ est manifestement explorée; et toute ville de $X$, puisqu'elle est bonne, est donc à l'origine d'au plus une route allant vers une autre ville de $X$. Il y a donc au plus $x$ routes entre villes de $X$, ce qui signifie que $x \leqslant 3$.
Alice n'a donc plus qu'à interroger le roi de cœur sur toutes les paires $\{v, x\}$ où $x \in X$ : cela fera $n x \leqslant 3 n$ questions supplémentaires, à l'issue desquelles Alice saura exactement combien de routes partent de chacune des villes de $X$. Si, à cette étape de l'algorithme, il reste une bonne ville $v$, c'est qu'il n'y avait effectivement pas plus d'une route qui partait de $v$.
Commentaire des correcteurs Du fait de sa difficulté, cet exercice a été résolu par un faible nombre d'élèves. Nombreux sont ceux qui ont remarqué que, pour $n \leqslant 11$, Alice pouvait se contenter de demander le sens de toutes les routes; malheureusement, cela ne faisait pas avancer le problème. La clé consistait à s'apercevoir que, en général, il fallait éviter de poser une question sur une ville dont deux routes sortaient.
Quelques élèves ont proposé des stratégies qui ne marchaient pas en $5 n$ questions, mais en $6 n$ questions ou plus (par exemple 10n questions) et cela a été valorisé. Quelques élèves ont également obtenu des points en montrant qu'au plus 3 villes pouvaient avoir moins de 2 routes sortantes.
## Exercices Senior
|
{
"exam": "French_tests",
"problem_label": "5",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T1",
"year": "2019"
}
|
In the land of wonders, there are $n$ cities. Each pair of cities is connected by a one-way road, which starts from one of the two cities and arrives at the other. To find her way, Alice questions the King of Hearts: with each question, Alice chooses a pair of cities, and the King of Hearts tells her which is the starting city of the road connecting these two cities.
Prove that, in $5 n$ questions or fewer, Alice can determine whether there exists a city from which at most one road starts.
|
We will describe a strategy that Alice can implement to achieve her goal in $5 n$ questions or fewer. At any time, we will say that a city $v$ is bad if Alice has already found two roads that leave from $v$, and that $v$ is good otherwise. Similarly, we will say that a pair of cities $\{v, w\}$ is explored if Alice has already asked the Queen of Hearts about this pair, and unexplored otherwise.
In addition, in parallel with these questions, Alice has drawn a map on which the $n$ cities are represented by $n$ vertices, and she adds an edge on this map, between the cities $v$ and $w$ for each question she asks about the pair $\{v, w\}$. In the following, we will identify Wonderland with the graph that Alice is building.
First of all, Alice clearly has no interest in asking the Queen of Hearts about a pair of cities that would both be bad, or about a pair of cities already explored. Alice's strategy therefore begins as follows. As long as there is an unexplored pair $\{v, w\}$ formed of two good cities, Alice chooses such a pair and asks the Queen of Hearts about this pair. At the end of this first step, no vertex in our graph has strictly more than two outgoing edges. Alice has therefore asked at most $2 n$ questions.
Furthermore, let $X$ be the set of cities that are still good at the end of this step, and let $x$ be the cardinality of $X$, so that there are $x(x-1) / 2$ roads between cities in $X$. Every pair $\{v, w\}$ formed of two cities in $X$ is clearly explored; and every city in $X$, since it is good, is therefore the origin of at most one road going to another city in $X$. There are therefore at most $x$ roads between cities in $X$, which means that $x \leqslant 3$.
Alice therefore only has to ask the Queen of Hearts about all pairs $\{v, x\}$ where $x \in X$: this will make $n x \leqslant 3 n$ additional questions, at the end of which Alice will know exactly how many roads leave from each of the cities in $X$. If, at this stage of the algorithm, there is a good city $v$, it is because there was indeed no more than one road that left from $v$.
Comment from the graders: Due to its difficulty, this problem was solved by a small number of students. Many noticed that for $n \leqslant 11$, Alice could simply ask the direction of all the roads; unfortunately, this did not advance the problem. The key was to realize that, in general, it was necessary to avoid asking a question about a city from which two roads left.
Some students proposed strategies that did not work in $5 n$ questions, but in $6 n$ questions or more (for example, 10n questions), and this was valued. Some students also earned points by showing that at most 3 cities could have fewer than 2 outgoing roads.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Au pays des merveilles se trouvent $n$ villes. Chaque paire de villes est reliée par une route à sens unique, qui part d'une des deux villes et arrive à l'autre. Afin de s'y retrouver, Alice interroge le roi de cœur : à chaque question, Alice choisit une paire de villes, et le roi de cœur lui dit quelle est la ville de départ de la route qui relie ces deux villes.
Démontrer que, en $5 n$ questions ou moins, Alice peut arriver à savoir s'il existe une ville d'où part au plus une route.
|
Nous allons décrire une stratégie qu'Alice peut mettre en place pour aboutir à ses fins en $5 n$ questions ou moins. À tout moment, on dira qu'une ville $v$ est mauvaise si Alice a déjà trouvé deux routes qui partent de $v$, et que $v$ est bonne sinon. De même, on dira qu'une paire de villes $\{v, w\}$ est explorée si Alice a déjà interrogé le roi de cœur sur cette paire-là, et inexplorée sinon.
Enfin, en parallèle de ces questions, Alice a dessiné une carte sur laquelle les $n$ villes sont représentées par $n$ sommets, et elle ajoute une arête sur cette carte, entre les villes $v$ et $w$ à chaque question qu'elle pose sur la paire $\{v, w\}$. Dans la suite, nous allons identifier le pays des merveilles au graphe qu'Alice est en train de construire.
Tout d'abord, Alice n'a manifestement jamais intérêt à interroger le roi de cœur sur une paire de villes qui seraient toutes deux mauvaises, ou sur une paire de villes déjà explorée. La stratégie d'Alice débute donc comme suit. Tant qu'il existe une paire inexplorée $\{v, w\}$ formée de deux bonnes villes, Alice choisit une telle paire et interroge le roi de cœur sur cette paire. À la fin de cette première étape, nul sommet de notre graphe n'a strictement plus de deux arêtes sortantes. Alice a donc posé au plus $2 n$ questions.
En outre, soit $X$ l'ensemble des villes toujours bonnes à l'issue de cette étape, et soit $x$ le cardinal de $X$, de sorte qu'il y a $x(x-1) / 2$ routes entre villes de $X$. Toute paire $\{v, w\}$ formée de deux villes de $X$ est manifestement explorée; et toute ville de $X$, puisqu'elle est bonne, est donc à l'origine d'au plus une route allant vers une autre ville de $X$. Il y a donc au plus $x$ routes entre villes de $X$, ce qui signifie que $x \leqslant 3$.
Alice n'a donc plus qu'à interroger le roi de cœur sur toutes les paires $\{v, x\}$ où $x \in X$ : cela fera $n x \leqslant 3 n$ questions supplémentaires, à l'issue desquelles Alice saura exactement combien de routes partent de chacune des villes de $X$. Si, à cette étape de l'algorithme, il reste une bonne ville $v$, c'est qu'il n'y avait effectivement pas plus d'une route qui partait de $v$.
Commentaire des correcteurs Du fait de sa difficulté, cet exercice a été résolu par un faible nombre d'élèves. Nombreux sont ceux qui ont remarqué que, pour $n \leqslant 11$, Alice pouvait se contenter de demander le sens de toutes les routes; malheureusement, cela ne faisait pas avancer le problème. La clé consistait à s'apercevoir que, en général, il fallait éviter de poser une question sur une ville dont deux routes sortaient.
Quelques élèves ont proposé des stratégies qui ne marchaient pas en $5 n$ questions, mais en $6 n$ questions ou plus (par exemple 10n questions) et cela a été valorisé. Quelques élèves ont également obtenu des points en montrant qu'au plus 3 villes pouvaient avoir moins de 2 routes sortantes.
|
{
"exam": "French_tests",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T1",
"year": "2019"
}
|
Let $ABC$ be an acute triangle such that $\widehat{CAB} > \widehat{BCA}$, and let $P$ be the point on the segment $[BC]$ such that $\widehat{PAB} = \widehat{BCA}$. Let $Q$ be the intersection point, other than $A$, between the circumcircle of $ABP$ and the line $(AC)$. Let $D$ be the point on the segment $[AP]$ such that $\widehat{QDC} = \widehat{CAP}$, and let $E$ be the point on $(BD)$, other than $D$, such that $CE = CD$. Finally, let $F$ be the intersection point, other than $C$, between the circumcircle of $CQE$ and the line $(CD)$, and let $G$ be the intersection point of the lines $(QF)$ and $(BC)$.
Prove that the points $B, D, F$, and $G$ are concyclic.
|
Let's start by drawing a figure. The first difficulty is to construct point $P$: a simple way to proceed is to construct the intersection point, other than $A$, between the circumcircle of $A B C$ and the circle centered at $B$ with radius $A$. Indeed, if we denote this point by $P^{\prime}$, the arcs $\overline{A B}$ and $\overline{B P^{\prime}}$ have the same measure, so $\widehat{B C A}=\widehat{P^{\prime} A B}=\widehat{P A B}$, and it suffices to construct $P$ as the intersection of the lines $(B C)$ and $\left(A P^{\prime}\right)$.
Similarly, since we want $\widehat{Q D C}=\widehat{C A P}=\widehat{Q A P}=\widehat{Q B P}=\widehat{Q B C}$, we can construct point $D$ as the intersection of the line $(A P)$ and the circumcircle of $B C Q$.
We then obtain the following figure, where we have drawn in dashed lines all the circles useful for our construction, in gray the circle we wish to show exists, and of course marked the angles $\widehat{P A B}=\widehat{B C A}$ and $\widehat{Q D C}=\widehat{C A P}$, which are likely to play a role in the following.
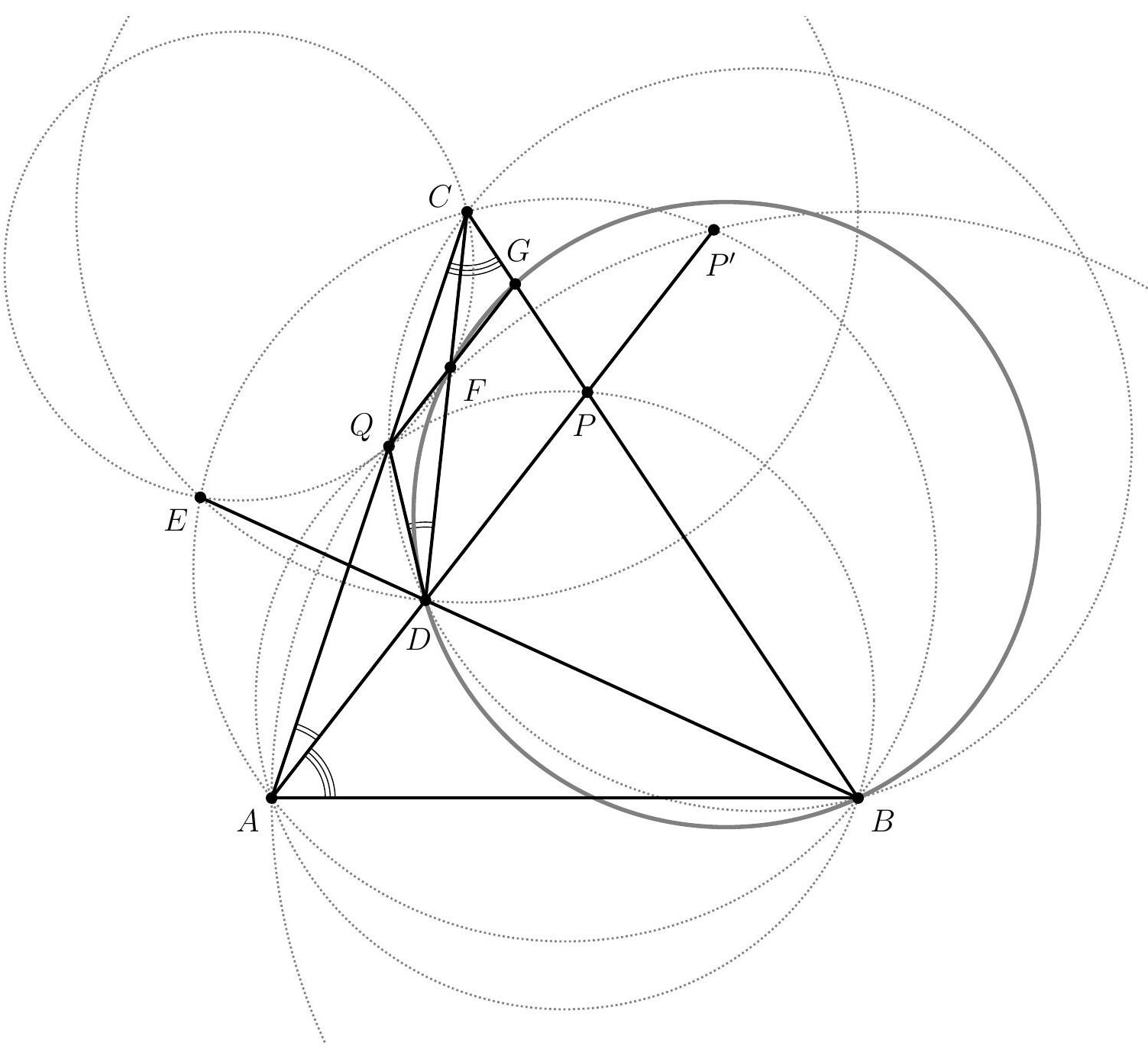
A first clear observation from the figure is that points $A, B, P^{\prime}, C$ and $E$ appear to be concyclic. We therefore start by proving this, using the following angle chasing:
$$
\begin{aligned}
(E C, E B) & =(D B, D C)=(Q B, Q C)=(Q B, Q A)=(P B, P A) \\
& =(C B, P A)=(C B, A B)+(A B, P A) \\
& =(C B, A B)+(A C, C B)=(A C, A B) .
\end{aligned}
$$
Since no other observation is immediately apparent, we focus on the property to be proven, with the aim of transforming it into an equivalent property that is more likely to be easier to observe. Thus, it is necessary to prove that
$$
(D F, D B)=(G F, G B)=(Q F, B C)=(Q F, C F)+(C F, B C)=(Q E, C E)+(D F, B C)
$$
that is, $(Q E, C E)=(B C, D B)=(B C, B E)=(A C, A E)$, or that the triangles $A C E$ and $E C Q$ are (indirectly) similar, since they already have the same angle at $\widehat{C}$.
Given the relation $C D^{2}=C E^{2}$, our goal is therefore to prove that $C A \cdot C Q=$ $C E^{2}=C D^{2}$. But the equality $C A \cdot C Q=C D^{2}$ follows precisely from the fact that the triangles $C A D$ and $C D Q$ are similar, since they have the same angle at $\widehat{C}$ and $\widehat{C A D}=\widehat{Q D C}$. This concludes our solution.
Comment from the graders: The exercise was very successful! Several approaches were possible. Some students were, without knowing it, very close to the conclusion. Others performed an interesting angle chasing without seeing that it implied that certain points were concyclic or that certain lines were parallel, which is always a pity.
Several students attempted to reduce the problem or to bring it back to the proof of another property of the figure. This is a good idea, but most of the time, proving this other property is not particularly simpler than the original problem.
It is worth noting that it was not necessary to deploy technical tools for this exercise, and a simple angle chasing or the use of the power of a point with respect to a circle was more than sufficient.
Once again, we deplore the case of students who did not follow the instructions regarding the figures. We emphasize the importance of neat and accurate figures, which are the basis of geometric reasoning, especially when the exercise becomes really challenging. The habit of drawing accurate figures is therefore essential. Conversely, many students were able to use their figures to conjecture various properties and provide a start to the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle acutangle tel que $\widehat{C A B}>\widehat{B C A}$ et soit $P$ le point du segment $[B C]$ tel que $\widehat{P A B}=\widehat{B C A}$. Soit $Q$ le point d'intersection, autre que $A$, entre le cercle circonscrit à $A B P$ et la droite $(A C)$. Soit ensuite $D$ le point du segment $[A P]$ tel que $\widehat{Q D C}=\widehat{C A P}$, puis $E$ le point de $(B D)$, autre que $D$, tel que $C E=C D$. Enfin, soit $F$ le point d'intersection, autre que $C$, entre le cercle circonscrit à $C Q E$ et la droite ( $C D$ ), et soit $G$ le point d'intersection des droites $(Q F)$ et $(B C)$.
Démontrer que les points $B, D, F$ et $G$ sont cocycliques.
|
Commençons par tracer une figure. Une première difficulté est de construire le point $P$ : une manière simple de procéder est alors de construire le point d'intersection, autre que $A$, entre le cercle circonscrit à $A B C$ et le cercle de centre $B$ et de rayon $A$. En effet, si l'on note $P^{\prime}$ ce point, les arcs $\overline{A B}$ et $\overline{B P^{\prime}}$ ont même mesure, donc $\widehat{B C A}=\widehat{P^{\prime} A B}=\widehat{P A B}$, et il suffit de construire $P$ comme le point d'intersection des droites $(B C)$ et $\left(A P^{\prime}\right)$.
De même, puisque l'on souhaite que $\widehat{Q D C}=\widehat{C A P}=\widehat{Q A P}=\widehat{Q B P}=\widehat{Q B C}$, on peut construire le point $D$ comme le point d'intersection entre la droite $(A P)$ et le cercle circonscrit à $B C Q$.
On obtient alors la figure suivante, où l'on a tracé en pointillés tous les cercle utiles à notre construction, en gris le cercle dont on souhaite montrer qu'il existe, et où l'on a bien sûr marqué les angles $\widehat{P A B}=\widehat{B C A}$ et $\widehat{Q D C}=\widehat{C A P}$, qui ont de fortes chances d'avoir un rôle à jouer dans la suite.

Une première remarque qui apparaît nettement sur la figure est que les points $A, B, P^{\prime}, C$ et $E$ semblent cocycliques. On commence donc par le démontrer, au moyen de la chasse aux angles de droites suivante:
$$
\begin{aligned}
(E C, E B) & =(D B, D C)=(Q B, Q C)=(Q B, Q A)=(P B, P A) \\
& =(C B, P A)=(C B, A B)+(A B, P A) \\
& =(C B, A B)+(A C, C B)=(A C, A B) .
\end{aligned}
$$
Puisque aucune autre remarque ne saute manifestement aux yeux, on se concentre alors sur la propriété à démontrer, dans le but de la transformer en une propriété équivalente qui aura des chances d'être plus facile à observer. Ainsi, il s'agit de démontrer que
$$
(D F, D B)=(G F, G B)=(Q F, B C)=(Q F, C F)+(C F, B C)=(Q E, C E)+(D F, B C)
$$
c'est-à-dire que $(Q E, C E)=(B C, D B)=(B C, B E)=(A C, A E)$, ou encore que les triangles $A C E$ et $E C Q$ sont (indirectement) semblables, puisqu'ils ont déjà même angle en $\widehat{C}$.
Au vu de la relation $C D^{2}=C E^{2}$, notre objectif devient donc de démontrer que $C A \cdot C Q=$ $C E^{2}=C D^{2}$. Mais l'égalité $C A \cdot C Q=C D^{2}$ découle justement du fait que les triangles $C A D$ et $C D Q$ sont semblables, puisqu'ils ont même angle en $\widehat{C}$ et que $\widehat{C A D}=\widehat{Q D C}$. Ceci conclut donc notre solution.
Commentaire des correcteurs L'exercice a été très réussi! Plusieurs approches étaient possibles. Quelques élèves étaient, sans le savoir, très proches de la conclusion. D'autres ont effectué une chasse aux angles intéressante sans pour autant voir que cela impliquait que des points étaient cocycliques ou que des droites étaient parallèles, ce qui est toujours dommage.
Plusieurs élèves ont tenté de réduire le problème ou de le ramener à la démonstration d'une autre propriété de la figure. C'est une bonne idée mais, la plupart du temps, démontrer cette autre propriété n'est pas spécialement plus simple que le problème de départ.
On notera qu'il n'était pas nécessaire de déployer des outils techniques pour cet exercice et qu'une simple chasse aux angles ou l'usage de la puissance d'un point par rapport à un cercle était largement suffisants.
Une fois de plus, on déplore le cas d'élèves n'ayant pas respecté la consigne concernant les figures. On insiste sur l'intérêt de figures propres et exactes qui sont la base de la réflexion en géométrie, surtout lorsque l'exercice devient rééllement corsé. L'habitude de tracer des figures exactes est donc essentiel. À l'inverse, de nombreux élèves ont su utiliser leur figure pour conjecturer diverses propriétés et en fournir un début de démonstration.
|
{
"exam": "French_tests",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T1",
"year": "2019"
}
|
Let $C$ be a non-zero natural number. Find all functions $f: \mathbb{N}^{*} \rightarrow \mathbb{N}^{*}$ such that for all integers $a$ and $b$ with sum $a+b \geqslant C$, the integer $a+f(b)$ divides $a^{2}+b f(a)$.
|
First, any strictly increasing linear function is a solution. Indeed, for any integer $k \geqslant 1$, the integer $a+k b$ divides $a^{2}+b \times(k a)=a(a+k b)$. Conversely, let's show that any solution is a linear function (which will be strictly increasing, since it takes values in $\mathbb{N}^{*}$).
Consider an integer $n \geqslant C$, and let $\varphi=f(1)$. Then
$$
\varphi^{2}+f(n) \equiv n^{2}+f(n) \equiv 0 \quad(\bmod n+\varphi)
$$
so $f(n)+\varphi^{2}$ is a non-zero multiple of $n+\varphi$, which means that $f(n) \geqslant n+\varphi-\varphi^{2}$.
On the other hand, since $1+f(n)$ divides $1+\varphi n$, let $g(n)=(1+\varphi n) /(1+f(n))$. Then
$$
\varphi(1+f(n)) \geqslant \varphi\left(n+1+\varphi-\varphi^{2}\right)=(1+f(n)) g(n)-1+\left(1+\varphi-\varphi^{2}\right) \varphi
$$
This means that $\Phi \geqslant(1+f(n))(g(n)-\varphi)$, where we have set $\Phi=\varphi^{3}-\varphi^{2}-\varphi+1$. Consequently, if $n \geqslant \Phi+\varphi^{2}-\varphi$, we know that $1+f(n)>\Phi$, and thus that $g(n) \leqslant \varphi$.
Now choose an integer $a \geqslant 1$, and let's prove that $f(a)=\varphi a$. To do this, we construct an integer $n \geqslant \max \left\{\Phi+\varphi^{2}-\varphi, C\right\}$ as follows:
$\triangleright$ we take $n \equiv 2(\bmod 4)$ if $\varphi$ is odd, and $n$ odd if $\varphi$ is even: in all cases, $n \varphi+1$ is odd;
$\triangleright$ for any prime $p \leqslant \max \{a, \varphi\}$ odd, we choose $n \equiv 1(\bmod p)$ or $n \equiv 2$ $(\bmod p)$ so that $n \varphi \not \equiv-1(\bmod p)$.
By the Chinese remainder theorem, such a choice is feasible, and for infinitely many integers $n$. Without loss of generality, we even assume that $n \geqslant 2 \max \{\varphi a, f(a)\}$.
Then $g(n)$ is a divisor of $1+\varphi n$, and we know that $g(n) \leqslant \varphi$. By construction, the integer $1+\varphi n$ has no prime factor $p \leqslant \varphi$, so $g(n)=1$, and thus $f(n)=\varphi n$. But then $a+\varphi n=a+f(n)$ divides
$$
\left(a^{2}+n f(a)\right)+(a+\varphi n)(\varphi n-a)=(\varphi n)^{2}+n f(a)=\left(\varphi^{2} n+f(a)\right) n
$$
However, we have constructed $n$ so that it has no common odd prime factor with $a$, and is not divisible by 4. Therefore, if we set $d=\operatorname{PGCD}(a+\varphi n, n)$, then $d=\operatorname{PGCD}(a, n)$ divides 2. Then, if we set $\alpha=(a+\varphi n) / d$ and $n^{\prime}=n / d$, we observe that $\operatorname{PGCD}\left(\alpha, n^{\prime}\right)=1$ and that $\alpha$ divides $\left(\varphi^{2} n+f(a)\right) n^{\prime}$, so $\alpha$ divides $\varphi^{2} n+f(a)$. The integer $\alpha$ therefore also divides
$$
\left(\varphi^{2} n+f(a)\right)-d \varphi \alpha=f(a)-\varphi a
$$
However, since $n \geqslant 2 \max \{\varphi a, f(a)\}$, we know that
$$
\alpha>\varphi n / d \geqslant \varphi n / 2 \geqslant \max \{\varphi a, f(a)\} \geqslant|f(a)-\varphi a| .
$$
Therefore, $f(a)=\varphi a$, which concludes.
|
f(a)=\varphi a
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Soit $C$ un entier naturel non nul. Trouver toutes les fonctions $f: \mathbb{N}^{*} \rightarrow \mathbb{N}^{*}$ telles que, pour tous les entiers $a$ et $b$ de somme $a+b \geqslant C$, l'entier $a+f(b)$ divise $a^{2}+b f(a)$.
|
Tout d'abord, toute fonction linéaire strictement croissante est solution. En effet, pour tout entier $k \geqslant 1$, l'entier $a+k b$ divise bien $a^{2}+b \times(k a)=a(a+k b)$. Réciproquement, montrons que toute solution est une fonction linéaire (qui sera strictement croissante, puisque à valeurs dans $\mathbb{N}^{*}$ ).
Considérons un entier $n \geqslant C$, et posons $\varphi=f(1)$. Alors
$$
\varphi^{2}+f(n) \equiv n^{2}+f(n) \equiv 0 \quad(\bmod n+\varphi)
$$
donc $f(n)+\varphi^{2}$ est un multiple non nul de $n+\varphi$, de sorte que $f(n) \geqslant n+\varphi-\varphi^{2}$.
D'autre part, puisque $1+f(n)$ divise $1+\varphi n$, soit $g(n)=(1+\varphi n) /(1+f(n))$. Alors
$$
\varphi(1+f(n)) \geqslant \varphi\left(n+1+\varphi-\varphi^{2}\right)=(1+f(n)) g(n)-1+\left(1+\varphi-\varphi^{2}\right) \varphi
$$
Cela signifie que $\Phi \geqslant(1+f(n))(g(n)-\varphi)$, où l'on a posé $\Phi=\varphi^{3}-\varphi^{2}-\varphi+1$. Par conséquent, si $n \geqslant \Phi+\varphi^{2}-\varphi$, on sait que $1+f(n)>\Phi$, et donc que $g(n) \leqslant \varphi$.
Choisissons maintenant un entier $a \geqslant 1$, et démontrons que $f(a)=\varphi a$. Pour ce faire, on construit un entier $n \geqslant \max \left\{\Phi+\varphi^{2}-\varphi, C\right\}$ comme suit :
$\triangleright$ on prend $n \equiv 2(\bmod 4)$ si $\varphi$ est impair, et $n$ impair si $\varphi$ est pair : dans tous les cas, $n \varphi+1$ est impair;
$\triangleright$ pour tout nombre premier $p \leqslant \max \{a, \varphi\}$ impair, on choisit $n \equiv 1(\bmod p)$ ou $n \equiv 2$ $(\bmod p)$ de sorte que $n \varphi \not \equiv-1(\bmod p)$.
D'après le théorème chinois, un tel choix est bien faisable, et ce pour une infinité d'entiers $n$. Sans perte de généralité, on suppose donc même que $n \geqslant 2 \max \{\varphi a, f(a)\}$.
Alors $g(n)$ est un diviseur de $1+\varphi n$, et l'on sait que $g(n) \leqslant \varphi$. Par construction, l'entier $1+\varphi n$ n'a aucun facteur premier $p \leqslant \varphi$, de sorte que $g(n)=1$, et donc que $f(n)=\varphi n$. Mais alors $a+\varphi n=a+f(n)$ divise
$$
\left(a^{2}+n f(a)\right)+(a+\varphi n)(\varphi n-a)=(\varphi n)^{2}+n f(a)=\left(\varphi^{2} n+f(a)\right) n
$$
Or, on a construit $n$ de sorte qu'il n'ait aucun facteur premier impair commun avec $a$, et ne soit pas divisible par 4. Par conséquent, si l'on pose $d=\operatorname{PGCD}(a+\varphi n, n)$, alors $d=\operatorname{PGCD}(a, n)$ divise 2. Puis, si l'on pose $\alpha=(a+\varphi n) / d$ et $n^{\prime}=n / d$, on constate que $\operatorname{PGCD}\left(\alpha, n^{\prime}\right)=1$ et que $\alpha$ divise $\left(\varphi^{2} n+f(a)\right) n^{\prime}$, de sorte que $\alpha$ divise $\varphi^{2} n+f(a)$. L'entier $\alpha$ divise donc également
$$
\left(\varphi^{2} n+f(a)\right)-d \varphi \alpha=f(a)-\varphi a
$$
Or, comme $n \geqslant 2 \max \{\varphi a, f(a)\}$, on sait que
$$
\alpha>\varphi n / d \geqslant \varphi n / 2 \geqslant \max \{\varphi a, f(a)\} \geqslant|f(a)-\varphi a| .
$$
C'est donc que $f(a)=\varphi a$, ce qui conclut.
|
{
"exam": "French_tests",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web.jsonl",
"solution_match": "\nSolution de l'exercice 7",
"tier": "T1",
"year": "2019"
}
|
Let $C$ be a non-zero natural number. Find all functions $f: \mathbb{N}^{*} \rightarrow \mathbb{N}^{*}$ such that for all integers $a$ and $b$ with sum $a+b \geqslant C$, the integer $a+f(b)$ divides $a^{2}+b f(a)$.
|
$n^{\circ} 1$ As previously, we set $\varphi=f(1)$, and we prove that if $f$ is a solution function, then $f(n)=\varphi n$ for all integers $n \geqslant 1$.
First, for all integers $n \geqslant C$, the statement indicates that $1+f(n)$ divides $1+n \varphi$. We deduce that $1+f(n) \leqslant 1+n \varphi$, hence that $f(n) \leqslant n \varphi$.
Now consider any integer $m \geqslant 2$, and an integer $k \geqslant 1$ such that $k m - f(m) \geqslant C$. If we set $a=k m - f(m)$, and since $a+m \geqslant a \geqslant C$, the statement indicates that
$$
f(m)^{2} + n f(a) \equiv f(m)^{2} + b f(a) \equiv (-a)^{2} + m f(a) \equiv 0 \quad(\bmod a+f(m)) .
$$
The integer $f(m)^{2} + m f(a)$ is therefore divisible by $a+f(m)=k m$, and by $m$ as well. We conclude that $f(m)^{2}$ is also divisible by $m$; of course, this divisibility relation is also valid for $m=1$, but we will not need it.
In particular, if $p$ is a prime number, and since $p$ divides $f(p)^{2}$, the integer $p$ also divides $f(p)$: in the following, we set $g(p)=f(p) / p$, and we know that $1 \leqslant g(p) \leqslant \varphi$. If, moreover, $p \geqslant \max \{C, \varphi+1\}$, then $p+1 \geqslant C$, and the statement indicates that $p+\varphi$ divides $p^{2}+f(p)=p(p+g(p))$. Since $p>\varphi$, $p$ and $p+\varphi$ are coprime, so $p+\varphi$ divides $p+g(p)$. Given that $1 \leqslant g(p) \leqslant \varphi$, we deduce that $g(p)=\varphi$, that is, $f(p)=\varphi p$.
Finally, let $\ell \geqslant 1$ be any integer, and let $p$ be a prime number such that $p \geqslant \max \{C, \varphi+1, \ell+1\}$. We have just seen that $f(p)=\varphi p$. Furthermore, since $\ell+p \geqslant p \geqslant C$, the statement indicates that
$$
p(f(\ell)-\varphi \ell) \equiv p f(\ell) - \ell f(p) \equiv p f(\ell) + \ell^{2} \equiv 0 \quad(\bmod \ell+f(p))
$$
Since $1 \leqslant \ell \leqslant p-1$, we know that $p$ is coprime with $\ell$, and therefore with $\ell+\varphi p=\ell+f(p)$ as well. We deduce that $\ell+\varphi p=\ell+f(p)$ divides $f(\ell)-\varphi \ell$. Since this is valid for arbitrarily large prime numbers $p$, we conclude that $f(\ell)=\ell \varphi$, which concludes the proof.
|
f(n)=\varphi n
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Soit $C$ un entier naturel non nul. Trouver toutes les fonctions $f: \mathbb{N}^{*} \rightarrow \mathbb{N}^{*}$ telles que, pour tous les entiers $a$ et $b$ de somme $a+b \geqslant C$, l'entier $a+f(b)$ divise $a^{2}+b f(a)$.
|
$n^{\circ} 1$ Comme précédemment, on pose $\varphi=f(1)$, et on démontre que, si $f$ est une fonction solution, alors $f(n)=\varphi n$ pour tout entier $n \geqslant 1$.
Tout d'abord, pour tout entier $n \geqslant C$, l'énoncé indique que $1+f(n)$ divise $1+n \varphi$. On en déduit que $1+f(n) \leqslant 1+n \varphi$, donc que $f(n) \leqslant n \varphi$.
On considère maintenant un entier $m \geqslant 2$ quelconque, puis un entier $k \geqslant 1$ tel que $k m-$ $f(m) \geqslant C$. Si l'on pose $a=k m-f(m)$, et puique $a+m \geqslant a \geqslant C$, l'énoncé indique que
$$
f(m)^{2}+n f(a) \equiv f(m)^{2}+b f(a) \equiv(-a)^{2}+m f(a) \equiv 0 \quad(\bmod a+f(m)) .
$$
L'entier $f(m)^{2}+m f(a)$ est donc divisible par $a+f(m)=k m$, et par $m$ également. On en conclut que $f(m)^{2}$ est lui aussi divisible par $m$; bien sûr, cette relation de divisibilité également valable pour $m=1$, mais on n'en aura pas besoin.
En particulier, si $p$ est un nombre premier, et comme $p$ divise $f(p)^{2}$, l'entier $p$ divise aussi $f(p)$ : dans la suite, on pose $g(p)=f(p) / p$, et l'on sait que $1 \leqslant g(p) \leqslant \varphi$. Si, en outre, $p \geqslant$ $\max \{C, \varphi+1\}$, alors $p+1 \geqslant C$, et l'énoncé indique donc que $p+\varphi$ divise $p^{2}+f(p)=p(p+g(p))$. Puisque $p>\varphi$, c'est que $p$ et $p+\varphi$ sont premiers entre eux, donc que $p+\varphi$ divise $p+g(p)$. Comme $1 \leqslant g(p) \leqslant \varphi$, on en déduit que $g(p)=\varphi$, c'est-à-dire que $f(p)=\varphi p$.
Enfin, soit $\ell \geqslant 1$ un entier quelconque, et soit $p$ un nombre premier tel que $p \geqslant \max \{C, \varphi+$ $1, \ell+1\}$. On vient de voir que $f(p)=\varphi p$. En outre, puisque $\ell+p \geqslant p \geqslant C$, l'énoncé indique que
$$
p(f(\ell)-\varphi \ell) \equiv p f(\ell)-\ell f(p) \equiv p f(\ell)+\ell^{2} \equiv 0 \quad(\bmod \ell+f(p))
$$
Or, comme $1 \leqslant \ell \leqslant p-1$, on sait que $p$ est premier avec $\ell$, donc avec $\ell+\varphi p=\ell+f(p)$ également. On en déduit que $\ell+\varphi p=\ell+f(p)$ divise $f(\ell)-\varphi \ell$. Ceci étant valable pour des nombres premiers $p$ arbitrairement grands, on en déduit que $f(\ell)=\ell \varphi$, ce qui conclut.
|
{
"exam": "French_tests",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2019"
}
|
Let $C$ be a non-zero natural number. Find all functions $f: \mathbb{N}^{*} \rightarrow \mathbb{N}^{*}$ such that for all integers $a$ and $b$ with sum $a+b \geqslant C$, the integer $a+f(b)$ divides $a^{2}+b f(a)$.
|
$n^{\circ} 2$ We present another slightly different way to conclude once we have shown that $p$ divides $f(p)$ for all prime numbers $p$.
Let $p$ be a prime number, and let $g(p)$ be the integer $f(p) / p$. Since $g(p) \leqslant \varphi$ whenever $p \geqslant C$, the function $g$ is bounded. Therefore, there exists an integer $\gamma$ and an infinite number of prime numbers $p$ for which $g(p)=\gamma$.
Let $\ell$ be an integer, and let $p \geqslant \max \{C, \ell+1\}$ be a prime number for which $g(p)=\gamma$. Then $p$ is coprime with $\ell$, and hence with $\ell+\gamma p=\ell+f(p)$. Since $\ell+p \geqslant p \geqslant C$, the statement indicates that
$$
p(f(\ell)-\gamma \ell) \equiv p f(\ell)-\ell f(p) \equiv p f(\ell)+\ell^{2} \equiv 0 \quad(\bmod \ell+f(p))
$$
We deduce that $\ell+\gamma p=\ell+f(p)$ divides $f(\ell)-\gamma \ell$. Since this is true for arbitrarily large prime numbers $p$, we conclude that $f(\ell)=\gamma \ell$, which completes the proof.
Comment from the graders: This difficult problem was fully solved by five students, which is very satisfying, especially since two other students had almost a complete solution!
There were many different proofs, some of which contained almost no arithmetic manipulation. Many students mentioned the Dirichlet theorem, very judiciously, either to prove that every prime number $p$ divides $f(p)$, or to directly prove that there are infinitely many integers $b$ such that $f(b)=b f(1)$. Other students clearly did not know this theorem: it is not a problem, and it is the right time to discover it!
By far, the most common mistake was not making the variables you introduce depend on the parameters $a$ and $b$. For example, it is better to write $a^{2}+b f(a)=k_{a, b}(a+f(b))$ rather than simply $a^{2}+b f(a)=k(a+f(b))$. Indeed, in the sequel, and because of this notation, many students forgot that $k$ depended on both $a$ and $b$, and then used the following false reasoning:
"By choosing $a=b$, we get $(a-k)(a+f(a))$, so $k=a$. Therefore, in the general case, since $k=a$, this means that $a^{2}+b f(a)=a^{2}+a f(b)$, i.e., that $f$ is linear!"
Obviously, we had $k_{a, a}=a$, but nothing indicated that $k_{a, b}=a$ when $a \neq b$.
Another tip: even though conjecturing that affine functions were solutions was not directly valued here, looking for simple solutions, such as the identity, is always a good idea. Indeed, several students wasted time trying to see what a lack of injectivity of $f$ would imply and based their work on this; if they had noticed that the identity was a solution, they would have quickly concluded that focusing on non-injective functions was actually far from sufficient, and that they should therefore concentrate on other approaches.
|
f(\ell)=\gamma \ell
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Soit $C$ un entier naturel non nul. Trouver toutes les fonctions $f: \mathbb{N}^{*} \rightarrow \mathbb{N}^{*}$ telles que, pour tous les entiers $a$ et $b$ de somme $a+b \geqslant C$, l'entier $a+f(b)$ divise $a^{2}+b f(a)$.
|
$n^{\circ} 2$ On présente une autre façon, légèrement différente, de conclure une fois que l'on a montré que $p$ divise $f(p)$ pour tout nombre premier $p$.
Soit $p$ un nombre premier, et soit $g(p)$ l'entier $f(p) / p$. Puisque $g(p) \leqslant \varphi$ dès lors que $p \geqslant C$, la fonction $g$ est bornée. Il existe donc un entier $\gamma$ et une infinité de nombres premiers $p$ pour lesquels $g(p)=\gamma$.
Soit alors $\ell$ un entier, puis $p \geqslant \max \{C, \ell+1\}$ un nombre premier pour lequel $g(p)=\gamma$. Alors $p$ est premier avec $\ell$, donc avec $\ell+\gamma p=\ell+f(p)$. Or, puisque $\ell+p \geqslant p \geqslant C$, l'énoncé indique que
$$
p(f(\ell)-\gamma \ell) \equiv p f(\ell)-\ell f(p) \equiv p f(\ell)+\ell^{2} \equiv 0 \quad(\bmod \ell+f(p))
$$
On en déduit que $\ell+\gamma p=\ell+f(p)$ divise $f(\ell)-\gamma \ell$. Ceci étant valable pour des nombres premiers $p$ arbitrairement grands, on en déduit que $f(\ell)=\gamma \ell$, ce qui conclut.
Commentaire des correcteurs Cet exercice difficile a été résolu entièrement par cinq élèves, ce qui est très satisfaisant, d'autant que deux autres élèves avaient presque une solution complète!
Il y avait de très nombreuses preuves différentes, certaines ne contenant même presque aucune manipulation arithmétique. Beaucoup d'élèves mentionnent le théorème de Dirichlet, de manière très judicieuse, soit pour démontrer que tout nombre $p$ premier divise $f(p)$, soit pour démontrer directement qu'il existe une infinité d'entiers $b$ tels que $f(b)=b f(1)$. D'autres élèves ne connaissaient manifestement pas ce théorème : ce n'est pas grave, et c'est le moment de le découvrir!
De très loin, l'erreur la plus fréquente est de ne pas faire dépendre les variables que vous introduisez des paramètres $a$ et $b$. Par exemple, mieux vaut écrire $a^{2}+b f(a)=k_{a, b}(a+f(b))$ plutôt que simplement $a^{2}+b f(a)=k(a+f(b))$. En effet, dans la suite, et à cause de cette notation, de nombreux élèves ont oublié que $k$ dépendait à la fois de $a$ et de $b$, et ont alors utilisé le raisonnement faux suivant:
«En choisissant $a=b$, on obtient $(a-k)(a+f(a))$, donc $k=a$. Par conséquent, dans le cas général, puisque $k=a$, cela signifie que $a^{2}+b f(a)=a^{2}+a f(b)$, c'est-à-dire que $f$ est linéaire! »
Évidemment, on avait bien $k_{a, a}=a$, mais rien $\mathrm{n}^{\prime}$ indiquait que $k_{a, b}=a$ quand $a \neq b$.
Autre conseil : même si conjecturer que les fonctions affines étaient solutions n'était pas valorisé directement ici, rechercher des solutions simples, telles que l'identité, est toujours une bonne idée. En effet, plusieurs élèves ont perdu du temps à essayer de voir ce qu'impliquerait un défaut d'injectivité de $f$ et ont fondé leur copie là-dessus; s'ils avaient remarqué que l'identité était solution, ils en auraient vite conclu que se focaliser sur les cas des fonctions non injectives était en fait loin de suffire, et qu'il fallait donc se concentrer sur d'autres approches.
|
{
"exam": "French_tests",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/tests/fr-2019-2020-Corrigé-Web.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2019"
}
|
Clara and Isabelle are playing the following game. At the beginning of the game, they choose an integer $n \geqslant 1$, then put $n$ candies in a bowl. Then they take turns, starting with Clara. On each turn, if the bowl contains $k$ candies, the player whose turn it is chooses an integer $\ell$ that is coprime with $k$, such that $\ell \leqslant k$, and then eats $\ell$ candies; it is then the other player's turn. The player who eats the last candy wins the game.
For which values of $n$ does Clara have a winning strategy?
|
First, if $n$ is odd, Clara can start by choosing $\ell = n-2$. Indeed, since $n$ is odd, we know that $\operatorname{GCD}(n, n-2) = \operatorname{GCD}(n, 2) = 1$. But then Isabelle is left with two candies, she is forced to eat one, and leaves the last candy to Clara, who therefore wins.
On the contrary, if $n$ is even, Clara is forced to choose an odd integer $\ell$, and she leaves $k = n - \ell$ candies to Isabelle, the integer $k$ being therefore odd. If $k = 1$, Isabelle has already won, and if $k \geq 3$, Isabelle can copy the strategy presented above, and eat $k-2$ candies, thus ensuring her victory.
The integers $n$ sought are therefore the odd integers.
Comment from the graders: This problem was generally well solved. However, the graders noticed some recurring errors:
$\triangleright$ Several students misunderstood the statement: they were not supposed to remove a prime number of marbles, but a number that is coprime with the total number of marbles.
$\triangleright$ After observing that Clara wins when $n$ is odd, it was necessary not to forget to prove that Isabelle wins when $n$ is even.
$\triangleright$ Some students did not see that Clara could simply remove one marble: even if 1 divides the number $n$ of marbles, 1 and $n$ are still coprime!
$\triangleright$ Others considered that the only winning strategy was to remove $n-2$ marbles because 2 is a losing position: this was indeed a winning strategy, but not the only one, and making such a statement rendered the proof invalid.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Clara et Isabelle jouent au jeu suivant. Au début du jeu, elles choisissent un entier $n \geqslant 1$, puis mettent $n$ bonbons dans un saladier. Puis elles jouent à tour de rôle, en commençant par Clara. À chaque tour, si le saladier contient $k$ bonbons, la joueuse dont c'est le tour choisit un entier $\ell$ premier avec $k$, tel que $\ell \leqslant k$, puis elle mange $\ell$ bonbons; c'est alors à l'autre joueuse de jouer. La joueuse qui mange le dernier bonbon gagne la partie.
Pour quelles valeurs de $n$ Clara dispose-t-elle d'une stratégie gagnante?
|
Tout d'abord, si $n$ est impair, Clara peut commencer par choisir $\ell=$ $n-2$. En effet, puisque $n$ est impair, on sait que $\operatorname{PGCD}(n, n-2)=\operatorname{PGCD}(n, 2)=1$. Mais alors Isabelle se retrouve avec deux bonbons, elle est obligée d'en manger un seul, et laisse le dernier bonbon à Clara, qui gagne donc.
Au contraire, si $n$ est pair, Clara est obligée de choisir un entier $\ell$ impair, et elle laisse donc $k=n-\ell$ bonbons à Isabelle, l'entier $k$ étant donc impair. Si $k=1$, Isabelle a déjà gagné, et si $k \geqslant 3$, Isabelle peut copier la stratégie présentée ci-dessus, et manger $k-2$ bonbons, s'assurant ainsi la victoire.
Les entiers $n$ recherchés sont donc les entiers impairs.
Commentaire des correcteurs Ce problème a été globalement bien réussi. Cependant, les correcteurs y ont repéré quelques erreurs récurrentes :
$\triangleright$ Plusieurs élèves ont mal compris l'énoncé : il ne fallait pas retirer un nombre premier de billes, mais un nombre premier avec le nombre total de billes.
$\triangleright$ Après avoir constaté que Clara gagnait lorsque $n$ était impair, il ne fallait pas oublié de démontrer qu'Isabelle gagnait lorsque $n$ étiat pair.
$\triangleright$ Certains élèves n'ont pas vu que Clara pouvait se contenter d'enlever une seule bille : même si 1 divise le nombre $n$ de billes, 1 et $n$ sont quand même premiers entre eux!
$\triangleright$ D'autres ont considéré que la seule stratégie gagnante était d'enlever $n-2$ billes car 2 est une position perdante : il s'agissait certes d'une stratégie gagnante, mais pas de la seule, et formuler une telle affirmation rendait donc la preuve invalide.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2019-2020-corrigé-test-janvier.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T1",
"year": "2019"
}
|
Let $ABC$ be a triangle and let $\Gamma$ be its circumcircle. Let $P$ be the intersection point of the line $(BC)$ and the tangent to $\Gamma$ at $A$. Let $D$ and $E$ be the symmetrical points of $B$ and $A$ with respect to $P$.
Let $\omega_{1}$ be the circumcircle of triangle $DAC$ and let $\omega_{2}$ be the circumcircle of triangle $APB$. We denote by $F$ the intersection point of the circles $\omega_{1}$ and $\omega_{2}$ other than $A$, and then we denote by $G$ the intersection point, other than $F$, of the circle $\omega_{1}$ with the line $(BF)$.
Prove that the lines $(BC)$ and $(EG)$ are parallel.
|
Let's start by drawing a figure.
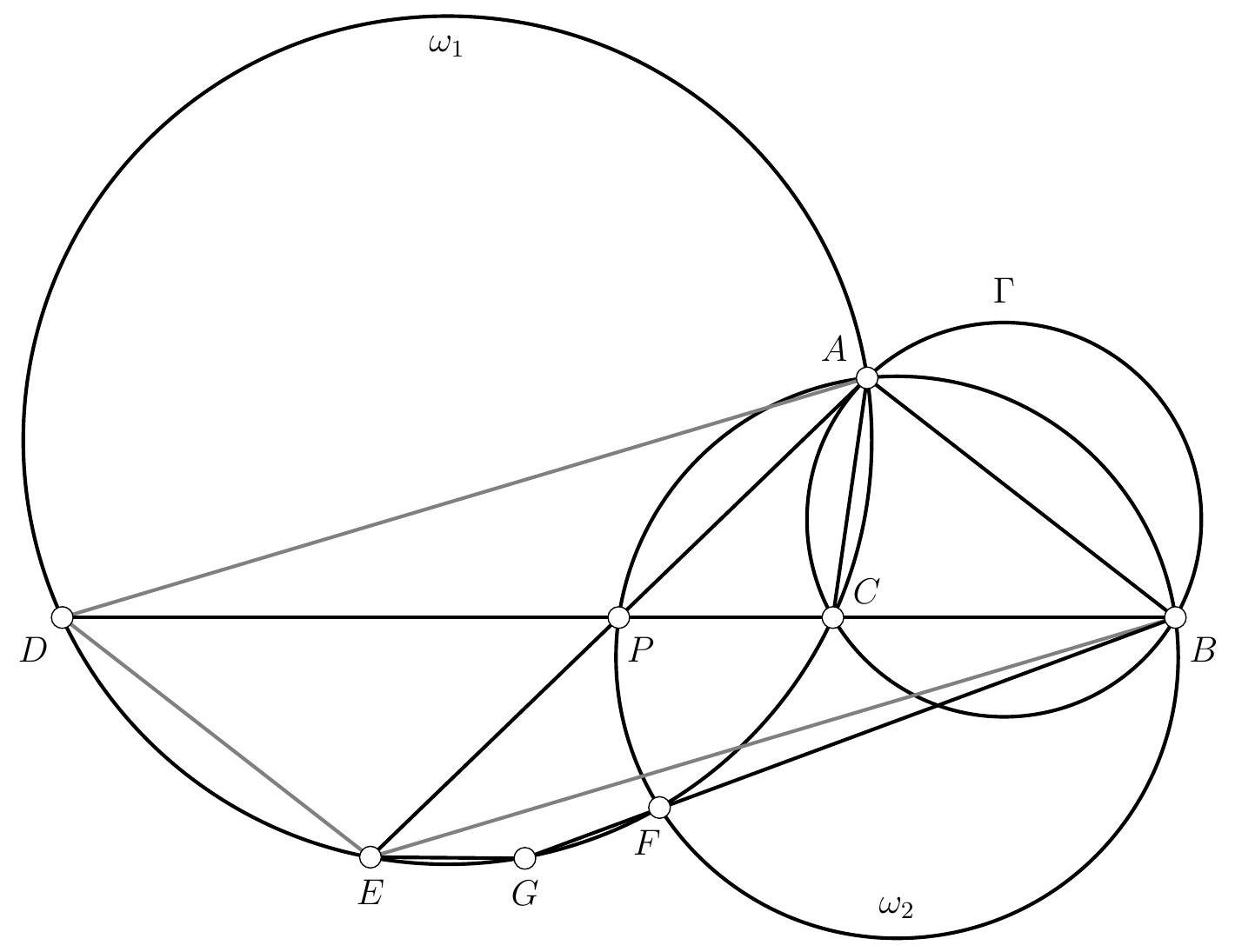
A first observation we can make is that, since $P$ is the midpoint of segments $[A E]$ and $[B D]$, the quadrilateral $A B E D$ is a parallelogram. Therefore, lines $(A B)$ and $(D E)$ are parallel, as are lines $(A D)$ and $(B E)$.
A striking second observation is that $E$ appears to lie on the circle $\omega_{1}$. After verifying on a second figure that this is indeed the case, we promptly set out to prove this first result. To do so, we embark on an angle chase:
$$
(E A, E D)=(E A, A B)=(C A, C B)=(C A, C D)
$$
An angle chase then indicates that
$(B C, E G)=(B C, B G)+(B G, E G)=(P B, B F)+(G F, G E)=(P A, A F)+(A F, A E)=0^{\circ}$, which means that $(B C)$ and $(E G)$ are parallel.
Comment from the graders: One of the reasons we require the presence of a figure is that it serves as a good means of forming intuitions about the problem; it is then necessary to prove that these intuitions are correct. Thus, on many drawings, it was clearly visible that $E$ lies on the circle $\omega_{1}$; however, few students noticed this. Similarly, several students saw on the drawing that $E$ seemed to lie on the circle $\omega_{1}$, and then used this property, but forgot to prove it!
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et soit $\Gamma$ son cercle circonscrit. Soit $P$ le point d'intersection de la droite $(B C)$ et de la tangente à $\Gamma$ en $A$. Soit $D$ et $E$ les symétriques respectifs des points $B$ et $A$ par rapport à $P$.
Soit alors $\omega_{1}$ le cercle circonscrit au triangle $D A C$ et soit $\omega_{2}$ le cercle circonscrit au triangle $A P B$. On note $F$ le point d'intersection des cercles $\omega_{1}$ et $\omega_{2}$ autre que $A$, puis on note $G$ le point d'intersection, autre que $F$, du cercle $\omega_{1}$ avec la droite $(B F)$.
Démontrer que les droites $(B C)$ et $(E G)$ sont parallèles.
|
Commençons par tracer une figure.

Une première remarque que l'on peut formuler est que, puisque $P$ est le milieu des segments $[A E]$ et $[B D]$, le quadrilatère $A B E D$ et un parallélogramme. Les droites $(A B)$ et $(D E)$ sont donc parallèles, de même que les droites $(A D)$ et $(B E)$.
Une seconde remarque frappante est que $E$ semble appartenir au cercle $\omega_{1}$. Après avoir vérifié sur une deuxième figure que c'était bien le cas, on s'empresse donc de démontrer ce premier résultat. Pour ce faire, on entame donc une chasse aux angles de droites :
$$
(E A, E D)=(E A, A B)=(C A, C B)=(C A, C D)
$$
Une chasse aux angles de droites indique alors que
$(B C, E G)=(B C, B G)+(B G, E G)=(P B, B F)+(G F, G E)=(P A, A F)+(A F, A E)=0^{\circ}$, ce qui signifie bien que $(B C)$ et $(E G)$ sont parallèles.
Commentaire des correcteurs Une des raisons pour lesquelles on exige la présence d'une figure est qu'elle constitue un bon moyen de se forger des intuitions sur le problème; c'est alors qu'il faut démontrer que ces intuitions sont correctes. Ainsi, sur beaucoup de dessins on voyait clairement que $E$ est sur le cercle $\omega_{1}$; cependant, peu d'élèves l'ont remarqué. Parallèlement, plusieurs élèves ont vu sur le dessin que $E$ semblait appartenir au cercle $\omega_{1}$, et ont alors utilisé cette propriété, mais ont oublié de la démontrer!
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2019-2020-corrigé-test-janvier.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T1",
"year": "2019"
}
|
Let $n$ be a non-zero natural number. We say that a function $f: \mathbb{R} \rightarrow \mathbb{R}$ is $n$-positive if, for all real numbers $x_{1}, \ldots, x_{n}$ such that $x_{1}+\ldots+x_{n}=0$, we have $f\left(x_{1}\right)+\ldots+f\left(x_{n}\right) \geqslant 0$.
a) Is every 2020-positive function necessarily 1010-positive?
b) Is every 1010-positive function necessarily 2020-positive?
|
In both solutions, we set $n=1010$.
a) Let $f$ be a $2n$-positive function, and let $x_{1}, \ldots, x_{n}$ be real numbers such that $x_{1}+\ldots+x_{n}=0$. Noting that $x_{1}+\ldots+x_{n}+x_{1}+\ldots+x_{n}=0$ and that $f$ is $2n$-positive, we observe that
$$
0 \leqslant f\left(x_{1}\right)+\ldots+f\left(x_{n}\right)+f\left(x_{1}\right)+\ldots+f\left(x_{n}\right)=2\left(f\left(x_{1}\right)+\ldots+f\left(x_{n}\right)\right),
$$
which shows that $f\left(x_{1}\right)+\ldots+f\left(x_{n}\right) \geqslant 0$, and thus that $f$ is $n$-positive. The answer is therefore yes!
b) Let $f$ be the function defined by $f(x)=-1$ if $x$ is an integer such that $x \equiv 1(\bmod 2n)$, and by $f(x)=n$ otherwise. Then $f$ is $n$-positive. Indeed, let $x_{1}, \ldots, x_{n}$ be real numbers such that $x_{1}+\ldots+x_{n}=0:$
$\triangleright$ If there exists an integer $k$ such that $f\left(x_{k}\right)=n$, and since $f\left(x_{i}\right) \geqslant-1$ for all $i \neq k$, we know that $f\left(x_{1}\right)+\ldots+f\left(x_{k}\right) \geqslant f\left(x_{k}\right)-(n-1) \geqslant 1$.
$\triangleright$ Otherwise, then $x_{k} \equiv 1(\bmod 2n)$ for all $k$, so $x_{1}+\ldots+x_{n} \equiv n \not \equiv 0(\bmod 2n)$, which means that this case is actually impossible.
However, $f$ is not $2n$-positive. Indeed, if $x_{1}=1-2n$ and $x_{2}=x_{3}=\ldots=x_{2n}=1$, then $x_{1}+\ldots+x_{2n}=0$ but $f\left(x_{1}\right)+\ldots+f\left(x_{2n}\right)=-2n<0$. The answer is therefore no!
Graders' Comments The graders noted several confusions about the concept of a function. Indeed, the function $f$ considered does not change depending on whether there are 1010 or 2020 real numbers.
Furthermore, if one wants to prove that a statement is false (for example, if one wishes to prove that any function $f$ that is $n$-positive is not necessarily $2n$-positive), the simplest way to proceed is still to present a counterexample.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $n$ un entier naturel non nul. On dit qu'une fonction $f: \mathbb{R} \rightarrow \mathbb{R}$ est $n$-positive si, pour tous les réels $x_{1}, \ldots, x_{n}$ tels que $x_{1}+\ldots+x_{n}=0$, on a $f\left(x_{1}\right)+\ldots+f\left(x_{n}\right) \geqslant 0$.
a) Toute fonction 2020-positive est-elle nécessairement 1010-positive?
b) Toute fonction 1010-positive est-elle nécessairement 2020-positive?
|
Dans les deux solutions, on pose $n=1010$.
a) Soit $f$ une fonction $2 n$-positive, et soit $x_{1}, \ldots, x_{n}$ des réels tels que $x_{1}+\ldots+x_{n}=0$. En notant que $x_{1}+\ldots+x_{n}+x_{1}+\ldots+x_{n}=0$ et que $f$ est $2 n$-positive, on constate que
$$
0 \leqslant f\left(x_{1}\right)+\ldots+f\left(x_{n}\right)+f\left(x_{1}\right)+\ldots+f\left(x_{n}\right)=2\left(f\left(x_{1}\right)+\ldots+f\left(x_{n}\right)\right),
$$
ce qui montre bien que $f\left(x_{1}\right)+\ldots+f\left(x_{n}\right) \geqslant 0$, et donc que $f$ est $n$-positive. La réponse est donc oui!
b) Soit $f$ la fonction définie par $f(x)=-1$ si $x$ est un entier tel que $x \equiv 1(\bmod 2 n)$, et par $f(x)=n$ sinon. Alors $f$ est $n$-positive. En effet, soit $x_{1}, \ldots, x_{n}$ des réels tels que $x_{1}+\ldots+x_{n}=0:$
$\triangleright$ S'il existe un entier $k$ tel que $f\left(x_{k}\right)=n$, et puisque $f\left(x_{i}\right) \geqslant-1$ pour tout $i \neq k$, on sait que $f\left(x_{1}\right)+\ldots+f\left(x_{k}\right) \geqslant f\left(x_{k}\right)-(n-1) \geqslant 1$.
$\triangleright$ Sinon, alors $x_{k} \equiv 1(\bmod 2 n)$ pour tout $k$, donc $x_{1}+\ldots+x_{n} \equiv n \not \equiv 0(\bmod 2 n)$, de sorte que ce cas est en fait impossible.
Cependant, $f$ n'est pas $2 n$-positive. En effet, si $x_{1}=1-2 n$ et $x_{2}=x_{3}=\ldots=x_{2 n}=1$, alors $x_{1}+\ldots+x_{2 n}=0$ mais $f\left(x_{1}\right)+\ldots+f\left(x_{2 n}\right)=-2 n<0$. La réponse est donc non!
Commentaire des correcteurs Les correcteurs ont repéré plusieurs confusions sur la notion de fonction. En effet, lafonction $f$ considérée ne change pas selon qu'il y a 1010 ou 2020 nombres réels.
D'autre part, si l'on veut démontrer qu'une assertion est fausse (par exemple, si l'on souhaite démontrer que toute fonction $f$ qui serait $n$-positive n'est pas nécessairement $2 n$-positive), la manière la plus simple de procéder reste encore de présenter un contre-exemple.
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2019-2020-corrigé-test-janvier.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T1",
"year": "2019"
}
|
Let $a_{0}, a_{1}, a_{2}, \ldots$ be a sequence of non-zero natural numbers, and let $b_{0}, b_{1}, b_{2}, \ldots$ be the sequence such that $b_{n}=\operatorname{GCD}\left(a_{n}, a_{n+1}\right)$ for all integers $n \geqslant 0$. Is it possible that every non-zero natural number is equal to exactly one of the terms $b_{0}, b_{1}, b_{2}, \ldots$?
|
The answer is yes!
In the following, we will say that a sequence $\left(b_{k}\right)_{k \geqslant 0}$ is pleasant if, for all $k \geqslant 0$, the integers $b_{k}$ and $b_{k+2}$ are coprime. Given a pleasant sequence $\left(b_{k}\right)_{k \geqslant 0}$, let $a_{0}=b_{0}$ and then $a_{k}=b_{k-1} b_{k}$ for all $k \geqslant 0$. We then observe that $\operatorname{PGCD}\left(a_{0}, a_{1}\right)=b_{0}$ and that $\operatorname{PGCD}\left(a_{k}, a_{k+1}\right)=b_{k} \operatorname{PGCD}\left(b_{k-1}, b_{k+1}\right)=b_{k}$ for all $k \geqslant 1$. Therefore, it suffices to construct a pleasant sequence $\left(b_{k}\right)_{k \geqslant 0}$ such that every positive integer is equal to exactly one of the integers $b_{0}, b_{1}, b_{2}, \ldots$
To this end, and for all $k \geqslant 1$, let $p_{k}$ be the $k^{\text {th }}$ smallest prime number, and $q_{k}$ the $k^{\text {th }}$ smallest composite number and greater than or equal to 1. It is easily observed that $p_{k} \geqslant 2 k-1$ and that $q_{k} \leqslant 2 k$, hence that $p_{k} \geqslant q_{k}-1$. We deduce that $q_{k} \leqslant p_{k}+1<2 p_{k}<2 p_{k+2}$, and thus that $\operatorname{PGCD}\left(q_{k}, p_{k}\right)=\operatorname{PGCD}\left(q_{k}, p_{k+2}\right)=1$.
We then set $b_{4 k}=p_{2 k+1}, b_{4 k+1}=p_{2 k+2}, b_{4 k+2}=q_{2 k+1}$ and $b_{4 k+3}=q_{2 k+2}$ for all $k \geqslant 0$. First, every positive integer is indeed equal to exactly one of the integers $b_{0}, b_{1}, b_{2}, \ldots$. Furthermore, for all $k \geqslant 0$, and as shown above:
$\triangleright \operatorname{PGCD}\left(b_{4 k}, b_{4 k+2}\right)=\operatorname{PGCD}\left(p_{2 k+1}, q_{2 k+1}\right)=1$,
$\triangleright \operatorname{PGCD}\left(b_{4 k+1}, b_{4 k+3}\right)=\operatorname{PGCD}\left(p_{2 k+2}, q_{2 k+2}\right)=1$,
$\triangleright \operatorname{PGCD}\left(b_{4 k+2}, b_{4 k+4}\right)=\operatorname{PGCD}\left(p_{2 k+3}, q_{2 k+1}\right)=1$ and
$\triangleright \operatorname{PGCD}\left(b_{4 k+3}, b_{4 k+5}\right)=\operatorname{PGCD}\left(p_{2 k+4}, q_{2 k+2}\right)=1$.
The sequence $\left(b_{k}\right)_{k \geqslant 0}$ is therefore indeed a sequence as sought, which concludes the proof.
Comment from the graders: Many different constructions were found, leading to proofs of varying difficulty. A key idea was to think about choosing the sequence $\left(a_{n}\right)$ to have a simple expression for the sequence $\left(b_{n}\right)$.
Often, a proof by algorithm was used: after reducing the problem to finding a sequence $\left(b_{n}\right)$ such that $b_{n}$ and $b_{n+2}$ would be coprime, some students invoked a greedy algorithm, where at each step the smallest integer $b_{n}$ not yet chosen and suitable was chosen. This algorithm does indeed work, but the proof of its correctness was often incomplete:
$\triangleright$ it is necessary to first specify that such an integer $b_{n}$ can indeed be chosen at each step, for example by invoking the infinitude of the set of prime numbers;
$\triangleright$ it is then necessary to demonstrate that, in this case, all integers will indeed be chosen; for this purpose, it was sufficient, for example, to indicate that an infinite number of integers $b_{n}$ would be prime numbers, and to deduce that every number was indeed chosen.
## Senior Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $a_{0}, a_{1}, a_{2}, \ldots$ une suite d'entiers naturels non nuls, et soit $b_{0}, b_{1}, b_{2}, \ldots$ la suite telle que $b_{n}=\operatorname{PGCD}\left(a_{n}, a_{n+1}\right)$ pour tout entier $n \geqslant 0$. Est-il possible que tout entier naturel non nul soit égal à exactement un des termes $b_{0}, b_{1}, b_{2}, \ldots$ ?
|
La réponse est oui!
Dans la suite, on dira qu'une suite $\left(b_{k}\right)_{k \geqslant 0}$ est agréable si, pour tout $k \geqslant 0$, les entiers $b_{k}$ et $b_{k+2}$ sont premiers entre eux. Étant donnée une suite $\left(b_{k}\right)_{k \geqslant 0}$ agréable, posons $a_{0}=b_{0}$ puis $a_{k}=b_{k-1} b_{k}$ pour tout $k \geqslant 0$. On constate alors que $\operatorname{PGCD}\left(a_{0}, a_{1}\right)=b_{0}$ et que $\operatorname{PGCD}\left(a_{k}, a_{k+1}\right)=b_{k} \operatorname{PGCD}\left(b_{k-1}, b_{k+1}\right)=b_{k}$ pour tout $k \geqslant 1$. Il nous suffit donc de construire une suite $\left(b_{k}\right)_{k \geqslant 0}$ agréable telle que tout entier naturel non nul soit égal à exactement un des entiers $b_{0}, b_{1}, b_{2}, \ldots$
À cette fin, et pour tout $k \geqslant 1$, notons $p_{k}$ le $k^{\text {ème }}$ plus petit nombre premier, et $q_{k}$ le $k^{\text {ème }}$ plus petit entier composé et supérieur ou égal à 1 . On remarque aisément que $p_{k} \geqslant 2 k-1$ et que $q_{k} \leqslant 2 k$, donc que $p_{k} \geqslant q_{k}-1$. On en déduit que $q_{k} \leqslant p_{k}+1<2 p_{k}<2 p_{k+2}$, donc que $\operatorname{PGCD}\left(q_{k}, p_{k}\right)=\operatorname{PGCD}\left(q_{k}, p_{k+2}\right)=1$.
On pose alors $b_{4 k}=p_{2 k+1}, b_{4 k+1}=p_{2 k+2}, b_{4 k+2}=q_{2 k+1}$ et $b_{4 k+3}=q_{2 k+2}$ pour tout $k \geqslant 0$. Tout d'abord, tout entier naturel non nul est bien égal à exactement un des entiers $b_{0}, b_{1}, b_{2}, \ldots$. En outre, pour tout $k \geqslant 0$, et comme démontré ci-dessus :
$\triangleright \operatorname{PGCD}\left(b_{4 k}, b_{4 k+2}\right)=\operatorname{PGCD}\left(p_{2 k+1}, q_{2 k+1}\right)=1$ ,
$\triangleright \operatorname{PGCD}\left(b_{4 k+1}, b_{4 k+3}\right)=\operatorname{PGCD}\left(p_{2 k+2}, q_{2 k+2}\right)=1$ ,
$\triangleright \operatorname{PGCD}\left(b_{4 k+2}, b_{4 k+4}\right)=\operatorname{PGCD}\left(p_{2 k+3}, q_{2 k+1}\right)=1$ et
$\triangleright \operatorname{PGCD}\left(b_{4 k+3}, b_{4 k+5}\right)=\operatorname{PGCD}\left(p_{2 k+4}, q_{2 k+2}\right)=1$.
La suite $\left(b_{k}\right)_{k \geqslant 0}$ est donc bien une suite telle que recherchée, ce qui conclut.
Commentaire des correcteurs Beaucoup de constructions différentes ont été trouvées, menant à des preuves plus ou moins faciles. Une idée clé était de penser à choisir la suite $\left(a_{n}\right)$ pour avoir une expression simple de la suite $\left(b_{n}\right)$.
Souvent, une preuve par algorithme a été utilisée : après s'être ramenés à trouver une suite $\left(b_{n}\right)$ telle que $b_{n}$ et $b_{n+2}$ seraient premiers entre eux, certains élèves ont invoqué un algorithme glouton, où l'on choisissait à chaque fois le plus petit entier $b_{n}$ non pris qui convenait. Cet algorithme fonctionne effectivement, mais la preuve de correction de cet algorithme était très souvent incomplète :
$\triangleright$ il faut tout d'abord préciser que l'on peut bien choisir un tel entier $b_{n}$ à chaque étape, par exemple en invoquant l'infinité de l'ensemble des nombres premiers;
$\triangleright$ il faut ensuite démontrer que, dans ce cas, tous les entiers seront bien pris ; à cette fin, il suffisait par exemple de signaler qu'une infinité d'entiers $b_{n}$ seraient des nombres premiers, et en déduire que tout nombre était effectivement pris.
## Exercices Senior
|
{
"exam": "French_tests",
"problem_label": "5",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/tests/fr-2019-2020-corrigé-test-janvier.jsonl",
"solution_match": "## Solution de l'exercice 4",
"tier": "T1",
"year": "2019"
}
|
Let $a_{0}, a_{1}, a_{2}, \ldots$ be a sequence of non-zero natural numbers, and let $b_{0}, b_{1}, b_{2}, \ldots$ be the sequence such that $b_{n}=\operatorname{GCD}\left(a_{n}, a_{n+1}\right)$ for all integers $n \geqslant 0$. Is it possible that every non-zero natural number is equal to exactly one of the terms $b_{0}, b_{1}, b_{2}, \ldots$?
|
The answer is yes!
In the following, we will say that a sequence $\left(b_{k}\right)_{k \geqslant 0}$ is pleasant if, for all $k \geqslant 0$, the integers $b_{k}$ and $b_{k+2}$ are coprime. Given a pleasant sequence $\left(b_{k}\right)_{k \geqslant 0}$, let $a_{0}=b_{0}$ and then $a_{k}=b_{k-1} b_{k}$ for all $k \geqslant 0$. We then observe that $\operatorname{PGCD}\left(a_{0}, a_{1}\right)=b_{0}$ and that $\operatorname{PGCD}\left(a_{k}, a_{k+1}\right)=b_{k} \operatorname{PGCD}\left(b_{k-1}, b_{k+1}\right)=b_{k}$ for all $k \geqslant 1$. Therefore, it suffices to construct a pleasant sequence $\left(b_{k}\right)_{k \geqslant 0}$ such that every positive integer is equal to exactly one of the integers $b_{0}, b_{1}, b_{2}, \ldots$
To this end, and for all $k \geqslant 1$, let $p_{k}$ be the $k^{\text {th }}$ smallest prime number, and $q_{k}$ the $k^{\text {th }}$ smallest composite number and greater than or equal to 1. It is easily observed that $p_{k} \geqslant 2 k-1$ and that $q_{k} \leqslant 2 k$, hence that $p_{k} \geqslant q_{k}-1$. We deduce that $q_{k} \leqslant p_{k}+1<2 p_{k}<2 p_{k+2}$, thus $\operatorname{PGCD}\left(q_{k}, p_{k}\right)=\operatorname{PGCD}\left(q_{k}, p_{k+2}\right)=1$.
We then set $b_{4 k}=p_{2 k+1}, b_{4 k+1}=p_{2 k+2}, b_{4 k+2}=q_{2 k+1}$ and $b_{4 k+3}=q_{2 k+2}$ for all $k \geqslant 0$. First, every positive integer is indeed equal to exactly one of the integers $b_{0}, b_{1}, b_{2}, \ldots$. Furthermore, for all $k \geqslant 0$, and as shown above:
$$
\begin{aligned}
& \triangleright \operatorname{PGCD}\left(b_{4 k}, b_{4 k+2}\right)=\operatorname{PGCD}\left(p_{2 k+1}, q_{2 k+1}\right)=1, \\
& \triangleright \operatorname{PGCD}\left(b_{4 k+1}, b_{4 k+3}\right)=\operatorname{PGCD}\left(p_{2 k+2}, q_{2 k+2}\right)=1, \\
& \triangleright \operatorname{PGCD}\left(b_{4 k+2}, b_{4 k+4}\right)=\operatorname{PGCD}\left(p_{2 k+3}, q_{2 k+1}\right)=1 \text { and } \\
& \triangleright \operatorname{PGCD}\left(b_{4 k+3}, b_{4 k+5}\right)=\operatorname{PGCD}\left(p_{2 k+4}, q_{2 k+2}\right)=1 .
\end{aligned}
$$
The sequence $\left(b_{k}\right)_{k \geqslant 0}$ is therefore indeed a sequence as sought, which concludes.
Comment from the graders: Many different constructions were found, leading to proofs of varying difficulty. A key idea was to think of choosing the sequence $\left(a_{n}\right)$ to have a simple expression for the sequence $\left(b_{n}\right)$.
Often, a proof by algorithm was used: after reducing to finding a sequence $\left(b_{n}\right)$ such that $b_{n}$ and $b_{n+2}$ would be coprime, some students invoked a greedy algorithm, where at each step the smallest integer $b_{n}$ not yet taken that worked was chosen. This algorithm does indeed work, but the proof of correctness of this algorithm was often incomplete:
$\triangleright$ it is necessary to first specify that one can indeed choose such an integer $b_{n}$ at each step, for example by invoking the infinitude of the set of prime numbers;
$\triangleright$ it is then necessary to show that, in this case, all integers will indeed be taken; for this purpose, it was sufficient, for example, to indicate that an infinite number of integers $b_{n}$ would be prime numbers, and to deduce that every number was indeed taken.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $a_{0}, a_{1}, a_{2}, \ldots$ une suite d'entiers naturels non nuls, et soit $b_{0}, b_{1}, b_{2}, \ldots$ la suite telle que $b_{n}=\operatorname{PGCD}\left(a_{n}, a_{n+1}\right)$ pour tout entier $n \geqslant 0$. Est-il possible que tout entier naturel non nul soit égal à exactement un des termes $b_{0}, b_{1}, b_{2}, \ldots$ ?
|
La réponse est oui!
Dans la suite, on dira qu'une suite $\left(b_{k}\right)_{k \geqslant 0}$ est agréable si, pour tout $k \geqslant 0$, les entiers $b_{k}$ et $b_{k+2}$ sont premiers entre eux. Étant donnée une suite $\left(b_{k}\right)_{k \geqslant 0}$ agréable, posons $a_{0}=b_{0}$ puis $a_{k}=b_{k-1} b_{k}$ pour tout $k \geqslant 0$. On constate alors que $\operatorname{PGCD}\left(a_{0}, a_{1}\right)=b_{0}$ et que $\operatorname{PGCD}\left(a_{k}, a_{k+1}\right)=b_{k} \operatorname{PGCD}\left(b_{k-1}, b_{k+1}\right)=b_{k}$ pour tout $k \geqslant 1$. Il nous suffit donc de construire une suite $\left(b_{k}\right)_{k \geqslant 0}$ agréable telle que tout entier naturel non nul soit égal à exactement un des entiers $b_{0}, b_{1}, b_{2}, \ldots$
À cette fin, et pour tout $k \geqslant 1$, notons $p_{k}$ le $k^{\text {ème }}$ plus petit nombre premier, et $q_{k}$ le $k^{\text {ème }}$ plus petit entier composé et supérieur ou égal à 1 . On remarque aisément que $p_{k} \geqslant 2 k-1$ et que $q_{k} \leqslant 2 k$, donc que $p_{k} \geqslant q_{k}-1$. On en déduit que $q_{k} \leqslant p_{k}+1<2 p_{k}<2 p_{k+2}$, donc que $\operatorname{PGCD}\left(q_{k}, p_{k}\right)=\operatorname{PGCD}\left(q_{k}, p_{k+2}\right)=1$.
On pose alors $b_{4 k}=p_{2 k+1}, b_{4 k+1}=p_{2 k+2}, b_{4 k+2}=q_{2 k+1}$ et $b_{4 k+3}=q_{2 k+2}$ pour tout $k \geqslant 0$. Tout d'abord, tout entier naturel non nul est bien égal à exactement un des entiers $b_{0}, b_{1}, b_{2}, \ldots$. En outre, pour tout $k \geqslant 0$, et comme démontré ci-dessus:
$$
\begin{aligned}
& \triangleright \operatorname{PGCD}\left(b_{4 k}, b_{4 k+2}\right)=\operatorname{PGCD}\left(p_{2 k+1}, q_{2 k+1}\right)=1, \\
& \triangleright \operatorname{PGCD}\left(b_{4 k+1}, b_{4 k+3}\right)=\operatorname{PGCD}\left(p_{2 k+2}, q_{2 k+2}\right)=1, \\
& \triangleright \operatorname{PGCD}\left(b_{4 k+2}, b_{4 k+4}\right)=\operatorname{PGCD}\left(p_{2 k+3}, q_{2 k+1}\right)=1 \text { et } \\
& \triangleright \operatorname{PGCD}\left(b_{4 k+3}, b_{4 k+5}\right)=\operatorname{PGCD}\left(p_{2 k+4}, q_{2 k+2}\right)=1 .
\end{aligned}
$$
La suite $\left(b_{k}\right)_{k \geqslant 0}$ est donc bien une suite telle que recherchée, ce qui conclut.
Commentaire des correcteurs Beaucoup de constructions différentes ont été trouvées, menant à des preuves plus ou moins faciles. Une idée clé était de penser à choisir la suite $\left(a_{n}\right)$ pour avoir une expression simple de la suite $\left(b_{n}\right)$.
Souvent, une preuve par algorithme a été utilisée : après s'être ramenés à trouver une suite $\left(b_{n}\right)$ telle que $b_{n}$ et $b_{n+2}$ seraient premiers entre eux, certains élèves ont invoqué un algorithme glouton, où l'on choisissait à chaque fois le plus petit entier $b_{n}$ non pris qui convenait. Cet algorithme fonctionne effectivement, mais la preuve de correction de cet algorithme était très souvent incomplète :
$\triangleright$ il faut tout d'abord préciser que l'on peut bien choisir un tel entier $b_{n}$ à chaque étape, par exemple en invoquant l'infinité de l'ensemble des nombres premiers;
$\triangleright$ il faut ensuite démontrer que, dans ce cas, tous les entiers seront bien pris; à cette fin, il suffisait par exemple de signaler qu'une infinité d'entiers $b_{n}$ seraient des nombres premiers, et en déduire que tout nombre était effectivement pris.
|
{
"exam": "French_tests",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/tests/fr-2019-2020-corrigé-test-janvier.jsonl",
"solution_match": "## Solution de l'exercice 5",
"tier": "T1",
"year": "2019"
}
|
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
f(x+f(y))+x=f(f(2 x)+y)
$$
for all real numbers $x$ and $y$.
|
First, it is easily observed that for any real number $a$, the function $f: x \rightarrow x+a$ is a solution to the problem. Conversely, we will show that there are no other solutions.
In what follows, we consider a solution function $f$, we set $a=f(0)$, and we will denote by $\mathbf{E}(x, y)$ the equation
$$
f(x+f(y))+x=f(f(2 x)+y)
$$
First, the equations $\mathbf{E}(x, 0)$ and $\mathbf{E}(0,2 x)$ show that $f(f(2 x))=f(x+a)+x$ and that $f(f(2 x))=f(2 x+a)$. We deduce that
$$
f(2 x+a)=f(f(2 x))=f(x+a)+x
$$
and, if we set $x=-a$, it follows that $f(-a)=f(0)-a=0$.
We then consider an arbitrary real number $x$, and we set $y=-f(-2 x)-a$ and $z=-x+f(y)$. Since $f(-a)=0$, the equation $\mathbf{E}(-x, y)$ shows that $f(z)-x=f(-a)=0$, that is, $f(z)=x$. The function $f$ is therefore surjective.
Let us prove that $f$ is also injective. Let $x$ and $y$ be two real numbers such that $f(x)=f(y)$, and let $d=y-x$. Let $t$ be an arbitrary real number, and let $z$ be a preimage of $t$ by $f$. The equations $\mathbf{E}(z / 2, x)$ and $\mathbf{E}(z / 2, y)$ show that
$$
f(t+x)=f(f(2 z / 2)+x)=f(z / 2+f(x))+z / 2=f(z / 2+f(y))+z / 2=f(t+y)
$$
If $d \neq 0$, this means that $f$ is $d$-periodic, which proves that $f(2 x)=f(2 x+2 d)=f(2 y)$ and that $f(x+a)=f(x+a+d)=f(y+a)$. But then the equation $\mathbf{E}(x, 0)$ indicates that
$$
x=f^{2}(2 x)-f(x+a)=f^{2}(2 y)-f(y+a)=y
$$
contradicting the fact that $d \neq 0$.
The function $f$ is therefore indeed injective. Since $\mathbf{E}(0, y)$ shows that $f(f(y))=f(y+a)$, as mentioned above, it follows that $f(y)=y+a$ for all real $y$, which concludes the proof.
|
f(x) = x + a
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Trouver toutes les fonctions $f: \mathbb{R} \rightarrow \mathbb{R}$ telles que
$$
f(x+f(y))+x=f(f(2 x)+y)
$$
pour tous les réels $x$ et $y$.
|
Tout d'abord, on constate aisément que, pour tout réel $a$, la fonction $f: x \rightarrow x+a$ est une solution du problème. Réciproquement, on va montrer qu'il n'existe pas d'autre solution.
Dans ce qui suit, on considère une fonction solution $f$, on pose $a=f(0)$, et on notera $\mathbf{E}(x, y)$ l'équation
$$
f(x+f(y))+x=f(f(2 x)+y)
$$
Tout d'abord, les équations $\mathbf{E}(x, 0)$ et $\mathbf{E}(0,2 x)$ montrent que $f(f(2 x))=f(x+a)+x$ et que $f(f(2 x))=f(2 x+a)$. On en déduit que
$$
f(2 x+a)=f(f(2 x))=f(x+a)+x
$$
et, si l'on pose $x=-a$, il s'ensuit même que $f(-a)=f(0)-a=0$.
On considère alors un réel $x$ quelconque, et on pose $y=-f(-2 x)-a$ puis $z=-x+f(y)$. Comme $f(-a)=0$, l'équation $\mathbf{E}(-x, y)$ montre que $f(z)-x=f(-a)=0$, c'est-à-dire que $f(z)=x$. La fonction $f$ est donc surjective.
Démontrons que $f$ est également injective. Soit $x$ et $y$ deux réels tels que $f(x)=f(y)$, et soit $d=y-x$. Soit également $t$ un réel quelconque, et soit $z$ un antécédent de $t$ par $f$. Les équations $\mathbf{E}(z / 2, x)$ et $\mathbf{E}(z / 2, y)$ démontrent que
$$
f(t+x)=f(f(2 z / 2)+x)=f(z / 2+f(x))+z / 2=f(z / 2+f(y))+z / 2=f(t+y)
$$
Si $d \neq 0$, cela signifie que $f$ est $d$-périodique, ce qui prouve que $f(2 x)=f(2 x+2 d)=f(2 y)$ et que $f(x+a)=f(x+a+d)=f(y+a)$. Mais alors l'équation $\mathbf{E}(x, 0)$ indique que
$$
x=f^{2}(2 x)-f(x+a)=f^{2}(2 y)-f(y+a)=y
$$
contredisant le fait que $d \neq 0$.
La fonction $f$ est donc bien injective. Puisque $\mathbf{E}(0, y)$ montre que $f(f(y))=f(y+a)$, comme on l'a déjà mentionné ci-dessus, il s'ensuit que $f(y)=y+a$ pour tout réel $y$, ce qui conclut.
|
{
"exam": "French_tests",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/tests/fr-2019-2020-corrigé-test-janvier.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T1",
"year": "2019"
}
|
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
f(x+f(y))+x=f(f(2 x)+y)
$$
for all real numbers $x$ and $y$.
|
$n^{\circ} 1$ As previously, observe that functions of the form $f: x \rightarrow x+a$ are solutions, and we will show that these are the only ones. To this end, let $a=f(0)$ and denote $\mathbf{E}(x, y)$ the equation
$$
f(x+f(y))+x=f(f(2 x)+y)
$$
Let then $y$ be any real number, and $x=y+a-f(y)$. Then
$$
\begin{aligned}
f(f(2 x)+y+a) & =f(f(f(2 x)+y)) & & \text { according to } \mathbf{E}(0, f(2 x)+y) \\
& =f(f(x+f(y))+x) & & \text { according to } \mathbf{E}(x, y) \\
& =f(f(2 x)+x+f(y))-x & & \text { according to } \mathbf{E}(x, x+f(y)) \\
& =f(f(2 x)+y+a)-x & & \text { since } f(2 x)+y+a=f(2 x)+x+f(y)
\end{aligned}
$$
This means that $x=0$, or equivalently that $f(y)=y+a$, which concludes the proof.
Comment from the graders Many students provided a complete solution. Some proofs were impressively efficient! Moreover, no student forgot to verify that the solutions found indeed satisfy the functional equation, which is very pleasing to see. However, here are some errors that recurred:
$\triangleright$ Several students reasoned using the continuity or differentiability of the function. No continuity hypothesis was given in the statement, and these arguments are therefore not valid. Similarly, several students assumed that $f$ was a polynomial. Finally, a few students tried to interpret, in a sentence, the behavior of $f$ from the equation in the statement: however, since no "obvious" property of the function $f$ could be deduced, these attempts were all unsuccessful.
$\triangleright$ Some students confused the notions of surjectivity and injectivity: after showing that $f$ was surjective, they performed simplifications by $f$ of the equation invoking surjectivity, whereas this property pertains to injectivity.
$\triangleright$ When composing with $f$ multiple times, it can be wise to use different sizes or colors of parentheses: several students unfortunately made calculation errors in their manipulations by forgetting or moving parentheses.
Finally, in the context of a functional equation, we recommend clearly writing each substitution made and, if combining different equations, clearly writing which equations are combined. This attention to structure not only helps the grader understand that the student knows what they are doing and follow the student's reasoning, but it also helps the student not get lost in their equations and make calculation errors. In particular, it greatly facilitates the student's proofreading, and will often help them detect and correct calculation errors that would have cost them points if they had not seen them.
|
f(x) = x + a
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Trouver toutes les fonctions $f: \mathbb{R} \rightarrow \mathbb{R}$ telles que
$$
f(x+f(y))+x=f(f(2 x)+y)
$$
pour tous les réels $x$ et $y$.
|
$n^{\circ} 1$ Comme précédemment, constate que les fonctions de la forme $f$ : $x \rightarrow x+a$ sont des solutions, et on va montrer que ce sont les seules. À cette fin, on pose $a=f(0)$ et on note $\mathbf{E}(x, y)$ l'équation
$$
f(x+f(y))+x=f(f(2 x)+y)
$$
Soit alors $y$ un nombre réel quelconque, et $x=y+a-f(y)$. Alors
$$
\begin{aligned}
f(f(2 x)+y+a) & =f(f(f(2 x)+y)) & & \text { d'après } \mathbf{E}(0, f(2 x)+y) \\
& =f(f(x+f(y))+x) & & \text { d'après } \mathbf{E}(x, y) \\
& =f(f(2 x)+x+f(y))-x & & \text { d'après } \mathbf{E}(x, x+f(y)) \\
& =f(f(2 x)+y+a)-x & & \text { car } f(2 x)+y+a=f(2 x)+x+f(y)
\end{aligned}
$$
Cela signifie que $x=0$, ou encore que $f(y)=y+a$, ce qui conclut.
Commentaire des correcteurs De nombreux élèves ont fourni une solution complète. Certaines preuves étaient impressionnantes par leur efficacité! Par ailleurs, aucun élève n'a oublié de vérifier que les solutions trouvées vérifiaient bien l'équation fonctionnelle, ce qui fait très plaisir à voir. Voici, cependant, quelques erreurs qui sont revenues à plusieurs reprises:
$\triangleright$ Plusieurs élèves ont raisonné en utilisant la continuité ou la dérivablité de la fonction. Aucune hypothèse concernant la continuité ne figurait dans l'énoncé, et ces raisonnements ne sont donc pas valides. De même, plusieurs élèves ont supposé d'office que $f$ était un polynôme. Enfin, quelques élèves ont tenté d'interpréter, par une phrase, le comportement de $f$ à partir de l'équation de l'énoncé : cependant, comme aucune propriété « évidente » de la fonction $f$ ne se dégageait, ces tentatives se sont toutes avérées infructueuses.
$\triangleright$ Quelques élèves ont confondu les notions de surjectivité et d'injectivité : après avoir montré que $f$ était surjective, ils ont opéré des simplifications par $f$ de l'équation en invoquant la surjectivité, alors que cette propriété relève de l'injectivité.
$\triangleright$ Lorsqu'il faut composer plusieurs fois par $f$, il peut être judicieux d'employer différentes tailles ou couleurs de parenthésage : plusieurs élèves ont malheureusement fait des erreurs de calcul lors de leurs manipulations en oubliant ou en déplaçant des parenthèses.
Enfin, dans le cadre d'une équation fonctionnelle, nous recommandons de bien écrire à chaque fois les substitutions effectuées et, si l'on combine différentes équations, de bien écrire quelles équations sont combinées. Ce souci de structure permet non seulement au correcteur de comprendre que l'élève sait ce qu'il fait et de suivre le raisonnement de celuici, mais il permet également à l'élève de ne pas se perdre dans ses équations et faire des erreurs de calcul. En particulier, cela facilite grandement le travail de relecture par l'élève, et l'aidera donc souvent à détecter puis corriger des erreurs de calcul qui lui auraient coûté des points s'il ne les avait pas vues.
|
{
"exam": "French_tests",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/tests/fr-2019-2020-corrigé-test-janvier.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2019"
}
|
Let $k$ and $n$ be two non-zero natural numbers, such that $k \leqslant 2^{n}$. Morgane has written, in her notebook, the set of $n$-tuples formed of 0 and 1: there are $2^{n}$ of them. We say that two $n$-tuples $\left(x_{1}, \ldots, x_{n}\right)$ and $\left(y_{1}, \ldots, y_{n}\right)$ are neighbors if they have $n-1$ terms in common, that is, if there is only one integer $i$ such that $x_{i} \neq y_{i}$. Then Morgane chooses $k$ of these $n$-tuples and underlines them. She then performs the following operations: in each operation, she chooses an $n$-tuple whose two neighbors are underlined, and she also underlines this $n$-tuple.
For which values of $k$ can Morgane manage to underline all the $n$-tuples?
|
Throughout the following, we will identify our $n$-tuples with vectors in $(\mathbb{Z} / 2 \mathbb{Z})^{n}$, that is, vectors whose $n$ coordinates are elements of $\mathbb{Z} / 2 \mathbb{Z}$. Thus, we denote:
$\triangleright 0$ the vector whose all coordinates are zero,
$\triangleright \mathbf{a}_{i}$ the vector whose $i^{\text{th}}$ coordinate is 1 and the others are 0,
$\triangleright \mathbf{b}_{i, j}$ the vector whose $i$-th and $j^{\text{th}}$ coordinates are 1 and the others are 0;
First, we will show that the integer $k=1+\lceil n / 2\rceil$ works, where $\lceil x\rceil$ denotes the ceiling of the real number $x$, that is, the smallest integer greater than or equal to $x$. To do this, we can assume that Morgane first underlined the vectors $\mathbf{0}, \mathbf{b}_{1,2}, \mathbf{b}_{3,4}, \ldots, \mathbf{b}_{2 k-3,2 k-2}$; if $n$ is even, the last vector is $\mathbf{b}_{n-1, n}$ and, if $n$ is odd, by abuse of notation, we identify the vector $\mathbf{b}_{n, n+1}$ with the vector $\mathbf{a}_{n}$. Under these conditions:
$\triangleright$ if $i$ is even, then $\mathbf{a}_{i}$ is a neighbor of the two vectors $\mathbf{0}$ and $\mathbf{b}_{i-1, i}$;
$\triangleright$ if $i$ is odd, with $i \leqslant n-1$, then $\mathbf{a}_{i}$ is a neighbor of the two vectors $\mathbf{0}$ and $\mathbf{b}_{i, i+1}$;
$\triangleright$ if $i=n$ is odd, then $\mathbf{a}_{i}=\mathbf{a}_{n}=\mathbf{b}_{2 k-3,2 k-2}$ is already underlined.
Thus, Morgane can underline each of the vectors $\mathbf{a}_{i}$.
An immediate induction on $\ell$ then shows that Morgane can underline any vector with $\ell$ coordinates equal to 1, and the $n-\ell$ others equal to 0. We conclude that any integer $k$ between $1+\lceil n / 2\rceil$ and $2^{n}$ works.
Conversely, let $k$ be one of the integers sought: let us show that $k \geqslant 1+\lceil n / 2\rceil$. To do this, we first construct the directed graph whose vertices are the vectors in $(\mathbb{Z} / 2 \mathbb{Z})^{n}$ and whose edges are constructed as follows:
$\triangleright$ if a vector $\mathbf{t}$ was one of the $k$ vectors that Morgane had initially underlined, then no edge arrives at $\mathbf{t}$;
$\triangleright$ otherwise, let $\mathbf{u}$ and $\mathbf{v}$ be two neighbors of $\mathbf{t}$ that Morgane had underlined before underlining $\mathbf{t}$: the graph contains an edge from $\mathbf{u}$ to $\mathbf{t}$, and another edge from $\mathbf{v}$ to $\mathbf{t}$.
Now introduce some notions and concepts. We say that a set $S$ of vectors is an initial set if every edge entering a vertex of $S$ comes from another vertex of $S$. We also say that $S$ is connected if, by taking the edges in the wrong direction, we can connect any vector in $S$ to any other without leaving $S$. Furthermore, we say that the sources of $S$ are the vectors in $S$ that Morgane had initially underlined, that is, those in which no edge enters. Finally, we say that a coordinate $i$ is a variable of $S$ if there exist two vectors $\mathbf{t}$ and $\mathbf{t}^{\prime}$ in $S$ such that $\mathbf{t}_{i} \neq \mathbf{t}_{i}^{\prime}$.
We will now prove the property $\mathcal{P}_{\ell}$ by strong induction on $\ell$:
Let $S$ be an initial connected set containing $\ell$ vectors and $m$ sources. Then $S$ has at most $2(m-1)$ variable coordinates.
First, the property $\mathcal{P}_{1}$ is obvious, since $S$ is then reduced to a single vector, which is itself a source, and therefore has no variable coordinate. Now let $\ell \geqslant 2$ be an integer such that the properties $\mathcal{P}_{1}, \ldots, \mathcal{P}_{\ell-1}$ are all true, and let $S$ be an initial connected set containing $\ell$ vectors, $m$ sources, and $c$ variable coordinates.
Let $\mathbf{t}$ be the last vector, among those belonging to $S$, that Morgane underlined. If $\mathbf{t}$ is a source, then $S$ is formed only of sources, which contains no edge, in contradiction with the fact that $S$ is connected and that $\ell \geqslant 2$. Thus, there exist two edges $\mathbf{u} \rightarrow \mathbf{t}$ and $\mathbf{v} \rightarrow \mathbf{t}$, coming from two other vectors $\mathbf{u}$ and $\mathbf{v}$ in $S$. Let $i$ and $j$ be the two coordinates such that $\mathbf{t}_{i} \neq \mathbf{u}_{i}$ and $\mathbf{t}_{j} \neq \mathbf{v}_{j}$, and let $S^{\prime}$ be the set $\backslash \backslash\{\mathbf{t}\}$.
$\triangleright$ If $S^{\prime}$ is connected, we easily observe that the variable coordinates of $S$ are those of $S^{\prime}$. Since $S^{\prime}$ contains $\ell-1$ vertices and $m$ sources, the sets $S$ and $S^{\prime}$ therefore have at most $2(m-1)$ variable coordinates.
$\triangleright$ If $S^{\prime}$ is not connected, then we can split it into two initial connected sets, $U$ and $V$, which contain the vectors $\mathbf{u}$ and $\mathbf{v}$, respectively. One contains $\ell_{u}$ vectors, $m_{u}$ sources, and $c_{u}$ variable coordinates, while the other contains $\ell_{v}$ vectors, $m_{v}$ sources, and $c_{v}$ variable coordinates. Since $\ell_{u} \leqslant \ell-1$ and $\ell_{v} \leqslant \ell-1$, we know that $c_{u} \leqslant 2\left(m_{u}-1\right)$ and that $c_{v} \leqslant 2\left(m_{v}-1\right)$.
Moreover, the sources of $S$ are those of $U$ and $V$, and no source can belong to both $U$ and $V$, so $m=m_{u}+m_{v}$. On the other hand, we easily observe that the variable coordinates of $S$ are either those of $U$, those of $V$, or $i$ and $j$. Thus, the set $S$ has at most $c_{u}+c_{v}+2 \leqslant 2\left(m_{u}+m_{v}-1\right)=2(m-1)$ variable coordinates, which proves $\mathcal{P}_{\ell}$.
Finally, note that the set $(\mathbb{Z} / 2 \mathbb{Z})^{n}$ itself is an initial connected set, and it contains $n$ variables and $k$ sources. The property $\mathcal{P}_{2^{n}}$ therefore shows that $n \leqslant 2(k-1)$, that is, $k \geqslant 1+\lceil n / 2\rceil$. The integers sought are therefore the integers between $1+\lceil n / 2\rceil$ and $2^{n}$.
|
k \geqslant 1+\lceil n / 2\rceil
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Soit $k$ et $n$ deux entiers naturels non nuls, tels que $k \leqslant 2^{n}$. Morgane a écrit, sur son cahier, l'ensemble des $n$-uplets formés de 0 et de 1 :il y en a $2^{n}$. On dit que deux $n$-uplets $\left(x_{1}, \ldots, x_{n}\right)$ et $\left(y_{1}, \ldots, y_{n}\right)$ sont voisins s'ils ont $n-1$ termes en commun, c'est-à-dire s'il existe un seul entier $i$ tel que $x_{i} \neq y_{i}$. Puis Morgane choisit $k$ de ces $n$-uplets et les souligne. Elle effectue ensuite les opérations suivantes : lors de chaque opération, elle choisit un $n$-uplet dont deux voisins sont soulignés, et elle souligne également ce $n$-uplet.
Pour quelles valeurs de $k$ Morgane peut-elle parvenir à souligner l'ensemble des $n$-uplets?
|
Dans toute la suite, on assimilera nos $n$-uplets à des vecteurs de $(\mathbb{Z} / 2 \mathbb{Z})^{n}$, c'est-à-dire des vecteurs dont les $n$ coordonnées sont des éléments de $\mathbb{Z} / 2 \mathbb{Z}$. Ainsi, on note
$\triangleright 0$ le vecteur dont toutes les coordonnées sont nulles,
$\triangleright \mathbf{a}_{i}$ le vecteur dont la $i^{\text {ème }}$ coordonnée vaut 1 et les autres valent 0
$\triangleright \mathbf{b}_{i, j}$ le vecteur dont les $i$ ème et $j^{\text {ème }}$ coordonnées valent 1 et les autres valent 0 ;
Dans un premier temps, nous allons montrer que l'entier $k=1+\lceil n / 2\rceil$ convient, où $\lceil x\rceil$ désigne la partie entière supérieure du réel $x$, c'est-à-dire le plus petit entier supérieur ou égal à $x$. Pour ce faire, on peut supposer que Morgane a d'abord souligné les vecteurs $\mathbf{0}, \mathbf{b}_{1,2}, \mathbf{b}_{3,4}, \ldots, \mathbf{b}_{2 k-3,2 k-2}$; si $n$ est pair, ce dernier vecteur est le vecteur $\mathbf{b}_{n-1, n}$ et, si $n$ est impair, par abus de notation, on identifiera le vecteur $\mathbf{b}_{n, n+1}$ au vecteur $\mathbf{a}_{n}$. Dans ces conditions:
$\triangleright \operatorname{si} i$ est pair, alors $\mathbf{a}_{i}$ est voisin des deux vecteurs $\mathbf{0}$ et $\mathbf{b}_{i-1, i}$;
$\triangleright \operatorname{si} i$ est impair, avec $i \leqslant n-1$, alors $\mathbf{a}_{i}$ est voisin des deux vecteurs $\mathbf{0}$ et $\mathbf{b}_{i, i+1}$;
$\triangleright \operatorname{si} i=n$ est impair, alors $\mathbf{a}_{i}=\mathbf{a}_{n}=\mathbf{b}_{2 k-3,2 k-2}$ est déjà souligné.
Ainsi, Morgane peut souligner chacun des vecteurs $\mathbf{a}_{i}$.
Une récurrence immédiate sur $\ell$ permet alors de montrer que Morgane peut souligner tout vecteur dont $\ell$ coordonnées sont égales à 1 , et les $n-\ell$ autres sont égales à 0 . On en conclut que tout entier $k$ compris entre $1+\lceil n / 2\rceil$ et $2^{n}$ convient.
Réciproquement, soit $k$ un des entiers recherchés : démontrons que $k \geqslant 1+\lceil n / 2\rceil$. Pour ce faire, on construit d'abord le graphe orienté dont les sommets sont les vecteurs de $(\mathbb{Z} / 2 \mathbb{Z})^{n}$ et dont les arêtes sont construites comme suit:
$\triangleright$ si un vecteur t était un des $k$ vecteurs que Morgane avait soulignés initialement, alors aucune arête n'arrive en $t$;
$\triangleright$ sinon, soit $\mathbf{u}$ et $\mathbf{v}$ deux voisins de $\mathbf{t}$ que Morgane avait soulignés avant de souligner $\mathbf{t}$ : le graphe contient une arête qui va de $\mathbf{u}$ vers $t$, et une autre arête qui va de $\mathbf{v}$ vers $t$.
Introduisons maintenant quelques notions et concepts. On dit qu'un ensemble $S$ de vecteurs est un ensemble initial si toute arête entrant en un sommet de $S$ provient d'un autre sommet de $S$. On dit également que $S$ est connexe si, quitte à prendre les arêtes dans le mauvais sens, on peut relier n'importe quel vecteur de $S$ à n'importe quel autre sans sortir de $S$. En outre, on dit que les sources de $S$ sont les vecteurs de $S$ que Morgane avait soulignés initialement, c'est-à-dire ceux en lesquels n'entre aucune arête. Enfin, on dit qu'une coordonnée $i$ est une variable de $S$ s'il existe deux vecteurs $\mathbf{t}$ et $\mathbf{t}^{\prime}$ de $S$ tels que $\mathbf{t}_{i} \neq \mathbf{t}_{i}^{\prime}$.
Nous allons maintenant démontrer la propriété $\mathcal{P}_{\ell}$ par récurrence forte sur $\ell$ :
Soit $S$ un ensemble initial connexe contenant $\ell$ vecteurs et $m$ sources. Alors $S$ a au plus $2(m-1)$ coodonnées variables.
Tout d'abord, la propriété $\mathcal{P}_{1}$ est évidente, puisque $S$ est alors réduit à un seul vecteur, qui est lui-même une source, et n'a donc aucune coordonnée variable. Soit maintenant $\ell \geqslant 2$
un entier tel que les propriétés $\mathcal{P}_{1}, \ldots, \mathcal{P}_{\ell-1}$ soient toutes vraies, et soit $S$ un ensemble initial connexe contenant $\ell$ vecteurs, $m$ sources, et $c$ coordonnées variables.
Notons $\mathbf{t}$ le dernier vecteur, parmi ceux appartenant à $S$, que Morgane a souligné. Si t est une source, c'est que $S$ n'est formé que de sources, dont ne contient aucune arête, en contradiction avec le fait que $S$ soit connexe et que $\ell \geqslant 2$. Ainsi, il existe deux arêtes $\mathbf{u} \rightarrow \mathbf{t}$ et $\mathbf{v} \rightarrow \mathbf{t}$, provenant de deux autres vecteurs $\mathbf{u}$ et $\mathbf{v}$ de $S$. Soit $i$ et $j$ les deux coordonnées telles que $\mathbf{t}_{i} \neq \mathbf{u}_{i}$ et $\mathbf{t}_{j} \neq \mathbf{v}_{j}$, et soit $S^{\prime}$ l'ensemble $\backslash \backslash\{\mathbf{t}\}$.
$\triangleright$ Si $S^{\prime}$ est connexe, on constate aisément que les coordonnées variables de $S$ sont celles de $S^{\prime}$. Puisque $S^{\prime}$ contient $\ell-1$ sommets et $m$ sources, les ensembles $S$ et $S^{\prime}$ ont donc bien $2(m-1)$ coordonnées variables au maximum.
$\triangleright$ Si $S^{\prime}$ n'est pas connexe, alors on peut le couper en deux ensembles initiaux connexes, $U$ et $V$, qui contiennent respectivement les vecteurs $\mathbf{u}$ et $\mathbf{v}$. L'un contient $\ell_{u}$ vecteurs, $m_{u}$ sources, et $c_{u}$ coordonées variables, tandis que l'autre contient $\ell_{v}$ vecteurs, $m_{v}$ sources, et $c_{v}$ coordonées variables. Puisque $\ell_{u} \leqslant \ell-1$ et $\ell_{v} \leqslant \ell-1$, on sait que $c_{u} \leqslant 2\left(m_{u}-1\right)$ et que $c_{v} \leqslant 2\left(m_{v}-1\right)$.
Or, les sources de $S$ sont celles de $U$ et de $V$, et nulle source ne peut appartenir à la fois à $U$ et à $V$, de sorte que $m=m_{u}+m_{v}$. D'un autre côté, on constate aisément que les coordonnées variables de $S$ sont soit celles de $U$, soit celles de $V$, soit $i$ et $j$. Ainsi, l'ensemble $S$ a au plus $c_{u}+c_{v}+2 \leqslant 2\left(m_{u}+m_{v}-1\right)=2(m-1)$ coordonnées variables, ce qui démontre $\mathcal{P}_{\ell}$.
Remarquons enfin que l'ensemble $(\mathbb{Z} / 2 \mathbb{Z})^{n}$ lui-même est un ensemble initial connexe, et qu'il contient $n$ variables et $k$ sources. La propriété $\mathcal{P}_{2^{n}}$ montre donc que $n \leqslant 2(k-1)$, c'est-à-dire que $k \geqslant 1+\lceil n / 2\rceil$. Les entiers recherchés sont donc bien les entiers compris entre $1+\lceil n / 2\rceil$ et $2^{n}$.
|
{
"exam": "French_tests",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/tests/fr-2019-2020-corrigé-test-janvier.jsonl",
"solution_match": "\nSolution de l'exercice 7",
"tier": "T1",
"year": "2019"
}
|
Let $k$ and $n$ be two non-zero natural numbers, such that $k \leqslant 2^{n}$. Morgane has written, in her notebook, the set of $n$-tuples formed of 0 and 1: there are $2^{n}$ of them. We say that two $n$-tuples $\left(x_{1}, \ldots, x_{n}\right)$ and $\left(y_{1}, \ldots, y_{n}\right)$ are neighbors if they have $n-1$ terms in common, that is, if there is only one integer $i$ such that $x_{i} \neq y_{i}$. Then Morgane chooses $k$ of these $n$-tuples and underlines them. She then performs the following operations: in each operation, she chooses an $n$-tuple whose two neighbors are underlined, and she also underlines this $n$-tuple.
For which values of $k$ can Morgane manage to underline all the $n$-tuples?
|
$n^{\circ} 1$ We have shown above that any integer $k \geqslant 1+\lceil n / 2\rceil$ works, and it remains to show that we must necessarily have $k \geqslant 1+\lceil n / 2\rceil$. To do this, we will proceed by induction on $n$.
First, for $n=1$ and $n=2$, if Morgane underlines only one vector, none of the other non-underlined vectors will be able to have two underlined neighbors. We deduce, in these cases, that $k \geqslant 2$, that is, $k \geqslant 1+\lceil n / 2\rceil$.
Now suppose that $n \geqslant 3$, and that Morgane has underlined $k$ vectors, so that she will then be able to underline each of the $2^{n}-k$ remaining vectors. Morgane then numbers the $2^{n}$ vectors in the order in which she underlines them: she can therefore choose the vectors $v_{1}, \ldots, v_{k}$ arbitrarily, and she will then be able to underline the vectors $v_{k+1}, \ldots, v_{2^{n}}$. In particular, we observe that, for all $\ell \leqslant k+1$, the vector $v_{\ell}$ is a neighbor of two vectors $v_{i}$ and $v_{j}$ such that $1 \leqslant i<j<\ell$.
Let then $i$ and $j$ be two integers such that $1 \leqslant i<j \leqslant k$ and such that $v_{i}$ and $v_{j}$ are both neighbors of the vector $v_{k+1}$. Let then $s$ and $t$ be the two coordinates in which the vectors $v_{i}$ and $v_{j}$ differ from each other. Morgane then decides to erase the coordinates $s$ and $t$ from all $2^{n}$ vectors.
She is thus left with $2^{n-2}$ vectors with $n-2$ coordinates, each present in four copies. Let $\phi(v)$ be the vector with $n-2$ coordinates obtained by erasing the coordinates $s$ and $t$ from the vector $v$. Among the $2^{n-2}$ vectors obtained, Morgane decides, initially, to underline the vectors $\phi\left(v_{1}\right), \phi\left(v_{2}\right), \ldots, \phi\left(v_{k}\right)$: since $\phi\left(v_{i}\right)=\phi\left(v_{j}\right)$, she has underlined at most $k-1$ vectors.
Moreover, if two vectors $v$ and $v^{\prime}$, with $n$ coordinates, are neighbors of each other, then the vectors $\phi(v)$ and $\phi\left(v^{\prime}\right)$ are either equal or neighbors. Thus, Morgane can always underline, in this order, the vectors $\phi\left(v_{k+1}\right)$ - which is equal to $\phi\left(v_{i}\right)$ and $\phi\left(v_{j}\right)$ - then $\phi\left(v_{k+2}\right), \ldots, \phi\left(v_{2^{n}}\right)$, possibly re-underlining a vector already underlined.
Consequently, by underlining $k-1$ vectors with $n-2$ coordinates at the start, Morgane has indeed managed to underline all $2^{n-2}$ vectors with $n-2$ coordinates. The induction hypothesis then indicates that $k-1 \geqslant\lceil(n-2) / 2\rceil+1$, that is, $k \geqslant\lceil n / 2\rceil+1$, which concludes.
Comment from the graders This very difficult exercise consisted of two parts:
$\triangleright$ First, it was necessary to observe, then prove, that $k=\lceil n / 2\rceil+1$ works.
$\triangleright$ Then it was necessary to prove that one could not do better.
The first part was already difficult. Many students noticed that $k=n$ works, except for $n=1$, and then tried (in vain!) to prove that one could not do better, by proceeding by induction on $n$. The fact that the proposed bound, and therefore the prototype of induction on $n$, does not work for $n=1$, could have been a clue that one should look for another solution.
Moreover, the graders were pleased to note that, among the students who obtained one of the two bounds $k=n$ or $k=\lceil n / 2\rceil+1$, the vast majority succeeded in proving that their construction indeed worked.
The second part, on the other hand, was clearly very difficult. Consequently, only one student managed to prove that one could indeed not do better than $k=\lceil n / 2\rceil+1$.
|
k \geqslant 1+\lceil n / 2\rceil
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Soit $k$ et $n$ deux entiers naturels non nuls, tels que $k \leqslant 2^{n}$. Morgane a écrit, sur son cahier, l'ensemble des $n$-uplets formés de 0 et de 1 :il y en a $2^{n}$. On dit que deux $n$-uplets $\left(x_{1}, \ldots, x_{n}\right)$ et $\left(y_{1}, \ldots, y_{n}\right)$ sont voisins s'ils ont $n-1$ termes en commun, c'est-à-dire s'il existe un seul entier $i$ tel que $x_{i} \neq y_{i}$. Puis Morgane choisit $k$ de ces $n$-uplets et les souligne. Elle effectue ensuite les opérations suivantes : lors de chaque opération, elle choisit un $n$-uplet dont deux voisins sont soulignés, et elle souligne également ce $n$-uplet.
Pour quelles valeurs de $k$ Morgane peut-elle parvenir à souligner l'ensemble des $n$-uplets?
|
$n^{\circ} 1$ On démontre comme ci-dessus que tout entier $k \geqslant 1+\lceil n / 2\rceil$ convient, et il ne nous reste maintenant plus qu'à montrer que l'on doit nécessairement avoir $k \geqslant 1+\lceil n / 2\rceil$. Pour ce faire, on va procéder par récurrence sur $n$.
Tout d'abord, pour $n=1$ et $n=2$, si Morgane ne souligne qu'un seul vecteur, aucun des autres vecteurs non soulignés ne pourra avoir deux voisins soulignés. On en déduit, dans ces cas-là, que $k \geqslant 2$, c'est-à-dire que $k \geqslant 1+\lceil n / 2\rceil$.
Supposons maintenant que $n \geqslant 3$, et que Morgane a souligné $k$ vecteurs, de sorte qu'elle pourra ensuite parvenir à souligner chacun des $2^{n}-k$ vecteurs restants. Morgane numérote alors les $2^{n}$ vecteurs dans l'ordre dans lequel elle les a soulignés : elle peut donc choisir les vecteurs $v_{1}, \ldots, v_{k}$ de manière arbitraire, et elle pourra ensuite souligner les vecteurs $v_{k+1}, \ldots, v_{2^{n}}$. En particulier, on constate que, pour tout $\ell \leqslant k+1$, le vecteur $v_{\ell}$ est voisin de deux vecteurs $v_{i}$ et $v_{j}$ tels que $1 \leqslant i<j<\ell$.
Soit alors $i$ et $j$ deux entiers tels que $1 \leqslant i<j \leqslant k$ et tels que $v_{i}$ et $v_{j}$ soient tous les deux voisins du vecteur $v_{k+1}$. Soit ensuite $s$ et $t$ les deux coordonnées en lesquelles les vecteurs $v_{i}$ et $v_{j}$ diffèrent l'un de l'autre. Morgane décide alors d'effacer les coordonnées $s$ et $t$ de l'ensemble des $2^{n}$ vecteurs.
Elle se retrouve ainsi avec $2^{n-2}$ vecteurs à $n-2$ coordonnées, chacun étant présent en quatre exemplaires. Notons $\phi(v)$ le vecteur à $n-2$ coordonnées obtenu en effaçant les coordonnées $s$ et $t$ du vecteur $v$. Parmi les $2^{n-2}$ vecteurs obtenus, Morgane décide, initialement, de souligner les vecteurs $\phi\left(v_{1}\right), \phi\left(v_{2}\right), \ldots, \phi\left(v_{k}\right)$ : puisque $\phi\left(v_{i}\right)=\phi\left(v_{j}\right)$, elle a souligné au plus $k-1$ vecteurs.
En outre, si deux vecteurs $v$ et $v^{\prime}$, à $n$ coordonnées, sont voisins l'un de l'autre, alors les vecteurs $\phi(v)$ et $\phi\left(v^{\prime}\right)$ sont soit égaux, soit voisins. Ainsi, Morgane peut toujours souligner,
dans cet ordre, les vecteurs $\phi\left(v_{k+1}\right)$ - qui est égal à $\phi\left(v_{i}\right)$ et à $\phi\left(v_{j}\right)$ - puis $\phi\left(v_{k+2}\right), \ldots, \phi\left(v_{2^{n}}\right)$, quitte à resouligner un vecteur déjà souligné.
Par conséquent, en soulignant au départ $k-1$ vecteurs à $n-2$ coordonnées, Morgane est bien parvenue à souligner l'intégralité des $2^{n-2}$ vecteurs à $n-2$ coordonnées. L'hypothèse de récurrence indique donc que $k-1 \geqslant\lceil(n-2) / 2\rceil+1$, c'est-à-dire que $k \geqslant\lceil n / 2\rceil+1$, ce qui conclut.
Commentaire des correcteurs Cet exercice très difficile se composait de deux parties :
$\triangleright$ Tout d'abord, il fallait constater, puis démontrer, que $k=\lceil n / 2\rceil+1$ convenait.
$\triangleright$ Puis il fallait démontrer qu'on ne pouvait pas faire mieux.
La première partie était déjà difficile. De nombreux élèves ont remarqué que $k=n$ convenait, sauf pour $n=1$, et ont ensuite tenté (en vain!) de démontrer qu'on ne pouvait pas faire mieux, en procédant par récurrence sur $n$. Le fait que la borne proposée, et donc le prototype de récurrence sur $n$, ne fonctionne pas pour $n=1$, aurait pu être un indice qu'il fallait rechercher une autre solution.
Par ailleurs, les correcteurs ont constaté avec plaisir que, parmi les élèves ayant obtenu une des deux bornes $k=n$ ou bien $k=\lceil n / 2\rceil+1$, la quasi-totalité a réussi à démontrer que leur construction fonctionnait effectivement.
La seconde partie, quant à elle, était manifestement très difficile. Par conséquent, seul un élève est parvenu à démontrer que l'on ne pouvait effectivement pas faire mieux que $k=$ $\lceil n / 2\rceil+1$.
|
{
"exam": "French_tests",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/tests/fr-2019-2020-corrigé-test-janvier.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2019"
}
|
Let $ABC$ be a triangle with all angles acute, and $AB \neq AC$. Let $\Gamma$ be the circumcircle of $ABC$, and $D$ the midpoint of the arc $\widehat{BC}$ not containing $A$. Let $E$ and $F$ be points on segments $[AB]$ and $[AC]$, respectively, such that $AE = AF$. Let $P$ be the intersection point, other than $A$, between $\Gamma$ and the circumcircle of $AEF$.
Let $G$ and $H$ be the intersection points, other than $P$, between $\Gamma$ and the lines $(PE)$ and $(PF)$, respectively. Finally, let $J$ be the intersection point between the lines $(AB)$ and $(DG)$, and let $K$ be the intersection point between the lines $(AC)$ and $(DH)$.
Prove that the midpoint of segment $[BC]$ lies on the line $(JK)$.
|
Let's start by drawing a figure, and let $X$ be the midpoint of $[B C]$, which we hope is also the intersection point of the lines $(B C)$ and $(J K)$. Without loss of generality, we assume that $A B > A C$.
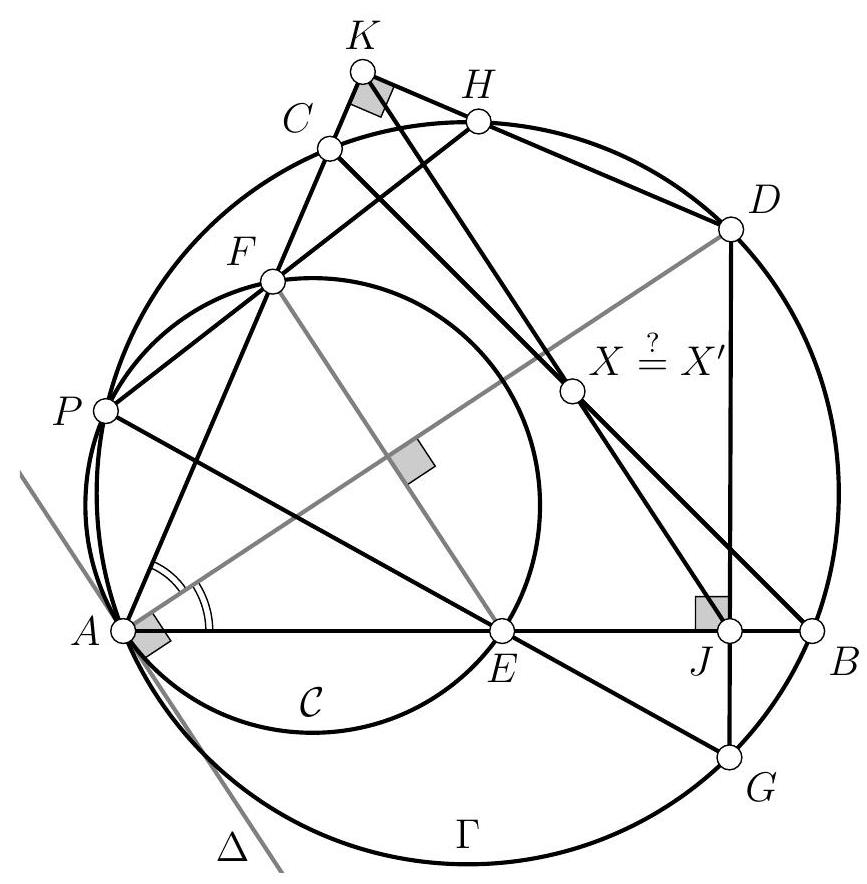
A first observation we can make is that, since the arcs $\widehat{B D}$ and $\widehat{D C}$ have the same measure, the angles $\widehat{B A D}$ and $\widehat{D A C}$ are in fact equal. This means that the line $(A D)$ is the angle bisector of $\widehat{B A C}$; more precisely, the point $D$ is actually the South Pole of $A$ in the triangle $A B C$. We therefore draw this bisector, especially since the equality $A E = E F$ means that the points $E$ and $F$ are in fact symmetric with respect to the line $(A D)$.
A striking second observation is that the angle $\widehat{A J D}$ appears to be a right angle. After verifying that it indeed is on a second figure, we promptly set out to prove this first result. To do this, we embark on an angle chase:
$$
(A J, D J) = (A J, P G) + (P G, D J) = (A E, P E) + (P G, D G) = (A E, P E) + (P A, A D)
$$
To go further, we want to replace the angle $(A E, P E)$ with an angle involving the line $(P A)$. We then use the limiting case of the inscribed angle theorem, as follows.
Let $\mathcal{C}$ be the circumcircle of $A E F$ and $\Delta$ its tangent at $A$. Then we know that $(A E, P E) = (\Delta, P A)$, and therefore that $(A J, D J) = (\Delta, A D)$. The line $(A D)$ is an axis of symmetry of $\mathcal{C}$, and it is therefore perpendicular to $\Delta$. As desired, we have $(A J, D J) = 90^{\circ}$.
But then $J$ and $K$ are the orthogonal projections of $D$ onto the lines $(A B)$ and $(A C)$. Since $D$ lies on the bisector of $\widehat{B A C}$, we have $D J = D K$ and $A J = A K$. Furthermore, since $A$ is the midpoint of the arc $\overparen{B C}$, we know that $B D = C D$. The triangles $B J D$ and $C K D$ are therefore isometric.
Since $A C = |x \pm y|, A B = |x \pm y|$, and $A B > A C$, it follows that $A B = x + y$ and $A C = |x - y|$. In other words, we have $\overrightarrow{A C} = (1 - y / x) \overrightarrow{A K}$ and $\overrightarrow{A B} = (1 + y / x) \overrightarrow{A J}$. But then
$$
\overrightarrow{A X} = (\overrightarrow{A B} + \overrightarrow{A C}) / 2 = (1 - y / x) \overrightarrow{A K} / 2 + (1 + y / x) \overrightarrow{A J} / 2 = \overrightarrow{A X} + \overrightarrow{X K} + (1 + y / x) \overrightarrow{K J} / 2
$$
which means that $\overrightarrow{K X} = (1 + y / x) \overrightarrow{K J} / 2$, and therefore that $X$ lies on the line $(J K)$, as we needed to prove.
$\underline{\text{Alternative Solution } n^{\circ} 1}$ We propose another way to complete the problem once we have obtained that the angles $\widehat{A J D}$ and $\widehat{A K D}$ are right angles.
Since $(A J, D J) = 90^{\circ} = (D K, A K)$, the points $K, A, J$, and $D$ are concyclic. Let $X^{\prime}$ be the intersection point of the lines $(B C)$ and $(J K)$. Since
$$
\left(D K, K X^{\prime}\right) = (D K, K J) = (D A, A J) = (D A, A B) = (D C, C B) = \left(D C, C X^{\prime}\right)
$$
the points $D, C, K$, and $X^{\prime}$ are also concyclic.
But then $\left(C X^{\prime}, X^{\prime} D\right) = (C K, K D) = 90^{\circ}$, so $X^{\prime}$ is actually the orthogonal projection of $D$ onto the line $(B C)$. Since $D$ lies on the perpendicular bisector of the segment $[B C]$, the point $X^{\prime}$ is therefore the midpoint of this segment, which concludes the proof.
$\underline{\text{Alternative Solution } n^{\circ} 2}$ We propose a third way to complete the problem: this is a variant of the alternative solution $n^{\circ} 1$.
Since $B D = C D$, the point $X$ is also the orthogonal projection of $D$ onto the line $(B C)$. But then, since $D$ lies on the circumcircle of $A B C$, the points $J, K$, and $X$ are in fact collinear on the Simson line of $D$, which concludes the proof.
Comment from the graders The problem was well solved. However, some frequent errors occurred:
$\triangleright$ Several students introduced the point $X^{\prime}$ before proving that the lines $(J K)$ and $(B C)$ actually intersect. For some proofs, this omission could be quite penalizing.
An effective way to handle all configurations and thus eliminate these penalizing pathological cases was to use directed angles, or even directed angles of lines, which few students thought to do.
$\triangleright$ Several students confused the points $X$ and $X^{\prime}$, since they appeared at the same place on their figure. For example, after defining the point $X^{\prime}$, they used the fact that it was the midpoint of $[B C]$, which was precisely the property that needed to be proven! Such an error, while understandable, proved to be fatal whenever it occurred, as it brought the proof to an end.
Moreover, many students demonstrated good knowledge by recognizing in the figure a South Pole, a similarity, a Miquel point, or the Simson line relative to the point $D$. Very beautiful figures were also seen! Conversely, one student, who had provided a correct solution to the problem, submitted only a rough sketch rather than a complete figure with ruler and compass. Consequently, instead of the 7 points that were within reach, they were given a score of $0 / 7$.
|
proof
|
Yes
|
Incomplete
|
proof
|
Geometry
|
Soit $A B C$ un triangle dont tous les angles sont aigus, avec $A B \neq A C$. Soit $\Gamma$ le cercle circonscrit à $A B C$, et $D$ le milieu de l'arc $\widehat{B C}$ ne contenant pas $A$. Soit $E$ et $F$ des points appartenant respectivement aux segments $[A B]$ et $[A C]$, de sorte que $A E=A F$. Soit $P$ le point d'intersection, autre que $A$, entre $\Gamma$ et le cercle circonscrit à $A E F$.
Soit $G$ et $H$ les points d'intersection respectifs, autres que $P$, entre $\Gamma$ et les droites $(P E)$ et $(P F)$. Enfin, soit $J$ le point d'intersection entre les droites $(A B)$ et $(D G)$, et soit $K$ le point d'intersection entre les droites $(A C)$ et $(D H)$.
Démontrer que le milieu du segment $[B C]$ appartient à la droite $(J K)$.
|
Commençons par tracer une figure, et notons $X$ le milieu de $[B C]$, que l'on espère être également le point d'intersection des droites $(B C)$ et $(J K)$. Sans perte de généralité, on suppose également que $A B>A C$.

Une première remarque que l'on peut formuler est que, puisque les arcs $\widehat{B D}$ et $\widehat{D C}$ ont même mesure, les angles $\widehat{B A D}$ et $\widehat{D A C}$ sont en fait égaux. Cela signifie que la droite $(A D)$ est la bissectrice de l'angle $\widehat{B A C}$; plus précisément, le point $D$ est en fait le pôle Sud de $A$ dans le triangle $A B C$. On s'empresse donc de dessiner cette bissectrice, d'autant plus que l'égalité $A E=E F$ revient alors à dire que les points $E$ et $F$ sont en fait symétriques par rapport à la droite ( $A D$ ).
Une seconde remarque frappante est que l'angle $\widehat{A J D}$ semble droit. Après avoir vérifié qu'il l'était bien sur une deuxième figure, on s'empresse donc de démontrer ce premier résultat. Pour ce faire, on entame donc une chasse aux angles de droites :
$$
(A J, D J)=(A J, P G)+(P G, D J)=(A E, P E)+(P G, D G)=(A E, P E)+(P A, A D)
$$
Pour aller plus loin, on voudrait remplacer l'angle $(A E, P E)$ par un angle faisant intervenir la droite $(P A)$. On utilise alors le cas limite du théorème de l'angle au centre, comme suit.
Soit $\mathcal{C}$ le cercle circonscrit à $A E F$ et $\Delta$ sa tangente en $A$. Alors on sait que $(A E, P E)=$ $(\Delta, P A)$, et donc que $(A J, D J)=(\Delta, A D)$. Or, la droite $(A D)$ est un axe de symétrie de $\mathcal{C}$, et elle est donc perpendiculaire à $\Delta$. Comme souhaité, on a donc $(A J, D J)=90^{\circ}$.
Mais alors $J$ et $K$ sont les projetés orthogonaux de $D$ sur les droites $(A B)$ et $(A C)$. Puisque $D$ appartient à la bissectrice de $\widehat{B A C}$, on a donc $D J=D K$ et $A J=A K$. Par ailleurs, comme $A$ est le milieu de l'arc $\overparen{B C}$, on sait que $B D=C D$. Les triangles $B J D$ et $C K D$ étant respectivement rectangles en $J$ et en $K$, ils sont donc isométriques.
Puisque $A C=|x \pm y|, A B=|x \pm y|$ et $A B>A C, \mathrm{c}^{\prime}$ est donc que $A B=x+y$ et $A C=|x-y|$. Autrement dit, on a $\overrightarrow{A C}=(1-y / x) \overrightarrow{A K}$ et $\overrightarrow{A B}=(1+y / x) \overrightarrow{A J}$. Mais alors
$$
\overrightarrow{A X}=(\overrightarrow{A B}+\overrightarrow{A C}) / 2=(1-y / x) \overrightarrow{A K} / 2+(1+y / x) \overrightarrow{A J} / 2=\overrightarrow{A X}+\overrightarrow{X K}+(1+y / x) \overrightarrow{K J} / 2
$$
ce qui signifie que $\overrightarrow{K X}=(1+y / x) \overrightarrow{K J} / 2$, et donc que $X$ se trouve bien sur la droite $(J K)$, comme on devait le démontrer.
$\underline{\text { Solution alternative } n^{\circ} 1}$ On propose une autre façon de terminer le problème une fois que l'on a obtenu que les angles $\widehat{A J D}$ et $\widehat{A K D}$ sont droits.
Comme $(A J, D J)=90^{\circ}=(D K, A K)$, les points $K, A, J$ et $D$ sont cocycliques. Soit alors $X^{\prime}$ le point d'intersection des droites $(B C)$ et $(J K)$. Puisque
$$
\left(D K, K X^{\prime}\right)=(D K, K J)=(D A, A J)=(D A, A B)=(D C, C B)=\left(D C, C X^{\prime}\right)
$$
les points $D, C, K$ et $X^{\prime}$ sont eux aussi cocycliques.
Mais alors $\left(C X^{\prime}, X^{\prime} D\right)=(C K, K D)=90^{\circ}$, donc $X^{\prime}$ est en fait le projeté orthogonal de $D$ sur la droite $(B C)$. Comme $D$ se trouve sur la médiatrice du segment $[B C]$, le point $X^{\prime}$ est donc le milieu de ce segment, ce qui conclut.
$\underline{\text { Solution alternative } n^{\circ} 2}$ On propose une troisième façon de terminer le problème : il s'agit là d'une variante de la solution alternative $\mathrm{n}^{\circ} 1$.
Puisque $B D=C D$, le point $X$ est également le projeté orthogonal de $D$ sur la droite $(B C)$. Mais alors, puisque $D$ appartient au cercle circonscrit à $A B C$, les points $J, K$ et $X$ sont en fait alignés sur la droite de Simson de $D$, ce qui conclut.
Commentaire des correcteurs Le problème a été bien réussi. Cependant, quelques erreurs sont revenues fréquemment:
$\triangleright$ Plusieurs élèves ont introduit le point $X^{\prime}$ avant d'avoir démontré que les droites $(J K)$ et $(B C)$ avaient effectivement un point d'intersection. Pour certaines preuves, cette omission pouvait se montrer assez pénalisante.
Une façon efficace de traiter toutes les configurations, et donc d'éliminer ces cas pathologiques pénalisants, était d'utiliser des angles orientés, voire des angles de droites orientés, ce que peu d'élèves ont pensé à faire.
$\triangleright$ Plusieurs élèves ont confondu les points $X$ et $X^{\prime}$, puisque ceux-ci apparaissaient au même endroit sur leur figure. Par exemple, après avoir défini le point $X^{\prime}$, ils ont utilisé le fait qu'il s'agissait du milieu de $[B C]$, alors que c'est justement la propriété qu'il fallait démontrer! Une telle erreur, si elle se comprend aisément, s'est néanmoins avérée rédhibitoire dès qu'elle survenait, puisqu'elle mettait un terme à la démonstration.
Par ailleurs, beaucoup d'élèves montrent une bonne culture, en reconnaissant dans la figure un pôle Sud, une similitude, un point de Miquel ou la droite de Simson relative au point $D$. On a également pu voir de très jolies figures! À l'inverse, un élève, qui avait pourtant fourni une solution correcte à l'exercice, n'a fourni qu'un simple schéma à main levée plutôt qu'une figure complète à la règle et au compas. Par conséquent, et au lieu des 7 points qui lui tendaient les bras, il s'est vu attribuer la note de $0 / 7$.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2019-2020-corrigé-test-novembre.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T1",
"year": "2019"
}
|
Each cell of an $8 \times 8$ table can be colored white or black, such that each rectangle of size $2 \times 3$ or $3 \times 2$ contains two black cells that share a side. Determine the minimum number of black cells that can be on the table.
|
As usual in this kind of problem, we start by searching for upper (by exhibiting a configuration) and lower bounds (by double counting and/or tiling arguments) on the minimum number of black squares the board must contain.
For example, the configuration below (on the left) ensures that 28 black squares are sufficient; indeed, any vertical rectangle (of size $3 \times 2$) contains two squares on one of the rows 3 or 6, and any horizontal rectangle (of size $2 \times 3$) contains two squares on one of the columns 3 or 6. On the other hand, each of the 10 rectangles in the partial tiling below (on the right) must contain at least 2 black squares, so 20 black squares are necessary.
Unfortunately, these two bounds are not equal. We need to improve both of them until they are equal.
By trial and error, we eventually find a new configuration that satisfies the conditions of the problem but contains only 24 black squares. It is the configuration below.
On the other hand, using a simple tiling by rectangles seems a bit too brutal to indicate the best possible lower bound on the number of black squares needed. We study a given rectangle:
Here we observe that, among the 3 hatched squares, at least one must be a black square, otherwise our rectangle will never contain two adjacent black squares. In particular, the square in row 1, column 2 must have a black neighbor within this rectangle. Similarly, the square in row 2, column 2 must also have a black neighbor within our rectangle.
Armed with this observation, we focus on the minimum number of black neighbors that each square $c$ on the chessboard has:
$\triangleright$ if $c$ is one of the four corners, it could a priori have no black neighbors (which is indeed the case in our previous configuration);
$\triangleright$ if $c$ is one of the $2 \times 6=12$ squares on the top or bottom edge, it belongs to the central column of a horizontal rectangle, so it has at least one black neighbor;
$\triangleright$ similarly, if $c$ is one of the $2 \times 6=12$ squares on the left or right edge, it belongs to the central row of a vertical rectangle, so it has at least one black neighbor;
$\triangleright$ finally, if $c$ is one of the $6 \times 6=36$ squares in the center of the chessboard, it already has one black neighbor (say $d$); but then $c$ also belongs to the column (respectively, the row) of another horizontal (resp., vertical) rectangle that does not contain $d$, so $c$ has a second black neighbor.
In conclusion, we actually have at least $12+12+36 \times 2=96$ pairs $(c, d)$ of adjacent squares such that $d$ is a black square. Since each black square has at most four neighbors, it belongs to at most four such pairs. Therefore, we have at least $96 / 4=24$ black squares on our chessboard, which matches the upper bound found previously, and thus concludes the problem.
|
24
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Chaque case d'un tableau de taille $8 \times 8$ peut être coloriée en blanc ou en noir, de telle sorte que chaque rectangle de taille $2 \times 3$ ou $3 \times 2$ contient deux cases noires ayant un côté en commun. Déterminer le nombre minimal de cases noires qu'il peut y avoir sur le tableau.
|
Comme d'habitude dans ce genre de problèmes, on commence par rechercher des bornes supérieures (en exhibant une configuration) et inférieures (par des arguments de double comptage et/ou de pavage) sur le nombre minimal de cases noires que doit contenir le tableau.
Par exemple, la configuration ci-dessous (à gauche) nous assure que 28 cases noires sont suffisantes; en effet, tout rectangle vertical (de taille $3 \times 2$ ) contient deux cases sur l'une des lignes 3 ou 6 , et tout rectangle horizontal (de taille $2 \times 3$ ) contient deux cases sur l'une des colonnes 3 ou 6. D'autre part, chacun des 10 rectangles du pavage partiel ci-dessous (à droite) doit contenir au moins 2 cases noires, de sorte que 20 cases noires ont nécessaires.
Malheureusement, ces deux bornes ne sont pas égales l'une à l'autre. Il nous faut donc chercher à les améliorer toutes les deux jusqu'à les rendre égales.


En tâtonnant, on finit par trouver une nouvelle configuration satisfaisant les conditions de l'énoncé, mais qui ne contient que 24 cases noires. Il s'agit de la configuration ci-dessous.

D'autre part, utiliser un simple pavage par des rectangles semble un peu trop brutal pour nous indiquer la meilleure borne inférieure possible sur le nombre de cases noires nécessaires. On étudie un rectangle quelconque donné :

On constate ici que, parmi les 3 cases hachurées, au moins une doit être une case noire, ce sans quoi notre rectangle ne contiendra jamais deux cases noires adjacentes. En particulier, la case en ligne 1 , colonne 2 a nécessairement une voisine noire au sein de ce rectangle. De même, la case en ligne 2, colonne 2 , a aussi une voisine noire au sein de notre rectangle.
Forts de ce constat, on s'intéresse, pour chaque case $c$ de l'échiquier, au nombre minimal de voisines noires que possède la case $c$ :
$\triangleright$ si $c$ est un des quatre coins, a priori, elle pourrait n'avoir aucune voisine noire (c'est d'ailleurs le cas dans notre configuration précédente);
$\triangleright$ si $c$ est une des $2 \times 6=12$ cases situées sur le côté haut ou bas, elle appartient à la colonne centrale d'un rectangle horizontal, donc elle a au moins une voisine noire;
$\triangleright$ de même, si $c$ est une des $2 \times 6=12$ cases situées sur le côté gauche ou droit, elle appartient à la ligne centrale d'un rectangle vertical, donc elle a au moins une voisine noire;
$\triangleright$ enfin, si $c$ est une des $6 \times 6=36$ cases situées au centre de l'échiquier, elle a déjà une voisine noire au minimum (disons $d$ ) ; mais alors $c$ appartient également à la colonne (respectivement, à la ligne) d'un autre rectangle horizontal (resp., vertical) ne contenant pas $d$, donc $c$ a une deuxième voisine noire.
En conclusion, on dispose en fait d'au moins $12+12+36 \times 2=96$ paires $(c, d)$ de cases adjacentes telles que $d$ est une case noire. Or, chaque case noire a au plus quatre voisines, donc appartient à au plus quatre telles paires. On a donc au moins $96 / 4=24$ cases noires sur notre échiquier, ce qui rejoint la borne supérieure trouvée précédemment, et conclut donc.
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2019-2020-corrigé-test-novembre.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T1",
"year": "2019"
}
|
Each cell of an $8 \times 8$ table can be colored white or black, such that each rectangle of size $2 \times 3$ or $3 \times 2$ contains two black cells that share a side. Determine the minimum number of black cells that can be on the table.
|
$n^{\circ} 1$ Here is another way to prove that 24 black squares are necessary once we know that each square at the center of the chessboard has at least two black neighbors. Indeed, this means that each occurrence of the pattern shown below must contain at least two black squares.
We can then place such patterns of three or four squares, without overlap, on our $8 \times 8$ chessboard, for example by proceeding as follows: in the drawing below, we connect the centers of the squares belonging to the same pattern.
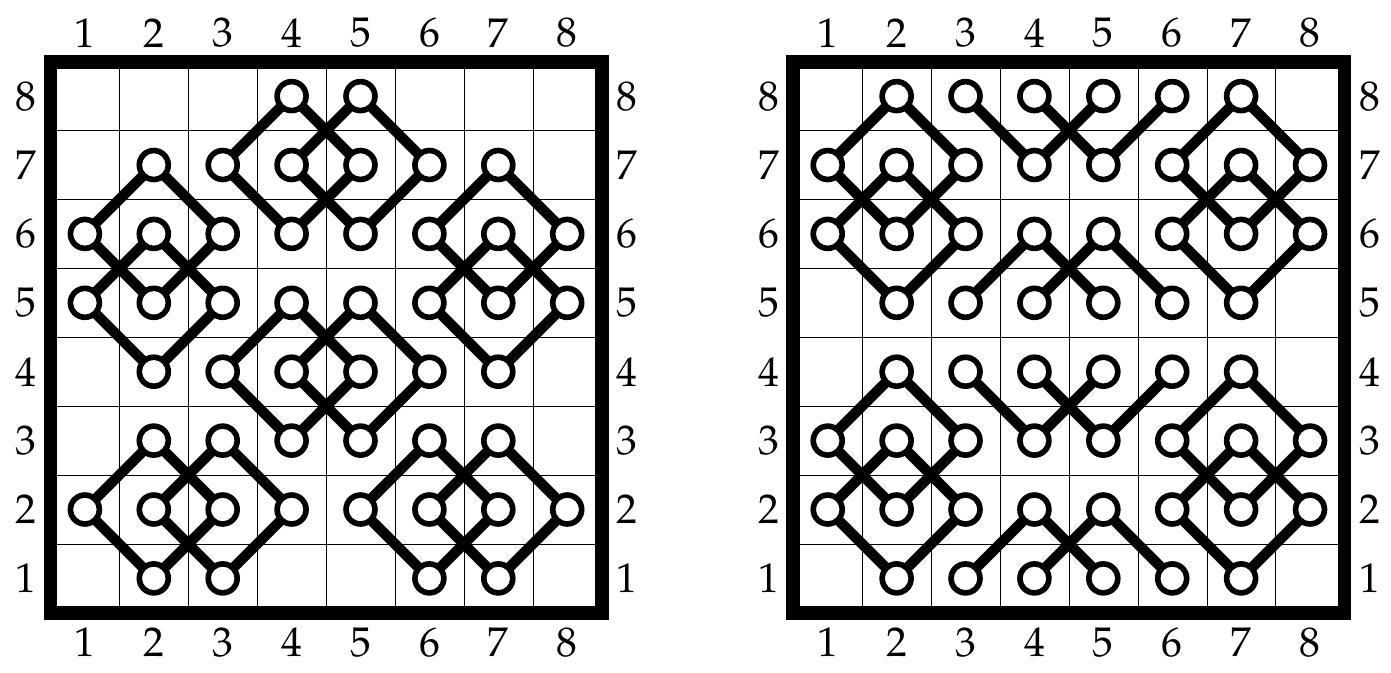
We have thus managed to place 12 instances of our four-square pattern, or 8 instances of the four-square pattern and 8 instances of the three-square pattern, without overlap. In each case, these patterns contain a total of at least 24 black squares, which concludes the proof.
Comment from the graders: The exercise was generally well done considering its level of difficulty. Identifying a configuration with 24 black squares was not obvious, and many students managed to do so. Showing that it could not be better was then very difficult. Moreover, many students made several avoidable errors, which we summarize below.
$\triangleright$ Just because a suitable configuration (such as every $2 \times 3$ or $3 \times 2$ rectangle containing two adjacent black squares) is minimal for inclusion (i.e., if any black square is removed, the configuration will no longer be suitable) does not mean it is also minimal for the number of black squares used.
We leave it to the reader to verify that the first configuration mentioned in this solution, which contained 28 black squares, was indeed a minimal suitable configuration for inclusion, but clearly not for the number of black squares used.
$\triangleright$ Just because a suitable configuration is minimal does not mean that, on any part extracted from the $8 \times 8$ chessboard, it still induces a minimal configuration. An obvious example of this phenomenon appears if the part in question is a $2 \times 2$ square, since no black square is then necessary.
$\triangleright$ Just because the chessboard is invariant under certain axial symmetries or rotations does not mean that a minimal suitable configuration is also invariant under these transformations. For example, in the case of a $3 \times 3$ chessboard, it is easily shown that the configuration below is minimal, and yet it is not invariant under rotation or many axial symmetries.
|
24
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Chaque case d'un tableau de taille $8 \times 8$ peut être coloriée en blanc ou en noir, de telle sorte que chaque rectangle de taille $2 \times 3$ ou $3 \times 2$ contient deux cases noires ayant un côté en commun. Déterminer le nombre minimal de cases noires qu'il peut y avoir sur le tableau.
|
$n^{\circ} 1$ Voici une autre manière de démontrer que 24 cases noires sont nécessaires une fois que l'on sait que chaque case située au centre de l'échiquier a au moins deux voisines noires. En effet, cela signifie que chaque occurrence du motif représenté ci-dessous doit contenir au moins deux cases noires.

On peut alors placer de tels motifs à trois ou à quatre cases, sans recouvrement, dans notre échiquier $8 \times 8$, par exemple en procédant comme suit : dans le dessin ci-dessous, on relie les centres des cases appartenant à un même motif.

On a donc réussi à placer dans l'échiquier 12 exemplaires de notre motif à quatre cases, ou bien 8 exemplaires du motif à quatre cases et 8 exemplaires du motif à trois cases, ne se chevauchant pas. Dans chaque cas, ces motifs contiennent bien un total de 24 cases noires au minimum, ce qui conclut.
Commentaire des correcteurs L'exercice a été globalement bien réussi compte tenu de son niveau de difficulté. Identifier une configuration à 24 cases noires était peu évident, et de nombreaux élèves y sont cependant parvenus. Montrer que l'on ne pouvait pas faire mieux était ensuite très difficile. Par ailleurs, de nombreux élèves ont commis plusieurs erreurs évitables, que nous récapitulons ci-dessous.
$\triangleright$ Ce n'est pas parce qu'une configuration adéquate (telle que tout rectangle $2 \times 3$ ou $3 \times 2$ contient deux cases noires adjacentes) est minimale pour l'inclusion (c'est-à-dire que, si on retire n'importe quelle case noire, notre configuration ne sera plus adéquate) qu'elle est également minimale pour le nombre de cases noires utilisées.
On laisse ainsi au lecteur le plaisir de vérifier que la première configuration mentionnée dans cette solution, et qui contenait 28 cases, était bien une configuration adéquate minimale pour l'inclusion, mais manifestement pas pour le nombre de cases noires utilisées.
$\triangleright$ Ce n'est pas parce qu'une configuration adéquate est minimale que, sur toute partie extraite de l'échiquier $8 \times 8$, elle induit encore une configuration minimale. Un exemple évident de ce phénomène apparaît si la partie en question est un carré $2 \times 2$, puisque aucun carré noir n'est alors nécessaire.
$\triangleright$ Ce n'est pas parce que l'échiquier est invariant selon certaines symétries axiales ou rotations qu'une configuration adéquate minimale est également invariante selon ces transformations. Par exemple, dans le cas d'un échiquier $3 \times 3$, on montre aisément que la configuration ci-dessous est minimale, et elle n'est pourtant pas invariante par rotation, ou par de nombreuses symétries axiales.

|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2019-2020-corrigé-test-novembre.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2019"
}
|
Let $P_{1}, P_{2}, \ldots, P_{2019}$ be non-constant polynomials with real coefficients such that
$$
P_{1}\left(P_{2}(x)\right)=P_{2}\left(P_{3}(x)\right)=\ldots=P_{2019}\left(P_{1}(x)\right)
$$
for all real $x$. Prove that $P_{1}=P_{2}=\ldots=P_{2019}$.
|
We will in fact demonstrate the more general result that if $P_{1}, \ldots, P_{2 n+1}$ are non-constant polynomials with real coefficients such that $P_{1} \circ P_{2} = P_{2} \circ P_{3} = \ldots = P_{2 n+1} \circ P_{1}$, then $P_{1} = \ldots = P_{2 n+1}$. For convenience, in the following, we set $P_{2 n+1+k} = P_{k}$ for all $k \geq 1$.
First, we denote $d_{k}$ as the degree of $P_{k}$. Since $P_{k} \circ P_{k+1}$ is a polynomial of degree $d_{k} d_{k+1}$, it follows that $d_{k} d_{k+1} = d_{k+1} d_{k+2}$, and thus $d_{k} = d_{k+2}$ for all $k$. We deduce that all polynomials $P_{k}$ have degree $d_{1}$, and we simply set $d = d_{1}$.
Next, let $p_{k}$ be the leading coefficient of $P_{k}$, i.e., its coefficient of degree $d$, and set $q_{k} = p_{k} / p_{k+1}$. The leading coefficient of $P_{k} \circ P_{k+1}$ is equal to $p_{k} p_{k+1}^{d}$. We deduce that $p_{k} p_{k+1}^{d} = p_{k+1} p_{k+2}^{d}$, which means $q_{k} = q_{k+1}^{-d}$. But then
$$
1 = \prod_{i=k+1}^{k+2 n+1} q_{i} = q_{k}^{s}
$$
where we have set
$$
s = \sum_{i=0}^{2 n} (-d)^{i} \equiv 1 \quad (\bmod 2).
$$
Since $s$ is an odd integer, it follows that $q_{k} = 1$. This means that all polynomials $P_{k}$ have the same leading coefficient $p_{1}$, and we simply set $p = p_{1}$.
Now suppose that $d = 1$. In this case, we can write each polynomial $P_{k}$ in the form $P_{k}(X) = p X + b_{k}$, and then $P_{k}(P_{k+1}(X)) = p^{2} X + p b_{k+1} + b_{k}$. We set $c_{k} = b_{k+1} - b_{k}$, and since the statement indicates that $p b_{k+1} + b_{k} = p b_{k+2} + b_{k+1}$, this means that $c_{k} = -p c_{k+1}$. Again, we deduce that $c_{k} = (-p)^{2 n+1} c_{k}$, so that $c_{k} = 0$ for all $k$, or that $p = -1$; but in the latter case, we still have $c_{k} = c_{k+1}$ for all $k$, so that $0 = \sum_{i=1}^{2 n+1} c_{i} = (2 n+1) c_{k}$ and thus $c_{k} = 0$ in any case. Thus, when $d = 1$, the polynomials $P_{k}$ are indeed equal to each other.
Finally, suppose that $d \geq 2$. We denote $p_{k, \ell}$ as the coefficient of $P_{k}$ of degree $\ell$, and we will prove by induction on $d - \ell$ that $p_{k, \ell} = p_{1, \ell}$. First, for $\ell = d$, we have $p_{k, d} = p = p_{1, d}$. We now assume that $p_{k, m} = p_{1, m}$ for all integers $m \geq \ell + 1$, and we study the coefficient of degree $d^{2} - d + \ell$ of the polynomial $P_{k} \circ P_{k+1}$. Writing $A \approx B$ whenever two polynomials $A$ and $B$ have the same coefficient of degree $d^{2} - d + \ell$, we observe that
$$
\begin{aligned}
P_{k}(P_{k+1}(X)) & = \sum_{i=0}^{d} p_{k, i} \left( \sum_{j=0}^{d} p_{k+1, j} X^{j} \right)^{i} \\
& \approx p \left( \sum_{j=0}^{d} p_{k+1, j} X^{j} \right)^{d} + p_{k, d-1} \left( \sum_{j=0}^{d} p_{k+1, j} X^{j} \right)^{d-1} \\
& \approx p \left( p_{k+1, \ell} X^{\ell} + \sum_{j=\ell+1}^{d} p_{1, j} X^{j} \right)^{d} + p_{k, d-1} (p X^{d})^{d-1} \\
& \approx d p_{k+1, \ell} p^{d} X^{d^{2} - d + \ell} + p \left( \sum_{j=\ell+1}^{d} p_{1, j} X^{j} \right)^{d} + p_{k, d-1} p^{d-1} X^{d^{2} - d}
\end{aligned}
$$
For $\ell \geq 1$, we deduce that $d p_{k+1, \ell} p^{d} = d p_{1, \ell} p^{d}$, which means that $p_{k+1, \ell} = p_{1, \ell}$. Then, for $\ell = 0$, we deduce that $d p_{k+1, 0} p^{d} + p_{k, d-1} = d p_{1, 0} p^{d} + p_{2 n+1, d-1}$. Since $d \geq 2$, when we reach the case $\ell = 0$, we already know that $p_{k, d-1} = p_{2 n+1, d-1}$. We thus deduce as expected that $p_{k+1, 0} = p_{1, 0}$, which concludes the proof.
Comment from the graders: This problem was extremely difficult, and scoring points on it was therefore challenging. Unfortunately, several students lost these hard-earned points by making avoidable errors, which we list below:
$\triangleright$ Many students confused the composition and the product of two polynomials. Thus, the composition $P \circ Q$ of two polynomials $P$ and $Q$ of degrees $d$ and $d'$ is a polynomial of degree $d \times d'$, not $d + d'$. Similarly, if $P$ and $Q$ have leading coefficients $p$ and $q$, then the leading coefficient of $P \circ Q$ is $p \times q^{d}$, not $p \times q$. Finally, the polynomials $P \circ (Q + R)$ and $(P \circ Q) + (P \circ R)$ are, in general, distinct polynomials.
$\triangleright$ Some students did not prove that the polynomials $P_{i}$ have the same degree, claiming it was obvious. However, this assertion depended on the oddness of 2019, making it far less obvious: it is advisable to avoid losing 1 point by saving a line of writing.
$\triangleright$ It is recommended not to call a polynomial $P'$ that one introduces, as $P'$ already denotes the derivative of $P$. Such notation can be confusing, both for the grader and for the student themselves!
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $P_{1}, P_{2}, \ldots, P_{2019}$ des polynômes non constants à coefficients réels tels que
$$
P_{1}\left(P_{2}(x)\right)=P_{2}\left(P_{3}(x)\right)=\ldots=P_{2019}\left(P_{1}(x)\right)
$$
pour tout réel $x$. Démontrer que $P_{1}=P_{2}=\ldots=P_{2019}$.
|
Nous allons en fait démontrer le résultat plus général suivant : si $P_{1}, \ldots, P_{2 n+1}$ sont des polynômes non constants à coefficients réels et tels que $P_{1} \circ P_{2}=$ $P_{2} \circ P_{3}=\ldots=P_{2 n+1} \circ P_{1}$, alors $P_{1}=\ldots=P_{2 n+1}$. Par commodité, dans la suite, on pose $P_{2 n+1+k}=P_{k}$ pour tout $k \geqslant 1$.
Tout d'abord, on note $d_{k}$ le degré de $P_{k}$. Puisque $P_{k} \circ P_{k+1}$ est un polynôme de degré $d_{k} d_{k+1}$, $c^{\prime}$ est que $d_{k} d_{k+1}=d_{k+1} d_{k+2}$, et donc $d_{k}=d_{k+2}$, pour tout $k$. On en déduit que tous les polynômes $P_{k}$ ont degré $d_{1}$, et on pose simplement $d=d_{1}$.
Ensuite, soit $p_{k}$ le coefficient dominant de $P_{k}$, c'est-à-dire son coefficient de degré $d$, et posons $q_{k}=p_{k} / p_{k+1}$. Le coefficient dominant de $P_{k} \circ P_{k+1}$ est égal à $p_{k} p_{k+1}^{d}$. On en déduit que $p_{k} p_{k+1}^{d}=$ $p_{k+1} p_{k+2}^{d}$ , c'est-à-dire que $q_{k}=q_{k+1}^{-d}$. Mais alors
$$
1=\prod_{i=k+1}^{k+2 n+1} q_{i}=q_{k}^{s}
$$
où l'on a posé
$$
s=\sum_{i=0}^{2 n}(-d)^{i} \equiv 1 \quad(\bmod 2) .
$$
Puisque $s$ est un entier impair, $\mathrm{c}^{\prime}$ est donc que $q_{k}=1$. Cela signifie donc que tous les polynômes $P_{k}$ sont de coefficient dominant $p_{1}$, et on pose simplement $p=p_{1}$.
Supposons maintenant que $d=1$. Dans ce cas, on peut écrire chaque polynôme $P_{k}$ sous la forme $P_{k}(X)=p X+b_{k}$, et alors $P_{k}\left(P_{k+1}(X)\right)=p^{2} X+p b_{k+1}+b_{k}$. On pose alors $c_{k}=b_{k+1}-b_{k}$, et puisque l'énoncé indique entre autres que $p b_{k+1}+b_{k}=p b_{k+2}+b_{k+1}$, cela signifie en fait que $c_{k}=-p c_{k+1}$. Là encore, on en déduit que $c_{k}=(-p)^{2 n+1} c_{k}$, de sorte que $c_{k}=0$ pour tout $k$, ou bien que $p=-1$; mais, dans ce second cas, on a tout de même $c_{k}=c_{k+1}$ pour tout $k$, de sorte que $0=\sum_{i=1}^{2 n+1} c_{i}=(2 n+1) c_{k}$ et que l'on a $c_{k}=0$ de toute façon. Ainsi, quand $d=1$, les polynômes $P_{k}$ sont bien égaux deux à deux.
Supposons enfin que $d \geqslant 2$. On note $p_{k, \ell}$ le coefficient de $P_{k}$ de degré $\ell$, et on va prouver par récurrence sur $d-\ell$ que $p_{k, \ell}=p_{1, \ell}$. Tout d'abord, pour $\ell=d$, on a bien $p_{k, d}=p=p_{1, d}$. On suppose donc maintenant que $p_{k, m}=p_{1, m}$ pour tout entier $m \geqslant \ell+1$, et on étudie le coefficient de degré $d^{2}-d+\ell$ du polynôme $P_{k} \circ P_{k+1}$. En écrivant $A \approx B$ dès lors que deux polynômes $A$ et $B$ ont même coefficient de degré $d^{2}-d+\ell$, on constate que
$$
\begin{aligned}
P_{k}\left(P_{k+1}(X)\right) & =\sum_{i=0}^{d} p_{k, i}\left(\sum_{j=0}^{d} p_{k+1, j} X^{j}\right)^{i} \\
& \approx p\left(\sum_{j=0}^{d} p_{k+1, j} X^{j}\right)^{d}+p_{k, d-1}\left(\sum_{j=0}^{d} p_{k+1, j} X^{j}\right)^{d-1} \\
& \approx p\left(p_{k+1, \ell} X^{\ell}+\sum_{j=\ell+1}^{d} p_{1, j} X^{j}\right)^{d}+p_{k, d-1}\left(p X^{d}\right)^{d-1} \\
& \approx d p_{k+1, \ell} p^{d} X^{d^{2}-d+\ell}+p\left(\sum_{j=\ell+1}^{d} p_{1, j} X^{j}\right)^{d}+p_{k, d-1} p^{d-1} X^{d^{2}-d}
\end{aligned}
$$
Pour $\ell \geqslant 1$, on en déduit que $d p_{k+1, \ell} p^{d}=d p_{1, \ell} p^{d}$, ce qui signifie bien que $p_{k+1, \ell}=p_{1, \ell}$. Puis, pour $\ell=0$, on en déduit aussi que $d p_{k+1,0} p^{d}+p_{k, d-1}=d p_{1,0} p^{d}+p_{2 n+1, d-1}$. Or, puisque $d \geqslant 2$, quand on en arrive à étudier le cas $\ell=0$, on sait déjà que $p_{k, d-1}=p_{2 n+1, d-1}$. On en déduit donc comme prévu que $p_{k+1,0}=p_{1,0}$, ce qui conclut.
Commentaire des correcteurs Ce problème était extrêmement difficile, et y obtenir des points était donc ardu. Malheureusement, plusieurs élèves ont perdu ces points si durement acquis en commettant des erreurs évitables, que nous listons ci-dessous :
$\triangleright$ De nombreux élèves ont confondu la composée et le produit de deux polynômes. Ainsi, la composée $P \circ Q$ de deux polynômes $P$ et $Q$ de degrés $d$ et $d^{\prime}$ est un polynôme de degré $d \times d^{\prime}$, et non pas $d+d^{\prime}$. De même, si $P$ et $Q$ sont de coefficients dominants $p$ et $q$, alors le coefficient dominant de $P \circ Q$ est $p \times q^{d}$, et non pas $p \times q$. Enfin, les polynômes $P \circ(Q+R)$ et $(P \circ Q)+(P \circ R)$ sont, dans le cas général, des polynômes distincts l'un de l'autre.
$\triangleright$ Certains élèves n'ont pas démontré que les polynômes $P_{i}$ avaient même degré, affirmant qu'il s'agissait là d'une évidence. Cependant, cette affirmation dépendait de l'imparité de 2019, ce qui la rendait nettement moins évidente : il faut éviter de perdre bêtement 1 point pour économiser une ligne de rédaction.
$\triangleright$ Il est recommandé de ne pas appeler $P^{\prime}$ un polynôme que l'on introduit, car $P^{\prime}$ désigne déjà le polynôme dérivé de $P$. Une telle notation peut donc prêter à confusion, pour le correcteur mais aussi pour l'élève lui-même !
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2019-2020-corrigé-test-novembre.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T1",
"year": "2019"
}
|
A grid of dimensions $20 \times 20$ is divided into 400 unit squares of dimensions $1 \times 1$. Clara colors each square either white or black, and then Isabelle cuts the grid into rectangles whose sides lie along the grid lines. Each of these rectangles must contain at most 2 black squares, and she gives Clara a chocolate for each rectangle that contains 0 or 1 black square.
Isabelle chooses her cutting to give the fewest chocolates possible to Clara, and Clara chooses her initial coloring to get the most chocolates possible from Isabelle. How many chocolates will Isabelle give to Clara?
|
We will demonstrate for all integers $n \geqslant 3$ that, if Clara and Isabelle play on a grid of dimensions $n \times n$, Isabelle will give $n$ chocolates to Clara.
First, to limit the number of chocolates she will give to Clara, Isabelle can proceed as follows. She starts by cutting the rectangle into $n$ rows, and prepares to subdivide each row into rectangles. To do this, she numbers the black squares in the row from left to right, then she cuts just to the right of each of the black squares numbered $2, 4, 6, \ldots$ By doing so, all the rectangles obtained, except possibly the last one, contain two black squares. Thus, Isabelle gives at most $n$ chocolates to Clara.

Conversely, suppose Clara colors her $n \times n$ grid with the following coloring, where we have distinguished with two shades of gray the squares that Clara colors black, and where $k$ and $\ell$ are two non-negative integers whose sum is $k+\ell=n-1$.
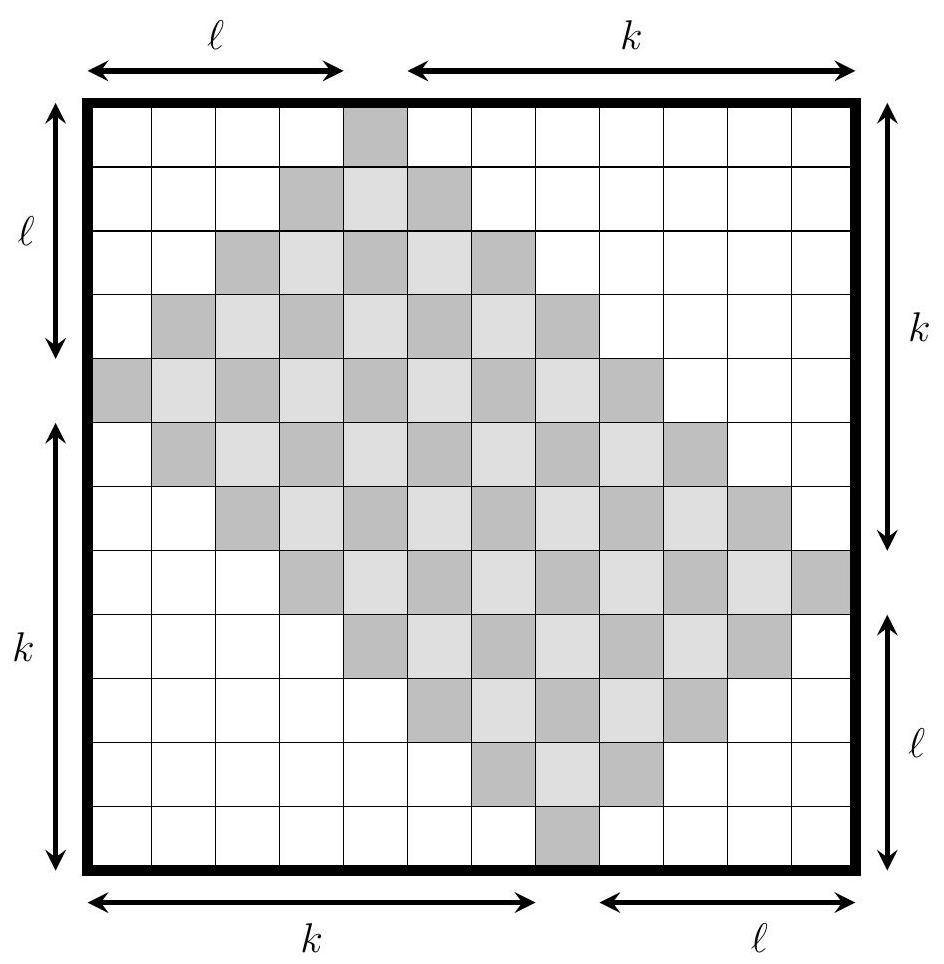
If a rectangle contains exactly two black squares, they are adjacent: one dark gray and one light gray. There are $(k+1)(\ell+1)$ dark gray squares and $k \ell$ light gray squares. Therefore, Isabelle can draw at most $k \ell$ rectangles covering exactly two black squares, and these rectangles leave aside $k+\ell+1=n$ dark gray squares. This forces Isabelle to give at least $n=20$ chocolates to Clara.
Comment from the graders The main difficulties of this problem were as follows:
1. convincing oneself that Clara can force Isabelle to give her at least 2 chocolates;
2. finding a coloring that forces Isabelle to give at least 20 chocolates;
3. proving that this coloring indeed forces Isabelle to give at least 20 chocolates;
4. finding a simple strategy that allows Isabelle to give at most $n$ chocolates.
Many students were stuck at the first difficulty, simply noting that Isabelle would give at least one chocolate if the grid was empty or contained an odd number of black squares, but making the incorrect assertion:
If Clara draws a non-zero even number of black squares, Isabelle can pair these squares to give no chocolates to Clara.
Once such a property was incorrectly considered as established, these students did not even address difficulties 2 to 4.
From a methodological point of view, it is a pity that these students did not take the time to carefully study the cases of small grids, since the $2 \times 3$ and $3 \times 3$ rectangular grids provided a clear counterexample to this assertion, as illustrated below.
Moreover, by looking for the simplest possible arguments to explain why such configurations forced Isabelle to give 2 or even 3 chocolates, students could have had the idea of the gray shade coloring; or, at the very least, noticed that two black squares contained in the same rectangle of Isabelle were necessarily adjacent.
Furthermore, several students correctly identified the cross-shaped motif in the $3 \times 3$ grid, but did not think to try to generalize it to the $4 \times 4$ case: the few students who followed such an approach all arrived at a complete solution, proposing the construction presented above in the case where $k=\lfloor n / 2\rfloor$ or $k=1$.
Several students, having searched for but not found a coloring that would force Isabelle to give $n$ chocolates, nonetheless successfully undertook to show that Isabelle would give between $n / 2$ and $n$ chocolates to Clara. More generally, the graders are pleased to note that many students had the idea of separately seeking lower and upper bounds on the number of chocolates Isabelle would give, that is, of seeking a good strategy for Isabelle and a good coloring for Clara, and then proving that such a coloring was good. In fact, students who followed such an approach were very often rewarded with a substantial number of points, even when they did not find an optimal coloring.
Finally, here are three very avoidable errors that the graders found in many papers.
$\triangleright$ Several students, explaining how Isabelle could manage to give no more than 20 chocolates, incorrectly wrote that, in the case of a row with an even number of black squares, Isabelle would give no chocolates. This assertion is incorrect, as Isabelle must still give a chocolate if the row contains no black squares.
$\triangleright$ Other students, while attempting to prove that a coloring by Clara would force Isabelle to give her at least 20 chocolates, assumed that Isabelle would cut the grid into rectangles of width 1. Even though such considerations indeed showed that the technique of cutting the grid into strips would not allow Isabelle to give fewer than 20 chocolates, this assumption was unfounded, as Isabelle would already have to give 20 chocolates even when the grid is empty.
$\triangleright$ Finally, some students, starting from an optimal configuration, attempted to prove that it could not be improved by changing the color of a single square. But nothing prevented changing the color of several squares, and such reasoning was therefore null and void: exhibiting a local maximum (which was done here) is clearly insufficient to prove that it is in fact a global maximum.
|
20
|
Yes
|
Incomplete
|
math-word-problem
|
Combinatorics
|
Une grille de dimensions $20 \times 20$ est divisée en 400 cases unité de dimensions $1 \times 1$. Clara colorie chaque case en blanc ou en noir, puis Isabelle découpe la grille en rectangles dont les côtés sont contenus dans la grille. Chacun de ces rectangles doit contenir au plus 2 cases noires, et elle donne un chocolat à Clara à chaque fois qu'elle découpe un rectangle qui contient 0 ou 1 case noire.
Isabelle choisit son découpage de manière à donner le moins de chocolats possibles à Clara, et Clara choisit son coloriage initial de manière à obtenir le plus de chocolats possibles d'Isabelle. Combien de chocolats Isabelle donnera-t-elle à Clara?
|
Nous allons démontrer pour tout entier $n \geqslant 3$ que, si Clara et Isabelle jouent sur une grille de dimensions $n \times n$, Isabelle donnera $n$ chocolats à Clara.
Tout d'abord, pour limiter le nombre de chocolats qu'elle donnera à Clara, Isabelle peut procéder comme suit. Elle commence par découper le rectangle en $n$ lignes, et s'apprête à subdiviser chaque ligne en rectangles. Pour ce faire, elle numérote les cases noires de la ligne de gauche à droite, puis elle donne un coup de ciseaux juste à droite de chacune des cases noires $\mathrm{n}^{\circ} 2,4,6, \ldots$ Ce faisant, tous les rectangles obtenus, sauf éventuellement le dernier, comptent deux cases noires. Ainsi, Isabelle donne au plus $n$ chocolats à Clara.

Réciproquement, supposons que Clara colorie sa grille $n \times n$ avec le coloriage suivant, où nous avons distingué avec deux niveaux de gris les cases que Clara colorie en noir, et où $k$ et $\ell$ sont deux entiers naturels non nuls de somme $k+\ell=n-1$.

Si un rectangle contient exactement deux cases noires, il s'agit de cases adjacentes : une gris foncé et une gris clair. Or, il y a $(k+1)(\ell+1)$ cases gris foncé et $k \ell$ cases gris clair. Isabelle dessine donc au plus $k \ell$ rectangles recouvrant exactement deux cases noires, et ces rectangles laissent de côté $k+\ell+1=n$ cases gris foncé. Cela force donc Isabelle à donner au moins $n=20$ chocolats à Clara.
Commentaire des correcteurs Les difficultés principales de cet exercice étaient les suivantes:
1. se convaincre que Clara peut forcer Isabelle à lui donner au moins 2 chocolats;
2. trouver un coloriage qui force Isabelle à donner au moins 20 chocolats;
3. démontrer que ce coloriage force en effet Isabelle à donner au moins 20 chocolats;
4. trouver une stratégie simple permettant à Isabelle de donner au plus $n$ chocolats.
De nombreux élèves ont été bloqués à la première difficulté, remarquant simplement qu'Isabelle donnerait au moins un chocolat si la grille était vide ou contenait un nombre impair de cases noires, mais formulant tout de go l'affirmation incorrecte suivante :
Si Clara dessine un nombre pair non nul de cases noires, Isabelle peut apparier ces cases pour ne donner aucun chocolat à Clara.
Une fois une telle propriété indûment considérée comme acquise, ces élèves n'ont donc tout simplement pas abordé les difficultés 2 à 4.
D'un point de vue méthodologique, il est dommage que ces élèves n'aient pas pris la peine d'étudier soigneusement le cas des grilles de petites dimensions, puisque les grilles rectangulaires $2 \times 3$ et $3 \times 3$ fournissaient un contre-exemple manifeste à cette affirmation, comme illustré ci-dessous.

En outre, en cherchant des arguments aussi simples que possibles pour expliquer pourquoi de telles configurations forçaient Isabelle à donner 2 voire 3 chocolats, les élèves auraient pu avoir l'idée du coloriage entre nuances de gris; ou, au minimum, constater que deux cases noires contenues dans un même rectangle d'Isabelle étaient nécessairement contiguës.
Par ailleurs, plusieurs élèves ont bien identifié le motif en forme de croix dans la grille $3 \times 3$, mais n'ont ensuite pas pensé à tenter de le généraliser au cas de la grille $4 \times 4$ : les quelques élèves qui ont suivi une telle approche sont tous parvenus à une solution complète, proposant la construction présentée ci-dessus dans le cas où $k=\lfloor n / 2\rfloor$ ou bien $k=1$.
Plusieurs élèves, ayant cherché sans le trouver un coloriage qui forcerait Isabelle à donner $n$ chocolats, ont néanmoins entrepris avec succès qu'Isabelle donnerait entre $n / 2$ et $n$ chocolats à Clara. Plus généralement, les correcteurs tiennent à souligner leur satisfaction de constater que de nombreux élèves ont eu l'idée de chercher séparément des bornes inférieures et supérieures sur le nombre de chocolats que donnerait Isabelle, c'est-à-dire de chercher une bonne stratégie pour Isabelle et un bon coloriage pour Clara, puis à démontrer qu'un tel coloriage était bon. De fait, les élèves qui ont suivi une telle approche ont très souvent été récompensés par un nombre substantiel de points, et ce même quand ils ne parvenaient pas à trouver un coloriage optimal.
Enfin, voici trois erreurs très évitables que les correcteurs ont retrouvées dans de nombreuses copies.
$\triangleright$ Plusieurs élèves, expliquant comment Isabelle pouvait se débrouiller pour ne pas donner plus de 20 chocolats, ont indûment écrit que, dans le cas d'une ligne avec un nombre pair de cases noires, Isabelle ne donnerait aucun chocolat. Cette assertion est incorrecte, car Isabelle doit quand même donner un chocolat si la ligne ne contient aucune case noire.
$\triangleright$ D'autres élèves, alors qu'ils tentaient de démontrer qu'un coloriage de Clara contraindrait Isabelle à lui donner au moins 20 chocolats, ont supposé qu'Isabelle découperait la grille en rectangles de largeur 1 . Même si de telles considérations permettaient en effet de montrer que la technique consistant à découper la grille en lamelles n'aurait pas permis à Isabelle de donner moins de 20 chocolats, cette supposition était infondée, ce sans quoi Isabelle devrait déjà donner 20 chocolats même quand la grille est vide.
$\triangleright$ Enfin, certains élèves, partant d'une configuration optimale, ont tenté de démontrer que celle-ci ne pouvait pas être améliorée si on changeait la couleur d'une seule case. Mais rien n'empêchait de changer la couleur de plusieurs cases, et un tel raisonnement était donc nul et non avenu : exhiber un maximum local (ce qui était fait ici) est clairement insuffisant pour démontrer qu'il s'agit en fait d'un maximum global.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-1.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T1",
"year": "2020"
}
|
It is said that a sequence $\left(u_{n}\right)_{n \geqslant 0}$ of non-zero natural numbers is Sicilian if $^{-10}$
$$
u_{n+1} \in\left\{u_{n} / 2, u_{n} / 3,2 u_{n}+1,3 u_{n}+1\right\}
$$
for all $n \geqslant 0$. Prove that, for every integer $k \geqslant 1$, there exists a Sicilian sequence $\left(u_{n}\right)_{n \geqslant 0}$ and an integer $\ell \geqslant 0$ such that $u_{0}=k$ and $u_{\ell}=1$.
|
We will demonstrate, for any integer $k \geqslant 2$, the property $\mathcal{P}_{k}$ as follows: there exists a finite Sicilian sequence $\left(u_{0}, \ldots, u_{\ell}\right)$ such that $u_{0}=k$ and $u_{\ell}<k$.
The property $\mathcal{P}_{k}$ is immediate if $k$ is even, since it suffices to choose $u_{1}=k / 2$. Therefore, we assume $k$ is odd. Let $\alpha$ and $\kappa$ be non-zero natural numbers such that $k=2^{\alpha} \kappa-1$, with the integer $\kappa$ being odd. We then construct our Sicilian sequence as follows.
First, for all $i \leqslant \alpha-1$, we set $u_{2 i}=2^{\alpha-i} 3^{i} \kappa-1$ and $u_{2 i+1}=2^{\alpha-i} 3^{i+1} \kappa-2$. We then set $u_{2 \alpha}=3^{\alpha} \kappa-1$ and $u_{2 \alpha+1}=\left(3^{\alpha} \kappa-1\right) / 2$, which is indeed an integer since $\kappa$ is odd. Finally, for all $i \leqslant \alpha$, we set $u_{2 \alpha+2+i}=3^{\alpha-i} \kappa$. We then easily verify that the sequence $\left(u_{0}, \ldots, u_{3 \alpha+2}\right)$ is Sicilian. Indeed, we have $u_{2 i+1}=3 u_{2 i}+1$ and $u_{2 i+2}=u_{2 i+1} / 2$ for all $i \leqslant \alpha$, then $u_{2 \alpha+1}=u_{2 \alpha} / 2$ and $u_{2 \alpha+2}=2 u_{2 \alpha+1}+1$, and we also have $u_{2 \alpha+3+i}=u_{2 \alpha+2+i} / 3$ for all $i \leqslant \alpha-1$. Since $u_{0}=k$ and $u_{3 \alpha+2}=\kappa \leqslant(k+1) / 2<k$, this completes the proof of the property $\mathcal{P}_{k}$.
Armed with this property, we finally prove the statement in the problem by induction on $k$.
Comment from the graders: On this problem, many students had relevant ideas: performing a strong induction or trying to reduce to a term smaller than $u_{0}$ to ensure reaching 1. However, numerous calculation errors were observed when manipulating congruences: to divide a congruence modulo $m$ by $k$, one must also divide $m$ by $\operatorname{PGCD}(k, m)$. For example, we have $6 \equiv 2(\bmod 4)$, so we can deduce that $3 \equiv 1(\bmod 2)$, but certainly not that $3 \equiv 1(\bmod 4)$.
Some students managed to set up rigorous arguments to obtain the result for all values of $k$. Some treated many cases, reducing to increasingly complex cases: $k \equiv 3(\bmod 4)$, then $k \equiv 7(\bmod 8)$, and so on. The key insight was to consider the integer $k+1$ and its 2-adic valuation.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
On dit qu'une suite $\left(u_{n}\right)_{n \geqslant 0}$ d'entiers naturels non nuls est sicilienne si $^{-10}$
$$
u_{n+1} \in\left\{u_{n} / 2, u_{n} / 3,2 u_{n}+1,3 u_{n}+1\right\}
$$
pour tout $n \geqslant 0$. Démontrer que, pour tout entier $k \geqslant 1$, il existe une suite sicilienne $\left(u_{n}\right)_{n \geqslant 0}$ et un entier $\ell \geqslant 0$ tels que $u_{0}=k$ et $u_{\ell}=1$.
|
Nous allons démontrer, pour tout entier $k \geqslant 2$, la propriété $\mathcal{P}_{k}$ suivante : il existe une suite sicilienne finie $\left(u_{0}, \ldots, u_{\ell}\right)$ telle que $u_{0}=k$ et $u_{\ell}<k$.
La propriété $\mathcal{P}_{k}$ est immédiate si $k$ est pair, puisqu'il suffit de choisir $u_{1}=k / 2$. On suppose donc $k$ impair. Soit $\alpha$ et $\kappa$ les entiers naturels non nuls tels que $k=2^{\alpha} \kappa-1$, l'entier $\kappa$ étant impair. On construit alors notre suite sicilienne comme suit.
Tout d'abord, pour tout $i \leqslant \alpha-1$, on pose $u_{2 i}=2^{\alpha-i} 3^{i} \kappa-1$ et $u_{2 i+1}=2^{\alpha-i} 3^{i+1} \kappa-2$. On pose ensuite $u_{2 \alpha}=3^{\alpha} \kappa-1$ et $u_{2 \alpha+1}=\left(3^{\alpha} \kappa-1\right) / 2$, qui est bien un entier puisque $\kappa$ est impair. Enfin, pour tout $i \leqslant \alpha$, on pose $u_{2 \alpha+2+i}=3^{\alpha-i} \kappa$. On vérifie alors aisément que la suite $\left(u_{0}, \ldots, u_{3 \alpha+2}\right)$ est sicilienne. En effet, on a $u_{2 i+1}=3 u_{2 i}+1$ et $u_{2 i+2}=u_{2 i+1} / 2$ pour tout $i \leqslant \alpha$, puis $u_{2 \alpha+1}=u_{2 \alpha} / 2$ et $u_{2 \alpha+2}=2 u_{2 \alpha+1}+1$, et on a également $u_{2 \alpha+3+i}=u_{2 \alpha+2+i} / 3$ pour tout $i \leqslant \alpha-1$. Puisque $u_{0}=k$ et $u_{3 \alpha+2}=\kappa \leqslant(k+1) / 2<k$, cela achève de démontrer la propriété $\mathcal{P}_{k}$.
Forts de cette propriété, on démontre enfin l'assertion de l'énoncé par récurrence sur $k$.
Commentaire des correcteurs Sur ce problème, beaucoup d'élèves ont eu des idées pertinentes : faire une récurrence forte ou essayer de se ramener à un terme plus petit que $u_{0}$ pour s'assurer d'aboutir à 1 . Toutefois, on a constaté de nombreuses erreurs de calcul lors de la manipulation de congruences : pour diviser une égalité modulo $m$ par $k$, il faut également diviser $m$ par $\operatorname{PGCD}(k, m)$. Par exemple, on a $6 \equiv 2(\bmod 4)$, donc on peut en déduire que $3 \equiv 1(\bmod 2)$, mais certainement pas que $3 \equiv 1(\bmod 4)$.
Quelques élèves ont réussi à mettre en place des arguments rigoureux pour obtenir le résultat pour toute valeur de $k$. Certains ont traité de nombreux cas, se ramenant à des cas de plus en plus compliqués : $k \equiv 3(\bmod 4)$, puis $k \equiv 7(\bmod 8)$, et ainsi de suite. Il fallait alors se rendre compte que la bonne idée à avoir était de considérer l'entier $k+1$ et sa valuation 2 -adique.
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-1.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T1",
"year": "2020"
}
|
Let $ABC$ be a triangle with acute angles, and let $D$ be the foot of the altitude from vertex $A$. Let $X$ and $Y$ be the two points on the circumcircle of $ABC$ such that $AX = AY = AD$, and such that $B$ and $X$ are on the same side of the line $(AD)$. Let $E$ be the intersection point of the lines $(BX)$ and $(CY)$. Finally, let $F$ be the intersection point, other than $E$, between the line $(DE)$ and the circumcircle of $EXY$.
Prove that the circumcircles of triangles $BCF$ and $EXY$ are tangent.
|
In the following, we denote $\mathcal{C}_{U V W}$ as the circumcircle of a triangle $U V W$. Let $i$ be the inversion centered at $E$ that leaves the circle $\mathcal{C}_{A B C}$ globally invariant. This inversion exchanges the points $B$ and $X$, as well as the points $C$ and $Y$. Therefore, it exchanges the circle $\mathcal{C}_{E X Y}$ and the line $(B C)$. Since $i$ leaves the line $(D E)$ globally invariant, it exchanges $F$ with the intersection point of $(D E)$ and $(B C)$, which is the point $D$.
Consequently, the inversion $i$ exchanges the circles $\mathcal{C}_{B C F}$ and $\mathcal{C}_{X Y D}$. The latter circle has a radius $[A D]$, and it is therefore tangent to the line $(B C)$. Thus, the circles $\mathcal{C}_{B C F}$ and $\mathcal{C}_{E X Y}$ are themselves tangent.
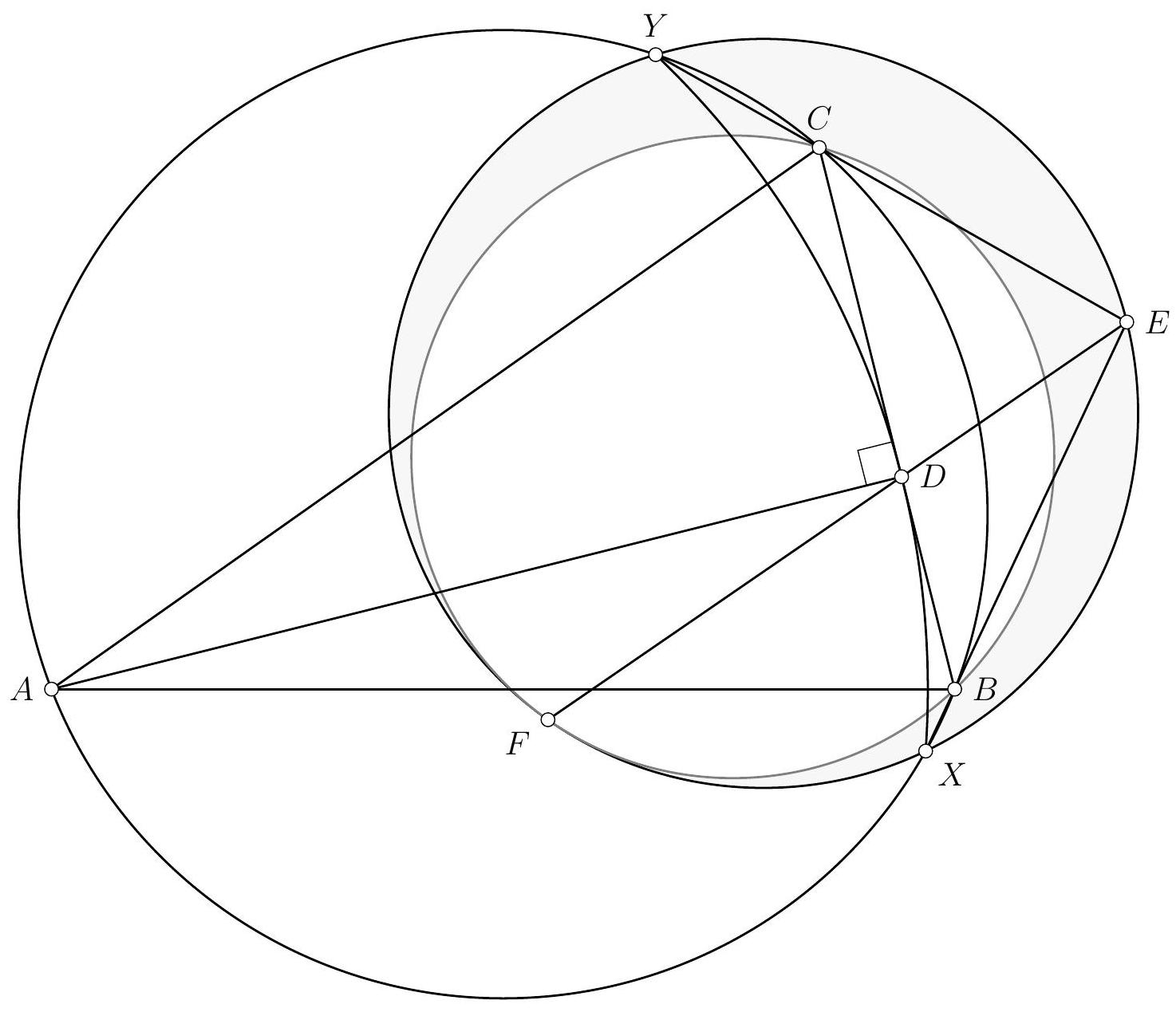
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle dont les angles sont aigus, et soit $D$ le pied de la hauteur issue du sommet $A$. Soit $X$ et $Y$ les deux points du cercle circonscrit à $A B C$ tels que $A X=A Y=A D$, et tels que $B$ et $X$ se trouvent du même côté de la droite $(A D)$. Soit $E$ le point d'intersection des droites $(B X)$ et $(C Y)$. Enfin, soit $F$ le point d'intersection, autre que $E$, entre la droite $(D E)$ et le cercle circonscrit à $E X Y$.
Démontrer que les cercles circonscrits aux triangles $B C F$ et $E X Y$ sont tangents.
|
Dans la suite, on note $\mathcal{C}_{U V W}$ le cercle circonscrit à un triangle $U V W$. Soit $i$ l'inversion de centre $E$ qui laisse le cercle $\mathcal{C}_{A B C}$ globalement invariant. Cette inversion échange les points $B$ et $X$, ainsi que les points $C$ et $Y$. Elle échange donc le cercle $\mathcal{C}_{E X Y}$ et la droite $(B C)$. Puisque $i$ laisse la droite $(D E)$ globalement invariante, elle échange donc $F$ avec le point d'intersection de $(D E)$ et $(B C)$, c'est-à-dire avec le point $D$.
Par conséquent, l'inversion $i$ échange les cercles $\mathcal{C}_{B C F}$ et $\mathcal{C}_{X Y D}$. Or, ce dernier cercle a pour rayon $[A D]$, et il est donc tangent à la droite ( $B C$ ). Ainsi, les cercles $\mathcal{C}_{B C F}$ et $\mathcal{C}_{E X Y}$ sont euxmêmes tangents.

|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-1.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T1",
"year": "2020"
}
|
Let $ABC$ be a triangle with acute angles, and let $D$ be the foot of the altitude from vertex $A$. Let $X$ and $Y$ be the two points on the circumcircle of $ABC$ such that $AX = AY = AD$, and such that $B$ and $X$ are on the same side of the line $(AD)$. Let $E$ be the intersection point of the lines $(BX)$ and $(CY)$. Finally, let $F$ be the intersection point, other than $E$, between the line $(DE)$ and the circumcircle of $EXY$.
Prove that the circumcircles of triangles $BCF$ and $EXY$ are tangent.
|
$n^{\circ} 1$ In the following, we denote $\mathcal{C}_{U V W}$ as the circumcircle of triangle $U V W$. If $A B C$ is isosceles at $A$, the line $(A D)$ constitutes an axis of symmetry of the figure, and the result is immediate. Therefore, without loss of generality, we assume that $A B \neq A C$.
When drawing the figure, it is obviously important to highlight the triangle $A B C$ first, the isosceles triangles $A D X, A D Y$, and $A X Y$, and what appears to be the common tangent to the two circles $\mathcal{C}_{B C F}$ and $\mathcal{C}_{E X Y}$. We then notice that these three lines seem to be concurrent, and this is what we set out to prove.
Let $I$ be the intersection point of the lines $(X Y)$ and $(B C)$: this point exists because $A B C$ is not isosceles at $A$. We will prove that the line $(I F)$ is tangent to the circles $\mathcal{C}_{F B C}$ and $\mathcal{C}_{F X Y}$, which will give the desired result. By considering the power of the point $I$ with respect to the circles $\mathcal{C}_{F B C}$ and $\mathcal{C}_{F X Y}$, it is therefore necessary to prove that $I F^{2}$ is equal to $I X \cdot I Y$ and to $I B \cdot I C$. Since the lines $(B C)$ and $(A D)$ are perpendicular, the circle $\mathcal{C}_{X Y D}$ is tangent to the line $(B C)$. By considering the power of the point $I$ with respect to the circles $\mathcal{C}_{X Y D}$ and $\mathcal{C}_{A B C}$, we deduce that $I D^{2}=I X \cdot I Y=I B \cdot I C$. It is therefore necessary to prove that $I F=I D$. From there, we seek additional properties of the point $D$. If $(I F)$ is the common tangent sought and if $I F D$ is isosceles at $I$, then
$$
(F B, F D)=(F B, F I)+(F I, F D)=(C B, C F)+(F D, D I)=(F D, F C),
$$
and $(F D)$ is therefore the bisector of the angle $\widehat{B F C}$.
Conversely, if $(F D)$ is the bisector of $\widehat{B F C}$, and if $J$ is the intersection point between $(B C)$ and the tangent to $\mathcal{C}_{B C F}$ at $F$, the angle chasing above indicates that $J F D$ is isosceles at $J$, so $J D^{2}=J F^{2}=J B \cdot J C$. The point $J$ therefore has the same power with respect to the circles $\mathcal{C}_{B C F}$ and $\mathcal{C}_{D X Y}$, so it lies on their radical axis $(X Y)$, hence $I=J$. Thus, our problem is equivalent to proving that $(F D)$ is the bisector of the angle $\widehat{B F C}$.
To do this, we denote $G$ as the intersection point, other than $D$, between the circles $\mathcal{C}_{D B X}$ and $\mathcal{C}_{C D Y}$. Since
$$
(G Y, G X)=(G Y, G D)+(G D, G X)=(C Y, C D)+(B D, B X)=(E Y, E X)
$$
the point $G$ lies on the circle $\mathcal{C}_{E X Y}$. Furthermore, $E$ is the intersection point of the radical axes of $\mathcal{C}_{A B C}$ with $\mathcal{C}_{D B X}$ and $\mathcal{C}_{C D Y}$. It is therefore the radical center of these three circles, and $E$ lies on the radical axis of $\mathcal{C}_{D B X}$ and $\mathcal{C}_{C D Y}$, which is the line $(G D)$. This means that $F=G$.
We then conclude by simple angle chasing. Indeed,
$$
\begin{aligned}
(F B, F D)+(F C, F D) & =(G B, G D)+(G C, G D) \\
& =(X B, X D)+(Y C, Y D) \\
& =(B X, B C)+(D B, D X)+(C Y, C B)+(D C, D Y) \\
& =(Y X, Y C)+(Y D, Y X)+(X Y, X B)+(X D, X Y) \\
& =(Y D, Y C)+(X D, X B) .
\end{aligned}
$$
Thus, $2(X B, X D)+2(Y C, Y D)=0^{\circ}$, so the angles $\widehat{D F B}$ and $\widehat{C F D}$ are equal modulo $90^{\circ}$. Since $\widehat{D F B}=\widehat{D X B} \leqslant \widehat{C X B}=\widehat{C A B}<90^{\circ}$ and, similarly, $\widehat{C F D}<90^{\circ}$, we deduce that $\widehat{D F B}=\widehat{C F D}$, which concludes the problem.
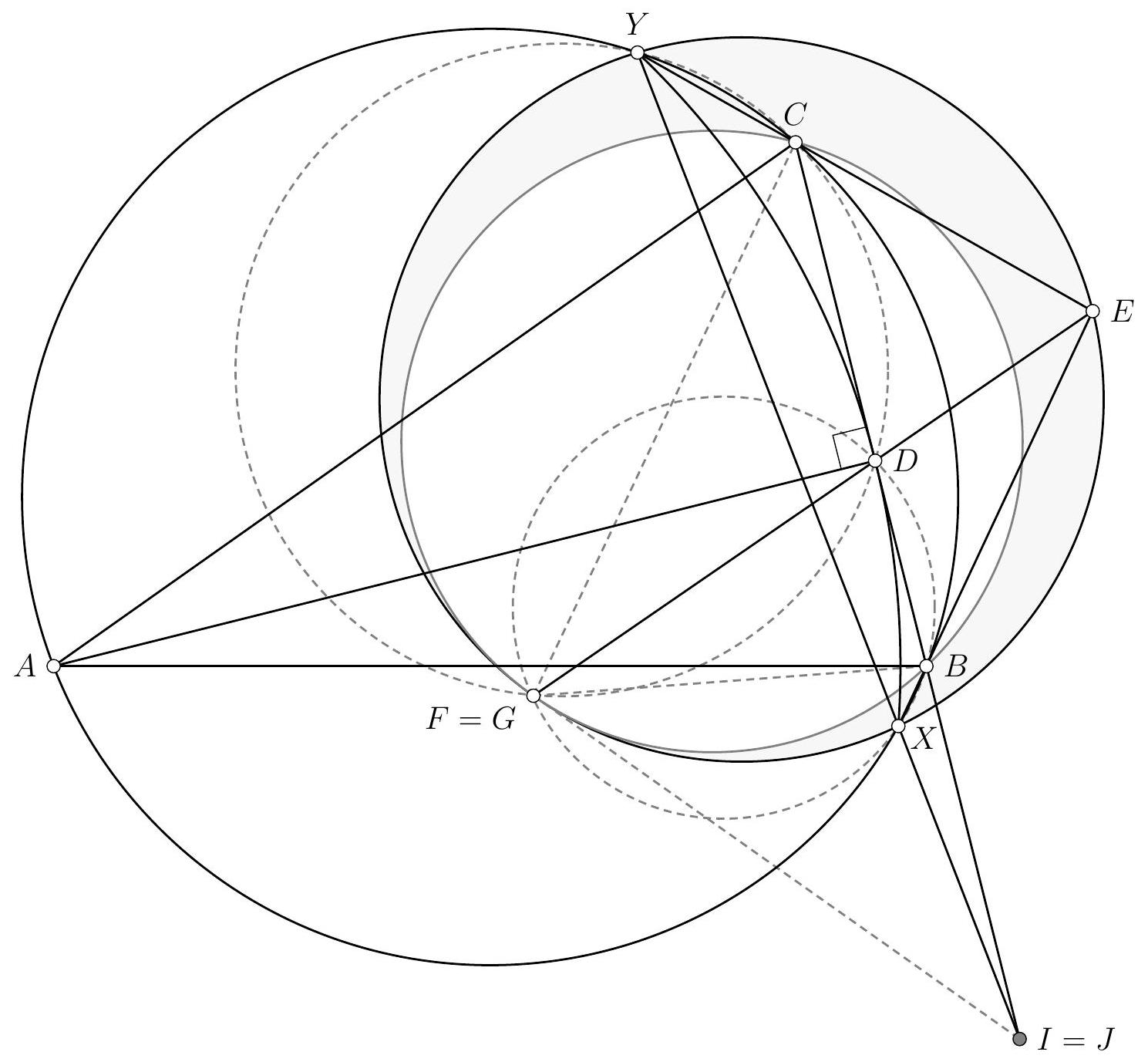
Comment from the graders: For this problem, several students highlighted a solution by inversion that the graders had not thought of: this is the solution $\mathrm{n}^{\circ} 1$ presented above. This method made the exercise significantly less difficult than the difficulty level estimated by the correction team.
Thus, a strong dichotomy was observed between students who recognized this inversion solution and those who did not recognize it or who are not adept at inversion and who, for the most part, were not able to make significant progress in the exercise. However, we commend the efforts and the approaches advanced by the students who attempted the exercise and who sometimes earned their author 1 or 2 partial points.
|
proof
|
Yes
|
Incomplete
|
proof
|
Geometry
|
Soit $A B C$ un triangle dont les angles sont aigus, et soit $D$ le pied de la hauteur issue du sommet $A$. Soit $X$ et $Y$ les deux points du cercle circonscrit à $A B C$ tels que $A X=A Y=A D$, et tels que $B$ et $X$ se trouvent du même côté de la droite $(A D)$. Soit $E$ le point d'intersection des droites $(B X)$ et $(C Y)$. Enfin, soit $F$ le point d'intersection, autre que $E$, entre la droite $(D E)$ et le cercle circonscrit à $E X Y$.
Démontrer que les cercles circonscrits aux triangles $B C F$ et $E X Y$ sont tangents.
|
$n^{\circ} 1$ Dans la suite, on note $\mathcal{C}_{U V W}$ le cercle circonscrit au triangle $U V W . \mathrm{Si}$ $A B C$ est isocèle en $A$, la droite $(A D)$ constitue un axe de symétrie de la figure et le résultat est immédiat. On suppose donc, sans perte de généralité, que $A B \neq A C$.
Lorsque l'on trace la figure, il est évidemment important de mettre en évidence le triangle $A B C$ et départ, les triangles isocèles $A D X, A D Y$ et $A X Y$, et ce qui semble être la tangente commune aux deux cercles $\mathcal{C}_{B C F}$ et $\mathcal{C}_{E X Y}$. On remarque alors que ces trois droites semblent concourantes, et c'est donc ce que l'on entreprend de démontrer.
Soit $I$ le point d'intersection des droites $(X Y)$ et $(B C)$ : ce point existe bien, car $A B C$ n'est pas isocèle en $A$. Nous allons démontrer que la droite $(I F)$ est tangente aux cercles $\mathcal{C}_{F B C}$ et $\mathcal{C}_{F X Y}$, ce qui donnera le résultat désiré. En considérant la puissance du point $I$ par rapport aux cercles $\mathcal{C}_{F B C}$ et $\mathcal{C}_{F X Y}$, il s'agit donc de démontrer que $I F^{2}$ est égal à $I X \cdot I Y$ et à $I B \cdot I C$. Or, puisque les droites $(B C)$ et $(A D)$ sont perpendiculaires, le cercle $\mathcal{C}_{X Y D}$ est tangent à la droite $(B C)$. En considérant la puissance du point $I$ par rapport aux cercles $\mathcal{C}_{X Y D}$ et $\mathcal{C}_{A B C}$, on en déduit donc que $I D^{2}=I X \cdot I Y=I B \cdot I C$. Il s'agit donc de démontrer que $I F=I D$. Dès lors, on cherche des propriétés supplémentaires sur le point $D$. Si $(I F)$ est la tangente commune recherchée et si $I F D$ est isocèle en $I$, alors
$$
(F B, F D)=(F B, F I)+(F I, F D)=(C B, C F)+(F D, D I)=(F D, F C),
$$
et $(F D)$ est donc la bissectrice de l'angle $\widehat{B F C}$.
Réciproquement, si $(F D)$ est la bissectrice de $\widehat{B F C}$, et en notant $J$ le point d'intersection entre $(B C)$ et la tangente à $\mathcal{C}_{B C F}$ en $F$, la chasse aux angles ci-dessus indique que $J F D$ est isocèle en $J$, donc que $J D^{2}=J F^{2}=J B \cdot J C$. Le point $J$ a donc même puissance par rapport aux cercles $\mathcal{C}_{B C F}$ et $\mathcal{C}_{D X Y}$, donc il appartient à leur axe radical $(X Y)$, de sorte que $I=J$. Ainsi, notre problème est équivalent à démontrer que $(F D)$ est donc la bissectrice de l'angle $\widehat{B F C}$.
Pour cela, on note $G$ le point d'intersection, autre que $D$, entre les cercles $\mathcal{C}_{D B X}$ et $\mathcal{C}_{C D Y}$. Puisque
$$
(G Y, G X)=(G Y, G D)+(G D, G X)=(C Y, C D)+(B D, B X)=(E Y, E X)
$$
les point $G$ appartient au cercle $\mathcal{C}_{E X Y}$. En outre, $E$ est le point de concourt des axes radicaux de $\mathcal{C}_{A B C}$ avec $\mathcal{C}_{D B X}$ et $\mathcal{C}_{C D Y}$. Il s'agit donc du centre radical de ces trois cercles, et $E$ appartient donc à l'axe radical de $\mathcal{C}_{D B X}$ et $\mathcal{C}_{C D Y}$, c'est-à-dire à la droite (GD). Cela signifie que $F=G$.
On conclut alors par simple chasse aux angles. En effet,
$$
\begin{aligned}
(F B, F D)+(F C, F D) & =(G B, G D)+(G C, G D) \\
& =(X B, X D)+(Y C, Y D) \\
& =(B X, B C)+(D B, D X)+(C Y, C B)+(D C, D Y) \\
& =(Y X, Y C)+(Y D, Y X)+(X Y, X B)+(X D, X Y) \\
& =(Y D, Y C)+(X D, X B) .
\end{aligned}
$$
Ainsi, $2(X B, X D)+2(Y C, Y D)=0^{\circ}$, de sorte que les angles $\widehat{D F B}$ et $\widehat{C F D}$ sont égaux modulo $90^{\circ}$. Comme $\widehat{D F B}=\widehat{D X B} \leqslant \widehat{C X B}=\widehat{C A B}<90^{\circ}$ et, de même, $\widehat{C F D}<90^{\circ}$, on en déduit que $\widehat{D F B}=\widehat{C F D}$, ce qui conclut le problème.

Commentaire des correcteurs Pour ce problème, plusieurs élèves ont mis en évidence une solution par inversion à laquelle les correcteurs n'avaient pas pensé : il s'agit de la solution $\mathrm{n}^{\circ} 1$ présentée ci-dessus. Cette méthode rendait l'exercice nettement moins difficile que le niveau de difficulté estimé par l'équipe de correction.
Ainsi, on a observé une forte dichotomie entre les élèves ayant repéré cette solution par inversion et les élèves qui ne l'ont pas repérée ou qui ne sont pas adeptes de l'inversion et qui n'ont, pour la plupart, pas pu avancer de façon significative dans l'exercice. Toutefois, nous saluons les efforts et les pistes avancées par les élèves ayant tenté l'exercice et qui ont parfois pu rapporter à leur auteur 1 ou 2 points partiels.
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-1.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2020"
}
|
Let $n=2021$. Prove that the number $3^{2 n+1}+2^{n+2}$ is divisible by 35.
|
We will demonstrate that the number $S_{n}=3^{2 n+1}+2^{n+2}$ is simultaneously divisible by 5 and by 7 when $n=2021$.
We immediately verify that
$$
S_{n} \equiv 9^{n} \times 3+2^{n} \times 4 \equiv 2^{n} \times 3+2^{n} \times 4 \equiv 2^{n} \times 7 \equiv 0 \quad(\bmod 7),
$$
which means that $S_{n}$ is indeed divisible by 7.
We then verify that
$$
S_{n} \equiv 9^{n} \times 3+2^{n} \times 4 \equiv(-1)^{n} \times 3+2^{n} \times(-1) \equiv-3-2^{n} \quad(\bmod 5).
$$
The required property clearly depends on the value of $n$, as it would have been invalid if we had chosen $n=3$.
We therefore calculate the first few values of $S_{n}(\bmod 5)$ to get some ideas:
$$
\begin{array}{ll}
\triangleright S_{0} \equiv-3-1 \equiv 1(\bmod 5) ; & \triangleright S_{4} \equiv-3-16 \equiv 1(\bmod 5) ; \\
\triangleright S_{1} \equiv-3-2 \equiv 0(\bmod 5) ; & \triangleright S_{5} \equiv-3-32 \equiv 0(\bmod 5) ; \\
\triangleright S_{2} \equiv-3-4 \equiv 3(\bmod 5) ; & \triangleright S_{6} \equiv-3-64 \equiv 3(\bmod 5) ; \\
\triangleright S_{3} \equiv-3-8 \equiv 4(\bmod 5) ; & \triangleright S_{7} \equiv-3-128 \equiv 4(\bmod 5) .
\end{array}
$$
It is clearly visible that $S_{n} \equiv 0(\bmod 5)$ when $n \equiv 1(\bmod 4)$, and we therefore set out to prove this. If we set $n=4 k+1$, then
$$
S_{n} \equiv-3-2^{4 k+1} \equiv-3-16^{k} \times 2 \equiv-3-1^{k} \times 2 \equiv-3-2 \equiv 0 \quad(\bmod 5)
$$
Thus, when $n=2021$, we indeed have $n \equiv 1(\bmod 4)$, and the integer $S_{n}$ is therefore divisible by 5.
In conclusion, the integer $S_{n}$ is divisible by both 5 and 7, so it is also divisible by their LCM, which is 35.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
On pose $n=2021$. Démontrer que le nombre $3^{2 n+1}+2^{n+2}$ est divisible par 35.
|
Nous allons démontrer que le nombre $S_{n}=3^{2 n+1}+2^{n+2}$ est divisible simultanément par 5 et par 7 lorsque $n=2021$.
On vérifie immédiatement que
$$
S_{n} \equiv 9^{n} \times 3+2^{n} \times 4 \equiv 2^{n} \times 3+2^{n} \times 4 \equiv 2^{n} \times 7 \equiv 0 \quad(\bmod 7),
$$
ce qui signifie bien que $S_{n}$ est divisible par 7 .
On vérifie ensuite que
$$
S_{n} \equiv 9^{n} \times 3+2^{n} \times 4 \equiv(-1)^{n} \times 3+2^{n} \times(-1) \equiv-3-2^{n} \quad(\bmod 5) .
$$
La propriété demandée dépend donc manifestement de la valeur de $n$, puisqu'elle aurait été invalide si on avait choisi $n=3$.
On calcule donc les premières valeurs de $S_{n}(\bmod 5)$ pour se donner des idées :
$$
\begin{array}{ll}
\triangleright S_{0} \equiv-3-1 \equiv 1(\bmod 5) ; & \triangleright S_{4} \equiv-3-16 \equiv 1(\bmod 5) ; \\
\triangleright S_{1} \equiv-3-2 \equiv 0(\bmod 5) ; & \triangleright S_{5} \equiv-3-32 \equiv 0(\bmod 5) ; \\
\triangleright S_{2} \equiv-3-4 \equiv 3(\bmod 5) ; & \triangleright S_{6} \equiv-3-64 \equiv 3(\bmod 5) ; \\
\triangleright S_{3} \equiv-3-8 \equiv 4(\bmod 5) ; & \triangleright S_{7} \equiv-3-128 \equiv 4(\bmod 5) .
\end{array}
$$
Il apparaît visiblement que $S_{n} \equiv 0(\bmod 5)$ lorsque $n \equiv 1(\bmod 4)$, et on entreprend donc de le démontrer. Si l'on pose $n=4 k+1$, alors
$$
S_{n} \equiv-3-2^{4 k+1} \equiv-3-16^{k} \times 2 \equiv-3-1^{k} \times 2 \equiv-3-2 \equiv 0 \quad(\bmod 5)
$$
Ainsi, lorsque $n=2021$, on a bien $n \equiv 1(\bmod 4)$, et l'entier $S_{n}$ est donc divisible par 5 .
En conclusion, l'entier $S_{n}$ est divisible à la fois par 5 et par 7, donc il est également divisible par leur PPCM, c'est-à-dire 35.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-2.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T1",
"year": "2020"
}
|
Let $n=2021$. Prove that the number $3^{2 n+1}+2^{n+2}$ is divisible by 35.
|
$n^{\circ} 1$ Fermat's little theorem assures us that $2^{4} \equiv 3^{4} \equiv 1(\bmod 5)$. Since $2 n+1 \equiv 4043 \equiv 3(\bmod 4)$ and $n+2 \equiv 2023 \equiv 3(\bmod 4)$, we deduce that $S_{n} \equiv$ $3^{3}+2^{3} \equiv 35 \equiv 0(\bmod 5)$.
Similarly, Fermat's little theorem assures us that $2^{6} \equiv 3^{6} \equiv 1(\bmod 7)$. Since $2 n+1 \equiv$ $4043 \equiv-1(\bmod 6)$ and $n+2 \equiv 2023 \equiv 1(\bmod 6)$, we deduce that $S_{n} \equiv 3^{5}+2^{1} \equiv 245 \equiv 0$ $(\bmod 7)$.
In conclusion, the sum $S_{n}$ is divisible by 5 and by 7, hence by 35.
Examiner's Comment This problem was generally well done, to the great satisfaction of the examiners. Most students had good ideas and good reflexes:
$\triangleright$ to reduce the problem to studying the divisibility of $S_{n}$ by 5 and by 7;
$\triangleright$ to study small values of $n$;
$\triangleright$ to consider the powers of 2 and 3 separately and study their last digits, i.e., their congruence modulo 10;
$\triangleright$ to notice that a pattern was repeating.
These are very encouraging signs!
Some students also directly invoked Fermat's little theorem, which states that $a^{p-1} \equiv 1(\bmod p)$ when $p$ is a prime number that does not divide $a$. This result allowed them to reach the solution more quickly, and also made the divisibility by 5 and by 7 symmetric.
However, the examiners also noted several mathematical or strategic errors, which they wish to highlight to prevent students from making them again. Here, first, are the most frequent mathematical errors:
$\triangleright$ Several students made mistakes in manipulating powers and wrote, incorrectly, equalities of the form $a^{k}+b^{\ell}=(a+b)^{k+\ell}$. When one "invents" such an algebraic identity, there is a strong chance that it is false, and a very important step is therefore to look for possible counterexamples: if one does not find any, one will have more confidence in one's identity. Here, taking $a=b=k=\ell=1$ is enough to confirm that $a^{k}+b^{\ell}=1+1=2 \neq 4=2^{2}=(a+b)^{k+\ell}$.
$\triangleright$ Several students incorrectly believed that one could reduce the exponents modulo $m$. Certainly, if $a \equiv b(\bmod m)$, then $a+c \equiv b+c(\bmod m)$ and $a c \equiv b c(\bmod m)$ for any $c$. However, in general, $c^{a} \not \equiv c^{b}(\bmod m)$. This is the case, for example, when $a=1, b=4$, $c=2$ and $m=3$, since then $c^{a} \equiv 2^{1} \equiv 2 \not \equiv 16 \equiv 2^{4} \equiv c^{b}(\bmod m)$.
$\triangleright$ Several students incorrectly claimed that a number is divisible by 7 if and only if the number formed by its last two digits is divisible by 7. This divisibility criterion is clearly incorrect, since 100 and 700 have the same last digits but only 700 is divisible by 7. Moreover, if such a criterion existed, and given its simplicity, it would certainly be taught in school, which is not the case.
$\triangleright$ Many students confused necessary and sufficient conditions. They thus claimed that "if $S_{n}$ is divisible by $35=5 \times 7$", it is also divisible by 5 and by 7. This information is certainly true, but it is also useless to us. What was expected of students was to formulate the reciprocal implication, which is also the one they used: "if $S_{n}$ is divisible by 5 and by 7, it is also divisible by $35=5 \times 7$".
Here are, next, the most frequent strategic errors:
$\triangleright$ Several students believed, based on a false reasoning or a calculation error, that they had demonstrated that 35 does not divide $S_{n}$. Instead of concluding that the statement was incorrect, it would have been more judicious to first question themselves and recheck the calculations made and the correctness of the arguments invoked.
$\triangleright$ Many students, after studying the last digit of $2^{n}$ and $3^{n}$ to deduce that 5 divides $S_{n}$, did not think to take a step back to realize that it would suffice to do the same but write all our numbers in base 7 rather than base 10. In general, when one breaks down a problem into two sub-problems that appear analogous and solves one of the two sub-problems, it is very useful to take the time to think about how one could adapt the reasoning used to solve the other sub-problem.
$\triangleright$ Many students, after noticing that the last digits of $2^{n}$ seemed to repeat in the cycle $2,4,8,6,2,4,8,6, \ldots$, claimed that this was the case without trying to prove it. Instead of a proof, they relied on a mere conjecture. Since this conjecture played a central role in their solution, it was essential to prove it.
The examiners here decided not to penalize the lack of this proof, as it was the first timed POFM test of their lives for most candidates.
However, in other circumstances, omitting this proof could have been quite heavily penalized, to the tune of 2 or 3 points out of 7.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
On pose $n=2021$. Démontrer que le nombre $3^{2 n+1}+2^{n+2}$ est divisible par 35.
|
$n^{\circ} 1$ Le petit théorème de Fermat nous assure que $2^{4} \equiv 3^{4} \equiv 1(\bmod 5)$. Comme $2 n+1 \equiv 4043 \equiv 3(\bmod 4)$ et $n+2 \equiv 2023 \equiv 3(\bmod 4)$, on en déduit que $S_{n} \equiv$ $3^{3}+2^{3} \equiv 35 \equiv 0(\bmod 5)$.
De même, le petit théorème de Fermat nous assure que $2^{6} \equiv 3^{6} \equiv 1(\bmod 7)$. Comme $2 n+1 \equiv$ $4043 \equiv-1(\bmod 6)$ et $n+2 \equiv 2023 \equiv 1(\bmod 6)$, on en déduit que $S_{n} \equiv 3^{5}+2^{1} \equiv 245 \equiv 0$ $(\bmod 7)$.
En conclusion, la somme $S_{n}$ est divisible par 5 et par 7, donc par 35.
Commentaire des correcteurs Cet exercice a été globalement bien réussi, à la grande satisfaction des correcteurs. La plupart des élèves ont eu bonnes idées et de bons réflexes :
$\triangleright$ se ramener à étudier la divisibilité de $S_{n}$ par 5 et par 7;
$\triangleright$ étudier les petites valeurs de $n$;
$\triangleright$ considérer séparément les puissances de 2 et de 3 et étudier leur chiffre des unités, c'est-à-dire leur congruence modulo 10;
$\triangleright$ repérer qu'un motif se répétait.
Il s'agit là de signes très encourageants!
Certains élèves ont aussi invoqué directement le petit théorème de Fermat, qui stipule que $a^{p-1} \equiv 1(\bmod p)$ quand $p$ est un nombre premier qui ne divise pas $a$. Ce résultat permettait d'aboutir plus rapidement à la solution, et avait aussi le bon goût de rendre les divisibilités par 5 et par 7 symétriques.
Néanmoins, les correcteurs ont également repéré plusieurs erreurs, mathématiques ou stratégiques, qu'ils tiennent à souligner pour éviter aux élèves de les commettre à nouveau. Voici, tout d'abord, les erreurs mathématiques les plus fréquentes:
$\triangleright$ Plusieurs élèves se sont trompés en manipulant les puissances, et ont écrit, à tort, des égalités de la forme $a^{k}+b^{\ell}=(a+b)^{k+\ell}$. Quand on « invente» une telle identité algébrique, il y a de fortes chances qu'elle soit fausse, et une étape très importante est donc de rechercher des contre-exemples éventuels : si on n'en trouve pas, on aura davantage confiance en notre identité. Ici, prendre $a=b=k=\ell=1$ suffit à confirmer que $a^{k}+b^{\ell}=1+1=2 \neq 4=2^{2}=(a+b)^{k+\ell}$.
$\triangleright$ Plusieurs élèves ont cru à tort que l'on pouvait réduire les exposants modulo $m$. Certes, si $a \equiv b(\bmod m)$, on a bien $a+c \equiv b+c(\bmod m)$ et $a c \equiv b c(\bmod m)$ pour tout $c$. En revanche, en général, $c^{a} \not \equiv c^{b}(\bmod m)$. C'est le cas, par exemple, quand $a=1, b=4$, $c=2$ et $m=3$, puisque alors $c^{a} \equiv 2^{1} \equiv 2 \not \equiv 16 \equiv 2^{4} \equiv c^{b}(\bmod m)$.
$\triangleright$ Plusieurs élèves ont affirmé, à tort, qu'un nombre est divisible par 7 si et seulement si le nombre formé par ses deux derniers chiffres est divisible par 7. Ce critère de divisibilité est manifestement incorrect, puisque 100 et 700 ont les mêmes derniers chiffres mais que seul 700 est divisible par 7 . En outre, si un tel critère existait, et au vu de sa simplicité, il serait certainement enseigné à l'école, ce qui n'est pas le cas.
$\triangleright$ De nombreux élèves ont confondu conditions nécessaires et suffisantes. Ils ont ainsi affirmé que « si $S_{n}$ est divisible par $35=5 \times 7$ », il est aussi divisible par 5 et par 7 ». Cette information est certes vraie, mais elle nous est aussi inutile. On attendait des élèves qu'ils formulent l'implication réciproque, qui est d'ailleurs celle qu'ils ont utilisée : «si $S_{n}$ est divisible par 5 et par 7, il est aussi divisible par $35=5 \times 7$ ».
Voici, ensuite, les erreurs stratégiques les plus fréquentes :
$\triangleright$ Plusieurs élèves ont cru, en s'appuyant sur un raisonnement faux ou sur une erreur de calcul, démontrer que 35 ne divisait pas $S_{n}$. Dans pareil cas, au lieu de conclure au fait que l'énoncé était incorrect, il aurait été plus judicieux de se remettre d'abord en question, et revérifiant les calculs effectués et la correction des arguments invoqués.
$\triangleright$ De nombreux élèves, après avoir étudié le chiffre des unités de $2^{n}$ et $3^{n}$ pour en déduire que 5 divisait $S_{n}$, n'ont pas pensé à prendre du recul pour se dire qu'il suffisait de faire la même chose mais en écrivant tous nos nombres en base 7 plutôt qu'en base 10. De manière générale, quand on découpe un problème en deux sous-problèmes d'apparences analogues et que l'on résout un des deux sous-problèmes, il est très utile de prendre le temps de réfléchir à la façon dont on pourrait adapter le raisonnement utilisé pour résoudre l'autre sous-problème.
$\triangleright$ De nombreux élèves, après avoir repéré que les chiffres des unités de $2^{n}$ semblaient se répéter en formant le cycle $2,4,8,6,2,4,8,6, \ldots$, ont affirmé que c'était le cas sans essayer de le démontrer. Au lieu d'une démonstration, ils se sont donc appuyés sur une simple conjecture. Puisque cette conjecture tenait un rôle central dans leur solution, il était cependant indispensable de la démontrer.
Les correcteurs ont ici décidé de ne pas pénaliser l'absence de cette démonstration, car il s'agissait du premier test POFM en temps limité de leur vie pour la plupart des candidats.
Cependant, en d'autres circonstances, omettre cette démonstration aurait pu être assez lourdement sanctionné, à hauteur de 2 ou 3 points sur 7.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-2.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2020"
}
|
Let $n$ and $k$ be integers such that $n \geqslant 3$. Théo is organizing the class representative elections for his class of $n$ students: each student must vote for one of their classmates (everyone is a candidate), and no one votes for themselves. Then Théo divides the students into groups so that, if a student is in a group, the student they voted for is not in the same group.
For which values of $k$ is Théo sure to be able to divide the students into at most $k$ groups, regardless of how the students vote?
|
First, if we have three students (let's say Anna, Martin, and Vincent) such that Anna voted for Martin, Martin voted for Vincent, and Vincent voted for Anna, it is clear that Théo will need at least three groups.
Conversely, let's prove by induction on \( n \) that Théo can manage with only three groups, even if some students vote blank.
The base case is clear for \( n=3 \). So, we assume \( n \geqslant 4 \). Since there were at most \( n \) votes, there is at least one student who received at most one vote: we call this student Donald. By forgetting Donald and fraudulently "forgetting" the vote he might have received, replacing it with a blank vote, Théo can distribute the remaining \( n-1 \) students into at most three groups.
Then Théo brings Donald back to the class: among the three groups, there is at least one that does not contain the person for whom Donald might have voted, nor the potential voter of Donald. Théo then places Donald in this group, which concludes the induction.
In summary, the integers sought are the integers \( k \geqslant 3 \).
Comment from the graders: Many students understood that certain cases forced Théo to choose \( k \geqslant 3 \). It was then necessary, for all \( n \), to provide an example of a vote for which 3 groups were necessary.
Subsequently, numerous strategies for distributing the students into 3 groups were proposed, but few were correct. In such a case, trying to prove that the distribution works is always useful: either the distribution is correct, and proving it is necessary to get all the points; or it is not, and failing to prove it often helps to understand why the strategy fails. It is also important not to hesitate to test the distribution given for certain votes: this often easily reveals the problems.
Finally, some students transformed the problem into a graph coloring problem, then claimed that if one could color any subset of 4 vertices of the graph without having two adjacent vertices of the same color, one could color the entire graph without having two adjacent vertices of the same color. This statement is actually invalid, as illustrated by the counterexample below. To avoid such disappointments, we encourage students to provide a proper proof of the different elements they state.
|
k \geqslant 3
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Soit $n$ et $k$ deux entiers, tels que $n \geqslant 3$. Théo organise les élections des délégués de sa classe de $n$ élèves : chaque élève doit voter pour un de ses camarades (tout le monde est candidat), et nul ne vote pour lui-même. Puis Théo répartit les élèves en groupes de sorte que, si un élève est dans un groupe, l'élève pour lequel il a voté n'y soit pas.
Pour quelles valeurs de $k$ Théo est-il sûr de pouvoir répartir les élèves en au plus $k$ groupes, et ce quelle que soit la manière dont les élèves auront voté?
|
Tout d'abord, si on a trois élèves (disons Anna, Martin et Vincent) tels qu'Anna a voté pour Martin, Martin a voté pour Vincent, et Vincent a voté pour Anna, il est clair que Théo aura besoin d'au moins trois groupes.
Réciproquement, démontrons par récurrence sur $n$ que Théo peut s'en sortir avec trois groupes seulement, et ce même si certains élèves votent blanc.
L'initialisation est claire pour $n=3$. On suppose donc que $n \geqslant 4$. Puisqu'il y a eu au plus $n$ votes, il y a au moins un élève qui a reçu au plus un vote : on l'appelle Donald. Quitte à oublier Donald et à frauder en « oubliant» le vote que celui-ci aurait reçu pour le remplacer par un vote blanc, Théo peut répartir les $n-1$ élèves restants en au plus trois groupes.
Puis Théo fait revenir Donald dans la classe : sur les trois groupes, il y en a au moins un qui ne contient ni la personne pour laquelle Donald a pu voter, ni l'électeur éventuel de Donald. Théo met alors Donald dans ce groupe-là, ce qui conclut la récurrence.
En résumé, les entiers recherchés sont les entiers $k \geqslant 3$.
Commentaire des correcteurs Beaucoup d'élèves ont bien compris que certains cas forçaient Théo à choisir $k \geqslant 3$. Il fallait alors, pour tout $n$, donner un exemple de vote pour lequel 3 groupes étaient nécessaires.
Par la suite, de nombreuses stratégies pour répartir les élèves en 3 groupes ont été proposées, mais peu étaient correctes. Dans un tel cas, essayer de prouver que la répartition convient est toujours utile : en effet, soit la répartition est correcte, et alors démontrer qu'elle l'est est nécessaire pour obtenir tous les points; soit elle ne l'est pas, et échouer dans cette tentative de preuve permet souvent de comprendre pourquoi la stratégie échoue en fait. Il ne faut pas non plus hésiter à tester la répartition qui est donnée pour certains votes : en effet, cela permet souvent facilement de voir les problèmes.
Enfin, quelques élèves ont transformé le problème en un problème de coloriage de graphes, puis ont affirmé que, si l'on pouvait colorier toute partie de 4 sommets du graphe sans avoir deux sommets de même couleur adjacents, on pouvait colorier le graphe entier sans avoir deux sommets de même couleur adjacents. Cette affirmation est en fait invalide, comme l'illustre le contre-exemple ci-dessous. Afin d'éviter aux élèves ce genre de déconvenues, nous les encourageons encore une fois à tenter de fournir une vraie preuve des différents éléments qu'ils énoncent.

|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-2.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T1",
"year": "2020"
}
|
We define the sequence $a_{1}, a_{2}, a_{3} \ldots$ as follows: $a_{1}=63$ and, for all integers $n \geqslant 2, a_{n}$ is the smallest multiple of $n$ that is greater than or equal to $a_{n-1}$. Prove that the terms of our sequence are pairwise distinct.
|
It is clear that the sequence $\left(a_{n}\right)_{n \geqslant 1}$ is increasing. Therefore, it is necessary to prove that it is strictly increasing.
We calculate the first terms of the sequence: $a_{1}=63, a_{2}=64, a_{3}=66, a_{4}=68, a_{5}=70$, $a_{6}=72, a_{7}=77, a_{8}=80, a_{9}=81, a_{10}=90, a_{11}=99, a_{12}=108, a_{13}=117 . .$.
A property then becomes apparent: it seems that $a_{n}=9 n$ for all $n \geqslant 9$. In practice, it is good to verify this conjecture on a few additional values of $n$ to be convinced that it is true. We therefore set out to prove this property by induction.
First, as mentioned above, we have $a_{9}=9^{2}$. Then, for any integer $n \geqslant 9$ such that $a_{n}=9 n$, we observe that $8(n+1)=a_{n}-(n-8)<a_{n}<9(n+1)$, so that $a_{n+1}=9(n+1)$.
In conclusion, the sequence $\left(a_{n}\right)_{n \geqslant 1}$ is strictly increasing as long as $n \leqslant 9$, and it is clearly so when $n \geqslant 9$. Its terms are therefore indeed distinct from each other.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
On définit la suite $a_{1}, a_{2}, a_{3} \ldots$ de la façon suivante : $a_{1}=63$ et, pour tout entier $n \geqslant 2, a_{n}$ est le plus petit multiple de $n$ qui soit supérieur ou égal à $a_{n-1}$. Démontrer que les termes de notre suite sont deux à deux distincts.
|
Il est clair que la suite $\left(a_{n}\right)_{n \geqslant 1}$ est croissante. Il s'agit donc de démontrer qu'elle est strictement croissante.
On calcule donc les premiers termes de la suite : $a_{1}=63, a_{2}=64, a_{3}=66, a_{4}=68, a_{5}=70$, $a_{6}=72, a_{7}=77, a_{8}=80, a_{9}=81, a_{10}=90, a_{11}=99, a_{12}=108, a_{13}=117 . .$.
Une propriété se dessine alors sous nos yeux : il semble que $a_{n}=9 n$ pour tout $n \geqslant 9$. En pratique, il est bon de vérifier cette conjecture sur quelques valeurs supplémentaires de $n$, pour se convaincre qu'elle est vraie. On entreprend donc de démontrer cette propriété par récurrence.
Tout d'abord, comme mentionné ci-dessus, on a bien $a_{9}=9^{2}$. Puis, pour tout entier $n \geqslant 9$ tel que $a_{n}=9 n$, on constate que $8(n+1)=a_{n}-(n-8)<a_{n}<9(n+1)$, de sorte que $a_{n+1}=9(n+1)$.
En conclusion, la suite $\left(a_{n}\right)_{n \geqslant 1}$ est strictement croissante tant que $n \leqslant 9$, et elle l'est manifestement quand $n \geqslant 9$. Ses termes sont donc en effet distincts deux à deux.
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-2.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T1",
"year": "2020"
}
|
We define the sequence $a_{1}, a_{2}, a_{3} \ldots$ as follows: $a_{1}=63$ and, for all integers $n \geqslant 2, a_{n}$ is the smallest multiple of $n$ that is greater than or equal to $a_{n-1}$. Prove that the terms of our sequence are pairwise distinct.
|
$n^{\circ} 1$ As in the previous solution, it is clear that the sequence $\left(a_{n}\right)_{n \geqslant 1}$ is increasing. Therefore, it is necessary to prove, for all integers $n \geqslant 1$, that $a_{n} \neq a_{n+1}$, that is, $n(n+1)$ does not divide $a_{n}$.
We then calculate the first terms of the sequence, up to $a_{9}=81$, and observe that $n(n+1)$ does not divide $a_{n}$ when $n \leqslant 9$. We then prove that $a_{n}<n(n+1)$ for all integers $n \geqslant 9$.
Indeed, this is the case if $n=9$. Then, for all integers $n \geqslant 9$ such that $a_{n}<n(n+1)$, we observe that $a_{n+1} \leqslant a_{n}+n<n(n+2)<(n+1)^{2}$, which concludes the proof.
Comment from the graders: Many students had interesting ideas that allowed them to make progress in solving this difficult problem. When faced with such a statement, it is important to look at how the sequence $\left(a_{n}\right)$ behaves, and therefore to calculate its first terms: one can try to look at the first 10 or 20 terms to get an idea of the sequence. This idea proved particularly fruitful here, as it allowed conjecturing that $a_{n}=9 n$ when $n \geqslant 9$, which seems a priori easier to prove than the initial statement.
However, be careful with the writing! Students who started a recurrence often wrote that $a_{n}=9 n$ since $a_{n+1}=k(n+1)$ for some $k$, and then tried to find $k$, but only managed to show that $k \leqslant 9$ or that $k \geqslant 9$, forgetting the other inequality: it is important to properly justify why $k=9$.
Moreover, in this exercise, it was possible to empirically notice that $a_{n}=9 n$ when $n \geqslant 9$, but without being able to prove it. In such a case, it is obviously necessary to mention such a conjecture, and then see how it could be used to solve the problem. Indeed, the more complete the reasoning is and the fewer elements are missing to justify, the more points it will be worth. Admitting a result obviously costs points (and if the result that is admitted is as difficult to prove as the initial statement, it can even cost all the points), but it is often possible to formulate a conjecture and then deduce the desired result from it.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
On définit la suite $a_{1}, a_{2}, a_{3} \ldots$ de la façon suivante : $a_{1}=63$ et, pour tout entier $n \geqslant 2, a_{n}$ est le plus petit multiple de $n$ qui soit supérieur ou égal à $a_{n-1}$. Démontrer que les termes de notre suite sont deux à deux distincts.
|
$n^{\circ} 1$ Comme dans la solution précédente, il est clair que la suite $\left(a_{n}\right)_{n \geqslant 1}$ est croissante. Il s'agit donc de démontrer, pour tout entier $n \geqslant 1$, que $a_{n} \neq a_{n+1}$, c'est-à-dire que $n(n+1)$ ne divise pas $a_{n}$.
On calcule alors les premiers termes de la suite, jusqu'à $a_{9}=81$, et l'on constate bien que $n(n+1)$ ne divise pas $a_{n}$ lorsque $n \leqslant 9$. On démontre ensuite que $a_{n}<n(n+1)$ pour tout entier $n \geqslant 9$.
En effet, c'est bien le cas si $n=9$. Puis, pour tout entier $n \geqslant 9$ tel que $a_{n}<n(n+1)$, on constate que $a_{n+1} \leqslant a_{n}+n<n(n+2)<(n+1)^{2}$, ce qui conclut.
Commentaire des correcteurs De nombreux élèves ont eu des idées intéressantes et leur permettant d'avancer dans la résolution de ce problème pourtant difficile. Face à un tel énoncé, il est important de regarder comment la suite $\left(a_{n}\right)$ se comporte, et donc en calculer les premiers termes : on peut essayer de regarder les 10 ou 20 premiers termes pour se faire une idée de la suite. Cette idée s'avérait particulièrement fructueuse ici, puisqu'elle permettait de conjecturer que $a_{n}=9 n$ lorsque $n \geqslant 9$, ce qui semble a priori plus facile à prouver que l'énoncé initial.
Néanmoins, attention à la rédaction! Les élèves qui ont entamé une récurrence on souvent écrit que $a_{n}=9 n$ puisque $a_{n+1}=k(n+1)$ pour un certain $k$, et ont ensuite tenté de trouver $k$, mais ont uniquement démontré que $k \leqslant 9$ ou que $k \geqslant 9$, oubliant l'autre inégalité : il est important de bien justifier pourquoi $k=9$.
Par ailleurs, dans cet exercice, il était possible de remarquer empiriquement que $a_{n}=9 n$ lorsque $n \geqslant 9$, mais sans parvenir à le démontrer. Dans ce cas, il faut évidemment mentionner une telle conjecture, puis voir comment on pourrait l'utiliser pour résoudre l'exercice. En effet, plus le raisonnement est complet et moins il manque d'éléments à justifier, et plus il vaudra de points. Admettre un résultat coûte évidemment des points (et si le résultat que l'on admet est aussi difficile à démontrer que l'énoncé initial, cela peut même coûter l'intégralité des points), mais il est souvent possible de formuler une conjecture puis d'en déduire le résultat désiré.
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-2.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2020"
}
|
Let $P_{1} P_{2} \ldots P_{2021}$ be a convex polygon with 2021 vertices such that, for each vertex $P_{i}$, the 2018 diagonals emanating from $P_{i}$ divide the angle $\widehat{P}_{i}$ into 2019 equal angles.
Prove that $P_{1} P_{2} \ldots P_{2021}$ is a regular polygon, that is, a polygon where all angles have the same measure and all sides have the same length.
|
In the following, we set \( n=2019 \) and, for any vertex \( P_{i} \), we denote \( a_{i} \) as the angle \( \widehat{P}_{i} / n \). Let \( P_{k} \), \( P_{k+1} \), \( P_{k+2} \), \( P_{k+3} \), and \( P_{k+4} \) be four consecutive vertices, with the indices of the vertices considered modulo \( n+2 \).
The sum of the angles in a triangle is \( 180^{\circ} \). By considering the triangles \( P_{i} P_{i+1} P_{i+2} \), \( P_{i} P_{i+1} P_{i+3} \), and \( P_{i} P_{i+1} P_{i+4} \), we observe that
\[
\begin{aligned}
a_{i} + n a_{i+1} + a_{i+2} & = 180^{\circ} \\
2 a_{i} + (n-1) a_{i+1} + a_{i+3} & = 180^{\circ} \\
3 a_{i} + (n-2) a_{i+1} + a_{i+4} & = 180^{\circ}
\end{aligned}
\]
We will then subtract these equations two by two:
\(\triangleright (1)-(2)\) indicates that \( a_{i+1} + a_{i+2} = a_{i} + a_{i+3} \), which means \( a_{i+1} - a_{i} = a_{i+3} - a_{i+2} \);
\(\triangleright (2)-(3)\) indicates that \( a_{i+1} + a_{i+3} = a_{i} + a_{i+4} \), which means \( a_{i+1} - a_{i} = a_{i+4} - a_{i+3} \).
We observe that \( a_{i+4} - a_{i+3} = a_{i+3} - a_{i+2} \). The difference between two consecutive angles \( a_{j} \) and \( a_{j+1} \) is therefore equal to a constant \( \mathbf{c} \).
This means that \( a_{i+k} = a_{i} + k \mathbf{c} \) for all integers \( i \) and \( k \). In particular, \( a_{1} = a_{n+3} = a_{1} + (n+2) \mathbf{c} \), so \( \mathbf{c} = 0^{\circ} \). Thus, our polygon has all its vertices equal.
The triangle \( P_{i} P_{i+1} P_{i+2} \) is therefore isosceles at \( P_{i+1} \), so that \( P_{i} P_{i+1} = P_{i+1} P_{i+2} \). Since two consecutive sides are of the same length, our polygon has all its sides of the same length, and it is indeed a regular polygon.
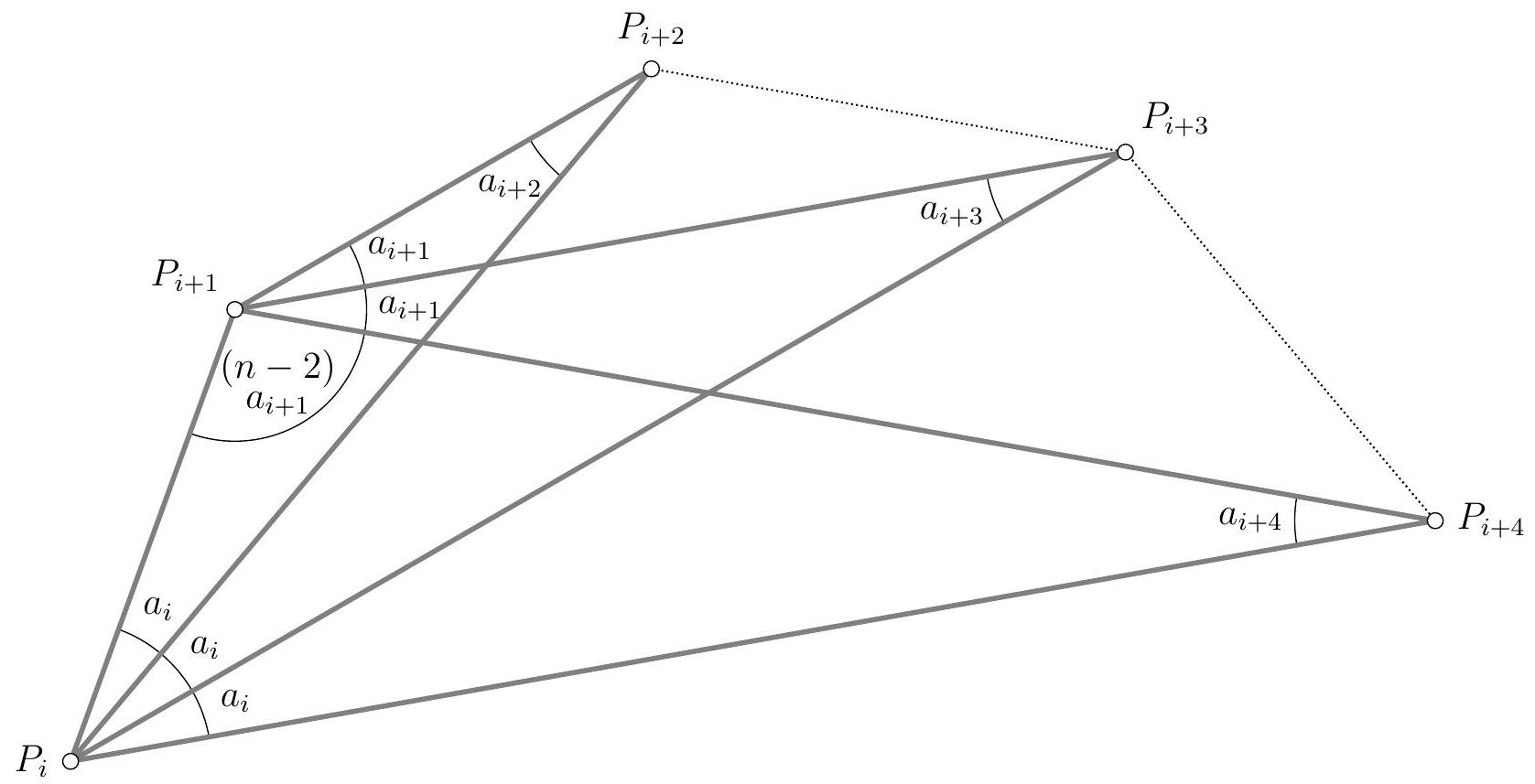
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $P_{1} P_{2} \ldots P_{2021}$ un polygone convexe à 2021 sommets tel que, pour chaque sommet $P_{i}$, les 2018 diagonales issues de $P_{i}$ divisent l'angle $\widehat{P}_{i}$ en 2019 angles égaux.
Démontrer que $P_{1} P_{2} \ldots P_{2021}$ est un polygone régulier, c'est-à-dire un polygone dont tous les angles ont même mesure et tous les côtés ont même longueur.
|
Dans la suite, on pose $n=2019$ et, pour tout sommet $P_{i}$, on note $a_{i}$ l'angle $\widehat{P}_{i} / n$. Soit alors $P_{k}$, $P_{k+1}, P_{k+2}, P_{k+3}$ et $P_{k+4}$ quatre sommets consécutifs, les indices des sommets étant considérés modulo $n+2$.
La somme des angles d'un triangle vaut $180^{\circ}$. En considérant respectivement les triangles $P_{i} P_{i+1} P_{i+2}, P_{i} P_{i+1} P_{i+3}$ et $P_{i} P_{i+1} P_{i+4}$, on constate que
$$
\begin{aligned}
a_{i}+n a_{i+1}+a_{i+2} & =180^{\circ} \\
2 a_{i}+(n-1) a_{i+1}+a_{i+3} & =180^{\circ} \\
3 a_{i}+(n-2) a_{i+1}+a_{i+4} & =180^{\circ}
\end{aligned}
$$
Nous allons alors soustraire deux à deux ces équations :
$\triangleright(11)-(2)$ indique que $a_{i+1}+a_{i+2}=a_{i}+a_{i+3}$, c'est-à-dire que $a_{i+1}-a_{i}=a_{i+3}-a_{i+2}$;
$\triangleright(2)-(3)$ indique que $a_{i+1}+a_{i+3}=a_{i}+a_{i+4}$, c'est-à-dire que $a_{i+1}-a_{i}=a_{i+4}-a_{i+3}$.
On constate donc que $a_{i+4}-a_{i+3}=a_{i+3}-a_{i+2}$. La différence entre deux angles $a_{j}$ et $a_{j+1}$ consécutifs est donc égale à une constante $\mathbf{c}$.
Cela signifie que $a_{i+k}=a_{i}+k \mathbf{c}$ pour tous les entiers $i$ et $k$. En particulier, $a_{1}=a_{n+3}=$ $a_{1}+(n+2) \mathbf{c}$, donc $\mathbf{c}=0^{\circ}$. Ainsi, notre polygone a tous ses sommets égaux.
Le triangle $P_{i} P_{i+1} P_{i+2}$ est donc isocèle en $P_{i+1}$, de sorte que $P_{i} P_{i+1}=P_{i+1} P_{i+2}$. Deux côtés consécutifs étant de même longueur, notre polygone a donc tous ses côtés de même longueur, et il s'agit bien d'un polygone régulier.

|
{
"exam": "French_tests",
"problem_label": "5",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-2.jsonl",
"solution_match": "## Solution de l'exercice 4",
"tier": "T1",
"year": "2020"
}
|
Let $P_{1} P_{2} \ldots P_{2021}$ be a convex polygon with 2021 vertices such that, for each vertex $P_{i}$, the 2018 diagonals emanating from $P_{i}$ divide the angle $\widehat{P}_{i}$ into 2019 equal angles.
Prove that $P_{1} P_{2} \ldots P_{2021}$ is a regular polygon, that is, a polygon where all angles have the same measure and all sides have the same length.
|
$n^{\circ} 1$ As in the previous solution, we prove equalities (1) and (2) to deduce that $a_{i+1}-a_{i}=a_{i+3}-a_{i+2}$. If we set $\mathbf{c}=a_{2}-a_{1}$, an immediate induction proves that $a_{2 k}-a_{2 k-1}=\mathbf{c}$ for all integers $k \geqslant 1$.
Since our indices are considered modulo $n+2=2021$, which is odd, we deduce that $a_{i+1}-a_{i}=\mathbf{c}$ for all indices $i$. We conclude as before.
|
proof
|
Yes
|
Incomplete
|
proof
|
Geometry
|
Soit $P_{1} P_{2} \ldots P_{2021}$ un polygone convexe à 2021 sommets tel que, pour chaque sommet $P_{i}$, les 2018 diagonales issues de $P_{i}$ divisent l'angle $\widehat{P}_{i}$ en 2019 angles égaux.
Démontrer que $P_{1} P_{2} \ldots P_{2021}$ est un polygone régulier, c'est-à-dire un polygone dont tous les angles ont même mesure et tous les côtés ont même longueur.
|
$n^{\circ} 1$ Comme dans la solution précédente, on démontre les égalités (1) et (2) pour en déduire que $a_{i+1}-a_{i}=a_{i+3}-a_{i+2}$. Si l'on pose $\mathbf{c}=a_{2}-a_{1}$, une récurrence immédiate démontre alors que $a_{2 k}-a_{2 k-1}=\mathbf{c}$ pour tout entier $k \geqslant 1$.
Or, nos indices sont considérés modulo $n+2=2021$, qui est impair. On en déduit que $a_{i+1}-a_{i}=\mathbf{c}$ pour tout indice $i$. On conclut alors comme précédemment.
|
{
"exam": "French_tests",
"problem_label": "5",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-2.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2020"
}
|
Let $P_{1} P_{2} \ldots P_{2021}$ be a convex polygon with 2021 vertices such that, for each vertex $P_{i}$, the 2018 diagonals emanating from $P_{i}$ divide the angle $\widehat{P}_{i}$ into 2019 equal angles.
Prove that $P_{1} P_{2} \ldots P_{2021}$ is a regular polygon, that is, a polygon where all angles have the same measure and all sides have the same length.
|
$n^{\circ} 2$ As previously, we prove the equality (1). If we set $b_{i}=a_{i}-180^{\circ} /(n+2)$, this equality can be rewritten as $b_{i}+n b_{i+1}+b_{i+2}=0$.
The sequence $\left(b_{i}\right)_{i \geqslant 1}$ is therefore a linear recurrence. If we denote $r_{+}$ and $r_{-}$ the two roots of the polynomial $1+n X+X^{2}$, that is,
$$
r_{ \pm}=\frac{-n \pm \sqrt{n^{2}-4}}{2}
$$
there exist two numbers $\lambda_{+}$ and $\lambda_{-}$ such that
$$
b_{i}=\lambda_{+} r_{+}^{i}+\lambda_{-} r_{-}^{i}
$$
for all $i \geqslant 0$.
Since $n \geqslant 5$, we know that
$$
\left(n^{2}-4\right)-(n-2)^{2}=2(n-4)>0
$$
so that $r_{-} \leqslant-n / 2<-1<r_{+}<0$ and that we know $\left|r_{-}\right|>1>\left|r_{+}\right|$. Consequently, we know that, if $\lambda_{-} \neq 0$, the fraction $b_{i} /\left(\lambda_{-} r_{-}^{i}\right)$ tends to 1 as $i \rightarrow+\infty$. However, the sequence $\left(b_{i}\right)_{i \geqslant 1}$ is $(n+2)$-periodic. We deduce that $\lambda_{-}=0$.
Similarly, if $\lambda_{+} \neq 0$, the fraction $b_{i} /\left(\lambda_{+} r_{+}^{i}\right)$ tends to 1 as $i \rightarrow+\infty$, in contradiction with the $(n+2)$-periodic nature of the sequence $\left(b_{i}\right)_{i \geqslant 1}$. We deduce that $\lambda_{+}=0$, so that $b_{i}=0$ for all $i \geqslant 1$.
In conclusion, all the angles $a_{i}$ are equal, and we prove as previously that the sides of the polygon are equal as well.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $P_{1} P_{2} \ldots P_{2021}$ un polygone convexe à 2021 sommets tel que, pour chaque sommet $P_{i}$, les 2018 diagonales issues de $P_{i}$ divisent l'angle $\widehat{P}_{i}$ en 2019 angles égaux.
Démontrer que $P_{1} P_{2} \ldots P_{2021}$ est un polygone régulier, c'est-à-dire un polygone dont tous les angles ont même mesure et tous les côtés ont même longueur.
|
$n^{\circ} 2$ Comme précédemment, on démontre l'égalité (1). Si l'on pose $b_{i}=a_{i}-180^{\circ} /(n+2)$, cette égalité se réécrit comme $b_{i}+n b_{i+1}+b_{i+2}=0$.
La suite $\left(b_{i}\right)_{i \geqslant 1}$ est donc récurrente linéaire. Si l'on note $r_{+}$et $r_{-}$les deux racines du polynôme $1+n X+X^{2}$, c'est-à-dire
$$
r_{ \pm}=\frac{-n \pm \sqrt{n^{2}-4}}{2}
$$
il existe donc deux nombres $\lambda_{+}$et $\lambda_{-}$tels que
$$
b_{i}=\lambda_{+} r_{+}^{i}+\lambda_{-} r_{-}^{i}
$$
pour tout $i \geqslant 0$.
Puisque $n \geqslant 5$, on sait que
$$
\left(n^{2}-4\right)-(n-2)^{2}=2(n-4)>0
$$
donc que $r_{-} \leqslant-n / 2<-1<r_{+}<0$ et que on sait que $\left|r_{-}\right|>1>\left|r_{+}\right|$. Par conséquent, on sait que, si $\lambda_{-} \neq 0$, la fraction $b_{i} /\left(\lambda_{-} r_{-}^{i}\right)$ tend vers 1 quand $i \rightarrow+\infty$. Or, la suite $\left(b_{i}\right)_{i \geqslant 1}$ est $(n+2)$-périodique. On en déduit que $\lambda_{-}=0$.
De même, si $\lambda_{+} \neq 0$, la fraction $b_{i} /\left(\lambda_{+} r_{+}^{i}\right)$ tend vers 1 quand $i \rightarrow+\infty$, en contradiction avec le caractère $(n+2)$-périodique de la suite $\left(b_{i}\right)_{i \geqslant 1}$. On en déduit que $\lambda_{+}=0$, donc que $b_{i}=0$ pour tout $i \geqslant 1$.
En conclusion, tous les angles $a_{i}$ sont égaux, et on démontre comme précédemment que les côtés du polygone sont égaux eux aussi.
|
{
"exam": "French_tests",
"problem_label": "5",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-2.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2020"
}
|
Let $P_{1} P_{2} \ldots P_{2021}$ be a convex polygon with 2021 vertices such that, for each vertex $P_{i}$, the 2018 diagonals emanating from $P_{i}$ divide the angle $\widehat{P}_{i}$ into 2019 equal angles.
Prove that $P_{1} P_{2} \ldots P_{2021}$ is a regular polygon, that is, a polygon where all angles have the same measure and all sides have the same length.
|
$n^{\circ} 3$ As before, we prove the equality (1). By writing this equality for two consecutive integers $i$, and subtracting the two obtained equalities, we observe that
$$
a_{i}+(n-1) a_{i+1}-(n-1) a_{i+2}-a_{i+3}=0.
$$
The sequence $a_{i}$ is therefore linearly recurrent. This time, the roots of the polynomial
$$
1+(n-1) X-(n-1) X^{2}-X^{3}=(1-X)\left(1+n X+X^{2}\right)
$$
are $r_{\pm}$ and 1. Since $n \geqslant 5$, we know that
$$
\left(n^{2}-4\right)-(n-2)^{2}=2(n-4)>0
$$
so that $r_{-} \leqslant -n / 2 < -1 < r_{+} < 0 < 1$ and that $\left|r_{-}\right| > 1 > \left|r_{+}\right|$.
Therefore, there exist three numbers $\lambda_{+}, \lambda_{1}$, and $\lambda_{-}$ such that
$$
a_{i}=\lambda_{+} r_{+}^{i}+\lambda_{1}+\lambda_{-} r_{-}^{i}
$$
for all $i \in \mathbb{Z}$. As in the previous solution, we prove that $\lambda_{-}=0$. Similarly, if $\lambda_{+} \neq 0$, then $a_{i} / \left(\lambda_{+} r_{+}^{i}\right) \rightarrow 1$ as $i \rightarrow -\infty$, contradicting the periodicity of $\left(a_{i}\right)$. Thus, $\lambda_{+}=0.1$
[^0]In conclusion, all the angles $a_{i}$ are equal to $\lambda_{1}$, and we prove as before that the sides of the polygon are also equal.
Remark: This problem was proposed in 2003, at the First Year Mathematical Olympiads, in the Academy of Versailles, but with intermediate questions included. Out of the 623 candidates present in the academy, including two national laureates, none managed to solve this problem, which proved to be particularly difficult despite requiring few technical tools.
Comment from the graders: The problem, being difficult, was fully solved by only a very few students. Many students, however, managed to earn partial points by establishing interesting equations between the angles, or by showing that if all the angles of the polygon were equal, then all the sides of the polygon were also of the same length.
## Senior Problems
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $P_{1} P_{2} \ldots P_{2021}$ un polygone convexe à 2021 sommets tel que, pour chaque sommet $P_{i}$, les 2018 diagonales issues de $P_{i}$ divisent l'angle $\widehat{P}_{i}$ en 2019 angles égaux.
Démontrer que $P_{1} P_{2} \ldots P_{2021}$ est un polygone régulier, c'est-à-dire un polygone dont tous les angles ont même mesure et tous les côtés ont même longueur.
|
$n^{\circ} 3$ Comme précédemment, on démontre l'égalité (1). En écrivant cette égalité pour deux entiers $i$ consécutifs, et en soustrayant les deux égalités obtenues, on constate que
$$
a_{i}+(n-1) a_{i+1}-(n-1) a_{i+2}-a_{i+3}=0 .
$$
La suite $a_{i}$ est donc récurrente linéaire. Cette fois-ci, les racines du polynôme
$$
1+(n-1) X-(n-1) X^{2}-X^{3}=(1-X)\left(1+n X+X^{2}\right)
$$
sont $r_{ \pm}$et 1 . Puisque $n \geqslant 5$, on sait que
$$
\left(n^{2}-4\right)-(n-2)^{2}=2(n-4)>0
$$
donc que $r_{-} \leqslant-n / 2<-1<r_{+}<0<1$ et que on sait que $\left|r_{-}\right|>1>\left|r_{+}\right|$.
Il existe donc trois nombres $\lambda_{+}, \lambda_{1}$ et $\lambda_{-}$tels que
$$
a_{i}=\lambda_{+} r_{+}^{i}+\lambda_{1}+\lambda_{-} r_{-}^{i}
$$
pour tout $i \in \mathbb{Z}$. On démontre comme dans la solution précédente que $\lambda_{-}=0$. De même, si $\lambda_{+} \neq 0$, alors $a_{i} /\left(\lambda_{+} r_{+}^{i}\right) \rightarrow 1$ quand $i \rightarrow-\infty$, en contradiction avec le caractère périodique de $\left(a_{i}\right)$. Ainsi, $\lambda_{+}=0.1$
[^0]En conclusion, tous les angles $a_{i}$ sont égaux à $\lambda_{1}$, et on démontre comme précédemment que les côtés du polygone sont égaux eux aussi.
Remarque : Cet exercice avait été proposé en 2003, aux Olympiades mathématiques de première, dans l'académie de Versailles, mais en incluant des questions intermédiaires. Sur les 623 candidats présents dans l'académie, dont deux lauréats nationaux, aucun n'était parvenu à résoudre cet exercice, qui s'était donc révélé particulièrement difficile bien qu'abordable avec peu d'outils techniques.
Commentaire des correcteurs L'exercice, difficile, n'a été complètement résolu que par très peu d'élèves. Un grand nombre d'élèves ont tout de même réussi à obtenir des points partiels en établissant des équations intéressantes entre les angles, ou bien en montrant que, si tous les angles du polygone étaient égaux, alors tous les côtés du polygone étaient également de même longueur.
## Problèmes Senior
|
{
"exam": "French_tests",
"problem_label": "5",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-2.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2020"
}
|
Let $P_{1} P_{2} \ldots P_{2021}$ be a convex polygon with 2021 vertices such that, for each vertex $P_{i}$, the 2018 diagonals emanating from $P_{i}$ divide the angle $\widehat{P}_{i}$ into 2019 equal angles.
Prove that $P_{1} P_{2} \ldots P_{2021}$ is a regular polygon, that is, a polygon where all angles have the same measure and all sides have the same length.
|
In the following, we set \( n=2019 \) and, for any vertex \( P_{i} \), we denote \( a_{i} \) as the angle \( \widehat{P}_{i} / n \). Let \( P_{k} \), \( P_{k+1} \), \( P_{k+2} \), \( P_{k+3} \), and \( P_{k+4} \) be four consecutive vertices, with the indices of the vertices considered modulo \( n+2 \).
The sum of the angles in a triangle is \( 180^{\circ} \). By considering the triangles \( P_{i} P_{i+1} P_{i+2} \), \( P_{i} P_{i+1} P_{i+3} \), and \( P_{i} P_{i+1} P_{i+4} \), we observe that
\[
\begin{aligned}
a_{i} + n a_{i+1} + a_{i+2} & = 180^{\circ} \\
2 a_{i} + (n-1) a_{i+1} + a_{i+3} & = 180^{\circ} \\
3 a_{i} + (n-2) a_{i+1} + a_{i+4} & = 180^{\circ}
\end{aligned}
\]
We will then subtract these equations two by two:
\(\triangleright\) (1) - (2) indicates that \( a_{i+1} + a_{i+2} = a_{i} + a_{i+3} \), which means \( a_{i+1} - a_{i} = a_{i+3} - a_{i+2} \);
\(\triangleright\) (2) - (3) indicates that \( a_{i+1} + a_{i+3} = a_{i} + a_{i+4} \), which means \( a_{i+1} - a_{i} = a_{i+4} - a_{i+3} \).
We observe that \( a_{i+4} - a_{i+3} = a_{i+3} - a_{i+2} \). The difference between two consecutive angles \( a_{j} \) and \( a_{j+1} \) is therefore equal to a constant \(\mathbf{c}\).
This means that \( a_{i+k} = a_{i} + k \mathbf{c} \) for all integers \( i \) and \( k \). In particular, \( a_{1} = a_{n+3} = a_{1} + (n+2) \mathbf{c} \), so \(\mathbf{c} = 0^{\circ}\). Thus, our polygon has all its vertices equal.
The triangle \( P_{i} P_{i+1} P_{i+2} \) is therefore isosceles at \( P_{i+1} \), so that \( P_{i} P_{i+1} = P_{i+1} P_{i+2} \). Since two consecutive sides are of the same length, our polygon has all its sides of the same length, and it is indeed a regular polygon.
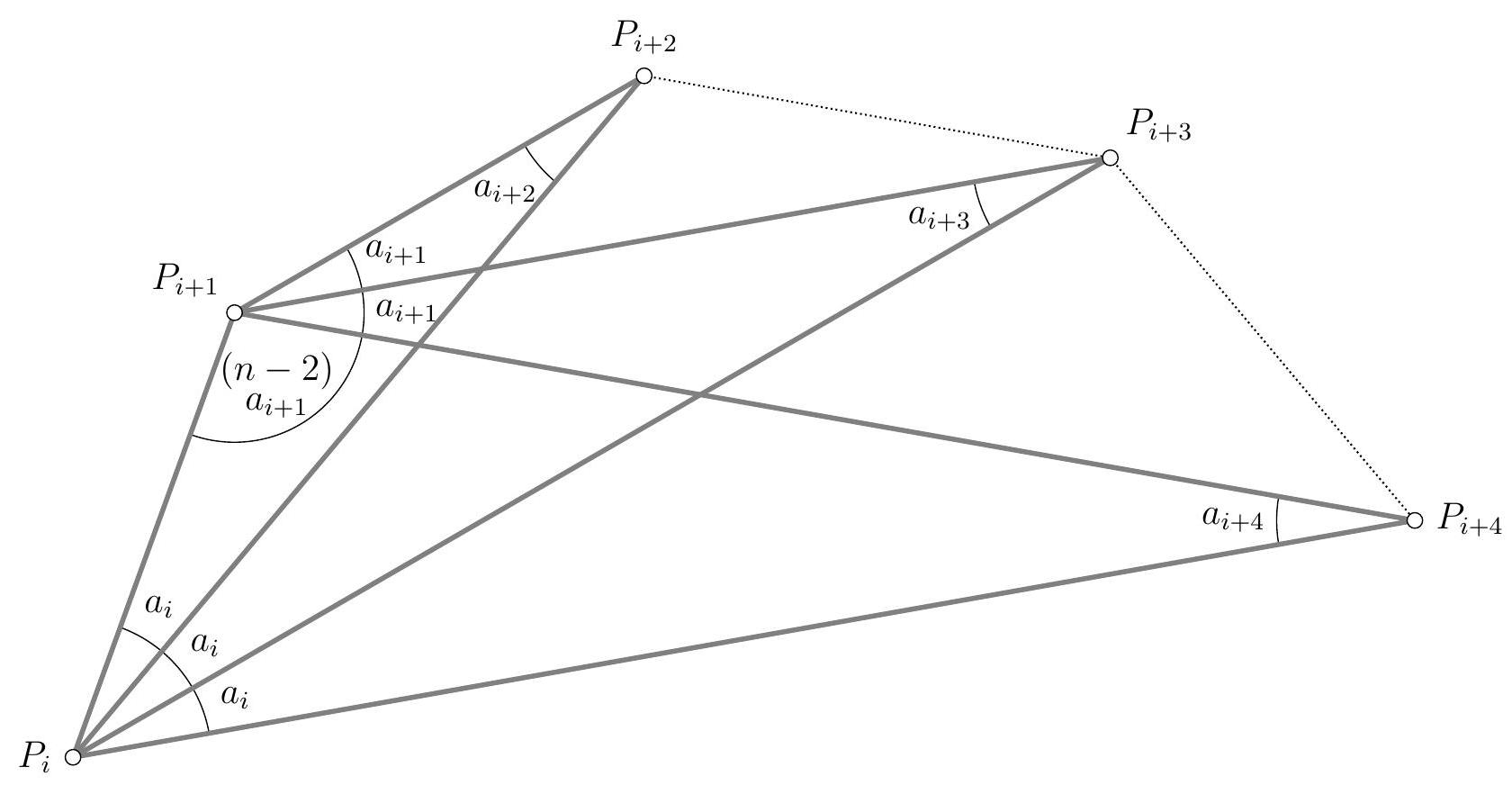
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $P_{1} P_{2} \ldots P_{2021}$ un polygone convexe à 2021 sommets tel que, pour chaque sommet $P_{i}$, les 2018 diagonales issues de $P_{i}$ divisent l'angle $\widehat{P}_{i}$ en 2019 angles égaux.
Démontrer que $P_{1} P_{2} \ldots P_{2021}$ est un polygone régulier, c'est-à-dire un polygone dont tous les angles ont même mesure et tous les côtés ont même longueur.
|
Dans la suite, on pose $n=2019$ et, pour tout sommet $P_{i}$, on note $a_{i}$ l'angle $\widehat{P}_{i} / n$. Soit alors $P_{k}$, $P_{k+1}, P_{k+2}, P_{k+3}$ et $P_{k+4}$ quatre sommets consécutifs, les indices des sommets étant considérés modulo $n+2$.
La somme des angles d'un triangle vaut $180^{\circ}$. En considérant respectivement les triangles $P_{i} P_{i+1} P_{i+2}, P_{i} P_{i+1} P_{i+3}$ et $P_{i} P_{i+1} P_{i+4}$, on constate que
$$
\begin{aligned}
a_{i}+n a_{i+1}+a_{i+2} & =180^{\circ} \\
2 a_{i}+(n-1) a_{i+1}+a_{i+3} & =180^{\circ} \\
3 a_{i}+(n-2) a_{i+1}+a_{i+4} & =180^{\circ}
\end{aligned}
$$
Nous allons alors soustraire deux à deux ces équations :
$\triangleright$ (1) - (2) indique que $a_{i+1}+a_{i+2}=a_{i}+a_{i+3}$, c'est-à-dire que $a_{i+1}-a_{i}=a_{i+3}-a_{i+2}$;
$\triangleright(2)-(3)$ indique que $a_{i+1}+a_{i+3}=a_{i}+a_{i+4}$, c'est-à-dire que $a_{i+1}-a_{i}=a_{i+4}-a_{i+3}$.
On constate donc que $a_{i+4}-a_{i+3}=a_{i+3}-a_{i+2}$. La différence entre deux angles $a_{j}$ et $a_{j+1}$ consécutifs est donc égale à une constante $\mathbf{c}$.
Cela signifie que $a_{i+k}=a_{i}+k \mathbf{c}$ pour tous les entiers $i$ et $k$. En particulier, $a_{1}=a_{n+3}=$ $a_{1}+(n+2) \mathbf{c}$, donc $\mathbf{c}=0^{\circ}$. Ainsi, notre polygone a tous ses sommets égaux.
Le triangle $P_{i} P_{i+1} P_{i+2}$ est donc isocèle en $P_{i+1}$, de sorte que $P_{i} P_{i+1}=P_{i+1} P_{i+2}$. Deux côtés consécutifs étant de même longueur, notre polygone a donc tous ses côtés de même longueur, et il s'agit bien d'un polygone régulier.

|
{
"exam": "French_tests",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-2.jsonl",
"solution_match": "## Solution de l'exercice 5",
"tier": "T1",
"year": "2020"
}
|
Let $P_{1} P_{2} \ldots P_{2021}$ be a convex polygon with 2021 vertices such that, for each vertex $P_{i}$, the 2018 diagonals emanating from $P_{i}$ divide the angle $\widehat{P}_{i}$ into 2019 equal angles.
Prove that $P_{1} P_{2} \ldots P_{2021}$ is a regular polygon, that is, a polygon where all angles have the same measure and all sides have the same length.
|
$n^{\circ} 1$ As in the previous solution, we prove equalities (1) and (2) to deduce that $a_{i+1}-a_{i}=a_{i+3}-a_{i+2}$. If we set $\mathbf{c}=a_{2}-a_{1}$, an immediate induction proves that $a_{2 k}-a_{2 k-1}=\mathbf{c}$ for all integers $k \geqslant 1$.
Since our indices are considered modulo $n+2=2021$, which is odd, we deduce that $a_{i+1}-a_{i}=\mathbf{c}$ for all indices $i$. We conclude as before.
|
proof
|
Yes
|
Incomplete
|
proof
|
Geometry
|
Soit $P_{1} P_{2} \ldots P_{2021}$ un polygone convexe à 2021 sommets tel que, pour chaque sommet $P_{i}$, les 2018 diagonales issues de $P_{i}$ divisent l'angle $\widehat{P}_{i}$ en 2019 angles égaux.
Démontrer que $P_{1} P_{2} \ldots P_{2021}$ est un polygone régulier, c'est-à-dire un polygone dont tous les angles ont même mesure et tous les côtés ont même longueur.
|
$n^{\circ} 1$ Comme dans la solution précédente, on démontre les égalités (1) et (2) pour en déduire que $a_{i+1}-a_{i}=a_{i+3}-a_{i+2}$. Si l'on pose $\mathbf{c}=a_{2}-a_{1}$, une récurrence immédiate démontre alors que $a_{2 k}-a_{2 k-1}=\mathbf{c}$ pour tout entier $k \geqslant 1$.
Or, nos indices sont considérés modulo $n+2=2021$, qui est impair. On en déduit que $a_{i+1}-a_{i}=\mathbf{c}$ pour tout indice $i$. On conclut alors comme précédemment.
|
{
"exam": "French_tests",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-2.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2020"
}
|
Let $P_{1} P_{2} \ldots P_{2021}$ be a convex polygon with 2021 vertices such that, for each vertex $P_{i}$, the 2018 diagonals emanating from $P_{i}$ divide the angle $\widehat{P}_{i}$ into 2019 equal angles.
Prove that $P_{1} P_{2} \ldots P_{2021}$ is a regular polygon, that is, a polygon where all angles have the same measure and all sides have the same length.
|
$n^{\circ} 2$ As previously, we prove the equality (1). If we set $b_{i}=a_{i}-180^{\circ} /(n+2)$, this equality can be rewritten as $b_{i}+n b_{i+1}+b_{i+2}=0$.
The sequence $\left(b_{i}\right)_{i \geqslant 1}$ is therefore a linear recurrence. If we denote $r_{+}$ and $r_{-}$ the two roots of the polynomial $1+n X+X^{2}$, that is,
$$
r_{ \pm}=\frac{-n \pm \sqrt{n^{2}-4}}{2}
$$
there exist two numbers $\lambda_{+}$ and $\lambda_{-}$ such that
$$
b_{i}=\lambda_{+} r_{+}^{i}+\lambda_{-} r_{-}^{i}
$$
for all $i \geqslant 0$.
Since $n \geqslant 5$, we know that
$$
\left(n^{2}-4\right)-(n-2)^{2}=2(n-4)>0
$$
so that $r_{-} \leqslant-n / 2<-1<r_{+}<0$ and that we know $\left|r_{-}\right|>1>\left|r_{+}\right|$. Consequently, we know that, if $\lambda_{-} \neq 0$, the fraction $b_{i} /\left(\lambda_{-} r_{-}^{i}\right)$ tends to 1 as $i \rightarrow+\infty$. However, the sequence $\left(b_{i}\right)_{i \geqslant 1}$ is $(n+2)$-periodic. We deduce that $\lambda_{-}=0$.
Similarly, if $\lambda_{+} \neq 0$, the fraction $b_{i} /\left(\lambda_{+} r_{+}^{i}\right)$ tends to 1 as $i \rightarrow+\infty$, in contradiction with the $(n+2)$-periodic nature of the sequence $\left(b_{i}\right)_{i \geqslant 1}$. We deduce that $\lambda_{+}=0$, so that $b_{i}=0$ for all $i \geqslant 1$.
In conclusion, all the angles $a_{i}$ are equal, and we prove as previously that the sides of the polygon are equal as well.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $P_{1} P_{2} \ldots P_{2021}$ un polygone convexe à 2021 sommets tel que, pour chaque sommet $P_{i}$, les 2018 diagonales issues de $P_{i}$ divisent l'angle $\widehat{P}_{i}$ en 2019 angles égaux.
Démontrer que $P_{1} P_{2} \ldots P_{2021}$ est un polygone régulier, c'est-à-dire un polygone dont tous les angles ont même mesure et tous les côtés ont même longueur.
|
$n^{\circ} 2$ Comme précédemment, on démontre l'égalité (1). Si l'on pose $b_{i}=a_{i}-180^{\circ} /(n+2)$, cette égalité se réécrit comme $b_{i}+n b_{i+1}+b_{i+2}=0$.
La suite $\left(b_{i}\right)_{i \geqslant 1}$ est donc récurrente linéaire. Si l'on note $r_{+}$et $r_{-}$les deux racines du polynôme $1+n X+X^{2}$, c'est-à-dire
$$
r_{ \pm}=\frac{-n \pm \sqrt{n^{2}-4}}{2}
$$
il existe donc deux nombres $\lambda_{+}$et $\lambda_{-}$tels que
$$
b_{i}=\lambda_{+} r_{+}^{i}+\lambda_{-} r_{-}^{i}
$$
pour tout $i \geqslant 0$.
Puisque $n \geqslant 5$, on sait que
$$
\left(n^{2}-4\right)-(n-2)^{2}=2(n-4)>0
$$
donc que $r_{-} \leqslant-n / 2<-1<r_{+}<0$ et que on sait que $\left|r_{-}\right|>1>\left|r_{+}\right|$. Par conséquent, on sait que, si $\lambda_{-} \neq 0$, la fraction $b_{i} /\left(\lambda_{-} r_{-}^{i}\right)$ tend vers 1 quand $i \rightarrow+\infty$. Or, la suite $\left(b_{i}\right)_{i \geqslant 1}$ est $(n+2)$-périodique. On en déduit que $\lambda_{-}=0$.
De même, si $\lambda_{+} \neq 0$, la fraction $b_{i} /\left(\lambda_{+} r_{+}^{i}\right)$ tend vers 1 quand $i \rightarrow+\infty$, en contradiction avec le caractère $(n+2)$-périodique de la suite $\left(b_{i}\right)_{i \geqslant 1}$. On en déduit que $\lambda_{+}=0$, donc que $b_{i}=0$ pour tout $i \geqslant 1$.
En conclusion, tous les angles $a_{i}$ sont égaux, et on démontre comme précédemment que les côtés du polygone sont égaux eux aussi.
|
{
"exam": "French_tests",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-2.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2020"
}
|
Let $P_{1} P_{2} \ldots P_{2021}$ be a convex polygon with 2021 vertices such that, for each vertex $P_{i}$, the 2018 diagonals emanating from $P_{i}$ divide the angle $\widehat{P}_{i}$ into 2019 equal angles.
Prove that $P_{1} P_{2} \ldots P_{2021}$ is a regular polygon, that is, a polygon where all angles have the same measure and all sides have the same length.
|
$n^{\circ} 3$ As previously, we prove the equality (1). By writing this equality for two consecutive integers $i$, and subtracting the two obtained equalities, we observe that
$$
a_{i}+(n-1) a_{i+1}-(n-1) a_{i+2}-a_{i+3}=0 .
$$
The sequence $a_{i}$ is therefore linearly recurrent. This time, the roots of the polynomial
$$
1+(n-1) X-(n-1) X^{2}-X^{3}=(1-X)\left(1+n X+X^{2}\right)
$$
are $r_{ \pm}$ and 1. Since $n \geqslant 5$, we know that
$$
\left(n^{2}-4\right)-(n-2)^{2}=2(n-4)>0
$$
so that $r_{-} \leqslant-n / 2<-1<r_{+}<0<1$ and that $\left|r_{-}\right|>1>\left|r_{+}\right|$.
There therefore exist three numbers $\lambda_{+}, \lambda_{1}$ and $\lambda_{-}$ such that
$$
a_{i}=\lambda_{+} r_{+}^{i}+\lambda_{1}+\lambda_{-} r_{-}^{i}
$$
for all $i \in \mathbb{Z}$. As in the previous solution, we prove that $\lambda_{-}=0$. Similarly, if $\lambda_{+} \neq 0$, then $a_{i} /\left(\lambda_{+} r_{+}^{i}\right) \rightarrow 1$ as $i \rightarrow-\infty$, in contradiction with the periodicity of $\left(a_{i}\right)$. Thus, $\lambda_{+}=0 .{ }^{2}$
2. One could also consider the periodicity of the sequence $a_{i}-\lambda_{1}$, but then we would fall back into the alternative solution $\mathrm{n}^{\circ} 2$.
In conclusion, all the angles $a_{i}$ are equal to $\lambda_{1}$, and we prove as previously that the sides of the polygon are equal as well.
Remark: This exercise was proposed in 2003, at the first-year Mathematical Olympiads, in the Academy of Versailles, but with intermediate questions included. Out of the 623 candidates present in the academy, including two national laureates, none managed to solve this exercise, which thus proved to be particularly difficult despite requiring few technical tools.
Comment from the graders: The exercise was solved by a large number of students. Almost all students managed to obtain at least partial points by establishing interesting equations between the angles associated with two or three consecutive vertices. However, here are several frequent errors:
$\triangleright$ A non-negligible portion of students stop after showing that all angles are equal. This, however, is not enough to show that the polygon is regular, as it is also necessary to show that all lengths are equal.
$\triangleright$ Some students provided the following reasoning: they start from the configuration of the regular polygon and show that it is not possible, by moving the vertices from this configuration while respecting the hypothesis of the statement, to obtain another polygon that satisfies the condition. However, this reasoning relies on continuity assumptions that have no basis, and therefore does not show that there are no other polygons that satisfy the property given by the statement. Often, the transformations proposed do not allow moving from a square to a non-square rhombus, although both quadrilaterals satisfy the condition of the statement.
$\triangleright$ Many students content themselves with treating the case of the pentagon instead of the 2021-gon and say that the result can be easily extended to the case of the 2021-gon. While a large part of their reasoning is indeed applicable to solving the case $n=2021$, one aspect of the problem is precisely to be able to fully generalize the reasoning on small polygons. Therefore, to be fully convincing, the proof should have been redone in the general case. Indeed, often the reasoning on the pentagon produced equations relating the angles to each other that were much simpler than the general case.
$\triangleright$ Some students content themselves with noting that there are many equations between the angles and that one therefore has a system with 2021 equations and 2021 unknowns, before asserting that such a system always admits a unique solution (here, the constant solution). However, it was necessary to specify the 2021 equations involved (too many students only note that there are more than 2021 equations) and show that these equations were independent of each other. The fact that a linear system of 2021 equations and 2021 unknowns admits a unique solution is only true in this context.
Other students, after stating the system, assert that "after calculations," the unique solution is given by all angles being equal. But this assertion is far from convincing without the calculations to support it.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $P_{1} P_{2} \ldots P_{2021}$ un polygone convexe à 2021 sommets tel que, pour chaque sommet $P_{i}$, les 2018 diagonales issues de $P_{i}$ divisent l'angle $\widehat{P}_{i}$ en 2019 angles égaux.
Démontrer que $P_{1} P_{2} \ldots P_{2021}$ est un polygone régulier, c'est-à-dire un polygone dont tous les angles ont même mesure et tous les côtés ont même longueur.
|
$n^{\circ} 3$ Comme précédemment, on démontre l'égalité (1). En écrivant cette égalité pour deux entiers $i$ consécutifs, et en soustrayant les deux égalités obtenues, on constate que
$$
a_{i}+(n-1) a_{i+1}-(n-1) a_{i+2}-a_{i+3}=0 .
$$
La suite $a_{i}$ est donc récurrente linéaire. Cette fois-ci, les racines du polynôme
$$
1+(n-1) X-(n-1) X^{2}-X^{3}=(1-X)\left(1+n X+X^{2}\right)
$$
sont $r_{ \pm}$et 1 . Puisque $n \geqslant 5$, on sait que
$$
\left(n^{2}-4\right)-(n-2)^{2}=2(n-4)>0
$$
donc que $r_{-} \leqslant-n / 2<-1<r_{+}<0<1$ et que on sait que $\left|r_{-}\right|>1>\left|r_{+}\right|$.
Il existe donc trois nombres $\lambda_{+}, \lambda_{1}$ et $\lambda_{-}$tels que
$$
a_{i}=\lambda_{+} r_{+}^{i}+\lambda_{1}+\lambda_{-} r_{-}^{i}
$$
pour tout $i \in \mathbb{Z}$. On démontre comme dans la solution précédente que $\lambda_{-}=0$. De même, si $\lambda_{+} \neq 0$, alors $a_{i} /\left(\lambda_{+} r_{+}^{i}\right) \rightarrow 1$ quand $i \rightarrow-\infty$, en contradiction avec le caractère périodique de $\left(a_{i}\right)$. Ainsi, $\lambda_{+}=0 .{ }^{2}$
2. On pourrait aussi considérer le caractère périodique de la suite $a_{i}-\lambda_{1}$, mais alors on retomberait dans la solution alternative $\mathrm{n}^{\circ} 2$.
En conclusion, tous les angles $a_{i}$ sont égaux à $\lambda_{1}$, et on démontre comme précédemment que les côtés du polygone sont égaux eux aussi.
Remarque : Cet exercice avait été proposé en 2003, aux Olympiades mathématiques de première, dans l'académie de Versailles, mais en incluant des questions intermédiaires. Sur les 623 candidats présents dans l'académie, dont deux lauréats nationaux, aucun n'était parvenu à résoudre cet exercice, qui s'était donc révélé particulièrement difficile bien qu'abordable avec peu d'outils techniques.
Commentaire des correcteurs L'exercice a été résolu par un grand nombre d'élèves. Pratiquement tous les élèves ont su obtenir au moins des points partiels en établissant des équations intéressantes entre les angles associés à deux ou trois sommets consécutifs. Voici cependant plusieurs erreurs rencontrées fréquemment:
$\triangleright$ Une partie non négligeable des élèves s'arrête après avoir montré que tous les angles sont égaux. Cela ne suffit pourtant pas à montrer que le polygone est régulier, puisqu'il faut aussi montrer que toutes les longueurs sont égales.
$\triangleright$ Quelques élèves ont donné le raisonnement suivant : ils partent de la configuration du polygone régulier et montrent qu'il n'est pas possible, en bougeant les sommets à partir de cette configuration de manière à respecter l'hypothèse de l'énoncé, d'obtenir un autre polygone respectant la condition. Cependant ce raisonnement repose sur des hypothèses de continuité qui n'ont aucune raison d'être, et ne permet donc pas de montrer qu'il n'existe pas d'autres polygones respectant la propriété donnée par l'énoncé. Bien souvent, les transformations proposées ne permettent pas de passer du carré au losange non carré, alors que les deux quadrilatères respectent la condition de l'énoncé.
$\triangleright$ Beaucoup d'élèves se contentent de traiter le cas du pentagone au lieu du 2021-gone et disent qu'on étend aisément le résultat pour le cas du 2021-gone. Si une grande partie de leurs raisonnement est effectivement utilisable pour la résolution du cas $n=2021$, l'un des aspects du problème est justement d'être capable de généraliser complètement le raisonnement sur des petits polygones. Il fallait donc, pour être parfaitement convaincant, effectuer de nouveau la preuve dans le cas général. En effet, bien souvent, le raisonnement sur le pentagone produisait des équations reliant les angles entre eux qui étaient beaucoup plus simples que le cas général.
$\triangleright$ Quelques élèves se contentent de signaler qu'il y a beaucoup d'équations entre les angles et qu'on a donc un système avec 2021 équations à 2021 inconnues, avant d'affirmer qu'un tel système admet toujours une unique solution (ici, la solution constante). Mais il fallait alors préciser les 2021 équations mises en jeu (trop d'élèves ne font que signaler qu'il y a bien plus que 2021 équations) et montrer que ces équations étaient indépendantes les unes des autres. Le fait qu'un système linéaire de 2021 équations à 2021 inconnues admet une unique solution n'est vrai que dans ce cadre.
D'autres élèves, après avoir énoncé le système, affirment que « après calculs », l'unique solution est donnée par des angles tous égaux. Mais cette affirmation est loin d'être convaincante sans les calculs à l'appui.
|
{
"exam": "French_tests",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-2.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2020"
}
|
The sequences $\left(a_{n}\right)_{n \geqslant 0}$ and $\left(b_{n}\right)_{n \geqslant 0}$ are defined by
$$
\left\{\begin{array} { l l }
{ a _ { n } = 0 } & { \text { if } n = 0 ; } \\
{ a _ { n } = 2 a _ { \lfloor n / 2 \rfloor } + n } & { \text { if } n \geqslant 1 ; }
\end{array} \quad \text { and } \quad \left\{\begin{array}{ll}
b_{n}=0 & \text { if } n=0 ; \\
b_{n}=3 b_{\lfloor n / 3\rfloor}+n & \text { if } n \geqslant 1 .
\end{array}\right.\right.
$$
Prove that the sequence with general term $2^{a_{n}}-3^{b_{n}}$ changes sign infinitely often.
|
First, we show by induction on $n$ that $a_{n} \leqslant n\left\lfloor\log _{2}(2 n)\right\rfloor$ for all integers $n \geqslant 1$, with equality when $n$ is a power of 2. Indeed, for $n=1$, we have $a_{n}=1=n \log _{2}(2 n)$. Then, if $n \geqslant 2$,
$$
a_{n}=2 a_{\lfloor n / 2\rfloor}+n \leqslant 2\lfloor n / 2\rfloor\left\lfloor\log _{2}(2\lfloor n / 2\rfloor)\right\rfloor+n \leqslant n\left\lfloor\log _{2}(n)+1\right\rfloor=n\left\lfloor\log _{2}(2 n)\right\rfloor \text {, }
$$
with equality when $n / 2=\lfloor n / 2\rfloor$ and $n / 2$ is a power of 2.
Similarly, we show that $b_{n} \leqslant n\left\lfloor\log _{3}(3 n)\right\rfloor$ for all integers $n \geqslant 1$, with equality when $n$ is a power of 3. We already deduce, if $n$ is a power of 3, that
$$
2^{a_{n}}-3^{b_{n}}=2^{a_{n}}-(3 n)^{n} \leqslant(2 n)^{n}-(3 n)^{n}<0 .
$$
Conversely, let $k$ and $\ell$ be two non-zero natural numbers such that $2^{\ell}<3^{k} \leqslant 2^{\ell+1}$, and let $n=2^{\ell}$. Then $k \log _{2}(3) \leqslant \ell+1$, so
$$
\log _{2}(3) b_{n} \leqslant \log _{2}(3) n\left\lfloor\log _{3}(3 n)\right\rfloor=\log _{2}(3) k n \leqslant(\ell+1) n=a_{n}
$$
so that $2^{a_{n}}-3^{b_{n}}=2^{a_{n}}-2^{\log _{2}(3) b_{n}} \geqslant 0$. Since $2^{a_{n}} \neq 3^{b_{n}}$, as one is odd and the other is not, we deduce that $2^{a_{n}}-3^{b_{n}}>0$, which concludes this solution.
Remark: In fact, we could have shown that, if
$$
n=\sum_{k \geqslant 0} \alpha_{k} 2^{k}=\sum_{\ell \geqslant 0} \beta_{\ell} 3^{\ell},
$$
then
$$
a_{n}=\sum_{k \geqslant 0}(k+1) \alpha_{k} 2^{k} \text { and } b_{n}=\sum_{\ell \geqslant 0}(\ell+1) \beta_{\ell} 3^{\ell} .
$$
Remark: It would have been tempting to show that $2^{a_{n}}>3^{b_{n}}$ as soon as $n$ is a power of 2 or $n+1$ is a power of 3. However, this is not the case: by noting $\langle x\rangle$ the fractional part of a real number $x$, i.e., $\langle x\rangle=x-\lfloor x\rfloor$, we can in fact show that $2^{a_{n}}<3^{b_{n}}$ as soon as $\left\langle\log _{3}(n)\right\rangle<7 / 100$ or $\left\langle\log _{2}(n)\right\rangle>98 / 100$.
Examiner's Comment: This problem was difficult, and only five students solved it completely. In practice, many students had good ideas but stopped halfway, instead of stepping back to see how to generalize or exploit their discoveries. Thus,
$\triangleright$ Several students empirically noticed and proved that the value of $a_{n+1}-a_{n}$ depended on the 2-adic valuation of $n$, deriving horrible sums for the expression of $a_{n}$, whereas using a double-counting method, they could have obtained the rather cute expressions given above.
$\triangleright$ Many students empirically noticed that $a_{n}$ grew quickly when $n$ was a power of 2, and thus expressed their desire to prove that $2^{a_{n}}>3^{b_{n}}$ when $n$ was a power of 2. However, they stopped there, or simply verified that $a_{n}=n\left(1+\log _{2}(n)\right)$ when $n$ is a power of 2, but did not think to look for an upper bound for the term $b_{n}$ when $n$ is any number.
$\triangleright$ Several students, after successfully proving that $3^{b_{n}}>2^{a_{n}}$ when $n$ was a power of 3, conjectured and tried to prove that $2^{a_{n}}>3^{b_{n}}$ when $n$ was a power of 2. Unfortunately for them, this was the main (and particularly insidious!) difficulty of the problem, since this tempting conjecture was invalid, the first counterexample being $n=2^{8}$.
This is where it would have been useful to step back to see where the proof of this conjecture failed, before refining it to focus simultaneously on integers $n$ for which $a_{n}$ is "large" (i.e., $n$ is not much larger than a power of 2) and $b_{n}$ is "small" (i.e., $n$ is not much smaller than a power of 3). The students who had this idea all did very well.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Les suites $\left(a_{n}\right)_{n \geqslant 0}$ et $\left(b_{n}\right)_{n \geqslant 0}$ sont définies par
$$
\left\{\begin{array} { l l }
{ a _ { n } = 0 } & { \text { si } n = 0 ; } \\
{ a _ { n } = 2 a _ { \lfloor n / 2 \rfloor } + n } & { \text { si } n \geqslant 1 ; }
\end{array} \quad \text { et } \quad \left\{\begin{array}{ll}
b_{n}=0 & \text { si } n=0 ; \\
b_{n}=3 b_{\lfloor n / 3\rfloor}+n & \text { si } n \geqslant 1 .
\end{array}\right.\right.
$$
Démontrer que la suite de terme général $2^{a_{n}}-3^{b_{n}}$ change de signe infiniment souvent.
|
On montre tout d'abord, par récurrence sur $n$, que $a_{n} \leqslant n\left\lfloor\log _{2}(2 n)\right\rfloor$ pour tout entier $n \geqslant 1$, avec égalité lorsque $n$ est une puissance de 2 . En effet, pour $n=1$, on a bien $a_{n}=1=n \log _{2}(2 n)$. Puis, si $n \geqslant 2$,
$$
a_{n}=2 a_{\lfloor n / 2\rfloor}+n \leqslant 2\lfloor n / 2\rfloor\left\lfloor\log _{2}(2\lfloor n / 2\rfloor)\right\rfloor+n \leqslant n\left\lfloor\log _{2}(n)+1\right\rfloor=n\left\lfloor\log _{2}(2 n)\right\rfloor \text {, }
$$
avec égalité lorsque $n / 2=\lfloor n / 2\rfloor$ et $n / 2$ est une puissance de 2 .
On montre de même que $b_{n} \leqslant n\left\lfloor\log _{3}(3 n)\right\rfloor$ pour tout entier $n \geqslant 1$, avec égalité lorsque $n$ est une puissance de 3 . On en déduit déjà, si $n$ est une puissance de 3 , que
$$
2^{a_{n}}-3^{b_{n}}=2^{a_{n}}-(3 n)^{n} \leqslant(2 n)^{n}-(3 n)^{n}<0 .
$$
Réciproquement, soit $k$ et $\ell$ deux entiers naturels non nuls tels que $2^{\ell}<3^{k} \leqslant 2^{\ell+1}$, et soit $n=2^{\ell}$. Alors $k \log _{2}(3) \leqslant \ell+1$, donc
$$
\log _{2}(3) b_{n} \leqslant \log _{2}(3) n\left\lfloor\log _{3}(3 n)\right\rfloor=\log _{2}(3) k n \leqslant(\ell+1) n=a_{n}
$$
de sorte que $2^{a_{n}}-3^{b_{n}}=2^{a_{n}}-2^{\log _{2}(3) b_{n}} \geqslant 0$. Puisque $2^{a_{n}} \neq 3^{b_{n}}$, car l'un est impair et l'autre non, on en déduit que $2^{a_{n}}-3^{b_{n}}>0$, ce qui conclut cette solution.
Remarque: On pouvait en fait démontrer que, si
$$
n=\sum_{k \geqslant 0} \alpha_{k} 2^{k}=\sum_{\ell \geqslant 0} \beta_{\ell} 3^{\ell},
$$
alors
$$
a_{n}=\sum_{k \geqslant 0}(k+1) \alpha_{k} 2^{k} \text { et } b_{n}=\sum_{\ell \geqslant 0}(\ell+1) \beta_{\ell} 3^{\ell} .
$$
Remarque: Il eût été tentant de démontrer que $2^{a_{n}}>3^{b_{n}}$ dès lors que $n$ est une puissance de 2 ou que $n+1$ est une puissance de 3 . Cependant, il n'en est rien : en notant $\langle x\rangle$ la partie fractionnaire d'un réel $x$, c'est-à-dire $\langle x\rangle=x-\lfloor x\rfloor$, on peut en fait démontrer que $2^{a_{n}}<3^{b_{n}}$ dès lors que $\left\langle\log _{3}(n)\right\rangle<7 / 100$ ou que $\left\langle\log _{2}(n)\right\rangle>98 / 100$.
Commentaire des correcteurs Cet exercice était difficile, et seuls cinq élèves l'ont intégralement résolu. En pratique, de nombreux élèves ont eu de bonnes idées mais se sont arrêtés en cours de route, au lieu de prendre du recul pour voir comment généraliser ou exploiter leurs découvertes. Ainsi,
$\triangleright$ Plusieurs élèves ont remarqué empiriquement, puis démontré, que la valeur de $a_{n+1}-$ $a_{n}$ dépendait de la valuation 2-adique de $n$, en déduisant des sommes horribles pour l'expression de $a_{n}$, alors qu'en utiisant un double-comptage, ils auraient pu obtenir les expressions somme toute mignonnes obtenues ci-dessus.
$\triangleright$ De nombreux élèves ont remarqué empiriquement que $a_{n}$ croissait vite quand $n$ était une puissance de 2, et ont donc exprimé leur envie de démontrer que $2^{a_{n}}>3^{b_{n}}$ quand $n$ était une puissance de 2 . Cependant, ils se sont arrêtés là, ou bien se sont contentés de vérifier que $a_{n}=n\left(1+\log _{2}(n)\right)$ quand $n$ est une puissance de 2, mais n'ont pas pensé à rechercher de borne supérieure pour le terme $b_{n}$ quand $n$ est un nombre quelconque.
$\triangleright$ Plusieurs élèves, après avoir réussi à démontrer que $3^{b_{n}}>2^{a_{n}}$ lorsque $n$ était une puissance de 3 , ont conjecturé et cherché à démontrer que $2^{a_{n}}>3^{b_{n}}$ lorsque $n$ était une puissance de 2 . Malheureusement pour eux, là résidait la difficulté principale (et particulièrement sournoise!) du problème, puisque cette conjecture pourtant très tentante était invalide, le premier contre-exemple étant $n=2^{8}$.
C'est là qu'il aurait été utile de prendre du recul pour voir où la preuve de cette conjecture pêchait, avant de l'affiner pour se concentrer simultanément sur les entiers $n$ pour lesquels $a_{n}$ est « grand » (c'est-à-dire que $n$ n'est pas beaucoup plus grand qu'une puissance de 2) et $b_{n}$ est « petit » (c'est-à-dire que $n$ n'est pas beaucoup plus petit qu'une puissance de 3). Les élèves qui ont eu cette idée s'en sont tous tirés avec brio.
|
{
"exam": "French_tests",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-2.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T1",
"year": "2020"
}
|
Morgane wrote the three integers 3, 4, and 12 on the board. She then makes successive changes as follows: she chooses two numbers $a$ and $b$ written on the board, erases them, and replaces them with $(3a + 4b) / 5$ and $(4a - 3b) / 5$.
Can Morgane, after a finite number of such changes,
a) manage to write the number 13 on the board?
b) manage to write the number -12 on the board?
|
We will show that the answer is negative in both cases. Let $\mathcal{S}$ be the sum of the squares of the numbers written on the board, and let $f$ and $g$ be the functions defined by $f:(x, y) \rightarrow(3 x+4 y) / 5$ and $g:(x, y) \rightarrow(4 x-3 y) / 5$. The relation
$$
f(x, y)^{2}+g(x, y)^{2}=x^{2}+y^{2}
$$
ensures that, when Morgane replaces two numbers $a$ and $b$ with $f(a, b)$ and $g(a, b)$, she does not change the value of $\mathcal{S}$.
Moreover, the equalities $f(f(x, y), g(x, y))=x$ and $g(f(x, y), g(x, y))=y$ indicate that the changes Morgane makes are reversible: if she transforms an unordered triplet $\mathbf{t}=(a, b, c)$ into another triplet $\mathbf{t}^{\prime}=\left(a^{\prime}, b^{\prime}, c\right)$ such that $a^{\prime}=f(a, b)$ and $b^{\prime}=g(a, b)$, she can retransform $\mathbf{t}^{\prime}$ into $\mathbf{t}$.
We now treat the two questions separately.
a) If she ever manages to write three numbers $x, y$ and $z$ such that $z=13$, then
$$
x^{2}+y^{2}+13^{2}=x^{2}+y^{2}+z^{2}=\mathcal{S}=3^{2}+4^{2}+12^{2}=13^{2}
$$
so that $x=y=0$. This means that Morgane can transform, in several steps, the triplet $(3,4,12)$ into $(0,0,13)$. She can therefore also transform $(0,0,13)$ and $(3,4,12)$.
We then say that a triplet $(x, y, z)$ of rational numbers is sympathetic if $v_{13}(u) \geqslant 1$ for all $u \in\{x, y, z\}$. If Morgane transforms a sympathetic triplet $(x, y, z)$ into a new triplet $\left(x^{\prime}, y^{\prime}, z^{\prime}\right)$, the latter is clearly sympathetic as well. Thus, starting from the sympathetic triplet $(0,0,13)$, Morgane can only obtain sympathetic triplets. She cannot therefore obtain the triplet $(3,4,12)$. This proves that she could not transform the triplet $(3,4,12)$ into $(0,0,13)$.
b) We will even show that Morgane cannot write any integer other than the elements of the set $\Omega=\{0, \pm 3, \pm 4, \pm 5,12\} \cdot{ }^{3}$
Consider an ordered triplet ( $x_{1}, x_{2}, x_{3}$ ). For all integers $i$ and $j$ distinct from each other, we denote $\Theta_{i, j}\left(x_{1}, x_{2}, x_{3}\right)$ the triplet obtained from $\left(x_{1}, x_{2}, x_{3}\right)$ by replacing the numbers $x_{i}$ and $x_{j}$ with $f\left(x_{i}, x_{j}\right)$ and $g\left(x_{i}, x_{j}\right)$. Furthermore, we say that $\left(x_{1}, x_{2}, x_{3}\right)$ is of order $n$ if $\min \left\{v_{5}\left(x_{1}\right), v_{5}\left(x_{2}\right), v_{5}\left(x_{3}\right)\right\}=-n$, and that it is an egalitarian triplet if there are at least two indices $i$ such that $v_{5}\left(x_{i}\right)=-n$.
Any triplet of order $n \geqslant 1$ that Morgane obtains is egalitarian. Indeed, suppose this is not the case. Without loss of generality, we have $v_{5}\left(x_{1}\right)=-n, v_{5}\left(x_{2}\right) \geqslant 1-n$ and $v_{5}\left(x_{3}\right) \geqslant 1-n$. Then, by setting $X_{i}=5^{n} x_{i}$, we observe that $X_{1} \not \equiv 0(\bmod 5)$ and that $X_{2} \equiv X_{3} \equiv 0(\bmod 5)$, so that
$$
0 \equiv 5^{2 n} \times 13^{2} \equiv 5^{2 n}\left(x_{1}^{2}+x_{2}^{2}+x_{3}^{2}\right) \equiv X_{1}^{2}+X_{2}^{2}+X_{3}^{2} \equiv X_{1}^{2} \not \equiv 0 \quad(\bmod 5),
$$
which is absurd.
3. This would also answer question a), but in a much more complicated way.
Let then $n \geqslant 0$ be an integer, and $\left(x_{1}, x_{2}, x_{3}\right)$ and $\left(y_{1}, y_{2}, y_{3}\right)$ be two triplets of orders $\ell \leqslant n$ and $n+1$ that Morgane can obtain successively. There exist two integers $i$ and $j$ such that $\Theta_{i, j}\left(x_{1}, x_{2}, x_{3}\right)=\left(y_{1}, y_{2}, y_{3}\right)$, and the triplet $\left(y_{1}, y_{2}, y_{3}\right)$ is egalitarian. By denoting $k$ the element of $\{1,2,3\}$ other than $i$ and $j$, and $X_{u}=5^{n} x_{u}$ and $Y_{u}=5^{n+1} y_{u}$ for all $u \in\{1,2,3\}$, we observe that
$$
Y_{i}=3 X_{i}+4 X_{j} \not \equiv 0(\bmod 5), Y_{j}=4 X_{i}-3 X_{j} \not \equiv 0(\bmod 5) \text { and } Y_{k} \equiv 0(\bmod 5) .
$$
We immediately deduce that the triplets $\Theta_{i, k}\left(y_{1}, y_{2}, y_{3}\right)$, $\Theta_{j, k}\left(y_{1}, y_{2}, y_{3}\right)$, $\Theta_{k, i}\left(y_{1}, y_{2}, y_{3}\right)$ and $\Theta_{k, j}\left(y_{1}, y_{2}, y_{3}\right)$ are all of order $n+2$. Similarly,
$$
f\left(y_{j}, y_{i}\right)=\left(24 X_{i}+7 X_{j}\right) / 5^{n+2} \text { and } g\left(y_{j}, y_{i}\right)=\left(7 X_{i}-24 X_{j}\right) / 5^{n+2}
$$
Since $24 X_{i}+7 X_{j} \equiv Y_{j}(\bmod 5)$ and $7 X_{i}-24 X_{j} \equiv-Y_{i}(\bmod 5)$, the triplet $\Theta_{j, i}\left(y_{1}, y_{2}, y_{3}\right)$ is also of order $n+2$. Finally, as in solution $\mathrm{n}^{\circ} 1$, we easily verify that $\Theta_{i, j}$ is an involution, so that $\Theta_{i, j}\left(y_{1}, y_{2}, y_{3}\right)$ is of order $\ell \leqslant n$.
To finish, let $\mathbf{T}$ be a triplet, with at least one integer coordinate $x$, that Morgane can write. Suppose that Morgane has successively written triplets $\mathbf{T}_{0}, \ldots, \mathbf{T}_{k}$ such that $\mathbf{T}_{0}=(3,4,12)$ and $\mathbf{T}_{k}=\mathbf{T}$ is with integer coordinates, with $k$ minimal.
Let $\mathbf{T}_{i}$ be a triplet of maximal order $n$ among the triplets $\mathbf{T}_{0}, \ldots, \mathbf{T}_{k}$. If $n \geqslant 1$ and if $i \leqslant k-1$, we have just shown that $\mathbf{T}_{i-1}=\mathbf{T}_{i+1}$, which contradicts the minimality of $k$. If $n \geqslant 1$ and if $i=k$, then $\mathbf{T}_{k}$ contains a coordinate already present in $\mathbf{T}_{k-1}$ and two coordinates of 5-adic valuation equal to $-n$, distinct from $x$. This again contradicts the minimality of $k$.
It now suffices to show that, starting from a triplet $\mathbf{t}=\left(x_{1}, x_{2}, x_{3}\right)$ of elements of $\Omega$ such that $x_{1}^{2}+x_{2}^{2}+x_{3}^{2}=13^{2}$, any triplet $\mathbf{t}^{\prime}=\left(y_{1}, y_{2}, y_{3}\right)$ with integer coordinates that Morgane can form has coordinates in $\Omega$. First, we can assume without loss of generality that $\left|x_{1}\right| \leqslant\left|x_{2}\right| \leqslant\left|x_{3}\right|$, so that $3 \times 5^{2}<13^{2} \leqslant 3 x_{3}^{2}$, hence $x_{3}=12$ and $\left(x_{1}, x_{2}\right) \in\{(0, \pm 5),( \pm 3, \pm 4)\}$.
We then assume that $\mathbf{t}^{\prime}$ has an integer coordinate that does not belong to $\Omega$. Let $i$ and $j$ be the integers such that $\mathbf{t}^{\prime}=\Theta_{i, j}(\mathbf{t})$. If $\left\{x_{i}, x_{j}\right\} \subseteq\{0, \pm 3, \pm 4, \pm 5\}$, then $y_{i}^{2}+y_{j}^{2}=x_{i}^{2}+x_{j}^{2}=5^{2}$, so $\left\{y_{i}, y_{j}\right\} \subseteq \Omega$. Thus, one of the two integers $x_{i}$ and $x_{j}$ is equal to 12. Now,
$$
0 \equiv 5 y_{i} \equiv 3 x_{i}+4 x_{j} \equiv 3\left(x_{i}-2 x_{j}\right)(\bmod 5)
$$
so $x_{i} \equiv 2 x_{j}(\bmod 5)$.
If $x_{i}=12$, then $x_{j} \equiv 1(\bmod 5)$, so $x_{j}=-4$, and $\left(y_{i}, y_{j}\right)=(4,12)$; if $x_{j}=12$, then $x_{i} \equiv-1(\bmod 5)$, so $x_{j}=4$, and $\left(y_{i}, y_{j}\right)=(12,-4)$. In both cases, we have $\left\{y_{i}, y_{j}\right\} \subseteq \Omega$. In conclusion, any integer that Morgane can write necessarily belongs to $\Omega$. She cannot therefore write the number -12 on the board.
$\underline{\text { Alternative solution } n^{\circ} 1}$ We can present the solution to part a) in another way. First, any number that Morgane writes will necessarily belong to the set $\mathbb{L}=\left\{d / 5^{k}: d, k \in \mathbb{Z}\right\}$. Since 5 and 13 are coprime, we identify each element of $\mathbb{L}$ with its residue modulo 13.
But then, if Morgane manages to replace two numbers $a$ and $b$ with numbers $a^{\prime}=f(a, b)$ and $b^{\prime}=g(a, b)$ such that $a^{\prime} \equiv b^{\prime} \equiv 0(\bmod 13)$, this means that $3 a+4 b \equiv 4 a-3 b \equiv 0(\bmod 13)$, and therefore that
$$
\begin{aligned}
a & \equiv-25 a \\
b & \equiv-3(3 a+4 b)-4(4 a-3 b) \\
b & \equiv 0 \quad(\bmod 13) ; \\
& \
|
proof
|
Yes
|
Incomplete
|
math-word-problem
|
Algebra
|
Morgane a écrit les trois entiers 3, 4 et 12 au tableau. Elle effectue ensuite des changements successifs en procédant comme suit : elle choisit deux nombres $a$ et $b$ écrits au tableau, les efface, et les remplace par $(3 a+4 b) / 5$ et $(4 a-3 b) / 5$.
Morgane peut-elle, après un nombre fini de tels changements,
a) parvenir à écrire le nombre 13 au tableau?
b) parvenir à écrire le nombre - 12 au tableau?
|
Nous allons démontrer que la réponse est négative dans les deux cas. Soit $\mathcal{S}$ la somme des carrés des nombres écrits au tableau, et soit $f$ et $g$ les fonctions définies par $f:(x, y) \rightarrow(3 x+4 y) / 5$ et $g:(x, y) \rightarrow(4 x-3 y) / 5$. La relation
$$
f(x, y)^{2}+g(x, y)^{2}=x^{2}+y^{2}
$$
nous assure que, lorsque Morgane remplace deux nombres $a$ et $b$ par $f(a, b)$ et $g(a, b)$, elle ne change pas la valeur de $\mathcal{S}$.
En outre, les égalités $f(f(x, y), g(x, y))=x$ et $g(f(x, y), g(x, y))=y$ nous indiquent que les changements qu'effectue Morgane sont réversible : si elle transforme un triplet non ordonné $\mathbf{t}=(a, b, c)$ en un autre triplet $\mathbf{t}^{\prime}=\left(a^{\prime}, b^{\prime}, c\right)$ tel que $a^{\prime}=f(a, b)$ et $b^{\prime}=g(a, b)$, elle peut retransformer $\mathbf{t}^{\prime}$ en $\mathbf{t}$.
On traite maintenant les deux questions séparément.
a) Si jamais elle réussit à écrire trois nombres $x, y$ et $z$ tels que $z=13$, alors
$$
x^{2}+y^{2}+13^{2}=x^{2}+y^{2}+z^{2}=\mathcal{S}=3^{2}+4^{2}+12^{2}=13^{2}
$$
de sorte que $x=y=0$. Cela signifie que Morgane peut transformer, en plusieurs étapes, le triplet $(3,4,12)$ en $(0,0,13)$. Elle peut donc également transformer $(0,0,13)$ et $(3,4,12)$.
On dit alors qu'un triplet $(x, y, z)$ de nombres rationnelles est sympathique si $v_{13}(u) \geqslant$ 1 pour tout $u \in\{x, y, z\}$. Si Morgane transforme un triplet $(x, y, z)$ sympathique en un nouveau triplet $\left(x^{\prime}, y^{\prime}, z^{\prime}\right)$, ce dernier est clairement sympathique lui aussi. Ainsi, à partir du triplet sympathique $(0,0,13)$, Morgane ne peut obtenir que des triplets sympathiques. Elle ne peut donc pas obtenir le triplet $(3,4,12)$. Ceci démontre bien qu'elle ne pouvait pas transformer le triplet $(3,4,12)$ en $(0,0,13)$.
b) Nous allons carrément démontrer que Morgane ne peut pas écrire d'entier autre que les éléments de l'ensemble $\Omega=\{0, \pm 3, \pm 4, \pm 5,12\} \cdot{ }^{3}$
Considérons un triplet ordonné ( $x_{1}, x_{2}, x_{3}$ ). Pour tous les entiers $i$ et $j$ distincts l'un de l'autre, on note $\Theta_{i, j}\left(x_{1}, x_{2}, x_{3}\right)$ le triplet obtenu à partir de $\left(x_{1}, x_{2}, x_{3}\right)$ en remplaçant les nombres $x_{i}$ et $x_{j}$ par $f\left(x_{i}, x_{j}\right)$ et $g\left(x_{i}, x_{j}\right)$. Par ailleurs, on dit que $\left(x_{1}, x_{2}, x_{3}\right)$ est d'ordre $n$ si $\min \left\{v_{5}\left(x_{1}\right), v_{5}\left(x_{2}\right), v_{5}\left(x_{3}\right)\right\}=-n$, et qu'il s'agit d'un triplet égalitaire s'il y a au moins deux indices $i$ tels qu $v_{5}\left(x_{i}\right)=-n$.
Tout triplet d'ordre $n \geqslant 1$ qu'obtiendra Morgane est égalitaire. En effet, supposons que cela ne soit pas le cas. Sans perte de généralité, on a $v_{5}\left(x_{1}\right)=-n, v_{5}\left(x_{2}\right) \geqslant 1-n$ et $v_{5}\left(x_{3}\right) \geqslant 1-n$. Alors, en posant $X_{i}=5^{n} x_{i}$, on constate que $X_{1} \not \equiv 0(\bmod 5)$ et que $X_{2} \equiv X_{3} \equiv 0(\bmod 5)$, de sorte que
$$
0 \equiv 5^{2 n} \times 13^{2} \equiv 5^{2 n}\left(x_{1}^{2}+x_{2}^{2}+x_{3}^{2}\right) \equiv X_{1}^{2}+X_{2}^{2}+X_{3}^{2} \equiv X_{1}^{2} \not \equiv 0 \quad(\bmod 5),
$$
ce qui est absurde.
3. Cela répondrait aussi à la question a), mais de manière nettement plus compliquée.
Soit alors $n \geqslant 0$ un entier, puis $\left(x_{1}, x_{2}, x_{3}\right)$ et $\left(y_{1}, y_{2}, y_{3}\right)$ deux triplets d'ordres $\ell \leqslant n$ et $n+1$ que Morgane peut obtenir successivement. Il existe deux entiers $i$ et $j$ tels que $\Theta_{i, j}\left(x_{1}, x_{2}, x_{3}\right)=\left(y_{1}, y_{2}, y_{3}\right)$, et le triplet $\left(y_{1}, y_{2}, y_{3}\right)$ est égalitaire. En notant $k$ l'élément de $\{1,2,3\}$ autre que $i$ et $j$, puis $X_{u}=5^{n} x_{u}$ et $Y_{u}=5^{n+1} y_{u}$ pour tout $u \in\{1,2,3\}$, on constate que
$$
Y_{i}=3 X_{i}+4 X_{j} \not \equiv 0(\bmod 5), Y_{j}=4 X_{i}-3 X_{j} \not \equiv 0(\bmod 5) \text { et } Y_{k} \equiv 0(\bmod 5) .
$$
On en déduit immédiatement que les triplets $\Theta_{i, k}\left(y_{1}, y_{2}, y_{3}\right)$, $\Theta_{j, k}\left(y_{1}, y_{2}, y_{3}\right)$, $\Theta_{k, i}\left(y_{1}, y_{2}, y_{3}\right)$ et $\Theta_{k, j}\left(y_{1}, y_{2}, y_{3}\right)$ sont tous d'ordre $n+2$. De même,
$$
f\left(y_{j}, y_{i}\right)=\left(24 X_{i}+7 X_{j}\right) / 5^{n+2} \text { et } g\left(y_{j}, y_{i}\right)=\left(7 X_{i}-24 X_{j}\right) / 5^{n+2}
$$
Puisque $24 X_{i}+7 X_{j} \equiv Y_{j}(\bmod 5)$ et $7 X_{i}-24 X_{j} \equiv-Y_{i}(\bmod 5)$, le triplet $\Theta_{j, i}\left(y_{1}, y_{2}, y_{3}\right)$ est lui aussi d'ordre $n+2$. Enfin, comme dans la solution $\mathrm{n}^{\circ} 1$, on vérifie aisément que $\Theta_{i, j}$ est une involution, de sorte que $\Theta_{i, j}\left(y_{1}, y_{2}, y_{3}\right)$ est d'ordre $\ell \leqslant n$.
Pour finir, soit $\mathbf{T}$ un triplet, avec au moins une coordonnée $x$ entière, que Morgane peut écrire. Supposons que Morgane a écrit successivement des triplets $\mathbf{T}_{0}, \ldots, \mathbf{T}_{k}$ tels que $\mathbf{T}_{0}=(3,4,12)$ et $\mathbf{T}_{k}=\mathbf{T}$ soit à coordonnées entières, avec $k$ minimal.
Soit $\mathbf{T}_{i}$ un triplet d'ordre $n$ maximal parmi les triplets $\mathbf{T}_{0}, \ldots, \mathbf{T}_{k}$. Si $n \geqslant 1$ et si $i \leqslant k-1$, on vient de démontrer que $\mathbf{T}_{i-1}=\mathbf{T}_{i+1}$, ce qui vient contredire la minimalité de $k$. Si $n \geqslant 1$ et si $i=k$, alors $\mathbf{T}_{k}$ contient une coordonnée déjà présente dans $\mathbf{T}_{k-1}$ et deux coordonnées de valuation 5 -adique égale à $-n$, donc distinctes de $x$. Ceci vient là encore contredire la minimalité de $k$.
Il suffit maintenant de démontrer que, partant d'un triplet $\mathbf{t}=\left(x_{1}, x_{2}, x_{3}\right)$ d'éléments de $\Omega$ tel que $x_{1}^{2}+x_{2}^{2}+x_{3}^{2}=13^{2}$, tout triplet $\mathbf{t}^{\prime}=\left(y_{1}, y_{2}, y_{3}\right)$ à coordonnées entières que Morgane peut former est à coordonnées dans $\Omega$. Tout d'abord, on peut supposer sans perte de généralité que $\left|x_{1}\right| \leqslant\left|x_{2}\right| \leqslant\left|x_{3}\right|$, de sorte que $3 \times 5^{2}<13^{2} \leqslant 3 x_{3}^{2}$, donc que $x_{3}=12$ et que $\left(x_{1}, x_{2}\right) \in\{(0, \pm 5),( \pm 3, \pm 4)\}$.
On suppose alors que $\mathbf{t}^{\prime}$ a une coordonnée entière qui n'appartient pas à $\Omega$. Soit $i$ et $j$ les entiers tels que $\mathbf{t}^{\prime}=\Theta_{i, j}(\mathbf{t})$. Si $\left\{x_{i}, x_{j}\right\} \subseteq\{0, \pm 3, \pm 4, \pm 5\}$, alors $y_{i}^{2}+y_{j}^{2}=x_{i}^{2}+x_{j}^{2}=5^{2}$, donc $\left\{y_{i}, y_{j}\right\} \subseteq \Omega$. Ainsi, l'un des deux entiers $x_{i}$ et $x_{j}$ est égal à 12 . Or,
$$
0 \equiv 5 y_{i} \equiv 3 x_{i}+4 x_{j} \equiv 3\left(x_{i}-2 x_{j}\right)(\bmod 5)
$$
donc $x_{i} \equiv 2 x_{j}(\bmod 5)$.
Si $x_{i}=12$, alors $x_{j} \equiv 1(\bmod 5)$, donc $x_{j}=-4$, et $\left(y_{i}, y_{j}\right)=(4,12)$; si $x_{j}=12$, alors $x_{i} \equiv-1(\bmod 5)$, donc $x_{j}=4$, et $\left(y_{i}, y_{j}\right)=(12,-4)$. Dans les deux cas, on a bien $\left\{y_{i}, y_{j}\right\} \subseteq \Omega$. En conclusion, tout nombre entier que peut écrire Morgane appartient nécessairement à $\Omega$. Elle ne peut donc pas écrire le nombre -12 au tableau.
$\underline{\text { Solution alternative } n^{\circ} 1}$ On peut présenter la solution à la partie a) d'une autre manière. Tout d'abord, tout nombre qu'écrira Morgane appartiendra nécessairement à l'ensemble $\mathbb{L}=\left\{d / 5^{k}: d, k \in \mathbb{Z}\right\}$. Puisque 5 et 13 sont premiers entre eux, on identifie chaque élément de $\mathbb{L}$ à son résidu modulo 13.
Mais alors, si Morgane parvient à remplacer deux nombres $a$ et $b$ par des nombres $a^{\prime}=f(a, b)$ et $b^{\prime}=g(a, b)$ tels que $a^{\prime} \equiv b^{\prime} \equiv 0(\bmod 13)$, cela signifie que $3 a+4 b \equiv 4 a-3 b \equiv 0(\bmod 13)$, et donc que
$$
\begin{aligned}
a & \equiv-25 a \\
b & \equiv-3(3 a+4 b)-4(4 a-3 b) \\
b & \equiv 0 \quad(\bmod 13) ; \\
& \equiv-4(3 a+4 b)+3(4 a-3 b) \equiv 0 \quad(\bmod 13)
\end{aligned}
$$
Par conséquent, une récurrence immédiate indique que les nombres que Morgane écrira au tableau ne seront jamais tous congrus à 0 modulo 13.
|
{
"exam": "French_tests",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-2.jsonl",
"solution_match": "\nSolution de l'exercice 7",
"tier": "T1",
"year": "2020"
}
|
Morgane wrote the three integers 3, 4, and 12 on the board. She then makes successive changes as follows: she chooses two numbers $a$ and $b$ written on the board, erases them, and replaces them with $(3a + 4b) / 5$ and $(4a - 3b) / 5$.
Can Morgane, after a finite number of such changes,
a) manage to write the number 13 on the board?
b) manage to write the number -12 on the board?
|
$n^{\circ} 2$ We can also answer part a) with a simplified version of the reasoning used for part b).
Indeed, it involves proving that the triplet $\mathbf{T}=(0,0,13)$, in any order of the coordinates, cannot be reached. If Morgane reaches this triplet, and reasoning as above, she must have written triplets $\mathbf{T}_{0}=(3,4,12), \mathbf{T}_{1}, \ldots, \mathbf{T}_{k}=\mathbf{T}$, each $\mathbf{T}_{i}$ having integer coordinates.
However, since each operation $\Theta_{i, j}$ is an involution, we can write $\mathbf{T}_{k-1}$ in the form $\Theta_{i, j}(\mathbf{T})$. To the order of its coordinates, the triplet $\mathbf{T}_{k-1}$ is therefore equal to $\Theta_{2,3}(0,0,13)$ or to $\Theta_{3,2}(0,0,13)$, that is, to $(0,52 / 5,-39 / 5)$ or to $(0,39 / 5,52 / 5)$. This contradiction proves that Morgane will never be able to write the number 13 on the board.
Comment from the correctors The exercise was very difficult, and few students managed to find truly interesting elements. Several students understood the importance of the 5-adic valuation of the numbers written: it was necessary to succeed in formalizing this idea and looking at the evolution of the 5-adic valuations written.
[^0]: 1. We could also consider the periodic nature of the sequence $a_{i}-\lambda_{1}$, but then we would fall back into the alternative solution $\mathrm{n}^{\circ} 2$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Morgane a écrit les trois entiers 3, 4 et 12 au tableau. Elle effectue ensuite des changements successifs en procédant comme suit : elle choisit deux nombres $a$ et $b$ écrits au tableau, les efface, et les remplace par $(3 a+4 b) / 5$ et $(4 a-3 b) / 5$.
Morgane peut-elle, après un nombre fini de tels changements,
a) parvenir à écrire le nombre 13 au tableau?
b) parvenir à écrire le nombre - 12 au tableau?
|
$n^{\circ} 2$ On peut également répondre à la partie a) avec une version simplifiée du raisonnement utilisé pour la partie b).
En effet, il s'agit de démontrer que l'on ne peut pas atteindre le triplet $\mathbf{T}=(0,0,13)$, à l'ordre près des coordonnées. Si Morgane atteint ce triplet, et en raisonnant comme ci-dessus, elle a nécessairement dû écrire des triplets $\mathbf{T}_{0}=(3,4,12), \mathbf{T}_{1}, \ldots, \mathbf{T}_{k}=\mathbf{T}$, chaque $\mathbf{T}_{i}$ étant à coordonnées entières.
Mais alors, puisque chaque opération $\Theta_{i, j}$ est une involution, on peut écrire $\mathbf{T}_{k-1}$ sous la forme $\Theta_{i, j}(\mathbf{T})$. À l'ordre près de ses coordonnées, le triplet $\mathbf{T}_{k-1}$ donc est égal à $\Theta_{2,3}(0,0,13)$ ou à $\Theta_{3,2}(0,0,13)$, c'est-à-dire à $(0,52 / 5,-39 / 5)$ ou à $(0,39 / 5,52 / 5)$. Cette contradiction démontre que Morgane ne pourra jamais écrire le nombre 13 au tableau.
Commentaire des correcteurs L'exercice était très difficile, et peu d'élèves ont réussi à trouver des éléments véritablement intéressants. Plusieurs élèves ont compris l'importance de la valuation 5 adique des nombres écrits : il fallait réussir à formaliser cette idée et regarder l'évolution des valuations 5 -adiques écrites.
[^0]: 1. On pourrait aussi considérer le caractère périodique de la suite $a_{i}-\lambda_{1}$, mais alors on retomberait dans la solution alternative $\mathrm{n}^{\circ} 2$.
|
{
"exam": "French_tests",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-2.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2020"
}
|
Let $a, b, c$ and $d$ be four real numbers. Suppose there exists a permutation $(x, y, z, t)$ of the numbers $a, b, c$ and $d$ such that
$$
x \leqslant 2 a-b, y \leqslant 2 b-c, z \leqslant 2 c-d \text { and } t \leqslant 2 d-a .
$$
Prove that $a=b=c=d$.
|
To better exploit the first inequality, which we rewrite as $x + b \leqslant 2a$, it would be ideal for $x$ and $b$ to be maximal, or for $a$ to be minimal. Obviously, it is quite possible that neither $a$, nor $b$, nor $x$ is extremal. Nevertheless, since the variables play cyclic roles, we can still hope, at our choice, that $a$ is minimal, or that $b$ is maximal, or that $x$ is maximal. However, hoping that $b$ and $x$ would be simultaneously maximal would be too much to ask. Instead, we assume, without loss of generality, that $a$ is the smallest of the four real numbers. Under these conditions, $2a \leqslant b + x \leqslant 2a$, so $a = b$. But then $b$ is also the smallest of the four real numbers, so $b = c$, and we similarly prove that $c = d$.
$\underline{\text{Alternative Solution } n^{\circ} 1}$ By summing the four inequalities given in the problem, we obtain the inequality $x + y + z + t \leqslant a + b + c + d$. Since $(x, y, z, t)$ is a permutation of $(a, b, c, d)$, this last inequality is actually an equality, so each of the inequalities given in the problem is also an equality: $x = 2a - b$, $y = 2b - c$, $z = 2c - d$, and $t = 2d - a$.
By squaring each side and adding the resulting equalities, we observe that
$$
a^{2} + b^{2} + c^{2} + d^{2} = x^{2} + y^{2} + z^{2} + t^{2} = 5\left(a^{2} + b^{2} + c^{2} + d^{2}\right) - 4(ab + bc + cd + da)
$$
This means that $ab + bc + cd + da = a^{2} + b^{2} + c^{2} + d^{2}$, or equivalently,
$$
0 = 2\left(a^{2} + b^{2} + c^{2} + d^{2}\right) - 2(ab + bc + cd + da) = (a - b)^{2} + (b - c)^{2} + (c - d)^{2} + (d - a)^{2},
$$
so $a = b = c = d$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $a, b, c$ et $d$ quatre nombres réels. On suppose qu'il existe une permutation $(x, y, z, t)$ des nombres $a, b, c$ et $d$ telle que
$$
x \leqslant 2 a-b, y \leqslant 2 b-c, z \leqslant 2 c-d \text { et } t \leqslant 2 d-a .
$$
Démontrer que $a=b=c=d$.
|
Pour mieux exploiter la première inégalité, que l'on réécrit comme $x+b \leqslant 2 a$, l'idéal serait que $x$ et $b$ soient maximaux, ou bien que $a$ soit minimal. Évidemment, il se pourrait très bien que ni $a$, ni $b$, ni $x$ ne soit extrémal. Néanmoins, puisque les variables jouent des rôles cycliques, on peut tout de même espérer, au choix, que $a$ soit minimal, ou que $b$ soit maximal, ou que $x$ soit maximal.
Cependant, espérer que $b$ et $x$ seraient simultanément maximaux serait trop demander. À la place, on se contente de supposer, sans perte de généralité, que $a$ est le plus petit des quatre nombres réels. Dans ces conditions, $2 a \leqslant b+x \leqslant 2 a$, donc $a=b$. Mais alors $b$ est aussi le plus petit des quatre nombres réels, donc $b=c$, et on démontre de même que $c=d$.
$\underline{\text { Solution alternative } n^{\circ} 1}$ En sommant les quatre inégalités de l'énoncé, on obtient l'inégalité $x+y+z+t \leqslant a+b+c+d$. Puisque $(x, y, z, t)$ est une permutation de $(a, b, c, d)$, cette dernière inégalité est en fait une égalité, donc chacune des inégalités de l'énoncé est également une égalité : $x=2 a-b, y=2 b-c, z=2 c-d$ et $t=2 d-a$.
En élevant chaque membre au carré et en additionnant les égalités ainsi obtenues, on constate alors que
$$
a^{2}+b^{2}+c^{2}+d^{2}=x^{2}+y^{2}+z^{2}+t^{2}=5\left(a^{2}+b^{2}+c^{2}+d^{2}\right)-4(a b+b c+c d+d a)
$$
Cela signifie que $a b+b c+c d+d a=a^{2}+b^{2}+c^{2}+d^{2}$, ou encore que
$$
0=2\left(a^{2}+b^{2}+c^{2}+d^{2}\right)-2(a b+b c+c d+d a)=(a-b)^{2}+(b-c)^{2}+(c-d)^{2}+(d-a)^{2},
$$
de sorte que $a=b=c=d$.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T1",
"year": "2020"
}
|
Let $a, b, c$ and $d$ be four real numbers. Suppose there exists a permutation $(x, y, z, t)$ of the numbers $a, b, c$ and $d$ such that
$$
x \leqslant 2 a-b, y \leqslant 2 b-c, z \leqslant 2 c-d \text { and } t \leqslant 2 d-a .
$$
Prove that $a=b=c=d$.
|
$n^{\circ} 2$ Another way to conclude is to note that the equality $a b+b c+c d+d a=a^{2}+b^{2}+c^{2}+d^{2}$ is a case of equality in the Cauchy-Schwarz inequality, which is only achieved if the quadruples $(a, b, c, d)$ and $(b, c, d, a)$ are proportional to each other. Since these have the same sum, they are therefore equal, which indeed concludes the proof.
|
proof
|
Yes
|
Incomplete
|
proof
|
Algebra
|
Soit $a, b, c$ et $d$ quatre nombres réels. On suppose qu'il existe une permutation $(x, y, z, t)$ des nombres $a, b, c$ et $d$ telle que
$$
x \leqslant 2 a-b, y \leqslant 2 b-c, z \leqslant 2 c-d \text { et } t \leqslant 2 d-a .
$$
Démontrer que $a=b=c=d$.
|
$n^{\circ} 2$ Une autre manière de conclure consiste à remarquer que l'égalité $a b+b c+c d+d a=a^{2}+b^{2}+c^{2}+d^{2}$ est un cas d'égalité de l'inégalité de Cauchy-Schwarz, qui n'est atteint que si les quadruplets $(a, b, c, d)$ et $(b, c, d, a)$ sont proportionnels l'un à l'autre. Puisque ceux-ci sont de même somme, ils sont donc égaux, ce qui conclut en effet.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2020"
}
|
Let $a, b, c$ and $d$ be four real numbers. Suppose there exists a permutation $(x, y, z, t)$ of the numbers $a, b, c$ and $d$ such that
$$
x \leqslant 2 a-b, y \leqslant 2 b-c, z \leqslant 2 c-d \text { and } t \leqslant 2 d-a .
$$
Prove that $a=b=c=d$.
|
$n^{\circ} 3$ Another variant of the two previous solutions is as follows: by subtracting a sufficiently large real number $\lambda$ from all our numbers, we assume that each member of each inequality is negative. By squaring these members and adding the inequalities thus obtained, we then observe that
$$
a^{2}+b^{2}+c^{2}+d^{2}=x^{2}+y^{2}+z^{2}+t^{2} \geqslant 5\left(a^{2}+b^{2}+c^{2}+d^{2}\right)-4(a b+b c+c d+d a) .
$$
This means once again that $a b+b c+c d+d a \geqslant a^{2}+b^{2}+c^{2}+d^{2}$, and we conclude as before.
|
a=b=c=d
|
Yes
|
Yes
|
proof
|
Algebra
|
Soit $a, b, c$ et $d$ quatre nombres réels. On suppose qu'il existe une permutation $(x, y, z, t)$ des nombres $a, b, c$ et $d$ telle que
$$
x \leqslant 2 a-b, y \leqslant 2 b-c, z \leqslant 2 c-d \text { et } t \leqslant 2 d-a .
$$
Démontrer que $a=b=c=d$.
|
$n^{\circ} 3$ Une autre variante des deux solutions précédentes est la suivante: quitte à soustraire un réel $\lambda$ suffisamment grand à tous nos nombres, on suppose que chaque membre de chaque inégalité est négatif. En élevant ces membres au carré et en additionnant les inégalités ainsi obtenues, on constate alors que
$$
a^{2}+b^{2}+c^{2}+d^{2}=x^{2}+y^{2}+z^{2}+t^{2} \geqslant 5\left(a^{2}+b^{2}+c^{2}+d^{2}\right)-4(a b+b c+c d+d a) .
$$
Cela signifie une fois de plus que $a b+b c+c d+d a \geqslant a^{2}+b^{2}+c^{2}+d^{2}$, et l'on conclut alors comme précédemment.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2020"
}
|
Let $a, b, c$ and $d$ be four real numbers. Suppose there exists a permutation $(x, y, z, t)$ of the numbers $a, b, c$ and $d$ such that
$$
x \leqslant 2 a-b, y \leqslant 2 b-c, z \leqslant 2 c-d \text { and } t \leqslant 2 d-a .
$$
Prove that $a=b=c=d$.
|
$n^{\circ} 4$ We proceed in a brute force manner, studying each of the $4!=24$ possible permutations $(x, y, z, t)$ separately. In each case, we will express the numbers $a-b, b-c, c-d$, and $d-a$ as linear combinations, with positive coefficients, of the numbers $\alpha=(2 a-b-x) / 60, \beta=(2 b-c-y) / 60, \gamma=(2 c-d-z) / 60$, and $\delta=(2 d-a-t) / 60$; the denominators were chosen a posteriori so that all our coefficients are integers. This will show that they are non-negative numbers, and since their sum is 0, we will conclude that $a=b=c=d$.
However, let us not be misled! We present this solution solely to convince the reader that, while theoretically feasible within the four hours of the exam, it is very risky and intellectually unsatisfying. Moreover, such a method would be impractical if there were 2021 variables instead of four. For information, the examiners needed a computer program to write the cells of this table, which they did not have the courage to calculate by hand after spending more than two hours on it.
| Case | $(x, y, z, t)$ | $a-b$ | $b-c$ | $c-d$ | $d-a$ |
| :---: | :---: | :---: | :---: | :---: | :---: |
| 1 | $(a, b, c, d)$ | $60 \alpha$ | $60 \beta$ | $60 \gamma$ | $60 \delta$ |
| 2 | $(a, b, d, c)$ | $60 \alpha$ | $60 \beta$ | $30 \gamma$ | $30 \gamma+60 \delta$ |
| 3 | $(a, c, b, d)$ | $60 \alpha$ | $30 \beta$ | $30 \beta+60 \gamma$ | $60 \delta$ |
| 4 | $(a, c, d, b)$ | $60 \alpha$ | $30 \beta$ | $30 \gamma$ | $30 \beta+30 \gamma+60 \delta$ |
| 5 | $(a, d, b, c)$ | $60 \alpha$ | $20 \alpha+40 \beta+20 \delta$ | $20 \beta+40 \gamma$ | $20 \beta+40 \gamma+60 \delta$ |
| 6 | $(a, d, c, b)$ | $60 \alpha$ | $30 \alpha+60 \beta+30 \delta$ | $60 \gamma$ | $30 \beta+30 \gamma+60 \delta$ |
| 7 | $(b, a, c, d)$ | $30 \alpha$ | $30 \alpha+60 \beta$ | $60 \gamma$ | $60 \delta$ |
| 8 | $(b, a, d, c)$ | $30 \alpha$ | $30 \alpha+60 \beta$ | $30 \gamma$ | $30 \gamma+60 \delta$ |
| 9 | $(b, c, a, d)$ | $30 \alpha$ | $30 \beta$ | $30 \alpha+30 \beta+60 \gamma$ | $60 \delta$ |
| 10 | $(b, c, d, a)$ | $30 \alpha$ | $30 \beta$ | $30 \gamma$ | $30 \delta$ |
| 11 | $(b, d, a, c)$ | $30 \alpha$ | $10 \alpha+40 \beta+20 \delta$ | $20 \alpha+20 \beta+40 \gamma$ | $30 \alpha+20 \gamma+40 \delta$ |
| 12 | $(b, d, c, a)$ | $30 \alpha$ | $30 \alpha+60 \beta+30 \delta$ | $60 \gamma$ | $30 \delta$ |
| 13 | $(c, a, b, d)$ | $40 \alpha+20 \gamma+20 \delta$ | $20 \alpha+40 \beta$ | $20 \alpha+40 \beta+60 \gamma$ | $60 \delta$ |
| 14 | $(c, a, d, b)$ | $40 \alpha+20 \gamma+20 \delta$ | $20 \alpha+40 \beta$ | $30 \gamma$ | $20 \beta+10 \gamma+40 \delta$ |
| 15 | $(c, b, a, d)$ | $60 \alpha+30 \gamma+30 \delta$ | $60 \beta$ | $30 \alpha+30 \beta+60 \gamma$ | $60 \delta$ |
| 16 | $(c, b, d, a)$ | $60 \alpha+30 \gamma+30 \delta$ | $60 \beta$ | $30 \gamma$ | $30 \delta$ |
| 17 | $(c, d, a, b)$ | $48 \alpha+24 \gamma+12 \delta$ | $12 \alpha+48 \beta+24 \delta$ | $24 \alpha+12 \beta+48 \delta$ | $24 \beta+12 \gamma+48 \delta$ |
| 18 | $(c, d, b, a)$ | $40 \alpha+20 \gamma+10 \delta$ | $20 \alpha+40 \beta+20 \delta$ | $20 \beta+40 \gamma$ | $30 \delta$ |
| 19 | $(d, a, b, c)$ | $45 \alpha+15 \gamma+30 \delta$ | $30 \alpha+45 \beta+15 \delta$ | $15 \alpha+30 \beta+45 \gamma$ | $15 \beta+30 \gamma+45 \delta$ |
| 20 | $(d, a, c, b)$ | $40 \alpha+20 \delta$ | $40 \alpha+60 \beta+20 \delta$ | $60 \gamma$ | $20 \beta+20 \gamma+40 \delta$ |
| 21 | $(d, b, a, c)$ | $60 \alpha+20 \gamma+40 \delta$ | $60 \beta$ | $20 \alpha+20 \beta+40 \gamma$ | $20 \gamma+40 \delta$ |
| 22 | $(d, b, c, a)$ | $60 \alpha+30 \delta$ | $60 \beta$ | $60 \gamma$ | $30 \delta$ |
| 23 | $(d, c, a, b)$ | $40 \alpha+20 \delta$ | $30 \beta$ | $20 \alpha+10 \beta+40 \gamma$ | $20 \beta+20 \gamma+40 \delta$ |
| 24 | $(d, c, b, a)$ | $60 \alpha+30 \delta$ | $30 \beta$ | $30 \beta+60 \gamma$ | $30 \delta$ |
Remark: The pairs of variables $(a, x),(b, y),(c, z)$, and $(d, t)$ play cyclic roles. In the previous solution, it is therefore possible to treat several permutations at once. For example, the cases where $(x, y, z, t)=(a, b, d, c)$ and $(y, z, t, x)=(b, c, a, d)$ are treated in the same way, since treating the second permutation is equivalent to treating the first, but replacing the numbers $\alpha, \beta, \gamma$, and $\delta$ with $\beta, \gamma, \delta$, and $\beta$, respectively. More generally, if we denote $\sigma$ as the function such that $\sigma(a)=b, \sigma(b)=c, \sigma(c)=d$, and $\sigma(d)=a$, each permutation $(x, y, z, t)$ is treated in the same way as the permutation $(\sigma(t), \sigma(x), \sigma(y), \sigma(z))$.
This observation allows us to group the cases
$\triangleright 2,22,7$ and 3,
$\triangleright 4,16,12$ and 9,
and thus to study "only" 10 permutations rather than 24 (for example, the permutations in gray), which allows us to obtain a horrible solution rather than an inhumane one.
Remark: Alternatively, and given the cyclic role of our variables, it is in fact sufficient to prove the inequality $a \geqslant b$ for each permutation $(x, y, z, t)$, to then deduce the analogous inequalities $b \geqslant c, c \geqslant d$, and $d \geqslant a$. Such an approach, while no longer allowing the grouping mentioned in the previous remark, allows us to focus on the first column of the table.
Moreover, since $a-b=60 \alpha$ when $x=a$, and $a-b=30 \alpha$ when $x=b$, it is in fact sufficient to study the 12 permutations for which $x=c$ or $x=d$, i.e., 12 cells out of the $24 \times 4=96$ cells of the table. Some cases, however, remain particularly tedious to handle, for example, case 17.
Examiner's Comment: Relatively few students obtained all the points on the problem. Several approaches were possible. The riskiest strategy was to test the 24 possible cases, possibly invoking symmetry arguments to dispose of some cases. Among the students who attempted this approach, very few managed to complete it. Here are some general remarks following the review of the proposed attempts:
$\triangleright$ Many students thought to sum the inequalities to show that they were in fact equalities. This is an excellent reflex!
$\triangleright$ Many students consider $a$ as the minimum and assume by contradiction that $a<b, a<c$, and $a<d$. After obtaining a contradiction (for example, by showing that $a=b$), they immediately conclude that $a=b=c=d$. However, the contradiction obtained here only allowed them to assert that at least one of the strict inequalities was invalid, but not necessarily all three at the same time.
$\triangleright$ The most important remark is perhaps the following: Many students claim that one can assume without loss of generality that $a \leqslant b \leqslant c \leqslant d$. This assumption is only possible if the inequalities are completely symmetric, i.e., if swapping two variables does not change the inequalities. Here, if we swap the variables $a$ and $b$, the system of inequalities changes completely.
The inequalities do, however, have a cyclic symmetry: replacing $(a, b, c, d)$ with $(d, a, b, c)$ does not change the inequalities. This cyclic symmetry does not allow us to order the variables, but only to choose one variable to be the minimum or maximum of the 4 reals.
|
proof
|
Yes
|
Incomplete
|
proof
|
Algebra
|
Soit $a, b, c$ et $d$ quatre nombres réels. On suppose qu'il existe une permutation $(x, y, z, t)$ des nombres $a, b, c$ et $d$ telle que
$$
x \leqslant 2 a-b, y \leqslant 2 b-c, z \leqslant 2 c-d \text { et } t \leqslant 2 d-a .
$$
Démontrer que $a=b=c=d$.
|
$n^{\circ} 4$ On procède de manière brutale, étudiant séparément chacune des $4!=24$ permutations $(x, y, z, t)$ possibles. Dans chaque cas, nous allons exprimer les nombres $a-b, b-c, c-d$ et $d-a$ comme combinaisons linéaires, à coefficients positifs, des
nombres $\alpha=(2 a-b-x) / 60, \beta=(2 b-c-y) / 60, \gamma=(2 c-d-z) / 60$ et $\delta=(2 d-a-t) / 60$; les dénominateurs ont été choisis a posteriori pour que tous nos coefficients soient entiers. Cela démontrera qu'il s'agit de nombres positifs ou nuls, et puisque leur somme vaut 0 , on en conclura que $a=b=c=d$.
Cependant, que l'on ne se méprenne pas! Nous présentons cette solution dans le seul but de le convaincre le lecteur que, si celle-ci est théoriquement faisable dans le temps imparti des quatre heures de l'épreuve, elle est très risquée, et intellectuellement très peu satisfaisante. En outre, on serait bien en peine d'appliquer une telle méthode si on avait 2021 variables plutôt que quatre. Pour information, les correcteurs ont eu besoin d'un programme informatique pour écrire les cases de ce tableau, qu'ils n'ont pas eu le courage de calculer à la main après y avoir passé plus de deux heures.
| Cas | $(x, y, z, t)$ | $a-b$ | $b-c$ | $c-d$ | $d-a$ |
| :---: | :---: | :---: | :---: | :---: | :---: |
| 1 | $(a, b, c, d)$ | $60 \alpha$ | $60 \beta$ | $60 \gamma$ | $60 \delta$ |
| 2 | $(a, b, d, c)$ | $60 \alpha$ | $60 \beta$ | $30 \gamma$ | $30 \gamma+60 \delta$ |
| 3 | $(a, c, b, d)$ | $60 \alpha$ | $30 \beta$ | $30 \beta+60 \gamma$ | $60 \delta$ |
| 4 | $(a, c, d, b)$ | $60 \alpha$ | $30 \beta$ | $30 \gamma$ | $30 \beta+30 \gamma+60 \delta$ |
| 5 | $(a, d, b, c)$ | $60 \alpha$ | $20 \alpha+40 \beta+20 \delta$ | $20 \beta+40 \gamma$ | $20 \beta+40 \gamma+60 \delta$ |
| 6 | $(a, d, c, b)$ | $60 \alpha$ | $30 \alpha+60 \beta+30 \delta$ | $60 \gamma$ | $30 \beta+30 \gamma+60 \delta$ |
| 7 | $(b, a, c, d)$ | $30 \alpha$ | $30 \alpha+60 \beta$ | $60 \gamma$ | $60 \delta$ |
| 8 | $(b, a, d, c)$ | $30 \alpha$ | $30 \alpha+60 \beta$ | $30 \gamma$ | $30 \gamma+60 \delta$ |
| 9 | $(b, c, a, d)$ | $30 \alpha$ | $30 \beta$ | $30 \alpha+30 \beta+60 \gamma$ | $60 \delta$ |
| 10 | $(b, c, d, a)$ | $30 \alpha$ | $30 \beta$ | $30 \gamma$ | $30 \delta$ |
| 11 | $(b, d, a, c)$ | $30 \alpha$ | $10 \alpha+40 \beta+20 \delta$ | $20 \alpha+20 \beta+40 \gamma$ | $30 \alpha+20 \gamma+40 \delta$ |
| 12 | $(b, d, c, a)$ | $30 \alpha$ | $30 \alpha+60 \beta+30 \delta$ | $60 \gamma$ | $30 \delta$ |
| 13 | $(c, a, b, d)$ | $40 \alpha+20 \gamma+20 \delta$ | $20 \alpha+40 \beta$ | $20 \alpha+40 \beta+60 \gamma$ | $60 \delta$ |
| 14 | $(c, a, d, b)$ | $40 \alpha+20 \gamma+20 \delta$ | $20 \alpha+40 \beta$ | $30 \gamma$ | $20 \beta+10 \gamma+40 \delta$ |
| 15 | $(c, b, a, d)$ | $60 \alpha+30 \gamma+30 \delta$ | $60 \beta$ | $30 \alpha+30 \beta+60 \gamma$ | $60 \delta$ |
| 16 | $(c, b, d, a)$ | $60 \alpha+30 \gamma+30 \delta$ | $60 \beta$ | $30 \gamma$ | $30 \delta$ |
| 17 | $(c, d, a, b)$ | $48 \alpha+24 \gamma+12 \delta$ | $12 \alpha+48 \beta+24 \delta$ | $24 \alpha+12 \beta+48 \delta$ | $24 \beta+12 \gamma+48 \delta$ |
| 18 | $(c, d, b, a)$ | $40 \alpha+20 \gamma+10 \delta$ | $20 \alpha+40 \beta+20 \delta$ | $20 \beta+40 \gamma$ | $30 \delta$ |
| 19 | $(d, a, b, c)$ | $45 \alpha+15 \gamma+30 \delta$ | $30 \alpha+45 \beta+15 \delta$ | $15 \alpha+30 \beta+45 \gamma$ | $15 \beta+30 \gamma+45 \delta$ |
| 20 | $(d, a, c, b)$ | $40 \alpha+20 \delta$ | $40 \alpha+60 \beta+20 \delta$ | $60 \gamma$ | $20 \beta+20 \gamma+40 \delta$ |
| 21 | $(d, b, a, c)$ | $60 \alpha+20 \gamma+40 \delta$ | $60 \beta$ | $20 \alpha+20 \beta+40 \gamma$ | $20 \gamma+40 \delta$ |
| 22 | $(d, b, c, a)$ | $60 \alpha+30 \delta$ | $60 \beta$ | $60 \gamma$ | $30 \delta$ |
| 23 | $(d, c, a, b)$ | $40 \alpha+20 \delta$ | $30 \beta$ | $20 \alpha+10 \beta+40 \gamma$ | $20 \beta+20 \gamma+40 \delta$ |
| 24 | $(d, c, b, a)$ | $60 \alpha+30 \delta$ | $30 \beta$ | $30 \beta+60 \gamma$ | $30 \delta$ |
Remarque : Les paires de variables $(a, x),(b, y),(c, z)$ et $(d, t)$ jouent des rôles cycliques. Dans la solution précédente, il est donc possible de traiter plusieurs permutations d'un coup. Par exemple, les cas où $(x, y, z, t)=(a, b, d, c)$ et $(y, z, t, x)=(b, c, a, d)$ se traitent de la même manière, puisque traiter la seconde permutation revient à traiter la première, mais en remplaçant respectivement les nombres $\alpha, \beta, \gamma$ et $\delta \operatorname{par} \beta, \gamma, \delta$ et $\beta$. Plus généralement, si on note $\sigma$ la fonction telle que $\sigma(a)=b, \sigma(b)=c, \sigma(c)=d$ et $\sigma(d)=a$, chaque permutation $(x, y, z, t)$ se traite de la même manière que la permutation $(\sigma(t), \sigma(x), \sigma(y), \sigma(z))$.
Cette observation permet de regrouper les cas
$\triangleright 2,22,7$ et 3 ,
$\triangleright 4,16,12$ et 9 ,
et donc de n'étudier « que » 10 permutations plutôt que 24 (par exemple les permutations sur fond gris), ce qui permet d'obtenir une solution horrible plutôt qu'inhumaine.
Remarque: Alternativement, et au vu du rôle cyclique de nos variables, il est en fait suffisant de démontrer l'inégalité $a \geqslant b$ pour chaque permutation $(x, y, z, t)$, pour en déduire ensuite les inégalités analogues $b \geqslant c, c \geqslant d$ et $d \geqslant a$. Une telle approche, si elle ne permet plus le regroupement mentionné à la remarque précédente, nous permet de nous concentrer sur la première colonne du tableau.
De surcroît, puisque $a-b=60 \alpha$ lorsque $x=a$, et $a-b=30 \alpha$ lorsque $x=b$, il suffit en fait d'étudier que les 12 permutations pour lesquelles $x=c$ ou $x=d$, soit 12 cases sur les $24 \times 4=96$ cases du tableau. Certains cas restent cependant particulièrement pénibles à traiter, par exemple le cas 17.
Commentaire des correcteurs Relativement peu d'élèves ont obtenu tous les points sur le problème. Plusieurs approches étaient possibles. La stratégie la plus risquée consistait à tester les 24 cas possibles, éventuellement en invoquant des arguments de symétrie pour se débarrasser de certains cas. Parmi les élèves qui ont tenté cette approche, très peu en sont arrivés à bout. Voici quelques remarques générales à la suite de la lecture des tentatives proposées:
$\triangleright$ De nombreux élèves ont pensé à sommer les inégalités pour montrer qu'il s'agissait en fait d'égalités. Il s'agit là d'un excellent réflexe!
$\triangleright$ De nombreux élèves pensent à considérer $a$ comme le minimum et supposent par l'absurde que $a<b, a<c$ et $a<d$. Après avoir obtenu une contradiction, (par exemple en montrant que $a=b$ ), ils en déduisent immédiatement que $a=b=c=d$. Toutefois, la contradiction obtenue ici permettait simplement d'affirmer qu'au moins l'une des inégalités strictes était invalide, mais pas forcément les trois en même temps.
$\triangleright$ La remarque la plus importante est sans doute la suivante: De nombreux élèves affirment que l'on peut supposer sans perte de généralité que $a \leqslant b \leqslant c \leqslant d$. Cette supposition n'est possible que si les inégalités sont totalement symétriques, c'est-àdire si échanger deux variables ne changent pas les inégalités. Or, ici, si on échange les variables $a$ et $b$, le système d'inégalités change complètement.
Les inégalités possèdent toutefois une symétrie cyclique : remplacer ( $a, b, c, d$ ) par $(d, a, b, c)$ ne change pas les inégalités. Cette symétrie cyclique ne nous permet donc pas d'ordonner les variables, mais seulement de choisir une variable pour être le minimum ou le maximum des 4 réels.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2020"
}
|
Let $ABC$ be a triangle with acute angles. We denote $D$ as the foot of the altitude from $A$ in triangle $ABC$, then $E$ as the midpoint of the segment $[AD]$, and $\omega$ as the circle with diameter $[AD]$. Next, let $X$ be the intersection point between $\omega$ and the line $(BE)$, such that $B$ and $X$ are on opposite sides of the line $(AD)$. Similarly, let $Y$ be the intersection point between $\omega$ and the line $(CE)$, such that $C$ and $Y$ are on opposite sides of the line $(AD)$. Finally, suppose there exists a point $Z$, other than $D$, lying on the line $(AD)$ and on both circumcircles of $BDX$ and $CDY$. Prove that $AB = AC$.
|
Let $\omega^{\prime}$ be the circle with diameter $[E Z]$ and $\omega_{b}$ the circle passing through $B, D, X$ and $Z$. Since $\widehat{B D Z}=90^{\circ}$, we know that $[B Z]$ is a diameter of $\omega_{b}$. It follows that $\widehat{E X Z}=\widehat{B X Z}=90^{\circ}$, so $X$ is a point of intersection between $\omega$ and $\omega^{\prime}$. Similarly, $Y$ is a point of intersection between $\omega$ and $\omega^{\prime}$.
Let $s$ be the symmetry with axis $(A D)$: it leaves the circles $\omega$ and $\omega^{\prime}$ globally invariant, so it exchanges $X$ and $Y$. Since $E=s(E)$, the symmetry $s$ exchanges the lines $(E X)$ and $(E Y)$. Furthermore, $s$ also leaves the line $(B C)$ globally invariant. Thus, $s$ exchanges $B$ and $C$. Since $A=s(A)$, we conclude that $A B=A C$.
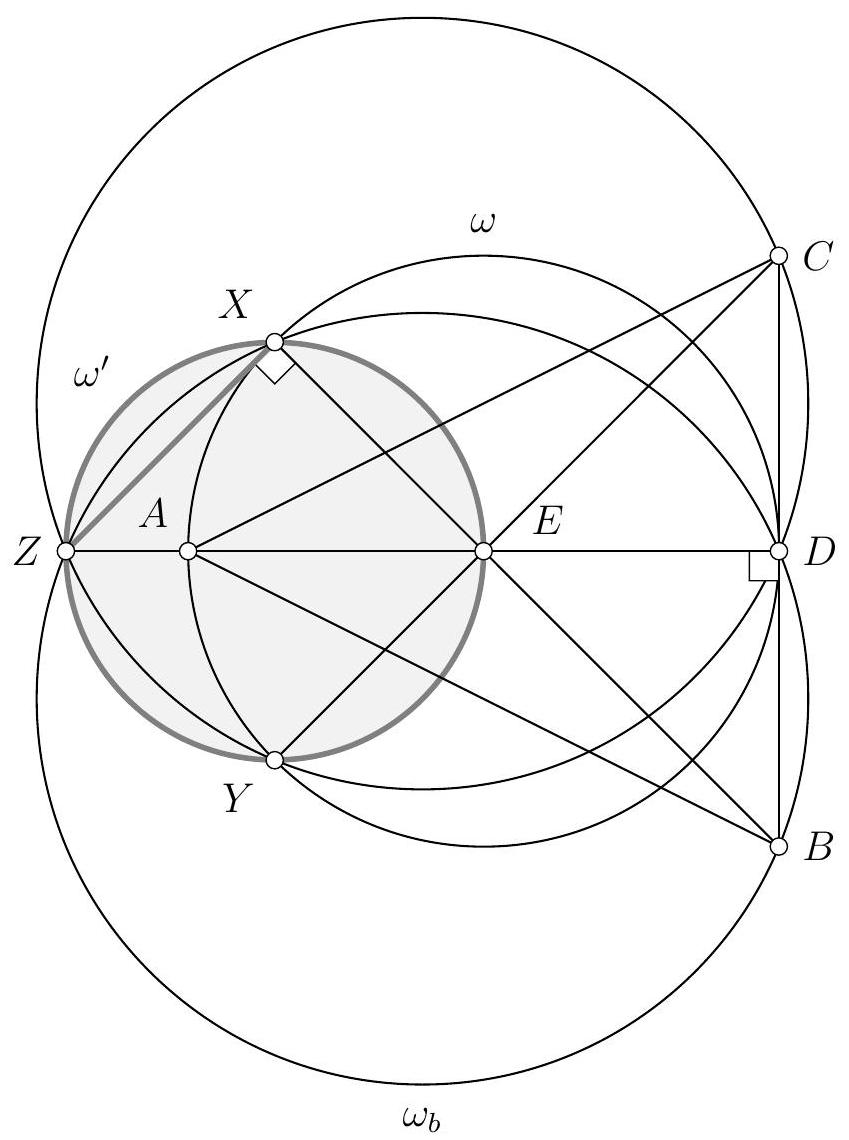
|
AB = AC
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle dont les angles sont aigus. On note $D$ le pied de la hauteur issue de $A$ dans le triangle $A B C$, puis $E$ le milieu du segment $[A D]$, et $\omega$ le cercle de diamètre $[A D]$. Ensuite, soit $X$ le point d'intersection entre $\omega$ et la droite $(B E)$, tel que $B$ et $X$ soient situés de part et d'autre de la droite $(A D)$. De même, soit $Y$ le point d'intersection entre $\omega$ et la droite $(C E)$, tel que $C$ et $Y$ soient situés de part et d'autre de la droite $(A D)$. Enfin, on suppose qu'il existe un point $Z$, autre que $D$, appartenant à la droite $(A D)$ et aux deux cercles circonscrits à $B D X$ et à $C D Y$. Démontrer que $A B=A C$.
|
Soit $\omega^{\prime}$ le cercle de diamètre $[E Z]$ et $\omega_{b}$ le cercle passant par $B, D$, $X$ et $Z$. Puisque $\widehat{B D Z}=90^{\circ}$, on sait que $[B Z]$ est un diamètre de $\omega_{b}$. On en déduit que $\widehat{E X Z}=\widehat{B X Z}=90^{\circ}$, donc que $X$ est un point d'intersection entre $\omega$ et $\omega^{\prime}$. De même, $Y$ est un point d'intersection entre $\omega$ et $\omega^{\prime}$.
Soit $s$ la symétrie d'axe $(A D)$ : elle laisse les cercles $\omega$ et $\omega^{\prime}$ globalement invariants, donc elle échange $X$ et $Y$. Puisque $E=s(E)$, la symétrie $s$ échange donc les droites $(E X)$ et $(E Y)$. En outre, $s$ laisse également la droite $(B C)$ globalement invariante. Ainsi, $s$ échange $B$ et $C$. Puisque $A=s(A)$, on en conclut que $A B=A C$.

|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T1",
"year": "2020"
}
|
Let $ABC$ be a triangle with acute angles. We denote $D$ as the foot of the altitude from $A$ in triangle $ABC$, then $E$ as the midpoint of the segment $[AD]$, and $\omega$ as the circle with diameter $[AD]$. Next, let $X$ be the intersection point between $\omega$ and the line $(BE)$, such that $B$ and $X$ are on opposite sides of the line $(AD)$. Similarly, let $Y$ be the intersection point between $\omega$ and the line $(CE)$, such that $C$ and $Y$ are on opposite sides of the line $(AD)$. Finally, suppose there exists a point $Z$, other than $D$, lying on the line $(AD)$ and on both circumcircles of $BDX$ and $CDY$. Prove that $AB = AC$.
|
$n^{\circ} 1$ Let $\omega_{b}$ and $\omega_{c}$ be the circumcircles of $B D X Z$ and $C D Y Z$. The line $(D Z)$ is the radical axis of these two circles. Since $E$ lies on this radical axis, it has the same power with respect to the circles $\omega_{b}$ and $\omega_{c}$, which means that $E X \cdot E B = E Y \cdot E C$. Since $E$ is the center of the circle $\omega$, we deduce that $E X = E Y$, and therefore that $E B = E C$.
Consequently, the line $(A D)$, which is the perpendicular to $(B C)$ passing through $E$, is also the perpendicular bisector of $[B C]$. We conclude as expected that $A B = A C$.
Comment from the graders: One of the first difficulties of the exercise was to figure out how to draw the figure in a relevant way. Indeed, drawing an isosceles triangle right away risked giving false intuitions about the figure. This was detrimental to many students who, after drawing the figure for an isosceles triangle $A B C$ at $A$, claimed certain angle equalities without proving them because they appeared true on the figure. After drawing this first figure, it would have been better to draw a new figure by forgetting one of the hypotheses, for example, by constructing a side $A B$ slightly longer than the side $A C$; this new figure could then serve as an alternative support for reflection, to ensure not to be misled by one's own sketch. In general, this advice remains valid for all geometry exercises with a format similar to the statement.
It was then necessary to figure out how to exploit the hypothesis given by the statement. The inscribed angle theorem was the key here, and very few students noted the equality $\widehat{Z X B} = \widehat{Z D B} = 90^{\circ}$, which was the starting point of the reasoning. Most students who noted this equality managed to conclude the exercise.
Here are some elements found repeatedly in the proposed solutions:
$\triangleright$ Many students claim to provide a complete solution to the problem, but in reality, it did not work or had a significant gap. Most of the time, this is because an assertion is given without proof, perhaps because it appears visually on the figure (see the remark above). The assertion is often true, but proving it often amounts to proving the exercise.
One way to avoid this pitfall is to reread, check that all assertions are justified, and verify if all the hypotheses of the statement have been used! Some students claim to prove that the triangle $A B C$ is isosceles without ever mentioning the point $Z$ or noting that the point $E$ is defined as the midpoint of the segment $[A D]$.
In fact, drawing an alternative figure where one forgets such and such hypothesis (for example, the hypotheses that were not used) allows checking if what one is saying has a chance of being true.
$\triangleright$ Many students notice that the line $(A D)$ is the radical axis of two circles. This observation could lead to another way (rather effective) to solve the exercise. However, it is frustrating to see that most students who made this observation stopped at this observation without continuing their reasoning.
The interest in identifying a radical axis is to then look at the power of a well-chosen point on this axis with respect to the two circles concerned. Here, very few students point out that the point $E$ belongs to the radical axis and therefore has the same power with respect to the two given circles.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle dont les angles sont aigus. On note $D$ le pied de la hauteur issue de $A$ dans le triangle $A B C$, puis $E$ le milieu du segment $[A D]$, et $\omega$ le cercle de diamètre $[A D]$. Ensuite, soit $X$ le point d'intersection entre $\omega$ et la droite $(B E)$, tel que $B$ et $X$ soient situés de part et d'autre de la droite $(A D)$. De même, soit $Y$ le point d'intersection entre $\omega$ et la droite $(C E)$, tel que $C$ et $Y$ soient situés de part et d'autre de la droite $(A D)$. Enfin, on suppose qu'il existe un point $Z$, autre que $D$, appartenant à la droite $(A D)$ et aux deux cercles circonscrits à $B D X$ et à $C D Y$. Démontrer que $A B=A C$.
|
$n^{\circ} 1$ Notons $\omega_{b}$ et $\omega_{c}$ les cercles circonscrits à $B D X Z$ et à $C D Y Z$. La droite $(D Z)$ est l'axe radical de ces deux cercles. Puisque $E$ appartient à cet axe radical, il a mêmes puissances par rapport aux cercles $\omega_{b}$ et $\omega_{c}$, ce qui signifie que $E X \cdot E B=E Y \cdot E C$. Or, $E$ est le centre du cercle $\omega$. On en déduit que $E X=E Y$, et donc que $E B=E C$.
Par conséquent, la droite $(A D)$, qui est la perpendiculaire à $(B C)$ passant par $E$, est aussi la médiatrice de $[B C]$. On en conclut comme prévu que $A B=A C$.
Commentaire des correcteurs Une première difficulté de l'exercice était de trouver comment tracer sa figure de façon pertinente. En effet, tracer d'emblée un triangle isocèle risquait
de donner de fausses intuitions sur la figure. Cela a été dommageable pour des nombreux élèves qui, après avoir tracé la figure pour un triangle $A B C$ isocèle en $A$, ont affirmé sans les démontrer certaines égalités d'angles parce qu'elles apparaissaient comme vraies sur la figure. Après avoir tracé cette première figure, il aurait en fait fallu tracer une nouvelle figure obtenue en oubliant l'une des hypothèses, par exemple en construisant un côté $A B$ légèrement plus grand que le côté $A C$; cette nouvelle figure pouvant alors servir comme support de réflexion alternatif, pour être sûr de ne pas être trompé par son propre brouillon. De manière générale, ce conseil reste valide pour tous les exercices de géométrie ayant un format analogue à celui de l'énoncé.
Il fallait ensuite trouver comment exploiter l'hypothèse donnée par l'énoncé. Le théorème de l'angle inscrit était de mise ici, et très peu d'élèves ont relevé l'égalité $\widehat{Z X B}=\widehat{Z D B}=90^{\circ}$, qui était pourtant le point de départ du raisonnement. La plupart des élèves qui ont noté cette égalité sont parvenus à conclure l'exercice.
Voici quelques éléments trouvés de façon récurrente dans les réponses proposées :
$\triangleright$ Beaucoup d'élèves prétendent donner une solution complète du problème, mais qui en réalité ne fonctionnait pas ou comportait un trou important. La plupart du temps, cela vient du fait qu'une affirmation est donnée sans démonstration, sans doute parce qu'elle apparaît visuellement sur la figure (cf la remarque plus haut). L'affirmation est souvent vraie mais la démontrer revient souvent à démontrer l'exercice.
Une façon de ne pas tomber dans cet écueil est de se relire, de vérifier que toutes les affirmations sont justifiées, et de vérifier si toutes les hypothèses de l'énoncé ont été utilisées! Certains élèves affirment ainsi démontrer que le triangle $A B C$ est isocèle sans évoquer une seule fois le point $Z$ ou sans mentionner que le point $E$ est défini comme le milieu du segment $[A D]$.
De fait, tracer une figure alternative où l'on oublie telle ou telle hypothèse (par exemple les hypothèses que l'on n'a pas utilisées) permet de vérifier si ce que l'on raconte a une chance d'être vrai.
$\triangleright$ Beaucoup d'élèves remarquent que la droite $(A D)$ est l'axe radical de deux cercles. Cette remarque pouvait conduire à une autre façon (plutôt efficace) de résoudre l'exercice. Toutefois, il est frustrant de voir que la plupart des élèves ayant formulé cette remarque se sont arrêtés à cette remarque sans continuer leur raisonnement.
L'intérêt de repérer un axe radical est de pouvoir ensuite regarder la puissance d'un point bien choisi sur cet axe par rapport aux deux cercles concernés. Ici, très peu d'élèves signalent que le point $E$ appartenait à l'axe radical et a donc la même puissance par rapport aux deux cercles donnés.
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2020"
}
|
Let $k \geqslant 1$ be an integer, and let $A$ be a subset of $\{1,2, \ldots, 3 k\}$ such that, for all elements $a, b, c$ of $A$, if $a+b=2 c$, then $a=b=c$. For any integer $n \geqslant 1$, we denote $r_{k}(n)$ as the smallest non-zero natural number such that $3 k$ divides $n-r_{k}(n)$. Furthermore, we say that $n$ is small if $n \leqslant k$, that $n$ is medium if $k+1 \leqslant n \leqslant 2 k$, and that $n$ is large if $2 k+1 \leqslant n$. Finally, we assume that we have two non-zero natural numbers $x$ and $d$ such that $r_{k}(x), r_{k}(x+d)$, and $r_{k}(x+2 d)$ all belong to $A$, and such that $r_{k}(x) \neq r_{k}(x+d)$.
Can we necessarily affirm, given the information above, that
a) at least one of the two integers $r_{k}(x)$ and $r_{k}(x+d)$ is medium or large?
b) at least one of the two integers $r_{k}(x)$ and $r_{k}(x+d)$ is small or large?
c) at least one of the two integers $r_{k}(x)$ and $r_{k}(x+d)$ is small or medium?
|
This statement may seem long and complicated. It therefore contains key elements to retain to better understand what is happening. Here, we want the set $A$ not to contain any arithmetic progression ($a, c, b$). This means finding two integers $x$ and $d$ such that, even though $x, x+d$, and $x+2d$ are clearly in arithmetic progression, the remainders $r_{k}(x), r_{k}(x+d)$, and $r_{k}(x+2d)$ in the Euclidean division by $3k$ are not in arithmetic progression.
One idea to achieve this is to construct $x$ and $d$, possibly choosing them to be negative if it suits us (it will always be time to add arbitrarily large multiples of $3k$ to $x$ and $d$) such that $x$ and $x+d$ are between 1 and $3k$, but $x+2d$ exceeds the interval $\{1,2, \ldots, 3k\}$. Once this preparatory reflection work is done, we can now address each of the three questions in the statement: we will seek to construct integers $x$ and $x+d$ that are both small, or both medium, or both large.
a) Let's try to construct small integers $x$ and $x+d$ such that $x+2d \leq 0$ and $x+2d \geq 3k+1$. Since $x+2d=2(x+d)-x \leq 2k-1 < 2k+1$, we need to ensure that $x+2d \leq 0$, so $d < 0$. The simplest way to proceed is then to choose $d=-1, x=2$, and $k \geq 2$. Obviously, we are not really allowed to choose $d=-1$; as mentioned earlier, we will therefore choose $d=3k-1$, which is the same but conforms to the constraints of the statement.
In practice, if $k=2, A=\{1,2,6\}, x=2$ and $d=5$, then $r_{k}(x)=2$ and $r_{k}(x+d)=1$ are two small elements of $A$, and $r_{k}(x+2d)=6$ also belongs to $A$. The answer is therefore negative.
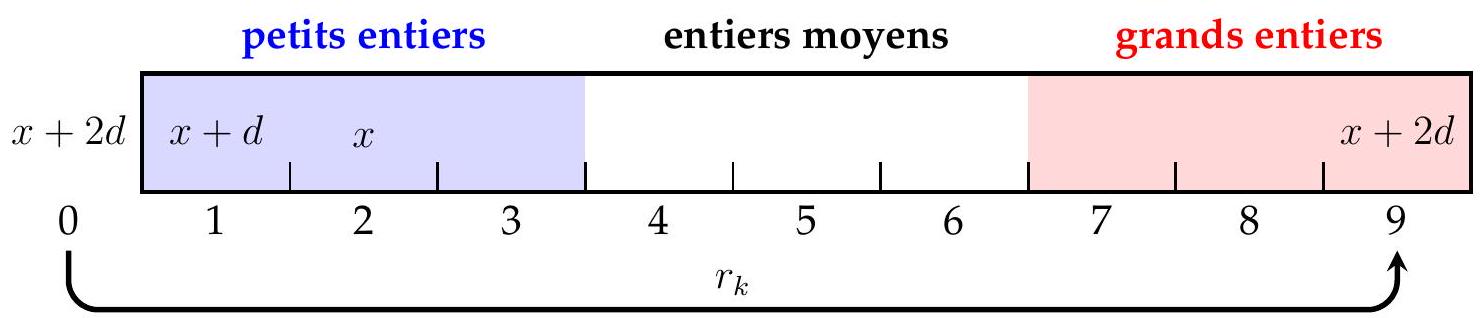
b) Suppose that $r_{k}(x)$ and $r_{k}(x+d)$ are both medium, and let $t=2r_{k}(x+d)-r_{k}(x)$. We know that
$$
2=2(k+1)-2k \leq t \leq 2 \times 2k - (k+1) = 3k-1
$$
and that
$$
t \equiv 2(x+d) - x \equiv x + 2d \quad (\bmod 3k),
$$
so $t = r_{k}(x+2d)$. But then $t + r_{k}(x) = 2r_{k}(x+d)$, which contradicts the initial characterization of $A$. This invalidates our assumption, and the answer is therefore positive.
c) Given the manifest symmetry between left and right, it suffices to adapt the construction proposed in question a), by replacing $x$ with $3k+1-x$ and $d$ with $3k-d$.
In practice, if $k=2, A=\{1,5,6\}, x=5$ and $d=1$, then $r_{k}(x)=5$ and $r_{k}(x+d)=6$ are two large elements of $A$, and $r_{k}(x+2d)=1$ also belongs to $A$. The answer is therefore negative.

Comment from the graders: One of the main difficulties of this exercise was to understand the statement in detail, without forgetting any constraints here and there. The idea was then to highlight three integers that are in arithmetic progression if considered modulo $3k$, but not if considered as integers. Students who had this idea generally achieved excellent results.
However, several avoidable errors trapped many students. We list them here to prevent them from recurring:
$\triangleright$ Several students confused the integers $x, x+d$, and $x+2d$ with their remainders $r_{k}(x), r_{k}(x+d)$, and $r_{k}(x+2d)$. In particular, they believed that $x, x+d$, and $x+2d$ must necessarily be between 1 and $3k$.
$\triangleright$ Several students incorrectly believed that, to divide $x$ by $3k$, the quotient of this division must necessarily be non-zero.
$\triangleright$ Several students provided counterexamples that were actually false because they had forgotten some constraints in the statement. Generally, once a counterexample is available, it is very important to carefully reread the statement to verify that it is indeed a counterexample: indeed, if one is content with exhibiting this counterexample but has actually made a mistake, one no longer provides the grader with elements that will allow points to be given, and the grader is therefore left with no other choice but to give no points for the relevant question.
$\triangleright$ Finally, surprisingly, and even though it is not a strict error, several students treated case a) but not case c), or vice versa, even though the ideas involved were exactly the same.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Soit $k \geqslant 1$ un entier, et soit $A$ un sous-ensemble de $\{1,2, \ldots, 3 k\}$ tel que, pour tous les éléments $a, b, c$ de $A$, si $a+b=2 c$, alors $a=b=c$. Pour tout entier $n \geqslant 1$, on note $r_{k}(n)$ le plus petit entier naturel non nul tel que $3 k$ divise $n-r_{k}(n)$. En outre, on dit que $n$ est petit si $n \leqslant k$, que $n$ est moyen si $k+1 \leqslant n \leqslant 2 k$, et que $n$ est grand si $2 k+1 \leqslant n$. Enfin, on suppose que l'on dispose de deux entiers naturels non nuls $x$ et $d$ tels que $r_{k}(x), r_{k}(x+d)$ et $r_{k}(x+2 d)$ appartiennent tous trois à $A$, et tels que $r_{k}(x) \neq r_{k}(x+d)$.
Peut-on nécessairement affirmer, au vu des informations ci-dessus, que
a) au moins l'un des deux entiers $r_{k}(x)$ et $r_{k}(x+d)$ est moyen ou grand?
b) au moins l'un des deux entiers $r_{k}(x)$ et $r_{k}(x+d)$ est petit ou grand?
c) au moins l'un des deux entiers $r_{k}(x)$ et $r_{k}(x+d)$ est petit ou moyen?
|
Cet énoncé peut paraître long et compliqué. Il contient donc d'en retenir les éléments saillants, pour mieux comprendre ce qui se passe. Ici, on souhaite que l'ensemble $A$ ne contienne pas de progression arithmétique ( $a, c, b$ ). Il s'agit donc de trouver deux entiers $x$ et $d$ pour lesquels, quand bien même $x, x+d$ et $x+2 d$ sont manifestement en progression arithmétique, les restes $r_{k}(x), r_{k}(x+d)$ et $r_{k}(x+2 d)$ dans la division euclidienne par $3 k$ ne seront pas en progression arithmétique.
Une idée, pour ce faire, est de construire $x$ et $d$, éventuellement en les choisissant négatifs si ça nous arrange (il sera toujours temps d'ajouter à $x$ et à $d$ des multiples de $3 k$ arbitrairement grands) tels que $x$ et $x+d$ soient compris entre 1 et $3 k$, mais $x+2 d$ dépasse de l'intervalle $\{1,2, \ldots, 3 k\}$. Une fois effectué ce travail de réflexion préparatoire, on peut maintenant traiter une à une les trois questions de l'énoncé : on cherchera à construire des entiers $x$ et $x+d$ qui sont tous deux petits, ou tous deux moyens, ou tous deux grands.
a) Cherchons à construire de petits entiers $x$ et $x+d$ tels que $x+2 d \leqslant 0$ et $x+2 d \geqslant 3 k+1$. Puisque $x+2 d=2(x+d)-x \leqslant 2 k-1<2 k+1$, il nous faut faire en sorte que $x+2 d \leqslant 0$, donc que $d<0$. La manière la plus simple de procéder est alors de choisir $d=-1, x=2$, et $k \geqslant 2$. Évidemment, on n'a pas vraiment le droit de choisir $d=-1$; comme mentionné précédemment, on choisira donc $d=3 k-1$, ce qui revient au même mais est conforme aux contraintes de l'énoncé.
En pratique, si $k=2, A=\{1,2,6\}, x=2$ et $d=5$, alors $r_{k}(x)=2$ et $r_{k}(x+d)=1$ sont deux petits éléments de $A$, et $r_{k}(x+2 d)=6$ appartient à $A$ également. La réponse est donc négative.

b) Supposons que $r_{k}(x)$ et $r_{k}(x+d)$ soient tous deux moyens, puis soit $t=2 r_{k}(x+d)-r_{k}(x)$. On sait que
$$
2=2(k+1)-2 k \leqslant t \leqslant 2 \times 2 k-(k+1)=3 k-1
$$
et que
$$
t \equiv 2(x+d)-x \equiv x+2 d \quad(\bmod 3 k),
$$
donc que $t=r_{k}(x+2 d)$. Mais alors $t+r_{k}(x)=2 r_{k}(x+d)$, en contradiction avec la caractérisation initiale de $A$. Ceci invalide notre supposition, et la réponse est donc positive.
c) Au vu de la symétrie manifeste entre gauche et droite, il suffit d'adapter la construction proposée en question a), en remplaçant $x$ par $3 k+1-x$ et $d$ par $3 k-d$.
En pratique, si $k=2, A=\{1,5,6\}, x=5$ et $d=1$, alors $r_{k}(x)=5$ et $r_{k}(x+d)=6$ sont deux grands éléments de $A$, et $r_{k}(x+2 d)=1$ appartient à $A$ également. La réponse est donc négative.

Commentaire des correcteurs Une des difficultés principales de cet exercice était d'en comprendre l'énoncé en détail, sans oublier des contraintes de ci de là. L'idée était ensuite de mettre en évidence trois entiers qui sont en progression arithmétique si on les considère modulo $3 k$, mais pas si on les considère en tant qu'entiers. Les élèves qui ont eu cette idée ont en général obtenu d'excellents résultats.
On peut cependant noter que plusieurs erreurs évitables ont piégé de nombreux élèves. Nous les listons ici pour éviter qu'elles ne se reproduisent:
$\triangleright$ Plusieurs élèves ont confondu les entiers $x, x+d$ et $x+2 d$ avec leurs restes $r_{k}(x), r_{k}(x+d)$ et $r_{k}(x+2 d)$. En particulier, ils ont cru que $x, x+d$ et $x+2 d$ devaient forcément être compris entre 1 et $3 k$.
$\triangleright$ Plusieurs élèves ont cru à tort que, pour que l'on puisse diviser $x$ par $3 k$, il fallait nécessairement que le quotient de cette division soit non nul.
$\triangleright$ Plusieurs élèves ont cru fournir des contre-exemples qui étaient en fait faux, parce qu'ils avaient oublié certaines contraintes de l'énoncé. De manière générale, une fois que l'on dispose d'un contre-exemple, il est très important de relire attentivement l'énoncé pour vérifier qu'il s'agit bien d'un contre-exemple : en effet, si on se contente d'exhiber ce contre-exemple mais que l'on s'est en fait trompé, on ne fournit plus au correcteur d'éléments qui lui permettront de donner des points, et il se retrouve donc sans autre choix que de n'en donner aucun pour la question concernée.
$\triangleright$ Enfin, de manière surprenante, et même s'il ne s'agit pas d'une erreur stricto sensu, plusieurs élèves on traité le cas a) mais pas le cas c), ou l'inverse, alors même que les idées mises en jeu étaient exactement les mêmes.
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T1",
"year": "2020"
}
|
Let $\left(F_{k}\right)_{k \geqslant 0}$ be the sequence defined by $F_{0}=0, F_{1}=1$, and $F_{k+2}=F_{k}+F_{k+1}$ for all integers $k \geqslant 0$. Let then $n \geqslant 1$ be an integer. Prove that there are exactly $F_{n+1}$ ways to order the numbers $1,2, \ldots, n$ to obtain an $n$-tuple $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ such that
$$
a_{1} \leqslant 2 a_{2} \leqslant 3 a_{3} \leqslant \ldots \leqslant n a_{n} .
$$
|
A permutation $\mathbf{a}=\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ of the integers $1,2, \ldots, n$ is said to be pretty if it satisfies the inequalities $a_{1} \leqslant 2 a_{2} \leqslant \ldots \leqslant n a_{n}$.
First, let $a$ be a pretty permutation. If there exists an integer $k$ for which $a_{k} \leqslant k-2$, we choose the minimal $k$. In this case, we know that $k \geqslant 2$ and that $a_{k-1} \geqslant k-2 \geqslant a_{k}$, so $a_{k-1} \geqslant a_{k}+1$. We conclude that
$$
(k-1) a_{k-1} \geqslant(k-1)\left(a_{k}+1\right)=k a_{k}+\left(k-a_{k}-1\right) \geqslant k a_{k}+1,
$$
and thus that $a$ is not pretty. Therefore, we conclude that $a_{k} \geqslant k-1$ for all $k \leqslant n$.
On the other hand, let $\ell$ be the integer such that $a_{\ell}=n$. Given the result obtained previously, an immediate downward induction on $k$ ensures that $a_{k}=k-1$ for all integers $k$ such that $\ell+1 \leqslant k \leqslant n$. Since
$$
\ell n=\ell a_{\ell} \leqslant(\ell+1) a_{\ell+1}=(\ell+1) \ell
$$
we conclude that $\ell \in\{n-1, n\}$.
Thus, for $a$ to be pretty, we have two choices a priori:
$\triangleright$ either $\ell=n$, in which case $a$ is indeed pretty if and only if the permutation $\left(a_{1}, a_{2}, \ldots, a_{n-1}\right)$ of the integers $1,2, \ldots, n-1$ is pretty;
$\triangleright$ or $\ell=n-1$, in which case $a_{n}=n-1$, and then $a$ is indeed pretty if the permutation $\left(a_{1}, a_{2}, \ldots, a_{n-2}\right)$ of the integers $1,2, \ldots, n-2$ is pretty.
Consequently, if we denote by $J_{n}$ the number of pretty permutations of $1,2, \ldots, n$, we note that $J_{n}=J_{n-1}+J_{n-2}$ as soon as $n \geqslant 3$. We conclude by verifying that $J_{1}=1=F_{2}$ and that $J_{2}=2=F_{3}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soit $\left(F_{k}\right)_{k \geqslant 0}$ la suite définie par $F_{0}=0, F_{1}=1$, et $F_{k+2}=F_{k}+F_{k+1}$ pour tout entier $k \geqslant 0$. Soit ensuite $n \geqslant 1$ un entier. Démontrer qu'il existe exactement $F_{n+1}$ façons d'ordonner les nombres $1,2, \ldots, n$ de manière à obtenir un $n$-uplet $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ tel que
$$
a_{1} \leqslant 2 a_{2} \leqslant 3 a_{3} \leqslant \ldots \leqslant n a_{n} .
$$
|
On dit qu'une permutation $\mathbf{a}=\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ des entiers $1,2, \ldots, n$ est jolie si elle satisfait les inégalités $a_{1} \leqslant 2 a_{2} \leqslant \ldots \leqslant n a_{n}$.
Tout d'abord, soit a une jolie permutation. S'il existe un entier $k$ pour lequel $a_{k} \leqslant k-2$, on choisit $k$ minimal. Dans ces conditions, on sait que $k \geqslant 2$ et que $a_{k-1} \geqslant k-2 \geqslant a_{k}$, de sorte que $a_{k-1} \geqslant a_{k}+1$. On en conclut que
$$
(k-1) a_{k-1} \geqslant(k-1)\left(a_{k}+1\right)=k a_{k}+\left(k-a_{k}-1\right) \geqslant k a_{k}+1,
$$
et donc que a n'est pas jolie. On en conclut donc que $a_{k} \geqslant k-1$ pour tout $k \leqslant n$.
D'autre part, soit $\ell$ l'entier tel que $a_{\ell}=n$. Au vu du résultat obtenu précédemment, une récurrence descendante immédiate sur $k$ nous assure que $a_{k}=k-1$ pour tout entier $k$ tel que $\ell+1 \leqslant k \leqslant n$. Puisque
$$
\ell n=\ell a_{\ell} \leqslant(\ell+1) a_{\ell+1}=(\ell+1) \ell
$$
on en conclut que $\ell \in\{n-1, n\}$.
Ainsi, pour que a soit jolie, on dispose a priori de deux choix :
$\triangleright$ soit $\ell=n$, auquel cas a est effectivement jolie si et seulement si la permutation $\left(a_{1}, a_{2}, \ldots, a_{n-1}\right)$ des entiers $1,2, \ldots, n-1$ est jolie;
$\triangleright$ soit $\ell=n-1$, auquel cas $a_{n}=n-1$, et alors a est effectivement jolie si la permutation $\left(a_{1}, a_{2}, \ldots, a_{n-2}\right)$ des entiers $1,2, \ldots, n-2$ est jolie.
Par conséquent, si on note $J_{n}$ le nombre de jolies permutations de $1,2, \ldots, n$, on remarque bien que $J_{n}=J_{n-1}+J_{n-2}$ dès lors que $n \geqslant 3$. On conclut en vérifiant que $J_{1}=1=F_{2}$ et que $J_{2}=2=F_{3}$ 。
|
{
"exam": "French_tests",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T1",
"year": "2020"
}
|
Let $\left(F_{k}\right)_{k \geqslant 0}$ be the sequence defined by $F_{0}=0, F_{1}=1$, and $F_{k+2}=F_{k}+F_{k+1}$ for all integers $k \geqslant 0$. Let then $n \geqslant 1$ be an integer. Prove that there are exactly $F_{n+1}$ ways to order the numbers $1,2, \ldots, n$ to obtain an $n$-tuple $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ such that
$$
a_{1} \leqslant 2 a_{2} \leqslant 3 a_{3} \leqslant \ldots \leqslant n a_{n} .
$$
|
$n^{\circ} 1$ As previously, we consider a permutation $a$ and the integer $\ell$ such that $a_{\ell}=n$. Since $n a_{k} \geqslant k a_{k} \geqslant \ell a_{\ell}=\ell n$ for all $k \geqslant \ell$, we know that $a$ induces a permutation of $1,2, \ldots, \ell-1$ and of $\ell, \ell+1, \ldots, n$.
If $\ell \leqslant n-1$, let $m$ be the unique integer such that $a_{m}=\ell$. Since $m \geqslant \ell$, we know that
$$
m \ell=m a_{m} \geqslant \ell a_{\ell}=\ell n
$$
thus $m=n$. But then $k a_{k}=\ell n$ for all integers $k$ such that $\ell \leqslant k \leqslant n$. We deduce in particular that $n-1$ divides $(n-1) a_{n-1}=\ell n$, and thus divides $\ell$ as well, which means that $\ell=n-1$. Now that we have established that $\ell \in\{n-1, n\}$, we conclude as previously.
Comment from the graders: This problem was difficult. Nevertheless, a good number of students had the good idea to try to find a recurrence relation on the number of permutations satisfying the statement and succeeded, by analyzing the recurrence relation, to understand the structure of the permutations satisfying the statement.
However, very few students managed to formalize this, in particular to show that the integer $\ell$ defined in the solution was indeed greater than or equal to $n-1$. Some used the fact that $n(n-2)<(n-1)^{2}$ to conclude in the general case. If this argument worked for $\ell=n-2$, it was unfortunately impossible to adapt it directly for arbitrary $\ell$.
Also be careful with the recurrence! Several students showed, if we denote by $k_{n}$ the number of permutations of $\{1, \ldots, n\}$ satisfying the statement, that $k_{n}=k_{n-1}+k_{n-2}$. They then performed a strong induction, initialized at $n=1$, to prove that $k_{n}=F_{n+1}$. Here, for $n=2$, the formula $k_{2}=k_{1}+k_{0}$ does not make sense because $k_{0}$ is not even defined. This inductive reasoning therefore did not allow proving that $k_{2}=F_{3}$, and it would have been necessary to treat this equality in the initialization of our recurrence. Here, to avoid this error, it would have been better to perform a double induction, which requires explicitly initializing at $n=1$ and $n=2$.
## Senior Problems
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soit $\left(F_{k}\right)_{k \geqslant 0}$ la suite définie par $F_{0}=0, F_{1}=1$, et $F_{k+2}=F_{k}+F_{k+1}$ pour tout entier $k \geqslant 0$. Soit ensuite $n \geqslant 1$ un entier. Démontrer qu'il existe exactement $F_{n+1}$ façons d'ordonner les nombres $1,2, \ldots, n$ de manière à obtenir un $n$-uplet $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ tel que
$$
a_{1} \leqslant 2 a_{2} \leqslant 3 a_{3} \leqslant \ldots \leqslant n a_{n} .
$$
|
$n^{\circ} 1$ Comme précédemment, on considère une permutation a puis l'entier $\ell$ tel que $a_{\ell}=n$. Puisque $n a_{k} \geqslant k a_{k} \geqslant \ell a_{\ell}=\ell$ n pour tout $k \geqslant \ell$, on sait que a induit une permutation de $1,2, \ldots, \ell-1$ et de $\ell, \ell+1, \ldots, n$.
Si $\ell \leqslant n-1$, soit $m$ l'unique entier tel que $a_{m}=\ell$. Puisque $m \geqslant \ell$, on sait que
$$
m \ell=m a_{m} \geqslant \ell a_{\ell}=\ell n
$$
donc que $m=n$. Mais alors $k a_{k}=\ell n$ pour tout entier $k$ tel que $\ell \leqslant k \leqslant n$. On en déduit en particulier que $n-1$ divise $(n-1) a_{n-1}=\ell n$, donc divise $\ell$ aussi, ce qui signifie que $\ell=n-1$. Maintenant acquis le fait que $\ell \in\{n-1, n\}$, on conclut comme précédemment.
Commentaire des correcteurs Cet exercice était difficile. Néanmoins, une bonne partie des élèves a eu la bonne idée d'essayer de trouver une relation de récurrence sur le nombre de permutations vérifiant l'énoncé et a réussi, en analysant la relation de récurrence, à comprendre la structure des permutations vérifiant l'énoncé.
Toutefois, très peu d'élèves ont réussi à formaliser cela, en particulier à montrer que l'entier $\ell$ défini dans la correction était bien supérieur ou égal à $n-1$. Certains ont utilisé le fait que $n(n-2)<(n-1)^{2}$ pour conclure dans le cas général. Si cet argument fonctionnait
pour $\ell=n-2$, il était malheureusement impossible de l'adapter directement pour des $\ell$ quelconques.
Attention aussi à la récurrence! Plusieurs élèves ont montré, si on note $k_{n}$ le nombre de permutations de $\{1, \ldots, n\}$ vérifiant l'énoncé, que $k_{n}=k_{n-1}+k_{n-2}$. Ils ont ensuite fait une récurrence forte, initialisée à $n=1$, pour prouver que $k_{n}=F_{n+1}$. Ici pour $n=2$, la formule $k_{2}=k_{1}+k_{0}$ n'a pas de sens car $k_{0}$ n'est même pas défini. Ce raisonnement par récurrence ne permettait donc pas de prouver que $k_{2}=F_{3}$, et il aurait fallu traiter cette égalité dans le cadre de l'initialisation de notre récurrence. Ici, pour éviter cette erreur, il valait mieux faire une récurrence double, qui nécessite explicitement d'initialiser à $n=1$ et $n=2$.
## Problèmes Senior
|
{
"exam": "French_tests",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2020"
}
|
Pierre and Clara are playing the following game. First, Clara chooses an integer $c$. Then Pierre chooses a prime number $p \geqslant c$ and writes two integers $a$ and $b$ on the board. Clara is then allowed to perform the following operations: she chooses one of the two numbers written on the board, say $n$, erases it, and writes another integer, say $m$, such that $p$ divides $\left(n^{2}-m+1\right)\left(m^{2}-n+1\right)$. Clara wins if she manages to make the two integers on the board identical after a finite number of such operations. Otherwise, she loses, and Pierre wins.
Prove that Pierre can prevent Clara from winning.
|
Let $p$ be a prime number, arbitrarily large, that Pierre is likely to choose, and let $f: \mathbb{Z} / p \mathbb{Z} \mapsto \mathbb{Z} / p \mathbb{Z}$ be the function defined by $f(x)=x^{2}+1$.
When Clara replaces an integer $n$ by an integer $m$, one of the two equalities $n=f(m)$ or $m=f(n)$ is necessarily satisfied, so that $m$ and $n$ belong to the same orbit of $f$. We then say that two residues $u$ and $v$ modulo $p$ are connected if there exist two integers $k \geqslant 0$ and $\ell \geqslant 0$ such that $f^{k}(u)=f^{\ell}(v)$. It is immediately apparent that if Clara manages to transform a residue $m$ into a residue $n$, these two residues are connected; the converse is also true, although we will not need it.
Pierre's goal is therefore to find a prime number $p \geqslant c$, and two residues $a$ and $b$ modulo $p$ that are not connected to each other. The simplest way is for $a$ and $b$ to be fixed points of $f$, i.e., such that $(X-a)(X-b) \equiv X^{2}-X+1(\bmod p)$.
Now, if $X^{2}-X+1$ has a root $a$ modulo $p$, the other root is $1 / a$ (since $a$ is non-zero), or $1-a$. These two roots are therefore equal only if $1-a \equiv a \equiv 1 / a(\bmod p)$, i.e., if $p \neq 2$ and $1 / 2 \equiv a \equiv \pm 1(\bmod p)$. We know that $1 / 2 \equiv \pm 1(\bmod p)$ if and only if $p=3$. Consequently, Pierre only needs to choose a prime number $p>\max \{c, 3\}$ that divides a number of the form $n^{2}-n+1$. In practice, to do this, he just needs to define $p$ as the smallest prime factor of the number $S_{m}=(m!)^{2}-m!+1$, where he has set $m=\max \{c, 3\}$. Indeed, we know that $S_{m} \geqslant 2$ and that $S_{m}$ is coprime with $m!$. Thus, the smallest prime factor of $S_{m}$ exists, and it is coprime with $m!$, hence strictly greater than $m$. Pierre will then choose $a=m!$ and $b=1-m!$ to finally savor a well-deserved victory.
$\underline{\text { Alternative Solution } n^{\circ} 1}$ Given a prime number $p$, we will construct the graph $G$ whose vertices are the elements of $\mathbb{Z} / p \mathbb{Z}$ and the edges are the pairs $(m, n)$ such that $\left(n^{2}-m+1\right)\left(m^{2}-n+1\right) \equiv 0(\bmod p)$. We will say that an edge $(m, n)$ is useful if $m \neq n$, and useless otherwise, i.e., if it is a loop. If $G$ contains at most $p-2$ useful edges, then it is not connected, and Pierre only needs to choose integers belonging to two distinct connected components.
We then say that an edge $(m, n)$ is generated by $n$ if $m \equiv n^{2}+1(\bmod m)$. Every edge is generated by one of its endpoints, and each vertex generates a unique edge, so $G$ contains at most $p$ edges. Therefore, if $G$ contains two useless edges, i.e., if there exist two distinct residues $u$ and $v$ such that $u \equiv u^{2}+1(\bmod p)$ and $v \equiv v^{2}+1(\bmod p)$, Pierre is assured of winning.
He then only needs to proceed as in the previous solution.
Remark: In fact, it can be shown that any graph $G$ constructed as above contains at least $p-1$ edges. Indeed, if this is not the case, there exist two edges $(m, n)$ and $(u, v)$, each generated by their two endpoints, and such that $m, n, u$ and $v$ are pairwise distinct modulo $p$. These are four distinct roots of the polynomial $P(X)=\left(X^{2}+1\right)^{2}+1-X$
in $\mathbb{Z} / p \mathbb{Z}$, such that $m=f(n), n=f(m), u=f(v)$ and $v=f(u)$.
Now, any fixed point of $f$ is a root of $P$, which means that $P$ is divisible by the polynomial $Q(X)=X^{2}+1-X$. We deduce the factorization $P(X)=\left(X^{2}+X+2\right) Q(X)$. Thus, among $m, n, u$ and $v$, two are roots of $Q$, i.e., fixed points of $f$, in contradiction with our assumption.
In particular, it was therefore essential to focus on the fixed points of $f$, or at least on its small cycles.
$\underline{\text { Alternative Solution } n^{\circ} 2}$ The solution below uses more advanced concepts, but this allows a lax approach to the combinatorial dimension of the problem. Below, we consider directly that Pierre chooses residues modulo $p$ rather than integers, and we denote $f: \mathbb{Z} / p \mathbb{Z}$ the function defined by $f(x)=x^{2}+1$. When $x$ and $y$ are residues modulo $p$, we will abusively write $x=y$ and $x \neq y$ the relations $x \equiv y(\bmod p)$ and $x \not \equiv y(\bmod p)$.
Suppose Pierre has chosen a prime number $p$ and two residues $a$ and $b$ such that $b \neq \pm a$ such that $a=f(a)$, but Clara wins anyway. Since every operation of Clara can be reversed, we assume without loss of generality that she gradually transformed $a$ into $b$, in the smallest number of steps possible.
The first step of Clara consists in transforming $a$ into $f(a)=a$, which would be silly, or into an antecedent $x \neq a$ of $a$ by $f$. The two antecedents of $a$ by $f$ are opposite to each other, and one is equal to $a$, so the other is $-a$. Thus, Clara has transformed $a$ into $-a$.
Since $b \neq -a$, Clara had to transform $-a$ into $f(-a)=a$ again, which would be silly again, or into an antecedent $y$ of $-a$ by $f$, so that $-a-1=f(y)-1=y^{2}$ is a quadratic residue modulo $p$.
Therefore, Pierre will win if he finds a prime number $p \geqslant 3$ for which $f$ has a fixed point $a$ such that $-a-1$ is not a quadratic residue modulo $p$. Now, if $a$ is a fixed point of $f$, we know that $f(1-a)=a^{2}-2 a+2=f(a)-2 a+1=1-a$, so $1-a$ is also a fixed point of $f$. It is therefore sufficient that either $-a-1$ or $a-2$ is not a quadratic residue (or both).
The simplest way to ensure that two numbers are not both quadratic residues is to make sure that their product is not a quadratic residue. This technique will be advantageous here, as it allows us not to distinguish the residues $-a-1$ and $a-2$, which had been defined symmetrically. Here, Pierre will therefore choose $p$ so that $(a-2)(-a-1)=2+a-a^{2}=3$ is not a quadratic residue.
Finally, he must ensure that $f$ has a fixed point. Now, if he immerses himself in the field $\mathbb{C}$ of complex numbers, Pierre knows well that the roots of the polynomial $f(X)-X=X^{2}-X+1$ are $(1+\sqrt{-3}) / 2$ and $(1-\sqrt{-3}) / 2$. We recognize that $a$ is a fixed point of $f$ if and only if $(2 a-1)^{2}=-3$, and such a fixed point exists if and only if -3 is a quadratic residue. It is therefore for Pierre to choose a prime number $p$ for which -3 is a quadratic residue and -1 is not.
Now, if there exists a residue $z$ such that $z^{2}=-1$, we know that $z$ is of order 4, so $p \equiv 1(\bmod 4)$. Pierre will therefore look for $p$ among the prime factors not congruent to $1(\bmod 4)$ of an integer of the form $n^{2}+3$. Choosing $n$ coprime with 3 ensures that $p \neq 3$. Then, choosing $n$ even ensures that $n^{2}+3 \equiv 3(\bmod 4)$, so $n$ necessarily has a prime factor $p \equiv 3(\bmod 4)$. It is therefore sufficient to define $n$ as the least common multiple of the prime numbers less than or equal to max $\{c, 2\}$ and different from $3$: the factor $p$ that Pierre will choose will be coprime with all these prime numbers, but also with 3, so that $p>c$, and the considerations of the previous paragraphs ensure that Pierre can choose integers $a$ and $b$ appropriately.
Remark: Once resolved to choose a prime number $p$ for which neither $3$ nor $-1$ are quadratic residues, Pierre can also rely on powerful theorems that he does not necessarily know how to prove, which will leave him a slight taste of incompleteness.
Quadratic Reciprocity Theorem. Let $p$ be a prime number and $n$ an integer not divisible by $p$. We set $\binom{n}{p}=1$ if $n$ is a quadratic residue modulo $p$, and $\binom{n}{p}=-1$ otherwise.
$\triangleright$ If $p$ and $q$ are two distinct odd prime numbers, $\binom{p}{q}\binom{q}{p}=(-1)^{(p-1)(q-1) / 4}$.
$\triangleright$ For any odd prime number $p$, $\binom{-1}{p}=(-1)^{(p-1) / 2}$ and $\binom{2}{p}=(-1)^{\left(p^{2}-1\right) / 8}$.
Dirichlet's Theorem on Primes. Let $a$ and $b$ be two coprime integers. There are infinitely many prime numbers $p$ such that $p \equiv a(\bmod b)$.
Equipped with these two results, Pierre therefore chooses a prime number $p$ such that $p \equiv 3(\bmod 4)$ and $\binom{p}{3}=-\binom{3}{p}=1$, i.e., $p \equiv 1(\bmod 3)$. It is thus a matter of choosing a prime number $p \geqslant c$ such that $p \equiv 7(\bmod 12)$, and Dirichlet's theorem indicates that such a prime number exists.
Comment from the graders Very few students fully solved this difficult problem, which could have been a difficult problem 1 or 4 at the International Olympiad. It involves the study of a dynamical system presented in the form of a game with a winning strategy. Two main approaches were possible here: a combinatorial approach translating the problem into terms of a graph whose vertices belonged to $\mathbb{Z} / p \mathbb{Z}$, as in the first two proposed solutions, and a very arithmetic approach passing through a study of squares modulo $p$, as in the alternative solution $\mathrm{n}^{\circ} 2$. Each of the two approaches required the implementation of many ideas, and obtaining points therefore required establishing significant results.
This problem involved the study of a dynamical system, i.e., a system (here, a pair of integers) on which one acts via an operation (here, one replaces an integer by another according to certain constraints). In such a case, it is crucial to study the small cases. Many students presented their study for particular $p$, most often for $p=7$. Even if this initiative was not rewarded with a point here, we strongly encourage it!
Another important reflex to have is to consider the possible fixed points of the operation. This was here, whatever the approach, the starting point of the problem, and several students had this reflex, to the great satisfaction of the graders. A few students looked for invariants of the system, and this is obviously a very good idea. Even if it did not allow them to progress in this problem, this attempt was very relevant. Similarly, several students mentioned that Clara's operations were reversible: this point was certainly easy to prove, but it is a characteristic that it is useful to study in general. We hope that these reminders will allow students to progress and be better armed the next time they encounter a similar problem.
We now list some errors encountered in the solution attempts.
$\triangleright$
|
proof
|
Yes
|
Incomplete
|
proof
|
Number Theory
|
Pierre et Clara jouent au jeu suivant. Tout d'abord, Clara choisit un entier $c$. Puis Pierre choisit un nombre premier $p \geqslant c$ et écrit deux entiers $a$ et $b$ au tableau. Clara se permet alors d'effectuer les opérations suivantes : elle choisit un des deux nombres écrits au tableau, disons $n$, l'efface, et écrit à la place un autre entier, disons $m$, tel que $p$ divise $\left(n^{2}-m+1\right)\left(m^{2}-n+1\right)$. Clara gagne si elle réussit à faire en sorte, au bout d'un nombre fini de telles opérations, que les deux entiers écrits au tableau soient identiques. Sinon, elle perd, et c'est Pierre qui gagne.
Démontrer que Pierre peut empêcher Clara de gagner.
|
Soit $p$ un nombre premier, arbitrairement grand, que Pierre est susceptible de choisir, et soit $f: \mathbb{Z} / p \mathbb{Z} \mapsto \mathbb{Z} / p \mathbb{Z}$ la fonction définie par $f(x)=x^{2}+1$.
Lorsque Clara remplace un entier $n$ par un entier $m$, l'une des deux égalités $n=f(m)$ ou $m=f(n)$ est nécessairement vérifiée, de sorte que $m$ et $n$ appartiennent à une même orbite de $f$. On dit alors que deux résidus $u$ et $v$ modulo $p$ sont reliés s'il existe deux entiers $k \geqslant 0$ et $\ell \geqslant 0$ tels que $f^{k}(u)=f^{\ell}(v)$. Il apparaît directement que, si Clara parvient à transformer un résidu $m$ en un résidu $n$, ces deux résidus sont reliés; la réciproque est d'ailleurs vraie, même si nous n'en aurons pas besoin.
Pierre a donc pour but de trouver un nombre premier $p \geqslant c$, puis deux résidus $a$ et $b$ modulo $p$ qui ne sont pas reliés l'un à l'autre. Pour ce faire, le plus simple est que $a$ et $b$ soient des points fixes de $f$, c'est-à-dire que $(X-a)(X-b) \equiv X^{2}-X+1(\bmod p)$.
Or, si $X^{2}-X+1$ admet une racine $a$ modulo $p$, l'autre racine vaut $1 / a$ (car $a$ est non nul), ou encore $1-a$. Ces deux racines ne sont donc égales que si $1-a \equiv a \equiv 1 / a(\bmod p)$, c'est-à-dire si $p \neq 2$ et $1 / 2 \equiv a \equiv \pm 1(\bmod p)$. Or, on sait que $1 / 2 \equiv \pm 1(\bmod p)$ si et seulement si $p=3$. Par conséquent, Pierre n'a qu'à choisir un nombre premier $p>\max \{c, 3\}$ qui divise un nombre de la forme $n^{2}-n+1$. En pratique, pour ce faire, il lui suffit de définir $p$ comme le plus petit facteur premier du nombre $S_{m}=(m!)^{2}-m!+1$, où l'on a posé $m=\max \{c, 3\}$. En effet, on sait que $S_{m} \geqslant 2$ et que $S_{m}$ est premier avec $m!$. Ainsi, le plus petit facteur premier de $S_{m}$ existe bien, et il est premier avec $m$ !, donc strictement supérieur à $m$. Pierre s'empressera ensuite de choisir $a=m$ ! et $b=1-m$ ! pour enfin savourer une victoire amplement méritée.
$\underline{\text { Solution alternative } n^{\circ} 1}$ Étant donné un nombre premier $p$, nous allons construire le graphe $G$ dont les sommets sont les éléments de $\mathbb{Z} / p \mathbb{Z}$ et les arêtes sont les paires $(m, n)$ telles que $\left(n^{2}-m+1\right)\left(m^{2}-n+1\right) \equiv 0(\bmod p)$. On dira qu'une arête $(m, n)$ est utile si $m \neq n$, et qu'elle est inutile sinon, c'est-à-dire s'il s'agit d'une boucle. Si $G$ contient au plus $p-2$ arêtes utiles, alors il n'est pas connexe, et Pierre n'a plus qu'à choisir des entiers appartenant à deux composantes connexes distinctes.
On dit ensuite qu'une arête $(m, n)$ est engendrée par $n$ si $m \equiv n^{2}+1(\bmod m)$. Toute arête est engendrée par une de ses extrémités, et chaque sommet engendre une unique arête, donc $G$ contient au plus $p$ arêtes. Par conséquent, si $G$ contient deux arêtes inutiles, c'est-à-dire s'il existe deux résidus distincts $u$ et $v$ tels que $u \equiv u^{2}+1(\bmod p)$ et $v \equiv v^{2}+1(\bmod p)$, Pierre est assuré de pouvoir gagner.
Il lui suffit alors de procéder comme dans la solution précédente.
Remarque: On peut en fait démontrer que tout graphe $G$ construit comme ci-dessus contient au moins $p-1$ arêtes. En effet, si ce n'est pas le cas, il existe deux arêtes $(m, n)$ et $(u, v)$, dont chacune est engendrée par ses deux extrémités, et telles que $m, n, u$ et $v$ sont deux à deux distincts modulo $p$. Ce sont là quatre racines distinctes du polynôme $P(X)=\left(X^{2}+1\right)^{2}+1-X$
dans $\mathbb{Z} / p \mathbb{Z}$, telles que $m=f(n), n=f(m), u=f(v)$ et $v=f(u)$.
Or, tout point fixe de $f$ est racine de $P$, ce qui signifie que $P$ est divisible par le polynôme $Q(X)=X^{2}+1-X$. On en déduit la factorisation $P(X)=\left(X^{2}+X+2\right) Q(X)$. Ainsi, parmi $m, n, u$ et $v$, deux sont des racines de $Q$, c'est-à-dire des points fixes de $f$, en contradiction avec notre hypothèse.
En particulier, s'intéresser aux points fixes de $f$, ou au minimum à ses cycles de petite taille, était donc indispensable.
$\underline{\text { Solution alternative } n^{\circ} 2}$ La solution ci-dessous fait appel à des notions plus avancées, mais cela permet une approche laxiste de la dimension combinatoire du problème. Ci-dessous, on considère directement que Pierre choisit des résidus modulo $p$ plutôt que des entiers, et on note $f: \mathbb{Z} / p \mathbb{Z}$ la fonction définie par $f(x)=x^{2}+1$. Lorsque $x$ et $y$ sont des résidus modulo $p$, on notera abusivement $x=y$ et $x \neq y$ les relations $x \equiv y(\bmod p)$ et $x \not \equiv y(\bmod p)$.
Supposons que Pierre a choisi un nombre premier $p$ et deux résidus $a$ et $b$ tels que $b \neq \pm a$ tels que $a=f(a)$, mais que Clara gagne malgré tout. Puisque toute opération de Clara peut être inversée, on suppose sans perte de généralité que celle-ci a graduellement transformé $a$ en $b$, en le plus petit nombre d'étapes possibles.
La première étape de Clara consiste à transformer $a$ en $f(a)=a$, ce qui serait stupide, ou en un antécédent $x \neq a$ de $a$ par $f$. Les deux antécédents de $a$ par $f$ sont opposés l'un à l'autre, et l'un est égal à $a$, donc l'autre vaut $-a$. Ainsi, Clara a transformé $a$ en $-a$.
Puisque $b \neq-a$, Clara a de nouveau dû transformer $-a$ en $f(-a)=a$, ce qui serait encore une fois stupide, ou bien en un antécédent $y$ de $-a$ par $f$, de sorte que $-a-1=f(y)-1=y^{2}$ est un résidu quadratique modulo $p$.
Par conséquent, Pierre gagnera s'il trouve un nombre premier $p \geqslant 3$ pour lequel $f$ a un point fixe $a$ tel que $-a-1$ ne soit pas un résidu quadratique modulo $p$. Or, si $a$ est un point fixe de $f$, on sait que $f(1-a)=a^{2}-2 a+2=f(a)-2 a+1=1-a$, donc que $1-a$ est aussi un point fixe de $f$. Il suffit donc que soit $-a-1$, soit $a-2$ ne soit pas un résidu quadratique (soit les deux).
La manière la plus simple pour s'assurer que deux nombres ne seront pas tous deux des résidus quadratiques est de faire en sorte que leur produit n'en soit pas un. Cette technique sera ici avantageuse, puisqu'elle nous permettra de ne pas devoir distinguer les résidus $-a-1$ et $a-2$, qui avaient été définis de manière symétrique. Ici, Pierre va donc choisir $p$ de sorte que $(a-2)(-a-1)=2+a-a^{2}=3$ ne soit pas un résidu quadratique.
Enfin, il doit s'assurer que $f$ ait bien un point fixe. Or, s'il se plonge dans le corps $\mathbb{C}$ des nombres complexes, Pierre sait bien que les racines du polynôme $f(X)-X=X^{2}-X+1$ sont $(1+\sqrt{-3}) / 2$ et $(1-\sqrt{-3}) / 2$. On reconnaît donc là que $a$ est un point fixe de $f$ si et seulement si $(2 a-1)^{2}=-3$, et un tel point fixe existe donc si et seulement si -3 est un résidu quadratique. Il s'agit donc, pour Pierre, de choisir un nombre premier $p$ pour lequel -3 est un résidu quadratique et -1 n'en est pas un.
Or, s'il existe un résidu $z$ tel que $z^{2}=-1$, on sait que $z$ est d'ordre 4 , donc que $p \equiv 1(\bmod 4)$. Pierre va donc chercher $p$ parmi les facteurs premiers non congrus à $1(\bmod 4) \mathrm{d}$ 'un entier de la forme $n^{2}+3$. Choisir $n$ premier avec 3 nous assure déjà que $p \neq 3$. Ensuite, choisir $n$ pair nous assure que $n^{2}+3 \equiv 3(\bmod 4)$, donc que $n$ admet nécessairement un facteur premier $p \equiv 3(\bmod 4)$. Il suffit donc de définir $n$ comme le PPCM des nombres premiers inférieurs ou égaux à max $\{c, 2\}$ et différents de $3:$ le facteur $p$ que choisira Pierre sera premier avec tous ces nombres premiers, mais aussi avec 3 , de sorte que $p>c$, et les considérations des paragraphes précédents nous assurent alors que Pierre peut choisir des entiers $a$ et $b$ de façon adéquate.
Remarque: Une fois résolu à choisir un nombre premier $p$ pour lequel ni $3 \mathrm{ni}-1$ ne sont des résidus quadratiques, Pierre peut aussi se reposer sur des théorèmes puissants mais qu'il ne sait pas nécessairement démontrer, ce qui lui laissera un léger goût d'inachevé.
Théorème de la réciprocité quadratique. Soit $p$ un nombre premier et $n$ un entier non divisible par $p$. On pose $\binom{n}{p}=1$ si $n$ est un résidu quadratique modulo $p$, et $\binom{n}{p}=-1$ sinon.
$\triangleright$ Si $p$ et $q$ sont deux nombres premiers impairs distincts, $\binom{p}{q}\binom{q}{p}=(-1)^{(p-1)(q-1) / 4}$.
$\triangleright$ Pour tout nombre premier $p$ impair, $\binom{-1}{p}=(-1)^{(p-1) / 2}$ et $\binom{2}{p}=(-1)^{\left(p^{2}-1\right) / 8}$.
Théorème de Dirichlet sur les nombres premiers. Soit $a$ et $b$ deux entiers premiers entre eux. Il existe une infinité de nombres premiers $p$ tels que $p \equiv a(\bmod b)$.
Muni de ces deux résultats, Pierre choisit donc un nombre premier $p$ tel que $p \equiv 3(\bmod 4)$ et $\binom{p}{3}=-\binom{3}{p}=1$, c'est-à-dire $p \equiv 1(\bmod 3)$. Il s'agit ainsi de choisir un nombre premier $p \geqslant c$ tel que $p \equiv 7(\bmod 12)$, et le théorème de Dirichlet indique qu'un tel nombre premier existe bien.
Commentaire des correcteurs Très peu d'élèves ont entièrement résolu ce problème difficile, qui aurait pu faire figure de problème 1 ou 4 difficile à l'Olympiade Internationale. Il s'agit de l'étude d'un système dynamique présentée sous la forme d'un jeu à stratégie gagnante. Deux approches principales étaient possibles ici : une approche combinatoire traduisant le problème en termes d'un graphe dont les sommets appartenaient à $\mathbb{Z} / p \mathbb{Z}$, comme dans les deux premières solutions proposées, et une approche très arithmétique passant par une étude des carrés modulo $p$, comme dans la solution alternative $\mathrm{n}^{\circ} 2$. Chacune des deux approches nécessitait la mise en place de nombreuses idées, et obtenir des points nécessitait donc d'établir des résultats significatifs.
Ce problème consistait en l'étude d'un système dynamique, c'est-à-dire un système (ici, un couple d'entiers) sur lequel on agit via une opération (ici, on remplace un entier par un autre selon certaines contraintes). Dans un tel cas, il est primordial d'étudier les petits cas. De nombreux élèves ont présenté leur étude pour des $p$ particuliers, le plus souvent pour $p=7$. Même si cette initiative n'était pas récompensée par un point ici, nous l'encourageons fortement!
Un autre réflexe important à avoir est de considérer les éventuels points fixes de l'opération. C'était ici, quelle que soit l'approche, le point de départ du problème, et plusieurs élèves ont eu ce réflexe, à la grande satisfaction des correcteurs. Quelques élèves ont cherché des invariants au système et c'est évidemment une très bonne idée. Même si elle ne permettait pas d'avancer dans ce problème, cette tentative était très pertinente. De même, plusieurs élèves ont mentionné la que les opérations de Clara étaient réversibles : ce point était certes facile à démontrer, mais il s'agit là d'une caractéristique qu'il est utile à étudier de manière générale. Nous espérons que ces rappels permettront aux élèves de progresser et d'être mieux armés la prochaine fois qu'ils tombent sur un problème similaire.
Nous listons maintenant quelques erreurs rencontrées dans les tentatives de solutions.
$\triangleright$ Attention à bien lire l'énoncé! Nous déplorons que plusieurs raisonnements soient voués à l'échec car l'énoncé de départ n'est pas compris correctement. Quelques élèves ont par exemple cru que les entiers $m$ et $n$ de l'hypothèse $p \mid\left(m^{2}-n+1\right)\left(n^{2}-m+1\right)$
étaient les deux entiers écrits au tableau. D'autres élèves font d'emblée une erreur de signe dans leur congruence, en écrivant que que $m^{2} \equiv n+1(\bmod p)$.
$\triangleright$ Une fois supposée ou acquise l'existence d'un point fixe pour l'opération de Clara, c'est-à-dire d'un entier $a$ et d'un nombre premier $p$ tels que $a^{2}+1 \equiv a(\bmod p)$, plusieurs élèves étudient les antécédents possibles de $a$ par l'opération, dans l'espoir de montrer que $a$ ne peut pas être obtenu à partir de tous les autres restes modulo $p$. La plupart remarquent que $-a$ est lui aussi un antécédent de $a$, car $a^{2} \equiv b^{2}(\bmod p)$ si et seulement si $a \equiv \pm b(\bmod p)$ ). Mais certains concluent trop hâtivement qu'alors $a$ et $-a$ sont isolés et ne peuvent être atteints par d'autres entiers; il restait cependant possible que $-a$ ait plusieurs antécédents autres que $\pm a$.
Nous terminons par avouer notre surprise devant les statistiques : de nombreux élèves ayant passé le test n'ont rien rendu pour ce problème en particulier, pourtant censé être plus abordable que les deux suivants. S'il est bon de regarder tous les problèmes, il est stratégique de passer une grande partie du temps donné sur le problème classé comme le plus abordable, puisqu'on peut plus facilement espérer y avoir des idées intéressantes et donc y récolter des points.
|
{
"exam": "French_tests",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T1",
"year": "2020"
}
|
Find the largest integer $n \geqslant 3$ for which there exists a set $\mathcal{S}$ of $n$ points in the plane with the following property: every triangle (even degenerate) whose vertices belong to $\mathcal{S}$ is isosceles but not equilateral.
|
It is said that a set $\mathcal{S}$ having the required property is cute. We will prove that any cute set contains at most 6 elements. Furthermore, we will denote by $\omega_{A, B}$ the circle centered at $A$ passing through $B$, and by $\ell_{A, B}$ the perpendicular bisector of the segment $[A B]$.
First, if $\mathcal{S}$ consists of the five vertices $P_{1}, \ldots, P_{5}$ of a regular pentagon and its center $O$, it is easily verified that $\mathcal{S}$ is cute.
Conversely, let $\mathcal{S}$ be a cute set with $n \geqslant 6$ points: we will prove that $n=6$. For all points $X, Y$ and $Z$ in $\mathcal{S}$, we know that $Z$ belongs to one of the three sets $\omega_{X, Y}, \omega_{Y, X}$, or $\ell_{X, Y}$. This observation already allows us to prove the following result.
Lemma 1. Any three points in $\mathcal{S}$ are never collinear.
Proof: Suppose $\mathcal{S}$ contains three points $A, B$, and $C$, aligned in that order. Since $A B C$ is isosceles, $B$ is the midpoint of $[A C]$. Now let $D$ be another point in $\mathcal{S}$. Without loss of generality, assume that $A D \leqslant C D$.
Since $D$ cannot belong to the circle $\omega_{C, B}$ or the line $\ell_{B, C}$, it must necessarily belong to the circle $\omega_{B, C}=\omega_{B, A}$. But then $D$ cannot belong to either the circle $\omega_{C, A}$ or the circle $\omega_{A, C}$, and it must therefore necessarily belong to the line $\ell_{A, C}$. This situation repeats for each of the $n-3$ points in $\mathcal{S} \backslash\{A, B, C\}$, which therefore belong both to $\omega_{B, C}$ and to $\ell_{A, C}$.
However, a line and a circle have at most two points of intersection. Our initial assumption was therefore invalid, which proves the lemma.
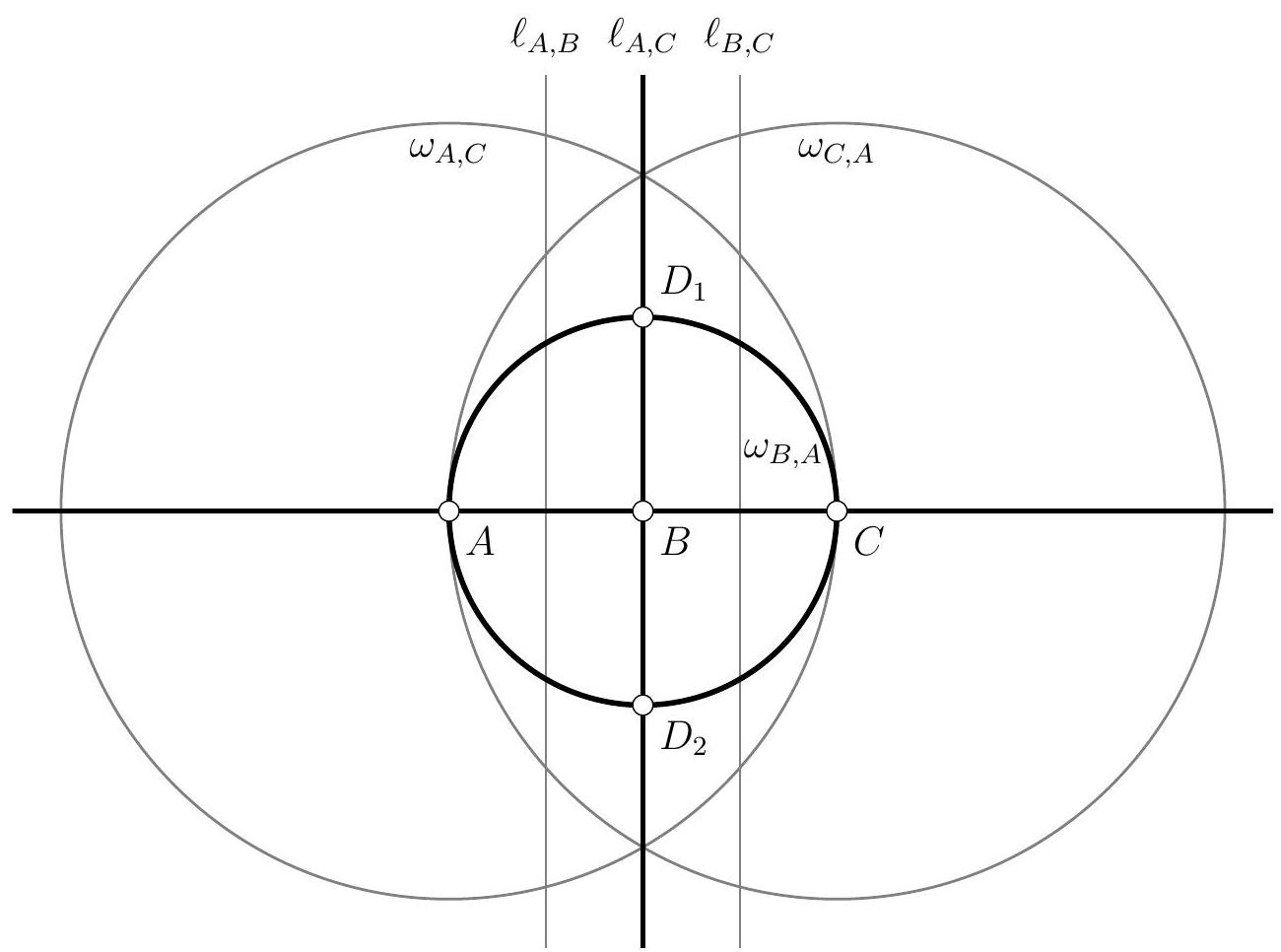
We then continue and focus on pairs of circles $\omega_{A, B}$ and $\omega_{B, A}$.
Lemma 2. Let $A$ and $B$ be two points in $\mathcal{S}$. If $\mathcal{S}$ contains points in both $\omega_{A, B}$ and $\omega_{B, A}$ other than $A$ and $B$, then $n \leqslant 6$.
Proof: Suppose $\mathcal{S}$ contains two points $C$ and $D$, distinct from $A$ and $B$, which belong respectively to the circles $\omega_{B, A}$ and $\omega_{A, B}$. They cannot be equal to each other, otherwise the triangle $A B C$ would be equilateral. We will first prove that $(A B)$ is parallel to $(C D)$.
Indeed, if $A B = C D$, then $A B = B C = C D = D A$, and the quadrilateral $A B C D$ is a rhombus, so $(A B)$ is indeed parallel to $(C D)$. We therefore assume that $A B \neq C D$, that is, $A D \neq C D$. Since $A C \neq A D$ and $A C D$ is isosceles, we deduce that $A C = C D$. We similarly prove that $B D = C D$, so $A C = B D$, and therefore the triangles $A B C$ and $D A B$ are isometric.
Next, suppose that $C$ and $D$ are on opposite sides of the line $(A B)$. If we denote by $\theta$ the angle $\widehat{A B C}$, we can then verify, for example using Cartesian coordinates, that $A C^2 = B D^2 = (2 - 2 \cos (\theta)) A B^2$ and that $C D^2 = (5 - 4 \cos (\theta)) A B^2$. Since $A C = C D$, we conclude that $2 \cos (\theta) = 3$, which is absurd. Our assumption is therefore invalid, so $C$ and $D$ must necessarily be on the same side of $(A B)$, and therefore $(A B)$ is indeed parallel to $(C D)$.
Once this parallelism is established, we conclude that any point in $\mathcal{S}$ belongs to the line $(A B)$, the perpendicular bisector $\ell_{A, B}$, or a parallel to $(A B)$ passing through $C$ or $D$, that is, $(C D)$. Lemma 1 ensures that none of these lines contains more than two points of $\mathcal{S}$, which proves that $n \leqslant 6$ and proves the lemma.
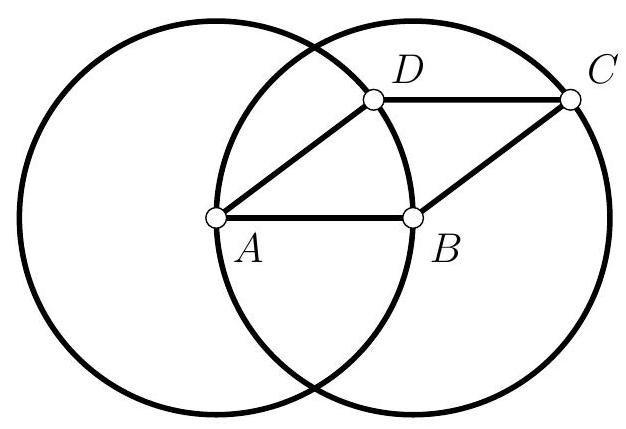
Case 1: $A B = B C = C D = D A$

Case 2: $A C = C D = D B$
Lemma 3. Let $A$ and $B$ be two points in $\mathcal{S}$. If $n \geqslant 7$, then either $\omega_{A, B}$ contains at least $n-2$ points of $\mathcal{S}$, or $B$ is the only point of $\mathcal{S}$ belonging to $\omega_{A, B}$.
|
6
|
Yes
|
Incomplete
|
math-word-problem
|
Geometry
|
Trouver le plus grand entier $n \geqslant 3$ pour lequel il existe un ensemble $\mathcal{S}$ de $n$ points du plan avec la propriété suivante : tout triangle (même plat) dont les sommets appartiennent à $\mathcal{S}$ est isocèle mais pas équilatéral.
|
On dit qu'un ensemble $\mathcal{S}$ ayant la propriété requise est mignon. Nous allons démontrer que tout ensemble mignon contient au plus 6 éléments. En outre, on notera $\omega_{A, B}$ le cercle de centre $A$ passant par $B$, et par $\ell_{A, B}$ la médiatrice du segment $[A B]$.
Tout d'abord, si $\mathcal{S}$ est formé des cinq sommets $P_{1}, \ldots, P_{5}$ d'un pentagone régulier ainsi que de son centre $O$, on vérifie aisément que $\mathcal{S}$ est mignon.
Réciproquement, soit $\mathcal{S}$ un ensemble mignon à $n \geqslant 6$ points : nous allons démontrer que $n=6$. Pour tous les points $X, Y$ et $Z$ de $\mathcal{S}$, on sait que $Z$ appartient à un seul des trois ensembles $\omega_{X, Y}, \omega_{Y, X}$ et $\ell_{X, Y}$. Cette remarque nous permet déjà de démontrer le résultat suivant.
Lemme 1. Trois points quelconques de $\mathcal{S}$ ne sont jamais alignés.
Démonstration : Supposons que $\mathcal{S}$ contient trois points $A, B$ et $C$, alignés dans cet ordre. Puisque $A B C$ est isocèle, $B$ est le milieu de $[A C]$. Soit maintenant $D$ un autre point de $\mathcal{S}$. Sans perte de généralité, on suppose que $A D \leqslant C D$.
Comme $D$ ne peut appartenir ni au cercle $\omega_{C, B}$ ni à la droite $\ell_{B, C}$, il appartient nécessairement au cercle $\omega_{B, C}=\omega_{B, A}$. Mais alors $D$ ne peut appartenir ni au cercle $\omega_{C, A}$, ni au cercle $\omega_{A, C}$, et il appartient donc nécessairement à la droite $\ell_{A, C}$. Cette situation se répète pour chacun des $n-3$ points de $\mathcal{S} \backslash\{A, B, C\}$, qui appartiennent donc à la fois à $\omega_{B, C}$ et à $\ell_{A, C}$.
Or, une droite et un cercle ont au plus deux points d'intersection. Notre supposition initiale était donc invalide, ce qui démontre le lemme.

On continue alors, et on s'intéresse aux paires de cercles $\omega_{A, B}$ et $\omega_{B, A}$.
Lemme 2. Soit $A$ et $B$ deux points de $\mathcal{S}$. Si $\mathcal{S}$ contient à la fois des points de $\omega_{A, B}$ et de $\omega_{B, A}$ autres que $A$ et $B$, alors $n \leqslant 6$.
Démonstration : Supposons que $\mathcal{S}$ contient deux points $C$ et $D$, distincts de $A$ et de $B$, qui appartiennent respectivement aux cercles $\omega_{B, A}$ et $\omega_{A, B}$. Ils ne peuvent être égaux l'un à l'autre, ce sans quoi le triangle $A B C$ serait équilatéral. Nous allons d'abord démontrer que $(A B)$ est parallèle à $(C D)$.
En effet, si $A B=C D$, alors $A B=B C=C D=D A$, et le quadrilatère $A B C D$ est un losange, donc $(A B)$ est bien parallèle à $(C D)$. On suppose donc que $A B \neq C D$, c'est-à-dire que $A D \neq C D$. Puisque $A C \neq A D$ et que $A C D$ est isocèle, on en déduit que $A C=C D$. On démontre de même que $B D=C D$, de sorte que $A C=B D$, et donc que les triangles $A B C$ et $D A B$ sont isométriques.
Supposons ensuite que $C$ et $D$ se trouvent de part et d'autre de la droite $(A B)$. Si l'on note $\theta$ l'angle $\widehat{A B C}$, on peut alors vérifier, par exemple en utilisant des coordonnées cartésiennes, que $A C^{2}=B D^{2}=(2-2 \cos (\theta)) A B^{2}$ et que $C D^{2}=(5-4 \cos (\theta)) A B^{2}$. Comme $A C=C D$, on en conclut alors que $2 \cos (\theta)=3$, ce qui est absurde. Notre supposition est donc invalide, de sorte que $C$ et $D$ sont nécessairement du même côté de $(A B)$, et donc que $(A B)$ est bien parallèle à $(C D)$.
Une fois cette relation de parallélisme acquise, on conclut que tout point de $\mathcal{S}$ appartient à la droite $(A B)$, à la médiatrice $\ell_{A, B}$, ou encore à une parallèle à $(A B)$ passant par $C$ ou par $D$, c'est-à-dire à $(C D)$. Le lemme 1 nous assure que nulle de ces droites ne contient plus de deux points de $\mathcal{S}$, ce qui prouve que $n \leqslant 6$ et démontre le lemme.

Cas 1: $A B=B C=C D=D A$

Cas 2: $A C=C D=D B$
Lemme 3. Soit $A$ et $B$ deux points de $\mathcal{S}$. Si $n \geqslant 7$, alors soit $\omega_{A, B}$ contient au moins $n-2$ points de $\mathcal{S}$, soit $B$ est le seul point de $\mathcal{S}$ appartenant à $\omega_{A, B}$.
|
{
"exam": "French_tests",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T1",
"year": "2020"
}
|
Find the largest integer $n \geqslant 3$ for which there exists a set $\mathcal{S}$ of $n$ points in the plane with the following property: every triangle (even degenerate) whose vertices belong to $\mathcal{S}$ is isosceles but not equilateral.
|
Suppose $n \geqslant 7$ and that the circle $\omega_{A, B}$ contains $k \geqslant 2$ points of $\mathcal{S}$. Lemmas 1 and 2 respectively ensure that $\ell_{A, B}$ contains at most two points of $\mathcal{S}$, and that $A$ is the only point of $\mathcal{S}$ belonging to $\omega_{B, A}$. We deduce that $k \geqslant n-3$, with equality if and only if $\ell_{A, B}$ contains exactly two points of $\mathcal{S}$, none of which belong to $\omega_{A, B}$. If $k=n-3$, let $C$ be another point on $\omega_{A, B}$. For the same reasons as before, the line $\ell_{A, C}$ contains two points of $\mathcal{S}$, none of which belong to $\omega_{A, C}=\omega_{A, B}$. Since $\ell_{A, B}$ and $\ell_{A, C}$ have at most one point in common, they therefore contain at least, between the two of them, three points of $\mathcal{S}$. If we add the point $A$ and the $k$ points of $\mathcal{S}$ belonging to $\omega_{A, B}$, this gives us a total of $k+4=n+1$ points in $\mathcal{S}$. Our initial assumption was therefore invalid, which proves the lemma.
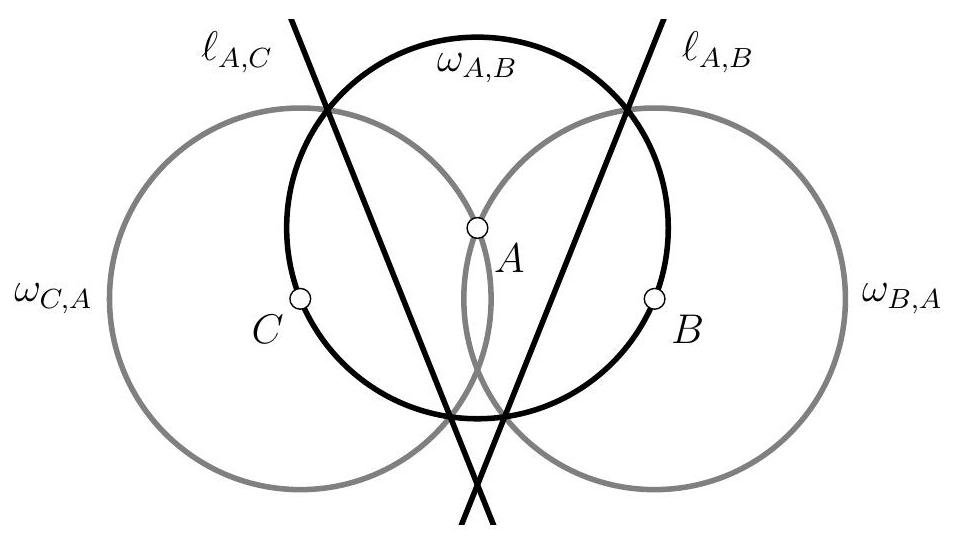
In conclusion, let's return to the statement itself. We will assume that $n \geqslant 7$ and arrive at a contradiction. Let $A, B$, and $C$ be three points of $\mathcal{S}$. The line $\ell_{A, B}$ contains at most two points of $\mathcal{S}$, so one of the circles $\omega_{A, B}$ and $\omega_{B, A}$ (say $\omega_{A, B}$) contains at least two points. Lemma 3 then ensures that $\omega_{A, B}$ contains at least $n-2$ points of $\mathcal{S}$. Similarly, one of the circles $\omega_{B, C}$ and $\omega_{C, B}$ (say $\omega_{X, Y}$) contains at least $n-2$ points of $\mathcal{S}$. We then have two circles, with centers $A$ and $X$, each containing $n-2$ points of $\mathcal{S}$. They therefore have at least $n-4 \geqslant 3$ points in common, which is absurd since their centers are distinct. We have thus reached the desired contradiction, which concludes our solution.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Trouver le plus grand entier $n \geqslant 3$ pour lequel il existe un ensemble $\mathcal{S}$ de $n$ points du plan avec la propriété suivante : tout triangle (même plat) dont les sommets appartiennent à $\mathcal{S}$ est isocèle mais pas équilatéral.
|
Supposons que $n \geqslant 7$ et que le cercle $\omega_{A, B}$ contient $k \geqslant 2$ points de $\mathcal{S}$. Les lemmes 1 et 2 nous assurent respectivement que $\ell_{A, B}$ contient au plus deux points de $\mathcal{S}$, et que $A$ est le seul point de $\mathcal{S}$ appartenant à $\omega_{B, A}$. On en déduit que $k \geqslant n-3$, avec égalité si et seulement si $\ell_{A, B}$ contient exactement deux points de $\mathcal{S}$, dont aucun n'appartient à $\omega_{A, B}$. Si $k=n-3$, soit $C$ un autre point de $\omega_{A, B}$. Pour les mêmes raisons que précédemment, la droite $\ell_{A, C}$ contient deux points de $\mathcal{S}$, dont aucun n'appartient à $\omega_{A, C}=\omega_{A, B}$. Or, puisque $\ell_{A, B}$ et $\ell_{A, C}$ ont au plus un point commun, elles contiennent donc au moins, à elles deux, trois points de $\mathcal{S}$. Si l'on ajoute le point $A$ et les $k$ points de $\mathcal{S}$ appartenant à $\omega_{A, B}$, cela nous fait un total de $k+4=n+1$ points dans $\mathcal{S}$. Notre supposition initiale était donc invalide, ce qui démontre le lemme.

En conclusion, revenons à l'énoncé lui-même. Nous allons supposer que $n \geqslant 7$ et aboutir à une absurdité. Soit $A, B$ et $C$ trois points de $\mathcal{S}$. La droite $\ell_{A, B}$ contient au plus deux points de $\mathcal{S}$, donc l'un des cercles $\omega_{A, B}$ et $\omega_{B, A}$ (disons $\omega_{A, B}$ ) en contient au moins deux. Le lemme 3 nous assure alors que $\omega_{A, B}$ contient au moins $n-2$ points de $\mathcal{S}$.
De même, l'un des cercles $\omega_{B, C}$ et $\omega_{C, B}$ (disons $\omega_{X, Y}$ ) contient au moins $n-2$ points de $\mathcal{S}$. On dispose alors de deux cercles, de centres $A$ et $X$, qui contiennent chacun $n-2$ points de $\mathcal{S}$. Ils ont donc au moins $n-4 \geqslant 3$ points communs, ce qui est absurde puisque leurs centres sont distincts. On tient donc ici l'absurdité tant désirée, qui conclut notre solution.
|
{
"exam": "French_tests",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"solution_match": "\nDémonstration:",
"tier": "T1",
"year": "2020"
}
|
Find the largest integer $n \geqslant 3$ for which there exists a set $\mathcal{S}$ of $n$ points in the plane with the following property: every triangle (even degenerate) whose vertices belong to $\mathcal{S}$ is isosceles but not equilateral.
|
$n^{\circ} 1$ Reusing the notations from the previous solution, we prove as before that there exists a cute set with 6 elements, and we proceed by contradiction, assuming that we have a cute set $\mathcal{S}$ with 7 elements. As in the previous solution, we prove that no 3 points of $\mathcal{S}$ are collinear. We then prove the following result.
Lemma 4. Let $A$ and $B$ be two points of $\mathcal{S}$. If $n \geqslant 7$, then $\omega_{A, B}$ contains at most 3 points of $\mathcal{S}$.
Proof: Suppose that $\omega_{A, B}$ contains at least four points $B, C, D$, and $E$, such that $B C=C D$. Since $B$ and $D$ are the only two points of intersection of $\omega_{A, B}$ and $\omega_{C, B}=\omega_{C, D}$, and $A$ is the unique point of intersection of $\omega_{B, C}$ and $\omega_{D, C}$, we know that $E$ is, in one of the following cases:
1. on $\omega_{A, B}, \ell_{C, D}$, and $\omega_{B, C}$;
2. on $\omega_{A, B}, \ell_{B, C}$, and $\omega_{D, C}$;
3. on $\omega_{A, B}, \omega_{B, C}$, and $\omega_{D, C}$.
In the third case, we have $B C=C D=D E=E B$, so $B C D E$ is a rhombus whose vertices are concyclic, i.e., a square, and thus $A, B$, and $D$ are collinear. This case is therefore impossible. Moreover, the first and second cases are symmetric to each other. We assume we are in the second case.
We then observe that $B, C, D$, and $E$ are four consecutive vertices of a regular pentagon centered at $A$, and we denote the side length by $d$. Among the two other points of $\mathcal{S}$, one does not belong to $\ell_{C, D}$, which already contains $A$: we denote this point by $X$. Each of the lines $\ell_{B, C}$ and $\ell_{D, E}$ already contains two points of $\mathcal{S}$ among $A, B, C, D$, and $E$, and thus does not contain $X$. We deduce that
$$
\left\{\begin{array}{l}
B X=d \text { or } C X=d \\
C X=d \text { or } D X=d ; \\
D X=d \text { or } E X=d
\end{array}\right.
$$
Consequently, $X$ is on $\ell_{B, D}$ (if $B X=D X=d$) or on $\ell_{C, E}$ (if $C X=E X=d$). Both cases are impossible, since $\ell_{B, D}$ already contains $A$ and $C$, while $\ell_{C, E}$ already contains $A$ and $D$. Our initial assumption was therefore invalid, which proves the lemma.
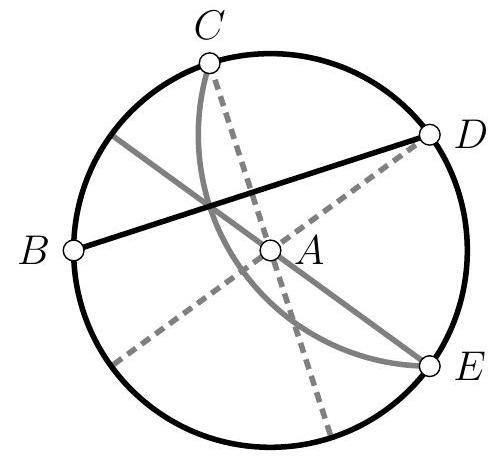
Case 2: $E \in \ell_{B, C} \cap \omega_{D, C}$
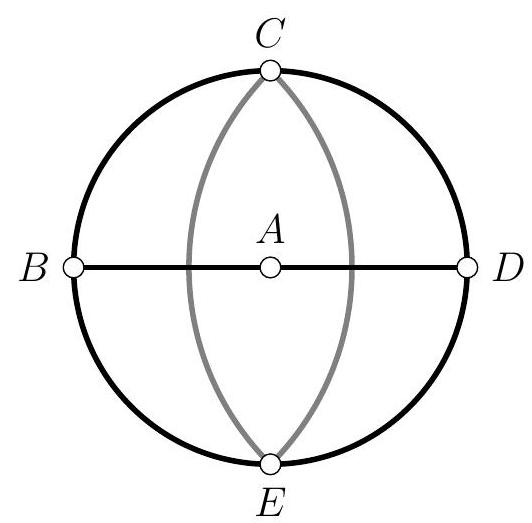
Case 3: $E \in \omega_{B, C} \cap \omega_{D, C}$
For any segment $[A, B]$ whose endpoints are in $\mathcal{S}$, we denote by $p_{A, B}$ the number of points of $\mathcal{S}$ located on the perpendicular bisector $\ell_{A, B}$: we say that this is the weight of $[A, B]$. Since there are $\binom{7}{3}=35$ isosceles (but not equilateral) triangles with vertices in $\mathcal{S}$, the sum of the weights of the segments is 35. There are $\binom{7}{2}=21$ segments, none of which has a weight $p_{A, B} \geqslant 3$. If we denote by $a_{i}$ the number of segments of weight $i$, we observe that
$$
35=2 a_{2}+a_{1} \leqslant\left(a_{0}+a_{1}+a_{2}\right)+a_{2}=21+a_{2},
$$
so that $a_{2} \geqslant 14$. Since $2 a_{2}=28 \geqslant 24.5=(1-1 / 2) \times 7^{2}$, Turán's theorem indicates that there exists a triangle $A B C$, isosceles at $A$, whose three sides $[A, B],[B, C]$, and $[C, A]$ are of weight 2.
Among $A, B$, and $C$, only $A$ belongs to one of the three perpendicular bisectors $\ell_{A, B}, \ell_{B, C}$, or $\ell_{C, A}$. Moreover, these three perpendicular bisectors intersect at $O$, the center of the circumcircle of $A B C$. Therefore, if $O \notin \mathcal{S}$, we know that $\mathcal{S}$ contains 8 distinct points, which are $B, C$, and two points on each of the perpendicular bisectors $\ell_{A, B}, \ell_{B, C}$, and $\ell_{C, A}$. We deduce that $O \in \mathcal{S}$.
Let then $D$ be the second point of $\mathcal{S}$ located on $\ell_{A, B}$. Since $D \notin \omega_{O, B}$, we know that $D \in \omega_{B, O}$, in which case $D$ coincides with the reflection of $O$ with respect to $(A B)$, or that $D \in \ell_{B, O}$, in which case $D$ coincides with the center of the circumcircle of $A B O$. In both cases, note that $D \notin \omega_{A, B}=\omega_{A, C}$ and that $D \notin \ell_{A, C}$, so $D \in \omega_{C, A}$.
In the first case, we also know that $B D=B O \neq B C$, so $D \notin \omega_{B, C}$, and that $D \notin \ell_{B, C}$, so $D \in \omega_{C, B}$. This means that $C D=C B \neq C O$, so $D \notin \omega_{C, O}$. Since $D \notin \omega_{O, C}$, we deduce that $D \in \ell_{C, O}$. Thus, and since $D \in \omega_{C, A}$, we know that $O D=C D=C A=B A$, so $A D B O$ is a rhombus whose diagonals are of the same length, i.e., a square. But then $\widehat{A O B}$ is a right angle, and $\widehat{A O C}$ is a right angle too, so $B, O$, and $C$ are collinear, which contradicts Lemma 1. This case is therefore impossible.
We are thus in the second case and, similarly, $\mathcal{S}$ contains the center of the circumcircle of $A C O$, which we denote by $E$. Since $C D=C A \neq C O$ and $D \notin \omega_{O, C}$, we know that $D \in \ell_{C, O}$. Thus, $D$ belongs to the two lines $\ell_{B, O}$ and $\ell_{C, O}$ and, for symmetry reasons, $E$ also belongs to these two lines. Since these two lines cannot be the same, this second case is also impossible, which concludes.
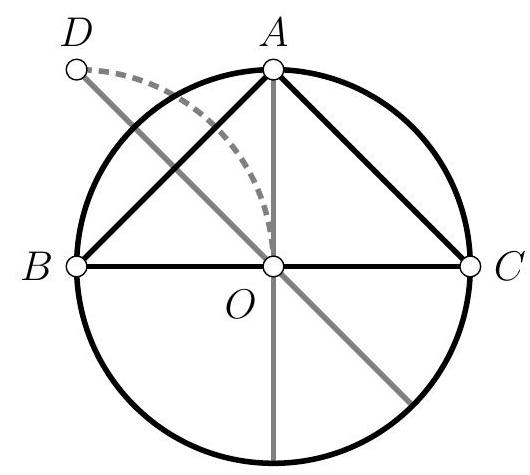
Case 1: $D \in \ell_{A, B} \cap \omega_{B, O}$
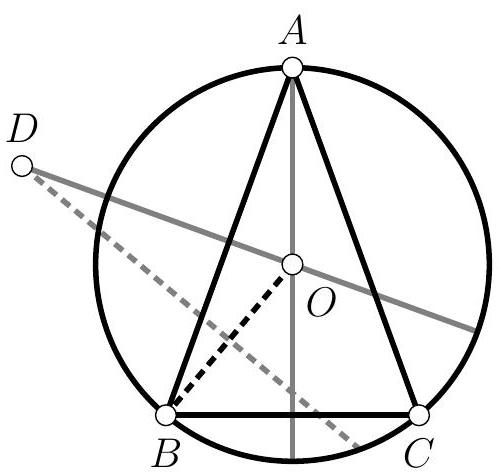
Case $2: D \in \ell_{A, B} \cap \ell_{B, O}$
|
6
|
Yes
|
Incomplete
|
math-word-problem
|
Geometry
|
Trouver le plus grand entier $n \geqslant 3$ pour lequel il existe un ensemble $\mathcal{S}$ de $n$ points du plan avec la propriété suivante : tout triangle (même plat) dont les sommets appartiennent à $\mathcal{S}$ est isocèle mais pas équilatéral.
|
$n^{\circ} 1$ Réutilisons les notations de la solution ci-dessus. On démontre comme précédemment qu'il existe un ensemble mignon à 6 éléments, et on procède désormais par l'absurde, en supposant que l'on dispose d'un ensemble $\mathcal{S}$ mignon à 7 éléments. Comme dans la solution précédente, on démontre que 3 points de $\mathcal{S}$ ne sont jamais alignés. On démontre ensuite le résultat suivant.
Lemme 4. Soit $A$ et $B$ deux points de $\mathcal{S}$. Si $n \geqslant 7$, alors $\omega_{A, B}$ contient au plus 3 points de $\mathcal{S}$.
Démonstration : Supposons que $\omega_{A, B}$ contient au moins quatre points $B, C, D$ et $E$, tels que $B C=C D$. Puisque $B$ et $D$ sont les deux seuls points d'intersection de $\omega_{A, B}$ et $\omega_{C, B}=\omega_{C, D}$, et que $A$ est l'unique point d'intersection de $\omega_{B, C}$ et $\omega_{D, C}$, on sait que $E$ est, au choix :
1. $\operatorname{sur} \omega_{A, B}, \ell_{C, D}$ et $\omega_{B, C}$;
2. sur $\omega_{A, B}, \ell_{B, C}$ et $\omega_{D, C}$;
3. $\operatorname{sur} \omega_{A, B}, \omega_{B, C}$ et $\omega_{D, C}$.
Dans le troisième cas, on a donc $B C=C D=D E=E B$, de sorte que $B C D E$ est un losange dont les sommets sont cocycliques, c'est-à-dire un carré, et donc que $A, B$ et $D$ sont alignés. Ce cas est donc impossible. Par ailleurs, les premier et deuxième cas sont symétriques l'un de l'autre. On suppose donc que l'on est dans le deuxième cas.
On observe alors que $B, C, D$ et $E$ sont quatre sommets consécutifs d'un pentagone régulier de centre $A$, et dont on note $d$ la longueur des côtés. Parmi les deux autres points de $\mathcal{S}$, l'un n'appartient pas à $\ell_{C, D}$, qui contient déjà $A$ : on note $X$ ce point. Chacune des droites $\ell_{B, C}$ et $\ell_{D, E}$ contient déjà deux points de $\mathcal{S}$ parmi $A, B, C, D$ et $E$, et ne contient donc pas $X$. On en déduit que
$$
\left\{\begin{array}{l}
B X=d \text { ou } C X=d \\
C X=d \text { ou } D X=d ; \\
D X=d \text { ou } E X=d
\end{array}\right.
$$
Par conséquent, $X$ est sur $\ell_{B, D}$ (si $B X=D X=d$ ) ou sur $\ell_{C, E}$ (si $C X=E X=d$ ). Ces deux cas sont impossibles, puisque $\ell_{B, D}$ contient déjà $A$ et $C$, tandis que $\ell_{C, E}$ contient déjà $A$ et $D$. Note supposition initiale était donc invalide, ce qui démontre le lemme.

Cas 2: $E \in \ell_{B, C} \cap \omega_{D, C}$

Cas 3: $E \in \omega_{B, C} \cap \omega_{D, C}$
Pour tout segment $[A, B]$ dont les extrémités sont dans $\mathcal{S}$, on note maintenant $p_{A, B}$ le nombre de points de $\mathcal{S}$ situés sur la médiatrice $\ell_{A, B}$ : on dit qu'il s'agit du poids de $[A, B]$. Puisqu'il existe $\binom{7}{3}=35$ triangles isocèles (mais pas équilatéraux) à sommets dans $\mathcal{S}$, la somme des poids des segments vaut 35 . Or, il y a $\binom{7}{2}=21$ segments, dont aucun n'est de poids $p_{A, B} \geqslant 3$. Si on note $a_{i}$ le nombre de segments de poids $i$, on constate donc que
$$
35=2 a_{2}+a_{1} \leqslant\left(a_{0}+a_{1}+a_{2}\right)+a_{2}=21+a_{2},
$$
de sorte que $a_{2} \geqslant 14$. Comme $2 a_{2}=28 \geqslant 24,5=(1-1 / 2) \times 7^{2}$, le théorème de Turan indique qu'il existe un triangle $A B C$, isocèle en $A$, dont les trois côtés $[A, B],[B, C]$ et $[C, A]$ sont de poids 2.
Parmi $A, B$ et $C$, seul $A$ appartient à l'une des trois médiatrices $\ell_{A, B}, \ell_{B, C}$ ou $\ell_{C, A}$. En outre, ces trois médiatrices concourent en $O$, le centre du cercle circonscrit à $A B C$. Par conséquent, si $O \notin \mathcal{S}$, on sait que $\mathcal{S}$ contient 8 points distincts, que sont $B, C$, et deux points sur chacune des médiatrices $\ell_{A, B}, \ell_{B, C}$ et $\ell_{C, A}$. On en déduit que $O \in \mathcal{S}$.
Soit alors $D$ le second point de $\mathcal{S}$ situé sur $\ell_{A, B}$. Puisque $D \notin \omega_{O, B}$, on sait que $D \in \omega_{B, O}$, auquel cas $D$ coïncide avec le symétrique de $O$ par rapport à $(A B)$, ou bien que $D \in \ell_{B, O}$, auquel cas $D$ coïncide avec le centre du cercle circonscrit à $A B O$. Dans les deux cas, remarquons que $D \notin \omega_{A, B}=\omega_{A, C}$ et que $D \notin \ell_{A, C}$, de sorte que $D \in \omega_{C, A}$.
Dans le premier cas, on sait en outre que $B D=B O \neq B C$, donc que $D \notin \omega_{B, C}$, et que $D \notin \ell_{B, C}$, de sorte que $D \in \omega_{C, B}$. Cela signifie que $C D=C B \neq C O$, donc que $D \notin \omega_{C, O}$. Puisque $D \notin \omega_{O, C}$, on en déduit que $D \in \ell_{C, O}$. Ainsi, et puisque $D \in \omega_{C, A}$, on sait que $O D=C D=C A=B A$, donc que $A D B O$ est un losange dont les diagonales sont de même longueur, c'est-à-dire un carré. Mais alors $\widehat{A O B}$ est droit, et $\widehat{A O C}$ est droit aussi, donc $B, O$ et $C$ sont alignés, ce qui contrevient au lemme 1. Ce cas est donc impossible.
On est donc dans le deuxième cas et, de même, $\mathcal{S}$ contient le centre du cercle circonscrit à $A C O$, que l'on note $E$. Puisque $C D=C A \neq C O$ et que $D \notin \omega_{O, C}$, on sait que $D \in \ell_{C, O}$. Ainsi, $D$ appartient aux deux droites $\ell_{B, O}$ et $\ell_{C, O}$ et, pour des raisons de symétrie, $E$ appartient également à ces deux droites. Puisque ces deux droites ne sauraient être confondues, ce second cas est lui aussi impossible, ce qui conclut.

Cas 1: $D \in \ell_{A, B} \cap \omega_{B, O}$

Cas $2: D \in \ell_{A, B} \cap \ell_{B, O}$
|
{
"exam": "French_tests",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2020"
}
|
Find the largest integer $n \geqslant 3$ for which there exists a set $\mathcal{S}$ of $n$ points in the plane with the following property: every triangle (even degenerate) whose vertices belong to $\mathcal{S}$ is isosceles but not equilateral.
|
$n^{\circ} 2$ Let's reuse the notations from the previous solution. As before, we prove that there exists a "cute" set with 6 elements, and we proceed by contradiction, assuming that we have a "cute" set $\mathcal{S}$ with 7 elements. As in the previous solution, we prove that no three points in $\mathcal{S}$ are collinear.
Now consider an isosceles triangle $ABC$ with vertex $A$, whose vertices belong to $\mathcal{S}$, and let $D$ be another point in $\mathcal{S}$. Since the triangles $ABD$, $BCD$, and $CAD$ are isosceles but not equilateral, we know that $D$ belongs to:
$\triangleright$ one of the three sets $\omega_{A, B}$, $\omega_{B, A}$, and $\ell_{A, B}$;
$\triangleright$ one of the three sets $\omega_{A, C}$, $\omega_{C, A}$, and $\ell_{A, C}$;
$\triangleright$ one of the three sets $\omega_{B, C}$, $\omega_{C, B}$, and $\ell_{B, C}$.
The circles and lines $\omega_{A, B}$, $\omega_{B, A}$, $\omega_{B, C}$, $\omega_{C, B}$, $\ell_{A, B}$, and $\ell_{B, C}$ are all distinct and, taken two at a time, intersect at most at two points. We can therefore consider each possible point $D$ one by one.
1. If $D$ belongs to $\omega_{A, B} = \omega_{A, C}$ and to $\omega_{B, C}$, then $D$ is the reflection $C^{\bullet}$ of $C$ with respect to $(AB)$.
2. If $D$ belongs to $\omega_{A, B} = \omega_{A, C}$ and to $\omega_{C, B}$, then $D$ is the reflection $B^{\bullet}$ of $B$ with respect to $(AC)$.
3. If $D$ belongs to $\omega_{A, B} = \omega_{A, C}$ and to $\ell_{B, C}$, then $D$ is the midpoint of one of the two arcs $\overline{BC}$ on $\omega_{A, B}$, which we denote as $M$ and $M^{\prime}$.
4. If $D$ belongs to at least two perpendicular bisectors, then $D$ is the circumcenter $O$ of the triangle $ABC$.
5. If $D$ belongs to $\omega_{B, A}$ and to $\omega_{C, A}$, then $D$ is the reflection $A^{\bullet}$ of $A$ with respect to $(BC)$.
6. If $D$ belongs to $\omega_{B, A}$ and to $\ell_{A, C}$, and to no other perpendicular bisector, then $D$ cannot belong to $\omega_{B, C}$, so it belongs to $\omega_{C, B}$. We then have $BD = BA = CA$ and $AD = CD = BC$. Thus, the triangles $ABC$ and $ABD$ are isometric, as are the triangles $ACD$ and $BCD$. By setting $x = \widehat{BAC}$ and $y = \widehat{CAD}$, we can easily calculate each angle in the figure, so that $3x + 2y = x + 4y = 180^{\circ}$ (thus $x = y = 36^{\circ}$) if $ABCD$ is crossed. If $ABCD$ is not crossed, we recover a totally analogous figure, up to the order of the points, so that $x = 108^{\circ}$. In these circumstances, we denote by $B^{\boldsymbol{k}}$ the point of intersection of $\omega_{B, A}$, $\omega_{C, B}$, and $\ell_{A, C}$.
7. If $D$ belongs to $\omega_{C, A}$, to $\ell_{A, B}$, and to no other perpendicular bisector, the situation is totally analogous, and $x = 36^{\circ}$ or $108^{\circ}$. It then coincides with the point of intersection of $\omega_{C, A}$, $\omega_{B, C}$, and $\ell_{A, B}$, which we denote as $C^{\boldsymbol{\alpha}}$.
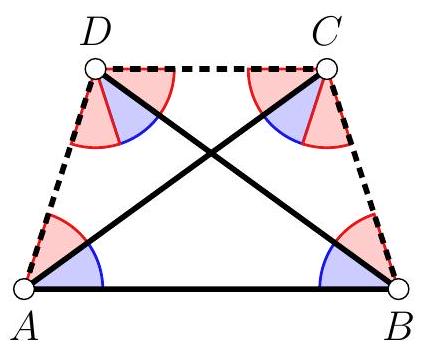
Case 6: $ABCD$ crossed
Case 6: $ABCD$ not crossed
Since $A$ already belongs to $\ell_{B, C}$, Lemma 1 ensures that $\mathcal{S}$ contains at most one of the points $A^{\bullet}$, $O$, $M$, and $M^{\prime}$. Therefore, $\mathcal{S}$ contains at least three of the four points $B^{\bullet}$, $C^{\bullet}$, $B^{\boldsymbol{\omega}}$, and $C^{\boldsymbol{\omega}}$, which means that $x = 36^{\circ}$ or $108^{\circ}$. By repeating this reasoning for each triangle, we conclude that every triangle has angles of $36^{\circ}$ and $108^{\circ}$, or $36^{\circ}$ and $72^{\circ}$.
But then, if a segment $[AB]$ is on the convex hull of $\mathcal{S}$, the other five points $P_{1}, P_{2}, \ldots, P_{5}$ of $\mathcal{S}$ are in the same half-plane delimited by $(AB)$, and every angle $\widehat{P_{i}AB}$ is $36^{\circ}$, $72^{\circ}$, or $108^{\circ}$. Thus, two of these angles are equal, so we have three collinear points, which contradicts Lemma 1 and concludes the proof.
|
6
|
Yes
|
Incomplete
|
math-word-problem
|
Geometry
|
Trouver le plus grand entier $n \geqslant 3$ pour lequel il existe un ensemble $\mathcal{S}$ de $n$ points du plan avec la propriété suivante : tout triangle (même plat) dont les sommets appartiennent à $\mathcal{S}$ est isocèle mais pas équilatéral.
|
$n^{\circ} 2$ Réutilisons les notations de la solution ci-dessus. On démontre comme précédemment qu'il existe un ensemble mignon à 6 éléments, et on procède désormais par l'absurde, en supposant que l'on dispose d'un ensemble $\mathcal{S}$ mignon à 7 éléments. Comme dans la solution précédente, on démontre que 3 points de $\mathcal{S}$ ne sont jamais alignés.
Considérons maintenant un triangle $A B C$, isocèle en $A$, dont les sommets appartiennent à $\mathcal{S}$, puis soit $D$ un autre point de $\mathcal{S}$. Puisque les triangles $A B D, B C D$ et $C A D$ sont isocèles mais pas équilatéraux, on sait que $D$ appartient à
$\triangleright$ un seul des trois ensembles $\omega_{A, B}, \omega_{B, A}$ et $\ell_{A, B}$;
$\triangleright$ un seul des trois ensembles $\omega_{A, C}, \omega_{C, A}$ et $\ell_{A, C}$;
$\triangleright$ un seul des trois ensembles $\omega_{B, C}, \omega_{C, B}$ et $\ell_{B, C}$.
Or, les cercles et droites $\omega_{A, B}, \omega_{B, A}, \omega_{B, C}, \omega_{C, B}, \ell_{A, B}$ et $\ell_{B, C}$ sont deux à deux distincts et, pris deux à deux, ont au plus deux points d'intersection. On peut donc considérer un à un tous les points $D$ possibles.
1. Si $D$ appartient à $\omega_{A, B}=\omega_{A, C}$ et à $\omega_{B, C}, \mathrm{c}^{\prime}$ est le symétrique $C^{\bullet}$ de $C$ par rapport à $(A B)$.
2. Si $D$ appartient à $\omega_{A, B}=\omega_{A, C}$ et à $\omega_{C, B}, \mathrm{C}^{\prime}$ est le symétrique $B^{\bullet}$ de $B$ par rapport à $(A C)$.
3. Si $D$ appartient à $\omega_{A, B}=\omega_{A, C}$ et à $\ell_{B, C}$, c'est le milieu d'un des deux arcs de cercles $\overline{B C}$ sur $\omega_{A, B}$, que l'on note $M$ et $M^{\prime}$.
4. Si $D$ appartient à au moins deux médiatrices, c'est le centre $O$ du cercle circonscrit à $A B C$.
5. Si $D$ appartient à $\omega_{B, A}$ et à $\omega_{C, A}, \mathrm{c}^{\prime}$ est le symétrique $A^{\bullet}$ de $A$ par rapport à $(B C)$.
6. Si $D$ appartient à $\omega_{B, A}$ à $\ell_{A, C}$, et à aucune autre médiatrice, il ne peut appartenir à $\omega_{B, C}$, donc il appartient à $\omega_{C, B}$. On a alors $B D=B A=C A$ et $A D=C D=B C$. Ainsi, les triangles $A B C$ et $A B D$ sont isométriques, de même que les triangles $A C D$ et $B C D$. En posant $x=\widehat{B A C}$ et $y=\widehat{C A D}$, on calcule aisément chacun des angles de la figure, de sorte que $3 x+2 y=x+4 y=180^{\circ}$ (donc $x=y=36^{\circ}$ ) si $A B C D$ est croisé. Si $A B C D$ est non croisé, on récupère une figure totalement analogue, à l'ordre près des points, de sorte que $x=108^{\circ}$. Dans ces circonstances, on note $B^{\boldsymbol{k}}$ le point de concours de $\omega_{B, A}$, $\omega_{C, B}$ et $\ell_{A, C}$.
7. Si $D$ appartient à $\omega_{C, A}$, à $\ell_{A, B}$, et à aucune autre médiatrice, la situation est totalement analogue, et $x=36^{\circ}$ ou $108^{\circ}$. Il coïncide alors avec le point de concours de $\omega_{C, A}, \omega_{B, C}$ et $\ell_{A, B}$, que l'on note $C^{\boldsymbol{\alpha}}$.

Cas 6: $A B C D$ croisé

Cas 6 : $A B C D$ non croisé
Puisque $A$ appartient déjà à $\ell_{B, C}$, le lemme 1 nous assure que $\mathcal{S}$ contient au plus un des points $A^{\bullet}, O, M$ et $M^{\prime}$. L'ensemble $\mathcal{S}$ contient donc au moins trois des quatre points $B^{\bullet}, C^{\bullet}$, $B^{\boldsymbol{\omega}}$ et $C^{\boldsymbol{\omega}}$, ce qui signifie que $x=36^{\circ}$ ou $108^{\circ}$. En répétant ce raisonnement pour chaque triangle, on en conclut que tout triangle a pour angles $36^{\circ}$ et $108^{\circ}$, ou bien $36^{\circ}$ et $72^{\circ}$.
Mais alors, si un segment $[A B]$ est situé sur l'enveloppe convexe de $\mathcal{S}$, les cinq autres points $P_{1}, P_{2}, \ldots, P_{5}$ de $\mathcal{S}$ sont situés dans un même demi-plan délimité par $(A B)$, et tout angle $\widehat{P_{i} A B}$ vaut $36^{\circ}, 72^{\circ}$ ou $108^{\circ}$. Ainsi, deux de ces angles sont égaux, donc on a trois points alignés, ce qui contrevient au lemme 1 et conclut.
|
{
"exam": "French_tests",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2020"
}
|
Find the largest integer $n \geqslant 3$ for which there exists a set $\mathcal{S}$ of $n$ points in the plane with the following property: every triangle (even degenerate) whose vertices belong to $\mathcal{S}$ is isosceles but not equilateral.
|
$n^{\circ} 3$ Here is another way to prove that any cute set has at most 6 elements. As above, we proceed by contradiction and assume that we have a cute set $\mathcal{S}$ with 7 elements. Once again, we prove that 3 points of $\mathcal{S}$ are never collinear.
The score of a point $A$ in $\mathcal{S}$ is the number of segments $[B C]$ with endpoints in $\mathcal{S}$ such that $A B C$ is isosceles at $A$. Since there are $\binom{7}{3}=35$ isosceles (but not equilateral) triangles with vertices in $\mathcal{S}$, the sum of the scores of the vertices is 35. Since $\mathcal{S}$ has 7 vertices, one of them, say $O$, has a score $s \geqslant 5$.
However, the score of $O$ cannot be due to $s$ segments with distinct endpoints. Therefore, there exist three points $A, B$, and $C$ in $\mathcal{S}$ such that $A O = B O = C O$. Without loss of generality, we assume even $A B = A C \neq B C$. We then set $A O = x$, $A B = y$, and $B C = z$, and we know that $x, y$, and $z$ are pairwise distinct.
Suppose now that $\mathcal{S}$ contains a point $D \neq O$ that is not on $\omega_{O, A}$. The perpendicular bisector $\ell_{B, C}$ already contains $A$ and $O$, so it does not contain $D$. Without loss of generality, we assume that $D \in \omega_{B, C}$. Since $O B D$ is isosceles and $O B = x \neq O D$ and $B D = B C = z$, it follows that $O D = z$. Furthermore, $B C D$ is isosceles at $C$ but not equilateral, so $C D \neq z$. Since $O C D$ is isosceles, $O D = z \neq C D$ and $O C = x$, it follows that $C D = x$. Therefore:
$\triangleright A B D$ is isosceles, $A B = y$ and $B D = x$, so $A D$ is $x$ or $y$;
$\triangleright A O D$ is isosceles, $A O = x$ and $O D = z$, so $A D$ is $x$ or $z$;
$\triangleright A C D$ is isosceles, $A C = y$ and $C D = z$, so $A D$ is $y$ or $z$.
We thus have a contradiction.
Thus, except for $O$, every point in $\mathcal{S}$ lies on $\omega_{O, A}$, and also on $\omega_{A, B}$, $\omega_{B, A}$, or $\ell_{A, B}$. The circles $\omega_{A, B}$ and $\omega_{B, A}$ each have two points of intersection with $\omega_{O, A}$. As for the perpendicular bisector $\ell_{A, B}$, it already contains $O$, and thus contains at most one point of $\omega_{O, A}$. Therefore, $\mathcal{S}$ has at most six elements, which concludes the proof.
Comment from the graders Despite its difficulty, this problem was the one for which we received the most solutions. Many approaches were attempted: considering the convex hull, the extreme points, the number of points on a perpendicular bisector or on a circle, the number of times a point is the vertex of an isosceles triangle, ... While these approaches, taken individually, rarely led to a conclusion, each provided information about the shape of a set satisfying the constraints of the problem, and combining these approaches allowed one to arrive at a complete solution. The solutions we had in mind when proposing this problem were of this nature. We therefore encourage students to try this kind of combinatorial geometry approach and to use all the tools at their disposal to cross-reference the information obtained. However, the majority of the solutions were quite different. The two most followed approaches to solve the problem were:
$\triangleright$ Start from an isosceles triangle and determine which points can be added to the set, then exclude simultaneous choices of these points to show that only 3 points can be added, thus establishing the bound of 6, or
$\triangleright$ Establish a list of all possible configurations satisfying the statement.
Here, these two approaches were indeed realistic. However, it was easy to accidentally forget some cases, and many did. For example, the first approach required noticing that, in an isosceles triangle $A B C$ at $A$, the perpendicular bisector of $A B$, the circle centered at $B$ passing through $C$, and the circle centered at $C$ passing through $A$ can intersect provided that $\hat{A}=36^{\circ}$, which not everyone saw. These omissions were severely penalized, as the basis of any case disjunction consists precisely in being sufficiently rigorous to not forget any case.
Finally, the graders were surprised by the number of students who did not recognize the six-point configuration (a pentagon and its center), which had appeared in the 2015 International Olympiad problem 1. We hope that this configuration will join the "standard toolkit" of students in the future.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Trouver le plus grand entier $n \geqslant 3$ pour lequel il existe un ensemble $\mathcal{S}$ de $n$ points du plan avec la propriété suivante : tout triangle (même plat) dont les sommets appartiennent à $\mathcal{S}$ est isocèle mais pas équilatéral.
|
$n^{\circ} 3$ Voici une autre manière de démontrer que tout ensemble mignon compte au plus 6 éléments. Comme ci-dessus, on procède par l'absurde, et l'on suppose que l'on dispose d'un ensemble $\mathcal{S}$ mignon à 7 éléments. Une fois de plus, on démontre que 3 points de $\mathcal{S}$ ne sont jamais alignés.
Le score d'un point $A$ de $\mathcal{S}$ est le nombre de segments $[B C]$ à extrémités dans $\mathcal{S}$ tels que $A B C$ soit isocèle en $A$. Puisqu'il existe $\binom{7}{3}=35$ triangles isocèles (mais pas équilatéraux) à sommets dans $\mathcal{S}$, la somme des scores des sommets vaut 35 . Comme $\mathcal{S}$ compte 7 sommets, l'un d'entre eux, disons $O$, est de score $s \geqslant 5$.
Or, le score de $O$ ne peut pas être dû à $s$ segments d'extrémités deux à deux distinctes. Il existe donc trois points $A, B$ et $C$ dans $\mathcal{S}$ tels que $A O=B O=C O$. Sans perte de généralité, on suppose même $A B=A C \neq B C$. On pose alors $A O=x, A B=y$ et $B C=z$, et l'on sait que $x, y$ et $z$ sont deux à deux distincts.
Supposons maintenant que $\mathcal{S}$ contient un point $D \neq O$ qui n'est pas sur $\omega_{O, A}$. La médiatrice $\ell_{B, C}$ contient déjà $A$ et $O$, donc ne contient pas $D$. Sans perte de généralité, on suppose donc que $D \in \omega_{B, C}$. Puisque $O B D$ est isocèle et que $O B=x \neq O D$ et $B D=B C=z, \mathrm{c}^{\prime}$ est donc que $O D=z$. Par ailleurs, $B C D$ est isocèle en $C$ mais pas équilatéral, donc $C D \neq z$. Puisque $O C D$ est isocèle, que $O D=z \neq C D$ et que $O C=x, \mathrm{c}^{\prime}$ est donc que $C D=x$. Dès lors :
$\triangleright A B D$ est isocèle, $A B=y$ et $B D=x$, donc $A D$ vaut $x$ ou $y$;
$\triangleright A O D$ est isocèle, $A O=x$ et $O D=z$, donc $A D$ vaut $x$ ou $z$;
$\triangleright A C D$ est isocèle, $A C=y$ et $C D=z$, donc $A D$ vaut $y$ ou $z$.
On dispose ainsi d'une contradiction.
Ainsi, à l'exception de $O$, tout point de $\mathcal{S}$ se trouve sur $\omega_{O, A}$, mais également sur $\omega_{A, B}, \omega_{B, A}$ ou $\ell_{A, B}$. Or, les cercles $\omega_{A, B}$ et $\omega_{B, A}$ ont chacun deux points d'intersection avec $\omega_{O, A}$. Quant à la médiatrice $\ell_{A, B}$, elle contient déjà $O$, et contient donc au plus un point de $\omega_{O, A}$. Ainsi, $\mathcal{S}$ est de taille au plus six, ce qui conclut.
Commentaire des correcteurs Malgré sa difficulté, ce problème est celui pour lequel nous avons reçu le plus de solutions. De nombreuses approches ont été tentées : considérer l'enveloppe convexe, les points extrémaux, le nombre de points sur une médiatrice ou sur un cercle, le nombre de fois qu'un point est sommet d'un triangle isocèle,...Si ces
approches, prises isolément, permettaient rarement de conclure, chacune donnait toutefois des informations sur la forme d'un ensemble vérifiant les contraintes de l'énoncé, et combiner ces approches permettait donc d'aboutir à une solution complète. Les solutions auxquelles nous avions pensé en proposant ce problème étaient de cette nature. Nous encourageons donc les élèves à essayer ce genre d'approche de géométrie combinatoire, et à utiliser tous les outils à leur disposition pour pouvoir croiser les informations obtenues. Cependant, la majorité des solutions était bien différente. Les deux approches les plus suivies pour résoudre le problème étaient:
$\triangleright$ Partir d'un triangle isocèle, et déterminer quels points peuvent être ajoutés à l'ensemble, puis exclure des choix simultanés de ces points pour montrer qu'on ne peut ajouter que 3 points, établissant ainsi la borne de 6, ou bien
$\triangleright$ Établir une liste de toutes les configurations possibles vérifiant l'énoncé.
Ici, ces deux approches étaient effectivement réalistes. Cependant, il était aisé d'oublier accidentellement des cas, et c'est ce que beaucoup ont fait. Par exemple, la première approche nécessitait de remarquer que, dans un triangle $A B C$ isocèle en $A$, la médiatrice de $A B$, le cercle de centre $B$ passant par $C$ et le cercle de centre $C$ passant par $A$ peuvent s'intersecter à condition que $\hat{A}=36^{\circ}$, ce que tout le monde n'a pas vu. Ces oublis ont été sévèrement sanctionnés, puisque la base de toute disjonction de cas consiste précisément à être suffisamment rigoureux pour n'oublier aucun cas.
Enfin, les correcteurs ont été surpris du nombre d'élèves qui n'ont pas repéré la configuration à six points (un pentagone et son centre), qui était pourtant apparue dans le problème 1 de l'Olympiade Internationale de 2015. Nous espérons que cette configuration rejoindra le « bagage standard » des élèves à l'avenir.
|
{
"exam": "French_tests",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2020"
}
|
We denote by $\mathbb{R}_{>0}$ the set of strictly positive real numbers. Find all functions $f: \mathbb{R}_{>0} \mapsto \mathbb{R}_{>0}$ such that
$$
f(x+f(x y))+y=f(x) f(y)+1
$$
for all strictly positive real numbers $x$ and $y$.
|
Let $f$ be a potential solution to the problem. In the following, we will denote $\mathbf{E}_{x, y}$ the given equality. Let $a$ and $b$ be two strictly positive real numbers such that $f(a)=f(b)$. The equalities $\mathbf{E}_{1, a}$ and $\mathbf{E}_{1, b}$ indicate that
$$
a=f(1) f(a)+1-f(1+f(a))=f(1) f(b)+1-f(1+f(b))=b
$$
which means that $f$ is injective.
Next, let $c$ and $d$ be two real numbers such that $0<c<d$, and let $t$ be a strictly positive real number. Since $f$ is injective, the equalities $\mathbf{E}_{c / t, t}$ and $\mathbf{E}_{d / t, t}$ indicate that
$$
f(c / t+f(c))=f(c / t) f(t)+1-t \neq f(d / t) f(t)+1-t=f(d / t+f(d))
$$
so that $c / t+f(c) \neq d / t+f(d)$, or equivalently that $f(d)-f(c) \neq (c-d) / t$. Since this inequality holds for all $t>0$, we deduce that $f(d) \geqslant f(c)$, which means that $f$ is increasing.
We then set $p=\inf \{f(x): x>0\}$ and $q=\inf \{f(x): x>p\}$. Since $f$ is increasing, we know that $f(x) \rightarrow p$ as $x \rightarrow 0$ and $x>0$, and that $f(y) \rightarrow q$ as $y \rightarrow p$ and $y>p$. For a fixed positive real number $y$, if we let $x$ tend to 0, we deduce that $f(x) \rightarrow p$ and that $f(x y) \rightarrow p$, so that $x+f(x y) \rightarrow p$ and that $f(x+f(x y)) \rightarrow q$. Consequently, the equality $\mathbf{E}_{x, y}$ indicates that
$$
y-1=f(x) f(y)-f(x+f(x y)) \rightarrow p f(y)-q,
$$
which means that $f(y)=y+(q-1) / p$.
The function $f$ is therefore an affine function, of the form $f: t \mapsto u t+v$. Conversely, once the coefficients $u$ and $v$ are fixed, the equality $\mathbf{E}_{x, y}$ indicates that
$$
u^{2} x y+u x+u v+v+y=f(x+f(x y))+y=f(x) f(y)+1=u^{2} x y+u v x+u v y+v^{2}+1
$$
or equivalently that $u(v-1) x+(u v-1) y=u v+v-v^{2}-1$. This means that
$$
u v-u=u v-1=u v+v-v^{2}-1=0
$$
We deduce that $u-1=(u v-1)-(u v-u)=0$, that is, $u=1$, and then that $v-1=u v-u=0$, that is, $v=1$. But then the triple equality
$$
u v-u=u v-1=u v+v-v^{2}-1=0
$$
is indeed satisfied.
In conclusion, the function $f: t \mapsto t+1$ is the unique solution to the problem.
Comment from the graders This problem was extremely difficult, and no student (nor any mentor from the POFM) managed to pass the crucial step of proving that $f$ is increasing. Several students had excellent reflexes: looking for a particular solution (the function $f: t \mapsto t+1$), examining specific values of $x$ and $y$ (here, $x=1$), investigating the injectivity of $f$, conjecturing that $f$ is increasing (by identifying an infinity of values $x<y$ such that $f(x)<f(y)$), and then using this conjecture. These excellent initiatives almost always earned their authors some points.
However, the graders noted a few avoidable errors or missteps, in the hope that students will avoid them in other situations:
$\triangleright$ Several students looked at what happened when $x=0$ or $y=0$. This often allowed them to identify the function $f: t \mapsto t+1$, which was very positive. However, of course, one could not base any proof on the equalities obtained when $x=0$ or $y=0$, since the function $f$ was only defined on $\mathbb{R}_{>0}$.
$\triangleright$ Many students looked at what happened when $y=1$, but not when $x=1$. Others looked at the case where $x=1$, but did not think to deduce the injectivity of $f$, even though they had the equality $f(1+f(x))+x=1+f(1) f(x)$, which made the injectivity of $f$ immediate.
$\triangleright$ Several students checked if the identity or constant functions could be solutions. It is a pity that they did not directly treat the case of affine functions, which was just as easy to handle, and which would have allowed them to identify the only solution to the problem.
|
f: t \mapsto t+1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
On note $\mathbb{R}_{>0}$ l'ensemble des réels strictement positifs. Trouver toutes les fonctions $f: \mathbb{R}_{>0} \mapsto \mathbb{R}_{>0}$ telles que
$$
f(x+f(x y))+y=f(x) f(y)+1
$$
pour tous les réels strictement positifs $x$ et $y$.
|
Soit $f$ une solution éventuelle du problème. Dans la suite, on notera $\mathbf{E}_{x, y}$ l'égalité de l'énoncé. Soit $a$ et $b$ deux réels strictement positifs tels que $f(a)=f(b)$. Les égalités $\mathbf{E}_{1, a}$ et $\mathbf{E}_{1, b}$ indiquent que
$$
a=f(1) f(a)+1-f(1+f(a))=f(1) f(b)+1-f(1+f(b))=b
$$
ce qui signifie que $f$ est injective.
Soit ensuite $c$ et $d$ deux réels tels que $0<c<d$, puis soit $t$ un réel strictement positif. Puisque $f$ est injective, les égalités $\mathbf{E}_{c / t, t}$ et $\mathbf{E}_{d / t, t}$ indiquent que
$$
f(c / t+f(c))=f(c / t) f(t)+1-t \neq f(d / t) f(t)+1-t=f(d / t+f(d))
$$
de sorte que $c / t+f(c) \neq d / t+f(d)$, ou encore que $f(d)-f(c) \neq(c-d) / t$. Cette dernière inégalité étant valide pour tout $t>0$, on en déduit que $f(d) \geqslant f(c)$, ce qui signifie que $f$ est croissante.
On pose alors $p=\inf \{f(x): x>0\}$ et $q=\inf \{f(x): x>p\}$. Puisque $f$ est croissante, on sait que $f(x) \rightarrow p$ lorsque $x \rightarrow 0$ et que $x>0$, et que $f(y) \rightarrow q$ lorsque $y \rightarrow p$ et que $y>p$. Un réel $y>0$ étant fixé, si on fait tendre $x$ vers 0 , on en déduit que $f(x) \rightarrow p$ et que $f(x y) \rightarrow p$, de sorte que $x+f(x y) \rightarrow p$ et que $f(x+f(x y)) \rightarrow q$. Par conséquent, l'égalité $\mathbf{E}_{x, y}$ indique que
$$
y-1=f(x) f(y)-f(x+f(x y)) \rightarrow p f(y)-q,
$$
ce qui signifie que $f(y)=y+(q-1) / p$.
La fonction $f$ est donc une fonction affine, de la forme $f: t \mapsto u t+v$. Réciproquement, une fois les coefficients $u$ et $v$ fixés, l'égalité $\mathbf{E}_{x, y}$ indique que
$$
u^{2} x y+u x+u v+v+y=f(x+f(x y))+y=f(x) f(y)+1=u^{2} x y+u v x+u v y+v^{2}+1
$$
ou encore que $u(v-1) x+(u v-1) y=u v+v-v^{2}-1$. Cela signifie que
$$
u v-u=u v-1=u v+v-v^{2}-1=0
$$
On en déduit que $u-1=(u v-1)-(u v-u)=0$, c'est-à-dire que $u=1$, puis que $v-1=$ $u v-u=0$, c'est-à-dire que $v=1$. Mais alors la triple égalité
$$
u v-u=u v-1=u v+v-v^{2}-1=0
$$
est bien respectée.
En conclusion, la fonction $f: t \mapsto t+1$ est l'unique solution du problème.
Commentaire des correcteurs Cet exercice était extrêmement difficile, et aucun élève (ni encadrant de la POFM) n'est parvenu à passer l'étape cruciale qui consistait à démontrer que $f$ était croissante. Plusieurs élèves ont eu d'excellents réflexes : rechercher une solution particulière (la fonction $f: t \mapsto t+1$ ), regarder des valeurs particulières de $x$ et $y$ (ici, $x=1$ ), s'intéresser à l'injectivité de $f$, conjecturer que $f$ était croissante (en repérant une infinité de valeurs $x<y$ telles que $f(x)<f(y)$ ), puis utiliser cette conjecture. Ces excellentes initiatives ont à peu près toutes permis à leur auteur d'obtenir quelques points.
Mentionnons cependant quelques erreurs ou maladresses évitables que les correcteurs ont repérées, dans l'espoir que les élèves les éviteront en d'autres occasions:
$\triangleright$ Plusieurs élèves ont regardé ce qui se passait lorsque $x=0$ ou $y=0$. Cela leur a souvent permis de repérer la fonction $f: t \mapsto t+1$, ce qui était très positif. Cependant, on ne pouvait bien sûr pas se baser sur les égalités obtenues lorsque $x=0$ ou $y=0$ pour démontrer quoi que ce soit, puisque la fonction $f$ n'était définie que sur $\mathbb{R}_{>0}$.
$\triangleright$ De nombreux élèves ont regardé ce qui se passait lorsque $y=1$, mais pas lorsque $x=1$. D'autres ont regardé le cas où $x=1$, mais n'ont pas pensé à en déduire l'injectivité de $f$, alors même qu'ils disposaient de l'égalité $f(1+f(x))+x=1+f(1) f(x)$, ce qui rendait l'injectivité de $f$ immédiate.
$\triangleright$ Plusieurs élèves ont regardé si l'identité ou les fonctions constantes pouvaient être solutions. Il est dommage de ne pas avoir traité directement le cas des fonctions affines, qui était aussi facile à traiter, et qui leur aurait permis d'identifier la seule solution du problème.
## Problèmes EGMO
|
{
"exam": "French_tests",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"solution_match": "\nSolution de l'exercice 7",
"tier": "T1",
"year": "2020"
}
|
Let $\left(F_{k}\right)_{k \geqslant 0}$ be the sequence defined by $F_{0}=0, F_{1}=1$, and $F_{k+2}=F_{k}+F_{k+1}$ for all integers $k \geqslant 0$. Let then $n \geqslant 1$ be an integer. Prove that there are exactly $F_{n+1}$ ways to order the numbers $1,2, \ldots, n$ to obtain an $n$-tuple $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ such that
$$
a_{1} \leqslant 2 a_{2} \leqslant 3 a_{3} \leqslant \ldots \leqslant n a_{n}
$$
|
A permutation $\mathbf{a}=\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ of the integers $1,2, \ldots, n$ is said to be pretty if it satisfies the inequalities $a_{1} \leqslant 2 a_{2} \leqslant \ldots \leqslant n a_{n}$.
First, let a be a pretty permutation. If there exists an integer $k$ for which $a_{k} \leqslant k-2$, we choose the minimal $k$. In this case, we know that $k \geqslant 2$ and that $a_{k-1} \geqslant k-2 \geqslant a_{k}$, so that $a_{k-1} \geqslant a_{k}+1$. We conclude that
$$
(k-1) a_{k-1} \geqslant(k-1)\left(a_{k}+1\right)=k a_{k}+\left(k-a_{k}-1\right) \geqslant k a_{k}+1,
$$
and thus that a is not pretty. Therefore, we conclude that $a_{k} \geqslant k-1$ for all $k \leqslant n$.
On the other hand, let $\ell$ be the integer such that $a_{\ell}=n$. Given the result obtained previously, an immediate downward induction on $k$ ensures that $a_{k}=k-1$ for all integers $k$ such that $\ell+1 \leqslant k \leqslant n$. Since
$$
\ell n=\ell a_{\ell} \leqslant(\ell+1) a_{\ell+1}=(\ell+1) \ell
$$
we conclude that $\ell \in\{n-1, n\}$.
Thus, for a to be pretty, we have two choices a priori:
$\triangleright$ either $\ell=n$, in which case a is indeed pretty if and only if the permutation $\left(a_{1}, a_{2}, \ldots, a_{n-1}\right)$ of the integers $1,2, \ldots, n-1$ is pretty;
$\triangleright$ or $\ell=n-1$, in which case $a_{n}=n-1$, and then a is indeed pretty if the permutation $\left(a_{1}, a_{2}, \ldots, a_{n-2}\right)$ of the integers $1,2, \ldots, n-2$ is pretty.
Consequently, if we denote by $J_{n}$ the number of pretty permutations of $1,2, \ldots, n$, we note that $J_{n}=J_{n-1}+J_{n-2}$ as soon as $n \geqslant 3$. We conclude by verifying that $J_{1}=1=F_{2}$ and that $J_{2}=2=F_{3}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soit $\left(F_{k}\right)_{k \geqslant 0}$ la suite définie par $F_{0}=0, F_{1}=1$, et $F_{k+2}=F_{k}+F_{k+1}$ pour tout entier $k \geqslant 0$. Soit ensuite $n \geqslant 1$ un entier. Démontrer qu'il existe exactement $F_{n+1}$ façons d'ordonner les nombres $1,2, \ldots, n$ de manière à obtenir un $n$-uplet $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ tel que
$$
a_{1} \leqslant 2 a_{2} \leqslant 3 a_{3} \leqslant \ldots \leqslant n a_{n}
$$
|
On dit qu'une permutation $\mathbf{a}=\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ des entiers $1,2, \ldots, n$ est jolie si elle satisfait les inégalités $a_{1} \leqslant 2 a_{2} \leqslant \ldots \leqslant n a_{n}$.
Tout d'abord, soit a une jolie permutation. S'il existe un entier $k$ pour lequel $a_{k} \leqslant k-2$, on choisit $k$ minimal. Dans ces conditions, on sait que $k \geqslant 2$ et que $a_{k-1} \geqslant k-2 \geqslant a_{k}$, de sorte que $a_{k-1} \geqslant a_{k}+1$. On en conclut que
$$
(k-1) a_{k-1} \geqslant(k-1)\left(a_{k}+1\right)=k a_{k}+\left(k-a_{k}-1\right) \geqslant k a_{k}+1,
$$
et donc que a n'est pas jolie. On en conclut donc que $a_{k} \geqslant k-1$ pour tout $k \leqslant n$.
D'autre part, soit $\ell$ l'entier tel que $a_{\ell}=n$. Au vu du résultat obtenu précédemment, une récurrence descendante immédiate sur $k$ nous assure que $a_{k}=k-1$ pour tout entier $k$ tel que $\ell+1 \leqslant k \leqslant n$. Puisque
$$
\ell n=\ell a_{\ell} \leqslant(\ell+1) a_{\ell+1}=(\ell+1) \ell
$$
on en conclut que $\ell \in\{n-1, n\}$.
Ainsi, pour que a soit jolie, on dispose a priori de deux choix :
$\triangleright$ soit $\ell=n$, auquel cas a est effectivement jolie si et seulement si la permutation $\left(a_{1}, a_{2}, \ldots, a_{n-1}\right)$ des entiers $1,2, \ldots, n-1$ est jolie;
$\triangleright$ soit $\ell=n-1$, auquel cas $a_{n}=n-1$, et alors a est effectivement jolie si la permutation $\left(a_{1}, a_{2}, \ldots, a_{n-2}\right)$ des entiers $1,2, \ldots, n-2$ est jolie.
Par conséquent, si on note $J_{n}$ le nombre de jolies permutations de $1,2, \ldots, n$, on remarque bien que $J_{n}=J_{n-1}+J_{n-2}$ dès lors que $n \geqslant 3$. On conclut en vérifiant que $J_{1}=1=F_{2}$ et que $J_{2}=2=F_{3}$.
|
{
"exam": "French_tests",
"problem_label": "8",
"problem_match": "\nExercice 8.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"solution_match": "\nSolution de l'exercice 8",
"tier": "T1",
"year": "2020"
}
|
Let $\left(F_{k}\right)_{k \geqslant 0}$ be the sequence defined by $F_{0}=0, F_{1}=1$, and $F_{k+2}=F_{k}+F_{k+1}$ for all integers $k \geqslant 0$. Let then $n \geqslant 1$ be an integer. Prove that there are exactly $F_{n+1}$ ways to order the numbers $1,2, \ldots, n$ to obtain an $n$-tuple $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ such that
$$
a_{1} \leqslant 2 a_{2} \leqslant 3 a_{3} \leqslant \ldots \leqslant n a_{n}
$$
|
$n^{\circ} 1$ As previously, we consider a permutation $a$ and the integer $\ell$ such that $a_{\ell}=n$. Since $n a_{k} \geqslant k a_{k} \geqslant \ell a_{\ell}=\ell n$ for all $k \geqslant \ell$, we know that $a$ induces a permutation of $1,2, \ldots, \ell-1$ and of $\ell, \ell+1, \ldots, n$.
If $\ell \leqslant n-1$, let $m$ be the unique integer such that $a_{m}=\ell$. Since $m \geqslant \ell$, we know that
$$
m \ell=m a_{m} \geqslant \ell a_{\ell}=\ell n
$$
thus $m=n$. But then $k a_{k}=\ell n$ for all integers $k$ such that $\ell \leqslant k \leqslant n$. We deduce in particular that $n-1$ divides $(n-1) a_{n-1}=\ell n$, and thus divides $\ell$ as well, which means that $\ell=n-1$. Now that we have established that $\ell \in\{n-1, n\}$, we conclude as previously.
Comment from the graders This problem was difficult. Nevertheless, a good number of students had the good idea to try to find a recurrence relation on the number of permutations satisfying the statement and succeeded, by analyzing the recurrence relation, to understand the structure of the permutations satisfying the statement.
However, very few students managed to formalize this, in particular to show that the integer $\ell$ defined in the solution was indeed greater than or equal to $n-1$. Some used the fact that $n(n-2)<(n-1)^{2}$ to conclude in the general case. While this argument worked for $\ell=n-2$, it was unfortunately impossible to adapt it directly for arbitrary $\ell$.
Also be careful with the recurrence! Several students showed, if we denote by $k_{n}$ the number of permutations of $\{1, \ldots, n\}$ satisfying the statement, that $k_{n}=k_{n-1}+k_{n-2}$. They then performed a strong induction, initialized at $n=1$, to prove that $k_{n}=F_{n+1}$. Here, for $n=2$, the formula $k_{2}=k_{1}+k_{0}$ does not make sense because $k_{0}$ is not even defined. This inductive reasoning therefore did not allow proving that $k_{2}=F_{3}$, and it would have been necessary to treat this equality in the initialization of our induction. Here, to avoid this error, it would have been better to perform a double induction, which requires explicitly initializing at $n=1$ and $n=2$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soit $\left(F_{k}\right)_{k \geqslant 0}$ la suite définie par $F_{0}=0, F_{1}=1$, et $F_{k+2}=F_{k}+F_{k+1}$ pour tout entier $k \geqslant 0$. Soit ensuite $n \geqslant 1$ un entier. Démontrer qu'il existe exactement $F_{n+1}$ façons d'ordonner les nombres $1,2, \ldots, n$ de manière à obtenir un $n$-uplet $\left(a_{1}, a_{2}, \ldots, a_{n}\right)$ tel que
$$
a_{1} \leqslant 2 a_{2} \leqslant 3 a_{3} \leqslant \ldots \leqslant n a_{n}
$$
|
$n^{\circ} 1$ Comme précédemment, on considère une permutation a puis l'entier $\ell$ tel que $a_{\ell}=n$. Puisque $n a_{k} \geqslant k a_{k} \geqslant \ell a_{\ell}=\ell$ n pour tout $k \geqslant \ell$, on sait que a induit une permutation de $1,2, \ldots, \ell-1$ et de $\ell, \ell+1, \ldots, n$.
Si $\ell \leqslant n-1$, soit $m$ l'unique entier tel que $a_{m}=\ell$. Puisque $m \geqslant \ell$, on sait que
$$
m \ell=m a_{m} \geqslant \ell a_{\ell}=\ell n
$$
donc que $m=n$. Mais alors $k a_{k}=\ell n$ pour tout entier $k$ tel que $\ell \leqslant k \leqslant n$. On en déduit en particulier que $n-1$ divise $(n-1) a_{n-1}=\ell n$, donc divise $\ell$ aussi, ce qui signifie que $\ell=n-1$. Maintenant acquis le fait que $\ell \in\{n-1, n\}$, on conclut comme précédemment.
Commentaire des correcteurs Cet exercice était difficile. Néanmoins, une bonne partie des élèves a eu la bonne idée d'essayer de trouver une relation de récurrence sur le nombre de permutations vérifiant l'énoncé et a réussi, en analysant la relation de récurrence, à comprendre la structure des permutations vérifiant l'énoncé.
Toutefois, très peu d'élèves ont réussi à formaliser cela, en particulier à montrer que l'entier $\ell$ défini dans la correction était bien supérieur ou égal à $n-1$. Certains ont utilisé le fait que $n(n-2)<(n-1)^{2}$ pour conclure dans le cas général. Si cet argument fonctionnait pour $\ell=n-2$, il était malheureusement impossible de l'adapter directement pour des $\ell$ quelconques.
Attention aussi à la récurrence! Plusieurs élèves ont montré, si on note $k_{n}$ le nombre de permutations de $\{1, \ldots, n\}$ vérifiant l'énoncé, que $k_{n}=k_{n-1}+k_{n-2}$. Ils ont ensuite fait une récurrence forte, initialisée à $n=1$, pour prouver que $k_{n}=F_{n+1}$. Ici pour $n=2$, la formule $k_{2}=k_{1}+k_{0}$ n'a pas de sens car $k_{0}$ n'est même pas défini. Ce raisonnement par récurrence ne permettait donc pas de prouver que $k_{2}=F_{3}$, et il aurait fallu traiter cette égalité dans le cadre de l'initialisation de notre récurrence. Ici, pour éviter cette erreur, il valait mieux faire une récurrence double, qui nécessite explicitement d'initialiser à $n=1$ et $n=2$.
|
{
"exam": "French_tests",
"problem_label": "8",
"problem_match": "\nExercice 8.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2020"
}
|
Let $n$ be a natural number. Prove that the binary representation of the integer $n\left(2^{n}-1\right)$ contains exactly $n$ occurrences of the digit 1.
|
Let $s_{n}$ be the integer $n\left(2^{n}-1\right)$. Since $s_{0}=0$ and $s_{1}=1$, the statement is verified for $n \leqslant 1$. We therefore assume from now on that $n \geqslant 2$.
We then set $t=2^{n}-n$ and $s=n-1$, so that $n\left(2^{n}-1\right)=2^{n} s+t$ and $s+t=2^{n}-1$. By the binomial theorem, we know that $2^{n} \geqslant(1+1)^{n} \geqslant\binom{ n}{0}+\binom{n}{1}=n+1$. Thus, $s$ and $t$ are two natural numbers whose sum is $2^{n}-1$. Consequently, they can be written respectively as
$$
{\overline{a_{n-1} a_{n-2} \ldots a_{0}}}^{2} \text { and }{\overline{b_{n-1} b_{n-2} \ldots b_{0}}}^{2}
$$
in base 2, and we are assured that $a_{i}+b_{i}=1$ for all $i \leqslant n-1$.
Furthermore, since $t<2^{n}$, the base 2 representation of $2^{n} s+t$ starts with the $n$ digits of $s$ and ends with the $n$ digits of $t$. The integer $n\left(2^{n}-1\right)=2^{n} s+t$ is therefore written as
$$
{\overline{a_{n-1} a_{n-2} \ldots a_{0} b_{n-1} b_{n-2} \ldots b_{0}}}^{2}
$$
in base 2. The sum of these digits is therefore $\left(a_{0}+b_{0}\right)+\left(a_{1}+b_{1}\right)+\ldots+\left(a_{n-1}+b_{n-1}\right)=n$, which concludes the proof.
Grader's Comment This problem was difficult. The key was to recognize that the $k^{\text {th }}$ and $(n+k)^{\text {th }}$ digits of $n\left(2^{n}-1\right)$ were a 0 and a 1, which a systematic study of small cases (say, up to 8) could have helped to observe. The only student who noticed this phenomenon is also the only one who provided a complete solution.
Moreover, it is unfortunate that several students, having had the good idea of writing $2^{n}-1$ in base 2, then prematurely claimed that any number of the form $k\left(2^{n}-1\right)$ contains $n$ occurrences of the digit 1 when written in base 2: this is true only if $1 \leqslant k \leqslant 2^{n}$. Any proof intended to work for all integers $k$ was therefore doomed to fail, which was predictable by looking at the case where $n=1$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $n$ un entier naturel. Démontrer que l'écriture de l'entier $n\left(2^{n}-1\right)$ en base 2 compte exactement $n$ occurrences du chiffre 1.
|
Notons $s_{n}$ l'entier $n\left(2^{n}-1\right)$. Puisque $s_{0}=0$ et $s_{1}=1$, l'énoncé est bien vérifié lorsque $n \leqslant 1$. On suppose donc désormais que $n \geqslant 2$.
On pose alors $t=2^{n}-n$ et $s=n-1$, de sorte que $n\left(2^{n}-1\right)=2^{n} s+t$ et que $s+t=2^{n}-1$. En vertu du binôme de Newton, on sait que $2^{n} \geqslant(1+1)^{n} \geqslant\binom{ n}{0}+\binom{n}{1}=n+1$. Ainsi, $s$ et $t$ sont deux entiers naturels de somme $2^{n}-1$. Par conséquent, ils s'écrivent respectivement comme
$$
{\overline{a_{n-1} a_{n-2} \ldots a_{0}}}^{2} \text { et }{\overline{b_{n-1} b_{n-2} \ldots b_{0}}}^{2}
$$
en base 2 , et on est assuré que $a_{i}+b_{i}=1$ pour tout $i \leqslant n-1$.
En outre, comme $t<2^{n}$, l'écriture de $2^{n} s+t$ en base 2 commence avec les $n$ chiffres de $s$ puis se termine avec les $n$ chiffres de $t$. L'entier $n\left(2^{n}-1\right)=2^{n} s+t$ s'écrit donc
$$
{\overline{a_{n-1} a_{n-2} \ldots a_{0} b_{n-1} b_{n-2} \ldots b_{0}}}^{2}
$$
en base 2. La somme de ces chiffres vaut donc $\left(a_{0}+b_{0}\right)+\left(a_{1}+b_{1}\right)+\ldots+\left(a_{n-1}+b_{n-1}\right)=n$ , ce qui conclut.
Commentaire des correcteurs Cet exercice était difficile. Le point crucial consistait à repérer que les $k^{\text {ème }}$ et $(n+k)^{\text {ème }}$ chiffres de $n\left(2^{n}-1\right)$ étaient un 0 et un 1 , ce qu'une étude systématique des petits cas (disons, jusqu'à 8) aurait pu aider à constater. La seule élève qui a remarqué ce phénomène est également la seule qui a fourni une solution complète.
Par ailleurs, il est dommage que plusieurs élèves, ayant eu la bonne idée d'écrire $2^{n}-1$ en base 2, aient ensuite prématurément affirmé que tout nombre de la forme $k\left(2^{n}-1\right)$ contenait $n$ occurrences du chiffre 1 quand on l'écrivait en base 2 : ceci n'est vrai que si $1 \leqslant k \leqslant 2^{n}$. Toute preuve censée fonctionner pour tout entier $k$ était donc vouée à l'échec, ce qui était prévisible en regardant le cas où $n=1$.
|
{
"exam": "French_tests",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"solution_match": "\nSolution de l'exercice 9",
"tier": "T1",
"year": "2020"
}
|
Let $ABC$ be a triangle. We denote $H_{A}$ as the foot of the altitude from $A$ in $\triangle ABC$, and $A^{\prime}$ as the midpoint of the segment $[BC]$. We then denote $Q_{A}$ as the symmetric point of $H_{A}$ with respect to $A^{\prime}$. We define the points $Q_{B}$ and $Q_{C}$ similarly. Finally, we denote $R$ as the intersection point, other than $Q_{A}$, of the circumcircles of triangles $Q_{A} Q_{B} C$ and $Q_{A} B Q_{C}$.
Prove that the lines $\left(Q_{A} R\right)$ and $(BC)$ are perpendicular.
|
Let $H$ be the orthocenter of $ABC$, $O$ the center of the circumcircle of $ABC$, and $R'$ the symmetric point of $H$ with respect to $O$. The orthogonal projections of $H$ and $O$ on $(BC)$ are $H_a$ and $A'$, so the orthogonal projection of $R'$ on $(BC)$ is $Q_A$. Similarly, the orthogonal projections of $R'$ on $(CA)$ and $(AB)$ are $Q_B$ and $Q_C$.
This means, among other things, that $\widehat{C Q_A R'} = \widehat{Q C_B R'} = 90^\circ$, so $Q_A$ and $Q_B$ belong to the circle with diameter $[CR']$. This circle therefore coincides with the circumcircle of $Q_A Q_B C$. Similarly, the points $Q_A$ and $Q_C$ belong to the circle with diameter $[BR']$, which coincides with the circumcircle of $Q_A B Q_C$. Consequently, the points $R$ and $R'$ are coincident, and $(Q_A R)$ is indeed perpendicular to $(BC)$.
$\underline{\text{Alternative Solution } n^\circ 1}$ Below, we denote by $\Gamma_A, \Gamma_B$, and $\Gamma_C$ the circumcircles of $A Q_B Q_C$, $Q_A B Q_C$, and $Q_A Q_B C$, respectively. Since $R$ belongs to $\Gamma_B$ and $\Gamma_C$, we know that
\[
\left(Q_C A, Q_C R\right) = \left(Q_C B, Q_C R\right) = \left(Q_A B, Q_A R\right) = \left(Q_A C, Q_A R\right) = \left(Q_B C, Q_B R\right) = \left(Q_B A, Q_B R\right)
\]
This means that $R$ also belongs to $\Gamma_A$, and thus $A, B$, and $C$ play symmetric roles. With this observation, we introduce the circumcircle of $ABC$, which we denote by $\Omega$. In search of remarkable circles, we also notice that the right angles at $H_A, H_B$, and $H_C$ suggest drawing the circles $\Xi_A, \Xi_B$, and $\Xi_C$, with diameters $[BC]$, $[CA]$, and $[AB]$, respectively.
Finally, if we denote by $m$ the perpendicular bisector of $[BC]$, the problem asks us to prove that $(Q_A R)$ and $(A H_A)$ are symmetric with respect to $m$. We therefore focus more closely on the symmetry with axis $m$ and the circles for which $m$ is an axis of symmetry: these are the circles $\Omega, \Xi_A$, and, at least in appearance, $\Gamma_A$.
Lacking a proof that the center of the latter circle lies on $m$, we can attempt to prove that the radical axes of $\Gamma_A$ with $\Omega$ or $\Xi_A$ are parallel to $(BC)$. The first would then clearly be the line parallel to $(BC)$ passing through $A$, while the second appears to be the line $(B' C')$.
Since $B'$ is the midpoint of $[AC]$ and $[H_B Q_B]$, we know that $B' H_B \cdot B' C = B' Q_B \cdot B' A$, which means that $B'$ belongs to the radical axis of $\Gamma_A$ and $\Xi_A$. Similarly, $C'$ belongs to this radical axis, which is therefore coincident with $(B' C')$, so $\Gamma_A$ is indeed symmetric with respect to $m$.
Consequently, the circles $\Omega$ and $\Gamma_A$ intersect at a point $X$ which is none other than the symmetric point of $A$ with respect to $m$. Let us then denote by $R'$ the intersection of $(Q_A X)$ and $\Gamma_C$. We know that $\widehat{C Q_B R'} = \widehat{C Q_A R'} = 90^\circ$. Since we also have $\widehat{A X R'} = 90^\circ$, the point $R'$ is therefore diametrically opposite to $A$ in the circumcircle of $A Q_B X$. This proves that $R'$ belongs to $\Gamma_A$, and thus coincides with $R$, which concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle. On note $H_{A}$ le pied de la hauteur de $A B C$ issue de $A$, et $A^{\prime}$ le milieu du segment $[B C]$. On note ensuite $Q_{A}$ le symétrique de $H_{A}$ par rapport à $A^{\prime}$. On définit de même les points $Q_{B}$ et $Q_{C}$. Enfin, on note $R$ le point d'intersection, autre que $Q_{A}$, entre les cercles circonscrits aux triangles $Q_{A} Q_{B} C$ et $Q_{A} B Q_{C}$.
Démontrer que les droites $\left(Q_{A} R\right)$ et $(B C)$ sont perpendiculaires.
|
Soit $H$ l'orthocentre de $A B C, O$ le centre du cercle circonscrit à $A B C$, et $R^{\prime}$ le symétrique de $H$ par rapport à $O$. Les projetés orthogonaux de $H$ et $O \operatorname{sur}(B C)$ sont $H_{a}$ et $A^{\prime}$, donc le projeté orthogonal de $R^{\prime}$ sur $(B C)$ est $Q_{A}$. De même, les projetés orthogonaux de $R^{\prime}$ sur $(C A)$ et sur $(A B)$ sont $Q_{B}$ et $Q_{C}$.
Cela signifie entre autres que $\widehat{C Q_{A} R^{\prime}}=\widehat{Q C_{B} R^{\prime}}=90^{\circ}$, donc que $Q_{A}$ et $Q_{B}$ appartiennent au cercle de diamètre $\left[C R^{\prime}\right]$. Ce cercle coïncide donc avec le cercle circonscrit à $Q_{A} Q_{B} C$. De même, les points $Q_{A}$ et $Q_{C}$ appartiennent au cercle de diamètre [ $B R^{\prime}$ ], qui coïncide avec le cercle circonscrit à $Q_{A} B Q_{C}$. Par conséquent, les points $R$ et $R^{\prime}$ sont confondus, et ( $Q_{A} R$ ) est bien perpendiculaire à $(B C)$.

$\underline{\text { Solution alternative } n^{\circ} 1}$ Ci-dessous, on note $\Gamma_{A}, \Gamma_{B}$ et $\Gamma_{C}$ les cercles circonscrits respectifs à $A Q_{B} Q_{C}, Q_{A} B Q_{C}$ et $Q_{A} Q_{B} C$. Puisque $R$ appartient à $\Gamma_{B}$ et à $\Gamma_{C}$, on sait que
$$
\left(Q_{C} A, Q_{C} R\right)=\left(Q_{C} B, Q_{C} R\right)=\left(Q_{A} B, Q_{A} R\right)=\left(Q_{A} C, Q_{A} R\right)=\left(Q_{B} C, Q_{B} R\right)=\left(Q_{B} A, Q_{B} R\right)
$$
Cela signifie que $R$ appartient aussi à $\Gamma_{A}$, et donc que $A, B$ et $C$ jouent des rôles symétriques. Forts de ce constat, on introduit donc également le cercle circonscrit à $A B C$, que l'on note $\Omega$. Toujours à la recherche de cercles remarquables, on remarque alors que les angles droits en $H_{A}, H_{B}$ et $H_{C}$ suggèrent aussi de tracer les cercles $\Xi_{A}, \Xi_{B}$ et $\Xi_{C}$, de diamètres respectifs $[B C],[C A]$ et $[A B]$.
Enfin, si l'on note $m$ la médiatrice de $[B C]$, l'énoncé nous demande de démontrer que ( $Q_{A} R$ ) et $\left(A H_{A}\right)$ sont symétriques l'une de l'autre par rapport à $m$. On s'intéresse donc de plus près à la symétrie d'axe $m$ et aux cercles dont $m$ est un axe de symétrie : il s'agit des cercles $\Omega, \Xi_{A}$ et, ne serait-ce qu'en apparence, $\Gamma_{A}$.
À défaut de démontrer que le centre de ce dernier cercle se trouve sur $m$, on peut tenter de démontrer que les axes radicaux de $\Gamma_{A}$ avec $\Omega$ ou $\Xi_{A}$ sont parallèles à $(B C)$. Le premier serait alors manifestement la parallèle à $(B C)$ passant par $A$, tandis que le deuxième a l'air $d^{\prime}$ être la droite $\left(B^{\prime} C^{\prime}\right)$.
Comme $B^{\prime}$ est le milieu de $[A C]$ et de $\left[H_{B} Q_{B}\right.$, on sait que $B^{\prime} H_{B} \cdot B^{\prime} C=B^{\prime} Q_{B} \cdot B^{\prime} A$, ce qui signifie bien que $B^{\prime}$ appartient à l'axe radical de $\Gamma_{A}$ et $\Xi_{A}$. De même, $C^{\prime}$ appartient à cet axe radical, qui est donc confondu avec $\left(B^{\prime} C^{\prime}\right)$, de sorte que $\Gamma_{A}$ est bien symétrique par rapport à $m$.
Par conséquent, les cercles $\Omega$ et $\Gamma_{A}$ se rencontrent en un point $X$ qui n'est autre que le symétrique de $A$ par rapport à $m$. Notons alors $R^{\prime}$ le point d'intersection entre $\left(Q_{A} X\right)$ et $\Gamma_{C}$. On sait que $\widehat{C Q_{B} R^{\prime}}=\widehat{C Q_{A} R^{\prime}}=90^{\circ}$. Puisque l'on a également $\widehat{A X R^{\prime}}=90^{\circ}$, le point $R^{\prime}$ est donc diamétralement opposé à $A$ dans le cercle circonscrit à $A Q_{B} X$. Cela démontre que $R^{\prime}$ appartient à $\Gamma_{A}$, donc coïncide avec $R$, ce qui conclut.

|
{
"exam": "French_tests",
"problem_label": "10",
"problem_match": "\nExercice 10.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"solution_match": "\nSolution de l'exercice 10",
"tier": "T1",
"year": "2020"
}
|
Let $ABC$ be a triangle. We denote $H_{A}$ as the foot of the altitude from $A$ in $\triangle ABC$, and $A^{\prime}$ as the midpoint of the segment $[BC]$. We then denote $Q_{A}$ as the symmetric point of $H_{A}$ with respect to $A^{\prime}$. We define the points $Q_{B}$ and $Q_{C}$ similarly. Finally, we denote $R$ as the intersection point, other than $Q_{A}$, of the circumcircles of triangles $Q_{A} Q_{B} C$ and $Q_{A} B Q_{C}$.
Prove that the lines $\left(Q_{A} R\right)$ and $(BC)$ are perpendicular.
|
$n^{\circ} 2$ We resume the notations from the previous solution. Since the line $\left(Q_{A} R\right)$ is the radical axis of the circles $\Gamma_{B}$ and $\Gamma_{C}$, it is tempting to look for the radical axes of these two circles with another circle. For this purpose, we could consider the circle $\Gamma_{A}$, and observe as before that $R$ is the radical center of the three circles $\Gamma_{A}, \Gamma_{B}$, and $\Gamma_{C}$. Given this symmetry of roles, we also consider the circle $\Omega$, and denote by $Y$ the radical center of $\Gamma_{B}, \Gamma_{C}$, and $\Omega$.
It seems that $B A C Y$ is a parallelogram, and we therefore set out to prove this. To do so, we proceed as in the previous solution. Since $A^{\prime}$ is the midpoint of $[B C]$ and of $\left[H_{A} Q_{A}\right]$, it has the same power with respect to $\Gamma_{C}$ and $\Xi_{C}$. Similarly, $B^{\prime}$ has the same power with respect to $\Gamma_{C}$ and $\Xi_{C}$. We deduce that $\left(A^{\prime} B^{\prime}\right)$ is the radical axis of $\Gamma_{C}$ and $\Xi_{C}$. Since $(A B)$ is the radical axis of $\Xi_{C}$ and $\Omega$ and that $(A B)$ is parallel to $\left(A^{\prime} B^{\prime}\right)$, we deduce that $(A B)$ is parallel to the third radical axis $(C Y)$ between $\Gamma_{C}$ and $\Omega$. Similarly, $(A C)$ is parallel to $(B Y)$.
The symmetry with center $A^{\prime}$ therefore exchanges the line $\left(A H_{A}\right)$ with $\left(Y Q_{A}\right)$, that is, with $\left(Q_{A} R\right)$. The line $\left(Q_{A} R\right)$ is therefore indeed perpendicular to $(B C)$.
Graders' Comments Very few points were awarded on this problem, for which no student provided a complete solution. The graders nevertheless wish to commend the numerous attempts that were submitted, demonstrating a genuine effort to solve the problem.
Often, the relationships established around the points $H_{A}, H_{B}$, and $H_{C}$ were entirely correct, and we encourage students to remember these as they are true and applicable in many contexts. However, here they were not sufficient on their own to approach the solution and therefore did not earn points.
The problem required a bit of perspective on the definition of the points $Q_{A}, Q_{B}$, and $Q_{C}$. A few students managed to add symmetry to the problem by showing that the point $R$ defined also belongs to the circle $\Gamma_{C}$. It was by examining the many symmetries offered by the figure that it was possible to gain an intuition of the numerous properties of the point $R$, such as the fact that it is the symmetric of $H$ with respect to $O$.
Here are some recurring elements in the proposed solutions:
$\triangleright$ Some students identified the line $\left(Q_{A} R\right)$ as a radical axis. This is indeed the starting point of a possible approach. It would have been necessary to extend this radical axis to guess some of its properties or to introduce other interesting points lying on it, for example, the symmetric of point $A$ with respect to $A^{\prime}$.
$\triangleright$ Some students claimed to submit a complete solution but which in reality did not work. To avoid falling into this trap, it is important to reread and verify that each statement is true and justified. Another way to reread is to check that all the hypotheses of the problem statement have been used.
For example, the fact of having used the point $R$'s belonging to only one of the two circles should be a clue that one has been too hasty.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle. On note $H_{A}$ le pied de la hauteur de $A B C$ issue de $A$, et $A^{\prime}$ le milieu du segment $[B C]$. On note ensuite $Q_{A}$ le symétrique de $H_{A}$ par rapport à $A^{\prime}$. On définit de même les points $Q_{B}$ et $Q_{C}$. Enfin, on note $R$ le point d'intersection, autre que $Q_{A}$, entre les cercles circonscrits aux triangles $Q_{A} Q_{B} C$ et $Q_{A} B Q_{C}$.
Démontrer que les droites $\left(Q_{A} R\right)$ et $(B C)$ sont perpendiculaires.
|
$n^{\circ} 2$ On reprend les notations de la solution précédente. Puisque la droite $\left(Q_{A} R\right)$ est l'axe radical des cercles $\Gamma_{B}$ et $\Gamma_{C}$, il est tentant de rechercher les axes radicaux de ces deux cercles avec un autre cercle. À cette fin, on pourrait considérer le cercle $\Gamma_{A}$, et constater comme précédemment que $R$ est le centre radical des trois cercles $\Gamma_{A}, \Gamma_{B}$ et $\Gamma_{C}$. Au vu de cette symétrie des rôles, on considère également le cercle $\Omega$, et on note alors $Y$ le centre radical de $\Gamma_{B}, \Gamma_{C}$ et $\Omega$.
Il semble que $B A C Y$ soit un parallélogramme, et on entreprend donc de le démontrer. Pour ce faire, on procède comme dans la solution précédente. Puisque $A^{\prime}$ est le milieu de $[B C]$ et de $\left[H_{A} Q_{A}\right]$, il a même puissance par rapport à $\Gamma_{C}$ et $\Xi_{C}$. De même, $B^{\prime}$ a même puissance par rapport à $\Gamma_{C}$ et $\Xi_{C}$. On en déduit que $\left(A^{\prime} B^{\prime}\right)$ est l'axe radical de $\Gamma_{C}$ et $\Xi_{C}$. Puisque $(A B)$ est l'axe radical de $\Xi_{C}$ et $\Omega$ et que $(A B)$ est parallèle à $\left(A^{\prime} B^{\prime}\right)$, on en déduit que $(A B)$ est parallèle au troisième axe radical $(C Y)$ entre $\Gamma_{C}$ et $\Omega$. De même, $(A C)$ est parallèle à $(B Y)$.
La symétrie de centre $A^{\prime}$ échange donc la droite $\left(A H_{A}\right)$ avec $\left(Y Q_{A}\right)$, c'est-à-dire avec $\left(Q_{A} R\right)$. La droite $\left(Q_{A} R\right)$ est donc bien perpendiculaire à $(B C)$.

Commentaire des correcteurs Très peu de points ont été distribués sur cet exercice, pour lequel aucune élève n'a proposé de solution complète. Les correcteurs tiennent toutefois à saluer les nombreuses tentatives qui ont été rendues, témoignant d'un réel effort de recherche sur le problème.
Bien souvent, les relations établies autour des points $H_{A}, H_{B}$ et $H_{C}$ sont tout à fait correctes, et nous encourageons les élèves à les retenir car elles sont vraies et applicables dans de nombreux contextes. Toutefois ici, elles ne suffisaient pas à elles seules à se rapprocher de la solution et ne rapportaient donc pas de points.
L'exercice nécessitait un peu de recul sur la définition des points $Q_{A}, Q_{B}$ et $Q_{C}$. De rares élèves ont pu donc rajouté de la symétrie au problème en montrant que le point $R$ défini appartenait également au cercle $\Gamma_{C}$. C'est en examinant les nombreuses symétries offertes par la figure qu'il était possible d'acquérir l'intuition des nombreuses propriétés sur le point $R$, comme le fait qu'il s'agit du symétrique de $H$ par rapport à $O$.
Voici quelques éléments récurrents dans les solutions proposées:
$\triangleright$ Quelques élèves ont identifié la droite $\left(Q_{A} R\right)$ comme un axe radical. C'est en effet le point de départ d'une approche possible. Il aurait fallu prolonger cet axe radical pour en deviner quelques propriétés ou pour introduire d'autres points intéressants y appartenant, par exemple le symétrique du point $A$ par rapport à $A^{\prime}$.
$\triangleright$ Quelques élèves ont prétendu rendre une solution complète mais qui ne fonctionnait en réalité pas. Pour éviter de tomber dans cet écueil, il est important de se relire et de vérifier que chaque affirmation est vraie et justifiée. Une autre façon de se relire est de vérifier que toutes les hypothèses de l'énoncé ont été utilisées.
Par exemple, le fait de n'avoir utilisé l'appartenance du point $R$ qu'à un seul des deux cercles doit mettre sur la piste que l'on a été trop vite.
|
{
"exam": "French_tests",
"problem_label": "10",
"problem_match": "\nExercice 10.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-3-Web.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2020"
}
|
Morgane and Bosphore are playing the following game. Morgane has written the integers from 1 to 8 on the vertices of a regular octagon: each integer is written on one of the eight vertices of the octagon. Bosphore then chooses a vertex and calculates the sum of the numbers written on that vertex and its two neighbors. He notes this sum as $s$, and gives $s$ candies to Morgane.
Bosphore chooses a vertex so as to give the fewest candies to Morgane, and Morgane writes the integers from 1 to 8 so as to receive as many candies as possible. Prove that Bosphore will give her 12 candies.
|
First, if Morgane distributes the integers from 1 to 8 as follows, we indeed observe that Bosphore will have to give her at least 12 candies; next to each vertex, we have indicated the sum $s$ that Bosphore would calculate if he chose this vertex.
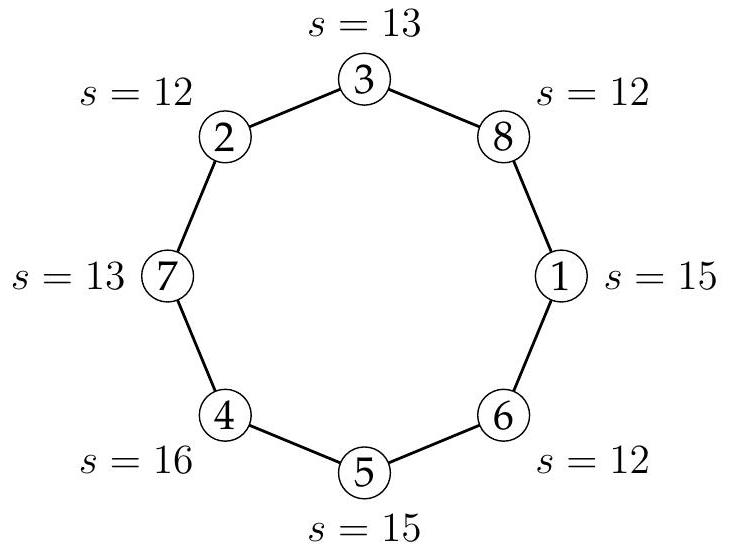
Conversely, regardless of the distribution chosen by Morgane, Bosphore can proceed as follows to avoid giving her 13 or more candies. Below, each vertex is identified with the integer that Morgane wrote on that vertex.
If the two neighbors of vertex 8 are vertices 1 and 2, Bosphore only needs to choose vertex 8, and he will give only 11 candies to Morgane. Otherwise, one of the two neighbors of vertex 8 is an integer $k \geqslant 3$. Bosphore divides the remaining six vertices into two groups of three consecutive vertices, as illustrated below. The sum of the values of these two groups is $(1+2+\ldots+8)-(k+8)=28-k \leqslant 25$, so one of the two groups has a sum $s \leqslant 12$. Bosphore ensures that he gives at most 12 candies to Morgane by choosing the vertex in the middle of this group.
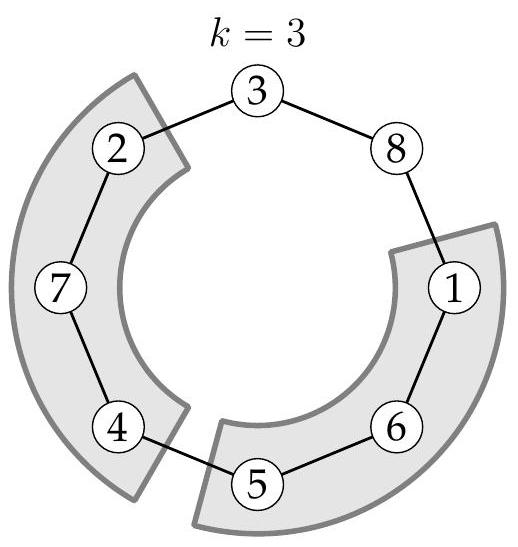
|
12
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Morgane et Bosphore jouent au jeu suivant. Morgane a écrit les entiers de 1 à 8 sur les sommets d'un octogone régulier : chaque entier est écrit sur un des huit sommets de l'octogone. Bosphore choisit ensuite un sommet et calcule la somme des nombres écrits sur ce sommet et sur ses deux voisins. Il note $s$ cette somme, et donne $s$ bonbons à Morgane.
Bosphore choisit un sommet de sorte à donner le moins possible de bonbons à Morgane, et Morgane écrit les entiers de 1 à 8 de sorte à recevoir autant de bonbons que possible. Démontrer que Bosphore lui donnera 12 bonbons.
|
Tout d'abord, si Morgane répartit les entiers de 1 à 8 comme suit, on constate en effet que Bosphore devra lui donner au moins 12 bonbons; on a indiqué, à côté de chaque sommet, la somme $s$ que calculerait Bosphore s'il choisissait ce sommet.

Réciproquement, quel que soit la répartition que choisit Morgane, Bosphore peut procéder comme suit pour éviter de lui donner 13 bonbons ou plus. Ci-dessous, on identifie chaque sommet à l'entier que Morgane a écrit sur ce sommet.
Si les deux voisins du sommet 8 sont les sommets 1 et 2, Bosphore n'a qu'à choisir le sommet 8 , et il ne donnera que 11 bonbons à Morgane. Sinon, l'un des deux sommets de 8 est un entier $k \geqslant 3$. Bosphore répartit les six sommets restants en deux groupes de trois sommets consécutifs, comme illustré ci-dessous. La somme des valeurs de ces deux groupes de sommets vaut $(1+2+\ldots+8)-(k+8)=28-k \leqslant 25$, donc l'un des deux groupes est de somme $s \leqslant 12$. Bosphore s'assure alors de donner au plus 12 bonbons à Morgane en choisissant le sommet au milieu de ce groupe.

|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-4-Web.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T1",
"year": "2020"
}
|
Morgane and Bosphore are playing the following game. Morgane has written the integers from 1 to 8 on the vertices of a regular octagon: each integer is written on one of the eight vertices of the octagon. Bosphore then chooses a vertex and calculates the sum of the numbers written on that vertex and its two neighbors. He notes this sum as $s$, and gives $s$ candies to Morgane.
Bosphore chooses a vertex so as to give the fewest candies to Morgane, and Morgane writes the integers from 1 to 8 so as to receive as many candies as possible. Prove that Bosphore will give her 12 candies.
|
$n^{\circ} 1$ Bosphore has other ways to proceed, for example this one. Group the vertices into three groups of three, so that the vertex of value 1 is the only vertex belonging to two groups. The sum of the values of these groups of vertices is $1+(1+2+\ldots+8)=37<3 \times 13$, so one of these groups has a value $s \leqslant 12$, and Bosphore just needs to choose the vertex in the middle of this group.
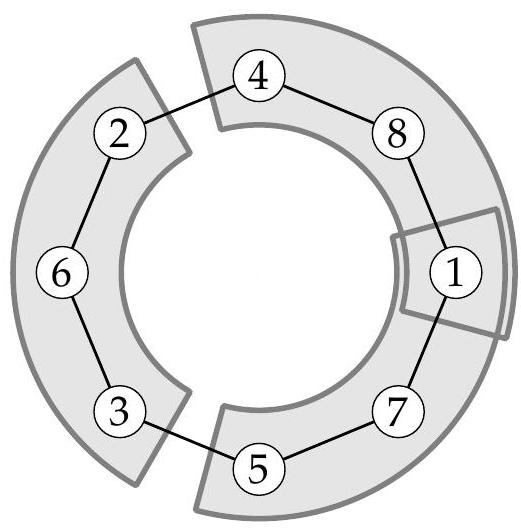
|
12
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Morgane et Bosphore jouent au jeu suivant. Morgane a écrit les entiers de 1 à 8 sur les sommets d'un octogone régulier : chaque entier est écrit sur un des huit sommets de l'octogone. Bosphore choisit ensuite un sommet et calcule la somme des nombres écrits sur ce sommet et sur ses deux voisins. Il note $s$ cette somme, et donne $s$ bonbons à Morgane.
Bosphore choisit un sommet de sorte à donner le moins possible de bonbons à Morgane, et Morgane écrit les entiers de 1 à 8 de sorte à recevoir autant de bonbons que possible. Démontrer que Bosphore lui donnera 12 bonbons.
|
$n^{\circ} 1$ Bosphore a d'autres manières de procéder, par exemple celle-ci. Regroupons les sommets en trois groupes de trois, de sorte que le sommet de valeur 1 soit le seul sommet appartenant à deux groupes. La somme des valeurs de ces groupes de sommets vaut $1+(1+2+\ldots+8)=37<3 \times 13$, donc l'un de ces groupes est de valeur $s \leqslant 12$, et Bosphore n'a qu'à choisir le sommet au milieu de ce groupe.

|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-4-Web.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2020"
}
|
Morgane and Bosphore are playing the following game. Morgane has written the integers from 1 to 8 on the vertices of a regular octagon: each integer is written on one of the eight vertices of the octagon. Bosphore then chooses a vertex and calculates the sum of the numbers written on that vertex and its two neighbors. He notes this sum as $s$, and gives $s$ candies to Morgane.
Bosphore chooses a vertex so as to give the fewest candies to Morgane, and Morgane writes the integers from 1 to 8 so as to receive as many candies as possible. Prove that Bosphore will give her 12 candies.
|
$n^{\circ} 2$ Here is a third way for Bosphore to ensure that he will give at most 12 candies to Morgane. Let $a$ and $b$ be the two neighbors of vertex 5, with $a \geqslant b$. If $b \leqslant 4$, then $a \leqslant 3$, so $a+b+5 \leqslant 12$ and Bosphore directly chooses vertex 5. Otherwise, we know that $b \geqslant 6$. Bosphore then eliminates vertices 5 and $b$, which are contiguous, and distributes the six remaining vertices into two groups of three consecutive vertices. As in the previous solution, the sum of the values of these two groups of vertices is $(1+2+\ldots+8)-(5+b)=31-b \leqslant 25$, so one of the two groups has a sum $s \leqslant 12$. Bosphore then chooses the vertex in the middle of this group.
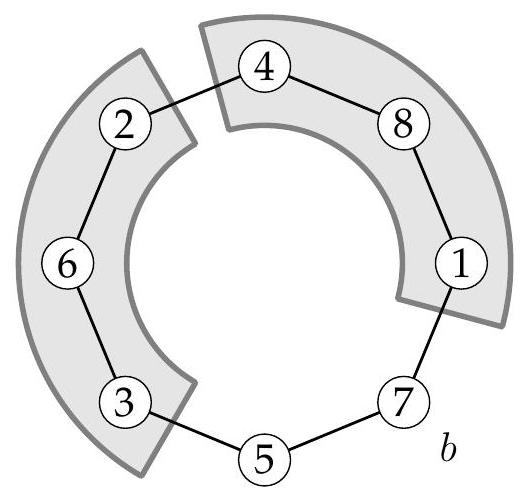
|
12
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Morgane et Bosphore jouent au jeu suivant. Morgane a écrit les entiers de 1 à 8 sur les sommets d'un octogone régulier : chaque entier est écrit sur un des huit sommets de l'octogone. Bosphore choisit ensuite un sommet et calcule la somme des nombres écrits sur ce sommet et sur ses deux voisins. Il note $s$ cette somme, et donne $s$ bonbons à Morgane.
Bosphore choisit un sommet de sorte à donner le moins possible de bonbons à Morgane, et Morgane écrit les entiers de 1 à 8 de sorte à recevoir autant de bonbons que possible. Démontrer que Bosphore lui donnera 12 bonbons.
|
$n^{\circ} 2$ Voici une troisième manière, pour Bosphore, de s'assurer qu'il donnera au plus 12 bonbons à Morgane. Soit $a$ et $b$ les deux voisins du sommet 5 , avec $a \geqslant b$. Si $b \leqslant 4$, alors $a \leqslant 3$, donc $a+b+5 \leqslant 12$ et Bosphore choisit directement le sommet 5 . Sinon, on sait que $b \geqslant 6$. Bosphore élimine alors les sommets 5 et $b$, qui sont contigus, et répartit les six sommets restants en deux groupes de trois sommets consécutifs. Comme dans la solution précédente, la somme des valeurs de ces deux groupes de sommets vaut $(1+2+\ldots+8)-(5+b)=31-b \leqslant 25$, donc l'un des deux groupes est de somme $s \leqslant 12$. Bosphore choisit alors le sommet au milieu de ce groupe.

|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-4-Web.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2020"
}
|
Morgane and Bosphore are playing the following game. Morgane has written the integers from 1 to 8 on the vertices of a regular octagon: each integer is written on one of the eight vertices of the octagon. Bosphore then chooses a vertex and calculates the sum of the numbers written on that vertex and its two neighbors. He notes this sum as $s$, and gives $s$ candies to Morgane.
Bosphore chooses a vertex so as to give the fewest candies to Morgane, and Morgane writes the integers from 1 to 8 so as to receive as many candies as possible. Prove that Bosphore will give her 12 candies.
|
$n^{\circ} 3$ Here is yet another way to prove that Bosphore will necessarily manage to give Morgane at most 12 candies. Unlike the previous solutions, this one does not provide an explicit strategy for Bosphore.
Suppose Morgane has found a configuration that forces Bosphore to give her at least 13 candies. We number the vertices of the octagon from 1 to 8, these numbers being considered modulo 8. We then denote $a_{i}$ as the number Morgane has written on vertex $i$, and we denote $s_{i}$ as the sum $a_{i-1}+a_{i}+a_{i+1}$.
Notice that $s_{i+1}-s_{i}=a_{i+2}-a_{i-1} \neq 0$, regardless of the value of $i$. Thus, the sum of two consecutive numbers $s_{i}$ is at least $13+14=27$. Furthermore, the sum of the integers $s_{i}$ is $3\left(a_{1}+a_{2}+\ldots+a_{8}\right)=3(1+2+\ldots+8)=108=4 \times 27$. Consequently, the sum of two consecutive numbers $s_{i}$ is always 27, and the $s_{i}$ alternate between the values 13 and 14, so that $s_{1}=s_{3}=s_{5}=s_{7}$ and $s_{2}=s_{4}=s_{6}=s_{8}$.
Under these conditions, we observe that
$$
0=\left(s_{2}-s_{3}\right)+\left(s_{5}-s_{6}\right)=\left(a_{1}-a_{4}\right)+\left(a_{4}-a_{7}\right)=a_{4}-a_{7},
$$
which is impossible. Thus, Morgane will never be able to force Bosphore to give her 13 or more candies.
Comment from the graders: This problem was very well done overall, to the great satisfaction of the graders. The vast majority of students had identified the two key points, which were to prove, using a possible configuration example, that Morgane could force Bosphore to give her at least 12 candies, and then to prove that she could not do better.
A very large number of students thought to look at the sum of the scores of the eight groups of three, which was $3 \times(1+2+\ldots+8)=108=13 \times 8+4$, to deduce instantly that Morgane could win at most 13 candies. This did not, of course, directly answer the question, but it brought them closer, which is always positive. Such a result was therefore certainly not valued, but the elements of reasoning that led to it, and which could be reused to get to 12 candies, were of course valued.
However, note some blunders that were found in many papers, and which systematically cost their authors points:
$\triangleright$ Several students made mistakes in their counter-examples, allowing Bosphore to give Morgane 11 candies or fewer, or writing an integer between 1 and 8 twice and not at all another. In general, it is of course essential to proofread, especially since verifying these counter-examples generally took about 20 to 30 seconds, which is clearly not wasted time.
$\triangleright$ Several students made mistakes in their calculations, for example indicating that $108<13 \times 8$, which would have allowed them to get out of it by using the pigeonhole principle (or the average principle, which is the same thing). As in the previous point, once a solution is written, and especially if it is simple and short, proofreading is essential and always beneficial: either the student spots an error and has the opportunity to correct it, or he ensures that he very likely has a correct solution.
$\triangleright$ Finally, several students proceeded by case disjunction, often using symmetry arguments, but without specifying them, or even without specifying at all how their case disjunction worked. In such a situation, these students very often lost one or more points, as it was impossible to distinguish the student who really proceeded to a case disjunction without forgetting any from the student who bluffed because he trusted the statement and knew what result he wanted to achieve.
|
12
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Morgane et Bosphore jouent au jeu suivant. Morgane a écrit les entiers de 1 à 8 sur les sommets d'un octogone régulier : chaque entier est écrit sur un des huit sommets de l'octogone. Bosphore choisit ensuite un sommet et calcule la somme des nombres écrits sur ce sommet et sur ses deux voisins. Il note $s$ cette somme, et donne $s$ bonbons à Morgane.
Bosphore choisit un sommet de sorte à donner le moins possible de bonbons à Morgane, et Morgane écrit les entiers de 1 à 8 de sorte à recevoir autant de bonbons que possible. Démontrer que Bosphore lui donnera 12 bonbons.
|
$n^{\circ} 3$ Voici encore une manière de démontrer que Bosphore pourra nécessairement se débrouiller pour donner au plus 12 bonbons à Morgane. À la différence des solutions précédentes, celle-ci ne fournit pas de stratégie explicite pour Bosphore.
Supposons que Morgane ait trouvé une configuration qui force Bosphore à lui donner au moins 13 bonbons. On numérote les sommets de l'octogone de 1 à 8 , ces numéros étant considérés modulo 8. On note alors $a_{i}$ le nombre que Morgane a écrit sur le sommet $i$, et on note $s_{i}$ la somme $a_{i-1}+a_{i}+a_{i+1}$.
Remarquons que $s_{i+1}-s_{i}=a_{i+2}-a_{i-1} \neq 0$, et ce quelle que soit la valeur de $i$. Ainsi, la somme de deux nombres $s_{i}$ consécutifs vaut au minimum $13+14=27$. En outre, la somme des entiers $s_{i}$ vaut $3\left(a_{1}+a_{2}+\ldots+a_{8}\right)=3(1+2+\ldots+8)=108=4 \times 27$. Par conséquent, la
somme de deux nombres $s_{i}$ consécutifs vaut toujours 27 , et les $s_{i}$ alternent entre les valeurs 13 et 14 , de sorte que $s_{1}=s_{3}=s_{5}=s_{7}$ et $s_{2}=s_{4}=s_{6}=s_{8}$.
Dans ces conditions, on constate que
$$
0=\left(s_{2}-s_{3}\right)+\left(s_{5}-s_{6}\right)=\left(a_{1}-a_{4}\right)+\left(a_{4}-a_{7}\right)=a_{4}-a_{7},
$$
ce qui est impossible. Ainsi, Morgane ne pourra jamais forcer Bosphore à lui donner 13 bonbons ou plus.
Commentaire des correcteurs Cet exercice a été très réussi dans l'ensemble, à la grande satisfaction des correcteurs. La grande majorité des élèves avait identifié les deux enjeux, qui consistaient à démontrer, à l'aide d'un exemple de configuration possible, que Morgane pouvait forcer Bosphore à lui donner au moins 12 bonbons, puis à démontrer qu'elle ne pouvait pas faire mieux.
Un très grand nombre d'élèves a pensé à regarder la somme des scores des huit groupes de trois, qui valait $3 \times(1+2+\ldots+8)=108=13 \times 8+4$, pour en déduire instantanément que Morgane pourrait gagner au plus 13 bonbons. Cela ne répondait bien sûr pas directement à l'énoncé, mais permettait de s'en approcher, ce qui est toujours positif. Un tel résultat n'était donc certes pas valorisé, mais les éléments de raisonnement qui y avaient mené, et qui étaient réutilisables pour se ramener à 12 bonbons, l'ont bien sûr été.
Notons néanmoins quelques bévues que l'on a retrouvé dans de multiples copies, et qui ont systématiquement coûté des points à leurs auteurs :
$\triangleright$ Plusieurs élèves se sont trompés dans leur contre-exemple, permettant à Bosphore de donner 11 bonbons ou moins à Morgane, ou bien écrivant deux fois un entier entre 1 et 8 et zéro fois un autre. En règle générale, il est bien sûr indispensable de se relire, d'autant plus que vérifier ces contre-exemples prenait généralement de l'ordre de 20 à 30 secondes, qui ne sont donc manifestement pas du temps perdu.
$\triangleright$ Plusieurs élèves se sont trompés dans leurs calculs, par exemple en indiquant que $108<13 \times 8$, ce qui aurait permis de s'en sortir en utilisant le principe des tiroirs (ou de la moyenne, ce qui revient au même). Comme au point précédent, une fois une solution écrite, et d'autant plus si elle est simple et courte, se relire est indispensable et toujours salutaire : soit l'élève repère une erreur et a la possibilité de la corriger, soit il s'assure d'avoir très vraisemblablement une solution correcte.
$\triangleright$ Enfin, plusieurs élèves ont procédé par disjonction de cas, utilisant souvent des arguments de symétrie, mais sans les préciser, voire sans préciser du tout comment fonctionnait leur disjonction de cas. Dans une telle situation, ces élèves ont très souvent perdu un ou plusieurs points, car il était impossible distinguer l'élève qui a vraiment procédé à une disjonction de cas sans en oublier un seul de l'élève qui bluffe car il a confiance en l'énoncé et sait à quel résultat il souhaite aboutir.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-4-Web.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2020"
}
|
Let $x, y$ and $z$ be three real numbers such that $0 \leqslant x \leqslant y \leqslant z$ and $x+y+z=1$. Find the maximum value that the expression
$$
(x-y z)^{2}+(y-z x)^{2}+(z-x y)^{2} .
$$
can take.
|
The quantity we wish to maximize can be rewritten as
$$
\begin{aligned}
\mathcal{S} & =\left(x^{2}+y^{2}+z^{2}\right)+\left((x y)^{2}+(y z)^{2}+(z x)^{2}\right)-6 x y z \\
& =(x+y+z)^{2}-2(x y+y z+z x)+(x y+y z+z x)^{2}-2 x y z(x+y+z)-6 x y z \\
& =1-2(x y+y z+z x)+(x y+y z+z x)^{2}-8 x y z \\
& =(x y+y z+z x-1)^{2}-8 x y z .
\end{aligned}
$$
Since $0 \leqslant x y+y z+z x \leqslant(x+y+z)^{2} / 2=1 / 2$, we deduce that $\mathcal{S} \leqslant 1$. Conversely, if $x=y=0$ and $z=1$, we have $\mathcal{S}=1$, which concludes the proof.
|
1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Soit $x, y$ et $z$ trois nombres réels tels que $0 \leqslant x \leqslant y \leqslant z$ et $x+y+z=1$. Trouver la valeur maximale que peut prendre l'expression
$$
(x-y z)^{2}+(y-z x)^{2}+(z-x y)^{2} .
$$
|
La quantité que l'on souhaite maximiser peut se récrire comme
$$
\begin{aligned}
\mathcal{S} & =\left(x^{2}+y^{2}+z^{2}\right)+\left((x y)^{2}+(y z)^{2}+(z x)^{2}\right)-6 x y z \\
& =(x+y+z)^{2}-2(x y+y z+z x)+(x y+y z+z x)^{2}-2 x y z(x+y+z)-6 x y z \\
& =1-2(x y+y z+z x)+(x y+y z+z x)^{2}-8 x y z \\
& =(x y+y z+z x-1)^{2}-8 x y z .
\end{aligned}
$$
Puisque $0 \leqslant x y+y z+z x \leqslant(x+y+z)^{2} / 2=1 / 2$, on en déduit que $\mathcal{S} \leqslant 1$. Réciproquement, si $x=y=0$ et $z=1$, on a bien $\mathcal{S}=1$, ce qui conclut.
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-4-Web.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T1",
"year": "2020"
}
|
Let $x, y$ and $z$ be three real numbers such that $0 \leqslant x \leqslant y \leqslant z$ and $x+y+z=1$. Find the maximum value that the expression
$$
(x-y z)^{2}+(y-z x)^{2}+(z-x y)^{2} .
$$
can take.
|
$n^{\circ} 1$ The quantity we wish to maximize can be rewritten as
$$
\begin{aligned}
\mathcal{S} & =\left(x^{2}+y^{2}+z^{2}\right)+\left((x y)^{2}+(y z)^{2}+(z x)^{2}\right)-6 x y z \\
& =(x+y+z)^{2}-2(x y+y z+z x)+\left((x y)^{2}+(y z)^{2}+(z x)^{2}\right)-6 x y z
\end{aligned}
$$
The statement indicates that $0 \leqslant x \leqslant y \leqslant z \leqslant 1$, so $0 \leqslant x y \leqslant x z \leqslant y z \leqslant 1$. Since any number $t$ such that $0 \leqslant t$ satisfies the inequality $t^{2} \leqslant 2 t$, we deduce that $\mathcal{S} \leqslant(x+y+z)^{2}-6 x y z \leqslant 1$. Conversely, if $x=y=0$ and $z=1$, we indeed have $\mathcal{S}=1$, which concludes the proof.
|
1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Soit $x, y$ et $z$ trois nombres réels tels que $0 \leqslant x \leqslant y \leqslant z$ et $x+y+z=1$. Trouver la valeur maximale que peut prendre l'expression
$$
(x-y z)^{2}+(y-z x)^{2}+(z-x y)^{2} .
$$
|
$n^{\circ} 1$ La quantité que l'on souhaite maximiser peut se réécrire comme
$$
\begin{aligned}
\mathcal{S} & =\left(x^{2}+y^{2}+z^{2}\right)+\left((x y)^{2}+(y z)^{2}+(z x)^{2}\right)-6 x y z \\
& =(x+y+z)^{2}-2(x y+y z+z x)+\left((x y)^{2}+(y z)^{2}+(z x)^{2}\right)-6 x y z
\end{aligned}
$$
Or, l'énoncé indique que $0 \leqslant x \leqslant y \leqslant z \leqslant 1$, de sorte que $0 \leqslant x y \leqslant x z \leqslant y z \leqslant 1$. Puisque tout nombre $t$ tel que $0 \leqslant t$ satisfait l'inégalité $t^{2} \leqslant 2 t$, on en déduit que $\mathcal{S} \leqslant(x+y+z)^{2}-6 x y z \leqslant 1$. Réciproquement, si $x=y=0$ et $z=1$, on a bien $\mathcal{S}=1$, ce qui conclut.
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-4-Web.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2020"
}
|
Let $x, y$ and $z$ be three real numbers such that $0 \leqslant x \leqslant y \leqslant z$ and $x+y+z=1$. Find the maximum value that the expression
$$
(x-y z)^{2}+(y-z x)^{2}+(z-x y)^{2} .
$$
can take.
|
$n^{\circ} 2$ The inequalities $0 \leqslant x \leqslant y \leqslant z \leqslant x+y+z=1$ indicate that $z \geqslant y \geqslant x y$ and $y \geqslant x \geqslant z x$, so that the quantity we wish to maximize satisfies the inequality
$$
\mathcal{S} \leqslant \max \{x, y z\}^{2}+y^{2}+z^{2}
$$
Since $x^{2}+y^{2}+z^{2} \leqslant(x+y+z)^{2}=1$ and $(y z)^{2}+y^{2}+z^{2} \leqslant 2 y z+y^{2}+z^{2}=(y+z)^{2}=(1-x)^{2} \leqslant 1$, we deduce that $\mathcal{S} \leqslant 1$. Conversely, if $x=y=0$ and $z=1$, we indeed have $\mathcal{S}=1$, which concludes the proof.
Comment from the graders The proposed inequality was unusual in that the optimum sought was achieved when the variables were not equal to each other, which is uncommon. Many students had the (correct) intuition that the maximum sought was equal to 1, and that it was achieved when $x=y=0$ and $z=1$. They then focused on proving that the expression could never exceed 1, which was the expected approach, much to the graders' delight.
However, here are some avoidable errors that several students made:
$\triangleright$ Some students simply tried to find upper bounds for the expression being studied, without even looking at particular cases, such as the case where $x=y=0$ and $z=1$, to get an idea. Others outright stated that they wished to prove the inequality $\mathcal{S} \leqslant 1$, but did not think to indicate that $\mathcal{S}=1$ when $x=y=0$ and $z=1$. Such omissions are regrettable, as the student thus forfeits points that were readily available.
$\triangleright$ Several students wrote inequalities that were all correct, but were clearly too weak to conclude. Thus, one student began by proving that $\mathcal{S} \leqslant 3(z-x y)^{2}$. While this inequality is correct, it is also useless for showing that $\mathcal{S} \leqslant 1$, since the right-hand side is 3 when $x=y=0$ and $z=1$.
In general, when one wishes to prove an inequality by introducing intermediate inequalities, it is of course essential to ensure, even by looking at simple examples, that they have a chance of being precise enough to lead to a conclusion. In our case, any intermediate inequality that could be used had to be an equality when $x=y=0$ and $z=1$.
|
1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Soit $x, y$ et $z$ trois nombres réels tels que $0 \leqslant x \leqslant y \leqslant z$ et $x+y+z=1$. Trouver la valeur maximale que peut prendre l'expression
$$
(x-y z)^{2}+(y-z x)^{2}+(z-x y)^{2} .
$$
|
$n^{\circ} 2$ Les inégalités $0 \leqslant x \leqslant y \leqslant z \leqslant x+y+z=1$ indiquent que $z \geqslant y \geqslant x y$ et $y \geqslant x \geqslant z x$, de sorte que la quantité que l'on souhaite maximiser satisfait l'inégalité
$$
\mathcal{S} \leqslant \max \{x, y z\}^{2}+y^{2}+z^{2}
$$
Puisque $x^{2}+y^{2}+z^{2} \leqslant(x+y+z)^{2}=1$ et $(y z)^{2}+y^{2}+z^{2} \leqslant 2 y z+y^{2}+z^{2}=(y+z)^{2}=(1-x)^{2} \leqslant 1$, on en déduit que $\mathcal{S} \leqslant 1$. Réciproquement, si $x=y=0$ et $z=1$, on a bien $\mathcal{S}=1$, ce qui conclut.
Commentaire des correcteurs L'inégalité proposée était inhabituelle, en ce sens que l'optimum recherché était obtenu lorsque les variables n'étaient pas égales l'une à l'autre, ce qui est peu courant. De nombreux élèves ont eu l'intuition (correcte) selon laquelle le maximum recherché était égal à 1 , et qu'il était obtenu lorsque $x=y=0$ et $z=1$. Ils se sont ensuite attachés à démontrer que l'expression recherchée ne pouvait jamais dépasser 1, et il s'agissait là de la démarche attendue, ce qui a ravi les correcteurs.
Cependant, voici quelques erreurs évitables que plusieurs élèves ont commises:
$\triangleright$ Certains élèves ont simplement cherché à trouver des majorations de l'expression étudiée, sans même regarder des cas particulier, dont le cas où $x=y=0$ et $z=1$, pour se faire une idée. D'autres ont carrément dit qu'ils souhaitaient démontrer l'inégalité $\mathcal{S} \leqslant 1$, mais n'ont pas pensé à indiquer que $\mathcal{S}=1$ quand $x=y=0$ et $z=1$. De telles omissions sont regrettables, car l'élève renonce ainsi purement et simplement à des points qui lui tendaient la main.
$\triangleright$ Plusieurs élèves ont écrit des inégalités qui étaient toutes correctes, mais qui étaient manifestement trop faibles pour conclure. Ainsi, un élève a commencé par démontrer que $\mathcal{S} \leqslant 3(z-x y)^{2}$. Si cette inégalité est correcte, elle est également inutile pour montrer que $\mathcal{S} \leqslant 1$, puisque le membre de droite vaut 3 lorsque $x=y=0$ et $z=1$.
De manière générale, lorsque l'on souhaite démontrer une inégalité en introduisant des inégalités intermédiaires, il est bien sûr indispensable de s'assurer, ne seraitce qu'en regardant des exemples simples, que celles-ci ont une chance d'être suffisamment précises pour aboutir. Dans notre cas, toute inégalité intermédiaire utilisable devait en fait être une égalité lorsque $x=y=0$ et $z=1$.
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-4-Web.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2020"
}
|
Let $ABC$ be a triangle such that $90^{\circ}>\widehat{ABC}>\widehat{BCA}$. Let $D$ be the point on the segment $[BC]$ such that $2 \widehat{DAC}=\widehat{ABC}-\widehat{BCA}$. We denote $E$ as the intersection point, other than $A$, between $(AB)$ and the circumcircle of $ACD$, and $P$ as the intersection point between $(AB)$ and the angle bisector of $\widehat{BDE}$. Similarly, we denote $F$ as the intersection point, other than $A$, between $(AC)$ and the circumcircle of $ABD$, and $Q$ as the intersection point between $(AC)$ and the angle bisector of $\widehat{CDF}$.
Prove that $(AB)$ and $(PQ)$ are perpendicular.
|
As usual, we start with a figure that is sufficiently beautiful and large to serve as a support for reflection. For this purpose, we first construct a triangle $A'BC'$ isometric to $ABC$, such that $C'$ lies on the ray $[BA)$, then we draw the bisector of the angle $\widehat{CBA'}$, which we denote as $d$. We can then transfer the angle between the lines $(BC)$ and $d$ to $A$ to construct the ray $[AD)$.
Alternatively, the cocyclicity of points $A, B, D$, and $F$ ensures the equality
$$
\widehat{DBF} = \widehat{DAF} = \widehat{DAC} = \widehat{CBA'}/2
$$
Thus, $F$ is the intersection point of the lines $(AC)$ and $d$, and $D$ is the intersection point, other than $B$, of the line $(BC)$ with the circumcircle of $ABF$.
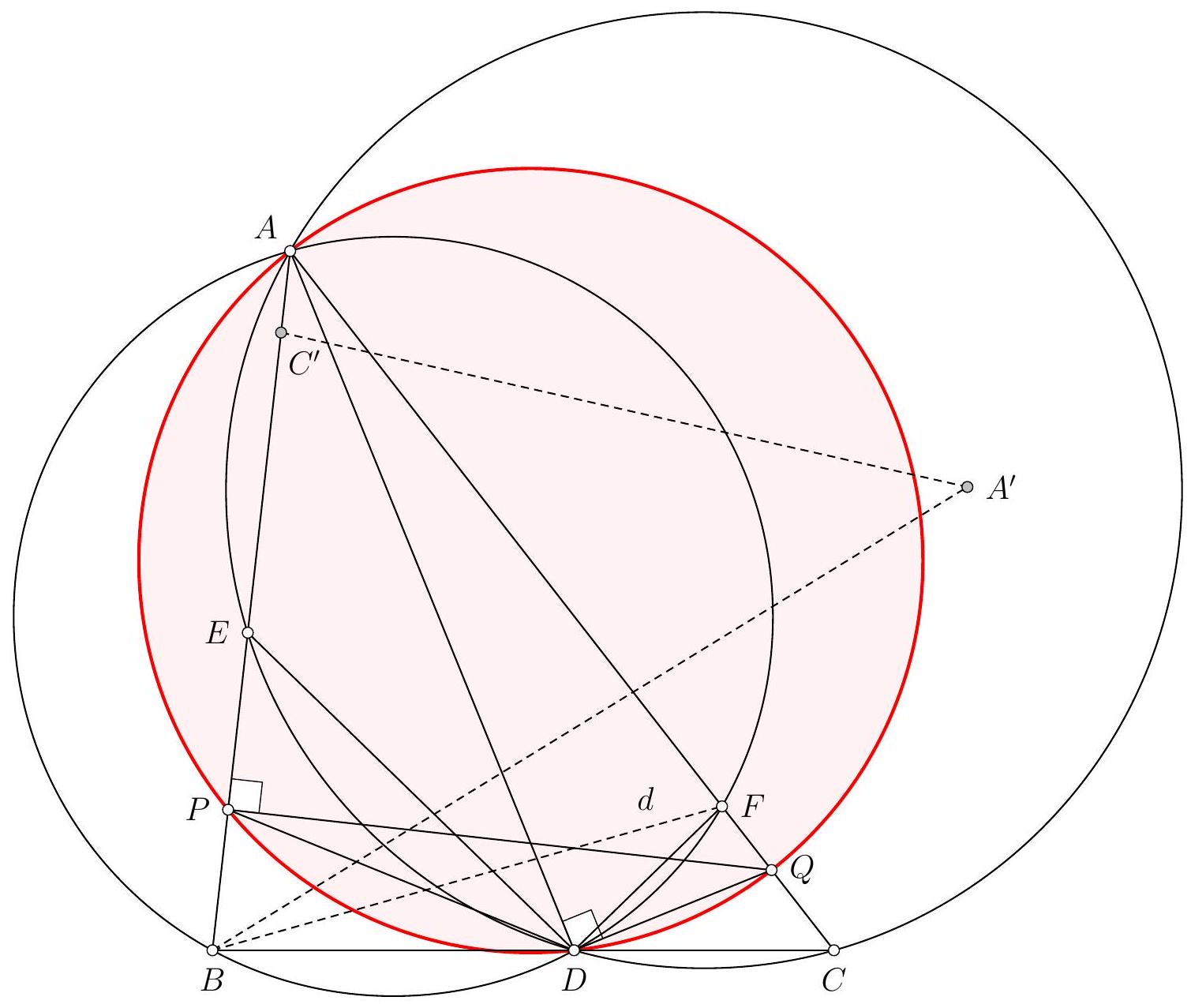
Given the statement, an angle chase is necessary. We set $x = \widehat{BCA}$ and $y = \widehat{DAC}$, and observe that
$$
2 \widehat{CDQ} = \widehat{CDF} = 180^\circ - \widehat{FDB} = \widehat{BAF} = \widehat{BAC} = 180^\circ - 2(x + y),
$$
so $\widehat{CDQ} = 90^\circ - (x + y)$. Similarly,
$$
2 \widehat{PDB} = \widehat{EDB} = 180^\circ - \widehat{CDE} = \widehat{EAC} = \widehat{BAC}
$$
so $\widehat{PDB} = 90^\circ - (x + y)$.
We continue our angle chase, from which we deduce that
$\widehat{QDA} = 180^\circ - \widehat{DAQ} - \widehat{AQD} = 180^\circ - y - (180^\circ - \widehat{DQC}) = (180^\circ - \widehat{CDQ} - \widehat{QCD}) - y = 90^\circ$.
Thus, we need to prove that $A, P, D$, and $Q$ are concyclic. We verify that
$$
\widehat{DPA} = 180^\circ - \widehat{BPD} = \widehat{PDB} + \widehat{DBP} = (90^\circ - x - y) + (x + 2y) = 90^\circ + y = 180^\circ - \widehat{AQD},
$$
which concludes the proof.
Comment from the graders The exercise had two difficulties:
$\triangleright$ The first difficulty was to draw the figure. It was certainly possible to solve the problem without an exact figure, but it is always good to focus on the exact construction of the figure because often, finding how to construct a figure with a complicated hypothesis is already starting to solve the exercise. Moreover, an exact figure allowed one to visually observe that the angle $\widehat{QDA}$ was a right angle, which was a crucial step in the proof.
$\triangleright$ The second difficulty was to express all the angles in the figure solely in terms of the angles $\widehat{CAB}$, $\widehat{ABC}$, and $\widehat{BCA}$. The few students who managed this work mostly solved the exercise immediately.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle tel que $90^{\circ}>\widehat{A B C}>\widehat{B C A}$. Soit $D$ le point sur le segment $[B C]$ tel que $2 \widehat{D A C}=\widehat{A B C}-\widehat{B C A}$. On note $E$ le point d'intersection, autre que $A$, entre $(A B)$ et le cercle circonscrit à $A C D$, puis $P$ le point d'intersection entre $(A B)$ et la bissectrice de $\widehat{B D E}$. De même, on note $F$ le point d'intersection, autre que $A$, entre $(A C)$ et le cercle circonscrit à $A B D$, puis $Q$ le point d'intersection entre $(A C)$ et la bissectrice de $\widehat{C D F}$.
Démontrer que $(A B)$ et $(P Q)$ sont perpendiculaires.
|
Comme d'habitude, on commence par une figure suffisamment belle et grande pour servir de support à la réflexion. À cette fin, on construit tout d'abord un triangle $A^{\prime} B C^{\prime}$ isométrique à $A B C$, tel que $C^{\prime}$ se trouve sur la demi-droite $[B A)$, puis on trace la bissectrice de l'angle $\widehat{C B A^{\prime}}$, que l'on note $d$. On peut alors reporter en $A$ l'angle en entre les droites $(B C)$ et $d$, pour construire la demi-droite $[A D)$.
Alternativement, la cocyclicité des points $A, B, D$ et $F$ nous assure de l'égalité
$$
\widehat{D B F}=\widehat{D A F}=\widehat{D A C}=\widehat{C B A^{\prime}} / 2
$$
Ainsi, $F$ est le point d'intersection des droites $(A C)$ et $d$, et $D$ est le point d'intersection, autre que $B$, de la droite $(B C)$ avec le cercle circonscrit à $A B F$.

Au vu de l'énoncé, une chasse aux angles s'impose. On pose donc $x=\widehat{B C A}$ et $y=\widehat{D A C}$, puis l'on constate que
$$
2 \widehat{C D Q}=\widehat{C D F}=180^{\circ}-\widehat{F D B}=\widehat{B A F}=\widehat{B A C}=180^{\circ}-2(x+y),
$$
de sorte que $\widehat{C D Q}=90^{\circ}-(x+y)$. De même,
$$
2 \widehat{P D B}=\widehat{E D B}=180^{\circ}-\widehat{C D E}=\widehat{E A C}=\widehat{B A C}
$$
de sorte que $\widehat{P D B}=90^{\circ}-(x+y)$.
On continue notre chasse aux angles, d'où l'on déduit que
$\widehat{Q D A}=180^{\circ}-\widehat{D A Q}-\widehat{A Q D}=180^{\circ}-y-\left(180^{\circ}-\widehat{D Q C}\right)=\left(180^{\circ}-\widehat{C D Q}-\widehat{Q C D}\right)-y=90^{\circ}$.
Il s'agit donc de démontrer que $A, P, D$ et $Q$ sont cocycliques. On vérifie alors que
$$
\widehat{D P A}=180^{\circ}-\widehat{B P D}=\widehat{P D B}+\widehat{D B P}=\left(90^{\circ}-x-y\right)+(x+2 y)=90^{\circ}+y=180^{\circ}-\widehat{A Q D},
$$
ce qui conclut.
Commentaire des correcteurs L'exercice comportait deux difficultés:
$\triangleright$ La première difficulté était de tracer la figure. Ici il était certes possible de résoudre le problème sans avoir une figure exacte, mais il est toujours bon de s'intéresser à a construction exacte de la figure car bien souvent, trouver comment construire une figure comportant une hypothèse compliquée, c'est déjà commencer à résoudre l'exercice. De plus, une figure exacte permettait de constater visuellement que l'angle $\widehat{Q D A}$ était droit, ce qui constituait une étape cruciale de la preuve.
$\triangleright$ La deuxième difficulté était d'exprimer tous les angles de la figures uniquement en fonction des angles $\widehat{C A B}, \widehat{A B C}$ et $\widehat{B C A}$. Les quelques élèves ayant réussi ce travail ont pour la plupart résolu l'exercice dans la foulée.
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-4-Web.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T1",
"year": "2020"
}
|
Find all triplets of non-zero natural numbers $(a, b, c)$ such that
$$
2021^{a}+4=3^{b} \times 5^{c}
$$
|
In a Diophantine equation, one always starts by looking at small values of the parameters. Here, it suffices to factorize $2021^{a}+4$ into prime factors, so we look at the small values of $a$. Here, when $a=1$, the equation becomes $2025=3^{b} \times 5^{c}$, so $(a, b, c)=(1,4,2)$ is a solution. Moreover, if $a \geqslant 2$, no one wants to factorize $2021^{a}+4$, so we stop here our exploration of small cases.
In a second step, one should either proceed with factorizations or look at the equation modulo a well-chosen number $n$ to reduce the set of possible values of $a, b$, and $c$. The numbers 3 and 5 are clearly prime, and our study of the case $a=1$ indicates that $2021=45^{2}-4=43 \times 47$. We note this relation in a corner of our scratch paper for later use.
Finally, using the Chinese Remainder Theorem, we reduce our equation modulo $n$ when $n$ is a power of a prime. For example:
$\triangleright n=1, n=2$ and $n=5$ do not provide any information;
$\triangleright n=3$ indicates that $a$ is odd;
$\triangleright n=4$ indicates that $b$ is even;
$\triangleright n=7$ does not provide any easy-to-exploit information;
$\triangleright n=8$ indicates, since $a$ is odd and $b$ is even, that $c$ is even.
We then set $\beta=b / 2$ and $\gamma=c / 2$. Moreover, two of the three terms in our equation are squares, which allows us to obtain the factorization
$$
43^{a} \times 47^{a}=2021^{a}=\left(3^{\beta} \times 5^{\gamma}\right)^{2}-2^{2}=\left(3^{\beta} \times 5^{\gamma}+2\right)\left(3^{\beta} \times 5^{\gamma}-2\right) .
$$
Since $3^{\beta} \times 5^{\gamma}+2$ and $3^{\beta} \times 5^{\gamma}-2$ are two odd integers whose difference is 4, they are coprime.
Only one of these two factors is divisible by 43, and only one is divisible by 47. Several cases are possible a priori:
$\triangleright$ if 47 divides $3^{\beta} \times 5^{\gamma}-2$, then $47^{a}$ divides $3^{\beta} \times 5^{\gamma}-2$, so $3^{\beta} \times 5^{\gamma}-2 \geqslant 47^{a} \geqslant 43^{a} \geqslant 3^{\beta} \times 5^{\gamma}+2$, which is impossible;
$\triangleright$ if 43 and 47 divide $3^{\beta} \times 5^{\gamma}+2$, then $3^{\beta} \times 5^{\gamma}+2=43^{a} \times 47^{a}$ and $3^{\beta} \times 5^{\gamma}-2=1$, which is impossible since $3^{\beta} \times 5^{\gamma}-2 \geqslant 3 \times 5-2=13$.
Thus, 47 divides $3^{\beta} \times 5^{\gamma}+2$ and 43 divides $3^{\beta} \times 5^{\gamma}-2$, so that $3^{\beta} \times 5^{\gamma}+2=47^{a}$ and $3^{\beta} \times 5^{\gamma}-2=43^{a}$. But then
$$
4=\left(3^{\beta} \times 5^{\gamma}+2\right)-\left(3^{\beta} \times 5^{\gamma}-2\right)=47^{a}-43^{a} \geqslant 47^{a}-43 \times 47^{a-1}=4 \times 47^{a-1}
$$
which shows that $a \leqslant 1$.
In conclusion, the only solution to the problem is $(a, b, c)=(1,4,2)$.
Comment from the graders The problem was difficult, but many students managed to score points thanks to intelligent reflections. Finding a particular solution is always a step forward, as it allows one to see what can or cannot be proven: here $(1,4,2)$ was a solution, so one could expect to prove that $b$ or $c$ was even, and it was futile to prove that $b$ or $c$ was odd without additional assumptions on $a$.
Let's recall that looking modulo a composite number is rarely intelligent: looking modulo 15, for example, serves no purpose, since the same observations can be made modulo 3 and 5, and since the calculations are simpler, it allows one to avoid making mistakes.
Here, the key to the problem was to question the parity of $b, c$ to obtain a square: obtaining squares in Diophantine equations is crucial, as it allows one to factorize and thus simplify the problem. However, once the equation is factorized, some forget to specify that the two terms are positive and even strictly greater than 1, which means one cannot immediately conclude that one of the factors is $47^{a}$ and the other is $43^{a}$. Moreover, it would be good to rigorously justify at the end that $47^{a}=43^{a}+4$ implies $a=1$. For example, one can invoke that $47^{2}>43^{2}+4$ and say that by immediate induction $47^{k}>43^{k}+4$ if $k \geqslant 2$.
## Senior Problems
|
(1,4,2)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Trouver tous les triplets d'entiers naturels non nuls $(a, b, c)$ tels que
$$
2021^{a}+4=3^{b} \times 5^{c}
$$
|
Dans une équation diophantienne, on commence toujours par regarder de petites valeurs des paramètres. Ici, il suffit de factoriser $2021^{a}+4$ en produit de facteurs premiers, donc on regarde les petites valeurs de $a$. Ici, lorsque $a=1$, l'équation devient $2025=3^{b} \times 5^{c}$, donc $(a, b, c)=(1,4,2)$ est solution. Par ailleurs, si $a \geqslant 2$, personne n'a envie de factoriser $2021^{a}+4$, donc on arrête ici notre exploration des petits cas.
Dans un deuxième temps, il faudra soit procéder à des factorisations, soit regarder l'équation modulo un nombre $n$ bien choisi pour réduire l'ensemble des valeurs possibles de $a, b$ et $c$. Les nombres 3 et 5 sont manifestement des nombres premiers, et notre étude du cas $a=1$ indique que $2021=45^{2}-4=43 \times 47$. On note donc cette relation dans un coin de notre brouillon en attendant de pouvoir en faire usage.
Enfin, quitte à utiliser le théorème chinois, on réduit notre équation modulo $n$ lorsque $n$ est une puissance de nombre premier. Par exemple :
$\triangleright n=1, n=2$ et $n=5$ ne nous apportent aucune information;
$\triangleright n=3$ indique que $a$ est impair;
$\triangleright n=4$ indique que $b$ est pair;
$\triangleright n=7$ ne nous apporte aucune information facile à exploiter;
$\triangleright n=8$ indique, puisque $a$ est impair et $b$ est pair, que $c$ est pair.
On pose alors $\beta=b / 2$ et $\gamma=c / 2$. En outre, deux des trois termes de notre équation sont des carrés, ce qui nous permet d'obtenir la factorisation
$$
43^{a} \times 47^{a}=2021^{a}=\left(3^{\beta} \times 5^{\gamma}\right)^{2}-2^{2}=\left(3^{\beta} \times 5^{\gamma}+2\right)\left(3^{\beta} \times 5^{\gamma}-2\right) .
$$
Puisque $3^{\beta} \times 5^{\gamma}+2$ et $3^{\beta} \times 5^{\gamma}-2$ sont deux entiers impairs dont la différence vaut 4 , ils sont premiers entre eux.
Seul l'un de ces deux facteurs est divisible par 43, et seul l'un est divisible par 47. Plusieurs cas sont donc possibles a priori :
$\triangleright \operatorname{si} 47$ divise $3^{\beta} \times 5^{\gamma}-2$, alors $47^{a}$ divise $3^{\beta} \times 5^{\gamma}-2$, donc $3^{\beta} \times 5^{\gamma}-2 \geqslant 47^{a} \geqslant 43^{a} \geqslant 3^{\beta} \times 5^{\gamma}+2$, ce qui est impossible;
$\triangleright$ si 43 et 47 divisent $3^{\beta} \times 5^{\gamma}+2$, on a $3^{\beta} \times 5^{\gamma}+2=43^{a} \times 47^{a}$ et $3^{\beta} \times 5^{\gamma}-2=1$, ce qui est impossible puisque $3^{\beta} \times 5^{\gamma}-2 \geqslant 3 \times 5-2=13$.
Ainsi, 47 divise $3^{\beta} \times 5^{\gamma}+2$ et 43 divise $3^{\beta} \times 5^{\gamma}-2$, de sorte que $3^{\beta} \times 5^{\gamma}+2=47^{a}$ et $3^{\beta} \times 5^{\gamma}-2=43^{a}$. Mais alors
$$
4=\left(3^{\beta} \times 5^{\gamma}+2\right)-\left(3^{\beta} \times 5^{\gamma}-2\right)=47^{a}-43^{a} \geqslant 47^{a}-43 \times 47^{a-1}=4 \times 47^{a-1}
$$
ce qui démontre que $a \leqslant 1$.
En conclusion, la seule solution du problème est $(a, b, c)=(1,4,2)$.
Commentaire des correcteurs L'exercice était difficile, mais de nombreux élèves ont réussi à obtenir des points grâce à des réflexions intelligentes. Trouver une solution particulière est toujours une avancée, puisqu'elle permet de voir ce qu'on pourra ou non prouver : ici $(1,4,2)$ était solution, donc on pouvait s'attendre à avoir $b$ ou $c$ pair, en tout cas il était illusoire de prouver que $b$ ou $c$ était impair sans hypothèses supplémentaires sur $a$.
Rappelons que regarder modulo un nombre composé est très rarement intelligent : regarder modulo 15 par exemple ne sert à rien, puisqu'on peut faire les mêmes observations modulo 3 et 5 , et comme les calculs sont plus simples, cela permet de ne pas faire d'erreur.
Ici la clé du problème était de s'interroger sur les parité de $b, c$ pour obtenir un carré : obtenir des carrés en équation diophantienne est crucial, car cela permet de factoriser et donc de rendre le problème plus simple. Néanmoins, une fois l'équation factorisée, certains oublient de préciser que les deux termes sont positifs, et qu'ils sont même strictement plus grand que 1 , ce qui fait qu'on ne peut pas conclure immédiatement qu'un des facteurs vaut $47^{a}$ et l'autre $43^{a}$. De plus, il serait bien de justifier rigoureusement à la fin que $47^{a}=43^{a}+4$ implique $a=1$. Par exemple, on peut invoquer que $47^{2}>43^{2}+4$ et dire que par récurrence immédiate $47^{k}>43^{k}+4$ si $k \geqslant 2$.
## Énoncés Senior
|
{
"exam": "French_tests",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-4-Web.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T1",
"year": "2020"
}
|
We denote by $\mathbb{Z}[x, y, z]$ the set of polynomials with integer coefficients in the three variables $x, y$, and $z$. We then say that a polynomial $P \in \mathbb{Z}[x, y, z]$ is Olympic if $\mathbb{Z}[x, y, z]$ contains polynomials $A, B$, and $C$ such that
$$
P(x, y, z)=(x+y+z) A(x, y, z)+(x y+y z+z x) B(x, y, z)+x y z C(x, y, z).
$$
Find the largest integer $n$ for which there exist natural numbers $i, j$, and $k$ with sum $i+j+k=n$ and such that the polynomial $x^{i} y^{j} z^{k}$ is not Olympic.
Note: A polynomial with integer coefficients in the variables $x, y$, and $z$ is a function that can be written as a sum of terms of the form $\lambda x^{i} y^{j} z^{k}$, where $\lambda$ is an integer and $i, j$, and $k$ are natural numbers. For example, $x-y+1$ and $x y+y z+z x$ are such polynomials, but $\pi x y z, \exp (x), x /\left(y^{2}+1\right)$, and $\sqrt{x y+z}$ are not.
|
Let $s_{1}=x+y+z, s_{2}=x y+y z+z x$ and $s_{3}=x y z$. We observe that
$$
\begin{cases}x^{3} \equiv-x^{2}(y+z) \equiv-x(x y+x z) \equiv x y z \equiv 0 & \left(\bmod s_{1}, s_{2}, s_{3}\right) \\ x^{2} y^{2} \equiv x y(-x z-y z) \equiv-x y z(x+y) \equiv 0 & \left(\bmod s_{1}, s_{2}, s_{3}\right)\end{cases}
$$
which means that $x^{3}$ and $x^{2} y^{2}$ are Olympic. Moreover, the set of Olympic polynomials is stable under multiplication by any polynomial and permutation of the variables.
Therefore, consider a polynomial $x^{i} y^{j} z^{k}$, which is not Olympic. Without loss of generality, we assume that $i \geqslant j \geqslant k$. If $i \geqslant 3, j \geqslant 2$ or $k \geqslant 1$, our polynomial is a multiple of $x^{3}$, $x^{2} y^{2}$, or $x y z$, so it is Olympic. We deduce that $i \leqslant 2, j \leqslant 1$ and $k \leqslant 0$, so that $i+j+k \leqslant 3$. This already ensures that $n \leqslant 3$.
Conversely, let us consider the set $\mathcal{E}$ of Olympic polynomials whose monomials all have a total degree of 3, i.e., polynomials $x^{i} y^{j} z^{k}$ such that $i+j+k=3$. By restricting $A, B$ and $C$ to their monomials of total degrees 2, 1, and 0 respectively, each polynomial in $\mathcal{E}$ can be written in the form
$$
\begin{aligned}
P= & (x+y+z)\left(a x^{2}+b y^{2}+c z^{2}+d x y+e x z+f y z\right)+(x y+y z+z x)(g x+h y+i z)+j x y z \\
= & a x^{3}+b y^{2}+c z^{3}+(a+d+g) x^{2} y+(a+e+g) x^{2} z+(b+d+h) y^{2} x+(b+f+h) y^{2} z \\
& \quad+(c+e+i) z^{2} x+(c+f+i) z^{2} y+(d+e+f+g+h+i+j) x y z .
\end{aligned}
$$
If $x^{2} y$ is Olympic, we then have
$$
1=(a+d+g)+(b+f+h)+(c+e+i)-(a+e+g)-(b+d+h)-(c+f+i)=0,
$$
which is absurd. Thus, the polynomial $x^{2} y$ is not Olympic, and the largest integer sought is $n=3$.
**Comment from the graders** The problem was difficult, but many students made significant progress by showing that several polynomials were Olympic. However, be careful of calculation errors!
Some tried to show that $x^{2} y$ was not Olympic by doing arithmetic on polynomials in several variables. This approach was risky and, like any complicated path to the solution, led to many errors.
Here, the key was to look at the terms of degree 3 but in two variables, i.e., $x^{2} y, x^{2} z, z^{2} x, z^{2} y, y^{2} x$ and $y^{2} z$. However, be careful: some students proceeded by contradiction and, from polynomials $(A, B, C)$ that allowed obtaining $x^{2} y$, exhibited new $\left(A^{\prime}, B^{\prime}, C^{\prime}\right)$ that allowed obtaining $\pm y^{2} x$, and then concluded directly that since they reduced to the same case (up to symmetry) it was impossible. There is no a priori reason for this to be the case: there could be many triplets $(A, B, C)$ that allow obtaining that $x^{2} y$ is Olympic!
Finally, after restricting to terms of degree 3, some forgot the terms in $x^{2}, y^{2}$ and $z^{2}$ in $A$, which is a pity.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
On note $\mathbb{Z}[x, y, z]$ l'ensemble des polynômes à coefficients entiers en les trois variables $x, y$ et $z$. On dit ensuite qu'un polynôme $P \in \mathbb{Z}[x, y, z]$ est olympique si $\mathbb{Z}[x, y, z]$ contient des polynômes $A, B$ et $C$ tels que
$$
P(x, y, z)=(x+y+z) A(x, y, z)+(x y+y z+z x) B(x, y, z)+x y z C(x, y, z) .
$$
Trouver le plus grand entier $n$ pour lequel il existe des entiers naturels $i, j$ et $k$ de somme $i+j+k=n$ et tels que le polynôme $x^{i} y^{j} z^{k}$ ne soit pas olympique.
Note : Un polynôme à coefficients entiers en les variables $x, y$ et $z$ est une fonction que l'on peut écrire comme une somme de termes de la forme $\lambda x^{i} y^{j} z^{k}$, où $\lambda$ est un entier relatif et $i, j$ et $k$ sont des entiers naturels. Par exemple, $x-y+1$ et $x y+y z+z x$ sont de tels polynômes, mais $\pi x y z, \exp (x), x /\left(y^{2}+1\right)$ et $\sqrt{x y+z}$ n'en sont pas.
|
Posons $s_{1}=x+y+z, s_{2}=x y+y z+z x$ et $s_{3}=x y z$. On constate que
$$
\begin{cases}x^{3} \equiv-x^{2}(y+z) \equiv-x(x y+x z) \equiv x y z \equiv 0 & \left(\bmod s_{1}, s_{2}, s_{3}\right) \\ x^{2} y^{2} \equiv x y(-x z-y z) \equiv-x y z(x+y) \equiv 0 & \left(\bmod s_{1}, s_{2}, s_{3}\right)\end{cases}
$$
ce qui signifie que $x^{3}$ et $x^{2} y^{2}$ sont olympiques. Or, l'ensemble des polynômes olympiques est stable par multiplication par tout polynôme et par permutation des variables.
Par conséquent, considérons un polynôme $x^{i} y^{j} z^{k}$, non olympique. Sans perte de généralité, on suppose que $i \geqslant j \geqslant k$. Si $i \geqslant 3, j \geqslant 2$ ou $k \geqslant 1$, notre polynôme est un multiple de $x^{3}$, de $x^{2} y^{2}$ ou de $x y z$, donc il est olympique. On en déduit que $i \leqslant 2, j \leqslant 1$ et $k \leqslant 0$, de sorte que $i+j+k \leqslant 3$. Cela nous assure déjà que $n \leqslant 3$.
Réciproquement, intéressons-nous à l'ensemble $\mathcal{E}$ des polynômes olympiques dont tous les monômes sont de degré total 3, c'est-à-dire sont des polynômes $x^{i} y^{j} z^{k}$ tels que $i+j+k=3$. Quitte à restreindre respectivement $A, B$ et $C$ à leurs monômes de degrés totaux 2,1 et 0 , chaque polynôme de $\mathcal{E}$ s'écrit sous la forme
$$
\begin{aligned}
P= & (x+y+z)\left(a x^{2}+b y^{2}+c z^{2}+d x y+e x z+f y z\right)+(x y+y z+z x)(g x+h y+i z)+j x y z \\
= & a x^{3}+b y^{2}+c z^{3}+(a+d+g) x^{2} y+(a+e+g) x^{2} z+(b+d+h) y^{2} x+(b+f+h) y^{2} z \\
& \quad+(c+e+i) z^{2} x+(c+f+i) z^{2} y+(d+e+f+g+h+i+j) x y z .
\end{aligned}
$$
Si $x^{2} y$ est olympique, on a alors
$$
1=(a+d+g)+(b+f+h)+(c+e+i)-(a+e+g)-(b+d+h)-(c+f+i)=0,
$$
ce qui est absurde. Ainsi, le polynôme $x^{2} y$ n'est pas olympique, et le plus grand entier recherché est $n=3$.
Commentaire des correcteurs L'exercice était difficile, mais de nombreux élèves ont bien avancé sur le problème, en montrant que plusieurs polynômes étaient olympiques. Attention néanmoins aux erreurs de calcul!
Certains ont essayé de montrer que $x^{2} y$ n'était pas olympique en faisant de l'arithmétique sur les polynômes à plusieurs variables. Cette approche était risquée et, comme toute voie compliquée pour obtenir la solution, elle a mené à de nombreuses erreurs.
Ici, la la clé était de regarder les termes de degré 3 mais en deux variables, c'est-à-dire en $x^{2} y, x^{2} z, z^{2} x, z^{2} y, y^{2} x$ et $y^{2} z$. Attention, toutefois: certains élèves ont procédé par l'absurde
et, à partir de polynômes $(A, B, C)$ qui permettaient d'obtenir $x^{2} y$, ont exhibé de nouveaux $\left(A^{\prime}, B^{\prime}, C^{\prime}\right)$ qui permettaient d'obtenir $\pm y^{2} x$, puis en ont conclu directement que comme on se ramenait au même cas (à symétrie près) c'était impossible. Il n'y a à priori pas de raison que ce soit le cas : il pourrait y avoir de nombreux triplets $(A, B, C)$ permettant d'obtenir que $x^{2} y$ est olympique!
Enfin, après s'être restreints aux termes de degré 3 , certains oublient les termes en $x^{2}, y^{2}$ et $z^{2}$ dans $A$, ce qui est dommage.
|
{
"exam": "French_tests",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-4-Web.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T1",
"year": "2020"
}
|
Let $ABC$ be an isosceles triangle at $A$, and let $D$ be a point on the segment $[BC]$ such that $BD \neq CD$. Let $P$ and $Q$ be the orthogonal projections of $D$ onto $(AB)$ and $(AC)$. Finally, let $E$ be the point of intersection, other than $A$, between the circumcircles of $ABC$ and $APQ$.
Prove that, if the lines $(EP)$, $(AC)$, and the perpendicular bisector of $[PQ]$ are concurrent, the triangle $ABC$ is right-angled at $A$.
|
A first reflex is to draw a figure where the triangle $ABC$ is isosceles right-angled, but without indicating that it is. Many symmetries then appear. Let $X$ be the intersection point of the lines $(AC)$ and $(EP)$, $\ell$ the perpendicular bisector of $[PQ]$, $O$ the center of the circumcircle of $ABC$, and $M$ the midpoint of $[BC]$: it is a matter of proving that $M=O$.
Since $PQX$ is isosceles at $X$, the symmetry with axis $\ell$ exchanges the lines $(AQ)$ and $(PE)$, so that $\widehat{AQP}=\widehat{QPE}$. Since $A, E, P$, and $Q$ are concyclic, the quadrilateral $AEPQ$ is therefore an isosceles trapezoid, which is easily verified since
$$
(AE, PQ) = (AE, AQ) + (AQ, PQ) = (PE, PQ) + (QA, QP) = 0^{\circ}
$$
The symmetry with axis $\ell$ therefore exchanges the points $A$ and $E$, and $\ell$ is in fact the perpendicular bisector of $[AE]$. It therefore contains, in particular, the centers $O$ and $O'$ of the circumcircles of $ABC$ and $AEPQ$.
Given the right angles at $P, Q$, and $M$, the latter circle is in fact the circle with diameter $[AD]$, and it contains $D$ and $M$. Moreover, $(AM)$ is the angle bisector of $\widehat{BAC}$, so $M$ is the South pole of $A$ in the triangle $APQ$, and $PQM$ is isosceles at $M$. Thus, $M$ lies on $\ell$.
In conclusion, $M$ and $O$ both belong to $(AM)$ and to $\ell$. Since $D \neq M$, we also know that $O'$, the midpoint of $[AD]$, is not on $(AM)$. Since $\ell$ contains $O'$, it is therefore not coincident with $(AM)$, and $M$ must coincide with $O$, which concludes.
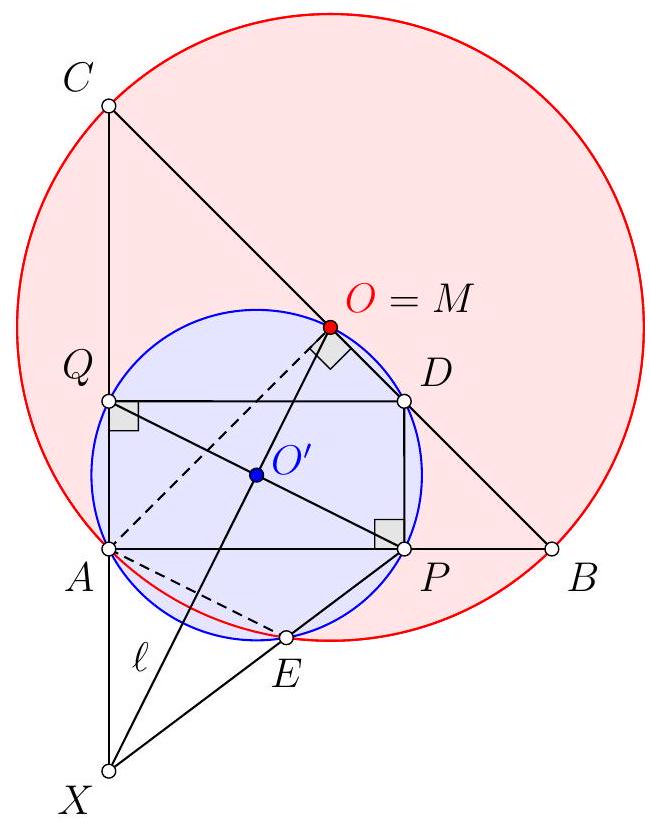
Comment from the graders: The exercise was very well done. Many students manage, through the development of simple ideas like angle chasing, to make significant progress in solving the problem, while some others force the use of very advanced results like Pascal's or Desargues' theorems but without obtaining significant results.
The figures provided are often very precise, and it was sometimes frustrating to see that the midpoint of the segment $[BC]$ belongs to the circle passing through the points $A, P$, and $Q$ appear on them without the student mentioning this midpoint in their attempt.
We noted a significant number of incorrect solutions. The errors are often due to the use of a property that is evident on the figure but not yet proven. Often, to avoid this pitfall, it is good to ask oneself if all the hypotheses of the statement have been used. Thus, several students believe they have solved the exercise without using either that the triangle $ABC$ is isosceles or that the point $E$ belongs to its circumcircle.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle isocèle en $A$, puis $D$ un point du segment $[B C]$ tel que $B D \neq C D$. Soit $P$ et $Q$ les projetés orthogonaux de $D$ sur $(A B)$ et $(A C)$. Enfin, soit $E$ le point d'intersection, autre que $A$, entre les cercles circonscrits à $A B C$ et $A P Q$.
Démontrer que, si les droites $(E P),(A C)$ et la médiatrice de $[P Q]$ sont concourantes, le triangle $A B C$ est rectangle en $A$.
|
Un premier réflexe est de dessiner une figure où le triangle $A B C$ est isocèle rectangle, mais sans indiquer qu'il l'est. De nombreuses symétries apparaissent alors. Notons $X$ le point d'intersection des droites $(A C)$, et $(E P), \ell$ la médiatrice de $[P Q]$, $O$ le centre du cercle circonscrit à $A B C$ et $M$ le milieu de $[B C]$ : il s'agit de démontrer que $M=O$.
Comme $P Q X$ est isocèle en $X$, la symétrie d'axe $\ell$ échange les droites $(A Q)$ et $(P E)$, de sorte que $\widehat{A Q P}=\widehat{Q P E}$. Puisque $A, E, P$ et $Q$ sont cocycliques, le quadrilatère $A E P Q$ est donc un trapèze isocèle, ce qui se vérifie aisément puisque
$$
(A E, P Q)=(A E, A Q)+(A Q, P Q)=(P E, P Q)+(Q A, Q P)=0^{\circ}
$$
La symétrie d'axe $\ell$ échange donc les points $A$ et $E$, et $\ell$ est en fait la médiatrice de $[A E]$. Elle contient donc, en particulier, les centres $O$ et $O^{\prime}$ des cercles circonscrits à $A B C$ et $A E P Q$.
Au vu des angles droits en $P, Q$ et $M$, ce dernier cercle est en fait le cercle de diamètre $[A D]$, et il contient $D$ et $M$. En outre, $(A M)$ est la bissectrice de $\widehat{B A C}$, donc $M$ est le pôle Sud de $A$ dans le triangle $A P Q$, et $P Q M$ est isocèle en $M$. Ainsi, $M$ appartient à $\ell$.
En conclusion, $M$ et $O$ appartiennent tous deux à $(A M)$ et à $\ell$. Puisque $D \neq M$, on sait aussi que $O^{\prime}$, le milieu de $[A D]$, n'est pas sur $(A M)$. Puisque $\ell$ contient $O^{\prime}$, elle n'est donc pas confondue avec ( $A M)$, et $M$ coïncide donc avec $O$, ce qui conclut.

Commentaire des correcteurs L'exercice a été très bien réussi. Beaucoup d'élèves arrivent, par le développement d'idées simples comme une chasse aux angles, à avancer significativement dans la résolution du problème, quand certains autres forcent l'utilisation de résultats très avancés comme le théorème de Pascal ou de Desargues mais sans en obtenir des résultats conséquents.
Les figures fournies sont souvent très précises et il a été parfois frustrant de voir apparaître sur celles-ci que le milieu du segment $[B C]$ appartient au cercle passant par les points $A, P$ et $Q$ sans que l'élève n'évoque ce milieu dans sa tentative.
Nous avons noté une quantité significative de solutions erronées. Les erreurs sont souvent dues à l'utilisation d'une propriété manifeste sur la figure mais qui n'est pas encore démontrée. Bien souvent, pour éviter cet écueil, il est bon de se demander si toutes les hypothèses de l'énoncé ont été utilisées. Ainsi, plusieurs élèves croient avoir résolu l'exercice sans avoir utilisé ni que le triangle $A B C$ est isocèle, ni que le point $E$ appartient à son cercle circonscrit.
|
{
"exam": "French_tests",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-4-Web.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T1",
"year": "2020"
}
|
Let $n \geqslant 6$ be an integer. In the plane, we have arranged $n$ pairwise disjoint disks $D_{1}, D_{2}, \ldots, D_{n}$ with radii $r_{1} \geqslant r_{2} \geqslant \ldots \geqslant r_{n}$. For every integer $i \leqslant n$, consider a point $P_{i}$ inside the disk $D_{i}$. Finally, let $A$ be any point in the plane. Prove that
$$
A P_{1}+A P_{2}+\ldots+A P_{n} \geqslant r_{6}+r_{7}+\ldots+r_{n}
$$
|
Given such a statement, and not necessarily knowing where to start, we wish to use induction on $n$. In these conditions, it turns out that the key property of our induction will be the following.
Lemma. If $n=6$, there exists an integer $i$ such that $A P_{i} \geqslant r_{6}$.
|
proof
|
Yes
|
Incomplete
|
proof
|
Inequalities
|
Soit $n \geqslant 6$ un entier. On a disposé, dans le plan, $n$ disques $D_{1}, D_{2}, \ldots, D_{n}$ deux à deux disjoints, de rayons $r_{1} \geqslant r_{2} \geqslant \ldots \geqslant r_{n}$. Pour tout entier $i \leqslant n$, on considère un point $P_{i}$ à l'intérieur du disque $D_{i}$. Enfin, soit $A$ un point quelconque du plan. Démontrer que
$$
A P_{1}+A P_{2}+\ldots+A P_{n} \geqslant r_{6}+r_{7}+\ldots+r_{n}
$$
|
Au vu d'un tel énoncé, et ne sachant pas nécessairement par où commencer, on souhaite utiliser une récurrence sur $n$. Dans ces conditions, il s'avère que la propriété clé de notre récurrence sera la suivante.
Lemme. Si $n=6$, il existe un entier $i$ tel que $A P_{i} \geqslant r_{6}$.
|
{
"exam": "French_tests",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-4-Web.jsonl",
"solution_match": "\nSolution de l'exercice 7",
"tier": "T1",
"year": "2020"
}
|
Let $n \geqslant 6$ be an integer. In the plane, we have arranged $n$ pairwise disjoint disks $D_{1}, D_{2}, \ldots, D_{n}$ with radii $r_{1} \geqslant r_{2} \geqslant \ldots \geqslant r_{n}$. For every integer $i \leqslant n$, consider a point $P_{i}$ inside the disk $D_{i}$. Finally, let $A$ be any point in the plane. Prove that
$$
A P_{1}+A P_{2}+\ldots+A P_{n} \geqslant r_{6}+r_{7}+\ldots+r_{n}
$$
|
Let $O_{i}$ be the center of the disk $D_{i}$. If $A$ coincides with one of the points $O_{i}$, the desired result is immediate. Otherwise, we sort the centers $O_{i}$ clockwise around $A$. These define six angles whose sum is $360^{\circ}$, so one of the angles, say $\widehat{O_{i} A O_{j}}$, is at most $60^{\circ}$. If we assume without loss of generality that $A O_{i} \geqslant A O_{j}$, the Law of Cosines (Al-Kashi's theorem) then indicates that
$$
\begin{aligned}
\left(r_{i}+r_{j}\right)^{2} & \leqslant O_{i} O_{j}^{2}=A O_{i}^{2}+A O_{j}^{2}-2 \cos \left(\widehat{O_{i} A O_{j}}\right) A O_{i} \cdot A O_{j} \leqslant A O_{i}^{2}-A O_{i} \cdot A O_{j}+A O_{j}^{2} \\
& \leqslant A O_{i}^{2} \leqslant\left(A P_{i}+r_{i}\right)^{2},
\end{aligned}
$$
so that $A P_{i} \geqslant r_{j} \geqslant r_{6}$.
We now proceed by induction on $n$. First, if $n=6$, the statement of the problem is a simple corollary of our lemma. Then, if $n \geqslant 7$, we apply our lemma to the disks $D_{1}, \ldots, D_{6}$. There exists an integer $i \leqslant 6$ such that $A P_{i} \geqslant r_{6}$. We now remove the disk $D_{i}$ and apply the induction hypothesis to the remaining $n-1$ disks, so that
$$
A P_{i}+\sum_{j \neq i} A P_{j} \geqslant r_{6}+\left(r_{7}+\ldots+r_{n}\right)
$$
which concludes the proof.
Comment from the graders: The proposed problem was very difficult and was only tackled by about twenty students. The graders were amazed to see that two students had solved it brilliantly.
Many students first made the relevant observation that one could always assume that $A P_{i}=A O_{i}-r_{i}$ when $A$ does not belong to $D_{i}$, where $O_{i}$ is the center of the disk $D_{i}$. However, the graders were surprised to find sometimes very complicated proofs for this result, which is yet very simple and geometrically clear. Unfortunately, given the difficulty of the exercise, this observation did not earn any points, but it does not detract from its relevance. The key was therefore to find a stronger intermediate statement from which the desired conclusion could be deduced.
Several students thought about the case $n=6$, which was very good, but the two who rigorously treated this case are also the only two to have concluded the exercise. In general, asserting outright that "the worst situation is when the disks have the same radius and their centers form a regular hexagon centered at $A$" is a welcome heuristic, but it is not proven, and it is clear that this statement cannot earn any points until it is supported.
Similarly, several students tried to prove that when $A$ does not belong to any disk $D_{i}$, there exists such a disk for which $A P_{i} \geqslant r_{i}$. However, it was easy to construct a counterexample to this inequality, for example if $A$ and the points $P_{i}$ and $O_{i}$ are
aligned, with $A O_{i}=5^{i}, r_{i}=3 \times 5^{i-1}$ and $A P_{i}=2 \times 5^{i-1}$. Indeed, when formulating an idea for a lemma, it is very important to look for simple counterexamples to this lemma, which would invalidate it, and this in order to limit the time wasted trying to prove something false. Such a phase often allows, at little cost, to refine the formulation of the lemma, or to realize that the underlying idea is completely wrong; when it does not lead to anything, that is, when no counterexample has been found, one has more confidence in the lemma, and this is also encouraging, therefore positive.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $n \geqslant 6$ un entier. On a disposé, dans le plan, $n$ disques $D_{1}, D_{2}, \ldots, D_{n}$ deux à deux disjoints, de rayons $r_{1} \geqslant r_{2} \geqslant \ldots \geqslant r_{n}$. Pour tout entier $i \leqslant n$, on considère un point $P_{i}$ à l'intérieur du disque $D_{i}$. Enfin, soit $A$ un point quelconque du plan. Démontrer que
$$
A P_{1}+A P_{2}+\ldots+A P_{n} \geqslant r_{6}+r_{7}+\ldots+r_{n}
$$
|
Soit $O_{i}$ le centre du disque $D_{i}$. Si $A$ coïncide avec l'un des points $O_{i}$, le résultat désiré est immédiat. Sinon, on trie les centres $O_{i}$ dans le sens horaire autour de $A$. Ceux-ci définissent six angles de somme $360^{\circ}$, donc l'un des angles, disons $\widehat{O_{i} A O_{j}}$, vaut au plus $60^{\circ}$. Si l'on suppose sans perte de généralité que $A O_{i} \geqslant A O_{j}$, le théorème d'Al-Kashi indique alors que
$$
\begin{aligned}
\left(r_{i}+r_{j}\right)^{2} & \leqslant O_{i} O_{j}^{2}=A O_{i}^{2}+A O_{j}^{2}-2 \cos \left(\widehat{O_{i} A O_{j}}\right) A O_{i} \cdot A O_{j} \leqslant A O_{i}^{2}-A O_{i} \cdot A O_{j}+A O_{j}^{2} \\
& \leqslant A O_{i}^{2} \leqslant\left(A P_{i}+r_{i}\right)^{2},
\end{aligned}
$$
de sorte que $A P_{i} \geqslant r_{j} \geqslant r_{6}$.
On procède maintenant par récurrence sur $n$. Tout d'abord, si $n=6$, le résultat de l'énoncé est un simple corollaire de notre lemme. Puis, si $n \geqslant 7$, on applique notre lemme aux disques $D_{1}, \ldots, D_{6}$. Il existe donc un entier $i \leqslant 6$ tel que $A P_{i} \geqslant r_{6}$. On supprime maintenant le disque $D_{i}$ et on applique l'hypothèse de récurrence aux $n-1$ disques restants, de sorte que
$$
A P_{i}+\sum_{j \neq i} A P_{j} \geqslant r_{6}+\left(r_{7}+\ldots+r_{n}\right)
$$
ce qui conclut.
Commentaire des correcteurs Le problème proposé était très difficile, et il n'a été abordé que par une vingtaine d'élèves. Les correcteurs se sont émerveillés de constater que deux élèves l'avaient résolu avec brio.
De nombreux élèves ont tout d'abord formulé la remarque pertinente selon laquelle on pouvait toujours supposer que $A P_{i}=A O_{i}-r_{i}$ quand $A$ n'appartient pas à $D_{i}$, où $O_{i}$ est le centre du disque $D_{i}$. Toutefois, les correcteurs ont été surpris de découvrir des preuves parfois très compliquées pour ce résultat pourtant fort simple et géométriquement clair. Malheureusement, au vu de la difficulté de l'exercice, cette remarque ne rapportait aucun point, mais cela n'enlève rien à sa pertinence. La clé consistait donc à trouver un énoncé intermédiaire plus fort, dont on pourrait déduire la conclusion demandée.
Plusieurs élèves ont pensé à regarder le cas $n=6$, ce qui était très bien, mais les deux seuls qui ont traité ce cas rigoureusement sont aussi les deux seuls à avoir conclu l'exercice. De manière générale, affirmer tout de go que « la pire situation est celle où les disques sont de même rayon et où leurs centres forment un hexagone régulier de centre $A$ » repose sur une heuristique bienvenue, mais nullement prouvée, et il est clair que cette affirmation ne peut pas rapporter le moindre point tant qu'elle n'est pas étayée.
De même, plusieurs élèves ont cherché à démontrer que lorsque $A$ n'appartient à aucun disque $D_{i}$, il existait un tel disque pour lequel $A P_{i} \geqslant r_{i}$. Cependant, il était facile de construire un contre-exemple à cette inégalité, par exemple si $A$ et les points $P_{i}$ et $O_{i}$ sont
alignés, avec $A O_{i}=5^{i}, r_{i}=3 \times 5^{i-1}$ et $A P_{i}=2 \times 5^{i-1}$. De fait, lorsque l'on formule une idée de lemme, il est très important de rechercher des contre-exemples simples à ce lemme, qui seraient de nature à l'invalider, et ce dans le but de limiter le temps perdu à tenter de démontrer quelque chose de faux. Une telle phase permet souvent, à peu de frais, d'affiner la formulation du lemme, ou bien de se rendre compte que l'idée sous-jacente est complètement fausse; quand elle n'aboutit pas, c'est-à-dire quand on n'a pas trouvé de contre-exemple, on a plus confiance dans le lemme, et c'est là aussi encourageant, donc positif.
|
{
"exam": "French_tests",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Test-4-Web.jsonl",
"solution_match": "\nDémonstration.",
"tier": "T1",
"year": "2020"
}
|
Let $A B C D E$ be a convex pentagon such that $\widehat{A B E}=\widehat{A C E}=\widehat{A D E}=90^{\circ}$ and $B C=C D$. Finally, let $K$ be a point on the ray $[A B]$ such that $A K=A D$, and let $L$ be a point on the ray $[E D)$ such that $E L=B E$. Prove that the points $B, D, K$ and $L$ lie on the same circle with center $C$.
|
Given the right angles at $B, C$, and $D$, the points $A, B, C, D$, and $E$ lie on the same semicircle with diameter $[A E]$. Since $B C = C D$, point $C$ is the South Pole of $A$ in triangle $A B D$. Therefore, $(A C)$ is the angle bisector of $\widehat{D A B}$, which means it is the perpendicular bisector of $[K D]$. Similarly, $(C E)$ is the perpendicular bisector of $[B L]$. This implies that $C L = B C = D C = C K$, which concludes the proof.
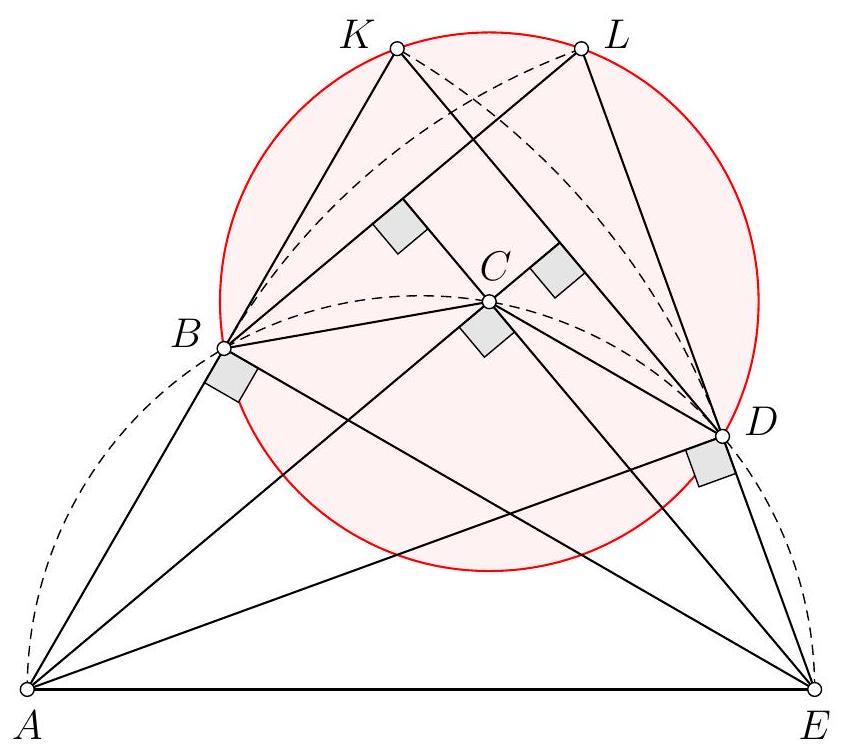
Comment from the graders: The problem was well approached. Many students managed to show that points $B, D, L$, and $K$ are concyclic. Once this step was achieved, most students attempted to show that $\widehat{B C D} = 2 \widehat{B K D}$ to apply the converse of the inscribed angle theorem.
Unfortunately, the angle equality alone is not sufficient to establish that point $C$ is the center of the circumcircle of triangle $B K D$. Indeed, any point $X$ on the arc $B D$ containing $C$ in the circumcircle of triangle $B C D$ also satisfies this angle equality.
It was necessary to invoke the hypothesis given in the problem statement, which is that $B C = C D$. The equalities $B C = C D$ and $\widehat{B C D} = 2 \widehat{B K D}$ were then sufficient to conclude, since on the perpendicular bisector of segment $[B D]$, there is only one point $X$ that satisfies $\widehat{B X D} = 2 \widehat{B K D}$. Since this property is satisfied by the center of the circumcircle of triangle $B K D$, such a point $X$ is indeed the center sought. This recurring error prevented many students from earning full points.
It is also worth noting that very few students recognized the South Pole configuration, which is present in many geometry problems and should therefore be remembered.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D E$ un pentagone convexe tel que $\widehat{A B E}=\widehat{A C E}=\widehat{A D E}=90^{\circ}$ et $B C=C D$. Enfin, soit $K$ un point sur la demi-droite $[A B]$ tel que $A K=A D$, et soit $L$ un point sur la demi-droite $[E D)$ tel que $E L=B E$. Démontrer que les points $B, D, K$ et $L$ appartiennent à un même cercle de centre $C$.
|
Au vu des angles droits dont on dispose en $B, C$ et $D$, les points $A$, $B, C, D$ et $E$ appartiennent à un même demi-cercle de diamètre $[A E]$. Comme $B C=C D$, le point $C$ est donc le pôle Sud issu de $A$ dans le triangle $A B D$. Ainsi, $(A C)$ est la bissectrice de $\widehat{D A B}$, c'est-à-dire la médiatrice de $[K D]$. De même, $(C E)$ est la médiatrice de $[B L]$. Cela signifie que $C L=B C=D C=C K$, ce qui conclut.

Commentaire des correcteurs Le problème a été bien abordé. Une bonne partie des élèves parvient à montrer que les points $B, D, L$ et $K$ sont cocycliques. Une fois cette étape franchie, la plupart des élèves tentent de montrer que $\widehat{B C D}=2 \widehat{B K D}$ pour appliquer une réciproque du théorème de l'angle au centre.
Malheureusement, l'égalité d'angle seule ne permet pas d'établir que le point $C$ est le centre du cercle circonscrit au triangle $B K D$. En effet, tout point $X$ sur l'arc $B D$ contenant $C$ dans le cercle circonscrit au triangle $B C D$ vérifie également cette égalité d'angle.
Il fallait encore invoquer l'hypothèse donnée par l'énoncé qui est que $B C=C D$. Les égalités $B C=C D$ et $\widehat{B C D}=2 \widehat{B K D}$ étaient alors suffisantes pour conclure, puisque sur la médiatrice du segment $[B D]$, il n'y a qu'un seul point $X$ vérifiant $\widehat{B X D}=2 \widehat{B K D}$, et comme cette propriété est vérifiée par le centre du cercle circonscrit au triangle $B K D$, un tel point $X$ est bien le centre recherché. Cette erreur récurrente a empêché de nombreux élèves d'avoir la totalité des points.
Mentionnons également que très peu d'élèves ont reconnu la configuration du pôle Sud, qui est pourtant présente dans de nombreux problèmes de géométrie et qui est donc à retenir.
|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Web-Test-5.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T1",
"year": "2020"
}
|
Find all quadruplets of integers $(a, b, c, p)$ such that $p$ is a prime number and for which
$$
73 p^{2}+6=9 a^{2}+17 b^{2}+17 c^{2}
$$
|
The equality in the statement involves many squares. The first thing to do is to study it modulo a number $n$ for which there are few quadratic residues. We therefore study the case $n=8$, as the squares modulo 8 are 0, 1, and 4.
In particular, if $p$ is odd, the equation becomes $a^{2}+b^{2}+c^{2} \equiv -1 \pmod{8}$, and this equation has no solutions. We deduce that $p=2$, and it is now a matter of finding the integers $a, b$, and $c$ such that $298=9 a^{2}+17 b^{2}+17 c^{2}$.
Without loss of generality, we assume that $a, b$, and $c$ are positive or zero. Since $b$ and $c$ play symmetric roles, we assume even that $b \leqslant c$. We then observe that $9 \times 6^{2}=324 > 298 \geqslant 9 a^{2}$, so that $0 \leqslant a \leqslant 5$. Since $9 a^{2}+17 b^{2}+17 c^{2} \equiv 298 \equiv 9 \pmod{17}$, we deduce in addition that 17 divides $9(a-1)(a+1)$. This means that $a=1$, and our equation becomes $17=b^{2}+c^{2}$, which means that $b=1$ and $c=4$.
In conclusion, the only possible solutions are
$$
(a, b, c, p)=( \pm 1, \pm 1, \pm 4,2) \text { and }( \pm 1, \pm 4, \pm 1,2)
$$
Conversely, and by virtue of the equality $73 \times 2^{2}+6=298=9 \times 1^{2}+17 \times 1^{2}+17 \times 4^{2}$, these quadruplets indeed work.
Examiner's Comment: Many students approached the problem but few managed to make significant progress. The exercise consisted of two parts: looking modulo 8 to show that $p=2$, and then finding the solutions. It is a pity that many students attempted simplifications without ultimately looking for the case $p=2$, which was quite easy to handle and could have earned points. This case is also more relevant than cases like $a=b$ or $a=b=c$, as there is little chance of achieving such an equality.
Regarding the modular studies of the first equation, looking modulo 8 is quite natural in the presence of squares. When there are multiple squares present, one should study modulo 4, 3, and then 8 first, as these are three moduli very well suited for these equations. To succeed, one needs to look at what the squares modulo 8 are, which are 0, 1, and 4, and deduce that $p$ cannot be odd.
It is also worth noting that it is unnecessary to look at the equation modulo a number $n$ that has two different prime factors, such as $n=6$ or $n=10$. For $n=6$, the equation provides as much information as the equation taken modulo 2 and then modulo 3, and the calculations are simpler in this case.
|
(a, b, c, p)=( \pm 1, \pm 1, \pm 4,2) \text { and }( \pm 1, \pm 4, \pm 1,2)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Trouver tous les quadruplets d'entiers relatifs $(a, b, c, p)$ tels que $p$ soit un nombre premier et pour lesquels
$$
73 p^{2}+6=9 a^{2}+17 b^{2}+17 c^{2}
$$
|
L'égalité de l'énoncé met en jeu de nombreux carrés. La première chose à faire consiste donc à l'étudier modulo un nombre $n$ pour lequel il y a peu de résidus quadratiques. On étudie donc le cas $n=8$, car les carrés modulo 8 sont 0,1 et 4 .
En particulier, si $p$ est impair, l'équation devient $a^{2}+b^{2}+c^{2} \equiv-1(\bmod 8)$, et cette équation n'a aucune solution. On en déduit que $p=2$, et il s'agit désormais de trouver les entiers $a, b$ et $c$ tels que $298=9 a^{2}+17 b^{2}+17 c^{2}$.
Sans perte de généralité, on suppose que $a, b$ et $c$ sont positifs ou nuls. Puisque $b$ et $c$ jouent des rôles symétriques, on suppose même que $b \leqslant c$. On constate alors que $9 \times 6^{2}=324>$ $298 \geqslant 9 a^{2}$, de sorte que $0 \leqslant a \leqslant 5$. Puisque $9 a^{2}+17 b^{2}+17 c^{2} \equiv 298 \equiv 9(\bmod 17)$, on en déduit en outre que 17 divise $9(a-1)(a+1)$. Cela signifie que $a=1$, et notre équation devient $17=b^{2}+c^{2}$, ce qui signifie que $b=1$ et $c=4$.
En conclusion, les seules solutions possibles sont
$$
(a, b, c, p)=( \pm 1, \pm 1, \pm 4,2) \text { et }( \pm 1, \pm 4, \pm 1,2)
$$
Réciproquement, et en vertu de l'égalité $73 \times 2^{2}+6=298=9 \times 1^{2}+17 \times 1^{2}+17 \times 4^{2}$, ces quadruplets conviennent effectivement.
Commentaire des correcteurs Beaucoup d'élèves ont abordé l'exercice mais peu ont réussi à véritablement avancer. L'exercice consistait en deux parties : regarder modulo 8 pour montrer que $p=2$, puis trouver les solutions. Il est dommage que beaucoup d'élèves aient tenté des simplifications, sans finalement chercher le cas $p=2$, qui était assez facile à traiter et aurait pu rapporter des points. Ce cas est d'ailleurs plus pertinent que des cas comme $a=b$ ou $a=b=c$, puisqu'il y a peu de chances d'aboutir à une telle égalité.
Concernant les études modulo de la première équation, regarder modulo 8 est assez naturel en présence de carrés. Quand il y a plusieurs carrés présents, il faut étudier modulo 4, 3 puis 8 en premier, ce sont trois modulos très adaptés pour ces équations. Pour réussir, il faut ici regarder quels sont les carrés modulo 8 , qui sont 0,1 et 4 , et en déduit que $p$ ne peut pas être impair.
Rappelons aussi qu'il est inutile de regarder l'équation modulo un nombre $n$ qui a deux facteurs premiers différents, par exemple comme $n=6$ ou $n=10$. Pour $n=6$, l'équation donne autant d'information que l'équation prise modulo 2 puis modulo 3 , et les calculs sont plus simples dans ce cas.
|
{
"exam": "French_tests",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Web-Test-5.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T1",
"year": "2020"
}
|
To prepare for the final POFM test of the year, Jean-Baptiste and Marie-Odile have collected 100 math problems and are now working on creating a revision schedule. Over the 100 days leading up to the POFM test, each of them will solve one problem per day. Let \( x \) be the number of problems Jean-Baptiste solves strictly before Marie-Odile, and \( y \) be the number of problems Marie-Odile solves strictly before Jean-Baptiste. Finally, we say that the revision schedule is fair if \( x = y \).
Prove that there are at least \( 100! \times \left(2^{50} + (50!)^2\right) \) fair schedules.
|
First, there are 100! ways to choose the order in which Jean-Baptiste will handle the problems. These 100! ways all play symmetric roles. Without loss of generality, we number the problems from 1 to 100, in the order Jean-Baptiste deals with them, and it is necessary to prove that there are at least \(2^{50}+(50!)^{2}\) permutations \(\sigma\) of the set \(\{1,2, \ldots, 100\}\) for which the sets \(\{k: \sigma(k)<k\}\) and \(\{k: \sigma(k)>k\}\) have the same cardinality. We will say that these permutations are fair.
First, we can construct \(2^{50}\) fair permutations as follows: given a subset \(X\) of \(\{1,2, \ldots, 50\}\), among the \(2^{50}\) possible subsets, we construct the permutation \(\sigma_{X}\) such that
\[
\sigma_{X}(2 k-1)=\left\{\begin{array}{ll}
2 k & \text { if } k \in X \\
2 k-1 & \text { if } k \notin X
\end{array} \text { and } \sigma_{X}(2 k)= \begin{cases}2 k-1 & \text { if } k \in X \\
2 k & \text { if } k \notin X .\end{cases}\right.
\]
For such a permutation, we observe that \(\sigma_{X}(k)<k\) if and only if \(k / 2 \in X\), and that \(\sigma_{X}(k)>k\) if and only if \((k+1) / 2 \in X\). Consequently, \(\sigma_{X}\) is fair.
We then construct \((50! )^{2}\) fair permutations as follows: given two permutations \(\tau\) and \(\pi\) of \(\{1,2, \ldots, 50\}\) among the \((50!)^{2}\) pairs of possible permutations, we construct the permutation \(\sigma_{\pi, \tau}\) such that
\[
\sigma_{\pi, \tau}(k)= \begin{cases}50+\pi(k) & \text { if } 1 \leqslant k \leqslant 50 \\ \tau(k-50) & \text { if } 51 \leqslant k \leqslant 100\end{cases}
\]
For such a permutation, we observe that \(\sigma_{\pi, \tau}(k)<k\) if and only if \(51 \leqslant k \leqslant 100\), and that \(\sigma_{X}(k)>k\) if and only if \(1 \leqslant k \leqslant 50\). Consequently, \(\sigma_{\pi, \tau}\) is fair.
Finally, we of course verify that two permutations \(\sigma_{X}\) and \(\sigma_{\pi, \tau}\) are never equal, since \(\sigma_{X}(1) \leqslant 2<51 \leqslant \sigma_{\pi, \tau}(1)\).
Examiner's Comment The problem was difficult and few students managed to make significant progress. Some tried to invoke possible meanings of \(100!, 2^{50}\), and \((50!)^{2}\) somewhat randomly, hoping it would work. It is important to remain rigorous: trying to interpret each of these quantities is obviously a good idea, but one must carefully examine the expression.
Here, the term 100! invites us to fix an initial permutation for one of the two people, for which there are 100! choices. Then, we wanted to find \(2^{50}+(50!)^{2}\) permutations. Here, the plus sign suggests that we need to find at least two types of permutations: ideally, one type with \((50!)^{2}\) permutations, and another with \(2^{50}\) permutations.
Some students, in their vague justifications, did not understand this and tried to show that there were \(2^{50}\) possibilities for something, and \((50!)^{2}\) for something else, which here would have given a product. Moreover, several students, once the two sets of permutations were created, did not verify that these sets were disjoint, which is necessary to conclude: it must obviously be done!
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Pour s'entraîner en prévision du dernier test POFM de l'année, Jean-Baptiste et Marie-Odile ont collecté 100 problèmes de mathématiques, et s'attellent désormais à la confection d'un programme de révisions. Pendant les 100 jours qui les séparent du test POFM, chacun devra traiter un problème par jour. On note $x$ le nombre de problèmes que Jean-Baptiste a traités strictement avant Marie-Odile, et $y$ le nombre de problèmes que Marie-Odile a traités strictement avant Jean-Baptiste. Enfin, on dit que le programme de révisions est équitable si $x=y$.
Démontrer qu'il existe au moins $100!\times\left(2^{50}+(50!)^{2}\right)$ programmes équitables.
|
Tout d'abord, il existe 100! manières de choisir l'ordre dans lequel Jean-Baptiste traitera les problèmes. Ces 100! manières jouent toutes des rôles symétriques. Sans perte de généralité, on numérote les problèmes de 1 à 100, dans l'ordre où Jean-Baptiste les traite, et il s'agit de démontrer qu'il existe au moins $2^{50}+(50!)^{2}$ permutations $\sigma$ de l'ensemble $\{1,2, \ldots, 100\}$ pour lesquelles les ensembles $\{k: \sigma(k)<k\}$ et $\{k: \sigma(k)>k\}$ ont même cardinal. On dira que ces permutations sont équitables.
Tout d'abord, on peut construire $2^{50}$ permutations équitables comme suit : étant donné un sous-ensemble $X$ de $\{1,2, \ldots, 50\}$, parmi les $2^{50}$ possibles, on construit la permutation $\sigma_{X}$ telle que
$$
\sigma_{X}(2 k-1)=\left\{\begin{array}{ll}
2 k & \text { si } k \in X \\
2 k-1 & \text { si } k \notin X
\end{array} \text { et } \sigma_{X}(2 k)= \begin{cases}2 k-1 & \text { si } k \in X \\
2 k & \text { si } k \notin X .\end{cases}\right.
$$
Pour une telle permutation, on constate que $\sigma_{X}(k)<k$ si et seulement $k / 2 \in X$, et que $\sigma_{X}(k)>k$ si et seulement si $(k+1) / 2 \in X$. Par conséquent, $\sigma_{X}$ est équitable.
On construit ensuite (50! $)^{2}$ permutations équitables comme suit : étant données deux permutations $\tau$ et $\pi$ de $\{1,2, \ldots, 50\}$ parmi les $(50!)^{2}$ paires de permutations possibles, on construit la permutation $\sigma_{\pi, \tau}$ telle que
$$
\sigma_{\pi, \tau}(k)= \begin{cases}50+\pi(k) & \text { si } 1 \leqslant k \leqslant 50 \\ \tau(k-50) & \text { si } 51 \leqslant k \leqslant 100\end{cases}
$$
Pour une telle permutation, on constate que $\sigma_{\pi, \tau}(k)<k$ si et seulement $51 \leqslant k \leqslant 100$, et que $\sigma_{X}(k)>k$ si et seulement si $1 \leqslant k \leqslant 50$. Par conséquent, $\sigma_{\pi, \tau}$ est équitable.
Enfin, on vérifie bien sûr que deux permutations $\sigma_{X}$ et $\sigma_{\pi, \tau}$ ne sont jamais égales, puisque $\sigma_{X}(1) \leqslant 2<51 \leqslant \sigma_{\pi, \tau}(1)$.
Commentaire des correcteurs L'exercice était difficile et peu d'élèves ont réussi à bien avancer dessus. Certains ont tenté d'invoquer parfois un peu au hasard des significations possibles de $100!, 2^{50}$ et $(50!)^{2}$ en espérant que cela fonctionnait. Il faut rester rigoureux : essayer d'interpréter chacune de ces quantités est évidemment une bonne idée, mais il faut bien regarder l'expression.
Ici, le terme 100! nous invitait à fixer une permutation initiale pour une des deux personnes, pour laquelle il y a 100! choix. Ensuite, on voulait trouver $2^{50}+(50!)^{2}$ permutations. Ici, le fait d'avoir un plus nous fait comprendre qu'il faut trouver deux types de permutations au moins : idéalement, un type avec (50!) $)^{2}$ permutations, et un autre avec $2^{50}$ permutations.
Certains élèves, dans leurs justifications très vagues, n'ont pas compris cela, et essayaient de montrer qu'il y avait $2^{50}$ possibilités pour quelque chose, puis (50!) ${ }^{2}$ pour autre chose, ce qui ici aurait donné un produit. Par ailleurs, plusieurs élèves, une fois les deux ensembles de permutations créés, n'ont pas vérifié que ces ensembles étaient disjoints, chose pourtant nécessaire pour conclure : il faut évidemment le faire!
|
{
"exam": "French_tests",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Web-Test-5.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T1",
"year": "2020"
}
|
Find all real numbers $x$ and $y$ such that
$$
\left(x-\sqrt{x^{2}+1}\right)\left(y-\sqrt{y^{2}+1}\right)=1 \text { and }\left(x^{2}+y+2\right)\left(y^{2}+x+2\right)=8 .
$$
|
Let $(x, y)$ be a potential solution. The equalities
$$
\left\{\begin{array}{l}
\left(x-\sqrt{x^{2}+1}\right)\left(x+\sqrt{x^{2}+1}\right)=x^{2}-\left(x^{2}+1\right)=-1 \\
\left(y-\sqrt{y^{2}+1}\right)\left(y+\sqrt{y^{2}+1}\right)=y^{2}-\left(y^{2}+1\right)=-1
\end{array}\right.
$$
indicate that
$$
\left\{\begin{array}{l}
x+\sqrt{x^{2}+1}=\sqrt{y^{2}+1}-y \\
\sqrt{x^{2}+1}-x=y+\sqrt{y^{2}+1}
\end{array}\right.
$$
Subtracting equation (2) from equation (1) indicates that $x=-y$, and the equation $\left(x^{2}+y+2\right)\left(y^{2}+x+2\right)=8$ can then be rewritten as
$$
8=\left(x^{2}-x+2\right)\left(x^{2}+x+2\right)=\left(x^{2}+2\right)^{2}-x^{2}
$$
If we let $z=x^{2}$, it then becomes necessary to solve the equation
$0=(z+2)^{2}-z-8=z^{2}+3z-4=(z+3/2)^{2}-25/4=(z+3/2)^{2}-(5/2)^{2}=(z+4)(z-1)$.
Since we know that $z=x^{2} \geqslant 0$, we deduce that $z=1$, hence $x= \pm 1$ and $y=-x= \pm 1$.
Conversely, when $(x, y)=( \pm 1, \mp 1)$, it is easily verified that both equalities in the problem statement are satisfied. In conclusion, the two solutions are
$$
(x, y)=(1,-1) \text { and }(x, y)=(-1,1)
$$
**Graders' Comments** This very challenging problem was tackled by only a few students, and the graders were pleased to note that five students managed to solve it.
The key idea for this problem was to recognize what are called the conjugates of a difference of the form $a-b$ where $a$ and $b$ are terms whose squares $a^{2}$ and $b^{2}$ are very close. Indeed, in such cases, it is often useful to also study the term $a+b$, which is called the conjugate of the term $a-b$, and this is due to the remarkable identity $a^{2}-b^{2}=(a+b)(a-b)$. This is exactly how the solution above begins, and the students who solved this problem are those who had the idea to introduce these conjugates.
Moreover, several students mistakenly believed that $x$ and $y$ had to be integers, or even that the terms $x-\sqrt{x^{2}+1}$ and $y-\sqrt{y^{2}+1}$ had to be integers as well. It is important to read the problem statement carefully!
Similarly, several students had the very good reflex to look for particular solutions, but many of them stopped at the cases where $x=0$ (or $y=0$), $x=y=1$, or more generally at the case where $x=y$, without considering the analogous case where $x=-y$. What a pity! In such an equation, it is always important not to forget the case where one of the two unknowns (or both) could be negative.
|
(x, y)=(1,-1) \text { and }(x, y)=(-1,1)
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Trouver tous les nombres réels $x$ et $y$ tels que
$$
\left(x-\sqrt{x^{2}+1}\right)\left(y-\sqrt{y^{2}+1}\right)=1 \text { et }\left(x^{2}+y+2\right)\left(y^{2}+x+2\right)=8 .
$$
|
Soit $(x, y)$ une solution éventuelle. Les égalités
$$
\left\{\begin{array}{l}
\left(x-\sqrt{x^{2}+1}\right)\left(x+\sqrt{x^{2}+1}\right)=x^{2}-\left(x^{2}+1\right)=-1 \\
\left(y-\sqrt{y^{2}+1}\right)\left(y+\sqrt{y^{2}+1}\right)=y^{2}-\left(y^{2}+1\right)=-1
\end{array}\right.
$$
indiquent en fait que
$$
\left\{\begin{array}{l}
x+\sqrt{x^{2}+1}=\sqrt{y^{2}+1}-y \\
\sqrt{x^{2}+1}-x=y+\sqrt{y^{2}+1}
\end{array}\right.
$$
L'équation (1) - (2) indique que $x=-y$, et l'égalité $\left(x^{2}+y+2\right)\left(y^{2}+x+2\right)=8$ se réécrit alors comme
$$
8=\left(x^{2}-x+2\right)\left(x^{2}+x+2\right)=\left(x^{2}+2\right)^{2}-x^{2}
$$
Si l'on pose $z=x^{2}$, il s'agit donc de résoudre l'équation
$0=(z+2)^{2}-z-8=z^{2}+3 z-4=(z+3 / 2)^{2}-25 / 4=(z+3 / 2)^{2}-(5 / 2)^{2}=(z+4)(z-1)$.
Or, on sait que $z=x^{2} \geqslant 0$. On en déduit que $z=1$, donc que $x= \pm 1$ et $y=-x= \pm 1$.
Réciproquement, lorsque $(x, y)=( \pm 1, \mp 1)$, on vérifie aisément que les deux égalités de l'énoncé sont vérifiées. En conclusion, les deux solutions sont
$$
(x, y)=(1,-1) \text { et }(x, y)=(-1,1)
$$
Commentaire des correcteurs Ce problème fort difficile a été assez peu abordé, et les correcteurs ont eu le plaisir de constater que cinq élèves en étaient venus à bout.
L'idée clé pour ce problème consistait à reconnaître ce que l'on appelle les conjugués d'une différence de la forme $a-b$ où $a$ et $b$ sont deux termes dont les carrés $a^{2}$ et $b^{2}$ sont très proches. En effet, dans ces cas-là, il est souvent pertinent d'étudier également le terme $a+b$, que l'on appelle conjugué du terme $a-b$, et ce en vertu de l'identité remarquable $a^{2}-b^{2}=(a+b)(a-b)$. C'est exactement ainsi que commence la solution ci-dessus, et les élèves qui ont réussi ce problème sont peu ou prou ceux qui ont eu l'idée d'introduire ces conjugués.
Par ailleurs, plusieurs élèves ont abusivement cru que $x$ et $y$ devaient être des entiers, voire que les termes $x-\sqrt{x^{2}+1}$ et $y-\sqrt{y^{2}+1}$ devaient eux aussi être des entiers. Il est important de lire attentivement l'énoncé!
De même, plusieurs élèves ont eu le très bon réflexe de rechercher des solutions particulières, mais beaucoup d'entre eux se sont arrêtés aux cas où $x=0$ (ou $y=0$ ), $x=y=1$, ou plus généralement au cas où $x=y$, mais sans considérer le cas pourtant analogue où $x=-y$. C'est dommage! De manière générale, dans une telle équation, il est toujours important de ne pas oublier le cas où une des deux inconnues (voire les deux) pourrait être négative.
## Énoncés Senior
|
{
"exam": "French_tests",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Web-Test-5.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T1",
"year": "2020"
}
|
Let $ABCD$ be a convex quadrilateral where the angles at $B$ and $D$ are obtuse, and the angles at $A$ and $C$ are equal to each other. Let $E$ and $F$ be the reflections of $A$ with respect to $(BC)$ and $(CD)$. Let $K$ and $L$ be the points of intersection of $(BD)$ with $(AE)$ and $(AF)$. Prove that the circumcircles of triangles $BEK$ and $DFL$ are tangent to each other.
|
The most practical way to construct point $A$ is to first construct its symmetric point $A^{\prime}$ with respect to $(B D)$, since $A^{\prime}$ is cocyclic with $B, C$, and $D$. By doing so, we observe that $A^{\prime}$ seems to belong to the circumcircles of triangles $B E K$ and $D F L$, and an angle chase indeed shows that
$$
\begin{aligned}
\left(K E, K A^{\prime}\right) & =(K E, B C)+(B C, B D)+\left(B D, K A^{\prime}\right) \\
& =90^{\circ}+(B C, B D)+(K A, B D) \\
& =90^{\circ}+(B C, B D)+(K A, B C)+(B C, B D) \\
& =2(B C, B D) \\
\left(B E, B A^{\prime}\right) & =(B E, B C)+(B C, B D)+\left(B D, B A^{\prime}\right) \\
& =(B C, B A)+(B C, B D)+(B A, B D) \\
& =2(B C, B D) .
\end{aligned}
$$
This means that $A^{\prime}, B, K$, and $E$ lie on a circle $\omega_{b}$, and similarly, that $A^{\prime}, D, L$, and $F$ lie on a circle $\omega_{d}$. Let $t$ and $t^{\prime}$ be the tangents to $\omega_{b}$ and $\omega_{d}$ at $A^{\prime}$. Another angle chase shows that
$$
\begin{aligned}
(t, B D) & =\left(t, A^{\prime} B\right)+\left(A^{\prime} B, B D\right) \\
& =\left(K A^{\prime}, K B\right)+(B D, B A) \\
& =(K B, K A)+(B D, B A) \\
& =(B D, B C)+90^{\circ}+(B D, B A) \\
\left(t^{\prime}, B D\right) & =\left(t^{\prime}, A^{\prime} D\right)+\left(A^{\prime} D, B D\right) \\
& =\left(L A^{\prime}, L D\right)+(B D, A D) \\
& =(L D, L A)+(B D, A D) \\
& =(B D, D C)+90^{\circ}+(B D, A D) .
\end{aligned}
$$
Finally, we verify that
$$
\begin{aligned}
(B D, B C)+(B D, B A) & =(B D, B C)+(B D, A D)+(A D, A B) \\
& =(B D, B C)+(B D, A D)+(B C, C D) \\
& =(B D, D C)+(B D, A D),
\end{aligned}
$$
which concludes the proof.
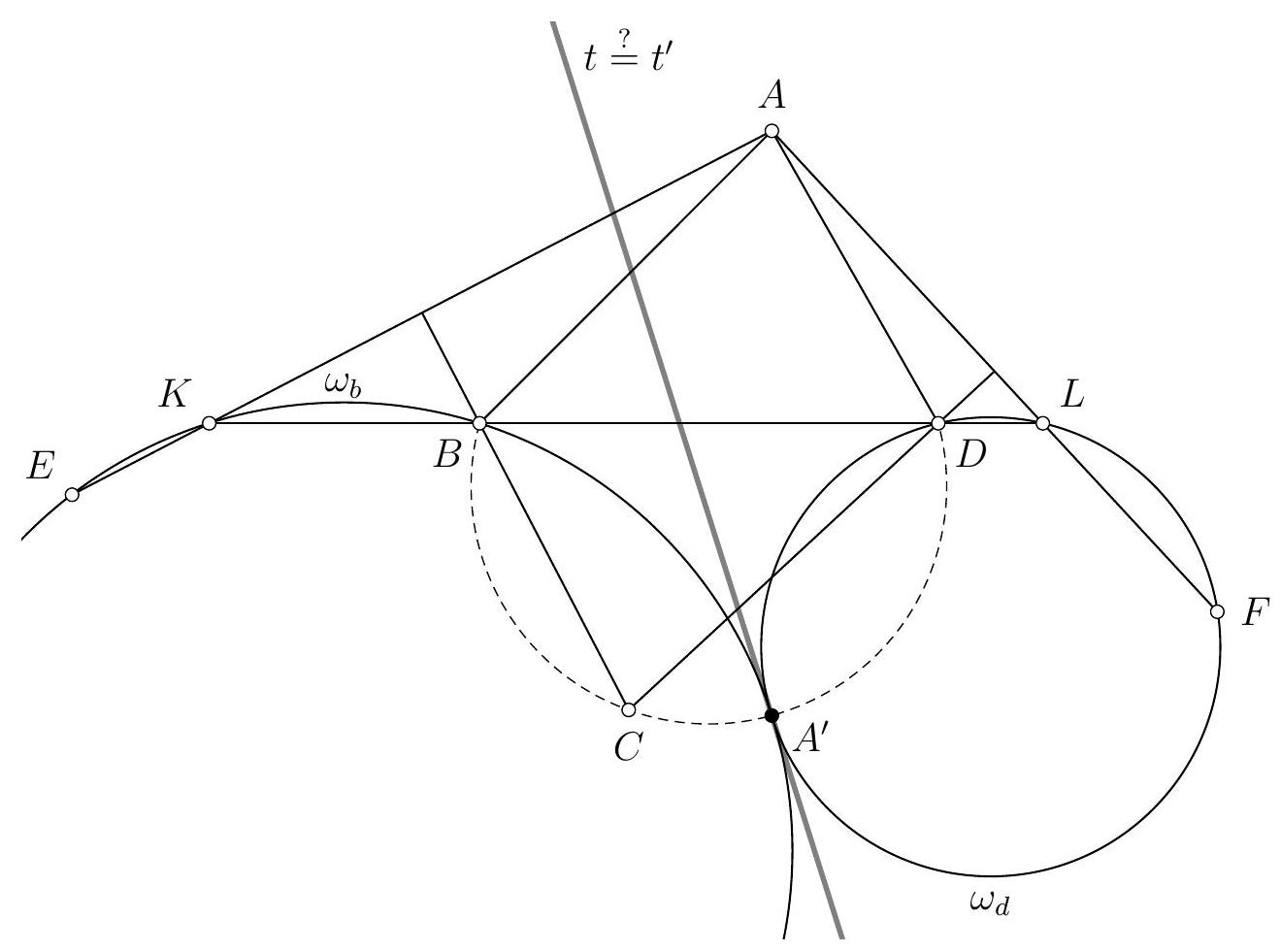
Comment from the graders: Only half of the students who took the test attempted this problem. It is very concerning to note that students' strategy when facing an Olympiad problem does not take into account the fact that the problems are ranked in increasing order of difficulty. Of course, students are encouraged to look at each of the problems on the test. However, unless a student has a very particular interest in a specific area of the Olympiads, to the point of being able to completely solve problems of any difficulty in that area, it is much more profitable to devote the majority of their time to the problem ranked as the easiest, regardless of its theme, since they are more likely to have interesting ideas.
It is naive to think that one can skip one of the four themes of the Olympiads, especially geometry, which has been the theme of a problem 1 or 4 in the International Olympiads 8 times in the last 10 years. The strategy of not reflecting on the geometry problem in this test to focus on the other two problems often backfired against the students, as problems 6 and 7 were very difficult and required many ideas to hope to obtain a significant number of points. We hope that students who have the opportunity will adjust their strategy for next year.
Regarding this problem, finding how to draw the exact figure was essential to get started. Indeed, looking for how to draw the exact figure pushed students to introduce additional points necessary for the subsequent steps. To construct a point $C$ such that $\widehat{B C D}=\widehat{B A D}$, one needed to find a particular point $X$ that satisfies $\widehat{B X D}=\widehat{B A D}$ but such that $X$ and $A$ are on opposite sides of the line $(B D)$, and then construct $C$ anywhere on the circle $\mathcal{C}_{B X D}$. This reasoning (which can be used whenever one is faced with an angle condition to realize with a ruler and compass) pushed to introduce the symmetric point of $A$ with respect to the line $(B D)$. Once the figure was completed, it was then legitimate to conjecture that this symmetric point was the desired point of tangency. This conjecture work was the most difficult part of the task, and often students who made this conjecture managed to completely prove it.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un quadrilatère convexe dont les angles en $B$ et en $D$ sont obtus, et dont les angles en $A$ et en $C$ sont égaux l'un à l'autre. Soit $E$ et $F$ les symétriques de $A$ par rapport à $(B C)$ et $(C D)$. Soit $K$ et $L$ les points d'intersection de $(B D)$ avec $(A E)$ et $(A F)$. Démontrer que les cercles circonscrits aux triangles $B E K$ et $D F L$ sont tangents l'un à l'autre.
|
La manière la plus pratique de construire le point $A$ est d'en construire tout d'abord son symétrique $A^{\prime}$ par rapport à $(B D)$, puisque $A^{\prime}$ est cocyclique avec $B, C$ et $D$. Ce faisant, on constate que $A^{\prime}$ semble appartenir aux deux cercles circonscrits aux triangles $B E K$ et $D F L$, et une chasse aux angles indique en effet que
$$
\begin{aligned}
\left(K E, K A^{\prime}\right) & =(K E, B C)+(B C, B D)+\left(B D, K A^{\prime}\right) \\
& =90^{\circ}+(B C, B D)+(K A, B D) \\
& =90^{\circ}+(B C, B D)+(K A, B C)+(B C, B D) \\
& =2(B C, B D) \\
\left(B E, B A^{\prime}\right) & =(B E, B C)+(B C, B D)+\left(B D, B A^{\prime}\right) \\
& =(B C, B A)+(B C, B D)+(B A, B D) \\
& =2(B C, B D) .
\end{aligned}
$$
Cela signifie bien que $A^{\prime}, B, K$ et $E$ appartiennent à un cercle $\omega_{b}$ et, de même, que $A^{\prime}, D, L$ et $F$ appartiennent à un cercle $\omega_{d}$.
Soit alors $t$ et $t^{\prime}$ les tangentes à $\omega_{b}$ et $\omega_{d}$ en $A^{\prime}$. Une nouvelle chasse aux angles indique que
$$
\begin{aligned}
(t, B D) & =\left(t, A^{\prime} B\right)+\left(A^{\prime} B, B D\right) \\
& =\left(K A^{\prime}, K B\right)+(B D, B A) \\
& =(K B, K A)+(B D, B A) \\
& =(B D, B C)+90^{\circ}+(B D, B A) \\
\left(t^{\prime}, B D\right) & =\left(t^{\prime}, A^{\prime} D\right)+\left(A^{\prime} D, B D\right) \\
& =\left(L A^{\prime}, L D\right)+(B D, A D) \\
& =(L D, L A)+(B D, A D) \\
& =(B D, D C)+90^{\circ}+(B D, A D) .
\end{aligned}
$$
On vérifie enfin que
$$
\begin{aligned}
(B D, B C)+(B D, B A) & =(B D, B C)+(B D, A D)+(A D, A B) \\
& =(B D, B C)+(B D, A D)+(B C, C D) \\
& =(B D, D C)+(B D, A D),
\end{aligned}
$$
ce qui conclut.

Commentaire des correcteurs Seule la moitié des élèves ayant pris part au test ont abordé cet exercice. Il est très préoccupant de constater que la stratégie des élèves face à un sujet d'Olympiade ne prend pas en compte le fait que les problèmes sont classés par ordre de difficulté croissante. On encourage bien sûr les élèves à regarder chacun des problèmes du sujet. Mais, à moins d'avoir une appétence très particulière pour un domaine des olympiades, au point d'être capable de résoudre complètement des problèmes de toute difficulté portant sur ce thème, il est bien plus rentable de consacrer la majeure partie de son temps au problème classé comme le plus facile, quel que soit son thème, puisqu'on a plus de chances d'y avoir des idées intéressantes.
Il est bien naïf de penser pouvoir faire l'impasse sur l'un des 4 thèmes des olympiades, en particulier la géométrie qui, ces 10 dernières années, a été 8 fois le thème d'un problème 1 ou 4 des Olympiades Internationales. La stratégie de ne pas réfléchir au problème de géométrie du présent test pour se consacrer aux deux autres problèmes s'est bien souvent retournée contre les élèves, puisque les problèmes 6 et 7 étaient très difficiles et demandaient de nombreuses idées pour espérer obtenir une quantité significative de points. Nous espérons donc que les élèves qui en ont l'occasion adapteront leur stratégie pour l'année prochaine.
Concernant ce problème, trouver comment tracer la figure exacte était essentiel pour démarrer. En effet, chercher comment tracer la figure exacte poussait à introduire des points supplémentaires nécessaires dans la suite. Pour construire un point $C$ tel que $\widehat{B C D}=\widehat{B A D}$, il fallait trouver un point $X$ particulier qui vérifie $\widehat{B X D}=\widehat{B A D}$ mais tel que $X$ et $A$ soient de part et d'autre de l'axe $(B D)$, puis construire $C$ quelconque sur le cercle $\mathcal{C}_{B X D}$. Ce raisonnement (qui peut être employé dès que l'on se retrouve face à une hypothèse d'angle à réaliser à la règle et au compas) poussait à introduire le symétrique du point $A$ par rapport à la droite $(B D)$. Une fois la figure complétée, il était alors légitime de conjecturer que ce symétrique était le point de tangence recherché. Ce travail de conjecture était la partie la plus difficile du travail, et bien souvent les élèves ayant fait cette conjecture ont réussi à la démontrer complètement.
|
{
"exam": "French_tests",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Web-Test-5.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T1",
"year": "2020"
}
|
For every integer $k \geqslant 0$, we denote $F_{k}$ as the $k^{\text {th }}$ Fibonacci number, defined by $F_{0}=0$, $F_{1}=1$, and $F_{k}=F_{k-2}+F_{k-1}$ when $k \geqslant 2$. Let $n \geqslant 2$ be an integer, and let $S$ be a set of integers with the following property:
For every integer $k$ such that $2 \leqslant k \leqslant n$, the set $S$ contains two integers $x$ and $y$ such that $x-y=F_{k}$.
What is the smallest possible number of elements in such a set $S$?
|
First, let $m=\lceil n / 2\rceil$, and let $S$ be the set $\left\{F_{2 \ell}: 0 \leqslant \ell \leqslant m\right\}$. For any integer $k$ such that $2 \leqslant k \leqslant n$, we choose $x=F_{k}$ and $y=F_{0}=0$ if $k$ is even, or $x=F_{k+1}$ and $y=F_{k-1}$ if $k$ is odd. In both cases, $x$ and $y$ are two elements of $S$ such that $x-y=F_{k}$.
Conversely, let $S$ be a set as described in the statement. We will prove that $|S| \geqslant m+1$. To do this, we construct a weighted, undirected graph $G$ as follows. The vertices of our graph are the elements of the set $S$. Then, for every odd integer $k$ such that $1 \leqslant k \leqslant n$, and recalling that $F_{1}=F_{2}$, we choose two elements $x$ and $y$ of $S$ such that $x-y=F_{k}$. We then insert the edge $\{x, y\}$ into our graph $G$, and assign it the weight $F_{k}$.
The graph thus obtained has $m$ edges. Furthermore, suppose it contains a cycle $c=x_{0} x_{1} \ldots x_{\ell}$, with $x_{0}=x_{\ell}$, which we choose to have minimal length $\ell$. Without loss of generality, we assume that $x_{0}>x_{1}$, and that $\left\{x_{0}, x_{1}\right\}$ is the edge of $c$ with the maximum weight. We denote this weight by $F_{2 k+1}$. The cumulative weight of the other edges does not exceed $F_{1}+F_{3}+\ldots+F_{2 k-1}$ and, by construction, it is equal to
$$
\left|x_{1}-x_{2}\right|+\left|x_{2}-x_{3}\right|+\ldots+\left|x_{\ell-1}-x_{\ell}\right| \geqslant\left|x_{\ell}-x_{1}\right|=F_{2 k+1}
$$
However, a straightforward induction on $k$ shows that $F_{1}+F_{3}+\ldots+F_{2 k-1}=F_{2 k}<F_{2 k+1}$. Consequently, our graph is acyclic, and since it has $m$ edges, it has at least $m+1$ vertices.
The minimal cardinality sought is therefore equal to $m+1$.
|
m+1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Pour tout entier $k \geqslant 0$, on note $F_{k}$ le $k^{\text {ème }}$ nombre de Fibonacci, défini par $F_{0}=0$, $F_{1}=1$, et $F_{k}=F_{k-2}+F_{k-1}$ lorsque $k \geqslant 2$. Soit $n \geqslant 2$ un entier, et soit $S$ un ensemble d'entiers ayant la propriété suivante :
Pour tout entier $k$ tel que $2 \leqslant k \leqslant n$, l'ensemble $S$ contient deux entiers $x$ et $y$ tels que $x-y=F_{k}$.
Quel est le plus petit nombre possible d'éléments d'un tel ensemble $S$ ?
|
Tout d'abord, soit $m=\lceil n / 2\rceil$, et soit $S$ l'ensemble $\left\{F_{2 \ell}: 0 \leqslant \ell \leqslant m\right\}$. Pour tout entier $k$ tel que $2 \leqslant k \leqslant n$, on choisit $x=F_{k}$ et $y=F_{0}=0$ si $k$ est pair, ou bien $x=F_{k+1}$ et $y=F_{k-1}$ si $k$ est impair. Dans les deux cas, $x$ et $y$ sont deux éléments de $S$ tels que $x-y=F_{k}$.
Réciproquement, soit $S$ un ensemble tel que décrit dans l'énoncé. Nous allons démontrer que $|S| \geqslant m+1$. Pour ce faire, on construit un graphe pondéré $G$, non orienté, en procédant comme suit. Les sommets de notre graphe sont les éléments de l'ensemble $S$. Puis, pour tout entier $k$ impair tel que $1 \leqslant k \leqslant n$, et en se rappelant que $F_{1}=F_{2}$, on choisit deux éléments $x$ et $y$ de $S$ tels que $x-y=F_{k}$. On insère alors dans notre graphe $G$ l'arête $\{x, y\}$, à qui l'on affecte le poids $F_{k}$.
Le graphe ainsi obtenu compte $m$ arêtes. En outre, supposons qu'il contienne un cycle $c=x_{0} x_{1} \ldots x_{\ell}$, avec $x_{0}=x_{\ell}$, que l'on choisit de longueur $\ell$ minimale. Sans perte de généralité, on suppose que $x_{0}>x_{1}$, et que $\left\{x_{0}, x_{1}\right\}$ est l'arête de $c$ de poids maximal. On note $F_{2 k+1}$ ce poids. Le poids cumulé des autres arêtes ne dépasse pas $F_{1}+F_{3}+\ldots+F_{2 k-1}$ et, par construction, il est égal à
$$
\left|x_{1}-x_{2}\right|+\left|x_{2}-x_{3}\right|+\ldots+\left|x_{\ell-1}-x_{\ell}\right| \geqslant\left|x_{\ell}-x_{1}\right|=F_{2 k+1}
$$
Cependant, une récurrence immédiate sur $k$ montre que $F_{1}+F_{3}+\ldots+F_{2 k-1}=F_{2 k}<F_{2 k+1}$. Par conséquent, notre graphe est acyclique, et puisqu'il compte $m$ arêtes, il compte au moins $m+1$ sommets.
Le cardinal minimal recherché est donc égal à $m+1$.
|
{
"exam": "French_tests",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Web-Test-5.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T1",
"year": "2020"
}
|
For every integer $k \geqslant 0$, we denote $F_{k}$ as the $k^{\text {th }}$ Fibonacci number, defined by $F_{0}=0$, $F_{1}=1$, and $F_{k}=F_{k-2}+F_{k-1}$ when $k \geqslant 2$. Let $n \geqslant 2$ be an integer, and let $S$ be a set of integers with the following property:
For every integer $k$ such that $2 \leqslant k \leqslant n$, the set $S$ contains two integers $x$ and $y$ such that $x-y=F_{k}$.
What is the smallest possible number of elements in such a set $S$?
|
$n^{\circ} 1$ It is said that a set as described in the statement is $n$-cute. Let $S_{n}$ be an $n$-cute set of the smallest possible cardinality. We will prove, by induction on $n$, that $\left|S_{n}\right| \geqslant\lceil n / 2\rceil+1$. First, for $n=2$, the desired result is immediate. We now assume that $n \geqslant 3$.
This time, we introduce the weighted graph $G$ whose vertices are the elements of $S_{n}$ and which contains, for every integer $k$ such that $2 \leqslant k \leqslant n-2$, an edge $(x, y)$ of weight $F_{k}$ between two vertices $x$ and $y$ such that $|x-y|=F_{k}$. Finally, let $u$ and $v$ be two elements of $S_{n}$ such that $|u-v|=F_{n}$.
An immediate induction on $k$ shows that $F_{2}+F_{3}+\ldots+F_{k-2}=F_{k}-3$ for all integers $k \geqslant 4$. Consequently, two vertices of $S_{n}$ belonging to the same connected component of $G$ are at most $F_{n}-3$ apart, and $u$ and $v$ cannot belong to the same connected component of $G$.
Let $U_{n}$ be the set of elements of $S_{n}$ that belong to the same connected component of $G$ as $u$, and let $V_{n}$ be the other elements of $S_{n}$. No edge of $G$ has one endpoint in $U_{n}$ and the other in $V_{n}$. Therefore, if we replace each vertex $x$ of $U_{n}$ by $x+v-u$, we obtain a new set $S_{n}^{\prime}=\left\{x+v-u: x \in U_{n}\right\} \cup V_{n}$ of cardinality $\left|S_{n}^{\prime}\right| \leqslant\left|S_{n}\right|-1$ and which is $(n-2)$-cute. We conclude as expected that
$$
\left|S_{n}\right| \geqslant\left|S_{n}^{\prime}\right|+1 \geqslant\lceil(n-2) / 2\rceil+1+2=\lceil n / 2\rceil+1
$$
Graders' Comments This problem was very difficult. The vast majority of students who tackled it indeed found a suitable set of minimal cardinality, but very few found arguments to prove that this cardinality was indeed minimal. This difficulty was clearly perceived by many students, and it is very surprising that half of the students who tackled problem 6 did not even submit a figure for problem 5.
Many students identified constructions similar to the one proposed above, even if they sometimes appeared in much more complicated forms. Let us recall here that it is always good to start by looking at particular cases for small values of $n$ (here, $2 \leqslant n \leqslant 4$ or 5, for example) to form an intuition about the general form of the objects one is about to construct.
The idea of considering an implicitly or explicitly weighted graph was then crucial, and could in fact arise naturally when one tried to highlight "essential" edges to the $n$-cuteness of the sets considered. In general, trying to highlight a simple and common combinatorial structure (here, a graph) to characterize a property is often a good idea.
Finally, many students wrongly claimed that every $n$-cute set of minimal cardinality already contained an $(n-2)$-cute set of minimal cardinality. The alternative solution above shows that such a statement is true, but in the absolute, this statement is by no means obvious, and there are many analogous problems for which it is grossly false.
|
\lceil n / 2\rceil+1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Pour tout entier $k \geqslant 0$, on note $F_{k}$ le $k^{\text {ème }}$ nombre de Fibonacci, défini par $F_{0}=0$, $F_{1}=1$, et $F_{k}=F_{k-2}+F_{k-1}$ lorsque $k \geqslant 2$. Soit $n \geqslant 2$ un entier, et soit $S$ un ensemble d'entiers ayant la propriété suivante :
Pour tout entier $k$ tel que $2 \leqslant k \leqslant n$, l'ensemble $S$ contient deux entiers $x$ et $y$ tels que $x-y=F_{k}$.
Quel est le plus petit nombre possible d'éléments d'un tel ensemble $S$ ?
|
$n^{\circ} 1$ On dit qu'un ensemble tel que décrit dans l'énoncé est $n$-mignon. Soit $S_{n}$ un ensemble $n$-mignon de cardinal aussi petit que possible. Nous allons démontrer, par récurrence sur $n$, que $\left|S_{n}\right| \geqslant\lceil n / 2\rceil+1$. Tout d'abord, pour $n=2$, le résultat désiré est immédiat. On suppose désormais que $n \geqslant 3$.
Cette fois-ci, on introduit le graphe pondéré $G$ dont les sommets sont les éléments de $S_{n}$ et qui contient, pour tout entier $k$ tel que $2 \leqslant k \leqslant n-2$, une arête $(x, y)$ de poids $F_{k}$ entre deux sommets $x$ et $y$ tels que $|x-y|=F_{k}$. Enfin, soit $u$ et $v$ deux éléments de $S_{n}$ tels que $|u-v|=F_{n}$.
Une récurrence immédiate sur $k$ montre que $F_{2}+F_{3}+\ldots+F_{k-2}=F_{k}-3$ pour tout entier $k \geqslant 4$. Par conséquent, deux sommets de $S_{n}$ appartenant à une même composante connexe de $G$ sont distants d'au plus $F_{n}-3$, et $u$ et $v$ ne peuvent pas appartenir à la même composante connexe de $G$.
Soit $U_{n}$ l'ensemble des éléments de $S_{n}$ qui appartiennent à la même composante connexe de $G$ que $u$, et soit $V_{n}$ les autres éléments de $S_{n}$. Nulle arête de $G$ n'a une extrémité dans $U_{n}$ et une autre dans $V_{n}$. Par conséquent, si l'on remplace chaque sommet $x$ de $U_{n}$ par $x+v-u$, on obtient un nouvel ensemble $S_{n}^{\prime}=\left\{x+v-u: x \in U_{n}\right\} \cup V_{n}$ de cardinal $\left|S_{n}^{\prime}\right| \leqslant\left|S_{n}\right|-1$ et qui est $(n-2)$-mignon. On en conclut comme prévu que
$$
\left|S_{n}\right| \geqslant\left|S_{n}^{\prime}\right|+1 \geqslant\lceil(n-2) / 2\rceil+1+2=\lceil n / 2\rceil+1
$$
Commentaire des correcteurs Ce problème était très difficile. La grande majorité des élèves qui l'ont abordé ont effectivement trouvé un ensemble adéquat de cardinal minimal, mais très peu ont trouvé des arguments permettant de démontrer que ce cardinal était effectivement minimal. Cette difficulté a manifestement été perçue par de nombreux élèves, et cela rend très surprenant que la moitié des élèves qui ont abordé le problème 6 n'aient pas même rendu de figure pour le problème 5.
De nombreux élèves ont identifié des constructions semblables à celle proposée ci-dessus, même si elles sont parfois apparues sous des formes beaucoup trop compliquées. Rappelons ici qu'il est toujours bon de commencer par regarder des cas particuliers pour de petites valeurs de $n$ (ici, $2 \leqslant n \leqslant 4$ ou 5 , par exemple) pour se forger une intuition sur la forme générale des objets que l'on s'apprête à construire.
L'idée de considérer un graphe implicitement ou explicitement pondéré était ensuite cruciale, et pouvait en fait survenir naturellement lorsque l'on essayait de mettre en évidence des arêtes « indispensables » à la $n$-mignonitude des ensembles considérés. De manière générale, tenter de mettre en évidence une structure combinatoire à la fois simple et usuelle (ici, un graphe) pour caractériser une propriété est souvent une bonne idée.
Enfin, de nombreux élèves on indûment affirmé que tout ensemble $n$-mignon de cardinal minimal contenait déjà un ensemble ( $n-2$ )-mignon de cardinal minimal. La solution alternative ci-dessus démontre qu'une telle affirmation est vraie, mais dans l'absolu, cette affirmation n'a rien d'évident, et il existe de nombreux problèmes analogues pour lesquels elle est grossièrement fausse.
|
{
"exam": "French_tests",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Web-Test-5.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2020"
}
|
Find the functions $f: \mathbb{N}_{\geqslant 1} \mapsto \mathbb{N}_{\geqslant 0}$ satisfying the following two conditions:
1. $f(x y)=f(x)+f(y)$ for all integers $x \geqslant 1$ and $y \geqslant 1$;
2. there exists an infinite number of integers $n \geqslant 1$ such that the equality $f(k)=f(n-k)$ holds for every integer $k$ such that $1 \leqslant k \leqslant n-1$.
We denote $\mathbb{N}_{\geqslant 0}$ the set of integers greater than or equal to 0, and $\mathbb{N}_{\geqslant 1}$ the set of integers greater than or equal to 1.
|
The sought functions are of the form $f: n \mapsto c v_{p}(n)$, where $c$ is a natural number, $p$ is a prime number, and $v_{p}(n)$ is the $p$-adic valuation of $n$. First, it is clear that these functions are indeed solutions to the problem.
Conversely, let $f$ be a non-zero solution to the problem. We say that an integer $n$ is $j o l i$ if the equality $f(k)=f(n-k)$ holds for all integers $k \leqslant 1$. Note that any divisor of a joli integer is joli. Indeed, if $d$ divides a joli integer $n=a d$, then
$$
f(k)=f(a k)-f(a)=f(n-a k)-f(a)=f(a(d-k))-f(a)=f(d-k)
$$
for all integers $k \leqslant d-1$.
Furthermore, condition 1 means that $f\left(\prod_{i} p_{i}^{\alpha_{i}}\right)=\sum_{i} \alpha_{i} f\left(p_{i}\right)$ for any prime factorization. Therefore, it is necessary to show that there is at most one prime $p$ for which $f(p)>0$. We then consider the smallest integer $p$ such that $f(p)>0$. The above formula indicates that $p$ is prime, and we set $c=f(p)$.
If there exists a joli integer $n \geqslant p$ that $p$ does not divide, let $n=p q+r$, with $q$ an integer and $1 \leqslant r \leqslant p-1$. Since $n$ is joli, we know that $f(r)=f(n-p q)=f(p q) \geqslant f(p)>0$, which contradicts the definition of $p$. Thus, every joli integer is of the form $a p^{b}$ with $b$ an integer and $1 \leqslant a \leqslant p-1$. Conversely, since there are infinitely many joli integers and $a$ can only take a finite number of values, every power of $p$ divides a joli integer, and is therefore joli itself.
Consequently, for any prime $q$ different from $p$, the integer $p^{q-1}$ is joli. Since $q$ divides $p^{q-1}-1$, we deduce in particular that $0=f(1)=f\left(p^{q-1}-1\right) \geqslant f(q)$, which concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Trouver les fonctions $f: \mathbb{N}_{\geqslant 1} \mapsto \mathbb{N}_{\geqslant 0}$ vérifiant les deux conditions suivantes :
1. $f(x y)=f(x)+f(y)$ pour tous les entiers $x \geqslant 1$ et $y \geqslant 1$;
2. il existe une infinité d'entiers $n \geqslant 1$ tels que l'égalité $f(k)=f(n-k)$ est vraie pour tout entier $k$ tel que $1 \leqslant k \leqslant n-1$.
On note $\mathbb{N}_{\geqslant 0}$ l'ensemble des entiers supérieurs ou égaux à 0 , et $\mathbb{N}_{\geqslant 1}$ l'ensemble des entiers supérieurs ou égauxà 1.
|
Les fonctions recherchées sont les fonctions de la forme $f: n \mapsto c v_{p}(n)$, où $c$ est un entier naturel, $p$ est un nombre premier, et $v_{p}(n)$ et la valuation $p$-adique de $n$. Tout d'abord, il est clair que ces fonctions sont bien solutions du problème.
Réciproquement, soit $f$ une solution non nulle du problème. On dit qu'un entier $n$ est $j o l i$ si l'égalité $f(k)=f(n-k)$ est vraie pour tout entier $k \leqslant 1$. Remarquons que tout diviseur d'un joli entier est joli. En effet, si $d$ divise un joli entier $n=a d$, alors
$$
f(k)=f(a k)-f(a)=f(n-a k)-f(a)=f(a(d-k))-f(a)=f(d-k)
$$
pour tout entier $k \leqslant d-1$.
En outre, la condition 1 signifie que $f\left(\prod_{i} p_{i}^{\alpha_{i}}\right)=\sum_{i} \alpha_{i} f\left(p_{i}\right)$ pour toute décomposition en produit de facteurs premiers. Il s'agit donc de démontrer qu'il existe au plus un nombre premier $p$ pour lequel $f(p)>0$. On considère alors le plus petit entier $p$ tel que $f(p)>0$. La formule ci-dessus indique que $p$ est premier, et on pose $c=f(p)$.
S'il existe un joli entier $n \geqslant p$ que $p$ ne divise pas, posons $n=p q+r$, avec $q$ entier et $1 \leqslant r \leqslant p-1$. Puisque $n$ est joli, on sait que $f(r)=f(n-p q)=f(p q) \geqslant f(p)>0$, en contradiction avec la définition de $p$. Ainsi, tout entier joli est de la forme $a p^{b}$ avec $b$ entier et $1 \leqslant a \leqslant p-1$. Réciproquement, puisqu'il existe une infinité d'entiers jolis et que $a$ ne peut prendre qu'un nombre fini de valeurs, toute puissance de $p$ divise un joli entier, et est donc elle-même jolie.
Par conséquent, pour tout nombre premier $q$ distinct de $p, l^{\prime}$ entier $p^{q-1}$ est joli. Puisque $q$ divise $p^{q-1}-1$, on en déduit en particulier que $0=f(1)=f\left(p^{q-1}-1\right) \geqslant f(q)$, ce qui conclut.
|
{
"exam": "French_tests",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Web-Test-5.jsonl",
"solution_match": "\nSolution de l'exercice 7",
"tier": "T1",
"year": "2020"
}
|
Find the functions $f: \mathbb{N}_{\geqslant 1} \mapsto \mathbb{N}_{\geqslant 0}$ satisfying the following two conditions:
1. $f(x y)=f(x)+f(y)$ for all integers $x \geqslant 1$ and $y \geqslant 1$;
2. there exists an infinite number of integers $n \geqslant 1$ such that the equality $f(k)=f(n-k)$ holds for every integer $k$ such that $1 \leqslant k \leqslant n-1$.
We denote $\mathbb{N}_{\geqslant 0}$ the set of integers greater than or equal to 0, and $\mathbb{N}_{\geqslant 1}$ the set of integers greater than or equal to 1.
|
$n^{\circ} 1$ Once it is established that every pretty integer is of the form $a p^{b}$, with $b$ an integer and $1 \leqslant a \leqslant p-1$, and that every divisor of a pretty integer is pretty, one can also proceed as follows.
Suppose there exists a prime number $q \neq p$ for which $f(q)>0$, and let $q$ be the smallest such prime number. We then consider the smallest pretty integer $n>q$, and write $n$ in the form $n=a p^{b}=u q+v$, with $u$ an integer and $0 \leqslant v \leqslant q-1$.
Since $n>q>p$, we know that $b \geqslant 1$, so $p$ divides $n$, and since $q$ does not divide $n$, we know that $v \geqslant 1$. Under these conditions, $f(v)=f(u q)>0$, and the minimality of $q$ indicates that $p$ divides $v$. But then $p$ also divides $u q=n-v$, and $p$ is coprime with $q$, so $p$ divides $u$. We deduce that $n>p q$, so the pretty integer $n / p$ also satisfies the inequality $n / p>q$, contradicting the minimality of $n$. Our assumption is thus invalid, which concludes the proof.
Comment from the graders The problem was very difficult and, even though it was widely attempted, very few students managed to score even a point. The first thing to understand in such a problem is the set of solutions: indeed, many students tried to prove that $f$ was zero, when many other functions were solutions. Any proof that did not take this into account could not succeed, nor introduce the right tools as in the given solution: thus, it was difficult to score points without understanding the solutions.
It is also regrettable that many students sought, without success, conclusive elements for problem 7 without even addressing problem 5. As in the International Mathematical Olympiads, the problems are presented in increasing order of difficulty. Thus, basic remarks on problems 5 and 6 are more likely to score points than on problem 7. This does not mean, however, that one should automatically "forget" to tackle problem 7: it is obviously advisable to at least look at each problem, but one must know how to focus efforts on the more accessible problems.
|
proof
|
Yes
|
Incomplete
|
proof
|
Number Theory
|
Trouver les fonctions $f: \mathbb{N}_{\geqslant 1} \mapsto \mathbb{N}_{\geqslant 0}$ vérifiant les deux conditions suivantes :
1. $f(x y)=f(x)+f(y)$ pour tous les entiers $x \geqslant 1$ et $y \geqslant 1$;
2. il existe une infinité d'entiers $n \geqslant 1$ tels que l'égalité $f(k)=f(n-k)$ est vraie pour tout entier $k$ tel que $1 \leqslant k \leqslant n-1$.
On note $\mathbb{N}_{\geqslant 0}$ l'ensemble des entiers supérieurs ou égaux à 0 , et $\mathbb{N}_{\geqslant 1}$ l'ensemble des entiers supérieurs ou égauxà 1.
|
$n^{\circ} 1$ Une fois acquis le fait que tout entier joli est de la forme $a p^{b}$, avec $b$ entier et $1 \leqslant a \leqslant p-1$, et que tout diviseur d'un entier joli est joli, on peut aussi procéder comme suit.
Supposons qu'il existe un nombre premier $q \neq p$ pour lequel $f(q)>0$, et soit $q$ le plus petit tel nombre premier. On considère alors le plus petit entier joli $n>q$, puis on écrit $n$ sous la forme $n=a p^{b}=u q+v$, avec $u$ entier et $0 \leqslant v \leqslant q-1$.
Puisque $n>q>p$, on sait que $b \geqslant 1$, donc que $p$ divise $n$, et comme $q$ ne divise pas $n$, on sait que $v \geqslant 1$. Dans ces conditions, $f(v)=f(u q)>0$, et la minimalité de $q$ indique que $p$ divise $v$. Mais alors $p$ divise aussi $u q=n-v$, et $p$ est premier avec $q$, donc $p$ divise $u$. On en déduit que $n>p q$, donc que le joli entier $n / p$ satisfait lui aussi l'inégalité $n / p>q$, en contradiction avec la minimalité de $n$. Notre supposition est ainsi invalide, ce qui conclut.
Commentaire des correcteurs L'exercice était très difficile et, même s'il a été beaucoup traité, très peu d'élèves ont réussi à avoir ne serait-ce qu'un point. Dans un tel exercice, la première chose à comprendre est l'ensemble des solutions : en effet, beaucoup d'élèves ont tenté de prouver que $f$ était nulle, quand beaucoup d'autres fonctions étaient des solutions. En particulier, toute preuve qui ne prenait pas en compte cela ne pouvait pas aboutir, ni introduire les bons outils comme dans la solution donnée : ainsi il était difficile d'avoir des points sans comprendre les solutions.
Il est aussi regrettable que de nombreux élèves aient cherché sans aboutir à des éléments concluant le problème 7 sans même aborder le problème 5. Comme aux Olympiades Internationales, les énoncés sont proposés par ordre de difficulté croissante. Ainsi, des remarques basiques sur les problèmes 5 et 6 ont plus de chance de rapporter des points que sur le problème 7. Cela ne veut pas dire pour autant qu'il faut « oublier » d'office de s'attaquer au problème 7 : il est évidemment conseillé de regarder au moins un peu chaque problème, mais il faut savoir consacrer ses efforts sur les problèmes plus accessibles.
|
{
"exam": "French_tests",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/tests/fr-2020-2021-Corrigé-Web-Test-5.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T1",
"year": "2020"
}
|
Let $ABCD$ be a parallelogram. The internal bisector of angle $\widehat{BAC}$ intersects the segment $[BC]$ at $E$, while its external bisector intersects the line $(CD)$ at $F$. Let $M$ be the midpoint of the segment $[AE]$.
Prove that the lines $(EF)$ and $(BM)$ are parallel.
|
Let $G$ be the intersection point of the lines $(A B)$ and $(E F)$. The problem reduces to proving that $(M B)$ is a midline of the triangle $A E G$, that is, that $B$ is the midpoint of $[A G]$.
Similarly, let $H$ be the intersection point of the lines $(A E)$ and $(C D)$. The homothety centered at $E$ that maps $(A B)$ to $(C D)$ maps the points $A, B$ and $G$ to $H, C$ and $F$. Equivalently, the problem reduces to proving that $C$ is the midpoint of $[H F]$.
Now, in terms of angles between lines,
$$
\begin{aligned}
(A C, A F) & =(A C, A E)+(A E, A F)=(A E, A B)+90^{\circ}=(A E, A B)+(A F, A E)=(A F, A B) \\
& =(F A, F C)
\end{aligned}
$$
which means that the triangle $A C F$ is isosceles at $C$. Similarly,
$$
(H A, H C)=(E A, C D)=(A E, A B)=(A C, A E)=(A C, A H)
$$
so $A C H$ is isosceles at $C$.
We conclude that $C F=C A=C H$, hence $C$ is indeed the midpoint of $[\mathrm{CH}]$.
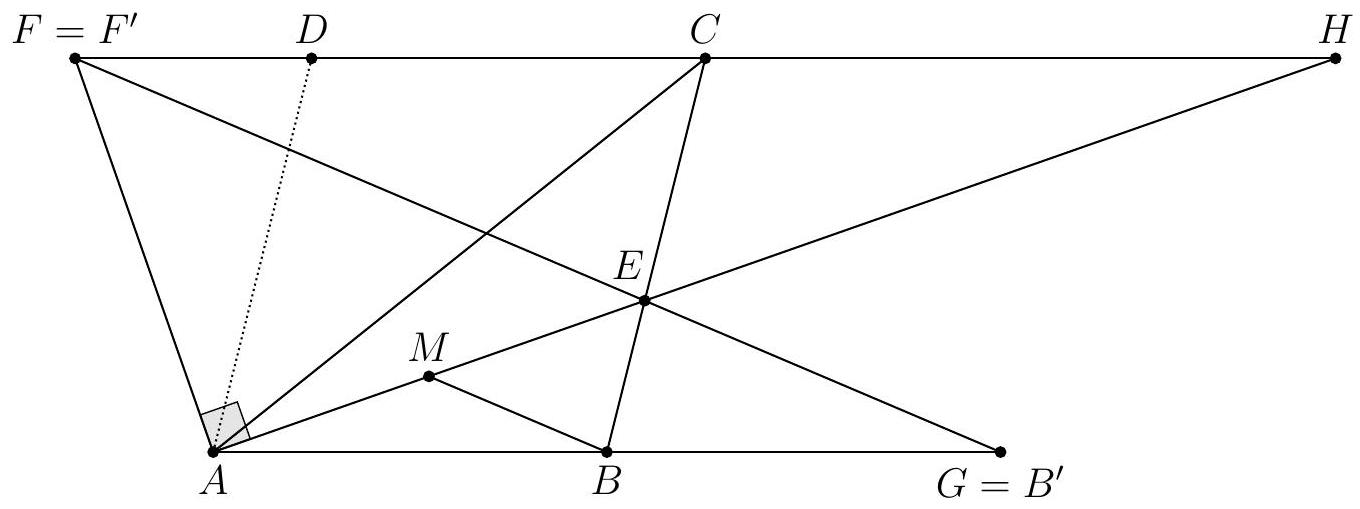
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un parallélogramme. La bissectrice intérieure de l'angle $\widehat{B A C}$ coupe le segment $[B C]$ en $E$ tandis que sa bissectrice extérieure coupe la droite ( $C D)$ en $F$. Soit $M$ le milieu du segment $[A E]$.
Démontrer que les droites $(E F)$ et $(B M)$ sont parallèles.
|
Soit $G$ le point d'intersection des droites $(A B)$ et $(E F)$. Le problème revient à démontrer que $(M B)$ est une droite des milieux du triangle $A E G$, c'est-à-dire que $B$ est le milieu de $[A G]$.
De même, soit $H$ le point d'intersection des droites $(A E)$ et $(C D)$. L'homothétie de centre $E$ qui envoie $(A B)$ sur $(C D)$ envoie les points $A, B$ et $G \operatorname{sur} H, C$ et $F$. De manière équivalente, le problème revient donc à démontrer que $C$ est le milieu de $[H F]$.
Or, en angles de droites,
$$
\begin{aligned}
(A C, A F) & =(A C, A E)+(A E, A F)=(A E, A B)+90^{\circ}=(A E, A B)+(A F, A E)=(A F, A B) \\
& =(F A, F C)
\end{aligned}
$$
ce qui signifie que le triangle $A C F$ est isocèle en $C$. De même,
$$
(H A, H C)=(E A, C D)=(A E, A B)=(A C, A E)=(A C, A H)
$$
donc $A C H$ est isocèle en $C$.
On en conclut que $C F=C A=C H$, donc que $C$ est bien le milieu de $[\mathrm{CH}]$.

|
{
"exam": "French_tests",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/tests/fr-2021-2022-Corrigé-Web-Test-1.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T1",
"year": "2021"
}
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.