problem
stringlengths 14
10.4k
| solution
stringlengths 1
24.1k
| answer
stringlengths 1
250
⌀ | problem_is_valid
stringclasses 4
values | solution_is_valid
stringclasses 3
values | question_type
stringclasses 4
values | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
10.4k
| solution_raw
stringlengths 1
24.1k
| metadata
dict |
|---|---|---|---|---|---|---|---|---|---|
Do there exist strictly positive integers $a$ and $b$ such that $a^{n}+n^{b}$ and $b^{n}+n^{a}$ are coprime for all integers $n \geqslant 0$?
|
By contradiction: suppose there exist such integers $a$ and $b$.
By symmetry, we can assume that $a \geqslant b$.
If $d=\operatorname{gcd}(a, b)$, then for $n=d$, it is clear that $d$ divides $a^{d}+d^{b}$ and $b^{d}+d^{a}$. Since these two numbers are supposed to be coprime, it follows that $d=1$.
Let $N=a^{a}+b^{b}$. We have $N>1$ so there exists a prime number $p$ that divides $N$. Moreover, $p$ cannot divide $a$ without also dividing $b$, which contradicts $d=1$. Thus, $a$ is invertible modulo $p$ and there exists an integer $k \in\{0, \cdots, p-1\}$ such that $k a=b \bmod [p]$.
We then choose $n=k+p(a-b-k+p-1)$. By Fermat's little theorem, we get:
$$
a^{n}+n^{b} \equiv a^{k} \cdot a^{a-b-k+p-1}+k^{b} \equiv a^{a-b}+k^{b} \bmod [p]
$$
where $a^{b}\left(a^{n}+n^{b}\right) \equiv a^{a}+b^{b} \equiv 0 \bmod [p]$,
and since $p$ does not divide $a$, we have $a^{n}+n^{b} \equiv 0 \bmod [p]$.
Similarly, we have $b^{n}+n^{a} \equiv 0 \bmod [p]$.
But then $p$ divides both $a^{n}+n^{b}$ and $b^{n}+n^{a}$, which contradicts their being coprime.
Finally, there do not exist such integers.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Existe-t-il des entiers strictement positifs $a$ et $b$ tels que $a^{n}+n^{b}$ et $b^{n}+n^{a}$ soient premiers entre eux pour tout entier $n \geqslant 0$ ?
|
Par l'absurde : supposons qu'il existe de tels entiers a et b.
Par symétrie, on peut supposer que $a \geqslant b$.
Si $d=\operatorname{pgcd}(a, b)$ alors, pour $n=d$, il est clair que $d$ divise $a^{d}+d^{b}$ et $b^{d}+d^{a}$. Or ces deux nombres étant censés être premiers entre eux, c'est que $d=1$.
Soit $N=a^{a}+b^{b}$. On a $N>1$ donc il existe un nombre premier $p$ qui divise $N$. De plus, $p$ ne peut diviser a sans quoi il devrait diviser également $b$, en contradiction avec $d=1$. Ainsi, $a$ est inversible modulo $p$ et il existe un entier $k \in\{0, \cdots, p-1\}$ tel que $k a=b \bmod [p]$.
On choisit alors $n=k+p(a-b-k+p-1)$. D'après le petit théorème de Fermat, il vient :
$$
a^{n}+n^{b} \equiv a^{k} \cdot a^{a-b-k+p-1}+k^{b} \equiv a^{a-b}+k^{b} \bmod [p]
$$
$d^{\prime}$ où $a^{b}\left(a^{n}+n^{b}\right) \equiv a^{a}+b^{b} \equiv 0 \bmod [p]$,
et, puisque $p$ ne divise par $a$, on a alors $a^{n}+n^{b} \equiv 0 \bmod [p]$.
On prouve de même, on a $b^{n}+n^{a} \equiv 0 \bmod [p]$.
Mais, alors $p$ divise à la fois $a^{n}+n^{b}$ et $b^{n}+n^{a}$, ce qui contredit qu'ils soient premiers entre eux.
Finalement, il n'existe pas de tels entiers.
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/envois/fr-ofm-2014-2015-envoi-6-solutions.jsonl",
"solution_match": "## Solution de l'exercice 6",
"tier": "T2",
"year": "2015"
}
|
The Xantians are the inhabitants, potentially in infinite number, of the planet Xanta. Regarding themselves and their peers, the Xantians are capable of feeling two types of emotions, which they call love and respect. It has been observed that:
- Each Xantian loves one and only one Xantian, and respects one and only one Xantian.
- If $A$ loves $B$, then any Xantian who respects $A$ also loves $B$.
- If $A$ respects $B$, then any Xantian who loves $A$ also respects $B$.
- Each Xantian is loved by at least one Xantian.
Is it true that each Xantian respects the Xantian they love?
|
For each Xantian $x$, let $f(x)$ and $g(x)$ denote the Xantians loved and respected by $x$.
The first condition ensures that we have well-defined functions $f$ and $g$ from the set $X$ of Xantiens to itself.
The question is whether, for all $x$, we have $f(x)=g(x)$.
In fact, we will even prove that, for all $x$, we have $f(x)=g(x)=x$.
Let $x$ be a Xantian.
He respects $g(x)$, who, in turn, loves $f(g(x))$.
The second condition therefore ensures that $f(g(x))=f(x)$ for all $x$. (1)
Similarly, the third condition leads to $g(f(x))=g(x)$ for all $x$. (2)
Finally, the fourth condition means that $f$ is surjective.
Let $x$ be a Xantian. There therefore exists a Xantian $y$ such that $f(y)=x$.
We have $f(g(f(y)))=f(g(y))$ according to (2),
and thus, according to (1), it follows that $f(f(y))=f(y)$, or $f(x)=x$.
From (1), we immediately deduce that $g(x)=x$.
Ultimately, for all $x$, we have $f(x)=g(x)=x$.
|
proof
|
Yes
|
Yes
|
proof
|
Logic and Puzzles
|
Les Xantiens sont les habitants, en nombre éventuellement infini, de la planète Xanta. Vis-à-vis d'eux-mêmes et de leurs semblables, les Xantiens sont capables de ressentir deux types d'émotions, qu'ils appellent amour et respect. Il a été observé que:
- Chaque Xantien aime un et un seul Xantien, et respecte un et un seul Xantien.
- Si $A$ aime $B$, alors tout Xantien qui respecte $A$ aime également $B$.
- Si $A$ respecte $B$, alors tout Xantien qui aime $A$ respecte également $B$.
- Chaque Xantien est aimé d'au moins un Xantien.
Est-il vrai que chaque Xantien respecte le Xantien qu'il aime?
|
Pour chaque Xantien $x$, désignons respectivement par $f(x)$ et $g(x)$ les Xantiens aimés et respectés par $x$.
La première condition assure que l'on a bien défini des fonctions $f$ et $g$ de l'ensemble $X$ des Xantiens sur lui-même.
Il s'agit de savoir si, pour tout $x$, on a $f(x)=g(x)$.
En fait, nous allons même prouver que, pour tout $x$, on a $f(x)=g(x)=x$.
Soit $x$ un Xantien.
Il respecte $g(x)$ qui, de son côté, aime $f(g(x))$.
La seconde condition assure donc que $f(g(x))=f(x)$ pour tout $x$. (1)
De même, la troisième condition conduit à $g(f(x))=g(x)$ pour tout $x$. (2)
Enfin, la quatrième condition signifie que f est surjective.
Soit $x$ un Xantien. Il existe donc un Xantien $y$ tel que $f(y)=x$.
Or, on a $f(g(f(y)))=f(g(y))$ d'après (2)
et ainsi, d'après (1), il vient $f(f(y))=f(y)$, ou encore $f(x)=x$.
De (1), on déduit alors immédiatement que $g(x)=x$.
Finalement, pour tout $x$, on a bien $f(x)=g(x)=x$.
|
{
"exam": "French_envois",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/envois/fr-ofm-2014-2015-envoi-6-solutions.jsonl",
"solution_match": "## Solution de l'exercice 7",
"tier": "T2",
"year": "2015"
}
|
Determine all strictly positive integers \(a\) and \(b\) such that \(4a+1\) and \(4b-1\) are coprime, and such that \(a+b\) divides \(16ab+1\).
|
Let's denote (C) as the condition in the statement. The integers $4 \mathbf{a}+1$ and $4 \mathrm{~b}-1$ are coprime if and only if $4 \boldsymbol{a}+1$ is coprime with $(4 a+1)+(4 b-1)=4(a+b)$. Since $4 \boldsymbol{a}+1$ is odd, it is automatically coprime with 4. We deduce that $4 \boldsymbol{a}+1$ and $4 \boldsymbol{b}-1$ are coprime if and only if $4 a+1$ is coprime with $a+b$.
On the other hand, $16 a b+1=16 a(a+b)+\left(1-16 a^{2}\right)=16 a(a+b)-(4 a-1)(1+4 a)$, so $a+b$ divides $16 a b+1$ if and only if $a+b$ divides $(4 a-1)(1+4 a)$. If $a+b$ is coprime with $1+4 a$, then this is equivalent to $a+b \mid 4 a-1$.
We deduce that (C) is equivalent to $\operatorname{pgcd}(a+b, 4 a+1)=1$ and $a+b \mid 4 a-1$.
On the other hand, let's show that if $a+b \mid 4 a-1$ then we automatically have $\operatorname{pgcd}(a+b, 4 a+1)=1$. Indeed, if a prime number $p$ divides $a+b$ and $4 a+1$, then it divides $4 a-1$ and $4 a+1$, so it divides $(4 a+1)-(4 a-1)=2$. Thus, $p=2$, and $2 \mid 4 a-1$. Impossible.
Finally, (C) is equivalent to $\mathrm{a}+\mathrm{b} \mid 4 \mathrm{a}-1$.
Since $\mathrm{a}+\mathrm{b}>\mathrm{a}>\frac{4 \mathrm{a}-1}{4}$, $\mathrm{a}+\mathrm{b} \mid 4 \mathrm{a}-1$ can only occur if $\mathrm{a}+\mathrm{b}=4 \mathrm{a}-1$ or $\mathrm{a}+\mathrm{b}=\frac{4 \mathrm{a}-1}{2}$ or $\mathrm{a}+\mathrm{b}=\frac{4 \mathrm{a}-1}{3}$.
The second case cannot occur because $4 a-1$ is odd.
(C) is therefore equivalent to $\mathrm{a}+\mathrm{b}=4 \mathrm{a}-1$ or $\mathrm{a}+\mathrm{b}=\frac{4 \mathrm{a}-1}{3}$, i.e., $\mathrm{b}=3 \mathrm{a}-1$ or $\mathrm{a}=3 \mathrm{~b}+1$.
|
b=3a-1 \text{ or } a=3b+1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer tous les entiers strictement positifs a et $b$ tels que $4 \boldsymbol{a}+1$ et $4 \boldsymbol{b}-1$ soient premiers entre eux, et tels que $a+b$ divise $16 a b+1$.
|
Notons (C) la condition de l'énoncé. Les entiers $4 \mathbf{a}+1$ et $4 \mathrm{~b}-1$ sont premiers entre eux si et seulement si $4 \boldsymbol{a}+1$ est premier avec $(4 a+1)+(4 b-1)=4(a+b)$. Or, $4 \boldsymbol{a}+1$ est impair donc il est automatiquement premier avec 4 . On en déduit que $4 \boldsymbol{a}+1$ et $4 \boldsymbol{b}-1$ sont premiers entre eux si et seulement si $4 a+1$ est premier avec $a+b$.
D'autre part, $16 a b+1=16 a(a+b)+\left(1-16 a^{2}\right)=16 a(a+b)-(4 a-1)(1+4 a)$, donc $a+b$ divise $16 a b+1$ si et seulement si $a+b$ divise $(4 a-1)(1+4 a)$. Or, si $a+b$ est premier avec $1+4 a$ alors ceci équivaut à $a+b \mid 4 a-1$.
On en déduit que (C) équivaut à ce que $\operatorname{pgcd}(a+b, 4 a+1)=1$ et $a+b \mid 4 a-1$.
D'autre part, montrons que si $a+b \mid 4 a-1$ alors on a automatiquement $\operatorname{pgcd}(a+b, 4 a+1)=1$. En effet, si un nombre premier $p$ divise $a+b$ et $4 a+1$, alors il divise $4 a-1$ et $4 a+1$, donc il divise $(4 a+1)-(4 a-1)=2$. Il vient $p=2$, puis $2 \mid 4 a-1$. Impossible.
Finalement, (C) équivaut à $\mathrm{a}+\mathrm{b} \mid 4 \mathrm{a}-1$.
Or, $\mathrm{a}+\mathrm{b}>\mathrm{a}>\frac{4 \mathrm{a}-1}{4}$, donc $\mathrm{a}+\mathrm{b} \mid 4 \mathrm{a}-1$ ne peut se produire que si $\mathrm{a}+\mathrm{b}=4 \mathrm{a}-1$ ou $\mathrm{a}+\mathrm{b}=\frac{4 \mathrm{a}-1}{2}$ ou $\mathrm{a}+\mathrm{b}=\frac{4 \mathrm{a}-1}{3}$.
Le deuxième cas ne peut pas se produire car $4 a-1$ est impair.
(C) équivaut donc à $\mathrm{a}+\mathrm{b}=4 \mathrm{a}-1$ ou $\mathrm{a}+\mathrm{b}=\frac{4 \mathrm{a}-1}{3}$, $\mathrm{c}^{\prime}$ est-à-dire $\mathrm{b}=3 \mathrm{a}-1$ ou $\mathrm{a}=3 \mathrm{~b}+1$.
|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "\nExercice 8.",
"resource_path": "French/segmented/envois/fr-ofm-2014-2015-envoi-6-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 8",
"tier": "T2",
"year": "2015"
}
|
Let $ABC$ be a triangle such that $\widehat{A}=40^{\circ}$ and $\widehat{B}=60^{\circ}$. Let $D$ and $E$ be points on $[AC]$ and $[\mathrm{AB}]$ such that $\widehat{\mathrm{CBD}}=40^{\circ}$ and $\widehat{\mathrm{ECB}}=70^{\circ}$. We denote $F$ as the intersection of $(BD)$ and $(CE)$. Show that $(A F) \perp(B C)$.
|
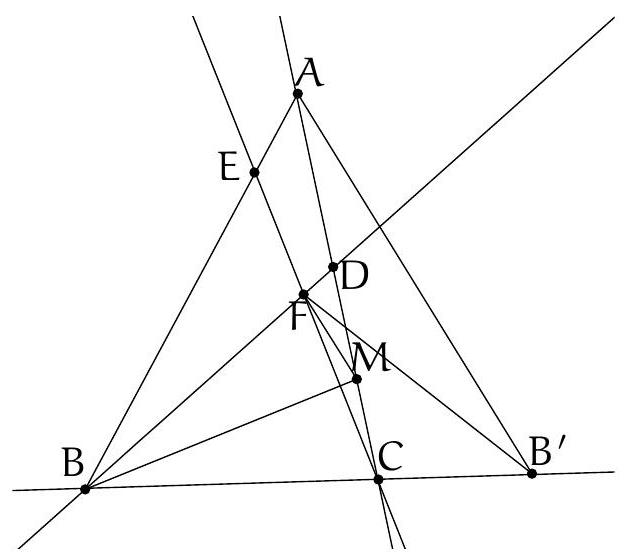
In $\widehat{\mathrm{BFC}}=180^{\circ}-\widehat{\mathrm{CBF}}-\widehat{\mathrm{FCB}}=180^{\circ}-40^{\circ}-70^{\circ}=70^{\circ}=\widehat{\mathrm{FCB}}$, so BCF is isosceles at B. It follows that $B C=B F$.
Let $M$ be the intersection point between the bisector of $\widehat{C B F}$ and ( $A C$ ). We have $\widehat{B M A}=40^{\circ}=\widehat{B A M}$, so $M A=M B$.
On the other hand, $\widehat{B M C}=180^{\circ}-\widehat{C B M}-\widehat{M C B}=180^{\circ}-20^{\circ}-80^{\circ}=80^{\circ}=\widehat{M C B}$, so $B C=B M$.
From the above, we deduce that $M A=B F$.
Let $\mathrm{B}^{\prime} \in(\mathrm{BC})$ such that $A B^{\prime}$ is equilateral. Let $\Delta$ be the bisector of $\widehat{\mathrm{B}^{\prime} \mathrm{BA}}$. Since $\mathrm{BF}=\mathrm{BM}$ and $\widehat{\mathrm{FBA}}=\widehat{\mathrm{CBM}}$, the points $M$ and $F$ are symmetric with respect to $\Delta$. Also, $A$ and $B^{\prime}$ are symmetric with respect to $\Delta$, so $M A=\mathrm{FB}^{\prime}$.
Finally, $\mathrm{FB}^{\prime}=\mathrm{FB}$, so $F$ lies on the perpendicular bisector of $\left[\mathrm{BB}^{\prime}\right]$, which is also the altitude ( $A F$ ) of the triangle $A B B^{\prime}$.
Another solution. Let $H$ be the projection of $F$ on $[B C]$ and $H^{\prime}$ the projection of $A$ on [BC]. It suffices to show that $\mathrm{H}=\mathrm{H}^{\prime}$. For this, it is enough to see that $\mathrm{BH}=\mathrm{BH}^{\prime}$.
We have $B^{\prime}=A B \cos 60$ and $B H=B F \cos 40=B C \cos 40$. Since $\frac{A B}{B C}=\frac{\sin 80}{\sin 40}$, it suffices to show that $\sin 80 \cos 60=\sin 40 \cos 40$, which is equivalent (given that $\cos 60=\frac{1}{2}$) to $\sin 80=2 \sin 40 \cos 40$, which is true according to the general formula $\sin 2 x=2 \sin x \cos x$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle tel que $\widehat{A}=40^{\circ}$ et $\widehat{B}=60^{\circ}$. Soient $D$ et $E$ des points de [AC] et $[\mathrm{AB}]$ tels que $\widehat{\mathrm{CBD}}=40^{\circ}$ et $\widehat{\mathrm{ECB}}=70^{\circ}$. On note F l'intersection de (BD) et (CE). Monter que $(A F) \perp(B C)$.
|

On a $\widehat{\mathrm{BFC}}=180^{\circ}-\widehat{\mathrm{CBF}}-\widehat{\mathrm{FCB}}=180^{\circ}-40^{\circ}-70^{\circ}=70^{\circ}=\widehat{\mathrm{FCB}}$ donc BCF est isocèle en B . Il vient $B C=B F$.
Soit $M$ le point d'intersection entre la bissectrice de $\widehat{C B F}$ et ( $A C$ ). On a $\widehat{B M A}=40^{\circ}=\widehat{B A M}$ donc $M A=M B$.
D'autre part, $\widehat{B M C}=180^{\circ}-\widehat{C B M}-\widehat{M C B}=180^{\circ}-20^{\circ}-80^{\circ}=80^{\circ}=\widehat{M C B}$ donc $B C=B M$.
On déduit de ce qui précède que $M A=B F$.
Soit $\mathrm{B}^{\prime} \in(\mathrm{BC})$ tel que $A B^{\prime}$ est équilatéral. Soit $\Delta$ la bissectrice de $\widehat{\mathrm{B}^{\prime} \mathrm{BA}}$. Comme $\mathrm{BF}=\mathrm{BM}$ et $\widehat{\mathrm{FBA}}=\widehat{\mathrm{CBM}}$, les points $M$ et $F$ sont symétriques par rapport à $\Delta$. Or, $A$ et $B^{\prime}$ sont aussi symétriques par rapport à $\Delta$, donc $M A=\mathrm{FB}^{\prime}$.
Finalement, $\mathrm{FB}^{\prime}=\mathrm{FB}$, donc $F$ appartient à la médiatrice de $\left[\mathrm{BB}^{\prime}\right]$, qui est aussi la hauteur ( $A F$ ) du triangle $A B B^{\prime}$.
Autre solution. Notons $H$ le projeté de $F$ sur $[B C]$ et $H^{\prime}$ le projeté de $A$ sur [BC]. Il s'agit de montrer que $\mathrm{H}=\mathrm{H}^{\prime}$. Pour cela, il suffit de voir que $\mathrm{BH}=\mathrm{BH}^{\prime}$.
On a $B^{\prime}=A B \cos 60$ et $B H=B F \cos 40=B C \cos 40$. Comme $\frac{A B}{B C}=\frac{\sin 80}{\sin 40}$, il suffit de montrer que $\sin 80 \cos 60=\sin 40 \cos 40$, c'est-à-dire (compte tenu de $\cos 60=\frac{1}{2}$ ) que $\sin 80=$ $2 \sin 40 \cos 40$, ce qui est vrai d'après la formule générale $\sin 2 x=2 \sin x \cos x$.
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-ofm-2014-2015-envoi-6-solutions.jsonl",
"solution_match": "## Solution de l'exercice 9",
"tier": "T2",
"year": "2015"
}
|
For any strictly positive integer $x$, we denote $S(x)$ as the sum of the digits of its decimal representation.
Let $k>0$ be an integer. We define the sequence $\left(x_{n}\right)$ by $x_{1}=1$ and $x_{n+1}=S\left(k x_{n}\right)$ for all $n>0$.
Prove that $x_{n}<27 \sqrt{k}$, for all $n>0$.
|
Lemme. For any integer $s \geqslant 0$, we have $10^{s} \geqslant(s+1)^{3}$.
Proof of the lemma. We reason by induction on $s$.
For $s=0$, we have $10^{0}=1=(0+1)^{3}$.
Suppose the inequality is true for the value $s$. Then:
$10^{\mathrm{s}+1} \geqslant 10(\mathrm{~s}+1)^{3}$ according to the induction hypothesis
$=10 s^{3}+30 s^{2}+30 s+10$
$\geqslant \mathrm{s}^{3}+6 \mathrm{~s}^{2}+12 \mathrm{~s}+8$
$=(s+2)^{3}$, which completes the proof.
If $x>0$ is an integer whose decimal representation uses $s+1$ digits, we have $S(x) \leqslant 9(s+1)$ and $10^{s} \leqslant x<10^{s+1}$. From the lemma, we have $s+1 \leqslant 10^{\frac{s}{3}}$, so $s+1 \leqslant x^{\frac{1}{3}}$ and thus $S(x) \leqslant 9 x^{\frac{1}{3}}$.
Now let's show by induction that $x_{n}<27 \sqrt{k}$ for all $n$. The statement is clear for $n=1$. Suppose $x_{n}<27 \sqrt{k}$, then $x_{n+1}=S\left(k x_{n}\right) \leqslant 9\left(k x_{n}\right)^{\frac{1}{3}}<9(27 k \sqrt{k})^{\frac{1}{3}}=9 \times 3 \times \sqrt{k}=$ $27 \sqrt{\mathrm{k}}$, hence the result.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Pour tout entier strictement positif $x$, on note $S(x)$ la somme des chiffres de son écriture décimale.
Soit $k>0$ un entier. On définit la suite $\left(x_{n}\right)$ par $x_{1}=1$ et $x_{n+1}=S\left(k x_{n}\right)$ pour tout $n>0$.
Prouver que $x_{n}<27 \sqrt{k}$, pour tout $n>0$.
|
Lemme. Pour tout entier $s \geqslant 0$, on a $10^{s} \geqslant(s+1)^{3}$.
Preuve du lemme. On raisonne par récurrence sur s.
Pour $s=0$, on a $10^{0}=1=(0+1)^{3}$.
Supposons l'inégalité vraie pour la valeur s. Alors :
$10^{\mathrm{s}+1} \geqslant 10(\mathrm{~s}+1)^{3}$ d'après l'hypothèse de récurrence
$=10 s^{3}+30 s^{2}+30 s+10$
$\geqslant \mathrm{s}^{3}+6 \mathrm{~s}^{2}+12 \mathrm{~s}+8$
$=(s+2)^{3}$, ce qui achève la preuve.
Si $x>0$ est un entier dont l'écriture décimale utilise $s+1$ chiffres, on a $S(x) \leqslant 9(s+1)$ et $10^{s} \leqslant x<10^{s+1}$. Or, d'après le lemme, on a $s+1 \leqslant 10^{\frac{s}{3}}$, donc $s+1 \leqslant x^{\frac{1}{3}}$ et ainsi $S(x) \leqslant 9 x^{\frac{1}{3}}$.
Montrons maintenant par récurrence que $x_{n}<27 \sqrt{k}$ pour tout $n$. L'assertion est claire pour $n=1$. Supposons $x_{n}<27 \sqrt{k}$, alors $x_{n+1}=S\left(k x_{n}\right) \leqslant 9\left(k x_{n}\right)^{\frac{1}{3}}<9(27 k \sqrt{k})^{\frac{1}{3}}=9 \times 3 \times \sqrt{k}=$ $27 \sqrt{\mathrm{k}}$, d'où le résultat.
|
{
"exam": "French_envois",
"problem_label": "10",
"problem_match": "\nExercice 10.",
"resource_path": "French/segmented/envois/fr-ofm-2014-2015-envoi-6-solutions.jsonl",
"solution_match": "## Solution de l'exercice 10",
"tier": "T2",
"year": "2015"
}
|
Let $a, b, c$ be three strictly positive real numbers such that $a+b+c=9$. Show that
$$
\frac{a^{3}+b^{3}}{a b+9}+\frac{b^{3}+c^{3}}{b c+9}+\frac{c^{3}+a^{3}}{c a+9} \geqslant 9
$$
|
We are looking for a lower bound of the form $\frac{a^{3}+b^{3}}{a b+9} \geqslant u(a+b)+v$, that is, $f(a) \geqslant 0$ where $f(a)=a^{3}+b^{3}-(u(a+b)+v)(a b+9)$.
By summing the three inequalities, we would deduce $\frac{a^{3}+b^{3}}{a b+9}+\frac{b^{3}+c^{3}}{b c+9}+\frac{c^{3}+a^{3}}{c a+9} \geqslant 2 u(a+b+c)+3 v = 3(6 u+v)$, so it suffices that $6 u+v=3$.
On the other hand, if such a lower bound exists, since the inequality becomes an equality when $a = b = c = 3$, we must have $f(3)=0$ if $b=3$. Since $f(a) \geqslant 0$ for all $a$, we must necessarily have $f'(3)=0$ for $b=3$.
This imposes the condition $0=f'(3)=27-18 u-(6 u+v) \times 3=18(1-u)$, so $u=1$ and $v=-3$.
Let's show $\frac{a^{3}+b^{3}}{a b+9} \geqslant(a+b)-3$. Since $a^{3}+b^{3} \geqslant \frac{(a+b)^{3}}{4}$ and $a b+9 \leqslant\left(\frac{a+b}{2}\right)^{2}+9$, it suffices to show that
$$
\frac{s^{3}}{s^{2}+36} \geqslant s-3
$$
where $s=a+b$. We reduce to a common denominator; the inequality simplifies to $3 s^{2}-36 s+108 \geqslant 0$, or equivalently $3(s-6)^{2} \geqslant 0$, which is true.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soient $a, b, c$ trois nombres réels strictement positifs tels que $a+b+c=9$. Montrer que
$$
\frac{a^{3}+b^{3}}{a b+9}+\frac{b^{3}+c^{3}}{b c+9}+\frac{c^{3}+a^{3}}{c a+9} \geqslant 9
$$
|
On cherche une minoration de la forme $\frac{a^{3}+b^{3}}{a b+9} \geqslant u(a+b)+v, c^{\prime}$ est-àdire $f(a) \geqslant 0$ où $f(a)=a^{3}+b^{3}-(u(a+b)+v)(a b+9)$.
En sommant les trois inégalités, on en déduirait $\frac{a^{3}+b^{3}}{a b+9}+\frac{b^{3}+c^{3}}{b c+9}+\frac{c^{3}+a^{3}}{c a+9} \geqslant 2 u(a+b+c)+3 v=$ $3(6 u+v)$, donc il suffit que $6 u+v=3$.
D'autre part, si une telle minoration existe, comme l'inégalité devient une égalité lorsque $\mathrm{a}=$ $\mathrm{b}=\mathrm{c}=3$, on doit avoir $\mathrm{f}(3)=0$ si $\mathrm{b}=3$. Comme de plus $\mathrm{f}(\mathrm{a}) \geqslant 0$ pour tout a , on doit nécessairement avoir $\mathrm{f}^{\prime}(3)=0$ pour $\mathrm{b}=3$.
Ceci impose la condition $0=f^{\prime}(3)=27-18 \mathbf{u}-(6 \mathbf{u}+\boldsymbol{v}) \times 3=18(1-\mathfrak{u})$, donc $\mathbf{u}=1$ et $v=-3$.
Montrons donc $\frac{a^{3}+b^{3}}{a b+9} \geqslant(a+b)-3$. Comme $a^{3}+b^{3} \geqslant \frac{(a+b)^{3}}{4}$ et $a b+9 \leqslant\left(\frac{a+b}{2}\right)^{2}+9$, il suffit de montrer que
$$
\frac{s^{3}}{s^{2}+36} \geqslant s-3
$$
où $s=a+b$. On réduit au même dénominateur; l'inégalité se simplifie en $3 s^{2}-36 s+108 \geqslant 0$, ou encore en $3(s-6)^{2} \geqslant 0$, ce qui est vrai.
|
{
"exam": "French_envois",
"problem_label": "11",
"problem_match": "\nExercice 11.",
"resource_path": "French/segmented/envois/fr-ofm-2014-2015-envoi-6-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 11",
"tier": "T2",
"year": "2015"
}
|
Determine all integers $\mathrm{n}>0$ having the following property: "any strictly positive number that can be written as the sum of the squares of $n$ integers that are multiples of $n$ can also be written as the sum of the squares of $n$ integers, none of which is a multiple of $\mathrm{n}^{\prime \prime}$.
Determine all integers $\mathrm{n}>0$ having the following property: "any strictly positive number that can be written as the sum of the squares of $n$ integers that are multiples of $n$ can also be written as the sum of the squares of $n$ integers, none of which is a multiple of $\mathrm{n}^{\prime \prime}$.
|
An integer n having the desired property will be called good.
Let $\mathrm{n} \geqslant 2$ be a good integer. Then 2n is also good: indeed, let $\mathrm{m}=2 \mathrm{n}$ and let $x_{1}, \cdots, x_{m}$ be integers divisible by m. If two of these integers are non-zero, we can assume without loss of generality that they are $x_{1}$ and $x_{m}$. Since $n$ is good, there then exist integers $y_{i}$ not divisible by $n$ (and therefore not divisible by $m$) such that $\sum_{i=1}^{n} x_{i}^{2}=\sum_{i=1}^{n} y_{i}^{2}$ and $\sum_{i=n+1}^{2 n} x_{i}^{2}=\sum_{i=n+1}^{2 n} y_{i}^{2}$. Thus, $\sum_{i=1}^{m} x_{i}^{2}=\sum_{i=1}^{m} y_{i}^{2}$ with each $y_{i}$ not divisible by $m$.
If exactly one of the $x_{i}$ is non-zero, then $\sum_{i=1}^{m} x_{i}^{2}$ is of the form $(2 a)^{2}=a^{2}+a^{2}+a^{2}+a^{2}$ where $a>0$ is divisible by n, and we reason in the same way.
Lemma. Let $\mathrm{n}>0$ be an odd integer and $x_{1}, \cdots, x_{n}$ be integers, at least one of which is not divisible by $n$. Then there exist integers $y_{1}, \cdots, y_{n}$ not divisible by $n$ such that $\sum_{i=1}^{n}\left(n x_{i}\right)^{2}=\sum_{i=1}^{n} y_{i}^{2}$.
 set $X=2 \sum_{i=1}^{n} x_{i}$.
If $n$ divides $X$, we replace $x_{1}$ by $-x_{1}$. The new value $X^{\prime}$ satisfies $X^{\prime}=X-4 x_{1}$. Since $n$ divides $X$ but not $4 x_{1}$ (recall that $n$ is assumed to be odd), it does not divide $X^{\prime}$. Thus, without loss of generality, we can assume that $n$ does not divide $X$.
It is easy to verify that $\sum_{i=1}^{n}\left(n x_{i}\right)^{2}=\sum_{i=1}^{n}\left(X-n x_{i}\right)^{2}$. By setting $y_{i}=X-n x_{i}$ for all $i$, the desired conclusion follows.
We can now prove that every $n \geqslant 3$ odd is good. Indeed, if $a>0$ is an integer that can be written as the sum of $n$ squares of integers all divisible by $n$, then, by considering the highest power of $n$ that divides these integers, there exists an integer $r>0$ and integers $x_{1}, \cdots, x_{n}$, at least one of which is not divisible by $n$, such that $a=\sum_{i=1}^{n}\left(n^{r} x_{i}\right)^{2}$.
According to the lemma, there exist integers $y_{1}, \cdots, y_{n}$ not divisible by $n$ such that $\sum_{i=1}^{n}\left(n x_{i}\right)^{2}=\sum_{i=1}^{n} y_{i}^{2}$, and thus $\sum_{i=1}^{n}\left(n^{r} x_{i}\right)^{2}=\sum_{i=1}^{n}\left(n^{r-1} y_{i}\right)^{2}$. Therefore, by applying the lemma $r$ times in succession, we are assured of the existence of integers $z_{1}, \cdots, z_{n}$ not divisible by $n$ such that $a=\sum_{i=1}^{n} z_{i}^{2}$. This proves that $n$ is good.
Since the double of any good integer is good, any integer that is not a power of 2 is good.
We now prove that 8 is good: Indeed, if $a$ is the sum of 8 squares of integers divisible by 8, then $a$ is divisible by 64. In particular, $a \geqslant 64$ and, according to Lagrange's four-square theorem, there exist integers $x_{1}, x_{2}$, $x_{3}, x_{4}$ such that $a=1^{2}+4^{2}+4^{2}+4^{2}+x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}$. Note that, since $a \equiv 0 \bmod [8]$, we have $x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2} \equiv 7 \bmod [8]$. Since a square is congruent to 0, 1, or 4 modulo 8, the only way to obtain a sum of four squares congruent to 7 modulo 8 is to have $1,1,1,4$ in some order. Thus, none of the $x_{i}$ is divisible by 8, which concludes the proof.
Finally, we prove that 4 is not good. For this, it suffices to observe that $32=4^{2}+4^{2}+0^{2}+0^{2}$. On the other hand, to obtain $32=x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}$, we must have $\left|x_{i}\right| \leqslant 5$ for all $i$. Moreover, to avoid multiples of 4, the only remaining possibilities are $\left|x_{i}\right|=1,2,3$ or 5. As above, reasoning modulo 8, the only possibility is to have $\left|x_{i}\right|=2$ for all $i$. But, we have $32 \neq 2^{2}+2^{2}+2^{2}+2^{2}$, which ensures that 4 is not good.
Thus, any divisor of 4 cannot be good.
Finally, all integers $\mathrm{n}>0$ are good except 1, 2, and 4.
|
all integers \mathrm{n}>0 are good except 1, 2, and 4
|
Incomplete
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer tous les entiers $\mathrm{n}>0$ ayant la propriété suivante: "tout nombre strictement positif qui s'écrit comme la somme des carrés de $n$ entiers multiples de $n$ peut également s'écrire comme la somme des carrés de $n$ entiers dont aucun n'est un multiple de $\mathrm{n}^{\prime \prime}$.
|
Un entier n ayant la propriété désirée sera dit bon.
Soit $\mathrm{n} \geqslant 2$ un entier bon. Alors 2 n est également bon : en effet, soit $\mathrm{m}=2 \mathrm{n}$ et soit $x_{1}, \cdots, x_{m}$ des entiers divisibles par m. Si deux de ces entiers sont non nuls, on peut supposer sans perte de généralité qu'il s'agit de $x_{1}$ et $x_{m}$. Puisque $n$ est bon, il existe alors des entiers $y_{i}$ non divisibles par $n$ (donc non divisibles par $m$ ) tels que $\sum_{i=1}^{n} x_{i}^{2}=\sum_{i=1}^{n} y_{i}^{2}$ et $\sum_{i=n+1}^{2 n} x_{i}^{2}=\sum_{i=n+1}^{2 n} y_{i}^{2}$. Ainsi, $\sum_{i=1}^{m} x_{i}^{2}=\sum_{i=1}^{m} y_{i}^{2}$ avec chaque $y_{i}$ non divisible par $m$.
Si un et un seul des $x_{i}$ est non nul, alors $\sum_{i=1}^{m} x_{i}^{2}$ est de la forme $(2 a)^{2}=a^{2}+a^{2}+a^{2}+a^{2}$ où $a>0$ est divisible par n et on raisonne de la même manière.
Lemme. Soit $\mathrm{n}>0$ un entier impair et $x_{1}, \cdots, x_{n}$ des entiers dont au moins un n'est pas divisible par $n$. Alors il existe des entiers $y_{1}, \cdots, y_{n}$ non divisibles par $n$ tels que $\sum_{i=1}^{n}\left(n x_{i}\right)^{2}=\sum_{i=1}^{n} y_{i}^{2}$.
 pose $X=2 \sum_{i=1}^{n} x_{i}$.
Si $n$ divise $X$, on remplace $x_{1}$ par $-x_{1}$. La nouvelle valeur $X^{\prime}$ vérifie $X^{\prime}=X-4 x_{1}$. Comme $n$ divise $X$ mais pas $4 x_{1}$ (rappelons que $n$ est supposé impair), il ne divise pas $X^{\prime}$. Ainsi, sans perte de généralité, on peut supposer que $n$ ne divise pas $X$.
Il est facile de vérifier que $\sum_{i=1}^{n}\left(n x_{i}\right)^{2}=\sum_{i=1}^{n}\left(X-n x_{i}\right)^{2}$. En posant $y_{i}=X-n x_{i}$ pour tout $i$, la conclusion souhaitée en découle.
On peut maintenant prouver que tout $n \geqslant 3$ impair est bon. En effet, si $a>0$ est un entier qui peut s'écrire comme la somme de $n$ carrés d'entiers tous divisibles par $n$ alors, en considérant la plus grande puissance de $n$ qui divise ces entiers, il existe donc un entier $r>0$ et des entiers $x_{1}, \cdots, x_{n}$ dont au moins un n'est pas divisible par $n$ tels que $a=\sum_{i=1}^{n}\left(n^{r} x_{i}\right)^{2}$.
D'après le lemme, il existe des entiers $y_{1}, \cdots, y_{n}$ non divisibles par $n$ tels que $\sum_{i=1}^{n}\left(n x_{i}\right)^{2}=\sum_{i=1}^{n} y_{i}^{2}$, et donc $\sum_{i=1}^{n}\left(n^{r} x_{i}\right)^{2}=\sum_{i=1}^{n}\left(n^{r-1} y_{i}\right)^{2}$. Ainsi, en appliquant le lemme $r$ fois de suite, on est assuré de l'existence d'entiers $z_{1}, \cdots, z_{n}$ non divisibles par $n$ tels que $a=\sum_{i=1}^{n} z_{i}^{2}$. Cela prouve que $n$ est bon.
Puisque le double de tout entier bon est bon, tout entier qui n'est pas une puissance de 2 est bon.
On prouve maintenant que 8 est bon : En effet, si a est la somme de 8 carrés d'entiers divisibles par 8 alors a est divisible par 64 . En particulier $a \geqslant 64 \mathrm{et}$, d'après le théorème des quatre carrés de Lagrange, il existe des entiers $x_{1}, x_{2}$, $x_{3}, x_{4}$ tels que $a=1^{2}+4^{2}+4^{2}+4^{2}+x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}$. Notons que, puisque $a \equiv 0 \bmod [8]$, on a $x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2} \equiv 7 \bmod$ [8]. Or, un carré étant congru à 0,1 ou 4 modulo 8 , la seule façon d'obtenir une somme de quatre carrés congrue à 7 modulo 8 est d'avoir $1,1,1,4$ à l'ordre près. Ainsi, aucun des $x_{i}$ n'est divisible par 8 , ce qui conclut.
Enfin, on prouve que 4 n'est pas bon. Pour cela, il suffit de constater que $32=4^{2}+4^{2}+0^{2}+0^{2}$. D'autre part, pour obtenir $32=x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}$, on doit avoir $\left|x_{i}\right| \leqslant 5$ pour tout i. De plus, si l'on veut éviter les multiples de 4 , il ne reste plus que $\left|x_{i}\right|=1,2,3$ ou 5 . Or, comme ci-dessus en raisonnant modulo 8 , la seule possibilités est d'avoir $\left|x_{i}\right|=2$ pour tout $i$. Mais, on a $32 \neq$ $2^{2}+2^{2}+2^{2}+2^{2}$, ce qui assure que $4 \mathrm{n}^{\prime}$ est pas bon.
Ainsi, tout diviseur de 4 ne peut être bon.
Finalement, tous les entiers $\mathrm{n}>0$ sont bons sauf 1,2 et 4 .
|
{
"exam": "French_envois",
"problem_label": "12",
"problem_match": "\nExercice 12.",
"resource_path": "French/segmented/envois/fr-ofm-2014-2015-envoi-6-solutions.jsonl",
"solution_match": "## Solution de l'exercice 12",
"tier": "T2",
"year": "2015"
}
|
Prove that there are only a finite number of prime numbers that can be written in the form $n^{3}+2 n+3$ with $n \in \mathbb{N}$.
|
Note that $n^{3}-n=n(n-1)(n+1)$ is a product of three consecutive integers. Since among three consecutive integers there is always a multiple of 3, we obtain that $n^{3}-n$ is divisible by 3, that is, $n^{3} \equiv n(\bmod 3)$. (This can also be seen using Fermat's little theorem.) Therefore, $n^{3}+2 n+3 \equiv n+2 n+3 \equiv 3 n+3 \equiv 0(\bmod 3)$, so $n^{3}+2 n+3$ is always divisible by 3. On the other hand, it can only be equal to 3 for a finite number of values of $n$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prouver qu'il n'existe qu'un nombre fini de nombres premiers s'écrivant sous la forme $n^{3}+2 n+3$ avec $n \in \mathbb{N}$.
|
: Remarquons que $n^{3}-n=n(n-1)(n+1)$ est un produit de trois entiers consécutifs. Puisque parmi trois entiers consécutifs il y a toujours un multiple de 3 , on obtient que $n^{3}-n$ est divisible par 3, c'est-à-dire $n^{3} \equiv n(\bmod 3)$. (On peut le voir aussi en utilisant le petit théorème de Fermat.) On a donc $n^{3}+2 n+3 \equiv n+2 n+3 \equiv 3 n+3 \equiv 0(\bmod 3)$, donc $n^{3}+2 n+3$ est toujours divisible par 3 . D'autre part, il ne peut être égal à 3 que pour un nombre fini de valeurs de $n$.
|
{
"exam": "French_envois",
"problem_label": "1",
"problem_match": "\nExercice 1",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-1-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T2",
"year": "2016"
}
|
Solve $x^{4}-6 x^{2}+1=7 \times 2^{y}$ for $x$ and $y$ integers.
|
: The equation can be rewritten as $\left(x^{2}-3\right)^{2}=7 \times 2^{y}+8$. If $y \geq 3$, then the right side can be written as $8\left(7 \times 2^{y-3}+1\right)$. Since the left side is a square, its 2-adic valuation is even. Thus, $7 \times 2^{y-3}+1$ must be even, so $y=3$. In this case, $x^{2}-3=8$ so $x^{2}=11$, which is impossible. Therefore, $y \leq 2$. If $y=2$, we find $x= \pm 3$. For $y<0$, as well as for $y=0$ or $y=1$, there are no solutions. The only pairs of solutions are therefore $(x, y)=(3,2)$ and $(-3,2)$.
|
(3,2) \text{ and } (-3,2)
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Résoudre $x^{4}-6 x^{2}+1=7 \times 2^{y}$ pour $x$ et $y$ entiers.
|
: L'équation se réécrit $\left(x^{2}-3\right)^{2}=7 \times 2^{y}+8$. Si $y \geq 3$, alors le côté droit s'écrit $8\left(7 \times 2^{y-3}+1\right)$. Le côté gauche étant un carré, sa valuation 2 -adique est paire. Ainsi, $7 \times 2^{y-3}+1$ doit être pair, donc $y=3$. Dans ce cas $x^{2}-3=8$ donc $x^{2}=11$, impossible. Donc $y \leq 2$. Si $y=2$, on trouve $x= \pm 3$. Pour $y<0$, ainsi que pour $y=0$ ou $y=1$ il n'y a pas de solution. Les seuls couples de solutions sont donc $(x, y)=(3,2)$ et $(-3,2)$.
|
{
"exam": "French_envois",
"problem_label": "2",
"problem_match": "\nExercice 2",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-1-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T2",
"year": "2016"
}
|
Find the smallest positive integer that cannot be written in the form $\frac{2^{a}-2^{b}}{2^{c}-2^{d}}$ for $a, b, c, d \in \mathbb{N}$.
|
Let $E$ be the set of strictly positive integers that can be written in this form. Let's start by noting that
$$
\frac{2^{a}-2^{b}}{2^{c}-2^{d}}=2^{b-d} \frac{2^{a-b}-1}{2^{c-d}-1}
$$
Thus, if $x>0$ is written as $x=\frac{2^{a}-2^{b}}{2^{c}-2^{d}}$, then $b-d=v_{2}(x)$ and if we call $y$ the odd integer such that $x=2^{v_{2}(x)} y$, then $y$ can be written in the form $\frac{2^{n}-1}{2^{m}-1}$. In particular, the integer we are looking for is necessarily odd. On the other hand, we can immediately exclude integers of the form $2^{n}-1$, which are reached with $m=1$.
It is classical that if $2^{m}-1$ divides $2^{n}-1$, then $m$ divides $n$. Thus, by writing $n=m d, y$ is of the form
$$
y=\frac{2^{m d}-1}{2^{m}-1}=2^{(d-1) m}+2^{(d-2) m}+\ldots+2^{m}+1
$$
In other words, denoting $u=\underbrace{0 \ldots 0}_{m-1 \text { zeros }} 1$, the binary representation of $y$ is of the form $\overline{1 u \ldots u}^{2}$, with $u$ appearing $d-1$ times. The odd integers belonging to $E$ are exactly those having such a binary representation for well-chosen $m$ and $d$. The binary representations of the first odd integers that are not of the form $2^{n}-1$ are
$$
5=\overline{101}^{2}, 9={\overline{1001}^{2}}^{2}, 11={\overline{1011}^{2}}^{2}
$$
According to the criterion above, the smallest integer sought is 11.
Remark: This exercise can also be done by finding ways to write the integers 1 to 10 in this form, then showing that 11 cannot be written in this form: indeed, since 11 is odd, we can assume $b=d=1$. Then
$$
\left(2^{a}-1\right)=11\left(2^{c}-1\right)
$$
rewrites as
$$
10=2^{c} \times 11-2^{a}
$$
Since $10=2 \times 5$, we have $a=1$ or $c=1$. If $a=1$, we get $2^{c} \times 11=12$, which has no solution, and if $c=1$, we get $2^{a}=12$, which has no solution either. Therefore, 11 is the integer sought.
## 2 Common Exercises
|
11
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Trouver le plus petit entier positif qui ne s'écrit pas sous la forme $\frac{2^{a}-2^{b}}{2^{c}-2^{d}}$ pour $a, b, c, d \in \mathbb{N}$.
|
: Soit E l'ensemble des entiers strictement positifs s'écrivant sous cette forme. Commençons par remarquer que
$$
\frac{2^{a}-2^{b}}{2^{c}-2^{d}}=2^{b-d} \frac{2^{a-b}-1}{2^{c-d}-1}
$$
Ainsi, si $x>0$ s'écrit $x=\frac{2^{a}-2^{b}}{2^{c}-2^{d}}$, alors $b-d=v_{2}(x)$ et si on appelle $y$ l'entier impair tel que $x=2^{v_{2}(x)} y$, alors $y$ s'écrit sous la forme $\frac{2^{n}-1}{2^{m}-1}$. En particulier, l'entier que nous cherchons est nécessairement impair. D'autre part, on peut tout de suite exclure les entiers de la forme $2^{n}-1$, atteints avec $m=1$.
Il est classique que si $2^{m}-1$ divise $2^{n}-1$, alors $m$ divise $n$. Ainsi, en écrivant $n=m d, y$ est de la forme
$$
y=\frac{2^{m d}-1}{2^{m}-1}=2^{(d-1) m}+2^{(d-2) m}+\ldots+2^{m}+1
$$
Autrement dit, en notant $u=\underbrace{0 \ldots 0}_{m-1 \text { zéros }} 1$, l'écriture en base 2 de $y$ est de la forme $\overline{1 u \ldots u}^{2}$, avec $u$ apparaissant $d-1$ fois. Les entiers impairs appartenant à $E$ sont exactement ceux ayant une telle écriture binaire pour $m$ et $d$ bien choisis. Les écritures binaires des premiers entiers impairs qui ne sont pas de la forme $2^{n}-1$ sont
$$
5=\overline{101}^{2}, 9={\overline{1001}^{2}}^{2}, 11={\overline{1011}^{2}}^{2}
$$
D'après le critère ci-dessus, le plus petit entier cherché est 11.
Remarque : cet exercice peut aussi se faire en trouvant des manières d'écrire les entiers 1 à 10 sous cette forme, puis en montrant que 11 ne s'écrit pas sous cette forme : en effet, vu que 11 est impair, on peut supposer $b=d=1$. Ensuite
$$
\left(2^{a}-1\right)=11\left(2^{c}-1\right)
$$
se réécrit
$$
10=2^{c} \times 11-2^{a}
$$
Puisque $10=2 \times 5$, nous avons $a=1$ ou $c=1$. Si $a=1$, on trouve $2^{c} \times 11=12$, qui n'a pas de solution, et si $c=1$, on trouve $2^{a}=12$, qui n'a pas de solution non plus. Donc 11 est l'entier cherché.
## 2 Exercices communs
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-1-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T2",
"year": "2016"
}
|
Find all triplets of prime numbers $(p, q, r)$ such that $(p+1)(q+2)(r+3)=4 p q r$.
|
If $p=2$ then we have $3(q+2)(r+3)=8 q r$ which implies $q=3$ or $r=3$. We then have the solution $(2,3,5)$.
If $q=2$ and $p, r>2$ then we have $(p+1)(r+3)=2 p r$. Since $p$ and $r$ are odd, the left-hand side is divisible by 4, while the right-hand side is divisible by 2, but not by 4, leading to a contradiction. Therefore, $p$ or $r$ must be 2, but no valid solution follows from this.
If $r=2$ then $5(p+1)(q+2)=8 p q$ and so $p$ or $q$ must be 5. We obtain the solution $(7,5,2)$.
Otherwise, $(p+1)$ is even and $(r+3)$ is even. Thus, we reduce to
$$
\left(\frac{p+1}{2}\right)(q+2)\left(\frac{r+3}{2}\right)=p q r .
$$
We have thus written $pqr$ as a product of three factors each strictly greater than 1. We deduce that $\left(\frac{p+1}{2}, q+2, \frac{r+3}{2}\right)$ is a permutation of $(p, q, r)$.
Clearly, $p \neq \frac{p+1}{2}$ since $p>\frac{p+1}{2}$.
If $p=\frac{r+3}{2}$, then since $q \neq q+2$, we must have $q=\frac{p+1}{2}=\frac{r+5}{4}$. Then $r=q+2=\frac{r+13}{4}$, and thus $r$ is not an integer.
If $p=q+2$, then there are two cases to consider:
- $r=\frac{p+1}{2}=\frac{q+3}{2}$ and $q=\frac{r+3}{2}=\frac{q+9}{4}$. So $q=3$ and we obtain the solution $(5,3,3)$.
- $r=\frac{r+3}{2}$ and $q=\frac{p+1}{2}=\frac{q+3}{2}$, which gives $r=q=3$. We then obtain the same solution $(5,3,3)$.
Finally, the only solutions are $(2,3,5),(7,5,2)$ and $(5,3,3)$.
|
(2,3,5),(7,5,2),(5,3,3)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Trouver tous les triplets de nombres premiers $(p, q, r)$ tels que $(p+1)(q+2)(r+3)=4 p q r$.
|
: Si $p=2$ alors on a $3(q+2)(r+3)=8 q r$ ce qui implique $q=3$ ou $r=3$. On a alors la solution $(2,3,5)$.
Si $q=2$ et $p, r>2$ alors on a $(p+1)(r+3)=2 p r$. Puisque $p$ et $r$ sont impairs, le membre de gauche est divisible par 4 , alors que le membre de droite est divisible par 2 , mais pas par 4 , contradiction. Donc $p$ ou $r$ vaut 2 mais aucune solution valide n'en découle.
Si $r=2$ alors $5(p+1)(q+2)=8 p q$ et donc $p$ ou $q$ vaut 5 . On obtient la solution $(7,5,2)$.
Sinon, $(p+1)$ est pair et $(r+3)$ est pair. Donc on se ramène à
$$
\left(\frac{p+1}{2}\right)(q+2)\left(\frac{r+3}{2}\right)=p q r .
$$
Nous avons donc écrit pqr comme un produit de trois facteurs strictement plus grands que 1. On en déduit que $\left(\frac{p+1}{2}, q+2, \frac{r+3}{2}\right)$ est une permutation de $(p, q, r)$.
Clairement, $p \neq \frac{p+1}{2}$ puisque $p>\frac{p+1}{2}$.
Si $p=\frac{r+3}{2}$, alors puisque $q \neq q+2$, nous avons nécessairement $q=\frac{p+1}{2}=\frac{r+5}{4}$. Alors $r=q+2=\frac{r+13}{4}$, et donc $r$ n'est pas entier.
Si $p=q+2$, alors il y a deux cas à considérer :
$-r=\frac{p+1}{2}=\frac{q+3}{2}$ et $q=\frac{r+3}{2}=\frac{q+9}{4}$. Donc $q=3$ et on obtient la solution $(5,3,3)$.
$-r=\frac{r+3}{2}$ et $q=\frac{p+1}{2}=\frac{q+3}{2}$, ce qui donne $r=q=3$. On obtient alors cette même solution $(5,3,3)$.
Finalement, les seules solutions sont $(2,3,5),(7,6,2)$ et $(5,3,3)$.
|
{
"exam": "French_envois",
"problem_label": "4",
"problem_match": "\nExercice 4",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-1-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T2",
"year": "2016"
}
|
Find all strictly positive integers $n$ such that $2^{n-1} n+1$ is a perfect square.
|
We want to solve $2^{n-1} n+1=m^{2}$, that is, $2^{n-1} n=(m-1)(m+1)$. Since $n=1$ is not a solution, we have $n \geq 2$, and therefore $m$ must be odd, and $m-1$ and $m+1$ are even (in particular, $n \geq 3$). We set $k=\frac{m-1}{2}$. It then suffices to solve $2^{n-3} n=k(k+1)$. Among the integers $k$ and $k+1$, exactly one is even, and thus they are of the form $2^{n-3} d$ and $\frac{n}{d}$ with $d$ a divisor of $n$. A divisor of $n$ cannot be at a distance of 1 from an integer greater than $2^{n-3}$ if $n$ is too large. More precisely, we have $2^{n-3} d \geq 2^{n-3} \geq n+2$ if $n \geq 6$, so we must have $n \leq 5$. For $n=5$, we find $2^{4} \times 5+1=9^{2}$, so 5 is a solution. We verify that $2,3,4$ are not solutions. Therefore, $n=5$ is the only solution.
|
5
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Trouver tous les entiers strictement positifs $n$ tels que $2^{n-1} n+1$ soit un carré parfait.
|
: On veut résoudre $2^{n-1} n+1=m^{2}$, c'est-à-dire $2^{n-1} n=(m-1)(m+1)$. Puisque $n=1$ n'est pas solution, on a $n \geq 2$, et donc $m$ est nécessairement impair, et $m-1$ et $m+1$ sont pairs (en particulier $n \geq 3$ ). On pose $k=\frac{m-1}{2}$. Il suffit alors de résoudre $2^{n-3} n=k(k+1)$. Parmi les entiers $k$ et $k+1$ exactement un est pair, et donc ils sont de la forme $2^{n-3} d$ et $\frac{n}{d}$ avec $d$ un diviseur de $n$. Or un diviseur de $n$ ne peut pas être à distance 1 d'un entier supérieur à $2^{n-3}$ si $n$ est trop grand. Plus précisément, on a $2^{n-3} d \geq 2^{n-3} \geq n+2$ si $n \geq 6$, donc on a nécessairement $n \leq 5$. Pour $n=5$, on trouve $2^{4} \times 5+1=9^{2}$, donc 5 est solution. On vérifie que $2,3,4$ ne sont pas solutions. Donc $n=5$ est la seule solution.
|
{
"exam": "French_envois",
"problem_label": "5",
"problem_match": "\nExercice 5",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-1-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T2",
"year": "2016"
}
|
Let $x>1$ and $y$ be integers satisfying $2 x^{2}-1=y^{15}$. Show that $x$ is divisible by 5.
|
The integer $y$ is clearly odd and strictly greater than 1. We factorize the equation as follows:
$$
x^{2}=\left(\frac{y^{5}+1}{2}\right)\left(y^{10}-y^{5}+1\right)
$$
Notice that
$$
y^{10}-y^{5}+1 \equiv 3\left(\bmod y^{5}+1\right)
$$
and thus $\operatorname{pgcd}\left(y^{5}+1, y^{10}-y^{5}+1\right)$ is equal to 1 or 3. If it were 1, then $y^{10}-y^{5}+1$ would be a square. However, for $y>0$ we have
$$
\left(y^{5}-1\right)^{2}=y^{10}-2 y^{5}+1<y^{10}-y^{5}+1<y^{10}=\left(y^{5}\right)^{2},
$$
which means that $y^{10}-y^{5}+1$ is strictly between two consecutive squares and cannot be a square itself. Therefore, $\operatorname{pgcd}\left(y^{5}+1, y^{10}-y^{5}+1\right)=3$, so there exist integers $a$ and $b$ such that
$$
y^{5}+1=6 a^{2} \quad \text { and } \quad y^{10}-y^{5}+1=3 b^{2} .
$$
We can factorize $(y+1)\left(y^{4}-y^{3}+y^{2}-y+1\right)=6 a^{2}$. Since $y^{5} \equiv-1(\bmod 3)$, we must have $y \equiv-1$ $(\bmod 3)$, so $y+1$ is divisible by 6. Similarly as above, we have
$$
y^{4}-y^{3}+y^{2}-y+1 \equiv 5(\bmod y+1)
$$
and thus $\operatorname{pgcd}\left(y+1, y^{4}-y^{3}+y^{2}-y+1\right)$ is equal to 1 or 5. If it is 5, then $a$ is divisible by 5 and so is $x$, and we are done. Suppose it is 1. Then $y^{4}-y^{3}+y^{2}-y+1$ is a square. In this case, $4\left(y^{4}-y^{3}+y^{2}-y+1\right)$ is also a square, which is impossible, because for $y>1$, we have
$$
\left(2 y^{2}-y\right)^{2}=4 y^{4}-4 y^{3}+y^{2}<4\left(y^{4}-y^{3}+y^{2}-y+1\right)<4 y^{4}-4 y^{3}+5 y^{2}-2 y+1=\left(2 y^{2}-y+1\right)^{2}
$$
## 3 Exercices groupe A
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soient $x>1$ et $y$ des entiers vérifiant $2 x^{2}-1=y^{15}$. Montrer que $x$ est divisible par 5 .
|
: L'entier $y$ est clairement impair et strictement plus grand que 1. On factorise l'équation sous la forme
$$
x^{2}=\left(\frac{y^{5}+1}{2}\right)\left(y^{10}-y^{5}+1\right)
$$
Remarquons que
$$
y^{10}-y^{5}+1 \equiv 3\left(\bmod y^{5}+1\right)
$$
et que donc $\operatorname{pgcd}\left(y^{5}+1, y^{10}-y^{5}+1\right)$ est égal à 1 ou à 3 . S'il valait 1 , alors $y^{10}-y^{5}+1$ serait un carré. Or pour $y>0$ nous avons
$$
\left(y^{5}-1\right)^{2}=y^{10}-2 y^{5}+1<y^{10}-y^{5}+1<y^{10}=\left(y^{5}\right)^{2},
$$
c'est-à-dire que $y^{10}-y^{5}+1$ est strictement compris entre deux carrés consécutifs, et ne peut pas être lui-même un carré. Donc $\operatorname{pgcd}\left(y^{5}+1, y^{10}-y^{5}+1\right)=3$, de sorte qu'il existe des entiers $a$ et $b$ tels que
$$
y^{5}+1=6 a^{2} \quad \text { et } \quad y^{10}-y^{5}+1=3 b^{2} .
$$
On peut factoriser $(y+1)\left(y^{4}-y^{3}+y^{2}-y+1\right)=6 a^{2}$. Puisque $y^{5} \equiv-1(\bmod 3)$, on a nécessairement $y \equiv-1$ $(\bmod 3)$, donc $y+1$ est divisible par 6 . De même que plus haut, on a
$$
y^{4}-y^{3}+y^{2}-y+1 \equiv 5(\bmod y+1)
$$
et donc $\operatorname{pgcd}\left(y+1, y^{4}-y^{3}+y^{2}-y+1\right)$ est égal à 1 ou à 5 . S'il vaut 5 , alors $a$ est divisible par 5 et donc $x$ aussi, et nous avons terminé. Supposons donc qu'il vaut 1. Alors $y^{4}-y^{3}+y^{2}-y+1$ est un carré. Dans ce cas, $4\left(y^{4}-y^{3}+y^{2}-y+1\right)$ est aussi un carré, ce qui est impossible, car pour $y>1$, on a
$$
\left(2 y^{2}-y\right)^{2}=4 y^{4}-4 y^{3}+y^{2}<4\left(y^{4}-y^{3}+y^{2}-y+1\right)<4 y^{4}-4 y^{3}+5 y^{2}-2 y+1=\left(2 y^{2}-y+1\right)^{2}
$$
## 3 Exercices groupe A
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "\nExercice 6",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-1-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T2",
"year": "2016"
}
|
Characterize the integers $n \geq 2$ such that for any integer $a$ we have $a^{n+1}=a(\bmod n)$.
|
Here are the $n$ satisfying this property: $2,2 \cdot 3,2 \cdot 3 \cdot 7,2 \cdot 3 \cdot 7 \cdot 43$.
To prove that this is exhaustive, we proceed as follows: we start by noting that $n$ has no square factor. Indeed, if $p^{2}$ divides $n$, then $p^{n+1}-p$ is divisible by $p^{2}$, which is not possible. Thus, $n$ must necessarily be a product $p_{1} \ldots p_{k}$ of distinct prime numbers. Consequently, by the Chinese Remainder Theorem, the condition in the statement is equivalent to $a^{n+1} \equiv a(\bmod p)$ for all integers $a$ and all $p \in\left\{p_{1}, \ldots, p_{k}\right\}$. By choosing $a$ of order $p-1$ modulo $p$, we see that this is equivalent to $p-1$ dividing $n$ for all $p \in\left\{p_{1}, \ldots, p_{k}\right\}$.
In summary: $n$ is a product of distinct primes $p_{1}, \ldots, p_{k}$, and $p_{i}-1$ divides $n$ for all $i$. We deduce that for all $i, p_{i}-1$ is square-free and $p_{i}-1=q_{1} \ldots q_{m}$ where the $q_{j}$ are primes taken from the $p_{r}, r \neq i$.
Assuming without loss of generality that $p_{1}<p_{2}<\ldots<p_{k}$. From the above condition, we necessarily have $p_{1}=2$. If $k=1$, this gives the integer $n=2$. If $k>1$, then $p_{2}-1$ must be equal to 2, so $p_{2}=3$. If $k=2$, this gives the solution $n=6$. If $k>2$, we continue by saying that $p_{3}-1$ cannot be equal to 2 or 3, so it must be equal to $p_{1} p_{2}=6$, hence $p_{3}=7$. If $k=3$, this gives the solution $n=2 \cdot 3 \cdot 7=42$. If $k>3$, we see that the only possible value for $p_{4}$ is $2 \times 3 \times 7+1=43$. For $k=4$, this gives the solution $n=2 \cdot 3 \cdot 7 \cdot 43$. Finally, suppose that $k>4$. Then $p_{5}-1$ must be even and strictly greater than 43, so the only possible values are $2 \cdot 43,2 \cdot 3 \cdot 43,2 \cdot 7 \cdot 43,2 \cdot 3 \cdot 7 \cdot 43$. We check that none of these possibilities provide a prime $p_{5}$. Thus, we must have $k \leq 4$ and the solutions we have found are the only ones.
|
2, 2 \cdot 3, 2 \cdot 3 \cdot 7, 2 \cdot 3 \cdot 7 \cdot 43
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Caractériser les entiers $n \geq 2$ tels que pour tout entier $a$ on ait $a^{n+1}=a(\bmod n)$.
|
: Voici les $n$ vérifiant cette propriété : $2,2 \cdot 3,2 \cdot 3 \cdot 7,2 \cdot 3 \cdot 7 \cdot 43$.
Pour prouver que c'est exhaustif on procède de la façon suivante : on commence par remarquer que $n$ n'a pas de facteur carré. En effet, si $p^{2}$ divise $n$, alors $p^{n+1}-p$ est divisible par $p^{2}$, ce qui n'est pas possible. Ainsi, $n$ est forcément un produit $p_{1} \ldots p_{k}$ de nombres premiers distincts. Par conséquent, par le lemme chinois la condition de l'énoncé est équivalente à $a^{n+1} \equiv a(\bmod p)$ pour tout entier $a$ et tout $p \in\left\{p_{1}, \ldots, p_{k}\right\}$. En choisissant $a$ d'ordre $p-1$ modulo $p$, on obtient que cela est équivalent à ce que $p-1$ divise $n$ pour tout $p \in\left\{p_{1}, \ldots, p_{k}\right\}$.
En résumé : $n$ est produit de premiers distincts $p_{1}, \ldots, p_{k}$, et $p_{i}-1$ divise $n$ pour tout $i$. On en déduit que pour tout $i, p_{i}-1$ est sans facteur carré et $p_{i}-1=q_{1} \ldots q_{m}$ où les $q_{j}$ sont des nombres premiers pris parmi les $p_{r}, r \neq i$.
Quitte à re-numéroter les $p_{i}$, on peut supposer que $p_{1}<p_{2}<\ldots<p_{k}$. D'après la condition ci-dessus, nous avons nécessairement $p_{1}=2$. Si $k=1$, cela nous donne l'entier $n=2$. Si $k>1$, alors $p_{2}-1$ est nécessairement égal à 2 , donc $p_{2}=3$. Si $k=2$, cela nous donne la solution $n=6$. Si $k>2$ on continue en disant que $p_{3}-1$ ne peut être égal à 2 ou 3 , donc il est égal à $p_{1} p_{2}=6$, d'où $p_{3}=7$. Si $k=3$, cela donne la solution $n=2 \cdot 3 \cdot 7=42$. Si $k>3$, on voit que de même la seule valeur possible pour $p_{4}$ est $2 \times 3 \times 7+1=43$. Pour $k=4$, cela donne la solution $n=2 \cdot 3 \cdot 7 \cdot 43$. Enfin, supposons que $k>4$. Alors $p_{5}-1$ doit être pair et strictement supérieur à 43 , donc les seules valeurs possibles sont $2 \cdot 43,2 \cdot 3 \cdot 43,2 \cdot 7 \cdot 43,2 \cdot 3 \cdot 7 \cdot 43$. On vérifie qu'aucune de ces possibilités ne fournit un $p_{5}$ premier. Ainsi on a nécessairement $k \leq 4$ et les solutions que nous avons trouvées sont les seules.
|
{
"exam": "French_envois",
"problem_label": "7",
"problem_match": "\nExercice 7",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-1-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 7",
"tier": "T2",
"year": "2016"
}
|
Let $k \geq 3$ be an integer. We define the sequence $\left(a_{n}\right)_{n \geq k}$ by $a_{k}=2 k$, and
$$
a_{n}= \begin{cases}a_{n-1}+1 & \text { if } \operatorname{gcd}\left(a_{n-1}, n\right)=1 \\ 2 n & \text { otherwise. }\end{cases}
$$
Show that the sequence $\left(a_{n+1}-a_{n}\right)_{n \geq k}$ has infinitely many terms that are prime numbers.
|
: Let's start with an integer $n$ such that $a_{n}=2 n$. We will show by induction that if $p$ is the smallest prime factor of $n-1$, then for all $i \in\{0, \ldots, p-2\}, a_{n+i}=2 n+i$. Indeed, it is true for $i=0$, and if it is true for some $i<p-2$, then
$$
\operatorname{gcd}(n+i+1,2 n+i)=\operatorname{gcd}(n+i+1, n-1)=\operatorname{gcd}(i+2, n-1)=1
$$
since $i+2<p$, and thus $i+2$ is coprime with $n-1$ by the definition of $p$, which concludes the induction. Similarly, $\operatorname{gcd}(n+p-1,2 n+p-2)=\operatorname{gcd}(p, n-1)=p \neq 1$, and thus $a_{n+p-1}=2(n+p-1)$. In particular,
$$
a_{n+p-1}-a_{n+p-2}=2 n+2 p-2-(2 n+p-2)=p
$$
is prime.
Since $a_{k}=2 k$, we have thus shown that there are infinitely many $n$ satisfying $\operatorname{gcd}\left(a_{n-1}, n\right) \neq 1$, and that for such values of $n, a_{n}-a_{n-1}$ is prime.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $k \geq 3$ un entier. On définit la suite $\left(a_{n}\right)_{n \geq k}$ par $a_{k}=2 k$, et
$$
a_{n}= \begin{cases}a_{n-1}+1 & \text { si } \operatorname{pgcd}\left(a_{n-1}, n\right)=1 \\ 2 n & \text { sinon. }\end{cases}
$$
Montrer que la suite $\left(a_{n+1}-a_{n}\right)_{n \geq k}$ a une infinité de termes qui sont des nombres premiers.
|
: Partons d'un entier $n$ tel que $a_{n}=2 n$. Montrons par récurrence que si $p$ est le plus petit facteur premier de $n-1$, alors pour tout $i \in\{0, \ldots, p-2\}, a_{n+i}=2 n+i$. En effet, c'est vrai pour $i=0$, et si c'est vrai pour un certain $i<p-2$, alors
$$
\operatorname{pgcd}(n+i+1,2 n+i)=\operatorname{pgcd}(n+i+1, n-1)=\operatorname{pgcd}(i+2, n-1)=1
$$
car $i+2<p$, et donc $i+2$ est premier avec $n-1$ par définition de $p$, ce qui conclut la récurrence. De même, $\operatorname{pgcd}(n+p-1,2 n+p-2)=\operatorname{pgcd}(p, n-1)=p \neq 1$, et donc $a_{n+p-1}=2(n+p-1)$. En particulier,
$$
a_{n+p-1}-a_{n+p-2}=2 n+2 p-2-(2 n+p-2)=p
$$
est premier.
Puisque $a_{k}=2 k$, avons donc montré qu'il existe une infinité de $n$ satisfaisant $\operatorname{pgcd}\left(a_{n-1}, n\right) \neq 1$, et que pour de telles valeurs de $n, a_{n}-a_{n-1}$ est premier.
|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "\nExercice 8",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-1-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 8",
"tier": "T2",
"year": "2016"
}
|
Let $t$ be a non-zero natural number. Show that there exists an integer $n>1$ coprime with $t$ such that for any integer $k \geq 1$, the integer $n^{k}+t$ is not a power (i.e., it is not of the form $m^{r}$ with $m \geq 1$ and $r \geq 2$).
|
To ensure that $n$ is coprime with $t$, we will look for it in the form $1 + ts$ where $s$ is an integer. We will then have $n^{k} + t \equiv 1 + t \pmod{s}$. In particular, if $s$ is divisible by $(t+1)$, then $n^{k} + t$ is also divisible by $(t+1)$.
First, we will handle the case where $t+1$ is not a power. In this case, it would suffice to ensure that we can choose $s$ such that $n^{k} + t$ is divisible by $t+1$, and that the quotient is coprime with $t+1$. For this, let's take $s = (t+1)^2$. Then $n = 1 + t(t+1)^2$, and
$$
n^{k} + t = \underbrace{\sum_{i=1}^{k} \binom{k}{i} t^i (t+1)^{2i}}_{\text{terms divisible by } (t+1)^2} + 1 + t = (t+1)(a(t+1) + 1)
$$
for some integer $a$, so we are done.
Now suppose that $t+1$ is a power: $t+1 = m^r$ with $m$ not a power. If we keep the same $n$ as above, we see that if $n^{k} + t = b^d$ is a power (with $d \geq 2$), then $t+1$ must necessarily be a $d$-th power, and thus $d$ divides $r$. Therefore, we have a bound on the $d$ such that $n^{k} + t$ is a $d$-th power for some $k$. We then observe that by replacing $n$ with its $r$-th power, i.e., by setting $n = n_0^r$ where $n_0 = 1 + t(t+1)^2$ (which does not change the fact that $t+1$ divides $n^{k} + t$, that the quotient is coprime with $t+1$, and that $n^{k} + t = b^d$ implies $d \mid r$ as above), we can write $t$ as the difference of two $d$-th powers:
$$
t = b^d - (n_0^{ke})^d
$$
where $e$ is the natural number such that $r = de$. This is not possible because $n_0$ is large relative to $t$. More precisely, we have:
$$
t = b^d - (n_0^{ke})^d = (b - n_0^{ke})(b^{d-1} + b^{d-2} n_0^{ke} + \ldots + b n_0^{ke(d-2)} + n_0^{ke(d-1)}) \geq n_0 > t
$$
contradiction. Therefore, for all $k$ and for all $d$, $n^{k} + t$ is not a $d$-th power, and we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $t$ un entier naturel non-nul. Montrer qu'il existe un entier $n>1$ premier avec $t$ tel que pour tout entier $k \geq 1$, l'entier $n^{k}+t$ ne soit pas une puissance (c'est-à-dire qu'il ne soit pas de la forme $m^{r}$ avec $m \geq 1$ et $r \geq 2$ ).
|
: Pour que $n$ soit premier avec $t$, on va le chercher sous la forme $1+t s$ où $s$ est entier. On aura alors $n^{k}+t \equiv 1+t(\bmod s)$. En particulier, si $s$ est divisible par $(t+1)$, alors $n^{k}+t$ l'est également.
On va d'abord traiter le cas où $t+1$ n'est pas une puissance. Dans ce cas, il suffirait de s'assurer qu'on peut choisir $s$ de telle sorte que $n^{k}+t$ soit divisible par $t+1$, et que le quotient soit premier avec $t+1$. Pour cela, prenons $s=(t+1)^{2}$. Alors $n=1+t(t+1)^{2}$, et
$$
n^{k}+t=\underbrace{\sum_{i=1}^{k}\binom{k}{i} t^{i}(t+1)^{2 i}}_{\text {termes divisibles par }(t+1)^{2}}+1+t=(t+1)(a(t+1)+1)
$$
pour un certain entier $a$, donc on a gagné.
Supposons maintenant que $t+1$ soit une puissance : $t+1=m^{r}$ avec $m$ qui n'est pas une puissance. Si on garde le même $n$ que ci-dessus, on voit que si $n^{k}+t=b^{d}$ est une puissance (avec $d \geq 2$ ), alors $t+1$ est nécessairement une puissance $d$-ième, et donc $d$ divise $r$. Ainsi, nous avons une borne sur les $d$ tels que $n^{k}+t$ est puissance $d$-ième pour un certain $k$. On constate alors qu'en remplaçant $n$ par sa puissance $r$-ième, c'est-à-dire en posant $n=n_{0}^{r}$ où $n_{0}=1+t(t+1)^{2}$ (ce qui ne change pas le fait que $t+1$ divise $n^{k}+t$, que le quotient soit premier avec $t+1$, et que donc $n^{k}+t=b^{d}$ implique $d \mid r$ comme ci-dessus), on arrive à écrire $t$ comme une différence de deux puissances $d$-ièmes :
$$
t=b^{d}-\left(n_{0}^{k e}\right)^{d}
$$
où $e$ est l'entier naturel tel que $r=d e$. Cela n'est pas possible car $n_{0}$ est grand par rapport à $t$. Plus précisément, nous avons:
$$
t=b^{d}-\left(n_{0}^{k e}\right)^{d}=\left(b-n_{0}^{k e}\right)\left(b^{d-1}+b^{d-2} n_{0}^{k e}+\ldots+b n_{0}^{k e(d-2)}+n_{0}^{k e(d-1)}\right) \geq n_{0}>t
$$
contradiction. Donc pour tout $k$ et pour tout $d, n^{k}+t$ n'est pas une puissance $d$-ième et nous avons terminé.
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-1-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 9",
"tier": "T2",
"year": "2016"
}
|
Let $A$ be a point outside a circle $\mathscr{C}$ with center $O$. A point $P$ moves on $\mathscr{C}$. Let $M$ be the intersection point between $(A P)$ and the bisector of $\widehat{P O A}$. Show that $M$ moves on a circle that we will describe.
|
Let $d=OA$ and $R$ be the radius of the circle.
According to the Angle Bisector Theorem, we have $MP/MA = OP/OA$, so $\frac{MA}{AP} = \frac{MA}{MA + MP} = \frac{1}{1 + \frac{MP}{MA}} = \frac{1}{1 + \frac{OP}{OA}} = \frac{OA}{OA + OP} = \frac{d}{d + R}$. Let $k$ be this value. Let $O'$ be the point on $[AO]$ such that $AO' = kAO$. According to Thales' Theorem, the lines $(O'M)$ and $(OP)$ are parallel, so $\frac{O'M}{OP} = \frac{AM}{AP} = k$, thus $O'M = kR$. This proves that $M$ describes the circle with center $O'$ and radius $kR$.
Notice that $AO' + kR = k(d + R) = d$, so this circle passes through $O$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A$ un point extérieur à un cercle $\mathscr{C}$ de centre $O$. Un point $P$ se déplace sur $\mathscr{C}$. Soit $M$ le point d'intersection entre $(A P)$ et la bissectrice de $\widehat{P O A}$. Montrer que $M$ se déplace sur un cercle que l'on décrira.
|
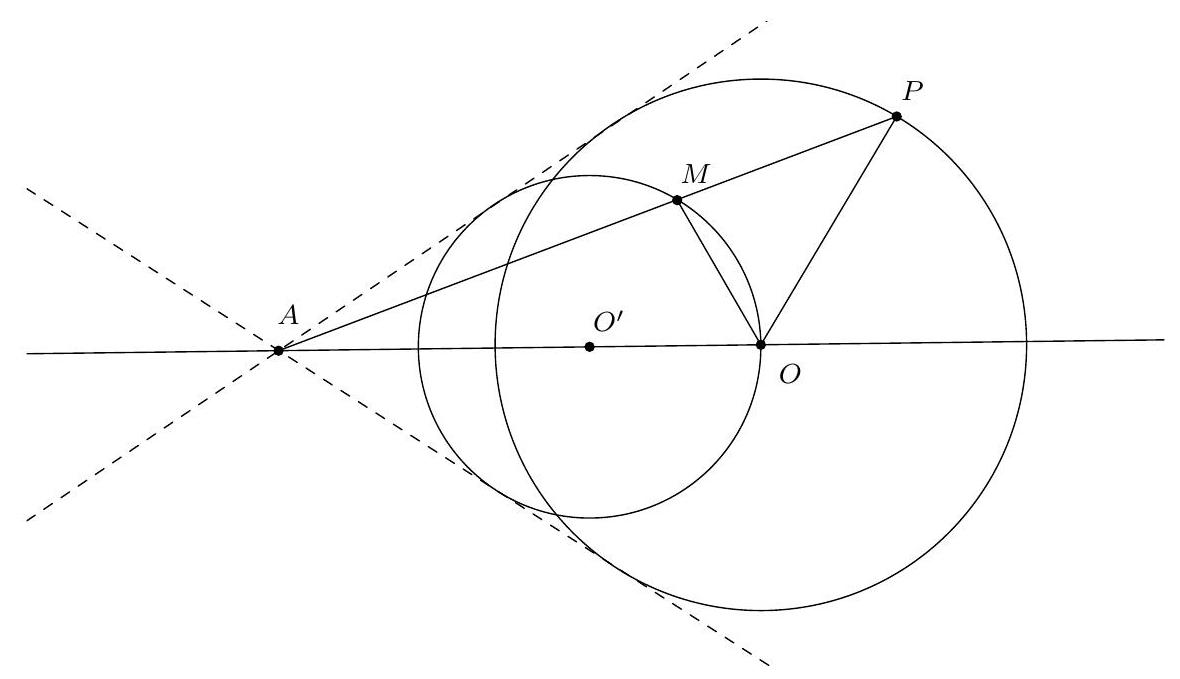
Notons $d=O A$ et $R$ le rayon du cercle.
D'après le théorème de la bissectrice, on a $M P / M A=O P / O A$, donc $\frac{M A}{A P}=\frac{M A}{M A+M P}=$ $\frac{1}{1+\frac{M P}{M A}}=\frac{1}{1+\frac{O P}{O A}}=\frac{O A}{O A+O P}=\frac{d}{d+R}$. Notons $k$ cette valeur. Soit $O^{\prime}$ le point de $[A O]$ tel que $A O^{\prime}=k A O$. D'après le théorème de Thalès, les droites $\left(O^{\prime} M\right)$ et $(O P)$ sont parallèles, donc $\frac{O^{\prime} M}{O P}=\frac{A M}{A P}=k$, donc $O^{\prime} M=k R$. Ceci prouve que $M$ décrit le cercle de centre $O^{\prime}$ et de rayon kR.
Remarquons que $A O^{\prime}+k R=k(d+R)=d$, donc ce cercle passe par $O$.
|
{
"exam": "French_envois",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-2-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T2",
"year": "2016"
}
|
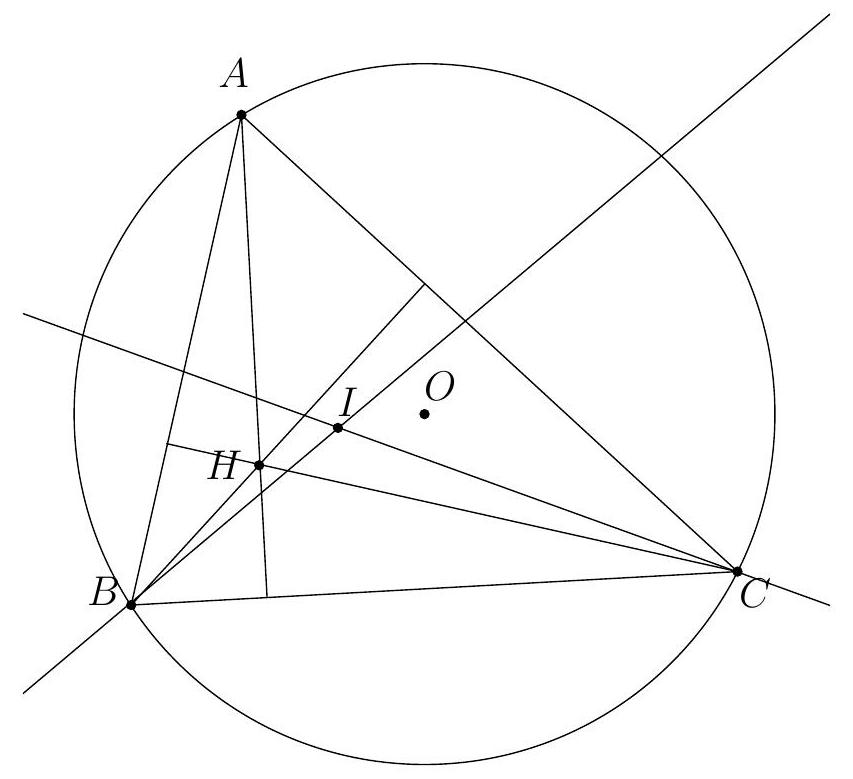
Let $ABC$ be a triangle such that $\widehat{A}=60^{\circ}$. We denote $O$ as the center of the circumcircle, $I$ as the center of the incircle, and $H$ as the orthocenter. Show that
1) $B, C, O, I, H$ are concyclic
2) $OIH$ is isosceles.
|
We use angles of lines. The angles are modulo $180^{\circ}$.
1) $(H B, H C)=(H B, A C)+(A C, A B)+(A B, H C)=D-(A B, A C)+D=-(A B, A C)=-60^{\circ}=$ $120^{\circ}=(O B, O C)$ (where we have denoted $D$ as the right angle), so $B, H, O, C$ are concyclic.
$(I B, I C)=(I B, B C)+(B C, I C)=-\widehat{B} / 2-\widehat{C} / 2=-120 / 2=-60^{\circ}=120^{\circ}$, so $I$ is also on this circle.
2) $(C O, C I)-(C I, C H)=(C O, C B)+(C B, C I)-(C I, C B)-(C B, C H)=(C O, C B)+$ $(C H, C B)+2(C B, C I)=(90-\widehat{A})+(90-\widehat{B})-\widehat{C}=0$, so $(C O, C I)=(C I, C H)$. Therefore, $(O I, O H)=(C I, C H)=(C O, C I)=(H O, H I)$, so $O I H$ is isosceles at $I$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle tel que $\widehat{A}=60^{\circ}$. On note $O$ le centre du cercle circonscrit, $I$ le centre du cercle inscrit et $H$ l'orthocentre. Montrer que
1) $B, C, O, I, H$ sont cocycliques
2) $O I H$ est isocèle.
|

On utilise les angles de droites. Les angles sont modulo $180^{\circ}$.
1) $(H B, H C)=(H B, A C)+(A C, A B)+(A B, H C)=D-(A B, A C)+D=-(A B, A C)=-60^{\circ}=$ $120^{\circ}=(O B, O C)$ (où on a noté $D$ l'angle droit), donc $B, H, O, C$ sont cocycliques.
$(I B, I C)=(I B, B C)+(B C, I C)=-\widehat{B} / 2-\widehat{C} / 2=-120 / 2=-60^{\circ}=120^{\circ}$, donc $I$ se trouve également sur ce cercle.
2) $(C O, C I)-(C I, C H)=(C O, C B)+(C B, C I)-(C I, C B)-(C B, C H)=(C O, C B)+$ $(C H, C B)+2(C B, C I)=(90-\widehat{A})+(90-\widehat{B})-\widehat{C}=0$, donc $(C O, C I)=(C I, C H)$. On a donc $(O I, O H)=(C I, C H)=(C O, C I)=(H O, H I)$, donc $O I H$ est isocèle en $I$.
|
{
"exam": "French_envois",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-2-solutions.jsonl",
"solution_match": "## Solution de l'exercice 2",
"tier": "T2",
"year": "2016"
}
|
From a point $A$ on a circle with center $O$, a tangent to this circle is drawn, and two points $B$ and $C$ are taken on this tangent, with $C$ between $A$ and $B$. From $B$ and $C$, $(B D)$ and $(C E)$ are drawn tangent to the circle. Prove that $\widehat{B O C}=\widehat{D A E}$.
|
Let $\alpha=\widehat{B D E}$ and $\beta=\widehat{C E A}$. According to the inscribed angle theorem, we have $\alpha=\widehat{D A E}$.
Since $(C A)$ and $(C E)$ are the two tangents drawn from $C$, we have $\widehat{E A C}=\widehat{C E A}=\beta$. $\widehat{B O C}=\widehat{B O A}-\widehat{C O A}$. Now, $(B O) \perp(A D)$ and $(O A) \perp(A C)$, so $\widehat{B O A}=\widehat{D A C}=\alpha+\beta$, and similarly $\widehat{C O A}=\beta$, thus $\widehat{B O C}=\alpha=\widehat{D A E}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Par un point $A$ d'un cercle de centre $O$, on mène une tangente à ce cercle, et on prend deux points $B$ et $C$ sur cette tangente, avec $C$ entre $A$ et $B$. De $B$ et $C$, on mène $(B D)$ et $(C E)$ tangentes au cercle. Démontrer que $\widehat{B O C}=\widehat{D A E}$.
|
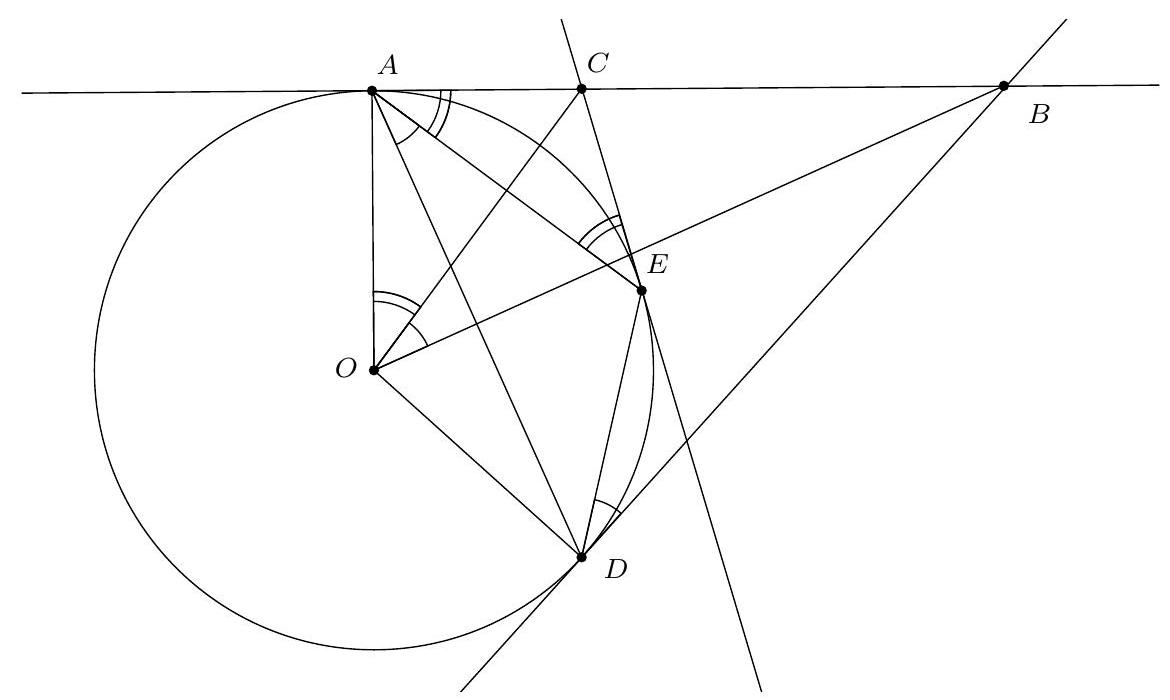
Notons $\alpha=\widehat{B D E}$ et $\beta=\widehat{C E A}$. D'après le théorème de l'angle inscrit, on a $\alpha=\widehat{D A E}$.
Comme $(C A)$ et $(C E)$ sont les deux tangentes menées à partir de $C$, on a $\widehat{E A C}=\widehat{C E A}=\beta$. $\widehat{B O C}=\widehat{B O A}-\widehat{C O A} . \mathrm{Or},(B O) \perp(A D)$ et $(O A) \perp(A C)$, donc $\widehat{B O A}=\widehat{D A C}=\alpha+\beta$, et de même $\widehat{C O A}=\beta$, donc $\widehat{B O C}=\alpha=\widehat{D A E}$.
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-2-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T2",
"year": "2016"
}
|
Let $ABC$ be a triangle. Let $P$ belong to the circumcircle. We know that the projections of $P$ onto $(BC)$, $(CA)$, and $(AB)$ are aligned on the line known as the Simson line. We assume that this line passes through the point diametrically opposite to $P$. Show that it also passes through the centroid of $ABC$.
|
Let $P^{\prime}$ be the point diametrically opposite to $P$. Let $\Delta$ be the Simson line. Let $h$ be the homothety with center $P$ and ratio 2. Then $h(\Delta)$ is the Steiner line. We know that it passes through the orthocenter $H$, so $\Delta$ passes through the midpoint of $[P H]$. We deduce that $\Delta$ is the median of $P P^{\prime} H$ from $P^{\prime}$.
Furthermore, (HO) is the median of $P P^{\prime} H$ from $H$. Since $\overrightarrow{H G}=\frac{2}{3} \overrightarrow{H O}$, the point $G$ is the centroid of $P H P^{\prime}$, so $\Delta$ passes through $G$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle. Soit $P$ appartenant au cercle circonscrit. On sait que les projetés de $P$ sur $(B C),(C A)$ et $(A B)$ sont alignés sur la droite dite de Simson. On suppose que cette droite passe par le point diamétralement opposé à $P$. Montrer qu'elle passe également par le centre de gravité de $A B C$.
|
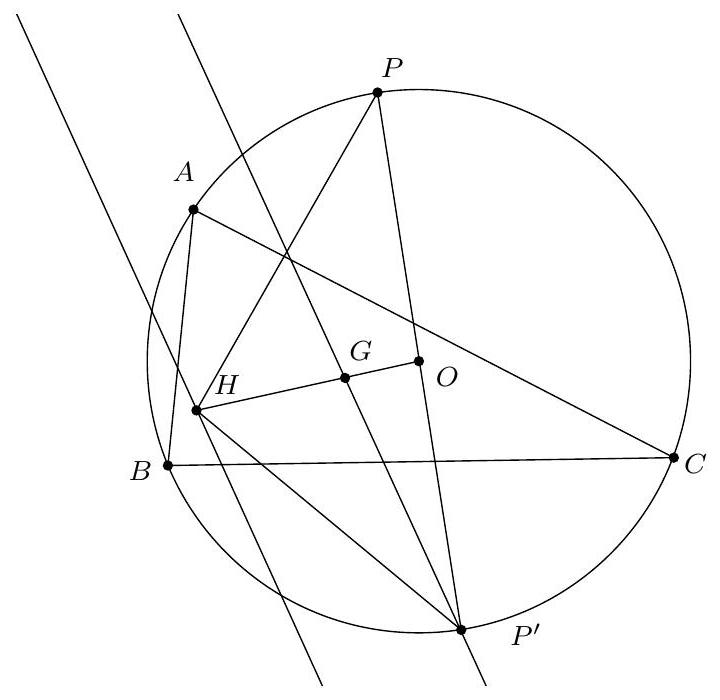
Notons $P^{\prime}$ le point diamétralement opposé à $P$. Soit $\Delta$ la droite de Simson. Soit $h$ l'homothétie de centre $P$ et de rapport 2. Alors $h(\Delta)$ est la droite de Steiner. On sait qu'elle passe par l'orthocentre $H$, donc $\Delta$ passe par le milieu de $[P H]$. On en déduit que $\Delta$ est la médiane de $P P^{\prime} H$ issue de $P^{\prime}$.
Par ailleurs, (HO) est la médiane de $P P^{\prime} H$ issue de $H$. Comme $\overrightarrow{H G}=\frac{2}{3} \overrightarrow{H O}$, le point $G$ est le centre de gravité de $P H P^{\prime}$, donc $\Delta$ passe par $G$.
|
{
"exam": "French_envois",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-2-solutions.jsonl",
"solution_match": "## Solution de l'exercice 4",
"tier": "T2",
"year": "2016"
}
|
Let $ABC$ be a triangle. Suppose that the median $(BM)$ and the angle bisector $(CD)$ intersect at a point $J$ such that $JB=JC$. Let $H$ be the foot of the altitude from $A$. Show that $JM=JH$.
Soit $ABC$ un triangle. On suppose que la médiane $(BM)$ et la bissectrice $(CD)$ se coupent en un point $J$ tel que $JB=JC$. Soit $H$ le pied de la hauteur issue de $A$. Montrer que $JM=JH$.
(Note: The second part is the original French text, which is kept as requested.)
|
Let $\gamma=\widehat{A C B}$. We have $M A=M C=M H$, so $\widehat{C H M}=\gamma$.
We also have $\widehat{C H M}=180^{\circ}-\widehat{M H B}=\widehat{H B M}+\widehat{B M H}$.
Furthermore, $\widehat{H B M}=\widehat{D C B}=\gamma / 2$, so $\widehat{B M H}=\widehat{H M B}=\gamma / 2$.
We deduce that $B H=H M=M C$. The triangles $B H J$ and $C M J$ satisfy $B J=C J, \widehat{H B J}=$ $\widehat{M C J}$ and $B H=C M$ so they are congruent. Consequently, $J H=H M$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle. On suppose que la médiane $(B M)$ et la bissectrice $(C D)$ se coupent en un point $J$ tel que $J B=J C$. Soit $H$ le pied de la hauteur issue de $A$. Montrer que $J M=J H$.
|
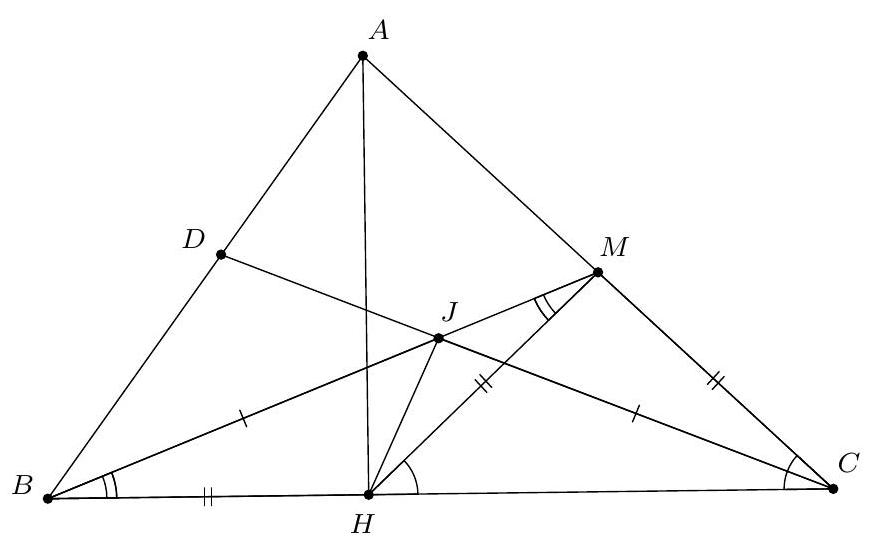
Notons $\gamma=\widehat{A C B}$. On a $M A=M C=M H$, donc $\widehat{C H M}=\gamma$.
On a aussi $\widehat{C H M}=180^{\circ}-\widehat{M H B}=\widehat{H B M}+\widehat{B M H}$.
De plus, $\widehat{H B M}=\widehat{D C B}=\gamma / 2$, donc $\widehat{B M H}=\widehat{H M B}=\gamma / 2$.
On en déduit que $B H=H M=M C$. Les triangles $B H J$ et $C M J$ vérifient $B J=C J, \widehat{H B J}=$ $\widehat{M C J}$ et $B H=C M$ donc sont isométriques. Par conséquent, $J H=H M$.
|
{
"exam": "French_envois",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-2-solutions.jsonl",
"solution_match": "## \nSolution de l'exercice 5",
"tier": "T2",
"year": "2016"
}
|
Let $ABC$ be a triangle, and $D, E, F$ the feet of the altitudes from $A, B, C$ respectively. We also define $H$ as the orthocenter of $ABC$, $O$ as the center of its circumcircle, and $X$ as the point on the line $(EF)$ that satisfies $XA = XD$. Show that the lines $(AX)$ and $(OH)$ are perpendicular.
|
We know that the radical axis of two circles is a line perpendicular to the line passing through the centers of the two circles.
The condition \( XA = XD \) means that \( X \) is on the perpendicular bisector of \([AD]\), which is none other than the midline \((B' C')\) (with \( B' \) and \( C' \) being the midpoints of \([AC]\) and \([AB]\)). We also know that the points \( A, E, F, H \) are concyclic according to the converse of the inscribed angle theorem. Furthermore, since \([AH]\) is a diameter of the circle passing through these four points, the midpoint \( H' \) of \([AH]\) is the center of this circle.
The center of the circle passing through \( A, B', C' \) is the midpoint \( O' \) of \([AO]\) (by the property of the homothety centered at \( A \) with a ratio of 1/2). We know that \((O' H')\) and \((OH)\) are parallel. The problem thus reduces to showing that \((AX)\) and \((O' H')\) are perpendicular. We will show here that \((AX)\) is actually the radical axis of the two circles mentioned earlier, which will complete the exercise according to the property mentioned at the beginning of the proof.
Since \( A \) is on both circles, it is indeed on their radical axis. We also know that \( B', C', E, F \) are concyclic on the Euler circle of triangle \( ABC \). Thus, we have the equality of lengths: \( XC' \times XB' = XE \times XF \), which means that \( X \) is indeed on the radical axis of our two circles.
Therefore, we have \((AX)\) and \((OH)\) being perpendicular.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle, et $D, E, F$ les pieds des hauteurs de $A, B, C$ respectivement. On définit aussi $H$ l'orthocentre de $A B C, O$ le centre de son cercle circonscrit, et $X$ le point de la droite $(E F)$ qui vérifie $X A=X D$. Montrer que les droites $(A X)$ et $(O H)$ sont perpendiculaires.
|
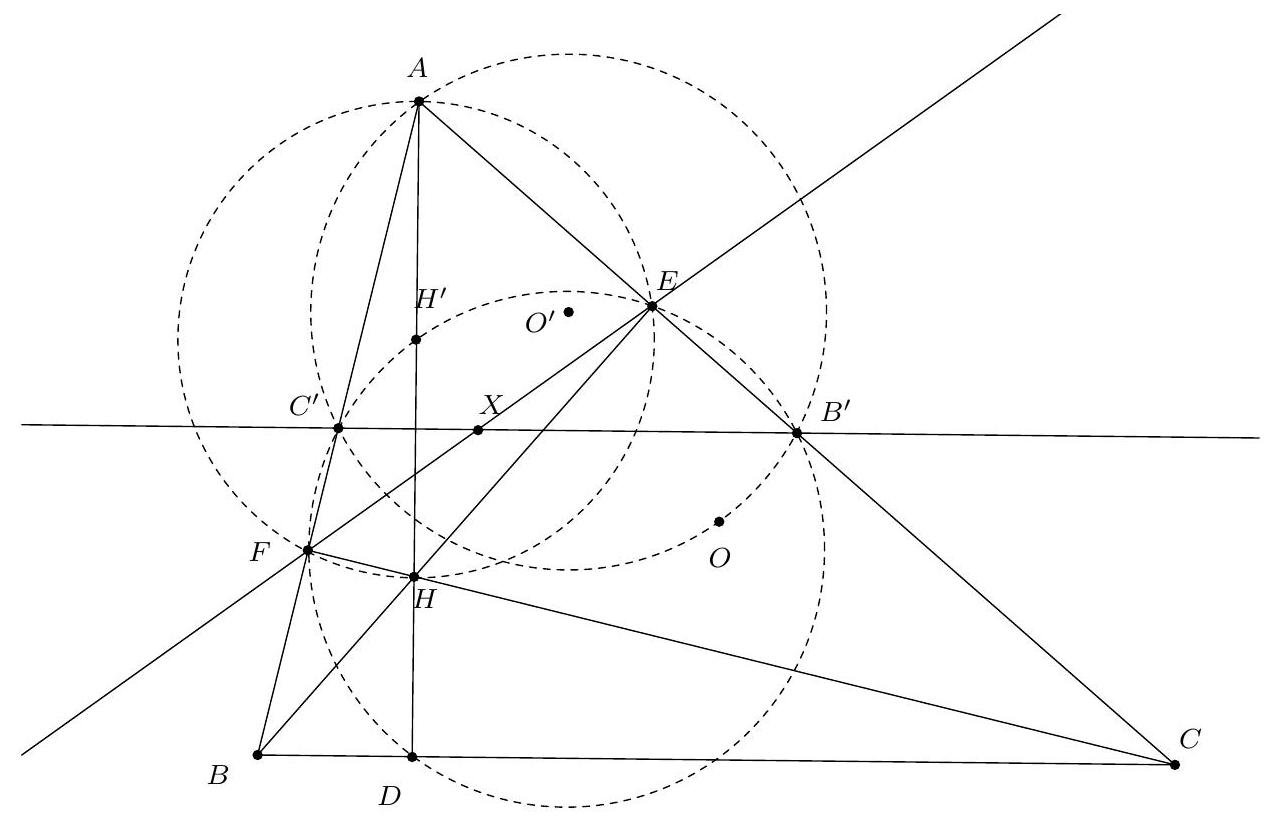
On sait que l'axe radical de deux cercles est une droite perpendiculaire à la droite passant par les centres des deux cercles.
La condition $X A=X D$ signifie que X est sur la médiatrice de $[A D]$, qui n'est autre que le droite des milieux $\left(B^{\prime} C^{\prime}\right)$ (avec $B^{\prime}$ et $C^{\prime}$ les milieux de $[A C]$ et de $[A B]$ ). On sait aussi que les points
$A, E, F, H$ sont cocycliques d'après la réciproque du théorème de l'angle inscrit. De, plus $[A H]$ étant un diamètre du cercle passant par ces quatre points, le milieu $H^{\prime}$ de $[A H]$ est le centre de ce cercle.
Le centre du cercle passant par $A, B^{\prime}, C^{\prime}$ est le milieu $O^{\prime}$ de $[A O]$ (par propriété de l'homothétie de centre $A$ et de rapport 1/2). On sait que $\left(O^{\prime} H^{\prime}\right)$ et $(O H)$ sont parallèles. Le problème revient donc à montrer que $(A X)$ et $\left(O^{\prime} H^{\prime}\right)$ sont perpendiculaires. Nous allons montrer ici que $(A X)$ est en fait l'axe radical des deux cercles évoqués précédemment, ce qui terminera l'exercice d'après la propriété évoquée au début de la preuve.
$A$ étant sur les deux cercles, est bien sur leur axe radical. On sait de plus que $B^{\prime}, C^{\prime}, E, F$ sont cocycliques sur le cercle d'Euler du triangle $A B C$. Ainsi on a l'égalité de longueurs : $X C^{\prime} \times X B^{\prime}=X E \times X F$, ce qui signifie que $X$ est bien sur l'axe radical de nos deux cercles.
Ainsi on a bien $(A X)$ et $(O H)$ qui sont perpendiculaires.
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-2-solutions.jsonl",
"solution_match": "## Solution de l'exercice 6",
"tier": "T2",
"year": "2016"
}
|
Let $ABC$ be a triangle, and $\Gamma$ its circumcircle. Let $M$ be the midpoint of the arc $BC$ not containing $A$. A circle $\mathscr{C}$ is tangent to $[AB), [AC)$ at $D$ and $E$ respectively, and internally tangent to $\Gamma$ at $F$. Show that $(DE), (BC)$, and $(FM)$ are concurrent.
|
Let $I$ be the center of the incircle of $ABC$. The line $(EF)$ intersects $\Gamma$ at a point $H$. Let $J$ be the intersection of $(BC)$ with $(FM)$.
It is easy to see that $H$ is the midpoint of the arc $AC$ not containing $B$: indeed, the homothety centered at $F$ that maps $\mathscr{C}$ to $\Gamma$ maps $(AC)$ to the tangent at $H$ to $\Gamma$; this tangent is parallel to $(AC)$, which implies that $H$ is the midpoint of the arc, and consequently $B, I, H$ are collinear.
By applying Pascal's theorem to the hexagon $AMFHB C$, we obtain that $I, E, J$ are collinear. Similarly, $D, I, J$ are collinear. Thus, $(DE)$, $(BC)$, and $(FM)$ meet at $J$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle, et $\Gamma$ son cercle circonscrit. Soit $M$ le milieu de l'arc $B C$ ne contenant pas $A$. Un cercle $\mathscr{C}$ est tangent à $[A B),[A C)$ en $D$ et $E$ respectivement, et tangent intérieurement à $\Gamma$ en $F$. Montrer que $(D E),(B C)$ et $(F M)$ sont concourantes.
|
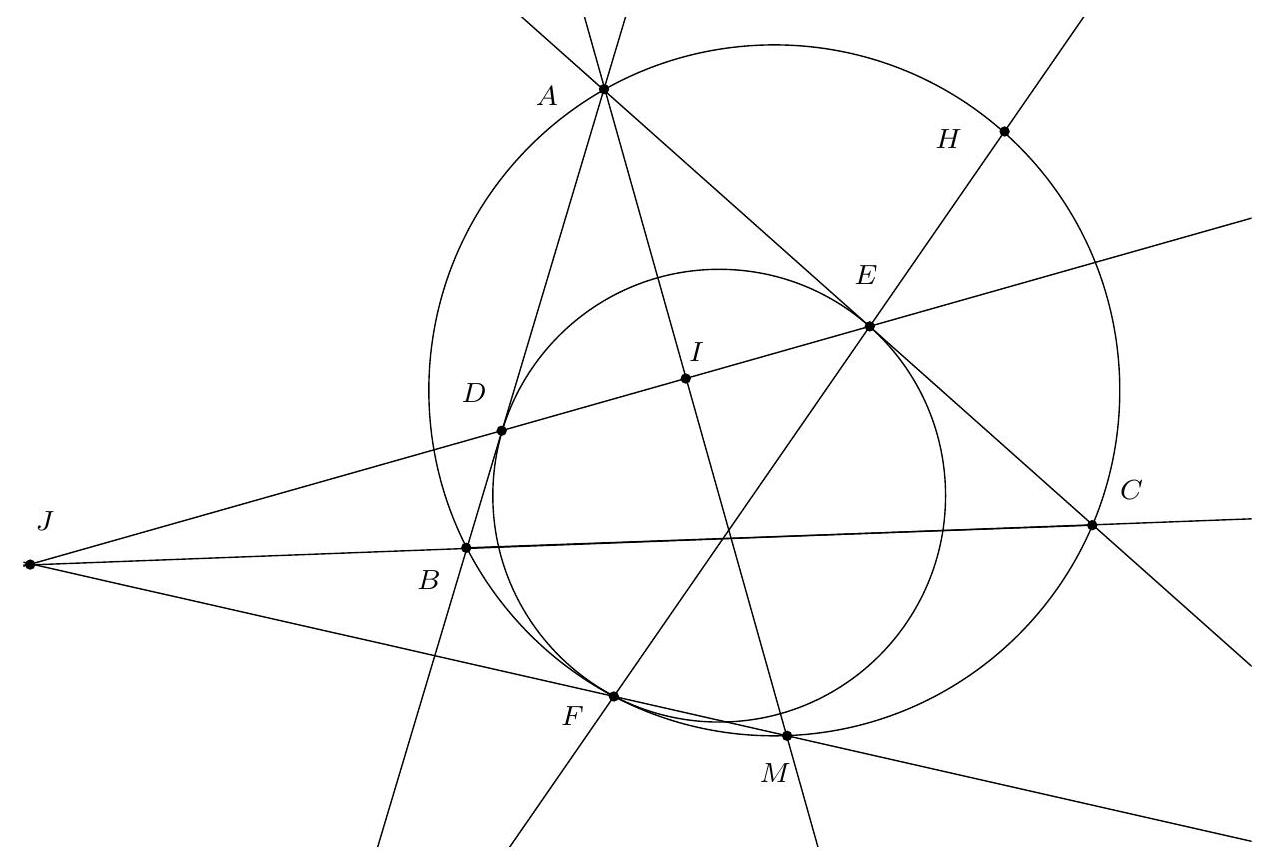
Soit $I$ le centre du cercle inscrit dans $A B C$. La droite $(E F)$ recoupe $\Gamma$ en un point $H$. Soit $J$ le point d'intersection de $(B C)$ avec $(F M)$.
Il est facile de voir que $H$ est le milieu de l'arc $A C$ ne contenant pas $B$ : en effet, l'homothétie de centre $F$ qui envoie $\mathscr{C}$ sur $\Gamma$ envoie $(A C)$ sur la tangente en $H$ à $\Gamma$; celle-ci est parallèle à $(A C)$, ce qui entraîne que $H$ est le milieu de l'arc, et par conséquent $B, I, H$ sont alignés.
En appliquant le théorème de Pascal à l'hexagone $A M F H B C$, on obtient que $I, E, J$ sont alignés. De même, $D, I, J$ sont alignés. Ainsi, $(D E),(B C)$ et $(F M)$ se rencontrent en $J$.
|
{
"exam": "French_envois",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-2-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 7",
"tier": "T2",
"year": "2016"
}
|
Let $ABC$ be a triangle, $D, E, F$ the points of tangency of the incircle on the sides $(BC), (AC)$, and $(AB)$, $M$ the midpoint of $[BC]$, $I$ the incenter of $ABC$. $G$ and $H$ are defined as the reflections of $E$ and $F$ with respect to $I$. We denote $Q$ as the intersection between the lines $(BC)$ and $(GH)$. Show that the lines $(IQ)$ and $(IM)$ are perpendicular.
|
Let $\omega$ be the incircle of $ABC$.
We will denote for any point $X$ in the plane $p(X)$ the polar of $X$ with respect to $\omega$. We know that for any point $X$ in the plane, $p(X)$ is a line perpendicular to $(IX)$. We will therefore show that $p(Q)$ and $(IM)$ are parallel to deduce the result.
We know that $p(D) = (BC)$, and that $Q \in (BC)$, so $Q \in p(D)$. Thus, by the property of polars (with respect to a fixed circle), we deduce that $D \in p(Q)$. Moreover, by the construction of the polar, we know that $A'$, the intersection of the tangents to $\omega$ at $G$ and $H$, is also on the polar of $Q$. Thus we have: $p(Q) = (DA')$. By symmetry of the construction, we know that $A$ and $A'$ are symmetric with respect to $I$.
Now let $D'$ be the symmetric of $D$ with respect to $I$ (which is therefore on $\omega$) and $D''$ the point on $(BC)$ such that $M$ is the midpoint of $[D D'']$. Since a homothety maps a line to a parallel line, we know that the lines $(DA')$ and $(D'A)$ are parallel, as well as the lines $(IM)$ and $(D'D'')$. It is known that the points $A, D', D''$ are collinear (which can be shown by a homothety centered at $A$).
Thus the lines $(DA')$ and $(IM)$ are parallel, and since $(DA')$ and $(QI)$ are perpendicular, we deduce that $(IQ)$ and $(IM)$ are indeed perpendicular.
Another solution. Let $\alpha, \beta$, and $\gamma$ be the angles of $DEF$ and $R$ the radius of the circumcircle of $DEF$. We have $BD = R \tan \beta, CD = R \tan \gamma$ so
$$
2DM = BC - 2BD = R(\tan \gamma - \tan \beta) = R \frac{\sin \gamma \cos \beta - \sin \beta \cos \gamma}{\cos \beta \cos \gamma} = R \frac{\sin (\gamma - \beta)}{\cos \beta \cos \gamma}.
$$
On the other hand, the law of sines in $QDH$ gives $DQ = DH \frac{\cos \gamma}{\sin (\beta - \gamma)} = 2R \frac{\cos \beta \cos \gamma}{\sin (\beta - \gamma)}$ so $QD \cdot DM = R^2 = DI^2$. Since $[ID]$ is the altitude of $IQM$ from $I$, $IQM$ is a right triangle at $I$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle, $D, E, F$ les points de tangence du cercle inscrit sur les côtés $(B C),(A C)$ et $(A B), M$ le milieu de $[B C], I$ le centre du cercle inscrit de $A B C . G$ et $H$ sont définis comme les symétriques de $E$ et $F$ par rapport à $I$. On note $Q$ l'intersection entre les droites $(B C)$ et $(G H)$. Montrer que les droites $(I Q)$ et $(I M)$ sont perpendiculaires.
|
Soit $\omega$ le cercle inscrit de $A B C$.
On notera pour tout point $X$ du plan $p(X)$ la polaire de $X$ par rapport à $\omega$. On sait que pour tout point $X$ du plan, $p(X)$ est une droite perpendiculaire à $(I X)$. Nous allons donc montrer que $p(Q)$ et $(I M)$ sont parallèles pour en déduire le résultat.
On sait que $p(D)=(B C)$, et que $Q \in(B C)$ donc $Q \in p(D)$. Ainsi par propriété des polaires (par rapport à un cercle fixé), on en déduit que $D \in p(Q)$. De plus par construction de la polaire, on sait que $A^{\prime}$ le point d'intersection des tangentes à $\omega$ en $G$ et $H$ est aussi sur la polaire de $Q$. Ainsi on a : $p(Q)=\left(D A^{\prime}\right)$. Par symétrie de la construction, on sait que $A$ et $A^{\prime}$ sont symétriques par rapport à $I$.
Soit maintenant $D^{\prime}$ le symétrique de $D$ par rapport à $I$ (qui est donc sur $\omega$ ) et $D^{\prime \prime}$ le point de $(B C)$ tel que $M$ soit le milieu de [ $\left.D D^{\prime \prime}\right]$. Une homothétie envoyant une droite sur une droite qui lui est parallèle, on sait que les droites $\left(D A^{\prime}\right)$ et $\left(D^{\prime} A\right)$ sont parallèles, ainsi que les droites $(I M)$ et $\left(D^{\prime} D^{\prime \prime}\right)$. Or il est connu que les points $A, D^{\prime}, D^{\prime \prime}$ sont alignés (se montre par une homothétie de centre $A$ ).
Ainsi les droites $\left(D A^{\prime}\right)$ et $(I M)$ sont parallèles, et $\left(D A^{\prime}\right)$ et $(Q I)$ étant perpendiculaires, on en déduit que $(I Q)$ et $(I M)$ sont bien perpendiculaires.
Autre solution. Notons $\alpha, \beta$ et $\gamma$ les angles de $D E F$ et $R$ le rayon du cercle circonscrit à $D E F$. On a $B D=R \tan \beta, C D=R \tan \gamma$ donc
$$
2 D M=B C-2 B D=R(\tan \gamma-\tan \beta)=R \frac{\sin \gamma \cos \beta-\sin \beta \cos \gamma}{\cos \beta \cos \gamma}=R \frac{\sin (\gamma-\beta)}{\cos \beta \cos \gamma} .
$$
D'autre part, la loi des sinus dans $Q D H$ donne $D Q=D H \frac{\cos \gamma}{\sin (\beta-\gamma)}=2 R \frac{\cos \beta \cos \gamma}{\sin (\beta-\gamma)}$ donc $Q D . D M=R^{2}=D I^{2}$. Or, $[I D]$ est la hauteur de $I Q M$ issue de $I$, donc $I Q M$ est rectangle en $I$.
|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "\nExercice 8.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-2-solutions.jsonl",
"solution_match": "## Solution de l'exercice 8",
"tier": "T2",
"year": "2016"
}
|
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that $f(x) f(y)-f(x y)=x+y$ for all $x, y \in \mathbb{R}$.
|
Let $f$ be a function satisfying the condition of the statement. By taking $x=y=0$, we obtain $f(0)(f(0)-1)=0$ hence $f(0)=0$ or $f(0)=1$.
First case: suppose that $f(0)=0$. By taking $y=0$ in the initial equation, we get $0=\chi$ for all $x \in \mathbb{R}$, which is absurd.
Second case: suppose that $f(0)=1$. By taking $y=0$ in the initial equation, we get $f(x)=x+1$ for all $x \in \mathbb{R}$.
Conversely, we verify that the function $f(x)=x+1$ for all $x \in \mathbb{R}$ is a solution because we indeed have $(x+1)(y+1)-(x y+1)=x+y$ for all $x, y \in \mathbb{R}$.
Remark. It is important to verify that conversely, the function $f(x)=x+1$ works. Indeed, we reasoned by successive implications and not by equivalences. For example, if the statement was "Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that $f(x) f(y)-f(x y)=x+y$ for all $x, y \in \mathbb{R}$ and $f(2)=2$", we would have concluded that conversely, the function $f(x)=x+1$ does not work (since $f(2)=3$) and that in this case there is no solution.
|
f(x)=x+1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Trouver toutes les fonctions $f: \mathbb{R} \rightarrow \mathbb{R}$ telles que $f(x) f(y)-f(x y)=x+y$ pour tous $x, y \in \mathbb{R}$.
|
Soit f une fonction vérifiant la condition de l'énoncé. En prenant $x=y=$ 0 , on obtient $f(0)(f(0)-1)=0$ donc $f(0)=0$ ou $f(0)=1$.
Premier cas : supposons que $f(0)=0$. En prenant $y=0$ dans l'équation initiale, on obtient $0=\chi$ pour tout $x \in \mathbb{R}$, ce qui est absurde.
Deuxième cas : supposons que $f(0)=1$. En prenant $y=0$ dans l'équation initiale, on obtient $f(x)=x+1$ pour tout $x \in \mathbb{R}$.
Réciproquement, on vérifie que la fonction $f(x)=x+1$ pour tout $x \in \mathbb{R}$ est solution car on a bien $(x+1)(y+1)-(x y+1)=x+y$ pour tous $x, y, \in \mathbb{R}$.
Remarque. Il est important de vérifier que réciproquement, la fonction $f(x)=x+1$ convient. En effet, nous avons raisonné par implications successives et non pas par équivalences. Par exemple, si l'énoncé était "Trouver toutes les fonctions $f: \mathbb{R} \rightarrow \mathbb{R}$ telles que $f(x) f(y)-f(x y)=$ $x+y$ pour tous $x, y \in \mathbb{R}$ et $f(2)=2$ ", nous aurions conclu que réciproquement, la fonction $f(x)=x+1$ ne convient pas $(\operatorname{car} f(2)=3)$ et que dans ce cas il n'y a pas de solution.
|
{
"exam": "French_envois",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-3-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T2",
"year": "2016"
}
|
Let $n \geqslant 3$ be an integer and $a_{1}, a_{2}, \ldots, a_{n}$ be real numbers.
(a) Suppose that $a_{i}<\max \left(a_{i-1}, a_{i+1}\right)$ for all $i \in\{2,3, \ldots, n-1\}$. Show that $a_{i}<$ $\max \left(a_{1}, a_{n}\right)$ for all $i \in\{2,3, \ldots, n-1\}$.
(b) Suppose that $a_{i} \leqslant \max \left(a_{i-1}, a_{i+1}\right)$ for all $i \in\{2,3, \ldots, n-1\}$. Is it true that $a_{i} \leqslant \max \left(a_{1}, a_{n}\right)$ for all $i \in\{2,3, \ldots, n-1\}$?
N.B. If $x$ and $y$ are two real numbers, we denote $\max (x, y)$ the largest of the two.
|
(a) Let $i \in\{1,2, \ldots, n\}$ be an integer such that $a_{i}=\max \left(a_{1}, \ldots, a_{n}\right)$. The statement indicates that $i \notin\{2,3, \ldots, n-1\}$. This shows both that $i \in\{1, n\}$, and thus that $a_{i}=\max \left(a_{1}, a_{n}\right)$, and that $a_{k}<a_{i}$ if $k \in\{2,3, \ldots, n-1\}$, which is the required inequality.
(b) The result is clearly true for $n=3$. Let's show that it is not always true for $n \geqslant 4$ by providing a counterexample: take $a_{1}=a_{n}=1$ and $a_{i}=2$. The condition of the statement is satisfied, but $a_{i}>\max \left(a_{1}, a_{n}\right)$ for all $2 \leqslant i \leqslant n-1$.
Another solution for (a). The idea is to look at where the sequence "rises" for the first time. For this, we will distinguish two cases:
First case: there exists a smallest integer $1 \leqslant \mathfrak{i}_{0} \leqslant n-1$ such that $a_{i_{0}} \leqslant a_{i_{0}+1}$. Thus, $a_{1}>\cdots>a_{i_{0}}$ and $a_{i_{0}} \leqslant a_{i_{0}+1}$. In particular, if $i_{0}=n-1$, we note that we have the desired result (since then $a_{n-1}<a_{1}$ and $a_{n-1} \leqslant a_{n}$). Suppose now that $\mathfrak{i}_{0}<n-1$ and show that $a_{j}<a_{j+1}$ for all integers $\mathfrak{i}_{0}+1 \leqslant j \leqslant n-1$ by induction on $j$.
Initialization: we have $a_{i_{0}+1}<\max \left(a_{i_{0}}, a_{i_{0}+2}\right)$. Since $a_{i_{0}} \leqslant a_{i_{0}+1}$, we must have $\max \left(a_{i_{0}}, a_{i_{0}+2}\right)=$ $a_{i_{0}+2}$, which implies that $a_{i_{0}+1}<a_{i_{0}+2}$.
Induction step: let $\mathfrak{i}_{0}+1 \leqslant \mathfrak{j}<n-1$ be an integer such that $a_{j}<a_{j+1}$. Show that $a_{j+1}<a_{j+2}$. Since $a_{\mathfrak{j}+1}<\max \left(a_{\mathfrak{j}}, a_{\mathfrak{j}+2}\right)$ and $a_{\mathfrak{j}}<\mathfrak{a}_{\mathfrak{j}+1}$, we must have $\max \left(a_{j}, a_{j+2}\right)=a_{j+2}$, which implies that $a_{j+1}<a_{j+2}$.
We therefore have:
$$
a_{1}>\cdots>a_{i_{0}} \leqslant a_{i_{0}+1}<a_{i_{0}+2}<a_{i_{0}+3}<\cdots<a_{n}
$$
which implies that $a_{i}<\max \left(a_{1}, a_{n}\right)$ for all $i \in\{2,3, \ldots, n-1\}$.
Second case: there does not exist an integer $1 \leqslant \mathfrak{i}_{0} \leqslant n-1$ such that $a_{i_{0}} \leqslant a_{i_{0}+1}$. Then $a_{1}>a_{2}>\cdots>$ $a_{n}$ and we have the desired result.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $n \geqslant 3$ un nombre entier et $a_{1}, a_{2}, \ldots, a_{n}$ des nombres réels.
(a) On suppose que $a_{i}<\max \left(a_{i-1}, a_{i+1}\right)$ pour tout $i \in\{2,3, \ldots, n-1\}$. Montrer que $a_{i}<$ $\max \left(a_{1}, a_{n}\right)$ pour tout $i \in\{2,3, \ldots, n-1\}$.
(b) On suppose que $a_{i} \leqslant \max \left(a_{i-1}, a_{i+1}\right)$ pour tout $i \in\{2,3, \ldots, n-1\}$. Est-il vrai que $a_{i} \leqslant \max \left(a_{1}, a_{n}\right)$ pour tout $i \in\{2,3, \ldots, n-1\}$ ?
N.B. Si $x$ et y sont deux nombres réels, on note $\max (x, y)$ le plus grand des deux.
|
(a) Soit $i \in\{1,2, \ldots, n\}$ un entier tel que $a_{i}=\max \left(a_{1}, \ldots, a_{n}\right)$. L'énoncé indique que $i \notin\{2,3, \ldots, n-1\}$. Cela montre à la fois que $i \in\{1, n\}$, donc que $a_{i}=\max \left(a_{1}, a_{n}\right)$, et que $a_{k}<a_{i}$ si $k \in\{2,3, \ldots, n-1\}$, ce qui était l'inégalité demandée.
(b) Le résultat est clairement vrai pour $\mathrm{n}=3$. Montrons qu'il n'est pas toujours vrai pour $\mathrm{n} \geqslant 4$ en exhibant un contre-exemple : prenons $a_{1}=a_{n}=1$ et $a_{i}=2$. La consigne de l'énoncé est respectée mais $a_{i}>\max \left(a_{1}, a_{n}\right)$ pour tout $2 \leqslant i \leqslant n-1$.
Autre solution pour (a). L'idée est de regarder où la suite "remonte" pour la première fois. Pour cela, nous allons distinguer deux cas :
Premier cas : il existe un plus petit entier $1 \leqslant \mathfrak{i}_{0} \leqslant n-1$ tel que $a_{i_{0}} \leqslant a_{i_{0}+1}$. Ainsi, $a_{1}>\cdots>a_{i_{0}}$ et $a_{i_{0}} \leqslant a_{i_{0}+1}$. En particulier, si $i_{0}=n-1$, on remarque qu'on a bien le résultat voulu (car alors $a_{n-1}<a_{1}$ at $a_{n-1} \leqslant a_{n}$ ). Supposons maintenant que $\mathfrak{i}_{0}<n-1$ et montrons que $a_{j}<a_{j+1}$ pour tout entier $\mathfrak{i}_{0}+1 \leqslant j \leqslant n-1$ par récurrence sur $j$.
Initialisation : on a $a_{i_{0}+1}<\max \left(a_{i_{0}}, a_{i_{0}+2}\right)$. Comme $a_{i_{0}} \leqslant a_{i_{0}+1}$, on doit avoir max $\left(a_{i_{0}}, a_{i_{0}+2}\right)=$ $a_{i_{0}+2}$, ce qui implique que $a_{i_{0}+1}<a_{i_{0}+2}$.
Hérédité : soit $\mathfrak{i}_{0}+1 \leqslant \mathfrak{j}<n-1$ un entier tel que $a_{j}<a_{j+1}$. Montrons que $a_{j+1}<a_{j+2}$. Comme $a_{\mathfrak{j}+1}<\max \left(a_{\mathfrak{j}}, a_{\mathfrak{j}+2}\right)$ et $a_{\mathfrak{j}}<\mathfrak{a}_{\mathfrak{j}+1}$, on doit avoir $\max \left(a_{j}, a_{j+2}\right)=a_{j+2}$, ce qui implique que $a_{j+1}<a_{j+2}$.
On a donc:
$$
a_{1}>\cdots>a_{i_{0}} \leqslant a_{i_{0}+1}<a_{i_{0}+2}<a_{i_{0}+3}<\cdots<a_{n}
$$
ce qui implique que $a_{i}<\max \left(a_{1}, a_{n}\right)$ pour tout $i \in\{2,3, \ldots, n-1\}$.
Deuxième cas : il n'existe pas d'entier $1 \leqslant \mathfrak{i}_{0} \leqslant n-1$ tel que $a_{i_{0}} \leqslant a_{i_{0}+1}$. Alors $a_{1}>a_{2}>\cdots>$ $a_{n}$ et on a bien le résultat voulu.
|
{
"exam": "French_envois",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-3-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T2",
"year": "2016"
}
|
Let $0 \leqslant a, b, c, d, e \leqslant 1$ be real numbers. Show that
$$
(1+a+b+c+d+e)^{2} \geqslant 4\left(a^{2}+b^{2}+c^{2}+d^{2}+e^{2}\right)
$$
|
The idea is to use the inequality $(x+y)^{2} \geqslant 4 x y$ for $x=1$ and a particular value of $y$.
More precisely, for all $x, y \geqslant 0$, we have $(x-y)^{2} \geqslant 0$, and thus $(x+y)^{2} \geqslant 4 x y$ (this inequality is also the arithmetic-geometric mean inequality for two variables). By evaluating this inequality with $x=1$ and $y=a+b+c+d+e$, we get:
$$
(1+a+b+c+d+e)^{2} \geqslant 4(a+b+c+d+e)
$$
For any real number $x$ such that $0 \leqslant x \leqslant 1$, we have $x \geqslant x^{2}$. Therefore,
$$
4(a+b+c+d+e) \geqslant 4\left(a^{2}+b^{2}+c^{2}+d^{2}+e^{2}\right)
$$
which finally shows that $(1+a+b+c+d+e)^{2} \geqslant 4\left(a^{2}+b^{2}+c^{2}+d^{2}+e^{2}\right)$.
## Common Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soient $0 \leqslant a, b, c, d, e \leqslant 1$ des nombres réels. Montrer que
$$
(1+a+b+c+d+e)^{2} \geqslant 4\left(a^{2}+b^{2}+c^{2}+d^{2}+e^{2}\right)
$$
|
L'idée est d'utiliser l'inégalité $(x+y)^{2} \geqslant 4 x y$ pour $x=1$ et une valeur particulière de $y$.
Plus précisément, pour tous $x, y \geqslant 0$, on a $(x-y)^{2} \geqslant 0$, et donc $(x+y)^{2} \geqslant 4 x y$ (cette inégalité est aussi l'inégalité arithmético-géométrique à deux variables). En évaluant cette inégalité avec $x=1$ et $y=a+b+c+d+e$, on obtient:
$$
(1+a+b+c+d+e)^{2} \geqslant 4(a+b+c+d+e)
$$
Or pour tout nombre réel $x$ tel que $0 \leqslant x \leqslant 1$, on a $x \geqslant x^{2}$. Donc
$$
4(a+b+c+d+e) \geqslant 4\left(a^{2}+b^{2}+c^{2}+d^{2}+e^{2}\right)
$$
ce qui montre finalement que $(1+a+b+c+d+e)^{2} \geqslant 4\left(a^{2}+b^{2}+c^{2}+d^{2}+e^{2}\right)$.
## Exercices communs
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-3-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T2",
"year": "2016"
}
|
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that $f(f(x)+3 y)=12 x+f(f(y)-x)$ for all $x, y \in \mathbb{R}$.
|
Let $f$ be a function satisfying the condition of the statement. The idea is to show that $f$ is injective by using the fact that it is surjective. First, let's show that $f$ is surjective. By taking $y=-f(x) / 3$ in the functional equation, we get $f(f(y)-x) = f(0)-12 x$. By varying $x$, we see that the right-hand side of this last equality can take any real number value, and therefore the left-hand side can as well, which implies that $f$ is surjective.
Let's show that $f$ is injective. Let $a, b \in \mathbb{R}$ such that $f(a)=f(b)$. We will show that $a=b$. By taking $y=a$ and $y=b$ in the functional equation, we get for all $x \in \mathbb{R}$
$$
\mathbf{f}(\mathbf{f}(\mathrm{x})+3 \mathbf{a})=12 x+f(f(a)-x)=12 x+f(f(b)-x)=f(f(x)+3 b)
$$
where we used the fact that $\mathrm{f}(\mathrm{a})=\mathrm{f}(\mathrm{b})$ for the second equality. This implies that for all $y \in \mathbb{R}$,
$$
f(y)=f(y+3(b-a))
$$
Indeed, if we fix $y \in \mathbb{R}$, by surjectivity there exists $x$ such that $f(x)=y-3 a$ and by substituting into (1), this gives (2). In particular, $f(0)=f(3(b-a))$. Then
$$
\mathbf{f}(\mathbf{f}(0))=\mathbf{f}(\mathbf{f}(3(b-a))+3 \cdot 0)=12 \cdot 3(b-a)+\mathbf{f}(\mathbf{f}(0)-3(b-a))=12 \cdot 3(b-a)+\mathbf{f}(\mathbf{f}(0))
$$
where for the first equality we use the fact that $f(0)=f(3(b-a))$, for the second we use the functional equation from the statement (with $x=3(b-a)$ and $y=0$), and for the third equality we use (2) (with $y=f(0)-3(b-a)$). Therefore, $3(b-a)=0$ and $a=b$.
To conclude, by taking $x=0$ in the initial equation and using the injectivity of $f$, we get
$$
f(y)=f(0)+3 y
$$
for all real $y$.
Conversely, we verify that functions of the form $f(x)=a+3 x$ for all $x \in \mathbb{R}$ with $a \in \mathbb{R}$ satisfy the functional equation from the statement.
|
f(x)=a+3x
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Trouver toutes les fonctions $f: \mathbb{R} \rightarrow \mathbb{R}$ telles que $f(f(x)+3 y)=12 x+f(f(y)-x)$ pour tous $x, y \in \mathbb{R}$.
|
Soit f une fonction satisfaisant à la condition de l'énoncé. L'idée est de montrer que f est injective en utilisant le fait qu'elle est surjective. Montrons d'abord que f est surjective. En prenant $y=-f(x) / 3$ dans l'équation fonctionnelle, on obtient $f(f(y)-x)=$ $f(0)-12 x$. En faisant varier $x$, on voit que le membre de droite de cette dernière égalité peut prendre pour valeur n'importe quel nombre réel, et donc le membre de gauche aussi, ce qui implique que f est surjective.
Montrons que $f$ est injective. Soient $a, b \in \mathbb{R}$ tels que $f(a)=f(b)$. Nous allons montrer que $a=b$. En prenant $y=a$ et $y=b$ dans l'équation fonctionnelle, on obtient pour tout $x \in \mathbb{R}$
$$
\mathbf{f}(\mathbf{f}(\mathrm{x})+3 \mathbf{a})=12 x+f(f(a)-x)=12 x+f(f(b)-x)=f(f(x)+3 b)
$$
où on a utilisé le fait que $\mathrm{f}(\mathrm{a})=\mathrm{f}(\mathrm{b})$ pour la deuxième égalité. Ceci implique que pour tout $y \in \mathbb{R}$,
$$
f(y)=f(y+3(b-a))
$$
En effet, si on fixe $y \in \mathbb{R}$, par surjectivité il existe $x$ tel que $f(x)=y-3 a$ et en injectant dans (1), ceci donne (2). En particulier, $f(0)=f(3(b-a))$. Alors
$$
\mathbf{f}(\mathbf{f}(0))=\mathbf{f}(\mathbf{f}(3(b-a))+3 \cdot 0)=12 \cdot 3(b-a)+\mathbf{f}(\mathbf{f}(0)-3(b-a))=12 \cdot 3(b-a)+\mathbf{f}(\mathbf{f}(0))
$$
où pour la première égalité on utilise le fait que $f(0)=f(3(b-a))$, pour la deuxième on utilise l'équation fonctionnelle de l'énoncé (avec $x=3(b-a)$ et $y=0$ ), pour la troisième égalité on utilise (2) $(\operatorname{avec} y=f(0)-3(b-a)$ ). Donc $3(b-a)=0$ et $a=b$.
Pour conclure, en prenant $x=0$ dans l'équation de départ et en utilisant l'injectivité de f , on obtient
$$
f(y)=f(0)+3 y
$$
pour tout réel $y$.
Réciproquement, on vérifie que les fonctions de la forme $f(x)=a+3 x$ pour tout $x \in \mathbb{R}$ avec $a \in \mathbb{R}$ vérifient l'équation fonctionnelle de l'énoncé.
|
{
"exam": "French_envois",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-3-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T2",
"year": "2016"
}
|
Let \( a, b, c > 0 \). Show that
\[
\sqrt{\frac{a}{b+c}} + \sqrt{\frac{b}{c+a}} + \sqrt{\frac{c}{a+b}} > 2.
\]
|
The idea is to use the arithmetic-geometric mean inequality to lower bound $\frac{1}{\sqrt{x+y}}$. More precisely, by the arithmetic-geometric mean inequality:
$$
\sqrt{\frac{a}{b+c}}=\frac{a}{\sqrt{a(b+c)}} \geqslant \frac{a}{(a+b+c) / 2} \geqslant \frac{2 a}{a+b+c}
$$
We proceed similarly to show that $\sqrt{\frac{b}{c+a}} \geqslant \frac{2 b}{a+b+c}$ and that $\sqrt{\frac{c}{a+b}} \geqslant \frac{2 c}{a+b+c}$. We deduce that
$$
\sqrt{\frac{a}{b+c}}+\sqrt{\frac{b}{c+a}}+\sqrt{\frac{c}{a+b}} \geqslant 2
$$
Equality holds if and only if we are in the equality case of each of the three arithmetic-geometric mean inequalities used, i.e., $a=b+c, b=a+c$ and $c=a+b$, which is impossible.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soient a, b, $c>0$. Montrer que
$$
\sqrt{\frac{a}{b+c}}+\sqrt{\frac{b}{c+a}}+\sqrt{\frac{c}{a+b}}>2 .
$$
|
L'idée est d'utiliser inégalité arithmético-géométrique pour minorer $\frac{1}{\sqrt{x+y}}$. Plus précisément, on a, par inégalité arithmético-géométrique :
$$
\sqrt{\frac{a}{b+c}}=\frac{a}{\sqrt{a(b+c)}} \geqslant \frac{a}{(a+b+c) / 2} \geqslant \frac{2 a}{a+b+c}
$$
On procède de même pour montrer que $\sqrt{\frac{b}{c+a}} \geqslant \frac{2 b}{a+b+c}$ et que $\sqrt{\frac{c}{a+b}} \geqslant \frac{2 c}{a+b+c}$. On en déduit que
$$
\sqrt{\frac{a}{b+c}}+\sqrt{\frac{b}{c+a}}+\sqrt{\frac{c}{a+b}} \geqslant 2
$$
Il y a égalité seulement si et seulement si on est dans le cas d'égalité de chacune des trois inégalités arithmético-géométrique utilisées, soit : $a=b+c, b=a+c$ et $c=a+b$, ce qui est impossible.
|
{
"exam": "French_envois",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-3-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T2",
"year": "2016"
}
|
Let $n>1$ be an integer. Find all non-constant polynomials $P$ with real coefficients such that
$$
P(x) P\left(x^{2}\right) P\left(x^{3}\right) \cdots P\left(x^{n}\right)=P\left(x^{\frac{n(n+1)}{2}}\right)
$$
for all real numbers $x$.
|
We will show that the solutions are of the form $P(x)=x^{a}$ with $a \geqslant 0$ an integer if $n$ is even, and $P(x)=x^{a}$ or $P(x)=-x^{a}$ with $a \geqslant 0$ an integer if $n$ is odd. Since $1+2+\cdots+n=\frac{n(n+1)}{2}$, we first verify that these polynomials satisfy the equation given in the statement.
Let $P$ now be a polynomial solution. First, write $P$ in the form $P(x)=x^{a} Q(x)$ with $a \geqslant 0$ an integer and $Q$ a polynomial such that $c=Q(0) \neq 0$. Write $Q'$ in the form $Q'=x^{b} S(x)$ with $b \geqslant 0$ an integer and $S$ a polynomial such that $S(0) \neq 0$ (and thus $S$ is not divisible by the polynomial $x$), and set
$$
R(x)=Q(x) Q\left(x^{2}\right) Q\left(x^{3}\right) \cdots Q\left(x^{n}\right)
$$
The idea is to consider the quantity $R'(x) / R(x)$, where $R'$ is the derivative of $R$. Indeed, since $1+2+\cdots+n=\frac{n(n+1)}{2}$, $Q$ must also satisfy the equality
$$
Q(x) Q\left(x^{2}\right) Q\left(x^{3}\right) \cdots Q\left(x^{n}\right)=Q\left(x^{\frac{n(n+1)}{2}}\right) .
$$
By setting $x=0$, we find $c^{n-1}=1$, so $c=1$ if $n$ is even and $c= \pm 1$ if $n$ is odd. Suppose, for the sake of contradiction, that $Q$ is not constant (so that $Q'$ is not the zero polynomial), and differentiate (3):
$$
R(x)\left(\frac{Q'(x)}{Q(x)}+2 x \frac{Q'\left(x^{2}\right)}{Q\left(x^{2}\right)}+\cdots+n x^{n-1} \frac{Q'\left(x^{n}\right)}{Q\left(x^{n}\right)}\right)=\frac{n(n+1)}{2} x^{\frac{n(n+1)}{2}-1} Q'\left(x^{\frac{n(n+1)}{2}}\right) .
$$
Note that $R(0)=c^{n} \neq 0$ (and thus $R$ is not divisible by the polynomial $x$). The highest power of $x$ that divides the right-hand side of (4) is $x^{\frac{n(n+1)}{2}-1+b \frac{n(n+1)}{2}}$ while the highest power of $x$ that divides the left-hand side is $x^{b}$ (since all terms in the sum are divisible by $x^{b+1}$ except $\frac{Q'(x)}{Q(x)}$). Therefore,
$$
b=\frac{n(n+1)}{2}-1+b \frac{n(n+1)}{2}
$$
Since $n \geqslant 2$,
$$
b<b \frac{n(n+1)}{2}<\frac{n(n+1)}{2}-1+b \frac{n(n+1)}{2}
$$
which is absurd. Therefore, $Q$ is constant, which concludes the proof.
## Exercises of Group A
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Soit $n>1$ un entier. Trouver tous les polynômes $P$ non constants à coefficients réels tels que
$$
P(x) P\left(x^{2}\right) P\left(x^{3}\right) \cdots P\left(x^{n}\right)=P\left(x^{\frac{n(n+1)}{2}}\right)
$$
pour tout nombre réel $x$.
|
Nous allons montrer que les solutions sont de la forme $\mathrm{P}(\mathrm{x})=\mathrm{x}^{\mathrm{a}}$ avec $a \geqslant 0$ un entier si $n$ est pair, et $P(x)=x^{a}$ ou $P(x)=-x^{a}$ avec $a \geqslant 0$ un entier si $n$ est impair. Comme $1+2+\cdots+n=\frac{n(n+1)}{2}$, on vérifie tout d'abord que ces polynômes vérifient l'équation de l'énoncé.
Soit maintenant $P$ un polynôme solution. Écrivons d'abord $P$ sous la forme $P(x)=x^{a} Q(x)$ avec $a \geqslant 0$ un entier et $Q$ un polynôme tel que $c=Q(0) \neq 0$. Écrivons $Q^{\prime}$ sous la forme $Q^{\prime}=x^{b} S(x)$ avec $b \geqslant 0$ un entier et $S$ un polynôme tel que $S(0) \neq 0$ (et donc $S$ n'est pas divisible par le polynôme $x$ ), et posons
$$
R(x)=Q(x) Q\left(x^{2}\right) Q\left(x^{3}\right) \cdots Q\left(x^{n}\right)
$$
L'idée est de considérer la quantité $R^{\prime}(x) / R(x)$, où $R^{\prime}$ est le polynôme dérivé de R. En effet, comme $1+2+\cdots+n=\frac{\mathfrak{n}(\boldsymbol{n}+1)}{2}$, Q doit aussi vérifier l'égalité
$$
Q(x) Q\left(x^{2}\right) Q\left(x^{3}\right) \cdots Q\left(x^{n}\right)=Q\left(x^{\frac{n(n+1)}{2}}\right) .
$$
En faisant $x=0$, on trouve $\boldsymbol{c}^{n-1}=1$, de sorte que $\mathrm{c}=1$ si n est pair et $\mathrm{c}= \pm 1$ si n est impair. Supposons par l'absurde que $Q$ n'est pas constant (de sorte que $Q^{\prime} n^{\prime}$ est pas le polynôme nul), et dérivons (3) :
$$
R(x)\left(\frac{Q^{\prime}(x)}{Q(x)}+2 x \frac{Q^{\prime}\left(x^{2}\right)}{Q\left(x^{2}\right)}+\cdots+n x^{n-1} \frac{Q^{\prime}\left(x^{n}\right)}{Q\left(x^{n}\right)}\right)=\frac{n(n+1)}{2} x^{\frac{n(n+1)}{2}-1} Q^{\prime}\left(x^{\frac{n(n+1)}{2}}\right) .
$$
Notons que $R(0)=c^{n} \neq 0$ (et donc $R n^{\prime}$ est pas divisible par le polynôme $x$ ). La plus grande puissance de $x$ qui divise le membre de droite de (4) est $x^{\frac{n(n+1)}{2}-1+b \frac{n(n+1)}{2}}$ tandis que la plus grande puissance de $x$ qui divise celui de gauche est $x^{b}$ (car tous les termes de la somme sont divisibles par $x^{\mathrm{b}+1}$ sauf $\frac{\mathrm{Q}^{\prime}(x)}{\mathrm{Q}(x)}$ ). Donc
$$
\mathrm{b}=\frac{\mathrm{n}(\mathrm{n}+1)}{2}-1+\mathrm{b} \frac{\mathrm{n}(\mathrm{n}+1)}{2}
$$
Or $n \geqslant 2$, donc
$$
\mathrm{b}<\mathrm{b} \frac{\mathrm{n}(\mathrm{n}+1)}{2}<\frac{\mathrm{n}(\mathrm{n}+1)}{2}-1+\mathrm{b} \frac{\mathrm{n}(\mathrm{n}+1)}{2}
$$
ce qui est absurde. Donc $Q$ est constant, ce qui conclut.
## Exercices du groupe A
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-3-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T2",
"year": "2016"
}
|
. Let $n \geqslant 2$ be an integer and let $x_{1}, \ldots, x_{n}$ be positive real numbers such that $x_{1} x_{2} \cdots x_{n}=1$. Show that
$$
\frac{1}{n-1+x_{1}}+\frac{1}{n-1+x_{2}}+\cdots+\frac{1}{n-1+x_{n}} \leqslant 1
$$
|
By reducing to a common denominator, it is a matter of showing that
$$
\sum_{k=1}^{n} \prod_{j \neq k}\left(x_{j}+n-1\right) \leqslant \prod_{k=1}^{n}\left(x_{k}+n-1\right)
$$
We denote
$$
\sigma_{k}=\sum_{1 \leqslant i_{1}<\cdots<i_{k} \leqslant n} x_{i_{1}} x_{i_{2}} \cdots x_{i_{k}}
$$
the $k$-th elementary polynomial (of degree $k$) in $x_{1}, \cdots, x_{n}$. Then, by expanding both sides of (5), we see that the coefficient of $\sigma_{k}$ is $(n-1)^{n-k}$ on the right side for $1 \leqslant k \leqslant n$, and $(n-k)(n-1)^{n-k-1}$ on the left side for $1 \leqslant k \leqslant n-1$. The constant term is $(n-1)^{n}$ on the right and $n(n-1)^{n-1}$ on the left. In other words,
$$
\prod_{k=1}^{n}\left(x_{j}+n-1\right)=\sum_{k=1}^{n}(n-1)^{n-k} \sigma_{k}+(n-1)^{n}
$$
and
$$
\sum_{k=1}^{n} \prod_{j \neq k}\left(x_{j}+n-1\right)=\sum_{k=1}^{n-1}(n-k)(n-1)^{n-k-1} \sigma_{k}+n(n-1)^{n-1}
$$
By noting $D=\prod_{k=1}^{n}\left(x_{k}+n-1\right)-\sum_{k=1}^{n} \prod_{j \neq k}\left(x_{j}+n-1\right)$, we have
$$
D=x_{1} x_{2} \cdots x_{n}+\sum_{k=1}^{n-1}(k-1)(n-1)^{n-k-1} \sigma_{k}-(n-1)^{n-1}
$$
Since $\sigma_{k} \geqslant\binom{ n}{k}$ by the arithmetic-geometric inequality (since $x_{1} x_{2} \cdots x_{n}=1$), we have:
$$
D \geqslant \sum_{k=1}^{n}(k-1)(n-1)^{n-k-1}\binom{n}{k}-(n-1)^{n-1}
$$
or, by dividing both sides by $(n-1)^{n-1}$,
$$
\frac{D}{(n-1)^{n-1}} \geqslant \sum_{k=1}^{n}(k-1)(n-1)^{-k}\binom{n}{k}-1=\sum_{k=1}^{n} k(n-1)^{-k}\binom{n}{k}-\sum_{k=1}^{n}(n-1)^{-k}\binom{n}{k}-1 .
$$
Now,
$$
\sum_{k=1}^{n} k\binom{n}{k}(n-1)^{-k}=\frac{n}{n-1} \sum_{k=1}^{n}\binom{n-1}{k-1} \cdot\left(\frac{1}{n-1}\right)^{k-1}=\frac{n}{n-1} \times\left(\frac{n}{n-1}\right)^{n-1}=\left(\frac{n}{n-1}\right)^{n}
$$
and
$$
\sum_{k=1}^{n}(n-1)^{-k}\binom{n}{k}=\sum_{k=0}^{n}(n-1)^{-k}\binom{n}{k}-1=\left(\frac{n}{n-1}\right)^{n}-1 .
$$
We deduce that $D \geqslant 0$, which concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
. Soit $n \geqslant 2$ un nombre entier et soient $x_{1}, \ldots, x_{n}$ des nombres réels positifs tels que $x_{1} x_{2} \cdots x_{n}=1$. Montrer que
$$
\frac{1}{n-1+x_{1}}+\frac{1}{n-1+x_{2}}+\cdots+\frac{1}{n-1+x_{n}} \leqslant 1
$$
|
En réduisant au même dénominateur, il s'agit de montrer que
$$
\sum_{k=1}^{n} \prod_{j \neq k}\left(x_{j}+n-1\right) \leqslant \prod_{k=1}^{n}\left(x_{k}+n-1\right)
$$
On note
$$
\sigma_{k}=\sum_{1 \leqslant i_{1}<\cdots<i_{k} \leqslant n} x_{i_{1}} x_{i_{2}} \cdots x_{i_{k}}
$$
le $k$-ème polynôme élémentaire (de degré $k$ donc) en $x_{1}, \cdots, x_{n}$. Alors, en développant les deux côtés de (5), on voit que le coefficient de $\sigma_{k}$ est $(n-1)^{n-k}$ dans celui de droite pour $1 \leqslant k \leqslant n$, et $(n-k)(n-1)^{n-k-1}$ dans celui de gauche pour $1 \leqslant k \leqslant n-1$. Le coefficient constant vaut $(n-1)^{n}$ à droite et $n(n-1)^{n-1}$ à gauche. Autrement dit,
$$
\prod_{k=1}^{n}\left(x_{j}+n-1\right)=\sum_{k=1}^{n}(n-1)^{n-k} \sigma_{k}+(n-1)^{n}
$$
et
$$
\sum_{k=1}^{n} \prod_{j \neq k}\left(x_{j}+n-1\right)=\sum_{k=1}^{n-1}(n-k)(n-1)^{n-k-1} \sigma_{k}+n(n-1)^{n-1}
$$
En notant $D=\prod_{k=1}^{n}\left(x_{k}+n-1\right)-\sum_{k=1}^{n} \prod_{j \neq k}\left(x_{j}+n-1\right)$, on a donc
$$
D=x_{1} x_{2} \cdots x_{n}+\sum_{k=1}^{n-1}(k-1)(n-1)^{n-k-1} \sigma_{k}-(n-1)^{n-1}
$$
Or $\sigma_{k} \geqslant\binom{ n}{k}$ par l'inégalité arithmético-géométrique ( $\operatorname{car} x_{1} x_{2} \cdots x_{n}=1$,) de sorte que :
$$
D \geqslant \sum_{k=1}^{n}(k-1)(n-1)^{n-k-1}\binom{n}{k}-(n-1)^{n-1}
$$
ou encore, en divisant les deux côtés par $(\mathrm{n}-1)^{\mathrm{n}-1}$,
$$
\frac{D}{(n-1)^{n-1}} \geqslant \sum_{k=1}^{n}(k-1)(n-1)^{-k}\binom{n}{k}-1=\sum_{k=1}^{n} k(n-1)^{-k}\binom{n}{k}-\sum_{k=1}^{n}(n-1)^{-k}\binom{n}{k}-1 .
$$
Or
$$
\sum_{k=1}^{n} k\binom{n}{k}(n-1)^{-k}=\frac{n}{n-1} \sum_{k=1}^{n}\binom{n-1}{k-1} \cdot\left(\frac{1}{n-1}\right)^{k-1}=\frac{n}{n-1} \times\left(\frac{n}{n-1}\right)^{n-1}=\left(\frac{n}{n-1}\right)^{n}
$$
et
$$
\sum_{k=1}^{n}(n-1)^{-k}\binom{n}{k}=\sum_{k=0}^{n}(n-1)^{-k}\binom{n}{k}-1=\left(\frac{n}{n-1}\right)^{n}-1 .
$$
On en déduit que $D \geqslant 0$, ce qui conclut.
|
{
"exam": "French_envois",
"problem_label": "7",
"problem_match": "\nExercice 7",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-3-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 7",
"tier": "T2",
"year": "2016"
}
|
We denote $S(k)$ as the sum of the digits of an integer $k$. We say that an integer $a$ is of order $n$ if there exists a sequence of integers $a_{0}, a_{1}, \ldots, a_{n}$ such that $a_{n}=a$ and $a_{i+1}=a_{i}-S\left(a_{i}\right)$ for all $i=0,1, \ldots, n-1$. Show that for every integer $n \geqslant 1$ there exists an integer $b$ which is of order $n$ but not of order $n+1$.
|
We set $F(x)=x-S(x)$, and consider the sequence defined by $u_{0}=1$ and $u_{i+1}=10^{u_{i}}$ for $i \geqslant 0$. Let $n \geqslant 1$ be fixed, and consider an integer $N>u_{n+1}$. We will show that $X=F^{(n)}\left(10^{N}-5 N\right)$ (we iterate $F$ $n$ times) is of order $n$ but not $n+1$. For this, it suffices to show that $X$ is not of order $n+1$.
First, we note that $F(a)-F(b)$ is always divisible by 9, and that if $a$ and $b$ differ only in their last $k$ digits, then $|a-b| \leqslant 10^{k}$.
Now let's establish a kind of converse to this remark. Let $a, b$ be two integers and write $a=\sum_{i \geqslant 0} c_{i} 10^{i}$ and $b=\sum_{i \geqslant 0} c_{i}^{\prime} 10^{i}$. We have $F(a)-F(b)=\sum_{i \geqslant 0}\left(c_{i}-c_{i}^{\prime}\right)\left(10^{i}-1\right)$. If $j$ is the largest index such that $c_{j}>c_{j}^{\prime}$, then
$$
F(a)-F(b) \geqslant\left(10^{j}-1\right)+\sum_{i=0}^{j-1}\left(c_{i}-c_{i}^{\prime}\right)\left(10^{i}-1\right) \geqslant\left(10^{j}-1\right)-9 \sum_{i=0}^{j-1}\left(10^{i}-1\right)=9 j
$$
We deduce that if $|F(a)-F(b)|=9 k$, then $j \leqslant k$, and therefore
if $|F(a)-F(b)|=9 k$, then $a$ and $b$ can only differ in their last $k+1$ digits. (6)
Let's now prove the following lemma:
Lemma. If $F^{(n)}(a)=F^{(n)}(b)$, then $a$ and $b$ can only differ in their last $u_{n}$ digits.
Let's return to the proof of the lemma by induction on $n$. The initialization for $n=1$ comes from (6) applied with $k=0$. For the induction step, let $n \geqslant 1$ such that the lemma is true up to rank $n$. Let $a, b$ be two integers such that $F^{(n+1)}(a)=F^{(n+1)}(b)$. Then $F^{(n)}(F(a))=F^{(n)}(F(b))$, and therefore $|F(a)-F(b)| \leqslant 10^{u_{n}}$ by the induction hypothesis. Since $|F(a)-F(b)|$ is divisible by 9, write $|F(a)-F(b)|=9 k$ (with $9 k \leqslant 10^{u_{n}}$). Then, according to (6), $a$ and $b$ can only differ in their last $k+1$ digits. Since $k+1 \leqslant 10^{u_{n}} / 9+1 \leqslant 10^{u_{n}}$, $a$ and $b$ can only differ in their last $10^{u_{n}}=u_{n+1}$ digits, which concludes the proof.
Let's return to the exercise. Reason by contradiction, assuming the existence of an integer $y$ such that $X=F^{(n+1)}(y)=F^{(n)}\left(10^{N}-5 N\right)$. Then
$$
F^{(n)}\left(10^{N}-5 N\right)=F^{(n)}(F(y))
$$
and therefore, according to the lemma,
$$
\left|10^{\mathrm{N}}-5 \mathrm{~N}-\mathrm{F}(\mathrm{y})\right| \leqslant 10^{\mathbf{u}_{\mathrm{n}}} \leqslant \mathrm{~N} .
$$
Thus,
$$
10^{\mathrm{N}}-4 \mathrm{~N} \leqslant \mathrm{~F}(\mathrm{y}) \leqslant 10^{\mathrm{N}}-6 \mathrm{~N}
$$
However, we observe that if $\mathrm{y} \geqslant 10^{\mathrm{N}}$, then $\mathrm{F}(\mathrm{y}) \geqslant 10^{\mathrm{N}}-1$ (indeed, it is easily verified that $F$ is increasing and that $\left.F\left(10^{N}\right)=10^{N}-1\right)$. Moreover, if $y \leqslant 10^{N}-1$, then $F(y) \leqslant 10^{N}-9 \mathrm{~N}-1$; indeed, if $y=\sum_{i=0}^{N-1} c_{i} 10^{i}$, then
$$
F(y)=\sum_{i=0}^{N-1} c_{i}\left(10^{i}-1\right) \leqslant \sum_{i=0}^{N-1} 9\left(10^{i}-1\right)=10^{N}-9 N-1
$$
This contradicts (7), and $X$ satisfies the desired condition.
Another solution, a bit shorter: As above, we set $F(x)=x-S(x)$. It immediately follows that $F(a+1)=F(a)$ if $a \not \equiv 9(\bmod 10)$ and that $F(a+1)>F(a)$ if $a \equiv 9(\bmod 10)$. Consequently, any integer $k$ has at most 10 antecedents by $F$, and a fortiori it has at most $10^{\mathrm{n}}$ antecedents by $F^{(n)}$, where $F^{(n)}$ is the $n^{\text {th }}$ iterate of $F$. It follows that $F^{(n)}\left(k+10^{n}\right)>F^{(n)}(k)$ for any integer $k \geqslant 1$ (indeed, if $F^{(n)}\left(k+10^{n}\right)=F^{(n)}(k)$ for some integer $k \geqslant 1$, we would have $F^{(n)}(k)=F^{(n)}(i)$ for all $k \leqslant i \leqslant k+10^{n}$, so the integer $F^{(n)}(k)$ would have at least $10^{n}+1$ antecedents which are $\left.k, k+1, k+2, \ldots, k+10^{n}\right)$.
Now, let $\ell$ be an integer such that $9 \ell \geqslant 2 \cdot 10^{n}$. We observe that $F\left(10^{\ell}\right)=10^{\ell}-1$ and that $F\left(10^{\ell}-1\right)=10^{\ell}-1-9 \ell$, and we set $a_{k}=F^{(k)}\left(10^{\ell}-10^{n}-1\right)$ and $b_{k}=F^{(k)}\left(10^{\ell}-1\right)$, for $k \geqslant 0$. Since $b_{0} \geqslant a_{0}+10^{n}$, we deduce that $b_{n}>a_{n}$. Similarly, since $a_{0} \geqslant b_{1}+10^{n}$, we deduce that $a_{n}>b_{n+1}$. This shows that $b_{0}>i>b_{1}$ for any integer $i$ such that $a_{n}=F^{(n)}(i)$.
Now, we have $F(k) \geqslant b_{0}$ for all $k \geqslant 10^{\ell}$ and $F(k) \leqslant b_{1}$ for all $k \leqslant 10^{\ell}-1$, which shows that the elements of the set $\left\{b_{1}+1, \ldots, b_{0}-1\right\}$ are all of order 0 but not of order 1. It follows that $a_{n}$ is of order $n$ but not of order $n+1$, which concludes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
On note $S(k)$ la somme des chiffres d'un nombre entier $k$. On dit qu'un entier a est d'ordre $n$ s'il existe une suite d'entiers $a_{0}, a_{1}, \ldots, a_{n}$ tels que $a_{n}=a$ et $a_{i+1}=a_{i}-S\left(a_{i}\right)$ pour tout $i=0,1, \ldots, n-1$. Montrer que pour tout entier $n \geqslant 1$ il existe un entier $b$ qui soit d'ordre $n$ mais qui ne soit pas d'ordre $n+1$.
|
On pose $F(x)=x-S(x)$, et on considère la suite définie par $u_{0}=1$ et $u_{i+1}=10^{u_{i}}$ pour $i \geqslant 0$. Soit $n \geqslant 1$ fixé, et considérons un entier $N>u_{n+1}$. Nous allons montrer que $X=F^{(n)}\left(10^{N}-5 N\right.$ ) (on itère $n$ fois $F$ ) est d'ordre $n$ mais pas $n+1$. Pour cela, il suffit de montrer que X n'est pas d'ordre $\mathrm{n}+1$.
On remarque pour commencer que $F(a)-F(b)$ est toujours divisible par 9, et que si $a$ et $b$ ne différent que sur leurs $k$ derniers chiffres, alors $|a-b| \leqslant 10^{k}$.
Établissons maintenant une sorte de réciproque à cette remarque. Soient $a, b$ deux entiers et écrivons $a=\sum_{i \geqslant 0} c_{i} 10^{i}$ et $b=\sum_{i \geqslant 0} c_{i}^{\prime} 10^{i}$. On a $F(a)-F(b)=\sum_{i \geqslant 0}\left(c_{i}-c_{i}^{\prime}\right)\left(10^{i}-1\right)$. Si $j$ est le plus grand indice tel que $c_{j}>c_{j}^{\prime}$, alors
$$
F(a)-F(b) \geqslant\left(10^{j}-1\right)+\sum_{i=0}^{j-1}\left(c_{i}-c_{i}^{\prime}\right)\left(10^{i}-1\right) \geqslant\left(10^{j}-1\right)-9 \sum_{i=0}^{j-1}\left(10^{i}-1\right)=9 j
$$
On en déduit que si $|F(a)-F(b)|=9 k$, alors $j \leqslant k$, et donc
si $|F(a)-F(b)|=9 k, \quad$ alors $a$ et $b$ ne peuvent différer que sur leurs $k+1$ derniers chiffres. (6)
Montrons maintenant le lemme suivant:
Lemme. Si $F^{(n)}(a)=F^{(n)}(b)$ alors $a$ et b ne peuvent différer que sur leurs $u_{n}$ derniers chiffres.
Revenons maintenant à la preuve du lemme en raisonnant par récurrence sur n . L'initialisation pour $n=1$ provient de (6) appliqué avec $k=0$. Pour l'hérédité, soit $n \geqslant 1$ tel que le lemme est vrai jusqu'au rang $n$. Soient $a, b$ deux entiers tels que $F^{(n+1)}(a)=F^{(n+1)}(b)$. Alors $F^{(n)}(F(a))=$ $F^{(n)}(F(b))$, et donc $|F(a)-F(b)| \leqslant 10^{u_{n}}$ par hypothèse de récurrence. Comme $|F(a)-F(b)|$ est divisible par 9 , écrivons $|F(a)-F(b)|=9 k$ (avec $9 k \leqslant 10^{u_{n}}$ ). Alors d'après (6), a et b ne peuvent différer que sur leurs $k+1$ derniers chiffres. Comme $k+1 \leqslant 10^{u_{n}} / 9+1 \leqslant 10^{u_{n}}$, a et b ne peuvent différer que sur leurs $10^{u_{n}}=u_{n+1}$ derniers chiffres, ce qui conclut.
Revenons à l'exercice. Raisonnons par l'absurde en supposant l'existence d'un entier y tel que $X=F^{(n+1)}(y)=F^{(n)}\left(10^{N}-5 N\right)$. Alors
$$
F^{(n)}\left(10^{N}-5 N\right)=F^{(n)}(F(y))
$$
et donc d'après le lemme
$$
\left|10^{\mathrm{N}}-5 \mathrm{~N}-\mathrm{F}(\mathrm{y})\right| \leqslant 10^{\mathbf{u}_{\mathrm{n}}} \leqslant \mathrm{~N} .
$$
Donc
$$
10^{\mathrm{N}}-4 \mathrm{~N} \leqslant \mathrm{~F}(\mathrm{y}) \leqslant 10^{\mathrm{N}}-6 \mathrm{~N}
$$
Or on constate que si $\mathrm{y} \geqslant 10^{\mathrm{N}}$, alors $\mathrm{F}(\mathrm{y}) \geqslant 10^{\mathrm{N}}-1$ (en effet, on vérifie aisément que F est croissante et que $\left.F\left(10^{N}\right)=10^{N}-1\right)$. De plus, si $y \leqslant 10^{N}-1$, alors $F(y) \leqslant 10^{N}-9 \mathrm{~N}-1$; en effet si $y=\sum_{i=0}^{N-1} c_{i} 10^{i}$, alors
$$
F(y)=\sum_{i=0}^{N-1} c_{i}\left(10^{i}-1\right) \leqslant \sum_{i=0}^{N-1} 9\left(10^{i}-1\right)=10^{N}-9 N-1
$$
Ceci contredit (7), et $X$ vérifie bien la condition cherchée.
Autre solution, un peu plus courte : Comme ci-dessus, on pose $F(x)=x-S(x)$. Il vient immédiatement que $F(a+1)=F(a)$ si $a \not \equiv 9(\bmod 10)$ et que $F(a+1)>F(a)$ si $a \equiv 9(\bmod 10)$. Par conséquent, tout entier k a au plus 10 antécédents par F , et a fortiori il a au plus $10^{\mathrm{n}}$ antécédents par $F^{(n)}$, où $F^{(n)}$ est la $n^{\text {ème }}$ itérée de $F$. Il s'ensuit que $F^{(n)}\left(k+10^{n}\right)>F^{(n)}(k)$ pour tout entier $k \geqslant 1$ (en effet, si $F^{(n)}\left(k+10^{n}\right)=F^{(n)}(k)$ pour un certain entier $k \geqslant 1$, on aurait $F^{(n)}(k)=F^{(n)}(i)$ pour tout $k \leqslant i \leqslant k+10^{n}$, de sorte que $l^{\prime}$ entier $F^{(n)}(k)$ aurait au moins $10^{n}+1$ antécédents qui sont $\left.k, k+1, k+2, \ldots, k+10^{n}\right)$.
Maintenant, soit $\ell$ un entier tel que $9 \ell \geqslant 2 \cdot 10^{n}$. On observe que $F\left(10^{\ell}\right)=10^{\ell}-1$ et que $F\left(10^{\ell}-1\right)=10^{\ell}-1-9 \ell$, puis on pose $a_{k}=F^{(k)}\left(10^{\ell}-10^{n}-1\right)$ et $b_{k}=F^{(k)}\left(10^{\ell}-1\right)$, pour $k \geqslant 0$. Puisque $b_{0} \geqslant a_{0}+10^{n}$, on en déduit que $b_{n}>a_{n}$. De même, puisque $a_{0} \geqslant b_{1}+10^{n}$, on en déduit que $a_{n}>b_{n+1}$. Cela montre que $b_{0}>i>b_{1}$ pour tout entier $i$ tel que $a_{n}=F^{(n)}(i)$.
Or, on a $F(k) \geqslant b_{0}$ pour tout $k \geqslant 10^{\ell}$ et $F(k) \leqslant b_{1}$ pour tout $k \leqslant 10^{\ell}-1$, ce qui montre que les éléments de l'ensemble $\left\{b_{1}+1, \ldots, b_{0}-1\right\}$ sont tous d'ordre 0 mais pas d'ordre 1 . Il s'ensuit que $a_{n}$ est d'ordre $n$ mais pas d'ordre $n+1$, ce qui conclut.
|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "\nExercice 8.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-3-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 8",
"tier": "T2",
"year": "2016"
}
|
Find all functions $\mathrm{f}: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
f(x) f(y f(x)-1)=x^{2} f(y)-f(x)
$$
for all $x, y \in \mathbb{R}$.
|
First, we notice that the null function is a solution.
Let now $f$ be a solution. By taking $x=0$, we get $f(0)(f(y f(0)-1)+1)=0$. If $f(0) \neq 0$, then $f(y f(0)-1)=-1$ for all $y \in \mathbb{R}$. Since $y f(0)-1$ spans $\mathbb{R}$ as $y$ spans $\mathbb{R}$, we deduce that $f$ is then constantly equal to -1. By taking $x=1$, we get $(-1)^{2}=-1^{2}+1$, which is absurd. Therefore, $f(0)=0$.
Suppose now that $f$ is not the null function. Then there exists $a \in \mathbb{R}^{*}$ such that $f(a) \neq 0$. By taking $x=a$ and $y=0$, we get $f(-1)=-1$.
If $f(x)=0$, by taking $y=a$, we get $x^{2} f(a)=0$, and thus $x=0$. Therefore, $f(x)=0$ if and only if $x=0$.
By taking $x=y=1$, we get $f(1) f(f(1)-1)=0$, and thus, since $f(1) \neq 0$, $f(1)=1$.
By taking $x=1$, we get $f(y-1)=f(y)-1$, and using this in the initial equation, we get
$$
f(x) f(y f(x))=x^{2} f(y)
$$
By taking $x=-1$ in this last equation, we get $f(-y)=-f(y)$, and thus $f$ is odd. Combined with the fact that $f(y-1)=f(y)-1$, we deduce by induction that
$$
f(y-n)=f(y)-n
$$
for all integers $n \geqslant 0$, and then that $f(n)=n$ for all integers $n$. By taking $x=n$ in (8), we get
$$
f(yn)=n f(y)
$$
and we deduce that $f(r)=r$ for all rational numbers $r$.
By taking $y=1$ in (8), we get $f(x) f(f(x))=x^{2}$. By taking $x=y=f(x)$ in (8), we get $f(f(x)) f\left(f(x) f(f(x))=f(x)^{2} f(f(x))\right.$. For $x \neq 0, f(f(x)) \neq 0$, and thus by simplifying by $f(f(x))$ we get $f\left(x^{2}\right)=f\left(f(x) f(f(x))=f(x)^{2}\right.$. Therefore, $f(x)>0$ for $x>0$.
Let now $z>0$ be an irrational number, and suppose by contradiction that $f(z)>z$. Let $r=n / m$ be a rational number such that $f(z)>r>z$. Since $m(r-z)>0$, we have $f(m(r-z))>0$. But $f$ is odd (take $n=-1$ in (10)), so $m f(z)-n=f(m z)-n=f(m z-n)<0$, which contradicts the fact that $f(z)>r$. The case where $f(z)<z$ is treated similarly. Therefore, $f(x)=x$ for all $x \in \mathbb{R}$. Conversely, we verify that it works.
The solutions are therefore the null function and the identity function.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Trouver toutes les fonctions $\mathrm{f}: \mathbb{R} \rightarrow \mathbb{R}$ telles que
$$
f(x) f(y f(x)-1)=x^{2} f(y)-f(x)
$$
pour tous $x, y \in \mathbb{R}$.
|
Tout d'abord, on remarque que la fonction nulle est solution.
Soit maintenant une fonction f solution. En prenant $x=0$, on obtient $f(0)(f(y f(0)-1)+1)=0$. Si $f(0) \neq 0$, alors $f(y f(0)-1)=-1$ pour tout $y \in \mathbb{R}$. Comme $y f(0)-1$ parcourt $\mathbb{R}$ quand
y parcourt $\mathbb{R}$, on en déduit qu'alors f est constante égale à -1 . En prenant $x=1$, on obtient $(-1)^{2}=-1^{2}+1$, ce qui est absurde. Donc $f(0)=0$.
Supposons maintenant que $f n^{\prime}$ est pas la fonction nulle. Il existe alors $a \in \mathbb{R}^{*}$ tel que $f(a) \neq 0$. En prenant $x=a$ et $y=0$, on obtient $f(-1)=-1$.
Si $f(x)=0$, en prenant $y=a$, on obtient $x^{2} f(a)=0$, et donc $x=0$. Ainsi, $f(x)=0$ si et seulement si $x=0$.
En prenant $x=y=1$, on obtient $f(1) f(f(1)-1)=0$, et donc, comme $f(1) \neq 0, f(1)=1$.
En prenant $x=1$, on obtient $f(y-1)=f(y)-1$, et en utilisant ceci dans l'équation initiale on obtient
$$
f(x) f(y f(x))=x^{2} f(y)
$$
En prenant $x=-1$ dans cette dernière équation, on obtient $f(-y)=-f(y)$, et donc $f$ est impaire. Combiné avec le fait que $\mathrm{f}(\mathrm{y}-1)=\mathrm{f}(\mathrm{y})-1$, on en déduit par récurrence que
$$
f(y-n)=f(y)-n
$$
pour tout entier $n \geqslant 0$, puis que $f(n)=n$ pour tout nombre entier relatif $n$. En prenant $x=n$ dans (8), on obtient
$$
\mathrm{f}(\mathrm{yn})=\mathfrak{n f}(\mathrm{y})
$$
et on en déduit que $f(r)=r$ pour tout nombre rationnel $r$.
En prenant $y=1$ dans (8), on obtient $f(x) f(f(x))=x^{2}$. En prenant $x=y=f(x)$ dans (8), on obtient $f(f(x)) f\left(f(x) f(f(x))=f(x)^{2} f(f(x))\right.$. Pour $x \neq 0, f(f(x)) \neq 0$, et donc en simplifiant par $f(f(x))$ on obtient $f\left(x^{2}\right)=f\left(f(x) f(f(x))=f(x)^{2}\right.$. Ainsi, $f(x)>0$ pour $x>0$.
Soit maintenant $z>0$ un nombre irrationnel, et supposons par l'absurde que $f(z)>z$. Soit $r=n / m$ un nombre rationnel tel que $f(z)>r>z$. Comme $m(r-z)>0$, on a $f(m(r-z))>0$. Or f est impaire (prendre $n=-1$ dans (10)), donc $m f(z)-n=f(m z)-n=f(m z-n)<0$, ce qui contredit le fait que $f(z)>r$. Le cas où $f(z)<z$ se traite de la même manière. Donc $f(x)=x$ pour tout $x \in \mathbb{R}$. Réciproquement, on vérifie qu'elle convient.
Les solutions sont donc la fonction nulle et la fonction identité.
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-3-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 9",
"tier": "T2",
"year": "2016"
}
|
Let $n \geqslant 2$. We place a coin on each square of an $n \times n$ chessboard. A move consists of moving each coin to a square that touches the starting square exactly by a corner (multiple coins can end up on the same square).
What is the smallest integer $k$ such that it is possible that after a certain number of moves, only $k$ squares contain at least one coin?
|
The answer is 4.
We denote $\mathrm{A}, \mathrm{B}, \mathrm{C}$, and D as the four cells that form the $2 \times 2$ square in the top right:
Each piece can be moved to one of the cells $\mathrm{A}, \mathrm{B}, \mathrm{C}$, and D, and then oscillate between $A$ and $D$ or between $B$ and $C$ at each move. Therefore, it is possible that after a certain number of moves, all pieces are on one of the four cells $A, B, C$, and $D$.
It remains to show that it is not possible to do better than 4. We consider the following coloring of the chessboard (here for $\mathrm{n}=4$):
Since $n \geqslant 2$, there is at least one piece on a cell of each color at the beginning. But at each move, the pieces that are on blue cells move to red cells, those on red cells move to blue cells, those on yellow cells move to green cells, and those on green cells move to yellow cells. At each step, there are therefore always pieces on at least one cell of each color, so there are always at least 4 cells that contain at least one piece.
|
4
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Soit $n \geqslant 2$. On place une pièce sur chaque case d'un échiquier $n \times n$. Un mouvement consiste à déplacer chaque pièce sur une case qui touche la case de départ par un coin exactement (plusieurs pièces peuvent se retrouver sur la même case).
Quel est le plus petit entier $k$ tel qu'il est possible qu'après un certain nombre de mouvements, seules $k$ cases contiennent au moins une pièce?
|
La réponse est 4.
On note $\mathrm{A}, \mathrm{B}, \mathrm{C}$ et D les quatre cases quif forment le carré $2 \times 2$ en haut à droite :

Chaque pièce peut être amenée sur une des cases $\mathrm{A}, \mathrm{B}, \mathrm{C}$ et D , puis osciller à chaque mouvement entre $A$ et $D$ ou entre $B$ et $C$. Il est donc possible qu'après un certain nombre de mouvements, toutes les pièces soient sur une des quatre cases $A, B, C$ et $D$.
Il reste à montrer qu'on ne peut pas faire mieux que 4 . On considère le coloriage suivant de l'échiquier (ici pour $\mathrm{n}=4$ ) :

Comme $n \geqslant 2$, il y a au début au moins une pièce sur une case de chaque couleur. Mais à chaque mouvement, les pièces qui se trouvent sur des cases bleues passent sur des cases rouges, celles sur des cases rouges passent sur des bleues, celles sur des jaunes passent sur des vertes et celles sur des vertes passent sur des jaunes. A chaque étape, il y a donc des pièces sur au moins une case de chaque couleur, donc il y a toujours au moins 4 cases qui contiennent au moins une pièce.
|
{
"exam": "French_envois",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-4-solutions.jsonl",
"solution_match": "## Solution de l'exercice 1",
"tier": "T2",
"year": "2016"
}
|
Let A be a set of 13 integers between 1 and 37. Show that there exist four distinct numbers in $A$ such that the sum of two of them is equal to the sum of the other two.
|
A contains 13 integers, so there are $\frac{13 \times 12}{2}=78$ ways to choose two different numbers from A (13 ways to choose the first, 12 ways to choose the second, and we divide by 2 because we have counted each set of 2 numbers twice). Now, the sum of two numbers from $\mathcal{A}$ is always at least $1+2=3$ and at most $36+37=73$, so it can take 71 different values. According to the pigeonhole principle, there exist $\mathrm{a} \neq \mathrm{d}$ and $\mathrm{b} \neq \mathrm{c}$ in $A$ such that $\mathrm{a}+\mathrm{d}=\mathrm{b}+\mathrm{c}$, and the set $\{a, d\}$ is different from $\{b, c\}$. To conclude, we need to ensure that $a, b, c$ and $d$ are all distinct.
But if, for example, $a=b$, then since $a+d=b+c$, we must have $d=c$ so $\{a, d\}=\{b, c\}$, which is false. Therefore, we have indeed found 4 numbers that satisfy the desired property.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soit A un ensemble de 13 entiers entre 1 et 37 . Montrer qu'il existe quatre nombres deux à deux distincts dans $A$ tels que la somme de deux d'entre eux est égale à la somme des deux autres.
|
A contient 13 entiers, donc il y a $\frac{13 \times 12}{2}=78$ manières de choisir deux nombres de A différents ( 13 manières de choisir le premier, 12 manières de choisir le deuxième et on divise par 2 car on a compté deux fois chaque ensemble de 2 nombres). Or, la somme de deux nombres de $\mathcal{A}$ vaut toujours au moins $1+2=3$ et au plus $36+37=73$, donc elle peut prendre 71 valeurs différentes. D'après le principe des tiroirs, il existe donc $\mathrm{a} \neq \mathrm{d}$ et $\mathrm{b} \neq \mathrm{c}$ dans $A$ tels que $\mathrm{a}+\mathrm{d}=\mathrm{b}+\mathrm{c}$, et l'ensemble $\{a, d\}$ est différent de $\{b, c\}$. Pour conclure, il suffit de s'assurer que $a, b, c$ et $d$ sont deux à deux distincts.
Mais si par exemple $a=b$, alors comme $a+d=b+c$, on doit avoir $d=c$ donc $\{a, d\}=\{b, c\}$, ce qui est faux. On a donc bien trouvé 4 nombres qui vérifient la propriété voulue.
|
{
"exam": "French_envois",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-4-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T2",
"year": "2016"
}
|
The seven dwarfs have distinct heights. They go to the mine in a column in a certain order, such that the dwarf at the front is taller than the second, who is shorter than the third, who is taller than the fourth, and so on...
How many such ways are there to arrange the dwarfs?
|
We denote $u_{3}$ as the number of ways to arrange 3 dwarfs such that the first is taller than the second, who is taller than the third, $\mathfrak{u}_{5}$ as the number of similar ways to arrange 5 dwarfs, and $u_{7}$ as the solution to the exercise.
With 3 dwarfs, we are forced to place the shortest dwarf in the middle, and we can then place the other two as we wish.
With 5 dwarfs, the shortest dwarf can be in the second or fourth position:
- If he is in position 2, any dwarf can be first, so we have 4 choices for the first dwarf. It then remains to order the last three: there are $\mathfrak{u}_{3}$ ways to do this, so we get $4 \mathfrak{u}_{3}$ arrangements.
- If he is in position 4, we similarly have $4 u_{3}$ arrangements (by first choosing the fifth).
We therefore have $\mathfrak{u}_{5}=4 u_{3}+4 u_{3}=8 \times 2=16$.
With 7 dwarfs, the shortest dwarf can be in position 2, 4, or 6:
- If he is in position 2, any dwarf can be first (6 choices), and there are $u_{5}$ ways to order the last five, giving $6 \mathbf{u}_{5}$ possible orders.
- If he is in position 6, any dwarf can be last (6 choices), and there are $u_{5}$ ways to order the first five, giving $6 \mathfrak{u}_{5}$ possible orders.
- If he is in position 4, we can first sort the dwarfs who will be in front of him from those who will be behind. There are $\binom{6}{3}=20$ ways to do this sorting. Then there are $u_{3}$ ways to order the three in front and $u_{3}$ ways to order the three behind, giving $20 u_{3}^{2}$ possible orders.
We therefore have $\mathfrak{u}_{7}=6 \mathfrak{u}_{5}+6 \mathfrak{u}_{5}+20 \mathfrak{u}_{3}^{2}=6 \times 16+6 \times 16+20 \times 2^{2}=272$.
|
272
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Les sept nains ont des tailles deux à deux distinctes. Ils se rendent à la mine en colonne dans un certain ordre, de telle manière que le nain en tête est plus grand que le deuxième, qui est plus petit que le troisième, qui est plus grand que le quatrième et ainsi de suite...
Combien y a-t-il de telles manières d'arranger les nains?
|
On note $u_{3}$ le nombre de manières d'arranger 3 nains de manière à ce que le premier est plus grand que le second, qui est plus grand que le troisième, $\mathfrak{u}_{5}$ le nombre de manières similaires d'arranger 5 nains et $u_{7}$ la solution de l'exercice.
Avec 3 nains, on est obligé de mettre le nain le plus petit au milieu et on peut ensuite placer comme on veut les deux autres.
Avec 5 nains, le nain le plus petit peut être en deuxième ou quatrième position :
- S'il est en position 2, n'importe quel nain peut être en premier, donc on a 4 choix pour le premier nain. Il reste à ordonner les trois derniers : il y a $\mathfrak{u}_{3}$ manières de le faire, donc on obtient $4 \mathfrak{u}_{3}$ arrangements.
- S'il est en position 4 , on a de même $4 u_{3}$ arrangements (en choisissant d'abord le cinquième).
On a donc $\mathfrak{u}_{5}=4 u_{3}+4 u_{3}=8 \times 2=16$.
Avec 7 nains, le nain le plus petit peut être en position 2, 4 ou 6 :
- S'il est en position 2 , n'importe quel nain peut être en premier (soit 6 choix), puis il y a $u_{5}$ manières d'ordonner les cinq derniers, soit $6 \mathbf{u}_{5}$ ordres possibles.
- S'il est en position 6 , n'importe quel nain peut être en dernier (soit 6 choix), puis il y a $u_{5}$ manières d'ordonner les cinq premiers, soit $6 \mathfrak{u}_{5}$ ordres possibles.
- S'il est en position 4, on peut d'abord trier les nains qui seront devant lui de ceux qui seront derrière. Il y a $\binom{6}{3}=20$ manières de faire ce tri. Puis il y a $u_{3}$ manières d'ordonner les trois nains de devant et $u_{3}$ manières d'ordonner les trois de derrière, soit $20 u_{3}^{2}$ ordres popssibles.
On a donc $\mathfrak{u}_{7}=6 \mathfrak{u}_{5}+6 \mathfrak{u}_{5}+20 \mathfrak{u}_{3}^{2}=6 \times 16+6 \times 16+20 \times 2^{2}=272$.
## Exercices communs
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-4-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T2",
"year": "2016"
}
|
Let $n \geqslant 1$. We have a finite number of bottles, each containing an amount of water less than 1 liter, such that the total amount of water is $\frac{\mathfrak{n}}{2}$ liters. We also have $n$ empty buckets.
Show that it is possible to empty each bottle into a bucket (we can empty several bottles into the same bucket, but not empty a bottle partially into one bucket and partially into another) in such a way that there is at most 1 liter of water in each bucket.
|
We reason by induction on $n$: for $\mathrm{n}=1$, it suffices to empty everything into the unique bucket.
Suppose the result is true at rank $n$: if we manage to empty into a bucket a certain number of bottles representing in total at least $\frac{1}{2}$ liter and at most 1 liter, then there will remain $\frac{\mathrm{n}-1}{2}$ liters to empty into the $\mathrm{n}-1$ remaining buckets, and we can apply the induction hypothesis to conclude.
If there exists a bottle containing at least $\frac{1}{2}$ liter, we can therefore empty it into the first bucket. Otherwise, all the bottles contain less than $\frac{1}{2}$ liter. We therefore empty them one by one into the first bucket, and stop as soon as the content of the bucket exceeds $\frac{1}{2}$ liter: the bucket then contains more than $\frac{1}{2}$ liter. Moreover, just before emptying the last bottle, it contained less than $\frac{1}{2}$ liter, and we added a bottle, thus less than $\frac{1}{2}$ liter. The bucket therefore contains less than 1 liter, and we can conclude by induction hypothesis.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soit $n \geqslant 1$. On a un nombre fini de bouteilles, chacune contenant une quantité d'eau inférieure à 1 litre, telles que la quantité totale d'eau est de $\frac{\mathfrak{n}}{2}$ litres. On dispose également de n seaux vides.
Montrer qu'il est possible de vider chaque bouteille dans un seau (on peut vider plusieurs bouteilles dans le même seau, mais pas vider une bouteille en partie dans un seau et en partie dans un autre) de manière à avoir au plus 1 litre d'eau dans chaque seau.
|
On raisonne par récurrence sur $n$ : pour $\mathrm{n}=1$, il suffit de tout vider dans l'unique seau.
Supposons le résultat vrai au rang n : si on arrive à vider dans un seau un certain nombre de bouteilles représentant au total au moins $\frac{1}{2}$ litre et au plus 1 litre, alors il restera $\frac{\mathrm{n}-1}{2}$ litres à vider dans les $\mathrm{n}-1$ seaux restants, et on pourra appliquer l'hypothèse de récurrence pour conclure.
Si il existe une bouteille contenant au moins $\frac{1}{2}$ litre, on peut donc la vider dans le premier seau. Sinon, toutes les bouteilles contiennent moins de $\frac{1}{2}$ litre. On les vide donc une par une dans le premier seau, et on s'arrête dès que le contenu du seau dépasse $\frac{1}{2}$ litre : le seau contient alors plus de $\frac{1}{2}$ litre. De plus, juste avant de vider la dernière bouteille, il contenait moins de $\frac{1}{2}$ litre, et on a ajouté une bouteille, donc moins de $\frac{1}{2}$ litre. Le seau contient donc moins de 1 litre, et on peut conclure par hypothèse de récurrence.
|
{
"exam": "French_envois",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-4-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T2",
"year": "2016"
}
|
Let $S$ be the set of integers from 1 to 2016. How many ways are there to partition $S$ into two subsets $A$ and $B$ such that neither $A$ nor $B$ contains two integers whose sum is a power of 2?
Note. We say that $A$ and $B$ form a partition of $S$ if neither $A$ nor $B$ is empty, $A$ and $B$ are disjoint, and their union is equal to $S$.
|
The answer is $2^{11}=2048$. More precisely, we will show that it is possible to distribute the numbers $1,2,4,8, \ldots, 1024=2^{10}$ as we wish between $A$ and $B$, and that once these numbers are placed, there is a unique way to distribute the others. We can then conclude because there are $2^{11}=2048$ ways to distribute these 11 numbers between $A$ and $B$.
The fact that the distribution of $1,2,4,8, \ldots, 1024$ determines the position of $k$ can be shown by strong induction on $k$: the positions of 1 and 2 have already been fixed, and 3 must be in the set that does not contain $1$ because $3+1=2^{2}$. Suppose now that the positions of all numbers from 1 to $k-1$ are fixed: if $k$ is a power of 2, then the position of $k$ is fixed by hypothesis. Otherwise, there exists $a$ such that $2^{a-1}<k<2^{a}$. But then $0<2^{a}-k<k$, so $2^{a}-k$ is in $A$ or $B$, and its position has already been fixed. Therefore, $k$ must be in the other set. Thus, there is at most one partition that works once the distribution of the powers of 2 is fixed.
It remains to show that such a distribution exists. However, the previous proof provides an algorithm that allows distributing the integers that are not powers of 2 between $\mathcal{A}$ and $B$ in such a way that for all $k$ and $a$ such that $2^{a-1}<k<2^{a}$, the numbers $k$ and $2^{a}-k$ are not in the same set. If two numbers $x \neq y$ have a sum that is a power of 2, denoted by $2^{a}$, we can assume $x>y$. Then $x>\frac{x+y}{2}=2^{a-1}$, so $2^{a-1}<x<2^{a}$ and $y=2^{a}-x$, so $x$ and $y$ are not in the same set, hence there always exists a suitable distribution.
|
2048
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On note $S$ l'ensemble des entiers de 1 à 2016. Combien y a-t-il de manières de partitionner $S$ en deux sous-ensembles $A$ et $B$ de telle manière que ni $A$ ni $B$ ne contient deux entiers dont la somme est une puissance de 2 ?
Remarque. On dit que $A$ et $B$ forment une partition de $S$ si ni $A$ ni $B$ n'est vide, $A$ et $B$ sont d'intersection vide et si leur union est égale à $S$.
|
La réponse est $2^{11}=2048$. Plus précisément, on va montrer qu'il est possible de répartir comme on veut les nombres $1,2,4,8, \ldots, 1024=2^{10}$ comme on veut entre $A$ et $B$ et qu'une fois ces nombres placés il existe une unique manière de répartir les autres. On peut alors conclure car il y a $2^{11}=2048$ manières de répartir ces 11 nombres entre $A$ et $B$.
Le fait que la répartition de $1,2,4,8, \ldots, 1024$ impose la position de $k$ se montre par récurrence forte sur k : la position de 1 et 2 a déjà été fixée, et 3 doit être dans l'ensemble qui ne contient pas $1 \mathrm{car} 3+1=2^{2}$. Supposons maintenant que toutes les positions de nombres de 1 à $k-1$ soient fixées : si $k$ est une puissance de 2, alors la position de $k$ est fixée par hypothèse. Sinon, il existe a tel que $2^{a-1}<k<2^{a}$. Mais alors $0<2^{a}-k<k$ donc $2^{a}-k$ est dans $A$ ou $B$, et sa position a déjà été fixée. $k$ est donc nécessairement dans l'autre ensemble. Il existe donc au plus une partition qui convient une fois fixée la répartition des puissances de 2 .
Il reste à montrer qu'une telle répartition existe bien. Mais la preuve précédente fournit un algorithme qui permet de répartir les entiers qui ne sont pas des puissances de 2 entre $\mathcal{A}$ et $B$ de telle manière que pour tous $k$ et $a$ tel que $2^{a-1}<k<2^{a}$, les nombres $k$ et $2^{a}-k$ ne sont pas dans le même ensemble. Or, si deux nombres $x \neq y$ ont pour somme une puissance de 2 notée $2^{a}$, on peut supposer $x>y$. On a alors $x>\frac{x+y}{2}=2^{a-1}$, donc $2^{a-1}<x<2^{a}$ et $y=2^{a}-x$, donc $x$ et $y$ ne sont pas dans le même ensemble, donc il existe bien toujours une répartition qui convient.
|
{
"exam": "French_envois",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-4-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T2",
"year": "2016"
}
|
On each vertex of a regular n-gon, we place a sign $+\mathrm{or}-$. At each step, we are allowed to change the signs of three consecutive vertices of the n-gon.
For which n can we, starting from any initial configuration, achieve + signs on all vertices in a finite number of steps?
|
We will show that these are exactly the $n$ that are not divisible by 3.
If $n$ is divisible by 3, we denote $A_{1}, \ldots, A_{n}$ as the vertices of the polygon, and we denote $P$ as the number of $k$ that are not divisible by 3 and such that there is a sign $-\operatorname{on} A_{k}$. We show that at each step the parity of $P$ does not change: at each step, we change the signs of 3 consecutive vertices $A_{k}, A_{k-1}$, and $A_{k+1}$ (with the convention $A_{0}=A_{n}$ and $A_{n+1}=A_{1}$). Exactly one of the numbers $k-1, k$, and $k+1$ is divisible by 3, so we change the signs of exactly 2 vertices that are not divisible by 3. $P$ can therefore vary by -2 (if two - become +), by 0 (if one - becomes a + and one + becomes a -), or by 2 (if two + become two -), so its parity never changes. In particular, if $P=1$ at the start, it is impossible to obtain $P=0$, so it is impossible to have only +.
If $n$ is not divisible by 3, we show that it is possible to change exactly one sign. We can then easily conclude because it is sufficient to change the - signs one by one:
- If $n$ is of the form $3k-1$, we can change the signs of $A_{1}, A_{2}, A_{3}$, then of $A_{4}, A_{5}, A_{6}$, and so on until $A_{3k-2}, A_{3k-1}, A_{1}$, which changes the sign of everyone except $A_{1}$ (which has been touched twice). We can then change the sign of everyone except $A_{2}$, and then change the signs of $A_{1}, A_{2}, A_{3}$. This is equivalent to changing only the sign of $A_{3}$.
- If $n$ is of the form $3k+1$, we can change the signs of $A_{1}, A_{2}, A_{3}$, then of $A_{4}, A_{5}, A_{6}$, and so on until $A_{3k-2}, A_{3k-1}, A_{3k}$, which changes the sign of everyone except $A_{3k+1}$, and we conclude as above.
## Exercises of Group A
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Sur chaque sommet d'un n-gone régulier on place un signe $+\mathrm{ou}-$. A chaque étape, on a le droit de changer les signes de trois sommets consécutifs du n-gone.
Quels sont les n pour lesquels quelle que soit la configuration de départ on peut obtenir en un nombre fini d'étapes des + sur tous les sommets?
|
On va montrer que ce sont exactement les n qui ne sont pas divisibles par 3.
Si $n$ est divisible par 3 , on note $A_{1}, \ldots, A_{n}$ les sommets du polygone, et on note $P$ le nombre de $k$ qui ne sont pas divisibles par 3 et tels qu'il y a un signe $-\operatorname{sur} A_{k}$. On montre qu'à chaque étape la parité de $P$ ne change pas : à chaque étape, on change les signes de 3 sommets consécutifs $A_{k}, A_{k-1}$ et $A_{k+1}$ (avec la convention $A_{0}=A_{n}$ et $A_{n+1}=A_{1}$ ). Exactement un de des nombres $k-1, k$ et $k+1$ est divisible par 3, donc on change exactement les signes de 2 sommets non divisibles par 3. P peut donc varier de -2 (si deux - deviennent des + ), de 0 (si un - devient un + et un + devient un - ) ou de 2 (si deux +
deviennent deux -), donc sa parité ne change jamais. En particulier, si $P=1$ au départ, il est impossible d'obtenir $\mathrm{P}=0$ donc il est impossible de n'avoir que des + .
Si $n$ n'est pas divisible par 3, on montre qu'il est possible de modifier exactement un signe. On peut alors facilement conclure car il suffit de modifier un par un les signes - :
- Si $n$ est de la forme $3 k-1$, on peut modifier les signes de $A_{1}, A_{2}, A_{3}$ puis de $A_{4}, A_{5}, A_{6}$ et ainsi de suite jusqu'à $A_{3 \mathrm{k}-2}, A_{3 \mathrm{k}-1}, A_{1}$, ce qui modifie le signe de tout le monde sauf $A_{1}$ (qui a été touché deux fois). On peut ensuite modifier le signe de tout le monde sauf $A_{2}$, puis modifier les signes de $A_{1}, A_{2}, A_{3}$. Cela revient à ne changer que le signe de $A_{3}$.
- Si $n$ et de la forme $3 k+1$, on peut modifier les signes de $A_{1}, A_{2}, A_{3}$ puis de $A_{4}, A_{5}, A_{6}$ et ainsi de suite jusqu'à $A_{3 k-2}, A_{3 k-1}, A_{3 k}$, ce qui modifie le signe de tout le monde sauf $A_{3 k+1}$ et on conclut comme ci-dessus.
## Exercices du groupe A
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-4-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T2",
"year": "2016"
}
|
Let $n \geqslant 2$. We draw a circuit on an $n \times n$ chessboard that passes exactly once through each square and returns to its starting point (two consecutive squares on the circuit must share a side).
Show that there exist two adjacent squares on the chessboard such that, if we "cut" the circuit at these two squares, the two paths obtained have a length of at least a quarter of the length of the original circuit.
Note. The length of a path is the number of times it changes squares. In particular, if the circuit is cut into two paths, the sum of the lengths of the two paths will always be $n^2$.
|
First, note that if the chessboard is tiled in black and white in the usual way, the circuit must alternate between black and white squares and return to its starting square, so its length must be even, and thus $n^{2}$ must be even. We write $n=2 m$.

We consider the set of corners of the squares that are inside the circuit (these are the blue points in the figure), and we connect two of these points when they are 1 unit apart (these are the blue edges in the figure). The graph obtained is a tree: it is connected because the circuit is, and it has no cycle because a cycle would either create a second circuit inside the first, or enclose the center of a square that would therefore not be in the red circuit. Moreover, in this tree, each vertex has at most 4 neighbors.
The following lemma allows us to link the length of the red path to the number of vertices of the blue tree:
Lemma (Lemma 1). Let $T$ be a tree whose vertices are on the corners of a grid, and $C$ a circuit passing through the centers of the squares and surrounding the tree. We denote $|\mathrm{C}|$ the length of this circuit. Then $|C|=2|T|+2$.
Proof of Lemma 1. Each vertex of the tree is the center of a square of side 1. We compute the sum $S$ of the perimeters of these squares in two different ways. On one hand, we have $S=4|T|$. But on the other hand, to compute $S$, we take into account each edge of $C$ once, and each edge that separates two vertices of the tree twice. Since the tree has $|\mathrm{T}|-1$ edges, we have $S=|C|+2(|T|-1)$. We deduce the lemma from this.
We know that $|C|=n^{2}=4 m^{2}$. We deduce that $|T|=\frac{1}{2}(|C|-1)=2 m^{2}-1$. Moreover, cutting the circuit between two adjacent squares is essentially equivalent to cutting an edge of the tree. We will therefore show the following lemma:
Lemma (Lemma 2). We denote $|T|$ the number of vertices of a tree. Let $T$ be a tree with at least two vertices and where all vertices have a degree of at most 4. There exists an edge $e$ of $T$ such that by cutting the edge $e$, the tree $T$ is split into two trees $T_{1}$ and $T_{2}$ such that $\left|T_{1}\right| \geqslant \frac{1}{4}(|T|-1)$ and $\left|T_{2}\right| \geqslant \frac{1}{4}(|T|-1)$.
Proof of Lemma 2. We reason by contradiction. We fix $\mathrm{x}_{0}$ a vertex of $T$: removing $\mathrm{x}_{0}$ divides $T$ into $\mathrm{T}_{1}, \mathrm{~T}_{2}, \mathrm{~T}_{3}$ and $\mathrm{T}_{4}$ (if $\times$ does not have four neighbors, some of these trees have zero vertices). According to the pigeonhole principle, there exists $i$ such that $\left|T_{i}\right| \geqslant \frac{1}{4}(|T|-1)$. Suppose it is $T_{1}$, and we denote $x_{1}$ the vertex of $T_{1}$ that is connected to $x_{0}$. But if $T$ does not satisfy the lemma, then $\left|\mathrm{T}_{1}\right|>|\mathrm{T}|-\frac{1}{4}(|\mathrm{~T}|-1)=\frac{3}{4}(|\mathrm{~T}|-1)+1$.
We can now apply the same reasoning with $x_{1}$: it has at most three neighbors different from $x_{0}$ which correspond to three trees $\mathrm{T}_{1}^{\prime}, \mathrm{T}_{2}^{\prime}$ and $\mathrm{T}_{3}^{\prime}$, and the total number of vertices of these three trees is at least $\frac{3}{4}(|T|-1)$. By the pigeonhole principle, there exists $i$ such that $\left|T_{i}^{\prime}\right| \geqslant \frac{1}{4}(|T|-1)$, so, as $T$ does not satisfy the lemma, $\left|\mathrm{T}_{1}^{\prime}\right|>\frac{3}{4}(|\mathrm{~T}|-1)+1$. We denote $x_{2}$ the vertex by which $\mathrm{T}_{1}^{\prime}$ is connected to $x_{1}$. Since we only considered the neighbors of $x_{1}$ that are different from $x_{0}$, we have $x_{2} \neq x_{0}$. We can then iterate this argument. Since $T$ does not satisfy the lemma, the process never stops and we construct a sequence $\left(x_{n}\right)$ of vertices such that $x_{n+2} \neq x_{n}$ for all $n$. Since $T$ is a tree, $\left(x_{n}\right)$ never passes through the same vertex twice, so $T$ is infinite, which is absurd.
According to Lemma 2, there therefore exists an edge $e$ of the tree (in green in the figure) such that, if we cut $e$, we obtain $T_{1}$ and $T_{2}$ such that $\left|T_{1}\right|,\left|T_{2}\right| \geqslant \frac{1}{4}(|T|-1)=\frac{\mathrm{m}^{2}-1}{2}$. If we denote $C_{1}$ and $C_{2}$ the circuits that surround $T_{1}$ and $T_{2}$, we therefore have, according to Lemma 1, the inequalities $\left|C_{1}\right|,\left|C_{2}\right| \geqslant m^{2}+1$. But the two parts of the circuit obtained by cutting it have lengths $\left|C_{1}\right|-1$ and $\left|C_{2}\right|-1$ (we remove the orange edge) which are at least $\mathrm{m}^{2}$, hence the result.
|
proof
|
Yes
|
Incomplete
|
proof
|
Combinatorics
|
Soit $n \geqslant 2$. On trace un circuit sur un échiquier $n \times n$ qui passe exactement une fois par chaque case et revient à son point de départ (deux cases consécutives sur le circuit doivent avoir un côté commun).
Montrer qu'il existe deux cases voisines sur l'échiquier telles que, si on "coupe" le circuit en ces deux cases, les deux chemins obtenus ont pour longueur au moins le quart de la longueur du circuit de départ.
Remarque. La longueur d'un chemin est le nombre de fois où il change de case. En particulier, si le circuit est découpé en deux chemins, la somme des longueurs des deux chemins vaudra toujours $\mathrm{n}^{2}$.
|
Remarquons tout d'abord que si l'échiquier est pavé en noir et blanc de la manière habituelle, le circuit doit alterner des cases noires et blanches et revenir à sa case de départ donc sa longueur doit être paire donc $n^{2}$ et pair. On écrit donc $n=2 m$.

On considère l'ensemble des coins des carrés qui se trouvent à l'intérieur du circuit (ce sont les points bleus sur la figure), et on relie deux de ces points quand ils sont à distance 1 l'un de l'autre (ce sont les
arêtes bleues sur la figure). Le graphe obtenu est un arbre : il est connexe car le circuit l'est, et il n'a pas de cycle car un cycle soit créerait un deuxième circuit à l'intérieur du premier, soit enfermerait le centre d'une case qui ne serait donc pas dans le circuit rouge. De plus, dans cet arbre, chaque sommet a au plus 4 voisins.
Le lemme suivant permet de faire le lien entre la longueur du chemin rouge et le nombre de sommets de l'arbre bleu :
Lemme (Lemme 1). Soit $T$ un arbre dont les sommets sont sur les coins d'un quadrillage, et $C$ un circuit passant par les centres des cases et faisant le tour de l'arbre. On note $|\mathrm{C}|$ la longueur de ce circuit. Alors $|C|=2|T|+2$.
Preuve du lemme 1. Chaque sommet de l'arbre est le centre d'un carré de côté 1. On calcule de deux manières différentes la somme $S$ des périmètres de ces carrés. D'un part on a $S=4|T|$. Mais d'autre part, pour calculer $S$, on prend en compte une fois chaque arête de $C$, et deux fois chaque arête qui sépare deux sommets de l'arbre. Comme l'arbre a $|\mathrm{T}|-1$ arêtes, on a donc $S=|C|+2(|T|-1)$. On en déduit le lemme.
On sait que $|C|=n^{2}=4 m^{2}$. On en déduit $|T|=\frac{1}{2}(|C|-1)=2 m^{2}-1$. De plus, couper le circuit en deux cases voisines revient essentiellement à couper une arête de l'arbre. On va donc montrer le lemme suivant:
Lemme (Lemme 2). On note |T| le nombre de sommets d'un arbre. Soit T un arbre ayant au moins deux sommets et dont tous les sommets sont de degré au plus 4. Il existe une arête e de T telle qu'en coupant l'arête $e$, l'arbre $T$ est coupé en deux arbres $T_{1}$ et $T_{2}$ tels que $\left|T_{1}\right| \geqslant \frac{1}{4}(|T|-1)$ et $\left|T_{2}\right| \geqslant \frac{1}{4}(|T|-1)$.
Preuve du lemme 2. On raisonne par l'absurde. On fixe $\mathrm{x}_{0}$ un sommet de T : supprimer $\mathrm{x}_{0}$ divise T en $\mathrm{T}_{1}, \mathrm{~T}_{2}, \mathrm{~T}_{3}$ et $\mathrm{T}_{4}$ (si $\times$ n'a pas quatre voisins, certains de ces arbres ont un nombre de sommets nul). D'après le principe des tiroirs, il existe $i$ tel que $\left|T_{i}\right| \geqslant \frac{1}{4}(|T|-1)$. On suppose que c'est $T_{1}$, et on note $x_{1}$ le sommet de $T_{1}$ qui est relié à $x_{0}$. Mais si $T$ ne vérifie pas le lemme, alors $\left|\mathrm{T}_{1}\right|>|\mathrm{T}|-\frac{1}{4}(|\mathrm{~T}|-1)=\frac{3}{4}(|\mathrm{~T}|-1)+1$.
On peut maintenant effectuer le même raisonnement avec $x_{1}$ : il a au plus trois voisins différents de $x_{0}$ qui correspondent à trois arbres $\mathrm{T}_{1}^{\prime}, \mathrm{T}_{2}^{\prime}$ et $\mathrm{T}_{3}^{\prime}$, et le nombre total de sommets de ces trois arbres vaut au moins $\frac{3}{4}(|T|-1)$. Par le principe des tiroirs il existe $i$ tel que $\left|T_{i}^{\prime}\right| \geqslant \frac{1}{4}(|T|-1)$ donc, comme $T$ ne vérifie pas le lemme, $\left|\mathrm{T}_{1}^{\prime}\right|>\frac{3}{4}(|\mathrm{~T}|-1)+1$. On note $x_{2}$ le sommet par lequel $\mathrm{T}_{1}^{\prime}$ est relié à $x_{1}$. Comme on n'a considéré que les voisins de $x_{1}$ qui sont différents de $x_{0}$, on a $x_{2} \neq x_{0}$. On peut alors itérer cet argument. Comme T ne vérifie pas le lemme, le procédé ne s'arrête jamais et on construit une suite $\left(x_{n}\right)$ de sommets telle que $x_{n+2} \neq x_{n}$ pour tout $n$. Comme $T$ est un arbre, $\left(x_{n}\right)$ ne passe jamais deux fois par le même sommet donc $T$ est infini, ce qui est absurde.
D'après le lemme 2, il existe donc une arête $e$ de l'arbre (en vert sur la figure) telle que, si on coupe $e$, on obtient $T_{1}$ et $T_{2}$ tels que $\left|T_{1}\right|,\left|T_{2}\right| \geqslant \frac{1}{4}(|T|-1)=\frac{\mathrm{m}^{2}-1}{2}$. Si on note $C_{1}$ et $C_{2}$ les circuits qui font le tour
de $T_{1}$ et de $T_{2}$, on a donc d'après le lemme 1 les inégalités $\left|C_{1}\right|,\left|C_{2}\right| \geqslant m^{2}+1$. Mais les deux parties du circuit obtenues en le coupant ont pour longueurs $\left|C_{1}\right|-1$ et $\left|C_{2}\right|-1$ (on retire l'arête orange) qui valent au moins $\mathrm{m}^{2}$, d'où le résultat.
|
{
"exam": "French_envois",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-4-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 7",
"tier": "T2",
"year": "2016"
}
|
Let $n \in \mathbb{N}^{*}$. We place $1 \times n$ and $n \times 1$ rectangles on a $2 n \times 2 n$ chessboard, in such a way that no two rectangles intersect and each rectangle covers exactly $n$ squares. A set of such rectangles is said to be saturated if it is impossible to add another rectangle without intersecting a rectangle already in place.
Find the smallest $k$ such that there exists a saturated set of $k$ rectangles.
|
Let's start with the case $n \geqslant 3$: the answer is $k=2n+1$. The following set (in the case $n=5$, the construction generalizes easily) works:
It remains to show that with 2n rectangles, it is always possible to add one that does not intersect them. If the 2n rectangles are oriented in the same direction, for example, all horizontal, then there must be exactly one on each row (otherwise there would be an empty row), and it cannot be at the end of the row (if it were all the way to the left, one could add a rectangle to its right). Consequently, the first and last columns are empty, and it is possible to add a vertical rectangle.
If there are rectangles in both directions, we can assume there are at most n vertical rectangles. Suppose the configuration is saturated. Let $1 \leqslant k \leqslant n$ such that column $k$ contains a vertical rectangle denoted $r$. By shifting $r$ one cell to the left, it must intersect an already placed rectangle, denoted $r'$ (otherwise one could add a rectangle). However, if $r'$ were horizontal, it would have to intersect $r$ because there is not enough space for a horizontal rectangle to the left of $r$. The rectangle $r'$ is therefore vertical, and thus column $k-1$ contains a vertical rectangle, and similarly for columns $k-2, \ldots, 2,1$.
Similarly, if $n+1 \leqslant k \leqslant 2n$ is such that column $k$ contains a vertical rectangle, then all columns to its right contain a vertical rectangle. The set of columns not containing a vertical rectangle is therefore a set of at least $n$ consecutive columns. There is thus an $n \times 2n$ rectangle that does not intersect any of the vertical rectangles. If the configuration is saturated, it therefore requires 2n horizontal rectangles to "block" each row within this $n \times 2n$ rectangle. Since we have assumed there is at least one vertical rectangle, there are therefore at least $2n+1$ rectangles, which is absurd.
Let's move on to the cases $n=1$ and $n=2$: the case $n=1$ is trivial and the answer is 4 (one must cover everything, otherwise one could add a 1x1 square). For $n=2$, there is no saturated set of 5 rectangles.
To show this, one can either perform a somewhat tedious case disjunction, or adapt the previous proof: if all rectangles have the same direction, it is not possible (one row contains 2 rectangles, so only one rectangle can intersect the first column, leaving room for a vertical domino in the first column). Otherwise, we can assume there are at most 2 vertical dominos. The proof for $n \geqslant 3$ shows that there are two consecutive free columns, so at least 4 horizontal dominos, so only one vertical. Moreover, the columns without a vertical domino are consecutive, so we can assume the vertical domino is in column 1. It must be in the middle of the column to avoid leaving space, and it is then easy to see that it is impossible to "plug all the holes" with 4 horizontal dominos.
Finally, the following configuration works with $k=6$:
|
2n+1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Soit $n \in \mathbb{N}^{*}$. On place des rectangles $1 \times n$ et $n \times 1$ sur un échiquier $2 n \times 2 n$, de telle manière que deux rectangles ne s'intersectent jamais et que chaque rectangle recouvre exactement n cases. Un ensemble de tels rectangles est dit saturé s'il est impossible d'ajouter un rectangle sans intersecter un rectangle déjà en place.
Trouver le plus petit $k$ tel qu'il existe un ensemble saturé de $k$ rectangles.
|
Commençons par le cas $n \geqslant 3$ : la réponse est $k=2 n+1$. L'ensemble suivant (dans le cas $\mathrm{n}=5$, la construction se généralisant facilement) convient :

Il reste à montrer qu'avec 2 n rectangles il est toujours possible d'en ajouter un qui ne les intersecte pas. Si les 2 n rectangles sont orientés dans le même sens, par exemple tous horizontaux, alors il doit y en avoir exactement un sur chaque ligne (sinon il y aurait une ligne vide), et il ne peut pas être tout au bout de la ligne (s'il était tout à gauche, on pourrait ajouter un rectangle à sa droite). Par conséquent, la première et la dernière colonne sont vides, et il est possible d'ajouter un rectangle vertical.
S'il y a des rectangles dans les deux sens, on peut supposer qu'il y a au plus n rectangles verticaux. Supposons que la configuration soit saturée. Soit $1 \leqslant k \leqslant n$ tel que la colonne $k$ contient un rectangle vertical noté $r$. En décalant $r$ d'une case vers la gauche, on doit intersecter un rectangle déjà en place, noté $r^{\prime}$ (sinon on pourrait ajouter un rectangle). Cependant, si $r^{\prime}$ était horizontal, il devrait intersecter $r$ car il n'y a pas assez de place pour un rectangle horizontal à gauche de $r$. Le rectangle $r^{\prime}$ est donc vertical, donc la colonne $k-1$ contient un rectangle vertical et de même pour les colonnes $k-2, \ldots, 2,1$.
De même, si $\mathrm{n}+1 \leqslant \mathrm{k} \leqslant 2 \mathrm{n}$ est tel que la colonne k contient un rectangle vertical, alors toutes les colonnes à sa droite contiennent un rectangle vertical. L'ensemble des colonnes ne contenant pas de rectangle vertical est donc un ensemble d'au moins n colonnes consécutives. Il y a donc un rectangle $\mathrm{n} \times 2 \mathrm{n}$ qui ne rencontre aucun des rectangles verticaux. Si la configuration est saturée, il faut donc 2 n rectangles horizontaux pour "bloquer" chaque ligne dans ce rectangle $\mathrm{n} \times 2 \mathrm{n}$. Comme on a supposé qu'il y avait au moins un rectangle vertical, il y a donc au moins $2 \mathrm{n}+1$ rectangles, ce qui est absurde.
Passons aux cas $n=1$ et $n=2$ : le cas $n=1$ est trivial et la réponse est 4 (il faut tout couvrir, sinon on pourrait ajouter un carré 1 . Pour $n=2$, il n'y a pas d'ensemble saturé de 5 rectangles.
Pour le montrer, on peut soit effectuer une disjonction de cas un peu fastidieuse, soit adapter la preuve précédente : si tous les rectangles ont la même direction, ce n'est pas possible (une seule ligne contient 2 rectangles donc un seul rectangle peut intersecter la première colonne donc il reste la place pour un domino vertical dans la première colonne). Sinon, on peut supposer qu'il y a au plus 2 dominos verticaux. La preuve pour $n \geqslant 3$ montre qu'il y a deux colonnes consécutives libres, donc au moins 4 dominos horizontaux, donc un seul vertical. De plus, les colonnes sans domino vertical sont consécutives donc on peut supposer que le domino vertical est dans la colonne 1. Il doit être au milieu de la colonne pour ne pas laisser une place, et il est alors facile de voir qu'il est impossible de "boucher tous les trous" avec 4 dominos horizontaux.
Enfin, la configuration suivante marche avec $\mathrm{k}=6$ :

|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "\nExercice 8.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-4-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 8",
"tier": "T2",
"year": "2016"
}
|
Let $n \geqslant 2$ and $a_{1}, \ldots, a_{n}, b_{1}, \ldots, b_{n}$ be strictly positive real numbers. The $a_{i}$ are assumed to be pairwise distinct, as are the $b_{i}$. It is assumed that it is possible to separate the $a_{i}$ into two subsets of equal sum, and the same for the $b_{i}$.
Show that there exists a simple 2n-gon having exactly n horizontal sides and n vertical sides, the lengths of the horizontal sides being exactly the $a_{i}$ and the lengths of the vertical sides being exactly the $b_{i}$.
Note. A simple polygon is a polygon whose sides do not intersect, except of course two consecutive sides at their common endpoint.
|
By changing the indices and possibly swapping the roles of $a$ and $b$, we can assume that there exist $\ell \leqslant m \leqslant \frac{n}{2}$ such that $a_{1}+\cdots+a_{\ell}=a_{\ell+1}+\cdots+a_{n}=S_{a}$ and $b_{1}+\cdots+b_{m}=$ $b_{m+1}+\cdots+b_{n}$, that $b_{1} \geqslant \cdots \geqslant b_{m}$ and that $b_{m+1} \leqslant \cdots \leqslant b_{n}$. When we go around our polygon in a clockwise direction, the $a_{i}$ with $i \leqslant \ell$ will correspond to the lengths of the sides where we go to the right, the $a_{i}$ with $i \geqslant \ell+1$ to those where we go to the left, the $b_{i}$ with $i \leqslant m$ to those where we go up, and the $b_{i}$ with $i \geqslant m+1$ to those where we go down. It remains to place these sides correctly relative to each other, so that they do not intersect.
We denote $b_{i}^{\prime}=b_{i}$ for $i \leqslant m$ and $b_{i}^{\prime}=-b_{i}$ for $i \geqslant m+1$, so that $\sum_{i=1}^{n} b_{i}^{\prime}=0$ (this change of notation will allow us to measure the change in ordinate when moving from one vertex of the polygon to another). The $b_{i}^{\prime}$ are then arranged in decreasing order.
Lemma. There exists a subset $\mathrm{I} \subset \llbracket 2, n-1 \rrbracket$ of cardinality $\ell-1$ such that $b_{1}^{\prime}+\sum_{i \in I} b_{i}^{\prime}>0$ and $b_{n}^{\prime}+\sum_{i \in \mathrm{I}} \mathrm{b}_{\mathrm{i}}^{\prime}<0$.
Proof of the lemma. The statement of the lemma is equivalent to finding $\mathrm{I}$ of cardinality $\ell-1$ with $\left.\sum_{i \in I} b_{i}^{\prime} \in\right]-$ $\mathrm{b}_{1}^{\prime},-\mathrm{b}_{n}^{\prime}\left[\right.$. Let $\mathrm{I}_{\max }=\{2, \ldots, \ell\}$ and $\mathrm{I}_{\min }=\{\mathrm{n}-\ell+1, \ldots, \mathrm{n}-1\}$. It is clear that $\sum_{i \in \mathrm{I}_{\max }} \mathrm{b}_{\mathrm{i}}^{\prime}>-\mathrm{b}_{1}^{\prime}$ (if we have $n$ numbers with a sum of zero, the sum of the $\ell$ largest is positive) and that $\sum_{i \in \mathrm{I}_{\mathrm{min}}} b_{i}^{\prime}<$ $-b_{n}^{\prime}$.
If we replace one by one the elements of $I_{\min }$ with those of $I_{\max }$, the sum increases at each step by a number of the form $b_{i}^{\prime}-b_{j}^{\prime}<b_{1}^{\prime}-b_{n}^{\prime}$ (the inequality is strict because the $b_{i}$ are pairwise distinct). We thus pass from a number less than $-b_{n}^{\prime}$ to a number greater than $-b_{1}^{\prime}$, increasing at each step by a number strictly less than $b_{1}^{\prime}-b_{n}^{\prime}$, so at some point the sum will be strictly between $-b_{1}^{\prime}$ and $-b_{n}^{\prime}$.
We want to construct our polygon as follows: $b_{1}$ will be the length of the leftmost vertical side (we denote $A$ the bottom vertex and $B$ the top vertex of this side) and $b_{n}$ the length of the rightmost vertical side (we name $C$ the top vertex and $D$ the bottom vertex of this side), and the horizontal distance between these two sides is $S_{a}$. To go from $B$ to $C$, we use the horizontal sides of length $a_{i}$ with $1 \leqslant i \leqslant \ell$ between which we interleave the $\ell-1$ sides of lengths $b_{i}$ with $i \in I$, starting with those such that $i \leqslant m$. We thus obtain a broken line (in blue) that connects the top of $b_{1}$ to the top of $b_{n}$ by alternating moves to the right and up, then moves to the right and down.
Then, to connect $D$ to $A$, we use the $n-\ell$ horizontal sides of length $a_{i}$ with $\ell+1 \leqslant i \leqslant n$, between which we interleave the remaining $b_{i}$, this time starting with the $i \geqslant m+1$ to go down before going up (this corresponds to the green line in the figure).
The polygon thus constructed has the desired side lengths. It remains to verify that these sides do not intersect. The two red sides do not cut any other because by construction, they are respectively the farthest to the left and the farthest to the right of all the others. Moreover, two blue sides cannot intersect because there is always one to the left of the other, and the same for two green sides.
It is therefore sufficient to verify that a blue side cannot intersect a green vertex. We will show that in fact, the blue line is entirely above the green line. Since the blue line goes up and then down, its ordinate is everywhere greater than $\min \left\{\mathrm{y}_{\mathrm{B}}, \mathrm{y}_{\mathrm{C}}\right\}$. Similarly, the ordinate on the green line is everywhere less than $\max \left\{y_{A}, y_{D}\right\}$. It is therefore sufficient to show that $\min \left\{y_{B}, y_{C}\right\}>\max \left\{y_{A}, y_{D}\right\}$. Since it is obvious that $y_{B}>y_{A}$ and $y_{C}>y_{D}$, it is sufficient to show $y_{C}>y_{A}$ and $y_{B}>y_{D}$. Now, $y_{C}-y_{A}=$ $b_{1}+\sum_{i \in I} b_{i}^{\prime}$, which is strictly positive according to the lemma. Similarly, $y_{D}-y_{B}=\sum_{i \in I} b_{i}^{\prime}-b_{n}^{\prime}$, which is strictly negative according to the lemma. We can therefore draw a horizontal line (in orange in the figure) such that the blue line is strictly above and the green line is strictly below.
Remark. The original statement omitted the condition "the $b_{i}$ are pairwise distinct". A fairly simple counterexample without this hypothesis is the following: $n=4$ with $a_{1}=a_{2}=a_{3}=a_{4}$ and $b_{1}=b_{2}=b_{3}=b_{4}$. However, the proof above can be adapted as long as the $a_{i}$ are not all equal or the $b_{i}$ are not all equal.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $n \geqslant 2$ et $a_{1}, \ldots, a_{n}, b_{1}, \ldots, b_{n}$ des réels strictement positifs. Les $a_{i}$ sont supposés deux à deux distincts, de même que les $b_{i}$. On suppose qu'il est possible de séparer les $a_{i}$ en deux sous-ensembles de même somme, et de même pour les $b_{i}$.
Montrer qu'il existe un 2 n -gone simple ayant exactement n côtés horizontaux et n côtés verticaux, dont les longueurs des côtés horizontaux sont exactement les $a_{i}$ et dont les longueurs des côtés verticaux sont exactement les $b_{i}$.
Remarque. Un polygone simple est un polygone dont les côtés ne s'intersectent pas, sauf bien sûr deux côtés consécutifs en leur extrémité commune.
|
Quitte à changer les indices et éventuellement à échanger les rôles de $a$ et $b$, on peut supposer qu'il existe $\ell \leqslant m \leqslant \frac{n}{2}$ tels que $a_{1}+\cdots+a_{\ell}=a_{\ell+1}+\cdots+a_{n}=S_{a}$ et $b_{1}+\cdots+b_{m}=$ $b_{m+1}+\cdots+b_{n}$, que $b_{1} \geqslant \cdots \geqslant b_{m}$ et que $b_{m+1} \leqslant \cdots \leqslant b_{n}$. Quand on fait le tour de notre polygone dans le sens horaire, les $a_{i}$ avec $i \leqslant \ell$ correspondront aux longueurs des côtés où on va vers la droite, les $a_{i}$ avec $i \geqslant \ell+1$ à ceux où on va vers la gauche, les $b_{i}$ avec $i \leqslant m$ à ceux où on va vers le haut et les $b_{i}$ avec $i \geqslant m+1$ à ceux où on va vers le bas. Il reste à placer ces côtés correctement les uns par rapport aux autres, de manière à ce qu'ils ne s'intersectent pas.
On note $b_{i}^{\prime}=b_{i}$ pour $i \leqslant m$ et $b_{i}^{\prime}=-b_{i}$ pour $i \geqslant m+1$, de manière à avoir $\sum_{i=1}^{n} b_{i}^{\prime}=0$ (ce changement de notation permettra de mesurer la variation d'ordonnée quand on passe d'un sommet du polygone à un autre). Les $b_{i}^{\prime}$ sont alors rangés dans l'ordre décroissant.
Lemme. Il existe un sous-ensemble $\mathrm{I} \subset \llbracket 2, n-1 \rrbracket$ de cardinal $\ell-1$ tel que $b_{1}^{\prime}+\sum_{i \in I} b_{i}^{\prime}>0$ et $b_{n}^{\prime}+\sum_{i \in \mathrm{I}} \mathrm{b}_{\mathrm{i}}^{\prime}<0$.
Preuve du lemme. L'énoncé du lemme revient à trouver I de cardinal $\ell-1$ avec $\left.\sum_{i \in I} b_{i}^{\prime} \in\right]-$ $\mathrm{b}_{1}^{\prime},-\mathrm{b}_{n}^{\prime}\left[\right.$. Soient $\mathrm{I}_{\max }=\{2, \ldots, \ell\}$ et $\mathrm{I}_{\min }=\{\mathrm{n}-\ell+1, \ldots, \mathrm{n}-1\}$. Il est clair que $\sum_{i \in \mathrm{I}_{\max }} \mathrm{b}_{\mathrm{i}}^{\prime}>-\mathrm{b}_{1}^{\prime}$ (si on a $n$ nombres de somme nulle, la somme des $\ell$ plus grand est positive) et que $\sum_{i \in \mathrm{I}_{\mathrm{min}}} b_{i}^{\prime}<$ $-b_{n}^{\prime}$.
Si on remplace un par un les éléments de $I_{\min }$ par ceux de $I_{\max }$, la somme augmente à chaque étape d'un nombre de la forme $b_{i}^{\prime}-b_{j}^{\prime}<b_{1}^{\prime}-b_{n}^{\prime}$ (l'inégalité est stricte car les $b_{i}$ sont deux à deux distincts). On passe donc d'un nombre inférieur à $-b_{n}^{\prime}$ à un nombre supérieur à $-b_{1}^{\prime}$ en augmentant à chaque étape $d^{\prime}$ un nombre strictement inférieur à $b_{1}^{\prime}-b_{n}^{\prime}$ donc à un moment la somme se trouvera strictement entre $-b_{1}^{\prime}$ et $-b_{n}^{\prime}$.
On veut construire notre polygone de la manière suivante : $b_{1}$ sera la longueur du côté vertical le plus à gauche (on note $A$ le sommet en bas et $B$ le sommet en haut de ce côté) et $b_{n}$ celle du côté vertical le plus à droite (on nomme C le sommet en haut et D le sommet en bas de ce côté), et l'écart horizontal entre ces deux côtés vaut $S_{a}$. Pour passer de $B$ à $C$, on utilise les côtés horizontaux de longueur $a_{i}$ avec $1 \leqslant i \leqslant \ell$ entre lesquels on intercale les $\ell-1$ côtés de longueurs $b_{i}$ avec $i \in I$, en commençant par ceux tels que $i \leqslant m$. On obtient ainsi une ligne brisée (en bleu) qui relie le haut de $b_{1}$ au haut de $b_{n}$ en alternant les déplacements vers la droite et vers le haut, puis les déplacements vers la droite et vers le bas.
Puis, pour relier $D$ à $A$, on utilise les $n-\ell$ côtés horizontaux de longueur $a_{i}$ avec $\ell+1 \leqslant i \leqslant n$, entre lesquels on intercale les $b_{i}$ restants, cette fois en commençant par les $i \geqslant m+1$ pour descendre avant de remonter (cela correspond à la ligne verte sur la figure).

Le polygone ainsi construit a bien les longueurs de côtés voulues. il reste à vérifier que ces côtés ne s'intersectent pas. Les deux côtés rouges n'en coupent aucun autre car par construction, ils sont respec-
tivement plus à gauche et plus à droite que tous les autres. De plus, deux côtés bleus ne peuvent pas s'intersecter car il y en a toujours un plus à gauche que l'autre, et de même pour deux côtés verts.
Il suffit donc de vérifier qu'un côté bleu ne peut pas intersecter un sommet vert. On va montrer qu'en fait, la ligne bleue est entièrement située au-dessus de la ligne verte. Comme la ligne bleue monte puis redescend, son ordonnée est partout supérieure à $\min \left\{\mathrm{y}_{\mathrm{B}}, \mathrm{y}_{\mathrm{C}}\right\}$. De même, l'ordonnée sur la ligne verte est partout inférieure à $\max \left\{y_{A}, y_{D}\right\}$. Il suffit donc de montrer que $\min \left\{y_{B}, y_{C}\right\}>\max \left\{y_{A}, y_{D}\right\}$. Comme il est évident que $y_{B}>y_{A}$ et $y_{C}>y_{D}$, il suffit de montrer $y_{C}>y_{A}$ et $y_{B}>y_{D}$. Or, $y_{C}-y_{A}=$ $b_{1}+\sum_{i \in I} b_{i}^{\prime}$, qui est strictement positive d'après le lemme. De même, $y_{D}-y_{B}=\sum_{i \in I} b_{i}^{\prime}-b_{n}^{\prime}$ qui est strictement négative d'après le lemme. On peut donc tracer une ligne horizontale (en orange sur la figure) telle que la ligne bleue soit strictement au-dessus et la verte strictement en-dessous.
Remarque. L'énoncé original omettait la condition "les $b_{i}$ sont deux à deux distincts". Un contre-exemple assez simple sans cette hypothèse est le suivant: $n=4$ avec $a_{1}=a_{2}=a_{3}=a_{4}$ et $b_{1}=b_{2}=b_{3}=b_{4}$. En revanche, la preuve ci-dessus peut être adaptée dès que les $a_{i}$ ne sont pas tous égaux ou que les $b_{i}$ ne sont pas tous égaux.
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-4-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 9",
"tier": "T2",
"year": "2016"
}
|
Determine all natural numbers \( a \) for which there exist prime numbers \(\mathbf{p}, \mathbf{q}, \mathrm{r}\), not necessarily distinct, such that
\[
a=\frac{p+q}{r}+\frac{q+r}{p}+\frac{r+p}{q}
\]
|
First, if $p=q=r$, then we get $\mathrm{a}=6$, which is indeed a solution. Let's show that this is the only solution, and suppose there exists a solution $a=\frac{p+q}{r}+\frac{q+r}{p}+\frac{r+p}{q}$ with $p, q, r$ being primes and not all equal.
- If two of the numbers $p, q, r$ are equal, say $p=q \neq r$, then:
$$
\mathrm{a}=2\left(\frac{\mathrm{p}}{\mathrm{r}}+\frac{\mathrm{r}}{\mathrm{p}}\right)+2=\frac{2\left(\mathrm{p}^{2}+\mathrm{r}^{2}\right)}{\mathrm{pr}}+2
$$
Thus, $\frac{2\left(\mathfrak{p}^{2}+r^{2}\right)}{p r}$ is an integer. We deduce that the prime number $p$ divides $2 r^{2}$ while being coprime with $r$, and therefore that $p=2$. The same reasoning applies to show that $r=2$, which contradicts that $r \neq p$. Therefore, there is no solution in this case.
- If $p, q, r$ are pairwise distinct, then, without loss of generality, we can assume that $p>q>r$ (noting that then $p$ and $q$ are odd), and then
$$
\operatorname{apqr}=\mathrm{pq}(\mathrm{p}+\mathrm{q})+\mathrm{qr}(\mathbf{q}+\mathrm{r})+\mathrm{rp}(\mathrm{r}+\mathrm{p})
$$
Thus, $p$ divides $q r(q+r)$. Since $p$ is coprime with $q r$, it must divide $q+r$. But $0<q+r<2 p$ so $p=q+r$. This implies that $r$ is even, and therefore that $r=2$. We then have $p=q+2$ and $a=(q+1)+1+\frac{q+4}{q}=q+3+\frac{4}{q}$. In particular, $\frac{4}{q}$ must be an integer, which is impossible for $\mathrm{q}>1$ odd. Thus, there is no solution in this case, which concludes.
|
6
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer tous les entiers naturels a pour lesquels il existe des nombres premiers $\mathbf{p}, \mathbf{q}, \mathrm{r}$, pas forcément distincts, tels que
$$
a=\frac{p+q}{r}+\frac{q+r}{p}+\frac{r+p}{q}
$$
|
Tout d'abord, si $p=q=r$, alors on obtient $\mathrm{a}=6$, qui est bien une solution. Montrons qu'il s'agit de la seule solution, et supposons qu'il existe une solution $a=\frac{p+q}{r}+\frac{q+r}{p}+\frac{r+p}{q}$ avec $p, q, r$ premiers et non tous égaux.
- Si deux des nombres $p, q, r$ sont égaux, disons $p=q \neq r$, alors:
$$
\mathrm{a}=2\left(\frac{\mathrm{p}}{\mathrm{r}}+\frac{\mathrm{r}}{\mathrm{p}}\right)+2=\frac{2\left(\mathrm{p}^{2}+\mathrm{r}^{2}\right)}{\mathrm{pr}}+2
$$
Ainsi, $\frac{2\left(\mathfrak{p}^{2}+r^{2}\right)}{p r}$ est un entier. On en déduit que le nombre premier $p$ divise $2 r^{2}$ tout en étant premier avec $r$, et donc que $p=2$. Le raisonnement $s^{\prime}$ adapte mot pour mot pour prouver que $r=2$, ce qui contredit que $r \neq p$. Il n'y a donc pas de solution dans ce cas.
- Si $p, q, r$ sont deux à deux distincts alors, sans perte de généralité, on peut supposer que $p>q>$ $r$ (on note qu'alors $p$ et $q$ sont impairs), et alors
$$
\operatorname{apqr}=\mathrm{pq}(\mathrm{p}+\mathrm{q})+\mathrm{qr}(\mathbf{q}+\mathrm{r})+\mathrm{rp}(\mathrm{r}+\mathrm{p})
$$
Ainsi, $p$ divise $q r(q+r)$. Puisque $p$ est premier avec $q r$, il divise donc $q+r$. Mais $0<q+r<2 p$ donc $p=q+r$. Cela implique que $r$ est pair, et donc que $r=2$. On a alors $p=q+2$ et $a=(q+1)+1+\frac{q+4}{q}=q+3+\frac{4}{q}$. En particulier, $\frac{4}{q}$ soit être un entier, ce qui est impossible pour $\mathrm{q}>1$ impair. Il n'y a ainsi pas de solution dans ce cas, ce qui conclut.
|
{
"exam": "French_envois",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-5-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T2",
"year": "2016"
}
|
In a high school theater club, 14 groups of 4 students each have been formed to work on scenes from a play. Any two different groups always have exactly one student in common.
a) Prove that there exists a student who belongs to at least 5 groups.
b) Each student in the theater club is a member of at least one group. How many students are there in this club?
|
a) Let G be one of the groups. Each of the 13 other groups has a student in common with G. Since $13=3 \times 4+1$, according to the pigeonhole principle, one of the four students in G, say $x$, belongs to at least 4 of the other nine groups. Including G, this means that $x$ belongs to at least 5 groups.
b) Let's prove that $x$ belongs to all the groups. We denote $\mathrm{G}=\mathrm{G}_{1}, \mathrm{G}_{2}, \mathrm{G}_{3}, \mathrm{G}_{4}, \mathrm{G}_{5}$ as the groups to which $x$ belongs, and then proceed by contradiction: suppose there exists a group $\mathrm{G}^{\prime}$ such that $x \notin \mathrm{G}^{\prime}$.
Since $\mathrm{G}^{\prime}$ has a student in common with each of the groups $\mathrm{G}_{1}, \mathrm{G}_{2}, \mathrm{G}_{3}, \mathrm{G}_{4}, \mathrm{G}_{5}$ and, as $\mathrm{G}^{\prime}$ contains only four students, it follows that one of the members of $G^{\prime}$, say $y$, belongs to two of these five groups, say $G_{i}$ and $G_{j}$, with $1 \leqslant i<j \leqslant 5$. Clearly, $x \neq y$, because $x \notin G^{\prime}$ and $y \in G^{\prime}$. But then the groups $G_{i}$ and $G_{j}$ have both $x$ and $y$ in common, which contradicts the hypothesis of the problem.
Thus, $x$ belongs to all the groups. By removing $x$ from each of these 14 groups, we obtain 14 disjoint groups of 3 students, which is $14 \times 3=42$ students. We still need to add $x$ and, since each member of the club belongs to one of the groups, all members are then counted exactly once.
Therefore, there are exactly 43 members in the club.
|
43
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Au club théâtre d'un lycée, on a formé 14 groupes de 4 élèves afin de travailler les scènes d'une pièce. Deux groupes différents ont toujours un et un seul élève en commun.
a) Prouver qu'il existe un élève qui appartient à au moins 5 groupes.
b) Chaque élève du club théâtre est membre d'au moins un groupe. Combien y a-t-il d'élèves dans ce club?
|
a) Soit G un des groupes. Chacun des 13 autres groupes a un élève en commun avec G. Or $13=3 \times 4+1$ donc, d'après le principe des tiroirs, un des quatre élèves de G, disons $x$, appartient à au moins 4 des neuf autres groupes. Avec G, cela signifie que $x$ appartient à au moins 5 groupes.
b) Prouvons que $x$ appartient à tous les groupes. On note $\mathrm{G}=\mathrm{G}_{1}, \mathrm{G}_{2}, \mathrm{G}_{3}, \mathrm{G}_{4}, \mathrm{G}_{5}$ des groupes auxquels appartient $x$, puis on procède par l'absurde : supposons qu'il existe un groupe $\mathrm{G}^{\prime}$ tel que $x \notin \mathrm{G}^{\prime}$.
Puisque $\mathrm{G}^{\prime}$ a un élève en commun avec chacun des groupes $\mathrm{G}_{1}, \mathrm{G}_{2}, \mathrm{G}_{3}, \mathrm{G}_{4}, \mathrm{G}_{5}$ et, comme $\mathrm{G}^{\prime}$ ne contient que quatre élèves, c'est que l'un des membres de $G^{\prime}$, disons $y$, appartient à deux de ces cinq groupes, disons $G_{i}$ et $G_{j}$, avec $1 \leqslant i<j \leqslant 5$. Clairement, on a $x \neq y$, car $x \notin G^{\prime}$ et $y \in G^{\prime}$. Mais alors les groupes $G_{i}$ et $G_{j}$ ont $x$ et $y$ en commun, en contradiction avec l'hypothèse de l'énoncé.
Ainsi, $x$ appartient à tous les groupes. En enlevant $x$ de chacun de ces 14 groupes, on obtient alors 14 groupes deux à deux disjoints de 3 élèves, soit $14 \times 3=42$ élèves. Il faut encore y ajouter $x$ et, puisque chaque membre du club appartient à un des groupes, les membres sont alors bien tous comptés une et une seule fois.
Il y a donc exactement 43 membres dans le club.
|
{
"exam": "French_envois",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-5-solutions.jsonl",
"solution_match": "## Solution de l'exercice 2",
"tier": "T2",
"year": "2016"
}
|
Let $A B C D$ be a convex quadrilateral whose diagonals are not perpendicular and such that the lines $(A B)$ and $(C D)$ are not parallel. We denote by $O$ the point of intersection of $[A C]$ and $[B D]$. Let $\mathrm{H}_{1}$ and $\mathrm{H}_{2}$ be the orthocenters of triangles $A O B$ and $C O D$, respectively. We denote by $M$ and $N$ the midpoints of $[A B]$ and $[C D]$, respectively.
Prove that the lines $\left(H_{1} H_{2}\right)$ and $(M N)$ are parallel if and only if $A C = B D$.
|
Let $A^{\prime}$ and $B^{\prime}$ be the feet of the altitudes from $A$ and $B$ in $\triangle AOB$. Let $C^{\prime}$ and $D^{\prime}$ be the feet of the altitudes from $C$ and $D$ in $\triangle COD$.
The points $A^{\prime}$ and $D^{\prime}$ therefore belong to the circle $\Gamma_{1}$ with diameter $[AD]$, and the points $B^{\prime}$ and $C^{\prime}$ belong to the circle $\Gamma_{2}$ with diameter $[BC]$. The points $A^{\prime}$ and $B^{\prime}$ therefore belong to the circle $\Gamma_{3}$ with diameter $[AB]$. Using the power of $H_{1}$ with respect to $\Gamma_{3}$, we get $H_{1} A \cdot H_{1} A^{\prime} = H_{1} B \cdot H_{1} B^{\prime}$.
We deduce that $H_{1}$ has the same power with respect to $\Gamma_{1}$ and $\Gamma_{2}$, and therefore that $H_{1}$ lies on the radical axis of these two circles, which we denote by $\Delta$. Similarly, we have $H_{2} \in \Delta$. Since the radical axis of two circles is perpendicular to the line connecting their centers, we have $(H_{1} H_{2}) \perp (PQ)$, where $P$ and $Q$ are the midpoints of $[AD]$ and $[BC]$, respectively.
Thus, $(H_{1} H_{2}) \parallel (MN)$ if and only if $(MN) \perp (PQ)$. According to the midline theorem, it is easy to verify that $PMQN$ is a parallelogram and that $MP = \frac{1}{2} BD$ and $MQ = \frac{1}{2} AC$. Therefore, $(MN) \perp (PQ)$ if and only if $PMQN$ is a rhombus, which is equivalent to $MP = MQ$, i.e., $AC = BD$.
|
AC = BD
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un quadrilatère convexe dont les diagonales ne sont pas perpendiculaires et tel que les droites $(A B)$ et $(C D)$ ne sont pas parallèles. On note O le point d'intersection de $[A C]$ et $[B D]$. Soit $\mathrm{H}_{1}$ et $\mathrm{H}_{2}$ les orthocentres respectifs des triangles $A O B$ et $C O D$. On désigne par $M$ et $N$ les milieux respectifs de $[A B]$ et [CD].
Prouver que les droites $\left(H_{1} H_{2}\right)$ et $(M N)$ sont parallèles si et seulement si $A C=B D$.
|
Soit $A^{\prime}$ et $B^{\prime}$ les pieds des hauteurs issues respectivement de $A$ et $B$ dans $A O B$. Soit $\mathrm{C}^{\prime}$ et $\mathrm{D}^{\prime}$ les pieds des hauteurs issues respectivement de C et D dans COD.
Les points $A^{\prime}$ et $D^{\prime}$ appartiennent donc au cercle $\Gamma_{1}$ de diamètre $[A D]$, et les points $B^{\prime}$ et $C^{\prime}$ appartiennent au cercle $\Gamma_{2}$ de diamètre $[B C]$. Les points $A^{\prime}$ et $B^{\prime}$ appartiennent donc au cercle $\Gamma_{3}$ de diamètre $[A B]$. En utilisant la puissance de $H_{1}$ par rapport à $\Gamma_{3}$, il vient $H_{1} A \cdot H_{1} A^{\prime}=H_{1} B \cdot H_{1} B^{\prime}$.
On en déduit que $\mathrm{H}_{1}$ a la même puissance par rapport à $\Gamma_{1}$ et $\Gamma_{2}$, donc que $\mathrm{H}_{1}$ appartient à l'axe radical de ces deux cercles, que l'on note $\Delta$. De même, on a $\mathrm{H}_{2} \in \Delta$. Or, l'axe radical de deux cercles étant perpendiculaire à la droite qui relie leur centres, on a $\left(\mathrm{H}_{1} \mathrm{H}_{2}\right) \perp(\mathrm{PQ})$, où $P$ et $Q$ sont les milieux respectifs de $[A D]$ et $[B C]$.
Ainsi, $\left(\mathrm{H}_{1} \mathrm{H}_{2}\right) / /(\mathrm{MN})$ si et seulement si $(\mathrm{MN}) \perp(\mathrm{PQ})$. Or, d'après le théorème des milieux, il est facile de vérifier que $P M Q N$ est un parallélogramme et que $M P=\frac{1}{2} B D$ et $M Q=\frac{1}{2} A C$. Par suite, $(M N) \perp(P Q)$ si et seulement si $P M Q N$ est un losange, ce qui équivaut à $M P=M Q$, c'est-à-dire $A C=B D$.
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-5-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T2",
"year": "2016"
}
|
Let $A B C D$ be a convex quadrilateral whose diagonals are not perpendicular and such that the lines $(A B)$ and $(C D)$ are not parallel. We denote by $O$ the point of intersection of $[A C]$ and $[B D]$. Let $\mathrm{H}_{1}$ and $\mathrm{H}_{2}$ be the orthocenters of triangles $A O B$ and $C O D$, respectively. We denote by $M$ and $N$ the midpoints of $[A B]$ and $[C D]$, respectively.
Prove that the lines $\left(H_{1} H_{2}\right)$ and $(M N)$ are parallel if and only if $A C = B D$.
|
The points considered are defined only by intersections of lines and orthogonality relations (but do not involve equalities of angles or intersections of circles or circle and line), so we can attempt an analytical approach, which will be tedious but humanly feasible.
Let us place ourselves in an orthonormal frame centered at \(O\) such that the points \(A, B, C, D, O\) have the following coordinates respectively:
$$
\binom{-a}{0},\binom{-1}{-b},\binom{c}{0},\binom{d}{b \mathrm{~d}},\binom{0}{0}
$$
Then the points \(\mathrm{H}_{1}, \mathrm{H}_{2}, \mathrm{M}, \mathrm{N}\) have the following coordinates respectively:
$$
\binom{-1}{y_{1}}, \quad\binom{d}{y_{2}}, \quad\binom{-(a+1) / 2}{-b / 2}, \quad\binom{(c+d) / 2}{b d / 2}
$$
with \(\overrightarrow{\mathrm{AH}_{1}} \cdot \overrightarrow{\mathrm{OB}}=-(\mathrm{a}-1)-\mathrm{y}_{1} \mathrm{~b}=0\) and \(\overrightarrow{\mathrm{CH}_{2}} \cdot \overrightarrow{\mathrm{OD}}=(\mathrm{d}-\mathrm{c}) \mathrm{d}+\mathrm{y}_{2} \mathrm{bd}=0\), that is,
$$
\mathrm{y}_{1}=\frac{1-\mathrm{a}}{\mathrm{~b}} \text { and } \mathrm{y}_{2}=\frac{\mathrm{c}-\mathrm{d}}{\mathrm{~b}}
$$
The lines \(\left(\mathrm{H}_{1} \mathrm{H}_{2}\right)\) and \((\mathrm{MN})\) are parallel if and only if they have the same slope, that is, if the equality
$$
\frac{y_{2}-y_{1}}{d+1}=\frac{b d+b}{c+d+a+1}
$$
is satisfied. We therefore calculate that
$$
\text { (1) } \begin{aligned}
& \Leftrightarrow b(d+1)^{2}=(c+d+a+1)\left(y_{2}-y_{1}\right)=\frac{1}{b}(c+d+a+1)(c-d+a-1) \\
& \Leftrightarrow b^{2}(d+1)^{2}=(c+a)^{2}-(d+1)^{2} \\
& \Leftrightarrow B D^{2}=(d+1)^{2}\left(b^{2}+1\right)=(c+a)^{2}=A C^{2}
\end{aligned}
$$
which allows us to conclude.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un quadrilatère convexe dont les diagonales ne sont pas perpendiculaires et tel que les droites $(A B)$ et $(C D)$ ne sont pas parallèles. On note O le point d'intersection de $[A C]$ et $[B D]$. Soit $\mathrm{H}_{1}$ et $\mathrm{H}_{2}$ les orthocentres respectifs des triangles $A O B$ et $C O D$. On désigne par $M$ et $N$ les milieux respectifs de $[A B]$ et [CD].
Prouver que les droites $\left(H_{1} H_{2}\right)$ et $(M N)$ sont parallèles si et seulement si $A C=B D$.
|
Les points considérés étant définis uniquement par des intersections de droite et de relations d'orthogonalité (mais ne faisant intervenir ni égalités d'angles ni intersections de cercles ou de cercle et droite), on peut tenter une approche analytique, qui sera pénible mais humainement faisable.
Plaçons-nous dans un repère orthonormé de centre $O$ et tel que les points $A, B, C, D, O$ aient pour coordonnées respectives
$$
\binom{-a}{0},\binom{-1}{-b},\binom{c}{0},\binom{d}{b \mathrm{~d}},\binom{0}{0}
$$
Alors les points $\mathrm{H}_{1}, \mathrm{H}_{2}, \mathrm{M}, \mathrm{N}$ ont pour coordonnées respectives
$$
\binom{-1}{y_{1}}, \quad\binom{d}{y_{2}}, \quad\binom{-(a+1) / 2}{-b / 2}, \quad\binom{(c+d) / 2}{b d / 2}
$$
avec $\overrightarrow{\mathrm{AH}_{1}} \cdot \overrightarrow{\mathrm{OB}}=-(\mathrm{a}-1)-\mathrm{y}_{1} \mathrm{~b}=0$ et $\overrightarrow{\mathrm{CH}_{2}} \cdot \overrightarrow{\mathrm{OD}}=(\mathrm{d}-\mathrm{c}) \mathrm{d}+\mathrm{y}_{2} \mathrm{bd}=0$, c'est-à-dire
$$
\mathrm{y}_{1}=\frac{1-\mathrm{a}}{\mathrm{~b}} \text { et } \mathrm{y}_{2}=\frac{\mathrm{c}-\mathrm{d}}{\mathrm{~b}}
$$
Les droites $\left(\mathrm{H}_{1} \mathrm{H}_{2}\right)$ et $(\mathrm{MN})$ sont parallèles si et seulement si elles ont même pente, c'est-à-dire si l'égalité
$$
\frac{y_{2}-y_{1}}{d+1}=\frac{b d+b}{c+d+a+1}
$$
est vérifiée. On calcule donc que
$$
\text { (1) } \begin{aligned}
& \Leftrightarrow b(d+1)^{2}=(c+d+a+1)\left(y_{2}-y_{1}\right)=\frac{1}{b}(c+d+a+1)(c-d+a-1) \\
& \Leftrightarrow b^{2}(d+1)^{2}=(c+a)^{2}-(d+1)^{2} \\
& \Leftrightarrow B D^{2}=(d+1)^{2}\left(b^{2}+1\right)=(c+a)^{2}=A C^{2}
\end{aligned}
$$
ce qui permet de conclure.

|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-5-solutions.jsonl",
"solution_match": "\nSolution alternative",
"tier": "T2",
"year": "2016"
}
|
Let $S$ be a set of strictly positive integers such that
$$
\lfloor\sqrt{x}\rfloor=\lfloor\sqrt{y}\rfloor \text{ for all } x, y \in S
$$
Prove that if $x, y, z, t \in S$ with $(x, y) \neq(z, t)$ and $(x, y) \neq(t, z)$, then $x y \neq z t$.
( $\lfloor.$.$\rfloor$ denotes the floor function.)
|
Suppose first that there exist integers $x_{1}, x_{2}, x_{3}, x_{4}$ in $S$ such that $x_{1} x_{2} \leqslant x_{3} x_{4}$ and $x_{1}+x_{2}>x_{3}+x_{4}$. Since these are integers, we have $x_{1}+x_{2}-x_{3}-x_{4} \geqslant 1$. Let $n=\left\lfloor\sqrt{x_{1}}\right\rfloor$. By definition of $S$, for $i=1,2,3,4$, there exists an integer $w_{i}$ such that $0 \leqslant w_{i} \leqslant 2 n$ and $x_{i}=n^{2}+w_{i}$.
The inequalities $x_{1} x_{2} \leqslant x_{3} x_{4}$ and $x_{1}+x_{2}>x_{3}+x_{4}$ become respectively
$$
w_{1}+w_{2}-w_{3}-w_{4} \geqslant 1 \quad \text { and } \quad\left(w_{1}+w_{2}-w_{3}+w_{4}\right) n^{2} \leqslant w_{3} w_{4}-w_{1} w_{2}
$$
In particular, we must have $\boldsymbol{w}_{3}>0$, and therefore
$$
\begin{aligned}
\mathrm{n}^{2} & \leqslant\left(w_{1}+w_{2}-w_{3}+w_{4}\right) n^{2} \leqslant w_{3} w_{4}-w_{1} w_{2} \\
& <w_{3}\left(w_{1}+w_{2}-w_{3}\right)-w_{1} w_{2}=\left(w_{1}-w_{3}\right)\left(w_{3}-w_{2}\right) \\
& <\frac{\left(\left(w_{1}-w_{3}\right)+\left(w_{3}-w_{2}\right)\right)^{2}}{4}=\frac{\left(w_{1}-w_{2}\right)^{2}}{4} \leqslant n^{2}
\end{aligned}
$$
leading to a contradiction.
Let then $x_{1}, x_{2}, x_{3}, x_{4}$ in $S$ such that $x_{1} x_{2}=x_{3} x_{4}=a$. According to the lemma above, we have $x_{1}+x_{2}=$ $x_{3}+x_{4}=b$. The numbers $x_{1}$ and $x_{2}$ on one hand, $x_{3}$ and $x_{4}$ on the other hand, are then the roots of the polynomial $X^{2}-a X+b$. We then have $x_{1}=x_{3}$ and $x_{2}=x_{4}$, or $x_{1}=x_{4}$ and $x_{2}=x_{3}$, which concludes.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $S$ un ensemble d'entiers strictement positifs tel que
$$
\lfloor\sqrt{x}\rfloor=\lfloor\sqrt{y}\rfloor \text { pour tous } x, y \in S
$$
Prouver que si $x, y, z, t \in S$ avec $(x, y) \neq(z, t)$ et $(x, y) \neq(t, z)$, alors $x y \neq z t$.
( $\lfloor.$.$\rfloor désigne la partie entière.)$
|
Supposons tout d'abord qu'il existe des entiers $x_{1}, x_{2}, x_{3}, x_{4}$ dans $S$ tels que $x_{1} x_{2} \leqslant x_{3} x_{4}$ et $x_{1}+x_{2}>x_{3}+x_{4}$. Puisqu'il s'agit d'entiers, on a donc $x_{1}+x_{2}-x_{3}-x_{4} \geqslant 1$. Soit $n=\left\lfloor\sqrt{x_{1}}\right\rfloor$. Par définition de $S$, pour $i=1,2,3,4$, il existe donc un entier $w_{i}$ tel que $0 \leqslant w_{i} \leqslant 2 n$ et $x_{i}=n^{2}+w_{i}$.
Les inégalités $x_{1} x_{2} \leqslant x_{3} x_{4}$ et $x_{1}+x_{2}>x_{3}+x_{4}$ deviennent respectivement
$$
w_{1}+w_{2}-w_{3}-w_{4} \geqslant 1 \quad \text { et } \quad\left(w_{1}+w_{2}-w_{3}+w_{4}\right) n^{2} \leqslant w_{3} w_{4}-w_{1} w_{2}
$$
En particulier, on doit avoir $\boldsymbol{w}_{3}>0$, et donc
$$
\begin{aligned}
\mathrm{n}^{2} & \leqslant\left(w_{1}+w_{2}-w_{3}+w_{4}\right) n^{2} \leqslant w_{3} w_{4}-w_{1} w_{2} \\
& <w_{3}\left(w_{1}+w_{2}-w_{3}\right)-w_{1} w_{2}=\left(w_{1}-w_{3}\right)\left(w_{3}-w_{2}\right) \\
& <\frac{\left(\left(w_{1}-w_{3}\right)+\left(w_{3}-w_{2}\right)\right)^{2}}{4}=\frac{\left(w_{1}-w_{2}\right)^{2}}{4} \leqslant n^{2}
\end{aligned}
$$
d'où la contradiction.
Soit alors $x_{1}, x_{2}, x_{3}, x_{4}$ dans $S$ tels que $x_{1} x_{2}=x_{3} x_{4}=a$. D'après le lemme ci-dessus, on a donc $x_{1}+x_{2}=$ $x_{3}+x_{4}=b$. Les nombres $x_{1}$ et $x_{2}$ d'une part, $x_{3}$ et $x_{4}$ d'autre part, sont alors les racines du polynôme $X^{2}-a X+b$. On a alors $x_{1}=x_{3}$ et $x_{2}=x_{4}$, ou $x_{1}=x_{4}$ et $x_{2}=x_{3}$, ce qui conclut.
|
{
"exam": "French_envois",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-5-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T2",
"year": "2016"
}
|
Let $n \geqslant 5$ be an integer, and $\left\{a_{1}, a_{2}, \cdots, a_{n}\right\}=\{1,2, \cdots, n\}$. Prove that the numbers $a_{1}, a_{1}+a_{2}, a_{1}+a_{2}+a_{3}, \cdots, a_{1}+a_{2}+\cdots+a_{n}$ give at least $\lfloor\sqrt{n}\rfloor+1$ distinct remainders modulo $n$.
( $\lfloor.\rfloor$ denotes the floor function.)
|
For $i=1, \cdots, n$, let $b_{i}=a_{1}+\cdots+a_{i}$. Proceed by contradiction and assume that the numbers $b_{1}, \cdots, b_{n}$ give at most $\sqrt{n}$ distinct remainders modulo $n$.
Note that, for $i=1, \cdots, n-1$, we have $a_{i+1}=b_{i+1}-b_{i}$, and only the $a_{i}$ that equals $n$ can lead to $b_{i+1}-b_{i} \equiv 0(\bmod n)$. The numbers $b_{i+1}-b_{i}$ can therefore take, modulo $n$, at most $\sqrt{n}(\sqrt{n}-1)$ distinct non-zero values. Taking into account the $a_{i}$ that is equal to $n$ and $a_{n}$ (which is not of the form $b_{i+1}-b_{i}$), and since $n \geqslant 5$, the $a_{i}$ can therefore take at most
$$
n-\sqrt{n}+2 \leqslant n-\sqrt{5}+2<n
$$
distinct values modulo $n$. However, the $a_{i}$ form a permutation of $\{1, \cdots, n\}$, so they represent all the remainders modulo $n$: this is a contradiction.
The numbers $b_{1}, \cdots, b_{n}$ therefore give at least $\lfloor\sqrt{n}\rfloor+1$ distinct remainders modulo $n$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $n \geqslant 5$ un entier, et $\left\{a_{1}, a_{2}, \cdots, a_{n}\right\}=\{1,2, \cdots, n\}$. Prouver que les nombres $a_{1}, a_{1}+$ $a_{2}, a_{1}+a_{2}+a_{3}, \cdots, a_{1}+a_{2}+\cdots+a_{n}$ donnent au moins $\lfloor\sqrt{n}\rfloor+1$ restes distincts modulo $n$.
( $\lfloor.$.$\rfloor désigne la partie entière.)$
|
Pour $i=1, \cdots, n$, on pose $b_{i}=a_{1}+\cdots+a_{i}$. Procédons par l'absurde et supposons que les nombres $b_{1}, \cdots, b_{n}$ ne donnent qu'au plus $\sqrt{n}$ restes distincts modulo $n$.
Notons que, pour $i=1, \cdots, n-1$, on a $a_{i+1}=b_{i+1}-b_{i}$, et seul celui des $a_{i}$ qui vaut $n$ peut donc conduire à $b_{i+1}-b_{i} \equiv 0(\bmod n)$. Les nombres $b_{i+1}-b_{i}$ ne peuvent donc prendre, modulo $n$, qu'au plus $\sqrt{n}(\sqrt{n}-1)$ valeurs non nulles distinctes. En tenant compte du $a_{i}$ qui est égal à $n$ et de $a_{n}$ (qui n'est pas de la forme $b_{i+1}-b_{i}$ ), et puisque $n \geqslant 5$, les $a_{i}$ prennent donc au plus
$$
\mathrm{n}-\sqrt{\mathrm{n}}+2 \leqslant \mathrm{n}-\sqrt{5}+2<\mathrm{n}
$$
valeurs distinctes modulo $n$. Or, les $a_{i}$ forment une permutation de $\{1, \cdots, n\}$ donc ils représentent tous les restes modulo n : il y a là une contradiction.
Les nombres $b_{1}, \cdots, b_{n}$ donnent donc au moins $\lfloor\sqrt{n}\rfloor+1$ restes distincts modulo $n$.
|
{
"exam": "French_envois",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-5-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T2",
"year": "2016"
}
|
Let $H$ be the foot of the altitude from $A$ in the acute triangle $ABC$, and $H'$ be the symmetric point of $H$ with respect to the midpoint of $[BC]$. The tangents to the circumcircle of $ABC$ at $B$ and $C$ meet at $X$. The perpendicular to $(XH')$ at $H'$ intersects the line $(AB)$ at $Y$, and the line $(AC)$ at $Z$.
Prove that $\widehat{YXB} = \widehat{ZXC}$.
|
Let $P, Q$ and $M$ be the orthogonal projections of $X$ onto $(AB), (AC)$, and $(BC)$, respectively. Clearly, $M$ is the midpoint of $[BC]$. The points $X, H', Y, P$ lie on the circle with diameter $[XY]$, and the points $X, H', Z, Q$ lie on the circle with diameter $[XZ]$, hence
$$
\widehat{H'XY} = \widehat{YPH'} = \widehat{APH'} \text{ and } \widehat{H'XZ} = \widehat{ZQH'} = \widehat{AQH'},
$$
which shows that $\widehat{ZXY} = \widehat{ZXH'} + \widehat{H'XY} = \widehat{AQH'} + \widehat{APH'} = \widehat{PH'Q} - \widehat{ABC}$.
Since $\widehat{BXC} = 180^\circ - 2 \widehat{BAC}$, to conclude, it suffices to prove that $\widehat{PH'Q} = 180^\circ - \widehat{BAC}$. The points $B, P, X, M$ lie on the circle with diameter $[BX]$, so
$$
\widehat{APM} = \widehat{BPM} = \widehat{BXM} = 90^\circ - \widehat{BAC},
$$
which shows that $(PM) \perp (AQ)$.
Similarly, $(QM)$ is perpendicular to $(AP)$, and $M$ is therefore the orthocenter of triangle $APQ$. This ensures that $(AM) \perp (PQ)$ and that $AM = 2r \cos (\widehat{PAQ})$, where $r$ is the radius of the circumcircle of $APQ$.
Let $R$ be the orthogonal projection of $A$ onto $(XM)$. Then $ARHM$ is a parallelogram, so $ARH'M$ is also a parallelogram. The lines $(RH')$ and $(AM)$ are then parallel, and thus $(RH')$ and $(PQ)$ are perpendicular. On the other hand, since $A, R, Q, X$, and $P$ are all on the circle with diameter $[AX]$, we have $\widehat{PRQ} = \widehat{PAQ} = \widehat{BAC}$. Therefore, $RH' = AM = 2r \cos (\widehat{PAQ}) = 2r \cos (\widehat{PRQ})$, which proves that $H'$ is in fact the orthocenter of $PRQ$.
In particular, we have $\widehat{PH'Q} = 180^\circ - \widehat{PRQ} = 180^\circ - \widehat{BAC}$, which completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit H le pied de la hauteur issue de $A$ dans le triangle acutangle $A B C$, et $\mathrm{H}^{\prime}$ le symétrique de $H$ par rapport au milieu de $[B C]$. Les tangentes au cercle circonscrit à $A B C$ en $B$ et en $C$ se rencontrent en $X$. La perpendiculaire à $\left(\mathrm{XH}^{\prime}\right)$ en $\mathrm{H}^{\prime}$ rencontre la droite $(A B)$ en $Y$, et la droite $(A C)$ en $Z$.
Prouver que $\widehat{\mathrm{YXB}}=\widehat{\mathrm{ZXC}}$.
|
Soit $P, Q$ et $M$ les projetés orthogonaux respectifs de $X \operatorname{sur}(A B),(A C)$ et (BC). Clairement $M$ est le milieu de $[B C]$. Les points $X, H^{\prime}, Y, P$ sont sur le cercle de diamètre $[X Y]$, et les points $\mathrm{X}, \mathrm{H}^{\prime}, \mathrm{Z}, \mathrm{Q}$ sont sur le cercle de diamètre $[\mathrm{XZ}]$ donc
$$
\widehat{\mathrm{H}^{\prime} \mathrm{XY}}=\widehat{\mathrm{YPH}^{\prime}}=\widehat{\mathrm{APH}^{\prime}} \text { et } \widehat{\mathrm{H}^{\prime} \mathrm{XZ}}=\widehat{\mathrm{ZQH}^{\prime}}=\widehat{\mathrm{AQH}^{\prime}} \text {, }
$$
ce qui montre que $\widehat{Z X Y}=\widehat{\mathrm{ZXH}^{\prime}}+\widehat{\mathrm{H}^{\prime} X Y}=\widehat{\mathrm{AQH}^{\prime}}+\widehat{\mathrm{APH}^{\prime}}=\widehat{\mathrm{PH}^{\prime} \mathrm{Q}}-\widehat{\mathrm{ABC}}$.
Puisque $\widehat{\mathrm{BXC}}=180^{\circ}-2 \widehat{\mathrm{BAC}}$, pour conclure il suffit donc de prouver que $\widehat{\mathrm{PH}^{\prime} \mathrm{Q}}=180^{\circ}-\widehat{\mathrm{BAC}}$. Or, les points $B, P, X, M$ sont sur le cercle de diamètre $[B X]$, donc
$$
\widehat{A P M}=\widehat{B P M}=\widehat{B X M}=90^{\circ}-\widehat{B A C},
$$
ce qui montre que $(P M) \perp(A Q)$.
De même, $(Q M)$ est perpendiculaire à ( $A P)$, et $M$ est donc l'orthocentre du triangle $A P Q$. Cela assure que $(A M) \perp(P Q)$ et que $A M=2 r \cos (\widehat{P A Q})$, où $r$ est le rayon du cercle circonscrit à $A P Q$.
Soit $R$ le projeté orthogonal de $A$ sur ( $X M$ ). Alors $A R M H$ est un parallélogramme, donc $A R H^{\prime} M$ est aussi un parallélogramme. Les droites $\left(\mathrm{RH}^{\prime}\right)$ et $(A M)$ sont alors parallèles, et ainsi $\left(\mathrm{RH}^{\prime}\right)$ et $(P Q)$ sont perpendiculaires. D'autre part, puisque $A, R, Q, X$ et $P$ sont tous sur le cercle de diamètre $[A X]$, on a $\widehat{\mathrm{PRQ}}=\widehat{\mathrm{PAQ}}=\widehat{\mathrm{BAC}}$. Par suite $\mathrm{RH}^{\prime}=\mathrm{AM}=2 \mathrm{r} \cos (\widehat{\mathrm{PAQ}})=2 \mathrm{r} \cos (\widehat{\mathrm{PRQ}})$, ce qui prouve que $\mathrm{H}^{\prime}$ est en fait l'orthocentre de PRQ.
En particulier, on a $\widehat{\mathrm{PH}^{\prime} \mathrm{Q}}=180^{\circ}-\widehat{\mathrm{PRQ}}=180^{\circ}-\widehat{\mathrm{BAC}}$, ce qui achève la démonstration.

|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-5-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T2",
"year": "2016"
}
|
Let $a_{1}, a_{2}, a_{3}$ be strictly positive integers. For any integer $n \geqslant 3$, we set
$$
a_{n+1}=\operatorname{lcm}\left(a_{n}, a_{n-1}\right)-\operatorname{lcm}\left(a_{n-1}, a_{n-2}\right)
$$
where it is understood that $\operatorname{lcm}(0, x)=0$ for any integer $x$.
Prove that there exists a natural number $k$ such that $k \leqslant a_{3}+4$ and $a_{k} \leqslant 0$.
|
If $x$ and $y$ are integers, we denote $x \vee y=\operatorname{ppcm}(x, y)$ and $x \wedge y=\operatorname{pgcd}(x, y)$, with $\operatorname{pgcd}(0, x)=x$ for all $x$. We recall that then $x y=(x \vee y)(x \wedge y)$.
For any integer $n \geqslant 3, a_{n-1}$ divides $a_{n} \vee a_{n-1}$ and $a_{n-1} \vee a_{n-2}$, and therefore $a_{n-1}$ also divides $a_{n+1}$. But then, for any $n \geqslant 4$, the number $a_{n-2}$ divides $a_{n}$, and thus divides $a_{n} \vee a_{n-1}$ and $a_{n-1} \vee a_{n-2}$, and finally divides $a_{n+1}$. The number $a_{n+1}$ is therefore divisible by $a_{n-1} \vee a_{n-2}$. We now set $c_{4}=\frac{a_{5}}{a_{2} \vee a_{3}}$. Let's show the equality ( $E_{n}$ ) for any integer $n \geqslant 4$ such that $a_{4}, \ldots, a_{n}>0$:
$$
\left(a_{n-1} \vee a_{n-2}\right)\left(4+c_{4}-n\right)=a_{n+1}
$$
First, by construction, the equality ( $E_{4}$ ) is true. Suppose now that the equality ( $E_{n-1}$ ) is true, and deduce that, if $a_{4}, \ldots, a_{n}>0$, then ( $E_{n}$ ) is also true. Since $a_{n-3}$ divides $a_{n-1}$, we observe that
$$
\begin{aligned}
\left(a_{n-1} \wedge a_{n}\right)\left(a_{n-1} \vee a_{n-2}\right) & =\left(a_{n-1} \wedge\left(a_{n-1} \vee a_{n-2}-a_{n-2} \vee a_{n-3}\right)\right) \cdot\left(a_{n-1} \vee a_{n-2} \vee a_{n-3}\right) \\
& =\left(a_{n-1} \wedge\left(a_{n-2} \vee a_{n-3}\right)\right) \cdot\left(a_{n-1} \vee\left(a_{n-2} \vee a_{n-3}\right)\right) \\
& =a_{n-1}\left(a_{n-2} \vee a_{n-3}\right) .
\end{aligned}
$$
Since
$$
\begin{aligned}
\left(E_{n}\right) & \Leftrightarrow \frac{a_{n+1}}{a_{n-1} \vee a_{n-2}}=4+c_{4}-n=\frac{a_{n}}{a_{n-2} \vee a_{n-3}}-1 \\
& \Leftrightarrow \frac{a_{n} \vee a_{n-1}}{a_{n-1} \vee a_{n-2}}=\frac{a_{n}}{a_{n-1} \vee a_{n-2}}+1=\frac{a_{n}}{a_{n-2} \vee a_{n-3}} \\
& \Leftrightarrow\left(a_{n-1} \vee a_{n-2}\right) a_{n}=\left(a_{n-2} \vee a_{n-3}\right)\left(a_{n} \vee a_{n-1}\right) \\
& \Leftrightarrow\left(a_{n-1} \vee a_{n-2}\right) a_{n}\left(a_{n} \wedge a_{n-1}\right)=\left(a_{n-2} \vee a_{n-3}\right) a_{n} a_{n-1},
\end{aligned}
$$
we deduce that ( $E_{n}$ ) is indeed true.
It follows that there exists a natural number $k$, minimal, such that $k \leqslant c_{4}+5$ and $a_{k} \leqslant 0$. If $k \leqslant 5$, then we have $k \leqslant a_{3}+4$. Otherwise, then $0<a_{5}<a_{3} \vee a_{4}$ and $0<a_{4}<a_{2} \vee a_{3}$, so
$$
c_{4}=\frac{a_{5}}{a_{2} \vee a_{3}}<\frac{a_{3} \vee a_{4}}{a_{2} \vee a_{3}} \leqslant \frac{a_{3} a_{4}}{a_{2} \vee a_{3}}<a_{3},
$$
thus $k \leqslant c_{4}+5 \leqslant a_{3}+4$, which concludes.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $a_{1}, a_{2} a_{3}$ des entiers strictement positifs. Pour tout entier $n \geqslant 3$, on pose
$$
a_{n+1}=\operatorname{ppcm}\left(a_{n}, a_{n-1}\right)-\operatorname{ppcm}\left(a_{n-1}, a_{n-2}\right)
$$
étant entendu que l'on a $\operatorname{ppcm}(0, x)=0$ pour tout entier $x$.
Prouver qu'il existe un entier naturel $k$ tel que $k \leqslant a_{3}+4$ et $a_{k} \leqslant 0$.
|
Si $x$ et $y$ sont des entiers, on note $x \vee y=\operatorname{ppcm}(x, y)$ et $x \wedge y=\operatorname{pgcd}(x, y)$, avec $\operatorname{pgcd}(0, x)=x$ pour tout $x$. On rappelle qu'alors $x y=(x \vee y)(x \wedge y)$.
Pour tout entier $n \geqslant 3, a_{n-1}$ divise $a_{n} \vee a_{n-1}$ et $a_{n-1} \vee a_{n-2}$, donc que $a_{n-1}$ divise $a_{n+1}$ également. Mais alors, pour tout $n \geqslant 4$, le nombre $a_{n-2}$ divise $a_{n}$, donc divise $a_{n} \vee a_{n-1}$ et $a_{n-1} \vee a_{n-2}$, et enfin divise $a_{n+1}$. Le nombre $a_{n+1}$ est donc divisible par $a_{n-1} \vee a_{n-2}$. On pose maintenant $c_{4}=\frac{a_{5}}{a_{2} \vee a_{3}}$. Montrons alors l'égalité ( $E_{n}$ ) suivante pour tout entier $n \geqslant 4$ tel que $a_{4}, \ldots, a_{n}>0$ :
$$
\left(a_{n-1} \vee a_{n-2}\right)\left(4+c_{4}-n\right)=a_{n+1}
$$
Tout d'abord, par construction, l'égalité ( $E_{4}$ ) est vraie. Supposons maintenant que l'égalités ( $E_{n-1}$ ) est vraie, et déduisons-en que, si $a_{4}, \ldots, a_{n}>0$, alors ( $E_{n}$ ) est vraie aussi. Puisque $a_{n-3}$ divise $a_{n-1}$, on observe que
$$
\begin{aligned}
\left(a_{n-1} \wedge a_{n}\right)\left(a_{n-1} \vee a_{n-2}\right) & =\left(a_{n-1} \wedge\left(a_{n-1} \vee a_{n-2}-a_{n-2} \vee a_{n-3}\right)\right) \cdot\left(a_{n-1} \vee a_{n-2} \vee a_{n-3}\right) \\
& =\left(a_{n-1} \wedge\left(a_{n-2} \vee a_{n-3}\right)\right) \cdot\left(a_{n-1} \vee\left(a_{n-2} \vee a_{n-3}\right)\right) \\
& =a_{n-1}\left(a_{n-2} \vee a_{n-3}\right) .
\end{aligned}
$$
Or, puisque
$$
\begin{aligned}
\left(E_{n}\right) & \Leftrightarrow \frac{a_{n+1}}{a_{n-1} \vee a_{n-2}}=4+c_{4}-n=\frac{a_{n}}{a_{n-2} \vee a_{n-3}}-1 \\
& \Leftrightarrow \frac{a_{n} \vee a_{n-1}}{a_{n-1} \vee a_{n-2}}=\frac{a_{n}}{a_{n-1} \vee a_{n-2}}+1=\frac{a_{n}}{a_{n-2} \vee a_{n-3}} \\
& \Leftrightarrow\left(a_{n-1} \vee a_{n-2}\right) a_{n}=\left(a_{n-2} \vee a_{n-3}\right)\left(a_{n} \vee a_{n-1}\right) \\
& \Leftrightarrow\left(a_{n-1} \vee a_{n-2}\right) a_{n}\left(a_{n} \wedge a_{n-1}\right)=\left(a_{n-2} \vee a_{n-3}\right) a_{n} a_{n-1},
\end{aligned}
$$
on en déduit que ( $E_{n}$ ) est bien vraie.
Il s'ensuit qu'il existe un entier naturel $k$, minimal, tel que $k \leqslant c_{4}+5$ et $a_{k} \leqslant 0$. Si $k \leqslant 5$, alors on a bien $k \leqslant a_{3}+4$. Sinon, alors $0<a_{5}<a_{3} \vee a_{4}$ et $0<a_{4}<a_{2} \vee a_{3}$, donc
$$
c_{4}=\frac{a_{5}}{a_{2} \vee a_{3}}<\frac{a_{3} \vee a_{4}}{a_{2} \vee a_{3}} \leqslant \frac{a_{3} a_{4}}{a_{2} \vee a_{3}}<a_{3},
$$
donc $k \leqslant \mathrm{c}_{4}+5 \leqslant \mathrm{a}_{3}+4$, ce qui conclut.
|
{
"exam": "French_envois",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-5-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 7",
"tier": "T2",
"year": "2016"
}
|
A finite and non-empty set E of strictly positive real numbers is said to be powerful when, for all $a, b \in E$ distinct, at least one of the numbers $a^{b}$ and $b^{a}$ also belongs to E. Determine the maximum number of elements that a powerful set can contain.
|
First, the set
$$
\left\{1, \frac{1}{2}, \frac{1}{4}, \frac{1}{16}\right\}
$$
is a powerful set containing four elements. Let $S$ be a powerful set, and $n$ its cardinality: we will show that $\mathrm{n} \leqslant 4$.
First, let's prove the following lemma: there do not exist elements $a$ and $b$ in $S$ such that $\mathrm{a}<1<\mathrm{b}$. Indeed, if we had $a<1<b$, then $a^{b}<a<1<b^{a}<b$; by taking $a=\min S$ and $b=\min \{s \in S: 1<s\}$, we would ensure that neither $a^{b}$ nor $b^{a}$ belongs to $S$, contradicting the fact that $S$ is powerful.
On the other hand, if $S$ is a powerful set, then $S \cup\{1\}$ is also powerful. Our search for a powerful set of maximum cardinality leads us to consider two cases.
1. If $S=\left\{a_{1}, a_{2}, \cdots, a_{n}\right\}$, with $n \geqslant 5$ and $1=a_{1}<a_{2}<\cdots<a_{n}$, then we observe that
$$
a_{n}<a_{n}^{a_{2}}<a_{n}^{a_{3}}<\ldots<a_{n}^{a_{n-1}}
$$
thus, $S$ contains the elements
$$
a_{2}<a_{2}^{a_{n}}<a_{3}^{a_{n}}<\ldots<a_{n-1}^{a_{n}} .
$$
This shows that $a_{i+1}=a_{i}^{a_{n}}$ for all $i \in\{2, \ldots, \mathfrak{n}-1\}$. However, we note that
$$
\mathrm{a}_{2}<\mathrm{a}_{2}^{\mathrm{a}_{3}}<\mathrm{a}_{2}^{\mathrm{a}_{\mathrm{n}}}=\mathrm{a}_{3}<\mathrm{a}_{3}^{\mathrm{a}_{2}}<\mathrm{a}_{3}^{\mathrm{a}_{\mathrm{n}}}=\mathrm{a}_{4}
$$
which shows that neither $a_{2}^{a_{3}}$ nor $a_{3}^{a_{2}}$ belongs to $S$, which therefore cannot be powerful.
2. If $S=\left\{a_{1}, a_{2}, \cdots, a_{n}\right\}$, with $n \geqslant 5$ and $a_{1}<a_{2}<\cdots<a_{n}=1$, then we observe that
$$
a_{n-1}<a_{n-1}^{a_{n-2}}<a_{n-1}^{a_{n-3}}<\ldots<a_{n-1}^{a_{1}}<a_{n}
$$
thus, $S$ contains the elements
$$
a_{1}<a_{1}^{a_{n-1}}<a_{2}^{a_{n-1}}<\ldots<a_{n-2}^{a_{n-1}}<a_{n}=1
$$
This shows that $a_{i+1}=a_{i}^{a_{n-1}}$ for all $i \in\{1, \ldots, n-2\}$. Similarly, we observe that
$$
a_{n-1}=a_{n-2}^{a_{n-1}}<a_{n-2}^{a_{n-3}}<\ldots<a_{n-2}^{a_{1}}<a_{n}=1
$$
thus, $S$ contains the elements
$$
a_{2}=a_{1}^{a_{n-1}}<a_{1}^{a_{n-2}}<a_{2}^{a_{n-2}}<\ldots<a_{n-3}^{a_{n-2}}<a_{n}=1 .
$$
This also shows that $a_{i+2}=a_{i}^{a_{n-2}}=a_{i}^{a_{n-1}^{2}}$ for all $i \in\{1, \ldots, n-3\}$.
We deduce that $a_{n-1}=a_{n-2}^{a_{n-1}}=a_{n-1}^{2 a_{n-1}}$ and then that $1=2 a_{n-1}$, so $a_{n-i}=2^{-2^{i}}$ for $i \in\{1, \ldots, n-1\}$. However, since $n \geqslant 5$, then $a_{n-4}^{a_{n-3}}=2^{-2^{-4}}$ and $a_{n-3}^{a_{n-4}}=2^{-2^{-13}}$, so $S$ does not contain either $a_{n-4}^{a_{n-3}}$ or $a_{n-3}^{a_{n-4}}$ and cannot be powerful.
|
4
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Un ensemble E fini et non vide de réels strictement positifs est dit puissant lorsque, pour tous $a, b \in E$ distincts, l'un au moins des nombres $a^{b}$ et $b^{a}$ appartient aussi à $E$. Déterminer le nombre maximal d'éléments que peut contenir un ensemble puissant.
|
Tout d'abord, l'ensemble
$$
\left\{1, \frac{1}{2}, \frac{1}{4}, \frac{1}{16}\right\}
$$
est un ensemble puissant qui contient quatre éléments. Soit S un ensemble puissant, et n son cardinal : nous allons montrer que $\mathrm{n} \leqslant 4$.
Démontrons d'abord le lemme suivant : il n'existe pas d'éléments a et b de $S$ tels que $\mathrm{a}<1<\mathrm{b}$. En effet, si l'on avait $a<1<b$, alors $a^{b}<a<1<b^{a}<b$; en prenant $a=\min S$ et $b=\min \{s \in S: 1<s\}$, on s'assurerait donc que ni $a^{b}$ ni $b^{a}$ n'appartient à $S$, contredisant le fait que $S$ est puissant.
D'autre part, si $S$ est un ensemble puissant, alors $S \cup\{1\}$ l'est aussi. Notre recherche d'un ensemble puissant de cardinal maximal nous amène donc à considérer deux cas.
1. Si $S=\left\{a_{1}, a_{2}, \cdots, a_{n}\right\}$, avec $n \geqslant 5$ et $1=a_{1}<a_{2}<\cdots<a_{n}$, alors on observe que
$$
a_{n}<a_{n}^{a_{2}}<a_{n}^{a_{3}}<\ldots<a_{n}^{a_{n-1}}
$$
donc que $S$ contient les éléments
$$
a_{2}<a_{2}^{a_{n}}<a_{3}^{a_{n}}<\ldots<a_{n-1}^{a_{n}} .
$$
Cela montre que $a_{i+1}=a_{i}^{a_{n}}$ pour tout $i \in\{2, \ldots, \mathfrak{n}-1\}$. On remarque cependant que
$$
\mathrm{a}_{2}<\mathrm{a}_{2}^{\mathrm{a}_{3}}<\mathrm{a}_{2}^{\mathrm{a}_{\mathrm{n}}}=\mathrm{a}_{3}<\mathrm{a}_{3}^{\mathrm{a}_{2}}<\mathrm{a}_{3}^{\mathrm{a}_{\mathrm{n}}}=\mathrm{a}_{4}
$$
ce qui montre que ni $a_{2}^{a_{3}} n i a_{3}^{a_{2}} n$ 'appartient à $S$, qui ne peut donc pas être puissant.
2. Si $S=\left\{a_{1}, a_{2}, \cdots, a_{n}\right\}$, avec $n \geqslant 5$ et $a_{1}<a_{2}<\cdots<a_{n}=1$, alors on observe que
$$
a_{n-1}<a_{n-1}^{a_{n-2}}<a_{n-1}^{a_{n-3}}<\ldots<a_{n-1}^{a_{1}}<a_{n}
$$
donc que $S$ contient les éléments
$$
a_{1}<a_{1}^{a_{n-1}}<a_{2}^{a_{n-1}}<\ldots<a_{n-2}^{a_{n-1}}<a_{n}=1
$$
Cela montre que $a_{i+1}=a_{i}^{a_{n-1}}$ pour tout $i \in\{1, \ldots, n-2\}$. De même, on observe que
$$
a_{n-1}=a_{n-2}^{a_{n-1}}<a_{n-2}^{a_{n-3}}<\ldots<a_{n-2}^{a_{1}}<a_{n}=1
$$
donc que $S$ contient les éléments
$$
a_{2}=a_{1}^{a_{n-1}}<a_{1}^{a_{n-2}}<a_{2}^{a_{n-2}}<\ldots<a_{n-3}^{a_{n-2}}<a_{n}=1 .
$$
Cela montre aussi que $a_{i+2}=a_{i}^{a_{n-2}}=a_{i}^{a_{n-1}^{2}}$ pour tout $i \in\{1, \ldots, n-3\}$.
On en déduit que $a_{n-1}=a_{n-2}^{a_{n-1}}=a_{n-1}^{2 a_{n-1}}$ puis que $1=2 a_{n-1}$, donc que $a_{n-i}=2^{-2^{i}}$ pour $i \in\{1, \ldots, n-1\}$. Cependant, puisque $n \geqslant 5$, alors $a_{n-4}^{a_{n-3}}=2^{-2^{-4}}$ et $a_{n-3}^{a_{n-4}}=2^{-2^{-13}}$, donc $S$ ne contient ni $a_{n-4}^{a_{n-3}}$ et $a_{n-3}^{a_{n-4}}$ et ne peut pas être puissant.
|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "\nExercice 8.",
"resource_path": "French/segmented/envois/fr-ofm-2015-2016-envoi-5-solutions.jsonl",
"solution_match": "## Solution de l'exercice 8",
"tier": "T2",
"year": "2016"
}
|
We define a sequence as follows:
$$
\left\{\begin{array}{l}
u_{0}=15, u_{1}=57 \\
u_{n}=u_{n-1}+u_{n-2} \text { for all } n \geq 2
\end{array}\right.
$$
Find the largest integer $k$ such that $3^{k} \mid u_{2017}$.
|
Let $k$ be the integer sought. The first terms of the sequence are 15, 57, 72, 129, 201, 330, 541,... apparently all divisible by 3. Indeed, $u_{0}$ and $u_{1}$ are multiples of 3, so $u_{2}=u_{0}+u_{1}$ is also. Similarly, $u_{3}$ is divisible by 3. More generally, if $u_{n-1}$ and $u_{n-2}$ are multiples of 3, then $u_{n}$ is as well. Thus, we prove step by step (by induction, in fact) that for all integers $n$, $u_{n}$ is divisible by 3, so $3 \mid u_{2017}$ and $k \geq 1$.
Now let's reason modulo 9 to see if $k \geq 2$. We find:
$u_{0} \equiv 6(\bmod 9)$
$u_{1} \equiv 3(\bmod 9)$
$u_{2} \equiv 0(\bmod 9)$
$u_{3} \equiv 3(\bmod 9)$
$u_{4} \equiv 3(\bmod 9)$
$u_{5} \equiv 6(\bmod 9)$
$u_{6} \equiv 0(\bmod 9)$
$u_{7} \equiv 6(\bmod 9)$
$u_{8} \equiv 6(\bmod 9)$
$u_{9} \equiv 3(\bmod 9)$
We observe that $u_{8} \equiv u_{0}(\bmod 9)$ and $u_{9} \equiv u_{1}(\bmod 9)$, so $u_{10} \equiv u_{2}(\bmod 9)$, since the modulos add up. More generally, we establish as before that $u_{n+8} \equiv u_{n}(\bmod 9)$ for all $n \in \mathbb{N}$. Thus, the sequence $\left(u_{n}(\bmod 9)\right)$ is periodic with period 8. Since $2017=252 \times 8+1$, we have $u_{2017} \equiv u_{1} \equiv 3(\bmod 9)$. Therefore, $k<2$. Conclusion: $k=1$.
Remark. If $l$ is any natural number, then the sequence $\left(v_{n}\right)$ defined by $v_{n}=u_{n}(\bmod l)$ is periodic from a certain rank. Indeed, there are $l \times l=l^{2}$ possibilities for the pair $\left(v_{n}, v_{n+1}\right)$. Therefore, if we look at $\left(v_{0}, v_{1}\right),\left(v_{1}, v_{2}\right), \cdots,\left(v_{l^{2}}, v_{l^{2}+1}\right)$, this makes $l^{2}+1$ pairs. According to the pigeonhole principle (i.e., if we put $c+1$ socks into $c$ drawers, one drawer will contain at least 2 socks), two pairs are equal, so there exist $0 \leqslant i<j \leqslant l^{2}$ such that $\left(v_{i}, v_{i+1}\right)=$ $\left(v_{j}, v_{j+1}\right)$. In other words, $u_{i} \equiv u_{j}(\bmod l)$ and $u_{i+1} \equiv u_{j+1}(\bmod l)$. Therefore, $u_{i+2} \equiv u_{j+2}(\bmod l)$, or $\left(v_{i+1}, v_{i+2}\right)=\left(v_{j+1}, v_{j+2}\right)$. We deduce similarly that $v_{i+3}=v_{j+3}, v_{i+4}=v_{j+4}$, etc. Thus, $\left(v_{n}\right)$ is periodic from rank $i$ (at the latest), with period $i-j$.
However, it may have a smaller period (exercise: show that the minimal period divides $i-j$).
|
1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
On définit une suite ainsi:
$$
\left\{\begin{array}{l}
u_{0}=15, u_{1}=57 \\
u_{n}=u_{n-1}+u_{n-2} \text { pour tout } n \geq 2
\end{array}\right.
$$
Trouver le plus grand entier $k$ tel que $3^{k} \mid u_{2017}$.
|
Soit $k$ l'entier cherché. Les premiers termes de la suite sont 15, 57, 72, 129, 201, 330, 541,... apparemment tous divisibles par 3 . En effet, $u_{0}$ et $u_{1}$ sont multiples de 3 , donc $u_{2}=u_{0}+u_{1}$ aussi. De même, $u_{3}$ est divisible par 3. Plus généralement, si $u_{n-1}$ et $u_{n-2}$ sont multiples de 3, alors $u_{n}$ aussi. On prouve ainsi de proche en proche (par récurrence, en fait) que pour tout entier $n$, $u_{n}$ est divisible par 3, donc $3 \mid u_{2017}$ et $k \geq 1$.
Raisonnons maintenant modulo 9 pour voir si $k \geq 2$. On trouve :
$u_{0} \equiv 6(\bmod 9)$
$u_{1} \equiv 3(\bmod 9)$
$u_{2} \equiv 0(\bmod 9)$
$u_{3} \equiv 3(\bmod 9)$
$u_{4} \equiv 3(\bmod 9)$
$u_{5} \equiv 6(\bmod 9)$
$u_{6} \equiv 0(\bmod 9)$
$u_{7} \equiv 6(\bmod 9)$
$u_{8} \equiv 6(\bmod 9)$
$u_{9} \equiv 3(\bmod 9)$
On constate que $u_{8} \equiv u_{0}(\bmod 9)$ et $u_{9} \equiv u_{1}(\bmod 9)$, donc $u_{10} \equiv u_{2}(\bmod 9)$, car les modulos s'additionnent. Plus généralement, on établit comme précédemment que $u_{n+8} \equiv u_{n}(\bmod 9)$ pour tout $n \in \mathbb{N}$. Ainsi, la suite $\left(u_{n}(\bmod 9)\right)$ est périodique de période 8 . Or $2017=252 \times 8+1$, donc $u_{2017} \equiv u_{1} \equiv 3(\bmod 9)$. Donc $k<2$. Conclusion : $k=1$.
Remarque. Si $l$ est un entier naturel quelconque, alors la suite $\left(v_{n}\right)$ définie par $v_{n}=u_{n}(\bmod l)$ est périodique artir d'un certain rang. En effet, il y a $l \times l=l^{2}$ possibilités pour le couple $\left(v_{n}, v_{n+1}\right)$. Donc, si on regarde $\left(v_{0}, v_{1}\right),\left(v_{1}, v_{2}\right), \cdots,\left(v_{l^{2}}, v_{l^{2}+1}\right)$, cela fait $l^{2}+1$ couples. D'après le principe des tiroirs (ie si on range $c+1$ chaussettes dans $c$ tiroirs, un tiroir contiendra au moins 2 chaussettes), deux couples sont égaux, il existe donc $0 \leqslant i<j \leqslant l^{2}$ tels que $\left(v_{i}, v_{i+1}\right)=$ $\left(v_{j}, v_{j+1}\right)$. Autrement dit, $u_{i} \equiv u_{j}(\bmod l)$ et $u_{i+1} \equiv u_{j+1}(\bmod l)$. Donc $u_{i+2} \equiv u_{j+2}(\bmod l)$, soit $\left(v_{i+1}, v_{i+2}\right)=\left(v_{j+1}, v_{j+2}\right)$. On en déduit de même que $v_{i+3}=v_{j+3}, v_{i+4}=v_{j+4}$, etc. Ainsi, $\left(v_{n}\right)$ est périodique artir du rang $i$ (au plus tard), de période $i-j$.
Elle peut toutefois avoir une période plus petite (exercice : montrer que la période minimale divise $i-j$ ).
|
{
"exam": "French_envois",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-1-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T2",
"year": "2017"
}
|
Find all natural numbers $n$ for which $2^{n}+12^{n}+2011^{n}$ is a perfect square.
|
Let $u_{n}=2^{n}+12^{n}+2011^{n}$. We look modulo 3: $2 \equiv-1(\bmod 3), 12 \equiv 0$ $(\bmod 3)$ and $2011 \equiv 1(\bmod 3)$, so
$$
u_{n} \equiv(-1)^{n}+0^{n}+1^{n} \equiv(-1)^{n}+1 \quad(\bmod 3)
$$
If $n$ is even, $u_{n} \equiv 2(\bmod 3)$. But no square can be congruent to 2 modulo 3: indeed, if $x \equiv 0$ $(\bmod 3), x^{2} \equiv 0(\bmod 3)$, if $x \equiv 1(\bmod 3), x^{2} \equiv 1(\bmod 3)$, and if $x \equiv 2(\bmod 3), x^{2} \equiv 1(\bmod 3)$. If $n$ is odd, we note that $u_{1}=2+12+2011=2025=45^{2}$, so $n=1$ works. If $n \geq 3$, $2^{n} \equiv 12^{n} \equiv 0(\bmod 4)$. And $2011 \equiv 3(\bmod 4)$. By writing $n=2 k+1, k \in \mathbb{N}$, we have
$$
u_{n} \equiv 3^{2 k+1} \equiv\left(3^{2}\right)^{k} \times 3 \equiv 9^{k} \times 3 \equiv 1^{k} \times 3 \equiv 3 \quad(\bmod 4) .
$$
But a square is never congruent to 3 modulo 4, indeed a table of congruences shows:
| $x(\bmod 4)$ | $x^{2}(\bmod 4)$ |
| :---: | :---: |
| 0 | 0 |
| 1 | 1 |
| 2 | 0 |
| 3 | 1 |
Therefore $u_{n}$ cannot be a square if $n \geq 3$ is odd. Conclusion: $n=1$ is the only solution.
|
n=1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Trouver tous les entiers naturels $n$ pour lesquels $2^{n}+12^{n}+2011^{n}$ est un carré parfait.
|
Posons $u_{n}=2^{n}+12^{n}+2011^{n}$. On regarde modulo 3: $2 \equiv-1(\bmod 3), 12 \equiv 0$ $(\bmod 3)$ et $2011 \equiv 1(\bmod 3)$, donc
$$
u_{n} \equiv(-1)^{n}+0^{n}+1^{n} \equiv(-1)^{n}+1 \quad(\bmod 3)
$$
Si $n$ est pair, $u_{n} \equiv 2(\bmod 3)$. Or aucun carré ne peut être congru 2modulo3: eneffet, six $\equiv 0$ $(\bmod 3), x^{2} \equiv 0(\bmod 3)$, si $x \equiv 1(\bmod 3), x^{2} \equiv 1(\bmod 3)$, et si $x \equiv 2(\bmod 3), x^{2} \equiv 1(\bmod 3)$. Si $n$ est impair, on remarque que $u_{1}=2+12+2011=2025=45^{2}$ donc $n=1$ convient. Si $n \geq 3$, $2^{n} \equiv 12^{n} \equiv 0(\bmod 4)$. Et $2011 \equiv 3(\bmod 4)$. En écrivant $n=2 k+1, k \in \mathbb{N}$, on a
$$
u_{n} \equiv 3^{2 k+1} \equiv\left(3^{2}\right)^{k} \times 3 \equiv 9^{k} \times 3 \equiv 1^{k} \times 3 \equiv 3 \quad(\bmod 4) .
$$
Or un carré n'est jamais congru 3 modulo 4 , sionfaituntableaudecongruence :
| $x(\bmod 4)$ | $x^{2}(\bmod 4)$ |
| :---: | :---: |
| 0 | 0 |
| 1 | 1 |
| 2 | 0 |
| 3 | 1 |
Doncu $_{n}$ ne peut pas être un carré si $n \geq 3$ est impair. Conclusion : $n=1$ est la seule solution.
|
{
"exam": "French_envois",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-1-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T2",
"year": "2017"
}
|
Show that for any integer $n \geq 1$, there exists $m$ a multiple of $n$ such that the sum of the digits of $m$ is $n$.
|
The sequence of powers of 10, i.e., $1, 10, 100, \cdots$, contains an infinite number of terms, which can take a finite number of residues modulo $n$. Therefore, there exists a residue $k$ such that an infinite number of powers of 10 are congruent to $k$ modulo $n$. Let $0 \leqslant a_{1}<a_{2}<a_{n}$ be integers such that
$$
10^{a_{i}} \equiv k \quad(\bmod n)
$$
for all $i \in\{1,2, \cdots, n\}$. We set $m=10^{a_{n}}+10^{a_{n-1}}+\cdots+10^{a_{2}}+10^{a_{1}}$. $m$ is written with $n$ digits "1" and a certain number of zeros, so the sum of its digits is $n$.
And $m \equiv k+\cdots+k \equiv k n \equiv 0(\bmod n)$, so $m$ is divisible by $n$, hence this integer satisfies the conditions of the statement.
## Common Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Montrer que pour tout entier $n \geq 1$, il existe $m$ un multiple de $n$ tel que la somme des chiffres de $m$ fasse $n$.
|
La suite des puissances de 10, donc $1,10,100, \cdots$ contient une infinité de termes, qui peuvent prendre un nombre fini de résidus modulo $n$. Il existe donc un résidu $k$ tel qu'une infinité de puissances de 10 soient congrues kmodulon.Soientdonc $0 \leqslant a_{1}<a_{2}<a_{n}$ des entiers tels que
$$
10^{a_{i}} \equiv k \quad(\bmod n)
$$
pour tout $i \in\{1,2, \cdots, n\}$. On pose $m=10^{a_{n}}+10^{a_{n-1}}+\cdots+10^{a_{2}}+10^{a_{1}}$. $m$ s'écrit avec $n$ chiffres "1" et un certain nombre de zéros, donc sa somme des chiffres vaut $n$.
Et $m \equiv k+\cdots+k \equiv k n \equiv 0(\bmod n)$, donc $m$ est divisible par $n$, donc cet entier satisfait aux conditions de l'énoncé.
## Exercices Communs
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-1-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T2",
"year": "2017"
}
|
Let $m, n$ be positive integers such that $\operatorname{gcd}(m, n)=1$, where $a \wedge b$ denotes the greatest common divisor of $a$ and $b$. What value(s) can
$$
\left(2^{m}-2^{n} \wedge 2^{m^{2}+m n+n^{2}}-1\right)
$$
take?
|
We use the following property: if $m \geq 1$ and $a, b \in \mathbb{N}$, then $\left(m^{a}-1\right) \wedge\left(m^{b}-1\right)=$ $m^{a \wedge b}-1$. We thus reduce the problem to studying $\left(m^{2}+m n+n^{2}\right) \wedge(m-n)$. If $d \mid m^{2}+m n+n^{2}$ and $d \mid m-n$, then $d \mid m^{2}+m n+n^{2}-(m-n)^{2}=3 m n$. Therefore, $d \mid 3 m n-3 n(m-n)=3 n^{2}$ and $d \mid 3 m n+3 m(m-n)=3 m^{2}$, so $d \mid\left(3 m^{2}, 3 n^{2}\right)$, hence $d \mid 3$. Thus, $\left(m^{2}+m n+n^{2}\right) \wedge(m-n) \mid 3$, and can take at most two values, 1 and 3. Let's verify that these values are realized.
If $m=2$ and $n=1,\left(m^{2}+m n+n^{2}\right) \wedge(m-n)=1$ and
$$
\left(2^{m}-2^{n}\right) \wedge\left(2^{m^{2}+m n+n^{2}}-1\right)=2^{\left(m^{2}+m n+n^{2}\right) \wedge(m-n)}-1=1
$$
If $m=n=1,\left(m^{2}+m n+n^{2}\right) \wedge(m-n)=3$ and
$$
\left(2^{m}-2^{n}\right) \wedge\left(2^{m^{2}+m n+n^{2}}-1\right)=2^{\left(m^{2}+m n+n^{2}\right) \wedge(m-n)}-1=7 .
$$
Thus, the possible values are 1 and 7.
Proof of the property: we can assume $a \geq b$. We write $a=b q+r$ for the Euclidean division of $a$ by $b$. Let $d:=\left(m^{a}-1\right) \wedge\left(m^{b}-1\right)$. Then $d \mid\left(m^{b}-1\right)+\left(m^{2 b}-m^{b}\right)+\left(m^{3 b}-m^{2 b}\right)+\cdots+\left(m^{q b}-m^{(q-1) b}\right)$, which is $d \mid m^{q b}-1$. Therefore, $d \mid m^{a}-m^{q b}$. But $m^{a}-m^{q b}=m^{q b}\left(m^{r}-1\right)$. Since $d$ is a divisor of $m^{b}-1$ which is coprime with $m$, then $d$ is coprime with $m^{q b}$. By Gauss's lemma, $d \mid m^{r}-1$. Thus, $d \mid\left(m^{b}-1\right) \wedge\left(m^{r}-1\right)$. We proceed similarly by performing the Euclidean division of $b$ by $r$ and so on. We thus reproduce the Euclidean algorithm. The latter terminates on $a \wedge b$, so we eventually get that $d$ divides $m^{a \wedge b}-1$. To conclude, it remains to show that $m^{a \wedge b}-1$ is a divisor of $m^{b}-1$ and $m^{a}-1$. If $i=k j$ for integers $i, j, k, m^{j}-1$ divides $m^{i}-1$, because:
$$
m^{i}-1=\left(m^{j}\right)^{k}-1=\left(m^{j}-1\right)\left(\left(m^{j}\right)^{k-1}+\left(m^{j}\right)^{k-2}+\cdots+m^{j}+1\right)
$$
This allows us to conclude.
|
1 \text{ and } 7
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Soit $m, n$ des entiers positifs tels que $\operatorname{pgcd}(m, n)=1$, où $a \wedge b$ désigne le plus grand diviseur commun de $a$ et $b$. Quelle(s) valeur(s) peut prendre
$$
\left(2^{m}-2^{n} \wedge 2^{m^{2}+m n+n^{2}}-1\right) ?
$$
|
On utilise la propriété suivante : si $m \geq 1$ et $a, b \in \mathbb{N}$, alors $\left(m^{a}-1\right) \wedge\left(m^{b}-1\right)=$ $m^{a \wedge b}-1$. On se ramène ainsi tudier $\left(m^{2}+m n+n^{2}\right) \wedge(m-n)$. Si $d \mid m^{2}+m n+n^{2}$ et $d \mid m-n$, alors $d \mid m^{2}+m n+n^{2}-(m-n)^{2}=3 m n$. Donc $d \mid 3 m n-3 n(m-n)=3 n^{2}$ et $d \mid 3 m n+3 m(m-n)=3 m^{2}$, donc $d \mid\left(3 m^{2}, 3 n^{2}\right)$, donc $d \mid 3$. Ainsi, $\left(m^{2}+m n+n^{2}\right) \wedge(m-n) \mid 3$, et ne peut prendre qu'au plus deux valeurs, 1 et 3 . Vérifions qu'elles sont réalisées.
Si $m=2$ et $n=1,\left(m^{2}+m n+n^{2}\right) \wedge(m-n)=1$ et
$$
\left(2^{m}-2^{n}\right) \wedge\left(2^{m^{2}+m n+n^{2}}-1\right)=2^{\left(m^{2}+m n+n^{2}\right) \wedge(m-n)}-1=1
$$
Si $m=n=1,\left(m^{2}+m n+n^{2}\right) \wedge(m-n)=3$ et
$$
\left(2^{m}-2^{n}\right) \wedge\left(2^{m^{2}+m n+n^{2}}-1\right)=2^{\left(m^{2}+m n+n^{2}\right) \wedge(m-n)}-1=7 .
$$
Donc les valeurs possibles sont 1 et 7 .
Preuve de la propriété : on peut supposer $a \geq b$. On écrit $a=b q+r$ la division euclidienne de $a$ par b. Soit $d:=\left(m^{a}-1\right) \wedge\left(m^{b}-1\right) . d \mid\left(m^{b}-1\right)+\left(m^{2 b}-m^{b}\right)+\left(m^{3 b}-m^{2 b}\right)+\cdots+\left(m^{q b}-m^{(q-1) b}\right)$, soit $d \mid m^{q b}-1$. Donc $d \mid m^{a}-m^{q b}$. Or $m^{a}-m^{q b}=m^{q b}\left(m^{r}-1\right)$. Comme $d$ est un diviseur de $m^{b}-1$ qui est premier avec $m$, alors $d$ est premier avec $m^{q b}$. D'après le lemme de Gauss, $d \mid m^{r}-1$. Ainsi, $d \mid\left(m^{b}-1\right) \wedge\left(m^{r}-1\right)$. On procède de même en faisant la division euclidienne de $b$ par $r$ et ainsi de
suite. On reproduit ainsi l'algorithme d'Euclide. Ce dernier termine sur $a \wedge b$, donc on obtient a fin que $d$ divise $m^{a \wedge b}-1$. Pour conclure, il reste rouver que $m^{a \wedge b}-1$ est un diviseur de $m^{b}-1$ et de $m^{a}-1$. Or, si $i=k j$ pour des entiers $i, j, k, m^{j}-1$ divise $m^{i}-1$, car :
$$
m^{i}-1=\left(m^{j}\right)^{k}-1=\left(m^{j}-1\right)\left(\left(m^{j}\right)^{k-1}+\left(m^{j}\right)^{k-2}+\cdots+m^{j}+1\right)
$$
Ceci permet de conclure.
|
{
"exam": "French_envois",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-1-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T2",
"year": "2017"
}
|
Find all triplets of natural numbers $(x, y, z)$ such that:
$$
x^{2}+y^{2}=3 \cdot 2016^{z}+77 \text{. }
$$
|
Let $(x, y, z)$ be a solution triplet. What can we necessarily say about it?
If $z=0$, we have $x^{2}+y^{2}=80$. We make a congruence table modulo 4: we show that if a sum of two squares is congruent modulo 4, then the two squares in question are both even. We can thus set $x=2 x_{0}, y=2 y_{0}$ with $x_{0}, y_{0}$ integers and $x_{0}^{2}+y_{0}^{2}=20$. By the same argument modulo 4, we arrive at $x=4 x_{1}, y=4 y_{1}$ with $x_{1}, y_{1}$ integers and $x_{1}^{2}+y_{1}^{2}=5$. The only pairs that satisfy this are $\left(x_{1}, y_{1}\right)=(1,2)$ or $(2,1)$.
If $z>0$, since $7 \mid 2016$, we have modulo $7 x^{2}+y^{2}=0$, which gives, by writing the table of squares modulo 7, $x$ and $y$ congruent modulo 7. We can thus set $x=7 x_{1}$ and $y=7 y_{1}$ with $x_{1}, y_{1}$ integers. Therefore, $49 \mid x^{2}+y^{2}$, that is, $49 \mid 3 \cdot 2016^{z}+77$ so $z=1$. It then follows that $x_{1}^{2}+y_{1}^{2}=125$. We test the remaining cases one by one to see which ones work by hand: $\left(x_{1}, y_{1}\right)=(5,10),(2,11),(10,5),(11,2)$. Thus, all solution triplets are in the set:
$$
\{(4,8,0),(8,4,0),(35,70,1),(70,35,1),(14,77,1),(77,14,1)\}
$$
and we verify that, conversely, all these triplets are indeed solutions.
## Exercises of Group A
|
(4,8,0),(8,4,0),(35,70,1),(70,35,1),(14,77,1),(77,14,1)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Trouver tous les triplets d'entiers naturels $(x, y, z)$ tels que :
$$
x^{2}+y^{2}=3 \cdot 2016^{z}+77 \text {. }
$$
|
Soit un triplet solution $(x, y, z)$. Que peut-on en dire de façon nécessaire ?
Si $z=0$, on a $x^{2}+y^{2}=80$. On fait une table de congruence modulo 4 : on montre ainsi que, si une somme de deux carrés est congrue modulo 4 , c'est que les deux carrés en question sot tous les deux pairs. On peut donc poser $x=2 x_{0}, y=2 y_{0}$ avec $x_{0}, y_{0}$ entiers et $x_{0}^{2}+y_{0}^{2}=20$. Par le même argument modulo 4 , on arrive $\mathrm{x}=4 \mathrm{x}_{1}, y=4 y_{1}$ avec $x_{1}, y_{1}$ entiers et $x_{1}^{2}+y_{1}^{2}=5$. Les seuls couples vérifiant cela sont $\left(x_{1}, y_{1}\right)=(1,2)$ ou $(2,1)$.
Si $z>0$, comme $7 \mid 2016$, on a modulo $7 x^{2}+y^{2}=0$, ce qui donne, en écrivant la table des carrés modulo 7, $x$ et $y$ congrus modulo 7. On peut donc poser $x=7 x_{1}$ et $y=7 y_{1}$ avec $x_{1}, y_{1}$ entiers. Donc $49 \mid x^{2}+y^{2}$, c'est-dire $49 \mid 3 \cdot 2016^{z}+77$ donc $z=1$. Il vient alors $x_{1}^{2}+y_{1}^{2}=125$. On teste les cas restants un par un pour voir ceux qui marchent a main : $\left(x_{1}, y_{1}\right)=(5,10),(2,11),(10,5),(11,2)$. Ainsi, tous les triplets solutions sont dans l'ensemble :
$$
\{(4,8,0),(8,4,0),(35,70,1),(70,35,1),(14,77,1),(77,14,1)\}
$$
et on vérifie que, réciproquement, tous ces triplets sont bien des solutions.
## Exercices du groupe A
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-1-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T2",
"year": "2017"
}
|
Let $p$ be a prime number, $m$ a natural integer. Find the smallest integer $d$ such that there exists a monic polynomial $Q$ of degree $d$ with integer coefficients such that, for all integers $n, p^{m} \mid Q(n)$.
|
Let's show that $d$ is the smallest integer such that $p^{m} \mid d$!. Let $k$ be the smallest integer such that $p^{m} \mid k$!.
First, let's show that $k \geq d$. Consider the polynomial $Q(x)=X(X+1) \cdots(X+k-1)$: it is monic, of degree $k$, with integer coefficients. Moreover, for all $n \in \mathbb{N}, Q(n)=k!\binom{n}{k}$ (this is a property of binomial coefficients), hence $p^{m}|k!| Q(n)$. Therefore, $k$ is an integer for which there exists a monic polynomial with integer coefficients of degree $k$ such that for all $n \in \mathbb{N}, p^{m} \mid Q(n)$. Therefore, $k \geq d$. It remains to show the reverse direction. In other words, let $Q$ be a monic polynomial with integer coefficients of degree $l$ such that for all integers $n, p^{m} \mid Q(n)$. Let's show that $k \leq l$. It suffices to show that $p^{m} \mid l$! (because, by definition, $k$ is the smallest integer to satisfy this).
We introduce the family of polynomials $P_{i}:=X(X+1) \cdots(X+i-1)$ for $i \in\{0, \ldots l\}\left(P_{0}:=1\right)$. By performing successive Euclidean divisions of $Q$ by $P_{l}, P_{l-1}, \ldots, P_{0}$, we show that $Q$ can be written as:
$$
Q=\sum_{i=0}^{l} c_{i} P_{i}
$$
where $c_{i} \in \mathbb{Z}$ for all $i$.
We then show by induction on $i \in\{0 \ldots l\}$ the following property:
$$
p^{m}\left|c_{i} P_{i}(-i)\right| c_{i} P_{i}(n) \text { for all } n \in \mathbb{Z}
$$
- for $i=0$, the only $P_{i}$ that does not vanish at zero is $P_{0}$, so $Q(0)=c_{0}$, hence $p^{m} \mid c_{0}=$ $c_{0} P_{0}(n)$ for all $n \in \mathbb{Z}$.
- let $i<l$. Suppose the property is true for all elements of $\{0, \ldots, i\}$ and show it for $i+1$. We observe that if $j>i+1,(X+i+1) \mid P_{j}$, so $P_{j}(-i-1)=0$. Thus,
$$
\underbrace{Q(-i-1)}_{p^{m} \mid}=\underbrace{\sum_{j=0}^{i} c_{j} P_{j}(-i-1)}_{p^{m} \mid}+c_{i+1} P_{i+1}(-i-1)
$$
by the induction hypothesis and by the definition of $Q$. Therefore, $p^{m} \mid c_{i+1} P_{i+1}(-i-1)$, and since $P_{i+1}(-i-1)=(i+1)!$ divides any product of $i+1$ consecutive integers (we can also see this using binomial coefficients), it divides $P_{i+1}(n)$ for all $n \in \mathbb{Z}$.
Thus, we obtain in particular $p^{m} \mid P_{l}(n)$ for all $n \in \mathbb{N}$, hence $p^{m} \mid l$!. Therefore, $k \leq l$, so $k \leq d$. By double inclusion, we have thus shown that $k=d$.
|
d = k
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Soit $p$ un nombre premier, $m$ un entier naturel. Trouver le plus petit entier $d$ tel qu'il existe un polynôme unitaire $Q$ de degré $d$ à coefficients entiers tel que, pour tout entier $n, p^{m} \mid Q(n)$.
|
Montrons que $d$ est le plus petit entier tel que $p^{m} \mid d$ !. Soit $k$ le plus petit entier tel que $p^{m} \mid k$ !.
Tout d'abord, montrons que $k \geq d$. On considère le polynôme $Q(x)=X(X+1) \cdots(X+k-1)$ : il est unitaire, de degré $k$, oefficients entiers. Qui plus est, pour tout $n \in \mathbb{N}, Q(n)=k!\binom{n}{k}$ (c'est une propriété des coefficients binomiaux), d'où $p^{m}|k!| Q(n)$. Donc $k$ est un entier pour lequel on dispose d'un polynôme $Q$ unitaire oefficients entiers de degré $k$ tel que pour tout $n \in \mathbb{N}, p^{m} \mid Q(n)$. Donc $k \geq d$. Reste ontrer le sens réciproque. Autrement dit, soit $Q$ un polynôme unitaire oefficients entiers de degré $l$ tel que pour tout entier $n, p^{m} \mid Q(n)$. Montrons que $k \leq l$. Il suffit de montrer que $p^{m} \mid l$ ! (car, par définition, $k$ est le plus petit entier érifier cela).
On introduit la famille des polynômes $P_{i}:=X(X+1) \cdots(X+i-1)$ pour $i \in\{0, \ldots l\}\left(P_{0}:=1\right)$. En effectuant les divisions euclidiennes successives de $Q$ par $P_{l}, P_{l-1}, \ldots, P_{0}$, on montre que $Q$ s'écrit :
$$
Q=\sum_{i=0}^{l} c_{i} P_{i}
$$
où $c_{i} \in \mathbb{Z}$ pour tout $i$.
On montre alors par récurrence sur $i \in\{0 \ldots l\}$ la propriété suivante :
$$
p^{m}\left|c_{i} P_{i}(-i)\right| c_{i} P_{i}(n) \text { pour tout } n \in \mathbb{Z}
$$
- pour $i=0$, le seul des $P_{i}$ qui ne s'annule pas en zéro est $P_{0}$, donc $Q(0)=c_{0}$, d'où $p^{m} \mid c_{0}=$ $c_{0} P_{0}(n)$ pour tout $n \in \mathbb{Z}$.
- soit $i<l$. Supposons que la propriété est vraie pour tous les éléments de $\{0, \ldots, i\}$ et montrons-la pour $i+1$. On constate que si $j>i+1,(X+i+1) \mid P_{j}$ donc $P_{j}(-i-1)=0$. Ainsi,
$$
\underbrace{Q(-i-1)}_{p^{m} \mid}=\underbrace{\sum_{j=0}^{i} c_{j} P_{j}(-i-1)}_{p^{m} \mid}+c_{i+1} P_{i+1}(-i-1)
$$
par hypothèse de récurrence et par définition de $Q$. Donc $p^{m} \mid c_{i+1} P_{i+1}(-i-1)$, et comme $P_{i+1}(-i-1)=(i+1)!$ divise tout produit de $i+1$ entiers consécutifs (on peut encore le voir grâce aux coefficients binomiaux), il divise $P_{i+1}(n)$ pour tout $n \in \mathbb{Z}$.
Ainsi, on obtient en particulier $p^{m} \mid P_{l}(n)$ pour tout $n \in \mathbb{N}$, donc $p^{m} \mid l$ !. Donc $k \leq l$, d'où $k \leq d$. Par double encadrement, on a donc bien montré que $k=d$.
|
{
"exam": "French_envois",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-1-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 7",
"tier": "T2",
"year": "2017"
}
|
If $n \in \mathbb{N}^{*}$, we denote $d(n)$ as its number of divisors. What are the strictly positive integers such that $d(n)^{3}=4 n$?
|
Let $f(n):=\frac{d(n)^{3}}{n}$, the problem is to find the preimages of 4 by $f$. We note that $f(a b)=f(a) f(b)$ if $a$ and $b$ are coprime. This suggests decomposing $n$ into a product of prime factors:
$$
n=p_{1}^{a_{1}} \times p_{2}^{a_{2}} \times \cdots \times p_{l}^{a_{l}},
$$
where the $p_{i}, 1 \leqslant i \leqslant l$, are primes and $a_{i} \geqslant 1$. Therefore, $f(n)=\prod_{i=1}^{l} f\left(p_{i}^{a_{i}}\right)$.
Let $n \in \mathbb{N}^{*}$ satisfy the problem, $n^{3}=2 \times(d(n) / 2)^{3}$ is twice a perfect cube ( $d(n)$ is necessarily even). We deduce that $v_{p}(n) \equiv 0(\bmod 3)$ for $p$ an odd prime, and $v_{2}(n) \equiv 1(\bmod 3)$. Here, $v_{p}(n)$ denotes the $p$-adic valuation of $n$, which is the largest integer $k$ such that $p^{k} \mid n$, so $v_{p_{i}}(n)=a_{i}$ with our notation. We can write
$$
f(n)=\frac{\left(\left(a_{1}+1\right)\left(a_{2}+1\right) \cdots\left(a_{l}+1\right)\right)^{3}}{p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{l}^{a_{l}}}
$$
From the previous remark, the numerator is not divisible by 3, so none of the $p_{i}$ can be 3. And $n$ is the product of powers of cubes of odd primes multiplied by twice a power of $2^{3}$.
It is easy to show that if $m$ is a power of the cube of a prime strictly greater than 3, then $f(m) \geqslant \frac{64}{125}$ with equality if and only if $m=5^{3}$. We prove at the end that for any prime $p \geqslant 5$, $k \rightarrow f\left(p^{3 k}\right)$ is strictly decreasing, and that for any $k \geqslant 1, p \rightarrow f\left(p^{3 k}\right)$ is also strictly decreasing. To have $f(n)=4$, it is necessary to use powers of 2. We have $f(2)=f\left(2^{7}\right)=4, f\left(2^{4}\right)=\frac{125}{16}$ and $f\left(2^{3 k+1}\right)<1$ for $k>2$.
Thus, 2 and 128 are solutions. And to find another one, we need to find $m$ a product of powers of cubes of odd primes such that $f(m)=\frac{64}{125}$. According to the previous study, only $m=5^{3}$ works. Therefore, there are 3 integers $n$ that solve the problem: $n=2, n=2^{7}$ and $n=2^{4} \times 5^{3}$.
|
n=2, n=2^{7}, n=2^{4} \times 5^{3}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Si $n \in \mathbb{N}^{*}$, on note $d(n)$ son nombre de diviseurs. Quels sont les entiers strictement positifs tels que $d(n)^{3}=4 n$ ?
|
Soit $f(n):=\frac{d(n)^{3}}{n}$, l'énoncé revient rouver les antécédents de 4 par $f$. On remarque que $f(a b)=f(a) f(b)$ si $a$ et $b$ sont premiers entre eux. Ceci nous incite écomposer $n$ en produit de facteurs premiers :
$$
n=p_{1}^{a_{1}} \times p_{2}^{a_{2}} \times \cdots \times p_{l}^{a_{l}},
$$
où les $p_{i}, 1 \leqslant i \leqslant l$, sont premiers et $a_{i} \geqslant 1$. On a donc $f(n)=\prod_{i=1}^{l} f\left(p_{i}^{a_{i}}\right)$.
Soit $n \in \mathbb{N}^{*}$ vérifiant l'énoncé, $n^{3}=2 \times(d(n) / 2)^{3}$ est le double d'un cube parfait ( $d(n)$ est nécessairement pair). On en déduit que $v_{p}(n) \equiv 0(\bmod 3)$ pour $p$ nombre premier impair, et $v_{2}(n) \equiv 1(\bmod 3)$. Ici, $v_{p}(n)$ désigne la valuation $p$-adique de $n$, soit le plus grand entier $k$ tel que $p^{k} \mid n$, donc $v_{p_{i}}(n)=a_{i}$ avec nos notations. On peut écrire
$$
f(n)=\frac{\left(\left(a_{1}+1\right)\left(a_{2}+1\right) \cdots\left(a_{l}+1\right)\right)^{3}}{p_{1}^{a_{1}} p_{2}^{a_{2}} \cdots p_{l}^{a_{l}}}
$$
D'après la remarque précédente, le numérateur n'est pas divisible par 3, donc aucun des $p_{i}$ ne peut valoir 3. Et $n$ est le produit de puissances de cubes de nombres premiers impairs que multplie le double d'une puissance de $2^{3}$.
On montre aisément que si $m$ est puissance du cube d'un nombre premier strictement plus grand que 3 , alors $f(m) \geqslant \frac{64}{125}$ avec égalité si et seulement si $m=5^{3}$. On prouve ette fin que pour tout premier $p \geqslant 5$, $k \rightarrow f\left(p^{3 k}\right)$ est strictement décroissante, et que pour tout $k \geqslant 1, p \rightarrow f\left(p^{3 k}\right)$ l'est aussi. Pour avoir $f(n)=4$, il faut donc utiliser des puissances de 2 . On a $f(2)=f\left(2^{7}\right)=4, f\left(2^{4}\right)=\frac{125}{16}$ et $f\left(2^{3 k+1}\right)<1$ pour $k>2$.
Ainsi, 2 et 128 sont solution. Et pour en avoir une autre, il faut trouver $m$ un produit de puissances de cubes de nombres premiers impairs tel que $f(m)=\frac{64}{125}$. D'après l'étude précédente, seul $m=5^{3}$ convient. Donc il y a 3 entiers $n$ solution au problème : $n=2, n=2^{7}$ et $n=2^{4} \times 5^{3}$.
|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "\nExercice 8.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-1-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 8",
"tier": "T2",
"year": "2017"
}
|
Prove that there are infinitely many integers $n$ such that $2^{2^{n}+1}+1$ is divisible by $n$, but $2^{n}+1$ is not.
|
For $m \geqslant 1$, let $a_{m}=2^{3^{m}}+1$. We have
$a_{m}=\left(2^{3^{m-1}}+1\right)\left(\left(2^{3^{m-1}}\right)^{2}-2^{3^{m-1}}+1\right)=a_{m-1}\left(\left(2^{3^{m-1}}\right)^{2}-2^{3^{m-1}}+1\right)$.
Note that for $a \in \mathbb{N}^{*}$, if $p \mid a+1$ and $p \mid a^{2}-a+1$, then $p \mid 2 a-1$ because $2 a-1=a(a+1)-\left(a^{2}-a+1\right)$. And $p \mid 2 a+2$, so $p \mid 3$. Therefore, $\left(a_{m-1} \wedge a_{m}\right) \mid 3$ for all $m \in \mathbb{N} *$. Therefore, $a_{m}$ has an odd prime factor (since $a_{m}$ is odd) other than 3 that does not divide $a_{m-1}$, unless possibly if $a_{m}$ is a power of 3, in which case $a_{m+1}$ has a prime factor that $a_{m}$ does not have.
Thus, for an infinite number of integers $m \in \mathbb{N}^{*}, a_{m}$ has a prime factor $p_{m}>3$ that does not divide $a_{m-1}$. Let $b_{m}=3^{m-1} p_{m}$. According to Fermat's Little Theorem,
$$
2^{b_{m}}+1 \equiv 2^{3^{m-1}}+1 \equiv a_{m-1} \quad(\bmod p)_{m}
$$
Therefore, $p_{m} \nmid 2^{b_{m}}+1$, so $b_{m} \nmid 2^{b_{m}}+1$.
Since $p_{m}$ and 3 are coprime, it suffices to show that $p_{m} \mid 2^{2^{b_{m}}+1}+1$ and that $3^{m_{1}} \mid 2^{2^{b_{m}}+1}+1$. This can be done quite directly with LTE, but we might find an alternative solution. Research is ongoing.
Thus, an infinite number of integers $b_{m}$ satisfy the condition of the statement.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prouver qu'il existe une infinité d'entiers $n$ tels que $2^{2^{n}+1}+1$ est divisible par $n$, mais $2^{n}+1$ ne l'est pas.
|
Pour $m \geqslant 1$, posons $a_{m}=2^{3^{m}}+1$. On a
$a_{m}=\left(2^{3^{m-1}}+1\right)\left(\left(2^{3^{m-1}}\right)^{2}-2^{3^{m-1}}+1\right)=a_{m-1}\left(\left(2^{3^{m-1}}\right)^{2}-2^{3^{m-1}}+1\right)$.
Notons que pour $a \in \mathbb{N}^{*}$, si $p \mid a+1$ et $p \mid a^{2}-a+1$, alors $p \mid 2 a-1$ car $2 a-1=a(a+1)-\left(a^{2}-a+1\right)$. Et $p \mid 2 a+2$, donc $p \mid 3$. Donc $\left(a_{m-1} \wedge a_{m}\right) \mid 3$ pour tout $m \in \mathbb{N} *$. Donc $a_{m}$ possède un facteur premier impair (car $a_{m}$ impair) autre que 3 qui ne divise pas $a_{m-1}$, sauf éventuellement si $a_{m}$ est une puissance de 3 , auquel cas $a_{m+1}$ possède un facteur premier que n'a pas $a_{m}$.
Donc pour une infinité d'entiers $m \in \mathbb{N}^{*}, a_{m}$ possède un facteur premier $p_{m}>3$ qui ne divise pas $a_{m-1}$. Posons $b_{m}=3^{m-1} p_{m}$. D'après le petit théorème de Fermat,
$$
2^{b_{m}}+1 \equiv 2^{3^{m-1}}+1 \equiv a_{m-1} \quad(\bmod p)_{m}
$$
Donc $p_{m} \nmid 2^{b_{m}}+1$, donc $b_{m} \nmid 2^{b_{m}}+1$.
Comme $p_{m}$ et 3 sont premiers entre eux, il suffit de montrer que $p_{m} \mid 2^{2^{b m}+1}+1$ et que $3^{m_{1}} \mid 2^{2^{b_{m}}+1}+1$. Cela se fait assez directement avec LTE mais on peut peut-être trouver une solution alternative. Recherche en cours.
Ainsi, une infinité d'entiers $b_{m}$ satisfont la condition de l'énoncé.
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-1-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 9",
"tier": "T2",
"year": "2017"
}
|
Determine the minimum value of
$$
\left\lfloor\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{\mathrm{~d}}\right\rfloor+\left\lfloor\frac{\mathrm{b}+\mathrm{c}+\mathrm{d}}{\mathrm{a}}\right\rfloor+\left\lfloor\frac{\mathrm{c}+\mathrm{d}+\mathrm{a}}{\mathrm{~b}}\right\rfloor+\left\lfloor\frac{\mathrm{d}+\mathrm{a}+\mathrm{b}}{\mathrm{c}}\right\rfloor
$$
when $\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}$ range over $\mathbb{N}^{*}$.
|
The minimum sought is 9.
Indeed, if a, b, c, d are non-zero natural numbers, we define
$$
f(a, b, c, d)=\left\lfloor\frac{a+b+c}{d}\right\rfloor+\left\lfloor\frac{b+c+d}{a}\right\rfloor+\left\lfloor\frac{c+d+a}{b}\right\rfloor+\left\lfloor\frac{d+a+b}{c}\right\rfloor .
$$
We recall that for any real number $x$, we have $\lfloor x\rfloor>x-1$. Thus, for all integers $a, b, c, d>0$, we have
$$
\begin{aligned}
f(a, b, c, d)+4 & >\frac{a+b+c}{d}+\frac{b+c+d}{a}+\frac{c+d+a}{b}+\frac{d+a+b}{c} \\
& >\left(\frac{a}{b}+\frac{b}{a}\right)+\left(\frac{a}{c}+\frac{c}{a}\right)+\left(\frac{a}{d}+\frac{d}{a}\right)+\left(\frac{b}{c}+\frac{c}{b}\right)+\left(\frac{b}{d}+\frac{d}{b}\right)+\left(\frac{c}{d}+\frac{d}{c}\right) \\
& >6 \times 2 \text{ since } t+\frac{1}{t} \geqslant 2 \text{ for all real } t>0 .
\end{aligned}
$$
Thus, $f(a, b, c, d)>8$. Since $f(a, b, c, d)$ is clearly an integer, it follows that $f(a, b, c, d) \geqslant$ 9. It remains to verify that $f(5,5,5,4)=9$ to conclude.
|
9
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Déterminer la valeur minimale de
$$
\left\lfloor\frac{\mathrm{a}+\mathrm{b}+\mathrm{c}}{\mathrm{~d}}\right\rfloor+\left\lfloor\frac{\mathrm{b}+\mathrm{c}+\mathrm{d}}{\mathrm{a}}\right\rfloor+\left\lfloor\frac{\mathrm{c}+\mathrm{d}+\mathrm{a}}{\mathrm{~b}}\right\rfloor+\left\lfloor\frac{\mathrm{d}+\mathrm{a}+\mathrm{b}}{\mathrm{c}}\right\rfloor
$$
lorsque $\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}$ décrivent $\mathbb{N}^{*}$.
|
Le minimum cherché est 9.
En effet, si a, b, c, d sont des entiers naturels non nuls, on pose
$$
f(a, b, c, d)=\left\lfloor\frac{a+b+c}{d}\right\rfloor+\left\lfloor\frac{b+c+d}{a}\right\rfloor+\left\lfloor\frac{c+d+a}{b}\right\rfloor+\left\lfloor\frac{d+a+b}{c}\right\rfloor .
$$
On rappelle que, pour tout réel $x$, on a $\lfloor x\rfloor>x-1$. Ainsi, pour tous entiers $a, b, c, d>0$, on a
$$
\begin{aligned}
f(a, b, c, d)+4 & >\frac{a+b+c}{d}+\frac{b+c+d}{a}+\frac{c+d+a}{b}+\frac{d+a+b}{c} \\
& >\left(\frac{a}{b}+\frac{b}{a}\right)+\left(\frac{a}{c}+\frac{c}{a}\right)+\left(\frac{a}{d}+\frac{d}{a}\right)+\left(\frac{b}{c}+\frac{c}{b}\right)+\left(\frac{b}{d}+\frac{d}{b}\right)+\left(\frac{c}{d}+\frac{d}{c}\right) \\
& >6 \times 2 \text { car } t+\frac{1}{t} \geqslant 2 \text { pour tout réel } t>0 .
\end{aligned}
$$
Ainsi, $f(a, b, c, d)>8$. Or, $f(a, b, c, d)$ étant clairement un entier, $c^{\prime}$ est donc que $f(a, b, c, d) \geqslant$ 9. Il reste à vérifier que $f(5,5,5,4)=9$ pour conclure.
|
{
"exam": "French_envois",
"problem_label": "1",
"problem_match": "## Exercice 1.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-2-solutions.jsonl",
"solution_match": "## Solution de l'exercice 1",
"tier": "T2",
"year": "2017"
}
|
Let $m$ and $n$ be non-zero natural numbers. Prove that
$$
\frac{(m+n)!}{(m+n)^{m+n}}<\frac{m!}{m^{m}} \frac{n!}{n^{n}}
$$
|
According to the binomial formula, we have
$$
(m+n)^{m+n}=\sum_{k=0}^{m+n}\binom{m+n}{k} m^{k} n^{m+n-k}
$$
The right-hand side being a sum of $m+n+1$ strictly positive numbers, it is strictly greater than any of these numbers. In particular, for $k=m$, we have
$$
(m+n)^{m+n}>\binom{m+n}{m} m^{m} n^{n}
$$
Since $\binom{m+n}{m}=\frac{(m+n)!}{m!n!}$, this concludes.
Remark The required inequality can be interpreted in probabilistic terms. Indeed, consider an urn containing $m$ white balls and $n$ black balls indistinguishable by touch, from which $m+n$ balls are drawn successively with replacement. It is easy to verify that the probability $p_{m}$ of obtaining exactly $m$ white balls during these $m+n$ draws is
$$
p_{m}=\binom{m+n}{m}\left(\frac{m}{m+n}\right)^{m}\left(\frac{n}{m+n}\right)^{n}
$$
If we denote $q_{m}$ as the probability of not obtaining exactly $m$ white balls, we have $q_{m}>0$ and $p_{m}+q_{m}=1$, hence $p_{m}=1-q_{m}<1$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soit $m$ et $n$ des entiers naturels non nuls. Prouver que
$$
\frac{(m+n)!}{(m+n)^{m+n}}<\frac{m!}{m^{m}} \frac{n!}{n^{n}}
$$
|
D'après la formule du binôme, on a
$$
(m+n)^{m+n}=\sum_{k=0}^{m+n}\binom{m+n}{k} m^{k} n^{m+n-k}
$$
Le membre de droite étant une somme de $m+n+1$ nombres strictement positifs, elle est strictement plus grande que n'importe lequel de ces nombres. En particulier, pour $k=m$, on a donc
$$
(m+n)^{m+n}>\binom{m+n}{m} m^{m} n^{n}
$$
Puisque $\binom{m+n}{m}=\frac{(m+n)!}{m!n!}$, cela conclut.
Remarque L'inégalité demandée peut s'interpréter en termes probabilistes. En effet, considérons une urne contenant $m$ boules blanches et $n$ boules noires indiscernables au toucher, et de laquelle on tire successivement $m+n$ boules avec remise. Il est facile de vérifier que la probabilité $p_{m}$ d'obtenir exactement $m$ boules blanches au cours de ces $m+n$ tirages est
$$
p_{m}=\binom{m+n}{m}\left(\frac{m}{m+n}\right)^{m}\left(\frac{n}{m+n}\right)^{n}
$$
Si on note $q_{m}$ la probabilité de ne pas obtenir exactement $m$ boules blanches, on a $q_{m}>0$ et $p_{m}+q_{m}=1$, d'où $p_{m}=1-q_{m}<1$.
|
{
"exam": "French_envois",
"problem_label": "2",
"problem_match": "## Exercice 2.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-2-solutions.jsonl",
"solution_match": "## Solution de l'exercice 2",
"tier": "T2",
"year": "2017"
}
|
Let $a_{0}<a_{1}<a_{2}<\ldots$ be an infinite sequence of strictly positive integers. Prove that there exists a unique integer $n \geqslant 1$ such that
$$
a_{n}<\frac{a_{0}+a_{1}+a_{2}+\cdots+a_{n}}{n} \leqslant a_{n+1} .
$$
|
For $n \geqslant 1$, we set $d_{n}=a_{0}+a_{1}+\cdots+a_{n}-n a_{n}$.
Clearly, the left inequality of the desired bound is equivalent to $d_{n}>0$.
On the other hand, we have $d_{n+1}=a_{0}+\cdots+a_{n}-n a_{n+1}$, so the right inequality is equivalent to $d_{n+1} \leqslant 0$. Therefore, it is necessary to prove that there exists a unique $n \geqslant 1$ such that $d_{n+1} \leqslant 0 < d_{n}$, which naturally leads us to study the variations of the sequence $(d_{i})$.
For all $n \geqslant 1$, we have $d_{n+1}-d_{n}=n(a_{n}-a_{n+1})<0$ because the sequence $(a_{i})$ is strictly increasing. Moreover, we have $d_{1}=a_{0}>0$.
Thus, the sequence $(d_{i})$ is a strictly decreasing sequence of integers, which ensures that it will only take non-positive values from a certain rank, and with a strictly positive first term. Therefore, there indeed exists a unique index $n$ for which $d_{n+1} \leqslant 0 < d_{n}$, namely the largest integer such that $d_{n}>0$.
Remark The conclusion is no longer guaranteed without the assumption that the $a_{i}$ are all integers. A counterexample is given by $a_{n}=2-\frac{1}{2^{n}}$ for all $n \geqslant 0$.
## Common Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $a_{0}<a_{1}<a_{2}<\ldots$ une suite infinie d'entiers strictement positifs. Prouver qu'il existe un unique entier $n \geqslant 1$ tel que
$$
a_{n}<\frac{a_{0}+a_{1}+a_{2}+\cdots+a_{n}}{n} \leqslant a_{n+1} .
$$
|
Pour $n \geqslant 1$, on pose $d_{n}=a_{0}+a_{1}+\cdots+a_{n}-n a_{n}$.
Clairement, l'inégalité de gauche de l'encadrement souhaité est équivalente à $\mathrm{d}_{\mathrm{n}}>0$.
D'autre part, on a $d_{n+1}=a_{0}+\cdots+a_{n}-n a_{n+1}$, donc l'inégalité de droite est équivalente à $d_{n+1} \leqslant 0$. Il s'agit donc de prouver qu'il existe un unique $n \geqslant 1$ tel que $d_{n+1} \leqslant 0<d_{n}$, ce qui nous pousse naturellement à étudier les variations de la suite ( $d_{i}$ ).
Pour tout $n \geqslant 1$, on a $d_{n+1}-d_{n}=n\left(a_{n}-a_{n+1}\right)<0$ car la suite $\left(a_{i}\right)$ est strictement croissante. De plus, on a $d_{1}=a_{0}>0$.
Ainsi, la suite ( $\mathrm{d}_{\mathrm{i}}$ ) est une suite strictement décroissante $\mathrm{d}^{\prime}$ entiers, ce qui assure qu'elle ne prendra des valeurs négatives ou nulles qu'à partir d'un certain rang, et de premier terme strictement positif. Il existe donc bien un unique indice $n$ pour lequel $d_{n+1} \leqslant 0<d_{n}$, à savoir le plus grand entier tel que $d_{n}>0$.
Remarque La conclusion n'est plus assurée sans l'hypothèse que les $a_{i}$ sont tous des entiers. Un contre-exemple est donné par $a_{n}=2-\frac{1}{2^{n}}$ pour tout $n \geqslant 0$.
## Exercices communs
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "## Exercice 3.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-2-solutions.jsonl",
"solution_match": "## Solution de l'exercice 3",
"tier": "T2",
"year": "2017"
}
|
Determine all integers $n \geqslant 3$ for which there exist $n$ polynomials $P_{1}, \ldots, P_{n}$ with real coefficients such that for all distinct $i, j, k$: $P_{i}+P_{j}$ has no real roots and $P_{i}+P_{j}+P_{k}$ has at least one real root.
|
Let us prove that only $n=3$ has the desired property.
First, by setting $\mathrm{P}_{1}(x)=3 x^{2}+3$ and $\mathrm{P}_{2}(x)=P_{3}(x)=-x^{2}-2$, we easily verify that the polynomials $P_{1}(x)+P_{2}(x)=P_{1}(x)+P_{3}(x)=2 x^{2}+1$ and $P_{2}(x)+P_{3}(x)=-2 x^{2}-4$ have no real roots, while $P_{1}(x)+P_{2}(x)+P_{3}(x)=x^{2}-1$ has 1 and -1 as roots. Thus, $n=3$ is a solution to the problem.
Now, note that if $n \geqslant 4$ polynomials $\mathrm{P}_{1}, \ldots, \mathrm{P}_{n}$ satisfy the required conditions, then $\mathrm{P}_{1} \mathrm{P}_{2}, \mathrm{P}_{3}$, and $\mathrm{P}_{4}$ already satisfy these conditions. To conclude, it is therefore sufficient to prove that $n=4 n^{\prime}$ is not a solution.
The key is to note that if P and Q are polynomials such that $\mathrm{P}+\mathrm{Q}$ has no real root, then $\mathrm{P}+\mathrm{Q}$ maintains a constant sign on $\mathbb{R}$.
We proceed by contradiction: suppose that $\mathrm{P}_{1}, \mathrm{P}_{2}, \mathrm{P}_{3}$, and $\mathrm{P}_{4}$ are polynomials such that, for all distinct $i, j, k$, $P_{i}+P_{j}$ has no real root and $P_{i}+P_{j}+P_{k}$ has at least one real root.
Draw then the complete graph whose vertices are the polynomials $\mathrm{P}_{1}, \mathrm{P}_{2}, \mathrm{P}_{3}, \mathrm{P}_{4}$ and color the edge $P_{i} P_{j}$ in red if $P_{i}+P_{j}$ is strictly positive, and in green if $P_{i}+P_{j}$ is strictly negative. Each edge is necessarily colored. Moreover, this graph cannot contain a triangle whose three edges are of the same color, otherwise the sum of the three polynomials which are the vertices of this triangle would have no real root.
By changing each $P_{i}$ to $-P_{i}$ if necessary, we can assume that two of the three edges from $P_{1}$ are red, and by renumbering, we can assume that $P_{1} P_{2}$ and $P_{1} P_{4}$ are red. To avoid the red triangle $P_{1} P_{2} P_{4}$, it follows that $P_{2} P_{4}$ is green. Since $P_{2} P_{3} P_{4}$ cannot have all three edges green, it follows that $P_{2} P_{3}$ or $P_{4} P_{3}$ is red. By symmetry of roles, we can assume that $\mathrm{P}_{2} \mathrm{P}_{3}$ is red. But then $\mathrm{P}_{1} \mathrm{P}_{3}$ is green.
Thus, for any real $x$, we simultaneously have
$$
\begin{aligned}
& P_{1}(x)+P_{4}(x)>0 \text{ and } P_{2}(x)+P_{3}(x)>0 \text{, so } P_{1}(x)+P_{2}(x)+P_{3}(x)+P_{4}(x)>0 \text{, and } \\
& P_{1}(x)+P_{3}(x)<0 \text{ and } P_{2}(x)+P_{4}(x)<0 \text{, so } P_{1}(x)+P_{2}(x)+P_{3}(x)+P_{4}(x)<0,
\end{aligned}
$$
which is absurd. Thus, $n=4$ is not a solution, which concludes the proof.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Déterminer tous les entiers $n \geqslant 3$ pour lesquels il existe $n$ polynômes $P_{1}, \ldots, P_{n}$ à coefficients réels et tels que, pour tous $i, j, k$ distincts : $P_{i}+P_{j} n^{\prime}$ a aucune racine réelle et $P_{i}+P_{j}+P_{k}$ admet au moins une racine réelle.
|
Prouvons que seul $n=3$ a la propriété désirée.
Tout d'abord, en posant $\mathrm{P}_{1}(x)=3 x^{2}+3$ et $\mathrm{P}_{2}(x)=P_{3}(x)=-x^{2}-2$, on vérifie aisément que les polynômes $P_{1}(x)+P_{2}(x)=P_{1}(x)+P_{3}(x)=2 x^{2}+1$ et $P_{2}(x)+P_{3}(x)=-2 x^{2}-4$ n'ont aucune racine réelle, tandis que $P_{1}(x)+P_{2}(x)+P_{3}(x)=x^{2}-1$ admet 1 et -1 comme racines. Ainsi, $n=3$ est une solution du problème.
Remarquons maintenant que si $n \geqslant 4$ polynômes $\mathrm{P}_{1}, \ldots, \mathrm{P}_{n}$ vérifient les conditions requises, alors $\mathrm{P}_{1} \mathrm{P}_{2}, \mathrm{P}_{3}$ et $\mathrm{P}_{4}$ vérifient déjà ces conditions. Pour conclure, il suffit donc de prouver que $n=4 n^{\prime}$ est pas une solution.
La clé est alors de noter que si P et Q sont des polynômes tels que $\mathrm{P}+\mathrm{Q}$ n'a pas de racine rélle, alors $\mathrm{P}+\mathrm{Q}$ garde un signe constant sur $\mathbb{R}$.
On procède donc par l'absurde : supposons que $\mathrm{P}_{1}, \mathrm{P}_{2}, \mathrm{P}_{3}$ et $\mathrm{P}_{4}$ soient des polynômes tels que, pour tous $i, j, k$ distincts, $P_{i}+P_{j}$ n'a aucune racine réelle et $P_{i}+P_{j}+P_{k}$ admet au moins une racine réelle.
Traçons alors le graphe complet dont les sommets sont les polynômes $\mathrm{P}_{1}, \mathrm{P}_{2}, \mathrm{P}_{3}, \mathrm{P}_{4}$ et colorons l'arête $P_{i} P_{j}$ en rouge si $P_{i}+P_{j}$ est strictement positif, et en vert si $P_{i}+P_{j}$ est strictement négatif. Chaque arête est nécessairement colorée. De plus, ce graphe ne peut contenir de triangles dont les trois arêtes sont de la même couleur, ce sans quoi la somme des trois polynômes qui sont les sommets de ce triangle n'aurait pas de racine réelle.
Quitte à changer chaque $P_{i}$ en $-P_{i}$, on peut supposer que deux des trois arêtes issues de $P_{1}$ sont rouges et, quitte à renuméroter, on peut supposer que $P_{1} P_{2}$ et $P_{1} P_{4}$ sont rouges. Pour éviter le triangle rouge $P_{1} P_{2} P_{4}$, $c^{\prime}$ est donc que $P_{2} P_{4}$ est verte. Puisque $P_{2} P_{3} P_{4}$ ne peut avoir ses trois arêtes vertes, $c^{\prime}$ est donc que $P_{2} P_{3}$ ou $P_{4} P_{3}$ est rouge. Par symétrie des rôles, on peut supposer que $\mathrm{P}_{2} \mathrm{P}_{3}$ est rouge. Mais alors $\mathrm{P}_{1} \mathrm{P}_{3}$ est verte.
Ainsi, pour tout réel $x$, on a simultanement
$$
\begin{aligned}
& P_{1}(x)+P_{4}(x)>0 \text { et } P_{2}(x)+P_{3}(x)>0 \text {, donc } P_{1}(x)+P_{2}(x)+P_{3}(x)+P_{4}(x)>0 \text {, et } \\
& P_{1}(x)+P_{3}(x)<0 \text { et } P_{2}(x)+P_{4}(x)<0 \text {, donc } P_{1}(x)+P_{2}(x)+P_{3}(x)+P_{4}(x)<0,
\end{aligned}
$$
ce qui est absurde. Ainsi, $n=4$ n'est pas une solution, ce qui conclut.
|
{
"exam": "French_envois",
"problem_label": "4",
"problem_match": "## Exercice 4.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-2-solutions.jsonl",
"solution_match": "## Solution de l'exercice 4",
"tier": "T2",
"year": "2017"
}
|
a) Determine all functions $f: \mathbb{R} \longrightarrow \mathbb{Z}$ such that
$$
f(f(y)-x)^{2}+f(x)^{2}+f(y)^{2}=f(y)(1+2 f(f(y)))
$$
for all real numbers $x$ and $y$.
b) Determine all functions $f: \mathbb{R} \longrightarrow \mathbb{R}$ such that
$$
f(f(y)-x)^{2}+f(x)^{2}+f(y)^{2}=f(y)(1+2 f(f(y)))
$$
for all real numbers $x$ and $y$.
|
a) Let \( f \) be a potential solution to the problem. Denote \( \mathrm{P}(\mathrm{x}, \mathrm{y}) \) as the equality in the statement for the values \( x \) and \( y \). Let \( c = f(0) \).
For all \( x \), from \( P(0, x) \) we deduce that \( f(f(x))^2 + c^2 + f(x)^2 = f(x) + 2 f(f(x)) f(x) \), hence \( f(x) = c^2 + (f(f(x)) - f(x))^2 \). It follows that \( f(x) \geq c^2 \geq 0 \).
For \( x = 0 \), this gives \( c = c^2 + (f(c) - c)^2 \), hence \( c(1 - c) = (f(c) - c)^2 \geq 0 \). Since \( c \) is an integer, it follows that \( c = 0 \) or \( c = 1 \). In both cases, this shows that \( f(c) - c = 0 \). Thus, we know that \( f(c) = c \).
Finally, for all \( x \), from \( P(x, 0) \) we deduce that
\[
f(c - x)^2 + f(x)^2 + c^2 = c(1 + 2c)
\]
- If \( c = 0 \), the above equality can be rewritten as \( f(-x)^2 + f(x)^2 = 0 \), hence \( f(x) = 0 \).
- If \( c = 1 \), it can be rewritten as \( f(1 - x)^2 + f(x)^2 = 2 \). Since \( f(1 - x) \) and \( f(x) \) are non-negative integers, it follows that \( f(x) = f(1 - x) = 1 \).
Conversely, the functions \( f: x \longmapsto 0 \) and \( f: x \longmapsto 1 \) are clearly solutions to the problem.
b) Let \( f \) be a potential solution to the problem. Denote \( \mathrm{P}(\mathrm{x}, \mathrm{y}) \) as the equality in the statement for the values \( x \) and \( y \). Let \( c = f(0) \), \( d = f(c) \), and \( \mathcal{F} = \{ f(x) \mid x \in \mathbb{R} \} \).
For all \( x \in \mathbb{R} \), from \( P(0, x) \) we deduce that \( f(f(x))^2 + c^2 + f(x)^2 = f(x) + 2 f(f(x)) f(x) \), hence \( f(x) = c^2 + (f(f(x)) - f(x))^2 \). Consequently, for all \( x \in \mathcal{F} \), we have \( x \geq c^2 \geq 0 \) and \( f(x) = x \pm \sqrt{x - c^2} \).
It follows that \( c \geq c^2 \), i.e., \( c(1 - c) \geq 0 \), hence \( 0 \leq c \leq 1 \). We proceed by contradiction and assume that \( 0 < c < 1 \).
By the arithmetic-geometric mean inequality, we have \( 0 < c(1 - c) \leq \left( \frac{c + 1 - c}{2} \right)^2 = \frac{1}{4} \). On the other hand, for any real number \( x \in (0, 1) \), we know that \( x < \sqrt{x} \).
We have proven above that \( d = c + \epsilon \sqrt{c - c^2} \), with \( \epsilon = \pm 1 \). If \( \epsilon = -1 \), then \( d - c^2 = (c - c^2) - \sqrt{c - c^2} < 0 \), which is impossible. Therefore, \( \epsilon = 1 \), and \( d = c + \sqrt{c - c^2} \). Then we find \( f(d) = d + \varepsilon \sqrt{d - c^2} \), with \( \varepsilon = \pm 1 \). Observe that
\[
0 < c - c^2 \leq d - c^2 \leq (c - c^2) + \sqrt{c - c^2} \leq \frac{1}{4} + \frac{1}{2} = \frac{3}{4} < 1.
\]
Consequently, if \( \varepsilon = -1 \), then \( f(d) - c^2 = (d - c^2) - \sqrt{d - c^2} < 0 \), which is again impossible. Therefore, \( \varepsilon = 1 \), and \( f(d) = d + \sqrt{d - c^2} \).
Finally, \( P(d, 0) \) indicates that
\[
\begin{aligned}
0 & = f(c - d)^2 + f(d)^2 + c^2 - c(1 + 2d) = f(c - d)^2 + (d + \sqrt{d - c^2})^2 + c^2 - c(1 + 2d) \\
& \geq c^4 + d^2 + d - c^2 + c^2 - c(1 + 2d) = c^4 + (d - c)^2 + (d - c) - c^2 \\
& \geq c^4 + c - c^2 + \sqrt{c - c^2} - c^2 \geq c^4 + c - c^2 + c - c^2 - c^2 = c(c - 1)^2 (c + 2)
\end{aligned}
\]
which is impossible.
It follows that \( c = 0 \) or \( c = 1 \), hence \( c = c^2 \) and \( f(c) = c \pm \sqrt{c - c^2} = c \). Consequently, for all \( x \), \( P(x, 0) \) indicates that
\[
f(c - x)^2 + f(x)^2 + c^2 = c(1 + 2c)
\]
- If \( c = 0 \), the above equality can be rewritten as \( f(-x)^2 + f(x)^2 = 0 \), hence \( f(x) = 0 \).
- If \( c = 1 \), it can be rewritten as \( f(1 - x)^2 + f(x)^2 = 2 \). We have seen above that \( f(1 - x) \geq c^2 = 1 \) and \( f(x) \geq c^2 = 1 \), which shows that \( f(x) = f(1 - x) = 1 \).
Conversely, the functions \( f: x \longmapsto 0 \) and \( f: x \longmapsto 1 \) are clearly solutions to the problem.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
a) Déterminer toutes les fonctions $f: \mathbb{R} \longrightarrow \mathbb{Z}$ telles que
$$
f(f(y)-x)^{2}+f(x)^{2}+f(y)^{2}=f(y)(1+2 f(f(y)))
$$
pour tous réels $x$ et $y$.
b) Déterminer toutes les fonctions $f: \mathbb{R} \longrightarrow \mathbb{R}$ telles que
$$
f(f(y)-x)^{2}+f(x)^{2}+f(y)^{2}=f(y)(1+2 f(f(y)))
$$
pour tous réels $x$ et $y$.
|
a) Soit f une éventuelle solution du problème. Notons $\mathrm{P}(\mathrm{x}, \mathrm{y})$ l'égalité de l'énoncé pour les valeurs $x$ et $y$. On pose $c=f(0)$.
Pour tout $x$, de $P(0, x)$ on déduit que $f(f(x))^{2}+c^{2}+f(x)^{2}=f(x)+2 f(f(x)) f(x)$, d'où $f(x)=c^{2}+(f(f(x))-f(x))^{2}$. Il s'ensuit que $f(x) \geqslant c^{2} \geqslant 0$.
Pour $x=0$, cela donne $c=c^{2}+(f(c)-c)^{2}$, d'où $c(1-c)=(f(c)-c)^{2} \geqslant 0$. Puisque $c$ est un entier, il vient $c=0$ ou $c=1$. Dans les deux cas, cela montre que $f(c)-c=0$. Ainsi, on sait que $f(c)=c$.
Enfin, pour tout $x$, de $P(x, 0)$ on déduit que
$$
f(c-x)^{2}+f(x)^{2}+c^{2}=c(1+2 c)
$$
- Si $\mathrm{c}=0$, l'égalité ci-dessus se réécrit comme $f(-x)^{2}+f(x)^{2}=0$, donc $f(x)=0$.
- Si $\mathrm{c}=1$, elle se réécrit comme $f(1-x)^{2}+f(x)^{2}=2$. Or, $f(1-x)$ et $f(x)$ sont entiers naturels, donc $f(x)=f(1-x)=1$.
Réciproquement, les fonctions $\mathrm{f}: x \longmapsto 0$ et $\mathrm{f}: x \longmapsto 1$ sont clairement solutions du problème.
b) Soit $f$ une éventuelle solution du problème. Notons $\mathrm{P}(\mathrm{x}, \mathrm{y})$ l'égalité de l'énoncé pour les valeurs $x$ et $y$. On pose $c=f(0), d=f(c)$ et $\mathcal{F}=\{f(x) \mid x \in \mathbb{R}\}$.
Pour tout $x \in \mathbb{R}$, de $P(0, x)$ on déduit que $f(f(x))^{2}+c^{2}+f(x)^{2}=f(x)+2 f(f(x)) f(x)$, $d^{\prime}$ où $f(x)=c^{2}+(f(f(x))-f(x))^{2}$. Par conséquent, pour tout $x \in \mathcal{F}$, on a $x \geqslant c^{2} \geqslant 0$ et $f(x)=x \pm \sqrt{x-c^{2}}$.
Il s'ensuit que $c \geqslant c^{2}$, c'est-à-dire que $c(1-c) \geqslant 0$, donc que $0 \leqslant c \leqslant 1$. On procède alors par l'absurde, et on suppose que $0<c<1$.
Par inégalité arithmético-géométrique, il vient $0<\mathrm{c}(1-\mathrm{c}) \leqslant\left(\frac{\mathrm{c}+1-\mathrm{c}}{2}\right)^{2}=\frac{1}{4}$. D'autre part, de manière générale, pour tout réel $x \in] 0 ; 1[$, on sait que $x<\sqrt{x}$.
Or, on a prouvé ci-dessus que $d=c+\epsilon \sqrt{c-c^{2}}$, avec $\epsilon= \pm 1$. Si $\epsilon=-1$, alors $d-c^{2}=$ $\left(c-c^{2}\right)-\sqrt{c-c^{2}}<0$, ce qui est impossible. Il vient donc $\epsilon=1$, et $d=c+\sqrt{c-c^{2}}$. Puis on trouve $f(d)=d+\varepsilon \sqrt{d-c^{2}}$, avec $\varepsilon= \pm 1$. Observons que
$$
0<c-c^{2} \leqslant d-c^{2} \leqslant\left(c-c^{2}\right)+\sqrt{c-c^{2}} \leqslant \frac{1}{4}+\frac{1}{2}=\frac{3}{4}<1 .
$$
Par conséquent, si $\varepsilon=-1$, alors $f(d)-c^{2}=\left(d-c^{2}\right)-\sqrt{d-c^{2}}<0$, ce qui est encore une fois impossible. Il vient donc $\varepsilon=1$, et $f(d)=d+\sqrt{d-c^{2}}$.
Enfin, $P(d, 0)$ indique que
$$
\begin{aligned}
0 & =f(c-d)^{2}+f(d)^{2}+c^{2}-c(1+2 d)=f(c-d)^{2}+\left(d+\sqrt{d-c^{2}}\right)^{2}+c^{2}-c(1+2 d) \\
& \geqslant c^{4}+d^{2}+d-c^{2}+c^{2}-c(1+2 d)=c^{4}+(d-c)^{2}+(d-c)-c^{2} \\
& \geqslant c^{4}+c-c^{2}+\sqrt{c-c^{2}}-c^{2} \geqslant c^{4}+c-c^{2}+c-c^{2}-c^{2}=c(c-1)^{2}(c+2)
\end{aligned}
$$
ce qui est impossible.
Il s'ensuit que $c=0$ ou $c=1$, donc que $c=c^{2}$ et que $f(c)=c \pm \sqrt{c-c^{2}}=c$. Par conséquent, pour tout $x, P(x, 0)$ indique que
$$
f(c-x)^{2}+f(x)^{2}+c^{2}=c(1+2 c)
$$
- Si $\mathrm{c}=0$, l'égalité ci-dessus se réécrit comme $f(-x)^{2}+f(x)^{2}=0$, donc $f(x)=0$.
- Si $\mathrm{c}=1$, elle se réécrit comme $\mathrm{f}(1-x)^{2}+\mathrm{f}(\mathrm{x})^{2}=2$. Or, on a vu plus haut que $f(1-x) \geqslant c^{2}=1$ et que $f(x) \geqslant c^{2}=1$, ce qui montre que $f(x)=f(1-x)=1$.
Réciproquement, les fonctions $\mathrm{f}: x \longmapsto 0$ et $\mathrm{f}: \mathrm{x} \longmapsto 1$ sont clairement solutions du problème.
|
{
"exam": "French_envois",
"problem_label": "5",
"problem_match": "## Exercice 5.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-2-solutions.jsonl",
"solution_match": "## Solution de l'exercice 5",
"tier": "T2",
"year": "2017"
}
|
a) Let $x_{1} \geqslant x_{2}>0$ and $y_{1} \geqslant y_{2}>0$ be real numbers such that
$$
x_{1} \geqslant y_{1} \text { and } x_{1} x_{2} \geqslant y_{1} y_{2}
$$
Prove that
$$
x_{1}+x_{2} \geqslant y_{1}+y_{2}
$$
b) Let $x_{1} \geqslant x_{2} \geqslant \ldots \geqslant x_{n}>0$ and $y_{1} \geqslant y_{2} \geqslant \ldots \geqslant y_{n}>0$ be real numbers such that
$$
x_{1} x_{2} \cdots x_{i} \geqslant y_{1} y_{2} \cdots y_{i} \text { for } i=1, \ldots, n
$$
Prove that
$$
x_{1}+x_{2}+\cdots+x_{n} \geqslant y_{1}+y_{2}+\cdots+y_{n}
$$
|
a) Proceed by contradiction: suppose that $y_{1}+y_{2}>x_{1}+x_{2}$. Then $y_{2}>x_{1}+x_{2}-y_{1}$ and we have
$$
0 \geqslant y_{1} y_{2}-x_{1} x_{2}>y_{1}\left(x_{1}+x_{2}-y_{1}\right)-x_{1} x_{2}=\left(x_{1}-y_{1}\right)\left(y_{1}-x_{2}\right)
$$
Since $x_{1} \geqslant y_{1}$, then $y_{1}<x_{2}$. But then $x_{1}+x_{2} \geqslant 2 y_{1} \geqslant y_{1}+y_{2}$, which contradicts our assumption. Therefore, we must have $y_{1}+y_{2} \leqslant x_{1}+x_{2}$.
b) Proceed by strong induction on $n$. First, the result is obvious for $n=1$, and we have just proved it for $n=2$. Assume therefore that $n \geqslant 3$.
Let $\lambda=\min _{1 \leqslant k<n} \frac{x_{1}+\ldots+x_{k}}{y_{1}+\ldots+y_{k}}$, and let $\ell$ be an integer such that $1 \leqslant \ell<n$ and such that
$$
x_{1}+\ldots+x_{\ell}=\lambda\left(y_{1}+\ldots+y_{\ell}\right)
$$
We then set $y_{1}^{\prime}=\lambda y_{1}, y_{n}^{\prime}=\frac{y_{n}}{\lambda}$ and $y_{k}^{\prime}=y_{k}$ for $k=2, \ldots, n-1$. By construction, we have $y_{1}^{\prime} \geqslant y_{2} \geqslant \ldots \geqslant y_{n}^{\prime}$ and, for $k=1, \ldots, n$, we also have $x_{1} \ldots x_{k} \geqslant y_{1}^{\prime} \ldots y_{k}^{\prime}$, with equality when $k=\ell<n$. By the induction hypothesis, we know that $x_{1}+\ldots+x_{\ell} \geqslant y_{1}^{\prime}+\ldots+y_{\ell}^{\prime}$.
Furthermore, note that $y_{1}^{\prime} \geqslant y_{n}^{\prime}, y_{1} \geqslant y_{n}, y_{1}^{\prime} \geqslant y_{1}$ and $y_{1}^{\prime} y_{n}^{\prime}=y_{1} y_{n}$. Applying the induction hypothesis (for $n=2$), we get $y_{1}^{\prime}+y_{n}^{\prime} \geqslant y_{1}+y_{n}$, and even $y_{1}^{\prime}+y_{2}^{\prime}+\ldots+y_{n}^{\prime} \geqslant y_{1}+y_{2}+\ldots+y_{n}$.
Finally, let $\bar{x}_{i}=x_{\ell+i}$ and $\bar{y}_{i}=y_{\ell+1}^{\prime}$, for $i=1, \ldots, n-\ell$. Then $\bar{x}_{1} \geqslant \ldots \geqslant \bar{x}_{n-\ell}>0$ and $\bar{y}_{1} \geqslant \ldots \geqslant \bar{y}_{n-\ell}>0$. Moreover, for $i=1, \ldots, n-\ell$, we have
$$
\left(x_{1} \ldots x_{\ell}\right)\left(\bar{x}_{1} \ldots \bar{x}_{i}\right)=x_{1} \ldots x_{\ell+i} \geqslant y_{1}^{\prime} \ldots y_{\ell+i}^{\prime}=\left(y_{1}^{\prime} \ldots y_{\ell}^{\prime}\right)\left(\bar{y}_{1} \ldots \bar{y}_{i}\right)
$$
Since $x_{1} \ldots x_{\ell}=y_{1}^{\prime} \ldots y_{\ell}^{\prime}>0$, this shows that $\bar{x}_{1} \ldots \bar{x}_{i} \geqslant \bar{y}_{1} \ldots \bar{y}_{i}$. We have $n-\ell<n$, and the induction hypothesis shows that $\bar{x}_{1}+\ldots+\bar{x}_{n-\ell} \geqslant \bar{y}_{1}+\ldots+\bar{y}_{n-\ell}$.
Putting these inequalities together, we get
$$
\begin{aligned}
x_{1}+\ldots+x_{n} & =\left(x_{1}+\ldots+x_{\ell}\right)+\left(\bar{x}_{1}+\ldots+\bar{x}_{n-\ell}\right) \\
& \geqslant y_{1}^{\prime}+\ldots+y_{\ell}^{\prime}+\bar{y}_{1}+\ldots+\bar{y}_{n-\ell}=y_{1}^{\prime}+\ldots+y_{n}^{\prime} \\
& \geqslant y_{1}+\ldots+y_{n} .
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
a) Soit $x_{1} \geqslant x_{2}>0$ et $y_{1} \geqslant y_{2}>0$ des réels tels que
$$
x_{1} \geqslant y_{1} \text { et } x_{1} x_{2} \geqslant y_{1} y_{2}
$$
Prouver que
$$
x_{1}+x_{2} \geqslant y_{1}+y_{2}
$$
b) Soit $x_{1} \geqslant x_{2} \geqslant \ldots \geqslant x_{n}>0$ et $y_{1} \geqslant y_{2} \geqslant \ldots \geqslant y_{n}>0$ des réels tels que
$$
x_{1} x_{2} \cdots x_{i} \geqslant y_{1} y_{2} \cdots y_{i} \text { pour } i=1, \ldots, n
$$
Prouver que
$$
x_{1}+x_{2}+\cdots+x_{n} \geqslant y_{1}+y_{2}+\cdots+y_{n}
$$
|
a) Procédons par l'absurde: supposons que $y_{1}+y_{2}>x_{1}+x_{2}$. Alors $y_{2}>x_{1}+x_{2}-y_{1}$ et on a
$$
0 \geqslant y_{1} y_{2}-x_{1} x_{2}>y_{1}\left(x_{1}+x_{2}-y_{1}\right)-x_{1} x_{2}=\left(x_{1}-y_{1}\right)\left(y_{1}-x_{2}\right)
$$
Puisque $x_{1} \geqslant y_{1}$, alors $y_{1}<x_{2}$. Mais alors $x_{1}+x_{2} \geqslant 2 y_{1} \geqslant y_{1}+y_{2}$, ce qui contredit notre hypothèse. On a donc bien $y_{1}+y_{2} \leqslant x_{1}+x_{2}$.
b) Procédons par récurrence forte sur $n$. Tout d'abord, le résultat est évident pour $n=1$, et on vient de le prouver pour $\mathrm{n}=2$. On suppose donc $\mathrm{n} \geqslant 3$.
Soit $\lambda=\min _{1 \leqslant k<n} \frac{x_{1}+\ldots+x_{k}}{y_{1}+\ldots+y_{k}}$, et soit $\ell$ un entier tel que $1 \leqslant \ell<n$ et tel que
$$
x_{1}+\ldots+x_{\ell}=\lambda\left(y_{1}+\ldots+y_{\ell}\right)
$$
On pose alors $y_{1}^{\prime}=\lambda y_{1}, y_{n}^{\prime}=\frac{y_{n}}{\lambda}$ et $y_{k}^{\prime}=y_{k}$ pour $k=2, \ldots, n-1$. Par construction, on a bien $y_{1}^{\prime} \geqslant y_{2} \geqslant \ldots \geqslant y_{n}^{\prime}$ et, pour $k=1, \ldots, n$, on a également $x_{1} \ldots x_{k} \geqslant y_{1}^{\prime} \ldots y_{k}^{\prime}$, avec égalité quand $k=\ell<n$. Par hypothèse de récurrence, on sait que $x_{1}+\ldots+x_{\ell} \geqslant$ $y_{1}^{\prime}+\ldots+y_{\ell}^{\prime}$.
En outre, remarquons que $y_{1}^{\prime} \geqslant y_{n}^{\prime}, y_{1} \geqslant y_{n}, y_{1}^{\prime} \geqslant y_{1}$ et $y_{1}^{\prime} y_{n}^{\prime}=y_{1} y_{n}$. En appliquant l'hypothèse de récurrence (pour $n=2$ ), on obtient donc $y_{1}^{\prime}+y_{n}^{\prime} \geqslant y_{1}+y_{n}$, et même $y_{1}^{\prime}+y_{2}^{\prime}+\ldots+y_{n}^{\prime} \geqslant y_{1}+y_{2}+\ldots+y_{n}$.
Enfin, posons $\bar{x}_{i}=x_{\ell+i}$ et $\bar{y}_{i}=y_{\ell+1}^{\prime}$, pour $i=1, \ldots, n-\ell$. Alors $\bar{x}_{1} \geqslant \ldots \geqslant \bar{x}_{n-\ell}>0$ et $\bar{y}_{1} \geqslant \ldots \geqslant \bar{y}_{n-\ell}>0$. En outre, pour $i=1, \ldots, n-\ell$, on a
$$
\left(x_{1} \ldots x_{\ell}\right)\left(\bar{x}_{1} \ldots \bar{x}_{i}\right)=x_{1} \ldots x_{\ell+i} \geqslant y_{1}^{\prime} \ldots y_{\ell+i}^{\prime}=\left(y_{1}^{\prime} \ldots y_{\ell}^{\prime}\right)\left(\bar{y}_{1} \ldots \bar{y}_{i}\right)
$$
Puisque $x_{1} \ldots x_{\ell}=y_{1}^{\prime} \ldots y_{\ell}^{\prime}>0$, cela montre que $\bar{x}_{1} \ldots \bar{x}_{i} \geqslant \bar{y}_{1} \ldots \bar{y}_{i}$. On a $n-\ell<n$, et l'hypothèse de récurrence montre donc que $\bar{x}_{1}+\ldots+\bar{x}_{n-\ell} \geqslant \bar{y}_{1}+\ldots+\bar{y}_{n-\ell}$.
Mises bout à bout, ces inégalités montrent que
$$
\begin{aligned}
x_{1}+\ldots+x_{n} & =\left(x_{1}+\ldots+x_{\ell}\right)+\left(\bar{x}_{1}+\ldots+\bar{x}_{n-\ell}\right) \\
& \geqslant y_{1}^{\prime}+\ldots+y_{\ell}^{\prime}+\bar{y}_{1}+\ldots+\bar{y}_{n-\ell}=y_{1}^{\prime}+\ldots+y_{n}^{\prime} \\
& \geqslant y_{1}+\ldots+y_{n} .
\end{aligned}
$$
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "## Exercice 6.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-2-solutions.jsonl",
"solution_match": "## Solution de l'exercice 6",
"tier": "T2",
"year": "2017"
}
|
a) Let $x_{1} \geqslant x_{2}>0$ and $y_{1} \geqslant y_{2}>0$ be real numbers such that
$$
x_{1} \geqslant y_{1} \text { and } x_{1} x_{2} \geqslant y_{1} y_{2}
$$
Prove that
$$
x_{1}+x_{2} \geqslant y_{1}+y_{2}
$$
b) Let $x_{1} \geqslant x_{2} \geqslant \ldots \geqslant x_{n}>0$ and $y_{1} \geqslant y_{2} \geqslant \ldots \geqslant y_{n}>0$ be real numbers such that
$$
x_{1} x_{2} \cdots x_{i} \geqslant y_{1} y_{2} \cdots y_{i} \text { for } i=1, \ldots, n
$$
Prove that
$$
x_{1}+x_{2}+\cdots+x_{n} \geqslant y_{1}+y_{2}+\cdots+y_{n}
$$
|
We set
$$
x_{n+1}=\min \left(x_{n}, y_{n}\right) \frac{y_{1} \cdots y_{n}}{x_{1} \cdots x_{n}} \text { and } y_{n+1}=\min \left(x_{n}, y_{n}\right)
$$
We then have $0<x_{n+1} \leqslant x_{n}, 0<y_{n+1} \leqslant y_{n}, x_{n+1} \leqslant y_{n+1}$ and $x_{1} \cdots x_{n} x_{n+1}=y_{1} \cdots y_{n} y_{n+1}$. Since everything is homogeneous, by multiplying the $x_{i}$ and the $y_{i}$ by the same constant, we can assume that $x_{i}, y_{i}>1$ for all $i$. We then set $\alpha_{i}=\ln \left(x_{i}\right)$ and $\beta_{i}=\ln \left(y_{i}\right)$, for all $i$. We then have:
$-\alpha_{1} \geqslant \ldots \geqslant \alpha_{n+1}>0$ and $\beta_{1} \geqslant \ldots \geqslant \beta_{n+1}>0 ;$
$-\beta_{1}+\cdots+\beta_{i} \leqslant \alpha_{1}+\cdots+\alpha_{i}$, for $i=1, \ldots, n$;
$-\beta_{1}+\cdots \beta_{n+1}=\alpha_{1}+\cdots+\alpha_{n+1}$.
We can therefore use Muirhead's inequality, which ensures that, for all positive real numbers $\mathrm{x}_{1}, \ldots, \chi_{n+1}$, we have
$$
\sum_{\text {sym. }} x_{1}^{\beta_{1}} \cdots x_{n+1}^{\beta_{n+1}} \leqslant \sum_{\text {sym. }} x_{1}^{\alpha_{1}} \cdots x_{n+1}^{\alpha_{n+1}} .
$$
In particular, if $x_{1}=e$ and $x_{i}=1$ for $i \geqslant 2$, it follows that $\sum_{i=1}^{n+1} y_{i} \leqslant \sum_{i=1}^{n+1} x_{i}$. Since $x_{n+1} \leqslant y_{n+1}$, it actually follows that $\sum_{i=1}^{n} y_{i} \leqslant \sum_{i=1}^{n} x_{i}$.
Remark Once the numbers $\alpha_{i}$ and $\beta_{i}$ are introduced, instead of using Muirhead's inequality, we could have directly used Karamata's inequality with the exponential function (which is convex on $\mathbb{R}$ ).
## Exercises of group $\mathcal{A}$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
a) Soit $x_{1} \geqslant x_{2}>0$ et $y_{1} \geqslant y_{2}>0$ des réels tels que
$$
x_{1} \geqslant y_{1} \text { et } x_{1} x_{2} \geqslant y_{1} y_{2}
$$
Prouver que
$$
x_{1}+x_{2} \geqslant y_{1}+y_{2}
$$
b) Soit $x_{1} \geqslant x_{2} \geqslant \ldots \geqslant x_{n}>0$ et $y_{1} \geqslant y_{2} \geqslant \ldots \geqslant y_{n}>0$ des réels tels que
$$
x_{1} x_{2} \cdots x_{i} \geqslant y_{1} y_{2} \cdots y_{i} \text { pour } i=1, \ldots, n
$$
Prouver que
$$
x_{1}+x_{2}+\cdots+x_{n} \geqslant y_{1}+y_{2}+\cdots+y_{n}
$$
|
On pose
$$
x_{n+1}=\min \left(x_{n}, y_{n}\right) \frac{y_{1} \cdots y_{n}}{x_{1} \cdots x_{n}} \text { et } y_{n+1}=\min \left(x_{n}, y_{n}\right)
$$
On a alors $0<x_{n+1} \leqslant x_{n}, 0<y_{n+1} \leqslant y_{n}, x_{n+1} \leqslant y_{n+1}$ et $x_{1} \cdots x_{n} x_{n+1}=y_{1} \cdots y_{n} y_{n+1}$. Tout étant homogène, quitte à multiplier les $x_{i}$ et les $y_{i}$ par une même constante, on peut supposer que $x_{i}, y_{i}>1$ pour tout $i$. On pose ensuite $\alpha_{i}=\ln \left(x_{i}\right)$ et $\beta_{i}=\ln \left(y_{i}\right)$, pour tout i. On a alors:
$-\alpha_{1} \geqslant \ldots \geqslant \alpha_{n+1}>0$ et $\beta_{1} \geqslant \ldots \geqslant \beta_{n+1}>0 ;$
$-\beta_{1}+\cdots+\beta_{i} \leqslant \alpha_{1}+\cdots+\alpha_{i}$, pour $i=1, \ldots, n$;
$-\beta_{1}+\cdots \beta_{n+1}=\alpha_{1}+\cdots+\alpha_{n+1}$.
On peut donc utiliser l'inégalité de Muirhead, qui assure que, pour tous réels $\mathrm{x}_{1}, \ldots, \chi_{n+1}$ strictement positifs, on a
$$
\sum_{\text {sym. }} x_{1}^{\beta_{1}} \cdots x_{n+1}^{\beta_{n+1}} \leqslant \sum_{\text {sym. }} x_{1}^{\alpha_{1}} \cdots x_{n+1}^{\alpha_{n+1}} .
$$
En particulier, si $x_{1}=e$ et $x_{i}=1$ pour $i \geqslant 2$, il vient $\sum_{i=1}^{n+1} y_{i} \leqslant \sum_{i=1}^{n+1} x_{i}$. Puisque $x_{n+1} \leqslant y_{n+1}$, il s'ensuit en fait $\sum_{i=1}^{n} y_{i} \leqslant \sum_{i=1}^{n} x_{i}$.
Remarque Une fois introduits les nombres $\alpha_{i}$ et $\beta_{i}$, au lieu d'utiliser l'inégalité de Muirhead, on aurait pu directement utiliser l'inégalité de Karamata à la fonction exponentielle (qui est convexe sur $\mathbb{R}$ ).
## Exercices du groupe $\mathcal{A}$
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "## Exercice 6.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-2-solutions.jsonl",
"solution_match": "## Solution alternative",
"tier": "T2",
"year": "2017"
}
|
Let $a_{0}$ and $b_{0}$ be strictly positive integers. For all $i \geqslant 0$, we set
$$
a_{i+1}=a_{i}+\left\lfloor\sqrt{b_{i}}\right\rfloor \text { and } b_{i+1}=b_{i}+\left\lfloor\sqrt{a_{i}}\right\rfloor \text {. }
$$
Prove that there exists an integer $n \geqslant 0$ such that $a_{n}=b_{n}$.
|
For all $i \geqslant 0$, let $c_{i}=b_{i}-a_{i}, \alpha_{i}=\left\lfloor\sqrt{a_{i}}\right\rfloor$ and $\beta_{i}=\left\lfloor\sqrt{b_{i}}\right\rfloor$. Without loss of generality, we assume that $c_{0} \geqslant 0$. We first show by induction that $c_{i} \geqslant 0$ for all $i \geqslant 0$. Indeed, for all $n \geqslant 0$, we have $\lfloor\sqrt{n+1}\rfloor \leqslant\lfloor\sqrt{n}\rfloor+1$. The function $f: n \longmapsto n-\lfloor\sqrt{n}\rfloor$ is therefore increasing on $\mathbb{N}$, because
$$
f(n+1)-f(n)=n+1-\lfloor\sqrt{n+1}\rfloor-n+\lfloor\sqrt{n}\rfloor \geqslant n+1-\lfloor\sqrt{n}\rfloor-1-n+\lfloor\sqrt{n}\rfloor=0
$$
for all $n \geqslant 0$. Consequently, if $c_{i} \geqslant 0$, then $b_{i} \geqslant a_{i}$, so
$$
c_{i+1}=\left(b_{i}-\left\lfloor\sqrt{b_{i}}\right\rfloor\right)-\left(a_{i}-\left\lfloor\sqrt{a_{i}}\right\rfloor\right)=f\left(b_{i}\right)-f\left(a_{i}\right) \geqslant 0
$$
This concludes the induction, and shows that $\boldsymbol{c}_{\boldsymbol{i}} \geqslant 0$ for all $i \geqslant 0$.
On the other hand, if $c_{i} \geqslant 0$, and still since $b_{i} \geqslant a_{i}$, we also have $c_{i+1}=c_{i}+\left\lfloor\sqrt{a_{i}}\right\rfloor-\left\lfloor\sqrt{b_{i}}\right\rfloor \leqslant$ $c_{i}$. The sequence $\left(c_{i}\right)_{i \geqslant 0}$ is therefore decreasing, with values in the natural numbers. There exists an integer $n \geqslant 0$ such that $c_{i}=c_{n}$ for all $i \geqslant n$. It is therefore sufficient to prove that $c_{n}=0$.
Proceed by contradiction: suppose that $c_{n} \geqslant 1$. For all $i \geqslant n$, we know that $c_{i}=c_{i+1}=$ $c_{i}+\alpha_{i}-\beta_{i}$, so that $\alpha_{i}=\beta_{i}$. The sequence $\left(b_{i}-\beta_{i}^{2}\right)_{i \geqslant n}$ has positive integer values; there therefore exists an integer $m \geqslant n$ such that $b_{i}-\beta_{i}^{2} \geqslant b_{m}-\beta_{m}^{2}$ for all $i \geqslant n$. By increasing the value of $n$, we assume in addition that $m=n$.
Finally, note that the sequences $\left(a_{i}\right)_{i \geqslant 0}$ and $\left(\alpha_{i}\right)_{i \geqslant 0}$ are clearly increasing. Two cases are then possible:
— If $\alpha_{n}=\alpha_{n+1}$, then
$$
\begin{aligned}
& b_{n+2}=b_{n}+\alpha_{n}+\alpha_{n+1} \geqslant a_{n}+c_{n}+2 \beta_{n} \geqslant \beta_{n}^{2}+2 \beta_{n}+1=\left(\beta_{n}+1\right)^{2} \text { and } \\
& b_{n+2}=b_{n}+\alpha_{n}+\alpha_{n+1}<\left(\beta_{n}+1\right)^{2}+2 \beta_{n}<\left(\beta_{n}+2\right)^{2}
\end{aligned}
$$
so $\beta_{n+2}=\beta_{n}+1$. This shows that
$$
b_{n+2}-\beta_{n+2}^{2}=b_{n}+2 \beta_{n}-\left(\beta_{n}+1\right)^{2}=\left(b_{n}-\beta_{n}^{2}\right)-1<b_{n}-\beta_{n}^{2}
$$
which contradicts our assumption.
- If $\alpha_{n}<\alpha_{n+1}$, then
$$
\begin{aligned}
& b_{n+1} \geqslant \beta_{n+1}^{2}=\alpha_{n+1}^{2} \geqslant\left(\alpha_{n}+1\right)^{2}=\left(\beta_{n}+1\right)^{2} \text { and } \\
& b_{n+1}=b_{n}+\alpha_{n}<\left(\beta_{n}+1\right)^{2}+\beta_{n}<\left(\beta_{n}+2\right)^{2}
\end{aligned}
$$
so $\beta_{n+1}=\beta_{n}+1$. This shows that
$$
b_{n+1}-\beta_{n+1}^{2}=b_{n}+\beta_{n}-\left(\beta_{n}+1\right)^{2}=\left(b_{n}-\beta_{n}^{2}\right)-\beta_{n}-1<b_{n}-\beta_{n}^{2}
$$
which once again contradicts our assumption.
Our assumption that $c_{n} \geqslant 1$ was therefore false, which shows that $c_{n}=0$, thus concluding the exercise.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Soit $a_{0}$ et $b_{0}$ des entiers strictement positifs. Pour tout $i \geqslant 0$, on pose
$$
a_{i+1}=a_{i}+\left\lfloor\sqrt{b_{i}}\right\rfloor \text { et } b_{i+1}=b_{i}+\left\lfloor\sqrt{a_{i}}\right\rfloor \text {. }
$$
Prouver qu'il existe un entier $n \geqslant 0$ tel que $a_{n}=b_{n}$.
|
Pour tout $i \geqslant 0$, posons $c_{i}=b_{i}-a_{i}, \alpha_{i}=\left\lfloor\sqrt{a_{i}}\right\rfloor$ et $\beta_{i}=\left\lfloor\sqrt{b_{i}}\right\rfloor$. Sans perte de généralité, on suppose que $c_{0} \geqslant 0$. On montre tout d'abord par récurrence que $c_{i} \geqslant 0$ pour tout $i \geqslant 0$. En effet, pour tout $n \geqslant 0$, on a $\lfloor\sqrt{n+1}\rfloor \leqslant\lfloor\sqrt{n}\rfloor+1$. La fonction $f: n \longmapsto n-\lfloor\sqrt{n}\rfloor$ est donc croissante sur $\mathbb{N}$, car
$$
f(n+1)-f(n)=n+1-\lfloor\sqrt{n+1}\rfloor-n+\lfloor\sqrt{n}\rfloor \geqslant n+1-\lfloor\sqrt{n}\rfloor-1-n+\lfloor\sqrt{n}\rfloor=0
$$
pour tout $n \geqslant 0$. Par conséquent, si $c_{i} \geqslant 0$, alors $b_{i} \geqslant a_{i}$, donc
$$
c_{i+1}=\left(b_{i}-\left\lfloor\sqrt{b_{i}}\right\rfloor\right)-\left(a_{i}-\left\lfloor\sqrt{a_{i}}\right\rfloor\right)=f\left(b_{i}\right)-f\left(a_{i}\right) \geqslant 0
$$
Ceci conclut la récurrence, et montre bien que $\boldsymbol{c}_{\boldsymbol{i}} \geqslant 0$ pour tout $i \geqslant 0$.
D'autre part, si $c_{i} \geqslant 0$, et toujours puisque $b_{i} \geqslant a_{i}$, on a aussi $c_{i+1}=c_{i}+\left\lfloor\sqrt{a_{i}}\right\rfloor-\left\lfloor\sqrt{b_{i}}\right\rfloor \leqslant$ $c_{i}$. La suite $\left(c_{i}\right)_{i \geqslant 0}$ est donc décroissante, à valeurs dans les entiers naturels. Il existe donc un entier $n \geqslant 0$ tel que $c_{i}=c_{n}$ pour tout $i \geqslant n$. Il suffit donc de prouver que $c_{n}=0$.
Procédons par l'absurde : supposons que $c_{n} \geqslant 1$. Pour tout $i \geqslant n$, on sait que $c_{i}=c_{i+1}=$ $c_{i}+\alpha_{i}-\beta_{i}$, donc que $\alpha_{i}=\beta_{i}$. La suite $\left(b_{i}-\beta_{i}^{2}\right)_{i \geqslant n}$ est à valeurs entières positives ; il existe donc un entier $m \geqslant n$ tel que $b_{i}-\beta_{i}^{2} \geqslant b_{m}-\beta_{m}^{2}$ pour tout $i \geqslant n$. Quitte à augmenter la valeur de $n$, on suppose en outre que $m=n$.
Notons enfin que les suites $\left(a_{i}\right)_{i \geqslant 0}$ et $\left(\alpha_{i}\right)_{i \geqslant 0}$ sont clairement croissantes. Deux cas sont alors possibles :
— Si $\alpha_{n}=\alpha_{n+1}$, alors
$$
\begin{aligned}
& b_{n+2}=b_{n}+\alpha_{n}+\alpha_{n+1} \geqslant a_{n}+c_{n}+2 \beta_{n} \geqslant \beta_{n}^{2}+2 \beta_{n}+1=\left(\beta_{n}+1\right)^{2} \text { et } \\
& b_{n+2}=b_{n}+\alpha_{n}+\alpha_{n+1}<\left(\beta_{n}+1\right)^{2}+2 \beta_{n}<\left(\beta_{n}+2\right)^{2}
\end{aligned}
$$
donc $\beta_{n+2}=\beta_{n}+1$. Ceci montre que
$$
b_{n+2}-\beta_{n+2}^{2}=b_{n}+2 \beta_{n}-\left(\beta_{n}+1\right)^{2}=\left(b_{n}-\beta_{n}^{2}\right)-1<b_{n}-\beta_{n}^{2}
$$
ce qui contredit notre hypothèse.

- Si $\alpha_{n}<\alpha_{n+1}$, alors
$$
\begin{aligned}
& b_{n+1} \geqslant \beta_{n+1}^{2}=\alpha_{n+1}^{2} \geqslant\left(\alpha_{n}+1\right)^{2}=\left(\beta_{n}+1\right)^{2} \text { et } \\
& b_{n+1}=b_{n}+\alpha_{n}<\left(\beta_{n}+1\right)^{2}+\beta_{n}<\left(\beta_{n}+2\right)^{2}
\end{aligned}
$$
donc $\beta_{n+1}=\beta_{n}+1$. Ceci montre que
$$
b_{n+1}-\beta_{n+1}^{2}=b_{n}+\beta_{n}-\left(\beta_{n}+1\right)^{2}=\left(b_{n}-\beta_{n}^{2}\right)-\beta_{n}-1<b_{n}-\beta_{n}^{2}
$$
ce qui contredit une fois encore notre hypothèse.
Notre hypothèse selon laquelle $c_{n} \geqslant 1$ était donc fausse, ce qui montre que $c_{n}=0$, concluant donc l'exercice.
|
{
"exam": "French_envois",
"problem_label": "7",
"problem_match": "## Exercice 7.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-2-solutions.jsonl",
"solution_match": "## Solution de l'exercice 7",
"tier": "T2",
"year": "2017"
}
|
A polynomial is said to be "monic" if the coefficient of its highest degree monomial is 1. Let $a<b$ be real numbers, and let $P$ be a non-constant monic polynomial such that $\max _{x \in[a, b]}|P(x)|<2$.
Prove that there exists a non-constant monic polynomial $Q$ such that $\max _{x \in[\mathbf{a}, \mathbf{b}]}|\mathrm{Q}(\mathrm{x})|<\frac{1}{2017}$.
|
If $Q$ denotes a polynomial, we set
$$
\|Q\|=\frac{1}{2} \max _{x \in[a, b]}|Q(x)| \text { and } T(Q)(x)=Q(x)^{2}-2\|Q\|^{2}
$$
It is clear that if $Q$ is a non-constant unitary polynomial, then $T(Q)$ is also a non-constant unitary polynomial. Moreover, we have $\|T(Q)\|=\|Q\|^{2}$. If we denote $T^{n}$ as the $n$-th iterate of $T$, then an immediate induction ensures that for any integer $n \geqslant 0, T^{n}(Q)$ is a non-constant polynomial whose leading coefficient is 1 and that $\left\|T^{\mathrm{n}}(Q)\right\|=\|Q\|^{2^{n}}$. Let $P$ be a non-constant unitary polynomial such that $\max _{\mathrm{x} \in[\mathrm{a}, \mathbf{b}]}|\mathrm{P}(\mathrm{x})|<2$. Since $0<$ $\|P\|<1$, we have $\lim _{n \rightarrow+\infty}\left\|T^{n}(P)\right\|=0$. In particular, there exists $n \geqslant 0$ sufficiently large such that $\left\|\mathrm{T}^{\mathrm{n}}(\mathrm{P})\right\|<\frac{1}{2 \times 2017}$, and the polynomial $\mathrm{Q}=\mathrm{T}^{\mathrm{n}}(\mathrm{P})$ then answers the question.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Un polynôme est dit «unitaire » si le coefficient de son monôme de plus haut de degré vaut 1. Soit $a<b$ des réels, et soit $P$ un polynôme unitaire non constant tel que $\max _{x \in[a, b]}|P(x)|<2$.
Prouver qu'il existe un polynôme $Q$, unitaire et non constant, tel que $\max _{x \in[\mathbf{a}, \mathbf{b}]}|\mathrm{Q}(\mathrm{x})|<\frac{1}{2017}$.
|
Si Q désigne un polynôme, on pose
$$
\|Q\|=\frac{1}{2} \max _{x \in[a, b]}|Q(x)| \text { et } T(Q)(x)=Q(x)^{2}-2\|Q\|^{2}
$$
Il est clair que si Q est un polynôme unitaire non constant, alors $\mathrm{T}(\mathrm{Q})$ l'est également. De plus, on a $\|T(Q)\|=\|Q\|^{2}$. Si $l^{\prime}$ on note $T^{n}$ la $n$-ieme itérée de $T$, alors une récurrence immédiate assure que pour tout entier $n \geqslant 0, T^{n}(Q)$ est un polynôme non constant dont le coefficient du monôme de plus haut de degré vaut 1 et que $\left\|T^{\mathrm{n}}(Q)\right\|=\|Q\|^{2^{n}}$. Soit donc P un polynôme unitaire non constant, tel que $\max _{\mathrm{x} \in[\mathrm{a}, \mathbf{b}]}|\mathrm{P}(\mathrm{x})|<2$. Puisque $0<$ $\|P\|<1$, on a $\lim _{n \rightarrow+\infty}\left\|T^{n}(P)\right\|=0$. En particulier, il existe $n \geqslant 0$ suffisamment grand pour que $\left\|\mathrm{T}^{\mathrm{n}}(\mathrm{P})\right\|<\frac{1}{2 \times 2017}$, et le polynôme $\mathrm{Q}=\mathrm{T}^{\mathrm{n}}(\mathrm{P})$ répond alors à la question.
|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "## Exercice 8.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-2-solutions.jsonl",
"solution_match": "## Solution de l'exercice 8",
"tier": "T2",
"year": "2017"
}
|
a) Prove that there exist integers $\mathbf{a}, \boldsymbol{b}$, $\mathbf{c}$ such that $(\mathbf{a}, \mathbf{b}, \mathbf{c}) \neq (0,0,0)$ and $|\mathbf{a}|,|\mathbf{b}|,|\mathbf{c}| < 10^{6}$ for which
$$
|a + b \sqrt{2} + c \sqrt{3}| < 10^{-11}
$$
b) Let $\mathbf{a}, \mathbf{b}, \mathrm{c}$ be integers such that $(\mathbf{a}, \boldsymbol{b}, \mathrm{c}) \neq (0,0,0)$ and $|\mathbf{a}|,|\mathbf{b}|,|\mathbf{c}| < 10^{6}$. Prove that
$$
|a + b \sqrt{2} + c \sqrt{3}| > 10^{-21}
$$
|
a) Let E be the set of $10^{18}$ numbers of the form $a+b \sqrt{2}+c \sqrt{3}$, with $a, b, c$ natural integers and $a, b, c<10^{6}$. We set $d=(1+\sqrt{2}+\sqrt{3}) 10^{6}$.
For all $x \in \mathrm{E}$, we have $0 \leqslant x<\mathrm{d}$. Moreover, $0<\mathrm{d}<(1+2+3) \times 10^{6}<10^{7}-10^{-11}$. We then divide the interval [0; d[ into $10^{18}-1$ intervals
$$
\left[\frac{(\mathrm{k}-1) \mathrm{d}}{10^{18}-1} ; \frac{\mathrm{kd}}{10^{18}-1}[,\right.
$$
for $k=1, \ldots, 10^{18}-1$. According to the pigeonhole principle, at least two of the $10^{18}$ elements of $E$, say $x$ and $y$, belong to one of these intervals. Their difference $z=x-y$ is indeed of the form $z=a+b \sqrt{2}+c \sqrt{3}$ with $a, b, c$ integers and $|a|,|b|,|c|<10^{6}$. Moreover, $|z|=|x-y|<\frac{d}{10^{18}-1}<10^{-11}$.
b) Let $a, b, c$ be integers such that $(a, b, c) \neq(0,0,0)$ and $|a|,|b|,|c|<10^{6}$. For $\epsilon= \pm 1$ and $\varepsilon= \pm 1$, we set
$$
F_{\epsilon, \varepsilon}=a+\epsilon b \sqrt{2}+\varepsilon c \sqrt{3} .
$$
As above, we have $\left|\mathrm{F}_{\epsilon, \varepsilon}\right|<10^{7}$.
We easily verify that
$$
\begin{aligned}
F_{1,1} F_{1,-1} F_{-1,1} F_{-1,-1} & =\left((a+b \sqrt{2})^{2}-3 c^{2}\right)\left((a-b \sqrt{2})^{2}-3 c^{2}\right) \\
& =\left(a^{2}+2 b^{2}-3 c^{2}+2 a b \sqrt{2}\right)\left(a^{2}+2 b^{2}-3 c^{2}-2 a b \sqrt{2}\right) \\
& =\left(a^{2}+2 b^{2}-3 c^{2}\right)^{2}-2(2 a b)^{2}
\end{aligned}
$$
is an integer.
To show that it is non-zero, we proceed by contradiction and assume that
$$
\mathrm{F}_{1,1} \mathrm{~F}_{1,-1} \mathrm{~F}_{-1,1} \mathrm{~F}_{-1,-1}=0
$$
It follows that $x^{2}=2 y^{2}$, with $x=a^{2}+2 b^{2}-3 c^{2}$ and $y=2 a b$. If $x$ and $y$ are non-zero, by considering the 2-adic valuation, we get $2 v_{2}(x)=1+2 v_{2}(\mathrm{y})$. This is absurd, which shows that $x=y=0$. Then:
— if $a=0$, and since $x=0$, we have $2 b^{2}=3 c^{2}$, and the 2-adic valuation shows again that $\mathrm{b}=\mathrm{c}=0$;
- if $b=0$, and since $x=0$, we have $a^{2}=3 c^{2}$, and the 3-adic valuation also shows that $a=c=0$.
Consequently, if $(a, b, c) \neq 0$, the integer $F_{1,1} F_{1,-1} F_{-1,1} F_{-1,-1}$ is non-zero.
Thus, $\left|\mathrm{F}_{1,1} \mathrm{~F}_{1,-1} \mathrm{~F}_{-1,1} \mathrm{~F}_{-1,-1}\right| \geqslant 1$, so $\left|\mathrm{F}_{1,1}\right| \geqslant \frac{1}{\left|\mathrm{~F}_{1,-1} \mathrm{~F}_{-1,1} \mathrm{~F}_{-1,-1}\right|}>10^{-21}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
a) Prouver qu'il existe des entiers $\mathbf{a}, \boldsymbol{b}$, $\mathbf{c}$ tels que $(\mathbf{a}, \mathbf{b}, \mathbf{c}) \neq(0,0,0)$ et $|\mathbf{a}|,|\mathbf{b}|,|\mathbf{c}|<10^{6}$ pour lesquels
$$
|a+b \sqrt{2}+c \sqrt{3}|<10^{-11}
$$
b) Soit $\mathbf{a}, \mathbf{b}, \mathrm{c}$ des entiers tels que $(\mathbf{a}, \boldsymbol{b}, \mathrm{c}) \neq(0,0,0)$ et $|\mathbf{a}|,|\mathbf{b}|,|\mathbf{c}|<10^{6}$. Prouver que
$$
|a+b \sqrt{2}+c \sqrt{3}|>10^{-21}
$$
|
a) Soit E l'ensemble des $10^{18}$ nombres de la forme $a+b \sqrt{2}+c \sqrt{3}$, avec $a, b, c$ entiers naturels et $a, b, c<10^{6}$. On pose $d=(1+\sqrt{2}+\sqrt{3}) 10^{6}$.
Pour tout $x \in \mathrm{E}$, on a $0 \leqslant x<\mathrm{d}$. De plus $0<\mathrm{d}<(1+2+3) \times 10^{6}<10^{7}-10^{-11}$. On divise alors l'intervalle [0; d[ en $10^{18}-1$ intervalles
$$
\left[\frac{(\mathrm{k}-1) \mathrm{d}}{10^{18}-1} ; \frac{\mathrm{kd}}{10^{18}-1}[,\right.
$$
pour $k=1, \ldots, 10^{18}-1$. D'après le principe des tiroirs, au moins deux des $10^{18}$ élements de $E$, disons $x$ et $y$, appartiennent à un même de ces intervalles. Leur différence $z=x-y$ est bien de la forme $z=a+b \sqrt{2}+c \sqrt{3}$ avec $a, b, c$ entiers et $|a|,|b|,|c|<10^{6}$. De plus, $|z|=|x-y|<\frac{d}{10^{18}-1}<10^{-11}$.
b) Soit $a, b, c$ des entiers tels que $(a, b, c) \neq(0,0,0)$ et $|a|,|b|,|c|<10^{6}$. Pour $\epsilon= \pm 1$ et $\varepsilon= \pm 1$, on pose
$$
F_{\epsilon, \varepsilon}=a+\epsilon b \sqrt{2}+\varepsilon c \sqrt{3} .
$$
Comme ci-dessus, on a $\left|\mathrm{F}_{\epsilon, \varepsilon}\right|<10^{7}$.
On vérifie facilement que
$$
\begin{aligned}
F_{1,1} F_{1,-1} F_{-1,1} F_{-1,-1} & =\left((a+b \sqrt{2})^{2}-3 c^{2}\right)\left((a-b \sqrt{2})^{2}-3 c^{2}\right) \\
& =\left(a^{2}+2 b^{2}-3 c^{2}+2 a b \sqrt{2}\right)\left(a^{2}+2 b^{2}-3 c^{2}-2 a b \sqrt{2}\right) \\
& =\left(a^{2}+2 b^{2}-3 c^{2}\right)^{2}-2(2 a b)^{2}
\end{aligned}
$$
est un entier.
Afin de montrer qu'il est non nul, on procède par l'absurde, et on suppose que
$$
\mathrm{F}_{1,1} \mathrm{~F}_{1,-1} \mathrm{~F}_{-1,1} \mathrm{~F}_{-1,-1}=0
$$
Il s'ensuit que $x^{2}=2 y^{2}$, avec $x=a^{2}+2 b^{2}-3 c^{2}$ et $y=2 a b$. Si $x$ et $y$ sont non nuls, en considérant la valuation 2-adique, il vient $2 v_{2}(x)=1+2 v_{2}(\mathrm{y})$. C'est absurde, ce qui montre que $x=y=0$. Puis :
— si $a=0$, et puisque $x=0$, on a $2 b^{2}=3 c^{2}$, et la valuation 2 -adique montre de nouveau que $\mathrm{b}=\mathrm{c}=0$;
- si $b=0$, et puisque $x=0$, on a $a^{2}=3 c^{2}$, et la valuation 3-adique montre aussi que $a=c=0$.
Par conséquent, si $(a, b, c) \neq 0$, l'entier $F_{1,1} F_{1,-1} F_{-1,1} F_{-1,-1}$ est non nul.
Ainsi, $\left|\mathrm{F}_{1,1} \mathrm{~F}_{1,-1} \mathrm{~F}_{-1,1} \mathrm{~F}_{-1,-1}\right| \geqslant 1$, donc $\left|\mathrm{F}_{1,1}\right| \geqslant \frac{1}{\left|\mathrm{~F}_{1,-1} \mathrm{~F}_{-1,1} \mathrm{~F}_{-1,-1}\right|}>10^{-21}$.
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "## Exercice 9.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-2-solutions.jsonl",
"solution_match": "## Solution de l'exercice 9",
"tier": "T2",
"year": "2017"
}
|
Let $A B C D$ be a convex quadrilateral (i.e., its diagonals are inside $A B C D$), and $P$ the intersection of its diagonals $[A C]$ and $[B D]$. We denote $O_{1}, O_{2}, O_{3}$, and $O_{4}$ as the centers of the circumcircles of $A B P, B C P, C D P$, and $D A P$.
Show that $O_{1} O_{2} O_{3} O_{4}$ is a parallelogram.
|
$1 O_{1}$ and $O_{2}$ are on the perpendicular bisector of $[P B]$, so $O_{1} O_{2}$ is the perpendicular bisector of $[P B]$. Similarly, $\left(O_{3} O_{4}\right)$ is the perpendicular bisector of $[P D]$, so $\left(O_{1} O_{2}\right)$ and $\left(O_{3} O_{4}\right)$ are both perpendicular to $(B D)$, thus they are parallel. Similarly, $\left(O_{2} O_{3}\right)$ and $\left(O_{4} O_{1}\right)$ are both perpendicular to $(A C)$, so they are parallel.
$A B C D$ has its opposite sides parallel in pairs, so it is a parallelogram.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C D$ un quadrilatère convexe (c'est-à-dire que ses diagonales sont à l'intérieur de $A B C D)$, et $P$ l'intersection de ses diagonales $[A C]$ et $[B D]$. On note $O_{1}, O_{2}, O_{3}$ et $O_{4}$ les centres des cercles circonscrits à $A B P, B C P, C D P$ et $D A P$.
Montrer que $O_{1} O_{2} O_{3} O_{4}$ est un parallélogramme.

|
$1 O_{1}$ et $O_{2}$ sont sur la médiatrice de $[P B]$, donc $O_{1} O_{2}$ est la médiatrice de $[P B]$. De même, $\left(O_{3} O_{4}\right)$ est la médiatrice de $[P D]$, donc $\left(O_{1} O_{2}\right)$ et $\left(O_{3} O_{4}\right)$ sont toutes deux perpendiculaires à $(B D)$, donc elles sont parallèles. De même, $\left(O_{2} O_{3}\right)$ et $\left(O_{4} O_{1}\right)$ sont toutes deux perpendiculaires à $(A C)$, donc elles sont parallèles.
$A B C D$ a ses côtés opposés parallèles deux à deux, donc c'est un parallélogramme.
|
{
"exam": "French_envois",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-3-solutions.jsonl",
"solution_match": "\nSolution de l'exercice ",
"tier": "T2",
"year": "2017"
}
|
Let $ABC$ be a triangle. $H$ its orthocenter and $P, Q$ and $R$ the feet of the altitudes from $A$, $B$ and $C$.
Show that $H$ is the center of the inscribed circle of $PQR$.
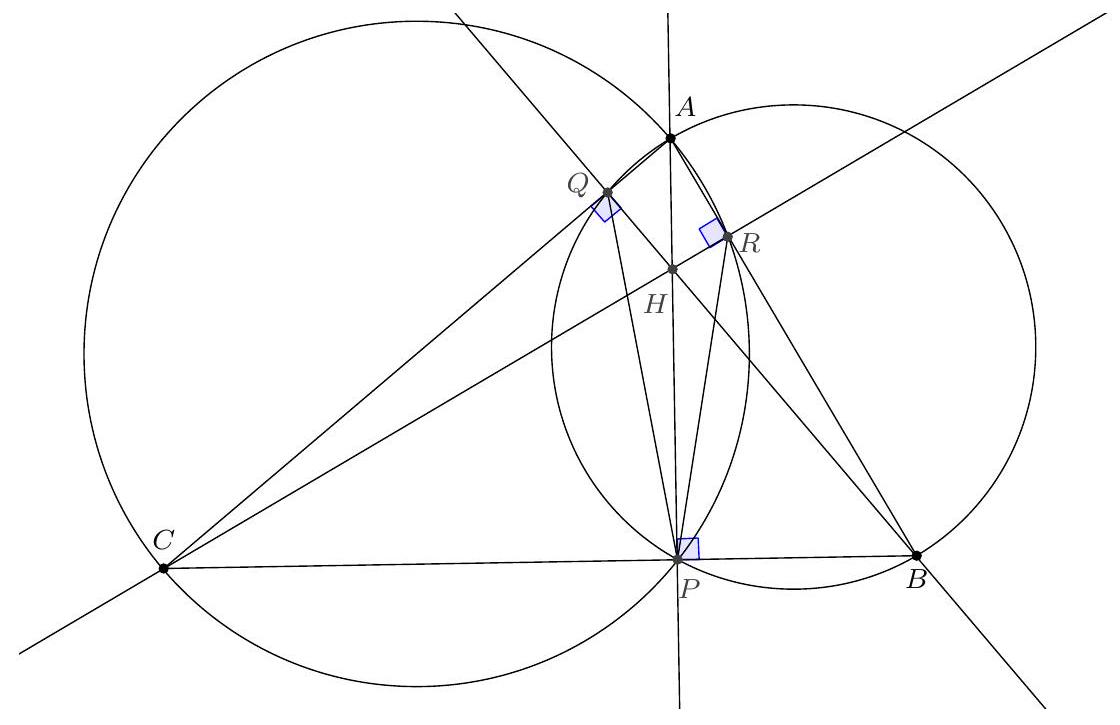
|
We know that points $A, B, P$ and $Q$ are concyclic on the circle with diameter $[A B]$, so:
$$
\widehat{H P Q}=\widehat{A P Q}=\widehat{A B Q}=90-\widehat{B A Q}=90-\widehat{B A C}
$$
Similarly, $A, C, P$ and $R$ are concyclic on the circle with diameter $[A C]$ so:
$$
\widehat{H P R}=\widehat{A P R}=\widehat{A C R}=90-\widehat{C A R}=90-\widehat{B A C}
$$
Therefore, $\widehat{H P Q}=\widehat{H P R}$, so $(P H)$ is the angle bisector of $\widehat{Q P R}$. Similarly, we can show that $(Q H)$ and $(R H)$ are the angle bisectors of $\widehat{P Q R}$ and $\widehat{P R Q}$, so $H$ is the incenter of $\triangle P Q R$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle. $H$ son orthocentre et $P, Q$ et $R$ les pieds des hauteurs issues de $A$, $B$ et $C$.
Montrer que $H$ est le centre du cercle inscrit à $P Q R$.

|
On sait que les points $A, B, P$ et $Q$ sont cocycliques sur le cercle de diamètre $[A B]$, donc :
$$
\widehat{H P Q}=\widehat{A P Q}=\widehat{A B Q}=90-\widehat{B A Q}=90-\widehat{B A C}
$$
De même, $A, C, P$ et $R$ sont cocycliques sur le cercle de diamètre $[A C]$ donc:
$$
\widehat{H P R}=\widehat{A P R}=\widehat{A C R}=90-\widehat{C A R}=90-\widehat{B A C}
$$
On a donc $\widehat{H P Q}=\widehat{H P R}$ donc $(P H)$ est la bissectrice de $\widehat{Q P R}$. On montre de même que $(Q H)$ et $(R H)$ sont les bissectrices de $\widehat{P Q R}$ et $\widehat{P R Q}$, donc $H$ est le centre du cercle inscrit à $P Q R$.
|
{
"exam": "French_envois",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-3-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 2",
"tier": "T2",
"year": "2017"
}
|
Points $D$ and $E$ divide the side $[A B]$ of an equilateral triangle into three equal parts, such that $D$ is located between $A$ and $E$. The point $F$ is located on $[B C]$ such that $C F=A D$. Calculate the sum of the angles $\widehat{C D F}+\widehat{C E F}$.
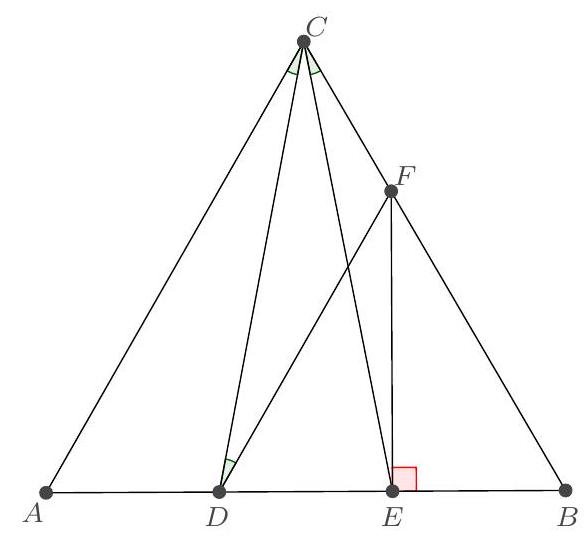
|
Given $B F = B D$ and $\widehat{D B F} = 60^{\circ}$, the triangle $D B F$ is equilateral. Therefore, $\widehat{B A C} = \widehat{B D F} = 60^{\circ}$, so $(D F) \parallel (A C)$, and thus $\widehat{C D F} = \widehat{A C D}$.
On the other hand, $\widehat{A C D} = \widehat{B C E}$ by symmetry, so $\widehat{C D F} = \widehat{B C E} = \widehat{F C E}$. The sum we are interested in is therefore $\widehat{F C E} + \widehat{C E F} = \widehat{B F E}$ according to the sum of the angles of triangle $F C E$. Since $(F E)$ is a median of the equilateral triangle $D B F$, it is also a bisector, so $\widehat{B F E} = \frac{1}{2} \widehat{B F D} = 30^{\circ}$ and our sum is equal to $30^{\circ}$.
## Common Exercises
|
30^{\circ}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Les points $D$ et $E$ divisent le côté $[A B]$ d'un triangle équilatéral en trois parties égales, de telle manière que $D$ est situé entre $A$ et $E$. Le point $F$ est situé sur $[B C]$ de sorte que $C F=A D$. Calculer la somme des angles $\widehat{C D F}+\widehat{C E F}$.

|
On a $B F=B D$ et $\widehat{D B F}=60^{\circ}$, donc le triangle $D B F$ est équilatéral. On a donc $\widehat{B A C}=\widehat{B D F}=60^{\circ}$ donc $(D F) \|(A C)$, donc $\widehat{C D F}=\widehat{A C D}$.
D'autre part, $\widehat{A C D}=\widehat{B C E}$ par symétrie, donc $\widehat{C D F}=\widehat{B C E}=\widehat{F C E}$. La somme qui nous intéresse vaut donc $\widehat{F C E}+\widehat{C E F}=\widehat{B F E}$ d'après la somme des angles du triangle $F C E$. Comme $(F E)$ est une médiane du triangle équilatéral $D B F$, c'est aussi une bissectrice, donc $\widehat{B F E}=\frac{1}{2} \widehat{B F D}=30^{\circ}$ et notre somme est égale à $30^{\circ}$.
## Exercices communs
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-3-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 3",
"tier": "T2",
"year": "2017"
}
|
Two circles $\mathcal{C}$ and $\mathcal{C}^{\prime}$ with centers $O$ and $O^{\prime}$ are externally tangent at $B$. A common external tangent touches $\mathcal{C}$ at $M$ and $\mathcal{C}^{\prime}$ at $N$. The common tangent to $\mathcal{C}$ and $\mathcal{C}^{\prime}$ at $B$ intersects $(M N)$ at $A$. We denote $C$ as the intersection of $(O A)$ and $(B M)$, and $D$ as the intersection of $\left(O^{\prime} A\right)$ and $(B N)$.
Show that $(C D)$ is parallel to $(M N)$.
|
Since $(A M)$ and $(A B)$ are tangent to the circle with center $O$, we have $A M=A B$. We also have $O M=O B$, so $(O A)$ is the perpendicular bisector of $[M B]$, and thus $C$ is the midpoint of $[M B]$. Similarly, $D$ is the midpoint of $[B N]$, so $(C D)$ is parallel to ( $M N$ ).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Deux cercles $\mathcal{C}$ et $\mathcal{C}^{\prime}$ de centres $O$ et $O^{\prime}$ sont tangents extérieurement en $B$. Une tangente commune extérieure touche $\mathcal{C}$ en $M$ et $\mathcal{C}^{\prime}$ en $N$. La tangente commune à $\mathcal{C}$ et $\mathcal{C}^{\prime}$ en $B$ coupe $(M N)$ en $A$. On note $C$ l'intersection de $(O A)$ et $(B M)$, et $D$ l'intersection de $\left(O^{\prime} A\right)$ et $(B N)$.
Montrer que $(C D)$ est parallèle à $(M N)$.
|
Comme $(A M)$ et $(A B)$ sont tangents au cercle de centre $O$, on a $A M=A B$. On a aussi $O M=O B$, donc $(O A)$ est la médiatrice de $[M B]$, et donc $C$ est le milieu de $[M B]$. De même, $D$ est le milieu de $[B N]$, donc $(C D)$ est parallèle à ( $M N$ ).
|
{
"exam": "French_envois",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-3-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T2",
"year": "2017"
}
|
Let $ABC$ be a triangle with all three angles acute and $\Gamma$ its circumcircle. The tangent to $\Gamma$ at $A$ intersects $(BC)$ at $P$. We denote $M$ as the midpoint of $[AP]$. The line $(BM)$ intersects $\Gamma$ at $R$ and the line $(PR)$ intersects $\Gamma$ at $S$.
Show that $(AP)$ and $(CS)$ are parallel.
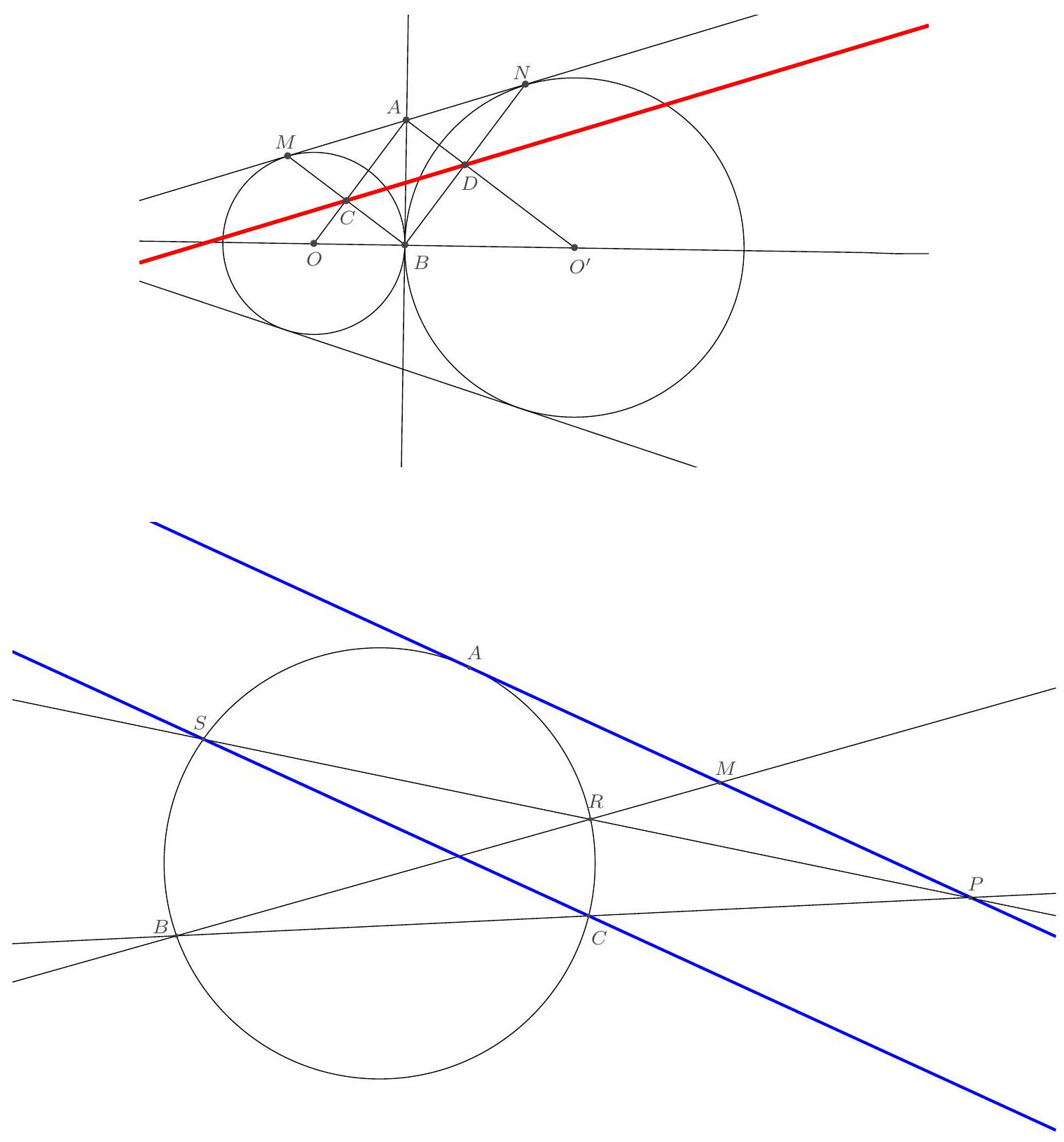
|
By writing the power of $M$ with respect to $\Gamma$ and the fact that $M$ is the midpoint of $[A P]$, we obtain
$$
M R \times M B=M A^{2}=M P^{2}
$$
The triangles $M R P$ and $M P B$ are therefore indirectly similar, so $\widehat{R P M}=\widehat{P B M}$. We thus have
$$
\begin{aligned}
\widehat{C S P} & =\widehat{C S R} \\
& =\widehat{C B R} \\
& =\widehat{P B M} \\
& =\widehat{R P M} \\
& =\widehat{S P A},
\end{aligned}
$$
where $\widehat{C S R}=\widehat{C B R}$ by the inscribed angle theorem. By alternate interior angles, the lines $(C S)$ and $(A P)$ are therefore parallel.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle dont les trois angles sont aigus et $\Gamma$ son cercle circonscrit. La tangente à $\Gamma$ en $A$ recoupe $(B C)$ en $P$. On note $M$ le milieu de $[A P]$. La droite $(B M)$ recoupe $\Gamma$ en $R$ et la droite $(P R)$ recoupe $\Gamma$ en $S$.
Montrer que $(A P)$ et $(C S)$ sont parallèles.

|
En écrivant la puissance de $M$ par rapport à $\Gamma$ puis le fait que $M$ est le milieu de $[A P]$, on obtient
$$
M R \times M B=M A^{2}=M P^{2}
$$
Les triangles $M R P$ et $M P B$ sont donc indirectement semblables, donc $\widehat{R P M}=\widehat{P B M}$. On a donc
$$
\begin{aligned}
\widehat{C S P} & =\widehat{C S R} \\
& =\widehat{C B R} \\
& =\widehat{P B M} \\
& =\widehat{R P M} \\
& =\widehat{S P A},
\end{aligned}
$$
où $\widehat{C S R}=\widehat{C B R}$ par le théorème de l'angle inscrit. Par angles alternes-internes, les droites $(C S)$ et $(A P)$ sont donc parallèles.
|
{
"exam": "French_envois",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-3-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T2",
"year": "2017"
}
|
Let $ABC$ be a triangle and $(I)$ the center of its inscribed circle. The line $(AI)$ intersects $[BC]$ at $D$. The perpendicular bisector of $[AD]$ intersects $(BI)$ at $M$ and $(CI)$ at $N$.
Show that $A, M, N$ and $I$ are concyclic.
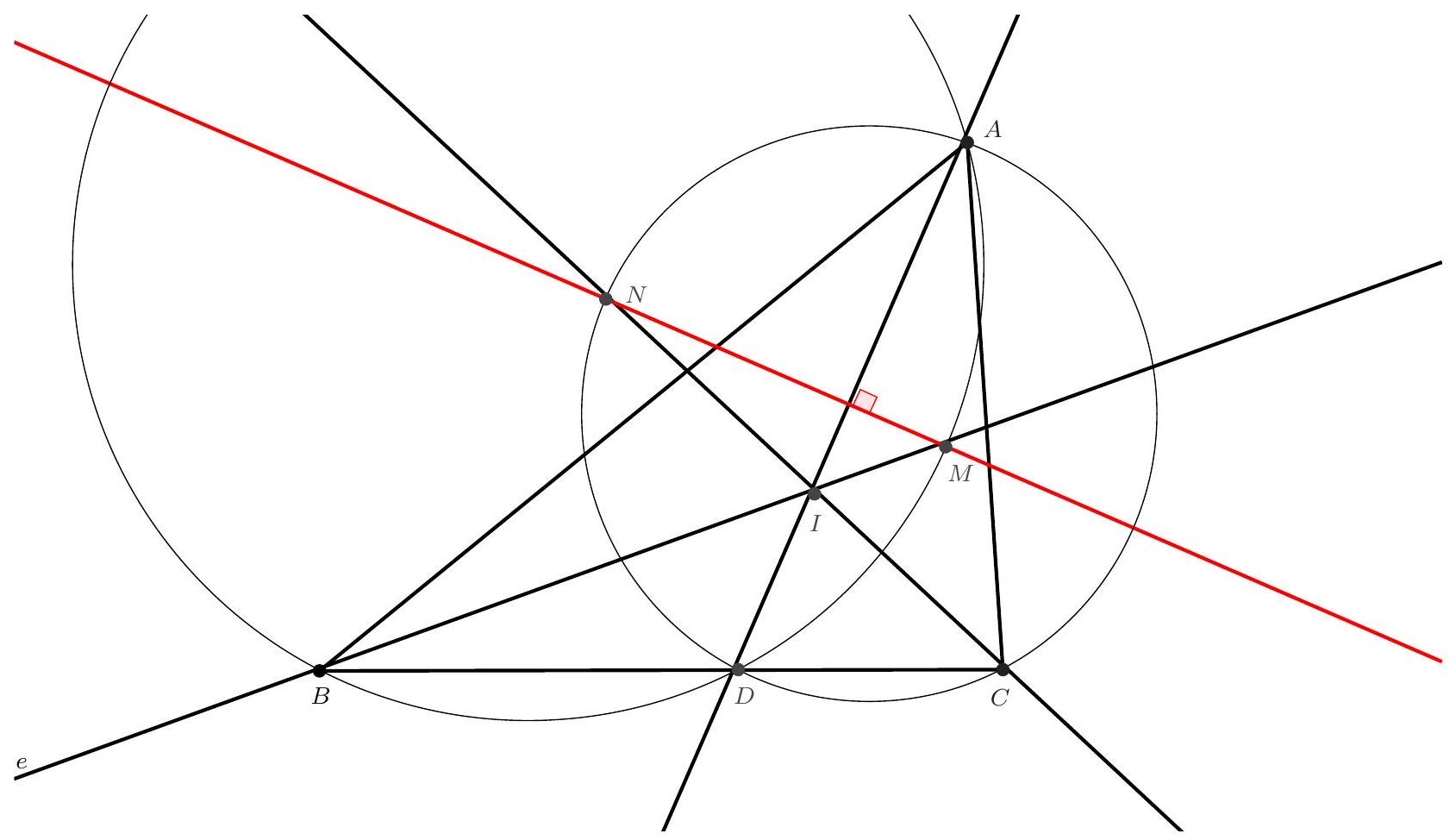
|
We start by recalling the South Pole Theorem:
Lemma 1 (South Pole Theorem). Let $ABC$ be a triangle, $\Gamma$ its circumcircle, and $I$ the center of its incircle. Let $S$ be the second intersection point of the angle bisector of $\widehat{BAC}$ with $\Gamma$. Then $SB = SC$. The point $S$ is called the South Pole of $A$ in the triangle $ABC$.
Proof of the lemma. The inscribed angle theorem in $\Gamma$ gives $\widehat{SBC} = \widehat{SAC}$ and $\widehat{SCB} = \widehat{SAB}$. Since $S$ is on the angle bisector of $\widehat{BAC}$, we have $\widehat{SAC} = \widehat{SAB}$, hence $\widehat{SBC} = \widehat{SCB}$, so $\triangle SCB$ is isosceles at $S$ and $SB = SC$.
Let's return to our exercise. Note that the South Pole of $A$ in a triangle $ABC$ lies on the angle bisector of $\widehat{BAC}$ and on the perpendicular bisector of $[BC]$, so it can be defined as the intersection of these two lines. We start by showing that $A, B, D$, and $M$ are concyclic. The point $M$ is on the perpendicular bisector of $[AD]$ and on the angle bisector of $\widehat{ABD}$. Therefore, it is the South Pole of $B$ in $\triangle ABD$, so it lies on the circumcircle of $\triangle ABD$. Similarly, the points $A, C, D$, and $N$ are concyclic. We can now do some angle chasing:
$$
\widehat{AMI} = \widehat{AMB} = \widehat{ADB} = 180^{\circ} - \widehat{ADC} = 180^{\circ} - \widehat{ANC} = 180^{\circ} - \widehat{ANI}
$$
Therefore, the points $A, I, M$, and $N$ are concyclic.
## Exercises of Group A
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle et $(I)$ le centre de son cercle inscrit. La droite ( $A I)$ recoupe $[B C]$ en $D$. La médiatrice de $[A D]$ recoupe $(B I)$ en $M$ et $(C I)$ en $N$.
Montrer que $A, M, N$ et $I$ sont cocycliques.

|
On commence par rappeler le théorème du Pôle Sud :
Lemme 1 (Théorème du Pôle Sud). Soit $A B C$ un triangle, $\Gamma$ son cercle circonscrit et $I$ le centre de son cercle inscrit. Soit $S$ le second point d'intersection de la bissectrice de $\widehat{B A C}$ avec $\Gamma$. Alors $S B=S C$. Le point $S$ est appelé Pôle Sud de $A$ dans le triangle $A B C$.
Preuve du lemme. Le théorème de l'angle inscrit dans $\Gamma$ donne $\widehat{S B C}=\widehat{S A C}$ et $\widehat{S C B}=\widehat{S A B}$. Or, comme $S$ est sur la bissectrice de $\widehat{B A C}$ on a $\widehat{S A C}=\widehat{S A B}$, d'où $\widehat{S B C}=\widehat{S C B}$, donc $S C B$ est isocèle en $S$ et $S B=S C$.
Revenons à notre exercice. Notons que le pôle Sud de $A$ dans un triangle $A B C$ est sur la bissectrice de $\widehat{B A C}$ et sur la médiatrice de $[B C]$, donc il peut être défini comme l'intersection de ces deux droites. On commence par montrer que $A, B, D$ et $M$ sont cocycliques. Le point $M$ est sur la médiatrice de $[A D]$ et sur la bissectrice de $\widehat{A B D}$. C'est donc le pôle Sud de $B$ dans $A B D$, donc il est sur le cercle circonscrit à $A B D$. De même, les points $A, C, D$ et $N$ sont cocycliques. On peut maintenant faire une chasse aux angles:
$$
\widehat{A M I}=\widehat{A M B}=\widehat{A D B}=180^{\circ}-\widehat{A D C}=180^{\circ}-\widehat{A N C}=180^{\circ}-\widehat{A N I}
$$
Les points $A, I, M$ et $N$ sont donc cocycliques.
## Exercices du groupe A
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-3-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T2",
"year": "2017"
}
|
Let $A B C$ be a triangle whose orthocenter $H$ is distinct from the vertices as well as from the center of the circumcircle $O$. We denote by $M, N, P$ the centers of the circumcircles of triangles $H B C, H C A$ and $H A B$.
Show that the lines $(A M),(B N),(C P)$ and $(O H)$ are concurrent.
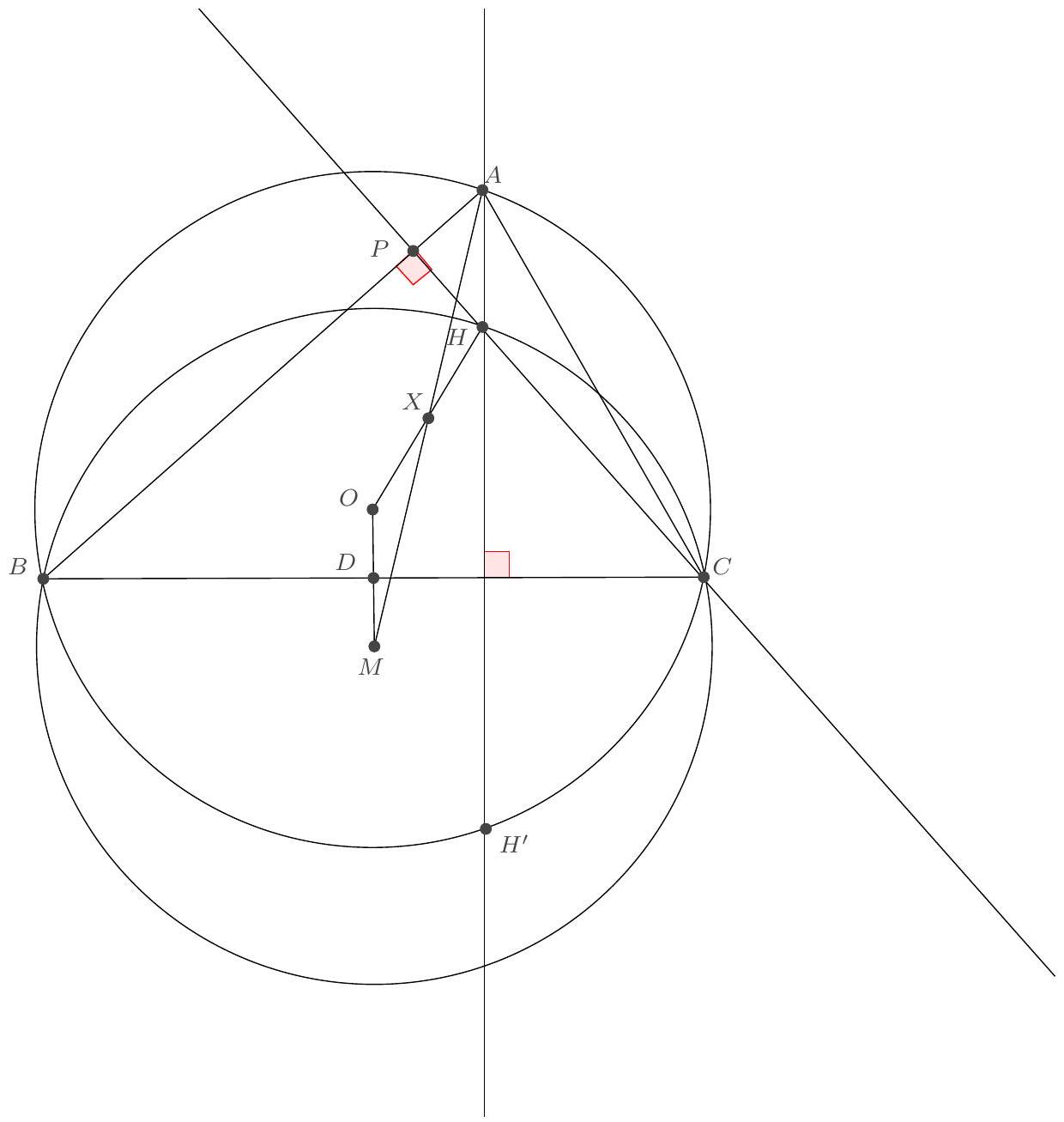
|
Let $H^{\prime}$ be the symmetric point of $H$ with respect to $(B C)$. We know that $H^{\prime}$ is on the circumcircle of $A B C$ (it is easy to verify $\widehat{B H^{\prime} C}=\widehat{B H C}=180^{\circ}-\widehat{B A C}$). The center of the circumcircle of $H^{\prime} B C$ is therefore 0. By symmetry with respect to $(B C)$, the center of the circumcircle of $B H C$ is the symmetric point of 0 with respect to $(B C)$, so $M$ is the symmetric point of $O$ with respect to $(B C)$. We will now show that $A H M O$ is a parallelogram. If this is true, then $[A M]$ and $[O H]$ intersect at their midpoints, so the midpoint of $[O H]$ is on $(A M)$ and, by the same reasoning, it is also on $(B N)$ and $(C P)$. If we denote $D$ as the midpoint of $[B C]$, then $\overrightarrow{O D}=\frac{1}{2}(\overrightarrow{O B}+\overrightarrow{O C})=\frac{1}{2}(\overrightarrow{O H}-\overrightarrow{O A})=\frac{1}{2} \overrightarrow{A H}$, so $\overrightarrow{O M}=\overrightarrow{A H}$. Using the relation $\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}=\overrightarrow{O H}$, which is equivalent to $\overrightarrow{O H}=3 \overrightarrow{O G}$ (Euler line).
We also provide another method, less quick but requiring less knowledge, to show that $A H M O$ is a parallelogram. The lines $(A H)$ and $(O M)$ are parallel, so it suffices to show that $A H=O M$. For this, we can use trigonometry. On the one hand, denoting $R$ as the radius of the circumcircle of $A B C$ and $\alpha, \beta, \gamma$ as its angles, we have
$$
O M=2 O D=2 O B \sin \widehat{O B C}=2 R \sin \left(90^{\circ}-\alpha\right)=2 R \cos \alpha
$$
On the other hand, denoting $P$ as the foot of the altitude from $C$, we have
$$
A H=\frac{A P}{\cos \widehat{P A H}}=\frac{A P}{\sin \beta}=\frac{A C \sin \widehat{A C P}}{\sin \beta}=2 R \sin \widehat{A C P}=2 R \sin \left(90^{\circ}-\alpha\right)=2 R \cos \alpha
$$
using the law of sines.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle dont l'orthocentre $H$ est distinct des sommets ainsi que du centre du cercle circonscrit $O$. On désigne par $M, N, P$ les centres des cercles circonscrits aux triangles $H B C, H C A$ et $H A B$.
Montrer que les droites $(A M),(B N),(C P)$ et $(O H)$ sont concourantes.

|
Soit $H^{\prime}$ le symétrique de $H$ par rapport à $(B C)$. On sait que $H^{\prime}$ est sur le cercle circonscrit à $A B C$ (il est facile de vérifier $\widehat{B H^{\prime} C}=\widehat{B H C}=180^{\circ}-\widehat{B A C}$ ). Le centre du cercle circonscrit à $H^{\prime} B C$ est donc 0 . Par symétrie par rapport à $(B C)$, le centre du cercle circonscrit à $B H C$ est donc le symétrique de 0 par rapport à $(B C)$, donc $M$ est le symétrique de $O$ par rapport à $(B C)$. On va maintenant montrer que $A H M O$ est un parallélogramme. Si c'est bien vrai, alors $[A M]$ et $[O H]$ se coupent en leur milieu, donc le milieu de $[O H]$ est sur $(A M)$ et, par le même raisonnement, il est aussi $\operatorname{sur}(B N)$ et $(C P)$. Si on note $D$ le milieu de $[B C]$, alors $\overrightarrow{O D}=\frac{1}{2}(\overrightarrow{O B}+\overrightarrow{O C})=\frac{1}{2}(\overrightarrow{O H}-\overrightarrow{O A})=\frac{1}{2} \overrightarrow{A H}$, donc $\overrightarrow{O M}=\overrightarrow{A H}$. En utilisant la relation $\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}=\overrightarrow{O H}$, qui est équivalente à $\overrightarrow{O H}=3 \overrightarrow{O G}$ (droite d'Euler).
On donne également une autre manière, moins rapide mais nécessitant moins de connaissances, de montrer que $A H M O$ est un parallélogramme. Les droites $(A H)$ et $(O M)$ sont parallèles, donc il suffit de montrer que $A H=O M$. Pour cela, on peut utiliser la trigonométrie. D'une part, en notant $R$ le rayon
du cercle circonscrit à $A B C$ et $\alpha, \beta, \gamma$ ses angles, on a
$$
O M=2 O D=2 O B \sin \widehat{O B C}=2 R \sin \left(90^{\circ}-\alpha\right)=2 R \cos \alpha
$$
D'autre part, en notant $P$ le pied de la hauteur issue de $C$, on a
$$
A H=\frac{A P}{\cos \widehat{P A H}}=\frac{A P}{\sin \beta}=\frac{A C \sin \widehat{A C P}}{\sin \beta}=2 R \sin \widehat{A C P}=2 R \sin \left(90^{\circ}-\alpha\right)=2 R \cos \alpha
$$
en utilisant la loi des sinus.
|
{
"exam": "French_envois",
"problem_label": "7",
"problem_match": "\nExercice 7.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-3-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 7",
"tier": "T2",
"year": "2017"
}
|
Let $ABC$ be a triangle with all three angles acute. Let $D \in [BC]$ such that $\widehat{BAC} = \widehat{ADB}$. Let $H$ be the foot of the altitude from $B$ in $ABC$. The perpendicular to $(BC)$ passing through $H$ intersects $(AD)$ at $K$. Assume that $K$ is inside the triangle $ABC$. Let $M$ be the midpoint of $[AC]$. Show that $MH = MK$.
|
Note that $\widehat{A B H}=90^{\circ}-\widehat{B A C}=90^{\circ}-\widehat{A D B}=\widehat{A K H}$. Therefore, the points $A, B, K$, $H$ are concyclic. Let $T$ be the foot of the altitude from $A$ in $A B C$. Then $\widehat{B T A}=\widehat{B H A}=90^{\circ}$, so $A, B, H$ and $T$ are concyclic, and the circle passing through these points also passes through $K$. We deduce that $\widehat{A T K}=180^{\circ}-\widehat{A H K}=\widehat{K H C}$.
We will now show that $M, K$ and $T$ are collinear. We have $(A T) \|(H K)$ because these two lines are perpendicular to $(B C)$, so $\widehat{A T K}=\widehat{K H C}=\widehat{T A C}$. But the triangle $A T C$ is right-angled at $T$ so $M A=M C=M T$ and $\widehat{T A M}=\widehat{A T M}$. We deduce that $\widehat{A T M}=\widehat{A T K}$, so $T, K$ and $M$ are collinear. Finally, $M H=M K$ because $A T \| H K$ and $M A=M T$.
|
MH = MK
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle dont les trois angles sont aigus. Soit $D \in[B C]$ tel que $\widehat{B A C}=$ $\widehat{A D B}$. Soit $H$ le pied de la hauteur issue de $B$ dans $A B C$. La perpendiculaire à $(B C)$ passant par $H$ coupe $(A D)$ en $K$. On suppose que $K$ est à l'intérieur du triangle $A B C$. Soit $M$ le milieu de $[A C]$. Montrer que $M H=M K$.
|
Notons que $\widehat{A B H}=90^{\circ}-\widehat{B A C}=90^{\circ}-\widehat{A D B}=\widehat{A K H}$. Les points $A, B, K$, $H$ sont donc cocycliques. Soit $T$ le pied de la hauteur issue de $A$ dans $A B C$. Alors $\widehat{B T A}=\widehat{B H A}=90^{\circ}$ donc $A, B, H$ et $T$ sont cocyliques et le cercle qui passe par ces points passe aussi par $K$. On en déduit $\widehat{A T K}=180^{\circ}-\widehat{A H K}=\widehat{K H C}$.
On va maintenant montrer que $M, K$ et $T$ sont alignés. On a $(A T) \|(H K)$ car ces deux droites sont perpendiculaires à $(B C)$, donc $\widehat{A T K}=\widehat{K H C}=\widehat{T A C}$. Mais le triangle $A T C$ est rectangle en $T$ donc $M A=M C=M T$ et $\widehat{T A M}=\widehat{A T M}$. On en déduit $\widehat{A T M}=\widehat{A T K}$ donc $T, K$ et $M$ sont alignés. Enfin, $M H=M K$ parce que $A T \| H K$ et $M A=M T$.
|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "\nExercice 8.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-3-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 8",
"tier": "T2",
"year": "2017"
}
|
Let ABC be a triangle with orthocenter H. Let $\left(d_{1}\right)$ and $\left(d_{2}\right)$ be two perpendicular lines intersecting at $H$. Let $A_{1}$ (respectively $B_{1}, C_{1}$) be the intersection of $\left(d_{1}\right)$ with $(B C)$ (respectively $(C A), (A B)$). Let $A_{2}$ (respectively $B_{2}, C_{2}$) be the intersection of $\left(d_{2}\right)$ with $(B C)$ (respectively $(C A)$, $(A B)$). Let $A_{3}, B_{3}, C_{3}$ be points in the plane such that $A_{1} A_{2} A_{3}, B_{1} B_{2} B_{3}, C_{1} C_{2} C_{3}$ are directly similar triangles.
Show that $A_{3}, B_{3}, C_{3}$ are collinear.
|
We provide a proof with direct similarities. There are other proofs, a bit shorter, which use complex numbers.
First, let us recall the following result:
Lemma 2. Let $ABC$ be a triangle, $\Gamma$ its circumcircle, and $H$ its orthocenter. Then the symmetrics $H_{A}, H_{B}$, and $H_{C}$ of $H$ with respect to $(BC), (CA)$, and $(AB)$ belong to $\Gamma$.
Proof. Let $H_{A}^{\prime}$ be the intersection of $AH$ and $\Gamma$. By the inscribed angle theorem, we have:
$$
\begin{aligned}
\widehat{H_{A}^{\prime} B C} & =\widehat{H_{A}^{\prime} A C} \\
& =90-\widehat{B C A} \\
& =\widehat{H B C}
\end{aligned}
$$
Thus, $(H_{A}^{\prime} B)$ and $(HB)$ are symmetric with respect to $(BC)$. We deduce that $H_{A}^{\prime}=H_{A} \in \Gamma$. Similarly, $H_{B}, H_{C} \in \Gamma$.
Let us resume the notations of the exercise and introduce $H_{A}, H_{B}$, and $H_{C}$ as in the previous lemma.
Lemma 3. Let $S$ be the intersection of $(A_{1} H_{A})$ and $(B_{1} H_{B})$. Then $S \in \Gamma$.
Proof. We denote by $\mathcal{S}_{yz}$ the symmetry with axis $(YZ)$. Then
$$
\begin{aligned}
\mathcal{S}_{AC}\left(\mathcal{S}_{BC}\left(H_{A} A_{1}\right)\right) & =\mathcal{S}_{AC}\left(A_{1} H\right) \text { since } H_{A} \text { and } H \text { are symmetric with respect to }(BC) \\
& =\mathcal{S}_{AC}\left(B_{1} H\right) \\
& =\left(H_{B} B_{1}\right) \text { since } H \text { and } H_{B} \text { are symmetric with respect to }(AC) .
\end{aligned}
$$
Let $(XY, ZW)$ denote the angle formed by the lines $XY$ and $ZW$. From Proposition 1, we deduce that $(H_{A} A_{1})$ and $(H_{B} B_{1})$ are images of each other by the rotation of angle $2 \cdot(CB, CA)$ centered at $C: (S H_{A}, S H_{B})=2 \cdot(CB, CA)$. Thus,
$$
\begin{aligned}
\left(S H_{A}, S H_{B}\right) & \equiv 2 \cdot(CB, CA) \\
& \equiv(CB, CA)+(CB, CH)+(CH, CA) \\
& \equiv(CB, CA)+\left(CH_{A}, CB\right)+\frac{\pi}{2}-(AC, AB) \\
& \equiv\left(CH_{A}, CA\right)+(BA, BH) \\
& \equiv\left(BH_{A}, BA\right)+\left(BA, BH_{B}\right) \\
& \equiv\left(BH_{A}, BH_{B}\right)[\pi]
\end{aligned}
$$
Thus, $S \in \Gamma$.
Lemma 4. The circles with diameters $[A_{1} A_{2}],[B_{1} B_{2}],[C_{1} C_{2}]$ are concurrent at a point $M$ belonging to $\Gamma$.
Proof. Let $M^{\prime}$ be the intersection point of the circles with diameters $[A_{1} A_{2}]$ (which therefore pass through $H$ and $H_{A}$) and $[B_{1} B_{2}]$ (which therefore pass through $H$ and $H_{B}$) different from $H$. We have:
$$
\begin{aligned}
\left(M^{\prime} H_{A}, M^{\prime} H_{B}\right) & \equiv\left(M^{\prime} H_{A}, M^{\prime} H\right)+\left(M^{\prime} H, M^{\prime} H_{B}\right) \\
& \equiv\left(A_{1} H_{A}, A_{1} H\right)+\left(B_{1} H, B_{1} H_{B}\right) \\
& \equiv 2 \cdot\left(A_{1} B, A_{1} H\right)+2 \cdot\left(B_{1} H, B_{1} A\right) \\
& \equiv 2 \cdot\left(\frac{\pi}{2}+\left(H H_{A}, H A_{1}\right)\right)+2 \cdot\left(H B_{2}, H H_{B}\right) \\
& \equiv 2 \cdot\left(H H_{A}, H A_{1}\right)+2 \cdot \frac{\pi}{2}+2 \cdot\left(H B_{2}, H H_{B}\right) \\
& \equiv 2 \cdot\left(H H_{A}, H H_{B}\right) \\
& \equiv 2 \cdot(CB, CA) \\
& \equiv\left(S H_{A}, S H_{B}\right)[\pi] .
\end{aligned}
$$
Thus, $M^{\prime} \in \Gamma$ by the inscribed angle theorem. Similarly, we show that the intersection of the circles with diameters $[B_{1} B_{2}]$ and $[C_{1} C_{2}]$ is a point $M^{\prime \prime} \in \Gamma$. Since the intersection of the circle with diameter $[B_{1} B_{2}]$ and $\Gamma$ is unique, we deduce that $M^{\prime}=M^{\prime \prime}=M$, that is, the four circles are concurrent at $M$.
We can now complete the exercise:
$$
\begin{aligned}
\left(C_{1} M, C_{1} C_{2}\right) & \equiv\left(H M, H C_{2}\right) \text { since } M, C_{1}, H, C_{2} \text { are concyclic } \\
& \equiv\left(H M, H B_{2}\right) \\
& \equiv\left(B_{1} M, B_{1} B_{2}\right)[\pi] \text { since } M, B_{1}, H, B_{2} \text { are concyclic. }
\end{aligned}
$$
Similarly, we prove that $\left(B_{1} M, B_{1} B_{2}\right) \equiv\left(C_{1} M, C_{1} C_{2}\right)$. Therefore, since $\left(M A_{1}, M A_{2}\right) \equiv$ $\left(M B_{1}, M C_{2}\right) \equiv\left(M C_{1}, M C_{2}\right) \equiv \frac{\pi}{2} \quad[\pi]$, we obtain that $M A_{1} A_{2}, M B_{1} B_{2}$, and $M C_{1} C_{2}$ are directly similar, which we will denote as $M A_{1} A_{2} \sim M B_{1} B_{2} \sim M C_{1} C_{2}$. Furthermore, $A_{1} A_{2} A_{3} \sim$ $B_{1} B_{2} B_{3} \sim C_{1} C_{2} C_{3}$ by hypothesis. Therefore, $M A_{1} A_{2} A_{3} \sim M B_{1} B_{2} B_{3} \sim M C_{1} C_{2} C_{3}$.
The use of direct similarities then allows us to conclude directly: a direct similarity $\mathcal{S}$ centered at $M$ sends $A_{1}$ to $A_{3}$, and also $B_{1}$ to $B_{3}$ and $C_{1}$ to $C_{3}$. Since $A_{1}, B_{1}$, and $C_{1}$ are collinear, we deduce that $A_{3}, B_{3}$, and $C_{3}$ are collinear as well.
$\mathcal{F i n}$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit ABC un triangle d'orthocentre H. Soient $\left(d_{1}\right)$ et $\left(d_{2}\right)$ deux droites perpendiculaires se coupant en $H$. Soit $A_{1}$ (respectivement $B_{1}, C_{1}$ ) l'intersection de $\left(d_{1}\right)$ avec $(B C)$ (respectivement $(C A),(A B)$ ). Soit $A_{2}$ (respectivement $B_{2}, C_{2}$ ) l'intersection de $\left(d_{2}\right)$ avec $(B C)$ (respectivement $(C A)$, $(A B)$ ). Soient $A_{3}, B_{3}, C_{3}$ des points dans le plan tels que $A_{1} A_{2} A_{3}, B_{1} B_{2} B_{3}, C_{1} C_{2} C_{3}$ soient des triangles directement semblables.
Montrer que $A_{3}, B_{3}, C_{3}$ sont alignés.

|
Nous donnons une preuve avec des similitudes directes. Il existe d'autres preuves, un peu plus courtes, qui utilisent des nombres complexes.
Rappelons tout d'abord le résultat suivant :
Lemme 2. Soit $A B C$ un triangle, $\Gamma$ son cercle circonscrit et $H$ son orthocentre. Alors les symétriques $H_{A}, H_{B}$ et $H_{C}$ de H par rapport à $(\mathrm{BC}),(\mathrm{CA})$ et $(\mathrm{AB})$ appartiennent à $\Gamma$.
Proof. Soit $H_{A}^{\prime}$ l'intersection de $A H$ et $\Gamma$. Par le théorème de l'angle inscrit, on a :
$$
\begin{aligned}
\widehat{H_{A}^{\prime} B C} & =\widehat{H_{A}^{\prime} A C} \\
& =90-\widehat{B C A} \\
& =\widehat{H B C}
\end{aligned}
$$
Ainsi, $\left(H_{A}^{\prime} B\right)$ et $(H B)$ sont symétriques par rapport à $(B C)$. On en déduit que $H_{A}^{\prime}=H_{A} \in \Gamma$. De même $H_{B}, H_{C} \in \Gamma$.
Reprenons les notations de l'exercice et introduisons $H_{A}, H_{B}$ et $H_{C}$ comme dans le lemme précédent.
Lemme 3. Soit S l'intersection de $\left(A_{1} H_{A}\right)$ et de $\left(B_{1} H_{B}\right)$. Alors $S \in \Gamma$.
Proof. On note $\mathcal{S}_{y z}$ la symétrie d'axe $(Y Z)$. Alors
$$
\begin{aligned}
\mathcal{S}_{\mathcal{A C}}\left(\mathcal{S}_{\mathcal{B C}}\left(H_{A} A_{1}\right)\right) & =\mathcal{S}_{\mathcal{A C}}\left(A_{1} H\right) \text { car } H_{A} \text { et } H \text { sont symétriques par rapport à }(B C) \\
& =\mathcal{S}_{\mathcal{A C}}\left(B_{1} H\right) \\
& =\left(H_{B} B_{1}\right) \text { car } H \text { et } H_{B} \text { sont symétriques par rapport à }(A C) .
\end{aligned}
$$
Notons ( $\mathrm{XY}, \mathrm{ZW}$ ) l'angle de droite formé par les droites XY et ZW . De la proposition 1, on déduit que $\left(H_{A} A_{1}\right)$ et $\left(H_{B} B_{1}\right)$ sont images l'une de l'autre par la rotation d'angle $2 \cdot(C B, C A)$ de centre $C:\left(S H_{A}, S H_{B}\right)=2 \cdot(C B, C A)$. Ainsi,
$$
\begin{aligned}
\left(S H_{A}, S H_{B}\right) & \equiv 2 \cdot(C B, C A) \\
& \equiv(C B, C A)+(C B, C H)+(C H, C A) \\
& \equiv(C B, C A)+\left(C H_{A}, C B\right)+\frac{\pi}{2}-(A C, A B) \\
& \equiv\left(C H_{A}, C A\right)+(B A, B H) \\
& \equiv\left(B H_{A}, B A\right)+\left(B A, B H_{B}\right) \\
& \equiv\left(B H_{A}, B H_{B}\right)[\pi]
\end{aligned}
$$
Ainsi, $S \in \Gamma$.
Lemme 4. Les cercles de diamètre $\left[A_{1} A_{2}\right],\left[B_{1} B_{2}\right],\left[C_{1} C_{2}\right]$ sont concourants en un point $M$ appartenant à $\Gamma$.
Proof. Soit $M^{\prime}$ le point d'intersection des cercles de diamètre $\left[A_{1} A_{2}\right]$ (passant donc par $H$ et $H_{A}$ ) et $\left[B_{1} B_{2}\right]$ (passant donc par $H$ et $H_{B}$ ) différent de $H$. On a :
$$
\begin{aligned}
\left(M^{\prime} H_{A}, M^{\prime} H_{B}\right) & \equiv\left(M^{\prime} H_{A}, M^{\prime} H\right)+\left(M^{\prime} H, M^{\prime} H_{B}\right) \\
& \equiv\left(A_{1} H_{A}, A_{1} H\right)+\left(B_{1} H, B_{1} H_{B}\right) \\
& \equiv 2 \cdot\left(A_{1} B, A_{1} H\right)+2 \cdot\left(B_{1} H, B_{1} A\right) \\
& \equiv 2 \cdot\left(\frac{\pi}{2}+\left(H H_{A}, H A_{1}\right)\right)+2 \cdot\left(H B_{2}, H H_{B}\right) \\
& \equiv 2 \cdot\left(H H_{A}, H A_{1}\right)+2 \cdot \frac{\pi}{2}+2 \cdot\left(H B_{2}, H H_{B}\right) \\
& \equiv 2 \cdot\left(H H_{A}, H H_{B}\right) \\
& \equiv 2 \cdot(C B, C A) \\
& \equiv\left(S H_{A}, S H_{B}\right)[\pi] .
\end{aligned}
$$
Ainsi, $M^{\prime} \in \Gamma$ par le théorème de l'angle inscrit. De la même façon, on montre que l'intersection des cercles de diamètre $\left[B_{1} B_{2}\right]$ et $\left[C_{1} C_{2}\right]$ est un point $M^{\prime \prime} \in \Gamma$. Comme l'intersection du cercle de diamètre $\left[B_{1} B_{2}\right]$ et de $\Gamma$ est unique, on en déduit que $M^{\prime}=M^{\prime \prime}=M$, c'est-à-dire que les quatre cercles sont concourants en $M$.
Nous pouvouns maintenant terminer l'exercice :
$$
\begin{aligned}
\left(C_{1} M, C_{1} C_{2}\right) & \equiv\left(H M, H C_{2}\right) \text { car } M, C_{1}, H, C_{2} \text { sont cocycliques } \\
& \equiv\left(H M, H B_{2}\right) \\
& \equiv\left(B_{1} M, B_{1} B_{2}\right)[\pi] \text { car } M, B_{1}, H, B_{2} \text { cocycliques. }
\end{aligned}
$$
De la même façon, on prouve que $\left(B_{1} M, B_{1} B_{2}\right) \equiv\left(C_{1} M, C_{1} C_{2}\right)$. Donc, comme $\left(M A_{1}, M A_{2}\right) \equiv$ $\left(M B_{1}, M C_{2}\right) \equiv\left(M C_{1}, M C_{2}\right) \equiv \frac{\pi}{2} \quad[\pi]$, on obtient que $M A_{1} A_{2}, M B_{1} B_{2}$ et $M C_{1} C_{2}$ sont directement semblables, ce que l'on notera désormais $M A_{1} A_{2} \sim M B_{1} B_{2} \sim M C_{1} C_{2}$. En outre, $A_{1} A_{2} A_{3} \sim$ $B_{1} B_{2} B_{3} \sim C_{1} C_{2} C_{3}$ par hypothèse. Donc $M A_{1} A_{2} A_{3} \sim M B_{1} B_{2} B_{3} \sim M C_{1} C_{2} C_{3}$.
L'utilisation de similitudes directes permet alors de conclure directement : une similitude directe $\mathcal{S}$ de centre $M$ envoie $A_{1}$ sur $A_{3}$, et également $B_{1}$ sur $B_{3}$ et $C_{1}$ sur $C_{3}$. Comme $A_{1}, B_{1}$ et $C_{1}$ sont alignés, on en déduit que $A_{3}, B_{3}$ et $C_{3}$ le sont également.
$\mathcal{F i n}$
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-3-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 9",
"tier": "T2",
"year": "2017"
}
|
We place four points in the plane, with no three points ever aligned, and connect each pair of points. We color each of the six segments obtained either blue or red. Show that there exist two different triangles that are colored in the same way. For example, in the following example (where red is replaced by thick and blue by dashed), ABD and ACD are colored in the same way.
|
There are four different ways to color a triangle (with zero, one, two, or three red segments) and there are four triangles drawn. Therefore, either two triangles are colored the same way, or all the triangles are different. Let's show that the second case is not possible. Indeed, two different triangles always share two vertices in common, and thus one side in common. However, if all the triangles are different, there is one triangle that is entirely blue, and another that is entirely red. Their common side would then be both red and blue, which is impossible. Ultimately, we do have two triangles colored the same way.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
On place quatre points dans le plan, trois jamais alignés, et on les relie tous deux à deux. On colorie chacun des six segments obtenus soit en bleu soit en rouge. Montrer qu'il existe deux triangles différents coloriés de la même façon. Par exemple, dans l'exemple suivant (où l'on a remplacé rouge par épais et bleu par pointillé), ABD et ACD sont coloriés de la même façon.

|
Il y a quatre façons différentes de colorier un triangle (avec zéro, un, deux ou trois segments rouges) et il y a quatre triangles dessinés. Donc, soit deux triangles sont coloriés de la même façon, soit tous les triangles sont différents. Montrons que le deuxième cas n'est pas possible. En effet, deux triangles différents partagent toujours deux sommets en commun, donc un côté en commun. Or, si tous les triangles sont différents, il y a un triangle entièrement bleu, et un autre entièrement rouge. Leur côté commun serait alors à la fois rouge et bleu, impossible. Finalement, on a bien deux triangles coloriés de la même façon.
|
{
"exam": "French_envois",
"problem_label": "1",
"problem_match": "## Exercice 1.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-4-solutions.jsonl",
"solution_match": "## Solution de l'exercice 1",
"tier": "T2",
"year": "2017"
}
|
For which $n \geqslant 1$ can one fill an $n \times n$ chessboard with pieces of the form
without them overlapping? (Rotations are allowed).
|
Suppose we have managed to cover an $\mathrm{n} \times \mathrm{n}$ chessboard. A piece covers 4 squares. Therefore, clearly 4 divides $n^{2}$, so $n$ is even. Now, each piece covers either three black squares and one white square of the chessboard, or the inverse. However, since $n$ is even, there are as many black squares as white squares. Therefore, there must be as many pieces covering three black squares as there are pieces covering three white squares. Consequently, there is an even number of pieces, hence 8 divides $n^{2}$. Therefore, if we manage to cover an $n \times n$ chessboard, then 4 divides $n$.
Conversely, if 4 divides $n$, we can easily cover the chessboard with $4 \times 4$ blocks.
|
4 \text{ divides } n
|
Incomplete
|
Yes
|
math-word-problem
|
Combinatorics
|
Pour quel $n \geqslant 1$ peut-on remplir un échiquier $n \times n$ avec des pièces de la forme

sans qu'elles se recouvrent? (Les rotations sont autorisées).
|
Supposons que nous avons réussi à recouvrir un échiquier $\mathrm{n} \times \mathrm{n}$. Une pièce recouvre 4 cases. Donc clairement 4 divise $n^{2}$ donc $n$ est pair. Maintenant, chaque pièce recouvre soit trois cases noires et une case blanche de l'échiquier, soit l'inverse. Or, comme n est pair, il y a autant de cases noires que de cases blanches. Il faut donc autant de pièces recouvrant trois cases noires que de pièces recouvrant trois cases blanches. Par conséquent, il y a un nombre pair de pièces, d'où 8 divise $n^{2}$. Donc, si l'on parvient à couvrir un échiquier $n \times n$, alors 4 divise n .
Réciproquement, si 4 divise $n$, on peut facilement recouvrir l'échiquier avec des blocs $4 \times 4$.

|
{
"exam": "French_envois",
"problem_label": "2",
"problem_match": "## Exercice 2.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-4-solutions.jsonl",
"solution_match": "## Solution de l'exercice 2",
"tier": "T2",
"year": "2017"
}
|
Let $A_{1}, A_{2}, \ldots, A_{m}$ be distinct subsets of $\{1,2, \ldots, n\}$ such that for all $1 \leqslant$ $\mathbf{i}, \mathbf{j} \leqslant \mathrm{n}$ we have $A_{i} \cap A_{j} \neq \emptyset$. Show $m \leqslant 2^{n-1}$.
|
Consider all pairs of sets $\left\{A, A^{c}\right\}$ for all $A \subset\{1,2, \ldots, n\}$. Since there are $2^{n-1}$ such pairs, if $m>2^{n-1}$ there would be $1 \leqslant i<j \leqslant m$ such that $A_{i}, A_{j} \in\left\{A, A^{c}\right\}$ for some $A \subset\{1,2, \ldots, n\}$. Therefore, $A_{i} \cap A_{j}=\emptyset$ which contradicts our assumption.
## Common Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soient $A_{1}, A_{2}, \ldots, A_{m}$ des sous-ensembles distincts de $\{1,2, \ldots, n\}$ tels que pour tout $1 \leqslant$ $\boldsymbol{i}, \mathbf{j} \leqslant \mathrm{n}$ on a $A_{i} \cap A_{j} \neq \emptyset$. Montrer $m \leqslant 2^{n-1}$.
|
Considérons toutes les paires d'ensembles $\left\{A, A^{c}\right\}$ pour tout $A \subset\{1,2, \ldots, n\}$. Puisqu'il y a $2^{n-1}$ telles paires, si $m>2^{n-1}$ on aurait $1 \leqslant i<j \leqslant m$ tels que $A_{i}, A_{j} \in\left\{A, A^{c}\right\}$ pour un $A \subset\{1,2, \ldots, n\}$. Donc $A_{i} \cap A_{j}=\emptyset$ ce qui contredit notre hypothèse.
## Exercices communs
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-4-solutions.jsonl",
"solution_match": "## Solution de l'exercice 3",
"tier": "T2",
"year": "2017"
}
|
How many $3 \times 3$ tables can be constructed by filling them with the numbers from 1 to 3 such that no number appears twice in the same row or column? And how many $4 \times 4$ tables with the numbers from 1 to 4?
|
We present below a complete proof of the exercise. It was not necessary to be so precise to get all the points, but it is good, when counting objects, to have an idea of the proof to show that we have not forgotten anything or counted anything twice.
We have six ways to fill the first row (three ways to place the 1, then two to place the 2, and one way to place the 3). Then, we have two ways to fill the column already containing a 1 (which makes twelve in total). We end up with, for example, the table
$$
\left[\begin{array}{lll}
2 & 1 & 3 \\
& 2 & A \\
& 3 &
\end{array}\right] .
$$
We realize that there is only one way to fill the cell $A$, that is, the one in the row containing a 2 and the column containing a 3. Then we complete the table in the only possible way.
Therefore, there are twelve ways to fill a $3 \times 3$ table as described in the statement.
For $4 \times 4$ tables, it is roughly the same idea. We have twenty-four ways to fill the first row and six ways to fill the column containing a 1. We obtain a table similar to
$$
\left[\begin{array}{cccc}
2 & 1 & 4 & 3 \\
& 4 & & \\
A_{3,2} & 3 & & \\
& 2 & &
\end{array}\right] .
$$
Now, let $A_{k, l}, k, l \in\{2,3,4\}$, be the cell in the row containing $k$ and the column containing $l$. We see that there are two possibilities for filling $A_{3,2}$:
- if we fill $A_{3,2}$ with 1, we will have only one possibility for $A_{4,2}$, and then, in order, $A_{2,2}, A_{3,4}, A_{3,3}, A_{4,4}, A_{4,3}, A_{2,4}$, and $A_{2,3}$. We obtain the unique table
$$
\left[\begin{array}{llll}
2 & 1 & 4 & 3 \\
3 & 4 & 1 & 2 \\
1 & 3 & 2 & 4 \\
4 & 2 & 3 & 1
\end{array}\right]
$$
- if we fill $A_{3,2}$ with 4, we have two possibilities again:
* we fill $A_{4,2}$ with 1 and then fill the other cells in the only possible way.
$$
\left[\begin{array}{llll}
2 & 1 & 4 & 3 \\
1 & 4 & 3 & 2 \\
4 & 3 & 2 & 1 \\
3 & 2 & 1 & 4
\end{array}\right] .
$$
* we fill $A_{4,2}$ with 3 and then fill $A_{2,2}, A_{2,4}$, and $A_{2,3}$ in the only possible way. There remain two ways to fill the obtained table.
$$
\left[\begin{array}{llll}
2 & 1 & 4 & 3 \\
3 & 4 & & \\
4 & 3 & & \\
1 & 2 & 3 & 4
\end{array}\right] .
$$
Note that all the statements are always true, not just in the example. Therefore, no matter how we fill the first row and the column containing a 1, there are always four ways to fill the table. There are thus $24 \cdot 6 \cdot 4=576$ ways to fill a $4 \times 4$ table according to the statement.
|
576
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Combien de tableaux $3 \times 3$ peut-on construire en les remplissant avec les nombres de 1 à 3 tels qu'il n'y ait pas deux fois le même nombre dans une ligne ni dans une colonne. Et de tableaux $4 \times 4$ avec les nombres de 1 à 4 ?
|
Nous présentons ci-dessous une preuve complète de l'exercice. Il n'était pas nécessaire d'être aussi précis pour avoir tous les points mais il est bon, lorsque que l'on compte des objets, d'avoir une idée de la preuve pour démontrer que nous n'avons rien oublié ni compté en double.
Nous avons six façons de remplir la première rangée (trois façons de placer le 1 puis deux de placer le 2 puis une seule possibilité pour placer le 3). Ensuite, il nous reste deux façons de remplir la colonne contenant déjà un 1 (ce qui fait douze en tout). On se retrouve avec, par exemple, le tableau
$$
\left[\begin{array}{lll}
2 & 1 & 3 \\
& 2 & A \\
& 3 &
\end{array}\right] .
$$
On se rend compte qu'il n'y a qu'une seule façon de remplir la case $A$, c'est-à-dire celle qui est dans la rangée contenant un 2 et dans la colonne contenant un 3 . Puis on complète le tableau de la seule manière possible.
On a donc douze façons de remplir un tableau $3 \times 3$ comme dans l'énoncé.
Pour les tableaux $4 \times 4$, c'est à peu près la même idée. Nous avons vingt-quatre façons de remplir la première rangée et six façons de remplir la colonne contenant un 1 . Nous obtenons un tableau ressemblant à
$$
\left[\begin{array}{cccc}
2 & 1 & 4 & 3 \\
& 4 & & \\
A_{3,2} & 3 & & \\
& 2 & &
\end{array}\right] .
$$
Maintenant, notons $A_{k, l}, k, l \in\{2,3,4\}$, la case dans la rangée contenant $k$ et la colonne contenant l. Nous voyons qu'il y a deux possibilités pour remplir $A_{3,2}$ :
- si l'on remplit $A_{3,2}$ avec 1 , nous n'aurons plus qu'une seule possibilité pour $A_{4,2}$ puis, dans l'ordre, $A_{2,2}, A_{3,4}, A_{3,3}, A_{4,4}, A_{4,3}, A_{2,4}$ et $A_{2,3}$. On obtient l'unique tableau
$$
\left[\begin{array}{llll}
2 & 1 & 4 & 3 \\
3 & 4 & 1 & 2 \\
1 & 3 & 2 & 4 \\
4 & 2 & 3 & 1
\end{array}\right]
$$
- si l'on remplit $A_{3,2}$ avec 4 nous avons de nouveau deux possibilités:
* on remplit $A_{4,2}$ avec 1 puis on remplit les autres cases de la seule façon possible.
$$
\left[\begin{array}{llll}
2 & 1 & 4 & 3 \\
1 & 4 & 3 & 2 \\
4 & 3 & 2 & 1 \\
3 & 2 & 1 & 4
\end{array}\right] .
$$
* on remplit $A_{4,2}$ avec 3 puis on remplit $A_{2,2}, A_{2,4}$ et $A_{2,3}$ de la seule façon possible. Il reste deux façons de remplir le tableau obtenu.
$$
\left[\begin{array}{llll}
2 & 1 & 4 & 3 \\
3 & 4 & & \\
4 & 3 & & \\
1 & 2 & 3 & 4
\end{array}\right] .
$$
Remarque que toutes les affirmations sont toujours vraies, pas seulement dans l'exemple. Donc, quelque soit la façon de remplir la première rangée et la colonne contenant un 1, il reste toujours quatre façons de remplir le tableau. Il y a donc en tout $24 \cdot 6 \cdot 4=576$ façons de remplir un tableau $4 \times 4$ selon l'énoncé.
|
{
"exam": "French_envois",
"problem_label": "4",
"problem_match": "## Exercice 4.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-4-solutions.jsonl",
"solution_match": "## Solution de l'exercice 4",
"tier": "T2",
"year": "2017"
}
|
Can the numbers $1,1,2,2, \ldots, 50,50$ be arranged such that, for all $1 \leqslant k \leqslant 50$, there are exactly $k$ elements between the two numbers $k$.
|
The answer is no. Suppose, for the sake of contradiction, that it is possible. For all $1 \leqslant k \leqslant 50$, let $a_{k}$ be an integer such that $a_{k}$ and $a_{k}+k+1$ are the positions of the two $k$. Clearly, we have
$$
\sum_{k=1}^{50}\left(a_{k}+a_{k}+k+1\right)=1+2+\ldots+100
$$
By looking at the previous equality modulo 2, we must have $51 \times 26-1 \equiv 50 \times 101(\bmod 2)$, which is false.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Peut-on arranger les nombres $1,1,2,2, \ldots, 50,50$ tels que, pour tout $1 \leqslant k \leqslant 50$, entre les deux nombres $k$ il y ait exactement $k$ éléments.
|
La réponse est non. Supposons, par l'absurde, qu'on le peut. Pour tout $1 \leqslant k \leqslant 50$, soit $a_{k}$ un entier tel que $a_{k}$ et $a_{k}+k+1$ sont les positions des deux $k$. Évidemment, on a
$$
\sum_{k=1}^{50}\left(a_{k}+a_{k}+k+1\right)=1+2+\ldots+100
$$
En regardant l'égalité précédente modulos 2 , on doit avoir $51 \times 26-1 \equiv 50 \times 101(\bmod 2)$ ce qui est faux.
|
{
"exam": "French_envois",
"problem_label": "5",
"problem_match": "## Exercice 5.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-4-solutions.jsonl",
"solution_match": "## Solution de l'exercice 5",
"tier": "T2",
"year": "2017"
}
|
Let $n \geqslant 2$ be an integer and $X$ a set with $n$ elements. Show that the number of functions $f: X \rightarrow X$ such that $f \circ f$ is a constant function is equal to
$$
n \sum_{i=1}^{n-1}\binom{n-1}{i} i^{n-i-1}
$$
|
Let $\mathrm{f}: \mathrm{X} \rightarrow \mathrm{X}$ such that f o $\mathrm{f}=\mathrm{c}$ for a $\mathrm{c} \in X$. First, we have $\mathrm{f}(\mathrm{c})=\mathrm{c}$ because
$$
f \circ f(c)=c \Rightarrow f \circ f \circ f(c)=f(c),
$$
and according to the definition $\mathrm{f} \circ \mathrm{f} \circ \mathrm{f}(\mathrm{c})=\mathrm{f} \circ \mathrm{f}(\mathrm{f}(\mathrm{c}))=\mathrm{c}$, which gives us $\mathrm{f}(\mathrm{c})=\mathrm{c}$. Let's define the set
$$
A=\{x \in X \mid f(x)=c\}
$$
We have shown that it contains $c$. According to the definition, we have $f(x) \in A \backslash\{c\}$ for all $x \in A^{c}$ where $A^{c}$ is the complement of $A$.
Therefore, to determine all functions $f: X \rightarrow X$ such that $f \circ f$ is constant, we must first choose a $c \in X$ ( $n$ ways to do this) then a subset $A \subset X$ containing $c\left(\binom{n-1}{i}\right.$ ways to do this if $|A|=i+1)$ and then choose the values $f(x)$ for each $x \in A^{c}$ in $A \backslash\{c\}$ ( $i^{n-i-1}$ ways to do this). Thus, the number of such functions will be
$$
n \sum_{i=1}^{n-1}\binom{n-1}{i} i^{n-i-1}
$$
|
n \sum_{i=1}^{n-1}\binom{n-1}{i} i^{n-i-1}
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soient $n \geqslant 2$ un entier et $X$ un ensemble à $n$ éléments. Montrer que le nombre de fonctions $f: X \rightarrow X$ telles que $f \circ f$ soit une fonction constante est égale à
$$
n \sum_{i=1}^{n-1}\binom{n-1}{i} i^{n-i-1}
$$
|
Soit $\mathrm{f}: \mathrm{X} \rightarrow \mathrm{X}$ telle que f o $\mathrm{f}=\mathrm{c}$ pour un $\mathrm{c} \in X$. D'abord on a $\mathrm{f}(\mathrm{c})=\mathrm{c}$ parce que
$$
f \circ f(c)=c \Rightarrow f \circ f \circ f(c)=f(c),
$$
et selon la définition $\mathrm{f} \circ \mathrm{f} \circ \mathrm{f}(\mathrm{c})=\mathrm{f} \circ \mathrm{f}(\mathrm{f}(\mathrm{c}))=\mathrm{c}$, ce qui nous donne $\mathrm{f}(\mathrm{c})=\mathrm{c}$. Posons l'ensemble
$$
A=\{x \in X \mid f(x)=c\}
$$
On a montré qu'il contient $c$. Selon la définition, on a $f(x) \in A \backslash\{c\}$ pour tout $x \in A^{c}$ où $A^{c}$ est le complémentaire de $A$.
Donc, pour déterminer toutes les fonctions $f: X \rightarrow X$ telles que $f \circ f$ est constante, on doit d'abord choisir un $c \in X$ ( $n$ manières de faire) puis un $A \subset X$ contenant $c\left(\binom{n-1}{i}\right.$ manières de faire si $|A|=i+1)$ et ensuite choisir les valeurs $f(x)$ pour chaque $x \in A^{c}$ dans $A \backslash\{c\}$ ( $i^{n-i-1}$ manières de faire). Alors le nombre de telles fonctions sera
$$
n \sum_{i=1}^{n-1}\binom{n-1}{i} i^{n-i-1}
$$
|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "## Exercice 6.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-4-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T2",
"year": "2017"
}
|
A toy manufacturer creates at least one toy per day. They are not capable of creating more than 725 toys per year. For any $\mathrm{n} \in \mathbb{N}$, show that there exist consecutive days during which they created exactly n toys.
|
Let $x_{i} \in \mathbb{N}$ be the number of toys created on the $i-$th day. If
$$
\mathrm{x}_{1}+\mathrm{x}_{2}+\ldots+\mathrm{x}_{\mathrm{n}}<2 \mathrm{n}
$$
consider the following numbers:
$$
1 \leqslant x_{1}<x_{1}+x_{2}<\ldots<x_{1}+x_{2}+\ldots+x_{n}<2 n .
$$
We have two cases. Either they represent all residues modulo $n$, or there exist $1 \leqslant i<j \leqslant n$ such that
$$
x_{1}+x_{2}+\ldots+x_{i} \equiv x_{1}+x_{2}+\ldots+x_{j} \quad(\bmod n)
$$
The latter case gives us
$$
\mathrm{n} \mid \mathrm{x}_{\mathrm{i}+1}+\ldots+\mathrm{x}_{\mathrm{j}}
$$
and thus
$$
x_{i+1}+\ldots+x_{j}=n
$$
In the first case, there exists $1 \leqslant \mathfrak{j} \leqslant n$ such that
$$
\mathrm{n} \mid \mathrm{x}_{1}+\mathrm{x}_{2}+\ldots+\mathrm{x}_{\mathrm{j}}
$$
so
$$
\mathrm{x}_{1}+\mathrm{x}_{2}+\ldots+\mathrm{x}_{\mathrm{j}}=\mathrm{n}
$$
In both cases, the problem is solved. Now consider what happens if, for any $n$ consecutive days, the total number of toys is greater than $2 n$. Then
$$
2 \mathrm{n} \times 365 \leqslant \sum_{i=1}^{365 n} x_{i} \leqslant 725 n
$$
we reach a contradiction.
## Exercises of group $\mathcal{A}$
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Un constructeur de jouets crée au moins un jouet par jour. Il n'est pas capable de créer plus de 725 jouets par an. Pour tout $\mathrm{n} \in \mathbb{N}$, montrer qu'il existe des jours consécutifs pendant lesquels il a créé exactement n jouets.
|
Soit $x_{i} \in \mathbb{N}$ le nombre de jouets qu'il a crée pendant le $i-$ ème jour. Si
$$
\mathrm{x}_{1}+\mathrm{x}_{2}+\ldots+\mathrm{x}_{\mathrm{n}}<2 \mathrm{n}
$$
étudions les nombres suivants :
$$
1 \leqslant x_{1}<x_{1}+x_{2}<\ldots<x_{1}+x_{2}+\ldots+x_{n}<2 n .
$$
On a deux cas. Soit ils représentent tous les résidus modulo $n$, soit il existe $1 \leqslant i<j \leqslant n$ tels que
$$
x_{1}+x_{2}+\ldots+x_{i} \equiv x_{1}+x_{2}+\ldots+x_{j} \quad(\bmod n)
$$
Ce dernier cas nous donne
$$
\mathrm{n} \mid \mathrm{x}_{\mathrm{i}+1}+\ldots+\mathrm{x}_{\mathrm{j}}
$$
puis
$$
x_{i+1}+\ldots+x_{j}=n
$$
Dans le premier cas, il existe $1 \leqslant \mathfrak{j} \leqslant n$ tel que
$$
\mathrm{n} \mid \mathrm{x}_{1}+\mathrm{x}_{2}+\ldots+\mathrm{x}_{\mathrm{j}}
$$
donc
$$
\mathrm{x}_{1}+\mathrm{x}_{2}+\ldots+\mathrm{x}_{\mathrm{j}}=\mathrm{n}
$$
Dans les deux cas, le problème est résolu. Étudions maintenant ce qui se passe si, pour tous n jours consécutifs, le nombre total de jouets est plus grand que 2 n . Alors
$$
2 \mathrm{n} \times 365 \leqslant \sum_{i=1}^{365 n} x_{i} \leqslant 725 n
$$
on aboutit à une contradiction.
## Exercices dugroupe $\mathcal{A}$
|
{
"exam": "French_envois",
"problem_label": "7",
"problem_match": "## Exercice 7.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-4-solutions.jsonl",
"solution_match": "## Solution de l'exercice 7",
"tier": "T2",
"year": "2017"
}
|
Let $A_{1}, A_{2}, \ldots, A_{n}, B_{1}, B_{2}, \ldots, B_{n}$ be sets of $k$ elements. Show that if $\sin < 2^{k-1}$, then there exist elements $a_{1}, a_{2}, \ldots, a_{n}, b_{1}, b_{2}, \ldots, b_{n}$ such that:
$$
a_{i} \in A_{i}, b_{j} \in B_{j}, a_{i} \neq b_{j}
$$
for all $1 \leqslant i, j \leqslant n$.
|
Let $X$ be the union of all $A_{i}$ and $B_{j}$ for all $1 \leqslant i, j \leqslant n$ and let $m=|X|$. We want to show that there is a coloring of the elements of $X$ in red and blue such that
- None of the $A_{1}, A_{2}, \ldots, A_{n}$ is entirely red,
- None of the $B_{1}, B_{2}, \ldots, B_{n}$ is entirely blue.
For each $A_{i}$, the number of colorings such that $A_{i}$ is all red is equal to $2^{m-k}$. Therefore, since $2n\left(2^{m-k}\right) < 2^{m}$, we will have a coloring with the above property. With such a coloring, we choose each $a_{i}$ from the blue elements of $A_{i}$ and each $b_{j}$ from the red elements of $B_{j}$. This works.
|
proof
|
Incomplete
|
Yes
|
proof
|
Combinatorics
|
Soient $A_{1}, A_{2}, \ldots, A_{n}, B_{1}, B_{2}, \ldots, B_{n}$ des ensembles de kéléments. Montrer que $\sin <2^{k-1}$ alors il existe des éléments $a_{1}, a_{2}, \ldots, a_{n}, b_{1}, b_{2}, \ldots, b_{n}$ tels que:
$$
a_{i} \in A_{i}, b_{j} \in B_{j}, a_{i} \neq b_{j}
$$
pour tout $1 \leqslant i, j \leqslant n$.
|
Soit $X$ l'union de tous les $A_{i}$ et $B_{j}$ pour tous $1 \leqslant i, j \leqslant n$ et soit $m=|X|$. On veut montrer qu'il y a un coloriage des éléments de $X$ en rouge et bleu telle que
- Aucun des $A_{1}, A_{2}, \ldots, A_{n}$ ne soit totalement rouge,
- Aucun des $B_{1}, B_{2}, \ldots, B_{n}$ ne soit totalement bleu.
Pour chaque $A_{i}$, le nombre de coloriages tels que $A_{i}$ soit tout en rouge est égal $2^{m-k}$. Donc, puisque $2 \mathrm{n}\left(2^{\mathrm{m}-\mathrm{k}}\right)<2^{\mathrm{m}}$, on aura un coloriage avec la propriété précédente. Avec un tel coloriage, on choisit chaque $a_{i}$ parmi les éléments bleus de $A_{i}$ et chaque $b_{j}$ parmi les éléments rouges de $B_{j}$. Ce qui convient.
|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "## Exercice 8.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-4-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 8",
"tier": "T2",
"year": "2017"
}
|
Let $n$ be a positive integer. Show that in a set $A$ of $2^{n}$ strictly positive numbers, one can choose a subset $B$ of size $n+1$ such that the sum of any two different numbers in $B$ is never in $A$.
|
Let $n$ and $A$ be as in the statement. We will show, by induction on $m \leqslant n+1$, that the greedy algorithm consisting of always taking the largest number that does not cause a problem works.
Set $A_{0}=A$, and $B_{0}=B$. Suppose that, for $m<n+1$, we have constructed $A_{m}$ and $B_{m}$, subsets of $A$ such that:
1. the sum of two different elements of $B_{m}$ is never in $A$,
2. the sum of an element of $A_{m}$ and an element of $B_{m}$ is never in $A$,
3. $A_{m}$ and $B_{m}$ are disjoint,
4. $\operatorname{card}\left(A_{m}\right) \geqslant 2^{n}-2^{m}+1$ and
5. $\operatorname{card}\left(B_{m}\right)=m$.
In this case, $A_{m}$ is non-empty because $m \leqslant n$ so $2^{n}-2^{m}+1 \geqslant 1$. Let $b_{m+1}$ be the largest element of $A_{m}$. We set $B_{m+1}=B_{m} \cup\left\{b_{m+1}\right\}$. By hypothesis 3 for order $m$, we obtain 5 for order $m+1$. Similarly, hypotheses 1 and 2 give us 1 for the higher order. Now, we set
$$
A_{m+1}=\left\{a \in A_{m} \mid a \neq b_{m+1} \text { and } a+b_{m+1} \notin A\right\} .
$$
By definition, and by hypothesis 2, $A_{m+1}$ satisfies 2 and 3. The only less obvious point is 4. We want to show that $\operatorname{card}\left(A_{m}\right)-\operatorname{card}\left(A_{m+1}\right) \leqslant 2^{m}$. Now,
$$
\begin{aligned}
A_{\mathfrak{m}} \backslash A_{\mathfrak{m}+1} & =\left\{\mathbf{b}_{\mathfrak{m}+1}\right\} \cup\left\{a \in A_{\mathfrak{m}} \mid a+b_{\mathfrak{m}+1} \in A\right\} \\
& \subset\left\{b_{\mathfrak{m}+1}\right\} \cup\left\{a \in A \mid a>b_{\mathfrak{m}+1}\right\} \\
& \subset\left\{\mathbf{b}_{\mathfrak{m}+1}\right\} \cup\left(A \backslash A_{\mathfrak{m}}\right) .
\end{aligned}
$$
The latter set has size at most $1+\left(2^{n}-\left(2^{n}-2^{m}+1\right)\right)=2^{m}$. Therefore, $\operatorname{card}\left(A_{m}\right)-$ $\operatorname{card}\left(A_{m+1}\right) \leqslant 2^{m}$, and we obtain 4 at order $m+1$. This concludes the induction.
Now, we apply the induction up to $m=n+1$ and we obtain a set $B_{n+1}$ of size $n+1$ that satisfies hypothesis 1, and is thus a solution to the exercise.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Soit $n$ un entier positif. Montrer que dans un ensemble $A$ de $2^{n}$ nombres strictement positifs, on peut choisir un sous-ensemble B de taille $n+1$ tel que la somme de deux nombres différents dans $B$ ne soit jamais dans $A$.
|
Soient $n$ et $A$ comme dans l'énoncé. Nous allons montrer, par récurrence sur $m \leqslant n+1$, que l'algorithme glouton consistant à toujours prendre le plus grand nombre qui ne pose pas de problème convient.
Posons $A_{0}=A$, et $B_{0}=B$. Supposons que, pour $m<n+1$, on a construit $A_{m}$ et $B_{m}$ des sous-ensembles de $A$ tels que :
1. la somme de deux éléments différents de $B_{m}$ ne soit jamais dans $A$,
2. la somme d'un élément de $A_{m}$ et d'un élément de $B_{m}$ ne soit jamais dans $A$,
3. $A_{m}$ et $B_{m}$ sont disjoints,
4. $\operatorname{card}\left(A_{m}\right) \geqslant 2^{n}-2^{m}+1$ et
5. $\operatorname{card}\left(B_{m}\right)=m$.
Dans ce cas, $A_{m}$ est non vide car $m \leqslant n$ donc $2^{n}-2^{m}+1 \geqslant 1$. Soit $b_{m+1}$ le plus grand élément de $A_{m}$. On pose $B_{m+1}=B_{m} \cup\left\{b_{m+1}\right\}$. Par l'hypothèse 3 pour l'ordre $m$, on obtient 5 pour l'ordre $m+1$. De même, les hypothèses 1 et 2 nous donne 1 pour l'ordre supérieur. Maintenant, on pose
$$
A_{m+1}=\left\{a \in A_{m} \mid a \neq b_{m+1} \text { et } a+b_{m+1} \notin A\right\} .
$$
Par définition, et par l'hypothèse $2, A_{m+1}$ vérifie 2 et 3 . Le seul point moins évident est 4 . Nous voulons montrer que $\operatorname{card}\left(A_{m}\right)-\operatorname{card}\left(A_{m+1}\right) \leqslant 2^{m}$. Or,
$$
\begin{aligned}
A_{\mathfrak{m}} \backslash A_{\mathfrak{m}+1} & =\left\{\mathbf{b}_{\mathfrak{m}+1}\right\} \cup\left\{a \in A_{\mathfrak{m}} \mid a+b_{\mathfrak{m}+1} \in A\right\} \\
& \subset\left\{b_{\mathfrak{m}+1}\right\} \cup\left\{a \in A \mid a>b_{\mathfrak{m}+1}\right\} \\
& \subset\left\{\mathbf{b}_{\mathfrak{m}+1}\right\} \cup\left(A \backslash A_{\mathfrak{m}}\right) .
\end{aligned}
$$
Or ce dernier ensemble est de taille au plus $1+\left(2^{n}-\left(2^{n}-2^{m}+1\right)\right)=2^{m}$. Donc, $\operatorname{card}\left(A_{m}\right)-$ $\operatorname{card}\left(A_{m+1}\right) \leqslant 2^{m}$, puis on obtient 4 à l'ordre $m+1$. Ce qui conclut la récurrence.
Maintenant, on applique la récurrence jusqu'à $m=n+1$ et on obtient un ensemble $B_{n+1}$ de taille $n+1$ qui vérifie l'hypothèse 1 , donc qui est bien solution de l'exercice.
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "## Exercice 9.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-4-solutions.jsonl",
"solution_match": "## Solution de l'exercice 9",
"tier": "T2",
"year": "2017"
}
|
We have an infinite list of cells, the cells being numbered by $1, 2, \ldots$. Initially, all cells contain the number 1. At each step, we choose a number $a \in \mathbb{N}^{*}$ such that:
- either all the cells numbered by a multiple of $a$ contain 1, in which case we replace these 1s with 0s,
- or all the cells numbered by a multiple of $a$ contain 0, in which case we replace these 0s with 1s.
Show that, for all $n \geqslant 2$, we can ensure that all the cells numbered at most $n$ contain a 0 except the first cell which contains a 1.
|
We will first rephrase the problem. We are working in $\mathbb{N}^{*}$. If $A$, $B$ are two sets (in $\mathbb{N}^{*}$), we denote
- $A \oplus B:=A \cup B$ if $A \cap B=\emptyset$, otherwise the operation is forbidden, and
- $A \ominus B:=A \backslash B$ if $B \subset A$, otherwise the operation is forbidden.
We add the convention that $\oplus$ and $\ominus$ are left-associative, meaning operations are performed from left to right. For example, $\{1\} \oplus\{2\} \ominus\{1,2\}=(\{1\} \oplus \{2\}) \ominus\{1,2\}=\emptyset$, whereas $\{1\} \oplus\{1,2\} \ominus\{1\}$ is forbidden.
The problem can thus be restated as: for $n \in \mathbb{N}^{*}$, there exists a formula starting with $\mathbb{N}^{*}$, containing only sets of multiples of integers and using the operations $\oplus$ and $\ominus$ that results in a set $E$ such that $E \cap\{1, \ldots, \mathbf{n}\}=\{1\}$. To prove this, we will use a lemma, which we will prove later, and which is nothing more than an improved variant of the principle of inclusion-exclusion.
Lemma: If $m \in \mathbb{N}^{*}$ and $A_{1}, \ldots, A_{m}$ are sets, then there exists a formula using the operations $\oplus$ and $\ominus$ and consisting only of arbitrary intersections of the sets $A_{1}, \ldots, A_{m}$ whose value is $A_{1} \cup \cdots \cup A_{m}$.
For example, in the case $m=2, A_{1} \cup A_{2}=A_{1} \ominus\left(A_{1} \cap A_{2}\right) \oplus A_{2}$.
Now, let $\mathrm{p}_{1}, \mathrm{p}_{2}, \ldots$ be the prime numbers in order. Let $A_{i}$ be the set of multiples (strictly positive) of $p_{i}$, for all $i \in \mathbb{N}^{*}$. Take $n \geqslant 2$ and let $m$ be the number of prime numbers less than or equal to $n$. According to the lemma, there exists a formula whose value is $A_{1} \cup \cdots \cup A_{m}$. This union is the set of numbers that are multiples of at least one number among $p_{1}, p_{2}, \ldots$ and $p_{m}$. It therefore contains all numbers less than or equal to $n$ except 1. By replacing the $\oplus$ with $\ominus$ and vice versa in the formula and adding $\mathbb{N}^{*} \ominus$ in front, we obtain an authorized formula whose value satisfies what we want. It remains to add that, if $1 \leqslant \mathrm{l} \leqslant \mathrm{m}$ and if $1 \leqslant \mathfrak{i}_{1}<\mathfrak{i}_{2}<\cdots<\mathfrak{i}_{l} \leqslant \mathfrak{m}$, then $A_{i_{1}} \cap A_{i_{2}} \cap \cdots \cap A_{i_{l}}$ is nothing other than the set of multiples of $p_{i_{1}} p_{i_{2}} \ldots p_{i_{l}}$. Therefore, the formula we have obtained consists only of sets of multiples of integers and thus is suitable.
Now let's prove the lemma by induction on $m$. The case $m=1$ is trivial. Moreover, we have treated the case $m=2$ above as an example. Let $m \geqslant 2$ and suppose the theorem is true for $m$ sets. Let $A_{1}, \ldots, A_{m+1}$ be $m+1$ sets. We have
\[
\begin{aligned}
& A_{1} \cup \cdots \cup A_{m+1}=A_{1} \cup \cdots \cup A_{m} \ominus\left(\left(A_{1} \cup \cdots \cup A_{m}\right) \cap A_{m+1}\right) \oplus A_{m+1} \\
& A_{1} \cup \cdots \cup A_{m+1}=A_{1} \cup \cdots \cup A_{m} \ominus\left(\left(A_{1} \cap A_{m+1}\right) \cup \cdots \cup\left(A_{m} \cap A_{m+1}\right)\right) \oplus A_{m+1}
\end{aligned}
\]
By the induction hypothesis, there exists a formula for the second term consisting only of arbitrary intersections of $A_{1} \cap A_{m+1}, \ldots, A_{m} \cap A_{m+1}$; thus, only of arbitrary intersections of $A_{1}, \ldots, A_{m+1}$. Now, we can insert the formula for the second term into the large formula by replacing, in the formula for the second term, the $\oplus$ with $\ominus$ and vice versa. By directly replacing the first term with the formula obtained by the induction hypothesis, we get the desired formula.
We conclude the proof of the lemma by induction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
On possède une liste infinie de cases, les cases étant numérotées par $1,2, \ldots$. Au départ, toutes les cases contiennent le nombre 1 . À chaque étape, on choisit un nombre $a \in \mathbb{N}^{*}$ tel que:
- soit toutes les cases numérotées par un multiple de a contiennent 1 auquel cas on remplace ces 1 par des 0 ,
- soit toutes les cases numérotées par un multiple de a contiennent 0 auquel cas on remplace ces 0 par des 1 .
Montrer que, pour tout $n \geqslant 2$, on peut faire en sorte que toutes les cases de numéro au plus n contiennent un 0 sauf la première case qui contient un 1.
|
Nous allons d'abord reformuler le problème. On se place dans $\mathbb{N}^{*}$. Si $A$, B sont deux ensembles (dans $\mathbb{N}^{*}$ ), on note
- $A \oplus B:=A \cup B$ si $A \cap B=\emptyset$, sinon l'opération est interdite, et
- $A \ominus B:=A \backslash B$ si $B \subset A$, sinon l'opération est interdite.
On ajoute la convention que $\oplus$ et $\ominus$ sont associatives à gauche, c'est-à-dire que les opérations sont effectuées de la gauche vers la droite. Par exemple, $\{1\} \oplus\{2\} \ominus\{1,2\}=(\{1\} \oplus$ $\{2\}) \ominus\{1,2\}=\emptyset$, par contre $\{1\} \oplus\{1,2\} \ominus\{1\}$ est interdit.
Le problème se reformule donc par : montrer que, pour $n \in \mathbb{N}^{*}$, il existe une formule commençant par $\mathbb{N}^{*}$, contenant que des ensembles de multiples d'entiers et utilisant les opérations $\oplus$ et $\ominus$ aboutissant à un ensemble $E$ tel que $E \cap\{1, \ldots, \mathbf{n}\}=\{1\}$. Pour montrer cela, nous allons utiliser un lemme, que nous démontrerons plus tard, et qui n'est rien d'autre qu'une variante améliorée du principe d'inclusion-exclusion.
Lemme: Si $m \in \mathbb{N}^{*}$ et $A_{1}, \ldots, A_{m}$ sont des ensembles, alors il existe une formule utilisant les opérations $\oplus$ et $\ominus$ et constituée uniquement d'intersections quelconques des ensembles $A_{1}, \ldots, A_{m}$ dont la valeur est $A_{1} \cup \cdots \cup A_{m}$.
Par exemple, dans le cas $m=2, A_{1} \cup A_{2}=A_{1} \ominus\left(A_{1} \cap A_{2}\right) \oplus A_{2}$.
Maintenant, notons $\mathrm{p}_{1}, \mathrm{p}_{2}, \ldots$ les nombres premiers dans l'ordre. Notons $A_{i}$ l'ensemble des multiples (strictement positifs) de $p_{i}$, pour tout $i \in \mathbb{N}^{*}$. Prenons $n \geqslant 2$ et soit $m$ le nombre de nombres premiers inférieurs ou égaux à $n$. D'après le lemme, il existe une formule dont la valeur est $A_{1} \cup \cdots \cup A_{m}$. Or cette union est l'ensemble des nombres qui sont multiples d'au moins un nombre parmi $p_{1}, p_{2}, \ldots$ et $p_{m}$. Il contient donc tous les nombres inférieurs ou égaux à $n$ sauf 1 . En remplaçant les $\oplus$ par des $\ominus$ et vice-versa dans la formule et en ajoutant $\mathbb{N}^{*} \ominus$ devant, nous obtenons donc une formule autorisée dont la valeur vérifie ce que nous voulons. Il reste à ajouter pour conclure que, si $1 \leqslant \mathrm{l} \leqslant \mathrm{m}$ et si $1 \leqslant \mathfrak{i}_{1}<\mathfrak{i}_{2}<\cdots<\mathfrak{i}_{l} \leqslant \mathfrak{m}$, alors $A_{i_{1}} \cap A_{i_{2}} \cap \cdots \cap A_{i_{l}} n^{\prime}$ est rien d'autre que l'ensemble des multiples de $p_{i_{1}} p_{i_{2}} \ldots p_{i_{l}}$. Donc la formule que l'on a obtenue n'est constituée que d'ensembles de multiples d'entier et donc convient.
Montrons maintenant le lemme par récurrence sur $m$. Le cas $m=1$ est trivial. De plus, nous avons traité le cas $m=2$, pour l'exemple, ci-dessus. Soit $m \geqslant 2$ et supposons le théorème vrai pour $m$ ensembles. Soient $A_{1}, \ldots, A_{m+1} m+1$ ensembles. On a
$$
\begin{aligned}
& A_{1} \cup \cdots \cup A_{m+1}=A_{1} \cup \cdots \cup A_{m} \ominus\left(\left(A_{1} \cup \cdots \cup A_{m}\right) \cap A_{m+1}\right) \oplus A_{m+1} \\
& A_{1} \cup \cdots \cup A_{m+1}=A_{1} \cup \cdots \cup A_{m} \ominus\left(\left(A_{1} \cap A_{m+1}\right) \cup \cdots \cup\left(A_{m} \cap A_{m+1}\right)\right) \oplus A_{m+1}
\end{aligned}
$$
Par hypothèse de récurrence, il existe une formule pour le deuxième terme constituée uniquement d'intersections quelconques de $A_{1} \cap A_{m+1}, \ldots, A_{m} \cap A_{m+1}$; donc uniquement d'intersections quelconques de $A_{1}, \ldots, A_{m+1}$. Maintenant, on peut insérer la formule du deuxième terme dans la grosse formule en remplaçant, dans la formule du deuxième terme, les $\oplus$ par des $\ominus$ et vice-versa. En remplaçant directement le premier terme par la formule obtenue par l'hypothèse de récurrence, on obtient la formule voulue.
On conclut la preuve du lemme par récurrence.
|
{
"exam": "French_envois",
"problem_label": "10",
"problem_match": "## Exercice 10.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-4-solutions.jsonl",
"solution_match": "## Solution de l'exercice 10",
"tier": "T2",
"year": "2017"
}
|
Consider a $3 \times 3$ chessboard. At the beginning, the digit 0 is written in each of the 9 squares. Then, at each step, the following operation is performed: choose two adjacent squares (sharing a side), and either add 1 to the numbers written in these two squares, or subtract 1 from the numbers written in these two squares. Is it possible to obtain a configuration where the number 2017 is written in all 9 squares?
|
It is not possible. We color the $3 \times 3$ chessboard in black and white in the usual way (so that a black square only has white squares as neighbors and a white square only has black squares as neighbors). We check that the sum of the numbers on the black squares is always equal to the sum of the numbers on the white squares. Indeed, this is the case at the beginning, and if the sum of the numbers on the black squares is equal to the sum of the numbers on the white squares, then it is always the case after performing the operation described in the statement.
When the number 2017 is written in all 9 squares, these two sums are not equal, hence the result.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
On considère un échiquier $3 \times 3$. Au début, on écrit le chiffre 0 dans chacune des 9 cases. Ensuite, à chaque étape, on effectue l'opération suivante : on choisit deux cases ayant un côté commun, puis on rajoute 1 au nombre écrit dans ces deux cases, ou bien on retranche 1 au nombre écrit dans ces deux cases. Est-il possible d'obtenir une configuration où le nombre 2017 est écrit dans les 9 cases?
|
Ce n'est pas possible. On colorie l'échiquier $3 \times 3$ en noir et blanc de manière usuelle (de sorte qu'une case noire n'ait que des cases blanches comme voisins et qu'une case blanche n'ait que des cases noires comme voisins). On vérifie que la somme des nombres sur les cases noires est toujours égale à la somme des nombres sur les cases blanches. En effet, c'est le cas au début, et si la somme des nombres sur les cases noires est égale à la somme des nombres sur les cases blanches, alors c'est toujours le cas après avoir effectué l'opération de l'énoncé.
Lorsque le nombre 2017 est écrit dans les 9 cases, ces deux sommes ne sont pas égales, d'où le résultat.
|
{
"exam": "French_envois",
"problem_label": "1",
"problem_match": "\nExercice 1.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-5-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 1",
"tier": "T2",
"year": "2017"
}
|
Let $ABC$ be an acute triangle. We denote $O$ as the center of its circumcircle. Consider the circle $\Gamma_{B}$ passing through $A$ and $B$ and tangent to $(AC)$, as well as the circle $\Gamma_{C}$ passing through $A$ and $C$ and tangent to $(AB)$. A line $\Delta$ passing through $A$ intersects $\Gamma_{B}$ at $X$ and $\Gamma_{C}$ at $Y$. Show that $\mathrm{OX}=\mathrm{OY}$.
|
Let $Z$ be the intersection point of the circumcircle of $A B C$ with $\Delta$. By angle chasing, we find that $\widehat{X B A}=\widehat{Z A C}=\widehat{Z B C}$. We deduce that $\widehat{X B Z}=\widehat{A B C}$. Since $\widehat{B C A}=\widehat{B Z A}$, we deduce that triangles $A B C$ and $X B Z$ are similar. Therefore,
$$
\frac{X Z}{A C}=\frac{B Z}{B C} .
$$
Similarly, we show that triangles $C A Y$ and $C B Z$ are similar, so that
$$
\frac{A Y}{B Z}=\frac{A C}{B C}
$$
We deduce that $A Y=X Z$, and then that $A X=Z Y$. This implies that the perpendicular bisectors of segments $[X Y]$ and $[A Z]$ are the same. Therefore, $O$ lies on the perpendicular bisector of $[X Y]$. Therefore, $O X=O Y$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soit $A B C$ un triangle acutangle. On note O le centre de son cercle circonscrit. On considère le cercle $\Gamma_{B}$ passant par $A$ et $B$ et qui est tangent à ( $A C$ ), ainsi que le cercle $\Gamma_{C}$ passant par $A$ et $C$ qui est tangent à $(A B)$. Une droite $\Delta$ passant par $A$ recoupe $\Gamma_{B}$ en $X$ et $\Gamma_{C}$ en $Y$. Montrer que $\mathrm{OX}=\mathrm{OY}$.
|
Soit $Z$ le point d'intersection du cercle circonscrit de $A B C$ avec $\Delta$. En faisant une chasse aux angles, on trouve que $\widehat{X B A}=\widehat{Z A C}=\widehat{Z B C}$. On en déduit que $\widehat{X B Z}=\widehat{A B C}$. Or, comme $\widehat{B C A}=$ $\widehat{B Z A}$, on en déduit que les triangles $A B C$ et $X B Z$ sont semblables. Donc
$$
\frac{X Z}{A C}=\frac{B Z}{B C} .
$$
On montre de même que les triangles CAY et CBZ sont semblables, de sorte que
$$
\frac{A Y}{B Z}=\frac{A C}{B C}
$$
On en déduit que $A Y=X Z$, puis que $A X=Z Y$. Ceci implique que les médiatrices des segments $[X Y]$ et $[A Z]$ sont les mêmes. Donc $O$ appartient à la médiatrice de $[X Y]$. Donc $O X=O Y$.

|
{
"exam": "French_envois",
"problem_label": "2",
"problem_match": "\nExercice 2.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-5-solutions.jsonl",
"solution_match": "## Solution de l'exercice 2",
"tier": "T2",
"year": "2017"
}
|
Find all strictly positive integers $a, b$ and $c$ such that $\operatorname{GCD}(a, b, c)=1$,
$$
a\left|(b-c)^{2}, \quad b\right|(a-c)^{2}, \quad c \mid(a-b)^{2}
$$
and such that it is possible to construct a non-degenerate triangle with sides of lengths $\mathrm{a}, \mathrm{b}$ and c.
|
First, let's check that $\operatorname{GCD}(a, b)=1$. Reason by contradiction, assuming that $p$ is a prime number that divides both $a$ and $b$. Then $p$ divides $a$, which itself divides
$$
(b-c)^{2}=b(b-2 c)+c^{2}
$$
so $p$ divides $c^{2}$ and thus $p$ divides $c$. This contradicts the fact that $\operatorname{GCD}(a, b, c)=1$.
Suppose first that two of the numbers are equal, for example $a=b$ by symmetry. Since $a$ and $b$ are coprime, we have $a = b = 1$. The only way to construct a non-degenerate triangle is to take $c=1$.
Now suppose that $a, b, c$ are pairwise distinct. Reason by contradiction, assuming that it is possible to construct a non-degenerate triangle whose sides have lengths $a, b$, and $c$. By symmetry, assume that $c>b>a$.
Show that $a$ divides $(a+b-c)^{2}$ and that $b$ divides $(a+b-c)^{2}$. We have $a(a+b-c)^{2}=a^{2}+2 a(b-$ $c)+(b-c)^{2}$, so $a$ divides $(a+b-c)^{2}$. Similarly, $b$ divides $(a+b-c)^{2}$.
Since $a$ and $b$ are coprime, we deduce that $ab$ divides $(a+b-c)^{2}$. But $0<$ $a+b-c<a$, so
$$
ab>a^{2}>(a+b-c)^{2}
$$
which is absurd.
Thus, the only solution is $a=b=c=1$.
## Common exercises
|
a=b=c=1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Trouver tous les entiers strictement positifs $a, b$ et $c$ tels que $\operatorname{PGCD}(a, b, c)=1$,
$$
a\left|(b-c)^{2}, \quad b\right|(a-c)^{2}, \quad c \mid(a-b)^{2}
$$
et tels qu'il est possible de construire un triangle non aplati dont les côtés ont pour longueurs $\mathrm{a}, \mathrm{b}$ et c .
|
Tout d'abord, vérifions que $\operatorname{PGCD}(a, b)=1$. Raisonnons par l'absurde en supposant que $p$ est un nombre premier qui divise à la fois $a$ et $b$. Alors $p$ divise $a$, qui lui même divise
$$
(b-c)^{2}=b(b-2 c)+c^{2}
$$
donc $p$ divise $c^{2}$ et donc $p$ divise $c$. Ceci contredit le fait que $\operatorname{PGCD}(a, b, c)=1$.
Supposons tout d'abord que deux des nombres sont égaux, par exemple $a=b$ par symétrie. Comme $a$ et $b$ sont premiers entre eux, on $a \mathrm{a}=\mathrm{b}=1$. La seule possibilité pour construire un triangle non-aplati est de prendre $\mathrm{c}=1$.
Supposons maintenant que $a, b, c$ sont deux à deux différents. Raisonnons par l'absurde, en supposant qu'il est possible de construire un triangle non aplati dont les côtés ont pour longueur a, b et c. Par symétrie, supposons que $c>b>a$.
Montrons que $a$ divise $(a+b-c)^{2}$ et que $b$ divise $(a+b-c)^{2}$. On $a(a+b-c)^{2}=a^{2}+2 a(b-$ $c)+(b-c)^{2}$, donc a divise $(a+b-c)^{2}$. De même $b$ divise $(a+b-c)^{2}$.
Comme $a$ et $b$ sont premiers entre eux, on en déduit que $a b$ divise $(a+b-c)^{2}$. Or $0<$ $a+b-c<a$, donc
$$
a b>a^{2}>(a+b-c)^{2}
$$
ce qui est absurde.
Ainsi, la seule solution est $\mathrm{a}=\mathrm{b}=\mathrm{c}=1$.
## Exercices communs
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-5-solutions.jsonl",
"solution_match": "## Solution de l'exercice 3",
"tier": "T2",
"year": "2017"
}
|
Let $\mathrm{a}, \mathrm{b}$, and $\mathrm{c}$ be three strictly positive numbers such that $\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{abc}=4$. Show that
$$
\left(1+\frac{\mathrm{a}}{\mathrm{~b}}+\mathrm{ca}\right)\left(1+\frac{\mathrm{b}}{\mathrm{c}}+\mathrm{ab}\right)\left(1+\frac{\mathrm{c}}{\mathrm{a}}+\mathrm{bc}\right) \geqslant 27
$$
|
Using the arithmetic-geometric mean inequality, we find that
$$
4=a+b+c+a b c \geqslant 4\left((a b c)^{2}\right)^{\frac{1}{4}}
$$
and thus $a b c \leqslant 1$. Next, using the arithmetic-geometric mean inequality again,
$$
\left(1+\frac{a}{b}+c a\right)\left(1+\frac{b}{c}+a b\right)\left(1+\frac{c}{a}+b c\right)=\frac{(4-a)(4-b)(4-c)}{a b c}=15+4\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)
$$
and using the arithmetic-geometric mean inequality again, we deduce that
$$
\left(1+\frac{a}{b}+c a\right)\left(1+\frac{b}{c}+a b\right)\left(1+\frac{c}{a}+b c\right) \geqslant 15+12\left(\frac{1}{a b c}\right)^{1 / 3} \geqslant 27
$$
|
27
|
Yes
|
Yes
|
proof
|
Inequalities
|
Soient $\mathrm{a}, \mathrm{b}$ et c trois nombres strictement positifs tels que $\mathrm{a}+\mathrm{b}+\mathrm{c}+\mathrm{abc}=4$. Montrer que
$$
\left(1+\frac{\mathrm{a}}{\mathrm{~b}}+\mathrm{ca}\right)\left(1+\frac{\mathrm{b}}{\mathrm{c}}+\mathrm{ab}\right)\left(1+\frac{\mathrm{c}}{\mathrm{a}}+\mathrm{bc}\right) \geqslant 27
$$
|
En utilisant l'inégalité arithmético-géométrique, on trouve que
$$
4=a+b+c+a b c \geqslant 4\left((a b c)^{2}\right)^{\frac{1}{4}}
$$
et donc $a b c \leqslant 1$. Ensuite, en utilisant encore l'inégalité arithmético-géométrique,
$$
\left(1+\frac{a}{b}+c a\right)\left(1+\frac{b}{c}+a b\right)\left(1+\frac{c}{a}+b c\right)=\frac{(4-a)(4-b)(4-c)}{a b c}=15+4\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)
$$
et en utilisant encore l'inégalité arithmético-géométrique on en déduit que
$$
\left(1+\frac{\mathrm{a}}{\mathrm{~b}}+\mathrm{ca}\right)\left(1+\frac{\mathrm{b}}{\mathrm{c}}+\mathrm{ab}\right)\left(1+\frac{\mathrm{c}}{\mathrm{a}}+\mathrm{bc}\right) \geqslant 15+12\left(\frac{1}{\mathrm{abc}}\right)^{1 / 3} \geqslant 27
$$
|
{
"exam": "French_envois",
"problem_label": "4",
"problem_match": "\nExercice 4.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-5-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 4",
"tier": "T2",
"year": "2017"
}
|
Find all functions $\mathrm{f}: \mathbb{R} \rightarrow \mathbb{R}$ such that for all real numbers $x, y \in \mathbb{R}$ we have
$$
f(x+y)+f(x) f(y)=f(x y)+f(x)+f(y)
$$
|
By setting $y=0$, we find that $f(0)(f(x)-2)=0$ for all $x \in \mathbb{R}$. If $f(0) \neq 0$, we deduce that $f(x)=2$ for all $x \in \mathbb{R}$. Suppose henceforth that $f(0)=0$ and let $a=f(1)$.
By setting $y=1$, we obtain
$$
f(x+1)=(2-a) f(x)+a
$$
for all $x \in \mathbb{R}$.
By setting $y+1$ instead of $y$ in the functional equation, we obtain
$$
\begin{aligned}
(2-a) f(x+y)+a+f(x)((2-a) f(y)+a) & =f(x+y+1)+f(x) f(y+1) \\
& =f(x y+x)+f(x)+f(y+1) \\
& =f(x y+x)+f(x)+(2-a) f(y)+x
\end{aligned}
$$
By subtracting $(2-a) f(x+y)+(2-a) f(x) f(y)=(2-a) f(x y)+(2-a) f(x)+(2-a) f(y)$ from this equality, we obtain
$$
f(x)+(2-a) f(x y)=f(x y+x)
$$
By setting $y=-1$, we deduce that $f(x)=-(2-a) f(-x)$, and thus $f(x)=(2-a)^{2} f(x)$ for all $x \in \mathbb{R}$. If $f$ is not the zero function, by choosing $x$ such that $f(x) \neq 0$, we obtain that $a=1$ or $a=3$.
First case. We assume that $a=1$. Then $f(x y+x)=f(x y)+f(x)$ for all $x, y \in \mathbb{R}$. We deduce that
$$
f(x+y)=f(x)+f(y)
$$
for all $x, y \in \mathbb{R}$. By injecting this into the functional equation, we obtain that $f(x y)=$ $f(x) f(y)$. By setting $x=y$, we deduce that $f(x) \geqslant 0$ for $x \geqslant 0$, and with (1) we deduce that $f$ is increasing. It is then classical that (1) and the increasing nature of $f$ imply that $f$ is of the form $f(x)=\operatorname{ax}$ with $x \in \mathbb{R}$, and thus $f(x)=x$ for all $x \in \mathbb{R}$.
Second case. We assume that $a=3$. Starting from $\mathbf{f}(x+1)=(2-a) f(x)+\boldsymbol{a}$, we deduce that $f(x+2)=f(x)$ for all $x \in \mathbb{R}$. By setting $y+2$ instead of $y$ in the functional equation, we deduce that
$f(x+y)+f(x) f(y)=f(x+y+2)+f(x) f(y+2)=f(x y+2 x)+f(x)+f(y+2)=f(x y+2 x)+f(x)+f(y)$
for all $x, y \in \mathbb{R}$. By comparing with the initial functional equation, we deduce that $f(x y+$ $2 x)=f(x y)$ for all $x, y \in \mathbb{R}$, and thus that $f$ is constant, which contradicts the fact that $f(0)=0$ and $f(1)=3$.
Conversely, we verify that the three solutions $f(x)=0$ for all $x \in \mathbb{R}, f(x)=2$ for all $x \in \mathbb{R}$ and $f(x)=x$ for all $x \in \mathbb{R}$ are valid.
|
f(x)=0, f(x)=2, f(x)=x
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Trouver toutes les fonctions $\mathrm{f}: \mathbb{R} \rightarrow \mathbb{R}$ telles que pour tous nombres réels $x, y \in \mathbb{R}$ on ait
$$
f(x+y)+f(x) f(y)=f(x y)+f(x)+f(y)
$$
|
En prenant $y=0$, on trouve que $f(0)(f(x)-2)=0$ pour tout $x \in \mathbb{R}$. Si $f(0) \neq 0$, on en déduit que $f(x)=2$ pour tout $x \in \mathbb{R}$. Supposons donc dans la suite que $f(0)=0$ et notons $a=f(1)$.
En prenant $y=1$, on obtient
$$
f(x+1)=(2-a) f(x)+a
$$
pour tout $x \in \mathbb{R}$.
En prenant $y+1$ à la place de $y$ dans l'équation fonctionnelle, on obtient
$$
\begin{aligned}
(2-a) f(x+y)+a+f(x)((2-a) f(y)+a) & =f(x+y+1)+f(x) f(y+1) \\
& =f(x y+x)+f(x)+f(y+1) \\
& =f(x y+x)+f(x)+(2-a) f(y)+x
\end{aligned}
$$
En retranchant $(2-a) f(x+y)+(2-a) f(x) f(y)=(2-a) f(x y)+(2-a) f(x)+(2-a) f(y)$ à cette égalité, on obtient
$$
f(x)+(2-a) f(x y)=f(x y+x)
$$
En prenant $y=-1$, on en déduit que $f(x)=-(2-a) f(-x)$, et donc $f(x)=(2-a)^{2} f(x)$ pour tout $x \in \mathbb{R}$. Si f n'est pas la fonction nulle, en choisissant $x$ tel que $f(x) \neq 0$, on obtient que $a=1$ ou a $=3$.
Premier cas. On suppose que $a=1$. Alors $f(x y+x)=f(x y)+f(x)$ pour tous $x, y \in \mathbb{R}$. On en déduit que
$$
f(x+y)=f(x)+f(y)
$$
pour tout $x, y \in \mathbb{R}$. En injectant ceci dans l'équation fonctionnelle, on obtient que $f(x y)=$ $f(x) f(y)$. En prenant $x=y$, on en déduit que $f(x) \geqslant 0$ pour $x \geqslant 0$, et avec (1) on en déduit que $f$ est croissante. Il est alors classique que (1) et la croissance de $f$ entraînent que $f$ est de la forme $f(x)=\operatorname{ax}$ avec $x \in \mathbb{R}$, et donc $f(x)=x$ pour tout $x \in \mathbb{R}$.
Deuxième cas. On suppose que $a=3$. Partant de $\mathbf{f}(x+1)=(2-a) f(x)+\boldsymbol{a}$, on en déduit que $f(x+2)=f(x)$ pour tout $x \in \mathbb{R}$. En prenant $y+2$ à la place de $y$ dans l'équation fonctionnelle, on en déduit que
$f(x+y)+f(x) f(y)=f(x+y+2)+f(x) f(y+2)=f(x y+2 x)+f(x)+f(y+2)=f(x y+2 x)+f(x)+f(y)$
pour tous $x, y \in \mathbb{R}$. En comparant avec l'équation fonctionnelle initiale, on en déduit que $f(x y+$ $2 x)=f(x y)$ pour tous $x, y \in \mathbb{R}$, et donc que $f$ est constante, ce qui contredit le fait que $f(0)=0$ et $f(1)=3$.
Réciproquement, on vérifie que les trois solutions $f(x)=0$ pour tout $x \in \mathbb{R}, f(x)=2$ pour tout $x \in \mathbb{R}$ et $f(x)=x$ pour tout $x \in \mathbb{R}$ conviennent.
|
{
"exam": "French_envois",
"problem_label": "5",
"problem_match": "\nExercice 5.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-5-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 5",
"tier": "T2",
"year": "2017"
}
|
Consider a convex quadrilateral ABCD whose diagonals are perpendicular and intersect at $E$. Let $P \in [AD]$ be a point such that $P \neq A$ and $PE = EC$. Suppose that the circumcircle of triangle $BCD$ intersects $[AD]$ at a point $Q$ different from $A$. Let $R$ be the second intersection point of $[AC]$ with the circle passing through $A$ and tangent to $(EP)$ at $P$. Assume that the points $B, R, Q$ are collinear. Show that $\widehat{BCD} = 90^{\circ}$.
|
Introduce $F$, the intersection point of the circumcircle of triangle ARD and the segment [DE]. The power of E with respect to the circle passing through $A, R, F, D$ is $E R \cdot E A = E F \cdot E D$. Furthermore, the power of $E$ with respect to the circle passing through $A, R, P$ is $E R \cdot E A = E P^2 = E C^2$. We deduce that $E D \cdot E F = E C^2$, which shows that the circle passing through $F, C, D$ is tangent to (CE).
We deduce that $\widehat{E C F} = \widehat{\mathrm{EDC}}$. Furthermore, since $A, R, F, D$ are concyclic, we have $\widehat{A D E} = \widehat{\mathrm{ERF}}$. We deduce that $\widehat{\mathrm{QDB}} + \widehat{\mathrm{BDC}} = \widehat{\mathrm{FRC}} + \widehat{\mathrm{RCF}}$, which implies that $\widehat{\mathrm{RBC}} = \widehat{\mathrm{RFC}}$. Since $(B F)$ and $(C R)$ are perpendicular, this implies that $F$ is the reflection of $B$ with respect to the line $(A C)$. It follows that $\widehat{B C R} = \widehat{R C F} = \widehat{\mathrm{BDC}}$. Since $\widehat{\mathrm{BEC}} = 90^{\circ}$, we have $\widehat{\mathrm{ECD}} = 90^{\circ} - \widehat{\mathrm{BCE}}$ and conclude that $\widehat{B C D} = 90^{\circ}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
On considère un quadrilatère convexe ABCD dont les diagonales sont perpendiculaires et se coupent en $E$. Soit $P \in[A D]$ un point tel que $P \neq A$ et $P E=E C$. On suppose que le cercle circonscrit du triangle $B C D$ recoupe $[A D]$ en un point $Q$ différent de $A$. On note $R$ le deuxième point d'intersection de $[A C]$ avec le cercle passant par $A$ et tangent à (EP) en $P$. On suppose que les points $B, R, Q$ sont alignés. Montrer que $\widehat{B C D}=90^{\circ}$.
|
Introduisons $F$, le point d'intersection du cercle circonscrit du triangle ARD et du segment [DE]. La puissance de E par rapport au cercle passant par $A, R, F, D$ est $E R \cdot E A=E F \cdot E D$. Par ailleurs, la puissance de $E$ par rapport au cercle passant par $A, R, P$ est
$E R \cdot E A=E P^{2}=E C^{2}$. On en déduit que $E D \cdot E F=E C^{2}$, ce qui montre que le cercle passant par $\mathrm{F}, \mathrm{C}, \mathrm{D}$ est tangent à (CE).
On en déduit que $\widehat{E C F}=\widehat{\mathrm{EDC}}$. Par ailleurs, comme $A, R, F, D$ sont cocycliques, on a $\widehat{A D E}=$ $\widehat{\mathrm{ERF}}$. On en déduit que $\widehat{\mathrm{QDB}}+\widehat{\mathrm{BDC}}=\widehat{\mathrm{FRC}}+\widehat{\mathrm{RCF}}$, ce qui implique que $\widehat{\mathrm{RBC}}=\widehat{\mathrm{RFC}}$. Comme $(B F)$ et $(C R)$ sont perpendiculaires, ceci implique que $F$ est le symétrique de $B$ par rapport à la droite ( $A C$ ). Il en découle que $\widehat{B C R}=\widehat{R C F}=\widehat{\mathrm{BDC}}$. Comme $\widehat{\mathrm{BEC}}=90^{\circ}$, on a $\widehat{\mathrm{ECD}}=90^{\circ}-\widehat{\mathrm{BCE}}$ et conclut que $\widehat{B C D}=90^{\circ}$.

|
{
"exam": "French_envois",
"problem_label": "6",
"problem_match": "\nExercice 6.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-5-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 6",
"tier": "T2",
"year": "2017"
}
|
Find all polynomials P with integer coefficients such that $\mathrm{P}(\mathrm{P}(\mathrm{n})+\mathrm{n})$ is a prime number for an infinite number of integers n.
|
Let $P$ be a non-constant polynomial solution. We can write $\mathrm{P}(\mathrm{X} + P(X)) = P(X) Q(X)$, where $Q$ is a polynomial with integer coefficients. Indeed, if $P(X) = \sum_{i=0}^{k} a_{i} X^{i}$, with $a_{i} \in \mathbb{Z}$, we have
\[ P(P(X) + X) = \sum_{i=0}^{k} a_{i}(P(X) + X)^{i} = a_{0} + \sum_{i=1}^{k} a_{i}\left(P(X) Q_{i}(X) + X^{i}\right) = P(X) + P(X) \sum_{i=1}^{k} a_{i} Q_{i}(X) = P(X) Q(X), \]
where the $\mathrm{Q}_{i}$ are polynomials with integer coefficients, and thus $Q$ is also a polynomial with integer coefficients.
Since $P(X) + 1$ and $P(X) - 1$ have a finite number of roots and $P(n + P(n))$ is prime for an infinite number of integers $n$, we deduce that $Q(n) = 1$ or $Q(n) = -1$ for an infinite number of integers $n$, which implies that $Q$ is constant. Denoting $k$ as the degree of $P$, we have $\operatorname{deg}(P(P(X) + X)) = k^{2}$, which implies $k = k^{2}$ and thus $k = 1$. If $P(X) = a X + b$ with $a \neq 0$, we have $P(P(n) + n) = (a + 1)(a n + b)$. Since $a \neq 0$, for this number to be prime for an infinite number of integers $n$, we must have $|a + 1| = 1$, which implies that $a = -2$. For $2n - b$ to be a prime number for an infinite number of integers $n$, it is necessary and sufficient that $b$ be odd.
Thus, the solutions are the constant polynomials equal to a prime number and the polynomials $P$ of the form $P(X) = -2X + b$ with $b$ an odd integer.
|
P(X) = -2X + b \text{ with } b \text{ an odd integer, and constant polynomials equal to a prime number}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Trouver tous les polynômes P à coefficients entiers tels que $\mathrm{P}(\mathrm{P}(\mathrm{n})+\mathrm{n})$ est un nombre premier pour une infinité d'entiers n .
|
Soit P un polynôme solution qui n'est pas constant. On peut écrire $\mathrm{P}(\mathrm{X}+$ $P(X))=P(X) Q(X)$, avec $Q$ un polynôme à coefficients entiers. En effet, si $P(X)=\sum_{i=0}^{k} a_{i} X^{i}$, avec $a_{i} \in \mathbb{Z}$, on a
$P(P(X)+X)=\sum_{i=0}^{k} a_{i}(P(X)+X)^{i}=a_{0}+\sum_{i=1}^{k} a_{i}\left(P(X) Q_{i}(X)+X^{i}\right)=P(X)+P(X) \sum_{i=1}^{k} a_{i} Q_{i}(X)=P(X) Q(X)$,
où les $\mathrm{Q}_{i}$ sont des polynômes à coefficients entiers, et donc $Q$ également.
Comme $P(X)+1$ et $P(X)-1$ ont un nombre fini de racines et que $P(n+P(n))$ est premier pour une infinité de nombres entiers $n$, on en déduit que $Q(n)=1$ ou $Q(n)=-1$ pour une infinité d'entiers $n$, ce qui implique que $Q$ est constant. En notant $k$ le degré de $P$, on a $\operatorname{deg}(P(P(X)+$ $X))=k^{2}$, ce qui implique $k=k^{2}$ et donc $k=1$. Si $P(X)=a X+b$ avec $a \neq 0$, on a $P(P(n)+n)=$ $(a+1)(a n+b)$. Comme $a \neq 0$, pour que ce nombre soit premier pour une infinité d'entiers $n$, on doit avoir $|a+1|=1$, ce qui implique que $a=-2$. Pour que $2 \mathfrak{n}-\mathrm{b}$ soit un nombre premier pour une infinité de nombres entiers $n$, il faut et il suffit que $b$ soit impair.
Ainsi, les solutions sont les polynômes constants égaux à un nombre premier et les polynômes $P$ de la forme $P(X)=-2 X+b$ avec $b$ un entier impair.
|
{
"exam": "French_envois",
"problem_label": "8",
"problem_match": "\nExercice 8.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-5-solutions.jsonl",
"solution_match": "\nSolution de l'exercice 8",
"tier": "T2",
"year": "2017"
}
|
Let $ABCD$ be a quadrilateral inscribed in a circle. We denote $\Delta_{1}$ as the line parallel to $(BC)$ passing through $A$ and $\Delta_{2}$ as the line parallel to $(AD)$ passing through $B$. We denote $E$ as the intersection point of $\Delta_{1}$ with $(CD)$ and $F$ as the intersection point of $\Delta_{2}$ with $(CD)$. The line perpendicular to $\Delta_{1}$ passing through $A$ intersects $(BC)$ at $P$, and the line perpendicular to $\Delta_{2}$ passing through $B$ intersects $(AD)$ at $Q$. We denote $\Gamma_{1}$ as the circumcircle of triangle $ADE$ and $\Gamma_{2}$ as the circumcircle of triangle $BFC$. Show that $\Gamma_{1}$ and $\Gamma_{2}$ are tangent if and only if $(DP)$ and $(CQ)$ are perpendicular.
FIGURE 1 - Proof of the first implication
|
We start with some preliminary remarks. We have $\widehat{\mathrm{EDA}}=180^{\circ}-\widehat{\mathrm{ADC}}=\widehat{\mathrm{ABC}}=180^{\circ}-\widehat{\mathrm{EAB}}$, so $(\mathrm{AB})$ and $\Gamma_{1}$ are tangent. Similarly, $\Gamma_{2}$ and $(AB)$ are tangent. Next, since $(AP) \perp (BC)$ and $(AD) \perp (BQ)$, we have $(PD) \perp (CQ)$ if and only if the triangles $APD$ and $BCQ$ are similar, that is, if and only if $\frac{AP}{AD}=\frac{BC}{CQ}$. Since the triangles $ADE$ and $BFC$ are similar, we have $\frac{AD}{AE}=\frac{BF}{BC}$. We deduce that $\frac{AP}{AD}=\frac{BC}{CQ}$ if and only if $\frac{AP}{AE}=\frac{BF}{BQ}$ if and only if $PAE$ and $FBQ$ are similar (since $\widehat{\mathrm{PAE}}=\widehat{\mathrm{FBQ}}=90^{\circ}$).
Now suppose that $\Gamma_{1}$ and $\Gamma_{2}$ are tangent at $R$. It is easy to see that $\widehat{ARB}=90^{\circ}$, which implies that the points $A, Q, P, B, R$ all lie on the circle with diameter $[AB]$. We deduce that $\widehat{ARP}=180^{\circ}-\widehat{ABP}=180^{\circ}-\widehat{ABC}=180^{\circ}-\widehat{ADE}=180^{\circ}-\widehat{ARE}$. Therefore, $E, R, P$ are collinear. Similarly, we show that $F, R, Q$ are collinear. Thus, $\widehat{PEA}=\widehat{REA}=\widehat{RAB}=\widehat{RQB}=\widehat{FQB}$. We deduce that $PEA$ and $FQB$ are similar.
Now suppose that $PEA$ and $FQB$ are similar. Let $S$ be the intersection of $(PE)$ and $(QF)$. We will show that $\Gamma_{1}$ and $\Gamma_{2}$ are tangent at $S$. We have the equality of angles
$$
\widehat{\mathrm{SQB}}=\widehat{\mathrm{FQB}}=\widehat{\mathrm{PEA}}=\widehat{\mathrm{EPC}}=180^{\circ}-\widehat{\mathrm{SPB}}
$$
We deduce that $S, Q, B, P$ are concyclic. Thus, $A, Q, P, B, S$ are concyclic. It follows that
$$
\widehat{ASE}=180^{\circ}-\widehat{ASP}=\widehat{ABP}=\widehat{ABC}=180^{\circ}-\widehat{ADC}=\widehat{ADE}
$$
Therefore, $S \in \Gamma_{1}$. We show similarly that $S \in \Gamma_{2}$. To conclude, we write
$$
\widehat{BSA}=90^{\circ}=\widehat{SAB}+\widehat{ABS}=\widehat{SDA}+\widehat{BCS}
$$
This easily implies that the tangent to $\Gamma_{1}$ passing through $S$ is tangent to $\Gamma_{2}$.
Figure 2 - Proof of the second implication.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Soient $A B C D$ un quadrilatère inscrit dans un cercle. On note $\Delta_{1}$ la droite parallèle à $(B C)$ passant par $A$ et $\Delta_{2}$ la droite parallèle à $(A D)$ passant par $B$. On note $E$ le point d'intersection de $\Delta_{1}$ avec (CD) et $F$ le point d'intersection de $\Delta_{2}$ avec (CD). La droite perpendiculaire à $\Delta_{1}$ passant $A$ coupe $(B C)$ en $P$, et la droite perpendiculaire à $\Delta_{2}$ passant par $B$ coupe ( $\left.A D\right)$ en Q. On note $\Gamma_{1}$ le cercle circonscrit du triangle $A D E$ et $\Gamma_{2}$ le cercle circonscrit du triangle BFC. Montrer que $\Gamma_{1}$ et $\Gamma_{2}$ sont tangents si et seulement si (DP) et (CQ) sont perpendiculaires.

FIGURE 1 - Preuve de la première implication
|
On commence par quelques remarques préliminaires. On a $\widehat{\mathrm{EDA}}=180^{\circ}-\widehat{\mathrm{ADC}}=\widehat{\mathrm{ABC}}=$ $180^{\circ}-\widehat{\mathrm{EAB}}$, donc $(\mathrm{AB})$ et $\Gamma_{1}$ sont tangents. De même, $\Gamma_{2}$ et $(A B)$ sont tangents. Ensuite, comme $(A P) \perp(B C)$ et $(A D) \perp(B Q)$, on a $(P D) \perp(C Q)$ si et seulement si les triangles $A P D$ et $B C Q$ sont semblables, c'est-à-dire si et seulement si $\frac{A P}{A D}=\frac{B C}{C O}$. Or les triangles $A D E$ et $B F C$ sont semblables, donc $\frac{A D}{A E}=\frac{B F}{B C}$. On en déduit que $\frac{A P}{A D}=\frac{B C}{C Q}$ si et seulement si $\frac{A P}{A E}=\frac{B F}{B Q}$ si et seulement si PAE et FBQ sont semblables ( $\operatorname{car} \widehat{\mathrm{PAE}}=\widehat{\mathrm{FBQ}}=90^{\circ}$ ).
Supposons maintenant que $\Gamma_{1}$ et $\Gamma_{2}$ sont tangents en $R$. On vois facilement que $\widehat{A R B}=90^{\circ}$, ce qui implique que les points $A, Q, P, B, R$ appartiennent tous au cercle de diamètre $[A B]$. On en déduit que $\widehat{A R P}=180^{\circ}-\widehat{A B P}=180^{\circ}-\widehat{A B C}=180^{\circ}-\widehat{A D E}=180^{\circ}-\widehat{A R E}$. Donc E, $R, P$ sont alignés. On montre de même que $F, R$, $Q$ sont alignés. Ainsi, $\widehat{P E A}=\widehat{R E A}=\widehat{R A B}=\widehat{R Q B}=\widehat{F Q B}$. On en déduit que $P E A$ et $F Q B$ sont semblables.
Supposons maintenant que PEA et FQB sont semblables. Soit $S$ le point d'intersection de (PE) et (QF). Nous allons montrer que $\Gamma_{1}$ et $\Gamma_{2}$ sont tangents en $S$. On a l'égalité des angles
$$
\widehat{\mathrm{SQB}}=\widehat{\mathrm{FQB}}=\widehat{\mathrm{PEA}}=\widehat{\mathrm{EPC}}=180^{\circ}-\widehat{\mathrm{SPB}}
$$
On en déduit que $S, Q, B, P$ sont cocycliques. Ainsi, $A, Q, P, B, S$ sont cocycliques. Il en découle que
$$
\widehat{A S E}=180^{\circ}-\widehat{A S P}=\widehat{A B P}=\widehat{A B C}=180^{\circ}-\widehat{A D C}=\widehat{A D E}
$$
Donc $S \in \Gamma_{1}$. On montre de même que $S \in \Gamma_{2}$. Pour conclure, on écrit
$$
\widehat{B S A}=90^{\circ}=\widehat{S A B}+\widehat{A B S}=\widehat{S D A}+\widehat{B C S}
$$
$\qquad$

Figure 2 - Preuve de la deuxième implication.
Ceci entraîne aisément que la tangente à $\Gamma_{1}$ passant par $S$ est tangente à $\Gamma_{2}$.
|
{
"exam": "French_envois",
"problem_label": "9",
"problem_match": "\nExercice 9.",
"resource_path": "French/segmented/envois/fr-ofm-2016-2017-envoi-5-solutions.jsonl",
"solution_match": "## Solution de l'exercice 9",
"tier": "T2",
"year": "2017"
}
|
A cell can divide into 42 or 44 smaller cells. How many divisions are needed to obtain exactly 2017 cells from one cell?
|
A division increases the number of cells by 41 or 43. Let $a$ be the number of divisions into 42 cells, and $b$ the number of divisions into 44 cells. We want to find $a+b$, given that
$$
2017=1+41 a+43 b=1+41(a+b)+2 b=1+43(a+b)-2 b
$$
We see that $41(a+b) \leq 2016$, so $a+b<50$.
Similarly, $43(a+b) \geq 2016$, so $a+b>46$.
Now, $2017=1+41 \times 49+7=1+41 \times 48+48=1+41 \times 47+89$. Since $2 b$ is even, the only solution is $a+b=48$ (with $2 b=48$ thus $a=b=24$).
|
48
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Une cellule peut se diviser en 42 ou en 44 petites cellules. Combien de divisions faut-il pour obtenir, à partir d'une cellule, exactement 2017 cellules?
|
Une division augmente de 41 ou 43 le nombre de cellules. Soit $a$ le nombre de divisions en 42 cellules, et $b$ le nombre de divisions en 44 cellules. On veut trouver $a+b$, sachant que
$$
2017=1+41 a+43 b=1+41(a+b)+2 b=1+43(a+b)-2 b
$$
On voit que $41(a+b) \leq 2016$, donc $a+b<50$.
De même, $43(a+b) \geq 2016$, donc $a+b>46$.
Or $2017=1+41 \times 49+7=1+41 \times 48+48=1+41 \times 47+89$. Comme $2 b$ est pair, la seule solution est $a+b=48$ (avec $2 b=48$ donc $a=b=24$ ).
|
{
"exam": "French_envois",
"problem_label": "1",
"problem_match": "\nExercice 1",
"resource_path": "French/segmented/envois/fr-pofm-2017-2018-envoi1-corrige.jsonl",
"solution_match": "\nSolution ",
"tier": "T2",
"year": "2018"
}
|
On a $n$ lamps, each with a switch. Each lamp works normally, pressing its switch turns it off if it is on, and turns it on if it is off. Every minute, we touch the switches.
At the first minute: we press all the switches $(1,2,3, \ldots, n)$.
At the second minute: we press all the switches whose lamp has an even number $(2,4,6, \ldots)$.
At the third minute: we press all the switches whose lamp has a number divisible by $3(3,6,9, \ldots)$.
And so on, at the $k$-th minute, we press the switches with a number divisible by $k$.
Which lamps are on after $n$ minutes, given that at the beginning all the lamps are off?
|
Let $i \in\{1, \ldots, n\}$ be the number of one of the lamps. We press the switch $i$ at the $k$-th minute if and only if $k$ is a divisor of $i$, so we have pressed the switch $i$ $d(i)$ times, where $d(i)$ is the number of divisors of $i$. Let's decompose $i$ into prime factors: $i=p_{1}^{\alpha_{1}} \times \cdots \times p_{r}^{\alpha_{r}}$, with $p_{1}, \ldots, p_{r}$ distinct prime numbers and $\alpha_{1}, \ldots, \alpha_{r}$ integers. The divisors of $i$ are the integers
of the form $p_{1}^{\beta_{1}} \times \cdots \times p_{r}^{\beta_{r}}$, with $\beta_{1} \in\left\{0,1, \ldots, \alpha_{1}\right\}, \ldots, \beta_{r} \in\left\{0,1, \ldots, \alpha_{r}\right\}$, so there are $d(i)=\left(\alpha_{1}+1\right) \ldots\left(\alpha_{r}+1\right)$ (number of choices of $\left.\beta_{1}, \ldots, \beta_{r}\right)$.
For the lamp $i$ to be on at the end, it is necessary and sufficient that we have pressed the switch an odd number of times, so that $d(i)$ is odd, so that all $\alpha_{j}, j \in\{1, \ldots, r\}$, are even, that is, $i$ is a perfect square.
Thus, the lamps that are on after $n$ minutes are those whose number is a perfect square.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
On a $n$ lampes, chacune avec un interrupteur. Chaque lampe fonctionne normalement, appuyer sur son interrupteur l'éteint si elle est allumée, et l'allume si elle est éteinte. Toutes les minutes on touche aux interrupteurs.
À la première minute : on appuie sur tous les interrupteurs $(1,2,3, \ldots, n)$.
À la deuxième minute : on appuie sur tous les interrupteurs dont la lampe a un numéro pair $(2,4,6, \ldots)$.
À la troisième minute : on appuie sur tous les interrupteurs dont la lampe a un numéro divisible par $3(3,6,9, \ldots)$.
Et ainsi de suite, à la $k$-ième minute, on appuie sur les interrupteurs avec un numéro divisible par $k$.
Quelles sont les lampes qui sont allumées après $n$ minutes sachant qu'au début toutes les lampes sont éteintes ?
|
Soit $i \in\{1, \ldots, n\}$ le numéro d'une des lampes. On appuie sur l'interrupteur $i$ à la $k$-ième minute si et seulement si $k$ est un diviseur de $i$, donc on a appuyé $d(i)$ fois sur l'interrupteur $i$, avec $d(i)$ le nombre de diviseurs de $i$. Décomposons $i$ en facteurs premiers : $i=p_{1}^{\alpha_{1}} \times \cdots \times p_{r}^{\alpha_{r}}$, avec $p_{1}, \ldots, p_{r}$ des nombres premiers distincts et $\alpha_{1}, \ldots, \alpha_{r}$ des entiers. Les diviseurs de $i$ sont les entiers
de la forme $p_{1}^{\beta_{1}} \times \cdots \times p_{r}^{\beta_{r}}$, avec $\beta_{1} \in\left\{0,1, \ldots, \alpha_{1}\right\}, \ldots, \beta_{r} \in\left\{0,1, \ldots, \alpha_{r}\right\}$, il y en a donc $d(i)=\left(\alpha_{1}+1\right) \ldots\left(\alpha_{r}+1\right)$ (nombres de choix de $\left.\beta_{1}, \ldots, \beta_{r}\right)$.
Pour que la lampe $i$ soit allumée à la fin, il faut et il suffit qu'on ait appuyé un nombre impair de fois sur l'interrupteur, donc que $d(i)$ soit impair, donc que tous les $\alpha_{j}, j \in\{1, \ldots, r\}$, soient pairs, c'est-à-dire que $i$ soit un carré parfait.
Ainsi, les lampes allumées après $n$ minutes sont celles dont le numéro est un carré parfait.
|
{
"exam": "French_envois",
"problem_label": "2",
"problem_match": "\nExercice 2",
"resource_path": "French/segmented/envois/fr-pofm-2017-2018-envoi1-corrige.jsonl",
"solution_match": "\nSolution ",
"tier": "T2",
"year": "2018"
}
|
Consider 5 positive integers. By adding them two at a time in all possible ways, 10 integers are generated. Show that these 10 integers cannot be 10 consecutive integers.
|
Suppose the 10 integers are consecutive, and we denote $n$ as the smallest. Their sum is $n+(n+1)+\cdots+(n+9)=10n+45$. But this is also the sum of the 5 initial numbers, each counted 4 times, so it is a multiple of 4. This is impossible because for any integer $n$, $10n+45$ is odd. We arrive at a contradiction, so the 10 integers cannot be consecutive.
## Common Exercises
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
On considère 5 nombres entiers positifs. En les ajoutant deux à deux de toutes les façons possibles, on génère 10 entiers. Montrer que ces 10 entiers ne peuvent pas être 10 entiers consécutifs.
|
On suppose que les 10 entiers sont consécutifs, et on note $n$ le plus petit. Leur somme est $n+(n+1)+\cdots+(n+9)=10 n+45$. Mais c'est aussi la somme des 5 nombres de départ, comptés 4 fois chacun, donc c'est un multiple de 4. C'est impossible car pour tout entier $n, 10 n+45$ est impair. On aboutit à une contradiction, donc les 10 entiers ne peuvent pas être consécutifs.
## Exercices Communs
|
{
"exam": "French_envois",
"problem_label": "3",
"problem_match": "\nExercice 3",
"resource_path": "French/segmented/envois/fr-pofm-2017-2018-envoi1-corrige.jsonl",
"solution_match": "\nSolution ",
"tier": "T2",
"year": "2018"
}
|
In the remote region of Torturie, the vizier arranges $n$ condemned prisoners in a circle, numbered in order from 1 to $n$. Unrelentingly, he sends every second condemned prisoner to the executioner: prisoners $2, 4, \ldots$ and so on, circling around and skipping one person between each execution, until only one remains. Calculate, as a function of $n$, the number of the last condemned prisoner remaining.
|
We denote $f(n)$ as the number of the survivor. First, let's consider the case where $n$ is a power of 2. We will show by induction that in this case, $f(n)=1$. If $n=1$, this is indeed the case. If $n=2^{a}$, with $a \geq 1$, the vizier first eliminates all the even numbers. There then remain $\frac{n}{2}=2^{a-1}$ condemned individuals, and the next to be sent to the executioner is number 3, which is the second remaining person. By the induction hypothesis, the survivor will be the first remaining person, i.e., number 1. Thus $f\left(2^{a}\right)=1$ for any integer $a$.
Now let's consider the general case. We write $n=2^{a}+b$, where $a$ and $b$ are integers such that $0 \leq b<2^{a}$. The vizier first sends to the executioner the numbers $2,4, \ldots, 2 b$. There then remain $2^{a}$ condemned individuals. According to the previous case, the survivor is the one just before the next victim, namely number $2 b+1$, since $2 b+1 \leq n$. Thus $f\left(2^{a}+b\right)=2 b+1$.
|
f\left(2^{a}+b\right)=2 b+1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Dans la région reculée de Torturie, le vizir dispose en cercle $n$ condamnés, numérotés dans l'ordre entre 1 et $n$. Implacablement, il envoie au bourreau un condamné sur deux : les condamnés $2,4, \ldots$ et ainsi de suite en tournant autour du cercle, en sautant une personne entre deux supplices, jusqu'au moment où il n'en reste plus qu'un. Calculer en fonction de $n$ le numéro du dernier condamné restant.
|
On note $f(n)$ le numéro du survivant. Traitons d'abord le cas où $n$ est une puissance de 2 . Montrons par récurrence que dans ce cas, $f(n)=1$. Si $n=1$, c'est bien le cas. Si $n=2^{a}$, avec $a \geq 1$, le vizir élimine d'abord tous les numéros pairs. Il reste alors $\frac{n}{2}=2^{a-1}$ condamnés, et le prochain à être envoyé au bourreau est le numéro 3, qui est la deuxième personne restante. Par hypothèse de récurrence, le survivant sera la première personne restante, c'est-à-dire le numéro 1 . Ainsi $f\left(2^{a}\right)=1$ pour tout entier $a$.
Traitons maintenant le cas général. On écrit $n=2^{a}+b$, où $a$ et $b$ sont des entiers tels que $0 \leq b<2^{a}$. Le vizir envoie d'abord au bourreau les numéros $2,4, \ldots, 2 b$. Il reste alors $2^{a}$ condamnés. D'après le cas précédent, le survivant est celui situé juste avant la prochaine victime, à savoir le numéro $2 b+1$, car $2 b+1 \leq n$. Ainsi $f\left(2^{a}+b\right)=2 b+1$.
|
{
"exam": "French_envois",
"problem_label": "1",
"problem_match": "\nExercice 1",
"resource_path": "French/segmented/envois/fr-pofm-2017-2018-envoi1-corrige.jsonl",
"solution_match": "\nSolution ",
"tier": "T2",
"year": "2018"
}
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.