problem
stringlengths 14
10.4k
| solution
stringlengths 1
24.1k
| answer
stringlengths 1
250
⌀ | problem_is_valid
stringclasses 4
values | solution_is_valid
stringclasses 3
values | question_type
stringclasses 4
values | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
10.4k
| solution_raw
stringlengths 1
24.1k
| metadata
dict |
|---|---|---|---|---|---|---|---|---|---|
My friend and I are playing a game with the following rules: If one of us says an integer $n$, the opponent then says an integer of their choice between $2 n$ and $3 n$, inclusive. Whoever first says 2007 or greater loses the game, and their opponent wins. I must begin the game by saying a positive integer less than 10 . With how many of them can I guarantee a win?
|
6. We assume optimal play and begin working backward. I win if I say any number between 1004 and 2006. Thus, by saying such a number, my friend can force a win for himself if I ever say a number between 335 and 1003. Then I win if I say any number between 168 and 334 , because my friend must then say one of the losing numbers just considered. Similarly, I lose by saying 56 through 167 , win by saying 28 through 55 , lose with 10 through 17 , win with 5 through 9 , lose with 2 through 4 , and win with 1 .
|
6
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
My friend and I are playing a game with the following rules: If one of us says an integer $n$, the opponent then says an integer of their choice between $2 n$ and $3 n$, inclusive. Whoever first says 2007 or greater loses the game, and their opponent wins. I must begin the game by saying a positive integer less than 10 . With how many of them can I guarantee a win?
|
6. We assume optimal play and begin working backward. I win if I say any number between 1004 and 2006. Thus, by saying such a number, my friend can force a win for himself if I ever say a number between 335 and 1003. Then I win if I say any number between 168 and 334 , because my friend must then say one of the losing numbers just considered. Similarly, I lose by saying 56 through 167 , win by saying 28 through 55 , lose with 10 through 17 , win with 5 through 9 , lose with 2 through 4 , and win with 1 .
|
{
"exam": "HMMT",
"problem_label": "7",
"problem_match": "\n7. [4]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Compute the number of sequences of numbers $a_{1}, a_{2}, \ldots, a_{10}$ such that
$$
\begin{aligned}
& \text { I. } a_{i}=0 \text { or } 1 \text { for all } i \\
& \text { II. } a_{i} \cdot a_{i+1}=0 \text { for } i=1,2, \ldots, 9 \\
& \text { III. } a_{i} \cdot a_{i+2}=0 \text { for } i=1,2, \ldots, 8
\end{aligned}
$$
|
60. Call such a sequence "good," and let $A_{n}$ be the number of good sequences of length $n$. Let $a_{1}, a_{2}, \ldots, a_{n}$ be a good sequence. If $a_{1}=0$, then $a_{1}, a_{2}, \ldots, a_{n}$ is a good sequence if and only if $a_{2}, \ldots, a_{n}$ is a good sequence, so there are $A_{n-1}$ of them. If $a_{1}=1$, then we must have $a_{2}=a_{3}=0$, and in this case, $a_{1}, a_{2}, \ldots, a_{n}$ is a good sequence if and only if $a_{4}, a_{5}, \ldots, a_{n}$ is a good sequence, so there are $A_{n-3}$ of them. We thus obtain the recursive relation $A_{n}=A_{n-1}+A_{n-3}$. Note that $A_{1}=2, A_{2}=3, A_{3}=4$. Plugging these into the recursion eventually yields $A_{10}=60$.
|
60
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Compute the number of sequences of numbers $a_{1}, a_{2}, \ldots, a_{10}$ such that
$$
\begin{aligned}
& \text { I. } a_{i}=0 \text { or } 1 \text { for all } i \\
& \text { II. } a_{i} \cdot a_{i+1}=0 \text { for } i=1,2, \ldots, 9 \\
& \text { III. } a_{i} \cdot a_{i+2}=0 \text { for } i=1,2, \ldots, 8
\end{aligned}
$$
|
60. Call such a sequence "good," and let $A_{n}$ be the number of good sequences of length $n$. Let $a_{1}, a_{2}, \ldots, a_{n}$ be a good sequence. If $a_{1}=0$, then $a_{1}, a_{2}, \ldots, a_{n}$ is a good sequence if and only if $a_{2}, \ldots, a_{n}$ is a good sequence, so there are $A_{n-1}$ of them. If $a_{1}=1$, then we must have $a_{2}=a_{3}=0$, and in this case, $a_{1}, a_{2}, \ldots, a_{n}$ is a good sequence if and only if $a_{4}, a_{5}, \ldots, a_{n}$ is a good sequence, so there are $A_{n-3}$ of them. We thus obtain the recursive relation $A_{n}=A_{n-1}+A_{n-3}$. Note that $A_{1}=2, A_{2}=3, A_{3}=4$. Plugging these into the recursion eventually yields $A_{10}=60$.
|
{
"exam": "HMMT",
"problem_label": "8",
"problem_match": "\n8. [5]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Let $A:=\mathbb{Q} \backslash\{0,1\}$ denote the set of all rationals other than 0 and 1. A function $f: A \rightarrow \mathbb{R}$ has the property that for all $x \in A$,
$$
f(x)+f\left(1-\frac{1}{x}\right)=\log |x|
$$
Compute the value of $f(2007)$.
|
$\log (\mathbf{2 0 0 7} / \mathbf{2 0 0 6})$. Same as Algebra \#8.
|
\log (2007 / 2006)
|
Yes
|
Incomplete
|
math-word-problem
|
Algebra
|
Let $A:=\mathbb{Q} \backslash\{0,1\}$ denote the set of all rationals other than 0 and 1. A function $f: A \rightarrow \mathbb{R}$ has the property that for all $x \in A$,
$$
f(x)+f\left(1-\frac{1}{x}\right)=\log |x|
$$
Compute the value of $f(2007)$.
|
$\log (\mathbf{2 0 0 7} / \mathbf{2 0 0 6})$. Same as Algebra \#8.
|
{
"exam": "HMMT",
"problem_label": "9",
"problem_match": "\n9. [6]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
$A B C D$ is a convex quadrilateral such that $A B=2, B C=3, C D=7$, and $A D=6$. It also has an incircle. Given that $\angle A B C$ is right, determine the radius of this incircle.
|
$\frac{1+\sqrt{13}}{3}$. Same as Geometry $\# 10$.
|
\frac{1+\sqrt{13}}{3}
|
Yes
|
Incomplete
|
math-word-problem
|
Geometry
|
$A B C D$ is a convex quadrilateral such that $A B=2, B C=3, C D=7$, and $A D=6$. It also has an incircle. Given that $\angle A B C$ is right, determine the radius of this incircle.
|
$\frac{1+\sqrt{13}}{3}$. Same as Geometry $\# 10$.
|
{
"exam": "HMMT",
"problem_label": "10",
"problem_match": "\n10. [7]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-gen2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
A cube of edge length $s>0$ has the property that its surface area is equal to the sum of its volume and five times its edge length. Compute all possible values of $s$.
|
1,5. The volume of the cube is $s^{3}$ and its surface area is $6 s^{2}$, so we have $6 s^{2}=s^{3}+5 s$, or $0=s^{3}-6 s^{2}+5 s=s(s-1)(s-5)$.
|
1,5
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
A cube of edge length $s>0$ has the property that its surface area is equal to the sum of its volume and five times its edge length. Compute all possible values of $s$.
|
1,5. The volume of the cube is $s^{3}$ and its surface area is $6 s^{2}$, so we have $6 s^{2}=s^{3}+5 s$, or $0=s^{3}-6 s^{2}+5 s=s(s-1)(s-5)$.

|
{
"exam": "HMMT",
"problem_label": "1",
"problem_match": "\n1. [3]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-geo-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
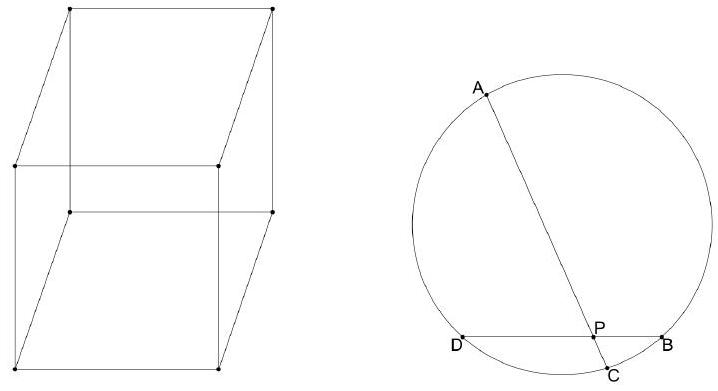
$A, B, C$, and $D$ are points on a circle, and segments $\overline{A C}$ and $\overline{B D}$ intersect at $P$, such that $A P=8$, $P C=1$, and $B D=6$. Find $B P$, given that $B P<D P$.
|
2. Writing $B P=x$ and $P D=6-x$, we have that $B P<3$. Power of a point at $P$ gives $A P \cdot P C=B P \cdot P D$ or $8=x(6-x)$. This can be solved for $x=2$ and $x=4$, and we discard the latter.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
$A, B, C$, and $D$ are points on a circle, and segments $\overline{A C}$ and $\overline{B D}$ intersect at $P$, such that $A P=8$, $P C=1$, and $B D=6$. Find $B P$, given that $B P<D P$.
|
2. Writing $B P=x$ and $P D=6-x$, we have that $B P<3$. Power of a point at $P$ gives $A P \cdot P C=B P \cdot P D$ or $8=x(6-x)$. This can be solved for $x=2$ and $x=4$, and we discard the latter.
|
{
"exam": "HMMT",
"problem_label": "2",
"problem_match": "\n2. [3]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-geo-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Circles $\omega_{1}, \omega_{2}$, and $\omega_{3}$ are centered at $M, N$, and $O$, respectively. The points of tangency between $\omega_{2}$ and $\omega_{3}, \omega_{3}$ and $\omega_{1}$, and $\omega_{1}$ and $\omega_{2}$ are tangent at $A, B$, and $C$, respectively. Line $M O$ intersects $\omega_{3}$ and $\omega_{1}$ again at $P$ and $Q$ respectively, and line $A P$ intersects $\omega_{2}$ again at $R$. Given that $A B C$ is an equilateral triangle of side length 1 , compute the area of $P Q R$.
|
$\mathbf{2 \sqrt { 3 }}$. Note that $O N M$ is an equilateral triangle of side length 2, so $m \angle B P A=m \angle B O A / 2=$ $\pi / 6$. Now $B P A$ is a $30-60-90$ triangle with short side length 1 , so $A P=\sqrt{3}$. Now $A$ and $B$ are the midpoints of segments $P R$ and $P Q$, so $[P Q R]=\frac{P R}{P A} \cdot \frac{P Q}{P B}[P B A]=2 \cdot 2[P B A]=2 \sqrt{3}$.

|
2 \sqrt{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Circles $\omega_{1}, \omega_{2}$, and $\omega_{3}$ are centered at $M, N$, and $O$, respectively. The points of tangency between $\omega_{2}$ and $\omega_{3}, \omega_{3}$ and $\omega_{1}$, and $\omega_{1}$ and $\omega_{2}$ are tangent at $A, B$, and $C$, respectively. Line $M O$ intersects $\omega_{3}$ and $\omega_{1}$ again at $P$ and $Q$ respectively, and line $A P$ intersects $\omega_{2}$ again at $R$. Given that $A B C$ is an equilateral triangle of side length 1 , compute the area of $P Q R$.
|
$\mathbf{2 \sqrt { 3 }}$. Note that $O N M$ is an equilateral triangle of side length 2, so $m \angle B P A=m \angle B O A / 2=$ $\pi / 6$. Now $B P A$ is a $30-60-90$ triangle with short side length 1 , so $A P=\sqrt{3}$. Now $A$ and $B$ are the midpoints of segments $P R$ and $P Q$, so $[P Q R]=\frac{P R}{P A} \cdot \frac{P Q}{P B}[P B A]=2 \cdot 2[P B A]=2 \sqrt{3}$.

|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n3. [4]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-geo-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Circle $\omega$ has radius 5 and is centered at $O$. Point $A$ lies outside $\omega$ such that $O A=13$. The two tangents to $\omega$ passing through $A$ are drawn, and points $B$ and $C$ are chosen on them (one on each tangent), such that line $B C$ is tangent to $\omega$ and $\omega$ lies outside triangle $A B C$. Compute $A B+A C$ given that $B C=7$.
|
17. Let $T_{1}, T_{2}$, and $T_{3}$ denote the points of tangency of $A B, A C$, and $B C$ with $\omega$, respectively. Then $7=B C=B T_{3}+T_{3} C=B T_{1}+C T_{2}$. By Pythagoras, $A T_{1}=A T_{2}=\sqrt{13^{2}-5^{2}}=12$. Now note that $24=A T_{1}+A T_{2}=A B+B T_{1}+A C+C T_{2}=A B+A C+7$.
|
17
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Circle $\omega$ has radius 5 and is centered at $O$. Point $A$ lies outside $\omega$ such that $O A=13$. The two tangents to $\omega$ passing through $A$ are drawn, and points $B$ and $C$ are chosen on them (one on each tangent), such that line $B C$ is tangent to $\omega$ and $\omega$ lies outside triangle $A B C$. Compute $A B+A C$ given that $B C=7$.
|
17. Let $T_{1}, T_{2}$, and $T_{3}$ denote the points of tangency of $A B, A C$, and $B C$ with $\omega$, respectively. Then $7=B C=B T_{3}+T_{3} C=B T_{1}+C T_{2}$. By Pythagoras, $A T_{1}=A T_{2}=\sqrt{13^{2}-5^{2}}=12$. Now note that $24=A T_{1}+A T_{2}=A B+B T_{1}+A C+C T_{2}=A B+A C+7$.
|
{
"exam": "HMMT",
"problem_label": "4",
"problem_match": "\n4. [4]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-geo-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
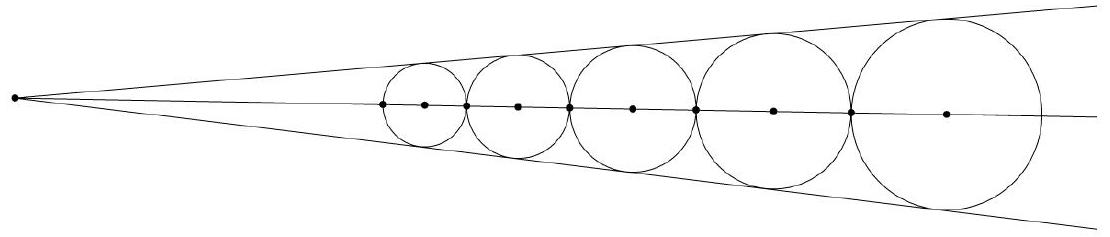
Five marbles of various sizes are placed in a conical funnel. Each marble is in contact with the adjacent marble(s). Also, each marble is in contact all around the funnel wall. The smallest marble has a radius of 8 , and the largest marble has a radius of 18 . What is the radius of the middle marble?
|
12. One can either go through all of the algebra, find the slope of the funnel wall and go from there to figure out the radius of the middle marble. Or one can notice that the answer will just be the geometric mean of 18 and 8 which is 12 .
|
12
|
Yes
|
Incomplete
|
math-word-problem
|
Geometry
|
Five marbles of various sizes are placed in a conical funnel. Each marble is in contact with the adjacent marble(s). Also, each marble is in contact all around the funnel wall. The smallest marble has a radius of 8 , and the largest marble has a radius of 18 . What is the radius of the middle marble?
|
12. One can either go through all of the algebra, find the slope of the funnel wall and go from there to figure out the radius of the middle marble. Or one can notice that the answer will just be the geometric mean of 18 and 8 which is 12 .

|
{
"exam": "HMMT",
"problem_label": "5",
"problem_match": "\n5. [5]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-geo-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Triangle $A B C$ has $\angle A=90^{\circ}$, side $B C=25, A B>A C$, and area 150. Circle $\omega$ is inscribed in $A B C$, with $M$ its point of tangency on $A C$. Line $B M$ meets $\omega$ a second time at point $L$. Find the length of segment $B L$.
|
$4 \mathbf{4 5} \sqrt{\mathbf{1 7} / 17}$. Let $D$ be the foot of the altitude from $A$ to side $B C$. The length of $A D$ is $2 \cdot 150 / 25=12$. Triangles $A D C$ and $B D A$ are similar, so $C D \cdot D B=A D^{2}=144 \Rightarrow B D=16$ and $C D=9 \Rightarrow A B=20$ and $A C=15$. Using equal tangents or the formula inradius as area divided by semiperimeter, we can find the radius of $\omega$ to be 5 . Now, let $N$ be the tangency point of $\omega$ on $A B$. By power of a point, we have $B L \cdot B M=B N^{2}$. Since the center of $\omega$ together with $M, A$, and $N$ determines a square, $B N=15$ and $B M=5 \sqrt{17}$, and we have $B L=45 \sqrt{17} / 17$.

|
\frac{45\sqrt{17}}{17}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Triangle $A B C$ has $\angle A=90^{\circ}$, side $B C=25, A B>A C$, and area 150. Circle $\omega$ is inscribed in $A B C$, with $M$ its point of tangency on $A C$. Line $B M$ meets $\omega$ a second time at point $L$. Find the length of segment $B L$.
|
$4 \mathbf{4 5} \sqrt{\mathbf{1 7} / 17}$. Let $D$ be the foot of the altitude from $A$ to side $B C$. The length of $A D$ is $2 \cdot 150 / 25=12$. Triangles $A D C$ and $B D A$ are similar, so $C D \cdot D B=A D^{2}=144 \Rightarrow B D=16$ and $C D=9 \Rightarrow A B=20$ and $A C=15$. Using equal tangents or the formula inradius as area divided by semiperimeter, we can find the radius of $\omega$ to be 5 . Now, let $N$ be the tangency point of $\omega$ on $A B$. By power of a point, we have $B L \cdot B M=B N^{2}$. Since the center of $\omega$ together with $M, A$, and $N$ determines a square, $B N=15$ and $B M=5 \sqrt{17}$, and we have $B L=45 \sqrt{17} / 17$.

|
{
"exam": "HMMT",
"problem_label": "6",
"problem_match": "\n6. [5]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-geo-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Convex quadrilateral $A B C D$ has sides $A B=B C=7, C D=5$, and $A D=3$. Given additionally that $m \angle A B C=60^{\circ}$, find $B D$.
|
8. Triangle $A B C$ is equilateral, so $A C=7$ as well. Now the law of cosines shows that $m \angle C D A=120^{\circ}$; i.e., $A B C D$ is cyclic. Ptolemy's theorem now gives $A C \cdot B D=A B \cdot C D+A D \cdot B C$, or simply $B D=C D+A D=8$.
|
8
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Convex quadrilateral $A B C D$ has sides $A B=B C=7, C D=5$, and $A D=3$. Given additionally that $m \angle A B C=60^{\circ}$, find $B D$.
|
8. Triangle $A B C$ is equilateral, so $A C=7$ as well. Now the law of cosines shows that $m \angle C D A=120^{\circ}$; i.e., $A B C D$ is cyclic. Ptolemy's theorem now gives $A C \cdot B D=A B \cdot C D+A D \cdot B C$, or simply $B D=C D+A D=8$.
|
{
"exam": "HMMT",
"problem_label": "7",
"problem_match": "\n7. [5]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-geo-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
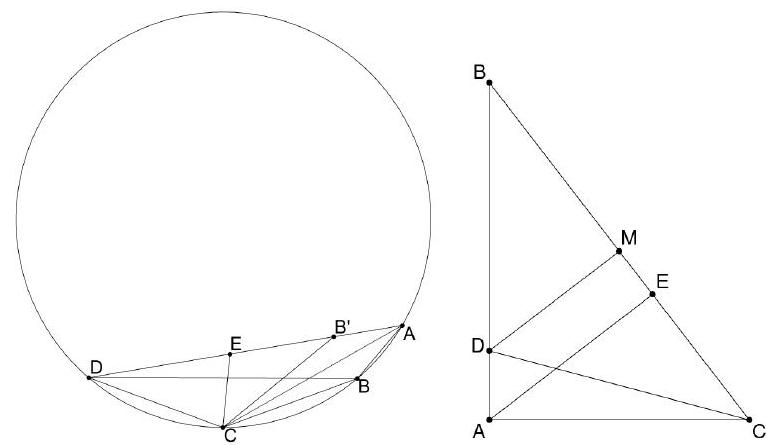
$A B C D$ is a convex quadrilateral such that $A B<A D$. The diagonal $\overline{A C}$ bisects $\angle B A D$, and $m \angle A B D=130^{\circ}$. Let $E$ be a point on the interior of $\overline{A D}$, and $m \angle B A D=40^{\circ}$. Given that $B C=$ $C D=D E$, determine $m \angle A C E$ in degrees.
|
55 ${ }^{\circ}$. First, we check that $A B C D$ is cyclic. Reflect $B$ over $\overline{A C}$ to $B^{\prime}$ on $\overline{A D}$, and note that $B^{\prime} C=C D$. Therefore, $m \angle A D C=m \angle B^{\prime} D C=m \angle C B^{\prime} D=180^{\circ}-m \angle A B^{\prime} C=180^{\circ}-m \angle C B A$. Now $m \angle C B D=m \angle C A D=20^{\circ}$ and $m \angle A D C=180^{\circ}-m \angle C B A=30^{\circ}$. Triangle $C D E$ is isosceles, so $m \angle C E D=75^{\circ}$ and $m \angle A E C=105^{\circ}$. It follows that $m \angle E C A=180^{\circ}-m \angle A E C-m \angle C A E=55^{\circ}$.
|
55^{\circ}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
$A B C D$ is a convex quadrilateral such that $A B<A D$. The diagonal $\overline{A C}$ bisects $\angle B A D$, and $m \angle A B D=130^{\circ}$. Let $E$ be a point on the interior of $\overline{A D}$, and $m \angle B A D=40^{\circ}$. Given that $B C=$ $C D=D E$, determine $m \angle A C E$ in degrees.
|
55 ${ }^{\circ}$. First, we check that $A B C D$ is cyclic. Reflect $B$ over $\overline{A C}$ to $B^{\prime}$ on $\overline{A D}$, and note that $B^{\prime} C=C D$. Therefore, $m \angle A D C=m \angle B^{\prime} D C=m \angle C B^{\prime} D=180^{\circ}-m \angle A B^{\prime} C=180^{\circ}-m \angle C B A$. Now $m \angle C B D=m \angle C A D=20^{\circ}$ and $m \angle A D C=180^{\circ}-m \angle C B A=30^{\circ}$. Triangle $C D E$ is isosceles, so $m \angle C E D=75^{\circ}$ and $m \angle A E C=105^{\circ}$. It follows that $m \angle E C A=180^{\circ}-m \angle A E C-m \angle C A E=55^{\circ}$.

|
{
"exam": "HMMT",
"problem_label": "8",
"problem_match": "\n8. [6]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-geo-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
$\triangle A B C$ is right angled at $A . D$ is a point on $A B$ such that $C D=1 . A E$ is the altitude from $A$ to $B C$. If $B D=B E=1$, what is the length of $A D$ ?
|
$\sqrt[3]{2}-1$. Let $A D=x$, angle $A B C=t$. We also have $\angle B C A=90-t$ and $\angle D C A=90-2 t$ so that $\angle A D C=2 t$. Considering triangles $A B E$ and $A D C$, we obtain, respectively,
$\cos (t)=1 /(1+x)$ and $\cos (2 t)=x$. By the double angle formula we get, $(1+x)^{3}=2$.
Alternatively, construct $M$, the midpoint of segment $B C$, and note that triangles $A B C, E B A$, and $M B D$ are similar. Thus, $A B^{2}=B C \cdot B E=B C$. In particular,
$$
A B=\frac{B C}{A B}=\frac{A B}{B E}=\frac{B D}{B M}=\frac{2 B D}{B C}=\frac{2}{A B^{2}}
$$
from which $A B=\sqrt[3]{2}$ and $A D=\sqrt[3]{2}-1$.
|
\sqrt[3]{2}-1
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
$\triangle A B C$ is right angled at $A . D$ is a point on $A B$ such that $C D=1 . A E$ is the altitude from $A$ to $B C$. If $B D=B E=1$, what is the length of $A D$ ?
|
$\sqrt[3]{2}-1$. Let $A D=x$, angle $A B C=t$. We also have $\angle B C A=90-t$ and $\angle D C A=90-2 t$ so that $\angle A D C=2 t$. Considering triangles $A B E$ and $A D C$, we obtain, respectively,
$\cos (t)=1 /(1+x)$ and $\cos (2 t)=x$. By the double angle formula we get, $(1+x)^{3}=2$.
Alternatively, construct $M$, the midpoint of segment $B C$, and note that triangles $A B C, E B A$, and $M B D$ are similar. Thus, $A B^{2}=B C \cdot B E=B C$. In particular,
$$
A B=\frac{B C}{A B}=\frac{A B}{B E}=\frac{B D}{B M}=\frac{2 B D}{B C}=\frac{2}{A B^{2}}
$$
from which $A B=\sqrt[3]{2}$ and $A D=\sqrt[3]{2}-1$.
|
{
"exam": "HMMT",
"problem_label": "9",
"problem_match": "\n9. [7]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-geo-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
$A B C D$ is a convex quadrilateral such that $A B=2, B C=3, C D=7$, and $A D=6$. It also has an incircle. Given that $\angle A B C$ is right, determine the radius of this incircle.

|
$\frac{1+\sqrt{13}}{\mathbf{3}}$. Note that $A C^{2}=A B^{2}+B C^{2}=13=C D^{2}-D A^{2}$. It follows that $\angle D A C$ is right, and so
$$
[A B C D]=[A B C]+[D A C]=2 \cdot 3 / 2+6 \cdot \sqrt{13} / 2=3+3 \sqrt{13}
$$
On the other hand, if $I$ denotes the incenter and $r$ denotes the inradius,
$$
[A B C D]=[A I B]+[B I C]+[C I D]+[D I A]=A B \cdot r / 2+B C \cdot r / 2+C D \cdot r / 2+D A \cdot r / 2=9 r
$$
Therefore, $r=(3+3 \sqrt{13}) / 9=\frac{1+\sqrt{13}}{3}$.
|
\frac{1+\sqrt{13}}{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
$A B C D$ is a convex quadrilateral such that $A B=2, B C=3, C D=7$, and $A D=6$. It also has an incircle. Given that $\angle A B C$ is right, determine the radius of this incircle.

|
$\frac{1+\sqrt{13}}{\mathbf{3}}$. Note that $A C^{2}=A B^{2}+B C^{2}=13=C D^{2}-D A^{2}$. It follows that $\angle D A C$ is right, and so
$$
[A B C D]=[A B C]+[D A C]=2 \cdot 3 / 2+6 \cdot \sqrt{13} / 2=3+3 \sqrt{13}
$$
On the other hand, if $I$ denotes the incenter and $r$ denotes the inradius,
$$
[A B C D]=[A I B]+[B I C]+[C I D]+[D I A]=A B \cdot r / 2+B C \cdot r / 2+C D \cdot r / 2+D A \cdot r / 2=9 r
$$
Therefore, $r=(3+3 \sqrt{13}) / 9=\frac{1+\sqrt{13}}{3}$.
|
{
"exam": "HMMT",
"problem_label": "10",
"problem_match": "\n10. [8]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-geo-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Define the sequence of positive integers $a_{n}$ recursively by $a_{1}=7$ and $a_{n}=7^{a_{n-1}}$ for all $n \geq 2$. Determine the last two digits of $a_{2007}$.
|
43. Note that the last two digits of $7^{4}$ are 01. Also, $a_{2006}=7^{a_{2005}}=(-1)^{a_{2005}}=-1=3$ $(\bmod 4)$ since $a_{2005}$ is odd. Therefore, $a_{2007}=7^{a_{2006}}=7^{3}=43(\bmod 100)$.
|
43
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Define the sequence of positive integers $a_{n}$ recursively by $a_{1}=7$ and $a_{n}=7^{a_{n-1}}$ for all $n \geq 2$. Determine the last two digits of $a_{2007}$.
|
43. Note that the last two digits of $7^{4}$ are 01. Also, $a_{2006}=7^{a_{2005}}=(-1)^{a_{2005}}=-1=3$ $(\bmod 4)$ since $a_{2005}$ is odd. Therefore, $a_{2007}=7^{a_{2006}}=7^{3}=43(\bmod 100)$.
|
{
"exam": "HMMT",
"problem_label": "1",
"problem_match": "\n1. [5]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
A candy company makes 5 colors of jellybeans, which come in equal proportions. If I grab a random sample of 5 jellybeans, what is the probability that I get exactly 2 distinct colors?
|
$\frac{\mathbf{1 2}}{\mathbf{1 2 5}}$. There are $\binom{5}{2}=10$ possible pairs of colors. Each pair of colors contributes $2^{5}-2=30$ sequences of beans that use both colors. Thus, the answer is $10 \cdot 30 / 5^{5}=12 / 125$.
|
\frac{12}{125}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A candy company makes 5 colors of jellybeans, which come in equal proportions. If I grab a random sample of 5 jellybeans, what is the probability that I get exactly 2 distinct colors?
|
$\frac{\mathbf{1 2}}{\mathbf{1 2 5}}$. There are $\binom{5}{2}=10$ possible pairs of colors. Each pair of colors contributes $2^{5}-2=30$ sequences of beans that use both colors. Thus, the answer is $10 \cdot 30 / 5^{5}=12 / 125$.
|
{
"exam": "HMMT",
"problem_label": "2",
"problem_match": "\n2. [5]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
The equation $x^{2}+2 x=i$ has two complex solutions. Determine the product of their real parts.
|
$\frac{1-\sqrt{2}}{\mathbf{2}}$. Complete the square by adding 1 to each side. Then $(x+1)^{2}=1+i=e^{\frac{i \pi}{4}} \sqrt{2}$, so $x+1= \pm e^{\frac{i \pi}{8}} \sqrt[4]{2}$. The desired product is then
$$
\left(-1+\cos \left(\frac{\pi}{8}\right) \sqrt[4]{2}\right)\left(-1-\cos \left(\frac{\pi}{8}\right) \sqrt[4]{2}\right)=1-\cos ^{2}\left(\frac{\pi}{8}\right) \sqrt{2}=1-\frac{\left(1+\cos \left(\frac{\pi}{4}\right)\right)}{2} \sqrt{2}=\frac{1-\sqrt{2}}{2}
$$
$10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
\frac{1-\sqrt{2}}{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
The equation $x^{2}+2 x=i$ has two complex solutions. Determine the product of their real parts.
|
$\frac{1-\sqrt{2}}{\mathbf{2}}$. Complete the square by adding 1 to each side. Then $(x+1)^{2}=1+i=e^{\frac{i \pi}{4}} \sqrt{2}$, so $x+1= \pm e^{\frac{i \pi}{8}} \sqrt[4]{2}$. The desired product is then
$$
\left(-1+\cos \left(\frac{\pi}{8}\right) \sqrt[4]{2}\right)\left(-1-\cos \left(\frac{\pi}{8}\right) \sqrt[4]{2}\right)=1-\cos ^{2}\left(\frac{\pi}{8}\right) \sqrt{2}=1-\frac{\left(1+\cos \left(\frac{\pi}{4}\right)\right)}{2} \sqrt{2}=\frac{1-\sqrt{2}}{2}
$$
$10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n3. [5]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
A sequence consists of the digits $122333444455555 \ldots$ such that the each positive integer $n$ is repeated $n$ times, in increasing order. Find the sum of the 4501 st and 4052 nd digits of this sequence.
|
13. Note that $n$ contributes $n \cdot d(n)$ digits, where $d(n)$ is the number of digits of $n$. Then because $1+\cdots+99=4950$, we know that the digits of interest appear amongst copies of two digit numbers. Now for $10 \leq n \leq 99$, the number of digits in the subsequence up to the last copy of $n$ is
$$
1+2+3+\cdots+9+2 \cdot(10+\cdots+n)=2 \cdot(1+\cdots+n)-45=n^{2}+n-45
$$
Since $67^{2}+67-45=4511$, the two digits are 6 and 7 in some order, so have sum 13 .
|
13
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A sequence consists of the digits $122333444455555 \ldots$ such that the each positive integer $n$ is repeated $n$ times, in increasing order. Find the sum of the 4501 st and 4052 nd digits of this sequence.
|
13. Note that $n$ contributes $n \cdot d(n)$ digits, where $d(n)$ is the number of digits of $n$. Then because $1+\cdots+99=4950$, we know that the digits of interest appear amongst copies of two digit numbers. Now for $10 \leq n \leq 99$, the number of digits in the subsequence up to the last copy of $n$ is
$$
1+2+3+\cdots+9+2 \cdot(10+\cdots+n)=2 \cdot(1+\cdots+n)-45=n^{2}+n-45
$$
Since $67^{2}+67-45=4511$, the two digits are 6 and 7 in some order, so have sum 13 .
|
{
"exam": "HMMT",
"problem_label": "4",
"problem_match": "\n4. [6]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Compute the largest positive integer such that $\frac{2007!}{2007^{n}}$ is an integer.
|
9. Note that $2007=3^{2} \cdot 223$. Using the fact that the number of times a prime $p$ divides $n$ ! is given by
$$
\left\lfloor\frac{n}{p}\right\rfloor+\left\lfloor\frac{n}{p^{2}}\right\rfloor+\left\lfloor\frac{n}{p^{3}}\right\rfloor+\cdots
$$
it follows that the answer is 9 .
|
9
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Compute the largest positive integer such that $\frac{2007!}{2007^{n}}$ is an integer.
|
9. Note that $2007=3^{2} \cdot 223$. Using the fact that the number of times a prime $p$ divides $n$ ! is given by
$$
\left\lfloor\frac{n}{p}\right\rfloor+\left\lfloor\frac{n}{p^{2}}\right\rfloor+\left\lfloor\frac{n}{p^{3}}\right\rfloor+\cdots
$$
it follows that the answer is 9 .
|
{
"exam": "HMMT",
"problem_label": "5",
"problem_match": "\n5. [6]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
There are three video game systems: the Paystation, the WHAT, and the ZBoz2 $\pi$, and none of these systems will play games for the other systems. Uncle Riemann has three nephews: Bernoulli, Galois, and Dirac. Bernoulli owns a Paystation and a WHAT, Galois owns a WHAT and a ZBoz2r, and Dirac owns a ZBoz2 $\pi$ and a Paystation. A store sells 4 different games for the Paystation, 6 different games for the WHAT, and 10 different games for the ZBoz2 $\pi$. Uncle Riemann does not understand the
difference between the systems, so he walks into the store and buys 3 random games (not necessarily distinct) and randomly hands them to his nephews. What is the probability that each nephew receives a game he can play?
|
$\frac{\mathbf{7}}{\mathbf{2 5}}$. Since the games are not necessarily distinct, probabilities are independent. Multiplying the odds that each nephew receives a game he can play, we get $10 / 20 \cdot 14 / 20 \cdot 16 / 20=7 / 25$.
$10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
\frac{7}{25}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There are three video game systems: the Paystation, the WHAT, and the ZBoz2 $\pi$, and none of these systems will play games for the other systems. Uncle Riemann has three nephews: Bernoulli, Galois, and Dirac. Bernoulli owns a Paystation and a WHAT, Galois owns a WHAT and a ZBoz2r, and Dirac owns a ZBoz2 $\pi$ and a Paystation. A store sells 4 different games for the Paystation, 6 different games for the WHAT, and 10 different games for the ZBoz2 $\pi$. Uncle Riemann does not understand the
difference between the systems, so he walks into the store and buys 3 random games (not necessarily distinct) and randomly hands them to his nephews. What is the probability that each nephew receives a game he can play?
|
$\frac{\mathbf{7}}{\mathbf{2 5}}$. Since the games are not necessarily distinct, probabilities are independent. Multiplying the odds that each nephew receives a game he can play, we get $10 / 20 \cdot 14 / 20 \cdot 16 / 20=7 / 25$.
$10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
{
"exam": "HMMT",
"problem_label": "6",
"problem_match": "\n6. [6]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
A student at Harvard named Kevin
Was counting his stones by 11
He messed up $n$ times
And instead counted 9s
And wound up at 2007.
How many values of $n$ could make this limerick true?
|
21. The mathematical content is that $9 n+11 k=2007$, for some nonnegative integers $n$ and $k$. As $2007=9 \cdot 223, k$ must be divisible by 9 . Using modulo 11 , we see that $n$ is 3 more than a multiple of 11 . Thus, the possibilities are $n=223,212,201, \ldots, 3$, which are 21 in number.
|
21
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A student at Harvard named Kevin
Was counting his stones by 11
He messed up $n$ times
And instead counted 9s
And wound up at 2007.
How many values of $n$ could make this limerick true?
|
21. The mathematical content is that $9 n+11 k=2007$, for some nonnegative integers $n$ and $k$. As $2007=9 \cdot 223, k$ must be divisible by 9 . Using modulo 11 , we see that $n$ is 3 more than a multiple of 11 . Thus, the possibilities are $n=223,212,201, \ldots, 3$, which are 21 in number.
|
{
"exam": "HMMT",
"problem_label": "7",
"problem_match": "\n7. [7]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
A circle inscribed in a square,
Has two chords as shown in a pair.
It has radius 2,
And $P$ bisects $T U$.
The chords' intersection is where?
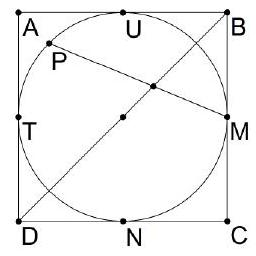
Answer the question by giving the distance of the point of intersection from the center of the circle.
|
$\sqrt[2]{\mathbf{2} \sqrt{\mathbf{2}}-\mathbf{2} .}$ Let $O B$ intersect the circle at $X$ and $Y$, and the chord $P M$ at $Q$, such that $O$ lies between $X$ and $Q$. Then $M N X Q$ is a parallelogram. For, $O B \| N M$ by homothety at $C$ and $P M \| N X$ because $M N X P$ is an isoceles trapezoid. It follows that $Q X=M N$. Considering that the center of the circle together with points $M, C$, and $N$ determines a square of side length 2 , it follows that $M N=2 \sqrt{2}$, so the answer is $2 \sqrt{2}-2$.
|
\sqrt{2 \sqrt{2} - 2}
|
Incomplete
|
Yes
|
math-word-problem
|
Geometry
|
A circle inscribed in a square,
Has two chords as shown in a pair.
It has radius 2,
And $P$ bisects $T U$.
The chords' intersection is where?

Answer the question by giving the distance of the point of intersection from the center of the circle.
|
$\sqrt[2]{\mathbf{2} \sqrt{\mathbf{2}}-\mathbf{2} .}$ Let $O B$ intersect the circle at $X$ and $Y$, and the chord $P M$ at $Q$, such that $O$ lies between $X$ and $Q$. Then $M N X Q$ is a parallelogram. For, $O B \| N M$ by homothety at $C$ and $P M \| N X$ because $M N X P$ is an isoceles trapezoid. It follows that $Q X=M N$. Considering that the center of the circle together with points $M, C$, and $N$ determines a square of side length 2 , it follows that $M N=2 \sqrt{2}$, so the answer is $2 \sqrt{2}-2$.
|
{
"exam": "HMMT",
"problem_label": "8",
"problem_match": "\n8. [7]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
I ponder some numbers in bed,
All products of three primes I've said,
Apply $\phi$ they're still fun:
now Elev'n cubed plus one.
$$
\begin{gathered}
n=37^{2} \cdot 3 \ldots \\
\phi(n)= \\
11^{3}+1 ?
\end{gathered}
$$
What numbers could be in my head?
|
2007, 2738,3122. The numbers expressible as a product of three primes are each of the form $p^{3}, p^{2} q$, or $p q r$, where $p, q$, and $r$ are distinct primes. Now, $\phi\left(p^{3}\right)=p^{2}(p-1), \phi\left(p^{2} q\right)=$ $p(p-1)(q-1)$, and $\phi(p q r)=(p-1)(q-1)(r-1)$. We require $11^{3}+1=12 \cdot 111=2^{2} 3^{2} 37$. The first case is easy to rule out, since necessarily $p=2$ or $p=3$, which both fail. The second case requires $p=2, p=3$, or $p=37$. These give $q=667,223$, and 2 , respectively. As $667=23 \cdot 29$, we reject $2^{2} \cdot 667$, but $3^{2} 233=2007$ and $37^{2} 2=2738$. In the third case, exactly one of the primes is 2 , since all other primes are odd. So say $p=2$. There are three possibilities for $(q, r):\left(2 \cdot 1+1,2 \cdot 3^{2} \cdot 37+1\right),(2 \cdot 3+1,2 \cdot 3 \cdot 37+1)$, and $\left(2 \cdot 3^{2}+1,2 \cdot 37+1\right)$. Those are $(3,667),(7,223)$, and $(19,75)$, respectively, of which only $(7,223)$ is a pair of primes. So the third and final possibility is $2 \cdot 7 \cdot 223=3122$.
$10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
2007, 2738, 3122
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
I ponder some numbers in bed,
All products of three primes I've said,
Apply $\phi$ they're still fun:
now Elev'n cubed plus one.
$$
\begin{gathered}
n=37^{2} \cdot 3 \ldots \\
\phi(n)= \\
11^{3}+1 ?
\end{gathered}
$$
What numbers could be in my head?
|
2007, 2738,3122. The numbers expressible as a product of three primes are each of the form $p^{3}, p^{2} q$, or $p q r$, where $p, q$, and $r$ are distinct primes. Now, $\phi\left(p^{3}\right)=p^{2}(p-1), \phi\left(p^{2} q\right)=$ $p(p-1)(q-1)$, and $\phi(p q r)=(p-1)(q-1)(r-1)$. We require $11^{3}+1=12 \cdot 111=2^{2} 3^{2} 37$. The first case is easy to rule out, since necessarily $p=2$ or $p=3$, which both fail. The second case requires $p=2, p=3$, or $p=37$. These give $q=667,223$, and 2 , respectively. As $667=23 \cdot 29$, we reject $2^{2} \cdot 667$, but $3^{2} 233=2007$ and $37^{2} 2=2738$. In the third case, exactly one of the primes is 2 , since all other primes are odd. So say $p=2$. There are three possibilities for $(q, r):\left(2 \cdot 1+1,2 \cdot 3^{2} \cdot 37+1\right),(2 \cdot 3+1,2 \cdot 3 \cdot 37+1)$, and $\left(2 \cdot 3^{2}+1,2 \cdot 37+1\right)$. Those are $(3,667),(7,223)$, and $(19,75)$, respectively, of which only $(7,223)$ is a pair of primes. So the third and final possibility is $2 \cdot 7 \cdot 223=3122$.
$10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
{
"exam": "HMMT",
"problem_label": "9",
"problem_match": "\n9. [7]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Let $A_{12}$ denote the answer to problem 12. There exists a unique triple of digits $(B, C, D)$ such that $10>A_{12}>B>C>D>0$ and
$$
\overline{A_{12} B C D}-\overline{D C B A_{12}}=\overline{B D A_{12} C}
$$
where $\overline{A_{12} B C D}$ denotes the four digit base 10 integer. Compute $B+C+D$.
|
11. Since $D<A_{12}$, when $A$ is subtracted from $D$ we must carry over from $C$. Thus, $D+10-\overline{A_{12}}=C$. Next, since $C-1<C<B$, we must carry over from the tens digit, so that $(C-1+10)-B=A_{12}$. Now $B>C$ so $B-1 \geq C$, and $(B-1)-C=D$. Similarly, $A_{12}-D=B$. Solving this system of four equations produces $\left(A_{12}, B, C, D\right)=(7,6,4,1)$.
|
11
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $A_{12}$ denote the answer to problem 12. There exists a unique triple of digits $(B, C, D)$ such that $10>A_{12}>B>C>D>0$ and
$$
\overline{A_{12} B C D}-\overline{D C B A_{12}}=\overline{B D A_{12} C}
$$
where $\overline{A_{12} B C D}$ denotes the four digit base 10 integer. Compute $B+C+D$.
|
11. Since $D<A_{12}$, when $A$ is subtracted from $D$ we must carry over from $C$. Thus, $D+10-\overline{A_{12}}=C$. Next, since $C-1<C<B$, we must carry over from the tens digit, so that $(C-1+10)-B=A_{12}$. Now $B>C$ so $B-1 \geq C$, and $(B-1)-C=D$. Similarly, $A_{12}-D=B$. Solving this system of four equations produces $\left(A_{12}, B, C, D\right)=(7,6,4,1)$.
|
{
"exam": "HMMT",
"problem_label": "10",
"problem_match": "\n10. [8]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
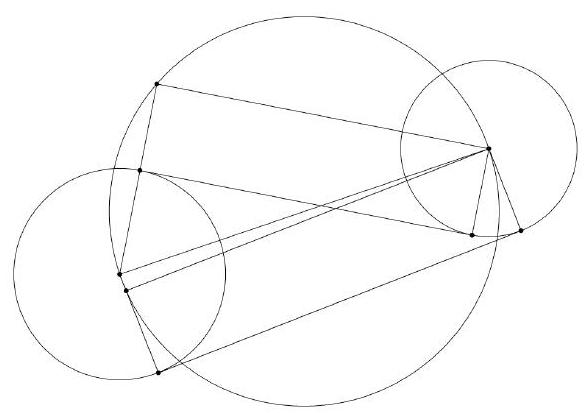
Let $A_{10}$ denote the answer to problem 10. Two circles lie in the plane; denote the lengths of the internal and external tangents between these two circles by $x$ and $y$, respectively. Given that the product of the radii of these two circles is $15 / 2$, and that the distance between their centers is $A_{10}$, determine $y^{2}-x^{2}$.
|
30. Suppose the circles have radii $r_{1}$ and $r_{2}$. Then using the tangents to build right triangles, we have $x^{2}+\left(r_{1}+r_{2}\right)^{2}=A_{10}^{2}=y^{2}+\left(r_{1}-r_{2}\right)^{2}$. Thus, $y^{2}-x^{2}=\left(r_{1}+r_{2}\right)^{2}-\left(r_{1}-r_{2}\right)^{2}=$ $4 r_{1} r_{2}=30$.
|
30
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A_{10}$ denote the answer to problem 10. Two circles lie in the plane; denote the lengths of the internal and external tangents between these two circles by $x$ and $y$, respectively. Given that the product of the radii of these two circles is $15 / 2$, and that the distance between their centers is $A_{10}$, determine $y^{2}-x^{2}$.
|
30. Suppose the circles have radii $r_{1}$ and $r_{2}$. Then using the tangents to build right triangles, we have $x^{2}+\left(r_{1}+r_{2}\right)^{2}=A_{10}^{2}=y^{2}+\left(r_{1}-r_{2}\right)^{2}$. Thus, $y^{2}-x^{2}=\left(r_{1}+r_{2}\right)^{2}-\left(r_{1}-r_{2}\right)^{2}=$ $4 r_{1} r_{2}=30$.

|
{
"exam": "HMMT",
"problem_label": "11",
"problem_match": "\n11. [8]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Let $A_{11}$ denote the answer to problem 11. Determine the smallest prime $p$ such that the arithmetic sequence $p, p+A_{11}, p+2 A_{11}, \ldots$ begins with the largest possible number of primes.
|
7. First, note that the maximal number of initial primes is bounded above by the smallest prime not dividing $A_{11}$, with equality possible only if $p$ is this prime. For, if $q$ is the smallest prime not dividing $A_{11}$, then the first $q$ terms of the arithmetic sequence determine a complete residue class modulo $q$, and the multiple of $q$ is nonprime unless it equals $q$. If $q<A_{11}$, then $q$ must appear first in the sequence, and thus divide the $(q+1)$ st term. If $q>A_{11}$, then $A_{11}=2$ and $q=3$ by Bertrand's postulate, so $q$ must appear first by inspection.
Now since $A_{11}=30$, the bound is 7 . In fact, $7,37,67,97,127$, and 157 are prime, but 187 is not. Then on the one hand, our bound of seven initial primes is not realizable. On the other hand, this implies an upper bound of six, and this bound is achieved by $p=7$. Smaller primes $p$ yield only one initial prime, so 7 is the answer.
Remarks. A number of famous theorems are concerned with the distribution of prime numbers. For two relatively prime positive integers $a$ and $b$, the arithmetic progression $a, a+b, a+2 b, \ldots$ contains infinitely many primes, a result known as Dirichlet's theorem. It was shown recently (c. 2004) that there exist arbitrarily long arithmetic progressions consisting of primes only. Bertrand's postulate states that for any positive integer $n$, there exists a prime $p$ such that $n<p \leq 2 n$. This is an unfortunate misnomer, as the statement is known to be true. As with many theorems concerning the distributions of primes, these results are easily stated in elementary terms, concealing elaborate proofs.
There is just one triple of possible $\left(A_{10}, A_{11}, A_{12}\right)$ of answers to these three problems. Your team will receive credit only for answers matching these. (So, for example, submitting a wrong answer for problem 11 will not alter the correctness of your answer to problem 12.)
|
7
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $A_{11}$ denote the answer to problem 11. Determine the smallest prime $p$ such that the arithmetic sequence $p, p+A_{11}, p+2 A_{11}, \ldots$ begins with the largest possible number of primes.
|
7. First, note that the maximal number of initial primes is bounded above by the smallest prime not dividing $A_{11}$, with equality possible only if $p$ is this prime. For, if $q$ is the smallest prime not dividing $A_{11}$, then the first $q$ terms of the arithmetic sequence determine a complete residue class modulo $q$, and the multiple of $q$ is nonprime unless it equals $q$. If $q<A_{11}$, then $q$ must appear first in the sequence, and thus divide the $(q+1)$ st term. If $q>A_{11}$, then $A_{11}=2$ and $q=3$ by Bertrand's postulate, so $q$ must appear first by inspection.
Now since $A_{11}=30$, the bound is 7 . In fact, $7,37,67,97,127$, and 157 are prime, but 187 is not. Then on the one hand, our bound of seven initial primes is not realizable. On the other hand, this implies an upper bound of six, and this bound is achieved by $p=7$. Smaller primes $p$ yield only one initial prime, so 7 is the answer.
Remarks. A number of famous theorems are concerned with the distribution of prime numbers. For two relatively prime positive integers $a$ and $b$, the arithmetic progression $a, a+b, a+2 b, \ldots$ contains infinitely many primes, a result known as Dirichlet's theorem. It was shown recently (c. 2004) that there exist arbitrarily long arithmetic progressions consisting of primes only. Bertrand's postulate states that for any positive integer $n$, there exists a prime $p$ such that $n<p \leq 2 n$. This is an unfortunate misnomer, as the statement is known to be true. As with many theorems concerning the distributions of primes, these results are easily stated in elementary terms, concealing elaborate proofs.
There is just one triple of possible $\left(A_{10}, A_{11}, A_{12}\right)$ of answers to these three problems. Your team will receive credit only for answers matching these. (So, for example, submitting a wrong answer for problem 11 will not alter the correctness of your answer to problem 12.)
|
{
"exam": "HMMT",
"problem_label": "12",
"problem_match": "\n12. [8]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Determine the largest integer $n$ such that $7^{2048}-1$ is divisible by $2^{n}$.
|
14. We have
$$
7^{2048}-1=(7-1)(7+1)\left(7^{2}+1\right)\left(7^{4}+1\right) \cdots\left(7^{1024}+1\right)
$$
In the expansion, the eleven terms other than $7+1$ are divisible by 2 exactly once, as can be checked easily with modulo 4 .
|
14
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Determine the largest integer $n$ such that $7^{2048}-1$ is divisible by $2^{n}$.
|
14. We have
$$
7^{2048}-1=(7-1)(7+1)\left(7^{2}+1\right)\left(7^{4}+1\right) \cdots\left(7^{1024}+1\right)
$$
In the expansion, the eleven terms other than $7+1$ are divisible by 2 exactly once, as can be checked easily with modulo 4 .
|
{
"exam": "HMMT",
"problem_label": "13",
"problem_match": "\n13. [9]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
We are given some similar triangles. Their areas are $1^{2}, 3^{2}, 5^{2} \ldots$, and $49^{2}$. If the smallest triangle has a perimeter of 4 , what is the sum of all the triangles' perimeters?
|
2500. Because the triangles are all similar, they all have the same ratio of perimeter squared to area, or, equivalently, the same ratio of perimeter to the square root of area. Because the latter ratio is 4 for the smallest triangle, it is 4 for all the triangles, and thus their perimeters are $4 \cdot 1,4 \cdot 3,4 \cdot 5, \ldots, 4 \cdot 49$, and the sum of these numbers is $\left[4(1+3+5+\cdots+49)=4\left(25^{2}\right)=2500\right.$.
|
2500
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
We are given some similar triangles. Their areas are $1^{2}, 3^{2}, 5^{2} \ldots$, and $49^{2}$. If the smallest triangle has a perimeter of 4 , what is the sum of all the triangles' perimeters?
|
2500. Because the triangles are all similar, they all have the same ratio of perimeter squared to area, or, equivalently, the same ratio of perimeter to the square root of area. Because the latter ratio is 4 for the smallest triangle, it is 4 for all the triangles, and thus their perimeters are $4 \cdot 1,4 \cdot 3,4 \cdot 5, \ldots, 4 \cdot 49$, and the sum of these numbers is $\left[4(1+3+5+\cdots+49)=4\left(25^{2}\right)=2500\right.$.
|
{
"exam": "HMMT",
"problem_label": "14",
"problem_match": "\n14. [9]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
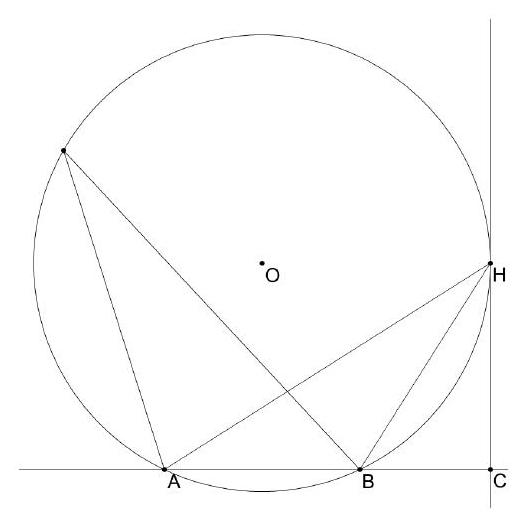
Points $A, B$, and $C$ lie in that order on line $\ell$, such that $A B=3$ and $B C=2$. Point $H$ is such that $C H$ is perpendicular to $\ell$. Determine the length $C H$ such that $\angle A H B$ is as large as possible.
|
$\sqrt{\sqrt{\mathbf{1 0}}}$. Let $\omega$ denote the circumcircle of triangle $A B H$. Since $A B$ is fixed, the smaller the radius of $\omega$, the bigger the angle $A H B$. If $\omega$ crosses the line $C H$ in more than one point, then there exists a smaller circle that goes through $A$ and $B$ that crosses $C H$ at a point $H^{\prime}$. But angle $A H^{\prime} B$ is greater than $A H B$, contradicting our assumption that $H$ is the optimal spot. Thus the circle $\omega$ crosses the line $C H$ at exactly one spot: ie, $\omega$ is tangent to $C H$ at $H$. By Power of a Point, $C H^{2}=C A C B=5 \cdot 2=10$, so $C H=\sqrt{10}$.
$10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
\sqrt{10}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Points $A, B$, and $C$ lie in that order on line $\ell$, such that $A B=3$ and $B C=2$. Point $H$ is such that $C H$ is perpendicular to $\ell$. Determine the length $C H$ such that $\angle A H B$ is as large as possible.

|
$\sqrt{\sqrt{\mathbf{1 0}}}$. Let $\omega$ denote the circumcircle of triangle $A B H$. Since $A B$ is fixed, the smaller the radius of $\omega$, the bigger the angle $A H B$. If $\omega$ crosses the line $C H$ in more than one point, then there exists a smaller circle that goes through $A$ and $B$ that crosses $C H$ at a point $H^{\prime}$. But angle $A H^{\prime} B$ is greater than $A H B$, contradicting our assumption that $H$ is the optimal spot. Thus the circle $\omega$ crosses the line $C H$ at exactly one spot: ie, $\omega$ is tangent to $C H$ at $H$. By Power of a Point, $C H^{2}=C A C B=5 \cdot 2=10$, so $C H=\sqrt{10}$.
$10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
{
"exam": "HMMT",
"problem_label": "15",
"problem_match": "\n15. [9]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
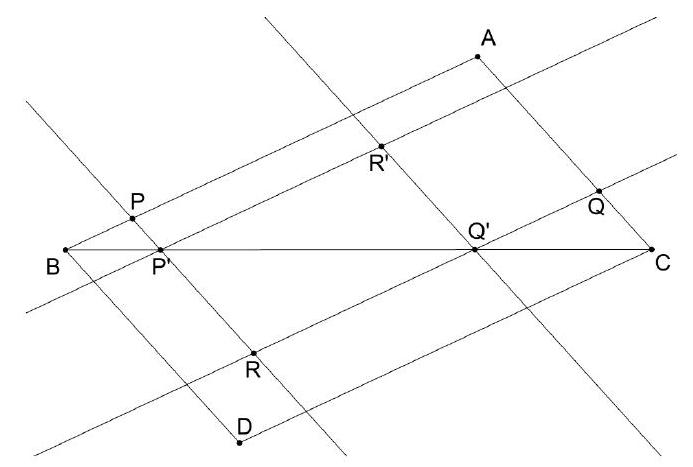
Let $A B C$ be a triangle with $A B=7, B C=9$, and $C A=4$. Let $D$ be the point such that $A B \| C D$ and $C A \| B D$. Let $R$ be a point within triangle $B C D$. Lines $\ell$ and $m$ going through $R$ are parallel to $C A$ and $A B$ respectively. Line $\ell$ meets $A B$ and $B C$ at $P$ and $P^{\prime}$ respectively, and $m$ meets $C A$ and $B C$ at $Q$ and $Q^{\prime}$ respectively. If $S$ denotes the largest possible sum of the areas of triangles $B P P^{\prime}, R P^{\prime} Q^{\prime}$, and $C Q Q^{\prime}$, determine the value of $S^{2}$.
|
180. Let $R^{\prime}$ denote the intersection of the lines through $Q^{\prime}$ and $P^{\prime}$ parallel to $\ell$ and $m$ respectively. Then $\left[R P^{\prime} Q^{\prime}\right]=\left[R^{\prime} P^{\prime} Q^{\prime}\right]$. Triangles $B P P^{\prime}, R^{\prime} P^{\prime} Q^{\prime}$, and $C Q Q^{\prime}$ lie in $A B C$ without overlap, so that on the one hand, $S \leq A B C$. On the other, this bound is realizable by taking $R$ to be a vertex of triangle $B C D$. We compute the square of the area of $A B C$ to be $10 \cdot(10-9) \cdot(10-7) \cdot(10-4)=$ 180.
|
180
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle with $A B=7, B C=9$, and $C A=4$. Let $D$ be the point such that $A B \| C D$ and $C A \| B D$. Let $R$ be a point within triangle $B C D$. Lines $\ell$ and $m$ going through $R$ are parallel to $C A$ and $A B$ respectively. Line $\ell$ meets $A B$ and $B C$ at $P$ and $P^{\prime}$ respectively, and $m$ meets $C A$ and $B C$ at $Q$ and $Q^{\prime}$ respectively. If $S$ denotes the largest possible sum of the areas of triangles $B P P^{\prime}, R P^{\prime} Q^{\prime}$, and $C Q Q^{\prime}$, determine the value of $S^{2}$.

|
180. Let $R^{\prime}$ denote the intersection of the lines through $Q^{\prime}$ and $P^{\prime}$ parallel to $\ell$ and $m$ respectively. Then $\left[R P^{\prime} Q^{\prime}\right]=\left[R^{\prime} P^{\prime} Q^{\prime}\right]$. Triangles $B P P^{\prime}, R^{\prime} P^{\prime} Q^{\prime}$, and $C Q Q^{\prime}$ lie in $A B C$ without overlap, so that on the one hand, $S \leq A B C$. On the other, this bound is realizable by taking $R$ to be a vertex of triangle $B C D$. We compute the square of the area of $A B C$ to be $10 \cdot(10-9) \cdot(10-7) \cdot(10-4)=$ 180.
|
{
"exam": "HMMT",
"problem_label": "16",
"problem_match": "\n16. [10]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
During the regular season, Washington Redskins achieve a record of 10 wins and 6 losses. Compute the probability that their wins came in three streaks of consecutive wins, assuming that all possible arrangements of wins and losses are equally likely. (For example, the record LLWWWWWLWWLWWWLL contains three winning streaks, while WWWWWWWLLLLLLWWW has just two.)
|
\( \frac{45}{286} \). Suppose the winning streaks consist of \( w_1, w_2, \) and \( w_3 \) wins, in chronological order, where the first winning streak is preceded by $l_{0}$ consecutive losses and the $i$ winning streak is immediately succeeded by $l_{i}$ losses. Then $w_{1}, w_{2}, w_{3}, l_{1}, l_{2}>0$ are positive and $l_{0}, l_{3} \geq 0$ are nonnegative. The equations
$$
w_{1}+w_{2}+w_{3}=10 \quad \text { and } \quad\left(l_{0}+1\right)+l_{1}+l_{2}+\left(l_{3}+1\right)=8
$$
are independent, and have $\binom{9}{2}$ and $\binom{7}{3}$ solutions, respectively. It follows that the answer is
$$
\frac{\binom{9}{2}\binom{7}{3}}{\binom{16}{6}}=\frac{315}{2002}
$$
|
\frac{315}{2002}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
During the regular season, Washington Redskins achieve a record of 10 wins and 6 losses. Compute the probability that their wins came in three streaks of consecutive wins, assuming that all possible arrangements of wins and losses are equally likely. (For example, the record LLWWWWWLWWLWWWLL contains three winning streaks, while WWWWWWWLLLLLLWWW has just two.)
|
\( \frac{45}{286} \). Suppose the winning streaks consist of \( w_1, w_2, \) and \( w_3 \) wins, in chronological order, where the first winning streak is preceded by $l_{0}$ consecutive losses and the $i$ winning streak is immediately succeeded by $l_{i}$ losses. Then $w_{1}, w_{2}, w_{3}, l_{1}, l_{2}>0$ are positive and $l_{0}, l_{3} \geq 0$ are nonnegative. The equations
$$
w_{1}+w_{2}+w_{3}=10 \quad \text { and } \quad\left(l_{0}+1\right)+l_{1}+l_{2}+\left(l_{3}+1\right)=8
$$
are independent, and have $\binom{9}{2}$ and $\binom{7}{3}$ solutions, respectively. It follows that the answer is
$$
\frac{\binom{9}{2}\binom{7}{3}}{\binom{16}{6}}=\frac{315}{2002}
$$
|
{
"exam": "HMMT",
"problem_label": "17",
"problem_match": "\n17. [10]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
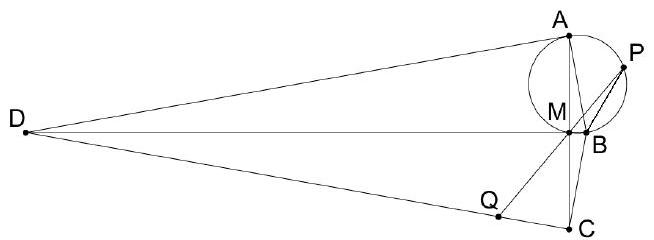
Convex quadrilateral $A B C D$ has right angles $\angle A$ and $\angle C$ and is such that $A B=B C$ and $A D=C D$. The diagonals $A C$ and $B D$ intersect at point $M$. Points $P$ and $Q$ lie on the circumcircle of triangle $A M B$ and segment $C D$, respectively, such that points $P, M$, and $Q$ are collinear. Suppose that $m \angle A B C=160^{\circ}$ and $m \angle Q M C=40^{\circ}$. Find $M P \cdot M Q$, given that $M C=6$.
|
36. Note that $m \angle Q P B=m \angle M P B=m \angle M A B=m \angle C A B=\angle B C A=\angle C D B$. Thus, $M P \cdot M Q=M B \cdot M D$. On the other hand, segment $C M$ is an altitude of right triangle $B C D$, so $M B \cdot M D=M C^{2}=36$.
$10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
36
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Convex quadrilateral $A B C D$ has right angles $\angle A$ and $\angle C$ and is such that $A B=B C$ and $A D=C D$. The diagonals $A C$ and $B D$ intersect at point $M$. Points $P$ and $Q$ lie on the circumcircle of triangle $A M B$ and segment $C D$, respectively, such that points $P, M$, and $Q$ are collinear. Suppose that $m \angle A B C=160^{\circ}$ and $m \angle Q M C=40^{\circ}$. Find $M P \cdot M Q$, given that $M C=6$.

|
36. Note that $m \angle Q P B=m \angle M P B=m \angle M A B=m \angle C A B=\angle B C A=\angle C D B$. Thus, $M P \cdot M Q=M B \cdot M D$. On the other hand, segment $C M$ is an altitude of right triangle $B C D$, so $M B \cdot M D=M C^{2}=36$.
$10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
{
"exam": "HMMT",
"problem_label": "18",
"problem_match": "\n18. [10]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Define $x \star y=\frac{\sqrt{x^{2}+3 x y+y^{2}-2 x-2 y+4}}{x y+4}$. Compute
$$
((\cdots((2007 \star 2006) \star 2005) \star \cdots) \star 1) .
$$
|
$\frac{\sqrt{\mathbf{1 5}}}{\mathbf{9}}$. Note that $x \star 2=\frac{\sqrt{x^{2}+6 x+4-2 x-4+4}}{2 x+4}=\frac{\sqrt{(x+2)^{2}}}{2(x+2)}=\frac{1}{2}$ for $x>-2$. Because $x \star y>0$ if $x, y>0$, we need only compute $\frac{1}{2} \star 1=\frac{\sqrt{\frac{1}{4}+\frac{3}{2}+1-3+4}}{\frac{1}{2}+4}=\frac{\sqrt{15}}{9}$.
|
\frac{\sqrt{15}}{9}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Define $x \star y=\frac{\sqrt{x^{2}+3 x y+y^{2}-2 x-2 y+4}}{x y+4}$. Compute
$$
((\cdots((2007 \star 2006) \star 2005) \star \cdots) \star 1) .
$$
|
$\frac{\sqrt{\mathbf{1 5}}}{\mathbf{9}}$. Note that $x \star 2=\frac{\sqrt{x^{2}+6 x+4-2 x-4+4}}{2 x+4}=\frac{\sqrt{(x+2)^{2}}}{2(x+2)}=\frac{1}{2}$ for $x>-2$. Because $x \star y>0$ if $x, y>0$, we need only compute $\frac{1}{2} \star 1=\frac{\sqrt{\frac{1}{4}+\frac{3}{2}+1-3+4}}{\frac{1}{2}+4}=\frac{\sqrt{15}}{9}$.
|
{
"exam": "HMMT",
"problem_label": "19",
"problem_match": "\n19. [10]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
For $a$ a positive real number, let $x_{1}, x_{2}, x_{3}$ be the roots of the equation $x^{3}-a x^{2}+a x-a=0$. Determine the smallest possible value of $x_{1}^{3}+x_{2}^{3}+x_{3}^{3}-3 x_{1} x_{2} x_{3}$.
|
-4 . Note that $x_{1}+x_{2}+x_{3}=x_{1} x_{2}+x_{2} x_{3}+x_{3} x_{1}=a$. Then
$$
\begin{aligned}
& x_{1}^{3}+x_{2}^{3}+x_{3}^{3}-3 x_{1} x_{2} x_{3}=\left(x_{1}+x_{2}+x_{3}\right)\left(x_{1}^{2}+x_{2}^{2}+x_{3}^{2}-\left(x_{1} x_{2}+x_{2} x_{3}+x_{3} x_{1}\right)\right) \\
& \quad=\left(x_{1}+x_{2}+x_{3}\right)\left(\left(x_{1}+x_{2}+x_{3}\right)^{2}-3\left(x_{1} x_{2}+x_{2} x_{3}+x_{3} x_{1}\right)\right)=a \cdot\left(a^{2}-3 a\right)=a^{3}-3 a^{2}
\end{aligned}
$$
The expression is negative only where $0<a<3$, so we need only consider these values of $a$. Finally, AM-GM gives $\sqrt[3]{(6-2 a)(a)(a)} \leq \frac{(6-2 a)+a+a}{3}=2$, with equality where $a=2$, and this rewrites as $(a-3) a^{2} \geq-4$.
|
-4
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
For $a$ a positive real number, let $x_{1}, x_{2}, x_{3}$ be the roots of the equation $x^{3}-a x^{2}+a x-a=0$. Determine the smallest possible value of $x_{1}^{3}+x_{2}^{3}+x_{3}^{3}-3 x_{1} x_{2} x_{3}$.
|
-4 . Note that $x_{1}+x_{2}+x_{3}=x_{1} x_{2}+x_{2} x_{3}+x_{3} x_{1}=a$. Then
$$
\begin{aligned}
& x_{1}^{3}+x_{2}^{3}+x_{3}^{3}-3 x_{1} x_{2} x_{3}=\left(x_{1}+x_{2}+x_{3}\right)\left(x_{1}^{2}+x_{2}^{2}+x_{3}^{2}-\left(x_{1} x_{2}+x_{2} x_{3}+x_{3} x_{1}\right)\right) \\
& \quad=\left(x_{1}+x_{2}+x_{3}\right)\left(\left(x_{1}+x_{2}+x_{3}\right)^{2}-3\left(x_{1} x_{2}+x_{2} x_{3}+x_{3} x_{1}\right)\right)=a \cdot\left(a^{2}-3 a\right)=a^{3}-3 a^{2}
\end{aligned}
$$
The expression is negative only where $0<a<3$, so we need only consider these values of $a$. Finally, AM-GM gives $\sqrt[3]{(6-2 a)(a)(a)} \leq \frac{(6-2 a)+a+a}{3}=2$, with equality where $a=2$, and this rewrites as $(a-3) a^{2} \geq-4$.
|
{
"exam": "HMMT",
"problem_label": "20",
"problem_match": "\n20. [10]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Bob the bomb-defuser has stumbled upon an active bomb. He opens it up, and finds the red and green wires conveniently located for him to cut. Being a seasoned member of the bomb-squad, Bob quickly determines that it is the green wire that he should cut, and puts his wirecutters on the green wire. But just before he starts to cut, the bomb starts to count down, ticking every second. Each time the bomb ticks, starting at time $t=15$ seconds, Bob panics and has a certain chance to move his wirecutters to the other wire. However, he is a rational man even when panicking, and has a $\frac{1}{2 t^{2}}$ chance of switching wires at time $t$, regardless of which wire he is about to cut. When the bomb ticks at $t=1$, Bob cuts whatever wire his wirecutters are on, without switching wires. What is the probability that Bob cuts the green wire?
|
$\frac{\mathbf{2 3}}{\mathbf{3 0}}$. Suppose Bob makes $n$ independent decisions, with probabilities of switching $p_{1}, p_{2}, \ldots, p_{n}$. Then in the expansion of the product
$$
P(x)=\left(p_{1}+\left(1-p_{1}\right) x\right)\left(p_{2}+\left(1-p_{2}\right) x\right) \cdots\left(p_{n}+\left(1-p_{n}\right) x\right)
$$
the sum of the coefficients of even powers of $x$ gives the probability that Bob makes his original decision. This is just $(P(1)+P(-1)) / 2$, so the probability is just
$$
\frac{1+\left(1-\frac{1}{1515}\right)\left(1-\frac{1}{1414}\right) \cdots\left(1-\frac{1}{22}\right)}{2}=\frac{1+\frac{1416 \frac{1315}{1515} 1414}{\cdots \frac{13}{22}}}{2}=\frac{1+\frac{8}{15}}{2}=\frac{23}{30} .
$$
$10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
\frac{23}{30}
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
Bob the bomb-defuser has stumbled upon an active bomb. He opens it up, and finds the red and green wires conveniently located for him to cut. Being a seasoned member of the bomb-squad, Bob quickly determines that it is the green wire that he should cut, and puts his wirecutters on the green wire. But just before he starts to cut, the bomb starts to count down, ticking every second. Each time the bomb ticks, starting at time $t=15$ seconds, Bob panics and has a certain chance to move his wirecutters to the other wire. However, he is a rational man even when panicking, and has a $\frac{1}{2 t^{2}}$ chance of switching wires at time $t$, regardless of which wire he is about to cut. When the bomb ticks at $t=1$, Bob cuts whatever wire his wirecutters are on, without switching wires. What is the probability that Bob cuts the green wire?
|
$\frac{\mathbf{2 3}}{\mathbf{3 0}}$. Suppose Bob makes $n$ independent decisions, with probabilities of switching $p_{1}, p_{2}, \ldots, p_{n}$. Then in the expansion of the product
$$
P(x)=\left(p_{1}+\left(1-p_{1}\right) x\right)\left(p_{2}+\left(1-p_{2}\right) x\right) \cdots\left(p_{n}+\left(1-p_{n}\right) x\right)
$$
the sum of the coefficients of even powers of $x$ gives the probability that Bob makes his original decision. This is just $(P(1)+P(-1)) / 2$, so the probability is just
$$
\frac{1+\left(1-\frac{1}{1515}\right)\left(1-\frac{1}{1414}\right) \cdots\left(1-\frac{1}{22}\right)}{2}=\frac{1+\frac{1416 \frac{1315}{1515} 1414}{\cdots \frac{13}{22}}}{2}=\frac{1+\frac{8}{15}}{2}=\frac{23}{30} .
$$
$10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
{
"exam": "HMMT",
"problem_label": "21",
"problem_match": "\n21. [10]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
The sequence $\left\{a_{n}\right\}_{n \geq 1}$ is defined by $a_{n+2}=7 a_{n+1}-a_{n}$ for positive integers $n$ with initial values $a_{1}=1$ and $a_{2}=8$. Another sequence, $\left\{b_{n}\right\}$, is defined by the rule $b_{n+2}=3 b_{n+1}-b_{n}$ for positive integers $n$ together with the values $b_{1}=1$ and $b_{2}=2$. Find $\operatorname{gcd}\left(a_{5000}, b_{501}\right)$.
|
89. We show by induction that $a_{n}=F_{4 n-2}$ and $b_{n}=F_{2 n-1}$, where $F_{k}$ is the $k$ th Fibonacci number. The base cases are clear. As for the inductive steps, note that
$$
F_{k+2}=F_{k+1}+F_{k}=2 F_{k}+F_{k-1}=3 F_{k}-F_{k-2}
$$
and
$$
F_{k+4}=3 F_{k+2}-F_{k}=8 F_{k}+3 F_{k-2}=7 F_{k}-F_{k-4}
$$
We wish to compute the greatest common denominator of $F_{19998}$ and $F_{1001}$. The Fibonacci numbers satisfy the property that $\operatorname{gcd}\left(F_{m}, F_{n}\right)=F_{\operatorname{gcd}(m, n)}$, which can be proven by noting that they are periodic modulo any positive integer. So since $\operatorname{gcd}(19998,1001)=11$, the answer is $F_{11}=89$.
|
89
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
The sequence $\left\{a_{n}\right\}_{n \geq 1}$ is defined by $a_{n+2}=7 a_{n+1}-a_{n}$ for positive integers $n$ with initial values $a_{1}=1$ and $a_{2}=8$. Another sequence, $\left\{b_{n}\right\}$, is defined by the rule $b_{n+2}=3 b_{n+1}-b_{n}$ for positive integers $n$ together with the values $b_{1}=1$ and $b_{2}=2$. Find $\operatorname{gcd}\left(a_{5000}, b_{501}\right)$.
|
89. We show by induction that $a_{n}=F_{4 n-2}$ and $b_{n}=F_{2 n-1}$, where $F_{k}$ is the $k$ th Fibonacci number. The base cases are clear. As for the inductive steps, note that
$$
F_{k+2}=F_{k+1}+F_{k}=2 F_{k}+F_{k-1}=3 F_{k}-F_{k-2}
$$
and
$$
F_{k+4}=3 F_{k+2}-F_{k}=8 F_{k}+3 F_{k-2}=7 F_{k}-F_{k-4}
$$
We wish to compute the greatest common denominator of $F_{19998}$ and $F_{1001}$. The Fibonacci numbers satisfy the property that $\operatorname{gcd}\left(F_{m}, F_{n}\right)=F_{\operatorname{gcd}(m, n)}$, which can be proven by noting that they are periodic modulo any positive integer. So since $\operatorname{gcd}(19998,1001)=11$, the answer is $F_{11}=89$.
|
{
"exam": "HMMT",
"problem_label": "22",
"problem_match": "\n22. [12]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
In triangle $A B C, \angle A B C$ is obtuse. Point $D$ lies on side $A C$ such that $\angle A B D$ is right, and point $E$ lies on side $A C$ between $A$ and $D$ such that $B D$ bisects $\angle E B C$. Find $C E$, given that $A C=35, B C=7$, and $B E=5$.

|
10. Reflect $A$ and $E$ over $B D$ to $A^{\prime}$ and $E^{\prime}$ respectively. Note that the angle conditions show that $A^{\prime}$ and $E^{\prime}$ lie on $A B$ and $B C$ respectively. $B$ is the midpoint of segment $A A^{\prime}$ and $C E^{\prime}=$ $B C-B E^{\prime}=2$. Menelaus' theorem now gives
$$
\frac{C D}{D A} \cdot \frac{A A^{\prime}}{A^{\prime} B} \cdot \frac{B E^{\prime}}{E^{\prime} C}=1
$$
from which $D A=5 C D$ or $C D=A C / 6$. By the angle bisector theorem, $D E=5 C D / 7$, so that $C E=12 C D / 7=10$.
|
10
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
In triangle $A B C, \angle A B C$ is obtuse. Point $D$ lies on side $A C$ such that $\angle A B D$ is right, and point $E$ lies on side $A C$ between $A$ and $D$ such that $B D$ bisects $\angle E B C$. Find $C E$, given that $A C=35, B C=7$, and $B E=5$.

|
10. Reflect $A$ and $E$ over $B D$ to $A^{\prime}$ and $E^{\prime}$ respectively. Note that the angle conditions show that $A^{\prime}$ and $E^{\prime}$ lie on $A B$ and $B C$ respectively. $B$ is the midpoint of segment $A A^{\prime}$ and $C E^{\prime}=$ $B C-B E^{\prime}=2$. Menelaus' theorem now gives
$$
\frac{C D}{D A} \cdot \frac{A A^{\prime}}{A^{\prime} B} \cdot \frac{B E^{\prime}}{E^{\prime} C}=1
$$
from which $D A=5 C D$ or $C D=A C / 6$. By the angle bisector theorem, $D E=5 C D / 7$, so that $C E=12 C D / 7=10$.
|
{
"exam": "HMMT",
"problem_label": "23",
"problem_match": "\n23. [12]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Let $x, y, n$ be positive integers with $n>1$. How many ordered triples $(x, y, n)$ of solutions are there to the equation $x^{n}-y^{n}=2^{100}$ ?
|
49. Break all possible values of $n$ into the four cases: $n=2, n=4, n>4$ and $n$ odd. By Fermat's theorem, no solutions exist for the $n=4$ case because we may write $y^{4}+\left(2^{25}\right)^{4}=x^{4}$.
We show that for $n$ odd, no solutions exist to the more general equation $x^{n}-y^{n}=2^{k}$ where $k$ is a positive integer. Assume otherwise for contradiction's sake, and suppose on the grounds of well ordering that $k$ is the least exponent for which a solution exists. Clearly $x$ and $y$ must both be even or both odd. If both are odd, we have $(x-y)\left(x^{n-1}+\ldots+y^{n-1}\right)$. The right factor of this expression contains an odd number of odd terms whose sum is an odd number greater than 1 , impossible. Similarly if $x$ and $y$ are even, write $x=2 u$ and $y=2 v$. The equation becomes $u^{n}-v^{n}=2^{k-n}$. If $k-n$ is greater than 0 , then our choice $k$ could not have been minimal. Otherwise, $k-n=0$, so that two consecutive positive integers are perfect $n$th powers, which is also absurd.
For the case that $n$ is even and greater than 4, consider the same generalization and hypotheses. Writing $n=2 m$, we find $\left(x^{m}-y^{m}\right)\left(x^{m}+y^{m}\right)=2^{k}$. Then $x^{m}-y^{m}=2^{a}<2^{k}$. By our previous work, we see that $m$ cannot be an odd integer greater than 1 . But then $m$ must also be even, contrary to the minimality of $k$.
Finally, for $n=2$ we get $x^{2}-y^{2}=2^{100}$. Factoring the left hand side gives $x-y=2^{a}$ and $x+y=2^{b}$, where implicit is $a<b$. Solving, we get $x=2^{b-1}+2^{a-1}$ and $y=2^{b-1}-2^{a-1}$, for a total of 49 solutions. Namely, those corresponding to $(a, b)=(1,99),(2,98), \cdots,(49,51)$.
$10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
49
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $x, y, n$ be positive integers with $n>1$. How many ordered triples $(x, y, n)$ of solutions are there to the equation $x^{n}-y^{n}=2^{100}$ ?
|
49. Break all possible values of $n$ into the four cases: $n=2, n=4, n>4$ and $n$ odd. By Fermat's theorem, no solutions exist for the $n=4$ case because we may write $y^{4}+\left(2^{25}\right)^{4}=x^{4}$.
We show that for $n$ odd, no solutions exist to the more general equation $x^{n}-y^{n}=2^{k}$ where $k$ is a positive integer. Assume otherwise for contradiction's sake, and suppose on the grounds of well ordering that $k$ is the least exponent for which a solution exists. Clearly $x$ and $y$ must both be even or both odd. If both are odd, we have $(x-y)\left(x^{n-1}+\ldots+y^{n-1}\right)$. The right factor of this expression contains an odd number of odd terms whose sum is an odd number greater than 1 , impossible. Similarly if $x$ and $y$ are even, write $x=2 u$ and $y=2 v$. The equation becomes $u^{n}-v^{n}=2^{k-n}$. If $k-n$ is greater than 0 , then our choice $k$ could not have been minimal. Otherwise, $k-n=0$, so that two consecutive positive integers are perfect $n$th powers, which is also absurd.
For the case that $n$ is even and greater than 4, consider the same generalization and hypotheses. Writing $n=2 m$, we find $\left(x^{m}-y^{m}\right)\left(x^{m}+y^{m}\right)=2^{k}$. Then $x^{m}-y^{m}=2^{a}<2^{k}$. By our previous work, we see that $m$ cannot be an odd integer greater than 1 . But then $m$ must also be even, contrary to the minimality of $k$.
Finally, for $n=2$ we get $x^{2}-y^{2}=2^{100}$. Factoring the left hand side gives $x-y=2^{a}$ and $x+y=2^{b}$, where implicit is $a<b$. Solving, we get $x=2^{b-1}+2^{a-1}$ and $y=2^{b-1}-2^{a-1}$, for a total of 49 solutions. Namely, those corresponding to $(a, b)=(1,99),(2,98), \cdots,(49,51)$.
$10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
{
"exam": "HMMT",
"problem_label": "24",
"problem_match": "\n24. [12]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Two real numbers $x$ and $y$ are such that $8 y^{4}+4 x^{2} y^{2}+4 x y^{2}+2 x^{3}+2 y^{2}+2 x=x^{2}+1$. Find all possible values of $x+2 y^{2}$.
|
$\frac{\mathbf{1}}{\mathbf{2}}$. Writing $a=x+2 y^{2}$, the given quickly becomes $4 y^{2} a+2 x^{2} a+a+x=x^{2}+1$. We can rewrite $4 y^{2} a$ for further reduction to $a(2 a-2 x)+2 x^{2} a+a+x=x^{2}+1$, or
$$
2 a^{2}+\left(2 x^{2}-2 x+1\right) a+\left(-x^{2}+x-1\right)=0
$$
The quadratic formula produces the discriminant
$$
\left(2 x^{2}-2 x+1\right)^{2}+8\left(x^{2}-x+1\right)=\left(2 x^{2}-2 x+3\right)^{2},
$$
an identity that can be treated with the difference of squares, so that $a=\frac{-2 x^{2}+2 x-1 \pm\left(2 x^{2}-2 x+3\right)}{4}=$ $\frac{1}{2},-x^{2}+x-1$. Now $a$ was constructed from $x$ and $y$, so is not free. Indeed, the second expression flies in the face of the trivial inequality: $a=-x^{2}+x-1<-x^{2}+x \leq x+2 y^{2}=a$. On the other hand, $a=1 / 2$ is a bona fide solution to $\left(^{*}\right)$, which is identical to the original equation.
|
\frac{1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Two real numbers $x$ and $y$ are such that $8 y^{4}+4 x^{2} y^{2}+4 x y^{2}+2 x^{3}+2 y^{2}+2 x=x^{2}+1$. Find all possible values of $x+2 y^{2}$.
|
$\frac{\mathbf{1}}{\mathbf{2}}$. Writing $a=x+2 y^{2}$, the given quickly becomes $4 y^{2} a+2 x^{2} a+a+x=x^{2}+1$. We can rewrite $4 y^{2} a$ for further reduction to $a(2 a-2 x)+2 x^{2} a+a+x=x^{2}+1$, or
$$
2 a^{2}+\left(2 x^{2}-2 x+1\right) a+\left(-x^{2}+x-1\right)=0
$$
The quadratic formula produces the discriminant
$$
\left(2 x^{2}-2 x+1\right)^{2}+8\left(x^{2}-x+1\right)=\left(2 x^{2}-2 x+3\right)^{2},
$$
an identity that can be treated with the difference of squares, so that $a=\frac{-2 x^{2}+2 x-1 \pm\left(2 x^{2}-2 x+3\right)}{4}=$ $\frac{1}{2},-x^{2}+x-1$. Now $a$ was constructed from $x$ and $y$, so is not free. Indeed, the second expression flies in the face of the trivial inequality: $a=-x^{2}+x-1<-x^{2}+x \leq x+2 y^{2}=a$. On the other hand, $a=1 / 2$ is a bona fide solution to $\left(^{*}\right)$, which is identical to the original equation.
|
{
"exam": "HMMT",
"problem_label": "25",
"problem_match": "\n25. [12]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
$A B C D$ is a cyclic quadrilateral in which $A B=4, B C=3, C D=2$, and $A D=5$. Diagonals $A C$ and $B D$ intersect at $X$. A circle $\omega$ passes through $A$ and is tangent to $B D$ at $X$. $\omega$ intersects $A B$ and $A D$ at $Y$ and $Z$ respectively. Compute $Y Z / B D$.
|
$\frac{\mathbf{1 1 5}}{\mathbf{1 4 3}}$. Denote the lengths $A B, B C, C D$, and $D A$ by $a, b, c$, and $d$ respectively. Because $A B C D$ is cyclic, $\triangle A B X \sim \triangle D C X$ and $\triangle A D X \sim \triangle B C X$. It follows that $\frac{A X}{D X}=\frac{B X}{C X}=\frac{a}{c}$ and $\frac{A X}{B X}=\frac{D X}{C X}=\frac{d}{b}$. Therefore we may write $A X=a d k, B X=a b k, C X=b c k$, and $D X=c d k$ for some $k$. Now, $\angle X D C=\angle B A X=\angle Y X B$ and $\angle D C X=\angle X B Y$, so $\triangle B X Y \sim \triangle C D X$. Thus, $X Y=$ $D X \cdot \frac{B X}{C D}=c d k \cdot \frac{a b k}{c}=a b d k^{2}$. Analogously, $X Y=a c d k^{2}$. Note that $X Y / X Z=C B / C D$. Since $\angle Y X Z=\pi-\angle Z A \stackrel{c}{Y}=\angle B C D$, we have that $\triangle X Y Z \sim \triangle C B D$. Thus, $Y Z / B D=X Y / C B=a d k^{2}$.
Finally, Ptolemy's theorem applied to $A B C D$ gives
$$
(a d+b c) k \cdot(a b+c d) k=a c+b d
$$
It follows that the answer is
$$
\frac{a d(a c+b d)}{(a b+c d)(a d+b c)}=\frac{20 \cdot 23}{22 \cdot 26}=\frac{115}{143}
$$
|
\frac{115}{143}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
$A B C D$ is a cyclic quadrilateral in which $A B=4, B C=3, C D=2$, and $A D=5$. Diagonals $A C$ and $B D$ intersect at $X$. A circle $\omega$ passes through $A$ and is tangent to $B D$ at $X$. $\omega$ intersects $A B$ and $A D$ at $Y$ and $Z$ respectively. Compute $Y Z / B D$.

|
$\frac{\mathbf{1 1 5}}{\mathbf{1 4 3}}$. Denote the lengths $A B, B C, C D$, and $D A$ by $a, b, c$, and $d$ respectively. Because $A B C D$ is cyclic, $\triangle A B X \sim \triangle D C X$ and $\triangle A D X \sim \triangle B C X$. It follows that $\frac{A X}{D X}=\frac{B X}{C X}=\frac{a}{c}$ and $\frac{A X}{B X}=\frac{D X}{C X}=\frac{d}{b}$. Therefore we may write $A X=a d k, B X=a b k, C X=b c k$, and $D X=c d k$ for some $k$. Now, $\angle X D C=\angle B A X=\angle Y X B$ and $\angle D C X=\angle X B Y$, so $\triangle B X Y \sim \triangle C D X$. Thus, $X Y=$ $D X \cdot \frac{B X}{C D}=c d k \cdot \frac{a b k}{c}=a b d k^{2}$. Analogously, $X Y=a c d k^{2}$. Note that $X Y / X Z=C B / C D$. Since $\angle Y X Z=\pi-\angle Z A \stackrel{c}{Y}=\angle B C D$, we have that $\triangle X Y Z \sim \triangle C B D$. Thus, $Y Z / B D=X Y / C B=a d k^{2}$.
Finally, Ptolemy's theorem applied to $A B C D$ gives
$$
(a d+b c) k \cdot(a b+c d) k=a c+b d
$$
It follows that the answer is
$$
\frac{a d(a c+b d)}{(a b+c d)(a d+b c)}=\frac{20 \cdot 23}{22 \cdot 26}=\frac{115}{143}
$$
|
{
"exam": "HMMT",
"problem_label": "26",
"problem_match": "\n26. [12]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Find the number of 7 -tuples $\left(n_{1}, \ldots, n_{7}\right)$ of integers such that
$$
\sum_{i=1}^{7} n_{i}^{6}=96957
$$
|
2688. Consider the equation in modulo 9. All perfect 6 th powers are either 0 or 1 . Since 9 divides 96957 , it must be that each $n_{i}$ is a multiple of 3 . Writing $3 a_{i}=n_{i}$ and dividing both sides by $3^{6}$, we have $a_{1}^{6}+\cdots+a_{7}^{6}=133$. Since sixth powers are nonnegative, $\left|a_{i}\right| \leq 2$. Again considering modulo 9 , we see that $a_{i} \neq 0$. Thus, $a_{i}^{6} \in\{1,64\}$. The only possibility is $133=64+64+1+1+1+1+1$, so $\left|a_{1}\right|, \ldots,\left|a_{7}\right|$ consists of 22 's and 51 's. It follows that the answer is $\binom{7}{2} \cdot 2^{7}=2688$.
$10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
2688
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the number of 7 -tuples $\left(n_{1}, \ldots, n_{7}\right)$ of integers such that
$$
\sum_{i=1}^{7} n_{i}^{6}=96957
$$
|
2688. Consider the equation in modulo 9. All perfect 6 th powers are either 0 or 1 . Since 9 divides 96957 , it must be that each $n_{i}$ is a multiple of 3 . Writing $3 a_{i}=n_{i}$ and dividing both sides by $3^{6}$, we have $a_{1}^{6}+\cdots+a_{7}^{6}=133$. Since sixth powers are nonnegative, $\left|a_{i}\right| \leq 2$. Again considering modulo 9 , we see that $a_{i} \neq 0$. Thus, $a_{i}^{6} \in\{1,64\}$. The only possibility is $133=64+64+1+1+1+1+1$, so $\left|a_{1}\right|, \ldots,\left|a_{7}\right|$ consists of 22 's and 51 's. It follows that the answer is $\binom{7}{2} \cdot 2^{7}=2688$.
$10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
{
"exam": "HMMT",
"problem_label": "27",
"problem_match": "\n27. [12]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Compute the circumradius of cyclic hexagon $A B C D E F$, which has side lengths $A B=B C=$ $2, C D=D E=9$, and $E F=F A=12$.
|
8. Construct point $E^{\prime}$ on the circumcircle of $A B C D E F$ such that $D E^{\prime}=E F=12$ and $E^{\prime} F=D E=9$; then $\overline{B E^{\prime}}$ is a diameter. Let $B E^{\prime}=d$. Then $C E^{\prime}=\sqrt{B E^{\prime 2}-B C^{2}}=\sqrt{d^{2}-4}$ and $B D=\sqrt{B E^{\prime 2}-D E^{\prime 2}}=\sqrt{d^{2}-144}$. Applying Ptolemy's theorem to $B C D E^{\prime}$ now yields
$$
9 \cdot d+2 \cdot 12=\sqrt{\left(d^{2}-4\right)\left(d^{2}-144\right)}
$$
Squaring and rearranging, we find $0=d^{4}-229 d^{2}-432 d=d(d-16)\left(d^{2}+16 d+27\right)$. Since $d$ is a positive real number, $d=16$, and the circumradius is 8 .
|
8
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Compute the circumradius of cyclic hexagon $A B C D E F$, which has side lengths $A B=B C=$ $2, C D=D E=9$, and $E F=F A=12$.

|
8. Construct point $E^{\prime}$ on the circumcircle of $A B C D E F$ such that $D E^{\prime}=E F=12$ and $E^{\prime} F=D E=9$; then $\overline{B E^{\prime}}$ is a diameter. Let $B E^{\prime}=d$. Then $C E^{\prime}=\sqrt{B E^{\prime 2}-B C^{2}}=\sqrt{d^{2}-4}$ and $B D=\sqrt{B E^{\prime 2}-D E^{\prime 2}}=\sqrt{d^{2}-144}$. Applying Ptolemy's theorem to $B C D E^{\prime}$ now yields
$$
9 \cdot d+2 \cdot 12=\sqrt{\left(d^{2}-4\right)\left(d^{2}-144\right)}
$$
Squaring and rearranging, we find $0=d^{4}-229 d^{2}-432 d=d(d-16)\left(d^{2}+16 d+27\right)$. Since $d$ is a positive real number, $d=16$, and the circumradius is 8 .
|
{
"exam": "HMMT",
"problem_label": "28",
"problem_match": "\n28. [15]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
A sequence $\left\{a_{n}\right\}_{n \geq 1}$ of positive reals is defined by the rule $a_{n+1} a_{n-1}^{5}=a_{n}^{4} a_{n-2}^{2}$ for integers $n>2$ together with the initial values $a_{1}=8$ and $a_{2}=64$ and $a_{3}=1024$. Compute
$$
\sqrt{a_{1}+\sqrt{a_{2}+\sqrt{a_{3}+\cdots}}}
$$
|
$\mathbf{3} \sqrt{\mathbf{2}}$. Taking the base- $2 \log$ of the sequence $\left\{a_{n}\right\}$ converts the multiplicative rule to a more familiar additive rule: $\log _{2}\left(a_{n+1}\right)-4 \log _{2}\left(a_{n}\right)+5 \log _{2}\left(a_{n-1}\right)-2 \log _{2}\left(a_{n-2}\right)=0$. The characteristic equation is $0=x^{3}-4 x^{2}+5 x-2=(x-1)^{2}(x-2)$, so $\log _{2}\left(a_{n}\right)$ is of the form $a \cdot n+b+c \cdot 2^{n}$ and we find $a_{n}=2^{2 n+2^{n-1}}$. Now,
$$
\sqrt{a_{1}+\sqrt{a_{2}+\sqrt{a_{3}+\cdots}}}=\sqrt{2} \cdot \sqrt{4+\sqrt{16+\sqrt{64+\cdots}}}
$$
We can estimate the new nested radical expression as 3 , which expands thus
$$
3=\sqrt{4+5}=\sqrt{4+\sqrt{16+9}}=\sqrt{4+\sqrt{16+\sqrt{64+17}}}=\cdots
$$
As a rigorous confirmation, we have $2^{k}+1=\sqrt{4^{k}+\left(2^{k+1}+1\right)}$, as desired. It follows that the answer is $3 \sqrt{2}$.
|
3 \sqrt{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
A sequence $\left\{a_{n}\right\}_{n \geq 1}$ of positive reals is defined by the rule $a_{n+1} a_{n-1}^{5}=a_{n}^{4} a_{n-2}^{2}$ for integers $n>2$ together with the initial values $a_{1}=8$ and $a_{2}=64$ and $a_{3}=1024$. Compute
$$
\sqrt{a_{1}+\sqrt{a_{2}+\sqrt{a_{3}+\cdots}}}
$$
|
$\mathbf{3} \sqrt{\mathbf{2}}$. Taking the base- $2 \log$ of the sequence $\left\{a_{n}\right\}$ converts the multiplicative rule to a more familiar additive rule: $\log _{2}\left(a_{n+1}\right)-4 \log _{2}\left(a_{n}\right)+5 \log _{2}\left(a_{n-1}\right)-2 \log _{2}\left(a_{n-2}\right)=0$. The characteristic equation is $0=x^{3}-4 x^{2}+5 x-2=(x-1)^{2}(x-2)$, so $\log _{2}\left(a_{n}\right)$ is of the form $a \cdot n+b+c \cdot 2^{n}$ and we find $a_{n}=2^{2 n+2^{n-1}}$. Now,
$$
\sqrt{a_{1}+\sqrt{a_{2}+\sqrt{a_{3}+\cdots}}}=\sqrt{2} \cdot \sqrt{4+\sqrt{16+\sqrt{64+\cdots}}}
$$
We can estimate the new nested radical expression as 3 , which expands thus
$$
3=\sqrt{4+5}=\sqrt{4+\sqrt{16+9}}=\sqrt{4+\sqrt{16+\sqrt{64+17}}}=\cdots
$$
As a rigorous confirmation, we have $2^{k}+1=\sqrt{4^{k}+\left(2^{k+1}+1\right)}$, as desired. It follows that the answer is $3 \sqrt{2}$.
|
{
"exam": "HMMT",
"problem_label": "29",
"problem_match": "\n29. [15]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
$A B C D$ is a cyclic quadrilateral in which $A B=3, B C=5, C D=6$, and $A D=10 . M, I$, and $T$ are the feet of the perpendiculars from $D$ to lines $A B, A C$, and $B C$ respectively. Determine the value of $M I / I T$.
|
$\frac{\mathbf{2 5}}{\mathbf{9}}$. Quadrilaterals $A M I D$ and $D I C T$ are cyclic, having right angles $\angle A M D, \angle A I D$, and $\angle C I D, \angle C T D$ respectively. We see that $M, I$, and $T$ are collinear. For, $m \angle M I D=\pi-m \angle D A M=$ $\pi-m \angle D A B=m \angle B C D=\pi-m \angle D C T=\pi-m \angle D I T$. Therefore, Menelaus' theorem applied to triangle $M T B$ and line $I C A$ gives
$$
\frac{M I}{I T} \cdot \frac{T C}{C B} \cdot \frac{B A}{A M}=1
$$
On the other hand, triangle $A D M$ is similar to triangle $C D T$ since $\angle A M D \cong \angle C T D$ and $\angle D A M \cong$ $\angle D C T$ and thus $A M / C T=A D / C D$. It follows that
$$
\frac{M I}{I T}=\frac{B C \cdot A M}{A B \cdot C T}=\frac{B C \cdot A D}{A B \cdot C D}=\frac{5 \cdot 10}{3 \cdot 6}=\frac{25}{9}
$$
Remarks. The line MIT, constructed in this problem by taking perpendiculars from a point on the circumcircle of $A B C$, is known as the Simson line. It is often helpful for us to use directed angles while angle chasing to avoid supplementary configuration issues, such as those arising while establishing the collinearity of $M, I$, and $T$.
## $10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
\frac{25}{9}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
$A B C D$ is a cyclic quadrilateral in which $A B=3, B C=5, C D=6$, and $A D=10 . M, I$, and $T$ are the feet of the perpendiculars from $D$ to lines $A B, A C$, and $B C$ respectively. Determine the value of $M I / I T$.

|
$\frac{\mathbf{2 5}}{\mathbf{9}}$. Quadrilaterals $A M I D$ and $D I C T$ are cyclic, having right angles $\angle A M D, \angle A I D$, and $\angle C I D, \angle C T D$ respectively. We see that $M, I$, and $T$ are collinear. For, $m \angle M I D=\pi-m \angle D A M=$ $\pi-m \angle D A B=m \angle B C D=\pi-m \angle D C T=\pi-m \angle D I T$. Therefore, Menelaus' theorem applied to triangle $M T B$ and line $I C A$ gives
$$
\frac{M I}{I T} \cdot \frac{T C}{C B} \cdot \frac{B A}{A M}=1
$$
On the other hand, triangle $A D M$ is similar to triangle $C D T$ since $\angle A M D \cong \angle C T D$ and $\angle D A M \cong$ $\angle D C T$ and thus $A M / C T=A D / C D$. It follows that
$$
\frac{M I}{I T}=\frac{B C \cdot A M}{A B \cdot C T}=\frac{B C \cdot A D}{A B \cdot C D}=\frac{5 \cdot 10}{3 \cdot 6}=\frac{25}{9}
$$
Remarks. The line MIT, constructed in this problem by taking perpendiculars from a point on the circumcircle of $A B C$, is known as the Simson line. It is often helpful for us to use directed angles while angle chasing to avoid supplementary configuration issues, such as those arising while establishing the collinearity of $M, I$, and $T$.
## $10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
{
"exam": "HMMT",
"problem_label": "30",
"problem_match": "\n30. [15]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
A sequence $\left\{a_{n}\right\}_{n \geq 0}$ of real numbers satisfies the recursion $a_{n+1}=a_{n}^{3}-3 a_{n}^{2}+3$ for all positive integers $n$. For how many values of $a_{0}$ does $a_{2007}=a_{0}$ ?
|
$\mathbf{3}^{\mathbf{2 0 0 7}}$. If $x$ appears in the sequence, the next term $x^{3}-3 x^{2}+3$ is the same if and only if $0=x^{3}-3 x^{2}-x+3=(x-3)(x-1)(x+1)$. Moreover, that next term is strictly larger if $x>3$ and strictly smaller if $x<-1$. It follows that no values of $a_{0}$ with $\left|a_{0}-1\right|>2$ yield $a_{0}=a_{2007}$.
Now suppose $a_{0}=a_{2007}$ and write $a_{0}=1+e^{\alpha i}+e^{-\alpha i}$; the values $a_{0}$ we seek will be in bijective correspondence with solutions $\alpha$ where $0 \leq \alpha \leq \pi$. Then
$$
a_{1}=\left(a_{0}-1\right)^{3}-3 a_{0}+4=e^{3 \alpha i}+3 e^{\alpha i}+3 e^{-\alpha i}+e^{-3 \alpha i}-3 e^{\alpha i}-3 e^{-\alpha i}-3+4=e^{3 \alpha i}+e^{-3 \alpha i}+1
$$
and an easy inductive argument gives $a_{2007}=e^{3^{2007} \alpha i}+e^{-3^{2007} \alpha i}+1$. It follows that $a_{0}=a_{2007}$ is equivalent to $\cos (\alpha)=\cos \left(3^{2007} \alpha\right)$. Now,
$$
\cos \left(3^{2007} \alpha\right)-\cos (\alpha)=2 \sin \left(\left(\frac{3^{2007}+1}{2}\right) \alpha\right) \sin \left(\left(\frac{3^{2007}-1}{2}\right) \alpha\right)
$$
so $\operatorname{since} \sin (k x)=0$ for a positive integer $k$ if and only if $x$ is a multiple of $\frac{\pi}{k}$, the solutions $\alpha$ are $\left\{0, \frac{2 \pi}{3^{2007}-1}, \frac{4 \pi}{3^{2007}-1}, \ldots, \pi\right\} \cup\left\{0, \frac{2 \pi}{3^{2007}+1}, \ldots, \pi\right\}$. Because our values $k$ are consecutive, these sets overlap only at 0 and $\pi$, so there are $3^{2007}$ distinct $\alpha$.
|
3^{2007}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
A sequence $\left\{a_{n}\right\}_{n \geq 0}$ of real numbers satisfies the recursion $a_{n+1}=a_{n}^{3}-3 a_{n}^{2}+3$ for all positive integers $n$. For how many values of $a_{0}$ does $a_{2007}=a_{0}$ ?
|
$\mathbf{3}^{\mathbf{2 0 0 7}}$. If $x$ appears in the sequence, the next term $x^{3}-3 x^{2}+3$ is the same if and only if $0=x^{3}-3 x^{2}-x+3=(x-3)(x-1)(x+1)$. Moreover, that next term is strictly larger if $x>3$ and strictly smaller if $x<-1$. It follows that no values of $a_{0}$ with $\left|a_{0}-1\right|>2$ yield $a_{0}=a_{2007}$.
Now suppose $a_{0}=a_{2007}$ and write $a_{0}=1+e^{\alpha i}+e^{-\alpha i}$; the values $a_{0}$ we seek will be in bijective correspondence with solutions $\alpha$ where $0 \leq \alpha \leq \pi$. Then
$$
a_{1}=\left(a_{0}-1\right)^{3}-3 a_{0}+4=e^{3 \alpha i}+3 e^{\alpha i}+3 e^{-\alpha i}+e^{-3 \alpha i}-3 e^{\alpha i}-3 e^{-\alpha i}-3+4=e^{3 \alpha i}+e^{-3 \alpha i}+1
$$
and an easy inductive argument gives $a_{2007}=e^{3^{2007} \alpha i}+e^{-3^{2007} \alpha i}+1$. It follows that $a_{0}=a_{2007}$ is equivalent to $\cos (\alpha)=\cos \left(3^{2007} \alpha\right)$. Now,
$$
\cos \left(3^{2007} \alpha\right)-\cos (\alpha)=2 \sin \left(\left(\frac{3^{2007}+1}{2}\right) \alpha\right) \sin \left(\left(\frac{3^{2007}-1}{2}\right) \alpha\right)
$$
so $\operatorname{since} \sin (k x)=0$ for a positive integer $k$ if and only if $x$ is a multiple of $\frac{\pi}{k}$, the solutions $\alpha$ are $\left\{0, \frac{2 \pi}{3^{2007}-1}, \frac{4 \pi}{3^{2007}-1}, \ldots, \pi\right\} \cup\left\{0, \frac{2 \pi}{3^{2007}+1}, \ldots, \pi\right\}$. Because our values $k$ are consecutive, these sets overlap only at 0 and $\pi$, so there are $3^{2007}$ distinct $\alpha$.
|
{
"exam": "HMMT",
"problem_label": "31",
"problem_match": "\n31. [18]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Triangle $A B C$ has $A B=4, B C=6$, and $A C=5$. Let $O$ denote the circumcenter of $A B C$. The circle $\Gamma$ is tangent to and surrounds the circumcircles of triangles $A O B, B O C$, and $A O C$. Determine the diameter of $\Gamma$.
|
$\frac{\mathbf{2 5 6} \sqrt{\mathbf{7}}}{\mathbf{1 7}}$. Denote by $\omega, \Gamma_{1}, \Gamma_{2}$, and $\Gamma_{3}$ the circumcenters of triangles $A B C, B O C, C O A$, and $A O B$, respectively. An inversion about $\omega$ interchanges $\Gamma_{1}$ and line $B C, \Gamma_{2}$ and line $C A$, and $\Gamma_{3}$ and line $A B$. This inversion also preserves tangency between generalized circles, so the image of $\Gamma$ is a circle tangent to $A B, B C$, and $C A$. It is the incircle of $A B C$ because it is closer to $O$ than these lines and $A B C$ is acute.
Now we run a few standard calculations. Where $s, r$, and $R$ denote the semiperimeter, inradius, and circumradius of $A B C$, respectively, we have the following:
$$
\begin{aligned}
& {[A B C]=\sqrt{s(s-a)(s-b)(s-c)}=\frac{15 \sqrt{7}}{4}} \\
& r=[A B C] / s=\sqrt{7} / 2 \\
& R=\frac{a b c}{4[A B C]}=\frac{8}{\sqrt{7}} \\
& O I^{2}=R(R-2 r)=\frac{8}{7}
\end{aligned}
$$
Let $O I$ intersect the incircle of $A B C$ at $P$ and $Q$, with $I$ between $P$ and $O$. Then $O P=r+O I$ and $O Q=r-O I$, and $\overline{P Q}$ is a diameter. Under the inversion, $P$ and $Q$ map to $P^{\prime}$ and $Q^{\prime}$ respectively. Because $P, I, O$, and $Q$ are collinear in that order, $P^{\prime}$ and $Q^{\prime}$ are diametrically opposed on $\Gamma$. It follows that the diameter of $\Gamma$ is
$$
P^{\prime} Q^{\prime}=O P^{\prime}+O Q^{\prime}=\frac{R^{2}}{O P}+\frac{R^{2}}{O Q}=R^{2}\left(\frac{1}{r+O I}+\frac{1}{r-O I}\right)=\frac{2 r R^{2}}{r^{2}-O I^{2}} .
$$
We plug in the values found above to arrive at $\frac{256 \sqrt{7}}{17}$.
|
\frac{256 \sqrt{7}}{17}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Triangle $A B C$ has $A B=4, B C=6$, and $A C=5$. Let $O$ denote the circumcenter of $A B C$. The circle $\Gamma$ is tangent to and surrounds the circumcircles of triangles $A O B, B O C$, and $A O C$. Determine the diameter of $\Gamma$.
|
$\frac{\mathbf{2 5 6} \sqrt{\mathbf{7}}}{\mathbf{1 7}}$. Denote by $\omega, \Gamma_{1}, \Gamma_{2}$, and $\Gamma_{3}$ the circumcenters of triangles $A B C, B O C, C O A$, and $A O B$, respectively. An inversion about $\omega$ interchanges $\Gamma_{1}$ and line $B C, \Gamma_{2}$ and line $C A$, and $\Gamma_{3}$ and line $A B$. This inversion also preserves tangency between generalized circles, so the image of $\Gamma$ is a circle tangent to $A B, B C$, and $C A$. It is the incircle of $A B C$ because it is closer to $O$ than these lines and $A B C$ is acute.
Now we run a few standard calculations. Where $s, r$, and $R$ denote the semiperimeter, inradius, and circumradius of $A B C$, respectively, we have the following:
$$
\begin{aligned}
& {[A B C]=\sqrt{s(s-a)(s-b)(s-c)}=\frac{15 \sqrt{7}}{4}} \\
& r=[A B C] / s=\sqrt{7} / 2 \\
& R=\frac{a b c}{4[A B C]}=\frac{8}{\sqrt{7}} \\
& O I^{2}=R(R-2 r)=\frac{8}{7}
\end{aligned}
$$
Let $O I$ intersect the incircle of $A B C$ at $P$ and $Q$, with $I$ between $P$ and $O$. Then $O P=r+O I$ and $O Q=r-O I$, and $\overline{P Q}$ is a diameter. Under the inversion, $P$ and $Q$ map to $P^{\prime}$ and $Q^{\prime}$ respectively. Because $P, I, O$, and $Q$ are collinear in that order, $P^{\prime}$ and $Q^{\prime}$ are diametrically opposed on $\Gamma$. It follows that the diameter of $\Gamma$ is
$$
P^{\prime} Q^{\prime}=O P^{\prime}+O Q^{\prime}=\frac{R^{2}}{O P}+\frac{R^{2}}{O Q}=R^{2}\left(\frac{1}{r+O I}+\frac{1}{r-O I}\right)=\frac{2 r R^{2}}{r^{2}-O I^{2}} .
$$
We plug in the values found above to arrive at $\frac{256 \sqrt{7}}{17}$.

|
{
"exam": "HMMT",
"problem_label": "32",
"problem_match": "\n32. [18]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Compute
$$
\int_{1}^{2} \frac{9 x+4}{x^{5}+3 x^{2}+x} d x
$$
(No, your TI-89 doesn't know how to do this one. Yes, the end is near.)
|
$\ln \frac{\mathbf{8 0}}{\mathbf{2 3}}$. We break the given integral into two pieces:
$$
\int_{1}^{2} \frac{9 x+4}{x^{5}+3 x^{2}+x} d x=5 \int_{1}^{2} \frac{x^{4}+3 x+1}{x^{5}+3 x^{2}+x} d x-\int_{1}^{2} \frac{5 x^{4}+6 x+1}{x^{5}+3 x^{2}+x} d x
$$
These two new integrals are easily computed; for, the first integrand reduces to $1 / x$ and the second is of the form $f^{\prime}(x) / f(x)$. We obtain
$$
\left[5 \ln |x|-\ln \left|x^{5}+3 x^{2}+x\right|\right]_{1}^{2}=\ln 32-\ln 46+\ln 5=\ln \frac{80}{23}
$$
Motivation. Writing $f(x)=9 x+4$ and $g(x)=x^{5}+3 x^{2}+x=x\left(x^{4}+3 x+1\right)$, we wish to find the antiderivative of $f(x) / g(x)$. It makes sense to consider other rational functions with denominator $g(x)$ that have an exact antiderivative. Clearly, if the numerator were $f_{1}(x)=x^{4}+3 x+1$ or a constant multiple, then we can integrate the function. Another trivial case is if the numerator were $f_{2}(x)=g^{\prime}(x)=5 x^{4}+6 x+1$ or a constant multiple. Guessing that $f(x)$ is a linear combination of $f_{1}(x)$ and $f_{2}(x)$, we easily find that $f(x)=9 x+4=5 f_{1}(x)-f_{2}(x)$.
$10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
\ln \frac{80}{23}
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Compute
$$
\int_{1}^{2} \frac{9 x+4}{x^{5}+3 x^{2}+x} d x
$$
(No, your TI-89 doesn't know how to do this one. Yes, the end is near.)
|
$\ln \frac{\mathbf{8 0}}{\mathbf{2 3}}$. We break the given integral into two pieces:
$$
\int_{1}^{2} \frac{9 x+4}{x^{5}+3 x^{2}+x} d x=5 \int_{1}^{2} \frac{x^{4}+3 x+1}{x^{5}+3 x^{2}+x} d x-\int_{1}^{2} \frac{5 x^{4}+6 x+1}{x^{5}+3 x^{2}+x} d x
$$
These two new integrals are easily computed; for, the first integrand reduces to $1 / x$ and the second is of the form $f^{\prime}(x) / f(x)$. We obtain
$$
\left[5 \ln |x|-\ln \left|x^{5}+3 x^{2}+x\right|\right]_{1}^{2}=\ln 32-\ln 46+\ln 5=\ln \frac{80}{23}
$$
Motivation. Writing $f(x)=9 x+4$ and $g(x)=x^{5}+3 x^{2}+x=x\left(x^{4}+3 x+1\right)$, we wish to find the antiderivative of $f(x) / g(x)$. It makes sense to consider other rational functions with denominator $g(x)$ that have an exact antiderivative. Clearly, if the numerator were $f_{1}(x)=x^{4}+3 x+1$ or a constant multiple, then we can integrate the function. Another trivial case is if the numerator were $f_{2}(x)=g^{\prime}(x)=5 x^{4}+6 x+1$ or a constant multiple. Guessing that $f(x)$ is a linear combination of $f_{1}(x)$ and $f_{2}(x)$, we easily find that $f(x)=9 x+4=5 f_{1}(x)-f_{2}(x)$.
$10^{\text {th }}$ HARVARD-MIT MATHEMATICS TOURNAMENT, 24 FEBRUARY 2007 - GUTS ROUND
|
{
"exam": "HMMT",
"problem_label": "33",
"problem_match": "\n33. [18]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
The Game. Eric and Greg are watching their new favorite TV show, The Price is Right. Bob Barker recently raised the intellectual level of his program, and he begins the latest installment with bidding on following question: How many Carmichael numbers are there less than 100,000?
Each team is to list one nonnegative integer not greater than 100,000. Let $X$ denote the answer to Bob's question. The teams listing $N$, a maximal bid (of those submitted) not greater than $X$, will receive $N$ points, and all other teams will neither receive nor lose points. (A Carmichael number is an odd composite integer $n$ such that $n$ divides $a^{n-1}-1$ for all integers $a$ relatively prime to $n$ with $1<a<n$.)
|
16? There are 16 such numbers: 561, 1105, 1729, 2465, 2821, 6601, 8911, 10585, 15841, $29341,41041,46657,52633,62745,63973$, and 75361 . The next, 101101 , is too large to be counted. Their distribution is considerably more subtle than that of the primes, and it was only recently proven that there are infinitely many Carmichael numbers. For sufficiently large $n, C(n)>n^{2 / 7}$, although this bound has been subsequently improved. (For details, see Alford, W. R.; Granville, A.; and Pomerance, C. "There are Infinitely Many Carmichael Numbers." Annals of Mathematics. 139 (1994), 703-722.) The expectation is that teams are unable to determine that $X=16$; otherwise, the obvious dominant play is listing 16. The Problem Czar, anticipating that teams will attempt to deduce $X$ by considering the point values of the other problems in the triplet, has chosen a value $X$ that is considerably lower. Teams may of course speculate whether this action has been taken, and to what extent, etc... On the actual TV show, many contestants win by guessing prices of 1 , or other numbers dramatically lower than the actual price. This strategy is enhanced because of the show's ordered bidding, and will be more difficult here. It will be interesting to see the submissions.
|
16
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
The Game. Eric and Greg are watching their new favorite TV show, The Price is Right. Bob Barker recently raised the intellectual level of his program, and he begins the latest installment with bidding on following question: How many Carmichael numbers are there less than 100,000?
Each team is to list one nonnegative integer not greater than 100,000. Let $X$ denote the answer to Bob's question. The teams listing $N$, a maximal bid (of those submitted) not greater than $X$, will receive $N$ points, and all other teams will neither receive nor lose points. (A Carmichael number is an odd composite integer $n$ such that $n$ divides $a^{n-1}-1$ for all integers $a$ relatively prime to $n$ with $1<a<n$.)
|
16? There are 16 such numbers: 561, 1105, 1729, 2465, 2821, 6601, 8911, 10585, 15841, $29341,41041,46657,52633,62745,63973$, and 75361 . The next, 101101 , is too large to be counted. Their distribution is considerably more subtle than that of the primes, and it was only recently proven that there are infinitely many Carmichael numbers. For sufficiently large $n, C(n)>n^{2 / 7}$, although this bound has been subsequently improved. (For details, see Alford, W. R.; Granville, A.; and Pomerance, C. "There are Infinitely Many Carmichael Numbers." Annals of Mathematics. 139 (1994), 703-722.) The expectation is that teams are unable to determine that $X=16$; otherwise, the obvious dominant play is listing 16. The Problem Czar, anticipating that teams will attempt to deduce $X$ by considering the point values of the other problems in the triplet, has chosen a value $X$ that is considerably lower. Teams may of course speculate whether this action has been taken, and to what extent, etc... On the actual TV show, many contestants win by guessing prices of 1 , or other numbers dramatically lower than the actual price. This strategy is enhanced because of the show's ordered bidding, and will be more difficult here. It will be interesting to see the submissions.
|
{
"exam": "HMMT",
"problem_label": "34",
"problem_match": "\n34. [?]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
The Algorithm. There are thirteen broken computers situated at the following set $S$ of thirteen points in the plane:
$$
\begin{array}{lll}
A=(1,10) & B=(976,9) & C=(666,87) \\
D=(377,422) & E=(535,488) & F=(775,488) \\
G=(941,500) & H=(225,583) & I=(388,696) \\
J=(3,713) & K=(504,872) & L=(560,934) \\
& M=(22,997) &
\end{array}
$$
At time $t=0$, a repairman begins moving from one computer to the next, traveling continuously in straight lines at unit speed. Assuming the repairman begins and $A$ and fixes computers instantly, what path does he take to minimize the total downtime of the computers? List the points he visits in order. Your score will be $\left\lfloor\frac{N}{40}\right\rfloor$, where
$$
N=1000+\lfloor\text { the optimal downtime }\rfloor-\lfloor\text { your downtime }\rfloor,
$$
or 0 , whichever is greater. By total downtime we mean the sum
$$
\sum_{P \in S} t_{P}
$$
where $t_{P}$ is the time at which the repairman reaches $P$.
|
ADHIKLEFGBCJM. This is an instance of the minimum-latency problem, which is at least NP-hard. There is an easy $O(n!)$ algorithm, but this is unavailable to teams on computational grounds ( 100 MHz calculators used to seem fast...) The best strategy may be drawing an accurate picture and exercising geometric intuition. The distribution of the points somewhat resembles a short, four-pronged fork with its outermost prongs bent apart; it is plausible to assume that the optimal order respects this shape. The optimal downtime is 24113.147907 , realized by ADHIKLEFGBCJM, though a number of others also receive positive marks.
|
24113.147907
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
The Algorithm. There are thirteen broken computers situated at the following set $S$ of thirteen points in the plane:
$$
\begin{array}{lll}
A=(1,10) & B=(976,9) & C=(666,87) \\
D=(377,422) & E=(535,488) & F=(775,488) \\
G=(941,500) & H=(225,583) & I=(388,696) \\
J=(3,713) & K=(504,872) & L=(560,934) \\
& M=(22,997) &
\end{array}
$$
At time $t=0$, a repairman begins moving from one computer to the next, traveling continuously in straight lines at unit speed. Assuming the repairman begins and $A$ and fixes computers instantly, what path does he take to minimize the total downtime of the computers? List the points he visits in order. Your score will be $\left\lfloor\frac{N}{40}\right\rfloor$, where
$$
N=1000+\lfloor\text { the optimal downtime }\rfloor-\lfloor\text { your downtime }\rfloor,
$$
or 0 , whichever is greater. By total downtime we mean the sum
$$
\sum_{P \in S} t_{P}
$$
where $t_{P}$ is the time at which the repairman reaches $P$.
|
ADHIKLEFGBCJM. This is an instance of the minimum-latency problem, which is at least NP-hard. There is an easy $O(n!)$ algorithm, but this is unavailable to teams on computational grounds ( 100 MHz calculators used to seem fast...) The best strategy may be drawing an accurate picture and exercising geometric intuition. The distribution of the points somewhat resembles a short, four-pronged fork with its outermost prongs bent apart; it is plausible to assume that the optimal order respects this shape. The optimal downtime is 24113.147907 , realized by ADHIKLEFGBCJM, though a number of others also receive positive marks.
|
{
"exam": "HMMT",
"problem_label": "35",
"problem_match": "\n35. [ $\\leq \\mathbf{2 5}]$",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
The Marathon. Let $\omega$ denote the incircle of triangle $A B C$. The segments $B C, C A$, and $A B$ are tangent to $\omega$ at $D, E$, and $F$, respectively. Point $P$ lies on $E F$ such that segment $P D$ is perpendicular to $B C$. The line $A P$ intersects $B C$ at $Q$. The circles $\omega_{1}$ and $\omega_{2}$ pass through $B$ and $C$, respectively, and are tangent to $A Q$ at $Q$; the former meets $A B$ again at $X$, and the latter meets $A C$ again at $Y$. The line $X Y$ intersects $B C$ at $Z$. Given that $A B=15, B C=14$, and $C A=13$, find $\lfloor X Z \cdot Y Z\rfloor$.
|
101. Construct $D^{\prime}$ diametrically opposed to $D$, so that $\angle D F D^{\prime}$ and $\angle D E D^{\prime}$ are right, and note that $P$ lies on $D D^{\prime}$. By standard angle chasing, $m \angle F D D^{\prime}=\beta$ (half angle $B$ ) and $m \angle D^{\prime} D E=\gamma$. Thus, $m \angle D D^{\prime} F=90^{\circ}-\beta$ and $m \angle E D^{\prime} D=90^{\circ}-\gamma$. Then by the law of sines, $D E: E D^{\prime}: D^{\prime} F$ : $F D=\cos (\gamma): \sin (\gamma): \sin (\beta): \sin (\gamma)$. Now using $\triangle D E P \sim \triangle F D^{\prime} P$ and $\triangle D F P \sim \triangle E D^{\prime} P$, we have
$$
\frac{E P}{P F}=\frac{E D \cdot E D^{\prime}}{F D \cdot F D^{\prime}}=\frac{\sin (\gamma) \cos (\gamma)}{\sin (\beta) \sin (\beta)}=\frac{c}{b}
$$
Let the dilation centered at $A$ sending $E$ to $C$ map $P$ and $F$ to $P^{\prime}$ and $F^{\prime}$, respectively. Note that $A F^{\prime}=A C$ as $A E$ and $A F$ are equal tangents, and $C P^{\prime}: P^{\prime} F^{\prime}=E P: P F=c: b$ by similarity. Then by Menelaus' theorem,
$$
1=\frac{B Q}{Q C} \frac{C P^{\prime}}{P^{\prime} F^{\prime}} \frac{F^{\prime} A}{A B}=\frac{B Q}{Q C} \frac{c}{b} \frac{b}{c}
$$
so that $B Q=Q C$ and $A Q$ is actually a median. So, $A Q^{2}=\frac{1}{4}\left(2 b^{2}+2 c^{2}-a^{2}\right)=148$. Now by Power of a Point, $A B \cdot A X=A Q^{2}=A C \cdot A Y$, so $A X=148 / 15$ and $A Y=148 / 13$. Moreover, $B X C Y$ is cyclic as $\triangle A B C \sim \triangle A Y X$. Thus, $X Z \cdot Y Z=B Z \cdot C Z$, and it suffices to compute $B Z / C Z$. Menelaus once more gives
$$
1=\frac{B Z}{Z C} \frac{C Y}{Y A} \frac{A X}{X B}
$$
whence, $B Z / C Z=(A Y / A X)(B X / C Y)=(15 / 13)((77 \cdot 13) /(21 \cdot 15))=11 / 3$. We write $C Z=3 d$ and $B Z=11 d$. Because $A X<A B$ and $A Y<A C, Z$ does not lie on segment $B C$. Given the configuration information, $B C=8 d=14$, so $d=7 / 4$, and finally $\lfloor B Z \cdot C Z\rfloor=\left\lfloor 33 d^{2}\right\rfloor=\left\lfloor\frac{1617}{16}\right\rfloor=101$.
|
101
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
The Marathon. Let $\omega$ denote the incircle of triangle $A B C$. The segments $B C, C A$, and $A B$ are tangent to $\omega$ at $D, E$, and $F$, respectively. Point $P$ lies on $E F$ such that segment $P D$ is perpendicular to $B C$. The line $A P$ intersects $B C$ at $Q$. The circles $\omega_{1}$ and $\omega_{2}$ pass through $B$ and $C$, respectively, and are tangent to $A Q$ at $Q$; the former meets $A B$ again at $X$, and the latter meets $A C$ again at $Y$. The line $X Y$ intersects $B C$ at $Z$. Given that $A B=15, B C=14$, and $C A=13$, find $\lfloor X Z \cdot Y Z\rfloor$.

|
101. Construct $D^{\prime}$ diametrically opposed to $D$, so that $\angle D F D^{\prime}$ and $\angle D E D^{\prime}$ are right, and note that $P$ lies on $D D^{\prime}$. By standard angle chasing, $m \angle F D D^{\prime}=\beta$ (half angle $B$ ) and $m \angle D^{\prime} D E=\gamma$. Thus, $m \angle D D^{\prime} F=90^{\circ}-\beta$ and $m \angle E D^{\prime} D=90^{\circ}-\gamma$. Then by the law of sines, $D E: E D^{\prime}: D^{\prime} F$ : $F D=\cos (\gamma): \sin (\gamma): \sin (\beta): \sin (\gamma)$. Now using $\triangle D E P \sim \triangle F D^{\prime} P$ and $\triangle D F P \sim \triangle E D^{\prime} P$, we have
$$
\frac{E P}{P F}=\frac{E D \cdot E D^{\prime}}{F D \cdot F D^{\prime}}=\frac{\sin (\gamma) \cos (\gamma)}{\sin (\beta) \sin (\beta)}=\frac{c}{b}
$$
Let the dilation centered at $A$ sending $E$ to $C$ map $P$ and $F$ to $P^{\prime}$ and $F^{\prime}$, respectively. Note that $A F^{\prime}=A C$ as $A E$ and $A F$ are equal tangents, and $C P^{\prime}: P^{\prime} F^{\prime}=E P: P F=c: b$ by similarity. Then by Menelaus' theorem,
$$
1=\frac{B Q}{Q C} \frac{C P^{\prime}}{P^{\prime} F^{\prime}} \frac{F^{\prime} A}{A B}=\frac{B Q}{Q C} \frac{c}{b} \frac{b}{c}
$$
so that $B Q=Q C$ and $A Q$ is actually a median. So, $A Q^{2}=\frac{1}{4}\left(2 b^{2}+2 c^{2}-a^{2}\right)=148$. Now by Power of a Point, $A B \cdot A X=A Q^{2}=A C \cdot A Y$, so $A X=148 / 15$ and $A Y=148 / 13$. Moreover, $B X C Y$ is cyclic as $\triangle A B C \sim \triangle A Y X$. Thus, $X Z \cdot Y Z=B Z \cdot C Z$, and it suffices to compute $B Z / C Z$. Menelaus once more gives
$$
1=\frac{B Z}{Z C} \frac{C Y}{Y A} \frac{A X}{X B}
$$
whence, $B Z / C Z=(A Y / A X)(B X / C Y)=(15 / 13)((77 \cdot 13) /(21 \cdot 15))=11 / 3$. We write $C Z=3 d$ and $B Z=11 d$. Because $A X<A B$ and $A Y<A C, Z$ does not lie on segment $B C$. Given the configuration information, $B C=8 d=14$, so $d=7 / 4$, and finally $\lfloor B Z \cdot C Z\rfloor=\left\lfloor 33 d^{2}\right\rfloor=\left\lfloor\frac{1617}{16}\right\rfloor=101$.
|
{
"exam": "HMMT",
"problem_label": "36",
"problem_match": "\n36. [25]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-guts-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Evaluate the functions $\phi(n), \sigma(n)$, and $\tau(n)$ for $n=12, n=2007$, and $n=2^{2007}$.
|
For $n=12=2^{2} \cdot 3^{1}$,
$$
\phi(12)=2(2-1)(3-1)=4, \quad \sigma(12)=(1+2+4)(1+3)=28, \quad \tau(12)=(2+1)(1+1)=6
$$
for $n=2007=3^{2} \cdot 223$,
$\phi(2007)=3(3-1)(223-1)=1332, \quad \sigma(2007)=(1+3+9)(1+223)=2912, \quad \tau(2007)=(2+1)(1+1)=6 ;$
and for $n=2^{2007}$,
$$
\phi\left(2^{2007}\right)=2^{2006}, \quad \sigma\left(2^{2007}\right)=\left(1+2+\cdots+2^{2007}\right)=2^{2008}-1, \quad \tau\left(2^{2007}\right)=2007+1=2008
$$
|
4, 28, 6, 1332, 2912, 6, 2^{2006}, 2^{2008}-1, 2008
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Evaluate the functions $\phi(n), \sigma(n)$, and $\tau(n)$ for $n=12, n=2007$, and $n=2^{2007}$.
|
For $n=12=2^{2} \cdot 3^{1}$,
$$
\phi(12)=2(2-1)(3-1)=4, \quad \sigma(12)=(1+2+4)(1+3)=28, \quad \tau(12)=(2+1)(1+1)=6
$$
for $n=2007=3^{2} \cdot 223$,
$\phi(2007)=3(3-1)(223-1)=1332, \quad \sigma(2007)=(1+3+9)(1+223)=2912, \quad \tau(2007)=(2+1)(1+1)=6 ;$
and for $n=2^{2007}$,
$$
\phi\left(2^{2007}\right)=2^{2006}, \quad \sigma\left(2^{2007}\right)=\left(1+2+\cdots+2^{2007}\right)=2^{2008}-1, \quad \tau\left(2^{2007}\right)=2007+1=2008
$$
|
{
"exam": "HMMT",
"problem_label": "1",
"problem_match": "\n1. [15]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team1-solutions.jsonl",
"solution_match": "\nSolution. ",
"tier": "T4",
"year": "2007"
}
|
Solve for the positive integer(s) $n$ such that $\phi\left(n^{2}\right)=1000 \phi(n)$.
|
1000.
|
1000
|
Yes
|
Problem not solved
|
math-word-problem
|
Number Theory
|
Solve for the positive integer(s) $n$ such that $\phi\left(n^{2}\right)=1000 \phi(n)$.
|
1000.
|
{
"exam": "HMMT",
"problem_label": "2",
"problem_match": "\n2. [20]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team1-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Solve for the positive integer(s) $n$ such that $\phi\left(n^{2}\right)=1000 \phi(n)$.
|
The unique solution is $n=1000$. For, $\phi(p n)=p \phi(n)$ for every prime $p$ dividing $n$, so that $\phi\left(n^{2}\right)=n \phi(n)$ for all positive integers $n$.
|
1000
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Solve for the positive integer(s) $n$ such that $\phi\left(n^{2}\right)=1000 \phi(n)$.
|
The unique solution is $n=1000$. For, $\phi(p n)=p \phi(n)$ for every prime $p$ dividing $n$, so that $\phi\left(n^{2}\right)=n \phi(n)$ for all positive integers $n$.
|
{
"exam": "HMMT",
"problem_label": "2",
"problem_match": "\n2. [20]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team1-solutions.jsonl",
"solution_match": "\nSolution. ",
"tier": "T4",
"year": "2007"
}
|
Prove that for every integer $n$ greater than 1 ,
$$
\sigma(n) \phi(n) \leq n^{2}-1
$$
When does equality hold?
|
Note that
$$
\sigma(m n) \phi(m n)=\sigma(m) \phi(m) \sigma(n) \phi(n) \leq\left(m^{2}-1\right)\left(n^{2}-1\right)=(m n)^{2}-\left(m^{2}+n^{2}-1\right)<(m n)^{2}-1
$$
for any pair of relatively prime positive integers $(m, n)$ other than $(1,1)$. Now, for $p$ a prime and $k$ a positive integer, $\sigma\left(p^{k}\right)=1+p+\cdots+p^{k}=\frac{p^{k+1}-1}{p-1}$ and $\phi\left(p^{k}\right)=p^{k}-\frac{1}{p} \cdot p^{k}=(p-1) p^{k-1}$. Thus,
$$
\sigma\left(p^{k}\right) \phi\left(p^{k}\right)=\frac{p^{k+1}-1}{p-1} \cdot(p-1) p^{k-1}=\left(p^{k+1}-1\right) p^{k-1}=p^{2 k}-p^{k-1} \leq p^{2 k}-1
$$
with equality where $k=1$. It follows that equality holds in the given inequality if and only if $n$ is prime.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that for every integer $n$ greater than 1 ,
$$
\sigma(n) \phi(n) \leq n^{2}-1
$$
When does equality hold?
|
Note that
$$
\sigma(m n) \phi(m n)=\sigma(m) \phi(m) \sigma(n) \phi(n) \leq\left(m^{2}-1\right)\left(n^{2}-1\right)=(m n)^{2}-\left(m^{2}+n^{2}-1\right)<(m n)^{2}-1
$$
for any pair of relatively prime positive integers $(m, n)$ other than $(1,1)$. Now, for $p$ a prime and $k$ a positive integer, $\sigma\left(p^{k}\right)=1+p+\cdots+p^{k}=\frac{p^{k+1}-1}{p-1}$ and $\phi\left(p^{k}\right)=p^{k}-\frac{1}{p} \cdot p^{k}=(p-1) p^{k-1}$. Thus,
$$
\sigma\left(p^{k}\right) \phi\left(p^{k}\right)=\frac{p^{k+1}-1}{p-1} \cdot(p-1) p^{k-1}=\left(p^{k+1}-1\right) p^{k-1}=p^{2 k}-p^{k-1} \leq p^{2 k}-1
$$
with equality where $k=1$. It follows that equality holds in the given inequality if and only if $n$ is prime.
|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n3. [25]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team1-solutions.jsonl",
"solution_match": "\nSolution. ",
"tier": "T4",
"year": "2007"
}
|
Prove the identity
$$
\sum_{d \mid n} \tau(d)^{3}=\left(\sum_{d \mid n} \tau(d)\right)^{2}
$$
|
Note that $\tau^{3}$ is multiplicative; in light of the convolution property just shown, it follows that both sides of the posed equality are multiplicative. Thus, it would suffice to prove the claim for $n$ a power of a prime. So, write $n=p^{k}$ where $p$ is a prime and $k$ is a nonnegative integer. Then
$$
\begin{aligned}
& \sum_{d \mid n} \tau(d)^{3}=\sum_{i=0}^{k} \tau\left(p^{i}\right)^{3}=\sum_{i=0}^{k}(i+1)^{3} \\
& \quad=1^{3}+\cdots+(k+1)^{3}=\frac{(k+1)^{2}(k+2)^{2}}{4}=\left(\frac{(k+1)(k+2)}{2}\right)^{2} \\
& \quad=\left(\sum_{i=0}^{k} \tau\left(p^{i}\right)\right)^{2}=\left(\sum_{d \mid n} \tau(d)\right)^{2}
\end{aligned}
$$
as required.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove the identity
$$
\sum_{d \mid n} \tau(d)^{3}=\left(\sum_{d \mid n} \tau(d)\right)^{2}
$$
|
Note that $\tau^{3}$ is multiplicative; in light of the convolution property just shown, it follows that both sides of the posed equality are multiplicative. Thus, it would suffice to prove the claim for $n$ a power of a prime. So, write $n=p^{k}$ where $p$ is a prime and $k$ is a nonnegative integer. Then
$$
\begin{aligned}
& \sum_{d \mid n} \tau(d)^{3}=\sum_{i=0}^{k} \tau\left(p^{i}\right)^{3}=\sum_{i=0}^{k}(i+1)^{3} \\
& \quad=1^{3}+\cdots+(k+1)^{3}=\frac{(k+1)^{2}(k+2)^{2}}{4}=\left(\frac{(k+1)(k+2)}{2}\right)^{2} \\
& \quad=\left(\sum_{i=0}^{k} \tau\left(p^{i}\right)\right)^{2}=\left(\sum_{d \mid n} \tau(d)\right)^{2}
\end{aligned}
$$
as required.
|
{
"exam": "HMMT",
"problem_label": "5",
"problem_match": "\n5. [30]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team1-solutions.jsonl",
"solution_match": "\nSolution. ",
"tier": "T4",
"year": "2007"
}
|
Show that for positive integers $n$,
$$
\sum_{d \mid n} \phi(d)=n
$$
|
Both sides are multiplicative functions of $n$, the right side trivially and the left because for relatively prime positive integers $n$ and $n^{\prime}$,
$$
\left(\sum_{d \mid n} \phi(d)\right)\left(\sum_{d^{\prime} \mid n^{\prime}} \phi\left(d^{\prime}\right)\right)=\sum_{d\left|n, d^{\prime}\right| n^{\prime}} \phi(d) \phi\left(d^{\prime}\right),
$$
and $\phi(d) \phi\left(d^{\prime}\right)=\phi\left(d d^{\prime}\right)$. The identity is then easy to check; since $\phi\left(p^{k}\right)=p^{k-1}(p-1)$ for positive integers $k$ and $\phi(1)=1$, we have $\phi(1)+\phi(p)+\cdots+\phi\left(p^{k}\right)=1+(p-1)+\left(p^{2}-p\right)+\cdots+\left(p^{k}-p^{k-1}\right)=p^{k}$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Show that for positive integers $n$,
$$
\sum_{d \mid n} \phi(d)=n
$$
|
Both sides are multiplicative functions of $n$, the right side trivially and the left because for relatively prime positive integers $n$ and $n^{\prime}$,
$$
\left(\sum_{d \mid n} \phi(d)\right)\left(\sum_{d^{\prime} \mid n^{\prime}} \phi\left(d^{\prime}\right)\right)=\sum_{d\left|n, d^{\prime}\right| n^{\prime}} \phi(d) \phi\left(d^{\prime}\right),
$$
and $\phi(d) \phi\left(d^{\prime}\right)=\phi\left(d d^{\prime}\right)$. The identity is then easy to check; since $\phi\left(p^{k}\right)=p^{k-1}(p-1)$ for positive integers $k$ and $\phi(1)=1$, we have $\phi(1)+\phi(p)+\cdots+\phi\left(p^{k}\right)=1+(p-1)+\left(p^{2}-p\right)+\cdots+\left(p^{k}-p^{k-1}\right)=p^{k}$, as desired.
|
{
"exam": "HMMT",
"problem_label": "6",
"problem_match": "\n6. [25]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team1-solutions.jsonl",
"solution_match": "\nSolution. ",
"tier": "T4",
"year": "2007"
}
|
Show that for positive integers $n$,
$$
\sum_{d \mid n} \frac{\mu(d)}{d}=\frac{\phi(n)}{n}
$$
|
On the grounds of the previous problem, Möbius inversion with $f(k)=\phi(k)$ and $g(k)=k$ gives:
$$
\phi(n)=f(n)=\sum_{d \mid n} g(d) \mu\left(\frac{n}{d}\right)=\sum_{d^{\prime} \mid n} g\left(\frac{n}{d^{\prime}}\right) \mu\left(d^{\prime}\right)=\sum_{d^{\prime} \mid n} \frac{n}{d^{\prime}} \mu\left(d^{\prime}\right)
$$
Alternatively, one uses the convolution of the functions $f(k)=n$ and $g(k)=\frac{\mu(d)}{d}$. The strategy is the same as the previous convolution proof. For $n=p^{k}$ with $k$ a positive integer, we have $\phi(n)=p^{k}-p^{k-1}$, while the series reduces to $p^{k} \cdot \mu(1)+p^{k} \cdot \mu(p) / p=p^{k}-p^{k-1}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Show that for positive integers $n$,
$$
\sum_{d \mid n} \frac{\mu(d)}{d}=\frac{\phi(n)}{n}
$$
|
On the grounds of the previous problem, Möbius inversion with $f(k)=\phi(k)$ and $g(k)=k$ gives:
$$
\phi(n)=f(n)=\sum_{d \mid n} g(d) \mu\left(\frac{n}{d}\right)=\sum_{d^{\prime} \mid n} g\left(\frac{n}{d^{\prime}}\right) \mu\left(d^{\prime}\right)=\sum_{d^{\prime} \mid n} \frac{n}{d^{\prime}} \mu\left(d^{\prime}\right)
$$
Alternatively, one uses the convolution of the functions $f(k)=n$ and $g(k)=\frac{\mu(d)}{d}$. The strategy is the same as the previous convolution proof. For $n=p^{k}$ with $k$ a positive integer, we have $\phi(n)=p^{k}-p^{k-1}$, while the series reduces to $p^{k} \cdot \mu(1)+p^{k} \cdot \mu(p) / p=p^{k}-p^{k-1}$.
|
{
"exam": "HMMT",
"problem_label": "7",
"problem_match": "\n7. [25]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team1-solutions.jsonl",
"solution_match": "\nSolution. ",
"tier": "T4",
"year": "2007"
}
|
Determine with proof, a simple closed form expression for
$$
\sum_{d \mid n} \phi(d) \tau\left(\frac{n}{d}\right)
$$
|
We claim the series reduces to $\sigma(n)$. The series counts the ordered triples $(d, x, y)$ with $d|n ; x| d ; 0<y \leq n / d ;$ and $(y, n / d)=1$. To see this, write
$$
\sum_{d \mid n} \phi(d) \tau\left(\frac{n}{d}\right)=\sum_{d^{\prime} \mid n} \phi\left(\frac{n}{d^{\prime}}\right) \tau\left(d^{\prime}\right)
$$
so that for a given $d^{\prime} \mid n$ we may choose $x$ and $y$ as described above. On the other hand, we can count these triples by groups sharing a given $x$. Fixing $x$ as a divisor of $n$ fixes an integer $\frac{n}{x}$. Then $d$ varies such that $\frac{n}{d}$ is a divisor of $\frac{n}{x}$. For each divisor $\frac{n}{d}$ of $\frac{n}{x}$ there are precisely $\phi\left(\frac{n}{d}\right)$ choices $y$, so that by the lemma from the previous problem, there are $\frac{n}{x}$ triples $(d, x, y)$ for a given $x$. It follows that there are precisely $\sigma(n)$ such triples $(d, x, y)$.
Again, an alternative is to use the multiplicativity of the convolution, although it is now a little more difficult. Write $n=p^{k}$ so that
$$
\begin{aligned}
\sum_{d \mid n} & \phi(d) \tau\left(\frac{n}{d}\right)=\sum_{m=0}^{k} \phi\left(p^{m}\right) \tau\left(p^{k-m}\right)=k+1+\sum_{m=1}^{k} p^{m-1}(p-1)(k-m+1) \\
& =k+1+\left(\sum_{m=1}^{k} p^{m}(k-m+1)\right)-\left(\sum_{m=1}^{k} p^{m-1}(k-m+1)\right)=k+1+p^{k}-k+\sum_{m^{\prime}=1}^{k-1} p^{m^{\prime}} \\
& =1+p+\cdots+p^{k}=\sigma\left(p^{k}\right)
\end{aligned}
$$
|
\sigma(n)
|
Yes
|
Yes
|
proof
|
Number Theory
|
Determine with proof, a simple closed form expression for
$$
\sum_{d \mid n} \phi(d) \tau\left(\frac{n}{d}\right)
$$
|
We claim the series reduces to $\sigma(n)$. The series counts the ordered triples $(d, x, y)$ with $d|n ; x| d ; 0<y \leq n / d ;$ and $(y, n / d)=1$. To see this, write
$$
\sum_{d \mid n} \phi(d) \tau\left(\frac{n}{d}\right)=\sum_{d^{\prime} \mid n} \phi\left(\frac{n}{d^{\prime}}\right) \tau\left(d^{\prime}\right)
$$
so that for a given $d^{\prime} \mid n$ we may choose $x$ and $y$ as described above. On the other hand, we can count these triples by groups sharing a given $x$. Fixing $x$ as a divisor of $n$ fixes an integer $\frac{n}{x}$. Then $d$ varies such that $\frac{n}{d}$ is a divisor of $\frac{n}{x}$. For each divisor $\frac{n}{d}$ of $\frac{n}{x}$ there are precisely $\phi\left(\frac{n}{d}\right)$ choices $y$, so that by the lemma from the previous problem, there are $\frac{n}{x}$ triples $(d, x, y)$ for a given $x$. It follows that there are precisely $\sigma(n)$ such triples $(d, x, y)$.
Again, an alternative is to use the multiplicativity of the convolution, although it is now a little more difficult. Write $n=p^{k}$ so that
$$
\begin{aligned}
\sum_{d \mid n} & \phi(d) \tau\left(\frac{n}{d}\right)=\sum_{m=0}^{k} \phi\left(p^{m}\right) \tau\left(p^{k-m}\right)=k+1+\sum_{m=1}^{k} p^{m-1}(p-1)(k-m+1) \\
& =k+1+\left(\sum_{m=1}^{k} p^{m}(k-m+1)\right)-\left(\sum_{m=1}^{k} p^{m-1}(k-m+1)\right)=k+1+p^{k}-k+\sum_{m^{\prime}=1}^{k-1} p^{m^{\prime}} \\
& =1+p+\cdots+p^{k}=\sigma\left(p^{k}\right)
\end{aligned}
$$
|
{
"exam": "HMMT",
"problem_label": "8",
"problem_match": "\n8. [30]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team1-solutions.jsonl",
"solution_match": "\nSolution. ",
"tier": "T4",
"year": "2007"
}
|
Find all positive integers $n$ such that
$$
\sum_{k=1}^{n} \phi(k)=\frac{3 n^{2}+5}{8}
$$
|
1, 3,5.
|
1, 3, 5
|
Yes
|
Problem not solved
|
math-word-problem
|
Number Theory
|
Find all positive integers $n$ such that
$$
\sum_{k=1}^{n} \phi(k)=\frac{3 n^{2}+5}{8}
$$
|
1, 3,5.
|
{
"exam": "HMMT",
"problem_label": "9",
"problem_match": "\n9. [35]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team1-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Find all positive integers $n$ such that
$$
\sum_{k=1}^{n} \phi(k)=\frac{3 n^{2}+5}{8}
$$
|
We contend that the proper relation is
$$
\sum_{k=1}^{n} \phi(k) \leq \frac{3 n^{2}+5}{8}
$$
Let $\Phi(k)$ denote the left hand side of $(*)$. It is trivial to see that for $n \leq 7$ the posed inequality holds, has equality where $n=1,3,5$, and holds strictly for $n=7$. Note that $\phi(2 k) \leq k$ and $\phi(2 k+1) \leq 2 k$, the former because $2,4, \ldots, 2 k$ share a common divisor. It follows that $\phi(2 k)+\phi(2 k+1) \leq 3 k$. Suppose for the sake of induction that $\Phi(2 k-1)<\frac{3(2 k-1)^{2}+5}{8}$. Then
$$
\Phi(2 k+1)=\Phi(2 k-1)+\phi(2 k)+\phi(2 k+1)<\frac{3(2 k-1)^{2}+5}{8}+3 k=\frac{3(2 k+1)^{2}+5}{8}
$$
To complete the proof, it is enough to note that for a positive integer $k$,
$$
\frac{3(2 k-1)^{2}+5}{8}+k<\frac{3(2 k)^{2}+5}{8}
$$
|
not found
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all positive integers $n$ such that
$$
\sum_{k=1}^{n} \phi(k)=\frac{3 n^{2}+5}{8}
$$
|
We contend that the proper relation is
$$
\sum_{k=1}^{n} \phi(k) \leq \frac{3 n^{2}+5}{8}
$$
Let $\Phi(k)$ denote the left hand side of $(*)$. It is trivial to see that for $n \leq 7$ the posed inequality holds, has equality where $n=1,3,5$, and holds strictly for $n=7$. Note that $\phi(2 k) \leq k$ and $\phi(2 k+1) \leq 2 k$, the former because $2,4, \ldots, 2 k$ share a common divisor. It follows that $\phi(2 k)+\phi(2 k+1) \leq 3 k$. Suppose for the sake of induction that $\Phi(2 k-1)<\frac{3(2 k-1)^{2}+5}{8}$. Then
$$
\Phi(2 k+1)=\Phi(2 k-1)+\phi(2 k)+\phi(2 k+1)<\frac{3(2 k-1)^{2}+5}{8}+3 k=\frac{3(2 k+1)^{2}+5}{8}
$$
To complete the proof, it is enough to note that for a positive integer $k$,
$$
\frac{3(2 k-1)^{2}+5}{8}+k<\frac{3(2 k)^{2}+5}{8}
$$
|
{
"exam": "HMMT",
"problem_label": "9",
"problem_match": "\n9. [35]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team1-solutions.jsonl",
"solution_match": "\nSolution. ",
"tier": "T4",
"year": "2007"
}
|
Find all pairs $(n, k)$ of positive integers such that
$$
\sigma(n) \phi(n)=\frac{n^{2}}{k}
$$
|
(1, 1).
|
(1, 1)
|
Yes
|
Problem not solved
|
math-word-problem
|
Number Theory
|
Find all pairs $(n, k)$ of positive integers such that
$$
\sigma(n) \phi(n)=\frac{n^{2}}{k}
$$
|
(1, 1).
|
{
"exam": "HMMT",
"problem_label": "10",
"problem_match": "\n10. [40]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team1-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Find all pairs $(n, k)$ of positive integers such that
$$
\sigma(n) \phi(n)=\frac{n^{2}}{k}
$$
|
It is clear that for a given integer $n$, there is at most one integer $k$ for which the equation holds. For $n=1$ this is $k=1$. But, for $n>1$, problem 1 asserts that $\sigma(n) \phi(n) \leq n^{2}-1<n^{2}$, so that $k \geq 2$. We now claim that $2>\frac{n^{2}}{\sigma(n) \phi(n)}$. Write $n=p_{1}^{e_{1}} \cdots p_{k}^{e_{k}}$, where the $p_{i}$ are distinct primes and $e_{i} \geq 1$ for all $i$, and let $q_{1}<q_{2}<\cdots$ be the primes in ascending order. Then
$$
\begin{aligned}
& \frac{n^{2}}{\sigma(n) \phi(n)}=\prod_{i=1}^{k} \frac{p_{i}^{2 e_{i}}}{\frac{p_{i}^{e_{i}+1}-1}{p_{i}-1} \cdot\left(p_{i}-1\right) p_{i}^{e_{i}-1}}=\prod_{i=1}^{k} \frac{p_{i}^{2 e_{i}}}{p_{i}^{2 e_{i}}-p_{i}^{e_{i}-1}} \\
& \quad=\prod_{i=1}^{k} \frac{1}{1-p_{i}^{-1-e_{i}}} \leq \prod_{i=1}^{k} \frac{1}{1-p_{i}^{-2}}<\prod_{i=1}^{\infty} \frac{1}{1-q_{i}^{-2}} \\
& \quad=\prod_{i=1}^{\infty}\left(\sum_{j=0}^{\infty} \frac{1}{q_{i}^{2 j}}\right)=\sum_{n=1}^{\infty} \frac{1}{n^{2}} \\
& \quad<1+\sum_{n=2}^{\infty} \frac{1}{n^{2}-1}=1+\frac{1}{2}\left(\left(\frac{1}{1}-\frac{1}{3}\right)+\left(\frac{1}{2}-\frac{1}{4}\right)+\left(\frac{1}{3}-\frac{1}{5}\right)+\cdots\right)=\frac{7}{4}<2 .
\end{aligned}
$$
It follows that there can be no solutions to $k=\frac{n^{2}}{\sigma(n) \phi(n)}$ other than $n=k=1$.
## Grab Bag - Miscellaneous Problems [130]
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all pairs $(n, k)$ of positive integers such that
$$
\sigma(n) \phi(n)=\frac{n^{2}}{k}
$$
|
It is clear that for a given integer $n$, there is at most one integer $k$ for which the equation holds. For $n=1$ this is $k=1$. But, for $n>1$, problem 1 asserts that $\sigma(n) \phi(n) \leq n^{2}-1<n^{2}$, so that $k \geq 2$. We now claim that $2>\frac{n^{2}}{\sigma(n) \phi(n)}$. Write $n=p_{1}^{e_{1}} \cdots p_{k}^{e_{k}}$, where the $p_{i}$ are distinct primes and $e_{i} \geq 1$ for all $i$, and let $q_{1}<q_{2}<\cdots$ be the primes in ascending order. Then
$$
\begin{aligned}
& \frac{n^{2}}{\sigma(n) \phi(n)}=\prod_{i=1}^{k} \frac{p_{i}^{2 e_{i}}}{\frac{p_{i}^{e_{i}+1}-1}{p_{i}-1} \cdot\left(p_{i}-1\right) p_{i}^{e_{i}-1}}=\prod_{i=1}^{k} \frac{p_{i}^{2 e_{i}}}{p_{i}^{2 e_{i}}-p_{i}^{e_{i}-1}} \\
& \quad=\prod_{i=1}^{k} \frac{1}{1-p_{i}^{-1-e_{i}}} \leq \prod_{i=1}^{k} \frac{1}{1-p_{i}^{-2}}<\prod_{i=1}^{\infty} \frac{1}{1-q_{i}^{-2}} \\
& \quad=\prod_{i=1}^{\infty}\left(\sum_{j=0}^{\infty} \frac{1}{q_{i}^{2 j}}\right)=\sum_{n=1}^{\infty} \frac{1}{n^{2}} \\
& \quad<1+\sum_{n=2}^{\infty} \frac{1}{n^{2}-1}=1+\frac{1}{2}\left(\left(\frac{1}{1}-\frac{1}{3}\right)+\left(\frac{1}{2}-\frac{1}{4}\right)+\left(\frac{1}{3}-\frac{1}{5}\right)+\cdots\right)=\frac{7}{4}<2 .
\end{aligned}
$$
It follows that there can be no solutions to $k=\frac{n^{2}}{\sigma(n) \phi(n)}$ other than $n=k=1$.
## Grab Bag - Miscellaneous Problems [130]
|
{
"exam": "HMMT",
"problem_label": "10",
"problem_match": "\n10. [40]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team1-solutions.jsonl",
"solution_match": "\nSolution. ",
"tier": "T4",
"year": "2007"
}
|
Find all functions $f: \mathbb{Q} \rightarrow \mathbb{Q}$ such that
$$
\begin{aligned}
f(x) f(y) & =f(x)+f(y)-f(x y) \\
1+f(x+y) & =f(x y)+f(x) f(y)
\end{aligned}
$$
for all rational numbers $x, y$.
|
$\mathbf{f}(\mathbf{x})=\mathbf{1} \forall \mathbf{x}$, and $\mathbf{f}(\mathbf{x})=\mathbf{1}-\mathbf{x} \forall \mathbf{x}$.
|
f(x)=1 \text{ and } f(x)=1-x
|
Yes
|
Incomplete
|
math-word-problem
|
Algebra
|
Find all functions $f: \mathbb{Q} \rightarrow \mathbb{Q}$ such that
$$
\begin{aligned}
f(x) f(y) & =f(x)+f(y)-f(x y) \\
1+f(x+y) & =f(x y)+f(x) f(y)
\end{aligned}
$$
for all rational numbers $x, y$.
|
$\mathbf{f}(\mathbf{x})=\mathbf{1} \forall \mathbf{x}$, and $\mathbf{f}(\mathbf{x})=\mathbf{1}-\mathbf{x} \forall \mathbf{x}$.
|
{
"exam": "HMMT",
"problem_label": "11",
"problem_match": "\n11. $[30]$",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team1-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Find all functions $f: \mathbb{Q} \rightarrow \mathbb{Q}$ such that
$$
\begin{aligned}
f(x) f(y) & =f(x)+f(y)-f(x y) \\
1+f(x+y) & =f(x y)+f(x) f(y)
\end{aligned}
$$
for all rational numbers $x, y$.
|
Considering the first equation, either side of the second equation is equal to $f(x)+f(y)$. Now write $g(x)=1-f(x)$, so that
$$
\begin{aligned}
& g(x y)=1-f(x y)=1-f(x)-f(y)+f(x) f(y)=(1-f(x))(1-f(y))=g(x) g(y) \\
& g(x+y)=1-f(x+y)=1-f(x)+1-f(y)=g(x)+g(y)
\end{aligned}
$$
By induction, $g(n x)=n g(x)$ for all integers $n$, so that $g(p / q)=(p / q) g(1)$ for integers $p$ and $q$ with $q$ nonzero; i.e., $g(x)=x g(1)$. As $g$ is multiplicative, $g(1)=g(1)^{2}$, so the only possibilities are $g(1)=1$ and $g(1)=0$. These give $g(x)=x$ and $g(x)=0$, or $f(x)=1-x$ and $f(x)=1$, respectively. One easily checks that these functions are satisfactory.
|
f(x)=1-x \text{ and } f(x)=1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all functions $f: \mathbb{Q} \rightarrow \mathbb{Q}$ such that
$$
\begin{aligned}
f(x) f(y) & =f(x)+f(y)-f(x y) \\
1+f(x+y) & =f(x y)+f(x) f(y)
\end{aligned}
$$
for all rational numbers $x, y$.
|
Considering the first equation, either side of the second equation is equal to $f(x)+f(y)$. Now write $g(x)=1-f(x)$, so that
$$
\begin{aligned}
& g(x y)=1-f(x y)=1-f(x)-f(y)+f(x) f(y)=(1-f(x))(1-f(y))=g(x) g(y) \\
& g(x+y)=1-f(x+y)=1-f(x)+1-f(y)=g(x)+g(y)
\end{aligned}
$$
By induction, $g(n x)=n g(x)$ for all integers $n$, so that $g(p / q)=(p / q) g(1)$ for integers $p$ and $q$ with $q$ nonzero; i.e., $g(x)=x g(1)$. As $g$ is multiplicative, $g(1)=g(1)^{2}$, so the only possibilities are $g(1)=1$ and $g(1)=0$. These give $g(x)=x$ and $g(x)=0$, or $f(x)=1-x$ and $f(x)=1$, respectively. One easily checks that these functions are satisfactory.
|
{
"exam": "HMMT",
"problem_label": "11",
"problem_match": "\n11. $[30]$",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team1-solutions.jsonl",
"solution_match": "\nSolution. ",
"tier": "T4",
"year": "2007"
}
|
Let $A B C D$ be a cyclic quadrilateral, and let $P$ be the intersection of its two diagonals. Points $R, S, T$, and $U$ are feet of the perpendiculars from $P$ to sides $A B, B C, C D$, and $A D$, respectively. Show that quadrilateral $R S T U$ is bicentric if and only if $A C \perp B D$. (Note that a quadrilateral is called inscriptible if it has an incircle; a quadrilateral is called bicentric if it is both cyclic and inscriptible.)
|
First we show that $R S T U$ is always inscriptible. Note that in addition to $A B C D$, we have cyclic quadrilaterals $A R P U$ and $B S P R$. Thus,
$$
\angle P R U=\angle P A U=\angle C A D=\angle C B D=\angle S B P=\angle S R P
$$
and it follows that $P$ lies on the bisector of $\angle S R U$. Analogously, $P$ lies on the bisectors of $\angle T S R$ and $\angle U T S$, so is equidistant from lines $U R, R S, S T$, and $T U$, and $R S T U$ is inscriptible having incenter $P$. Now we show that $R S T U$ is cyclic if and only if the diagonals of $A B C D$ are orthogonal. We have
$$
\begin{aligned}
& \angle A P B=\pi-\angle B A P-\angle P B A=\pi-\angle R A P-\angle P B R=\pi-\angle R U P-\angle P S R \\
& \quad=\pi-\frac{1}{2}(\angle R U T+\angle T S R)
\end{aligned}
$$
It follows that $\angle A P B=\frac{\pi}{2}$ if and only if $\angle R U T+\angle T S R=\pi$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral, and let $P$ be the intersection of its two diagonals. Points $R, S, T$, and $U$ are feet of the perpendiculars from $P$ to sides $A B, B C, C D$, and $A D$, respectively. Show that quadrilateral $R S T U$ is bicentric if and only if $A C \perp B D$. (Note that a quadrilateral is called inscriptible if it has an incircle; a quadrilateral is called bicentric if it is both cyclic and inscriptible.)

|
First we show that $R S T U$ is always inscriptible. Note that in addition to $A B C D$, we have cyclic quadrilaterals $A R P U$ and $B S P R$. Thus,
$$
\angle P R U=\angle P A U=\angle C A D=\angle C B D=\angle S B P=\angle S R P
$$
and it follows that $P$ lies on the bisector of $\angle S R U$. Analogously, $P$ lies on the bisectors of $\angle T S R$ and $\angle U T S$, so is equidistant from lines $U R, R S, S T$, and $T U$, and $R S T U$ is inscriptible having incenter $P$. Now we show that $R S T U$ is cyclic if and only if the diagonals of $A B C D$ are orthogonal. We have
$$
\begin{aligned}
& \angle A P B=\pi-\angle B A P-\angle P B A=\pi-\angle R A P-\angle P B R=\pi-\angle R U P-\angle P S R \\
& \quad=\pi-\frac{1}{2}(\angle R U T+\angle T S R)
\end{aligned}
$$
It follows that $\angle A P B=\frac{\pi}{2}$ if and only if $\angle R U T+\angle T S R=\pi$, as desired.
|
{
"exam": "HMMT",
"problem_label": "12",
"problem_match": "\n12. [30]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team1-solutions.jsonl",
"solution_match": "\nSolution. ",
"tier": "T4",
"year": "2007"
}
|
Find all nonconstant polynomials $P(x)$, with real coefficients and having only real zeros, such that $P(x+1) P\left(x^{2}-x+1\right)=P\left(x^{3}+1\right)$ for all real numbers $x$.
|
$\left\{\mathbf{P}(\mathbf{x})=\mathbf{x}^{\mathbf{k}} \mid \mathbf{k} \in \mathbb{Z}^{+}\right\}$.
|
P(x)=x^k \mid k \in \mathbb{Z}^{+}
|
Yes
|
Problem not solved
|
math-word-problem
|
Algebra
|
Find all nonconstant polynomials $P(x)$, with real coefficients and having only real zeros, such that $P(x+1) P\left(x^{2}-x+1\right)=P\left(x^{3}+1\right)$ for all real numbers $x$.
|
$\left\{\mathbf{P}(\mathbf{x})=\mathbf{x}^{\mathbf{k}} \mid \mathbf{k} \in \mathbb{Z}^{+}\right\}$.
|
{
"exam": "HMMT",
"problem_label": "13",
"problem_match": "\n13. [30]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team1-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Find all nonconstant polynomials $P(x)$, with real coefficients and having only real zeros, such that $P(x+1) P\left(x^{2}-x+1\right)=P\left(x^{3}+1\right)$ for all real numbers $x$.
|
Note that if $P(\alpha)=0$, then by setting $x=\alpha-1$ in the given equation, we find $0=P\left(x^{3}+\right.$ $1)=P\left(\alpha^{3}-3 \alpha^{2}+3 \alpha\right)$. Because $P$ is nonconstant, it has at least one zero. Because $P$ has finite degree, there exist minimal and maximal roots of $P$. Writing $\alpha^{3}-3 \alpha^{2}+3 \alpha \geq \alpha \Longleftrightarrow \alpha(\alpha-1)(\alpha-2) \geq 0$, we see that the largest zero of $P$ cannot exceed 2 . Likewise, the smallest zero cannot be negative, so all of the zeroes of $P$ lie in [0,2]. Moreover, if $\alpha \notin\{0,1,2\}$ is a zero of $P$, then $\alpha^{\prime}=\alpha^{3}-3 \alpha^{2}+3 \alpha$ is another zero of $P$ that lies strictly between $\alpha$ and 1. Because $P$ has only finitely many zeroes, all of its zeroes must lie in $\{0,1,2\}$. Now write $P(x)=k x^{p}(x-1)^{q}(x-2)^{r}$ for nonnegative integers $p, q$ and $r$ having a positive sum. The given equation becomes
$$
\begin{aligned}
& k^{2}(x+1)^{p} x^{q}(x-1)^{r}\left(x^{2}-x+1\right)^{p}\left(x^{2}-x\right)^{q}\left(x^{2}-x-1\right)^{r}=P(x+1) P\left(x^{2}-x+1\right) \\
& \quad=P\left(x^{3}+1\right)=k\left(x^{3}+1\right)^{p} x^{3 q}\left(x^{3}-1\right)^{r}
\end{aligned}
$$
For the leading coefficients to agree, we require $k=k^{2}$. Because the leading coefficient is nonzero, $P$ must be monic. In $(*), r$ must be zero lest $P\left(x^{3}+1\right)=0$ have complex roots. Then $q$ must be zero as well. For, if $q$ is positive, then $P\left(x^{2}-x+1\right)=0$ has 1 as a root while $P\left(x^{3}+1\right)$ does not. Finally, the remaining possibilities are $P(x)=x^{p}$ for $p$ an arbitrary positive integer. It is easily seen that these polynomials are satisfactory.
|
P(x)=x^{p}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all nonconstant polynomials $P(x)$, with real coefficients and having only real zeros, such that $P(x+1) P\left(x^{2}-x+1\right)=P\left(x^{3}+1\right)$ for all real numbers $x$.
|
Note that if $P(\alpha)=0$, then by setting $x=\alpha-1$ in the given equation, we find $0=P\left(x^{3}+\right.$ $1)=P\left(\alpha^{3}-3 \alpha^{2}+3 \alpha\right)$. Because $P$ is nonconstant, it has at least one zero. Because $P$ has finite degree, there exist minimal and maximal roots of $P$. Writing $\alpha^{3}-3 \alpha^{2}+3 \alpha \geq \alpha \Longleftrightarrow \alpha(\alpha-1)(\alpha-2) \geq 0$, we see that the largest zero of $P$ cannot exceed 2 . Likewise, the smallest zero cannot be negative, so all of the zeroes of $P$ lie in [0,2]. Moreover, if $\alpha \notin\{0,1,2\}$ is a zero of $P$, then $\alpha^{\prime}=\alpha^{3}-3 \alpha^{2}+3 \alpha$ is another zero of $P$ that lies strictly between $\alpha$ and 1. Because $P$ has only finitely many zeroes, all of its zeroes must lie in $\{0,1,2\}$. Now write $P(x)=k x^{p}(x-1)^{q}(x-2)^{r}$ for nonnegative integers $p, q$ and $r$ having a positive sum. The given equation becomes
$$
\begin{aligned}
& k^{2}(x+1)^{p} x^{q}(x-1)^{r}\left(x^{2}-x+1\right)^{p}\left(x^{2}-x\right)^{q}\left(x^{2}-x-1\right)^{r}=P(x+1) P\left(x^{2}-x+1\right) \\
& \quad=P\left(x^{3}+1\right)=k\left(x^{3}+1\right)^{p} x^{3 q}\left(x^{3}-1\right)^{r}
\end{aligned}
$$
For the leading coefficients to agree, we require $k=k^{2}$. Because the leading coefficient is nonzero, $P$ must be monic. In $(*), r$ must be zero lest $P\left(x^{3}+1\right)=0$ have complex roots. Then $q$ must be zero as well. For, if $q$ is positive, then $P\left(x^{2}-x+1\right)=0$ has 1 as a root while $P\left(x^{3}+1\right)$ does not. Finally, the remaining possibilities are $P(x)=x^{p}$ for $p$ an arbitrary positive integer. It is easily seen that these polynomials are satisfactory.
|
{
"exam": "HMMT",
"problem_label": "13",
"problem_match": "\n13. [30]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team1-solutions.jsonl",
"solution_match": "\nSolution. ",
"tier": "T4",
"year": "2007"
}
|
Find an explicit, closed form formula for
$$
\sum_{k=1}^{n} \frac{k \cdot(-1)^{k} \cdot\binom{n}{k}}{n+k+1}
$$
|
$\frac{-\mathbf{1}}{\binom{2 \mathbf{1}+1}{\mathbf{n}}}$ or $-\frac{\mathbf{n}!(\mathbf{n}+\mathbf{1})!}{(\mathbf{2 n}+\mathbf{1})!}$ or obvious equivalent.
|
-\frac{n!(n+1)!}{(2n+1)!}
|
Yes
|
Problem not solved
|
math-word-problem
|
Combinatorics
|
Find an explicit, closed form formula for
$$
\sum_{k=1}^{n} \frac{k \cdot(-1)^{k} \cdot\binom{n}{k}}{n+k+1}
$$
|
$\frac{-\mathbf{1}}{\binom{2 \mathbf{1}+1}{\mathbf{n}}}$ or $-\frac{\mathbf{n}!(\mathbf{n}+\mathbf{1})!}{(\mathbf{2 n}+\mathbf{1})!}$ or obvious equivalent.
|
{
"exam": "HMMT",
"problem_label": "14",
"problem_match": "\n14. [40]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team1-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Find an explicit, closed form formula for
$$
\sum_{k=1}^{n} \frac{k \cdot(-1)^{k} \cdot\binom{n}{k}}{n+k+1}
$$
|
Consider the interpolation of the polynomial $P(x)=x \cdot n!$ at $x=0,1, \ldots, n$. We obtain the identity
$$
\begin{aligned}
P(x) & =x \cdot n!=\sum_{k=0}^{n} k \cdot n!\prod_{j \neq k} \frac{x-j}{k-j} \\
& =\sum_{k=0}^{n} k \cdot n!\cdot \frac{x(x-1) \cdots(x-k+1)(x-k-1) \cdots(x-n)}{k!(n-k)!(-1)^{n-k}} \\
& =\sum_{k=1}^{n} k \cdot(-1)^{n-k} \cdot\binom{n}{k} \cdot x(x-1) \cdots(x-k+1)(x-k-1) \cdots(x-n)
\end{aligned}
$$
This identity is valid for all complex numbers $x$, but, to extract a factor $\frac{1}{n+k+1}$ from the valid product of each summand, we set $x=-n-1$, so that
$-(n+1)!=\sum_{k=1}^{n} k(-1)^{n-k}\binom{n}{k}(-n-1) \cdots(-n-k)(-n-k-2) \cdots(-2 n-1)=\sum_{k=1}^{n} \frac{k(-1)^{k}\binom{n}{k}(2 n+1)!}{n!(n+k+1)}$.
Finally,
$$
\sum_{k=1}^{n} \frac{k \cdot(-1)^{k} \cdot\binom{n}{k}}{n+k+1}=\frac{-n!(n+1)!}{(2 n+1)!}=\frac{-1}{\binom{2 n+1}{n}} \cdot \square
$$
|
\frac{-1}{\binom{2 n+1}{n}}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Find an explicit, closed form formula for
$$
\sum_{k=1}^{n} \frac{k \cdot(-1)^{k} \cdot\binom{n}{k}}{n+k+1}
$$
|
Consider the interpolation of the polynomial $P(x)=x \cdot n!$ at $x=0,1, \ldots, n$. We obtain the identity
$$
\begin{aligned}
P(x) & =x \cdot n!=\sum_{k=0}^{n} k \cdot n!\prod_{j \neq k} \frac{x-j}{k-j} \\
& =\sum_{k=0}^{n} k \cdot n!\cdot \frac{x(x-1) \cdots(x-k+1)(x-k-1) \cdots(x-n)}{k!(n-k)!(-1)^{n-k}} \\
& =\sum_{k=1}^{n} k \cdot(-1)^{n-k} \cdot\binom{n}{k} \cdot x(x-1) \cdots(x-k+1)(x-k-1) \cdots(x-n)
\end{aligned}
$$
This identity is valid for all complex numbers $x$, but, to extract a factor $\frac{1}{n+k+1}$ from the valid product of each summand, we set $x=-n-1$, so that
$-(n+1)!=\sum_{k=1}^{n} k(-1)^{n-k}\binom{n}{k}(-n-1) \cdots(-n-k)(-n-k-2) \cdots(-2 n-1)=\sum_{k=1}^{n} \frac{k(-1)^{k}\binom{n}{k}(2 n+1)!}{n!(n+k+1)}$.
Finally,
$$
\sum_{k=1}^{n} \frac{k \cdot(-1)^{k} \cdot\binom{n}{k}}{n+k+1}=\frac{-n!(n+1)!}{(2 n+1)!}=\frac{-1}{\binom{2 n+1}{n}} \cdot \square
$$
|
{
"exam": "HMMT",
"problem_label": "14",
"problem_match": "\n14. [40]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team1-solutions.jsonl",
"solution_match": "\nSolution. ",
"tier": "T4",
"year": "2007"
}
|
Find the sum of the positive integer divisors of $2^{2007}$.
|
$\mathbf{2}^{\mathbf{2 0 0 8}}-\mathbf{1}$. The divisors are the powers of two not exceeding $2^{2007}$. So the sum is
$1+2+2^{2}+\cdots+2^{2007}=-1+2+2+2^{2}+\cdots+2^{2007}=-1+2^{2}+2^{2}+\cdots+2^{2007}=\cdots=-1+2^{2008}$.
|
2^{2008}-1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the sum of the positive integer divisors of $2^{2007}$.
|
$\mathbf{2}^{\mathbf{2 0 0 8}}-\mathbf{1}$. The divisors are the powers of two not exceeding $2^{2007}$. So the sum is
$1+2+2^{2}+\cdots+2^{2007}=-1+2+2+2^{2}+\cdots+2^{2007}=-1+2^{2}+2^{2}+\cdots+2^{2007}=\cdots=-1+2^{2008}$.
|
{
"exam": "HMMT",
"problem_label": "1",
"problem_match": "\n1. [20]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
The four sides of quadrilateral $A B C D$ are equal in length. Determine the perimeter of $A B C D$ given that it has area 120 and $A C=10$.
|
52. Let $M$ be the midpoint of $A C$. Then triangles $A M B, B M C, C M D$, and $D M A$ are all right triangles having legs 5 and $h$ for some $h$. The area of $A B C D$ is 120 , but also $4 \cdot\left(\frac{1}{2} \cdot 5 \cdot h\right)=10 h$, so $h=12$. Then $A B=B C=C D=D A=\sqrt{12^{2}+5^{2}}=13$, and the perimeter of $A B C D$ is 52 .
|
52
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
The four sides of quadrilateral $A B C D$ are equal in length. Determine the perimeter of $A B C D$ given that it has area 120 and $A C=10$.

|
52. Let $M$ be the midpoint of $A C$. Then triangles $A M B, B M C, C M D$, and $D M A$ are all right triangles having legs 5 and $h$ for some $h$. The area of $A B C D$ is 120 , but also $4 \cdot\left(\frac{1}{2} \cdot 5 \cdot h\right)=10 h$, so $h=12$. Then $A B=B C=C D=D A=\sqrt{12^{2}+5^{2}}=13$, and the perimeter of $A B C D$ is 52 .
|
{
"exam": "HMMT",
"problem_label": "2",
"problem_match": "\n2. [20]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Five people are crowding into a booth against a wall at a noisy restaurant. If at most three can fit on one side, how many seating arrangements accomodate them all?
|
240. Three people will sit on one side and two sit on the other, giving a factor of two. Then there are 5 ! ways to permute the people.
|
240
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Five people are crowding into a booth against a wall at a noisy restaurant. If at most three can fit on one side, how many seating arrangements accomodate them all?
|
240. Three people will sit on one side and two sit on the other, giving a factor of two. Then there are 5 ! ways to permute the people.
|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n3. [20]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Thomas and Michael are just two people in a large pool of well qualified candidates for appointment to a problem writing committee for a prestigious college math contest. It is 40 times more likely that both will serve if the size of the committee is increased from its traditional 3 members to a whopping $n$ members. Determine $n$. (Each person in the pool is equally likely to be chosen.)
|
16. Suppose there are $k$ candidates. Then the probability that both serve on a 3 membered committee is $(k-2) /\binom{k}{3}$, and the odds that both serve on an $n$ membered committee are $\binom{k-2}{n-2} /\binom{k}{n}$. The ratio of the latter to the former is
$$
\frac{\binom{k}{3}\binom{k-2}{n-2}}{(k-2)\binom{k}{n}}=\frac{k!(k-2)!1!(k-3)!n!(k-n)!}{k!(k-2)!(n-2)!(k-n)!3!(k-3)!}=\frac{n \cdot(n-1)}{3!}
$$
Solving $n \cdot(n-1)=240$ produces $n=16,-15$, and we discard the latter.
|
16
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Thomas and Michael are just two people in a large pool of well qualified candidates for appointment to a problem writing committee for a prestigious college math contest. It is 40 times more likely that both will serve if the size of the committee is increased from its traditional 3 members to a whopping $n$ members. Determine $n$. (Each person in the pool is equally likely to be chosen.)
|
16. Suppose there are $k$ candidates. Then the probability that both serve on a 3 membered committee is $(k-2) /\binom{k}{3}$, and the odds that both serve on an $n$ membered committee are $\binom{k-2}{n-2} /\binom{k}{n}$. The ratio of the latter to the former is
$$
\frac{\binom{k}{3}\binom{k-2}{n-2}}{(k-2)\binom{k}{n}}=\frac{k!(k-2)!1!(k-3)!n!(k-n)!}{k!(k-2)!(n-2)!(k-n)!3!(k-3)!}=\frac{n \cdot(n-1)}{3!}
$$
Solving $n \cdot(n-1)=240$ produces $n=16,-15$, and we discard the latter.
|
{
"exam": "HMMT",
"problem_label": "4",
"problem_match": "\n4. [20]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
The curves $y=x^{2}(x-3)^{2}$ and $y=\left(x^{2}-1\right)(x-2)$ intersect at a number of points in the real plane. Determine the sum of the $x$-coordinates of these points of intersection.
|
7. Because the first curve touches the $x$-axis at $x=0$ and $x=3$ while the second curve crosses the $x$-axis at $x= \pm 1$ and $x=2$, there are four points of intersection. In particular, the points of intersection have $x$-coordinates determined by the difference of the two curves:
$$
0=x^{2}(x-3)^{2}-\left(x^{2}-1\right)(x-2)=\left(x^{4}-6 x^{3}+\cdots\right)-\left(x^{3}+\cdots\right)=x^{4}-7 x^{3}+\cdots
$$
We need only the first two coefficients to determine $x_{1}+x_{2}+x_{3}+x_{4}=-\left(\frac{-7}{1}\right)=7$.
|
7
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
The curves $y=x^{2}(x-3)^{2}$ and $y=\left(x^{2}-1\right)(x-2)$ intersect at a number of points in the real plane. Determine the sum of the $x$-coordinates of these points of intersection.
|
7. Because the first curve touches the $x$-axis at $x=0$ and $x=3$ while the second curve crosses the $x$-axis at $x= \pm 1$ and $x=2$, there are four points of intersection. In particular, the points of intersection have $x$-coordinates determined by the difference of the two curves:
$$
0=x^{2}(x-3)^{2}-\left(x^{2}-1\right)(x-2)=\left(x^{4}-6 x^{3}+\cdots\right)-\left(x^{3}+\cdots\right)=x^{4}-7 x^{3}+\cdots
$$
We need only the first two coefficients to determine $x_{1}+x_{2}+x_{3}+x_{4}=-\left(\frac{-7}{1}\right)=7$.
|
{
"exam": "HMMT",
"problem_label": "5",
"problem_match": "\n5. [20]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Andrew has a fair six sided die labeled with 1 through 6 as usual. He tosses it repeatedly, and on every third roll writes down the number facing up as long as it is not the 6 . He stops as soon as the last two numbers he has written down are squares or one is a prime and the other is a square. What is the probability that he stops after writing squares consecutively?
|
$4 / \mathbf{2 5}$. We can safely ignore all of the rolls he doesn't record. The probability that he stops after writing two squares consecutively is the same as the probability that he never rolls a prime. For, as soon as the first prime is written, either it must have been preceded by a square or it will be followed by a nonnegative number of additional primes and then a square. So we want the probability that two numbers chosen uniformly with replacement from $\{1,2,3,4,5\}$ are both squares, which is $(2 / 5)^{2}$.
|
\frac{4}{25}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Andrew has a fair six sided die labeled with 1 through 6 as usual. He tosses it repeatedly, and on every third roll writes down the number facing up as long as it is not the 6 . He stops as soon as the last two numbers he has written down are squares or one is a prime and the other is a square. What is the probability that he stops after writing squares consecutively?
|
$4 / \mathbf{2 5}$. We can safely ignore all of the rolls he doesn't record. The probability that he stops after writing two squares consecutively is the same as the probability that he never rolls a prime. For, as soon as the first prime is written, either it must have been preceded by a square or it will be followed by a nonnegative number of additional primes and then a square. So we want the probability that two numbers chosen uniformly with replacement from $\{1,2,3,4,5\}$ are both squares, which is $(2 / 5)^{2}$.
|
{
"exam": "HMMT",
"problem_label": "6",
"problem_match": "\n6. [20]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Three positive reals $x, y$, and $z$ are such that
$$
\begin{aligned}
x^{2}+2(y-1)(z-1) & =85 \\
y^{2}+2(z-1)(x-1) & =84 \\
z^{2}+2(x-1)(y-1) & =89
\end{aligned}
$$
Compute $x+y+z$.
|
18. Add the three equations to obtain
$$
x^{2}+y^{2}+z^{2}+2 x y+2 y z+2 z x-4 x-4 y-4 z+6=258
$$
which rewrites as $(x+y+z-2)^{2}=256$. Evidently, $x+y+z=2 \pm 16$. Since $x, y$, and $z$ are positive, $x+y+z>0$ so $x+y+z=2+16=18$.
|
18
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Three positive reals $x, y$, and $z$ are such that
$$
\begin{aligned}
x^{2}+2(y-1)(z-1) & =85 \\
y^{2}+2(z-1)(x-1) & =84 \\
z^{2}+2(x-1)(y-1) & =89
\end{aligned}
$$
Compute $x+y+z$.
|
18. Add the three equations to obtain
$$
x^{2}+y^{2}+z^{2}+2 x y+2 y z+2 z x-4 x-4 y-4 z+6=258
$$
which rewrites as $(x+y+z-2)^{2}=256$. Evidently, $x+y+z=2 \pm 16$. Since $x, y$, and $z$ are positive, $x+y+z>0$ so $x+y+z=2+16=18$.
|
{
"exam": "HMMT",
"problem_label": "7",
"problem_match": "\n7. [20]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Find the positive real number(s) $x$ such that $\frac{1}{2}\left(3 x^{2}-1\right)=\left(x^{2}-50 x-10\right)\left(x^{2}+25 x+5\right)$.
|
$\mathbf{2 5}+\mathbf{2} \sqrt{\mathbf{1 5 9}}$. Write $a=x^{2}-50 x-10$ and $b=x^{2}+25 x+5$; the given becomes $\frac{a+2 b-1}{2}=a b$, so $0=2 a b-a-2 b+1=(a-1)(2 b-1)$. Then $a-1=x^{2}-50 x-11=0$ or $2 b-1=2 x^{2}+50 x+9=0$. The former has a positive root, $x=25+2 \sqrt{159}$, while the latter cannot, for obvious reasons.
|
25+2 \sqrt{159}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find the positive real number(s) $x$ such that $\frac{1}{2}\left(3 x^{2}-1\right)=\left(x^{2}-50 x-10\right)\left(x^{2}+25 x+5\right)$.
|
$\mathbf{2 5}+\mathbf{2} \sqrt{\mathbf{1 5 9}}$. Write $a=x^{2}-50 x-10$ and $b=x^{2}+25 x+5$; the given becomes $\frac{a+2 b-1}{2}=a b$, so $0=2 a b-a-2 b+1=(a-1)(2 b-1)$. Then $a-1=x^{2}-50 x-11=0$ or $2 b-1=2 x^{2}+50 x+9=0$. The former has a positive root, $x=25+2 \sqrt{159}$, while the latter cannot, for obvious reasons.
|
{
"exam": "HMMT",
"problem_label": "8",
"problem_match": "\n8. [20]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Cyclic quadrilateral $A B C D$ has side lengths $A B=1, B C=2, C D=3$, and $A D=4$. Determine $A C / B D$.
|
5/7. Let the diagonals intersect at $P$. Note that triangles $A B P$ and $D C P$ are similar, so that $3 A P=D P$ and $3 B P=C P$. Additionally, triangles $B C P$ and $A D P$ are similar, so that $2 B P=A P$. It follows that
$$
\frac{A C}{B D}=\frac{A P+P C}{B P+P D}=\frac{2 B P+3 B P}{B P+6 B P}=\frac{5}{7}
$$
|
\frac{5}{7}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Cyclic quadrilateral $A B C D$ has side lengths $A B=1, B C=2, C D=3$, and $A D=4$. Determine $A C / B D$.

|
5/7. Let the diagonals intersect at $P$. Note that triangles $A B P$ and $D C P$ are similar, so that $3 A P=D P$ and $3 B P=C P$. Additionally, triangles $B C P$ and $A D P$ are similar, so that $2 B P=A P$. It follows that
$$
\frac{A C}{B D}=\frac{A P+P C}{B P+P D}=\frac{2 B P+3 B P}{B P+6 B P}=\frac{5}{7}
$$
|
{
"exam": "HMMT",
"problem_label": "9",
"problem_match": "\n9. [20]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
A positive real number $x$ is such that
$$
\sqrt[3]{1-x^{3}}+\sqrt[3]{1+x^{3}}=1
$$
Find $x^{2}$.
|
$\frac{\sqrt[3]{28}}{\mathbf{3}}$. Cubing the given equation yields
$$
1=\left(1-x^{3}\right)+3 \sqrt[3]{\left(1-x^{3}\right)\left(1+x^{3}\right)}\left(\sqrt[3]{1-x^{3}}+\sqrt[3]{1+x^{3}}\right)+\left(1+x^{3}\right)=2+3 \sqrt[3]{1-x^{6}}
$$
Then $\frac{-1}{3}=\sqrt[3]{1-x^{6}}$, so $\frac{-1}{27}=1-x^{6}$ and $x^{6}=\frac{28}{27}$ and $x^{2}=\frac{\sqrt[3]{28}}{3}$.
## Adult Acorns - Gee, I'm a Tree! [200]
In this section of the team round, your team will derive some basic results concerning tangential quadrilaterals. Tangential quadrilaterals have an incircle, or a circle lying within them that is tangent to all four sides. If a quadrilateral has an incircle, then the center of this circle is the incenter of the quadrilateral. As you shall see, tangential quadrilaterals are related to cyclic quadrilaterals. For reference, a review of cyclic quadrilaterals is given at the end of this section.
Your answers for this section of the team test should be proofs. Note that you may use any standard facts about cyclic quadrilaterals, such as those listed at the end of this test, without proving them. Additionally, you may cite the results of previous problems, even if you were unable to prove them.
For these problems, $A B C D$ is a tangential quadrilateral having incenter $I$. For the first three problems, the point $P$ is constructed such that triangle $P A B$ is similar to triangle $I D C$ and lies outside $A B C D$.
|
\frac{\sqrt[3]{28}}{3}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
A positive real number $x$ is such that
$$
\sqrt[3]{1-x^{3}}+\sqrt[3]{1+x^{3}}=1
$$
Find $x^{2}$.
|
$\frac{\sqrt[3]{28}}{\mathbf{3}}$. Cubing the given equation yields
$$
1=\left(1-x^{3}\right)+3 \sqrt[3]{\left(1-x^{3}\right)\left(1+x^{3}\right)}\left(\sqrt[3]{1-x^{3}}+\sqrt[3]{1+x^{3}}\right)+\left(1+x^{3}\right)=2+3 \sqrt[3]{1-x^{6}}
$$
Then $\frac{-1}{3}=\sqrt[3]{1-x^{6}}$, so $\frac{-1}{27}=1-x^{6}$ and $x^{6}=\frac{28}{27}$ and $x^{2}=\frac{\sqrt[3]{28}}{3}$.
## Adult Acorns - Gee, I'm a Tree! [200]
In this section of the team round, your team will derive some basic results concerning tangential quadrilaterals. Tangential quadrilaterals have an incircle, or a circle lying within them that is tangent to all four sides. If a quadrilateral has an incircle, then the center of this circle is the incenter of the quadrilateral. As you shall see, tangential quadrilaterals are related to cyclic quadrilaterals. For reference, a review of cyclic quadrilaterals is given at the end of this section.
Your answers for this section of the team test should be proofs. Note that you may use any standard facts about cyclic quadrilaterals, such as those listed at the end of this test, without proving them. Additionally, you may cite the results of previous problems, even if you were unable to prove them.
For these problems, $A B C D$ is a tangential quadrilateral having incenter $I$. For the first three problems, the point $P$ is constructed such that triangle $P A B$ is similar to triangle $I D C$ and lies outside $A B C D$.
|
{
"exam": "HMMT",
"problem_label": "10",
"problem_match": "\n10. [20]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team2-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2007"
}
|
Show that $P A I B$ is cyclic by proving that $\angle I A P$ is supplementary to $\angle P B I$.
|
Note that $I$ lies on the angle bisectors of the angles of quadrilateral $A B C D$. So writing $\angle D A B=2 \alpha, \angle A B C=2 \beta, \angle B C D=2 \gamma$, and $\angle C D A=2 \delta$, we have
$$
\begin{aligned}
\angle I A P+\angle P B I & =\angle I A B+\angle B A P+\angle P B A+\angle A B I \\
& =\angle I A B+\angle C D I+\angle I C D+\angle A B I \\
& =\alpha+\beta+\gamma+\delta .
\end{aligned}
$$
We are done because the angles in quadrilateral $A B C D$ add up to $360^{\circ}$.

|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Show that $P A I B$ is cyclic by proving that $\angle I A P$ is supplementary to $\angle P B I$.
|
Note that $I$ lies on the angle bisectors of the angles of quadrilateral $A B C D$. So writing $\angle D A B=2 \alpha, \angle A B C=2 \beta, \angle B C D=2 \gamma$, and $\angle C D A=2 \delta$, we have
$$
\begin{aligned}
\angle I A P+\angle P B I & =\angle I A B+\angle B A P+\angle P B A+\angle A B I \\
& =\angle I A B+\angle C D I+\angle I C D+\angle A B I \\
& =\alpha+\beta+\gamma+\delta .
\end{aligned}
$$
We are done because the angles in quadrilateral $A B C D$ add up to $360^{\circ}$.

|
{
"exam": "HMMT",
"problem_label": "1",
"problem_match": "\n1. $[\\mathbf{3 0}]$",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team2-solutions.jsonl",
"solution_match": "\nSolution. ",
"tier": "T4",
"year": "2007"
}
|
Show that triangle $P A I$ is similar to triangle $B I C$. Then conclude that
$$
P A=\frac{P I}{B C} \cdot B I
$$
|
We have $\angle I B C=\angle A B I$ because $I$ lies on the angle bisector, and $\angle A B I=\angle A P I$ because $P A I B$ is cyclic. Additionally,
$$
\angle B C I=\angle I C D=\angle P B A=\angle P I A
$$
by the angle bisector $C I$, that triangles $P A B$ and $I D C$ are similar, and the fact that $P A I B$ is cyclic, respectively. It follows that triangles $P A I$ and $B I C$ are similar. In particular, it follows that $I P / P A=B C / B I$, as required.
|
P A=\frac{P I}{B C} \cdot B I
|
Yes
|
Yes
|
proof
|
Geometry
|
Show that triangle $P A I$ is similar to triangle $B I C$. Then conclude that
$$
P A=\frac{P I}{B C} \cdot B I
$$
|
We have $\angle I B C=\angle A B I$ because $I$ lies on the angle bisector, and $\angle A B I=\angle A P I$ because $P A I B$ is cyclic. Additionally,
$$
\angle B C I=\angle I C D=\angle P B A=\angle P I A
$$
by the angle bisector $C I$, that triangles $P A B$ and $I D C$ are similar, and the fact that $P A I B$ is cyclic, respectively. It follows that triangles $P A I$ and $B I C$ are similar. In particular, it follows that $I P / P A=B C / B I$, as required.
|
{
"exam": "HMMT",
"problem_label": "2",
"problem_match": "\n2. [40]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team2-solutions.jsonl",
"solution_match": "\nSolution. ",
"tier": "T4",
"year": "2007"
}
|
Deduce from the above that
$$
\frac{B C}{A D} \cdot \frac{A I}{B I} \cdot \frac{D I}{C I}=1
$$
|
Exchanging the roles of $A$ and $D$ with $B$ and $C$, respectively, converts the formula from problem 2 into another formula:
$$
P B=\frac{P I}{A D} \cdot A D
$$
Then one the one hand, dividing the two gives $P A / P B=(A D \cdot B I) /(B C \cdot A I)$. On the other hand, $P A / P B=D I / C I$ because triangles $P A B$ and $I D C$ are similar. Clearing the denominators in the equation
$$
\frac{D I}{C I}=\frac{A D \cdot B I}{B C \cdot A I}
$$
yields the desired form.
|
\frac{B C}{A D} \cdot \frac{A I}{B I} \cdot \frac{D I}{C I}=1
|
Incomplete
|
Yes
|
proof
|
Geometry
|
Deduce from the above that
$$
\frac{B C}{A D} \cdot \frac{A I}{B I} \cdot \frac{D I}{C I}=1
$$
|
Exchanging the roles of $A$ and $D$ with $B$ and $C$, respectively, converts the formula from problem 2 into another formula:
$$
P B=\frac{P I}{A D} \cdot A D
$$
Then one the one hand, dividing the two gives $P A / P B=(A D \cdot B I) /(B C \cdot A I)$. On the other hand, $P A / P B=D I / C I$ because triangles $P A B$ and $I D C$ are similar. Clearing the denominators in the equation
$$
\frac{D I}{C I}=\frac{A D \cdot B I}{B C \cdot A I}
$$
yields the desired form.
|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n3. [25]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team2-solutions.jsonl",
"solution_match": "\nSolution. ",
"tier": "T4",
"year": "2007"
}
|
Show that $A B+C D=A D+B C$. Use the above to conclude that for some positive number $\alpha$,
$$
\begin{array}{ll}
A B=\alpha \cdot\left(\frac{A I}{C I}+\frac{B I}{D I}\right) & B C=\alpha \cdot\left(\frac{B I}{D I}+\frac{C I}{A I}\right) \\
C D=\alpha \cdot\left(\frac{C I}{A I}+\frac{D I}{B I}\right) & D A=\alpha \cdot\left(\frac{D I}{B I}+\frac{A I}{C I}\right) .
\end{array}
$$
|
Draw in the points of tangency $P, Q, R$, and $S$, of the incircle with sides $A B, B C, C D$, and $A D$, as shown. Then we have equal tangents $A P=A S, B P=B Q, C Q=C R$, and $D R=D S$. Then
$$
A B+C D=A P+B P+C R+D R=A S+(B Q+C Q)+D S=B C+A D
$$
Using the result of problem 3, we set $B C=x \cdot B I \cdot C I$ and $A D=x \cdot A I \cdot D I$ for some $x$, and $A B=y \cdot A I \cdot B I$ and $C D=y \cdot C I \cdot D I$ for some $y$. Now because $A B+C D=B C+A D$, we obtain
$$
y(A I \cdot B I+C I \cdot D I)=x(B I \cdot C I+A I \cdot D I)
$$
So it follows that the ratio $A B: B C: C D: D A$ is uniquely determined. One easily checks that the posed ratio satisfies the three required relations.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Show that $A B+C D=A D+B C$. Use the above to conclude that for some positive number $\alpha$,
$$
\begin{array}{ll}
A B=\alpha \cdot\left(\frac{A I}{C I}+\frac{B I}{D I}\right) & B C=\alpha \cdot\left(\frac{B I}{D I}+\frac{C I}{A I}\right) \\
C D=\alpha \cdot\left(\frac{C I}{A I}+\frac{D I}{B I}\right) & D A=\alpha \cdot\left(\frac{D I}{B I}+\frac{A I}{C I}\right) .
\end{array}
$$
|
Draw in the points of tangency $P, Q, R$, and $S$, of the incircle with sides $A B, B C, C D$, and $A D$, as shown. Then we have equal tangents $A P=A S, B P=B Q, C Q=C R$, and $D R=D S$. Then
$$
A B+C D=A P+B P+C R+D R=A S+(B Q+C Q)+D S=B C+A D
$$
Using the result of problem 3, we set $B C=x \cdot B I \cdot C I$ and $A D=x \cdot A I \cdot D I$ for some $x$, and $A B=y \cdot A I \cdot B I$ and $C D=y \cdot C I \cdot D I$ for some $y$. Now because $A B+C D=B C+A D$, we obtain
$$
y(A I \cdot B I+C I \cdot D I)=x(B I \cdot C I+A I \cdot D I)
$$
So it follows that the ratio $A B: B C: C D: D A$ is uniquely determined. One easily checks that the posed ratio satisfies the three required relations.

|
{
"exam": "HMMT",
"problem_label": "4",
"problem_match": "\n4. [25]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team2-solutions.jsonl",
"solution_match": "\nSolution. ",
"tier": "T4",
"year": "2007"
}
|
Show that
$$
A B \cdot B C=B I^{2}+\frac{A I \cdot B I \cdot C I}{D I}
$$
|
Returning to the original set up, Ptolemy's theorem applied to quadrilateral $P A I B$ gives $A B \cdot P I=P A \cdot B I+P B \cdot A I$. Substituting equation $P A=\frac{P I}{B C} \cdot B I$ from problem 2 and its cousin $P B=\frac{P I}{A D} \cdot A I$ allows us to write
$$
A B \cdot P I=\frac{P I}{B C} \cdot B I^{2}+\frac{P I}{A D} \cdot A I^{2}
$$
or
$$
A B \cdot B C=B I^{2}+\frac{B C}{A D} \cdot A I^{2}
$$
Substituting the formula $B C / A D=\frac{B I \cdot C I}{A I \cdot D I}$ from problem 3 finishes the problem.
|
proof
|
Incomplete
|
Yes
|
proof
|
Geometry
|
Show that
$$
A B \cdot B C=B I^{2}+\frac{A I \cdot B I \cdot C I}{D I}
$$
|
Returning to the original set up, Ptolemy's theorem applied to quadrilateral $P A I B$ gives $A B \cdot P I=P A \cdot B I+P B \cdot A I$. Substituting equation $P A=\frac{P I}{B C} \cdot B I$ from problem 2 and its cousin $P B=\frac{P I}{A D} \cdot A I$ allows us to write
$$
A B \cdot P I=\frac{P I}{B C} \cdot B I^{2}+\frac{P I}{A D} \cdot A I^{2}
$$
or
$$
A B \cdot B C=B I^{2}+\frac{B C}{A D} \cdot A I^{2}
$$
Substituting the formula $B C / A D=\frac{B I \cdot C I}{A I \cdot D I}$ from problem 3 finishes the problem.
|
{
"exam": "HMMT",
"problem_label": "5",
"problem_match": "\n5. [40]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team2-solutions.jsonl",
"solution_match": "\nSolution. ",
"tier": "T4",
"year": "2007"
}
|
Let the incircle of $A B C D$ be tangent to sides $A B, B C, C D$, and $A D$ at points $P, Q, R$, and $S$, respectively. Show that $A B C D$ is cyclic if and only if $P R \perp Q S$.
|
Let the diagonals of $P Q R S$ intersect at $T$. Because $\overline{A P}$ and $\overline{A S}$ are tangent to $\omega$ at $P$ and $S$, we may write $\alpha=\angle A S P=\angle S P A=\angle S Q P$ and $\beta=\angle C Q R=\angle Q R C=\angle Q P R$. Then $\angle P T Q=\pi-\alpha-\beta$. On the other hand, $\angle P A S=\pi-2 \alpha$ and $\angle R C Q=\pi-2 \beta$, so that $A B C D$ is cyclic if and only if
$$
\pi=\angle B A D+\angle D C B=2 \pi-2 \alpha-2 \beta
$$
or simply
$$
\pi / 2=\pi-\alpha-\beta=\angle P T Q
$$
as desired.
A brief review of cyclic Quadrilaterals.
The following discussion of cyclic quadrilaterals is included for reference. Any of the results given here may be cited without proof in your writeups.
A cyclic quadrilateral is a quadrilateral whose four vertices lie on a circle called the circumcircle (the circle is unique if it exists.) If a quadrilateral has a circumcircle, then the center of this circumcircle is called the circumcenter of the quadrilateral. For a convex quadrilateral $A B C D$, the following are equivalent:
- Quadrilateral $A B C D$ is cyclic;
- $\angle A B D=\angle A C D$ (or $\angle B C A=\angle B D A$, etc.);
- Angles $\angle A B C$ and $\angle C D A$ are supplementary, that is, $m \angle A B C+m \angle C D A=180^{\circ}$ (or angles $\angle B C D$ and $\angle B A D$ are supplementary);
Cyclic quadrilaterals have a number of interesting properties. A cyclic quadrilateral $A B C D$ satisfies
$$
A C \cdot B D=A B \cdot C D+A D \cdot B C
$$
a result known as Ptolemy's theorem. Another result, typically called Power of a Point, asserts that given a circle $\omega$, a point $P$ anywhere in the plane of $\omega$, and a line $\ell$ through $P$ intersecting $\omega$ at points $A$ and $B$, the value of $A P \cdot B P$ is independent of $\ell$; i.e., if a second line $\ell^{\prime}$ through $P$ intersects $\omega$ at $A^{\prime}$ and $B^{\prime}$, then $A P \cdot B P=A^{\prime} P \cdot B^{\prime} P$. This second theorem is proved via similar triangles. Say $P$ lies outside of $\omega$, that $\ell$ and $\ell^{\prime}$ are as before and that $A$ and $A^{\prime}$ lie on segments $B P$ and $B^{\prime} P$ respectively. Then triangle $A A^{\prime} P$ is similar to triangle $B^{\prime} B P$ because the triangles share an angle at $P$ and we have
$$
m \angle A A^{\prime} P=180^{\circ}-m \angle B^{\prime} A^{\prime} A=m \angle A B B^{\prime}=m \angle P B B^{\prime}
$$
The case where $A=B$ is valid and describes the tangents to $\omega$. A similar proof works for $P$ inside $\omega$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let the incircle of $A B C D$ be tangent to sides $A B, B C, C D$, and $A D$ at points $P, Q, R$, and $S$, respectively. Show that $A B C D$ is cyclic if and only if $P R \perp Q S$.
|
Let the diagonals of $P Q R S$ intersect at $T$. Because $\overline{A P}$ and $\overline{A S}$ are tangent to $\omega$ at $P$ and $S$, we may write $\alpha=\angle A S P=\angle S P A=\angle S Q P$ and $\beta=\angle C Q R=\angle Q R C=\angle Q P R$. Then $\angle P T Q=\pi-\alpha-\beta$. On the other hand, $\angle P A S=\pi-2 \alpha$ and $\angle R C Q=\pi-2 \beta$, so that $A B C D$ is cyclic if and only if
$$
\pi=\angle B A D+\angle D C B=2 \pi-2 \alpha-2 \beta
$$
or simply
$$
\pi / 2=\pi-\alpha-\beta=\angle P T Q
$$
as desired.
A brief review of cyclic Quadrilaterals.
The following discussion of cyclic quadrilaterals is included for reference. Any of the results given here may be cited without proof in your writeups.
A cyclic quadrilateral is a quadrilateral whose four vertices lie on a circle called the circumcircle (the circle is unique if it exists.) If a quadrilateral has a circumcircle, then the center of this circumcircle is called the circumcenter of the quadrilateral. For a convex quadrilateral $A B C D$, the following are equivalent:
- Quadrilateral $A B C D$ is cyclic;
- $\angle A B D=\angle A C D$ (or $\angle B C A=\angle B D A$, etc.);
- Angles $\angle A B C$ and $\angle C D A$ are supplementary, that is, $m \angle A B C+m \angle C D A=180^{\circ}$ (or angles $\angle B C D$ and $\angle B A D$ are supplementary);
Cyclic quadrilaterals have a number of interesting properties. A cyclic quadrilateral $A B C D$ satisfies
$$
A C \cdot B D=A B \cdot C D+A D \cdot B C
$$
a result known as Ptolemy's theorem. Another result, typically called Power of a Point, asserts that given a circle $\omega$, a point $P$ anywhere in the plane of $\omega$, and a line $\ell$ through $P$ intersecting $\omega$ at points $A$ and $B$, the value of $A P \cdot B P$ is independent of $\ell$; i.e., if a second line $\ell^{\prime}$ through $P$ intersects $\omega$ at $A^{\prime}$ and $B^{\prime}$, then $A P \cdot B P=A^{\prime} P \cdot B^{\prime} P$. This second theorem is proved via similar triangles. Say $P$ lies outside of $\omega$, that $\ell$ and $\ell^{\prime}$ are as before and that $A$ and $A^{\prime}$ lie on segments $B P$ and $B^{\prime} P$ respectively. Then triangle $A A^{\prime} P$ is similar to triangle $B^{\prime} B P$ because the triangles share an angle at $P$ and we have
$$
m \angle A A^{\prime} P=180^{\circ}-m \angle B^{\prime} A^{\prime} A=m \angle A B B^{\prime}=m \angle P B B^{\prime}
$$
The case where $A=B$ is valid and describes the tangents to $\omega$. A similar proof works for $P$ inside $\omega$.
|
{
"exam": "HMMT",
"problem_label": "6",
"problem_match": "\n6. [40]",
"resource_path": "HarvardMIT/segmented/en-102-2007-feb-team2-solutions.jsonl",
"solution_match": "\nSolution. ",
"tier": "T4",
"year": "2007"
}
|
Positive real numbers $x, y$ satisfy the equations $x^{2}+y^{2}=1$ and $x^{4}+y^{4}=\frac{17}{18}$. Find $x y$.
|
$\sqrt[\frac{1}{6}]{ }$ We have $2 x^{2} y^{2}=\left(x^{2}+y^{2}\right)^{2}-\left(x^{4}+y^{4}\right)=\frac{1}{18}$, so $x y=\frac{1}{6}$.
|
\frac{1}{6}
|
Yes
|
Incomplete
|
math-word-problem
|
Algebra
|
Positive real numbers $x, y$ satisfy the equations $x^{2}+y^{2}=1$ and $x^{4}+y^{4}=\frac{17}{18}$. Find $x y$.
|
$\sqrt[\frac{1}{6}]{ }$ We have $2 x^{2} y^{2}=\left(x^{2}+y^{2}\right)^{2}-\left(x^{4}+y^{4}\right)=\frac{1}{18}$, so $x y=\frac{1}{6}$.
|
{
"exam": "HMMT",
"problem_label": "4",
"problem_match": "\n1. [3]",
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-alg-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Let $f(n)$ be the number of times you have to hit the $\sqrt{ }$ key on a calculator to get a number less than 2 starting from $n$. For instance, $f(2)=1, f(5)=2$. For how many $1<m<2008$ is $f(m)$ odd?
|
242 This is $\left[2^{1}, 2^{2}\right) \cup\left[2^{4}, 2^{8}\right) \cup\left[2^{16}, 2^{32}\right) \ldots$, and $2^{8}<2008<2^{16}$ so we have exactly the first two intervals.
|
242
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $f(n)$ be the number of times you have to hit the $\sqrt{ }$ key on a calculator to get a number less than 2 starting from $n$. For instance, $f(2)=1, f(5)=2$. For how many $1<m<2008$ is $f(m)$ odd?
|
242 This is $\left[2^{1}, 2^{2}\right) \cup\left[2^{4}, 2^{8}\right) \cup\left[2^{16}, 2^{32}\right) \ldots$, and $2^{8}<2008<2^{16}$ so we have exactly the first two intervals.
|
{
"exam": "HMMT",
"problem_label": "2",
"problem_match": "\n2. [3]",
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-alg-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Determine all real numbers $a$ such that the inequality $\left|x^{2}+2 a x+3 a\right| \leq 2$ has exactly one solution in $x$.
|
1,2 Let $f(x)=x^{2}+2 a x+3 a$. Note that $f(-3 / 2)=9 / 4$, so the graph of $f$ is a parabola that goes through $(-3 / 2,9 / 4)$. Then, the condition that $\left|x^{2}+2 a x+3 a\right| \leq 2$ has exactly one solution means that the parabola has exactly one point in the strip $-1 \leq y \leq 1$, which is possible if and only if the parabola is tangent to $y=1$. That is, $x^{2}+2 a x+3 a=2$ has exactly one solution. Then, the discriminant $\Delta=4 a^{2}-4(3 a-2)=4 a^{2}-12 a+8$ must be zero. Solving the equation yields $a=1,2$.
|
1,2
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Determine all real numbers $a$ such that the inequality $\left|x^{2}+2 a x+3 a\right| \leq 2$ has exactly one solution in $x$.
|
1,2 Let $f(x)=x^{2}+2 a x+3 a$. Note that $f(-3 / 2)=9 / 4$, so the graph of $f$ is a parabola that goes through $(-3 / 2,9 / 4)$. Then, the condition that $\left|x^{2}+2 a x+3 a\right| \leq 2$ has exactly one solution means that the parabola has exactly one point in the strip $-1 \leq y \leq 1$, which is possible if and only if the parabola is tangent to $y=1$. That is, $x^{2}+2 a x+3 a=2$ has exactly one solution. Then, the discriminant $\Delta=4 a^{2}-4(3 a-2)=4 a^{2}-12 a+8$ must be zero. Solving the equation yields $a=1,2$.
|
{
"exam": "HMMT",
"problem_label": "6",
"problem_match": "\n3. [4]",
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-alg-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
The function $f$ satisfies
$$
f(x)+f(2 x+y)+5 x y=f(3 x-y)+2 x^{2}+1
$$
for all real numbers $x, y$. Determine the value of $f(10)$.
|
$\quad-49$ Setting $x=10$ and $y=5$ gives $f(10)+f(25)+250=f(25)+200+1$, from which we get $f(10)=-49$.
Remark: By setting $y=\frac{x}{2}$, we see that the function is $f(x)=-\frac{1}{2} x^{2}+1$, and it can be checked that this function indeed satisfies the given equation.
|
-49
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
The function $f$ satisfies
$$
f(x)+f(2 x+y)+5 x y=f(3 x-y)+2 x^{2}+1
$$
for all real numbers $x, y$. Determine the value of $f(10)$.
|
$\quad-49$ Setting $x=10$ and $y=5$ gives $f(10)+f(25)+250=f(25)+200+1$, from which we get $f(10)=-49$.
Remark: By setting $y=\frac{x}{2}$, we see that the function is $f(x)=-\frac{1}{2} x^{2}+1$, and it can be checked that this function indeed satisfies the given equation.
|
{
"exam": "HMMT",
"problem_label": "5",
"problem_match": "\n4. [4]",
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-alg-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Let $f(x)=x^{3}+x+1$. Suppose $g$ is a cubic polynomial such that $g(0)=-1$, and the roots of $g$ are the squares of the roots of $f$. Find $g(9)$.
|
899 Let $a, b, c$ be the zeros of $f$. Then $f(x)=(x-a)(x-b)(x-c)$. Then, the roots of $g$ are $a^{2}, b^{2}, c^{2}$, so $g(x)=k\left(x-a^{2}\right)\left(x-b^{2}\right)\left(x-c^{2}\right)$ for some constant $k$. Since $a b c=-f(0)=-1$, we have $k=k a^{2} b^{2} c^{2}=-g(0)=1$. Thus,
$$
g\left(x^{2}\right)=\left(x^{2}-a^{2}\right)\left(x^{2}-b^{2}\right)\left(x^{2}-c^{2}\right)=(x-a)(x-b)(x-c)(x+a)(x+b)(x+c)=-f(x) f(-x)
$$
Setting $x=3$ gives $g(9)=-f(3) f(-3)=-(31)(-29)=899$.
|
899
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $f(x)=x^{3}+x+1$. Suppose $g$ is a cubic polynomial such that $g(0)=-1$, and the roots of $g$ are the squares of the roots of $f$. Find $g(9)$.
|
899 Let $a, b, c$ be the zeros of $f$. Then $f(x)=(x-a)(x-b)(x-c)$. Then, the roots of $g$ are $a^{2}, b^{2}, c^{2}$, so $g(x)=k\left(x-a^{2}\right)\left(x-b^{2}\right)\left(x-c^{2}\right)$ for some constant $k$. Since $a b c=-f(0)=-1$, we have $k=k a^{2} b^{2} c^{2}=-g(0)=1$. Thus,
$$
g\left(x^{2}\right)=\left(x^{2}-a^{2}\right)\left(x^{2}-b^{2}\right)\left(x^{2}-c^{2}\right)=(x-a)(x-b)(x-c)(x+a)(x+b)(x+c)=-f(x) f(-x)
$$
Setting $x=3$ gives $g(9)=-f(3) f(-3)=-(31)(-29)=899$.
|
{
"exam": "HMMT",
"problem_label": "5",
"problem_match": "\n5. [5]",
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-alg-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
A root of unity is a complex number that is a solution to $z^{n}=1$ for some positive integer $n$. Determine the number of roots of unity that are also roots of $z^{2}+a z+b=0$ for some integers $a$ and $b$.
|
8 The only real roots of unity are 1 and -1 . If $\zeta$ is a complex root of unity that is also a root of the equation $z^{2}+a z+b$, then its conjugate $\bar{\zeta}$ must also be a root. In this case, $|a|=|\zeta+\bar{\zeta}| \leq|\zeta|+|\bar{\zeta}|=$ 2 and $b=\zeta \bar{\zeta}=1$. So we only need to check the quadratics $z^{2}+2 z+1, z^{2}+z+1, z^{2}+1, z^{2}-z+1, z^{2}-2 z+1$. We find 8 roots of unity: $\pm 1, \pm i, \frac{1}{2}( \pm 1 \pm \sqrt{3} i)$.
|
8
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
A root of unity is a complex number that is a solution to $z^{n}=1$ for some positive integer $n$. Determine the number of roots of unity that are also roots of $z^{2}+a z+b=0$ for some integers $a$ and $b$.
|
8 The only real roots of unity are 1 and -1 . If $\zeta$ is a complex root of unity that is also a root of the equation $z^{2}+a z+b$, then its conjugate $\bar{\zeta}$ must also be a root. In this case, $|a|=|\zeta+\bar{\zeta}| \leq|\zeta|+|\bar{\zeta}|=$ 2 and $b=\zeta \bar{\zeta}=1$. So we only need to check the quadratics $z^{2}+2 z+1, z^{2}+z+1, z^{2}+1, z^{2}-z+1, z^{2}-2 z+1$. We find 8 roots of unity: $\pm 1, \pm i, \frac{1}{2}( \pm 1 \pm \sqrt{3} i)$.
|
{
"exam": "HMMT",
"problem_label": "7",
"problem_match": "\n6. [5]",
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-alg-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Compute $\sum_{n=1}^{\infty} \sum_{k=1}^{n-1} \frac{k}{2^{n+k}}$.
|
$\frac{4}{9}$ We change the order of summation:
$$
\sum_{n=1}^{\infty} \sum_{k=1}^{n-1} \frac{k}{2^{n+k}}=\sum_{k=1}^{\infty} \frac{k}{2^{k}} \sum_{n=k+1}^{\infty} \frac{1}{2^{n}}=\sum_{k=1}^{\infty} \frac{k}{4^{k}}=\frac{4}{9} .
$$
(The last two steps involve the summation of an infinite geometric series, and what is sometimes called an infinite arithmetico-geometric series. These summations are quite standard, and thus we omit the details here.)
|
\frac{4}{9}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Compute $\sum_{n=1}^{\infty} \sum_{k=1}^{n-1} \frac{k}{2^{n+k}}$.
|
$\frac{4}{9}$ We change the order of summation:
$$
\sum_{n=1}^{\infty} \sum_{k=1}^{n-1} \frac{k}{2^{n+k}}=\sum_{k=1}^{\infty} \frac{k}{2^{k}} \sum_{n=k+1}^{\infty} \frac{1}{2^{n}}=\sum_{k=1}^{\infty} \frac{k}{4^{k}}=\frac{4}{9} .
$$
(The last two steps involve the summation of an infinite geometric series, and what is sometimes called an infinite arithmetico-geometric series. These summations are quite standard, and thus we omit the details here.)
|
{
"exam": "HMMT",
"problem_label": "7",
"problem_match": "\n7. [5]",
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-alg-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Compute $\arctan \left(\tan 65^{\circ}-2 \tan 40^{\circ}\right)$. (Express your answer in degrees as an angle between $0^{\circ}$ and $180^{\circ}$.)
|
$25^{\circ}$ First Solution: We have
$$
\tan 65^{\circ}-2 \tan 40^{\circ}=\cot 25^{\circ}-2 \cot 50^{\circ}=\cot 25^{\circ}-\frac{\cot ^{2} 25^{\circ}-1}{\cot 25^{\circ}}=\frac{1}{\cot 25^{\circ}}=\tan 25^{\circ} .
$$
Therefore, the answer is $25^{\circ}$.
Second Solution: We have
$\tan 65^{\circ}-2 \tan 40^{\circ}=\frac{1+\tan 20^{\circ}}{1-\tan 20^{\circ}}-\frac{4 \tan 20^{\circ}}{1-\tan ^{2} 20^{\circ}}=\frac{\left(1-\tan 20^{\circ}\right)^{2}}{\left(1-\tan 20^{\circ}\right)\left(1+\tan 20^{\circ}\right)}=\tan \left(45^{\circ}-20^{\circ}\right)=\tan 25^{\circ}$.
Again, the answer is $25^{\circ}$.
|
25^{\circ}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Compute $\arctan \left(\tan 65^{\circ}-2 \tan 40^{\circ}\right)$. (Express your answer in degrees as an angle between $0^{\circ}$ and $180^{\circ}$.)
|
$25^{\circ}$ First Solution: We have
$$
\tan 65^{\circ}-2 \tan 40^{\circ}=\cot 25^{\circ}-2 \cot 50^{\circ}=\cot 25^{\circ}-\frac{\cot ^{2} 25^{\circ}-1}{\cot 25^{\circ}}=\frac{1}{\cot 25^{\circ}}=\tan 25^{\circ} .
$$
Therefore, the answer is $25^{\circ}$.
Second Solution: We have
$\tan 65^{\circ}-2 \tan 40^{\circ}=\frac{1+\tan 20^{\circ}}{1-\tan 20^{\circ}}-\frac{4 \tan 20^{\circ}}{1-\tan ^{2} 20^{\circ}}=\frac{\left(1-\tan 20^{\circ}\right)^{2}}{\left(1-\tan 20^{\circ}\right)\left(1+\tan 20^{\circ}\right)}=\tan \left(45^{\circ}-20^{\circ}\right)=\tan 25^{\circ}$.
Again, the answer is $25^{\circ}$.
|
{
"exam": "HMMT",
"problem_label": "8",
"problem_match": "\n8. [6]",
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-alg-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Let $S$ be the set of points $(a, b)$ with $0 \leq a, b \leq 1$ such that the equation
$$
x^{4}+a x^{3}-b x^{2}+a x+1=0
$$
has at least one real root. Determine the area of the graph of $S$.
|
$\frac{1}{4}$ After dividing the equation by $x^{2}$, we can rearrange it as
$$
\left(x+\frac{1}{x}\right)^{2}+a\left(x+\frac{1}{x}\right)-b-2=0
$$
Let $y=x+\frac{1}{x}$. We can check that the range of $x+\frac{1}{x}$ as $x$ varies over the nonzero reals is $(-\infty,-2] \cup[2, \infty)$. Thus, the following equation needs to have a real root:
$$
y^{2}+a y-b-2=0 .
$$
Its discriminant, $a^{2}+4(b+2)$, is always positive since $a, b \geq 0$. Then, the maximum absolute value of the two roots is
$$
\frac{a+\sqrt{a^{2}+4(b+2)}}{2} .
$$
We need this value to be at least 2 . This is equivalent to
$$
\sqrt{a^{2}+4(b+2)} \geq 4-a .
$$
We can square both sides and simplify to obtain
$$
2 a \geq 2-b
$$
This equation defines the region inside $[0,1] \times[0,1]$ that is occupied by $S$, from which we deduce that the desired area is $1 / 4$.
|
\frac{1}{4}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $S$ be the set of points $(a, b)$ with $0 \leq a, b \leq 1$ such that the equation
$$
x^{4}+a x^{3}-b x^{2}+a x+1=0
$$
has at least one real root. Determine the area of the graph of $S$.
|
$\frac{1}{4}$ After dividing the equation by $x^{2}$, we can rearrange it as
$$
\left(x+\frac{1}{x}\right)^{2}+a\left(x+\frac{1}{x}\right)-b-2=0
$$
Let $y=x+\frac{1}{x}$. We can check that the range of $x+\frac{1}{x}$ as $x$ varies over the nonzero reals is $(-\infty,-2] \cup[2, \infty)$. Thus, the following equation needs to have a real root:
$$
y^{2}+a y-b-2=0 .
$$
Its discriminant, $a^{2}+4(b+2)$, is always positive since $a, b \geq 0$. Then, the maximum absolute value of the two roots is
$$
\frac{a+\sqrt{a^{2}+4(b+2)}}{2} .
$$
We need this value to be at least 2 . This is equivalent to
$$
\sqrt{a^{2}+4(b+2)} \geq 4-a .
$$
We can square both sides and simplify to obtain
$$
2 a \geq 2-b
$$
This equation defines the region inside $[0,1] \times[0,1]$ that is occupied by $S$, from which we deduce that the desired area is $1 / 4$.
|
{
"exam": "HMMT",
"problem_label": "9",
"problem_match": "\n9. [7]",
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-alg-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Evaluate the infinite sum
$$
\sum_{n=0}^{\infty}\binom{2 n}{n} \frac{1}{5^{n}}
$$
|
$\sqrt{5}$ First Solution: Note that
$$
\begin{aligned}
\binom{2 n}{n} & =\frac{(2 n)!}{n!\cdot n!}=\frac{(2 n)(2 n-2)(2 n-4) \cdots(2)}{n!} \cdot \frac{(2 n-1)(2 n-3)(2 n-5) \cdots(1)}{n!} \\
& =2^{n} \cdot \frac{(-2)^{n}}{n!}\left(-\frac{1}{2}\right)\left(-\frac{1}{2}-1\right)\left(-\frac{1}{2}-2\right) \cdots\left(-\frac{1}{2}-n+1\right) \\
& =(-4)^{n}\binom{-\frac{1}{2}}{n}
\end{aligned}
$$
Then, by the binomial theorem, for any real $x$ with $|x|<\frac{1}{4}$, we have
$$
(1-4 x)^{-1 / 2}=\sum_{n=0}^{\infty}\binom{-\frac{1}{2}}{n}(-4 x)^{n}=\sum_{n=0}^{\infty}\binom{2 n}{n} x^{n} .
$$
Therefore,
$$
\sum_{n=0}^{\infty}\binom{2 n}{n}\left(\frac{1}{5}\right)^{n}=\frac{1}{\sqrt{1-\frac{4}{5}}}=\sqrt{5}
$$
Second Solution: Consider the generating function
$$
f(x)=\sum_{n=0}^{\infty}\binom{2 n}{n} x^{n}
$$
It has formal integral given by
$$
g(x)=I(f(x))=\sum_{n=0}^{\infty} \frac{1}{n+1}\binom{2 n}{n} x^{n+1}=\sum_{n=0}^{\infty} C_{n} x^{n+1}=x \sum_{n=0}^{\infty} C_{n} x^{n}
$$
where $C_{n}=\frac{1}{n+1}\binom{2 n}{n}$ is the $n$th Catalan number. Let $h(x)=\sum_{n=0}^{\infty} C_{n} x^{n}$; it suffices to compute this generating function. Note that
$$
1+x h(x)^{2}=1+x \sum_{i, j \geq 0} C_{i} C_{j} x^{i+j}=1+x \sum_{k \geq 0}\left(\sum_{i=0}^{k} C_{i} C_{k-i}\right) x^{k}=1+\sum_{k \geq 0} C_{k+1} x^{k+1}=h(x)
$$
where we've used the recurrence relation for the Catalan numbers. We now solve for $h(x)$ with the quadratic equation to obtain
$$
h(x)=\frac{1 / x \pm \sqrt{1 / x^{2}-4 / x}}{2}=\frac{1 \pm \sqrt{1-4 x}}{2 x}
$$
Note that we must choose the - sign in the $\pm$, since the + would lead to a leading term of $\frac{1}{x}$ for $h$ (by expanding $\sqrt{1-4 x}$ into a power series). Therefore, we see that
$$
f(x)=D(g(x))=D(x h(x))=D\left(\frac{1-\sqrt{1-4 x}}{2}\right)=\frac{1}{\sqrt{1-4 x}}
$$
and our answer is hence $f(1 / 5)=\sqrt{5}$.
|
\sqrt{5}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Evaluate the infinite sum
$$
\sum_{n=0}^{\infty}\binom{2 n}{n} \frac{1}{5^{n}}
$$
|
$\sqrt{5}$ First Solution: Note that
$$
\begin{aligned}
\binom{2 n}{n} & =\frac{(2 n)!}{n!\cdot n!}=\frac{(2 n)(2 n-2)(2 n-4) \cdots(2)}{n!} \cdot \frac{(2 n-1)(2 n-3)(2 n-5) \cdots(1)}{n!} \\
& =2^{n} \cdot \frac{(-2)^{n}}{n!}\left(-\frac{1}{2}\right)\left(-\frac{1}{2}-1\right)\left(-\frac{1}{2}-2\right) \cdots\left(-\frac{1}{2}-n+1\right) \\
& =(-4)^{n}\binom{-\frac{1}{2}}{n}
\end{aligned}
$$
Then, by the binomial theorem, for any real $x$ with $|x|<\frac{1}{4}$, we have
$$
(1-4 x)^{-1 / 2}=\sum_{n=0}^{\infty}\binom{-\frac{1}{2}}{n}(-4 x)^{n}=\sum_{n=0}^{\infty}\binom{2 n}{n} x^{n} .
$$
Therefore,
$$
\sum_{n=0}^{\infty}\binom{2 n}{n}\left(\frac{1}{5}\right)^{n}=\frac{1}{\sqrt{1-\frac{4}{5}}}=\sqrt{5}
$$
Second Solution: Consider the generating function
$$
f(x)=\sum_{n=0}^{\infty}\binom{2 n}{n} x^{n}
$$
It has formal integral given by
$$
g(x)=I(f(x))=\sum_{n=0}^{\infty} \frac{1}{n+1}\binom{2 n}{n} x^{n+1}=\sum_{n=0}^{\infty} C_{n} x^{n+1}=x \sum_{n=0}^{\infty} C_{n} x^{n}
$$
where $C_{n}=\frac{1}{n+1}\binom{2 n}{n}$ is the $n$th Catalan number. Let $h(x)=\sum_{n=0}^{\infty} C_{n} x^{n}$; it suffices to compute this generating function. Note that
$$
1+x h(x)^{2}=1+x \sum_{i, j \geq 0} C_{i} C_{j} x^{i+j}=1+x \sum_{k \geq 0}\left(\sum_{i=0}^{k} C_{i} C_{k-i}\right) x^{k}=1+\sum_{k \geq 0} C_{k+1} x^{k+1}=h(x)
$$
where we've used the recurrence relation for the Catalan numbers. We now solve for $h(x)$ with the quadratic equation to obtain
$$
h(x)=\frac{1 / x \pm \sqrt{1 / x^{2}-4 / x}}{2}=\frac{1 \pm \sqrt{1-4 x}}{2 x}
$$
Note that we must choose the - sign in the $\pm$, since the + would lead to a leading term of $\frac{1}{x}$ for $h$ (by expanding $\sqrt{1-4 x}$ into a power series). Therefore, we see that
$$
f(x)=D(g(x))=D(x h(x))=D\left(\frac{1-\sqrt{1-4 x}}{2}\right)=\frac{1}{\sqrt{1-4 x}}
$$
and our answer is hence $f(1 / 5)=\sqrt{5}$.
|
{
"exam": "HMMT",
"problem_label": "10",
"problem_match": "\n10. [8]",
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-alg-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Let $f(x)=1+x+x^{2}+\cdots+x^{100}$. Find $f^{\prime}(1)$.
|
5050 Note that $f^{\prime}(x)=1+2 x+3 x^{2}+\cdots+100 x^{99}$, so $f^{\prime}(1)=1+2+\cdots+100=\frac{100 \cdot 101}{2}=$ 5050.
|
5050
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Let $f(x)=1+x+x^{2}+\cdots+x^{100}$. Find $f^{\prime}(1)$.
|
5050 Note that $f^{\prime}(x)=1+2 x+3 x^{2}+\cdots+100 x^{99}$, so $f^{\prime}(1)=1+2+\cdots+100=\frac{100 \cdot 101}{2}=$ 5050.
|
{
"exam": "HMMT",
"problem_label": "1",
"problem_match": "\n1. [3]",
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-calc-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Let $\ell$ be the line through $(0,0)$ and tangent to the curve $y=x^{3}+x+16$. Find the slope of $\ell$.
|
13 Let the point of tangency be $\left(t, t^{3}+t+16\right)$, then the slope of $\ell$ is $\left(t^{3}+t+16\right) / t$. On the other hand, since $d y / d x=3 x^{2}+1$, the slope of $\ell$ is $3 t^{2}+1$. Therefore,
$$
\frac{t^{3}+t+16}{t}=3 t^{2}+1
$$
Simplifying, we get $t^{3}=8$, so $t=2$. It follows that the slope is $3(2)^{2}+1=13$.
|
13
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Let $\ell$ be the line through $(0,0)$ and tangent to the curve $y=x^{3}+x+16$. Find the slope of $\ell$.
|
13 Let the point of tangency be $\left(t, t^{3}+t+16\right)$, then the slope of $\ell$ is $\left(t^{3}+t+16\right) / t$. On the other hand, since $d y / d x=3 x^{2}+1$, the slope of $\ell$ is $3 t^{2}+1$. Therefore,
$$
\frac{t^{3}+t+16}{t}=3 t^{2}+1
$$
Simplifying, we get $t^{3}=8$, so $t=2$. It follows that the slope is $3(2)^{2}+1=13$.
|
{
"exam": "HMMT",
"problem_label": "2",
"problem_match": "\n2. [3]",
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-calc-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Find all $y>1$ satisfying $\int_{1}^{y} x \ln x d x=\frac{1}{4}$.
|
$\sqrt{\sqrt{e}}$ Applying integration by parts with $u=\ln x$ and $v=\frac{1}{2} x^{2}$, we get
$$
\int_{1}^{y} x \ln x d x=\left.\frac{1}{2} x^{2} \ln x\right|_{1} ^{y}-\frac{1}{2} \int_{1}^{y} x d x=\frac{1}{2} y^{2} \ln y-\frac{1}{4} y^{2}+\frac{1}{4}
$$
So $y^{2} \ln y=\frac{1}{2} y^{2}$. Since $y>1$, we obtain $\ln y=\frac{1}{2}$, and thus $y=\sqrt{e}$.
|
\sqrt{e}
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Find all $y>1$ satisfying $\int_{1}^{y} x \ln x d x=\frac{1}{4}$.
|
$\sqrt{\sqrt{e}}$ Applying integration by parts with $u=\ln x$ and $v=\frac{1}{2} x^{2}$, we get
$$
\int_{1}^{y} x \ln x d x=\left.\frac{1}{2} x^{2} \ln x\right|_{1} ^{y}-\frac{1}{2} \int_{1}^{y} x d x=\frac{1}{2} y^{2} \ln y-\frac{1}{4} y^{2}+\frac{1}{4}
$$
So $y^{2} \ln y=\frac{1}{2} y^{2}$. Since $y>1$, we obtain $\ln y=\frac{1}{2}$, and thus $y=\sqrt{e}$.
|
{
"exam": "HMMT",
"problem_label": "3",
"problem_match": "\n3. [4]",
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-calc-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Let $a, b$ be constants such that $\lim _{x \rightarrow 1} \frac{(\ln (2-x))^{2}}{x^{2}+a x+b}=1$. Determine the pair $(a, b)$.
|
$(-2,1)$ When $x=1$, the numerator is 0 , so the denominator must be zero as well, so $1+a+b=0$. Using l'Hôpital's rule, we must have
$$
1=\lim _{x \rightarrow 1} \frac{(\ln (2-x))^{2}}{x^{2}+a x+b}=\lim _{x \rightarrow 1} \frac{2 \ln (2-x)}{(x-2)(2 x+a)}
$$
and by the same argument we find that $2+a=0$. Thus, $a=-2$ and $b=1$. This is indeed a solution, as can be seen by finishing the computation.
|
(-2,1)
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Let $a, b$ be constants such that $\lim _{x \rightarrow 1} \frac{(\ln (2-x))^{2}}{x^{2}+a x+b}=1$. Determine the pair $(a, b)$.
|
$(-2,1)$ When $x=1$, the numerator is 0 , so the denominator must be zero as well, so $1+a+b=0$. Using l'Hôpital's rule, we must have
$$
1=\lim _{x \rightarrow 1} \frac{(\ln (2-x))^{2}}{x^{2}+a x+b}=\lim _{x \rightarrow 1} \frac{2 \ln (2-x)}{(x-2)(2 x+a)}
$$
and by the same argument we find that $2+a=0$. Thus, $a=-2$ and $b=1$. This is indeed a solution, as can be seen by finishing the computation.
|
{
"exam": "HMMT",
"problem_label": "4",
"problem_match": "\n4. [4]",
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-calc-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Let $f(x)=\sin ^{6}\left(\frac{x}{4}\right)+\cos ^{6}\left(\frac{x}{4}\right)$ for all real numbers $x$. Determine $f^{(2008)}(0)$ (i.e., $f$ differentiated 2008 times and then evaluated at $x=0$ ).
|
| $\frac{3}{8}$ |
| :---: |
| We have |
$$
\begin{aligned}
\sin ^{6} x+\cos ^{6} x & =\left(\sin ^{2} x+\cos ^{2} x\right)^{3}-3 \sin ^{2} x \cos ^{2} x\left(\sin ^{2} x+\cos ^{2} x\right) \\
& =1-3 \sin ^{2} x \cos ^{2} x=1-\frac{3}{4} \sin ^{2} 2 x=1-\frac{3}{4}\left(\frac{1-\cos 4 x}{2}\right) \\
& =\frac{5}{8}+\frac{3}{8} \cos 4 x
\end{aligned}
$$
It follows that $f(x)=\frac{5}{8}+\frac{3}{8} \cos x$. Thus $f^{(2008)}(x)=\frac{3}{8} \cos x$. Evaluating at $x=0$ gives $\frac{3}{8}$.
|
\frac{3}{8}
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Let $f(x)=\sin ^{6}\left(\frac{x}{4}\right)+\cos ^{6}\left(\frac{x}{4}\right)$ for all real numbers $x$. Determine $f^{(2008)}(0)$ (i.e., $f$ differentiated 2008 times and then evaluated at $x=0$ ).
|
| $\frac{3}{8}$ |
| :---: |
| We have |
$$
\begin{aligned}
\sin ^{6} x+\cos ^{6} x & =\left(\sin ^{2} x+\cos ^{2} x\right)^{3}-3 \sin ^{2} x \cos ^{2} x\left(\sin ^{2} x+\cos ^{2} x\right) \\
& =1-3 \sin ^{2} x \cos ^{2} x=1-\frac{3}{4} \sin ^{2} 2 x=1-\frac{3}{4}\left(\frac{1-\cos 4 x}{2}\right) \\
& =\frac{5}{8}+\frac{3}{8} \cos 4 x
\end{aligned}
$$
It follows that $f(x)=\frac{5}{8}+\frac{3}{8} \cos x$. Thus $f^{(2008)}(x)=\frac{3}{8} \cos x$. Evaluating at $x=0$ gives $\frac{3}{8}$.
|
{
"exam": "HMMT",
"problem_label": "5",
"problem_match": "\n5. [4]",
"resource_path": "HarvardMIT/segmented/en-112-2008-feb-calc-solutions.jsonl",
"solution_match": "\nAnswer: ",
"tier": "T4",
"year": "2008"
}
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.