problem
stringlengths 14
10.4k
| solution
stringlengths 1
24.1k
| answer
stringlengths 1
250
⌀ | problem_is_valid
stringclasses 4
values | solution_is_valid
stringclasses 3
values | question_type
stringclasses 4
values | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
10.4k
| solution_raw
stringlengths 1
24.1k
| metadata
dict |
|---|---|---|---|---|---|---|---|---|---|
A graph has $N$ vertices. An invisible hare sits in one of the vertices. A group of hunters tries to kill the hare. In each move all of them shoot simultaneously: each hunter shoots at a single vertex, they choose the target vertices cooperatively. If the hare was in one of the target vertices during a shoot, the hunt is finished. Otherwise the hare can stay in its vertex or jump to one of the neighboring vertices.
The hunters know an algorithm that allows them to kill the hare in at most $N$ ! moves. Prove that then there exists an algorithm that allows them to kill the hare in at most $2^{N}$ moves.
|
Let hunters apply optimal (fastest) algorithm. Let say that a vertex has a smell of a hare, if there exists an initial vertex and a sequence of moves of the hare for which the hare is still alive and now occupies this vertex. After every shoot mark the set of all the vertices that have a smell of a hare. In the beginning all the vertices of the graph have a smell of hare, and after finish of hunting this set is empty. The idea is that in optimal strategy these sets can not repeat!
Indeed, the hunting does not imply feedback, the hunters' shoots do not depend on hare's moves because the hunters try to foresee all possible moves of hare. So if a set of vertices $A$ appears after the k-th shoot and once again after the $m$-th shoot, then then the strategy is not optimal because all shoots form $k$-th to $(m-1)$-th can be omitted with the same result of hunting.
Since it is possible to mark at most $2^{N}$ sets the hunting will finish in at most $2^{N}-1$ shoots.
|
2^{N}-1
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A graph has $N$ vertices. An invisible hare sits in one of the vertices. A group of hunters tries to kill the hare. In each move all of them shoot simultaneously: each hunter shoots at a single vertex, they choose the target vertices cooperatively. If the hare was in one of the target vertices during a shoot, the hunt is finished. Otherwise the hare can stay in its vertex or jump to one of the neighboring vertices.
The hunters know an algorithm that allows them to kill the hare in at most $N$ ! moves. Prove that then there exists an algorithm that allows them to kill the hare in at most $2^{N}$ moves.
|
Let hunters apply optimal (fastest) algorithm. Let say that a vertex has a smell of a hare, if there exists an initial vertex and a sequence of moves of the hare for which the hare is still alive and now occupies this vertex. After every shoot mark the set of all the vertices that have a smell of a hare. In the beginning all the vertices of the graph have a smell of hare, and after finish of hunting this set is empty. The idea is that in optimal strategy these sets can not repeat!
Indeed, the hunting does not imply feedback, the hunters' shoots do not depend on hare's moves because the hunters try to foresee all possible moves of hare. So if a set of vertices $A$ appears after the k-th shoot and once again after the $m$-th shoot, then then the strategy is not optimal because all shoots form $k$-th to $(m-1)$-th can be omitted with the same result of hunting.
Since it is possible to mark at most $2^{N}$ sets the hunting will finish in at most $2^{N}-1$ shoots.
|
{
"exam": "BalticWay",
"problem_label": "8",
"problem_match": "\n8.",
"resource_path": "BalticWay/segmented/en-bw18sol.jsonl",
"solution_match": "# Solution.",
"tier": "T3",
"year": "2018"
}
|
Olga and Sasha play a game on an infinite hexagonal grid. They take turns in placing a stone on a free hexagon of their choice. Olga starts the game. Just before the 2018th stone is placed, a new rule comes into play. A stone may now be placed only on those free hexagons having at least two occupied neighbors.
A player loses when she or he either is unable to make a move, or has filled a pattern of the rhomboid shape as shown (rotated in any possible way). Determine which player, if any, possesses a winning strategy.
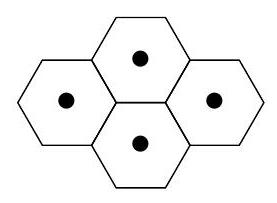
|
Answer: Olga has a winning strategy.
The game cannot go on forever. Draw a large hexagon enclosing all 2017 counters in play after the 2017th move, as in Figure ??. While it will be possible to place future counters in the hexagonal frame at distance 1 from the shaded part (i.e. immediately surrounding it), where $D$ and $E$ are located, it will be impossible to reach cells at distance 2 from the shaded part, where $F$ is located. Indeed, in order to place a counter at $F$, first counters must be placed on cells $D$ and $E$.
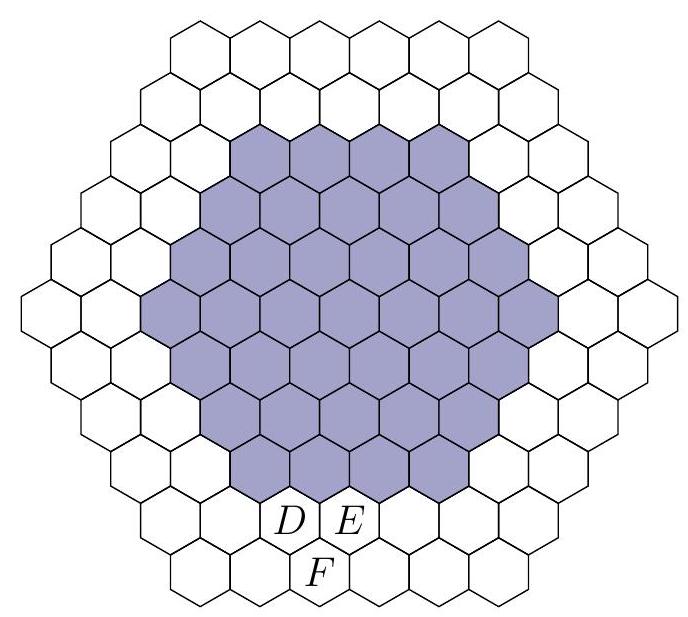
Figure 1: A large shaded hexagon enclosing all 2017 counters in play after the 2017th move.
Assume that the cells $E_{1}, E_{2}, \ldots, E_{n}$ to the right of $E$ contain counters, but the next cell to the right is $E_{n+1}$ and it is empty. Observe that the counter on $E_{n-1}$ has been placed before the counter on $E_{n}$, because otherwise the forbidden rhombus is formed by the cells $E_{n-1}, E_{n}$ and two ancestors of $E_{n}$ in the previous row. By analogous reasoning considering the moment of placing the counter on $E_{n-1}$ one can prove that the counter on $E_{n-2}$ has been placed before the counter on $E_{n-1}$, etc. Thus we conclude that the counter on $D$ has been placed before the counter on $E$. But changing the direction of our reasoning to the left we similarly conclude that counter on $E$ has been placed before the counter on $D$. A contradiction.
Now, let Olga place her first counter in any hexagon $H$, and then respond to each of Sasha's successive moves by symmetry, choosing to place her counter on the reflexion in $H$ of his chosen hexagon (in other words, diametrically opposite to his with respect to $H$ ). It is clear that the gameplay will be completely symmetrical after each of Olga's moves. Hence she may respond, even under the additional rule, to any move Sasha might make. It is also evident that she will never complete a forbidden rhombus if Sasha did not already do so before. Hence Olga is always certain to have a legal move at her disposal, and so will eventually win.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Olga and Sasha play a game on an infinite hexagonal grid. They take turns in placing a stone on a free hexagon of their choice. Olga starts the game. Just before the 2018th stone is placed, a new rule comes into play. A stone may now be placed only on those free hexagons having at least two occupied neighbors.
A player loses when she or he either is unable to make a move, or has filled a pattern of the rhomboid shape as shown (rotated in any possible way). Determine which player, if any, possesses a winning strategy.

|
Answer: Olga has a winning strategy.
The game cannot go on forever. Draw a large hexagon enclosing all 2017 counters in play after the 2017th move, as in Figure ??. While it will be possible to place future counters in the hexagonal frame at distance 1 from the shaded part (i.e. immediately surrounding it), where $D$ and $E$ are located, it will be impossible to reach cells at distance 2 from the shaded part, where $F$ is located. Indeed, in order to place a counter at $F$, first counters must be placed on cells $D$ and $E$.

Figure 1: A large shaded hexagon enclosing all 2017 counters in play after the 2017th move.
Assume that the cells $E_{1}, E_{2}, \ldots, E_{n}$ to the right of $E$ contain counters, but the next cell to the right is $E_{n+1}$ and it is empty. Observe that the counter on $E_{n-1}$ has been placed before the counter on $E_{n}$, because otherwise the forbidden rhombus is formed by the cells $E_{n-1}, E_{n}$ and two ancestors of $E_{n}$ in the previous row. By analogous reasoning considering the moment of placing the counter on $E_{n-1}$ one can prove that the counter on $E_{n-2}$ has been placed before the counter on $E_{n-1}$, etc. Thus we conclude that the counter on $D$ has been placed before the counter on $E$. But changing the direction of our reasoning to the left we similarly conclude that counter on $E$ has been placed before the counter on $D$. A contradiction.
Now, let Olga place her first counter in any hexagon $H$, and then respond to each of Sasha's successive moves by symmetry, choosing to place her counter on the reflexion in $H$ of his chosen hexagon (in other words, diametrically opposite to his with respect to $H$ ). It is clear that the gameplay will be completely symmetrical after each of Olga's moves. Hence she may respond, even under the additional rule, to any move Sasha might make. It is also evident that she will never complete a forbidden rhombus if Sasha did not already do so before. Hence Olga is always certain to have a legal move at her disposal, and so will eventually win.
|
{
"exam": "BalticWay",
"problem_label": "9",
"problem_match": "\n9.",
"resource_path": "BalticWay/segmented/en-bw18sol.jsonl",
"solution_match": "# Solution.",
"tier": "T3",
"year": "2018"
}
|
The integers from 1 to $n$ are written, one on each of $n$ cards. The first player removes one card. Then the second player removes two cards with consecutive integers. After that the first player removes three cards with consecutive integers. Finally, the second player removes four cards with consecutive integers. What is the smallest value of $n$ for which the second player can ensure that he completes both his moves?
|
Answer: $n=14$.
At first, let's show that for $n=13$ the first player can ensure that after his second move no 4 consecutive numbers are left. In the first move he can erase number 4 and in the second move he can ensure that numbers 8,9 and 10 are erased. No interval of length 4 is left.
If $n=14$ the second player can use the following strategy. Let the first player erase number $k$ in his first move, because of symmetry assume that that $k \leq 7$. If $k \geq 5$ then the second player can erase $k+1$ and $k+2$ and there are two intervals left of length at least 4: 1.. $(k-1)$ and $(k+3) . .14$, but the first player can destroy at most one of them. But if $k \leq 4$, then the second player can erase numbers 9 and 10 in his first move and again there are two intervals left of length at least 4: $(k+1) . .8$ and 11..14.
## 3 Geometry
|
14
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
The integers from 1 to $n$ are written, one on each of $n$ cards. The first player removes one card. Then the second player removes two cards with consecutive integers. After that the first player removes three cards with consecutive integers. Finally, the second player removes four cards with consecutive integers. What is the smallest value of $n$ for which the second player can ensure that he completes both his moves?
|
Answer: $n=14$.
At first, let's show that for $n=13$ the first player can ensure that after his second move no 4 consecutive numbers are left. In the first move he can erase number 4 and in the second move he can ensure that numbers 8,9 and 10 are erased. No interval of length 4 is left.
If $n=14$ the second player can use the following strategy. Let the first player erase number $k$ in his first move, because of symmetry assume that that $k \leq 7$. If $k \geq 5$ then the second player can erase $k+1$ and $k+2$ and there are two intervals left of length at least 4: 1.. $(k-1)$ and $(k+3) . .14$, but the first player can destroy at most one of them. But if $k \leq 4$, then the second player can erase numbers 9 and 10 in his first move and again there are two intervals left of length at least 4: $(k+1) . .8$ and 11..14.
## 3 Geometry
|
{
"exam": "BalticWay",
"problem_label": "10",
"problem_match": "\n10.",
"resource_path": "BalticWay/segmented/en-bw18sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2018"
}
|
The points $A, B, C, D$ lie, in this order, on a circle $\omega$, where $A D$ is a diameter of $\omega$. Furthermore, $A B=B C=a$ and $C D=c$ for some relatively prime integers $a$ and $c$. Show that if the diameter $d$ of $\omega$ is also an integer, then either $d$ or $2 d$ is a perfect square.
|
By Pythagoras, the lengths of the diagonals of quadrangle $A B C D$ are $\sqrt{d^{2}-a^{2}}$ and $\sqrt{d^{2}-c^{2}}$. Applying Ptolemaios' Theorem to the quadrilateral $A B C D$ gives
$$
\sqrt{d^{2}-a^{2}} \cdot \sqrt{d^{2}-c^{2}}=a b+a c,
$$
which after squaring and simplifying becomes
$$
d^{3}-\left(2 a^{2}+c^{2}\right) d-2 a^{2} c=0 .
$$
Then $d=-c$ is a root of this equation, hence, $c+d$ is a positive factor of the left-hand side. Hence, the remaining factor (which is quadratic in $d$ ) must vanish, and we obtain $d^{2}=c d+2 a^{2}$. Let $e=2 d-c$. The number $c^{2}+8 a^{2}=(2 d-c)^{2}=e^{2}$ is a square, and it follows that $8 a^{2}=e^{2}-c^{2}$. If $e$ and $c$ both were even, then by $8 \mid\left(e^{2}-c^{2}\right)$ we also have $16 \mid\left(e^{2}-c^{2}\right)=8 a^{2}$ which implies $2 \mid a$, a contradiction to the fact that $a$ and $c$ are relatively prime. Hence, $e$ and $c$ both must be odd. Moreover, $e$ and $c$ are obviously relatively prime. Consequently, the factors on the right-hand side of $2 a^{2}=\frac{e-c}{2} \cdot \frac{e+c}{2}$ are relatively prime. It follows that $d=\frac{e+c}{2}$ is a perfect square or twice a perfect square.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The points $A, B, C, D$ lie, in this order, on a circle $\omega$, where $A D$ is a diameter of $\omega$. Furthermore, $A B=B C=a$ and $C D=c$ for some relatively prime integers $a$ and $c$. Show that if the diameter $d$ of $\omega$ is also an integer, then either $d$ or $2 d$ is a perfect square.
|
By Pythagoras, the lengths of the diagonals of quadrangle $A B C D$ are $\sqrt{d^{2}-a^{2}}$ and $\sqrt{d^{2}-c^{2}}$. Applying Ptolemaios' Theorem to the quadrilateral $A B C D$ gives
$$
\sqrt{d^{2}-a^{2}} \cdot \sqrt{d^{2}-c^{2}}=a b+a c,
$$
which after squaring and simplifying becomes
$$
d^{3}-\left(2 a^{2}+c^{2}\right) d-2 a^{2} c=0 .
$$
Then $d=-c$ is a root of this equation, hence, $c+d$ is a positive factor of the left-hand side. Hence, the remaining factor (which is quadratic in $d$ ) must vanish, and we obtain $d^{2}=c d+2 a^{2}$. Let $e=2 d-c$. The number $c^{2}+8 a^{2}=(2 d-c)^{2}=e^{2}$ is a square, and it follows that $8 a^{2}=e^{2}-c^{2}$. If $e$ and $c$ both were even, then by $8 \mid\left(e^{2}-c^{2}\right)$ we also have $16 \mid\left(e^{2}-c^{2}\right)=8 a^{2}$ which implies $2 \mid a$, a contradiction to the fact that $a$ and $c$ are relatively prime. Hence, $e$ and $c$ both must be odd. Moreover, $e$ and $c$ are obviously relatively prime. Consequently, the factors on the right-hand side of $2 a^{2}=\frac{e-c}{2} \cdot \frac{e+c}{2}$ are relatively prime. It follows that $d=\frac{e+c}{2}$ is a perfect square or twice a perfect square.
|
{
"exam": "BalticWay",
"problem_label": "11",
"problem_match": "\n11.",
"resource_path": "BalticWay/segmented/en-bw18sol.jsonl",
"solution_match": "# Solution.",
"tier": "T3",
"year": "2018"
}
|
The altitudes $B B_{1}$ and $C C_{1}$ of an acute triangle $A B C$ intersect in point $H$. Let $B_{2}$ and $C_{2}$ be points on the segments $B H$ and $C H$, respectively, such that $B B_{2}=B_{1} H$ and $C C_{2}=C_{1} H$. The circumcircle of the triangle $B_{2} H C_{2}$ intersects the circumcircle of the triangle $A B C$ in points $D$ and $E$. Prove that the triangle $D E H$ is right-angled.
|
Despite of the logical symmetry of the picture the right angle in triangle $\triangle D E H$ is not $H$ but either $D$ or $E$.
Denote by $w$ the circumcircle of the triangle $\mathrm{B}_{2} \mathrm{HC}_{2}$. Midperpendicular to the segment $\mathrm{C}_{2} \mathrm{H}$ is also the midperpendicular to $C C_{1}$ therefore it passes through the midpoint $X$ of side $B C$. By the similar reasoning the midperpendicular to $B_{2} H$ passes through $X$. Therefore $X$ is the center of the circle $w$.
It is well known that the point which is symmetrical to the orthocenter $H$ with respect to the side $B C$ belongs to the circumcircle of the triangle $A B C$. The distance from this point to $X$ equals $X H$ due to symmetry, hence this point belongs $w$, therefore it coincides with $D$ or $E$, without loss of generality with $D$. Thus $D H \perp B C$.
Finally, the centers of $w$ and circumcircle $(A B C)$ belong to the midperpendicular of $B C$, therefore their common chord $D E$ is parallel $B C$. Thus $\angle H D E=90^{\circ}$.
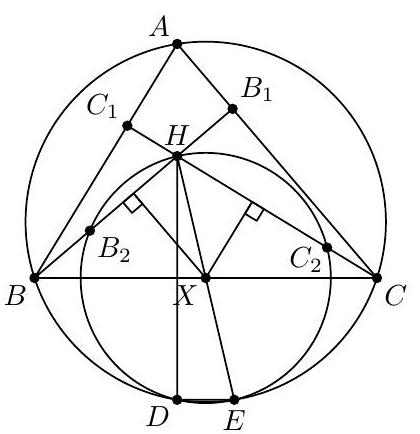
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The altitudes $B B_{1}$ and $C C_{1}$ of an acute triangle $A B C$ intersect in point $H$. Let $B_{2}$ and $C_{2}$ be points on the segments $B H$ and $C H$, respectively, such that $B B_{2}=B_{1} H$ and $C C_{2}=C_{1} H$. The circumcircle of the triangle $B_{2} H C_{2}$ intersects the circumcircle of the triangle $A B C$ in points $D$ and $E$. Prove that the triangle $D E H$ is right-angled.
|
Despite of the logical symmetry of the picture the right angle in triangle $\triangle D E H$ is not $H$ but either $D$ or $E$.
Denote by $w$ the circumcircle of the triangle $\mathrm{B}_{2} \mathrm{HC}_{2}$. Midperpendicular to the segment $\mathrm{C}_{2} \mathrm{H}$ is also the midperpendicular to $C C_{1}$ therefore it passes through the midpoint $X$ of side $B C$. By the similar reasoning the midperpendicular to $B_{2} H$ passes through $X$. Therefore $X$ is the center of the circle $w$.
It is well known that the point which is symmetrical to the orthocenter $H$ with respect to the side $B C$ belongs to the circumcircle of the triangle $A B C$. The distance from this point to $X$ equals $X H$ due to symmetry, hence this point belongs $w$, therefore it coincides with $D$ or $E$, without loss of generality with $D$. Thus $D H \perp B C$.
Finally, the centers of $w$ and circumcircle $(A B C)$ belong to the midperpendicular of $B C$, therefore their common chord $D E$ is parallel $B C$. Thus $\angle H D E=90^{\circ}$.

|
{
"exam": "BalticWay",
"problem_label": "12",
"problem_match": "\n12.",
"resource_path": "BalticWay/segmented/en-bw18sol.jsonl",
"solution_match": "# Solution.",
"tier": "T3",
"year": "2018"
}
|
The bisector of the angle $A$ of a triangle $A B C$ intersects $B C$ in a point $D$ and intersects the circumcircle of the triangle $A B C$ in a point $E$. Let $K, L, M$ and $N$ be the midpoints of the segments $A B, B D, C D$ and $A C$, respectively. Let $P$ be the circumcenter of the triangle $E K L$, and $Q$ be the circumcenter of the triangle $E M N$. Prove that $\angle P E Q=\angle B A C$.
|
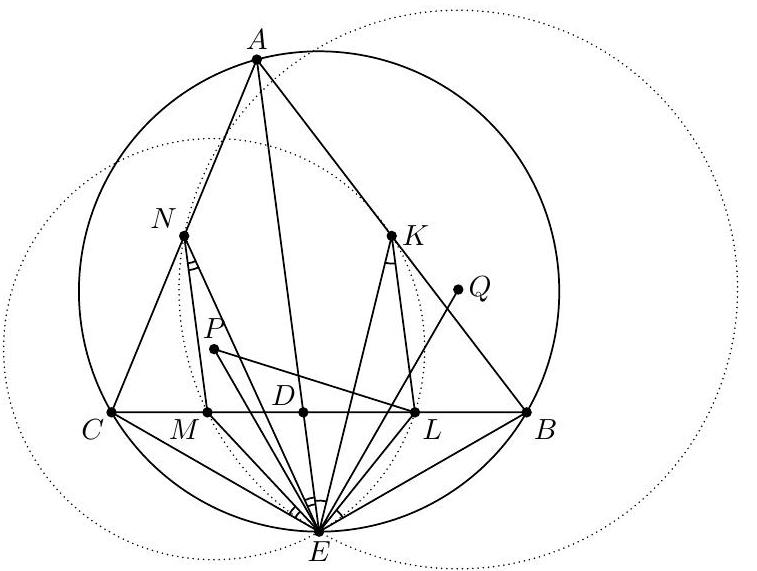
Triangles $A E B$ and $B E D$ are similar since $\angle B A E=\angle E A C=\angle D B E$. Hence $\angle A E K=$ $\angle B E L$ as the angles between a median and a side in similar triangles. Denote these angles by $\varphi$. Then $\angle E K L=\varphi$ since $K L$ is a midline of $\triangle A B D$. Analogously, let $\psi=\angle A E N=\angle C E M=$ $\angle E N M$. And let $\beta=\angle A B C, \gamma=\angle A C B$.
The triangle $P E L$ is isosceles, therefore $\angle P E L=90^{\circ}-\frac{1}{2} \angle E P L=90^{\circ}-\angle E K L=90^{\circ}-\varphi$ and
$$
\angle P E A=\angle P E L-\angle A E L=\angle P E L-(\angle A E B-\angle B E L)=90^{\circ}-\varphi-(\gamma-\varphi)=90^{\circ}-\gamma .
$$
Analogously $\angle Q E A=90^{\circ}-\beta$.
Thus $\angle P E Q=\angle P E A+\angle Q E A=180^{\circ}-\beta-\gamma=\angle B A C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The bisector of the angle $A$ of a triangle $A B C$ intersects $B C$ in a point $D$ and intersects the circumcircle of the triangle $A B C$ in a point $E$. Let $K, L, M$ and $N$ be the midpoints of the segments $A B, B D, C D$ and $A C$, respectively. Let $P$ be the circumcenter of the triangle $E K L$, and $Q$ be the circumcenter of the triangle $E M N$. Prove that $\angle P E Q=\angle B A C$.
|

Triangles $A E B$ and $B E D$ are similar since $\angle B A E=\angle E A C=\angle D B E$. Hence $\angle A E K=$ $\angle B E L$ as the angles between a median and a side in similar triangles. Denote these angles by $\varphi$. Then $\angle E K L=\varphi$ since $K L$ is a midline of $\triangle A B D$. Analogously, let $\psi=\angle A E N=\angle C E M=$ $\angle E N M$. And let $\beta=\angle A B C, \gamma=\angle A C B$.
The triangle $P E L$ is isosceles, therefore $\angle P E L=90^{\circ}-\frac{1}{2} \angle E P L=90^{\circ}-\angle E K L=90^{\circ}-\varphi$ and
$$
\angle P E A=\angle P E L-\angle A E L=\angle P E L-(\angle A E B-\angle B E L)=90^{\circ}-\varphi-(\gamma-\varphi)=90^{\circ}-\gamma .
$$
Analogously $\angle Q E A=90^{\circ}-\beta$.
Thus $\angle P E Q=\angle P E A+\angle Q E A=180^{\circ}-\beta-\gamma=\angle B A C$.
|
{
"exam": "BalticWay",
"problem_label": "13",
"problem_match": "\n13.",
"resource_path": "BalticWay/segmented/en-bw18sol.jsonl",
"solution_match": "# Solution.",
"tier": "T3",
"year": "2018"
}
|
A quadrilateral $A B C D$ is circumscribed about a circle $\omega$. The intersection point of $\omega$ and the diagonal $A C$, closest to $A$, is $E$. The point $F$ is diametrically opposite to the point $E$ on the circle $\omega$. The tangent to $\omega$ at the point $F$ intersects lines $A B$ and $B C$ in points $A_{1}$ and $C_{1}$, and lines $A D$ and $C D$ in points $A_{2}$ and $C_{2}$, respectively. Prove that $A_{1} C_{1}=A_{2} C_{2}$.
|
Denote by $X$ the intersection point of the lines $A_{1} A_{2}$ and $A C$. Prove that $X$ is a contact point of escribed circle of $\triangle A A_{1} A_{2}$ with side $A_{1} A_{2}$. Indeed, consider a homothety with center $A$ which maps incircle $\omega$ of $\triangle A A_{1} A_{2}$ to its escribed circle. This homothety maps the line that is tangent to $\omega$ in point $E$ to the parallel line which is tangent to the escribed circle, i.e. to the line $A_{1} A_{2}$. Therefore the point $E$ maps to the point $X$, hence $A_{1} A_{2}$ is tangent to the escribed circle of $\triangle A A_{1} A_{2}$ in the point $X$.
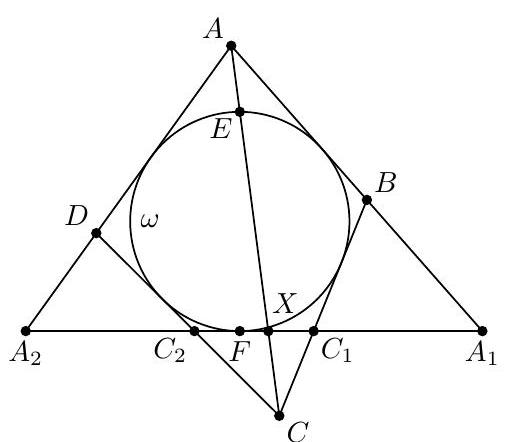
One can similarly prove that $X$ is a tangent point of the line c $C_{1} C_{2}$ and incircle of $\triangle C_{1} C C_{2}$.
From the first statement we conclude that $A_{1} X=F A_{2}$, and from the second one that $C_{1} X=$ $F C_{2}$. It remains to subtract the second equality from the first one.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A quadrilateral $A B C D$ is circumscribed about a circle $\omega$. The intersection point of $\omega$ and the diagonal $A C$, closest to $A$, is $E$. The point $F$ is diametrically opposite to the point $E$ on the circle $\omega$. The tangent to $\omega$ at the point $F$ intersects lines $A B$ and $B C$ in points $A_{1}$ and $C_{1}$, and lines $A D$ and $C D$ in points $A_{2}$ and $C_{2}$, respectively. Prove that $A_{1} C_{1}=A_{2} C_{2}$.
|
Denote by $X$ the intersection point of the lines $A_{1} A_{2}$ and $A C$. Prove that $X$ is a contact point of escribed circle of $\triangle A A_{1} A_{2}$ with side $A_{1} A_{2}$. Indeed, consider a homothety with center $A$ which maps incircle $\omega$ of $\triangle A A_{1} A_{2}$ to its escribed circle. This homothety maps the line that is tangent to $\omega$ in point $E$ to the parallel line which is tangent to the escribed circle, i.e. to the line $A_{1} A_{2}$. Therefore the point $E$ maps to the point $X$, hence $A_{1} A_{2}$ is tangent to the escribed circle of $\triangle A A_{1} A_{2}$ in the point $X$.

One can similarly prove that $X$ is a tangent point of the line c $C_{1} C_{2}$ and incircle of $\triangle C_{1} C C_{2}$.
From the first statement we conclude that $A_{1} X=F A_{2}$, and from the second one that $C_{1} X=$ $F C_{2}$. It remains to subtract the second equality from the first one.
|
{
"exam": "BalticWay",
"problem_label": "14",
"problem_match": "\n14.",
"resource_path": "BalticWay/segmented/en-bw18sol.jsonl",
"solution_match": "# Solution.",
"tier": "T3",
"year": "2018"
}
|
Two circles in the plane do not intersect and do not lie inside each other. We choose diameters $A_{1} B_{1}$ and $A_{2} B_{2}$ of these circles such that the segments $A_{1} A_{2}$ and $B_{1} B_{2}$ intersect. Let $A$ and $B$ be the midpoints of the segments $A_{1} A_{2}$ and $B_{1} B_{2}$, and $C$ be the intersection point of these segments. Prove that the orthocenter of the triangle $A B C$ belongs to a fixed line that does not depend on the choice of the diameters.
|
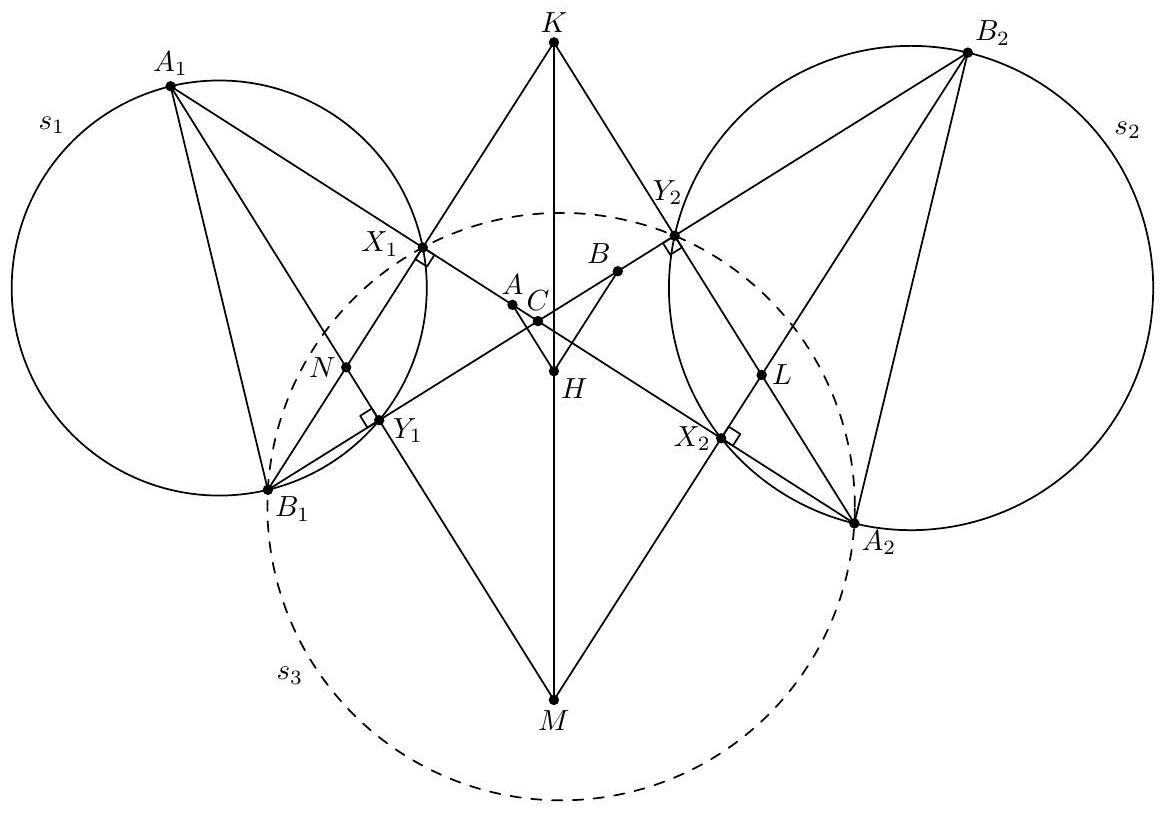
Prove that the orthocenter $H$ of $\triangle A B C$ belongs to their radical axe.
Denote the circles by $s_{1}$ и $s_{2}$. Let the line $A_{1} A_{2}$ intrersect circles $s_{1}$ and $s_{2}$ second time in points $X_{1}$ and $X_{2}$ respectively, and the line $B_{1} B_{2}$ intrersect the circles second time in points $Y_{1}$ and $Y_{2}$.
The lines $A_{1} Y_{1}$ and $A_{2} Y_{2}$ are parallel (because both of them are orthogonal to $B_{1} B_{2}$ ), analogously $B_{1} X_{1}$ and $B_{2} X_{2}$ are parallel. Hence these four lines form a parallelogram $K L M N$ (see fig.). It is clear that perpendiculars from the point $A$ to the line $B C$ and from the point $B$ to the line $A C$ lay on the midlines of this parallelogram. Therefore $H$ is the center of parallelogram $K L M N$ and coincide with the midpoint of segment $K M$.
In order to prove that $H$ lays on the radical axe of $s_{1}$ and $s_{2}$ it is sufficient to show that both points $K$ and $M$ belong to that radical axe.
The points $X_{1}$ and $Y_{2}$ lay on the circle $s_{3}$ with diameter $B_{1} A_{2}$. The line $B_{1} X_{1}$ is radical axe of $s_{1}$ and $s_{3}$, and the line $A_{2} Y_{2}$ is radical axe of $s_{2}$ and $s_{3}$. Therefore $k$ is radical center of these three circles and hence $K$ lays on the radical axe of $s_{1}$ and $s_{2}$. Analogously $M$ lays on the radical axe of $s_{1}$ and $s_{2}$.
## 4 Number Theory
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Two circles in the plane do not intersect and do not lie inside each other. We choose diameters $A_{1} B_{1}$ and $A_{2} B_{2}$ of these circles such that the segments $A_{1} A_{2}$ and $B_{1} B_{2}$ intersect. Let $A$ and $B$ be the midpoints of the segments $A_{1} A_{2}$ and $B_{1} B_{2}$, and $C$ be the intersection point of these segments. Prove that the orthocenter of the triangle $A B C$ belongs to a fixed line that does not depend on the choice of the diameters.
|

Prove that the orthocenter $H$ of $\triangle A B C$ belongs to their radical axe.
Denote the circles by $s_{1}$ и $s_{2}$. Let the line $A_{1} A_{2}$ intrersect circles $s_{1}$ and $s_{2}$ second time in points $X_{1}$ and $X_{2}$ respectively, and the line $B_{1} B_{2}$ intrersect the circles second time in points $Y_{1}$ and $Y_{2}$.
The lines $A_{1} Y_{1}$ and $A_{2} Y_{2}$ are parallel (because both of them are orthogonal to $B_{1} B_{2}$ ), analogously $B_{1} X_{1}$ and $B_{2} X_{2}$ are parallel. Hence these four lines form a parallelogram $K L M N$ (see fig.). It is clear that perpendiculars from the point $A$ to the line $B C$ and from the point $B$ to the line $A C$ lay on the midlines of this parallelogram. Therefore $H$ is the center of parallelogram $K L M N$ and coincide with the midpoint of segment $K M$.
In order to prove that $H$ lays on the radical axe of $s_{1}$ and $s_{2}$ it is sufficient to show that both points $K$ and $M$ belong to that radical axe.
The points $X_{1}$ and $Y_{2}$ lay on the circle $s_{3}$ with diameter $B_{1} A_{2}$. The line $B_{1} X_{1}$ is radical axe of $s_{1}$ and $s_{3}$, and the line $A_{2} Y_{2}$ is radical axe of $s_{2}$ and $s_{3}$. Therefore $k$ is radical center of these three circles and hence $K$ lays on the radical axe of $s_{1}$ and $s_{2}$. Analogously $M$ lays on the radical axe of $s_{1}$ and $s_{2}$.
## 4 Number Theory
|
{
"exam": "BalticWay",
"problem_label": "15",
"problem_match": "\n15.",
"resource_path": "BalticWay/segmented/en-bw18sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2018"
}
|
Let $p$ be an odd prime. Find all positive integers $n$ for which $\sqrt{n^{2}-n p}$ is a positive integer.
|
Answer: $n=\left(\frac{p+1}{2}\right)^{2}$.
Assume that $\sqrt{n^{2}-p n}=m$ is a positive integer. Then $n^{2}-p n-m^{2}=0$, and hence
$$
n=\frac{p \pm \sqrt{p^{2}+4 m^{2}}}{2}
$$
Now $p^{2}+4 m^{2}=k^{2}$ for some positive integer $k$, and $n=\frac{p+k}{2}$ since $k>p$. Thus $p^{2}=(k+2 m)(k-2 m)$, and since $p$ is prime we get $p^{2}=k+2 m$ and $k-2 m=1$. Hence $k=\frac{p^{2}+1}{2}$ and
$$
n=\frac{p+\frac{p^{2}+1}{2}}{2}=\left(\frac{p+1}{2}\right)^{2}
$$
is the only possible value of $n$. In this case we have
$$
\sqrt{n^{2}-p n}=\sqrt{\left(\frac{p+1}{2}\right)^{4}-p\left(\frac{p+1}{2}\right)^{2}}=\frac{p+1}{2} \sqrt{\left(\frac{p^{2}+1}{2}\right)^{2}-p}=\frac{p+1}{2} \cdot \frac{p-1}{2} .
$$
|
n=\left(\frac{p+1}{2}\right)^{2}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $p$ be an odd prime. Find all positive integers $n$ for which $\sqrt{n^{2}-n p}$ is a positive integer.
|
Answer: $n=\left(\frac{p+1}{2}\right)^{2}$.
Assume that $\sqrt{n^{2}-p n}=m$ is a positive integer. Then $n^{2}-p n-m^{2}=0$, and hence
$$
n=\frac{p \pm \sqrt{p^{2}+4 m^{2}}}{2}
$$
Now $p^{2}+4 m^{2}=k^{2}$ for some positive integer $k$, and $n=\frac{p+k}{2}$ since $k>p$. Thus $p^{2}=(k+2 m)(k-2 m)$, and since $p$ is prime we get $p^{2}=k+2 m$ and $k-2 m=1$. Hence $k=\frac{p^{2}+1}{2}$ and
$$
n=\frac{p+\frac{p^{2}+1}{2}}{2}=\left(\frac{p+1}{2}\right)^{2}
$$
is the only possible value of $n$. In this case we have
$$
\sqrt{n^{2}-p n}=\sqrt{\left(\frac{p+1}{2}\right)^{4}-p\left(\frac{p+1}{2}\right)^{2}}=\frac{p+1}{2} \sqrt{\left(\frac{p^{2}+1}{2}\right)^{2}-p}=\frac{p+1}{2} \cdot \frac{p-1}{2} .
$$
|
{
"exam": "BalticWay",
"problem_label": "16",
"problem_match": "\n16.",
"resource_path": "BalticWay/segmented/en-bw18sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2018"
}
|
Prove that for any positive integers $p, q$ such that $\sqrt{11}>\frac{p}{q}$, the following inequality holds:
$$
\sqrt{11}-\frac{p}{q}>\frac{1}{2 p q}
$$
|
We can assume that $p$ and $q$ are coprime, and since both sides of first inequality are positive, we can change it to $11 q^{2}>p^{2}$. The same way we can change second inequality:
$$
11 p^{2} q^{2}>p^{4}+p^{2}+\frac{1}{4}
$$
To see this one holds, we will prove stronger one:
$$
11 p^{2} q^{2} \geq p^{4}+2 p^{2} \text {. }
$$
Indeed, dividing this inequality by $p^{2}$ we get $11 q^{2} \geq p^{2}+2$, and since we already know that $11 q^{2}>p^{2}$ we only have to see, that $11 q^{2}$ can't be equal to $p^{2}+1$. Since we know that the only reminders of squares $(\bmod 11)$ are $0,1,3,4,5$ and $9, p^{2}+1$ can't be divisible by 11 , and therefore $11 q^{2} \neq p^{2}+1$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that for any positive integers $p, q$ such that $\sqrt{11}>\frac{p}{q}$, the following inequality holds:
$$
\sqrt{11}-\frac{p}{q}>\frac{1}{2 p q}
$$
|
We can assume that $p$ and $q$ are coprime, and since both sides of first inequality are positive, we can change it to $11 q^{2}>p^{2}$. The same way we can change second inequality:
$$
11 p^{2} q^{2}>p^{4}+p^{2}+\frac{1}{4}
$$
To see this one holds, we will prove stronger one:
$$
11 p^{2} q^{2} \geq p^{4}+2 p^{2} \text {. }
$$
Indeed, dividing this inequality by $p^{2}$ we get $11 q^{2} \geq p^{2}+2$, and since we already know that $11 q^{2}>p^{2}$ we only have to see, that $11 q^{2}$ can't be equal to $p^{2}+1$. Since we know that the only reminders of squares $(\bmod 11)$ are $0,1,3,4,5$ and $9, p^{2}+1$ can't be divisible by 11 , and therefore $11 q^{2} \neq p^{2}+1$.
|
{
"exam": "BalticWay",
"problem_label": "17",
"problem_match": "\n17.",
"resource_path": "BalticWay/segmented/en-bw18sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2018"
}
|
Let $n \geq 3$ be an integer such that $4 n+1$ is a prime number. Prove that $4 n+1$ divides $n^{2 n}-1$.
|
Since $p:=4 n+1$ is a prime number, each non-zero remainder modulo $p$ possesses a unique multiplicative inverse. Since $-4 \cdot n \equiv 1 \bmod p$, we have $n \equiv(-4)^{-1} \bmod p$, from which we deduce that $n \equiv-\left(2^{-1}\right)^{2}$. Consequently,
$$
n^{2 n}-1 \equiv\left(-\left(2^{-1}\right)^{2}\right)^{2 n}-1 \equiv\left(2^{-1}\right)^{4 n}-1 \equiv 0 \bmod p
$$
by Fermat's Little Theorem.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n \geq 3$ be an integer such that $4 n+1$ is a prime number. Prove that $4 n+1$ divides $n^{2 n}-1$.
|
Since $p:=4 n+1$ is a prime number, each non-zero remainder modulo $p$ possesses a unique multiplicative inverse. Since $-4 \cdot n \equiv 1 \bmod p$, we have $n \equiv(-4)^{-1} \bmod p$, from which we deduce that $n \equiv-\left(2^{-1}\right)^{2}$. Consequently,
$$
n^{2 n}-1 \equiv\left(-\left(2^{-1}\right)^{2}\right)^{2 n}-1 \equiv\left(2^{-1}\right)^{4 n}-1 \equiv 0 \bmod p
$$
by Fermat's Little Theorem.
|
{
"exam": "BalticWay",
"problem_label": "18",
"problem_match": "\n18.",
"resource_path": "BalticWay/segmented/en-bw18sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2018"
}
|
An infinite set $B$ consisting of positive integers has the following property. For each $a, b \in B$ with $a>b$ the number $\frac{a-b}{(a, b)}$ belongs to $B$. Prove that $B$ contains all positive integers. Here $(a, b)$ is the greatest common divisor of numbers $a$ and $b$.
|
If $d$ is g.c.d. of all the numbers in set $B$, let $A=\{b / d: b \in B\}$. Then for each $a, b \in A(a>b)$ we have
$$
\frac{a-b}{d(a, b)} \in A
$$
Observe that g.c.d of the set $A$ equals 1 , therefore we can find a finite subset $A_{1} \in A$ for which the $\operatorname{gcd} A_{1}=1$. We may think that the sum of elements of $A_{1}$ is minimal possible. Choose numbers $a, b \in A_{1}(a>b)$ and replace $a$ in the set $A_{1}$ with $\frac{a-b}{d(a, b)}$. The g.c.d. of the obtained set equals 1 . But the sum of numbers decreases by this operations that contradicts minimality of $A_{1}$.
Thus, $A_{1}=\{1\}$. Therefore all the numbers in the set $A$ have residue 1 modulo $d$. Take an arbitrary $a=k d+1 \in A$ and $b=1$. Then $k \in A$ by $(*)$ and hence $k=d s+1$. But $(k, k d+1)=1$, therefore $\frac{k d+1-d s-1}{d}=k-s=(d-1) s+1 \in A$, so $s$ is divisible by $d$. But $s \in A$, therefore $s-1$ is also divisible by $d$, hence $d=1$ (that means that $B=A$ ). Thus we have checked that if $a=k d+1=k+1 \in A$ then $a-1=k \in A$. Then all non-negative integers belong to $A$ because it is infinite.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
An infinite set $B$ consisting of positive integers has the following property. For each $a, b \in B$ with $a>b$ the number $\frac{a-b}{(a, b)}$ belongs to $B$. Prove that $B$ contains all positive integers. Here $(a, b)$ is the greatest common divisor of numbers $a$ and $b$.
|
If $d$ is g.c.d. of all the numbers in set $B$, let $A=\{b / d: b \in B\}$. Then for each $a, b \in A(a>b)$ we have
$$
\frac{a-b}{d(a, b)} \in A
$$
Observe that g.c.d of the set $A$ equals 1 , therefore we can find a finite subset $A_{1} \in A$ for which the $\operatorname{gcd} A_{1}=1$. We may think that the sum of elements of $A_{1}$ is minimal possible. Choose numbers $a, b \in A_{1}(a>b)$ and replace $a$ in the set $A_{1}$ with $\frac{a-b}{d(a, b)}$. The g.c.d. of the obtained set equals 1 . But the sum of numbers decreases by this operations that contradicts minimality of $A_{1}$.
Thus, $A_{1}=\{1\}$. Therefore all the numbers in the set $A$ have residue 1 modulo $d$. Take an arbitrary $a=k d+1 \in A$ and $b=1$. Then $k \in A$ by $(*)$ and hence $k=d s+1$. But $(k, k d+1)=1$, therefore $\frac{k d+1-d s-1}{d}=k-s=(d-1) s+1 \in A$, so $s$ is divisible by $d$. But $s \in A$, therefore $s-1$ is also divisible by $d$, hence $d=1$ (that means that $B=A$ ). Thus we have checked that if $a=k d+1=k+1 \in A$ then $a-1=k \in A$. Then all non-negative integers belong to $A$ because it is infinite.
|
{
"exam": "BalticWay",
"problem_label": "19",
"problem_match": "\n19.",
"resource_path": "BalticWay/segmented/en-bw18sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2018"
}
|
Find all the triples of positive integers $(a, b, c)$ for which the number
$$
\frac{(a+b)^{4}}{c}+\frac{(b+c)^{4}}{a}+\frac{(c+a)^{4}}{b}
$$
is an integer and $a+b+c$ is a prime.
|
Answer $(1,1,1),(1,2,2),(2,3,6)$.
Let $p=a+b+c$, then $a+b=p-c, b+c=p-a, c+a=p-b$ and
$$
\frac{(p-c)^{4}}{c}+\frac{(p-a)^{4}}{a}+\frac{(p-b)^{4}}{b}
$$
is a non-negative integer. By expanding brackets we obtain that the number $p^{4}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)$ is integer, too. But the numbers $a, b, c$ are not divisible by $p$, therefore the number $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$ is (non negative) integer. That is possible for the triples $(1,1,1),(1,2,2),(2,3,6)$ only.
|
(1,1,1),(1,2,2),(2,3,6)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all the triples of positive integers $(a, b, c)$ for which the number
$$
\frac{(a+b)^{4}}{c}+\frac{(b+c)^{4}}{a}+\frac{(c+a)^{4}}{b}
$$
is an integer and $a+b+c$ is a prime.
|
Answer $(1,1,1),(1,2,2),(2,3,6)$.
Let $p=a+b+c$, then $a+b=p-c, b+c=p-a, c+a=p-b$ and
$$
\frac{(p-c)^{4}}{c}+\frac{(p-a)^{4}}{a}+\frac{(p-b)^{4}}{b}
$$
is a non-negative integer. By expanding brackets we obtain that the number $p^{4}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)$ is integer, too. But the numbers $a, b, c$ are not divisible by $p$, therefore the number $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$ is (non negative) integer. That is possible for the triples $(1,1,1),(1,2,2),(2,3,6)$ only.
|
{
"exam": "BalticWay",
"problem_label": "20",
"problem_match": "\n20.",
"resource_path": "BalticWay/segmented/en-bw18sol.jsonl",
"solution_match": "# Solution.",
"tier": "T3",
"year": "2018"
}
|
Let $a_{0}>0$ be a real number, and let
$$
a_{n}=\frac{a_{n-1}}{\sqrt{1+2020 \cdot a_{n-1}^{2}}}, \quad \text { for } n=1,2, \ldots, 2020
$$
Show that $a_{2020}<\frac{1}{2020}$.
|
Let $b_{n}=\frac{1}{a_{n}^{2}}$. Then $b_{0}=\frac{1}{a_{0}^{2}}$ and
$$
b_{n}=\frac{1+2020 \cdot a_{n-1}^{2}}{a_{n-1}^{2}}=b_{n-1}\left(1+2020 \cdot \frac{1}{b_{n-1}}\right)=b_{n-1}+2020 .
$$
Hence $b_{2020}=b_{0}+2020^{2}=\frac{1}{a_{0}^{2}}+2020^{2}$ and $a_{2020}^{2}=\frac{1}{\frac{1}{a_{0}^{2}}+2020^{2}}<\frac{1}{2020^{2}}$ which shows that $a_{2020}<\frac{1}{2020}$.
|
a_{2020}<\frac{1}{2020}
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $a_{0}>0$ be a real number, and let
$$
a_{n}=\frac{a_{n-1}}{\sqrt{1+2020 \cdot a_{n-1}^{2}}}, \quad \text { for } n=1,2, \ldots, 2020
$$
Show that $a_{2020}<\frac{1}{2020}$.
|
Let $b_{n}=\frac{1}{a_{n}^{2}}$. Then $b_{0}=\frac{1}{a_{0}^{2}}$ and
$$
b_{n}=\frac{1+2020 \cdot a_{n-1}^{2}}{a_{n-1}^{2}}=b_{n-1}\left(1+2020 \cdot \frac{1}{b_{n-1}}\right)=b_{n-1}+2020 .
$$
Hence $b_{2020}=b_{0}+2020^{2}=\frac{1}{a_{0}^{2}}+2020^{2}$ and $a_{2020}^{2}=\frac{1}{\frac{1}{a_{0}^{2}}+2020^{2}}<\frac{1}{2020^{2}}$ which shows that $a_{2020}<\frac{1}{2020}$.
|
{
"exam": "BalticWay",
"problem_label": "1",
"problem_match": "\nProblem 1.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2020"
}
|
Let $a, b, c$ be positive real numbers such that $a b c=1$. Prove that
$$
\frac{1}{a \sqrt{c^{2}+1}}+\frac{1}{b \sqrt{a^{2}+1}}+\frac{1}{c \sqrt{b^{2}+1}}>2 .
$$
|
Denote $a=\frac{x}{y}, b=\frac{y}{z}, c=\frac{z}{x}$. Then
$$
\frac{1}{a \sqrt{c^{2}+1}}=\frac{1}{\frac{x}{y} \sqrt{\frac{z^{2}}{x^{2}}+1}}=\frac{y}{\sqrt{z^{2}+x^{2}}} \geqslant \frac{2 y^{2}}{x^{2}+y^{2}+z^{2}}
$$
where the last inequality follows from the AM-GM inequality
$$
y \sqrt{x^{2}+z^{2}} \leqslant \frac{y^{2}+\left(x^{2}+z^{2}\right)}{2} .
$$
If we do the same estimation also for the two other terms of the original inequality then we get
$$
\frac{1}{a \sqrt{c^{2}+1}}+\frac{1}{b \sqrt{a^{2}}+1}+\frac{1}{c \sqrt{b^{2}+1}} \geqslant \frac{2 y^{2}}{x^{2}+y^{2}+z^{2}}+\frac{2 z^{2}}{x^{2}+y^{2}+z^{2}}+\frac{2 x^{2}}{x^{2}+y^{2}+z^{2}}=2 .
$$
Equality holds only if $y^{2}=x^{2}+z^{2}, z^{2}=x^{2}+y^{2}$ and $x^{2}=y^{2}+z^{2}$ what is impossible.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers such that $a b c=1$. Prove that
$$
\frac{1}{a \sqrt{c^{2}+1}}+\frac{1}{b \sqrt{a^{2}+1}}+\frac{1}{c \sqrt{b^{2}+1}}>2 .
$$
|
Denote $a=\frac{x}{y}, b=\frac{y}{z}, c=\frac{z}{x}$. Then
$$
\frac{1}{a \sqrt{c^{2}+1}}=\frac{1}{\frac{x}{y} \sqrt{\frac{z^{2}}{x^{2}}+1}}=\frac{y}{\sqrt{z^{2}+x^{2}}} \geqslant \frac{2 y^{2}}{x^{2}+y^{2}+z^{2}}
$$
where the last inequality follows from the AM-GM inequality
$$
y \sqrt{x^{2}+z^{2}} \leqslant \frac{y^{2}+\left(x^{2}+z^{2}\right)}{2} .
$$
If we do the same estimation also for the two other terms of the original inequality then we get
$$
\frac{1}{a \sqrt{c^{2}+1}}+\frac{1}{b \sqrt{a^{2}}+1}+\frac{1}{c \sqrt{b^{2}+1}} \geqslant \frac{2 y^{2}}{x^{2}+y^{2}+z^{2}}+\frac{2 z^{2}}{x^{2}+y^{2}+z^{2}}+\frac{2 x^{2}}{x^{2}+y^{2}+z^{2}}=2 .
$$
Equality holds only if $y^{2}=x^{2}+z^{2}, z^{2}=x^{2}+y^{2}$ and $x^{2}=y^{2}+z^{2}$ what is impossible.
|
{
"exam": "BalticWay",
"problem_label": "2",
"problem_match": "\nProblem 2.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2020"
}
|
A real sequence $\left(a_{n}\right)_{n=0}^{\infty}$ is defined recursively by $a_{0}=2$ and the recursion formula
$$
a_{n}= \begin{cases}a_{n-1}^{2} & \text { if } a_{n-1}<\sqrt{3} \\ \frac{a_{n-1}^{2}}{3} & \text { if } a_{n-1} \geqslant \sqrt{3}\end{cases}
$$
Another real sequence $\left(b_{n}\right)_{n=1}^{\infty}$ is defined in terms of the first by the formula
$$
b_{n}= \begin{cases}0 & \text { if } a_{n-1}<\sqrt{3} \\ \frac{1}{2^{n}} & \text { if } a_{n-1} \geqslant \sqrt{3}\end{cases}
$$
valid for each $n \geqslant 1$. Prove that
$$
b_{1}+b_{2}+\cdots+b_{2020}<\frac{2}{3}
$$
|
The first step is to prove, using induction, the formula
$$
a_{n}=\frac{2^{2^{n}}}{3^{2^{n}\left(b_{1}+b_{2}+\cdots+b_{n}\right)}} .
$$
The base case $n=0$ is trivial. Assume the formula is valid for $a_{n-1}$, that is,
$$
a_{n-1}=\frac{2^{2^{n-1}}}{3^{2^{n-1}\left(b_{1}+b_{2}+\cdots+b_{n-1}\right)}} .
$$
If now $a_{n-1}<\sqrt{3}$, then $b_{n}=0$, and so
$$
a_{n}=a_{n-1}^{2}=\frac{2^{2^{n}}}{3^{2^{n}\left(b_{1}+b_{2}+\cdots+b_{n-1}\right)}}=\frac{2^{2^{n}}}{3^{2^{n}\left(b_{1}+b_{2}+\cdots+b_{n-1}+b_{n}\right)}}
$$
whereas if $a_{n-1} \geqslant \sqrt{3}$, then $b_{n}=\frac{1}{2^{n}}$, and so
$$
a_{n}=\frac{a_{n-1}^{2}}{3}=\frac{2^{2^{n}}}{3^{2^{n}\left(b_{1}+b_{2}+\cdots+b_{n-1}\right)+1}}=\frac{2^{2^{n}}}{3^{2^{n}\left(b_{1}+b_{2}+\cdots+b_{n-1}+b_{n}\right)}} .
$$
This completes the induction.
Next, we inductively establish the inequality $a_{n} \geqslant 1$. The base case $n=0$ is again trivial. Suppose $a_{n-1} \geqslant 1$. If $a_{n-1}<\sqrt{3}$, then
$$
a_{n}=a_{n-1}^{2} \geqslant 1^{2}=1,
$$
whereas if $a_{n-1} \geqslant \sqrt{3}$, then
$$
a_{n}=\frac{a_{n-1}^{2}}{3} \geqslant \frac{(\sqrt{3})^{2}}{3}=1
$$
and the induction is complete.
From
$$
1 \leqslant a_{n}=\frac{2^{2^{n}}}{3^{2^{n}\left(b_{1}+b_{2}+\cdots+b_{n}\right)}}=\left(\frac{2}{3^{b_{1}+b_{2}+\cdots+b_{n}}}\right)^{2^{n}},
$$
we may then draw the conclusion
$$
3^{b_{1}+b_{2}+\cdots+b_{n}} \leqslant 2 .
$$
Since $3^{2 / 3}>2$ (and the function $x \mapsto 3^{x}$ is strictly increasing), we must have
$$
b_{1}+b_{2}+\cdots+b_{n}<\frac{2}{3}
$$
for all $n$, and we are finished.
Remark. Using only slightly more work, it may be proved that
$$
1 \leqslant a_{n}=\frac{2^{2^{n}}}{3^{2^{n}\left(b_{1}+b_{2}+\cdots+b_{n}\right)}}<3
$$
which entails
$$
1^{\frac{1}{2^{n}}} \leqslant \frac{2}{3^{b_{1}+b_{2}+\cdots+b_{n}}}<3^{\frac{1}{2^{n}}}
$$
for all $n$, hence
$$
3^{b_{1}+b_{2}+\cdots}=2 \text {. }
$$
The problem thus provides an algorithm for calculating
$$
b_{1}+b_{2}+\cdots=\log _{3} 2 \approx 0.63
$$
in binary.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
A real sequence $\left(a_{n}\right)_{n=0}^{\infty}$ is defined recursively by $a_{0}=2$ and the recursion formula
$$
a_{n}= \begin{cases}a_{n-1}^{2} & \text { if } a_{n-1}<\sqrt{3} \\ \frac{a_{n-1}^{2}}{3} & \text { if } a_{n-1} \geqslant \sqrt{3}\end{cases}
$$
Another real sequence $\left(b_{n}\right)_{n=1}^{\infty}$ is defined in terms of the first by the formula
$$
b_{n}= \begin{cases}0 & \text { if } a_{n-1}<\sqrt{3} \\ \frac{1}{2^{n}} & \text { if } a_{n-1} \geqslant \sqrt{3}\end{cases}
$$
valid for each $n \geqslant 1$. Prove that
$$
b_{1}+b_{2}+\cdots+b_{2020}<\frac{2}{3}
$$
|
The first step is to prove, using induction, the formula
$$
a_{n}=\frac{2^{2^{n}}}{3^{2^{n}\left(b_{1}+b_{2}+\cdots+b_{n}\right)}} .
$$
The base case $n=0$ is trivial. Assume the formula is valid for $a_{n-1}$, that is,
$$
a_{n-1}=\frac{2^{2^{n-1}}}{3^{2^{n-1}\left(b_{1}+b_{2}+\cdots+b_{n-1}\right)}} .
$$
If now $a_{n-1}<\sqrt{3}$, then $b_{n}=0$, and so
$$
a_{n}=a_{n-1}^{2}=\frac{2^{2^{n}}}{3^{2^{n}\left(b_{1}+b_{2}+\cdots+b_{n-1}\right)}}=\frac{2^{2^{n}}}{3^{2^{n}\left(b_{1}+b_{2}+\cdots+b_{n-1}+b_{n}\right)}}
$$
whereas if $a_{n-1} \geqslant \sqrt{3}$, then $b_{n}=\frac{1}{2^{n}}$, and so
$$
a_{n}=\frac{a_{n-1}^{2}}{3}=\frac{2^{2^{n}}}{3^{2^{n}\left(b_{1}+b_{2}+\cdots+b_{n-1}\right)+1}}=\frac{2^{2^{n}}}{3^{2^{n}\left(b_{1}+b_{2}+\cdots+b_{n-1}+b_{n}\right)}} .
$$
This completes the induction.
Next, we inductively establish the inequality $a_{n} \geqslant 1$. The base case $n=0$ is again trivial. Suppose $a_{n-1} \geqslant 1$. If $a_{n-1}<\sqrt{3}$, then
$$
a_{n}=a_{n-1}^{2} \geqslant 1^{2}=1,
$$
whereas if $a_{n-1} \geqslant \sqrt{3}$, then
$$
a_{n}=\frac{a_{n-1}^{2}}{3} \geqslant \frac{(\sqrt{3})^{2}}{3}=1
$$
and the induction is complete.
From
$$
1 \leqslant a_{n}=\frac{2^{2^{n}}}{3^{2^{n}\left(b_{1}+b_{2}+\cdots+b_{n}\right)}}=\left(\frac{2}{3^{b_{1}+b_{2}+\cdots+b_{n}}}\right)^{2^{n}},
$$
we may then draw the conclusion
$$
3^{b_{1}+b_{2}+\cdots+b_{n}} \leqslant 2 .
$$
Since $3^{2 / 3}>2$ (and the function $x \mapsto 3^{x}$ is strictly increasing), we must have
$$
b_{1}+b_{2}+\cdots+b_{n}<\frac{2}{3}
$$
for all $n$, and we are finished.
Remark. Using only slightly more work, it may be proved that
$$
1 \leqslant a_{n}=\frac{2^{2^{n}}}{3^{2^{n}\left(b_{1}+b_{2}+\cdots+b_{n}\right)}}<3
$$
which entails
$$
1^{\frac{1}{2^{n}}} \leqslant \frac{2}{3^{b_{1}+b_{2}+\cdots+b_{n}}}<3^{\frac{1}{2^{n}}}
$$
for all $n$, hence
$$
3^{b_{1}+b_{2}+\cdots}=2 \text {. }
$$
The problem thus provides an algorithm for calculating
$$
b_{1}+b_{2}+\cdots=\log _{3} 2 \approx 0.63
$$
in binary.
|
{
"exam": "BalticWay",
"problem_label": "3",
"problem_match": "\nProblem 3.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2020"
}
|
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ so that
$$
f(f(x)+x+y)=f(x+y)+y f(y)
$$
for all real numbers $x, y$.
|
.
Answer: $f(x)=0$ for all $x$.
We first notice that if there exists a number $\alpha$ so that $f(\alpha)=0$, then $f(\alpha+y)=$ $f(f(\alpha)+\alpha+y)=f(\alpha+y)+y f(y)$ for all real $y$. Hence $y f(y)=0$ for all $y$, meaning that $f(y)=0$ for all $y \neq 0$. We are therefore done if we can show that $f(0)=0$, as then $f(x)=0$ for all $x$, which is a solution.
Substituting $y=0$ in the equation yields that:
$$
f(f(x)+x)=f(x) \quad \forall x
$$
Substituting $y=f(x)$ in the equation yields that:
$$
f(f(x)+x+f(x))=f(x+f(x))+f(x) f(f(x))
$$
Let $z=x+f(x)$. Then:
$$
\begin{aligned}
f(x) & =f(x+f(x))=f(z)=f(f(z)+z) \\
& =f(f(x+f(x))+x+f(x)) \\
& =f(f(x)+x+f(x)) \\
& =f(x+f(x))+f(x) f(f(x)) \\
& =f(x)+f(x) f(f(x))
\end{aligned}
$$
Hence $f(x) f(f(x))=0$ for all $x$. Letting $x=0$ in (1), we get that $f(f(0))=f(0)$, which means that $f(0)^{2}=f(0) f(f(0))=0$. But then we must have $f(0)=0$.
|
f(x)=0
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ so that
$$
f(f(x)+x+y)=f(x+y)+y f(y)
$$
for all real numbers $x, y$.
|
.
Answer: $f(x)=0$ for all $x$.
We first notice that if there exists a number $\alpha$ so that $f(\alpha)=0$, then $f(\alpha+y)=$ $f(f(\alpha)+\alpha+y)=f(\alpha+y)+y f(y)$ for all real $y$. Hence $y f(y)=0$ for all $y$, meaning that $f(y)=0$ for all $y \neq 0$. We are therefore done if we can show that $f(0)=0$, as then $f(x)=0$ for all $x$, which is a solution.
Substituting $y=0$ in the equation yields that:
$$
f(f(x)+x)=f(x) \quad \forall x
$$
Substituting $y=f(x)$ in the equation yields that:
$$
f(f(x)+x+f(x))=f(x+f(x))+f(x) f(f(x))
$$
Let $z=x+f(x)$. Then:
$$
\begin{aligned}
f(x) & =f(x+f(x))=f(z)=f(f(z)+z) \\
& =f(f(x+f(x))+x+f(x)) \\
& =f(f(x)+x+f(x)) \\
& =f(x+f(x))+f(x) f(f(x)) \\
& =f(x)+f(x) f(f(x))
\end{aligned}
$$
Hence $f(x) f(f(x))=0$ for all $x$. Letting $x=0$ in (1), we get that $f(f(0))=f(0)$, which means that $f(0)^{2}=f(0) f(f(0))=0$. But then we must have $f(0)=0$.
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "\nProblem 4.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "\nSolution 1",
"tier": "T3",
"year": "2020"
}
|
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ so that
$$
f(f(x)+x+y)=f(x+y)+y f(y)
$$
for all real numbers $x, y$.
|
.
Substitute $x=0$ and $y=-1$. We obtain $f(f(0)-1)=f(-1)+(-1) \cdot f(-1)=0$.
Substitute $x=f(0)-1$. Then $f(x)=0$ and therefore $f(f(x)+x+y)$ and $f(x+y)$ cancel out. We obtain $0=y f(y)$ for all $y$. It follows that if $y \neq 0$ then $f(y)=0$.
Now, substitute $x=y=0$. We obtain $f(f(0))=f(0)$. Substituting $y=f(0)$ to $0=y f(y)$ yields $f(0) f(f(0))=0$, which means $f(0)^{2}=0$, and finally $f(0)=0$.
Therefore $f(x)=0$ for all $x$, which clearly satisfies the equation.
|
f(x)=0
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ so that
$$
f(f(x)+x+y)=f(x+y)+y f(y)
$$
for all real numbers $x, y$.
|
.
Substitute $x=0$ and $y=-1$. We obtain $f(f(0)-1)=f(-1)+(-1) \cdot f(-1)=0$.
Substitute $x=f(0)-1$. Then $f(x)=0$ and therefore $f(f(x)+x+y)$ and $f(x+y)$ cancel out. We obtain $0=y f(y)$ for all $y$. It follows that if $y \neq 0$ then $f(y)=0$.
Now, substitute $x=y=0$. We obtain $f(f(0))=f(0)$. Substituting $y=f(0)$ to $0=y f(y)$ yields $f(0) f(f(0))=0$, which means $f(0)^{2}=0$, and finally $f(0)=0$.
Therefore $f(x)=0$ for all $x$, which clearly satisfies the equation.
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "\nProblem 4.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "# Solution 2",
"tier": "T3",
"year": "2020"
}
|
Find all real numbers $x, y, z$ so that
$$
\begin{aligned}
x^{2} y+y^{2} z+z^{2} & =0 \\
z^{3}+z^{2} y+z y^{3}+x^{2} y & =\frac{1}{4}\left(x^{4}+y^{4}\right)
\end{aligned}
$$
|
Answer: $x=y=z=0$.
$y=0 \Longrightarrow z^{2}=0 \Longrightarrow z=0 \Longrightarrow \frac{1}{4} x^{4}=0 \Longrightarrow x=0 . x=y=z=0$ is a solution, so assume that $y \neq 0$. Then $z=0 \Longrightarrow x^{2} y=0 \Longrightarrow x=0 \Longrightarrow \frac{1}{4} y^{4}=0$, which is a contradiction. Hence $z \neq 0$. Now we solve the quadratic (first) equation w.r.t. $x, y$, and $z$.
$$
\begin{aligned}
& x= \pm \frac{\sqrt{-4 y^{3} z-4 y z^{2}}}{2 y} \\
& y=\frac{-x^{2} \pm \sqrt{x^{4}-4 z^{3}}}{2 z} \\
& z=\frac{-y^{2} \pm \sqrt{y^{4}-4 x^{2} y}}{2}
\end{aligned}
$$
The discriminants must be non-negative.
$$
\begin{gathered}
-4 y^{3} z-4 y z^{2} \geqslant 0 \\
x^{4}-4 z^{3} \geqslant 0 \\
y^{4}-4 x^{2} y \geqslant 0
\end{gathered}
$$
Adding the inequalities we get
$$
\begin{gathered}
y^{4}-4 x^{2} y+x^{4}-4 z^{3}-4 y^{3} z-4 y z^{2} \geqslant 0 \\
\frac{1}{4}\left(x^{4}+y^{4}\right) \geqslant z^{3}+z^{2} y+z y^{3}+x^{2} y
\end{gathered}
$$
But equation 2 says that $\frac{1}{4}\left(x^{4}+y^{4}\right)=z^{3}+z^{2} y+z y^{3}+x^{2} y$. This is only possible if all of the inequalities are in fact equalities, so we have
$$
\begin{gathered}
-4 y^{3} z-4 y z^{2}=0 \\
x^{4}-4 z^{3}=0 \\
y^{4}-4 x^{2} y=0
\end{gathered}
$$
This means that $x= \pm \frac{\sqrt{0}}{2 y}=0 \Longrightarrow y=\frac{-0^{2} \pm \sqrt{0}}{2 z}=0$, which is a contradiction. Hence the only solution is $x=y=z=0$.
|
x=y=z=0
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all real numbers $x, y, z$ so that
$$
\begin{aligned}
x^{2} y+y^{2} z+z^{2} & =0 \\
z^{3}+z^{2} y+z y^{3}+x^{2} y & =\frac{1}{4}\left(x^{4}+y^{4}\right)
\end{aligned}
$$
|
Answer: $x=y=z=0$.
$y=0 \Longrightarrow z^{2}=0 \Longrightarrow z=0 \Longrightarrow \frac{1}{4} x^{4}=0 \Longrightarrow x=0 . x=y=z=0$ is a solution, so assume that $y \neq 0$. Then $z=0 \Longrightarrow x^{2} y=0 \Longrightarrow x=0 \Longrightarrow \frac{1}{4} y^{4}=0$, which is a contradiction. Hence $z \neq 0$. Now we solve the quadratic (first) equation w.r.t. $x, y$, and $z$.
$$
\begin{aligned}
& x= \pm \frac{\sqrt{-4 y^{3} z-4 y z^{2}}}{2 y} \\
& y=\frac{-x^{2} \pm \sqrt{x^{4}-4 z^{3}}}{2 z} \\
& z=\frac{-y^{2} \pm \sqrt{y^{4}-4 x^{2} y}}{2}
\end{aligned}
$$
The discriminants must be non-negative.
$$
\begin{gathered}
-4 y^{3} z-4 y z^{2} \geqslant 0 \\
x^{4}-4 z^{3} \geqslant 0 \\
y^{4}-4 x^{2} y \geqslant 0
\end{gathered}
$$
Adding the inequalities we get
$$
\begin{gathered}
y^{4}-4 x^{2} y+x^{4}-4 z^{3}-4 y^{3} z-4 y z^{2} \geqslant 0 \\
\frac{1}{4}\left(x^{4}+y^{4}\right) \geqslant z^{3}+z^{2} y+z y^{3}+x^{2} y
\end{gathered}
$$
But equation 2 says that $\frac{1}{4}\left(x^{4}+y^{4}\right)=z^{3}+z^{2} y+z y^{3}+x^{2} y$. This is only possible if all of the inequalities are in fact equalities, so we have
$$
\begin{gathered}
-4 y^{3} z-4 y z^{2}=0 \\
x^{4}-4 z^{3}=0 \\
y^{4}-4 x^{2} y=0
\end{gathered}
$$
This means that $x= \pm \frac{\sqrt{0}}{2 y}=0 \Longrightarrow y=\frac{-0^{2} \pm \sqrt{0}}{2 z}=0$, which is a contradiction. Hence the only solution is $x=y=z=0$.
|
{
"exam": "BalticWay",
"problem_label": "5",
"problem_match": "\nProblem 5.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2020"
}
|
Let $n>2$ be a given positive integer. There are $n$ guests at Georg's bachelor party and each guest is friends with at least one other guest. Georg organizes a party game among the guests. Each guest receives a jug of water such that there are no two guests with the same amount of water in their jugs. All guests now proceed simultaneously as follows. Every guest takes one cup for each of his friends at the party and distributes all the water from his jug evenly in the cups. He then passes a cup to each of his friends. Each guest having received a cup of water from each of his friends pours the water he has received into his jug. What is the smallest possible number of guests that do not have the same amount of water as they started with?
|
Answer: 2 .
If there are guests $1,2, \ldots, n$ and guest $i$ is friends with guest $i-1$ and $i+1$ modulo $n$ (e.g. guest 1 and guest $n$ are friends). Then if guest $i$ has $i$ amount of water in their jug at the start of the game, then only guest 1 and $n$ end up with a different amount of water than they started with.
To show that there always will be at least two guests with a different amount of water at the end of the game than they started with, let $x_{i}$ and $d_{i}$ be the amount of water and number of friends, respectively, that guest $i$ has. Define $z_{v}=x_{v} / d_{v}$ and assume without loss of generality that the friendship graph of the party is connected. Since every friend has at least one friend, there must exist two guests $a$ and $b$ at the party with the same number of friends by the pigeonhole principle. They must satisfy $z_{a} \neq z_{b}$. Thus, the sets
$$
S=\left\{c \mid z_{c}=\min _{d} z_{d}\right\} \text { and } T=\left\{c \mid z_{c}=\max _{d} z_{d}\right\}
$$
are non-empty and disjoint. Since we assumed the friendship graph to be connected, there exists a guest $c \in S$ that has a friend $d$ not in $S$. Let $F$ be the friends of $c$ at the party. Then the amount of water in $c$ 's cup at the end of the game is
$$
\sum_{f \in F} z_{f} \geqslant z_{d}+\left(d_{c}-1\right) z_{c}>d_{c} \cdot z_{c}=x_{c}
$$
Thus, $c$ ends up with a different amount of water at the end of the game. Similarly, there is a guest in $T$ that ends up with a different amount of water at the end of the game than what they started with.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n>2$ be a given positive integer. There are $n$ guests at Georg's bachelor party and each guest is friends with at least one other guest. Georg organizes a party game among the guests. Each guest receives a jug of water such that there are no two guests with the same amount of water in their jugs. All guests now proceed simultaneously as follows. Every guest takes one cup for each of his friends at the party and distributes all the water from his jug evenly in the cups. He then passes a cup to each of his friends. Each guest having received a cup of water from each of his friends pours the water he has received into his jug. What is the smallest possible number of guests that do not have the same amount of water as they started with?
|
Answer: 2 .
If there are guests $1,2, \ldots, n$ and guest $i$ is friends with guest $i-1$ and $i+1$ modulo $n$ (e.g. guest 1 and guest $n$ are friends). Then if guest $i$ has $i$ amount of water in their jug at the start of the game, then only guest 1 and $n$ end up with a different amount of water than they started with.
To show that there always will be at least two guests with a different amount of water at the end of the game than they started with, let $x_{i}$ and $d_{i}$ be the amount of water and number of friends, respectively, that guest $i$ has. Define $z_{v}=x_{v} / d_{v}$ and assume without loss of generality that the friendship graph of the party is connected. Since every friend has at least one friend, there must exist two guests $a$ and $b$ at the party with the same number of friends by the pigeonhole principle. They must satisfy $z_{a} \neq z_{b}$. Thus, the sets
$$
S=\left\{c \mid z_{c}=\min _{d} z_{d}\right\} \text { and } T=\left\{c \mid z_{c}=\max _{d} z_{d}\right\}
$$
are non-empty and disjoint. Since we assumed the friendship graph to be connected, there exists a guest $c \in S$ that has a friend $d$ not in $S$. Let $F$ be the friends of $c$ at the party. Then the amount of water in $c$ 's cup at the end of the game is
$$
\sum_{f \in F} z_{f} \geqslant z_{d}+\left(d_{c}-1\right) z_{c}>d_{c} \cdot z_{c}=x_{c}
$$
Thus, $c$ ends up with a different amount of water at the end of the game. Similarly, there is a guest in $T$ that ends up with a different amount of water at the end of the game than what they started with.
|
{
"exam": "BalticWay",
"problem_label": "6",
"problem_match": "\nProblem 6.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2020"
}
|
A mason has bricks with dimensions $2 \times 5 \times 8$ and other bricks with dimensions $2 \times 3 \times 7$. She also has a box with dimensions $10 \times 11 \times 14$. The bricks and the box are all rectangular parallelepipeds. The mason wants to pack bricks into the box filling its entire volume and with no bricks sticking out. Find all possible values of the total number of bricks that she can pack.
|
Answer: 24.
Let the number of $2 \times 5 \times 8$ bricks in the box be $x$, and the number of $2 \times 3 \times 7$ bricks $y$. We must figure out the sum $x+y$. The volume of the box is divisible by 7 , and so is the volume of any $2 \times 3 \times 7$ brick. The volume of a $2 \times 5 \times 8$ brick is not divisible by 7 , which means that $x$ must be divisible by 7 .
The volume of the box is $10 \cdot 11 \cdot 14$. The volume of the $2 \times 5 \times 8$ bricks in the box is $x \cdot 2 \cdot 5 \cdot 8=80 x$. Since this volume cannot exceed the volume of the box, we must have
$$
x \leqslant \frac{10 \cdot 11 \cdot 14}{80}=\frac{11 \cdot 7}{4}=\frac{77}{4}<20 .
$$
Since $x$ was divisible by 7 , and certainly nonnegative, we conclude that $x$ must be 0,7 or 14 . Let us explore each of these possibilities separately.
If we had $x=0$, then the volume of the $2 \times 3 \times 7$ bricks, which is $y \cdot 2 \cdot 3 \cdot 7$, would be equal to the volume of the box, which is $10 \cdot 11 \cdot 14$. However, this is not possible since the volume of the $2 \times 3 \times 7$ bricks is divisible by three whereas the volume of the box is not. Thus $x$ must be 7 or 14 .
If we had $x=7$, then equating the total volume of the bricks with the volume of the box would give
$$
7 \cdot 2 \cdot 5 \cdot 8+y \cdot 2 \cdot 3 \cdot 7=10 \cdot 11 \cdot 14
$$
so that
$$
y \cdot 2 \cdot 3 \cdot 7=10 \cdot 11 \cdot 14-7 \cdot 2 \cdot 5 \cdot 8=1540-560=980 .
$$
However, again the left-hand side, the volume of the $2 \times 3 \times 7$ bricks, is divisible by three, whereas the right-hand side, 980, is not. Thus we cannot have have $x=7$ either, and the only possibility is $x=14$.
Since $x=14$, equating the volumes of the bricks and the box gives
$$
14 \cdot 2 \cdot 5 \cdot 8+y \cdot 2 \cdot 3 \cdot 7=10 \cdot 11 \cdot 14
$$
which in turn leads to
$$
y \cdot 2 \cdot 3 \cdot 7=10 \cdot 11 \cdot 14-14 \cdot 2 \cdot 5 \cdot 8=1540-1120=420
$$
so that
$$
y=\frac{420}{2 \cdot 3 \cdot 7}=\frac{420}{42}=10
$$
Thus the number of bricks in the box can only be $14+10=24$. Finally, for completeness, let us observe that 14 bricks with dimensions $2 \times 5 \times 8$ can be used to fill a volume with dimensions $10 \times 8 \times 14$, and 10 bricks with dimensions $2 \times 3 \times 7$ can be used to fill a volume with dimensions $10 \times 3 \times 14$, so that these 24 bricks can indeed be packed in the box.
|
24
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A mason has bricks with dimensions $2 \times 5 \times 8$ and other bricks with dimensions $2 \times 3 \times 7$. She also has a box with dimensions $10 \times 11 \times 14$. The bricks and the box are all rectangular parallelepipeds. The mason wants to pack bricks into the box filling its entire volume and with no bricks sticking out. Find all possible values of the total number of bricks that she can pack.
|
Answer: 24.
Let the number of $2 \times 5 \times 8$ bricks in the box be $x$, and the number of $2 \times 3 \times 7$ bricks $y$. We must figure out the sum $x+y$. The volume of the box is divisible by 7 , and so is the volume of any $2 \times 3 \times 7$ brick. The volume of a $2 \times 5 \times 8$ brick is not divisible by 7 , which means that $x$ must be divisible by 7 .
The volume of the box is $10 \cdot 11 \cdot 14$. The volume of the $2 \times 5 \times 8$ bricks in the box is $x \cdot 2 \cdot 5 \cdot 8=80 x$. Since this volume cannot exceed the volume of the box, we must have
$$
x \leqslant \frac{10 \cdot 11 \cdot 14}{80}=\frac{11 \cdot 7}{4}=\frac{77}{4}<20 .
$$
Since $x$ was divisible by 7 , and certainly nonnegative, we conclude that $x$ must be 0,7 or 14 . Let us explore each of these possibilities separately.
If we had $x=0$, then the volume of the $2 \times 3 \times 7$ bricks, which is $y \cdot 2 \cdot 3 \cdot 7$, would be equal to the volume of the box, which is $10 \cdot 11 \cdot 14$. However, this is not possible since the volume of the $2 \times 3 \times 7$ bricks is divisible by three whereas the volume of the box is not. Thus $x$ must be 7 or 14 .
If we had $x=7$, then equating the total volume of the bricks with the volume of the box would give
$$
7 \cdot 2 \cdot 5 \cdot 8+y \cdot 2 \cdot 3 \cdot 7=10 \cdot 11 \cdot 14
$$
so that
$$
y \cdot 2 \cdot 3 \cdot 7=10 \cdot 11 \cdot 14-7 \cdot 2 \cdot 5 \cdot 8=1540-560=980 .
$$
However, again the left-hand side, the volume of the $2 \times 3 \times 7$ bricks, is divisible by three, whereas the right-hand side, 980, is not. Thus we cannot have have $x=7$ either, and the only possibility is $x=14$.
Since $x=14$, equating the volumes of the bricks and the box gives
$$
14 \cdot 2 \cdot 5 \cdot 8+y \cdot 2 \cdot 3 \cdot 7=10 \cdot 11 \cdot 14
$$
which in turn leads to
$$
y \cdot 2 \cdot 3 \cdot 7=10 \cdot 11 \cdot 14-14 \cdot 2 \cdot 5 \cdot 8=1540-1120=420
$$
so that
$$
y=\frac{420}{2 \cdot 3 \cdot 7}=\frac{420}{42}=10
$$
Thus the number of bricks in the box can only be $14+10=24$. Finally, for completeness, let us observe that 14 bricks with dimensions $2 \times 5 \times 8$ can be used to fill a volume with dimensions $10 \times 8 \times 14$, and 10 bricks with dimensions $2 \times 3 \times 7$ can be used to fill a volume with dimensions $10 \times 3 \times 14$, so that these 24 bricks can indeed be packed in the box.
|
{
"exam": "BalticWay",
"problem_label": "7",
"problem_match": "\nProblem 7.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2020"
}
|
Let $n$ be a given positive integer. A restaurant offers a choice of $n$ starters, $n$ main dishes, $n$ desserts and $n$ wines. A merry company dines at the restaurant, with each guest choosing a starter, a main dish, a dessert and a wine. No two people place exactly the same order. It turns out that there is no collection of $n$ guests such that their orders coincide in three of these aspects, but in the fourth one they all differ. (For example, there are no $n$ people that order exactly the same three courses of food, but $n$ different wines.) What is the maximal number of guests?
|
Answer: The maximal number of guests is $n^{4}-n^{3}$.
The possible menus are represented by quadruples
$$
(a, b, c, d), \quad 1 \leqslant a, b, c, d \leqslant n .
$$
Let us count those menus satisfying
$$
a+b+c+d \not \equiv 0 \quad(\bmod n)
$$
The numbers $a, b, c$ may be chosen arbitrarily ( $n$ choices for each), and then $d$ is required to satisfy only $d \not \equiv-a-b-c$. Hence there are
$$
n^{3}(n-1)=n^{4}-n^{3}
$$
such menus.
If there are $n^{4}-n^{3}$ guests, and they have chosen precisely the $n^{4}-n^{3}$ menus satisfying $a+b+c+d \not \equiv 0(\bmod n)$, we claim that the condition of the problem is fulfilled. So suppose there is a collection of $n$ people whose orders coincide in three aspects, but differ in the fourth. With no loss of generality, we may assume they have ordered exactly the same food, but $n$ different wines. This means they all have the same value of $a, b$ and $c$, but their values of $d$ are distinct. A contradiction arises since, given $a, b$ and $c$, there are only $n-1$ values available for $d$.
We now show that for $n^{4}-n^{3}+1$ guests (or more), it is impossible to obtain the situation stipulated in the problem. The $n^{3}$ sets
$$
M_{a, b, c}=\{(a, b, c, d) \mid 1 \leqslant d \leqslant n\}, \quad 1 \leqslant a, b, c \leqslant n
$$
form a partition of the set of possible menus, totalling $n^{4}$. When the number of guests is at least $n^{4}-n^{3}+1$, there are at most $n^{3}-1$ unselected menus. Therefore, there exists a set $M_{a, b, c}$ which contains no unselected menus. That is, all the $n$ menus in $M_{a, b, c}$ have been selected, and the condition of the problem is violated.
|
n^{4}-n^{3}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be a given positive integer. A restaurant offers a choice of $n$ starters, $n$ main dishes, $n$ desserts and $n$ wines. A merry company dines at the restaurant, with each guest choosing a starter, a main dish, a dessert and a wine. No two people place exactly the same order. It turns out that there is no collection of $n$ guests such that their orders coincide in three of these aspects, but in the fourth one they all differ. (For example, there are no $n$ people that order exactly the same three courses of food, but $n$ different wines.) What is the maximal number of guests?
|
Answer: The maximal number of guests is $n^{4}-n^{3}$.
The possible menus are represented by quadruples
$$
(a, b, c, d), \quad 1 \leqslant a, b, c, d \leqslant n .
$$
Let us count those menus satisfying
$$
a+b+c+d \not \equiv 0 \quad(\bmod n)
$$
The numbers $a, b, c$ may be chosen arbitrarily ( $n$ choices for each), and then $d$ is required to satisfy only $d \not \equiv-a-b-c$. Hence there are
$$
n^{3}(n-1)=n^{4}-n^{3}
$$
such menus.
If there are $n^{4}-n^{3}$ guests, and they have chosen precisely the $n^{4}-n^{3}$ menus satisfying $a+b+c+d \not \equiv 0(\bmod n)$, we claim that the condition of the problem is fulfilled. So suppose there is a collection of $n$ people whose orders coincide in three aspects, but differ in the fourth. With no loss of generality, we may assume they have ordered exactly the same food, but $n$ different wines. This means they all have the same value of $a, b$ and $c$, but their values of $d$ are distinct. A contradiction arises since, given $a, b$ and $c$, there are only $n-1$ values available for $d$.
We now show that for $n^{4}-n^{3}+1$ guests (or more), it is impossible to obtain the situation stipulated in the problem. The $n^{3}$ sets
$$
M_{a, b, c}=\{(a, b, c, d) \mid 1 \leqslant d \leqslant n\}, \quad 1 \leqslant a, b, c \leqslant n
$$
form a partition of the set of possible menus, totalling $n^{4}$. When the number of guests is at least $n^{4}-n^{3}+1$, there are at most $n^{3}-1$ unselected menus. Therefore, there exists a set $M_{a, b, c}$ which contains no unselected menus. That is, all the $n$ menus in $M_{a, b, c}$ have been selected, and the condition of the problem is violated.
|
{
"exam": "BalticWay",
"problem_label": "8",
"problem_match": "\nProblem 8.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "# Solution.",
"tier": "T3",
"year": "2020"
}
|
Each vertex $v$ and each edge $e$ of a graph $G$ are assigned numbers $f(v) \in\{1,2\}$ and $f(e) \in\{1,2,3\}$, respectively. Let $S(v)$ be the sum of numbers assigned to the edges incident to $v$ plus the number $f(v)$. We say that an assignment $f$ is cool if $S(u) \neq S(v)$ for every pair $(u, v)$ of adjacent (i.e. connected by an edge) vertices in $G$. Prove that for every graph there exists a cool assignment.
|
Let $v_{1}, v_{2}, \ldots, v_{n}$ be any ordering of the vertices of $G$. Initially each vertex assigned number 1 , and each edge assigned number 2. One may imagine that there is a chip lying on each vertex, while two chips are lying on each edge. We are going to refine this assignment so as to get a cool one by performing the following greedy procedure. To explain what we do in the $i$ th step, denote by $x_{1}, x_{2}, \ldots, x_{k}$ denote all neighbours of $v_{i}$ with lower index, and let $e_{j}=v_{i} x_{j}$, with $j=1,2, \ldots, k$, denote the corresponding backward edges. For each edge $e_{j}$ we have two possibilities:
(a) if there is only one chip on $x_{j}$, then we may move one chip from $e_{j}$ to $x_{j}$ or do nothing;
(b) if there are two chips on $x_{j}$ we may move one chip from $x_{j}$ to $e_{j}$ or do nothing.
Notice that none of the sums $S\left(x_{j}\right)$ may change as a result of such action. Also, any action on each edge may change the total sum for $v_{i}$ just by one. Hence there are $k+1$ possible values for $S\left(v_{i}\right)$. So, at least one combination of chips gives a sum which is different from each of $S\left(x_{j}\right)$. We fix this combination and go to the next step.
To see that this algorithm ends in a desired configuration, note the following:
- by the definition of the steps, no vertex value ever leaves the set $\{1,2\}$;
- each edge $v_{m} v_{i}$ with $m<i$ is only considered at step $i$, so its value may change only once, staying in $2+\{-1,0,+1\}=\{1,2,3\}$;
- $S\left(v_{i}\right)$ can only change in the $i$-th step, when it is made to differ from all $S\left(v_{m}\right)$ with $m<i$ and $v_{m} v_{i}$ being an edge - hence all neighbouring pairs of values $S(\cdot)$ will end up being different.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Each vertex $v$ and each edge $e$ of a graph $G$ are assigned numbers $f(v) \in\{1,2\}$ and $f(e) \in\{1,2,3\}$, respectively. Let $S(v)$ be the sum of numbers assigned to the edges incident to $v$ plus the number $f(v)$. We say that an assignment $f$ is cool if $S(u) \neq S(v)$ for every pair $(u, v)$ of adjacent (i.e. connected by an edge) vertices in $G$. Prove that for every graph there exists a cool assignment.
|
Let $v_{1}, v_{2}, \ldots, v_{n}$ be any ordering of the vertices of $G$. Initially each vertex assigned number 1 , and each edge assigned number 2. One may imagine that there is a chip lying on each vertex, while two chips are lying on each edge. We are going to refine this assignment so as to get a cool one by performing the following greedy procedure. To explain what we do in the $i$ th step, denote by $x_{1}, x_{2}, \ldots, x_{k}$ denote all neighbours of $v_{i}$ with lower index, and let $e_{j}=v_{i} x_{j}$, with $j=1,2, \ldots, k$, denote the corresponding backward edges. For each edge $e_{j}$ we have two possibilities:
(a) if there is only one chip on $x_{j}$, then we may move one chip from $e_{j}$ to $x_{j}$ or do nothing;
(b) if there are two chips on $x_{j}$ we may move one chip from $x_{j}$ to $e_{j}$ or do nothing.
Notice that none of the sums $S\left(x_{j}\right)$ may change as a result of such action. Also, any action on each edge may change the total sum for $v_{i}$ just by one. Hence there are $k+1$ possible values for $S\left(v_{i}\right)$. So, at least one combination of chips gives a sum which is different from each of $S\left(x_{j}\right)$. We fix this combination and go to the next step.
To see that this algorithm ends in a desired configuration, note the following:
- by the definition of the steps, no vertex value ever leaves the set $\{1,2\}$;
- each edge $v_{m} v_{i}$ with $m<i$ is only considered at step $i$, so its value may change only once, staying in $2+\{-1,0,+1\}=\{1,2,3\}$;
- $S\left(v_{i}\right)$ can only change in the $i$-th step, when it is made to differ from all $S\left(v_{m}\right)$ with $m<i$ and $v_{m} v_{i}$ being an edge - hence all neighbouring pairs of values $S(\cdot)$ will end up being different.
|
{
"exam": "BalticWay",
"problem_label": "9",
"problem_match": "\nProblem 9.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "# Solution.",
"tier": "T3",
"year": "2020"
}
|
Alice and Bob are playing hide and seek. Initially, Bob chooses a secret fixed point $B$ in the unit square. Then Alice chooses a sequence of points $P_{0}, P_{1}, \ldots, P_{N}$ in the plane. After choosing $P_{k}$ (but before choosing $P_{k+1}$ ) for $k \geqslant 1$, Bob tells "warmer" if $P_{k}$ is closer to $B$ than $P_{k-1}$, otherwise he says "colder". After Alice has chosen $P_{N}$ and heard Bob's answer, Alice chooses a final point $A$. Alice wins if the distance $A B$ is at most $\frac{1}{2020}$, otherwise Bob wins. Show that if $N=18$, Alice cannot guarantee a win.
|
Let $S_{0}$ be the set of all points in the square, and for each $1 \leqslant k \leqslant N$, let $S_{k}$ be the set of possible points $B$ consistent with everything Bob has said. For each $k$, we then have that $S_{k}$ is the disjoint union of the two possible values $S_{k+1}$ can take for each of Bob's possible answers. Hence once of these must have area $\leqslant \frac{\left|S_{k+1}\right|}{2}$, and the other must have area $\geqslant \frac{\left|S_{k+1}\right|}{2}$. Suppose now that Alice always receives the answer resulting in the greater half. After receiving $N$ answers, then, $\left|S_{N}\right| \geqslant \frac{1}{2^{N}}$. If Alice has a winning strategy, there must be a point $A$ in $S_{N}$ so that the circle of radius $\frac{1}{2020}$ centered at $A$ contains $S_{N}$. Hence $\frac{\pi}{2020^{2}} \geqslant \frac{1}{2^{N}}$. It therefore suffices to show that this inequality does not hold for $N=18$. This follows from the estimates $\pi \leqslant 2^{2}$ and $2020>1024=2^{10}$, meaning that $\frac{\pi}{2020^{2}}>\frac{2^{2}}{2^{20}}=\frac{1}{2^{18}}$.
Comment. In fact, it also holds for $N=20$, but this requires some more estimation work to show by hand. Also, there is a winning strategy for $N=22$, where the square is dissected into right isosceles triangles of successively smaller sizes. This can evidently always be done exactly by choosing $P_{k}$ outside the square. It also seems possible to do this for $P_{k}$ restricted to the interior of the square, but is harder to write up precisely.
|
proof
|
Yes
|
Yes
|
proof
|
Logic and Puzzles
|
Alice and Bob are playing hide and seek. Initially, Bob chooses a secret fixed point $B$ in the unit square. Then Alice chooses a sequence of points $P_{0}, P_{1}, \ldots, P_{N}$ in the plane. After choosing $P_{k}$ (but before choosing $P_{k+1}$ ) for $k \geqslant 1$, Bob tells "warmer" if $P_{k}$ is closer to $B$ than $P_{k-1}$, otherwise he says "colder". After Alice has chosen $P_{N}$ and heard Bob's answer, Alice chooses a final point $A$. Alice wins if the distance $A B$ is at most $\frac{1}{2020}$, otherwise Bob wins. Show that if $N=18$, Alice cannot guarantee a win.
|
Let $S_{0}$ be the set of all points in the square, and for each $1 \leqslant k \leqslant N$, let $S_{k}$ be the set of possible points $B$ consistent with everything Bob has said. For each $k$, we then have that $S_{k}$ is the disjoint union of the two possible values $S_{k+1}$ can take for each of Bob's possible answers. Hence once of these must have area $\leqslant \frac{\left|S_{k+1}\right|}{2}$, and the other must have area $\geqslant \frac{\left|S_{k+1}\right|}{2}$. Suppose now that Alice always receives the answer resulting in the greater half. After receiving $N$ answers, then, $\left|S_{N}\right| \geqslant \frac{1}{2^{N}}$. If Alice has a winning strategy, there must be a point $A$ in $S_{N}$ so that the circle of radius $\frac{1}{2020}$ centered at $A$ contains $S_{N}$. Hence $\frac{\pi}{2020^{2}} \geqslant \frac{1}{2^{N}}$. It therefore suffices to show that this inequality does not hold for $N=18$. This follows from the estimates $\pi \leqslant 2^{2}$ and $2020>1024=2^{10}$, meaning that $\frac{\pi}{2020^{2}}>\frac{2^{2}}{2^{20}}=\frac{1}{2^{18}}$.
Comment. In fact, it also holds for $N=20$, but this requires some more estimation work to show by hand. Also, there is a winning strategy for $N=22$, where the square is dissected into right isosceles triangles of successively smaller sizes. This can evidently always be done exactly by choosing $P_{k}$ outside the square. It also seems possible to do this for $P_{k}$ restricted to the interior of the square, but is harder to write up precisely.
|
{
"exam": "BalticWay",
"problem_label": "10",
"problem_match": "\nProblem 10.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "# Solution.",
"tier": "T3",
"year": "2020"
}
|
Let $A B C$ be a triangle with $A B>A C$. The internal angle bisector of $\angle B A C$ intersects the side $B C$ at $D$. The circles with diameters $B D$ and $C D$ intersect the circumcircle of $\triangle A B C$ a second time at $P \neq B$ and $Q \neq C$, respectively. The lines $P Q$ and $B C$ intersect at $X$. Prove that $A X$ is tangent to the circumcircle of $\triangle A B C$.
|
.
The key observation is that the circumcircle of $\triangle D P Q$ is tangent to $B C$. This can be proved by angle chasing:
$$
\begin{aligned}
\measuredangle B D P & =90^{\circ}-\measuredangle P B D=90^{\circ}-\measuredangle P B C=90^{\circ}-\left(180^{\circ}-\measuredangle C Q P\right) \\
& =\measuredangle C Q P-90^{\circ}=\measuredangle D Q P .
\end{aligned}
$$
Now let the tangent to the circumcircle of $\triangle A B C$ at $A$ intersect $B C$ at $Y$. It is well-known (and easy to show) that $Y A=Y D$. This implies that $Y$ lies on the radical axis of the circumcircles of $\triangle A B C$ and $\triangle P D Q$, which is the line $P Q$. Thus $Y \equiv X$, and the claim follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $A B>A C$. The internal angle bisector of $\angle B A C$ intersects the side $B C$ at $D$. The circles with diameters $B D$ and $C D$ intersect the circumcircle of $\triangle A B C$ a second time at $P \neq B$ and $Q \neq C$, respectively. The lines $P Q$ and $B C$ intersect at $X$. Prove that $A X$ is tangent to the circumcircle of $\triangle A B C$.
|
.
The key observation is that the circumcircle of $\triangle D P Q$ is tangent to $B C$. This can be proved by angle chasing:
$$
\begin{aligned}
\measuredangle B D P & =90^{\circ}-\measuredangle P B D=90^{\circ}-\measuredangle P B C=90^{\circ}-\left(180^{\circ}-\measuredangle C Q P\right) \\
& =\measuredangle C Q P-90^{\circ}=\measuredangle D Q P .
\end{aligned}
$$
Now let the tangent to the circumcircle of $\triangle A B C$ at $A$ intersect $B C$ at $Y$. It is well-known (and easy to show) that $Y A=Y D$. This implies that $Y$ lies on the radical axis of the circumcircles of $\triangle A B C$ and $\triangle P D Q$, which is the line $P Q$. Thus $Y \equiv X$, and the claim follows.
|
{
"exam": "BalticWay",
"problem_label": "11",
"problem_match": "\nProblem 11.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "# Solution 1",
"tier": "T3",
"year": "2020"
}
|
Let $A B C$ be a triangle with $A B>A C$. The internal angle bisector of $\angle B A C$ intersects the side $B C$ at $D$. The circles with diameters $B D$ and $C D$ intersect the circumcircle of $\triangle A B C$ a second time at $P \neq B$ and $Q \neq C$, respectively. The lines $P Q$ and $B C$ intersect at $X$. Prove that $A X$ is tangent to the circumcircle of $\triangle A B C$.
|
.
Apply an inversion with center $D$. Let $A^{\prime}$ denote the image of point $A$, etc. Then $\measuredangle C^{\prime} B^{\prime} A^{\prime}=$ $\measuredangle D B^{\prime} A^{\prime}=\measuredangle B A D=\measuredangle D A C=\measuredangle A^{\prime} C^{\prime} D=\measuredangle A^{\prime} C^{\prime} B^{\prime}$, which means that the triangle $\triangle A^{\prime} B^{\prime} C^{\prime}$ is isosceles at $A^{\prime}$. The images of the circles with diameters $B D$ and $C D$ are the lines perpendicular to $B^{\prime} C^{\prime}$ through $B^{\prime}$ and $C^{\prime}$, respectively, and $P^{\prime}, Q^{\prime}$ are the second intersections of these lines with the circumcircle of $\triangle A^{\prime} B^{\prime} C^{\prime}$.
Now let $\rho$ denote the reflection with respect to the perpendicular bisector of $B^{\prime} C^{\prime}$. By symmetry, $\rho$ maps the circumcircle of $\triangle A^{\prime} B^{\prime} C^{\prime}$ to itself and swaps $B^{\prime}, C^{\prime}$, thus it follows that $\rho$ swaps $P^{\prime}$ and $Q^{\prime}$. The point $X^{\prime}$ is the second intersection of the circumcircle of $\triangle D P^{\prime} Q^{\prime}$ with $B^{\prime} C^{\prime}$. Since $\rho$ maps the line $B^{\prime} C^{\prime}$ to itself, this implies that $\rho$ swaps $D$ and $X^{\prime}$. By symmetry, this yields that the circumcircles of $\triangle A^{\prime} B^{\prime} C^{\prime}$ and $\triangle A^{\prime} D X^{\prime}$ are tangent at $A^{\prime}$, which is what we needed to show.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $A B>A C$. The internal angle bisector of $\angle B A C$ intersects the side $B C$ at $D$. The circles with diameters $B D$ and $C D$ intersect the circumcircle of $\triangle A B C$ a second time at $P \neq B$ and $Q \neq C$, respectively. The lines $P Q$ and $B C$ intersect at $X$. Prove that $A X$ is tangent to the circumcircle of $\triangle A B C$.
|
.
Apply an inversion with center $D$. Let $A^{\prime}$ denote the image of point $A$, etc. Then $\measuredangle C^{\prime} B^{\prime} A^{\prime}=$ $\measuredangle D B^{\prime} A^{\prime}=\measuredangle B A D=\measuredangle D A C=\measuredangle A^{\prime} C^{\prime} D=\measuredangle A^{\prime} C^{\prime} B^{\prime}$, which means that the triangle $\triangle A^{\prime} B^{\prime} C^{\prime}$ is isosceles at $A^{\prime}$. The images of the circles with diameters $B D$ and $C D$ are the lines perpendicular to $B^{\prime} C^{\prime}$ through $B^{\prime}$ and $C^{\prime}$, respectively, and $P^{\prime}, Q^{\prime}$ are the second intersections of these lines with the circumcircle of $\triangle A^{\prime} B^{\prime} C^{\prime}$.
Now let $\rho$ denote the reflection with respect to the perpendicular bisector of $B^{\prime} C^{\prime}$. By symmetry, $\rho$ maps the circumcircle of $\triangle A^{\prime} B^{\prime} C^{\prime}$ to itself and swaps $B^{\prime}, C^{\prime}$, thus it follows that $\rho$ swaps $P^{\prime}$ and $Q^{\prime}$. The point $X^{\prime}$ is the second intersection of the circumcircle of $\triangle D P^{\prime} Q^{\prime}$ with $B^{\prime} C^{\prime}$. Since $\rho$ maps the line $B^{\prime} C^{\prime}$ to itself, this implies that $\rho$ swaps $D$ and $X^{\prime}$. By symmetry, this yields that the circumcircles of $\triangle A^{\prime} B^{\prime} C^{\prime}$ and $\triangle A^{\prime} D X^{\prime}$ are tangent at $A^{\prime}$, which is what we needed to show.
|
{
"exam": "BalticWay",
"problem_label": "11",
"problem_match": "\nProblem 11.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "\nSolution 2",
"tier": "T3",
"year": "2020"
}
|
Let $A B C$ be a triangle with $A B>A C$. The internal angle bisector of $\angle B A C$ intersects the side $B C$ at $D$. The circles with diameters $B D$ and $C D$ intersect the circumcircle of $\triangle A B C$ a second time at $P \neq B$ and $Q \neq C$, respectively. The lines $P Q$ and $B C$ intersect at $X$. Prove that $A X$ is tangent to the circumcircle of $\triangle A B C$.
|
.
Define $Y$ as in the first solution. Since $Y D^{2}=Y A^{2}=Y B \cdot Y C$, it follows that the inversion with center $Y$ and radius $Y D$ swaps $B$ and $C$. Since inversion preserves angles, this implies that the circles with diameters $B D$ and $C D$ are mapped to each other. Moreover, the circumcircle of $\triangle A B C$ is mapped to itself. This implies that $P$ and $Q$ are swapped under the inversion, and therefore $P, Q, Y$ are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with $A B>A C$. The internal angle bisector of $\angle B A C$ intersects the side $B C$ at $D$. The circles with diameters $B D$ and $C D$ intersect the circumcircle of $\triangle A B C$ a second time at $P \neq B$ and $Q \neq C$, respectively. The lines $P Q$ and $B C$ intersect at $X$. Prove that $A X$ is tangent to the circumcircle of $\triangle A B C$.
|
.
Define $Y$ as in the first solution. Since $Y D^{2}=Y A^{2}=Y B \cdot Y C$, it follows that the inversion with center $Y$ and radius $Y D$ swaps $B$ and $C$. Since inversion preserves angles, this implies that the circles with diameters $B D$ and $C D$ are mapped to each other. Moreover, the circumcircle of $\triangle A B C$ is mapped to itself. This implies that $P$ and $Q$ are swapped under the inversion, and therefore $P, Q, Y$ are collinear.
|
{
"exam": "BalticWay",
"problem_label": "11",
"problem_match": "\nProblem 11.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "# Solution 3",
"tier": "T3",
"year": "2020"
}
|
Let $A B C$ be a triangle with circumcircle $\omega$. The internal angle bisectors of $\angle A B C$ and $\angle A C B$ intersect $\omega$ at $X \neq B$ and $Y \neq C$, respectively. Let $K$ be a point on $C X$ such that $\angle K A C=90^{\circ}$. Similarly, let $L$ be a point on $B Y$ such that $\angle L A B=90^{\circ}$. Let $S$ be the midpoint of $\operatorname{arc} C A B$ of $\omega$. Prove that $S K=S L$.
|
.
W.l.o.g. let $A B<A C$. We will prove that triangles $K X S$ and $S Y L$ are congruent by SAS, which will finish the proof.
As $B X$ and $C Y$ are angle bisectors, we obtain:
$$
\frac{1}{2} C \overparen{A} B=C \overparen{X} S=\overparen{C X}+\overparen{X S}=\frac{1}{2} C \overparen{X} A+\overparen{X S}
$$
This implies $\widehat{X S}=\frac{1}{2} A \widehat{Y} B=\widehat{Y B}$ and therefore $S X=Y B$. Note that $B Y=Y A$, hence $Y$ is the midpoint of the hypotenuse $B L$ in $\triangle A B L$. Thus $S X=Y B=Y L$. Similarly, we get $S Y=X K$.
Finally, as $S$ is the midpoint of $\operatorname{arc} C \widehat{A} B$, we obtain $\angle S X C=\angle B Y S$, thus $\angle K X S=\angle S Y L$, finishing the proof of congruency.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcircle $\omega$. The internal angle bisectors of $\angle A B C$ and $\angle A C B$ intersect $\omega$ at $X \neq B$ and $Y \neq C$, respectively. Let $K$ be a point on $C X$ such that $\angle K A C=90^{\circ}$. Similarly, let $L$ be a point on $B Y$ such that $\angle L A B=90^{\circ}$. Let $S$ be the midpoint of $\operatorname{arc} C A B$ of $\omega$. Prove that $S K=S L$.
|
.
W.l.o.g. let $A B<A C$. We will prove that triangles $K X S$ and $S Y L$ are congruent by SAS, which will finish the proof.
As $B X$ and $C Y$ are angle bisectors, we obtain:
$$
\frac{1}{2} C \overparen{A} B=C \overparen{X} S=\overparen{C X}+\overparen{X S}=\frac{1}{2} C \overparen{X} A+\overparen{X S}
$$
This implies $\widehat{X S}=\frac{1}{2} A \widehat{Y} B=\widehat{Y B}$ and therefore $S X=Y B$. Note that $B Y=Y A$, hence $Y$ is the midpoint of the hypotenuse $B L$ in $\triangle A B L$. Thus $S X=Y B=Y L$. Similarly, we get $S Y=X K$.
Finally, as $S$ is the midpoint of $\operatorname{arc} C \widehat{A} B$, we obtain $\angle S X C=\angle B Y S$, thus $\angle K X S=\angle S Y L$, finishing the proof of congruency.
|
{
"exam": "BalticWay",
"problem_label": "12",
"problem_match": "\nProblem 12.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "\nSolution 1",
"tier": "T3",
"year": "2020"
}
|
Let $A B C$ be a triangle with circumcircle $\omega$. The internal angle bisectors of $\angle A B C$ and $\angle A C B$ intersect $\omega$ at $X \neq B$ and $Y \neq C$, respectively. Let $K$ be a point on $C X$ such that $\angle K A C=90^{\circ}$. Similarly, let $L$ be a point on $B Y$ such that $\angle L A B=90^{\circ}$. Let $S$ be the midpoint of $\operatorname{arc} C A B$ of $\omega$. Prove that $S K=S L$.
|
.
Let $I$ be the incenter of $\triangle A B C$. It is well-known that $A Y=B Y=I Y$ and $A X=C X=I X$. By Thales, this implies that $Y$ is the midpoint of $B L$ and $X$ is the midpoint of $C K$. In particular, $I Y=L Y$ and $I X=K X$.
Next, observe that $\measuredangle S Y L=180^{\circ}-\measuredangle B Y S=\measuredangle S C B=\measuredangle C B S=\measuredangle C Y S=\measuredangle I Y S$, which means that $S Y$ is the angle bisector of $\angle I Y L$. Since $I Y=L Y$, this implies that $I S=L S$. Analogously, we can show that $I S=K S$, which completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcircle $\omega$. The internal angle bisectors of $\angle A B C$ and $\angle A C B$ intersect $\omega$ at $X \neq B$ and $Y \neq C$, respectively. Let $K$ be a point on $C X$ such that $\angle K A C=90^{\circ}$. Similarly, let $L$ be a point on $B Y$ such that $\angle L A B=90^{\circ}$. Let $S$ be the midpoint of $\operatorname{arc} C A B$ of $\omega$. Prove that $S K=S L$.
|
.
Let $I$ be the incenter of $\triangle A B C$. It is well-known that $A Y=B Y=I Y$ and $A X=C X=I X$. By Thales, this implies that $Y$ is the midpoint of $B L$ and $X$ is the midpoint of $C K$. In particular, $I Y=L Y$ and $I X=K X$.
Next, observe that $\measuredangle S Y L=180^{\circ}-\measuredangle B Y S=\measuredangle S C B=\measuredangle C B S=\measuredangle C Y S=\measuredangle I Y S$, which means that $S Y$ is the angle bisector of $\angle I Y L$. Since $I Y=L Y$, this implies that $I S=L S$. Analogously, we can show that $I S=K S$, which completes the proof.
|
{
"exam": "BalticWay",
"problem_label": "12",
"problem_match": "\nProblem 12.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "\nSolution 2",
"tier": "T3",
"year": "2020"
}
|
Let $A B C$ be an acute triangle with circumcircle $\omega$. Let $\ell$ be the tangent line to $\omega$ at $A$. Let $X$ and $Y$ be the projections of $B$ onto lines $\ell$ and $A C$, respectively. Let $H$ be the orthocenter of $B X Y$. Let $C H$ intersect $\ell$ at $D$. Prove that $B A$ bisects angle $C B D$.
|
.
Note that $X H \perp B Y \perp A C$ and $Y H \perp B X \perp A D$. Therefore $X H \| A C$ and $Y H \| A D$. It follows that
$$
\frac{A D}{A X}=\frac{C D}{C H}=\frac{C A}{C Y} \Longrightarrow \frac{A D}{C A}=\frac{A X}{C Y}=\frac{A B \cos \angle X A B}{C B \cos \angle Y C B}
$$
Since $\ell$ is tangent to $\omega$, we have $\angle X A B=\angle Y C B$. Thus the cosines in the equality above cancel out and we obtain
$$
\frac{A D}{C A}=\frac{A B}{C B}
$$
This, along with $\angle D A B=\angle A C B$, proves that $\triangle D A B \sim \triangle A C B$ by SAS. Therefore $\angle C B A=$ $\angle A B D$. This shows that $B A$ bisects angle $C B D$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with circumcircle $\omega$. Let $\ell$ be the tangent line to $\omega$ at $A$. Let $X$ and $Y$ be the projections of $B$ onto lines $\ell$ and $A C$, respectively. Let $H$ be the orthocenter of $B X Y$. Let $C H$ intersect $\ell$ at $D$. Prove that $B A$ bisects angle $C B D$.
|
.

Note that $X H \perp B Y \perp A C$ and $Y H \perp B X \perp A D$. Therefore $X H \| A C$ and $Y H \| A D$. It follows that
$$
\frac{A D}{A X}=\frac{C D}{C H}=\frac{C A}{C Y} \Longrightarrow \frac{A D}{C A}=\frac{A X}{C Y}=\frac{A B \cos \angle X A B}{C B \cos \angle Y C B}
$$
Since $\ell$ is tangent to $\omega$, we have $\angle X A B=\angle Y C B$. Thus the cosines in the equality above cancel out and we obtain
$$
\frac{A D}{C A}=\frac{A B}{C B}
$$
This, along with $\angle D A B=\angle A C B$, proves that $\triangle D A B \sim \triangle A C B$ by SAS. Therefore $\angle C B A=$ $\angle A B D$. This shows that $B A$ bisects angle $C B D$.
|
{
"exam": "BalticWay",
"problem_label": "13",
"problem_match": "\nProblem 13.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "# Solution 1",
"tier": "T3",
"year": "2020"
}
|
Let $A B C$ be an acute triangle with circumcircle $\omega$. Let $\ell$ be the tangent line to $\omega$ at $A$. Let $X$ and $Y$ be the projections of $B$ onto lines $\ell$ and $A C$, respectively. Let $H$ be the orthocenter of $B X Y$. Let $C H$ intersect $\ell$ at $D$. Prove that $B A$ bisects angle $C B D$.
|
.
Let $D^{\prime}$ be a point on $\ell$ such that $\angle C B A=\angle A B D^{\prime}$. Let $Z$ and $T$ be projections of $A$ onto $B C$ and $B D^{\prime}$, respectively. Note that the circle with diameter $A B$ passes through $X, Y, Z, T$. By Pascal's theorem for hexagon $A X Z B T Y$, points $D^{\prime}, C$, and $H^{\prime}:=X Z \cap T Y$ are collinear.
We have
$$
\angle X Z B=\angle X A B=\angle C A B=90^{\circ}-\angle Z B Y
$$
which shows that $X Z \perp B Y$.
By definition of $D^{\prime}$,
$$
\angle B D^{\prime} A=180^{\circ}-\angle D^{\prime} A B-\angle A B D^{\prime}=180^{\circ}-\angle A C B-\angle C B A=\angle B A C .
$$
Therefore
$$
\angle D^{\prime} A T=90^{\circ}-\angle T D^{\prime} A=90^{\circ}-\angle B A C,
$$
hence
$$
\angle X Y T+\angle B X Y=\angle X A T+\angle B A Y=90^{\circ}-\angle B A C+\angle B A C=90^{\circ} .
$$
This shows that $Y T \perp B X$.
Since $X Z \perp B Y$ and $Y T \perp B X$, it follows that $H^{\prime}$ is the orthocenter of $B X Y$, i.e. $H^{\prime}=H$. Since $D^{\prime}, C, H^{\prime}$ are collinear and $D^{\prime}$ lies on $\ell$, it follows that $D^{\prime}=D$. Therefore $\angle A B D=\angle C B A$ and we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with circumcircle $\omega$. Let $\ell$ be the tangent line to $\omega$ at $A$. Let $X$ and $Y$ be the projections of $B$ onto lines $\ell$ and $A C$, respectively. Let $H$ be the orthocenter of $B X Y$. Let $C H$ intersect $\ell$ at $D$. Prove that $B A$ bisects angle $C B D$.
|
.
Let $D^{\prime}$ be a point on $\ell$ such that $\angle C B A=\angle A B D^{\prime}$. Let $Z$ and $T$ be projections of $A$ onto $B C$ and $B D^{\prime}$, respectively. Note that the circle with diameter $A B$ passes through $X, Y, Z, T$. By Pascal's theorem for hexagon $A X Z B T Y$, points $D^{\prime}, C$, and $H^{\prime}:=X Z \cap T Y$ are collinear.

We have
$$
\angle X Z B=\angle X A B=\angle C A B=90^{\circ}-\angle Z B Y
$$
which shows that $X Z \perp B Y$.
By definition of $D^{\prime}$,
$$
\angle B D^{\prime} A=180^{\circ}-\angle D^{\prime} A B-\angle A B D^{\prime}=180^{\circ}-\angle A C B-\angle C B A=\angle B A C .
$$
Therefore
$$
\angle D^{\prime} A T=90^{\circ}-\angle T D^{\prime} A=90^{\circ}-\angle B A C,
$$
hence
$$
\angle X Y T+\angle B X Y=\angle X A T+\angle B A Y=90^{\circ}-\angle B A C+\angle B A C=90^{\circ} .
$$
This shows that $Y T \perp B X$.
Since $X Z \perp B Y$ and $Y T \perp B X$, it follows that $H^{\prime}$ is the orthocenter of $B X Y$, i.e. $H^{\prime}=H$. Since $D^{\prime}, C, H^{\prime}$ are collinear and $D^{\prime}$ lies on $\ell$, it follows that $D^{\prime}=D$. Therefore $\angle A B D=\angle C B A$ and we are done.
|
{
"exam": "BalticWay",
"problem_label": "13",
"problem_match": "\nProblem 13.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "# Solution 2",
"tier": "T3",
"year": "2020"
}
|
An acute triangle $A B C$ is given and let $H$ be its orthocenter. Let $\omega$ be the circle through $B, C$ and $H$, and let $\Gamma$ be the circle with diameter $A H$. Let $X \neq H$ be the other intersection point of $\omega$ and $\Gamma$, and let $\gamma$ be the reflection of $\Gamma$ over $A X$.
Suppose $\gamma$ and $\omega$ intersect again at $Y \neq X$, and line $A H$ and $\omega$ intersect again at $Z \neq H$. Show that the circle through $A, Y, Z$ passes through the midpoint of segment $B C$.
|
Let $M$ be the midpoint of $B C$. We first show that $X$ lies on $A M$. Consider $A^{\prime}$, the reflection of $A$ across $M$. As $A B A^{\prime} C$ is a parallelogram, we have that $\angle B A^{\prime} C=\angle B A C=180^{\circ}-\angle B H C$, which in turn gives us that $A^{\prime}$ lies on $\omega$. Now $\angle H B A^{\prime}=\angle H B C+\angle C B A^{\prime}=\angle H B C+\angle A C B=$ $90^{\circ}$. Hence $H A$ is a diameter of $\omega$. In particular we must have $\angle H X A^{\prime}=90^{\circ}$. Consequently $\angle A X A^{\prime}=\angle A X H+\angle H X A^{\prime}=90^{\circ}+90^{\circ}=180^{\circ}$, i.e. $A, X, A^{\prime}$ are collinear. But $A, M, A^{\prime}$ collinear by definition, hence $X$ lies on the $A$-median.
Now it suffices to show that $\angle A Y Z=\angle A M Z$. We note the two following facts:
- $\angle A H X=\angle A Y X$, since $\omega$ and $\Gamma$ have the same radius and the two angles span the same chord $A X$.
- $\omega$ is the reflection of the circumcircle of $A B C$ across $B C$. That gives us that $Z$ is the reflection of $A$ across $D$, the feet of the $A$-altitude to $B C$.
Hence we can write: $\angle A Y Z=\angle A Y X+\angle X Y Z=\angle A H X+\left(180^{\circ}-\angle X H Z\right)=2 \angle A H X=$ $2 \angle A M D=\angle A M Z$, which is what we wanted.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
An acute triangle $A B C$ is given and let $H$ be its orthocenter. Let $\omega$ be the circle through $B, C$ and $H$, and let $\Gamma$ be the circle with diameter $A H$. Let $X \neq H$ be the other intersection point of $\omega$ and $\Gamma$, and let $\gamma$ be the reflection of $\Gamma$ over $A X$.
Suppose $\gamma$ and $\omega$ intersect again at $Y \neq X$, and line $A H$ and $\omega$ intersect again at $Z \neq H$. Show that the circle through $A, Y, Z$ passes through the midpoint of segment $B C$.
|
Let $M$ be the midpoint of $B C$. We first show that $X$ lies on $A M$. Consider $A^{\prime}$, the reflection of $A$ across $M$. As $A B A^{\prime} C$ is a parallelogram, we have that $\angle B A^{\prime} C=\angle B A C=180^{\circ}-\angle B H C$, which in turn gives us that $A^{\prime}$ lies on $\omega$. Now $\angle H B A^{\prime}=\angle H B C+\angle C B A^{\prime}=\angle H B C+\angle A C B=$ $90^{\circ}$. Hence $H A$ is a diameter of $\omega$. In particular we must have $\angle H X A^{\prime}=90^{\circ}$. Consequently $\angle A X A^{\prime}=\angle A X H+\angle H X A^{\prime}=90^{\circ}+90^{\circ}=180^{\circ}$, i.e. $A, X, A^{\prime}$ are collinear. But $A, M, A^{\prime}$ collinear by definition, hence $X$ lies on the $A$-median.
Now it suffices to show that $\angle A Y Z=\angle A M Z$. We note the two following facts:
- $\angle A H X=\angle A Y X$, since $\omega$ and $\Gamma$ have the same radius and the two angles span the same chord $A X$.
- $\omega$ is the reflection of the circumcircle of $A B C$ across $B C$. That gives us that $Z$ is the reflection of $A$ across $D$, the feet of the $A$-altitude to $B C$.
Hence we can write: $\angle A Y Z=\angle A Y X+\angle X Y Z=\angle A H X+\left(180^{\circ}-\angle X H Z\right)=2 \angle A H X=$ $2 \angle A M D=\angle A M Z$, which is what we wanted.
|
{
"exam": "BalticWay",
"problem_label": "14",
"problem_match": "\nProblem 14.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "# Solution.",
"tier": "T3",
"year": "2020"
}
|
On a plane, Bob chooses 3 points $A_{0}, B_{0}, C_{0}$ (not necessarily distinct) such that $A_{0} B_{0}+B_{0} C_{0}+C_{0} A_{0}=1$. Then he chooses points $A_{1}, B_{1}, C_{1}$ (not necessarily distinct) in such a way that $A_{1} B_{1}=A_{0} B_{0}$ and $B_{1} C_{1}=B_{0} C_{0}$. Next he chooses points $A_{2}, B_{2}, C_{2}$ as a permutation of points $A_{1}, B_{1}, C_{1}$. Finally, Bob chooses points $A_{3}, B_{3}, C_{3}$ (not necessarily distinct) in such a way that $A_{3} B_{3}=A_{2} B_{2}$ and $B_{3} C_{3}=B_{2} C_{2}$. What are the smallest and the greatest possible values of $A_{3} B_{3}+B_{3} C_{3}+C_{3} A_{3}$ Bob can obtain?
|
Answer: $\frac{1}{3}$ and 3 .
Denote the lengths $A_{0} B_{0}, B_{0} C_{0}, C_{0} A_{0}$ by $x, y, z$ in non-increasing order. Similarly, denote the lengths $A_{1} B_{1}, B_{1} C_{1}, C_{1} A_{1}$ by $x^{\prime}, y^{\prime}, z^{\prime}$ in non-increasing order, and the lengths $A_{3} B_{3}, B_{3} C_{3}$, $C_{3} A_{3}$ by $x^{\prime \prime}, y^{\prime \prime}, z^{\prime \prime}$ in non-increasing order. (As permuting the points does not change the distances, we do not need a separate vector for $A_{2} B_{2}, B_{2} C_{2}, C_{2} A_{2}$.) Then we have $x+y+z=1$, $y+z \geqslant x, y^{\prime}+z^{\prime} \geqslant x^{\prime}, y^{\prime \prime}+z^{\prime \prime} \geqslant x^{\prime \prime}$. By construction, triples $(x, y, z)$ and $\left(x^{\prime}, y^{\prime}, z^{\prime}\right)$ have two values in common (but not necessarily at corresponding places), similarly $\left(x^{\prime}, y^{\prime}, z^{\prime}\right)$ and $\left(x^{\prime \prime}, y^{\prime \prime}, z^{\prime \prime}\right)$ have two values in common.
Using these observations, calculate:
$$
\begin{aligned}
x^{\prime \prime}+y^{\prime \prime}+z^{\prime \prime} & \leqslant 2\left(y^{\prime \prime}+z^{\prime \prime}\right) \leqslant 2\left(x^{\prime}+y^{\prime}\right) \leqslant 2\left(y^{\prime}+y^{\prime}+z^{\prime}\right) \\
& \leqslant 2(x+x+y) \leqslant 6 x \leqslant 3(x+y+z)=3 .
\end{aligned}
$$
We can achieve the value 3 as follows. Let $A_{0} B_{0}=\frac{1}{2}$ and $C_{0}=A_{0}$. Let $A_{1}=A_{0}$, $B_{1}=B_{0}$ and $\overrightarrow{B_{1} C_{1}}=-\overrightarrow{B_{0} C_{0}}$. Let $A_{2}=A_{1}$ and $B_{2}=C_{1}, C_{2}=B_{1}$. Finally, let $A_{3}=A_{2}$, $B_{3}=B_{2}$ and $\overrightarrow{B_{3} C_{3}}=-\overrightarrow{B_{2} C_{2}}$. By construction, $A_{3} B_{3}=1, B_{3} C_{3}=\frac{1}{2}$ and $C_{3} A_{3}=\frac{3}{2}$, so $A_{3} B_{3}+B_{3} C_{3}+C_{3} A_{3}=3$.
This establishes the upper bound. For the lower bound, note that all steps are reversible and the 3-step process itself is symmetric. By scaling, we can also make the initial configuration to satisfy the conditions of the problem. Hence all processes satisfying the conditions of the problem and achieving a final value $t$ are in one-to-one correspondence with processes satisfying the conditions of the problem and achieving the final value $\frac{1}{t}$. This shows that the lower bound is $\frac{1}{3}$.
|
\frac{1}{3} \text{ and } 3
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
On a plane, Bob chooses 3 points $A_{0}, B_{0}, C_{0}$ (not necessarily distinct) such that $A_{0} B_{0}+B_{0} C_{0}+C_{0} A_{0}=1$. Then he chooses points $A_{1}, B_{1}, C_{1}$ (not necessarily distinct) in such a way that $A_{1} B_{1}=A_{0} B_{0}$ and $B_{1} C_{1}=B_{0} C_{0}$. Next he chooses points $A_{2}, B_{2}, C_{2}$ as a permutation of points $A_{1}, B_{1}, C_{1}$. Finally, Bob chooses points $A_{3}, B_{3}, C_{3}$ (not necessarily distinct) in such a way that $A_{3} B_{3}=A_{2} B_{2}$ and $B_{3} C_{3}=B_{2} C_{2}$. What are the smallest and the greatest possible values of $A_{3} B_{3}+B_{3} C_{3}+C_{3} A_{3}$ Bob can obtain?
|
Answer: $\frac{1}{3}$ and 3 .
Denote the lengths $A_{0} B_{0}, B_{0} C_{0}, C_{0} A_{0}$ by $x, y, z$ in non-increasing order. Similarly, denote the lengths $A_{1} B_{1}, B_{1} C_{1}, C_{1} A_{1}$ by $x^{\prime}, y^{\prime}, z^{\prime}$ in non-increasing order, and the lengths $A_{3} B_{3}, B_{3} C_{3}$, $C_{3} A_{3}$ by $x^{\prime \prime}, y^{\prime \prime}, z^{\prime \prime}$ in non-increasing order. (As permuting the points does not change the distances, we do not need a separate vector for $A_{2} B_{2}, B_{2} C_{2}, C_{2} A_{2}$.) Then we have $x+y+z=1$, $y+z \geqslant x, y^{\prime}+z^{\prime} \geqslant x^{\prime}, y^{\prime \prime}+z^{\prime \prime} \geqslant x^{\prime \prime}$. By construction, triples $(x, y, z)$ and $\left(x^{\prime}, y^{\prime}, z^{\prime}\right)$ have two values in common (but not necessarily at corresponding places), similarly $\left(x^{\prime}, y^{\prime}, z^{\prime}\right)$ and $\left(x^{\prime \prime}, y^{\prime \prime}, z^{\prime \prime}\right)$ have two values in common.
Using these observations, calculate:
$$
\begin{aligned}
x^{\prime \prime}+y^{\prime \prime}+z^{\prime \prime} & \leqslant 2\left(y^{\prime \prime}+z^{\prime \prime}\right) \leqslant 2\left(x^{\prime}+y^{\prime}\right) \leqslant 2\left(y^{\prime}+y^{\prime}+z^{\prime}\right) \\
& \leqslant 2(x+x+y) \leqslant 6 x \leqslant 3(x+y+z)=3 .
\end{aligned}
$$
We can achieve the value 3 as follows. Let $A_{0} B_{0}=\frac{1}{2}$ and $C_{0}=A_{0}$. Let $A_{1}=A_{0}$, $B_{1}=B_{0}$ and $\overrightarrow{B_{1} C_{1}}=-\overrightarrow{B_{0} C_{0}}$. Let $A_{2}=A_{1}$ and $B_{2}=C_{1}, C_{2}=B_{1}$. Finally, let $A_{3}=A_{2}$, $B_{3}=B_{2}$ and $\overrightarrow{B_{3} C_{3}}=-\overrightarrow{B_{2} C_{2}}$. By construction, $A_{3} B_{3}=1, B_{3} C_{3}=\frac{1}{2}$ and $C_{3} A_{3}=\frac{3}{2}$, so $A_{3} B_{3}+B_{3} C_{3}+C_{3} A_{3}=3$.
This establishes the upper bound. For the lower bound, note that all steps are reversible and the 3-step process itself is symmetric. By scaling, we can also make the initial configuration to satisfy the conditions of the problem. Hence all processes satisfying the conditions of the problem and achieving a final value $t$ are in one-to-one correspondence with processes satisfying the conditions of the problem and achieving the final value $\frac{1}{t}$. This shows that the lower bound is $\frac{1}{3}$.
|
{
"exam": "BalticWay",
"problem_label": "15",
"problem_match": "\nProblem 15.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "# Solution.",
"tier": "T3",
"year": "2020"
}
|
Richard and Kaarel are taking turns to choose numbers from the set $\{1, \ldots, p-1\}$ where $p>3$ is a prime. Richard is the first one to choose. A number which has been chosen by one of the players cannot be chosen again by either of the players. Every number chosen by Richard is multiplied with the next number chosen by Kaarel. Kaarel wins the game if at any moment after his turn the sum of all of the products calculated so far is divisible by $p$. Richard wins if this does not happen, i.e. the players run out of numbers before any of the sums is divisible by $p$. Can either of the players guarantee their victory regardless of their opponent's moves and if so, which one?
|
.
Answer: Yes, Kaarel.
Let us split the numbers in the set to the following pairs: $(1, p-1),(2, p-2), \ldots,\left(\frac{p-1}{2}, \frac{p+1}{2}\right)$. If Richard chooses some number $a$, then let Kaarel choose the other number from the pair i.e. $p-a$. This forces Richard to choose a number from a pair in which both of the numbers have not been chosen yet and hence Kaarel can make his desired move. The residues modulo $p$ of the products are of the form $-a^{2}$. The residue of the sum of all the products is congruent to $-\left(1^{2}+2^{2}+\ldots+\left(\frac{p-1}{2}\right)^{2}\right)$. For every natural number $n$, we have $1^{2}+2^{2}+\ldots+n^{2}=\frac{n(n+1)(2 n+1)}{6}$, therefore $1^{2}+2^{2}+\ldots+\left(\frac{p-1}{2}\right)^{2}=\frac{(p-1) p(p+1)}{24}$. This must be an integer and as $p$ and 24 are coprime, $\frac{(p-1) p(p+1)}{24}$ must be divisible by $p$. Therefore, when the last number is chosen from the set, the sum of the products is divisible by $p$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Richard and Kaarel are taking turns to choose numbers from the set $\{1, \ldots, p-1\}$ where $p>3$ is a prime. Richard is the first one to choose. A number which has been chosen by one of the players cannot be chosen again by either of the players. Every number chosen by Richard is multiplied with the next number chosen by Kaarel. Kaarel wins the game if at any moment after his turn the sum of all of the products calculated so far is divisible by $p$. Richard wins if this does not happen, i.e. the players run out of numbers before any of the sums is divisible by $p$. Can either of the players guarantee their victory regardless of their opponent's moves and if so, which one?
|
.
Answer: Yes, Kaarel.
Let us split the numbers in the set to the following pairs: $(1, p-1),(2, p-2), \ldots,\left(\frac{p-1}{2}, \frac{p+1}{2}\right)$. If Richard chooses some number $a$, then let Kaarel choose the other number from the pair i.e. $p-a$. This forces Richard to choose a number from a pair in which both of the numbers have not been chosen yet and hence Kaarel can make his desired move. The residues modulo $p$ of the products are of the form $-a^{2}$. The residue of the sum of all the products is congruent to $-\left(1^{2}+2^{2}+\ldots+\left(\frac{p-1}{2}\right)^{2}\right)$. For every natural number $n$, we have $1^{2}+2^{2}+\ldots+n^{2}=\frac{n(n+1)(2 n+1)}{6}$, therefore $1^{2}+2^{2}+\ldots+\left(\frac{p-1}{2}\right)^{2}=\frac{(p-1) p(p+1)}{24}$. This must be an integer and as $p$ and 24 are coprime, $\frac{(p-1) p(p+1)}{24}$ must be divisible by $p$. Therefore, when the last number is chosen from the set, the sum of the products is divisible by $p$.
|
{
"exam": "BalticWay",
"problem_label": "16",
"problem_match": "\nProblem 16.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "# Solution 1",
"tier": "T3",
"year": "2020"
}
|
Richard and Kaarel are taking turns to choose numbers from the set $\{1, \ldots, p-1\}$ where $p>3$ is a prime. Richard is the first one to choose. A number which has been chosen by one of the players cannot be chosen again by either of the players. Every number chosen by Richard is multiplied with the next number chosen by Kaarel. Kaarel wins the game if at any moment after his turn the sum of all of the products calculated so far is divisible by $p$. Richard wins if this does not happen, i.e. the players run out of numbers before any of the sums is divisible by $p$. Can either of the players guarantee their victory regardless of their opponent's moves and if so, which one?
|
.
If Richard initially chooses some number $x$, then Kaarel chooses $p-x$ as above (distinct from $x$ as $p$ is odd). Since $p-1>2$, there are still numbers left, so the game continues.
If next Richard chooses $y$ as his second number, then Kaarel wins by choosing the unique number $1 \leqslant a \leqslant p-1$ congruent to $x^{2} \cdot y^{-1}$ modulo $p$. In order for Kaarel's second move to be legal, we must confirm that $a$ is different from $x,-x$ and $y$ modulo $p$.
If $a \equiv x(\bmod p)$, then $y \equiv x(\bmod p)$ contradicting Richards second move. If $a \equiv-x$ $(\bmod p)$, then $y \equiv-x(\bmod p)$ also contradicting Richards second move. Finally, if $a \equiv y$ $(\bmod p)$, then $x^{2} \equiv y^{2}(\bmod p)$ implying $y \equiv \pm x(\bmod p)$ with the same contradictions once more.
We conclude that $a$ is distinct from the previous numbers, and $x \cdot(p-x)+y \cdot a \equiv 0(\bmod p)$, so Kaarel wins.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Richard and Kaarel are taking turns to choose numbers from the set $\{1, \ldots, p-1\}$ where $p>3$ is a prime. Richard is the first one to choose. A number which has been chosen by one of the players cannot be chosen again by either of the players. Every number chosen by Richard is multiplied with the next number chosen by Kaarel. Kaarel wins the game if at any moment after his turn the sum of all of the products calculated so far is divisible by $p$. Richard wins if this does not happen, i.e. the players run out of numbers before any of the sums is divisible by $p$. Can either of the players guarantee their victory regardless of their opponent's moves and if so, which one?
|
.
If Richard initially chooses some number $x$, then Kaarel chooses $p-x$ as above (distinct from $x$ as $p$ is odd). Since $p-1>2$, there are still numbers left, so the game continues.
If next Richard chooses $y$ as his second number, then Kaarel wins by choosing the unique number $1 \leqslant a \leqslant p-1$ congruent to $x^{2} \cdot y^{-1}$ modulo $p$. In order for Kaarel's second move to be legal, we must confirm that $a$ is different from $x,-x$ and $y$ modulo $p$.
If $a \equiv x(\bmod p)$, then $y \equiv x(\bmod p)$ contradicting Richards second move. If $a \equiv-x$ $(\bmod p)$, then $y \equiv-x(\bmod p)$ also contradicting Richards second move. Finally, if $a \equiv y$ $(\bmod p)$, then $x^{2} \equiv y^{2}(\bmod p)$ implying $y \equiv \pm x(\bmod p)$ with the same contradictions once more.
We conclude that $a$ is distinct from the previous numbers, and $x \cdot(p-x)+y \cdot a \equiv 0(\bmod p)$, so Kaarel wins.
|
{
"exam": "BalticWay",
"problem_label": "16",
"problem_match": "\nProblem 16.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "\nSolution 2",
"tier": "T3",
"year": "2020"
}
|
For a prime number $p$ and a positive integer $n$, denote by $f(p, n)$ the largest integer $k$ such that $p^{k} \mid n$ !. Let $p$ be a given prime number and let $m$ and $c$ be given positive integers. Prove that there exist infinitely many positive integers $n$ such that $f(p, n) \equiv c$ $(\bmod m)$.
|
.
We start by noting that
$$
f(p, n)=\left\lfloor\frac{n}{p}\right\rfloor+\left\lfloor\frac{n}{p^{2}}\right\rfloor+\left\lfloor\frac{n}{p^{3}}\right\rfloor+\ldots
$$
which is the well-known Legendre Formula. Now, if we choose
$$
n=p^{a_{1}}+p^{a_{2}}+\cdots+p^{a_{k}}
$$
for positive integers $a_{1}>a_{2}>\cdots>a_{k}$ to be determined, this formula immediately shows that
$$
\begin{aligned}
f(p, n) & =\left(p^{a_{1}-1}+p^{a_{1}-2}+\cdots+p+1\right)+\left(p^{a_{2}-1}+p^{a_{2}-2}+\cdots+p+1\right)+\ldots \\
& =\frac{p^{a_{1}}-1}{p-1}+\frac{p^{a_{2}}-1}{p-1}+\ldots
\end{aligned}
$$
We thus consider the numbers $\left(p^{a}-1\right) /(p-1)$. If we can show that there is a residue class $C$ $(\bmod m)$ which is coprime to $m$ occuring infinitely often among these numbers, we will be done since we can choose $a_{1}, \ldots, a_{k}$ with $k C \equiv c(\bmod m)$ arbitrarily among these numbers. Now, how to find such a number $C$ ?
To this end, write $m=p^{t} \cdot m^{\prime}$ with $p \nmid m^{\prime}$. Since $p^{a}$ is certainly periodic modulo $m^{\prime} \cdot(p-1)$, the sequence $\left(p^{a}-1\right) /(p-1)$ is periodic modulo $m^{\prime}$ with some period $d$ and hence for $a \equiv 1(\bmod d)$, the numbers are always $1\left(\bmod m^{\prime}\right)$. Moreover, for $a \geq t$, all the numbers are equal to $\left(p^{t}-1\right) /(p-1)$ modulo $p^{t}$ and hence by the Chinese Remainder Theorem, all the numbers $\left(p^{a}-1\right) /(p-1)$ for $a \geq t$ and $a \equiv 1(\bmod d)$ are in the same residue class $C$ $(\bmod m)$, with $C$ coprime to $m$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For a prime number $p$ and a positive integer $n$, denote by $f(p, n)$ the largest integer $k$ such that $p^{k} \mid n$ !. Let $p$ be a given prime number and let $m$ and $c$ be given positive integers. Prove that there exist infinitely many positive integers $n$ such that $f(p, n) \equiv c$ $(\bmod m)$.
|
.
We start by noting that
$$
f(p, n)=\left\lfloor\frac{n}{p}\right\rfloor+\left\lfloor\frac{n}{p^{2}}\right\rfloor+\left\lfloor\frac{n}{p^{3}}\right\rfloor+\ldots
$$
which is the well-known Legendre Formula. Now, if we choose
$$
n=p^{a_{1}}+p^{a_{2}}+\cdots+p^{a_{k}}
$$
for positive integers $a_{1}>a_{2}>\cdots>a_{k}$ to be determined, this formula immediately shows that
$$
\begin{aligned}
f(p, n) & =\left(p^{a_{1}-1}+p^{a_{1}-2}+\cdots+p+1\right)+\left(p^{a_{2}-1}+p^{a_{2}-2}+\cdots+p+1\right)+\ldots \\
& =\frac{p^{a_{1}}-1}{p-1}+\frac{p^{a_{2}}-1}{p-1}+\ldots
\end{aligned}
$$
We thus consider the numbers $\left(p^{a}-1\right) /(p-1)$. If we can show that there is a residue class $C$ $(\bmod m)$ which is coprime to $m$ occuring infinitely often among these numbers, we will be done since we can choose $a_{1}, \ldots, a_{k}$ with $k C \equiv c(\bmod m)$ arbitrarily among these numbers. Now, how to find such a number $C$ ?
To this end, write $m=p^{t} \cdot m^{\prime}$ with $p \nmid m^{\prime}$. Since $p^{a}$ is certainly periodic modulo $m^{\prime} \cdot(p-1)$, the sequence $\left(p^{a}-1\right) /(p-1)$ is periodic modulo $m^{\prime}$ with some period $d$ and hence for $a \equiv 1(\bmod d)$, the numbers are always $1\left(\bmod m^{\prime}\right)$. Moreover, for $a \geq t$, all the numbers are equal to $\left(p^{t}-1\right) /(p-1)$ modulo $p^{t}$ and hence by the Chinese Remainder Theorem, all the numbers $\left(p^{a}-1\right) /(p-1)$ for $a \geq t$ and $a \equiv 1(\bmod d)$ are in the same residue class $C$ $(\bmod m)$, with $C$ coprime to $m$, as desired.
|
{
"exam": "BalticWay",
"problem_label": "17",
"problem_match": "\nProblem 17.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "\nSolution 1",
"tier": "T3",
"year": "2020"
}
|
For a prime number $p$ and a positive integer $n$, denote by $f(p, n)$ the largest integer $k$ such that $p^{k} \mid n$ !. Let $p$ be a given prime number and let $m$ and $c$ be given positive integers. Prove that there exist infinitely many positive integers $n$ such that $f(p, n) \equiv c$ $(\bmod m)$.
|
.
We denote $v_{p}(n)$ for the largest power of $p$ dividing $n$.
We start with a lemma.
Lemma. For any prime $q$ and modulus $m^{\prime}$ not divisible by $q$, there exists infinitely many powers $q^{n}$ of $q$ such that $v_{p}\left(q^{n} !\right) \equiv 1\left(\bmod m^{\prime}\right)$.
Proof. Define $a_{k}=v_{q}\left(q^{k} !\right)$. We then have $a_{k+1}=q a_{k}+1$. This sequence is eventually periodic modulo $m^{\prime}$. It must actually be periodic starting from 0 , as $a_{i} \equiv a_{i+T}\left(\bmod m^{\prime}\right)$ implies $q a_{i-1} \equiv q a_{i+T-1}\left(\bmod m^{\prime}\right)$ and therefore $a_{i-1} \equiv a_{i+T-1}\left(\bmod m^{\prime}\right)$, since $q \nmid m^{\prime}$. Thus, for infinitely many $n$ we have $a_{n} \equiv a_{1}=1\left(\bmod m^{\prime}\right)$.
We now turn to solving the problem. Write $m=p^{t} m^{\prime}$, where $p \nmid m^{\prime}$. The sequence $v_{p}(p !), v_{p}\left(p^{2} !\right), v_{p}\left(p^{3} !\right), \ldots$ is eventually constant modulo $p^{t}$. Denote this constant by $C$. Since $p \nmid C$, by the Chinese remainder theorem there exists a positive integer $s$ such that $C s \equiv c$ $\left(\bmod p^{t}\right)$ and $s \equiv c\left(\bmod m^{\prime}\right)$. Now, choose
$$
n=p^{b_{1}}+p^{b_{2}}+\ldots+p^{b_{s}}
$$
where $b_{i}$ are distinct positive integers such that $v_{p}\left(p_{i}^{b} !\right) \equiv 1\left(\bmod m^{\prime}\right)($ possible by the lemma) and large enough such that $v_{p}\left(p_{i}^{b} !\right) \equiv C\left(\bmod p^{t}\right)$. We have
$$
v_{p}(n !)=v_{p}\left(p_{1}^{b} !\right)+\ldots+v_{p}\left(p^{b_{s}} !\right) \equiv C s \equiv c \quad\left(\bmod p^{t}\right)
$$
and
$$
v_{p}(n !)=v_{p}\left(p_{1}^{b} !\right)+\ldots+v_{p}\left(p^{b_{s}} !\right) \equiv s \equiv c \quad\left(\bmod m^{\prime}\right)
$$
which proves $v_{p}(n !) \equiv c(\bmod m)$. Since there are infinitely many of possible choices $n$, we are done.
Comment. IMO shortlist 2007 N7 asks to prove that for given $d$ and primes $p_{1}, \ldots, p_{k}$ there exists infinitely many integers $n$ such that $d \mid v_{p_{i}}(n !)$ for all $i$. While the IMO shortlist problem is of similar flavor, it would seem that it is more difficult than the problem above, and the methods are a bit different. (There is no clear way to use prime powers in the IMO SL problem similarly to the solution above.)
Comment. As a vast generalization of the problem above and the IMO shortlist problem, one could ask whether the following holds: For any modulus $m$ and distinct primes $p_{1}, \ldots, p_{k}$, the function
$$
n \rightarrow\left(v_{p_{1}}(n !) \quad(\bmod m), v_{p_{2}}(n !) \quad(\bmod m), \ldots, v_{p_{k}}(n !) \quad(\bmod m)\right)
$$
(viewed as a function $\mathbb{Z}_{+} \rightarrow\left(\mathbb{Z}_{m}\right)^{k}$ ) is equidistributed. The author of the problem believes this generalization to hold, but he has no proof.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For a prime number $p$ and a positive integer $n$, denote by $f(p, n)$ the largest integer $k$ such that $p^{k} \mid n$ !. Let $p$ be a given prime number and let $m$ and $c$ be given positive integers. Prove that there exist infinitely many positive integers $n$ such that $f(p, n) \equiv c$ $(\bmod m)$.
|
.
We denote $v_{p}(n)$ for the largest power of $p$ dividing $n$.
We start with a lemma.
Lemma. For any prime $q$ and modulus $m^{\prime}$ not divisible by $q$, there exists infinitely many powers $q^{n}$ of $q$ such that $v_{p}\left(q^{n} !\right) \equiv 1\left(\bmod m^{\prime}\right)$.
Proof. Define $a_{k}=v_{q}\left(q^{k} !\right)$. We then have $a_{k+1}=q a_{k}+1$. This sequence is eventually periodic modulo $m^{\prime}$. It must actually be periodic starting from 0 , as $a_{i} \equiv a_{i+T}\left(\bmod m^{\prime}\right)$ implies $q a_{i-1} \equiv q a_{i+T-1}\left(\bmod m^{\prime}\right)$ and therefore $a_{i-1} \equiv a_{i+T-1}\left(\bmod m^{\prime}\right)$, since $q \nmid m^{\prime}$. Thus, for infinitely many $n$ we have $a_{n} \equiv a_{1}=1\left(\bmod m^{\prime}\right)$.
We now turn to solving the problem. Write $m=p^{t} m^{\prime}$, where $p \nmid m^{\prime}$. The sequence $v_{p}(p !), v_{p}\left(p^{2} !\right), v_{p}\left(p^{3} !\right), \ldots$ is eventually constant modulo $p^{t}$. Denote this constant by $C$. Since $p \nmid C$, by the Chinese remainder theorem there exists a positive integer $s$ such that $C s \equiv c$ $\left(\bmod p^{t}\right)$ and $s \equiv c\left(\bmod m^{\prime}\right)$. Now, choose
$$
n=p^{b_{1}}+p^{b_{2}}+\ldots+p^{b_{s}}
$$
where $b_{i}$ are distinct positive integers such that $v_{p}\left(p_{i}^{b} !\right) \equiv 1\left(\bmod m^{\prime}\right)($ possible by the lemma) and large enough such that $v_{p}\left(p_{i}^{b} !\right) \equiv C\left(\bmod p^{t}\right)$. We have
$$
v_{p}(n !)=v_{p}\left(p_{1}^{b} !\right)+\ldots+v_{p}\left(p^{b_{s}} !\right) \equiv C s \equiv c \quad\left(\bmod p^{t}\right)
$$
and
$$
v_{p}(n !)=v_{p}\left(p_{1}^{b} !\right)+\ldots+v_{p}\left(p^{b_{s}} !\right) \equiv s \equiv c \quad\left(\bmod m^{\prime}\right)
$$
which proves $v_{p}(n !) \equiv c(\bmod m)$. Since there are infinitely many of possible choices $n$, we are done.
Comment. IMO shortlist 2007 N7 asks to prove that for given $d$ and primes $p_{1}, \ldots, p_{k}$ there exists infinitely many integers $n$ such that $d \mid v_{p_{i}}(n !)$ for all $i$. While the IMO shortlist problem is of similar flavor, it would seem that it is more difficult than the problem above, and the methods are a bit different. (There is no clear way to use prime powers in the IMO SL problem similarly to the solution above.)
Comment. As a vast generalization of the problem above and the IMO shortlist problem, one could ask whether the following holds: For any modulus $m$ and distinct primes $p_{1}, \ldots, p_{k}$, the function
$$
n \rightarrow\left(v_{p_{1}}(n !) \quad(\bmod m), v_{p_{2}}(n !) \quad(\bmod m), \ldots, v_{p_{k}}(n !) \quad(\bmod m)\right)
$$
(viewed as a function $\mathbb{Z}_{+} \rightarrow\left(\mathbb{Z}_{m}\right)^{k}$ ) is equidistributed. The author of the problem believes this generalization to hold, but he has no proof.
|
{
"exam": "BalticWay",
"problem_label": "17",
"problem_match": "\nProblem 17.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "# Solution 2",
"tier": "T3",
"year": "2020"
}
|
Let $n \geqslant 1$ be a positive integer. We say that an integer $k$ is a fan of $n$ if $0 \leqslant k \leqslant n-1$ and there exist integers $x, y, z \in \mathbb{Z}$ such that
$$
\begin{aligned}
x^{2}+y^{2}+z^{2} & \equiv 0 \quad(\bmod n) ; \\
x y z & \equiv k \quad(\bmod n) .
\end{aligned}
$$
Let $f(n)$ be the number of fans of $n$. Determine $f(2020)$.
|
Answer: $f(2020)=f(4) \cdot f(5) \cdot f(101)=1 \cdot 1 \cdot 101=101$.
To prove our claim we show that $f$ is multiplicative, that is, $f(r s)=f(r) f(s)$ for coprime numbers $r, s \in \mathbb{N}$, and that
(i) $f(4)=1$,
(ii) $f(5)=1$,
(iii) $f(101)=101$.
The multiplicative property follows from the Chinese Remainder Theorem.
(i) Integers $x, y$ and $z$ satisfy $x^{2}+y^{2}+z^{2} \equiv 0 \bmod 4$ if and only if they are all even. In this case $x y z \equiv 0 \bmod 4$. Hence 0 is the only fan of 4 .
(ii) Integers $x, y$ and $z$ satisfy $x^{2}+y^{2}+z^{2} \equiv 0 \bmod 5$ if and only if at least one of them is divisible by 5 . In this case $x y z \equiv 0 \bmod 5$. Hence 5 is the only fan of 5 .
(iii) We have $9^{2}+4^{2}+2^{2}=81+16+4=101$. Hence $(9 x)^{2}+(4 x)^{2}+(2 x)^{2}$ is divisible by 101 for every integer $x$. Hence the residue of $9 x \cdot 4 x \cdot 2 x=72 x^{3}$ upon division by 101 is a fan of 101 for every $x \in \mathbb{Z}$. If we substitute $x=t^{67}$, then $x^{3}=t^{201} \equiv t \bmod 101$. Since 72 is coprime to 101 , the number $72 x^{3} \equiv 72 t$ can take any residue modulo 101 .
Note: In general for $p \not \equiv 1(\bmod 3)$, we have $f(p)=p$ as soon as we have at least one non-zero fan.
|
101
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $n \geqslant 1$ be a positive integer. We say that an integer $k$ is a fan of $n$ if $0 \leqslant k \leqslant n-1$ and there exist integers $x, y, z \in \mathbb{Z}$ such that
$$
\begin{aligned}
x^{2}+y^{2}+z^{2} & \equiv 0 \quad(\bmod n) ; \\
x y z & \equiv k \quad(\bmod n) .
\end{aligned}
$$
Let $f(n)$ be the number of fans of $n$. Determine $f(2020)$.
|
Answer: $f(2020)=f(4) \cdot f(5) \cdot f(101)=1 \cdot 1 \cdot 101=101$.
To prove our claim we show that $f$ is multiplicative, that is, $f(r s)=f(r) f(s)$ for coprime numbers $r, s \in \mathbb{N}$, and that
(i) $f(4)=1$,
(ii) $f(5)=1$,
(iii) $f(101)=101$.
The multiplicative property follows from the Chinese Remainder Theorem.
(i) Integers $x, y$ and $z$ satisfy $x^{2}+y^{2}+z^{2} \equiv 0 \bmod 4$ if and only if they are all even. In this case $x y z \equiv 0 \bmod 4$. Hence 0 is the only fan of 4 .
(ii) Integers $x, y$ and $z$ satisfy $x^{2}+y^{2}+z^{2} \equiv 0 \bmod 5$ if and only if at least one of them is divisible by 5 . In this case $x y z \equiv 0 \bmod 5$. Hence 5 is the only fan of 5 .
(iii) We have $9^{2}+4^{2}+2^{2}=81+16+4=101$. Hence $(9 x)^{2}+(4 x)^{2}+(2 x)^{2}$ is divisible by 101 for every integer $x$. Hence the residue of $9 x \cdot 4 x \cdot 2 x=72 x^{3}$ upon division by 101 is a fan of 101 for every $x \in \mathbb{Z}$. If we substitute $x=t^{67}$, then $x^{3}=t^{201} \equiv t \bmod 101$. Since 72 is coprime to 101 , the number $72 x^{3} \equiv 72 t$ can take any residue modulo 101 .
Note: In general for $p \not \equiv 1(\bmod 3)$, we have $f(p)=p$ as soon as we have at least one non-zero fan.
|
{
"exam": "BalticWay",
"problem_label": "18",
"problem_match": "\nProblem 18.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2020"
}
|
Denote by $d(n)$ the number of positive divisors of a positive integer $n$. Prove that there are infinitely many positive integers $n$ such that $|\sqrt{3} \cdot d(n)|$ divides $n$.
|
.
Note that $\lfloor\sqrt{3} \cdot 8\rfloor=13$. Therefore all numbers with 8 divisors that are divisible by 13 satisfy the condition. There are infinitely many of those, for example, all numbers in the form $13 p^{3}$, where $p$ is a prime different from 13 .
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Denote by $d(n)$ the number of positive divisors of a positive integer $n$. Prove that there are infinitely many positive integers $n$ such that $|\sqrt{3} \cdot d(n)|$ divides $n$.
|
.
Note that $\lfloor\sqrt{3} \cdot 8\rfloor=13$. Therefore all numbers with 8 divisors that are divisible by 13 satisfy the condition. There are infinitely many of those, for example, all numbers in the form $13 p^{3}$, where $p$ is a prime different from 13 .
|
{
"exam": "BalticWay",
"problem_label": "19",
"problem_match": "\nProblem 19.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "\nSolution 1",
"tier": "T3",
"year": "2020"
}
|
Denote by $d(n)$ the number of positive divisors of a positive integer $n$. Prove that there are infinitely many positive integers $n$ such that $|\sqrt{3} \cdot d(n)|$ divides $n$.
|
.
Based on the solution by the Finnish team: Instead of finding infinitely many solutions with $d(n)=2^{3}$, we prove that every power $2^{k}, k \geqslant 0$, has at least one solution with $d(n)=2^{k}$.
Let $k \geqslant 0$ be given, and let $p_{1}, p_{2}, \ldots$ be the sequence of all prime numbers. We then write the prime factorization of $\left\lfloor 2^{k} \sqrt{3}\right\rfloor$ as
$$
\left\lfloor 2^{k} \sqrt{3}\right\rfloor=\prod_{i=1}^{\infty} p_{i}^{b_{i}}
$$
with $b_{i} \geqslant 0$ and only finitely many $b_{i}$ different from 0 .
Since $\sqrt{3}<2$, we have
$$
2^{k+1}>\left\lfloor 2^{k} \sqrt{3}\right\rfloor=\prod_{i=1}^{\infty} p_{i}^{b_{i}} \geqslant \prod_{i=1}^{\infty} 2^{b_{i}}=2^{\sum_{i=1}^{\infty} b_{i}}
$$
and from this we conclude $\sum_{i=1}^{\infty} b_{i} \leqslant k$. We know that $m+1 \leqslant 2^{m}$ for any integer $m \geqslant 0$, and this brings us a further estimate
$$
\sum_{i=1}^{\infty}\left\lceil\log _{2}\left(b_{i}+1\right)\right\rceil \leqslant \sum_{i=1}^{\infty} b_{i} \leqslant k
$$
By increasing values if necessary, we can choose a sequence of non-negative integers $a_{1}, a_{2}, \ldots$ such that $a_{i} \geqslant\left\lceil\log _{2}\left(b_{i}+1\right)\right\rceil$ for all $i$, and $\sum_{i=1}^{\infty} a_{i}=k$. [Editor's note: In fact, unless $\sum_{i=1}^{\infty}\left\lceil\log _{2}\left(b_{i}+1\right)\right\rceil=k$ already, we have an infinite choice of such sequences - each leading to a distinct $n$ with the required properties.] We now define
$$
n=\prod_{i=1}^{\infty} p_{i}^{2^{a_{i}}-1}
$$
which is a valid product since all but finitely many $a_{i}$ are equal to zero. By construction we have $2^{a_{i}}-1 \geqslant b_{i}$ for all $i$, so $\left\lfloor 2^{k} \sqrt{3}\right\rfloor$ divides $n$. Finally, the number of divisors in $n$ can be calculated as
$$
d(n)=\prod_{i=1}^{\infty}\left(\left(2^{a_{i}}-1\right)+1\right)=\prod_{i=1}^{\infty} 2^{a_{i}}=2^{\sum_{i=1}^{\infty} a_{i}}=2^{k}
$$
so $n$ satisfies that $\lfloor d(n) \sqrt{3}\rfloor=\left\lfloor 2^{k} \sqrt{3}\right\rfloor$ divides $n$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Denote by $d(n)$ the number of positive divisors of a positive integer $n$. Prove that there are infinitely many positive integers $n$ such that $|\sqrt{3} \cdot d(n)|$ divides $n$.
|
.
Based on the solution by the Finnish team: Instead of finding infinitely many solutions with $d(n)=2^{3}$, we prove that every power $2^{k}, k \geqslant 0$, has at least one solution with $d(n)=2^{k}$.
Let $k \geqslant 0$ be given, and let $p_{1}, p_{2}, \ldots$ be the sequence of all prime numbers. We then write the prime factorization of $\left\lfloor 2^{k} \sqrt{3}\right\rfloor$ as
$$
\left\lfloor 2^{k} \sqrt{3}\right\rfloor=\prod_{i=1}^{\infty} p_{i}^{b_{i}}
$$
with $b_{i} \geqslant 0$ and only finitely many $b_{i}$ different from 0 .
Since $\sqrt{3}<2$, we have
$$
2^{k+1}>\left\lfloor 2^{k} \sqrt{3}\right\rfloor=\prod_{i=1}^{\infty} p_{i}^{b_{i}} \geqslant \prod_{i=1}^{\infty} 2^{b_{i}}=2^{\sum_{i=1}^{\infty} b_{i}}
$$
and from this we conclude $\sum_{i=1}^{\infty} b_{i} \leqslant k$. We know that $m+1 \leqslant 2^{m}$ for any integer $m \geqslant 0$, and this brings us a further estimate
$$
\sum_{i=1}^{\infty}\left\lceil\log _{2}\left(b_{i}+1\right)\right\rceil \leqslant \sum_{i=1}^{\infty} b_{i} \leqslant k
$$
By increasing values if necessary, we can choose a sequence of non-negative integers $a_{1}, a_{2}, \ldots$ such that $a_{i} \geqslant\left\lceil\log _{2}\left(b_{i}+1\right)\right\rceil$ for all $i$, and $\sum_{i=1}^{\infty} a_{i}=k$. [Editor's note: In fact, unless $\sum_{i=1}^{\infty}\left\lceil\log _{2}\left(b_{i}+1\right)\right\rceil=k$ already, we have an infinite choice of such sequences - each leading to a distinct $n$ with the required properties.] We now define
$$
n=\prod_{i=1}^{\infty} p_{i}^{2^{a_{i}}-1}
$$
which is a valid product since all but finitely many $a_{i}$ are equal to zero. By construction we have $2^{a_{i}}-1 \geqslant b_{i}$ for all $i$, so $\left\lfloor 2^{k} \sqrt{3}\right\rfloor$ divides $n$. Finally, the number of divisors in $n$ can be calculated as
$$
d(n)=\prod_{i=1}^{\infty}\left(\left(2^{a_{i}}-1\right)+1\right)=\prod_{i=1}^{\infty} 2^{a_{i}}=2^{\sum_{i=1}^{\infty} a_{i}}=2^{k}
$$
so $n$ satisfies that $\lfloor d(n) \sqrt{3}\rfloor=\left\lfloor 2^{k} \sqrt{3}\right\rfloor$ divides $n$.
|
{
"exam": "BalticWay",
"problem_label": "19",
"problem_match": "\nProblem 19.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "# Solution 2",
"tier": "T3",
"year": "2020"
}
|
Denote by $d(n)$ the number of positive divisors of a positive integer $n$. Prove that there are infinitely many positive integers $n$ such that $|\sqrt{3} \cdot d(n)|$ divides $n$.
|
.
Based on the solution by the Norwegian team: In this third solution, instead of letting $d(n)$ be a power of 2 , we prove that there a infinitely many solutions with $n=2^{k}$.
Consider the sequence $a_{i}=\lfloor i \sqrt{3}\rfloor$ for $i \geqslant 1$. If $k \geqslant 3$, then $(k+1) \sqrt{3}<2(k+1) \leqslant 2^{k}$. Consequently, whenever $a_{k+1}=2^{m}$ and $k \geqslant 3$, we get
$$
\left\lfloor d\left(2^{k}\right) \sqrt{3}\right\rfloor=\lfloor(k+1) \sqrt{3}\rfloor=a_{k+1}=2^{m} \mid 2^{k}
$$
so $n=2^{k}$ satisfies the properties of the problem. It is therefore sufficient to prove that the integer sequence $a_{i}=\lfloor i \sqrt{3}\rfloor$ contains infinitely many powers of 2 . Since $\sqrt{3}>1$, the sequence is strictly increasing, and since $\sqrt{3}<2$, we have
$$
a_{i+1}-a_{i}=\lfloor(i+1) \sqrt{3}\rfloor-\lfloor i \sqrt{3}\rfloor<(i+1) \sqrt{3}-(i \sqrt{3}-1)=\sqrt{3}+1<3 .
$$
Hence the sequence jump by at most 2 at each step.
Suppose for contradiction that the sequence constains only finitely many powers of two, say the largest is $2^{N}$. Then for every $m>N$ we can find a unique index $k$ such that $a_{k}=2^{m}-1$ and $a_{k+1}=2^{m}+1$.
Define $d_{i}=i \sqrt{3}-a_{i}$ to be the fractional part for each $i$, so that $0 \leqslant d_{i}<1$. For $k$ as above we then have
$$
\begin{aligned}
k \sqrt{3}-\left(2^{m}-1\right) & =d_{k} \geqslant 0, \\
(k+1) \sqrt{3}-\left(2^{m}+1\right) & =d_{k+1} \geqslant 0, \\
\text { and thus }(2 k+1) \sqrt{3}-2^{m+1} & =d_{k}+d_{k+1} \geqslant 0
\end{aligned}
$$
If $d_{k}+d_{k+1}<1$, we would have $a_{2 k+1}=2^{m+1}$ contrary to our assumptions, hence $1 \leqslant d_{k}+d_{k+1}<2$ and consequently $a_{2 k+1}=2^{m+1}+1$ and $a_{2 k}=2^{m+1}-1$.
Since $a_{2 k}=2^{m+1}-1$, we have a recursive expression for $d_{2 k}$ as well:
$$
d_{2 k}=2 k \sqrt{3}-\left(2^{m+1}-1\right)=2\left(d_{k}+2^{m}-1\right)-\left(2^{m+1}-1\right)=2 d_{k}-1 .
$$
We can now repeat the process with $2 k$ and $2 k+1$ in place of $k$ and $k+1$ in order to prove the following statements by induction for all $j \geqslant 0$ :
- $a_{2^{j} k}=2^{m+j}-1$ and $a_{2^{j} k+1}=2^{m+j}+1$
- $d_{2^{j} k}=2^{j} d_{k}-\left(2^{j}-1\right)=2^{j}\left(d_{k}-1\right)+1$
Finally, since $d_{k}-1<0$, the second property implies that $d_{2 j k}$ tends to $-\infty$ as $j$ tends to $\infty$. This clearly contradicts that $d_{2^{j} k} \geqslant 0$ for all $k$ and $j$, hence we conclude that the sequence $a_{i}$ contains infinitely many powers of 2 as required.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Denote by $d(n)$ the number of positive divisors of a positive integer $n$. Prove that there are infinitely many positive integers $n$ such that $|\sqrt{3} \cdot d(n)|$ divides $n$.
|
.
Based on the solution by the Norwegian team: In this third solution, instead of letting $d(n)$ be a power of 2 , we prove that there a infinitely many solutions with $n=2^{k}$.
Consider the sequence $a_{i}=\lfloor i \sqrt{3}\rfloor$ for $i \geqslant 1$. If $k \geqslant 3$, then $(k+1) \sqrt{3}<2(k+1) \leqslant 2^{k}$. Consequently, whenever $a_{k+1}=2^{m}$ and $k \geqslant 3$, we get
$$
\left\lfloor d\left(2^{k}\right) \sqrt{3}\right\rfloor=\lfloor(k+1) \sqrt{3}\rfloor=a_{k+1}=2^{m} \mid 2^{k}
$$
so $n=2^{k}$ satisfies the properties of the problem. It is therefore sufficient to prove that the integer sequence $a_{i}=\lfloor i \sqrt{3}\rfloor$ contains infinitely many powers of 2 . Since $\sqrt{3}>1$, the sequence is strictly increasing, and since $\sqrt{3}<2$, we have
$$
a_{i+1}-a_{i}=\lfloor(i+1) \sqrt{3}\rfloor-\lfloor i \sqrt{3}\rfloor<(i+1) \sqrt{3}-(i \sqrt{3}-1)=\sqrt{3}+1<3 .
$$
Hence the sequence jump by at most 2 at each step.
Suppose for contradiction that the sequence constains only finitely many powers of two, say the largest is $2^{N}$. Then for every $m>N$ we can find a unique index $k$ such that $a_{k}=2^{m}-1$ and $a_{k+1}=2^{m}+1$.
Define $d_{i}=i \sqrt{3}-a_{i}$ to be the fractional part for each $i$, so that $0 \leqslant d_{i}<1$. For $k$ as above we then have
$$
\begin{aligned}
k \sqrt{3}-\left(2^{m}-1\right) & =d_{k} \geqslant 0, \\
(k+1) \sqrt{3}-\left(2^{m}+1\right) & =d_{k+1} \geqslant 0, \\
\text { and thus }(2 k+1) \sqrt{3}-2^{m+1} & =d_{k}+d_{k+1} \geqslant 0
\end{aligned}
$$
If $d_{k}+d_{k+1}<1$, we would have $a_{2 k+1}=2^{m+1}$ contrary to our assumptions, hence $1 \leqslant d_{k}+d_{k+1}<2$ and consequently $a_{2 k+1}=2^{m+1}+1$ and $a_{2 k}=2^{m+1}-1$.
Since $a_{2 k}=2^{m+1}-1$, we have a recursive expression for $d_{2 k}$ as well:
$$
d_{2 k}=2 k \sqrt{3}-\left(2^{m+1}-1\right)=2\left(d_{k}+2^{m}-1\right)-\left(2^{m+1}-1\right)=2 d_{k}-1 .
$$
We can now repeat the process with $2 k$ and $2 k+1$ in place of $k$ and $k+1$ in order to prove the following statements by induction for all $j \geqslant 0$ :
- $a_{2^{j} k}=2^{m+j}-1$ and $a_{2^{j} k+1}=2^{m+j}+1$
- $d_{2^{j} k}=2^{j} d_{k}-\left(2^{j}-1\right)=2^{j}\left(d_{k}-1\right)+1$
Finally, since $d_{k}-1<0$, the second property implies that $d_{2 j k}$ tends to $-\infty$ as $j$ tends to $\infty$. This clearly contradicts that $d_{2^{j} k} \geqslant 0$ for all $k$ and $j$, hence we conclude that the sequence $a_{i}$ contains infinitely many powers of 2 as required.
|
{
"exam": "BalticWay",
"problem_label": "19",
"problem_match": "\nProblem 19.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "\nSolution 3",
"tier": "T3",
"year": "2020"
}
|
Let $A$ and $B$ be sets of positive integers with $|A| \geq 2$ and $|B| \geq 2$. Let $S$ be a set consisting of $|A|+|B|-1$ numbers of the form $a b$ where $a \in A$ and $b \in B$. Prove that there exist pairwise distinct $x, y, z \in S$ such that $x$ is a divisor of $y z$.
|
.
We use induction on $k=|A|+|B|-1$.
For $k=3$ we have $|A|=|B|=2$. Let $A=\{x, y\}, B=\{z, t\}$. Then $S$ consists of three numbers from the set $\{x z, y z, x t, y t\}$. Relabelling the elements of $A$ and $B$ if necessary, we can assume without loss of generality that the missing number is $y t$. Then $x z, x t, y z \in S$ and $x z \mid x t \cdot y z$ which concludes the base case of induction.
For the inductive step, suppose the thesis holds for some $k-1 \geq 3$. Since $k=|A|+|B|-1 \geq$ 4, we have that $\max (|A|,|B|) \geq 3$, WLOG assume $|B| \geq 3$. Since the set $S$ consists of $k=|A|+|B|-1>|A|$ elements, by pigeonhole principle there exists a number $x \in A$ which appears as the first of the two factors of at least two elements of $S$. So, there exist $y, z \in B$ with $x y, x z \in S$. If there exists $t \in A \backslash\{x\}$ such that $t y \in S$ and $t y \neq x z$, then we are done because $x y \mid x z \cdot t y$. If there exists no such $t$ then apply the inductive hypothesis to the sets $A$, $B \backslash\{y\}$ and $S \backslash\{x y\}$ - note here that every element of $S \backslash\{x y\}$ still has the form $a b$ for $a \in A$ and $b \in B \backslash\{y\}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $A$ and $B$ be sets of positive integers with $|A| \geq 2$ and $|B| \geq 2$. Let $S$ be a set consisting of $|A|+|B|-1$ numbers of the form $a b$ where $a \in A$ and $b \in B$. Prove that there exist pairwise distinct $x, y, z \in S$ such that $x$ is a divisor of $y z$.
|
.
We use induction on $k=|A|+|B|-1$.
For $k=3$ we have $|A|=|B|=2$. Let $A=\{x, y\}, B=\{z, t\}$. Then $S$ consists of three numbers from the set $\{x z, y z, x t, y t\}$. Relabelling the elements of $A$ and $B$ if necessary, we can assume without loss of generality that the missing number is $y t$. Then $x z, x t, y z \in S$ and $x z \mid x t \cdot y z$ which concludes the base case of induction.
For the inductive step, suppose the thesis holds for some $k-1 \geq 3$. Since $k=|A|+|B|-1 \geq$ 4, we have that $\max (|A|,|B|) \geq 3$, WLOG assume $|B| \geq 3$. Since the set $S$ consists of $k=|A|+|B|-1>|A|$ elements, by pigeonhole principle there exists a number $x \in A$ which appears as the first of the two factors of at least two elements of $S$. So, there exist $y, z \in B$ with $x y, x z \in S$. If there exists $t \in A \backslash\{x\}$ such that $t y \in S$ and $t y \neq x z$, then we are done because $x y \mid x z \cdot t y$. If there exists no such $t$ then apply the inductive hypothesis to the sets $A$, $B \backslash\{y\}$ and $S \backslash\{x y\}$ - note here that every element of $S \backslash\{x y\}$ still has the form $a b$ for $a \in A$ and $b \in B \backslash\{y\}$.
|
{
"exam": "BalticWay",
"problem_label": "20",
"problem_match": "\nProblem 20.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "\nSolution 1",
"tier": "T3",
"year": "2020"
}
|
Let $A$ and $B$ be sets of positive integers with $|A| \geq 2$ and $|B| \geq 2$. Let $S$ be a set consisting of $|A|+|B|-1$ numbers of the form $a b$ where $a \in A$ and $b \in B$. Prove that there exist pairwise distinct $x, y, z \in S$ such that $x$ is a divisor of $y z$.
|
.
Based on the solution by the Latvian team: We construct a bipartite graph $G$ where the elements of $A$ form one class of vertices, and the elements of $B$ form the other class of vertices. For each element $s \in S$ write $s=a b$ with $a \in A$ and $b \in B$ then put a single edge between $a$ and $b$ in $G$ (if $s$ decomposes as $a b$ in multiple ways, only place an edge for one of these decompositions). Now suppose $G$ has a path of length 3, i.e.
then $x \mid y z$ and since each element of $S$ only labels one edge, $x, y$ and $z$ are distinct. It is thus sufficient to show that if $|A|,|B| \geqslant 2$ and $|S|=|A|+|B|-1$, then $G$ has a path of length 3 . We shall prove the contrapositive statement: If $|S|=|A|+|B|-1$ and $G$ has no path of length 3 , then $|A|=1$ or $|B|=1$.
Suppose $G$ is bipartite and has no path of length 3, then in particular $G$ has no cycles, so $G$ is a forest (a collection of trees). The number of trees in a forest can be calculated as
$$
\# \text { vertices }-\# \text { edges }=(|A|+|B|)-(|A|+|B|-1)=1
$$
hence $G$ is a single tree. If $G$ is a tree and has not path of length 3, then $G$ has to be a star graph. A bipartite star graph necessarily has the central vertex in one class and all the leaves in the other class, hence either $|A|=1$ or $|B|=1$ as required.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $A$ and $B$ be sets of positive integers with $|A| \geq 2$ and $|B| \geq 2$. Let $S$ be a set consisting of $|A|+|B|-1$ numbers of the form $a b$ where $a \in A$ and $b \in B$. Prove that there exist pairwise distinct $x, y, z \in S$ such that $x$ is a divisor of $y z$.
|
.
Based on the solution by the Latvian team: We construct a bipartite graph $G$ where the elements of $A$ form one class of vertices, and the elements of $B$ form the other class of vertices. For each element $s \in S$ write $s=a b$ with $a \in A$ and $b \in B$ then put a single edge between $a$ and $b$ in $G$ (if $s$ decomposes as $a b$ in multiple ways, only place an edge for one of these decompositions). Now suppose $G$ has a path of length 3, i.e.
then $x \mid y z$ and since each element of $S$ only labels one edge, $x, y$ and $z$ are distinct. It is thus sufficient to show that if $|A|,|B| \geqslant 2$ and $|S|=|A|+|B|-1$, then $G$ has a path of length 3 . We shall prove the contrapositive statement: If $|S|=|A|+|B|-1$ and $G$ has no path of length 3 , then $|A|=1$ or $|B|=1$.
Suppose $G$ is bipartite and has no path of length 3, then in particular $G$ has no cycles, so $G$ is a forest (a collection of trees). The number of trees in a forest can be calculated as
$$
\# \text { vertices }-\# \text { edges }=(|A|+|B|)-(|A|+|B|-1)=1
$$
hence $G$ is a single tree. If $G$ is a tree and has not path of length 3, then $G$ has to be a star graph. A bipartite star graph necessarily has the central vertex in one class and all the leaves in the other class, hence either $|A|=1$ or $|B|=1$ as required.
|
{
"exam": "BalticWay",
"problem_label": "20",
"problem_match": "\nProblem 20.",
"resource_path": "BalticWay/segmented/en-bw20sol.jsonl",
"solution_match": "\nSolution 2",
"tier": "T3",
"year": "2020"
}
|
Let $n$ be a positive integer. Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ that satisfy the equation
$$
(f(x))^{n} f(x+y)=(f(x))^{n+1}+x^{n} f(y)
$$
for all $x, y \in \mathbb{R}$.
|
The functions we are looking for are $f: \mathbb{R} \rightarrow \mathbb{R}, f(x)=0$ and $f: \mathbb{R} \rightarrow \mathbb{R}, f(x)=x$. For $n$ even $f: \mathbb{R} \rightarrow \mathbb{R}, f(x)=-x$ is also a solution.
Throughout the solution, $P\left(x_{0}, y_{0}\right)$ will denote the substitution of $x_{0}$ and $y_{0}$ for $x$ and $y$, respectively, in the given equation.
$P(x, 0)$ for $x \neq 0$ gives
$$
f(x)^{n+1}=f(x)^{n+1}+x^{n} f(0)
$$
and therefore
$$
f(0)=\frac{f(x)^{n+1}-f(x)^{n+1}}{x^{n}}=0 .
$$
$P(x,-x)$ for $x \neq 0$ gives
$$
0=f(x)^{n} f(0)=f(x)^{n+1}+x^{n} f(-x)
$$
and therefore
$$
f(-x)=-\frac{f(x)^{n+1}}{x^{n}}
$$
Applying this identity twice, we get
$$
f(x)=f(-(-x))=-\frac{f(-x)^{n+1}}{(-x)^{n}}=-\frac{\left(-\frac{f(x)^{n+1}}{x^{n}}\right)^{n+1}}{(-x)^{n}}=\frac{f(x)^{n^{2}+2 n+1}}{x^{n^{2}+2 n}}
$$
which after rearranging yields
$$
f(x)\left(x^{n^{2}+2 n}-f(x)^{n^{2}+2 n}\right)=0 .
$$
If there exists an $a \neq 0$ for which $f(a)=0$, then $P(a, y)$ yields
$$
0=a^{n} f(y)
$$
which means that $f(y)=0$ for all $y \in \mathbb{R}$. This is a solution to the equation for all $n$.
If instead $f(x) \neq 0$ for all $x \neq 0$, then we have
$$
x^{n^{2}+2 n}=f(x)^{n^{2}+2 n} .
$$
If $n$ is odd, then so is $n(n+2)=\left(n^{2}+2 n\right)$, meaning $f(x)=x$ for all $x \in \mathbb{R}$. This is a solution to the equation.
## Baltic Way
If $n$ is even, then so is $n(n+2)=\left(n^{2}+2 n\right)$, meaning $f(x)= \pm x$ for all $x \in \mathbb{R}$. Both $f(x)=x$ and $f(x)=-x$ are solutions to the equation. In all other cases there must exist $x, y \neq 0$ such that $f(x)=x$ and $f(y)=-y$. Then $P(x, y)$ yields
$$
x^{n} f(x+y)=x^{n+1}-x^{n} y
$$
which after dividing by $x^{n} \neq 0$ yields
$$
f(x+y)=x-y .
$$
Since $(f(x))^{2}=x^{2}$ for all $x \in \mathbb{R}$, we have $(x+y)^{2}=(x-y)^{2}$. That is $4 x y=0$ which is impossible as $x, y \neq 0$.
There are therefore no more solutions to the equation.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $n$ be a positive integer. Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ that satisfy the equation
$$
(f(x))^{n} f(x+y)=(f(x))^{n+1}+x^{n} f(y)
$$
for all $x, y \in \mathbb{R}$.
|
The functions we are looking for are $f: \mathbb{R} \rightarrow \mathbb{R}, f(x)=0$ and $f: \mathbb{R} \rightarrow \mathbb{R}, f(x)=x$. For $n$ even $f: \mathbb{R} \rightarrow \mathbb{R}, f(x)=-x$ is also a solution.
Throughout the solution, $P\left(x_{0}, y_{0}\right)$ will denote the substitution of $x_{0}$ and $y_{0}$ for $x$ and $y$, respectively, in the given equation.
$P(x, 0)$ for $x \neq 0$ gives
$$
f(x)^{n+1}=f(x)^{n+1}+x^{n} f(0)
$$
and therefore
$$
f(0)=\frac{f(x)^{n+1}-f(x)^{n+1}}{x^{n}}=0 .
$$
$P(x,-x)$ for $x \neq 0$ gives
$$
0=f(x)^{n} f(0)=f(x)^{n+1}+x^{n} f(-x)
$$
and therefore
$$
f(-x)=-\frac{f(x)^{n+1}}{x^{n}}
$$
Applying this identity twice, we get
$$
f(x)=f(-(-x))=-\frac{f(-x)^{n+1}}{(-x)^{n}}=-\frac{\left(-\frac{f(x)^{n+1}}{x^{n}}\right)^{n+1}}{(-x)^{n}}=\frac{f(x)^{n^{2}+2 n+1}}{x^{n^{2}+2 n}}
$$
which after rearranging yields
$$
f(x)\left(x^{n^{2}+2 n}-f(x)^{n^{2}+2 n}\right)=0 .
$$
If there exists an $a \neq 0$ for which $f(a)=0$, then $P(a, y)$ yields
$$
0=a^{n} f(y)
$$
which means that $f(y)=0$ for all $y \in \mathbb{R}$. This is a solution to the equation for all $n$.
If instead $f(x) \neq 0$ for all $x \neq 0$, then we have
$$
x^{n^{2}+2 n}=f(x)^{n^{2}+2 n} .
$$
If $n$ is odd, then so is $n(n+2)=\left(n^{2}+2 n\right)$, meaning $f(x)=x$ for all $x \in \mathbb{R}$. This is a solution to the equation.
## Baltic Way
If $n$ is even, then so is $n(n+2)=\left(n^{2}+2 n\right)$, meaning $f(x)= \pm x$ for all $x \in \mathbb{R}$. Both $f(x)=x$ and $f(x)=-x$ are solutions to the equation. In all other cases there must exist $x, y \neq 0$ such that $f(x)=x$ and $f(y)=-y$. Then $P(x, y)$ yields
$$
x^{n} f(x+y)=x^{n+1}-x^{n} y
$$
which after dividing by $x^{n} \neq 0$ yields
$$
f(x+y)=x-y .
$$
Since $(f(x))^{2}=x^{2}$ for all $x \in \mathbb{R}$, we have $(x+y)^{2}=(x-y)^{2}$. That is $4 x y=0$ which is impossible as $x, y \neq 0$.
There are therefore no more solutions to the equation.
|
{
"exam": "BalticWay",
"problem_label": "1",
"problem_match": "\nProblem 1.",
"resource_path": "BalticWay/segmented/en-bw21sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2021"
}
|
Let $a, b, c$ be the side lengths of a triangle. Prove that
$$
\sqrt[3]{\left(a^{2}+b c\right)\left(b^{2}+c a\right)\left(c^{2}+a b\right)}>\frac{a^{2}+b^{2}+c^{2}}{2} .
$$
|
We claim that
$$
a^{2}+b c>\frac{a^{2}+b^{2}+c^{2}}{2}
$$
which will finish the proof. Note that the claimed inequality is equivalent to
$$
\begin{aligned}
a^{2}+b c>\frac{a^{2}+b^{2}+c^{2}}{2} & \Longleftrightarrow 2 a^{2}+2 b c>a^{2}+b^{2}+c^{2} \\
& \Longleftrightarrow a^{2}>(b-c)^{2} \Longleftrightarrow a>|b-c|,
\end{aligned}
$$
which holds due to the assumption of $a, b, c$ being side lengths of a triangle.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be the side lengths of a triangle. Prove that
$$
\sqrt[3]{\left(a^{2}+b c\right)\left(b^{2}+c a\right)\left(c^{2}+a b\right)}>\frac{a^{2}+b^{2}+c^{2}}{2} .
$$
|
We claim that
$$
a^{2}+b c>\frac{a^{2}+b^{2}+c^{2}}{2}
$$
which will finish the proof. Note that the claimed inequality is equivalent to
$$
\begin{aligned}
a^{2}+b c>\frac{a^{2}+b^{2}+c^{2}}{2} & \Longleftrightarrow 2 a^{2}+2 b c>a^{2}+b^{2}+c^{2} \\
& \Longleftrightarrow a^{2}>(b-c)^{2} \Longleftrightarrow a>|b-c|,
\end{aligned}
$$
which holds due to the assumption of $a, b, c$ being side lengths of a triangle.
|
{
"exam": "BalticWay",
"problem_label": "2",
"problem_match": "\nProblem 2.",
"resource_path": "BalticWay/segmented/en-bw21sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2021"
}
|
Determine all infinite sequences $\left(a_{1}, a_{2}, \ldots\right)$ of positive integers satisfying
$$
a_{n+1}^{2}=1+(n+2021) a_{n}
$$
for all $n \geq 1$.

BALTIC WAY
REYKJAVÍK$\cdot$ 2021
## Baltic Way
Reykjavík, November 11th - 15th
Solutions
|
Clearly $\left(a_{n}\right)_{n=1}^{\infty}=(n+2019)_{n=1}^{\infty}$ is a solution. We claim that it is the only one. Assume $\left(a_{n}\right)_{n=1}^{\infty}$ is a solution. Let $\left(b_{n}\right)_{n=1}^{\infty}=\left(a_{n}-n\right)_{n=1}^{\infty}$. We claim:
1) If $b_{n}<2019$, then $2019>b_{n+1}>b_{n}$.
2) If $b_{n}>2019$, then $2019<b_{n+1}<b_{n}$.
It is clear that these claims imply that $b_{n}=2019$ for all $n$.
Let us prove the claims:
1) Clearly $a_{n}<n+2019$ implies that $a_{n+1}<(n+1)+2019$ which already proves one part of the inequality. Suppose that $b_{n+1} \leq b_{n}$. Then
$$
\left(n+1+b_{n}\right)^{2} \geq a_{n+1}^{2}=1+(n+2021)\left(n+b_{n}\right) .
$$
Expanding gives
$$
\left(n+b_{n}\right)\left(b_{n}-2019\right) \geq 0
$$
which shows that $b_{n} \geq 2019$ contradicting our assumption.
2) It follows in exactly the same way, by just reversing all the inequality signs.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Determine all infinite sequences $\left(a_{1}, a_{2}, \ldots\right)$ of positive integers satisfying
$$
a_{n+1}^{2}=1+(n+2021) a_{n}
$$
for all $n \geq 1$.

BALTIC WAY
REYKJAVÍK$\cdot$ 2021
## Baltic Way
Reykjavík, November 11th - 15th
Solutions
|
Clearly $\left(a_{n}\right)_{n=1}^{\infty}=(n+2019)_{n=1}^{\infty}$ is a solution. We claim that it is the only one. Assume $\left(a_{n}\right)_{n=1}^{\infty}$ is a solution. Let $\left(b_{n}\right)_{n=1}^{\infty}=\left(a_{n}-n\right)_{n=1}^{\infty}$. We claim:
1) If $b_{n}<2019$, then $2019>b_{n+1}>b_{n}$.
2) If $b_{n}>2019$, then $2019<b_{n+1}<b_{n}$.
It is clear that these claims imply that $b_{n}=2019$ for all $n$.
Let us prove the claims:
1) Clearly $a_{n}<n+2019$ implies that $a_{n+1}<(n+1)+2019$ which already proves one part of the inequality. Suppose that $b_{n+1} \leq b_{n}$. Then
$$
\left(n+1+b_{n}\right)^{2} \geq a_{n+1}^{2}=1+(n+2021)\left(n+b_{n}\right) .
$$
Expanding gives
$$
\left(n+b_{n}\right)\left(b_{n}-2019\right) \geq 0
$$
which shows that $b_{n} \geq 2019$ contradicting our assumption.
2) It follows in exactly the same way, by just reversing all the inequality signs.
|
{
"exam": "BalticWay",
"problem_label": "3",
"problem_match": "\nProblem 3.",
"resource_path": "BalticWay/segmented/en-bw21sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2021"
}
|
Let $\Gamma$ be a circle in the plane and $S$ be a point on $\Gamma$. Mario and Luigi drive around the circle $\Gamma$ with their go-karts. They both start at $S$ at the same time. They both drive for exactly 6 minutes at constant speed counterclockwise around the track. During these 6 minutes, Luigi makes exactly one lap around $\Gamma$ while Mario, who is three times as fast, makes three laps.
While Mario and Luigi drive their go-karts, Princess Daisy positions herself such that she is always exactly in the middle of the chord between them. When she reaches a point she has already visited, she marks it with a banana.
How many points in the plane, apart from $S$, are marked with a banana by the end of the race?
|
. Without loss of generality, we assume that $\Gamma$ is the unit circle and $S=(1,0)$. Three points are marked with bananas:
(i) After 45 seconds, Luigi has passed through an arc with a subtended angle of $45^{\circ}$ and is at the point $\left(\sqrt{2} / 2, \sqrt{2} / 2\right.$ ), whereas Mario has passed through an arc with a subtended angle of $135^{\circ}$ and is at the point $(-\sqrt{2} / 2, \sqrt{2} / 2)$. Therefore Daisy is at the point $(0, \sqrt{2} / 2)$ after 45 seconds. After 135 seconds, Mario and Luigi's positions are exactly the other way round, so the princess is again at the point $(0, \sqrt{2} / 2)$ and puts a banana there.
## Baltic Way
Reykjavík, November 11th - 15th
Solutions
(ii) Similarly, after 225 seconds and after 315 seconds, Princess Daisy is at the point $(0,-\sqrt{2} / 2)$ and puts a banana there.
(iii) After 90 seconds, Luigi is at $(0,1)$ and Mario at $(0,-1)$, so that Daisy is at the origin of the plane. After 270 seconds, Mario and Luigi's positions are exactly the other way round, hence Princess Daisy drops a banana at the point $(0,0)$.
We claim that no other point in the plane, apart from these three points and $S$, is marked with a banana. Let $t_{1}$ and $t_{2}$ be two different times when Daisy is at the same place. For $n \in\{1,2\}$ we write Luigis position at time $t_{n}$ as a complex number $z_{n}=\exp \left(i x_{n}\right)$ with $\left.x_{n} \in\right] 0,2 \pi[$. At this time, Mario is located at $z_{i}^{3}$ and Daisy at $\left(z_{i}^{3}+z_{i}\right) / 2$. According to our assumption we have $\left(z_{1}^{3}+z_{1}\right) / 2=\left(z_{2}^{3}+z_{2}\right) / 2$ or, equivalently, $\left(z_{1}-z_{2}\right)\left(z_{1}^{2}+z_{1} z_{2}+z_{2}^{2}+1\right)=0$. We have $z_{1} \neq z_{2}$, so that we must have $z_{1}^{2}+z_{1} z_{2}+z_{2}^{2}=-1$.
We proceed with an observation of the structure of $\Gamma$ as a set of complex numbers. Suppose that $z \in \Gamma \backslash\{S\}$. Then $z+1+z^{-1} \in \Gamma$ if and only if $z \in\{i,-1,-i\}$. For a proof of the observation note that $z+1+z^{-1}=z+1+\bar{z}$ is a real number for every $z \in \mathbb{C}$ with norm $|z|=1$. So it lies on the unit circle if and only if it is equal to 1 , in which case the real part of $z$ is equal to 0 , or it is equal to -1 , in which case the real part of $z$ is equal to -1 . We apply the observation to the number $z=z_{1} / z_{2}$, which satisfies the premise since $z+1+\bar{z}=-\overline{z_{1}} \cdot \overline{z_{2}} \in \Gamma$. Therefore, one of the following cases must occur.
(i) We have $z= \pm i$, that is, $z_{1}= \pm i z_{2}$. Without loss of generality we may assume $z_{2}=i z_{1}$. It follows that $-1=z_{1}^{2}+z_{1} z_{2}+z_{2}^{2}=i z_{1}^{2}$, so that $z_{1}=\exp (i \pi / 4)$ or $z_{1}=\exp (5 i \pi / 4)$. In the former case $\left(z_{1}, z_{2}\right)=(\exp (i \pi / 4), \exp (3 i \pi / 4))$, which matches case (1) above. In the latter case $\left(z_{1}, z_{2}\right)=(\exp (5 i \pi / 4), \exp (7 i \pi / 4))$, which matches case (2) above.
(ii) We have $z=-1$, that is, $z_{2}=-z_{1}$. It follows that $-1=z_{1}^{2}+z_{1} z_{2}+z_{2}^{2}=z_{1}^{2}$, so that $z_{1}=i$ or $z_{1}=-i$. This matches case (3) above.
Depiction of the path Daisy takes
## Baltic Way
Reykjavík, November 11th - 15th
Solutions
|
3
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $\Gamma$ be a circle in the plane and $S$ be a point on $\Gamma$. Mario and Luigi drive around the circle $\Gamma$ with their go-karts. They both start at $S$ at the same time. They both drive for exactly 6 minutes at constant speed counterclockwise around the track. During these 6 minutes, Luigi makes exactly one lap around $\Gamma$ while Mario, who is three times as fast, makes three laps.
While Mario and Luigi drive their go-karts, Princess Daisy positions herself such that she is always exactly in the middle of the chord between them. When she reaches a point she has already visited, she marks it with a banana.
How many points in the plane, apart from $S$, are marked with a banana by the end of the race?
|
. Without loss of generality, we assume that $\Gamma$ is the unit circle and $S=(1,0)$. Three points are marked with bananas:
(i) After 45 seconds, Luigi has passed through an arc with a subtended angle of $45^{\circ}$ and is at the point $\left(\sqrt{2} / 2, \sqrt{2} / 2\right.$ ), whereas Mario has passed through an arc with a subtended angle of $135^{\circ}$ and is at the point $(-\sqrt{2} / 2, \sqrt{2} / 2)$. Therefore Daisy is at the point $(0, \sqrt{2} / 2)$ after 45 seconds. After 135 seconds, Mario and Luigi's positions are exactly the other way round, so the princess is again at the point $(0, \sqrt{2} / 2)$ and puts a banana there.
## Baltic Way
Reykjavík, November 11th - 15th
Solutions
(ii) Similarly, after 225 seconds and after 315 seconds, Princess Daisy is at the point $(0,-\sqrt{2} / 2)$ and puts a banana there.
(iii) After 90 seconds, Luigi is at $(0,1)$ and Mario at $(0,-1)$, so that Daisy is at the origin of the plane. After 270 seconds, Mario and Luigi's positions are exactly the other way round, hence Princess Daisy drops a banana at the point $(0,0)$.
We claim that no other point in the plane, apart from these three points and $S$, is marked with a banana. Let $t_{1}$ and $t_{2}$ be two different times when Daisy is at the same place. For $n \in\{1,2\}$ we write Luigis position at time $t_{n}$ as a complex number $z_{n}=\exp \left(i x_{n}\right)$ with $\left.x_{n} \in\right] 0,2 \pi[$. At this time, Mario is located at $z_{i}^{3}$ and Daisy at $\left(z_{i}^{3}+z_{i}\right) / 2$. According to our assumption we have $\left(z_{1}^{3}+z_{1}\right) / 2=\left(z_{2}^{3}+z_{2}\right) / 2$ or, equivalently, $\left(z_{1}-z_{2}\right)\left(z_{1}^{2}+z_{1} z_{2}+z_{2}^{2}+1\right)=0$. We have $z_{1} \neq z_{2}$, so that we must have $z_{1}^{2}+z_{1} z_{2}+z_{2}^{2}=-1$.
We proceed with an observation of the structure of $\Gamma$ as a set of complex numbers. Suppose that $z \in \Gamma \backslash\{S\}$. Then $z+1+z^{-1} \in \Gamma$ if and only if $z \in\{i,-1,-i\}$. For a proof of the observation note that $z+1+z^{-1}=z+1+\bar{z}$ is a real number for every $z \in \mathbb{C}$ with norm $|z|=1$. So it lies on the unit circle if and only if it is equal to 1 , in which case the real part of $z$ is equal to 0 , or it is equal to -1 , in which case the real part of $z$ is equal to -1 . We apply the observation to the number $z=z_{1} / z_{2}$, which satisfies the premise since $z+1+\bar{z}=-\overline{z_{1}} \cdot \overline{z_{2}} \in \Gamma$. Therefore, one of the following cases must occur.
(i) We have $z= \pm i$, that is, $z_{1}= \pm i z_{2}$. Without loss of generality we may assume $z_{2}=i z_{1}$. It follows that $-1=z_{1}^{2}+z_{1} z_{2}+z_{2}^{2}=i z_{1}^{2}$, so that $z_{1}=\exp (i \pi / 4)$ or $z_{1}=\exp (5 i \pi / 4)$. In the former case $\left(z_{1}, z_{2}\right)=(\exp (i \pi / 4), \exp (3 i \pi / 4))$, which matches case (1) above. In the latter case $\left(z_{1}, z_{2}\right)=(\exp (5 i \pi / 4), \exp (7 i \pi / 4))$, which matches case (2) above.
(ii) We have $z=-1$, that is, $z_{2}=-z_{1}$. It follows that $-1=z_{1}^{2}+z_{1} z_{2}+z_{2}^{2}=z_{1}^{2}$, so that $z_{1}=i$ or $z_{1}=-i$. This matches case (3) above.

Depiction of the path Daisy takes
## Baltic Way
Reykjavík, November 11th - 15th
Solutions
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "\nProblem 4.",
"resource_path": "BalticWay/segmented/en-bw21sol.jsonl",
"solution_match": "\nSolution 1",
"tier": "T3",
"year": "2021"
}
|
Let $\Gamma$ be a circle in the plane and $S$ be a point on $\Gamma$. Mario and Luigi drive around the circle $\Gamma$ with their go-karts. They both start at $S$ at the same time. They both drive for exactly 6 minutes at constant speed counterclockwise around the track. During these 6 minutes, Luigi makes exactly one lap around $\Gamma$ while Mario, who is three times as fast, makes three laps.
While Mario and Luigi drive their go-karts, Princess Daisy positions herself such that she is always exactly in the middle of the chord between them. When she reaches a point she has already visited, she marks it with a banana.
How many points in the plane, apart from $S$, are marked with a banana by the end of the race?
|
. We represent the position of Luigi and Mario by $(t, 3 t)(\bmod 1)$, so when Luigi is at angle $t \cdot 2 \pi$, Mario is at angle $3 t \cdot 2 \pi$.
A chord (if it is not the diameter is determined by its midpoint. Therefore Daisy revisit a location only if
$$
(x, 3 x) \equiv(3 y, y) \quad(\bmod 1)
$$
for different value of $x, y(\bmod 1)$. By inspection, the three locations are visited twice.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $\Gamma$ be a circle in the plane and $S$ be a point on $\Gamma$. Mario and Luigi drive around the circle $\Gamma$ with their go-karts. They both start at $S$ at the same time. They both drive for exactly 6 minutes at constant speed counterclockwise around the track. During these 6 minutes, Luigi makes exactly one lap around $\Gamma$ while Mario, who is three times as fast, makes three laps.
While Mario and Luigi drive their go-karts, Princess Daisy positions herself such that she is always exactly in the middle of the chord between them. When she reaches a point she has already visited, she marks it with a banana.
How many points in the plane, apart from $S$, are marked with a banana by the end of the race?
|
. We represent the position of Luigi and Mario by $(t, 3 t)(\bmod 1)$, so when Luigi is at angle $t \cdot 2 \pi$, Mario is at angle $3 t \cdot 2 \pi$.
A chord (if it is not the diameter is determined by its midpoint. Therefore Daisy revisit a location only if
$$
(x, 3 x) \equiv(3 y, y) \quad(\bmod 1)
$$
for different value of $x, y(\bmod 1)$. By inspection, the three locations are visited twice.

|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "\nProblem 4.",
"resource_path": "BalticWay/segmented/en-bw21sol.jsonl",
"solution_match": "\nSolution 2",
"tier": "T3",
"year": "2021"
}
|
Let $x, y \in \mathbb{R}$ be such that $x=y(3-y)^{2}$ and $y=x(3-x)^{2}$. Find all possible values of $x+y$.
|
. The set $\{0,3,4,5,8\}$ contains all possible values for $x+y$.
A pair $(x, x) \in \mathbb{R}^{2}$ satisfies the equations if and only if $x=x(3-x)^{2}$, and it is easy to see that this cubic equation has the solution set $\{0,2,4\}$. These pairs give us 0,4 and 8 as possible values for $x+y$.
Assuming $x \neq y$ let $s$ be the sum $x+y$ and $p$ be the product $x y$. Subtracting the first equation from the second and cancelling out the term $x-y$ we get
$$
p=s^{2}-6 s+10 \text {. }
$$
Adding the two equations gives
$$
0=s\left(s^{2}-3 p\right)-6\left(s^{2}-2 p\right)+8 s .
$$
Together the equations give
$$
0=s^{3}-12 s^{2}+47 s-60=(s-3)(s-4)(s-5) \text {. }
$$
## Baltic Way
Reykjavík, November 11th - 15th
Solutions
The only possible values for $x+y$ when $x \neq y$ are therefore 3,4 and 5 . We have already seen that $x+y=4$ has a solution $x=y=2$.
Next we investigate the case $x+y=3$. Here we can simplify the given equations as $x=y x^{2}$ and $y=x y^{2}$. The number $x$ cannot be zero in this case, since otherwise $y$ and $k$ would also be zero. We can conclude that $x y=1$. The equations $x+y=3$ and $x y=1$, according to Vieta's Theorem, imply that $x$ and $y$ are the solutions of the equation $\lambda^{2}-3 \lambda+1=0$. Hence
$$
(x, y)=\left(\frac{3+\sqrt{5}}{2}, \frac{3-\sqrt{5}}{2}\right) \quad \text { or } \quad(x, y)=\left(\frac{3-\sqrt{5}}{2}, \frac{3+\sqrt{5}}{2}\right)
$$
and it is easy to verify that both pairs satisfy the equations. These pairs give us 3 as a possible value for $x+y$.
A simple calculation shows that if a pair $(x, y) \in \mathbb{R}^{2}$ satisfy the equations, then the pair (4-x,4-y) is solution to the equations. From the pairs we have just found, we can therefore construct pairs of solutions
$$
(x, y)=\left(\frac{5-\sqrt{5}}{2}, \frac{5+\sqrt{5}}{2}\right) \text { and }(x, y)=\left(\frac{5+\sqrt{5}}{2}, \frac{5-\sqrt{5}}{2}\right),
$$
which give us 5 as a possible value for $x+y$.
|
\{0,3,4,5,8\}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $x, y \in \mathbb{R}$ be such that $x=y(3-y)^{2}$ and $y=x(3-x)^{2}$. Find all possible values of $x+y$.
|
. The set $\{0,3,4,5,8\}$ contains all possible values for $x+y$.
A pair $(x, x) \in \mathbb{R}^{2}$ satisfies the equations if and only if $x=x(3-x)^{2}$, and it is easy to see that this cubic equation has the solution set $\{0,2,4\}$. These pairs give us 0,4 and 8 as possible values for $x+y$.
Assuming $x \neq y$ let $s$ be the sum $x+y$ and $p$ be the product $x y$. Subtracting the first equation from the second and cancelling out the term $x-y$ we get
$$
p=s^{2}-6 s+10 \text {. }
$$
Adding the two equations gives
$$
0=s\left(s^{2}-3 p\right)-6\left(s^{2}-2 p\right)+8 s .
$$
Together the equations give
$$
0=s^{3}-12 s^{2}+47 s-60=(s-3)(s-4)(s-5) \text {. }
$$
## Baltic Way
Reykjavík, November 11th - 15th
Solutions
The only possible values for $x+y$ when $x \neq y$ are therefore 3,4 and 5 . We have already seen that $x+y=4$ has a solution $x=y=2$.
Next we investigate the case $x+y=3$. Here we can simplify the given equations as $x=y x^{2}$ and $y=x y^{2}$. The number $x$ cannot be zero in this case, since otherwise $y$ and $k$ would also be zero. We can conclude that $x y=1$. The equations $x+y=3$ and $x y=1$, according to Vieta's Theorem, imply that $x$ and $y$ are the solutions of the equation $\lambda^{2}-3 \lambda+1=0$. Hence
$$
(x, y)=\left(\frac{3+\sqrt{5}}{2}, \frac{3-\sqrt{5}}{2}\right) \quad \text { or } \quad(x, y)=\left(\frac{3-\sqrt{5}}{2}, \frac{3+\sqrt{5}}{2}\right)
$$
and it is easy to verify that both pairs satisfy the equations. These pairs give us 3 as a possible value for $x+y$.
A simple calculation shows that if a pair $(x, y) \in \mathbb{R}^{2}$ satisfy the equations, then the pair (4-x,4-y) is solution to the equations. From the pairs we have just found, we can therefore construct pairs of solutions
$$
(x, y)=\left(\frac{5-\sqrt{5}}{2}, \frac{5+\sqrt{5}}{2}\right) \text { and }(x, y)=\left(\frac{5+\sqrt{5}}{2}, \frac{5-\sqrt{5}}{2}\right),
$$
which give us 5 as a possible value for $x+y$.
|
{
"exam": "BalticWay",
"problem_label": "5",
"problem_match": "\nProblem 5.",
"resource_path": "BalticWay/segmented/en-bw21sol.jsonl",
"solution_match": "\nSolution 1",
"tier": "T3",
"year": "2021"
}
|
Let $x, y \in \mathbb{R}$ be such that $x=y(3-y)^{2}$ and $y=x(3-x)^{2}$. Find all possible values of $x+y$.
|
. Let $f(x)=x(3-x)^{2}$. It is easy to check that if $x<0$ then $f(x)<x$. In particular $f(f(x))<f(x)<x$ in this case, so that the pair $(x, f(x))$ cannot be a solution. Similarly, $f(x)>x$ if $x>4$, so the pair $(x, f(x))$ cannot be a solution in this case either.
Suppose that $(x, y) \in \mathbb{R}^{2}$ is a solution. According to the previous remark $x \in[0,4]$, and similarly, $y \in[0,4]$. Hence we may write $x=2+2 r$ and $y=2+2 s$ with $r, s \in[-1,1]$. After substitution and simplification, the equation $x=y(3-y)^{2}$ transforms into the equation $r=4 s^{3}-3 s$. Recall the trigonometric identities for threefold angles. If $s=\cos (\alpha)$ for some $\alpha \in \mathbb{R}$, then $r=4 \cos ^{3}(\alpha)-$ $3 \cos (\alpha)=\cos (3 \alpha)$. In the same way $s=4 r^{3}-3 r=\cos (9 \alpha)$.
We can deduce that $9 \alpha=2 \pi m+\alpha$ or $9 \alpha=2 \pi l-\alpha$ for some integers $m$ and $l$. In the former case we have $8 \alpha=2 \pi m$, so that $m \in\{0,1,2,3,4\}$, and the corresponding possible pairs of solutions can be found in Figure 1. In the former case we have $10 \alpha=2 \pi l$, so that $l \in\{0,1,2,3,4,5\}$, where $l=0$ and $l=5$ result in angles that we have already considered in the first case. We consider the other options in Figure 2 taking into account the well-known identities $\cos (\pi / 5)=(1+\sqrt{5}) / 4$ and $\cos (3 \pi / 5)=(1-\sqrt{5}) / 4$.
## Baltic Way
Reykjavík, November 11th - 15th
Solutions
| $m$ | $8 \alpha$ | $\alpha$ | $r$ | $s$ | $x$ | $y$ | $x+y$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 0 | 0 | 0 | 1 | 1 | 4 | 4 | 8 |
| 1 | $2 \pi$ | $\pi / 4$ | $\sqrt{2} / 2$ | $-\sqrt{2} / 2$ | $2+\sqrt{2}$ | $2-\sqrt{2}$ | 4 |
| 2 | $4 \pi$ | $\pi / 2$ | 0 | 0 | 2 | 2 | 4 |
| 3 | $6 \pi$ | $3 \pi / 4$ | $-\sqrt{2} / 2$ | $\sqrt{2} / 2$ | $2-\sqrt{2}$ | $2+\sqrt{2}$ | 4 |
| 4 | $8 \pi$ | $\pi$ | -1 | -1 | 0 | 0 | 0 |
Figure 1: Pairs of solutions and their sums
| $l$ | $10 \alpha$ | $\alpha$ | $r$ | $s$ | $x$ | $y$ | $x+y$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 1 | $2 \pi$ | $\pi / 5$ | $(1+\sqrt{5}) / 4$ | $(1-\sqrt{5}) / 4$ | $(5+\sqrt{5}) / 2$ | $(5-\sqrt{5}) / 2$ | 5 |
| 2 | $4 \pi$ | $2 \pi / 5$ | $(-1+\sqrt{5}) / 4$ | $(-1-\sqrt{5}) / 4$ | $(3+\sqrt{5}) / 2$ | $(3-\sqrt{5}) / 2$ | 3 |
| 3 | $6 \pi$ | $3 \pi / 5$ | $(1-\sqrt{5}) / 4$ | $(1+\sqrt{5}) / 4$ | $(5-\sqrt{5}) / 2$ | $(5+\sqrt{5}) / 2$ | 5 |
| 4 | $8 \pi$ | $4 \pi / 5$ | $(-1-\sqrt{5}) / 4$ | $(-1+\sqrt{5}) / 4$ | $(3-\sqrt{5}) / 2$ | $(3+\sqrt{5}) / 2$ | 3 |
Figure 2: Pairs of solutions and their sums
|
0, 3, 4, 5, 8
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $x, y \in \mathbb{R}$ be such that $x=y(3-y)^{2}$ and $y=x(3-x)^{2}$. Find all possible values of $x+y$.
|
. Let $f(x)=x(3-x)^{2}$. It is easy to check that if $x<0$ then $f(x)<x$. In particular $f(f(x))<f(x)<x$ in this case, so that the pair $(x, f(x))$ cannot be a solution. Similarly, $f(x)>x$ if $x>4$, so the pair $(x, f(x))$ cannot be a solution in this case either.
Suppose that $(x, y) \in \mathbb{R}^{2}$ is a solution. According to the previous remark $x \in[0,4]$, and similarly, $y \in[0,4]$. Hence we may write $x=2+2 r$ and $y=2+2 s$ with $r, s \in[-1,1]$. After substitution and simplification, the equation $x=y(3-y)^{2}$ transforms into the equation $r=4 s^{3}-3 s$. Recall the trigonometric identities for threefold angles. If $s=\cos (\alpha)$ for some $\alpha \in \mathbb{R}$, then $r=4 \cos ^{3}(\alpha)-$ $3 \cos (\alpha)=\cos (3 \alpha)$. In the same way $s=4 r^{3}-3 r=\cos (9 \alpha)$.
We can deduce that $9 \alpha=2 \pi m+\alpha$ or $9 \alpha=2 \pi l-\alpha$ for some integers $m$ and $l$. In the former case we have $8 \alpha=2 \pi m$, so that $m \in\{0,1,2,3,4\}$, and the corresponding possible pairs of solutions can be found in Figure 1. In the former case we have $10 \alpha=2 \pi l$, so that $l \in\{0,1,2,3,4,5\}$, where $l=0$ and $l=5$ result in angles that we have already considered in the first case. We consider the other options in Figure 2 taking into account the well-known identities $\cos (\pi / 5)=(1+\sqrt{5}) / 4$ and $\cos (3 \pi / 5)=(1-\sqrt{5}) / 4$.
## Baltic Way
Reykjavík, November 11th - 15th
Solutions
| $m$ | $8 \alpha$ | $\alpha$ | $r$ | $s$ | $x$ | $y$ | $x+y$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 0 | 0 | 0 | 1 | 1 | 4 | 4 | 8 |
| 1 | $2 \pi$ | $\pi / 4$ | $\sqrt{2} / 2$ | $-\sqrt{2} / 2$ | $2+\sqrt{2}$ | $2-\sqrt{2}$ | 4 |
| 2 | $4 \pi$ | $\pi / 2$ | 0 | 0 | 2 | 2 | 4 |
| 3 | $6 \pi$ | $3 \pi / 4$ | $-\sqrt{2} / 2$ | $\sqrt{2} / 2$ | $2-\sqrt{2}$ | $2+\sqrt{2}$ | 4 |
| 4 | $8 \pi$ | $\pi$ | -1 | -1 | 0 | 0 | 0 |
Figure 1: Pairs of solutions and their sums
| $l$ | $10 \alpha$ | $\alpha$ | $r$ | $s$ | $x$ | $y$ | $x+y$ |
| :---: | :---: | :---: | :---: | :---: | :---: | :---: | :---: |
| 1 | $2 \pi$ | $\pi / 5$ | $(1+\sqrt{5}) / 4$ | $(1-\sqrt{5}) / 4$ | $(5+\sqrt{5}) / 2$ | $(5-\sqrt{5}) / 2$ | 5 |
| 2 | $4 \pi$ | $2 \pi / 5$ | $(-1+\sqrt{5}) / 4$ | $(-1-\sqrt{5}) / 4$ | $(3+\sqrt{5}) / 2$ | $(3-\sqrt{5}) / 2$ | 3 |
| 3 | $6 \pi$ | $3 \pi / 5$ | $(1-\sqrt{5}) / 4$ | $(1+\sqrt{5}) / 4$ | $(5-\sqrt{5}) / 2$ | $(5+\sqrt{5}) / 2$ | 5 |
| 4 | $8 \pi$ | $4 \pi / 5$ | $(-1-\sqrt{5}) / 4$ | $(-1+\sqrt{5}) / 4$ | $(3-\sqrt{5}) / 2$ | $(3+\sqrt{5}) / 2$ | 3 |
Figure 2: Pairs of solutions and their sums
|
{
"exam": "BalticWay",
"problem_label": "5",
"problem_match": "\nProblem 5.",
"resource_path": "BalticWay/segmented/en-bw21sol.jsonl",
"solution_match": "\nSolution 2",
"tier": "T3",
"year": "2021"
}
|
Let $n$ be a positive integer and $t$ be a non-zero real number. Let $a_{1}, a_{2}, \ldots, a_{2 n-1}$ be real numbers (not necessarily distinct). Prove that there exist distinct indices $i_{1}, i_{2}, \ldots, i_{n}$ such that, for all $1 \leq k, l \leq n$, we have $a_{i_{k}}-a_{i_{l}} \neq t$.
|
Let $G=(V, E)$ be a graph with vertex set $V=\{1,2, \ldots, 2 n-1\}$ and edge set $E=$ $\left\{\{i, j\}:\left|a_{i}-a_{j}\right|=t\right\}$.
Note that $G$ has no odd cycles. Indeed, if $j_{1}, \ldots, j_{2 k+1}$ is a cycle, then for all $\ell=1,3,5, \ldots, 2 k-1$ the number $a_{j_{\ell}}$ differs from $a_{j_{\ell+2}}$ by $2 t$ or 0 . Hence $a_{j_{1}}$ differs from $a_{j_{2 k+1}}$ by an even multiple of $t$. Therefore there is no edge between $j_{1}$ and $j_{2 k+1}$ contradicting the assumption that $j_{1}, \ldots, j_{2 k+1}$ is a cycle.
Since $G$ has no odd cycles, it is bipartite. Therefore $V$ can be split into two disjoint sets $V_{1}, V_{2}$ such that there is no edge between any two vertices of $V_{1}$ and there are no edges between any two vertices in $V_{2}$. Since $V$ has $2 n-1$ elements, one of the sets $V_{1}, V_{2}$ has at least $n$ elements. Without loss of generality assume that $V_{1}$ has at least $n$ elements. Then for $k=1,2, \ldots, n$ simply define $i_{k}$ to be the $k$-th least element of $V_{1}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ be a positive integer and $t$ be a non-zero real number. Let $a_{1}, a_{2}, \ldots, a_{2 n-1}$ be real numbers (not necessarily distinct). Prove that there exist distinct indices $i_{1}, i_{2}, \ldots, i_{n}$ such that, for all $1 \leq k, l \leq n$, we have $a_{i_{k}}-a_{i_{l}} \neq t$.
|
Let $G=(V, E)$ be a graph with vertex set $V=\{1,2, \ldots, 2 n-1\}$ and edge set $E=$ $\left\{\{i, j\}:\left|a_{i}-a_{j}\right|=t\right\}$.
Note that $G$ has no odd cycles. Indeed, if $j_{1}, \ldots, j_{2 k+1}$ is a cycle, then for all $\ell=1,3,5, \ldots, 2 k-1$ the number $a_{j_{\ell}}$ differs from $a_{j_{\ell+2}}$ by $2 t$ or 0 . Hence $a_{j_{1}}$ differs from $a_{j_{2 k+1}}$ by an even multiple of $t$. Therefore there is no edge between $j_{1}$ and $j_{2 k+1}$ contradicting the assumption that $j_{1}, \ldots, j_{2 k+1}$ is a cycle.
Since $G$ has no odd cycles, it is bipartite. Therefore $V$ can be split into two disjoint sets $V_{1}, V_{2}$ such that there is no edge between any two vertices of $V_{1}$ and there are no edges between any two vertices in $V_{2}$. Since $V$ has $2 n-1$ elements, one of the sets $V_{1}, V_{2}$ has at least $n$ elements. Without loss of generality assume that $V_{1}$ has at least $n$ elements. Then for $k=1,2, \ldots, n$ simply define $i_{k}$ to be the $k$-th least element of $V_{1}$.
|
{
"exam": "BalticWay",
"problem_label": "6",
"problem_match": "\nProblem 6.",
"resource_path": "BalticWay/segmented/en-bw21sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2021"
}
|
Let $n>2$ be an integer. Anna, Edda and Magni play a game on a hexagonal board tiled with regular hexagons, with $n$ tiles on each side. The figure shows a board with 5 tiles on each side. The central tile is marked.
## Baltic Way
Reykjavík, November 11th - 15th
Solutions
The game begins with a stone on a tile in one corner of the board. Edda and Magni are on the same team, playing against Anna, and they win if the stone is on the central tile at the end of any player's turn. Anna, Edda and Magni take turns moving the stone: Anna begins, then Edda and then Magni, and so on.
The rules for each player's turn are:
- Anna has to move the stone to an adjacent tile, in any direction.
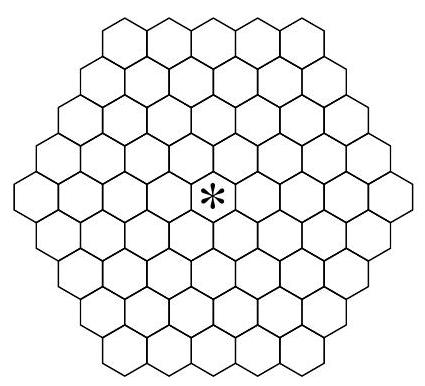
- Edda has to move the stone straight by two tiles in any of the 6 possible directions.
- Magni has a choice of passing his turn, or moving the stone straight by three tiles in any of the 6 possible directions.
Find all $n$ for which Edda and Magni have a winning strategy.
|
We colour the board in three colours in such a way that no neighbouring tiles are of the same colour. We can give each hexagon a coordinate using $\overrightarrow{e_{1}}=(1,0)$ and $\overrightarrow{e_{2}}=\left(\cos \left(120^{\circ}, \sin \left(120^{\circ}\right)\right)=\right.$ $\left(\frac{-1}{2}, \frac{\sqrt{3}}{2}\right)$ as basis. Let the central tile be the origin. Then each hexagon has center at $a \cdot \overrightarrow{e_{1}}+b \cdot \overrightarrow{e_{2}},(a, b) \in$ $\mathbb{Z}^{2}$. The tuple $(a, b)$ is the coordinate for a given hexagon its neighbours are $(a+1, b),(a+1, b+1)$, $(a, b+1),(a-1, b),(a-1, b-1)$ and $(a, b-1)$. We colour the hexagon with coordinates $(a, b)$ with colour number $(a+b)(\bmod 3)$. It is clear that neighbouring hexagons do not share a colour. (In fact this is the only three colouring of a hexagonal tiling). See figure 3 .

Figure 3: Three colouring of the hexagonal tiling for 5 hexagons on each side
We see that if $n \equiv 1(\bmod 3)$, the stone begins in a tile in the same colour as the central tile, let that colour be grey. By regarding a few cases, we see that whatever Anna does, Edda and Magni can end

BALTIC WAY
REYKJAVÍK$\cdot$ 2021
## Baltic Way
Reykjavík, November 11th - 15th
Solutions
their turns by getting the stone to a prescribed grey tile of the closest grey tiles. Therefore they can get the stone to the central tile.
If $n \not \equiv 1(\bmod 3)$, the stone does not begin on the same grey colour as the central tile. Say the stone begins on a white tile, and say the third colour is black. Anna can always move the stone to a grey tile that is not on the same horizontal/diagonal line as the central tile. Then Anna moves the stone to a white or black tile. After Magni moves the stone is still again on a white/black tile. Anna can continue this indefinitely, with the stone never reaching the central tile.
|
n \equiv 1(\bmod 3)
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n>2$ be an integer. Anna, Edda and Magni play a game on a hexagonal board tiled with regular hexagons, with $n$ tiles on each side. The figure shows a board with 5 tiles on each side. The central tile is marked.
## Baltic Way
Reykjavík, November 11th - 15th
Solutions
The game begins with a stone on a tile in one corner of the board. Edda and Magni are on the same team, playing against Anna, and they win if the stone is on the central tile at the end of any player's turn. Anna, Edda and Magni take turns moving the stone: Anna begins, then Edda and then Magni, and so on.
The rules for each player's turn are:
- Anna has to move the stone to an adjacent tile, in any direction.

- Edda has to move the stone straight by two tiles in any of the 6 possible directions.
- Magni has a choice of passing his turn, or moving the stone straight by three tiles in any of the 6 possible directions.
Find all $n$ for which Edda and Magni have a winning strategy.
|
We colour the board in three colours in such a way that no neighbouring tiles are of the same colour. We can give each hexagon a coordinate using $\overrightarrow{e_{1}}=(1,0)$ and $\overrightarrow{e_{2}}=\left(\cos \left(120^{\circ}, \sin \left(120^{\circ}\right)\right)=\right.$ $\left(\frac{-1}{2}, \frac{\sqrt{3}}{2}\right)$ as basis. Let the central tile be the origin. Then each hexagon has center at $a \cdot \overrightarrow{e_{1}}+b \cdot \overrightarrow{e_{2}},(a, b) \in$ $\mathbb{Z}^{2}$. The tuple $(a, b)$ is the coordinate for a given hexagon its neighbours are $(a+1, b),(a+1, b+1)$, $(a, b+1),(a-1, b),(a-1, b-1)$ and $(a, b-1)$. We colour the hexagon with coordinates $(a, b)$ with colour number $(a+b)(\bmod 3)$. It is clear that neighbouring hexagons do not share a colour. (In fact this is the only three colouring of a hexagonal tiling). See figure 3 .

Figure 3: Three colouring of the hexagonal tiling for 5 hexagons on each side
We see that if $n \equiv 1(\bmod 3)$, the stone begins in a tile in the same colour as the central tile, let that colour be grey. By regarding a few cases, we see that whatever Anna does, Edda and Magni can end

BALTIC WAY
REYKJAVÍK$\cdot$ 2021
## Baltic Way
Reykjavík, November 11th - 15th
Solutions
their turns by getting the stone to a prescribed grey tile of the closest grey tiles. Therefore they can get the stone to the central tile.
If $n \not \equiv 1(\bmod 3)$, the stone does not begin on the same grey colour as the central tile. Say the stone begins on a white tile, and say the third colour is black. Anna can always move the stone to a grey tile that is not on the same horizontal/diagonal line as the central tile. Then Anna moves the stone to a white or black tile. After Magni moves the stone is still again on a white/black tile. Anna can continue this indefinitely, with the stone never reaching the central tile.
|
{
"exam": "BalticWay",
"problem_label": "7",
"problem_match": "\nProblem 7.",
"resource_path": "BalticWay/segmented/en-bw21sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2021"
}
|
We are given a collection of $2^{2^{k}}$ coins, where $k$ is a non-negative integer. Exactly one coin is fake. We have an unlimited number of service dogs. One dog is sick but we do not know which one. A test consists of three steps: select some coins from the collection of all coins; choose a service dog; the dog smells all of the selected coins at once. A healthy dog will bark if and only if the fake coin is amongst them. Whether the sick dog will bark or not is random.
Devise a strategy to find the fake coin, using at most $2^{k}+k+2$ tests, and prove that it works.
|
Number the coins by $2^{k}$-digit binary numbers from $\overbrace{00 \ldots 0}^{\text {length } 2^{k}}$ to $\overbrace{11 \ldots 1}^{\text {length } 2^{k}}$. Let $A_{i}$ be the set of coins which have 0 in $i$-th position of the binary number. The first $2^{k}$ tests we perform with the help of $2^{k}$ different dogs. In the $i$-th test we determine whether the set $A_{i}$ contains the fake coin. With out loss of generality we may assume that the dogs determined that all the digits in the number of the fake coin are 0 's. Due to the possible presence of the sick dog in these tests, it means in fact that the binary number of the fake coin contains at most one 1 .
$$
\text { length } 2^{k}
$$
In the next test we let a new dog determine whether the coin $00 \ldots 0$ is genuine. If the new dog barks then the coin is really fake, for otherwise two dogs had given us a false answer. If the new dog does not bark we find a dog we have not used before to test the suspected coin.
(i) If the last two dogs disagree one of them must be sick and hence the first $k$ dogs must be healthy. length $2^{k}$
In this case the coin $\overbrace{00 \ldots 0}$ is the fake one.
(ii) If the last two dogs agree (by not barking) it follows that both of them are healthy. The reason is that if one of the last two dogs was sick and did not bark, it would mean that the first $k$ dogs were length $2^{k}$
healthy, implying that the coin $00 \ldots 0$ is fake, but then the other of the last two dogs is healthy and did not bark at the fake coin, a contradiction.

## Baltic Way
Reykjavík, November 11th - 15th
Solutions
Therefore one of the first $2^{k}$ dogs gave a wrong verdict. In this case we have $2^{k}$ possible candidates for the fake coin. We can find the fake coin using the last dog and $k$ tests using binary search.
It follows that no more than $2^{k}+k+2$ tests are needed.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
We are given a collection of $2^{2^{k}}$ coins, where $k$ is a non-negative integer. Exactly one coin is fake. We have an unlimited number of service dogs. One dog is sick but we do not know which one. A test consists of three steps: select some coins from the collection of all coins; choose a service dog; the dog smells all of the selected coins at once. A healthy dog will bark if and only if the fake coin is amongst them. Whether the sick dog will bark or not is random.
Devise a strategy to find the fake coin, using at most $2^{k}+k+2$ tests, and prove that it works.
|
Number the coins by $2^{k}$-digit binary numbers from $\overbrace{00 \ldots 0}^{\text {length } 2^{k}}$ to $\overbrace{11 \ldots 1}^{\text {length } 2^{k}}$. Let $A_{i}$ be the set of coins which have 0 in $i$-th position of the binary number. The first $2^{k}$ tests we perform with the help of $2^{k}$ different dogs. In the $i$-th test we determine whether the set $A_{i}$ contains the fake coin. With out loss of generality we may assume that the dogs determined that all the digits in the number of the fake coin are 0 's. Due to the possible presence of the sick dog in these tests, it means in fact that the binary number of the fake coin contains at most one 1 .
$$
\text { length } 2^{k}
$$
In the next test we let a new dog determine whether the coin $00 \ldots 0$ is genuine. If the new dog barks then the coin is really fake, for otherwise two dogs had given us a false answer. If the new dog does not bark we find a dog we have not used before to test the suspected coin.
(i) If the last two dogs disagree one of them must be sick and hence the first $k$ dogs must be healthy. length $2^{k}$
In this case the coin $\overbrace{00 \ldots 0}$ is the fake one.
(ii) If the last two dogs agree (by not barking) it follows that both of them are healthy. The reason is that if one of the last two dogs was sick and did not bark, it would mean that the first $k$ dogs were length $2^{k}$
healthy, implying that the coin $00 \ldots 0$ is fake, but then the other of the last two dogs is healthy and did not bark at the fake coin, a contradiction.

## Baltic Way
Reykjavík, November 11th - 15th
Solutions
Therefore one of the first $2^{k}$ dogs gave a wrong verdict. In this case we have $2^{k}$ possible candidates for the fake coin. We can find the fake coin using the last dog and $k$ tests using binary search.
It follows that no more than $2^{k}+k+2$ tests are needed.
|
{
"exam": "BalticWay",
"problem_label": "8",
"problem_match": "\nProblem 8.",
"resource_path": "BalticWay/segmented/en-bw21sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2021"
}
|
We are given 2021 points on a plane, no three of which are collinear. Among any 5 of these points, at least 4 lie on the same circle. Is it necessarily true that at least 2020 of the points lie on the same circle?
|
The answer is positive.
Let us first prove a lemma that if 4 points $A, B, C, D$ all lie on circle $\Gamma$ and some two points $X, Y$ do not lie on $\Gamma$, then these 6 points are pairs of intersections of three circles, circle $\Gamma$ and two other circles. Indeed, according to the problem statement there are 4 points among $A, B, C, X, Y$ which are concyclic. These 4 points must include points $X$ and $Y$ because if one of them is not, then the other one must lie on $\Gamma$. Without loss of generality, take $A, B, X, Y$ to lie on the same circle. Similarly for points $A, C, D, X, Y$ there must be 4 points which are concyclic. Analogously, they must include points $X$ and $Y$. Point $A$ cannot be one of them because two circles cannot have more than two common points. Therefore, points $C, D, X, Y$ are concyclic which proves the lemma.
Let us first solve the problem for the case for which there exist 5 points which lie on one circle $\Gamma$. Label these points $A, B, C, D, E$. Let us assume that there exists two points which do not lie on $\Gamma$, label them $X$ and $Y$. According to the previously proven lemma, points $A, B, C, D, X, Y$ must be the pairwise intersections of 3 circles. Without loss of generality, let the intersections of $\Gamma$ with one of the other circles be $A$ and $B$ and with the other circle $C$ and $D$. Similarly, $A, B, C, E, X, Y$ must be the pairwise intersections of three circles one of which is $\Gamma$. This is not possible as none of the points $A, B, C$ lies on the circumcircle of triangle $E X Y$. This contradiction shows that at most 1 point can lie outside circle $\Gamma$, i.e. at least 2020 points lie on circle $\Gamma$.
It remains to look at the case for which no 5 points lie on the same circle. Let $A, B, C, D, E$ be arbitrary 5 points. Without loss of generality, let $A, B, C, D$ be concyclic and $E$ a point not on this circle. According to the lemma, for every other point $F$ and points $A, B, C, D, E$, the 6 points are the intersections of circle $\Gamma$ and some two other circles. But in total, there are 3 such points because one of the two circles must go through $E$ and some 2 points out of $A, B, C, D$, while the other circle must go through point $E$ and the other two points out of $A, B, C, D$. There are only three partitions of $A, B, C, D$ into two sets. There is a contradiction, as there are $2021>5+3$ points in total.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
We are given 2021 points on a plane, no three of which are collinear. Among any 5 of these points, at least 4 lie on the same circle. Is it necessarily true that at least 2020 of the points lie on the same circle?
|
The answer is positive.
Let us first prove a lemma that if 4 points $A, B, C, D$ all lie on circle $\Gamma$ and some two points $X, Y$ do not lie on $\Gamma$, then these 6 points are pairs of intersections of three circles, circle $\Gamma$ and two other circles. Indeed, according to the problem statement there are 4 points among $A, B, C, X, Y$ which are concyclic. These 4 points must include points $X$ and $Y$ because if one of them is not, then the other one must lie on $\Gamma$. Without loss of generality, take $A, B, X, Y$ to lie on the same circle. Similarly for points $A, C, D, X, Y$ there must be 4 points which are concyclic. Analogously, they must include points $X$ and $Y$. Point $A$ cannot be one of them because two circles cannot have more than two common points. Therefore, points $C, D, X, Y$ are concyclic which proves the lemma.
Let us first solve the problem for the case for which there exist 5 points which lie on one circle $\Gamma$. Label these points $A, B, C, D, E$. Let us assume that there exists two points which do not lie on $\Gamma$, label them $X$ and $Y$. According to the previously proven lemma, points $A, B, C, D, X, Y$ must be the pairwise intersections of 3 circles. Without loss of generality, let the intersections of $\Gamma$ with one of the other circles be $A$ and $B$ and with the other circle $C$ and $D$. Similarly, $A, B, C, E, X, Y$ must be the pairwise intersections of three circles one of which is $\Gamma$. This is not possible as none of the points $A, B, C$ lies on the circumcircle of triangle $E X Y$. This contradiction shows that at most 1 point can lie outside circle $\Gamma$, i.e. at least 2020 points lie on circle $\Gamma$.
It remains to look at the case for which no 5 points lie on the same circle. Let $A, B, C, D, E$ be arbitrary 5 points. Without loss of generality, let $A, B, C, D$ be concyclic and $E$ a point not on this circle. According to the lemma, for every other point $F$ and points $A, B, C, D, E$, the 6 points are the intersections of circle $\Gamma$ and some two other circles. But in total, there are 3 such points because one of the two circles must go through $E$ and some 2 points out of $A, B, C, D$, while the other circle must go through point $E$ and the other two points out of $A, B, C, D$. There are only three partitions of $A, B, C, D$ into two sets. There is a contradiction, as there are $2021>5+3$ points in total.
|
{
"exam": "BalticWay",
"problem_label": "9",
"problem_match": "\nProblem 9.",
"resource_path": "BalticWay/segmented/en-bw21sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2021"
}
|
John has a string of paper where $n$ real numbers $a_{i} \in[0,1]$, for all $i \in\{1, \ldots, n\}$, are written in a row. Show that for any given $k<n$, he can cut the string of paper into $k$ non-empty pieces, between adjacent numbers, in such a way that the sum of the numbers on each piece does not differ from any other sum by more than 1 .
## Baltic Way
Reykjavík, November 11th - 15th
Solutions
|
. Denote the sums on each piece by
$$
\begin{aligned}
& S_{1}=a_{1}+a_{2}+\ldots+a_{m_{1}}, \\
& S_{2}=a_{m_{1}+1}+a_{m_{1}+2}+\ldots+a_{m_{2}}, \\
& \quad \ldots \\
& S_{k}=a_{m_{k-1}+1}+\ldots+a_{m_{k}} .
\end{aligned}
$$
By abuse of notation $S_{i}$ will both denote the set of numbers enclosed by cuts and its sum, the meaning of which must be determined by the context.
We will start the following algorithm. During this algorithm we will move some elements to the neighbouring piece and construct new sequence of pieces $S^{\star}=\left(S_{1}^{\star}, S_{2}^{\star}, \ldots, S_{k}^{\star}\right)$. Empty pieces may appear, but we will consider that case in the end.
(1) Find $p \leq k$ such that $S_{p}$ is the piece with the maximum sum of elements.
(2) If $S_{p} \leq \min \left(S_{1}, \ldots, S_{k}\right)+1$ we are done.
(3) If $S_{p}>\min \left(S_{1}, \ldots, S_{k}\right)+1$, let $S_{q}$ be the pieces with minimum sum of elements nearest to $S_{p}$ (ties broken arbitrarily) and let $S_{h}$ be the next pieces to $S_{q}$ between $S_{p}$ and $S_{q}$ (it is non empty by the choice of $S_{q}$ ). Then either $p<q$ and then $h=q-1$ and we define $S^{\star}$ by moving the last element from $S_{h}=S_{q-1}$ to $S_{q}$, or $q<p$, and then $h=q+1$ and $S^{\star}$ is obtained by moving the first element of $S_{h}=S_{q+1}$ to $S_{q}$. If $p=h$ then set $S=S^{\star}$ and go to step (1). If $p \neq h$ then set $S=S^{\star}$ and proceed to step (2).
Note that in step (3) each number $S_{i}^{\star}$ is at most $S_{p}$ and no new piece with sum $S_{p}$ is created. Indeed, $S_{h}^{\star}<S_{h} \leq S_{p}$, and for some $j$ we have $S_{q}^{\star}=S_{q}+a_{j}<S_{p}$ since $a_{j} \in[0,1]$ and $S_{p}>$ $\min \left(S_{1}, \ldots, S_{k}\right)+1$. It is clear also that $\max \left(S_{1}, \ldots, S_{k}\right)$ does not increase during the algorithm.
Note also that in step (3) the pieces $S_{h}$ may become empty. Then, in the next iteration of the algorithm, $q=h$ will be chosen since $\min \left(S_{1}, \ldots, S_{k}\right)=S_{h}=0$ and in step (3) $S_{h}^{\star}$ will become non empty (but one of its neighbours may become empty, etc.).
Claim: In the algorithm above, Step (3) is repeated at most $k n$ times with $S_{p}$ being the same maximal pieces in $S^{\star}$ and in $S$.
Proof. Let $s_{i}$ be the number of elements in $i$-th pieces. Then the number
$$
\sum_{i=1}^{k}|i-p| s_{i}
$$
takes positive integral values and is always less than $k n$. It is clear that this number decreases during the algorithm.
## Baltic Way
Thus after at most $k n$ iteration of (3), the algorithm decreases the value of $S_{p}$ and so goes to (1). Consequently it decreases either the number of pieces with maximal sums or $\max \left(S_{1}, \ldots, S_{k}\right)$. As there are only finitely many ways to split the sum onto pieces, the algorithm eventually terminates at (2).
When the algorithm teminates, we are left with a sequence $S=\left(S_{1}, S_{2}, \ldots, S_{k}\right)$ where the piece $S_{p}$ with maximum sum is such that $S_{p} \leq \min \left(S_{1}, \ldots, S_{k}\right)+1$. If there is an empty piece $S_{h}$ in the sequence, then the sum of any piece is in $[0,1]$. We can for any empty piece create a cut in any place between numbers where there was not previously a cut, and discard the empty pieces. This is possible since the cuts are $k \leq n-1$, and $n-1$ is the number of places in between numbers. This operation will only possibly decrease the maximum sum, and still all sums will be in $[0,1]$, so all conditions are satisfied.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
John has a string of paper where $n$ real numbers $a_{i} \in[0,1]$, for all $i \in\{1, \ldots, n\}$, are written in a row. Show that for any given $k<n$, he can cut the string of paper into $k$ non-empty pieces, between adjacent numbers, in such a way that the sum of the numbers on each piece does not differ from any other sum by more than 1 .
## Baltic Way
Reykjavík, November 11th - 15th
Solutions
|
. Denote the sums on each piece by
$$
\begin{aligned}
& S_{1}=a_{1}+a_{2}+\ldots+a_{m_{1}}, \\
& S_{2}=a_{m_{1}+1}+a_{m_{1}+2}+\ldots+a_{m_{2}}, \\
& \quad \ldots \\
& S_{k}=a_{m_{k-1}+1}+\ldots+a_{m_{k}} .
\end{aligned}
$$
By abuse of notation $S_{i}$ will both denote the set of numbers enclosed by cuts and its sum, the meaning of which must be determined by the context.
We will start the following algorithm. During this algorithm we will move some elements to the neighbouring piece and construct new sequence of pieces $S^{\star}=\left(S_{1}^{\star}, S_{2}^{\star}, \ldots, S_{k}^{\star}\right)$. Empty pieces may appear, but we will consider that case in the end.
(1) Find $p \leq k$ such that $S_{p}$ is the piece with the maximum sum of elements.
(2) If $S_{p} \leq \min \left(S_{1}, \ldots, S_{k}\right)+1$ we are done.
(3) If $S_{p}>\min \left(S_{1}, \ldots, S_{k}\right)+1$, let $S_{q}$ be the pieces with minimum sum of elements nearest to $S_{p}$ (ties broken arbitrarily) and let $S_{h}$ be the next pieces to $S_{q}$ between $S_{p}$ and $S_{q}$ (it is non empty by the choice of $S_{q}$ ). Then either $p<q$ and then $h=q-1$ and we define $S^{\star}$ by moving the last element from $S_{h}=S_{q-1}$ to $S_{q}$, or $q<p$, and then $h=q+1$ and $S^{\star}$ is obtained by moving the first element of $S_{h}=S_{q+1}$ to $S_{q}$. If $p=h$ then set $S=S^{\star}$ and go to step (1). If $p \neq h$ then set $S=S^{\star}$ and proceed to step (2).
Note that in step (3) each number $S_{i}^{\star}$ is at most $S_{p}$ and no new piece with sum $S_{p}$ is created. Indeed, $S_{h}^{\star}<S_{h} \leq S_{p}$, and for some $j$ we have $S_{q}^{\star}=S_{q}+a_{j}<S_{p}$ since $a_{j} \in[0,1]$ and $S_{p}>$ $\min \left(S_{1}, \ldots, S_{k}\right)+1$. It is clear also that $\max \left(S_{1}, \ldots, S_{k}\right)$ does not increase during the algorithm.
Note also that in step (3) the pieces $S_{h}$ may become empty. Then, in the next iteration of the algorithm, $q=h$ will be chosen since $\min \left(S_{1}, \ldots, S_{k}\right)=S_{h}=0$ and in step (3) $S_{h}^{\star}$ will become non empty (but one of its neighbours may become empty, etc.).
Claim: In the algorithm above, Step (3) is repeated at most $k n$ times with $S_{p}$ being the same maximal pieces in $S^{\star}$ and in $S$.
Proof. Let $s_{i}$ be the number of elements in $i$-th pieces. Then the number
$$
\sum_{i=1}^{k}|i-p| s_{i}
$$
takes positive integral values and is always less than $k n$. It is clear that this number decreases during the algorithm.
## Baltic Way
Thus after at most $k n$ iteration of (3), the algorithm decreases the value of $S_{p}$ and so goes to (1). Consequently it decreases either the number of pieces with maximal sums or $\max \left(S_{1}, \ldots, S_{k}\right)$. As there are only finitely many ways to split the sum onto pieces, the algorithm eventually terminates at (2).
When the algorithm teminates, we are left with a sequence $S=\left(S_{1}, S_{2}, \ldots, S_{k}\right)$ where the piece $S_{p}$ with maximum sum is such that $S_{p} \leq \min \left(S_{1}, \ldots, S_{k}\right)+1$. If there is an empty piece $S_{h}$ in the sequence, then the sum of any piece is in $[0,1]$. We can for any empty piece create a cut in any place between numbers where there was not previously a cut, and discard the empty pieces. This is possible since the cuts are $k \leq n-1$, and $n-1$ is the number of places in between numbers. This operation will only possibly decrease the maximum sum, and still all sums will be in $[0,1]$, so all conditions are satisfied.
|
{
"exam": "BalticWay",
"problem_label": "10",
"problem_match": "\nProblem 10.",
"resource_path": "BalticWay/segmented/en-bw21sol.jsonl",
"solution_match": "\nSolution 1",
"tier": "T3",
"year": "2021"
}
|
John has a string of paper where $n$ real numbers $a_{i} \in[0,1]$, for all $i \in\{1, \ldots, n\}$, are written in a row. Show that for any given $k<n$, he can cut the string of paper into $k$ non-empty pieces, between adjacent numbers, in such a way that the sum of the numbers on each piece does not differ from any other sum by more than 1 .
## Baltic Way
Reykjavík, November 11th - 15th
Solutions
|
. This problem can be solved by finding a certain graph having a directed path of length $k$. For real $x$ let $\left(V_{x}, E_{x}\right)$ be a directed graph having vertices $V_{x}=\{0,1, \ldots, n\}$. If $i, j \in V_{x}$ we have a directed edge $(i, j) \in V_{x}$ iff $i \leq j$ and $\sum_{l=i+1}^{j} \in[x, x+1]$.
Suppose that for some $x \in \mathbb{R}$ there exist such a graph $\left(V_{x}, E_{x}\right)$ such that there exist a path of length $k$ from vertex 0 to vertex $n$. Let $0=v_{0}, v_{1}, \ldots, v_{k}=n$ be an path of length $k$. If we cut the paper string between numbers $v_{i}$ and $v_{i}+1$ for $i \in\{1, \ldots, k-1\}$ we have that the sum of the $i$-th part is $a_{v_{i-1}+1}+\ldots+a_{v_{i}} \in[x, x+1]$. In particular the sum of the number of each piece does not differ from the sum of any other piece by more than 1 .
It is therefore evident that the statement of the problem is equivalent to the existence of a real $x$ such that there exists a path of length $k$ form vertex 0 to vertex $n$ in graph $\left(E_{x}, V_{x}\right)$.
For a real $x$ let $s_{x}$ be the least vertex in $\left(V_{x}, E_{x}\right)$ such that there exists a path of length $k$ from 0 to $s_{x}$ and let $t_{x}$ be the greatest, provided that such a path exists. It is not difficult to prove (by induction on $k$ ) that for each vertex $v \in E_{x}$ such that $s_{x} \leq v \leq t_{x}$ there exists a path of length $k$ for 0 to $v$.
Start with $x=0$. As $x$ increases both $s_{x}$ and $t_{x}$ increase. As there are only finitely many different sums formed by taking a subset of the $a_{i}$-s it follows that the graph $\left(V_{x}, E_{x}\right)$ changes at discrete values of $x$. It is not hard to see that if the graph makes one change between reals $x_{1}<x_{2}$ and $s_{x_{1}}, s_{x_{2}}, t_{x_{1}}, t_{x_{2}}$ exist then $s_{x_{1}} \leq s_{x_{2}} \leq t_{x_{1}} \leq t_{x_{2}}$.
For $s=\sum_{i=1}^{n} a_{i}+1$ it is clear that there $\left(V_{s}, E_{s}\right)$ has no edges. It is not hard to see that as $x$ increases we will eventually find a value for $x$ such that $\left(V_{x}, E_{x}\right)$ has a path of length $k$ for 0 to $n$ as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
John has a string of paper where $n$ real numbers $a_{i} \in[0,1]$, for all $i \in\{1, \ldots, n\}$, are written in a row. Show that for any given $k<n$, he can cut the string of paper into $k$ non-empty pieces, between adjacent numbers, in such a way that the sum of the numbers on each piece does not differ from any other sum by more than 1 .
## Baltic Way
Reykjavík, November 11th - 15th
Solutions
|
. This problem can be solved by finding a certain graph having a directed path of length $k$. For real $x$ let $\left(V_{x}, E_{x}\right)$ be a directed graph having vertices $V_{x}=\{0,1, \ldots, n\}$. If $i, j \in V_{x}$ we have a directed edge $(i, j) \in V_{x}$ iff $i \leq j$ and $\sum_{l=i+1}^{j} \in[x, x+1]$.
Suppose that for some $x \in \mathbb{R}$ there exist such a graph $\left(V_{x}, E_{x}\right)$ such that there exist a path of length $k$ from vertex 0 to vertex $n$. Let $0=v_{0}, v_{1}, \ldots, v_{k}=n$ be an path of length $k$. If we cut the paper string between numbers $v_{i}$ and $v_{i}+1$ for $i \in\{1, \ldots, k-1\}$ we have that the sum of the $i$-th part is $a_{v_{i-1}+1}+\ldots+a_{v_{i}} \in[x, x+1]$. In particular the sum of the number of each piece does not differ from the sum of any other piece by more than 1 .
It is therefore evident that the statement of the problem is equivalent to the existence of a real $x$ such that there exists a path of length $k$ form vertex 0 to vertex $n$ in graph $\left(E_{x}, V_{x}\right)$.
For a real $x$ let $s_{x}$ be the least vertex in $\left(V_{x}, E_{x}\right)$ such that there exists a path of length $k$ from 0 to $s_{x}$ and let $t_{x}$ be the greatest, provided that such a path exists. It is not difficult to prove (by induction on $k$ ) that for each vertex $v \in E_{x}$ such that $s_{x} \leq v \leq t_{x}$ there exists a path of length $k$ for 0 to $v$.
Start with $x=0$. As $x$ increases both $s_{x}$ and $t_{x}$ increase. As there are only finitely many different sums formed by taking a subset of the $a_{i}$-s it follows that the graph $\left(V_{x}, E_{x}\right)$ changes at discrete values of $x$. It is not hard to see that if the graph makes one change between reals $x_{1}<x_{2}$ and $s_{x_{1}}, s_{x_{2}}, t_{x_{1}}, t_{x_{2}}$ exist then $s_{x_{1}} \leq s_{x_{2}} \leq t_{x_{1}} \leq t_{x_{2}}$.
For $s=\sum_{i=1}^{n} a_{i}+1$ it is clear that there $\left(V_{s}, E_{s}\right)$ has no edges. It is not hard to see that as $x$ increases we will eventually find a value for $x$ such that $\left(V_{x}, E_{x}\right)$ has a path of length $k$ for 0 to $n$ as desired.
|
{
"exam": "BalticWay",
"problem_label": "10",
"problem_match": "\nProblem 10.",
"resource_path": "BalticWay/segmented/en-bw21sol.jsonl",
"solution_match": "\nSolution 2",
"tier": "T3",
"year": "2021"
}
|
A point $P$ lies inside a triangle $A B C$. The points $K$ and $L$ are the projections of $P$ onto $A B$ and $A C$, respectively. The point $M$ lies on the line $B C$ so that $K M=L M$, and the point $P^{\prime}$ is symmetric to $P$ with respect to $M$. Prove that $\angle B A P=\angle P^{\prime} A C$.
## Baltic Way
Reykjavík, November 11th - 15th
Solutions
Figure 4
|
For points $X, Y, Z, X \neq Y$ and $Z \neq Y$ let rot $X Y Z$ denote the rotation that takes rotates line $X Y$ to line $Z Y$ modulo half turns. We consider two rotations equivalent one of them is a composition of some translation and the other rotation. It is clear that this is indeed an equivalence relation (as the Euclidean plane is Desarguean).
Let $K^{\prime}$ and $L^{\prime}$ be the projections of $P^{\prime}$ onto $A B$ and $A C$ respectively, as in figure 4 . Let $\ell$ be the perpendicular line to line $A B$ passing through $M$. From symmetries it follows that $L^{\prime}$ is the refection of $L$ over $\ell$. In particular segments $M L$ and $M L^{\prime}$ are congruent. Similarly segments $M K$ and $M K^{\prime}$ are congruent. It follows that $M$ is a center of circle passing through $L, K, L^{\prime}$ and $K^{\prime}$.
As line $P L$ is perpendicular to line $A C$ and line $P K$ is perpendicular to line $A B$ it follows that quadrilateral $A K P L$ is cyclic. Similarly quadrilateral $A K^{\prime} P L^{\prime}$ is also cyclic.
From the theorem on inscribed angles in cyclic quadrilaterals it follows that
$$
\begin{gathered}
\operatorname{rot} B A P \equiv \operatorname{rot} K A P \equiv \operatorname{rot} K L P, \\
\operatorname{rot} P^{\prime} A C \equiv \operatorname{rot} P^{\prime} A L \equiv \operatorname{rot} P^{\prime} K^{\prime} L \quad \text { and } \\
\operatorname{rot} K L L^{\prime} \equiv \operatorname{rot} K K^{\prime} L^{\prime}
\end{gathered}
$$
As $\angle P L L^{\prime}$ and $\angle K K^{\prime} P^{\prime}$ are right it follows that $\operatorname{rot} P L L^{\prime} \equiv \operatorname{rot} K K^{\prime} P^{\prime}$ modulo half turns. Now $\operatorname{rot} K L L^{\prime} \equiv \operatorname{rot} K L P+\operatorname{rot} P L L^{\prime} \quad$ and $\quad \operatorname{rot} K K^{\prime} L^{\prime} \equiv \operatorname{rot} P^{\prime} K^{\prime} L+\operatorname{rot} K K^{\prime} P$
## Baltic Way
Reykjavík, November 11th - 15th
Solutions
and $\operatorname{rot} K L L^{\prime} \equiv \operatorname{rot} K K^{\prime} L^{\prime}$ so we decuce that $\operatorname{rot} K L P \equiv \operatorname{rot} P^{\prime} K^{\prime} L$.
Putting everything together gives
$$
\operatorname{rot} B A P \equiv \operatorname{rot} P^{\prime} A L^{\prime}
$$
which gives the desired result.
Remark. This method can be applied to prove the existence of isogonal conjugates in triangles.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A point $P$ lies inside a triangle $A B C$. The points $K$ and $L$ are the projections of $P$ onto $A B$ and $A C$, respectively. The point $M$ lies on the line $B C$ so that $K M=L M$, and the point $P^{\prime}$ is symmetric to $P$ with respect to $M$. Prove that $\angle B A P=\angle P^{\prime} A C$.
## Baltic Way
Reykjavík, November 11th - 15th
Solutions

Figure 4
|
For points $X, Y, Z, X \neq Y$ and $Z \neq Y$ let rot $X Y Z$ denote the rotation that takes rotates line $X Y$ to line $Z Y$ modulo half turns. We consider two rotations equivalent one of them is a composition of some translation and the other rotation. It is clear that this is indeed an equivalence relation (as the Euclidean plane is Desarguean).
Let $K^{\prime}$ and $L^{\prime}$ be the projections of $P^{\prime}$ onto $A B$ and $A C$ respectively, as in figure 4 . Let $\ell$ be the perpendicular line to line $A B$ passing through $M$. From symmetries it follows that $L^{\prime}$ is the refection of $L$ over $\ell$. In particular segments $M L$ and $M L^{\prime}$ are congruent. Similarly segments $M K$ and $M K^{\prime}$ are congruent. It follows that $M$ is a center of circle passing through $L, K, L^{\prime}$ and $K^{\prime}$.
As line $P L$ is perpendicular to line $A C$ and line $P K$ is perpendicular to line $A B$ it follows that quadrilateral $A K P L$ is cyclic. Similarly quadrilateral $A K^{\prime} P L^{\prime}$ is also cyclic.
From the theorem on inscribed angles in cyclic quadrilaterals it follows that
$$
\begin{gathered}
\operatorname{rot} B A P \equiv \operatorname{rot} K A P \equiv \operatorname{rot} K L P, \\
\operatorname{rot} P^{\prime} A C \equiv \operatorname{rot} P^{\prime} A L \equiv \operatorname{rot} P^{\prime} K^{\prime} L \quad \text { and } \\
\operatorname{rot} K L L^{\prime} \equiv \operatorname{rot} K K^{\prime} L^{\prime}
\end{gathered}
$$
As $\angle P L L^{\prime}$ and $\angle K K^{\prime} P^{\prime}$ are right it follows that $\operatorname{rot} P L L^{\prime} \equiv \operatorname{rot} K K^{\prime} P^{\prime}$ modulo half turns. Now $\operatorname{rot} K L L^{\prime} \equiv \operatorname{rot} K L P+\operatorname{rot} P L L^{\prime} \quad$ and $\quad \operatorname{rot} K K^{\prime} L^{\prime} \equiv \operatorname{rot} P^{\prime} K^{\prime} L+\operatorname{rot} K K^{\prime} P$
## Baltic Way
Reykjavík, November 11th - 15th
Solutions
and $\operatorname{rot} K L L^{\prime} \equiv \operatorname{rot} K K^{\prime} L^{\prime}$ so we decuce that $\operatorname{rot} K L P \equiv \operatorname{rot} P^{\prime} K^{\prime} L$.
Putting everything together gives
$$
\operatorname{rot} B A P \equiv \operatorname{rot} P^{\prime} A L^{\prime}
$$
which gives the desired result.
Remark. This method can be applied to prove the existence of isogonal conjugates in triangles.
|
{
"exam": "BalticWay",
"problem_label": "11",
"problem_match": "\nProblem 11.",
"resource_path": "BalticWay/segmented/en-bw21sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2021"
}
|
Let $I$ be the incentre of a triangle $A B C$. Let $F$ and $G$ be the projections of $A$ onto the lines $B I$ and $C I$, respectively. Rays $A F$ and $A G$ intersect the circumcircles of the triangles $C F I$ and $B G I$ for the second time at points $K$ and $L$, respectively. Prove that the line $A I$ bisects the segment $K L$.
|
Since $\angle I F K=90^{\circ}$, then $I K$ is the diameter of the circumcircle of $C F I$, hence also $\angle I C K=90^{\circ}$. Similarly is $I L$ the diameter of the circumcircle of $B G I$ and $\angle I B L=90^{\circ}$. Therefore are the lines $C K$ and $G L$ parallel, also $B L$ and $F K$ are parallel.
Let the lines $C K$ and $B L$ intersect at $D$, as seen in figure 5. From the above we get that $D K A L$ is a parallelogram. Note that $D$ is the excenter with respect to the vertex $A$ of the triangle $A B C$, since the lines $B L$ and $C K$ are perpendicular to the corresponding internal angle bisectors. The excenter lies on the internal angle bisector $A I$, hence $A I$ bisects the diagonal $K L$.
Figure 5
## Baltic Way
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $I$ be the incentre of a triangle $A B C$. Let $F$ and $G$ be the projections of $A$ onto the lines $B I$ and $C I$, respectively. Rays $A F$ and $A G$ intersect the circumcircles of the triangles $C F I$ and $B G I$ for the second time at points $K$ and $L$, respectively. Prove that the line $A I$ bisects the segment $K L$.
|
Since $\angle I F K=90^{\circ}$, then $I K$ is the diameter of the circumcircle of $C F I$, hence also $\angle I C K=90^{\circ}$. Similarly is $I L$ the diameter of the circumcircle of $B G I$ and $\angle I B L=90^{\circ}$. Therefore are the lines $C K$ and $G L$ parallel, also $B L$ and $F K$ are parallel.
Let the lines $C K$ and $B L$ intersect at $D$, as seen in figure 5. From the above we get that $D K A L$ is a parallelogram. Note that $D$ is the excenter with respect to the vertex $A$ of the triangle $A B C$, since the lines $B L$ and $C K$ are perpendicular to the corresponding internal angle bisectors. The excenter lies on the internal angle bisector $A I$, hence $A I$ bisects the diagonal $K L$.

Figure 5
## Baltic Way
|
{
"exam": "BalticWay",
"problem_label": "12",
"problem_match": "\nProblem 12.",
"resource_path": "BalticWay/segmented/en-bw21sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2021"
}
|
Let $D$ be the foot of the $A$-altitude of an acute triangle $A B C$. The internal bisector of the angle $D A C$ intersects $B C$ at $K$. Let $L$ be the projection of $K$ onto $A C$. Let $M$ be the intersection point of $B L$ and $A D$. Let $P$ be the intersection point of $M C$ and $D L$. Prove that $P K \perp A B$.
|
. Let $X$ be a point on $B C$ such that $L X \perp A B$, as seen in figure 6. It is enough to prove that
because then $P K \| L X$ and $L X \perp A B$.
$$
\frac{D P}{P L}=\frac{D K}{K X}
$$
Applying Menelaos for triangle $B D L$ and transversal $M P C$ we get
$$
\frac{D P}{P L} \cdot \frac{L M}{M B} \cdot \frac{B C}{C D}=1
$$
and Menelaus for triangle $B L C$ and transversal $A M D$ gives
$$
\frac{B M}{M L} \cdot \frac{L A}{A C} \cdot \frac{C D}{D B}=1
$$
Multiplying these two equalities yields
$$
\frac{D P \cdot B C \cdot A L}{P L \cdot B D \cdot A C}=1
$$
Note, however, that $A L=A D=A C \sin \gamma, B D=A B \cos \beta$, and, by the sine rule, $\frac{A B}{B C}=\frac{\sin \gamma}{\sin \alpha}$, where $\alpha=\angle B A C, \beta=\angle C B A$ and $\gamma=\angle A C B$. Therefore
$$
\frac{D P}{P L}=\frac{B D \cdot A C}{B C \cdot A L}=\frac{A B \cos \beta \cdot A C}{B C \cdot A C \sin \gamma}=\frac{\sin \gamma \cos \beta}{\sin \alpha \sin \gamma}=\frac{\cos \beta}{\sin \alpha} .
$$
On the other hand, since $D K=K L, \angle K L X=\pi-\alpha$, and $\angle L X K=\frac{\pi}{2}-\beta$, we have by the sine rule
$$
\frac{D K}{K X}=\frac{L K}{K X}=\frac{\sin \left(\frac{\pi}{2}-\beta\right)}{\sin (\pi-\alpha)}=\frac{\cos \beta}{\sin \alpha} .
$$
Therefore
$$
\frac{D P}{P L}=\frac{\cos \beta}{\sin \alpha}=\frac{D K}{K X}
$$
which finishes the proof.
## Baltic Way
Figure 6
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $D$ be the foot of the $A$-altitude of an acute triangle $A B C$. The internal bisector of the angle $D A C$ intersects $B C$ at $K$. Let $L$ be the projection of $K$ onto $A C$. Let $M$ be the intersection point of $B L$ and $A D$. Let $P$ be the intersection point of $M C$ and $D L$. Prove that $P K \perp A B$.
|
. Let $X$ be a point on $B C$ such that $L X \perp A B$, as seen in figure 6. It is enough to prove that
because then $P K \| L X$ and $L X \perp A B$.
$$
\frac{D P}{P L}=\frac{D K}{K X}
$$
Applying Menelaos for triangle $B D L$ and transversal $M P C$ we get
$$
\frac{D P}{P L} \cdot \frac{L M}{M B} \cdot \frac{B C}{C D}=1
$$
and Menelaus for triangle $B L C$ and transversal $A M D$ gives
$$
\frac{B M}{M L} \cdot \frac{L A}{A C} \cdot \frac{C D}{D B}=1
$$
Multiplying these two equalities yields
$$
\frac{D P \cdot B C \cdot A L}{P L \cdot B D \cdot A C}=1
$$
Note, however, that $A L=A D=A C \sin \gamma, B D=A B \cos \beta$, and, by the sine rule, $\frac{A B}{B C}=\frac{\sin \gamma}{\sin \alpha}$, where $\alpha=\angle B A C, \beta=\angle C B A$ and $\gamma=\angle A C B$. Therefore
$$
\frac{D P}{P L}=\frac{B D \cdot A C}{B C \cdot A L}=\frac{A B \cos \beta \cdot A C}{B C \cdot A C \sin \gamma}=\frac{\sin \gamma \cos \beta}{\sin \alpha \sin \gamma}=\frac{\cos \beta}{\sin \alpha} .
$$
On the other hand, since $D K=K L, \angle K L X=\pi-\alpha$, and $\angle L X K=\frac{\pi}{2}-\beta$, we have by the sine rule
$$
\frac{D K}{K X}=\frac{L K}{K X}=\frac{\sin \left(\frac{\pi}{2}-\beta\right)}{\sin (\pi-\alpha)}=\frac{\cos \beta}{\sin \alpha} .
$$
Therefore
$$
\frac{D P}{P L}=\frac{\cos \beta}{\sin \alpha}=\frac{D K}{K X}
$$
which finishes the proof.
## Baltic Way

Figure 6
|
{
"exam": "BalticWay",
"problem_label": "13",
"problem_match": "\nProblem 13.",
"resource_path": "BalticWay/segmented/en-bw21sol.jsonl",
"solution_match": "\nSolution 1",
"tier": "T3",
"year": "2021"
}
|
Let $D$ be the foot of the $A$-altitude of an acute triangle $A B C$. The internal bisector of the angle $D A C$ intersects $B C$ at $K$. Let $L$ be the projection of $K$ onto $A C$. Let $M$ be the intersection point of $B L$ and $A D$. Let $P$ be the intersection point of $M C$ and $D L$. Prove that $P K \perp A B$.
|
. Let $\omega$ be the circle with center $K$ an radius $K D$, as in figure 7. Then $\omega$ is tangent to $A D$ and $A L$. Let $B C$ intersect $\omega$ at $D$ and $Q$. Let $B M$ intersect $\omega$ at $L$ and $R$. Let $Q P$ intersect $B L$ at $S$.
Cross-ratio chasing gives, through the projections $B L \rightarrow D$-pencil $\rightarrow \omega \rightarrow L$-pencil $\rightarrow B C \rightarrow P-$ pencil $\rightarrow B L$,
$$
\begin{aligned}
(L, R ; M, B) & =(D L, D R ; D M, D B)=(L, R ; D, Q)=(L C, L B ; L D, L Q) \\
& =(C, B ; D, Q)=(P C, P B ; P D, P Q)=(M, B ; L, S)=(L, S ; M, B),
\end{aligned}
$$
therefore $R=S$.
It is clear now that $P$ lies on the polar lines of both $A$ and $B$ with respect to $\omega$, therefore $A B$ is the polar line of $P$. This implies that $P K \perp A B$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $D$ be the foot of the $A$-altitude of an acute triangle $A B C$. The internal bisector of the angle $D A C$ intersects $B C$ at $K$. Let $L$ be the projection of $K$ onto $A C$. Let $M$ be the intersection point of $B L$ and $A D$. Let $P$ be the intersection point of $M C$ and $D L$. Prove that $P K \perp A B$.
|
. Let $\omega$ be the circle with center $K$ an radius $K D$, as in figure 7. Then $\omega$ is tangent to $A D$ and $A L$. Let $B C$ intersect $\omega$ at $D$ and $Q$. Let $B M$ intersect $\omega$ at $L$ and $R$. Let $Q P$ intersect $B L$ at $S$.
Cross-ratio chasing gives, through the projections $B L \rightarrow D$-pencil $\rightarrow \omega \rightarrow L$-pencil $\rightarrow B C \rightarrow P-$ pencil $\rightarrow B L$,
$$
\begin{aligned}
(L, R ; M, B) & =(D L, D R ; D M, D B)=(L, R ; D, Q)=(L C, L B ; L D, L Q) \\
& =(C, B ; D, Q)=(P C, P B ; P D, P Q)=(M, B ; L, S)=(L, S ; M, B),
\end{aligned}
$$
therefore $R=S$.
It is clear now that $P$ lies on the polar lines of both $A$ and $B$ with respect to $\omega$, therefore $A B$ is the polar line of $P$. This implies that $P K \perp A B$.
|
{
"exam": "BalticWay",
"problem_label": "13",
"problem_match": "\nProblem 13.",
"resource_path": "BalticWay/segmented/en-bw21sol.jsonl",
"solution_match": "\nSolution 2",
"tier": "T3",
"year": "2021"
}
|
Let $A B C$ be a triangle with circumcircle $\Gamma$ and circumcentre $O$. Denote by $M$ the midpoint of $B C$. The point $D$ is the reflection of $A$ over $B C$, and the point $E$ is the intersection of $\Gamma$ and the ray $M D$. Let $S$ be the circumcentre of the triangle $A D E$. Prove that the points $A, E, M, O$, and $S$ lie on the same circle.
|
First we prove that $A, M, E, S$ are concyclic. Note that $B C$ is the perpendicular bisector of $A D$, so $S$ lies on $B C$. Let $X$ be the intersection of $A D$ and $B C$ as in figure 8 . Then, using directed
## Baltic Way
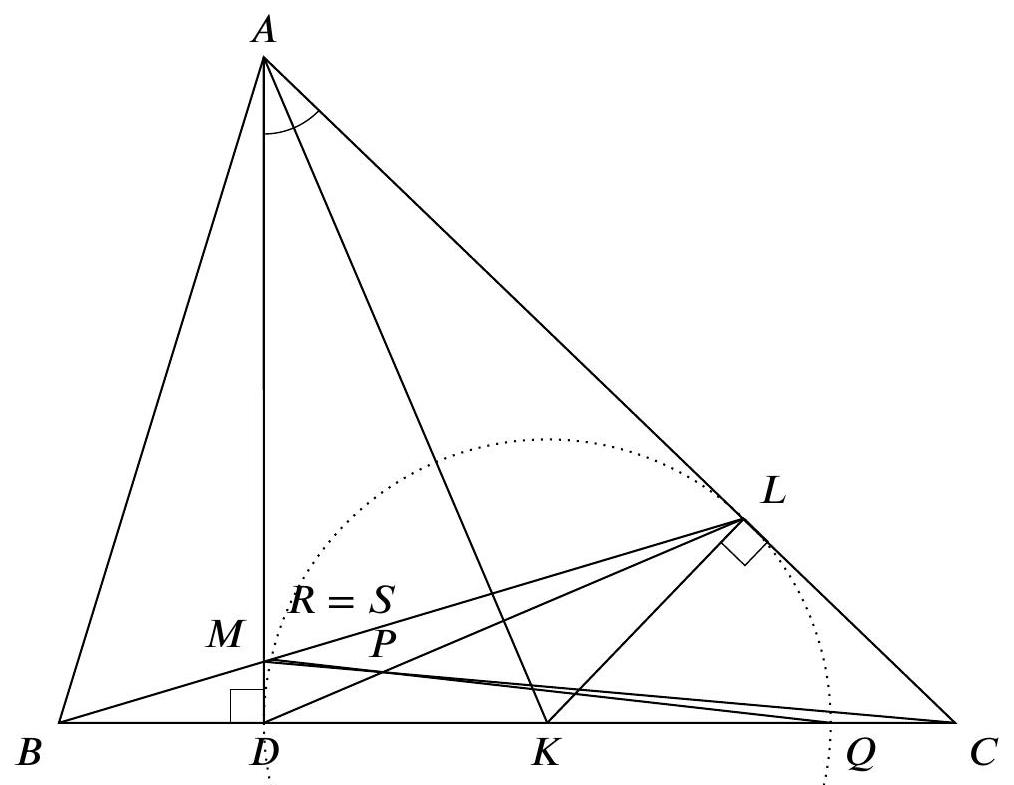
Figure 7
## Baltic Way
Reykjavík, November 11th - 15th
Solutions
angles,
$$
\begin{aligned}
\angle E M S & =\angle D M X \\
& =90^{\circ}-\angle X D M \\
& =90^{\circ}-\angle A D E \\
& =\angle S E A \\
& =\angle E A S,
\end{aligned}
$$
so $A M E S$ is cyclic as claimed.
Now we prove that $A, M, E, O$ are concyclic. Let $F$ be the reflection of $D$ over $M$. Then $F$ lies on the same side of $B C$ as $A$ and satisfies $F C B \cong D B C \cong A B C$, so $F$ must be the point such that $A F C B$ is an isosceles trapezoid. In particular, $F$ lies on $\Gamma$. Consequently,
$$
\angle O A E=90^{\circ}-\angle E F A=90^{\circ}-\angle E M B=\angle O M B+\angle B M E=\angle O M E \text {, }
$$
so $A M E O$ is also cyclic as claimed.
Thus $A, E, M, O, S$ are concyclic, as desired.
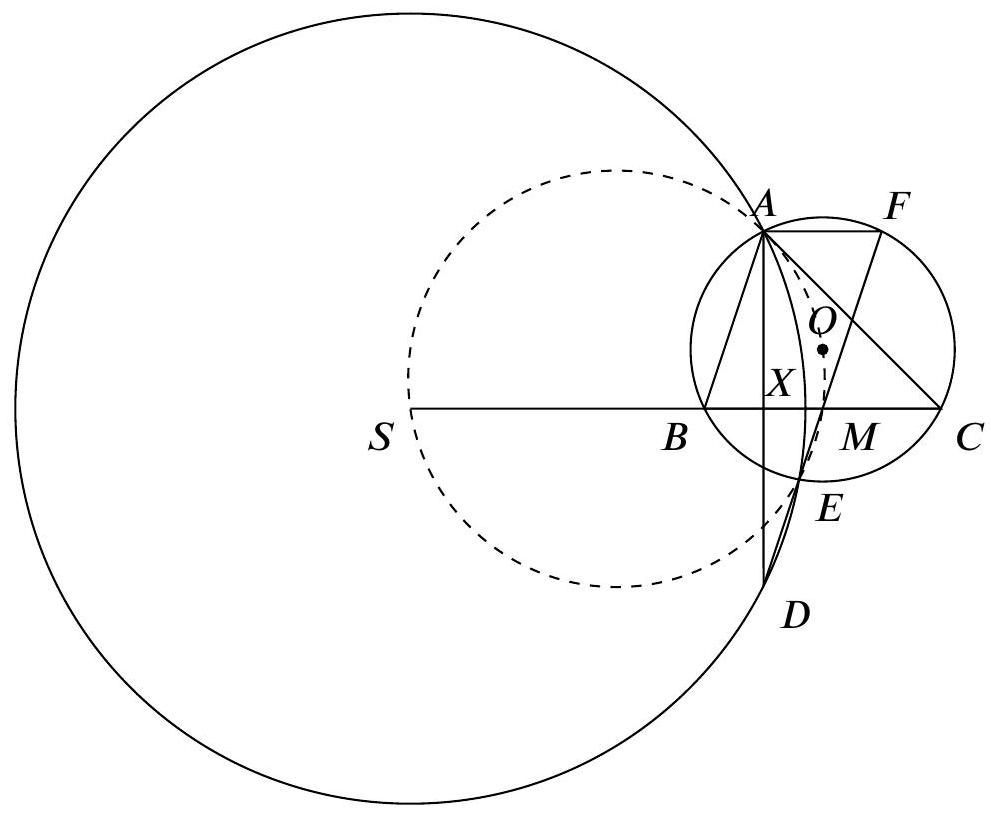
Figure 8
## Baltic Way
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with circumcircle $\Gamma$ and circumcentre $O$. Denote by $M$ the midpoint of $B C$. The point $D$ is the reflection of $A$ over $B C$, and the point $E$ is the intersection of $\Gamma$ and the ray $M D$. Let $S$ be the circumcentre of the triangle $A D E$. Prove that the points $A, E, M, O$, and $S$ lie on the same circle.
|
First we prove that $A, M, E, S$ are concyclic. Note that $B C$ is the perpendicular bisector of $A D$, so $S$ lies on $B C$. Let $X$ be the intersection of $A D$ and $B C$ as in figure 8 . Then, using directed
## Baltic Way

Figure 7
## Baltic Way
Reykjavík, November 11th - 15th
Solutions
angles,
$$
\begin{aligned}
\angle E M S & =\angle D M X \\
& =90^{\circ}-\angle X D M \\
& =90^{\circ}-\angle A D E \\
& =\angle S E A \\
& =\angle E A S,
\end{aligned}
$$
so $A M E S$ is cyclic as claimed.
Now we prove that $A, M, E, O$ are concyclic. Let $F$ be the reflection of $D$ over $M$. Then $F$ lies on the same side of $B C$ as $A$ and satisfies $F C B \cong D B C \cong A B C$, so $F$ must be the point such that $A F C B$ is an isosceles trapezoid. In particular, $F$ lies on $\Gamma$. Consequently,
$$
\angle O A E=90^{\circ}-\angle E F A=90^{\circ}-\angle E M B=\angle O M B+\angle B M E=\angle O M E \text {, }
$$
so $A M E O$ is also cyclic as claimed.
Thus $A, E, M, O, S$ are concyclic, as desired.

Figure 8
## Baltic Way
|
{
"exam": "BalticWay",
"problem_label": "14",
"problem_match": "\nProblem 14.",
"resource_path": "BalticWay/segmented/en-bw21sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2021"
}
|
For which positive integers $n \geq 4$ does there exist a convex $n$-gon with side lengths $1,2, \ldots, n$ (in some order) and with all of its sides tangent to the same circle?
|
It exists if $n=4 k$ or $n=4 k+1$ where $k$ is a positive integer.
Let us consider $n$-gon $P_{1} P_{2} \ldots P_{n}$. Tangent points of the inscribed circle divide each of its sides in two segments. Lengths of these segments that has a common vertex $P_{i}$ are equal. Denote the length of tangent segments that originate at point $P_{i}$ by $A_{i}$. It means that side lengths of the $n$-gon can be expressed as $P_{i} P_{i+1}=A_{i}+A_{i+1}$ for all $i=1,2, \ldots, n$ where we consider points cyclically $\left(P_{n+1}=P_{1}\right.$ and $A_{n+1}=A_{1}$ ).
We can show that the converse is true as well. That is, if we can find $n$ positive real numbers $A_{i}$, $i=1,2, \ldots, n$ such that the sequence $\left(A_{1}+A_{2}, A_{2}+A_{3}, \ldots, A_{n}+A_{1}\right)$ is a permutation of $(1,2, \ldots, n)$ then there is a circumscribed polygon $P_{1} P_{2} \ldots P_{n}$ with side lengths $1,2, \ldots, n$.
To show this we start with a circle of arbitrary radius $R$ and construct points $P_{1}, P_{2}, \ldots, P_{n}$ outside this circle so that the length of the tangent segments from $P_{i}$ to the circle are of length $A_{i}$ and the "right" tangent segment from $P_{i}$ touches the circle at the same point as the "left" tangent segment from $P_{i-1}$.
Now we almost have the $n$-gon except that possibly the "right" tangent point of $P_{1}$ does not match the "left" touching point of $P_{n}$. This can be easily fixed by adjusting the radius $R$ of the circle, using continuity.
Now we solve the problem by considering 4 cases:
(i) First let's consider the case when $n=4 k$. In this case such circumscribed $n$-gon exists. The $4 k$ segments $A_{i}$ can be of lengths
$$
\begin{array}{r}
A_{1}=\frac{1}{2}, A_{2}=\frac{1}{2}, A_{3}=\frac{3}{2}, A_{4}=\frac{3}{2}, \ldots, A_{2 k-1}=\frac{2 k-1}{2}, A_{2 k}=\frac{2 k-1}{2}, \\
A_{2 k+1}=\frac{2 k+1}{2}, A_{2 k+2}=\frac{6 k-1}{2}, A_{2 k+3}=\frac{2 k-1}{2}, A_{2 k+4}=\frac{6 k-3}{2}, \ldots, \\
A_{4 k-1}=\frac{3}{2}, A_{4 k}=\frac{4 k+1}{2} .
\end{array}
$$
One can see that the values of the sums of the consecutive elements $A_{1}+A_{2}, A_{2}+A_{3}, \ldots, A_{4 k-1}+$ $A_{4 k}, A_{4 k}+A_{4 k+1}$ are exactly $1,2, \ldots, 2 k, 4 k, 4 k-1, \ldots, 2 k+1$, respectively.
(ii) In the case $n=4 k+1$ the construction is similar, we can choose $4 k+1$ segments of length
$$
\begin{aligned}
& A_{1}=\frac{1}{2}, \quad A_{2}=\frac{1}{2}, \quad A_{3}=\frac{5}{2}, \quad A_{4}=\frac{5}{2}, \ldots, \\
& A_{2 k+1}=\frac{4 k+1}{2}, \quad A_{2 k+2}=\frac{4 k+1}{2}, \quad A_{2 k+3}=\frac{4 k-1}{2}, \\
& A_{2 k+4}=\frac{4 k-3}{2}, \quad A_{2 k+5}=\frac{4 k-5}{2}, \quad \ldots, A_{4 k+1}=\frac{3}{2}
\end{aligned}
$$
## Baltic Way
In this case the values of the sums of consecutive elements $A_{1}+A_{2}, A_{2}+A_{3}, \ldots, A_{4 k-1}+A_{4 k}$, $A_{4 k}+A_{4 k+1}$ are $1,3,5, \ldots, 4 k+1,4 k, 4 k-2, \ldots, 2$, respectively.
(iii) In case when $n=4 k+2$ such a polygon does not exist. To prove this we note that in case if the number of the sides of the circumscribed polygon is even then the sum of the odd numbered sides is equal to the sum of the even numbered sides. It is evident as two segments of equal length that originate from the same vertex contribute to different sums. But the total sum of the side lengths is an odd number what means that it is impossible to split the sides on two parts with equal sum of lengths.
(iv) In case $n=4 k+3$ such a polygon also does not exist. In this case we can express $A_{1}$ as
$$
\begin{aligned}
A_{1} & =\left(A_{1}+A_{2}+\ldots+A_{n}\right)-\left(A_{2}+A_{3}\right)-\left(A_{4}+A_{5}\right)-\ldots-\left(A_{4 k+2}+A_{4 k+3}\right)= \\
& =\frac{P_{1} P_{2}+P_{2} P_{3}+\cdots+P_{4 k+3} P_{1}}{2}-P_{2} P_{3}-P_{4} P_{5}-\ldots-P_{4 k+2} P_{4 k+3}
\end{aligned}
$$
As the sum of the length of the sides is an even number then we conclude that $A_{1}$ is a positive integer. The same is true for all $A_{2}, A_{3}, \ldots$ as well. But now we have a contradiction as the side of length 1 cannot be split in two parts, each of which has positive integer length.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
For which positive integers $n \geq 4$ does there exist a convex $n$-gon with side lengths $1,2, \ldots, n$ (in some order) and with all of its sides tangent to the same circle?
|
It exists if $n=4 k$ or $n=4 k+1$ where $k$ is a positive integer.
Let us consider $n$-gon $P_{1} P_{2} \ldots P_{n}$. Tangent points of the inscribed circle divide each of its sides in two segments. Lengths of these segments that has a common vertex $P_{i}$ are equal. Denote the length of tangent segments that originate at point $P_{i}$ by $A_{i}$. It means that side lengths of the $n$-gon can be expressed as $P_{i} P_{i+1}=A_{i}+A_{i+1}$ for all $i=1,2, \ldots, n$ where we consider points cyclically $\left(P_{n+1}=P_{1}\right.$ and $A_{n+1}=A_{1}$ ).
We can show that the converse is true as well. That is, if we can find $n$ positive real numbers $A_{i}$, $i=1,2, \ldots, n$ such that the sequence $\left(A_{1}+A_{2}, A_{2}+A_{3}, \ldots, A_{n}+A_{1}\right)$ is a permutation of $(1,2, \ldots, n)$ then there is a circumscribed polygon $P_{1} P_{2} \ldots P_{n}$ with side lengths $1,2, \ldots, n$.
To show this we start with a circle of arbitrary radius $R$ and construct points $P_{1}, P_{2}, \ldots, P_{n}$ outside this circle so that the length of the tangent segments from $P_{i}$ to the circle are of length $A_{i}$ and the "right" tangent segment from $P_{i}$ touches the circle at the same point as the "left" tangent segment from $P_{i-1}$.
Now we almost have the $n$-gon except that possibly the "right" tangent point of $P_{1}$ does not match the "left" touching point of $P_{n}$. This can be easily fixed by adjusting the radius $R$ of the circle, using continuity.
Now we solve the problem by considering 4 cases:
(i) First let's consider the case when $n=4 k$. In this case such circumscribed $n$-gon exists. The $4 k$ segments $A_{i}$ can be of lengths
$$
\begin{array}{r}
A_{1}=\frac{1}{2}, A_{2}=\frac{1}{2}, A_{3}=\frac{3}{2}, A_{4}=\frac{3}{2}, \ldots, A_{2 k-1}=\frac{2 k-1}{2}, A_{2 k}=\frac{2 k-1}{2}, \\
A_{2 k+1}=\frac{2 k+1}{2}, A_{2 k+2}=\frac{6 k-1}{2}, A_{2 k+3}=\frac{2 k-1}{2}, A_{2 k+4}=\frac{6 k-3}{2}, \ldots, \\
A_{4 k-1}=\frac{3}{2}, A_{4 k}=\frac{4 k+1}{2} .
\end{array}
$$
One can see that the values of the sums of the consecutive elements $A_{1}+A_{2}, A_{2}+A_{3}, \ldots, A_{4 k-1}+$ $A_{4 k}, A_{4 k}+A_{4 k+1}$ are exactly $1,2, \ldots, 2 k, 4 k, 4 k-1, \ldots, 2 k+1$, respectively.
(ii) In the case $n=4 k+1$ the construction is similar, we can choose $4 k+1$ segments of length
$$
\begin{aligned}
& A_{1}=\frac{1}{2}, \quad A_{2}=\frac{1}{2}, \quad A_{3}=\frac{5}{2}, \quad A_{4}=\frac{5}{2}, \ldots, \\
& A_{2 k+1}=\frac{4 k+1}{2}, \quad A_{2 k+2}=\frac{4 k+1}{2}, \quad A_{2 k+3}=\frac{4 k-1}{2}, \\
& A_{2 k+4}=\frac{4 k-3}{2}, \quad A_{2 k+5}=\frac{4 k-5}{2}, \quad \ldots, A_{4 k+1}=\frac{3}{2}
\end{aligned}
$$
## Baltic Way
In this case the values of the sums of consecutive elements $A_{1}+A_{2}, A_{2}+A_{3}, \ldots, A_{4 k-1}+A_{4 k}$, $A_{4 k}+A_{4 k+1}$ are $1,3,5, \ldots, 4 k+1,4 k, 4 k-2, \ldots, 2$, respectively.
(iii) In case when $n=4 k+2$ such a polygon does not exist. To prove this we note that in case if the number of the sides of the circumscribed polygon is even then the sum of the odd numbered sides is equal to the sum of the even numbered sides. It is evident as two segments of equal length that originate from the same vertex contribute to different sums. But the total sum of the side lengths is an odd number what means that it is impossible to split the sides on two parts with equal sum of lengths.
(iv) In case $n=4 k+3$ such a polygon also does not exist. In this case we can express $A_{1}$ as
$$
\begin{aligned}
A_{1} & =\left(A_{1}+A_{2}+\ldots+A_{n}\right)-\left(A_{2}+A_{3}\right)-\left(A_{4}+A_{5}\right)-\ldots-\left(A_{4 k+2}+A_{4 k+3}\right)= \\
& =\frac{P_{1} P_{2}+P_{2} P_{3}+\cdots+P_{4 k+3} P_{1}}{2}-P_{2} P_{3}-P_{4} P_{5}-\ldots-P_{4 k+2} P_{4 k+3}
\end{aligned}
$$
As the sum of the length of the sides is an even number then we conclude that $A_{1}$ is a positive integer. The same is true for all $A_{2}, A_{3}, \ldots$ as well. But now we have a contradiction as the side of length 1 cannot be split in two parts, each of which has positive integer length.
|
{
"exam": "BalticWay",
"problem_label": "15",
"problem_match": "\nProblem 15.",
"resource_path": "BalticWay/segmented/en-bw21sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2021"
}
|
Show that no non-zero integers $a, b, x, y$ satisfy
$$
\left\{\begin{array}{l}
a x-b y=16, \\
a y+b x=1 .
\end{array}\right.
$$
|
If we use the Diophantus sum of squares equality
$$
(a x-b y)^{2}+(a y+b x)^{2}=\left(a^{2}+b^{2}\right)\left(x^{2}+y^{2}\right)
$$
then we can see that for a system
$$
\left\{\begin{array}{l}
a x-b y=s \\
a y+b x=t
\end{array}\right.
$$
to have a solution in positive integers the number $s^{2}+t^{2}$ must be a composite number.
The number corresponding to the equation, $16^{2}+1^{2}=257$, is a prime number. This shows that no solution can exist in non-zero integers, as it would give a factorisation of the prime with each factor $>1$.

## Baltic Way
Reykjavík, November 11th - 15th
Solutions
Remark. Note that $(a+b i)(x+y i)=(a x-b y)+(a y+b x) i$. Finding a solution to the system of equations is therefore equivalent to finding a factorization of $s+t i$ in Gaussian integers $\mathbb{Z}[i]$ with non-negative real and imaginary component. It is known that the Gaussian integers form a Euclidean domain and hence a unique factorization domain. The form for primes in $\mathbb{Z}[i]$ has been thoroughly studied.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Show that no non-zero integers $a, b, x, y$ satisfy
$$
\left\{\begin{array}{l}
a x-b y=16, \\
a y+b x=1 .
\end{array}\right.
$$
|
If we use the Diophantus sum of squares equality
$$
(a x-b y)^{2}+(a y+b x)^{2}=\left(a^{2}+b^{2}\right)\left(x^{2}+y^{2}\right)
$$
then we can see that for a system
$$
\left\{\begin{array}{l}
a x-b y=s \\
a y+b x=t
\end{array}\right.
$$
to have a solution in positive integers the number $s^{2}+t^{2}$ must be a composite number.
The number corresponding to the equation, $16^{2}+1^{2}=257$, is a prime number. This shows that no solution can exist in non-zero integers, as it would give a factorisation of the prime with each factor $>1$.

## Baltic Way
Reykjavík, November 11th - 15th
Solutions
Remark. Note that $(a+b i)(x+y i)=(a x-b y)+(a y+b x) i$. Finding a solution to the system of equations is therefore equivalent to finding a factorization of $s+t i$ in Gaussian integers $\mathbb{Z}[i]$ with non-negative real and imaginary component. It is known that the Gaussian integers form a Euclidean domain and hence a unique factorization domain. The form for primes in $\mathbb{Z}[i]$ has been thoroughly studied.
|
{
"exam": "BalticWay",
"problem_label": "16",
"problem_match": "\nProblem 16.",
"resource_path": "BalticWay/segmented/en-bw21sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2021"
}
|
Distinct positive integers $a, b, c, d$ satisfy
$$
\left\{\begin{array}{l}
a \mid b^{2}+c^{2}+d^{2}, \\
b \mid a^{2}+c^{2}+d^{2}, \\
c \mid a^{2}+b^{2}+d^{2}, \\
d \mid a^{2}+b^{2}+c^{2},
\end{array}\right.
$$
and none of them is larger than the product of the three others. What is the largest possible number of primes among them?
|
At first we note that the given condition is equivalent to $a, b, c, d \mid a^{2}+b^{2}+c^{2}+d^{2}$.
It is possible that three of the given numbers are primes, for example for $a=2, b=3, c=13$ and $d=26$. In this case $2^{2}+3^{2}+13^{2}+26^{2}=13 \cdot 66$ which is divisible by all four given numbers. Furthermore we will show that it is impossible that all four of them are primes.
Let us assume that $a, b, c$ and $d$ are primes. As the sum $a^{2}+b^{2}+c^{2}+d^{2}$ is divisible by each of them then it is divisible also by their product $a b c d$. If one of the primes is equal to 2 , then we obtain a contradiction: the sum of four squares is odd, but its divisor $a b c d$ is even. Therefore all four primes are odd, and $a^{2}+b^{2}+c^{2}+d^{2}=0(\bmod 4)$. Hence $a^{2}+b^{2}+c^{2}+d^{2}$ is divisible by $4 a b c d$ which leads to a contradiction as it is easy to see that $a^{2}+b^{2}+c^{2}+d^{2}<4 a b c d$. Indeed, this is equivalent to
$$
\frac{a}{b c d}+\frac{b}{a c d}+\frac{c}{a b d}+\frac{d}{a b c}<4
$$
which is true as none of the numbers exceed the product of three three other and equality can hold only for the largest of the four.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Distinct positive integers $a, b, c, d$ satisfy
$$
\left\{\begin{array}{l}
a \mid b^{2}+c^{2}+d^{2}, \\
b \mid a^{2}+c^{2}+d^{2}, \\
c \mid a^{2}+b^{2}+d^{2}, \\
d \mid a^{2}+b^{2}+c^{2},
\end{array}\right.
$$
and none of them is larger than the product of the three others. What is the largest possible number of primes among them?
|
At first we note that the given condition is equivalent to $a, b, c, d \mid a^{2}+b^{2}+c^{2}+d^{2}$.
It is possible that three of the given numbers are primes, for example for $a=2, b=3, c=13$ and $d=26$. In this case $2^{2}+3^{2}+13^{2}+26^{2}=13 \cdot 66$ which is divisible by all four given numbers. Furthermore we will show that it is impossible that all four of them are primes.
Let us assume that $a, b, c$ and $d$ are primes. As the sum $a^{2}+b^{2}+c^{2}+d^{2}$ is divisible by each of them then it is divisible also by their product $a b c d$. If one of the primes is equal to 2 , then we obtain a contradiction: the sum of four squares is odd, but its divisor $a b c d$ is even. Therefore all four primes are odd, and $a^{2}+b^{2}+c^{2}+d^{2}=0(\bmod 4)$. Hence $a^{2}+b^{2}+c^{2}+d^{2}$ is divisible by $4 a b c d$ which leads to a contradiction as it is easy to see that $a^{2}+b^{2}+c^{2}+d^{2}<4 a b c d$. Indeed, this is equivalent to
$$
\frac{a}{b c d}+\frac{b}{a c d}+\frac{c}{a b d}+\frac{d}{a b c}<4
$$
which is true as none of the numbers exceed the product of three three other and equality can hold only for the largest of the four.
|
{
"exam": "BalticWay",
"problem_label": "17",
"problem_match": "\nProblem 17.",
"resource_path": "BalticWay/segmented/en-bw21sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2021"
}
|
Find all integer triples $(a, b, c)$ satisfying the equation
$$
5 a^{2}+9 b^{2}=13 c^{2}
$$
## Baltic Way
Solutions
|
Observe that $(a, b, c)=(0,0,0)$ is a solution. Assume that the equation has a solution $\left(a_{0}, b_{0}, c_{0}\right) \neq(0,0,0)$. Let $d=\operatorname{gcd}\left(a_{0}, b_{0}, c_{0}\right)>0$. Let $(a, b, c)=\left(a_{0} / d, b_{0} / d, c_{0} / d\right)$. Then $\operatorname{gcd}(a, b, c)$ $=1$. From $5 a_{0}{ }^{2}+9 b_{0}{ }^{2}=13 c_{0}{ }^{2}$ it follows that:
$$
5 a^{2}+9 b^{2}=5\left(\frac{a_{0}}{d}\right)^{2}+9\left(\frac{b_{0}}{d}\right)^{2}=\frac{5 a_{0}{ }^{2}+9 b_{0}{ }^{2}}{d^{2}}=\frac{13 c_{0}{ }^{2}}{d^{2}}=13\left(\frac{c_{0}}{d}\right)^{2}=13 c^{2}
$$
hence $(a, b, c)$ is also a solution.
As $\left(a_{0}, b_{0}, c_{0}\right) \neq(0,0,0)$ it follows that $(a, b, c) \neq(0,0,0)$. Consider the equation modulo 5. It follows that $4 b^{2} \equiv 5 a^{2}+9 b^{2}=13 c^{2} \equiv 3 c^{2}(\bmod 5)$, that is $4 b^{2} \equiv 3 c^{2}(\bmod 5)$. Multiplying by 4 gives:
$$
b^{2} \equiv 16 b^{2}=4 \cdot 4 b^{2} \equiv 4 \cdot 3 c^{2}=12 c^{2} \equiv 2 \cdot c^{2} \quad(\bmod 5)
$$
If $5 \mid c$ then $2 c^{2} \equiv 2 \cdot 0^{2}=0(\bmod 5)$ and therefore $a^{2} \equiv 0(\bmod 5)$, that is $5 \mid b^{2}$. As 5 is prime it follows that $5 \mid b$. Hence 5 divides $b$ and $c$. It follows that $5^{2} \mid 13 c^{2}-9 b^{2}=5 a^{2}$. Consequently 5 divides $a^{2}$. As 5 is prime, $5 \mid a$. This means that 5 divides $a, b$ and $c$ contradicting the fact that $\operatorname{gcd}(a, b, c)=1$. We conclude that $5 \mid c$ does not hold.
As $5 \mid c$ does not hold and 5 is a prime it follows that $c$ and 5 are relative prime. Therefore there exists $x \in \mathbb{Z}$ such that $c \cdot x \equiv 1(\bmod 5)$. Multiplying by $x^{2}$ gives:
$$
(b \cdot x)^{2}=b^{2} \cdot x^{2} \equiv 2 \cdot c^{2} \cdot x^{2}=2 \cdot(c \cdot x)^{2} \equiv 2 \cdot 1^{2}=2
$$
That is $y^{2} \equiv 2(\bmod 5)$ where $y=b \cdot x$. As $y^{2} \equiv 2(\bmod 5)$ it follows that $y$ and 5 are relative prime. By Fermat's little theorem it follows that $y^{4} \equiv 1(\bmod 5)$. Hence:
$$
1 \equiv y^{4}=\left(y^{2}\right)^{2} \equiv 2^{2}=4 \quad(\bmod 5)
$$
but $1 \not \equiv 4(\bmod 5)$ so we have a contradiction. We conclude that the equation $5 a^{2}+9 b^{2}=13 c^{2}$ has no solution besides the solution $(a, b, c)=(0,0,0)$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all integer triples $(a, b, c)$ satisfying the equation
$$
5 a^{2}+9 b^{2}=13 c^{2}
$$
## Baltic Way
Solutions
|
Observe that $(a, b, c)=(0,0,0)$ is a solution. Assume that the equation has a solution $\left(a_{0}, b_{0}, c_{0}\right) \neq(0,0,0)$. Let $d=\operatorname{gcd}\left(a_{0}, b_{0}, c_{0}\right)>0$. Let $(a, b, c)=\left(a_{0} / d, b_{0} / d, c_{0} / d\right)$. Then $\operatorname{gcd}(a, b, c)$ $=1$. From $5 a_{0}{ }^{2}+9 b_{0}{ }^{2}=13 c_{0}{ }^{2}$ it follows that:
$$
5 a^{2}+9 b^{2}=5\left(\frac{a_{0}}{d}\right)^{2}+9\left(\frac{b_{0}}{d}\right)^{2}=\frac{5 a_{0}{ }^{2}+9 b_{0}{ }^{2}}{d^{2}}=\frac{13 c_{0}{ }^{2}}{d^{2}}=13\left(\frac{c_{0}}{d}\right)^{2}=13 c^{2}
$$
hence $(a, b, c)$ is also a solution.
As $\left(a_{0}, b_{0}, c_{0}\right) \neq(0,0,0)$ it follows that $(a, b, c) \neq(0,0,0)$. Consider the equation modulo 5. It follows that $4 b^{2} \equiv 5 a^{2}+9 b^{2}=13 c^{2} \equiv 3 c^{2}(\bmod 5)$, that is $4 b^{2} \equiv 3 c^{2}(\bmod 5)$. Multiplying by 4 gives:
$$
b^{2} \equiv 16 b^{2}=4 \cdot 4 b^{2} \equiv 4 \cdot 3 c^{2}=12 c^{2} \equiv 2 \cdot c^{2} \quad(\bmod 5)
$$
If $5 \mid c$ then $2 c^{2} \equiv 2 \cdot 0^{2}=0(\bmod 5)$ and therefore $a^{2} \equiv 0(\bmod 5)$, that is $5 \mid b^{2}$. As 5 is prime it follows that $5 \mid b$. Hence 5 divides $b$ and $c$. It follows that $5^{2} \mid 13 c^{2}-9 b^{2}=5 a^{2}$. Consequently 5 divides $a^{2}$. As 5 is prime, $5 \mid a$. This means that 5 divides $a, b$ and $c$ contradicting the fact that $\operatorname{gcd}(a, b, c)=1$. We conclude that $5 \mid c$ does not hold.
As $5 \mid c$ does not hold and 5 is a prime it follows that $c$ and 5 are relative prime. Therefore there exists $x \in \mathbb{Z}$ such that $c \cdot x \equiv 1(\bmod 5)$. Multiplying by $x^{2}$ gives:
$$
(b \cdot x)^{2}=b^{2} \cdot x^{2} \equiv 2 \cdot c^{2} \cdot x^{2}=2 \cdot(c \cdot x)^{2} \equiv 2 \cdot 1^{2}=2
$$
That is $y^{2} \equiv 2(\bmod 5)$ where $y=b \cdot x$. As $y^{2} \equiv 2(\bmod 5)$ it follows that $y$ and 5 are relative prime. By Fermat's little theorem it follows that $y^{4} \equiv 1(\bmod 5)$. Hence:
$$
1 \equiv y^{4}=\left(y^{2}\right)^{2} \equiv 2^{2}=4 \quad(\bmod 5)
$$
but $1 \not \equiv 4(\bmod 5)$ so we have a contradiction. We conclude that the equation $5 a^{2}+9 b^{2}=13 c^{2}$ has no solution besides the solution $(a, b, c)=(0,0,0)$.
|
{
"exam": "BalticWay",
"problem_label": "18",
"problem_match": "\nProblem 18.",
"resource_path": "BalticWay/segmented/en-bw21sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2021"
}
|
Find all polynomials $p$ with integer coefficients such that the number $p(a)-p(b)$ is divisible by $a+b$ for all integers $a, b$, provided that $a+b \neq 0$.
|
The polynomials we are looking for are those whose every odd-degree term has zero coefficient.
Let $P(x)=P_{0}(x)+P_{1}(x)$, where $P_{0}$ and $P_{1}$ are polynomials whose all non-zero terms have either even or odd degree, respectively.
Then we can write $P_{0}(x)=Q\left(x^{2}\right)$, where polynomial $Q$ is obtained from polynomial $P_{0}$ by dividing degrees of all non-zero terms by 2 . Now, for any integers $a, b$ the number $P_{0}(a)-P_{0}(b)=Q\left(a^{2}\right)-Q\left(b^{2}\right)$

BALTIC WAY
REYKJAVÍK$\cdot$ 2021
## Baltic Way
Reykjavík, November 11th - 15th
Solutions
is divisible by $a^{2}-b^{2}$, and hence also by $a+b$. Thus, if every odd-degree term of $P$ has zero coefficient, then the condition of the problem is satisfied.
On the other hand, if polynomial $P$ satisfies the condition of the problem, then also $P-P_{0}=P_{1}$ must satisfy it. Note that for every real $x, P_{1}(-x)=-P_{1}(x)$, i.e. $P_{1}$ is an odd function. By substituting $b$ by $-b$ in the condition of the problem we obtain that $a-b \mid P_{1}(a)+P_{1}(b)$ holds for any distinct integers $a$ and $b$. Since also $a-b \mid P_{1}(a)-P_{1}(b)$, then for any integers $a$, $b$ we have $a-b \mid 2 P_{1}(a)$. But for any $a$ there exists such $b$ that $|a-b|>2 P_{1}(a)$. From this we conclude that $P_{1}(a)=0$ for any integer $a$. Altogether we have $P=P_{0}$, i.e. coefficients of all odd-degree terms are zero.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all polynomials $p$ with integer coefficients such that the number $p(a)-p(b)$ is divisible by $a+b$ for all integers $a, b$, provided that $a+b \neq 0$.
|
The polynomials we are looking for are those whose every odd-degree term has zero coefficient.
Let $P(x)=P_{0}(x)+P_{1}(x)$, where $P_{0}$ and $P_{1}$ are polynomials whose all non-zero terms have either even or odd degree, respectively.
Then we can write $P_{0}(x)=Q\left(x^{2}\right)$, where polynomial $Q$ is obtained from polynomial $P_{0}$ by dividing degrees of all non-zero terms by 2 . Now, for any integers $a, b$ the number $P_{0}(a)-P_{0}(b)=Q\left(a^{2}\right)-Q\left(b^{2}\right)$

BALTIC WAY
REYKJAVÍK$\cdot$ 2021
## Baltic Way
Reykjavík, November 11th - 15th
Solutions
is divisible by $a^{2}-b^{2}$, and hence also by $a+b$. Thus, if every odd-degree term of $P$ has zero coefficient, then the condition of the problem is satisfied.
On the other hand, if polynomial $P$ satisfies the condition of the problem, then also $P-P_{0}=P_{1}$ must satisfy it. Note that for every real $x, P_{1}(-x)=-P_{1}(x)$, i.e. $P_{1}$ is an odd function. By substituting $b$ by $-b$ in the condition of the problem we obtain that $a-b \mid P_{1}(a)+P_{1}(b)$ holds for any distinct integers $a$ and $b$. Since also $a-b \mid P_{1}(a)-P_{1}(b)$, then for any integers $a$, $b$ we have $a-b \mid 2 P_{1}(a)$. But for any $a$ there exists such $b$ that $|a-b|>2 P_{1}(a)$. From this we conclude that $P_{1}(a)=0$ for any integer $a$. Altogether we have $P=P_{0}$, i.e. coefficients of all odd-degree terms are zero.
|
{
"exam": "BalticWay",
"problem_label": "19",
"problem_match": "\nProblem 19.",
"resource_path": "BalticWay/segmented/en-bw21sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2021"
}
|
Let $n \geq 2$ be an integer. Given numbers $a_{1}, a_{2}, \ldots, a_{n} \in\{1,2,3, \ldots, 2 n\}$ such that $\operatorname{lcm}\left(a_{i}, a_{j}\right)>2 n$ for all $1 \leq i<j \leq n$, prove that
$$
a_{1} a_{2} \cdots a_{n} \mid(n+1)(n+2) \cdots(2 n-1)(2 n) .
$$
|
For every $i=1,2, \ldots, n$ let $b_{i}=\max \left\{k \cdot a_{i} \mid k \in \mathbb{Z}, k \cdot a_{i} \leq 2 n\right\}$, that is $b_{i}$ is the greatest multiple of $a_{i}$ in $\{1,2, \ldots, 2 n\}$. It is clear that $b_{i} \in\{n+1, n+2, \ldots, 2 n\}$ because if $b_{i} \leq n$ then $2 b_{i} \leq 2 n$ is a greater multiple of $a_{i}$.
If $1 \leq i<j \leq n$ then $a_{i}+b_{j}$ because else $b_{j} \leq 2 n$ would be a common multiple of $a_{i}$ and $a_{j}$ smaller than their least common multiple $\operatorname{lcm}\left(a_{i}, a_{j}\right)>2 n$. In particular $b_{i} \neq b_{j}$. It follows that the map $\{1,2, \ldots, n\} \rightarrow\{n+1, n+2, \ldots, 2 n\}, i \mapsto b_{i}$ is injective. As both sets $\{1,2, \ldots, n\}$ and $\{n+1, n+2, \ldots, 2 n\}$ have the same finite cardinality it follows that the map is also a surjection and hence a bijection. In particular $b_{1} b_{2} \cdots b_{n}=(n+1)(n+2) \cdots(2 n)$ by associativity and commutativity.
As each $a_{i} \mid b_{i}$ it follows that
$$
a_{1} a_{2} \cdots a_{n} \mid b_{1} b_{2} \cdots b_{n}=(n+1)(n+2) \cdots(2 n)
$$
as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n \geq 2$ be an integer. Given numbers $a_{1}, a_{2}, \ldots, a_{n} \in\{1,2,3, \ldots, 2 n\}$ such that $\operatorname{lcm}\left(a_{i}, a_{j}\right)>2 n$ for all $1 \leq i<j \leq n$, prove that
$$
a_{1} a_{2} \cdots a_{n} \mid(n+1)(n+2) \cdots(2 n-1)(2 n) .
$$
|
For every $i=1,2, \ldots, n$ let $b_{i}=\max \left\{k \cdot a_{i} \mid k \in \mathbb{Z}, k \cdot a_{i} \leq 2 n\right\}$, that is $b_{i}$ is the greatest multiple of $a_{i}$ in $\{1,2, \ldots, 2 n\}$. It is clear that $b_{i} \in\{n+1, n+2, \ldots, 2 n\}$ because if $b_{i} \leq n$ then $2 b_{i} \leq 2 n$ is a greater multiple of $a_{i}$.
If $1 \leq i<j \leq n$ then $a_{i}+b_{j}$ because else $b_{j} \leq 2 n$ would be a common multiple of $a_{i}$ and $a_{j}$ smaller than their least common multiple $\operatorname{lcm}\left(a_{i}, a_{j}\right)>2 n$. In particular $b_{i} \neq b_{j}$. It follows that the map $\{1,2, \ldots, n\} \rightarrow\{n+1, n+2, \ldots, 2 n\}, i \mapsto b_{i}$ is injective. As both sets $\{1,2, \ldots, n\}$ and $\{n+1, n+2, \ldots, 2 n\}$ have the same finite cardinality it follows that the map is also a surjection and hence a bijection. In particular $b_{1} b_{2} \cdots b_{n}=(n+1)(n+2) \cdots(2 n)$ by associativity and commutativity.
As each $a_{i} \mid b_{i}$ it follows that
$$
a_{1} a_{2} \cdots a_{n} \mid b_{1} b_{2} \cdots b_{n}=(n+1)(n+2) \cdots(2 n)
$$
as desired.
|
{
"exam": "BalticWay",
"problem_label": "20",
"problem_match": "\nProblem 20.",
"resource_path": "BalticWay/segmented/en-bw21sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2021"
}
|
Find all strictly increasing sequences $1=a_{1}<a_{2}<a_{3}<\cdots$ of positive integers satisfying
$$
3\left(a_{1}+a_{2}+\cdots+a_{n}\right)=a_{n+1}+a_{n+2}+\cdots+a_{2 n}
$$
for all positive integers $n$.
|
The strictly increasing sequence $\left(a_{n}\right)$ with $a_{n}=2 n-1$ for all $n \in \mathbb{Z}^{+}$ satisfies $a_{1}=1$ and solves the given equation, since $1+3+\cdots+(2 n-1)=n^{2}$ and $(2 n+1)+(2 n+3)+\cdots+(4 n-1)=(2 n)^{2}-n^{2}=3 n^{2}$ for all $n \in \mathbb{Z}^{+}$.
We claim that no other sequence is suitable. Let $\left(b_{n}\right)$ be a sequence that meets all requirements of the problem.
Let $k \in \mathbb{Z}^{+}$. Note that the given equation for $k$ and $k+1$ implies
$$
\begin{aligned}
& 3 \cdot \sum_{l=1}^{k} b_{\ell}=\sum_{l=k+1}^{2 k} b \ell \\
& 3 \cdot \sum_{l=1}^{k+1} b_{\ell}=\sum_{l=k+2}^{2 k+2} b_{\ell} ;
\end{aligned}
$$
the difference of the two equations yields $3 b_{k+1}=-b_{k+1}+b_{2 k+1}+b_{2 k+2}$. In other words, the equation
$$
4 b_{k+1}=b_{2 k+1}+b_{2 k+2}
$$
holds for all $k \in \mathbb{Z}^{+}$.
Equation $(*)$ implies that the numbers $b_{2 k+1}$ and $b_{2 k+2}$ have the same parity for every $k \in \mathbb{Z}^{+}$. Since $\left(b_{n}\right)$ is strictly increasing, we can deduce that $b_{2 k+2} \geq b_{2 k+1}+2$. Shifting indices we also obtain $4 b_{k+2}=b_{2 k+3}+b_{2 k+4}$ from equation $\left(^{*}\right)$. Note that $b_{2 k+3} \geq b_{2 k+2}+1 \geq b_{2 k+1}+3$. Similarly, since $b_{2 k+3}$ and $b_{2 k+4}$ must have the same parity, $b_{2 k+4} \geq b_{2 k+3}+2 \geq b_{2 k+2}+3$, so that
$$
\begin{aligned}
4 b_{k+2} & =b_{2 k+3}+b_{2 k+4} \\
& \geq\left(b_{2 k+1}+3\right)+\left(b_{2 k+2}+3\right) \\
& =4 b_{k+1}+6
\end{aligned}
$$
We can conclude that
$$
b_{k+2} \geq b_{k+1}+2 \text { for all } k \in \mathbb{Z}^{+}
$$
Now we are ready to show that $f(n)=2 n-1$ for all $n \in \mathbb{Z}^{+}$. More precisely, we use strong induction to show that $f(2 k-1)=4 k-3$ and $f(2 k)=4 k-1$ for all $k \in \mathbb{Z}^{+}$. The claim implies $f(n)=2 n-1$ for all $n \in \mathbb{Z}^{+}$.
For the start of the induction, note that we have $f(1)=1$ by definition; the given condition for $n=1$ implies $f(2)=3 f(1)=3$. Hence, the equations $f(2 k-1)=4 k-3$ and $f(2 k)=4 k-1$ are true for $k=1$.
For the induction step, let $k \geq 1$ and assume that $f(2 l-1)=4 l-3$ and $f(2 l)=4 l-1$ for all $l \in\{1, \ldots, k\}$. We want to show that $f(2 k+1)=4 k+1$ and $f(2 k+2)=$ $4 k+3$.
Since $k+1 \leq 2 k$ the induction hypothesis implies $f(k+1)=2 k+1$. Equation $(*)$ implies $f(2 k+1)+f(2 k+2)=8 k+4$. By induction hypothesis $f(2 k)=4 k-1$, so that by virtue of inequality $\left({ }^{* *}\right)$ we have $f(2 k+1) \geq 4 k+1$ and $f(2 k+2) \geq 4 k+3$. Since the sum of the two function values is $8 k+4$, we must have $f(2 k+1)=4 k+1$ and $f(2 k+2)=4 k+3$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all strictly increasing sequences $1=a_{1}<a_{2}<a_{3}<\cdots$ of positive integers satisfying
$$
3\left(a_{1}+a_{2}+\cdots+a_{n}\right)=a_{n+1}+a_{n+2}+\cdots+a_{2 n}
$$
for all positive integers $n$.
|
The strictly increasing sequence $\left(a_{n}\right)$ with $a_{n}=2 n-1$ for all $n \in \mathbb{Z}^{+}$ satisfies $a_{1}=1$ and solves the given equation, since $1+3+\cdots+(2 n-1)=n^{2}$ and $(2 n+1)+(2 n+3)+\cdots+(4 n-1)=(2 n)^{2}-n^{2}=3 n^{2}$ for all $n \in \mathbb{Z}^{+}$.
We claim that no other sequence is suitable. Let $\left(b_{n}\right)$ be a sequence that meets all requirements of the problem.
Let $k \in \mathbb{Z}^{+}$. Note that the given equation for $k$ and $k+1$ implies
$$
\begin{aligned}
& 3 \cdot \sum_{l=1}^{k} b_{\ell}=\sum_{l=k+1}^{2 k} b \ell \\
& 3 \cdot \sum_{l=1}^{k+1} b_{\ell}=\sum_{l=k+2}^{2 k+2} b_{\ell} ;
\end{aligned}
$$
the difference of the two equations yields $3 b_{k+1}=-b_{k+1}+b_{2 k+1}+b_{2 k+2}$. In other words, the equation
$$
4 b_{k+1}=b_{2 k+1}+b_{2 k+2}
$$
holds for all $k \in \mathbb{Z}^{+}$.
Equation $(*)$ implies that the numbers $b_{2 k+1}$ and $b_{2 k+2}$ have the same parity for every $k \in \mathbb{Z}^{+}$. Since $\left(b_{n}\right)$ is strictly increasing, we can deduce that $b_{2 k+2} \geq b_{2 k+1}+2$. Shifting indices we also obtain $4 b_{k+2}=b_{2 k+3}+b_{2 k+4}$ from equation $\left(^{*}\right)$. Note that $b_{2 k+3} \geq b_{2 k+2}+1 \geq b_{2 k+1}+3$. Similarly, since $b_{2 k+3}$ and $b_{2 k+4}$ must have the same parity, $b_{2 k+4} \geq b_{2 k+3}+2 \geq b_{2 k+2}+3$, so that
$$
\begin{aligned}
4 b_{k+2} & =b_{2 k+3}+b_{2 k+4} \\
& \geq\left(b_{2 k+1}+3\right)+\left(b_{2 k+2}+3\right) \\
& =4 b_{k+1}+6
\end{aligned}
$$
We can conclude that
$$
b_{k+2} \geq b_{k+1}+2 \text { for all } k \in \mathbb{Z}^{+}
$$
Now we are ready to show that $f(n)=2 n-1$ for all $n \in \mathbb{Z}^{+}$. More precisely, we use strong induction to show that $f(2 k-1)=4 k-3$ and $f(2 k)=4 k-1$ for all $k \in \mathbb{Z}^{+}$. The claim implies $f(n)=2 n-1$ for all $n \in \mathbb{Z}^{+}$.
For the start of the induction, note that we have $f(1)=1$ by definition; the given condition for $n=1$ implies $f(2)=3 f(1)=3$. Hence, the equations $f(2 k-1)=4 k-3$ and $f(2 k)=4 k-1$ are true for $k=1$.
For the induction step, let $k \geq 1$ and assume that $f(2 l-1)=4 l-3$ and $f(2 l)=4 l-1$ for all $l \in\{1, \ldots, k\}$. We want to show that $f(2 k+1)=4 k+1$ and $f(2 k+2)=$ $4 k+3$.
Since $k+1 \leq 2 k$ the induction hypothesis implies $f(k+1)=2 k+1$. Equation $(*)$ implies $f(2 k+1)+f(2 k+2)=8 k+4$. By induction hypothesis $f(2 k)=4 k-1$, so that by virtue of inequality $\left({ }^{* *}\right)$ we have $f(2 k+1) \geq 4 k+1$ and $f(2 k+2) \geq 4 k+3$. Since the sum of the two function values is $8 k+4$, we must have $f(2 k+1)=4 k+1$ and $f(2 k+2)=4 k+3$.
|
{
"exam": "BalticWay",
"problem_label": "1",
"problem_match": "\nProblem 1:",
"resource_path": "BalticWay/segmented/en-bw23sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2023"
}
|
Let $a_{1}, a_{2}, \ldots, a_{2023}$ be positive real numbers with
$$
a_{1}+a_{2}^{2}+a_{3}^{3}+\cdots+a_{2023}^{2023}=2023
$$
Show that
$$
a_{1}^{2023}+a_{2}^{2022}+\cdots+a_{2022}^{2}+a_{2023}>1+\frac{1}{2023} .
$$
|
Let us prove that conversely, the condition
$$
a_{1}^{2023}+a_{2}^{2022}+\cdots+a_{2023} \leq 1+\frac{1}{2023}
$$
implies that
$$
S:=a_{1}+a_{2}^{2}+\cdots+a_{2023}^{2023}<2023 .
$$
This is trivial if all $a_{i}$ are less than 1 . So suppose that there is an $i$ with $a_{i} \geq 1$, clearly it is unique and $a_{i}<1+\frac{1}{2023}$. Then we have
$$
\begin{aligned}
a_{i}^{i} & <\left(1+\frac{1}{2023}\right)^{2023}=1+\sum_{k=1}^{2023} \frac{1}{k !} \cdot \frac{2023}{2023} \cdot \frac{2022}{2023} \ldots \cdot \frac{2023-k+1}{2023} \\
& <1+\sum_{k=1}^{2023} \frac{1}{k !} \leq 1+\sum_{k=0}^{2022} \frac{1}{2^{k}}<3, \\
\sum_{\substack{k=1, k \neq i}}^{1011} a_{k}^{k} & \leq 1011 \text { and } \sum_{\substack{k=1012, k \neq i}}^{2023} a_{k}^{k} \leq \sum_{\substack{k=1012, k \neq i}}^{2023} a_{k}^{2024-k}<\frac{1}{2023} .
\end{aligned}
$$
Hence we have
$$
S=a_{i}^{i}+\sum_{\substack{k=1, k \neq i}}^{1011} a_{k}^{k}+\sum_{\substack{k=1012, k \neq i}}^{2023} a_{k}^{k}<3+1011+\frac{1}{2023}<2023
$$
Remark: While the estimates might seem crude, the resulting bound is not so far away from the truth: If we replace 2023 by $n$ and the bound by $1+c_{n}$, then our argument shows that $c_{n} \geq \frac{1}{n}$, at least for large $n$, while the optimal bound has $c_{n} \asymp \frac{\log n}{n}$ (as in fact a slightly more careful version of our argument immediately shows!).
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a_{1}, a_{2}, \ldots, a_{2023}$ be positive real numbers with
$$
a_{1}+a_{2}^{2}+a_{3}^{3}+\cdots+a_{2023}^{2023}=2023
$$
Show that
$$
a_{1}^{2023}+a_{2}^{2022}+\cdots+a_{2022}^{2}+a_{2023}>1+\frac{1}{2023} .
$$
|
Let us prove that conversely, the condition
$$
a_{1}^{2023}+a_{2}^{2022}+\cdots+a_{2023} \leq 1+\frac{1}{2023}
$$
implies that
$$
S:=a_{1}+a_{2}^{2}+\cdots+a_{2023}^{2023}<2023 .
$$
This is trivial if all $a_{i}$ are less than 1 . So suppose that there is an $i$ with $a_{i} \geq 1$, clearly it is unique and $a_{i}<1+\frac{1}{2023}$. Then we have
$$
\begin{aligned}
a_{i}^{i} & <\left(1+\frac{1}{2023}\right)^{2023}=1+\sum_{k=1}^{2023} \frac{1}{k !} \cdot \frac{2023}{2023} \cdot \frac{2022}{2023} \ldots \cdot \frac{2023-k+1}{2023} \\
& <1+\sum_{k=1}^{2023} \frac{1}{k !} \leq 1+\sum_{k=0}^{2022} \frac{1}{2^{k}}<3, \\
\sum_{\substack{k=1, k \neq i}}^{1011} a_{k}^{k} & \leq 1011 \text { and } \sum_{\substack{k=1012, k \neq i}}^{2023} a_{k}^{k} \leq \sum_{\substack{k=1012, k \neq i}}^{2023} a_{k}^{2024-k}<\frac{1}{2023} .
\end{aligned}
$$
Hence we have
$$
S=a_{i}^{i}+\sum_{\substack{k=1, k \neq i}}^{1011} a_{k}^{k}+\sum_{\substack{k=1012, k \neq i}}^{2023} a_{k}^{k}<3+1011+\frac{1}{2023}<2023
$$
Remark: While the estimates might seem crude, the resulting bound is not so far away from the truth: If we replace 2023 by $n$ and the bound by $1+c_{n}$, then our argument shows that $c_{n} \geq \frac{1}{n}$, at least for large $n$, while the optimal bound has $c_{n} \asymp \frac{\log n}{n}$ (as in fact a slightly more careful version of our argument immediately shows!).
|
{
"exam": "BalticWay",
"problem_label": "2",
"problem_match": "\nProblem 2:",
"resource_path": "BalticWay/segmented/en-bw23sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2023"
}
|
Denote a set of equations in the real numbers with variables $x_{1}, x_{2}, x_{3} \in \mathbb{R}$ Flensburgian if there exists an $i \in\{1,2,3\}$ such that every solution of the set of equations where all the variables are pairwise different, satisfies $x_{i}>x_{j}$ for all $j \neq i$.
Determine for which positive integers $n \geq 2$, the following set of two equations
$$
a^{n}+b=a \text { and } c^{n+1}+b^{2}=a b
$$
in the three real variables $a, b, c$ is Flensburgian.
|
The set of equations given in the problem statement is Flensburgian precisely when $n$ is even.
To see that it is not Flensburgian when $n \geq 3$ is odd, notice that if $(a, b, c)$ satisfies the set of equations then so does $(-a,-b,-c)$. Hence, if there exists a single solution to the set of equation where all the variables are different then the set of equations cannot be Flensburgian. This is in fact the case, e.g., consider $(a, b, c)=$ $\left(\frac{1}{2}, \frac{2^{n-1}-1}{2^{n}},\left(\frac{2^{n-1}-1}{2^{2 n}}\right)^{\frac{1}{n+1}}\right)$.
The rest of the solution is dedicated to prove that the set of equations is indeed Flensburgian when $n$ is even.
The first equation yields $b=a-a^{n} \leq a$, since $a^{n} \geq 0$ when $n$ is even. The inequality is strict whenever $a \neq 0$ and the case $a=0$ implies $b=0$, i.e. $a=b$, which we can disregard. Substituting the relation $b=a-a^{n}$ into the second equation yields
$$
\begin{aligned}
& 0=c^{n+1}+\left(a-a^{n}\right)^{2}-a\left(a-a^{n}\right)=c^{n+1}+a^{2 n}-a^{n+1}, \text { i.e. } \\
& c^{n+1}=a^{n+1}-a^{2 n}<a^{n+1}
\end{aligned}
$$
since we can disregard $a=0$ and $2 n$ is even. Since $n+1$ is odd, the polynomial $x^{n+1}$ is strictly increasing, implying that $c<a$. Hence, when $n$ is even, all solutions of the set of equations where $a, b, c$ are pairwise different satisfy $a>b$ and $a>c$.
|
n \text{ is even}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Denote a set of equations in the real numbers with variables $x_{1}, x_{2}, x_{3} \in \mathbb{R}$ Flensburgian if there exists an $i \in\{1,2,3\}$ such that every solution of the set of equations where all the variables are pairwise different, satisfies $x_{i}>x_{j}$ for all $j \neq i$.
Determine for which positive integers $n \geq 2$, the following set of two equations
$$
a^{n}+b=a \text { and } c^{n+1}+b^{2}=a b
$$
in the three real variables $a, b, c$ is Flensburgian.
|
The set of equations given in the problem statement is Flensburgian precisely when $n$ is even.
To see that it is not Flensburgian when $n \geq 3$ is odd, notice that if $(a, b, c)$ satisfies the set of equations then so does $(-a,-b,-c)$. Hence, if there exists a single solution to the set of equation where all the variables are different then the set of equations cannot be Flensburgian. This is in fact the case, e.g., consider $(a, b, c)=$ $\left(\frac{1}{2}, \frac{2^{n-1}-1}{2^{n}},\left(\frac{2^{n-1}-1}{2^{2 n}}\right)^{\frac{1}{n+1}}\right)$.
The rest of the solution is dedicated to prove that the set of equations is indeed Flensburgian when $n$ is even.
The first equation yields $b=a-a^{n} \leq a$, since $a^{n} \geq 0$ when $n$ is even. The inequality is strict whenever $a \neq 0$ and the case $a=0$ implies $b=0$, i.e. $a=b$, which we can disregard. Substituting the relation $b=a-a^{n}$ into the second equation yields
$$
\begin{aligned}
& 0=c^{n+1}+\left(a-a^{n}\right)^{2}-a\left(a-a^{n}\right)=c^{n+1}+a^{2 n}-a^{n+1}, \text { i.e. } \\
& c^{n+1}=a^{n+1}-a^{2 n}<a^{n+1}
\end{aligned}
$$
since we can disregard $a=0$ and $2 n$ is even. Since $n+1$ is odd, the polynomial $x^{n+1}$ is strictly increasing, implying that $c<a$. Hence, when $n$ is even, all solutions of the set of equations where $a, b, c$ are pairwise different satisfy $a>b$ and $a>c$.
|
{
"exam": "BalticWay",
"problem_label": "3",
"problem_match": "\nProblem 3:",
"resource_path": "BalticWay/segmented/en-bw23sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2023"
}
|
Determine all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ that satisfy
$$
f(f(x)+y)+x f(y)=f(x y+y)+f(x)
$$
for all real numbers $x$ and $y$.
|
Let $P(x, y)$ denote the assertion of the given functional equation.
Claim 1: $f(0)=0$.
Proof. Note that $P(0, y)$ and $P(x, 0)$ gives us the following:
$$
\begin{aligned}
f(y+f(0)) & =f(y)+f(0) \\
f(f(x))+x f(0) & =f(0)+f(x) .
\end{aligned}
$$
Consider the first expression. Plugging $y=-f(0)$ in it yields
$$
f(-f(0)+f(0))=f(-f(0))+f(0) \text {, i.e. } f(-f(0))=0 \text {. }
$$
If we denote $-f(0)=a$, then we have $f(a)=0$. Plugging $x=a$ in the second expression gives us:
$$
f(f(a))+a f(0)=f(0)+f(a) \text {, i.e. } a f(0)=0 \text {. }
$$
This either means that $a=0$, i.e. $f(0)=0$ or $f(0)=0$. In both cases the claim is proved.
Since $f(0)=0$, the expression $P(x, 0)$ becomes
$$
f(f(x))=f(x) .
$$
Claim 2: $f(1)=1$ or $f(x)=0$ for all real numbers $x$.
Proof. Consider $P(x, 1)$ :
$$
f(f(x)+1)+x f(1)=f(x+1)+f(x) .
$$
Replacing $x$ by $f(x)$ and using $(*)$ leads to:
$$
\begin{aligned}
f(f(f(x))+1)+f(x) f(1) & =f(f(x)+1)+f(f(x)) \\
f(f(x)+1)+f(x) f(1) & =f(f(x)+1)+f(x) \\
f(x) f(1) & =f(x) .
\end{aligned}
$$
Suppose that there does not exist such $b$ that $f(b) \neq 0$, then $f(x)=0$ for all real numbers $x$. Otherwise $f(b) f(1)=f(b)$ implies $f(1)=1$ as desired.
Claim 3: If $f(1)=1$ and $f(a)=0$, then $a=0$.
Proof. Suppose $f(a)=0$ for some real number $a$. Then $P(a, 1)$ gives us
$$
\begin{aligned}
f(f(a)+1)+a f(1) & =f(a+1)+f(a) \\
f(1)+a=f(a+1) & =a+1
\end{aligned}
$$
On the other hand $P(1, a)$ leads us to the following:
$$
\begin{aligned}
f(f(1)+a)+f(a) & =f(2 a)+f(1) \\
f(a+1) & =f(2 a)+1 \\
a+1 & =f(2 a)+1 \\
f(2 a) & =a .
\end{aligned}
$$
Taking $f$ from both sides in the last relation and using $(*)$ leads to:
$$
0=f(a)=f(f(2 a))=f(2 a)=a .
$$
This proves the claim.
To finish the problem, consider $P(x, x-f(x))$ :
$$
x f(x-f(x))=f((x-f(x)) \cdot(x+1)) .
$$
Setting $x=-1$ gives us
$$
-f(-1-f(-1))=f((-1-f(-1)) \cdot 0)=f(0)=0 .
$$
From Claim 3 for $f \not \equiv 0$ we obtain that $-1-f(-1)=0$ implies $f(-1)=-1$. Now looking at $P(-1, y)$ and replacing $y$ by $y+1$, we get that
$$
f(y-1)=f(y)-1 \text { implies } f(y+1)=f(y)+1 \text {. }
$$
On the other hand, $P(x, 1)$, the previous relation and $\left(^{*}\right)$ give us the following:
$$
\begin{aligned}
f(f(x)+1)+x & =f(x+1)+f(x) \\
f(f(x))+1+x & =f(x)+1+f(x) \\
f(x)+x & =2 f(x) \\
f(x) & =x .
\end{aligned}
$$
Thus, the only possible functions that satisfy the given relation are $f(x)=x$ and $f(x)=0$. It is easy to check that they indeed solve the functional equation.
|
f(x)=x \text{ and } f(x)=0
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Determine all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ that satisfy
$$
f(f(x)+y)+x f(y)=f(x y+y)+f(x)
$$
for all real numbers $x$ and $y$.
|
Let $P(x, y)$ denote the assertion of the given functional equation.
Claim 1: $f(0)=0$.
Proof. Note that $P(0, y)$ and $P(x, 0)$ gives us the following:
$$
\begin{aligned}
f(y+f(0)) & =f(y)+f(0) \\
f(f(x))+x f(0) & =f(0)+f(x) .
\end{aligned}
$$
Consider the first expression. Plugging $y=-f(0)$ in it yields
$$
f(-f(0)+f(0))=f(-f(0))+f(0) \text {, i.e. } f(-f(0))=0 \text {. }
$$
If we denote $-f(0)=a$, then we have $f(a)=0$. Plugging $x=a$ in the second expression gives us:
$$
f(f(a))+a f(0)=f(0)+f(a) \text {, i.e. } a f(0)=0 \text {. }
$$
This either means that $a=0$, i.e. $f(0)=0$ or $f(0)=0$. In both cases the claim is proved.
Since $f(0)=0$, the expression $P(x, 0)$ becomes
$$
f(f(x))=f(x) .
$$
Claim 2: $f(1)=1$ or $f(x)=0$ for all real numbers $x$.
Proof. Consider $P(x, 1)$ :
$$
f(f(x)+1)+x f(1)=f(x+1)+f(x) .
$$
Replacing $x$ by $f(x)$ and using $(*)$ leads to:
$$
\begin{aligned}
f(f(f(x))+1)+f(x) f(1) & =f(f(x)+1)+f(f(x)) \\
f(f(x)+1)+f(x) f(1) & =f(f(x)+1)+f(x) \\
f(x) f(1) & =f(x) .
\end{aligned}
$$
Suppose that there does not exist such $b$ that $f(b) \neq 0$, then $f(x)=0$ for all real numbers $x$. Otherwise $f(b) f(1)=f(b)$ implies $f(1)=1$ as desired.
Claim 3: If $f(1)=1$ and $f(a)=0$, then $a=0$.
Proof. Suppose $f(a)=0$ for some real number $a$. Then $P(a, 1)$ gives us
$$
\begin{aligned}
f(f(a)+1)+a f(1) & =f(a+1)+f(a) \\
f(1)+a=f(a+1) & =a+1
\end{aligned}
$$
On the other hand $P(1, a)$ leads us to the following:
$$
\begin{aligned}
f(f(1)+a)+f(a) & =f(2 a)+f(1) \\
f(a+1) & =f(2 a)+1 \\
a+1 & =f(2 a)+1 \\
f(2 a) & =a .
\end{aligned}
$$
Taking $f$ from both sides in the last relation and using $(*)$ leads to:
$$
0=f(a)=f(f(2 a))=f(2 a)=a .
$$
This proves the claim.
To finish the problem, consider $P(x, x-f(x))$ :
$$
x f(x-f(x))=f((x-f(x)) \cdot(x+1)) .
$$
Setting $x=-1$ gives us
$$
-f(-1-f(-1))=f((-1-f(-1)) \cdot 0)=f(0)=0 .
$$
From Claim 3 for $f \not \equiv 0$ we obtain that $-1-f(-1)=0$ implies $f(-1)=-1$. Now looking at $P(-1, y)$ and replacing $y$ by $y+1$, we get that
$$
f(y-1)=f(y)-1 \text { implies } f(y+1)=f(y)+1 \text {. }
$$
On the other hand, $P(x, 1)$, the previous relation and $\left(^{*}\right)$ give us the following:
$$
\begin{aligned}
f(f(x)+1)+x & =f(x+1)+f(x) \\
f(f(x))+1+x & =f(x)+1+f(x) \\
f(x)+x & =2 f(x) \\
f(x) & =x .
\end{aligned}
$$
Thus, the only possible functions that satisfy the given relation are $f(x)=x$ and $f(x)=0$. It is easy to check that they indeed solve the functional equation.
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "\nProblem 4:",
"resource_path": "BalticWay/segmented/en-bw23sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2023"
}
|
Find the smallest positive real number $\alpha$, such that
$$
\frac{x+y}{2} \geq \alpha \sqrt{x y}+(1-\alpha) \sqrt{\frac{x^{2}+y^{2}}{2}}
$$
for all positive real numbers $x$ and $y$.
|
Let us prove that $\alpha=\frac{1}{2}$ works. Then the following inequality should hold for all positive real numbers $x$ and $y$ :
$$
\begin{aligned}
& \frac{x+y}{2} \geq \frac{1}{2} \sqrt{x y}+\frac{1}{2} \sqrt{\frac{x^{2}+y^{2}}{2}} \\
\Longleftrightarrow & (x+y)^{2} \geq x y+\frac{x^{2}+y^{2}}{2}+2 \sqrt{x y \cdot \frac{x^{2}+y^{2}}{2}} \\
\Longleftrightarrow & (x+y)^{2} \geq 4 \sqrt{x y \cdot \frac{x^{2}+y^{2}}{2}} \\
\Longleftrightarrow & (x+y)^{4} \geq 8 x y\left(x^{2}+y^{2}\right) \\
\Longleftrightarrow & (x-y)^{4} \geq 0
\end{aligned}
$$
which is true, so we showed that $\alpha=\frac{1}{2}$ actually works.
Now it remains to show that $\alpha \geq \frac{1}{2}$. Let's consider $x=1+\varepsilon$ and $y=1-\varepsilon$ where $\varepsilon<1$. Then the inequality becomes
$$
1 \geq \alpha \sqrt{1-\varepsilon^{2}}+(1-\alpha) \sqrt{1+\varepsilon^{2}} \text {, i.e. } \alpha \geq \frac{\sqrt{1+\varepsilon^{2}}-1}{\sqrt{1+\varepsilon^{2}}-\sqrt{1-\varepsilon^{2}}} \text {. }
$$
Notice that
$$
\begin{aligned}
& \frac{\sqrt{1+\varepsilon^{2}}-1}{\sqrt{1+\varepsilon^{2}}-\sqrt{1-\varepsilon^{2}}} \\
= & \frac{\left(\sqrt{1+\varepsilon^{2}}-1\right)\left(\sqrt{1+\varepsilon^{2}}+1\right)\left(\sqrt{1+\varepsilon^{2}}+\sqrt{1-\varepsilon^{2}}\right)}{\left(\sqrt{1+\varepsilon^{2}}-\sqrt{1-\varepsilon^{2}}\right)\left(\sqrt{1+\varepsilon^{2}}+\sqrt{1-\varepsilon^{2}}\right)\left(\sqrt{1+\varepsilon^{2}}+1\right)} \\
= & \frac{\varepsilon^{2}\left(\sqrt{1+\varepsilon^{2}}+\sqrt{1-\varepsilon^{2}}\right)}{2 \varepsilon^{2}\left(\sqrt{1+\varepsilon^{2}}+1\right)}=\frac{\sqrt{1+\varepsilon^{2}}+1-1+\sqrt{1-\varepsilon^{2}}}{2\left(\sqrt{1+\varepsilon^{2}}+1\right)} \\
= & \frac{1}{2}-\frac{1-\sqrt{1-\varepsilon^{2}}}{2\left(\sqrt{1+\varepsilon^{2}}+1\right)}=\frac{1}{2}-\frac{\left(1-\sqrt{1-\varepsilon^{2}}\right)\left(1+\sqrt{1-\varepsilon^{2}}\right)}{2\left(\sqrt{1+\varepsilon^{2}}+1\right)\left(1+\sqrt{1-\varepsilon^{2}}\right)} \\
= & \frac{1}{2}-\frac{\varepsilon^{2}}{2\left(\sqrt{1+\varepsilon^{2}}+1\right)\left(1+\sqrt{1-\varepsilon^{2}}\right)}>\frac{1}{2}-\frac{\varepsilon^{2}}{4 \cdot(1+\sqrt{2})} .
\end{aligned}
$$
As $\varepsilon$ can be arbitrarily small this expression can get arbitrarily close to $\frac{1}{2}$. This means that $\alpha<\frac{1}{2}$ cannot hold, as desired.
|
\alpha = \frac{1}{2}
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Find the smallest positive real number $\alpha$, such that
$$
\frac{x+y}{2} \geq \alpha \sqrt{x y}+(1-\alpha) \sqrt{\frac{x^{2}+y^{2}}{2}}
$$
for all positive real numbers $x$ and $y$.
|
Let us prove that $\alpha=\frac{1}{2}$ works. Then the following inequality should hold for all positive real numbers $x$ and $y$ :
$$
\begin{aligned}
& \frac{x+y}{2} \geq \frac{1}{2} \sqrt{x y}+\frac{1}{2} \sqrt{\frac{x^{2}+y^{2}}{2}} \\
\Longleftrightarrow & (x+y)^{2} \geq x y+\frac{x^{2}+y^{2}}{2}+2 \sqrt{x y \cdot \frac{x^{2}+y^{2}}{2}} \\
\Longleftrightarrow & (x+y)^{2} \geq 4 \sqrt{x y \cdot \frac{x^{2}+y^{2}}{2}} \\
\Longleftrightarrow & (x+y)^{4} \geq 8 x y\left(x^{2}+y^{2}\right) \\
\Longleftrightarrow & (x-y)^{4} \geq 0
\end{aligned}
$$
which is true, so we showed that $\alpha=\frac{1}{2}$ actually works.
Now it remains to show that $\alpha \geq \frac{1}{2}$. Let's consider $x=1+\varepsilon$ and $y=1-\varepsilon$ where $\varepsilon<1$. Then the inequality becomes
$$
1 \geq \alpha \sqrt{1-\varepsilon^{2}}+(1-\alpha) \sqrt{1+\varepsilon^{2}} \text {, i.e. } \alpha \geq \frac{\sqrt{1+\varepsilon^{2}}-1}{\sqrt{1+\varepsilon^{2}}-\sqrt{1-\varepsilon^{2}}} \text {. }
$$
Notice that
$$
\begin{aligned}
& \frac{\sqrt{1+\varepsilon^{2}}-1}{\sqrt{1+\varepsilon^{2}}-\sqrt{1-\varepsilon^{2}}} \\
= & \frac{\left(\sqrt{1+\varepsilon^{2}}-1\right)\left(\sqrt{1+\varepsilon^{2}}+1\right)\left(\sqrt{1+\varepsilon^{2}}+\sqrt{1-\varepsilon^{2}}\right)}{\left(\sqrt{1+\varepsilon^{2}}-\sqrt{1-\varepsilon^{2}}\right)\left(\sqrt{1+\varepsilon^{2}}+\sqrt{1-\varepsilon^{2}}\right)\left(\sqrt{1+\varepsilon^{2}}+1\right)} \\
= & \frac{\varepsilon^{2}\left(\sqrt{1+\varepsilon^{2}}+\sqrt{1-\varepsilon^{2}}\right)}{2 \varepsilon^{2}\left(\sqrt{1+\varepsilon^{2}}+1\right)}=\frac{\sqrt{1+\varepsilon^{2}}+1-1+\sqrt{1-\varepsilon^{2}}}{2\left(\sqrt{1+\varepsilon^{2}}+1\right)} \\
= & \frac{1}{2}-\frac{1-\sqrt{1-\varepsilon^{2}}}{2\left(\sqrt{1+\varepsilon^{2}}+1\right)}=\frac{1}{2}-\frac{\left(1-\sqrt{1-\varepsilon^{2}}\right)\left(1+\sqrt{1-\varepsilon^{2}}\right)}{2\left(\sqrt{1+\varepsilon^{2}}+1\right)\left(1+\sqrt{1-\varepsilon^{2}}\right)} \\
= & \frac{1}{2}-\frac{\varepsilon^{2}}{2\left(\sqrt{1+\varepsilon^{2}}+1\right)\left(1+\sqrt{1-\varepsilon^{2}}\right)}>\frac{1}{2}-\frac{\varepsilon^{2}}{4 \cdot(1+\sqrt{2})} .
\end{aligned}
$$
As $\varepsilon$ can be arbitrarily small this expression can get arbitrarily close to $\frac{1}{2}$. This means that $\alpha<\frac{1}{2}$ cannot hold, as desired.
|
{
"exam": "BalticWay",
"problem_label": "5",
"problem_match": "\nProblem 5:",
"resource_path": "BalticWay/segmented/en-bw23sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2023"
}
|
Let $n$ be a positive integer. Each cell of an $n \times n$ table is coloured in one of $k$ colours where every colour is used at least once. Two different colours $A$ and $B$ are said to touch each other, if there exists a cell coloured in $A$ sharing a side with a cell coloured in $B$. The table is coloured in such a way that each colour touches at most 2 other colours. What is the maximal value of $k$ in terms of $n$ ?
|
$k=2 n-1$ when $n \neq 2$ and $k=4$ when $n=2$.
$k=2 n-1$ is possible by colouring diagonally as shown in the figure below and when $n=2, k=4$ is possible by colouring each cell in a unique colour.

We consider the graph, where each node represents a colour and two nodes are linked, if the colours they represent touch. This graph is connected and since each colour touches at most 2 colours every node has at most degree 2 . This means that the graph is either one long chain or one big cycle.
We now look at the case when $n$ is odd. Consider the cell in the center of the table. From this cell we can get to any other cell by passing through at most $n-1$ cells. Therefore from the node representing this cell, we can get to any node through at most $n-1$ edges. But if the graph has $2 n$ or more nodes, then for every node there is a node which is more than $n-1$ edges away. So we must have $k \leq 2 n-1$ for all odd $n$.
When $n$ is even we consider the 4 center cells. If they all have a different colour, then they form a 4-cycle in the graph, meaning the graph has only 4 nodes. If two of the center cells have the same colour, then from this colour you will be able to get to all other cells passing thorugh at most $n-1$ cells. By same the arguments as in the odd case, we get $k \leq \max (2 n-1,4)$ for even $n$.
So overall we have $k \leq 2 n-1$ for $n \neq 2$ and $k \leq 4$ for $n=2$ as desired.
|
k=2n-1 \text{ when } n \neq 2 \text{ and } k=4 \text{ when } n=2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be a positive integer. Each cell of an $n \times n$ table is coloured in one of $k$ colours where every colour is used at least once. Two different colours $A$ and $B$ are said to touch each other, if there exists a cell coloured in $A$ sharing a side with a cell coloured in $B$. The table is coloured in such a way that each colour touches at most 2 other colours. What is the maximal value of $k$ in terms of $n$ ?
|
$k=2 n-1$ when $n \neq 2$ and $k=4$ when $n=2$.
$k=2 n-1$ is possible by colouring diagonally as shown in the figure below and when $n=2, k=4$ is possible by colouring each cell in a unique colour.

We consider the graph, where each node represents a colour and two nodes are linked, if the colours they represent touch. This graph is connected and since each colour touches at most 2 colours every node has at most degree 2 . This means that the graph is either one long chain or one big cycle.

We now look at the case when $n$ is odd. Consider the cell in the center of the table. From this cell we can get to any other cell by passing through at most $n-1$ cells. Therefore from the node representing this cell, we can get to any node through at most $n-1$ edges. But if the graph has $2 n$ or more nodes, then for every node there is a node which is more than $n-1$ edges away. So we must have $k \leq 2 n-1$ for all odd $n$.
When $n$ is even we consider the 4 center cells. If they all have a different colour, then they form a 4-cycle in the graph, meaning the graph has only 4 nodes. If two of the center cells have the same colour, then from this colour you will be able to get to all other cells passing thorugh at most $n-1$ cells. By same the arguments as in the odd case, we get $k \leq \max (2 n-1,4)$ for even $n$.
So overall we have $k \leq 2 n-1$ for $n \neq 2$ and $k \leq 4$ for $n=2$ as desired.
|
{
"exam": "BalticWay",
"problem_label": "6",
"problem_match": "\nProblem 6:",
"resource_path": "BalticWay/segmented/en-bw23sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2023"
}
|
A robot moves in the plane in a straight line, but every one meter it turns $90^{\circ}$ to the right or to the left. At some point it reaches its starting point without having visited any other point more than once, and stops immediately. What are the possible path lengths of the robot?
|
Let us define the coordinates system with unit length of one meter, point of origin in the starting point and vertical-horizontal axes. W.l.o.g. assume that the first move was east and the path had length of $n$. Then each odd move changed $x$ coordinate of the robot by 1 and each even move changed $y$ coordinate by 1 .
At the end of the day both coordinates were equal to zero again, so there had to be even number of odd and even number of even moves. That implies that only $n$ divisible by 4 can fulfill the conditions.
For $n=4$ we have a square path. For $n=8$ we had 4 changes of $x$ coordinate and 4 changes of $y$, so the whole path was inside some $2 \times 2$ square. Unfortunately that's not possible without reaching some point twice.
Now, we will prove that all $n>8$ divisible by 4 are good. For $n=12$ there is a path in shape of "+" with first 4 moves like $(\rightarrow, \uparrow, \rightarrow, \uparrow)$. Now we can change the middle $(\uparrow, \rightarrow)$ sequence by $(\downarrow, \rightarrow, \uparrow, \rightarrow, \uparrow, \leftarrow)$. Thanks to this change the robot explored new territory south-east from the one before explored. We got +4 of length of the path. There we can do it again and again, reaching any length of $4 k+8$ for all $k \in \mathbb{Z}^{+}$.
|
4k+8 \text{ for all } k \in \mathbb{Z}^{+}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A robot moves in the plane in a straight line, but every one meter it turns $90^{\circ}$ to the right or to the left. At some point it reaches its starting point without having visited any other point more than once, and stops immediately. What are the possible path lengths of the robot?
|
Let us define the coordinates system with unit length of one meter, point of origin in the starting point and vertical-horizontal axes. W.l.o.g. assume that the first move was east and the path had length of $n$. Then each odd move changed $x$ coordinate of the robot by 1 and each even move changed $y$ coordinate by 1 .
At the end of the day both coordinates were equal to zero again, so there had to be even number of odd and even number of even moves. That implies that only $n$ divisible by 4 can fulfill the conditions.
For $n=4$ we have a square path. For $n=8$ we had 4 changes of $x$ coordinate and 4 changes of $y$, so the whole path was inside some $2 \times 2$ square. Unfortunately that's not possible without reaching some point twice.
Now, we will prove that all $n>8$ divisible by 4 are good. For $n=12$ there is a path in shape of "+" with first 4 moves like $(\rightarrow, \uparrow, \rightarrow, \uparrow)$. Now we can change the middle $(\uparrow, \rightarrow)$ sequence by $(\downarrow, \rightarrow, \uparrow, \rightarrow, \uparrow, \leftarrow)$. Thanks to this change the robot explored new territory south-east from the one before explored. We got +4 of length of the path. There we can do it again and again, reaching any length of $4 k+8$ for all $k \in \mathbb{Z}^{+}$.
|
{
"exam": "BalticWay",
"problem_label": "7",
"problem_match": "\nProblem 7:",
"resource_path": "BalticWay/segmented/en-bw23sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2023"
}
|
In the city of Flensburg there is a single, infinitely long, street with houses numbered 2, 3, .. The police in Flensburg is trying to catch a thief who every night moves from the house where she is currently hiding to one of its neighbouring houses.
To taunt the local law enforcement the thief reveals every morning the highest prime divisor of the number of the house she has moved to.
Every Sunday afternoon the police searches a single house, and they catch the thief if they search the house she is currently occupying. Does the police have a strategy to catch the thief in finite time?
|
We will prove that the police are always able to catch the thief in finite time.
Let $h_{i}$ denote the house the thief stays at the $i$-th night and $p_{i}$ denote the greatest prime divisor of $h_{i}$.
The police knows that she stays at different neighbouring houses every night, so $h_{i+1}-h_{i}=1$ for all non-negative integers $i$. Let us assume that the police are given the address of the thief's first two hiding spots, then we will prove by induction that the police can determine $h_{i}$ precisely except being unable to distinguish between houses numbered 2 and 4.
Assume the police knows $h_{i-2}$ and $h_{i-1}$, then they known that $h_{i}=h_{i-2}$ or $h_{i}=$ $2 h_{i-1}-h_{i-2}$. In the first case they will receive $p_{i}=p_{i-2}$ and in the latter case they will receive $p_{i}$ as the biggest prime divisor of $2 h_{i-1}-h_{i-2}$. Assume that they are unable to distinguish between these two cases, i.e., that $p_{i}=p_{i-2}$, which implies
$$
p_{i-2} \mid 2 h_{i-1}-h_{i-2} \text {, i.e. } p_{i-2} \mid 2 h_{i-1} \text {, i.e. } p_{i-2} \mid 2 \text {, i.e. } p_{i-2}=2
$$
since $h_{i-1}-h_{i-2}=1$ implies $\operatorname{gcd}\left(h_{i-1}, h_{i-1}\right)=1$. Moreover, since $p_{i}=p_{i-2}=2$ are the biggest prime divisors of $h_{i}=2 h_{i-1}-h_{i-2}$ and $h_{i-2}$ they must both be powers of 2 . However, the only powers of two with a difference of exactly 2 are 2 and 4 . Hence $\left\{h_{i-2}, 2 h_{i-1}-h_{i-2}\right\}=\{2,4\}$, i.e. $h_{i-1}=\frac{2+4}{2}=3$.
Thus, either the police will with certainty be able to determine $h_{i}$ or $h_{i-1}=3$, in which case $h_{i}$ may equal either 2 or 4 . To complete the inductive step we observe that the police are always able to determine the parity of $h_{j}$, since it changes every day. Thus, in the future if the police know that $h_{j} \in[2,4]$, then they can either determine $h_{j}=3$ or $h_{j} \in\{2,4\}$. However, the only way for the thief to leave the interval $[2,4]$ is to go to house number 5 , in which case the police will be alerted by receiving $p_{j}=5$, and they can again with certainty determine $h_{j}=5$ and $h_{j-1}=4$ preserving our inductive hypothesis.
To summarize, if the police knows both $h_{0}$ and $h_{1}$, then they can always determine $h_{i}$ with certainty until $h_{i-1}=3$. After this point they will with known the two last hiding places of the thief if she leaves the interval $[2,4]$, restoring the inductive hypothesis, or otherwise, if she never leaves $[2,4]$ be able to determine his position, up to confusion about 2 and 4 using the parity of the day.
Now, to catch the thief in finite time, they may methodically try to guess all viable pairs of $\left(h_{0}, h_{1}\right)$, i.e $h_{0}, h_{1} \in \mathbb{N}_{\geq 2}$ and $h_{0}-h_{1}=1$, of which there are countably many.
For each viable starting position, let us consider either the immediate Sunday or the one after that, since each week has an odd amount of days, we are certain that exactly one of these days gives us that the thief is hiding in an odd house (given our assumption on his starting position). Thus, due to our inductive hypothesis, we can precisely determine where the thief will be, and search this house.
If the thief is hiding in that house, the police wins, and if not, they will with certainty know that their guess of starting positions was incorrect, and move onto the next guess. By the above argument, each guess of initial starting positions requires at most two weeks, meaning that the police will catch the thief in finite time.
Remark: Note that if a week contained an even number of days then the police would not be able to guarantee that they would be able to catch the thief, if the thief moves between houses number 3 and $\{2,4\}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
In the city of Flensburg there is a single, infinitely long, street with houses numbered 2, 3, .. The police in Flensburg is trying to catch a thief who every night moves from the house where she is currently hiding to one of its neighbouring houses.
To taunt the local law enforcement the thief reveals every morning the highest prime divisor of the number of the house she has moved to.
Every Sunday afternoon the police searches a single house, and they catch the thief if they search the house she is currently occupying. Does the police have a strategy to catch the thief in finite time?
|
We will prove that the police are always able to catch the thief in finite time.
Let $h_{i}$ denote the house the thief stays at the $i$-th night and $p_{i}$ denote the greatest prime divisor of $h_{i}$.
The police knows that she stays at different neighbouring houses every night, so $h_{i+1}-h_{i}=1$ for all non-negative integers $i$. Let us assume that the police are given the address of the thief's first two hiding spots, then we will prove by induction that the police can determine $h_{i}$ precisely except being unable to distinguish between houses numbered 2 and 4.
Assume the police knows $h_{i-2}$ and $h_{i-1}$, then they known that $h_{i}=h_{i-2}$ or $h_{i}=$ $2 h_{i-1}-h_{i-2}$. In the first case they will receive $p_{i}=p_{i-2}$ and in the latter case they will receive $p_{i}$ as the biggest prime divisor of $2 h_{i-1}-h_{i-2}$. Assume that they are unable to distinguish between these two cases, i.e., that $p_{i}=p_{i-2}$, which implies
$$
p_{i-2} \mid 2 h_{i-1}-h_{i-2} \text {, i.e. } p_{i-2} \mid 2 h_{i-1} \text {, i.e. } p_{i-2} \mid 2 \text {, i.e. } p_{i-2}=2
$$
since $h_{i-1}-h_{i-2}=1$ implies $\operatorname{gcd}\left(h_{i-1}, h_{i-1}\right)=1$. Moreover, since $p_{i}=p_{i-2}=2$ are the biggest prime divisors of $h_{i}=2 h_{i-1}-h_{i-2}$ and $h_{i-2}$ they must both be powers of 2 . However, the only powers of two with a difference of exactly 2 are 2 and 4 . Hence $\left\{h_{i-2}, 2 h_{i-1}-h_{i-2}\right\}=\{2,4\}$, i.e. $h_{i-1}=\frac{2+4}{2}=3$.
Thus, either the police will with certainty be able to determine $h_{i}$ or $h_{i-1}=3$, in which case $h_{i}$ may equal either 2 or 4 . To complete the inductive step we observe that the police are always able to determine the parity of $h_{j}$, since it changes every day. Thus, in the future if the police know that $h_{j} \in[2,4]$, then they can either determine $h_{j}=3$ or $h_{j} \in\{2,4\}$. However, the only way for the thief to leave the interval $[2,4]$ is to go to house number 5 , in which case the police will be alerted by receiving $p_{j}=5$, and they can again with certainty determine $h_{j}=5$ and $h_{j-1}=4$ preserving our inductive hypothesis.
To summarize, if the police knows both $h_{0}$ and $h_{1}$, then they can always determine $h_{i}$ with certainty until $h_{i-1}=3$. After this point they will with known the two last hiding places of the thief if she leaves the interval $[2,4]$, restoring the inductive hypothesis, or otherwise, if she never leaves $[2,4]$ be able to determine his position, up to confusion about 2 and 4 using the parity of the day.
Now, to catch the thief in finite time, they may methodically try to guess all viable pairs of $\left(h_{0}, h_{1}\right)$, i.e $h_{0}, h_{1} \in \mathbb{N}_{\geq 2}$ and $h_{0}-h_{1}=1$, of which there are countably many.
For each viable starting position, let us consider either the immediate Sunday or the one after that, since each week has an odd amount of days, we are certain that exactly one of these days gives us that the thief is hiding in an odd house (given our assumption on his starting position). Thus, due to our inductive hypothesis, we can precisely determine where the thief will be, and search this house.
If the thief is hiding in that house, the police wins, and if not, they will with certainty know that their guess of starting positions was incorrect, and move onto the next guess. By the above argument, each guess of initial starting positions requires at most two weeks, meaning that the police will catch the thief in finite time.
Remark: Note that if a week contained an even number of days then the police would not be able to guarantee that they would be able to catch the thief, if the thief moves between houses number 3 and $\{2,4\}$.
|
{
"exam": "BalticWay",
"problem_label": "8",
"problem_match": "\nProblem 8:",
"resource_path": "BalticWay/segmented/en-bw23sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2023"
}
|
Determine if there exists a triangle that can be cut into 101 congruent triangles.
|
Answer: Yes, there is.
Choose an arbitrary positive integer $m$ and draw a height in the right triangle with ratio of legs $1: m$. This height cuts the triangle in two similar triangles with similarity coefficient $m$. The largest of them can further be cut into $m^{2}$ smaller equal triangles by splitting all sides in $m$ equal parts and connecting corresponding points with parallel lines. Thus a triangle can be split into $m^{2}+1$ equal triangles.
The figure shows this for $m=4$, but in our problem we must take $m=10$.
|
Yes, there is.
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Determine if there exists a triangle that can be cut into 101 congruent triangles.
|
Answer: Yes, there is.
Choose an arbitrary positive integer $m$ and draw a height in the right triangle with ratio of legs $1: m$. This height cuts the triangle in two similar triangles with similarity coefficient $m$. The largest of them can further be cut into $m^{2}$ smaller equal triangles by splitting all sides in $m$ equal parts and connecting corresponding points with parallel lines. Thus a triangle can be split into $m^{2}+1$ equal triangles.
The figure shows this for $m=4$, but in our problem we must take $m=10$.

|
{
"exam": "BalticWay",
"problem_label": "9",
"problem_match": "\nProblem 9:",
"resource_path": "BalticWay/segmented/en-bw23sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2023"
}
|
On a circle, $n \geq 3$ points are marked. Each marked point is coloured red, green or blue. In one step, one can erase two neighbouring marked points of different colours and mark a new point between the locations of the erased points with the third colour. In a final state, all marked points have the same colour which is called the colour of the final state. Find all $n$ for which there exists an initial state of $n$ marked points with one missing colour, from which one can reach a final state of any of the three colours by applying a suitable sequence of steps.
|
Answer: All even numbers $n$ greater than 2 .
We show first that required initial states are impossible for odd $n$. Note that if one colour is missing then the numbers of marked points of existing two colours have different parities, i.e., the difference of these numbers is odd. Each step keeps the parity of the difference of the numbers of marked points of these two colours unchanged. Hence in every intermediate state and also in the final state, one of these two colours is represented. Consequently, a final state of the third colour is impossible.
For every even number $n>2$, an initial state with 2 consecutive points marked with one colour and $n-2$ points marked with another colour satisfies the conditions of the problem. Indeed, if $n>4$ then with two symmetric steps, one can reach a similar state where the number of points marked with the more popular colour is 2 less. Hence it suffices to solve the case $n=4$. In this case, making one step leads to a state with 3 marked points, all with different colours. In order to obtain a final state of any given colour, one can replace points of the other two colours with a new point of the given colour. This completes the solution.
## 2nd Solution:
Definition: Call a configuration colourful, if the final state may have any of the three colours.
The case of $n$ being odd is excluded as in the first solution, so let $n>2$ be even. To construct colourful configurations, we consider linear configurations, i.e. one where the points are placed on a line instead of a circle. There is only difference to the circular situaton: We may not choose the two end points for the replacement step. So it suffices to construct linear colourful configurations.
We start by providing explicit examples for $n=4$ and $n=6$ (with the bold letters being replaced):
$$
\begin{aligned}
& \mathbf{R G} R G \rightarrow B \mathbf{R G} \rightarrow B B \\
& R \mathbf{G R} G \rightarrow R \mathbf{B G} \rightarrow R R \\
& R \mathbf{G R} G \rightarrow \mathbf{R B} G \rightarrow G G \\
& \mathbf{R G} R R G R \rightarrow B R R \mathbf{G R} \rightarrow B R \mathbf{R B} \rightarrow B \mathbf{R G} \rightarrow B B \\
& R \mathbf{G R} R G R \rightarrow R B \mathbf{R G} R \rightarrow \mathbf{R B} B R \rightarrow \mathbf{G B} R \rightarrow R R \\
& R \mathbf{G R} R G R \rightarrow R B \mathbf{R G} R \rightarrow \mathbf{R B} B R \rightarrow G \mathbf{B R} \rightarrow G G .
\end{aligned}
$$
Next observe that the concatenation of several linear colourful configurations is again colourful: Indeed, each part can be transformed into the desired colour independently. So the building blocks for $n=4$ and $n=6$ can produce colourful configurations of any even length.
Actually one can prove a lot more about colourful configurations:
Proposition: Denote the number of red resp. green resp. blue points in the initial state by $R$ resp. $G$ resp. $B$. A circular configuration is colourful if and only if
$$
R \equiv G \equiv B \quad(\bmod 2)
$$
and it contains at least two colours.
Proof. We have already seen in the solution above that $R-G \bmod 2, G-B \bmod 2$ and $B-R$ mod 2 are invariants. Moreover it is obvious that we need at least two colours to be able to do anything. So the conditions are necessary.
We prove that they are sufficient: For $n=3$ the conditions require $R=G=B=1$ and the configuration indeed colourful. We continue by induction for $n>3$ : As $n>3$, there is at least one colour with more than one point, so assume wlog. $R>1$. Having at least two colours, we can find a pair of two different colours, one of which is red. Assume w.l.o.g. that the other is green. As a first step replace these two points. The resulting configuration has $R-1$ red, $G-1$ green and $B+1$ blue points, so it satisfies $R-1=G-1=B+1 \bmod 2$. Moreover due to $R>1$ is has at least one red and one blue point. So by induction the configuration is colourful, and hence so was our original state.
This classification of colourful configuration, has some nice consequences:
Proposition: If a circular configuration is colourful, then so is any permutation of its points.
Proof. Immediate.
|
All even numbers n greater than 2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On a circle, $n \geq 3$ points are marked. Each marked point is coloured red, green or blue. In one step, one can erase two neighbouring marked points of different colours and mark a new point between the locations of the erased points with the third colour. In a final state, all marked points have the same colour which is called the colour of the final state. Find all $n$ for which there exists an initial state of $n$ marked points with one missing colour, from which one can reach a final state of any of the three colours by applying a suitable sequence of steps.
|
Answer: All even numbers $n$ greater than 2 .
We show first that required initial states are impossible for odd $n$. Note that if one colour is missing then the numbers of marked points of existing two colours have different parities, i.e., the difference of these numbers is odd. Each step keeps the parity of the difference of the numbers of marked points of these two colours unchanged. Hence in every intermediate state and also in the final state, one of these two colours is represented. Consequently, a final state of the third colour is impossible.
For every even number $n>2$, an initial state with 2 consecutive points marked with one colour and $n-2$ points marked with another colour satisfies the conditions of the problem. Indeed, if $n>4$ then with two symmetric steps, one can reach a similar state where the number of points marked with the more popular colour is 2 less. Hence it suffices to solve the case $n=4$. In this case, making one step leads to a state with 3 marked points, all with different colours. In order to obtain a final state of any given colour, one can replace points of the other two colours with a new point of the given colour. This completes the solution.
## 2nd Solution:
Definition: Call a configuration colourful, if the final state may have any of the three colours.
The case of $n$ being odd is excluded as in the first solution, so let $n>2$ be even. To construct colourful configurations, we consider linear configurations, i.e. one where the points are placed on a line instead of a circle. There is only difference to the circular situaton: We may not choose the two end points for the replacement step. So it suffices to construct linear colourful configurations.
We start by providing explicit examples for $n=4$ and $n=6$ (with the bold letters being replaced):
$$
\begin{aligned}
& \mathbf{R G} R G \rightarrow B \mathbf{R G} \rightarrow B B \\
& R \mathbf{G R} G \rightarrow R \mathbf{B G} \rightarrow R R \\
& R \mathbf{G R} G \rightarrow \mathbf{R B} G \rightarrow G G \\
& \mathbf{R G} R R G R \rightarrow B R R \mathbf{G R} \rightarrow B R \mathbf{R B} \rightarrow B \mathbf{R G} \rightarrow B B \\
& R \mathbf{G R} R G R \rightarrow R B \mathbf{R G} R \rightarrow \mathbf{R B} B R \rightarrow \mathbf{G B} R \rightarrow R R \\
& R \mathbf{G R} R G R \rightarrow R B \mathbf{R G} R \rightarrow \mathbf{R B} B R \rightarrow G \mathbf{B R} \rightarrow G G .
\end{aligned}
$$
Next observe that the concatenation of several linear colourful configurations is again colourful: Indeed, each part can be transformed into the desired colour independently. So the building blocks for $n=4$ and $n=6$ can produce colourful configurations of any even length.
Actually one can prove a lot more about colourful configurations:
Proposition: Denote the number of red resp. green resp. blue points in the initial state by $R$ resp. $G$ resp. $B$. A circular configuration is colourful if and only if
$$
R \equiv G \equiv B \quad(\bmod 2)
$$
and it contains at least two colours.
Proof. We have already seen in the solution above that $R-G \bmod 2, G-B \bmod 2$ and $B-R$ mod 2 are invariants. Moreover it is obvious that we need at least two colours to be able to do anything. So the conditions are necessary.
We prove that they are sufficient: For $n=3$ the conditions require $R=G=B=1$ and the configuration indeed colourful. We continue by induction for $n>3$ : As $n>3$, there is at least one colour with more than one point, so assume wlog. $R>1$. Having at least two colours, we can find a pair of two different colours, one of which is red. Assume w.l.o.g. that the other is green. As a first step replace these two points. The resulting configuration has $R-1$ red, $G-1$ green and $B+1$ blue points, so it satisfies $R-1=G-1=B+1 \bmod 2$. Moreover due to $R>1$ is has at least one red and one blue point. So by induction the configuration is colourful, and hence so was our original state.
This classification of colourful configuration, has some nice consequences:
Proposition: If a circular configuration is colourful, then so is any permutation of its points.
Proof. Immediate.
|
{
"exam": "BalticWay",
"problem_label": "10",
"problem_match": "\nProblem 10:",
"resource_path": "BalticWay/segmented/en-bw23sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2023"
}
|
$\quad$ Let $A B C$ be a triangle and let $J$ be the centre of the $A$-excircle. The reflection of $J$ in $B C$ is $K$. The points $E$ and $F$ are on $B J$ and $C J$, respectively, such that $\angle E A B=\angle C A F=90^{\circ}$. Prove that $\angle F K E+\angle F J E=$ $180^{\circ}$.
Remark: The $A$-excircle is the circle that touches the side $B C$ and the extensions of $A C$ and $A B$.
|
Let $J K$ intersect $B C$ at $X$. We will prove a key claim:
Claim: $B E K$ is similar to $B A X$.
Proof. Note that $\angle E A B=90^{\circ}=\angle K X B$. Also, since $B J$ bisects $\angle C B A$, we get $\angle A B E=\angle J B X=\angle X B K$. Hence $E B A \sim K B X$. From that, we see that the spiral similarity that sends the line segment $E A$ to $K X$ has centre $B$. So the spiral similarity that sends the line segment $E K$ to $A X$ has centre $B$. Thus $B E K \sim B A X$.
In a similar manner, we get $C F K$ is similar to $C A X$.
Now, using the similar triangles and the fact that $K$ and $J$ are symmetric in $B C$, we have
$$
\begin{aligned}
\angle F K E+\angle F J E & =\angle F K E+\angle B K C \\
& =360^{\circ}-\angle E K B-\angle C K F \\
& =360^{\circ}-\angle A X B-\angle C X A \\
& =360^{\circ}-180^{\circ} \\
& =180^{\circ}
\end{aligned}
$$
as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
$\quad$ Let $A B C$ be a triangle and let $J$ be the centre of the $A$-excircle. The reflection of $J$ in $B C$ is $K$. The points $E$ and $F$ are on $B J$ and $C J$, respectively, such that $\angle E A B=\angle C A F=90^{\circ}$. Prove that $\angle F K E+\angle F J E=$ $180^{\circ}$.
Remark: The $A$-excircle is the circle that touches the side $B C$ and the extensions of $A C$ and $A B$.
|

Let $J K$ intersect $B C$ at $X$. We will prove a key claim:
Claim: $B E K$ is similar to $B A X$.
Proof. Note that $\angle E A B=90^{\circ}=\angle K X B$. Also, since $B J$ bisects $\angle C B A$, we get $\angle A B E=\angle J B X=\angle X B K$. Hence $E B A \sim K B X$. From that, we see that the spiral similarity that sends the line segment $E A$ to $K X$ has centre $B$. So the spiral similarity that sends the line segment $E K$ to $A X$ has centre $B$. Thus $B E K \sim B A X$.
In a similar manner, we get $C F K$ is similar to $C A X$.
Now, using the similar triangles and the fact that $K$ and $J$ are symmetric in $B C$, we have
$$
\begin{aligned}
\angle F K E+\angle F J E & =\angle F K E+\angle B K C \\
& =360^{\circ}-\angle E K B-\angle C K F \\
& =360^{\circ}-\angle A X B-\angle C X A \\
& =360^{\circ}-180^{\circ} \\
& =180^{\circ}
\end{aligned}
$$
as desired.
|
{
"exam": "BalticWay",
"problem_label": "11",
"problem_match": "\nProblem 11:",
"resource_path": "BalticWay/segmented/en-bw23sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2023"
}
|
Let $A B C$ be an acute triangle with $A B>A C$. The internal angle bisector of $\angle B A C$ intersects $B C$ at $D$. Let $O$ be the circumcentre of $A B C$. Let $A O$ intersect the segment $B C$ at $E$. Let $J$ be the incentre of $A E D$. Prove that if $\angle A D O=45^{\circ}$ then $O J=J D$.
|
Let $\alpha=\angle B A C, \beta=\angle C B A, \gamma=\angle A C B$. We have
$$
\begin{aligned}
\angle D J A & =90^{\circ}+\frac{1}{2} \angle D E A=90^{\circ}+\frac{1}{2}(\angle E B A+\angle B A E) \\
& =90^{\circ}+\frac{1}{2}\left(\beta+90^{\circ}-\gamma\right)=135^{\circ}+\frac{\beta}{2}-\frac{\gamma}{2}
\end{aligned}
$$
and
$$
\begin{aligned}
\angle D O A & =180^{\circ}-\angle O A D-\angle A D O=180^{\circ}-(\angle O A C-\angle D A C)-45^{\circ} \\
& =135^{\circ}-\left(90^{\circ}-\beta-\frac{\alpha}{2}\right)=135^{\circ}-\left(\frac{1}{2}(\alpha+\beta+\gamma)-\beta-\frac{\alpha}{2}\right) \\
& =135^{\circ}+\frac{\beta}{2}-\frac{\gamma}{2} .
\end{aligned}
$$
Therefore, $\angle D J A=\angle D O A$, hence quadrilateral $A D J O$ is cyclic. Since $A J$ is the bisector of $\angle O A D$, the $\operatorname{arcs} O J$ and $J D$ are equal. Hence $O J=J D$.
## B ALTIC
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with $A B>A C$. The internal angle bisector of $\angle B A C$ intersects $B C$ at $D$. Let $O$ be the circumcentre of $A B C$. Let $A O$ intersect the segment $B C$ at $E$. Let $J$ be the incentre of $A E D$. Prove that if $\angle A D O=45^{\circ}$ then $O J=J D$.
|
Let $\alpha=\angle B A C, \beta=\angle C B A, \gamma=\angle A C B$. We have
$$
\begin{aligned}
\angle D J A & =90^{\circ}+\frac{1}{2} \angle D E A=90^{\circ}+\frac{1}{2}(\angle E B A+\angle B A E) \\
& =90^{\circ}+\frac{1}{2}\left(\beta+90^{\circ}-\gamma\right)=135^{\circ}+\frac{\beta}{2}-\frac{\gamma}{2}
\end{aligned}
$$
and
$$
\begin{aligned}
\angle D O A & =180^{\circ}-\angle O A D-\angle A D O=180^{\circ}-(\angle O A C-\angle D A C)-45^{\circ} \\
& =135^{\circ}-\left(90^{\circ}-\beta-\frac{\alpha}{2}\right)=135^{\circ}-\left(\frac{1}{2}(\alpha+\beta+\gamma)-\beta-\frac{\alpha}{2}\right) \\
& =135^{\circ}+\frac{\beta}{2}-\frac{\gamma}{2} .
\end{aligned}
$$
Therefore, $\angle D J A=\angle D O A$, hence quadrilateral $A D J O$ is cyclic. Since $A J$ is the bisector of $\angle O A D$, the $\operatorname{arcs} O J$ and $J D$ are equal. Hence $O J=J D$.

## B ALTIC
|
{
"exam": "BalticWay",
"problem_label": "12",
"problem_match": "\nProblem 12:",
"resource_path": "BalticWay/segmented/en-bw23sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2023"
}
|
Let $A B C$ be an acute triangle with $A B<A C$ and incentre $I$. Let $D$ be the projection of $I$ onto $B C$. Let $H$ be the orthocentre of $A B C$. Given $\angle I D H=\angle C B A-\angle A C B$, prove that $A H=2 \cdot I D$.
|
Let $H^{\prime}$ be the reflection of $H$ in $B C$. It is well-known (and easy to prove) that $H^{\prime}$ lies on the circumcircle of $A B C$. Let $O$ be the circumcentre of $A B C$. We have
$$
\begin{aligned}
\angle O H^{\prime} A & =\angle H A O=\angle B A C-\angle B A H-\angle O A C \\
& =\angle B A C-2\left(90^{\circ}-\angle C B A\right)=\angle C B A-\angle A C B \\
& =\angle I D H=\angle H^{\prime} H D=\angle D H^{\prime} A,
\end{aligned}
$$
hence $O, D, H^{\prime}$ are collinear. Also note that $\angle H A O=\angle H^{\prime} H D$ implies that $A O \| H D$.
Let $M$ be the midpoint of $B C$. Let $E$ be the reflection of $D$ in $M$. We have
$$
\angle M O E=\angle D O M=\angle O H^{\prime} A=\angle H A O \text {. }
$$
Since $O M \| A H$, the above equality gives that $A, O, E$ are collinear.
Let $D^{\prime}$ be the reflection of $D$ in $I$. It is well-known (and easy to prove) that $D^{\prime}$ lies on $A E$. Since $A H \| O M$ and $A D^{\prime} \| H D$, quadrilateral $A H D D^{\prime}$ is a parallelogram. Therefore $A H=D D^{\prime}=2 \cdot I D$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with $A B<A C$ and incentre $I$. Let $D$ be the projection of $I$ onto $B C$. Let $H$ be the orthocentre of $A B C$. Given $\angle I D H=\angle C B A-\angle A C B$, prove that $A H=2 \cdot I D$.
|
Let $H^{\prime}$ be the reflection of $H$ in $B C$. It is well-known (and easy to prove) that $H^{\prime}$ lies on the circumcircle of $A B C$. Let $O$ be the circumcentre of $A B C$. We have
$$
\begin{aligned}
\angle O H^{\prime} A & =\angle H A O=\angle B A C-\angle B A H-\angle O A C \\
& =\angle B A C-2\left(90^{\circ}-\angle C B A\right)=\angle C B A-\angle A C B \\
& =\angle I D H=\angle H^{\prime} H D=\angle D H^{\prime} A,
\end{aligned}
$$
hence $O, D, H^{\prime}$ are collinear. Also note that $\angle H A O=\angle H^{\prime} H D$ implies that $A O \| H D$.
Let $M$ be the midpoint of $B C$. Let $E$ be the reflection of $D$ in $M$. We have
$$
\angle M O E=\angle D O M=\angle O H^{\prime} A=\angle H A O \text {. }
$$
Since $O M \| A H$, the above equality gives that $A, O, E$ are collinear.
Let $D^{\prime}$ be the reflection of $D$ in $I$. It is well-known (and easy to prove) that $D^{\prime}$ lies on $A E$. Since $A H \| O M$ and $A D^{\prime} \| H D$, quadrilateral $A H D D^{\prime}$ is a parallelogram. Therefore $A H=D D^{\prime}=2 \cdot I D$.

|
{
"exam": "BalticWay",
"problem_label": "13",
"problem_match": "\nProblem 13:",
"resource_path": "BalticWay/segmented/en-bw23sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2023"
}
|
Let $A B C$ be a triangle with centroid $G$. Let $D, E$ and $F$ be the circumcentres of $B C G, C A G$ and $A B G$, respectively. Let $X$ be the intersection of the perpendiculars from $E$ to $A B$ and from $F$ to $A C$. Prove that $D X$ bisects the segment $E F$.
|
In all three solutions we will prove that the $D$ median coincides with the perpendicular bisector of the segment $B C$. Thus the solutions con- sist of two parts, proving that $X$ lies on the perpendicular bisector of $\mathrm{BC}$ and proving that the midpoint of $E F$ lies on the perpendicular bisector of $B C$.
The two parts may be completed independently, and in the three solutions below we demonstrate different approaches to both parts, though one can create valid solutions combining either first part with either second part.
Let $\omega_{B}, \omega_{C}$ denote the circumcircles of triangles $A B G$ and $A C G$ respectively, and the points $Y$ and $Z$ the second intersection of the line through $B$ parallel to $A C$ and $\omega_{B}$ and the second intersection of the line through $C$ parallel to $A B$ and $\omega_{C}$.
The lines $B Y$ and $C Z$ thus intersects at $A^{\prime}$, the reflection of $A$ across the midpoint of $B C$, and in particular on the $A$-median. Using Power of a Point from $A^{\prime}$ with respect to the circles $\omega_{B}$ and $\omega_{C}$ we obtain $A^{\prime} B \cdot A^{\prime} Y=A^{\prime} A \cdot A^{\prime} G=A^{\prime} C \cdot A^{\prime} E$ implying from the converse of Power of a Point that the quadrilateral $Y B C Z$ is cyclic. The perpendicular bisector of $B Y$ is orthogonal to $B Y \| A C$ and passes through $F$ and thus $X$ as well. Similarly, the perpendicular bisector of $C Z$ passes through $Z$. Hence $X$ is the centre of circle $(Y B C Z)$ and thus on the perpendicular bisector of the line $B C$.
Let $M$ and $N$ denote the midpoints of $B C$ and $E F$, respectively. To prove that $N$ lies on the perpendicular bisector of $B C$, let $V$ and $W$ denote the second intersections of $\omega_{B}$ and $\omega_{C}$ with the line $B C$, respectively.
From Power of a Point from $M$ with respect to $\omega_{B}$ and $\omega_{C}$ we obtain $M V \cdot M B=$ $M G \cdot M A=W M \cdot C M$, i.e. $M V=W M$, so $M$ is the midpoint of the segment $V W$. Let $E^{\prime}, N^{\prime}, F^{\prime}$ denote the projections of $E, N$ and $F$ onto $B C$ respectively. Since $N$ is the midpoint of $E F, N^{\prime}$ will be the midpoint of $E^{\prime} F^{\prime}$.
Moreover, from the fact that $E$ and $F$ are the centres of $\omega_{B}$ and $\omega_{C}$ we get that $E^{\prime}$ and $F^{\prime}$ are the midpoints of $B V$ and $W C$, and hence $M$ is the midpoint $E^{\prime} F^{\prime}$ as well, implying $N^{\prime}=M$ and that $N$ is on the perpendicular bisector of $B C$.
2nd Solution: Let $G^{\prime}$ denote the reflection of $G$ across the midpoint of $B C$. We begin by proving that triangles $A B C$ and $D F E$ are orthological, with orthology centres $G^{\prime}$ and $X$.
Observe that $G^{\prime}$ is on the $A$-median and thus $A G^{\prime} \perp E F$. Furthermore, quadrilateral $B G C G^{\prime}$ is a parellelogram and hence $B G^{\prime} \| C G \perp D E$ and $C G^{\prime} \| B G \perp D F$. Hence, $G^{\prime}$ is the first orthology centre of $A B C$ and $D F E$.
Thus, by the property of orthologoical triangle, the second orthology centre must exists, which is defined as the common intersection of the normal from $D$ to $B C$, $E$ to $A B$ and $F$ to $A C$, i.e. the point $X$. Since $D$ is on the perpendicular bisector of $B C$, by virtue of being the circumcentre of triangle $B G C$, and $X D \perp B C$ so must point $X$.
Moreover, let $O$ denote the circumcentre of triangle $A B C$. Then $E O \perp A C \perp$ $F X$ implies $E O \| F X$ and $F O \perp A B \perp E X$ implies $F O \| E X$, meaning that quadrilateral $F O E X$ is a parallelogram. Hence, the midpoint of $E F$ lies on the line $\overline{X O D}$ i.e. the perpendicular bisector of segment $B C$.
3rd Solution: Let $M$ be the midpoint of $B C$. Let $N$ be the intersection of $E F$ and $D M$. We claim that $N$ is the midpoint of $E F$.
Namely, we have $D E N \sim C G M$ because corresponding pairs of sides are orthogonal. Similarly, $D F N \sim B G M$. Hence
$$
\frac{E N}{N D}=\frac{G M}{M C}=\frac{G M}{M B}=\frac{F N}{N D}
$$
proving that $E N=F N$, as desired.
Next, let $X^{\prime}$ resp. $X^{\prime \prime}$ denote the intersection of $D N$ with the perpendicular from $E$ to $A B$ resp. the perpendicular from $F$ to $A C$. Just as above we have $E N X^{\prime} \sim A M B$ and $F N X^{\prime \prime} \sim A M C$, thus
$$
\frac{X^{\prime} N}{N E}=\frac{B M}{M A}=\frac{C M}{M A}=\frac{X^{\prime \prime} N}{N F}
$$
Since $N$ is the midpoint of $E F$, we get $X^{\prime} N=X^{\prime \prime} N$, hence $X^{\prime}=X^{\prime \prime}$ for orientation reasons (note that by the above similarities, $X^{\prime}$ and $X^{\prime \prime}$ must lie on the same side of $E F$ ).
This shows that $X=X^{\prime}=X^{\prime \prime}$ lies on $D N$.
Remark: That the medians of triangle $D E F$ coincide with the perpendicular bisectors of triangle $A B C$ implies that the centroid of $D E F$ coincides with the circumcentre of $A B C$. It is possible to ask for this in the problem instead, but then the problem becomes significantly easier, only requiring the second part of the first solution.
|
proof
|
Yes
|
Incomplete
|
proof
|
Geometry
|
Let $A B C$ be a triangle with centroid $G$. Let $D, E$ and $F$ be the circumcentres of $B C G, C A G$ and $A B G$, respectively. Let $X$ be the intersection of the perpendiculars from $E$ to $A B$ and from $F$ to $A C$. Prove that $D X$ bisects the segment $E F$.
|

In all three solutions we will prove that the $D$ median coincides with the perpendicular bisector of the segment $B C$. Thus the solutions con- sist of two parts, proving that $X$ lies on the perpendicular bisector of $\mathrm{BC}$ and proving that the midpoint of $E F$ lies on the perpendicular bisector of $B C$.
The two parts may be completed independently, and in the three solutions below we demonstrate different approaches to both parts, though one can create valid solutions combining either first part with either second part.
Let $\omega_{B}, \omega_{C}$ denote the circumcircles of triangles $A B G$ and $A C G$ respectively, and the points $Y$ and $Z$ the second intersection of the line through $B$ parallel to $A C$ and $\omega_{B}$ and the second intersection of the line through $C$ parallel to $A B$ and $\omega_{C}$.
The lines $B Y$ and $C Z$ thus intersects at $A^{\prime}$, the reflection of $A$ across the midpoint of $B C$, and in particular on the $A$-median. Using Power of a Point from $A^{\prime}$ with respect to the circles $\omega_{B}$ and $\omega_{C}$ we obtain $A^{\prime} B \cdot A^{\prime} Y=A^{\prime} A \cdot A^{\prime} G=A^{\prime} C \cdot A^{\prime} E$ implying from the converse of Power of a Point that the quadrilateral $Y B C Z$ is cyclic. The perpendicular bisector of $B Y$ is orthogonal to $B Y \| A C$ and passes through $F$ and thus $X$ as well. Similarly, the perpendicular bisector of $C Z$ passes through $Z$. Hence $X$ is the centre of circle $(Y B C Z)$ and thus on the perpendicular bisector of the line $B C$.
Let $M$ and $N$ denote the midpoints of $B C$ and $E F$, respectively. To prove that $N$ lies on the perpendicular bisector of $B C$, let $V$ and $W$ denote the second intersections of $\omega_{B}$ and $\omega_{C}$ with the line $B C$, respectively.
From Power of a Point from $M$ with respect to $\omega_{B}$ and $\omega_{C}$ we obtain $M V \cdot M B=$ $M G \cdot M A=W M \cdot C M$, i.e. $M V=W M$, so $M$ is the midpoint of the segment $V W$. Let $E^{\prime}, N^{\prime}, F^{\prime}$ denote the projections of $E, N$ and $F$ onto $B C$ respectively. Since $N$ is the midpoint of $E F, N^{\prime}$ will be the midpoint of $E^{\prime} F^{\prime}$.
Moreover, from the fact that $E$ and $F$ are the centres of $\omega_{B}$ and $\omega_{C}$ we get that $E^{\prime}$ and $F^{\prime}$ are the midpoints of $B V$ and $W C$, and hence $M$ is the midpoint $E^{\prime} F^{\prime}$ as well, implying $N^{\prime}=M$ and that $N$ is on the perpendicular bisector of $B C$.
2nd Solution: Let $G^{\prime}$ denote the reflection of $G$ across the midpoint of $B C$. We begin by proving that triangles $A B C$ and $D F E$ are orthological, with orthology centres $G^{\prime}$ and $X$.
Observe that $G^{\prime}$ is on the $A$-median and thus $A G^{\prime} \perp E F$. Furthermore, quadrilateral $B G C G^{\prime}$ is a parellelogram and hence $B G^{\prime} \| C G \perp D E$ and $C G^{\prime} \| B G \perp D F$. Hence, $G^{\prime}$ is the first orthology centre of $A B C$ and $D F E$.
Thus, by the property of orthologoical triangle, the second orthology centre must exists, which is defined as the common intersection of the normal from $D$ to $B C$, $E$ to $A B$ and $F$ to $A C$, i.e. the point $X$. Since $D$ is on the perpendicular bisector of $B C$, by virtue of being the circumcentre of triangle $B G C$, and $X D \perp B C$ so must point $X$.
Moreover, let $O$ denote the circumcentre of triangle $A B C$. Then $E O \perp A C \perp$ $F X$ implies $E O \| F X$ and $F O \perp A B \perp E X$ implies $F O \| E X$, meaning that quadrilateral $F O E X$ is a parallelogram. Hence, the midpoint of $E F$ lies on the line $\overline{X O D}$ i.e. the perpendicular bisector of segment $B C$.
3rd Solution: Let $M$ be the midpoint of $B C$. Let $N$ be the intersection of $E F$ and $D M$. We claim that $N$ is the midpoint of $E F$.
Namely, we have $D E N \sim C G M$ because corresponding pairs of sides are orthogonal. Similarly, $D F N \sim B G M$. Hence
$$
\frac{E N}{N D}=\frac{G M}{M C}=\frac{G M}{M B}=\frac{F N}{N D}
$$
proving that $E N=F N$, as desired.
Next, let $X^{\prime}$ resp. $X^{\prime \prime}$ denote the intersection of $D N$ with the perpendicular from $E$ to $A B$ resp. the perpendicular from $F$ to $A C$. Just as above we have $E N X^{\prime} \sim A M B$ and $F N X^{\prime \prime} \sim A M C$, thus
$$
\frac{X^{\prime} N}{N E}=\frac{B M}{M A}=\frac{C M}{M A}=\frac{X^{\prime \prime} N}{N F}
$$
Since $N$ is the midpoint of $E F$, we get $X^{\prime} N=X^{\prime \prime} N$, hence $X^{\prime}=X^{\prime \prime}$ for orientation reasons (note that by the above similarities, $X^{\prime}$ and $X^{\prime \prime}$ must lie on the same side of $E F$ ).
This shows that $X=X^{\prime}=X^{\prime \prime}$ lies on $D N$.
Remark: That the medians of triangle $D E F$ coincide with the perpendicular bisectors of triangle $A B C$ implies that the centroid of $D E F$ coincides with the circumcentre of $A B C$. It is possible to ask for this in the problem instead, but then the problem becomes significantly easier, only requiring the second part of the first solution.
|
{
"exam": "BalticWay",
"problem_label": "14",
"problem_match": "\nProblem 14:",
"resource_path": "BalticWay/segmented/en-bw23sol.jsonl",
"solution_match": "# Solution:",
"tier": "T3",
"year": "2023"
}
|
Let $\omega_{1}$ and $\omega_{2}$ be circles with no common points, such that neither circle lies inside the other. Points $M$ and $N$ are chosen on the circles $\omega_{1}$ and $\omega_{2}$, respectively, such that the tangent to the circle $\omega_{1}$ at $M$ and the tangent to the circle $\omega_{2}$ at $N$ intersect at $P$ and such that $P M N$ is an isosceles triangle with $P M=P N$. The circles $\omega_{1}$ and $\omega_{2}$ meet the segment $M N$ again at $A$ and $B$, respectively. The line $P A$ meets the circle $\omega_{1}$ again at $C$ and the line $P B$ meets the circle $\omega_{2}$ again at $D$. Prove that $\angle B C N=\angle A D M$.
|
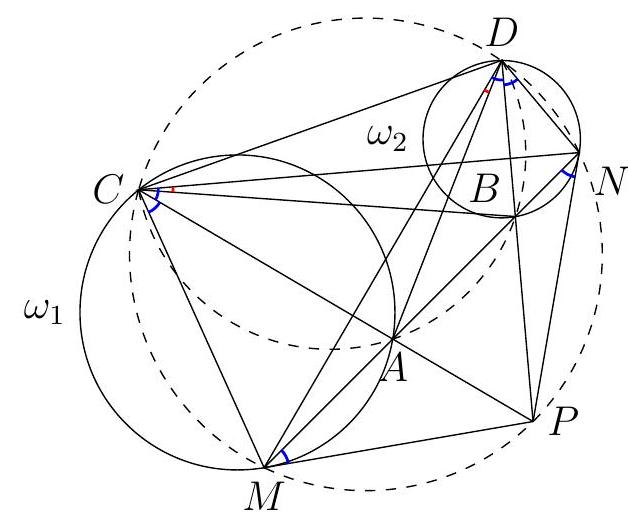
Since $M P N$ is an isosceles triangle, we have $\angle P M A=\angle P M N=\angle M N P=\angle B N P$. By tangent and chord theorem, $\angle M C A=$ $\angle P M A=\angle B N P=\angle B D N$.
Since $\angle M C P=\angle M N P$, the quadrilateral $C M P N$ is cyclic. Analogously, from $\angle P D N=\angle P M N$, we get that $N D M P$ is cyclic. Since $C$ and $D$ both lie on the circumcircle of $N P M$, points $P, N, M, C$ and $D$ are concyclic.
From inscribed angles subtending arcs with the same length, we get that $\angle M D P=$ $\angle M C P=\angle M N P=\angle P D N=\angle P M N=\angle P C N$.
The power of $P$ with respect to $\omega_{1}$ gives us that $P M^{2}=P A \cdot P C$. The power of $P$ with respect to $\omega_{2}$ gives us that $P N^{2}=P B \cdot P D$. Since $P M=P N$, the powers of $P$ with respect to $\omega_{1}$ and $\omega_{2}$ are equal ( $P$ lies on the radical axis). Hence, $P A \cdot P C=P B \cdot P D$, which implies that $A B D C$ is cyclic. From inscribed angles subtending the $\operatorname{arc} A B$, we get that $\angle A C B=\angle A D B$.
Hence, $\angle B C N=\angle A C N-\angle A C B=\angle M D B-\angle A D B=\angle M D A$.
2nd Solution: Since $M P N$ is an isosceles triangle, we have $\angle P M A=\angle P M N=$ $\angle M N P=\angle B N P$. By tangent and chord theorem, $\angle M C A=\angle P M A=\angle B N P=$ $\angle B D N$.
Since $\angle M C P=\angle M N P$, the quadrilateral $M P N C$ is cyclic, which means that $P$ lies on the circumcircle of $M N C$. Since $M P N$ is isosceles, the perpendicular bisector of $M N$ passes through $P$. Since the intersection point of the angle bisector and the perpendicular bisector of the opposite side of the triangle lies on the circumcircle, it follows that $C P$ bisects angle $\angle M C N$. Hence, $\angle M C P=\angle P C N$. Analogously, since $\angle P D N=\angle P M N$, it follows that $N D M P$ is cyclic and the circumcircle of $M N D$, the perpendicular bisector of $M N$ and the angle bisector of $\angle M D N$ meet at $P$. Hence, $\angle M D P=\angle P D N=\angle M C P=\angle P C N$.
Now we continue as in the previous solution.
## BALTIC
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\omega_{1}$ and $\omega_{2}$ be circles with no common points, such that neither circle lies inside the other. Points $M$ and $N$ are chosen on the circles $\omega_{1}$ and $\omega_{2}$, respectively, such that the tangent to the circle $\omega_{1}$ at $M$ and the tangent to the circle $\omega_{2}$ at $N$ intersect at $P$ and such that $P M N$ is an isosceles triangle with $P M=P N$. The circles $\omega_{1}$ and $\omega_{2}$ meet the segment $M N$ again at $A$ and $B$, respectively. The line $P A$ meets the circle $\omega_{1}$ again at $C$ and the line $P B$ meets the circle $\omega_{2}$ again at $D$. Prove that $\angle B C N=\angle A D M$.
|

Since $M P N$ is an isosceles triangle, we have $\angle P M A=\angle P M N=\angle M N P=\angle B N P$. By tangent and chord theorem, $\angle M C A=$ $\angle P M A=\angle B N P=\angle B D N$.
Since $\angle M C P=\angle M N P$, the quadrilateral $C M P N$ is cyclic. Analogously, from $\angle P D N=\angle P M N$, we get that $N D M P$ is cyclic. Since $C$ and $D$ both lie on the circumcircle of $N P M$, points $P, N, M, C$ and $D$ are concyclic.
From inscribed angles subtending arcs with the same length, we get that $\angle M D P=$ $\angle M C P=\angle M N P=\angle P D N=\angle P M N=\angle P C N$.
The power of $P$ with respect to $\omega_{1}$ gives us that $P M^{2}=P A \cdot P C$. The power of $P$ with respect to $\omega_{2}$ gives us that $P N^{2}=P B \cdot P D$. Since $P M=P N$, the powers of $P$ with respect to $\omega_{1}$ and $\omega_{2}$ are equal ( $P$ lies on the radical axis). Hence, $P A \cdot P C=P B \cdot P D$, which implies that $A B D C$ is cyclic. From inscribed angles subtending the $\operatorname{arc} A B$, we get that $\angle A C B=\angle A D B$.
Hence, $\angle B C N=\angle A C N-\angle A C B=\angle M D B-\angle A D B=\angle M D A$.
2nd Solution: Since $M P N$ is an isosceles triangle, we have $\angle P M A=\angle P M N=$ $\angle M N P=\angle B N P$. By tangent and chord theorem, $\angle M C A=\angle P M A=\angle B N P=$ $\angle B D N$.
Since $\angle M C P=\angle M N P$, the quadrilateral $M P N C$ is cyclic, which means that $P$ lies on the circumcircle of $M N C$. Since $M P N$ is isosceles, the perpendicular bisector of $M N$ passes through $P$. Since the intersection point of the angle bisector and the perpendicular bisector of the opposite side of the triangle lies on the circumcircle, it follows that $C P$ bisects angle $\angle M C N$. Hence, $\angle M C P=\angle P C N$. Analogously, since $\angle P D N=\angle P M N$, it follows that $N D M P$ is cyclic and the circumcircle of $M N D$, the perpendicular bisector of $M N$ and the angle bisector of $\angle M D N$ meet at $P$. Hence, $\angle M D P=\angle P D N=\angle M C P=\angle P C N$.
Now we continue as in the previous solution.
## BALTIC
|
{
"exam": "BalticWay",
"problem_label": "15",
"problem_match": "\nProblem 15:",
"resource_path": "BalticWay/segmented/en-bw23sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2023"
}
|
Prove that there exist nonconstant polynomials $f$ and $g$ with integer coefficients such that, for infinitely many primes $p$, there are no integers $x$ and $y$ with $p \mid f(x)-g(y)$.
|
We take $f(x)=\left(x^{2}+1\right)^{2}$ and $g(y)=-\left(y^{2}+1\right)^{2}$ and prove for all $p \equiv 3(\bmod 4)$ that $f(x) \equiv g(y)(\bmod p)$ has no solution. Famously, there are infinitely many primes congruent to 3 modulo 4 .
Recall the fact that if $p \equiv 3(\bmod 4)$ then the only solution to $a^{2}+b^{2} \equiv 0(\bmod p)$ is $a \equiv b \equiv 0(\bmod p)$. Hence, for $f(x) \equiv g(y)(\bmod p)$ to hold, we need
$$
\left(x^{2}+1\right)^{2}+\left(y^{2}+1\right)^{2} \equiv 0 \quad(\bmod p)
$$
and thus
$$
x^{2}+1 \equiv y^{2}+1 \equiv 0 \quad(\bmod p)
$$
which is impossible for $p \equiv 3(\bmod 4)$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that there exist nonconstant polynomials $f$ and $g$ with integer coefficients such that, for infinitely many primes $p$, there are no integers $x$ and $y$ with $p \mid f(x)-g(y)$.
|
We take $f(x)=\left(x^{2}+1\right)^{2}$ and $g(y)=-\left(y^{2}+1\right)^{2}$ and prove for all $p \equiv 3(\bmod 4)$ that $f(x) \equiv g(y)(\bmod p)$ has no solution. Famously, there are infinitely many primes congruent to 3 modulo 4 .
Recall the fact that if $p \equiv 3(\bmod 4)$ then the only solution to $a^{2}+b^{2} \equiv 0(\bmod p)$ is $a \equiv b \equiv 0(\bmod p)$. Hence, for $f(x) \equiv g(y)(\bmod p)$ to hold, we need
$$
\left(x^{2}+1\right)^{2}+\left(y^{2}+1\right)^{2} \equiv 0 \quad(\bmod p)
$$
and thus
$$
x^{2}+1 \equiv y^{2}+1 \equiv 0 \quad(\bmod p)
$$
which is impossible for $p \equiv 3(\bmod 4)$.
|
{
"exam": "BalticWay",
"problem_label": "16",
"problem_match": "\nProblem 16:",
"resource_path": "BalticWay/segmented/en-bw23sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2023"
}
|
Let $S(m)$ be the sum of the digits of the positive integer $m$. Find all pairs $(a, b)$ of positive integers such that $S\left(a^{b+1}\right)=a^{b}$.
|
Answer: $(a, b) \in\left\{(1, b) \mid b \in \mathbb{Z}^{+}\right\} \cup\{(3,2),(9,1)\}$.
Let $k$ denote the number of digits of $a$. Then $10^{k-1} \leq a<10^{k}$ and, therefore, $10^{(k-1) b} \leq a^{b}$ and $a^{b+1}<10^{k(b+1)}$. Of course, the digits are at most 9, so $S\left(a^{b+1}\right) \leq 9 \cdot k(b+1)$. We get
$$
10^{(k-1) b} \leq a^{b}=S\left(a^{b+1}\right) \leq 9 \cdot k(b+1) \text {, i.e. } 10^{(k-1) b} \leq 9 \cdot k(b+1)
$$
Let us consider the case where $k \geq 2$. Then $k \leq 2(k-1)$ and note that $b+1 \leq 2 b$ as $b \geq 1$. Put $(k-1) b=: x$, then $k(b+1) \leq 4(k-1) b=4 x$. So $10^{x} \leq 36 x$. It is obvious that the only solutions in nonnegative integers to this inequality are $x=0$ and $x=1$. Indeed, for $x \geq 2$, the left hand side grows faster. Therefore, either $k=1$ or $k=2$ and $b=1$.
Now we have only two cases left.
Case 1: $b=1$ and $k=2$. We are left with the equation $S\left(a^{2}\right)=a$, for $10 \leq a<100$. Then $a^{2}<10^{4}$, so $a=S\left(a^{2}\right) \leq 9 \cdot 4=36$.
Moreover, taking into account the fact that the sum of digits does not change the number modulo $9, a^{2} \equiv a(\bmod 9)$, i.e., $a(a-1) \equiv 0(\bmod 9)$, therefore $a \equiv 0(\bmod 9)$ or $a \equiv 1(\bmod 9)$. So now we are left only with numbers $a \in$ $\{10,18,19,27,28,36\}$, which we can easily check by substitution and see that there are no solutions.
Case 2: $k=1$. In the same way, looking modulo 9, we get that $a^{b+1} \equiv a^{b}(\bmod 9)$ implies $a^{b}(a-1) \equiv 0(\bmod 9)$. Therefore either $a=1$ or $a$ is divisible by 3 . $a=1$ is an obvious solution with all $b \in \mathbb{Z}^{+}$.
Otherwise, $a \in\{3,6,9\}$. But then $a^{b+1}<10^{b+1}$ and $S\left(a^{b+1}\right) \leq 9(b+1)$. Therefore, $3^{b} \leq a^{b}=S\left(a^{b+1}\right) \leq 9(b+1)$. But from $3^{b} \leq 9(b+1)$, we can conclude $b \leq 3$. Indeed, for $b \geq 4$, the left hand side increases faster. So we are left with $a \in\{3,6,9\}$ and $b \leq 3$. We check all these cases to determine that only $(a, b)=(3,2)$ or $(a, b)=(9,1)$ are solutions.
|
(a, b) \in\left\{(1, b) \mid b \in \mathbb{Z}^{+}\right\} \cup\{(3,2),(9,1)\}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $S(m)$ be the sum of the digits of the positive integer $m$. Find all pairs $(a, b)$ of positive integers such that $S\left(a^{b+1}\right)=a^{b}$.
|
Answer: $(a, b) \in\left\{(1, b) \mid b \in \mathbb{Z}^{+}\right\} \cup\{(3,2),(9,1)\}$.
Let $k$ denote the number of digits of $a$. Then $10^{k-1} \leq a<10^{k}$ and, therefore, $10^{(k-1) b} \leq a^{b}$ and $a^{b+1}<10^{k(b+1)}$. Of course, the digits are at most 9, so $S\left(a^{b+1}\right) \leq 9 \cdot k(b+1)$. We get
$$
10^{(k-1) b} \leq a^{b}=S\left(a^{b+1}\right) \leq 9 \cdot k(b+1) \text {, i.e. } 10^{(k-1) b} \leq 9 \cdot k(b+1)
$$
Let us consider the case where $k \geq 2$. Then $k \leq 2(k-1)$ and note that $b+1 \leq 2 b$ as $b \geq 1$. Put $(k-1) b=: x$, then $k(b+1) \leq 4(k-1) b=4 x$. So $10^{x} \leq 36 x$. It is obvious that the only solutions in nonnegative integers to this inequality are $x=0$ and $x=1$. Indeed, for $x \geq 2$, the left hand side grows faster. Therefore, either $k=1$ or $k=2$ and $b=1$.
Now we have only two cases left.
Case 1: $b=1$ and $k=2$. We are left with the equation $S\left(a^{2}\right)=a$, for $10 \leq a<100$. Then $a^{2}<10^{4}$, so $a=S\left(a^{2}\right) \leq 9 \cdot 4=36$.
Moreover, taking into account the fact that the sum of digits does not change the number modulo $9, a^{2} \equiv a(\bmod 9)$, i.e., $a(a-1) \equiv 0(\bmod 9)$, therefore $a \equiv 0(\bmod 9)$ or $a \equiv 1(\bmod 9)$. So now we are left only with numbers $a \in$ $\{10,18,19,27,28,36\}$, which we can easily check by substitution and see that there are no solutions.
Case 2: $k=1$. In the same way, looking modulo 9, we get that $a^{b+1} \equiv a^{b}(\bmod 9)$ implies $a^{b}(a-1) \equiv 0(\bmod 9)$. Therefore either $a=1$ or $a$ is divisible by 3 . $a=1$ is an obvious solution with all $b \in \mathbb{Z}^{+}$.
Otherwise, $a \in\{3,6,9\}$. But then $a^{b+1}<10^{b+1}$ and $S\left(a^{b+1}\right) \leq 9(b+1)$. Therefore, $3^{b} \leq a^{b}=S\left(a^{b+1}\right) \leq 9(b+1)$. But from $3^{b} \leq 9(b+1)$, we can conclude $b \leq 3$. Indeed, for $b \geq 4$, the left hand side increases faster. So we are left with $a \in\{3,6,9\}$ and $b \leq 3$. We check all these cases to determine that only $(a, b)=(3,2)$ or $(a, b)=(9,1)$ are solutions.
|
{
"exam": "BalticWay",
"problem_label": "17",
"problem_match": "\nProblem 17:",
"resource_path": "BalticWay/segmented/en-bw23sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2023"
}
|
Let $p>7$ be a prime number and let $A$ be a subset of $\{0,1, \ldots, p-1\}$ consisting of at least $\frac{p-1}{2}$ elements. Show that for each integer $r$, there exist (not necessarily distinct) numbers $a, b, c, d \in A$ such that
$$
a b-c d \equiv r \quad(\bmod p)
$$
|
Let $P$ be the set of residues modulo of possible products $a b$, for $a, b \in A$. Clearly, we have $|P| \geq \frac{p-1}{2}$, since we get $|A|$ different products by fixing an arbitrary $0 \neq a \in A$ and let run $b$ through $A$. If $|P| \geq \frac{p+1}{2}$, then $|r+P| \geq \frac{p+1}{2}$, too. Hence, $|P|+|r+P| \geq p+1>p$, so, by the Pigeonhole Principle, $P$ and $r+P$ must have an element in common. In other words, there are $p_{1}, p_{2}$ with $p_{1} \equiv r+p_{2}(\bmod p)$ and hence $p_{1}-p_{2} \equiv r(\bmod p)$, which gives a solution of the desired shape from the definition of $P$. So the only remaining case is that of $|P|=|A|=\frac{p-1}{2}$.
Multiplying all elements of $A$ with the same constant and reducing modulo $p$, if necessary, we may assume w.l.o.g. that $1 \in A$. Then $A \subseteq P$ and hence $A=P$. This means that the product of each two non-zero elements of $A$ is an element of $A$, too. Furthermore, for a fixed $0 \neq a \in A$ the products $a b$ all differ modulolo $p$. (It follows, that for every $0 \neq a \in A$ there is a $b \in A$ with $a b \equiv 1(\bmod p)$. Hence, the non-zero elements of $A$ form a group.) Thus, if we denote $A^{\star}:=A \backslash\{0\}$, for a fixed non-zero $a \in A$ we have
$$
\prod_{b \in A^{\star}} b \equiv \prod_{b \in A^{\star}}(a b)=a^{\left|A^{\star}\right|} \cdot \prod_{b \in A^{\star}} b(\bmod p) .
$$
Hence $a^{\left|A^{\star}\right|} \equiv 1(\bmod p)$.
If $0 \in A$ we have $\left|A^{\star}\right|=\frac{p-3}{2}$. So $a^{p-3}=a^{2 \mid A^{\star}} \equiv 1(\bmod p)$. But from Fermat's little theorem we know $a^{p-1} \equiv 1(\bmod p)$, hence $a^{2} \equiv 1(\bmod p)$ and $a \equiv \pm 1(\bmod p)$. We get $\frac{p-3}{2}=\left|A^{\star}\right| \leq 2$. This is impossible for $p>7$.
Consequently, $0 \notin A$ and we have $A^{\star}=A$.
We now use the well-known fact that for every prime $p$ there exists a primitive root, that is an integer $0<q<p$ where the residues modulo $p$ of the powers $q^{1}, q^{2}$, $\ldots, q^{p-1}$ are (in some order) $1,2, \ldots, p-1$. That is, we can write every non-zero element $a \in A$ as $q^{i}$ with some $1 \leq i \leq p-1$.
If $A$ is not the set of quadratic residues modulo $p$, that is the set of residues of $q^{2 \cdot 1}$, $q^{2 \cdot 2}, \ldots, q^{2 \cdot \frac{p-1}{2}}$, then it would contain two elements with consequtive exponents, say $q^{i}$ and $q^{i+1}$. But then we have $q^{(i+1)-i}=q \in A$ and, therefore, all powers of $q$. This contradicts $|A|=\frac{p-1}{2}<p-1$. Hence $A$ exactly the set of the quadratic residues modulo $p$.
Replacing $r$ by $r+p$, if necessary, one may assume $r$ to be odd. Then we can put $b:=d:=1 \in A$, as well as
$$
a \equiv\left(\frac{r+1}{2}\right)^{2} \quad(\bmod p) \quad \text { and } \quad c \equiv\left(\frac{r-1}{2}\right)^{2} \quad(\bmod p) \text {. }
$$
Then $a, c \in A$, too. This yields
$$
a d-b c \equiv a-c \equiv\left(\frac{r+1}{2}\right)^{2}-\left(\frac{r-1}{2}\right)^{2} \equiv r \quad(\bmod p)
$$
as required.
Remark: This solution avoids using knowledge from basic group theory. But clearly, with this, it could be stated in a shorter way.
Probably the result is also very far from being sharp and the $\frac{p-1}{2}$ can be replaced by something even smaller. Determining the sharp bound (or even its order of magnitude) here is most likely a very difficult problem.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $p>7$ be a prime number and let $A$ be a subset of $\{0,1, \ldots, p-1\}$ consisting of at least $\frac{p-1}{2}$ elements. Show that for each integer $r$, there exist (not necessarily distinct) numbers $a, b, c, d \in A$ such that
$$
a b-c d \equiv r \quad(\bmod p)
$$
|
Let $P$ be the set of residues modulo of possible products $a b$, for $a, b \in A$. Clearly, we have $|P| \geq \frac{p-1}{2}$, since we get $|A|$ different products by fixing an arbitrary $0 \neq a \in A$ and let run $b$ through $A$. If $|P| \geq \frac{p+1}{2}$, then $|r+P| \geq \frac{p+1}{2}$, too. Hence, $|P|+|r+P| \geq p+1>p$, so, by the Pigeonhole Principle, $P$ and $r+P$ must have an element in common. In other words, there are $p_{1}, p_{2}$ with $p_{1} \equiv r+p_{2}(\bmod p)$ and hence $p_{1}-p_{2} \equiv r(\bmod p)$, which gives a solution of the desired shape from the definition of $P$. So the only remaining case is that of $|P|=|A|=\frac{p-1}{2}$.
Multiplying all elements of $A$ with the same constant and reducing modulo $p$, if necessary, we may assume w.l.o.g. that $1 \in A$. Then $A \subseteq P$ and hence $A=P$. This means that the product of each two non-zero elements of $A$ is an element of $A$, too. Furthermore, for a fixed $0 \neq a \in A$ the products $a b$ all differ modulolo $p$. (It follows, that for every $0 \neq a \in A$ there is a $b \in A$ with $a b \equiv 1(\bmod p)$. Hence, the non-zero elements of $A$ form a group.) Thus, if we denote $A^{\star}:=A \backslash\{0\}$, for a fixed non-zero $a \in A$ we have
$$
\prod_{b \in A^{\star}} b \equiv \prod_{b \in A^{\star}}(a b)=a^{\left|A^{\star}\right|} \cdot \prod_{b \in A^{\star}} b(\bmod p) .
$$
Hence $a^{\left|A^{\star}\right|} \equiv 1(\bmod p)$.
If $0 \in A$ we have $\left|A^{\star}\right|=\frac{p-3}{2}$. So $a^{p-3}=a^{2 \mid A^{\star}} \equiv 1(\bmod p)$. But from Fermat's little theorem we know $a^{p-1} \equiv 1(\bmod p)$, hence $a^{2} \equiv 1(\bmod p)$ and $a \equiv \pm 1(\bmod p)$. We get $\frac{p-3}{2}=\left|A^{\star}\right| \leq 2$. This is impossible for $p>7$.
Consequently, $0 \notin A$ and we have $A^{\star}=A$.
We now use the well-known fact that for every prime $p$ there exists a primitive root, that is an integer $0<q<p$ where the residues modulo $p$ of the powers $q^{1}, q^{2}$, $\ldots, q^{p-1}$ are (in some order) $1,2, \ldots, p-1$. That is, we can write every non-zero element $a \in A$ as $q^{i}$ with some $1 \leq i \leq p-1$.
If $A$ is not the set of quadratic residues modulo $p$, that is the set of residues of $q^{2 \cdot 1}$, $q^{2 \cdot 2}, \ldots, q^{2 \cdot \frac{p-1}{2}}$, then it would contain two elements with consequtive exponents, say $q^{i}$ and $q^{i+1}$. But then we have $q^{(i+1)-i}=q \in A$ and, therefore, all powers of $q$. This contradicts $|A|=\frac{p-1}{2}<p-1$. Hence $A$ exactly the set of the quadratic residues modulo $p$.
Replacing $r$ by $r+p$, if necessary, one may assume $r$ to be odd. Then we can put $b:=d:=1 \in A$, as well as
$$
a \equiv\left(\frac{r+1}{2}\right)^{2} \quad(\bmod p) \quad \text { and } \quad c \equiv\left(\frac{r-1}{2}\right)^{2} \quad(\bmod p) \text {. }
$$
Then $a, c \in A$, too. This yields
$$
a d-b c \equiv a-c \equiv\left(\frac{r+1}{2}\right)^{2}-\left(\frac{r-1}{2}\right)^{2} \equiv r \quad(\bmod p)
$$
as required.
Remark: This solution avoids using knowledge from basic group theory. But clearly, with this, it could be stated in a shorter way.
Probably the result is also very far from being sharp and the $\frac{p-1}{2}$ can be replaced by something even smaller. Determining the sharp bound (or even its order of magnitude) here is most likely a very difficult problem.
|
{
"exam": "BalticWay",
"problem_label": "18",
"problem_match": "\nProblem 18:",
"resource_path": "BalticWay/segmented/en-bw23sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2023"
}
|
Show that the sum of the digits of $2^{2^{2 \cdot 2023}}$ is greater than 2023 .
|
We will prove the more general statement that, for every positive integer $n$, the sum of decimal digits of $2^{2^{2 n}}$ is greater than $n$.
Let $m=2^{2 n}=4^{n}$, so that we need to consider the digits of $2^{m}$. It will suffice to prove that at least $n$ of these digits are different from 0 , since the last digit is at least 2 .
Let $0=e_{0}<e_{1}<\cdots<e_{k}$ be the positions of non-zero digits, so that $2^{m}=\sum_{i=0}^{k} d_{i} \cdot 10^{e_{i}}$ with $1 \leq d_{i} \leq 9$. Considering this number modulo $10^{e_{j}}$, for some $0<j \leq k$, the residue $\sum_{i=0}^{j-1} d_{i} \cdot 10^{e_{i}}$ is a multiple of $2^{e_{j}}$, hence at least $2^{e_{j}}$, but on the other hand it is bounded by $10^{e_{j-1}+1}$.
It follows that $2^{e_{j}}<10^{e_{j-1}+1}<16^{e_{j-1}+1}$, and hence $e_{j}<4\left(e_{j-1}+1\right)$. With $e_{0}=4^{0}-1$ and $e_{j} \leq 4\left(e_{j-1}+1\right)-1$, it follows that $e_{j} \leq 4^{j}-1$, for all $0 \leq j \leq k$. In particular, $e_{k} \leq 4^{k}-1$ and hence
$$
2^{m}=\sum_{i=0}^{k} d_{i} \cdot 10^{e_{i}}<10^{4^{k}}<16^{4^{k}}=2^{4 \cdot 4^{k}}=2^{4^{k+1}}
$$
which yields $4^{n}=m<4^{k+1}$, i.e., $n-1<k$. In other words, $2^{m}$ has $k \geq n$ non-zero decimal digits, as claimed.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Show that the sum of the digits of $2^{2^{2 \cdot 2023}}$ is greater than 2023 .
|
We will prove the more general statement that, for every positive integer $n$, the sum of decimal digits of $2^{2^{2 n}}$ is greater than $n$.
Let $m=2^{2 n}=4^{n}$, so that we need to consider the digits of $2^{m}$. It will suffice to prove that at least $n$ of these digits are different from 0 , since the last digit is at least 2 .
Let $0=e_{0}<e_{1}<\cdots<e_{k}$ be the positions of non-zero digits, so that $2^{m}=\sum_{i=0}^{k} d_{i} \cdot 10^{e_{i}}$ with $1 \leq d_{i} \leq 9$. Considering this number modulo $10^{e_{j}}$, for some $0<j \leq k$, the residue $\sum_{i=0}^{j-1} d_{i} \cdot 10^{e_{i}}$ is a multiple of $2^{e_{j}}$, hence at least $2^{e_{j}}$, but on the other hand it is bounded by $10^{e_{j-1}+1}$.
It follows that $2^{e_{j}}<10^{e_{j-1}+1}<16^{e_{j-1}+1}$, and hence $e_{j}<4\left(e_{j-1}+1\right)$. With $e_{0}=4^{0}-1$ and $e_{j} \leq 4\left(e_{j-1}+1\right)-1$, it follows that $e_{j} \leq 4^{j}-1$, for all $0 \leq j \leq k$. In particular, $e_{k} \leq 4^{k}-1$ and hence
$$
2^{m}=\sum_{i=0}^{k} d_{i} \cdot 10^{e_{i}}<10^{4^{k}}<16^{4^{k}}=2^{4 \cdot 4^{k}}=2^{4^{k+1}}
$$
which yields $4^{n}=m<4^{k+1}$, i.e., $n-1<k$. In other words, $2^{m}$ has $k \geq n$ non-zero decimal digits, as claimed.
|
{
"exam": "BalticWay",
"problem_label": "19",
"problem_match": "\nProblem 19:",
"resource_path": "BalticWay/segmented/en-bw23sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2023"
}
|
Let $n$ be a positive integer. A German set in an $n \times n$ square grid is a set of $n$ cells which contains exactly one cell in each row and column. Given a labelling of the cells with the integers from 1 to $n^{2}$ using each integer exactly once, we say that an integer is a German product if it is the product of the labels of the cells in a German set.
(a) Let $n=8$. Determine whether there exists a labelling of an $8 \times 8$ grid such that the following condition is fulfilled: The difference of any two German products is always divisible by 65 .
(b) Let $n=10$. Determine whether there exists a labelling of a $10 \times 10$ grid such that the following condition is fulfilled: The difference of any two German products is always divisible by 101.
|
(a) No, there is no such labelling.
On the contrary, we show that for every labelling there exist two German products whose difference is not divisible by 65 . Suppose that an $8 \times 8$ square grid is labelled with the numbers $1,2, \ldots, 64$ such that no number is used twice.
We can construct a German product that is divisible by 13 by choosing a German set that includes the cell with the label 13 and seven others in different rows and columns, but otherwise arbitrarily.
We can construct a German product that is not divisible by 13 as follows. Notice that only four labels are divisible by 13, namely $13,26,39$, and 52 . These four labels are located in at most four rows; we denote the index set of these rows $R \subseteq[1,8]$. Similarly, there are at least four columns that do not contain any of these four labels; we denote the index set of these columns $C \subseteq[1,8]$. Since $R \leq C$ it is possible to choose cells of a German set from rows $R$ using only columns from $C$. The remaining cells are chosen from the remaining rows accordingly to the definition, but otherwise arbitrarily. The resulting German product is not divisible by 13 since the German set avoids the cells whose labels are divisible by 13 .
The difference of the two German products is not divisible by 13, since one German product is divisible by 13 whereas the other one is not. Hence the difference is not divisible by 65 .
(b) Yes, there is such a labelling.
For $k \in[0,99]$ we define $a_{k}=2^{k}(\bmod 101)$; in other words, $a_{k}$ is the remainder of $2^{k}$ when divided by 101. Note that $a_{k} \neq 0$ since no power of 2 is divisible by 101 . Hence $1 \leq a_{k} \leq 100$ for all $k \in[0,99]$.
We label the cells of the square grid with the numbers $a_{k}$ as follows:
| $a_{0}$ | $a_{1}$ | $a_{2}$ | $\cdots$ | $a_{9}$ |
| :---: | :---: | :---: | :---: | :---: |
| $a_{10}$ | $a_{11}$ | $a_{12}$ | $\cdots$ | $a_{19}$ |
| $a_{20}$ | $a_{21}$ | $a_{22}$ | $\cdots$ | $a_{29}$ |
| $\vdots$ | $\vdots$ | $\vdots$ | $\ddots$ | $\vdots$ |
| $a_{90}$ | $a_{91}$ | $a_{92}$ | $\cdots$ | $a_{99}$ |
More precisely, if we label the rows and columns of the chessboard by $\{0,1,2, \ldots, 9\}$, then the cell with coordinates $(i, j)$ gets the label $a_{10 i+j}$.
Note that $a_{10 i+j} \equiv 2^{10 i+j}(\bmod 101)$ and that $2^{10 i+j}=\left(2^{10}\right)^{i} \cdot 2^{j}$. Hence for this labelling any rook product is congruent to
$$
\left(2^{10}\right)^{0+1+2+\ldots+9} \cdot 2^{0+1+2+\ldots+9}
$$
modulo 101. Hence the difference of any two German products is divisible by 101 for this labelling.
It remains to show that the $a_{k}$ are pairwise different. (In more elaborate language, we would say that 2 is a primitive root modulo 101.) To do this, we denote by $s$ the smallest positive integer such that $2^{s} \equiv 1(\bmod 101)$. Using long division, we may write $100=q s+r$ with non-negative integers $q$ and $r$ such that $0 \leq r \leq s-1$. By virtue of Fermat's little theorem we have
$$
1 \equiv 2^{100} \equiv 2^{q s+r} \equiv\left(2^{s}\right)^{q} \cdot 2^{r} \equiv 1^{q} \cdot 2^{r} \equiv 2^{r} \quad(\bmod 101) .
$$
Since $r<s$ and $s$ is the smallest positive integer with $2^{s} \equiv 1(\bmod 101)$, we must have $r=0$. In other words, 100 is divisible by $s$; in other words, $s$ is a divisor of 100 .
We claim that $s=100$. If this was not the case, we would have $s \mid 20$ or $s \mid 50$, which implies that $2^{20} \equiv 1(\bmod 101)$ or $2^{50} \equiv 1(\bmod 101)$. However $2^{10}=1024 \equiv 14(\bmod 101)$, so that $2^{20} \equiv 14^{2} \equiv 196 \equiv-6 \not \equiv 1(\bmod 101)$ and $2^{50} \equiv\left(2^{20}\right)^{2} \cdot 2^{10} \equiv(-6)^{2} \cdot 14 \equiv 504 \equiv-1$ 丰 $1(\bmod 101)$.
Now assume that $k, \ell \in[0,99]$ are positive integers with $k>\ell$ and $a_{k}=a_{\ell}$. Then we have $2^{k} \equiv 2^{\ell}(\bmod 101)$ and $0 \equiv 2^{k}-2^{\ell} \equiv 2^{\ell} \cdot\left(2^{k-\ell}-1\right)(\bmod 101)$. Since $2^{\ell}$ and 101 are coprime, it follows that $2^{k-\ell}-1 \equiv 0(\bmod 101)$ and $2^{k-\ell} \equiv 1(\bmod 101)$. This cannot be true, since $k-\ell \in[1,99]$, but $s=100$ is the smallest positive integer with $2^{s} \equiv 1(\bmod 101)$. Hence $a_{k} \neq a_{\ell}$.
We conclude that the numbers $a_{k}$ with $k \in[0,99]$ are a hundred pairwise different numbers from the set $[1,100]$, hence they are a permutation of the set $[1,100]$ as it was required.
2nd Solution:
Definition: Let $p$ be a prime. Consider an $n \times n$ square grid of elements $a_{i, j} \in \mathbb{F}_{p}^{*}$ (for $i, j=1, \ldots, n$ ), which are not necessarily distinct. We call it rooky, if all its German products are equal as elements in $\mathbb{F}_{p}^{*}$.
We will provide a classification of all rooky square grids. Of course, most of this is not necessary when writing down a solution to the given problem, but it may still be interesting...
Lemma: A square grid is rooky if and only if for all $i, j, k, \ell$ :
$$
a_{i, j} \cdot a_{k, \ell}=a_{i, \ell} \cdot a_{k, j}
$$
Proof. If we swap the rows of two cells in a German set and keep their columns, it turns one valid German set into another. When comparing their German products, we can ignore all $n-2$ labels of cells that were not moved. The remaining values are $a_{i, j} \cdot a_{k, \ell}$ resp. $a_{i, \ell} \cdot a_{k, j}$ for certain $i, j, k, \ell$. This gives equality (1) for rooky square grids.
Conversely assume that (1) holds. Then we have to compare two arbitrary German products. But they can transformed into each other by a sequence of several swaps of two cells. Due to (1) the German product does not change at any of these steps, so the rook products of the original configurations are the same as well.
Lemma: A rooky square grid is uniquely determined by the elements of its first row and first column.
Proof. Indeed the previous lemma implies that
$$
a_{i, j} \cdot a_{1,1}=a_{i, 1} \cdot a_{1, j}
$$
which determines $a_{i, j}$ uniquely because $a_{1,1}$ is a unit.
One can actually prove directly that the square grid obtained that way is rooky, but it is simpler to continue directly to
Proposition: Let $\lambda_{i} \in \mathbb{F}_{p}^{*}(i=1, \ldots, n)$ and $\mu_{j} \in \mathbb{F}_{p}^{*}(j=1, \ldots, n)$ arbitrary elements. Then the square grid with
$$
a_{i, j}=\lambda_{i} \cdot \mu_{j}
$$
is rooky. Moreover any rooky square grid can be obtained this way.
Proof. The square grid with $a_{i, j}=\lambda_{i} \cdot \mu_{j}$ is rooky, because any German product has the value
$$
\prod_{i} \lambda_{i} \cdot \prod_{j} \mu_{j} .
$$
## B ALTIC <br> Way <br> FLENSBURG 2023
Let us prove the converse: By the previous lemma, it suffices to find $\lambda_{i} \mathrm{~s}$ and $\mu_{j} \mathrm{~s}$ that recreate the values of the first row and column. For this simply set $\lambda_{i}=a_{i, 1}$ and $\mu_{j}=\frac{a_{1, j}}{a_{1,1}}$.
Proposition: For any prime $p>n^{2}$, there exists a rooky square grid with only distinct elements.
Proof. Choose any primitive root $\alpha \in \mathbb{F}_{p}^{*}$. Then set $\lambda_{i}=\alpha^{i-1}, \mu_{j}=\alpha^{n \cdot(j-1)}$ and $a_{i, j}=\lambda_{i} \cdot \mu_{j}=\alpha^{i-1+n \cdot(j-1)}$. This provides indeed a rooky square grid. The values in the square are $\alpha^{0}, \alpha^{1}, \ldots, \alpha^{n^{2}-1}$. As we have chosen a primitive root, these are all distinct.
For $n=10, p=101$ and $\alpha=2$, this reproduces exactly the construction given in the previous solution.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be a positive integer. A German set in an $n \times n$ square grid is a set of $n$ cells which contains exactly one cell in each row and column. Given a labelling of the cells with the integers from 1 to $n^{2}$ using each integer exactly once, we say that an integer is a German product if it is the product of the labels of the cells in a German set.
(a) Let $n=8$. Determine whether there exists a labelling of an $8 \times 8$ grid such that the following condition is fulfilled: The difference of any two German products is always divisible by 65 .
(b) Let $n=10$. Determine whether there exists a labelling of a $10 \times 10$ grid such that the following condition is fulfilled: The difference of any two German products is always divisible by 101.
|
(a) No, there is no such labelling.
On the contrary, we show that for every labelling there exist two German products whose difference is not divisible by 65 . Suppose that an $8 \times 8$ square grid is labelled with the numbers $1,2, \ldots, 64$ such that no number is used twice.
We can construct a German product that is divisible by 13 by choosing a German set that includes the cell with the label 13 and seven others in different rows and columns, but otherwise arbitrarily.
We can construct a German product that is not divisible by 13 as follows. Notice that only four labels are divisible by 13, namely $13,26,39$, and 52 . These four labels are located in at most four rows; we denote the index set of these rows $R \subseteq[1,8]$. Similarly, there are at least four columns that do not contain any of these four labels; we denote the index set of these columns $C \subseteq[1,8]$. Since $R \leq C$ it is possible to choose cells of a German set from rows $R$ using only columns from $C$. The remaining cells are chosen from the remaining rows accordingly to the definition, but otherwise arbitrarily. The resulting German product is not divisible by 13 since the German set avoids the cells whose labels are divisible by 13 .
The difference of the two German products is not divisible by 13, since one German product is divisible by 13 whereas the other one is not. Hence the difference is not divisible by 65 .
(b) Yes, there is such a labelling.
For $k \in[0,99]$ we define $a_{k}=2^{k}(\bmod 101)$; in other words, $a_{k}$ is the remainder of $2^{k}$ when divided by 101. Note that $a_{k} \neq 0$ since no power of 2 is divisible by 101 . Hence $1 \leq a_{k} \leq 100$ for all $k \in[0,99]$.
We label the cells of the square grid with the numbers $a_{k}$ as follows:
| $a_{0}$ | $a_{1}$ | $a_{2}$ | $\cdots$ | $a_{9}$ |
| :---: | :---: | :---: | :---: | :---: |
| $a_{10}$ | $a_{11}$ | $a_{12}$ | $\cdots$ | $a_{19}$ |
| $a_{20}$ | $a_{21}$ | $a_{22}$ | $\cdots$ | $a_{29}$ |
| $\vdots$ | $\vdots$ | $\vdots$ | $\ddots$ | $\vdots$ |
| $a_{90}$ | $a_{91}$ | $a_{92}$ | $\cdots$ | $a_{99}$ |
More precisely, if we label the rows and columns of the chessboard by $\{0,1,2, \ldots, 9\}$, then the cell with coordinates $(i, j)$ gets the label $a_{10 i+j}$.
Note that $a_{10 i+j} \equiv 2^{10 i+j}(\bmod 101)$ and that $2^{10 i+j}=\left(2^{10}\right)^{i} \cdot 2^{j}$. Hence for this labelling any rook product is congruent to
$$
\left(2^{10}\right)^{0+1+2+\ldots+9} \cdot 2^{0+1+2+\ldots+9}
$$
modulo 101. Hence the difference of any two German products is divisible by 101 for this labelling.
It remains to show that the $a_{k}$ are pairwise different. (In more elaborate language, we would say that 2 is a primitive root modulo 101.) To do this, we denote by $s$ the smallest positive integer such that $2^{s} \equiv 1(\bmod 101)$. Using long division, we may write $100=q s+r$ with non-negative integers $q$ and $r$ such that $0 \leq r \leq s-1$. By virtue of Fermat's little theorem we have
$$
1 \equiv 2^{100} \equiv 2^{q s+r} \equiv\left(2^{s}\right)^{q} \cdot 2^{r} \equiv 1^{q} \cdot 2^{r} \equiv 2^{r} \quad(\bmod 101) .
$$
Since $r<s$ and $s$ is the smallest positive integer with $2^{s} \equiv 1(\bmod 101)$, we must have $r=0$. In other words, 100 is divisible by $s$; in other words, $s$ is a divisor of 100 .
We claim that $s=100$. If this was not the case, we would have $s \mid 20$ or $s \mid 50$, which implies that $2^{20} \equiv 1(\bmod 101)$ or $2^{50} \equiv 1(\bmod 101)$. However $2^{10}=1024 \equiv 14(\bmod 101)$, so that $2^{20} \equiv 14^{2} \equiv 196 \equiv-6 \not \equiv 1(\bmod 101)$ and $2^{50} \equiv\left(2^{20}\right)^{2} \cdot 2^{10} \equiv(-6)^{2} \cdot 14 \equiv 504 \equiv-1$ 丰 $1(\bmod 101)$.
Now assume that $k, \ell \in[0,99]$ are positive integers with $k>\ell$ and $a_{k}=a_{\ell}$. Then we have $2^{k} \equiv 2^{\ell}(\bmod 101)$ and $0 \equiv 2^{k}-2^{\ell} \equiv 2^{\ell} \cdot\left(2^{k-\ell}-1\right)(\bmod 101)$. Since $2^{\ell}$ and 101 are coprime, it follows that $2^{k-\ell}-1 \equiv 0(\bmod 101)$ and $2^{k-\ell} \equiv 1(\bmod 101)$. This cannot be true, since $k-\ell \in[1,99]$, but $s=100$ is the smallest positive integer with $2^{s} \equiv 1(\bmod 101)$. Hence $a_{k} \neq a_{\ell}$.
We conclude that the numbers $a_{k}$ with $k \in[0,99]$ are a hundred pairwise different numbers from the set $[1,100]$, hence they are a permutation of the set $[1,100]$ as it was required.
2nd Solution:
Definition: Let $p$ be a prime. Consider an $n \times n$ square grid of elements $a_{i, j} \in \mathbb{F}_{p}^{*}$ (for $i, j=1, \ldots, n$ ), which are not necessarily distinct. We call it rooky, if all its German products are equal as elements in $\mathbb{F}_{p}^{*}$.
We will provide a classification of all rooky square grids. Of course, most of this is not necessary when writing down a solution to the given problem, but it may still be interesting...
Lemma: A square grid is rooky if and only if for all $i, j, k, \ell$ :
$$
a_{i, j} \cdot a_{k, \ell}=a_{i, \ell} \cdot a_{k, j}
$$
Proof. If we swap the rows of two cells in a German set and keep their columns, it turns one valid German set into another. When comparing their German products, we can ignore all $n-2$ labels of cells that were not moved. The remaining values are $a_{i, j} \cdot a_{k, \ell}$ resp. $a_{i, \ell} \cdot a_{k, j}$ for certain $i, j, k, \ell$. This gives equality (1) for rooky square grids.
Conversely assume that (1) holds. Then we have to compare two arbitrary German products. But they can transformed into each other by a sequence of several swaps of two cells. Due to (1) the German product does not change at any of these steps, so the rook products of the original configurations are the same as well.
Lemma: A rooky square grid is uniquely determined by the elements of its first row and first column.
Proof. Indeed the previous lemma implies that
$$
a_{i, j} \cdot a_{1,1}=a_{i, 1} \cdot a_{1, j}
$$
which determines $a_{i, j}$ uniquely because $a_{1,1}$ is a unit.
One can actually prove directly that the square grid obtained that way is rooky, but it is simpler to continue directly to
Proposition: Let $\lambda_{i} \in \mathbb{F}_{p}^{*}(i=1, \ldots, n)$ and $\mu_{j} \in \mathbb{F}_{p}^{*}(j=1, \ldots, n)$ arbitrary elements. Then the square grid with
$$
a_{i, j}=\lambda_{i} \cdot \mu_{j}
$$
is rooky. Moreover any rooky square grid can be obtained this way.
Proof. The square grid with $a_{i, j}=\lambda_{i} \cdot \mu_{j}$ is rooky, because any German product has the value
$$
\prod_{i} \lambda_{i} \cdot \prod_{j} \mu_{j} .
$$
## B ALTIC <br> Way <br> FLENSBURG 2023
Let us prove the converse: By the previous lemma, it suffices to find $\lambda_{i} \mathrm{~s}$ and $\mu_{j} \mathrm{~s}$ that recreate the values of the first row and column. For this simply set $\lambda_{i}=a_{i, 1}$ and $\mu_{j}=\frac{a_{1, j}}{a_{1,1}}$.
Proposition: For any prime $p>n^{2}$, there exists a rooky square grid with only distinct elements.
Proof. Choose any primitive root $\alpha \in \mathbb{F}_{p}^{*}$. Then set $\lambda_{i}=\alpha^{i-1}, \mu_{j}=\alpha^{n \cdot(j-1)}$ and $a_{i, j}=\lambda_{i} \cdot \mu_{j}=\alpha^{i-1+n \cdot(j-1)}$. This provides indeed a rooky square grid. The values in the square are $\alpha^{0}, \alpha^{1}, \ldots, \alpha^{n^{2}-1}$. As we have chosen a primitive root, these are all distinct.
For $n=10, p=101$ and $\alpha=2$, this reproduces exactly the construction given in the previous solution.
|
{
"exam": "BalticWay",
"problem_label": "20",
"problem_match": "\nProblem 20:",
"resource_path": "BalticWay/segmented/en-bw23sol.jsonl",
"solution_match": "# Solution:",
"tier": "T3",
"year": "2023"
}
|
Let $\alpha$ be a non-zero real number. Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
x f(x+y)=(x+\alpha y) f(x)+x f(y)
$$
for all $x, y \in \mathbb{R}$.
Answer: $f(x)=c x^{2}$ for any real constant $c$ if $\alpha=2 ; f(x)=0$ otherwise.
|
Let $P(x, y)$ denote the assertion of the given functional equation. Note that $P(1,0)$ is $f(1)=f(1)+f(0)$ which implies
$$
f(0)=0
$$
Applying this result to $P(x,-x)$ and $P(-x, x)$ where $x \neq 0$ we get:
$$
\begin{aligned}
& 0=(1-\alpha) x f(x)+x f(-x) \\
& 0=(\alpha-1) x f(-x)-x f(x)
\end{aligned}
$$
By adding (1) and (2) and simplifying, we get $0=\alpha x f(-x)-\alpha x f(x)$ which implies
$$
f(x)=f(-x)
$$
for all $x \neq 0$. Since $f(0)=0=f(-0)$, we can conclude that $f$ is even. Therefore (1) simplifies to
$$
0=x f(x)(2-\alpha)
$$
which implies that if $\alpha \neq 2$ then $f(x)=0$ for all $x \in \mathbb{R}$. It is easy to check that this function works. Now let us consider the case $\alpha=2$. The initial functional equation becomes
$$
x f(x+y)=(x+2 y) f(x)+x f(y)
$$
which can be rewritten as
$$
x f(x+y)-(x+y) f(x)=y f(x)+x f(y)
$$
Note that the right hand side is symmetric with respect to $x$ and $y$. From this we can deduce that $x f(x+y)-(x+y) f(x)=y f(x+y)-(x+y) f(y)$ where factorizing yields
$$
(x-y) f(x+y)=(x+y)(f(x)-f(y)) .
$$
By replacing $y$ with $-y$ and using the fact that $f$ is even, we get
$$
(x+y) f(x-y)=(x-y)(f(x)-f(y))
$$
Taking $x=\frac{z+1}{2}$ and $y=\frac{z-1}{2}$ in both (3) and 4, we get
$$
\begin{aligned}
f(z) & =z\left(f\left(\frac{z+1}{2}\right)-f\left(\frac{z-1}{2}\right)\right) \\
z f(1) & =f\left(\frac{z+1}{2}\right)-f\left(\frac{z-1}{2}\right)
\end{aligned}
$$
respectively. Equations (5) and (6) together yield $f(z)=z \cdot z f(1)=z^{2} f(1)$ which must hold for all $z \in \mathbb{R}$.
Thus, the only possible functions that satisfy the given relation for $\alpha=2$ are $f(x)=c x^{2}$ for some real constant $c$. It is easy to check that they indeed work.
|
f(x)=c x^{2} \text{ for any real constant } c \text{ if } \alpha=2 ; f(x)=0 \text{ otherwise}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $\alpha$ be a non-zero real number. Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
x f(x+y)=(x+\alpha y) f(x)+x f(y)
$$
for all $x, y \in \mathbb{R}$.
Answer: $f(x)=c x^{2}$ for any real constant $c$ if $\alpha=2 ; f(x)=0$ otherwise.
|
Let $P(x, y)$ denote the assertion of the given functional equation. Note that $P(1,0)$ is $f(1)=f(1)+f(0)$ which implies
$$
f(0)=0
$$
Applying this result to $P(x,-x)$ and $P(-x, x)$ where $x \neq 0$ we get:
$$
\begin{aligned}
& 0=(1-\alpha) x f(x)+x f(-x) \\
& 0=(\alpha-1) x f(-x)-x f(x)
\end{aligned}
$$
By adding (1) and (2) and simplifying, we get $0=\alpha x f(-x)-\alpha x f(x)$ which implies
$$
f(x)=f(-x)
$$
for all $x \neq 0$. Since $f(0)=0=f(-0)$, we can conclude that $f$ is even. Therefore (1) simplifies to
$$
0=x f(x)(2-\alpha)
$$
which implies that if $\alpha \neq 2$ then $f(x)=0$ for all $x \in \mathbb{R}$. It is easy to check that this function works. Now let us consider the case $\alpha=2$. The initial functional equation becomes
$$
x f(x+y)=(x+2 y) f(x)+x f(y)
$$
which can be rewritten as
$$
x f(x+y)-(x+y) f(x)=y f(x)+x f(y)
$$
Note that the right hand side is symmetric with respect to $x$ and $y$. From this we can deduce that $x f(x+y)-(x+y) f(x)=y f(x+y)-(x+y) f(y)$ where factorizing yields
$$
(x-y) f(x+y)=(x+y)(f(x)-f(y)) .
$$
By replacing $y$ with $-y$ and using the fact that $f$ is even, we get
$$
(x+y) f(x-y)=(x-y)(f(x)-f(y))
$$
Taking $x=\frac{z+1}{2}$ and $y=\frac{z-1}{2}$ in both (3) and 4, we get
$$
\begin{aligned}
f(z) & =z\left(f\left(\frac{z+1}{2}\right)-f\left(\frac{z-1}{2}\right)\right) \\
z f(1) & =f\left(\frac{z+1}{2}\right)-f\left(\frac{z-1}{2}\right)
\end{aligned}
$$
respectively. Equations (5) and (6) together yield $f(z)=z \cdot z f(1)=z^{2} f(1)$ which must hold for all $z \in \mathbb{R}$.
Thus, the only possible functions that satisfy the given relation for $\alpha=2$ are $f(x)=c x^{2}$ for some real constant $c$. It is easy to check that they indeed work.
|
{
"exam": "BalticWay",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "BalticWay/segmented/en-bw24sol.jsonl",
"solution_match": "\nSolution 1:",
"tier": "T3",
"year": "2024"
}
|
Let $\alpha$ be a non-zero real number. Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
x f(x+y)=(x+\alpha y) f(x)+x f(y)
$$
for all $x, y \in \mathbb{R}$.
Answer: $f(x)=c x^{2}$ for any real constant $c$ if $\alpha=2 ; f(x)=0$ otherwise.
|
Multiplying the given equation by $y$ gives
$$
x y f(x+y)=(x+\alpha y) y f(x)+x y f(y)
$$
which is equivalent to
$$
x y(f(x+y)-f(x)-f(y))=\alpha y^{2} f(x)
$$
The left-hand side of this equation is symmetric in $x$ and $y$. Hence the right-hand side must also stay the same if we swap $x$ and $y$, i.e.,
$$
\alpha y^{2} f(x)=\alpha x^{2} f(y)
$$
As $\alpha \neq 0$, this implies
$$
y^{2} f(x)=x^{2} f(y)
$$
Setting $y=1$ in this equation immediately gives $f(x)=c x^{2}$ where $c=f(1)$. Plugging $f(x)=c x^{2}$ into the original equation gives
$$
c x(x+y)^{2}=c(x+\alpha y) x^{2}+c x y^{2}
$$
where terms can be rearranged to obtain
$$
c x(x+y)^{2}=c x\left(x^{2}+\alpha x y+y^{2}\right)
$$
If $c=0$ then (7) is satisfied. Hence for every $\alpha$, the function $f(x)=0$ is a solution. If $c \neq 0$ then (7) is satisfied if and only if $\alpha=2$. Hence in the case $\alpha=2$, all functions $f(x)=c x^{2}$ (where $c \neq 0$ ) are also solutions.
|
f(x)=c x^{2} \text{ for any real constant } c \text{ if } \alpha=2 ; f(x)=0 \text{ otherwise}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $\alpha$ be a non-zero real number. Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
x f(x+y)=(x+\alpha y) f(x)+x f(y)
$$
for all $x, y \in \mathbb{R}$.
Answer: $f(x)=c x^{2}$ for any real constant $c$ if $\alpha=2 ; f(x)=0$ otherwise.
|
Multiplying the given equation by $y$ gives
$$
x y f(x+y)=(x+\alpha y) y f(x)+x y f(y)
$$
which is equivalent to
$$
x y(f(x+y)-f(x)-f(y))=\alpha y^{2} f(x)
$$
The left-hand side of this equation is symmetric in $x$ and $y$. Hence the right-hand side must also stay the same if we swap $x$ and $y$, i.e.,
$$
\alpha y^{2} f(x)=\alpha x^{2} f(y)
$$
As $\alpha \neq 0$, this implies
$$
y^{2} f(x)=x^{2} f(y)
$$
Setting $y=1$ in this equation immediately gives $f(x)=c x^{2}$ where $c=f(1)$. Plugging $f(x)=c x^{2}$ into the original equation gives
$$
c x(x+y)^{2}=c(x+\alpha y) x^{2}+c x y^{2}
$$
where terms can be rearranged to obtain
$$
c x(x+y)^{2}=c x\left(x^{2}+\alpha x y+y^{2}\right)
$$
If $c=0$ then (7) is satisfied. Hence for every $\alpha$, the function $f(x)=0$ is a solution. If $c \neq 0$ then (7) is satisfied if and only if $\alpha=2$. Hence in the case $\alpha=2$, all functions $f(x)=c x^{2}$ (where $c \neq 0$ ) are also solutions.
|
{
"exam": "BalticWay",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "BalticWay/segmented/en-bw24sol.jsonl",
"solution_match": "\nSolution 2:",
"tier": "T3",
"year": "2024"
}
|
Let $\mathbb{R}^{+}$be the set of all positive real numbers. Find all functions $f: \mathbb{R}^{+} \rightarrow \mathbb{R}^{+}$such that
$$
\frac{f(a)}{1+a+c a}+\frac{f(b)}{1+b+a b}+\frac{f(c)}{1+c+b c}=1
$$
for all $a, b, c \in \mathbb{R}^{+}$that satisfy $a b c=1$.
Answer: $f(x)=k x+1-k$ where $k$ is any real number such that $0 \leq k \leq 1$.
|
Note that $\frac{1}{1+a+c a}=b c \cdot \frac{1}{1+c+b c}$ since $a b c=1$. Similarly,
$$
\frac{1}{1+b+a b}=a c \cdot \frac{1}{1+a+c a}=c \cdot \frac{1}{1+c+b c}
$$
So the initial equality becomes $\frac{b c f(a)+c f(b)+f(c)}{1+c+b c}=1$ which yields
$$
b c f\left(\frac{1}{b c}\right)+c f(b)+f(c)=1+c+b c
$$
Taking $a=b=c=1$ in (8) gives $f(1)+f(1)+f(1)=3$ which implies $f(1)=1$. Using this fact after substituting $c=1$ into 8 yields $b f\left(\frac{1}{b}\right)+f(b)=1+b$, so $b f\left(\frac{1}{b}\right)=1+b-f(b)$ for all $b \in \mathbb{R}^{+}$. Applying this in (8) gives $1+b c-f(b c)+c f(b)+f(c)=1+c+b c$, so
$$
c f(b)+f(c)=c+f(b c)
$$
Swapping $b$ and $c$ here gives
$$
b f(c)+f(b)=b+f(b c)
$$
Subtracting the last equality from the second last one and rearranging the terms gives
$$
c f(b)-f(b)+f(c)-b f(c)=c-b
$$
Substituting $c=2$ into (9) gives $f(b)+f(2)-b f(2)=2-b$, so $f(b)=b(f(2)-1)+2-f(2)$. Denoting $f(2)-1=k$, we get $f(b)=k b+1-k$ for all $b \in \mathbb{R}^{+}$.
Note that if $k<0$, then for large enough $b$ the value of $f(b)$ would become negative. If $k>1$, then for small enough $b$ the value of $f(b)$ would become negative. Therefore $k \in[0,1]$. After substituting $f(x)=k x+1-k$ into 8e can see that it is satisfied. Hence this function satisfies the original equality for all $a, b, c \in \mathbb{R}^{+}$such that $a b c=1$.
|
f(x)=k x+1-k
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $\mathbb{R}^{+}$be the set of all positive real numbers. Find all functions $f: \mathbb{R}^{+} \rightarrow \mathbb{R}^{+}$such that
$$
\frac{f(a)}{1+a+c a}+\frac{f(b)}{1+b+a b}+\frac{f(c)}{1+c+b c}=1
$$
for all $a, b, c \in \mathbb{R}^{+}$that satisfy $a b c=1$.
Answer: $f(x)=k x+1-k$ where $k$ is any real number such that $0 \leq k \leq 1$.
|
Note that $\frac{1}{1+a+c a}=b c \cdot \frac{1}{1+c+b c}$ since $a b c=1$. Similarly,
$$
\frac{1}{1+b+a b}=a c \cdot \frac{1}{1+a+c a}=c \cdot \frac{1}{1+c+b c}
$$
So the initial equality becomes $\frac{b c f(a)+c f(b)+f(c)}{1+c+b c}=1$ which yields
$$
b c f\left(\frac{1}{b c}\right)+c f(b)+f(c)=1+c+b c
$$
Taking $a=b=c=1$ in (8) gives $f(1)+f(1)+f(1)=3$ which implies $f(1)=1$. Using this fact after substituting $c=1$ into 8 yields $b f\left(\frac{1}{b}\right)+f(b)=1+b$, so $b f\left(\frac{1}{b}\right)=1+b-f(b)$ for all $b \in \mathbb{R}^{+}$. Applying this in (8) gives $1+b c-f(b c)+c f(b)+f(c)=1+c+b c$, so
$$
c f(b)+f(c)=c+f(b c)
$$
Swapping $b$ and $c$ here gives
$$
b f(c)+f(b)=b+f(b c)
$$
Subtracting the last equality from the second last one and rearranging the terms gives
$$
c f(b)-f(b)+f(c)-b f(c)=c-b
$$
Substituting $c=2$ into (9) gives $f(b)+f(2)-b f(2)=2-b$, so $f(b)=b(f(2)-1)+2-f(2)$. Denoting $f(2)-1=k$, we get $f(b)=k b+1-k$ for all $b \in \mathbb{R}^{+}$.
Note that if $k<0$, then for large enough $b$ the value of $f(b)$ would become negative. If $k>1$, then for small enough $b$ the value of $f(b)$ would become negative. Therefore $k \in[0,1]$. After substituting $f(x)=k x+1-k$ into 8e can see that it is satisfied. Hence this function satisfies the original equality for all $a, b, c \in \mathbb{R}^{+}$such that $a b c=1$.
|
{
"exam": "BalticWay",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "BalticWay/segmented/en-bw24sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2024"
}
|
Positive real numbers $a_{1}, a_{2}, \ldots, a_{2024}$ are written on the blackboard. A move consists of choosing two numbers $x$ and $y$ on the blackboard, erasing them and writing the number $\frac{x^{2}+6 x y+y^{2}}{x+y}$ on the blackboard. After 2023 moves, only one number $c$ will remain on the blackboard. Prove that
$$
c<2024\left(a_{1}+a_{2}+\ldots+a_{2024}\right)
$$
|
Note that by GM-HM we have
$$
\frac{x^{2}+6 x y+y^{2}}{x+y}=x+y+\frac{4 x y}{x+y}=x+y+2 \cdot \frac{2}{\frac{1}{x}+\frac{1}{y}} \leq x+y+2 \sqrt{x y}=(\sqrt{x}+\sqrt{y})^{2}
$$
which means that
$$
\sqrt{\frac{x^{2}+6 x y+y^{2}}{x+y}} \leq \sqrt{x}+\sqrt{y}
$$
Therefore after each move the sum of square roots of all numbers on the blackboard decreases or stays the same. This implies that
$$
\sqrt{c} \leq \sqrt{a_{1}}+\sqrt{a_{2}}+\ldots+\sqrt{a_{2024}}
$$
By QM-AM we have
$$
\sqrt{a_{1}}+\sqrt{a_{2}}+\ldots+\sqrt{a_{2024}} \leq 2024 \sqrt{\frac{a_{1}+a_{2}+\ldots+a_{2024}}{2024}}
$$
Hence $c \leq 2024\left(a_{1}+a_{2}+\ldots+a_{2024}\right)$.
It remains to show that the equality cannot hold. Suppose, for the sake of contradiction, that
$$
c=2024\left(a_{1}+a_{2}+\ldots+a_{2024}\right)
$$
For this to occur, all the inequalities used must be equalities. Note that the last equality holds if and only if $a_{1}=a_{2}=\cdots=a_{2024}$. Also to reach the equality we must have $x=y$ at each move, so that the sum of square roots of all numbers on the blackboard stays the same all the time. So the square root of the number occurring 2024 times on the blackboard in the beginning is $\frac{\sqrt{c}}{2024}$, and choosing two copies of any number $x$ with square root $\sqrt{x}$ yields a number with square root $2 \sqrt{x}$ after the move. Hence the square root of any number occurring on the blackboard during the process must be of the form $\frac{\sqrt{c}}{2024} \cdot 2^{k}$ for a natural number $k$. But the square root of the number in the blackboard in the end is $\sqrt{c}$ which is not of this form since 2024 is not a power of 2 . The contradiction shows that the equality cannot be achieved and we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Positive real numbers $a_{1}, a_{2}, \ldots, a_{2024}$ are written on the blackboard. A move consists of choosing two numbers $x$ and $y$ on the blackboard, erasing them and writing the number $\frac{x^{2}+6 x y+y^{2}}{x+y}$ on the blackboard. After 2023 moves, only one number $c$ will remain on the blackboard. Prove that
$$
c<2024\left(a_{1}+a_{2}+\ldots+a_{2024}\right)
$$
|
Note that by GM-HM we have
$$
\frac{x^{2}+6 x y+y^{2}}{x+y}=x+y+\frac{4 x y}{x+y}=x+y+2 \cdot \frac{2}{\frac{1}{x}+\frac{1}{y}} \leq x+y+2 \sqrt{x y}=(\sqrt{x}+\sqrt{y})^{2}
$$
which means that
$$
\sqrt{\frac{x^{2}+6 x y+y^{2}}{x+y}} \leq \sqrt{x}+\sqrt{y}
$$
Therefore after each move the sum of square roots of all numbers on the blackboard decreases or stays the same. This implies that
$$
\sqrt{c} \leq \sqrt{a_{1}}+\sqrt{a_{2}}+\ldots+\sqrt{a_{2024}}
$$
By QM-AM we have
$$
\sqrt{a_{1}}+\sqrt{a_{2}}+\ldots+\sqrt{a_{2024}} \leq 2024 \sqrt{\frac{a_{1}+a_{2}+\ldots+a_{2024}}{2024}}
$$
Hence $c \leq 2024\left(a_{1}+a_{2}+\ldots+a_{2024}\right)$.
It remains to show that the equality cannot hold. Suppose, for the sake of contradiction, that
$$
c=2024\left(a_{1}+a_{2}+\ldots+a_{2024}\right)
$$
For this to occur, all the inequalities used must be equalities. Note that the last equality holds if and only if $a_{1}=a_{2}=\cdots=a_{2024}$. Also to reach the equality we must have $x=y$ at each move, so that the sum of square roots of all numbers on the blackboard stays the same all the time. So the square root of the number occurring 2024 times on the blackboard in the beginning is $\frac{\sqrt{c}}{2024}$, and choosing two copies of any number $x$ with square root $\sqrt{x}$ yields a number with square root $2 \sqrt{x}$ after the move. Hence the square root of any number occurring on the blackboard during the process must be of the form $\frac{\sqrt{c}}{2024} \cdot 2^{k}$ for a natural number $k$. But the square root of the number in the blackboard in the end is $\sqrt{c}$ which is not of this form since 2024 is not a power of 2 . The contradiction shows that the equality cannot be achieved and we are done.
|
{
"exam": "BalticWay",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "BalticWay/segmented/en-bw24sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2024"
}
|
Find the largest real number $\alpha$ such that, for all non-negative real numbers $x, y$ and $z$, the following inequality holds:
$$
(x+y+z)^{3}+\alpha\left(x^{2} z+y^{2} x+z^{2} y\right) \geq \alpha\left(x^{2} y+y^{2} z+z^{2} x\right) .
$$
Answer: $6 \sqrt{3}$.
|
Without loss of generality, $x$ is the largest amongst the three variables. By moving $\alpha\left(x^{2} z+y^{2} x+z^{2} y\right)$ to the right-hand side and factoring, we get the equivalent inequality
$$
(x+y+z)^{3} \geq \alpha(x-y)(x-z)(y-z)
$$
If $z>y$, then the right-hand side is non-positive, so we can assume $x \geq y \geq z$.
Note that
$$
\begin{aligned}
x+y+z & \geq x+y-2 z \\
& =\frac{1}{\sqrt{3}}(x-y)+\left(1-\frac{1}{\sqrt{3}}\right)(x-z)+\left(1+\frac{1}{\sqrt{3}}\right)(y-z) \\
& \geq 3 \sqrt[3]{\frac{2}{3 \sqrt{3}}(x-y)(x-z)(y-z)} .
\end{aligned}
$$
Cubing both sides gives $(x+y+z)^{3} \geq 6 \sqrt{3}(x-y)(x-z)(y-z)$. The equality holds when $z=0$ and $x=y(2+\sqrt{3})$. So $\alpha=6 \sqrt{3}$.
|
6 \sqrt{3}
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Find the largest real number $\alpha$ such that, for all non-negative real numbers $x, y$ and $z$, the following inequality holds:
$$
(x+y+z)^{3}+\alpha\left(x^{2} z+y^{2} x+z^{2} y\right) \geq \alpha\left(x^{2} y+y^{2} z+z^{2} x\right) .
$$
Answer: $6 \sqrt{3}$.
|
Without loss of generality, $x$ is the largest amongst the three variables. By moving $\alpha\left(x^{2} z+y^{2} x+z^{2} y\right)$ to the right-hand side and factoring, we get the equivalent inequality
$$
(x+y+z)^{3} \geq \alpha(x-y)(x-z)(y-z)
$$
If $z>y$, then the right-hand side is non-positive, so we can assume $x \geq y \geq z$.
Note that
$$
\begin{aligned}
x+y+z & \geq x+y-2 z \\
& =\frac{1}{\sqrt{3}}(x-y)+\left(1-\frac{1}{\sqrt{3}}\right)(x-z)+\left(1+\frac{1}{\sqrt{3}}\right)(y-z) \\
& \geq 3 \sqrt[3]{\frac{2}{3 \sqrt{3}}(x-y)(x-z)(y-z)} .
\end{aligned}
$$
Cubing both sides gives $(x+y+z)^{3} \geq 6 \sqrt{3}(x-y)(x-z)(y-z)$. The equality holds when $z=0$ and $x=y(2+\sqrt{3})$. So $\alpha=6 \sqrt{3}$.
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "BalticWay/segmented/en-bw24sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2024"
}
|
Find all positive real numbers $\lambda$ such that every sequence $a_{1}, a_{2}, \ldots$ of positive real numbers satisfying
$$
a_{n+1}=\lambda \cdot \frac{a_{1}+a_{2}+\ldots+a_{n}}{n}
$$
for all $n \geq 2024^{2024}$ is bounded.
Remark: A sequence $a_{1}, a_{2}, \ldots$ of positive real numbers is bounded if there exists a real number $M$ such that $a_{i}<M$ for all $i=1,2, \ldots$
Answer: All positive real numbers $\lambda \leq 1$.
|
First we will show that for all $\lambda>1$ every such sequence is unbounded. Note that $a_{n}=\lambda \cdot \frac{a_{1}+a_{2}+\ldots+a_{n-1}}{n-1}$ implies
$$
\frac{a_{n}(n-1)}{\lambda}=a_{1}+a_{2}+\ldots+a_{n-1}
$$
for all $n>2024^{2024}$. Therefore
$$
\begin{aligned}
a_{n+1} & =\lambda \cdot \frac{a_{1}+a_{2}+\ldots+a_{n}}{n} \\
& =\lambda\left(\frac{a_{1}+a_{2}+\ldots+a_{n-1}}{n}+\frac{a_{n}}{n}\right) \\
& =\lambda\left(\frac{a_{n}(n-1)}{\lambda n}+\frac{a_{n}}{n}\right) \\
& =a_{n}\left(\frac{n-1}{n}+\frac{\lambda}{n}\right) \\
& =a_{n}\left(1+\frac{\lambda-1}{n}\right)
\end{aligned}
$$
Hence for all $n>2024^{2024}$ and positive integers $k$ we have
$$
a_{n+k}=a_{n} \cdot\left(1+\frac{\lambda-1}{n}\right)\left(1+\frac{\lambda-1}{n+1}\right) \ldots\left(1+\frac{\lambda-1}{n+k-1}\right) .
$$
This implies that
$$
\begin{aligned}
\frac{a_{n+k}}{a_{n}} & =\left(1+\frac{\lambda-1}{n}\right)\left(1+\frac{\lambda-1}{n+1}\right) \ldots\left(1+\frac{\lambda-1}{n+k-1}\right) \\
& >\frac{\lambda-1}{n}+\frac{\lambda-1}{n+1}+\ldots+\frac{\lambda-1}{n+k-1} \\
& =(\lambda-1) \cdot\left(\frac{1}{n}+\frac{1}{n+1}+\ldots+\frac{1}{n+k-1}\right) .
\end{aligned}
$$
As the sequence $\left(1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{m}\right)_{m \geq 1}$ is unbounded and $\lambda-1>0$, the ratio $\frac{a_{n+k}}{a_{n}}$ is unbounded, implying that the sequence $\left(a_{n}\right)_{n \geq 1}$ is also unbounded.
Now it remains to show that for all $\lambda \leq 1$ every such sequence is bounded. To this end, define $M=\max \left(a_{1}, a_{2}, \ldots, a_{20242024}\right)$. We will show by induction on $n$ that $a_{n} \leq M$ for all $n$. This holds trivially for $n=1,2, \ldots, 2024^{2024}$. For the induction step, assume the desired inequality for some $n \geq 2024^{2024}$ and note that
$$
a_{n+1}=\lambda \cdot \frac{a_{1}+a_{2}+\ldots+a_{n}}{n} \leq \frac{a_{1}+a_{2}+\ldots+a_{n}}{n} \leq \max \left(a_{1}, a_{2}, \ldots, a_{n}\right)=M
$$
The required result follows.
|
\lambda \leq 1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all positive real numbers $\lambda$ such that every sequence $a_{1}, a_{2}, \ldots$ of positive real numbers satisfying
$$
a_{n+1}=\lambda \cdot \frac{a_{1}+a_{2}+\ldots+a_{n}}{n}
$$
for all $n \geq 2024^{2024}$ is bounded.
Remark: A sequence $a_{1}, a_{2}, \ldots$ of positive real numbers is bounded if there exists a real number $M$ such that $a_{i}<M$ for all $i=1,2, \ldots$
Answer: All positive real numbers $\lambda \leq 1$.
|
First we will show that for all $\lambda>1$ every such sequence is unbounded. Note that $a_{n}=\lambda \cdot \frac{a_{1}+a_{2}+\ldots+a_{n-1}}{n-1}$ implies
$$
\frac{a_{n}(n-1)}{\lambda}=a_{1}+a_{2}+\ldots+a_{n-1}
$$
for all $n>2024^{2024}$. Therefore
$$
\begin{aligned}
a_{n+1} & =\lambda \cdot \frac{a_{1}+a_{2}+\ldots+a_{n}}{n} \\
& =\lambda\left(\frac{a_{1}+a_{2}+\ldots+a_{n-1}}{n}+\frac{a_{n}}{n}\right) \\
& =\lambda\left(\frac{a_{n}(n-1)}{\lambda n}+\frac{a_{n}}{n}\right) \\
& =a_{n}\left(\frac{n-1}{n}+\frac{\lambda}{n}\right) \\
& =a_{n}\left(1+\frac{\lambda-1}{n}\right)
\end{aligned}
$$
Hence for all $n>2024^{2024}$ and positive integers $k$ we have
$$
a_{n+k}=a_{n} \cdot\left(1+\frac{\lambda-1}{n}\right)\left(1+\frac{\lambda-1}{n+1}\right) \ldots\left(1+\frac{\lambda-1}{n+k-1}\right) .
$$
This implies that
$$
\begin{aligned}
\frac{a_{n+k}}{a_{n}} & =\left(1+\frac{\lambda-1}{n}\right)\left(1+\frac{\lambda-1}{n+1}\right) \ldots\left(1+\frac{\lambda-1}{n+k-1}\right) \\
& >\frac{\lambda-1}{n}+\frac{\lambda-1}{n+1}+\ldots+\frac{\lambda-1}{n+k-1} \\
& =(\lambda-1) \cdot\left(\frac{1}{n}+\frac{1}{n+1}+\ldots+\frac{1}{n+k-1}\right) .
\end{aligned}
$$
As the sequence $\left(1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{m}\right)_{m \geq 1}$ is unbounded and $\lambda-1>0$, the ratio $\frac{a_{n+k}}{a_{n}}$ is unbounded, implying that the sequence $\left(a_{n}\right)_{n \geq 1}$ is also unbounded.
Now it remains to show that for all $\lambda \leq 1$ every such sequence is bounded. To this end, define $M=\max \left(a_{1}, a_{2}, \ldots, a_{20242024}\right)$. We will show by induction on $n$ that $a_{n} \leq M$ for all $n$. This holds trivially for $n=1,2, \ldots, 2024^{2024}$. For the induction step, assume the desired inequality for some $n \geq 2024^{2024}$ and note that
$$
a_{n+1}=\lambda \cdot \frac{a_{1}+a_{2}+\ldots+a_{n}}{n} \leq \frac{a_{1}+a_{2}+\ldots+a_{n}}{n} \leq \max \left(a_{1}, a_{2}, \ldots, a_{n}\right)=M
$$
The required result follows.
|
{
"exam": "BalticWay",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "BalticWay/segmented/en-bw24sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2024"
}
|
A labyrinth is a system of 2024 caves and 2023 non-intersecting (bidirectional) corridors, each of which connects exactly two caves, where each pair of caves is connected through some sequence of corridors. Initially, Erik is standing in a corridor connecting some two caves. In a move, he can walk through one of the caves to another corridor that connects that cave to a third cave. However, when doing so, the corridor he was just in will magically disappear and get replaced by a new one connecting the end of his new corridor to the beginning of his old one (i.e., if Erik was in a corridor connecting caves $a$ and $b$ and he walked through cave $b$ into a corridor that connects caves $b$ and $c$, then the corridor between caves $a$ and $b$ will disappear and a new corridor between caves $a$ and $c$ will appear).
Since Erik likes designing labyrinths and has a specific layout in mind for his next one, he is wondering whether he can transform the labyrinth into that layout using these moves. Prove that this is in fact possible, regardless of the original layout and his starting position there.
|
Throughout the solution, we denote a corridor directly connecting caves $a$ and $b$ by $a b$.
First we show that Erik can reverse his moves. Indeed, consider three caves $a, b, c$ such that $a b$ and $b c$ are corridors, and assume that Erik stands in the corridor $a b$. He can then perform the moves $a b \rightarrow b c \rightarrow c a \rightarrow a b$ in succession (Fig. 1\} note that after each move, the edge he is about to walk to in the sequence has just appeared as a consequence of his last move). But this will take him back to where he started as well as make sure that the layout of the labyrinth has not changed. Hence after performing the first move, he can "undo" it by performing the remaining two moves in this sequence.
Figure 1
Figure 2
This means that it is enough to show that Erik can turn any layout into the star shape (i.e., a layout with one central cave that all the remaining caves are directly connected to), since if he can get from any layout to the star shape he can also get from the star shape to any layout. Let us prove this by induction on the number $n$ of caves.
For $n=3$, any allowed layout has the star shape, so let us assume $n \geq 4$. It is easy to see that there has to exist at least two caves, each of which being connected to only one other cave. These caves cannot be directly connected to each other (otherwise they could not be connected to other caves). Hence one of these two caves, say $v$, is such that Erik is not initially standing in the only corridor adjacent to it. By the induction hypothesis, Erik can then perform some sequence of moves that will transform the labyrinth excluding $v$ into the star shape with $n-1$ caves. Let the central cave of the star be $c$ and assume that Erik is standing in the corridor $c w$. We have to consider three cases for how $v$ is connected to other caves:
- The cave $v$ is directly connected to $c$. In this case we already have the star shape with $n$ caves, and so we are done.
- The cave $v$ is directly connected to $w$. In this case Erik can make the moves $c w \rightarrow w v \rightarrow v c$ (Fig. 2). Then the resulting layout has the star shape.
- The cave $v$ is directly connected to some other non-central cave $u$. In this case Erik can make the moves
$$
w c \rightarrow c u \rightarrow u w \rightarrow u v \rightarrow v w \rightarrow w c \rightarrow w u \rightarrow u c
$$
(Fig. 3). Then the resulting layout has the star shape.
In all cases, we have shown that we can turn the labyrinth into the star shape. So we are done by induction.

Figure 3
A $45 \times 45$ grid has had the central unit square removed. For which positive integers $n$ is it possible to cut the remaining area into $1 \times n$ and $n \times 1$ rectangles?
Answer: 1, 2, 11, 22, 23.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A labyrinth is a system of 2024 caves and 2023 non-intersecting (bidirectional) corridors, each of which connects exactly two caves, where each pair of caves is connected through some sequence of corridors. Initially, Erik is standing in a corridor connecting some two caves. In a move, he can walk through one of the caves to another corridor that connects that cave to a third cave. However, when doing so, the corridor he was just in will magically disappear and get replaced by a new one connecting the end of his new corridor to the beginning of his old one (i.e., if Erik was in a corridor connecting caves $a$ and $b$ and he walked through cave $b$ into a corridor that connects caves $b$ and $c$, then the corridor between caves $a$ and $b$ will disappear and a new corridor between caves $a$ and $c$ will appear).
Since Erik likes designing labyrinths and has a specific layout in mind for his next one, he is wondering whether he can transform the labyrinth into that layout using these moves. Prove that this is in fact possible, regardless of the original layout and his starting position there.
|
Throughout the solution, we denote a corridor directly connecting caves $a$ and $b$ by $a b$.
First we show that Erik can reverse his moves. Indeed, consider three caves $a, b, c$ such that $a b$ and $b c$ are corridors, and assume that Erik stands in the corridor $a b$. He can then perform the moves $a b \rightarrow b c \rightarrow c a \rightarrow a b$ in succession (Fig. 1\} note that after each move, the edge he is about to walk to in the sequence has just appeared as a consequence of his last move). But this will take him back to where he started as well as make sure that the layout of the labyrinth has not changed. Hence after performing the first move, he can "undo" it by performing the remaining two moves in this sequence.

Figure 1

Figure 2
This means that it is enough to show that Erik can turn any layout into the star shape (i.e., a layout with one central cave that all the remaining caves are directly connected to), since if he can get from any layout to the star shape he can also get from the star shape to any layout. Let us prove this by induction on the number $n$ of caves.
For $n=3$, any allowed layout has the star shape, so let us assume $n \geq 4$. It is easy to see that there has to exist at least two caves, each of which being connected to only one other cave. These caves cannot be directly connected to each other (otherwise they could not be connected to other caves). Hence one of these two caves, say $v$, is such that Erik is not initially standing in the only corridor adjacent to it. By the induction hypothesis, Erik can then perform some sequence of moves that will transform the labyrinth excluding $v$ into the star shape with $n-1$ caves. Let the central cave of the star be $c$ and assume that Erik is standing in the corridor $c w$. We have to consider three cases for how $v$ is connected to other caves:
- The cave $v$ is directly connected to $c$. In this case we already have the star shape with $n$ caves, and so we are done.
- The cave $v$ is directly connected to $w$. In this case Erik can make the moves $c w \rightarrow w v \rightarrow v c$ (Fig. 2). Then the resulting layout has the star shape.
- The cave $v$ is directly connected to some other non-central cave $u$. In this case Erik can make the moves
$$
w c \rightarrow c u \rightarrow u w \rightarrow u v \rightarrow v w \rightarrow w c \rightarrow w u \rightarrow u c
$$
(Fig. 3). Then the resulting layout has the star shape.
In all cases, we have shown that we can turn the labyrinth into the star shape. So we are done by induction.

Figure 3
A $45 \times 45$ grid has had the central unit square removed. For which positive integers $n$ is it possible to cut the remaining area into $1 \times n$ and $n \times 1$ rectangles?
Answer: 1, 2, 11, 22, 23.
|
{
"exam": "BalticWay",
"problem_label": "6",
"problem_match": "\n6.",
"resource_path": "BalticWay/segmented/en-bw24sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2024"
}
|
A labyrinth is a system of 2024 caves and 2023 non-intersecting (bidirectional) corridors, each of which connects exactly two caves, where each pair of caves is connected through some sequence of corridors. Initially, Erik is standing in a corridor connecting some two caves. In a move, he can walk through one of the caves to another corridor that connects that cave to a third cave. However, when doing so, the corridor he was just in will magically disappear and get replaced by a new one connecting the end of his new corridor to the beginning of his old one (i.e., if Erik was in a corridor connecting caves $a$ and $b$ and he walked through cave $b$ into a corridor that connects caves $b$ and $c$, then the corridor between caves $a$ and $b$ will disappear and a new corridor between caves $a$ and $c$ will appear).
Since Erik likes designing labyrinths and has a specific layout in mind for his next one, he is wondering whether he can transform the labyrinth into that layout using these moves. Prove that this is in fact possible, regardless of the original layout and his starting position there.
|
Clearly, any $n$ that works must be a divisor of the number $45^{2}-1=2024$ of unit squares. Furthermore, it must not be greater than 45 , or else we cannot fit any $1 \times n$ rectangles in the grid. This leaves the options $n=1, n=2, n=4, n=8, n=11, n=22, n=23$ and $n=44$. Note that any divisor $d$ of a length $n$ that works also works, since we can just divide each of the $1 \times n$ and $n \times 1$ pieces into $1 \times d$ and $d \times 1$ pieces.
For $n=22$, we can cover the grid as in Fig. 4. By the above, this shows that $n=1, n=2$ and $n=11$ all work.
For $n=23$, we can cover the grid as in Fig. 5 .

Figure 4

Figure 5
The remaining possibilities are $n=4, n=8$ and $n=44$. All of these are divisible by 4 , and hence if any of them work $n=4$ would also have to work. However, $n=4$ does not work. Indeed, color gray all rows with row numbers congruent to 1 or 2 modulo 4 (Fig. 6). Then any $1 \times 4$ or $4 \times 1$ piece will cover an even number of gray squares. But there is an odd number of gray squares in total, since the number of gray rows is odd, as well as the length of any row, and the center square is white as it is in row 23 . So it is impossible to cover all of them.
Consequently, $n=1,2,11,22,23$ are the only values that work.

Figure 6
|
proof
|
Yes
|
Incomplete
|
proof
|
Combinatorics
|
A labyrinth is a system of 2024 caves and 2023 non-intersecting (bidirectional) corridors, each of which connects exactly two caves, where each pair of caves is connected through some sequence of corridors. Initially, Erik is standing in a corridor connecting some two caves. In a move, he can walk through one of the caves to another corridor that connects that cave to a third cave. However, when doing so, the corridor he was just in will magically disappear and get replaced by a new one connecting the end of his new corridor to the beginning of his old one (i.e., if Erik was in a corridor connecting caves $a$ and $b$ and he walked through cave $b$ into a corridor that connects caves $b$ and $c$, then the corridor between caves $a$ and $b$ will disappear and a new corridor between caves $a$ and $c$ will appear).
Since Erik likes designing labyrinths and has a specific layout in mind for his next one, he is wondering whether he can transform the labyrinth into that layout using these moves. Prove that this is in fact possible, regardless of the original layout and his starting position there.
|
Clearly, any $n$ that works must be a divisor of the number $45^{2}-1=2024$ of unit squares. Furthermore, it must not be greater than 45 , or else we cannot fit any $1 \times n$ rectangles in the grid. This leaves the options $n=1, n=2, n=4, n=8, n=11, n=22, n=23$ and $n=44$. Note that any divisor $d$ of a length $n$ that works also works, since we can just divide each of the $1 \times n$ and $n \times 1$ pieces into $1 \times d$ and $d \times 1$ pieces.
For $n=22$, we can cover the grid as in Fig. 4. By the above, this shows that $n=1, n=2$ and $n=11$ all work.
For $n=23$, we can cover the grid as in Fig. 5 .

Figure 4

Figure 5
The remaining possibilities are $n=4, n=8$ and $n=44$. All of these are divisible by 4 , and hence if any of them work $n=4$ would also have to work. However, $n=4$ does not work. Indeed, color gray all rows with row numbers congruent to 1 or 2 modulo 4 (Fig. 6). Then any $1 \times 4$ or $4 \times 1$ piece will cover an even number of gray squares. But there is an odd number of gray squares in total, since the number of gray rows is odd, as well as the length of any row, and the center square is white as it is in row 23 . So it is impossible to cover all of them.
Consequently, $n=1,2,11,22,23$ are the only values that work.

Figure 6
|
{
"exam": "BalticWay",
"problem_label": "6",
"problem_match": "\n6.",
"resource_path": "BalticWay/segmented/en-bw24sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2024"
}
|
Let $a, b, n$ be positive integers such that $a+b \leq n^{2}$. Alice and Bob play a game on an (initially uncoloured) $n \times n$ grid as follows:
- First, Alice paints $a$ cells green.
- Then, Bob paints $b$ other (i.e. uncoloured) cells blue.
Alice wins if she can find a path of non-blue cells starting with the bottom left cell and ending with the top right cell (where a path is a sequence of cells such that any two consecutive ones have a common side), otherwise Bob wins. Determine, in terms of $a, b$ and $n$, who has a winning strategy. Answer: If $a \geq \min (2 b, 2 n-1)$, Alice wins, otherwise Bob wins.

Figure 7

Figure 8
|
If $a \geq 2 n-1$, Alice can win, for example by painting all the cells in the leftmost column and the topmost row green, ensuring that there will be a green path (Fig. 77).
If $2 n-1>a \geq 2 b$, Alice can also win. Indeed, note that $n>b$, so Alice can make sure to color (at least) the bottommost $b$ cells in the leftmost column and the rightmost $b$ cells in the topmost row green. There are now $b+1$ disjoint paths from some green square in the leftmost column to some green square in the topmost row (Fig. 8d), so there is no way for Bob to block all of the paths.
If however $a<\min (2 b, 2 n-1)$, Bob wins. Indeed, note that $\min (2 b, 2 n-1)$ is the number of all descending diagonals of length at most $b$. Hence after Alice has made her move, there must still be some of these diagonals with no green cells in it. Bob can color all cells in it blue and win.
Hence Alice wins iff $a \geq \min (2 b, 2 n-1)$.
|
a \geq \min (2 b, 2 n-1)
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $a, b, n$ be positive integers such that $a+b \leq n^{2}$. Alice and Bob play a game on an (initially uncoloured) $n \times n$ grid as follows:
- First, Alice paints $a$ cells green.
- Then, Bob paints $b$ other (i.e. uncoloured) cells blue.
Alice wins if she can find a path of non-blue cells starting with the bottom left cell and ending with the top right cell (where a path is a sequence of cells such that any two consecutive ones have a common side), otherwise Bob wins. Determine, in terms of $a, b$ and $n$, who has a winning strategy. Answer: If $a \geq \min (2 b, 2 n-1)$, Alice wins, otherwise Bob wins.

Figure 7

Figure 8
|
If $a \geq 2 n-1$, Alice can win, for example by painting all the cells in the leftmost column and the topmost row green, ensuring that there will be a green path (Fig. 77).
If $2 n-1>a \geq 2 b$, Alice can also win. Indeed, note that $n>b$, so Alice can make sure to color (at least) the bottommost $b$ cells in the leftmost column and the rightmost $b$ cells in the topmost row green. There are now $b+1$ disjoint paths from some green square in the leftmost column to some green square in the topmost row (Fig. 8d), so there is no way for Bob to block all of the paths.
If however $a<\min (2 b, 2 n-1)$, Bob wins. Indeed, note that $\min (2 b, 2 n-1)$ is the number of all descending diagonals of length at most $b$. Hence after Alice has made her move, there must still be some of these diagonals with no green cells in it. Bob can color all cells in it blue and win.
Hence Alice wins iff $a \geq \min (2 b, 2 n-1)$.
|
{
"exam": "BalticWay",
"problem_label": "8",
"problem_match": "\n8.",
"resource_path": "BalticWay/segmented/en-bw24sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2024"
}
|
Let $S$ be a finite set. For a positive integer $n$, we say that a function $f: S \rightarrow S$ is an $n$-th power if there exists some function $g: S \rightarrow S$ such that
$$
f(x)=\underbrace{g(g(\ldots g(x) \ldots))}_{g \text { applied } n \text { times }}
$$
for each $x \in S$.
Suppose that a function $f: S \rightarrow S$ is an $n$-th power for each positive integer $n$. Is it necessarily true that $f(f(x))=f(x)$ for each $x \in S$ ?
Answer: Yes.
|
Since $S$ is finite, there is a finite set of all functions $\left\{g_{1}, g_{2}, \ldots, g_{k}\right\}$ from $S$ to itself. Consider a function $F$ that assigns to each positive integer $n$ one of these functions such that $f$ is the $n$-th power of the function $F(n)$. So $F$ induces a partition of the set of all positive integers into sets $P_{i}$ consisting of all the integers $n$ such that $F(n)=g_{i}$.
For any positive integer $N$, consider the complete graph $K_{N}$ on $N$ vertices labeled 1 through $N$. We will colour the edges of $K_{N}$ in $k$ colours $C_{1}, C_{2}, \ldots, C_{k}$ according to the partition in the following way: If $|x-y|$ lies in $P_{i}$, colour the edge between $x$ and $y$ in the colour $C_{i}$. By Ramsey's theorem we can take $N$ to be large enough that there is a monochromatic triangle in $K_{N}$. This means that there are three integers $x, y$ and $z$ and an index $i$ for which $|x-y|,|y-z|,|z-x| \in P_{i}$. Hence there are three integers $a, b, c \in P_{i}$ such that $a+b=c$.
Therefore, some function $g_{i}: S \rightarrow S$ satisfies $f(x)=g_{i}^{a}(x)=g_{i}^{b}(x)=g_{i}^{a+b}(x)$ for each $x \in S$. Hence, $f(f(x))=g_{i}^{a}\left(g_{i}^{b}(x)\right)=g_{i}^{a+b}(x)=f(x)$ for each $x \in S$.
Remark: The fact that there is an index $i$ for which $P_{i}$ contains three integers $a, b, c$ such that $a+b=c$ is known as Schur's theorem.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $S$ be a finite set. For a positive integer $n$, we say that a function $f: S \rightarrow S$ is an $n$-th power if there exists some function $g: S \rightarrow S$ such that
$$
f(x)=\underbrace{g(g(\ldots g(x) \ldots))}_{g \text { applied } n \text { times }}
$$
for each $x \in S$.
Suppose that a function $f: S \rightarrow S$ is an $n$-th power for each positive integer $n$. Is it necessarily true that $f(f(x))=f(x)$ for each $x \in S$ ?
Answer: Yes.
|
Since $S$ is finite, there is a finite set of all functions $\left\{g_{1}, g_{2}, \ldots, g_{k}\right\}$ from $S$ to itself. Consider a function $F$ that assigns to each positive integer $n$ one of these functions such that $f$ is the $n$-th power of the function $F(n)$. So $F$ induces a partition of the set of all positive integers into sets $P_{i}$ consisting of all the integers $n$ such that $F(n)=g_{i}$.
For any positive integer $N$, consider the complete graph $K_{N}$ on $N$ vertices labeled 1 through $N$. We will colour the edges of $K_{N}$ in $k$ colours $C_{1}, C_{2}, \ldots, C_{k}$ according to the partition in the following way: If $|x-y|$ lies in $P_{i}$, colour the edge between $x$ and $y$ in the colour $C_{i}$. By Ramsey's theorem we can take $N$ to be large enough that there is a monochromatic triangle in $K_{N}$. This means that there are three integers $x, y$ and $z$ and an index $i$ for which $|x-y|,|y-z|,|z-x| \in P_{i}$. Hence there are three integers $a, b, c \in P_{i}$ such that $a+b=c$.
Therefore, some function $g_{i}: S \rightarrow S$ satisfies $f(x)=g_{i}^{a}(x)=g_{i}^{b}(x)=g_{i}^{a+b}(x)$ for each $x \in S$. Hence, $f(f(x))=g_{i}^{a}\left(g_{i}^{b}(x)\right)=g_{i}^{a+b}(x)=f(x)$ for each $x \in S$.
Remark: The fact that there is an index $i$ for which $P_{i}$ contains three integers $a, b, c$ such that $a+b=c$ is known as Schur's theorem.
|
{
"exam": "BalticWay",
"problem_label": "9",
"problem_match": "\n9.",
"resource_path": "BalticWay/segmented/en-bw24sol.jsonl",
"solution_match": "\nSolution 1:",
"tier": "T3",
"year": "2024"
}
|
Let $S$ be a finite set. For a positive integer $n$, we say that a function $f: S \rightarrow S$ is an $n$-th power if there exists some function $g: S \rightarrow S$ such that
$$
f(x)=\underbrace{g(g(\ldots g(x) \ldots))}_{g \text { applied } n \text { times }}
$$
for each $x \in S$.
Suppose that a function $f: S \rightarrow S$ is an $n$-th power for each positive integer $n$. Is it necessarily true that $f(f(x))=f(x)$ for each $x \in S$ ?
Answer: Yes.
|
Pick $x \in S$ arbitrarily and denote $y=f(x)$. We need to prove that $f(y)=y$. Let $n=|S|$ and consider the function $g: S \rightarrow S$ such that $f=g^{n!}$. As we must have $g^{n!}(x)=y$, the element $y$ must occur among the first $n$ terms of the sequence $x, g(x), g^{2}(x), \ldots$, i.e., $g^{k}(x)=y$ for
some $k<n$. So $g^{n!-k}(y)=y$, or putting it otherwise, $g^{n!-k-1}(g(y))=y$. Like before, we obtain that $y$ must occur among the first $n$ terms of the sequence $g(y), g^{2}(y), \ldots$, i.e., $g^{l}(y)=y$ for some $l \leq n$. So certainly $g^{n!}(y)=y$ as $l \mid n$ !. This proves the claim.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $S$ be a finite set. For a positive integer $n$, we say that a function $f: S \rightarrow S$ is an $n$-th power if there exists some function $g: S \rightarrow S$ such that
$$
f(x)=\underbrace{g(g(\ldots g(x) \ldots))}_{g \text { applied } n \text { times }}
$$
for each $x \in S$.
Suppose that a function $f: S \rightarrow S$ is an $n$-th power for each positive integer $n$. Is it necessarily true that $f(f(x))=f(x)$ for each $x \in S$ ?
Answer: Yes.
|
Pick $x \in S$ arbitrarily and denote $y=f(x)$. We need to prove that $f(y)=y$. Let $n=|S|$ and consider the function $g: S \rightarrow S$ such that $f=g^{n!}$. As we must have $g^{n!}(x)=y$, the element $y$ must occur among the first $n$ terms of the sequence $x, g(x), g^{2}(x), \ldots$, i.e., $g^{k}(x)=y$ for
some $k<n$. So $g^{n!-k}(y)=y$, or putting it otherwise, $g^{n!-k-1}(g(y))=y$. Like before, we obtain that $y$ must occur among the first $n$ terms of the sequence $g(y), g^{2}(y), \ldots$, i.e., $g^{l}(y)=y$ for some $l \leq n$. So certainly $g^{n!}(y)=y$ as $l \mid n$ !. This proves the claim.
|
{
"exam": "BalticWay",
"problem_label": "9",
"problem_match": "\n9.",
"resource_path": "BalticWay/segmented/en-bw24sol.jsonl",
"solution_match": "\nSolution 2:",
"tier": "T3",
"year": "2024"
}
|
A frog is located on a unit square of an infinite grid oriented according to the cardinal directions. The frog makes moves consisting of jumping either one or two squares in the direction it is facing, and then turning according to the following rules:
(i) If the frog jumps one square, it then turns $90^{\circ}$ to the right;
(ii) If the frog jumps two squares, it then turns $90^{\circ}$ to the left.
Is it possible for the frog to reach the square exactly 2024 squares north of the initial square after some finite number of moves if it is initially facing:
(a) North;
(b) East?
Answer: (a) No; (b) Yes.
|
(a) We color the grid with 5 colors so that the color of a square is determined by the expression $2 x+y$ modulo 5 , where $(x, y)$ are the coordinates of the square (we assume that the side length of the square is 1 ; see Fig. 9). Without loss of generality, let the color of the target square be 0 , and let the frog be there facing in the positive $y$-direction. Before the move that brought the frog to this position, it must have been either on a square of color 1 , facing in the positive $x$ direction, or on a square of color 2 , facing in the negative $x$-direction. In either case, one move earlier, the frog must have been either on a square of color 3 , facing in the negative $y$-direction, or on a square of color 0 , facing in the positive $y$-direction. If at some point the frog was on a square of color 3 , facing in the negative $y$-direction, then before the move that brought it there, it must have been either on a square of color 1 , facing in the positive $x$-direction, or on a square of color 2 , facing in the negative $x$-direction. This exhausts all possible cases, showing that throughout the entire process, the frog could only be in one of the following four positions:
- On a square of color 0 , facing in the positive $y$-direction;
- On a square of color 1 , facing in the positive $x$-direction;
- On a square of color 2 , facing in the negative $x$-direction;
- On a square of color 3 , facing in the negative $y$-direction.
Based on this, we examine all possibilities:
| | | | | | | | | | | | | |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| | 0 | 2 | 4 | 1 | 3 | 0 | 2 | 4 | 1 | 3 | 0 | |
| | 4 | 1 | 3 | 0 | 2 | 4 | 1 | 3 | 0 | 2 | 4 | |
| | 3 | 0 | 2 | 4 | 1 | 3 | 0 | 2 | 4 | 1 | 3 | |
| | 2 | 4 | 1 | 3 | 0 | 2 | 4 | 1 | 3 | 0 | 2 | |
| | 1 | 3 | 0 | 2 | 4 | 1 | 3 | 0 | 2 | 4 | 1 | |
| | 0 | 2 | 4 | 1 | 3 | 0 | 2 | 4 | 1 | 3 | 0 | |
| | 4 | 1 | 3 | 0 | 2 | 4 | 1 | 3 | 0 | 2 | 4 | |
| | 3 | 0 | 2 | 4 | 1 | 3 | 0 | 2 | 4 | 1 | 3 | |
| | 2 | 4 | 1 | 3 | 0 | 2 | 4 | 1 | 3 | 0 | 2 | |
| | 1 | 3 | 0 | 2 | 4 | 1 | 3 | 0 | 2 | 4 | 1 | |
| | 0 | 2 | 4 | 1 | 3 | 0 | 2 | 4 | 1 | 3 | 0 | |
| | | | | | | | | | | | | |
Figure 9
Figure 10
- If the positive $y$-direction corresponds to north, then the color of the initial square is 1 , and the frog must have been facing in the positive $x$-direction, that is, east.
- If the positive $y$-direction corresponds to east, then the color of the initial square is 3 , and the frog must have been facing in the negative $y$-direction, that is, west.
- If the positive $y$-direction corresponds to west, then the color of the initial square is 2 , and the frog must have been facing in the negative $x$-direction, that is, south.
- If the positive $y$-direction corresponds to south, then the color of the initial square is 4 , from which the frog could not reach the target square at all.
This demonstrates that if the frog reaches the target square, it cannot have been facing north at the initial square.
(b) Let the frog at some point face east. Then it can make the following moves: east 2 squares, north 2 squares, west 1 square, north 2 squares, west 1 square, north 1 square (Fig. 10). This way, the frog has moved a total of 5 squares north, and after these moves, it is again facing east. Therefore, by repeating this sequence of moves 405 times, the frog can reach a point 2025 squares north of the initial square. By omitting the last move, the frog reaches exactly the square that is 2024 squares north of the initial square.
Remark: Similarly to the solution of part (b), one can show that the frog can reach the desired square also after making its first move to the south or to the west.
Let $A B C D$ be a cyclic quadrilateral with circumcentre $O$ and with $A C$ perpendicular to $B D$. Points $X$ and $Y$ lie on the circumcircle of the triangle $B O D$ such that $\angle A X O=\angle C Y O=90^{\circ}$. Let $M$ be the midpoint of $A C$. Prove that $B D$ is tangent to the circumcircle of the triangle $M X Y$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
A frog is located on a unit square of an infinite grid oriented according to the cardinal directions. The frog makes moves consisting of jumping either one or two squares in the direction it is facing, and then turning according to the following rules:
(i) If the frog jumps one square, it then turns $90^{\circ}$ to the right;
(ii) If the frog jumps two squares, it then turns $90^{\circ}$ to the left.
Is it possible for the frog to reach the square exactly 2024 squares north of the initial square after some finite number of moves if it is initially facing:
(a) North;
(b) East?
Answer: (a) No; (b) Yes.
|
(a) We color the grid with 5 colors so that the color of a square is determined by the expression $2 x+y$ modulo 5 , where $(x, y)$ are the coordinates of the square (we assume that the side length of the square is 1 ; see Fig. 9). Without loss of generality, let the color of the target square be 0 , and let the frog be there facing in the positive $y$-direction. Before the move that brought the frog to this position, it must have been either on a square of color 1 , facing in the positive $x$ direction, or on a square of color 2 , facing in the negative $x$-direction. In either case, one move earlier, the frog must have been either on a square of color 3 , facing in the negative $y$-direction, or on a square of color 0 , facing in the positive $y$-direction. If at some point the frog was on a square of color 3 , facing in the negative $y$-direction, then before the move that brought it there, it must have been either on a square of color 1 , facing in the positive $x$-direction, or on a square of color 2 , facing in the negative $x$-direction. This exhausts all possible cases, showing that throughout the entire process, the frog could only be in one of the following four positions:
- On a square of color 0 , facing in the positive $y$-direction;
- On a square of color 1 , facing in the positive $x$-direction;
- On a square of color 2 , facing in the negative $x$-direction;
- On a square of color 3 , facing in the negative $y$-direction.
Based on this, we examine all possibilities:
| | | | | | | | | | | | | |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| | 0 | 2 | 4 | 1 | 3 | 0 | 2 | 4 | 1 | 3 | 0 | |
| | 4 | 1 | 3 | 0 | 2 | 4 | 1 | 3 | 0 | 2 | 4 | |
| | 3 | 0 | 2 | 4 | 1 | 3 | 0 | 2 | 4 | 1 | 3 | |
| | 2 | 4 | 1 | 3 | 0 | 2 | 4 | 1 | 3 | 0 | 2 | |
| | 1 | 3 | 0 | 2 | 4 | 1 | 3 | 0 | 2 | 4 | 1 | |
| | 0 | 2 | 4 | 1 | 3 | 0 | 2 | 4 | 1 | 3 | 0 | |
| | 4 | 1 | 3 | 0 | 2 | 4 | 1 | 3 | 0 | 2 | 4 | |
| | 3 | 0 | 2 | 4 | 1 | 3 | 0 | 2 | 4 | 1 | 3 | |
| | 2 | 4 | 1 | 3 | 0 | 2 | 4 | 1 | 3 | 0 | 2 | |
| | 1 | 3 | 0 | 2 | 4 | 1 | 3 | 0 | 2 | 4 | 1 | |
| | 0 | 2 | 4 | 1 | 3 | 0 | 2 | 4 | 1 | 3 | 0 | |
| | | | | | | | | | | | | |
Figure 9

Figure 10
- If the positive $y$-direction corresponds to north, then the color of the initial square is 1 , and the frog must have been facing in the positive $x$-direction, that is, east.
- If the positive $y$-direction corresponds to east, then the color of the initial square is 3 , and the frog must have been facing in the negative $y$-direction, that is, west.
- If the positive $y$-direction corresponds to west, then the color of the initial square is 2 , and the frog must have been facing in the negative $x$-direction, that is, south.
- If the positive $y$-direction corresponds to south, then the color of the initial square is 4 , from which the frog could not reach the target square at all.
This demonstrates that if the frog reaches the target square, it cannot have been facing north at the initial square.
(b) Let the frog at some point face east. Then it can make the following moves: east 2 squares, north 2 squares, west 1 square, north 2 squares, west 1 square, north 1 square (Fig. 10). This way, the frog has moved a total of 5 squares north, and after these moves, it is again facing east. Therefore, by repeating this sequence of moves 405 times, the frog can reach a point 2025 squares north of the initial square. By omitting the last move, the frog reaches exactly the square that is 2024 squares north of the initial square.
Remark: Similarly to the solution of part (b), one can show that the frog can reach the desired square also after making its first move to the south or to the west.
Let $A B C D$ be a cyclic quadrilateral with circumcentre $O$ and with $A C$ perpendicular to $B D$. Points $X$ and $Y$ lie on the circumcircle of the triangle $B O D$ such that $\angle A X O=\angle C Y O=90^{\circ}$. Let $M$ be the midpoint of $A C$. Prove that $B D$ is tangent to the circumcircle of the triangle $M X Y$.
|
{
"exam": "BalticWay",
"problem_label": "10",
"problem_match": "\n10.",
"resource_path": "BalticWay/segmented/en-bw24sol.jsonl",
"solution_match": "# Solution:",
"tier": "T3",
"year": "2024"
}
|
A frog is located on a unit square of an infinite grid oriented according to the cardinal directions. The frog makes moves consisting of jumping either one or two squares in the direction it is facing, and then turning according to the following rules:
(i) If the frog jumps one square, it then turns $90^{\circ}$ to the right;
(ii) If the frog jumps two squares, it then turns $90^{\circ}$ to the left.
Is it possible for the frog to reach the square exactly 2024 squares north of the initial square after some finite number of moves if it is initially facing:
(a) North;
(b) East?
Answer: (a) No; (b) Yes.
|
Denote the circumradius of $A B C D$ by $r$ and the circumcircle of triangle $B O D$ by $\omega$. Let $T=A C \cap B D$, let $O T$ meet $\omega$ again at $S$, and let $O E$ be a diameter of $\omega$ (Fig. 11). We see that $A C \| O E$ as $A C \perp B D$ and $B D \perp O E$. Furthermore, note that
$$
\measuredangle D S T=\measuredangle D S O=\measuredangle D B O=\measuredangle O D B=\measuredangle O D T
$$
so $O D$ is tangent to the circumcircle of the triangle $D S T$ and thus $O T \cdot O S=O D^{2}=r^{2}$.
Figure 11
We find $\angle A X O=90^{\circ}=\angle O X E$ so $A, X, E$ are collinear. Since also $\angle A M O=90^{\circ}$, points $A$, $O, X, M$ are concyclic. Next, we can see that points $A, X, T, S$ are concyclic since $\measuredangle X A T=$ $\measuredangle E A C=\measuredangle A E O=\measuredangle X E O=\measuredangle X S O=\measuredangle X S T$. Moreover, $A O$ is tangent to this circle as $O T \cdot O S=r^{2}=O A^{2}$. Hence $\measuredangle M T X=\measuredangle A T X=\measuredangle O A X=\measuredangle O M X$, so $O M$ is tangent to the circumcircle of triangle $X M T$ at $M$.
By interchanging the roles of $A$ and $C$ and the roles of $X$ and $Y$, we can similarly prove that $O M$ is also tangent to the circumcircle of triangle $Y M T$ at $M$. But then these two circles must coincide. Now $O M \perp A C$ implies that $M T$ is a diameter of this one circle, and $A C \perp B D$ implies that $B D$ is tangent to it. The desired result follows.
|
not found
|
Yes
|
Incomplete
|
math-word-problem
|
Logic and Puzzles
|
A frog is located on a unit square of an infinite grid oriented according to the cardinal directions. The frog makes moves consisting of jumping either one or two squares in the direction it is facing, and then turning according to the following rules:
(i) If the frog jumps one square, it then turns $90^{\circ}$ to the right;
(ii) If the frog jumps two squares, it then turns $90^{\circ}$ to the left.
Is it possible for the frog to reach the square exactly 2024 squares north of the initial square after some finite number of moves if it is initially facing:
(a) North;
(b) East?
Answer: (a) No; (b) Yes.
|
Denote the circumradius of $A B C D$ by $r$ and the circumcircle of triangle $B O D$ by $\omega$. Let $T=A C \cap B D$, let $O T$ meet $\omega$ again at $S$, and let $O E$ be a diameter of $\omega$ (Fig. 11). We see that $A C \| O E$ as $A C \perp B D$ and $B D \perp O E$. Furthermore, note that
$$
\measuredangle D S T=\measuredangle D S O=\measuredangle D B O=\measuredangle O D B=\measuredangle O D T
$$
so $O D$ is tangent to the circumcircle of the triangle $D S T$ and thus $O T \cdot O S=O D^{2}=r^{2}$.

Figure 11
We find $\angle A X O=90^{\circ}=\angle O X E$ so $A, X, E$ are collinear. Since also $\angle A M O=90^{\circ}$, points $A$, $O, X, M$ are concyclic. Next, we can see that points $A, X, T, S$ are concyclic since $\measuredangle X A T=$ $\measuredangle E A C=\measuredangle A E O=\measuredangle X E O=\measuredangle X S O=\measuredangle X S T$. Moreover, $A O$ is tangent to this circle as $O T \cdot O S=r^{2}=O A^{2}$. Hence $\measuredangle M T X=\measuredangle A T X=\measuredangle O A X=\measuredangle O M X$, so $O M$ is tangent to the circumcircle of triangle $X M T$ at $M$.
By interchanging the roles of $A$ and $C$ and the roles of $X$ and $Y$, we can similarly prove that $O M$ is also tangent to the circumcircle of triangle $Y M T$ at $M$. But then these two circles must coincide. Now $O M \perp A C$ implies that $M T$ is a diameter of this one circle, and $A C \perp B D$ implies that $B D$ is tangent to it. The desired result follows.
|
{
"exam": "BalticWay",
"problem_label": "10",
"problem_match": "\n10.",
"resource_path": "BalticWay/segmented/en-bw24sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2024"
}
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.