problem
stringlengths 14
10.4k
| solution
stringlengths 1
24.1k
| answer
stringlengths 1
250
⌀ | problem_is_valid
stringclasses 4
values | solution_is_valid
stringclasses 3
values | question_type
stringclasses 4
values | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
10.4k
| solution_raw
stringlengths 1
24.1k
| metadata
dict |
|---|---|---|---|---|---|---|---|---|---|
Let $A B C$ be an acute triangle with circumcircle $\omega$ such that $A B<A C$. Let $M$ be the midpoint of the arc $B C$ of $\omega$ containing the point $A$, and let $X \neq M$ be the other point on $\omega$ such that $A X=A M$. Points $E$ and $F$ are chosen on sides $A C$ and $A B$ of the triangle $A B C$, respectively, such that $E X=E C$ and $F X=F B$. Prove that $A E=A F$.
|
Triangles $X F B$ and $X E C$ are isosceles (Fig. 12). Note that $X$ lies on the shorter arc $A B$ of $\omega$ since otherwise the perpendicular bisector of $B X$ could not intersect side $A B$. Hence $\angle X B F=\angle X B A=\angle X C A=\angle X C E$ which implies that triangles $X F B$ and $X E C$ are similar. Therefore $\angle X F A=\angle X E A$. Hence $A E F X$ is a cyclic quadrilateral.
Let $X F$ intersect $\omega$ again at $X^{\prime} \neq X$ (Fig. 13). By $\angle B X X^{\prime}=\angle B X F=\angle X B F=\angle X B A$, arcs $B X^{\prime}$ and $A X$ of $\omega$ are equal, i.e. $B X^{\prime}=A X$. Since $A X=A M$, it follows that $B X^{\prime}=A M$. So $A B X^{\prime} M$ is an isosceles trapezoid which implies also $A X^{\prime}=B M$, i.e. arcs $A X^{\prime}$ and $B M$ of $\omega$ are equal. Therefore
$$
\angle A E F=180^{\circ}-\angle A X F=180^{\circ}-\angle A X X^{\prime}=180^{\circ}-\angle M A B=\angle M C B .
$$
By considering the second intersection point of $X E$ with $\omega$, we can analgously prove the equality $\angle E F A=\angle C B M$. Since arcs $M B$ and $M C$ of $\omega$ are equal, $\angle M C B=\angle C B M$, so $\angle A E F=\angle E F A$. Hence $A E=A F$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with circumcircle $\omega$ such that $A B<A C$. Let $M$ be the midpoint of the arc $B C$ of $\omega$ containing the point $A$, and let $X \neq M$ be the other point on $\omega$ such that $A X=A M$. Points $E$ and $F$ are chosen on sides $A C$ and $A B$ of the triangle $A B C$, respectively, such that $E X=E C$ and $F X=F B$. Prove that $A E=A F$.
|
Triangles $X F B$ and $X E C$ are isosceles (Fig. 12). Note that $X$ lies on the shorter arc $A B$ of $\omega$ since otherwise the perpendicular bisector of $B X$ could not intersect side $A B$. Hence $\angle X B F=\angle X B A=\angle X C A=\angle X C E$ which implies that triangles $X F B$ and $X E C$ are similar. Therefore $\angle X F A=\angle X E A$. Hence $A E F X$ is a cyclic quadrilateral.
Let $X F$ intersect $\omega$ again at $X^{\prime} \neq X$ (Fig. 13). By $\angle B X X^{\prime}=\angle B X F=\angle X B F=\angle X B A$, arcs $B X^{\prime}$ and $A X$ of $\omega$ are equal, i.e. $B X^{\prime}=A X$. Since $A X=A M$, it follows that $B X^{\prime}=A M$. So $A B X^{\prime} M$ is an isosceles trapezoid which implies also $A X^{\prime}=B M$, i.e. arcs $A X^{\prime}$ and $B M$ of $\omega$ are equal. Therefore
$$
\angle A E F=180^{\circ}-\angle A X F=180^{\circ}-\angle A X X^{\prime}=180^{\circ}-\angle M A B=\angle M C B .
$$
By considering the second intersection point of $X E$ with $\omega$, we can analgously prove the equality $\angle E F A=\angle C B M$. Since arcs $M B$ and $M C$ of $\omega$ are equal, $\angle M C B=\angle C B M$, so $\angle A E F=\angle E F A$. Hence $A E=A F$, as desired.
|
{
"exam": "BalticWay",
"problem_label": "12",
"problem_match": "\n12.",
"resource_path": "BalticWay/segmented/en-bw24sol.jsonl",
"solution_match": "\nSolution 1:",
"tier": "T3",
"year": "2024"
}
|
Let $A B C$ be an acute triangle with circumcircle $\omega$ such that $A B<A C$. Let $M$ be the midpoint of the arc $B C$ of $\omega$ containing the point $A$, and let $X \neq M$ be the other point on $\omega$ such that $A X=A M$. Points $E$ and $F$ are chosen on sides $A C$ and $A B$ of the triangle $A B C$, respectively, such that $E X=E C$ and $F X=F B$. Prove that $A E=A F$.
|
Triangles $X F B, X E C$ and $X A M$ are isosceles (Fig. 144. In addition, note that $\measuredangle F B X=\measuredangle A B X=\measuredangle A M X$ and $\measuredangle F B X=\measuredangle A B X=\measuredangle A C X=\measuredangle E C X$, from which it follows that triangles $X F B, X E C$ and $X A M$ are directly similar (i.e., similar with the same orientation).
Denote $\frac{X F}{X B}=\frac{X E}{X C}=\frac{X A}{X M}=k$ and $\measuredangle B X F=\measuredangle C X E=\measuredangle M X A=\alpha$. Then the rotation with center $X$ by angle $\alpha$ along with scaling by ratio $k$ maps points $B, C, M$ to points $F, E, A$, respectively. Thus triangle $A F E$ is similar to triangle $M B C$ by spiral similarity. But $M B=M C$ as $M$ is the midpoint of arc $B C$. Hence also $A E=A F$.
Remark: The problem can be approached using complex numbers, taking $\omega$ as a unit circle.
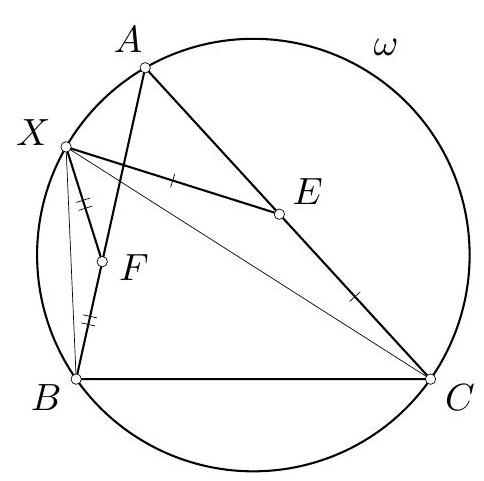
Figure 12
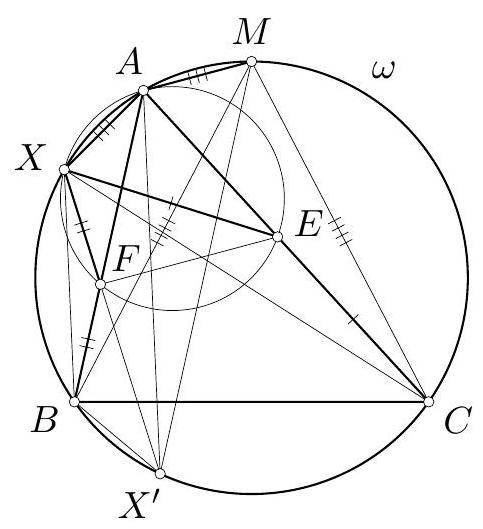
Figure 13
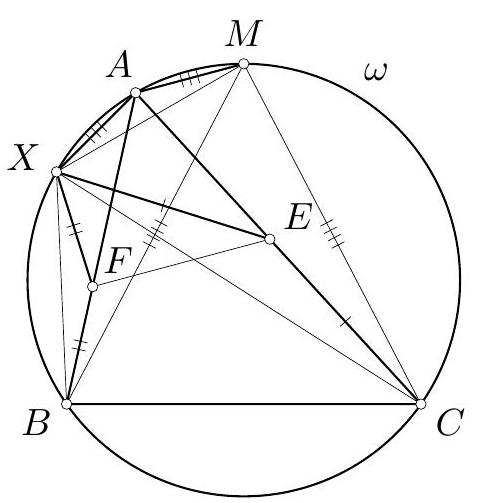
Figure 14
|
A E=A F
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with circumcircle $\omega$ such that $A B<A C$. Let $M$ be the midpoint of the arc $B C$ of $\omega$ containing the point $A$, and let $X \neq M$ be the other point on $\omega$ such that $A X=A M$. Points $E$ and $F$ are chosen on sides $A C$ and $A B$ of the triangle $A B C$, respectively, such that $E X=E C$ and $F X=F B$. Prove that $A E=A F$.
|
Triangles $X F B, X E C$ and $X A M$ are isosceles (Fig. 144. In addition, note that $\measuredangle F B X=\measuredangle A B X=\measuredangle A M X$ and $\measuredangle F B X=\measuredangle A B X=\measuredangle A C X=\measuredangle E C X$, from which it follows that triangles $X F B, X E C$ and $X A M$ are directly similar (i.e., similar with the same orientation).
Denote $\frac{X F}{X B}=\frac{X E}{X C}=\frac{X A}{X M}=k$ and $\measuredangle B X F=\measuredangle C X E=\measuredangle M X A=\alpha$. Then the rotation with center $X$ by angle $\alpha$ along with scaling by ratio $k$ maps points $B, C, M$ to points $F, E, A$, respectively. Thus triangle $A F E$ is similar to triangle $M B C$ by spiral similarity. But $M B=M C$ as $M$ is the midpoint of arc $B C$. Hence also $A E=A F$.
Remark: The problem can be approached using complex numbers, taking $\omega$ as a unit circle.

Figure 12

Figure 13

Figure 14
|
{
"exam": "BalticWay",
"problem_label": "12",
"problem_match": "\n12.",
"resource_path": "BalticWay/segmented/en-bw24sol.jsonl",
"solution_match": "\nSolution 2:",
"tier": "T3",
"year": "2024"
}
|
Let $A B C$ be an acute triangle with orthocentre $H$. Let $D$ be a point outside the circumcircle of triangle $A B C$ such that $\angle A B D=\angle D C A$. The reflection of $A B$ in $B D$ intersects $C D$ at $X$. The reflection of $A C$ in $C D$ intersects $B D$ at $Y$. The lines through $X$ and $Y$ perpendicular to $A C$ and $A B$, respectively, intersect at $P$. Prove that points $D, P$ and $H$ are collinear.
|
From the reflections, we have
$$
\angle D B X=180^{\circ}-\angle D B A=180^{\circ}-\angle D C A=\angle D C Y
$$
(Fig. 15), so points $B, C, X, Y$ are concyclic.
Define $Q=X P \cap B D$ and $R=Y P \cap C D$ (Fig. 16). Then due to the right angles, we find $\angle D Y R=\angle D X Q$. Hence points $Q, R, X, Y$ are concyclic, too.
Consequently, $\angle D Q R=\angle D X Y=\angle D B C$, so $B C \| Q R$. Since also $B H \| P Q$ and $C H \| P R$, it follows that triangle $B H C$ is a homothetic image of triangle $Q P R$ with center $D$. Hence $D, P$ and $H$ are collinear.
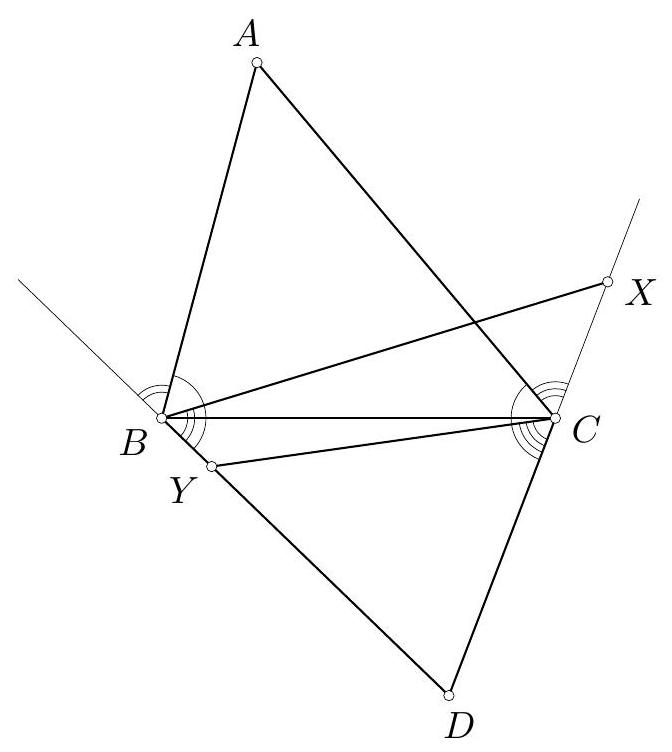
Figure 15
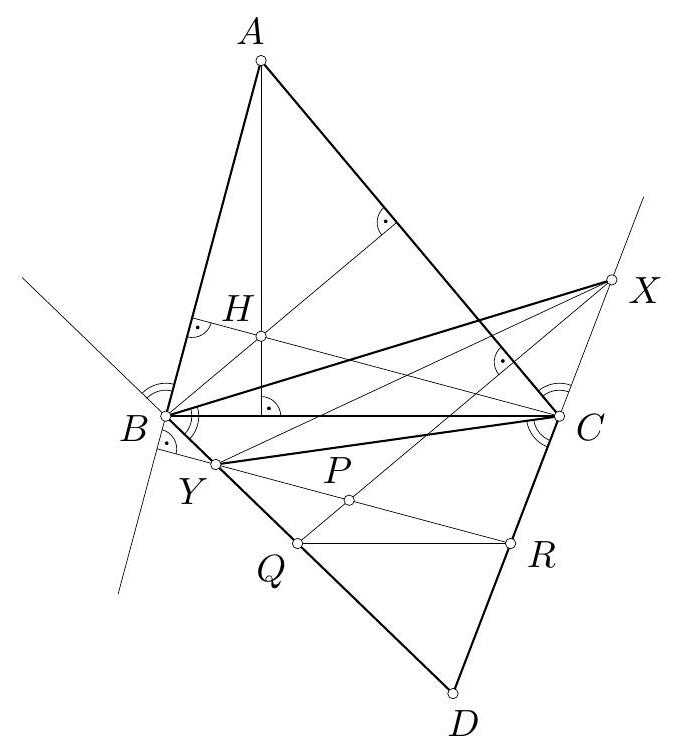
Figure 16
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with orthocentre $H$. Let $D$ be a point outside the circumcircle of triangle $A B C$ such that $\angle A B D=\angle D C A$. The reflection of $A B$ in $B D$ intersects $C D$ at $X$. The reflection of $A C$ in $C D$ intersects $B D$ at $Y$. The lines through $X$ and $Y$ perpendicular to $A C$ and $A B$, respectively, intersect at $P$. Prove that points $D, P$ and $H$ are collinear.
|
From the reflections, we have
$$
\angle D B X=180^{\circ}-\angle D B A=180^{\circ}-\angle D C A=\angle D C Y
$$
(Fig. 15), so points $B, C, X, Y$ are concyclic.
Define $Q=X P \cap B D$ and $R=Y P \cap C D$ (Fig. 16). Then due to the right angles, we find $\angle D Y R=\angle D X Q$. Hence points $Q, R, X, Y$ are concyclic, too.
Consequently, $\angle D Q R=\angle D X Y=\angle D B C$, so $B C \| Q R$. Since also $B H \| P Q$ and $C H \| P R$, it follows that triangle $B H C$ is a homothetic image of triangle $Q P R$ with center $D$. Hence $D, P$ and $H$ are collinear.

Figure 15

Figure 16
|
{
"exam": "BalticWay",
"problem_label": "13",
"problem_match": "\n13.",
"resource_path": "BalticWay/segmented/en-bw24sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2024"
}
|
Let $A B C$ be an acute triangle with circumcircle $\omega$. The altitudes $A D, B E$ and $C F$ of the triangle $A B C$ intersect at point $H$. A point $K$ is chosen on the line $E F$ such that $K H \| B C$. Prove that the reflection of $H$ in $K D$ lies on $\omega$.
|
Since $\angle A E H=90^{\circ}=\angle A F H$, we know that $A E H F$ is a cyclic quadrilateral and $A H$ is a diameter of its circumcircle. As $K H \| B C$ and $A H \perp B C$, we have $\angle K H A=90^{\circ}$, so $K H$ is tangent to the circumcircle of $A E H F$.
Denote by $H^{\prime}$ the reflection of $H$ in $K D$ and by $L$ the intersection of lines $K D$ and $H H^{\prime}$ (Fig. 17). Clearly $\angle H L D=90^{\circ}$ and from the equality $\angle K H D=180^{\circ}-\angle H L D$ it follows that $K H$ is also tangent to the circumcircle of $D L H$. From the power of the point $K$ with respect to the circumcircles of $A E H F$ and $D L H$ we obtain $K E \cdot K F=K H^{2}=K L \cdot K D$. Hence points $E, F, D, L$ lie on a common circle.
By a known fact of triangle geometry, reflections of $H$ in the points $D, E$ and $F$ lie on $\omega$. Hence the homothety with center $H$ and ratio 2 maps the circumcircle of triangle $D E F$ to $\omega$. As this homothety maps $L$ to $H^{\prime}$ and $L$ lies on the circumcircle of triangle $D E F$, the point $H^{\prime}$ must lie on $\omega$.
Remark: The problem can be approached using computational methods, namely complex numbers and Cartesian coordinates.
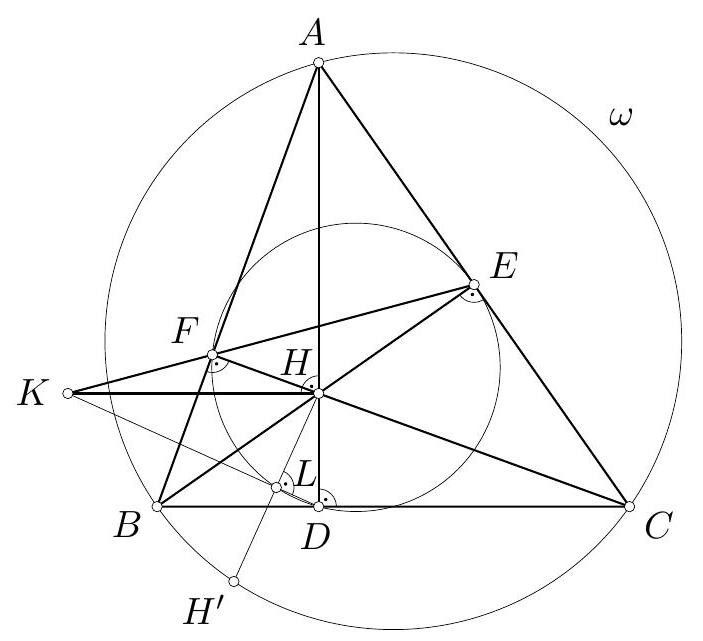
Figure 17
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute triangle with circumcircle $\omega$. The altitudes $A D, B E$ and $C F$ of the triangle $A B C$ intersect at point $H$. A point $K$ is chosen on the line $E F$ such that $K H \| B C$. Prove that the reflection of $H$ in $K D$ lies on $\omega$.
|
Since $\angle A E H=90^{\circ}=\angle A F H$, we know that $A E H F$ is a cyclic quadrilateral and $A H$ is a diameter of its circumcircle. As $K H \| B C$ and $A H \perp B C$, we have $\angle K H A=90^{\circ}$, so $K H$ is tangent to the circumcircle of $A E H F$.
Denote by $H^{\prime}$ the reflection of $H$ in $K D$ and by $L$ the intersection of lines $K D$ and $H H^{\prime}$ (Fig. 17). Clearly $\angle H L D=90^{\circ}$ and from the equality $\angle K H D=180^{\circ}-\angle H L D$ it follows that $K H$ is also tangent to the circumcircle of $D L H$. From the power of the point $K$ with respect to the circumcircles of $A E H F$ and $D L H$ we obtain $K E \cdot K F=K H^{2}=K L \cdot K D$. Hence points $E, F, D, L$ lie on a common circle.
By a known fact of triangle geometry, reflections of $H$ in the points $D, E$ and $F$ lie on $\omega$. Hence the homothety with center $H$ and ratio 2 maps the circumcircle of triangle $D E F$ to $\omega$. As this homothety maps $L$ to $H^{\prime}$ and $L$ lies on the circumcircle of triangle $D E F$, the point $H^{\prime}$ must lie on $\omega$.
Remark: The problem can be approached using computational methods, namely complex numbers and Cartesian coordinates.

Figure 17
|
{
"exam": "BalticWay",
"problem_label": "14",
"problem_match": "\n14.",
"resource_path": "BalticWay/segmented/en-bw24sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2024"
}
|
There is a set of $N \geq 3$ points in the plane, such that no three of them are collinear. Three points $A$, $B, C$ in the set are said to form a Baltic triangle if no other point in the set lies on the circumcircle of triangle $A B C$. Assume that there exists at least one Baltic triangle.
Show that there exist at least $\frac{N}{3}$ Baltic triangles.
|
If $N=3$, the number of Baltic triangles is 1 which is $\frac{N}{3}$.
To show that there always exist at least $\frac{N}{3}$ Baltic triangles, we prove that every point is a vertex of at least one Baltic triangle. This implies the desired result because every Baltic triangle consists of exactly 3 points.
First we prove a useful lemma: Given $n \geq 2$ points in the plane, either all are collinear or there exists a line passing through exactly 2 points.
Proof: Take a line $l$ going through at least 2 points, and a point $Q$ not on the line $l$ such that the distance from $Q$ to $l$ is minimal over all such pairs. Denote $Q^{\prime}$ as the projection of $Q$ to $l$. If $l$ contains at least 3 points, two of them must be on the same side of $Q^{\prime}$ (or coincide with $Q^{\prime}$ ). Say those points are $X$ and $Y$, with $X$ lying between $Y$ and $Q^{\prime}$ (Fig. 18). But then the distance from $X$ to the line $Q Y$ is smaller than $Q Q^{\prime}$ and this contradicts minimality.
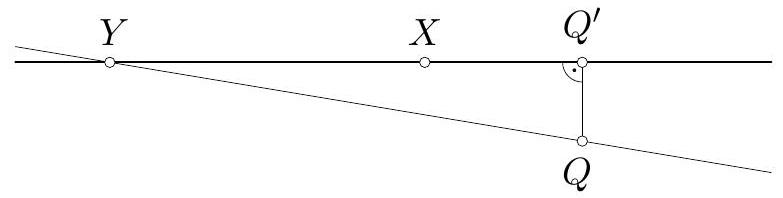
Figure 18
Now assume $N \geq 4$ and apply an inversion of the plane with center $O$ where $O$ is any point in the given set. Consider the $N-1$ other points after the inversion. By our lemma, there exists a line going through exactly 2 of them, because if they were all collinear, all points would have been concyclic before the inversion, contradicting the assumption about the existence of a Baltic triangle. Denote these points as $P$ and $Q$. The line $P Q$ cannot go through $O$, because this would mean that these 3 points were collinear before the inversion. But then before the inversion, no other point lied on the circumcircle of triangle $O P Q$, meaning that $O, P, Q$ formed a Baltic triangle.
So every single point in the given set is a vertex of at least one Baltic triangle and we are done.
Remark: The lemma proved in the solution is known as the Sylvester-Gallai theorem.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
There is a set of $N \geq 3$ points in the plane, such that no three of them are collinear. Three points $A$, $B, C$ in the set are said to form a Baltic triangle if no other point in the set lies on the circumcircle of triangle $A B C$. Assume that there exists at least one Baltic triangle.
Show that there exist at least $\frac{N}{3}$ Baltic triangles.
|
If $N=3$, the number of Baltic triangles is 1 which is $\frac{N}{3}$.
To show that there always exist at least $\frac{N}{3}$ Baltic triangles, we prove that every point is a vertex of at least one Baltic triangle. This implies the desired result because every Baltic triangle consists of exactly 3 points.
First we prove a useful lemma: Given $n \geq 2$ points in the plane, either all are collinear or there exists a line passing through exactly 2 points.
Proof: Take a line $l$ going through at least 2 points, and a point $Q$ not on the line $l$ such that the distance from $Q$ to $l$ is minimal over all such pairs. Denote $Q^{\prime}$ as the projection of $Q$ to $l$. If $l$ contains at least 3 points, two of them must be on the same side of $Q^{\prime}$ (or coincide with $Q^{\prime}$ ). Say those points are $X$ and $Y$, with $X$ lying between $Y$ and $Q^{\prime}$ (Fig. 18). But then the distance from $X$ to the line $Q Y$ is smaller than $Q Q^{\prime}$ and this contradicts minimality.

Figure 18
Now assume $N \geq 4$ and apply an inversion of the plane with center $O$ where $O$ is any point in the given set. Consider the $N-1$ other points after the inversion. By our lemma, there exists a line going through exactly 2 of them, because if they were all collinear, all points would have been concyclic before the inversion, contradicting the assumption about the existence of a Baltic triangle. Denote these points as $P$ and $Q$. The line $P Q$ cannot go through $O$, because this would mean that these 3 points were collinear before the inversion. But then before the inversion, no other point lied on the circumcircle of triangle $O P Q$, meaning that $O, P, Q$ formed a Baltic triangle.
So every single point in the given set is a vertex of at least one Baltic triangle and we are done.
Remark: The lemma proved in the solution is known as the Sylvester-Gallai theorem.
|
{
"exam": "BalticWay",
"problem_label": "15",
"problem_match": "\n15.",
"resource_path": "BalticWay/segmented/en-bw24sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2024"
}
|
Determine all composite positive integers $n$ such that, for each positive divisor $d$ of $n$, there are integers $k \geq 0$ and $m \geq 2$ such that $d=k^{m}+1$.
Answer: 10.
|
Call a positive integer $n$ powerless if, for each positive divisor $d$ of $n$, there are integers $k \geq 0$ and $m \geq 2$ such that $d=k^{m}+1$. The solution is composed of proofs of three claims.
Claim 1: If $n$ is powerless, then each positive divisor $d$ of $n$ can be written as $k^{2}+1$ for some integer $k$.
Proof: We will prove this by strong induction on the divisors of $n$. First, we have that $1=0^{2}+1$. Now let $d=k^{m}+1>1$ be a divisor of $n$, and assume that all divisors less than $d$ can be written on the desired form. If $m$ is even, we are done, and if $m$ is odd, we have
$$
d=(k+1)\left(k^{m-1}-k^{m-2}+\cdots+1\right) .
$$
Then, either $k+1=d$, meaning that $k^{m}=k$ so $k=1$ and $d=1^{2}+1$, or $k+1$ is a divisor of $n$ stricly less than $d$, so we can write $k+1=l^{2}+1$ for some integer $l$. Hence $d=\left(l^{2}\right)^{m}+1=\left(l^{m}\right)^{2}+1$.
Claim 2: If $n$ is powerless, then $n$ is square-free.
Proof: Suppose for contradiction that there is a prime $p$ such that $p^{2} \mid n$. Then by Claim 1 we may write $p^{2}=l^{2}+1$. As the difference of square numbers are sums of consecutive odd integers, this leaves only the solution $l=0, p=1$, a contradiction.
Claim 3: The only composite powerless positive integer is 10.
We will give two proofs for this claim.
Proof 1: Suppose $n$ is a composite powerless number with prime divisors $p<q$. By Claim 1, we write $p=a^{2}+1, q=b^{2}+1$ and $p q=c^{2}+1$. Then we have $c^{2}<p q<q^{2}$, so $c<q$. However, as $b^{2}+1=q \mid c^{2}+1$, we have $c^{2} \equiv-1 \equiv b^{2}(\bmod q)$, so $c \equiv \pm b(\bmod q)$ and thus either $c=b$ or $c=q-b$. In the first case, we get $p=1$, a contradiction. In the second case, we get
$$
p q=c^{2}+1=(q-b)^{2}+1=q^{2}-2 b q+b^{2}+1=q^{2}-2 b q+q=(q-2 b+1) q
$$
so $p=q-2 b+1$ and thus $p$ is even. Therefore, $p=2$, and so $b^{2}+1=q=2 b+1$, which means $b=2$, and thus $q=5$. By Claim 2, this implies $n=10$, and since $1=0^{2}+1,2=1^{2}+1,5=2^{2}+1$ and $10=3^{2}+1$, this is indeed a powerless number.
Proof 2: Again, let $p \neq q$ be prime divisors of $n$ and write $p=a^{2}+1, q=b^{2}+1$ and $p q=c^{2}+1$. Factorizing in gaussian integers, this yields
$$
(a+\mathrm{i})(a-\mathrm{i})(b+\mathrm{i})(b-\mathrm{i})=(c+\mathrm{i})(c-\mathrm{i})
$$
We note that all the factors on the left, and none of the factors on the right, are gaussian primes. Thus, each factor on the right must be the product of two factors on the left. As $(a+i)(a-i)$ and $(b+i)(b-i)$ both are real, the unique factorization of $\mathbb{Z}[\mathrm{i}]$ leaves us without loss of generality with three cases:
$$
c+\mathrm{i}=(a+\mathrm{i})(b+\mathrm{i}), \quad c+\mathrm{i}=(a-\mathrm{i})(b-\mathrm{i}), \quad c+\mathrm{i}=(a+\mathrm{i})(b-\mathrm{i})
$$
In the first two cases, we have $a+b= \pm 1$, both contradictions. In the third case, we get $b-a=1$, and thus, $q=a^{2}+2 a+2$. As this makes $q-p$ odd, we get $p=2$ meaning $a=1$ so that $q=5$. Now we finish as in proof 1.
Remark: Claim 2 can also be proven independently of Claim 1 with the help of Mihailescu's theorem.
Do there exist infinitely many quadruples $(a, b, c, d)$ of positive integers such that the number $a^{a!}+$ $b^{b!}-c^{c!}-d^{d!}$ is prime and $2 \leq d \leq c \leq b \leq a \leq d^{2024} ?$
Answer: No.
|
10
|
Incomplete
|
Yes
|
math-word-problem
|
Number Theory
|
Determine all composite positive integers $n$ such that, for each positive divisor $d$ of $n$, there are integers $k \geq 0$ and $m \geq 2$ such that $d=k^{m}+1$.
Answer: 10.
|
Call a positive integer $n$ powerless if, for each positive divisor $d$ of $n$, there are integers $k \geq 0$ and $m \geq 2$ such that $d=k^{m}+1$. The solution is composed of proofs of three claims.
Claim 1: If $n$ is powerless, then each positive divisor $d$ of $n$ can be written as $k^{2}+1$ for some integer $k$.
Proof: We will prove this by strong induction on the divisors of $n$. First, we have that $1=0^{2}+1$. Now let $d=k^{m}+1>1$ be a divisor of $n$, and assume that all divisors less than $d$ can be written on the desired form. If $m$ is even, we are done, and if $m$ is odd, we have
$$
d=(k+1)\left(k^{m-1}-k^{m-2}+\cdots+1\right) .
$$
Then, either $k+1=d$, meaning that $k^{m}=k$ so $k=1$ and $d=1^{2}+1$, or $k+1$ is a divisor of $n$ stricly less than $d$, so we can write $k+1=l^{2}+1$ for some integer $l$. Hence $d=\left(l^{2}\right)^{m}+1=\left(l^{m}\right)^{2}+1$.
Claim 2: If $n$ is powerless, then $n$ is square-free.
Proof: Suppose for contradiction that there is a prime $p$ such that $p^{2} \mid n$. Then by Claim 1 we may write $p^{2}=l^{2}+1$. As the difference of square numbers are sums of consecutive odd integers, this leaves only the solution $l=0, p=1$, a contradiction.
Claim 3: The only composite powerless positive integer is 10.
We will give two proofs for this claim.
Proof 1: Suppose $n$ is a composite powerless number with prime divisors $p<q$. By Claim 1, we write $p=a^{2}+1, q=b^{2}+1$ and $p q=c^{2}+1$. Then we have $c^{2}<p q<q^{2}$, so $c<q$. However, as $b^{2}+1=q \mid c^{2}+1$, we have $c^{2} \equiv-1 \equiv b^{2}(\bmod q)$, so $c \equiv \pm b(\bmod q)$ and thus either $c=b$ or $c=q-b$. In the first case, we get $p=1$, a contradiction. In the second case, we get
$$
p q=c^{2}+1=(q-b)^{2}+1=q^{2}-2 b q+b^{2}+1=q^{2}-2 b q+q=(q-2 b+1) q
$$
so $p=q-2 b+1$ and thus $p$ is even. Therefore, $p=2$, and so $b^{2}+1=q=2 b+1$, which means $b=2$, and thus $q=5$. By Claim 2, this implies $n=10$, and since $1=0^{2}+1,2=1^{2}+1,5=2^{2}+1$ and $10=3^{2}+1$, this is indeed a powerless number.
Proof 2: Again, let $p \neq q$ be prime divisors of $n$ and write $p=a^{2}+1, q=b^{2}+1$ and $p q=c^{2}+1$. Factorizing in gaussian integers, this yields
$$
(a+\mathrm{i})(a-\mathrm{i})(b+\mathrm{i})(b-\mathrm{i})=(c+\mathrm{i})(c-\mathrm{i})
$$
We note that all the factors on the left, and none of the factors on the right, are gaussian primes. Thus, each factor on the right must be the product of two factors on the left. As $(a+i)(a-i)$ and $(b+i)(b-i)$ both are real, the unique factorization of $\mathbb{Z}[\mathrm{i}]$ leaves us without loss of generality with three cases:
$$
c+\mathrm{i}=(a+\mathrm{i})(b+\mathrm{i}), \quad c+\mathrm{i}=(a-\mathrm{i})(b-\mathrm{i}), \quad c+\mathrm{i}=(a+\mathrm{i})(b-\mathrm{i})
$$
In the first two cases, we have $a+b= \pm 1$, both contradictions. In the third case, we get $b-a=1$, and thus, $q=a^{2}+2 a+2$. As this makes $q-p$ odd, we get $p=2$ meaning $a=1$ so that $q=5$. Now we finish as in proof 1.
Remark: Claim 2 can also be proven independently of Claim 1 with the help of Mihailescu's theorem.
Do there exist infinitely many quadruples $(a, b, c, d)$ of positive integers such that the number $a^{a!}+$ $b^{b!}-c^{c!}-d^{d!}$ is prime and $2 \leq d \leq c \leq b \leq a \leq d^{2024} ?$
Answer: No.
|
{
"exam": "BalticWay",
"problem_label": "16",
"problem_match": "\n16.",
"resource_path": "BalticWay/segmented/en-bw24sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2024"
}
|
Determine all composite positive integers $n$ such that, for each positive divisor $d$ of $n$, there are integers $k \geq 0$ and $m \geq 2$ such that $d=k^{m}+1$.
Answer: 10.
|
Assume that there exists a prime $p<d$ such that $p \nmid a b c d$. Then, since $p-1 \mid d$ ! and $p \nmid d$, by Fermat's little theorem $d^{d!} \equiv\left(d^{p-1}\right)^{\frac{d!}{p-1}} \equiv 1(\bmod p)$. By the same argument $a^{a!} \equiv b^{b!} \equiv c^{c!} \equiv 1$ $(\bmod p)$, and therefore $a^{a!}+b^{b!}-c^{c!}-d^{d!} \equiv 1+1-1-1 \equiv 0(\bmod p)$.
Now we prove that for big enough $d$, the product $P$ of primes less than $d$ is at least $d^{10000}$. Assume $d>2^{\frac{10001 \cdot 10002}{2}}$. Notice that by Bertrand's postulate, the biggest prime less than $d$ is at least $\frac{d}{2}$, the second biggest is at least $\frac{d}{4}$ etc., and 10001-th biggest is at least $\frac{d}{2^{10001}}$. So
$$
P \geq \frac{d}{2} \frac{d}{4} \cdots \frac{d}{2^{10001}}=\frac{d^{10001}}{2^{\frac{10001 \cdot 10002}{2}}} \geq d^{10000}
$$
Now note that the number of quadruples where $d<2^{\frac{10001 \cdot 10002}{2}}$ is finite, because all the number are bounded above by $d^{2024}$ and hence by $2^{\frac{10001 \cdot 10002}{2}} \cdot 2024$. When $d \geq 2^{\frac{10001 \cdot 10002}{2}}$ we have $a b c d \leq$ $d^{1+3 \cdot 2024}<d^{7000}$ and since $P \geq d^{10000}$, there exist at least two primes $p$ and $q$, less than $d$, that do not divide $a b c d$. But then by our first result, we have $p q \mid a^{a!}+b^{b!}-c^{c!}-d^{d!}$, so it cannot be prime.
Remark: The solution can be modified as follows. We can proceed in the first paragraph to conclude that $a^{a!}+b^{b!}-c^{c!}-d^{d!}$ is not prime. Indeed, if $a^{a!}+b^{b!}-c^{c!}-d^{d!}=p$ where $p<d$ then definitely $a>d$ (otherwise $a=b=c=d$ and $a^{a!}+b^{b!}-c^{c!}-d^{d!}=0$ ). Hence
$$
\begin{aligned}
d & >p=a^{a!}+b^{b!}-c^{c!}-d^{d!} \geq a^{a!}-d^{d!}=\left(a^{(d+1) \cdot \ldots \cdot a}\right)^{d!}-d^{d!} \\
& \geq\left(a^{d+1}\right)^{d!}-d^{d!} \geq a^{d+1}-d>d^{d+1}-d>d^{2}-d=(d-1) d \geq d
\end{aligned}
$$
contradiction. Then in the last paragraph, there is no need to find two primes less than $d$ that do not divide $a b c d$, one is enough.
|
10
|
Incomplete
|
Incomplete
|
math-word-problem
|
Number Theory
|
Determine all composite positive integers $n$ such that, for each positive divisor $d$ of $n$, there are integers $k \geq 0$ and $m \geq 2$ such that $d=k^{m}+1$.
Answer: 10.
|
Assume that there exists a prime $p<d$ such that $p \nmid a b c d$. Then, since $p-1 \mid d$ ! and $p \nmid d$, by Fermat's little theorem $d^{d!} \equiv\left(d^{p-1}\right)^{\frac{d!}{p-1}} \equiv 1(\bmod p)$. By the same argument $a^{a!} \equiv b^{b!} \equiv c^{c!} \equiv 1$ $(\bmod p)$, and therefore $a^{a!}+b^{b!}-c^{c!}-d^{d!} \equiv 1+1-1-1 \equiv 0(\bmod p)$.
Now we prove that for big enough $d$, the product $P$ of primes less than $d$ is at least $d^{10000}$. Assume $d>2^{\frac{10001 \cdot 10002}{2}}$. Notice that by Bertrand's postulate, the biggest prime less than $d$ is at least $\frac{d}{2}$, the second biggest is at least $\frac{d}{4}$ etc., and 10001-th biggest is at least $\frac{d}{2^{10001}}$. So
$$
P \geq \frac{d}{2} \frac{d}{4} \cdots \frac{d}{2^{10001}}=\frac{d^{10001}}{2^{\frac{10001 \cdot 10002}{2}}} \geq d^{10000}
$$
Now note that the number of quadruples where $d<2^{\frac{10001 \cdot 10002}{2}}$ is finite, because all the number are bounded above by $d^{2024}$ and hence by $2^{\frac{10001 \cdot 10002}{2}} \cdot 2024$. When $d \geq 2^{\frac{10001 \cdot 10002}{2}}$ we have $a b c d \leq$ $d^{1+3 \cdot 2024}<d^{7000}$ and since $P \geq d^{10000}$, there exist at least two primes $p$ and $q$, less than $d$, that do not divide $a b c d$. But then by our first result, we have $p q \mid a^{a!}+b^{b!}-c^{c!}-d^{d!}$, so it cannot be prime.
Remark: The solution can be modified as follows. We can proceed in the first paragraph to conclude that $a^{a!}+b^{b!}-c^{c!}-d^{d!}$ is not prime. Indeed, if $a^{a!}+b^{b!}-c^{c!}-d^{d!}=p$ where $p<d$ then definitely $a>d$ (otherwise $a=b=c=d$ and $a^{a!}+b^{b!}-c^{c!}-d^{d!}=0$ ). Hence
$$
\begin{aligned}
d & >p=a^{a!}+b^{b!}-c^{c!}-d^{d!} \geq a^{a!}-d^{d!}=\left(a^{(d+1) \cdot \ldots \cdot a}\right)^{d!}-d^{d!} \\
& \geq\left(a^{d+1}\right)^{d!}-d^{d!} \geq a^{d+1}-d>d^{d+1}-d>d^{2}-d=(d-1) d \geq d
\end{aligned}
$$
contradiction. Then in the last paragraph, there is no need to find two primes less than $d$ that do not divide $a b c d$, one is enough.
|
{
"exam": "BalticWay",
"problem_label": "16",
"problem_match": "\n16.",
"resource_path": "BalticWay/segmented/en-bw24sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2024"
}
|
An infinite sequence $a_{1}, a_{2}, \ldots$ of positive integers is such that $a_{n} \geq 2$ and $a_{n+2}$ divides $a_{n+1}+a_{n}$ for all $n \geq 1$. Prove that there exists a prime which divides infinitely many terms of the sequence.
|
Assume that every prime divides only finitely many terms of the sequence. In particular this means that there exists an integer $N>1$ such that $2 \nmid a_{n}$ for all $n \geq N$. Let $M=\max \left(a_{N}, a_{N+1}\right)$ We will now show by induction that $a_{n} \leq M$ for all $n \geq N$. This is obvious for $n=N$ and $n=N+1$. Now let $n \geq N+2$ be arbitrary and assume that $a_{n-1}, a_{n-2} \leq M$. By the definition of $N$, it is clear that $a_{n-2}, a_{n-1}, a_{n}$ are all odd and so $a_{n} \neq a_{n-1}+a_{n-2}$, but we know that $a_{n} \mid a_{n-1}+a_{n-2}$ and therefore
$$
a_{n} \leq \frac{a_{n-1}+a_{n-2}}{2} \leq \max \left(a_{n-1}, a_{n-2}\right) \leq M
$$
by the induction hypothesis. This completes the induction.
This shows that the sequence is bounded and therefore there are only finitely many primes which divide a term of the sequence. However there are infinitely many terms, that all have a prime divisor, hence some prime must divide infinitely many terms of the sequence.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
An infinite sequence $a_{1}, a_{2}, \ldots$ of positive integers is such that $a_{n} \geq 2$ and $a_{n+2}$ divides $a_{n+1}+a_{n}$ for all $n \geq 1$. Prove that there exists a prime which divides infinitely many terms of the sequence.
|
Assume that every prime divides only finitely many terms of the sequence. In particular this means that there exists an integer $N>1$ such that $2 \nmid a_{n}$ for all $n \geq N$. Let $M=\max \left(a_{N}, a_{N+1}\right)$ We will now show by induction that $a_{n} \leq M$ for all $n \geq N$. This is obvious for $n=N$ and $n=N+1$. Now let $n \geq N+2$ be arbitrary and assume that $a_{n-1}, a_{n-2} \leq M$. By the definition of $N$, it is clear that $a_{n-2}, a_{n-1}, a_{n}$ are all odd and so $a_{n} \neq a_{n-1}+a_{n-2}$, but we know that $a_{n} \mid a_{n-1}+a_{n-2}$ and therefore
$$
a_{n} \leq \frac{a_{n-1}+a_{n-2}}{2} \leq \max \left(a_{n-1}, a_{n-2}\right) \leq M
$$
by the induction hypothesis. This completes the induction.
This shows that the sequence is bounded and therefore there are only finitely many primes which divide a term of the sequence. However there are infinitely many terms, that all have a prime divisor, hence some prime must divide infinitely many terms of the sequence.
|
{
"exam": "BalticWay",
"problem_label": "18",
"problem_match": "\n18.",
"resource_path": "BalticWay/segmented/en-bw24sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2024"
}
|
Does there exist a positive integer $N$ which is divisible by at least 2024 distinct primes and whose positive divisors $1=d_{1}<d_{2}<\ldots<d_{k}=N$ are such that the number
$$
\frac{d_{2}}{d_{1}}+\frac{d_{3}}{d_{2}}+\ldots+\frac{d_{k}}{d_{k-1}}
$$
is an integer?
Answer: Yes.
|
For arbitrary positive integer $N$, we will write $f(N)=\frac{d_{2}}{d_{1}}+\frac{d_{3}}{d_{2}}+\ldots+\frac{d_{k}}{d_{k-1}}$ where $1=d_{1}<d_{2}<\ldots<d_{k}=N$ are all positive divisors of $N$. Let us prove by induction that for any positive integer $M$ there is a positive integer $N$ with exactly $M$ different prime divisors such that $f(N)$ is an integer.
- Base case: If $M=1$, this is clearly true (any prime power $N>1$ works).
- Induction step: Assume that the claim holds for $M$ prime divisors. Let $N$ be a positive integer with exactly $M$ prime divisors such that $f(N)$ is an integer. Pick a prime $p>N$. We claim that there is some choice of $\alpha$ such that $f\left(N \cdot p^{\alpha}\right)$ is an integer. Note that since $p>N$, the divisors of $N \cdot p^{\alpha}$ in the ascending order are
$$
\begin{aligned}
& d_{1}, d_{2}, \ldots, d_{k} \\
& p d_{1}, p d_{2}, \ldots, p d_{k} \\
& \ldots \ldots \ldots \ldots \ldots \ldots \ldots \\
& p^{\alpha} d_{1}, p^{\alpha} d_{2}, \ldots, p^{\alpha} d_{k}
\end{aligned}
$$
Hence we get that
$$
f\left(N \cdot p^{\alpha}\right)=(\alpha+1) f(N)+\alpha \cdot \frac{p d_{1}}{d_{k}}
$$
The term $(\alpha+1) f(N)$ is an integer by the choice of $N$. If we pick $\alpha=N$ then $\alpha \cdot \frac{p d_{1}}{d_{k}}=N \cdot \frac{p}{N}=p$ is an integer, too. Thus $f\left(N \cdot p^{\alpha}\right)$ is an integer and we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Does there exist a positive integer $N$ which is divisible by at least 2024 distinct primes and whose positive divisors $1=d_{1}<d_{2}<\ldots<d_{k}=N$ are such that the number
$$
\frac{d_{2}}{d_{1}}+\frac{d_{3}}{d_{2}}+\ldots+\frac{d_{k}}{d_{k-1}}
$$
is an integer?
Answer: Yes.
|
For arbitrary positive integer $N$, we will write $f(N)=\frac{d_{2}}{d_{1}}+\frac{d_{3}}{d_{2}}+\ldots+\frac{d_{k}}{d_{k-1}}$ where $1=d_{1}<d_{2}<\ldots<d_{k}=N$ are all positive divisors of $N$. Let us prove by induction that for any positive integer $M$ there is a positive integer $N$ with exactly $M$ different prime divisors such that $f(N)$ is an integer.
- Base case: If $M=1$, this is clearly true (any prime power $N>1$ works).
- Induction step: Assume that the claim holds for $M$ prime divisors. Let $N$ be a positive integer with exactly $M$ prime divisors such that $f(N)$ is an integer. Pick a prime $p>N$. We claim that there is some choice of $\alpha$ such that $f\left(N \cdot p^{\alpha}\right)$ is an integer. Note that since $p>N$, the divisors of $N \cdot p^{\alpha}$ in the ascending order are
$$
\begin{aligned}
& d_{1}, d_{2}, \ldots, d_{k} \\
& p d_{1}, p d_{2}, \ldots, p d_{k} \\
& \ldots \ldots \ldots \ldots \ldots \ldots \ldots \\
& p^{\alpha} d_{1}, p^{\alpha} d_{2}, \ldots, p^{\alpha} d_{k}
\end{aligned}
$$
Hence we get that
$$
f\left(N \cdot p^{\alpha}\right)=(\alpha+1) f(N)+\alpha \cdot \frac{p d_{1}}{d_{k}}
$$
The term $(\alpha+1) f(N)$ is an integer by the choice of $N$. If we pick $\alpha=N$ then $\alpha \cdot \frac{p d_{1}}{d_{k}}=N \cdot \frac{p}{N}=p$ is an integer, too. Thus $f\left(N \cdot p^{\alpha}\right)$ is an integer and we are done.
|
{
"exam": "BalticWay",
"problem_label": "19",
"problem_match": "\n19.",
"resource_path": "BalticWay/segmented/en-bw24sol.jsonl",
"solution_match": "\nSolution:",
"tier": "T3",
"year": "2024"
}
|
Positive integers $a, b$ and $c$ satisfy the system of equations
$$
\left\{\begin{aligned}
(a b-1)^{2} & =c\left(a^{2}+b^{2}\right)+a b+1 \\
a^{2}+b^{2} & =c^{2}+a b
\end{aligned}\right.
$$
(a) Prove that $c+1$ is a perfect square.
(b) Find all such triples $(a, b, c)$.
Answer: (b) $a=b=c=3$.
|
(a) Rearranging terms in the first equation gives
$$
a^{2} b^{2}-2 a b=c\left(a^{2}+b^{2}\right)+a b
$$
By substituting $a b=a^{2}+b^{2}-c^{2}$ into the right-hand side and rearranging the terms we get
$$
a^{2} b^{2}+c^{2}=(c+1)\left(a^{2}+b^{2}\right)+2 a b
$$
By adding $2 a b c$ to both sides and factorizing we get
$$
(a b+c)^{2}=(c+1)(a+b)^{2}
$$
Now it is obvious that $c+1$ has to be a square of an integer.
(b) Let us say $c+1=d^{2}$, where $d>1$ and is an integer. Then substituting this into the equation (10) and taking the square root of both sides (we can do that as all the terms are positive) we get
$$
a b+d^{2}-1=d(a+b)
$$
We can rearrange it to $(a-d)(b-d)=1$, which immediately tells us that either $a=b=d+1$ or $a=b=d-1$. Note that in either case $a=b$. Substituting this into the second equation of the given system we get $a^{2}=c^{2}$, implying $a=c$ (as $\left.a, c>0\right)$.
- If $a=b=d-1$, then $a=c$ gives $d-1=d^{2}-1$, so $d=0$ or $d=1$, neither of which gives a positive $c$, so cannot be a solution.
- If $a=b=d+1$, then $a=c$ gives $d+1=d^{2}-1$, so $d^{2}-d-2=0$. The only positive solution is $d=2$ which gives $a=b=c=3$. Substituting it once again into both equations we indeed get a solution.
|
a=b=c=3
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Positive integers $a, b$ and $c$ satisfy the system of equations
$$
\left\{\begin{aligned}
(a b-1)^{2} & =c\left(a^{2}+b^{2}\right)+a b+1 \\
a^{2}+b^{2} & =c^{2}+a b
\end{aligned}\right.
$$
(a) Prove that $c+1$ is a perfect square.
(b) Find all such triples $(a, b, c)$.
Answer: (b) $a=b=c=3$.
|
(a) Rearranging terms in the first equation gives
$$
a^{2} b^{2}-2 a b=c\left(a^{2}+b^{2}\right)+a b
$$
By substituting $a b=a^{2}+b^{2}-c^{2}$ into the right-hand side and rearranging the terms we get
$$
a^{2} b^{2}+c^{2}=(c+1)\left(a^{2}+b^{2}\right)+2 a b
$$
By adding $2 a b c$ to both sides and factorizing we get
$$
(a b+c)^{2}=(c+1)(a+b)^{2}
$$
Now it is obvious that $c+1$ has to be a square of an integer.
(b) Let us say $c+1=d^{2}$, where $d>1$ and is an integer. Then substituting this into the equation (10) and taking the square root of both sides (we can do that as all the terms are positive) we get
$$
a b+d^{2}-1=d(a+b)
$$
We can rearrange it to $(a-d)(b-d)=1$, which immediately tells us that either $a=b=d+1$ or $a=b=d-1$. Note that in either case $a=b$. Substituting this into the second equation of the given system we get $a^{2}=c^{2}$, implying $a=c$ (as $\left.a, c>0\right)$.
- If $a=b=d-1$, then $a=c$ gives $d-1=d^{2}-1$, so $d=0$ or $d=1$, neither of which gives a positive $c$, so cannot be a solution.
- If $a=b=d+1$, then $a=c$ gives $d+1=d^{2}-1$, so $d^{2}-d-2=0$. The only positive solution is $d=2$ which gives $a=b=c=3$. Substituting it once again into both equations we indeed get a solution.
|
{
"exam": "BalticWay",
"problem_label": "20",
"problem_match": "\n20.",
"resource_path": "BalticWay/segmented/en-bw24sol.jsonl",
"solution_match": "# Solution 1:",
"tier": "T3",
"year": "2024"
}
|
Positive integers $a, b$ and $c$ satisfy the system of equations
$$
\left\{\begin{aligned}
(a b-1)^{2} & =c\left(a^{2}+b^{2}\right)+a b+1 \\
a^{2}+b^{2} & =c^{2}+a b
\end{aligned}\right.
$$
(a) Prove that $c+1$ is a perfect square.
(b) Find all such triples $(a, b, c)$.
Answer: (b) $a=b=c=3$.
|
(a) Substituting $a^{2}+b^{2}$ from the second equation to the first one gives
$$
(a b-1)^{2}=c\left(c^{2}+a b\right)+a b+1
$$
Rearranging terms in the obtained equation gives
$$
(a b)^{2}-(c+3) a b-c^{3}=0
$$
which we can consider as a quadratic equation in $a b$. Its discriminant is
$$
D=(c+3)^{2}+4 c^{3}=4 c^{3}+c^{2}+6 c+9=(c+1)\left(4 c^{2}-3 c+9\right)=(c+1)\left(4(c-1)^{2}+5(c+1)\right)
$$
To have solutions in integers, $D$ must be a perfect square. Note that $c+1$ and $4(c-1)^{2}+5(c+1)$ can have no common odd prime factors. Hence $\operatorname{gcd}\left(c+1,4(c-1)^{2}+5(c+1)\right)$ is a power of 2 , so $c+1$ and $4(c-1)^{2}+5(c+1)$ are either both perfect squares or both twice of some perfect squares. In the first case, we are done. In the second case, note that
$$
4(c-1)^{2}+5(c+1) \equiv 4(c-1)^{2}=(2(c-1))^{2} \quad(\bmod 5)
$$
so $4(c-1)^{2}+5(c+1)$ must be $0,1,4$ modulo 5 . On the other hand, twice of a perfect square is $0,2,3$ modulo 5 . Consequently, $c+1 \equiv 0(\bmod 5)$ and $4(c-1)^{2}+5(c+1) \equiv 0(\bmod 5)$, the latter of which implies $c-1 \equiv 0(\bmod 5)$. This leads to contradiction since $c-1$ and $c+1$ cannot be both divisible by 5 .
(b) By the solution of part (a), both $c+1$ and $4 c^{2}-3 c+9$ are perfect squares. However, due to $c>0$ we have $(2 c-1)^{2}=4 c^{2}-4 c+1<4 c^{2}-3 c+9$, and for $c>3$ we also have $(2 c)^{2}=4 c^{2}>4 c^{2}-3 c+9$. Thus $4 c^{2}-3 c+9$ is located between two consecutive perfect squares, which gives a contradiction with it being a square itself.
Out of $c=1,2,3$, only $c=3$ makes $c+1$ a perfect square. In this case, the quadratic equation $(a b)^{2}-(c+3) a b-c^{3}=0$ yields $a b=9$, so $a=1, b=9$ or $a=3, b=3$ or $a=9, b=1$. Out of those, only $a=3, b=3$ satisfies the equations.
Remark: Part (a) of the problem can be solved yet another way. By substituting $a^{2}+b^{2}$ from the second equation to the first one, we obtain
$$
(a b-1)^{2}=c\left(c^{2}+a b\right)+a b+1=c^{3}+1+a b c+a b=(c+1)\left(c^{2}-c+1+a b\right)
$$
Whenever an integer $n$ divides $c+1$, it also divides $a b-1$. Therefore $c \equiv-1(\bmod n)$ and $a b \equiv 1$ $(\bmod n)$. But then $c^{2}-c+1+a b \equiv 4(\bmod n)$, i.e., $n$ divides $c^{2}-c+1+a b-4$. Thus the greatest common divisor of $c+1$ and $c^{2}-c+1+a b$ divides 4 , i.e., it is either 1,2 or 4 . In the first and third case we are done. If their greatest common divisor is 2 , then clearly all three of $a, b, c$ are odd, so $a^{2} \equiv b^{2} \equiv c^{2} \equiv 1(\bmod 8)$. Thus from the second equation we have $a b=a^{2}+b^{2}-c^{2} \equiv 1$ $(\bmod 8)$, so $(a b-1)^{2}$ is divisible by 64 . Now, if $c \equiv 1(\bmod 4)$, then $c^{2}-c+1+a b \equiv 2(\bmod 4)$, which means that $(c+1)\left(c^{2}-c+1+a b\right) \equiv 4(\bmod 8)$, giving a contradiction with $(a b-1)^{2}$ being divisible by 64 . If instead $c \equiv 3(\bmod 4)$, then $c^{2}-c+1+a b \equiv 0(\bmod 4)$. This means that both $c+1$ and $c^{2}-c+1+a b$ are divisible by 4 , giving a contradiction with the assumption that their greatest common divisor is 2 . Therefore $c+1$ must be a perfect square.
|
a=b=c=3
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Positive integers $a, b$ and $c$ satisfy the system of equations
$$
\left\{\begin{aligned}
(a b-1)^{2} & =c\left(a^{2}+b^{2}\right)+a b+1 \\
a^{2}+b^{2} & =c^{2}+a b
\end{aligned}\right.
$$
(a) Prove that $c+1$ is a perfect square.
(b) Find all such triples $(a, b, c)$.
Answer: (b) $a=b=c=3$.
|
(a) Substituting $a^{2}+b^{2}$ from the second equation to the first one gives
$$
(a b-1)^{2}=c\left(c^{2}+a b\right)+a b+1
$$
Rearranging terms in the obtained equation gives
$$
(a b)^{2}-(c+3) a b-c^{3}=0
$$
which we can consider as a quadratic equation in $a b$. Its discriminant is
$$
D=(c+3)^{2}+4 c^{3}=4 c^{3}+c^{2}+6 c+9=(c+1)\left(4 c^{2}-3 c+9\right)=(c+1)\left(4(c-1)^{2}+5(c+1)\right)
$$
To have solutions in integers, $D$ must be a perfect square. Note that $c+1$ and $4(c-1)^{2}+5(c+1)$ can have no common odd prime factors. Hence $\operatorname{gcd}\left(c+1,4(c-1)^{2}+5(c+1)\right)$ is a power of 2 , so $c+1$ and $4(c-1)^{2}+5(c+1)$ are either both perfect squares or both twice of some perfect squares. In the first case, we are done. In the second case, note that
$$
4(c-1)^{2}+5(c+1) \equiv 4(c-1)^{2}=(2(c-1))^{2} \quad(\bmod 5)
$$
so $4(c-1)^{2}+5(c+1)$ must be $0,1,4$ modulo 5 . On the other hand, twice of a perfect square is $0,2,3$ modulo 5 . Consequently, $c+1 \equiv 0(\bmod 5)$ and $4(c-1)^{2}+5(c+1) \equiv 0(\bmod 5)$, the latter of which implies $c-1 \equiv 0(\bmod 5)$. This leads to contradiction since $c-1$ and $c+1$ cannot be both divisible by 5 .
(b) By the solution of part (a), both $c+1$ and $4 c^{2}-3 c+9$ are perfect squares. However, due to $c>0$ we have $(2 c-1)^{2}=4 c^{2}-4 c+1<4 c^{2}-3 c+9$, and for $c>3$ we also have $(2 c)^{2}=4 c^{2}>4 c^{2}-3 c+9$. Thus $4 c^{2}-3 c+9$ is located between two consecutive perfect squares, which gives a contradiction with it being a square itself.
Out of $c=1,2,3$, only $c=3$ makes $c+1$ a perfect square. In this case, the quadratic equation $(a b)^{2}-(c+3) a b-c^{3}=0$ yields $a b=9$, so $a=1, b=9$ or $a=3, b=3$ or $a=9, b=1$. Out of those, only $a=3, b=3$ satisfies the equations.
Remark: Part (a) of the problem can be solved yet another way. By substituting $a^{2}+b^{2}$ from the second equation to the first one, we obtain
$$
(a b-1)^{2}=c\left(c^{2}+a b\right)+a b+1=c^{3}+1+a b c+a b=(c+1)\left(c^{2}-c+1+a b\right)
$$
Whenever an integer $n$ divides $c+1$, it also divides $a b-1$. Therefore $c \equiv-1(\bmod n)$ and $a b \equiv 1$ $(\bmod n)$. But then $c^{2}-c+1+a b \equiv 4(\bmod n)$, i.e., $n$ divides $c^{2}-c+1+a b-4$. Thus the greatest common divisor of $c+1$ and $c^{2}-c+1+a b$ divides 4 , i.e., it is either 1,2 or 4 . In the first and third case we are done. If their greatest common divisor is 2 , then clearly all three of $a, b, c$ are odd, so $a^{2} \equiv b^{2} \equiv c^{2} \equiv 1(\bmod 8)$. Thus from the second equation we have $a b=a^{2}+b^{2}-c^{2} \equiv 1$ $(\bmod 8)$, so $(a b-1)^{2}$ is divisible by 64 . Now, if $c \equiv 1(\bmod 4)$, then $c^{2}-c+1+a b \equiv 2(\bmod 4)$, which means that $(c+1)\left(c^{2}-c+1+a b\right) \equiv 4(\bmod 8)$, giving a contradiction with $(a b-1)^{2}$ being divisible by 64 . If instead $c \equiv 3(\bmod 4)$, then $c^{2}-c+1+a b \equiv 0(\bmod 4)$. This means that both $c+1$ and $c^{2}-c+1+a b$ are divisible by 4 , giving a contradiction with the assumption that their greatest common divisor is 2 . Therefore $c+1$ must be a perfect square.
|
{
"exam": "BalticWay",
"problem_label": "20",
"problem_match": "\n20.",
"resource_path": "BalticWay/segmented/en-bw24sol.jsonl",
"solution_match": "# Solution 2:",
"tier": "T3",
"year": "2024"
}
|
Integers $1,2, \ldots, n$ are written (in some order) on the circumference of a circle. What is the smallest possible sum of moduli of the differences of neighbouring numbers?
|
Let $a_{1}=1, a_{2}, \ldots, a_{k}=n, a_{k+1}, \ldots, a_{n}$ be the order in which the numbers $1,2, \ldots, n$ are written around the circle. Then the sum of moduli of the differences of neighbouring numbers is
$$
\begin{aligned}
& \left|1-a_{2}\right|+\left|a_{2}-a_{3}\right|+\cdots+\left|a_{k}-n\right|+\left|n-a_{k+1}\right|+\cdots+\left|a_{n}-1\right| \\
& \geq\left|1-a_{2}+a_{2}-a_{3}+\cdots+a_{k}-n\right|+\left|n-a_{k+1}+\cdots+a_{n}-1\right| \\
& =|1-n|+|n-1|=2 n-2 .
\end{aligned}
$$
This minimum is achieved if the numbers are written around the circle in increasing order.
|
2n-2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Integers $1,2, \ldots, n$ are written (in some order) on the circumference of a circle. What is the smallest possible sum of moduli of the differences of neighbouring numbers?
|
Let $a_{1}=1, a_{2}, \ldots, a_{k}=n, a_{k+1}, \ldots, a_{n}$ be the order in which the numbers $1,2, \ldots, n$ are written around the circle. Then the sum of moduli of the differences of neighbouring numbers is
$$
\begin{aligned}
& \left|1-a_{2}\right|+\left|a_{2}-a_{3}\right|+\cdots+\left|a_{k}-n\right|+\left|n-a_{k+1}\right|+\cdots+\left|a_{n}-1\right| \\
& \geq\left|1-a_{2}+a_{2}-a_{3}+\cdots+a_{k}-n\right|+\left|n-a_{k+1}+\cdots+a_{n}-1\right| \\
& =|1-n|+|n-1|=2 n-2 .
\end{aligned}
$$
This minimum is achieved if the numbers are written around the circle in increasing order.
|
{
"exam": "BalticWay",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "BalticWay/segmented/en-bw90sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1990"
}
|
The squares of a squared paper are enumerated as follows:
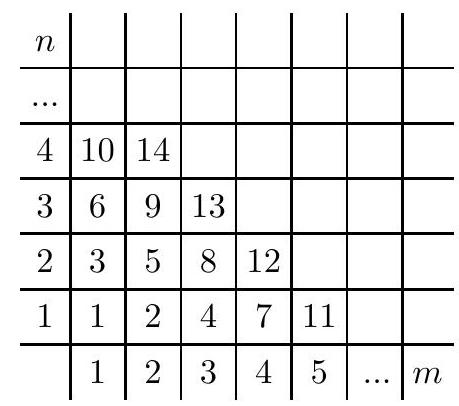
Devise a polynomial $p(m, n)$ of two variables $m, n$ such that for any positive integers $m$ and $n$ the number written in the square with coordinates $(m, n)$ will be equal to $p(m, n)$.
|
Since the square with the coordinates $(m, n)$ is $n$th on the $(n+m-1)$-th diagonal, it contains the number
$$
P(m, n)=\sum_{i=1}^{n+m-2} i+n=\frac{(n+m-1)(n+m-2)}{2}+n
$$
|
\frac{(n+m-1)(n+m-2)}{2}+n
|
Incomplete
|
Yes
|
math-word-problem
|
Algebra
|
The squares of a squared paper are enumerated as follows:

Devise a polynomial $p(m, n)$ of two variables $m, n$ such that for any positive integers $m$ and $n$ the number written in the square with coordinates $(m, n)$ will be equal to $p(m, n)$.
|
Since the square with the coordinates $(m, n)$ is $n$th on the $(n+m-1)$-th diagonal, it contains the number
$$
P(m, n)=\sum_{i=1}^{n+m-2} i+n=\frac{(n+m-1)(n+m-2)}{2}+n
$$
|
{
"exam": "BalticWay",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "BalticWay/segmented/en-bw90sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1990"
}
|
Let $a_{0}>0, c>0$ and
$$
a_{n+1}=\frac{a_{n}+c}{1-a_{n} c}, \quad n=0,1, \ldots
$$
Is it possible that the first 1990 terms $a_{0}, a_{1}, \ldots, a_{1989}$ are all positive but $a_{1990}<0$ ?
|
Obviously we can find angles $0<\alpha, \beta<90^{\circ}$ such that $\tan \alpha>0, \tan (\alpha+\beta)>0, \ldots$, $\tan (\alpha+1989 \beta)>0$ but $\tan (\alpha+1990 \beta)<0$. Now it suffices to note that if we take $a_{0}=\tan \alpha$ and $c=\tan \beta$ then $a_{n}=\tan (\alpha+n \beta)$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $a_{0}>0, c>0$ and
$$
a_{n+1}=\frac{a_{n}+c}{1-a_{n} c}, \quad n=0,1, \ldots
$$
Is it possible that the first 1990 terms $a_{0}, a_{1}, \ldots, a_{1989}$ are all positive but $a_{1990}<0$ ?
|
Obviously we can find angles $0<\alpha, \beta<90^{\circ}$ such that $\tan \alpha>0, \tan (\alpha+\beta)>0, \ldots$, $\tan (\alpha+1989 \beta)>0$ but $\tan (\alpha+1990 \beta)<0$. Now it suffices to note that if we take $a_{0}=\tan \alpha$ and $c=\tan \beta$ then $a_{n}=\tan (\alpha+n \beta)$.
|
{
"exam": "BalticWay",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "BalticWay/segmented/en-bw90sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1990"
}
|
Prove that, for any real $a_{1}, a_{2}, \ldots, a_{n}$,
$$
\sum_{i, j=1}^{n} \frac{a_{i} a_{j}}{i+j-1} \geq 0
$$
|
Consider the polynomial $P(x)=a_{1}+a_{2} x+\cdots+a_{n} x^{n-1}$. Then $P^{2}(x)=\sum_{k, l=1}^{n} a_{k} a_{l} x^{k+l-2}$ and $\int_{0}^{1} P^{2}(x) d x=\sum_{k, l=1}^{n} \frac{a_{k} a_{l}}{k+l-1}$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that, for any real $a_{1}, a_{2}, \ldots, a_{n}$,
$$
\sum_{i, j=1}^{n} \frac{a_{i} a_{j}}{i+j-1} \geq 0
$$
|
Consider the polynomial $P(x)=a_{1}+a_{2} x+\cdots+a_{n} x^{n-1}$. Then $P^{2}(x)=\sum_{k, l=1}^{n} a_{k} a_{l} x^{k+l-2}$ and $\int_{0}^{1} P^{2}(x) d x=\sum_{k, l=1}^{n} \frac{a_{k} a_{l}}{k+l-1}$.
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "BalticWay/segmented/en-bw90sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1990"
}
|
Let $*$ denote an operation, assigning a real number $a * b$ to each pair of real numbers ( $a, b)$ (e.g., $a * b=$ $a+b^{2}-17$ ). Devise an equation which is true (for all possible values of variables) provided the operation $*$ is commutative or associative and which can be false otherwise.
|
A suitable equation is $x *(x * x)=(x * x) * x$ which is obviously true if $*$ is any commutative or associative operation but does not hold in general, e.g., $1-(1-1) \neq(1-1)-1$.
|
1-(1-1) \neq (1-1)-1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $*$ denote an operation, assigning a real number $a * b$ to each pair of real numbers ( $a, b)$ (e.g., $a * b=$ $a+b^{2}-17$ ). Devise an equation which is true (for all possible values of variables) provided the operation $*$ is commutative or associative and which can be false otherwise.
|
A suitable equation is $x *(x * x)=(x * x) * x$ which is obviously true if $*$ is any commutative or associative operation but does not hold in general, e.g., $1-(1-1) \neq(1-1)-1$.
|
{
"exam": "BalticWay",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "BalticWay/segmented/en-bw90sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1990"
}
|
Let $A B C D$ be a quadrangle, $|A D|=|B C|, \angle A+\angle B=120^{\circ}$ and let $P$ be a point exterior to the quadrangle such that $P$ and $A$ lie at opposite sides of the line $D C$ and the triangle $D P C$ is equilateral. Prove that the triangle $A P B$ is also equilateral.
|
Note that $\angle A D C+\angle C D P+\angle B C D+\angle D C P=360^{\circ}$ (see Figure 1). Thus $\angle A D P=360^{\circ}-$ $\angle B C D-\angle D C P=\angle B C P$. As we have $|D P|=|C P|$ and $|A D|=|B C|$, the triangles $A D P$ and $B C P$ are congruent and $|A P|=|B P|$. Moreover, $\angle A P B=60^{\circ}$ since $\angle D P C=60^{\circ}$ and $\angle D P A=\angle C P B$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a quadrangle, $|A D|=|B C|, \angle A+\angle B=120^{\circ}$ and let $P$ be a point exterior to the quadrangle such that $P$ and $A$ lie at opposite sides of the line $D C$ and the triangle $D P C$ is equilateral. Prove that the triangle $A P B$ is also equilateral.
|
Note that $\angle A D C+\angle C D P+\angle B C D+\angle D C P=360^{\circ}$ (see Figure 1). Thus $\angle A D P=360^{\circ}-$ $\angle B C D-\angle D C P=\angle B C P$. As we have $|D P|=|C P|$ and $|A D|=|B C|$, the triangles $A D P$ and $B C P$ are congruent and $|A P|=|B P|$. Moreover, $\angle A P B=60^{\circ}$ since $\angle D P C=60^{\circ}$ and $\angle D P A=\angle C P B$.
|
{
"exam": "BalticWay",
"problem_label": "6",
"problem_match": "\n6.",
"resource_path": "BalticWay/segmented/en-bw90sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1990"
}
|
The midpoint of each side of a convex pentagon is connected by a segment with the intersection point of the medians of the triangle formed by the remaining three vertices of the pentagon. Prove that all five such segments intersect at one point.
|
Let $A, B, C, D$ and $E$ be the vertices of the pentagon (in order), and take any point $O$ as origin. Let $M$ be the intersection point of the medians of the triangle $C D E$, and let $N$ be the midpoint of the segment $A B$. We have
$$
\overline{O M}=\frac{1}{3}(\overline{O C}+\overline{O D}+\overline{O E})
$$
and
$$
\overline{O N}=\frac{1}{2}(\overline{O A}+\overline{O B})
$$
The segment $N M$ may be written as
$$
\overline{O N}+t(\overline{O M}-\overline{O N}), \quad 0 \leq t \leq 1
$$
Taking $t=\frac{3}{5}$ we get the point
$$
P=\frac{1}{5}(\overline{O A}+\overline{O B}+\overline{O C}+\overline{O D}+\overline{O E}),
$$
the centre of gravity of the pentagon. Choosing a different side of the pentagon, we clearly get the same point $P$, which thus lies on all such line segments.
Remark. The problem expresses the idea of subdividing a system of five equal masses placed at the vertices of the pentagon into two subsystems, one of which consists of the two masses at the endpoints of the side under consideration, and one consisting of the three remaining masses. The segment mentioned in the problem connects the centres of gravity of these two subsystems, and hence it contains the centre of gravity of the whole system.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The midpoint of each side of a convex pentagon is connected by a segment with the intersection point of the medians of the triangle formed by the remaining three vertices of the pentagon. Prove that all five such segments intersect at one point.
|
Let $A, B, C, D$ and $E$ be the vertices of the pentagon (in order), and take any point $O$ as origin. Let $M$ be the intersection point of the medians of the triangle $C D E$, and let $N$ be the midpoint of the segment $A B$. We have
$$
\overline{O M}=\frac{1}{3}(\overline{O C}+\overline{O D}+\overline{O E})
$$
and
$$
\overline{O N}=\frac{1}{2}(\overline{O A}+\overline{O B})
$$
The segment $N M$ may be written as
$$
\overline{O N}+t(\overline{O M}-\overline{O N}), \quad 0 \leq t \leq 1
$$
Taking $t=\frac{3}{5}$ we get the point
$$
P=\frac{1}{5}(\overline{O A}+\overline{O B}+\overline{O C}+\overline{O D}+\overline{O E}),
$$
the centre of gravity of the pentagon. Choosing a different side of the pentagon, we clearly get the same point $P$, which thus lies on all such line segments.
Remark. The problem expresses the idea of subdividing a system of five equal masses placed at the vertices of the pentagon into two subsystems, one of which consists of the two masses at the endpoints of the side under consideration, and one consisting of the three remaining masses. The segment mentioned in the problem connects the centres of gravity of these two subsystems, and hence it contains the centre of gravity of the whole system.
|
{
"exam": "BalticWay",
"problem_label": "7",
"problem_match": "\n7.",
"resource_path": "BalticWay/segmented/en-bw90sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1990"
}
|
Let $P$ be a point on the circumcircle of a triangle $A B C$. It is known that the base points of the perpendiculars drawn from $P$ onto the lines $A B, B C$ and $C A$ lie on one straight line (called a Simson line). Prove that the Simson lines of two diametrically opposite points $P_{1}$ and $P_{2}$ are perpendicular.
|
Let $O$ be the circumcentre of the triangle $A B C$ and $\angle B$ be its maximal angle (so that $\angle A$ and $\angle C$ are necessarily acute). Further, let $B_{1}$ and $C_{1}$ be the base points of the perpendiculars drawn from the point $P$ to the sides $A C$ and $A B$ respectively and let $\alpha$ be the angle between the Simson line $l$ of point $P$ and the height $h$ of the triangle drawn to the side $A C$. It is sufficient to prove that $\alpha=\frac{1}{2} \angle P O B$. To show this, first note that the points $P, C_{1}, B_{1}, A$ all belong to a certain circle. Now we have to consider several sub-cases depending on the order of these points on that circle and the location of point $P$ on the circumcircle of triangle $A B C$. Figure 2 shows one of these cases - here we have $\alpha=\angle P B_{1} C_{1}=\angle P B_{1} C_{1}=$ $\angle P A B=\frac{1}{2} \angle P O B$. The other cases can be treated in a similar manner.
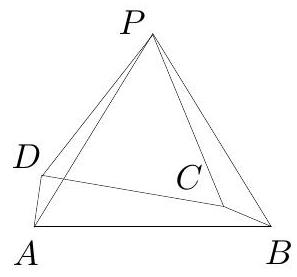
Figure 1
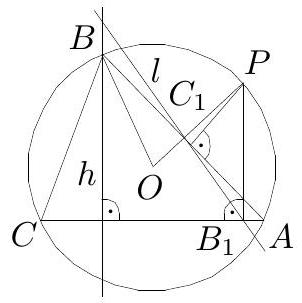
Figure 2
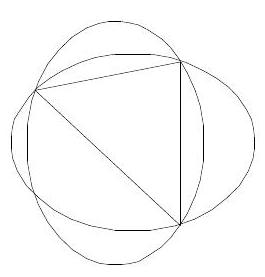
Figure 3
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $P$ be a point on the circumcircle of a triangle $A B C$. It is known that the base points of the perpendiculars drawn from $P$ onto the lines $A B, B C$ and $C A$ lie on one straight line (called a Simson line). Prove that the Simson lines of two diametrically opposite points $P_{1}$ and $P_{2}$ are perpendicular.
|
Let $O$ be the circumcentre of the triangle $A B C$ and $\angle B$ be its maximal angle (so that $\angle A$ and $\angle C$ are necessarily acute). Further, let $B_{1}$ and $C_{1}$ be the base points of the perpendiculars drawn from the point $P$ to the sides $A C$ and $A B$ respectively and let $\alpha$ be the angle between the Simson line $l$ of point $P$ and the height $h$ of the triangle drawn to the side $A C$. It is sufficient to prove that $\alpha=\frac{1}{2} \angle P O B$. To show this, first note that the points $P, C_{1}, B_{1}, A$ all belong to a certain circle. Now we have to consider several sub-cases depending on the order of these points on that circle and the location of point $P$ on the circumcircle of triangle $A B C$. Figure 2 shows one of these cases - here we have $\alpha=\angle P B_{1} C_{1}=\angle P B_{1} C_{1}=$ $\angle P A B=\frac{1}{2} \angle P O B$. The other cases can be treated in a similar manner.

Figure 1

Figure 2

Figure 3
|
{
"exam": "BalticWay",
"problem_label": "8",
"problem_match": "\n8.",
"resource_path": "BalticWay/segmented/en-bw90sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1990"
}
|
Two equal triangles are inscribed into an ellipse. Are they necessarily symmetrical with respect either to the axes or to the centre of the ellipse?
|
No, not necessarily (see Figure 3 where the two ellipses are equal).
|
not found
|
Yes
|
Problem not solved
|
math-word-problem
|
Geometry
|
Two equal triangles are inscribed into an ellipse. Are they necessarily symmetrical with respect either to the axes or to the centre of the ellipse?
|
No, not necessarily (see Figure 3 where the two ellipses are equal).
|
{
"exam": "BalticWay",
"problem_label": "9",
"problem_match": "\n9.",
"resource_path": "BalticWay/segmented/en-bw90sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1990"
}
|
A segment $A B$ of unit length is marked on the straight line $t$. The segment is then moved on the plane so that it remains parallel to $t$ at all times, the traces of the points $A$ and $B$ do not intersect and finally the segment returns onto $t$. How far can the point $A$ now be from its initial position?
|
The point $A$ can move any distance from its initial position - see Figure 4 and note that we can make the height $h$ arbitrarily small.
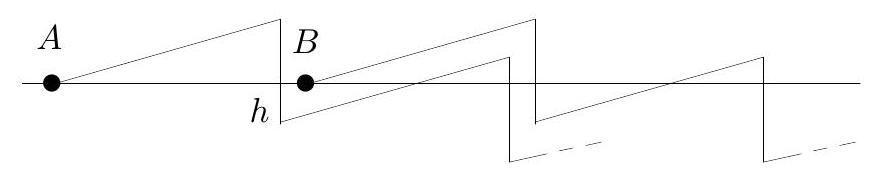
Figure 4
|
any\ distance
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
A segment $A B$ of unit length is marked on the straight line $t$. The segment is then moved on the plane so that it remains parallel to $t$ at all times, the traces of the points $A$ and $B$ do not intersect and finally the segment returns onto $t$. How far can the point $A$ now be from its initial position?
|
The point $A$ can move any distance from its initial position - see Figure 4 and note that we can make the height $h$ arbitrarily small.

Figure 4
|
{
"exam": "BalticWay",
"problem_label": "10",
"problem_match": "\n10.",
"resource_path": "BalticWay/segmented/en-bw90sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1990"
}
|
Prove that the modulus of an integer root of a polynomial with integer coefficients cannot exceed the maximum of the moduli of the coefficients.
|
For a non-zero polynomial $P(x)=a_{n} x^{n}+\cdots+a_{1} x+a_{0}$ with integer coefficients, let $k$ be the smallest index such that $a_{k} \neq 0$. Let $c$ be an integer root of $P(x)$. If $c=0$, the statement is obvious. If $c \neq 0$, then using $P(c)=0$ we get $a_{k}=-x\left(a_{k+1}+a_{k+2} x+\cdots+a_{n} x^{n-k-1}\right)$. Hence $c$ divides $a_{k}$, and since $a_{k} \neq 0$ we must have $|c| \leq\left|a_{k}\right|$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Prove that the modulus of an integer root of a polynomial with integer coefficients cannot exceed the maximum of the moduli of the coefficients.
|
For a non-zero polynomial $P(x)=a_{n} x^{n}+\cdots+a_{1} x+a_{0}$ with integer coefficients, let $k$ be the smallest index such that $a_{k} \neq 0$. Let $c$ be an integer root of $P(x)$. If $c=0$, the statement is obvious. If $c \neq 0$, then using $P(c)=0$ we get $a_{k}=-x\left(a_{k+1}+a_{k+2} x+\cdots+a_{n} x^{n-k-1}\right)$. Hence $c$ divides $a_{k}$, and since $a_{k} \neq 0$ we must have $|c| \leq\left|a_{k}\right|$.
|
{
"exam": "BalticWay",
"problem_label": "11",
"problem_match": "\n11.",
"resource_path": "BalticWay/segmented/en-bw90sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1990"
}
|
Let $m$ and $n$ be positive integers. Prove that $25 m+3 n$ is divisible by 83 if and only if $3 m+7 n$ is divisible by 83 .
|
Use the equality $2 \cdot(25 x+3 y)+11 \cdot(3 x+7 y)=83 x+83 y$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $m$ and $n$ be positive integers. Prove that $25 m+3 n$ is divisible by 83 if and only if $3 m+7 n$ is divisible by 83 .
|
Use the equality $2 \cdot(25 x+3 y)+11 \cdot(3 x+7 y)=83 x+83 y$.
|
{
"exam": "BalticWay",
"problem_label": "12",
"problem_match": "\n12.",
"resource_path": "BalticWay/segmented/en-bw90sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1990"
}
|
Prove that the equation $x^{2}-7 y^{2}=1$ has infinitely many solutions in natural numbers.
|
For any solution $(m, n)$ of the equation we have $m^{2}-7 n^{2}=1$ and
$$
1=\left(m^{2}-7 n^{2}\right)^{2}=\left(m^{2}+7 n^{2}\right)^{2}-7 \cdot(2 m n)^{2} .
$$
Thus $\left(m^{2}+7 n^{2}, 2 m n\right)$ is also a solution. Therefore it is sufficient to note that the equation $x^{2}-7 y^{2}=1$ has at least one solution, for example $x=8, y=3$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that the equation $x^{2}-7 y^{2}=1$ has infinitely many solutions in natural numbers.
|
For any solution $(m, n)$ of the equation we have $m^{2}-7 n^{2}=1$ and
$$
1=\left(m^{2}-7 n^{2}\right)^{2}=\left(m^{2}+7 n^{2}\right)^{2}-7 \cdot(2 m n)^{2} .
$$
Thus $\left(m^{2}+7 n^{2}, 2 m n\right)$ is also a solution. Therefore it is sufficient to note that the equation $x^{2}-7 y^{2}=1$ has at least one solution, for example $x=8, y=3$.
|
{
"exam": "BalticWay",
"problem_label": "13",
"problem_match": "\n13.",
"resource_path": "BalticWay/segmented/en-bw90sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1990"
}
|
Do there exist 1990 relatively prime numbers such that all possible sums of two or more of these numbers are composite numbers?
|
Such numbers do exist. Let $M=1990$ ! and consider the sequence of numbers $1+M, 1+2 M$, $1+3 M, \ldots$ For any natural number $2 \leq k \leq 1990$, any sum of exactly $k$ of these numbers (not necessarily different) is divisible by $k$, and hence is composite. number. It remains to show that we can choose 1990 numbers $a_{1}, \ldots, a_{1990}$ from this sequence which are relatively prime. Indeed, let $a_{1}=1+M$, $a_{2}=1+2 M$ and for $a_{1}, \ldots, a_{n}$ already chosen take $a_{n+1}=1+a_{1} \cdots a_{n} \cdot M$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Do there exist 1990 relatively prime numbers such that all possible sums of two or more of these numbers are composite numbers?
|
Such numbers do exist. Let $M=1990$ ! and consider the sequence of numbers $1+M, 1+2 M$, $1+3 M, \ldots$ For any natural number $2 \leq k \leq 1990$, any sum of exactly $k$ of these numbers (not necessarily different) is divisible by $k$, and hence is composite. number. It remains to show that we can choose 1990 numbers $a_{1}, \ldots, a_{1990}$ from this sequence which are relatively prime. Indeed, let $a_{1}=1+M$, $a_{2}=1+2 M$ and for $a_{1}, \ldots, a_{n}$ already chosen take $a_{n+1}=1+a_{1} \cdots a_{n} \cdot M$.
|
{
"exam": "BalticWay",
"problem_label": "14",
"problem_match": "\n14.",
"resource_path": "BalticWay/segmented/en-bw90sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1990"
}
|
Prove that none of the numbers
$$
F_{n}=2^{2^{n}}+1, \quad n=0,1,2, \ldots,
$$
is a cube of an integer.
|
Assume there exist such natural numbers $k$ and $n$ that $2^{2^{n}}+1=k^{3}$. Then $k$ must be an odd number and we have $2^{2^{n}}=k^{3}-1=(k-1)\left(k^{2}+k+1\right)$. Hence $k-1=2^{s}$ and $k^{2}+k+1=2^{t}$ where $s$ and $t$ are some positive integers. Now $2^{2 s}=(k-1)^{2}=k^{2}-2 k+1$ and $2^{t}-2^{2 s}=3 k$. But $2^{t}-2^{2 s}$ is even while $3 k$ is odd, a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that none of the numbers
$$
F_{n}=2^{2^{n}}+1, \quad n=0,1,2, \ldots,
$$
is a cube of an integer.
|
Assume there exist such natural numbers $k$ and $n$ that $2^{2^{n}}+1=k^{3}$. Then $k$ must be an odd number and we have $2^{2^{n}}=k^{3}-1=(k-1)\left(k^{2}+k+1\right)$. Hence $k-1=2^{s}$ and $k^{2}+k+1=2^{t}$ where $s$ and $t$ are some positive integers. Now $2^{2 s}=(k-1)^{2}=k^{2}-2 k+1$ and $2^{t}-2^{2 s}=3 k$. But $2^{t}-2^{2 s}$ is even while $3 k$ is odd, a contradiction.
|
{
"exam": "BalticWay",
"problem_label": "15",
"problem_match": "\n15.",
"resource_path": "BalticWay/segmented/en-bw90sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1990"
}
|
A closed polygonal line is drawn on squared paper so that its links lie on the lines of the paper (the sides of the squares are equal to 1). The lengths of all links are odd numbers. Prove that the number of links is divisible by 4 .
|
There must be an equal number of horizontal and vertical links, and hence it suffices to show that the number of vertical links is even. Let's pass the whole polygonal line in a chosen direction and mark each vertical link as "up" or "down" according to the direction we pass it. As the sum of lengths of the "up" links is equal to that of the "down" ones and each link is of odd length, we have an even or odd number of links of both kinds depending on the parity of the sum of their lengths.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A closed polygonal line is drawn on squared paper so that its links lie on the lines of the paper (the sides of the squares are equal to 1). The lengths of all links are odd numbers. Prove that the number of links is divisible by 4 .
|
There must be an equal number of horizontal and vertical links, and hence it suffices to show that the number of vertical links is even. Let's pass the whole polygonal line in a chosen direction and mark each vertical link as "up" or "down" according to the direction we pass it. As the sum of lengths of the "up" links is equal to that of the "down" ones and each link is of odd length, we have an even or odd number of links of both kinds depending on the parity of the sum of their lengths.
|
{
"exam": "BalticWay",
"problem_label": "16",
"problem_match": "\n16.",
"resource_path": "BalticWay/segmented/en-bw90sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1990"
}
|
In two piles there are 72 and 30 sweets respectively. Two students take, one after another, some sweets from one of the piles. Each time the number of sweets taken from a pile must be an integer multiple of the number of sweets in the other pile. Is it the beginner of the game or his adversary who can always assure taking the last sweet from one of the piles?
|
Note that one of the players must have a winning strategy. Assume that it is the player making the second move who has it. Then his strategy will assure taking the last sweet also in the case when the beginner takes $2 \cdot 30$ sweets as his first move. But now, if the beginner takes $1 \cdot 30$ sweets then the second player has no choice but to take another 30 sweets from the same pile, and hence the beginner can use the same strategy to assure taking the last sweet himself. This contradiction shows that it must be the beginner who has the winning strategy.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
In two piles there are 72 and 30 sweets respectively. Two students take, one after another, some sweets from one of the piles. Each time the number of sweets taken from a pile must be an integer multiple of the number of sweets in the other pile. Is it the beginner of the game or his adversary who can always assure taking the last sweet from one of the piles?
|
Note that one of the players must have a winning strategy. Assume that it is the player making the second move who has it. Then his strategy will assure taking the last sweet also in the case when the beginner takes $2 \cdot 30$ sweets as his first move. But now, if the beginner takes $1 \cdot 30$ sweets then the second player has no choice but to take another 30 sweets from the same pile, and hence the beginner can use the same strategy to assure taking the last sweet himself. This contradiction shows that it must be the beginner who has the winning strategy.
|
{
"exam": "BalticWay",
"problem_label": "17",
"problem_match": "\n17.",
"resource_path": "BalticWay/segmented/en-bw90sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1990"
}
|
Positive integers $1,2, \ldots, 100,101$ are written in the cells of a $101 \times 101$ square grid so that each number is repeated 101 times. Prove that there exists either a column or a row containing at least 11 different numbers.
|
Let $a_{k}$ denote the total number of rows and columns containing the number $k$ at least once. As $i \cdot(20-i)<101$ for any natural number $i$, we have $a_{k} \geq 21$ for all $k=1,2, \ldots, 101$. Hence $a_{1}+\cdots+a_{101} \geq 21 \cdot 101=2121$. On the other hand, assuming any row and any column contains no more than 10 different numbers we have $a_{1}+\cdots+a_{101} \leq 202 \cdot 10=2020$, a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Positive integers $1,2, \ldots, 100,101$ are written in the cells of a $101 \times 101$ square grid so that each number is repeated 101 times. Prove that there exists either a column or a row containing at least 11 different numbers.
|
Let $a_{k}$ denote the total number of rows and columns containing the number $k$ at least once. As $i \cdot(20-i)<101$ for any natural number $i$, we have $a_{k} \geq 21$ for all $k=1,2, \ldots, 101$. Hence $a_{1}+\cdots+a_{101} \geq 21 \cdot 101=2121$. On the other hand, assuming any row and any column contains no more than 10 different numbers we have $a_{1}+\cdots+a_{101} \leq 202 \cdot 10=2020$, a contradiction.
|
{
"exam": "BalticWay",
"problem_label": "18",
"problem_match": "\n18.",
"resource_path": "BalticWay/segmented/en-bw90sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1990"
}
|
What is the largest possible number of subsets of the set $\{1,2, \ldots, 2 n+1\}$ such that the intersection of any two subsets consists of one or several consecutive integers?
|
Consider any subsets $A_{1}, \ldots, A_{s}$ satisfying the condition of the problem and let $A_{i}=$ $\left\{a_{i 1}, \ldots, a_{i, k_{i}}\right\}$ where $a_{i 1}<\cdots<a_{i, k_{i}}$. Replacing each $A_{i}$ by $A_{i}^{\prime}=\left\{a_{i 1}, a_{i 1}+1, \ldots, a_{i, k_{i}}-1, a_{i, k_{i}}\right\}$ (i.e., adding to it all "missing" numbers) yields a collection of different subsets $A_{1}^{\prime}, \ldots, A_{s}^{\prime}$ which also satisfies the required condition. Now, let $b_{i}$ and $c_{i}$ be the smallest and largest elements of the subset $A_{i}^{\prime}$, respectively. Then $\min _{1 \leq i \leq s} c_{i} \geq \max _{1 \leq i \leq s} b_{i}$, as otherwise some subsets $A_{k}^{\prime}$ and $A_{l}^{\prime}$ would not intersect. Hence there exists an element $a \in \bigcap_{1<i<s} A_{i}^{\prime}$. As the number of subsets of the set $\{1,2, \ldots, 2 n+1\}$ containing $a$ and consisting of $k$ consecutive integers does not exceed $\min (k, 2 n+2-k)$ we have $s \leq(n+1)+2 \cdot(1+2+\cdots+n)=(n+1)^{2}$. This maximum will be reached if we take $a=n+1$.
|
(n+1)^2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
What is the largest possible number of subsets of the set $\{1,2, \ldots, 2 n+1\}$ such that the intersection of any two subsets consists of one or several consecutive integers?
|
Consider any subsets $A_{1}, \ldots, A_{s}$ satisfying the condition of the problem and let $A_{i}=$ $\left\{a_{i 1}, \ldots, a_{i, k_{i}}\right\}$ where $a_{i 1}<\cdots<a_{i, k_{i}}$. Replacing each $A_{i}$ by $A_{i}^{\prime}=\left\{a_{i 1}, a_{i 1}+1, \ldots, a_{i, k_{i}}-1, a_{i, k_{i}}\right\}$ (i.e., adding to it all "missing" numbers) yields a collection of different subsets $A_{1}^{\prime}, \ldots, A_{s}^{\prime}$ which also satisfies the required condition. Now, let $b_{i}$ and $c_{i}$ be the smallest and largest elements of the subset $A_{i}^{\prime}$, respectively. Then $\min _{1 \leq i \leq s} c_{i} \geq \max _{1 \leq i \leq s} b_{i}$, as otherwise some subsets $A_{k}^{\prime}$ and $A_{l}^{\prime}$ would not intersect. Hence there exists an element $a \in \bigcap_{1<i<s} A_{i}^{\prime}$. As the number of subsets of the set $\{1,2, \ldots, 2 n+1\}$ containing $a$ and consisting of $k$ consecutive integers does not exceed $\min (k, 2 n+2-k)$ we have $s \leq(n+1)+2 \cdot(1+2+\cdots+n)=(n+1)^{2}$. This maximum will be reached if we take $a=n+1$.
|
{
"exam": "BalticWay",
"problem_label": "19",
"problem_match": "\n19.",
"resource_path": "BalticWay/segmented/en-bw90sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1990"
}
|
Find the smallest positive integer $n$ having the property: for any set of $n$ distinct integers $a_{1}, a_{2}, \ldots, a_{n}$ the product of all differences $a_{i}-a_{j}, i<j$ is divisible by 1991 .
|
Let $S=\prod_{1 \leq i<j \leq n}\left(a_{i}-a_{j}\right)$. Note that $1991=11 \cdot 181$. Therefore $S$ is divisible by 1991 if and only if it is divisible by both 11 and 181 . If $n \leq 181$ then we can take the numbers $a_{1}, \ldots, a_{n}$ from distinct congruence classes modulo 181 so that $S$ will not be divisible by 181 . On the other hand, if $n \geq 182$ then according to the pigeonhole principle there always exist $a_{i}$ and $a_{j}$ such that $a_{i}-a_{j}$ is divisible by 181 (and of course there exist $a_{k}$ and $a_{l}$ such that $a_{k}-a_{l}$ is divisible by 11).
|
182
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the smallest positive integer $n$ having the property: for any set of $n$ distinct integers $a_{1}, a_{2}, \ldots, a_{n}$ the product of all differences $a_{i}-a_{j}, i<j$ is divisible by 1991 .
|
Let $S=\prod_{1 \leq i<j \leq n}\left(a_{i}-a_{j}\right)$. Note that $1991=11 \cdot 181$. Therefore $S$ is divisible by 1991 if and only if it is divisible by both 11 and 181 . If $n \leq 181$ then we can take the numbers $a_{1}, \ldots, a_{n}$ from distinct congruence classes modulo 181 so that $S$ will not be divisible by 181 . On the other hand, if $n \geq 182$ then according to the pigeonhole principle there always exist $a_{i}$ and $a_{j}$ such that $a_{i}-a_{j}$ is divisible by 181 (and of course there exist $a_{k}$ and $a_{l}$ such that $a_{k}-a_{l}$ is divisible by 11).
|
{
"exam": "BalticWay",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "BalticWay/segmented/en-bw91sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1991"
}
|
Prove that there are no positive integers $n$ and $m>1$ such that $102^{1991}+103^{1991}=n^{m}$.
|
Factorizing, we get
$$
102^{1991}+103^{1991}=(102+103)\left(102^{1990}-102^{1989} \cdot 103+102^{1988} \cdot 103^{2}-\cdots+103^{1990}\right),
$$
where $102+103=205=5 \cdot 41$. It suffices to show that the other factor is not divisible by 5 . Let $a_{k}=102^{k} \cdot 103^{1990-k}$, then $a_{k} \equiv 4(\bmod 5)$ if $k$ is even and $a_{k} \equiv-4(\bmod 5)$ if $k$ is odd. Thus the whole second factor is congruent to $4 \cdot 1991 \equiv 4(\bmod 5)$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that there are no positive integers $n$ and $m>1$ such that $102^{1991}+103^{1991}=n^{m}$.
|
Factorizing, we get
$$
102^{1991}+103^{1991}=(102+103)\left(102^{1990}-102^{1989} \cdot 103+102^{1988} \cdot 103^{2}-\cdots+103^{1990}\right),
$$
where $102+103=205=5 \cdot 41$. It suffices to show that the other factor is not divisible by 5 . Let $a_{k}=102^{k} \cdot 103^{1990-k}$, then $a_{k} \equiv 4(\bmod 5)$ if $k$ is even and $a_{k} \equiv-4(\bmod 5)$ if $k$ is odd. Thus the whole second factor is congruent to $4 \cdot 1991 \equiv 4(\bmod 5)$.
|
{
"exam": "BalticWay",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "BalticWay/segmented/en-bw91sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1991"
}
|
There are 20 cats priced from $\$ 12$ to $\$ 15$ and 20 sacks priced from 10 cents to $\$ 1$ for sale (all prices are different). Prove that each of two boys, John and Peter, can buy a cat in a sack paying the same amount of money.
|
The number of different possibilities for buying a cat and a sack is $20 \cdot 20=400$ while the number of different possible prices is $1600-1210+1=391$. Thus by the pigeonhole principle there exist two combinations of a cat and a sack costing the same amount of money. Note that the two cats (and also the two sacks) involved must be different as otherwise the two sacks (respectively, cats) would have equal prices.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
There are 20 cats priced from $\$ 12$ to $\$ 15$ and 20 sacks priced from 10 cents to $\$ 1$ for sale (all prices are different). Prove that each of two boys, John and Peter, can buy a cat in a sack paying the same amount of money.
|
The number of different possibilities for buying a cat and a sack is $20 \cdot 20=400$ while the number of different possible prices is $1600-1210+1=391$. Thus by the pigeonhole principle there exist two combinations of a cat and a sack costing the same amount of money. Note that the two cats (and also the two sacks) involved must be different as otherwise the two sacks (respectively, cats) would have equal prices.
|
{
"exam": "BalticWay",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "BalticWay/segmented/en-bw91sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1991"
}
|
Let $p$ be a polynomial with integer coefficients such that $p(-n)<p(n)<n$ for some integer $n$. Prove that $p(-n)<-n$.
|
As $a^{n}-b^{n}=(a-b)\left(a^{n-1}+a^{n-2} b+\cdots+b^{n-1}\right)$, then for any distinct integers $a, b$ and for any polynomial $p(x)$ with integer coefficients $p(a)-p(b)$ is divisible by $a-b$. Thus, $p(n)-p(-n) \neq 0$ is divisible by $2 n$ and consequently $p(-n) \leq p(n)-2 n<n-2 n=-n$.
|
p(-n) < -n
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $p$ be a polynomial with integer coefficients such that $p(-n)<p(n)<n$ for some integer $n$. Prove that $p(-n)<-n$.
|
As $a^{n}-b^{n}=(a-b)\left(a^{n-1}+a^{n-2} b+\cdots+b^{n-1}\right)$, then for any distinct integers $a, b$ and for any polynomial $p(x)$ with integer coefficients $p(a)-p(b)$ is divisible by $a-b$. Thus, $p(n)-p(-n) \neq 0$ is divisible by $2 n$ and consequently $p(-n) \leq p(n)-2 n<n-2 n=-n$.
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "BalticWay/segmented/en-bw91sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1991"
}
|
For any positive numbers $a, b, c$ prove the inequalities
$$
\frac{1}{a}+\frac{1}{b}+\frac{1}{c} \geq \frac{2}{a+b}+\frac{2}{b+c}+\frac{2}{c+a} \geq \frac{9}{a+b+c} .
$$
|
To prove the first inequality, note that $\frac{2}{a+b} \leq \frac{1}{2}\left(\frac{1}{a}+\frac{1}{b}\right)$ and similarly $\frac{2}{b+c} \leq \frac{1}{2}\left(\frac{1}{b}+\frac{1}{c}\right), \frac{2}{c+a} \leq$ $\frac{1}{2}\left(\frac{1}{c}+\frac{1}{a}\right)$. For the second part, use the inequality $\frac{3}{x+y+z} \leq \frac{1}{3}\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)$ for $x=a+b, y=b+c$ and $z=c+a$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
For any positive numbers $a, b, c$ prove the inequalities
$$
\frac{1}{a}+\frac{1}{b}+\frac{1}{c} \geq \frac{2}{a+b}+\frac{2}{b+c}+\frac{2}{c+a} \geq \frac{9}{a+b+c} .
$$
|
To prove the first inequality, note that $\frac{2}{a+b} \leq \frac{1}{2}\left(\frac{1}{a}+\frac{1}{b}\right)$ and similarly $\frac{2}{b+c} \leq \frac{1}{2}\left(\frac{1}{b}+\frac{1}{c}\right), \frac{2}{c+a} \leq$ $\frac{1}{2}\left(\frac{1}{c}+\frac{1}{a}\right)$. For the second part, use the inequality $\frac{3}{x+y+z} \leq \frac{1}{3}\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)$ for $x=a+b, y=b+c$ and $z=c+a$.
|
{
"exam": "BalticWay",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "BalticWay/segmented/en-bw91sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1991"
}
|
Let $[x]$ be the integer part of a number $x$, and $\{x\}=x-[x]$. Solve the equation
$$
[x] \cdot\{x\}=1991 x .
$$
|
Let $f(x)=[x] \cdot\{x\}$. Then we have to solve the equation $f(x)=1991 x$. Obviously, $x=0$ is a solution. For any $x>0$ we have $0 \leq[x] \leq x$ and $0 \leq\{x\}<1$ which imply $f(x)<x<1991 x$. For $x \leq-1$ we have $0>[x]>x-1$ and $0 \leq\{x\}<1$ which imply $f(x)>x-1>1991 x$. Finally, if $-1<x<0$, then $[x]=-1,\{x\}=x-[x]=x+1$ and $f(x)=-x-1$. The only solution of the equation $-x-1=1991 x$ is $x=-\frac{1}{1992}$.
|
-\frac{1}{1992}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $[x]$ be the integer part of a number $x$, and $\{x\}=x-[x]$. Solve the equation
$$
[x] \cdot\{x\}=1991 x .
$$
|
Let $f(x)=[x] \cdot\{x\}$. Then we have to solve the equation $f(x)=1991 x$. Obviously, $x=0$ is a solution. For any $x>0$ we have $0 \leq[x] \leq x$ and $0 \leq\{x\}<1$ which imply $f(x)<x<1991 x$. For $x \leq-1$ we have $0>[x]>x-1$ and $0 \leq\{x\}<1$ which imply $f(x)>x-1>1991 x$. Finally, if $-1<x<0$, then $[x]=-1,\{x\}=x-[x]=x+1$ and $f(x)=-x-1$. The only solution of the equation $-x-1=1991 x$ is $x=-\frac{1}{1992}$.
|
{
"exam": "BalticWay",
"problem_label": "6",
"problem_match": "\n6.",
"resource_path": "BalticWay/segmented/en-bw91sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1991"
}
|
Let $A, B, C$ be the angles of an acute-angled triangle. Prove the inequality
$$
\sin A+\sin B>\cos A+\cos B+\cos C
$$
|
In an acute-angled triangle we have $A+B>\frac{\pi}{2}$. Hence we have $\sin A>\sin \left(\frac{\pi}{2}-B\right)=\cos B$ and $\sin B>\cos A$. Using these inequalities we get $(1-\sin A)(1-\sin B)<(1-\cos A)(1-\cos B)$ and
$$
\begin{aligned}
\sin A+\sin B & >\cos A+\cos B-\cos A \cos B+\sin A \sin B \\
& =\cos A+\cos B-\cos (A+B)=\cos A+\cos B+\cos C
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $A, B, C$ be the angles of an acute-angled triangle. Prove the inequality
$$
\sin A+\sin B>\cos A+\cos B+\cos C
$$
|
In an acute-angled triangle we have $A+B>\frac{\pi}{2}$. Hence we have $\sin A>\sin \left(\frac{\pi}{2}-B\right)=\cos B$ and $\sin B>\cos A$. Using these inequalities we get $(1-\sin A)(1-\sin B)<(1-\cos A)(1-\cos B)$ and
$$
\begin{aligned}
\sin A+\sin B & >\cos A+\cos B-\cos A \cos B+\sin A \sin B \\
& =\cos A+\cos B-\cos (A+B)=\cos A+\cos B+\cos C
\end{aligned}
$$
|
{
"exam": "BalticWay",
"problem_label": "7",
"problem_match": "\n7.",
"resource_path": "BalticWay/segmented/en-bw91sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1991"
}
|
Let $a, b, c, d, e$ be distinct real numbers. Prove that the equation
$$
\begin{aligned}
& (x-a)(x-b)(x-c)(x-d) \\
& +(x-a)(x-b)(x-c)(x-e) \\
& +(x-a)(x-b)(x-d)(x-e) \\
& +(x-a)(x-c)(x-d)(x-e) \\
& +(x-b)(x-c)(x-d)(x-e)=0
\end{aligned}
$$
has 4 distinct real solutions.
|
On the left-hand side of the equation we have the derivative of the function
$$
f(x)=(x-a)(x-b)(x-c)(x-d)(x-e)
$$
which is continuous and has five distinct real roots.
|
proof
|
Yes
|
Incomplete
|
proof
|
Algebra
|
Let $a, b, c, d, e$ be distinct real numbers. Prove that the equation
$$
\begin{aligned}
& (x-a)(x-b)(x-c)(x-d) \\
& +(x-a)(x-b)(x-c)(x-e) \\
& +(x-a)(x-b)(x-d)(x-e) \\
& +(x-a)(x-c)(x-d)(x-e) \\
& +(x-b)(x-c)(x-d)(x-e)=0
\end{aligned}
$$
has 4 distinct real solutions.
|
On the left-hand side of the equation we have the derivative of the function
$$
f(x)=(x-a)(x-b)(x-c)(x-d)(x-e)
$$
which is continuous and has five distinct real roots.
|
{
"exam": "BalticWay",
"problem_label": "8",
"problem_match": "\n8.",
"resource_path": "BalticWay/segmented/en-bw91sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1991"
}
|
Find the number of solutions of the equation $a e^{x}=x^{3}$.
|
Studying the graphs of the functions $a e^{x}$ and $x^{3}$ it is easy to see that the equation always has one solution if $a<0$ and can have 0,1 or 2 solutions if $a>0$. Moreover, in the case $a>0$ the number of solutions can only decrease as $a$ increases and we have exactly one positive value of $a$ for which the equation has one solution - this is the case when the graphs of $a e^{x}$ and $x^{3}$ are tangent to each other, i.e., there exists $x_{0}$ such that $a e^{x_{0}}=x_{0}^{3}$ and $a e^{x_{0}}=3 x_{0}^{2}$. From these two equations we get $x_{0}=3$ and $a=\frac{27}{e^{3}}$. Summarizing: the equation $a e^{x}=x^{3}$ has one solution for $a \leq 0$ and $a=\frac{27}{e^{3}}$, two solutions for $0<a<\frac{27}{e^{3}}$ and no solutions for $a>\frac{27}{e^{3}}$.
|
a \leq 0 \text{ or } a = \frac{27}{e^3} \text{ (1 solution)}, 0 < a < \frac{27}{e^3} \text{ (2 solutions)}, a > \frac{27}{e^3} \text{ (0 solutions)}
|
Yes
|
Yes
|
math-word-problem
|
Calculus
|
Find the number of solutions of the equation $a e^{x}=x^{3}$.
|
Studying the graphs of the functions $a e^{x}$ and $x^{3}$ it is easy to see that the equation always has one solution if $a<0$ and can have 0,1 or 2 solutions if $a>0$. Moreover, in the case $a>0$ the number of solutions can only decrease as $a$ increases and we have exactly one positive value of $a$ for which the equation has one solution - this is the case when the graphs of $a e^{x}$ and $x^{3}$ are tangent to each other, i.e., there exists $x_{0}$ such that $a e^{x_{0}}=x_{0}^{3}$ and $a e^{x_{0}}=3 x_{0}^{2}$. From these two equations we get $x_{0}=3$ and $a=\frac{27}{e^{3}}$. Summarizing: the equation $a e^{x}=x^{3}$ has one solution for $a \leq 0$ and $a=\frac{27}{e^{3}}$, two solutions for $0<a<\frac{27}{e^{3}}$ and no solutions for $a>\frac{27}{e^{3}}$.
|
{
"exam": "BalticWay",
"problem_label": "9",
"problem_match": "\n9.",
"resource_path": "BalticWay/segmented/en-bw91sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1991"
}
|
Express the value of $\sin 3^{\circ}$ in radicals.
|
We use the equality
$$
\sin 3^{\circ}=\sin \left(18^{\circ}-15^{\circ}\right)=\sin 18^{\circ} \cos 15^{\circ}+\cos 18^{\circ} \sin 15^{\circ}
$$
where
$$
\sin 15^{\circ}=\sin \frac{30^{\circ}}{2}=\sqrt{\frac{1-\cos 30^{\circ}}{2}}=\frac{\sqrt{6}-\sqrt{2}}{4}
$$
and
$$
\cos 15^{\circ}=\sqrt{1-\sin ^{2} 15^{\circ}}=\frac{\sqrt{6}+\sqrt{2}}{4} .
$$
To calculate $\cos 18^{\circ}$ and $\sin 18^{\circ}$ note that $\cos \left(3 \cdot 18^{\circ}\right)=\sin \left(2 \cdot 18^{\circ}\right)$. As $\cos 3 x=\cos ^{3} x-3 \cos x \sin ^{2} x=$ $\cos x\left(1-4 \sin ^{2} x\right)$ and $\sin 2 x=2 \sin x \cos x$ we get $1-4 \sin ^{2} 18^{\circ}=2 \sin 18^{\circ}$. Solving this quadratic equation yields $\sin 18^{\circ}=\frac{\sqrt{5}-1}{4}$ (we discard $\frac{-\sqrt{5}-1}{4}$ which is negative) and $\cos 18^{\circ}=\frac{\sqrt{10+2 \sqrt{5}}}{4}$.
| null |
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Express the value of $\sin 3^{\circ}$ in radicals.
|
We use the equality
$$
\sin 3^{\circ}=\sin \left(18^{\circ}-15^{\circ}\right)=\sin 18^{\circ} \cos 15^{\circ}+\cos 18^{\circ} \sin 15^{\circ}
$$
where
$$
\sin 15^{\circ}=\sin \frac{30^{\circ}}{2}=\sqrt{\frac{1-\cos 30^{\circ}}{2}}=\frac{\sqrt{6}-\sqrt{2}}{4}
$$
and
$$
\cos 15^{\circ}=\sqrt{1-\sin ^{2} 15^{\circ}}=\frac{\sqrt{6}+\sqrt{2}}{4} .
$$
To calculate $\cos 18^{\circ}$ and $\sin 18^{\circ}$ note that $\cos \left(3 \cdot 18^{\circ}\right)=\sin \left(2 \cdot 18^{\circ}\right)$. As $\cos 3 x=\cos ^{3} x-3 \cos x \sin ^{2} x=$ $\cos x\left(1-4 \sin ^{2} x\right)$ and $\sin 2 x=2 \sin x \cos x$ we get $1-4 \sin ^{2} 18^{\circ}=2 \sin 18^{\circ}$. Solving this quadratic equation yields $\sin 18^{\circ}=\frac{\sqrt{5}-1}{4}$ (we discard $\frac{-\sqrt{5}-1}{4}$ which is negative) and $\cos 18^{\circ}=\frac{\sqrt{10+2 \sqrt{5}}}{4}$.
|
{
"exam": "BalticWay",
"problem_label": "10",
"problem_match": "\n10.",
"resource_path": "BalticWay/segmented/en-bw91sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1991"
}
|
All positive integers from 1 to 1000000 are divided into two groups consisting of numbers with odd or even sums of digits respectively. Which group contains more numbers?
|
Among any ten integers $\overline{a_{1} \ldots a_{n} 0}, \overline{a_{1} \ldots a_{n} 1}, \ldots, \overline{a_{1} \ldots a_{n} 9}$ there are exactly five numbers with odd digit sum and five numbers with even digit sum. Thus, among the integers 0, 1, . , 999999 we have equally many numbers of both kinds. After substituting 1000000 instead of 0 we shall have more numbers with odd digit sum.
|
not found
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
All positive integers from 1 to 1000000 are divided into two groups consisting of numbers with odd or even sums of digits respectively. Which group contains more numbers?
|
Among any ten integers $\overline{a_{1} \ldots a_{n} 0}, \overline{a_{1} \ldots a_{n} 1}, \ldots, \overline{a_{1} \ldots a_{n} 9}$ there are exactly five numbers with odd digit sum and five numbers with even digit sum. Thus, among the integers 0, 1, . , 999999 we have equally many numbers of both kinds. After substituting 1000000 instead of 0 we shall have more numbers with odd digit sum.
|
{
"exam": "BalticWay",
"problem_label": "11",
"problem_match": "\n11.",
"resource_path": "BalticWay/segmented/en-bw91sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1991"
}
|
The vertices of a convex 1991-gon are enumerated with integers from 1 to 1991. Each side and diagonal of the 1991-gon is coloured either red or blue. Prove that, for an arbitrary renumeration of vertices, one can find integers $k$ and $l$ such that the line connecting vertices with numbers $k$ and $l$ before the renumeration has the same colour as the line between the vertices having these numbers after the renumeration.
|
Assume there exists a renumeration such that for any numbers $1 \leq k<l \leq n$ the segment connecting vertices numbered $k$ and $l$ before the renumeration has a different colour than the segment connecting vertices with the same numbers after the renumeration. Then there has to be an equal number of red and blue segments, and thus the total number of segments must be even. However, the number of segments is $\left(\begin{array}{c}1991 \\ 2\end{array}\right)=995 \cdot 1991$, an odd number.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
The vertices of a convex 1991-gon are enumerated with integers from 1 to 1991. Each side and diagonal of the 1991-gon is coloured either red or blue. Prove that, for an arbitrary renumeration of vertices, one can find integers $k$ and $l$ such that the line connecting vertices with numbers $k$ and $l$ before the renumeration has the same colour as the line between the vertices having these numbers after the renumeration.
|
Assume there exists a renumeration such that for any numbers $1 \leq k<l \leq n$ the segment connecting vertices numbered $k$ and $l$ before the renumeration has a different colour than the segment connecting vertices with the same numbers after the renumeration. Then there has to be an equal number of red and blue segments, and thus the total number of segments must be even. However, the number of segments is $\left(\begin{array}{c}1991 \\ 2\end{array}\right)=995 \cdot 1991$, an odd number.
|
{
"exam": "BalticWay",
"problem_label": "12",
"problem_match": "\n12.",
"resource_path": "BalticWay/segmented/en-bw91sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1991"
}
|
An equilateral triangle is divided into 25 congruent triangles enumerated with numbers from 1 to 25 . Prove that one can find two triangles having a common side and with the difference of the numbers assigned to them greater than 3 .
|
Define the distance between two small triangles to be the minimal number of steps one needs to move from one of the triangles to the other (a step here means transition from one triangle to another having a common side with it). The maximum distance between two small triangles is 8 and this maximum is achieved if and only if one of these lies at a corner of the big triangle and the other lies anywhere at the opposite side of it. Assume now that we have assigned the numbers 1, .., 25 to the small triangles so that the difference of the numbers assigned to any two adjacent triangles does not exceed 3 . Then the distance between the triangles numbered 1 and $25 ; 1$ and $24 ; 2$ and $25 ; 2$ and 24 must be equal to 8 . However, this is not possible since it implies that either the numbers 1 and 2 or 24 and 25 are assigned to the same "corner" triangle.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
An equilateral triangle is divided into 25 congruent triangles enumerated with numbers from 1 to 25 . Prove that one can find two triangles having a common side and with the difference of the numbers assigned to them greater than 3 .
|
Define the distance between two small triangles to be the minimal number of steps one needs to move from one of the triangles to the other (a step here means transition from one triangle to another having a common side with it). The maximum distance between two small triangles is 8 and this maximum is achieved if and only if one of these lies at a corner of the big triangle and the other lies anywhere at the opposite side of it. Assume now that we have assigned the numbers 1, .., 25 to the small triangles so that the difference of the numbers assigned to any two adjacent triangles does not exceed 3 . Then the distance between the triangles numbered 1 and $25 ; 1$ and $24 ; 2$ and $25 ; 2$ and 24 must be equal to 8 . However, this is not possible since it implies that either the numbers 1 and 2 or 24 and 25 are assigned to the same "corner" triangle.
|
{
"exam": "BalticWay",
"problem_label": "13",
"problem_match": "\n13.",
"resource_path": "BalticWay/segmented/en-bw91sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1991"
}
|
A castle has a number of halls and $n$ doors. Every door leads into another hall or outside. Every hall has at least two doors. A knight enters the castle. In any hall, he can choose any door for exit except the one he just used to enter that hall. Find a strategy allowing the knight to get outside after visiting no more than $2 n$ halls (a hall is counted each time it is entered).
|
The knight can use the following strategy: exit from any hall through the door immediately to the right of the one he used to enter that hall. Then, knowing which door was passed last and in which direction we can uniquely restore the whole path of the knight up to that point. Therefore, he will not be able to pass any door twice in the same direction unless he has been outside the castle in between.
|
not found
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A castle has a number of halls and $n$ doors. Every door leads into another hall or outside. Every hall has at least two doors. A knight enters the castle. In any hall, he can choose any door for exit except the one he just used to enter that hall. Find a strategy allowing the knight to get outside after visiting no more than $2 n$ halls (a hall is counted each time it is entered).
|
The knight can use the following strategy: exit from any hall through the door immediately to the right of the one he used to enter that hall. Then, knowing which door was passed last and in which direction we can uniquely restore the whole path of the knight up to that point. Therefore, he will not be able to pass any door twice in the same direction unless he has been outside the castle in between.
|
{
"exam": "BalticWay",
"problem_label": "14",
"problem_match": "\n14.",
"resource_path": "BalticWay/segmented/en-bw91sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1991"
}
|
In each of the squares of a chess board an arbitrary integer is written. A king starts to move on the board. As the king moves, 1 is added to the number in each square it "visits". Is it always possible to make the numbers on the chess board:
(a) all even;
(b) all divisible by 3 ;
(c) all equal?
|
Figure 1 demonstrates a possible king's path passing through each square exactly once and finally returning to the initial square. Thus, it suffices to prove part (c) as we can always increase the numbers in all the squares by 1 or 2 if necessary. Moreover, note that for any given square it is possible to modify the path shown in Figure 1 in such a way that this particular square will be passed twice while any other square will still be passed exactly once. Repeating this procedure a suitable number of times for each square we can make all the numbers on the chess board equal.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Logic and Puzzles
|
In each of the squares of a chess board an arbitrary integer is written. A king starts to move on the board. As the king moves, 1 is added to the number in each square it "visits". Is it always possible to make the numbers on the chess board:
(a) all even;
(b) all divisible by 3 ;
(c) all equal?
|
Figure 1 demonstrates a possible king's path passing through each square exactly once and finally returning to the initial square. Thus, it suffices to prove part (c) as we can always increase the numbers in all the squares by 1 or 2 if necessary. Moreover, note that for any given square it is possible to modify the path shown in Figure 1 in such a way that this particular square will be passed twice while any other square will still be passed exactly once. Repeating this procedure a suitable number of times for each square we can make all the numbers on the chess board equal.
|
{
"exam": "BalticWay",
"problem_label": "15",
"problem_match": "\n15.",
"resource_path": "BalticWay/segmented/en-bw91sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1991"
}
|
Let two circles $C_{1}$ and $C_{2}$ (with radii $r_{1}$ and $r_{2}$ ) touch each other externally, and let $l$ be their common tangent. A third circle $C_{3}$ (with radius $r_{3}<\min \left(r_{1}, r_{2}\right)$ ) is externally tangent to the two given circles and tangent to the line $l$. Prove that
$$
\frac{1}{\sqrt{r_{3}}}=\frac{1}{\sqrt{r_{1}}}+\frac{1}{\sqrt{r_{2}}}
$$
|
Let $O_{1}, O_{2}, O_{3}$ be the centres of the circles $C_{1}, C_{2}, C_{3}$, respectively. Let $P_{1}, P_{2}, P_{3}$ be the perpendicular projections of $O_{1}, O_{2}, O_{3}$ onto the line $l$ and let $Q$ be the perpendicular projection of $O_{3}$ onto the line $P_{1} O_{1}$ (see Figure 2). Then $\left|P_{1} P_{3}\right|^{2}=\left|Q O_{3}\right|^{2}=\left|O_{1} O_{3}\right|^{2}-\left|Q O_{1}\right|^{2}=\left(r_{1}+r_{3}\right)^{2}-\left(r_{1}-r_{3}\right)^{2}=4 r_{1} r_{3}$. Similarly we get $\left|P_{1} P_{2}\right|^{2}=4 r_{1} r_{2}$ and $\left|P_{2} P_{3}\right|^{2}=4 r_{2} r_{3}$. Since $\left|P_{1} P_{2}\right|=\left|P_{1} P_{3}\right|+\left|P_{2} P_{3}\right|$ we have $\sqrt{r_{1} r_{2}}=$ $\sqrt{r_{1} r_{3}}+\sqrt{r_{2} r_{3}}$, which implies the required equality.
Figure 1
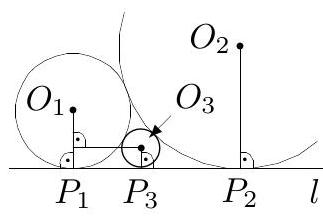
Figure 2
Figure 3
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let two circles $C_{1}$ and $C_{2}$ (with radii $r_{1}$ and $r_{2}$ ) touch each other externally, and let $l$ be their common tangent. A third circle $C_{3}$ (with radius $r_{3}<\min \left(r_{1}, r_{2}\right)$ ) is externally tangent to the two given circles and tangent to the line $l$. Prove that
$$
\frac{1}{\sqrt{r_{3}}}=\frac{1}{\sqrt{r_{1}}}+\frac{1}{\sqrt{r_{2}}}
$$
|
Let $O_{1}, O_{2}, O_{3}$ be the centres of the circles $C_{1}, C_{2}, C_{3}$, respectively. Let $P_{1}, P_{2}, P_{3}$ be the perpendicular projections of $O_{1}, O_{2}, O_{3}$ onto the line $l$ and let $Q$ be the perpendicular projection of $O_{3}$ onto the line $P_{1} O_{1}$ (see Figure 2). Then $\left|P_{1} P_{3}\right|^{2}=\left|Q O_{3}\right|^{2}=\left|O_{1} O_{3}\right|^{2}-\left|Q O_{1}\right|^{2}=\left(r_{1}+r_{3}\right)^{2}-\left(r_{1}-r_{3}\right)^{2}=4 r_{1} r_{3}$. Similarly we get $\left|P_{1} P_{2}\right|^{2}=4 r_{1} r_{2}$ and $\left|P_{2} P_{3}\right|^{2}=4 r_{2} r_{3}$. Since $\left|P_{1} P_{2}\right|=\left|P_{1} P_{3}\right|+\left|P_{2} P_{3}\right|$ we have $\sqrt{r_{1} r_{2}}=$ $\sqrt{r_{1} r_{3}}+\sqrt{r_{2} r_{3}}$, which implies the required equality.

Figure 1

Figure 2

Figure 3
|
{
"exam": "BalticWay",
"problem_label": "16",
"problem_match": "\n16.",
"resource_path": "BalticWay/segmented/en-bw91sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1991"
}
|
Let the coordinate planes have the reflection property. A beam falls onto one of them. How does the final direction of the beam after reflecting from all three coordinate planes depend on its initial direction?
|
Let the velocity vector of the beam be $\vec{v}=(\alpha, \beta, \gamma)$. Reflection from each of the coordinate planes changes the sign of exactly one of the coordinates $\alpha, \beta$ and $\gamma$, and thus the final direction will be opposite to the initial one.
|
(-\alpha, -\beta, -\gamma)
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let the coordinate planes have the reflection property. A beam falls onto one of them. How does the final direction of the beam after reflecting from all three coordinate planes depend on its initial direction?
|
Let the velocity vector of the beam be $\vec{v}=(\alpha, \beta, \gamma)$. Reflection from each of the coordinate planes changes the sign of exactly one of the coordinates $\alpha, \beta$ and $\gamma$, and thus the final direction will be opposite to the initial one.
|
{
"exam": "BalticWay",
"problem_label": "17",
"problem_match": "\n17.",
"resource_path": "BalticWay/segmented/en-bw91sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1991"
}
|
Is it possible to put two tetrahedra of volume $\frac{1}{2}$ without intersection into a sphere with radius 1 ?
|
No, it is not. Any tetrahedron that does not contain the centre of the sphere as an internal point has a height drawn to one of its faces less than or equal to the radius of the sphere. As each of the faces of the tetrahedron is contained in a circle with radius not greater than 1 , its area cannot exceed $\frac{3 \sqrt{3}}{4}$. Thus, the volume of such a tetrahedron must be less or equal than $\frac{1}{3} \cdot 1 \cdot \frac{3 \sqrt{3}}{4}=\frac{\sqrt{3}}{4}<\frac{1}{2}$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Is it possible to put two tetrahedra of volume $\frac{1}{2}$ without intersection into a sphere with radius 1 ?
|
No, it is not. Any tetrahedron that does not contain the centre of the sphere as an internal point has a height drawn to one of its faces less than or equal to the radius of the sphere. As each of the faces of the tetrahedron is contained in a circle with radius not greater than 1 , its area cannot exceed $\frac{3 \sqrt{3}}{4}$. Thus, the volume of such a tetrahedron must be less or equal than $\frac{1}{3} \cdot 1 \cdot \frac{3 \sqrt{3}}{4}=\frac{\sqrt{3}}{4}<\frac{1}{2}$.
|
{
"exam": "BalticWay",
"problem_label": "18",
"problem_match": "\n18.",
"resource_path": "BalticWay/segmented/en-bw91sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1991"
}
|
Let's expand a little bit three circles, touching each other externally, so that three pairs of intersection points appear. Denote by $A_{1}, B_{1}, C_{1}$ the three so obtained "external" points and by $A_{2}, B_{2}, C_{2}$ the corresponding "internal" points. Prove the equality
$$
\left|A_{1} B_{2}\right| \cdot\left|B_{1} C_{2}\right| \cdot\left|C_{1} A_{2}\right|=\left|A_{1} C_{2}\right| \cdot\left|C_{1} B_{2}\right| \cdot\left|B_{1} A_{2}\right| .
$$
|
First, note that the three straight lines $A_{1} A_{2}, B_{1} B_{2}$ and $C_{1} C_{2}$ intersect in a single point $O$. Indeed, each of the lines is the locus of points from which the tangents to two of the circles are of equal length (it is easy to check that this locus has the form of a straight line and obviously it contains the two intersection points of the circles). Now, we have $\left|O A_{1}\right| \cdot\left|O A_{2}\right|=\left|O B_{1}\right| \cdot\left|O B_{2}\right|$ (as both of these products are equal to $|O T|^{2}$ where $O T$ is a tangent line to the circle containing $A_{1}, A_{2}, B_{1}, B_{2}$, and $T$ is the corresponding point of tangency). Hence $\frac{\left|O A_{1}\right|}{\left|O B_{2}\right|}=\frac{\left|O B_{1}\right|}{\left|O A_{2}\right|}$ which implies that the triangles $O A_{1} B_{2}$ and $O B_{1} A_{2}$ are similar and $\frac{\left|A_{1} B_{2}\right|}{\left|A_{2} B_{1}\right|}=\frac{\left|O A_{1}\right|}{\left|O B_{1}\right|}$. Similarly we get $\frac{\left|B_{1} C_{2}\right|}{\left|B_{2} C_{1}\right|}=\frac{\left|O B_{1}\right|}{\left|O C_{1}\right|}$ and $\frac{\left|C_{1} A_{2}\right|}{\left|C_{2} A_{1}\right|}=\frac{\left|O C_{1}\right|}{\left|O A_{1}\right|}$. Multiplying these three equalities gives the desired result.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let's expand a little bit three circles, touching each other externally, so that three pairs of intersection points appear. Denote by $A_{1}, B_{1}, C_{1}$ the three so obtained "external" points and by $A_{2}, B_{2}, C_{2}$ the corresponding "internal" points. Prove the equality
$$
\left|A_{1} B_{2}\right| \cdot\left|B_{1} C_{2}\right| \cdot\left|C_{1} A_{2}\right|=\left|A_{1} C_{2}\right| \cdot\left|C_{1} B_{2}\right| \cdot\left|B_{1} A_{2}\right| .
$$
|
First, note that the three straight lines $A_{1} A_{2}, B_{1} B_{2}$ and $C_{1} C_{2}$ intersect in a single point $O$. Indeed, each of the lines is the locus of points from which the tangents to two of the circles are of equal length (it is easy to check that this locus has the form of a straight line and obviously it contains the two intersection points of the circles). Now, we have $\left|O A_{1}\right| \cdot\left|O A_{2}\right|=\left|O B_{1}\right| \cdot\left|O B_{2}\right|$ (as both of these products are equal to $|O T|^{2}$ where $O T$ is a tangent line to the circle containing $A_{1}, A_{2}, B_{1}, B_{2}$, and $T$ is the corresponding point of tangency). Hence $\frac{\left|O A_{1}\right|}{\left|O B_{2}\right|}=\frac{\left|O B_{1}\right|}{\left|O A_{2}\right|}$ which implies that the triangles $O A_{1} B_{2}$ and $O B_{1} A_{2}$ are similar and $\frac{\left|A_{1} B_{2}\right|}{\left|A_{2} B_{1}\right|}=\frac{\left|O A_{1}\right|}{\left|O B_{1}\right|}$. Similarly we get $\frac{\left|B_{1} C_{2}\right|}{\left|B_{2} C_{1}\right|}=\frac{\left|O B_{1}\right|}{\left|O C_{1}\right|}$ and $\frac{\left|C_{1} A_{2}\right|}{\left|C_{2} A_{1}\right|}=\frac{\left|O C_{1}\right|}{\left|O A_{1}\right|}$. Multiplying these three equalities gives the desired result.
|
{
"exam": "BalticWay",
"problem_label": "19",
"problem_match": "\n19.",
"resource_path": "BalticWay/segmented/en-bw91sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1991"
}
|
Consider two points $A\left(x_{1}, y_{1}\right)$ and $B\left(x_{2}, y_{2}\right)$ on the graph of the function $y=\frac{1}{x}$ such that $0<x_{1}<x_{2}$ and $|A B|=2 \cdot|O A|(O$ is the reference point, i.e., $O(0,0))$. Let $C$ be the midpoint of the segment $A B$. Prove that the angle between the $x$-axis and the ray $O A$ is equal to three times the angle between $x$-axis and the ray $O C$.
|
We have $A\left(x_{1}, \frac{1}{x_{1}}\right), B\left(x_{2}, \frac{1}{x_{2}}\right)$ and $C\left(\frac{x_{1}+x_{2}}{2}, \frac{1}{2 x_{1}}+\frac{1}{2 x_{2}}\right)$. Computing the coordinates of $\bar{v}=$ $|O C| \cdot \overline{A C}+|A C| \cdot \overline{O C}$ we find that the vector $\bar{v}-$ and hence also the bisector of the angle $\angle O C A-$ is parallel to the $x$-axis. Since $|O A|=|A C|$ this yields $\angle A O C=\angle A C O=2 \cdot \angle C O x$ (see Figure 3) and $\angle A O x=\angle A O C+\angle C O x=3 \cdot \angle C O x$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Consider two points $A\left(x_{1}, y_{1}\right)$ and $B\left(x_{2}, y_{2}\right)$ on the graph of the function $y=\frac{1}{x}$ such that $0<x_{1}<x_{2}$ and $|A B|=2 \cdot|O A|(O$ is the reference point, i.e., $O(0,0))$. Let $C$ be the midpoint of the segment $A B$. Prove that the angle between the $x$-axis and the ray $O A$ is equal to three times the angle between $x$-axis and the ray $O C$.
|
We have $A\left(x_{1}, \frac{1}{x_{1}}\right), B\left(x_{2}, \frac{1}{x_{2}}\right)$ and $C\left(\frac{x_{1}+x_{2}}{2}, \frac{1}{2 x_{1}}+\frac{1}{2 x_{2}}\right)$. Computing the coordinates of $\bar{v}=$ $|O C| \cdot \overline{A C}+|A C| \cdot \overline{O C}$ we find that the vector $\bar{v}-$ and hence also the bisector of the angle $\angle O C A-$ is parallel to the $x$-axis. Since $|O A|=|A C|$ this yields $\angle A O C=\angle A C O=2 \cdot \angle C O x$ (see Figure 3) and $\angle A O x=\angle A O C+\angle C O x=3 \cdot \angle C O x$.
|
{
"exam": "BalticWay",
"problem_label": "20",
"problem_match": "\n20.",
"resource_path": "BalticWay/segmented/en-bw91sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1991"
}
|
Let $p$ and $q$ be two consecutive odd prime numbers. Prove that $p+q$ is a product of at least three positive integers greater than 1 (not necessarily different).
|
Since $q-p=2 k$ is even, we have $p+q=2(p+k)$. It is clear that $p<p+k<p+2 k=q$. Therefore $p+k$ is not prime and, consequently, is a product of two positive integers greater than 1 .
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $p$ and $q$ be two consecutive odd prime numbers. Prove that $p+q$ is a product of at least three positive integers greater than 1 (not necessarily different).
|
Since $q-p=2 k$ is even, we have $p+q=2(p+k)$. It is clear that $p<p+k<p+2 k=q$. Therefore $p+k$ is not prime and, consequently, is a product of two positive integers greater than 1 .
|
{
"exam": "BalticWay",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "BalticWay/segmented/en-bw92sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1992"
}
|
Denote by $d(n)$ the number of all positive divisors of a positive integer $n$ (including 1 and $n$ ). Prove that there are infinitely many $n$ such that $\frac{n}{d(n)}$ is an integer.
|
Consider numbers of the form $p^{p^{n}-1}$ where $p$ is an arbitrary prime number and $n=1,2, \ldots$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Denote by $d(n)$ the number of all positive divisors of a positive integer $n$ (including 1 and $n$ ). Prove that there are infinitely many $n$ such that $\frac{n}{d(n)}$ is an integer.
|
Consider numbers of the form $p^{p^{n}-1}$ where $p$ is an arbitrary prime number and $n=1,2, \ldots$
|
{
"exam": "BalticWay",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "BalticWay/segmented/en-bw92sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1992"
}
|
Find an infinite non-constant arithmetic progression of positive integers such that each term is neither a sum of two squares, nor a sum of two cubes (of positive integers).
|
For any natural number $n$, we have $n^{2} \equiv 0$ or $n^{2} \equiv 1(\bmod 4)$ and $n^{3} \equiv 0$ or $n^{3} \equiv \pm 1(\bmod 9)$. Thus $\{36 n+3 \mid n=1,2, \ldots\}$ is a progression with the required property.
|
\{36 n+3 \mid n=1,2, \ldots\}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find an infinite non-constant arithmetic progression of positive integers such that each term is neither a sum of two squares, nor a sum of two cubes (of positive integers).
|
For any natural number $n$, we have $n^{2} \equiv 0$ or $n^{2} \equiv 1(\bmod 4)$ and $n^{3} \equiv 0$ or $n^{3} \equiv \pm 1(\bmod 9)$. Thus $\{36 n+3 \mid n=1,2, \ldots\}$ is a progression with the required property.
|
{
"exam": "BalticWay",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "BalticWay/segmented/en-bw92sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1992"
}
|
Is it possible to draw a hexagon with vertices in the knots of an integer lattice so that the squares of the lengths of the sides are six consecutive positive integers?
|
The sum of any six consecutive positive integers is odd. On the other hand, the sum of the squares of the lengths of the sides of the hexagon is equal to the sum of the squares of their projections onto the two axes. But this number has the same parity as the sum of the projections themselves, the latter being obviously even.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Is it possible to draw a hexagon with vertices in the knots of an integer lattice so that the squares of the lengths of the sides are six consecutive positive integers?
|
The sum of any six consecutive positive integers is odd. On the other hand, the sum of the squares of the lengths of the sides of the hexagon is equal to the sum of the squares of their projections onto the two axes. But this number has the same parity as the sum of the projections themselves, the latter being obviously even.
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "BalticWay/segmented/en-bw92sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1992"
}
|
Given that $a^{2}+b^{2}+(a+b)^{2}=c^{2}+d^{2}+(c+d)^{2}$, prove that $a^{4}+b^{4}+(a+b)^{4}=c^{4}+d^{4}+(c+d)^{4}$.
|
Use the identity $\left(a^{2}+b^{2}+(a+b)^{2}\right)^{2}=2\left(a^{4}+b^{4}+(a+b)^{4}\right)$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Given that $a^{2}+b^{2}+(a+b)^{2}=c^{2}+d^{2}+(c+d)^{2}$, prove that $a^{4}+b^{4}+(a+b)^{4}=c^{4}+d^{4}+(c+d)^{4}$.
|
Use the identity $\left(a^{2}+b^{2}+(a+b)^{2}\right)^{2}=2\left(a^{4}+b^{4}+(a+b)^{4}\right)$.
|
{
"exam": "BalticWay",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "BalticWay/segmented/en-bw92sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1992"
}
|
Prove that the product of the 99 numbers of the form $\frac{k^{3}-1}{k^{3}+1}$ where $k=2,3, \ldots, 100$, is greater than $\frac{2}{3}$.
|
Note that
$$
\frac{k^{3}-1}{k^{3}+1}=\frac{(k-1)\left(k^{2}+k+1\right)}{(k+1)\left(k^{2}-k+1\right)}=\frac{(k-1)\left(k^{2}+k+1\right)}{(k+1)\left((k-1)^{2}+(k-1)+1\right)}
$$
After obvious cancellations we get
$$
\prod_{k=2}^{100} \frac{k^{3}-1}{k^{3}+1}=\frac{1 \cdot 2 \cdot\left(100^{2}+100+1\right)}{100 \cdot 101 \cdot\left(1^{2}+1+1\right)}>\frac{2}{3}
$$
|
\frac{1 \cdot 2 \cdot\left(100^{2}+100+1\right)}{100 \cdot 101 \cdot\left(1^{2}+1+1\right)}>\frac{2}{3}
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that the product of the 99 numbers of the form $\frac{k^{3}-1}{k^{3}+1}$ where $k=2,3, \ldots, 100$, is greater than $\frac{2}{3}$.
|
Note that
$$
\frac{k^{3}-1}{k^{3}+1}=\frac{(k-1)\left(k^{2}+k+1\right)}{(k+1)\left(k^{2}-k+1\right)}=\frac{(k-1)\left(k^{2}+k+1\right)}{(k+1)\left((k-1)^{2}+(k-1)+1\right)}
$$
After obvious cancellations we get
$$
\prod_{k=2}^{100} \frac{k^{3}-1}{k^{3}+1}=\frac{1 \cdot 2 \cdot\left(100^{2}+100+1\right)}{100 \cdot 101 \cdot\left(1^{2}+1+1\right)}>\frac{2}{3}
$$
|
{
"exam": "BalticWay",
"problem_label": "6",
"problem_match": "\n6.",
"resource_path": "BalticWay/segmented/en-bw92sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1992"
}
|
Let $a=\sqrt[1992]{1992}$. Which number is greater:
$$
\left.a^{a^{a^{a}}}\right\} 1992
$$
or 1992 ?
|
The first of these numbers is less than
$$
\left.\left.a^{a^{a^{. \cdot}}}\right\}^{1992}=a^{a^{a^{. \cdot}}}\right\}^{1991}=\ldots=1992 .
$$
|
1992
|
Incomplete
|
Yes
|
math-word-problem
|
Algebra
|
Let $a=\sqrt[1992]{1992}$. Which number is greater:
$$
\left.a^{a^{a^{a}}}\right\} 1992
$$
or 1992 ?
|
The first of these numbers is less than
$$
\left.\left.a^{a^{a^{. \cdot}}}\right\}^{1992}=a^{a^{a^{. \cdot}}}\right\}^{1991}=\ldots=1992 .
$$
|
{
"exam": "BalticWay",
"problem_label": "7",
"problem_match": "\n7.",
"resource_path": "BalticWay/segmented/en-bw92sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1992"
}
|
Find all integers satisfying the equation $2^{x} \cdot(4-x)=2 x+4$.
|
Since $2^{x}$ must be positive, we have $\frac{2 x+4}{4-x}>0$ yielding $-2<x<4$. Thus it suffices to check the points $-1,0,1,2,3$. The three solutions are $x=0,1,2$.
|
x=0,1,2
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all integers satisfying the equation $2^{x} \cdot(4-x)=2 x+4$.
|
Since $2^{x}$ must be positive, we have $\frac{2 x+4}{4-x}>0$ yielding $-2<x<4$. Thus it suffices to check the points $-1,0,1,2,3$. The three solutions are $x=0,1,2$.
|
{
"exam": "BalticWay",
"problem_label": "8",
"problem_match": "\n8.",
"resource_path": "BalticWay/segmented/en-bw92sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1992"
}
|
A polynomial $f(x)=x^{3}+a x^{2}+b x+c$ is such that $b<0$ and $a b=9 c$. Prove that the polynomial has three different real roots.
|
Consider the derivative $f^{\prime}(x)=3 x^{2}+2 a x+b$. Since $b<0$, it has two real roots $x_{1}$ and $x_{2}$. Since $f(x) \rightarrow \pm \infty$ as $x \rightarrow \pm \infty$, it is sufficient to check that $f\left(x_{1}\right)$ and $f\left(x_{2}\right)$ have different signs, i.e., $f\left(x_{1}\right) f\left(x_{2}\right)<0$. Dividing $f(x)$ by $f^{\prime}(x)$ and using the equality $a b=9 c$ we find that the remainder is equal to $x\left(\frac{2}{3} b-\frac{2}{9} a^{2}\right)$. Now, as $x_{1} x_{2}=\frac{b}{3}<0$ we have $f\left(x_{1}\right) f\left(x_{2}\right)=x_{1} x_{2}\left(\frac{2}{3} b-\frac{2}{9} a^{2}\right)^{2}<0$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
A polynomial $f(x)=x^{3}+a x^{2}+b x+c$ is such that $b<0$ and $a b=9 c$. Prove that the polynomial has three different real roots.
|
Consider the derivative $f^{\prime}(x)=3 x^{2}+2 a x+b$. Since $b<0$, it has two real roots $x_{1}$ and $x_{2}$. Since $f(x) \rightarrow \pm \infty$ as $x \rightarrow \pm \infty$, it is sufficient to check that $f\left(x_{1}\right)$ and $f\left(x_{2}\right)$ have different signs, i.e., $f\left(x_{1}\right) f\left(x_{2}\right)<0$. Dividing $f(x)$ by $f^{\prime}(x)$ and using the equality $a b=9 c$ we find that the remainder is equal to $x\left(\frac{2}{3} b-\frac{2}{9} a^{2}\right)$. Now, as $x_{1} x_{2}=\frac{b}{3}<0$ we have $f\left(x_{1}\right) f\left(x_{2}\right)=x_{1} x_{2}\left(\frac{2}{3} b-\frac{2}{9} a^{2}\right)^{2}<0$.
|
{
"exam": "BalticWay",
"problem_label": "9",
"problem_match": "\n9.",
"resource_path": "BalticWay/segmented/en-bw92sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1992"
}
|
Find all fourth degree polynomials $p(x)$ such that the following four conditions are satisfied:
(i) $p(x)=p(-x)$ for all $x$.
(ii) $p(x) \geq 0$ for all $x$.
(iii) $p(0)=1$.
(iv) $p(x)$ has exactly two local minimum points $x_{1}$ and $x_{2}$ such that $\left|x_{1}-x_{2}\right|=2$.
|
Let $p(x)=a x^{4}+b x^{3}+c x^{2}+d x+e$ with $a \neq 0$. From $(i)-(i i i)$ we get $b=d=0, a>0$ and $e=1$. From (iv) it follows that $p^{\prime}(x)=4 a x^{3}+2 c x$ has at least two different real roots. Since $a>0$, we have $c<0$ and $p^{\prime}(x)$ has three roots $x=0, x= \pm \sqrt{-c /(2 a)}$. The minimum points mentioned in $(i v)$ must be $x= \pm \sqrt{-c /(2 a)}$, so $2 \sqrt{-c /(2 a)}=2$ and $c=-2 a$. Finally, by $(i i)$ we have $p(x)=a\left(x^{2}-1\right)^{2}+1-a \geq 0$ for all $x$, which implies $0<a \leq 1$. It is easy to check that every such polynomial satisfies the conditions (i)-(iv).
|
0<a \leq 1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all fourth degree polynomials $p(x)$ such that the following four conditions are satisfied:
(i) $p(x)=p(-x)$ for all $x$.
(ii) $p(x) \geq 0$ for all $x$.
(iii) $p(0)=1$.
(iv) $p(x)$ has exactly two local minimum points $x_{1}$ and $x_{2}$ such that $\left|x_{1}-x_{2}\right|=2$.
|
Let $p(x)=a x^{4}+b x^{3}+c x^{2}+d x+e$ with $a \neq 0$. From $(i)-(i i i)$ we get $b=d=0, a>0$ and $e=1$. From (iv) it follows that $p^{\prime}(x)=4 a x^{3}+2 c x$ has at least two different real roots. Since $a>0$, we have $c<0$ and $p^{\prime}(x)$ has three roots $x=0, x= \pm \sqrt{-c /(2 a)}$. The minimum points mentioned in $(i v)$ must be $x= \pm \sqrt{-c /(2 a)}$, so $2 \sqrt{-c /(2 a)}=2$ and $c=-2 a$. Finally, by $(i i)$ we have $p(x)=a\left(x^{2}-1\right)^{2}+1-a \geq 0$ for all $x$, which implies $0<a \leq 1$. It is easy to check that every such polynomial satisfies the conditions (i)-(iv).
|
{
"exam": "BalticWay",
"problem_label": "10",
"problem_match": "\n10.",
"resource_path": "BalticWay/segmented/en-bw92sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1992"
}
|
Let $\mathbb{Q}^{+}$denote the set of positive rational numbers. Show that there exists one and only one function $f: \mathbb{Q}^{+} \rightarrow \mathbb{Q}^{+}$satisfying the following conditions:
(i) If $0<q<\frac{1}{2}$ then $f(q)=1+f\left(\frac{q}{1-2 q}\right)$.
(ii) If $1<q \leq 2$ then $f(q)=1+f(q-1)$.
(iii) $f(q) \cdot f\left(\frac{1}{q}\right)=1$ for all $q \in \mathbb{Q}^{+}$.
|
By condition (iii) we have $f(1)=1$. Applying condition (iii) to each of (i) and (ii) gives two new conditions $\left(i^{\prime}\right)$ and $\left(i i^{\prime}\right)$ taking care of $q>2$ and $\frac{1}{2} \leq q<1$ respectively. Now, for any rational number $\frac{a}{b} \neq 1$ we can use $(i),\left(i^{\prime}\right),(i i)$ or $\left(i i^{\prime}\right)$ to express $f\left(\frac{a}{b}\right)$ in terms of $f\left(\frac{a^{\prime}}{b^{\prime}}\right)$ where $a^{\prime}+b^{\prime}<a+b$. The recursion therefore finishes in a finite number of steps, when we can use $f(1)=1$. Thus we have established that such a function $f$ exists, and is uniquely determined by the given conditions.
Remark. Initially it was also required to determine all fixed points of the function $f$, i.e., all solutions $q$ of the equation $f(q)=q$, but the Jury of the contest decided to simplify the problem. Here we present a solution. First note that if $q$ is a fixed point, then so is $\frac{1}{q}$. By $(i)$, if $0<q<\frac{1}{2}$ is a fixed point, then $f\left(\frac{q}{1-2 q}\right)=q-1<0$ which is impossible, so there are no fixed points $0<q<\frac{1}{2}$ or $q>2$. Now, for a fixed point $1<\frac{a}{b} \leq 2$ (ii) easily gives us that $\frac{a}{b}-1=\frac{a-b}{b}$ and $\frac{b}{a-b}$ are fixed points too. It is easy to see that $1 \leq \frac{b}{a-b} \leq 2$ (the latter holds because $\frac{b}{a-b}$ is a fixed point). As the sum of the numerator and denominator of the new fixed point is strictly less than $a+b$ we can continue in this manner until, in a finite number of steps, we arrive at the fixed point 1. By reversing the process, any fixed point $q>1$ can be constructed by repeatedly using the condition that if $\frac{a}{b}>1$ is a fixed point then so is $\frac{a+b}{a}$, starting with $a=b=1$. It is now an easy exercise to see that these fixed points have the form $\frac{F_{n+1}}{F_{n}}$ where $\left\{F_{n}\right\}_{n \in \mathbb{N}}$ is the sequence of Fibonacci numbers.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $\mathbb{Q}^{+}$denote the set of positive rational numbers. Show that there exists one and only one function $f: \mathbb{Q}^{+} \rightarrow \mathbb{Q}^{+}$satisfying the following conditions:
(i) If $0<q<\frac{1}{2}$ then $f(q)=1+f\left(\frac{q}{1-2 q}\right)$.
(ii) If $1<q \leq 2$ then $f(q)=1+f(q-1)$.
(iii) $f(q) \cdot f\left(\frac{1}{q}\right)=1$ for all $q \in \mathbb{Q}^{+}$.
|
By condition (iii) we have $f(1)=1$. Applying condition (iii) to each of (i) and (ii) gives two new conditions $\left(i^{\prime}\right)$ and $\left(i i^{\prime}\right)$ taking care of $q>2$ and $\frac{1}{2} \leq q<1$ respectively. Now, for any rational number $\frac{a}{b} \neq 1$ we can use $(i),\left(i^{\prime}\right),(i i)$ or $\left(i i^{\prime}\right)$ to express $f\left(\frac{a}{b}\right)$ in terms of $f\left(\frac{a^{\prime}}{b^{\prime}}\right)$ where $a^{\prime}+b^{\prime}<a+b$. The recursion therefore finishes in a finite number of steps, when we can use $f(1)=1$. Thus we have established that such a function $f$ exists, and is uniquely determined by the given conditions.
Remark. Initially it was also required to determine all fixed points of the function $f$, i.e., all solutions $q$ of the equation $f(q)=q$, but the Jury of the contest decided to simplify the problem. Here we present a solution. First note that if $q$ is a fixed point, then so is $\frac{1}{q}$. By $(i)$, if $0<q<\frac{1}{2}$ is a fixed point, then $f\left(\frac{q}{1-2 q}\right)=q-1<0$ which is impossible, so there are no fixed points $0<q<\frac{1}{2}$ or $q>2$. Now, for a fixed point $1<\frac{a}{b} \leq 2$ (ii) easily gives us that $\frac{a}{b}-1=\frac{a-b}{b}$ and $\frac{b}{a-b}$ are fixed points too. It is easy to see that $1 \leq \frac{b}{a-b} \leq 2$ (the latter holds because $\frac{b}{a-b}$ is a fixed point). As the sum of the numerator and denominator of the new fixed point is strictly less than $a+b$ we can continue in this manner until, in a finite number of steps, we arrive at the fixed point 1. By reversing the process, any fixed point $q>1$ can be constructed by repeatedly using the condition that if $\frac{a}{b}>1$ is a fixed point then so is $\frac{a+b}{a}$, starting with $a=b=1$. It is now an easy exercise to see that these fixed points have the form $\frac{F_{n+1}}{F_{n}}$ where $\left\{F_{n}\right\}_{n \in \mathbb{N}}$ is the sequence of Fibonacci numbers.
|
{
"exam": "BalticWay",
"problem_label": "11",
"problem_match": "\n11.",
"resource_path": "BalticWay/segmented/en-bw92sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1992"
}
|
Let $\mathbb{N}$ denote the set of positive integers. Let $\varphi: \mathbb{N} \rightarrow \mathbb{N}$ be a bijective function and assume that there exists a finite limit
$$
\lim _{n \rightarrow \infty} \frac{\varphi(n)}{n}=L
$$
What are the possible values of $L$ ?
|
In this solution we allow $L$ to be $\infty$ as well. We show that $L=1$ is the only possible value. Assume that $L>1$. Then there exists a number $N$ such that for any $n \geq N$ we have $\frac{\varphi(n)}{n}>1$ and thus $\varphi(n) \geq n+1 \geq N+1$. But then $\varphi$ cannot be bijective, since the numbers $1,2, \ldots, N-1$ cannot be bijectively mapped onto $1,2, \ldots, N$.
Now assume that $L<1$. Since $\varphi$ is bijective we clearly have $\varphi(n) \rightarrow \infty$ as $n \rightarrow \infty$. Then
$$
\lim _{n \rightarrow \infty} \frac{\varphi^{-1}(n)}{n}=\lim _{n \rightarrow \infty} \frac{\varphi^{-1}(\varphi(n))}{\varphi(n)}=\lim _{n \rightarrow \infty} \frac{n}{\varphi(n)}=\frac{1}{L}>1,
$$
i.e., $\lim _{n \rightarrow \infty} \frac{\varphi^{-1}(n)}{n}>1$, which is a contradiction since $\varphi^{-1}$ is also bijective. (When $L=0$ we interpret $\frac{1}{L}$ as $\infty$ ).
|
L=1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $\mathbb{N}$ denote the set of positive integers. Let $\varphi: \mathbb{N} \rightarrow \mathbb{N}$ be a bijective function and assume that there exists a finite limit
$$
\lim _{n \rightarrow \infty} \frac{\varphi(n)}{n}=L
$$
What are the possible values of $L$ ?
|
In this solution we allow $L$ to be $\infty$ as well. We show that $L=1$ is the only possible value. Assume that $L>1$. Then there exists a number $N$ such that for any $n \geq N$ we have $\frac{\varphi(n)}{n}>1$ and thus $\varphi(n) \geq n+1 \geq N+1$. But then $\varphi$ cannot be bijective, since the numbers $1,2, \ldots, N-1$ cannot be bijectively mapped onto $1,2, \ldots, N$.
Now assume that $L<1$. Since $\varphi$ is bijective we clearly have $\varphi(n) \rightarrow \infty$ as $n \rightarrow \infty$. Then
$$
\lim _{n \rightarrow \infty} \frac{\varphi^{-1}(n)}{n}=\lim _{n \rightarrow \infty} \frac{\varphi^{-1}(\varphi(n))}{\varphi(n)}=\lim _{n \rightarrow \infty} \frac{n}{\varphi(n)}=\frac{1}{L}>1,
$$
i.e., $\lim _{n \rightarrow \infty} \frac{\varphi^{-1}(n)}{n}>1$, which is a contradiction since $\varphi^{-1}$ is also bijective. (When $L=0$ we interpret $\frac{1}{L}$ as $\infty$ ).
|
{
"exam": "BalticWay",
"problem_label": "12",
"problem_match": "\n12.",
"resource_path": "BalticWay/segmented/en-bw92sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1992"
}
|
Prove that for any positive $x_{1}, x_{2}, \ldots, x_{n}$ and $y_{1}, y_{2}, \ldots, y_{n}$ the inequality
$$
\sum_{i=1}^{n} \frac{1}{x_{i} y_{i}} \geq \frac{4 n^{2}}{\sum_{i=1}^{n}\left(x_{i}+y_{i}\right)^{2}}
$$
holds.
|
Since $\left(x_{i}+y_{i}\right)^{2} \geq 4 x_{i} y_{i}$, it is sufficient to prove that
$$
\left(\sum_{i=1}^{n} \frac{1}{x_{i} y_{i}}\right)\left(\sum_{i=1}^{n} x_{i} y_{i}\right) \geq n^{2}
$$
This can easily be done by induction using the fact that $a+\frac{1}{a} \geq 2$ for any $a>0$. It also follows directly from the Cauchy-Schwarz inequality.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that for any positive $x_{1}, x_{2}, \ldots, x_{n}$ and $y_{1}, y_{2}, \ldots, y_{n}$ the inequality
$$
\sum_{i=1}^{n} \frac{1}{x_{i} y_{i}} \geq \frac{4 n^{2}}{\sum_{i=1}^{n}\left(x_{i}+y_{i}\right)^{2}}
$$
holds.
|
Since $\left(x_{i}+y_{i}\right)^{2} \geq 4 x_{i} y_{i}$, it is sufficient to prove that
$$
\left(\sum_{i=1}^{n} \frac{1}{x_{i} y_{i}}\right)\left(\sum_{i=1}^{n} x_{i} y_{i}\right) \geq n^{2}
$$
This can easily be done by induction using the fact that $a+\frac{1}{a} \geq 2$ for any $a>0$. It also follows directly from the Cauchy-Schwarz inequality.
|
{
"exam": "BalticWay",
"problem_label": "13",
"problem_match": "\n13.",
"resource_path": "BalticWay/segmented/en-bw92sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1992"
}
|
There is a finite number of towns in a country. They are connected by one direction roads. It is known that, for any two towns, one of them can be reached from the other one. Prove that there is a town such that all the remaining towns can be reached from it.
|
Consider a town $A$ from which a maximal number of towns can be reached. Suppose there is a town $B$ which cannot be reached from $A$. Then $A$ can be reached from $B$ and so one can reach more towns from $B$ than from $A$, a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
There is a finite number of towns in a country. They are connected by one direction roads. It is known that, for any two towns, one of them can be reached from the other one. Prove that there is a town such that all the remaining towns can be reached from it.
|
Consider a town $A$ from which a maximal number of towns can be reached. Suppose there is a town $B$ which cannot be reached from $A$. Then $A$ can be reached from $B$ and so one can reach more towns from $B$ than from $A$, a contradiction.
|
{
"exam": "BalticWay",
"problem_label": "14",
"problem_match": "\n14.",
"resource_path": "BalticWay/segmented/en-bw92sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1992"
}
|
Noah has to fit 8 species of animals into 4 cages of the ark. He plans to put species in each cage. It turns out that, for each species, there are at most 3 other species with which it cannot share the accommodation. Prove that there is a way to assign the animals to their cages so that each species shares a cage with compatible species.
|
Start assigning the species to cages in an arbitrary order. Since for each species there are at most three species incompatible with it, we can always add it to one of the four cages.
Remark. Initially the problem was posed as follows: "...He plans to put two species in each cage..." Because of a misprint the word "two" disappeared, and the problem became trivial. We give a solution to the original problem. Start with the distribution obtained above. If in some cage $A$ there are more than three species, then there is also a cage $B$ with at most one species and this species is compatible with at least one species in cage $A$, which we can then transfer to cage $B$. Thus we may assume that there are at most three species in each cage. If there are two cages with 3 species, then we can obviously transfer one of these 6 species to one of the remaining two cages. Now, assume the four cages contain 1, 2, 2 and 3 species respectively. If the species in the first cage is compatible with one in the fourth cage, we can transfer that species to the first cage, and we are done. Otherwise, for an arbitrary species $X$ in the fourth cage there exists a species compatible with it in either the second or the third cage. Transfer the other species from that cage to the first cage, and then $X$ to that cage.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Noah has to fit 8 species of animals into 4 cages of the ark. He plans to put species in each cage. It turns out that, for each species, there are at most 3 other species with which it cannot share the accommodation. Prove that there is a way to assign the animals to their cages so that each species shares a cage with compatible species.
|
Start assigning the species to cages in an arbitrary order. Since for each species there are at most three species incompatible with it, we can always add it to one of the four cages.
Remark. Initially the problem was posed as follows: "...He plans to put two species in each cage..." Because of a misprint the word "two" disappeared, and the problem became trivial. We give a solution to the original problem. Start with the distribution obtained above. If in some cage $A$ there are more than three species, then there is also a cage $B$ with at most one species and this species is compatible with at least one species in cage $A$, which we can then transfer to cage $B$. Thus we may assume that there are at most three species in each cage. If there are two cages with 3 species, then we can obviously transfer one of these 6 species to one of the remaining two cages. Now, assume the four cages contain 1, 2, 2 and 3 species respectively. If the species in the first cage is compatible with one in the fourth cage, we can transfer that species to the first cage, and we are done. Otherwise, for an arbitrary species $X$ in the fourth cage there exists a species compatible with it in either the second or the third cage. Transfer the other species from that cage to the first cage, and then $X$ to that cage.
|
{
"exam": "BalticWay",
"problem_label": "15",
"problem_match": "\n15.",
"resource_path": "BalticWay/segmented/en-bw92sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1992"
}
|
All faces of a convex polyhedron are parallelograms. Can the polyhedron have exactly 1992 faces?
|
No, it cannot. Let us call a series of faces $F_{1}, F_{2}, \ldots, F_{k}$ a ring if the pairs $\left(F_{1}, F_{2}\right),\left(F_{2}, F_{3}\right), \ldots$, $\left(F_{k-1}, F_{k}\right),\left(F_{k}, F_{1}\right)$ each have a common edge and all these common edges are parallel. It is not difficult to see that any two rings have exactly two common faces and, conversely, each face belongs to exactly two rings. Therefore, if there are $n$ rings then the total number of faces must be $2\left(\begin{array}{l}n \\ 2\end{array}\right)=n(n-1)$. But there is no positive integer $n$ such that $n(n-1)=1992$.
Remark. The above solution, which is the only one proposed that is known to us, is not correct. For a counterexample, consider a cube with side 2 built up of four unit cubes, and take the polyhedron with 24 faces built up of the faces of the unit cubes that face the outside. This polyhedron has rings that do not have any faces in common. Moreover, by subdividing faces into rectangles sufficiently many times, we can obtain a polyhedron with 1992 faces.
|
proof
|
Yes
|
Incomplete
|
math-word-problem
|
Geometry
|
All faces of a convex polyhedron are parallelograms. Can the polyhedron have exactly 1992 faces?
|
No, it cannot. Let us call a series of faces $F_{1}, F_{2}, \ldots, F_{k}$ a ring if the pairs $\left(F_{1}, F_{2}\right),\left(F_{2}, F_{3}\right), \ldots$, $\left(F_{k-1}, F_{k}\right),\left(F_{k}, F_{1}\right)$ each have a common edge and all these common edges are parallel. It is not difficult to see that any two rings have exactly two common faces and, conversely, each face belongs to exactly two rings. Therefore, if there are $n$ rings then the total number of faces must be $2\left(\begin{array}{l}n \\ 2\end{array}\right)=n(n-1)$. But there is no positive integer $n$ such that $n(n-1)=1992$.
Remark. The above solution, which is the only one proposed that is known to us, is not correct. For a counterexample, consider a cube with side 2 built up of four unit cubes, and take the polyhedron with 24 faces built up of the faces of the unit cubes that face the outside. This polyhedron has rings that do not have any faces in common. Moreover, by subdividing faces into rectangles sufficiently many times, we can obtain a polyhedron with 1992 faces.
|
{
"exam": "BalticWay",
"problem_label": "16",
"problem_match": "\n16.",
"resource_path": "BalticWay/segmented/en-bw92sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1992"
}
|
Quadrangle $A B C D$ is inscribed in a circle with radius 1 in such a way that one diagonal, $A C$, is a diameter of the circle, while the other diagonal, $B D$, is as long as $A B$. The diagonals intersect in $P$. It is known that the length of $P C$ is $\frac{2}{5}$. How long is the side $C D$ ?
Figure 1
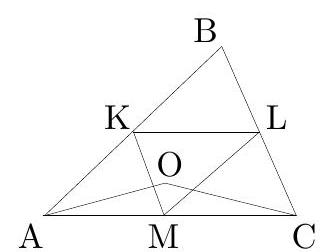
Figure 2
Figure 3
|
Let $\angle A C D=2 \alpha$ (see Figure 1). Then $\angle C A D=\frac{\pi}{2}-2 \alpha, \angle A B D=2 \alpha, \angle A D B=\frac{\pi}{2}-\alpha$ and $\angle C D B=\alpha$. The sine theorem applied to triangles $D C P$ and $D A P$ yields
$$
\frac{|D P|}{\sin 2 \alpha}=\frac{2}{5 \sin \alpha}
$$
and
$$
\frac{|D P|}{\sin \left(\frac{\pi}{2}-2 \alpha\right)}=\frac{8}{5 \sin \left(\frac{\pi}{2}-\alpha\right)}
$$
Combining these equalities we have
$$
\frac{2 \sin 2 \alpha}{5 \sin \alpha}=\frac{8 \cos 2 \alpha}{5 \cos \alpha}
$$
which gives $4 \sin \alpha \cos ^{2} \alpha=8 \cos 2 \alpha \sin \alpha$ and $\cos 2 \alpha+1=4 \cos 2 \alpha$. So we get $\cos 2 \alpha=\frac{1}{3}$ and $|C D|=$ $2 \cos 2 \alpha=\frac{2}{3}$.
|
\frac{2}{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Quadrangle $A B C D$ is inscribed in a circle with radius 1 in such a way that one diagonal, $A C$, is a diameter of the circle, while the other diagonal, $B D$, is as long as $A B$. The diagonals intersect in $P$. It is known that the length of $P C$ is $\frac{2}{5}$. How long is the side $C D$ ?

Figure 1

Figure 2

Figure 3
|
Let $\angle A C D=2 \alpha$ (see Figure 1). Then $\angle C A D=\frac{\pi}{2}-2 \alpha, \angle A B D=2 \alpha, \angle A D B=\frac{\pi}{2}-\alpha$ and $\angle C D B=\alpha$. The sine theorem applied to triangles $D C P$ and $D A P$ yields
$$
\frac{|D P|}{\sin 2 \alpha}=\frac{2}{5 \sin \alpha}
$$
and
$$
\frac{|D P|}{\sin \left(\frac{\pi}{2}-2 \alpha\right)}=\frac{8}{5 \sin \left(\frac{\pi}{2}-\alpha\right)}
$$
Combining these equalities we have
$$
\frac{2 \sin 2 \alpha}{5 \sin \alpha}=\frac{8 \cos 2 \alpha}{5 \cos \alpha}
$$
which gives $4 \sin \alpha \cos ^{2} \alpha=8 \cos 2 \alpha \sin \alpha$ and $\cos 2 \alpha+1=4 \cos 2 \alpha$. So we get $\cos 2 \alpha=\frac{1}{3}$ and $|C D|=$ $2 \cos 2 \alpha=\frac{2}{3}$.
|
{
"exam": "BalticWay",
"problem_label": "17",
"problem_match": "\n17.",
"resource_path": "BalticWay/segmented/en-bw92sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1992"
}
|
Show that in a non-obtuse triangle the perimeter of the triangle is always greater than two times the diameter of the circumcircle.
|
Let $K, L, M$ be the midpoints of the sides $A B, B C, A C$ of a non-obtuse triangle $A B C$ (see Figure 2). Note that the centre $O$ of the circumcircle is inside the triangle $K L M$ (or at one of its vertices if $A B C$ is a right-angled triangle). Therefore $|A K|+|K L|+|L C|>|A O|+|O C|$ and hence $|A B|+|A C|+|B C|>$ $2(|A O|+|O C|)=2 d$, where $d$ is the diameter of the circumcircle.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Show that in a non-obtuse triangle the perimeter of the triangle is always greater than two times the diameter of the circumcircle.
|
Let $K, L, M$ be the midpoints of the sides $A B, B C, A C$ of a non-obtuse triangle $A B C$ (see Figure 2). Note that the centre $O$ of the circumcircle is inside the triangle $K L M$ (or at one of its vertices if $A B C$ is a right-angled triangle). Therefore $|A K|+|K L|+|L C|>|A O|+|O C|$ and hence $|A B|+|A C|+|B C|>$ $2(|A O|+|O C|)=2 d$, where $d$ is the diameter of the circumcircle.
|
{
"exam": "BalticWay",
"problem_label": "18",
"problem_match": "\n18.",
"resource_path": "BalticWay/segmented/en-bw92sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1992"
}
|
Let $C$ be a circle in the plane. Let $C_{1}$ and $C_{2}$ be non-intersecting circles touching $C$ internally at points $A$ and $B$ respectively. Let $t$ be a common tangent of $C_{1}$ and $C_{2}$, touching them at points $D$ and $E$ respectively, such that both $C_{1}$ and $C_{2}$ are on the same side of $t$. Let $F$ be the point of intersection of $A D$ and $B E$. Show that $F$ lies on $C$.
|
Let $F_{1}$ be the second intersection point of the line $A D$ and the circle $C$ (see Figure 3). Consider the homothety with centre $A$ which maps $D$ onto $F_{1}$. This homothety maps the circle $C_{1}$ onto $C$ and the tangent line $t$ of $C_{1}$ onto the tangent line of the circle $C$ at $F_{1}$. Let us do the same with the circle $C_{2}$ and the line $B E$ : let $F_{2}$ be their intersection point and consider the homothety with centre $B$, mapping $E$ onto $F_{2}$, $C_{2}$ onto $C$ and $t$ onto the tangent of $C$ at point $F_{2}$. Since the tangents of $C$ at $F_{1}$ and $F_{2}$ are both parallel to $t$, they must coincide, and so must the points $F_{1}$ and $F_{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $C$ be a circle in the plane. Let $C_{1}$ and $C_{2}$ be non-intersecting circles touching $C$ internally at points $A$ and $B$ respectively. Let $t$ be a common tangent of $C_{1}$ and $C_{2}$, touching them at points $D$ and $E$ respectively, such that both $C_{1}$ and $C_{2}$ are on the same side of $t$. Let $F$ be the point of intersection of $A D$ and $B E$. Show that $F$ lies on $C$.
|
Let $F_{1}$ be the second intersection point of the line $A D$ and the circle $C$ (see Figure 3). Consider the homothety with centre $A$ which maps $D$ onto $F_{1}$. This homothety maps the circle $C_{1}$ onto $C$ and the tangent line $t$ of $C_{1}$ onto the tangent line of the circle $C$ at $F_{1}$. Let us do the same with the circle $C_{2}$ and the line $B E$ : let $F_{2}$ be their intersection point and consider the homothety with centre $B$, mapping $E$ onto $F_{2}$, $C_{2}$ onto $C$ and $t$ onto the tangent of $C$ at point $F_{2}$. Since the tangents of $C$ at $F_{1}$ and $F_{2}$ are both parallel to $t$, they must coincide, and so must the points $F_{1}$ and $F_{2}$.
|
{
"exam": "BalticWay",
"problem_label": "19",
"problem_match": "\n19.",
"resource_path": "BalticWay/segmented/en-bw92sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1992"
}
|
Let $a \leq b \leq c$ be the sides of a right triangle, and let $2 p$ be its perimeter. Show that
$$
p(p-c)=(p-a)(p-b)=S
$$
where $S$ is the area of the triangle.
|
By straightforward computation, we find:
$$
\begin{aligned}
& p(p-c)=\frac{1}{4}\left((a+b)^{2}-c^{2}\right)=\frac{a b}{2}=S, \\
& (p-a)(p-b)=\frac{1}{4}\left(c^{2}-(a-b)^{2}\right)=\frac{a b}{2}=S .
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $a \leq b \leq c$ be the sides of a right triangle, and let $2 p$ be its perimeter. Show that
$$
p(p-c)=(p-a)(p-b)=S
$$
where $S$ is the area of the triangle.
|
By straightforward computation, we find:
$$
\begin{aligned}
& p(p-c)=\frac{1}{4}\left((a+b)^{2}-c^{2}\right)=\frac{a b}{2}=S, \\
& (p-a)(p-b)=\frac{1}{4}\left(c^{2}-(a-b)^{2}\right)=\frac{a b}{2}=S .
\end{aligned}
$$
|
{
"exam": "BalticWay",
"problem_label": "20",
"problem_match": "\n20.",
"resource_path": "BalticWay/segmented/en-bw92sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1992"
}
|
$\overline{a_{1} a_{2} a_{3}}$ and $\overline{a_{3} a_{2} a_{1}}$ are two three-digit decimal numbers, with $a_{1}, a_{3}$ being different non-zero digits. The squares of these numbers are five-digit numbers $\overline{b_{1} b_{2} b_{3} b_{4} b_{5}}$ and $\overline{b_{5} b_{4} b_{3} b_{2} b_{1}}$ respectively. Find all such threedigit numbers.
|
Assume $a_{1}>a_{3}>0$. As the square of $\overline{a_{1} a_{2} a_{3}}$ must be a five-digit number we have $a_{1} \leq 3$. Now a straightforward case study shows that $\overline{a_{1} a_{2} a_{3}}$ can be 301, 311, 201, 211 or 221 .
|
301, 311, 201, 211, 221
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
$\overline{a_{1} a_{2} a_{3}}$ and $\overline{a_{3} a_{2} a_{1}}$ are two three-digit decimal numbers, with $a_{1}, a_{3}$ being different non-zero digits. The squares of these numbers are five-digit numbers $\overline{b_{1} b_{2} b_{3} b_{4} b_{5}}$ and $\overline{b_{5} b_{4} b_{3} b_{2} b_{1}}$ respectively. Find all such threedigit numbers.
|
Assume $a_{1}>a_{3}>0$. As the square of $\overline{a_{1} a_{2} a_{3}}$ must be a five-digit number we have $a_{1} \leq 3$. Now a straightforward case study shows that $\overline{a_{1} a_{2} a_{3}}$ can be 301, 311, 201, 211 or 221 .
|
{
"exam": "BalticWay",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "BalticWay/segmented/en-bw93sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1993"
}
|
Do there exist positive integers $a>b>1$ such that for each positive integer $k$ there exists a positive integer $n$ for which $a n+b$ is a $k$ th power of a positive integer?
|
Let $a=6, b=3$ and denote $x_{n}=a n+b$. Then we have $x_{l} \cdot x_{m}=x_{6 l m+3(l+m)+1}$ for any natural numbers $l$ and $m$. Thus, any powers of the numbers $x_{n}$ belong to the same sequence.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Do there exist positive integers $a>b>1$ such that for each positive integer $k$ there exists a positive integer $n$ for which $a n+b$ is a $k$ th power of a positive integer?
|
Let $a=6, b=3$ and denote $x_{n}=a n+b$. Then we have $x_{l} \cdot x_{m}=x_{6 l m+3(l+m)+1}$ for any natural numbers $l$ and $m$. Thus, any powers of the numbers $x_{n}$ belong to the same sequence.
|
{
"exam": "BalticWay",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "BalticWay/segmented/en-bw93sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1993"
}
|
Let's call a positive integer "interesting" if it is a product of two (distinct or equal) prime numbers. What is the greatest number of consecutive positive integers all of which are "interesting"?
|
The three consecutive numbers $33=3 \cdot 11,34=2 \cdot 17$ and $35=5 \cdot 7$ are all "interesting". On the other hand, among any four consecutive numbers there is one of the form $4 k$ which is "interesting" only if $k=1$. But then we have either 3 or 5 among the four numbers, neither of which is "interesting".
|
3
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let's call a positive integer "interesting" if it is a product of two (distinct or equal) prime numbers. What is the greatest number of consecutive positive integers all of which are "interesting"?
|
The three consecutive numbers $33=3 \cdot 11,34=2 \cdot 17$ and $35=5 \cdot 7$ are all "interesting". On the other hand, among any four consecutive numbers there is one of the form $4 k$ which is "interesting" only if $k=1$. But then we have either 3 or 5 among the four numbers, neither of which is "interesting".
|
{
"exam": "BalticWay",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "BalticWay/segmented/en-bw93sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1993"
}
|
Determine all integers $n$ for which
$$
\sqrt{\frac{25}{2}+\sqrt{\frac{625}{4}-n}}+\sqrt{\frac{25}{2}-\sqrt{\frac{625}{4}-n}}
$$
is an integer.
|
Let
$$
p=\sqrt{\frac{25}{2}+\sqrt{\frac{625}{4}-n}}+\sqrt{\frac{25}{2}-\sqrt{\frac{625}{4}-n}}=\sqrt{25+2 \sqrt{n}} .
$$
Then $n=\left(\frac{p^{2}-25}{2}\right)^{2}$ and obviously $p$ is an odd number not less than 5. If $p \geq 9$ then $n>\frac{625}{4}$ and the initial expression would be undefined. The two remaining values $p=5$ and $p=7$ give $n=0$ and $n=144$ respectively.
|
n=0 \text{ and } n=144
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Determine all integers $n$ for which
$$
\sqrt{\frac{25}{2}+\sqrt{\frac{625}{4}-n}}+\sqrt{\frac{25}{2}-\sqrt{\frac{625}{4}-n}}
$$
is an integer.
|
Let
$$
p=\sqrt{\frac{25}{2}+\sqrt{\frac{625}{4}-n}}+\sqrt{\frac{25}{2}-\sqrt{\frac{625}{4}-n}}=\sqrt{25+2 \sqrt{n}} .
$$
Then $n=\left(\frac{p^{2}-25}{2}\right)^{2}$ and obviously $p$ is an odd number not less than 5. If $p \geq 9$ then $n>\frac{625}{4}$ and the initial expression would be undefined. The two remaining values $p=5$ and $p=7$ give $n=0$ and $n=144$ respectively.
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "BalticWay/segmented/en-bw93sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1993"
}
|
Prove that for any odd positive integer $n, n^{12}-n^{8}-n^{4}+1$ is divisible by $2^{9}$.
|
Factorizing the expression, we get
$$
n^{12}-n^{8}-n^{4}+1=\left(n^{4}+1\right)\left(n^{2}+1\right)^{2}(n-1)^{2}(n+1)^{2} .
$$
Now note that one of the two even numbers $n-1$ and $n+1$ is divisible by 4 .
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Prove that for any odd positive integer $n, n^{12}-n^{8}-n^{4}+1$ is divisible by $2^{9}$.
|
Factorizing the expression, we get
$$
n^{12}-n^{8}-n^{4}+1=\left(n^{4}+1\right)\left(n^{2}+1\right)^{2}(n-1)^{2}(n+1)^{2} .
$$
Now note that one of the two even numbers $n-1$ and $n+1$ is divisible by 4 .
|
{
"exam": "BalticWay",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "BalticWay/segmented/en-bw93sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1993"
}
|
Suppose two functions $f(x)$ and $g(x)$ are defined for all $x$ such that $2<x<4$ and satisfy $2<f(x)<4$, $2<g(x)<4, f(g(x))=g(f(x))=x$ and $f(x) \cdot g(x)=x^{2}$ for all such values of $x$. Prove that $f(3)=g(3)$.
|
Let $h(x)=\frac{f(x)}{x}$. Then we have $g(x)=\frac{x^{2}}{f(x)}=\frac{x}{h(x)}$ and $g(f(x))=\frac{f(x)}{h(f(x))}=x$ which yields $h(f(x))=\frac{f(x)}{x}=h(x)$. Using induction we easily get $h\left(f^{(k)}(x)\right)=h(x)$ for any natural number $k$ where $f^{(k)}(x)$ denotes $\underbrace{f(f(\ldots f}_{k}(x) \ldots))$. Now
$$
f^{(k+1)}(x)=f\left(f^{(k)}(x)\right)=f^{(k)}(x) \cdot h\left(f^{(k)}(x)\right)=f^{(k)}(x) \cdot h(x)
$$
and $\frac{f^{(k+1)}(x)}{f^{(k)}(x)}=h(x)$ for any natural number $k$. Thus
$$
\frac{f^{(k)}(x)}{x}=\frac{f^{(k)}(x)}{f^{(k-1)}(x)} \cdots \cdot \frac{f(x)}{x}=(h(x))^{k}
$$
and $\frac{f^{(k)}(3)}{3}=(h(3))^{k} \in\left(\frac{2}{3}, \frac{4}{3}\right)$ for all $k$. This is only possible if $h(3)=1$ and thus $f(3)=g(3)=3$.
|
f(3)=g(3)=3
|
Yes
|
Yes
|
proof
|
Algebra
|
Suppose two functions $f(x)$ and $g(x)$ are defined for all $x$ such that $2<x<4$ and satisfy $2<f(x)<4$, $2<g(x)<4, f(g(x))=g(f(x))=x$ and $f(x) \cdot g(x)=x^{2}$ for all such values of $x$. Prove that $f(3)=g(3)$.
|
Let $h(x)=\frac{f(x)}{x}$. Then we have $g(x)=\frac{x^{2}}{f(x)}=\frac{x}{h(x)}$ and $g(f(x))=\frac{f(x)}{h(f(x))}=x$ which yields $h(f(x))=\frac{f(x)}{x}=h(x)$. Using induction we easily get $h\left(f^{(k)}(x)\right)=h(x)$ for any natural number $k$ where $f^{(k)}(x)$ denotes $\underbrace{f(f(\ldots f}_{k}(x) \ldots))$. Now
$$
f^{(k+1)}(x)=f\left(f^{(k)}(x)\right)=f^{(k)}(x) \cdot h\left(f^{(k)}(x)\right)=f^{(k)}(x) \cdot h(x)
$$
and $\frac{f^{(k+1)}(x)}{f^{(k)}(x)}=h(x)$ for any natural number $k$. Thus
$$
\frac{f^{(k)}(x)}{x}=\frac{f^{(k)}(x)}{f^{(k-1)}(x)} \cdots \cdot \frac{f(x)}{x}=(h(x))^{k}
$$
and $\frac{f^{(k)}(3)}{3}=(h(3))^{k} \in\left(\frac{2}{3}, \frac{4}{3}\right)$ for all $k$. This is only possible if $h(3)=1$ and thus $f(3)=g(3)=3$.
|
{
"exam": "BalticWay",
"problem_label": "6",
"problem_match": "\n6.",
"resource_path": "BalticWay/segmented/en-bw93sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1993"
}
|
Solve the system of equations in integers:
$$
\left\{\begin{array}{l}
z^{x}=y^{2 x} \\
2^{z}=4^{x} \\
x+y+z=20 .
\end{array}\right.
$$
|
From the second and third equation we find $z=2 x$ and $x=\frac{20-y}{3}$. Substituting these into the first equation yields $\left(\frac{40-2 y}{3}\right)^{x}=\left(y^{2}\right)^{x}$. As $x \neq 0$ (otherwise we have $0^{0}$ in the first equation which is usually considered undefined) we have $y^{2}= \pm \frac{40-2 y}{3}$ (the ' - ' case occurring only if $x$ is even). The equation $y^{2}=-\frac{40-2 y}{3}$ has no integer solutions; from $y^{2}=\frac{40-2 y}{3}$ we get $y=-4, x=8, z=16$ (the other solution $y=\frac{10}{3}$ is not an integer).
Remark. If we accept the definition $0^{0}=1$, then we get the additional solution $x=0, y=20, z=0$. Defining $0^{0}=0$ gives no additional solution.
|
x=8, y=-4, z=16
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Solve the system of equations in integers:
$$
\left\{\begin{array}{l}
z^{x}=y^{2 x} \\
2^{z}=4^{x} \\
x+y+z=20 .
\end{array}\right.
$$
|
From the second and third equation we find $z=2 x$ and $x=\frac{20-y}{3}$. Substituting these into the first equation yields $\left(\frac{40-2 y}{3}\right)^{x}=\left(y^{2}\right)^{x}$. As $x \neq 0$ (otherwise we have $0^{0}$ in the first equation which is usually considered undefined) we have $y^{2}= \pm \frac{40-2 y}{3}$ (the ' - ' case occurring only if $x$ is even). The equation $y^{2}=-\frac{40-2 y}{3}$ has no integer solutions; from $y^{2}=\frac{40-2 y}{3}$ we get $y=-4, x=8, z=16$ (the other solution $y=\frac{10}{3}$ is not an integer).
Remark. If we accept the definition $0^{0}=1$, then we get the additional solution $x=0, y=20, z=0$. Defining $0^{0}=0$ gives no additional solution.
|
{
"exam": "BalticWay",
"problem_label": "7",
"problem_match": "\n7.",
"resource_path": "BalticWay/segmented/en-bw93sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1993"
}
|
Compute the sum of all positive integers whose digits form either a strictly increasing or a strictly decreasing sequence.
|
Denote by $I$ and $D$ the sets of all positive integers with strictly increasing (respectively, decreasing) sequence of digits. Let $D_{0}, D_{1}, D_{2}$ and $D_{3}$ be the subsets of $D$ consisting of all numbers starting with 9 , not starting with 9 , ending in 0 and not ending in 0 , respectively. Let $S(A)$ denote the sum of all numbers belonging to a set $A$. All numbers in $I$ are obtained from the number 123456789 by deleting some of its digits. Thus, for any $k=0,1, \ldots, 9$ there are $\left(\begin{array}{l}9 \\ k\end{array}\right) k$-digit numbers in $I$ (here we consider 0 a 0 -digit number). Every $k$-digit number $a \in I$ can be associated with a unique number $b_{0} \in D_{0}, b_{1} \in D_{1}$ and $b_{3} \in D_{3}$ such that
$$
\begin{aligned}
& a+b_{0}=999 \ldots 9=10^{k+1}-1 \\
& a+b_{1}=99 \ldots 9=10^{k}-1 \\
& a+b_{3}=111 \ldots 10=\frac{10}{9}\left(10^{k}-1\right)
\end{aligned}
$$
Hence we have
$$
\begin{aligned}
& S(I)+S\left(D_{0}\right)=\sum_{k=0}^{9}\left(\begin{array}{l}
9 \\
k
\end{array}\right)\left(10^{k+1}-1\right)=10 \cdot 11^{9}-2^{9} \\
& S(I)+S\left(D_{1}\right)=\sum_{k=0}^{9}\left(\begin{array}{l}
9 \\
k
\end{array}\right)\left(10^{k}-1\right)=11^{9}-2^{9} \\
& S(I)+S\left(D_{3}\right)=\frac{10}{9}\left(11^{9}-2^{9}\right)
\end{aligned}
$$
Noting that $S\left(D_{0}\right)+S\left(D_{1}\right)=S\left(D_{2}\right)+S\left(D_{3}\right)=S(D)$ and $S\left(D_{2}\right)=10 S\left(D_{3}\right)$ we obtain the system of equations
$$
\left\{\begin{aligned}
2 S(I)+S(D) & =11^{10}-2^{10} \\
S(I)+\frac{1}{11} S(D) & =\frac{10}{9}\left(11^{9}-2^{9}\right)
\end{aligned}\right.
$$
which yields
$$
S(I)+S(D)=\frac{80}{81} \cdot 11^{10}-\frac{35}{81} \cdot 2^{10} .
$$
This sum contains all one-digit numbers twice, so the final answer is
$$
\frac{80}{81} \cdot 11^{10}-\frac{35}{81} \cdot 2^{10}-45=25617208995
$$
|
25617208995
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Compute the sum of all positive integers whose digits form either a strictly increasing or a strictly decreasing sequence.
|
Denote by $I$ and $D$ the sets of all positive integers with strictly increasing (respectively, decreasing) sequence of digits. Let $D_{0}, D_{1}, D_{2}$ and $D_{3}$ be the subsets of $D$ consisting of all numbers starting with 9 , not starting with 9 , ending in 0 and not ending in 0 , respectively. Let $S(A)$ denote the sum of all numbers belonging to a set $A$. All numbers in $I$ are obtained from the number 123456789 by deleting some of its digits. Thus, for any $k=0,1, \ldots, 9$ there are $\left(\begin{array}{l}9 \\ k\end{array}\right) k$-digit numbers in $I$ (here we consider 0 a 0 -digit number). Every $k$-digit number $a \in I$ can be associated with a unique number $b_{0} \in D_{0}, b_{1} \in D_{1}$ and $b_{3} \in D_{3}$ such that
$$
\begin{aligned}
& a+b_{0}=999 \ldots 9=10^{k+1}-1 \\
& a+b_{1}=99 \ldots 9=10^{k}-1 \\
& a+b_{3}=111 \ldots 10=\frac{10}{9}\left(10^{k}-1\right)
\end{aligned}
$$
Hence we have
$$
\begin{aligned}
& S(I)+S\left(D_{0}\right)=\sum_{k=0}^{9}\left(\begin{array}{l}
9 \\
k
\end{array}\right)\left(10^{k+1}-1\right)=10 \cdot 11^{9}-2^{9} \\
& S(I)+S\left(D_{1}\right)=\sum_{k=0}^{9}\left(\begin{array}{l}
9 \\
k
\end{array}\right)\left(10^{k}-1\right)=11^{9}-2^{9} \\
& S(I)+S\left(D_{3}\right)=\frac{10}{9}\left(11^{9}-2^{9}\right)
\end{aligned}
$$
Noting that $S\left(D_{0}\right)+S\left(D_{1}\right)=S\left(D_{2}\right)+S\left(D_{3}\right)=S(D)$ and $S\left(D_{2}\right)=10 S\left(D_{3}\right)$ we obtain the system of equations
$$
\left\{\begin{aligned}
2 S(I)+S(D) & =11^{10}-2^{10} \\
S(I)+\frac{1}{11} S(D) & =\frac{10}{9}\left(11^{9}-2^{9}\right)
\end{aligned}\right.
$$
which yields
$$
S(I)+S(D)=\frac{80}{81} \cdot 11^{10}-\frac{35}{81} \cdot 2^{10} .
$$
This sum contains all one-digit numbers twice, so the final answer is
$$
\frac{80}{81} \cdot 11^{10}-\frac{35}{81} \cdot 2^{10}-45=25617208995
$$
|
{
"exam": "BalticWay",
"problem_label": "8",
"problem_match": "\n8.",
"resource_path": "BalticWay/segmented/en-bw93sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1993"
}
|
Solve the system of equations:
$$
\left\{\begin{array}{l}
x^{5}=y+y^{5} \\
y^{5}=z+z^{5} \\
z^{5}=t+t^{5} \\
t^{5}=x+x^{5} .
\end{array}\right.
$$
|
Adding all four equations we get $x+y+z+t=0$. On the other hand, the numbers $x, y, z, t$ are simultaneously positive, negative or equal to zero. Thus, $x=y=z=t=0$ is the only solution.
|
x=y=z=t=0
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Solve the system of equations:
$$
\left\{\begin{array}{l}
x^{5}=y+y^{5} \\
y^{5}=z+z^{5} \\
z^{5}=t+t^{5} \\
t^{5}=x+x^{5} .
\end{array}\right.
$$
|
Adding all four equations we get $x+y+z+t=0$. On the other hand, the numbers $x, y, z, t$ are simultaneously positive, negative or equal to zero. Thus, $x=y=z=t=0$ is the only solution.
|
{
"exam": "BalticWay",
"problem_label": "9",
"problem_match": "\n9.",
"resource_path": "BalticWay/segmented/en-bw93sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1993"
}
|
Let $a_{1}, a_{2}, \ldots, a_{n}$ and $b_{1}, b_{2}, \ldots, b_{n}$ be two finite sequences consisting of $2 n$ different real numbers. Rearranging each of the sequences in the increasing order we obtain $a_{1}^{\prime}, a_{2}^{\prime}, \ldots, a_{n}^{\prime}$ and $b_{1}^{\prime}, b_{2}^{\prime}, \ldots, b_{n}^{\prime}$. Prove that
$$
\max _{1 \leq i \leq n}\left|a_{i}-b_{i}\right| \geq \max _{1 \leq i \leq n}\left|a_{i}^{\prime}-b_{i}^{\prime}\right| .
$$
|
Let $m$ be such index that $\left|a_{m}^{\prime}-b_{m}^{\prime}\right|=\max _{1 \leq i \leq n}\left|a_{i}^{\prime}-b_{i}^{\prime}\right|=c$. Without loss of generality we may assume $a_{m}^{\prime}>b_{m}^{\prime}$. Consider the numbers $a_{m}^{\prime}, a_{m+1}^{\prime}, \ldots, a_{n}^{\prime}$ and $b_{1}^{\prime}, b_{2}^{\prime}, \ldots, b_{m}^{\prime}$. As there are $n+1$ numbers altogether and only $n$ places in the initial sequence there must exist an index $j$ such that we have $a_{j}$ among $a_{m}^{\prime}, a_{m+1}^{\prime}, \ldots, a_{n}^{\prime}$ and $b_{j}$ among $b_{1}^{\prime}, b_{2}^{\prime}, \ldots, b_{m}^{\prime}$. Now, as $b_{j} \leq b_{m}^{\prime}<a_{m}^{\prime} \leq a_{j}$ we have $\left|a_{j}-b_{j}\right| \geq\left|a_{m}^{\prime}-b_{m}^{\prime}\right|=c$ and $\max _{1 \leq i \leq n}\left|a_{i}-b_{i}\right| \geq c=\max _{1 \leq i \leq n}\left|a_{i}^{\prime}-b_{i}^{\prime}\right|$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a_{1}, a_{2}, \ldots, a_{n}$ and $b_{1}, b_{2}, \ldots, b_{n}$ be two finite sequences consisting of $2 n$ different real numbers. Rearranging each of the sequences in the increasing order we obtain $a_{1}^{\prime}, a_{2}^{\prime}, \ldots, a_{n}^{\prime}$ and $b_{1}^{\prime}, b_{2}^{\prime}, \ldots, b_{n}^{\prime}$. Prove that
$$
\max _{1 \leq i \leq n}\left|a_{i}-b_{i}\right| \geq \max _{1 \leq i \leq n}\left|a_{i}^{\prime}-b_{i}^{\prime}\right| .
$$
|
Let $m$ be such index that $\left|a_{m}^{\prime}-b_{m}^{\prime}\right|=\max _{1 \leq i \leq n}\left|a_{i}^{\prime}-b_{i}^{\prime}\right|=c$. Without loss of generality we may assume $a_{m}^{\prime}>b_{m}^{\prime}$. Consider the numbers $a_{m}^{\prime}, a_{m+1}^{\prime}, \ldots, a_{n}^{\prime}$ and $b_{1}^{\prime}, b_{2}^{\prime}, \ldots, b_{m}^{\prime}$. As there are $n+1$ numbers altogether and only $n$ places in the initial sequence there must exist an index $j$ such that we have $a_{j}$ among $a_{m}^{\prime}, a_{m+1}^{\prime}, \ldots, a_{n}^{\prime}$ and $b_{j}$ among $b_{1}^{\prime}, b_{2}^{\prime}, \ldots, b_{m}^{\prime}$. Now, as $b_{j} \leq b_{m}^{\prime}<a_{m}^{\prime} \leq a_{j}$ we have $\left|a_{j}-b_{j}\right| \geq\left|a_{m}^{\prime}-b_{m}^{\prime}\right|=c$ and $\max _{1 \leq i \leq n}\left|a_{i}-b_{i}\right| \geq c=\max _{1 \leq i \leq n}\left|a_{i}^{\prime}-b_{i}^{\prime}\right|$.
|
{
"exam": "BalticWay",
"problem_label": "10",
"problem_match": "\n10.",
"resource_path": "BalticWay/segmented/en-bw93sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1993"
}
|
An equilateral triangle is divided into $n^{2}$ congruent equilateral triangles. A spider stands at one of the vertices, a fly at another. Alternately each of them moves to a neighbouring vertex. Prove that the spider can always catch the fly.
|
Assume that the big triangle lies on one of its sides. Then a suitable strategy for the spider will be as follows:
(1) First, move to the lower left vertex of the big triangle.
(2) Then, as long as the fly is higher than the spider, move upwards along the left side of the big triangle.
(3) After reaching the horizontal line where the fly is, retain this situation while moving to the right (more precisely: move "right", "right and up" or "right and down" depending on the last move of the fly).
|
proof
|
Yes
|
Yes
|
proof
|
Logic and Puzzles
|
An equilateral triangle is divided into $n^{2}$ congruent equilateral triangles. A spider stands at one of the vertices, a fly at another. Alternately each of them moves to a neighbouring vertex. Prove that the spider can always catch the fly.
|
Assume that the big triangle lies on one of its sides. Then a suitable strategy for the spider will be as follows:
(1) First, move to the lower left vertex of the big triangle.
(2) Then, as long as the fly is higher than the spider, move upwards along the left side of the big triangle.
(3) After reaching the horizontal line where the fly is, retain this situation while moving to the right (more precisely: move "right", "right and up" or "right and down" depending on the last move of the fly).
|
{
"exam": "BalticWay",
"problem_label": "11",
"problem_match": "\n11.",
"resource_path": "BalticWay/segmented/en-bw93sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1993"
}
|
There are 13 cities in a certain kingdom. Between some pairs of cities two-way direct bus, train or plane connections are established. What is the least possible number of connections to be established in order that choosing any two means of transportation one can go from any city to any other without using the third kind of vehicle?
|
An example for 18 connections is shown in Figure 1 (where single, double and dashed lines denote the three different kinds of transportation). On the other hand, a connected graph with 13 vertices has at least 12 edges, so the total number of connections for any two kinds of vehicle is at least 12 . Thus, twice the total number of all connections is at least $12+12+12=36$.
Figure 1
Figure 2
|
18
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There are 13 cities in a certain kingdom. Between some pairs of cities two-way direct bus, train or plane connections are established. What is the least possible number of connections to be established in order that choosing any two means of transportation one can go from any city to any other without using the third kind of vehicle?
|
An example for 18 connections is shown in Figure 1 (where single, double and dashed lines denote the three different kinds of transportation). On the other hand, a connected graph with 13 vertices has at least 12 edges, so the total number of connections for any two kinds of vehicle is at least 12 . Thus, twice the total number of all connections is at least $12+12+12=36$.

Figure 1

Figure 2
|
{
"exam": "BalticWay",
"problem_label": "12",
"problem_match": "\n12.",
"resource_path": "BalticWay/segmented/en-bw93sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1993"
}
|
An equilateral triangle $A B C$ is divided into 100 congruent equilateral triangles. What is the greatest number of vertices of small triangles that can be chosen so that no two of them lie on a line that is parallel to any of the sides of the triangle $A B C$ ?
|
An example for 7 vertices is shown in Figure 2. Now assume we have chosen 8 vertices satisfying the conditions of the problem. Let the height of each small triangle be equal to 1 and denote by $a_{i}, b_{i}, c_{i}$ the distance of the $i$ th point from the three sides of the big triangle. For any $i=1,2, \ldots, 8$ we then have $a_{i}, b_{i}, c_{i} \geq 0$ and $a_{i}+b_{i}+c_{i}=10$. Thus, $\left(a_{1}+a_{2}+\cdots+a_{8}\right)+\left(b_{1}+b_{2}+\cdots+b_{8}\right)+\left(c_{1}+c_{2}+\cdots+c_{8}\right)=80$. On the other hand, each of the sums in the brackets is not less than $0+1+\cdots+7=28$, but $3 \cdot 28=84>80$, a contradiction.
|
7
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
An equilateral triangle $A B C$ is divided into 100 congruent equilateral triangles. What is the greatest number of vertices of small triangles that can be chosen so that no two of them lie on a line that is parallel to any of the sides of the triangle $A B C$ ?
|
An example for 7 vertices is shown in Figure 2. Now assume we have chosen 8 vertices satisfying the conditions of the problem. Let the height of each small triangle be equal to 1 and denote by $a_{i}, b_{i}, c_{i}$ the distance of the $i$ th point from the three sides of the big triangle. For any $i=1,2, \ldots, 8$ we then have $a_{i}, b_{i}, c_{i} \geq 0$ and $a_{i}+b_{i}+c_{i}=10$. Thus, $\left(a_{1}+a_{2}+\cdots+a_{8}\right)+\left(b_{1}+b_{2}+\cdots+b_{8}\right)+\left(c_{1}+c_{2}+\cdots+c_{8}\right)=80$. On the other hand, each of the sums in the brackets is not less than $0+1+\cdots+7=28$, but $3 \cdot 28=84>80$, a contradiction.
|
{
"exam": "BalticWay",
"problem_label": "13",
"problem_match": "\n13.",
"resource_path": "BalticWay/segmented/en-bw93sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1993"
}
|
A square is divided into 16 equal squares, obtaining the set of 25 different vertices. What is the least number of vertices one must remove from this set, so that no 4 points of the remaining set are the vertices of any square with sides parallel to the sides of the initial square?
Remark. The proposed solution to this problem claimed that it is enough to remove 7 vertices but the example to demonstrate this appeared to be incorrect. Below we show that removing 6 vertices is not sufficient but removing 8 vertices is. It seems that removing 7 vertices is not sufficient but we currently know no potential way to prove this, apart from a tedious case study.
|
The example in Figure 3a demonstrates that it suffices to remove 8 vertices to "destroy" all squares. Assume now that we have managed to do that by removing only 6 vertices. Denote the horizontal and vertical lines by $A, B, \ldots, E$ and $1,2, \ldots, 5$ respectively. Obviously, one of the removed vertices must be a vertex of the big square - let this be vertex $A 1$. Then, in order to "destroy" all the squares shown in Figure $3 \mathrm{~b}-\mathrm{e}$ we have to remove vertices $B 2, C 3, D 4, D 2$ and $B 4$. Thus we have removed 6 vertices without having any choice but a square shown in Figure $3 \mathrm{f}$ is still left intact.
12345
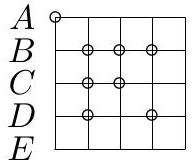
$\mathrm{a}$
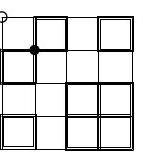
$\mathrm{b}$
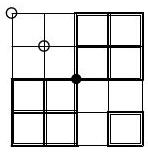
c
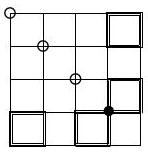
d
e
f
Figure 3
|
8
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A square is divided into 16 equal squares, obtaining the set of 25 different vertices. What is the least number of vertices one must remove from this set, so that no 4 points of the remaining set are the vertices of any square with sides parallel to the sides of the initial square?
Remark. The proposed solution to this problem claimed that it is enough to remove 7 vertices but the example to demonstrate this appeared to be incorrect. Below we show that removing 6 vertices is not sufficient but removing 8 vertices is. It seems that removing 7 vertices is not sufficient but we currently know no potential way to prove this, apart from a tedious case study.
|
The example in Figure 3a demonstrates that it suffices to remove 8 vertices to "destroy" all squares. Assume now that we have managed to do that by removing only 6 vertices. Denote the horizontal and vertical lines by $A, B, \ldots, E$ and $1,2, \ldots, 5$ respectively. Obviously, one of the removed vertices must be a vertex of the big square - let this be vertex $A 1$. Then, in order to "destroy" all the squares shown in Figure $3 \mathrm{~b}-\mathrm{e}$ we have to remove vertices $B 2, C 3, D 4, D 2$ and $B 4$. Thus we have removed 6 vertices without having any choice but a square shown in Figure $3 \mathrm{f}$ is still left intact.
12345

$\mathrm{a}$

$\mathrm{b}$

c

d

e

f
Figure 3
|
{
"exam": "BalticWay",
"problem_label": "14",
"problem_match": "\n14.",
"resource_path": "BalticWay/segmented/en-bw93sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1993"
}
|
On each face of two dice some positive integer is written. The two dice are thrown and the numbers on the top faces are added. Determine whether one can select the integers on the faces so that the possible sums are $2,3,4,5,6,7,8,9,10,11,12,13$, all equally likely?
|
We can write 1, 2, 3, 4, 5, 6 on the sides of one die and 1, 1, 1, 7, 7, 7 on the sides of the other. Then each of the 12 possible sums appears in exactly 3 cases.
|
3
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On each face of two dice some positive integer is written. The two dice are thrown and the numbers on the top faces are added. Determine whether one can select the integers on the faces so that the possible sums are $2,3,4,5,6,7,8,9,10,11,12,13$, all equally likely?
|
We can write 1, 2, 3, 4, 5, 6 on the sides of one die and 1, 1, 1, 7, 7, 7 on the sides of the other. Then each of the 12 possible sums appears in exactly 3 cases.
|
{
"exam": "BalticWay",
"problem_label": "15",
"problem_match": "\n15.",
"resource_path": "BalticWay/segmented/en-bw93sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1993"
}
|
Two circles, both with the same radius $r$, are placed in the plane without intersecting each other. A line in the plane intersects the first circle at the points $A, B$ and the other at the points $C, D$ so that $|A B|=|B C|=|C D|=14 \mathrm{~cm}$. Another line intersects the circles at points $E, F$ and $G, H$ respectively, so that $|E F|=|F G|=|G H|=6 \mathrm{~cm}$. Find the radius $r$.
|
First, note that the centres $O_{1}$ and $O_{2}$ of the two circles lie on different sides of the line $E H-$ otherwise we have $r<12$ and $A B$ cannot be equal to 14 . Let $P$ be the intersection point of $E H$ and $O_{1} O_{2}$ (see Figure 4). Points $A$ and $D$ lie on the same side of the line $O_{1} O_{2}$ (otherwise the three lines $A D, E H$ and $O_{1} O_{2}$ would intersect in $P$ and $|A B|=|B C|=|C D|,|E F|=|F G|=|G H|$ would imply $|B C|=|F G|$, a contradiction). It is easy to see that $\left|O_{1} O_{2}\right|=2 \cdot\left|O_{1} P\right|=|A C|=28 \mathrm{~cm}$. Let $h=\left|O_{1} T\right|$ be the height of triangle $O_{1} E P$. Then we have $h^{2}=14^{2}-6^{2}=160$ from triangle $O_{1} T P$ and $r^{2}=h^{2}+3^{2}=169$ from triangle $O_{1} T F$. Thus $r=13 \mathrm{~cm}$.

Figure 4
Figure 5
|
13 \text{ cm}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Two circles, both with the same radius $r$, are placed in the plane without intersecting each other. A line in the plane intersects the first circle at the points $A, B$ and the other at the points $C, D$ so that $|A B|=|B C|=|C D|=14 \mathrm{~cm}$. Another line intersects the circles at points $E, F$ and $G, H$ respectively, so that $|E F|=|F G|=|G H|=6 \mathrm{~cm}$. Find the radius $r$.
|
First, note that the centres $O_{1}$ and $O_{2}$ of the two circles lie on different sides of the line $E H-$ otherwise we have $r<12$ and $A B$ cannot be equal to 14 . Let $P$ be the intersection point of $E H$ and $O_{1} O_{2}$ (see Figure 4). Points $A$ and $D$ lie on the same side of the line $O_{1} O_{2}$ (otherwise the three lines $A D, E H$ and $O_{1} O_{2}$ would intersect in $P$ and $|A B|=|B C|=|C D|,|E F|=|F G|=|G H|$ would imply $|B C|=|F G|$, a contradiction). It is easy to see that $\left|O_{1} O_{2}\right|=2 \cdot\left|O_{1} P\right|=|A C|=28 \mathrm{~cm}$. Let $h=\left|O_{1} T\right|$ be the height of triangle $O_{1} E P$. Then we have $h^{2}=14^{2}-6^{2}=160$ from triangle $O_{1} T P$ and $r^{2}=h^{2}+3^{2}=169$ from triangle $O_{1} T F$. Thus $r=13 \mathrm{~cm}$.

Figure 4

Figure 5
|
{
"exam": "BalticWay",
"problem_label": "16",
"problem_match": "\n16.",
"resource_path": "BalticWay/segmented/en-bw93sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1993"
}
|
Let's consider three pairwise non-parallel straight lines in the plane. Three points are moving along these lines with different non-zero velocities, one on each line (we consider the movement as having taken place for infinite time and continuing infinitely in the future). Is it possible to determine these straight lines, the velocities of each moving point and their positions at some "zero" moment in such a way that the points never were, are or will be collinear?
|
Yes, it is. First, place the three points at the vertices of an equilateral triangle at the "zero" moment and let them move with equal velocities along the straight lines determined by the sides of the
triangle as shown in Figure 5. Then, at any moment in the past or future, the points are located at the vertices of some equilateral triangle, and thus cannot be collinear. Finally, to make the velocities of the points also differ, take any non-zero constant vector such that its projections on the three lines have different lengths and add it to each of the velocity vectors. This is equivalent to making the whole picture "drift" across the plane with constant velocity, so the non-collinearity of our points is preserved (in fact, they are still located at the vertices of an equilateral triangle at any given moment).
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let's consider three pairwise non-parallel straight lines in the plane. Three points are moving along these lines with different non-zero velocities, one on each line (we consider the movement as having taken place for infinite time and continuing infinitely in the future). Is it possible to determine these straight lines, the velocities of each moving point and their positions at some "zero" moment in such a way that the points never were, are or will be collinear?
|
Yes, it is. First, place the three points at the vertices of an equilateral triangle at the "zero" moment and let them move with equal velocities along the straight lines determined by the sides of the
triangle as shown in Figure 5. Then, at any moment in the past or future, the points are located at the vertices of some equilateral triangle, and thus cannot be collinear. Finally, to make the velocities of the points also differ, take any non-zero constant vector such that its projections on the three lines have different lengths and add it to each of the velocity vectors. This is equivalent to making the whole picture "drift" across the plane with constant velocity, so the non-collinearity of our points is preserved (in fact, they are still located at the vertices of an equilateral triangle at any given moment).
|
{
"exam": "BalticWay",
"problem_label": "17",
"problem_match": "\n17.",
"resource_path": "BalticWay/segmented/en-bw93sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1993"
}
|
A convex quadrangle $A B C D$ is inscribed in a circle with the centre $O$. The angles $\angle A O B, \angle B O C, \angle C O D$ and $\angle D O A$, taken in some order, are of the same size as the angles of quadrangle $A B C D$. Prove that $A B C D$ is a square.
|
As the quadrangle $A B C D$ is inscribed in a circle, we have $\angle A B C+\angle C D A=\angle B C D+\angle D A B=$ $180^{\circ}$. It suffices to show that if each of these angles is equal to $90^{\circ}$, then each of the angles $A O B, B O C$, $C O D$ and $D O A$ is also equal to $90^{\circ}$ and thus $A B C D$ is a square. We consider the two possible situations:
(a) At least one of the diagonals of $A B C D$ is a diameter - say, $\angle A O B+\angle B O C=180^{\circ}$. Then $\angle A B C=$ $\angle C D A=90^{\circ}$ and at least two of the angles $A O B, B O C, C O D$ and $D O A$ must be $90^{\circ}$ : say, $\angle A O B=$ $\angle B O C=90^{\circ}$. Now, $\angle C O D=\angle D A B$ and $\angle D O A=\angle B C D$ (see Figure 7). Using the fact that $\frac{1}{2} \angle D O A=\angle D C A=\angle B C D-45^{\circ}$ we have $\angle B C D=\angle D A B=90^{\circ}$.
(b) None of the diagonals of the quadrangle $A B C D$ is a diameter. Then $\angle A O B+\angle C O D=\angle B O C+$ $\angle D O A=180^{\circ}$ and no angle of the quadrangle $A B C D$ is equal to $90^{\circ}$. Consequently, none of the angles $A O B, B O C, C O D$ and $D O A$ is equal to $90^{\circ}$. Without loss of generality we assume that $\angle A O B>90^{\circ}$, $\angle B O C>90^{\circ}$ (see Figure 8). Then $\angle A B C<90^{\circ}$ and thus $\angle A B C=\angle C O D$ or $\angle A B C=\angle D O A$. As $\angle C O D+\angle D O A=\angle A O C=2 \angle A B C$, we have $\angle C O D=\angle D O A$ and $\angle A O B+\angle D O A=180^{\circ}$, a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A convex quadrangle $A B C D$ is inscribed in a circle with the centre $O$. The angles $\angle A O B, \angle B O C, \angle C O D$ and $\angle D O A$, taken in some order, are of the same size as the angles of quadrangle $A B C D$. Prove that $A B C D$ is a square.
|
As the quadrangle $A B C D$ is inscribed in a circle, we have $\angle A B C+\angle C D A=\angle B C D+\angle D A B=$ $180^{\circ}$. It suffices to show that if each of these angles is equal to $90^{\circ}$, then each of the angles $A O B, B O C$, $C O D$ and $D O A$ is also equal to $90^{\circ}$ and thus $A B C D$ is a square. We consider the two possible situations:
(a) At least one of the diagonals of $A B C D$ is a diameter - say, $\angle A O B+\angle B O C=180^{\circ}$. Then $\angle A B C=$ $\angle C D A=90^{\circ}$ and at least two of the angles $A O B, B O C, C O D$ and $D O A$ must be $90^{\circ}$ : say, $\angle A O B=$ $\angle B O C=90^{\circ}$. Now, $\angle C O D=\angle D A B$ and $\angle D O A=\angle B C D$ (see Figure 7). Using the fact that $\frac{1}{2} \angle D O A=\angle D C A=\angle B C D-45^{\circ}$ we have $\angle B C D=\angle D A B=90^{\circ}$.
(b) None of the diagonals of the quadrangle $A B C D$ is a diameter. Then $\angle A O B+\angle C O D=\angle B O C+$ $\angle D O A=180^{\circ}$ and no angle of the quadrangle $A B C D$ is equal to $90^{\circ}$. Consequently, none of the angles $A O B, B O C, C O D$ and $D O A$ is equal to $90^{\circ}$. Without loss of generality we assume that $\angle A O B>90^{\circ}$, $\angle B O C>90^{\circ}$ (see Figure 8). Then $\angle A B C<90^{\circ}$ and thus $\angle A B C=\angle C O D$ or $\angle A B C=\angle D O A$. As $\angle C O D+\angle D O A=\angle A O C=2 \angle A B C$, we have $\angle C O D=\angle D O A$ and $\angle A O B+\angle D O A=180^{\circ}$, a contradiction.
|
{
"exam": "BalticWay",
"problem_label": "19",
"problem_match": "\n19.",
"resource_path": "BalticWay/segmented/en-bw93sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1993"
}
|
Let $Q$ be a unit cube. We say a tetrahedron is "good" if all its edges are equal and all its vertices lie on the boundary of $Q$. Find all possible volumes of "good" tetrahedra.
|
Clearly, the volume of a regular tetrahedron contained in a sphere reaches its maximum value if and only if all four vertices of the tetrahedron lie on the surface of the sphere. Therefore, a "good" tetrahedron with maximum volume must have its vertices at the vertices of the cube (for a proof, inscribe the cube in a sphere). There are exactly two such tetrahedra, their volume being equal to $1-4 \cdot \frac{1}{6}=\frac{1}{3}$. On the other hand, one can find arbitrarily small "good" tetrahedra by applying homothety to the maximal tetrahedron, with the centre of the homothety in one of its vertices.
|
\frac{1}{3}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $Q$ be a unit cube. We say a tetrahedron is "good" if all its edges are equal and all its vertices lie on the boundary of $Q$. Find all possible volumes of "good" tetrahedra.
|
Clearly, the volume of a regular tetrahedron contained in a sphere reaches its maximum value if and only if all four vertices of the tetrahedron lie on the surface of the sphere. Therefore, a "good" tetrahedron with maximum volume must have its vertices at the vertices of the cube (for a proof, inscribe the cube in a sphere). There are exactly two such tetrahedra, their volume being equal to $1-4 \cdot \frac{1}{6}=\frac{1}{3}$. On the other hand, one can find arbitrarily small "good" tetrahedra by applying homothety to the maximal tetrahedron, with the centre of the homothety in one of its vertices.
|
{
"exam": "BalticWay",
"problem_label": "20",
"problem_match": "\n20.",
"resource_path": "BalticWay/segmented/en-bw93sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1993"
}
|
Let $a \circ b=a+b-a b$. Find all triples $(x, y, z)$ of integers such that $(x \circ y) \circ z+(y \circ z) \circ x+(z \circ x) \circ y=0$.
|
Note that
$$
(x \circ y) \circ z=x+y+z-x y-y z-x z+x y z=(x-1)(y-1)(z-1)+1 .
$$
Hence
$$
(x \circ y) \circ z+(y \circ z) \circ x+(z \circ x) \circ y=3((x-1)(y-1)(z-1)+1) \text {. }
$$
Now, if the required equality holds we have $(x-1)(y-1)(z-1)=-1$. There are only four possible decompositions of -1 into a product of three integers. Thus we have four such triples, namely $(0,0,0)$, $(0,2,2),(2,0,2)$ and $(2,2,0)$.
|
(0,0,0), (0,2,2), (2,0,2), (2,2,0)
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $a \circ b=a+b-a b$. Find all triples $(x, y, z)$ of integers such that $(x \circ y) \circ z+(y \circ z) \circ x+(z \circ x) \circ y=0$.
|
Note that
$$
(x \circ y) \circ z=x+y+z-x y-y z-x z+x y z=(x-1)(y-1)(z-1)+1 .
$$
Hence
$$
(x \circ y) \circ z+(y \circ z) \circ x+(z \circ x) \circ y=3((x-1)(y-1)(z-1)+1) \text {. }
$$
Now, if the required equality holds we have $(x-1)(y-1)(z-1)=-1$. There are only four possible decompositions of -1 into a product of three integers. Thus we have four such triples, namely $(0,0,0)$, $(0,2,2),(2,0,2)$ and $(2,2,0)$.
|
{
"exam": "BalticWay",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "BalticWay/segmented/en-bw94sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1994"
}
|
Let $a_{1}, a_{2}, \ldots, a_{9}$ be any non-negative numbers such that $a_{1}=a_{9}=0$ and at least one of the numbers is non-zero. Prove that for some $i, 2 \leq i \leq 8$, the inequality $a_{i-1}+a_{i+1}<2 a_{i}$ holds. Will the statement remain true if we change the number 2 in the last inequality to $1.9 ?$
|
Suppose we have the opposite inequality $a_{i-1}+a_{i+1} \geq 2 a_{i}$ for all $i=2, \ldots, 8$. Let $a_{k}=\max _{1 \leq i \leq 9} a_{i}$. Then we have $a_{k-1}=a_{k+1}=a_{k}, a_{k-2}=a_{k-1}=a_{k}$, etc. Finally we get $a_{1}=a_{k}$, a contradiction.
Suppose now $a_{i-1}+a_{i+1} \geq 1.9 a_{i}$, i.e., $a_{i+1} \geq 1.9 a_{i}-a_{i-1}$ for all $i=2, \ldots, 8$, and let $a_{k}=\max _{1 \leq i \leq 9} a_{i}$. We can multiply all numbers $a_{1}, \ldots, a_{9}$ by the same positive constant without changing the situation in any way, so we assume $a_{k}=1$. Then we have $a_{k-1}+a_{k+1} \geq 1.9$ and hence $0.9 \leq a_{k-1}, a_{k+1} \leq 1$. Moreover, at least one of the numbers $a_{k-1}, a_{k+1}$ must be greater than or equal to 0.95 - let us assume $a_{k+1} \geq 0.95$. Now, we consider two sub-cases:
(a) $k \geq 5$. Then we have
$$
\begin{aligned}
1 \geq a_{k+1} & \geq 0.95>0 \\
1 \geq a_{k+2} & \geq 1.9 a_{k+1}-a_{k} \geq 1.9 \cdot 0.95-1=0.805>0 \\
a_{k+3} & \geq 1.9 a_{k+2}-a_{k+1} \geq 1.9 \cdot 0.805-1=0.5295>0 \\
a_{k+4} & \geq 1.9 a_{k+3}-a_{k+2} \geq 1.9 \cdot 0.5295-1=0.00605>0
\end{aligned}
$$
So in any case we have $a_{9}>0$, a contradiction.
(b) $k \leq 4$. In this case we obtain
$$
\begin{aligned}
1 \geq a_{k-1} & \geq 0.9>0 \\
a_{k-2} & \geq 1.9 a_{k-1}-a_{k} \geq 1.9 \cdot 0.9-1=0.71>0 \\
a_{k-3} & \geq 1.9 a_{k-2}-a_{k-1} \geq 1.9 \cdot 0.71-1=0.349>0
\end{aligned}
$$
and hence $a_{1}>0$, contrary to the condition of the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a_{1}, a_{2}, \ldots, a_{9}$ be any non-negative numbers such that $a_{1}=a_{9}=0$ and at least one of the numbers is non-zero. Prove that for some $i, 2 \leq i \leq 8$, the inequality $a_{i-1}+a_{i+1}<2 a_{i}$ holds. Will the statement remain true if we change the number 2 in the last inequality to $1.9 ?$
|
Suppose we have the opposite inequality $a_{i-1}+a_{i+1} \geq 2 a_{i}$ for all $i=2, \ldots, 8$. Let $a_{k}=\max _{1 \leq i \leq 9} a_{i}$. Then we have $a_{k-1}=a_{k+1}=a_{k}, a_{k-2}=a_{k-1}=a_{k}$, etc. Finally we get $a_{1}=a_{k}$, a contradiction.
Suppose now $a_{i-1}+a_{i+1} \geq 1.9 a_{i}$, i.e., $a_{i+1} \geq 1.9 a_{i}-a_{i-1}$ for all $i=2, \ldots, 8$, and let $a_{k}=\max _{1 \leq i \leq 9} a_{i}$. We can multiply all numbers $a_{1}, \ldots, a_{9}$ by the same positive constant without changing the situation in any way, so we assume $a_{k}=1$. Then we have $a_{k-1}+a_{k+1} \geq 1.9$ and hence $0.9 \leq a_{k-1}, a_{k+1} \leq 1$. Moreover, at least one of the numbers $a_{k-1}, a_{k+1}$ must be greater than or equal to 0.95 - let us assume $a_{k+1} \geq 0.95$. Now, we consider two sub-cases:
(a) $k \geq 5$. Then we have
$$
\begin{aligned}
1 \geq a_{k+1} & \geq 0.95>0 \\
1 \geq a_{k+2} & \geq 1.9 a_{k+1}-a_{k} \geq 1.9 \cdot 0.95-1=0.805>0 \\
a_{k+3} & \geq 1.9 a_{k+2}-a_{k+1} \geq 1.9 \cdot 0.805-1=0.5295>0 \\
a_{k+4} & \geq 1.9 a_{k+3}-a_{k+2} \geq 1.9 \cdot 0.5295-1=0.00605>0
\end{aligned}
$$
So in any case we have $a_{9}>0$, a contradiction.
(b) $k \leq 4$. In this case we obtain
$$
\begin{aligned}
1 \geq a_{k-1} & \geq 0.9>0 \\
a_{k-2} & \geq 1.9 a_{k-1}-a_{k} \geq 1.9 \cdot 0.9-1=0.71>0 \\
a_{k-3} & \geq 1.9 a_{k-2}-a_{k-1} \geq 1.9 \cdot 0.71-1=0.349>0
\end{aligned}
$$
and hence $a_{1}>0$, contrary to the condition of the problem.
|
{
"exam": "BalticWay",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "BalticWay/segmented/en-bw94sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1994"
}
|
Find the largest value of the expression
$$
x y+x \sqrt{1-y^{2}}+y \sqrt{1-x^{2}}-\sqrt{\left(1-x^{2}\right)\left(1-y^{2}\right)}
$$
|
The expression is well-defined only for $|x|,|y| \leq 1$ and we can assume that $x, y \geq 0$. Let $x=\cos \alpha$ and $y=\cos \beta$ for some $0 \leq \alpha, \beta \leq \frac{\pi}{2}$. This reduces the expression to
$$
\cos \alpha \cos \beta+\cos \alpha \sin \beta+\cos \beta \sin \alpha-\sin \alpha \sin \beta=\cos (\alpha+\beta)+\sin (\alpha+\beta)=\sqrt{2} \cdot \sin \left(\alpha+\beta+\frac{\pi}{4}\right)
$$
which does not exceed $\sqrt{2}$. The equality holds when $\alpha+\beta+\frac{\pi}{4}=\frac{\pi}{2}$, for example when $\alpha=\frac{\pi}{4}$ and $\beta=0$, i.e., $x=\frac{\sqrt{2}}{2}$ and $y=1$.
|
\sqrt{2}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find the largest value of the expression
$$
x y+x \sqrt{1-y^{2}}+y \sqrt{1-x^{2}}-\sqrt{\left(1-x^{2}\right)\left(1-y^{2}\right)}
$$
|
The expression is well-defined only for $|x|,|y| \leq 1$ and we can assume that $x, y \geq 0$. Let $x=\cos \alpha$ and $y=\cos \beta$ for some $0 \leq \alpha, \beta \leq \frac{\pi}{2}$. This reduces the expression to
$$
\cos \alpha \cos \beta+\cos \alpha \sin \beta+\cos \beta \sin \alpha-\sin \alpha \sin \beta=\cos (\alpha+\beta)+\sin (\alpha+\beta)=\sqrt{2} \cdot \sin \left(\alpha+\beta+\frac{\pi}{4}\right)
$$
which does not exceed $\sqrt{2}$. The equality holds when $\alpha+\beta+\frac{\pi}{4}=\frac{\pi}{2}$, for example when $\alpha=\frac{\pi}{4}$ and $\beta=0$, i.e., $x=\frac{\sqrt{2}}{2}$ and $y=1$.
|
{
"exam": "BalticWay",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "BalticWay/segmented/en-bw94sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1994"
}
|
Is there an integer $n$ such that $\sqrt{n-1}+\sqrt{n+1}$ is a rational number?
|
Inverting the relation gives
$$
\frac{q}{p}=\frac{1}{\sqrt{n+1}+\sqrt{n-1}}=\frac{\sqrt{n+1}-\sqrt{n-1}}{(\sqrt{n+1}+\sqrt{n-1})(\sqrt{n+1}-\sqrt{n-1})}=\frac{\sqrt{n+1}-\sqrt{n-1}}{2} .
$$
Hence we get the system of equations
$$
\left\{\begin{array}{l}
\sqrt{n+1}+\sqrt{n-1}=\frac{p}{q} \\
\sqrt{n+1}-\sqrt{n-1}=\frac{2 q}{p}
\end{array}\right.
$$
Adding these equations and dividing by 2 gives $\sqrt{n+1}=\frac{2 q^{2}+p^{2}}{2 p q}$. This implies $4 n p^{2} q^{2}=4 q^{4}+p^{4}$.
Suppose now that $n, p$ and $q$ are all positive integers with $p$ and $q$ relatively prime. The relation $4 n p^{2} q^{2}=$ $4 q^{4}+p^{4}$ shows that $p^{4}$, and hence $p$, is divisible by 2 . Letting $p=2 P$ we obtain $4 n P^{2} q^{2}=q^{4}+4 P^{4}$ which shows that $q$ must also be divisible by 2 . This contradicts the assumption that $p$ and $q$ are relatively prime.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Is there an integer $n$ such that $\sqrt{n-1}+\sqrt{n+1}$ is a rational number?
|
Inverting the relation gives
$$
\frac{q}{p}=\frac{1}{\sqrt{n+1}+\sqrt{n-1}}=\frac{\sqrt{n+1}-\sqrt{n-1}}{(\sqrt{n+1}+\sqrt{n-1})(\sqrt{n+1}-\sqrt{n-1})}=\frac{\sqrt{n+1}-\sqrt{n-1}}{2} .
$$
Hence we get the system of equations
$$
\left\{\begin{array}{l}
\sqrt{n+1}+\sqrt{n-1}=\frac{p}{q} \\
\sqrt{n+1}-\sqrt{n-1}=\frac{2 q}{p}
\end{array}\right.
$$
Adding these equations and dividing by 2 gives $\sqrt{n+1}=\frac{2 q^{2}+p^{2}}{2 p q}$. This implies $4 n p^{2} q^{2}=4 q^{4}+p^{4}$.
Suppose now that $n, p$ and $q$ are all positive integers with $p$ and $q$ relatively prime. The relation $4 n p^{2} q^{2}=$ $4 q^{4}+p^{4}$ shows that $p^{4}$, and hence $p$, is divisible by 2 . Letting $p=2 P$ we obtain $4 n P^{2} q^{2}=q^{4}+4 P^{4}$ which shows that $q$ must also be divisible by 2 . This contradicts the assumption that $p$ and $q$ are relatively prime.
|
{
"exam": "BalticWay",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "BalticWay/segmented/en-bw94sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1994"
}
|
Let $p(x)$ be a polynomial with integer coefficients such that both equations $p(x)=1$ and $p(x)=3$ have integer solutions. Can the equation $p(x)=2$ have two different integer solutions?
|
Observe first that if $a$ and $b$ are two different integers then $p(a)-p(b)$ is divisible by $a-b$. Suppose now that $p(a)=1$ and $p(b)=3$ for some integers $a$ and $b$. If we have $p(c)=2$ for some integer $c$, then $c-b= \pm 1$ and $c-a= \pm 1$, hence there can be at most one such integer $c$.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $p(x)$ be a polynomial with integer coefficients such that both equations $p(x)=1$ and $p(x)=3$ have integer solutions. Can the equation $p(x)=2$ have two different integer solutions?
|
Observe first that if $a$ and $b$ are two different integers then $p(a)-p(b)$ is divisible by $a-b$. Suppose now that $p(a)=1$ and $p(b)=3$ for some integers $a$ and $b$. If we have $p(c)=2$ for some integer $c$, then $c-b= \pm 1$ and $c-a= \pm 1$, hence there can be at most one such integer $c$.
|
{
"exam": "BalticWay",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "BalticWay/segmented/en-bw94sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1994"
}
|
Prove that any irreducible fraction $\frac{p}{q}$, where $p$ and $q$ are positive integers and $q$ is odd, is equal to a fraction $\frac{n}{2^{k}-1}$ for some positive integers $n$ and $k$.
|
Since the number of congruence classes modulo $q$ is finite, there exist two non-negative integers $i$ and $j$ with $i>j$ which satisfy $2^{i} \equiv 2^{j}(\bmod q)$. Hence, $q$ divides the number $2^{i}-2^{j}=2^{j}\left(2^{i-j}-1\right)$. Since $q$ is odd, $q$ has to divide $2^{i-j}-1$. Now it suffices to multiply the numerator and denominator of the fraction $\frac{p}{q}$ by $\frac{2^{i-j}-1}{q}$.
|
proof
|
Incomplete
|
Yes
|
proof
|
Number Theory
|
Prove that any irreducible fraction $\frac{p}{q}$, where $p$ and $q$ are positive integers and $q$ is odd, is equal to a fraction $\frac{n}{2^{k}-1}$ for some positive integers $n$ and $k$.
|
Since the number of congruence classes modulo $q$ is finite, there exist two non-negative integers $i$ and $j$ with $i>j$ which satisfy $2^{i} \equiv 2^{j}(\bmod q)$. Hence, $q$ divides the number $2^{i}-2^{j}=2^{j}\left(2^{i-j}-1\right)$. Since $q$ is odd, $q$ has to divide $2^{i-j}-1$. Now it suffices to multiply the numerator and denominator of the fraction $\frac{p}{q}$ by $\frac{2^{i-j}-1}{q}$.
|
{
"exam": "BalticWay",
"problem_label": "6",
"problem_match": "\n6.",
"resource_path": "BalticWay/segmented/en-bw94sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1994"
}
|
Let $p>2$ be a prime number and $1+\frac{1}{2^{3}}+\frac{1}{3^{3}}+\cdots+\frac{1}{(p-1)^{3}}=\frac{m}{n}$ where $m$ and $n$ are relatively prime. Show that $m$ is a multiple of $p$.
|
The sum has an even number of terms; they can be joined in pairs in such a way that the sum is the sum of the terms
$$
\frac{1}{k^{3}}+\frac{1}{(p-k)^{3}}=\frac{p^{3}-3 p^{2} k+3 p k^{2}}{k^{3}(p-k)^{3}} .
$$
The sum of all terms of this type has a denominator in which every prime factor is less than $p$ while the numerator has $p$ as a factor.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $p>2$ be a prime number and $1+\frac{1}{2^{3}}+\frac{1}{3^{3}}+\cdots+\frac{1}{(p-1)^{3}}=\frac{m}{n}$ where $m$ and $n$ are relatively prime. Show that $m$ is a multiple of $p$.
|
The sum has an even number of terms; they can be joined in pairs in such a way that the sum is the sum of the terms
$$
\frac{1}{k^{3}}+\frac{1}{(p-k)^{3}}=\frac{p^{3}-3 p^{2} k+3 p k^{2}}{k^{3}(p-k)^{3}} .
$$
The sum of all terms of this type has a denominator in which every prime factor is less than $p$ while the numerator has $p$ as a factor.
|
{
"exam": "BalticWay",
"problem_label": "7",
"problem_match": "\n7.",
"resource_path": "BalticWay/segmented/en-bw94sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1994"
}
|
Show that for any integer $a \geq 5$ there exist integers $b$ and $c, c \geq b \geq a$, such that $a, b, c$ are the lengths of the sides of a right-angled triangle.
|
We first show this for odd numbers $a=2 i+1 \geq 3$. Put $c=2 k+1$ and $b=2 k$. Then $c^{2}-b^{2}=(2 k+1)^{2}-(2 k)^{2}=4 k+1=a^{2}$. Now $a=2 i+1$ and thus $a^{2}=4 i^{2}+4 i+1$ and $k=i^{2}+i$. Furthermore, $c>b=2 i^{2}+2 i>2 i+1=a$.
Since any multiple of a Pythagorean triple (i.e., a triple of integers $(x, y, z)$ such that $x^{2}+y^{2}=z^{2}$ ) is also a Pythagorean triple we see that the statement is also true for all even numbers which have an odd factor. Hence only the powers of 2 remain. But for 8 we have the triple $(8,15,17)$ and hence all higher powers of 2 are also minimum values of such a triple.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Show that for any integer $a \geq 5$ there exist integers $b$ and $c, c \geq b \geq a$, such that $a, b, c$ are the lengths of the sides of a right-angled triangle.
|
We first show this for odd numbers $a=2 i+1 \geq 3$. Put $c=2 k+1$ and $b=2 k$. Then $c^{2}-b^{2}=(2 k+1)^{2}-(2 k)^{2}=4 k+1=a^{2}$. Now $a=2 i+1$ and thus $a^{2}=4 i^{2}+4 i+1$ and $k=i^{2}+i$. Furthermore, $c>b=2 i^{2}+2 i>2 i+1=a$.
Since any multiple of a Pythagorean triple (i.e., a triple of integers $(x, y, z)$ such that $x^{2}+y^{2}=z^{2}$ ) is also a Pythagorean triple we see that the statement is also true for all even numbers which have an odd factor. Hence only the powers of 2 remain. But for 8 we have the triple $(8,15,17)$ and hence all higher powers of 2 are also minimum values of such a triple.
|
{
"exam": "BalticWay",
"problem_label": "8",
"problem_match": "\n8.",
"resource_path": "BalticWay/segmented/en-bw94sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1994"
}
|
Find all pairs of positive integers $(a, b)$ such that $2^{a}+3^{b}$ is the square of an integer.
|
Considering the equality $2^{a}+3^{b}=n^{2}$ modulo 3 it is easy to see that $a$ must be even. Obviously $n$ is odd so we may take $a=2 x, n=2 y+1$ and write the equality as $4^{x}+3^{b}=(2 y+1)^{2}=4 y^{2}+4 y+1$. Hence $3^{b} \equiv 1(\bmod 4)$ which implies $b=2 z$ for some positive integer $z$. So we get $4^{x}+9^{z}=(2 y+1)^{2}$ and $4^{x}=\left(2 y+1-3^{z}\right)\left(2 y+1+3^{z}\right)$. Both factors on the right-hand side are even numbers but at most one of them is divisible by 4 (since their sum is not divisible by 4 ). Hence $2 y+1-3^{z}=2$ and $2 y+1+3^{z}=2^{2 x-1}$. These two equalities yield $2 \cdot 3^{z}=2^{2 x-1}-2$ and $3^{z}=4^{x-1}-1$. Clearly $x>1$ and a simple argument
modulo 10 gives $z=4 d+1, x-1=2 e+1$ for some non-negative integers $d$ and $e$. Substituting, we get $3^{4 d+1}=4^{2 e+1}-1$ and $3 \cdot(80+1)^{d}=4^{2 e+1}-1$. If $d \geq 1$ then $e \geq 1$, a contradiction (expanding the left-hand expression and moving everything to the left we find that all summands but one are divisible by $4^{2}$ ). Hence $e=d=0, z=1, b=2, x=2$ and $a=4$, and we obtain the classical $2^{4}+3^{2}=4^{2}+3^{2}=5^{2}$.
|
2^{4}+3^{2}=5^{2}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all pairs of positive integers $(a, b)$ such that $2^{a}+3^{b}$ is the square of an integer.
|
Considering the equality $2^{a}+3^{b}=n^{2}$ modulo 3 it is easy to see that $a$ must be even. Obviously $n$ is odd so we may take $a=2 x, n=2 y+1$ and write the equality as $4^{x}+3^{b}=(2 y+1)^{2}=4 y^{2}+4 y+1$. Hence $3^{b} \equiv 1(\bmod 4)$ which implies $b=2 z$ for some positive integer $z$. So we get $4^{x}+9^{z}=(2 y+1)^{2}$ and $4^{x}=\left(2 y+1-3^{z}\right)\left(2 y+1+3^{z}\right)$. Both factors on the right-hand side are even numbers but at most one of them is divisible by 4 (since their sum is not divisible by 4 ). Hence $2 y+1-3^{z}=2$ and $2 y+1+3^{z}=2^{2 x-1}$. These two equalities yield $2 \cdot 3^{z}=2^{2 x-1}-2$ and $3^{z}=4^{x-1}-1$. Clearly $x>1$ and a simple argument
modulo 10 gives $z=4 d+1, x-1=2 e+1$ for some non-negative integers $d$ and $e$. Substituting, we get $3^{4 d+1}=4^{2 e+1}-1$ and $3 \cdot(80+1)^{d}=4^{2 e+1}-1$. If $d \geq 1$ then $e \geq 1$, a contradiction (expanding the left-hand expression and moving everything to the left we find that all summands but one are divisible by $4^{2}$ ). Hence $e=d=0, z=1, b=2, x=2$ and $a=4$, and we obtain the classical $2^{4}+3^{2}=4^{2}+3^{2}=5^{2}$.
|
{
"exam": "BalticWay",
"problem_label": "9",
"problem_match": "\n9.",
"resource_path": "BalticWay/segmented/en-bw94sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1994"
}
|
How many positive integers satisfy the following three conditions:
(i) All digits of the number are from the set $\{1,2,3,4,5\}$;
(ii) The absolute value of the difference between any two consecutive digits is 1 ;
(iii) The integer has 1994 digits?
|
Consider all positive integers with $2 n$ digits satisfying conditions $(i)$ and (ii) of the problem. Let the number of such integers beginning with $1,2,3,4$ and 5 be $a_{n}, b_{n}, c_{n}, d_{n}$ and $e_{n}$, respectively. Then, for $n=1$ we have $a_{1}=1$ (integer 12), $b_{1}=2$ (integers 21 and 23), $c_{1}=2$ (integers 32 and 34$), d_{1}=2$ (integers 43 and 45) and $e_{1}=1$ (integer 54). Observe that $c_{1}=a_{1}+e_{1}$.
Suppose now that $n>1$, i.e., the integers have at least four digits. If an integer begins with the digit 1 then the second digit is 2 while the third can be 1 or 3 . This gives the relation
$$
a_{n}=a_{n-1}+c_{n-1} \text {. }
$$
Similarly, if the first digit is 5 , then the second is 4 while the third can be 3 or 5 . This implies
$$
e_{n}=c_{n-1}+e_{n-1}
$$
If the integer begins with 23 then the third digit is 2 or 4 . If the integer begins with 21 then the third digit is 2 . From this we can conclude that
$$
b_{n}=2 b_{n-1}+d_{n-1} \text {. }
$$
In the same manner we can show that
$$
d_{n}=b_{n-1}+2 d_{n-1} .
$$
If the integer begins with 32 then the third digit must be 1 or 3 , and if it begins with 34 the third digit is 3 or 5 . Hence
$$
c_{n}=a_{n-1}+2 c_{n-1}+e_{n-1} \text {. }
$$
From (1), (2) and (5) it follows that $c_{n}=a_{n}+e_{n}$, which is true for all $n \geq 1$. On the other hand, adding the relations (1)-(5) results in
$$
a_{n}+b_{n}+c_{n}+d_{n}+e_{n}=2 a_{n-1}+3 b_{n-1}+4 c_{n-1}+3 d_{n-1}+2 e_{n-1}
$$
and, since $c_{n-1}=a_{n-1}+e_{n-1}$,
$$
a_{n}+b_{n}+c_{n}+d_{n}+e_{n}=3\left(a_{n-1}+b_{n-1}+c_{n-1}+d_{n-1}+e_{n-1}\right)
$$
Thus the number of integers satisfying conditions $(i)$ and $(i i)$ increases three times when we increase the number of digits by 2 . Since the number of such integers with two digits is 8 , and $1994=2+2 \cdot 996$, the number of integers satisfying all three conditions is $8 \cdot 3^{996}$.
|
8 \cdot 3^{996}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
How many positive integers satisfy the following three conditions:
(i) All digits of the number are from the set $\{1,2,3,4,5\}$;
(ii) The absolute value of the difference between any two consecutive digits is 1 ;
(iii) The integer has 1994 digits?
|
Consider all positive integers with $2 n$ digits satisfying conditions $(i)$ and (ii) of the problem. Let the number of such integers beginning with $1,2,3,4$ and 5 be $a_{n}, b_{n}, c_{n}, d_{n}$ and $e_{n}$, respectively. Then, for $n=1$ we have $a_{1}=1$ (integer 12), $b_{1}=2$ (integers 21 and 23), $c_{1}=2$ (integers 32 and 34$), d_{1}=2$ (integers 43 and 45) and $e_{1}=1$ (integer 54). Observe that $c_{1}=a_{1}+e_{1}$.
Suppose now that $n>1$, i.e., the integers have at least four digits. If an integer begins with the digit 1 then the second digit is 2 while the third can be 1 or 3 . This gives the relation
$$
a_{n}=a_{n-1}+c_{n-1} \text {. }
$$
Similarly, if the first digit is 5 , then the second is 4 while the third can be 3 or 5 . This implies
$$
e_{n}=c_{n-1}+e_{n-1}
$$
If the integer begins with 23 then the third digit is 2 or 4 . If the integer begins with 21 then the third digit is 2 . From this we can conclude that
$$
b_{n}=2 b_{n-1}+d_{n-1} \text {. }
$$
In the same manner we can show that
$$
d_{n}=b_{n-1}+2 d_{n-1} .
$$
If the integer begins with 32 then the third digit must be 1 or 3 , and if it begins with 34 the third digit is 3 or 5 . Hence
$$
c_{n}=a_{n-1}+2 c_{n-1}+e_{n-1} \text {. }
$$
From (1), (2) and (5) it follows that $c_{n}=a_{n}+e_{n}$, which is true for all $n \geq 1$. On the other hand, adding the relations (1)-(5) results in
$$
a_{n}+b_{n}+c_{n}+d_{n}+e_{n}=2 a_{n-1}+3 b_{n-1}+4 c_{n-1}+3 d_{n-1}+2 e_{n-1}
$$
and, since $c_{n-1}=a_{n-1}+e_{n-1}$,
$$
a_{n}+b_{n}+c_{n}+d_{n}+e_{n}=3\left(a_{n-1}+b_{n-1}+c_{n-1}+d_{n-1}+e_{n-1}\right)
$$
Thus the number of integers satisfying conditions $(i)$ and $(i i)$ increases three times when we increase the number of digits by 2 . Since the number of such integers with two digits is 8 , and $1994=2+2 \cdot 996$, the number of integers satisfying all three conditions is $8 \cdot 3^{996}$.
|
{
"exam": "BalticWay",
"problem_label": "10",
"problem_match": "\n10.",
"resource_path": "BalticWay/segmented/en-bw94sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1994"
}
|
Let $N S$ and $E W$ be two perpendicular diameters of a circle $\mathcal{C}$. A line $l$ touches $\mathcal{C}$ at point $S$. Let $A$ and $B$ be two points on $\mathcal{C}$, symmetric with respect to the diameter $E W$. Denote the intersection points of $l$ with the lines $N A$ and $N B$ by $A^{\prime}$ and $B^{\prime}$, respectively. Show that $\left|S A^{\prime}\right| \cdot\left|S B^{\prime}\right|=|S N|^{2}$.
|
We have $\angle N A S=\angle N B S=90^{\circ}$ (see Figure 1). Thus, the triangles $N A^{\prime} S$ and $N S A$ are similar. Also, the triangles $B^{\prime} N S$ and $S N B$ are similar and the triangles $N S A$ and $S N B$ are congruent. Hence, the triangles $N A^{\prime} S$ and $B^{\prime} N S$ are similar which implies $\frac{S A^{\prime}}{S N}=\frac{S N}{S B^{\prime}}$ and $S A^{\prime} \cdot S B^{\prime}=S N^{2}$.
Figure 1
|
S A^{\prime} \cdot S B^{\prime}=S N^{2}
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $N S$ and $E W$ be two perpendicular diameters of a circle $\mathcal{C}$. A line $l$ touches $\mathcal{C}$ at point $S$. Let $A$ and $B$ be two points on $\mathcal{C}$, symmetric with respect to the diameter $E W$. Denote the intersection points of $l$ with the lines $N A$ and $N B$ by $A^{\prime}$ and $B^{\prime}$, respectively. Show that $\left|S A^{\prime}\right| \cdot\left|S B^{\prime}\right|=|S N|^{2}$.
|
We have $\angle N A S=\angle N B S=90^{\circ}$ (see Figure 1). Thus, the triangles $N A^{\prime} S$ and $N S A$ are similar. Also, the triangles $B^{\prime} N S$ and $S N B$ are similar and the triangles $N S A$ and $S N B$ are congruent. Hence, the triangles $N A^{\prime} S$ and $B^{\prime} N S$ are similar which implies $\frac{S A^{\prime}}{S N}=\frac{S N}{S B^{\prime}}$ and $S A^{\prime} \cdot S B^{\prime}=S N^{2}$.

Figure 1
|
{
"exam": "BalticWay",
"problem_label": "11",
"problem_match": "\n11.",
"resource_path": "BalticWay/segmented/en-bw94sol.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "1994"
}
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.