problem
stringlengths 14
10.4k
| solution
stringlengths 1
24.1k
| answer
stringlengths 1
250
⌀ | problem_is_valid
stringclasses 4
values | solution_is_valid
stringclasses 3
values | question_type
stringclasses 4
values | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
10.4k
| solution_raw
stringlengths 1
24.1k
| metadata
dict |
|---|---|---|---|---|---|---|---|---|---|
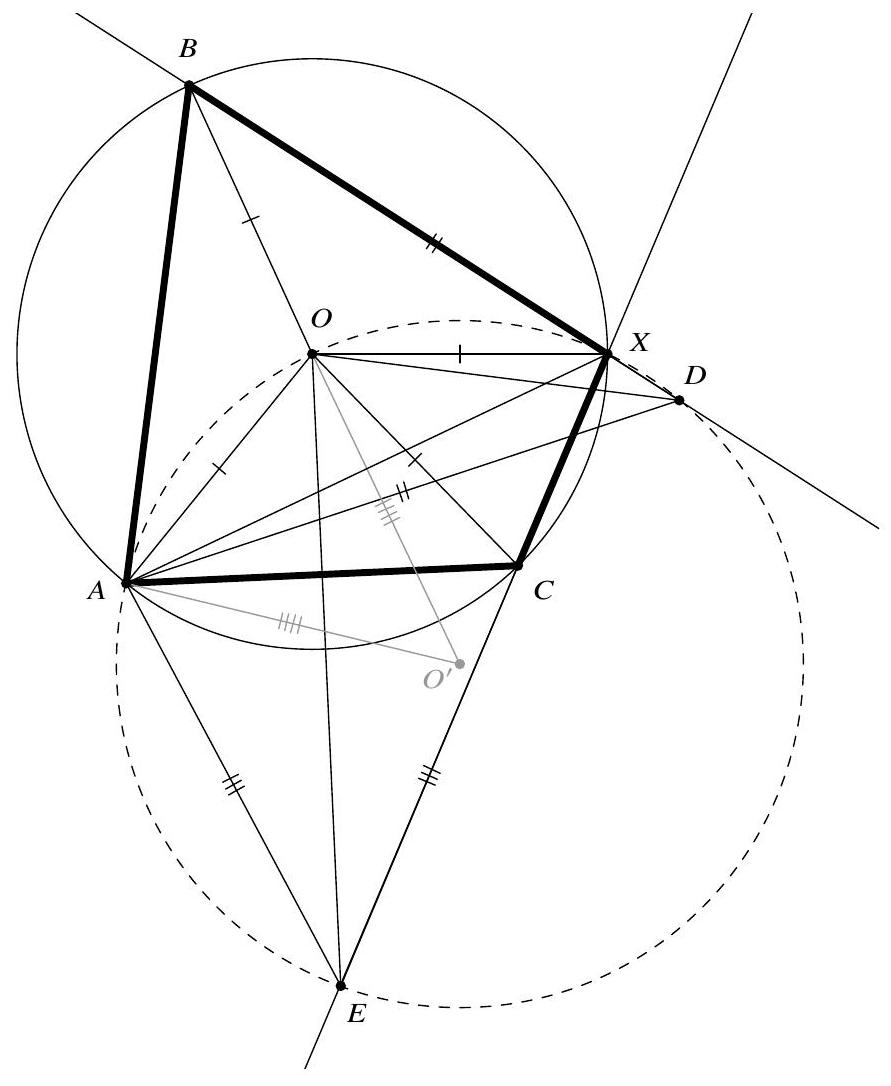
A cyclic quadrilateral $A B X C$ has circumcentre $O$. Let $D$ be a point on line $B X$ such that $|A D|=|B D|$. Let $E$ be a point on line $C X$ such that $|A E|=|C E|$. Prove that the circumcentre of triangle $\triangle D E X$ lies on the perpendicular bisector of $O A$.
#
|
First, note that $\angle A O X=2 \angle A B X=2\left(180^{\circ}-\angle A C X\right)=2 \angle A C E$ as $A B X C$ is cyclic. Secondly, both $\triangle D A B$ and $\triangle E A C$ are isosceles, which implies that $\angle A E X=\angle A E C=180^{\circ}-2 \angle A C E=180^{\circ}-\angle A O X$ and $\angle A D X=$ $\angle A D B=180^{\circ}-2 \angle A B D=180^{\circ}-2 \angle A B X=180^{\circ}-\angle A O X$. From this, see that respectively $A E X O$ and $A D X O$ are cyclic, i.e. $A E D X O$ is cyclic.
Hence, the circumcentre of $\triangle D E X$ is also the circumcentre of $A E D X O$. However, as in a circle any perpendicular bisector of a chord goes through the centre of the circle, we find that the circumcentre of $\triangle D E X$ lies on the perpendicular bisector of $O A$.
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A cyclic quadrilateral $A B X C$ has circumcentre $O$. Let $D$ be a point on line $B X$ such that $|A D|=|B D|$. Let $E$ be a point on line $C X$ such that $|A E|=|C E|$. Prove that the circumcentre of triangle $\triangle D E X$ lies on the perpendicular bisector of $O A$.
#
|
First, note that $\angle A O X=2 \angle A B X=2\left(180^{\circ}-\angle A C X\right)=2 \angle A C E$ as $A B X C$ is cyclic. Secondly, both $\triangle D A B$ and $\triangle E A C$ are isosceles, which implies that $\angle A E X=\angle A E C=180^{\circ}-2 \angle A C E=180^{\circ}-\angle A O X$ and $\angle A D X=$ $\angle A D B=180^{\circ}-2 \angle A B D=180^{\circ}-2 \angle A B X=180^{\circ}-\angle A O X$. From this, see that respectively $A E X O$ and $A D X O$ are cyclic, i.e. $A E D X O$ is cyclic.
Hence, the circumcentre of $\triangle D E X$ is also the circumcentre of $A E D X O$. However, as in a circle any perpendicular bisector of a chord goes through the centre of the circle, we find that the circumcentre of $\triangle D E X$ lies on the perpendicular bisector of $O A$.

#
|
{
"exam": "Benelux_MO",
"problem_label": "3",
"problem_match": "# Problem 3",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2021-zz.jsonl",
"solution_match": "# Solution 1",
"tier": "T3",
"year": "2021"
}
|
A cyclic quadrilateral $A B X C$ has circumcentre $O$. Let $D$ be a point on line $B X$ such that $|A D|=|B D|$. Let $E$ be a point on line $C X$ such that $|A E|=|C E|$. Prove that the circumcentre of triangle $\triangle D E X$ lies on the perpendicular bisector of $O A$.
#
|
In this solution, we use directed angles $\measuredangle$. We have $\measuredangle A B D=\measuredangle A B X=\measuredangle A C X=\measuredangle A C E$ and since $\triangle A B D$ and $\triangle A C E$ are both isosceles, we see that $\triangle A B D \sim \triangle A C E$ with equal orientation. This means that there exists a spiral symmetry $T$ with centre $A$ such that $T(B)=D$ and $T(C)=E$. Now let $O^{\prime}$ be the centre of $\odot D E X$. Then we find $\measuredangle D O^{\prime} E=2 \measuredangle D X E=2 \measuredangle B X C=\measuredangle B O C$. Moreover, $\triangle D O^{\prime} E$ and $\triangle B O C$ are isosceles, so we have $\triangle D O^{\prime} E \sim \triangle B O C$ with equal orientation. This means that $T$ must send $O$ to $O^{\prime}$, so in particular, $\triangle A O O^{\prime}$ is similar to $\triangle A B D$ and $\triangle A C E$. We conclude that $\left|A O^{\prime}\right|=\left|O O^{\prime}\right|$, from which the result follows.
# BxMO 2021: Problems and Solutions
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A cyclic quadrilateral $A B X C$ has circumcentre $O$. Let $D$ be a point on line $B X$ such that $|A D|=|B D|$. Let $E$ be a point on line $C X$ such that $|A E|=|C E|$. Prove that the circumcentre of triangle $\triangle D E X$ lies on the perpendicular bisector of $O A$.
#
|
In this solution, we use directed angles $\measuredangle$. We have $\measuredangle A B D=\measuredangle A B X=\measuredangle A C X=\measuredangle A C E$ and since $\triangle A B D$ and $\triangle A C E$ are both isosceles, we see that $\triangle A B D \sim \triangle A C E$ with equal orientation. This means that there exists a spiral symmetry $T$ with centre $A$ such that $T(B)=D$ and $T(C)=E$. Now let $O^{\prime}$ be the centre of $\odot D E X$. Then we find $\measuredangle D O^{\prime} E=2 \measuredangle D X E=2 \measuredangle B X C=\measuredangle B O C$. Moreover, $\triangle D O^{\prime} E$ and $\triangle B O C$ are isosceles, so we have $\triangle D O^{\prime} E \sim \triangle B O C$ with equal orientation. This means that $T$ must send $O$ to $O^{\prime}$, so in particular, $\triangle A O O^{\prime}$ is similar to $\triangle A B D$ and $\triangle A C E$. We conclude that $\left|A O^{\prime}\right|=\left|O O^{\prime}\right|$, from which the result follows.
# BxMO 2021: Problems and Solutions
#
|
{
"exam": "Benelux_MO",
"problem_label": "3",
"problem_match": "# Problem 3",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2021-zz.jsonl",
"solution_match": "# Solution 2",
"tier": "T3",
"year": "2021"
}
|
A sequence $a_{1}, a_{2}, a_{3}, \ldots$ of positive integers satisfies $a_{1}>5$ and $a_{n+1}=5+6+\cdots+a_{n}$ for all positive integers $n$. Determine all prime numbers $p$ such that, regardless of the value of $a_{1}$, this sequence must contain a multiple of $p$.
#
|
We claim that the only prime number of which the sequence must contain a multiple is $p=2$. To prove this, we begin by noting that
$$
a_{n+1}=\frac{a_{n}\left(a_{n}+1\right)}{2}-10=\frac{\left(a_{n}-4\right)\left(a_{n}+5\right)}{2}
$$
Let $p>2$ be an odd prime, and choose $a_{1} \equiv-4(\bmod p)$, so $2 a_{2} \equiv(-4-4)(-4+5) \equiv-8(\bmod p)$, whence $a_{2} \equiv-4(\bmod p)$, since $p$ is odd. By induction, $a_{n} \equiv-4(\bmod p) \not \equiv 0(\bmod p)$ for all $n$, and so the sequence need not contain a multiple of $p$.
We are left to show that the sequence must contain an even number. Suppose to the contrary that $a_{n}$ is odd for $n=1,2, \ldots$ We observe that
$$
a_{n+1}-a_{n}=\frac{a_{n}\left(a_{n}+1\right)}{2}-\frac{a_{n-1}\left(a_{n-1}+1\right)}{2}=\frac{a_{n}-a_{n-1}}{2}\left(a_{n}+a_{n-1}+1\right)
$$
By assumption, $a_{n}+a_{n-1}+1$ is odd for $n=1,2, \ldots$, so this shows that $v_{2}\left(a_{n+1}-a_{n}\right)=v_{2}\left(a_{n}-a_{n-1}\right)-1$, and so there exists $N$ such that $v_{2}\left(a_{N+1}-a_{N}\right)=0$. This is a contradiction, because $a_{n+1}-a_{n}$ is even for $n=1,2, \ldots$ by assumption, and thus completes the proof.
#
|
2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A sequence $a_{1}, a_{2}, a_{3}, \ldots$ of positive integers satisfies $a_{1}>5$ and $a_{n+1}=5+6+\cdots+a_{n}$ for all positive integers $n$. Determine all prime numbers $p$ such that, regardless of the value of $a_{1}$, this sequence must contain a multiple of $p$.
#
|
We claim that the only prime number of which the sequence must contain a multiple is $p=2$. To prove this, we begin by noting that
$$
a_{n+1}=\frac{a_{n}\left(a_{n}+1\right)}{2}-10=\frac{\left(a_{n}-4\right)\left(a_{n}+5\right)}{2}
$$
Let $p>2$ be an odd prime, and choose $a_{1} \equiv-4(\bmod p)$, so $2 a_{2} \equiv(-4-4)(-4+5) \equiv-8(\bmod p)$, whence $a_{2} \equiv-4(\bmod p)$, since $p$ is odd. By induction, $a_{n} \equiv-4(\bmod p) \not \equiv 0(\bmod p)$ for all $n$, and so the sequence need not contain a multiple of $p$.
We are left to show that the sequence must contain an even number. Suppose to the contrary that $a_{n}$ is odd for $n=1,2, \ldots$ We observe that
$$
a_{n+1}-a_{n}=\frac{a_{n}\left(a_{n}+1\right)}{2}-\frac{a_{n-1}\left(a_{n-1}+1\right)}{2}=\frac{a_{n}-a_{n-1}}{2}\left(a_{n}+a_{n-1}+1\right)
$$
By assumption, $a_{n}+a_{n-1}+1$ is odd for $n=1,2, \ldots$, so this shows that $v_{2}\left(a_{n+1}-a_{n}\right)=v_{2}\left(a_{n}-a_{n-1}\right)-1$, and so there exists $N$ such that $v_{2}\left(a_{N+1}-a_{N}\right)=0$. This is a contradiction, because $a_{n+1}-a_{n}$ is even for $n=1,2, \ldots$ by assumption, and thus completes the proof.
#
|
{
"exam": "Benelux_MO",
"problem_label": "4",
"problem_match": "# Problem 4",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2021-zz.jsonl",
"solution_match": "# Solution 1",
"tier": "T3",
"year": "2021"
}
|
A sequence $a_{1}, a_{2}, a_{3}, \ldots$ of positive integers satisfies $a_{1}>5$ and $a_{n+1}=5+6+\cdots+a_{n}$ for all positive integers $n$. Determine all prime numbers $p$ such that, regardless of the value of $a_{1}$, this sequence must contain a multiple of $p$.
#
|
For odd $p$, proceed as in solution 1 . Now let $p=2$, and suppose that every term of the sequence is odd. We claim that it follows that $a_{n} \equiv 5\left(\bmod 2^{k}\right)$ for every integer $n \geq 1$ and every integer $k \geq 1$. We proceed per induction on $k$. For $k=1$ this simply states that $a_{n}$ is odd for all integers $n \geq 1$, as assumed. Now suppose it is true for $k=r$. Let $k=r+1$. Take any integer $n \geq 1$. Note that, by the induction hypothesis, $a_{n} \equiv 5\left(\bmod 2^{r}\right)$. Therefore there exists an integer $s$ such that $a_{n}=2^{r} s+5$. Now note that
$$
a_{n+1}=\frac{\left(a_{n}-4\right)\left(a_{n}+5\right)}{2}=\frac{\left(2^{r} s+1\right)\left(2^{r} s+10\right)}{2}=\left(2^{r} s+1\right)\left(2^{r-1} s+5\right) \equiv 2^{r-1} s+5 \quad\left(\bmod 2^{r}\right)
$$
By the induction hypothesis, $a_{n+1} \equiv 5\left(\bmod 2^{r}\right)$. Therefore $s$ is even, such that $a_{n}$ is of the form $2^{r+1} s+5$ for any integer $n \geq 1$, which concludes the induction. From this property, it follows that $a_{1}-5$ is divisible by $2^{k}$ for every integer $k \geq 1$, which is only possible if $a_{1}=5$. But $a_{1}>5$, so this is a contradiction.
|
2
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A sequence $a_{1}, a_{2}, a_{3}, \ldots$ of positive integers satisfies $a_{1}>5$ and $a_{n+1}=5+6+\cdots+a_{n}$ for all positive integers $n$. Determine all prime numbers $p$ such that, regardless of the value of $a_{1}$, this sequence must contain a multiple of $p$.
#
|
For odd $p$, proceed as in solution 1 . Now let $p=2$, and suppose that every term of the sequence is odd. We claim that it follows that $a_{n} \equiv 5\left(\bmod 2^{k}\right)$ for every integer $n \geq 1$ and every integer $k \geq 1$. We proceed per induction on $k$. For $k=1$ this simply states that $a_{n}$ is odd for all integers $n \geq 1$, as assumed. Now suppose it is true for $k=r$. Let $k=r+1$. Take any integer $n \geq 1$. Note that, by the induction hypothesis, $a_{n} \equiv 5\left(\bmod 2^{r}\right)$. Therefore there exists an integer $s$ such that $a_{n}=2^{r} s+5$. Now note that
$$
a_{n+1}=\frac{\left(a_{n}-4\right)\left(a_{n}+5\right)}{2}=\frac{\left(2^{r} s+1\right)\left(2^{r} s+10\right)}{2}=\left(2^{r} s+1\right)\left(2^{r-1} s+5\right) \equiv 2^{r-1} s+5 \quad\left(\bmod 2^{r}\right)
$$
By the induction hypothesis, $a_{n+1} \equiv 5\left(\bmod 2^{r}\right)$. Therefore $s$ is even, such that $a_{n}$ is of the form $2^{r+1} s+5$ for any integer $n \geq 1$, which concludes the induction. From this property, it follows that $a_{1}-5$ is divisible by $2^{k}$ for every integer $k \geq 1$, which is only possible if $a_{1}=5$. But $a_{1}>5$, so this is a contradiction.
|
{
"exam": "Benelux_MO",
"problem_label": "4",
"problem_match": "# Problem 4",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2021-zz.jsonl",
"solution_match": "# Solution 2",
"tier": "T3",
"year": "2021"
}
|
Let $n \geqslant 0$ be an integer, and let $a_{0}, a_{1}, \ldots, a_{n}$ be real numbers. Show that there exists $k \in\{0,1, \ldots, n\}$ such that
$$
a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n} \leqslant a_{0}+a_{1}+\cdots+a_{k}
$$
for all real numbers $x \in[0,1]$.
#
|
The case $n=0$ is trivial; for $n>0$, the proof goes by induction on $n$. We need to make one preliminary observation:
Claim. For all reals $a, b, a+b x \leqslant \max \{a, a+b\}$ for all $x \in[0,1]$.
Proof. If $b \leqslant 0$, then $a+b x \leqslant a$ for all $x \in[0,1]$; otherwise, if $b>0, a+b x \leqslant a+b$ for all $x \in[0,1]$. This proves our claim.
This disposes of the base case $n=1$ of the induction: $a_{0}+a_{1} x \leqslant \max \left\{a_{0}, a_{0}+a_{1}\right\}$ for all $x \in[0,1]$. For $n \geqslant 2$, we note that, for all $x \in[0,1]$,
$$
\begin{aligned}
a_{0}+a_{1} x+\cdots+a_{n} x^{n} & =a_{0}+x\left(a_{1}+a_{2} x+\cdots+a_{n} x^{n-1}\right) \\
& \leqslant a_{0}+x\left(a_{1}+a_{2}+\cdots+a_{k}\right) \leqslant \max \left\{a_{0}, a_{0}+\left(a_{1}+\cdots+a_{k}\right)\right\},
\end{aligned}
$$
for some $k \in\{1,2, \ldots, n\}$ by the inductive hypothesis and our earlier claim. This completes the proof by induction.
#
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n \geqslant 0$ be an integer, and let $a_{0}, a_{1}, \ldots, a_{n}$ be real numbers. Show that there exists $k \in\{0,1, \ldots, n\}$ such that
$$
a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n} \leqslant a_{0}+a_{1}+\cdots+a_{k}
$$
for all real numbers $x \in[0,1]$.
#
|
The case $n=0$ is trivial; for $n>0$, the proof goes by induction on $n$. We need to make one preliminary observation:
Claim. For all reals $a, b, a+b x \leqslant \max \{a, a+b\}$ for all $x \in[0,1]$.
Proof. If $b \leqslant 0$, then $a+b x \leqslant a$ for all $x \in[0,1]$; otherwise, if $b>0, a+b x \leqslant a+b$ for all $x \in[0,1]$. This proves our claim.
This disposes of the base case $n=1$ of the induction: $a_{0}+a_{1} x \leqslant \max \left\{a_{0}, a_{0}+a_{1}\right\}$ for all $x \in[0,1]$. For $n \geqslant 2$, we note that, for all $x \in[0,1]$,
$$
\begin{aligned}
a_{0}+a_{1} x+\cdots+a_{n} x^{n} & =a_{0}+x\left(a_{1}+a_{2} x+\cdots+a_{n} x^{n-1}\right) \\
& \leqslant a_{0}+x\left(a_{1}+a_{2}+\cdots+a_{k}\right) \leqslant \max \left\{a_{0}, a_{0}+\left(a_{1}+\cdots+a_{k}\right)\right\},
\end{aligned}
$$
for some $k \in\{1,2, \ldots, n\}$ by the inductive hypothesis and our earlier claim. This completes the proof by induction.
#
|
{
"exam": "Benelux_MO",
"problem_label": "1",
"problem_match": "# Problem 1",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2022-zz.jsonl",
"solution_match": "# Solution 1",
"tier": "T3",
"year": "2022"
}
|
Let $n \geqslant 0$ be an integer, and let $a_{0}, a_{1}, \ldots, a_{n}$ be real numbers. Show that there exists $k \in\{0,1, \ldots, n\}$ such that
$$
a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n} \leqslant a_{0}+a_{1}+\cdots+a_{k}
$$
for all real numbers $x \in[0,1]$.
#
|
Define $s_{i}=a_{0}+a_{1}+\cdots+a_{i}$ for $i \in\{0,1, \ldots, n\}$. Thus $a_{0}=s_{0}$ and $a_{i}=s_{i}-s_{i-1}$ for all $i \in\{1,2, \ldots, n\}$. Hence
$$
\begin{aligned}
a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n} & =s_{0}+\left(s_{1}-s_{0}\right) x+\left(s_{2}-s_{1}\right) x^{2}+\ldots+\left(s_{n}-s_{n-1}\right) x^{n} \\
& =s_{0}(1-x)+s_{1}\left(x-x^{2}\right)+\ldots+s_{n-1}\left(x^{n-1}-x^{n}\right)+s_{n} x^{n}
\end{aligned}
$$
Now choose $k \in\{0,1, \ldots, n\}$ such that $s_{k}=\max \left\{s_{0}, s_{1}, \ldots, s_{n}\right\}$. Using the inequality $x^{i-1}-x^{i} \geqslant 0$, valid for all $i \in\{1,2, \ldots, n\}$ and all $x \in[0,1]$, in the right-hand side above, it follows that
$$
\begin{aligned}
a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n} \leqslant s_{k}(1- & x)+s_{k}\left(x-x^{2}\right)+\cdots+s_{k}\left(x^{n-1}-x^{n}\right)+s_{k} x^{n} \\
& =s_{k}\left[(1-x)+\left(x-x^{2}\right)+\cdots+\left(x^{n-1}-x^{n}\right)+x^{n}\right] \\
& =s_{k}=a_{0}+a_{1}+\cdots+a_{k} .
\end{aligned}
$$
This completes the proof.
## BxMO 2022: Problems and Solutions
#
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n \geqslant 0$ be an integer, and let $a_{0}, a_{1}, \ldots, a_{n}$ be real numbers. Show that there exists $k \in\{0,1, \ldots, n\}$ such that
$$
a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n} \leqslant a_{0}+a_{1}+\cdots+a_{k}
$$
for all real numbers $x \in[0,1]$.
#
|
Define $s_{i}=a_{0}+a_{1}+\cdots+a_{i}$ for $i \in\{0,1, \ldots, n\}$. Thus $a_{0}=s_{0}$ and $a_{i}=s_{i}-s_{i-1}$ for all $i \in\{1,2, \ldots, n\}$. Hence
$$
\begin{aligned}
a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n} & =s_{0}+\left(s_{1}-s_{0}\right) x+\left(s_{2}-s_{1}\right) x^{2}+\ldots+\left(s_{n}-s_{n-1}\right) x^{n} \\
& =s_{0}(1-x)+s_{1}\left(x-x^{2}\right)+\ldots+s_{n-1}\left(x^{n-1}-x^{n}\right)+s_{n} x^{n}
\end{aligned}
$$
Now choose $k \in\{0,1, \ldots, n\}$ such that $s_{k}=\max \left\{s_{0}, s_{1}, \ldots, s_{n}\right\}$. Using the inequality $x^{i-1}-x^{i} \geqslant 0$, valid for all $i \in\{1,2, \ldots, n\}$ and all $x \in[0,1]$, in the right-hand side above, it follows that
$$
\begin{aligned}
a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n} \leqslant s_{k}(1- & x)+s_{k}\left(x-x^{2}\right)+\cdots+s_{k}\left(x^{n-1}-x^{n}\right)+s_{k} x^{n} \\
& =s_{k}\left[(1-x)+\left(x-x^{2}\right)+\cdots+\left(x^{n-1}-x^{n}\right)+x^{n}\right] \\
& =s_{k}=a_{0}+a_{1}+\cdots+a_{k} .
\end{aligned}
$$
This completes the proof.
## BxMO 2022: Problems and Solutions
#
|
{
"exam": "Benelux_MO",
"problem_label": "1",
"problem_match": "# Problem 1",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2022-zz.jsonl",
"solution_match": "# Solution 2",
"tier": "T3",
"year": "2022"
}
|
Let $n \geqslant 0$ be an integer, and let $a_{0}, a_{1}, \ldots, a_{n}$ be real numbers. Show that there exists $k \in\{0,1, \ldots, n\}$ such that
$$
a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n} \leqslant a_{0}+a_{1}+\cdots+a_{k}
$$
for all real numbers $x \in[0,1]$.
#
|
The proof proceeds by induction on $n$. The base case $n=0$ is trivial. For $n \geqslant 1$, since $x \in[0,1]$, we have $x^{n} \leqslant x^{n-1}$. Thus, if $a_{n} \geqslant 0$, then $a_{n} x^{n} \leqslant a_{n} x^{n-1}$, while, if $a_{n}<0$, then $a_{n} x^{n}<0$ trivially. This shows that $a_{n} x^{n} \leqslant \max \left\{0, a_{n} x^{n-1}\right\}$, whence
$$
a_{0}+a_{1} x+\cdots+a_{n-1} x^{n-1}+a_{n} x^{n} \leqslant a_{0}+a_{1} x+\cdots+\max \left\{a_{n-1}, a_{n-1}+a_{n}\right\} x^{n-1}
$$
By the inductive hypothesis, the polynomial of degree $n-1$ on the right-hand side is bounded above by $a_{0}+\cdots+a_{k}$ for some $k \in\{0,1, \ldots, n-2\}$ or $a_{0}+\cdots+a_{n-2}+\max \left\{a_{n-1}, a_{n-1}+a_{n}\right\}$. But the latter is equal to one of $a_{0}+a_{1}+\cdots+a_{n-1}$ or $a_{0}+a_{1}+\cdots+a_{n}$; both are of the desired form, $a_{0}+a_{1}+\cdots+a_{k}$ for some $k \in\{n-1, n\}$. This completes the proof by induction.
## BxMO 2022: Problems and Solutions
#
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n \geqslant 0$ be an integer, and let $a_{0}, a_{1}, \ldots, a_{n}$ be real numbers. Show that there exists $k \in\{0,1, \ldots, n\}$ such that
$$
a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n} \leqslant a_{0}+a_{1}+\cdots+a_{k}
$$
for all real numbers $x \in[0,1]$.
#
|
The proof proceeds by induction on $n$. The base case $n=0$ is trivial. For $n \geqslant 1$, since $x \in[0,1]$, we have $x^{n} \leqslant x^{n-1}$. Thus, if $a_{n} \geqslant 0$, then $a_{n} x^{n} \leqslant a_{n} x^{n-1}$, while, if $a_{n}<0$, then $a_{n} x^{n}<0$ trivially. This shows that $a_{n} x^{n} \leqslant \max \left\{0, a_{n} x^{n-1}\right\}$, whence
$$
a_{0}+a_{1} x+\cdots+a_{n-1} x^{n-1}+a_{n} x^{n} \leqslant a_{0}+a_{1} x+\cdots+\max \left\{a_{n-1}, a_{n-1}+a_{n}\right\} x^{n-1}
$$
By the inductive hypothesis, the polynomial of degree $n-1$ on the right-hand side is bounded above by $a_{0}+\cdots+a_{k}$ for some $k \in\{0,1, \ldots, n-2\}$ or $a_{0}+\cdots+a_{n-2}+\max \left\{a_{n-1}, a_{n-1}+a_{n}\right\}$. But the latter is equal to one of $a_{0}+a_{1}+\cdots+a_{n-1}$ or $a_{0}+a_{1}+\cdots+a_{n}$; both are of the desired form, $a_{0}+a_{1}+\cdots+a_{k}$ for some $k \in\{n-1, n\}$. This completes the proof by induction.
## BxMO 2022: Problems and Solutions
#
|
{
"exam": "Benelux_MO",
"problem_label": "1",
"problem_match": "# Problem 1",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2022-zz.jsonl",
"solution_match": "# Solution 3",
"tier": "T3",
"year": "2022"
}
|
Let $n$ be a positive integer. There are $n$ ants walking along a line at constant nonzero speeds. Different ants need not walk at the same speed or walk in the same direction. Whenever two or more ants collide, all the ants involved in this collision instantly change directions. (Different ants need not be moving in opposite directions when they collide, since a faster ant may catch up with a slower one that is moving in the same direction.) The ants keep walking indefinitely.
Assuming that the total number of collisions is finite, determine the largest possible number of collisions in terms of $n$.
#
|
The order of the ants along the line does not change; denote by $v_{1}, v_{2}, \ldots, v_{n}$ the respective speeds of ants $1,2, \ldots, n$ in this order. If $v_{i-1}<v_{i}>v_{i+1}$ for some $i \in\{2, \ldots, n-1\}$, then, at each stage, ant $i$ can catch up with ants $i-1$ or $i+1$ irrespective of the latters' directions of motion, so the number of collisions is infinite. Hence, if the number of collisions is finite, then, up to switching the direction definining the order of the ants, (i) $v_{1} \geqslant \cdots \geqslant v_{n}$ or (ii) $v_{1} \geqslant \cdots \geqslant v_{k-1}>v_{k} \leqslant \cdots \leqslant v_{n}$ for some $k \in\{2, \ldots, n-1\}$. We need the following observation:
Claim. If $v_{1} \geqslant \cdots \geqslant v_{m}$, then ants $m-1$ and $m$ collide at most $m-1$ times.
Proof. The proof goes by induction on $m$, the case $m=1$ being trivial. Since $v_{m-1} \geqslant v_{m}$, ants $m-1$ and $m$ can only collide if the former is moving towards the latter. Hence, between successive collisions with ant $m$, ant $m-1$ must reverse direction by colliding with ant $m-2$. Since ants $m-1$ and $m-2$ collide at most $(m-1)-1=m-2$ times by the inductive hypothesis, ants $m$ and $m-1$ collide at most $(m-2)+1=m-1$ times.
Hence, in case (i), there are at most $0+1+\cdots+(n-1)=n(n-1) / 2$ collisions. In case (ii), applying the claim to ants $1,2, \ldots, k$ and also to ants $n, n-1, \ldots, k$ by switching their order, the number of collisions is at most $k(k-1) / 2+(n-k+1)(n-k) / 2=n(n-1) / 2-(k-1)(n-k)<n(n-1) / 2$.
Now take a coordinate $x$ along the line, and put ants at $x=1,2, \ldots, n$ with positive initial velocities and speeds $v_{1}=\cdots=v_{n-1}=1, v_{n}=\varepsilon$, for some $\varepsilon$. For $\varepsilon=0$, collisions occur according to the pattern shown below for $n=5$, which clearly extends to all values of $n$ in such a way that ants $m$ and $m+1$ collide exactly $m$ times for $m=1,2, \ldots, n-1$. This yield $1+2+\cdots+(n-1)=n(n-1) / 2$ collisions in total. For all sufficiently small $\varepsilon>0$, the number of collisions remains equal to $n(n-1) / 2$.
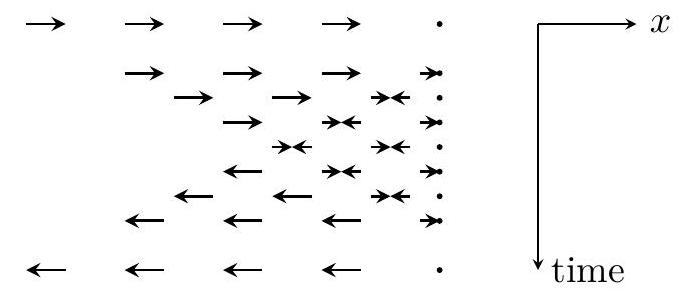
This shows that the upper bound obtained above can be attained. If the number of collisions is finite, the largest possible number of collisions is therefore indeed $n(n-1) / 2$.
## BxMO 2022: Problems and Solutions
#
|
n(n-1) / 2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be a positive integer. There are $n$ ants walking along a line at constant nonzero speeds. Different ants need not walk at the same speed or walk in the same direction. Whenever two or more ants collide, all the ants involved in this collision instantly change directions. (Different ants need not be moving in opposite directions when they collide, since a faster ant may catch up with a slower one that is moving in the same direction.) The ants keep walking indefinitely.
Assuming that the total number of collisions is finite, determine the largest possible number of collisions in terms of $n$.
#
|
The order of the ants along the line does not change; denote by $v_{1}, v_{2}, \ldots, v_{n}$ the respective speeds of ants $1,2, \ldots, n$ in this order. If $v_{i-1}<v_{i}>v_{i+1}$ for some $i \in\{2, \ldots, n-1\}$, then, at each stage, ant $i$ can catch up with ants $i-1$ or $i+1$ irrespective of the latters' directions of motion, so the number of collisions is infinite. Hence, if the number of collisions is finite, then, up to switching the direction definining the order of the ants, (i) $v_{1} \geqslant \cdots \geqslant v_{n}$ or (ii) $v_{1} \geqslant \cdots \geqslant v_{k-1}>v_{k} \leqslant \cdots \leqslant v_{n}$ for some $k \in\{2, \ldots, n-1\}$. We need the following observation:
Claim. If $v_{1} \geqslant \cdots \geqslant v_{m}$, then ants $m-1$ and $m$ collide at most $m-1$ times.
Proof. The proof goes by induction on $m$, the case $m=1$ being trivial. Since $v_{m-1} \geqslant v_{m}$, ants $m-1$ and $m$ can only collide if the former is moving towards the latter. Hence, between successive collisions with ant $m$, ant $m-1$ must reverse direction by colliding with ant $m-2$. Since ants $m-1$ and $m-2$ collide at most $(m-1)-1=m-2$ times by the inductive hypothesis, ants $m$ and $m-1$ collide at most $(m-2)+1=m-1$ times.
Hence, in case (i), there are at most $0+1+\cdots+(n-1)=n(n-1) / 2$ collisions. In case (ii), applying the claim to ants $1,2, \ldots, k$ and also to ants $n, n-1, \ldots, k$ by switching their order, the number of collisions is at most $k(k-1) / 2+(n-k+1)(n-k) / 2=n(n-1) / 2-(k-1)(n-k)<n(n-1) / 2$.
Now take a coordinate $x$ along the line, and put ants at $x=1,2, \ldots, n$ with positive initial velocities and speeds $v_{1}=\cdots=v_{n-1}=1, v_{n}=\varepsilon$, for some $\varepsilon$. For $\varepsilon=0$, collisions occur according to the pattern shown below for $n=5$, which clearly extends to all values of $n$ in such a way that ants $m$ and $m+1$ collide exactly $m$ times for $m=1,2, \ldots, n-1$. This yield $1+2+\cdots+(n-1)=n(n-1) / 2$ collisions in total. For all sufficiently small $\varepsilon>0$, the number of collisions remains equal to $n(n-1) / 2$.

This shows that the upper bound obtained above can be attained. If the number of collisions is finite, the largest possible number of collisions is therefore indeed $n(n-1) / 2$.
## BxMO 2022: Problems and Solutions
#
|
{
"exam": "Benelux_MO",
"problem_label": "2",
"problem_match": "# Problem 2",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2022-zz.jsonl",
"solution_match": "# Solution 1",
"tier": "T3",
"year": "2022"
}
|
Let $n$ be a positive integer. There are $n$ ants walking along a line at constant nonzero speeds. Different ants need not walk at the same speed or walk in the same direction. Whenever two or more ants collide, all the ants involved in this collision instantly change directions. (Different ants need not be moving in opposite directions when they collide, since a faster ant may catch up with a slower one that is moving in the same direction.) The ants keep walking indefinitely.
Assuming that the total number of collisions is finite, determine the largest possible number of collisions in terms of $n$.
#
|
We show that there are at most $n(n-1) / 2$ collisions if the number of collisions is finite as in Solution 1.
To show that the upper bound of $n(n-1) / 2$ collisions can be attained, we construct, inductively, an example of $n$ ants colliding $n(n-1) / 2$ times, the speeds of the ants decrease from left to right, and after all collisions all ants move towards the left, with the possible exception of the rightmost ant. In every case, we will label the ants $1,2, \ldots, n$ from left to right. For $n=1$ this is trivial. For $n \geqslant 2$, we use the construction for $n-1$ ants (now labelled $2,3, \ldots, n$ ). We add ant 1 on the left, moving towards the right, faster than all other ants (so that the speeds of the ants still decrease from left to right), and in such a way that its first collision (with ant 2) happens after all $(n-1)(n-2) / 2$ collisions of the other $n-1$ ants. Now the following events happen (in this order) for $i=1,2, \ldots, n-2$ : ants $i$ and $i+1$ collide, after which ant $i$ moves to the left and ant $i+1$ moves to the right. These collisions do happen because the speeds of the ants decrease from left to right. Then ants $n-1$ and $n$ also collide, resulting in ant $n-1$ moving to the left. This shows that there are (at least) $(n-1)(n-2) / 2+(n-1)=n(n-1) / 2$ collisions. There are in fact no more collisions since the speeds of the ants decrease from left to right; alternatively, this follows from the upper bound proved previously. Since all ants except ant $n$ are moving towards the left after the collisions, this completes the inductive construction.
## BxMO 2022: Problems and Solutions
#
|
n(n-1) / 2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be a positive integer. There are $n$ ants walking along a line at constant nonzero speeds. Different ants need not walk at the same speed or walk in the same direction. Whenever two or more ants collide, all the ants involved in this collision instantly change directions. (Different ants need not be moving in opposite directions when they collide, since a faster ant may catch up with a slower one that is moving in the same direction.) The ants keep walking indefinitely.
Assuming that the total number of collisions is finite, determine the largest possible number of collisions in terms of $n$.
#
|
We show that there are at most $n(n-1) / 2$ collisions if the number of collisions is finite as in Solution 1.
To show that the upper bound of $n(n-1) / 2$ collisions can be attained, we construct, inductively, an example of $n$ ants colliding $n(n-1) / 2$ times, the speeds of the ants decrease from left to right, and after all collisions all ants move towards the left, with the possible exception of the rightmost ant. In every case, we will label the ants $1,2, \ldots, n$ from left to right. For $n=1$ this is trivial. For $n \geqslant 2$, we use the construction for $n-1$ ants (now labelled $2,3, \ldots, n$ ). We add ant 1 on the left, moving towards the right, faster than all other ants (so that the speeds of the ants still decrease from left to right), and in such a way that its first collision (with ant 2) happens after all $(n-1)(n-2) / 2$ collisions of the other $n-1$ ants. Now the following events happen (in this order) for $i=1,2, \ldots, n-2$ : ants $i$ and $i+1$ collide, after which ant $i$ moves to the left and ant $i+1$ moves to the right. These collisions do happen because the speeds of the ants decrease from left to right. Then ants $n-1$ and $n$ also collide, resulting in ant $n-1$ moving to the left. This shows that there are (at least) $(n-1)(n-2) / 2+(n-1)=n(n-1) / 2$ collisions. There are in fact no more collisions since the speeds of the ants decrease from left to right; alternatively, this follows from the upper bound proved previously. Since all ants except ant $n$ are moving towards the left after the collisions, this completes the inductive construction.
## BxMO 2022: Problems and Solutions
#
|
{
"exam": "Benelux_MO",
"problem_label": "2",
"problem_match": "# Problem 2",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2022-zz.jsonl",
"solution_match": "# Solution 2",
"tier": "T3",
"year": "2022"
}
|
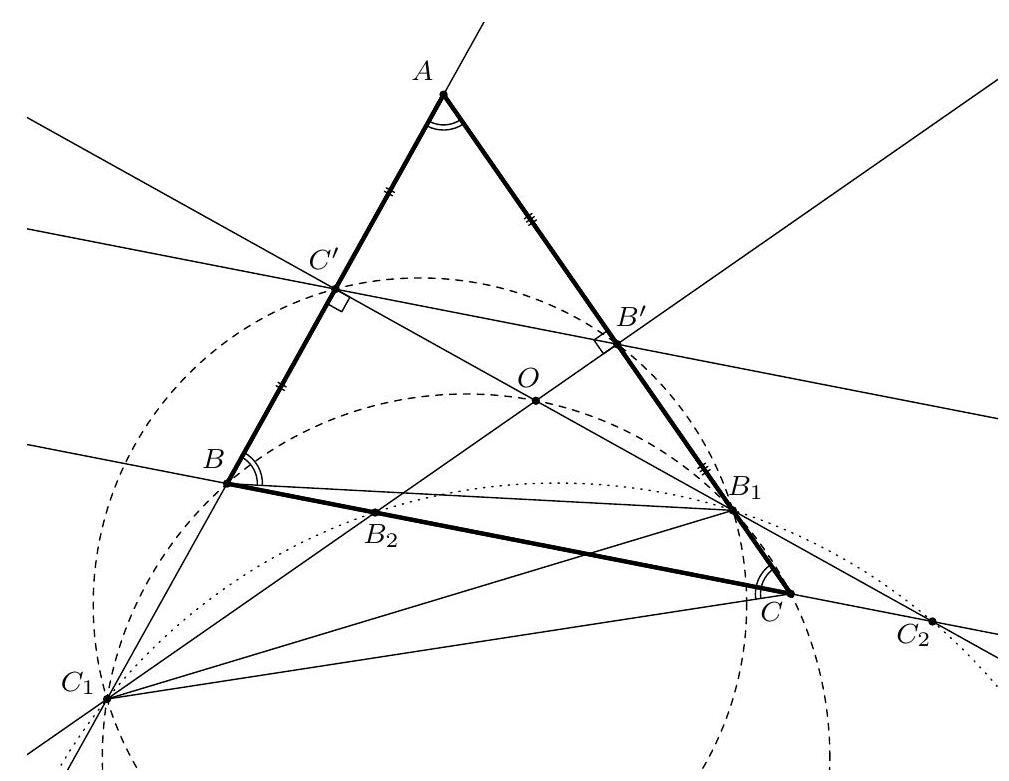
Let $A B C$ be a scalene acute triangle. Let $B_{1}$ be the point on ray $\left[A C\right.$ such that $\left|A B_{1}\right|=\left|B B_{1}\right|$. Let $C_{1}$ be the point on ray $\left[A B\right.$ such that $\left|A C_{1}\right|=\left|C C_{1}\right|$. Let $B_{2}$ and $C_{2}$ be the points on line $B C$ such that $\left|A B_{2}\right|=\left|C B_{2}\right|$ and $\left|B C_{2}\right|=\left|A C_{2}\right|$. Prove that $B_{1}, C_{1}, B_{2}, C_{2}$ are concyclic.
#
|
By construction, lines $B_{1} C_{2}$ and $B_{2} C_{1}$ bisect segments $[A B]$ and $[A C]$, respectively, so their intersection $O$ is the circumcentre of $A B C$. Hence $\angle B O C=2 \angle A$ and $\angle C B O=\angle O C B=90^{\circ}-\angle A$. Now, by construction, $\angle O C_{1} B=90^{\circ}-\angle A=\angle O C B$, so $B C_{1} C O$ is cyclic. Similarly, $B C B_{1} O$ is cyclic by construction because $\angle O B_{1} C=180^{\circ}-\angle A B_{1} O=90^{\circ}+\angle A=180^{\circ}-\angle C B O$. In particular, $B C_{1} C B_{1}$ is cyclic, too.
Now $\angle B_{1} C_{1} B_{2}=\angle B_{1} C_{1} B-\angle B_{2} C_{1} B$ and $\angle B_{1} C_{2} B_{2}=\angle B_{1} C B-\angle C B_{1} C_{2}$. But $\angle B_{1} C_{1} B=\angle B_{1} C B$ since $B C_{1} C B_{1}$ is cyclic and $\angle B_{2} C_{1} B=\angle O C_{1} B=90^{\circ}-\angle A=180^{\circ}-\angle O B_{1} C=\angle C B_{1} C_{2}$. Hence $\angle B_{1} C_{1} B_{2}=\angle B_{1} C_{2} B_{2}$, so $B_{1} B_{2} C_{1} C_{2}$ is cyclic, as required.
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene acute triangle. Let $B_{1}$ be the point on ray $\left[A C\right.$ such that $\left|A B_{1}\right|=\left|B B_{1}\right|$. Let $C_{1}$ be the point on ray $\left[A B\right.$ such that $\left|A C_{1}\right|=\left|C C_{1}\right|$. Let $B_{2}$ and $C_{2}$ be the points on line $B C$ such that $\left|A B_{2}\right|=\left|C B_{2}\right|$ and $\left|B C_{2}\right|=\left|A C_{2}\right|$. Prove that $B_{1}, C_{1}, B_{2}, C_{2}$ are concyclic.
#
|
By construction, lines $B_{1} C_{2}$ and $B_{2} C_{1}$ bisect segments $[A B]$ and $[A C]$, respectively, so their intersection $O$ is the circumcentre of $A B C$. Hence $\angle B O C=2 \angle A$ and $\angle C B O=\angle O C B=90^{\circ}-\angle A$. Now, by construction, $\angle O C_{1} B=90^{\circ}-\angle A=\angle O C B$, so $B C_{1} C O$ is cyclic. Similarly, $B C B_{1} O$ is cyclic by construction because $\angle O B_{1} C=180^{\circ}-\angle A B_{1} O=90^{\circ}+\angle A=180^{\circ}-\angle C B O$. In particular, $B C_{1} C B_{1}$ is cyclic, too.
Now $\angle B_{1} C_{1} B_{2}=\angle B_{1} C_{1} B-\angle B_{2} C_{1} B$ and $\angle B_{1} C_{2} B_{2}=\angle B_{1} C B-\angle C B_{1} C_{2}$. But $\angle B_{1} C_{1} B=\angle B_{1} C B$ since $B C_{1} C B_{1}$ is cyclic and $\angle B_{2} C_{1} B=\angle O C_{1} B=90^{\circ}-\angle A=180^{\circ}-\angle O B_{1} C=\angle C B_{1} C_{2}$. Hence $\angle B_{1} C_{1} B_{2}=\angle B_{1} C_{2} B_{2}$, so $B_{1} B_{2} C_{1} C_{2}$ is cyclic, as required.

#
|
{
"exam": "Benelux_MO",
"problem_label": "3",
"problem_match": "# Problem 3",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2022-zz.jsonl",
"solution_match": "# Solution 1",
"tier": "T3",
"year": "2022"
}
|
Let $A B C$ be a scalene acute triangle. Let $B_{1}$ be the point on ray $\left[A C\right.$ such that $\left|A B_{1}\right|=\left|B B_{1}\right|$. Let $C_{1}$ be the point on ray $\left[A B\right.$ such that $\left|A C_{1}\right|=\left|C C_{1}\right|$. Let $B_{2}$ and $C_{2}$ be the points on line $B C$ such that $\left|A B_{2}\right|=\left|C B_{2}\right|$ and $\left|B C_{2}\right|=\left|A C_{2}\right|$. Prove that $B_{1}, C_{1}, B_{2}, C_{2}$ are concyclic.
#
|
The isosceles triangles $A B_{1} B$ and $A C_{1} C$ have equal base angles $\angle B A B_{1}=\angle C_{1} A C=\angle A$, so are similar. In particular, $|A B| /\left|A B_{1}\right|=|A C| /\left|A C_{1}\right|$. Since $\angle B A C=\angle B_{1} A C_{1}=\angle A$, it follows that triangles $A B C$ and $A B_{1} C_{1}$ are similar, too. In particular, $\angle C B A=\angle A B_{1} C_{1}$.
By construction, lines $B_{1} C_{2}$ and $B_{2} C_{1}$ are the respective perpendicular bisectors of $[A B]$ and $[A C]$, so meet them at their respective midpoints $C^{\prime}$ and $B^{\prime}$. Hence
$$
\begin{aligned}
\angle B_{1} C_{2} B_{2} & =\angle C^{\prime} C_{2} B=90^{\circ}-\angle C_{2} B C^{\prime}=90^{\circ}-\angle C B A=90^{\circ}-\angle A B_{1} C_{1}=90^{\circ}-\angle B^{\prime} B_{1} C_{1} \\
& =\angle B_{1} C_{1} B^{\prime}=\angle B_{1} C_{1} B_{2} .
\end{aligned}
$$
Hence $B_{1} C_{2} C_{1} B_{2}$ is cyclic, which completes the proof.
## BxMO 2022: Problems and Solutions
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene acute triangle. Let $B_{1}$ be the point on ray $\left[A C\right.$ such that $\left|A B_{1}\right|=\left|B B_{1}\right|$. Let $C_{1}$ be the point on ray $\left[A B\right.$ such that $\left|A C_{1}\right|=\left|C C_{1}\right|$. Let $B_{2}$ and $C_{2}$ be the points on line $B C$ such that $\left|A B_{2}\right|=\left|C B_{2}\right|$ and $\left|B C_{2}\right|=\left|A C_{2}\right|$. Prove that $B_{1}, C_{1}, B_{2}, C_{2}$ are concyclic.
#
|
The isosceles triangles $A B_{1} B$ and $A C_{1} C$ have equal base angles $\angle B A B_{1}=\angle C_{1} A C=\angle A$, so are similar. In particular, $|A B| /\left|A B_{1}\right|=|A C| /\left|A C_{1}\right|$. Since $\angle B A C=\angle B_{1} A C_{1}=\angle A$, it follows that triangles $A B C$ and $A B_{1} C_{1}$ are similar, too. In particular, $\angle C B A=\angle A B_{1} C_{1}$.
By construction, lines $B_{1} C_{2}$ and $B_{2} C_{1}$ are the respective perpendicular bisectors of $[A B]$ and $[A C]$, so meet them at their respective midpoints $C^{\prime}$ and $B^{\prime}$. Hence
$$
\begin{aligned}
\angle B_{1} C_{2} B_{2} & =\angle C^{\prime} C_{2} B=90^{\circ}-\angle C_{2} B C^{\prime}=90^{\circ}-\angle C B A=90^{\circ}-\angle A B_{1} C_{1}=90^{\circ}-\angle B^{\prime} B_{1} C_{1} \\
& =\angle B_{1} C_{1} B^{\prime}=\angle B_{1} C_{1} B_{2} .
\end{aligned}
$$
Hence $B_{1} C_{2} C_{1} B_{2}$ is cyclic, which completes the proof.
## BxMO 2022: Problems and Solutions
#
|
{
"exam": "Benelux_MO",
"problem_label": "3",
"problem_match": "# Problem 3",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2022-zz.jsonl",
"solution_match": "# Solution 2",
"tier": "T3",
"year": "2022"
}
|
Let $A B C$ be a scalene acute triangle. Let $B_{1}$ be the point on ray $\left[A C\right.$ such that $\left|A B_{1}\right|=\left|B B_{1}\right|$. Let $C_{1}$ be the point on ray $\left[A B\right.$ such that $\left|A C_{1}\right|=\left|C C_{1}\right|$. Let $B_{2}$ and $C_{2}$ be the points on line $B C$ such that $\left|A B_{2}\right|=\left|C B_{2}\right|$ and $\left|B C_{2}\right|=\left|A C_{2}\right|$. Prove that $B_{1}, C_{1}, B_{2}, C_{2}$ are concyclic.
#
|
By construction, lines $B_{1} C_{2}$ and $B_{2} C_{1}$ are the respective perpendicular bisectors of $[A B]$ and $[A C]$, so meet them at their respective midpoints $C^{\prime}$ and $B^{\prime}$. Since $\angle B_{1} C^{\prime} C_{1}=90^{\circ}=\angle C_{1} B^{\prime} B_{1}, B_{1} C_{1} C^{\prime} B^{\prime}$ is cyclic. Together with the fact that $B^{\prime} C^{\prime} \| B C$ by construction, this implies
$$
\angle B_{1} C_{2} B_{2}=\angle C^{\prime} C_{2} B=\angle C_{2} C^{\prime} B^{\prime}=\angle B_{1} C^{\prime} B^{\prime}=\angle B_{1} C_{1} B^{\prime}=\angle B_{1} C_{1} B_{2},
$$
whence $B_{1} C_{2} C_{1} B_{2}$ is cyclic. This completes the proof.
# BxMO 2022: Problems and Solutions
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a scalene acute triangle. Let $B_{1}$ be the point on ray $\left[A C\right.$ such that $\left|A B_{1}\right|=\left|B B_{1}\right|$. Let $C_{1}$ be the point on ray $\left[A B\right.$ such that $\left|A C_{1}\right|=\left|C C_{1}\right|$. Let $B_{2}$ and $C_{2}$ be the points on line $B C$ such that $\left|A B_{2}\right|=\left|C B_{2}\right|$ and $\left|B C_{2}\right|=\left|A C_{2}\right|$. Prove that $B_{1}, C_{1}, B_{2}, C_{2}$ are concyclic.
#
|
By construction, lines $B_{1} C_{2}$ and $B_{2} C_{1}$ are the respective perpendicular bisectors of $[A B]$ and $[A C]$, so meet them at their respective midpoints $C^{\prime}$ and $B^{\prime}$. Since $\angle B_{1} C^{\prime} C_{1}=90^{\circ}=\angle C_{1} B^{\prime} B_{1}, B_{1} C_{1} C^{\prime} B^{\prime}$ is cyclic. Together with the fact that $B^{\prime} C^{\prime} \| B C$ by construction, this implies
$$
\angle B_{1} C_{2} B_{2}=\angle C^{\prime} C_{2} B=\angle C_{2} C^{\prime} B^{\prime}=\angle B_{1} C^{\prime} B^{\prime}=\angle B_{1} C_{1} B^{\prime}=\angle B_{1} C_{1} B_{2},
$$
whence $B_{1} C_{2} C_{1} B_{2}$ is cyclic. This completes the proof.
# BxMO 2022: Problems and Solutions
#
|
{
"exam": "Benelux_MO",
"problem_label": "3",
"problem_match": "# Problem 3",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2022-zz.jsonl",
"solution_match": "# Solution 3",
"tier": "T3",
"year": "2022"
}
|
A subset $A$ of the natural numbers $\mathbb{N}=\{0,1,2, \ldots\}$ is called good if every integer $n>0$ has at most one prime divisor $p$ such that $n-p \in A$.
(a) Show that the set $S=\{0,1,4,9, \ldots\}$ of perfect squares is good.
(b) Find an infinite good set disjoint from $S$.
(Two sets are disjoint if they have no common elements.)
#
|
(a) Suppose to the contrary that $S$ is not good, so there exists $n \in \mathbb{N}$ with two different prime factors $p \neq q$ such that $n-p, n-q$ are perfect squares. In particular $n$ is not prime. Write $n-p=m^{2}$, for some $m \in \mathbb{N}$. As $p \mid n$, it follows that $p \mid m$ and hence $p^{2} \mid m^{2}$ since $p$ is prime. Hence there exists $k \in \mathbb{N}$ such that $n-p=p^{2} k^{2}$. Similarly, there exists $\ell \in \mathbb{N}$ such that $n-q=q^{2} \ell^{2}$. We observe that $k, \ell \neq 0$ since $n$ is not prime.
Now we have $p-q=(n-q)-(n-p)=(\ell q-k p)(\ell q+k p)$. Since $p-q \neq 0, \ell q-k p \neq 0$, and hence $|p-q|=|k p-\ell q||k p+\ell q| \geqslant|k p+\ell q|=k p+\ell q$. This is a contradiction however, because, since $k, \ell \neq 0$, it is clear that $k p+\ell q \geqslant p+q>|p-q|$. Hence $S$ is good.
(b) Let $q$ be a prime, and let $Q=\left\{q, q^{3}, q^{5}, \ldots\right\}$ be the (infinite) set of odd powers of $q$, which is disjoint from $S$. We claim that $Q$ is good. Indeed, let $n \in \mathbb{N}$, and let $p \mid n$ be a prime such that $n-p \in Q$, i.e. $n-p=q^{2 k+1}$ for some $k \in \mathbb{N}$. Then $p \mid n-p$, so $p \mid q^{2 k+1}$, and hence $p=q$. Thus $Q$ is good.
#
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
A subset $A$ of the natural numbers $\mathbb{N}=\{0,1,2, \ldots\}$ is called good if every integer $n>0$ has at most one prime divisor $p$ such that $n-p \in A$.
(a) Show that the set $S=\{0,1,4,9, \ldots\}$ of perfect squares is good.
(b) Find an infinite good set disjoint from $S$.
(Two sets are disjoint if they have no common elements.)
#
|
(a) Suppose to the contrary that $S$ is not good, so there exists $n \in \mathbb{N}$ with two different prime factors $p \neq q$ such that $n-p, n-q$ are perfect squares. In particular $n$ is not prime. Write $n-p=m^{2}$, for some $m \in \mathbb{N}$. As $p \mid n$, it follows that $p \mid m$ and hence $p^{2} \mid m^{2}$ since $p$ is prime. Hence there exists $k \in \mathbb{N}$ such that $n-p=p^{2} k^{2}$. Similarly, there exists $\ell \in \mathbb{N}$ such that $n-q=q^{2} \ell^{2}$. We observe that $k, \ell \neq 0$ since $n$ is not prime.
Now we have $p-q=(n-q)-(n-p)=(\ell q-k p)(\ell q+k p)$. Since $p-q \neq 0, \ell q-k p \neq 0$, and hence $|p-q|=|k p-\ell q||k p+\ell q| \geqslant|k p+\ell q|=k p+\ell q$. This is a contradiction however, because, since $k, \ell \neq 0$, it is clear that $k p+\ell q \geqslant p+q>|p-q|$. Hence $S$ is good.
(b) Let $q$ be a prime, and let $Q=\left\{q, q^{3}, q^{5}, \ldots\right\}$ be the (infinite) set of odd powers of $q$, which is disjoint from $S$. We claim that $Q$ is good. Indeed, let $n \in \mathbb{N}$, and let $p \mid n$ be a prime such that $n-p \in Q$, i.e. $n-p=q^{2 k+1}$ for some $k \in \mathbb{N}$. Then $p \mid n-p$, so $p \mid q^{2 k+1}$, and hence $p=q$. Thus $Q$ is good.
#
|
{
"exam": "Benelux_MO",
"problem_label": "4",
"problem_match": "# Problem 4",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2022-zz.jsonl",
"solution_match": "# Solution 1",
"tier": "T3",
"year": "2022"
}
|
A subset $A$ of the natural numbers $\mathbb{N}=\{0,1,2, \ldots\}$ is called good if every integer $n>0$ has at most one prime divisor $p$ such that $n-p \in A$.
(a) Show that the set $S=\{0,1,4,9, \ldots\}$ of perfect squares is good.
(b) Find an infinite good set disjoint from $S$.
(Two sets are disjoint if they have no common elements.)
#
|
(a) Let $p \mid n$ be a prime such that $n-p=p(n / p-1)=m^{2}$, for some $m \in \mathbb{N}$. Since $p \mid m^{2}$ and $p$ is prime, $p^{2} \mid m^{2}$, and hence $p \mid n / p-1<n / p$, so $p<\sqrt{n}$.
Now suppose to the contrary that $S$ is not good, so there are primes $p_{1}>p_{2}$ dividing $n$ such that $n-p_{1}<n-p_{2}$ are perfect squares. Then
$$
n-p_{2} \geqslant\left(\sqrt{n-p_{1}}+1\right)^{2}>n-p_{1}+2 \sqrt{n-p_{1}} \quad \Longrightarrow \quad p_{1}>p_{2}+2 \sqrt{n-p_{1}} \geqslant 2+2 \sqrt{n-p_{1}} .
$$
The last condition implies that $p_{1}>2 \sqrt{n-1}$. But $p_{1}<\sqrt{n}$ by the first part, so $\sqrt{n}>2 \sqrt{n-1}$, which is a contradiction for $n>1$; the cases $n=0$ and $n=1$ are trivial. Thus $S$ is good.
(b) We claim that the infinite set $P=\{3,5,7,11, \ldots\}$ of odd primes, which is disjoint from $S$, is good. Indeed, let $n \in \mathbb{N}$ and let $p \mid n$ be a prime such that $n-p=q$, for some odd prime $q$. Then $p \mid n-p$, so $p \mid q$, i.e. $p=q$, and hence $n=2 q$. Since $q$ is the only odd prime divisor of $n=2 q$, $P$ is good.
The set $P^{\prime}=\{2,3,5,7,11, \ldots\}$ of all primes is also good. The proof is similar: let $n \in \mathbb{N}$ and let $p \mid n$ be a prime such that $n-p=q$, for some prime $q$. Then $p \mid n-p$, so $p \mid q$, i.e. $p=q$, and hence $n=2 q$. If $q=2$, then 2 is the only prime divisor of $n$; if $q \neq 2$, then the only prime divisor of $n$, apart from $q$, is 2 . However, $n-2=2(q-1) \notin P^{\prime}$ since $q-1>1$. Hence $P^{\prime}$ is good.
# BxMO 2022: Problems and Solutions
#
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
A subset $A$ of the natural numbers $\mathbb{N}=\{0,1,2, \ldots\}$ is called good if every integer $n>0$ has at most one prime divisor $p$ such that $n-p \in A$.
(a) Show that the set $S=\{0,1,4,9, \ldots\}$ of perfect squares is good.
(b) Find an infinite good set disjoint from $S$.
(Two sets are disjoint if they have no common elements.)
#
|
(a) Let $p \mid n$ be a prime such that $n-p=p(n / p-1)=m^{2}$, for some $m \in \mathbb{N}$. Since $p \mid m^{2}$ and $p$ is prime, $p^{2} \mid m^{2}$, and hence $p \mid n / p-1<n / p$, so $p<\sqrt{n}$.
Now suppose to the contrary that $S$ is not good, so there are primes $p_{1}>p_{2}$ dividing $n$ such that $n-p_{1}<n-p_{2}$ are perfect squares. Then
$$
n-p_{2} \geqslant\left(\sqrt{n-p_{1}}+1\right)^{2}>n-p_{1}+2 \sqrt{n-p_{1}} \quad \Longrightarrow \quad p_{1}>p_{2}+2 \sqrt{n-p_{1}} \geqslant 2+2 \sqrt{n-p_{1}} .
$$
The last condition implies that $p_{1}>2 \sqrt{n-1}$. But $p_{1}<\sqrt{n}$ by the first part, so $\sqrt{n}>2 \sqrt{n-1}$, which is a contradiction for $n>1$; the cases $n=0$ and $n=1$ are trivial. Thus $S$ is good.
(b) We claim that the infinite set $P=\{3,5,7,11, \ldots\}$ of odd primes, which is disjoint from $S$, is good. Indeed, let $n \in \mathbb{N}$ and let $p \mid n$ be a prime such that $n-p=q$, for some odd prime $q$. Then $p \mid n-p$, so $p \mid q$, i.e. $p=q$, and hence $n=2 q$. Since $q$ is the only odd prime divisor of $n=2 q$, $P$ is good.
The set $P^{\prime}=\{2,3,5,7,11, \ldots\}$ of all primes is also good. The proof is similar: let $n \in \mathbb{N}$ and let $p \mid n$ be a prime such that $n-p=q$, for some prime $q$. Then $p \mid n-p$, so $p \mid q$, i.e. $p=q$, and hence $n=2 q$. If $q=2$, then 2 is the only prime divisor of $n$; if $q \neq 2$, then the only prime divisor of $n$, apart from $q$, is 2 . However, $n-2=2(q-1) \notin P^{\prime}$ since $q-1>1$. Hence $P^{\prime}$ is good.
# BxMO 2022: Problems and Solutions
#
|
{
"exam": "Benelux_MO",
"problem_label": "4",
"problem_match": "# Problem 4",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2022-zz.jsonl",
"solution_match": "# Solution 2",
"tier": "T3",
"year": "2022"
}
|
A subset $A$ of the natural numbers $\mathbb{N}=\{0,1,2, \ldots\}$ is called good if every integer $n>0$ has at most one prime divisor $p$ such that $n-p \in A$.
(a) Show that the set $S=\{0,1,4,9, \ldots\}$ of perfect squares is good.
(b) Find an infinite good set disjoint from $S$.
(Two sets are disjoint if they have no common elements.)
#
|
(a) Suppose to the contrary that $S$ is not good, so there exists $n \in \mathbb{N}$ with two different prime factors $p \neq q$ such that $n-p, n-q$ are perfect squares. Write $n-p=m^{2}$, for some $m \in \mathbb{N}$. As $p \mid n$, it follows that $p \mid m$ and hence $p^{2} \mid m^{2}$ since $p$ is prime. Hence there exists $k \in \mathbb{N}$ such that $n-p=p^{2} k^{2}$. Similarly, there exists $\ell \in \mathbb{N}$ such that $n-q=q^{2} \ell^{2}$. By construction, $n$ is not prime, so $n-p, n-q \neq 0$, whence $k, \ell \geqslant 1$.
Hence $p^{2} k^{2}+p=q^{2} \ell^{2}+q$. Hence $p^{2} k^{2}<p^{2} k^{2}+p=q^{2} \ell^{2}+q<q^{2} \ell^{2}+2 q \ell+1=(q \ell+1)^{2}$. Similarly, $q^{2} \ell^{2}<(p k+1)^{2}$, whence $q \ell-1<p k<q \ell+1$. It follows that $p k=q \ell$, so $p^{2} k^{2}+p=q^{2} \ell^{2}+q$ yields the contradiction $p=q$. Hence $S$ is good.
(b) Let $A$ be a finite good set such that $0 \notin A$, and let $m=\max A$. Let $a \geqslant 2 m+1$ be an integer. We claim that $A^{\prime}=A \cup\{a\}$ is good. Indeed, suppose to the contrary that there exist $n \in \mathbb{N}$ and primes $p, q \mid n$ with $p \neq q$ such that $n-p, n-q \in A^{\prime}$. If $n<a$, then $n-p, n-q \in A$, which is a contradiction because $A$ is good. Hence $n \geqslant a$. Now $p \mid n-p$, so $n-p \geqslant p$ since $0 \notin A^{\prime}$. Thus $p \leqslant n / 2$ and hence $n-p \geqslant n / 2 \geqslant a / 2>m$. Similarly, $n-q>m$. It follows that $n-p=n-q=a$, which implies the contradiction $p=q$. Hence $A^{\prime}$ is good.
Now it is clear that any singleton set is good: indeed, if $A=\{a\}$, and $n \in \mathbb{N}$ has prime divisors $p, q$ such that $n-p, n-q \in A$, then $n-p=a=n-q$, so $p=q$. Starting from the singleton $T_{1}=\{2\}$, we use the above construction to obtain, iteratively, good sets $T_{2}, T_{3}, \ldots$ of $2,3, \ldots$ elements. It is clearly possibly to ensure that they are each disjoint from $S$ by not adding a perfect square at any stage. Then $T=T_{1} \cup T_{2} \cup \cdots$ is an infinite good set disjoint from $S$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
A subset $A$ of the natural numbers $\mathbb{N}=\{0,1,2, \ldots\}$ is called good if every integer $n>0$ has at most one prime divisor $p$ such that $n-p \in A$.
(a) Show that the set $S=\{0,1,4,9, \ldots\}$ of perfect squares is good.
(b) Find an infinite good set disjoint from $S$.
(Two sets are disjoint if they have no common elements.)
#
|
(a) Suppose to the contrary that $S$ is not good, so there exists $n \in \mathbb{N}$ with two different prime factors $p \neq q$ such that $n-p, n-q$ are perfect squares. Write $n-p=m^{2}$, for some $m \in \mathbb{N}$. As $p \mid n$, it follows that $p \mid m$ and hence $p^{2} \mid m^{2}$ since $p$ is prime. Hence there exists $k \in \mathbb{N}$ such that $n-p=p^{2} k^{2}$. Similarly, there exists $\ell \in \mathbb{N}$ such that $n-q=q^{2} \ell^{2}$. By construction, $n$ is not prime, so $n-p, n-q \neq 0$, whence $k, \ell \geqslant 1$.
Hence $p^{2} k^{2}+p=q^{2} \ell^{2}+q$. Hence $p^{2} k^{2}<p^{2} k^{2}+p=q^{2} \ell^{2}+q<q^{2} \ell^{2}+2 q \ell+1=(q \ell+1)^{2}$. Similarly, $q^{2} \ell^{2}<(p k+1)^{2}$, whence $q \ell-1<p k<q \ell+1$. It follows that $p k=q \ell$, so $p^{2} k^{2}+p=q^{2} \ell^{2}+q$ yields the contradiction $p=q$. Hence $S$ is good.
(b) Let $A$ be a finite good set such that $0 \notin A$, and let $m=\max A$. Let $a \geqslant 2 m+1$ be an integer. We claim that $A^{\prime}=A \cup\{a\}$ is good. Indeed, suppose to the contrary that there exist $n \in \mathbb{N}$ and primes $p, q \mid n$ with $p \neq q$ such that $n-p, n-q \in A^{\prime}$. If $n<a$, then $n-p, n-q \in A$, which is a contradiction because $A$ is good. Hence $n \geqslant a$. Now $p \mid n-p$, so $n-p \geqslant p$ since $0 \notin A^{\prime}$. Thus $p \leqslant n / 2$ and hence $n-p \geqslant n / 2 \geqslant a / 2>m$. Similarly, $n-q>m$. It follows that $n-p=n-q=a$, which implies the contradiction $p=q$. Hence $A^{\prime}$ is good.
Now it is clear that any singleton set is good: indeed, if $A=\{a\}$, and $n \in \mathbb{N}$ has prime divisors $p, q$ such that $n-p, n-q \in A$, then $n-p=a=n-q$, so $p=q$. Starting from the singleton $T_{1}=\{2\}$, we use the above construction to obtain, iteratively, good sets $T_{2}, T_{3}, \ldots$ of $2,3, \ldots$ elements. It is clearly possibly to ensure that they are each disjoint from $S$ by not adding a perfect square at any stage. Then $T=T_{1} \cup T_{2} \cup \cdots$ is an infinite good set disjoint from $S$.
|
{
"exam": "Benelux_MO",
"problem_label": "4",
"problem_match": "# Problem 4",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2022-zz.jsonl",
"solution_match": "# Solution 3",
"tier": "T3",
"year": "2022"
}
|
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
(x-y)(f(x)+f(y)) \leqslant f\left(x^{2}-y^{2}\right) \quad \text { for all } x, y \in \mathbb{R}
$$
#
|
Clearly, $f(x)=c x$ is a solution for each $c \in \mathbb{R}$ since $(x-y)(c x+c y)=c\left(x^{2}-y^{2}\right)$. To show that there are no other solutions, we observe that
(1) $x=y: \quad 0 \leqslant f(0)$;
$x=1, y=0: \quad f(0)+f(1) \leqslant f(1) \Rightarrow f(0) \leqslant 0$, whence $f(0)=0 ;$
(2) $y=-x: \quad 2 x(f(x)+f(-x)) \leqslant f(0)=0$;
$x \rightarrow-x: \quad-2 x(f(-x)+f(x)) \leqslant 0 \Rightarrow 2 x(f(x)+f(-x)) \geqslant 0 ;$
thus $2 x(f(x)+f(-x))=0$ for all $x$, so $f(-x)=-f(x)$ for all $x \neq 0$, and hence for all $x$, since $f(0)=0$;
(3) $x \leftrightarrow y: \quad(y-x)(f(y)+f(x)) \leqslant f\left(y^{2}-x^{2}\right)=-f\left(x^{2}-y^{2}\right) \Rightarrow(x-y)(f(x)+f(y)) \geqslant f\left(x^{2}-y^{2}\right)$;
which is the given inequality with the inequality sign reversed, so $(x-y)(f(x)+f(y))=f\left(x^{2}-y^{2}\right)$ must hold for all $x, y \in \mathbb{R}$;
(4) $y \leftrightarrow-y: \quad(x-y)(f(x)+f(y))=f\left(x^{2}-y^{2}\right)=f\left(x^{2}-(-y)^{2}\right)=(x+y)(f(x)+f(-y))=(x+y)(f(x)-f(y))$; expanding yields $f(x) y=f(y) x$ for all $x, y \in \mathbb{R}$.
Taking $y=1$ in the last result, $f(x)=f(1) x$, i.e. $f(x)=c x$, where $c=f(1)$, for all $x \in \mathbb{R}$. Since we have shown above that, conversely, all such functions are solutions, this completes the proof.
Alternative solution. A slight variation of this argument proves that $(x-y)(f(x)+f(y))=f\left(x^{2}-y^{2}\right)$ must hold for all $x, y \in \mathbb{R}$ as above, and then reaches $f(x)=c x$ as follows:
(4) $y= \pm 1: \quad(x \mp 1)(f(x) \pm f(1))=f\left(x^{2}-1\right)$ using $f(-1)=-f(1)$ from (2);
hence $(x-1)(f(x)+f(1))=(x+1)(f(x)-f(1)) \Rightarrow f(x)=f(1) x=c x$, where $c=f(1)$, on expanding.
# BxMO 2023: Problems and Solutions
#
|
f(x)=c x
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all functions $f: \mathbb{R} \rightarrow \mathbb{R}$ such that
$$
(x-y)(f(x)+f(y)) \leqslant f\left(x^{2}-y^{2}\right) \quad \text { for all } x, y \in \mathbb{R}
$$
#
|
Clearly, $f(x)=c x$ is a solution for each $c \in \mathbb{R}$ since $(x-y)(c x+c y)=c\left(x^{2}-y^{2}\right)$. To show that there are no other solutions, we observe that
(1) $x=y: \quad 0 \leqslant f(0)$;
$x=1, y=0: \quad f(0)+f(1) \leqslant f(1) \Rightarrow f(0) \leqslant 0$, whence $f(0)=0 ;$
(2) $y=-x: \quad 2 x(f(x)+f(-x)) \leqslant f(0)=0$;
$x \rightarrow-x: \quad-2 x(f(-x)+f(x)) \leqslant 0 \Rightarrow 2 x(f(x)+f(-x)) \geqslant 0 ;$
thus $2 x(f(x)+f(-x))=0$ for all $x$, so $f(-x)=-f(x)$ for all $x \neq 0$, and hence for all $x$, since $f(0)=0$;
(3) $x \leftrightarrow y: \quad(y-x)(f(y)+f(x)) \leqslant f\left(y^{2}-x^{2}\right)=-f\left(x^{2}-y^{2}\right) \Rightarrow(x-y)(f(x)+f(y)) \geqslant f\left(x^{2}-y^{2}\right)$;
which is the given inequality with the inequality sign reversed, so $(x-y)(f(x)+f(y))=f\left(x^{2}-y^{2}\right)$ must hold for all $x, y \in \mathbb{R}$;
(4) $y \leftrightarrow-y: \quad(x-y)(f(x)+f(y))=f\left(x^{2}-y^{2}\right)=f\left(x^{2}-(-y)^{2}\right)=(x+y)(f(x)+f(-y))=(x+y)(f(x)-f(y))$; expanding yields $f(x) y=f(y) x$ for all $x, y \in \mathbb{R}$.
Taking $y=1$ in the last result, $f(x)=f(1) x$, i.e. $f(x)=c x$, where $c=f(1)$, for all $x \in \mathbb{R}$. Since we have shown above that, conversely, all such functions are solutions, this completes the proof.
Alternative solution. A slight variation of this argument proves that $(x-y)(f(x)+f(y))=f\left(x^{2}-y^{2}\right)$ must hold for all $x, y \in \mathbb{R}$ as above, and then reaches $f(x)=c x$ as follows:
(4) $y= \pm 1: \quad(x \mp 1)(f(x) \pm f(1))=f\left(x^{2}-1\right)$ using $f(-1)=-f(1)$ from (2);
hence $(x-1)(f(x)+f(1))=(x+1)(f(x)-f(1)) \Rightarrow f(x)=f(1) x=c x$, where $c=f(1)$, on expanding.
# BxMO 2023: Problems and Solutions
#
|
{
"exam": "Benelux_MO",
"problem_label": "1",
"problem_match": "# Problem 1",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2023-zz.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2023"
}
|
Determine all integers $k \geqslant 1$ with the following property: given $k$ different colours, if each integer is coloured in one of these $k$ colours, then there must exist integers $a_{1}<a_{2}<\cdots<a_{2023}$ of the same colour such that the differences $a_{2}-a_{1}, a_{3}-a_{2}, \ldots, a_{2023}-a_{2022}$ are all powers of 2 .
#
|
We claim that only $k=1$ and $k=2$ satisfy the required property. First, if $k \geqslant 3$, we colour each integer with its residue class modulo 3, so that, whenever two integers have the same colour, their difference is divisible by 3 , so is not a power of 2 . This shows that no $k \geqslant 3$ has the required property.
In the case $k=1$, the sequence defined by $a_{n}=2 n$ for $n=1,2, \ldots, 2023$ clearly has the required property. In the case $k=2$, we call the colours "red" and "blue", and construct, for each $n \geqslant 1$ and by induction, integers $a_{1}<a_{2}<\cdots<a_{n}$ of the same colour such that $a_{m+1}-a_{m}$ is a power of 2 for $m=1,2, \ldots, n-1$. The statement is trivial for $n=1$. For $n>1$, let $a_{1}<a_{2}<\cdots<a_{n}$ be red integers (without loss of generality) having the desired property. Consider the $n+1$ integers $b_{i}=a_{n}+2^{i}$, for $i=1,2, \ldots, n+1$. If one of these, say $b_{j}$, is red, then, as $b_{j}-a_{n}=2^{j}$, the $n+1$ red integers $a_{1}<a_{2}<\cdots<a_{n}<b_{j}$ have the desired property. Otherwise, $b_{1}, b_{2}, \ldots, b_{n+1}$ are all blue, and $b_{i+1}-b_{i}=\left(a_{n}+2^{i+1}\right)-\left(a_{n}+2^{i}\right)=2^{i}$ for $i=1,2, \ldots, n$, so the $n+1$ blue integers $b_{1}<b_{2}<\cdots<b_{n+1}$ have the desired property. This completes the inductive step and hence the proof.
## BxMO 2023: Problems and Solutions
#
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Determine all integers $k \geqslant 1$ with the following property: given $k$ different colours, if each integer is coloured in one of these $k$ colours, then there must exist integers $a_{1}<a_{2}<\cdots<a_{2023}$ of the same colour such that the differences $a_{2}-a_{1}, a_{3}-a_{2}, \ldots, a_{2023}-a_{2022}$ are all powers of 2 .
#
|
We claim that only $k=1$ and $k=2$ satisfy the required property. First, if $k \geqslant 3$, we colour each integer with its residue class modulo 3, so that, whenever two integers have the same colour, their difference is divisible by 3 , so is not a power of 2 . This shows that no $k \geqslant 3$ has the required property.
In the case $k=1$, the sequence defined by $a_{n}=2 n$ for $n=1,2, \ldots, 2023$ clearly has the required property. In the case $k=2$, we call the colours "red" and "blue", and construct, for each $n \geqslant 1$ and by induction, integers $a_{1}<a_{2}<\cdots<a_{n}$ of the same colour such that $a_{m+1}-a_{m}$ is a power of 2 for $m=1,2, \ldots, n-1$. The statement is trivial for $n=1$. For $n>1$, let $a_{1}<a_{2}<\cdots<a_{n}$ be red integers (without loss of generality) having the desired property. Consider the $n+1$ integers $b_{i}=a_{n}+2^{i}$, for $i=1,2, \ldots, n+1$. If one of these, say $b_{j}$, is red, then, as $b_{j}-a_{n}=2^{j}$, the $n+1$ red integers $a_{1}<a_{2}<\cdots<a_{n}<b_{j}$ have the desired property. Otherwise, $b_{1}, b_{2}, \ldots, b_{n+1}$ are all blue, and $b_{i+1}-b_{i}=\left(a_{n}+2^{i+1}\right)-\left(a_{n}+2^{i}\right)=2^{i}$ for $i=1,2, \ldots, n$, so the $n+1$ blue integers $b_{1}<b_{2}<\cdots<b_{n+1}$ have the desired property. This completes the inductive step and hence the proof.
## BxMO 2023: Problems and Solutions
#
|
{
"exam": "Benelux_MO",
"problem_label": "2",
"problem_match": "# Problem 2",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2023-zz.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2023"
}
|
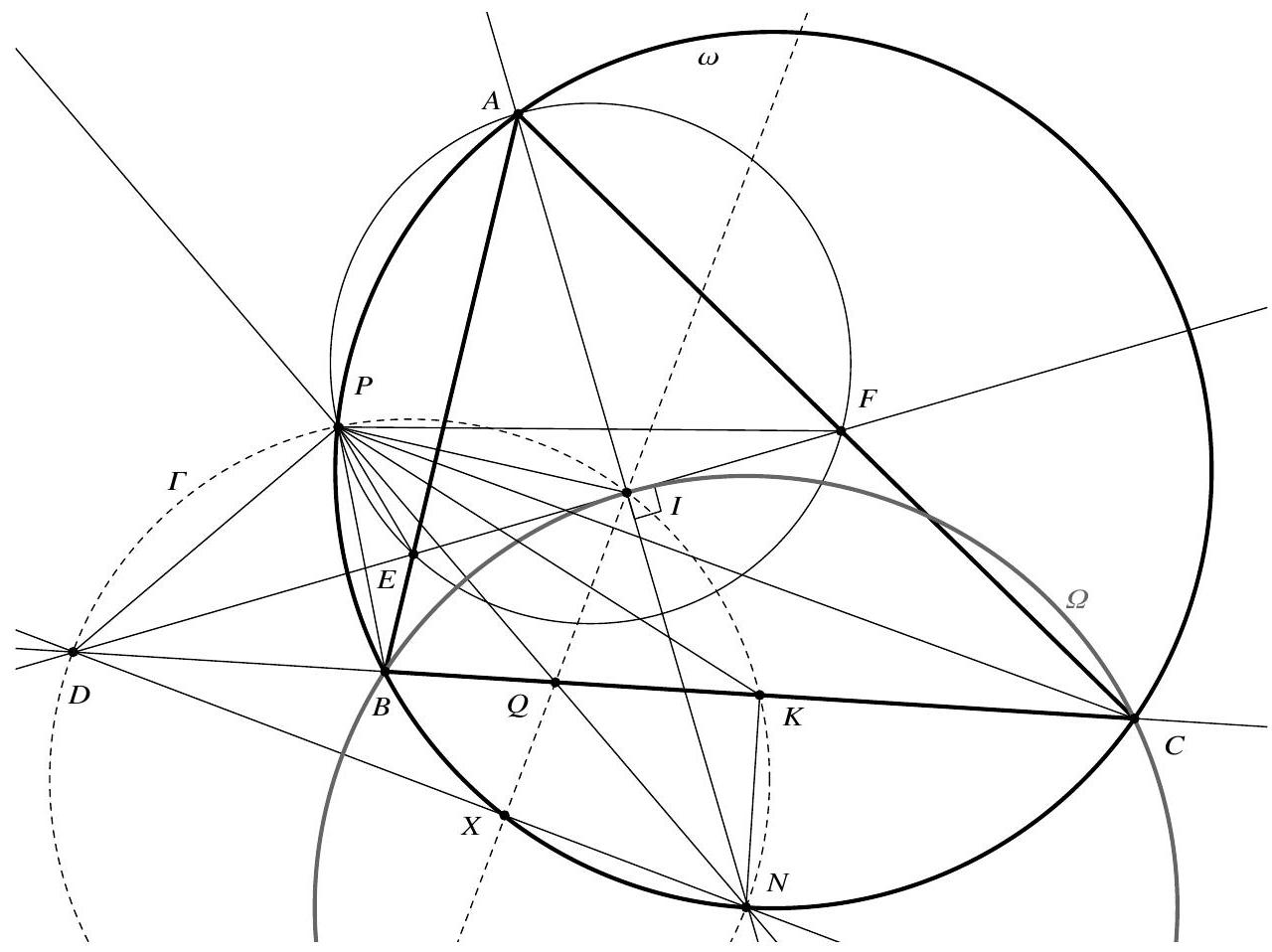
Let $A B C$ be a triangle with incentre $I$ and circumcircle $\omega$. Let $N$ denote the second point of intersection of line $A I$ and $\omega$. The line through $I$ perpendicular to $A I$ intersects line $B C$, segment $[A B]$, and segment $[A C]$ at the points $D, E$, and $F$, respectively. The circumcircle of triangle $A E F$ meets $\omega$ again at $P$, and lines $P N$ and $B C$ intersect at $Q$. Prove that lines $I Q$ and $D N$ intersect on $\omega$.
#
|
By construction, $A P E F$ and $A P B C$ are cyclic, and so
$$
\begin{aligned}
\angle B D E & =\angle C D F=\angle A F D-\angle F C D=\angle A F E-\angle A C B=\left(180^{\circ}-\angle E P A\right)-\left(180^{\circ}-\angle B P A\right) \\
& =\angle B P A-\angle E P A=\angle B P E .
\end{aligned}
$$
Hence $D B E P$ is cyclic, too. It follows that $\angle I D P=\angle E D P=\angle E B P=\angle A B P=\angle A N P=\angle I N P$ since $A P B N$ is cyclic, and so $P D N I$ is also cyclic. In particular, $\angle D P N=\angle D I N=90^{\circ}$. Let $R$ denote the second intersection of $D P$ and $\omega$, so $N Q \perp D R$. Then $\angle N P R=90^{\circ}$, so $R N$ is a diameter of $\omega$. It is well-known that $N$ is the midpoint of the arc $\widehat{B C}$ not containing $A$, whence $R N \perp B C$. Thus $D Q$ and $N Q$ are altitudes of triangle $R D N$, and so $Q$ is its orthocentre. This implies that $R Q \perp D N$, whence, since $R N$ is a diameter of $\omega$, the intersection $X$ of $R Q$ and $D N$ lies on $\omega$.
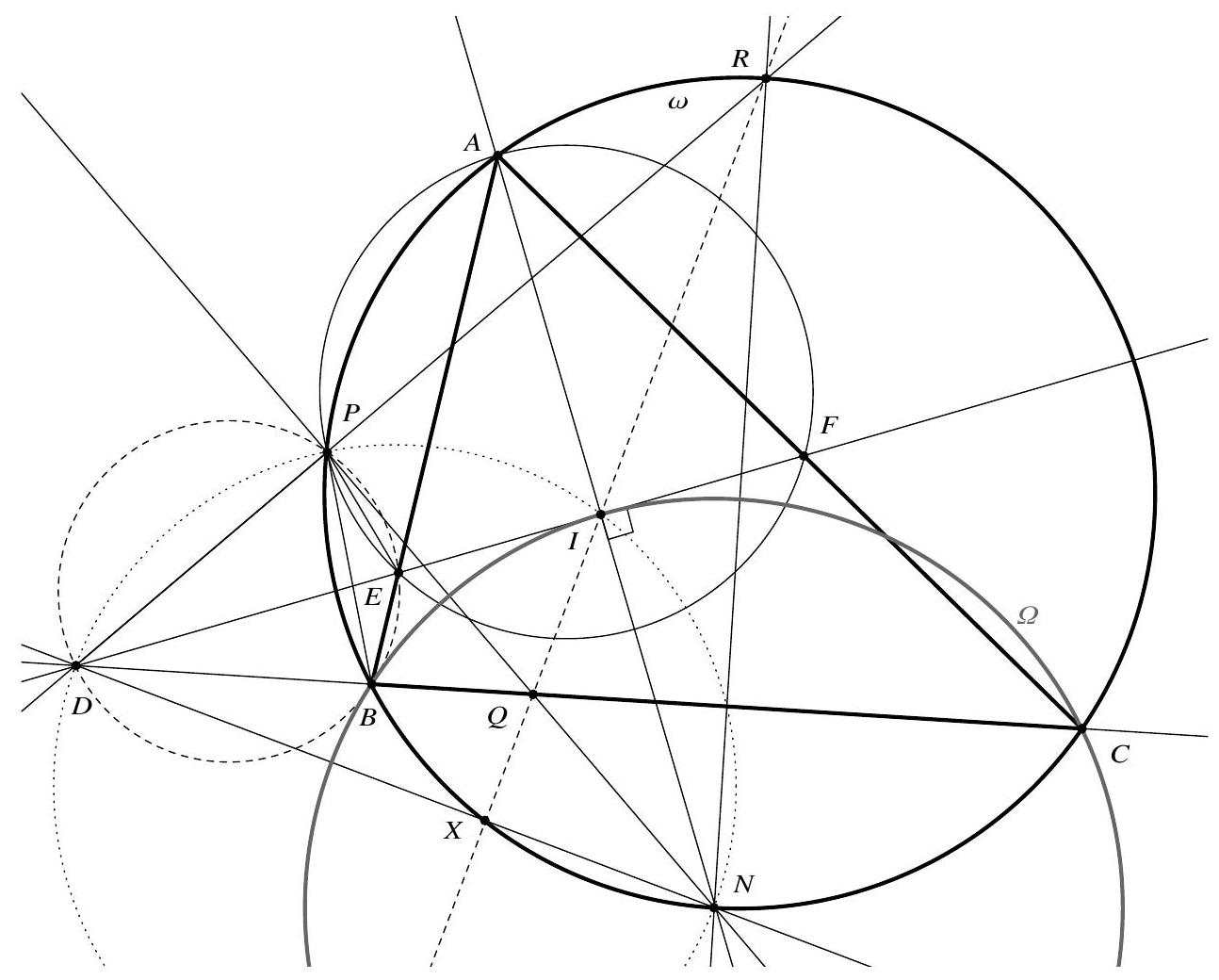
It is also well-known that $N$ is the centre of the circumcircle $\Omega$ of triangle $B C I$. Since $D I \perp I N$ by construction, $D I$ is tangent to $\Omega$ at $I$. As $D$ lies on the radical axis $B C$ of $\omega$ and $\Omega$, it follows that $|D I|^{2}=|D B||D C|=|D X||D N|$. Hence triangles $D N I$ and $D I X$ are similar; in particular, $\angle D X I=\angle D I N=90^{\circ}$. All of this shows that $R, I, Q, X$ lie on a line perpendicular to $D N$ that intersects $D N$ at $X \in \omega$. This completes the proof.
## BxMO 2023: Problems and Solutions
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incentre $I$ and circumcircle $\omega$. Let $N$ denote the second point of intersection of line $A I$ and $\omega$. The line through $I$ perpendicular to $A I$ intersects line $B C$, segment $[A B]$, and segment $[A C]$ at the points $D, E$, and $F$, respectively. The circumcircle of triangle $A E F$ meets $\omega$ again at $P$, and lines $P N$ and $B C$ intersect at $Q$. Prove that lines $I Q$ and $D N$ intersect on $\omega$.
#
|
By construction, $A P E F$ and $A P B C$ are cyclic, and so
$$
\begin{aligned}
\angle B D E & =\angle C D F=\angle A F D-\angle F C D=\angle A F E-\angle A C B=\left(180^{\circ}-\angle E P A\right)-\left(180^{\circ}-\angle B P A\right) \\
& =\angle B P A-\angle E P A=\angle B P E .
\end{aligned}
$$
Hence $D B E P$ is cyclic, too. It follows that $\angle I D P=\angle E D P=\angle E B P=\angle A B P=\angle A N P=\angle I N P$ since $A P B N$ is cyclic, and so $P D N I$ is also cyclic. In particular, $\angle D P N=\angle D I N=90^{\circ}$. Let $R$ denote the second intersection of $D P$ and $\omega$, so $N Q \perp D R$. Then $\angle N P R=90^{\circ}$, so $R N$ is a diameter of $\omega$. It is well-known that $N$ is the midpoint of the arc $\widehat{B C}$ not containing $A$, whence $R N \perp B C$. Thus $D Q$ and $N Q$ are altitudes of triangle $R D N$, and so $Q$ is its orthocentre. This implies that $R Q \perp D N$, whence, since $R N$ is a diameter of $\omega$, the intersection $X$ of $R Q$ and $D N$ lies on $\omega$.

It is also well-known that $N$ is the centre of the circumcircle $\Omega$ of triangle $B C I$. Since $D I \perp I N$ by construction, $D I$ is tangent to $\Omega$ at $I$. As $D$ lies on the radical axis $B C$ of $\omega$ and $\Omega$, it follows that $|D I|^{2}=|D B||D C|=|D X||D N|$. Hence triangles $D N I$ and $D I X$ are similar; in particular, $\angle D X I=\angle D I N=90^{\circ}$. All of this shows that $R, I, Q, X$ lie on a line perpendicular to $D N$ that intersects $D N$ at $X \in \omega$. This completes the proof.
## BxMO 2023: Problems and Solutions
#
|
{
"exam": "Benelux_MO",
"problem_label": "3",
"problem_match": "# Problem 3",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2023-zz.jsonl",
"solution_match": "# Solution 1",
"tier": "T3",
"year": "2023"
}
|
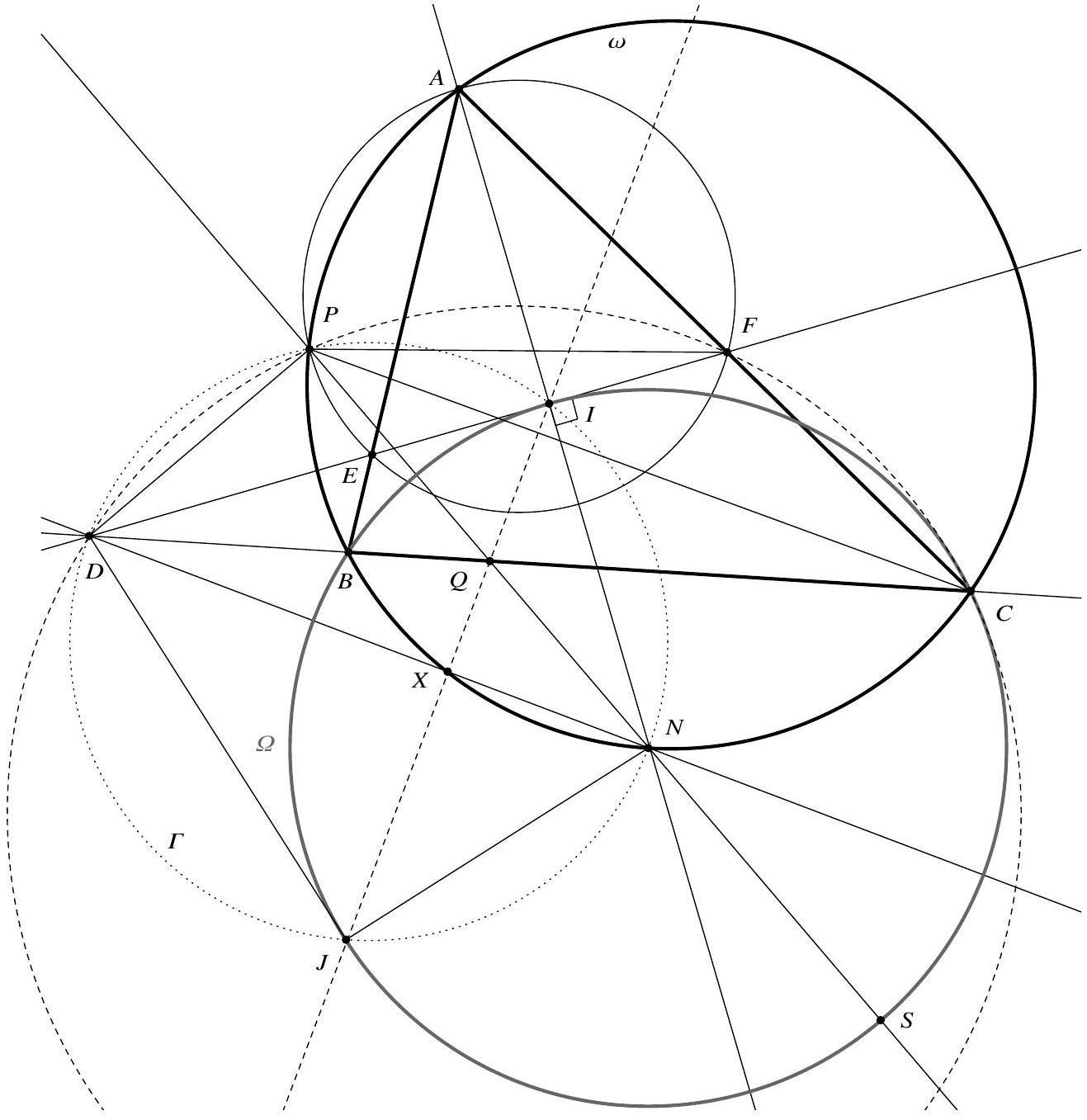
Let $A B C$ be a triangle with incentre $I$ and circumcircle $\omega$. Let $N$ denote the second point of intersection of line $A I$ and $\omega$. The line through $I$ perpendicular to $A I$ intersects line $B C$, segment $[A B]$, and segment $[A C]$ at the points $D, E$, and $F$, respectively. The circumcircle of triangle $A E F$ meets $\omega$ again at $P$, and lines $P N$ and $B C$ intersect at $Q$. Prove that lines $I Q$ and $D N$ intersect on $\omega$.
#
|
Let $K$ be the midpoint of segment [BC]. It is well-known that $N$ is the midpoint of the small arc $\widehat{B C}$ of $\omega$, so $B C \perp K N$. In particular, $\angle D K N=90^{\circ}$. But $\angle D I N=90^{\circ}$ by construction, so $D I K N$ is cyclic, with circumcircle $\Gamma$. Moreover, $\angle P E F=180^{\circ}-\angle P A F=180^{\circ}-\angle P A B=\angle P B C$ and $\angle P F E=\angle P A E=\angle P A B=\angle P C B$ since $A F E P$ and $A C B P$ are cyclic, so triangles $P E F$ and $P B C$ are similar. Now, by construction, $I$ is the midpoint of segment $[E F]$, so, $K$ being the midpoint of $[B C]$, triangles $P I F$ and $P K C$ are similar, too. It follows that $\angle P I D=180^{\circ}-\angle P I F=180^{\circ}-\angle P K C=\angle P K D$, whence $P$ lies on $\Gamma$.
Let $\Omega$ be the circumcircle of triangle $B C I$. By construction, $Q$ lies on the radical axes $P N$ of $\omega, \Gamma$ and $B C$ of $\omega, \Omega$, so is the radical centre of $\omega, \Gamma, \Omega$. In particular, $I Q$ is the radical axis of $\Gamma, \Omega$, so is perpendicular to the line joining the centres of $\Gamma, \Omega$. Now it is well-known that $N$ is the centre of $\Omega$, and, since $\angle D I N=90^{\circ}$, the centre of $\Gamma$ is the midpoint of segment $[D N]$. This shows that $I Q \perp D N$.
Finally, let $D N$ meet $\omega$ again at $X$. Since $D I \perp I N$ by construction and $N$ is the centre of $\Omega, D I$ is tangent to $\Omega$ at $I$. As $D$ lies on the radical axis $B C$ of $\omega, \Omega$, it follows that $|D I|^{2}=|D B||D C|=|D X||D N|$. Hence triangles $D N I$ and $D I X$ are similar; in particular, $\angle D X I=\angle D I N=90^{\circ}$, i.e. $I X \perp D N$. Since $I Q \perp D N$, it follows that $X$ is the intersection of $I Q$ and $D N$. Since $X$ lies on $\omega$ by construction, this completes the proof.
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incentre $I$ and circumcircle $\omega$. Let $N$ denote the second point of intersection of line $A I$ and $\omega$. The line through $I$ perpendicular to $A I$ intersects line $B C$, segment $[A B]$, and segment $[A C]$ at the points $D, E$, and $F$, respectively. The circumcircle of triangle $A E F$ meets $\omega$ again at $P$, and lines $P N$ and $B C$ intersect at $Q$. Prove that lines $I Q$ and $D N$ intersect on $\omega$.
#
|
Let $K$ be the midpoint of segment [BC]. It is well-known that $N$ is the midpoint of the small arc $\widehat{B C}$ of $\omega$, so $B C \perp K N$. In particular, $\angle D K N=90^{\circ}$. But $\angle D I N=90^{\circ}$ by construction, so $D I K N$ is cyclic, with circumcircle $\Gamma$. Moreover, $\angle P E F=180^{\circ}-\angle P A F=180^{\circ}-\angle P A B=\angle P B C$ and $\angle P F E=\angle P A E=\angle P A B=\angle P C B$ since $A F E P$ and $A C B P$ are cyclic, so triangles $P E F$ and $P B C$ are similar. Now, by construction, $I$ is the midpoint of segment $[E F]$, so, $K$ being the midpoint of $[B C]$, triangles $P I F$ and $P K C$ are similar, too. It follows that $\angle P I D=180^{\circ}-\angle P I F=180^{\circ}-\angle P K C=\angle P K D$, whence $P$ lies on $\Gamma$.

Let $\Omega$ be the circumcircle of triangle $B C I$. By construction, $Q$ lies on the radical axes $P N$ of $\omega, \Gamma$ and $B C$ of $\omega, \Omega$, so is the radical centre of $\omega, \Gamma, \Omega$. In particular, $I Q$ is the radical axis of $\Gamma, \Omega$, so is perpendicular to the line joining the centres of $\Gamma, \Omega$. Now it is well-known that $N$ is the centre of $\Omega$, and, since $\angle D I N=90^{\circ}$, the centre of $\Gamma$ is the midpoint of segment $[D N]$. This shows that $I Q \perp D N$.
Finally, let $D N$ meet $\omega$ again at $X$. Since $D I \perp I N$ by construction and $N$ is the centre of $\Omega, D I$ is tangent to $\Omega$ at $I$. As $D$ lies on the radical axis $B C$ of $\omega, \Omega$, it follows that $|D I|^{2}=|D B||D C|=|D X||D N|$. Hence triangles $D N I$ and $D I X$ are similar; in particular, $\angle D X I=\angle D I N=90^{\circ}$, i.e. $I X \perp D N$. Since $I Q \perp D N$, it follows that $X$ is the intersection of $I Q$ and $D N$. Since $X$ lies on $\omega$ by construction, this completes the proof.
#
|
{
"exam": "Benelux_MO",
"problem_label": "3",
"problem_match": "# Problem 3",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2023-zz.jsonl",
"solution_match": "# Solution 2",
"tier": "T3",
"year": "2023"
}
|
Let $A B C$ be a triangle with incentre $I$ and circumcircle $\omega$. Let $N$ denote the second point of intersection of line $A I$ and $\omega$. The line through $I$ perpendicular to $A I$ intersects line $B C$, segment $[A B]$, and segment $[A C]$ at the points $D, E$, and $F$, respectively. The circumcircle of triangle $A E F$ meets $\omega$ again at $P$, and lines $P N$ and $B C$ intersect at $Q$. Prove that lines $I Q$ and $D N$ intersect on $\omega$.
#
|
Since $A P E F$ and $A P B C$ are cyclic,
$$
\begin{aligned}
\angle C P F & =\angle B P A-\angle B P C-\angle F P A=\left(180^{\circ}-\angle B C A\right)-\angle B A C-\angle F E A \\
& =\left(180^{\circ}-\angle B C A-\angle B A C\right)-\angle B E D=\angle C B A-\angle B E D=\angle C B E-\angle B E D=\angle B D E=\angle C D F,
\end{aligned}
$$
so $D P F C$ is cyclic, too. Thence $\angle C P D=\angle C F D=180^{\circ}-\angle I F A=90^{\circ}+\angle I A F=90^{\circ}+\angle C A N=90^{\circ}+\angle C P N$. Hence $\angle D P N=\angle C P D-\angle C P N=90^{\circ}$. Since $\angle D I N=90^{\circ}$ by construction, it follows that DPIN is cyclic, with
## BxMO 2023: Problems and Solutions
circumcircle $\Gamma$. Let $J$ be the second intersection of line $I Q$ and $\Gamma$. Moreover, it is well-known that $N$ is the centre of the circumcircle $\Omega$ of BIC. In particular, $|N I|=|N B|$, and so, since $N I P J$ and $N B P C$ are cyclic,
$$
\frac{|J Q|}{|J P|}=\frac{|N Q|}{|N I|}=\frac{|N Q|}{|N B|}=\frac{|C Q|}{|C P|}
$$
Let $S$ now be the point of intersection of $P N$ and $\Omega$ such that $P, N, S$ lie on line $P N$ in this order. By construction, $\angle Q P C=\angle N P C=\angle N A C=\angle B A N=\angle B C N=\angle Q C N$, so triangles $C Q N$ and $P C N$ are similar, whence
$$
\frac{|C Q|}{|C P|}=\frac{|N C|}{|N P|}=\frac{|N Q|}{|N C|}=\frac{|N C|+|N Q|}{|N C|+|N P|}=\frac{|N S|+|N Q|}{|N S|+|N P|}=\frac{|S Q|}{|S P|}
$$
Combining (1) and (2) shows that $C, J, S$ lie on a circle of Apollonius, the centre of which lies on the line through $P, Q, N, S$, so, since $|N C|=|N S|$ by construction, is $N$. In other words, $J$ lies on $\Omega$.
In particular, $|N I|=|N J|$. Now, by construction, $\angle D I N=\angle D J N=90^{\circ}$, so the right-angled triangles $D I N$ and $D J N$ are congruent, whence $D I N J$ is a kite. In particular, $I J \perp D N$. Since $Q$ lies on $I J$ by definition, this shows that $I Q \perp D N$. We can now conclude as in Solution 2.
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incentre $I$ and circumcircle $\omega$. Let $N$ denote the second point of intersection of line $A I$ and $\omega$. The line through $I$ perpendicular to $A I$ intersects line $B C$, segment $[A B]$, and segment $[A C]$ at the points $D, E$, and $F$, respectively. The circumcircle of triangle $A E F$ meets $\omega$ again at $P$, and lines $P N$ and $B C$ intersect at $Q$. Prove that lines $I Q$ and $D N$ intersect on $\omega$.
#
|
Since $A P E F$ and $A P B C$ are cyclic,
$$
\begin{aligned}
\angle C P F & =\angle B P A-\angle B P C-\angle F P A=\left(180^{\circ}-\angle B C A\right)-\angle B A C-\angle F E A \\
& =\left(180^{\circ}-\angle B C A-\angle B A C\right)-\angle B E D=\angle C B A-\angle B E D=\angle C B E-\angle B E D=\angle B D E=\angle C D F,
\end{aligned}
$$
so $D P F C$ is cyclic, too. Thence $\angle C P D=\angle C F D=180^{\circ}-\angle I F A=90^{\circ}+\angle I A F=90^{\circ}+\angle C A N=90^{\circ}+\angle C P N$. Hence $\angle D P N=\angle C P D-\angle C P N=90^{\circ}$. Since $\angle D I N=90^{\circ}$ by construction, it follows that DPIN is cyclic, with
## BxMO 2023: Problems and Solutions
circumcircle $\Gamma$. Let $J$ be the second intersection of line $I Q$ and $\Gamma$. Moreover, it is well-known that $N$ is the centre of the circumcircle $\Omega$ of BIC. In particular, $|N I|=|N B|$, and so, since $N I P J$ and $N B P C$ are cyclic,
$$
\frac{|J Q|}{|J P|}=\frac{|N Q|}{|N I|}=\frac{|N Q|}{|N B|}=\frac{|C Q|}{|C P|}
$$
Let $S$ now be the point of intersection of $P N$ and $\Omega$ such that $P, N, S$ lie on line $P N$ in this order. By construction, $\angle Q P C=\angle N P C=\angle N A C=\angle B A N=\angle B C N=\angle Q C N$, so triangles $C Q N$ and $P C N$ are similar, whence
$$
\frac{|C Q|}{|C P|}=\frac{|N C|}{|N P|}=\frac{|N Q|}{|N C|}=\frac{|N C|+|N Q|}{|N C|+|N P|}=\frac{|N S|+|N Q|}{|N S|+|N P|}=\frac{|S Q|}{|S P|}
$$
Combining (1) and (2) shows that $C, J, S$ lie on a circle of Apollonius, the centre of which lies on the line through $P, Q, N, S$, so, since $|N C|=|N S|$ by construction, is $N$. In other words, $J$ lies on $\Omega$.

In particular, $|N I|=|N J|$. Now, by construction, $\angle D I N=\angle D J N=90^{\circ}$, so the right-angled triangles $D I N$ and $D J N$ are congruent, whence $D I N J$ is a kite. In particular, $I J \perp D N$. Since $Q$ lies on $I J$ by definition, this shows that $I Q \perp D N$. We can now conclude as in Solution 2.
#
|
{
"exam": "Benelux_MO",
"problem_label": "3",
"problem_match": "# Problem 3",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2023-zz.jsonl",
"solution_match": "# Solution 3",
"tier": "T3",
"year": "2023"
}
|
Let $A B C$ be a triangle with incentre $I$ and circumcircle $\omega$. Let $N$ denote the second point of intersection of line $A I$ and $\omega$. The line through $I$ perpendicular to $A I$ intersects line $B C$, segment $[A B]$, and segment $[A C]$ at the points $D, E$, and $F$, respectively. The circumcircle of triangle $A E F$ meets $\omega$ again at $P$, and lines $P N$ and $B C$ intersect at $Q$. Prove that lines $I Q$ and $D N$ intersect on $\omega$.
#
|
By construction, $P$ is the Miquel point of quadrilateral $B C F E$ (and the resulting complete quadrilateral with points $A$ and $D$ added) because it is the intersection of $\omega$ and the circumcircle of triangle $A E F$. In particular, $D B E P$ is
## BxMO 2023: Problems and Solutions
cyclic. It follows that $\angle I D P=\angle E D P=\angle E B P=\angle A B P=\angle A N P=\angle I N P$ since $A P B N$ is cyclic, and so $P D N I$ is also cyclic.
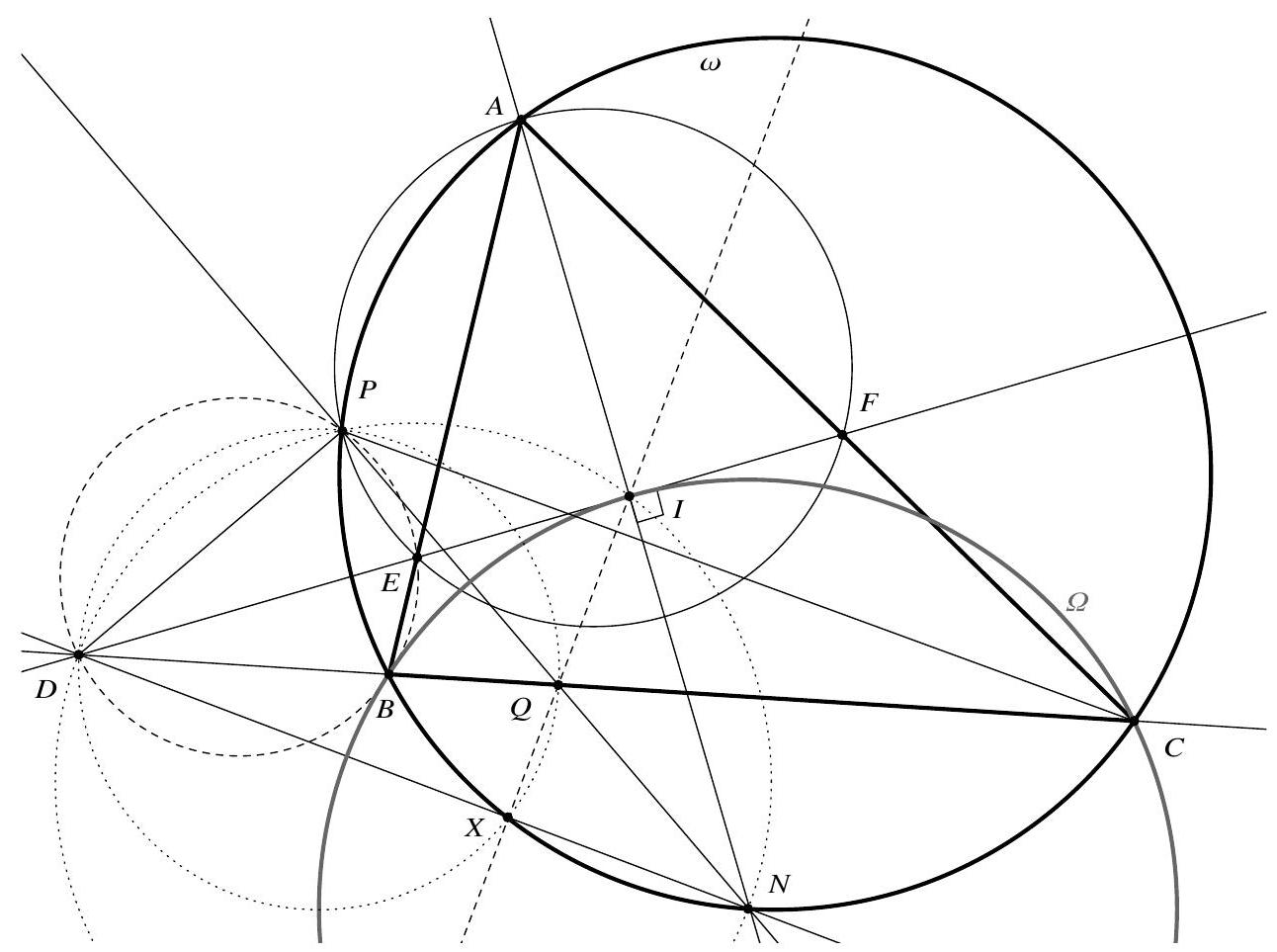
Next, let $X$ be the intersection of $D N$ and $\omega$ and let $A N$ meet $B C$ at $Y$. Then $\angle N A C=\angle A / 2=\angle N C B$, so $\angle B Y A=\angle C+\angle N A C=\angle C+\angle N C B=\angle N C A$ and hence
$$
\begin{aligned}
\angle D Q P & =\angle N Q Y=\angle Q Y A-\angle Q N Y=\angle B Y A-\angle P N A \\
& =\angle N C A-\angle P C A=\angle P C N=180^{\circ}-\angle N X P=\angle D X P
\end{aligned}
$$
This implies that $D X Q P$ is cyclic. In particular, $Q X \perp D N$. It now suffices to show that $I X \perp D N$, which we do in the same way as in Solution 2.
# BxMO 2023: Problems and Solutions
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incentre $I$ and circumcircle $\omega$. Let $N$ denote the second point of intersection of line $A I$ and $\omega$. The line through $I$ perpendicular to $A I$ intersects line $B C$, segment $[A B]$, and segment $[A C]$ at the points $D, E$, and $F$, respectively. The circumcircle of triangle $A E F$ meets $\omega$ again at $P$, and lines $P N$ and $B C$ intersect at $Q$. Prove that lines $I Q$ and $D N$ intersect on $\omega$.
#
|
By construction, $P$ is the Miquel point of quadrilateral $B C F E$ (and the resulting complete quadrilateral with points $A$ and $D$ added) because it is the intersection of $\omega$ and the circumcircle of triangle $A E F$. In particular, $D B E P$ is
## BxMO 2023: Problems and Solutions
cyclic. It follows that $\angle I D P=\angle E D P=\angle E B P=\angle A B P=\angle A N P=\angle I N P$ since $A P B N$ is cyclic, and so $P D N I$ is also cyclic.

Next, let $X$ be the intersection of $D N$ and $\omega$ and let $A N$ meet $B C$ at $Y$. Then $\angle N A C=\angle A / 2=\angle N C B$, so $\angle B Y A=\angle C+\angle N A C=\angle C+\angle N C B=\angle N C A$ and hence
$$
\begin{aligned}
\angle D Q P & =\angle N Q Y=\angle Q Y A-\angle Q N Y=\angle B Y A-\angle P N A \\
& =\angle N C A-\angle P C A=\angle P C N=180^{\circ}-\angle N X P=\angle D X P
\end{aligned}
$$
This implies that $D X Q P$ is cyclic. In particular, $Q X \perp D N$. It now suffices to show that $I X \perp D N$, which we do in the same way as in Solution 2.
# BxMO 2023: Problems and Solutions
#
|
{
"exam": "Benelux_MO",
"problem_label": "3",
"problem_match": "# Problem 3",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2023-zz.jsonl",
"solution_match": "# Solution 4",
"tier": "T3",
"year": "2023"
}
|
A positive integer $n$ is friendly if every pair of neighbouring digits of $n$, written in base 10, differs by exactly 1. For example, 6787 is friendly, but 211 and 901 are not.
Find all odd natural numbers $m$ for which there exists a friendly integer divisible by $64 m$.
#
|
Any friendly number divisible by 64 is divisible by 4 , and hence the number formed by its last two digits is a multiple of 4 , so ends in $00,04,08, \ldots$, or 96 . A friendly number divisible by 4 must therefore end in $12,32,56$, or 76 , so cannot be divisible by 5 . In particular, if $5 \mid \mathrm{m}$, then there is no friendly integer divisible by 64 m .
We claim that conversely, if $m$ is odd and $5 \nmid m$, then there exists a friendly integer divisible by $64 m$. First, we notice that $343232=64 \cdot 5363$ is a friendly number divisible by 64 , and hence so is
$$
N_{k}=343232343232 \cdots 343232=343232 \cdot\left(1+10^{6}+\cdots+10^{6 k}\right) \quad \text { for } k=0,1,2, \ldots
$$
Now the sequence $N_{0}, N_{1}, N_{2}, \ldots$ eventually repeats modulo $m$, i.e. there exist positive integers $k<\ell$ such that $N_{\ell} \equiv N_{k}(\bmod m)$. Hence $m \mid N_{\ell}-N_{k}=10^{6(k+1)} N_{\ell-k-1}$. Since $m$ is odd and $5 \nmid m,(10, m)=1$, so $m \mid N_{\ell-k-1}$. By construction, $64 \mid N_{\ell-k-1}$. Thus, as $m$ is odd and hence $(64, m)=1$, we conclude that $64 m \mid N_{\ell-k-1}$. This completes the proof.
The solution divides into two parts: (1) showing that, if $5 \mid m$, then there is no friendly integer divisible by $64 m$; (2) showing that, if $5 \nmid m$, then there is a friendly integer divisible by $64 m$.
Alternative solution for part (1). If $5 \mid m$, then $20 \mid 64 m$. The last two digits of a multiple of 20 are $00,20,40,60$, or 80 , so this number is not friendly. Thus, if $m$ is odd and $5 \mid m$, then there is no friendly integer divisible by $64 m$.
Alternative solution for part (2). Notice that $N_{k}=343232 \cdot\left(10^{6(k+1)}-1\right) /\left(10^{6}-1\right)$. Let $M=m\left(10^{6}-1\right)$. Since $5 \nmid m$ and $m$ is odd, $(10, M)=1$, so, taking $k=\varphi(M)-1$, we get $10^{6(k+1)}=10^{6 \varphi(M)} \equiv 1(\bmod M)$ by the Euler-Fermat theorem, i.e. $m \mid\left(10^{6(k+1)}-1\right) /\left(10^{6}-1\right)$, and hence $m \mid N_{k}$.
Alternative constructions of the integers $\boldsymbol{N}_{\boldsymbol{k}}$ for part (2). Direct calculation shows that friendly integers divisible by 64 end in $343232,543232,123456$, or 323456 , so the numbers $N_{k}$ defined in the solution of part (2) above may be replaced by, for instance,
$$
34543232 \cdot\left(1+10^{8}+\cdots+10^{8 k}\right), 5432123456 \cdot\left(1+10^{10}+\cdots+10^{10 k}\right), 54323456 \cdot\left(1+10^{8}+\cdots+10^{8 k}\right)
$$
Remark. Interestingly, friendly numbers cannot be divisible by arbitrarily high powers of 2. Direct calculation shows that the 60-digit friendly integer 101232121234323456543434343210121212323434343234565656543232 is divisible by $2^{60}$, but that there is no friendly integer divisible by $2^{61}$. The problem selection committee is not aware of a proof of this fact that eschews direct calculation.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A positive integer $n$ is friendly if every pair of neighbouring digits of $n$, written in base 10, differs by exactly 1. For example, 6787 is friendly, but 211 and 901 are not.
Find all odd natural numbers $m$ for which there exists a friendly integer divisible by $64 m$.
#
|
Any friendly number divisible by 64 is divisible by 4 , and hence the number formed by its last two digits is a multiple of 4 , so ends in $00,04,08, \ldots$, or 96 . A friendly number divisible by 4 must therefore end in $12,32,56$, or 76 , so cannot be divisible by 5 . In particular, if $5 \mid \mathrm{m}$, then there is no friendly integer divisible by 64 m .
We claim that conversely, if $m$ is odd and $5 \nmid m$, then there exists a friendly integer divisible by $64 m$. First, we notice that $343232=64 \cdot 5363$ is a friendly number divisible by 64 , and hence so is
$$
N_{k}=343232343232 \cdots 343232=343232 \cdot\left(1+10^{6}+\cdots+10^{6 k}\right) \quad \text { for } k=0,1,2, \ldots
$$
Now the sequence $N_{0}, N_{1}, N_{2}, \ldots$ eventually repeats modulo $m$, i.e. there exist positive integers $k<\ell$ such that $N_{\ell} \equiv N_{k}(\bmod m)$. Hence $m \mid N_{\ell}-N_{k}=10^{6(k+1)} N_{\ell-k-1}$. Since $m$ is odd and $5 \nmid m,(10, m)=1$, so $m \mid N_{\ell-k-1}$. By construction, $64 \mid N_{\ell-k-1}$. Thus, as $m$ is odd and hence $(64, m)=1$, we conclude that $64 m \mid N_{\ell-k-1}$. This completes the proof.
The solution divides into two parts: (1) showing that, if $5 \mid m$, then there is no friendly integer divisible by $64 m$; (2) showing that, if $5 \nmid m$, then there is a friendly integer divisible by $64 m$.
Alternative solution for part (1). If $5 \mid m$, then $20 \mid 64 m$. The last two digits of a multiple of 20 are $00,20,40,60$, or 80 , so this number is not friendly. Thus, if $m$ is odd and $5 \mid m$, then there is no friendly integer divisible by $64 m$.
Alternative solution for part (2). Notice that $N_{k}=343232 \cdot\left(10^{6(k+1)}-1\right) /\left(10^{6}-1\right)$. Let $M=m\left(10^{6}-1\right)$. Since $5 \nmid m$ and $m$ is odd, $(10, M)=1$, so, taking $k=\varphi(M)-1$, we get $10^{6(k+1)}=10^{6 \varphi(M)} \equiv 1(\bmod M)$ by the Euler-Fermat theorem, i.e. $m \mid\left(10^{6(k+1)}-1\right) /\left(10^{6}-1\right)$, and hence $m \mid N_{k}$.
Alternative constructions of the integers $\boldsymbol{N}_{\boldsymbol{k}}$ for part (2). Direct calculation shows that friendly integers divisible by 64 end in $343232,543232,123456$, or 323456 , so the numbers $N_{k}$ defined in the solution of part (2) above may be replaced by, for instance,
$$
34543232 \cdot\left(1+10^{8}+\cdots+10^{8 k}\right), 5432123456 \cdot\left(1+10^{10}+\cdots+10^{10 k}\right), 54323456 \cdot\left(1+10^{8}+\cdots+10^{8 k}\right)
$$
Remark. Interestingly, friendly numbers cannot be divisible by arbitrarily high powers of 2. Direct calculation shows that the 60-digit friendly integer 101232121234323456543434343210121212323434343234565656543232 is divisible by $2^{60}$, but that there is no friendly integer divisible by $2^{61}$. The problem selection committee is not aware of a proof of this fact that eschews direct calculation.
|
{
"exam": "Benelux_MO",
"problem_label": "4",
"problem_match": "# Problem 4",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2023-zz.jsonl",
"solution_match": "# Solution\n",
"tier": "T3",
"year": "2023"
}
|
(a) Let $a_{0}, a_{1}, \ldots, a_{2024}$ be real numbers such that $\left|a_{i+1}-a_{i}\right| \leqslant 1$ for $i=0,1, \ldots, 2023$.
Find the minimum possible value of
$$
a_{0} a_{1}+a_{1} a_{2}+\cdots+a_{2023} a_{2024}
$$
(b) Does there exist a real number $C$ such that
$$
a_{0} a_{1}-a_{1} a_{2}+a_{2} a_{3}-a_{3} a_{4}+\cdots+a_{2022} a_{2023}-a_{2023} a_{2024} \geqslant C
$$
for all real numbers $a_{0}, a_{1}, \ldots, a_{2024}$ such that $\left|a_{i+1}-a_{i}\right| \leqslant 1$ for $i=0,1, \ldots, 2023$ ?
#
|
(a) The minimum value is -506 . Note that from $\left|a_{i}-a_{i-1}\right| \leq 1$ it follows that
$$
a_{i} a_{i-1}=\frac{\left(a_{i}+a_{i-1}\right)^{2}-\left(a_{i}-a_{i-1}\right)^{2}}{4} \geq-\frac{\left(a_{i}-a_{i-1}\right)^{2}}{4} \geq-\frac{1}{4}
$$
Adding this for $i=1,2, \ldots, 2024$, we obtain that
$$
a_{0} a_{1}+a_{1} a_{2}+a_{2} a_{3}+\ldots+a_{2023} a_{2024} \geq 2024 \cdot-\frac{1}{4}=-506
$$
We now show that this value can be attained. Indeed, for the sequence $\left(a_{0}, a_{1}, \ldots, a_{2024}\right)=$ $\left(\frac{1}{2},-\frac{1}{2}, \frac{1}{2},-\frac{1}{2}, \frac{1}{2}, \ldots, \frac{1}{2}\right)$ with alternating $\frac{1}{2}$ 's and $-\frac{1}{2}$ 's, each term $a_{i} a_{i-1}$ is equal to $-\frac{1}{4}$, leading to $a_{0} a_{1}+a_{1} a_{2}+a_{2} a_{3}+\ldots+a_{2023} a_{2024}=2024 \cdot-\frac{1}{4}=-506$.
(b) No, such a $C$ does not exist. We argue by contradiction. Suppose $C$ has this property, and consider the sequence defined by $a_{0}=C$ and $a_{i}=C-1$ for $i=1,2, \ldots, 2024$ satisfies the condition in the problem. For this sequence, we have $a_{i} a_{i+1}-a_{i+1} a_{i+2}=0$ for $i=2,4, \ldots$, 2022, so the sum
$$
a_{0} a_{1}-a_{1} a_{2}+a_{2} a_{3}-a_{3} a_{4}+a_{4} a_{5}-a_{5} a_{6}+\ldots+a_{2022} a_{2023}-a_{2023} a_{2024}
$$
is equal to
$$
a_{0} a_{1}-a_{1} a_{2}=C(C-1)-(C-1)^{2}=C-1<C,
$$
contradiction.
#
|
-506
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
(a) Let $a_{0}, a_{1}, \ldots, a_{2024}$ be real numbers such that $\left|a_{i+1}-a_{i}\right| \leqslant 1$ for $i=0,1, \ldots, 2023$.
Find the minimum possible value of
$$
a_{0} a_{1}+a_{1} a_{2}+\cdots+a_{2023} a_{2024}
$$
(b) Does there exist a real number $C$ such that
$$
a_{0} a_{1}-a_{1} a_{2}+a_{2} a_{3}-a_{3} a_{4}+\cdots+a_{2022} a_{2023}-a_{2023} a_{2024} \geqslant C
$$
for all real numbers $a_{0}, a_{1}, \ldots, a_{2024}$ such that $\left|a_{i+1}-a_{i}\right| \leqslant 1$ for $i=0,1, \ldots, 2023$ ?
#
|
(a) The minimum value is -506 . Note that from $\left|a_{i}-a_{i-1}\right| \leq 1$ it follows that
$$
a_{i} a_{i-1}=\frac{\left(a_{i}+a_{i-1}\right)^{2}-\left(a_{i}-a_{i-1}\right)^{2}}{4} \geq-\frac{\left(a_{i}-a_{i-1}\right)^{2}}{4} \geq-\frac{1}{4}
$$
Adding this for $i=1,2, \ldots, 2024$, we obtain that
$$
a_{0} a_{1}+a_{1} a_{2}+a_{2} a_{3}+\ldots+a_{2023} a_{2024} \geq 2024 \cdot-\frac{1}{4}=-506
$$
We now show that this value can be attained. Indeed, for the sequence $\left(a_{0}, a_{1}, \ldots, a_{2024}\right)=$ $\left(\frac{1}{2},-\frac{1}{2}, \frac{1}{2},-\frac{1}{2}, \frac{1}{2}, \ldots, \frac{1}{2}\right)$ with alternating $\frac{1}{2}$ 's and $-\frac{1}{2}$ 's, each term $a_{i} a_{i-1}$ is equal to $-\frac{1}{4}$, leading to $a_{0} a_{1}+a_{1} a_{2}+a_{2} a_{3}+\ldots+a_{2023} a_{2024}=2024 \cdot-\frac{1}{4}=-506$.
(b) No, such a $C$ does not exist. We argue by contradiction. Suppose $C$ has this property, and consider the sequence defined by $a_{0}=C$ and $a_{i}=C-1$ for $i=1,2, \ldots, 2024$ satisfies the condition in the problem. For this sequence, we have $a_{i} a_{i+1}-a_{i+1} a_{i+2}=0$ for $i=2,4, \ldots$, 2022, so the sum
$$
a_{0} a_{1}-a_{1} a_{2}+a_{2} a_{3}-a_{3} a_{4}+a_{4} a_{5}-a_{5} a_{6}+\ldots+a_{2022} a_{2023}-a_{2023} a_{2024}
$$
is equal to
$$
a_{0} a_{1}-a_{1} a_{2}=C(C-1)-(C-1)^{2}=C-1<C,
$$
contradiction.
#
|
{
"exam": "Benelux_MO",
"problem_label": "1",
"problem_match": "# Problem 1",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2024-zz.jsonl",
"solution_match": "# Solution 1",
"tier": "T3",
"year": "2024"
}
|
(a) Let $a_{0}, a_{1}, \ldots, a_{2024}$ be real numbers such that $\left|a_{i+1}-a_{i}\right| \leqslant 1$ for $i=0,1, \ldots, 2023$.
Find the minimum possible value of
$$
a_{0} a_{1}+a_{1} a_{2}+\cdots+a_{2023} a_{2024}
$$
(b) Does there exist a real number $C$ such that
$$
a_{0} a_{1}-a_{1} a_{2}+a_{2} a_{3}-a_{3} a_{4}+\cdots+a_{2022} a_{2023}-a_{2023} a_{2024} \geqslant C
$$
for all real numbers $a_{0}, a_{1}, \ldots, a_{2024}$ such that $\left|a_{i+1}-a_{i}\right| \leqslant 1$ for $i=0,1, \ldots, 2023$ ?
#
|
We give an alternative construction for part (b). We choose a real constant $N$, from which we define $a_{i}=N+i$ for each $i=0,1, \ldots, 2024$, which clearly satisfies the requirement $\left|a_{i}-a_{i-1}\right| \leq 1$ for each $i=0,1, \ldots, 1011$. Then, it can be seen that for each $i=0,1, \ldots, 1011$ that
$$
a_{2 i} a_{2 i+1}-a_{2 i+1} a_{2 i+2}=a_{2 i+1}\left(a_{2 i}-a_{2 i+2}\right)=-2(N+2 i+1) \leqslant-2 N .
$$
From this, it can be concluded that
$a_{0} a_{1}-a_{1} a_{2}+a_{2} a_{3}-a_{3} a_{4}+a_{4} a_{5}-a_{5} a_{6}+\ldots+a_{2022} a_{2023}-a_{2023} a_{2024} \leqslant 1012 \cdot-2 N=-2024 N$.
As $N$ is a constant which can be arbitrarily chosen, there is no constant $C$ which lower bounds the given expression.
## BxMO 2024: Problems and Solutions
#
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
(a) Let $a_{0}, a_{1}, \ldots, a_{2024}$ be real numbers such that $\left|a_{i+1}-a_{i}\right| \leqslant 1$ for $i=0,1, \ldots, 2023$.
Find the minimum possible value of
$$
a_{0} a_{1}+a_{1} a_{2}+\cdots+a_{2023} a_{2024}
$$
(b) Does there exist a real number $C$ such that
$$
a_{0} a_{1}-a_{1} a_{2}+a_{2} a_{3}-a_{3} a_{4}+\cdots+a_{2022} a_{2023}-a_{2023} a_{2024} \geqslant C
$$
for all real numbers $a_{0}, a_{1}, \ldots, a_{2024}$ such that $\left|a_{i+1}-a_{i}\right| \leqslant 1$ for $i=0,1, \ldots, 2023$ ?
#
|
We give an alternative construction for part (b). We choose a real constant $N$, from which we define $a_{i}=N+i$ for each $i=0,1, \ldots, 2024$, which clearly satisfies the requirement $\left|a_{i}-a_{i-1}\right| \leq 1$ for each $i=0,1, \ldots, 1011$. Then, it can be seen that for each $i=0,1, \ldots, 1011$ that
$$
a_{2 i} a_{2 i+1}-a_{2 i+1} a_{2 i+2}=a_{2 i+1}\left(a_{2 i}-a_{2 i+2}\right)=-2(N+2 i+1) \leqslant-2 N .
$$
From this, it can be concluded that
$a_{0} a_{1}-a_{1} a_{2}+a_{2} a_{3}-a_{3} a_{4}+a_{4} a_{5}-a_{5} a_{6}+\ldots+a_{2022} a_{2023}-a_{2023} a_{2024} \leqslant 1012 \cdot-2 N=-2024 N$.
As $N$ is a constant which can be arbitrarily chosen, there is no constant $C$ which lower bounds the given expression.
## BxMO 2024: Problems and Solutions
#
|
{
"exam": "Benelux_MO",
"problem_label": "1",
"problem_match": "# Problem 1",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2024-zz.jsonl",
"solution_match": "# Solution 2",
"tier": "T3",
"year": "2024"
}
|
Let $n$ be a positive integer. In a coordinate grid, a path from $(0,0)$ to $(2 n, 2 n)$ consists of $4 n$ consecutive unit steps $(1,0)$ or $(0,1)$. Prove that the number of paths that divide the square with vertices $(0,0)$, $(2 n, 0),(2 n, 2 n),(0,2 n)$ into two regions with even areas is
$$
\frac{\binom{4 n}{2 n}+\binom{2 n}{n}}{2}
$$
#
|
Let $X$ denote the set of paths for which $A$ and $B$ have even area and let $Y$ denote the set of paths for which $A$ and $B$ both have odd area. Because $A$ and $B$ together form a square of area $4 n^{2}$, which is even, $|X|+|Y|$ equals the total number of paths from $(0,0)$ to $(2 n, 2 n)$, which is $\binom{4 n}{2 n}$.
Denoting a step to the right by $R$ and a step upwards by $U$, every path from $(0,0)$ to $(2 n, 2 n)$ can be described as a sequence of $4 n$ symbols, $2 n$ of which are $R$ and $2 n$ of which are $U$. We subdivide such a sequence into $2 n$ pairs of consecutive steps that can be $R R, U R, R U$ or $U U$. The number of possible paths for which neither $U R$ nor $R U$ occurs is $\binom{2 n}{n}$, because out of $2 n$ pairs that can be either $R R$ or $U U$ we have to choose $n$ that will be $R R$. These $\binom{2 n}{n}$ all belong to $X$; in fact, for these paths, $A$ and $B$ can be subdivided into $2 \times 2$-square, making their areas divisible by 4 . Now consider the paths that contain at least one $U R$ - or $R U$-pair. If in such a path we replace the first occurrence of a $U R$ or $R U$-pair by a pair of the other type (thus replacing $U R$ by $R U$ or vice versa), the areas of $A$ and $B$ each change by 1 and therefore become even if they were odd and odd if they were even. Because this modification is clearly reversible, we conclude that we can pair up all paths that contain at least one $U R$ - or $R U$-pair into pairs of paths, one of which belongs to $X$ and one of belongs to $Y$. This implies that $|X|-\binom{2 n}{n}=|Y|$. It follows that
$$
|X|=\frac{|X|+|Y|}{2}+\frac{|X|-|Y|}{2}=\frac{\binom{4 n}{2 n}}{2}+\frac{\binom{2 n}{n}}{2} .
$$
#
|
\frac{\binom{4 n}{2 n}+\binom{2 n}{n}}{2}
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ be a positive integer. In a coordinate grid, a path from $(0,0)$ to $(2 n, 2 n)$ consists of $4 n$ consecutive unit steps $(1,0)$ or $(0,1)$. Prove that the number of paths that divide the square with vertices $(0,0)$, $(2 n, 0),(2 n, 2 n),(0,2 n)$ into two regions with even areas is
$$
\frac{\binom{4 n}{2 n}+\binom{2 n}{n}}{2}
$$
#
|
Let $X$ denote the set of paths for which $A$ and $B$ have even area and let $Y$ denote the set of paths for which $A$ and $B$ both have odd area. Because $A$ and $B$ together form a square of area $4 n^{2}$, which is even, $|X|+|Y|$ equals the total number of paths from $(0,0)$ to $(2 n, 2 n)$, which is $\binom{4 n}{2 n}$.
Denoting a step to the right by $R$ and a step upwards by $U$, every path from $(0,0)$ to $(2 n, 2 n)$ can be described as a sequence of $4 n$ symbols, $2 n$ of which are $R$ and $2 n$ of which are $U$. We subdivide such a sequence into $2 n$ pairs of consecutive steps that can be $R R, U R, R U$ or $U U$. The number of possible paths for which neither $U R$ nor $R U$ occurs is $\binom{2 n}{n}$, because out of $2 n$ pairs that can be either $R R$ or $U U$ we have to choose $n$ that will be $R R$. These $\binom{2 n}{n}$ all belong to $X$; in fact, for these paths, $A$ and $B$ can be subdivided into $2 \times 2$-square, making their areas divisible by 4 . Now consider the paths that contain at least one $U R$ - or $R U$-pair. If in such a path we replace the first occurrence of a $U R$ or $R U$-pair by a pair of the other type (thus replacing $U R$ by $R U$ or vice versa), the areas of $A$ and $B$ each change by 1 and therefore become even if they were odd and odd if they were even. Because this modification is clearly reversible, we conclude that we can pair up all paths that contain at least one $U R$ - or $R U$-pair into pairs of paths, one of which belongs to $X$ and one of belongs to $Y$. This implies that $|X|-\binom{2 n}{n}=|Y|$. It follows that
$$
|X|=\frac{|X|+|Y|}{2}+\frac{|X|-|Y|}{2}=\frac{\binom{4 n}{2 n}}{2}+\frac{\binom{2 n}{n}}{2} .
$$
#
|
{
"exam": "Benelux_MO",
"problem_label": "2",
"problem_match": "# Problem 2",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2024-zz.jsonl",
"solution_match": "# Solution 1",
"tier": "T3",
"year": "2024"
}
|
Let $n$ be a positive integer. In a coordinate grid, a path from $(0,0)$ to $(2 n, 2 n)$ consists of $4 n$ consecutive unit steps $(1,0)$ or $(0,1)$. Prove that the number of paths that divide the square with vertices $(0,0)$, $(2 n, 0),(2 n, 2 n),(0,2 n)$ into two regions with even areas is
$$
\frac{\binom{4 n}{2 n}+\binom{2 n}{n}}{2}
$$
#
|
Define $Z_{m, n}$ to be the number of routes from $(0,0)$ to $(2 m, 2 n)$ that divide the rectangle with vertices $(0,0),(0,2 n),(2 m, 2 n)$ and $(2 m, 0)$ into two parts of even area. We call such paths good. We claim that
$$
2 Z_{m, n}=\binom{2 m+2 n}{2 m}+\binom{m+n}{m}
$$
for all $m, n$, which for $m=n$ establishes the desired result. We prove this formula by induction on $m+n$, noting first that it clearly holds when either $m$ or $n$ is zero, because $Z_{0, n}=Z_{m, 0}=1$ (there is only one path from $(0,0)$ to $(0,2 n)$ or $(2 m, 0)$, which is good). Therefore, suppose that $m, n \geq 1$ and consider a good path from $(0,0)$ to $(2 m, 2 n)$. This path passes through exactly one of $(2 m, 2 n-2)$,
## BxMO 2024: Problems and Solutions
$(2 m-1,2 n-1)$ and $(2 m-2,2 n)$. If it passes through $(2 m, 2 n-2)$ then the subpath from $(0,0)$ to $(2 m, 2 n-2)$ must also be good; moreover, for each good path from $(0,0)$ to $(2 m, 2 n-2)$ there is exactly one corresponding path from $(0,0)$ to $(2 m, 2 n)$, and that path is automatically good because the new area that gets added is even. Thus, there are $Z_{m, n-1}$ good paths from $(0,0)$ to $(2 m, 2 n)$ that pass through $(2 m, 2 n-2)$. Similarly, there are $Z_{m-1, n}$ good paths from $(0,0)$ to $(2 m, 2 n)$ that pass through $(2 m-2,2 n)$. Now notice that any path from $(0,0)$ to $(2 m-1,2 n-1)$ (of which there are $\binom{2 m+2 n-2}{2 m-1}$ ) can be extended in two ways to obtain a path from $(0,0)$ to $(2 m, 2 n)$; because the resulting areas for these paths differ by 1 , exactly one of these paths is good. All in all, we obtain the recursion
$$
Z_{m, n}=Z_{m, n-1}+Z_{m-1, n}+\binom{2 m+2 n-2}{2 m-1}
$$
By the inductive hypothesis, we have
$$
2 Z_{m, n-1}=\binom{2 m+2 n-2}{2 m}+\binom{m+n-1}{m}
$$
and
$$
2 Z_{m-1, n}=\binom{2 m+2 n-2}{2 m-2}+\binom{m+n-1}{m-1}
$$
Therefore, we obtain
$$
\begin{aligned}
2 Z_{m, n}= & 2 Z_{m, n-1}+2 Z_{m-1, n}+2\binom{2 m+2 n-2}{2 m-1} \\
= & \binom{2 m+2 n-2}{2 m}+\binom{m+n-1}{m}+\binom{2 m+2 n-2}{2 m-2}+\binom{m+n-1}{m-1} \\
& +2\binom{2 m+2 n-2}{2 m-1} .
\end{aligned}
$$
To simplify the expression on the right hand side, note that we can reorganize the terms
$$
\binom{2 m+2 n-2}{2 m}+\binom{2 m+2 n-2}{2 m-2}+2\binom{2 m+2 n-2}{2 m-1}
$$
as
$$
\left(\binom{2 m+2 n-2}{2 m}+\binom{2 m+2 n-2}{2 m-1}\right)+\left(\binom{2 m+2 n-2}{2 m-1}+\binom{2 m+2 n-2}{2 m-2}\right)
$$
which, using the addition rules for binomial coefficients, becomes
$$
\binom{2 m+2 n-1}{2 m}+\binom{2 m+2 n-1}{2 m-1}=\binom{2 m+2 n}{2 m}
$$
Similarly, we have
$$
\binom{m+n-1}{m}+\binom{m+n-1}{m-1}=\binom{m+n}{m}
$$
Putting everything together, we obtain that
$$
2 Z_{m, n}=\binom{2 m+2 n}{2 m}+\binom{m+n}{m}
$$
which completes the induction.
## Remark
The result from Solution 2 can also be proved using a combinatorial argument like in Solution 1.
## BxMO 2024: Problems and Solutions
#
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ be a positive integer. In a coordinate grid, a path from $(0,0)$ to $(2 n, 2 n)$ consists of $4 n$ consecutive unit steps $(1,0)$ or $(0,1)$. Prove that the number of paths that divide the square with vertices $(0,0)$, $(2 n, 0),(2 n, 2 n),(0,2 n)$ into two regions with even areas is
$$
\frac{\binom{4 n}{2 n}+\binom{2 n}{n}}{2}
$$
#
|
Define $Z_{m, n}$ to be the number of routes from $(0,0)$ to $(2 m, 2 n)$ that divide the rectangle with vertices $(0,0),(0,2 n),(2 m, 2 n)$ and $(2 m, 0)$ into two parts of even area. We call such paths good. We claim that
$$
2 Z_{m, n}=\binom{2 m+2 n}{2 m}+\binom{m+n}{m}
$$
for all $m, n$, which for $m=n$ establishes the desired result. We prove this formula by induction on $m+n$, noting first that it clearly holds when either $m$ or $n$ is zero, because $Z_{0, n}=Z_{m, 0}=1$ (there is only one path from $(0,0)$ to $(0,2 n)$ or $(2 m, 0)$, which is good). Therefore, suppose that $m, n \geq 1$ and consider a good path from $(0,0)$ to $(2 m, 2 n)$. This path passes through exactly one of $(2 m, 2 n-2)$,
## BxMO 2024: Problems and Solutions
$(2 m-1,2 n-1)$ and $(2 m-2,2 n)$. If it passes through $(2 m, 2 n-2)$ then the subpath from $(0,0)$ to $(2 m, 2 n-2)$ must also be good; moreover, for each good path from $(0,0)$ to $(2 m, 2 n-2)$ there is exactly one corresponding path from $(0,0)$ to $(2 m, 2 n)$, and that path is automatically good because the new area that gets added is even. Thus, there are $Z_{m, n-1}$ good paths from $(0,0)$ to $(2 m, 2 n)$ that pass through $(2 m, 2 n-2)$. Similarly, there are $Z_{m-1, n}$ good paths from $(0,0)$ to $(2 m, 2 n)$ that pass through $(2 m-2,2 n)$. Now notice that any path from $(0,0)$ to $(2 m-1,2 n-1)$ (of which there are $\binom{2 m+2 n-2}{2 m-1}$ ) can be extended in two ways to obtain a path from $(0,0)$ to $(2 m, 2 n)$; because the resulting areas for these paths differ by 1 , exactly one of these paths is good. All in all, we obtain the recursion
$$
Z_{m, n}=Z_{m, n-1}+Z_{m-1, n}+\binom{2 m+2 n-2}{2 m-1}
$$
By the inductive hypothesis, we have
$$
2 Z_{m, n-1}=\binom{2 m+2 n-2}{2 m}+\binom{m+n-1}{m}
$$
and
$$
2 Z_{m-1, n}=\binom{2 m+2 n-2}{2 m-2}+\binom{m+n-1}{m-1}
$$
Therefore, we obtain
$$
\begin{aligned}
2 Z_{m, n}= & 2 Z_{m, n-1}+2 Z_{m-1, n}+2\binom{2 m+2 n-2}{2 m-1} \\
= & \binom{2 m+2 n-2}{2 m}+\binom{m+n-1}{m}+\binom{2 m+2 n-2}{2 m-2}+\binom{m+n-1}{m-1} \\
& +2\binom{2 m+2 n-2}{2 m-1} .
\end{aligned}
$$
To simplify the expression on the right hand side, note that we can reorganize the terms
$$
\binom{2 m+2 n-2}{2 m}+\binom{2 m+2 n-2}{2 m-2}+2\binom{2 m+2 n-2}{2 m-1}
$$
as
$$
\left(\binom{2 m+2 n-2}{2 m}+\binom{2 m+2 n-2}{2 m-1}\right)+\left(\binom{2 m+2 n-2}{2 m-1}+\binom{2 m+2 n-2}{2 m-2}\right)
$$
which, using the addition rules for binomial coefficients, becomes
$$
\binom{2 m+2 n-1}{2 m}+\binom{2 m+2 n-1}{2 m-1}=\binom{2 m+2 n}{2 m}
$$
Similarly, we have
$$
\binom{m+n-1}{m}+\binom{m+n-1}{m-1}=\binom{m+n}{m}
$$
Putting everything together, we obtain that
$$
2 Z_{m, n}=\binom{2 m+2 n}{2 m}+\binom{m+n}{m}
$$
which completes the induction.
## Remark
The result from Solution 2 can also be proved using a combinatorial argument like in Solution 1.
## BxMO 2024: Problems and Solutions
#
|
{
"exam": "Benelux_MO",
"problem_label": "2",
"problem_match": "# Problem 2",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2024-zz.jsonl",
"solution_match": "# Solution 2",
"tier": "T3",
"year": "2024"
}
|
Let $n$ be a positive integer. In a coordinate grid, a path from $(0,0)$ to $(2 n, 2 n)$ consists of $4 n$ consecutive unit steps $(1,0)$ or $(0,1)$. Prove that the number of paths that divide the square with vertices $(0,0)$, $(2 n, 0),(2 n, 2 n),(0,2 n)$ into two regions with even areas is
$$
\frac{\binom{4 n}{2 n}+\binom{2 n}{n}}{2}
$$
#
|
We start by proving the following lemma: for a
$$
(2 m-1,2 n-1)
$$
-grid, there are equally many paths with a region of even area (called even paths), as there are with odd area (odd paths).
To prove this, we take a path and rotate it around the center of the grid. Then a path spanning a region with area $x$ is mapped on one spanning an area $(2 m-1)(2 n-1)-x$. This gives a bijection between paths creating an even region, and creating an odd region.
Now, for every path from
to $(2 n, 2 n)$, consider all the coordinates of the grid points it visits in order. There are $\binom{2 n}{n}$ of them which never visit a point with odd coordinates (which we call an odd point). Notice that such paths are all even.
We now construction a bijection between the remaining even paths and the odd paths. For each odd point, there are equally many even as odd paths from $(0,0)$ to that point. Define then a bijection $\phi$ between the sets of odd paths and even paths up to this point for each point. Notice that $\phi$ implicitly depends on the chosen odd point.
Now, for an arbitrary odd path $P$, consider the first odd point it passes through. Map $P$ to another path by changing the path up to this odd point to the $\phi$ of the path up to this point. As $\phi$ maps between even and odd paths, the resulting path is an even path. By the definition of $\phi$, and as each of the remaining paths goes to an odd point, this mapping defines a bijection.
We have hence found a bijection between the odd and even paths in the remaining $\binom{4 n}{2 n}-\binom{2 n}{n}$ paths, which yields the required result like in solution 1.
## BxMO 2024: Problems and Solutions
#
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ be a positive integer. In a coordinate grid, a path from $(0,0)$ to $(2 n, 2 n)$ consists of $4 n$ consecutive unit steps $(1,0)$ or $(0,1)$. Prove that the number of paths that divide the square with vertices $(0,0)$, $(2 n, 0),(2 n, 2 n),(0,2 n)$ into two regions with even areas is
$$
\frac{\binom{4 n}{2 n}+\binom{2 n}{n}}{2}
$$
#
|
We start by proving the following lemma: for a
$$
(2 m-1,2 n-1)
$$
-grid, there are equally many paths with a region of even area (called even paths), as there are with odd area (odd paths).
To prove this, we take a path and rotate it around the center of the grid. Then a path spanning a region with area $x$ is mapped on one spanning an area $(2 m-1)(2 n-1)-x$. This gives a bijection between paths creating an even region, and creating an odd region.
Now, for every path from
to $(2 n, 2 n)$, consider all the coordinates of the grid points it visits in order. There are $\binom{2 n}{n}$ of them which never visit a point with odd coordinates (which we call an odd point). Notice that such paths are all even.
We now construction a bijection between the remaining even paths and the odd paths. For each odd point, there are equally many even as odd paths from $(0,0)$ to that point. Define then a bijection $\phi$ between the sets of odd paths and even paths up to this point for each point. Notice that $\phi$ implicitly depends on the chosen odd point.
Now, for an arbitrary odd path $P$, consider the first odd point it passes through. Map $P$ to another path by changing the path up to this odd point to the $\phi$ of the path up to this point. As $\phi$ maps between even and odd paths, the resulting path is an even path. By the definition of $\phi$, and as each of the remaining paths goes to an odd point, this mapping defines a bijection.
We have hence found a bijection between the odd and even paths in the remaining $\binom{4 n}{2 n}-\binom{2 n}{n}$ paths, which yields the required result like in solution 1.
## BxMO 2024: Problems and Solutions
#
|
{
"exam": "Benelux_MO",
"problem_label": "2",
"problem_match": "# Problem 2",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2024-zz.jsonl",
"solution_match": "# Solution 3",
"tier": "T3",
"year": "2024"
}
|
Let $A B C$ be a triangle with incentre $I$ and circumcircle $\Omega$ such that $|A C| \neq|B C|$. The internal angle bisector of $\angle C A B$ intersects side [BC] in $D$, and the external angle bisectors of $\angle A B C$ and $\angle B C A$ intersect $\Omega$ again in $E$ and $F$, respectively. Let $G$ be the intersection of lines $A E$ and $F I$ and let $\Gamma$ be the circumcircle of triangle $B D I$. Show that $E$ lies on $\Gamma$ if and only if $G$ lies on $\Gamma$.
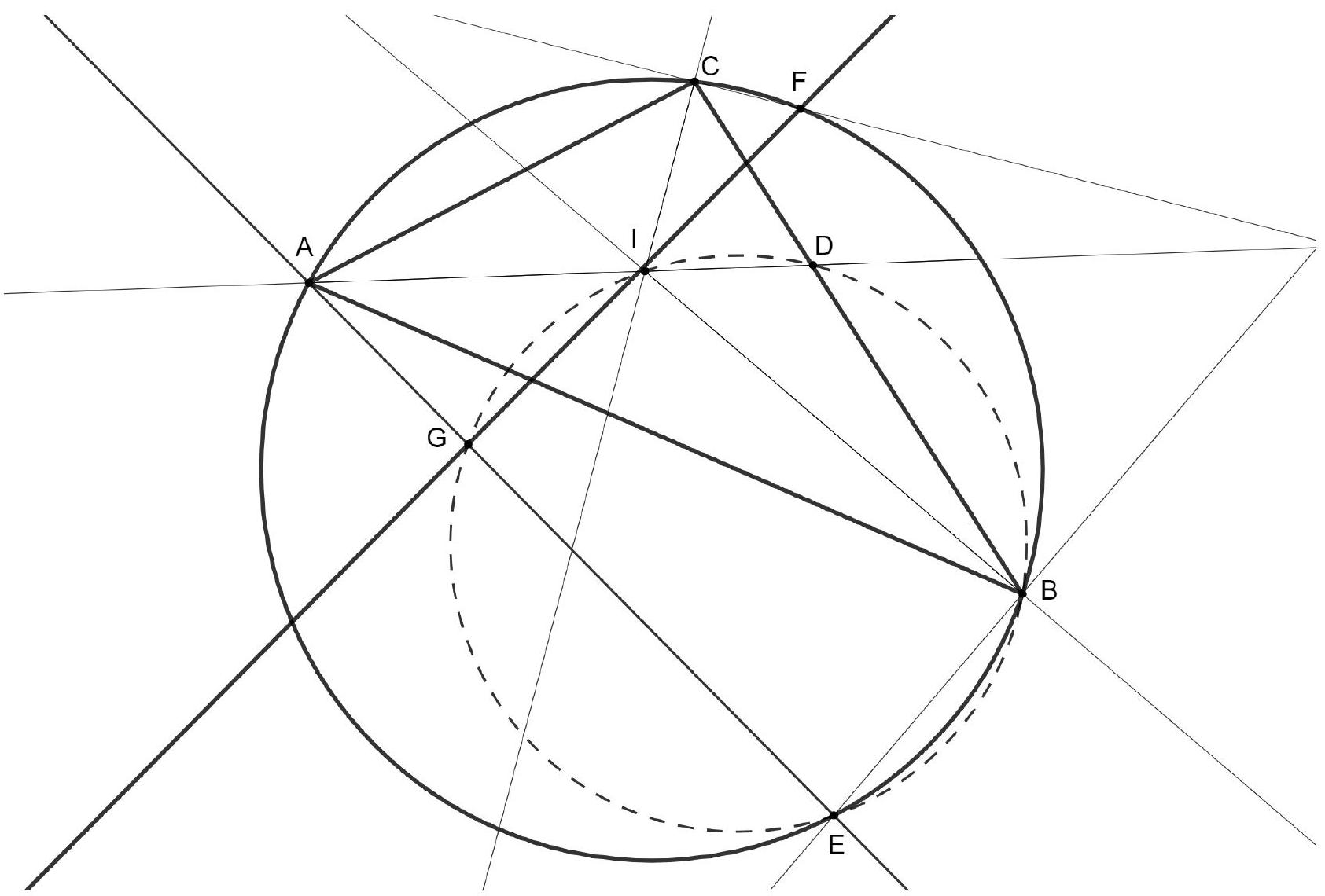
|
We first notice the general fact that $E F \perp A I$. This can be proved using the following argument. Denote $S$ for the intersection of $E F$ and $A I$. Then $\angle B I S=(\angle I B A+\angle I A B)=\frac{1}{2}(\angle A B C+\angle B A C)=$ $\frac{1}{2}\left(180^{\circ}-\angle B C A\right)=\angle B C F=\angle B E F=\angle B E S$. Thus $B, I, S, E$ form a cyclic quadrilateral, from which it can be concluded that $E F \perp A I$.
We will now continue to prove the problem by doing both directions separately. Assume first that $E$ lies on $\Gamma$. Then, as angle bisectors are perpendicular to one another, we have that $\angle I D E=\angle I B E=90^{\circ}$. Then, as $E F \perp A I$, it holds that $D$ lies on $E F$. It can then be concluded that $\angle I D F=90^{\circ}=\angle I C F$ (again due to perpendicular bisectors), from which it can be concluded that $I, D, C, F$ form a cyclic quadrilateral. We can now calculate that $\angle G I D=180^{\circ}-\angle F I D=180^{\circ}-\angle F C D=180^{\circ}-\angle F C B=$ $\angle A E F=\angle G E D$, where the second to last step follows from the fact that the arcs $B F$ and $A F$ have the
## BxMO 2024: Problems and Solutions
same length, as $F$ lies on the external bisector of $\angle A C B$. It now follows that $I, D, E, G$ form a cyclic quadrilteral, thus $G$ lies on $\Gamma$.
For the reverse implication, assume that $G$ lies on $\Gamma$. We can then compute that $\angle F A D=\angle F A S=$ $90^{\circ}-\angle A F S=90^{\circ}-\angle A F E=90^{\circ}-\angle A B E=\angle A B I=\angle I B D=\angle I G D=\angle F G D$, from which we can conclude that $A, G, D, F$ form a cyclic quadrilateral. Similarly to $\angle F A D=\angle I B D$, it holds that $\angle G A D=\angle I C D$. From this we can compute that $\angle I F D=\angle G F D=\angle G A D=\angle I C D$, thus $I, D, C, F$ forms a cyclic quadrilateral. Hence, $\angle I D F=180^{\circ}-\angle I C F=90^{\circ}$, so again $D=S$. We then see that $\angle I B E=90^{\circ}=\angle I D E$ from which we can conclude that $I, D, E, B$ form a cyclic quadrilateral. It then follows that $E$ lies on $\Gamma$.
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incentre $I$ and circumcircle $\Omega$ such that $|A C| \neq|B C|$. The internal angle bisector of $\angle C A B$ intersects side [BC] in $D$, and the external angle bisectors of $\angle A B C$ and $\angle B C A$ intersect $\Omega$ again in $E$ and $F$, respectively. Let $G$ be the intersection of lines $A E$ and $F I$ and let $\Gamma$ be the circumcircle of triangle $B D I$. Show that $E$ lies on $\Gamma$ if and only if $G$ lies on $\Gamma$.

|
We first notice the general fact that $E F \perp A I$. This can be proved using the following argument. Denote $S$ for the intersection of $E F$ and $A I$. Then $\angle B I S=(\angle I B A+\angle I A B)=\frac{1}{2}(\angle A B C+\angle B A C)=$ $\frac{1}{2}\left(180^{\circ}-\angle B C A\right)=\angle B C F=\angle B E F=\angle B E S$. Thus $B, I, S, E$ form a cyclic quadrilateral, from which it can be concluded that $E F \perp A I$.
We will now continue to prove the problem by doing both directions separately. Assume first that $E$ lies on $\Gamma$. Then, as angle bisectors are perpendicular to one another, we have that $\angle I D E=\angle I B E=90^{\circ}$. Then, as $E F \perp A I$, it holds that $D$ lies on $E F$. It can then be concluded that $\angle I D F=90^{\circ}=\angle I C F$ (again due to perpendicular bisectors), from which it can be concluded that $I, D, C, F$ form a cyclic quadrilateral. We can now calculate that $\angle G I D=180^{\circ}-\angle F I D=180^{\circ}-\angle F C D=180^{\circ}-\angle F C B=$ $\angle A E F=\angle G E D$, where the second to last step follows from the fact that the arcs $B F$ and $A F$ have the
## BxMO 2024: Problems and Solutions
same length, as $F$ lies on the external bisector of $\angle A C B$. It now follows that $I, D, E, G$ form a cyclic quadrilteral, thus $G$ lies on $\Gamma$.
For the reverse implication, assume that $G$ lies on $\Gamma$. We can then compute that $\angle F A D=\angle F A S=$ $90^{\circ}-\angle A F S=90^{\circ}-\angle A F E=90^{\circ}-\angle A B E=\angle A B I=\angle I B D=\angle I G D=\angle F G D$, from which we can conclude that $A, G, D, F$ form a cyclic quadrilateral. Similarly to $\angle F A D=\angle I B D$, it holds that $\angle G A D=\angle I C D$. From this we can compute that $\angle I F D=\angle G F D=\angle G A D=\angle I C D$, thus $I, D, C, F$ forms a cyclic quadrilateral. Hence, $\angle I D F=180^{\circ}-\angle I C F=90^{\circ}$, so again $D=S$. We then see that $\angle I B E=90^{\circ}=\angle I D E$ from which we can conclude that $I, D, E, B$ form a cyclic quadrilateral. It then follows that $E$ lies on $\Gamma$.
#
|
{
"exam": "Benelux_MO",
"problem_label": "3",
"problem_match": "# Problem 3",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2024-zz.jsonl",
"solution_match": "\nSolution 1",
"tier": "T3",
"year": "2024"
}
|
Let $A B C$ be a triangle with incentre $I$ and circumcircle $\Omega$ such that $|A C| \neq|B C|$. The internal angle bisector of $\angle C A B$ intersects side [BC] in $D$, and the external angle bisectors of $\angle A B C$ and $\angle B C A$ intersect $\Omega$ again in $E$ and $F$, respectively. Let $G$ be the intersection of lines $A E$ and $F I$ and let $\Gamma$ be the circumcircle of triangle $B D I$. Show that $E$ lies on $\Gamma$ if and only if $G$ lies on $\Gamma$.

|
The external angle bisectors $B E$ and $C F$ meet the internal bisector $I D$ at the $A$-excentre $J$ of triangle $A B C$. If one of BEDI and CFID is cyclic, then, as BECF is cyclic, $|J D||J I|=|J E||J B|=|J C||J F|$ by power of a point, and so the other is cyclic, too. This shows that
(1) $B E D I$ is cyclic if and only if CFID is cyclic.
Next, $\angle G A D=\angle E A D=\angle B A D-\angle B A E=\angle A / 2-\left(180^{\circ}-\angle A E B-\angle E B A\right)$, with $\angle A E B=\angle A C B=$ $\angle C$ and $\angle E B A=\angle E B I+\angle I B A=90^{\circ}+\angle B / 2$. Hence $\angle G A D=\angle A / 2+\angle B / 2+\angle C-90^{\circ}=\angle C / 2=$ $\angle I C D$. Thus, if one of $C F I D$ and $A G D F$ is cyclic, then $\angle I C D=\angle I F D=\angle G F D=\angle G A D$, and the other is cyclic, too. We have thus established that
(2) CFID is cyclic if and only if $A G D F$ is cylic.
Finally, let $A^{\prime}$ denote the second intersection of $A I$ with $\Omega$. Then $\angle D A F=\angle A^{\prime} A F=180^{\circ}-\angle F C A^{\prime}$, with $\angle F C A^{\prime}=\angle F C I+\angle I C B+\angle B C A^{\prime}=90^{\circ}+\angle C / 2+\angle B A A^{\prime}=90^{\circ}+\angle C / 2+\angle A / 2$. It follows that $\angle D A F=90^{\circ}-\angle A / 2-\angle C / 2=\angle B / 2=\angle D B I$. Hence, if one of $A G D F$ and $B D I G$ is cyclic, then $\angle D A F=\angle D G F=\angle D G I=\angle D B I$, and so the other is cyclic, too. Hence
(3) $A G D F$ is cyclic if and only if $B D I G$ is cylic.
These three equivalences prove that $B E D I$ is cyclic if and only if $B D I G$ is cyclic, i.e. $E$ lies on $\omega$ if and only if $G$ does. This completes the proof.
## BxMO 2024: Problems and Solutions
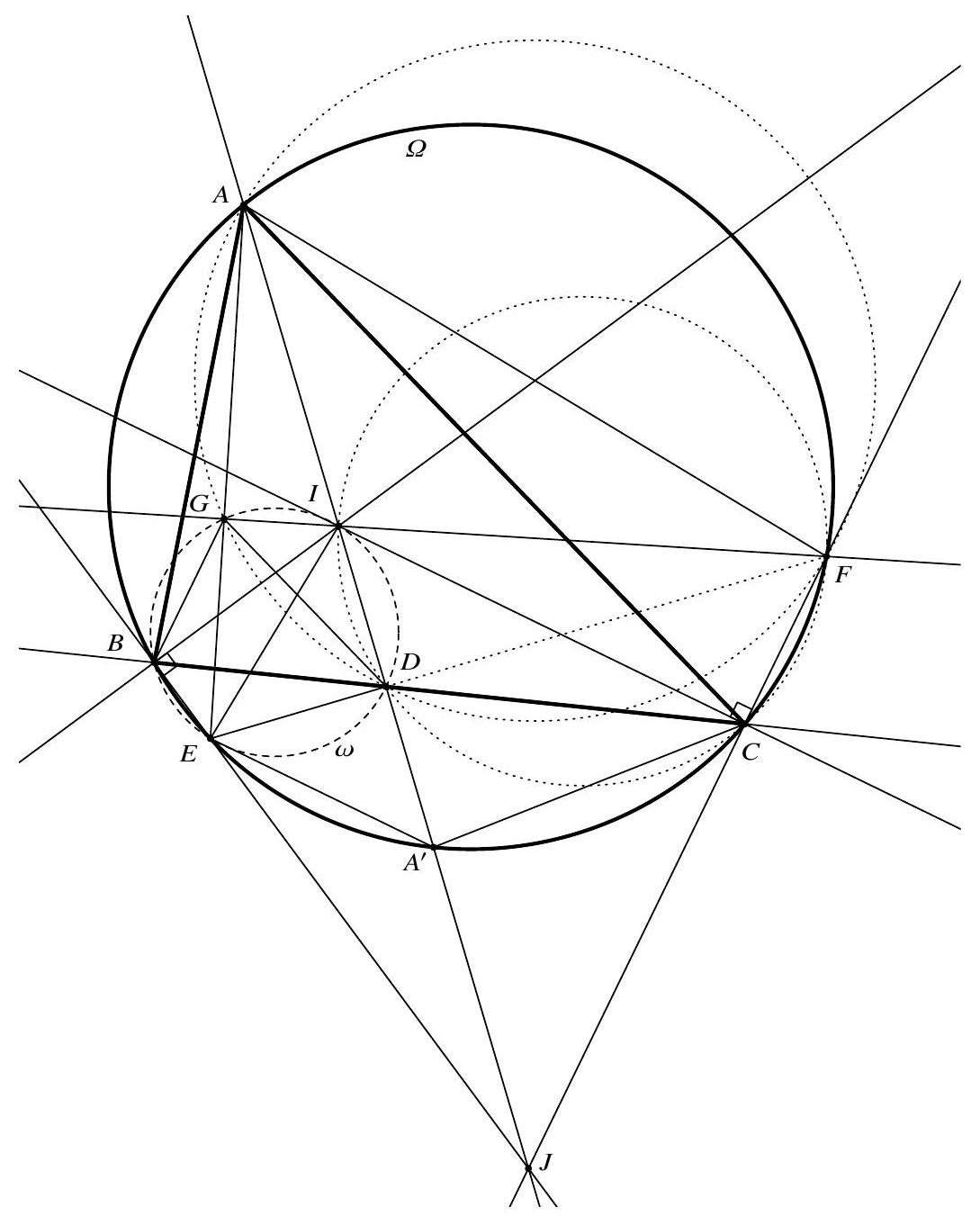
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incentre $I$ and circumcircle $\Omega$ such that $|A C| \neq|B C|$. The internal angle bisector of $\angle C A B$ intersects side [BC] in $D$, and the external angle bisectors of $\angle A B C$ and $\angle B C A$ intersect $\Omega$ again in $E$ and $F$, respectively. Let $G$ be the intersection of lines $A E$ and $F I$ and let $\Gamma$ be the circumcircle of triangle $B D I$. Show that $E$ lies on $\Gamma$ if and only if $G$ lies on $\Gamma$.

|
The external angle bisectors $B E$ and $C F$ meet the internal bisector $I D$ at the $A$-excentre $J$ of triangle $A B C$. If one of BEDI and CFID is cyclic, then, as BECF is cyclic, $|J D||J I|=|J E||J B|=|J C||J F|$ by power of a point, and so the other is cyclic, too. This shows that
(1) $B E D I$ is cyclic if and only if CFID is cyclic.
Next, $\angle G A D=\angle E A D=\angle B A D-\angle B A E=\angle A / 2-\left(180^{\circ}-\angle A E B-\angle E B A\right)$, with $\angle A E B=\angle A C B=$ $\angle C$ and $\angle E B A=\angle E B I+\angle I B A=90^{\circ}+\angle B / 2$. Hence $\angle G A D=\angle A / 2+\angle B / 2+\angle C-90^{\circ}=\angle C / 2=$ $\angle I C D$. Thus, if one of $C F I D$ and $A G D F$ is cyclic, then $\angle I C D=\angle I F D=\angle G F D=\angle G A D$, and the other is cyclic, too. We have thus established that
(2) CFID is cyclic if and only if $A G D F$ is cylic.
Finally, let $A^{\prime}$ denote the second intersection of $A I$ with $\Omega$. Then $\angle D A F=\angle A^{\prime} A F=180^{\circ}-\angle F C A^{\prime}$, with $\angle F C A^{\prime}=\angle F C I+\angle I C B+\angle B C A^{\prime}=90^{\circ}+\angle C / 2+\angle B A A^{\prime}=90^{\circ}+\angle C / 2+\angle A / 2$. It follows that $\angle D A F=90^{\circ}-\angle A / 2-\angle C / 2=\angle B / 2=\angle D B I$. Hence, if one of $A G D F$ and $B D I G$ is cyclic, then $\angle D A F=\angle D G F=\angle D G I=\angle D B I$, and so the other is cyclic, too. Hence
(3) $A G D F$ is cyclic if and only if $B D I G$ is cylic.
These three equivalences prove that $B E D I$ is cyclic if and only if $B D I G$ is cyclic, i.e. $E$ lies on $\omega$ if and only if $G$ does. This completes the proof.
## BxMO 2024: Problems and Solutions

#
|
{
"exam": "Benelux_MO",
"problem_label": "3",
"problem_match": "# Problem 3",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2024-zz.jsonl",
"solution_match": "# Solution 2",
"tier": "T3",
"year": "2024"
}
|
Let $A B C$ be a triangle with incentre $I$ and circumcircle $\Omega$ such that $|A C| \neq|B C|$. The internal angle bisector of $\angle C A B$ intersects side [BC] in $D$, and the external angle bisectors of $\angle A B C$ and $\angle B C A$ intersect $\Omega$ again in $E$ and $F$, respectively. Let $G$ be the intersection of lines $A E$ and $F I$ and let $\Gamma$ be the circumcircle of triangle $B D I$. Show that $E$ lies on $\Gamma$ if and only if $G$ lies on $\Gamma$.

|
This proof only shows $E \in \omega \Longrightarrow G \in \omega$. Note that this argument cannot be used straightforwardly to prove the converse implication.
If $B E D I$ is cyclic, let $A^{\prime}$ be the the second intersection of $A I$ with $\Omega$, so $\angle I A^{\prime} E=\angle A A^{\prime} E=$ $180^{\circ}-\angle E B A$, with $\angle E B A=\angle E B I+\angle I B A=90^{\circ}+\angle B / 2$, so $\angle I A^{\prime} E=90^{\circ}-\angle B / 2$. But $\angle E I A^{\prime}=\angle E B D$ since $E B D I$ is cyclic, with $\angle E B D=\angle E B I-\angle D B I=90^{\circ}-\angle B / 2$. Thus $\angle E A^{\prime} I=\angle E I A^{\prime}$, so $E A^{\prime} I$ is isosceles. Moreover, since $E B D I$ is cyclic and $\angle E B I$ is a right angle, so is $\angle I D E$. It follows that $D$ is the midpoint of $[A I]$. Next, the external bisectors $B E$ and $C F$ and the internal bisector $I D$ meet at the $A$-excentre $J$ of triangle $A B C$. By power of a point, since $B E D I$ and $B E C F$ are cyclic, $|J D||J I|=|J E||J B|=|J C||J F|$, so $C F I D$ is cyclic, too, with $\angle F D I=\angle F C I=90^{\circ}$. We have thus shown that $\angle A D E=\angle F D A=90^{\circ}$, so $D$ is the foot of the altitude from $A$ in triangle $A E F$. Moreover, all of this shows that $I$ is the reflection of $A^{\prime}$, which is the point at which this altitude meets the circumcircle $\Omega$ of $A E F$ again, in the side $[E F]$. Hence $I$ is the orthocentre of triangle $A E F$. By extension, $F I$ is its altitude from $F$, and $G$ is the foot of this altitude, so $\angle E G I=90^{\circ}=\angle I D E=\angle E B I$, and hence $B E D I G$ is cyclic. This shows that if $E$ lies on
## BxMO 2024: Problems and Solutions
$\omega$, then so does $G$.
## Remark
The equivalence $E \in \omega \Longleftrightarrow G \in \omega$ breaks down if triangle $A B C$ is not scalene. Indeed, if $A B C$ is isosceles with $\angle A=\angle B$, then $F=C$ and $G$ is the intersection of $C I$ and $A E$. Angle chasing as above then shows that $\angle G A D=\angle C / 2=\angle G C D$, so $A G D C$ is cyclic. Then $\angle D G I=\angle D G C=\angle D A C=$ $\angle A / 2=\angle B / 2=\angle D B I$, so $B D I G$ is cyclic, i.e. $G \in \omega$. Next, the $A$-excentre $J$ of triangle $A B C$ is the intersection of $B E, I D$, and the tangent to $\Omega$ at $C$, which, being the external bisector of $\angle C$, is perpendicular to $C I$. Hence, if $E \in \omega$, too, i.e. if $B E D I$ were cyclic, then by power of a point, $|J C|^{2}=|J E||J B|=|J D||J I|$, so the circumcircle of $C I D$ would be tangent to $J C$ at $C$, implying $\angle C D I=\angle I C J=90^{\circ}$. This is not however the case, unless $\angle B=\angle C$ and hence $A B C$ is equilateral. This shows that the condition in the problem statement that $A B C$ is scalene cannot be dropped.
## BxMO 2024: Problems and Solutions
#
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incentre $I$ and circumcircle $\Omega$ such that $|A C| \neq|B C|$. The internal angle bisector of $\angle C A B$ intersects side [BC] in $D$, and the external angle bisectors of $\angle A B C$ and $\angle B C A$ intersect $\Omega$ again in $E$ and $F$, respectively. Let $G$ be the intersection of lines $A E$ and $F I$ and let $\Gamma$ be the circumcircle of triangle $B D I$. Show that $E$ lies on $\Gamma$ if and only if $G$ lies on $\Gamma$.

|
This proof only shows $E \in \omega \Longrightarrow G \in \omega$. Note that this argument cannot be used straightforwardly to prove the converse implication.
If $B E D I$ is cyclic, let $A^{\prime}$ be the the second intersection of $A I$ with $\Omega$, so $\angle I A^{\prime} E=\angle A A^{\prime} E=$ $180^{\circ}-\angle E B A$, with $\angle E B A=\angle E B I+\angle I B A=90^{\circ}+\angle B / 2$, so $\angle I A^{\prime} E=90^{\circ}-\angle B / 2$. But $\angle E I A^{\prime}=\angle E B D$ since $E B D I$ is cyclic, with $\angle E B D=\angle E B I-\angle D B I=90^{\circ}-\angle B / 2$. Thus $\angle E A^{\prime} I=\angle E I A^{\prime}$, so $E A^{\prime} I$ is isosceles. Moreover, since $E B D I$ is cyclic and $\angle E B I$ is a right angle, so is $\angle I D E$. It follows that $D$ is the midpoint of $[A I]$. Next, the external bisectors $B E$ and $C F$ and the internal bisector $I D$ meet at the $A$-excentre $J$ of triangle $A B C$. By power of a point, since $B E D I$ and $B E C F$ are cyclic, $|J D||J I|=|J E||J B|=|J C||J F|$, so $C F I D$ is cyclic, too, with $\angle F D I=\angle F C I=90^{\circ}$. We have thus shown that $\angle A D E=\angle F D A=90^{\circ}$, so $D$ is the foot of the altitude from $A$ in triangle $A E F$. Moreover, all of this shows that $I$ is the reflection of $A^{\prime}$, which is the point at which this altitude meets the circumcircle $\Omega$ of $A E F$ again, in the side $[E F]$. Hence $I$ is the orthocentre of triangle $A E F$. By extension, $F I$ is its altitude from $F$, and $G$ is the foot of this altitude, so $\angle E G I=90^{\circ}=\angle I D E=\angle E B I$, and hence $B E D I G$ is cyclic. This shows that if $E$ lies on
## BxMO 2024: Problems and Solutions
$\omega$, then so does $G$.
## Remark
The equivalence $E \in \omega \Longleftrightarrow G \in \omega$ breaks down if triangle $A B C$ is not scalene. Indeed, if $A B C$ is isosceles with $\angle A=\angle B$, then $F=C$ and $G$ is the intersection of $C I$ and $A E$. Angle chasing as above then shows that $\angle G A D=\angle C / 2=\angle G C D$, so $A G D C$ is cyclic. Then $\angle D G I=\angle D G C=\angle D A C=$ $\angle A / 2=\angle B / 2=\angle D B I$, so $B D I G$ is cyclic, i.e. $G \in \omega$. Next, the $A$-excentre $J$ of triangle $A B C$ is the intersection of $B E, I D$, and the tangent to $\Omega$ at $C$, which, being the external bisector of $\angle C$, is perpendicular to $C I$. Hence, if $E \in \omega$, too, i.e. if $B E D I$ were cyclic, then by power of a point, $|J C|^{2}=|J E||J B|=|J D||J I|$, so the circumcircle of $C I D$ would be tangent to $J C$ at $C$, implying $\angle C D I=\angle I C J=90^{\circ}$. This is not however the case, unless $\angle B=\angle C$ and hence $A B C$ is equilateral. This shows that the condition in the problem statement that $A B C$ is scalene cannot be dropped.

## BxMO 2024: Problems and Solutions
#
|
{
"exam": "Benelux_MO",
"problem_label": "3",
"problem_match": "# Problem 3",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2024-zz.jsonl",
"solution_match": "# Solution 3",
"tier": "T3",
"year": "2024"
}
|
For each positive integer $n$, let $\operatorname{rad}(n)$ denote the product of the distinct prime factors of $n$. Show that there exist integers $a, b>1$ such that $\operatorname{gcd}(a, b)=1$ and
$$
\operatorname{rad}(a b(a+b))<\frac{a+b}{2024^{2024}}
$$
For example, $\operatorname{rad}(20)=\operatorname{rad}\left(2^{2} \cdot 5\right)=2 \cdot 5=10$ and $\operatorname{rad}(18)=\operatorname{rad}\left(2 \cdot 3^{2}\right)=2 \cdot 3=6$.
#
|
We show that the pair $(a, b)$ of the form $a=2^{p(p-1)}, b=3^{p(p-1)}-2^{p(p-1)}$ for sufficiently larger prime number $p$ satisfies the inequality. First, notice that $\operatorname{gcd}(a, b)=\operatorname{gcd}(a, a+b)=1$ indeed. In addition, see that $\operatorname{rad}(a)=2$, and $\operatorname{rad}(a+b)=3$. Because of Euler-Fermat, as $\phi\left(p^{2}\right)=p(p-1)$, it can directly be seen that $p^{2} \mid b$. In this case, $\operatorname{rad}(b) \leqslant \frac{b}{p}$. It then follows that, as rad is multiplicative for coprime numbers, that
$$
\operatorname{rad}(a b(a+b))=\operatorname{rad}(a) \operatorname{rad}(b) \operatorname{rad}(a+b) \leqslant 2 \cdot 3 \cdot \frac{b}{p} \leqslant \frac{6}{p}(a+b)
$$
Then, by choosing $p$ such that $\frac{6}{p}<\frac{1}{2024^{2024}}$, we found $a$ and $b$ satifying the inequality.
#
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For each positive integer $n$, let $\operatorname{rad}(n)$ denote the product of the distinct prime factors of $n$. Show that there exist integers $a, b>1$ such that $\operatorname{gcd}(a, b)=1$ and
$$
\operatorname{rad}(a b(a+b))<\frac{a+b}{2024^{2024}}
$$
For example, $\operatorname{rad}(20)=\operatorname{rad}\left(2^{2} \cdot 5\right)=2 \cdot 5=10$ and $\operatorname{rad}(18)=\operatorname{rad}\left(2 \cdot 3^{2}\right)=2 \cdot 3=6$.
#
|
We show that the pair $(a, b)$ of the form $a=2^{p(p-1)}, b=3^{p(p-1)}-2^{p(p-1)}$ for sufficiently larger prime number $p$ satisfies the inequality. First, notice that $\operatorname{gcd}(a, b)=\operatorname{gcd}(a, a+b)=1$ indeed. In addition, see that $\operatorname{rad}(a)=2$, and $\operatorname{rad}(a+b)=3$. Because of Euler-Fermat, as $\phi\left(p^{2}\right)=p(p-1)$, it can directly be seen that $p^{2} \mid b$. In this case, $\operatorname{rad}(b) \leqslant \frac{b}{p}$. It then follows that, as rad is multiplicative for coprime numbers, that
$$
\operatorname{rad}(a b(a+b))=\operatorname{rad}(a) \operatorname{rad}(b) \operatorname{rad}(a+b) \leqslant 2 \cdot 3 \cdot \frac{b}{p} \leqslant \frac{6}{p}(a+b)
$$
Then, by choosing $p$ such that $\frac{6}{p}<\frac{1}{2024^{2024}}$, we found $a$ and $b$ satifying the inequality.
#
|
{
"exam": "Benelux_MO",
"problem_label": "4",
"problem_match": "# Problem 4",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2024-zz.jsonl",
"solution_match": "# Solution 1",
"tier": "T3",
"year": "2024"
}
|
For each positive integer $n$, let $\operatorname{rad}(n)$ denote the product of the distinct prime factors of $n$. Show that there exist integers $a, b>1$ such that $\operatorname{gcd}(a, b)=1$ and
$$
\operatorname{rad}(a b(a+b))<\frac{a+b}{2024^{2024}}
$$
For example, $\operatorname{rad}(20)=\operatorname{rad}\left(2^{2} \cdot 5\right)=2 \cdot 5=10$ and $\operatorname{rad}(18)=\operatorname{rad}\left(2 \cdot 3^{2}\right)=2 \cdot 3=6$.
#
|
We show that the pair $(a, b)$ of the form $a=3^{2^{k}}, b=5^{2^{k}}-3^{2^{k}}$ for sufficiently large $k$ satisifies the inequality. Again, we have that $\operatorname{gcd}(a, b)=\operatorname{gcd}(a, a+b)=1$. Similarly to solution $1, \operatorname{rad}(a(a+b))=$ $\operatorname{rad}(a) \operatorname{rad}(a+b)=3 \cdot 5=15$. Then, we will show that $2^{k+1} \mid b$, from which it would follow that $\operatorname{rad}(b) \leqslant \frac{b}{2^{k}}$. From this, we then see that
$$
\operatorname{rad}(a b(a+b))=\operatorname{rad}(a(a+b)) \operatorname{rad}(b) \leqslant \frac{15 b}{2^{k}} .
$$
Like in solution 1, this gives a pair $(a, b)$ satisfying the inequality for sufficiently large $k$.
There are various ways to show that $2^{k+1} \mid 5^{2^{k}}-3^{2^{k}}$, for example directly by applying the Lifting-The-Exponent Lemma. For a more elementary proof, we can apply induction on $k$. The statement is clearly true for $k=0$, and if the statement holds for $k=n$, then for $k=n+1$ we see that
$$
5^{2^{k}}-3^{2^{k}}=5^{2^{n+1}}-3^{2^{n+1}}=\left(5^{2^{n}}\right)^{2}-\left(3^{2^{n}}\right)^{2}=\left(5^{2^{n}}-3^{2^{n}}\right)\left(5^{2^{n}}+3^{2^{n}}\right) .
$$
From the induction hypothesis, the first factor has $n+1$ factors of 2 . As the second factor is a sum of two odd numbers, the second term has at least one factor of 2 . The product thus has at least $n+2=k+1$ factors of 2 , from which the statement follows by induction.
#
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For each positive integer $n$, let $\operatorname{rad}(n)$ denote the product of the distinct prime factors of $n$. Show that there exist integers $a, b>1$ such that $\operatorname{gcd}(a, b)=1$ and
$$
\operatorname{rad}(a b(a+b))<\frac{a+b}{2024^{2024}}
$$
For example, $\operatorname{rad}(20)=\operatorname{rad}\left(2^{2} \cdot 5\right)=2 \cdot 5=10$ and $\operatorname{rad}(18)=\operatorname{rad}\left(2 \cdot 3^{2}\right)=2 \cdot 3=6$.
#
|
We show that the pair $(a, b)$ of the form $a=3^{2^{k}}, b=5^{2^{k}}-3^{2^{k}}$ for sufficiently large $k$ satisifies the inequality. Again, we have that $\operatorname{gcd}(a, b)=\operatorname{gcd}(a, a+b)=1$. Similarly to solution $1, \operatorname{rad}(a(a+b))=$ $\operatorname{rad}(a) \operatorname{rad}(a+b)=3 \cdot 5=15$. Then, we will show that $2^{k+1} \mid b$, from which it would follow that $\operatorname{rad}(b) \leqslant \frac{b}{2^{k}}$. From this, we then see that
$$
\operatorname{rad}(a b(a+b))=\operatorname{rad}(a(a+b)) \operatorname{rad}(b) \leqslant \frac{15 b}{2^{k}} .
$$
Like in solution 1, this gives a pair $(a, b)$ satisfying the inequality for sufficiently large $k$.
There are various ways to show that $2^{k+1} \mid 5^{2^{k}}-3^{2^{k}}$, for example directly by applying the Lifting-The-Exponent Lemma. For a more elementary proof, we can apply induction on $k$. The statement is clearly true for $k=0$, and if the statement holds for $k=n$, then for $k=n+1$ we see that
$$
5^{2^{k}}-3^{2^{k}}=5^{2^{n+1}}-3^{2^{n+1}}=\left(5^{2^{n}}\right)^{2}-\left(3^{2^{n}}\right)^{2}=\left(5^{2^{n}}-3^{2^{n}}\right)\left(5^{2^{n}}+3^{2^{n}}\right) .
$$
From the induction hypothesis, the first factor has $n+1$ factors of 2 . As the second factor is a sum of two odd numbers, the second term has at least one factor of 2 . The product thus has at least $n+2=k+1$ factors of 2 , from which the statement follows by induction.
#
|
{
"exam": "Benelux_MO",
"problem_label": "4",
"problem_match": "# Problem 4",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2024-zz.jsonl",
"solution_match": "# Solution 2",
"tier": "T3",
"year": "2024"
}
|
For each positive integer $n$, let $\operatorname{rad}(n)$ denote the product of the distinct prime factors of $n$. Show that there exist integers $a, b>1$ such that $\operatorname{gcd}(a, b)=1$ and
$$
\operatorname{rad}(a b(a+b))<\frac{a+b}{2024^{2024}}
$$
For example, $\operatorname{rad}(20)=\operatorname{rad}\left(2^{2} \cdot 5\right)=2 \cdot 5=10$ and $\operatorname{rad}(18)=\operatorname{rad}\left(2 \cdot 3^{2}\right)=2 \cdot 3=6$.
#
|
Choose $a=\left(4^{x}-1\right)^{2}, b=4^{x+1}$ and $a+b=\left(4^{x}+1\right)^{2}$. That is, $a, b$ and $a+b$ are squares, where $b$ only contains the factor 2 . Note that $a$ and $b$ are indeed coprime. Then $\operatorname{rad}(a b c)=2 \operatorname{rad}\left(16^{x}-1\right)$.
Choose then $x=5^{k}$ such that $x>2 \cdot 2024^{2024}$. By Lifting the exponent, we know that $5^{k+1} \mid 16^{5^{k}}-1$. This implies that $2 \operatorname{rad}\left(16^{x}-1\right) \leqslant 2\left(16^{x}-1\right) / 5^{k}<\left(4^{x}+1\right)^{2} / 2024^{2024}$.
This solution also works with Euler-Fermat, by choosing $x=\phi\left(5^{k+1}\right)$ with $5^{k}>2024^{2024}$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For each positive integer $n$, let $\operatorname{rad}(n)$ denote the product of the distinct prime factors of $n$. Show that there exist integers $a, b>1$ such that $\operatorname{gcd}(a, b)=1$ and
$$
\operatorname{rad}(a b(a+b))<\frac{a+b}{2024^{2024}}
$$
For example, $\operatorname{rad}(20)=\operatorname{rad}\left(2^{2} \cdot 5\right)=2 \cdot 5=10$ and $\operatorname{rad}(18)=\operatorname{rad}\left(2 \cdot 3^{2}\right)=2 \cdot 3=6$.
#
|
Choose $a=\left(4^{x}-1\right)^{2}, b=4^{x+1}$ and $a+b=\left(4^{x}+1\right)^{2}$. That is, $a, b$ and $a+b$ are squares, where $b$ only contains the factor 2 . Note that $a$ and $b$ are indeed coprime. Then $\operatorname{rad}(a b c)=2 \operatorname{rad}\left(16^{x}-1\right)$.
Choose then $x=5^{k}$ such that $x>2 \cdot 2024^{2024}$. By Lifting the exponent, we know that $5^{k+1} \mid 16^{5^{k}}-1$. This implies that $2 \operatorname{rad}\left(16^{x}-1\right) \leqslant 2\left(16^{x}-1\right) / 5^{k}<\left(4^{x}+1\right)^{2} / 2024^{2024}$.
This solution also works with Euler-Fermat, by choosing $x=\phi\left(5^{k+1}\right)$ with $5^{k}>2024^{2024}$.
|
{
"exam": "Benelux_MO",
"problem_label": "4",
"problem_match": "# Problem 4",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2024-zz.jsonl",
"solution_match": "# Solution 3",
"tier": "T3",
"year": "2024"
}
|
Does there exist a function \(f\colon \mathbb{R}\to \mathbb{R}\) such that
\[f\big(x^{2} + f(y)\big) = f(x)^{2} - y\]
for all \(x,y\in \mathbb{R}?\)
|
There does not exist such a function. Let us suppose by contradiction it does. By substituting \(x\gets 0\) , we get
\[f(f(y)) = f(0)^{2} - y\]
for all \(y\in \mathbb{R}\) . Since the right- hand side is bijective, this implies that \(f\) is also bijective. Taking \(y\gets 0\) we get
\[f\big(x^{2} + f(0)\big) = f(x)^{2}\]
for all \(x\in \mathbb{R}\) and so \(f(- x)^{2} = f(x^{2} + f(0)) = f(x)^{2}\) . Since \(f\) is injective, we get \(f(- x) = - f(x)\) for all \(x\neq 0\) . Since \(f\) is a surjection, there exists \(r\in \mathbb{R}\) such that \(f(r) = 0\) . If \(r\neq 0\) , \(f(- r) = - f(r) = 0 = f(r)\) contradicting the fact that \(f\) is injective. So \(r = 0\) and \(f(0) = 0\) . Substituting \((x,y)\gets (1,0)\) yields \(f(1) = f(1)^{2}\) and so \(f(1) = 1\) since \(f(0) = 0\) and \(f\) is injective. Taking \((x,y)\gets (0,1)\) , we finally get \(1 = f(f(1)) = - 1\) which is the desired contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Does there exist a function \(f\colon \mathbb{R}\to \mathbb{R}\) such that
\[f\big(x^{2} + f(y)\big) = f(x)^{2} - y\]
for all \(x,y\in \mathbb{R}?\)
|
There does not exist such a function. Let us suppose by contradiction it does. By substituting \(x\gets 0\) , we get
\[f(f(y)) = f(0)^{2} - y\]
for all \(y\in \mathbb{R}\) . Since the right- hand side is bijective, this implies that \(f\) is also bijective. Taking \(y\gets 0\) we get
\[f\big(x^{2} + f(0)\big) = f(x)^{2}\]
for all \(x\in \mathbb{R}\) and so \(f(- x)^{2} = f(x^{2} + f(0)) = f(x)^{2}\) . Since \(f\) is injective, we get \(f(- x) = - f(x)\) for all \(x\neq 0\) . Since \(f\) is a surjection, there exists \(r\in \mathbb{R}\) such that \(f(r) = 0\) . If \(r\neq 0\) , \(f(- r) = - f(r) = 0 = f(r)\) contradicting the fact that \(f\) is injective. So \(r = 0\) and \(f(0) = 0\) . Substituting \((x,y)\gets (1,0)\) yields \(f(1) = f(1)^{2}\) and so \(f(1) = 1\) since \(f(0) = 0\) and \(f\) is injective. Taking \((x,y)\gets (0,1)\) , we finally get \(1 = f(f(1)) = - 1\) which is the desired contradiction.
|
{
"exam": "Benelux_MO",
"problem_label": "1",
"problem_match": "\nProblem 1.",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2025-zz.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2025"
}
|
Does there exist a function \(f\colon \mathbb{R}\to \mathbb{R}\) such that
\[f\big(x^{2} + f(y)\big) = f(x)^{2} - y\]
for all \(x,y\in \mathbb{R}?\)
|
We observe that, for all \(y,z\in \mathbb{R}\) , we have
\[z\geqslant f(y)\Longrightarrow f(z)\geq -y.\]
Indeed, we can take \(x = \sqrt{z - f(y)}\) and get \(f(z) = f(x)^{2} - y\geq - y\) . We deduce that \(\lim_{z\to +\infty}f(z) =\) \(+\infty\) . Indeed, for any \(K\in \mathbb{R}\) , we have \(z\geqslant f(- K)\Longrightarrow f(z)\geqslant K\)
Let us now fix \(x\) , and let \(y\to +\infty\) . We have \(x^{2} + f(y)\to +\infty\) , hence \(f(x^{2} + f(y))\to +\infty\) . On the other side, we have \(f(x)^{2} - y\to -\infty\) , a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Does there exist a function \(f\colon \mathbb{R}\to \mathbb{R}\) such that
\[f\big(x^{2} + f(y)\big) = f(x)^{2} - y\]
for all \(x,y\in \mathbb{R}?\)
|
We observe that, for all \(y,z\in \mathbb{R}\) , we have
\[z\geqslant f(y)\Longrightarrow f(z)\geq -y.\]
Indeed, we can take \(x = \sqrt{z - f(y)}\) and get \(f(z) = f(x)^{2} - y\geq - y\) . We deduce that \(\lim_{z\to +\infty}f(z) =\) \(+\infty\) . Indeed, for any \(K\in \mathbb{R}\) , we have \(z\geqslant f(- K)\Longrightarrow f(z)\geqslant K\)
Let us now fix \(x\) , and let \(y\to +\infty\) . We have \(x^{2} + f(y)\to +\infty\) , hence \(f(x^{2} + f(y))\to +\infty\) . On the other side, we have \(f(x)^{2} - y\to -\infty\) , a contradiction.
|
{
"exam": "Benelux_MO",
"problem_label": "1",
"problem_match": "\nProblem 1.",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2025-zz.jsonl",
"solution_match": "\nAlternative Solution.",
"tier": "T3",
"year": "2025"
}
|
Let \(N \geq 2\) be a natural number. At a mathematical olympiad training camp, the same \(N\) courses are organised every day. Each student takes exactly one of the \(N\) courses each day. At the end of the camp, every student has taken each course exactly once, and any two students took the same course on at least one day, but took different courses on at least one other day. What is, in terms of \(N\) , the largest possible number of students at the camp?
|
The largest number of students at the camp is \((N - 1)!\) . Since each student takes exactly one course each day and, at the end, has taken each course exactly once, the schedule of a student can be represented by a permutation of the set of the \(N\) courses. To show that \((N - 1)!\) is possible, we can e.g. assign to each of the \((N - 1)!\) students a unique permutation of the \(N - 1\) first courses and making them all take the \(N\) - th course on the last day. It is easy to observe that such a construction satisfies the properties of the statement.
To prove that, for a set \(S\) of students, one has \(|S| \leq (N - 1)!\) , one first subdivides the set of permutations into disjoint subsets of size \(N\) . Two permutations are said to be in the same subset if and only if one can be obtained from the other by cyclically permute the order of the course. Clearly, this is a well- defined subdivision since cyclically permuting twice the order of the courses can be obtained by cyclically permute them only once. Moreover, each of these subsets contains exactly \(N\) permutations since there are \(N\) cycles of length \(N\) . There are thus \(\frac{N!}{N} = (N - 1)!\) such subsets. If \(|S| > (N - 1)!\) , two students will have their associated permutations in the same subset. However, they cannot be the same permutation (otherwise the two students took the same course every day), and they cannot be obtained by a non- trivial cyclic permutation from each other (otherwise the two students never took the same course).
|
(N - 1)!
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let \(N \geq 2\) be a natural number. At a mathematical olympiad training camp, the same \(N\) courses are organised every day. Each student takes exactly one of the \(N\) courses each day. At the end of the camp, every student has taken each course exactly once, and any two students took the same course on at least one day, but took different courses on at least one other day. What is, in terms of \(N\) , the largest possible number of students at the camp?
|
The largest number of students at the camp is \((N - 1)!\) . Since each student takes exactly one course each day and, at the end, has taken each course exactly once, the schedule of a student can be represented by a permutation of the set of the \(N\) courses. To show that \((N - 1)!\) is possible, we can e.g. assign to each of the \((N - 1)!\) students a unique permutation of the \(N - 1\) first courses and making them all take the \(N\) - th course on the last day. It is easy to observe that such a construction satisfies the properties of the statement.
To prove that, for a set \(S\) of students, one has \(|S| \leq (N - 1)!\) , one first subdivides the set of permutations into disjoint subsets of size \(N\) . Two permutations are said to be in the same subset if and only if one can be obtained from the other by cyclically permute the order of the course. Clearly, this is a well- defined subdivision since cyclically permuting twice the order of the courses can be obtained by cyclically permute them only once. Moreover, each of these subsets contains exactly \(N\) permutations since there are \(N\) cycles of length \(N\) . There are thus \(\frac{N!}{N} = (N - 1)!\) such subsets. If \(|S| > (N - 1)!\) , two students will have their associated permutations in the same subset. However, they cannot be the same permutation (otherwise the two students took the same course every day), and they cannot be obtained by a non- trivial cyclic permutation from each other (otherwise the two students never took the same course).
|
{
"exam": "Benelux_MO",
"problem_label": "2",
"problem_match": "\nProblem 2.",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2025-zz.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2025"
}
|
Let \(ABC\) be a triangle with incentre \(I\) and circumcircle \(\Omega\) . Let \(D, E, F\) be the midpoints of the arcs \(\overline{BC}, \overline{CA}, \overline{AB}\) of \(\Omega\) not containing \(A, B, C\) , respectively. Let \(D'\) be the point of \(\Omega\) diametrically opposite to \(D\) . Show that \(I, D'\) , and the midpoint \(M\) of \([EF]\) lie on a line.
|

By definition of \(D\) , \(E\) and \(F\) , we know that \(ID, IE\) and \(IF\) are the angle bisectors of \(ABC\) . Using angles in \(\Omega\) , we can compute
\[\overline{EFI} = \overline{EFC} = \overline{EBC} = \frac{\overline{ABC}}{2} = 90^{\circ} - \frac{\overline{ACB}}{2} - \frac{\overline{BAC}}{2}\] \[\qquad = 90^{\circ} - \overline{FCB} - \overline{BAD} = 90^{\circ} - \overline{FEB} - \overline{BED} = 90^{\circ} - \overline{FED} = \overline{D'EF}\]
proving that \(D'E\parallel FI\) . Moreover, we can also compute
\[\overline{FEI} = \overline{FEB} = \overline{FCB} = \frac{\overline{ACB}}{2} = 90^{\circ} - \frac{\overline{ABC}}{2} - \frac{\overline{CAB}}{2}\] \[\qquad = 90^{\circ} - \overline{EB} - \overline{CAD} = 90^{\circ} - \overline{EFC} - \overline{CFD} = 90^{\circ} - \overline{EFD} = \overline{D'FE}\]
proving that \(EI\parallel D'F\) . Therefore, \(ED'FI\) is a parallelogram and its diagonals intersect in their midpoints, proving that \(D'I\) contains \(M\) .

|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let \(ABC\) be a triangle with incentre \(I\) and circumcircle \(\Omega\) . Let \(D, E, F\) be the midpoints of the arcs \(\overline{BC}, \overline{CA}, \overline{AB}\) of \(\Omega\) not containing \(A, B, C\) , respectively. Let \(D'\) be the point of \(\Omega\) diametrically opposite to \(D\) . Show that \(I, D'\) , and the midpoint \(M\) of \([EF]\) lie on a line.
|

By definition of \(D\) , \(E\) and \(F\) , we know that \(ID, IE\) and \(IF\) are the angle bisectors of \(ABC\) . Using angles in \(\Omega\) , we can compute
\[\overline{EFI} = \overline{EFC} = \overline{EBC} = \frac{\overline{ABC}}{2} = 90^{\circ} - \frac{\overline{ACB}}{2} - \frac{\overline{BAC}}{2}\] \[\qquad = 90^{\circ} - \overline{FCB} - \overline{BAD} = 90^{\circ} - \overline{FEB} - \overline{BED} = 90^{\circ} - \overline{FED} = \overline{D'EF}\]
proving that \(D'E\parallel FI\) . Moreover, we can also compute
\[\overline{FEI} = \overline{FEB} = \overline{FCB} = \frac{\overline{ACB}}{2} = 90^{\circ} - \frac{\overline{ABC}}{2} - \frac{\overline{CAB}}{2}\] \[\qquad = 90^{\circ} - \overline{EB} - \overline{CAD} = 90^{\circ} - \overline{EFC} - \overline{CFD} = 90^{\circ} - \overline{EFD} = \overline{D'FE}\]
proving that \(EI\parallel D'F\) . Therefore, \(ED'FI\) is a parallelogram and its diagonals intersect in their midpoints, proving that \(D'I\) contains \(M\) .

|
{
"exam": "Benelux_MO",
"problem_label": "3",
"problem_match": "\nProblem 3.",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2025-zz.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2025"
}
|
Let \(ABC\) be a triangle with incentre \(I\) and circumcircle \(\Omega\) . Let \(D, E, F\) be the midpoints of the arcs \(\overline{BC}, \overline{CA}, \overline{AB}\) of \(\Omega\) not containing \(A, B, C\) , respectively. Let \(D'\) be the point of \(\Omega\) diametrically opposite to \(D\) . Show that \(I, D'\) , and the midpoint \(M\) of \([EF]\) lie on a line.
|
By definition of \(D, E\) and \(F\) , we know that \(ID, IE\) and \(IF\) are the angle bisectors of \(ABC\) . If \(D' = A\) , this means that \(\overrightarrow{OAB} = 90^\circ - \overrightarrow{ACB} = \frac{\overrightarrow{CAB}}{2}\) and \(ABC\) is isosceles in \(A\) . In that case, the symmetry with respect to \(AI\) sends \(E\) to \(F\) and so \(M \in AI\) . We can thus suppose that \(D' \neq A\) .
Let us consider \(I_A, I_B\) and \(I_C\) the excenters of \(ABC\) . The lines \(I_B AI_C, I_C BI_A\) and \(I_A CI_B\) are thus the exterior bisectors of the triangle. Hence, \(I_B IC \perp AI_A\) and, since \(\overrightarrow{D'AD} = 90^\circ\) , one has \(D' \in I_B IC\) . In the triangle \(I_A I_B IC\) , the points \(A, B\) and \(C\) are the feet of the heights and \(\Omega\) is thus the Euler circle of \(I_A I_B IC\) . Since \(D' \in [I_B IC] \cap \Omega\) and \(D' \neq A\) , it is the midpoint of \([I_B IC]\) . Moreover, \(E\) and \(F\) , being on the Euler circle and the heights, there are the midpoints of \([I_B I]\) and \([IC I]\) respectively. The homothety of centre \(I\) and ratio \(\frac{1}{2}\) sends \(I_B\) on \(E\) and \(IC\) on \(F\) . It thus also sends \(D'\) on \(M\) , proving that \(D', M\) and \(I\) are collinear.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let \(ABC\) be a triangle with incentre \(I\) and circumcircle \(\Omega\) . Let \(D, E, F\) be the midpoints of the arcs \(\overline{BC}, \overline{CA}, \overline{AB}\) of \(\Omega\) not containing \(A, B, C\) , respectively. Let \(D'\) be the point of \(\Omega\) diametrically opposite to \(D\) . Show that \(I, D'\) , and the midpoint \(M\) of \([EF]\) lie on a line.
|
By definition of \(D, E\) and \(F\) , we know that \(ID, IE\) and \(IF\) are the angle bisectors of \(ABC\) . If \(D' = A\) , this means that \(\overrightarrow{OAB} = 90^\circ - \overrightarrow{ACB} = \frac{\overrightarrow{CAB}}{2}\) and \(ABC\) is isosceles in \(A\) . In that case, the symmetry with respect to \(AI\) sends \(E\) to \(F\) and so \(M \in AI\) . We can thus suppose that \(D' \neq A\) .
Let us consider \(I_A, I_B\) and \(I_C\) the excenters of \(ABC\) . The lines \(I_B AI_C, I_C BI_A\) and \(I_A CI_B\) are thus the exterior bisectors of the triangle. Hence, \(I_B IC \perp AI_A\) and, since \(\overrightarrow{D'AD} = 90^\circ\) , one has \(D' \in I_B IC\) . In the triangle \(I_A I_B IC\) , the points \(A, B\) and \(C\) are the feet of the heights and \(\Omega\) is thus the Euler circle of \(I_A I_B IC\) . Since \(D' \in [I_B IC] \cap \Omega\) and \(D' \neq A\) , it is the midpoint of \([I_B IC]\) . Moreover, \(E\) and \(F\) , being on the Euler circle and the heights, there are the midpoints of \([I_B I]\) and \([IC I]\) respectively. The homothety of centre \(I\) and ratio \(\frac{1}{2}\) sends \(I_B\) on \(E\) and \(IC\) on \(F\) . It thus also sends \(D'\) on \(M\) , proving that \(D', M\) and \(I\) are collinear.
|
{
"exam": "Benelux_MO",
"problem_label": "3",
"problem_match": "\nProblem 3.",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2025-zz.jsonl",
"solution_match": "\nAlternative Solution.",
"tier": "T3",
"year": "2025"
}
|
Let \(a_{0},a_{1},\ldots ,a_{10}\) be integers such that, for each \(i\in \{0,1,\ldots ,2047\}\) , there exists a subset \(S\subseteq \{0,1,\ldots ,10\}\) with
\[\sum_{j\in S}a_{j}\equiv i\pmod {2048}.\]
Show that for each \(i\in \{0,1,\ldots ,10\}\) , there is exactly one \(j\in \{0,1,\ldots ,10\}\) such that \(a_{j}\) is divisible by \(2^{i}\) but not by \(2^{i + 1}\) .
Note: \(\sum_{j\in S}a_{j}\) is the summation notation, for instance, \(\sum_{j\in \{2,5\}}a_{j} = a_{2} + a_{5}\) , while, for the empty set \(\varnothing\) , one defines \(\sum_{j\in \varnothing}a_{j} = 0\) .
|
We denote by \(\nu_{2}(a)\) the valuation 2- adic of the integer \(a\) . Let us prove by induction the more general statement that, for \(n\in \mathbb{N}_{>0}\) , if \(a_{0},a_{1},\ldots ,a_{n - 1}\) are integers such that, for each \(i\in \{0,1,\ldots ,2^{n} - 1\}\) , there exists a subset \(S\subseteq \{0,1,\ldots ,n - 1\}\) with \(\sum_{j\in S}a_{j}\equiv i\) (mod \(2^{n}\) ), then, for each \(i\in \{0,1,\ldots ,n - 1\}\) , there is exactly one \(j\in \{0,1,\ldots ,n - 1\}\) such that \(\nu_{2}(a_{j}) = i\) . The result then follows by setting \(n = 11\) . The case \(n = 1\) is trivial.
We suppose by induction that the result is true for \(n - 1\) for prove it for \(n\geq 2\) . Let us first notice that, since there are \(2^{n}\) elements in \(\{0,1,\ldots ,2^{n} - 1\}\) and \(2^{n}\) subsets of \(\{0,1,\ldots ,n - 1\}\) , for each \(i\in\) \(\{0,1,\ldots ,2^{n} - 1\}\) , there exists exactly one \(S_{i}\subseteq \{0,1,\ldots ,n - 1\}\) such that \(\sum_{j\in S_{i}}a_{j}\equiv i\) (mod \(2^{n}\) ). By summing all these sums for all \(i\) , we obtain
\[\sum_{i = 0}^{2^{n} - 1}\sum_{j\in S_{i}}a_{j}\equiv \sum_{i = 0}^{2^{n} - 1}i = \frac{2^{n}\cdot(2^{n} - 1)}{2} = 2^{n - 1}\cdot (2^{n} - 1)\pmod {2^{n}}.\]
For a fixed \(j\in \{0,1,\ldots ,n - 1\}\) , \(a_{j}\) appears in exactly \(2^{n - 1}\) of these sums (since each of the \(n - 1\) remaining indices may or may not be in \(S_{i}\) ). Therefore,
\[2^{n - 1}\cdot \sum_{j = 0}^{n - 1}a_{j} = \sum_{i = 0}^{2^{n} - 1}\sum_{j\in S_{i}}a_{j}\equiv 2^{n - 1}\cdot (2^{n} - 1)\pmod {2^{n}}\]
which is equivalent to
\[\sum_{j = 0}^{n - 1}a_{j}\equiv 2^{n} - 1\equiv 1\pmod {2}.\]
Since \(\sum_{j = 0}^{n - 1}a_{j}\) is odd, at least one of the \(a_{j}\) 's is odd.
Let us suppose by contradiction that at least two of them are odd. We now sum all the \(\sum_{j\in S_{i}}a_{j}\) for which \(\sum_{j\in S_{i}}a_{j}\) (or, equivalently, \(i\) ) is even:
\[\sum_{i\in \{0,\ldots ,2^{n} - 1\}}\sum_{j\in S_{i}}a_{j}\equiv \sum_{i\in \{0,\ldots ,2^{n} - 1\}}i = 2^{n - 1}\cdot (2^{n - 1} - 1)\pmod {2^{n}}\]
For a fixed \(j\in \{0,1,\ldots ,n - 1\}\) , \(a_{j}\) appears in exactly \(2^{n - 2}\) of these sums. Indeed, since there is at least one \(k\in \{0,1,\ldots ,n - 1\} \backslash \{j\}\) such that \(a_{k}\) is odd, one can consider any \(S\subseteq \{0,1,\ldots ,n - 1\} \backslash \{j,k\}\) , add \(j\) to it, and potentially also \(k\) in order to make the partial sum even (exactly one possibility for each such \(S\) ). Therefore,
\[2^{n - 2}\cdot \sum_{j = 0}^{n - 1}a_{j} = \sum_{i\in \{0,\ldots ,2^{n} - 1\}}\sum_{j\in S_{i}}a_{j}\equiv 2^{n - 1}\cdot (2^{n - 1} - 1)\pmod {2^{n}}\]
or equivalently
\[\sum_{j = 0}^{n - 1}a_{j}\equiv 2\cdot (2^{n - 1} - 1)\pmod {4}.\]
Hence \(\sum_{j = 0}^{n - 1}a_{j}\) is even, which is a contradiction. Therefore, there is exactly one \(k\in \{0,1,\ldots ,n - 1\}\) such that \(a_{k}\) is odd.
A sum \(\sum_{j\in S}a_{j}\) is odd if and only if \(k\in S\) . Moreover, the sums \(\sum_{j\in S}a_{j}\) for which \(k\notin S\) cover all the even numbers modulo \(2^{n}\) . Thus, omitting \(a_{k}\) , the \(n - 1\) integers \(\frac{a_{0}}{2},\ldots ,\frac{a_{n - 1}}{2}\) satisfy the condition of the statement. By the induction hypothesis, for each \(i\in \{0,1,\ldots ,n - 2\}\) , there is exactly one \(j\in \{0,1,\ldots ,n - 1\} \backslash \{k\}\) such that \(\nu_{2}\left(\frac{a_{j}}{2}\right) = i\) , i.e., \(\nu_{2}(a_{j}) = i + 1\) . Since \(\nu_{2}(a_{k}) = 0\) , this concludes the proof.
Remark: If one considers the sum of all \(\sum_{j\in S_{i}}a_{j}\) such that \(i\) is odd, one obtains, in the case where at least two \(a_{i}\) 's are odd, that \(2^{n - 2}\cdot \sum_{j = 0}^{n - 1}a_{j}\equiv 0\) (mod \(2^{n}\) ) also reaching a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let \(a_{0},a_{1},\ldots ,a_{10}\) be integers such that, for each \(i\in \{0,1,\ldots ,2047\}\) , there exists a subset \(S\subseteq \{0,1,\ldots ,10\}\) with
\[\sum_{j\in S}a_{j}\equiv i\pmod {2048}.\]
Show that for each \(i\in \{0,1,\ldots ,10\}\) , there is exactly one \(j\in \{0,1,\ldots ,10\}\) such that \(a_{j}\) is divisible by \(2^{i}\) but not by \(2^{i + 1}\) .
Note: \(\sum_{j\in S}a_{j}\) is the summation notation, for instance, \(\sum_{j\in \{2,5\}}a_{j} = a_{2} + a_{5}\) , while, for the empty set \(\varnothing\) , one defines \(\sum_{j\in \varnothing}a_{j} = 0\) .
|
We denote by \(\nu_{2}(a)\) the valuation 2- adic of the integer \(a\) . Let us prove by induction the more general statement that, for \(n\in \mathbb{N}_{>0}\) , if \(a_{0},a_{1},\ldots ,a_{n - 1}\) are integers such that, for each \(i\in \{0,1,\ldots ,2^{n} - 1\}\) , there exists a subset \(S\subseteq \{0,1,\ldots ,n - 1\}\) with \(\sum_{j\in S}a_{j}\equiv i\) (mod \(2^{n}\) ), then, for each \(i\in \{0,1,\ldots ,n - 1\}\) , there is exactly one \(j\in \{0,1,\ldots ,n - 1\}\) such that \(\nu_{2}(a_{j}) = i\) . The result then follows by setting \(n = 11\) . The case \(n = 1\) is trivial.
We suppose by induction that the result is true for \(n - 1\) for prove it for \(n\geq 2\) . Let us first notice that, since there are \(2^{n}\) elements in \(\{0,1,\ldots ,2^{n} - 1\}\) and \(2^{n}\) subsets of \(\{0,1,\ldots ,n - 1\}\) , for each \(i\in\) \(\{0,1,\ldots ,2^{n} - 1\}\) , there exists exactly one \(S_{i}\subseteq \{0,1,\ldots ,n - 1\}\) such that \(\sum_{j\in S_{i}}a_{j}\equiv i\) (mod \(2^{n}\) ). By summing all these sums for all \(i\) , we obtain
\[\sum_{i = 0}^{2^{n} - 1}\sum_{j\in S_{i}}a_{j}\equiv \sum_{i = 0}^{2^{n} - 1}i = \frac{2^{n}\cdot(2^{n} - 1)}{2} = 2^{n - 1}\cdot (2^{n} - 1)\pmod {2^{n}}.\]
For a fixed \(j\in \{0,1,\ldots ,n - 1\}\) , \(a_{j}\) appears in exactly \(2^{n - 1}\) of these sums (since each of the \(n - 1\) remaining indices may or may not be in \(S_{i}\) ). Therefore,
\[2^{n - 1}\cdot \sum_{j = 0}^{n - 1}a_{j} = \sum_{i = 0}^{2^{n} - 1}\sum_{j\in S_{i}}a_{j}\equiv 2^{n - 1}\cdot (2^{n} - 1)\pmod {2^{n}}\]
which is equivalent to
\[\sum_{j = 0}^{n - 1}a_{j}\equiv 2^{n} - 1\equiv 1\pmod {2}.\]
Since \(\sum_{j = 0}^{n - 1}a_{j}\) is odd, at least one of the \(a_{j}\) 's is odd.
Let us suppose by contradiction that at least two of them are odd. We now sum all the \(\sum_{j\in S_{i}}a_{j}\) for which \(\sum_{j\in S_{i}}a_{j}\) (or, equivalently, \(i\) ) is even:
\[\sum_{i\in \{0,\ldots ,2^{n} - 1\}}\sum_{j\in S_{i}}a_{j}\equiv \sum_{i\in \{0,\ldots ,2^{n} - 1\}}i = 2^{n - 1}\cdot (2^{n - 1} - 1)\pmod {2^{n}}\]
For a fixed \(j\in \{0,1,\ldots ,n - 1\}\) , \(a_{j}\) appears in exactly \(2^{n - 2}\) of these sums. Indeed, since there is at least one \(k\in \{0,1,\ldots ,n - 1\} \backslash \{j\}\) such that \(a_{k}\) is odd, one can consider any \(S\subseteq \{0,1,\ldots ,n - 1\} \backslash \{j,k\}\) , add \(j\) to it, and potentially also \(k\) in order to make the partial sum even (exactly one possibility for each such \(S\) ). Therefore,
\[2^{n - 2}\cdot \sum_{j = 0}^{n - 1}a_{j} = \sum_{i\in \{0,\ldots ,2^{n} - 1\}}\sum_{j\in S_{i}}a_{j}\equiv 2^{n - 1}\cdot (2^{n - 1} - 1)\pmod {2^{n}}\]
or equivalently
\[\sum_{j = 0}^{n - 1}a_{j}\equiv 2\cdot (2^{n - 1} - 1)\pmod {4}.\]
Hence \(\sum_{j = 0}^{n - 1}a_{j}\) is even, which is a contradiction. Therefore, there is exactly one \(k\in \{0,1,\ldots ,n - 1\}\) such that \(a_{k}\) is odd.
A sum \(\sum_{j\in S}a_{j}\) is odd if and only if \(k\in S\) . Moreover, the sums \(\sum_{j\in S}a_{j}\) for which \(k\notin S\) cover all the even numbers modulo \(2^{n}\) . Thus, omitting \(a_{k}\) , the \(n - 1\) integers \(\frac{a_{0}}{2},\ldots ,\frac{a_{n - 1}}{2}\) satisfy the condition of the statement. By the induction hypothesis, for each \(i\in \{0,1,\ldots ,n - 2\}\) , there is exactly one \(j\in \{0,1,\ldots ,n - 1\} \backslash \{k\}\) such that \(\nu_{2}\left(\frac{a_{j}}{2}\right) = i\) , i.e., \(\nu_{2}(a_{j}) = i + 1\) . Since \(\nu_{2}(a_{k}) = 0\) , this concludes the proof.
Remark: If one considers the sum of all \(\sum_{j\in S_{i}}a_{j}\) such that \(i\) is odd, one obtains, in the case where at least two \(a_{i}\) 's are odd, that \(2^{n - 2}\cdot \sum_{j = 0}^{n - 1}a_{j}\equiv 0\) (mod \(2^{n}\) ) also reaching a contradiction.
|
{
"exam": "Benelux_MO",
"problem_label": "4",
"problem_match": "\nProblem 4.",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2025-zz.jsonl",
"solution_match": "\nSolution.",
"tier": "T3",
"year": "2025"
}
|
Let \(a_{0},a_{1},\ldots ,a_{10}\) be integers such that, for each \(i\in \{0,1,\ldots ,2047\}\) , there exists a subset \(S\subseteq \{0,1,\ldots ,10\}\) with
\[\sum_{j\in S}a_{j}\equiv i\pmod {2048}.\]
Show that for each \(i\in \{0,1,\ldots ,10\}\) , there is exactly one \(j\in \{0,1,\ldots ,10\}\) such that \(a_{j}\) is divisible by \(2^{i}\) but not by \(2^{i + 1}\) .
Note: \(\sum_{j\in S}a_{j}\) is the summation notation, for instance, \(\sum_{j\in \{2,5\}}a_{j} = a_{2} + a_{5}\) , while, for the empty set \(\varnothing\) , one defines \(\sum_{j\in \varnothing}a_{j} = 0\) .
|
We do the same induction as in the main Solution. If all \(a_{j}\) are even, then all the sums are even, contradicting the hypothesis. Therefore, without loss of generality, we can assume that \(a_{0}\) is odd. For each \(i\in \{0,1,2,\ldots ,2^{n} - 1\}\) , let \(S_{i}^{\prime}\subseteq \{0,1,\ldots ,n - 1\}\) be the subset such that \(\sum_{j\in S_{i}^{\prime}}a_{j}\equiv i\cdot a_{0}\) (mod \(2^{n}\) ) (this subset exists by the hypothesis and is unique since there are exactly \(2^{n}\) subsets of \(\{0,1,\ldots ,n - 1\}\) ). By definition, one has \(S_{0}^{\prime} = \emptyset\) and \(S_{1}^{\prime} = \{0\}\) .
Let us prove by induction that, for each \(i\in \{0,1,\ldots ,2^{n - 1} - 1\}\) , one has \(0\notin S_{2i}^{\prime}\) but \(0\in S_{2i + 1}^{\prime}\) . The case \(i = 0\) is trivial. For \(i > 0\) , if we suppose that \(0\in S_{2i - 1}^{\prime}\) , we prove that \(0\notin S_{2i}^{\prime}\) . Indeed, if \(0\in S_{2i}^{\prime}\) , then \(\sum_{j\in S_{2i}^{\prime}\backslash \{0\}}a_{j}\equiv 2i a_{0} - a_{0} = (2i - 1)a_{0}\equiv \sum_{j\in S_{2i - 1}^{\prime}}a_{j}\) (mod \(2^{n}\) ) and so \(S_{2i}^{\prime}\backslash \{0\} = S_{2i - 1}^{\prime}\) by uniqueness. But \(0\in S_{2i - 1}^{\prime}\) so this is a contradiction, proving that \(0\notin S_{2i}^{\prime}\) . Then, \(\sum_{j\in S_{2i}^{\prime}\cup \{0\}}a_{j}\equiv 2i a_{0} + a_{0} = (2i + 1)a_{0}\equiv \sum_{j\in S_{2i + 1}^{\prime}}a_{j}\) (mod \(2^{n}\) ). By uniqueness, \(S_{2i}^{\prime}\cup \{0\} = S_{2i + 1}^{\prime}\) and so \(0\in S_{2i + 1}^{\prime}\) .
Since \(a_{0}\) is odd, it is invertible modulo \(2^{n}\) and so \(0, a_{0}, 2a_{0}, \ldots , (2^{n} - 1)a_{0}\) is a permutation of 0, 1, 2, ..., \(2^{n} - 1\) modulo \(2^{n}\) . This shows that the subsets \(S_{0}^{\prime}, S_{2}^{\prime}, S_{4}^{\prime}, \ldots , S_{2^{n} - 2}^{\prime}\) are all distinct. There are thus \(2^{n - 1}\) subsets \(S_{2i}^{\prime}\) and they are a precisely the subsets of \(\{1,2,\ldots ,n - 1\}\) (since there are also \(2^{n - 1}\) such subsets). Moreover, their corresponding sums are all even. Since this list of subsets contains \(\{1\} , \{2\} , \ldots , \{n - 1\}\) , this shows that \(a_{1}, a_{2}, \ldots , a_{n - 1}\) are all even.
We then conclude the induction as in the main Solution.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let \(a_{0},a_{1},\ldots ,a_{10}\) be integers such that, for each \(i\in \{0,1,\ldots ,2047\}\) , there exists a subset \(S\subseteq \{0,1,\ldots ,10\}\) with
\[\sum_{j\in S}a_{j}\equiv i\pmod {2048}.\]
Show that for each \(i\in \{0,1,\ldots ,10\}\) , there is exactly one \(j\in \{0,1,\ldots ,10\}\) such that \(a_{j}\) is divisible by \(2^{i}\) but not by \(2^{i + 1}\) .
Note: \(\sum_{j\in S}a_{j}\) is the summation notation, for instance, \(\sum_{j\in \{2,5\}}a_{j} = a_{2} + a_{5}\) , while, for the empty set \(\varnothing\) , one defines \(\sum_{j\in \varnothing}a_{j} = 0\) .
|
We do the same induction as in the main Solution. If all \(a_{j}\) are even, then all the sums are even, contradicting the hypothesis. Therefore, without loss of generality, we can assume that \(a_{0}\) is odd. For each \(i\in \{0,1,2,\ldots ,2^{n} - 1\}\) , let \(S_{i}^{\prime}\subseteq \{0,1,\ldots ,n - 1\}\) be the subset such that \(\sum_{j\in S_{i}^{\prime}}a_{j}\equiv i\cdot a_{0}\) (mod \(2^{n}\) ) (this subset exists by the hypothesis and is unique since there are exactly \(2^{n}\) subsets of \(\{0,1,\ldots ,n - 1\}\) ). By definition, one has \(S_{0}^{\prime} = \emptyset\) and \(S_{1}^{\prime} = \{0\}\) .
Let us prove by induction that, for each \(i\in \{0,1,\ldots ,2^{n - 1} - 1\}\) , one has \(0\notin S_{2i}^{\prime}\) but \(0\in S_{2i + 1}^{\prime}\) . The case \(i = 0\) is trivial. For \(i > 0\) , if we suppose that \(0\in S_{2i - 1}^{\prime}\) , we prove that \(0\notin S_{2i}^{\prime}\) . Indeed, if \(0\in S_{2i}^{\prime}\) , then \(\sum_{j\in S_{2i}^{\prime}\backslash \{0\}}a_{j}\equiv 2i a_{0} - a_{0} = (2i - 1)a_{0}\equiv \sum_{j\in S_{2i - 1}^{\prime}}a_{j}\) (mod \(2^{n}\) ) and so \(S_{2i}^{\prime}\backslash \{0\} = S_{2i - 1}^{\prime}\) by uniqueness. But \(0\in S_{2i - 1}^{\prime}\) so this is a contradiction, proving that \(0\notin S_{2i}^{\prime}\) . Then, \(\sum_{j\in S_{2i}^{\prime}\cup \{0\}}a_{j}\equiv 2i a_{0} + a_{0} = (2i + 1)a_{0}\equiv \sum_{j\in S_{2i + 1}^{\prime}}a_{j}\) (mod \(2^{n}\) ). By uniqueness, \(S_{2i}^{\prime}\cup \{0\} = S_{2i + 1}^{\prime}\) and so \(0\in S_{2i + 1}^{\prime}\) .
Since \(a_{0}\) is odd, it is invertible modulo \(2^{n}\) and so \(0, a_{0}, 2a_{0}, \ldots , (2^{n} - 1)a_{0}\) is a permutation of 0, 1, 2, ..., \(2^{n} - 1\) modulo \(2^{n}\) . This shows that the subsets \(S_{0}^{\prime}, S_{2}^{\prime}, S_{4}^{\prime}, \ldots , S_{2^{n} - 2}^{\prime}\) are all distinct. There are thus \(2^{n - 1}\) subsets \(S_{2i}^{\prime}\) and they are a precisely the subsets of \(\{1,2,\ldots ,n - 1\}\) (since there are also \(2^{n - 1}\) such subsets). Moreover, their corresponding sums are all even. Since this list of subsets contains \(\{1\} , \{2\} , \ldots , \{n - 1\}\) , this shows that \(a_{1}, a_{2}, \ldots , a_{n - 1}\) are all even.
We then conclude the induction as in the main Solution.
|
{
"exam": "Benelux_MO",
"problem_label": "4",
"problem_match": "\nProblem 4.",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2025-zz.jsonl",
"solution_match": "\nAlternative Solution.",
"tier": "T3",
"year": "2025"
}
|
Let \(a_{0},a_{1},\ldots ,a_{10}\) be integers such that, for each \(i\in \{0,1,\ldots ,2047\}\) , there exists a subset \(S\subseteq \{0,1,\ldots ,10\}\) with
\[\sum_{j\in S}a_{j}\equiv i\pmod {2048}.\]
Show that for each \(i\in \{0,1,\ldots ,10\}\) , there is exactly one \(j\in \{0,1,\ldots ,10\}\) such that \(a_{j}\) is divisible by \(2^{i}\) but not by \(2^{i + 1}\) .
Note: \(\sum_{j\in S}a_{j}\) is the summation notation, for instance, \(\sum_{j\in \{2,5\}}a_{j} = a_{2} + a_{5}\) , while, for the empty set \(\varnothing\) , one defines \(\sum_{j\in \varnothing}a_{j} = 0\) .
|
We do the same induction as in the main Solution (except that we prove that for each \(i\in \{0,1,\ldots ,n - 1\}\) , there exists \(j\in \{0,1,\ldots ,n - 1\}\) with \(\nu_{2}(a_{j}) = i\) , uniqueness follows immediately). For the induction step, let us consider the polynomial
\[P(X) = \prod_{j = 0}^{n - 1}\left(X^{a_{j}} + 1\right).\]
The condition in the statement implies that
\[P(X)\equiv \sum_{i = 0}^{2^{n} - 1}X^{i}\pmod {X^{2^{n}} - 1}.\]
Since
\[\sum_{i = 0}^{2^{n} - 1}X^{i} = \frac{X^{2^{n}} - 1}{X - 1} = \frac{X^{2^{n} - 1} - 1}{X - 1}\cdot \left(X^{2^{n} - 1} + 1\right),\]
we know that \(P(X)\) is divisible by \(X^{2^{n} - 1} + 1\) . Let \(\omega \in \mathbb{C}\) be a primitive \(2^{n}\) - th root of unity. Thus \(\omega^{2^{n} - 1} = - 1\) and \(P(\omega) = 0\) . There exists thus \(j\in \{0,1,\ldots ,n - 1\}\) such that \(\omega^{a_{j}} = - 1\) . This means that \(a_{j} = (2k + 1)2^{n - 1}\) for some integer \(k\) , i.e., \(\nu_{2}(a_{j}) = n - 1\) . It is then obvious that the other ones satisfy the property for \(n - 1\) and we conclude by the inductive hypothesis.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let \(a_{0},a_{1},\ldots ,a_{10}\) be integers such that, for each \(i\in \{0,1,\ldots ,2047\}\) , there exists a subset \(S\subseteq \{0,1,\ldots ,10\}\) with
\[\sum_{j\in S}a_{j}\equiv i\pmod {2048}.\]
Show that for each \(i\in \{0,1,\ldots ,10\}\) , there is exactly one \(j\in \{0,1,\ldots ,10\}\) such that \(a_{j}\) is divisible by \(2^{i}\) but not by \(2^{i + 1}\) .
Note: \(\sum_{j\in S}a_{j}\) is the summation notation, for instance, \(\sum_{j\in \{2,5\}}a_{j} = a_{2} + a_{5}\) , while, for the empty set \(\varnothing\) , one defines \(\sum_{j\in \varnothing}a_{j} = 0\) .
|
We do the same induction as in the main Solution (except that we prove that for each \(i\in \{0,1,\ldots ,n - 1\}\) , there exists \(j\in \{0,1,\ldots ,n - 1\}\) with \(\nu_{2}(a_{j}) = i\) , uniqueness follows immediately). For the induction step, let us consider the polynomial
\[P(X) = \prod_{j = 0}^{n - 1}\left(X^{a_{j}} + 1\right).\]
The condition in the statement implies that
\[P(X)\equiv \sum_{i = 0}^{2^{n} - 1}X^{i}\pmod {X^{2^{n}} - 1}.\]
Since
\[\sum_{i = 0}^{2^{n} - 1}X^{i} = \frac{X^{2^{n}} - 1}{X - 1} = \frac{X^{2^{n} - 1} - 1}{X - 1}\cdot \left(X^{2^{n} - 1} + 1\right),\]
we know that \(P(X)\) is divisible by \(X^{2^{n} - 1} + 1\) . Let \(\omega \in \mathbb{C}\) be a primitive \(2^{n}\) - th root of unity. Thus \(\omega^{2^{n} - 1} = - 1\) and \(P(\omega) = 0\) . There exists thus \(j\in \{0,1,\ldots ,n - 1\}\) such that \(\omega^{a_{j}} = - 1\) . This means that \(a_{j} = (2k + 1)2^{n - 1}\) for some integer \(k\) , i.e., \(\nu_{2}(a_{j}) = n - 1\) . It is then obvious that the other ones satisfy the property for \(n - 1\) and we conclude by the inductive hypothesis.
|
{
"exam": "Benelux_MO",
"problem_label": "4",
"problem_match": "\nProblem 4.",
"resource_path": "Benelux_MO/segmented/Benelux_en-olympiad_en-bxmo-problems-2025-zz.jsonl",
"solution_match": "\nAlternative Solution.",
"tier": "T3",
"year": "2025"
}
|
Let $A B C D$ be a trapezoid with $A B$ parallel to $C D,|A B|>|C D|$, and equal edges $|A D|=|B C|$. Let $I$ be the center of the circle tangent to lines $A B, A C$ and $B D$, where $A$ and $I$ are on opposite sides of $B D$. Let $J$ be the center of the circle tangent to lines $C D, A C$ and $B D$, where $D$ and $J$ are on opposite sides of $A C$. Prove that $|I C|=|J B|$.
|
Let $\{P\}=A C \cap B D$ and let $\angle A P B=180-2 a$. Since $A B C D$ is an isosceles trapezoid, $A P B$ is an isosceles triangle. Therefore $\angle P B A=a$, which implies that $\angle P B I=90^{\circ}-a / 2$ since $I$ lies on the external bisector of $\angle P B A$. Since $I$ lies on the bisector of $\angle C P B$, it follows that $\angle B P I=a$ and hence that $I P B$ is isosceles with $|I P|=|P B|$. Similarly $J P C$ is isosceles with $|J P|=|P C|$. So, in the triangles $C P I$ and $B P J$ we have $P I \equiv P B$ and $P J \equiv C P$. Since $I$ and $J$ both lie on the internal bisector of $\angle B P C$, it follows that triangles $C P I$ and $B P J$ are congruent. Therefore $|I C|=|J B|$.
A competition of the Canadian Mathematical Society and supported by the Actuarial Profession.

Expertise. Insight. Solutions.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a trapezoid with $A B$ parallel to $C D,|A B|>|C D|$, and equal edges $|A D|=|B C|$. Let $I$ be the center of the circle tangent to lines $A B, A C$ and $B D$, where $A$ and $I$ are on opposite sides of $B D$. Let $J$ be the center of the circle tangent to lines $C D, A C$ and $B D$, where $D$ and $J$ are on opposite sides of $A C$. Prove that $|I C|=|J B|$.
|
Let $\{P\}=A C \cap B D$ and let $\angle A P B=180-2 a$. Since $A B C D$ is an isosceles trapezoid, $A P B$ is an isosceles triangle. Therefore $\angle P B A=a$, which implies that $\angle P B I=90^{\circ}-a / 2$ since $I$ lies on the external bisector of $\angle P B A$. Since $I$ lies on the bisector of $\angle C P B$, it follows that $\angle B P I=a$ and hence that $I P B$ is isosceles with $|I P|=|P B|$. Similarly $J P C$ is isosceles with $|J P|=|P C|$. So, in the triangles $C P I$ and $B P J$ we have $P I \equiv P B$ and $P J \equiv C P$. Since $I$ and $J$ both lie on the internal bisector of $\angle B P C$, it follows that triangles $C P I$ and $B P J$ are congruent. Therefore $|I C|=|J B|$.
A competition of the Canadian Mathematical Society and supported by the Actuarial Profession.

Expertise. Insight. Solutions.
|
{
"exam": "Canada_MO",
"problem_label": "1",
"problem_match": "\nProblem No. 1.",
"resource_path": "Canada_MO/segmented/en-2021CMO_solutions_en-1.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2021"
}
|
Let $n \geq 2$ be some fixed positive integer and suppose that $a_{1}, a_{2}, \ldots, a_{n}$ are positive real numbers satisfying $a_{1}+a_{2}+\cdots+a_{n}=2^{n}-1$.
Find the minimum possible value of
$$
\frac{a_{1}}{1}+\frac{a_{2}}{1+a_{1}}+\frac{a_{3}}{1+a_{1}+a_{2}}+\cdots+\frac{a_{n}}{1+a_{1}+a_{2}+\cdots+a_{n-1}} .
$$
|
We claim the the minimum possible value of this expression is $n$. Observe that by AM-GM, we have that
$$
\begin{aligned}
\frac{a_{1}}{1}+ & \frac{a_{2}}{1+a_{1}}+\cdots+\frac{a_{n}}{1+a_{1}+a_{2}+\cdots+a_{n-1}} \\
& =\frac{1+a_{1}}{1}+\frac{1+a_{1}+a_{2}}{1+a_{1}}+\cdots+\frac{1+a_{1}+a_{2}+\cdots+a_{n}}{1+a_{1}+a_{2}+\cdots+a_{n-1}}-n \\
& \geq n \cdot \sqrt[n]{\frac{1+a_{1}}{1} \cdot \frac{1+a_{1}+a_{2}}{1+a_{1}} \cdots \frac{1+a_{1}+a_{2}+\cdots+a_{n}}{1+a_{1}+a_{2}+\cdots+a_{n-1}}}-n \\
& =n \cdot \sqrt[n]{1+a_{1}+a_{2}+\cdots+a_{n}}-n \\
& =2 n-n=n .
\end{aligned}
$$
Furthermore, equality is achieved when $a_{k}=2^{k-1}$ for each $1 \leq k \leq n$.
|
n
|
Yes
|
Yes
|
math-word-problem
|
Inequalities
|
Let $n \geq 2$ be some fixed positive integer and suppose that $a_{1}, a_{2}, \ldots, a_{n}$ are positive real numbers satisfying $a_{1}+a_{2}+\cdots+a_{n}=2^{n}-1$.
Find the minimum possible value of
$$
\frac{a_{1}}{1}+\frac{a_{2}}{1+a_{1}}+\frac{a_{3}}{1+a_{1}+a_{2}}+\cdots+\frac{a_{n}}{1+a_{1}+a_{2}+\cdots+a_{n-1}} .
$$
|
We claim the the minimum possible value of this expression is $n$. Observe that by AM-GM, we have that
$$
\begin{aligned}
\frac{a_{1}}{1}+ & \frac{a_{2}}{1+a_{1}}+\cdots+\frac{a_{n}}{1+a_{1}+a_{2}+\cdots+a_{n-1}} \\
& =\frac{1+a_{1}}{1}+\frac{1+a_{1}+a_{2}}{1+a_{1}}+\cdots+\frac{1+a_{1}+a_{2}+\cdots+a_{n}}{1+a_{1}+a_{2}+\cdots+a_{n-1}}-n \\
& \geq n \cdot \sqrt[n]{\frac{1+a_{1}}{1} \cdot \frac{1+a_{1}+a_{2}}{1+a_{1}} \cdots \frac{1+a_{1}+a_{2}+\cdots+a_{n}}{1+a_{1}+a_{2}+\cdots+a_{n-1}}}-n \\
& =n \cdot \sqrt[n]{1+a_{1}+a_{2}+\cdots+a_{n}}-n \\
& =2 n-n=n .
\end{aligned}
$$
Furthermore, equality is achieved when $a_{k}=2^{k-1}$ for each $1 \leq k \leq n$.
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\n## Problem No. 2.",
"resource_path": "Canada_MO/segmented/en-2021CMO_solutions_en-1.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2021"
}
|
At a dinner party there are $N$ hosts and $N$ guests, seated around a circular table, where $N \geq 4$. A pair of two guests will chat with one another if either there is at most one person seated between them or if there are exactly two people between them, at least one of whom is a host. Prove that no matter how the 2 N people are seated at the dinner party, at least $N$ pairs of guests will chat with one another.
|
Let a run refer to a maximal group of consecutive dinner party guests all of whom are the same type (host or guest). Suppose that there are exactly $k$ runs of hosts and $k$ runs of guests. Let $G_{i}$ and $H_{i}$ denote the number of runs of guests and hosts, respectively, of length exactly $i$. Furthermore, let $X$ denote the number of hosts surrounded by two runs of guests, both of length exactly 1 . We claim that the number of pairs of guests who chat is at least
$$
2 N-3 k+G_{1}+2 H_{1}+H_{2}-X
$$
The number of pairs of guests who chat with no host between them is at least the sum of $\max \{2 \ell-3,0\}$ over all guest run lengths $\ell$. This sum is at least $2 N-3 k+G_{1}$. The number of pairs of guests who chat with exactly two hosts between them is $H_{2}$. Furthermore, the number of pairs of guests who chat with exactly one host between them is at least $2 H_{1}-X$. This is because any host surrounded by two runs of guests causes at least two pairs of guests to chat unless these runs are both of length exactly 1 . This proves the claim. Now note that
$$
2 H_{1}+H_{2}+N \geq 3 k
$$
because each run of hosts contributes at least three to the left hand side. Furthermore, pairing each run counted in $X$ with the guest run of length 1 immediately following it in clockwise order shows that $G_{1} \geq X$. Combining these inequalities yields that $2 N-3 k+G_{1}+2 H_{1}+H_{2}-X \geq N$, completing the proof of the desired result.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
At a dinner party there are $N$ hosts and $N$ guests, seated around a circular table, where $N \geq 4$. A pair of two guests will chat with one another if either there is at most one person seated between them or if there are exactly two people between them, at least one of whom is a host. Prove that no matter how the 2 N people are seated at the dinner party, at least $N$ pairs of guests will chat with one another.
|
Let a run refer to a maximal group of consecutive dinner party guests all of whom are the same type (host or guest). Suppose that there are exactly $k$ runs of hosts and $k$ runs of guests. Let $G_{i}$ and $H_{i}$ denote the number of runs of guests and hosts, respectively, of length exactly $i$. Furthermore, let $X$ denote the number of hosts surrounded by two runs of guests, both of length exactly 1 . We claim that the number of pairs of guests who chat is at least
$$
2 N-3 k+G_{1}+2 H_{1}+H_{2}-X
$$
The number of pairs of guests who chat with no host between them is at least the sum of $\max \{2 \ell-3,0\}$ over all guest run lengths $\ell$. This sum is at least $2 N-3 k+G_{1}$. The number of pairs of guests who chat with exactly two hosts between them is $H_{2}$. Furthermore, the number of pairs of guests who chat with exactly one host between them is at least $2 H_{1}-X$. This is because any host surrounded by two runs of guests causes at least two pairs of guests to chat unless these runs are both of length exactly 1 . This proves the claim. Now note that
$$
2 H_{1}+H_{2}+N \geq 3 k
$$
because each run of hosts contributes at least three to the left hand side. Furthermore, pairing each run counted in $X$ with the guest run of length 1 immediately following it in clockwise order shows that $G_{1} \geq X$. Combining these inequalities yields that $2 N-3 k+G_{1}+2 H_{1}+H_{2}-X \geq N$, completing the proof of the desired result.
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\n## Problem No. 3.",
"resource_path": "Canada_MO/segmented/en-2021CMO_solutions_en-1.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2021"
}
|
A function $f$ from the positive integers to the positive integers is called Canadian if it satisfies
$$
\operatorname{gcd}(f(f(x)), f(x+y))=\operatorname{gcd}(x, y)
$$
for all pairs of positive integers $x$ and $y$.
Find all positive integers $m$ such that $f(m)=m$ for all Canadian functions $f$.
|
Define an $m \in \mathbb{N}$ to be good if $f(m)=m$ for all such $f$. It will be shown that $m$ is good if and only if $m$ has two or more distinct prime divisors. Let $P(x, y)$ denote the assertion
$$
\operatorname{gcd}(f(f(x)), f(x+y))=\operatorname{gcd}(x, y)
$$
for a pair $x, y \in \mathbb{N}$. Let $x$ be a positive integer with two or more distinct prime divisors and let $p^{k}$ be largest power of one of these prime divisors such that $p^{k} \mid x$. If $x=p^{k} \cdot q$, then $p^{k}$ and $q$ are relatively prime and $x>p^{k}, q>1$. By $P(q, x-q)$,
$$
\operatorname{gcd}(f(f(q)), f(x-q+q))=\operatorname{gcd}(f(f(q)), f(x))=\operatorname{gcd}(q, x-q)=q
$$
which implies that $q \mid f(x)$. By $P\left(p^{k}, x-p^{k}\right)$,
$$
\operatorname{gcd}\left(f\left(f\left(p^{k}\right)\right), f\left(x-p^{k}+p^{k}\right)\right)=\operatorname{gcd}\left(f\left(f\left(p^{k}\right)\right), f(x)\right)=\operatorname{gcd}\left(p^{k}, x-p^{k}\right)=p^{k}
$$
which implies that $p^{k} \mid f(x)$. Since $p^{k}$ and $q$ are relatively prime, $x=p^{k} \cdot q$ divides $f(x)$, which implies that $f(x) \geq x$. Now assume for contradiction that $f(x)>x$. Let $y=f(x)-x>0$ and note that, by $P(x, y)$, it follows that
$$
f(f(x))=\operatorname{gcd}(f(f(x)), f(x+f(x)-x))=\operatorname{gcd}(x, f(x)-x)=\operatorname{gcd}(x, f(x)) .
$$
Therefore $f(f(x)) \mid x$ and $f(f(x)) \mid f(x)$. By $P(x, x)$, it follows that
$$
\operatorname{gcd}(f(f(x)), f(2 x))=\operatorname{gcd}(x, x)=x
$$
This implies that $x \mid f(f(x))$, which when combined with the above result, yields that $f(f(x))=x$. Since $x \mid f(x)$ and $x$ is divisible by at least two distinct prime numbers, $f(x)$ is also divisible by at least two distinct prime numbers. As shown previously, this implies that $f(x) \mid f(f(x))=x$, which is a contradiction since $f(x)>x$. Therefore $f(x)=x$ for all positive integers $x$ with two or more distinct prime divisors.
Now it will be shown that all $m \in \mathbb{N}$ such that either $m$ has one prime divisor or $m=1$ are not good. In either case, let $m=p^{k}$ where $k \geq 0$ and $p$ is a prime number and consider the function satisfying that $f\left(p^{k}\right)=p^{k+1}, f\left(p^{k+1}\right)=p^{k}$ and $f(x)=x$ for all $x \neq p^{k}, p^{k+1}$. Note that this function also satisfies that $f(f(x))=x$ for all positive integers $x$. If $x+y \neq p^{k}, p^{k+1}$, then $P(x, y)$ holds by the Euclidean
algorithm since $f\left(f((x))=x\right.$ and $f(x+y)=x+y$. If $x+y=p^{k+1}$, then $P(x, y)$ is equivalent to $\operatorname{gcd}\left(x, p^{k}\right)=\operatorname{gcd}\left(x, p^{k+1}-x\right)=\operatorname{gcd}\left(x, p^{k+1}\right)$ for all $x<p^{k+1}$ which holds since the greatest power of $p$ that can divide $x$ is $p^{k}$. If $x+y=p^{k}$, then $P(x, y)$ is equivalent to $\operatorname{gcd}\left(x, p^{k+1}\right)=\operatorname{gcd}\left(x, p^{k}-x\right)=\operatorname{gcd}\left(x, p^{k}\right)$ for all $x<p^{k}$ which holds as shown above. Note that if $m=1$ then this case cannot occur. Since this function satisfies $P(x, y), m$ is good if and only if $m$ has two or more distinct prime divisors.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
A function $f$ from the positive integers to the positive integers is called Canadian if it satisfies
$$
\operatorname{gcd}(f(f(x)), f(x+y))=\operatorname{gcd}(x, y)
$$
for all pairs of positive integers $x$ and $y$.
Find all positive integers $m$ such that $f(m)=m$ for all Canadian functions $f$.
|
Define an $m \in \mathbb{N}$ to be good if $f(m)=m$ for all such $f$. It will be shown that $m$ is good if and only if $m$ has two or more distinct prime divisors. Let $P(x, y)$ denote the assertion
$$
\operatorname{gcd}(f(f(x)), f(x+y))=\operatorname{gcd}(x, y)
$$
for a pair $x, y \in \mathbb{N}$. Let $x$ be a positive integer with two or more distinct prime divisors and let $p^{k}$ be largest power of one of these prime divisors such that $p^{k} \mid x$. If $x=p^{k} \cdot q$, then $p^{k}$ and $q$ are relatively prime and $x>p^{k}, q>1$. By $P(q, x-q)$,
$$
\operatorname{gcd}(f(f(q)), f(x-q+q))=\operatorname{gcd}(f(f(q)), f(x))=\operatorname{gcd}(q, x-q)=q
$$
which implies that $q \mid f(x)$. By $P\left(p^{k}, x-p^{k}\right)$,
$$
\operatorname{gcd}\left(f\left(f\left(p^{k}\right)\right), f\left(x-p^{k}+p^{k}\right)\right)=\operatorname{gcd}\left(f\left(f\left(p^{k}\right)\right), f(x)\right)=\operatorname{gcd}\left(p^{k}, x-p^{k}\right)=p^{k}
$$
which implies that $p^{k} \mid f(x)$. Since $p^{k}$ and $q$ are relatively prime, $x=p^{k} \cdot q$ divides $f(x)$, which implies that $f(x) \geq x$. Now assume for contradiction that $f(x)>x$. Let $y=f(x)-x>0$ and note that, by $P(x, y)$, it follows that
$$
f(f(x))=\operatorname{gcd}(f(f(x)), f(x+f(x)-x))=\operatorname{gcd}(x, f(x)-x)=\operatorname{gcd}(x, f(x)) .
$$
Therefore $f(f(x)) \mid x$ and $f(f(x)) \mid f(x)$. By $P(x, x)$, it follows that
$$
\operatorname{gcd}(f(f(x)), f(2 x))=\operatorname{gcd}(x, x)=x
$$
This implies that $x \mid f(f(x))$, which when combined with the above result, yields that $f(f(x))=x$. Since $x \mid f(x)$ and $x$ is divisible by at least two distinct prime numbers, $f(x)$ is also divisible by at least two distinct prime numbers. As shown previously, this implies that $f(x) \mid f(f(x))=x$, which is a contradiction since $f(x)>x$. Therefore $f(x)=x$ for all positive integers $x$ with two or more distinct prime divisors.
Now it will be shown that all $m \in \mathbb{N}$ such that either $m$ has one prime divisor or $m=1$ are not good. In either case, let $m=p^{k}$ where $k \geq 0$ and $p$ is a prime number and consider the function satisfying that $f\left(p^{k}\right)=p^{k+1}, f\left(p^{k+1}\right)=p^{k}$ and $f(x)=x$ for all $x \neq p^{k}, p^{k+1}$. Note that this function also satisfies that $f(f(x))=x$ for all positive integers $x$. If $x+y \neq p^{k}, p^{k+1}$, then $P(x, y)$ holds by the Euclidean
algorithm since $f\left(f((x))=x\right.$ and $f(x+y)=x+y$. If $x+y=p^{k+1}$, then $P(x, y)$ is equivalent to $\operatorname{gcd}\left(x, p^{k}\right)=\operatorname{gcd}\left(x, p^{k+1}-x\right)=\operatorname{gcd}\left(x, p^{k+1}\right)$ for all $x<p^{k+1}$ which holds since the greatest power of $p$ that can divide $x$ is $p^{k}$. If $x+y=p^{k}$, then $P(x, y)$ is equivalent to $\operatorname{gcd}\left(x, p^{k+1}\right)=\operatorname{gcd}\left(x, p^{k}-x\right)=\operatorname{gcd}\left(x, p^{k}\right)$ for all $x<p^{k}$ which holds as shown above. Note that if $m=1$ then this case cannot occur. Since this function satisfies $P(x, y), m$ is good if and only if $m$ has two or more distinct prime divisors.
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\n## Problem No. 4.",
"resource_path": "Canada_MO/segmented/en-2021CMO_solutions_en-1.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2021"
}
|
Nina and Tadashi play the following game. Initially, a triple $(a, b, c)$ of nonnegative integers with $a+b+c=$ 2021 is written on a blackboard. Nina and Tadashi then take moves in turn, with Nina first. A player making a move chooses a positive integer $k$ and one of the three entries on the board; then the player increases the chosen entry by $k$ and decreases the other two entries by $k$. A player loses if, on their turn, some entry on the board becomes negative.
Find the number of initial triples $(a, b, c)$ for which Tadashi has a winning strategy.
|
The answer is $3^{\text {number of 1's in binary expansion of } 2021}=3^{8}=6561$.
Throughout this solution, we say two nonnegative integers overlap in the $2^{\ell}$ position if their binary representations both have a 1 in that position. We say that two nonnegative integers overlap if they overlap in some position. Our central claim is the following.
Claim 1. A triple $(x, y, z)$ is losing if and only if no two of $x, y, z$ overlap.
Let $d_{\ell}(a)$ denote the bit in the $2^{\ell}$ position of the binary representation of $a$. Let $\&$ denote the bitwise and operation: $x \& y$ is the number satisfying $d_{\ell}(x \& y)=d_{\ell}(x) d_{\ell}(y)$ for all $\ell$.
Lemma 1. Let $x, y, z$ be nonnegative integers, at least one pair of which overlaps. Define $x^{\prime}=(x+y) \&(x+$ $z)$ and $y^{\prime}, z^{\prime}$ cyclically. At least one of the inequalities $x<x^{\prime}, y<y^{\prime}, z<z^{\prime}$ holds.
Proof. Let $\ell$ be maximal such that two of $x, y, z$ overlap in the $2^{\ell}$ position. We case on how many of the additions $x+y, x+z, y+z$ involve a carry from the $2^{\ell}$ position to the $2^{\ell+1}$ position, and on the values of $d_{\ell+1}(x), d_{\ell+1}(y), d_{\ell+1}(z)$. Because at least two of $d_{\ell}(x), d_{\ell}(y), d_{\ell}(z)$ equal 1 , at least one of the additions $x+y, x+z, y+z$ involves a carry from the $2^{\ell}$ position.
## Case 1. One carry.
WLOG let $x+y$ be the addition with the carry. Then, $d_{\ell}(x)=d_{\ell}(y)=1$ and $d_{\ell}(z)=0$. Since $x, y, z$ do not overlap in any position left of the $2^{\ell}$ position, the binary representations of $z, z^{\prime}$ agree left of the $2^{\ell}$ position. As the additions $x+z$ and $y+z$ do not involve a carry from the $2^{\ell}$ position, we have $d_{\ell}(x+z)=d_{\ell}(y+z)=1$, and thus $d_{\ell}\left(z^{\prime}\right)=1$. Thus $z^{\prime}>z$, as desired.
Case 2. At least two carries: $x+y$ and $x+z$ carry and $d_{\ell+1}(y)=d_{\ell+1}(z)=0$, or cyclic equivalent. ( $y+z$ may or may not carry.)
Let $i$ be maximal such that $d_{\ell+1}(x)=\cdots=d_{\ell+i}(x)=1$ (possibly $i=0$ ). By maximality of $\ell, d_{\ell+1}(y)=$ $\cdots=d_{\ell+i}(y)=d_{\ell+1}(z)=\cdots=d_{\ell+i}(z)=0$. By maximality of $i, d_{\ell+i+1}(x)=0$.
If $d_{\ell+i+1}(y)=d_{\ell+i+1}(z)=0$, then $d_{\ell+i+1}(x+y)=d_{\ell+i+1}(x+z)=1$, so $d_{\ell+i+1}\left(x^{\prime}\right)=1$. The binary representations of $x$ and $x^{\prime}$ agree to the left of the $2^{\ell+i+1}$ position, so $x^{\prime}>x$.
Otherwise, WLOG $d_{\ell+i+1}(y)=1$ and $d_{\ell+i+1}(z)=0$. (Note that, here we in fact have $i \geq 1$.) Then $d_{\ell+i+1}(y+z)=d_{\ell+i+1}(x+z)=1$, so $d_{\ell+i+1}\left(z^{\prime}\right)=1$. The binary representations of $z$ and $z^{\prime}$ agree to the left of the $2^{\ell+i+1}$ position, so $z^{\prime}>z$.
Case 3. At least two carries, and the condition in Case 2 does not occur.
WLOG let $x+y, x+z$ involve carries. Since the condition in Case 2 does not occur, $d_{\ell+1}(y)=1$ or $d_{\ell+1}(z)=1$. In either case, $d_{\ell+1}(x)=0$. WLOG $d_{\ell+1}(y)=1$ and $d_{\ell+1}(z)=0$.
Since the condition in Case 2 does not occur, $y+z$ does not involve a carry from the $2^{\ell}$ position. (Otherwise, $x+y$ and $y+z$ carry and $d_{\ell+1}(x)=d_{\ell+1}(z)=0$.) Then $d_{\ell+1}(x+z)=d_{\ell+1}(y+z)=1$, so $d_{\ell+1}\left(z^{\prime}\right)=1$. The binary representations of $z$ and $z^{\prime}$ agree to the left of the $2^{\ell+1}$ position, so $z^{\prime}>z$.
Proof of Claim 1. Proceed by strong induction on $x+y+z$. There is no base case.
Suppose by induction the claim holds for all $(x, y, z)$ with sum less than $N$. Consider a triple $(x, y, z)$ with $x+y+z=N$.
Suppose no two of $x, y, z$ overlap. If all moves from this position lead to positions with a negative coordinate, $(x, y, z)$ is a losing position, as claimed. Otherwise, the player increases or decreases all coordinates by $k$. Consider the smallest $m$ such that $d_{m}(k)=1$. The player's move will toggle each of $d_{m}(x), d_{m}(y), d_{m}(z)$. Since at most one of the original $d_{m}(x), d_{m}(y), d_{m}(z)$ is 1 , at least two of the new $d_{m}(x), d_{m}(y), d_{m}(z)$ will be 1 . So, two of the new $x, y, z$ overlap. By induction, the new $(x, y, z)$ is winning. Thus the original $(x, y, z)$ is losing, as claimed.
Conversely, suppose at least one pair of $x, y, z$ overlap. By Lemma 1, at least one of $x<x^{\prime}, y<y^{\prime}, z<z^{\prime}$ holds. WLOG $x<x^{\prime}$. Let the player to move choose $k=x^{\prime}-x$, decrease $y, z$ by $k$, and increase $x$ by $k$. The new coordinates are nonnegative, as
$$
y-k=x+y-x^{\prime} \geq 0
$$
because $x^{\prime} \leq x+y$, and similarly for the $z$ coordinate. Moreover, the binary representation of the new $x$ consists of the 1 's in the binary representations of both $x+y$ and $x+z$; the binary representation of the new $y$ consists of the 1 's in that of $x+y$ but not $x+z$; and the binary representation of the new $z$ consists of the 1's in that of $x+z$ but not $x+y$. So, no two of the new $x, y, z$ overlap. By induction, the new $(x, y, z)$ is losing. Thus the original $(x, y, z)$ is winning, as claimed.
We use Claim 1 to count the losing positions $(x, y, z)$ with
$$
x+y+z=2021=11111100101_{2}
$$
In each position where $d_{\ell}(2021)=0$, losing positions must have $d_{\ell}(x)=d_{\ell}(y)=d_{\ell}(z)=0$. In each position where $d_{\ell}(2021)=1$, the bit triplet $\left(d_{i}(x), d_{i}(y), d_{i}(z)\right)$ is one of $(1,0,0),(0,1,0),(0,0,1)$. This gives a count of $3^{8}=6561$.
|
6561
|
Yes
|
Incomplete
|
math-word-problem
|
Combinatorics
|
Nina and Tadashi play the following game. Initially, a triple $(a, b, c)$ of nonnegative integers with $a+b+c=$ 2021 is written on a blackboard. Nina and Tadashi then take moves in turn, with Nina first. A player making a move chooses a positive integer $k$ and one of the three entries on the board; then the player increases the chosen entry by $k$ and decreases the other two entries by $k$. A player loses if, on their turn, some entry on the board becomes negative.
Find the number of initial triples $(a, b, c)$ for which Tadashi has a winning strategy.
|
The answer is $3^{\text {number of 1's in binary expansion of } 2021}=3^{8}=6561$.
Throughout this solution, we say two nonnegative integers overlap in the $2^{\ell}$ position if their binary representations both have a 1 in that position. We say that two nonnegative integers overlap if they overlap in some position. Our central claim is the following.
Claim 1. A triple $(x, y, z)$ is losing if and only if no two of $x, y, z$ overlap.
Let $d_{\ell}(a)$ denote the bit in the $2^{\ell}$ position of the binary representation of $a$. Let $\&$ denote the bitwise and operation: $x \& y$ is the number satisfying $d_{\ell}(x \& y)=d_{\ell}(x) d_{\ell}(y)$ for all $\ell$.
Lemma 1. Let $x, y, z$ be nonnegative integers, at least one pair of which overlaps. Define $x^{\prime}=(x+y) \&(x+$ $z)$ and $y^{\prime}, z^{\prime}$ cyclically. At least one of the inequalities $x<x^{\prime}, y<y^{\prime}, z<z^{\prime}$ holds.
Proof. Let $\ell$ be maximal such that two of $x, y, z$ overlap in the $2^{\ell}$ position. We case on how many of the additions $x+y, x+z, y+z$ involve a carry from the $2^{\ell}$ position to the $2^{\ell+1}$ position, and on the values of $d_{\ell+1}(x), d_{\ell+1}(y), d_{\ell+1}(z)$. Because at least two of $d_{\ell}(x), d_{\ell}(y), d_{\ell}(z)$ equal 1 , at least one of the additions $x+y, x+z, y+z$ involves a carry from the $2^{\ell}$ position.
## Case 1. One carry.
WLOG let $x+y$ be the addition with the carry. Then, $d_{\ell}(x)=d_{\ell}(y)=1$ and $d_{\ell}(z)=0$. Since $x, y, z$ do not overlap in any position left of the $2^{\ell}$ position, the binary representations of $z, z^{\prime}$ agree left of the $2^{\ell}$ position. As the additions $x+z$ and $y+z$ do not involve a carry from the $2^{\ell}$ position, we have $d_{\ell}(x+z)=d_{\ell}(y+z)=1$, and thus $d_{\ell}\left(z^{\prime}\right)=1$. Thus $z^{\prime}>z$, as desired.
Case 2. At least two carries: $x+y$ and $x+z$ carry and $d_{\ell+1}(y)=d_{\ell+1}(z)=0$, or cyclic equivalent. ( $y+z$ may or may not carry.)
Let $i$ be maximal such that $d_{\ell+1}(x)=\cdots=d_{\ell+i}(x)=1$ (possibly $i=0$ ). By maximality of $\ell, d_{\ell+1}(y)=$ $\cdots=d_{\ell+i}(y)=d_{\ell+1}(z)=\cdots=d_{\ell+i}(z)=0$. By maximality of $i, d_{\ell+i+1}(x)=0$.
If $d_{\ell+i+1}(y)=d_{\ell+i+1}(z)=0$, then $d_{\ell+i+1}(x+y)=d_{\ell+i+1}(x+z)=1$, so $d_{\ell+i+1}\left(x^{\prime}\right)=1$. The binary representations of $x$ and $x^{\prime}$ agree to the left of the $2^{\ell+i+1}$ position, so $x^{\prime}>x$.
Otherwise, WLOG $d_{\ell+i+1}(y)=1$ and $d_{\ell+i+1}(z)=0$. (Note that, here we in fact have $i \geq 1$.) Then $d_{\ell+i+1}(y+z)=d_{\ell+i+1}(x+z)=1$, so $d_{\ell+i+1}\left(z^{\prime}\right)=1$. The binary representations of $z$ and $z^{\prime}$ agree to the left of the $2^{\ell+i+1}$ position, so $z^{\prime}>z$.
Case 3. At least two carries, and the condition in Case 2 does not occur.
WLOG let $x+y, x+z$ involve carries. Since the condition in Case 2 does not occur, $d_{\ell+1}(y)=1$ or $d_{\ell+1}(z)=1$. In either case, $d_{\ell+1}(x)=0$. WLOG $d_{\ell+1}(y)=1$ and $d_{\ell+1}(z)=0$.
Since the condition in Case 2 does not occur, $y+z$ does not involve a carry from the $2^{\ell}$ position. (Otherwise, $x+y$ and $y+z$ carry and $d_{\ell+1}(x)=d_{\ell+1}(z)=0$.) Then $d_{\ell+1}(x+z)=d_{\ell+1}(y+z)=1$, so $d_{\ell+1}\left(z^{\prime}\right)=1$. The binary representations of $z$ and $z^{\prime}$ agree to the left of the $2^{\ell+1}$ position, so $z^{\prime}>z$.
Proof of Claim 1. Proceed by strong induction on $x+y+z$. There is no base case.
Suppose by induction the claim holds for all $(x, y, z)$ with sum less than $N$. Consider a triple $(x, y, z)$ with $x+y+z=N$.
Suppose no two of $x, y, z$ overlap. If all moves from this position lead to positions with a negative coordinate, $(x, y, z)$ is a losing position, as claimed. Otherwise, the player increases or decreases all coordinates by $k$. Consider the smallest $m$ such that $d_{m}(k)=1$. The player's move will toggle each of $d_{m}(x), d_{m}(y), d_{m}(z)$. Since at most one of the original $d_{m}(x), d_{m}(y), d_{m}(z)$ is 1 , at least two of the new $d_{m}(x), d_{m}(y), d_{m}(z)$ will be 1 . So, two of the new $x, y, z$ overlap. By induction, the new $(x, y, z)$ is winning. Thus the original $(x, y, z)$ is losing, as claimed.
Conversely, suppose at least one pair of $x, y, z$ overlap. By Lemma 1, at least one of $x<x^{\prime}, y<y^{\prime}, z<z^{\prime}$ holds. WLOG $x<x^{\prime}$. Let the player to move choose $k=x^{\prime}-x$, decrease $y, z$ by $k$, and increase $x$ by $k$. The new coordinates are nonnegative, as
$$
y-k=x+y-x^{\prime} \geq 0
$$
because $x^{\prime} \leq x+y$, and similarly for the $z$ coordinate. Moreover, the binary representation of the new $x$ consists of the 1 's in the binary representations of both $x+y$ and $x+z$; the binary representation of the new $y$ consists of the 1 's in that of $x+y$ but not $x+z$; and the binary representation of the new $z$ consists of the 1's in that of $x+z$ but not $x+y$. So, no two of the new $x, y, z$ overlap. By induction, the new $(x, y, z)$ is losing. Thus the original $(x, y, z)$ is winning, as claimed.
We use Claim 1 to count the losing positions $(x, y, z)$ with
$$
x+y+z=2021=11111100101_{2}
$$
In each position where $d_{\ell}(2021)=0$, losing positions must have $d_{\ell}(x)=d_{\ell}(y)=d_{\ell}(z)=0$. In each position where $d_{\ell}(2021)=1$, the bit triplet $\left(d_{i}(x), d_{i}(y), d_{i}(z)\right)$ is one of $(1,0,0),(0,1,0),(0,0,1)$. This gives a count of $3^{8}=6561$.
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\n## Problem No. 5.",
"resource_path": "Canada_MO/segmented/en-2021CMO_solutions_en-1.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2021"
}
|
The \(n\) players of a hockey team gather to select their team captain. Initially, they stand in a circle, and each person votes for the person on their left.
The players will update their votes via a series of rounds. In one round, each player \(a\) updates their vote, one at a time, according to the following procedure: At the time of the update, if \(a\) is voting for \(b\) , and \(b\) is voting for \(c\) , then \(a\) updates their vote to \(c\) . (Note that \(a\) , \(b\) , and \(c\) need not be distinct; if \(b = c\) , then \(a\) 's vote does not change for this update.) Every player updates their vote exactly once in each round, in an order determined by the players (possibly different across different rounds).
They repeat this updating procedure for \(n\) rounds. Prove that at this time, all \(n\) players will unanimously vote for the same person.
|
Initially, all players are in a cycle. Note that once a player leaves the cycle, they cannot rejoin. Furthermore, a new cycle cannot be created. Hence, at any point in time, the graph corresponding to the votes will be a functional graph with a single cycle.
We will first prove that after \(\lfloor \log_{2}n\rfloor\) rounds, the cycle will become a self- loop. Then, we will show that in the next \(\lfloor \log_{2}n\rfloor\) rounds, all other players vote for the player in the self- loop.
To show the first step, assume the cycle has size \(K > 1\) at the beginning of a round. Consider arbitrary player \(a\) in the cycle who is updating their vote. Say \(a \to b \to c\) , all in the cycle. Then \(a \to c\) now, bumping \(b\) out of the cycle and reducing its size to \(K - 1\) . Note that \(b\) can now update their vote as well without affecting the size of the cycle. If we consider all \(K\) original players in the cycle, we see that at least \(\lceil \frac{K}{2} \rceil\) of them must still be in the cycle at the time of their update, and hence the cycle's size is reduced to at most \(\lfloor \frac{K}{2} \rfloor\) . After \(\lfloor \log_{2}n\rfloor\) rounds, the cycle must be reduced to size 1.
Now that the cycle has been reduced to a single player, say \(z\) , consider any path from a player \(a\) to \(z\) . No players can be added to this path now. With a similar argument as the cycle, the length of the path must halve each round. In particular, a path of length \(L\) to the cycle gets reduced to length \(\lceil \frac{L}{2} \rceil\) (note the ceiling, we had the floor for the cycle). After \(\lfloor \log_{2}n\rfloor\) rounds, the path must be reduced to length 1.
Thus, after \(\lfloor \log_{2}n\rfloor + \lfloor \log_{2}n\rfloor\) rounds, the graph has been completely reduced. For \(n \geq 5\) , \(\lfloor \log_{2}n\rfloor + \lfloor \log_{2}n\rfloor \leq 2 \lfloor \log_{2}n\rfloor + 1 \leq n\) . For the other \(n\) , we can manually check
that \(\lfloor \log_{2}n\rfloor +\lceil \log_{2}n\rceil \leq n\) .
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
The \(n\) players of a hockey team gather to select their team captain. Initially, they stand in a circle, and each person votes for the person on their left.
The players will update their votes via a series of rounds. In one round, each player \(a\) updates their vote, one at a time, according to the following procedure: At the time of the update, if \(a\) is voting for \(b\) , and \(b\) is voting for \(c\) , then \(a\) updates their vote to \(c\) . (Note that \(a\) , \(b\) , and \(c\) need not be distinct; if \(b = c\) , then \(a\) 's vote does not change for this update.) Every player updates their vote exactly once in each round, in an order determined by the players (possibly different across different rounds).
They repeat this updating procedure for \(n\) rounds. Prove that at this time, all \(n\) players will unanimously vote for the same person.
|
Initially, all players are in a cycle. Note that once a player leaves the cycle, they cannot rejoin. Furthermore, a new cycle cannot be created. Hence, at any point in time, the graph corresponding to the votes will be a functional graph with a single cycle.
We will first prove that after \(\lfloor \log_{2}n\rfloor\) rounds, the cycle will become a self- loop. Then, we will show that in the next \(\lfloor \log_{2}n\rfloor\) rounds, all other players vote for the player in the self- loop.
To show the first step, assume the cycle has size \(K > 1\) at the beginning of a round. Consider arbitrary player \(a\) in the cycle who is updating their vote. Say \(a \to b \to c\) , all in the cycle. Then \(a \to c\) now, bumping \(b\) out of the cycle and reducing its size to \(K - 1\) . Note that \(b\) can now update their vote as well without affecting the size of the cycle. If we consider all \(K\) original players in the cycle, we see that at least \(\lceil \frac{K}{2} \rceil\) of them must still be in the cycle at the time of their update, and hence the cycle's size is reduced to at most \(\lfloor \frac{K}{2} \rfloor\) . After \(\lfloor \log_{2}n\rfloor\) rounds, the cycle must be reduced to size 1.
Now that the cycle has been reduced to a single player, say \(z\) , consider any path from a player \(a\) to \(z\) . No players can be added to this path now. With a similar argument as the cycle, the length of the path must halve each round. In particular, a path of length \(L\) to the cycle gets reduced to length \(\lceil \frac{L}{2} \rceil\) (note the ceiling, we had the floor for the cycle). After \(\lfloor \log_{2}n\rfloor\) rounds, the path must be reduced to length 1.
Thus, after \(\lfloor \log_{2}n\rfloor + \lfloor \log_{2}n\rfloor\) rounds, the graph has been completely reduced. For \(n \geq 5\) , \(\lfloor \log_{2}n\rfloor + \lfloor \log_{2}n\rfloor \leq 2 \lfloor \log_{2}n\rfloor + 1 \leq n\) . For the other \(n\) , we can manually check
that \(\lfloor \log_{2}n\rfloor +\lceil \log_{2}n\rceil \leq n\) .
|
{
"exam": "Canada_MO",
"problem_label": "1",
"problem_match": "\nP1.",
"resource_path": "CANADA_MO/segmented/en-CMO2025-solutions.jsonl",
"solution_match": "\n## Solution 1",
"tier": "T2",
"year": "2025"
}
|
The \(n\) players of a hockey team gather to select their team captain. Initially, they stand in a circle, and each person votes for the person on their left.
The players will update their votes via a series of rounds. In one round, each player \(a\) updates their vote, one at a time, according to the following procedure: At the time of the update, if \(a\) is voting for \(b\) , and \(b\) is voting for \(c\) , then \(a\) updates their vote to \(c\) . (Note that \(a\) , \(b\) , and \(c\) need not be distinct; if \(b = c\) , then \(a\) 's vote does not change for this update.) Every player updates their vote exactly once in each round, in an order determined by the players (possibly different across different rounds).
They repeat this updating procedure for \(n\) rounds. Prove that at this time, all \(n\) players will unanimously vote for the same person.
|
We will use induction on \(n\) .
Inductive Hypothesis. Let \(G\) be any functional graph with \(n\) nodes and a single cycle. Then after \(n\) rounds of the given operation, \(G\) will become a self- loop with \(n - 1\) nodes pointing to it.
Base Case. The cases \(n \leq 2\) are clear.
Inductive Step. Assume that the hypothesis is proved for \(n = k - 1\) and \(n = k - 2\) . We will prove it for \(n = k\) . Consider any initial functional graph with \(k\) nodes and a single cycle. Note there is some node \(a\) which has in- degree 0 (i.e. no nodes point to it), or all \(k\) nodes are in the cycle.
In the first case, consider \(G\backslash \{a\}\) . Note that all operations except \(a\) 's own updates are independent of where \(a\) is. By the inductive hypothesis, after \(k - 1\) rounds, \(G\backslash \{a\}\) has become a single self- loop and \(k - 2\) nodes pointing to it. Regardless of where \(a\) is, it will point to the self- loop after one more round and we are done.
In the case where all \(k\) nodes are in a cycle, consider the very first operation \(z \to a \to b \implies z \to b, a \to b\) . This creates a zero in- degree node \(a\) , but \(z\) 's operation has been used for the first round so the inductive hypothesis cannot be naively applied. Instead, consider \(b \to c\) (possibly \(c = z\) if \(k = 3\) ). At some point in the first round, \(b\) will be updated. Either \(c\) will become another zero in- degree node, or \(a\) will be the only
node that points to \(c\) . Either way, consider \(G \setminus \{a, c\}\) . By the induction hypothesis, after rounds 2 through \(k - 1\) , this graph will become a self- loop with \(k - 3\) nodes pointing to it. It's also easy to see that \(a\) and \(c\) both have in- degree 0 after round 2. Then in one more round after round \(k - 1\) , we must have \(a\) and \(c\) pointing to the self- loop. So we are done for \(n = k\) .
By induction, we are done for all \(n\) .
|
proof
|
Yes
|
Incomplete
|
proof
|
Combinatorics
|
The \(n\) players of a hockey team gather to select their team captain. Initially, they stand in a circle, and each person votes for the person on their left.
The players will update their votes via a series of rounds. In one round, each player \(a\) updates their vote, one at a time, according to the following procedure: At the time of the update, if \(a\) is voting for \(b\) , and \(b\) is voting for \(c\) , then \(a\) updates their vote to \(c\) . (Note that \(a\) , \(b\) , and \(c\) need not be distinct; if \(b = c\) , then \(a\) 's vote does not change for this update.) Every player updates their vote exactly once in each round, in an order determined by the players (possibly different across different rounds).
They repeat this updating procedure for \(n\) rounds. Prove that at this time, all \(n\) players will unanimously vote for the same person.
|
We will use induction on \(n\) .
Inductive Hypothesis. Let \(G\) be any functional graph with \(n\) nodes and a single cycle. Then after \(n\) rounds of the given operation, \(G\) will become a self- loop with \(n - 1\) nodes pointing to it.
Base Case. The cases \(n \leq 2\) are clear.
Inductive Step. Assume that the hypothesis is proved for \(n = k - 1\) and \(n = k - 2\) . We will prove it for \(n = k\) . Consider any initial functional graph with \(k\) nodes and a single cycle. Note there is some node \(a\) which has in- degree 0 (i.e. no nodes point to it), or all \(k\) nodes are in the cycle.
In the first case, consider \(G\backslash \{a\}\) . Note that all operations except \(a\) 's own updates are independent of where \(a\) is. By the inductive hypothesis, after \(k - 1\) rounds, \(G\backslash \{a\}\) has become a single self- loop and \(k - 2\) nodes pointing to it. Regardless of where \(a\) is, it will point to the self- loop after one more round and we are done.
In the case where all \(k\) nodes are in a cycle, consider the very first operation \(z \to a \to b \implies z \to b, a \to b\) . This creates a zero in- degree node \(a\) , but \(z\) 's operation has been used for the first round so the inductive hypothesis cannot be naively applied. Instead, consider \(b \to c\) (possibly \(c = z\) if \(k = 3\) ). At some point in the first round, \(b\) will be updated. Either \(c\) will become another zero in- degree node, or \(a\) will be the only
node that points to \(c\) . Either way, consider \(G \setminus \{a, c\}\) . By the induction hypothesis, after rounds 2 through \(k - 1\) , this graph will become a self- loop with \(k - 3\) nodes pointing to it. It's also easy to see that \(a\) and \(c\) both have in- degree 0 after round 2. Then in one more round after round \(k - 1\) , we must have \(a\) and \(c\) pointing to the self- loop. So we are done for \(n = k\) .
By induction, we are done for all \(n\) .
|
{
"exam": "Canada_MO",
"problem_label": "1",
"problem_match": "\nP1.",
"resource_path": "CANADA_MO/segmented/en-CMO2025-solutions.jsonl",
"solution_match": "\n## Solution 2",
"tier": "T2",
"year": "2025"
}
|
Determine all positive integers \(a, b, c, p\) where \(p\) and \(p + 2\) are odd primes and
\[2^{a}p^{b} = (p + 2)^{c} - 1.\]
|
The only solution is \((a, b, c, p) = (3, 1, 2, 3)\) . First, factor the right hand side. This gives us
\[2^{a}p^{b} = (p + 1)((p + 2)^{c - 1} + (p + 2)^{c - 2} + \dots +(p + 2) + 1).\]
Since \(\gcd (p, p + 1) = 1\) it must be the case that \(p + 1 = 2^{x}\) for some positive integer \(x \leq a\) and so \(p = 2^{x} - 1\) and \(p + 2 = 2^{x} + 1\) . Now for \(x \geq 3\) , \(2^{x} + 1\) is not prime if \(x\) is odd (since it is 0 mod 3) and \(2^{x} - 1\) is not prime if \(x\) is even (since it is 0 mod 3). This means \(x \leq 2\) , and the only admissible such \(x\) is \(x = 2\) since otherwise \(p\) is not prime. So, the original equation becomes
\[2^{a}3^{b} = 5^{c} - 1.\]
Now \(3|(5^{c} - 1)\) , so evaluating \(5^{c} - 1\) mod 3 gives that \(c = 2d\) for some positive integer \(d\) and hence
\[2^{a}3^{b} = (5^{d} - 1)(5^{d} + 1).\]
Observe \(5^{d} - 1\) and \(5^{d} + 1\) are both even and have greatest common divisor 2 because they are 2 apart. Since \(4|(5^{d} - 1)\) this implies \(5^{d} - 1 = 2^{a - 1}\) and \(5^{d} + 1 = 2\cdot 3^{b}\) . Now, 3 is not a factor of \(5^{d} - 1\) because \(5^{d} - 1 = 2^{a - 1}\) . Thus, by evaluating mod 3, \(d\) must be odd. If \(d > 1\) , this is impossible as \(5^{d} - 1 = (5 - 1)(5^{d - 1} + 5^{d - 2} + \dots + 5 + 1)\) and the latter factor has an odd prime factor, contradicting \(5^{d} - 1\) is a power of 2. Thus \(d = 1\) and so \(c = 2\) , implying that \(2^{a}3^{b} = 24\) so \(a = 3\) and \(b = 1\) . Hence, the only solution is \((a, b, c, p) = (3, 1, 2, 3)\) .
|
(3, 1, 2, 3)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Determine all positive integers \(a, b, c, p\) where \(p\) and \(p + 2\) are odd primes and
\[2^{a}p^{b} = (p + 2)^{c} - 1.\]
|
The only solution is \((a, b, c, p) = (3, 1, 2, 3)\) . First, factor the right hand side. This gives us
\[2^{a}p^{b} = (p + 1)((p + 2)^{c - 1} + (p + 2)^{c - 2} + \dots +(p + 2) + 1).\]
Since \(\gcd (p, p + 1) = 1\) it must be the case that \(p + 1 = 2^{x}\) for some positive integer \(x \leq a\) and so \(p = 2^{x} - 1\) and \(p + 2 = 2^{x} + 1\) . Now for \(x \geq 3\) , \(2^{x} + 1\) is not prime if \(x\) is odd (since it is 0 mod 3) and \(2^{x} - 1\) is not prime if \(x\) is even (since it is 0 mod 3). This means \(x \leq 2\) , and the only admissible such \(x\) is \(x = 2\) since otherwise \(p\) is not prime. So, the original equation becomes
\[2^{a}3^{b} = 5^{c} - 1.\]
Now \(3|(5^{c} - 1)\) , so evaluating \(5^{c} - 1\) mod 3 gives that \(c = 2d\) for some positive integer \(d\) and hence
\[2^{a}3^{b} = (5^{d} - 1)(5^{d} + 1).\]
Observe \(5^{d} - 1\) and \(5^{d} + 1\) are both even and have greatest common divisor 2 because they are 2 apart. Since \(4|(5^{d} - 1)\) this implies \(5^{d} - 1 = 2^{a - 1}\) and \(5^{d} + 1 = 2\cdot 3^{b}\) . Now, 3 is not a factor of \(5^{d} - 1\) because \(5^{d} - 1 = 2^{a - 1}\) . Thus, by evaluating mod 3, \(d\) must be odd. If \(d > 1\) , this is impossible as \(5^{d} - 1 = (5 - 1)(5^{d - 1} + 5^{d - 2} + \dots + 5 + 1)\) and the latter factor has an odd prime factor, contradicting \(5^{d} - 1\) is a power of 2. Thus \(d = 1\) and so \(c = 2\) , implying that \(2^{a}3^{b} = 24\) so \(a = 3\) and \(b = 1\) . Hence, the only solution is \((a, b, c, p) = (3, 1, 2, 3)\) .
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\nP2.",
"resource_path": "CANADA_MO/segmented/en-CMO2025-solutions.jsonl",
"solution_match": "\n## Solution \n\n",
"tier": "T2",
"year": "2025"
}
|
A polynomial \(c_{d}x^{d} + c_{d - 1}x^{d - 1} + \dots + c_{1}x + c_{0}\) with degree \(d\) is reflexive if there is an integer \(n \geq d\) such that \(c_{i} = c_{n - i}\) for every \(0 \leq i \leq n\) , where \(c_{i} = 0\) for \(i > d\) . Let \(\ell \geq 2\) be an integer and \(p(x)\) be a polynomial with integer coefficients. Prove that there exist reflexive polynomials \(q(x), r(x)\) with integer coefficients such that
\[(1 + x + x^{2} + \dots + x^{\ell -1})p(x) = q(x) + x^{\ell}r(x).\]
|
Let \(d\) be the degree of \(p\) and let \(k\) be any non- negative integer. We will choose
\[q(x) = \frac{x^{d + k + \ell}p\left(\frac{1}{x}\right) - p(x)}{x - 1},\] \[r(x) = \frac{p(x) - x^{d + k}p\left(\frac{1}{x}\right)}{x - 1}.\]
First, we must show that both \(q\) and \(r\) are integer polynomials. Consider the numerator in \(q\) 's definition, \(x^{d + k + \ell}p\left(\frac{1}{x}\right) - p(x)\) . This is clearly an integer polynomial. As it is equal to 0 when evaluated at \(x - 1\) , \(x - 1\) divides it. Furthermore, as \(x - 1\) is monic, the quotient has integer coefficients. The argument for \(r\) is similar.
Next, we will show that this choice of \(q\) and \(r\) satisfies the desired equation. Plugging them into the RHS of the equation gives
\[q(x) + x^{\ell}r(x) = \frac{x^{d + k + \ell}p\left(\frac{1}{x}\right) - p(x)}{x - 1} +x^{\ell}\left(\frac{p(x) - x^{d + k}p\left(\frac{1}{x}\right)}{x - 1}\right)\] \[\qquad = \frac{x^{d + k + \ell}p\left(\frac{1}{x}\right) - p(x) + x^{\ell}p(x) - x^{d + k + \ell}p\left(\frac{1}{x}\right)}{x - 1}\] \[\qquad = \left(\frac{x^{\ell} - 1}{x - 1}\right)p(x)\] \[\qquad = (1 + x + \cdot \cdot \cdot +x^{\ell -1})p(x)\]
as desired.
Finally, we will show that \(q\) and \(r\) are indeed reflexive. We can re- interpret the reflexive condition as such:
Polynomial \(a(x)\) is reflexive iff there is an integer \(n \geq \deg (a)\) for which
\[a(x) = x^{n}a\left(\frac{1}{x}\right).\]
We have
\[q(x) = \frac{x^{d + k + \ell}p\left(\frac{1}{x}\right) - p(x)}{x - 1}\] \[\qquad = x^{d + k + \ell -1}\cdot \frac{p\left(\frac{1}{x}\right) - x^{-(d + k + \ell)}p(x)}{\frac{x - 1}{x}}\] \[\qquad = x^{d + k + \ell -1}\cdot \frac{x^{-(d + k + \ell)}p(x) - p\left(\frac{1}{x}\right)}{\frac{1}{x} - 1}\] \[\qquad = x^{d + k + \ell -1}q\left(\frac{1}{x}\right)\]
as desired. Similarly,
\[r(x) = \frac{p(x) - x^{d + k}p\left(\frac{1}{x}\right)}{x - 1}\] \[\qquad = x^{d + k - 1}\cdot \frac{x^{-(d + k)}p(x) - p\left(\frac{1}{x}\right)}{\frac{x - 1}{x}}\] \[\qquad = x^{d + k - 1}\cdot \frac{p\left(\frac{1}{x}\right) - x^{-(d + k)}p(x)}{\frac{1}{x} - 1}\] \[\qquad = x^{d + k - 1}r\left(\frac{1}{x}\right).\]
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
A polynomial \(c_{d}x^{d} + c_{d - 1}x^{d - 1} + \dots + c_{1}x + c_{0}\) with degree \(d\) is reflexive if there is an integer \(n \geq d\) such that \(c_{i} = c_{n - i}\) for every \(0 \leq i \leq n\) , where \(c_{i} = 0\) for \(i > d\) . Let \(\ell \geq 2\) be an integer and \(p(x)\) be a polynomial with integer coefficients. Prove that there exist reflexive polynomials \(q(x), r(x)\) with integer coefficients such that
\[(1 + x + x^{2} + \dots + x^{\ell -1})p(x) = q(x) + x^{\ell}r(x).\]
|
Let \(d\) be the degree of \(p\) and let \(k\) be any non- negative integer. We will choose
\[q(x) = \frac{x^{d + k + \ell}p\left(\frac{1}{x}\right) - p(x)}{x - 1},\] \[r(x) = \frac{p(x) - x^{d + k}p\left(\frac{1}{x}\right)}{x - 1}.\]
First, we must show that both \(q\) and \(r\) are integer polynomials. Consider the numerator in \(q\) 's definition, \(x^{d + k + \ell}p\left(\frac{1}{x}\right) - p(x)\) . This is clearly an integer polynomial. As it is equal to 0 when evaluated at \(x - 1\) , \(x - 1\) divides it. Furthermore, as \(x - 1\) is monic, the quotient has integer coefficients. The argument for \(r\) is similar.
Next, we will show that this choice of \(q\) and \(r\) satisfies the desired equation. Plugging them into the RHS of the equation gives
\[q(x) + x^{\ell}r(x) = \frac{x^{d + k + \ell}p\left(\frac{1}{x}\right) - p(x)}{x - 1} +x^{\ell}\left(\frac{p(x) - x^{d + k}p\left(\frac{1}{x}\right)}{x - 1}\right)\] \[\qquad = \frac{x^{d + k + \ell}p\left(\frac{1}{x}\right) - p(x) + x^{\ell}p(x) - x^{d + k + \ell}p\left(\frac{1}{x}\right)}{x - 1}\] \[\qquad = \left(\frac{x^{\ell} - 1}{x - 1}\right)p(x)\] \[\qquad = (1 + x + \cdot \cdot \cdot +x^{\ell -1})p(x)\]
as desired.
Finally, we will show that \(q\) and \(r\) are indeed reflexive. We can re- interpret the reflexive condition as such:
Polynomial \(a(x)\) is reflexive iff there is an integer \(n \geq \deg (a)\) for which
\[a(x) = x^{n}a\left(\frac{1}{x}\right).\]
We have
\[q(x) = \frac{x^{d + k + \ell}p\left(\frac{1}{x}\right) - p(x)}{x - 1}\] \[\qquad = x^{d + k + \ell -1}\cdot \frac{p\left(\frac{1}{x}\right) - x^{-(d + k + \ell)}p(x)}{\frac{x - 1}{x}}\] \[\qquad = x^{d + k + \ell -1}\cdot \frac{x^{-(d + k + \ell)}p(x) - p\left(\frac{1}{x}\right)}{\frac{1}{x} - 1}\] \[\qquad = x^{d + k + \ell -1}q\left(\frac{1}{x}\right)\]
as desired. Similarly,
\[r(x) = \frac{p(x) - x^{d + k}p\left(\frac{1}{x}\right)}{x - 1}\] \[\qquad = x^{d + k - 1}\cdot \frac{x^{-(d + k)}p(x) - p\left(\frac{1}{x}\right)}{\frac{x - 1}{x}}\] \[\qquad = x^{d + k - 1}\cdot \frac{p\left(\frac{1}{x}\right) - x^{-(d + k)}p(x)}{\frac{1}{x} - 1}\] \[\qquad = x^{d + k - 1}r\left(\frac{1}{x}\right).\]
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\nP3.",
"resource_path": "CANADA_MO/segmented/en-CMO2025-solutions.jsonl",
"solution_match": "\n## Solution 1",
"tier": "T2",
"year": "2025"
}
|
A polynomial \(c_{d}x^{d} + c_{d - 1}x^{d - 1} + \dots + c_{1}x + c_{0}\) with degree \(d\) is reflexive if there is an integer \(n \geq d\) such that \(c_{i} = c_{n - i}\) for every \(0 \leq i \leq n\) , where \(c_{i} = 0\) for \(i > d\) . Let \(\ell \geq 2\) be an integer and \(p(x)\) be a polynomial with integer coefficients. Prove that there exist reflexive polynomials \(q(x), r(x)\) with integer coefficients such that
\[(1 + x + x^{2} + \dots + x^{\ell -1})p(x) = q(x) + x^{\ell}r(x).\]
|
We write degree \(n\) polynomial \(p\) as
\[p(x):= \sum_{i = 0}^{n}p_{i}x^{i}.\]
Define vector \(P\in \mathbb{Z}^{n + 1}\) as
\[P:= \left(p_{0} p_{1} \dots p_{n}\right)^{T}.\]
We also denote \(X\in \mathbb{Z}[x]^{N}\) for \(N\) some sufficiently high degree (e.g. \(N > 2n + \ell\) ) as the vector of powers of \(x\) , i.e.
\[X:= \left(1 x x^{2}\dots x^{N - 1}\right)^{T}.\]
For a matrix \(M\in \mathbb{Z}^{(n + 1)\times N}\) , \(P^{T}M X\) is an integer polynomial of degree \(< N\) . Note that if the non- zero entries of matrix \(M\) are horizontally symmetric, then the resulting polynomial must be reflexive.
Then their total is the matrix whose entries are 1 at the parallelogram formed by
\[(0,0),(0,\ell -1),(n,n + \ell -1),(n,n),\]
which is precisely \(A\) .
|
proof
|
Yes
|
Incomplete
|
proof
|
Algebra
|
A polynomial \(c_{d}x^{d} + c_{d - 1}x^{d - 1} + \dots + c_{1}x + c_{0}\) with degree \(d\) is reflexive if there is an integer \(n \geq d\) such that \(c_{i} = c_{n - i}\) for every \(0 \leq i \leq n\) , where \(c_{i} = 0\) for \(i > d\) . Let \(\ell \geq 2\) be an integer and \(p(x)\) be a polynomial with integer coefficients. Prove that there exist reflexive polynomials \(q(x), r(x)\) with integer coefficients such that
\[(1 + x + x^{2} + \dots + x^{\ell -1})p(x) = q(x) + x^{\ell}r(x).\]
|
We write degree \(n\) polynomial \(p\) as
\[p(x):= \sum_{i = 0}^{n}p_{i}x^{i}.\]
Define vector \(P\in \mathbb{Z}^{n + 1}\) as
\[P:= \left(p_{0} p_{1} \dots p_{n}\right)^{T}.\]
We also denote \(X\in \mathbb{Z}[x]^{N}\) for \(N\) some sufficiently high degree (e.g. \(N > 2n + \ell\) ) as the vector of powers of \(x\) , i.e.
\[X:= \left(1 x x^{2}\dots x^{N - 1}\right)^{T}.\]
For a matrix \(M\in \mathbb{Z}^{(n + 1)\times N}\) , \(P^{T}M X\) is an integer polynomial of degree \(< N\) . Note that if the non- zero entries of matrix \(M\) are horizontally symmetric, then the resulting polynomial must be reflexive.
Then their total is the matrix whose entries are 1 at the parallelogram formed by
\[(0,0),(0,\ell -1),(n,n + \ell -1),(n,n),\]
which is precisely \(A\) .
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\nP3.",
"resource_path": "CANADA_MO/segmented/en-CMO2025-solutions.jsonl",
"solution_match": "\n## Solution 2",
"tier": "T2",
"year": "2025"
}
|
Let \(ABC\) be a triangle with circumcircle \(\Gamma\) and \(AB \neq AC\) . Let \(D\) and \(E\) lie on the arc \(BC\) of \(\Gamma\) not containing \(A\) such that \(\angle BAE = \angle DAC\) . Let the incenters of \(BAE\) and \(CAD\) be \(X\) and \(Y\) respectively, and let the external tangents of the incircles of \(BAE\) and \(CAD\) intersect at \(Z\) . Prove that \(Z\) lies on the common chord of \(\Gamma\) and the circumcircle of \(AXY\) .
|
Let \(AX\) and \(AY\) intersect \((ABC)\) again at \(P\) and \(Q\) , let the inradii of \(ABE\) and \(ACD\) be \(r_B\) and \(r_C\) , and let \((AXY)\) intersect \((ABC)\) again at \(N\) .
First note that \(\angle BAP = \frac{1}{2}\angle BAE = \frac{1}{2}\angle CAD = \angle QAC\) , so \(XP = BP = CQ = CY\) . This thus implies that, since \(NXP\) and \(NYQ\) are spirally similar, \(NX = NY\) and \(NP = NQ\) (in particular, \(N\) is the midpoint of arc \(XAY\) on \((AXY)\) ). Now, note that
\[\frac{ZX}{ZY} = \frac{r_b}{r_c\] \[\qquad = \frac{AX\sin(\angle PAE)}{AY\sin(\angle QAD)\] \[\qquad = \frac{AX}{AY}.\]
Since \(Z\) lies on the ray \(YX\) , we have that \(Z\) lies on the external angle bisector of \(\angle XAY\) . But so does \(N\) , hence \(Z\) , \(A\) , \(N\) are collinear, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let \(ABC\) be a triangle with circumcircle \(\Gamma\) and \(AB \neq AC\) . Let \(D\) and \(E\) lie on the arc \(BC\) of \(\Gamma\) not containing \(A\) such that \(\angle BAE = \angle DAC\) . Let the incenters of \(BAE\) and \(CAD\) be \(X\) and \(Y\) respectively, and let the external tangents of the incircles of \(BAE\) and \(CAD\) intersect at \(Z\) . Prove that \(Z\) lies on the common chord of \(\Gamma\) and the circumcircle of \(AXY\) .
|
Let \(AX\) and \(AY\) intersect \((ABC)\) again at \(P\) and \(Q\) , let the inradii of \(ABE\) and \(ACD\) be \(r_B\) and \(r_C\) , and let \((AXY)\) intersect \((ABC)\) again at \(N\) .
First note that \(\angle BAP = \frac{1}{2}\angle BAE = \frac{1}{2}\angle CAD = \angle QAC\) , so \(XP = BP = CQ = CY\) . This thus implies that, since \(NXP\) and \(NYQ\) are spirally similar, \(NX = NY\) and \(NP = NQ\) (in particular, \(N\) is the midpoint of arc \(XAY\) on \((AXY)\) ). Now, note that
\[\frac{ZX}{ZY} = \frac{r_b}{r_c\] \[\qquad = \frac{AX\sin(\angle PAE)}{AY\sin(\angle QAD)\] \[\qquad = \frac{AX}{AY}.\]
Since \(Z\) lies on the ray \(YX\) , we have that \(Z\) lies on the external angle bisector of \(\angle XAY\) . But so does \(N\) , hence \(Z\) , \(A\) , \(N\) are collinear, as desired.
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\nP4.",
"resource_path": "CANADA_MO/segmented/en-CMO2025-solutions.jsonl",
"solution_match": "\n## Solution \n\n",
"tier": "T2",
"year": "2025"
}
|
A rectangle \(R\) is divided into a set \(S\) of finitely many smaller rectangles with sides parallel to the sides of \(R\) such that no three rectangles in \(S\) share a common corner. An ant is initially located at the bottom-left corner of \(R\) . In one operation, we can choose a rectangle \(r \in S\) such that the ant is currently located at one of the corners of \(r\) , say \(c\) , and move the ant to one of the two corners of \(r\) adjacent to \(c\) .
Suppose that after a finite number of operations, the ant ends up at the top-right corner of \(R\) . Prove that some rectangle \(r \in S\) was chosen in at least two operations.
|
Consider the following version of the problem:
A rectangle \(R\) is divided into a set \(S\) of finitely many smaller rectangles such that no three rectangles in \(S\) share a common corner. For each \(r \in S\) , draw two non- intersecting arcs inside \(r\) , connecting the pairs of adjacent corners of \(r\) (there are two ways to do this, by connecting either the horizontally or vertically adjacent corners). Prove that there does not exist a path from the bottom- left corner of \(R\) to the top- right corner of \(R\) by walking only along these arcs.

<center>Figure 1: A possible diagram of all the arcs. </center>
In this problem, consider an undirected graph where nodes correspond to corners of rectangles in \(S\) and edges correspond to the arcs, connecting the two nodes that the arc connects. The degrees of the nodes corresponding to the corners of \(R\) are all exactly 1. Since no three rectangles in \(S\) share a common corner, all intersection points have a pattern like \(\vdash\) , \(\neg\) , \(\perp\) , or \(\top\) , so the degree of all other nodes is exactly 2. Therefore, this graph can be decomposed into several paths and cycles. The only possible endpoints of paths are the degree 1 nodes, which are the corners of \(R\) . It follows that if there exists a path from the bottom- left corner to the top- right corner of \(R\) , then there also exists a path from the bottom- right corner to the top- left corner of
\(R\) . However, this is impossible because these two paths (viewed as planar curves inside \(R\) ) must intersect, which cannot occur. Therefore, this claim is proved.
Returning to the original problem, suppose some operations were performed while choosing each rectangle at most once. Draw two arcs inside every rectangle, either both horizontal if the ant used this rectangle to move horizontally or both vertical if the ant used this rectangle to move vertically (or pick one arbitrarily if this rectangle was not used). By the new version of the problem, there does not exist a path from the bottom- left corner to the top- right corner of \(R\) , and it follows that it is impossible for the ant to have reached the top- right corner of \(R\) , finishing the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A rectangle \(R\) is divided into a set \(S\) of finitely many smaller rectangles with sides parallel to the sides of \(R\) such that no three rectangles in \(S\) share a common corner. An ant is initially located at the bottom-left corner of \(R\) . In one operation, we can choose a rectangle \(r \in S\) such that the ant is currently located at one of the corners of \(r\) , say \(c\) , and move the ant to one of the two corners of \(r\) adjacent to \(c\) .
Suppose that after a finite number of operations, the ant ends up at the top-right corner of \(R\) . Prove that some rectangle \(r \in S\) was chosen in at least two operations.
|
Consider the following version of the problem:
A rectangle \(R\) is divided into a set \(S\) of finitely many smaller rectangles such that no three rectangles in \(S\) share a common corner. For each \(r \in S\) , draw two non- intersecting arcs inside \(r\) , connecting the pairs of adjacent corners of \(r\) (there are two ways to do this, by connecting either the horizontally or vertically adjacent corners). Prove that there does not exist a path from the bottom- left corner of \(R\) to the top- right corner of \(R\) by walking only along these arcs.

<center>Figure 1: A possible diagram of all the arcs. </center>
In this problem, consider an undirected graph where nodes correspond to corners of rectangles in \(S\) and edges correspond to the arcs, connecting the two nodes that the arc connects. The degrees of the nodes corresponding to the corners of \(R\) are all exactly 1. Since no three rectangles in \(S\) share a common corner, all intersection points have a pattern like \(\vdash\) , \(\neg\) , \(\perp\) , or \(\top\) , so the degree of all other nodes is exactly 2. Therefore, this graph can be decomposed into several paths and cycles. The only possible endpoints of paths are the degree 1 nodes, which are the corners of \(R\) . It follows that if there exists a path from the bottom- left corner to the top- right corner of \(R\) , then there also exists a path from the bottom- right corner to the top- left corner of
\(R\) . However, this is impossible because these two paths (viewed as planar curves inside \(R\) ) must intersect, which cannot occur. Therefore, this claim is proved.
Returning to the original problem, suppose some operations were performed while choosing each rectangle at most once. Draw two arcs inside every rectangle, either both horizontal if the ant used this rectangle to move horizontally or both vertical if the ant used this rectangle to move vertically (or pick one arbitrarily if this rectangle was not used). By the new version of the problem, there does not exist a path from the bottom- left corner to the top- right corner of \(R\) , and it follows that it is impossible for the ant to have reached the top- right corner of \(R\) , finishing the proof.
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\nP5.",
"resource_path": "CANADA_MO/segmented/en-CMO2025-solutions.jsonl",
"solution_match": "\n## Solution 1",
"tier": "T2",
"year": "2025"
}
|
A rectangle \(R\) is divided into a set \(S\) of finitely many smaller rectangles with sides parallel to the sides of \(R\) such that no three rectangles in \(S\) share a common corner. An ant is initially located at the bottom-left corner of \(R\) . In one operation, we can choose a rectangle \(r \in S\) such that the ant is currently located at one of the corners of \(r\) , say \(c\) , and move the ant to one of the two corners of \(r\) adjacent to \(c\) .
Suppose that after a finite number of operations, the ant ends up at the top-right corner of \(R\) . Prove that some rectangle \(r \in S\) was chosen in at least two operations.
|
Suppose that no rectangle was chosen in at least two operations. In particular, a rectangle cannot be selected in two consecutive operations.
At any point in the process, consider whether the last move by the ant was horizontal or vertical, and whether the most recently chosen rectangle was to the left or the right of the ant's path. In the first move, either the ant moved horizontally and the rectangle was to the left, or the ant moved vertically and the rectangle was to the right. We claim that this invariant is preserved throughout the entire process (see Figure 2 for a sample path). Assuming this claim, the final move to the top right corner must select the top right rectangle. If it is vertical, this is to the left of the path, and if it is horizontal, it is to the right of the path, both of which are impossible, providing a contradiction.

<center>Figure 2: A possible path by the ant. The red arrows are all vertical, with the corresponding rectangle to the right. The blue arrows are all horizontal, with the corresponding rectangle to the left. </center>
It remains to show that the invariant is preserved. Since four rectangles cannot intersect at a corner, each intersection has a pattern like \(\vdash\) , \(\neg\) , \(\perp\) , or \(\top\) .
First, assume the ant moves up, hence the chosen rectangle \(r\) is on the right. The possible configurations are depicted in the first two diagrams in Figure 3.

<center>Figure 3: Possible ant moves going up or right. </center>
In each case, the ant must choose rectangle \(s\) next (to avoid repeating \(r\) twice), and we see that both side choices preserve a horizontal move with \(s\) left, or a vertical move with \(s\) right. By rotating the picture by \(180^{\circ}\) , we cover the two possibilities for the ant moving downward.
If the ant moves right, then \(r\) must occur on the left, and the possible configurations are the last two diagrams of Figure 3. Once again, rectangle \(s\) must be chosen next, and the invariant is similarly preserved. The case of the ant moving left is again handled by a \(180^{\circ}\) rotation, completing the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A rectangle \(R\) is divided into a set \(S\) of finitely many smaller rectangles with sides parallel to the sides of \(R\) such that no three rectangles in \(S\) share a common corner. An ant is initially located at the bottom-left corner of \(R\) . In one operation, we can choose a rectangle \(r \in S\) such that the ant is currently located at one of the corners of \(r\) , say \(c\) , and move the ant to one of the two corners of \(r\) adjacent to \(c\) .
Suppose that after a finite number of operations, the ant ends up at the top-right corner of \(R\) . Prove that some rectangle \(r \in S\) was chosen in at least two operations.
|
Suppose that no rectangle was chosen in at least two operations. In particular, a rectangle cannot be selected in two consecutive operations.
At any point in the process, consider whether the last move by the ant was horizontal or vertical, and whether the most recently chosen rectangle was to the left or the right of the ant's path. In the first move, either the ant moved horizontally and the rectangle was to the left, or the ant moved vertically and the rectangle was to the right. We claim that this invariant is preserved throughout the entire process (see Figure 2 for a sample path). Assuming this claim, the final move to the top right corner must select the top right rectangle. If it is vertical, this is to the left of the path, and if it is horizontal, it is to the right of the path, both of which are impossible, providing a contradiction.

<center>Figure 2: A possible path by the ant. The red arrows are all vertical, with the corresponding rectangle to the right. The blue arrows are all horizontal, with the corresponding rectangle to the left. </center>
It remains to show that the invariant is preserved. Since four rectangles cannot intersect at a corner, each intersection has a pattern like \(\vdash\) , \(\neg\) , \(\perp\) , or \(\top\) .
First, assume the ant moves up, hence the chosen rectangle \(r\) is on the right. The possible configurations are depicted in the first two diagrams in Figure 3.

<center>Figure 3: Possible ant moves going up or right. </center>
In each case, the ant must choose rectangle \(s\) next (to avoid repeating \(r\) twice), and we see that both side choices preserve a horizontal move with \(s\) left, or a vertical move with \(s\) right. By rotating the picture by \(180^{\circ}\) , we cover the two possibilities for the ant moving downward.
If the ant moves right, then \(r\) must occur on the left, and the possible configurations are the last two diagrams of Figure 3. Once again, rectangle \(s\) must be chosen next, and the invariant is similarly preserved. The case of the ant moving left is again handled by a \(180^{\circ}\) rotation, completing the proof.
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\nP5.",
"resource_path": "CANADA_MO/segmented/en-CMO2025-solutions.jsonl",
"solution_match": "\n## Solution 2",
"tier": "T2",
"year": "2025"
}
|
A rectangle \(R\) is divided into a set \(S\) of finitely many smaller rectangles with sides parallel to the sides of \(R\) such that no three rectangles in \(S\) share a common corner. An ant is initially located at the bottom-left corner of \(R\) . In one operation, we can choose a rectangle \(r \in S\) such that the ant is currently located at one of the corners of \(r\) , say \(c\) , and move the ant to one of the two corners of \(r\) adjacent to \(c\) .
Suppose that after a finite number of operations, the ant ends up at the top-right corner of \(R\) . Prove that some rectangle \(r \in S\) was chosen in at least two operations.
|
This is a variant of Solution 2. As in that proof, assume that no rectangle was chosen in two consecutive operations. We claim that for every move, the ant is in either the bottom- left or top- right corner of the chosen rectangle, and moves to the bottom- right or top- left corner.
This is clearly true of the first move. If the ant starts at the bottom- left or top- right corner on a move (choosing rectangle \(r\) ), it is clear that they must move to the bottom- right or top- left of \(r\) . Assume they moved to the bottom- right corner of \(r\) , and chose rectangle \(s\) in the next move. If they are at the bottom- right corner of \(s\) , then \(r\) and \(s\) are either equal or overlap, a contradiction. If they are at the top- left of \(s\) , then \(r\) and \(s\) intersect at a corner and no sides, and we must have 4 rectangles intersecting at a corner, again a contradiction.
Therefore they must be at the bottom- left or top- right corner of \(s\) , as desired. The case where the ant is at the top- left corner of \(r\) is analogous.
If the ant is able to make it to the top right corner, their final move must select \(r\) as the top- right rectangle, and they move to the top- right corner, which is therefore impossible.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A rectangle \(R\) is divided into a set \(S\) of finitely many smaller rectangles with sides parallel to the sides of \(R\) such that no three rectangles in \(S\) share a common corner. An ant is initially located at the bottom-left corner of \(R\) . In one operation, we can choose a rectangle \(r \in S\) such that the ant is currently located at one of the corners of \(r\) , say \(c\) , and move the ant to one of the two corners of \(r\) adjacent to \(c\) .
Suppose that after a finite number of operations, the ant ends up at the top-right corner of \(R\) . Prove that some rectangle \(r \in S\) was chosen in at least two operations.
|
This is a variant of Solution 2. As in that proof, assume that no rectangle was chosen in two consecutive operations. We claim that for every move, the ant is in either the bottom- left or top- right corner of the chosen rectangle, and moves to the bottom- right or top- left corner.
This is clearly true of the first move. If the ant starts at the bottom- left or top- right corner on a move (choosing rectangle \(r\) ), it is clear that they must move to the bottom- right or top- left of \(r\) . Assume they moved to the bottom- right corner of \(r\) , and chose rectangle \(s\) in the next move. If they are at the bottom- right corner of \(s\) , then \(r\) and \(s\) are either equal or overlap, a contradiction. If they are at the top- left of \(s\) , then \(r\) and \(s\) intersect at a corner and no sides, and we must have 4 rectangles intersecting at a corner, again a contradiction.
Therefore they must be at the bottom- left or top- right corner of \(s\) , as desired. The case where the ant is at the top- left corner of \(r\) is analogous.
If the ant is able to make it to the top right corner, their final move must select \(r\) as the top- right rectangle, and they move to the top- right corner, which is therefore impossible.
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\nP5.",
"resource_path": "CANADA_MO/segmented/en-CMO2025-solutions.jsonl",
"solution_match": "\n## Solution 3",
"tier": "T2",
"year": "2025"
}
|
Assume that real numbers $a$ and $b$ satisfy
$$
a b+\sqrt{a b+1}+\sqrt{a^{2}+b} \cdot \sqrt{b^{2}+a}=0
$$
Find, with proof, the value of
$$
a \sqrt{b^{2}+a}+b \sqrt{a^{2}+b}
$$
|
Let us rewrite the given equation as follows:
$$
a b+\sqrt{a^{2}+b} \sqrt{b^{2}+a}=-\sqrt{a b+1} .
$$
Squaring this gives us
$$
\begin{aligned}
a^{2} b^{2}+2 a b \sqrt{a^{2}+b} \sqrt{b^{2}+a}+\left(a^{2}+b\right)\left(b^{2}+a\right) & =a b+1 \\
\left(a^{2} b^{2}+a^{3}\right)+2 a b \sqrt{a^{2}+b} \sqrt{b^{2}+a}+\left(a^{2} b^{2}+b^{3}\right) & =1 \\
\left(a \sqrt{b^{2}+a}+b \sqrt{a^{2}+b}\right)^{2} & =1 \\
a \sqrt{b^{2}+a}+b \sqrt{a^{2}+b} & = \pm 1 .
\end{aligned}
$$
Next, we show that $a \sqrt{b^{2}+a}+b \sqrt{a^{2}+b}>0$. Note that
$$
a b=-\sqrt{a b+1}-\sqrt{a^{2}+b} \cdot \sqrt{b^{2}+a}<0
$$
so $a$ and $b$ have opposite signs. Without loss of generality, we may assume $a>0>b$. Then rewrite
$$
a \sqrt{b^{2}+a}+b \sqrt{a^{2}+b}=a\left(\sqrt{b^{2}+a}+b\right)-b\left(a-\sqrt{a^{2}+b}\right)
$$
and, since $\sqrt{b^{2}+a}+b$ and $a-\sqrt{a^{2}+b}$ are both positive, the expression above is positive. Therefore,
$$
a \sqrt{b^{2}+a}+b \sqrt{a^{2}+b}=1,
$$
and the proof is finished.
|
1
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Assume that real numbers $a$ and $b$ satisfy
$$
a b+\sqrt{a b+1}+\sqrt{a^{2}+b} \cdot \sqrt{b^{2}+a}=0
$$
Find, with proof, the value of
$$
a \sqrt{b^{2}+a}+b \sqrt{a^{2}+b}
$$
|
Let us rewrite the given equation as follows:
$$
a b+\sqrt{a^{2}+b} \sqrt{b^{2}+a}=-\sqrt{a b+1} .
$$
Squaring this gives us
$$
\begin{aligned}
a^{2} b^{2}+2 a b \sqrt{a^{2}+b} \sqrt{b^{2}+a}+\left(a^{2}+b\right)\left(b^{2}+a\right) & =a b+1 \\
\left(a^{2} b^{2}+a^{3}\right)+2 a b \sqrt{a^{2}+b} \sqrt{b^{2}+a}+\left(a^{2} b^{2}+b^{3}\right) & =1 \\
\left(a \sqrt{b^{2}+a}+b \sqrt{a^{2}+b}\right)^{2} & =1 \\
a \sqrt{b^{2}+a}+b \sqrt{a^{2}+b} & = \pm 1 .
\end{aligned}
$$
Next, we show that $a \sqrt{b^{2}+a}+b \sqrt{a^{2}+b}>0$. Note that
$$
a b=-\sqrt{a b+1}-\sqrt{a^{2}+b} \cdot \sqrt{b^{2}+a}<0
$$
so $a$ and $b$ have opposite signs. Without loss of generality, we may assume $a>0>b$. Then rewrite
$$
a \sqrt{b^{2}+a}+b \sqrt{a^{2}+b}=a\left(\sqrt{b^{2}+a}+b\right)-b\left(a-\sqrt{a^{2}+b}\right)
$$
and, since $\sqrt{b^{2}+a}+b$ and $a-\sqrt{a^{2}+b}$ are both positive, the expression above is positive. Therefore,
$$
a \sqrt{b^{2}+a}+b \sqrt{a^{2}+b}=1,
$$
and the proof is finished.
|
{
"exam": "Canada_MO",
"problem_label": "1",
"problem_match": "\nP1.",
"resource_path": "Canada_MO/segmented/en-cmo2022-solutions-en.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2022"
}
|
Let $d(k)$ denote the number of positive integer divisors of $k$. For example, $d(6)=4$ since 6 has 4 positive divisors, namely, $1,2,3$, and 6 . Prove that for all positive integers $n$,
$$
d(1)+d(3)+d(5)+\cdots+d(2 n-1) \leq d(2)+d(4)+d(6)+\cdots+d(2 n)
$$
|
For any integer $k$ and set of integers $S$, let $f_{S}(k)$ be the number of multiples of $k$ in $S$. We can count the number of pairs $(k, s)$ with $k \in \mathbb{N}$ dividing $s \in S$ in two different ways, as follows:
- For each $s \in S$, there are $d(s)$ pairs that include $s$, one for each divisor of $s$.
- For each $k \in \mathbb{N}$, there are $f_{k}(S)$ pairs that include $k$, one for each multiple of $k$.
Therefore,
$$
\sum_{s \in S} d(s)=\sum_{k \in \mathbb{N}} f_{S}(k)
$$
Let
$$
O=\{1,3,5, \ldots, 2 n-1\} \quad \text { and } \quad E=\{2,4,6, \ldots, 2 n\}
$$
be the set of odd and, respectively, the set of even integers between 1 and $2 n$. It suffices to show that
$$
\sum_{k \in \mathbb{N}} f_{O}(k) \leq \sum_{k \in \mathbb{N}} f_{E}(k)
$$
Since the elements of $O$ only have odd divisors,
$$
\sum_{k \in \mathbb{N}} f_{O}(k)=\sum_{k \text { odd }} f_{O}(k)
$$
For any odd $k$, consider the multiples of $k$ between 1 and $2 n$. They form a sequence
$$
k, 2 k, 3 k, \ldots,\left\lfloor\frac{2 n}{k}\right\rfloor k
$$
alternating between odd and even terms. There are either an equal number of odd and even terms, or there is one more odd term than even terms. Therefore, we have the inequality
$$
f_{O}(k) \leq f_{E}(k)+1
$$
for all odd $k$. Combining this with the previous observations gives us the desired inequality:
$$
\begin{aligned}
\sum_{k \in \mathbb{N}} f_{O}(k) & =\sum_{k \text { odd }} f_{O}(k) \\
& \leq \sum_{k \text { odd }}\left(f_{E}(k)+1\right) \\
& =\sum_{k \text { odd }} f_{E}(k)+n \\
& =\sum_{k \text { odd }} f_{E}(k)+f_{E}(2) \\
& \leq \sum_{k \in \mathbb{N}} f_{E}(k)
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $d(k)$ denote the number of positive integer divisors of $k$. For example, $d(6)=4$ since 6 has 4 positive divisors, namely, $1,2,3$, and 6 . Prove that for all positive integers $n$,
$$
d(1)+d(3)+d(5)+\cdots+d(2 n-1) \leq d(2)+d(4)+d(6)+\cdots+d(2 n)
$$
|
For any integer $k$ and set of integers $S$, let $f_{S}(k)$ be the number of multiples of $k$ in $S$. We can count the number of pairs $(k, s)$ with $k \in \mathbb{N}$ dividing $s \in S$ in two different ways, as follows:
- For each $s \in S$, there are $d(s)$ pairs that include $s$, one for each divisor of $s$.
- For each $k \in \mathbb{N}$, there are $f_{k}(S)$ pairs that include $k$, one for each multiple of $k$.
Therefore,
$$
\sum_{s \in S} d(s)=\sum_{k \in \mathbb{N}} f_{S}(k)
$$
Let
$$
O=\{1,3,5, \ldots, 2 n-1\} \quad \text { and } \quad E=\{2,4,6, \ldots, 2 n\}
$$
be the set of odd and, respectively, the set of even integers between 1 and $2 n$. It suffices to show that
$$
\sum_{k \in \mathbb{N}} f_{O}(k) \leq \sum_{k \in \mathbb{N}} f_{E}(k)
$$
Since the elements of $O$ only have odd divisors,
$$
\sum_{k \in \mathbb{N}} f_{O}(k)=\sum_{k \text { odd }} f_{O}(k)
$$
For any odd $k$, consider the multiples of $k$ between 1 and $2 n$. They form a sequence
$$
k, 2 k, 3 k, \ldots,\left\lfloor\frac{2 n}{k}\right\rfloor k
$$
alternating between odd and even terms. There are either an equal number of odd and even terms, or there is one more odd term than even terms. Therefore, we have the inequality
$$
f_{O}(k) \leq f_{E}(k)+1
$$
for all odd $k$. Combining this with the previous observations gives us the desired inequality:
$$
\begin{aligned}
\sum_{k \in \mathbb{N}} f_{O}(k) & =\sum_{k \text { odd }} f_{O}(k) \\
& \leq \sum_{k \text { odd }}\left(f_{E}(k)+1\right) \\
& =\sum_{k \text { odd }} f_{E}(k)+n \\
& =\sum_{k \text { odd }} f_{E}(k)+f_{E}(2) \\
& \leq \sum_{k \in \mathbb{N}} f_{E}(k)
\end{aligned}
$$
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\nP2.",
"resource_path": "Canada_MO/segmented/en-cmo2022-solutions-en.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2022"
}
|
Let $n \geq 2$ be an integer. Initially, the number 1 is written $n$ times on a board. Every minute, Vishal picks two numbers written on the board, say $a$ and $b$, erases them, and writes either $a+b$ or $\min \left\{a^{2}, b^{2}\right\}$. After $n-1$ minutes there is one number left on the board. Let the largest possible value for this final number be $f(n)$. Prove that
$$
2^{n / 3}<f(n) \leq 3^{n / 3}
$$
|
Clearly $f(n)$ is a strictly increasing function, as we can form $f(n-1)$ with $n-1$ ones, and add the final one. However, we can do better; assume Vishal generates $f(n)$ on the board. After $n-2$ minutes, there are two numbers left, say they were formed by $x$ ones and $y$ ones, where $x+y=n$. Clearly the numbers are at most $f(x), f(y)$ (and can be made to be equal to $f(x), f(y))$, and therefore we obtain
$$
f(n)=\max _{x+y=n, 1 \leq x \leq y \leq n-1}\left(\max \left(f(x)+f(y), f(x)^{2}\right)\right)
$$
where we used the fact that $f$ is increasing to get that $\min \left(f(x)^{2}, f(y)^{2}\right)=f(x)^{2}$ when $x \leq y$. In particular, $f(n+1) \geq f(n)+1$, and $f(2 n) \geq f(n)^{2}$ for all positive integers $n$.
Upper bound:
First proof of upper bound. We use induction. We can check that $f(n)=n$ for $n \leq 4$, and these all satisfy the bound $f(n)=n \leq 3^{n / 3}$. Assume it is true for all $m<n$ (some $n \geq 5$ ), and with $x, y$ as in equation ?? we have
$$
f(x)^{2} \leq f\left(\left\lfloor\frac{n}{2}\right\rfloor\right)^{2} \leq\left(3^{n / 6}\right)^{2}=3^{n / 3}
$$
as desired. It thus remains to show that $f(x)+f(y) \leq 3^{n / 3}$. By induction, it suffices to prove that
$$
3^{x / 3}+3^{y / 3} \leq 3^{(x+y) / 3}
$$
for $1 \leq x \leq y \leq n-1$ and $x+y=n$. This is equivalent to
$$
1+3^{(y-x) / 3} \leq 3^{y / 3}
$$
Let $w=3^{(y-x) / 3}$, and we require $3^{x / 3} w \geq w+1$. If $x \geq 2$, then this is true as $w \geq 1$, and if $x=1$ then $w=3^{(n-2) / 3} \geq 3$ and the result is still true. Thus all terms in equation ?? are at most $3^{n / 3}$, and so $f(n) \leq 3^{n / 3}$, and the upper bound is proven.
Second proof of upper bound. Consider a second game with the same rules but in which Vishal can replace $a$ and $b$ by either $a+b$ or $a b$. Let $g(n)$ be the largest possible value for this new game. Then $f(n) \leq g(n)$ because $\min \left\{a^{2}, b^{2}\right\} \leq a b$.
We can check $g(n)=n$ for $n \leq 4$, so $g(n) \leq 3^{n / 3}$ for these values. If $x$ and $y$ are both bigger than 1 , then $g(x)+g(y) \leq g(x) g(y)$. Therefore, for $n>4$, we have that
$$
g(n)=\max \left\{g(n-1)+1, \max _{1 \leq x \leq n-1} g(x) g(n-x)\right\}
$$
Now proceed similarly to the first proof. Assume $n>4$ and $g(m) \leq 3^{m / 3}$ for all $m<n$. If $1 \leq x \leq n-1$, then $g(x) g(n-x) \leq 3^{x / 3} 3^{(n-x) / 3}=3^{n / 3}$. And $g(n-1)+1 \leq 3^{(n-1) / 3}+1$, which is shown to be less than $3^{n / 3}$ in the first proof. It follows that $f(n) \leq g(n) \leq 3^{n / 3}$.
Lower bound:
First proof of lower bound. We begin with a lemma.
Lemma 1. Let $m$ be a nonnegative integer. Then
$$
f\left(2^{m}\right) \geq 2^{2^{m-1}} \quad \text { and } \quad f\left(3 \cdot 2^{m}\right) \geq 3^{2^{m}}
$$
Proof. We prove the lemma by induction. One can check that $f(n)=n$ for $n \leq 3$, which proves the lemma for $m=0$. For a general $m>0$, we get
$$
\begin{gathered}
f\left(2^{m}\right) \geq f\left(2^{m-1}\right)^{2} \geq\left(2^{2^{m-2}}\right)^{2}=2^{2^{m-1}} \\
f\left(3 \cdot 2^{m}\right) \geq f\left(3 \cdot 2^{m-1}\right)^{2} \geq\left(3^{2^{m-1}}\right)^{2}=3^{2^{m}}
\end{gathered}
$$
by induction, as required.
(This lemma can also be proved more constructively. Briefly, if $n=2^{m}$, then partition the 1 's on the board into $2^{m-1}$ pairs, and then add each pair to get $2^{m-1} 2^{\prime} \mathrm{s}\left(2=2^{2^{0}}\right)$; then multiply pairs of 2 's to get $2^{m-2} 4$ 's $\left(4=2^{2^{1}}\right)$; then multiply pairs of 4's to get $2^{m-3} 16$ 's $\left(16=2^{2^{2}}\right)$; and so on, until there are $2\left(=2^{1}\right)$ copies of $2^{2^{m-2}}$, which then gets replaced with $\left.\mathrm{a} 2^{2^{m-1}}\right)$. The process is similar for $n=3 \cdot 2^{m}$, except that the first step is to partition the 1 's into $2^{m}$ groups of 3 , and then use addition within each group to get $2^{m} 3$ 's on the board.)
Now assume $2^{x} \leq n<3 \cdot 2^{x-1}$ for some integer $x$. Then we have
$$
f(n) \geq f\left(2^{x}\right) \geq 2^{2^{x-1}}>2^{n / 3}
$$
as required. If no such $x$ exists, then there exists an integer $x$ such that $3 \cdot 2^{x-1} \leq n<2^{x+1}$. In this case, we have
$$
f(n) \geq f\left(3 \cdot 2^{x-1}\right) \geq 3^{2^{x-1}}>2^{2^{x+1} / 3}>2^{n / 3}
$$
where the second last inequality is equivalent to $2^{x-1} \log (3) \geq \frac{2^{x+1}}{3} \log (2)$, and by dividing out $2^{x}$ and clearing the denominator this is equivalent to $3 \log (3) \geq 4 \log 2$, which is true as $3^{3}=27>16=2^{4}$.
Second proof of lower bound. We shall prove the stronger result $f(n) \geq 2^{(n+1) / 3}$ for $n \geq 2$ by induction. One can check that $f(n)=n$ for $n=2,3,4$, which proves the result for these values. Assume that $n \geq 5$ and that $f(k) \geq 2^{(k+1) / 3}$ for all $k=2,3, \ldots, n-1$. Then
$$
\begin{array}{rlr}
f(n) & \geq f(\lfloor n / 2\rfloor)^{2} & \\
& \geq\left(2^{(\lfloor n / 2\rfloor+1) / 3}\right)^{2} \quad \quad \text { since }\left\lfloor\frac{n}{2}\right\rfloor \geq 2 \\
& =2^{(2\lfloor n / 2\rfloor+2) / 3} \quad \\
& \geq 2^{(n+1) / 3} \quad \text { since }\left\lfloor\frac{n}{2}\right\rfloor \geq \frac{n-1}{2} .
\end{array}
$$
The result follows by induction.
Remark 1. One can show that $f$ satisfies the recurrence $f(n)=n$ for $n=1,2, f(2 n)=f(n)^{2}$ for $n \geq 2$, and $f(2 n+1)=f(2 n)+1$ for $n \geq 1$. The upper bound in the problem is tight (equality holds for $n=3 \cdot 2^{x}$ ), but the lower bound is not.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $n \geq 2$ be an integer. Initially, the number 1 is written $n$ times on a board. Every minute, Vishal picks two numbers written on the board, say $a$ and $b$, erases them, and writes either $a+b$ or $\min \left\{a^{2}, b^{2}\right\}$. After $n-1$ minutes there is one number left on the board. Let the largest possible value for this final number be $f(n)$. Prove that
$$
2^{n / 3}<f(n) \leq 3^{n / 3}
$$
|
Clearly $f(n)$ is a strictly increasing function, as we can form $f(n-1)$ with $n-1$ ones, and add the final one. However, we can do better; assume Vishal generates $f(n)$ on the board. After $n-2$ minutes, there are two numbers left, say they were formed by $x$ ones and $y$ ones, where $x+y=n$. Clearly the numbers are at most $f(x), f(y)$ (and can be made to be equal to $f(x), f(y))$, and therefore we obtain
$$
f(n)=\max _{x+y=n, 1 \leq x \leq y \leq n-1}\left(\max \left(f(x)+f(y), f(x)^{2}\right)\right)
$$
where we used the fact that $f$ is increasing to get that $\min \left(f(x)^{2}, f(y)^{2}\right)=f(x)^{2}$ when $x \leq y$. In particular, $f(n+1) \geq f(n)+1$, and $f(2 n) \geq f(n)^{2}$ for all positive integers $n$.
Upper bound:
First proof of upper bound. We use induction. We can check that $f(n)=n$ for $n \leq 4$, and these all satisfy the bound $f(n)=n \leq 3^{n / 3}$. Assume it is true for all $m<n$ (some $n \geq 5$ ), and with $x, y$ as in equation ?? we have
$$
f(x)^{2} \leq f\left(\left\lfloor\frac{n}{2}\right\rfloor\right)^{2} \leq\left(3^{n / 6}\right)^{2}=3^{n / 3}
$$
as desired. It thus remains to show that $f(x)+f(y) \leq 3^{n / 3}$. By induction, it suffices to prove that
$$
3^{x / 3}+3^{y / 3} \leq 3^{(x+y) / 3}
$$
for $1 \leq x \leq y \leq n-1$ and $x+y=n$. This is equivalent to
$$
1+3^{(y-x) / 3} \leq 3^{y / 3}
$$
Let $w=3^{(y-x) / 3}$, and we require $3^{x / 3} w \geq w+1$. If $x \geq 2$, then this is true as $w \geq 1$, and if $x=1$ then $w=3^{(n-2) / 3} \geq 3$ and the result is still true. Thus all terms in equation ?? are at most $3^{n / 3}$, and so $f(n) \leq 3^{n / 3}$, and the upper bound is proven.
Second proof of upper bound. Consider a second game with the same rules but in which Vishal can replace $a$ and $b$ by either $a+b$ or $a b$. Let $g(n)$ be the largest possible value for this new game. Then $f(n) \leq g(n)$ because $\min \left\{a^{2}, b^{2}\right\} \leq a b$.
We can check $g(n)=n$ for $n \leq 4$, so $g(n) \leq 3^{n / 3}$ for these values. If $x$ and $y$ are both bigger than 1 , then $g(x)+g(y) \leq g(x) g(y)$. Therefore, for $n>4$, we have that
$$
g(n)=\max \left\{g(n-1)+1, \max _{1 \leq x \leq n-1} g(x) g(n-x)\right\}
$$
Now proceed similarly to the first proof. Assume $n>4$ and $g(m) \leq 3^{m / 3}$ for all $m<n$. If $1 \leq x \leq n-1$, then $g(x) g(n-x) \leq 3^{x / 3} 3^{(n-x) / 3}=3^{n / 3}$. And $g(n-1)+1 \leq 3^{(n-1) / 3}+1$, which is shown to be less than $3^{n / 3}$ in the first proof. It follows that $f(n) \leq g(n) \leq 3^{n / 3}$.
Lower bound:
First proof of lower bound. We begin with a lemma.
Lemma 1. Let $m$ be a nonnegative integer. Then
$$
f\left(2^{m}\right) \geq 2^{2^{m-1}} \quad \text { and } \quad f\left(3 \cdot 2^{m}\right) \geq 3^{2^{m}}
$$
Proof. We prove the lemma by induction. One can check that $f(n)=n$ for $n \leq 3$, which proves the lemma for $m=0$. For a general $m>0$, we get
$$
\begin{gathered}
f\left(2^{m}\right) \geq f\left(2^{m-1}\right)^{2} \geq\left(2^{2^{m-2}}\right)^{2}=2^{2^{m-1}} \\
f\left(3 \cdot 2^{m}\right) \geq f\left(3 \cdot 2^{m-1}\right)^{2} \geq\left(3^{2^{m-1}}\right)^{2}=3^{2^{m}}
\end{gathered}
$$
by induction, as required.
(This lemma can also be proved more constructively. Briefly, if $n=2^{m}$, then partition the 1 's on the board into $2^{m-1}$ pairs, and then add each pair to get $2^{m-1} 2^{\prime} \mathrm{s}\left(2=2^{2^{0}}\right)$; then multiply pairs of 2 's to get $2^{m-2} 4$ 's $\left(4=2^{2^{1}}\right)$; then multiply pairs of 4's to get $2^{m-3} 16$ 's $\left(16=2^{2^{2}}\right)$; and so on, until there are $2\left(=2^{1}\right)$ copies of $2^{2^{m-2}}$, which then gets replaced with $\left.\mathrm{a} 2^{2^{m-1}}\right)$. The process is similar for $n=3 \cdot 2^{m}$, except that the first step is to partition the 1 's into $2^{m}$ groups of 3 , and then use addition within each group to get $2^{m} 3$ 's on the board.)
Now assume $2^{x} \leq n<3 \cdot 2^{x-1}$ for some integer $x$. Then we have
$$
f(n) \geq f\left(2^{x}\right) \geq 2^{2^{x-1}}>2^{n / 3}
$$
as required. If no such $x$ exists, then there exists an integer $x$ such that $3 \cdot 2^{x-1} \leq n<2^{x+1}$. In this case, we have
$$
f(n) \geq f\left(3 \cdot 2^{x-1}\right) \geq 3^{2^{x-1}}>2^{2^{x+1} / 3}>2^{n / 3}
$$
where the second last inequality is equivalent to $2^{x-1} \log (3) \geq \frac{2^{x+1}}{3} \log (2)$, and by dividing out $2^{x}$ and clearing the denominator this is equivalent to $3 \log (3) \geq 4 \log 2$, which is true as $3^{3}=27>16=2^{4}$.
Second proof of lower bound. We shall prove the stronger result $f(n) \geq 2^{(n+1) / 3}$ for $n \geq 2$ by induction. One can check that $f(n)=n$ for $n=2,3,4$, which proves the result for these values. Assume that $n \geq 5$ and that $f(k) \geq 2^{(k+1) / 3}$ for all $k=2,3, \ldots, n-1$. Then
$$
\begin{array}{rlr}
f(n) & \geq f(\lfloor n / 2\rfloor)^{2} & \\
& \geq\left(2^{(\lfloor n / 2\rfloor+1) / 3}\right)^{2} \quad \quad \text { since }\left\lfloor\frac{n}{2}\right\rfloor \geq 2 \\
& =2^{(2\lfloor n / 2\rfloor+2) / 3} \quad \\
& \geq 2^{(n+1) / 3} \quad \text { since }\left\lfloor\frac{n}{2}\right\rfloor \geq \frac{n-1}{2} .
\end{array}
$$
The result follows by induction.
Remark 1. One can show that $f$ satisfies the recurrence $f(n)=n$ for $n=1,2, f(2 n)=f(n)^{2}$ for $n \geq 2$, and $f(2 n+1)=f(2 n)+1$ for $n \geq 1$. The upper bound in the problem is tight (equality holds for $n=3 \cdot 2^{x}$ ), but the lower bound is not.
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\nP3:",
"resource_path": "Canada_MO/segmented/en-cmo2022-solutions-en.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2022"
}
|
Let $n$ be a positive integer. A set of $n$ distinct lines divides the plane into various (possibly unbounded) regions. The set of lines is called "nice" if no three lines intersect at a single point. A "colouring" is an assignment of two colours to each region such that the first colour is from the set $\left\{A_{1}, A_{2}\right\}$, and the second colour is from the set $\left\{B_{1}, B_{2}, B_{3}\right\}$. Given a nice set of lines, we call it "colourable" if there exists a colouring such that
1). no colour is assigned to two regions that share an edge;
2). for each $i \in\{1,2\}$ and $j \in\{1,2,3\}$ there is at least one region that is assigned with both $A_{i}$ and $B_{j}$.
Determine all $n$ such that every nice configuration of $n$ lines is colourable.
|
The answer is $n \geq 5$. If $n \leq 4$, consider $n$ parallel lines. There are 6 total colour combinations required, and only $n+1 \leq 5$ total regions, hence the colouring is not possible.
Now, assume $n \geq 5$. Rotate the picture so that no line is horizontal, and orient each line so that the "forward" direction increases the $y$-value. In this way, each line divides the plane into a right and left hand side (with respect to this forward direction). Every region of the plane is on the right hand side of $k$ lines and on the left hand side of $n-k$ lines for some $0 \leq k \leq n$. Furthermore, there is a region for every $k$ : let $w$ be large enough so that $w$ is greater than the $y$-value of any intersection point of two lines. Consider the horizontal line $y=w$ : a point very far on the left of this line is left of every single line, and as we cross over all lines in the problem, we hit all values of $k$.
Finally, take a region that is on the right hand side of $k$ lines. Colour it $A_{1}$ if $k$ is odd, and $A_{2}$ if it is even. Similarly, colour it $B_{i}$ if $k \equiv i(\bmod 3)$. By the previous paragraph, there are regions for at least $k=0,1, \ldots, 5$, whence there is a region coloured $A_{i}$ and $B_{j}$ for all $(i, j)$. Furthermore, two regions that share an edge will be on the right hand side of $k$ and $k+1$ lines for some $k$. By construction, the $A_{i}$ and $B_{i}$ colours of the regions must differ, hence we have proven that the set of lines is colourable.
|
n \geq 5
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $n$ be a positive integer. A set of $n$ distinct lines divides the plane into various (possibly unbounded) regions. The set of lines is called "nice" if no three lines intersect at a single point. A "colouring" is an assignment of two colours to each region such that the first colour is from the set $\left\{A_{1}, A_{2}\right\}$, and the second colour is from the set $\left\{B_{1}, B_{2}, B_{3}\right\}$. Given a nice set of lines, we call it "colourable" if there exists a colouring such that
1). no colour is assigned to two regions that share an edge;
2). for each $i \in\{1,2\}$ and $j \in\{1,2,3\}$ there is at least one region that is assigned with both $A_{i}$ and $B_{j}$.
Determine all $n$ such that every nice configuration of $n$ lines is colourable.
|
The answer is $n \geq 5$. If $n \leq 4$, consider $n$ parallel lines. There are 6 total colour combinations required, and only $n+1 \leq 5$ total regions, hence the colouring is not possible.
Now, assume $n \geq 5$. Rotate the picture so that no line is horizontal, and orient each line so that the "forward" direction increases the $y$-value. In this way, each line divides the plane into a right and left hand side (with respect to this forward direction). Every region of the plane is on the right hand side of $k$ lines and on the left hand side of $n-k$ lines for some $0 \leq k \leq n$. Furthermore, there is a region for every $k$ : let $w$ be large enough so that $w$ is greater than the $y$-value of any intersection point of two lines. Consider the horizontal line $y=w$ : a point very far on the left of this line is left of every single line, and as we cross over all lines in the problem, we hit all values of $k$.
Finally, take a region that is on the right hand side of $k$ lines. Colour it $A_{1}$ if $k$ is odd, and $A_{2}$ if it is even. Similarly, colour it $B_{i}$ if $k \equiv i(\bmod 3)$. By the previous paragraph, there are regions for at least $k=0,1, \ldots, 5$, whence there is a region coloured $A_{i}$ and $B_{j}$ for all $(i, j)$. Furthermore, two regions that share an edge will be on the right hand side of $k$ and $k+1$ lines for some $k$. By construction, the $A_{i}$ and $B_{i}$ colours of the regions must differ, hence we have proven that the set of lines is colourable.
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\nP4.",
"resource_path": "Canada_MO/segmented/en-cmo2022-solutions-en.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2022"
}
|
Let $A B C D E$ be a convex pentagon such that the five vertices lie on a circle and the five sides are tangent to another circle inside the pentagon. There are $\binom{5}{3}=10$ triangles which can be formed by choosing 3 of the 5 vertices. For each of these 10 triangles, mark its incenter. Prove that these 10 incenters lie on two concentric circles.
|
Let $I$ be the incenter of pentagon $A B C D E$. Let $I_{A}$ denote the incenter of triangle $E A B$ and $I_{a}$ the incenter $D A C$. Define $I_{B}, I_{b}, I_{C}, I_{c}, I_{D}, I_{d}, I_{E}, I_{e}$ similarly.
We will first show that $I_{A} I_{B} I_{C} I_{D} I_{E}$ are concyclic. Let $\omega_{A}$ be the circle with center at the midpoint of arc $D E$ and passing through $D$ and $E$. Define $\omega_{B}, \omega_{C}, \omega_{D}, \omega_{E}$ similarly. It is well-known that the incenter of a triangle lies on such circles, in particular, $I_{A}$ lies on $\omega_{C}$ and $\omega_{D}$. So the radical axis of $\omega_{C}, \omega_{D}$ is the line $A I_{A}$. But this is just the angle bisector of $\angle E A B$, which $I$ also lies on. So $I$ is in fact the radical center of $\omega_{A}, \omega_{B}, \omega_{C}, \omega_{D}, \omega_{E}$ ! Inverting about $I$ swaps $I_{A}$ and $A$ and since $A B C D E$ are concyclic, $I_{A} I_{B} I_{C} I_{D} I_{E}$ are concyclic as well.
Let $O$ be the center of the circle $I_{A} I_{B} I_{C} I_{D} I_{E}$. We will now show that $O I_{a}=O I_{d}$ which finishes the problem as we can consider the cyclic versions of this equation to find that $O I_{a}=O I_{d}=O I_{b}=O I_{e}=O I_{c}$. Recall a well-known lemma: For any cyclic quadrilateral $W X Y Z$, the incenters of $X Y Z, Y Z W, Z W X, W X Y$ form a rectangle. Applying this lemma on $A B C D$, we see that $I_{B}, I_{C}, I_{a}, I_{d}$ form a rectangle in that order. Then the perpendicular bisector of $I_{B} I_{C}$ is exactly the perpendicular bisector of $I_{a} I_{d}$. Thus, $O$ is equidistant to $I_{a}$ and $I_{d}$ and we are done.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D E$ be a convex pentagon such that the five vertices lie on a circle and the five sides are tangent to another circle inside the pentagon. There are $\binom{5}{3}=10$ triangles which can be formed by choosing 3 of the 5 vertices. For each of these 10 triangles, mark its incenter. Prove that these 10 incenters lie on two concentric circles.
|
Let $I$ be the incenter of pentagon $A B C D E$. Let $I_{A}$ denote the incenter of triangle $E A B$ and $I_{a}$ the incenter $D A C$. Define $I_{B}, I_{b}, I_{C}, I_{c}, I_{D}, I_{d}, I_{E}, I_{e}$ similarly.
We will first show that $I_{A} I_{B} I_{C} I_{D} I_{E}$ are concyclic. Let $\omega_{A}$ be the circle with center at the midpoint of arc $D E$ and passing through $D$ and $E$. Define $\omega_{B}, \omega_{C}, \omega_{D}, \omega_{E}$ similarly. It is well-known that the incenter of a triangle lies on such circles, in particular, $I_{A}$ lies on $\omega_{C}$ and $\omega_{D}$. So the radical axis of $\omega_{C}, \omega_{D}$ is the line $A I_{A}$. But this is just the angle bisector of $\angle E A B$, which $I$ also lies on. So $I$ is in fact the radical center of $\omega_{A}, \omega_{B}, \omega_{C}, \omega_{D}, \omega_{E}$ ! Inverting about $I$ swaps $I_{A}$ and $A$ and since $A B C D E$ are concyclic, $I_{A} I_{B} I_{C} I_{D} I_{E}$ are concyclic as well.
Let $O$ be the center of the circle $I_{A} I_{B} I_{C} I_{D} I_{E}$. We will now show that $O I_{a}=O I_{d}$ which finishes the problem as we can consider the cyclic versions of this equation to find that $O I_{a}=O I_{d}=O I_{b}=O I_{e}=O I_{c}$. Recall a well-known lemma: For any cyclic quadrilateral $W X Y Z$, the incenters of $X Y Z, Y Z W, Z W X, W X Y$ form a rectangle. Applying this lemma on $A B C D$, we see that $I_{B}, I_{C}, I_{a}, I_{d}$ form a rectangle in that order. Then the perpendicular bisector of $I_{B} I_{C}$ is exactly the perpendicular bisector of $I_{a} I_{d}$. Thus, $O$ is equidistant to $I_{a}$ and $I_{d}$ and we are done.
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\nP5.",
"resource_path": "Canada_MO/segmented/en-cmo2022-solutions-en.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2022"
}
|
William is thinking of an integer between 1 and 50, inclusive. Victor can choose a positive integer $m$ and ask William: "does $m$ divide your number?", to which William must answer truthfully. Victor continues asking these questions until he determines William's number. What is the minimum number of questions that Victor needs to guarantee this?
|
The minimum number is 15 questions.
First, we show that 14 or fewer questions is not enough to guarantee success. Suppose Victor asks at most 14 questions, and William responds with "no" to each question unless $m=$ 1. Note that these responses are consistent with the secret number being 1. But since there are 15 primes less than 50 , some prime $p$ was never chosen as $m$. That means the responses are also consistent with the secret number being $p$. Therefore, Victor cannot determine the number for sure because 1 and $p$ are both possible options.
Now we show that Victor can always determine the number with 15 questions. Let $N$ be William's secret number. First, Victor asks 4 questions, with $m=2,3,5,7$. We then case on William's responses.
Case 1. William answers " $n o$ " to all four questions.
$N$ can only be divisible by primes that are 11 or larger. This means $N$ cannot have multiple prime factors (otherwise $N \geq 11^{2}>50$ ), so either $N=1$ or $N$ is one of the 11 remaining primes less than 50 . Victor can then ask 11 questions with $m=11,13,17, \ldots, 47$, one for each of the remaining primes, to determine the value of $N$.
Case 2. William answers "yes" to $m=2$, and " $n o$ " to $m=3,5,7$.
There are only 11 possible values of $N$ that match these answers $(2,4,8,16,22,26,32$, 34, 38, 44, and 46). Victor can use his remaining 11 questions on each of these possibilities.
Case 3. William answers "yes" to $m=3$, and " $n o$ " to $m=2,5,7$.
There are 5 possible values of $N(3,9,27,33$, and 39). Similar to Case 2, Victor can ask about these 5 numbers to determine the value of $N$.
Case 4. William answers "yes" to multiple questions, or one "yes" to $m=5$ or $m=7$.
Let $k$ be the product of all $m$ 's that received a "yes" response. Since $N$ is divisible by each of these $m$ 's, $N$ must be divisible by $k$. Since $k \geq 5$, there are at most 10 multiples of $k$ between 1 and 50 . Victor can ask about each of these multiples of $k$ with his remaining questions.
|
15
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
William is thinking of an integer between 1 and 50, inclusive. Victor can choose a positive integer $m$ and ask William: "does $m$ divide your number?", to which William must answer truthfully. Victor continues asking these questions until he determines William's number. What is the minimum number of questions that Victor needs to guarantee this?
|
The minimum number is 15 questions.
First, we show that 14 or fewer questions is not enough to guarantee success. Suppose Victor asks at most 14 questions, and William responds with "no" to each question unless $m=$ 1. Note that these responses are consistent with the secret number being 1. But since there are 15 primes less than 50 , some prime $p$ was never chosen as $m$. That means the responses are also consistent with the secret number being $p$. Therefore, Victor cannot determine the number for sure because 1 and $p$ are both possible options.
Now we show that Victor can always determine the number with 15 questions. Let $N$ be William's secret number. First, Victor asks 4 questions, with $m=2,3,5,7$. We then case on William's responses.
Case 1. William answers " $n o$ " to all four questions.
$N$ can only be divisible by primes that are 11 or larger. This means $N$ cannot have multiple prime factors (otherwise $N \geq 11^{2}>50$ ), so either $N=1$ or $N$ is one of the 11 remaining primes less than 50 . Victor can then ask 11 questions with $m=11,13,17, \ldots, 47$, one for each of the remaining primes, to determine the value of $N$.
Case 2. William answers "yes" to $m=2$, and " $n o$ " to $m=3,5,7$.
There are only 11 possible values of $N$ that match these answers $(2,4,8,16,22,26,32$, 34, 38, 44, and 46). Victor can use his remaining 11 questions on each of these possibilities.
Case 3. William answers "yes" to $m=3$, and " $n o$ " to $m=2,5,7$.
There are 5 possible values of $N(3,9,27,33$, and 39). Similar to Case 2, Victor can ask about these 5 numbers to determine the value of $N$.
Case 4. William answers "yes" to multiple questions, or one "yes" to $m=5$ or $m=7$.
Let $k$ be the product of all $m$ 's that received a "yes" response. Since $N$ is divisible by each of these $m$ 's, $N$ must be divisible by $k$. Since $k \geq 5$, there are at most 10 multiples of $k$ between 1 and 50 . Victor can ask about each of these multiples of $k$ with his remaining questions.
|
{
"exam": "Canada_MO",
"problem_label": "1",
"problem_match": "\nP1.",
"resource_path": "Canada_MO/segmented/en-cmo2023-solutions-en.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2023"
}
|
There are 20 students in a high school class, and each student has exactly three close friends in the class. Five of the students have bought tickets to an upcoming concert. If any student sees that at least two of their close friends have bought tickets, then they will buy a ticket too.
Is it possible that the entire class buys tickets to the concert?
(Assume that friendship is mutual; if student $A$ is close friends with student $B$, then $B$ is close friends with $A$.)
|
It is impossible for the whole class to buy tickets to the concert.
If two students $A$ and $B$ are close friends, and $A$ has bought a ticket to the concert while $B$ has not, then $A$ is enticing $B$. We call this pair $(A, B)$ an enticement.
In order for a student to change their mind and buy a ticket, they first be enticed by at least 2 of their 3 close friends. That means they can only entice at most 1 other friend. Therefore, the total number of enticements among the students decreases by 1 whenever a student changes their mind to buy a ticket.
Initially, the maximum number of enticements is 15 (each of the initial 5 students with tickets has 3 friends to entice). Assume, for the sake of contradiction, that the entire class ends up buying tickets. After the first 14 people buy tickets, the number of enticements is at most $15-14=1$. This is not enough to convince the last person to buy a ticket, since they need 2 enticements.
Therefore, it is impossible that the entire class buys tickets.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There are 20 students in a high school class, and each student has exactly three close friends in the class. Five of the students have bought tickets to an upcoming concert. If any student sees that at least two of their close friends have bought tickets, then they will buy a ticket too.
Is it possible that the entire class buys tickets to the concert?
(Assume that friendship is mutual; if student $A$ is close friends with student $B$, then $B$ is close friends with $A$.)
|
It is impossible for the whole class to buy tickets to the concert.
If two students $A$ and $B$ are close friends, and $A$ has bought a ticket to the concert while $B$ has not, then $A$ is enticing $B$. We call this pair $(A, B)$ an enticement.
In order for a student to change their mind and buy a ticket, they first be enticed by at least 2 of their 3 close friends. That means they can only entice at most 1 other friend. Therefore, the total number of enticements among the students decreases by 1 whenever a student changes their mind to buy a ticket.
Initially, the maximum number of enticements is 15 (each of the initial 5 students with tickets has 3 friends to entice). Assume, for the sake of contradiction, that the entire class ends up buying tickets. After the first 14 people buy tickets, the number of enticements is at most $15-14=1$. This is not enough to convince the last person to buy a ticket, since they need 2 enticements.
Therefore, it is impossible that the entire class buys tickets.
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\nP2.",
"resource_path": "Canada_MO/segmented/en-cmo2023-solutions-en.jsonl",
"solution_match": "\nSolution 1.",
"tier": "T2",
"year": "2023"
}
|
There are 20 students in a high school class, and each student has exactly three close friends in the class. Five of the students have bought tickets to an upcoming concert. If any student sees that at least two of their close friends have bought tickets, then they will buy a ticket too.
Is it possible that the entire class buys tickets to the concert?
(Assume that friendship is mutual; if student $A$ is close friends with student $B$, then $B$ is close friends with $A$.)
|
We shall use the term friendship to denote an unordered pair of students who are close friends. Since each of the 20 students is part of exactly 3 friendships, there are exactly 30 friendships in the class. (We could also represent friendships as edges in an undirected graph whose vertices are the 20 students.)
We say that a friendship is used if one of the students in that friendship buys a ticket after the original five buyers, and the other student already has a ticket at that time. Each time a ticket is purchased after the original five purchases, at least two friendships are used. Observe that no friendship gets used twice.
If all 20 students buy tickets, then three friendships are used when the last student buys a ticket. This would imply that the number of used friendships is at least $14 \times 2+3=31$, which is more than the number of friendships. This contradiction proves that it is not possible that the entire class buys tickets.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There are 20 students in a high school class, and each student has exactly three close friends in the class. Five of the students have bought tickets to an upcoming concert. If any student sees that at least two of their close friends have bought tickets, then they will buy a ticket too.
Is it possible that the entire class buys tickets to the concert?
(Assume that friendship is mutual; if student $A$ is close friends with student $B$, then $B$ is close friends with $A$.)
|
We shall use the term friendship to denote an unordered pair of students who are close friends. Since each of the 20 students is part of exactly 3 friendships, there are exactly 30 friendships in the class. (We could also represent friendships as edges in an undirected graph whose vertices are the 20 students.)
We say that a friendship is used if one of the students in that friendship buys a ticket after the original five buyers, and the other student already has a ticket at that time. Each time a ticket is purchased after the original five purchases, at least two friendships are used. Observe that no friendship gets used twice.
If all 20 students buy tickets, then three friendships are used when the last student buys a ticket. This would imply that the number of used friendships is at least $14 \times 2+3=31$, which is more than the number of friendships. This contradiction proves that it is not possible that the entire class buys tickets.
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\nP2.",
"resource_path": "Canada_MO/segmented/en-cmo2023-solutions-en.jsonl",
"solution_match": "\nSolution 2.",
"tier": "T2",
"year": "2023"
}
|
An acute triangle is a triangle that has all angles less than $90^{\circ}$ ( $90^{\circ}$ is a Right Angle). Let $A B C$ be an acute triangle with altitudes $A D, B E$, and $C F$ meeting at $H$. The circle passing through points $D, E$, and $F$ meets $A D, B E$, and $C F$ again at $X, Y$, and $Z$ respectively. Prove the following inequality:
$$
\frac{A H}{D X}+\frac{B H}{E Y}+\frac{C H}{F Z} \geq 3
$$
|
Let the circumcircle of $A B C$ meet the altitudes $A D, B E$, and $C F$ again at $I, J$, and $K$ respectively.
Lemma (9-point circle). $I, J, K$ are the reflections of $H$ across $B C, C A, A B$. Moreover, $D, E, F, X, Y, Z$ are the midpoints of $H I, H J, H K, H A, H B, H C$.
Proof. Since $A B D E$ and $A B I C$ are cyclic, we see that
$$
\angle E B D=\angle E A D=\angle C A I=\angle C B I .
$$
Hence the lines $B I$ and $B H$ are reflections across $B C$. Similarly, $C H$ and $C I$ are reflections across $B C$, so $I$ is the reflection of $H$ across $B C$. The analogous claims for $J$ and $K$ follow. A $\times 2$ dilation from $H$ now establishes the result.
From this lemma, we get $A I=2 X D, B J=2 E Y$, and $C K=2 F Z$. Hence it is equivalent to showing that
$$
\frac{A H}{2 D X}+\frac{B H}{2 E Y}+\frac{C H}{2 F Z} \geq \frac{3}{2}
$$
which is in turn equivalent to
$$
\frac{A H}{A I}+\frac{B H}{B J}+\frac{C H}{C K} \geq \frac{3}{2} .
$$
Let $a=J K, b=K I$ and $c=I J$. Again by the lemma we find $A H=A K=A J$, so by Ptolemy's theorem on $A K I J$,
$$
A J \cdot K I+A K \cdot I J=A I \cdot J K
$$
Substituting and rearranging,
$$
\begin{aligned}
A H \cdot b+A H \cdot c & =A I \cdot a \\
A H \cdot(b+c) & =A I \cdot a \\
\frac{A H}{A I} & =\frac{a}{b+c} .
\end{aligned}
$$
Similarly,
$$
\frac{B H}{B J}=\frac{b}{c+a} \quad \text { and } \quad \frac{C H}{C K}=\frac{c}{a+b}
$$
Plugging these back into $\left(^{*}\right)$, the desired inequality is now
$$
\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b} \geq \frac{3}{2} .
$$
This is known as Nesbitt's Inequality, which has many proofs. Below is one such proof.
Add 3 to both sides and rearrange:
$$
\begin{aligned}
\left(\frac{a}{b+c}+1\right)+\left(\frac{b}{c+a}+1\right)+\left(\frac{c}{a+b}+1\right) & \geq \frac{3}{2}+3 \\
\Longleftrightarrow \quad \frac{a+b+c}{b+c}+\frac{a+b+c}{c+a}+\frac{a+b+c}{a+b} & \geq \frac{9}{2} \\
\Longleftrightarrow \quad(a+b+c)\left(\frac{1}{b+c}+\frac{1}{c+a}+\frac{1}{a+b}\right) & \geq \frac{9}{2} \\
\Longleftrightarrow \quad & \frac{(b+c)+(c+a)+(a+b)}{3}
\end{aligned}
$$
which is true by the AM-HM inequality.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
An acute triangle is a triangle that has all angles less than $90^{\circ}$ ( $90^{\circ}$ is a Right Angle). Let $A B C$ be an acute triangle with altitudes $A D, B E$, and $C F$ meeting at $H$. The circle passing through points $D, E$, and $F$ meets $A D, B E$, and $C F$ again at $X, Y$, and $Z$ respectively. Prove the following inequality:
$$
\frac{A H}{D X}+\frac{B H}{E Y}+\frac{C H}{F Z} \geq 3
$$
|
Let the circumcircle of $A B C$ meet the altitudes $A D, B E$, and $C F$ again at $I, J$, and $K$ respectively.

Lemma (9-point circle). $I, J, K$ are the reflections of $H$ across $B C, C A, A B$. Moreover, $D, E, F, X, Y, Z$ are the midpoints of $H I, H J, H K, H A, H B, H C$.
Proof. Since $A B D E$ and $A B I C$ are cyclic, we see that
$$
\angle E B D=\angle E A D=\angle C A I=\angle C B I .
$$
Hence the lines $B I$ and $B H$ are reflections across $B C$. Similarly, $C H$ and $C I$ are reflections across $B C$, so $I$ is the reflection of $H$ across $B C$. The analogous claims for $J$ and $K$ follow. A $\times 2$ dilation from $H$ now establishes the result.
From this lemma, we get $A I=2 X D, B J=2 E Y$, and $C K=2 F Z$. Hence it is equivalent to showing that
$$
\frac{A H}{2 D X}+\frac{B H}{2 E Y}+\frac{C H}{2 F Z} \geq \frac{3}{2}
$$
which is in turn equivalent to
$$
\frac{A H}{A I}+\frac{B H}{B J}+\frac{C H}{C K} \geq \frac{3}{2} .
$$
Let $a=J K, b=K I$ and $c=I J$. Again by the lemma we find $A H=A K=A J$, so by Ptolemy's theorem on $A K I J$,
$$
A J \cdot K I+A K \cdot I J=A I \cdot J K
$$
Substituting and rearranging,
$$
\begin{aligned}
A H \cdot b+A H \cdot c & =A I \cdot a \\
A H \cdot(b+c) & =A I \cdot a \\
\frac{A H}{A I} & =\frac{a}{b+c} .
\end{aligned}
$$
Similarly,
$$
\frac{B H}{B J}=\frac{b}{c+a} \quad \text { and } \quad \frac{C H}{C K}=\frac{c}{a+b}
$$
Plugging these back into $\left(^{*}\right)$, the desired inequality is now
$$
\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b} \geq \frac{3}{2} .
$$
This is known as Nesbitt's Inequality, which has many proofs. Below is one such proof.
Add 3 to both sides and rearrange:
$$
\begin{aligned}
\left(\frac{a}{b+c}+1\right)+\left(\frac{b}{c+a}+1\right)+\left(\frac{c}{a+b}+1\right) & \geq \frac{3}{2}+3 \\
\Longleftrightarrow \quad \frac{a+b+c}{b+c}+\frac{a+b+c}{c+a}+\frac{a+b+c}{a+b} & \geq \frac{9}{2} \\
\Longleftrightarrow \quad(a+b+c)\left(\frac{1}{b+c}+\frac{1}{c+a}+\frac{1}{a+b}\right) & \geq \frac{9}{2} \\
\Longleftrightarrow \quad & \frac{(b+c)+(c+a)+(a+b)}{3}
\end{aligned}
$$
which is true by the AM-HM inequality.
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\nP3.",
"resource_path": "Canada_MO/segmented/en-cmo2023-solutions-en.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2023"
}
|
Let $f(x)$ be a non-constant polynomial with integer coefficients such that $f(1) \neq 1$. For a positive integer $n$, define $\operatorname{divs}(n)$ to be the set of positive divisors of $n$.
A positive integer $m$ is $f$-cool if there exists a positive integer $n$ for which
$$
f[\operatorname{divs}(m)]=\operatorname{divs}(n)
$$
Prove that for any such $f$, there are finitely many $f$-cool integers.
(The notation $f[S]$ for some set $S$ denotes the set $\{f(s): s \in S\}$.)
Remark 1. The original problem statement was "For a fixed non-constant polynomial $f(x) \neq$ $x$, prove that there are finitely many composite $f$-cool integers." Note that this allows $f(1)=1$. Try this problem for an added challenge!
|
Assume for the sake of contradiction that there are infinitely many $f$-cool integers.
If $f(x)$ has a negative leading coefficient, then a sufficiently large $f$-cool integer $m$ will have $f(m)<0$. But this implies $m$ is not $f$-cool, contradiction.
Thus $f(x)$ has a positive leading coefficient, so we can pick an $N$ such that for all $m>N$,
$$
f(m)>\max (f(1), f(2), \ldots, f(m-1))
$$
This means $f(m)$ is the largest value in $f[\operatorname{divs}(m)]$, so if $m$ is $f$-cool with $f[\operatorname{divs}(m)]=\operatorname{divs}(n)$, then we must have $n=f(m)$, since $n$ is the largest value in $\operatorname{divs}(n)$. In other words,
$$
f[\operatorname{divs}(m)]=\operatorname{divs}(f(m))
$$
for all $f$-cool $m>N$.
For each of those $m$ 's, $1 \in \operatorname{divs}(f(m))$, so there must be a $k \in \operatorname{divs}(m)$ such that $f(k)=1$. Let $k_{1}, k_{2}, \ldots, k_{n}$ be the solutions to $f(x)=1$. Thus every $f$-cool $m>N$ is divisible by some $k \in\left\{k_{1}, k_{2}, \ldots, k_{n}\right\}$. Since there are infinitely many such $m$ 's and finitely many $k$ 's, by the Pigeonhole Principle there is some $k$ which divides infinitely many $f$-cool integers $m$. (Note that $k \neq 1$ since $f(1) \neq 1$.)
For all $f$-cool $m>N$ divisible by $k$, we have
$$
\left.f\left(\frac{m}{k}\right) \in f[\operatorname{divs}(m)]=\operatorname{divs}(f(m)) \Longrightarrow f\left(\frac{m}{k}\right) \right\rvert\, f(m) .
$$
Thus, $f(x) \mid f(k x)$ has infinitely many positive integer solutions. Let $d=\operatorname{deg}(f)$, and write
$$
\frac{f(k x)}{f(x)}=k^{d}+\frac{g(x)}{f(x)}
$$
for some $g(x) \in \mathbb{Z}[x]$ with $\operatorname{deg}(g)<d$. If $g(x) \neq 0$, then for sufficiently large $x$ we have $0<|g(x)|<f(x)$, since $\operatorname{deg}(f)>\operatorname{deg}(g)$. But then $\frac{f(k x)}{f(x)}-k^{d}=\frac{g(x)}{f(x)}$ cannot be an integer, which gives us the desired contradiction.
Therefore $g(x)=0$, so $f(k x)=k^{d} f(x)$, i.e. $f(x)=a x^{d}$ for some positive integer $a$. If $a=1$ then $f(1)=1$, a contradiction. But if $a>1$, then $f(x)=1$ has no integer solutions, another contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $f(x)$ be a non-constant polynomial with integer coefficients such that $f(1) \neq 1$. For a positive integer $n$, define $\operatorname{divs}(n)$ to be the set of positive divisors of $n$.
A positive integer $m$ is $f$-cool if there exists a positive integer $n$ for which
$$
f[\operatorname{divs}(m)]=\operatorname{divs}(n)
$$
Prove that for any such $f$, there are finitely many $f$-cool integers.
(The notation $f[S]$ for some set $S$ denotes the set $\{f(s): s \in S\}$.)
Remark 1. The original problem statement was "For a fixed non-constant polynomial $f(x) \neq$ $x$, prove that there are finitely many composite $f$-cool integers." Note that this allows $f(1)=1$. Try this problem for an added challenge!
|
Assume for the sake of contradiction that there are infinitely many $f$-cool integers.
If $f(x)$ has a negative leading coefficient, then a sufficiently large $f$-cool integer $m$ will have $f(m)<0$. But this implies $m$ is not $f$-cool, contradiction.
Thus $f(x)$ has a positive leading coefficient, so we can pick an $N$ such that for all $m>N$,
$$
f(m)>\max (f(1), f(2), \ldots, f(m-1))
$$
This means $f(m)$ is the largest value in $f[\operatorname{divs}(m)]$, so if $m$ is $f$-cool with $f[\operatorname{divs}(m)]=\operatorname{divs}(n)$, then we must have $n=f(m)$, since $n$ is the largest value in $\operatorname{divs}(n)$. In other words,
$$
f[\operatorname{divs}(m)]=\operatorname{divs}(f(m))
$$
for all $f$-cool $m>N$.
For each of those $m$ 's, $1 \in \operatorname{divs}(f(m))$, so there must be a $k \in \operatorname{divs}(m)$ such that $f(k)=1$. Let $k_{1}, k_{2}, \ldots, k_{n}$ be the solutions to $f(x)=1$. Thus every $f$-cool $m>N$ is divisible by some $k \in\left\{k_{1}, k_{2}, \ldots, k_{n}\right\}$. Since there are infinitely many such $m$ 's and finitely many $k$ 's, by the Pigeonhole Principle there is some $k$ which divides infinitely many $f$-cool integers $m$. (Note that $k \neq 1$ since $f(1) \neq 1$.)
For all $f$-cool $m>N$ divisible by $k$, we have
$$
\left.f\left(\frac{m}{k}\right) \in f[\operatorname{divs}(m)]=\operatorname{divs}(f(m)) \Longrightarrow f\left(\frac{m}{k}\right) \right\rvert\, f(m) .
$$
Thus, $f(x) \mid f(k x)$ has infinitely many positive integer solutions. Let $d=\operatorname{deg}(f)$, and write
$$
\frac{f(k x)}{f(x)}=k^{d}+\frac{g(x)}{f(x)}
$$
for some $g(x) \in \mathbb{Z}[x]$ with $\operatorname{deg}(g)<d$. If $g(x) \neq 0$, then for sufficiently large $x$ we have $0<|g(x)|<f(x)$, since $\operatorname{deg}(f)>\operatorname{deg}(g)$. But then $\frac{f(k x)}{f(x)}-k^{d}=\frac{g(x)}{f(x)}$ cannot be an integer, which gives us the desired contradiction.
Therefore $g(x)=0$, so $f(k x)=k^{d} f(x)$, i.e. $f(x)=a x^{d}$ for some positive integer $a$. If $a=1$ then $f(1)=1$, a contradiction. But if $a>1$, then $f(x)=1$ has no integer solutions, another contradiction.
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\nP4.",
"resource_path": "Canada_MO/segmented/en-cmo2023-solutions-en.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2023"
}
|
A country with $n$ cities has some two-way roads connecting certain pairs of cities. Someone notices that if the country is split into two parts in any way, then there would be at most $k n$ roads between the two parts (where $k$ is a fixed positive integer). What is the largest integer $m$ (in terms of $n$ and $k$ ) such that there is guaranteed to be a set of $m$ cities, no two of which are directly connected by a road?
|
The answer is $m=\left\lceil\frac{n}{4 k}\right\rceil$
Call a collection of cities independent if no two cities in the collection are joined by a road. Let $r$ and $k$ be integers such that $n=4 k q+r$ where $1 \leq r \leq 4 k$.
First we show that $m \leq\left\lceil\frac{n}{4 k}\right\rceil=q+1$. Let $K_{i}$ denote a set of $i$ cities such that every pair of cities in $K_{i}$ is linked by a road. Consider a country containing $q$ copies of $K_{4 k}$ and one copy of $K_{r}$. An independent set of cities in this country contains at most one city from each $K_{4 k}$ or $K_{r}$ and therefore contains at most $q+1$ cities. Now note that any partition of the cities of the country into two new countries partitions each $K_{4 k}$ and $K_{r}$ into two sets. If $K_{i}$ where $i \leq 4 k$ is partitioned into two sets of cities of sizes $a$ and $b$, then the number of roads between the two sets is $a b \leq \frac{(a+b)^{2}}{4} \leq k i$. Summing this inequality over all copies of $K_{4 k}$ and $K_{r}$ yields that there are at most $k n$ roads between the two new countries. This implies that this particular country satisfies the given condition and it follows that $m \leq\left\lceil\frac{n}{4 k}\right\rceil$.
Now we show that any country satisfying the given condition has an independent set containing at least $\left\lceil\frac{n}{4 k}\right\rceil$ cities. Call a set of cities $i$-separable if it can be partitioned into $i$ disjoint independent sets of cities. Given a country satisfying the conditions, let $S$ be a largest set of cities in the country that is $2 k$-separable. We prove that $|S| \geq n / 2$. By definition of $S$, there exists a partition $A_{1}, A_{2}, \ldots, A_{2 k}$ of the cities in $S$ such that each $A_{i}$ is independent. Let $|S|=t$. Assume for contradiction that $t<\frac{n}{2}$. There are at most $k n$ roads between $S$ and the rest of the country, which by the pigeonhole principle implies that there is a city $u$ not in $S$ that is connected to at most $\frac{k n}{n-t}<2 k$ cities by road. Therefore $u$ is joined by a road to at most $2 k-1$ cities in $S$, and there must be an independent subset $A_{i}$ such that $u$ is not linked by a road to any city in $A_{i}$. Adding $u$ to $S$ maintains the fact that $S$ is $2 k$-separable but contradicts its maximality. Therefore it must follow that $t \geq \frac{n}{2}$. By the pigeonhole principle, one of the sets $A_{1}, A_{2}, \ldots, A_{2 k}$ must contain at least $\frac{t}{2 k} \geq \frac{n}{4 k}$ cities. This proves the claim and therefore $m=\left\lceil\frac{n}{4 k}\right\rceil$.
|
\left\lceil\frac{n}{4 k}\right\rceil
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A country with $n$ cities has some two-way roads connecting certain pairs of cities. Someone notices that if the country is split into two parts in any way, then there would be at most $k n$ roads between the two parts (where $k$ is a fixed positive integer). What is the largest integer $m$ (in terms of $n$ and $k$ ) such that there is guaranteed to be a set of $m$ cities, no two of which are directly connected by a road?
|
The answer is $m=\left\lceil\frac{n}{4 k}\right\rceil$
Call a collection of cities independent if no two cities in the collection are joined by a road. Let $r$ and $k$ be integers such that $n=4 k q+r$ where $1 \leq r \leq 4 k$.
First we show that $m \leq\left\lceil\frac{n}{4 k}\right\rceil=q+1$. Let $K_{i}$ denote a set of $i$ cities such that every pair of cities in $K_{i}$ is linked by a road. Consider a country containing $q$ copies of $K_{4 k}$ and one copy of $K_{r}$. An independent set of cities in this country contains at most one city from each $K_{4 k}$ or $K_{r}$ and therefore contains at most $q+1$ cities. Now note that any partition of the cities of the country into two new countries partitions each $K_{4 k}$ and $K_{r}$ into two sets. If $K_{i}$ where $i \leq 4 k$ is partitioned into two sets of cities of sizes $a$ and $b$, then the number of roads between the two sets is $a b \leq \frac{(a+b)^{2}}{4} \leq k i$. Summing this inequality over all copies of $K_{4 k}$ and $K_{r}$ yields that there are at most $k n$ roads between the two new countries. This implies that this particular country satisfies the given condition and it follows that $m \leq\left\lceil\frac{n}{4 k}\right\rceil$.
Now we show that any country satisfying the given condition has an independent set containing at least $\left\lceil\frac{n}{4 k}\right\rceil$ cities. Call a set of cities $i$-separable if it can be partitioned into $i$ disjoint independent sets of cities. Given a country satisfying the conditions, let $S$ be a largest set of cities in the country that is $2 k$-separable. We prove that $|S| \geq n / 2$. By definition of $S$, there exists a partition $A_{1}, A_{2}, \ldots, A_{2 k}$ of the cities in $S$ such that each $A_{i}$ is independent. Let $|S|=t$. Assume for contradiction that $t<\frac{n}{2}$. There are at most $k n$ roads between $S$ and the rest of the country, which by the pigeonhole principle implies that there is a city $u$ not in $S$ that is connected to at most $\frac{k n}{n-t}<2 k$ cities by road. Therefore $u$ is joined by a road to at most $2 k-1$ cities in $S$, and there must be an independent subset $A_{i}$ such that $u$ is not linked by a road to any city in $A_{i}$. Adding $u$ to $S$ maintains the fact that $S$ is $2 k$-separable but contradicts its maximality. Therefore it must follow that $t \geq \frac{n}{2}$. By the pigeonhole principle, one of the sets $A_{1}, A_{2}, \ldots, A_{2 k}$ must contain at least $\frac{t}{2 k} \geq \frac{n}{4 k}$ cities. This proves the claim and therefore $m=\left\lceil\frac{n}{4 k}\right\rceil$.
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\nP5.",
"resource_path": "Canada_MO/segmented/en-cmo2023-solutions-en.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2023"
}
|
Let $A B C$ be a triangle with incenter $I$. Suppose the reflection of $A B$ across $C I$ and the reflection of $A C$ across $B I$ intersect at a point $X$. Prove that $X I$ is perpendicular to $B C$.
(The incenter is the point where the three angle bisectors meet.)
|
Suppose the reflection of $A C$ across $B I$ intersects $B C$ at $E$. Define $F$ similarly for the reflection of $A B$ across $C I$. Also suppose $C I$ intersects $A B$ at $M$ and $B I$ intersects $A C$ at $N$. Since $C A$ and $C F=B C$ are reflections across $C I$, and so are $M A$ and $M F=X M$, we have that $A$ and $F$ are reflections across $C I$. Similarly $A$ and $E$ are reflections across $B I$. Thus $\angle X F C=\angle B A C=\angle X E B$ if $\angle B A C$ is acute (and $\angle X F C=\angle X E B=\pi-\angle B A C$, when $\angle B A C$ is obtuse), so $X F=X E$. Moreover we also find that $I F=I A=I E$ by the aforementioned reflection properties, so thus $X I$ is the perpendicular bisector of $E F$ and is hence perpendicular to $B C$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be a triangle with incenter $I$. Suppose the reflection of $A B$ across $C I$ and the reflection of $A C$ across $B I$ intersect at a point $X$. Prove that $X I$ is perpendicular to $B C$.
(The incenter is the point where the three angle bisectors meet.)
|
Suppose the reflection of $A C$ across $B I$ intersects $B C$ at $E$. Define $F$ similarly for the reflection of $A B$ across $C I$. Also suppose $C I$ intersects $A B$ at $M$ and $B I$ intersects $A C$ at $N$. Since $C A$ and $C F=B C$ are reflections across $C I$, and so are $M A$ and $M F=X M$, we have that $A$ and $F$ are reflections across $C I$. Similarly $A$ and $E$ are reflections across $B I$. Thus $\angle X F C=\angle B A C=\angle X E B$ if $\angle B A C$ is acute (and $\angle X F C=\angle X E B=\pi-\angle B A C$, when $\angle B A C$ is obtuse), so $X F=X E$. Moreover we also find that $I F=I A=I E$ by the aforementioned reflection properties, so thus $X I$ is the perpendicular bisector of $E F$ and is hence perpendicular to $B C$.
|
{
"exam": "Canada_MO",
"problem_label": "1",
"problem_match": "\nP1.",
"resource_path": "Canada_MO/segmented/en-cmo2024-solutions-en.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2024"
}
|
Jane writes down 2024 natural numbers around the perimeter of a circle. She wants the 2024 products of adjacent pairs of numbers to be exactly the set $\{1!, 2!, \ldots, 2024!\}$. Can she accomplish this?
|
Given any prime $p$ and positive integer $x$, let $v_{p}(x)$ denote the highest power of $p$ dividing $x$. We claim that Jane cannot write 2024 such numbers as that would imply that $1!\cdot 2!\cdots 2024$ ! is the square of the product of the 2024 numbers. Let $p$ be a prime and $k$ be a natural number such that $k<p, k p \leq 2024$, and $(k+1) p>2024$. Then note that
$$
v_{p}(1!\cdot 2!\cdots 2024!)=(2024-p+1)+(2024-2 p+1)+\ldots+(2024-k p+1)
$$
In particular, let $p$ be in $\left(\frac{2024}{4}, \frac{2024}{2}\right)$. By Bertrand's Postulate, such a prime $p$ exists (and $p$ must also be odd). Further, the corresponding $k$ is either 2 or 3 . Either way, $v_{p}(1!\cdot 2!\cdots 2024$ !) is odd from the above formula, and so $1!\cdot 2!\cdots 2024$ ! cannot be a perfect square.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Jane writes down 2024 natural numbers around the perimeter of a circle. She wants the 2024 products of adjacent pairs of numbers to be exactly the set $\{1!, 2!, \ldots, 2024!\}$. Can she accomplish this?
|
Given any prime $p$ and positive integer $x$, let $v_{p}(x)$ denote the highest power of $p$ dividing $x$. We claim that Jane cannot write 2024 such numbers as that would imply that $1!\cdot 2!\cdots 2024$ ! is the square of the product of the 2024 numbers. Let $p$ be a prime and $k$ be a natural number such that $k<p, k p \leq 2024$, and $(k+1) p>2024$. Then note that
$$
v_{p}(1!\cdot 2!\cdots 2024!)=(2024-p+1)+(2024-2 p+1)+\ldots+(2024-k p+1)
$$
In particular, let $p$ be in $\left(\frac{2024}{4}, \frac{2024}{2}\right)$. By Bertrand's Postulate, such a prime $p$ exists (and $p$ must also be odd). Further, the corresponding $k$ is either 2 or 3 . Either way, $v_{p}(1!\cdot 2!\cdots 2024$ !) is odd from the above formula, and so $1!\cdot 2!\cdots 2024$ ! cannot be a perfect square.
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\nP2.",
"resource_path": "Canada_MO/segmented/en-cmo2024-solutions-en.jsonl",
"solution_match": "\nSolution 1.",
"tier": "T2",
"year": "2024"
}
|
Jane writes down 2024 natural numbers around the perimeter of a circle. She wants the 2024 products of adjacent pairs of numbers to be exactly the set $\{1!, 2!, \ldots, 2024!\}$. Can she accomplish this?
|
As in the first solution, we prove $1!\cdot 2!\cdots 2024$ ! is not a perfect square. To do this, note that we can rewrite the product as $(1!)^{2} \cdot 2 \cdot(3!)^{2} \cdot 4 \cdots(2023!)^{2} \cdot 2024$ which is
$$
2 \cdot 4 \cdots 2024 \cdot(1!\cdot 3!\cdots 2023!)^{2}=1012!\cdot\left(2^{1012} \cdot 1!\cdot 3!\cdots 2023!\right)^{2}
$$
so it is sufficient to verify 1012 ! is not a perfect square. This can be verified by either noticing the prime 1009 only appears as a factor of 1012 ! once, or by evaluating $v_{2}(1012!)=1005$.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Jane writes down 2024 natural numbers around the perimeter of a circle. She wants the 2024 products of adjacent pairs of numbers to be exactly the set $\{1!, 2!, \ldots, 2024!\}$. Can she accomplish this?
|
As in the first solution, we prove $1!\cdot 2!\cdots 2024$ ! is not a perfect square. To do this, note that we can rewrite the product as $(1!)^{2} \cdot 2 \cdot(3!)^{2} \cdot 4 \cdots(2023!)^{2} \cdot 2024$ which is
$$
2 \cdot 4 \cdots 2024 \cdot(1!\cdot 3!\cdots 2023!)^{2}=1012!\cdot\left(2^{1012} \cdot 1!\cdot 3!\cdots 2023!\right)^{2}
$$
so it is sufficient to verify 1012 ! is not a perfect square. This can be verified by either noticing the prime 1009 only appears as a factor of 1012 ! once, or by evaluating $v_{2}(1012!)=1005$.
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\nP2.",
"resource_path": "Canada_MO/segmented/en-cmo2024-solutions-en.jsonl",
"solution_match": "\nSolution 2.",
"tier": "T2",
"year": "2024"
}
|
Let $N$ be the number of positive integers with 10 digits $\overline{d_{9} d_{8} \cdots d_{1} d_{0}}$ in base 10 (where $0 \leq d_{i} \leq 9$ for all $i$ and $d_{9}>0$ ) such that the polynomial
$$
d_{9} x^{9}+d_{8} x^{8}+\cdots+d_{1} x+d_{0}
$$
is irreducible in $\mathbb{Q}$. Prove that $N$ is even.
(A polynomial is irreducible in $\mathbb{Q}$ if it cannot be factored into two non-constant polynomials with rational coefficients.)
|
Let $f(x)=d_{9} x^{9}+d_{8} x^{8}+\cdots+d_{1} x+d_{0}$. If $d_{0}=0$, then $f(x)$ is divisible by $x$ and thus reducible, so we may ignore all such polynomials. The remaining polynomials all have nonzero leading and constant coefficients.
For any polynomial $p(x)$ of degree $n$ with nonzero leading and constant coefficients, say $p(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{1} x+a_{0}$, define $\bar{p}(x)$ to be the reversed polynomial $a_{0} x^{n}+$ $a_{1} x^{n-1}+\cdots+a_{n-1} x+a_{n}$. Observe that $\bar{p}(x)$ also has degree $n$ and furthermore, $\bar{p}(x)=$ $x^{n}\left(a_{0}+a_{1}\left(\frac{1}{x}\right)+\cdots+a_{n-1}\left(\frac{1}{x}\right)^{n-1}+a_{n}\left(\frac{1}{x}\right)^{n}\right)=x^{n} p\left(\frac{1}{x}\right)$.
Consider pairing each $f(x)$ with $\bar{f}(x)$ whenever $f(x) \neq \bar{f}(x)$. If $f(x)$ is reducible, it can be factored as $f(x)=g(x) h(x)$ where $\operatorname{deg} g, \operatorname{deg} h \geq 1$. Because the leading and constant coefficients of $f(x)$ are nonzero, so are the leading and constant coefficients of $g(x)$ and $h(x)$. Hence $\bar{g}(x)$ and $\bar{h}(x)$ are well defined with $\operatorname{deg} \bar{g}=\operatorname{deg} g \geq 1$ and $\operatorname{deg} \bar{h}=\operatorname{deg} h \geq 1$. Furthermore,
$$
\bar{f}(x)=x^{9} f\left(\frac{1}{x}\right)=x^{9} g\left(\frac{1}{x}\right) h\left(\frac{1}{x}\right)=\left(x^{\operatorname{deg} g} g\left(\frac{1}{x}\right)\right)\left(x^{\operatorname{deg} h} h\left(\frac{1}{x}\right)\right)=\bar{g}(x) \bar{h}(x)
$$
Thus $\bar{f}(x)=\bar{g}(x) \bar{h}(x)$ is a factorization of $\bar{f}(x)$ into two non-constant polynomials, so $\bar{f}(x)$ is also reducible. Therefore $f(x)$ is irreducible if and only if $\bar{f}(x)$ is irreducible, so considering each pair, there are an even number of irreducible polynomials with $f(x) \neq \bar{f}(x)$.
Finally, note that if $f(x)=\bar{f}(x)$, then $d_{i}=d_{9-i}$ for each $i$. In such a case, we have $f(-1)=$ $\left(d_{0}-d_{9}\right)+\left(d_{2}-d_{7}\right)+\left(d_{4}-d_{5}\right)+\left(d_{6}-d_{3}\right)+\left(d_{8}-d_{1}\right)=0$, so by the Factor Theorem, $(x+1)$ is a factor of $f(x)$. Therefore these remaining polynomials are all reducible.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $N$ be the number of positive integers with 10 digits $\overline{d_{9} d_{8} \cdots d_{1} d_{0}}$ in base 10 (where $0 \leq d_{i} \leq 9$ for all $i$ and $d_{9}>0$ ) such that the polynomial
$$
d_{9} x^{9}+d_{8} x^{8}+\cdots+d_{1} x+d_{0}
$$
is irreducible in $\mathbb{Q}$. Prove that $N$ is even.
(A polynomial is irreducible in $\mathbb{Q}$ if it cannot be factored into two non-constant polynomials with rational coefficients.)
|
Let $f(x)=d_{9} x^{9}+d_{8} x^{8}+\cdots+d_{1} x+d_{0}$. If $d_{0}=0$, then $f(x)$ is divisible by $x$ and thus reducible, so we may ignore all such polynomials. The remaining polynomials all have nonzero leading and constant coefficients.
For any polynomial $p(x)$ of degree $n$ with nonzero leading and constant coefficients, say $p(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{1} x+a_{0}$, define $\bar{p}(x)$ to be the reversed polynomial $a_{0} x^{n}+$ $a_{1} x^{n-1}+\cdots+a_{n-1} x+a_{n}$. Observe that $\bar{p}(x)$ also has degree $n$ and furthermore, $\bar{p}(x)=$ $x^{n}\left(a_{0}+a_{1}\left(\frac{1}{x}\right)+\cdots+a_{n-1}\left(\frac{1}{x}\right)^{n-1}+a_{n}\left(\frac{1}{x}\right)^{n}\right)=x^{n} p\left(\frac{1}{x}\right)$.
Consider pairing each $f(x)$ with $\bar{f}(x)$ whenever $f(x) \neq \bar{f}(x)$. If $f(x)$ is reducible, it can be factored as $f(x)=g(x) h(x)$ where $\operatorname{deg} g, \operatorname{deg} h \geq 1$. Because the leading and constant coefficients of $f(x)$ are nonzero, so are the leading and constant coefficients of $g(x)$ and $h(x)$. Hence $\bar{g}(x)$ and $\bar{h}(x)$ are well defined with $\operatorname{deg} \bar{g}=\operatorname{deg} g \geq 1$ and $\operatorname{deg} \bar{h}=\operatorname{deg} h \geq 1$. Furthermore,
$$
\bar{f}(x)=x^{9} f\left(\frac{1}{x}\right)=x^{9} g\left(\frac{1}{x}\right) h\left(\frac{1}{x}\right)=\left(x^{\operatorname{deg} g} g\left(\frac{1}{x}\right)\right)\left(x^{\operatorname{deg} h} h\left(\frac{1}{x}\right)\right)=\bar{g}(x) \bar{h}(x)
$$
Thus $\bar{f}(x)=\bar{g}(x) \bar{h}(x)$ is a factorization of $\bar{f}(x)$ into two non-constant polynomials, so $\bar{f}(x)$ is also reducible. Therefore $f(x)$ is irreducible if and only if $\bar{f}(x)$ is irreducible, so considering each pair, there are an even number of irreducible polynomials with $f(x) \neq \bar{f}(x)$.
Finally, note that if $f(x)=\bar{f}(x)$, then $d_{i}=d_{9-i}$ for each $i$. In such a case, we have $f(-1)=$ $\left(d_{0}-d_{9}\right)+\left(d_{2}-d_{7}\right)+\left(d_{4}-d_{5}\right)+\left(d_{6}-d_{3}\right)+\left(d_{8}-d_{1}\right)=0$, so by the Factor Theorem, $(x+1)$ is a factor of $f(x)$. Therefore these remaining polynomials are all reducible.
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\nP3.",
"resource_path": "Canada_MO/segmented/en-cmo2024-solutions-en.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2024"
}
|
Centuries ago, the pirate Captain Blackboard buried a vast amount of treasure in a single cell of an $M \times N(2 \leq M, N)$ grid-structured island. You and your crew have reached the island and have brought special treasure detectors to find the cell with the treasure. For each detector, you can set it up to scan a specific subgrid $[a, b] \times[c, d]$ with $1 \leq a \leq b \leq M$ and $1 \leq c \leq d \leq N$. Running the detector will tell you whether the treasure is in the region or not, though it cannot say where in the region the treasure was detected. You plan on setting up $Q$ detectors, which may only be run simultaneously after all $Q$ detectors are ready. In terms of $M$ and $N$, what is the minimum $Q$ required to guarantee your crew can determine the location of Blackboard's legendary treasure?
|
Let $m=\left\lceil\frac{M}{2}\right\rceil$ and $n=\left\lceil\frac{N}{2}\right\rceil$. We claim that the minimal $Q$ is $m+n$. For the construction, start with $m$ detectors covering $[i, i+m-1] \times[1, N]$ for $1 \leq i \leq m$. For every pair of rows, there is a detector that covers one row but not the other, hence this determines the row of the treasure. Similarly, placing $n$ detectors covering $[1, M] \times[i, i+n-1]$ for $1 \leq i \leq n$ determines the column, and thus the location of the treasure.
For the bound, we require the following lemma.
Lemma. $A 1 \times k$ island requires at least $\left\lceil\frac{k}{2}\right\rceil$ detectors.
Proof. Consider the $k-1$ lines separating the cells. If one of these lines is not covered by any detector, then these cells are indistinguishable. Similarly, if neither of the vertical lines at the ends are covered, then the first and last cells are indistinguishable. In particular, at least $k$ vertical lines need to be covered by the detectors. A detector covers 2 vertical lines, giving the result.
In general, consider the first row. Since the cells are distinguishable, by the lemma there must be at least $n$ detectors that intersect it non-trivially (as in, cover between 1 and $N-1$ of the cells). The analogous result holds for the last row and the first/last columns, giving $2 m+2 n$ detectors, where a detector may be counted multiple times.
If a detector intersected at least three of these sets, say it intersected the first row and the first and last columns. Therefore it covers the entire width of the island, and does not actually distinguish any cells in the first row, contradiction.
Therefore each detector contributes to at most 2 of the above $2 m+2 n$ detectors, giving the final lower bound of $\frac{2 m+2 n}{2}=m+n$ detectors required, as desired.
|
m+n
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Centuries ago, the pirate Captain Blackboard buried a vast amount of treasure in a single cell of an $M \times N(2 \leq M, N)$ grid-structured island. You and your crew have reached the island and have brought special treasure detectors to find the cell with the treasure. For each detector, you can set it up to scan a specific subgrid $[a, b] \times[c, d]$ with $1 \leq a \leq b \leq M$ and $1 \leq c \leq d \leq N$. Running the detector will tell you whether the treasure is in the region or not, though it cannot say where in the region the treasure was detected. You plan on setting up $Q$ detectors, which may only be run simultaneously after all $Q$ detectors are ready. In terms of $M$ and $N$, what is the minimum $Q$ required to guarantee your crew can determine the location of Blackboard's legendary treasure?
|
Let $m=\left\lceil\frac{M}{2}\right\rceil$ and $n=\left\lceil\frac{N}{2}\right\rceil$. We claim that the minimal $Q$ is $m+n$. For the construction, start with $m$ detectors covering $[i, i+m-1] \times[1, N]$ for $1 \leq i \leq m$. For every pair of rows, there is a detector that covers one row but not the other, hence this determines the row of the treasure. Similarly, placing $n$ detectors covering $[1, M] \times[i, i+n-1]$ for $1 \leq i \leq n$ determines the column, and thus the location of the treasure.
For the bound, we require the following lemma.
Lemma. $A 1 \times k$ island requires at least $\left\lceil\frac{k}{2}\right\rceil$ detectors.
Proof. Consider the $k-1$ lines separating the cells. If one of these lines is not covered by any detector, then these cells are indistinguishable. Similarly, if neither of the vertical lines at the ends are covered, then the first and last cells are indistinguishable. In particular, at least $k$ vertical lines need to be covered by the detectors. A detector covers 2 vertical lines, giving the result.
In general, consider the first row. Since the cells are distinguishable, by the lemma there must be at least $n$ detectors that intersect it non-trivially (as in, cover between 1 and $N-1$ of the cells). The analogous result holds for the last row and the first/last columns, giving $2 m+2 n$ detectors, where a detector may be counted multiple times.
If a detector intersected at least three of these sets, say it intersected the first row and the first and last columns. Therefore it covers the entire width of the island, and does not actually distinguish any cells in the first row, contradiction.
Therefore each detector contributes to at most 2 of the above $2 m+2 n$ detectors, giving the final lower bound of $\frac{2 m+2 n}{2}=m+n$ detectors required, as desired.
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\nP4.",
"resource_path": "Canada_MO/segmented/en-cmo2024-solutions-en.jsonl",
"solution_match": "\nSolution 1.",
"tier": "T2",
"year": "2024"
}
|
Centuries ago, the pirate Captain Blackboard buried a vast amount of treasure in a single cell of an $M \times N(2 \leq M, N)$ grid-structured island. You and your crew have reached the island and have brought special treasure detectors to find the cell with the treasure. For each detector, you can set it up to scan a specific subgrid $[a, b] \times[c, d]$ with $1 \leq a \leq b \leq M$ and $1 \leq c \leq d \leq N$. Running the detector will tell you whether the treasure is in the region or not, though it cannot say where in the region the treasure was detected. You plan on setting up $Q$ detectors, which may only be run simultaneously after all $Q$ detectors are ready. In terms of $M$ and $N$, what is the minimum $Q$ required to guarantee your crew can determine the location of Blackboard's legendary treasure?
|
The following alternative approach from CMO competitor Marvin Mao of Bergen County Academies is another full solution.
Take the same construction as in Solution 1. For the bound, consider the following sets:
- $S_{\mathrm{CR}}:=\{\{(1,1),(1, N)\},\{(M, 1),(M, N)\}\}$, i.e. the pairs of corners on the same row;
- $S_{\mathrm{CC}}:=\{\{(1,1),(M, 1)\},\{(1, N),(M, N)\}\}$, i.e. the pairs of corners on the same column;
- $S_{\mathrm{R}}:=\{\{(x, i),(x, i+1)\}: x \in\{1, M\}, 1 \leq i \leq N-1\}$, i.e. the pairs of adjacent edges on the first/last row;
- $S_{\mathrm{C}}:=\{\{(i, x),(i+1, x)\}: 1 \leq i \leq M-1, x \in\{1, N\}$, $\}$, i.e. the pairs of adjacent edges on the first/last column.
For each detector, we assign it a score $\left(x_{\mathrm{CR}}, x_{\mathrm{CC}}, x_{\mathrm{R}}, x_{\mathrm{C}}\right)$, where $x_{\mathrm{i}}$ is the number of pairs of cells in $S_{\mathrm{i}}$ for which the detector covers exactly one of the two cells. The possible scores of the detectors are as follows:
| What the detector hits | Score |
| :---: | :---: |
| No edges | $(0,0,0,0)$ |
| One edge, no corners | $(0,0,2,0)$ or $(0,0,0,2)$ |
| Two edges, no corners | $(0,0,4,0)$ or $(0,0,0,4)$ |
| One corner | $(1,1,1,1)$ |
| Two corners | $(2,0,2,0)$ or $(0,2,0,2)$ |
| $>2$ corners or edges | $(0,0,0,0)$ |
In order to determine the treasure, the total component-wise sum of scores of the detectors needs to be at least $(2,2,2 N-2,2 M-2)$, since we need to tell apart each of the pairs of cells. The sum of these components is $2 M+2 N$, and based on the analysis above, each detector adds a total component sum of at most 4 , giving at least $\left\lceil\frac{2 M+2 N}{4}\right\rceil=\left\lceil\frac{M+N}{2}\right\rceil$ detectors.
This is equal to $\left\lceil\frac{M}{2}\right\rceil+\left\lceil\frac{N}{2}\right\rceil$ except if both $M, N$ are odd. In this case, if there is at least one more detector, then we have the required bound, so assume otherwise. In particular, we must achieve exactly the score $(2,2,2 N-2,2 M-2)$, with each detector contributing 4 to the total component sum.
In particular, to fill out the first two components, we must either have two detectors scoring $(1,1,1,1)$, or two detectors scoring $(2,0,2,0)$ and $(0,2,0,2)$. This yields a total score of $(2,2,2,2)$, leaving us with achieving exactly $(0,0,2 N-4,2 M-4)$ from the rest. Since we cannot have a non-zero score in the first two entries and must have a total component sum of 4 , we can only use detectors scoring $(0,0,4,0)$ or $(0,0,0,4)$. But $2 N-4,2 M-4 \equiv 2$ $(\bmod 4)$, which is a contradiction.
Therefore all situations require at least $\left\lceil\frac{M}{2}\right\rceil+\left\lceil\frac{N}{2}\right\rceil$ detectors.
|
\left\lceil\frac{M}{2}\right\rceil+\left\lceil\frac{N}{2}\right\rceil
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Centuries ago, the pirate Captain Blackboard buried a vast amount of treasure in a single cell of an $M \times N(2 \leq M, N)$ grid-structured island. You and your crew have reached the island and have brought special treasure detectors to find the cell with the treasure. For each detector, you can set it up to scan a specific subgrid $[a, b] \times[c, d]$ with $1 \leq a \leq b \leq M$ and $1 \leq c \leq d \leq N$. Running the detector will tell you whether the treasure is in the region or not, though it cannot say where in the region the treasure was detected. You plan on setting up $Q$ detectors, which may only be run simultaneously after all $Q$ detectors are ready. In terms of $M$ and $N$, what is the minimum $Q$ required to guarantee your crew can determine the location of Blackboard's legendary treasure?
|
The following alternative approach from CMO competitor Marvin Mao of Bergen County Academies is another full solution.
Take the same construction as in Solution 1. For the bound, consider the following sets:
- $S_{\mathrm{CR}}:=\{\{(1,1),(1, N)\},\{(M, 1),(M, N)\}\}$, i.e. the pairs of corners on the same row;
- $S_{\mathrm{CC}}:=\{\{(1,1),(M, 1)\},\{(1, N),(M, N)\}\}$, i.e. the pairs of corners on the same column;
- $S_{\mathrm{R}}:=\{\{(x, i),(x, i+1)\}: x \in\{1, M\}, 1 \leq i \leq N-1\}$, i.e. the pairs of adjacent edges on the first/last row;
- $S_{\mathrm{C}}:=\{\{(i, x),(i+1, x)\}: 1 \leq i \leq M-1, x \in\{1, N\}$, $\}$, i.e. the pairs of adjacent edges on the first/last column.
For each detector, we assign it a score $\left(x_{\mathrm{CR}}, x_{\mathrm{CC}}, x_{\mathrm{R}}, x_{\mathrm{C}}\right)$, where $x_{\mathrm{i}}$ is the number of pairs of cells in $S_{\mathrm{i}}$ for which the detector covers exactly one of the two cells. The possible scores of the detectors are as follows:
| What the detector hits | Score |
| :---: | :---: |
| No edges | $(0,0,0,0)$ |
| One edge, no corners | $(0,0,2,0)$ or $(0,0,0,2)$ |
| Two edges, no corners | $(0,0,4,0)$ or $(0,0,0,4)$ |
| One corner | $(1,1,1,1)$ |
| Two corners | $(2,0,2,0)$ or $(0,2,0,2)$ |
| $>2$ corners or edges | $(0,0,0,0)$ |
In order to determine the treasure, the total component-wise sum of scores of the detectors needs to be at least $(2,2,2 N-2,2 M-2)$, since we need to tell apart each of the pairs of cells. The sum of these components is $2 M+2 N$, and based on the analysis above, each detector adds a total component sum of at most 4 , giving at least $\left\lceil\frac{2 M+2 N}{4}\right\rceil=\left\lceil\frac{M+N}{2}\right\rceil$ detectors.
This is equal to $\left\lceil\frac{M}{2}\right\rceil+\left\lceil\frac{N}{2}\right\rceil$ except if both $M, N$ are odd. In this case, if there is at least one more detector, then we have the required bound, so assume otherwise. In particular, we must achieve exactly the score $(2,2,2 N-2,2 M-2)$, with each detector contributing 4 to the total component sum.
In particular, to fill out the first two components, we must either have two detectors scoring $(1,1,1,1)$, or two detectors scoring $(2,0,2,0)$ and $(0,2,0,2)$. This yields a total score of $(2,2,2,2)$, leaving us with achieving exactly $(0,0,2 N-4,2 M-4)$ from the rest. Since we cannot have a non-zero score in the first two entries and must have a total component sum of 4 , we can only use detectors scoring $(0,0,4,0)$ or $(0,0,0,4)$. But $2 N-4,2 M-4 \equiv 2$ $(\bmod 4)$, which is a contradiction.
Therefore all situations require at least $\left\lceil\frac{M}{2}\right\rceil+\left\lceil\frac{N}{2}\right\rceil$ detectors.
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\nP4.",
"resource_path": "Canada_MO/segmented/en-cmo2024-solutions-en.jsonl",
"solution_match": "\nSolution 2.",
"tier": "T2",
"year": "2024"
}
|
Initially, three non-collinear points, $A, B$, and $C$, are marked on the plane. You have a pencil and a double-edged ruler of width 1. Using them, you may perform the following operations:
- Mark an arbitrary point in the plane.
- Mark an arbitrary point on an already drawn line.
- If two points $P_{1}$ and $P_{2}$ are marked, draw the line connecting $P_{1}$ and $P_{2}$.
- If two non-parallel lines $\ell_{1}$ and $\ell_{2}$ are drawn, mark the intersection of $\ell_{1}$ and $\ell_{2}$.
- If a line $\ell$ is drawn, draw a line parallel to $\ell$ that is at distance 1 away from $\ell$ (note that two such lines may be drawn).
Prove that it is possible to mark the orthocenter of $A B C$ using these operations.
|
Claim 1. It is possible to draw internal/external angle bisectors.
Proof. Let $A, B, C$ be marked. To bisect $\angle A B C$, draw the parallel line to $A B$ unit 1 away from it on the opposite side as $C$, and draw the parallel line to $B C$ unit 1 away from it on the opposite side as $A$. Let these lines intersect at $D$. Then $B D$ is the internal angle bisector of $\angle A B C$. We can construct external angle bisectors similarly by drawing the line on the same side as $A$ for the second line instead.
Corollary 2. It is possible to mark the incenters and excenters of a triangle $A B C$.
Proof. Draw in the internal/external bisectors of all three angles and intersect them.
Claim 3. It is possible to mark the midpoint of any segment $A B$.
Proof. Let $B$ and $C$ be marked. Draw an arbitrary point $A$ not on line $B C$. Draw a line parallel to $B C$ unit 1 away from it on the opposite side as $A$, and let this line intersect $A B$ at $D$ and $A C$ at $E$. Let $B E$ and $C D$ intersect at $F$, and let $A F$ intersect $B C$ at $M$. Then by Ceva's Theorem, $M$ is the midpoint of $B C$.
Corollary 4. It is possible to mark the centroid of $A B C$.
Proof. Draw the midpoint $D$ of $B C$ and the midpoint $E$ of $A C$, and intersect $A D$ with BE.
Claim 5. It is possible to draw the perpendicular bisector of any segment BC.
Proof. Let $B$ and $C$ be marked. Draw an arbitrary point $A$ not on line $B C$. Construct the incenter $I$ and $A$-excenter $I_{A}$ of $A B C$. Draw the midpoint $M$ of $B C$ and midpoint $N$ of $I I_{A}$. By the incenter-excenter lemma, $N$ is the midpoint of the $\operatorname{arc} \overparen{B C}$ not containing $A$, so $M N$ is the perpendicular bisector of $B C$.
Corollary 6. It is possible to mark the circumcenter of $A B C$.
Proof. Draw and intersect the perpendicular bisectors of $B C$ and $A C$.
Claim 7. Given two marked points $A$ and $B$, it is possible to mark the point $C$ such that $\overrightarrow{B C}=\frac{1}{2} \overrightarrow{A B}$.
Proof. Draw an arbitrary point $D$ not on line $A B$. Draw the midpoint $M$ of $A D$. Draw the midpoint $M_{1}$ of $B D$ and the midpoint $M_{2}$ of $M D$, and let $M_{1} M_{2}$ intersect $A B$ at $C$. Then $M_{1} M_{2} \| B M$ and $M M_{2}=\frac{1}{2} M D=\frac{1}{2} A M$, so $B C=\frac{1}{2} A B$.
Claim 8. Given two marked points $A$ and $B$ and any positive real number $k$ such that $2 k \in \mathbb{Z}$, it is possible to mark the point $C$ such that $\overrightarrow{B C}=k \overrightarrow{A B}$.
Proof. Note that by applying Claim 7 and marking the midpoint of $A B$, we can translate both $A$ and $B$ by $\frac{1}{2} \overrightarrow{A B}$. The claim now follows by applying this operation repeatedly.
To finish, take the given triangle $A B C$ and mark its circumcenter $O$ and centroid $G$. Note that its orthocenter $H$ satisfies that $\overrightarrow{G H}=2 \overrightarrow{O G}$, so applying Claim 8 to $k=2$ now finishes the problem.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Initially, three non-collinear points, $A, B$, and $C$, are marked on the plane. You have a pencil and a double-edged ruler of width 1. Using them, you may perform the following operations:
- Mark an arbitrary point in the plane.
- Mark an arbitrary point on an already drawn line.
- If two points $P_{1}$ and $P_{2}$ are marked, draw the line connecting $P_{1}$ and $P_{2}$.
- If two non-parallel lines $\ell_{1}$ and $\ell_{2}$ are drawn, mark the intersection of $\ell_{1}$ and $\ell_{2}$.
- If a line $\ell$ is drawn, draw a line parallel to $\ell$ that is at distance 1 away from $\ell$ (note that two such lines may be drawn).
Prove that it is possible to mark the orthocenter of $A B C$ using these operations.
|
Claim 1. It is possible to draw internal/external angle bisectors.
Proof. Let $A, B, C$ be marked. To bisect $\angle A B C$, draw the parallel line to $A B$ unit 1 away from it on the opposite side as $C$, and draw the parallel line to $B C$ unit 1 away from it on the opposite side as $A$. Let these lines intersect at $D$. Then $B D$ is the internal angle bisector of $\angle A B C$. We can construct external angle bisectors similarly by drawing the line on the same side as $A$ for the second line instead.
Corollary 2. It is possible to mark the incenters and excenters of a triangle $A B C$.
Proof. Draw in the internal/external bisectors of all three angles and intersect them.
Claim 3. It is possible to mark the midpoint of any segment $A B$.
Proof. Let $B$ and $C$ be marked. Draw an arbitrary point $A$ not on line $B C$. Draw a line parallel to $B C$ unit 1 away from it on the opposite side as $A$, and let this line intersect $A B$ at $D$ and $A C$ at $E$. Let $B E$ and $C D$ intersect at $F$, and let $A F$ intersect $B C$ at $M$. Then by Ceva's Theorem, $M$ is the midpoint of $B C$.
Corollary 4. It is possible to mark the centroid of $A B C$.
Proof. Draw the midpoint $D$ of $B C$ and the midpoint $E$ of $A C$, and intersect $A D$ with BE.
Claim 5. It is possible to draw the perpendicular bisector of any segment BC.
Proof. Let $B$ and $C$ be marked. Draw an arbitrary point $A$ not on line $B C$. Construct the incenter $I$ and $A$-excenter $I_{A}$ of $A B C$. Draw the midpoint $M$ of $B C$ and midpoint $N$ of $I I_{A}$. By the incenter-excenter lemma, $N$ is the midpoint of the $\operatorname{arc} \overparen{B C}$ not containing $A$, so $M N$ is the perpendicular bisector of $B C$.
Corollary 6. It is possible to mark the circumcenter of $A B C$.
Proof. Draw and intersect the perpendicular bisectors of $B C$ and $A C$.
Claim 7. Given two marked points $A$ and $B$, it is possible to mark the point $C$ such that $\overrightarrow{B C}=\frac{1}{2} \overrightarrow{A B}$.
Proof. Draw an arbitrary point $D$ not on line $A B$. Draw the midpoint $M$ of $A D$. Draw the midpoint $M_{1}$ of $B D$ and the midpoint $M_{2}$ of $M D$, and let $M_{1} M_{2}$ intersect $A B$ at $C$. Then $M_{1} M_{2} \| B M$ and $M M_{2}=\frac{1}{2} M D=\frac{1}{2} A M$, so $B C=\frac{1}{2} A B$.
Claim 8. Given two marked points $A$ and $B$ and any positive real number $k$ such that $2 k \in \mathbb{Z}$, it is possible to mark the point $C$ such that $\overrightarrow{B C}=k \overrightarrow{A B}$.
Proof. Note that by applying Claim 7 and marking the midpoint of $A B$, we can translate both $A$ and $B$ by $\frac{1}{2} \overrightarrow{A B}$. The claim now follows by applying this operation repeatedly.
To finish, take the given triangle $A B C$ and mark its circumcenter $O$ and centroid $G$. Note that its orthocenter $H$ satisfies that $\overrightarrow{G H}=2 \overrightarrow{O G}$, so applying Claim 8 to $k=2$ now finishes the problem.
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\nP5.",
"resource_path": "Canada_MO/segmented/en-cmo2024-solutions-en.jsonl",
"solution_match": "\n## Solution 1.",
"tier": "T2",
"year": "2024"
}
|
Initially, three non-collinear points, $A, B$, and $C$, are marked on the plane. You have a pencil and a double-edged ruler of width 1. Using them, you may perform the following operations:
- Mark an arbitrary point in the plane.
- Mark an arbitrary point on an already drawn line.
- If two points $P_{1}$ and $P_{2}$ are marked, draw the line connecting $P_{1}$ and $P_{2}$.
- If two non-parallel lines $\ell_{1}$ and $\ell_{2}$ are drawn, mark the intersection of $\ell_{1}$ and $\ell_{2}$.
- If a line $\ell$ is drawn, draw a line parallel to $\ell$ that is at distance 1 away from $\ell$ (note that two such lines may be drawn).
Prove that it is possible to mark the orthocenter of $A B C$ using these operations.
|
Ming Yang of Brophy College Preparatory submitted the following short, elegant solution which also creates tools that are able to extend beyond the problem. This solution has been designated by the CMO as the Best Solution for 2024 and earns Ming Yang the Matthew Brennan Award this year.
Start with Claims 1-3 of solution 1, allowing us to draw internal/external angle bisectors, in/excentres, and midpoints. We add one more claim.
Claim 9. Given a point $P$ and a line $\ell_{1}$, it is possible to draw a line through $P$ parallel to $\ell_{1}$.
Proof. Draw the line $\ell_{2}$ on the opposite side of $\ell_{1}$ to $P$, a distance 1 away. Draw arbitrary lines $P A B$ and $P C D$ with $A, C \in \ell_{1}, B, D \in \ell_{2}$. Let $E$ be the midpoint of $A C$, let $F=P E \cap \ell_{2}$, and let $Q=B E \cap F C$.
Since $\triangle Q E C \sim \triangle Q B F$ and $\triangle P A E \sim \triangle P B F$, we have
$$
\frac{Q E}{Q B}=\frac{E C}{B F}=\frac{A E}{B F}=\frac{P A}{P B}
$$
so $\triangle B A E \sim \triangle B P Q$. In particular, $P Q$ is parallel to $A E$, as desired.
In triangle $\triangle A B C$, draw the incentre $I$ and $A$-excentre $I_{A}$. Draw the midpoints $D$ of $B C$ and $M$ of $I I_{A}$. By the incentre-excentre lemma, $M$ is on the perpendicular bisector of $B C$, so $M D$ is perpendicular to $B C$. Finally, using Claim 9, we can draw a line through $A$ that is perpendicular to $B C$. Repeat this for $B$ and $A C$, and their intersection is the orthocentre of $\triangle A B C$, as required.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Initially, three non-collinear points, $A, B$, and $C$, are marked on the plane. You have a pencil and a double-edged ruler of width 1. Using them, you may perform the following operations:
- Mark an arbitrary point in the plane.
- Mark an arbitrary point on an already drawn line.
- If two points $P_{1}$ and $P_{2}$ are marked, draw the line connecting $P_{1}$ and $P_{2}$.
- If two non-parallel lines $\ell_{1}$ and $\ell_{2}$ are drawn, mark the intersection of $\ell_{1}$ and $\ell_{2}$.
- If a line $\ell$ is drawn, draw a line parallel to $\ell$ that is at distance 1 away from $\ell$ (note that two such lines may be drawn).
Prove that it is possible to mark the orthocenter of $A B C$ using these operations.
|
Ming Yang of Brophy College Preparatory submitted the following short, elegant solution which also creates tools that are able to extend beyond the problem. This solution has been designated by the CMO as the Best Solution for 2024 and earns Ming Yang the Matthew Brennan Award this year.
Start with Claims 1-3 of solution 1, allowing us to draw internal/external angle bisectors, in/excentres, and midpoints. We add one more claim.
Claim 9. Given a point $P$ and a line $\ell_{1}$, it is possible to draw a line through $P$ parallel to $\ell_{1}$.
Proof. Draw the line $\ell_{2}$ on the opposite side of $\ell_{1}$ to $P$, a distance 1 away. Draw arbitrary lines $P A B$ and $P C D$ with $A, C \in \ell_{1}, B, D \in \ell_{2}$. Let $E$ be the midpoint of $A C$, let $F=P E \cap \ell_{2}$, and let $Q=B E \cap F C$.
Since $\triangle Q E C \sim \triangle Q B F$ and $\triangle P A E \sim \triangle P B F$, we have
$$
\frac{Q E}{Q B}=\frac{E C}{B F}=\frac{A E}{B F}=\frac{P A}{P B}
$$
so $\triangle B A E \sim \triangle B P Q$. In particular, $P Q$ is parallel to $A E$, as desired.
In triangle $\triangle A B C$, draw the incentre $I$ and $A$-excentre $I_{A}$. Draw the midpoints $D$ of $B C$ and $M$ of $I I_{A}$. By the incentre-excentre lemma, $M$ is on the perpendicular bisector of $B C$, so $M D$ is perpendicular to $B C$. Finally, using Claim 9, we can draw a line through $A$ that is perpendicular to $B C$. Repeat this for $B$ and $A C$, and their intersection is the orthocentre of $\triangle A B C$, as required.
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\nP5.",
"resource_path": "Canada_MO/segmented/en-cmo2024-solutions-en.jsonl",
"solution_match": "\nSolution 2.",
"tier": "T2",
"year": "2024"
}
|
Let $S$ be a subset of $\{1,2, \ldots, 9\}$, such that the sums formed by adding each unordered pair of distinct numbers from $S$ are all different. For example, the subset $\{1,2,3,5\}$ has this property, but $\{1,2,3,4,5\}$ does not, since the pairs $\{1,4\}$ and $\{2,3\}$ have the same sum, namely 5 .
What is the maximum number of elements that $S$ can contain?
|
It can be checked that all the sums of pairs for the set $\{1,2,3,5,8\}$ are different.
Suppose, for a contradiction, that $S$ is a subset of $\{1, \ldots, 9\}$ containing 6 elements such that all the sums of pairs are different. Now the smallest possible sum for two numbers from $S$ is $1+2=3$ and the largest possible sum is $8+9=17$. That gives 15 possible sums: $3, \ldots, 17$.
Also there are $\left(\begin{array}{l}6 \\ 2\end{array}\right)=15$ pairs from $S$. Thus, each of $3, \ldots, 17$ is the sum of exactly one pair. The only pair from $\{1, \ldots, 9\}$ that adds to 3 is $\{1,2\}$ and to 17 is $\{8,9\}$. Thus $1,2,8,9$ are in $S$. But then $1+9=2+8$, giving a contradiction. It follows that the maximum number of elements that $S$ can contain is 5 .
|
5
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $S$ be a subset of $\{1,2, \ldots, 9\}$, such that the sums formed by adding each unordered pair of distinct numbers from $S$ are all different. For example, the subset $\{1,2,3,5\}$ has this property, but $\{1,2,3,4,5\}$ does not, since the pairs $\{1,4\}$ and $\{2,3\}$ have the same sum, namely 5 .
What is the maximum number of elements that $S$ can contain?
|
It can be checked that all the sums of pairs for the set $\{1,2,3,5,8\}$ are different.
Suppose, for a contradiction, that $S$ is a subset of $\{1, \ldots, 9\}$ containing 6 elements such that all the sums of pairs are different. Now the smallest possible sum for two numbers from $S$ is $1+2=3$ and the largest possible sum is $8+9=17$. That gives 15 possible sums: $3, \ldots, 17$.
Also there are $\left(\begin{array}{l}6 \\ 2\end{array}\right)=15$ pairs from $S$. Thus, each of $3, \ldots, 17$ is the sum of exactly one pair. The only pair from $\{1, \ldots, 9\}$ that adds to 3 is $\{1,2\}$ and to 17 is $\{8,9\}$. Thus $1,2,8,9$ are in $S$. But then $1+9=2+8$, giving a contradiction. It follows that the maximum number of elements that $S$ can contain is 5 .
|
{
"exam": "Canada_MO",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "Canada_MO/segmented/en-sol2002.jsonl",
"solution_match": "\n## Solution 1",
"tier": "T2",
"year": "2002"
}
|
Let $S$ be a subset of $\{1,2, \ldots, 9\}$, such that the sums formed by adding each unordered pair of distinct numbers from $S$ are all different. For example, the subset $\{1,2,3,5\}$ has this property, but $\{1,2,3,4,5\}$ does not, since the pairs $\{1,4\}$ and $\{2,3\}$ have the same sum, namely 5 .
What is the maximum number of elements that $S$ can contain?
|
It can be checked that all the sums of pairs for the set $\{1,2,3,5,8\}$ are different.
Suppose, for a contradiction, that $S$ is a subset of $\{1, \ldots 9\}$ such that all the sums of pairs are different and that $a_{1}<a_{2}<\ldots<a_{6}$ are the members of $S$.
Since $a_{1}+a_{6} \neq a_{2}+a_{5}$, it follows that $a_{6}-a_{5} \neq a_{2}-a_{1}$. Similarly $a_{6}-a_{5} \neq a_{4}-a_{3}$ and $a_{4}-a_{3} \neq a_{2}-a_{1}$. These three differences must be distinct positive integers, so,
$$
\left(a_{6}-a_{5}\right)+\left(a_{4}-a_{3}\right)+\left(a_{2}-a_{1}\right) \geq 1+2+3=6 .
$$
Similarly $a_{3}-a_{2} \neq a_{5}-a_{4}$, so
$$
\left(a_{3}-a_{2}\right)+\left(a_{5}-a_{4}\right) \geq 1+2=3 .
$$
Adding the above 2 inequalities yields
$$
a_{6}-a_{5}+a_{5}-a_{4}+a_{4}-a_{3}+a_{3}-a_{2}+a_{2}-a_{1} \geq 6+3=9,
$$
and hence $a_{6}-a_{1} \geq 9$. This is impossible since the numbers in $S$ are between 1 and 9 .
|
5
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $S$ be a subset of $\{1,2, \ldots, 9\}$, such that the sums formed by adding each unordered pair of distinct numbers from $S$ are all different. For example, the subset $\{1,2,3,5\}$ has this property, but $\{1,2,3,4,5\}$ does not, since the pairs $\{1,4\}$ and $\{2,3\}$ have the same sum, namely 5 .
What is the maximum number of elements that $S$ can contain?
|
It can be checked that all the sums of pairs for the set $\{1,2,3,5,8\}$ are different.
Suppose, for a contradiction, that $S$ is a subset of $\{1, \ldots 9\}$ such that all the sums of pairs are different and that $a_{1}<a_{2}<\ldots<a_{6}$ are the members of $S$.
Since $a_{1}+a_{6} \neq a_{2}+a_{5}$, it follows that $a_{6}-a_{5} \neq a_{2}-a_{1}$. Similarly $a_{6}-a_{5} \neq a_{4}-a_{3}$ and $a_{4}-a_{3} \neq a_{2}-a_{1}$. These three differences must be distinct positive integers, so,
$$
\left(a_{6}-a_{5}\right)+\left(a_{4}-a_{3}\right)+\left(a_{2}-a_{1}\right) \geq 1+2+3=6 .
$$
Similarly $a_{3}-a_{2} \neq a_{5}-a_{4}$, so
$$
\left(a_{3}-a_{2}\right)+\left(a_{5}-a_{4}\right) \geq 1+2=3 .
$$
Adding the above 2 inequalities yields
$$
a_{6}-a_{5}+a_{5}-a_{4}+a_{4}-a_{3}+a_{3}-a_{2}+a_{2}-a_{1} \geq 6+3=9,
$$
and hence $a_{6}-a_{1} \geq 9$. This is impossible since the numbers in $S$ are between 1 and 9 .
|
{
"exam": "Canada_MO",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "Canada_MO/segmented/en-sol2002.jsonl",
"solution_match": "\n## Solution 2.",
"tier": "T2",
"year": "2002"
}
|
Call a positive integer $n$ practical if every positive integer less than or equal to $n$ can be written as the sum of distinct divisors of $n$.
For example, the divisors of 6 are $\mathbf{1 , 2}, \mathbf{3}$, and $\mathbf{6}$. Since
$$
1=\mathbf{1}, \quad 2=\mathbf{2}, \quad 3=\mathbf{3}, \quad 4=\mathbf{1}+\mathbf{3}, \quad 5=\mathbf{2}+\mathbf{3}, \quad 6=\mathbf{6},
$$
we see that 6 is practical.
Prove that the product of two practical numbers is also practical.
|
Let $p$ and $q$ be practical. For any $k \leq p q$, we can write
$$
k=a q+b \text { with } 0 \leq a \leq p, 0 \leq b<q .
$$
Since $p$ and $q$ are practical, we can write
$$
a=c_{1}+\ldots+c_{m}, \quad b=d_{1}+\ldots+d_{n}
$$
where the $c_{i}$ 's are distinct divisors of $p$ and the $d_{j}$ 's are distinct divisors of $q$. Now
$$
\begin{aligned}
k & =\left(c_{1}+\ldots+c_{m}\right) q+\left(d_{1}+\ldots+d_{n}\right) \\
& =c_{1} q+\ldots+c_{m} q+d_{1}+\ldots+d_{n} .
\end{aligned}
$$
Each of $c_{i} q$ and $d_{j}$ divides $p q$. Since $d_{j}<q \leq c_{i} q$ for any $i, j$, the $c_{i} q$ 's and $d_{j}$ 's are all distinct, and we conclude that $p q$ is practical.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Call a positive integer $n$ practical if every positive integer less than or equal to $n$ can be written as the sum of distinct divisors of $n$.
For example, the divisors of 6 are $\mathbf{1 , 2}, \mathbf{3}$, and $\mathbf{6}$. Since
$$
1=\mathbf{1}, \quad 2=\mathbf{2}, \quad 3=\mathbf{3}, \quad 4=\mathbf{1}+\mathbf{3}, \quad 5=\mathbf{2}+\mathbf{3}, \quad 6=\mathbf{6},
$$
we see that 6 is practical.
Prove that the product of two practical numbers is also practical.
|
Let $p$ and $q$ be practical. For any $k \leq p q$, we can write
$$
k=a q+b \text { with } 0 \leq a \leq p, 0 \leq b<q .
$$
Since $p$ and $q$ are practical, we can write
$$
a=c_{1}+\ldots+c_{m}, \quad b=d_{1}+\ldots+d_{n}
$$
where the $c_{i}$ 's are distinct divisors of $p$ and the $d_{j}$ 's are distinct divisors of $q$. Now
$$
\begin{aligned}
k & =\left(c_{1}+\ldots+c_{m}\right) q+\left(d_{1}+\ldots+d_{n}\right) \\
& =c_{1} q+\ldots+c_{m} q+d_{1}+\ldots+d_{n} .
\end{aligned}
$$
Each of $c_{i} q$ and $d_{j}$ divides $p q$. Since $d_{j}<q \leq c_{i} q$ for any $i, j$, the $c_{i} q$ 's and $d_{j}$ 's are all distinct, and we conclude that $p q$ is practical.
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "Canada_MO/segmented/en-sol2002.jsonl",
"solution_match": "\n## Solution\n\n",
"tier": "T2",
"year": "2002"
}
|
Prove that for all positive real numbers $a, b$, and $c$,
$$
\frac{a^{3}}{b c}+\frac{b^{3}}{c a}+\frac{c^{3}}{a b} \geq a+b+c
$$
and determine when equality occurs.
Each of the inequalities used in the solutions below has the property that equality holds if and only if $a=b=c$. Thus equality holds for the given inequality if and only if $a=b=c$.
|
Note that $a^{4}+b^{4}+c^{4}=\frac{\left(a^{4}+b^{4}\right)}{2}+\frac{\left(b^{4}+c^{4}\right)}{2}+\frac{\left(c^{4}+a^{4}\right)}{2}$. Applying the arithmetic-geometric mean inequality to each term, we see that the right side is greater than or equal to
$$
a^{2} b^{2}+b^{2} c^{2}+c^{2} a^{2} \text {. }
$$
We can rewrite this as
$$
\frac{a^{2}\left(b^{2}+c^{2}\right)}{2}+\frac{b^{2}\left(c^{2}+a^{2}\right)}{2}+\frac{c^{2}\left(a^{2}+b^{2}\right)}{2} .
$$
Applying the arithmetic mean-geometric mean inequality again we obtain $a^{4}+b^{4}+c^{4} \geq$ $a^{2} b c+b^{2} c a+c^{2} a b$. Dividing both sides by $a b c$ (which is positive) the result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that for all positive real numbers $a, b$, and $c$,
$$
\frac{a^{3}}{b c}+\frac{b^{3}}{c a}+\frac{c^{3}}{a b} \geq a+b+c
$$
and determine when equality occurs.
Each of the inequalities used in the solutions below has the property that equality holds if and only if $a=b=c$. Thus equality holds for the given inequality if and only if $a=b=c$.
|
Note that $a^{4}+b^{4}+c^{4}=\frac{\left(a^{4}+b^{4}\right)}{2}+\frac{\left(b^{4}+c^{4}\right)}{2}+\frac{\left(c^{4}+a^{4}\right)}{2}$. Applying the arithmetic-geometric mean inequality to each term, we see that the right side is greater than or equal to
$$
a^{2} b^{2}+b^{2} c^{2}+c^{2} a^{2} \text {. }
$$
We can rewrite this as
$$
\frac{a^{2}\left(b^{2}+c^{2}\right)}{2}+\frac{b^{2}\left(c^{2}+a^{2}\right)}{2}+\frac{c^{2}\left(a^{2}+b^{2}\right)}{2} .
$$
Applying the arithmetic mean-geometric mean inequality again we obtain $a^{4}+b^{4}+c^{4} \geq$ $a^{2} b c+b^{2} c a+c^{2} a b$. Dividing both sides by $a b c$ (which is positive) the result follows.
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "Canada_MO/segmented/en-sol2002.jsonl",
"solution_match": "\n## Solution 1.",
"tier": "T2",
"year": "2002"
}
|
Prove that for all positive real numbers $a, b$, and $c$,
$$
\frac{a^{3}}{b c}+\frac{b^{3}}{c a}+\frac{c^{3}}{a b} \geq a+b+c
$$
and determine when equality occurs.
Each of the inequalities used in the solutions below has the property that equality holds if and only if $a=b=c$. Thus equality holds for the given inequality if and only if $a=b=c$.
|
Notice the inequality is homogeneous. That is, if $a, b, c$ are replaced by $k a, k b, k c, k>0$ we get the original inequality. Thus we can assume, without loss of generality, that $a b c=1$. Then
$$
\begin{aligned}
\frac{a^{3}}{b c}+\frac{b^{3}}{c a}+\frac{c^{3}}{a b} & =a b c\left(\frac{a^{3}}{b c}+\frac{b^{3}}{c a}+\frac{c^{3}}{a b}\right) \\
& =a^{4}+b^{4}+c^{4} .
\end{aligned}
$$
So we need prove that $a^{4}+b^{4}+c^{4} \geq a+b+c$.
By the Power Mean Inequality,
$$
\frac{a^{4}+b^{4}+c^{4}}{3} \geq\left(\frac{a+b+c}{3}\right)^{4}
$$
so $a^{4}+b^{4}+c^{4} \geq(a+b+c) \cdot \frac{(a+b+c)^{3}}{27}$.
By the arithmetic mean-geometric mean inequality, $\frac{a+b+c}{3} \geq \sqrt[3]{a b c}=1$, so $a+b+c \geq 3$.
Hence, $a^{4}+b^{4}+c^{4} \geq(a+b+c) \cdot \frac{(a+b+c)^{3}}{27} \geq(a+b+c) \frac{3^{3}}{27}=a+b+c$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that for all positive real numbers $a, b$, and $c$,
$$
\frac{a^{3}}{b c}+\frac{b^{3}}{c a}+\frac{c^{3}}{a b} \geq a+b+c
$$
and determine when equality occurs.
Each of the inequalities used in the solutions below has the property that equality holds if and only if $a=b=c$. Thus equality holds for the given inequality if and only if $a=b=c$.
|
Notice the inequality is homogeneous. That is, if $a, b, c$ are replaced by $k a, k b, k c, k>0$ we get the original inequality. Thus we can assume, without loss of generality, that $a b c=1$. Then
$$
\begin{aligned}
\frac{a^{3}}{b c}+\frac{b^{3}}{c a}+\frac{c^{3}}{a b} & =a b c\left(\frac{a^{3}}{b c}+\frac{b^{3}}{c a}+\frac{c^{3}}{a b}\right) \\
& =a^{4}+b^{4}+c^{4} .
\end{aligned}
$$
So we need prove that $a^{4}+b^{4}+c^{4} \geq a+b+c$.
By the Power Mean Inequality,
$$
\frac{a^{4}+b^{4}+c^{4}}{3} \geq\left(\frac{a+b+c}{3}\right)^{4}
$$
so $a^{4}+b^{4}+c^{4} \geq(a+b+c) \cdot \frac{(a+b+c)^{3}}{27}$.
By the arithmetic mean-geometric mean inequality, $\frac{a+b+c}{3} \geq \sqrt[3]{a b c}=1$, so $a+b+c \geq 3$.
Hence, $a^{4}+b^{4}+c^{4} \geq(a+b+c) \cdot \frac{(a+b+c)^{3}}{27} \geq(a+b+c) \frac{3^{3}}{27}=a+b+c$.
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "Canada_MO/segmented/en-sol2002.jsonl",
"solution_match": "\n## Solution 2.",
"tier": "T2",
"year": "2002"
}
|
Prove that for all positive real numbers $a, b$, and $c$,
$$
\frac{a^{3}}{b c}+\frac{b^{3}}{c a}+\frac{c^{3}}{a b} \geq a+b+c
$$
and determine when equality occurs.
Each of the inequalities used in the solutions below has the property that equality holds if and only if $a=b=c$. Thus equality holds for the given inequality if and only if $a=b=c$.
|
Rather than using the Power-Mean inequality to prove $a^{4}+b^{4}+c^{4} \geq a+b+c$ in Proof 2, the Cauchy-Schwartz-Bunjakovsky inequality can be used twice:
$$
\begin{aligned}
& \left(a^{4}+b^{4}+c^{4}\right)\left(1^{2}+1^{2}+1^{2}\right) \geq\left(a^{2}+b^{2}+c^{2}\right)^{2} \\
& \left(a^{2}+b^{2}+c^{2}\right)\left(1^{2}+1^{2}+1^{2}\right) \geq(a+b+c)^{2}
\end{aligned}
$$
So $\frac{a^{4}+b^{4}+c^{4}}{3} \geq \frac{\left(a^{2}+b^{2}+c^{2}\right)^{2}}{9} \geq \frac{(a+b+c)^{4}}{81}$. Continue as in Proof 2 .
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Prove that for all positive real numbers $a, b$, and $c$,
$$
\frac{a^{3}}{b c}+\frac{b^{3}}{c a}+\frac{c^{3}}{a b} \geq a+b+c
$$
and determine when equality occurs.
Each of the inequalities used in the solutions below has the property that equality holds if and only if $a=b=c$. Thus equality holds for the given inequality if and only if $a=b=c$.
|
Rather than using the Power-Mean inequality to prove $a^{4}+b^{4}+c^{4} \geq a+b+c$ in Proof 2, the Cauchy-Schwartz-Bunjakovsky inequality can be used twice:
$$
\begin{aligned}
& \left(a^{4}+b^{4}+c^{4}\right)\left(1^{2}+1^{2}+1^{2}\right) \geq\left(a^{2}+b^{2}+c^{2}\right)^{2} \\
& \left(a^{2}+b^{2}+c^{2}\right)\left(1^{2}+1^{2}+1^{2}\right) \geq(a+b+c)^{2}
\end{aligned}
$$
So $\frac{a^{4}+b^{4}+c^{4}}{3} \geq \frac{\left(a^{2}+b^{2}+c^{2}\right)^{2}}{9} \geq \frac{(a+b+c)^{4}}{81}$. Continue as in Proof 2 .
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "Canada_MO/segmented/en-sol2002.jsonl",
"solution_match": "\n## Solution 3.",
"tier": "T2",
"year": "2002"
}
|
Let $\Gamma$ be a circle with radius $r$. Let $A$ and $B$ be distinct points on $\Gamma$ such that $A B<\sqrt{3} r$. Let the circle with centre $B$ and radius $A B$ meet $\Gamma$ again at $C$. Let $P$ be the point inside $\Gamma$ such that triangle $A B P$ is equilateral. Finally, let $C P$ meet $\Gamma$ again at $Q$. Prove that $P Q=r$.
|
Let the center of $\Gamma$ be $O$, the radius $\mathrm{r}$. Since $B P=B C$, let $\theta=\measuredangle B P C=\measuredangle B C P$.
Quadrilateral $Q A B C$ is cyclic, so $\measuredangle B A Q=180^{\circ}-\theta$ and hence $\measuredangle P A Q=120^{\circ}-\theta$.
Also $\measuredangle A P Q=180^{\circ}-\measuredangle A P B-\measuredangle B P C=120^{\circ}-\theta$, so $P Q=A Q$ and $\measuredangle A Q P=2 \theta-60^{\circ}$.
Again because quadrilateral $Q A B C$ is cyclic, $\measuredangle A B C=180^{\circ}-\measuredangle A Q C=240^{\circ}-2 \theta$.
Triangles $O A B$ and $O C B$ are congruent, since $O A=O B=O C=r$ and $A B=B C$.
Thus $\measuredangle A B O=\measuredangle C B O=\frac{1}{2} \measuredangle A B C=120^{\circ}-\theta$.
We have now shown that in triangles $A Q P$ and $A O B, \measuredangle P A Q=\measuredangle B A O=\measuredangle A P Q=\measuredangle A B O$.
Also $A P=A B$, so $\triangle A Q P \cong \triangle A O B$. Hence $Q P=O B=r$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\Gamma$ be a circle with radius $r$. Let $A$ and $B$ be distinct points on $\Gamma$ such that $A B<\sqrt{3} r$. Let the circle with centre $B$ and radius $A B$ meet $\Gamma$ again at $C$. Let $P$ be the point inside $\Gamma$ such that triangle $A B P$ is equilateral. Finally, let $C P$ meet $\Gamma$ again at $Q$. Prove that $P Q=r$.

|
Let the center of $\Gamma$ be $O$, the radius $\mathrm{r}$. Since $B P=B C$, let $\theta=\measuredangle B P C=\measuredangle B C P$.
Quadrilateral $Q A B C$ is cyclic, so $\measuredangle B A Q=180^{\circ}-\theta$ and hence $\measuredangle P A Q=120^{\circ}-\theta$.
Also $\measuredangle A P Q=180^{\circ}-\measuredangle A P B-\measuredangle B P C=120^{\circ}-\theta$, so $P Q=A Q$ and $\measuredangle A Q P=2 \theta-60^{\circ}$.
Again because quadrilateral $Q A B C$ is cyclic, $\measuredangle A B C=180^{\circ}-\measuredangle A Q C=240^{\circ}-2 \theta$.
Triangles $O A B$ and $O C B$ are congruent, since $O A=O B=O C=r$ and $A B=B C$.
Thus $\measuredangle A B O=\measuredangle C B O=\frac{1}{2} \measuredangle A B C=120^{\circ}-\theta$.
We have now shown that in triangles $A Q P$ and $A O B, \measuredangle P A Q=\measuredangle B A O=\measuredangle A P Q=\measuredangle A B O$.
Also $A P=A B$, so $\triangle A Q P \cong \triangle A O B$. Hence $Q P=O B=r$.
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "Canada_MO/segmented/en-sol2002.jsonl",
"solution_match": "\n## Solution 1.",
"tier": "T2",
"year": "2002"
}
|
Let $\Gamma$ be a circle with radius $r$. Let $A$ and $B$ be distinct points on $\Gamma$ such that $A B<\sqrt{3} r$. Let the circle with centre $B$ and radius $A B$ meet $\Gamma$ again at $C$. Let $P$ be the point inside $\Gamma$ such that triangle $A B P$ is equilateral. Finally, let $C P$ meet $\Gamma$ again at $Q$. Prove that $P Q=r$.

|
Let the center of $\Gamma$ be $O$, the radius $r$. Since $A, P$ and $C$ lie on a circle centered at $B$, $60^{\circ}=\measuredangle A B P=2 \measuredangle A C P$, so $\measuredangle A C P=\measuredangle A C Q=30^{\circ}$.
Since $Q, A$, and $C$ lie on $\Gamma, \measuredangle Q O A=2 \measuredangle Q C A=60^{\circ}$.
So $Q A=r$ since if a chord of a circle subtends an angle of $60^{\circ}$ at the center, its length is the radius of the circle.
Now $B P=B C$, so $\measuredangle B P C=\measuredangle B C P=\measuredangle A C B+30^{\circ}$.
Thus $\measuredangle A P Q=180^{\circ}-\measuredangle A P B-\measuredangle B P C=90^{\circ}-\measuredangle A C B$.
Since $Q, A, B$ and $C$ lie on $\Gamma$ and $A B=B C, \measuredangle A Q P=\measuredangle A Q C=\measuredangle A Q B+\measuredangle B Q C=2 \measuredangle A C B$.
Finally, $\measuredangle Q A P=180-\measuredangle A Q P-\measuredangle A P Q=90-\measuredangle A C B$.
So $\measuredangle P A Q=\measuredangle A P Q$ hence $P Q=A Q=r$.
|
P Q=r
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\Gamma$ be a circle with radius $r$. Let $A$ and $B$ be distinct points on $\Gamma$ such that $A B<\sqrt{3} r$. Let the circle with centre $B$ and radius $A B$ meet $\Gamma$ again at $C$. Let $P$ be the point inside $\Gamma$ such that triangle $A B P$ is equilateral. Finally, let $C P$ meet $\Gamma$ again at $Q$. Prove that $P Q=r$.

|
Let the center of $\Gamma$ be $O$, the radius $r$. Since $A, P$ and $C$ lie on a circle centered at $B$, $60^{\circ}=\measuredangle A B P=2 \measuredangle A C P$, so $\measuredangle A C P=\measuredangle A C Q=30^{\circ}$.
Since $Q, A$, and $C$ lie on $\Gamma, \measuredangle Q O A=2 \measuredangle Q C A=60^{\circ}$.
So $Q A=r$ since if a chord of a circle subtends an angle of $60^{\circ}$ at the center, its length is the radius of the circle.
Now $B P=B C$, so $\measuredangle B P C=\measuredangle B C P=\measuredangle A C B+30^{\circ}$.
Thus $\measuredangle A P Q=180^{\circ}-\measuredangle A P B-\measuredangle B P C=90^{\circ}-\measuredangle A C B$.
Since $Q, A, B$ and $C$ lie on $\Gamma$ and $A B=B C, \measuredangle A Q P=\measuredangle A Q C=\measuredangle A Q B+\measuredangle B Q C=2 \measuredangle A C B$.
Finally, $\measuredangle Q A P=180-\measuredangle A Q P-\measuredangle A P Q=90-\measuredangle A C B$.
So $\measuredangle P A Q=\measuredangle A P Q$ hence $P Q=A Q=r$.
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "Canada_MO/segmented/en-sol2002.jsonl",
"solution_match": "\n## Solution 2.",
"tier": "T2",
"year": "2002"
}
|
Let $\mathbb{N}=\{0,1,2, \ldots\}$. Determine all functions $f: \mathbb{N} \rightarrow \mathbb{N}$ such that
$$
x f(y)+y f(x)=(x+y) f\left(x^{2}+y^{2}\right)
$$
for all $x$ and $y$ in $\mathbb{N}$.
|
We claim that $f$ is a constant function. Suppose, for a contradiction, that there exist $x$ and $y$ with $f(x)<f(y)$; choose $x, y$ such that $f(y)-f(x)>0$ is minimal. Then
$$
f(x)=\frac{x f(x)+y f(x)}{x+y}<\frac{x f(y)+y f(x)}{x+y}<\frac{x f(y)+y f(y)}{x+y}=f(y)
$$
so $f(x)<f\left(x^{2}+y^{2}\right)<f(y)$ and $0<f\left(x^{2}+y^{2}\right)-f(x)<f(y)-f(x)$, contradicting the choice of $x$ and $y$. Thus, $f$ is a constant function. Since $f(0)$ is in $\mathbb{N}$, the constant must be from $\mathbb{N}$.
Also, for any $c$ in $\mathbb{N}, x c+y c=(x+y) c$ for all $x$ and $y$, so $f(x)=c, c \in \mathbb{N}$ are the solutions to the equation.
|
f(x)=c, c \in \mathbb{N}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $\mathbb{N}=\{0,1,2, \ldots\}$. Determine all functions $f: \mathbb{N} \rightarrow \mathbb{N}$ such that
$$
x f(y)+y f(x)=(x+y) f\left(x^{2}+y^{2}\right)
$$
for all $x$ and $y$ in $\mathbb{N}$.
|
We claim that $f$ is a constant function. Suppose, for a contradiction, that there exist $x$ and $y$ with $f(x)<f(y)$; choose $x, y$ such that $f(y)-f(x)>0$ is minimal. Then
$$
f(x)=\frac{x f(x)+y f(x)}{x+y}<\frac{x f(y)+y f(x)}{x+y}<\frac{x f(y)+y f(y)}{x+y}=f(y)
$$
so $f(x)<f\left(x^{2}+y^{2}\right)<f(y)$ and $0<f\left(x^{2}+y^{2}\right)-f(x)<f(y)-f(x)$, contradicting the choice of $x$ and $y$. Thus, $f$ is a constant function. Since $f(0)$ is in $\mathbb{N}$, the constant must be from $\mathbb{N}$.
Also, for any $c$ in $\mathbb{N}, x c+y c=(x+y) c$ for all $x$ and $y$, so $f(x)=c, c \in \mathbb{N}$ are the solutions to the equation.
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "Canada_MO/segmented/en-sol2002.jsonl",
"solution_match": "\n## Solution 1.",
"tier": "T2",
"year": "2002"
}
|
Let $\mathbb{N}=\{0,1,2, \ldots\}$. Determine all functions $f: \mathbb{N} \rightarrow \mathbb{N}$ such that
$$
x f(y)+y f(x)=(x+y) f\left(x^{2}+y^{2}\right)
$$
for all $x$ and $y$ in $\mathbb{N}$.
|
We claim $f$ is a constant function. Define $g(x)=f(x)-f(0)$. Then $g(0)=0, g(x) \geq-f(0)$ and
$$
x g(y)+y g(x)=(x+y) g\left(x^{2}+y^{2}\right)
$$
for all $x, y$ in $\mathbb{N}$.
Letting $y=0$ shows $g\left(x^{2}\right)=0$ (in particular, $g(1)=g(4)=0$ ), and letting $x=y=1$ shows $g(2)=0$. Also, if $x, y$ and $z$ in $\mathbb{N}$ satisfy $x^{2}+y^{2}=z^{2}$, then
$$
g(y)=-\frac{y}{x} g(x) .
$$
Letting $x=4$ and $y=3,(*)$ shows that $g(3)=0$.
For any even number $x=2 n>4$, let $y=n^{2}-1$. Then $y>x$ and $x^{2}+y^{2}=\left(n^{2}+1\right)^{2}$. For any odd number $x=2 n+1>3$, let $y=2(n+1) n$. Then $y>x$ and $x^{2}+y^{2}=\left((n+1)^{2}+n^{2}\right)^{2}$. Thus for every $x>4$ there is $y>x$ such that $(*)$ is satisfied.
Suppose for a contradiction, that there is $x>4$ with $g(x)>0$. Then we can construct a
sequence $x=x_{0}<x_{1}<x_{2}<\ldots$ where $g\left(x_{i+1}\right)=-\frac{x_{i+1}}{x_{i}} g\left(x_{i}\right)$. It follows that $\left|g\left(x_{i+1}\right)\right|>$ $\left|g\left(x_{i}\right)\right|$ and the signs of $g\left(x_{i}\right)$ alternate. Since $g(x)$ is always an integer, $\left|g\left(x_{i+1}\right)\right| \geq\left|g\left(x_{i}\right)\right|+1$. Thus for some sufficiently large value of $i, g\left(x_{i}\right)<-f(0)$, a contradiction.
As for Proof 1, we now conclude that the functions that satisfy the given functional equation are $f(x)=c, c \in \mathbb{N}$.
|
f(x)=c, c \in \mathbb{N}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $\mathbb{N}=\{0,1,2, \ldots\}$. Determine all functions $f: \mathbb{N} \rightarrow \mathbb{N}$ such that
$$
x f(y)+y f(x)=(x+y) f\left(x^{2}+y^{2}\right)
$$
for all $x$ and $y$ in $\mathbb{N}$.
|
We claim $f$ is a constant function. Define $g(x)=f(x)-f(0)$. Then $g(0)=0, g(x) \geq-f(0)$ and
$$
x g(y)+y g(x)=(x+y) g\left(x^{2}+y^{2}\right)
$$
for all $x, y$ in $\mathbb{N}$.
Letting $y=0$ shows $g\left(x^{2}\right)=0$ (in particular, $g(1)=g(4)=0$ ), and letting $x=y=1$ shows $g(2)=0$. Also, if $x, y$ and $z$ in $\mathbb{N}$ satisfy $x^{2}+y^{2}=z^{2}$, then
$$
g(y)=-\frac{y}{x} g(x) .
$$
Letting $x=4$ and $y=3,(*)$ shows that $g(3)=0$.
For any even number $x=2 n>4$, let $y=n^{2}-1$. Then $y>x$ and $x^{2}+y^{2}=\left(n^{2}+1\right)^{2}$. For any odd number $x=2 n+1>3$, let $y=2(n+1) n$. Then $y>x$ and $x^{2}+y^{2}=\left((n+1)^{2}+n^{2}\right)^{2}$. Thus for every $x>4$ there is $y>x$ such that $(*)$ is satisfied.
Suppose for a contradiction, that there is $x>4$ with $g(x)>0$. Then we can construct a
sequence $x=x_{0}<x_{1}<x_{2}<\ldots$ where $g\left(x_{i+1}\right)=-\frac{x_{i+1}}{x_{i}} g\left(x_{i}\right)$. It follows that $\left|g\left(x_{i+1}\right)\right|>$ $\left|g\left(x_{i}\right)\right|$ and the signs of $g\left(x_{i}\right)$ alternate. Since $g(x)$ is always an integer, $\left|g\left(x_{i+1}\right)\right| \geq\left|g\left(x_{i}\right)\right|+1$. Thus for some sufficiently large value of $i, g\left(x_{i}\right)<-f(0)$, a contradiction.
As for Proof 1, we now conclude that the functions that satisfy the given functional equation are $f(x)=c, c \in \mathbb{N}$.
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "Canada_MO/segmented/en-sol2002.jsonl",
"solution_match": "\n## Solution 2.",
"tier": "T2",
"year": "2002"
}
|
Let $\mathbb{N}=\{0,1,2, \ldots\}$. Determine all functions $f: \mathbb{N} \rightarrow \mathbb{N}$ such that
$$
x f(y)+y f(x)=(x+y) f\left(x^{2}+y^{2}\right)
$$
for all $x$ and $y$ in $\mathbb{N}$.
|
Suppose that $W$ is the set of nonnegative integers and that $f: W \rightarrow W$ satisfies:
$$
x f(y)+y f(x)=(x+y) f\left(x^{2}+y^{2}\right) .
$$
We will show that $f$ is a constant function.
Let $f(0)=k$, and set $S=\{x \mid f(x)=k\}$.
Letting $y=0$ in $(*)$ shows that $f\left(x^{2}\right)=k \quad \forall x>0$, and so
$$
x^{2} \in S \quad \forall x>0
$$
In particular, $1 \in S$.
Suppose $x^{2}+y^{2}=z^{2}$. Then $y f(x)+x f(y)=(x+y) f\left(z^{2}\right)=(x+y) k$. Thus,
$$
x \in S \quad \text { iff } \quad y \in S
$$
whenever $x^{2}+y^{2}$ is a perfect square.
For a contradiction, let $n$ be the smallest non-negative integer such that $f\left(2^{n}\right) \neq k$. By (l) $n$ must be odd, so $\frac{n-1}{2}$ is an integer. Now $\frac{n-1}{2}<n$ so $f\left(2^{\frac{n-1}{2}}\right)=k$. Letting $x=y=2^{\frac{n-1}{2}}$ in (*) shows $f\left(2^{n}\right)=k$, a contradiction. Thus every power of 2 is an element of $S$.
For each integer $n \geq 2$ define $p(n)$ to be the largest prime such that $p(n) \mid n$.
Claim: For any integer $n>1$ that is not a power of 2 , there exists a sequence of integers $x_{1}, x_{2}, \ldots, x_{r}$ such that the following conditions hold:
a) $x_{1}=n$.
b) $x_{i}^{2}+x_{i+1}^{2}$ is a perfect square for each $i=1,2,3, \ldots, r-1$.
c) $p\left(x_{1}\right) \geq p\left(x_{2}\right) \geq \ldots \geq p\left(x_{r}\right)=2$.
Proof: Since $n$ is not a power of $2, p(n)=p\left(x_{1}\right) \geq 3$. Let $p\left(x_{1}\right)=2 m+1$, so $n=x_{1}=$ $b(2 m+1)^{a}$, for some $a$ and $b$, where $p(b)<2 m+1$.
Case 1: $a=1$. Since $\left(2 m+1,2 m^{2}+2 m, 2 m^{2}+2 m+1\right)$ is a Pythagorean Triple, if $x_{2}=b\left(2 m^{2}+\right.$ $2 m)$, then $x_{1}^{2}+x_{2}^{2}=b^{2}\left(2 m^{2}+2 m+1\right)^{2}$ is a perfect square. Furthermore, $x_{2}=2 b m(m+1)$, and so $p\left(x_{2}\right)<2 m+1=p\left(x_{1}\right)$.
Case 2: $a>1$. If $n=x_{1}=(2 m+1)^{a} \cdot b$, let $x_{2}=(2 m+1)^{a-1} \cdot b \cdot\left(2 m^{2}+2 m\right), x_{3}=$ $(2 m+1)^{a-2} \cdot b \cdot\left(2 m^{2}+2 m\right)^{2}, \ldots, x_{a+1}=(2 m+1)^{0} \cdot b \cdot\left(2 m^{2}+2 m\right)^{a}=b \cdot 2^{a} m^{a}(m+1)^{a}$. Note that for $1 \leq i \leq a, x_{i}^{2}+x_{i+1}^{2}$ is a perfect square and also note that $p\left(x_{a+1}\right)<2 m+1=p\left(x_{1}\right)$.
If $x_{a+1}$ is not a power of 2 , we extend the sequence $x_{i}$ using the same procedure described above. We keep doing this until $p\left(x_{r}\right)=2$, for some integer $r$.
By (2), $x_{i} \in S$ iff $x_{i+1} \in S$ for $i=1,2,3, \ldots, r-1$. Thus, $n=x_{1} \in S$ iff $x_{r} \in S$. But $x_{r}$ is a power of 2 because $p\left(x_{r}\right)=2$, and we earlier proved that powers of 2 are in $\mathrm{S}$. Therefore, $n \in S$, proving the claim.
We have proven that every integer $n \geq 1$ is an element of $S$, and so we have proven that $f(n)=k=f(0)$, for each $n \geq 1$. Therefore, $f$ is constant, Q.E.D.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Let $\mathbb{N}=\{0,1,2, \ldots\}$. Determine all functions $f: \mathbb{N} \rightarrow \mathbb{N}$ such that
$$
x f(y)+y f(x)=(x+y) f\left(x^{2}+y^{2}\right)
$$
for all $x$ and $y$ in $\mathbb{N}$.
|
Suppose that $W$ is the set of nonnegative integers and that $f: W \rightarrow W$ satisfies:
$$
x f(y)+y f(x)=(x+y) f\left(x^{2}+y^{2}\right) .
$$
We will show that $f$ is a constant function.
Let $f(0)=k$, and set $S=\{x \mid f(x)=k\}$.
Letting $y=0$ in $(*)$ shows that $f\left(x^{2}\right)=k \quad \forall x>0$, and so
$$
x^{2} \in S \quad \forall x>0
$$
In particular, $1 \in S$.
Suppose $x^{2}+y^{2}=z^{2}$. Then $y f(x)+x f(y)=(x+y) f\left(z^{2}\right)=(x+y) k$. Thus,
$$
x \in S \quad \text { iff } \quad y \in S
$$
whenever $x^{2}+y^{2}$ is a perfect square.
For a contradiction, let $n$ be the smallest non-negative integer such that $f\left(2^{n}\right) \neq k$. By (l) $n$ must be odd, so $\frac{n-1}{2}$ is an integer. Now $\frac{n-1}{2}<n$ so $f\left(2^{\frac{n-1}{2}}\right)=k$. Letting $x=y=2^{\frac{n-1}{2}}$ in (*) shows $f\left(2^{n}\right)=k$, a contradiction. Thus every power of 2 is an element of $S$.
For each integer $n \geq 2$ define $p(n)$ to be the largest prime such that $p(n) \mid n$.
Claim: For any integer $n>1$ that is not a power of 2 , there exists a sequence of integers $x_{1}, x_{2}, \ldots, x_{r}$ such that the following conditions hold:
a) $x_{1}=n$.
b) $x_{i}^{2}+x_{i+1}^{2}$ is a perfect square for each $i=1,2,3, \ldots, r-1$.
c) $p\left(x_{1}\right) \geq p\left(x_{2}\right) \geq \ldots \geq p\left(x_{r}\right)=2$.
Proof: Since $n$ is not a power of $2, p(n)=p\left(x_{1}\right) \geq 3$. Let $p\left(x_{1}\right)=2 m+1$, so $n=x_{1}=$ $b(2 m+1)^{a}$, for some $a$ and $b$, where $p(b)<2 m+1$.
Case 1: $a=1$. Since $\left(2 m+1,2 m^{2}+2 m, 2 m^{2}+2 m+1\right)$ is a Pythagorean Triple, if $x_{2}=b\left(2 m^{2}+\right.$ $2 m)$, then $x_{1}^{2}+x_{2}^{2}=b^{2}\left(2 m^{2}+2 m+1\right)^{2}$ is a perfect square. Furthermore, $x_{2}=2 b m(m+1)$, and so $p\left(x_{2}\right)<2 m+1=p\left(x_{1}\right)$.
Case 2: $a>1$. If $n=x_{1}=(2 m+1)^{a} \cdot b$, let $x_{2}=(2 m+1)^{a-1} \cdot b \cdot\left(2 m^{2}+2 m\right), x_{3}=$ $(2 m+1)^{a-2} \cdot b \cdot\left(2 m^{2}+2 m\right)^{2}, \ldots, x_{a+1}=(2 m+1)^{0} \cdot b \cdot\left(2 m^{2}+2 m\right)^{a}=b \cdot 2^{a} m^{a}(m+1)^{a}$. Note that for $1 \leq i \leq a, x_{i}^{2}+x_{i+1}^{2}$ is a perfect square and also note that $p\left(x_{a+1}\right)<2 m+1=p\left(x_{1}\right)$.
If $x_{a+1}$ is not a power of 2 , we extend the sequence $x_{i}$ using the same procedure described above. We keep doing this until $p\left(x_{r}\right)=2$, for some integer $r$.
By (2), $x_{i} \in S$ iff $x_{i+1} \in S$ for $i=1,2,3, \ldots, r-1$. Thus, $n=x_{1} \in S$ iff $x_{r} \in S$. But $x_{r}$ is a power of 2 because $p\left(x_{r}\right)=2$, and we earlier proved that powers of 2 are in $\mathrm{S}$. Therefore, $n \in S$, proving the claim.
We have proven that every integer $n \geq 1$ is an element of $S$, and so we have proven that $f(n)=k=f(0)$, for each $n \geq 1$. Therefore, $f$ is constant, Q.E.D.
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "Canada_MO/segmented/en-sol2002.jsonl",
"solution_match": "\nSolution 3.",
"tier": "T2",
"year": "2002"
}
|
Consider a standard twelve-hour clock whose hour and minute hands move continuously. Let $m$ be an integer, with $1 \leq m \leq 720$. At precisely $m$ minutes after 12:00, the angle made by the hour hand and minute hand is exactly $1^{\circ}$. Determine all possible values of $m$.
|
The minute hand makes a full revolution of $360^{\circ}$ every 60 minutes, so after $m$ minutes it has swept through $\frac{360}{60} m=6 m$ degrees. The hour hand makes a full revolution every 12 hours ( 720 minutes), so after $m$ minutes it has swept through $\frac{360}{720} m=m / 2$ degrees. Since both hands started in the same position at 12:00, the angle between the two hands will be $1^{\circ}$ if $6 m-m / 2= \pm 1+360 k$ for some integer $k$. Solving this equation we get
$$
m=\frac{720 k \pm 2}{11}=65 k+\frac{5 k \pm 2}{11}
$$
Since $1 \leq m \leq 720$, we have $1 \leq k \leq 11$. Since $m$ is an integer, $5 k \pm 2$ must be divisible by 11 , say $5 k \pm 2=11 q$. Then
$$
5 k=11 q \pm 2 \Rightarrow k=2 q+\frac{q \pm 2}{5}
$$
If is now clear that only $q=2$ and $q=3$ satisfy all the conditions. Thus $k=4$ or $k=7$ and substituting these values into the expression for $m$ we find that the only possible values of $m$ are 262 and 458 .
|
262, 458
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Consider a standard twelve-hour clock whose hour and minute hands move continuously. Let $m$ be an integer, with $1 \leq m \leq 720$. At precisely $m$ minutes after 12:00, the angle made by the hour hand and minute hand is exactly $1^{\circ}$. Determine all possible values of $m$.
|
The minute hand makes a full revolution of $360^{\circ}$ every 60 minutes, so after $m$ minutes it has swept through $\frac{360}{60} m=6 m$ degrees. The hour hand makes a full revolution every 12 hours ( 720 minutes), so after $m$ minutes it has swept through $\frac{360}{720} m=m / 2$ degrees. Since both hands started in the same position at 12:00, the angle between the two hands will be $1^{\circ}$ if $6 m-m / 2= \pm 1+360 k$ for some integer $k$. Solving this equation we get
$$
m=\frac{720 k \pm 2}{11}=65 k+\frac{5 k \pm 2}{11}
$$
Since $1 \leq m \leq 720$, we have $1 \leq k \leq 11$. Since $m$ is an integer, $5 k \pm 2$ must be divisible by 11 , say $5 k \pm 2=11 q$. Then
$$
5 k=11 q \pm 2 \Rightarrow k=2 q+\frac{q \pm 2}{5}
$$
If is now clear that only $q=2$ and $q=3$ satisfy all the conditions. Thus $k=4$ or $k=7$ and substituting these values into the expression for $m$ we find that the only possible values of $m$ are 262 and 458 .
|
{
"exam": "Canada_MO",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "Canada_MO/segmented/en-sol2003.jsonl",
"solution_match": "\n## Solution\n\n",
"tier": "T2",
"year": "2003"
}
|
Find the last three digits of the number $2003^{2002^{2001}}$.
|
We must find the remainder when $2003^{2002^{2001}}$ is divided by 1000 , which will be the same as the remainder when $3^{2002^{2001}}$ is divided by 1000 , since $2003 \equiv 3(\bmod 1000)$. To do this we will first find a positive integer $n$ such that $3^{n} \equiv 1(\bmod 1000)$ and then try to express $2002^{2001}$ in the form $n k+r$, so that
$$
2003^{2002^{2001}} \equiv 3^{n k+r} \equiv\left(3^{n}\right)^{k} \cdot 3^{r} \equiv 1^{k} \cdot 3^{r} \equiv 3^{r}(\bmod 1000)
$$
Since $3^{2}=10-1$, we can evaluate $3^{2 m}$ using the binomial theorem:
$$
3^{2 m}=(10-1)^{m}=(-1)^{m}+10 m(-1)^{m-1}+100 \frac{m(m-1)}{2}(-1)^{m-2}+\cdots+10^{m} .
$$
After the first 3 terms of this expansion, all remaining terms are divisible by 1000, so letting $m=2 q$, we have that
$$
3^{4 q} \equiv 1-20 q+100 q(2 q-1)(\bmod 1000)
$$
Using this, we can check that $3^{100} \equiv 1(\bmod 1000)$ and now we wish to find the remainder when $2002^{2001}$ is divided by 100 .
Now $2002^{2001} \equiv 2^{2001}(\bmod 100) \equiv 4 \cdot 2^{1999}(\bmod 4 \cdot 25)$, so we'll investigate powers of 2 modulo 25 . Noting that $2^{10}=1024 \equiv-1(\bmod 25)$, we have
$$
2^{1999}=\left(2^{10}\right)^{199} \cdot 2^{9} \equiv(-1)^{199} \cdot 512 \equiv-12 \equiv 13(\bmod 25) .
$$
Thus $2^{2001} \equiv 4 \cdot 13=52(\bmod 100)$. Therefore $2002^{2001}$ can be written in the form $100 k+52$ for some integer $k$, so
$$
2003^{2002^{2001}} \equiv 3^{52}(\bmod 1000) \equiv 1-20 \cdot 13+1300 \cdot 25 \equiv 241(\bmod 1000)
$$
using equation (1). So the last 3 digits of $2003^{2002^{2001}}$ are 241 .
|
241
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find the last three digits of the number $2003^{2002^{2001}}$.
|
We must find the remainder when $2003^{2002^{2001}}$ is divided by 1000 , which will be the same as the remainder when $3^{2002^{2001}}$ is divided by 1000 , since $2003 \equiv 3(\bmod 1000)$. To do this we will first find a positive integer $n$ such that $3^{n} \equiv 1(\bmod 1000)$ and then try to express $2002^{2001}$ in the form $n k+r$, so that
$$
2003^{2002^{2001}} \equiv 3^{n k+r} \equiv\left(3^{n}\right)^{k} \cdot 3^{r} \equiv 1^{k} \cdot 3^{r} \equiv 3^{r}(\bmod 1000)
$$
Since $3^{2}=10-1$, we can evaluate $3^{2 m}$ using the binomial theorem:
$$
3^{2 m}=(10-1)^{m}=(-1)^{m}+10 m(-1)^{m-1}+100 \frac{m(m-1)}{2}(-1)^{m-2}+\cdots+10^{m} .
$$
After the first 3 terms of this expansion, all remaining terms are divisible by 1000, so letting $m=2 q$, we have that
$$
3^{4 q} \equiv 1-20 q+100 q(2 q-1)(\bmod 1000)
$$
Using this, we can check that $3^{100} \equiv 1(\bmod 1000)$ and now we wish to find the remainder when $2002^{2001}$ is divided by 100 .
Now $2002^{2001} \equiv 2^{2001}(\bmod 100) \equiv 4 \cdot 2^{1999}(\bmod 4 \cdot 25)$, so we'll investigate powers of 2 modulo 25 . Noting that $2^{10}=1024 \equiv-1(\bmod 25)$, we have
$$
2^{1999}=\left(2^{10}\right)^{199} \cdot 2^{9} \equiv(-1)^{199} \cdot 512 \equiv-12 \equiv 13(\bmod 25) .
$$
Thus $2^{2001} \equiv 4 \cdot 13=52(\bmod 100)$. Therefore $2002^{2001}$ can be written in the form $100 k+52$ for some integer $k$, so
$$
2003^{2002^{2001}} \equiv 3^{52}(\bmod 1000) \equiv 1-20 \cdot 13+1300 \cdot 25 \equiv 241(\bmod 1000)
$$
using equation (1). So the last 3 digits of $2003^{2002^{2001}}$ are 241 .
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "Canada_MO/segmented/en-sol2003.jsonl",
"solution_match": "\n## Solution\n\n",
"tier": "T2",
"year": "2003"
}
|
Find all real positive solutions (if any) to
$$
\begin{gathered}
x^{3}+y^{3}+z^{3}=x+y+z, \text { and } \\
x^{2}+y^{2}+z^{2}=x y z .
\end{gathered}
$$
|
Let $f(x, y, z)=\left(x^{3}-x\right)+\left(y^{3}-y\right)+\left(z^{3}-z\right)$. The first equation above is equivalent to $f(x, y, z)=0$. If $x, y, z \geq 1$, then $f(x, y, z) \geq 0$ with equality only if $x=y=z=1$. But if $x=y=z=1$, then the second equation is not satisfied. So in any solution to the system of equations, at least one of the variables is less than 1. Without loss of generality, suppose that $x<1$. Then
$$
x^{2}+y^{2}+z^{2}>y^{2}+z^{2} \geq 2 y z>y z>x y z .
$$
Therefore the system has no real positive solutions.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all real positive solutions (if any) to
$$
\begin{gathered}
x^{3}+y^{3}+z^{3}=x+y+z, \text { and } \\
x^{2}+y^{2}+z^{2}=x y z .
\end{gathered}
$$
|
Let $f(x, y, z)=\left(x^{3}-x\right)+\left(y^{3}-y\right)+\left(z^{3}-z\right)$. The first equation above is equivalent to $f(x, y, z)=0$. If $x, y, z \geq 1$, then $f(x, y, z) \geq 0$ with equality only if $x=y=z=1$. But if $x=y=z=1$, then the second equation is not satisfied. So in any solution to the system of equations, at least one of the variables is less than 1. Without loss of generality, suppose that $x<1$. Then
$$
x^{2}+y^{2}+z^{2}>y^{2}+z^{2} \geq 2 y z>y z>x y z .
$$
Therefore the system has no real positive solutions.
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "Canada_MO/segmented/en-sol2003.jsonl",
"solution_match": "\n## Solution 1",
"tier": "T2",
"year": "2003"
}
|
Find all real positive solutions (if any) to
$$
\begin{gathered}
x^{3}+y^{3}+z^{3}=x+y+z, \text { and } \\
x^{2}+y^{2}+z^{2}=x y z .
\end{gathered}
$$
|
We will show that the system has no real positive solution. Assume otherwise.
The second equation can be written $x^{2}-(y z) x+\left(y^{2}+z^{2}\right)$. Since this quadratic in $x$ has a real solution by hypothesis, its discrimant is nonnegative. Hence
$$
y^{2} z^{2}-4 y^{2}-4 z^{2} \geq 0
$$
Dividing through by $4 y^{2} z^{2}$ yields
$$
\frac{1}{4} \geq \frac{1}{y^{2}}+\frac{1}{z^{2}} \geq \frac{1}{y^{2}}
$$
Hence $y^{2} \geq 4$ and so $y \geq 2, y$ being positive. A similar argument yields $x, y, z \geq 2$. But the first equation can be written as
$$
x\left(x^{2}-1\right)+y\left(y^{2}-1\right)+z\left(z^{2}-1\right)=0
$$
contradicting $x, y, z \geq 2$. Hence, a real positive solution cannot exist.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all real positive solutions (if any) to
$$
\begin{gathered}
x^{3}+y^{3}+z^{3}=x+y+z, \text { and } \\
x^{2}+y^{2}+z^{2}=x y z .
\end{gathered}
$$
|
We will show that the system has no real positive solution. Assume otherwise.
The second equation can be written $x^{2}-(y z) x+\left(y^{2}+z^{2}\right)$. Since this quadratic in $x$ has a real solution by hypothesis, its discrimant is nonnegative. Hence
$$
y^{2} z^{2}-4 y^{2}-4 z^{2} \geq 0
$$
Dividing through by $4 y^{2} z^{2}$ yields
$$
\frac{1}{4} \geq \frac{1}{y^{2}}+\frac{1}{z^{2}} \geq \frac{1}{y^{2}}
$$
Hence $y^{2} \geq 4$ and so $y \geq 2, y$ being positive. A similar argument yields $x, y, z \geq 2$. But the first equation can be written as
$$
x\left(x^{2}-1\right)+y\left(y^{2}-1\right)+z\left(z^{2}-1\right)=0
$$
contradicting $x, y, z \geq 2$. Hence, a real positive solution cannot exist.
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "Canada_MO/segmented/en-sol2003.jsonl",
"solution_match": "\n## Solution 2",
"tier": "T2",
"year": "2003"
}
|
Find all real positive solutions (if any) to
$$
\begin{gathered}
x^{3}+y^{3}+z^{3}=x+y+z, \text { and } \\
x^{2}+y^{2}+z^{2}=x y z .
\end{gathered}
$$
|
Applying the arithmetic-geometric mean inequality and the Power Mean Inequalities to $x, y, z$ we have
$$
\sqrt[3]{x y z} \leq \frac{x+y+z}{3} \leq \sqrt{\frac{x^{2}+y^{2}+z^{2}}{3}} \leq \sqrt[3]{\frac{x^{3}+y^{3}+z^{3}}{3}}
$$
Letting $S=x+y+z=x^{3}+y^{3}+z^{3}$ and $P=x y z=x^{2}+y^{2}+z^{2}$, this inequality can be written
$$
\sqrt[3]{P} \leq \frac{S}{3} \leq \sqrt{\frac{P}{3}} \leq \sqrt[3]{\frac{S}{3}}
$$
Now $\sqrt[3]{P} \leq \sqrt{\frac{P}{3}}$ implies $P^{2} \leq P^{3} / 27$, so $P \geq 27$. Also $\frac{S}{3} \leq \sqrt[3]{\frac{S}{3}}$ implies $S^{3} / 27 \leq S / 3$,
so $S \leq 3$. But then $\sqrt[3]{P} \geq 3$ and $\sqrt[3]{\frac{S}{3}} \leq 1$ which is inconsistent with $\sqrt[3]{P} \leq \sqrt[3]{\frac{S}{3}}$. Therefore the system cannot have a real positive solution.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all real positive solutions (if any) to
$$
\begin{gathered}
x^{3}+y^{3}+z^{3}=x+y+z, \text { and } \\
x^{2}+y^{2}+z^{2}=x y z .
\end{gathered}
$$
|
Applying the arithmetic-geometric mean inequality and the Power Mean Inequalities to $x, y, z$ we have
$$
\sqrt[3]{x y z} \leq \frac{x+y+z}{3} \leq \sqrt{\frac{x^{2}+y^{2}+z^{2}}{3}} \leq \sqrt[3]{\frac{x^{3}+y^{3}+z^{3}}{3}}
$$
Letting $S=x+y+z=x^{3}+y^{3}+z^{3}$ and $P=x y z=x^{2}+y^{2}+z^{2}$, this inequality can be written
$$
\sqrt[3]{P} \leq \frac{S}{3} \leq \sqrt{\frac{P}{3}} \leq \sqrt[3]{\frac{S}{3}}
$$
Now $\sqrt[3]{P} \leq \sqrt{\frac{P}{3}}$ implies $P^{2} \leq P^{3} / 27$, so $P \geq 27$. Also $\frac{S}{3} \leq \sqrt[3]{\frac{S}{3}}$ implies $S^{3} / 27 \leq S / 3$,
so $S \leq 3$. But then $\sqrt[3]{P} \geq 3$ and $\sqrt[3]{\frac{S}{3}} \leq 1$ which is inconsistent with $\sqrt[3]{P} \leq \sqrt[3]{\frac{S}{3}}$. Therefore the system cannot have a real positive solution.
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "Canada_MO/segmented/en-sol2003.jsonl",
"solution_match": "\n## Solution 3",
"tier": "T2",
"year": "2003"
}
|
Prove that when three circles share the same chord $A B$, every line through $A$ different from $A B$ determines the same ratio $X Y: Y Z$, where $X$ is an arbitrary point different from $B$ on the first circle while $Y$ and $Z$ are the points where $A X$ intersects the other two circles (labelled so that $Y$ is between $X$ and $Z$ ).
|
Let $l$ be a line through $A$ different from $A B$ and join $B$ to $A, X, Y$ and $Z$ as in the above diagram. No matter how $l$ is chosen, the angles $A X B, A Y B$ and $A Z B$ always subtend the chord $A B$. For this reason the angles in the triangles $B X Y$ and $B X Z$ are the same for all such $l$. Thus the ratio $X Y: Y Z$ remains constant by similar triangles.
Note that this is true no matter how $X, Y$ and $Z$ lie in relation to $A$. Suppose $X, Y$ and $Z$ all lie on the same side of $A$ (as in the diagram) and that $\measuredangle A X B=\alpha, \measuredangle A Y B=\beta$ and $\measuredangle A Z B=\gamma$. Then $\measuredangle B X Y=180^{\circ}-\alpha, \measuredangle B Y X=\beta, \measuredangle B Y Z=180^{\circ}-\beta$ and $\measuredangle B Z Y=\gamma$. Now suppose $l$ is chosen so that $X$ is now on the opposite side of $A$ from $Y$ and $Z$. Now since $X$ is on the other side of the chord $A B, \measuredangle A X B=180^{\circ}-\alpha$, but it is still the case that $\measuredangle B X Y=180^{\circ}-\alpha$ and all other angles in the two pertinent triangles remain unchanged. If $l$ is chosen so that $X$ is identical with $A$, then $l$ is tangent to the first circle and it is still the case that $\measuredangle B X Y=180^{\circ}-\alpha$. All other cases can be checked in a similar manner.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Prove that when three circles share the same chord $A B$, every line through $A$ different from $A B$ determines the same ratio $X Y: Y Z$, where $X$ is an arbitrary point different from $B$ on the first circle while $Y$ and $Z$ are the points where $A X$ intersects the other two circles (labelled so that $Y$ is between $X$ and $Z$ ).

|
Let $l$ be a line through $A$ different from $A B$ and join $B$ to $A, X, Y$ and $Z$ as in the above diagram. No matter how $l$ is chosen, the angles $A X B, A Y B$ and $A Z B$ always subtend the chord $A B$. For this reason the angles in the triangles $B X Y$ and $B X Z$ are the same for all such $l$. Thus the ratio $X Y: Y Z$ remains constant by similar triangles.
Note that this is true no matter how $X, Y$ and $Z$ lie in relation to $A$. Suppose $X, Y$ and $Z$ all lie on the same side of $A$ (as in the diagram) and that $\measuredangle A X B=\alpha, \measuredangle A Y B=\beta$ and $\measuredangle A Z B=\gamma$. Then $\measuredangle B X Y=180^{\circ}-\alpha, \measuredangle B Y X=\beta, \measuredangle B Y Z=180^{\circ}-\beta$ and $\measuredangle B Z Y=\gamma$. Now suppose $l$ is chosen so that $X$ is now on the opposite side of $A$ from $Y$ and $Z$. Now since $X$ is on the other side of the chord $A B, \measuredangle A X B=180^{\circ}-\alpha$, but it is still the case that $\measuredangle B X Y=180^{\circ}-\alpha$ and all other angles in the two pertinent triangles remain unchanged. If $l$ is chosen so that $X$ is identical with $A$, then $l$ is tangent to the first circle and it is still the case that $\measuredangle B X Y=180^{\circ}-\alpha$. All other cases can be checked in a similar manner.

|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "Canada_MO/segmented/en-sol2003.jsonl",
"solution_match": "\n## Solution 1",
"tier": "T2",
"year": "2003"
}
|
Prove that when three circles share the same chord $A B$, every line through $A$ different from $A B$ determines the same ratio $X Y: Y Z$, where $X$ is an arbitrary point different from $B$ on the first circle while $Y$ and $Z$ are the points where $A X$ intersects the other two circles (labelled so that $Y$ is between $X$ and $Z$ ).

|
Let $m$ be the perpendicular bisector of $A B$ and let $O_{1}, O_{2}, O_{3}$ be the centres of the three circles. Since $A B$ is a chord common to all three circles, $O_{1}, O_{2}, O_{3}$ all lie on $m$. Let $l$ be a line through $A$ different from $A B$ and suppose that $X, Y, Z$ all lie on the same side of $A B$, as in the above diagram. Let perpendiculars from $O_{1}, O_{2}, O_{3}$ meet $l$ at $P, Q, R$, respectively. Since a line through the centre of a circle bisects any chord,
$$
A X=2 A P, \quad A Y=2 A Q \quad \text { and } \quad A Z=2 A R
$$
Now
$$
X Y=A Y-A X=2(A Q-A P)=2 P Q \quad \text { and, similarly, } \quad Y Z=2 Q R \text {. }
$$
Therefore $X Y: Y Z=P Q: Q R$. But $O_{1} P\left\|O_{2} Q\right\| O_{3} R$, so $P Q: Q R=O_{1} O_{2}: O_{2} O_{3}$. Since the centres of the circles are fixed, the ratio $X Y: Y Z=O_{1} O_{2}: O_{2} O_{3}$ does not depend on the choice of $l$.
If $X, Y, Z$ do not all lie on the same side of $A B$, we can obtain the same result with a similar proof. For instance, if $X$ and $Y$ are opposite sides of $A B$, then we will have $X Y=A Y+A X$, but since in this case $P Q=A Q+A P$, it is still the case that $X Y=2 P Q$ and result still follows, etc.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Prove that when three circles share the same chord $A B$, every line through $A$ different from $A B$ determines the same ratio $X Y: Y Z$, where $X$ is an arbitrary point different from $B$ on the first circle while $Y$ and $Z$ are the points where $A X$ intersects the other two circles (labelled so that $Y$ is between $X$ and $Z$ ).

|
Let $m$ be the perpendicular bisector of $A B$ and let $O_{1}, O_{2}, O_{3}$ be the centres of the three circles. Since $A B$ is a chord common to all three circles, $O_{1}, O_{2}, O_{3}$ all lie on $m$. Let $l$ be a line through $A$ different from $A B$ and suppose that $X, Y, Z$ all lie on the same side of $A B$, as in the above diagram. Let perpendiculars from $O_{1}, O_{2}, O_{3}$ meet $l$ at $P, Q, R$, respectively. Since a line through the centre of a circle bisects any chord,
$$
A X=2 A P, \quad A Y=2 A Q \quad \text { and } \quad A Z=2 A R
$$
Now
$$
X Y=A Y-A X=2(A Q-A P)=2 P Q \quad \text { and, similarly, } \quad Y Z=2 Q R \text {. }
$$
Therefore $X Y: Y Z=P Q: Q R$. But $O_{1} P\left\|O_{2} Q\right\| O_{3} R$, so $P Q: Q R=O_{1} O_{2}: O_{2} O_{3}$. Since the centres of the circles are fixed, the ratio $X Y: Y Z=O_{1} O_{2}: O_{2} O_{3}$ does not depend on the choice of $l$.
If $X, Y, Z$ do not all lie on the same side of $A B$, we can obtain the same result with a similar proof. For instance, if $X$ and $Y$ are opposite sides of $A B$, then we will have $X Y=A Y+A X$, but since in this case $P Q=A Q+A P$, it is still the case that $X Y=2 P Q$ and result still follows, etc.
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "Canada_MO/segmented/en-sol2003.jsonl",
"solution_match": "\n## Solution 2",
"tier": "T2",
"year": "2003"
}
|
Let $S$ be a set of $n$ points in the plane such that any two points of $S$ are at least 1 unit apart. Prove there is a subset $T$ of $S$ with at least $n / 7$ points such that any two points of $T$ are at least $\sqrt{3}$ units apart.
|
We will construct the set $T$ in the following way: Assume the points of $S$ are in the $x y$-plane and let $P$ be a point in $S$ with maximum $y$-coordinate. This point $P$ will be a member of the set $T$ and now, from $S$, we will remove $P$ and all points in $S$ which are less than $\sqrt{3}$ units from $P$. From the remaining points we choose one with maximum $y$-coordinate to be a member of $T$ and remove from $S$ all points at distance less than $\sqrt{3}$ units from this new point. We continue in this way, until all the points of $S$ are exhausted. Clearly any two points in $T$ are at least $\sqrt{3}$ units apart. To show that $T$ has at least $n / 7$ points, we must prove that at each stage no more than 6 other points are removed along with $P$.
At a typical stage in this process, we've selected a point $P$ with maximum $y$-coordinate, so any points at distance less than $\sqrt{3}$ from $P$ must lie inside the semicircular region of radius $\sqrt{3}$ centred at $P$ shown in the first diagram below. Since points of $S$ are at least 1 unit apart, these points must lie outside (or on) the semicircle of radius 1. (So they lie in the shaded region of the first diagram.) Now divide this shaded region into 6 congruent regions $R_{1}, R_{2}, \ldots, R_{6}$ as shown in this diagram.
We will show that each of these regions contains at most one point of $S$. Since all 6 regions are congruent, consider one of them as depicted in the second diagram below. The distance between any two points in this shaded region must be less than the length of the line segment $A B$. The lengths of $P A$ and $P B$ are $\sqrt{3}$ and 1 , respectively, and angle $A P B=30^{\circ}$. If we construct a perpendicular from $B$ to $P A$ at $C$, then the length of $P C$ is $\cos 30^{\circ}=\sqrt{3} / 2$. Thus $B C$ is a perpendicular bisector of $P A$ and therefore $A B=P B=1$. So the distance between any two points in this region is less than 1. Therefore each of $R_{1}, \ldots, R_{6}$ can contain at most one point of $S$, which completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $S$ be a set of $n$ points in the plane such that any two points of $S$ are at least 1 unit apart. Prove there is a subset $T$ of $S$ with at least $n / 7$ points such that any two points of $T$ are at least $\sqrt{3}$ units apart.
|
We will construct the set $T$ in the following way: Assume the points of $S$ are in the $x y$-plane and let $P$ be a point in $S$ with maximum $y$-coordinate. This point $P$ will be a member of the set $T$ and now, from $S$, we will remove $P$ and all points in $S$ which are less than $\sqrt{3}$ units from $P$. From the remaining points we choose one with maximum $y$-coordinate to be a member of $T$ and remove from $S$ all points at distance less than $\sqrt{3}$ units from this new point. We continue in this way, until all the points of $S$ are exhausted. Clearly any two points in $T$ are at least $\sqrt{3}$ units apart. To show that $T$ has at least $n / 7$ points, we must prove that at each stage no more than 6 other points are removed along with $P$.
At a typical stage in this process, we've selected a point $P$ with maximum $y$-coordinate, so any points at distance less than $\sqrt{3}$ from $P$ must lie inside the semicircular region of radius $\sqrt{3}$ centred at $P$ shown in the first diagram below. Since points of $S$ are at least 1 unit apart, these points must lie outside (or on) the semicircle of radius 1. (So they lie in the shaded region of the first diagram.) Now divide this shaded region into 6 congruent regions $R_{1}, R_{2}, \ldots, R_{6}$ as shown in this diagram.
We will show that each of these regions contains at most one point of $S$. Since all 6 regions are congruent, consider one of them as depicted in the second diagram below. The distance between any two points in this shaded region must be less than the length of the line segment $A B$. The lengths of $P A$ and $P B$ are $\sqrt{3}$ and 1 , respectively, and angle $A P B=30^{\circ}$. If we construct a perpendicular from $B$ to $P A$ at $C$, then the length of $P C$ is $\cos 30^{\circ}=\sqrt{3} / 2$. Thus $B C$ is a perpendicular bisector of $P A$ and therefore $A B=P B=1$. So the distance between any two points in this region is less than 1. Therefore each of $R_{1}, \ldots, R_{6}$ can contain at most one point of $S$, which completes the proof.

|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "Canada_MO/segmented/en-sol2003.jsonl",
"solution_match": "\n## Solution\n\n",
"tier": "T2",
"year": "2003"
}
|
Find all ordered triples $(x, y, z)$ of real numbers which satisfy the following system of equations:
$$
\left\{\begin{array}{l}
x y=z-x-y \\
x z=y-x-z \\
y z=x-y-z
\end{array}\right.
$$
|
Subtracting the second equation from the first gives $x y-x z=2 z-2 y$. Factoring $y-z$ from each side and rearranging gives
$$
(x+2)(y-z)=0
$$
so either $x=-2$ or $z=y$.
If $x=-2$, the first equation becomes $-2 y=z+2-y$, or $y+z=-2$. Substituting $x=-2, y+z=-2$ into the third equation gives $y z=-2-(-2)=0$. Hence either $y$ or $z$ is 0 , so if $x=-2$, the only solutions are $(-2,0,-2)$ and $(-2,-2,0)$.
If $z=y$ the first equation becomes $x y=-x$, or $x(y+1)=0$. If $x=0$ and $z=y$, the third equation becomes $y^{2}=-2 y$ which gives $y=0$ or $y=-2$. If $y=-1$ and $z=y=-1$, the third equation gives $x=-1$. So if $y=z$, the only solutions are $(0,0,0),(0,-2,-2)$ and $(-1,-1,-1)$.
In summary, there are 5 solutions: $(-2,0,-2),(-2,-2,0),(0,0,0),(0,-2,-2)$ and $(-1,-1,-1)$.
|
(-2,0,-2),(-2,-2,0),(0,0,0),(0,-2,-2),(-1,-1,-1)
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all ordered triples $(x, y, z)$ of real numbers which satisfy the following system of equations:
$$
\left\{\begin{array}{l}
x y=z-x-y \\
x z=y-x-z \\
y z=x-y-z
\end{array}\right.
$$
|
Subtracting the second equation from the first gives $x y-x z=2 z-2 y$. Factoring $y-z$ from each side and rearranging gives
$$
(x+2)(y-z)=0
$$
so either $x=-2$ or $z=y$.
If $x=-2$, the first equation becomes $-2 y=z+2-y$, or $y+z=-2$. Substituting $x=-2, y+z=-2$ into the third equation gives $y z=-2-(-2)=0$. Hence either $y$ or $z$ is 0 , so if $x=-2$, the only solutions are $(-2,0,-2)$ and $(-2,-2,0)$.
If $z=y$ the first equation becomes $x y=-x$, or $x(y+1)=0$. If $x=0$ and $z=y$, the third equation becomes $y^{2}=-2 y$ which gives $y=0$ or $y=-2$. If $y=-1$ and $z=y=-1$, the third equation gives $x=-1$. So if $y=z$, the only solutions are $(0,0,0),(0,-2,-2)$ and $(-1,-1,-1)$.
In summary, there are 5 solutions: $(-2,0,-2),(-2,-2,0),(0,0,0),(0,-2,-2)$ and $(-1,-1,-1)$.
|
{
"exam": "Canada_MO",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "Canada_MO/segmented/en-sol2004.jsonl",
"solution_match": "\n## Solution 1",
"tier": "T2",
"year": "2004"
}
|
Find all ordered triples $(x, y, z)$ of real numbers which satisfy the following system of equations:
$$
\left\{\begin{array}{l}
x y=z-x-y \\
x z=y-x-z \\
y z=x-y-z
\end{array}\right.
$$
|
Adding $x$ to both sides of the first equation gives
$$
x(y+1)=z-y=(z+1)-(y+1) \Rightarrow(x+1)(y+1)=z+1 .
$$
Similarly manipulating the other two equations and letting $a=x+1, b=y+1$, $c=z+1$, we can write the system in the following way.
$$
\left\{\begin{array}{l}
a b=c \\
a c=b \\
b c=a
\end{array}\right.
$$
If any one of $a, b, c$ is 0 , then it's clear that all three are 0 . So $(a, b, c)=(0,0,0)$ is one solution and now suppose that $a, b, c$ are all nonzero. Substituting $c=a b$ into the second and third equations gives $a^{2} b=b$ and $b^{2} a=a$, respectively. Hence $a^{2}=1$, $b^{2}=1$ (since $a, b$ nonzero). This gives 4 more solutions: $(a, b, c)=(1,1,1),(1,-1,-1)$, $(-1,1,-1)$ or $(-1,-1,1)$. Reexpressing in terms of $x, y, z$, we obtain the 5 ordered triples listed in Solution 1.
|
(0,0,0), (1,1,1), (1,-1,-1), (-1,1,-1), (-1,-1,1)
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all ordered triples $(x, y, z)$ of real numbers which satisfy the following system of equations:
$$
\left\{\begin{array}{l}
x y=z-x-y \\
x z=y-x-z \\
y z=x-y-z
\end{array}\right.
$$
|
Adding $x$ to both sides of the first equation gives
$$
x(y+1)=z-y=(z+1)-(y+1) \Rightarrow(x+1)(y+1)=z+1 .
$$
Similarly manipulating the other two equations and letting $a=x+1, b=y+1$, $c=z+1$, we can write the system in the following way.
$$
\left\{\begin{array}{l}
a b=c \\
a c=b \\
b c=a
\end{array}\right.
$$
If any one of $a, b, c$ is 0 , then it's clear that all three are 0 . So $(a, b, c)=(0,0,0)$ is one solution and now suppose that $a, b, c$ are all nonzero. Substituting $c=a b$ into the second and third equations gives $a^{2} b=b$ and $b^{2} a=a$, respectively. Hence $a^{2}=1$, $b^{2}=1$ (since $a, b$ nonzero). This gives 4 more solutions: $(a, b, c)=(1,1,1),(1,-1,-1)$, $(-1,1,-1)$ or $(-1,-1,1)$. Reexpressing in terms of $x, y, z$, we obtain the 5 ordered triples listed in Solution 1.
|
{
"exam": "Canada_MO",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "Canada_MO/segmented/en-sol2004.jsonl",
"solution_match": "\n## Solution 2",
"tier": "T2",
"year": "2004"
}
|
How many ways can 8 mutually non-attacking rooks be placed on the $9 \times 9$ chessboard (shown here) so that all 8 rooks are on squares of the same colour?
[Two rooks are said to be attacking each other if they are placed in the same row or column of the board.]
|
We will first count the number of ways of placing 8 mutually non-attacking rooks on black squares and then count the number of ways of placing them on white squares. Suppose that the rows of the board have been numbered 1 to 9 from top to bottom.
First notice that a rook placed on a black square in an odd numbered row cannot attack a rook on a black square in an even numbered row. This effectively partitions the black squares into a $5 \times 5$ board and a $4 \times 4$ board (squares labelled $O$ and $E$ respectively, in the diagram at right) and rooks can be placed independently on these two boards. There are 5 ! ways to place 5 non-attacking rooks on the squares labelled $O$ and 4 ! ways to

place 4 non-attacking rooks on the squares labelled $E$.
This gives 5!4! ways to place 9 mutually non-attacking rooks on black squares and removing any one of these 9 rooks gives one of the desired configurations. Thus there are $9 \cdot 5 ! 4$ ! ways to place 8 mutually non-attacking rooks on black squares.
Using very similar reasoning we can partition the white squares as shown in the diagram at right. The white squares are partitioned into two $5 \times 4$ boards such that no rook on a square marked $O$ can attack a rook on a square mark $E$. At most 4 non-attacking rooks can be placed on a $5 \times 4$ board and they can be placed in $5 \cdot 4 \cdot 3 \cdot 2=5$ ! ways. Thus there are $(5 !)^{2}$ ways to place 8 mutually non-attacking rooks on white squares.

In total there are $9 \cdot 5 ! 4 !+(5 !)^{2}=(9+5) 5 ! 4 !=14 \cdot 5 ! 4 !=40320$ ways to place 8 mutually non-attacking rooks on squares of the same colour.
|
40320
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
How many ways can 8 mutually non-attacking rooks be placed on the $9 \times 9$ chessboard (shown here) so that all 8 rooks are on squares of the same colour?
[Two rooks are said to be attacking each other if they are placed in the same row or column of the board.]
|
We will first count the number of ways of placing 8 mutually non-attacking rooks on black squares and then count the number of ways of placing them on white squares. Suppose that the rows of the board have been numbered 1 to 9 from top to bottom.
First notice that a rook placed on a black square in an odd numbered row cannot attack a rook on a black square in an even numbered row. This effectively partitions the black squares into a $5 \times 5$ board and a $4 \times 4$ board (squares labelled $O$ and $E$ respectively, in the diagram at right) and rooks can be placed independently on these two boards. There are 5 ! ways to place 5 non-attacking rooks on the squares labelled $O$ and 4 ! ways to

place 4 non-attacking rooks on the squares labelled $E$.
This gives 5!4! ways to place 9 mutually non-attacking rooks on black squares and removing any one of these 9 rooks gives one of the desired configurations. Thus there are $9 \cdot 5 ! 4$ ! ways to place 8 mutually non-attacking rooks on black squares.
Using very similar reasoning we can partition the white squares as shown in the diagram at right. The white squares are partitioned into two $5 \times 4$ boards such that no rook on a square marked $O$ can attack a rook on a square mark $E$. At most 4 non-attacking rooks can be placed on a $5 \times 4$ board and they can be placed in $5 \cdot 4 \cdot 3 \cdot 2=5$ ! ways. Thus there are $(5 !)^{2}$ ways to place 8 mutually non-attacking rooks on white squares.

In total there are $9 \cdot 5 ! 4 !+(5 !)^{2}=(9+5) 5 ! 4 !=14 \cdot 5 ! 4 !=40320$ ways to place 8 mutually non-attacking rooks on squares of the same colour.
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "Canada_MO/segmented/en-sol2004.jsonl",
"solution_match": "\n## Solution 1",
"tier": "T2",
"year": "2004"
}
|
How many ways can 8 mutually non-attacking rooks be placed on the $9 \times 9$ chessboard (shown here) so that all 8 rooks are on squares of the same colour?
[Two rooks are said to be attacking each other if they are placed in the same row or column of the board.]
|
Consider rooks on black squares first. We have 8 rooks and 9 rows, so exactly one row will be without rooks. There are two cases: either the empty row has 5 black squares or it has 4 black squares. By permutation these rows can be made either last or second last. In each case we'll count the possible number of ways of placing the rooks on the board as we proceed row by row.
In the first case we have 5 choices for the empty row, then we can place a rook on any of the black squares in row 1 ( 5 possibilities) and any of the black squares in row 2 (4 possibilities). When we attempt to place a rook in row 3, we must avoid the column containing the rook that was placed in row 1 , so we have 4 possibilities. Using similar reasoning, we can place the rook on any of 3 possible black squares in row 4 , etc. The total number of possibilities for the first case is $5 \cdot 5 \cdot 4 \cdot 4 \cdot 3 \cdot 3 \cdot 2 \cdot 2 \cdot 1=(5 !)^{2}$. In the second case, we have 4 choices for the empty row (but assume it's the second last row). We now place rooks as before and using similar logic, we get that the total number of possibilities for the second case is $4 \cdot 5 \cdot 4 \cdot 4 \cdot 3 \cdot 3 \cdot 2 \cdot 1 \cdot 1=4(5 ! 4 !)$.
Now, do the same for the white squares. If a row with 4 white squares is empty ( 5 ways to choose it), then the total number of possibilities is $(5 !)^{2}$. It's impossible to have a row with 5 white squares empty, so the total number of ways to place rooks is
$$
(5 !)^{2}+4(5 ! 4 !)+(5 !)^{2}=(5+4+5) 5 ! 4 !=14(5 ! 4 !)
$$
|
14(5 ! 4 !)
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
How many ways can 8 mutually non-attacking rooks be placed on the $9 \times 9$ chessboard (shown here) so that all 8 rooks are on squares of the same colour?
[Two rooks are said to be attacking each other if they are placed in the same row or column of the board.]
|
Consider rooks on black squares first. We have 8 rooks and 9 rows, so exactly one row will be without rooks. There are two cases: either the empty row has 5 black squares or it has 4 black squares. By permutation these rows can be made either last or second last. In each case we'll count the possible number of ways of placing the rooks on the board as we proceed row by row.
In the first case we have 5 choices for the empty row, then we can place a rook on any of the black squares in row 1 ( 5 possibilities) and any of the black squares in row 2 (4 possibilities). When we attempt to place a rook in row 3, we must avoid the column containing the rook that was placed in row 1 , so we have 4 possibilities. Using similar reasoning, we can place the rook on any of 3 possible black squares in row 4 , etc. The total number of possibilities for the first case is $5 \cdot 5 \cdot 4 \cdot 4 \cdot 3 \cdot 3 \cdot 2 \cdot 2 \cdot 1=(5 !)^{2}$. In the second case, we have 4 choices for the empty row (but assume it's the second last row). We now place rooks as before and using similar logic, we get that the total number of possibilities for the second case is $4 \cdot 5 \cdot 4 \cdot 4 \cdot 3 \cdot 3 \cdot 2 \cdot 1 \cdot 1=4(5 ! 4 !)$.
Now, do the same for the white squares. If a row with 4 white squares is empty ( 5 ways to choose it), then the total number of possibilities is $(5 !)^{2}$. It's impossible to have a row with 5 white squares empty, so the total number of ways to place rooks is
$$
(5 !)^{2}+4(5 ! 4 !)+(5 !)^{2}=(5+4+5) 5 ! 4 !=14(5 ! 4 !)
$$
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "Canada_MO/segmented/en-sol2004.jsonl",
"solution_match": "\n## Solution 2",
"tier": "T2",
"year": "2004"
}
|
Let $A, B, C, D$ be four points on a circle (occurring in clockwise order), with $A B<A D$ and $B C>C D$. Let the bisector of angle $B A D$ meet the circle at $X$ and the bisector of angle $B C D$ meet the circle at $Y$. Consider the hexagon formed by these six points on the circle. If four of the six sides of the hexagon have equal length, prove that $B D$ must be a diameter of the circle.
|
We're given that $A B<A D$. Since $C Y$ bisects $\measuredangle B C D, B Y=Y D$, so $Y$ lies between $D$ and $A$ on the circle, as in the diagram above, and $D Y>Y A, D Y>A B$. Similar reasoning confirms that $X$ lies between $B$ and $C$ and $B X>X C, B X>C D$. So if $A B X C D Y$ has 4 equal sides, then it must be that $Y A=A B=X C=C D$.
Let $\measuredangle B A X=\measuredangle D A X=\alpha$ and let $\measuredangle B C Y=\measuredangle D C Y=\gamma$. Since $A B C D$ is cyclic, $\measuredangle A+\measuredangle C=180^{\circ}$, which implies that $\alpha+\gamma=90^{\circ}$. The fact that $Y A=A B=X C=C D$ means that the arc from $Y$ to $B$ (which is subtended by $\measuredangle Y C B$ ) is equal to the arc from $X$ to $D$ (which is subtended by $\measuredangle X A D$ ). Hence $\measuredangle Y C B=\measuredangle X A D$, so $\alpha=\gamma=45^{\circ}$. Finally, $B D$ is subtended by $\measuredangle B A D=2 \alpha=90^{\circ}$. Therefore $B D$ is a diameter of the circle.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A, B, C, D$ be four points on a circle (occurring in clockwise order), with $A B<A D$ and $B C>C D$. Let the bisector of angle $B A D$ meet the circle at $X$ and the bisector of angle $B C D$ meet the circle at $Y$. Consider the hexagon formed by these six points on the circle. If four of the six sides of the hexagon have equal length, prove that $B D$ must be a diameter of the circle.

|
We're given that $A B<A D$. Since $C Y$ bisects $\measuredangle B C D, B Y=Y D$, so $Y$ lies between $D$ and $A$ on the circle, as in the diagram above, and $D Y>Y A, D Y>A B$. Similar reasoning confirms that $X$ lies between $B$ and $C$ and $B X>X C, B X>C D$. So if $A B X C D Y$ has 4 equal sides, then it must be that $Y A=A B=X C=C D$.
Let $\measuredangle B A X=\measuredangle D A X=\alpha$ and let $\measuredangle B C Y=\measuredangle D C Y=\gamma$. Since $A B C D$ is cyclic, $\measuredangle A+\measuredangle C=180^{\circ}$, which implies that $\alpha+\gamma=90^{\circ}$. The fact that $Y A=A B=X C=C D$ means that the arc from $Y$ to $B$ (which is subtended by $\measuredangle Y C B$ ) is equal to the arc from $X$ to $D$ (which is subtended by $\measuredangle X A D$ ). Hence $\measuredangle Y C B=\measuredangle X A D$, so $\alpha=\gamma=45^{\circ}$. Finally, $B D$ is subtended by $\measuredangle B A D=2 \alpha=90^{\circ}$. Therefore $B D$ is a diameter of the circle.
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "Canada_MO/segmented/en-sol2004.jsonl",
"solution_match": "\n## Solution 1",
"tier": "T2",
"year": "2004"
}
|
Let $A, B, C, D$ be four points on a circle (occurring in clockwise order), with $A B<A D$ and $B C>C D$. Let the bisector of angle $B A D$ meet the circle at $X$ and the bisector of angle $B C D$ meet the circle at $Y$. Consider the hexagon formed by these six points on the circle. If four of the six sides of the hexagon have equal length, prove that $B D$ must be a diameter of the circle.

|
We're given that $A B<A D$. Since $C Y$ bisects $\measuredangle B C D, B Y=Y D$, so $Y$ lies between $D$ and $A$ on the circle, as in the diagram above, and $D Y>Y A, D Y>A B$. Similar reasoning confirms that $X$ lies between $B$ and $C$ and $B X>X C, B X>C D$. So if $A B X C D Y$ has 4 equal sides, then it must be that $Y A=A B=X C=C D$. This implies that the arc from $Y$ to $B$ is equal to the arc from $X$ to $D$ and hence that $Y B=X D$. Since $\measuredangle B A X=\measuredangle X A D, B X=X D$ and since $\measuredangle D C Y=\measuredangle Y C B$, $D Y=Y B$. Therefore $B X D Y$ is a square and its diagonal, $B D$, must be a diameter of the circle.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A, B, C, D$ be four points on a circle (occurring in clockwise order), with $A B<A D$ and $B C>C D$. Let the bisector of angle $B A D$ meet the circle at $X$ and the bisector of angle $B C D$ meet the circle at $Y$. Consider the hexagon formed by these six points on the circle. If four of the six sides of the hexagon have equal length, prove that $B D$ must be a diameter of the circle.

|
We're given that $A B<A D$. Since $C Y$ bisects $\measuredangle B C D, B Y=Y D$, so $Y$ lies between $D$ and $A$ on the circle, as in the diagram above, and $D Y>Y A, D Y>A B$. Similar reasoning confirms that $X$ lies between $B$ and $C$ and $B X>X C, B X>C D$. So if $A B X C D Y$ has 4 equal sides, then it must be that $Y A=A B=X C=C D$. This implies that the arc from $Y$ to $B$ is equal to the arc from $X$ to $D$ and hence that $Y B=X D$. Since $\measuredangle B A X=\measuredangle X A D, B X=X D$ and since $\measuredangle D C Y=\measuredangle Y C B$, $D Y=Y B$. Therefore $B X D Y$ is a square and its diagonal, $B D$, must be a diameter of the circle.
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "Canada_MO/segmented/en-sol2004.jsonl",
"solution_match": "\n## Solution 2",
"tier": "T2",
"year": "2004"
}
|
Let $p$ be an odd prime. Prove that
$$
\sum_{k=1}^{p-1} k^{2 p-1} \equiv \frac{p(p+1)}{2} \quad\left(\bmod p^{2}\right)
$$
[Note that $a \equiv b(\bmod m)$ means that $a-b$ is divisible by $m$.]
|
Since $p-1$ is even, we can pair up the terms in the summation in the following way (first term with last, 2nd term with 2nd last, etc.):
$$
\sum_{k=1}^{p-1} k^{2 p-1}=\sum_{k=1}^{\frac{p-1}{2}}\left(k^{2 p-1}+(p-k)^{2 p-1}\right)
$$
Expanding $(p-k)^{2 p-1}$ with the binomial theorem, we get
$$
(p-k)^{2 p-1}=p^{2 p-1}-\cdots-\left(\begin{array}{c}
2 p-1 \\
2
\end{array}\right) p^{2} k^{2 p-3}+\left(\begin{array}{c}
2 p-1 \\
1
\end{array}\right) p k^{2 p-2}-k^{2 p-1},
$$
where every term on the right-hand side is divisible by $p^{2}$ except the last two. Therefore
$$
k^{2 p-1}+(p-k)^{2 p-1} \equiv k^{2 p-1}+\left(\begin{array}{c}
2 p-1 \\
1
\end{array}\right) p k^{2 p-2}-k^{2 p-1} \equiv(2 p-1) p k^{2 p-2}\left(\bmod p^{2}\right)
$$
For $1 \leq k<p, k$ is not divisible by $p$, so $k^{p-1} \equiv 1(\bmod p)$, by Fermat's Little Theorem. So $(2 p-1) k^{2 p-2} \equiv(2 p-1)\left(1^{2}\right) \equiv-1(\bmod p)$, say $(2 p-1) k^{2 p-2}=m p-1$ for some integer $m$. Then
$$
(2 p-1) p k^{2 p-2}=m p^{2}-p \equiv-p\left(\bmod p^{2}\right)
$$
Finally,
$$
\begin{aligned}
\sum_{k=1}^{p-1} k^{2 p-1} & \equiv \sum_{k=1}^{\frac{p-1}{2}}(-p) \equiv\left(\frac{p-1}{2}\right)(-p)\left(\bmod p^{2}\right) \\
& \equiv \frac{p-p^{2}}{2}+p^{2} \equiv \frac{p(p+1)}{2}\left(\bmod p^{2}\right) .
\end{aligned}
$$
|
\frac{p(p+1)}{2}
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $p$ be an odd prime. Prove that
$$
\sum_{k=1}^{p-1} k^{2 p-1} \equiv \frac{p(p+1)}{2} \quad\left(\bmod p^{2}\right)
$$
[Note that $a \equiv b(\bmod m)$ means that $a-b$ is divisible by $m$.]
|
Since $p-1$ is even, we can pair up the terms in the summation in the following way (first term with last, 2nd term with 2nd last, etc.):
$$
\sum_{k=1}^{p-1} k^{2 p-1}=\sum_{k=1}^{\frac{p-1}{2}}\left(k^{2 p-1}+(p-k)^{2 p-1}\right)
$$
Expanding $(p-k)^{2 p-1}$ with the binomial theorem, we get
$$
(p-k)^{2 p-1}=p^{2 p-1}-\cdots-\left(\begin{array}{c}
2 p-1 \\
2
\end{array}\right) p^{2} k^{2 p-3}+\left(\begin{array}{c}
2 p-1 \\
1
\end{array}\right) p k^{2 p-2}-k^{2 p-1},
$$
where every term on the right-hand side is divisible by $p^{2}$ except the last two. Therefore
$$
k^{2 p-1}+(p-k)^{2 p-1} \equiv k^{2 p-1}+\left(\begin{array}{c}
2 p-1 \\
1
\end{array}\right) p k^{2 p-2}-k^{2 p-1} \equiv(2 p-1) p k^{2 p-2}\left(\bmod p^{2}\right)
$$
For $1 \leq k<p, k$ is not divisible by $p$, so $k^{p-1} \equiv 1(\bmod p)$, by Fermat's Little Theorem. So $(2 p-1) k^{2 p-2} \equiv(2 p-1)\left(1^{2}\right) \equiv-1(\bmod p)$, say $(2 p-1) k^{2 p-2}=m p-1$ for some integer $m$. Then
$$
(2 p-1) p k^{2 p-2}=m p^{2}-p \equiv-p\left(\bmod p^{2}\right)
$$
Finally,
$$
\begin{aligned}
\sum_{k=1}^{p-1} k^{2 p-1} & \equiv \sum_{k=1}^{\frac{p-1}{2}}(-p) \equiv\left(\frac{p-1}{2}\right)(-p)\left(\bmod p^{2}\right) \\
& \equiv \frac{p-p^{2}}{2}+p^{2} \equiv \frac{p(p+1)}{2}\left(\bmod p^{2}\right) .
\end{aligned}
$$
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "Canada_MO/segmented/en-sol2004.jsonl",
"solution_match": "\n## Solution\n\n",
"tier": "T2",
"year": "2004"
}
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.