problem
stringlengths 14
10.4k
| solution
stringlengths 1
24.1k
| answer
stringlengths 1
250
⌀ | problem_is_valid
stringclasses 4
values | solution_is_valid
stringclasses 3
values | question_type
stringclasses 4
values | problem_type
stringclasses 8
values | problem_raw
stringlengths 14
10.4k
| solution_raw
stringlengths 1
24.1k
| metadata
dict |
|---|---|---|---|---|---|---|---|---|---|
Let $T$ be the set of all positive integer divisors of $2004^{100}$. What is the largest possible number of elements that a subset $S$ of $T$ can have if no element of $S$ is an integer multiple of any other element of $S$ ?
|
Assume throughout that $a, b, c$ are nonnegative integers. Since the prime factorization of 2004 is $2004=2^{2} \cdot 3 \cdot 167$,
$$
T=\left\{2^{a} 3^{b} 167^{c} \mid 0 \leq a \leq 200,0 \leq b, c \leq 100\right\}
$$
Let
$$
S=\left\{2^{200-b-c} 3^{b} 167^{c} \mid 0 \leq b, c \leq 100\right\}
$$
For any $0 \leq b, c \leq 100$, we have $0 \leq 200-b-c \leq 200$, so $S$ is a subset of $T$. Since there are 101 possible values for $b$ and 101 possible values for $c, S$ contains $101^{2}$ elements. We will show that no element of $S$ is a multiple of another and that no larger subset of $T$ satisfies this condition.
Suppose $2^{200-b-c} 3^{b} 167^{c}$ is an integer multiple of $2^{200-j-k} 3^{j} 167^{k}$. Then
$$
200-b-c \geq 200-j-k, \quad b \geq j, \quad c \geq k
$$
But this first inequality implies $b+c \leq j+k$, which together with $b \geq j, c \geq k$ gives $b=j$ and $c=k$. Hence no element of $S$ is an integer multiple of another element of $S$.
Let $U$ be a subset of $T$ with more than $101^{2}$ elements. Since there are only $101^{2}$ distinct pairs $(b, c)$ with $0 \leq b, c \leq 100$, then (by the pigeonhole principle) $U$ must contain two elements $u_{1}=2^{a_{1}} 3^{b_{1}} 167^{c_{1}}$ and $u_{2}=2^{a_{2}} 3^{b_{2}} 167^{c_{2}}$, with $b_{1}=b_{2}$ and $c_{1}=c_{2}$, but $a_{1} \neq a_{2}$. If $a_{1}>a_{2}$, then $u_{1}$ is a multiple of $u_{2}$ and if $a_{1}<a_{2}$, then $u_{2}$ is a multiple of $u_{1}$. Hence $U$ does not satisfy the desired condition.
Therefore the largest possible number of elements that such a subset of $T$ can have is $101^{2}=10201$.
|
10201
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $T$ be the set of all positive integer divisors of $2004^{100}$. What is the largest possible number of elements that a subset $S$ of $T$ can have if no element of $S$ is an integer multiple of any other element of $S$ ?
|
Assume throughout that $a, b, c$ are nonnegative integers. Since the prime factorization of 2004 is $2004=2^{2} \cdot 3 \cdot 167$,
$$
T=\left\{2^{a} 3^{b} 167^{c} \mid 0 \leq a \leq 200,0 \leq b, c \leq 100\right\}
$$
Let
$$
S=\left\{2^{200-b-c} 3^{b} 167^{c} \mid 0 \leq b, c \leq 100\right\}
$$
For any $0 \leq b, c \leq 100$, we have $0 \leq 200-b-c \leq 200$, so $S$ is a subset of $T$. Since there are 101 possible values for $b$ and 101 possible values for $c, S$ contains $101^{2}$ elements. We will show that no element of $S$ is a multiple of another and that no larger subset of $T$ satisfies this condition.
Suppose $2^{200-b-c} 3^{b} 167^{c}$ is an integer multiple of $2^{200-j-k} 3^{j} 167^{k}$. Then
$$
200-b-c \geq 200-j-k, \quad b \geq j, \quad c \geq k
$$
But this first inequality implies $b+c \leq j+k$, which together with $b \geq j, c \geq k$ gives $b=j$ and $c=k$. Hence no element of $S$ is an integer multiple of another element of $S$.
Let $U$ be a subset of $T$ with more than $101^{2}$ elements. Since there are only $101^{2}$ distinct pairs $(b, c)$ with $0 \leq b, c \leq 100$, then (by the pigeonhole principle) $U$ must contain two elements $u_{1}=2^{a_{1}} 3^{b_{1}} 167^{c_{1}}$ and $u_{2}=2^{a_{2}} 3^{b_{2}} 167^{c_{2}}$, with $b_{1}=b_{2}$ and $c_{1}=c_{2}$, but $a_{1} \neq a_{2}$. If $a_{1}>a_{2}$, then $u_{1}$ is a multiple of $u_{2}$ and if $a_{1}<a_{2}$, then $u_{2}$ is a multiple of $u_{1}$. Hence $U$ does not satisfy the desired condition.
Therefore the largest possible number of elements that such a subset of $T$ can have is $101^{2}=10201$.
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "Canada_MO/segmented/en-sol2004.jsonl",
"solution_match": "\n## Solution\n\n",
"tier": "T2",
"year": "2004"
}
|
Consider an equilateral triangle of side length $n$, which is divided into unit triangles, as shown. Let $f(n)$ be the number of paths from the triangle in the top row to the middle triangle in the bottom row, such that adjacent triangles in our path share a common edge and the path never travels up (from a lower row to a higher row) or revisits a triangle. An example of one such path is illustrated below for $n=5$. Determine the value of $f(2005)$.
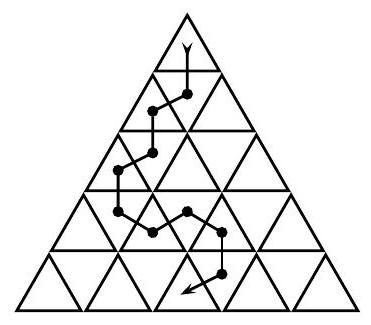
|
We shall show that $f(n)=(n-1)$ !.
Label the horizontal line segments in the triangle $l_{1}, l_{2}, \ldots$ as in the diagram below. Since the path goes from the top triangle to a triangle in the bottom row and never travels up, the path must cross each of $l_{1}, l_{2}, \ldots, l_{n-1}$ exactly once. The diagonal lines in the triangle divide $l_{k}$ into $k$ unit line segments and the path must cross exactly one of these $k$ segments for each $k$. (In the diagram below, these line segments have been highlighted.) The path is completely determined by the set of $n-1$ line segments which are crossed. So as the path moves from the $k$ th row to the $(k+1)$ st row, there are $k$ possible line segments where the path could cross $l_{k}$. Since there are $1 \cdot 2 \cdot 3 \cdots(n-1)=(n-1)$ ! ways that the path could cross the $n-1$ horizontal lines, and each one corresponds to a unique path, we get $f(n)=(n-1)$ !.
Therefore $f(2005)=(2004)$ !.
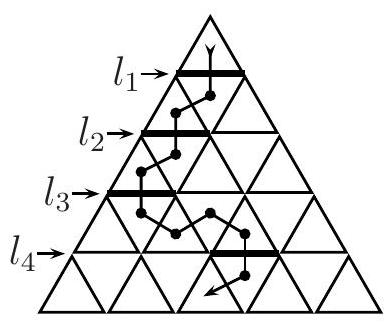
|
2004!
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Consider an equilateral triangle of side length $n$, which is divided into unit triangles, as shown. Let $f(n)$ be the number of paths from the triangle in the top row to the middle triangle in the bottom row, such that adjacent triangles in our path share a common edge and the path never travels up (from a lower row to a higher row) or revisits a triangle. An example of one such path is illustrated below for $n=5$. Determine the value of $f(2005)$.

|
We shall show that $f(n)=(n-1)$ !.
Label the horizontal line segments in the triangle $l_{1}, l_{2}, \ldots$ as in the diagram below. Since the path goes from the top triangle to a triangle in the bottom row and never travels up, the path must cross each of $l_{1}, l_{2}, \ldots, l_{n-1}$ exactly once. The diagonal lines in the triangle divide $l_{k}$ into $k$ unit line segments and the path must cross exactly one of these $k$ segments for each $k$. (In the diagram below, these line segments have been highlighted.) The path is completely determined by the set of $n-1$ line segments which are crossed. So as the path moves from the $k$ th row to the $(k+1)$ st row, there are $k$ possible line segments where the path could cross $l_{k}$. Since there are $1 \cdot 2 \cdot 3 \cdots(n-1)=(n-1)$ ! ways that the path could cross the $n-1$ horizontal lines, and each one corresponds to a unique path, we get $f(n)=(n-1)$ !.
Therefore $f(2005)=(2004)$ !.

|
{
"exam": "Canada_MO",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "Canada_MO/segmented/en-sol2005.jsonl",
"solution_match": "\n## Solution\n\n",
"tier": "T2",
"year": "2005"
}
|
Let $(a, b, c)$ be a Pythagorean triple, i.e., a triplet of positive integers with $a^{2}+b^{2}=c^{2}$.
a) Prove that $(c / a+c / b)^{2}>8$.
b) Prove that there does not exist any integer $n$ for which we can find a Pythagorean triple $(a, b, c)$ satisfying $(c / a+c / b)^{2}=n$.
## a) Solution 1
Let $(a, b, c)$ be a Pythagorean triple. View $a, b$ as lengths of the legs of a right angled triangle with hypotenuse of length $c$; let $\theta$ be the angle determined by the sides with lengths $a$ and $c$. Then
$$
\begin{aligned}
\left(\frac{c}{a}+\frac{c}{b}\right)^{2} & =\left(\frac{1}{\cos \theta}+\frac{1}{\sin \theta}\right)^{2}=\frac{\sin ^{2} \theta+\cos ^{2} \theta+2 \sin \theta \cos \theta}{(\sin \theta \cos \theta)^{2}} \\
& =4\left(\frac{1+\sin 2 \theta}{\sin ^{2} 2 \theta}\right)=\frac{4}{\sin ^{2} 2 \theta}+\frac{4}{\sin 2 \theta}
\end{aligned}
$$
Note that because $0<\theta<90^{\circ}$, we have $0<\sin 2 \theta \leq 1$, with equality only if $\theta=45^{\circ}$. But then $a=b$ and we obtain $\sqrt{2}=c / a$, contradicting $a, c$ both being integers. Thus, $0<\sin 2 \theta<1$ which gives $(c / a+c / b)^{2}>8$.
|
Defining $\theta$ as in Solution 1, we have $c / a+c / b=\sec \theta+\csc \theta$. By the AM-GM inequality, we have $(\sec \theta+\csc \theta) / 2 \geq \sqrt{\sec \theta \csc \theta}$. So
$$
c / a+c / b \geq \frac{2}{\sqrt{\sin \theta \cos \theta}}=\frac{2 \sqrt{2}}{\sqrt{\sin 2 \theta}} \geq 2 \sqrt{2}
$$
Since $a, b, c$ are integers, we have $c / a+c / b>2 \sqrt{2}$ which gives $(c / a+c / b)^{2}>8$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $(a, b, c)$ be a Pythagorean triple, i.e., a triplet of positive integers with $a^{2}+b^{2}=c^{2}$.
a) Prove that $(c / a+c / b)^{2}>8$.
b) Prove that there does not exist any integer $n$ for which we can find a Pythagorean triple $(a, b, c)$ satisfying $(c / a+c / b)^{2}=n$.
## a) Solution 1
Let $(a, b, c)$ be a Pythagorean triple. View $a, b$ as lengths of the legs of a right angled triangle with hypotenuse of length $c$; let $\theta$ be the angle determined by the sides with lengths $a$ and $c$. Then
$$
\begin{aligned}
\left(\frac{c}{a}+\frac{c}{b}\right)^{2} & =\left(\frac{1}{\cos \theta}+\frac{1}{\sin \theta}\right)^{2}=\frac{\sin ^{2} \theta+\cos ^{2} \theta+2 \sin \theta \cos \theta}{(\sin \theta \cos \theta)^{2}} \\
& =4\left(\frac{1+\sin 2 \theta}{\sin ^{2} 2 \theta}\right)=\frac{4}{\sin ^{2} 2 \theta}+\frac{4}{\sin 2 \theta}
\end{aligned}
$$
Note that because $0<\theta<90^{\circ}$, we have $0<\sin 2 \theta \leq 1$, with equality only if $\theta=45^{\circ}$. But then $a=b$ and we obtain $\sqrt{2}=c / a$, contradicting $a, c$ both being integers. Thus, $0<\sin 2 \theta<1$ which gives $(c / a+c / b)^{2}>8$.
|
Defining $\theta$ as in Solution 1, we have $c / a+c / b=\sec \theta+\csc \theta$. By the AM-GM inequality, we have $(\sec \theta+\csc \theta) / 2 \geq \sqrt{\sec \theta \csc \theta}$. So
$$
c / a+c / b \geq \frac{2}{\sqrt{\sin \theta \cos \theta}}=\frac{2 \sqrt{2}}{\sqrt{\sin 2 \theta}} \geq 2 \sqrt{2}
$$
Since $a, b, c$ are integers, we have $c / a+c / b>2 \sqrt{2}$ which gives $(c / a+c / b)^{2}>8$.
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "Canada_MO/segmented/en-sol2005.jsonl",
"solution_match": "\n## Solution 2",
"tier": "T2",
"year": "2005"
}
|
Let $(a, b, c)$ be a Pythagorean triple, i.e., a triplet of positive integers with $a^{2}+b^{2}=c^{2}$.
a) Prove that $(c / a+c / b)^{2}>8$.
b) Prove that there does not exist any integer $n$ for which we can find a Pythagorean triple $(a, b, c)$ satisfying $(c / a+c / b)^{2}=n$.
## a) Solution 1
Let $(a, b, c)$ be a Pythagorean triple. View $a, b$ as lengths of the legs of a right angled triangle with hypotenuse of length $c$; let $\theta$ be the angle determined by the sides with lengths $a$ and $c$. Then
$$
\begin{aligned}
\left(\frac{c}{a}+\frac{c}{b}\right)^{2} & =\left(\frac{1}{\cos \theta}+\frac{1}{\sin \theta}\right)^{2}=\frac{\sin ^{2} \theta+\cos ^{2} \theta+2 \sin \theta \cos \theta}{(\sin \theta \cos \theta)^{2}} \\
& =4\left(\frac{1+\sin 2 \theta}{\sin ^{2} 2 \theta}\right)=\frac{4}{\sin ^{2} 2 \theta}+\frac{4}{\sin 2 \theta}
\end{aligned}
$$
Note that because $0<\theta<90^{\circ}$, we have $0<\sin 2 \theta \leq 1$, with equality only if $\theta=45^{\circ}$. But then $a=b$ and we obtain $\sqrt{2}=c / a$, contradicting $a, c$ both being integers. Thus, $0<\sin 2 \theta<1$ which gives $(c / a+c / b)^{2}>8$.
|
By simplifying and using the AM-GM inequality,
$$
\left(\frac{c}{a}+\frac{c}{b}\right)^{2}=c^{2}\left(\frac{a+b}{a b}\right)^{2}=\frac{\left(a^{2}+b^{2}\right)(a+b)^{2}}{a^{2} b^{2}} \geq \frac{2 \sqrt{a^{2} b^{2}}(2 \sqrt{a b})^{2}}{a^{2} b^{2}}=8
$$
with equality only if $a=b$. By using the same argument as in Solution $1, a$ cannot equal $b$ and the inequality is strict.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $(a, b, c)$ be a Pythagorean triple, i.e., a triplet of positive integers with $a^{2}+b^{2}=c^{2}$.
a) Prove that $(c / a+c / b)^{2}>8$.
b) Prove that there does not exist any integer $n$ for which we can find a Pythagorean triple $(a, b, c)$ satisfying $(c / a+c / b)^{2}=n$.
## a) Solution 1
Let $(a, b, c)$ be a Pythagorean triple. View $a, b$ as lengths of the legs of a right angled triangle with hypotenuse of length $c$; let $\theta$ be the angle determined by the sides with lengths $a$ and $c$. Then
$$
\begin{aligned}
\left(\frac{c}{a}+\frac{c}{b}\right)^{2} & =\left(\frac{1}{\cos \theta}+\frac{1}{\sin \theta}\right)^{2}=\frac{\sin ^{2} \theta+\cos ^{2} \theta+2 \sin \theta \cos \theta}{(\sin \theta \cos \theta)^{2}} \\
& =4\left(\frac{1+\sin 2 \theta}{\sin ^{2} 2 \theta}\right)=\frac{4}{\sin ^{2} 2 \theta}+\frac{4}{\sin 2 \theta}
\end{aligned}
$$
Note that because $0<\theta<90^{\circ}$, we have $0<\sin 2 \theta \leq 1$, with equality only if $\theta=45^{\circ}$. But then $a=b$ and we obtain $\sqrt{2}=c / a$, contradicting $a, c$ both being integers. Thus, $0<\sin 2 \theta<1$ which gives $(c / a+c / b)^{2}>8$.
|
By simplifying and using the AM-GM inequality,
$$
\left(\frac{c}{a}+\frac{c}{b}\right)^{2}=c^{2}\left(\frac{a+b}{a b}\right)^{2}=\frac{\left(a^{2}+b^{2}\right)(a+b)^{2}}{a^{2} b^{2}} \geq \frac{2 \sqrt{a^{2} b^{2}}(2 \sqrt{a b})^{2}}{a^{2} b^{2}}=8
$$
with equality only if $a=b$. By using the same argument as in Solution $1, a$ cannot equal $b$ and the inequality is strict.
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "Canada_MO/segmented/en-sol2005.jsonl",
"solution_match": "\n## Solution 3",
"tier": "T2",
"year": "2005"
}
|
Let $(a, b, c)$ be a Pythagorean triple, i.e., a triplet of positive integers with $a^{2}+b^{2}=c^{2}$.
a) Prove that $(c / a+c / b)^{2}>8$.
b) Prove that there does not exist any integer $n$ for which we can find a Pythagorean triple $(a, b, c)$ satisfying $(c / a+c / b)^{2}=n$.
## a) Solution 1
Let $(a, b, c)$ be a Pythagorean triple. View $a, b$ as lengths of the legs of a right angled triangle with hypotenuse of length $c$; let $\theta$ be the angle determined by the sides with lengths $a$ and $c$. Then
$$
\begin{aligned}
\left(\frac{c}{a}+\frac{c}{b}\right)^{2} & =\left(\frac{1}{\cos \theta}+\frac{1}{\sin \theta}\right)^{2}=\frac{\sin ^{2} \theta+\cos ^{2} \theta+2 \sin \theta \cos \theta}{(\sin \theta \cos \theta)^{2}} \\
& =4\left(\frac{1+\sin 2 \theta}{\sin ^{2} 2 \theta}\right)=\frac{4}{\sin ^{2} 2 \theta}+\frac{4}{\sin 2 \theta}
\end{aligned}
$$
Note that because $0<\theta<90^{\circ}$, we have $0<\sin 2 \theta \leq 1$, with equality only if $\theta=45^{\circ}$. But then $a=b$ and we obtain $\sqrt{2}=c / a$, contradicting $a, c$ both being integers. Thus, $0<\sin 2 \theta<1$ which gives $(c / a+c / b)^{2}>8$.
|
$$
\begin{aligned}
\left(\frac{c}{a}+\frac{c}{b}\right)^{2} & =\frac{c^{2}}{a^{2}}+\frac{c^{2}}{b^{2}}+\frac{2 c^{2}}{a b}=1+\frac{b^{2}}{a^{2}}+\frac{a^{2}}{b^{2}}+1+\frac{2\left(a^{2}+b^{2}\right)}{a b} \\
& =2+\left(\frac{a}{b}-\frac{b}{a}\right)^{2}+2+\frac{2}{a b}\left((a-b)^{2}+2 a b\right) \\
& =4+\left(\frac{a}{b}-\frac{b}{a}\right)^{2}+\frac{2(a-b)^{2}}{a b}+4 \geq 8,
\end{aligned}
$$
with equality only if $a=b$, which (as argued previously) cannot occur.
## b) Solution 1
Since $c / a+c / b$ is rational, $(c / a+c / b)^{2}$ can only be an integer if $c / a+c / b$ is an integer. Suppose $c / a+c / b=m$. We may assume that $\operatorname{gcd}(a, b)=1$. (If not, divide the common factor from $(a, b, c)$, leaving $m$ unchanged.)
Since $c(a+b)=m a b$ and $\operatorname{gcd}(a, a+b)=1$, $a$ must divide $c$, say $c=a k$. This gives $a^{2}+b^{2}=a^{2} k^{2}$ which implies $b^{2}=\left(k^{2}-1\right) a^{2}$. But then $a$ divides $b$ contradicting the fact that $\operatorname{gcd}(a, b)=1$. Therefore $(c / a+c / b)^{2}$ is not equal to any integer $n$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $(a, b, c)$ be a Pythagorean triple, i.e., a triplet of positive integers with $a^{2}+b^{2}=c^{2}$.
a) Prove that $(c / a+c / b)^{2}>8$.
b) Prove that there does not exist any integer $n$ for which we can find a Pythagorean triple $(a, b, c)$ satisfying $(c / a+c / b)^{2}=n$.
## a) Solution 1
Let $(a, b, c)$ be a Pythagorean triple. View $a, b$ as lengths of the legs of a right angled triangle with hypotenuse of length $c$; let $\theta$ be the angle determined by the sides with lengths $a$ and $c$. Then
$$
\begin{aligned}
\left(\frac{c}{a}+\frac{c}{b}\right)^{2} & =\left(\frac{1}{\cos \theta}+\frac{1}{\sin \theta}\right)^{2}=\frac{\sin ^{2} \theta+\cos ^{2} \theta+2 \sin \theta \cos \theta}{(\sin \theta \cos \theta)^{2}} \\
& =4\left(\frac{1+\sin 2 \theta}{\sin ^{2} 2 \theta}\right)=\frac{4}{\sin ^{2} 2 \theta}+\frac{4}{\sin 2 \theta}
\end{aligned}
$$
Note that because $0<\theta<90^{\circ}$, we have $0<\sin 2 \theta \leq 1$, with equality only if $\theta=45^{\circ}$. But then $a=b$ and we obtain $\sqrt{2}=c / a$, contradicting $a, c$ both being integers. Thus, $0<\sin 2 \theta<1$ which gives $(c / a+c / b)^{2}>8$.
|
$$
\begin{aligned}
\left(\frac{c}{a}+\frac{c}{b}\right)^{2} & =\frac{c^{2}}{a^{2}}+\frac{c^{2}}{b^{2}}+\frac{2 c^{2}}{a b}=1+\frac{b^{2}}{a^{2}}+\frac{a^{2}}{b^{2}}+1+\frac{2\left(a^{2}+b^{2}\right)}{a b} \\
& =2+\left(\frac{a}{b}-\frac{b}{a}\right)^{2}+2+\frac{2}{a b}\left((a-b)^{2}+2 a b\right) \\
& =4+\left(\frac{a}{b}-\frac{b}{a}\right)^{2}+\frac{2(a-b)^{2}}{a b}+4 \geq 8,
\end{aligned}
$$
with equality only if $a=b$, which (as argued previously) cannot occur.
## b) Solution 1
Since $c / a+c / b$ is rational, $(c / a+c / b)^{2}$ can only be an integer if $c / a+c / b$ is an integer. Suppose $c / a+c / b=m$. We may assume that $\operatorname{gcd}(a, b)=1$. (If not, divide the common factor from $(a, b, c)$, leaving $m$ unchanged.)
Since $c(a+b)=m a b$ and $\operatorname{gcd}(a, a+b)=1$, $a$ must divide $c$, say $c=a k$. This gives $a^{2}+b^{2}=a^{2} k^{2}$ which implies $b^{2}=\left(k^{2}-1\right) a^{2}$. But then $a$ divides $b$ contradicting the fact that $\operatorname{gcd}(a, b)=1$. Therefore $(c / a+c / b)^{2}$ is not equal to any integer $n$.
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "Canada_MO/segmented/en-sol2005.jsonl",
"solution_match": "\n## Solution 4",
"tier": "T2",
"year": "2005"
}
|
Let $(a, b, c)$ be a Pythagorean triple, i.e., a triplet of positive integers with $a^{2}+b^{2}=c^{2}$.
a) Prove that $(c / a+c / b)^{2}>8$.
b) Prove that there does not exist any integer $n$ for which we can find a Pythagorean triple $(a, b, c)$ satisfying $(c / a+c / b)^{2}=n$.
## a) Solution 1
Let $(a, b, c)$ be a Pythagorean triple. View $a, b$ as lengths of the legs of a right angled triangle with hypotenuse of length $c$; let $\theta$ be the angle determined by the sides with lengths $a$ and $c$. Then
$$
\begin{aligned}
\left(\frac{c}{a}+\frac{c}{b}\right)^{2} & =\left(\frac{1}{\cos \theta}+\frac{1}{\sin \theta}\right)^{2}=\frac{\sin ^{2} \theta+\cos ^{2} \theta+2 \sin \theta \cos \theta}{(\sin \theta \cos \theta)^{2}} \\
& =4\left(\frac{1+\sin 2 \theta}{\sin ^{2} 2 \theta}\right)=\frac{4}{\sin ^{2} 2 \theta}+\frac{4}{\sin 2 \theta}
\end{aligned}
$$
Note that because $0<\theta<90^{\circ}$, we have $0<\sin 2 \theta \leq 1$, with equality only if $\theta=45^{\circ}$. But then $a=b$ and we obtain $\sqrt{2}=c / a$, contradicting $a, c$ both being integers. Thus, $0<\sin 2 \theta<1$ which gives $(c / a+c / b)^{2}>8$.
|
We begin as in Solution 1, supposing that $c / a+c / b=m$ with $\operatorname{gcd}(a, b)=1$. Hence $a$ and $b$ are not both even. It is also the case that $a$ and $b$ are not both odd, for then $c^{2}=a^{2}+b^{2} \equiv 2(\bmod 4)$, and perfect squares are congruent to either 0 or 1 modulo 4. So one of $a, b$ is odd and the other is even. Therefore $c$ must be odd.
Now $c / a+c / b=m$ implies $c(a+b)=m a b$, which cannot be true because $c(a+b)$ is odd and mab is even.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $(a, b, c)$ be a Pythagorean triple, i.e., a triplet of positive integers with $a^{2}+b^{2}=c^{2}$.
a) Prove that $(c / a+c / b)^{2}>8$.
b) Prove that there does not exist any integer $n$ for which we can find a Pythagorean triple $(a, b, c)$ satisfying $(c / a+c / b)^{2}=n$.
## a) Solution 1
Let $(a, b, c)$ be a Pythagorean triple. View $a, b$ as lengths of the legs of a right angled triangle with hypotenuse of length $c$; let $\theta$ be the angle determined by the sides with lengths $a$ and $c$. Then
$$
\begin{aligned}
\left(\frac{c}{a}+\frac{c}{b}\right)^{2} & =\left(\frac{1}{\cos \theta}+\frac{1}{\sin \theta}\right)^{2}=\frac{\sin ^{2} \theta+\cos ^{2} \theta+2 \sin \theta \cos \theta}{(\sin \theta \cos \theta)^{2}} \\
& =4\left(\frac{1+\sin 2 \theta}{\sin ^{2} 2 \theta}\right)=\frac{4}{\sin ^{2} 2 \theta}+\frac{4}{\sin 2 \theta}
\end{aligned}
$$
Note that because $0<\theta<90^{\circ}$, we have $0<\sin 2 \theta \leq 1$, with equality only if $\theta=45^{\circ}$. But then $a=b$ and we obtain $\sqrt{2}=c / a$, contradicting $a, c$ both being integers. Thus, $0<\sin 2 \theta<1$ which gives $(c / a+c / b)^{2}>8$.
|
We begin as in Solution 1, supposing that $c / a+c / b=m$ with $\operatorname{gcd}(a, b)=1$. Hence $a$ and $b$ are not both even. It is also the case that $a$ and $b$ are not both odd, for then $c^{2}=a^{2}+b^{2} \equiv 2(\bmod 4)$, and perfect squares are congruent to either 0 or 1 modulo 4. So one of $a, b$ is odd and the other is even. Therefore $c$ must be odd.
Now $c / a+c / b=m$ implies $c(a+b)=m a b$, which cannot be true because $c(a+b)$ is odd and mab is even.
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "Canada_MO/segmented/en-sol2005.jsonl",
"solution_match": "\n## Solution 2",
"tier": "T2",
"year": "2005"
}
|
Let $S$ be a set of $n \geq 3$ points in the interior of a circle.
a) Show that there are three distinct points $a, b, c \in S$ and three distinct points $A, B, C$ on the circle such that $a$ is (strictly) closer to $A$ than any other point in $S, b$ is closer to $B$ than any other point in $S$ and $c$ is closer to $C$ than any other point in $S$.
b) Show that for no value of $n$ can four such points in $S$ (and corresponding points on the circle) be guaranteed.
|
a) Let $H$ be the smallest convex set of points in the plane which contains $S . \dagger$ Take 3 points $a, b, c \in S$ which lie on the boundary of $H$. (There must always be at least 3 (but not necessarily 4) such points.)
Since $a$ lies on the boundary of the convex region $H$, we can construct a chord $L$ such that no two points of $H$ lie on opposite sides of $L$. Of the two points where the perpendicular to $L$ at $a$ meets the circle, choose one which is on a side of $L$ not containing any points of $H$ and call this point $A$. Certainly $A$ is closer to $a$ than to any other point on $L$ or on the other side of $L$. Hence $A$ is closer to $a$ than to any other point of $S$. We can find the required points $B$ and $C$ in an analogous way and the proof is complete.
[Note that this argument still holds if all the points of $S$ lie on a line.]
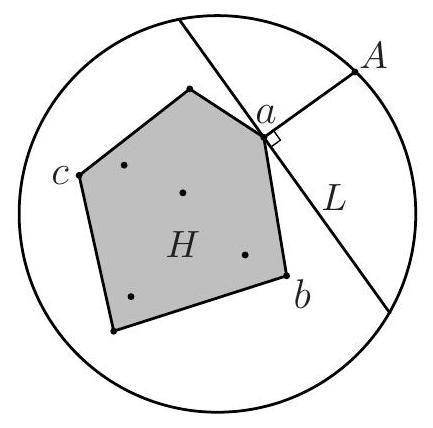
(a)
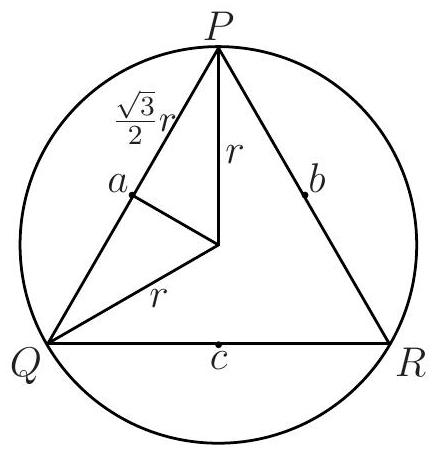
(b)
b) Let $P Q R$ be an equilateral triangle inscribed in the circle and let $a, b, c$ be midpoints of the three sides of $\triangle P Q R$. If $r$ is the radius of the circle, then every point on the circle is within $(\sqrt{3} / 2) r$ of one of $a, b$ or $c$. (See figure (b) above.) Now $\sqrt{3} / 2<9 / 10$, so if $S$ consists of $a, b, c$ and a cluster of points within $r / 10$ of the centre of the circle, then we cannot select 4 points from $S$ (and corresponding points on the circle) having the desired property.[^0]
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $S$ be a set of $n \geq 3$ points in the interior of a circle.
a) Show that there are three distinct points $a, b, c \in S$ and three distinct points $A, B, C$ on the circle such that $a$ is (strictly) closer to $A$ than any other point in $S, b$ is closer to $B$ than any other point in $S$ and $c$ is closer to $C$ than any other point in $S$.
b) Show that for no value of $n$ can four such points in $S$ (and corresponding points on the circle) be guaranteed.
|
a) Let $H$ be the smallest convex set of points in the plane which contains $S . \dagger$ Take 3 points $a, b, c \in S$ which lie on the boundary of $H$. (There must always be at least 3 (but not necessarily 4) such points.)
Since $a$ lies on the boundary of the convex region $H$, we can construct a chord $L$ such that no two points of $H$ lie on opposite sides of $L$. Of the two points where the perpendicular to $L$ at $a$ meets the circle, choose one which is on a side of $L$ not containing any points of $H$ and call this point $A$. Certainly $A$ is closer to $a$ than to any other point on $L$ or on the other side of $L$. Hence $A$ is closer to $a$ than to any other point of $S$. We can find the required points $B$ and $C$ in an analogous way and the proof is complete.
[Note that this argument still holds if all the points of $S$ lie on a line.]

(a)

(b)
b) Let $P Q R$ be an equilateral triangle inscribed in the circle and let $a, b, c$ be midpoints of the three sides of $\triangle P Q R$. If $r$ is the radius of the circle, then every point on the circle is within $(\sqrt{3} / 2) r$ of one of $a, b$ or $c$. (See figure (b) above.) Now $\sqrt{3} / 2<9 / 10$, so if $S$ consists of $a, b, c$ and a cluster of points within $r / 10$ of the centre of the circle, then we cannot select 4 points from $S$ (and corresponding points on the circle) having the desired property.[^0]
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "Canada_MO/segmented/en-sol2005.jsonl",
"solution_match": "\n## Solution 1",
"tier": "T2",
"year": "2005"
}
|
Let $S$ be a set of $n \geq 3$ points in the interior of a circle.
a) Show that there are three distinct points $a, b, c \in S$ and three distinct points $A, B, C$ on the circle such that $a$ is (strictly) closer to $A$ than any other point in $S, b$ is closer to $B$ than any other point in $S$ and $c$ is closer to $C$ than any other point in $S$.
b) Show that for no value of $n$ can four such points in $S$ (and corresponding points on the circle) be guaranteed.
|
a) If all the points of $S$ lie on a line $L$, then choose any 3 of them to be $a, b, c$. Let $A$ be a point on the circle which meets the perpendicular to $L$ at $a$. Clearly $A$ is closer to $a$ than to any other point on $L$, and hence closer than other other point in $S$. We find $B$ and $C$ in an analogous way.
Otherwise, choose $a, b, c$ from $S$ so that the triangle formed by these points has maximal area. Construct the altitude from the side $b c$ to the point $a$ and extend this line until it meets the circle at $A$. We claim that $A$ is closer to $a$ than to any other point in $S$.
Suppose not. Let $x$ be a point in $S$ for which the distance from $A$ to $x$ is less than the distance from $A$ to $a$. Then the perpendicular distance from $x$ to the line $b c$ must be greater than the perpendicular distance from $a$ to the line $b c$. But then the triangle formed by the points $x, b, c$ has greater area than the triangle formed by $a, b, c$, contradicting the original choice of these 3 points. Therefore $A$ is closer to $a$ than to any other point in $S$.
The points $B$ and $C$ are found by constructing similar altitudes through $b$ and $c$, respectively.
b) See Solution 1.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $S$ be a set of $n \geq 3$ points in the interior of a circle.
a) Show that there are three distinct points $a, b, c \in S$ and three distinct points $A, B, C$ on the circle such that $a$ is (strictly) closer to $A$ than any other point in $S, b$ is closer to $B$ than any other point in $S$ and $c$ is closer to $C$ than any other point in $S$.
b) Show that for no value of $n$ can four such points in $S$ (and corresponding points on the circle) be guaranteed.
|
a) If all the points of $S$ lie on a line $L$, then choose any 3 of them to be $a, b, c$. Let $A$ be a point on the circle which meets the perpendicular to $L$ at $a$. Clearly $A$ is closer to $a$ than to any other point on $L$, and hence closer than other other point in $S$. We find $B$ and $C$ in an analogous way.
Otherwise, choose $a, b, c$ from $S$ so that the triangle formed by these points has maximal area. Construct the altitude from the side $b c$ to the point $a$ and extend this line until it meets the circle at $A$. We claim that $A$ is closer to $a$ than to any other point in $S$.
Suppose not. Let $x$ be a point in $S$ for which the distance from $A$ to $x$ is less than the distance from $A$ to $a$. Then the perpendicular distance from $x$ to the line $b c$ must be greater than the perpendicular distance from $a$ to the line $b c$. But then the triangle formed by the points $x, b, c$ has greater area than the triangle formed by $a, b, c$, contradicting the original choice of these 3 points. Therefore $A$ is closer to $a$ than to any other point in $S$.
The points $B$ and $C$ are found by constructing similar altitudes through $b$ and $c$, respectively.
b) See Solution 1.
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "Canada_MO/segmented/en-sol2005.jsonl",
"solution_match": "\n## Solution 2",
"tier": "T2",
"year": "2005"
}
|
Let $A B C$ be a triangle with circumradius $R$, perimeter $P$ and area $K$. Determine the maximum value of $K P / R^{3}$.
|
Since similar triangles give the same value of $K P / R^{3}$, we can fix $R=1$ and maximize $K P$ over all triangles inscribed in the unit circle. Fix points $A$ and $B$ on the unit circle. The locus of points $C$ with a given perimeter $P$ is an ellipse that meets the circle in at most four points. The area $K$ is maximized (for a fixed $P$ ) when $C$ is chosen on the perpendicular bisector of $A B$, so we get a maximum value for $K P$ if $C$ is where the perpendicular bisector of $A B$ meets the circle. Thus the maximum value of $K P$ for a given $A B$ occurs when $A B C$ is an isosceles triangle. Repeating this argument with $B C$ fixed, we have that the maximum occurs when $A B C$ is an equilateral triangle.
Consider an equilateral triangle with side length $a$. It has $P=3 a$. It has height equal to $a \sqrt{3} / 2$ giving $K=a^{2} \sqrt{3} / 4$. ¿From the extended law of sines, $2 R=a / \sin (60)$ giving $R=a / \sqrt{3}$. Therefore the maximum value we seek is
$$
K P / R^{3}=\left(\frac{a^{2} \sqrt{3}}{4}\right)(3 a)\left(\frac{\sqrt{3}}{a}\right)^{3}=\frac{27}{4} .
$$
|
\frac{27}{4}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle with circumradius $R$, perimeter $P$ and area $K$. Determine the maximum value of $K P / R^{3}$.
|
Since similar triangles give the same value of $K P / R^{3}$, we can fix $R=1$ and maximize $K P$ over all triangles inscribed in the unit circle. Fix points $A$ and $B$ on the unit circle. The locus of points $C$ with a given perimeter $P$ is an ellipse that meets the circle in at most four points. The area $K$ is maximized (for a fixed $P$ ) when $C$ is chosen on the perpendicular bisector of $A B$, so we get a maximum value for $K P$ if $C$ is where the perpendicular bisector of $A B$ meets the circle. Thus the maximum value of $K P$ for a given $A B$ occurs when $A B C$ is an isosceles triangle. Repeating this argument with $B C$ fixed, we have that the maximum occurs when $A B C$ is an equilateral triangle.
Consider an equilateral triangle with side length $a$. It has $P=3 a$. It has height equal to $a \sqrt{3} / 2$ giving $K=a^{2} \sqrt{3} / 4$. ¿From the extended law of sines, $2 R=a / \sin (60)$ giving $R=a / \sqrt{3}$. Therefore the maximum value we seek is
$$
K P / R^{3}=\left(\frac{a^{2} \sqrt{3}}{4}\right)(3 a)\left(\frac{\sqrt{3}}{a}\right)^{3}=\frac{27}{4} .
$$
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "Canada_MO/segmented/en-sol2005.jsonl",
"solution_match": "\n## Solution 1",
"tier": "T2",
"year": "2005"
}
|
Let $A B C$ be a triangle with circumradius $R$, perimeter $P$ and area $K$. Determine the maximum value of $K P / R^{3}$.
|
From the extended law of sines, the lengths of the sides of the triangle are $2 R \sin A$, $2 R \sin B$ and $2 R \sin C$. So
$$
P=2 R(\sin A+\sin B+\sin C) \text { and } K=\frac{1}{2}(2 R \sin A)(2 R \sin B)(\sin C),
$$
giving
$$
\frac{K P}{R^{3}}=4 \sin A \sin B \sin C(\sin A+\sin B+\sin C)
$$
We wish to find the maximum value of this expression over all $A+B+C=180^{\circ}$. Using well-known identities for sums and products of sine functions, we can write
$$
\frac{K P}{R^{3}}=4 \sin A\left(\frac{\cos (B-C)}{2}-\frac{\cos (B+C)}{2}\right)\left(\sin A+2 \sin \left(\frac{B+C}{2}\right) \cos \left(\frac{B-C}{2}\right)\right) .
$$
If we first consider $A$ to be fixed, then $B+C$ is fixed also and this expression takes its maximum value when $\cos (B-C)$ and $\cos \left(\frac{B-C}{2}\right)$ equal 1 ; i.e. when $B=C$. In a similar way, one can show that for any fixed value of $B, K P / R^{3}$ is maximized when $A=C$. Therefore the maximum value of $K P / R^{3}$ occurs when $A=B=C=60^{\circ}$, and it is now an easy task to substitute this into the above expression to obtain the maximum value of $27 / 4$.
|
\frac{27}{4}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle with circumradius $R$, perimeter $P$ and area $K$. Determine the maximum value of $K P / R^{3}$.
|
From the extended law of sines, the lengths of the sides of the triangle are $2 R \sin A$, $2 R \sin B$ and $2 R \sin C$. So
$$
P=2 R(\sin A+\sin B+\sin C) \text { and } K=\frac{1}{2}(2 R \sin A)(2 R \sin B)(\sin C),
$$
giving
$$
\frac{K P}{R^{3}}=4 \sin A \sin B \sin C(\sin A+\sin B+\sin C)
$$
We wish to find the maximum value of this expression over all $A+B+C=180^{\circ}$. Using well-known identities for sums and products of sine functions, we can write
$$
\frac{K P}{R^{3}}=4 \sin A\left(\frac{\cos (B-C)}{2}-\frac{\cos (B+C)}{2}\right)\left(\sin A+2 \sin \left(\frac{B+C}{2}\right) \cos \left(\frac{B-C}{2}\right)\right) .
$$
If we first consider $A$ to be fixed, then $B+C$ is fixed also and this expression takes its maximum value when $\cos (B-C)$ and $\cos \left(\frac{B-C}{2}\right)$ equal 1 ; i.e. when $B=C$. In a similar way, one can show that for any fixed value of $B, K P / R^{3}$ is maximized when $A=C$. Therefore the maximum value of $K P / R^{3}$ occurs when $A=B=C=60^{\circ}$, and it is now an easy task to substitute this into the above expression to obtain the maximum value of $27 / 4$.
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "Canada_MO/segmented/en-sol2005.jsonl",
"solution_match": "\n## Solution 2",
"tier": "T2",
"year": "2005"
}
|
Let $A B C$ be a triangle with circumradius $R$, perimeter $P$ and area $K$. Determine the maximum value of $K P / R^{3}$.
|
As in Solution 2, we obtain
$$
\frac{K P}{R^{3}}=4 \sin A \sin B \sin C(\sin A+\sin B+\sin C)
$$
From the AM-GM inequality, we have
$$
\sin A \sin B \sin C \leq\left(\frac{\sin A+\sin B+\sin C}{3}\right)^{3},
$$
giving
$$
\frac{K P}{R^{3}} \leq \frac{4}{27}(\sin A+\sin B+\sin C)^{4}
$$
with equality when $\sin A=\sin B=\sin C$. Since the sine function is concave on the interval from 0 to $\pi$, Jensen's inequality gives
$$
\frac{\sin A+\sin B+\sin C}{3} \leq \sin \left(\frac{A+B+C}{3}\right)=\sin \frac{\pi}{3}=\frac{\sqrt{3}}{2} .
$$
Since equality occurs here when $\sin A=\sin B=\sin C$ also, we can conclude that the maximum value of $K P / R^{3}$ is $\frac{4}{27}\left(\frac{3 \sqrt{3}}{2}\right)^{4}=27 / 4$.
|
\frac{27}{4}
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be a triangle with circumradius $R$, perimeter $P$ and area $K$. Determine the maximum value of $K P / R^{3}$.
|
As in Solution 2, we obtain
$$
\frac{K P}{R^{3}}=4 \sin A \sin B \sin C(\sin A+\sin B+\sin C)
$$
From the AM-GM inequality, we have
$$
\sin A \sin B \sin C \leq\left(\frac{\sin A+\sin B+\sin C}{3}\right)^{3},
$$
giving
$$
\frac{K P}{R^{3}} \leq \frac{4}{27}(\sin A+\sin B+\sin C)^{4}
$$
with equality when $\sin A=\sin B=\sin C$. Since the sine function is concave on the interval from 0 to $\pi$, Jensen's inequality gives
$$
\frac{\sin A+\sin B+\sin C}{3} \leq \sin \left(\frac{A+B+C}{3}\right)=\sin \frac{\pi}{3}=\frac{\sqrt{3}}{2} .
$$
Since equality occurs here when $\sin A=\sin B=\sin C$ also, we can conclude that the maximum value of $K P / R^{3}$ is $\frac{4}{27}\left(\frac{3 \sqrt{3}}{2}\right)^{4}=27 / 4$.
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "Canada_MO/segmented/en-sol2005.jsonl",
"solution_match": "\n## Solution 3",
"tier": "T2",
"year": "2005"
}
|
Let's say that an ordered triple of positive integers $(a, b, c)$ is $n$-powerful if $a \leq b \leq c$, $\operatorname{gcd}(a, b, c)=1$, and $a^{n}+b^{n}+c^{n}$ is divisible by $a+b+c$. For example, $(1,2,2)$ is 5 -powerful.
a) Determine all ordered triples (if any) which are $n$-powerful for all $n \geq 1$.
b) Determine all ordered triples (if any) which are 2004-powerful and 2005-powerful, but not 2007-powerful.
[Note that $\operatorname{gcd}(a, b, c)$ is the greatest common divisor of $a, b$ and $c$.]
|
Let $T_{n}=a^{n}+b^{n}+c^{n}$ and consider the polynomial
$$
P(x)=(x-a)(x-b)(x-c)=x^{3}-(a+b+c) x^{2}+(a b+a c+b c) x-a b c .
$$
Since $P(a)=0$, we get $a^{3}=(a+b+c) a^{2}-(a b+a c+b c) a+a b c$ and multiplying both sides by $a^{n-3}$ we obtain $a^{n}=(a+b+c) a^{n-1}-(a b+a c+b c) a^{n-2}+(a b c) a^{n-3}$. Applying the same reasoning, we can obtain similar expressions for $b^{n}$ and $c^{n}$ and adding the three identities we get that $T_{n}$ satisfies the following 3 -term recurrence:
$$
T_{n}=(a+b+c) T_{n-1}-(a b+a c+b c) T_{n-2}+(a b c) T_{n-3} \text {, for all } n \geq 3
$$
¿From this we see that if $T_{n-2}$ and $T_{n-3}$ are divisible by $a+b+c$, then so is $T_{n}$. This immediately resolves part (b) - there are no ordered triples which are 2004-powerful and 2005-powerful, but not 2007-powerful-and reduces the number of cases to be considered in part (a): since all triples are 1-powerful, the recurrence implies that any ordered triple which is both 2 -powerful and 3 -powerful is $n$-powerful for all $n \geq 1$.
Putting $n=3$ in the recurrence, we have
$$
a^{3}+b^{3}+c^{3}=(a+b+c)\left(a^{2}+b^{2}+c^{2}\right)-(a b+a c+b c)(a+b+c)+3 a b c
$$
which implies that $(a, b, c)$ is 3 -powerful if and only if $3 a b c$ is divisible by $a+b+c$. Since
$$
a^{2}+b^{2}+c^{2}=(a+b+c)^{2}-2(a b+a c+b c),
$$
$(a, b, c)$ is 2 -powerful if and only if $2(a b+a c+b c)$ is divisible by $a+b+c$.
Suppose a prime $p \geq 5$ divides $a+b+c$. Then $p$ divides $a b c$. Since $\operatorname{gcd}(a, b, c)=1, p$ divides exactly one of $a, b$ or $c$; but then $p$ doesn't divide $2(a b+a c+b c)$.
Suppose $3^{2}$ divides $a+b+c$. Then 3 divides $a b c$, implying 3 divides exactly one of $a$, $b$ or $c$. But then 3 doesn't divide $2(a b+a c+b c)$.
Suppose $2^{2}$ divides $a+b+c$. Then 4 divides $a b c$. Since $\operatorname{gcd}(a, b, c)=1$, at most one of $a, b$ or $c$ is even, implying one of $a, b, c$ is divisible by 4 and the others are odd. But then $a b+a c+b c$ is odd and 4 doesn't divide $2(a b+a c+b c)$.
So if $(a, b, c)$ is 2 - and 3 -powerful, then $a+b+c$ is not divisible by 4 or 9 or any prime greater than 3. Since $a+b+c$ is at least $3, a+b+c$ is either 3 or 6 . It is now a simple matter to check the possibilities and conclude that the only triples which are $n$-powerful for all $n \geq 1$ are $(1,1,1)$ and $(1,1,4)$.
|
(1,1,1) \text{ and } (1,1,4)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let's say that an ordered triple of positive integers $(a, b, c)$ is $n$-powerful if $a \leq b \leq c$, $\operatorname{gcd}(a, b, c)=1$, and $a^{n}+b^{n}+c^{n}$ is divisible by $a+b+c$. For example, $(1,2,2)$ is 5 -powerful.
a) Determine all ordered triples (if any) which are $n$-powerful for all $n \geq 1$.
b) Determine all ordered triples (if any) which are 2004-powerful and 2005-powerful, but not 2007-powerful.
[Note that $\operatorname{gcd}(a, b, c)$ is the greatest common divisor of $a, b$ and $c$.]
|
Let $T_{n}=a^{n}+b^{n}+c^{n}$ and consider the polynomial
$$
P(x)=(x-a)(x-b)(x-c)=x^{3}-(a+b+c) x^{2}+(a b+a c+b c) x-a b c .
$$
Since $P(a)=0$, we get $a^{3}=(a+b+c) a^{2}-(a b+a c+b c) a+a b c$ and multiplying both sides by $a^{n-3}$ we obtain $a^{n}=(a+b+c) a^{n-1}-(a b+a c+b c) a^{n-2}+(a b c) a^{n-3}$. Applying the same reasoning, we can obtain similar expressions for $b^{n}$ and $c^{n}$ and adding the three identities we get that $T_{n}$ satisfies the following 3 -term recurrence:
$$
T_{n}=(a+b+c) T_{n-1}-(a b+a c+b c) T_{n-2}+(a b c) T_{n-3} \text {, for all } n \geq 3
$$
¿From this we see that if $T_{n-2}$ and $T_{n-3}$ are divisible by $a+b+c$, then so is $T_{n}$. This immediately resolves part (b) - there are no ordered triples which are 2004-powerful and 2005-powerful, but not 2007-powerful-and reduces the number of cases to be considered in part (a): since all triples are 1-powerful, the recurrence implies that any ordered triple which is both 2 -powerful and 3 -powerful is $n$-powerful for all $n \geq 1$.
Putting $n=3$ in the recurrence, we have
$$
a^{3}+b^{3}+c^{3}=(a+b+c)\left(a^{2}+b^{2}+c^{2}\right)-(a b+a c+b c)(a+b+c)+3 a b c
$$
which implies that $(a, b, c)$ is 3 -powerful if and only if $3 a b c$ is divisible by $a+b+c$. Since
$$
a^{2}+b^{2}+c^{2}=(a+b+c)^{2}-2(a b+a c+b c),
$$
$(a, b, c)$ is 2 -powerful if and only if $2(a b+a c+b c)$ is divisible by $a+b+c$.
Suppose a prime $p \geq 5$ divides $a+b+c$. Then $p$ divides $a b c$. Since $\operatorname{gcd}(a, b, c)=1, p$ divides exactly one of $a, b$ or $c$; but then $p$ doesn't divide $2(a b+a c+b c)$.
Suppose $3^{2}$ divides $a+b+c$. Then 3 divides $a b c$, implying 3 divides exactly one of $a$, $b$ or $c$. But then 3 doesn't divide $2(a b+a c+b c)$.
Suppose $2^{2}$ divides $a+b+c$. Then 4 divides $a b c$. Since $\operatorname{gcd}(a, b, c)=1$, at most one of $a, b$ or $c$ is even, implying one of $a, b, c$ is divisible by 4 and the others are odd. But then $a b+a c+b c$ is odd and 4 doesn't divide $2(a b+a c+b c)$.
So if $(a, b, c)$ is 2 - and 3 -powerful, then $a+b+c$ is not divisible by 4 or 9 or any prime greater than 3. Since $a+b+c$ is at least $3, a+b+c$ is either 3 or 6 . It is now a simple matter to check the possibilities and conclude that the only triples which are $n$-powerful for all $n \geq 1$ are $(1,1,1)$ and $(1,1,4)$.
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "Canada_MO/segmented/en-sol2005.jsonl",
"solution_match": "\n## Solution 1",
"tier": "T2",
"year": "2005"
}
|
Let's say that an ordered triple of positive integers $(a, b, c)$ is $n$-powerful if $a \leq b \leq c$, $\operatorname{gcd}(a, b, c)=1$, and $a^{n}+b^{n}+c^{n}$ is divisible by $a+b+c$. For example, $(1,2,2)$ is 5 -powerful.
a) Determine all ordered triples (if any) which are $n$-powerful for all $n \geq 1$.
b) Determine all ordered triples (if any) which are 2004-powerful and 2005-powerful, but not 2007-powerful.
[Note that $\operatorname{gcd}(a, b, c)$ is the greatest common divisor of $a, b$ and $c$.]
|
Let $p$ be a prime. By Fermat's Little Theorem,
$$
a^{p-1} \equiv \begin{cases}1(\bmod p), & \text { if } p \text { doesn't divide } a \\ 0(\bmod p), & \text { if } p \text { divides } a\end{cases}
$$
Since $\operatorname{gcd}(a, b, c)=1$, we have that $a^{p-1}+b^{p-1}+c^{p-1} \equiv 1,2$ or $3(\bmod p)$. Therefore if $p$ is a prime divisor of $a^{p-1}+b^{p-1}+c^{p-1}$, then $p$ equals 2 or 3 . So if $(a, b, c)$ is $n$-powerful for all $n \geq 1$, then the only primes which can divide $a+b+c$ are 2 or 3 .
We can proceed in a similar fashion to show that $a+b+c$ is not divisible by 4 or 9 .
Since
$$
a^{2} \equiv \begin{cases}0(\bmod 4), & \text { if } p \text { is even; } \\ 1(\bmod 4), & \text { if } p \text { is odd }\end{cases}
$$
and $a, b, c$ aren't all even, we have that $a^{2}+b^{2}+c^{2} \equiv 1,2$ or $3(\bmod 4)$.
By expanding $(3 k)^{3},(3 k+1)^{3}$ and $(3 k+2)^{3}$, we find that $a^{3}$ is congruent to 0,1 or -1 modulo 9. Hence
$$
a^{6} \equiv \begin{cases}0(\bmod 9), & \text { if } 3 \text { divides } a ; \\ 1(\bmod 9), & \text { if } 3 \text { doesn't divide } a .\end{cases}
$$
Since $a, b, c$ aren't all divisible by 3 , we have that $a^{6}+b^{6}+c^{6} \equiv 1,2$ or $3(\bmod 9)$.
So $a^{2}+b^{2}+c^{2}$ is not divisible by 4 and $a^{6}+b^{6}+c^{6}$ is not divisible by 9 . Thus if $(a, b, c)$ is $n$-powerful for all $n \geq 1$, then $a+b+c$ is not divisible by 4 or 9 . Therefore $a+b+c$ is either 3 or 6 and checking all possibilities, we conclude that the only triples which are $n$-powerful for all $n \geq 1$ are $(1,1,1)$ and $(1,1,4)$.
See Solution 1 for the (b) part.
[^0]: ${ }^{\dagger}$ By the way, $H$ is called the convex hull of $S$. If the points of $S$ lie on a line, then $H$ will be the shortest line segment containing the points of $S$. Otherwise, $H$ is a polygon whose vertices are all elements of $S$ and such that all other points in $S$ lie inside or on this polygon.
|
(1,1,1) \text{ and } (1,1,4)
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let's say that an ordered triple of positive integers $(a, b, c)$ is $n$-powerful if $a \leq b \leq c$, $\operatorname{gcd}(a, b, c)=1$, and $a^{n}+b^{n}+c^{n}$ is divisible by $a+b+c$. For example, $(1,2,2)$ is 5 -powerful.
a) Determine all ordered triples (if any) which are $n$-powerful for all $n \geq 1$.
b) Determine all ordered triples (if any) which are 2004-powerful and 2005-powerful, but not 2007-powerful.
[Note that $\operatorname{gcd}(a, b, c)$ is the greatest common divisor of $a, b$ and $c$.]
|
Let $p$ be a prime. By Fermat's Little Theorem,
$$
a^{p-1} \equiv \begin{cases}1(\bmod p), & \text { if } p \text { doesn't divide } a \\ 0(\bmod p), & \text { if } p \text { divides } a\end{cases}
$$
Since $\operatorname{gcd}(a, b, c)=1$, we have that $a^{p-1}+b^{p-1}+c^{p-1} \equiv 1,2$ or $3(\bmod p)$. Therefore if $p$ is a prime divisor of $a^{p-1}+b^{p-1}+c^{p-1}$, then $p$ equals 2 or 3 . So if $(a, b, c)$ is $n$-powerful for all $n \geq 1$, then the only primes which can divide $a+b+c$ are 2 or 3 .
We can proceed in a similar fashion to show that $a+b+c$ is not divisible by 4 or 9 .
Since
$$
a^{2} \equiv \begin{cases}0(\bmod 4), & \text { if } p \text { is even; } \\ 1(\bmod 4), & \text { if } p \text { is odd }\end{cases}
$$
and $a, b, c$ aren't all even, we have that $a^{2}+b^{2}+c^{2} \equiv 1,2$ or $3(\bmod 4)$.
By expanding $(3 k)^{3},(3 k+1)^{3}$ and $(3 k+2)^{3}$, we find that $a^{3}$ is congruent to 0,1 or -1 modulo 9. Hence
$$
a^{6} \equiv \begin{cases}0(\bmod 9), & \text { if } 3 \text { divides } a ; \\ 1(\bmod 9), & \text { if } 3 \text { doesn't divide } a .\end{cases}
$$
Since $a, b, c$ aren't all divisible by 3 , we have that $a^{6}+b^{6}+c^{6} \equiv 1,2$ or $3(\bmod 9)$.
So $a^{2}+b^{2}+c^{2}$ is not divisible by 4 and $a^{6}+b^{6}+c^{6}$ is not divisible by 9 . Thus if $(a, b, c)$ is $n$-powerful for all $n \geq 1$, then $a+b+c$ is not divisible by 4 or 9 . Therefore $a+b+c$ is either 3 or 6 and checking all possibilities, we conclude that the only triples which are $n$-powerful for all $n \geq 1$ are $(1,1,1)$ and $(1,1,4)$.
See Solution 1 for the (b) part.
[^0]: ${ }^{\dagger}$ By the way, $H$ is called the convex hull of $S$. If the points of $S$ lie on a line, then $H$ will be the shortest line segment containing the points of $S$. Otherwise, $H$ is a polygon whose vertices are all elements of $S$ and such that all other points in $S$ lie inside or on this polygon.
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "Canada_MO/segmented/en-sol2005.jsonl",
"solution_match": "\n## Solution 2",
"tier": "T2",
"year": "2005"
}
|
Let $f(n, k)$ be the number of ways of distributing $k$ candies to $n$ children so that each child receives at most 2 candies. For example, if $n=3$, then $f(3,7)=0, f(3,6)=1$ and $f(3,4)=6$.
Determine the value of
$$
f(2006,1)+f(2006,4)+f(2006,7)+\cdots+f(2006,1000)+f(2006,1003) .
$$
Comment. Unfortunately, there was an error in the statement of this problem. It was intended that the sum should continue to $f(2006,4012)$.
|
The number of ways of distributing $k$ candies to 2006 children is equal to the number of ways of distributing 0 to a particular child and $k$ to the rest, plus the number of ways of distributing 1 to the particular child and $k-1$ to the rest, plus the number of ways of distributing 2 to the particular child and $k-2$ to the rest. Thus $f(2006, k)=$ $f(2005, k)+f(2005, k-1)+f(2005, k-2)$, so that the required sum is
$$
1+\sum_{k=1}^{1003} f(2005, k)
$$
In evaluating $f(n, k)$, suppose that there are $r$ children who receive 2 candies; these $r$ children can be chosen in $\left(\begin{array}{l}n \\ r\end{array}\right)$ ways. Then there are $k-2 r$ candies from which at most one is given to each of $n-r$ children. Hence
$$
f(n, k)=\sum_{r=0}^{\lfloor k / 2\rfloor}\left(\begin{array}{l}
n \\
r
\end{array}\right)\left(\begin{array}{c}
n-r \\
k-2 r
\end{array}\right)=\sum_{r=0}^{\infty}\left(\begin{array}{l}
n \\
r
\end{array}\right)\left(\begin{array}{c}
n-r \\
k-2 r
\end{array}\right)
$$
with $\left(\begin{array}{l}x \\ y\end{array}\right)=0$ when $x<y$ and when $y<0$. The answer is
$$
\sum_{k=0}^{1003} \sum_{r=0}^{\infty}\left(\begin{array}{c}
2005 \\
r
\end{array}\right)\left(\begin{array}{c}
2005-r \\
k-2 r
\end{array}\right)=\sum_{r=0}^{\infty}\left(\begin{array}{c}
2005 \\
r
\end{array}\right) \sum_{k=0}^{1003}\left(\begin{array}{c}
2005-r \\
k-2 r
\end{array}\right)
$$
|
not found
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $f(n, k)$ be the number of ways of distributing $k$ candies to $n$ children so that each child receives at most 2 candies. For example, if $n=3$, then $f(3,7)=0, f(3,6)=1$ and $f(3,4)=6$.
Determine the value of
$$
f(2006,1)+f(2006,4)+f(2006,7)+\cdots+f(2006,1000)+f(2006,1003) .
$$
Comment. Unfortunately, there was an error in the statement of this problem. It was intended that the sum should continue to $f(2006,4012)$.
|
The number of ways of distributing $k$ candies to 2006 children is equal to the number of ways of distributing 0 to a particular child and $k$ to the rest, plus the number of ways of distributing 1 to the particular child and $k-1$ to the rest, plus the number of ways of distributing 2 to the particular child and $k-2$ to the rest. Thus $f(2006, k)=$ $f(2005, k)+f(2005, k-1)+f(2005, k-2)$, so that the required sum is
$$
1+\sum_{k=1}^{1003} f(2005, k)
$$
In evaluating $f(n, k)$, suppose that there are $r$ children who receive 2 candies; these $r$ children can be chosen in $\left(\begin{array}{l}n \\ r\end{array}\right)$ ways. Then there are $k-2 r$ candies from which at most one is given to each of $n-r$ children. Hence
$$
f(n, k)=\sum_{r=0}^{\lfloor k / 2\rfloor}\left(\begin{array}{l}
n \\
r
\end{array}\right)\left(\begin{array}{c}
n-r \\
k-2 r
\end{array}\right)=\sum_{r=0}^{\infty}\left(\begin{array}{l}
n \\
r
\end{array}\right)\left(\begin{array}{c}
n-r \\
k-2 r
\end{array}\right)
$$
with $\left(\begin{array}{l}x \\ y\end{array}\right)=0$ when $x<y$ and when $y<0$. The answer is
$$
\sum_{k=0}^{1003} \sum_{r=0}^{\infty}\left(\begin{array}{c}
2005 \\
r
\end{array}\right)\left(\begin{array}{c}
2005-r \\
k-2 r
\end{array}\right)=\sum_{r=0}^{\infty}\left(\begin{array}{c}
2005 \\
r
\end{array}\right) \sum_{k=0}^{1003}\left(\begin{array}{c}
2005-r \\
k-2 r
\end{array}\right)
$$
|
{
"exam": "Canada_MO",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "Canada_MO/segmented/en-sol2006.jsonl",
"solution_match": "\nSolution 1.",
"tier": "T2",
"year": "2006"
}
|
Let $f(n, k)$ be the number of ways of distributing $k$ candies to $n$ children so that each child receives at most 2 candies. For example, if $n=3$, then $f(3,7)=0, f(3,6)=1$ and $f(3,4)=6$.
Determine the value of
$$
f(2006,1)+f(2006,4)+f(2006,7)+\cdots+f(2006,1000)+f(2006,1003) .
$$
Comment. Unfortunately, there was an error in the statement of this problem. It was intended that the sum should continue to $f(2006,4012)$.
|
The desired number is the sum of the coefficients of the terms of degree not exceeding 1003 in the expansion of $\left(1+x+x^{2}\right)^{2005}$, which is equal to the coefficient of $x^{1003}$ in the expansion of
$$
\begin{aligned}
\left(1+x+x^{2}\right)^{2005}\left(1+x+\cdots+x^{1003}\right) & =\left[\left(1-x^{3}\right)^{2005}(1-x)^{-2005}\right]\left(1-x^{1004}\right)(1-x)^{-1} \\
& =\left(1-x^{3}\right)^{2005}(1-x)^{-2006}-\left(1-x^{3}\right)^{2005}(1-x)^{-2006} x^{1004}
\end{aligned}
$$
Since the degree of every term in the expansion of the second member on the right exceeds 1003, we are looking for the coefficient of $x^{1003}$ in the expansion of the first member:
$$
\left(1-x^{3}\right)^{2005}(1-x)^{-2006}=\sum_{i=0}^{2005}(-1)^{i}\left(\begin{array}{c}
2005 \\
i
\end{array}\right) x^{3 i} \sum_{j=0}^{\infty}(-1)^{j}\left(\begin{array}{c}
-2006 \\
j
\end{array}\right) x^{j}
$$
$$
\begin{aligned}
& =\sum_{i=0}^{2005} \sum_{j=0}^{\infty}(-1)^{i}\left(\begin{array}{c}
2005 \\
i
\end{array}\right)\left(\begin{array}{c}
2005+j \\
j
\end{array}\right) x^{3 i+j} \\
& =\sum_{k=0}^{\infty}\left(\sum_{i=1}^{2005}(-1)^{i}\left(\begin{array}{c}
2005 \\
i
\end{array}\right)\left(\begin{array}{c}
2005+k-3 i \\
2005
\end{array}\right)\right) x^{k} .
\end{aligned}
$$
The desired number is
$$
\sum_{i=1}^{334}(-1)^{i}\left(\begin{array}{c}
2005 \\
i
\end{array}\right)\left(\begin{array}{c}
3008-3 i \\
2005
\end{array}\right)=\sum_{i=1}^{334}(-1)^{i} \frac{(3008-3 i) !}{i !(2005-i) !(1003-3 i) !} .
$$
(Note that $\left(\begin{array}{c}3008-3 i \\ 2005\end{array}\right)=0$ when $i \geq 335$.)
|
\sum_{i=1}^{334}(-1)^{i} \frac{(3008-3 i) !}{i !(2005-i) !(1003-3 i) !}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $f(n, k)$ be the number of ways of distributing $k$ candies to $n$ children so that each child receives at most 2 candies. For example, if $n=3$, then $f(3,7)=0, f(3,6)=1$ and $f(3,4)=6$.
Determine the value of
$$
f(2006,1)+f(2006,4)+f(2006,7)+\cdots+f(2006,1000)+f(2006,1003) .
$$
Comment. Unfortunately, there was an error in the statement of this problem. It was intended that the sum should continue to $f(2006,4012)$.
|
The desired number is the sum of the coefficients of the terms of degree not exceeding 1003 in the expansion of $\left(1+x+x^{2}\right)^{2005}$, which is equal to the coefficient of $x^{1003}$ in the expansion of
$$
\begin{aligned}
\left(1+x+x^{2}\right)^{2005}\left(1+x+\cdots+x^{1003}\right) & =\left[\left(1-x^{3}\right)^{2005}(1-x)^{-2005}\right]\left(1-x^{1004}\right)(1-x)^{-1} \\
& =\left(1-x^{3}\right)^{2005}(1-x)^{-2006}-\left(1-x^{3}\right)^{2005}(1-x)^{-2006} x^{1004}
\end{aligned}
$$
Since the degree of every term in the expansion of the second member on the right exceeds 1003, we are looking for the coefficient of $x^{1003}$ in the expansion of the first member:
$$
\left(1-x^{3}\right)^{2005}(1-x)^{-2006}=\sum_{i=0}^{2005}(-1)^{i}\left(\begin{array}{c}
2005 \\
i
\end{array}\right) x^{3 i} \sum_{j=0}^{\infty}(-1)^{j}\left(\begin{array}{c}
-2006 \\
j
\end{array}\right) x^{j}
$$
$$
\begin{aligned}
& =\sum_{i=0}^{2005} \sum_{j=0}^{\infty}(-1)^{i}\left(\begin{array}{c}
2005 \\
i
\end{array}\right)\left(\begin{array}{c}
2005+j \\
j
\end{array}\right) x^{3 i+j} \\
& =\sum_{k=0}^{\infty}\left(\sum_{i=1}^{2005}(-1)^{i}\left(\begin{array}{c}
2005 \\
i
\end{array}\right)\left(\begin{array}{c}
2005+k-3 i \\
2005
\end{array}\right)\right) x^{k} .
\end{aligned}
$$
The desired number is
$$
\sum_{i=1}^{334}(-1)^{i}\left(\begin{array}{c}
2005 \\
i
\end{array}\right)\left(\begin{array}{c}
3008-3 i \\
2005
\end{array}\right)=\sum_{i=1}^{334}(-1)^{i} \frac{(3008-3 i) !}{i !(2005-i) !(1003-3 i) !} .
$$
(Note that $\left(\begin{array}{c}3008-3 i \\ 2005\end{array}\right)=0$ when $i \geq 335$.)
|
{
"exam": "Canada_MO",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "Canada_MO/segmented/en-sol2006.jsonl",
"solution_match": "\nSolution 2.",
"tier": "T2",
"year": "2006"
}
|
Let $A B C$ be an acute-angled triangle. Inscribe a rectangle $D E F G$ in this triangle so that $D$ is on $A B, E$ is on $A C$ and both $F$ and $G$ are on $B C$. Describe the locus of (i.e., the curve occupied by) the intersections of the diagonals of all possible rectangles $D E F G$.
|
The locus is the line segment joining the midpoint $M$ of $B C$ to the midpoint $K$ of the altitude $A H$. Note that a segment $D E$ with $D$ on $A B$ and $E$ on $A C$ determines an inscribed rectangle; the midpoint $F$ of $D E$ lies on the median $A M$, while the midpoint of the perpendicular from $F$ to $B C$ is the centre of the rectangle. This lies on the median $M K$ of the triangle $A M H$.
Conversely, any point $P$ on $M K$ is the centre of a rectangle with base along $B C$ whose height is double the distance from $K$ to $B C$.
|
not found
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Let $A B C$ be an acute-angled triangle. Inscribe a rectangle $D E F G$ in this triangle so that $D$ is on $A B, E$ is on $A C$ and both $F$ and $G$ are on $B C$. Describe the locus of (i.e., the curve occupied by) the intersections of the diagonals of all possible rectangles $D E F G$.
|
The locus is the line segment joining the midpoint $M$ of $B C$ to the midpoint $K$ of the altitude $A H$. Note that a segment $D E$ with $D$ on $A B$ and $E$ on $A C$ determines an inscribed rectangle; the midpoint $F$ of $D E$ lies on the median $A M$, while the midpoint of the perpendicular from $F$ to $B C$ is the centre of the rectangle. This lies on the median $M K$ of the triangle $A M H$.
Conversely, any point $P$ on $M K$ is the centre of a rectangle with base along $B C$ whose height is double the distance from $K$ to $B C$.
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "Canada_MO/segmented/en-sol2006.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2006"
}
|
In a rectangular array of nonnegative real numbers with $m$ rows and $n$ columns, each row and each column contains at least one positive element. Moreover, if a row and a column intersect in a positive element, then the sums of their elements are the same. Prove that $m=n$.
|
Consider first the case where all the rows have the same positive sum $s$; this covers the particular situation in which $m=1$. Then each column, sharing a positive element with some row, must also have the sum $s$. Then the sum of all the entries in the matrix is $m s=n s$, whence $m=n$.
We prove the general case by induction on $m$. The case $m=1$ is already covered. Suppose that we have an $m \times n$ array not all of whose rows have the same sum. Let $r<m$ of the rows have the sum $s$, and each of the of the other rows have a different sum. Then every column sharing a positive entry with one of these rows must also have sum $s$, and these are the only columns with the sum $s$. Suppose there are $c$ columns with sum $s$. The situation is essentially unchanged if we permute the rows and then the column so that the first $r$ rows have the sum $s$ and the first $c$ columns have the sum $s$. Since all the entries of the first $r$ rows not in the first $c$ columns and in the first $c$ columns not in the first $r$ rows must be 0 , we can partition the array into a $r \times c$ array in which all rows and columns have sum $s$ and which satisfies the hypothesis of the problem, two rectangular arrays of zeros in the upper right and lower left and a rectangular $(m-r) \times(n-c)$ array in the lower right that satisfies the conditions of the problem. By the induction hypothesis, we see that $r=c$ and so $m=n$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
In a rectangular array of nonnegative real numbers with $m$ rows and $n$ columns, each row and each column contains at least one positive element. Moreover, if a row and a column intersect in a positive element, then the sums of their elements are the same. Prove that $m=n$.
|
Consider first the case where all the rows have the same positive sum $s$; this covers the particular situation in which $m=1$. Then each column, sharing a positive element with some row, must also have the sum $s$. Then the sum of all the entries in the matrix is $m s=n s$, whence $m=n$.
We prove the general case by induction on $m$. The case $m=1$ is already covered. Suppose that we have an $m \times n$ array not all of whose rows have the same sum. Let $r<m$ of the rows have the sum $s$, and each of the of the other rows have a different sum. Then every column sharing a positive entry with one of these rows must also have sum $s$, and these are the only columns with the sum $s$. Suppose there are $c$ columns with sum $s$. The situation is essentially unchanged if we permute the rows and then the column so that the first $r$ rows have the sum $s$ and the first $c$ columns have the sum $s$. Since all the entries of the first $r$ rows not in the first $c$ columns and in the first $c$ columns not in the first $r$ rows must be 0 , we can partition the array into a $r \times c$ array in which all rows and columns have sum $s$ and which satisfies the hypothesis of the problem, two rectangular arrays of zeros in the upper right and lower left and a rectangular $(m-r) \times(n-c)$ array in the lower right that satisfies the conditions of the problem. By the induction hypothesis, we see that $r=c$ and so $m=n$.
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "Canada_MO/segmented/en-sol2006.jsonl",
"solution_match": "\nSolution 1.",
"tier": "T2",
"year": "2006"
}
|
In a rectangular array of nonnegative real numbers with $m$ rows and $n$ columns, each row and each column contains at least one positive element. Moreover, if a row and a column intersect in a positive element, then the sums of their elements are the same. Prove that $m=n$.
|
[Y. Zhao] Let the term in the $i$ th row and the $j$ th column of the array be denoted by $a_{i j}$, and let $S=\{(i, j)$ : $\left.a_{i j}>0\right\}$. Suppose that $r_{i}$ is the sum of the $i$ th row and $c_{j}$ the sum of the $j$ th column. Then $r_{i}=c_{j}$ whenever $(i, j) \in S$. Then we have that
$$
\sum\left\{\frac{a_{i j}}{r_{i}}:(i, j) \in S\right\}=\sum\left\{\frac{a_{i j}}{c_{j}}:(i, j) \in S\right\}
$$
We evaluate the sums on either side independently.
$$
\begin{aligned}
& \sum\left\{\frac{a_{i j}}{r_{i}}:(i, j) \in S\right\}=\sum\left\{\frac{a_{i j}}{r_{i}}: 1 \leq i \leq m, 1 \leq j \leq n\right\}=\sum_{i=1}^{m} \frac{1}{r_{i}} \sum_{j=1}^{n} a_{i j}=\sum_{i=1}^{m}\left(\frac{1}{r_{i}}\right) r_{i}=\sum_{i=1}^{m} 1=m . \\
& \sum\left\{\frac{a_{i j}}{c_{j}}:(i, j) \in S\right\}=\sum\left\{\frac{a_{i j}}{c_{j}}: 1 \leq i \leq m, 1 \leq j \leq n\right\}=\sum_{j=1}^{n} \frac{1}{c_{j}} \sum_{i=1}^{m} a_{i j}=\sum_{j=1}^{n}\left(\frac{1}{c_{j}}\right) c_{j}=\sum_{j=1}^{n} 1=n .
\end{aligned}
$$
Hence $m=n$.
Comment. The second solution can be made cleaner and more elegant by defining $u_{i j}=a_{i j} / r_{i}$ for all $(i, j)$. When $a_{i j}=0$, then $u_{i j}=0$. When $a_{i j}>0$, then, by hypothesis, $u_{i j}=a_{i j} / c_{j}$, a relation that in fact holds for all $(i, j)$. We find that
$$
\sum_{j=1}^{n} u_{i j}=1 \quad \text { and } \quad \sum_{i=1}^{n} u_{i j}=1
$$
for $1 \leq i \leq m$ and $1 \leq j \leq n$, so that $\left(u_{i j}\right)$ is an $m \times n$ array whose row sums and column sums are all equal to 1 . Hence
$$
m=\sum_{i=1}^{m}\left(\sum_{j=1}^{n} u_{i j}\right)=\sum\left\{u_{i j}: 1 \leq i \leq m, 1 \leq j \leq n\right\}=\sum_{j=1}^{n}\left(\sum_{i=1}^{m} u_{i j}\right)=n
$$
(being the sum of all the entries in the array).
|
m=n
|
Yes
|
Yes
|
proof
|
Combinatorics
|
In a rectangular array of nonnegative real numbers with $m$ rows and $n$ columns, each row and each column contains at least one positive element. Moreover, if a row and a column intersect in a positive element, then the sums of their elements are the same. Prove that $m=n$.
|
[Y. Zhao] Let the term in the $i$ th row and the $j$ th column of the array be denoted by $a_{i j}$, and let $S=\{(i, j)$ : $\left.a_{i j}>0\right\}$. Suppose that $r_{i}$ is the sum of the $i$ th row and $c_{j}$ the sum of the $j$ th column. Then $r_{i}=c_{j}$ whenever $(i, j) \in S$. Then we have that
$$
\sum\left\{\frac{a_{i j}}{r_{i}}:(i, j) \in S\right\}=\sum\left\{\frac{a_{i j}}{c_{j}}:(i, j) \in S\right\}
$$
We evaluate the sums on either side independently.
$$
\begin{aligned}
& \sum\left\{\frac{a_{i j}}{r_{i}}:(i, j) \in S\right\}=\sum\left\{\frac{a_{i j}}{r_{i}}: 1 \leq i \leq m, 1 \leq j \leq n\right\}=\sum_{i=1}^{m} \frac{1}{r_{i}} \sum_{j=1}^{n} a_{i j}=\sum_{i=1}^{m}\left(\frac{1}{r_{i}}\right) r_{i}=\sum_{i=1}^{m} 1=m . \\
& \sum\left\{\frac{a_{i j}}{c_{j}}:(i, j) \in S\right\}=\sum\left\{\frac{a_{i j}}{c_{j}}: 1 \leq i \leq m, 1 \leq j \leq n\right\}=\sum_{j=1}^{n} \frac{1}{c_{j}} \sum_{i=1}^{m} a_{i j}=\sum_{j=1}^{n}\left(\frac{1}{c_{j}}\right) c_{j}=\sum_{j=1}^{n} 1=n .
\end{aligned}
$$
Hence $m=n$.
Comment. The second solution can be made cleaner and more elegant by defining $u_{i j}=a_{i j} / r_{i}$ for all $(i, j)$. When $a_{i j}=0$, then $u_{i j}=0$. When $a_{i j}>0$, then, by hypothesis, $u_{i j}=a_{i j} / c_{j}$, a relation that in fact holds for all $(i, j)$. We find that
$$
\sum_{j=1}^{n} u_{i j}=1 \quad \text { and } \quad \sum_{i=1}^{n} u_{i j}=1
$$
for $1 \leq i \leq m$ and $1 \leq j \leq n$, so that $\left(u_{i j}\right)$ is an $m \times n$ array whose row sums and column sums are all equal to 1 . Hence
$$
m=\sum_{i=1}^{m}\left(\sum_{j=1}^{n} u_{i j}\right)=\sum\left\{u_{i j}: 1 \leq i \leq m, 1 \leq j \leq n\right\}=\sum_{j=1}^{n}\left(\sum_{i=1}^{m} u_{i j}\right)=n
$$
(being the sum of all the entries in the array).
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "Canada_MO/segmented/en-sol2006.jsonl",
"solution_match": "\nSolution 2.",
"tier": "T2",
"year": "2006"
}
|
Consider a round-robin tournament with $2 n+1$ teams, where each team plays each other team exactly once. We say that three teams $X, Y$ and $Z$, form a cycle triplet if $X$ beats $Y, Y$ beats $Z$, and $Z$ beats $X$. There are no ties.
(a) Determine the minimum number of cycle triplets possible.
(b) Determine the maximum number of cycle triplets possible.
|
(a) The minimum is 0 , which is achieved by a tournament in which team $T_{i}$ beats $T_{j}$ if and only if $i>j$.
(b) Any set of three teams constitutes either a cycle triplet or a "dominated triplet" in which one team beats the other two; let there be $c$ of the former and $d$ of the latter. Then $c+d=\left(\begin{array}{c}2 n+1 \\ 3\end{array}\right)$. Suppose that team $T_{i}$ beats $x_{i}$ other teams; then it is the winning team in exactly $\left(\begin{array}{c}x_{i} \\ 2\end{array}\right)$ dominated triples. Observe that $\sum_{i=1}^{2 n+1} x_{i}=\left(\begin{array}{c}2 n+1 \\ 2\end{array}\right)$, the total number of games. Hence
$$
d=\sum_{i=1}^{2 n+1}\left(\begin{array}{c}
x_{i} \\
2
\end{array}\right)=\frac{1}{2} \sum_{i=1}^{2 n+1} x_{i}^{2}-\frac{1}{2}\left(\begin{array}{c}
2 n+1 \\
2
\end{array}\right)
$$
By the Cauchy-Schwarz Inequality, $(2 n+1) \sum_{i=1}^{2 n+1} x_{i}^{2} \geq\left(\sum_{i=1}^{2 n+1} x_{i}\right)^{2}=n^{2}(2 n+1)^{2}$, whence
$$
c=\left(\begin{array}{c}
2 n+1 \\
3
\end{array}\right)-\sum_{i=1}^{2 n+1}\left(\begin{array}{c}
x_{i} \\
2
\end{array}\right) \leq\left(\begin{array}{c}
2 n+1 \\
3
\end{array}\right)-\frac{n^{2}(2 n+1)}{2}+\frac{1}{2}\left(\begin{array}{c}
2 n+1 \\
2
\end{array}\right)=\frac{n(n+1)(2 n+1)}{6} .
$$
To realize the upper bound, let the teams be $T_{1}=T_{2 n+2}, T_{2}=T_{2 n+3}$. $\cdots, T_{i}=T_{2 n+1+i}, \cdots, T_{2 n+1}=T_{4 n+2}$. For each $i$, let team $T_{i}$ beat $T_{i+1}, T_{i+2}, \cdots, T_{i+n}$ and lose to $T_{i+n+1}, \cdots, T_{i+2 n}$. We need to check that this is a consistent assignment of wins and losses, since the result for each pair of teams is defined twice. This can be seen by noting that $(2 n+1+i)-(i+j)=2 n+1-j \geq n+1$ for $1 \leq j \leq n$. The cycle triplets are $\left(T_{i}, T_{i+j}, T_{i+j+k}\right)$ where $1 \leq j \leq n$ and $(2 n+1+i)-(i+j+k) \leq n$, i.e., when $1 \leq j \leq n$ and $n+1-j \leq k \leq n$. For each $i$, this counts $1+2+\cdots+n=\frac{1}{2} n(n+1)$ cycle triplets. When we range over all $i$, each cycle triplet gets counted three times, so the number of cycle triplets is
$$
\frac{2 n+1}{3}\left(\frac{n(n+1)}{2}\right)=\frac{n(n+1)(2 n+1)}{6} .
$$
|
\frac{n(n+1)(2 n+1)}{6}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Consider a round-robin tournament with $2 n+1$ teams, where each team plays each other team exactly once. We say that three teams $X, Y$ and $Z$, form a cycle triplet if $X$ beats $Y, Y$ beats $Z$, and $Z$ beats $X$. There are no ties.
(a) Determine the minimum number of cycle triplets possible.
(b) Determine the maximum number of cycle triplets possible.
|
(a) The minimum is 0 , which is achieved by a tournament in which team $T_{i}$ beats $T_{j}$ if and only if $i>j$.
(b) Any set of three teams constitutes either a cycle triplet or a "dominated triplet" in which one team beats the other two; let there be $c$ of the former and $d$ of the latter. Then $c+d=\left(\begin{array}{c}2 n+1 \\ 3\end{array}\right)$. Suppose that team $T_{i}$ beats $x_{i}$ other teams; then it is the winning team in exactly $\left(\begin{array}{c}x_{i} \\ 2\end{array}\right)$ dominated triples. Observe that $\sum_{i=1}^{2 n+1} x_{i}=\left(\begin{array}{c}2 n+1 \\ 2\end{array}\right)$, the total number of games. Hence
$$
d=\sum_{i=1}^{2 n+1}\left(\begin{array}{c}
x_{i} \\
2
\end{array}\right)=\frac{1}{2} \sum_{i=1}^{2 n+1} x_{i}^{2}-\frac{1}{2}\left(\begin{array}{c}
2 n+1 \\
2
\end{array}\right)
$$
By the Cauchy-Schwarz Inequality, $(2 n+1) \sum_{i=1}^{2 n+1} x_{i}^{2} \geq\left(\sum_{i=1}^{2 n+1} x_{i}\right)^{2}=n^{2}(2 n+1)^{2}$, whence
$$
c=\left(\begin{array}{c}
2 n+1 \\
3
\end{array}\right)-\sum_{i=1}^{2 n+1}\left(\begin{array}{c}
x_{i} \\
2
\end{array}\right) \leq\left(\begin{array}{c}
2 n+1 \\
3
\end{array}\right)-\frac{n^{2}(2 n+1)}{2}+\frac{1}{2}\left(\begin{array}{c}
2 n+1 \\
2
\end{array}\right)=\frac{n(n+1)(2 n+1)}{6} .
$$
To realize the upper bound, let the teams be $T_{1}=T_{2 n+2}, T_{2}=T_{2 n+3}$. $\cdots, T_{i}=T_{2 n+1+i}, \cdots, T_{2 n+1}=T_{4 n+2}$. For each $i$, let team $T_{i}$ beat $T_{i+1}, T_{i+2}, \cdots, T_{i+n}$ and lose to $T_{i+n+1}, \cdots, T_{i+2 n}$. We need to check that this is a consistent assignment of wins and losses, since the result for each pair of teams is defined twice. This can be seen by noting that $(2 n+1+i)-(i+j)=2 n+1-j \geq n+1$ for $1 \leq j \leq n$. The cycle triplets are $\left(T_{i}, T_{i+j}, T_{i+j+k}\right)$ where $1 \leq j \leq n$ and $(2 n+1+i)-(i+j+k) \leq n$, i.e., when $1 \leq j \leq n$ and $n+1-j \leq k \leq n$. For each $i$, this counts $1+2+\cdots+n=\frac{1}{2} n(n+1)$ cycle triplets. When we range over all $i$, each cycle triplet gets counted three times, so the number of cycle triplets is
$$
\frac{2 n+1}{3}\left(\frac{n(n+1)}{2}\right)=\frac{n(n+1)(2 n+1)}{6} .
$$
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "Canada_MO/segmented/en-sol2006.jsonl",
"solution_match": "\nSolution 1.",
"tier": "T2",
"year": "2006"
}
|
Consider a round-robin tournament with $2 n+1$ teams, where each team plays each other team exactly once. We say that three teams $X, Y$ and $Z$, form a cycle triplet if $X$ beats $Y, Y$ beats $Z$, and $Z$ beats $X$. There are no ties.
(a) Determine the minimum number of cycle triplets possible.
(b) Determine the maximum number of cycle triplets possible.
|
[S. Eastwood] (b) Let $t$ be the number of cycle triplets and $u$ be the number of ordered triplets of teams $(X, Y, Z)$ where $X$ beats $Y$ and $Y$ beats $Z$. Each cycle triplet generates three ordered triplets while other triplets generate exactly one. The total number of triplets is
$$
\left(\begin{array}{c}
2 n+1 \\
3
\end{array}\right)=\frac{n\left(4 n^{2}-1\right)}{3} .
$$
The number of triples that are not cycle is
$$
\frac{n\left(4 n^{2}-1\right)}{3}-t
$$
Hence
$$
u=3 t+\left(\frac{n\left(4 n^{2}-1\right)}{3}-t\right) \Longrightarrow
$$
$$
t=\frac{3 u-n\left(4 n^{2}-1\right)}{6}=\frac{u-(2 n+1) n^{2}}{2}+\frac{n(n+1)(2 n+1)}{6}
$$
If team $Y$ beats $a$ teams and loses to $b$ teams, then the number of ordered triples with $Y$ as the central element is $a b$. Since $a+b=2 n$, by the Arithmetic-Geometric Means Inequality, we have that $a b \leq n 2$. Hence $u \leq(2 n+1) n 2$, so that
$$
t \leq \frac{n(n+1)(2 n+1)}{6}
$$
The maximum is attainable when $u=(2 n+1) n 2$, which can occur when we arrange all the teams in a circle with each team beating exactly the $n$ teams in the clockwise direction.
Comment. Interestingly enough, the maximum is $\sum_{i=1}^{n} i^{2}$; is there a nice argument that gives the answer in this form?
|
\frac{n(n+1)(2n+1)}{6}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Consider a round-robin tournament with $2 n+1$ teams, where each team plays each other team exactly once. We say that three teams $X, Y$ and $Z$, form a cycle triplet if $X$ beats $Y, Y$ beats $Z$, and $Z$ beats $X$. There are no ties.
(a) Determine the minimum number of cycle triplets possible.
(b) Determine the maximum number of cycle triplets possible.
|
[S. Eastwood] (b) Let $t$ be the number of cycle triplets and $u$ be the number of ordered triplets of teams $(X, Y, Z)$ where $X$ beats $Y$ and $Y$ beats $Z$. Each cycle triplet generates three ordered triplets while other triplets generate exactly one. The total number of triplets is
$$
\left(\begin{array}{c}
2 n+1 \\
3
\end{array}\right)=\frac{n\left(4 n^{2}-1\right)}{3} .
$$
The number of triples that are not cycle is
$$
\frac{n\left(4 n^{2}-1\right)}{3}-t
$$
Hence
$$
u=3 t+\left(\frac{n\left(4 n^{2}-1\right)}{3}-t\right) \Longrightarrow
$$
$$
t=\frac{3 u-n\left(4 n^{2}-1\right)}{6}=\frac{u-(2 n+1) n^{2}}{2}+\frac{n(n+1)(2 n+1)}{6}
$$
If team $Y$ beats $a$ teams and loses to $b$ teams, then the number of ordered triples with $Y$ as the central element is $a b$. Since $a+b=2 n$, by the Arithmetic-Geometric Means Inequality, we have that $a b \leq n 2$. Hence $u \leq(2 n+1) n 2$, so that
$$
t \leq \frac{n(n+1)(2 n+1)}{6}
$$
The maximum is attainable when $u=(2 n+1) n 2$, which can occur when we arrange all the teams in a circle with each team beating exactly the $n$ teams in the clockwise direction.
Comment. Interestingly enough, the maximum is $\sum_{i=1}^{n} i^{2}$; is there a nice argument that gives the answer in this form?
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "Canada_MO/segmented/en-sol2006.jsonl",
"solution_match": "\nSolution 2.",
"tier": "T2",
"year": "2006"
}
|
The vertices of a right triangle $A B C$ inscribed in a circle divide the circumference into three arcs. The right angle is at $A$, so that the opposite $\operatorname{arc} B C$ is a semicircle while $\operatorname{arc} A B$ and $\operatorname{arc} A C$ are supplementary. To each of the three arcs, we draw a tangent such that its point of tangency is the midpoint of that portion of the tangent intercepted by the extended lines $A B$ and $A C$. More precisely, the point $D$ on $\operatorname{arc} B C$ is the midpoint of the segment joining the points $D^{\prime}$ and $D^{\prime \prime}$ where the tangent at $D$ intersects the extended lines $A B$ and $A C$. Similarly for $E$ on arc $A C$ and $F$ on arc $A B$.
Prove that triangle $D E F$ is equilateral.
|
A prime indicates where a tangent meets $A B$ and a double prime where it meets $A C$. It is given that $D D^{\prime}=D D^{\prime \prime}, E E^{\prime}=E E^{\prime \prime}$ and $F F^{\prime}=F F^{\prime \prime}$. It is required to show that arc $E F$ is a third of the circumference as is arc $D B F$.
$A F$ is the median to the hypotenuse of right triangle $A F^{\prime} F^{\prime \prime}$, so that $F F^{\prime}=F A$ and therefore
$$
\operatorname{arc} A F=2 \angle F^{\prime \prime} F A=2\left(\angle F F^{\prime} A+\angle F A F^{\prime}\right)=4 \angle F A F^{\prime}=4 \angle F A B=2 \text { arc } B F \text {, }
$$
whence $\operatorname{arc} F A=(2 / 3)$ arc $B F A$. Similarly, arc $A E=(2 / 3)$ arc $A E C$. Therefore, $\operatorname{arc} F E$ is $2 / 3$ of the semicircle, or $1 / 3$ of the circumference as desired.
As for arc $D B F$, arc $B D=2 \angle B A D=\angle B A D+\angle B D^{\prime} D=\angle A D D^{\prime \prime}=(1 / 2)$ arc $A C D$. But, arc $B F=(1 / 2)$ arc $A F$, so arc $D B F=(1 / 2)$ arc $F A E D$. That is, arc $D B F$ is $1 / 3$ the circumference and the proof is complete.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The vertices of a right triangle $A B C$ inscribed in a circle divide the circumference into three arcs. The right angle is at $A$, so that the opposite $\operatorname{arc} B C$ is a semicircle while $\operatorname{arc} A B$ and $\operatorname{arc} A C$ are supplementary. To each of the three arcs, we draw a tangent such that its point of tangency is the midpoint of that portion of the tangent intercepted by the extended lines $A B$ and $A C$. More precisely, the point $D$ on $\operatorname{arc} B C$ is the midpoint of the segment joining the points $D^{\prime}$ and $D^{\prime \prime}$ where the tangent at $D$ intersects the extended lines $A B$ and $A C$. Similarly for $E$ on arc $A C$ and $F$ on arc $A B$.
Prove that triangle $D E F$ is equilateral.

|
A prime indicates where a tangent meets $A B$ and a double prime where it meets $A C$. It is given that $D D^{\prime}=D D^{\prime \prime}, E E^{\prime}=E E^{\prime \prime}$ and $F F^{\prime}=F F^{\prime \prime}$. It is required to show that arc $E F$ is a third of the circumference as is arc $D B F$.
$A F$ is the median to the hypotenuse of right triangle $A F^{\prime} F^{\prime \prime}$, so that $F F^{\prime}=F A$ and therefore
$$
\operatorname{arc} A F=2 \angle F^{\prime \prime} F A=2\left(\angle F F^{\prime} A+\angle F A F^{\prime}\right)=4 \angle F A F^{\prime}=4 \angle F A B=2 \text { arc } B F \text {, }
$$
whence $\operatorname{arc} F A=(2 / 3)$ arc $B F A$. Similarly, arc $A E=(2 / 3)$ arc $A E C$. Therefore, $\operatorname{arc} F E$ is $2 / 3$ of the semicircle, or $1 / 3$ of the circumference as desired.
As for arc $D B F$, arc $B D=2 \angle B A D=\angle B A D+\angle B D^{\prime} D=\angle A D D^{\prime \prime}=(1 / 2)$ arc $A C D$. But, arc $B F=(1 / 2)$ arc $A F$, so arc $D B F=(1 / 2)$ arc $F A E D$. That is, arc $D B F$ is $1 / 3$ the circumference and the proof is complete.
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "Canada_MO/segmented/en-sol2006.jsonl",
"solution_match": "\nSolution 1.",
"tier": "T2",
"year": "2006"
}
|
The vertices of a right triangle $A B C$ inscribed in a circle divide the circumference into three arcs. The right angle is at $A$, so that the opposite $\operatorname{arc} B C$ is a semicircle while $\operatorname{arc} A B$ and $\operatorname{arc} A C$ are supplementary. To each of the three arcs, we draw a tangent such that its point of tangency is the midpoint of that portion of the tangent intercepted by the extended lines $A B$ and $A C$. More precisely, the point $D$ on $\operatorname{arc} B C$ is the midpoint of the segment joining the points $D^{\prime}$ and $D^{\prime \prime}$ where the tangent at $D$ intersects the extended lines $A B$ and $A C$. Similarly for $E$ on arc $A C$ and $F$ on arc $A B$.
Prove that triangle $D E F$ is equilateral.

|
Since $A E^{\prime} E^{\prime \prime}$ is a right triangle, $A E=E E^{\prime}=E E^{\prime \prime}$ so that $\angle C A E=\angle C E^{\prime \prime} E$. Also $A D=D^{\prime} D=D D^{\prime \prime}$, so that $\angle C D D^{\prime \prime}=\angle C A D=\angle C D^{\prime \prime} D$. As $E A D C$ is a concyclic quadrilateral,
$$
\begin{aligned}
180^{\circ} & =\angle E A D+\angle E C D \\
& =\angle D A C+\angle C A E+\angle E C A+\angle A C D \\
& =\angle D A C+\angle C A E+\angle C E E^{\prime \prime}+\angle C E^{\prime \prime} E+\angle C D D^{\prime \prime}+\angle C D^{\prime \prime} D \\
& =\angle D A C+\angle C A E+\angle C A E+\angle C A E+\angle C A D+\angle C A D \\
& =3(\angle D A C+\angle D A E)=3(\angle D A E)
\end{aligned}
$$
Hence $\angle D F E=\angle D A E=60^{\circ}$. Similarly, $\angle D E F=60^{\circ}$. It follows that triangle $D E F$ is equilateral.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The vertices of a right triangle $A B C$ inscribed in a circle divide the circumference into three arcs. The right angle is at $A$, so that the opposite $\operatorname{arc} B C$ is a semicircle while $\operatorname{arc} A B$ and $\operatorname{arc} A C$ are supplementary. To each of the three arcs, we draw a tangent such that its point of tangency is the midpoint of that portion of the tangent intercepted by the extended lines $A B$ and $A C$. More precisely, the point $D$ on $\operatorname{arc} B C$ is the midpoint of the segment joining the points $D^{\prime}$ and $D^{\prime \prime}$ where the tangent at $D$ intersects the extended lines $A B$ and $A C$. Similarly for $E$ on arc $A C$ and $F$ on arc $A B$.
Prove that triangle $D E F$ is equilateral.

|
Since $A E^{\prime} E^{\prime \prime}$ is a right triangle, $A E=E E^{\prime}=E E^{\prime \prime}$ so that $\angle C A E=\angle C E^{\prime \prime} E$. Also $A D=D^{\prime} D=D D^{\prime \prime}$, so that $\angle C D D^{\prime \prime}=\angle C A D=\angle C D^{\prime \prime} D$. As $E A D C$ is a concyclic quadrilateral,
$$
\begin{aligned}
180^{\circ} & =\angle E A D+\angle E C D \\
& =\angle D A C+\angle C A E+\angle E C A+\angle A C D \\
& =\angle D A C+\angle C A E+\angle C E E^{\prime \prime}+\angle C E^{\prime \prime} E+\angle C D D^{\prime \prime}+\angle C D^{\prime \prime} D \\
& =\angle D A C+\angle C A E+\angle C A E+\angle C A E+\angle C A D+\angle C A D \\
& =3(\angle D A C+\angle D A E)=3(\angle D A E)
\end{aligned}
$$
Hence $\angle D F E=\angle D A E=60^{\circ}$. Similarly, $\angle D E F=60^{\circ}$. It follows that triangle $D E F$ is equilateral.
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "Canada_MO/segmented/en-sol2006.jsonl",
"solution_match": "\nSolution 2.",
"tier": "T2",
"year": "2006"
}
|
$A B C D$ is a convex quadrilateral in which $A B$ is the longest side. Points $M$ and $N$ are located on sides $A B$ and $B C$ respectively, so that each of the segments $A N$ and $C M$ divides the quadrilateral into two parts of equal area. Prove that the segment $M N$ bisects the diagonal $B D$.
|
Since $[M A D C]=\frac{1}{2}[A B C D]=[N A D C]$, it follows that $[A N C]=[A M C]$, so that $M N \| A C$. Let $m$ be a line through $D$ parallel to $A C$ and $M N$ and let $B A$ produced meet $m$ at $P$ and $B C$ produced meet $m$ at $Q$. Then
$$
[M P C]=[M A C]+[C A P]=[M A C]+[C A D]=[M A D C]=[B M C]
$$
whence $B M=M P$. Similarly $B N=N Q$, so that $M N$ is a midline of triangle $B P Q$ and must bisect $B D$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
$A B C D$ is a convex quadrilateral in which $A B$ is the longest side. Points $M$ and $N$ are located on sides $A B$ and $B C$ respectively, so that each of the segments $A N$ and $C M$ divides the quadrilateral into two parts of equal area. Prove that the segment $M N$ bisects the diagonal $B D$.
|
Since $[M A D C]=\frac{1}{2}[A B C D]=[N A D C]$, it follows that $[A N C]=[A M C]$, so that $M N \| A C$. Let $m$ be a line through $D$ parallel to $A C$ and $M N$ and let $B A$ produced meet $m$ at $P$ and $B C$ produced meet $m$ at $Q$. Then
$$
[M P C]=[M A C]+[C A P]=[M A C]+[C A D]=[M A D C]=[B M C]
$$
whence $B M=M P$. Similarly $B N=N Q$, so that $M N$ is a midline of triangle $B P Q$ and must bisect $B D$.
|
{
"exam": "Canada_MO",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "Canada_MO/segmented/en-sol2008.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2008"
}
|
Determine all functions $f$ defined on the set of rationals that take rational values for which
$$
f(2 f(x)+f(y))=2 x+y
$$
for each $x$ and $y$.
|
The only solutions are $f(x)=x$ for all rational $x$ and $f(x)=-x$ for all rational $x$. Both of these readily check out.
Setting $y=x$ yields $f(3 f(x))=3 x$ for all rational $x$. Now replacing $x$ by $3 f(x)$, we find that
$$
f(9 x)=f(3 f(3 f(x))=3[3 f(x)]=9 f(x),
$$
for all rational $x$. Setting $x=0$ yields $f(0)=9 f(0)$, whence $f(0)=0$.
Setting $x=0$ in the given functional equation yields $f(f(y))=y$ for all rational $y$. Thus $f$ is one-one onto. Applying $f$ to the functional equation yields that
$$
2 f(x)+f(y)=f(2 x+y)
$$
for every rational pair $(x, y)$.
Setting $y=0$ in the functional equation yields $f(2 f(x))=2 x$, whence $2 f(x)=f(2 x)$. Therefore $f(2 x)+f(y)=f(2 x+y)$ for each rational pair $(x, y)$, so that
$$
f(u+v)=f(u)+f(v)
$$
for each rational pair $(u, v)$.
Since $0=f(0)=f(-1)+f(1), f(-1)=-f(1)$. By induction, it can be established that for each intger $n$ and rational $x, f(n x)=n f(x)$. If $k=f(1)$, we can establish from this that $f(n)=n k, f(1 / n)=k / n$ and $f(m / n)=m k / n$ for each integer pair $(m, n)$. Thus $f(x)=k x$ for all rational $x$. Since $f(f(x))=x$, we must have $k 2=1$. Hence $f(x)=x$ or $f(x)=-x$. These check out.
|
f(x)=x \text{ or } f(x)=-x
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Determine all functions $f$ defined on the set of rationals that take rational values for which
$$
f(2 f(x)+f(y))=2 x+y
$$
for each $x$ and $y$.
|
The only solutions are $f(x)=x$ for all rational $x$ and $f(x)=-x$ for all rational $x$. Both of these readily check out.
Setting $y=x$ yields $f(3 f(x))=3 x$ for all rational $x$. Now replacing $x$ by $3 f(x)$, we find that
$$
f(9 x)=f(3 f(3 f(x))=3[3 f(x)]=9 f(x),
$$
for all rational $x$. Setting $x=0$ yields $f(0)=9 f(0)$, whence $f(0)=0$.
Setting $x=0$ in the given functional equation yields $f(f(y))=y$ for all rational $y$. Thus $f$ is one-one onto. Applying $f$ to the functional equation yields that
$$
2 f(x)+f(y)=f(2 x+y)
$$
for every rational pair $(x, y)$.
Setting $y=0$ in the functional equation yields $f(2 f(x))=2 x$, whence $2 f(x)=f(2 x)$. Therefore $f(2 x)+f(y)=f(2 x+y)$ for each rational pair $(x, y)$, so that
$$
f(u+v)=f(u)+f(v)
$$
for each rational pair $(u, v)$.
Since $0=f(0)=f(-1)+f(1), f(-1)=-f(1)$. By induction, it can be established that for each intger $n$ and rational $x, f(n x)=n f(x)$. If $k=f(1)$, we can establish from this that $f(n)=n k, f(1 / n)=k / n$ and $f(m / n)=m k / n$ for each integer pair $(m, n)$. Thus $f(x)=k x$ for all rational $x$. Since $f(f(x))=x$, we must have $k 2=1$. Hence $f(x)=x$ or $f(x)=-x$. These check out.
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "Canada_MO/segmented/en-sol2008.jsonl",
"solution_match": "\nSolution 1.",
"tier": "T2",
"year": "2008"
}
|
Determine all functions $f$ defined on the set of rationals that take rational values for which
$$
f(2 f(x)+f(y))=2 x+y
$$
for each $x$ and $y$.
|
In the functional equation, let
$$
x=y=2 f(z)+f(w)
$$
to obtain $f(x)=f(y)=2 z+w$ and
$$
f(6 z+3 w)=6 f(z)+3 f(w)
$$
for all rational pairs $(z, w)$. Set $(z, w)=(0,0)$ to obtain $f(0)=0, w=0$ to obtain $f(6 z)=6 f(z)$ and $z=0$ to obtain $f(3 w)=3 f(w)$ for all rationals $z$ and $w$. Hence $f(6 z+3 w)=f(6 z)+f(3 w)$. Replacing $(6 z, 3 w)$ by $(u, v)$ yields
$$
f(u+v)=f(u)+f(v)
$$
for all rational pairs $(u, v)$. Hence $f(x)=k x$ where $k=f(1)$ for all rational $x$. Substitution of this into the functional equation with $(x, y)=(1,1)$ leads to $3=f(3 f(1))=f(3 k)=3 k 2$, so that $k= \pm 1$. It can be checked that both $f(x) \equiv 1$ and $f(x) \equiv-1$ satisfy the equation.
Acknowledgment. The first solution is due to Man-Duen Choi and the second to Ed Doolittle.
|
f(x) = x \text{ or } f(x) = -x
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Determine all functions $f$ defined on the set of rationals that take rational values for which
$$
f(2 f(x)+f(y))=2 x+y
$$
for each $x$ and $y$.
|
In the functional equation, let
$$
x=y=2 f(z)+f(w)
$$
to obtain $f(x)=f(y)=2 z+w$ and
$$
f(6 z+3 w)=6 f(z)+3 f(w)
$$
for all rational pairs $(z, w)$. Set $(z, w)=(0,0)$ to obtain $f(0)=0, w=0$ to obtain $f(6 z)=6 f(z)$ and $z=0$ to obtain $f(3 w)=3 f(w)$ for all rationals $z$ and $w$. Hence $f(6 z+3 w)=f(6 z)+f(3 w)$. Replacing $(6 z, 3 w)$ by $(u, v)$ yields
$$
f(u+v)=f(u)+f(v)
$$
for all rational pairs $(u, v)$. Hence $f(x)=k x$ where $k=f(1)$ for all rational $x$. Substitution of this into the functional equation with $(x, y)=(1,1)$ leads to $3=f(3 f(1))=f(3 k)=3 k 2$, so that $k= \pm 1$. It can be checked that both $f(x) \equiv 1$ and $f(x) \equiv-1$ satisfy the equation.
Acknowledgment. The first solution is due to Man-Duen Choi and the second to Ed Doolittle.
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "Canada_MO/segmented/en-sol2008.jsonl",
"solution_match": "\nSolution 2.",
"tier": "T2",
"year": "2008"
}
|
Let $a, b, c$ be positive real numbers for which $a+b+c=1$. Prove that
$$
\frac{a-b c}{a+b c}+\frac{b-c a}{b+c a}+\frac{c-a b}{c+a b} \leq \frac{3}{2} .
$$
|
Note that
$$
1-\frac{a-b c}{a+b c}=\frac{2 b c}{1-b-c+b c}=\frac{2 b c}{(1-b)(1-c)}
$$
The inequality is equivalent to
$$
\frac{2 b c}{(1-b)(1-c)}+\frac{2 c a}{(1-c)(1-a)}+\frac{2 a b}{(1-a)(1-b)} \geq \frac{3}{2} .
$$
Manipulation yields the equivalent
$$
4(b c+c a+a b-3 a b c) \geq 3(b c+c a+a b+1-a-b-c-a b c) .
$$
This simplifies to $a b+b c+c a \geq 9 a b c$ or
$$
\frac{1}{a}+\frac{1}{b}+\frac{1}{c} \geq 9 \text {. }
$$
This is a consequence of the harmonic-arithmetic means inequality.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers for which $a+b+c=1$. Prove that
$$
\frac{a-b c}{a+b c}+\frac{b-c a}{b+c a}+\frac{c-a b}{c+a b} \leq \frac{3}{2} .
$$
|
Note that
$$
1-\frac{a-b c}{a+b c}=\frac{2 b c}{1-b-c+b c}=\frac{2 b c}{(1-b)(1-c)}
$$
The inequality is equivalent to
$$
\frac{2 b c}{(1-b)(1-c)}+\frac{2 c a}{(1-c)(1-a)}+\frac{2 a b}{(1-a)(1-b)} \geq \frac{3}{2} .
$$
Manipulation yields the equivalent
$$
4(b c+c a+a b-3 a b c) \geq 3(b c+c a+a b+1-a-b-c-a b c) .
$$
This simplifies to $a b+b c+c a \geq 9 a b c$ or
$$
\frac{1}{a}+\frac{1}{b}+\frac{1}{c} \geq 9 \text {. }
$$
This is a consequence of the harmonic-arithmetic means inequality.
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "Canada_MO/segmented/en-sol2008.jsonl",
"solution_match": "\nSolution 1.",
"tier": "T2",
"year": "2008"
}
|
Let $a, b, c$ be positive real numbers for which $a+b+c=1$. Prove that
$$
\frac{a-b c}{a+b c}+\frac{b-c a}{b+c a}+\frac{c-a b}{c+a b} \leq \frac{3}{2} .
$$
|
Observe that
$$
a+b c=a(a+b+c)+b c=(a+b)(a+c)
$$
and that $a+b=1-c$, with analogous relations for other permutations of the variables. Then
$$
(b+c)(c+a)(a+b)=(1-a)(1-b)(1-c)=(a b+b c+c a)-a b c .
$$
Putting the left side of the desired inequality over a common denominator, we find that it is equal to
$$
\begin{aligned}
\frac{(a-b c)(1-a)+(b-a c)(1-b)+(c-a b)(1-c)}{(b+c)(c+a)(a+b)} & =\frac{(a+b+c)-(a 2+b 2+c 2)-(b c+c a+a b)+3 a b c}{(b+c)(c+a)(a+b)} \\
& =\frac{1-(a+b+c) 2+(b c+c a+a b)+3 a b c}{(a b+b c+c a)-a b c} \\
& =\frac{(b c+c a+a b)+3 a b c}{(b c+b c+a b)-a b c} \\
& =1+\frac{4 a b c}{(a+b)(b+c)(c+a)} .
\end{aligned}
$$
Using the arithmetic-geometric means inequality, we obtain that
$$
\begin{aligned}
(a+b)(b+c)(c+a) & =\left(a^{2} b+b^{2} c+c^{2} a\right)+(a b 2+b c 2+c a 2)+2 a b c \\
& \geq 3 a b c+3 a b c+2 a b c=8 a b c
\end{aligned}
$$
whence $4 a b c /[(a+b)(b+c)(c+a)] \leq \frac{1}{2}$. The desired result follows. Equality occurs exactly when $a=b=$ $c=\frac{1}{3}$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b, c$ be positive real numbers for which $a+b+c=1$. Prove that
$$
\frac{a-b c}{a+b c}+\frac{b-c a}{b+c a}+\frac{c-a b}{c+a b} \leq \frac{3}{2} .
$$
|
Observe that
$$
a+b c=a(a+b+c)+b c=(a+b)(a+c)
$$
and that $a+b=1-c$, with analogous relations for other permutations of the variables. Then
$$
(b+c)(c+a)(a+b)=(1-a)(1-b)(1-c)=(a b+b c+c a)-a b c .
$$
Putting the left side of the desired inequality over a common denominator, we find that it is equal to
$$
\begin{aligned}
\frac{(a-b c)(1-a)+(b-a c)(1-b)+(c-a b)(1-c)}{(b+c)(c+a)(a+b)} & =\frac{(a+b+c)-(a 2+b 2+c 2)-(b c+c a+a b)+3 a b c}{(b+c)(c+a)(a+b)} \\
& =\frac{1-(a+b+c) 2+(b c+c a+a b)+3 a b c}{(a b+b c+c a)-a b c} \\
& =\frac{(b c+c a+a b)+3 a b c}{(b c+b c+a b)-a b c} \\
& =1+\frac{4 a b c}{(a+b)(b+c)(c+a)} .
\end{aligned}
$$
Using the arithmetic-geometric means inequality, we obtain that
$$
\begin{aligned}
(a+b)(b+c)(c+a) & =\left(a^{2} b+b^{2} c+c^{2} a\right)+(a b 2+b c 2+c a 2)+2 a b c \\
& \geq 3 a b c+3 a b c+2 a b c=8 a b c
\end{aligned}
$$
whence $4 a b c /[(a+b)(b+c)(c+a)] \leq \frac{1}{2}$. The desired result follows. Equality occurs exactly when $a=b=$ $c=\frac{1}{3}$.
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "Canada_MO/segmented/en-sol2008.jsonl",
"solution_match": "\nSolution 2.",
"tier": "T2",
"year": "2008"
}
|
Find all functions $f$ defined on the natural numbers that take values among the natural numbers for which
$$
(f(n))^{p} \equiv n \quad \bmod f(p)
$$
for all $n \in \mathbf{N}$ and all prime numbers $p$.
|
The substitution $n=p$, a prime, yields $p \equiv(f(p))^{p} \equiv 0(\bmod f(p))$, so that $p$ is divisible by $f(p)$. Hence, for each prime $p, f(p)=1$ or $f(p)=p$.
Let $S=\{p: p$ is prime and $f(p)=p\}$. If $S$ is infinite, then $f(n)^{p} \equiv n(\bmod p)$ for infinitely many primes $p$. By the little Fermat theorem, $n \equiv f(n)^{p} \equiv f(n)$, so that $f(n)-n$ is a multiple of $p$ for infinitely many primes $p$. This can happen only if $f(n)=n$ for all values of $n$, and it can be verified that this is a solution.
If $S$ is empty, then $f(p)=1$ for all primes $p$, and any function satisfying this condition is a solution.
Now suppose that $S$ is finite and non-empty. Let $q$ be the largest prime in $S$. Suppose, if possible, that $q \geq 3$. Therefore, for any prime $p$ exceeding $q, p \equiv 1(\bmod q)$. However, this is not true. Let $Q$ be the product of all the odd primes up to $q$. Then $Q+2$ must have a prime factor exceeding $q$ and at least one of them must be incongruent to $1(\bmod q)$. (An alternative argument notes that Bertrand's postulate can turn up a prime $p$ between $q$ and $2 q$ which fails to satisfy $p \equiv 1 \bmod q$.)
The only remaining case is that $S=\{2\}$. Then $f(2)=2$ and $f(p)=1$ for every odd prime $p$. Since $f(n) 2 \equiv n(\bmod 2), f(n)$ and $n$ must have the same parity. Conversely, any function $f$ for which $f(n) \equiv n$ $(\bmod 2)$ for all $n, f(2)=2$ and $f(p)=1$ for all odd primes $p$ satisfies the condition.
Therefore the only solutions are
- $f(n)=n$ for all $n \in \mathbf{N}$;
- any function $f$ with $f(p)=1$ for all primes $p$;
- any function for which $f(2)=2, f(p)=1$ for primes $p$ exceeding 2 and $f(n)$ and $n$ have the same parity.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all functions $f$ defined on the natural numbers that take values among the natural numbers for which
$$
(f(n))^{p} \equiv n \quad \bmod f(p)
$$
for all $n \in \mathbf{N}$ and all prime numbers $p$.
|
The substitution $n=p$, a prime, yields $p \equiv(f(p))^{p} \equiv 0(\bmod f(p))$, so that $p$ is divisible by $f(p)$. Hence, for each prime $p, f(p)=1$ or $f(p)=p$.
Let $S=\{p: p$ is prime and $f(p)=p\}$. If $S$ is infinite, then $f(n)^{p} \equiv n(\bmod p)$ for infinitely many primes $p$. By the little Fermat theorem, $n \equiv f(n)^{p} \equiv f(n)$, so that $f(n)-n$ is a multiple of $p$ for infinitely many primes $p$. This can happen only if $f(n)=n$ for all values of $n$, and it can be verified that this is a solution.
If $S$ is empty, then $f(p)=1$ for all primes $p$, and any function satisfying this condition is a solution.
Now suppose that $S$ is finite and non-empty. Let $q$ be the largest prime in $S$. Suppose, if possible, that $q \geq 3$. Therefore, for any prime $p$ exceeding $q, p \equiv 1(\bmod q)$. However, this is not true. Let $Q$ be the product of all the odd primes up to $q$. Then $Q+2$ must have a prime factor exceeding $q$ and at least one of them must be incongruent to $1(\bmod q)$. (An alternative argument notes that Bertrand's postulate can turn up a prime $p$ between $q$ and $2 q$ which fails to satisfy $p \equiv 1 \bmod q$.)
The only remaining case is that $S=\{2\}$. Then $f(2)=2$ and $f(p)=1$ for every odd prime $p$. Since $f(n) 2 \equiv n(\bmod 2), f(n)$ and $n$ must have the same parity. Conversely, any function $f$ for which $f(n) \equiv n$ $(\bmod 2)$ for all $n, f(2)=2$ and $f(p)=1$ for all odd primes $p$ satisfies the condition.
Therefore the only solutions are
- $f(n)=n$ for all $n \in \mathbf{N}$;
- any function $f$ with $f(p)=1$ for all primes $p$;
- any function for which $f(2)=2, f(p)=1$ for primes $p$ exceeding 2 and $f(n)$ and $n$ have the same parity.
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "Canada_MO/segmented/en-sol2008.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2008"
}
|
A self-avoiding rook walk on a chessboard (a rectangular grid of squares) is a path traced by a sequence of rook moves parallel to an edge of the board from one unit square to another, such that each begins where the previous move ended and such that no move ever crosses a square that has previously been crossed, i.e., the rook's path is non-self-intersecting.
Let $R(m, n)$ be the number of self-avoiding rook walks on an $m \times n$ ( $m$ rows, $n$ columns) chessboard which begin at the lower-left corner and end at the upper-left corner. For example, $R(m, 1)=1$ for all
natural numbers $m ; R(2,2)=2 ; R(3,2)=4 ; R(3,3)=11$. Find a formula for $R(3, n)$ for each natural number $n$.
|
Let $r_{n}=R(3, n)$. It can be checked directly that $r_{1}=1$ and $r_{2}=4$. Let $1 \leq i \leq 3$ and $1 \leq j$; let $(i, j)$ denote the cell in the $i$ th row from the bottom and the $j$ th column from the left, so that the paths in question go from $(1,1)$ to $(3,1)$.
Suppose that $n \geq 3$. The rook walks fall into exactly one of the following six categories:
(1) One walk given by $(1,1) \rightarrow(2,1) \rightarrow(3,1)$.
(2) Walks that avoid the cell $(2,1)$ : Any such walk must start with $(1,1) \rightarrow(1,2)$ and finish with $(3,2) \rightarrow$ $(3,1)$; there are $r_{n-1}$ such walks.
(3) Walks that begin with $(1,1) \rightarrow(2,1) \rightarrow(2,2)$ and never return to the first row: Such walks enter the third row from $(2, k)$ for some $k$ with $2 \leq k \leq n$ and then go along the third row leftwards to $(3,1)$; there are $n-1$ such walks.
(4) Walks that begin with $(1,1) \rightarrow(2,1) \rightarrow \cdots \rightarrow(2, k) \rightarrow(1, k) \rightarrow(1, k+1)$ and end with $(3, k+1) \rightarrow$ $(3, k) \rightarrow(3, k-1) \rightarrow \cdots \rightarrow(3,2) \rightarrow(3,1)$ for some $k$ with $2 \leq k \leq n-1$; there are $r_{n-2}+r_{n-3}+\cdots+r_{1}$ such walks.
(5) Walks that are the horizontal reflected images of walks in (3) that begin with $(1,1) \rightarrow(2,1)$ and never enter the third row until the final cell; there are $n-1$ such walks.
(6) Walks that are horizontal reflected images of walks in (5); there are $r_{n-2}+r_{n-3}+\cdots+r_{1}$ such walks.
Thus, $r_{3}=1+r_{2}+2\left(2+r_{1}\right)=11$ and, for $n \geq 3$,
$$
\begin{aligned}
r_{n} & =1+r_{n-1}+2\left[(n-1)+r_{n-2}+r_{n-3}+\cdots+r_{1}\right] \\
& =2 n-1+r_{n-1}+2\left(r_{n-2}+\cdots+r_{1}\right)
\end{aligned}
$$
and
$$
r_{n+1}=2 n+1+r_{n}+2\left(r_{n-1}+r_{n-2}+\cdots+r_{1}\right) .
$$
Therefore
$$
r_{n+1}-r_{n}=2+r_{n}+r_{n-1} \Longrightarrow r_{n+1}=2+2 r_{n}+r_{n-1}
$$
Thus
$$
r_{n+1}+1=2\left(r_{n}+1\right)+\left(r_{n-1}+1\right),
$$
whence
$$
r_{n}+1=\frac{1}{2 \sqrt{2}}(1+\sqrt{2})^{n+1}-\frac{1}{2 \sqrt{2}}(1-\sqrt{2})^{n+1},
$$
and
$$
r_{n}=\frac{1}{2 \sqrt{2}}(1+\sqrt{2})^{n+1}-\frac{1}{2 \sqrt{2}}(1-\sqrt{2})^{n+1}-1 .
$$
|
r_{n}=\frac{1}{2 \sqrt{2}}(1+\sqrt{2})^{n+1}-\frac{1}{2 \sqrt{2}}(1-\sqrt{2})^{n+1}-1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A self-avoiding rook walk on a chessboard (a rectangular grid of squares) is a path traced by a sequence of rook moves parallel to an edge of the board from one unit square to another, such that each begins where the previous move ended and such that no move ever crosses a square that has previously been crossed, i.e., the rook's path is non-self-intersecting.
Let $R(m, n)$ be the number of self-avoiding rook walks on an $m \times n$ ( $m$ rows, $n$ columns) chessboard which begin at the lower-left corner and end at the upper-left corner. For example, $R(m, 1)=1$ for all
natural numbers $m ; R(2,2)=2 ; R(3,2)=4 ; R(3,3)=11$. Find a formula for $R(3, n)$ for each natural number $n$.
|
Let $r_{n}=R(3, n)$. It can be checked directly that $r_{1}=1$ and $r_{2}=4$. Let $1 \leq i \leq 3$ and $1 \leq j$; let $(i, j)$ denote the cell in the $i$ th row from the bottom and the $j$ th column from the left, so that the paths in question go from $(1,1)$ to $(3,1)$.
Suppose that $n \geq 3$. The rook walks fall into exactly one of the following six categories:
(1) One walk given by $(1,1) \rightarrow(2,1) \rightarrow(3,1)$.
(2) Walks that avoid the cell $(2,1)$ : Any such walk must start with $(1,1) \rightarrow(1,2)$ and finish with $(3,2) \rightarrow$ $(3,1)$; there are $r_{n-1}$ such walks.
(3) Walks that begin with $(1,1) \rightarrow(2,1) \rightarrow(2,2)$ and never return to the first row: Such walks enter the third row from $(2, k)$ for some $k$ with $2 \leq k \leq n$ and then go along the third row leftwards to $(3,1)$; there are $n-1$ such walks.
(4) Walks that begin with $(1,1) \rightarrow(2,1) \rightarrow \cdots \rightarrow(2, k) \rightarrow(1, k) \rightarrow(1, k+1)$ and end with $(3, k+1) \rightarrow$ $(3, k) \rightarrow(3, k-1) \rightarrow \cdots \rightarrow(3,2) \rightarrow(3,1)$ for some $k$ with $2 \leq k \leq n-1$; there are $r_{n-2}+r_{n-3}+\cdots+r_{1}$ such walks.
(5) Walks that are the horizontal reflected images of walks in (3) that begin with $(1,1) \rightarrow(2,1)$ and never enter the third row until the final cell; there are $n-1$ such walks.
(6) Walks that are horizontal reflected images of walks in (5); there are $r_{n-2}+r_{n-3}+\cdots+r_{1}$ such walks.
Thus, $r_{3}=1+r_{2}+2\left(2+r_{1}\right)=11$ and, for $n \geq 3$,
$$
\begin{aligned}
r_{n} & =1+r_{n-1}+2\left[(n-1)+r_{n-2}+r_{n-3}+\cdots+r_{1}\right] \\
& =2 n-1+r_{n-1}+2\left(r_{n-2}+\cdots+r_{1}\right)
\end{aligned}
$$
and
$$
r_{n+1}=2 n+1+r_{n}+2\left(r_{n-1}+r_{n-2}+\cdots+r_{1}\right) .
$$
Therefore
$$
r_{n+1}-r_{n}=2+r_{n}+r_{n-1} \Longrightarrow r_{n+1}=2+2 r_{n}+r_{n-1}
$$
Thus
$$
r_{n+1}+1=2\left(r_{n}+1\right)+\left(r_{n-1}+1\right),
$$
whence
$$
r_{n}+1=\frac{1}{2 \sqrt{2}}(1+\sqrt{2})^{n+1}-\frac{1}{2 \sqrt{2}}(1-\sqrt{2})^{n+1},
$$
and
$$
r_{n}=\frac{1}{2 \sqrt{2}}(1+\sqrt{2})^{n+1}-\frac{1}{2 \sqrt{2}}(1-\sqrt{2})^{n+1}-1 .
$$
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "Canada_MO/segmented/en-sol2008.jsonl",
"solution_match": "\nSolution 1.",
"tier": "T2",
"year": "2008"
}
|
A self-avoiding rook walk on a chessboard (a rectangular grid of squares) is a path traced by a sequence of rook moves parallel to an edge of the board from one unit square to another, such that each begins where the previous move ended and such that no move ever crosses a square that has previously been crossed, i.e., the rook's path is non-self-intersecting.
Let $R(m, n)$ be the number of self-avoiding rook walks on an $m \times n$ ( $m$ rows, $n$ columns) chessboard which begin at the lower-left corner and end at the upper-left corner. For example, $R(m, 1)=1$ for all
natural numbers $m ; R(2,2)=2 ; R(3,2)=4 ; R(3,3)=11$. Find a formula for $R(3, n)$ for each natural number $n$.
|
Employ the same notation as in Solution 1. We have that $r_{1}=1, r_{2}=4$ and $r_{3}=11$. Let $n \geq 3$. Consider the situation that there are $r_{n+1}$ columns. There are basically three types of rook walks.
Type 1. There are four rook walks that enter only the first two columns.
Type 2. There are $3 r_{n-1}$ rooks walks that do not pass between the second and third columns in the middle row (in either direction), viz. $r_{n-1}$ of each of the types:
$$
\begin{gathered}
(1,1) \longrightarrow(1,2) \longrightarrow(1,3) \longrightarrow \cdots \longrightarrow(3,3) \longrightarrow(3,2) \longrightarrow(3,1) ; \\
(1,1) \longrightarrow(2,1) \longrightarrow(2,2) \longrightarrow(1,2) \longrightarrow(1,3) \longrightarrow \cdots \longrightarrow(3,3) \longrightarrow(3,2) \longrightarrow(3,1) ; \\
(1,1) \longrightarrow(1,2) \longrightarrow(1,3) \longrightarrow \cdots \longrightarrow(3,3) \longrightarrow(3,2) \longrightarrow(2,2) \longrightarrow(2,1) \longrightarrow(3,1) .
\end{gathered}
$$
Type 3. Consider the rook walks that pass between the second and third column along the middle row.
They are of Type 3a:
$$
(1,1) \longrightarrow * \longrightarrow(2,2) \longrightarrow(2,3) \longrightarrow \cdots \longrightarrow(3,3) \longrightarrow(3,2) \longrightarrow(3,1) \text {, }
$$
or Type $3 b$ :
$$
(1,1) \longrightarrow(1,2) \longrightarrow(1,3) \longrightarrow \cdots \longrightarrow(2,3) \longrightarrow(2,2) \longrightarrow * \longrightarrow(3,1) \text {, }
$$
where in each case the asterisk stands for one of two possible options.
We can associate in a two-one way the walks of Type 3a to a rook walk on the last $n$ columns, namely
$$
(1,2) \longrightarrow(2,2) \longrightarrow(2,3) \longrightarrow \cdots \longrightarrow(3,3) \longrightarrow(3,2)
$$
and the walks of Type $3 \mathrm{~b}$ to a rook walk on the last $n$ columns, namely
$$
(1,2) \longrightarrow(1,3) \longrightarrow \cdots \longrightarrow(2,3) \longrightarrow(2,2) \longrightarrow(3,2) \text {. }
$$
The number of rook walks of the latter two types together is $r_{n}-1-r_{n-1}$. From the number of rook walks on the last $n$ columns, we subtract one for $(1,2) \rightarrow(2,2) \rightarrow(3,2)$ and $r_{n-1}$ for those of the type
$$
(1,2) \longrightarrow(1,3) \longrightarrow \cdots \longrightarrow(3,3) \longrightarrow(2,3) \text {. }
$$
Therefore, the number of rook walks of Type 3 is $2\left(r_{n}-1-r_{n-1}\right)$ and we find that
$$
r_{n+1}=4+3 r_{n-1}+2\left(r_{n}-1-r_{n-1}\right)=2+2 r_{n}+r_{n-1} .
$$
We can now complete the solution as in Solution 1.
|
r_{n+1}=2+2r_{n}+r_{n-1}
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A self-avoiding rook walk on a chessboard (a rectangular grid of squares) is a path traced by a sequence of rook moves parallel to an edge of the board from one unit square to another, such that each begins where the previous move ended and such that no move ever crosses a square that has previously been crossed, i.e., the rook's path is non-self-intersecting.
Let $R(m, n)$ be the number of self-avoiding rook walks on an $m \times n$ ( $m$ rows, $n$ columns) chessboard which begin at the lower-left corner and end at the upper-left corner. For example, $R(m, 1)=1$ for all
natural numbers $m ; R(2,2)=2 ; R(3,2)=4 ; R(3,3)=11$. Find a formula for $R(3, n)$ for each natural number $n$.
|
Employ the same notation as in Solution 1. We have that $r_{1}=1, r_{2}=4$ and $r_{3}=11$. Let $n \geq 3$. Consider the situation that there are $r_{n+1}$ columns. There are basically three types of rook walks.
Type 1. There are four rook walks that enter only the first two columns.
Type 2. There are $3 r_{n-1}$ rooks walks that do not pass between the second and third columns in the middle row (in either direction), viz. $r_{n-1}$ of each of the types:
$$
\begin{gathered}
(1,1) \longrightarrow(1,2) \longrightarrow(1,3) \longrightarrow \cdots \longrightarrow(3,3) \longrightarrow(3,2) \longrightarrow(3,1) ; \\
(1,1) \longrightarrow(2,1) \longrightarrow(2,2) \longrightarrow(1,2) \longrightarrow(1,3) \longrightarrow \cdots \longrightarrow(3,3) \longrightarrow(3,2) \longrightarrow(3,1) ; \\
(1,1) \longrightarrow(1,2) \longrightarrow(1,3) \longrightarrow \cdots \longrightarrow(3,3) \longrightarrow(3,2) \longrightarrow(2,2) \longrightarrow(2,1) \longrightarrow(3,1) .
\end{gathered}
$$
Type 3. Consider the rook walks that pass between the second and third column along the middle row.
They are of Type 3a:
$$
(1,1) \longrightarrow * \longrightarrow(2,2) \longrightarrow(2,3) \longrightarrow \cdots \longrightarrow(3,3) \longrightarrow(3,2) \longrightarrow(3,1) \text {, }
$$
or Type $3 b$ :
$$
(1,1) \longrightarrow(1,2) \longrightarrow(1,3) \longrightarrow \cdots \longrightarrow(2,3) \longrightarrow(2,2) \longrightarrow * \longrightarrow(3,1) \text {, }
$$
where in each case the asterisk stands for one of two possible options.
We can associate in a two-one way the walks of Type 3a to a rook walk on the last $n$ columns, namely
$$
(1,2) \longrightarrow(2,2) \longrightarrow(2,3) \longrightarrow \cdots \longrightarrow(3,3) \longrightarrow(3,2)
$$
and the walks of Type $3 \mathrm{~b}$ to a rook walk on the last $n$ columns, namely
$$
(1,2) \longrightarrow(1,3) \longrightarrow \cdots \longrightarrow(2,3) \longrightarrow(2,2) \longrightarrow(3,2) \text {. }
$$
The number of rook walks of the latter two types together is $r_{n}-1-r_{n-1}$. From the number of rook walks on the last $n$ columns, we subtract one for $(1,2) \rightarrow(2,2) \rightarrow(3,2)$ and $r_{n-1}$ for those of the type
$$
(1,2) \longrightarrow(1,3) \longrightarrow \cdots \longrightarrow(3,3) \longrightarrow(2,3) \text {. }
$$
Therefore, the number of rook walks of Type 3 is $2\left(r_{n}-1-r_{n-1}\right)$ and we find that
$$
r_{n+1}=4+3 r_{n-1}+2\left(r_{n}-1-r_{n-1}\right)=2+2 r_{n}+r_{n-1} .
$$
We can now complete the solution as in Solution 1.
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "Canada_MO/segmented/en-sol2008.jsonl",
"solution_match": "\nSolution 2.",
"tier": "T2",
"year": "2008"
}
|
A self-avoiding rook walk on a chessboard (a rectangular grid of squares) is a path traced by a sequence of rook moves parallel to an edge of the board from one unit square to another, such that each begins where the previous move ended and such that no move ever crosses a square that has previously been crossed, i.e., the rook's path is non-self-intersecting.
Let $R(m, n)$ be the number of self-avoiding rook walks on an $m \times n$ ( $m$ rows, $n$ columns) chessboard which begin at the lower-left corner and end at the upper-left corner. For example, $R(m, 1)=1$ for all
natural numbers $m ; R(2,2)=2 ; R(3,2)=4 ; R(3,3)=11$. Find a formula for $R(3, n)$ for each natural number $n$.
|
Let $S(3, n)$ be the set of self-avoiding rook walks in which the rook occupies column $n$ but does not occupy column $n+1$. Then $R(3, n)=|S(3,1)|+|S(3,2)|+\cdots+|S(3, n)|$. Furthermore, topological considerations allow us to break $S(3, n)$ into three disjoint subsets $S_{1}(3, n)$, the set of paths in which corner $(1, n)$ is not occupied, but there is a path segment $(2, n) \longrightarrow(3, n) ; S_{2}(3, n)$, the set of paths in which corners $(1, n)$ and $(3, n)$ are both occupied by a path $(1, n) \longrightarrow(2, n) \longrightarrow(3, n)$; and $S_{3}(3, n)$, the set of paths in which corner $(3, n)$ is not occupied but there is a path segment $(1, n) \longrightarrow(2, n)$. Let $s_{i}(n)=\left|S_{i}(3, n)\right|$ for $i=1,2,3$. Note that $s_{1}(1)=0, s_{2}(1)=1$ and $s_{3}(1)=0$. By symmetry, $s_{1}(n)=s_{3}(n)$ for every positive $n$. Furthermore, we can construct paths in $S(3, n+1)$ by "bulging" paths in $S(3, n)$, from which we obtain
$$
\begin{aligned}
& s_{1}(n+1)=s_{1}(n)+s_{2}(n) ; \\
& s_{2}(n+1)=s_{1}(n)+s_{2}(n)+s_{3}(n) ; \\
& s_{3}(n+1)=s_{2}(n)+s_{3}(n) ;
\end{aligned}
$$
or, upon simplification,
$$
\begin{aligned}
& s_{1}(n+1)=s_{1}(n)+s_{2}(n) \\
& s_{2}(n+1)=2 s_{1}(n)+s_{2}(n)
\end{aligned}
$$
Hence, for $n \geq 2$,
$$
\begin{aligned}
s_{1}(n+1) & =s_{1}(n)+2 s_{1}(n-1)+s_{2}(n-1) \\
& =s_{1}(n)+2 s_{1}(n-1)+s_{1}(n)-s_{1}(n-1) \\
& =2 s_{1}(n)+s_{1}(n-1) .
\end{aligned}
$$
and
$$
\begin{aligned}
s_{2}(n+1) & =2 s_{1}(n)+s_{2}(n)=2 s_{1}(n-1)+2 s_{2}(n-1)+s_{2}(n) \\
& =s_{2}(n)-s_{2}(n-1)+2 s_{2}(n-1)+s_{2}(n) \\
& =2 s_{2}(n)+s_{2}(n-1) .
\end{aligned}
$$
We find that
$$
\begin{aligned}
& s_{1}(n)=\frac{1}{2 \sqrt{2}}(1+\sqrt{2})^{n-1}-\frac{1}{2 \sqrt{2}}(1-\sqrt{2})^{n-1} ; \\
& s_{2}(n)=\frac{1}{2}(1+\sqrt{2})^{n-1}+\frac{1}{2}(1-\sqrt{2})^{n-1} .
\end{aligned}
$$
Summing a geometric series yields that
$$
\begin{aligned}
R(3, n) & =\left(s_{2}(1)+\cdots+s_{2}(n)\right)+2\left(s_{1}(1)+\cdots+s_{1}(n)\right) \\
& =\left(\frac{1}{2}+\frac{1}{\sqrt{2}}\right)\left(\frac{(1+\sqrt{2})^{n}-1}{\sqrt{2}}\right)+\left(\frac{1}{2}-\frac{1}{\sqrt{2}}\right)\left(\frac{(1-\sqrt{2})^{n}-1}{-\sqrt{2}}\right) \\
& =\left(\frac{1}{2 \sqrt{2}}\right)\left[(1+\sqrt{2})^{n+1}-(1-\sqrt{2})^{n+1}\right]-1 .
\end{aligned}
$$
The formula agrees with $R(3,1)=1, R(3,2)=4$ and $R(3,3)=11$.
Acknowledgment. The first two solutions are due to Man-Duen Choi, and the third to Ed Doolittle.
|
R(3, n) = \left(\frac{1}{2 \sqrt{2}}\right)\left[(1+\sqrt{2})^{n+1}-(1-\sqrt{2})^{n+1}\right]-1
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A self-avoiding rook walk on a chessboard (a rectangular grid of squares) is a path traced by a sequence of rook moves parallel to an edge of the board from one unit square to another, such that each begins where the previous move ended and such that no move ever crosses a square that has previously been crossed, i.e., the rook's path is non-self-intersecting.
Let $R(m, n)$ be the number of self-avoiding rook walks on an $m \times n$ ( $m$ rows, $n$ columns) chessboard which begin at the lower-left corner and end at the upper-left corner. For example, $R(m, 1)=1$ for all
natural numbers $m ; R(2,2)=2 ; R(3,2)=4 ; R(3,3)=11$. Find a formula for $R(3, n)$ for each natural number $n$.
|
Let $S(3, n)$ be the set of self-avoiding rook walks in which the rook occupies column $n$ but does not occupy column $n+1$. Then $R(3, n)=|S(3,1)|+|S(3,2)|+\cdots+|S(3, n)|$. Furthermore, topological considerations allow us to break $S(3, n)$ into three disjoint subsets $S_{1}(3, n)$, the set of paths in which corner $(1, n)$ is not occupied, but there is a path segment $(2, n) \longrightarrow(3, n) ; S_{2}(3, n)$, the set of paths in which corners $(1, n)$ and $(3, n)$ are both occupied by a path $(1, n) \longrightarrow(2, n) \longrightarrow(3, n)$; and $S_{3}(3, n)$, the set of paths in which corner $(3, n)$ is not occupied but there is a path segment $(1, n) \longrightarrow(2, n)$. Let $s_{i}(n)=\left|S_{i}(3, n)\right|$ for $i=1,2,3$. Note that $s_{1}(1)=0, s_{2}(1)=1$ and $s_{3}(1)=0$. By symmetry, $s_{1}(n)=s_{3}(n)$ for every positive $n$. Furthermore, we can construct paths in $S(3, n+1)$ by "bulging" paths in $S(3, n)$, from which we obtain
$$
\begin{aligned}
& s_{1}(n+1)=s_{1}(n)+s_{2}(n) ; \\
& s_{2}(n+1)=s_{1}(n)+s_{2}(n)+s_{3}(n) ; \\
& s_{3}(n+1)=s_{2}(n)+s_{3}(n) ;
\end{aligned}
$$
or, upon simplification,
$$
\begin{aligned}
& s_{1}(n+1)=s_{1}(n)+s_{2}(n) \\
& s_{2}(n+1)=2 s_{1}(n)+s_{2}(n)
\end{aligned}
$$
Hence, for $n \geq 2$,
$$
\begin{aligned}
s_{1}(n+1) & =s_{1}(n)+2 s_{1}(n-1)+s_{2}(n-1) \\
& =s_{1}(n)+2 s_{1}(n-1)+s_{1}(n)-s_{1}(n-1) \\
& =2 s_{1}(n)+s_{1}(n-1) .
\end{aligned}
$$
and
$$
\begin{aligned}
s_{2}(n+1) & =2 s_{1}(n)+s_{2}(n)=2 s_{1}(n-1)+2 s_{2}(n-1)+s_{2}(n) \\
& =s_{2}(n)-s_{2}(n-1)+2 s_{2}(n-1)+s_{2}(n) \\
& =2 s_{2}(n)+s_{2}(n-1) .
\end{aligned}
$$
We find that
$$
\begin{aligned}
& s_{1}(n)=\frac{1}{2 \sqrt{2}}(1+\sqrt{2})^{n-1}-\frac{1}{2 \sqrt{2}}(1-\sqrt{2})^{n-1} ; \\
& s_{2}(n)=\frac{1}{2}(1+\sqrt{2})^{n-1}+\frac{1}{2}(1-\sqrt{2})^{n-1} .
\end{aligned}
$$
Summing a geometric series yields that
$$
\begin{aligned}
R(3, n) & =\left(s_{2}(1)+\cdots+s_{2}(n)\right)+2\left(s_{1}(1)+\cdots+s_{1}(n)\right) \\
& =\left(\frac{1}{2}+\frac{1}{\sqrt{2}}\right)\left(\frac{(1+\sqrt{2})^{n}-1}{\sqrt{2}}\right)+\left(\frac{1}{2}-\frac{1}{\sqrt{2}}\right)\left(\frac{(1-\sqrt{2})^{n}-1}{-\sqrt{2}}\right) \\
& =\left(\frac{1}{2 \sqrt{2}}\right)\left[(1+\sqrt{2})^{n+1}-(1-\sqrt{2})^{n+1}\right]-1 .
\end{aligned}
$$
The formula agrees with $R(3,1)=1, R(3,2)=4$ and $R(3,3)=11$.
Acknowledgment. The first two solutions are due to Man-Duen Choi, and the third to Ed Doolittle.
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "Canada_MO/segmented/en-sol2008.jsonl",
"solution_match": "\nSolution 3.",
"tier": "T2",
"year": "2008"
}
|
Given an $m \times n$ grid with squares coloured either black or white, we say that a black square in the grid is stranded if there is some square to its left in the same row that is white and there is some square above it in the same column that is white (see Figure).

FiguRE 1. A $4 \times 5$ grid with no stranded black squares
Find a closed formula for the number of $2 \times n$ grids with no stranded black squares.
|
There is no condition for squares in the first row. A square in the second row can be black only if the square above it is black or all squares to the left of it are black. Suppose the first $k$ squares in the second row are black and the $(k+1)$-st square is white or $k=n$. When $k<n$ then for each of the first $k+1$ squares in the first row we have 2 choices, and for each of the remaining $n-k-1$ columns we have 3 choices. When $k=n$, there are $2^{n}$ choices for the first row. The total number of choices is thus:
$$
\sum_{k=0}^{n-1} 2^{k+1} 3^{n-k-1}+2^{n}
$$
This expression simplifies to
$$
2 \cdot 3^{n}-2^{n}
$$
## CANADIAN MATHEMATICAL OLYMPIAD 2009 SOLUTIONS
|
2 \cdot 3^{n} - 2^{n}
|
Incomplete
|
Yes
|
math-word-problem
|
Combinatorics
|
Given an $m \times n$ grid with squares coloured either black or white, we say that a black square in the grid is stranded if there is some square to its left in the same row that is white and there is some square above it in the same column that is white (see Figure).

FiguRE 1. A $4 \times 5$ grid with no stranded black squares
Find a closed formula for the number of $2 \times n$ grids with no stranded black squares.
|
There is no condition for squares in the first row. A square in the second row can be black only if the square above it is black or all squares to the left of it are black. Suppose the first $k$ squares in the second row are black and the $(k+1)$-st square is white or $k=n$. When $k<n$ then for each of the first $k+1$ squares in the first row we have 2 choices, and for each of the remaining $n-k-1$ columns we have 3 choices. When $k=n$, there are $2^{n}$ choices for the first row. The total number of choices is thus:
$$
\sum_{k=0}^{n-1} 2^{k+1} 3^{n-k-1}+2^{n}
$$
This expression simplifies to
$$
2 \cdot 3^{n}-2^{n}
$$
## CANADIAN MATHEMATICAL OLYMPIAD 2009 SOLUTIONS
|
{
"exam": "Canada_MO",
"problem_label": "1",
"problem_match": "\nProblem 1.",
"resource_path": "Canada_MO/segmented/en-sol2009.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2009"
}
|
Two circles of different radii are cut out of cardboard. Each circle is subdivided into 200 equal sectors. On each circle 100 sectors are painted white and the other 100 are painted black. The smaller circle is then placed on top of the larger circle, so that their centers coincide. Show that one can rotate the small circle so that the sectors on the two circles line up and at least 100 sectors on the small circle lie over sectors of the same color on the big circle.
|
Let $x_{0}, \ldots, x_{199}$ be variables. Assign the value of +1 or -1 to $x_{i}$ depending on whether the $(i+1)$ st segment of the larger circle (counting counterclockwise) is black or white, respectively. Similarly, assign the value of +1 or -1 to the variable $y_{i}$ depending on whether the $(i+1)$ th segment of the smaller circle is black or white. We can now restate the problem in the following equivalent way: show that
$$
S_{j}=\sum_{i=1}^{200} x_{i} y_{i+j} \geq 0
$$
for some $j=0, \ldots, 199$. Here the subscript $i+j$ is understood modulo 200 .
Now observe that $y_{0}+\cdots+y_{199}=0$ and thus
$$
S_{0}+\cdots+S_{199}=\sum_{I=0}^{199} x_{i}\left(y_{0}+\cdots+y_{199}\right)=0 .
$$
Thus $S_{j} \geq 0$ for some $j=0, \ldots, 199$, as claimed.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Two circles of different radii are cut out of cardboard. Each circle is subdivided into 200 equal sectors. On each circle 100 sectors are painted white and the other 100 are painted black. The smaller circle is then placed on top of the larger circle, so that their centers coincide. Show that one can rotate the small circle so that the sectors on the two circles line up and at least 100 sectors on the small circle lie over sectors of the same color on the big circle.
|
Let $x_{0}, \ldots, x_{199}$ be variables. Assign the value of +1 or -1 to $x_{i}$ depending on whether the $(i+1)$ st segment of the larger circle (counting counterclockwise) is black or white, respectively. Similarly, assign the value of +1 or -1 to the variable $y_{i}$ depending on whether the $(i+1)$ th segment of the smaller circle is black or white. We can now restate the problem in the following equivalent way: show that
$$
S_{j}=\sum_{i=1}^{200} x_{i} y_{i+j} \geq 0
$$
for some $j=0, \ldots, 199$. Here the subscript $i+j$ is understood modulo 200 .
Now observe that $y_{0}+\cdots+y_{199}=0$ and thus
$$
S_{0}+\cdots+S_{199}=\sum_{I=0}^{199} x_{i}\left(y_{0}+\cdots+y_{199}\right)=0 .
$$
Thus $S_{j} \geq 0$ for some $j=0, \ldots, 199$, as claimed.
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\nProblem 2.",
"resource_path": "Canada_MO/segmented/en-sol2009.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2009"
}
|
Define
$$
f(x, y, z)=\frac{(x y+y z+z x)(x+y+z)}{(x+y)(x+z)(y+z)} .
$$
Determine the set of real numbers $r$ for which there exists a triplet $(x, y, z)$ of positive real numbers satisfying $f(x, y, z)=r$.
|
We prove that $1<f(x, y, z) \leq \frac{9}{8}$, and that $f(x, y, z)$ can take on any value within the range $\left(1, \frac{9}{8}\right]$.
The expression for $f(x, y, z)$ can be simplified to
$$
f(x, y, z)=1+\frac{x y z}{(x+y)(x+z)(y+z)} .
$$
Since $x, y, z$ are positive, we get $1<f(x, y, z)$.
The inequality $f(x, y, z) \leq \frac{9}{8}$ can be simplified to
$$
x^{2} y+x^{2} z+y^{2} x+y^{2} z+z^{2} x+z^{2} y-6 x y z \geq 0 .
$$
Rearrange the left hand side as follows:
$$
\begin{aligned}
& x^{2} y+x^{2} z+y^{2} x+y^{2} z+z^{2} x+z^{2} y-6 x y z= \\
& x\left(y^{2}+z^{2}\right)-2 x y z+y\left(x^{2}+z^{2}\right)-2 x y z+z\left(x^{2}+y^{2}\right)-2 x y z= \\
& x(y-z)^{2}+y(x-z)^{2}+z(x-y)^{2} .
\end{aligned}
$$
This expression is clearly non-negative when $x, y, z$ are non-negative. To prove that $f(x, y, z)$ takes any values in the interval $\left(1, \frac{9}{8}\right]$, define
$$
g(t)=f(t, 1,1)=1+\frac{t}{2(1+t)^{2}}
$$
Then $g(1)=\frac{9}{8}$ and $g(t)$ approaches 1 as $t$ approaches 0 . It follows from the continuity of $g(t)$ for $0<t \leq 1$ that it takes all values in the interval $\left(1, \frac{9}{8}\right]$. (Alternatively, one can check that the quadratic equation $g(t)=r$ has a solution $t$ for any number $r$ in the interval $\left(1, \frac{9}{8}\right]$.)
|
\left(1, \frac{9}{8}\right]
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Define
$$
f(x, y, z)=\frac{(x y+y z+z x)(x+y+z)}{(x+y)(x+z)(y+z)} .
$$
Determine the set of real numbers $r$ for which there exists a triplet $(x, y, z)$ of positive real numbers satisfying $f(x, y, z)=r$.
|
We prove that $1<f(x, y, z) \leq \frac{9}{8}$, and that $f(x, y, z)$ can take on any value within the range $\left(1, \frac{9}{8}\right]$.
The expression for $f(x, y, z)$ can be simplified to
$$
f(x, y, z)=1+\frac{x y z}{(x+y)(x+z)(y+z)} .
$$
Since $x, y, z$ are positive, we get $1<f(x, y, z)$.
The inequality $f(x, y, z) \leq \frac{9}{8}$ can be simplified to
$$
x^{2} y+x^{2} z+y^{2} x+y^{2} z+z^{2} x+z^{2} y-6 x y z \geq 0 .
$$
Rearrange the left hand side as follows:
$$
\begin{aligned}
& x^{2} y+x^{2} z+y^{2} x+y^{2} z+z^{2} x+z^{2} y-6 x y z= \\
& x\left(y^{2}+z^{2}\right)-2 x y z+y\left(x^{2}+z^{2}\right)-2 x y z+z\left(x^{2}+y^{2}\right)-2 x y z= \\
& x(y-z)^{2}+y(x-z)^{2}+z(x-y)^{2} .
\end{aligned}
$$
This expression is clearly non-negative when $x, y, z$ are non-negative. To prove that $f(x, y, z)$ takes any values in the interval $\left(1, \frac{9}{8}\right]$, define
$$
g(t)=f(t, 1,1)=1+\frac{t}{2(1+t)^{2}}
$$
Then $g(1)=\frac{9}{8}$ and $g(t)$ approaches 1 as $t$ approaches 0 . It follows from the continuity of $g(t)$ for $0<t \leq 1$ that it takes all values in the interval $\left(1, \frac{9}{8}\right]$. (Alternatively, one can check that the quadratic equation $g(t)=r$ has a solution $t$ for any number $r$ in the interval $\left(1, \frac{9}{8}\right]$.)
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\nPRoblem 3.",
"resource_path": "Canada_MO/segmented/en-sol2009.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2009"
}
|
Find all ordered pairs $(a, b)$ such that $a$ and $b$ are integers and $3^{a}+7^{b}$ is a perfect square.
|
It is obvious that $a$ and $b$ must be non-negative.
Suppose that $3^{a}+7^{b}=n^{2}$. We can assume that $n$ is positive. We first work modulo 4 . Since $3^{a}+7^{b}=n^{2}$, it follows that
$$
n^{2} \equiv(-1)^{a}+(-1)^{b} \quad(\bmod 4)
$$
Since no square can be congruent to 2 modulo 4 , it follows that we have either (i) $a$ is odd and $b$ is even or (ii) $a$ is even and $b$ is odd.
Case (i): Let $b=2 c$. Then
$$
3^{a}=\left(n-7^{c}\right)\left(n+7^{c}\right) .
$$
It cannot be the case that 3 divides both $n-7^{c}$ and $n+7^{c}$. But each of these is a power of 3. It follows that $n-7^{c}=1$, and therefore
$$
3^{a}=2 \cdot 7^{c}+1 .
$$
If $c=0$, then $a=1$, and we obtain the solution $a=1, b=0$. So suppose that $c \geq 1$. Then $3^{a} \equiv 1(\bmod 7)$. This is impossible, since the smallest positive value of $a$ such that $3^{a} \equiv 1(\bmod 7)$ is given by $a=6$, and therefore all $a$ such that $3^{a} \equiv 1(\bmod 7)$ are even, contradicting the fact that $a$ is odd.
Case (ii): Let $a=2 c$. Then
$$
7^{b}=\left(n-3^{c}\right)\left(n+3^{c}\right) .
$$
Thus each of $n-3^{c}$ and $n+3^{c}$ is a power of 7 . Since 7 cannot divide both of these, it follows that $n-3^{c}=1$, and therefore
$$
7^{b}=2 \cdot 3^{c}+1
$$
Look first at the case $c=1$. Then $b=1$, and we obtain the solution $a=2, b=1$. So from now on we may assume that $c>1$. Then $7^{b} \equiv 1(\bmod 9)$. The smallest positive integer $b$ such that $7^{b} \equiv 1(\bmod 9)$ is given by $b=3$. It follows that $b$ must be a multiple of 3 . Let $b=3 d$. Note that $d$ is odd, so in particular $d \geq 1$.
Let $y=7^{d}$. Then $y^{3}-1=2 \cdot 3^{c}$, and therefore
$$
2 \cdot 3^{c}=(y-1)\left(y^{2}+y+1\right) \text {. }
$$
It follows that $y-1=2 \cdot 3^{u}$ for some positive $u$, and that $y^{2}+y+1=3^{v}$ for some $v \geq 2$. But since
$$
3 y=\left(y^{2}+y+1\right)-(y-1)^{2},
$$
it follows that $3 \mid y$, which is impossible since $3 \mid(y-1)$.
|
a=1, b=0 \text{ and } a=2, b=1
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Find all ordered pairs $(a, b)$ such that $a$ and $b$ are integers and $3^{a}+7^{b}$ is a perfect square.
|
It is obvious that $a$ and $b$ must be non-negative.
Suppose that $3^{a}+7^{b}=n^{2}$. We can assume that $n$ is positive. We first work modulo 4 . Since $3^{a}+7^{b}=n^{2}$, it follows that
$$
n^{2} \equiv(-1)^{a}+(-1)^{b} \quad(\bmod 4)
$$
Since no square can be congruent to 2 modulo 4 , it follows that we have either (i) $a$ is odd and $b$ is even or (ii) $a$ is even and $b$ is odd.
Case (i): Let $b=2 c$. Then
$$
3^{a}=\left(n-7^{c}\right)\left(n+7^{c}\right) .
$$
It cannot be the case that 3 divides both $n-7^{c}$ and $n+7^{c}$. But each of these is a power of 3. It follows that $n-7^{c}=1$, and therefore
$$
3^{a}=2 \cdot 7^{c}+1 .
$$
If $c=0$, then $a=1$, and we obtain the solution $a=1, b=0$. So suppose that $c \geq 1$. Then $3^{a} \equiv 1(\bmod 7)$. This is impossible, since the smallest positive value of $a$ such that $3^{a} \equiv 1(\bmod 7)$ is given by $a=6$, and therefore all $a$ such that $3^{a} \equiv 1(\bmod 7)$ are even, contradicting the fact that $a$ is odd.
Case (ii): Let $a=2 c$. Then
$$
7^{b}=\left(n-3^{c}\right)\left(n+3^{c}\right) .
$$
Thus each of $n-3^{c}$ and $n+3^{c}$ is a power of 7 . Since 7 cannot divide both of these, it follows that $n-3^{c}=1$, and therefore
$$
7^{b}=2 \cdot 3^{c}+1
$$
Look first at the case $c=1$. Then $b=1$, and we obtain the solution $a=2, b=1$. So from now on we may assume that $c>1$. Then $7^{b} \equiv 1(\bmod 9)$. The smallest positive integer $b$ such that $7^{b} \equiv 1(\bmod 9)$ is given by $b=3$. It follows that $b$ must be a multiple of 3 . Let $b=3 d$. Note that $d$ is odd, so in particular $d \geq 1$.
Let $y=7^{d}$. Then $y^{3}-1=2 \cdot 3^{c}$, and therefore
$$
2 \cdot 3^{c}=(y-1)\left(y^{2}+y+1\right) \text {. }
$$
It follows that $y-1=2 \cdot 3^{u}$ for some positive $u$, and that $y^{2}+y+1=3^{v}$ for some $v \geq 2$. But since
$$
3 y=\left(y^{2}+y+1\right)-(y-1)^{2},
$$
it follows that $3 \mid y$, which is impossible since $3 \mid(y-1)$.
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\nProblem 4.",
"resource_path": "Canada_MO/segmented/en-sol2009.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2009"
}
|
A set of points is marked on the plane, with the property that any three marked points can be covered with a disk of radius 1. Prove that the set of all marked points can be covered with a disk of radius 1 .
|
(For a finite set of points only.) Let $D$ be a disk of smallest radius that covers all marked points. Consider the marked points on the boundary $C$ of this disk. Note that if all marked points on $C$ lie on an arc smaller than the half circle (ASTTHC for short), then the disk can be moved a little towards these points on the boundary and its radius can be decreased. Since we assumed that our disk has minimal radius, the marked points on its boundary do not lie on an ASTTHC.
If the two endpoints of a diagonal of $D$ are marked, then $D$ is the smallest disk containing these two points, hence must have radius at most 1 .
If there are 3 marked points on $C$ that do not lie on an ASTTHC, then $D$ is the smallest disk covering these 3 points and hence must have radius at most 1 . (In this case the triangle formed by the three points is acute and $C$ is its circumcircle.)
If there are more than 3 marked points on the boundary that do not lie on an ASTTHC, then we can remove one of them so that the remaining points again do not lie on an ASTTHC. By induction this leads us to the case of 3 points. Indeed, given 4 or more points on $C$, choose 3 points that lie on a half circle. Then the middle point can be removed.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A set of points is marked on the plane, with the property that any three marked points can be covered with a disk of radius 1. Prove that the set of all marked points can be covered with a disk of radius 1 .
|
(For a finite set of points only.) Let $D$ be a disk of smallest radius that covers all marked points. Consider the marked points on the boundary $C$ of this disk. Note that if all marked points on $C$ lie on an arc smaller than the half circle (ASTTHC for short), then the disk can be moved a little towards these points on the boundary and its radius can be decreased. Since we assumed that our disk has minimal radius, the marked points on its boundary do not lie on an ASTTHC.
If the two endpoints of a diagonal of $D$ are marked, then $D$ is the smallest disk containing these two points, hence must have radius at most 1 .
If there are 3 marked points on $C$ that do not lie on an ASTTHC, then $D$ is the smallest disk covering these 3 points and hence must have radius at most 1 . (In this case the triangle formed by the three points is acute and $C$ is its circumcircle.)
If there are more than 3 marked points on the boundary that do not lie on an ASTTHC, then we can remove one of them so that the remaining points again do not lie on an ASTTHC. By induction this leads us to the case of 3 points. Indeed, given 4 or more points on $C$, choose 3 points that lie on a half circle. Then the middle point can be removed.
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\nProblem 5.",
"resource_path": "Canada_MO/segmented/en-sol2009.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2009"
}
|
For a positive integer $n$, an $n$-staircase is a figure consisting of unit squares, with one square in the first row, two squares in the second row, and so on, up to $n$ squares in the $n^{\text {th }}$ row, such that all the left-most squares in each row are aligned vertically. For example, the 5 -staircase is shown below.

Let $f(n)$ denote the minimum number of square tiles required to tile the $n$ staircase, where the side lengths of the square tiles can be any positive integer. For example, $f(2)=3$ and $f(4)=7$.
(a) Find all $n$ such that $f(n)=n$.
(b) Find all $n$ such that $f(n)=n+1$.
|
(a) A diagonal square in an $n$-staircase is a unit square that lies on the diagonal going from the top-left to the bottom-right. A minimal tiling of an $n$-staircase is a tiling consisting of $f(n)$ square tiles.
Observe that $f(n) \geq n$ for all $n$. There are $n$ diagonal squares in an $n$-staircase, and a square tile can cover at most one diagonal square, so any tiling requires at least $n$ square tiles. In other words, $f(n) \geq n$. Hence, if $f(n)=n$, then each square tile covers exactly one diagonal square.
Let $n$ be a positive integer such that $f(n)=n$, and consider a minimal tiling of an $n$-staircase. The only square tile that can cover the unit square in the first row is the unit square itself.
Now consider the left-most unit square in the second row. The only square tile that can cover this unit square and a diagonal square is a $2 \times 2$ square tile.
## Sun <br> Life Financial
that can cover this unit square and a diagonal square is a $4 \times 4$ square tile.
Continuing this construction, we see that the side lengths of the square tiles we encounter will be $1,2,4$, and so on, up to $2^{k}$ for some nonnegative integer $k$. Therefore, $n$, the height of the $n$-staircase, is equal to $1+2+4+\cdots+2^{k}=2^{k+1}-1$. Alternatively, $n=2^{k}-1$ for some positive integer $k$. Let $p(k)=2^{k}-1$.
Conversely, we can tile a $p(k)$-staircase with $p(k)$ square tiles recursively as follows: We have that $p(1)=1$, and we can tile a 1 -staircase with 1 square tile. Assume that we can tile a $p(k)$-staircase with $p(k)$ square tiles for some positive integer $k$.
Consider a $p(k+1)$-staircase. Place a $2^{k} \times 2^{k}$ square tile in the bottom left corner. Note that this square tile covers a digaonal square. Then $p(k+1)-2^{k}=$ $2^{k+1}-1-2^{k}=2^{k}-1=p(k)$, so we are left with two $p(k)$-staircases.
Furthermore, these two $p(k)$-staircases can be tiled with $2 p(k)$ square tiles, which means we use $2 p(k)+1=p(k+1)$ square tiles.
Therefore, $f(n)=n$ if and only if $n=2^{k}-1=p(k)$ for some positive integer $k$. In other words, the binary representation of $n$ consists of all $1 \mathrm{~s}$, with no $0 \mathrm{~s}$.
(b) Let $n$ be a positive integer such that $f(n)=n+1$, and consider a minimal tiling of an $n$-staircase. Since there are $n$ diagonal squares, every square tile except one covers a diagonal square. We claim that the square tile that covers the bottom-left unit square must be the square tile that does not cover a diagonal square.
If $n$ is even, then this fact is obvious, because the square tile that covers the bottom-left unit square cannot cover any diagonal square, so assume that $n$ is odd. Let $n=2 m+1$. We may assume that $n>1$, so $m \geq 1$. Suppose that the square tile covering the bottom-left unit square also covers a diagonal square. Then the side length of this square tile must be $m+1$. After this $(m+1) \times(m+1)$ square tile has been placed, we are left with two $m$-staircases.

Hence, $f(n)=2 f(m)+1$. But $2 f(m)+1$ is odd, and $n+1=2 m+2$ is even, so $f(n)$ cannot be equal to $n+1$, contradiction. Therefore, the square tile that covers the bottom-left unit square is the square tile that does not cover a diagonal square.
Let $t$ be the side length of the square tile covering the bottom-left unit square. Then every other square tile must cover a diagonal square, so by the same construction as in part (a), $n=1+2+4+\cdots+2^{k-1}+t=2^{k}+t-1$ for some positive integer $k$. Furthermore, the top $p(k)=2^{k}-1$ rows of the $n$-staircase must be tiled the same way as the minimal tiling of a $p(k)$-staircase. Therefore, the horizontal line between rows $p(k)$ and $p(k)+1$ does not pass through any square tiles. Let us call such a line a fault line. Similarly, the vertical line between columns $t$ and $t+1$ is also a fault line. These two fault lines partition two $p(k)$-staircases.
If these two $p(k)$-staircases do not overlap, then $t=p(k)$, so $n=2 p(k)$. For example, the minimal tiling for $n=2 p(2)=6$ is shown below.
Hence, assume that the two $p(k)$-staircases do overlap. The intersection of the two $p(k)$-staircases is a $[p(k)-t]$-staircase. Since this $[p(k)-t]$-staircase is tiled the same way as the top $p(k)-t$ rows of a minimal tiling of a $p(k)$-staircase, $p(k)-t=p(l)$ for some positive integer $l<k$, so $t=p(k)-p(l)$. Then
$$
n=t+p(k)=2 p(k)-p(l)
$$
Since $p(0)=0$, we can summarize by saying that $n$ must be of the form
$$
n=2 p(k)-p(l)=2^{k+1}-2^{l}-1,
$$
## Sun $\underbrace{4}$ <br> Life Financial
where $k$ is a positive ger. Also, our argument shows how if $n$ is of this form, then an $n$-staircase can be tiled with $n+1$ square tiles.
Finally, we observe that $n$ is of this form if and only if the binary representation of $n$ contains exactly one 0 :
$$
2^{k+1}-2^{l}-1=\underbrace{11 \ldots 1}_{k-l 1 \mathrm{~s}} 0 \underbrace{11 \ldots 1}_{l 1 \mathrm{~s}} \text {. }
$$
|
proof
|
Yes
|
Incomplete
|
math-word-problem
|
Combinatorics
|
For a positive integer $n$, an $n$-staircase is a figure consisting of unit squares, with one square in the first row, two squares in the second row, and so on, up to $n$ squares in the $n^{\text {th }}$ row, such that all the left-most squares in each row are aligned vertically. For example, the 5 -staircase is shown below.

Let $f(n)$ denote the minimum number of square tiles required to tile the $n$ staircase, where the side lengths of the square tiles can be any positive integer. For example, $f(2)=3$ and $f(4)=7$.

(a) Find all $n$ such that $f(n)=n$.
(b) Find all $n$ such that $f(n)=n+1$.
|
(a) A diagonal square in an $n$-staircase is a unit square that lies on the diagonal going from the top-left to the bottom-right. A minimal tiling of an $n$-staircase is a tiling consisting of $f(n)$ square tiles.
Observe that $f(n) \geq n$ for all $n$. There are $n$ diagonal squares in an $n$-staircase, and a square tile can cover at most one diagonal square, so any tiling requires at least $n$ square tiles. In other words, $f(n) \geq n$. Hence, if $f(n)=n$, then each square tile covers exactly one diagonal square.
Let $n$ be a positive integer such that $f(n)=n$, and consider a minimal tiling of an $n$-staircase. The only square tile that can cover the unit square in the first row is the unit square itself.
Now consider the left-most unit square in the second row. The only square tile that can cover this unit square and a diagonal square is a $2 \times 2$ square tile.

## Sun <br> Life Financial
that can cover this unit square and a diagonal square is a $4 \times 4$ square tile.

Continuing this construction, we see that the side lengths of the square tiles we encounter will be $1,2,4$, and so on, up to $2^{k}$ for some nonnegative integer $k$. Therefore, $n$, the height of the $n$-staircase, is equal to $1+2+4+\cdots+2^{k}=2^{k+1}-1$. Alternatively, $n=2^{k}-1$ for some positive integer $k$. Let $p(k)=2^{k}-1$.
Conversely, we can tile a $p(k)$-staircase with $p(k)$ square tiles recursively as follows: We have that $p(1)=1$, and we can tile a 1 -staircase with 1 square tile. Assume that we can tile a $p(k)$-staircase with $p(k)$ square tiles for some positive integer $k$.
Consider a $p(k+1)$-staircase. Place a $2^{k} \times 2^{k}$ square tile in the bottom left corner. Note that this square tile covers a digaonal square. Then $p(k+1)-2^{k}=$ $2^{k+1}-1-2^{k}=2^{k}-1=p(k)$, so we are left with two $p(k)$-staircases.

Furthermore, these two $p(k)$-staircases can be tiled with $2 p(k)$ square tiles, which means we use $2 p(k)+1=p(k+1)$ square tiles.
Therefore, $f(n)=n$ if and only if $n=2^{k}-1=p(k)$ for some positive integer $k$. In other words, the binary representation of $n$ consists of all $1 \mathrm{~s}$, with no $0 \mathrm{~s}$.
(b) Let $n$ be a positive integer such that $f(n)=n+1$, and consider a minimal tiling of an $n$-staircase. Since there are $n$ diagonal squares, every square tile except one covers a diagonal square. We claim that the square tile that covers the bottom-left unit square must be the square tile that does not cover a diagonal square.
If $n$ is even, then this fact is obvious, because the square tile that covers the bottom-left unit square cannot cover any diagonal square, so assume that $n$ is odd. Let $n=2 m+1$. We may assume that $n>1$, so $m \geq 1$. Suppose that the square tile covering the bottom-left unit square also covers a diagonal square. Then the side length of this square tile must be $m+1$. After this $(m+1) \times(m+1)$ square tile has been placed, we are left with two $m$-staircases.

Hence, $f(n)=2 f(m)+1$. But $2 f(m)+1$ is odd, and $n+1=2 m+2$ is even, so $f(n)$ cannot be equal to $n+1$, contradiction. Therefore, the square tile that covers the bottom-left unit square is the square tile that does not cover a diagonal square.
Let $t$ be the side length of the square tile covering the bottom-left unit square. Then every other square tile must cover a diagonal square, so by the same construction as in part (a), $n=1+2+4+\cdots+2^{k-1}+t=2^{k}+t-1$ for some positive integer $k$. Furthermore, the top $p(k)=2^{k}-1$ rows of the $n$-staircase must be tiled the same way as the minimal tiling of a $p(k)$-staircase. Therefore, the horizontal line between rows $p(k)$ and $p(k)+1$ does not pass through any square tiles. Let us call such a line a fault line. Similarly, the vertical line between columns $t$ and $t+1$ is also a fault line. These two fault lines partition two $p(k)$-staircases.

If these two $p(k)$-staircases do not overlap, then $t=p(k)$, so $n=2 p(k)$. For example, the minimal tiling for $n=2 p(2)=6$ is shown below.

Hence, assume that the two $p(k)$-staircases do overlap. The intersection of the two $p(k)$-staircases is a $[p(k)-t]$-staircase. Since this $[p(k)-t]$-staircase is tiled the same way as the top $p(k)-t$ rows of a minimal tiling of a $p(k)$-staircase, $p(k)-t=p(l)$ for some positive integer $l<k$, so $t=p(k)-p(l)$. Then
$$
n=t+p(k)=2 p(k)-p(l)
$$
Since $p(0)=0$, we can summarize by saying that $n$ must be of the form
$$
n=2 p(k)-p(l)=2^{k+1}-2^{l}-1,
$$
## Sun $\underbrace{4}$ <br> Life Financial
where $k$ is a positive ger. Also, our argument shows how if $n$ is of this form, then an $n$-staircase can be tiled with $n+1$ square tiles.
Finally, we observe that $n$ is of this form if and only if the binary representation of $n$ contains exactly one 0 :
$$
2^{k+1}-2^{l}-1=\underbrace{11 \ldots 1}_{k-l 1 \mathrm{~s}} 0 \underbrace{11 \ldots 1}_{l 1 \mathrm{~s}} \text {. }
$$
|
{
"exam": "Canada_MO",
"problem_label": "1",
"problem_match": "\n(1) ",
"resource_path": "CANADA_MO/segmented/en-sol2010.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2010"
}
|
Let $A, B, P$ be three points on a circle. Prove that if $a$ and $b$ are the distances from $P$ to the tangents at $A$ and $B$ and $c$ is the distance from $P$ to the chord $A B$, then $c^{2}=a b$.
|
Let $r$ be the radius of the circle, and let $\mathrm{a}^{\prime}$ and $\mathrm{b}^{\prime}$ be the respective lengths of $P A$ and $P B$. Since $b^{\prime}=2 r \sin \angle P A B=2 r c / a^{\prime}, c=a^{\prime} b^{\prime} /(2 r)$. Let $A C$ be the diameter of the circle and $H$ the foot of the perpendicular from $P$ to $A C$. The similarity of the triangles $A C P$ and $A P H$ imply that $A H: A P=A P: A C$ or $\left(a^{\prime}\right)^{2}=2 r a$. Similarly, $\left(b^{\prime}\right)^{2}=2 r b$. Hence
$$
c^{2}=\frac{\left(a^{\prime}\right)^{2}}{2 r} \frac{\left(b^{\prime}\right)^{2}}{2 r}=a b
$$
as desired.
|
c^{2}=a b
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A, B, P$ be three points on a circle. Prove that if $a$ and $b$ are the distances from $P$ to the tangents at $A$ and $B$ and $c$ is the distance from $P$ to the chord $A B$, then $c^{2}=a b$.
|
Let $r$ be the radius of the circle, and let $\mathrm{a}^{\prime}$ and $\mathrm{b}^{\prime}$ be the respective lengths of $P A$ and $P B$. Since $b^{\prime}=2 r \sin \angle P A B=2 r c / a^{\prime}, c=a^{\prime} b^{\prime} /(2 r)$. Let $A C$ be the diameter of the circle and $H$ the foot of the perpendicular from $P$ to $A C$. The similarity of the triangles $A C P$ and $A P H$ imply that $A H: A P=A P: A C$ or $\left(a^{\prime}\right)^{2}=2 r a$. Similarly, $\left(b^{\prime}\right)^{2}=2 r b$. Hence
$$
c^{2}=\frac{\left(a^{\prime}\right)^{2}}{2 r} \frac{\left(b^{\prime}\right)^{2}}{2 r}=a b
$$
as desired.
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\n(2) ",
"resource_path": "CANADA_MO/segmented/en-sol2010.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2010"
}
|
Let $A, B, P$ be three points on a circle. Prove that if $a$ and $b$ are the distances from $P$ to the tangents at $A$ and $B$ and $c$ is the distance from $P$ to the chord $A B$, then $c^{2}=a b$.
|
Let $E, F, G$ be the feet of the perpendiculars to the tangents at $A$ and $B$ and the chord $A B$, respectively. We need to show that $P E: P G=P G: G F$, where $G$ is the foot of the perpendicular from $P$ to $A B$. This suggest that we try to prove that the triangles $E P G$ and $G P F$ are similar.
Since $P G$ is parallel to the bisector of the angle between the two tangents, $\angle E P G=\angle F P G$. Since $A E P G$ and $B F P G$ are concyclic quadrilaterals (having opposite angles right), $\angle P G E=\angle P A E$ and $\angle P F G=\angle P B G$. But $\angle P A E=$ $\angle P B A=\angle P B G$, whence $\angle P G E=\angle P F G$. Therefore triangles $E P G$ and $G P F$ are similar.
The argument above with concyclic quadrilaterals only works when $P$ lies on the shorter arc between $A$ and $B$. The other case can be proved similarly.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A, B, P$ be three points on a circle. Prove that if $a$ and $b$ are the distances from $P$ to the tangents at $A$ and $B$ and $c$ is the distance from $P$ to the chord $A B$, then $c^{2}=a b$.
|
Let $E, F, G$ be the feet of the perpendiculars to the tangents at $A$ and $B$ and the chord $A B$, respectively. We need to show that $P E: P G=P G: G F$, where $G$ is the foot of the perpendicular from $P$ to $A B$. This suggest that we try to prove that the triangles $E P G$ and $G P F$ are similar.
Since $P G$ is parallel to the bisector of the angle between the two tangents, $\angle E P G=\angle F P G$. Since $A E P G$ and $B F P G$ are concyclic quadrilaterals (having opposite angles right), $\angle P G E=\angle P A E$ and $\angle P F G=\angle P B G$. But $\angle P A E=$ $\angle P B A=\angle P B G$, whence $\angle P G E=\angle P F G$. Therefore triangles $E P G$ and $G P F$ are similar.
The argument above with concyclic quadrilaterals only works when $P$ lies on the shorter arc between $A$ and $B$. The other case can be proved similarly.
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\n(2) ",
"resource_path": "CANADA_MO/segmented/en-sol2010.jsonl",
"solution_match": "\nAlternate Solution.",
"tier": "T2",
"year": "2010"
}
|
Three speed skaters have a friendly race on a skating oval. They all start from the same point and skate in the same direction, but with different speeds that they maintain throughout the race. The slowest skater does 1 lap a minute, the fastest one does 3.14 laps a minute, and the middle one does $L$ laps a minute for some $1<L<3.14$. The race ends at the moment when all three skaters again come together to the same point on the oval (which may differ from the starting
## Sun $\mathscr{H}^{10}$
## Life Financial
point.) Find how mury uniusuru vnumu sue e we vine such that 117 passings occur before the end of the race. (A passing is defined when one skater passes another one. The beginning and the end of the race when all three skaters are at together are not counted as a passing.)
|
Assume that the length of the oval is one unit. Let $x(t)$ be the difference of distances that the slowest and the fastest skaters have skated by time $t$. Similarly, let $y(t)$ be the difference between the middle skater and the slowest skater. The path $(x(t), y(t))$ is a straight ray $R$ in $\mathbb{R}^{2}$, starting from the origin, with slope depending on $L$. By assumption, $0<y(t)<x(t)$.
One skater passes another one when either $x(t) \in \mathbb{Z}, y(t) \in \mathbb{Z}$ or $x(t)-y(t) \in \mathbb{Z}$. The race ends when both $x(t), y(t) \in \mathbb{Z}$.
Let $(a, b) \in \mathbb{Z}^{2}$ be the endpoint of the ray $R$. We need to find the number of such points satisfying:
(a) $0<b<a$
(b) The ray $R$ intersects $\mathbb{Z}^{2}$ at endpoints only.
(c) The ray $R$ crosses 357 times the lines $x \in \mathbb{Z}, y \in \mathbb{Z}, y-x \in \mathbb{Z}$.
The second condition says that $a$ and $b$ are relatively prime. The ray $R$ crosses $a-1$ of the lines $x \in \mathbb{Z}, b-1$ of the lines $y \in \mathbb{Z}$ and $a-b-1$ of the lines $x-y \in \mathbb{Z}$. Thus, we need $(a-1)+(b-1)+(a-b-1)=117$, or equivalently, $2 a-3=117$. That is $a=60$.
Now $b$ must be a positive integer less than and relatively prime to 60 . The number of such $b$ can be found using the Euler's $\phi$ function:
$$
\phi(60)=\phi\left(2^{2} \cdot 3 \cdot 5\right)=(2-1) \cdot 2 \cdot(3-1) \cdot(5-1)=16 .
$$
Thus the answer is 16 .
|
16
|
Incomplete
|
Yes
|
math-word-problem
|
Combinatorics
|
Three speed skaters have a friendly race on a skating oval. They all start from the same point and skate in the same direction, but with different speeds that they maintain throughout the race. The slowest skater does 1 lap a minute, the fastest one does 3.14 laps a minute, and the middle one does $L$ laps a minute for some $1<L<3.14$. The race ends at the moment when all three skaters again come together to the same point on the oval (which may differ from the starting
## Sun $\mathscr{H}^{10}$
## Life Financial
point.) Find how mury uniusuru vnumu sue e we vine such that 117 passings occur before the end of the race. (A passing is defined when one skater passes another one. The beginning and the end of the race when all three skaters are at together are not counted as a passing.)
|
Assume that the length of the oval is one unit. Let $x(t)$ be the difference of distances that the slowest and the fastest skaters have skated by time $t$. Similarly, let $y(t)$ be the difference between the middle skater and the slowest skater. The path $(x(t), y(t))$ is a straight ray $R$ in $\mathbb{R}^{2}$, starting from the origin, with slope depending on $L$. By assumption, $0<y(t)<x(t)$.
One skater passes another one when either $x(t) \in \mathbb{Z}, y(t) \in \mathbb{Z}$ or $x(t)-y(t) \in \mathbb{Z}$. The race ends when both $x(t), y(t) \in \mathbb{Z}$.
Let $(a, b) \in \mathbb{Z}^{2}$ be the endpoint of the ray $R$. We need to find the number of such points satisfying:
(a) $0<b<a$
(b) The ray $R$ intersects $\mathbb{Z}^{2}$ at endpoints only.
(c) The ray $R$ crosses 357 times the lines $x \in \mathbb{Z}, y \in \mathbb{Z}, y-x \in \mathbb{Z}$.
The second condition says that $a$ and $b$ are relatively prime. The ray $R$ crosses $a-1$ of the lines $x \in \mathbb{Z}, b-1$ of the lines $y \in \mathbb{Z}$ and $a-b-1$ of the lines $x-y \in \mathbb{Z}$. Thus, we need $(a-1)+(b-1)+(a-b-1)=117$, or equivalently, $2 a-3=117$. That is $a=60$.
Now $b$ must be a positive integer less than and relatively prime to 60 . The number of such $b$ can be found using the Euler's $\phi$ function:
$$
\phi(60)=\phi\left(2^{2} \cdot 3 \cdot 5\right)=(2-1) \cdot 2 \cdot(3-1) \cdot(5-1)=16 .
$$
Thus the answer is 16 .
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\n(3) ",
"resource_path": "CANADA_MO/segmented/en-sol2010.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2010"
}
|
Three speed skaters have a friendly race on a skating oval. They all start from the same point and skate in the same direction, but with different speeds that they maintain throughout the race. The slowest skater does 1 lap a minute, the fastest one does 3.14 laps a minute, and the middle one does $L$ laps a minute for some $1<L<3.14$. The race ends at the moment when all three skaters again come together to the same point on the oval (which may differ from the starting
## Sun $\mathscr{H}^{10}$
## Life Financial
point.) Find how mury uniusuru vnumu sue e we vine such that 117 passings occur before the end of the race. (A passing is defined when one skater passes another one. The beginning and the end of the race when all three skaters are at together are not counted as a passing.)
|
First, let us name our skaters. From fastest to slowest, call them: $A, B$ and $C$. (Abel, Bernoulli and Cayley?)
Now, it is helpful to consider the race from the viewpoint of $C$. Relative to $C$, both $A$ and $B$ complete a whole number of laps, since they both start and finish at $C$.
Let $n$ be the number of laps completed by $A$ relative to $C$, and let $m$ be the number of laps completed by $B$ relative to $C$. Note that: $n>m \in \mathbb{Z}^{+}$
Consider the number of minutes required to complete the race. Relative to $C$, $A$ is moving with a speed of $3.14-1=2.14$ laps per minute and completes the race in $\frac{n}{2.14}$ minutes. Also relative to $C, B$ is moving with a speed of $(L-1)$ laps per minute and completes the race in $\frac{m}{L-1}$ minutes. Since $A$ and $B$ finish the race together (when they both meet $C$ ):
$$
\frac{n}{2.14}=\frac{m}{L-1} \quad \Rightarrow \quad L=2.14\left(\frac{m}{n}\right)+1
$$
Hence, there is a one-to-one relation between values of $L$ and values of the postive proper fraction $\frac{m}{n}$. The fraction should be reduced, that is the pair $(m, n)$ should
## Sun Life Financial
$A$ and $m / k$ laps for $B$ when they first meet $C$ together.
It is also helpful to consider the race from the viewpoint of $B$. In this frame of reference, $A$ completes only $n-m$ laps. Hence $A$ passes $B$ only $(n-m)-1$ times, since the racers do not "pass" at the end of the race (nor at the beginning). Similarily $A$ passes $C$ only $n-1$ times and $B$ passes $C$ only $m-1$ times. The total number of passings is:
$$
117=(n-1)+(m-1)+(n-m-1)=2 n-3 \Rightarrow n=60
$$
Hence the number of values of $L$ equals the number of $m$ for which the fraction $\frac{m}{60}$ is positive, proper and reduced. That is the number of positive integer values smaller than and relatively prime to 60 . One could simply count: $\{1,7,11,13,17, \ldots\}$, but Euler's $\phi$ function gives this number:
$$
\phi(60)=\phi\left(2^{2} \cdot 3 \cdot 5\right)=(2-1) \cdot 2 \cdot(3-1) \cdot(5-1)=16 .
$$
Therefore, there are 16 values for $L$ which give the desired number of passings.
Note that the actual values for the speeds of $A$ and $C$ do not affect the result. They could be any values, rational or irrational, just so long as they are different, and there will be 16 possible values for the speed of $B$ between them.
|
16
|
Incomplete
|
Yes
|
math-word-problem
|
Combinatorics
|
Three speed skaters have a friendly race on a skating oval. They all start from the same point and skate in the same direction, but with different speeds that they maintain throughout the race. The slowest skater does 1 lap a minute, the fastest one does 3.14 laps a minute, and the middle one does $L$ laps a minute for some $1<L<3.14$. The race ends at the moment when all three skaters again come together to the same point on the oval (which may differ from the starting
## Sun $\mathscr{H}^{10}$
## Life Financial
point.) Find how mury uniusuru vnumu sue e we vine such that 117 passings occur before the end of the race. (A passing is defined when one skater passes another one. The beginning and the end of the race when all three skaters are at together are not counted as a passing.)
|
First, let us name our skaters. From fastest to slowest, call them: $A, B$ and $C$. (Abel, Bernoulli and Cayley?)
Now, it is helpful to consider the race from the viewpoint of $C$. Relative to $C$, both $A$ and $B$ complete a whole number of laps, since they both start and finish at $C$.
Let $n$ be the number of laps completed by $A$ relative to $C$, and let $m$ be the number of laps completed by $B$ relative to $C$. Note that: $n>m \in \mathbb{Z}^{+}$
Consider the number of minutes required to complete the race. Relative to $C$, $A$ is moving with a speed of $3.14-1=2.14$ laps per minute and completes the race in $\frac{n}{2.14}$ minutes. Also relative to $C, B$ is moving with a speed of $(L-1)$ laps per minute and completes the race in $\frac{m}{L-1}$ minutes. Since $A$ and $B$ finish the race together (when they both meet $C$ ):
$$
\frac{n}{2.14}=\frac{m}{L-1} \quad \Rightarrow \quad L=2.14\left(\frac{m}{n}\right)+1
$$
Hence, there is a one-to-one relation between values of $L$ and values of the postive proper fraction $\frac{m}{n}$. The fraction should be reduced, that is the pair $(m, n)$ should
## Sun Life Financial
$A$ and $m / k$ laps for $B$ when they first meet $C$ together.
It is also helpful to consider the race from the viewpoint of $B$. In this frame of reference, $A$ completes only $n-m$ laps. Hence $A$ passes $B$ only $(n-m)-1$ times, since the racers do not "pass" at the end of the race (nor at the beginning). Similarily $A$ passes $C$ only $n-1$ times and $B$ passes $C$ only $m-1$ times. The total number of passings is:
$$
117=(n-1)+(m-1)+(n-m-1)=2 n-3 \Rightarrow n=60
$$
Hence the number of values of $L$ equals the number of $m$ for which the fraction $\frac{m}{60}$ is positive, proper and reduced. That is the number of positive integer values smaller than and relatively prime to 60 . One could simply count: $\{1,7,11,13,17, \ldots\}$, but Euler's $\phi$ function gives this number:
$$
\phi(60)=\phi\left(2^{2} \cdot 3 \cdot 5\right)=(2-1) \cdot 2 \cdot(3-1) \cdot(5-1)=16 .
$$
Therefore, there are 16 values for $L$ which give the desired number of passings.
Note that the actual values for the speeds of $A$ and $C$ do not affect the result. They could be any values, rational or irrational, just so long as they are different, and there will be 16 possible values for the speed of $B$ between them.
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\n(3) ",
"resource_path": "CANADA_MO/segmented/en-sol2010.jsonl",
"solution_match": "\nAlternate Solution.",
"tier": "T2",
"year": "2010"
}
|
Each vertex of a finite graph can be colored either black or white. Initially all vertices are black. We are allowed to pick a vertex $\mathrm{P}$ and change the color of $P$ and all of its neighbours. Is it possible to change the colour of every vertex from black to white by a sequence of operations of this type?
|
The answer is yes. Proof by induction on the number $n$ of vertices. If $n=1$, this is obvious. For the induction assumption, suppose we can do this for any graph with $n-1$ vertices for some $n \geq 2$ and let $X$ be a graph with $n$ vertices which we will denote by $P_{1}, \ldots, P_{n+1}$.
Let us denote the "basic" operation of changing the color of $P_{i}$ and all of its neighbours by $f_{i}$. Removing a vertex $P_{i}$ from $X$ (along with all edges connecting to $P_{i}$ ) and applying the induction assumption to the resulting smaller graph, we see that there exists a sequence of operations $g_{i}$ (obtained by composing some $f_{j}$, with $j \neq i$ ) which changes the colour of every vertex in $X$, except for possibly $P_{i}$.
If $g_{i}$ it also changes the color of $P_{i}$ then we are done. So, we may assume that $g_{i}$ does not change the colour of $P$ for every $i=1, \ldots, n$. Now consider two cases.
Case 1: $n$ is even. Then composing $g_{1}, \ldots, g_{n}$ we will change the color of every vertex from white to black.
Case 2: $n$ is odd. I claim that in this case $X$ has a vertex with an even number of neighbours.
Indeed, denote the number of neighbours of $P_{i}$ (or equivalently, the number of edges connected to $P$ ) by $k_{i}$. Then $P_{1}+\cdots+P_{n+1}=2 e$, where $e$ is the number of edges of $X$. Thus one of the numbers $k_{i}$ has to be even as claimed.
## Sun $\Psi^{*}$ Life Financial
After renumbering vn vu vucu, wn nuy unwume vinu $?_{1}$ has $2 k$ neighbours, say $P_{2}, \ldots, P_{2 k+1}$. The composition of $f_{1}$ with $g_{1}, g_{2}, \ldots, g_{2 k+1}$ will then change the colour of every vertex, as desired.
|
proof
|
Yes
|
Incomplete
|
math-word-problem
|
Combinatorics
|
Each vertex of a finite graph can be colored either black or white. Initially all vertices are black. We are allowed to pick a vertex $\mathrm{P}$ and change the color of $P$ and all of its neighbours. Is it possible to change the colour of every vertex from black to white by a sequence of operations of this type?
|
The answer is yes. Proof by induction on the number $n$ of vertices. If $n=1$, this is obvious. For the induction assumption, suppose we can do this for any graph with $n-1$ vertices for some $n \geq 2$ and let $X$ be a graph with $n$ vertices which we will denote by $P_{1}, \ldots, P_{n+1}$.
Let us denote the "basic" operation of changing the color of $P_{i}$ and all of its neighbours by $f_{i}$. Removing a vertex $P_{i}$ from $X$ (along with all edges connecting to $P_{i}$ ) and applying the induction assumption to the resulting smaller graph, we see that there exists a sequence of operations $g_{i}$ (obtained by composing some $f_{j}$, with $j \neq i$ ) which changes the colour of every vertex in $X$, except for possibly $P_{i}$.
If $g_{i}$ it also changes the color of $P_{i}$ then we are done. So, we may assume that $g_{i}$ does not change the colour of $P$ for every $i=1, \ldots, n$. Now consider two cases.
Case 1: $n$ is even. Then composing $g_{1}, \ldots, g_{n}$ we will change the color of every vertex from white to black.
Case 2: $n$ is odd. I claim that in this case $X$ has a vertex with an even number of neighbours.
Indeed, denote the number of neighbours of $P_{i}$ (or equivalently, the number of edges connected to $P$ ) by $k_{i}$. Then $P_{1}+\cdots+P_{n+1}=2 e$, where $e$ is the number of edges of $X$. Thus one of the numbers $k_{i}$ has to be even as claimed.
## Sun $\Psi^{*}$ Life Financial
After renumbering vn vu vucu, wn nuy unwume vinu $?_{1}$ has $2 k$ neighbours, say $P_{2}, \ldots, P_{2 k+1}$. The composition of $f_{1}$ with $g_{1}, g_{2}, \ldots, g_{2 k+1}$ will then change the colour of every vertex, as desired.
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\n(4) ",
"resource_path": "CANADA_MO/segmented/en-sol2010.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2010"
}
|
Let $P(x)$ and $Q(x)$ be polynomials with integer coefficients. Let $a_{n}=n !+n$. Show that if $P\left(a_{n}\right) / Q\left(a_{n}\right)$ is an integer for every $n$, then $P(n) / Q(n)$ is an integer for every integer $n$ such that $Q(n) \neq 0$.
|
Imagine dividing $P(x)$ by $Q(x)$. We find that
$$
\frac{P(x)}{Q(x)}=A(x)+\frac{R(x)}{Q(x)}
$$
where $A(x)$ and $R(x)$ are polynomials with rational coefficients, and $R(x)$ is either identically 0 or has degree less than the degree of $Q(x)$.
By bringing the coefficients of $A(x)$ to their least common multiple, we can find a polynomial $B(x)$ with integer coefficients, and a positive integer $b$, such that $A(x)=B(x) / b$. Suppose first that $R(x)$ is not identically 0 . Note that for any integer $k$, either $A(k)=0$, or $|A(k)| \geq 1 / b$. But whenever $|k|$ is large enough, $0<|R(k) / Q(k)|<1 / b$, and therefore if $n$ is large enough, $P\left(a_{n}\right) / Q\left(a_{n}\right)$ cannot be an integer.
So $R(x)$ is identically 0 , and $P(x) / Q(x)=B(x) / b$ (at least whenever $Q(x) \neq 0$.)
Now let $n$ be an integer. Then there are infinitely many integers $k$ such that $n \equiv a_{k}(\bmod b)$. But $B\left(a_{k}\right) / b$ is an integer, or equivalently $b$ divides $B\left(a_{k}\right)$. It follows that $b$ divides $B(n)$, and therefore $P(n) / Q(n)$ is an integer.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
Let $P(x)$ and $Q(x)$ be polynomials with integer coefficients. Let $a_{n}=n !+n$. Show that if $P\left(a_{n}\right) / Q\left(a_{n}\right)$ is an integer for every $n$, then $P(n) / Q(n)$ is an integer for every integer $n$ such that $Q(n) \neq 0$.
|
Imagine dividing $P(x)$ by $Q(x)$. We find that
$$
\frac{P(x)}{Q(x)}=A(x)+\frac{R(x)}{Q(x)}
$$
where $A(x)$ and $R(x)$ are polynomials with rational coefficients, and $R(x)$ is either identically 0 or has degree less than the degree of $Q(x)$.
By bringing the coefficients of $A(x)$ to their least common multiple, we can find a polynomial $B(x)$ with integer coefficients, and a positive integer $b$, such that $A(x)=B(x) / b$. Suppose first that $R(x)$ is not identically 0 . Note that for any integer $k$, either $A(k)=0$, or $|A(k)| \geq 1 / b$. But whenever $|k|$ is large enough, $0<|R(k) / Q(k)|<1 / b$, and therefore if $n$ is large enough, $P\left(a_{n}\right) / Q\left(a_{n}\right)$ cannot be an integer.
So $R(x)$ is identically 0 , and $P(x) / Q(x)=B(x) / b$ (at least whenever $Q(x) \neq 0$.)
Now let $n$ be an integer. Then there are infinitely many integers $k$ such that $n \equiv a_{k}(\bmod b)$. But $B\left(a_{k}\right) / b$ is an integer, or equivalently $b$ divides $B\left(a_{k}\right)$. It follows that $b$ divides $B(n)$, and therefore $P(n) / Q(n)$ is an integer.
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\n(5) ",
"resource_path": "CANADA_MO/segmented/en-sol2010.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2010"
}
|
Consider 70-digit numbers $n$, with the property that each of the digits $1,2,3, \ldots, 7$ appears in the decimal expansion of $n$ ten times (and 8, 9, and 0 do not appear). Show that no number of this form can divide another number of this form.
|
Assume the contrary: there exist $a$ and $b$ of the prescribed form, such that $b \geq a$ and $a$ divides $b$. Then $a$ divides $b-a$.
Claim: $a$ is not divisible by 3 but $b-a$ is divisible by 9 . Indeed, the sum of the digits is $10(1+\cdots+7)=280$, for both $a$ and $b$. [Here one needs to know or prove that an integer $n$ is equivalent of the sum of its digits modulo 3 and modulo 9.]
We conclude that $b-a$ is divisible by $9 a$. But this is impossible, since $9 a$ has 71 digits and $b$ has only 70 digits, so $9 a>b>b-a$.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Consider 70-digit numbers $n$, with the property that each of the digits $1,2,3, \ldots, 7$ appears in the decimal expansion of $n$ ten times (and 8, 9, and 0 do not appear). Show that no number of this form can divide another number of this form.
|
Assume the contrary: there exist $a$ and $b$ of the prescribed form, such that $b \geq a$ and $a$ divides $b$. Then $a$ divides $b-a$.
Claim: $a$ is not divisible by 3 but $b-a$ is divisible by 9 . Indeed, the sum of the digits is $10(1+\cdots+7)=280$, for both $a$ and $b$. [Here one needs to know or prove that an integer $n$ is equivalent of the sum of its digits modulo 3 and modulo 9.]
We conclude that $b-a$ is divisible by $9 a$. But this is impossible, since $9 a$ has 71 digits and $b$ has only 70 digits, so $9 a>b>b-a$.
|
{
"exam": "Canada_MO",
"problem_label": "1",
"problem_match": "\n(1) ",
"resource_path": "CANADA_MO/segmented/en-sol2011.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2011"
}
|
Let $A B C D$ be a cyclic quadrilateral whose opposite sides are not parallel, $X$ the intersection of $A B$ and $C D$, and $Y$ the intersection of $A D$ and $B C$. Let the angle bisector of $\angle A X D$ intersect $A D, B C$ at $E, F$ respectively and let the angle bisector of $\angle A Y B$ intersect $A B, C D$ at $G, H$ respectively. Prove that $E G F H$ is a parallelogram. fore,
|
Since $A B C D$ is cyclic, $\triangle X A C \sim \triangle X D B$ and $\triangle Y A C \sim \triangle Y B D$. There-
$$
\frac{X A}{X D}=\frac{X C}{X B}=\frac{A C}{D B}=\frac{Y A}{Y B}=\frac{Y C}{Y D} .
$$
Let $s$ be this ratio. Therefore, by the angle bisector theorem,
$$
\frac{A E}{E D}=\frac{X A}{X D}=\frac{X C}{X B}=\frac{C F}{F B}=s,
$$
and
$$
\frac{A G}{G B}=\frac{Y A}{Y B}=\frac{Y C}{Y D}=\frac{C H}{H D}=s
$$
Hence, $\frac{A G}{G B}=\frac{C F}{F B}$ and $\frac{A E}{E D}=\frac{D H}{H C}$. Therefore, $E H\|A C\| G F$ and $E G\|D B\| H F$. Hence, $E G F H$ is a parallelogram.

## Life Financial
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a cyclic quadrilateral whose opposite sides are not parallel, $X$ the intersection of $A B$ and $C D$, and $Y$ the intersection of $A D$ and $B C$. Let the angle bisector of $\angle A X D$ intersect $A D, B C$ at $E, F$ respectively and let the angle bisector of $\angle A Y B$ intersect $A B, C D$ at $G, H$ respectively. Prove that $E G F H$ is a parallelogram. fore,
|
Since $A B C D$ is cyclic, $\triangle X A C \sim \triangle X D B$ and $\triangle Y A C \sim \triangle Y B D$. There-
$$
\frac{X A}{X D}=\frac{X C}{X B}=\frac{A C}{D B}=\frac{Y A}{Y B}=\frac{Y C}{Y D} .
$$
Let $s$ be this ratio. Therefore, by the angle bisector theorem,
$$
\frac{A E}{E D}=\frac{X A}{X D}=\frac{X C}{X B}=\frac{C F}{F B}=s,
$$
and
$$
\frac{A G}{G B}=\frac{Y A}{Y B}=\frac{Y C}{Y D}=\frac{C H}{H D}=s
$$
Hence, $\frac{A G}{G B}=\frac{C F}{F B}$ and $\frac{A E}{E D}=\frac{D H}{H C}$. Therefore, $E H\|A C\| G F$ and $E G\|D B\| H F$. Hence, $E G F H$ is a parallelogram.

## Life Financial
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\n(2) ",
"resource_path": "CANADA_MO/segmented/en-sol2011.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2011"
}
|
Amy has divided a square up into finitely many white and red rectangles, each with sides parallel to the sides of the square. Within each white rectangle, she writes down its width divided by its height. Within each red rectangle, she writes down its height divided by its width. Finally, she calculates $x$, the sum of these numbers. If the total area of the white rectangles equals the total area of the red rectangles, what is the smallest possible value of $x$ ?
|
Let $a_{i}$ and $b_{i}$ denote the width and height of each white rectangle, and let $c_{i}$ and $d_{i}$ denote the width and height of each red rectangle. Also, let $L$ denote the side length of the original square.
Lemma: Either $\sum a_{i} \geq L$ or $\sum d_{i} \geq L$.
Proof of lemma: Suppose there exists a horizontal line across the square that is covered entirely with white rectangles. Then, the total width of these rectangles is at least $L$, and the claim is proven. Otherwise, there is a red rectangle intersecting every horizontal line, and hence the total height of these rectangles is at least $L$.
Now, let us assume without loss of generality that $\sum a_{i} \geq L$. By the Cauchy-Schwarz inequality,
$$
\begin{aligned}
\left(\sum \frac{a_{i}}{b_{i}}\right) \cdot\left(\sum a_{i} b_{i}\right) & \geq\left(\sum a_{i}\right)^{2} \\
& \geq L^{2}
\end{aligned}
$$
But we know $\sum a_{i} b_{i}=\frac{L^{2}}{2}$, so it follows that $\sum \frac{a_{i}}{b_{i}} \geq 2$. Furthermore, each $c_{i} \leq L$, so
$$
\sum \frac{d_{i}}{c_{i}} \geq \frac{1}{L^{2}} \cdot \sum c_{i} d_{i}=\frac{1}{2}
$$
Therefore, $x$ is at least 2.5. Conversely, $x=2.5$ can be achieved by making the top half of the square one colour, and the bottom half the other colour.
|
2.5
|
Yes
|
Yes
|
math-word-problem
|
Geometry
|
Amy has divided a square up into finitely many white and red rectangles, each with sides parallel to the sides of the square. Within each white rectangle, she writes down its width divided by its height. Within each red rectangle, she writes down its height divided by its width. Finally, she calculates $x$, the sum of these numbers. If the total area of the white rectangles equals the total area of the red rectangles, what is the smallest possible value of $x$ ?
|
Let $a_{i}$ and $b_{i}$ denote the width and height of each white rectangle, and let $c_{i}$ and $d_{i}$ denote the width and height of each red rectangle. Also, let $L$ denote the side length of the original square.
Lemma: Either $\sum a_{i} \geq L$ or $\sum d_{i} \geq L$.
Proof of lemma: Suppose there exists a horizontal line across the square that is covered entirely with white rectangles. Then, the total width of these rectangles is at least $L$, and the claim is proven. Otherwise, there is a red rectangle intersecting every horizontal line, and hence the total height of these rectangles is at least $L$.
Now, let us assume without loss of generality that $\sum a_{i} \geq L$. By the Cauchy-Schwarz inequality,
$$
\begin{aligned}
\left(\sum \frac{a_{i}}{b_{i}}\right) \cdot\left(\sum a_{i} b_{i}\right) & \geq\left(\sum a_{i}\right)^{2} \\
& \geq L^{2}
\end{aligned}
$$
But we know $\sum a_{i} b_{i}=\frac{L^{2}}{2}$, so it follows that $\sum \frac{a_{i}}{b_{i}} \geq 2$. Furthermore, each $c_{i} \leq L$, so
$$
\sum \frac{d_{i}}{c_{i}} \geq \frac{1}{L^{2}} \cdot \sum c_{i} d_{i}=\frac{1}{2}
$$
Therefore, $x$ is at least 2.5. Conversely, $x=2.5$ can be achieved by making the top half of the square one colour, and the bottom half the other colour.
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\n(3) ",
"resource_path": "CANADA_MO/segmented/en-sol2011.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2011"
}
|
Show that there exists a positive integer $N$ such that for all integers $a>N$, there exists a contiguous substring of the decimal expansion of $a$ that is divisible by 2011. (For instance, if $a=153204$, then 15, 532, and 0 are all contiguous substrings of $a$. Note that 0 is divisible by 2011 .)
|
We claim that if the decimal expansion of $a$ has at least 2012 digits, then $a$ contains the required substring. Let the decimal expansion of $a$ be $a_{k} a_{k-1} \ldots a_{0}$. For $i=0, \ldots, 2011$, Let $b_{i}$ be the number with decimal expansion $a_{i} a_{i-1} \ldots a_{0}$. Then by pidgenhole principle, $b_{i} \equiv b_{j} \bmod 2011$ for some $i<j \leq 2011$. It follows that 2011 divides $b_{j}-b_{i}=c \cdot 10^{i}$. Here $c$ is the substring $a_{j} \ldots a_{i+1}$. Since 2011 and 10 are relatively prime, it follows that 2011 divides $c$.
## Life Financial
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Show that there exists a positive integer $N$ such that for all integers $a>N$, there exists a contiguous substring of the decimal expansion of $a$ that is divisible by 2011. (For instance, if $a=153204$, then 15, 532, and 0 are all contiguous substrings of $a$. Note that 0 is divisible by 2011 .)
|
We claim that if the decimal expansion of $a$ has at least 2012 digits, then $a$ contains the required substring. Let the decimal expansion of $a$ be $a_{k} a_{k-1} \ldots a_{0}$. For $i=0, \ldots, 2011$, Let $b_{i}$ be the number with decimal expansion $a_{i} a_{i-1} \ldots a_{0}$. Then by pidgenhole principle, $b_{i} \equiv b_{j} \bmod 2011$ for some $i<j \leq 2011$. It follows that 2011 divides $b_{j}-b_{i}=c \cdot 10^{i}$. Here $c$ is the substring $a_{j} \ldots a_{i+1}$. Since 2011 and 10 are relatively prime, it follows that 2011 divides $c$.
## Life Financial
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\n(4) ",
"resource_path": "CANADA_MO/segmented/en-sol2011.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2011"
}
|
Let $d$ be a positive integer. Show that for every integer $S$, there exists an integer $n>0$ and a sequence $\epsilon_{1}, \epsilon_{2}, \ldots, \epsilon_{n}$, where for any $k, \epsilon_{k}=1$ or $\epsilon_{k}=-1$, such that
$$
S=\epsilon_{1}(1+d)^{2}+\epsilon_{2}(1+2 d)^{2}+\epsilon_{3}(1+3 d)^{2}+\cdots+\epsilon_{n}(1+n d)^{2}
$$
|
Let $U_{k}=(1+k d)^{2}$. We calculate $U_{k+3}-U_{k+2}-U_{k+1}+U_{k}$. This turns out to be $4 d^{2}$, a constant. Changing signs, we obtain the sum $-4 d^{2}$.
Thus if we have found an expression for a certain number $S_{0}$ as a sum of the desired type, we can obtain an expression of the desired type for $S_{0}+\left(4 d^{2}\right) q$, for any integer $q$.
It remains to show that for any $S$, there exists an integer $S^{\prime}$ such that $S^{\prime} \equiv S$ $\left(\bmod 4 d^{2}\right)$ and $S^{\prime}$ can be expressed in the desired form. Look at the sum
$$
(1+d)^{2}+(1+2 d)^{2}+\cdots+(1+N d)^{2}
$$
where $N$ is "large." We can at will choose $N$ so that the sum is odd, or so that the sum is even.
By changing the sign in front of $(1+k d)^{2}$ to a minus sign, we decrease the sum by $2(1+k d)^{2}$. In particular, if $k \equiv 0(\bmod 2 d)$, we decrease the sum by $2\left(\operatorname{modulo} 4 d^{2}\right)$. So
If $N$ is large enough, there are many $k<N$ such that $k$ is a multiple of $2 d$. By switching the sign in front of $r$ of these, we change ("downward") the congruence class modulo $4 d^{2}$ by $2 r$. By choosing $N$ so that the original sum is odd, and choosing suitable $r<2 d^{2}$, we can obtain numbers congruent to all odd numbers modulo $4 d^{2}$. By choosing $N$ so that the original sum is even, we can obtain numbers congruent to all even numbers modulo $4 d^{2}$. This completes the proof.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $d$ be a positive integer. Show that for every integer $S$, there exists an integer $n>0$ and a sequence $\epsilon_{1}, \epsilon_{2}, \ldots, \epsilon_{n}$, where for any $k, \epsilon_{k}=1$ or $\epsilon_{k}=-1$, such that
$$
S=\epsilon_{1}(1+d)^{2}+\epsilon_{2}(1+2 d)^{2}+\epsilon_{3}(1+3 d)^{2}+\cdots+\epsilon_{n}(1+n d)^{2}
$$
|
Let $U_{k}=(1+k d)^{2}$. We calculate $U_{k+3}-U_{k+2}-U_{k+1}+U_{k}$. This turns out to be $4 d^{2}$, a constant. Changing signs, we obtain the sum $-4 d^{2}$.
Thus if we have found an expression for a certain number $S_{0}$ as a sum of the desired type, we can obtain an expression of the desired type for $S_{0}+\left(4 d^{2}\right) q$, for any integer $q$.
It remains to show that for any $S$, there exists an integer $S^{\prime}$ such that $S^{\prime} \equiv S$ $\left(\bmod 4 d^{2}\right)$ and $S^{\prime}$ can be expressed in the desired form. Look at the sum
$$
(1+d)^{2}+(1+2 d)^{2}+\cdots+(1+N d)^{2}
$$
where $N$ is "large." We can at will choose $N$ so that the sum is odd, or so that the sum is even.
By changing the sign in front of $(1+k d)^{2}$ to a minus sign, we decrease the sum by $2(1+k d)^{2}$. In particular, if $k \equiv 0(\bmod 2 d)$, we decrease the sum by $2\left(\operatorname{modulo} 4 d^{2}\right)$. So
If $N$ is large enough, there are many $k<N$ such that $k$ is a multiple of $2 d$. By switching the sign in front of $r$ of these, we change ("downward") the congruence class modulo $4 d^{2}$ by $2 r$. By choosing $N$ so that the original sum is odd, and choosing suitable $r<2 d^{2}$, we can obtain numbers congruent to all odd numbers modulo $4 d^{2}$. By choosing $N$ so that the original sum is even, we can obtain numbers congruent to all even numbers modulo $4 d^{2}$. This completes the proof.
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\n(5) ",
"resource_path": "CANADA_MO/segmented/en-sol2011.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2011"
}
|
Let $x, y$ and $z$ be positive real numbers. Show that $x^{2}+x y^{2}+x y z^{2} \geq 4 x y z-4$.
|
Note that
$$
x^{2} \geq 4 x-4, \quad y^{2} \geq 4 y-4, \quad \text { and } \quad z^{2} \geq 4 z-4
$$
and therefore
$$
x^{2}+x y^{2}+x y z^{2} \geq(4 x-4)+x(4 y-4)+x y(4 z-4)=4 x y z-4 .
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $x, y$ and $z$ be positive real numbers. Show that $x^{2}+x y^{2}+x y z^{2} \geq 4 x y z-4$.
|
Note that
$$
x^{2} \geq 4 x-4, \quad y^{2} \geq 4 y-4, \quad \text { and } \quad z^{2} \geq 4 z-4
$$
and therefore
$$
x^{2}+x y^{2}+x y z^{2} \geq(4 x-4)+x(4 y-4)+x y(4 z-4)=4 x y z-4 .
$$
|
{
"exam": "Canada_MO",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "Canada_MO/segmented/en-sol2012.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2012"
}
|
For any positive integers $n$ and $k$, let $L(n, k)$ be the least common multiple of the $k$ consecutive integers $n, n+1, \ldots, n+k-1$. Show that for any integer $b$, there exist integers $n$ and $k$ such that $L(n, k)>b L(n+1, k)$.
|
I. Let $p>b$ be prime, let $n=p^{3}$ and $k=p^{2}$. If $p^{3}<i<p^{3}+p^{2}$, then no power of $p$ greater than 1 divides $i$, while $p$ divides $p^{3}+p$. It follows that $L\left(p^{3}, p^{2}\right)=$ $p^{2} L\left(p^{3}+1, p^{2}-1\right)$. A similar calculation shows that $L\left(p^{3}+1, p^{2}\right)=p L\left(p^{3}+1, p^{2}-1\right)$. Thus $L\left(p^{3}, p^{2}\right)=p L\left(p^{3}+1, p^{2}\right)>b L\left(p^{3}+1, p^{2}\right)$.
II. Let $m>1$. Then $L(m !-1, m+1)$ is the least common multiple of the integers from $m !-1$ to $m !+m-1$. But $m !-1$ is relatively prime to all of $m !, m !+1, \ldots, m !+m-1$. It follows that $L(m !-1, m+1)=(m !-1) M$, where $M=\operatorname{lcm}(m !, m !+1, \ldots, m !+m-1)$.
Now consider $L(m !, m+1)$. This is $\operatorname{lcm}(M, m !+m)$. But $m !+m=m((m-1) !+1)$, and $m$ divides $M$. Thus $\operatorname{lcm}(M, m !+m) \leq M((m-1) !+1)$, and
$$
\frac{L(m !-1, m+1)}{L(m !, m+1)} \geq \frac{m !-1}{(m-1) !+1}
$$
Since $m$ can be arbitrarily large, so can $L(m !-1, m+1) / L(m !, m+1)$. Therefore taking $n=m$ ! - 1 for sufficiently large $m$, and $k=m+1$, works.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
For any positive integers $n$ and $k$, let $L(n, k)$ be the least common multiple of the $k$ consecutive integers $n, n+1, \ldots, n+k-1$. Show that for any integer $b$, there exist integers $n$ and $k$ such that $L(n, k)>b L(n+1, k)$.
|
I. Let $p>b$ be prime, let $n=p^{3}$ and $k=p^{2}$. If $p^{3}<i<p^{3}+p^{2}$, then no power of $p$ greater than 1 divides $i$, while $p$ divides $p^{3}+p$. It follows that $L\left(p^{3}, p^{2}\right)=$ $p^{2} L\left(p^{3}+1, p^{2}-1\right)$. A similar calculation shows that $L\left(p^{3}+1, p^{2}\right)=p L\left(p^{3}+1, p^{2}-1\right)$. Thus $L\left(p^{3}, p^{2}\right)=p L\left(p^{3}+1, p^{2}\right)>b L\left(p^{3}+1, p^{2}\right)$.
II. Let $m>1$. Then $L(m !-1, m+1)$ is the least common multiple of the integers from $m !-1$ to $m !+m-1$. But $m !-1$ is relatively prime to all of $m !, m !+1, \ldots, m !+m-1$. It follows that $L(m !-1, m+1)=(m !-1) M$, where $M=\operatorname{lcm}(m !, m !+1, \ldots, m !+m-1)$.
Now consider $L(m !, m+1)$. This is $\operatorname{lcm}(M, m !+m)$. But $m !+m=m((m-1) !+1)$, and $m$ divides $M$. Thus $\operatorname{lcm}(M, m !+m) \leq M((m-1) !+1)$, and
$$
\frac{L(m !-1, m+1)}{L(m !, m+1)} \geq \frac{m !-1}{(m-1) !+1}
$$
Since $m$ can be arbitrarily large, so can $L(m !-1, m+1) / L(m !, m+1)$. Therefore taking $n=m$ ! - 1 for sufficiently large $m$, and $k=m+1$, works.
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "Canada_MO/segmented/en-sol2012.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2012"
}
|
Let $A B C D$ be a convex quadrilateral and let $P$ be the point of intersection of $A C$ and $B D$. Suppose that $A C+A D=B C+B D$. Prove that the internal angle bisectors of $\angle A C B, \angle A D B$, and $\angle A P B$ meet at a common point.
|
I. Construct $A^{\prime}$ on $C A$ so that $A A^{\prime}=A D$ and $B^{\prime}$ on $C B$ such that $B B^{\prime}=B D$. Then we have three angle bisectors that correspond to the perpendicular bisectors of $A^{\prime} B^{\prime}, A^{\prime} D$, and $B^{\prime} D$. These perpendicular bisectors are concurrent, so the angle bisectors are also concurrent. This tells us that the external angle bisectors at $A$ and $B$ meet at the excentre of $P D B$. A symmetric argument for $C$ finishes the problem.
## Sun Life Financial Canadian Mathematical Olympiad
II. Note that the angle bisectors $\angle A C B$ and $\angle A P B$ intersect at the excentres of $\triangle P B C$ opposite $C$ and the angle bisectors of $\angle A D B$ and $\angle A P B$ intersect at the excentres of $\triangle P A D$ opposite $D$. Hence, it suffices to prove that these two excentres coincide.
Let the excircle of $\triangle P B C$ opposite $C$ touch side $P B$ at a point $X$, line $C P$ at a point $Y$ and line $C B$ at a point $Z$. Hence, $C Y=C Z, P X=P Y$ and $B X=B Z$. Therefore, $C P+P X=C B+B X$. Since $C P+P X+C B+B X$ is the perimeter of $\triangle C B P, C P+P X=C B+B X=s$, where $s$ is the semi-perimeter of $\triangle C B P$. Therefore,
$$
P X=C B+B X-C P=\frac{s}{2}-C P=\frac{C B+B P+P C}{2}-C P=\frac{C B+B P-P C}{2} .
$$
Similarly, if we let the excircle of $\triangle P A D$ opposite $D$ touch side $P A$ at a point $X^{\prime}$, then
$$
P X^{\prime}=\frac{D A+A P-P D}{2} .
$$
Since both excircles are tangent to $A C$ and $B D$, if we show that $P X=P X^{\prime}$, then we would show that the two excircles are tangent to $A C$ and $B D$ at the same points, i.e. the two excircles are identical. Hence, the two excentres coincide.
We will use the fact that $A C+A D=B C+B D$ to prove that $P X=P X^{\prime}$. Since $A C+A D=B C+B D, A P+P C+A D=B C+B P+P D$. Hence, $A P+A D-P D=$ $B C+B P-P C$. Therefore, $P X=P X^{\prime}$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C D$ be a convex quadrilateral and let $P$ be the point of intersection of $A C$ and $B D$. Suppose that $A C+A D=B C+B D$. Prove that the internal angle bisectors of $\angle A C B, \angle A D B$, and $\angle A P B$ meet at a common point.
|
I. Construct $A^{\prime}$ on $C A$ so that $A A^{\prime}=A D$ and $B^{\prime}$ on $C B$ such that $B B^{\prime}=B D$. Then we have three angle bisectors that correspond to the perpendicular bisectors of $A^{\prime} B^{\prime}, A^{\prime} D$, and $B^{\prime} D$. These perpendicular bisectors are concurrent, so the angle bisectors are also concurrent. This tells us that the external angle bisectors at $A$ and $B$ meet at the excentre of $P D B$. A symmetric argument for $C$ finishes the problem.
## Sun Life Financial Canadian Mathematical Olympiad
II. Note that the angle bisectors $\angle A C B$ and $\angle A P B$ intersect at the excentres of $\triangle P B C$ opposite $C$ and the angle bisectors of $\angle A D B$ and $\angle A P B$ intersect at the excentres of $\triangle P A D$ opposite $D$. Hence, it suffices to prove that these two excentres coincide.
Let the excircle of $\triangle P B C$ opposite $C$ touch side $P B$ at a point $X$, line $C P$ at a point $Y$ and line $C B$ at a point $Z$. Hence, $C Y=C Z, P X=P Y$ and $B X=B Z$. Therefore, $C P+P X=C B+B X$. Since $C P+P X+C B+B X$ is the perimeter of $\triangle C B P, C P+P X=C B+B X=s$, where $s$ is the semi-perimeter of $\triangle C B P$. Therefore,
$$
P X=C B+B X-C P=\frac{s}{2}-C P=\frac{C B+B P+P C}{2}-C P=\frac{C B+B P-P C}{2} .
$$
Similarly, if we let the excircle of $\triangle P A D$ opposite $D$ touch side $P A$ at a point $X^{\prime}$, then
$$
P X^{\prime}=\frac{D A+A P-P D}{2} .
$$
Since both excircles are tangent to $A C$ and $B D$, if we show that $P X=P X^{\prime}$, then we would show that the two excircles are tangent to $A C$ and $B D$ at the same points, i.e. the two excircles are identical. Hence, the two excentres coincide.
We will use the fact that $A C+A D=B C+B D$ to prove that $P X=P X^{\prime}$. Since $A C+A D=B C+B D, A P+P C+A D=B C+B P+P D$. Hence, $A P+A D-P D=$ $B C+B P-P C$. Therefore, $P X=P X^{\prime}$, as desired.
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "Canada_MO/segmented/en-sol2012.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2012"
}
|
A number of robots are placed on the squares of a finite, rectangular grid of squares. A square can hold any number of robots. Every edge of each square of the grid is classified as either passable or impassable. All edges on the boundary of the grid are impassable.
You can give any of the commands up, down, left, or right. All of the robots then simultaneously try to move in the specified direction. If the edge adjacent to a robot in that direction is passable, the robot moves across the edge and into the next square. Otherwise, the robot remains on its current square. You can then give another command of up, down, left, or right, then another, for as long as you want.
Suppose that for any individual robot, and any square on the grid, there is a finite sequence of commands that will move that robot to that square. Prove that you can also give a finite sequence of commands such that all of the robots end up on the same square at the same time.
|
We will prove any two robots can be moved to the same square. From that point on, they will always be on the same square. We can then similarly move
## Sun Life Financial Canadian Mathematical Olympiad

a third robot onto the same square as these two, and then a fourth, and so on, until all robots are on the same square.
Towards that end, consider two robots $A$ and $B$. Let $d(A, B)$ denote the minimum number of commands that need to be given in order to move $A$ to the square on which $B$ is currently standing. We will give a procedure that is guaranteed to decrease $d(A, B)$. Since $d(A, B)$ is a non-negative integer, this procedure will eventually decrease $n$ to 0 , which finishes the proof.
Let $n=d(A, B)$, and let $S=\left\{s_{1}, s_{2}, \ldots, s_{n}\right\}$ be a minimum sequence of moves that takes $A$ to the square where $B$ is currently standing. Certainly $A$ will not run into an impassable edge during this sequence, or we could get a shorter sequence by removing that command. Now suppose $B$ runs into an impassable edge after some command $s_{i}$. From that point, we can get $A$ to the square on which $B$ started with the commands $s_{i+1}, s_{i+2}, \ldots, s_{n}$ and then to the square where $B$ is currently with the commands $s_{1}, s_{2}, \ldots, s_{i-1}$. But this was only $n-1$ commands in total, and so we have decreased $d(A, B)$ as required.
Otherwise, we have given a sequence of $n$ commands to $A$ and $B$, and neither ran into an impassable edge during the execution of these commands. In particular, the vector $v$ connecting $A$ to $B$ on the grid must have never changed. We moved $A$ to the position $B=A+v$, and therefore we must have also moved $B$ to $B+v$. Repeating this process $k$ times, we will move $A$ to $A+k v$ and $B$ to $B+k v$. But if $v \neq(0,0)$, this will eventually force $B$ off the edge of the grid, giving a contradiction.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A number of robots are placed on the squares of a finite, rectangular grid of squares. A square can hold any number of robots. Every edge of each square of the grid is classified as either passable or impassable. All edges on the boundary of the grid are impassable.
You can give any of the commands up, down, left, or right. All of the robots then simultaneously try to move in the specified direction. If the edge adjacent to a robot in that direction is passable, the robot moves across the edge and into the next square. Otherwise, the robot remains on its current square. You can then give another command of up, down, left, or right, then another, for as long as you want.
Suppose that for any individual robot, and any square on the grid, there is a finite sequence of commands that will move that robot to that square. Prove that you can also give a finite sequence of commands such that all of the robots end up on the same square at the same time.
|
We will prove any two robots can be moved to the same square. From that point on, they will always be on the same square. We can then similarly move
## Sun Life Financial Canadian Mathematical Olympiad

a third robot onto the same square as these two, and then a fourth, and so on, until all robots are on the same square.
Towards that end, consider two robots $A$ and $B$. Let $d(A, B)$ denote the minimum number of commands that need to be given in order to move $A$ to the square on which $B$ is currently standing. We will give a procedure that is guaranteed to decrease $d(A, B)$. Since $d(A, B)$ is a non-negative integer, this procedure will eventually decrease $n$ to 0 , which finishes the proof.
Let $n=d(A, B)$, and let $S=\left\{s_{1}, s_{2}, \ldots, s_{n}\right\}$ be a minimum sequence of moves that takes $A$ to the square where $B$ is currently standing. Certainly $A$ will not run into an impassable edge during this sequence, or we could get a shorter sequence by removing that command. Now suppose $B$ runs into an impassable edge after some command $s_{i}$. From that point, we can get $A$ to the square on which $B$ started with the commands $s_{i+1}, s_{i+2}, \ldots, s_{n}$ and then to the square where $B$ is currently with the commands $s_{1}, s_{2}, \ldots, s_{i-1}$. But this was only $n-1$ commands in total, and so we have decreased $d(A, B)$ as required.
Otherwise, we have given a sequence of $n$ commands to $A$ and $B$, and neither ran into an impassable edge during the execution of these commands. In particular, the vector $v$ connecting $A$ to $B$ on the grid must have never changed. We moved $A$ to the position $B=A+v$, and therefore we must have also moved $B$ to $B+v$. Repeating this process $k$ times, we will move $A$ to $A+k v$ and $B$ to $B+k v$. But if $v \neq(0,0)$, this will eventually force $B$ off the edge of the grid, giving a contradiction.
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "Canada_MO/segmented/en-sol2012.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2012"
}
|
A bookshelf contains $n$ volumes, labelled 1 to $n$, in some order. The librarian wishes to put them in the correct order as follows. The librarian selects a volume that is too far to the right, say the volume with label $k$, takes it out, and inserts it in the $k$-th position. For example, if the bookshelf contains the volumes $1,3,2,4$ in that order, the librarian could take out volume 2 and place it in the second position. The books will then be in the correct order 1, 2, 3, 4 .
(a) Show that if this process is repeated, then, however the librarian makes the selections, all the volumes will eventually be in the correct order.
(b) What is the largest number of steps that this process can take?
|
(a) If $t_{k}$ is the number of times that volume $k$ is selected, then we have $t_{k} \leq 1+\left(t_{1}+t_{2}+\cdots+t_{k-1}\right)$. This is because volume $k$ must move to the right between selections, which means some volume was placed to its left. The only way that can happen is if a lower-numbered volume was selected. This leads to the bound $t_{k} \leq 2^{k-1}$. Furthermore, $t_{n}=0$ since the $n$th volume will never be too far to the right. Therefore if $N$ is the total number of moves then
$$
N=t_{1}+t_{2}+\cdots+t_{n-1} \leq 1+2+\cdots+2^{n-2}=2^{n-1}-1
$$
and in particular the process terminates.
(b) Conversely, $2^{n-1}-1$ moves are required for the configuration $(n, 1,2,3, \ldots, n-1)$ if the librarian picks the rightmost eligible volume each time.
This can be proved by induction: if at a certain stage we are at $(x, n-k, n-$ $k+1, \ldots, n-1)$, then after $2^{k}-1$ moves, we will have moved to $(n-k, n-k+$ $1, \ldots, n-1, x)$ without touching any of the volumes further to the left. Indeed, after $2^{k-1}-1$ moves, we get to $(x, n-k+1, n-k+2, \ldots, n-1, n-k)$, which becomes $(n-k, x, n-k+1, n-k+2, \ldots, n-1)$ after 1 more move, and then $(n-k, n-k+1, \ldots, n-1, x)$ after another $2^{k-1}-1$ moves. The result follows by taking $k=n-1$.
|
2^{n-1}-1
|
Yes
|
Yes
|
proof
|
Combinatorics
|
A bookshelf contains $n$ volumes, labelled 1 to $n$, in some order. The librarian wishes to put them in the correct order as follows. The librarian selects a volume that is too far to the right, say the volume with label $k$, takes it out, and inserts it in the $k$-th position. For example, if the bookshelf contains the volumes $1,3,2,4$ in that order, the librarian could take out volume 2 and place it in the second position. The books will then be in the correct order 1, 2, 3, 4 .
(a) Show that if this process is repeated, then, however the librarian makes the selections, all the volumes will eventually be in the correct order.
(b) What is the largest number of steps that this process can take?
|
(a) If $t_{k}$ is the number of times that volume $k$ is selected, then we have $t_{k} \leq 1+\left(t_{1}+t_{2}+\cdots+t_{k-1}\right)$. This is because volume $k$ must move to the right between selections, which means some volume was placed to its left. The only way that can happen is if a lower-numbered volume was selected. This leads to the bound $t_{k} \leq 2^{k-1}$. Furthermore, $t_{n}=0$ since the $n$th volume will never be too far to the right. Therefore if $N$ is the total number of moves then
$$
N=t_{1}+t_{2}+\cdots+t_{n-1} \leq 1+2+\cdots+2^{n-2}=2^{n-1}-1
$$
and in particular the process terminates.
(b) Conversely, $2^{n-1}-1$ moves are required for the configuration $(n, 1,2,3, \ldots, n-1)$ if the librarian picks the rightmost eligible volume each time.
This can be proved by induction: if at a certain stage we are at $(x, n-k, n-$ $k+1, \ldots, n-1)$, then after $2^{k}-1$ moves, we will have moved to $(n-k, n-k+$ $1, \ldots, n-1, x)$ without touching any of the volumes further to the left. Indeed, after $2^{k-1}-1$ moves, we get to $(x, n-k+1, n-k+2, \ldots, n-1, n-k)$, which becomes $(n-k, x, n-k+1, n-k+2, \ldots, n-1)$ after 1 more move, and then $(n-k, n-k+1, \ldots, n-1, x)$ after another $2^{k-1}-1$ moves. The result follows by taking $k=n-1$.
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "Canada_MO/segmented/en-sol2012.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2012"
}
|
Determine all polynomials $P(x)$ with real coefficients such that
$$
(x+1) P(x-1)-(x-1) P(x)
$$
is a constant polynomial.
|
The answer is $P(x)$ being any constant polynomial and $P(x) \equiv$ $k x^{2}+k x+c$ for any (nonzero) constant $k$ and constant $c$.
Let $\Lambda$ be the expression $(x+1) P(x-1)-(x-1) P(x)$, i.e. the expression in the problem statement.
Substituting $x=-1$ into $\Lambda$ yields $2 P(-1)$ and substituting $x=1$ into $\Lambda$ yield $2 P(0)$. Since $(x+1) P(x-1)-(x-1) P(x)$ is a constant polynomial, $2 P(-1)=2 P(0)$. Hence, $P(-1)=P(0)$.
Let $c=P(-1)=P(0)$ and $Q(x)=P(x)-c$. Then $Q(-1)=Q(0)=0$. Hence, $0,-1$ are roots of $Q(x)$. Consequently, $Q(x)=x(x+1) R(x)$ for some polynomial $R$. Then $P(x)-c=x(x+1) R(x)$, or equivalently, $P(x)=x(x+1) R(x)+c$.
Substituting this into $\Lambda$ yield
$$
(x+1)((x-1) x R(x-1)+c)-(x-1)(x(x+1) R(x)+c)
$$
This is a constant polynomial and simplifies to
$$
x(x-1)(x+1)(R(x-1)-R(x))+2 c .
$$
## Sun $\mathbb{E}^{\circ}$
## Life Financial
Since this expression is a constant, so is $x(x-1)(x+1)(R(x-1)-R(x))$. Therefore, $R(x-1)-R(x)=0$ as a polynomial. Therefore, $R(x)=R(x-1)$ for all $x \in \mathbb{R}$. Then $R(x)$ is a polynomial that takes on certain values for infinitely values of $x$. Let $k$ be such a value. Then $R(x)-k$ has infinitely many roots, which can occur if and only if $R(x)-k=0$. Therefore, $R(x)$ is identical to a constant $k$. Hence, $Q(x)=k x(x+1)$ for some constant $k$. Therefore, $P(x)=k x(x+1)+c=k x^{2}+k x+c$.
Finally, we verify that all such $P(x)=k x(x+1)+c$ work. Substituting this into $\Lambda$ yield
$$
\begin{aligned}
& (x+1)(k x(x-1)+c)-(x-1)(k x(x+1)+c) \\
= & k x(x+1)(x-1)+c(x+1)-k x(x+1)(x-1)-c(x-1)=2 c .
\end{aligned}
$$
Hence, $P(x)=k x(x+1)+c=k x^{2}+k x+c$ is a solution to the given equation for any constant $k$. Note that this solution also holds for $k=0$. Hence, constant polynomials are also solutions to this equation.
|
P(x) = kx^2 + kx + c
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Determine all polynomials $P(x)$ with real coefficients such that
$$
(x+1) P(x-1)-(x-1) P(x)
$$
is a constant polynomial.
|
The answer is $P(x)$ being any constant polynomial and $P(x) \equiv$ $k x^{2}+k x+c$ for any (nonzero) constant $k$ and constant $c$.
Let $\Lambda$ be the expression $(x+1) P(x-1)-(x-1) P(x)$, i.e. the expression in the problem statement.
Substituting $x=-1$ into $\Lambda$ yields $2 P(-1)$ and substituting $x=1$ into $\Lambda$ yield $2 P(0)$. Since $(x+1) P(x-1)-(x-1) P(x)$ is a constant polynomial, $2 P(-1)=2 P(0)$. Hence, $P(-1)=P(0)$.
Let $c=P(-1)=P(0)$ and $Q(x)=P(x)-c$. Then $Q(-1)=Q(0)=0$. Hence, $0,-1$ are roots of $Q(x)$. Consequently, $Q(x)=x(x+1) R(x)$ for some polynomial $R$. Then $P(x)-c=x(x+1) R(x)$, or equivalently, $P(x)=x(x+1) R(x)+c$.
Substituting this into $\Lambda$ yield
$$
(x+1)((x-1) x R(x-1)+c)-(x-1)(x(x+1) R(x)+c)
$$
This is a constant polynomial and simplifies to
$$
x(x-1)(x+1)(R(x-1)-R(x))+2 c .
$$
## Sun $\mathbb{E}^{\circ}$
## Life Financial
Since this expression is a constant, so is $x(x-1)(x+1)(R(x-1)-R(x))$. Therefore, $R(x-1)-R(x)=0$ as a polynomial. Therefore, $R(x)=R(x-1)$ for all $x \in \mathbb{R}$. Then $R(x)$ is a polynomial that takes on certain values for infinitely values of $x$. Let $k$ be such a value. Then $R(x)-k$ has infinitely many roots, which can occur if and only if $R(x)-k=0$. Therefore, $R(x)$ is identical to a constant $k$. Hence, $Q(x)=k x(x+1)$ for some constant $k$. Therefore, $P(x)=k x(x+1)+c=k x^{2}+k x+c$.
Finally, we verify that all such $P(x)=k x(x+1)+c$ work. Substituting this into $\Lambda$ yield
$$
\begin{aligned}
& (x+1)(k x(x-1)+c)-(x-1)(k x(x+1)+c) \\
= & k x(x+1)(x-1)+c(x+1)-k x(x+1)(x-1)-c(x-1)=2 c .
\end{aligned}
$$
Hence, $P(x)=k x(x+1)+c=k x^{2}+k x+c$ is a solution to the given equation for any constant $k$. Note that this solution also holds for $k=0$. Hence, constant polynomials are also solutions to this equation.
|
{
"exam": "Canada_MO",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "Canada_MO/segmented/en-sol2013.jsonl",
"solution_match": "\nSolution 1:",
"tier": "T2",
"year": "2013"
}
|
Determine all polynomials $P(x)$ with real coefficients such that
$$
(x+1) P(x-1)-(x-1) P(x)
$$
is a constant polynomial.
|
As in Solution 1, any constant polynomial $P$ satisfies the given property. Hence, we will assume that $P$ is not a constant polynomial.
Let $n$ be the degree of $P$. Since $P$ is not constant, $n \geq 1$. Let
$$
P(x)=\sum_{i=0}^{n} a_{i} x^{i}
$$
with $a_{n} \neq 0$. Then
$$
(x+1) \sum_{i=0}^{n} a_{i}(x-1)^{i}-(x-1) \sum_{i=0}^{n} a_{i} x^{i}=C,
$$
for some constant $C$. We will compare the coefficient of $x^{n}$ of the left-hand side of this equation with the right-hand side. Since $C$ is a constant and $n \geq 1$, the coefficient of $x^{n}$ of the right-hand side is equal to zero. We now determine the coefficient of $x^{n}$ of the left-hand side of this expression.
The left-hand side of the equation simplifies to
$$
x \sum_{i=0}^{n} a_{i}(x-1)^{i}+\sum_{i=0}^{n} a_{i}(x-1)^{i}-x \sum_{i=0}^{n} a_{i} x^{i}+\sum_{i=0}^{n} a_{i} x^{i}
$$
## Sun
## Life Financial
We will determine the coefficient $x^{n}$ of each of these four terms.
By the Binomial Theorem, the coefficient of $x^{n}$ of the first term is equal to that of $x\left(a_{n-1}(x-1)^{n-1}+a_{n}(x-1)^{n}\right)=a_{n-1}-\left(\begin{array}{c}n \\ n-1\end{array}\right) a_{n}=a_{n-1}-n a_{n}$.
The coefficient of $x^{n}$ of the second term is equal to that of $a_{n}(x-1)^{n}$, which is $a_{n}$.
The coefficient of $x^{n}$ of the third term is equal to $a_{n-1}$ and that of the fourth term is equal to $a_{n}$.
Summing these four coefficients yield $a_{n-1}-n a_{n}+a_{n}-a_{n-1}+a_{n}=(2-n) a_{n}$.
This expression is equal to 0 . Since $a_{n} \neq 0, n=2$. Hence, $P$ is a quadratic polynomial.
Let $P(x)=a x^{2}+b x+c$, where $a, b, c$ are real numbers with $a \neq 0$. Then
$$
(x+1)\left(a(x-1)^{2}+b(x-1)+c\right)-(x-1)\left(a x^{2}+b x+c\right)=C .
$$
Simplifying the left-hand side yields
$$
(b-a) x+2 c=2 C .
$$
Therefore, $b-a=0$ and $2 c=2 C$. Hence, $P(x)=a x^{2}+a x+c$. As in Solution 1, this is a valid solution for all $a \in \mathbb{R} \backslash\{0\}$.
## Sun
## Life Financial
|
P(x)=a x^{2}+a x+c
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Determine all polynomials $P(x)$ with real coefficients such that
$$
(x+1) P(x-1)-(x-1) P(x)
$$
is a constant polynomial.
|
As in Solution 1, any constant polynomial $P$ satisfies the given property. Hence, we will assume that $P$ is not a constant polynomial.
Let $n$ be the degree of $P$. Since $P$ is not constant, $n \geq 1$. Let
$$
P(x)=\sum_{i=0}^{n} a_{i} x^{i}
$$
with $a_{n} \neq 0$. Then
$$
(x+1) \sum_{i=0}^{n} a_{i}(x-1)^{i}-(x-1) \sum_{i=0}^{n} a_{i} x^{i}=C,
$$
for some constant $C$. We will compare the coefficient of $x^{n}$ of the left-hand side of this equation with the right-hand side. Since $C$ is a constant and $n \geq 1$, the coefficient of $x^{n}$ of the right-hand side is equal to zero. We now determine the coefficient of $x^{n}$ of the left-hand side of this expression.
The left-hand side of the equation simplifies to
$$
x \sum_{i=0}^{n} a_{i}(x-1)^{i}+\sum_{i=0}^{n} a_{i}(x-1)^{i}-x \sum_{i=0}^{n} a_{i} x^{i}+\sum_{i=0}^{n} a_{i} x^{i}
$$
## Sun
## Life Financial
We will determine the coefficient $x^{n}$ of each of these four terms.
By the Binomial Theorem, the coefficient of $x^{n}$ of the first term is equal to that of $x\left(a_{n-1}(x-1)^{n-1}+a_{n}(x-1)^{n}\right)=a_{n-1}-\left(\begin{array}{c}n \\ n-1\end{array}\right) a_{n}=a_{n-1}-n a_{n}$.
The coefficient of $x^{n}$ of the second term is equal to that of $a_{n}(x-1)^{n}$, which is $a_{n}$.
The coefficient of $x^{n}$ of the third term is equal to $a_{n-1}$ and that of the fourth term is equal to $a_{n}$.
Summing these four coefficients yield $a_{n-1}-n a_{n}+a_{n}-a_{n-1}+a_{n}=(2-n) a_{n}$.
This expression is equal to 0 . Since $a_{n} \neq 0, n=2$. Hence, $P$ is a quadratic polynomial.
Let $P(x)=a x^{2}+b x+c$, where $a, b, c$ are real numbers with $a \neq 0$. Then
$$
(x+1)\left(a(x-1)^{2}+b(x-1)+c\right)-(x-1)\left(a x^{2}+b x+c\right)=C .
$$
Simplifying the left-hand side yields
$$
(b-a) x+2 c=2 C .
$$
Therefore, $b-a=0$ and $2 c=2 C$. Hence, $P(x)=a x^{2}+a x+c$. As in Solution 1, this is a valid solution for all $a \in \mathbb{R} \backslash\{0\}$.
## Sun
## Life Financial
|
{
"exam": "Canada_MO",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "Canada_MO/segmented/en-sol2013.jsonl",
"solution_match": "\nSolution 2:",
"tier": "T2",
"year": "2013"
}
|
The sequence $a_{1}, a_{2}, \ldots, a_{n}$ consists of the numbers $1,2, \ldots, n$ in some order. For which positive integers $n$ is it possible that $0, a_{1}, a_{1}+a_{2}, \ldots, a_{1}+a_{2}+\ldots+a_{n}$ all have different remainders when divided by $n+1$ ?
|
It is possible if and only if $n$ is odd.
If $n$ is even, then $a_{1}+a_{2}+\ldots+a_{n}=1+2+\ldots+n=\frac{n}{2} \cdot(n+1)$, which is congruent to $0 \bmod n+1$. Therefore, the task is impossible.
Now suppose $n$ is odd. We will show that we can construct $a_{1}, a_{2}, \ldots, a_{n}$ that satisfy the conditions given in the problem. Then let $n=2 k+1$ for some non-negative integer $k$. Consider the sequence: $1,2 k, 3,2 k-2,5,2 k-3, \ldots, 2,2 k+1$, i.e. for each $1 \leq i \leq 2 k+1, a_{i}=i$ if $i$ is odd and $a_{i}=2 k+2-i$ if $i$ is even.
We first show that each term $1,2, \ldots, 2 k+1$ appears exactly once. Clearly, there are $2 k+1$ terms. For each odd number $m$ in $\{1,2, \ldots, 2 k+1\}, a_{m}=m$. For each even number $m$ in this set, $a_{2 k+2-m}=2 k+2-(2 k+2-m)=m$. Hence, every number appears in $a_{1}, \ldots, a_{2 k+1}$. Hence, $a_{1}, \ldots, a_{2 k+1}$ does consist of the numbers $1,2, \ldots, 2 k+1$ in some order.
We now determine $a_{1}+a_{2}+\ldots+a_{m}(\bmod 2 k+2)$. We will consider the cases when $m$ is odd and when $m$ is even separately. Let $b_{m}=a_{1}+a_{2} \ldots+a_{m}$.
If $m$ is odd, note that $a_{1} \equiv 1(\bmod 2 k+2), a_{2}+a_{3}=a_{4}+a_{5}=\ldots=a_{2 k}+$ $a_{2 k+1}=2 k+3 \equiv 1(\bmod 2 k+2)$. Therefore, $\left\{b_{1}, b_{3}, \ldots, b_{2 k+1}\right\}=\{1,2,3, \ldots, k+1\}$ $(\bmod 2 k+2)$.
If $m$ is even, note that $a_{1}+a_{2}=a_{3}+a_{4}=\ldots=a_{2 k-1}+a_{2 k}=2 k+1 \equiv-1$ $(\bmod 2 k+2)$. Therefore, $\left\{b_{2}, b_{4}, \ldots, b_{2 k}\right\}=\{-1,-2, \ldots,-k\}(\bmod 2 k+2) \equiv$ $\{2 k+1,2 k, \ldots, k+2\}(\bmod 2 k+2)$.
Therefore, $b_{1}, b_{2}, \ldots, b_{2 k+1}$ do indeed have different remainders when divided by $2 k+2$. This completes the problem.
## Sun
## Life Financial
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
The sequence $a_{1}, a_{2}, \ldots, a_{n}$ consists of the numbers $1,2, \ldots, n$ in some order. For which positive integers $n$ is it possible that $0, a_{1}, a_{1}+a_{2}, \ldots, a_{1}+a_{2}+\ldots+a_{n}$ all have different remainders when divided by $n+1$ ?
|
It is possible if and only if $n$ is odd.
If $n$ is even, then $a_{1}+a_{2}+\ldots+a_{n}=1+2+\ldots+n=\frac{n}{2} \cdot(n+1)$, which is congruent to $0 \bmod n+1$. Therefore, the task is impossible.
Now suppose $n$ is odd. We will show that we can construct $a_{1}, a_{2}, \ldots, a_{n}$ that satisfy the conditions given in the problem. Then let $n=2 k+1$ for some non-negative integer $k$. Consider the sequence: $1,2 k, 3,2 k-2,5,2 k-3, \ldots, 2,2 k+1$, i.e. for each $1 \leq i \leq 2 k+1, a_{i}=i$ if $i$ is odd and $a_{i}=2 k+2-i$ if $i$ is even.
We first show that each term $1,2, \ldots, 2 k+1$ appears exactly once. Clearly, there are $2 k+1$ terms. For each odd number $m$ in $\{1,2, \ldots, 2 k+1\}, a_{m}=m$. For each even number $m$ in this set, $a_{2 k+2-m}=2 k+2-(2 k+2-m)=m$. Hence, every number appears in $a_{1}, \ldots, a_{2 k+1}$. Hence, $a_{1}, \ldots, a_{2 k+1}$ does consist of the numbers $1,2, \ldots, 2 k+1$ in some order.
We now determine $a_{1}+a_{2}+\ldots+a_{m}(\bmod 2 k+2)$. We will consider the cases when $m$ is odd and when $m$ is even separately. Let $b_{m}=a_{1}+a_{2} \ldots+a_{m}$.
If $m$ is odd, note that $a_{1} \equiv 1(\bmod 2 k+2), a_{2}+a_{3}=a_{4}+a_{5}=\ldots=a_{2 k}+$ $a_{2 k+1}=2 k+3 \equiv 1(\bmod 2 k+2)$. Therefore, $\left\{b_{1}, b_{3}, \ldots, b_{2 k+1}\right\}=\{1,2,3, \ldots, k+1\}$ $(\bmod 2 k+2)$.
If $m$ is even, note that $a_{1}+a_{2}=a_{3}+a_{4}=\ldots=a_{2 k-1}+a_{2 k}=2 k+1 \equiv-1$ $(\bmod 2 k+2)$. Therefore, $\left\{b_{2}, b_{4}, \ldots, b_{2 k}\right\}=\{-1,-2, \ldots,-k\}(\bmod 2 k+2) \equiv$ $\{2 k+1,2 k, \ldots, k+2\}(\bmod 2 k+2)$.
Therefore, $b_{1}, b_{2}, \ldots, b_{2 k+1}$ do indeed have different remainders when divided by $2 k+2$. This completes the problem.
## Sun
## Life Financial
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "Canada_MO/segmented/en-sol2013.jsonl",
"solution_match": "\nSolution:",
"tier": "T2",
"year": "2013"
}
|
Let $G$ be the centroid of a right-angled triangle $A B C$ with $\angle B C A=90^{\circ}$. Let $P$ be the point on ray $A G$ such that $\angle C P A=\angle C A B$, and let $Q$ be the point on ray $B G$ such that $\angle C Q B=\angle A B C$. Prove that the circumcircles of triangles $A Q G$ and $B P G$ meet at a point on side $A B$.
|
Since $\angle C=90^{\circ}$, the point $C$ lies on the semicircle with diameter $A B$ which implies that, if $M$ is te midpoint of side $A B$, then $M A=M C=M B$. This implies that triangle $A M C$ is isosceles and hence that $\angle A C M=\angle A$. By definition, $G$ lies on segment $M$ and it follows that $\angle A C G=\angle A C M=\angle A=\angle C P A$. This implies that triangles $A P C$ and $A C G$ are similar and hence that $A C^{2}=A G \cdot A P$. Now if $D$ denotes the foot of the perpendicular from $C$ to $A B$, it follows that triangles $A C D$ and $A B C$ are similar which implies that $A C^{2}=A D \cdot A B$. Therefore $A G \cdot A P=$ $A C^{2}=A D \cdot A B$ and, by power of a point, quadrilateral $D G P B$ is cyclic. This implies that $D$ lies on the circumcircle of triangle $B P G$ and, by a symmetric argument, it follows that $D$ also lies on the circumcircle of triangle $A G Q$. Therefore these two circumcircles meet at the point $D$ on side $A B$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $G$ be the centroid of a right-angled triangle $A B C$ with $\angle B C A=90^{\circ}$. Let $P$ be the point on ray $A G$ such that $\angle C P A=\angle C A B$, and let $Q$ be the point on ray $B G$ such that $\angle C Q B=\angle A B C$. Prove that the circumcircles of triangles $A Q G$ and $B P G$ meet at a point on side $A B$.
|
Since $\angle C=90^{\circ}$, the point $C$ lies on the semicircle with diameter $A B$ which implies that, if $M$ is te midpoint of side $A B$, then $M A=M C=M B$. This implies that triangle $A M C$ is isosceles and hence that $\angle A C M=\angle A$. By definition, $G$ lies on segment $M$ and it follows that $\angle A C G=\angle A C M=\angle A=\angle C P A$. This implies that triangles $A P C$ and $A C G$ are similar and hence that $A C^{2}=A G \cdot A P$. Now if $D$ denotes the foot of the perpendicular from $C$ to $A B$, it follows that triangles $A C D$ and $A B C$ are similar which implies that $A C^{2}=A D \cdot A B$. Therefore $A G \cdot A P=$ $A C^{2}=A D \cdot A B$ and, by power of a point, quadrilateral $D G P B$ is cyclic. This implies that $D$ lies on the circumcircle of triangle $B P G$ and, by a symmetric argument, it follows that $D$ also lies on the circumcircle of triangle $A G Q$. Therefore these two circumcircles meet at the point $D$ on side $A B$.
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "Canada_MO/segmented/en-sol2013.jsonl",
"solution_match": "\nSolution 1.",
"tier": "T2",
"year": "2013"
}
|
Let $G$ be the centroid of a right-angled triangle $A B C$ with $\angle B C A=90^{\circ}$. Let $P$ be the point on ray $A G$ such that $\angle C P A=\angle C A B$, and let $Q$ be the point on ray $B G$ such that $\angle C Q B=\angle A B C$. Prove that the circumcircles of triangles $A Q G$ and $B P G$ meet at a point on side $A B$.
|
Define $D$ and $M$ as in Solution 1. Let $R$ be the point on side $A B$ such that $A C=C R$ and triangle $A C R$ is isosceles. Since $\angle C R A=\angle A=\angle C P A$, it follows that $C P R A$ is cyclic and hence that $\angle G P R=\angle A P R=\angle A C R=180^{\circ}-$ $2 \angle A$. As in Solution $1, M C=M B$ and hence $\angle G M R=\angle C M B=2 \angle A=180^{\circ}-$ $\angle G P R$. Therefore $G P R M$ is cyclic and, by power of a point, $A M \cdot A R=A G \cdot A P$. Since $A C R$ is isosceles, $D$ is the midpoint of $A R$ and thus, since $M$ is the midpoint of $A B$, it follows that $A M \cdot A R=A D \cdot A B=A G \cdot A P$. Therefore $D G P B$ is cyclic, implying the result as in Solution 1.
## Sun $\mathscr{H}^{*}$
## Life Financial
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $G$ be the centroid of a right-angled triangle $A B C$ with $\angle B C A=90^{\circ}$. Let $P$ be the point on ray $A G$ such that $\angle C P A=\angle C A B$, and let $Q$ be the point on ray $B G$ such that $\angle C Q B=\angle A B C$. Prove that the circumcircles of triangles $A Q G$ and $B P G$ meet at a point on side $A B$.
|
Define $D$ and $M$ as in Solution 1. Let $R$ be the point on side $A B$ such that $A C=C R$ and triangle $A C R$ is isosceles. Since $\angle C R A=\angle A=\angle C P A$, it follows that $C P R A$ is cyclic and hence that $\angle G P R=\angle A P R=\angle A C R=180^{\circ}-$ $2 \angle A$. As in Solution $1, M C=M B$ and hence $\angle G M R=\angle C M B=2 \angle A=180^{\circ}-$ $\angle G P R$. Therefore $G P R M$ is cyclic and, by power of a point, $A M \cdot A R=A G \cdot A P$. Since $A C R$ is isosceles, $D$ is the midpoint of $A R$ and thus, since $M$ is the midpoint of $A B$, it follows that $A M \cdot A R=A D \cdot A B=A G \cdot A P$. Therefore $D G P B$ is cyclic, implying the result as in Solution 1.
## Sun $\mathscr{H}^{*}$
## Life Financial
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "Canada_MO/segmented/en-sol2013.jsonl",
"solution_match": "\nSolution 2.",
"tier": "T2",
"year": "2013"
}
|
Let $n$ be a positive integer. For any positive integer $j$ and positive real number $r$, define
$$
f_{j}(r)=\min (j r, n)+\min \left(\frac{j}{r}, n\right), \quad \text { and } \quad g_{j}(r)=\min (\lceil j r\rceil, n)+\min \left(\left\lceil\frac{j}{r}\right\rceil, n\right) \text {, }
$$
where $\lceil x\rceil$ denotes the smallest integer greater than or equal to $x$. Prove that
$$
\sum_{j=1}^{n} f_{j}(r) \leq n^{2}+n \leq \sum_{j=1}^{n} g_{j}(r)
$$
|
We first prove the left hand side inequality. We begin by drawing an $n \times n$ board, with corners at $(0,0),(n, 0),(0, n)$ and $(n, n)$ on the Cartesian plane.
Consider the line $\ell$ with slope $r$ passing through $(0,0)$. For each $j \in\{1, \ldots, n\}$, consider the point $(j, \min (j r, n))$. Note that each such point either lies on $\ell$ or the top edge of the board. In the $j^{\text {th }}$ column from the left, draw the rectangle of height $\min (j r, n)$. Note that the sum of the $n$ rectangles is equal to the area of the board under the line $\ell$ plus $n$ triangles (possibly with area 0 ) each with width at most 1 and whose sum of the heights is at most $n$. Therefore, the sum of the areas of these $n$ triangles is at most $n / 2$. Therefore, $\sum_{j=1}^{n} \min (j r, n)$ is at most the area of the square under $\ell$ plus $n / 2$.
Consider the line with slope $1 / r$. By symmetry about the line $y=x$, the area of the square under the line with slope $1 / r$ is equal to the area of the square above the line $\ell$. Therefore, using the same reasoning as before, $\sum_{j=1}^{n} \min (j / r, n)$ is at most the area of the square above $\ell$ plus $n / 2$.
Therefore, $\sum_{j=1}^{n} f_{j}(r)=\sum_{j=1}^{n}\left(\min (j r, n)+\min \left(\frac{j}{r}, n\right)\right)$ is at most the area of the board plus $n$, which is $n^{2}+n$. This proves the left hand side inequality.
To prove the right hand side inequality, we will use the following lemma:
Lemma: Consider the line $\ell$ with slope $s$ passing through $(0,0)$. Then the number of squares on the board that contain an interior point below $\ell$ is $\sum_{j=1}^{n} \min (\lceil j s\rceil, n)$.
Proof of Lemma: For each $j \in\{1, \ldots, n\}$, we count the number of squares in the $j^{\text {th }}$ column (from the left) that contain an interior point lying below the line $\ell$. The line $x=j$ intersect the line $\ell$ at $(j, j s)$. Hence, since each column contains $n$ squares
## Sun
## Life Financial
total, the number of such squares is $\min (\lceil j s\rceil, n)$. Summing over all $j \in\{1,2, \ldots, n\}$ proves the lemma. End Proof of Lemma
By the lemma, the rightmost expression of the inequality is equal to the number of squares containing an interior point below the line with slope $r$ plus the number of squares containing an interior point below the line with slope $1 / r$. By symmetry about the line $y=x$, the latter number is equal to the number of squares containing an interior point above the line with slope $r$. Therefore, the rightmost expression of the inequality is equal to the number of squares of the board plus the number of squares of which $\ell$ passes through the interior. The former is equal to $n^{2}$. Hence, to prove the inequality, it suffices to show that every line passes through the interior of at least $n$ squares. Since $\ell$ has positive slope, each $\ell$ passes through either $n$ rows and/or $n$ columns. In either case, $\ell$ passes through the interior of at least $n$ squares. Hence, the right inequality holds.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n$ be a positive integer. For any positive integer $j$ and positive real number $r$, define
$$
f_{j}(r)=\min (j r, n)+\min \left(\frac{j}{r}, n\right), \quad \text { and } \quad g_{j}(r)=\min (\lceil j r\rceil, n)+\min \left(\left\lceil\frac{j}{r}\right\rceil, n\right) \text {, }
$$
where $\lceil x\rceil$ denotes the smallest integer greater than or equal to $x$. Prove that
$$
\sum_{j=1}^{n} f_{j}(r) \leq n^{2}+n \leq \sum_{j=1}^{n} g_{j}(r)
$$
|
We first prove the left hand side inequality. We begin by drawing an $n \times n$ board, with corners at $(0,0),(n, 0),(0, n)$ and $(n, n)$ on the Cartesian plane.
Consider the line $\ell$ with slope $r$ passing through $(0,0)$. For each $j \in\{1, \ldots, n\}$, consider the point $(j, \min (j r, n))$. Note that each such point either lies on $\ell$ or the top edge of the board. In the $j^{\text {th }}$ column from the left, draw the rectangle of height $\min (j r, n)$. Note that the sum of the $n$ rectangles is equal to the area of the board under the line $\ell$ plus $n$ triangles (possibly with area 0 ) each with width at most 1 and whose sum of the heights is at most $n$. Therefore, the sum of the areas of these $n$ triangles is at most $n / 2$. Therefore, $\sum_{j=1}^{n} \min (j r, n)$ is at most the area of the square under $\ell$ plus $n / 2$.
Consider the line with slope $1 / r$. By symmetry about the line $y=x$, the area of the square under the line with slope $1 / r$ is equal to the area of the square above the line $\ell$. Therefore, using the same reasoning as before, $\sum_{j=1}^{n} \min (j / r, n)$ is at most the area of the square above $\ell$ plus $n / 2$.
Therefore, $\sum_{j=1}^{n} f_{j}(r)=\sum_{j=1}^{n}\left(\min (j r, n)+\min \left(\frac{j}{r}, n\right)\right)$ is at most the area of the board plus $n$, which is $n^{2}+n$. This proves the left hand side inequality.
To prove the right hand side inequality, we will use the following lemma:
Lemma: Consider the line $\ell$ with slope $s$ passing through $(0,0)$. Then the number of squares on the board that contain an interior point below $\ell$ is $\sum_{j=1}^{n} \min (\lceil j s\rceil, n)$.
Proof of Lemma: For each $j \in\{1, \ldots, n\}$, we count the number of squares in the $j^{\text {th }}$ column (from the left) that contain an interior point lying below the line $\ell$. The line $x=j$ intersect the line $\ell$ at $(j, j s)$. Hence, since each column contains $n$ squares
## Sun
## Life Financial
total, the number of such squares is $\min (\lceil j s\rceil, n)$. Summing over all $j \in\{1,2, \ldots, n\}$ proves the lemma. End Proof of Lemma
By the lemma, the rightmost expression of the inequality is equal to the number of squares containing an interior point below the line with slope $r$ plus the number of squares containing an interior point below the line with slope $1 / r$. By symmetry about the line $y=x$, the latter number is equal to the number of squares containing an interior point above the line with slope $r$. Therefore, the rightmost expression of the inequality is equal to the number of squares of the board plus the number of squares of which $\ell$ passes through the interior. The former is equal to $n^{2}$. Hence, to prove the inequality, it suffices to show that every line passes through the interior of at least $n$ squares. Since $\ell$ has positive slope, each $\ell$ passes through either $n$ rows and/or $n$ columns. In either case, $\ell$ passes through the interior of at least $n$ squares. Hence, the right inequality holds.
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "Canada_MO/segmented/en-sol2013.jsonl",
"solution_match": "\nSolution 1:",
"tier": "T2",
"year": "2013"
}
|
Let $n$ be a positive integer. For any positive integer $j$ and positive real number $r$, define
$$
f_{j}(r)=\min (j r, n)+\min \left(\frac{j}{r}, n\right), \quad \text { and } \quad g_{j}(r)=\min (\lceil j r\rceil, n)+\min \left(\left\lceil\frac{j}{r}\right\rceil, n\right) \text {, }
$$
where $\lceil x\rceil$ denotes the smallest integer greater than or equal to $x$. Prove that
$$
\sum_{j=1}^{n} f_{j}(r) \leq n^{2}+n \leq \sum_{j=1}^{n} g_{j}(r)
$$
|
We first prove the left inequality. Define the function $f(r)=$ $\sum_{j=1}^{n} f_{j}(r)$. Note that $f(r)=f(1 / r)$ for all $r>0$. Therefore, we may assume that $r \geq 1$.
Let $m=\lfloor n / r\rfloor$, where $\lfloor x\rfloor$ denotes the largest integer less than or equal to $x$. Then $\min (j r, n)=j r$ for all $j \in\{1, \ldots, m\}$ and $\min (j r, n)=n$ for all $j \in\{m+1, \ldots, n\}$. Note that since $r \geq 1, \min (j / r, n) \leq n$ for all $j \in\{1, \ldots, n\}$. Therefore,
$$
\begin{gathered}
f(r)=\sum_{j=1}^{n} f_{j}(r)=(1+2+\ldots m) r+(n-m) n+(1+2+\ldots+n) \cdot \frac{1}{r} \\
=\frac{m(m+1)}{2} \cdot r+\frac{n(n+1)}{2} \cdot \frac{1}{r}+n(n-m)
\end{gathered}
$$
Then by (??), note that $f(r) \leq n^{2}+n$ if and only if
$$
\frac{m(m+1) r}{2}+\frac{n(n+1)}{2 r} \leq n(m+1)
$$
if and only if
$$
m(m+1) r^{2}+n(n+1) \leq 2 r n(m+1)
$$
Since $m=\lfloor n / r\rfloor$, there exist a real number $b$ satisfying $0 \leq b<r$ such that $n=m r+b$. Substituting this into (??) yields
$$
m(m+1) r^{2}+(m r+b)(m r+b+1) \leq 2 r(m r+b)(m+1),
$$
## Sun $\Psi^{*}$
## Life Financial
if and only if
$$
2 m^{2} r^{2}+m r^{2}+(2 m b+m) r+b^{2}+b \leq 2 m^{2} r^{2}+2 m r^{2}+2 m b r+2 b r,
$$
which simplifies to $m r+b^{2}+b \leq m r^{2}+2 b r \Leftrightarrow b(b+1-2 r) \leq m r(r-1) \Leftrightarrow$ $b((b-r)+(1-r)) \leq m r(r-1)$. This is true since
$$
b((b-r)+(1-r)) \leq 0 \leq m r(r-1),
$$
which holds since $r \geq 1$ and $b<r$. Therefore, the left inequality holds.
We now prove the right inequality. Define the function $g(r)=\sum_{j=1}^{n}=g_{j}(r)$. Note that $g(r)=g(1 / r)$ for all $r>0$. Therefore, we may assume that $r \geq 1$. We will consider two cases; $r \geq n$ and $1 \leq r<n$.
If $r \geq n$, then $\min (\lceil j r\rceil, n)=n$ and $\min (\lceil j / r\rceil, n)=1$ for all $j \in\{1, \ldots, n\}$. Hence, $g_{j}(r)=n+1$ for all $j \in\{1, \ldots, n\}$. Therefore, $g(r)=n(n+1)=n^{2}+n$, implying that the inequality is true.
Now we consider the case $1 \leq r<n$. Let $m=\lfloor n / r\rfloor$. Hence, $j r \leq n$ for all $j \in\{1, \ldots, m\}$, i.e. $\min (\lceil j r\rceil, n)=,\lceil j r\rceil$ and $j r \geq n$ for all $j \in\{m+1, \ldots, n\}$, i.e. $\min (\lceil j r\rceil, n)=n$. Therefore,
$$
\sum_{j=1}^{n} \min (\lceil j r\rceil, n)=\sum_{j=1}^{m}\lceil j r\rceil+(n-m) n
$$
We will now consider the second sum $\sum_{j=1}^{n} \min \{\lceil j / r\rceil, n\}$.
Since $r \geq 1, \min (\lceil j / r\rceil, n) \leq \min (\lceil n / r\rceil, n) \leq n$. Therefore, $\min (\lceil j / r\rceil, n)=$ $\lceil j / r\rceil$. Since $m=\lfloor n / r\rfloor,\lceil n / r\rceil \leq m+1$. Since $r>1, m<n$, which implies that $m+1 \leq n$. Therefore, $\min \{\lceil j / r\rceil, n\}=\lceil j / r\rceil \leq\lceil n / r\rceil \leq m+1$ for all $j \in\{1, \ldots, n\}$.
For each positive integer $k \in\{1, \ldots, m+1\}$, we now determine the number of positive integers $j \in\{1, \ldots, n\}$ such that $\lceil j / r\rceil=k$. We denote this number by $s_{k}$.
Note that $\lceil j / r\rceil=k$ if and only if $k-1<j / r \leq k$ if and only if $(k-1) r<j \leq$ $\min (k r, n)$, since $j \leq n$. We will handle the cases $k \in\{1, \ldots, m\}$ and $k=m+1$ separately. If $k \in\{1, \ldots, m\}$, then $\min (k r, n)=k r$, since $r \leq m$ and $m=\lfloor n / r\rfloor$.
## Sun 4
## Life Financial
The set of positive integers $j$ satisfying $(k-1) r<j \leq k r$ is $\{\lfloor(k-1) r\rfloor+1,\lfloor(k-$ 1) $r\rfloor+2, \ldots,\lfloor k r\rfloor\}$. Hence,
$$
s_{k}=\lfloor r k\rfloor-(\lfloor r(k-1)\rfloor+1)+1=\lfloor r k\rfloor-\lfloor r(k-1)\rfloor
$$
for all $k \in\{1, \ldots, m\}$. If $k=m+1$, then $(k-1) r<j \leq \min (k r, n)=n$. The set of positive integers $j$ satisfying $(k-1) r<j \leq k r$ is $\{\lfloor(k-1) r\rfloor+1, \ldots, n\}$. Then $s_{m+1}=n-\lfloor r(k-1)\rfloor=n-\lfloor m r\rfloor$. Note that this number is non-negative by the definition of $m$. Therefore, by the definition of $s_{k}$, we have
$$
\begin{aligned}
& \sum_{j=1}^{n} \min \left(\left\lceil\frac{j}{r}\right\rceil, n\right)=\sum_{k=1}^{m+1} k s_{k} \\
& \quad=\sum_{k=1}^{m}(k(\lfloor k r\rfloor-\lfloor(k-1) r\rfloor))+(m+1)(n-\lfloor r m\rfloor)=(m+1) n-\sum_{k=1}^{m}\lfloor k r\rfloor .
\end{aligned}
$$
Summing (??) and (??) yields that
$$
g(r)=n^{2}+n+\sum_{j=1}^{m}(\lceil j r\rceil-\lfloor j r\rfloor) \geq n^{2}+n
$$
which proves the right inequality.
## Sun
## Life Financial
|
proof
|
Yes
|
Incomplete
|
proof
|
Inequalities
|
Let $n$ be a positive integer. For any positive integer $j$ and positive real number $r$, define
$$
f_{j}(r)=\min (j r, n)+\min \left(\frac{j}{r}, n\right), \quad \text { and } \quad g_{j}(r)=\min (\lceil j r\rceil, n)+\min \left(\left\lceil\frac{j}{r}\right\rceil, n\right) \text {, }
$$
where $\lceil x\rceil$ denotes the smallest integer greater than or equal to $x$. Prove that
$$
\sum_{j=1}^{n} f_{j}(r) \leq n^{2}+n \leq \sum_{j=1}^{n} g_{j}(r)
$$
|
We first prove the left inequality. Define the function $f(r)=$ $\sum_{j=1}^{n} f_{j}(r)$. Note that $f(r)=f(1 / r)$ for all $r>0$. Therefore, we may assume that $r \geq 1$.
Let $m=\lfloor n / r\rfloor$, where $\lfloor x\rfloor$ denotes the largest integer less than or equal to $x$. Then $\min (j r, n)=j r$ for all $j \in\{1, \ldots, m\}$ and $\min (j r, n)=n$ for all $j \in\{m+1, \ldots, n\}$. Note that since $r \geq 1, \min (j / r, n) \leq n$ for all $j \in\{1, \ldots, n\}$. Therefore,
$$
\begin{gathered}
f(r)=\sum_{j=1}^{n} f_{j}(r)=(1+2+\ldots m) r+(n-m) n+(1+2+\ldots+n) \cdot \frac{1}{r} \\
=\frac{m(m+1)}{2} \cdot r+\frac{n(n+1)}{2} \cdot \frac{1}{r}+n(n-m)
\end{gathered}
$$
Then by (??), note that $f(r) \leq n^{2}+n$ if and only if
$$
\frac{m(m+1) r}{2}+\frac{n(n+1)}{2 r} \leq n(m+1)
$$
if and only if
$$
m(m+1) r^{2}+n(n+1) \leq 2 r n(m+1)
$$
Since $m=\lfloor n / r\rfloor$, there exist a real number $b$ satisfying $0 \leq b<r$ such that $n=m r+b$. Substituting this into (??) yields
$$
m(m+1) r^{2}+(m r+b)(m r+b+1) \leq 2 r(m r+b)(m+1),
$$
## Sun $\Psi^{*}$
## Life Financial
if and only if
$$
2 m^{2} r^{2}+m r^{2}+(2 m b+m) r+b^{2}+b \leq 2 m^{2} r^{2}+2 m r^{2}+2 m b r+2 b r,
$$
which simplifies to $m r+b^{2}+b \leq m r^{2}+2 b r \Leftrightarrow b(b+1-2 r) \leq m r(r-1) \Leftrightarrow$ $b((b-r)+(1-r)) \leq m r(r-1)$. This is true since
$$
b((b-r)+(1-r)) \leq 0 \leq m r(r-1),
$$
which holds since $r \geq 1$ and $b<r$. Therefore, the left inequality holds.
We now prove the right inequality. Define the function $g(r)=\sum_{j=1}^{n}=g_{j}(r)$. Note that $g(r)=g(1 / r)$ for all $r>0$. Therefore, we may assume that $r \geq 1$. We will consider two cases; $r \geq n$ and $1 \leq r<n$.
If $r \geq n$, then $\min (\lceil j r\rceil, n)=n$ and $\min (\lceil j / r\rceil, n)=1$ for all $j \in\{1, \ldots, n\}$. Hence, $g_{j}(r)=n+1$ for all $j \in\{1, \ldots, n\}$. Therefore, $g(r)=n(n+1)=n^{2}+n$, implying that the inequality is true.
Now we consider the case $1 \leq r<n$. Let $m=\lfloor n / r\rfloor$. Hence, $j r \leq n$ for all $j \in\{1, \ldots, m\}$, i.e. $\min (\lceil j r\rceil, n)=,\lceil j r\rceil$ and $j r \geq n$ for all $j \in\{m+1, \ldots, n\}$, i.e. $\min (\lceil j r\rceil, n)=n$. Therefore,
$$
\sum_{j=1}^{n} \min (\lceil j r\rceil, n)=\sum_{j=1}^{m}\lceil j r\rceil+(n-m) n
$$
We will now consider the second sum $\sum_{j=1}^{n} \min \{\lceil j / r\rceil, n\}$.
Since $r \geq 1, \min (\lceil j / r\rceil, n) \leq \min (\lceil n / r\rceil, n) \leq n$. Therefore, $\min (\lceil j / r\rceil, n)=$ $\lceil j / r\rceil$. Since $m=\lfloor n / r\rfloor,\lceil n / r\rceil \leq m+1$. Since $r>1, m<n$, which implies that $m+1 \leq n$. Therefore, $\min \{\lceil j / r\rceil, n\}=\lceil j / r\rceil \leq\lceil n / r\rceil \leq m+1$ for all $j \in\{1, \ldots, n\}$.
For each positive integer $k \in\{1, \ldots, m+1\}$, we now determine the number of positive integers $j \in\{1, \ldots, n\}$ such that $\lceil j / r\rceil=k$. We denote this number by $s_{k}$.
Note that $\lceil j / r\rceil=k$ if and only if $k-1<j / r \leq k$ if and only if $(k-1) r<j \leq$ $\min (k r, n)$, since $j \leq n$. We will handle the cases $k \in\{1, \ldots, m\}$ and $k=m+1$ separately. If $k \in\{1, \ldots, m\}$, then $\min (k r, n)=k r$, since $r \leq m$ and $m=\lfloor n / r\rfloor$.
## Sun 4
## Life Financial
The set of positive integers $j$ satisfying $(k-1) r<j \leq k r$ is $\{\lfloor(k-1) r\rfloor+1,\lfloor(k-$ 1) $r\rfloor+2, \ldots,\lfloor k r\rfloor\}$. Hence,
$$
s_{k}=\lfloor r k\rfloor-(\lfloor r(k-1)\rfloor+1)+1=\lfloor r k\rfloor-\lfloor r(k-1)\rfloor
$$
for all $k \in\{1, \ldots, m\}$. If $k=m+1$, then $(k-1) r<j \leq \min (k r, n)=n$. The set of positive integers $j$ satisfying $(k-1) r<j \leq k r$ is $\{\lfloor(k-1) r\rfloor+1, \ldots, n\}$. Then $s_{m+1}=n-\lfloor r(k-1)\rfloor=n-\lfloor m r\rfloor$. Note that this number is non-negative by the definition of $m$. Therefore, by the definition of $s_{k}$, we have
$$
\begin{aligned}
& \sum_{j=1}^{n} \min \left(\left\lceil\frac{j}{r}\right\rceil, n\right)=\sum_{k=1}^{m+1} k s_{k} \\
& \quad=\sum_{k=1}^{m}(k(\lfloor k r\rfloor-\lfloor(k-1) r\rfloor))+(m+1)(n-\lfloor r m\rfloor)=(m+1) n-\sum_{k=1}^{m}\lfloor k r\rfloor .
\end{aligned}
$$
Summing (??) and (??) yields that
$$
g(r)=n^{2}+n+\sum_{j=1}^{m}(\lceil j r\rceil-\lfloor j r\rfloor) \geq n^{2}+n
$$
which proves the right inequality.
## Sun
## Life Financial
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "Canada_MO/segmented/en-sol2013.jsonl",
"solution_match": "\nSolution 2:",
"tier": "T2",
"year": "2013"
}
|
Let $O$ denote the circumcentre of an acute-angled triangle $A B C$. A circle $\Gamma$ passing through vertex $A$ intersects segments $A B$ and $A C$ at points $P$ and $Q$ such that $\angle B O P=\angle A B C$ and $\angle C O Q=\angle A C B$. Prove that the reflection of $B C$ in the line $P Q$ is tangent to $\Gamma$.
|
Let the circumcircle of triangle $O B P$ intersect side $B C$ at the points $R$ and $B$ and let $\angle A, \angle B$ and $\angle C$ denote the angles at vertices $A, B$ and $C$, respectively.
Now note that since $\angle B O P=\angle B$ and $\angle C O Q=\angle C$, it follows that
$\angle P O Q=360^{\circ}-\angle B O P-\angle C O Q-\angle B O C=360^{\circ}-(180-\angle A)-2 \angle A=180^{\circ}-\angle A$.
This implies that $A P O Q$ is a cyclic quadrilateral. Since $B P O R$ is cyclic,
$\angle Q O R=360^{\circ}-\angle P O Q-\angle P O R=360^{\circ}-\left(180^{\circ}-\angle A\right)-\left(180^{\circ}-\angle B\right)=180^{\circ}-\angle C$.
This implies that $C Q O R$ is a cyclic quadrilateral. Since $A P O Q$ and $B P O R$ are cyclic,
$\angle Q P R=\angle Q P O+\angle O P R=\angle O A Q+\angle O B R=\left(90^{\circ}-\angle B\right)+\left(90^{\circ}-\angle A\right)=\angle C$.
Since $C Q O R$ is cyclic, $\angle Q R C=\angle C O Q=\angle C=\angle Q P R$ which implies that the circumcircle of triangle $P Q R$ is tangent to $B C$. Further, since $\angle P R B=\angle B O P=$ $\angle B$,
$$
\angle P R Q=180^{\circ}-\angle P R B-\angle Q R C=180^{\circ}-\angle B-\angle C=\angle A=\angle P A Q
$$
This implies that the circumcircle of $P Q R$ is the reflection of $\Gamma$ in line $P Q$. By symmetry in line $P Q$, this implies that the reflection of $B C$ in line $P Q$ is tangent to $\Gamma$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $O$ denote the circumcentre of an acute-angled triangle $A B C$. A circle $\Gamma$ passing through vertex $A$ intersects segments $A B$ and $A C$ at points $P$ and $Q$ such that $\angle B O P=\angle A B C$ and $\angle C O Q=\angle A C B$. Prove that the reflection of $B C$ in the line $P Q$ is tangent to $\Gamma$.
|
Let the circumcircle of triangle $O B P$ intersect side $B C$ at the points $R$ and $B$ and let $\angle A, \angle B$ and $\angle C$ denote the angles at vertices $A, B$ and $C$, respectively.
Now note that since $\angle B O P=\angle B$ and $\angle C O Q=\angle C$, it follows that
$\angle P O Q=360^{\circ}-\angle B O P-\angle C O Q-\angle B O C=360^{\circ}-(180-\angle A)-2 \angle A=180^{\circ}-\angle A$.
This implies that $A P O Q$ is a cyclic quadrilateral. Since $B P O R$ is cyclic,
$\angle Q O R=360^{\circ}-\angle P O Q-\angle P O R=360^{\circ}-\left(180^{\circ}-\angle A\right)-\left(180^{\circ}-\angle B\right)=180^{\circ}-\angle C$.
This implies that $C Q O R$ is a cyclic quadrilateral. Since $A P O Q$ and $B P O R$ are cyclic,
$\angle Q P R=\angle Q P O+\angle O P R=\angle O A Q+\angle O B R=\left(90^{\circ}-\angle B\right)+\left(90^{\circ}-\angle A\right)=\angle C$.
Since $C Q O R$ is cyclic, $\angle Q R C=\angle C O Q=\angle C=\angle Q P R$ which implies that the circumcircle of triangle $P Q R$ is tangent to $B C$. Further, since $\angle P R B=\angle B O P=$ $\angle B$,
$$
\angle P R Q=180^{\circ}-\angle P R B-\angle Q R C=180^{\circ}-\angle B-\angle C=\angle A=\angle P A Q
$$
This implies that the circumcircle of $P Q R$ is the reflection of $\Gamma$ in line $P Q$. By symmetry in line $P Q$, this implies that the reflection of $B C$ in line $P Q$ is tangent to $\Gamma$.
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "Canada_MO/segmented/en-sol2013.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2013"
}
|
Let $a_{1}, a_{2}, \ldots, a_{n}$ be positive real numbers whose product is 1 . Show that the sum $\frac{a_{1}}{1+a_{1}}+\frac{a_{2}}{\left(1+a_{1}\right)\left(1+a_{2}\right)}+\frac{a_{3}}{\left(1+a_{1}\right)\left(1+a_{2}\right)\left(1+a_{3}\right)}+\cdots+\frac{a_{n}}{\left(1+a_{1}\right)\left(1+a_{2}\right) \cdots\left(1+a_{n}\right)}$ is greater than or equal to $\frac{2^{n}-1}{2^{n}}$.
|
Note for that every positive integer $m$,
$$
\begin{aligned}
\frac{a_{m}}{\left(1+a_{1}\right)\left(1+a_{2}\right) \cdots\left(1+a_{m}\right)} & =\frac{1+a_{m}}{\left(1+a_{1}\right)\left(1+a_{2}\right) \cdots\left(1+a_{m}\right)}-\frac{1}{\left(1+a_{1}\right)\left(1+a_{2}\right) \cdots\left(1+a_{m}\right)} \\
& =\frac{1}{\left(1+a_{1}\right) \cdots\left(1+a_{m-1}\right)}-\frac{1}{\left(1+a_{1}\right) \cdots\left(1+a_{m}\right)} .
\end{aligned}
$$
Therefore, if we let $b_{j}=\left(1+a_{1}\right)\left(1+a_{2}\right) \cdots\left(1+a_{j}\right)$, with $b_{0}=0$, then by telescoping sums,
$$
\sum_{j=1}^{n} \frac{a_{j}}{\left(1+a_{1}\right) \cdots\left(1+a_{j}\right)}=\sum_{j=1}^{n}\left(\frac{1}{b_{j-1}}-\frac{1}{b_{j}}\right)=1-\frac{1}{b_{n}}
$$
Note that $b_{n}=\left(1+a_{1}\right)\left(1+a_{2}\right) \cdots\left(1+a_{n}\right) \geq\left(2 \sqrt{a_{1}}\right)\left(2 \sqrt{a_{2}}\right) \cdots\left(2 \sqrt{a_{n}}\right)=2^{n}$, with equality if and only if all $a_{i}$ 's equal to 1 . Therefore,
$$
1-\frac{1}{b_{n}} \geq 1-\frac{1}{2^{n}}=\frac{2^{n}-1}{2^{n}} .
$$
To check that this minimum can be obtained, substituting all $a_{i}=1$ to yield
$$
\frac{1}{2}+\frac{1}{2^{2}}+\frac{1}{2^{3}}+\ldots+\frac{1}{2^{n}}=\frac{2^{n-1}+2^{n-2}+\ldots+1}{2^{n}}=\frac{2^{n}-1}{2^{n}}
$$
as desired.

## Life Financial
|
\frac{2^{n}-1}{2^{n}}
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a_{1}, a_{2}, \ldots, a_{n}$ be positive real numbers whose product is 1 . Show that the sum $\frac{a_{1}}{1+a_{1}}+\frac{a_{2}}{\left(1+a_{1}\right)\left(1+a_{2}\right)}+\frac{a_{3}}{\left(1+a_{1}\right)\left(1+a_{2}\right)\left(1+a_{3}\right)}+\cdots+\frac{a_{n}}{\left(1+a_{1}\right)\left(1+a_{2}\right) \cdots\left(1+a_{n}\right)}$ is greater than or equal to $\frac{2^{n}-1}{2^{n}}$.
|
Note for that every positive integer $m$,
$$
\begin{aligned}
\frac{a_{m}}{\left(1+a_{1}\right)\left(1+a_{2}\right) \cdots\left(1+a_{m}\right)} & =\frac{1+a_{m}}{\left(1+a_{1}\right)\left(1+a_{2}\right) \cdots\left(1+a_{m}\right)}-\frac{1}{\left(1+a_{1}\right)\left(1+a_{2}\right) \cdots\left(1+a_{m}\right)} \\
& =\frac{1}{\left(1+a_{1}\right) \cdots\left(1+a_{m-1}\right)}-\frac{1}{\left(1+a_{1}\right) \cdots\left(1+a_{m}\right)} .
\end{aligned}
$$
Therefore, if we let $b_{j}=\left(1+a_{1}\right)\left(1+a_{2}\right) \cdots\left(1+a_{j}\right)$, with $b_{0}=0$, then by telescoping sums,
$$
\sum_{j=1}^{n} \frac{a_{j}}{\left(1+a_{1}\right) \cdots\left(1+a_{j}\right)}=\sum_{j=1}^{n}\left(\frac{1}{b_{j-1}}-\frac{1}{b_{j}}\right)=1-\frac{1}{b_{n}}
$$
Note that $b_{n}=\left(1+a_{1}\right)\left(1+a_{2}\right) \cdots\left(1+a_{n}\right) \geq\left(2 \sqrt{a_{1}}\right)\left(2 \sqrt{a_{2}}\right) \cdots\left(2 \sqrt{a_{n}}\right)=2^{n}$, with equality if and only if all $a_{i}$ 's equal to 1 . Therefore,
$$
1-\frac{1}{b_{n}} \geq 1-\frac{1}{2^{n}}=\frac{2^{n}-1}{2^{n}} .
$$
To check that this minimum can be obtained, substituting all $a_{i}=1$ to yield
$$
\frac{1}{2}+\frac{1}{2^{2}}+\frac{1}{2^{3}}+\ldots+\frac{1}{2^{n}}=\frac{2^{n-1}+2^{n-2}+\ldots+1}{2^{n}}=\frac{2^{n}-1}{2^{n}}
$$
as desired.

## Life Financial
|
{
"exam": "Canada_MO",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "Canada_MO/segmented/en-sol2014.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2014"
}
|
Let $m$ and $n$ be odd positive integers. Each square of an $m$ by $n$ board is coloured red or blue. A row is said to be red-dominated if there are more red squares than blue squares in the row. A column is said to be blue-dominated if there are more blue squares than red squares in the column. Determine the maximum possible value of the number of red-dominated rows plus the number of blue-dominated columns. Express your answer in terms of $m$ and $n$.
|
The answer is $m+n-2$ if $m, n \geq 3$ and $\max \{m, n\}$ if one of $m, n$ is equal to 1 .
Note that it is not possible that all rows are red-dominated and all columns are blue-dominated. This is true, since the number of rows and columns are both odd, the number of squares is odd. Hence, there are more squares of one color than the other. Without loss of generality, suppose there are more red squares than blue squares. Then it is not possible that for every column, there are more blue squares than red squares. Hence, every column cannot be blue-dominated.
If one of $m, n$ is equal to 1 , say $m$ without loss of generality, then by the claim, the answer is less than $n+1$. The example where there are $n$ blue-dominated columns is by painting every square blue. There are 0 red-dominated rows. The sum of the two is $n=\max \{m, n\}$.
Now we handle the case $m, n \geq 3$.
There are $m$ rows and $n$ columns on the board. Hence, the answer is at most $m+n$. We have already shown that the answer cannot be $m+n$.
Since $m, n$ are odd, let $m=2 a-1$ and $n=2 b-1$ for some positive integers $a, b$. Since $m, n \geq 3, a, b \geq 2$. We first show that the answer is not $m+n-1$. By symmetry, it suffices to show that we cannot have all rows red-dominated and all-butone column blue-dominated. If all rows are red dominated, then each row has at least $b$ red squares. Hence, there are at least $b m=(2 a-1) b$ red squares. Since all-but-one column is blue-dominated, there are at least $2 b-2$ blue-dominated columns. Each such column then has at least $a$ blue squares. Therefore, there are at least $a(2 b-2)$ blue squares. Therefore, the board has at least $(2 a-1) b+a(2 b-2)=4 a b-b-2 a$ squares. But the total number of squares on the board is
$$
(2 a-1)(2 b-1)=4 a b-2 a-2 b+1=4 a b-2 a-b-b+1<4 a b-2 a-b,
$$
which is true since $b \geq 2$. This is a contradiction. Therefore, the answer is less than $m+n-1$.
## Sun
## Life Financial
We now claim that there is a colouring of the board such that the number of bluedominated columns plus the number of red-dominated rows is $m+n-2$; Colour the first column entirely red, and the first row, minus the top-left corner, entirely blue. The remaining uncoloured square is an even-by-even board. Colour the remaining board in an alternating pattern (i.e. checkerboard pattern). Hence, on this evenby-even board, each row has the same number of red squares as blue squares and each column has the same number of red squares as blue squares. Then on the whole board, since the top row, minus the top-left square is blue, all columns, but the leftmost column, are blue-dominated. Hence, there are $n-1$ blue-dominated columns. Since the left column is red, all rows but the top row are red dominated. Hence, there are $m-1$ red-dominated rows. The sum of these two quantities is $m+n-2$, as desired.
|
m+n-2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $m$ and $n$ be odd positive integers. Each square of an $m$ by $n$ board is coloured red or blue. A row is said to be red-dominated if there are more red squares than blue squares in the row. A column is said to be blue-dominated if there are more blue squares than red squares in the column. Determine the maximum possible value of the number of red-dominated rows plus the number of blue-dominated columns. Express your answer in terms of $m$ and $n$.
|
The answer is $m+n-2$ if $m, n \geq 3$ and $\max \{m, n\}$ if one of $m, n$ is equal to 1 .
Note that it is not possible that all rows are red-dominated and all columns are blue-dominated. This is true, since the number of rows and columns are both odd, the number of squares is odd. Hence, there are more squares of one color than the other. Without loss of generality, suppose there are more red squares than blue squares. Then it is not possible that for every column, there are more blue squares than red squares. Hence, every column cannot be blue-dominated.
If one of $m, n$ is equal to 1 , say $m$ without loss of generality, then by the claim, the answer is less than $n+1$. The example where there are $n$ blue-dominated columns is by painting every square blue. There are 0 red-dominated rows. The sum of the two is $n=\max \{m, n\}$.
Now we handle the case $m, n \geq 3$.
There are $m$ rows and $n$ columns on the board. Hence, the answer is at most $m+n$. We have already shown that the answer cannot be $m+n$.
Since $m, n$ are odd, let $m=2 a-1$ and $n=2 b-1$ for some positive integers $a, b$. Since $m, n \geq 3, a, b \geq 2$. We first show that the answer is not $m+n-1$. By symmetry, it suffices to show that we cannot have all rows red-dominated and all-butone column blue-dominated. If all rows are red dominated, then each row has at least $b$ red squares. Hence, there are at least $b m=(2 a-1) b$ red squares. Since all-but-one column is blue-dominated, there are at least $2 b-2$ blue-dominated columns. Each such column then has at least $a$ blue squares. Therefore, there are at least $a(2 b-2)$ blue squares. Therefore, the board has at least $(2 a-1) b+a(2 b-2)=4 a b-b-2 a$ squares. But the total number of squares on the board is
$$
(2 a-1)(2 b-1)=4 a b-2 a-2 b+1=4 a b-2 a-b-b+1<4 a b-2 a-b,
$$
which is true since $b \geq 2$. This is a contradiction. Therefore, the answer is less than $m+n-1$.
## Sun
## Life Financial
We now claim that there is a colouring of the board such that the number of bluedominated columns plus the number of red-dominated rows is $m+n-2$; Colour the first column entirely red, and the first row, minus the top-left corner, entirely blue. The remaining uncoloured square is an even-by-even board. Colour the remaining board in an alternating pattern (i.e. checkerboard pattern). Hence, on this evenby-even board, each row has the same number of red squares as blue squares and each column has the same number of red squares as blue squares. Then on the whole board, since the top row, minus the top-left square is blue, all columns, but the leftmost column, are blue-dominated. Hence, there are $n-1$ blue-dominated columns. Since the left column is red, all rows but the top row are red dominated. Hence, there are $m-1$ red-dominated rows. The sum of these two quantities is $m+n-2$, as desired.
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "Canada_MO/segmented/en-sol2014.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2014"
}
|
Let $p$ be a fixed odd prime. A $p$-tuple $\left(a_{1}, a_{2}, a_{3}, \ldots, a_{p}\right)$ of integers is said to be good if
(i) $0 \leq a_{i} \leq p-1$ for all $i$, and
(ii) $a_{1}+a_{2}+a_{3}+\cdots+a_{p}$ is not divisible by $p$, and
(iii) $a_{1} a_{2}+a_{2} a_{3}+a_{3} a_{4}+\cdots+a_{p} a_{1}$ is divisible by $p$.
Determine the number of good $p$-tuples.
|
Let $S$ be the set of all sequences $\left(b_{1}, b_{2}, \ldots, b_{p}\right)$ of numbers from the set $\{0,1,2, \ldots, p-1\}$ such that $b_{1}+b_{2}+\cdots+b_{p}$ is not divisible by $p$. We show that $|S|=p^{p}-p^{p-1}$. For let $b_{1}, b_{2}, \ldots, b_{p-1}$ be an arbitrary sequence of numbers chosen from $\{0,1,2, \ldots, p-1\}$. There are exactly $p-1$ choices for $b_{p}$ such that $b_{1}+b_{2}+\cdots+b_{p-1}+b_{p} \not \equiv 0(\bmod p)$, and therefore $|S|=p^{p-1}(p-1)=p^{p}-p^{p-1}$.
Now it will be shown that the number of good sequences in $S$ is $\frac{1}{p}|S|$. For a sequence $B=\left(b_{1}, b_{2}, \ldots, b_{p}\right)$ in $S$, define the sequence $B_{k}=\left(a_{1}, a_{2}, \ldots, a_{p}\right)$ by
$$
a_{i}=b_{i}-b_{1}+k \bmod p
$$
for $1 \leq i \leq p$. Now note that $B$ in $S$ implies that
$a_{1}+a_{2}+\cdots+a_{p} \equiv\left(b_{1}+b_{2}+\cdots+b_{p}\right)-p b_{1}+p k \equiv\left(b_{1}+b_{2}+\cdots+b_{p}\right) \not \equiv 0 \quad(\bmod p)$
and therefore $B_{k}$ is in $S$ for all non-negative $k$. Now note that $B_{k}$ has first element $k$ for all $0 \leq k \leq p-1$ and therefore the sequences $B_{0}, B_{1}, \ldots, B_{p-1}$ are distinct.
Now define the cycle of $B$ as the set $\left\{B_{0}, B_{1}, \ldots, B_{p-1}\right\}$. Note that $B$ is in its own cycle since $B=B_{k}$ where $k=b_{1}$. Now note that since every sequence in $S$ is in exactly one cycle, $S$ is the disjoint union of cycles.
Now it will be shown that exactly one sequence per cycle is good. Consider an arbitrary cycle $B_{0}, B_{1}, \ldots, B_{p-1}$, and let $B_{0}=\left(b_{1}, b_{2}, \ldots, b_{p}\right)$ where $b_{0}=0$, and note that $B_{k}=\left(b_{1}+k, b_{2}+k, \ldots, b_{p}+k\right) \bmod p$. Let $u=b_{1}+b_{2}+\cdots+b_{p}$, and $v=b_{1} b_{2}+b_{2} b_{3}+\cdots+b_{p} b_{1}$ and note that $\left.\left(b_{1}+k\right)\left(b_{2}+k\right)+\left(b_{2}+k\right)\left(b_{3}+k\right)\right)+\cdots+$ $\left(b_{p}+k\right)\left(b_{1}+k\right)=u+2 k v \bmod p$ for all $0 \leq k \leq p-1$. Since $2 v$ is not divisible by $p$, there is exactly one value of $k$ with $0 \leq k \leq p-1$ such that $p$ divides $u+2 k v$ and it is exactly for this value of $k$ that $B_{k}$ is good. This shows that exactly one sequence per cycle is good and therefore that the number of good sequences in $S$ is $\frac{1}{p}|S|$, which is $p^{p-1}-p^{p-2}$.
|
p^{p-1}-p^{p-2}
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $p$ be a fixed odd prime. A $p$-tuple $\left(a_{1}, a_{2}, a_{3}, \ldots, a_{p}\right)$ of integers is said to be good if
(i) $0 \leq a_{i} \leq p-1$ for all $i$, and
(ii) $a_{1}+a_{2}+a_{3}+\cdots+a_{p}$ is not divisible by $p$, and
(iii) $a_{1} a_{2}+a_{2} a_{3}+a_{3} a_{4}+\cdots+a_{p} a_{1}$ is divisible by $p$.
Determine the number of good $p$-tuples.
|
Let $S$ be the set of all sequences $\left(b_{1}, b_{2}, \ldots, b_{p}\right)$ of numbers from the set $\{0,1,2, \ldots, p-1\}$ such that $b_{1}+b_{2}+\cdots+b_{p}$ is not divisible by $p$. We show that $|S|=p^{p}-p^{p-1}$. For let $b_{1}, b_{2}, \ldots, b_{p-1}$ be an arbitrary sequence of numbers chosen from $\{0,1,2, \ldots, p-1\}$. There are exactly $p-1$ choices for $b_{p}$ such that $b_{1}+b_{2}+\cdots+b_{p-1}+b_{p} \not \equiv 0(\bmod p)$, and therefore $|S|=p^{p-1}(p-1)=p^{p}-p^{p-1}$.
Now it will be shown that the number of good sequences in $S$ is $\frac{1}{p}|S|$. For a sequence $B=\left(b_{1}, b_{2}, \ldots, b_{p}\right)$ in $S$, define the sequence $B_{k}=\left(a_{1}, a_{2}, \ldots, a_{p}\right)$ by
$$
a_{i}=b_{i}-b_{1}+k \bmod p
$$
for $1 \leq i \leq p$. Now note that $B$ in $S$ implies that
$a_{1}+a_{2}+\cdots+a_{p} \equiv\left(b_{1}+b_{2}+\cdots+b_{p}\right)-p b_{1}+p k \equiv\left(b_{1}+b_{2}+\cdots+b_{p}\right) \not \equiv 0 \quad(\bmod p)$
and therefore $B_{k}$ is in $S$ for all non-negative $k$. Now note that $B_{k}$ has first element $k$ for all $0 \leq k \leq p-1$ and therefore the sequences $B_{0}, B_{1}, \ldots, B_{p-1}$ are distinct.
Now define the cycle of $B$ as the set $\left\{B_{0}, B_{1}, \ldots, B_{p-1}\right\}$. Note that $B$ is in its own cycle since $B=B_{k}$ where $k=b_{1}$. Now note that since every sequence in $S$ is in exactly one cycle, $S$ is the disjoint union of cycles.
Now it will be shown that exactly one sequence per cycle is good. Consider an arbitrary cycle $B_{0}, B_{1}, \ldots, B_{p-1}$, and let $B_{0}=\left(b_{1}, b_{2}, \ldots, b_{p}\right)$ where $b_{0}=0$, and note that $B_{k}=\left(b_{1}+k, b_{2}+k, \ldots, b_{p}+k\right) \bmod p$. Let $u=b_{1}+b_{2}+\cdots+b_{p}$, and $v=b_{1} b_{2}+b_{2} b_{3}+\cdots+b_{p} b_{1}$ and note that $\left.\left(b_{1}+k\right)\left(b_{2}+k\right)+\left(b_{2}+k\right)\left(b_{3}+k\right)\right)+\cdots+$ $\left(b_{p}+k\right)\left(b_{1}+k\right)=u+2 k v \bmod p$ for all $0 \leq k \leq p-1$. Since $2 v$ is not divisible by $p$, there is exactly one value of $k$ with $0 \leq k \leq p-1$ such that $p$ divides $u+2 k v$ and it is exactly for this value of $k$ that $B_{k}$ is good. This shows that exactly one sequence per cycle is good and therefore that the number of good sequences in $S$ is $\frac{1}{p}|S|$, which is $p^{p-1}-p^{p-2}$.
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "Canada_MO/segmented/en-sol2014.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2014"
}
|
The quadrilateral $A B C D$ is inscribed in a circle. The point $P$ lies in the interior of $A B C D$, and $\angle P A B=\angle P B C=\angle P C D=\angle P D A$. The lines $A D$ and $B C$ meet at $Q$, and the lines $A B$ and $C D$ meet at $R$. Prove that the lines $P Q$ and $P R$ form the same angle as the diagonals of $A B C D$.
|
. Let $\Gamma$ be the circumcircle of quadrilateral $A B C D$. Let $\alpha=\angle P A B=$ $\angle P B C \angle P C D=\angle P D A$ and let $T_{1}, T_{2}, T_{3}$ and $T_{4}$ denote the circumcircles of triangles $A P D, B P C, A P B$ and $C P D$, respectively. Let $M$ be the intersection of $T_{1}$ with line $R P$ and let $N$ be the intersection of $T_{3}$ with line $S P$. Also let $X$ denote the intersection of diagonals $A C$ and $B D$.
By power of a point for circles $T_{1}$ and $\Gamma$, it follows that $R M \cdot R P=R A \cdot R D=$ $R B \cdot R C$ which implies that the quadrilateral $B M P C$ is cyclic and $M$ lies on $T_{2}$. Therefore $\angle P M B=\angle P C B=\alpha=\angle P A B=\angle D M P$ where all angles are directed. This implies that $M$ lies on the diagonal $B D$ and also that $\angle X M P=\angle D M P=\alpha$. By a symmetric argument applied to $S, T_{3}$ and $T_{4}$, it follows that $N$ lies on $T_{4}$ and that $N$ lies on diagonal $A C$ with $\angle X N P=\alpha$. Therefore $\angle X M P=\angle X N P$ and $X, M, P$ and $N$ are concyclic. This implies that the angle formed by lines $M P$ and $N P$ is equal to one of the angles formed by lines $M X$ and $N X$. The fact that $M$ lies on $B D$ and $R P$ and $N$ lies on $A C$ and $S P$ now implies the desired result.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
The quadrilateral $A B C D$ is inscribed in a circle. The point $P$ lies in the interior of $A B C D$, and $\angle P A B=\angle P B C=\angle P C D=\angle P D A$. The lines $A D$ and $B C$ meet at $Q$, and the lines $A B$ and $C D$ meet at $R$. Prove that the lines $P Q$ and $P R$ form the same angle as the diagonals of $A B C D$.
|
. Let $\Gamma$ be the circumcircle of quadrilateral $A B C D$. Let $\alpha=\angle P A B=$ $\angle P B C \angle P C D=\angle P D A$ and let $T_{1}, T_{2}, T_{3}$ and $T_{4}$ denote the circumcircles of triangles $A P D, B P C, A P B$ and $C P D$, respectively. Let $M$ be the intersection of $T_{1}$ with line $R P$ and let $N$ be the intersection of $T_{3}$ with line $S P$. Also let $X$ denote the intersection of diagonals $A C$ and $B D$.
By power of a point for circles $T_{1}$ and $\Gamma$, it follows that $R M \cdot R P=R A \cdot R D=$ $R B \cdot R C$ which implies that the quadrilateral $B M P C$ is cyclic and $M$ lies on $T_{2}$. Therefore $\angle P M B=\angle P C B=\alpha=\angle P A B=\angle D M P$ where all angles are directed. This implies that $M$ lies on the diagonal $B D$ and also that $\angle X M P=\angle D M P=\alpha$. By a symmetric argument applied to $S, T_{3}$ and $T_{4}$, it follows that $N$ lies on $T_{4}$ and that $N$ lies on diagonal $A C$ with $\angle X N P=\alpha$. Therefore $\angle X M P=\angle X N P$ and $X, M, P$ and $N$ are concyclic. This implies that the angle formed by lines $M P$ and $N P$ is equal to one of the angles formed by lines $M X$ and $N X$. The fact that $M$ lies on $B D$ and $R P$ and $N$ lies on $A C$ and $S P$ now implies the desired result.
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "Canada_MO/segmented/en-sol2014.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2014"
}
|
Fix positive integers $n$ and $k \geq 2$. A list of $n$ integers is written in a row on a blackboard. You can choose a contiguous block of integers, and I will either add 1 to all of them or subtract 1 from all of them. You can repeat this step as often as you like, possibly adapting your selections based on what I do. Prove that after a finite number of steps, you can reach a state where at least $n-k+2$ of the numbers on the blackboard are all simultaneously divisible by $k$.
## Life Financial
|
We will think of all numbers as being residues mod $k$. Consider the following strategy:
- If there are less than $k-1$ non-zero numbers, then stop.
- If the first number is 0 , then recursively solve on the remaining numbers.
- If the first number is $j$ with $0<j<k$, then choose the interval stretching from the first number to the $j$ th-last non-zero number.
First note that this strategy is indeed well defined. The first number must have value between 0 and $k-1$, and if we do not stop immediately, then there are at least $k-1$ non-zero numbers, and hence the third step can be performed.
For each $j$ with $1 \leq j \leq k-2$, we claim the first number can take on the value of $j$ at most a finite number of times without taking on the value of $j-1$ in between. If this were to fail, then every time the first number became $j$, I would have to add 1 to the selected numbers to avoid making it $j-1$. This will always increase the $j$-th last non-zero number, and that number will never be changed by other steps. Therefore, that number would eventually become 0 , and the next last non-zero number would eventually become zero, and so on, until the first number itself becomes the $j$-th last non-zero number, at which point we are done since $j \leq k-2$.
Rephrasing slightly, if $1 \leq j \leq k-2$, the first number can take on the value of $j$ at most a finite number of times between each time it takes on the value of $j-1$. It then immediately follows that if the first number can take on the value of $j-1$ at most a finite number of times, then it can also only take on the value of $j$ a finite number of times. However, if it ever takes on the value of 0 , we have already reduced the problem to $n-1$, so we can assume that never happens. It then follows that the first number can take on all the values $0,1,2, \ldots, k-2$ at most a finite number of times.
Finally, every time the first number takes on the value of $k-1$, it must subsequently take on the value of $k-2$ or 0 , and so that can also happen only finitely many times.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Fix positive integers $n$ and $k \geq 2$. A list of $n$ integers is written in a row on a blackboard. You can choose a contiguous block of integers, and I will either add 1 to all of them or subtract 1 from all of them. You can repeat this step as often as you like, possibly adapting your selections based on what I do. Prove that after a finite number of steps, you can reach a state where at least $n-k+2$ of the numbers on the blackboard are all simultaneously divisible by $k$.
## Life Financial
|
We will think of all numbers as being residues mod $k$. Consider the following strategy:
- If there are less than $k-1$ non-zero numbers, then stop.
- If the first number is 0 , then recursively solve on the remaining numbers.
- If the first number is $j$ with $0<j<k$, then choose the interval stretching from the first number to the $j$ th-last non-zero number.
First note that this strategy is indeed well defined. The first number must have value between 0 and $k-1$, and if we do not stop immediately, then there are at least $k-1$ non-zero numbers, and hence the third step can be performed.
For each $j$ with $1 \leq j \leq k-2$, we claim the first number can take on the value of $j$ at most a finite number of times without taking on the value of $j-1$ in between. If this were to fail, then every time the first number became $j$, I would have to add 1 to the selected numbers to avoid making it $j-1$. This will always increase the $j$-th last non-zero number, and that number will never be changed by other steps. Therefore, that number would eventually become 0 , and the next last non-zero number would eventually become zero, and so on, until the first number itself becomes the $j$-th last non-zero number, at which point we are done since $j \leq k-2$.
Rephrasing slightly, if $1 \leq j \leq k-2$, the first number can take on the value of $j$ at most a finite number of times between each time it takes on the value of $j-1$. It then immediately follows that if the first number can take on the value of $j-1$ at most a finite number of times, then it can also only take on the value of $j$ a finite number of times. However, if it ever takes on the value of 0 , we have already reduced the problem to $n-1$, so we can assume that never happens. It then follows that the first number can take on all the values $0,1,2, \ldots, k-2$ at most a finite number of times.
Finally, every time the first number takes on the value of $k-1$, it must subsequently take on the value of $k-2$ or 0 , and so that can also happen only finitely many times.
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "Canada_MO/segmented/en-sol2014.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2014"
}
|
Let $\mathbb{N}=\{1,2,3, \ldots\}$ be the set of positive integers. Find all functions $f$, defined on $\mathbb{N}$ and taking values in $\mathbb{N}$, such that $(n-1)^{2}<f(n) f(f(n))<n^{2}+n$ for every positive integer $n$.
|
The only such function is $f(n)=n$.
Assume that $f$ satisfies the given condition. It will be shown by induction that $f(n)=n$ for all $n \in \mathbb{N}$. Substituting $n=1$ yields that $0<f(1) f(f(1))<2$ which implies the base case $f(1)=1$. Now assume that $f(k)=k$ for all $k<n$ and assume for contradiction that $f(n) \neq n$.
On the one hand, if $f(n) \leq n-1$ then $f(f(n))=f(n)$ and $f(n) f(f(n))=f(n)^{2} \leq(n-1)^{2}$ which is a contradiction. On the other hand, if $f(n) \geq n+1$ then there are several ways to proceed.
Method 1: Assume $f(n)=M \geq n+1$. Then $(n+1) f(M) \leq f(n) f(f(n))<n^{2}+n$. Therefore $f(M)<n$, and hence $f(f(M))=f(M)$ and $f(M) f(f(M))=f(M)^{2}<n^{2} \leq$ $(M-1)^{2}$, which is a contradiction. This completes the induction.
Method 2: First note that if $|a-b|>1$, then the intervals $\left((a-1)^{2}, a^{2}+a\right)$ and $\left((b-1)^{2}, b^{2}+b\right)$ are disjoint which implies that $f(a)$ and $f(b)$ cannot be equal.
Assuming $f(n) \geq n+1$, it follows that $f(f(n))<\frac{n^{2}+n}{f(n)} \leq n$. This implies that for some $a \leq n-1, f(a)=f(f(n))$ which is a contradiction since $|f(n)-a| \geq n+1-a \geq 2$. This completes the induction.
Method 3: Assuming $f(n) \geq n+1$, it follows that $f(f(n))<\frac{n^{2}+n}{f(n)} \leq n$ and $f(f(f(n)))=$ $f(f(n))$. This implies that $(f(n)-1)^{2}<f(f(n)) f(f(f(n)))=f(f(n))^{2}<f(n)^{2}+f(n)$ and therefore that $f(f(n))=f(n)$ since $f(n)^{2}$ is the unique square satisfying this constraint. This implies that $f(n) f(f(n))=f(n)^{2} \geq(n+1)^{2}$ which is a contradiction, completing the induction.
|
f(n)=n
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Let $\mathbb{N}=\{1,2,3, \ldots\}$ be the set of positive integers. Find all functions $f$, defined on $\mathbb{N}$ and taking values in $\mathbb{N}$, such that $(n-1)^{2}<f(n) f(f(n))<n^{2}+n$ for every positive integer $n$.
|
The only such function is $f(n)=n$.
Assume that $f$ satisfies the given condition. It will be shown by induction that $f(n)=n$ for all $n \in \mathbb{N}$. Substituting $n=1$ yields that $0<f(1) f(f(1))<2$ which implies the base case $f(1)=1$. Now assume that $f(k)=k$ for all $k<n$ and assume for contradiction that $f(n) \neq n$.
On the one hand, if $f(n) \leq n-1$ then $f(f(n))=f(n)$ and $f(n) f(f(n))=f(n)^{2} \leq(n-1)^{2}$ which is a contradiction. On the other hand, if $f(n) \geq n+1$ then there are several ways to proceed.
Method 1: Assume $f(n)=M \geq n+1$. Then $(n+1) f(M) \leq f(n) f(f(n))<n^{2}+n$. Therefore $f(M)<n$, and hence $f(f(M))=f(M)$ and $f(M) f(f(M))=f(M)^{2}<n^{2} \leq$ $(M-1)^{2}$, which is a contradiction. This completes the induction.
Method 2: First note that if $|a-b|>1$, then the intervals $\left((a-1)^{2}, a^{2}+a\right)$ and $\left((b-1)^{2}, b^{2}+b\right)$ are disjoint which implies that $f(a)$ and $f(b)$ cannot be equal.
Assuming $f(n) \geq n+1$, it follows that $f(f(n))<\frac{n^{2}+n}{f(n)} \leq n$. This implies that for some $a \leq n-1, f(a)=f(f(n))$ which is a contradiction since $|f(n)-a| \geq n+1-a \geq 2$. This completes the induction.
Method 3: Assuming $f(n) \geq n+1$, it follows that $f(f(n))<\frac{n^{2}+n}{f(n)} \leq n$ and $f(f(f(n)))=$ $f(f(n))$. This implies that $(f(n)-1)^{2}<f(f(n)) f(f(f(n)))=f(f(n))^{2}<f(n)^{2}+f(n)$ and therefore that $f(f(n))=f(n)$ since $f(n)^{2}$ is the unique square satisfying this constraint. This implies that $f(n) f(f(n))=f(n)^{2} \geq(n+1)^{2}$ which is a contradiction, completing the induction.
|
{
"exam": "Canada_MO",
"problem_label": "1",
"problem_match": "\nProblem 1.",
"resource_path": "Canada_MO/segmented/en-sol2015.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2015"
}
|
Let $A B C$ be an acute-angled triangle with altitudes $A D, B E$, and $C F$. Let $H$ be the orthocentre, that is, the point where the altitudes meet. Prove that
$$
\frac{A B \cdot A C+B C \cdot B A+C A \cdot C B}{A H \cdot A D+B H \cdot B E+C H \cdot C F} \leq 2 .
$$
|
Method 1: Let $A B=c, A C=b$, and $B C=a$ denote the three side lengths of the triangle.
As $\angle B F H=\angle B D H=90^{\circ}, F H D B$ is a cyclic quadrilateral. By the Power-of-a-Point Theorem, $A H \cdot A D=A F \cdot A B$. (We can derive this result in other ways: for example, see Method 2, below.)
Since $A F=A C \cdot \cos \angle A$, we have $A H \cdot A D=A C \cdot A B \cdot \cos \angle A=b c \cos \angle A$.
## Life Financial
Hence,By the Cosine Law, $\cos \angle A=\frac{b^{2}+c^{2}-a^{2}}{2 b c}$, which implies that $A H \cdot A D=\frac{b^{2}+c^{2}-a^{2}}{2}$.
By symmetry, we can show that $B H \cdot B E=\frac{a^{2}+c^{2}-b^{2}}{2}$ and $C H \cdot C F=\frac{a^{2}+b^{2}-c^{2}}{2}$.
$$
\begin{aligned}
A H \cdot A D+B H \cdot B E+C H \cdot C F & =\frac{b^{2}+c^{2}-a^{2}}{2}+\frac{a^{2}+c^{2}-b^{2}}{2}+\frac{a^{2}+b^{2}-c^{2}}{2} \\
& =\frac{a^{2}+b^{2}+c^{2}}{2} .
\end{aligned}
$$
Our desired inequality, $\frac{A B \cdot A C+B C \cdot B A+C A \cdot C B}{A H \cdot A D+B H \cdot B E+C H \cdot C F} \leq 2$, is equivalent to the inequality $\frac{c b+a c+b a}{\frac{a^{2}+b^{2}+c^{2}}{2}} \leq 2$, which simplifies to $2 a^{2}+2 b^{2}+2 c^{2} \geq 2 a b+2 b c+2 c a$.
But this last inequality is easy to prove, as it is equivalent to $(a-b)^{2}+(a-c)^{2}+(b-c)^{2} \geq 0$.
Therefore, we have established the desired inequality. The proof also shows that equality occurs if and only if $a=b=c$, i.e., $\triangle A B C$ is equilateral.
Method 2: Observe that
$$
\frac{A E}{A H}=\cos (\angle H A E)=\frac{A D}{A C} \quad \text { and } \quad \frac{A F}{A H}=\cos (\angle H A F)=\frac{A D}{A B} \text {. }
$$
It follows that
$$
A C \cdot A E=A H \cdot A D=A B \cdot A F .
$$
By symmetry, we similarly have
$$
B C \cdot B D=B H \cdot B E=B F \cdot B A \quad \text { and } \quad C D \cdot C B=C H \cdot C F=C E \cdot C A \text {. }
$$
Therefore
$$
\begin{aligned}
& 2(A H \cdot A D+B H \cdot B E+C H \cdot C F) \\
& \quad=A B(A F+B F)+A C(A E+C E)+B C(B D+C D) \\
& \quad=A B^{2}+A C^{2}+B C^{2} .
\end{aligned}
$$
This proves Equation (1) in Method 1. The rest of the proof is the same as the part of the proof of Method 1 that follows Equation (1).
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $A B C$ be an acute-angled triangle with altitudes $A D, B E$, and $C F$. Let $H$ be the orthocentre, that is, the point where the altitudes meet. Prove that
$$
\frac{A B \cdot A C+B C \cdot B A+C A \cdot C B}{A H \cdot A D+B H \cdot B E+C H \cdot C F} \leq 2 .
$$
|
Method 1: Let $A B=c, A C=b$, and $B C=a$ denote the three side lengths of the triangle.
As $\angle B F H=\angle B D H=90^{\circ}, F H D B$ is a cyclic quadrilateral. By the Power-of-a-Point Theorem, $A H \cdot A D=A F \cdot A B$. (We can derive this result in other ways: for example, see Method 2, below.)
Since $A F=A C \cdot \cos \angle A$, we have $A H \cdot A D=A C \cdot A B \cdot \cos \angle A=b c \cos \angle A$.
## Life Financial
Hence,By the Cosine Law, $\cos \angle A=\frac{b^{2}+c^{2}-a^{2}}{2 b c}$, which implies that $A H \cdot A D=\frac{b^{2}+c^{2}-a^{2}}{2}$.
By symmetry, we can show that $B H \cdot B E=\frac{a^{2}+c^{2}-b^{2}}{2}$ and $C H \cdot C F=\frac{a^{2}+b^{2}-c^{2}}{2}$.
$$
\begin{aligned}
A H \cdot A D+B H \cdot B E+C H \cdot C F & =\frac{b^{2}+c^{2}-a^{2}}{2}+\frac{a^{2}+c^{2}-b^{2}}{2}+\frac{a^{2}+b^{2}-c^{2}}{2} \\
& =\frac{a^{2}+b^{2}+c^{2}}{2} .
\end{aligned}
$$
Our desired inequality, $\frac{A B \cdot A C+B C \cdot B A+C A \cdot C B}{A H \cdot A D+B H \cdot B E+C H \cdot C F} \leq 2$, is equivalent to the inequality $\frac{c b+a c+b a}{\frac{a^{2}+b^{2}+c^{2}}{2}} \leq 2$, which simplifies to $2 a^{2}+2 b^{2}+2 c^{2} \geq 2 a b+2 b c+2 c a$.
But this last inequality is easy to prove, as it is equivalent to $(a-b)^{2}+(a-c)^{2}+(b-c)^{2} \geq 0$.
Therefore, we have established the desired inequality. The proof also shows that equality occurs if and only if $a=b=c$, i.e., $\triangle A B C$ is equilateral.
Method 2: Observe that
$$
\frac{A E}{A H}=\cos (\angle H A E)=\frac{A D}{A C} \quad \text { and } \quad \frac{A F}{A H}=\cos (\angle H A F)=\frac{A D}{A B} \text {. }
$$
It follows that
$$
A C \cdot A E=A H \cdot A D=A B \cdot A F .
$$
By symmetry, we similarly have
$$
B C \cdot B D=B H \cdot B E=B F \cdot B A \quad \text { and } \quad C D \cdot C B=C H \cdot C F=C E \cdot C A \text {. }
$$
Therefore
$$
\begin{aligned}
& 2(A H \cdot A D+B H \cdot B E+C H \cdot C F) \\
& \quad=A B(A F+B F)+A C(A E+C E)+B C(B D+C D) \\
& \quad=A B^{2}+A C^{2}+B C^{2} .
\end{aligned}
$$
This proves Equation (1) in Method 1. The rest of the proof is the same as the part of the proof of Method 1 that follows Equation (1).
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\nProblem 2.",
"resource_path": "Canada_MO/segmented/en-sol2015.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2015"
}
|
On a $(4 n+2) \times(4 n+2)$ square grid, a turtle can move between squares sharing a side. The turtle begins in a corner square of the grid and enters each square exactly once, ending in the square where she started. In terms of $n$, what is the largest positive integer $k$ such that there must be a row or column that the turtle has entered at least $k$ distinct times?
|
We shall prove that the answer is $2 n+2$. Number the rows in increasing order, from top to bottom, and number the columns from left to right. By symmetry, we may (and shall) assume that the turtle starts in the top right corner square.
First we shall prove that some row or column must be entered at least $2 n+2$ times. Let $m=4 n+2$. First note that each time the turtle moves, she enters either a row or a column. Let $r_{i}$ denote the number of times the turtle enters row $i$, and let $c_{i}$ be similarly defined for column $i$. Since the turtle moves $m^{2}$ times,
$$
r_{1}+r_{2}+\cdots+r_{m}+c_{1}+c_{2}+\cdots+c_{m}=m^{2}
$$
Now note that each time the turtle enters column 1, the next column she enters must be column 2. Therefore $c_{1}$ is equal to the number of times the turtle enters column 2 from column 1. Furthermore, the turtle must enter column 2 from column 3 at least once, which implies that $c_{2}>c_{1}$. Therefore since the $2 m$ terms $r_{i}$ and $c_{i}$ are not all equal, one must be strictly greater than $m^{2} /(2 m)=2 n+1$ and therefore at least $2 n+2$.
Now we construct an example to show that it is possible that no row or column is entered more than $2 n+2$ times. Partition the square grid into four $(2 n+1) \times(2 n+1)$ quadrants $A, B, C$, and $D$, containing the upper left, upper right, lower left, and lower right corners, respectively. The turtle begins at the top right corner square of $B$, moves one square down, and then moves left through the whole second row of $B$. She then moves one square down and moves right through the whole third row of $B$. She continues in this pattern, moving through each remaining row of $B$ in succession and moving one square down when each row is completed. Since $2 n+1$ is odd, the turtle ends at the bottom right corner of $B$. She then moves one square down into $D$ and through each column of $D$ in turn, moving one square to the left when each column is completed. She ends at the lower left corner of $D$ and moves left into $C$ and through the rows of $C$, moving one square up when each row is completed, ending in the upper left corner of $C$. She then enters $A$ and moves through the columns of $A$, moving one square right when each column is completed. This takes her to the upper right corner of $A$, whereupon she enters $B$ and moves right through the top row of $B$, which returns her to her starting point. Each row passing through $A$ and $B$ is entered at most $2 n+1$ times in $A$ and once in $B$, and thus at most $2 n+2$ times in total. Similarly, each row and column in the grid is entered at most $2 n+2$ times by this path. (See figure below.)
|
2n+2
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
On a $(4 n+2) \times(4 n+2)$ square grid, a turtle can move between squares sharing a side. The turtle begins in a corner square of the grid and enters each square exactly once, ending in the square where she started. In terms of $n$, what is the largest positive integer $k$ such that there must be a row or column that the turtle has entered at least $k$ distinct times?
|
We shall prove that the answer is $2 n+2$. Number the rows in increasing order, from top to bottom, and number the columns from left to right. By symmetry, we may (and shall) assume that the turtle starts in the top right corner square.
First we shall prove that some row or column must be entered at least $2 n+2$ times. Let $m=4 n+2$. First note that each time the turtle moves, she enters either a row or a column. Let $r_{i}$ denote the number of times the turtle enters row $i$, and let $c_{i}$ be similarly defined for column $i$. Since the turtle moves $m^{2}$ times,
$$
r_{1}+r_{2}+\cdots+r_{m}+c_{1}+c_{2}+\cdots+c_{m}=m^{2}
$$
Now note that each time the turtle enters column 1, the next column she enters must be column 2. Therefore $c_{1}$ is equal to the number of times the turtle enters column 2 from column 1. Furthermore, the turtle must enter column 2 from column 3 at least once, which implies that $c_{2}>c_{1}$. Therefore since the $2 m$ terms $r_{i}$ and $c_{i}$ are not all equal, one must be strictly greater than $m^{2} /(2 m)=2 n+1$ and therefore at least $2 n+2$.
Now we construct an example to show that it is possible that no row or column is entered more than $2 n+2$ times. Partition the square grid into four $(2 n+1) \times(2 n+1)$ quadrants $A, B, C$, and $D$, containing the upper left, upper right, lower left, and lower right corners, respectively. The turtle begins at the top right corner square of $B$, moves one square down, and then moves left through the whole second row of $B$. She then moves one square down and moves right through the whole third row of $B$. She continues in this pattern, moving through each remaining row of $B$ in succession and moving one square down when each row is completed. Since $2 n+1$ is odd, the turtle ends at the bottom right corner of $B$. She then moves one square down into $D$ and through each column of $D$ in turn, moving one square to the left when each column is completed. She ends at the lower left corner of $D$ and moves left into $C$ and through the rows of $C$, moving one square up when each row is completed, ending in the upper left corner of $C$. She then enters $A$ and moves through the columns of $A$, moving one square right when each column is completed. This takes her to the upper right corner of $A$, whereupon she enters $B$ and moves right through the top row of $B$, which returns her to her starting point. Each row passing through $A$ and $B$ is entered at most $2 n+1$ times in $A$ and once in $B$, and thus at most $2 n+2$ times in total. Similarly, each row and column in the grid is entered at most $2 n+2$ times by this path. (See figure below.)

|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\nProblem 3.",
"resource_path": "Canada_MO/segmented/en-sol2015.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2015"
}
|
Let $A B C$ be an acute-angled triangle with circumcenter $O$. Let $\Gamma$ be a circle with centre on the altitude from $A$ in $A B C$, passing through vertex $A$ and points $P$ and $Q$ on sides $A B$ and $A C$. Assume that $B P \cdot C Q=A P \cdot A Q$. Prove that $\Gamma$ is tangent to the circumcircle of triangle BOC.
|
Let $\omega$ be the circumcircle of $B O C$. Let $M$ be the point diametrically opposite to $O$ on $\omega$ and let the line $A M$ intersect $\omega$ at $M$ and $K$. Since $O$ is the circumcenter of $A B C$, it follows that $O B=O C$ and therefore that $O$ is the midpoint of the $\operatorname{arc} \widehat{B O C}$ of $\omega$. Since $M$ is diametrically opposite to $O$, it follows that $M$ is the midpoint of the arc $\widehat{B M C}$ of $\omega$. This implies since $K$ is on $\omega$ that $K M$ is the bisector of $\angle B K C$. Since $K$ is on $\omega$, this implies that $\angle B K M=\angle C K M$, i.e. $K M$ is the bisector of $\angle B K C$.
Since $O$ is the circumcenter of $A B C$, it follows that $\angle B O C=2 \angle B A C$. Since $B, K, O$ and $C$ all lie on $\omega$, it also follows that $\angle B K C=\angle B O C=2 \angle B A C$. Since $K M$ bisects $\angle B K C$, it follows that $\angle B K M=\angle C K M=\angle B A C$. The fact that $A, K$ and $M$ lie on a line therefore implies that $\angle A K B=\angle A K C=180^{\circ}-\angle B A C$. Now it follows that
$$
\angle K B A=180^{\circ}-\angle A K B-\angle K A B=\angle B A C-\angle K A B=\angle K A C .
$$
This implies that triangles $K B A$ and $K A C$ are similar. Rearranging the condition in the problem statement yields that $B P / A P=A Q / C Q$ which, when combined with the fact that $K B A$ and $K A C$ are similar, implies that triangles $K P A$ and $K Q C$ are similar. Therefore $\angle K P A=\angle K Q C=180^{\circ}-\angle K Q A$ which implies that $K$ lies on $\Gamma$.
Now let $S$ denote the centre of $\Gamma$ and let $T$ denote the centre of $\omega$. Note that $T$ is the midpoint of segment $O M$ and that $T M$ and $A S$, which are both perpendicular to $B C$, are parallel. This implies that $\angle K M T=\angle K A S$ since $A, K$ and $M$ are collinear. Further, since $K T M$ and $K S A$ are isosceles triangles, it follows that $\angle T K M=\angle K M T$ and $\angle S K A=$
$\angle K S A$. Therefore $\angle T K M=\angle S K A$ which implies that $S, T$ and $K$ are collinear. Therefore $\Gamma$ and $\omega$ intersect at a point $K$ which lies on the line $S T$ connecting the centres of the two circles. This implies that the circles $\Gamma$ and $\omega$ are tangent at $K$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $A B C$ be an acute-angled triangle with circumcenter $O$. Let $\Gamma$ be a circle with centre on the altitude from $A$ in $A B C$, passing through vertex $A$ and points $P$ and $Q$ on sides $A B$ and $A C$. Assume that $B P \cdot C Q=A P \cdot A Q$. Prove that $\Gamma$ is tangent to the circumcircle of triangle BOC.
|
Let $\omega$ be the circumcircle of $B O C$. Let $M$ be the point diametrically opposite to $O$ on $\omega$ and let the line $A M$ intersect $\omega$ at $M$ and $K$. Since $O$ is the circumcenter of $A B C$, it follows that $O B=O C$ and therefore that $O$ is the midpoint of the $\operatorname{arc} \widehat{B O C}$ of $\omega$. Since $M$ is diametrically opposite to $O$, it follows that $M$ is the midpoint of the arc $\widehat{B M C}$ of $\omega$. This implies since $K$ is on $\omega$ that $K M$ is the bisector of $\angle B K C$. Since $K$ is on $\omega$, this implies that $\angle B K M=\angle C K M$, i.e. $K M$ is the bisector of $\angle B K C$.
Since $O$ is the circumcenter of $A B C$, it follows that $\angle B O C=2 \angle B A C$. Since $B, K, O$ and $C$ all lie on $\omega$, it also follows that $\angle B K C=\angle B O C=2 \angle B A C$. Since $K M$ bisects $\angle B K C$, it follows that $\angle B K M=\angle C K M=\angle B A C$. The fact that $A, K$ and $M$ lie on a line therefore implies that $\angle A K B=\angle A K C=180^{\circ}-\angle B A C$. Now it follows that
$$
\angle K B A=180^{\circ}-\angle A K B-\angle K A B=\angle B A C-\angle K A B=\angle K A C .
$$
This implies that triangles $K B A$ and $K A C$ are similar. Rearranging the condition in the problem statement yields that $B P / A P=A Q / C Q$ which, when combined with the fact that $K B A$ and $K A C$ are similar, implies that triangles $K P A$ and $K Q C$ are similar. Therefore $\angle K P A=\angle K Q C=180^{\circ}-\angle K Q A$ which implies that $K$ lies on $\Gamma$.
Now let $S$ denote the centre of $\Gamma$ and let $T$ denote the centre of $\omega$. Note that $T$ is the midpoint of segment $O M$ and that $T M$ and $A S$, which are both perpendicular to $B C$, are parallel. This implies that $\angle K M T=\angle K A S$ since $A, K$ and $M$ are collinear. Further, since $K T M$ and $K S A$ are isosceles triangles, it follows that $\angle T K M=\angle K M T$ and $\angle S K A=$
$\angle K S A$. Therefore $\angle T K M=\angle S K A$ which implies that $S, T$ and $K$ are collinear. Therefore $\Gamma$ and $\omega$ intersect at a point $K$ which lies on the line $S T$ connecting the centres of the two circles. This implies that the circles $\Gamma$ and $\omega$ are tangent at $K$.
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\nProblem 4.",
"resource_path": "Canada_MO/segmented/en-sol2015.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2015"
}
|
Let $p$ be a prime number for which $\frac{p-1}{2}$ is also prime, and let a, $b, c$ be integers not divisible by $p$. Prove that there are at most $1+\sqrt{2 p}$ positive integers $n$ such that $n<p$ and $p$ divides $a^{n}+b^{n}+c^{n}$.
|
First suppose $b \equiv \pm a(\bmod p)$ and $c \equiv \pm b(\bmod p)$. Then, for any $n$, we have $a^{n}+b^{n}+c^{n} \equiv \pm a^{n}$ or $\pm 3 a^{n}(\bmod p)$. We are given that $p \neq 3\left(\right.$ since $\frac{3-1}{2}$ is not prime) and $p \not a$, so it follows that $a^{n}+b^{n}+c^{n} \not \equiv 0(\bmod p)$. The claim is trivial in this case. Otherwise, we may assume without loss of generality that $b \not \equiv \pm a(\bmod p) \Longrightarrow b a^{-1} \not \equiv \pm 1(\bmod p)$.
Now let $q=\frac{p-1}{2}$. By Fermat's little theorem, we know that the order of $b a^{-1} \bmod p$ divides $p-1=2 q$. However, since $b a^{-1} \not \equiv \pm 1(\bmod p)$, the order of $b a^{-1}$ does not divide 2 . Thus, the order must be either $q$ or $2 q$.
Next, let $S$ denote the set of positive integers $n<p$ such that $a^{n}+b^{n}+c^{n} \equiv 0(\bmod p)$, and let $s_{t}$ denote the number of ordered pairs $(i, j) \subset S$ such that $i-j \equiv t(\bmod p-1)$.
Lemma: If $t$ is a positive integer less than $2 q$ and not equal to $q$, then $s_{t} \leq 2$.
Proof: Consider $i, j \in S$ with $j-i \equiv t(\bmod p-1)$. Then we have
$$
\begin{aligned}
& a^{i}+b^{i}+c^{i} \equiv 0(\bmod p) \\
\Longrightarrow & a^{i} c^{j-i}+b^{i} c^{j-i}+c^{j} \equiv 0(\bmod p) \\
\Longrightarrow & a^{i} c^{j-i}+b^{i} c^{j-i}-a^{j}-b^{j} \equiv 0(\bmod p) \\
\Longrightarrow & a^{i} \cdot\left(c^{t}-a^{t}\right) \equiv b^{i} \cdot\left(b^{t}-c^{t}\right)(\bmod p) .
\end{aligned}
$$
If $c^{t} \equiv a^{t}(\bmod p)$, then this implies $c^{t} \equiv b^{t}(\bmod p)$ as well, so $\left(a b^{-1}\right)^{t} \equiv 1(\bmod p)$. However, we know the order of $a b^{-1}$ is $q$ or $2 q$, and $q \not t$, so this impossible. Thus, we can write
$$
\left(a b^{-1}\right)^{i} \equiv\left(b^{t}-c^{t}\right) \cdot\left(c^{t}-a^{t}\right)^{-1}(\bmod p)
$$
For a fixed $t$, the right-hand side of this equation is fixed, so $\left(a b^{-1}\right)^{i}$ is also fixed. Since the order of $a b^{-1}$ is either $q$ or $2 q$, it follows that there are at most 2 solutions for $i$, and the lemma is proven.
Now, for each element $i$ in $S$, there are at least $|S|-2$ other elements that differ from $i$ by a quantity other than $q(\bmod p-1)$. Therefore, the lemma implies that
$$
\begin{aligned}
|S| \cdot(|S|-2) & \leq \sum_{t \neq q} s_{t} \leq 2 \cdot(p-2) \\
\Longrightarrow \quad(|S|-1)^{2} & \leq 2 p-3 \\
\Longrightarrow \quad|S| & <\sqrt{2 p}+1 .
\end{aligned}
$$
|
|S| < \sqrt{2 p} + 1
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $p$ be a prime number for which $\frac{p-1}{2}$ is also prime, and let a, $b, c$ be integers not divisible by $p$. Prove that there are at most $1+\sqrt{2 p}$ positive integers $n$ such that $n<p$ and $p$ divides $a^{n}+b^{n}+c^{n}$.
|
First suppose $b \equiv \pm a(\bmod p)$ and $c \equiv \pm b(\bmod p)$. Then, for any $n$, we have $a^{n}+b^{n}+c^{n} \equiv \pm a^{n}$ or $\pm 3 a^{n}(\bmod p)$. We are given that $p \neq 3\left(\right.$ since $\frac{3-1}{2}$ is not prime) and $p \not a$, so it follows that $a^{n}+b^{n}+c^{n} \not \equiv 0(\bmod p)$. The claim is trivial in this case. Otherwise, we may assume without loss of generality that $b \not \equiv \pm a(\bmod p) \Longrightarrow b a^{-1} \not \equiv \pm 1(\bmod p)$.
Now let $q=\frac{p-1}{2}$. By Fermat's little theorem, we know that the order of $b a^{-1} \bmod p$ divides $p-1=2 q$. However, since $b a^{-1} \not \equiv \pm 1(\bmod p)$, the order of $b a^{-1}$ does not divide 2 . Thus, the order must be either $q$ or $2 q$.
Next, let $S$ denote the set of positive integers $n<p$ such that $a^{n}+b^{n}+c^{n} \equiv 0(\bmod p)$, and let $s_{t}$ denote the number of ordered pairs $(i, j) \subset S$ such that $i-j \equiv t(\bmod p-1)$.
Lemma: If $t$ is a positive integer less than $2 q$ and not equal to $q$, then $s_{t} \leq 2$.
Proof: Consider $i, j \in S$ with $j-i \equiv t(\bmod p-1)$. Then we have
$$
\begin{aligned}
& a^{i}+b^{i}+c^{i} \equiv 0(\bmod p) \\
\Longrightarrow & a^{i} c^{j-i}+b^{i} c^{j-i}+c^{j} \equiv 0(\bmod p) \\
\Longrightarrow & a^{i} c^{j-i}+b^{i} c^{j-i}-a^{j}-b^{j} \equiv 0(\bmod p) \\
\Longrightarrow & a^{i} \cdot\left(c^{t}-a^{t}\right) \equiv b^{i} \cdot\left(b^{t}-c^{t}\right)(\bmod p) .
\end{aligned}
$$
If $c^{t} \equiv a^{t}(\bmod p)$, then this implies $c^{t} \equiv b^{t}(\bmod p)$ as well, so $\left(a b^{-1}\right)^{t} \equiv 1(\bmod p)$. However, we know the order of $a b^{-1}$ is $q$ or $2 q$, and $q \not t$, so this impossible. Thus, we can write
$$
\left(a b^{-1}\right)^{i} \equiv\left(b^{t}-c^{t}\right) \cdot\left(c^{t}-a^{t}\right)^{-1}(\bmod p)
$$
For a fixed $t$, the right-hand side of this equation is fixed, so $\left(a b^{-1}\right)^{i}$ is also fixed. Since the order of $a b^{-1}$ is either $q$ or $2 q$, it follows that there are at most 2 solutions for $i$, and the lemma is proven.
Now, for each element $i$ in $S$, there are at least $|S|-2$ other elements that differ from $i$ by a quantity other than $q(\bmod p-1)$. Therefore, the lemma implies that
$$
\begin{aligned}
|S| \cdot(|S|-2) & \leq \sum_{t \neq q} s_{t} \leq 2 \cdot(p-2) \\
\Longrightarrow \quad(|S|-1)^{2} & \leq 2 p-3 \\
\Longrightarrow \quad|S| & <\sqrt{2 p}+1 .
\end{aligned}
$$
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\nProblem 5.",
"resource_path": "Canada_MO/segmented/en-sol2015.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2015"
}
|
The integers $1,2,3, \ldots, 2016$ are written on a board. You can choose any two numbers on the board and replace them with their average. For example, you can replace 1 and 2 with 1.5 , or you can replace 1 and 3 with a second copy of 2 . After 2015 replacements of this kind, the board will have only one number left on it.
(a) Prove that there is a sequence of replacements that will make the final number equal to 2 .
(b) Prove that there is a sequence of replacements that will make the final number equal to 1000 .
|
(a) First replace 2014 and 2016 with 2015, and then replace the two copies of 2015 with a single copy. This leaves us with $\{1,2, \ldots, 2013,2015\}$. From here, we can replace 2013 and 2015 with 2014 to get $\{1,2, \ldots, 2012,2014\}$. We can then replace 2012 and 2014 with 2013 , and so on, until we eventually get to $\{1,3\}$. We finish by replacing 1 and 3 with 2.
(b) Using the same construction as in (a), we can find a sequence of replacements that reduces $\{a, a+1, \ldots, b\}$ to just $\{a+1\}$. Similarly, can also find a sequence of replacements that reduces $\{a, a+1, \ldots, b\}$ to just $\{b-1\}$.
In particular, we can find sequences of replacements that reduce $\{1,2, \ldots, 999\}$
to just $\{998\}$, and that reduce $\{1001,1002, \ldots, 2016\}$ to just $\{1002\}$. This leaves us with $\{998,1000,1002\}$. We can replace 998 and 1002 with a second copy of 1000 , and then replace the two copies of 1000 with a single copy to complete the construction.
|
proof
|
Yes
|
Yes
|
proof
|
Algebra
|
The integers $1,2,3, \ldots, 2016$ are written on a board. You can choose any two numbers on the board and replace them with their average. For example, you can replace 1 and 2 with 1.5 , or you can replace 1 and 3 with a second copy of 2 . After 2015 replacements of this kind, the board will have only one number left on it.
(a) Prove that there is a sequence of replacements that will make the final number equal to 2 .
(b) Prove that there is a sequence of replacements that will make the final number equal to 1000 .
|
(a) First replace 2014 and 2016 with 2015, and then replace the two copies of 2015 with a single copy. This leaves us with $\{1,2, \ldots, 2013,2015\}$. From here, we can replace 2013 and 2015 with 2014 to get $\{1,2, \ldots, 2012,2014\}$. We can then replace 2012 and 2014 with 2013 , and so on, until we eventually get to $\{1,3\}$. We finish by replacing 1 and 3 with 2.
(b) Using the same construction as in (a), we can find a sequence of replacements that reduces $\{a, a+1, \ldots, b\}$ to just $\{a+1\}$. Similarly, can also find a sequence of replacements that reduces $\{a, a+1, \ldots, b\}$ to just $\{b-1\}$.
In particular, we can find sequences of replacements that reduce $\{1,2, \ldots, 999\}$
to just $\{998\}$, and that reduce $\{1001,1002, \ldots, 2016\}$ to just $\{1002\}$. This leaves us with $\{998,1000,1002\}$. We can replace 998 and 1002 with a second copy of 1000 , and then replace the two copies of 1000 with a single copy to complete the construction.
|
{
"exam": "Canada_MO",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "Canada_MO/segmented/en-sol2016.jsonl",
"solution_match": "\nSolution:",
"tier": "T2",
"year": "2016"
}
|
Consider the following system of 10 equations in 10 real variables $v_{1}, \ldots, v_{10}$ :
$$
v_{i}=1+\frac{6 v_{i}^{2}}{v_{1}^{2}+v_{2}^{2}+\cdots+v_{10}^{2}} \quad(i=1, \ldots, 10) .
$$
Find all 10-tuples $\left(v_{1}, v_{2}, \ldots, v_{10}\right)$ that are solutions of this system.
## Sun
Life Financial
|
For a particular solution $\left(v_{1}, v_{2}, \ldots, v_{10}\right)$, let $s=v_{1}^{2}+v_{2}^{2}+\cdots+v_{10}^{2}$. Then
$$
v_{i}=1+\frac{6 v_{i}^{2}}{s} \Rightarrow 6 v_{i}^{2}-s v_{i}+s=0
$$
Let $a$ and $b$ be the roots of the quadratic $6 x^{2}-s x+s=0$, so for each $i, v_{i}=a$ or $v_{i}=b$. We also have $a b=s / 6$ (by Vieta's formula, for example).
If all the $v_{i}$ are equal, then
$$
v_{i}=1+\frac{6}{10}=\frac{8}{5}
$$
for all $i$. Otherwise, let $5+k$ of the $v_{i}$ be $a$, and let $5-k$ of the $v_{i}$ be $b$, where $0<k \leq 4$. Then by the AM-GM inequality,
$$
6 a b=s=(5+k) a^{2}+(5-k) b^{2} \geq 2 a b \sqrt{25-k^{2}}
$$
From the given equations, $v_{i} \geq 1$ for all $i$, so $a$ and $b$ are positive. Then $\sqrt{25-k^{2}} \leq 3 \Rightarrow 25-k^{2} \leq 9 \Rightarrow k^{2} \geq 16 \Rightarrow k=4$. Hence, $6 a b=9 a^{2}+b^{2} \Rightarrow(b-3 a)^{2}=0 \Rightarrow b=3 a$.
Adding all given ten equations, we get
$$
v_{1}+v_{2}+\cdots+v_{10}=16
$$
But $v_{1}+v_{2}+\cdots+v_{10}=9 a+b=12 a$, so $a=16 / 12=4 / 3$ and $b=4$. Therefore, the solutions are $(8 / 5,8 / 5, \ldots, 8 / 5)$ and all ten permutations of $(4 / 3,4 / 3, \ldots, 4 / 3,4)$.
|
(8 / 5,8 / 5, \ldots, 8 / 5) \text{ and all ten permutations of } (4 / 3,4 / 3, \ldots, 4 / 3,4)
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Consider the following system of 10 equations in 10 real variables $v_{1}, \ldots, v_{10}$ :
$$
v_{i}=1+\frac{6 v_{i}^{2}}{v_{1}^{2}+v_{2}^{2}+\cdots+v_{10}^{2}} \quad(i=1, \ldots, 10) .
$$
Find all 10-tuples $\left(v_{1}, v_{2}, \ldots, v_{10}\right)$ that are solutions of this system.
## Sun
Life Financial
|
For a particular solution $\left(v_{1}, v_{2}, \ldots, v_{10}\right)$, let $s=v_{1}^{2}+v_{2}^{2}+\cdots+v_{10}^{2}$. Then
$$
v_{i}=1+\frac{6 v_{i}^{2}}{s} \Rightarrow 6 v_{i}^{2}-s v_{i}+s=0
$$
Let $a$ and $b$ be the roots of the quadratic $6 x^{2}-s x+s=0$, so for each $i, v_{i}=a$ or $v_{i}=b$. We also have $a b=s / 6$ (by Vieta's formula, for example).
If all the $v_{i}$ are equal, then
$$
v_{i}=1+\frac{6}{10}=\frac{8}{5}
$$
for all $i$. Otherwise, let $5+k$ of the $v_{i}$ be $a$, and let $5-k$ of the $v_{i}$ be $b$, where $0<k \leq 4$. Then by the AM-GM inequality,
$$
6 a b=s=(5+k) a^{2}+(5-k) b^{2} \geq 2 a b \sqrt{25-k^{2}}
$$
From the given equations, $v_{i} \geq 1$ for all $i$, so $a$ and $b$ are positive. Then $\sqrt{25-k^{2}} \leq 3 \Rightarrow 25-k^{2} \leq 9 \Rightarrow k^{2} \geq 16 \Rightarrow k=4$. Hence, $6 a b=9 a^{2}+b^{2} \Rightarrow(b-3 a)^{2}=0 \Rightarrow b=3 a$.
Adding all given ten equations, we get
$$
v_{1}+v_{2}+\cdots+v_{10}=16
$$
But $v_{1}+v_{2}+\cdots+v_{10}=9 a+b=12 a$, so $a=16 / 12=4 / 3$ and $b=4$. Therefore, the solutions are $(8 / 5,8 / 5, \ldots, 8 / 5)$ and all ten permutations of $(4 / 3,4 / 3, \ldots, 4 / 3,4)$.
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "Canada_MO/segmented/en-sol2016.jsonl",
"solution_match": "\n## Solution:",
"tier": "T2",
"year": "2016"
}
|
Find all polynomials $P(x)$ with integer coefficients such that $P(P(n)+$ $n$ ) is a prime number for infinitely many integers $n$.
Answer: $P(n)=p$ where $p$ is a prime number and $P(n)=-2 n+b$ where $b$ is odd.
|
Note that if $P(n)=0$ then $P(P(n)+n)=P(n)=0$ which is not prime. Let $P(x)$ be a degree $k$ polynomial of the form $P(x)=a_{k} x^{k}+a_{k-1} x^{k-1}+\cdots+a_{0}$ and note that if $P(n) \neq 0$ then
$$
\begin{aligned}
& P(P(n)+n)-P(n)= \\
& \quad a_{k}\left[(P(n)+n)^{k}-n^{k}\right]+a_{k-1}\left[(P(n)+n)^{k-1}-n^{k-1}\right]+\cdots+a_{1} P(n)
\end{aligned}
$$
which is divisible by $(P(n)+n)-n=P(n)$. Therefore if $P(P(n)+n)$ is prime then either $P(n)= \pm 1$ or $P(P(n)+n)= \pm P(n)=p$ for some prime number $p$. Since $P(x)$ is a polynomial, it follows that $P(n)= \pm 1$ for only finitely many integers $n$. Therefore either $P(n)=P(P(n)+n)$ for infinitely many integers $n$ or $P(n)=-P(P(n)+n)$ for infinitely many integers $n$. Suppose that $P(n)=P(P(n)+n)$ for infinitely many integers $n$. This implies that the polynomial $P(P(x)+x)-P(x)$ has infinitely many roots and thus is identically zero. Therefore $P(P(x)+$ $x)=P(x)$ holds identically. Now note that if $k \geq 2$ then $P(P(x)+x)$ has degree $k^{2}$ while $P(x)$ has degree $k$, which is not possible. Therefore $P(x)$ is at most linear with $P(x)=a x+b$ for some integers $a$ and $b$. Now note that
$$
P(P(x)+x)=a(a+1) x+a b+b
$$
and thus $a=a(a+1)$ and $a b+b=b$. It follows that $a=0$ which leads to the solution $P(n)=p$ where $p$ is a prime number. By the same argument if $P(n)=-P(P(n)+n)$ for infinitely many integers $n$ then $P(x)=-P(P(x)+x)$ holds identically and $P(x)$ is linear with $P(x)=a x+b$. In this case it follows that $a=-a(a+1)$ and $a b+b=-b$. This implies that either $a=0$ or $a=-2$. If $a=-2$ then $P(n)=-2 n+b$ which is prime for some integers $n$ only if $b$ is odd. Note that in this case $P(P(n)+n)=2 n-b$ which is indeed prime for infinitely many integers $n$ as long as $b$ is odd.
|
P(n)=p \text{ where } p \text{ is a prime number and } P(n)=-2 n+b \text{ where } b \text{ is odd}
|
Yes
|
Yes
|
math-word-problem
|
Algebra
|
Find all polynomials $P(x)$ with integer coefficients such that $P(P(n)+$ $n$ ) is a prime number for infinitely many integers $n$.
Answer: $P(n)=p$ where $p$ is a prime number and $P(n)=-2 n+b$ where $b$ is odd.
|
Note that if $P(n)=0$ then $P(P(n)+n)=P(n)=0$ which is not prime. Let $P(x)$ be a degree $k$ polynomial of the form $P(x)=a_{k} x^{k}+a_{k-1} x^{k-1}+\cdots+a_{0}$ and note that if $P(n) \neq 0$ then
$$
\begin{aligned}
& P(P(n)+n)-P(n)= \\
& \quad a_{k}\left[(P(n)+n)^{k}-n^{k}\right]+a_{k-1}\left[(P(n)+n)^{k-1}-n^{k-1}\right]+\cdots+a_{1} P(n)
\end{aligned}
$$
which is divisible by $(P(n)+n)-n=P(n)$. Therefore if $P(P(n)+n)$ is prime then either $P(n)= \pm 1$ or $P(P(n)+n)= \pm P(n)=p$ for some prime number $p$. Since $P(x)$ is a polynomial, it follows that $P(n)= \pm 1$ for only finitely many integers $n$. Therefore either $P(n)=P(P(n)+n)$ for infinitely many integers $n$ or $P(n)=-P(P(n)+n)$ for infinitely many integers $n$. Suppose that $P(n)=P(P(n)+n)$ for infinitely many integers $n$. This implies that the polynomial $P(P(x)+x)-P(x)$ has infinitely many roots and thus is identically zero. Therefore $P(P(x)+$ $x)=P(x)$ holds identically. Now note that if $k \geq 2$ then $P(P(x)+x)$ has degree $k^{2}$ while $P(x)$ has degree $k$, which is not possible. Therefore $P(x)$ is at most linear with $P(x)=a x+b$ for some integers $a$ and $b$. Now note that
$$
P(P(x)+x)=a(a+1) x+a b+b
$$
and thus $a=a(a+1)$ and $a b+b=b$. It follows that $a=0$ which leads to the solution $P(n)=p$ where $p$ is a prime number. By the same argument if $P(n)=-P(P(n)+n)$ for infinitely many integers $n$ then $P(x)=-P(P(x)+x)$ holds identically and $P(x)$ is linear with $P(x)=a x+b$. In this case it follows that $a=-a(a+1)$ and $a b+b=-b$. This implies that either $a=0$ or $a=-2$. If $a=-2$ then $P(n)=-2 n+b$ which is prime for some integers $n$ only if $b$ is odd. Note that in this case $P(P(n)+n)=2 n-b$ which is indeed prime for infinitely many integers $n$ as long as $b$ is odd.
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "Canada_MO/segmented/en-sol2016.jsonl",
"solution_match": "\nSolution:",
"tier": "T2",
"year": "2016"
}
|
Lavaman versus the Flea. Let $A, B$, and $F$ be positive integers, and assume $A<B<2 A$. A flea is at the number 0 on the number line. The flea can move by jumping to the right by $A$ or by $B$. Before the flea starts jumping, Lavaman chooses finitely many intervals $\{m+$ $1, m+2, \ldots, m+A\}$ consisting of $A$ consecutive positive integers, and places lava at all of the integers in the intervals. The intervals must be chosen so that:
(i) any two distinct intervals are disjoint and not adjacent;
(ii) there are at least $F$ positive integers with no lava between any two intervals; and
(iii) no lava is placed at any integer less than $F$.
Prove that the smallest $F$ for which the flea can jump over all the intervals and avoid all the lava, regardless of what Lavaman does,
is $F=(n-1) A+B$, where $n$ is the positive integer such that $\frac{A}{n+1} \leq B-A<\frac{A}{n}$.
|
Let $B=A+C$ where $A /(n+1) \leq C<A / n$.
First, here is an informal sketch of the proof.
Lavaman's strategy: Use only safe intervals with $n A+C-1$ integers. The flea will start at position $[1, C]$ from the left, which puts him at position $[n A, n A+C-1]$ from the right. After $n-1$ jumps, he will still have $n A-(n-1)(A+C)=A-(n-1) C>C$ distance to go, which is not enough for a big jump to clear the lava. Thus, he must do at least $n$ jumps in the safe interval, but that's possible only with all small jumps, and furthermore is impossible if the starting position is $C$. This gives him starting position 1 higher in the next safe interval, so sooner or later the flea is going to hit the lava.
Flea's strategy: The flea just does one interval at a time. If the safe interval has at least $n A+C$ integers in it, the flea has distance $d>n A$ to go to the next lava when it starts. Repeatedly do big jumps until $d$ is between 1 and $C \bmod A$, then small jumps until the remaining distance is between 1 and $C$, then a final big jump. This works as long as the first part does. However, we get at least $n$ big jumps since floor $((d-1) / A)$ can never go down two from a big jump (or we'd be done doing big jumps), so we get $n$ big jumps, and thus we are good if $d \bmod A$ is in any of $[1, C],[C+1,2 C], \ldots[n C+1,(n+1) C]$, but that's everything.
Let $C=B-A$. We shall write our intervals of lava in the form $\left(L_{i}, R_{i}\right]=\left\{L_{i}+1, L_{i}+2, \ldots, R_{i}\right\}$, where $R_{i}=L_{i}+A$ and $R_{i-1}<L_{i}$ for every $i \geq 1$. We also let $R_{0}=0$. We shall also represent a path for the flea as a sequence of integers $x_{0}, x_{1}, x_{2}, \ldots$ where $x_{0}=0$ and $x_{j}-x_{j-1} \in\{A, B\}$ for every $j \geq 0$.
Now here is a detailed proof.
First, assume $F<(n-1) A+B(=n A+C)$ : we must prove that Lavaman has a winning strategy. Let $L_{i}=R_{i-1}+n A+C-1$ for every $i \geq 1$. (Observe that $n A+C-1 \geq F$.)
Assume that the flea has an infinite path that avoids all the lava, which
means that $x_{j} \notin\left(L_{i}, R_{i}\right]$ for all $i, j \geq 1$. For each $i \geq 1$, let
$$
\begin{gathered}
M_{i}=\max \left\{x_{j}: x_{j} \leq L_{i}\right\}, \quad m_{i}=\min \left\{x_{j}: x_{j}>R_{i}\right\}, \\
\text { and } J(i)=\max \left\{j: x_{j} \leq L_{i}\right\}
\end{gathered}
$$
Also let $m_{0}=0$. Then for $i \geq 1$ we have
$$
M_{i}=x_{J(i)} \quad \text { and } \quad m_{i}=x_{J(i)+1} .
$$
Also, for every $i \geq 1$, we have
(a) $m_{i}=M_{i}+B$ (because $M_{i}+A \leq L_{i}+A=R_{i}$ );
(b) $L_{i} \geq M_{i}>L_{i}-C\left(\right.$ since $\left.M_{i}=m_{i}-B>R_{i}-B=L_{i}+A-B\right)$;
and
(c) $R_{i}<m_{i} \leq R_{i}+C\left(\right.$ since $\left.m_{i}=M_{i}+B \leq L_{i}+B=R_{i}+C\right)$.
Claim 1: $J(i+1)=J(i)+n+1$ for every $i \geq 1$. (That is, after jumping over one interval of lava, the flea must make exactly $n$ jumps before jumping over the next interval of lava.)
Proof:
$$
\begin{aligned}
x_{J(i)+n+1} & \leq x_{J(i)+1}+B n \\
& =m_{i}+B n \\
& <R_{i}+C+\left(A+\frac{A}{n}\right) n \\
& =L_{i+1}+A+1
\end{aligned}
$$
Because of the strict inequality, we have $x_{J(i)+n+1} \leq R_{i+1}$, and hence $x_{J(i)+n+1} \leq L_{i+1}$. Therefore $J(i)+n+1 \leq J(i+1)$. Next, we have
$$
\begin{aligned}
x_{J(i)+n+1} & \geq x_{J(i)+1}+A n \\
& =m_{i}+A n \\
& >R_{i}+A n \\
& =L_{i+1}-C+1 \\
& >L_{i+1}-A+1 \quad(\text { since } C<A) .
\end{aligned}
$$
Therefore $x_{J(i)+n+2} \geq x_{J(i)+n+1}+A>L_{i+1}$, and hence $J(i+1)<$ $J(i)+n+2$. Claim 1 follows.
Claim 2: $x_{j+1}-x_{j}=A$ for all $j=J(i)+1, \ldots, J(i+1)-1$, for all $i \geq 1$. (That is, the $n$ intermediate jumps of Claim 1 must all be of
length $A$.)
Proof: If Claim 2 is false, then
$$
\begin{aligned}
M_{i+1}=x_{J(i+1)}=x_{J(i)+n+1} & \geq x_{J(i)+1}+(n-1) A+B \\
& >R_{i}+n A+C \\
& =L_{i+1}+1 \\
& >M_{i+1}
\end{aligned}
$$
which is a contradiction. This proves Claim 2.
We can now conclude that
$$
\begin{aligned}
& x_{J(i+1)+1}=x_{J(i)+n+2}=x_{J(i)+1}+n A+B \\
& \text { i.e., } \quad m_{i+1}=m_{i}+n A+B \quad \text { for each } i \geq 1
\end{aligned}
$$
Therefore
$$
\begin{aligned}
m_{i+1}-R_{i+1} & =m_{i}+n A+B-\left(R_{i}+n A+C-1+A\right) \\
& =m_{i}-R_{i}+1
\end{aligned}
$$
Hence
$$
C \geq m_{C+1}-R_{C+1}=m_{1}-R_{1}+C>C
$$
which is a contradiction. Therefore no path for the flea avoids all the lava. We observe that Lavaman only needs to put lava on the first $C+1$ intervals.
Now assume $F \geq(n-1) A+B$. We will show that the flea can avoid all the lava. We shall need the following result:
Claim 3: Let $d \geq n A$. Then there exist nonnegative integers $s$ and $t$ such that $s A+t B \in(d-C, d]$.
We shall prove this result at the end.
First, observe that $L_{1} \geq n A$. By Claim 3 , it is possible for the flea to make a sequence of jumps starting from 0 and ending at a point of $\left(L_{1}-C, L_{1}\right]$. From any point of this interval, a single jump of size $B$ takes the flea over ( $L_{1}, R_{]}$to a point in $\left(R_{1}, R_{1}+C\right]$, which corresponds to the point $x_{J(1)+1}\left(=m_{1}\right)$ on the flea's path.
Now we use induction to prove that, for every $i \geq 1$, there is a path such that $x_{j}$ avoids lava for all $j \leq J(i)+1$. The case $i=1$ is done, so
assume that the assertion holds for a given $i$. Then $x_{J(i)+1}=m_{i} \in$ $\left(R_{i}, R_{i}+C\right]$. Therefore
$$
L_{i+1}-m_{i} \geq R_{i}+F-\left(R_{i}+C\right)=F-C \geq n A
$$
Applying Claim 3 with $d=L_{i+1}-m_{i}$ shows that the flea can jump from $m_{i}$ to a point of $\left(L_{i+1}-C, L_{i+1}\right]$. A single jump of size $B$ then takes the flea to a point of $\left(R_{i+1}, R_{i+1}+C\right]$ (without visiting $\left(L_{i+1}, R_{i+1}\right]$ ), and this point serves as $x_{J(i+1)+1}$. This completes the induction.
Proof of Claim 3: Let $u$ be the greatest integer that is less than or equal to $d / A$. Then $u \geq n$ and $u A \leq d<(u+1) A$. For $v=0, \ldots, n$, let
$$
z_{v}=(u-v) A+v B=u A+v C .
$$
Then
$$
\begin{aligned}
& \quad z_{0}=u A \leq d \\
& z_{n}=u A+n C=u A+(n+1) C-C \geq(u+1) A-C>d-C . \\
& \text { and } z_{v+1}-z_{v}=C \quad \text { for } v=0, \ldots, n-1
\end{aligned}
$$
Therefore we must have $z_{v} \in(d-C, d]$ for some $v$ in $\{0,1, \ldots, n\}$.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Lavaman versus the Flea. Let $A, B$, and $F$ be positive integers, and assume $A<B<2 A$. A flea is at the number 0 on the number line. The flea can move by jumping to the right by $A$ or by $B$. Before the flea starts jumping, Lavaman chooses finitely many intervals $\{m+$ $1, m+2, \ldots, m+A\}$ consisting of $A$ consecutive positive integers, and places lava at all of the integers in the intervals. The intervals must be chosen so that:
(i) any two distinct intervals are disjoint and not adjacent;
(ii) there are at least $F$ positive integers with no lava between any two intervals; and
(iii) no lava is placed at any integer less than $F$.
Prove that the smallest $F$ for which the flea can jump over all the intervals and avoid all the lava, regardless of what Lavaman does,
is $F=(n-1) A+B$, where $n$ is the positive integer such that $\frac{A}{n+1} \leq B-A<\frac{A}{n}$.
|
Let $B=A+C$ where $A /(n+1) \leq C<A / n$.
First, here is an informal sketch of the proof.
Lavaman's strategy: Use only safe intervals with $n A+C-1$ integers. The flea will start at position $[1, C]$ from the left, which puts him at position $[n A, n A+C-1]$ from the right. After $n-1$ jumps, he will still have $n A-(n-1)(A+C)=A-(n-1) C>C$ distance to go, which is not enough for a big jump to clear the lava. Thus, he must do at least $n$ jumps in the safe interval, but that's possible only with all small jumps, and furthermore is impossible if the starting position is $C$. This gives him starting position 1 higher in the next safe interval, so sooner or later the flea is going to hit the lava.
Flea's strategy: The flea just does one interval at a time. If the safe interval has at least $n A+C$ integers in it, the flea has distance $d>n A$ to go to the next lava when it starts. Repeatedly do big jumps until $d$ is between 1 and $C \bmod A$, then small jumps until the remaining distance is between 1 and $C$, then a final big jump. This works as long as the first part does. However, we get at least $n$ big jumps since floor $((d-1) / A)$ can never go down two from a big jump (or we'd be done doing big jumps), so we get $n$ big jumps, and thus we are good if $d \bmod A$ is in any of $[1, C],[C+1,2 C], \ldots[n C+1,(n+1) C]$, but that's everything.
Let $C=B-A$. We shall write our intervals of lava in the form $\left(L_{i}, R_{i}\right]=\left\{L_{i}+1, L_{i}+2, \ldots, R_{i}\right\}$, where $R_{i}=L_{i}+A$ and $R_{i-1}<L_{i}$ for every $i \geq 1$. We also let $R_{0}=0$. We shall also represent a path for the flea as a sequence of integers $x_{0}, x_{1}, x_{2}, \ldots$ where $x_{0}=0$ and $x_{j}-x_{j-1} \in\{A, B\}$ for every $j \geq 0$.
Now here is a detailed proof.
First, assume $F<(n-1) A+B(=n A+C)$ : we must prove that Lavaman has a winning strategy. Let $L_{i}=R_{i-1}+n A+C-1$ for every $i \geq 1$. (Observe that $n A+C-1 \geq F$.)
Assume that the flea has an infinite path that avoids all the lava, which
means that $x_{j} \notin\left(L_{i}, R_{i}\right]$ for all $i, j \geq 1$. For each $i \geq 1$, let
$$
\begin{gathered}
M_{i}=\max \left\{x_{j}: x_{j} \leq L_{i}\right\}, \quad m_{i}=\min \left\{x_{j}: x_{j}>R_{i}\right\}, \\
\text { and } J(i)=\max \left\{j: x_{j} \leq L_{i}\right\}
\end{gathered}
$$
Also let $m_{0}=0$. Then for $i \geq 1$ we have
$$
M_{i}=x_{J(i)} \quad \text { and } \quad m_{i}=x_{J(i)+1} .
$$
Also, for every $i \geq 1$, we have
(a) $m_{i}=M_{i}+B$ (because $M_{i}+A \leq L_{i}+A=R_{i}$ );
(b) $L_{i} \geq M_{i}>L_{i}-C\left(\right.$ since $\left.M_{i}=m_{i}-B>R_{i}-B=L_{i}+A-B\right)$;
and
(c) $R_{i}<m_{i} \leq R_{i}+C\left(\right.$ since $\left.m_{i}=M_{i}+B \leq L_{i}+B=R_{i}+C\right)$.
Claim 1: $J(i+1)=J(i)+n+1$ for every $i \geq 1$. (That is, after jumping over one interval of lava, the flea must make exactly $n$ jumps before jumping over the next interval of lava.)
Proof:
$$
\begin{aligned}
x_{J(i)+n+1} & \leq x_{J(i)+1}+B n \\
& =m_{i}+B n \\
& <R_{i}+C+\left(A+\frac{A}{n}\right) n \\
& =L_{i+1}+A+1
\end{aligned}
$$
Because of the strict inequality, we have $x_{J(i)+n+1} \leq R_{i+1}$, and hence $x_{J(i)+n+1} \leq L_{i+1}$. Therefore $J(i)+n+1 \leq J(i+1)$. Next, we have
$$
\begin{aligned}
x_{J(i)+n+1} & \geq x_{J(i)+1}+A n \\
& =m_{i}+A n \\
& >R_{i}+A n \\
& =L_{i+1}-C+1 \\
& >L_{i+1}-A+1 \quad(\text { since } C<A) .
\end{aligned}
$$
Therefore $x_{J(i)+n+2} \geq x_{J(i)+n+1}+A>L_{i+1}$, and hence $J(i+1)<$ $J(i)+n+2$. Claim 1 follows.
Claim 2: $x_{j+1}-x_{j}=A$ for all $j=J(i)+1, \ldots, J(i+1)-1$, for all $i \geq 1$. (That is, the $n$ intermediate jumps of Claim 1 must all be of
length $A$.)
Proof: If Claim 2 is false, then
$$
\begin{aligned}
M_{i+1}=x_{J(i+1)}=x_{J(i)+n+1} & \geq x_{J(i)+1}+(n-1) A+B \\
& >R_{i}+n A+C \\
& =L_{i+1}+1 \\
& >M_{i+1}
\end{aligned}
$$
which is a contradiction. This proves Claim 2.
We can now conclude that
$$
\begin{aligned}
& x_{J(i+1)+1}=x_{J(i)+n+2}=x_{J(i)+1}+n A+B \\
& \text { i.e., } \quad m_{i+1}=m_{i}+n A+B \quad \text { for each } i \geq 1
\end{aligned}
$$
Therefore
$$
\begin{aligned}
m_{i+1}-R_{i+1} & =m_{i}+n A+B-\left(R_{i}+n A+C-1+A\right) \\
& =m_{i}-R_{i}+1
\end{aligned}
$$
Hence
$$
C \geq m_{C+1}-R_{C+1}=m_{1}-R_{1}+C>C
$$
which is a contradiction. Therefore no path for the flea avoids all the lava. We observe that Lavaman only needs to put lava on the first $C+1$ intervals.
Now assume $F \geq(n-1) A+B$. We will show that the flea can avoid all the lava. We shall need the following result:
Claim 3: Let $d \geq n A$. Then there exist nonnegative integers $s$ and $t$ such that $s A+t B \in(d-C, d]$.
We shall prove this result at the end.
First, observe that $L_{1} \geq n A$. By Claim 3 , it is possible for the flea to make a sequence of jumps starting from 0 and ending at a point of $\left(L_{1}-C, L_{1}\right]$. From any point of this interval, a single jump of size $B$ takes the flea over ( $L_{1}, R_{]}$to a point in $\left(R_{1}, R_{1}+C\right]$, which corresponds to the point $x_{J(1)+1}\left(=m_{1}\right)$ on the flea's path.
Now we use induction to prove that, for every $i \geq 1$, there is a path such that $x_{j}$ avoids lava for all $j \leq J(i)+1$. The case $i=1$ is done, so
assume that the assertion holds for a given $i$. Then $x_{J(i)+1}=m_{i} \in$ $\left(R_{i}, R_{i}+C\right]$. Therefore
$$
L_{i+1}-m_{i} \geq R_{i}+F-\left(R_{i}+C\right)=F-C \geq n A
$$
Applying Claim 3 with $d=L_{i+1}-m_{i}$ shows that the flea can jump from $m_{i}$ to a point of $\left(L_{i+1}-C, L_{i+1}\right]$. A single jump of size $B$ then takes the flea to a point of $\left(R_{i+1}, R_{i+1}+C\right]$ (without visiting $\left(L_{i+1}, R_{i+1}\right]$ ), and this point serves as $x_{J(i+1)+1}$. This completes the induction.
Proof of Claim 3: Let $u$ be the greatest integer that is less than or equal to $d / A$. Then $u \geq n$ and $u A \leq d<(u+1) A$. For $v=0, \ldots, n$, let
$$
z_{v}=(u-v) A+v B=u A+v C .
$$
Then
$$
\begin{aligned}
& \quad z_{0}=u A \leq d \\
& z_{n}=u A+n C=u A+(n+1) C-C \geq(u+1) A-C>d-C . \\
& \text { and } z_{v+1}-z_{v}=C \quad \text { for } v=0, \ldots, n-1
\end{aligned}
$$
Therefore we must have $z_{v} \in(d-C, d]$ for some $v$ in $\{0,1, \ldots, n\}$.
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "Canada_MO/segmented/en-sol2016.jsonl",
"solution_match": "\nSolution:",
"tier": "T2",
"year": "2016"
}
|
Let $\triangle A B C$ be an acute-angled triangle with altitudes $A D$ and $B E$ meeting at $H$. Let $M$ be the midpoint of segment $A B$, and suppose that the circumcircles of $\triangle D E M$ and $\triangle A B H$ meet at points $P$ and $Q$ with $P$ on the same side of $C H$ as $A$. Prove that the lines $E D$, $P H$, and $M Q$ all pass through a single point on the circumcircle of $\triangle A B C$.
|
Let $R$ denote the intersection of lines $E D$ and $P H$. Since quadrilaterals $E C D H$ and $A P H B$ are cyclic, we have $\angle R D A=180^{\circ}-\angle E D A=$ $180^{\circ}-\angle E D H=180^{\circ}-\angle E C H=90^{\circ}+A$, and $\angle R P A=\angle H P A=$ $180^{\circ}-\angle H B A=90^{\circ}+A$. Therefore, $A P D R$ is cyclic. This in turn implies that $\angle P B E=\angle P B H=\angle P A H=\angle P A D=\angle P R D=\angle P R E$, and so $P B R E$ is also cyclic.
Let $F$ denote the base of the altitude from $C$ to $A B$. Then $D, E, F$, and $M$ all lie on the 9-point circle of $\triangle A B C$, and so are cyclic. We also know $A P D R, P B R E, B C E F$, and $A C D F$ are cyclic, which implies $\angle A R B=\angle P R B-\angle P R A=\angle P E B-\angle P D A=\angle P E F+\angle F E B-$ $\angle P D F+\angle A D F=\angle F E B+\angle A D F=\angle F C B+\angle A C F=C$. Therefore, $R$ lies on the circumcircle of $\triangle A B C$.
Now let $Q^{\prime}$ and $R^{\prime}$ denote the intersections of line $M Q$ with the circumcircle of $\triangle A B C$, chosen so that $Q^{\prime}, M, Q, R^{\prime}$ lie on the line in that order. We will show that $R^{\prime}=R$, which will complete the proof. However, first note that the circumcircle of $\triangle A B C$ has radius $\frac{A B}{2 \sin C}$, and the circumcircle of $\triangle A B H$ has radius $\frac{A B}{2 \sin \angle A H B}=\frac{A B}{2 \sin \left(180^{\circ}-C\right)}$. Thus the two circles have equal radius, and so they must be symmetrical about the point $M$. In particular, $M Q=M Q^{\prime}$.
Since $\angle A E B=\angle A D B=90^{\circ}$, we furthermore know that $M$ is the circumcenter of both $\triangle A E B$ and $\triangle A D B$. Thus, $M A=M E=M D=$ $M B$. By Power of a Point, we then have $M Q \cdot M R^{\prime}=M Q^{\prime} \cdot M R^{\prime}=$ $M A \cdot M B=M D^{2}$. In particular, this means that the circumcircle of
$\triangle D R^{\prime} Q$ is tangent to $M D$ at $D$, which means $\angle M R^{\prime} D=\angle M D Q$. Similarly $M Q \cdot M R^{\prime}=M E^{2}$, and so $\angle M R^{\prime} E=\angle M E Q=\angle M D Q=$ $\angle M R^{\prime} D$. Therefore, $R^{\prime}$ also lies on the line $E D$.
Finally, the same argument shows that $M P$ also intersects the circumcircle of $\triangle A B C$ at a point $R^{\prime \prime}$ on line $E D$. Thus, $R, R^{\prime}$, and $R^{\prime \prime}$ are all chosen from the intersection of the circumcircle of $\triangle A B C$ and the line $E D$. In particular, two of $R, R^{\prime}$, and $R^{\prime \prime}$ must be equal. However, $R^{\prime \prime} \neq R$ since $M P$ and $P H$ already intersect at $P$, and $R^{\prime \prime} \neq R^{\prime}$ since $M P$ and $M Q$ already intersect at $M$. Thus, $R^{\prime}=R$, and the proof is complete.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let $\triangle A B C$ be an acute-angled triangle with altitudes $A D$ and $B E$ meeting at $H$. Let $M$ be the midpoint of segment $A B$, and suppose that the circumcircles of $\triangle D E M$ and $\triangle A B H$ meet at points $P$ and $Q$ with $P$ on the same side of $C H$ as $A$. Prove that the lines $E D$, $P H$, and $M Q$ all pass through a single point on the circumcircle of $\triangle A B C$.
|

Let $R$ denote the intersection of lines $E D$ and $P H$. Since quadrilaterals $E C D H$ and $A P H B$ are cyclic, we have $\angle R D A=180^{\circ}-\angle E D A=$ $180^{\circ}-\angle E D H=180^{\circ}-\angle E C H=90^{\circ}+A$, and $\angle R P A=\angle H P A=$ $180^{\circ}-\angle H B A=90^{\circ}+A$. Therefore, $A P D R$ is cyclic. This in turn implies that $\angle P B E=\angle P B H=\angle P A H=\angle P A D=\angle P R D=\angle P R E$, and so $P B R E$ is also cyclic.
Let $F$ denote the base of the altitude from $C$ to $A B$. Then $D, E, F$, and $M$ all lie on the 9-point circle of $\triangle A B C$, and so are cyclic. We also know $A P D R, P B R E, B C E F$, and $A C D F$ are cyclic, which implies $\angle A R B=\angle P R B-\angle P R A=\angle P E B-\angle P D A=\angle P E F+\angle F E B-$ $\angle P D F+\angle A D F=\angle F E B+\angle A D F=\angle F C B+\angle A C F=C$. Therefore, $R$ lies on the circumcircle of $\triangle A B C$.
Now let $Q^{\prime}$ and $R^{\prime}$ denote the intersections of line $M Q$ with the circumcircle of $\triangle A B C$, chosen so that $Q^{\prime}, M, Q, R^{\prime}$ lie on the line in that order. We will show that $R^{\prime}=R$, which will complete the proof. However, first note that the circumcircle of $\triangle A B C$ has radius $\frac{A B}{2 \sin C}$, and the circumcircle of $\triangle A B H$ has radius $\frac{A B}{2 \sin \angle A H B}=\frac{A B}{2 \sin \left(180^{\circ}-C\right)}$. Thus the two circles have equal radius, and so they must be symmetrical about the point $M$. In particular, $M Q=M Q^{\prime}$.
Since $\angle A E B=\angle A D B=90^{\circ}$, we furthermore know that $M$ is the circumcenter of both $\triangle A E B$ and $\triangle A D B$. Thus, $M A=M E=M D=$ $M B$. By Power of a Point, we then have $M Q \cdot M R^{\prime}=M Q^{\prime} \cdot M R^{\prime}=$ $M A \cdot M B=M D^{2}$. In particular, this means that the circumcircle of
$\triangle D R^{\prime} Q$ is tangent to $M D$ at $D$, which means $\angle M R^{\prime} D=\angle M D Q$. Similarly $M Q \cdot M R^{\prime}=M E^{2}$, and so $\angle M R^{\prime} E=\angle M E Q=\angle M D Q=$ $\angle M R^{\prime} D$. Therefore, $R^{\prime}$ also lies on the line $E D$.
Finally, the same argument shows that $M P$ also intersects the circumcircle of $\triangle A B C$ at a point $R^{\prime \prime}$ on line $E D$. Thus, $R, R^{\prime}$, and $R^{\prime \prime}$ are all chosen from the intersection of the circumcircle of $\triangle A B C$ and the line $E D$. In particular, two of $R, R^{\prime}$, and $R^{\prime \prime}$ must be equal. However, $R^{\prime \prime} \neq R$ since $M P$ and $P H$ already intersect at $P$, and $R^{\prime \prime} \neq R^{\prime}$ since $M P$ and $M Q$ already intersect at $M$. Thus, $R^{\prime}=R$, and the proof is complete.
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "Canada_MO/segmented/en-sol2016.jsonl",
"solution_match": "\n## Solution:",
"tier": "T2",
"year": "2016"
}
|
Let $a, b$, and $c$ be non-negative real numbers, no two of which are equal. Prove that
$$
\frac{a^{2}}{(b-c)^{2}}+\frac{b^{2}}{(c-a)^{2}}+\frac{c^{2}}{(a-b)^{2}}>2
$$
|
The left-hand side is symmetric with respect to $a, b, c$. Hence, we may assume that $a>b>c \geq 0$. Note that replacing $(a, b, c)$ with $(a-c, b-c, 0)$ lowers the value of the lefthand side, since the numerators of each of the fractions would decrease and the denominators remain the same. Therefore, to obtain the minimum possible value of the left-hand side, we may assume that $c=0$.
Then the left-hand side becomes
$$
\frac{a^{2}}{b^{2}}+\frac{b^{2}}{a^{2}}
$$
which yields, by the Arithmetic Mean - Geometric Mean Inequality,
$$
\frac{a^{2}}{b^{2}}+\frac{b^{2}}{a^{2}} \geq 2 \sqrt{\frac{a^{2}}{b^{2}} \cdot \frac{b^{2}}{a^{2}}}=2
$$
with equality if and only if $a^{2} / b^{2}=b^{2} / a^{2}$, or equivalently, $a^{4}=b^{4}$. Since $a, b \geq 0, a=b$. But since no two of $a, b, c$ are equal, $a \neq b$. Hence, equality cannot hold. This yields
$$
\frac{a^{2}}{b^{2}}+\frac{b^{2}}{a^{2}}>2
$$
Ultimately, this implies the desired inequality.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b$, and $c$ be non-negative real numbers, no two of which are equal. Prove that
$$
\frac{a^{2}}{(b-c)^{2}}+\frac{b^{2}}{(c-a)^{2}}+\frac{c^{2}}{(a-b)^{2}}>2
$$
|
The left-hand side is symmetric with respect to $a, b, c$. Hence, we may assume that $a>b>c \geq 0$. Note that replacing $(a, b, c)$ with $(a-c, b-c, 0)$ lowers the value of the lefthand side, since the numerators of each of the fractions would decrease and the denominators remain the same. Therefore, to obtain the minimum possible value of the left-hand side, we may assume that $c=0$.
Then the left-hand side becomes
$$
\frac{a^{2}}{b^{2}}+\frac{b^{2}}{a^{2}}
$$
which yields, by the Arithmetic Mean - Geometric Mean Inequality,
$$
\frac{a^{2}}{b^{2}}+\frac{b^{2}}{a^{2}} \geq 2 \sqrt{\frac{a^{2}}{b^{2}} \cdot \frac{b^{2}}{a^{2}}}=2
$$
with equality if and only if $a^{2} / b^{2}=b^{2} / a^{2}$, or equivalently, $a^{4}=b^{4}$. Since $a, b \geq 0, a=b$. But since no two of $a, b, c$ are equal, $a \neq b$. Hence, equality cannot hold. This yields
$$
\frac{a^{2}}{b^{2}}+\frac{b^{2}}{a^{2}}>2
$$
Ultimately, this implies the desired inequality.
|
{
"exam": "Canada_MO",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "Canada_MO/segmented/en-sol2017.jsonl",
"solution_match": "\nSolution:",
"tier": "T2",
"year": "2017"
}
|
Let $a, b$, and $c$ be non-negative real numbers, no two of which are equal. Prove that
$$
\frac{a^{2}}{(b-c)^{2}}+\frac{b^{2}}{(c-a)^{2}}+\frac{c^{2}}{(a-b)^{2}}>2
$$
|
First, show that
$$
\begin{aligned}
& \frac{a^{2}}{(b-c)^{2}}+\frac{b^{2}}{(c-a)^{2}}+\frac{c^{2}}{(a-b)^{2}}-2= \\
& \frac{[a(a-b)(a-c)+b(b-a)(b-c)+c(c-a)(c-b)]^{2}}{[(a-b)(b-c)(c-a)]^{2}}
\end{aligned}
$$
Then Schur's Inequality tells us that the numerator of the right-hand side cannot be zero.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $a, b$, and $c$ be non-negative real numbers, no two of which are equal. Prove that
$$
\frac{a^{2}}{(b-c)^{2}}+\frac{b^{2}}{(c-a)^{2}}+\frac{c^{2}}{(a-b)^{2}}>2
$$
|
First, show that
$$
\begin{aligned}
& \frac{a^{2}}{(b-c)^{2}}+\frac{b^{2}}{(c-a)^{2}}+\frac{c^{2}}{(a-b)^{2}}-2= \\
& \frac{[a(a-b)(a-c)+b(b-a)(b-c)+c(c-a)(c-b)]^{2}}{[(a-b)(b-c)(c-a)]^{2}}
\end{aligned}
$$
Then Schur's Inequality tells us that the numerator of the right-hand side cannot be zero.
|
{
"exam": "Canada_MO",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "Canada_MO/segmented/en-sol2017.jsonl",
"solution_match": "\nAlternate solution:",
"tier": "T2",
"year": "2017"
}
|
Let $f$ be a function from the set of positive integers to itself such that, for every $n$, the number of positive integer divisors of $n$ is equal to $f(f(n))$. For example, $f(f(6))=4$ and $f(f(25))=3$. Prove that if $p$ is prime then $f(p)$ is also prime.
|
Let $d(n)=f(f(n))$ denote the number of divisors of $n$ and observe that $f(d(n))=$ $f(f(f(n)))=d(f(n))$ for all $n$. Also note that because all divisors of $n$ are distinct positive integers between 1 and $n$, including 1 and $n$, and excluding $n-1$ if $n>2$, it follows that $2 \leq d(n)<n$ for all $n>2$. Furthermore $d(1)=1$ and $d(2)=2$.
We first will show that $f(2)=2$. Let $m=f(2)$ and note that $2=d(2)=f(f(2))=f(m)$. If $m \geq 2$, then let $m_{0}$ be the smallest positive integer satisfying that $m_{0} \geq 2$ and $f\left(m_{0}\right)=2$. It follows that $f\left(d\left(m_{0}\right)\right)=d\left(f\left(m_{0}\right)\right)=d(2)=2$. By the minimality of $m_{0}$, it follows that $d\left(m_{0}\right) \geq m_{0}$, which implies that $m_{0}=2$. Therefore if $m \geq 2$, it follows that $f(2)=2$. It suffices to examine the case in which $f(2)=m=1$. If $m=1$, then $f(1)=f(f(2))=2$ and furthermore, each prime $p$ satisfies that $d(f(p))=f(d(p))=f(2)=1$ which implies that $f(p)=1$. Therefore $d\left(f\left(p^{2}\right)\right)=f\left(d\left(p^{2}\right)\right)=f(3)=1$ which implies that $f\left(p^{2}\right)=1$ for any prime $p$. This implies that $3=d\left(p^{2}\right)=f\left(f\left(p^{2}\right)\right)=f(1)=2$, which is a contradiction. Therefore $m \neq 1$ and $f(2)=2$.
It now follows that if $p$ is prime then $2=f(2)=f(d(p))=d(f(p))$ which implies that $f(p)$ is prime.
Remark. Such a function exists and can be constructed inductively.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $f$ be a function from the set of positive integers to itself such that, for every $n$, the number of positive integer divisors of $n$ is equal to $f(f(n))$. For example, $f(f(6))=4$ and $f(f(25))=3$. Prove that if $p$ is prime then $f(p)$ is also prime.
|
Let $d(n)=f(f(n))$ denote the number of divisors of $n$ and observe that $f(d(n))=$ $f(f(f(n)))=d(f(n))$ for all $n$. Also note that because all divisors of $n$ are distinct positive integers between 1 and $n$, including 1 and $n$, and excluding $n-1$ if $n>2$, it follows that $2 \leq d(n)<n$ for all $n>2$. Furthermore $d(1)=1$ and $d(2)=2$.
We first will show that $f(2)=2$. Let $m=f(2)$ and note that $2=d(2)=f(f(2))=f(m)$. If $m \geq 2$, then let $m_{0}$ be the smallest positive integer satisfying that $m_{0} \geq 2$ and $f\left(m_{0}\right)=2$. It follows that $f\left(d\left(m_{0}\right)\right)=d\left(f\left(m_{0}\right)\right)=d(2)=2$. By the minimality of $m_{0}$, it follows that $d\left(m_{0}\right) \geq m_{0}$, which implies that $m_{0}=2$. Therefore if $m \geq 2$, it follows that $f(2)=2$. It suffices to examine the case in which $f(2)=m=1$. If $m=1$, then $f(1)=f(f(2))=2$ and furthermore, each prime $p$ satisfies that $d(f(p))=f(d(p))=f(2)=1$ which implies that $f(p)=1$. Therefore $d\left(f\left(p^{2}\right)\right)=f\left(d\left(p^{2}\right)\right)=f(3)=1$ which implies that $f\left(p^{2}\right)=1$ for any prime $p$. This implies that $3=d\left(p^{2}\right)=f\left(f\left(p^{2}\right)\right)=f(1)=2$, which is a contradiction. Therefore $m \neq 1$ and $f(2)=2$.
It now follows that if $p$ is prime then $2=f(2)=f(d(p))=d(f(p))$ which implies that $f(p)$ is prime.
Remark. Such a function exists and can be constructed inductively.
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "Canada_MO/segmented/en-sol2017.jsonl",
"solution_match": "\nSolution:",
"tier": "T2",
"year": "2017"
}
|
Let $n$ be a positive integer, and define $S_{n}=\{1,2, \ldots, n\}$. Consider a non-empty subset $T$ of $S_{n}$. We say that $T$ is balanced if the median of $T$ is equal to the average of $T$. For example, for $n=9$, each of the subsets $\{7\},\{2,5\},\{2,3,4\},\{5,6,8,9\}$, and $\{1,4,5,7,8\}$ is balanced; however, the subsets $\{2,4,5\}$ and $\{1,2,3,5\}$ are not balanced. For each $n \geq 1$, prove that the number of balanced subsets of $S_{n}$ is odd.
(To define the median of a set of $k$ numbers, first put the numbers in increasing order; then the median is the middle number if $k$ is odd, and the average of the two middle numbers if $k$ is even. For example, the median of $\{1,3,4,8,9\}$ is 4 , and the median of $\{1,3,4,7,8,9\}$ is $(4+7) / 2=5.5$. $)$
|
The problem is to prove that there is an odd number of nonempty subsets $T$ of $S_{n}$ such that the average $A(T)$ and median $M(T)$ satisfy $A(T)=M(T)$. Given a subset $T$, consider the subset $T^{*}=\{n+1-t: t \in T\}$. It holds that $A\left(T^{*}\right)=n+1-A(T)$ and $M\left(T^{*}\right)=n+1-M(T)$, which implies that if $A(T)=M(T)$ then $A\left(T^{*}\right)=M\left(T^{*}\right)$. Pairing each set $T$ with $T^{*}$ yields that there are an even number of sets $T$ such that $A(T)=M(T)$ and $T \neq T^{*}$.
Thus it suffices to show that the number of nonempty subsets $T$ such that $A(T)=M(T)$ and $T=T^{*}$ is odd. Now note that if $T=T^{*}$, then $A(T)=M(T)=\frac{n+1}{2}$. Hence it suffices to show the number of nonempty subsets $T$ with $T=T^{*}$ is odd. Given such a set $T$, let $T^{\prime}$ be the largest nonempty subset of $\{1,2, \ldots,\lceil n / 2\rceil\}$ contained in $T$. Pairing $T$ with $T^{\prime}$ forms a bijection between these sets $T$ and the nonempty subsets of $\{1,2, \ldots,\lceil n / 2\rceil\}$. Thus there are $2^{\lceil n / 2\rceil}-1$ such subsets, which is odd as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ be a positive integer, and define $S_{n}=\{1,2, \ldots, n\}$. Consider a non-empty subset $T$ of $S_{n}$. We say that $T$ is balanced if the median of $T$ is equal to the average of $T$. For example, for $n=9$, each of the subsets $\{7\},\{2,5\},\{2,3,4\},\{5,6,8,9\}$, and $\{1,4,5,7,8\}$ is balanced; however, the subsets $\{2,4,5\}$ and $\{1,2,3,5\}$ are not balanced. For each $n \geq 1$, prove that the number of balanced subsets of $S_{n}$ is odd.
(To define the median of a set of $k$ numbers, first put the numbers in increasing order; then the median is the middle number if $k$ is odd, and the average of the two middle numbers if $k$ is even. For example, the median of $\{1,3,4,8,9\}$ is 4 , and the median of $\{1,3,4,7,8,9\}$ is $(4+7) / 2=5.5$. $)$
|
The problem is to prove that there is an odd number of nonempty subsets $T$ of $S_{n}$ such that the average $A(T)$ and median $M(T)$ satisfy $A(T)=M(T)$. Given a subset $T$, consider the subset $T^{*}=\{n+1-t: t \in T\}$. It holds that $A\left(T^{*}\right)=n+1-A(T)$ and $M\left(T^{*}\right)=n+1-M(T)$, which implies that if $A(T)=M(T)$ then $A\left(T^{*}\right)=M\left(T^{*}\right)$. Pairing each set $T$ with $T^{*}$ yields that there are an even number of sets $T$ such that $A(T)=M(T)$ and $T \neq T^{*}$.
Thus it suffices to show that the number of nonempty subsets $T$ such that $A(T)=M(T)$ and $T=T^{*}$ is odd. Now note that if $T=T^{*}$, then $A(T)=M(T)=\frac{n+1}{2}$. Hence it suffices to show the number of nonempty subsets $T$ with $T=T^{*}$ is odd. Given such a set $T$, let $T^{\prime}$ be the largest nonempty subset of $\{1,2, \ldots,\lceil n / 2\rceil\}$ contained in $T$. Pairing $T$ with $T^{\prime}$ forms a bijection between these sets $T$ and the nonempty subsets of $\{1,2, \ldots,\lceil n / 2\rceil\}$. Thus there are $2^{\lceil n / 2\rceil}-1$ such subsets, which is odd as desired.
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "Canada_MO/segmented/en-sol2017.jsonl",
"solution_match": "\nSolution:",
"tier": "T2",
"year": "2017"
}
|
Let $n$ be a positive integer, and define $S_{n}=\{1,2, \ldots, n\}$. Consider a non-empty subset $T$ of $S_{n}$. We say that $T$ is balanced if the median of $T$ is equal to the average of $T$. For example, for $n=9$, each of the subsets $\{7\},\{2,5\},\{2,3,4\},\{5,6,8,9\}$, and $\{1,4,5,7,8\}$ is balanced; however, the subsets $\{2,4,5\}$ and $\{1,2,3,5\}$ are not balanced. For each $n \geq 1$, prove that the number of balanced subsets of $S_{n}$ is odd.
(To define the median of a set of $k$ numbers, first put the numbers in increasing order; then the median is the middle number if $k$ is odd, and the average of the two middle numbers if $k$ is even. For example, the median of $\{1,3,4,8,9\}$ is 4 , and the median of $\{1,3,4,7,8,9\}$ is $(4+7) / 2=5.5$. $)$
|
Using the notation from the above solution: Let $B$ be the number of subsets $T$ with $M(T)>A(T), C$ be the number with $M(T)=A(T)$, and $D$ be the number with $M(T)<A(T)$. Pairing each set $T$ counted by $B$ with $T^{*}=\{n+1-t: t \in T\}$ shows that $B=D$. Now since $B+C+D=2^{n}-1$, we have that $C=2^{n}-1-2 B$, which is odd.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $n$ be a positive integer, and define $S_{n}=\{1,2, \ldots, n\}$. Consider a non-empty subset $T$ of $S_{n}$. We say that $T$ is balanced if the median of $T$ is equal to the average of $T$. For example, for $n=9$, each of the subsets $\{7\},\{2,5\},\{2,3,4\},\{5,6,8,9\}$, and $\{1,4,5,7,8\}$ is balanced; however, the subsets $\{2,4,5\}$ and $\{1,2,3,5\}$ are not balanced. For each $n \geq 1$, prove that the number of balanced subsets of $S_{n}$ is odd.
(To define the median of a set of $k$ numbers, first put the numbers in increasing order; then the median is the middle number if $k$ is odd, and the average of the two middle numbers if $k$ is even. For example, the median of $\{1,3,4,8,9\}$ is 4 , and the median of $\{1,3,4,7,8,9\}$ is $(4+7) / 2=5.5$. $)$
|
Using the notation from the above solution: Let $B$ be the number of subsets $T$ with $M(T)>A(T), C$ be the number with $M(T)=A(T)$, and $D$ be the number with $M(T)<A(T)$. Pairing each set $T$ counted by $B$ with $T^{*}=\{n+1-t: t \in T\}$ shows that $B=D$. Now since $B+C+D=2^{n}-1$, we have that $C=2^{n}-1-2 B$, which is odd.
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "Canada_MO/segmented/en-sol2017.jsonl",
"solution_match": "\nAlternate solution:",
"tier": "T2",
"year": "2017"
}
|
Points $P$ and $Q$ lie inside parallelogram $A B C D$ and are such that triangles $A B P$ and $B C Q$ are equilateral. Prove that the line through $P$ perpendicular to $D P$ and the line through $Q$ perpendicular to $D Q$ meet on the altitude from $B$ in triangle $A B C$.
|
Let $\angle A B C=m$ and let $O$ be the circumcenter of triangle $D P Q$. Since $P$ and $Q$ are in the interior of $A B C D$, it follows that $m=\angle A B C>60^{\circ}$ and $\angle D A B=180^{\circ}-m>60^{\circ}$ which together imply that $60^{\circ}<m<120^{\circ}$. Now note that $\angle D A P=\angle D A B-60^{\circ}=120^{\circ}-m$, $\angle D C Q=\angle D C B-60^{\circ}=120^{\circ}-m$ and that $\angle P B Q=60^{\circ}-\angle A B Q=60^{\circ}-\left(\angle A B C-60^{\circ}\right)=$ $120^{\circ}-\mathrm{m}$. This combined with the facts that $A D=B Q=C Q$ and $A P=B P=C D$ implies that triangles $D A P, Q B P$ and $Q C D$ are congruent. Therefore $D P=P Q=D Q$ and triangle $D P Q$ is equilateral. This implies that $\angle O D A=\angle P D A+30^{\circ}=\angle D Q C+30^{\circ}=\angle O Q C$. Combining this fact with $O Q=O D$ and $C Q=A D$ implies that triangles $O D A$ and $O Q C$ are congruent. Therefore $O A=O C$ and, if $M$ is the midpoint of segment $A C$, it follows that $O M$ is perpendicular to $A C$. Since $A B C D$ is a parallelogram, $M$ is also the midpoint of $D B$. If $K$ denotes the intersection of the line through $P$ perpendicular to $D P$ and the line through $Q$ perpendicular to $D Q$, then $K$ is diametrically opposite $D$ on the circumcircle of $D P Q$ and $O$ is the midpoint of segment $D K$. This implies that $O M$ is a midline of triangle $D B K$ and hence that $B K$ is parallel to $O M$ which is perpendicular to $A C$. Therefore $K$ lies on the altitude from $B$ in triangle $A B C$, as desired.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Points $P$ and $Q$ lie inside parallelogram $A B C D$ and are such that triangles $A B P$ and $B C Q$ are equilateral. Prove that the line through $P$ perpendicular to $D P$ and the line through $Q$ perpendicular to $D Q$ meet on the altitude from $B$ in triangle $A B C$.
|
Let $\angle A B C=m$ and let $O$ be the circumcenter of triangle $D P Q$. Since $P$ and $Q$ are in the interior of $A B C D$, it follows that $m=\angle A B C>60^{\circ}$ and $\angle D A B=180^{\circ}-m>60^{\circ}$ which together imply that $60^{\circ}<m<120^{\circ}$. Now note that $\angle D A P=\angle D A B-60^{\circ}=120^{\circ}-m$, $\angle D C Q=\angle D C B-60^{\circ}=120^{\circ}-m$ and that $\angle P B Q=60^{\circ}-\angle A B Q=60^{\circ}-\left(\angle A B C-60^{\circ}\right)=$ $120^{\circ}-\mathrm{m}$. This combined with the facts that $A D=B Q=C Q$ and $A P=B P=C D$ implies that triangles $D A P, Q B P$ and $Q C D$ are congruent. Therefore $D P=P Q=D Q$ and triangle $D P Q$ is equilateral. This implies that $\angle O D A=\angle P D A+30^{\circ}=\angle D Q C+30^{\circ}=\angle O Q C$. Combining this fact with $O Q=O D$ and $C Q=A D$ implies that triangles $O D A$ and $O Q C$ are congruent. Therefore $O A=O C$ and, if $M$ is the midpoint of segment $A C$, it follows that $O M$ is perpendicular to $A C$. Since $A B C D$ is a parallelogram, $M$ is also the midpoint of $D B$. If $K$ denotes the intersection of the line through $P$ perpendicular to $D P$ and the line through $Q$ perpendicular to $D Q$, then $K$ is diametrically opposite $D$ on the circumcircle of $D P Q$ and $O$ is the midpoint of segment $D K$. This implies that $O M$ is a midline of triangle $D B K$ and hence that $B K$ is parallel to $O M$ which is perpendicular to $A C$. Therefore $K$ lies on the altitude from $B$ in triangle $A B C$, as desired.
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "Canada_MO/segmented/en-sol2017.jsonl",
"solution_match": "\nSolution:",
"tier": "T2",
"year": "2017"
}
|
One hundred circles of radius one are positioned in the plane so that the area of any triangle formed by the centres of three of these circles is at most 2017. Prove that there is a line intersecting at least three of these circles.
|
We will prove that given $n$ circles, there is some line intersecting more than $\frac{n}{46}$ of them. Let $S$ be the set of centers of the $n$ circles. We will first show that there is a line $\ell$ such that the projections of the points in $S$ lie in an interval of length at most $\sqrt{8068}<90$ on $\ell$. Let $A$ and $B$ be the pair of points in $S$ that are farthest apart and let the distance between $A$ and $B$ be $d$. Now consider any point $C \in S$ distinct from $A$ and $B$. The distance from $C$ to the line $A B$ must be at most $\frac{4034}{d}$ since triangle $A B C$ has area at most 2017. Therefore if $\ell$ is a line perpendicular to $A B$, then the projections of $S$ onto $\ell$ lie in an interval of length $\frac{8068}{d}$ centered at the intersection of $\ell$ and $A B$. Furthermore, all of these projections must lie on an interval of length at most $d$ on $\ell$ since the largest distance between two of these projections is at most $d$. Since $\min (d, 8068 / d) \leq \sqrt{8068}<90$, this proves the claim.
Now note that the projections of the $n$ circles onto the line $\ell$ are intervals of length 2 , all contained in an interval of length at most $\sqrt{8068}+2<92$. Each point of this interval belongs to on average $\frac{2 n}{\sqrt{8068}+2}>\frac{n}{46}$ of the subintervals of length 2 corresponding to the projections of the $n$ circles onto $\ell$. Thus there is some point $x \in \ell$ belonging to the projections of more than $\frac{n}{46}$ circles. The line perpendicular to $\ell$ through $x$ has the desired property. Setting $n=100$ yields that there is a line intersecting at least three of the circles.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
One hundred circles of radius one are positioned in the plane so that the area of any triangle formed by the centres of three of these circles is at most 2017. Prove that there is a line intersecting at least three of these circles.
|
We will prove that given $n$ circles, there is some line intersecting more than $\frac{n}{46}$ of them. Let $S$ be the set of centers of the $n$ circles. We will first show that there is a line $\ell$ such that the projections of the points in $S$ lie in an interval of length at most $\sqrt{8068}<90$ on $\ell$. Let $A$ and $B$ be the pair of points in $S$ that are farthest apart and let the distance between $A$ and $B$ be $d$. Now consider any point $C \in S$ distinct from $A$ and $B$. The distance from $C$ to the line $A B$ must be at most $\frac{4034}{d}$ since triangle $A B C$ has area at most 2017. Therefore if $\ell$ is a line perpendicular to $A B$, then the projections of $S$ onto $\ell$ lie in an interval of length $\frac{8068}{d}$ centered at the intersection of $\ell$ and $A B$. Furthermore, all of these projections must lie on an interval of length at most $d$ on $\ell$ since the largest distance between two of these projections is at most $d$. Since $\min (d, 8068 / d) \leq \sqrt{8068}<90$, this proves the claim.
Now note that the projections of the $n$ circles onto the line $\ell$ are intervals of length 2 , all contained in an interval of length at most $\sqrt{8068}+2<92$. Each point of this interval belongs to on average $\frac{2 n}{\sqrt{8068}+2}>\frac{n}{46}$ of the subintervals of length 2 corresponding to the projections of the $n$ circles onto $\ell$. Thus there is some point $x \in \ell$ belonging to the projections of more than $\frac{n}{46}$ circles. The line perpendicular to $\ell$ through $x$ has the desired property. Setting $n=100$ yields that there is a line intersecting at least three of the circles.
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "Canada_MO/segmented/en-sol2017.jsonl",
"solution_match": "\nSolution:",
"tier": "T2",
"year": "2017"
}
|
Consider an arrangement of tokens in the plane, not necessarily at distinct points. We are allowed to apply a sequence of moves of the following kind: Select a pair of tokens at points $A$ and $B$ and move both of them to the midpoint of $A$ and $B$.
We say that an arrangement of $n$ tokens is collapsible if it is possible to end up with all $n$ tokens at the same point after a finite number of moves. Prove that every arrangement of $n$ tokens is collapsible if and only if $n$ is a power of 2 .
|
For a given positive integer $n$, consider an arrangement of $n$ tokens in the plane, where the tokens are at points $A_{1}, A_{2}, \ldots, A_{n}$. Let $G$ be the centroid of the $n$ points, so as vectors (after an arbitrary choice of origin),
$$
\vec{G}=\frac{\vec{A}_{1}+\vec{A}_{2}+\cdots+\vec{A}_{n}}{n}
$$
Note that any move leaves the centroid $G$ unchanged. Therefore, if all the tokens are eventually moved to the same point, then this point must be $G$.
First we prove that if $n=2^{k}$ for some nonnegative integer $k$, then all $n$ tokens can always be eventually moved to the same point. We shall use induction on $k$.
The result clearly holds for $n=2^{0}=1$. Assume that it holds when $n=2^{k}$ for some nonnegative integer $k$. Consider a set of $2^{k+1}$ tokens at $A_{1}, A_{2}, \ldots, A_{2^{k+1}}$. Let $M_{i}$ be the midpoint of $A_{2 i-1}$ and $A_{2 i}$ for $1 \leq i \leq 2^{k}$.
First we move the tokens at $A_{2 i-1}$ and $A_{2 i}$ to $M_{i}$, for $1 \leq i \leq 2^{k}$. Then, there are two tokens at $M_{i}$ for all $1 \leq i \leq 2^{k}$. If we take one token from each of $M_{1}, M_{2}, \ldots, M_{2^{k}}$, then by the induction hypothesis, we can move all of them to the same point, say $G$. We can do the same with the remaining tokens at $M_{1}, M_{2}, \ldots, M_{2^{k}}$. Thus, all $2^{k+1}$ tokens are now at $G$, which completes the induction argument.
(Here is an alternate approach to the induction step: Given the tokens at $A_{1}, A_{2}, \ldots, A_{2^{k+1}}$, move the first $2^{k}$ tokens to one point $G_{1}$, and move the remaining $2^{k}$ tokens to one point $G_{2}$. Then $2^{k}$ more moves can bring all the tokens to the midpoint of $G_{1}$ and $G_{2}$.)
Presented by the Canadian Mathematical Society and supported by the Actuarial Profession.

Expertise. Insight. Solutions.
Now, assume that $n$ is not a power of 2 . Take any line in the plane, and number it as a real number line. (Henceforth, when we refer to a token at a real number, we mean with respect to this real number line.)
At the start, place $n-1$ tokens at 0 and one token at 1 . We observed that if we can move all the tokens to the same point, then it must be the centroid of the $n$ points. Here, the centroid is at $\frac{1}{n}$. We now prove a lemma.
Lemma. The average of any two dyadic rationals is also a dyadic rational. (A dyadic rational is a rational number that can be expressed in the form $\frac{m}{2^{a}}$, where $m$ is an integer and $a$ is a nonnegative integer.)
Proof. Consider two dyadic rationals $\frac{m_{1}}{2^{a_{1}}}$ and $\frac{m_{2}}{2^{a_{2}}}$. Then their average is
$$
\frac{1}{2}\left(\frac{m_{1}}{2^{a_{1}}}+\frac{m_{2}}{2^{a_{2}}}\right)=\frac{1}{2}\left(\frac{2^{a_{2}} \cdot m_{1}+2^{a_{1}} \cdot m_{2}}{2^{a_{1}} \cdot 2^{a_{2}}}\right)=\frac{2^{a_{2}} \cdot m_{1}+2^{a_{1}} \cdot m_{2}}{2^{a_{1}+a_{2}+1}}
$$
which is another dyadic rational.
On this real number line, a move corresponds to taking a token at $x$ and a token at $y$ and moving both of them to $\frac{x+y}{2}$, the average of $x$ and $y$. At the start, every token is at a dyadic rational (namely 0 or 1 ), which means that after any number of moves, every token must still be at a dyadic rational.
But $n$ is not a power of 2 , so $\frac{1}{n}$ is not a dyadic rational. (Indeed, if we could express $\frac{1}{n}$ in dyadic form $\frac{m}{2^{a}}$, then we would have $2^{a}=m n$, which is impossible unless $m$ and $n$ are powers of 2.) This means that it is not possible for any token to end up at $\frac{1}{n}$, let alone all $n$ tokens.
We conclude that we can always move all $n$ tokens to the same point if and only if $n$ is a power of 2 .
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Consider an arrangement of tokens in the plane, not necessarily at distinct points. We are allowed to apply a sequence of moves of the following kind: Select a pair of tokens at points $A$ and $B$ and move both of them to the midpoint of $A$ and $B$.
We say that an arrangement of $n$ tokens is collapsible if it is possible to end up with all $n$ tokens at the same point after a finite number of moves. Prove that every arrangement of $n$ tokens is collapsible if and only if $n$ is a power of 2 .
|
For a given positive integer $n$, consider an arrangement of $n$ tokens in the plane, where the tokens are at points $A_{1}, A_{2}, \ldots, A_{n}$. Let $G$ be the centroid of the $n$ points, so as vectors (after an arbitrary choice of origin),
$$
\vec{G}=\frac{\vec{A}_{1}+\vec{A}_{2}+\cdots+\vec{A}_{n}}{n}
$$
Note that any move leaves the centroid $G$ unchanged. Therefore, if all the tokens are eventually moved to the same point, then this point must be $G$.
First we prove that if $n=2^{k}$ for some nonnegative integer $k$, then all $n$ tokens can always be eventually moved to the same point. We shall use induction on $k$.
The result clearly holds for $n=2^{0}=1$. Assume that it holds when $n=2^{k}$ for some nonnegative integer $k$. Consider a set of $2^{k+1}$ tokens at $A_{1}, A_{2}, \ldots, A_{2^{k+1}}$. Let $M_{i}$ be the midpoint of $A_{2 i-1}$ and $A_{2 i}$ for $1 \leq i \leq 2^{k}$.
First we move the tokens at $A_{2 i-1}$ and $A_{2 i}$ to $M_{i}$, for $1 \leq i \leq 2^{k}$. Then, there are two tokens at $M_{i}$ for all $1 \leq i \leq 2^{k}$. If we take one token from each of $M_{1}, M_{2}, \ldots, M_{2^{k}}$, then by the induction hypothesis, we can move all of them to the same point, say $G$. We can do the same with the remaining tokens at $M_{1}, M_{2}, \ldots, M_{2^{k}}$. Thus, all $2^{k+1}$ tokens are now at $G$, which completes the induction argument.
(Here is an alternate approach to the induction step: Given the tokens at $A_{1}, A_{2}, \ldots, A_{2^{k+1}}$, move the first $2^{k}$ tokens to one point $G_{1}$, and move the remaining $2^{k}$ tokens to one point $G_{2}$. Then $2^{k}$ more moves can bring all the tokens to the midpoint of $G_{1}$ and $G_{2}$.)
Presented by the Canadian Mathematical Society and supported by the Actuarial Profession.

Expertise. Insight. Solutions.
Now, assume that $n$ is not a power of 2 . Take any line in the plane, and number it as a real number line. (Henceforth, when we refer to a token at a real number, we mean with respect to this real number line.)
At the start, place $n-1$ tokens at 0 and one token at 1 . We observed that if we can move all the tokens to the same point, then it must be the centroid of the $n$ points. Here, the centroid is at $\frac{1}{n}$. We now prove a lemma.
Lemma. The average of any two dyadic rationals is also a dyadic rational. (A dyadic rational is a rational number that can be expressed in the form $\frac{m}{2^{a}}$, where $m$ is an integer and $a$ is a nonnegative integer.)
Proof. Consider two dyadic rationals $\frac{m_{1}}{2^{a_{1}}}$ and $\frac{m_{2}}{2^{a_{2}}}$. Then their average is
$$
\frac{1}{2}\left(\frac{m_{1}}{2^{a_{1}}}+\frac{m_{2}}{2^{a_{2}}}\right)=\frac{1}{2}\left(\frac{2^{a_{2}} \cdot m_{1}+2^{a_{1}} \cdot m_{2}}{2^{a_{1}} \cdot 2^{a_{2}}}\right)=\frac{2^{a_{2}} \cdot m_{1}+2^{a_{1}} \cdot m_{2}}{2^{a_{1}+a_{2}+1}}
$$
which is another dyadic rational.
On this real number line, a move corresponds to taking a token at $x$ and a token at $y$ and moving both of them to $\frac{x+y}{2}$, the average of $x$ and $y$. At the start, every token is at a dyadic rational (namely 0 or 1 ), which means that after any number of moves, every token must still be at a dyadic rational.
But $n$ is not a power of 2 , so $\frac{1}{n}$ is not a dyadic rational. (Indeed, if we could express $\frac{1}{n}$ in dyadic form $\frac{m}{2^{a}}$, then we would have $2^{a}=m n$, which is impossible unless $m$ and $n$ are powers of 2.) This means that it is not possible for any token to end up at $\frac{1}{n}$, let alone all $n$ tokens.
We conclude that we can always move all $n$ tokens to the same point if and only if $n$ is a power of 2 .
|
{
"exam": "Canada_MO",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "Canada_MO/segmented/en-sol2018.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2018"
}
|
Let five points on a circle be labelled $A, B, C, D$, and $E$ in clockwise order. Assume $A E=D E$ and let $P$ be the intersection of $A C$ and $B D$. Let $Q$ be the point on the line through $A$ and $B$ such that $A$ is between $B$ and $Q$ and $A Q=D P$. Similarly, let $R$ be the point on the line through $C$ and $D$ such that $D$ is between $C$ and $R$ and $D R=A P$. Prove that $P E$ is perpendicular to $Q R$.
|
We are given $A Q=D P$ and $A P=D R$. Additionally $\angle Q A P=180^{\circ}-\angle B A C=180^{\circ}-\angle B D C=\angle R D P$, and so triangles $A Q P$ and $D P R$ are congruent. Therefore $P Q=P R$. It follows that $P$ is on the perpendicular bisector of $Q R$.
We are also given $A P=D R$ and $A E=D E$. Additionally
$\angle P A E=\angle C A E=180^{\circ}-\angle C D E=\angle R D E$, and so triangles $P A E$ and $R D E$ are congruent.
Therefore $P E=R E$, and similarly $P E=Q E$. It follows that $E$ is on the perpendicular bisector of $P Q$.
Since both $P$ and $E$ are on the perpendicular bisector of $Q R$, the result follows.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Let five points on a circle be labelled $A, B, C, D$, and $E$ in clockwise order. Assume $A E=D E$ and let $P$ be the intersection of $A C$ and $B D$. Let $Q$ be the point on the line through $A$ and $B$ such that $A$ is between $B$ and $Q$ and $A Q=D P$. Similarly, let $R$ be the point on the line through $C$ and $D$ such that $D$ is between $C$ and $R$ and $D R=A P$. Prove that $P E$ is perpendicular to $Q R$.
|
We are given $A Q=D P$ and $A P=D R$. Additionally $\angle Q A P=180^{\circ}-\angle B A C=180^{\circ}-\angle B D C=\angle R D P$, and so triangles $A Q P$ and $D P R$ are congruent. Therefore $P Q=P R$. It follows that $P$ is on the perpendicular bisector of $Q R$.
We are also given $A P=D R$ and $A E=D E$. Additionally
$\angle P A E=\angle C A E=180^{\circ}-\angle C D E=\angle R D E$, and so triangles $P A E$ and $R D E$ are congruent.
Therefore $P E=R E$, and similarly $P E=Q E$. It follows that $E$ is on the perpendicular bisector of $P Q$.
Since both $P$ and $E$ are on the perpendicular bisector of $Q R$, the result follows.
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "Canada_MO/segmented/en-sol2018.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2018"
}
|
Two positive integers $a$ and $b$ are prime-related if $a=p b$ or $b=p a$ for some prime $p$. Find all positive integers $n$, such that $n$ has at least three divisors, and all the divisors can be arranged without repetition in a circle so that any two adjacent divisors are prime-related.
Note that 1 and $n$ are included as divisors.
|
We say that a positive integer is good if it has the given property. Let $n$ be a good number, and let $d_{1}, d_{2}, \ldots, d_{k}$ be the divisors of $n$ in the circle, in that order. Then for all $1 \leq i \leq k, d_{i+1} / d_{i}$ (taking the indices modulo $k$ ) is equal to either $p_{i}$ or $1 / p_{i}$ for some prime $p_{i}$. In other words, $d_{i+1} / d_{i}=p_{i}^{\epsilon_{i}}$, where $\epsilon_{i} \in\{1,-1\}$. Then
$$
p_{1}^{\epsilon_{1}} p_{2}^{\epsilon_{2}} \cdots p_{k}^{\epsilon_{k}}=\frac{d_{2}}{d_{1}} \cdot \frac{d_{3}}{d_{2}} \cdots \frac{d_{1}}{d_{k}}=1
$$
For the product $p_{1}^{\epsilon_{1}} p_{2}^{\epsilon_{2}} \cdots p_{k}^{\epsilon_{k}}$ to equal 1 , any prime factor $p$ must be paired with a factor of $1 / p$, and vice versa, so $k$ (the number of divisors of $n$ ) must be even. Hence, $n$ cannot be a perfect square.
Furthermore, $n$ cannot be the power of a prime (including a prime itself), because 1 always is a divisor of $n$, and if $n$ is a power of a prime, then the only divisor that can go next to 1 is the prime itself.
Now, let $n=p^{a} q^{b}$, where $p$ and $q$ are distinct primes, and $a$ is odd. We write the divisors of $n$ in a grid as follows: In the first row, write the numbers $1, q, q^{2}, \ldots, q^{b}$. In the next row, write the numbers $p, p q, p q^{2}, \ldots, p q^{b}$, and so on. The number of rows in the grid, $a+1$, is even. Note that if two squares are adjacent vertically or horizontally, then their corresponding numbers are prime-related. We start with the square with a 1 in the upper-left corner. We then move right along the first row, move down along the last column, move left along the last row, then zig-zag row by row, passing through every square, until we land on the square with a $p$. The following diagram gives the path for $a=3$ and $b=5$ :
Thus, we can write the divisors encountered on this path in a circle, so $n=p^{a} q^{b}$ is good.
Next, assume that $n$ is a good number. Let $d_{1}, d_{2}, \ldots, d_{k}$ be the divisors of $n$ in the circle, in that order. Let $p$ be a prime that does not divide $n$. We claim that $n \cdot p^{e}$ is also a good number. We
arrange the divisors of $n \cdot p^{e}$ that are not divisors of $n$ in a grid as follows:
$$
\begin{array}{cccc}
d_{1} p & d_{1} p^{2} & \ldots & d_{1} p^{e} \\
d_{2} p & d_{2} p^{2} & \ldots & d_{2} p^{e} \\
\vdots & \vdots & \ddots & \vdots \\
d_{k} p & d_{k} p^{2} & \ldots & d_{k} p^{e}
\end{array}
$$
Note that if two squares are adjacent vertically or horizontally, then their corresponding numbers are prime-related. Also, $k$ (the number of rows) is the number of factors of $n$, which must be even (since $n$ is good). Hence, we can use the same path described above, which starts at $d_{1} p$ and ends at $d_{2} p$. Since $d_{1}$ and $d_{2}$ are adjacent divisors in the circle for $n$, we can insert all the divisors in the grid above between $d_{1}$ and $d_{2}$, to obtain a circle for $n \cdot p^{e}$.
Finally, let $n$ be a positive integer that is neither a perfect square nor a power of a prime. Let the prime factorization of $n$ be
$$
n=p_{1}^{e_{1}} p_{2}^{e_{2}} \cdots p_{t}^{e_{t}}
$$
Since $n$ is not the power of a prime, $t \geq 2$. Also, since $n$ is not a perfect square, at least one exponent $e_{i}$ is odd. Without loss of generality, assume that $e_{1}$ is odd. Then from our work above, $p_{1}^{e_{1}} p_{2}^{e_{2}}$ is good, so $p_{1}^{e_{1}} p_{2}^{e_{2}} p_{3}^{e_{3}}$ is good, and so on, until $n=p_{1}^{e_{1}} p_{2}^{e_{2}} \cdots p_{t}^{e_{t}}$ is good.
Therefore, a positive integer $n$ has the given property if and only if it is neither a perfect square nor a power of a prime.
|
proof
|
Yes
|
Yes
|
math-word-problem
|
Number Theory
|
Two positive integers $a$ and $b$ are prime-related if $a=p b$ or $b=p a$ for some prime $p$. Find all positive integers $n$, such that $n$ has at least three divisors, and all the divisors can be arranged without repetition in a circle so that any two adjacent divisors are prime-related.
Note that 1 and $n$ are included as divisors.
|
We say that a positive integer is good if it has the given property. Let $n$ be a good number, and let $d_{1}, d_{2}, \ldots, d_{k}$ be the divisors of $n$ in the circle, in that order. Then for all $1 \leq i \leq k, d_{i+1} / d_{i}$ (taking the indices modulo $k$ ) is equal to either $p_{i}$ or $1 / p_{i}$ for some prime $p_{i}$. In other words, $d_{i+1} / d_{i}=p_{i}^{\epsilon_{i}}$, where $\epsilon_{i} \in\{1,-1\}$. Then
$$
p_{1}^{\epsilon_{1}} p_{2}^{\epsilon_{2}} \cdots p_{k}^{\epsilon_{k}}=\frac{d_{2}}{d_{1}} \cdot \frac{d_{3}}{d_{2}} \cdots \frac{d_{1}}{d_{k}}=1
$$
For the product $p_{1}^{\epsilon_{1}} p_{2}^{\epsilon_{2}} \cdots p_{k}^{\epsilon_{k}}$ to equal 1 , any prime factor $p$ must be paired with a factor of $1 / p$, and vice versa, so $k$ (the number of divisors of $n$ ) must be even. Hence, $n$ cannot be a perfect square.
Furthermore, $n$ cannot be the power of a prime (including a prime itself), because 1 always is a divisor of $n$, and if $n$ is a power of a prime, then the only divisor that can go next to 1 is the prime itself.
Now, let $n=p^{a} q^{b}$, where $p$ and $q$ are distinct primes, and $a$ is odd. We write the divisors of $n$ in a grid as follows: In the first row, write the numbers $1, q, q^{2}, \ldots, q^{b}$. In the next row, write the numbers $p, p q, p q^{2}, \ldots, p q^{b}$, and so on. The number of rows in the grid, $a+1$, is even. Note that if two squares are adjacent vertically or horizontally, then their corresponding numbers are prime-related. We start with the square with a 1 in the upper-left corner. We then move right along the first row, move down along the last column, move left along the last row, then zig-zag row by row, passing through every square, until we land on the square with a $p$. The following diagram gives the path for $a=3$ and $b=5$ :

Thus, we can write the divisors encountered on this path in a circle, so $n=p^{a} q^{b}$ is good.
Next, assume that $n$ is a good number. Let $d_{1}, d_{2}, \ldots, d_{k}$ be the divisors of $n$ in the circle, in that order. Let $p$ be a prime that does not divide $n$. We claim that $n \cdot p^{e}$ is also a good number. We
arrange the divisors of $n \cdot p^{e}$ that are not divisors of $n$ in a grid as follows:
$$
\begin{array}{cccc}
d_{1} p & d_{1} p^{2} & \ldots & d_{1} p^{e} \\
d_{2} p & d_{2} p^{2} & \ldots & d_{2} p^{e} \\
\vdots & \vdots & \ddots & \vdots \\
d_{k} p & d_{k} p^{2} & \ldots & d_{k} p^{e}
\end{array}
$$
Note that if two squares are adjacent vertically or horizontally, then their corresponding numbers are prime-related. Also, $k$ (the number of rows) is the number of factors of $n$, which must be even (since $n$ is good). Hence, we can use the same path described above, which starts at $d_{1} p$ and ends at $d_{2} p$. Since $d_{1}$ and $d_{2}$ are adjacent divisors in the circle for $n$, we can insert all the divisors in the grid above between $d_{1}$ and $d_{2}$, to obtain a circle for $n \cdot p^{e}$.
Finally, let $n$ be a positive integer that is neither a perfect square nor a power of a prime. Let the prime factorization of $n$ be
$$
n=p_{1}^{e_{1}} p_{2}^{e_{2}} \cdots p_{t}^{e_{t}}
$$
Since $n$ is not the power of a prime, $t \geq 2$. Also, since $n$ is not a perfect square, at least one exponent $e_{i}$ is odd. Without loss of generality, assume that $e_{1}$ is odd. Then from our work above, $p_{1}^{e_{1}} p_{2}^{e_{2}}$ is good, so $p_{1}^{e_{1}} p_{2}^{e_{2}} p_{3}^{e_{3}}$ is good, and so on, until $n=p_{1}^{e_{1}} p_{2}^{e_{2}} \cdots p_{t}^{e_{t}}$ is good.
Therefore, a positive integer $n$ has the given property if and only if it is neither a perfect square nor a power of a prime.
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "Canada_MO/segmented/en-sol2018.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2018"
}
|
Find all polynomials $p(x)$ with real coefficients that have the following property: There exists a polynomial $q(x)$ with real coefficients such that
$$
p(1)+p(2)+p(3)+\cdots+p(n)=p(n) q(n)
$$
for all positive integers $n$.
|
The property clearly holds whenever $p(x)$ is a constant polynomial, since we can take $q(x)=x$. Assume henceforth that $p(x)$ is nonconstant and has the stated property. Let $d$ be the degree of $p(x)$, so $p(x)$ is of the form
$$
p(x)=c x^{d}+\cdots .
$$
By a Lemma (which we will prove at the end), $\sum_{k=1}^{n} k^{d}$ is a polynomial in $n$ of degree $d+1$, so $p(1)+p(2)+\cdots+p(n)$ is a polynomial in $n$ of degree $d+1$. Hence, $q(n)$ is a polynomial of degree 1. Furthermore, the coefficient of $n^{d+1}$ in $\sum_{k=1}^{n} k^{d}$ is $\frac{1}{d+1}$, so the coefficient of $n$ in $q(n)$ is also $\frac{1}{d+1}$. Let $q(x)=\frac{1}{d+1}(x+r)$. We have that
$$
p(1)+p(2)+p(3)+\cdots+p(n)=p(n) q(n)
$$
and
$$
p(1)+p(2)+p(3)+\cdots+p(n)+p(n+1)=p(n+1) q(n+1) \text {. }
$$
Subtracting the first equation from the second, we get
$$
p(n+1)=p(n+1) q(n+1)-p(n) q(n),
$$
and hence
$$
p(n) q(n)=p(n+1)[q(n+1)-1] .
$$
Since this holds for all positive integers $n$, it follows that
$$
p(x) q(x)=p(x+1)[q(x+1)-1]
$$
for all real numbers $x$. We can then write
$$
p(x) \cdot \frac{1}{d+1}(x+r)=p(x+1)\left[\frac{1}{d+1}(x+r+1)-1\right]
$$
so
$$
(x+r) p(x)=(x+r-d) p(x+1) .
$$
Setting $x=-r$, we get
$$
(-d) p(-r+1)=0
$$
Hence, $-r+1$ is a root of $p(x)$. Let $p(x)=(x+r-1) p_{1}(x)$. Then
$$
(x+r)(x+r-1) p_{1}(x)=(x+r-d)(x+r) p_{1}(x+1),
$$
so
$$
(x+r-1) p_{1}(x)=(x+r-d) p_{1}(x+1) .
$$
If $d=1$, then $p_{1}(x)$ is a constant, so both sides are equal, and we can say $p(x)=c(x+r-1)$.
Otherwise, setting $x=-r+1$, we get
$$
(1-d) p_{1}(-r+2)=0
$$
Hence, $-r+2$ is a root of $p_{1}(x)$. Let $p_{1}(x)=(x+r-2) p_{2}(x)$. Then
$$
(x-r-1)(x+r-2) p_{2}(x)=(x+r-d)(x+r-1) p_{2}(x+1),
$$
so
$$
(x+r-2) p_{2}(x)=(x+r-d) p_{2}(x+1) \text {. }
$$
If $d=2$, then $p_{2}(x)$ is a constant, so both sides are equal, and we can say $p(x)=c(x+r-1)(x+r-2)$.
Otherwise, we can continue to substitute, giving us
$$
p(x)=c(x+r-1)(x+r-2) \cdots(x+r-d) .
$$
Conversely, if $p(x)$ is of this form, then
$$
\begin{aligned}
p(x)= & c(x+r-1)(x+r-2) \cdots(x+r-d) \\
= & \frac{c(d+1)(x+r-1)(x+r-2) \cdots(x+r-d)}{d+1} \\
= & \frac{c[(x+r)-(x+r-d-1)](x+r-1)(x+r-2) \cdots(x+r-d)}{d+1} \\
= & \frac{c(x+r)(x+r-1)(x+r-2) \cdots(x+r-d)}{d+1} \\
& -\frac{c(x+r-1)(x+r-2) \cdots(x+r-d)(x+r-d-1)}{d+1} .
\end{aligned}
$$
Then the sum $p(1)+p(2)+p(3)+\cdots+p(n)$ telescopes, and we are left with
$$
\begin{aligned}
p(1)+p(2)+p(3)+\cdots+p(n)= & \frac{c(n+r)(n+r-1)(n+r-2) \cdots(n+r-d)}{d+1} \\
& -\frac{c(r)(r-1) \cdots(r-d+1)(r-d)}{d+1} .
\end{aligned}
$$
We want this to be of the form
$$
p(n) q(n)=c(n+r-1)(n+r-2) \cdots(n+r-d) q(n)
$$
for some polynomial $q(n)$. The only way that this can hold for each positive integer $n$ is if the term
$$
\frac{c(r)(r-1) \cdots(r-d+1)(r-d)}{d+1}
$$
is equal to 0 . This means $r$ has to be one of the values $0,1,2, \ldots, d$. Therefore, the polynomials we seek are of the form
$$
p(x)=c(x+r-1)(x+r-2) \cdots(x+r-d)
$$
where $r \in\{0,1,2, \ldots, d\}$.
Lemma. For a positive integer $d$,
$$
\sum_{k=1}^{n} k^{d}
$$
is a polynomial in $n$ of degree $d+1$. Furthermore, the coefficient of $n^{d+1}$ is $\frac{1}{d+1}$.
Proof. We prove the result by strong induction. For $d=1$,
$$
\sum_{k=1}^{n} k=\frac{1}{2} n^{2}+\frac{1}{2} n
$$
so the result holds. Assume that the result holds for $d=1,2,3, \ldots, m$, for some positive integer $m$. By the Binomial Theorem,
$$
(k+1)^{m+2}-k^{m+2}=(m+2) k^{m+1}+c_{m} k^{m}+c_{m-1} k^{m-1}+\cdots+c_{1} k+c_{0},
$$
for some coefficients $c_{m}, c_{m-1}, \ldots, c_{1}, c_{0}$. Summing over $1 \leq k \leq n$, we get
$$
(n+1)^{m+2}-1=(m+2) \sum_{k=1}^{n} k^{m+1}+c_{m} \sum_{k=1}^{n} k^{m}+\cdots+c_{1} \sum_{k=1}^{n} k+c_{0} n .
$$
Then
$$
\sum_{k=1}^{n} k^{m+1}=\frac{(n+1)^{m+2}-c_{m} \sum_{k=1}^{n} k^{m}-\cdots-c_{1} \sum_{k=1}^{n} k-c_{0} n-1}{m+2} .
$$
By the induction hypothesis, the sums $\sum_{k=1}^{n} k^{m}, \ldots, \sum_{k=1}^{n} k$ are all polynomials in $n$ of degree less than $m+2$. Hence, the above expression is a polynomial in $n$ of degree $m+2$, and the coefficient of $n^{m+2}$ is $\frac{1}{m+2}$. Thus, the result holds for $d=m+1$, which completes the induction step.
|
p(x)=c(x+r-1)(x+r-2) \cdots(x+r-d)
|
Yes
|
Incomplete
|
math-word-problem
|
Algebra
|
Find all polynomials $p(x)$ with real coefficients that have the following property: There exists a polynomial $q(x)$ with real coefficients such that
$$
p(1)+p(2)+p(3)+\cdots+p(n)=p(n) q(n)
$$
for all positive integers $n$.
|
The property clearly holds whenever $p(x)$ is a constant polynomial, since we can take $q(x)=x$. Assume henceforth that $p(x)$ is nonconstant and has the stated property. Let $d$ be the degree of $p(x)$, so $p(x)$ is of the form
$$
p(x)=c x^{d}+\cdots .
$$
By a Lemma (which we will prove at the end), $\sum_{k=1}^{n} k^{d}$ is a polynomial in $n$ of degree $d+1$, so $p(1)+p(2)+\cdots+p(n)$ is a polynomial in $n$ of degree $d+1$. Hence, $q(n)$ is a polynomial of degree 1. Furthermore, the coefficient of $n^{d+1}$ in $\sum_{k=1}^{n} k^{d}$ is $\frac{1}{d+1}$, so the coefficient of $n$ in $q(n)$ is also $\frac{1}{d+1}$. Let $q(x)=\frac{1}{d+1}(x+r)$. We have that
$$
p(1)+p(2)+p(3)+\cdots+p(n)=p(n) q(n)
$$
and
$$
p(1)+p(2)+p(3)+\cdots+p(n)+p(n+1)=p(n+1) q(n+1) \text {. }
$$
Subtracting the first equation from the second, we get
$$
p(n+1)=p(n+1) q(n+1)-p(n) q(n),
$$
and hence
$$
p(n) q(n)=p(n+1)[q(n+1)-1] .
$$
Since this holds for all positive integers $n$, it follows that
$$
p(x) q(x)=p(x+1)[q(x+1)-1]
$$
for all real numbers $x$. We can then write
$$
p(x) \cdot \frac{1}{d+1}(x+r)=p(x+1)\left[\frac{1}{d+1}(x+r+1)-1\right]
$$
so
$$
(x+r) p(x)=(x+r-d) p(x+1) .
$$
Setting $x=-r$, we get
$$
(-d) p(-r+1)=0
$$
Hence, $-r+1$ is a root of $p(x)$. Let $p(x)=(x+r-1) p_{1}(x)$. Then
$$
(x+r)(x+r-1) p_{1}(x)=(x+r-d)(x+r) p_{1}(x+1),
$$
so
$$
(x+r-1) p_{1}(x)=(x+r-d) p_{1}(x+1) .
$$
If $d=1$, then $p_{1}(x)$ is a constant, so both sides are equal, and we can say $p(x)=c(x+r-1)$.
Otherwise, setting $x=-r+1$, we get
$$
(1-d) p_{1}(-r+2)=0
$$
Hence, $-r+2$ is a root of $p_{1}(x)$. Let $p_{1}(x)=(x+r-2) p_{2}(x)$. Then
$$
(x-r-1)(x+r-2) p_{2}(x)=(x+r-d)(x+r-1) p_{2}(x+1),
$$
so
$$
(x+r-2) p_{2}(x)=(x+r-d) p_{2}(x+1) \text {. }
$$
If $d=2$, then $p_{2}(x)$ is a constant, so both sides are equal, and we can say $p(x)=c(x+r-1)(x+r-2)$.
Otherwise, we can continue to substitute, giving us
$$
p(x)=c(x+r-1)(x+r-2) \cdots(x+r-d) .
$$
Conversely, if $p(x)$ is of this form, then
$$
\begin{aligned}
p(x)= & c(x+r-1)(x+r-2) \cdots(x+r-d) \\
= & \frac{c(d+1)(x+r-1)(x+r-2) \cdots(x+r-d)}{d+1} \\
= & \frac{c[(x+r)-(x+r-d-1)](x+r-1)(x+r-2) \cdots(x+r-d)}{d+1} \\
= & \frac{c(x+r)(x+r-1)(x+r-2) \cdots(x+r-d)}{d+1} \\
& -\frac{c(x+r-1)(x+r-2) \cdots(x+r-d)(x+r-d-1)}{d+1} .
\end{aligned}
$$
Then the sum $p(1)+p(2)+p(3)+\cdots+p(n)$ telescopes, and we are left with
$$
\begin{aligned}
p(1)+p(2)+p(3)+\cdots+p(n)= & \frac{c(n+r)(n+r-1)(n+r-2) \cdots(n+r-d)}{d+1} \\
& -\frac{c(r)(r-1) \cdots(r-d+1)(r-d)}{d+1} .
\end{aligned}
$$
We want this to be of the form
$$
p(n) q(n)=c(n+r-1)(n+r-2) \cdots(n+r-d) q(n)
$$
for some polynomial $q(n)$. The only way that this can hold for each positive integer $n$ is if the term
$$
\frac{c(r)(r-1) \cdots(r-d+1)(r-d)}{d+1}
$$
is equal to 0 . This means $r$ has to be one of the values $0,1,2, \ldots, d$. Therefore, the polynomials we seek are of the form
$$
p(x)=c(x+r-1)(x+r-2) \cdots(x+r-d)
$$
where $r \in\{0,1,2, \ldots, d\}$.
Lemma. For a positive integer $d$,
$$
\sum_{k=1}^{n} k^{d}
$$
is a polynomial in $n$ of degree $d+1$. Furthermore, the coefficient of $n^{d+1}$ is $\frac{1}{d+1}$.
Proof. We prove the result by strong induction. For $d=1$,
$$
\sum_{k=1}^{n} k=\frac{1}{2} n^{2}+\frac{1}{2} n
$$
so the result holds. Assume that the result holds for $d=1,2,3, \ldots, m$, for some positive integer $m$. By the Binomial Theorem,
$$
(k+1)^{m+2}-k^{m+2}=(m+2) k^{m+1}+c_{m} k^{m}+c_{m-1} k^{m-1}+\cdots+c_{1} k+c_{0},
$$
for some coefficients $c_{m}, c_{m-1}, \ldots, c_{1}, c_{0}$. Summing over $1 \leq k \leq n$, we get
$$
(n+1)^{m+2}-1=(m+2) \sum_{k=1}^{n} k^{m+1}+c_{m} \sum_{k=1}^{n} k^{m}+\cdots+c_{1} \sum_{k=1}^{n} k+c_{0} n .
$$
Then
$$
\sum_{k=1}^{n} k^{m+1}=\frac{(n+1)^{m+2}-c_{m} \sum_{k=1}^{n} k^{m}-\cdots-c_{1} \sum_{k=1}^{n} k-c_{0} n-1}{m+2} .
$$
By the induction hypothesis, the sums $\sum_{k=1}^{n} k^{m}, \ldots, \sum_{k=1}^{n} k$ are all polynomials in $n$ of degree less than $m+2$. Hence, the above expression is a polynomial in $n$ of degree $m+2$, and the coefficient of $n^{m+2}$ is $\frac{1}{m+2}$. Thus, the result holds for $d=m+1$, which completes the induction step.
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "Canada_MO/segmented/en-sol2018.jsonl",
"solution_match": "\nSolution.",
"tier": "T2",
"year": "2018"
}
|
Let $k$ be a given even positive integer. Sarah first picks a positive integer $N$ greater than 1 and proceeds to alter it as follows: every minute, she chooses a prime divisor $p$ of the current value of $N$, and multiplies the current $N$ by $p^{k}-p^{-1}$ to produce the next value of $N$. Prove that there are infinitely many even positive integers $k$ such that, no matter what choices Sarah makes, her number $N$ will at some point be divisible by 2018 .
|
Note that 1009 is prime. We will show that if $k=1009^{m}-1$ for some positive integer $m$, then Sarah's number must at some point be divisible by 2018 . Let $P$ be the largest divisor of $N$ not divisible by a prime congruent to 1 modulo 1009. Assume for contradiction that $N$ is never divisible by 2018. We will show that $P$ decreases each minute. Suppose that in the $t^{\text {th }}$ minute, Sarah chooses the prime divisor $p$ of $N$. First note that $N$ is replaced with $\frac{p^{k+1}-1}{p} \cdot N$ where
$$
p^{k+1}-1=p^{1009^{m}}-1=(p-1)\left(p^{1009^{m}-1}+p^{1009^{m}-2}+\cdots+1\right)
$$
Suppose that $q$ is a prime number dividing the second factor. Since $q$ divides $p^{1009^{m}}-1$, it follows that $q \neq p$ and the order of $p$ modulo $q$ must divide $1009^{m}$ and hence is either divisible by 1009 or is equal to 1 . If it is equal to 1 then $p \equiv 1(\bmod q)$, which implies that
$$
0 \equiv p^{1009^{m}-1}+p^{1009^{m}-2}+\cdots+1 \equiv 1009^{m} \quad(\bmod q)
$$
and thus $q=1009$. However, if $q=1009$ then $p \geq 1010$ and $p$ must be odd. Since $p-1$ now divides $N$, it follows that $N$ is divisible by 2018 in the $(t+1)^{\text {th }}$ minute, which is a contradiction. Therefore the order of $p$ modulo $q$ is divisible by 1009 and hence 1009 divides $q-1$. Therefore all of the prime divisors of the second factor are congruent to 1 modulo 1009. This implies that $P$ is replaced by a divisor of $\frac{p-1}{p} \cdot P$ in the $(t+1)^{\text {th }}$ minute and therefore decreases. Since $P \geq 1$ must always hold, $P$ cannot decrease forever. Therefore $N$ must at some point be divisible by 2018 .
Remark (no credit). If $k$ is allowed to be odd, then choosing $k+1$ to be divisible by $\phi(1009)=1008$ guarantees that Sarah's number will be divisible by 2018 the first time it is even, which is after either the first or second minute.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $k$ be a given even positive integer. Sarah first picks a positive integer $N$ greater than 1 and proceeds to alter it as follows: every minute, she chooses a prime divisor $p$ of the current value of $N$, and multiplies the current $N$ by $p^{k}-p^{-1}$ to produce the next value of $N$. Prove that there are infinitely many even positive integers $k$ such that, no matter what choices Sarah makes, her number $N$ will at some point be divisible by 2018 .
|
Note that 1009 is prime. We will show that if $k=1009^{m}-1$ for some positive integer $m$, then Sarah's number must at some point be divisible by 2018 . Let $P$ be the largest divisor of $N$ not divisible by a prime congruent to 1 modulo 1009. Assume for contradiction that $N$ is never divisible by 2018. We will show that $P$ decreases each minute. Suppose that in the $t^{\text {th }}$ minute, Sarah chooses the prime divisor $p$ of $N$. First note that $N$ is replaced with $\frac{p^{k+1}-1}{p} \cdot N$ where
$$
p^{k+1}-1=p^{1009^{m}}-1=(p-1)\left(p^{1009^{m}-1}+p^{1009^{m}-2}+\cdots+1\right)
$$
Suppose that $q$ is a prime number dividing the second factor. Since $q$ divides $p^{1009^{m}}-1$, it follows that $q \neq p$ and the order of $p$ modulo $q$ must divide $1009^{m}$ and hence is either divisible by 1009 or is equal to 1 . If it is equal to 1 then $p \equiv 1(\bmod q)$, which implies that
$$
0 \equiv p^{1009^{m}-1}+p^{1009^{m}-2}+\cdots+1 \equiv 1009^{m} \quad(\bmod q)
$$
and thus $q=1009$. However, if $q=1009$ then $p \geq 1010$ and $p$ must be odd. Since $p-1$ now divides $N$, it follows that $N$ is divisible by 2018 in the $(t+1)^{\text {th }}$ minute, which is a contradiction. Therefore the order of $p$ modulo $q$ is divisible by 1009 and hence 1009 divides $q-1$. Therefore all of the prime divisors of the second factor are congruent to 1 modulo 1009. This implies that $P$ is replaced by a divisor of $\frac{p-1}{p} \cdot P$ in the $(t+1)^{\text {th }}$ minute and therefore decreases. Since $P \geq 1$ must always hold, $P$ cannot decrease forever. Therefore $N$ must at some point be divisible by 2018 .
Remark (no credit). If $k$ is allowed to be odd, then choosing $k+1$ to be divisible by $\phi(1009)=1008$ guarantees that Sarah's number will be divisible by 2018 the first time it is even, which is after either the first or second minute.
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "Canada_MO/segmented/en-sol2018.jsonl",
"solution_match": "\nSolution:",
"tier": "T2",
"year": "2018"
}
|
Amy has drawn three points in a plane, $A, B$, and $C$, such that $A B=B C=C A=6$. Amy is allowed to draw a new point if it is the circumcenter of a triangle whose vertices she has already drawn. For example, she can draw the circumcenter $O$ of triangle $A B C$, and then afterwards she can draw the circumcenter of triangle $A B O$.
(a) Prove that Amy can eventually draw a point whose distance from a previously drawn point is greater than 7 .
(b) Prove that Amy can eventually draw a point whose distance from a previously drawn point is greater than 2019.
(Recall that the circumcenter of a triangle is the center of the circle that passes through its three vertices.)
|
(a) Given triangle $\triangle A B C$, Amy can draw the following points:
- $O$ is the circumcenter of $\triangle A B C$
- $A_{1}$ is the circumcenter of $\triangle B O C$
- $A_{2}$ is the circumcenter of $\triangle O B A_{1}$
- $A_{3}$ is the circumcenter of $\triangle B A_{2} A_{1}$
We claim that $A A_{3}>7$. We present two ways to prove this claim.
First Method: By symmetry of the equilateral triangle $\triangle A B C$, we have $\angle A O B=\angle B O C=\angle C O A=120^{\circ}$. Since $O B=O C$ and $A_{1} B=A_{1} O=A_{1} C$, we deduce that $\triangle A_{1} O B \cong \triangle A_{1} O C$, and hence $\angle B O A_{1}=\angle C O A_{1}=60^{\circ}$. Therefore, since $\triangle A_{1} O B$ is isosceles, it must be equilateral. As we found for our original triangle, we find $\angle B A_{2} A_{1}=120^{\circ}$, and so $\angle A_{2} B A_{1}=\angle A_{2} A_{1} B=30^{\circ}$ (since
A competition of the Canadian Mathematical Society and supported by the Actuarial Profession.

$\left.A_{2} B=A_{2} A_{1}\right)$. Also we see that $\angle O B A_{2}=30^{\circ}=\angle O B C$, which shows that $A_{2}$ lies on the segment $B C$.
Applying the Law of Sines to $\triangle B O C$, we obtain
$$
O C=\frac{B C \sin (\angle O B C)}{\sin (\angle B O C)}=\frac{6(1 / 2)}{\sqrt{3} / 2}=2 \sqrt{3} .
$$
By symmetry, we see that (i) $O A_{1}$ is the bisector of $\angle B O C$ and the perpendicular bisector of $B C$, and (ii) the three points $A, O$, and $A_{1}$ are collinear. Therefore $A_{1} A=A_{1} O+O A=2 O A=4 \sqrt{3}$.
The same argument that we used to show $\triangle A_{1} O B$ is equilateral with side $A C / \sqrt{3}$ shows that $\triangle A_{3} A_{2} A_{1}$ is equilateral with side $O B / \sqrt{3}=2$. Thus $\angle A_{3} A_{1} O=\angle O A_{1} B+\angle A_{3} A_{1} A_{2}-\angle A_{2} A_{1} B=$ $60^{\circ}+60^{\circ}-30^{\circ}=90^{\circ}$. Hence we can apply the Pythagorean Theorem:
$$
A_{3} A=\sqrt{\left(A_{3} A_{1}\right)^{2}+\left(A_{1} A\right)^{2}}=\sqrt{2^{2}+(4 \sqrt{3})^{2}}=\sqrt{52}>\sqrt{49}=7 .
$$
Second Method: (An alternative to writing the justifications of the constructions in the First Method is to use analytic geometry. Once the following coordinates are found using the kind of reasoning in the First Method or by other means, the writeup can justify them succinctly by computing distances.) Label $(0,0)$ as $B,(6,0)$ as $C$, and $(3, \sqrt{3})$ as $A$. Then we have $A B=B C=C A=6$.
The circumcenter $O$ of $\triangle A B C$ is $(3, \sqrt{3})$; this can be verified by observing $O A=O B=O C=2 \sqrt{3}$. Next, the point $A_{1}=(3,-\sqrt{3})$ satisfies $A_{1} O=A_{1} B=A_{1} C=2 \sqrt{3}$, so $A_{1}$ is the circumcenter of $\triangle B O C$.
The point $A_{2}=(2,0)$ satisfies $A_{2} O=A_{2} B=A_{2} A_{1}=2$, so this is the circumcenter of $\triangle O B A_{1}$.
And the point $A_{3}=(1,-\sqrt{3})$ satisfies $A_{3} B=A_{3} A_{2}=A_{3} A_{1}=2$, so this is the circumcenter of $\triangle B A_{2} A_{1}$.
Finally, we compute $A_{3} A=\sqrt{52}>\sqrt{49}=7$, and part (a) is proved.
(b) In part (a), using either method we find that $O A_{3}=4>2 \sqrt{3}=O A$. By rotating the construction of part (a) by $\pm 120^{\circ}$ about $O$, Amy can construct $B_{3}$ and $C_{3}$ such that $\triangle A_{3} B_{3} C_{3}$ is equilateral with circumcenter $O$ and circumradius 4 , which is strictly bigger than the circumradius $2 \sqrt{3}$ of $\triangle A B C$. Amy can repeat this process starting from $\triangle A_{3} B_{3} C_{3}$. After $n$ iterations of the process, Amy will have drawn the vertices of an equilateral triangle whose circumradius is $2 \sqrt{3}\left(\frac{4}{2 \sqrt{3}}\right)^{n}$, which is bigger than 2019 when $n$ is sufficiently large.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
Amy has drawn three points in a plane, $A, B$, and $C$, such that $A B=B C=C A=6$. Amy is allowed to draw a new point if it is the circumcenter of a triangle whose vertices she has already drawn. For example, she can draw the circumcenter $O$ of triangle $A B C$, and then afterwards she can draw the circumcenter of triangle $A B O$.
(a) Prove that Amy can eventually draw a point whose distance from a previously drawn point is greater than 7 .
(b) Prove that Amy can eventually draw a point whose distance from a previously drawn point is greater than 2019.
(Recall that the circumcenter of a triangle is the center of the circle that passes through its three vertices.)
|
(a) Given triangle $\triangle A B C$, Amy can draw the following points:
- $O$ is the circumcenter of $\triangle A B C$
- $A_{1}$ is the circumcenter of $\triangle B O C$
- $A_{2}$ is the circumcenter of $\triangle O B A_{1}$
- $A_{3}$ is the circumcenter of $\triangle B A_{2} A_{1}$
We claim that $A A_{3}>7$. We present two ways to prove this claim.
First Method: By symmetry of the equilateral triangle $\triangle A B C$, we have $\angle A O B=\angle B O C=\angle C O A=120^{\circ}$. Since $O B=O C$ and $A_{1} B=A_{1} O=A_{1} C$, we deduce that $\triangle A_{1} O B \cong \triangle A_{1} O C$, and hence $\angle B O A_{1}=\angle C O A_{1}=60^{\circ}$. Therefore, since $\triangle A_{1} O B$ is isosceles, it must be equilateral. As we found for our original triangle, we find $\angle B A_{2} A_{1}=120^{\circ}$, and so $\angle A_{2} B A_{1}=\angle A_{2} A_{1} B=30^{\circ}$ (since

A competition of the Canadian Mathematical Society and supported by the Actuarial Profession.

$\left.A_{2} B=A_{2} A_{1}\right)$. Also we see that $\angle O B A_{2}=30^{\circ}=\angle O B C$, which shows that $A_{2}$ lies on the segment $B C$.
Applying the Law of Sines to $\triangle B O C$, we obtain
$$
O C=\frac{B C \sin (\angle O B C)}{\sin (\angle B O C)}=\frac{6(1 / 2)}{\sqrt{3} / 2}=2 \sqrt{3} .
$$
By symmetry, we see that (i) $O A_{1}$ is the bisector of $\angle B O C$ and the perpendicular bisector of $B C$, and (ii) the three points $A, O$, and $A_{1}$ are collinear. Therefore $A_{1} A=A_{1} O+O A=2 O A=4 \sqrt{3}$.
The same argument that we used to show $\triangle A_{1} O B$ is equilateral with side $A C / \sqrt{3}$ shows that $\triangle A_{3} A_{2} A_{1}$ is equilateral with side $O B / \sqrt{3}=2$. Thus $\angle A_{3} A_{1} O=\angle O A_{1} B+\angle A_{3} A_{1} A_{2}-\angle A_{2} A_{1} B=$ $60^{\circ}+60^{\circ}-30^{\circ}=90^{\circ}$. Hence we can apply the Pythagorean Theorem:
$$
A_{3} A=\sqrt{\left(A_{3} A_{1}\right)^{2}+\left(A_{1} A\right)^{2}}=\sqrt{2^{2}+(4 \sqrt{3})^{2}}=\sqrt{52}>\sqrt{49}=7 .
$$
Second Method: (An alternative to writing the justifications of the constructions in the First Method is to use analytic geometry. Once the following coordinates are found using the kind of reasoning in the First Method or by other means, the writeup can justify them succinctly by computing distances.) Label $(0,0)$ as $B,(6,0)$ as $C$, and $(3, \sqrt{3})$ as $A$. Then we have $A B=B C=C A=6$.
The circumcenter $O$ of $\triangle A B C$ is $(3, \sqrt{3})$; this can be verified by observing $O A=O B=O C=2 \sqrt{3}$. Next, the point $A_{1}=(3,-\sqrt{3})$ satisfies $A_{1} O=A_{1} B=A_{1} C=2 \sqrt{3}$, so $A_{1}$ is the circumcenter of $\triangle B O C$.
The point $A_{2}=(2,0)$ satisfies $A_{2} O=A_{2} B=A_{2} A_{1}=2$, so this is the circumcenter of $\triangle O B A_{1}$.
And the point $A_{3}=(1,-\sqrt{3})$ satisfies $A_{3} B=A_{3} A_{2}=A_{3} A_{1}=2$, so this is the circumcenter of $\triangle B A_{2} A_{1}$.
Finally, we compute $A_{3} A=\sqrt{52}>\sqrt{49}=7$, and part (a) is proved.
(b) In part (a), using either method we find that $O A_{3}=4>2 \sqrt{3}=O A$. By rotating the construction of part (a) by $\pm 120^{\circ}$ about $O$, Amy can construct $B_{3}$ and $C_{3}$ such that $\triangle A_{3} B_{3} C_{3}$ is equilateral with circumcenter $O$ and circumradius 4 , which is strictly bigger than the circumradius $2 \sqrt{3}$ of $\triangle A B C$. Amy can repeat this process starting from $\triangle A_{3} B_{3} C_{3}$. After $n$ iterations of the process, Amy will have drawn the vertices of an equilateral triangle whose circumradius is $2 \sqrt{3}\left(\frac{4}{2 \sqrt{3}}\right)^{n}$, which is bigger than 2019 when $n$ is sufficiently large.
|
{
"exam": "Canada_MO",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "Canada_MO/segmented/en-sol2019.jsonl",
"solution_match": "\n## Solution.",
"tier": "T2",
"year": "2019"
}
|
Let $a$ and $b$ be positive integers such that $a+b^{3}$ is divisible by $a^{2}+3 a b+3 b^{2}-1$. Prove that $a^{2}+3 a b+3 b^{2}-1$ is divisible by the cube of an integer greater than 1 .
|
Let $Z=a^{2}+3 a b+3 b^{2}-1$. By assumption, there is a positive integer $c$ such that $c Z=a+b^{3}$. Noticing the resemblance between the first three terms of $Z$ and those of the expansion of $(a+b)^{3}$, we are led to
$$
(a+b)^{3}=a\left(a^{2}+3 a b+3 b^{2}\right)+b^{3}=a(Z+1)+b^{3}=a Z+a+b^{3}=a Z+c Z .
$$
Thus $Z$ divides $(a+b)^{3}$.
Let the prime factorization of $a+b$ be $p_{1}^{e_{1}} p_{2}^{e_{2}} \cdots p_{k}^{e_{k}}$ and let $Z=p_{1}^{f_{1}} p_{2}^{f_{2}} \cdots p_{k}^{f_{k}}$, where $f_{i} \leq 3 e_{i}$ for each $i$ since $Z$ divides $(a+b)^{3}$. If $Z$ is not divisible by a perfect cube greater than one, then $0 \leq f_{i} \leq 2$ and hence $f_{i} \leq 2 e_{i}$ for each $i$. This implies that $Z$ divides $(a+b)^{2}$. However, $(a+b)^{2}<a^{2}+3 a b+3 b^{2}-1=Z$ since $a, b \geq 1$, which is a contradiction. Thus $Z$ must be divisible by a perfect cube greater than one.
Remark. A brute force search yields many pairs $(a, b)$ satisfying this divisibility property. Examples include $(3,5),(19,11),(111,29)$ as well as twelve others satisfying that $a, b \leq 1000$. The values of $a^{2}+3 a b+3 b^{2}-1$ for these three pairs are $128=2^{7}, 1350=2 \times 3^{3} \times 5^{2}$ and $24500=2^{2} \times 5^{3} \times 7^{2}$, all of which have different perfect cube divisors.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $a$ and $b$ be positive integers such that $a+b^{3}$ is divisible by $a^{2}+3 a b+3 b^{2}-1$. Prove that $a^{2}+3 a b+3 b^{2}-1$ is divisible by the cube of an integer greater than 1 .
|
Let $Z=a^{2}+3 a b+3 b^{2}-1$. By assumption, there is a positive integer $c$ such that $c Z=a+b^{3}$. Noticing the resemblance between the first three terms of $Z$ and those of the expansion of $(a+b)^{3}$, we are led to
$$
(a+b)^{3}=a\left(a^{2}+3 a b+3 b^{2}\right)+b^{3}=a(Z+1)+b^{3}=a Z+a+b^{3}=a Z+c Z .
$$
Thus $Z$ divides $(a+b)^{3}$.
Let the prime factorization of $a+b$ be $p_{1}^{e_{1}} p_{2}^{e_{2}} \cdots p_{k}^{e_{k}}$ and let $Z=p_{1}^{f_{1}} p_{2}^{f_{2}} \cdots p_{k}^{f_{k}}$, where $f_{i} \leq 3 e_{i}$ for each $i$ since $Z$ divides $(a+b)^{3}$. If $Z$ is not divisible by a perfect cube greater than one, then $0 \leq f_{i} \leq 2$ and hence $f_{i} \leq 2 e_{i}$ for each $i$. This implies that $Z$ divides $(a+b)^{2}$. However, $(a+b)^{2}<a^{2}+3 a b+3 b^{2}-1=Z$ since $a, b \geq 1$, which is a contradiction. Thus $Z$ must be divisible by a perfect cube greater than one.
Remark. A brute force search yields many pairs $(a, b)$ satisfying this divisibility property. Examples include $(3,5),(19,11),(111,29)$ as well as twelve others satisfying that $a, b \leq 1000$. The values of $a^{2}+3 a b+3 b^{2}-1$ for these three pairs are $128=2^{7}, 1350=2 \times 3^{3} \times 5^{2}$ and $24500=2^{2} \times 5^{3} \times 7^{2}$, all of which have different perfect cube divisors.
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "Canada_MO/segmented/en-sol2019.jsonl",
"solution_match": "\n## Solution.",
"tier": "T2",
"year": "2019"
}
|
Let $m$ and $n$ be positive integers. A $2 m \times 2 n$ grid of squares is coloured in the usual chessboard fashion. Find the number of ways of placing $m n$ counters on the white squares, at most one counter per square, so that no two counters are on white squares that are diagonally adjacent. An example of a way to place the counters when $m=2$ and $n=3$ is shown below.
|
Divide the chessboard into $m n 2 \times 2$ squares.

Each $2 \times 2$ square can contain at most one counter. Since we want to place $m n$ counters, each $2 \times 2$ square must contain exactly one counter.
Assume that the lower-right corner of the $2 m \times 2 n$ chessboard is white, so in each $2 \times 2$ square, the upper-left and lower-right squares are white. Call a $2 \times 2$ square UL if the counter it contains is on the upper-left white square, and call it LR if the counter it contains is on the lower-right white square.
Suppose some $2 \times 2$ square is UL. Then the $2 \times 2$ square above it (if it exists) must also be UL, and the $2 \times 2$ square to the left of it (if it exists) must also be UL.
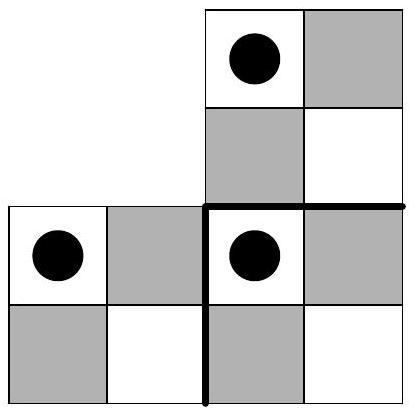
Similarly, if some $2 \times 2$ square is LR, then the $2 \times 2$ square below it (if it exists) must also be LR, and the $2 \times 2$ square to the right of it (if it exists) must also be LR.
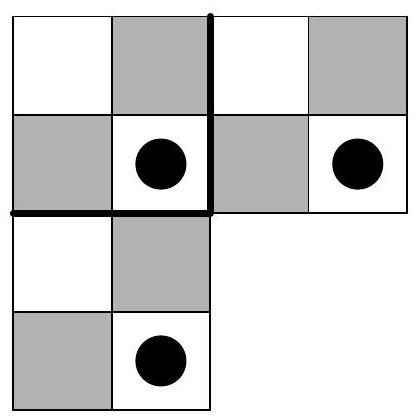
Then the collection of UL $2 \times 2$ squares form a region that is top-justified and left-justified, and the collection of LR $2 \times 2$ squares form a region that is bottom-justified and right-justified. This means that the boundary between the two regions forms a path between the lower-left corner and upper-right corner of the $2 m \times 2 n$ chessboard.
Conversely, any path from the lower-left corner to the upper-right corner, where each step consists of two units, can serve as the boundary of the UL squares and LR squares. Thus, the number of ways of placing the counters is equal to the number of paths, which is $\left(\begin{array}{c}m+n \\ m\end{array}\right)$.
|
\left(\begin{array}{c}m+n \\ m\end{array}\right)
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
Let $m$ and $n$ be positive integers. A $2 m \times 2 n$ grid of squares is coloured in the usual chessboard fashion. Find the number of ways of placing $m n$ counters on the white squares, at most one counter per square, so that no two counters are on white squares that are diagonally adjacent. An example of a way to place the counters when $m=2$ and $n=3$ is shown below.

|
Divide the chessboard into $m n 2 \times 2$ squares.

Each $2 \times 2$ square can contain at most one counter. Since we want to place $m n$ counters, each $2 \times 2$ square must contain exactly one counter.
Assume that the lower-right corner of the $2 m \times 2 n$ chessboard is white, so in each $2 \times 2$ square, the upper-left and lower-right squares are white. Call a $2 \times 2$ square UL if the counter it contains is on the upper-left white square, and call it LR if the counter it contains is on the lower-right white square.
Suppose some $2 \times 2$ square is UL. Then the $2 \times 2$ square above it (if it exists) must also be UL, and the $2 \times 2$ square to the left of it (if it exists) must also be UL.

Similarly, if some $2 \times 2$ square is LR, then the $2 \times 2$ square below it (if it exists) must also be LR, and the $2 \times 2$ square to the right of it (if it exists) must also be LR.

Then the collection of UL $2 \times 2$ squares form a region that is top-justified and left-justified, and the collection of LR $2 \times 2$ squares form a region that is bottom-justified and right-justified. This means that the boundary between the two regions forms a path between the lower-left corner and upper-right corner of the $2 m \times 2 n$ chessboard.

Conversely, any path from the lower-left corner to the upper-right corner, where each step consists of two units, can serve as the boundary of the UL squares and LR squares. Thus, the number of ways of placing the counters is equal to the number of paths, which is $\left(\begin{array}{c}m+n \\ m\end{array}\right)$.
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "Canada_MO/segmented/en-sol2019.jsonl",
"solution_match": "\n## Solution.",
"tier": "T2",
"year": "2019"
}
|
Let $n$ be an integer greater than 1 , and let $a_{0}, a_{1}, \ldots, a_{n}$ be real numbers with $a_{1}=a_{n-1}=0$. Prove that for any real number $k$,
$$
\left|a_{0}\right|-\left|a_{n}\right| \leq \sum_{i=0}^{n-2}\left|a_{i}-k a_{i+1}-a_{i+2}\right|
$$
|
Let $Q(x)=x^{2}-k x-1$ and let $P(x)=a_{0}+a_{1} x+\cdots+a_{n} x^{n}$. Note that the product of the two roots of $Q(x)$ is -1 and thus one of the two roots has magnitude at most 1. Let $z$ be this root. Now note that since $a_{1}=a_{n-1}=0$, we have that
$$
\begin{aligned}
0=Q(z) P(z) & =-a_{0}-k a_{0} z+\sum_{i=0}^{n-2}\left(a_{i}-k a_{i+1}-a_{i+2}\right) z^{i+2}-k a_{n} z^{n+1}+a_{n} z^{n+2} \\
& =a_{0}(-1-k z)+\sum_{i=0}^{n-2}\left(a_{i}-k a_{i+1}-a_{i+2}\right) z^{i+2}+a_{n} z^{n}\left(z^{2}-k z\right) \\
& =-a_{0} z^{2}+\sum_{i=0}^{n-2}\left(a_{i}-k a_{i+1}-a_{i+2}\right) z^{i+2}+a_{n} z^{n}
\end{aligned}
$$
where the third equality follows since $z^{2}-k z-1=0$. The triangle inequality now implies
$$
\begin{aligned}
\left|a_{0}\right| \cdot|z|^{2} & \leq\left|a_{n}\right| \cdot|z|^{n}+\sum_{i=0}^{n-2}\left|a_{i}-k a_{i+1}-a_{i+2}\right| \cdot|z|^{i+2} \\
& \leq\left|a_{n}\right| \cdot|z|^{2}+\sum_{i=0}^{n-2}\left|a_{i}-k a_{i+1}-a_{i+2}\right| \cdot|z|^{2}
\end{aligned}
$$
since $|z| \leq 1$ and $n \geq 2$. Since $z \neq 0$, the inequality is obtained on dividing by $|z|^{2}$.
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n$ be an integer greater than 1 , and let $a_{0}, a_{1}, \ldots, a_{n}$ be real numbers with $a_{1}=a_{n-1}=0$. Prove that for any real number $k$,
$$
\left|a_{0}\right|-\left|a_{n}\right| \leq \sum_{i=0}^{n-2}\left|a_{i}-k a_{i+1}-a_{i+2}\right|
$$
|
Let $Q(x)=x^{2}-k x-1$ and let $P(x)=a_{0}+a_{1} x+\cdots+a_{n} x^{n}$. Note that the product of the two roots of $Q(x)$ is -1 and thus one of the two roots has magnitude at most 1. Let $z$ be this root. Now note that since $a_{1}=a_{n-1}=0$, we have that
$$
\begin{aligned}
0=Q(z) P(z) & =-a_{0}-k a_{0} z+\sum_{i=0}^{n-2}\left(a_{i}-k a_{i+1}-a_{i+2}\right) z^{i+2}-k a_{n} z^{n+1}+a_{n} z^{n+2} \\
& =a_{0}(-1-k z)+\sum_{i=0}^{n-2}\left(a_{i}-k a_{i+1}-a_{i+2}\right) z^{i+2}+a_{n} z^{n}\left(z^{2}-k z\right) \\
& =-a_{0} z^{2}+\sum_{i=0}^{n-2}\left(a_{i}-k a_{i+1}-a_{i+2}\right) z^{i+2}+a_{n} z^{n}
\end{aligned}
$$
where the third equality follows since $z^{2}-k z-1=0$. The triangle inequality now implies
$$
\begin{aligned}
\left|a_{0}\right| \cdot|z|^{2} & \leq\left|a_{n}\right| \cdot|z|^{n}+\sum_{i=0}^{n-2}\left|a_{i}-k a_{i+1}-a_{i+2}\right| \cdot|z|^{i+2} \\
& \leq\left|a_{n}\right| \cdot|z|^{2}+\sum_{i=0}^{n-2}\left|a_{i}-k a_{i+1}-a_{i+2}\right| \cdot|z|^{2}
\end{aligned}
$$
since $|z| \leq 1$ and $n \geq 2$. Since $z \neq 0$, the inequality is obtained on dividing by $|z|^{2}$.
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "Canada_MO/segmented/en-sol2019.jsonl",
"solution_match": "\n## First Solution.",
"tier": "T2",
"year": "2019"
}
|
Let $n$ be an integer greater than 1 , and let $a_{0}, a_{1}, \ldots, a_{n}$ be real numbers with $a_{1}=a_{n-1}=0$. Prove that for any real number $k$,
$$
\left|a_{0}\right|-\left|a_{n}\right| \leq \sum_{i=0}^{n-2}\left|a_{i}-k a_{i+1}-a_{i+2}\right|
$$
|
Let $k$ be a real number. Put
$$
R= \begin{cases}\sqrt{k^{2}+4} & \text { if } k \geq 0 \\ -\sqrt{k^{2}+4} & \text { if } k<0\end{cases}
$$
Define the polynomial
$$
S(x)=x^{2}+R x+1
$$
The roots of $S$ are
$$
b=\frac{-R-k}{2} \quad \text { and } \quad c=\frac{-R+k}{2}
$$
Then we have
$$
b-c=-k, \quad b c=1, \quad \text { and } \quad|c| \leq 1
$$
(the inequality follows from $b c=1$ and $|c| \leq|b|$ ).
Put $d_{i}=a_{i}+b a_{i+1}$ for $i=0,1, \ldots, n-1$. Then, for $i=0,1, \ldots, n-2$, we have
$$
\begin{aligned}
d_{i}-c d_{i+1} & =a_{i}+(b-c) a_{i+1}-b c a_{i+2} \\
& =a_{i}-k a_{i+1}-a_{i+2}
\end{aligned}
$$
Therefore
$$
\begin{aligned}
\sum_{i=0}^{n-2}\left|a_{i}-k a_{i+1}-a_{i+2}\right| & =\sum_{i=0}^{n-2}\left|d_{i}-c d_{i+1}\right| \\
& \geq \sum_{i=0}^{n-2}\left(\left|d_{i}\right|-|c|\left|d_{i+1}\right|\right) \\
& =\left|d_{0}\right|+(1-|c|) \sum_{i=1}^{n-2}\left|d_{i}\right|-|c|\left|d_{n-1}\right| \\
& \geq\left|d_{0}\right|-|c|\left|d_{n-1}\right| \\
& =\left|a_{0}+b a_{1}\right|-|c|\left|a_{n-1}+b a_{n}\right| \\
& =\left|a_{0}\right|-|b c|\left|a_{n}\right| \\
& =\left|a_{0}\right|-\left|a_{n}\right|
\end{aligned}
$$
|
proof
|
Yes
|
Yes
|
proof
|
Inequalities
|
Let $n$ be an integer greater than 1 , and let $a_{0}, a_{1}, \ldots, a_{n}$ be real numbers with $a_{1}=a_{n-1}=0$. Prove that for any real number $k$,
$$
\left|a_{0}\right|-\left|a_{n}\right| \leq \sum_{i=0}^{n-2}\left|a_{i}-k a_{i+1}-a_{i+2}\right|
$$
|
Let $k$ be a real number. Put
$$
R= \begin{cases}\sqrt{k^{2}+4} & \text { if } k \geq 0 \\ -\sqrt{k^{2}+4} & \text { if } k<0\end{cases}
$$
Define the polynomial
$$
S(x)=x^{2}+R x+1
$$
The roots of $S$ are
$$
b=\frac{-R-k}{2} \quad \text { and } \quad c=\frac{-R+k}{2}
$$
Then we have
$$
b-c=-k, \quad b c=1, \quad \text { and } \quad|c| \leq 1
$$
(the inequality follows from $b c=1$ and $|c| \leq|b|$ ).
Put $d_{i}=a_{i}+b a_{i+1}$ for $i=0,1, \ldots, n-1$. Then, for $i=0,1, \ldots, n-2$, we have
$$
\begin{aligned}
d_{i}-c d_{i+1} & =a_{i}+(b-c) a_{i+1}-b c a_{i+2} \\
& =a_{i}-k a_{i+1}-a_{i+2}
\end{aligned}
$$
Therefore
$$
\begin{aligned}
\sum_{i=0}^{n-2}\left|a_{i}-k a_{i+1}-a_{i+2}\right| & =\sum_{i=0}^{n-2}\left|d_{i}-c d_{i+1}\right| \\
& \geq \sum_{i=0}^{n-2}\left(\left|d_{i}\right|-|c|\left|d_{i+1}\right|\right) \\
& =\left|d_{0}\right|+(1-|c|) \sum_{i=1}^{n-2}\left|d_{i}\right|-|c|\left|d_{n-1}\right| \\
& \geq\left|d_{0}\right|-|c|\left|d_{n-1}\right| \\
& =\left|a_{0}+b a_{1}\right|-|c|\left|a_{n-1}+b a_{n}\right| \\
& =\left|a_{0}\right|-|b c|\left|a_{n}\right| \\
& =\left|a_{0}\right|-\left|a_{n}\right|
\end{aligned}
$$
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "Canada_MO/segmented/en-sol2019.jsonl",
"solution_match": "\n## Second Solution.",
"tier": "T2",
"year": "2019"
}
|
David and Jacob are playing a game of connecting $n \geq 3$ points drawn in a plane. No three of the points are collinear. On each player's turn, he chooses two points to connect by a new line segment. The first player to complete a cycle consisting of an odd number of line segments loses the game. (Both endpoints of each line segment in the cycle must be among the $n$ given points, not points which arise later as intersections of segments.) Assuming David goes first, determine all $n$ for which he has a winning strategy.
|
Answer: David has a winning strategy if and only if $n \equiv 2(\bmod 4)$.
Call a move illegal if it would cause an odd cycle to be formed for the first time. First we show that if $n$ is odd, then any strategy where Jacob picks a legal move if one is available to him causes him to win. Assume for contradiction that Jacob at some point has no legal moves remaining. Since the graph representing the game state has no odd cycle, it must be bipartite. Let $a$ and $b$ be the sizes of the two sets in the bipartition of the graph. If there is some edge not already added between the two sets, adding this edge would be a legal move for Jacob. Therefore the graph must be a complete bipartite graph with all of its $a b$ edges present. However, since $a+b=n$ which is odd, one of $a$ or $b$ must be even and thus the graph contains an even number of edges. Moreover, since it is Jacob's turn, the graph must contain an odd number of edges, which is a contradiction. Therefore Jacob has a winning strategy for all odd $n$.
Now consider the case where $n$ is even. Call a graph good if the set of vertices of degree at least 1 are in a perfect matching (a set of non-adjacent edges that includes every vertex of the graph). The key observation is that either player has a strategy to preserve that the graph is good while increasing the number of vertices of degree at least 1 . More precisely, if the graph was good at the end of a player's previous turn and there are fewer than $n$ vertices of degree at least 1 , then at the end of his current turn he can always ensure that: (1) the graph is good and (2) there are at least two more vertices of degree 1 since the end of his previous turn. Let $A$ be the set of vertices of degree at least 1 at the end of the player's previous turn and $B$ be the set of remaining vertices where $|B|>0$. Since the vertices of $A$ have a perfect matching, $|A|$ is even, and since $n$ is even, so is $|B|$. If the other player adds an edge between two vertices of $A$, add an edge between two vertices of $B$. If the other player adds an edge between two vertices of $B$, add an edge between one of those vertices an a vertex of $A$ (but on the first round, when $A$ is empty, respond by adding an edge between two other vertices of $B)$. If the other player adds an edge between a vertex in $A$ and a vertex in $B$, then since $|B|$ is even, there must be another vertex of $B$. Connect these two vertices in $B$ with an edge. None of these moves can form a cycle and thus are legal. Furthermore, all of them achieve (1) and (2), proving the claim.
We now show that David has a winning strategy if $n \equiv 2(\bmod 4)$. Since the graph begins empty and therefore good, David has a strategy of legal moves to ensure that the graph contains a perfect matching after no more than $n$ moves. After this, let David implement any strategy where he picks a legal move if one is available to him. Assume for contradiction that there is a turn where David has no legal moves. This graph must be a complete bipartite graph containing a perfect matching. If one of the sets in the bipartition has size greater than $n / 2$, it must contain two vertices matched in the perfect matching, which is impossible. Therefore there are $n / 2$ vertices in each part and $n^{2} / 4$ edges have been added in total, which is an odd number. This contradicts the fact that it is David's turn, and proves the result for $n \equiv 2(\bmod 4)$.
Finally, consider the case that $n \equiv 0(\bmod 4)$. Note that after David's first turn, the graph contains a single edge and thus is good. This implies that Jacob can ensure the graph contains a perfect matching and win by the above parity argument.
|
David has a winning strategy if and only if n \equiv 2(\bmod 4)
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
David and Jacob are playing a game of connecting $n \geq 3$ points drawn in a plane. No three of the points are collinear. On each player's turn, he chooses two points to connect by a new line segment. The first player to complete a cycle consisting of an odd number of line segments loses the game. (Both endpoints of each line segment in the cycle must be among the $n$ given points, not points which arise later as intersections of segments.) Assuming David goes first, determine all $n$ for which he has a winning strategy.
|
Answer: David has a winning strategy if and only if $n \equiv 2(\bmod 4)$.
Call a move illegal if it would cause an odd cycle to be formed for the first time. First we show that if $n$ is odd, then any strategy where Jacob picks a legal move if one is available to him causes him to win. Assume for contradiction that Jacob at some point has no legal moves remaining. Since the graph representing the game state has no odd cycle, it must be bipartite. Let $a$ and $b$ be the sizes of the two sets in the bipartition of the graph. If there is some edge not already added between the two sets, adding this edge would be a legal move for Jacob. Therefore the graph must be a complete bipartite graph with all of its $a b$ edges present. However, since $a+b=n$ which is odd, one of $a$ or $b$ must be even and thus the graph contains an even number of edges. Moreover, since it is Jacob's turn, the graph must contain an odd number of edges, which is a contradiction. Therefore Jacob has a winning strategy for all odd $n$.
Now consider the case where $n$ is even. Call a graph good if the set of vertices of degree at least 1 are in a perfect matching (a set of non-adjacent edges that includes every vertex of the graph). The key observation is that either player has a strategy to preserve that the graph is good while increasing the number of vertices of degree at least 1 . More precisely, if the graph was good at the end of a player's previous turn and there are fewer than $n$ vertices of degree at least 1 , then at the end of his current turn he can always ensure that: (1) the graph is good and (2) there are at least two more vertices of degree 1 since the end of his previous turn. Let $A$ be the set of vertices of degree at least 1 at the end of the player's previous turn and $B$ be the set of remaining vertices where $|B|>0$. Since the vertices of $A$ have a perfect matching, $|A|$ is even, and since $n$ is even, so is $|B|$. If the other player adds an edge between two vertices of $A$, add an edge between two vertices of $B$. If the other player adds an edge between two vertices of $B$, add an edge between one of those vertices an a vertex of $A$ (but on the first round, when $A$ is empty, respond by adding an edge between two other vertices of $B)$. If the other player adds an edge between a vertex in $A$ and a vertex in $B$, then since $|B|$ is even, there must be another vertex of $B$. Connect these two vertices in $B$ with an edge. None of these moves can form a cycle and thus are legal. Furthermore, all of them achieve (1) and (2), proving the claim.
We now show that David has a winning strategy if $n \equiv 2(\bmod 4)$. Since the graph begins empty and therefore good, David has a strategy of legal moves to ensure that the graph contains a perfect matching after no more than $n$ moves. After this, let David implement any strategy where he picks a legal move if one is available to him. Assume for contradiction that there is a turn where David has no legal moves. This graph must be a complete bipartite graph containing a perfect matching. If one of the sets in the bipartition has size greater than $n / 2$, it must contain two vertices matched in the perfect matching, which is impossible. Therefore there are $n / 2$ vertices in each part and $n^{2} / 4$ edges have been added in total, which is an odd number. This contradicts the fact that it is David's turn, and proves the result for $n \equiv 2(\bmod 4)$.
Finally, consider the case that $n \equiv 0(\bmod 4)$. Note that after David's first turn, the graph contains a single edge and thus is good. This implies that Jacob can ensure the graph contains a perfect matching and win by the above parity argument.
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "Canada_MO/segmented/en-sol2019.jsonl",
"solution_match": "\n## Solution:",
"tier": "T2",
"year": "2019"
}
|
Let $S$ be a set of $n \geq 3$ positive real numbers. Show that the largest possible number of distinct integer powers of three that can be written as the sum of three distinct elements of $S$ is $n-2$.
|
We will show by induction that for all $n \geq 3$, it holds that at most $n-2$ powers of three are sums of three distinct elements of $S$ for any set $S$ of positive real numbers with $|S|=n$. This is trivially true when $n=3$. Let $n \geq 4$ and consider the largest element $x \in S$. The sum of $x$ and any two other elements of $S$ is strictly between $x$ and $3 x$. Therefore $x$ can be used as a summand for at most one power of three. By the induction hypothesis, at most $n-3$ powers of three are sums of three distinct elements of $S \backslash\{x\}$. This completes the induction.
Even if it was not asked to prove, we will now show that the optimal answer $n-2$ is reached. Observe that the set $S=\left\{1,2,3^{2}-3,3^{3}-3, \ldots, 3^{n}-3\right\}$ is such that $3^{2}, 3^{3}, \ldots, 3^{n}$ can be expressed as sums of three distinct elements of $S$. This makes use of the fact that each term of the form $3^{k}-3$ can be used in exactly one sum of three terms equal to $3^{k}$.
## A competition of the Canadian Mathematical Society and
supported by the Actuarial Profession.
## Expertise. Insight. Solutions.
|
proof
|
Yes
|
Yes
|
proof
|
Combinatorics
|
Let $S$ be a set of $n \geq 3$ positive real numbers. Show that the largest possible number of distinct integer powers of three that can be written as the sum of three distinct elements of $S$ is $n-2$.
|
We will show by induction that for all $n \geq 3$, it holds that at most $n-2$ powers of three are sums of three distinct elements of $S$ for any set $S$ of positive real numbers with $|S|=n$. This is trivially true when $n=3$. Let $n \geq 4$ and consider the largest element $x \in S$. The sum of $x$ and any two other elements of $S$ is strictly between $x$ and $3 x$. Therefore $x$ can be used as a summand for at most one power of three. By the induction hypothesis, at most $n-3$ powers of three are sums of three distinct elements of $S \backslash\{x\}$. This completes the induction.
Even if it was not asked to prove, we will now show that the optimal answer $n-2$ is reached. Observe that the set $S=\left\{1,2,3^{2}-3,3^{3}-3, \ldots, 3^{n}-3\right\}$ is such that $3^{2}, 3^{3}, \ldots, 3^{n}$ can be expressed as sums of three distinct elements of $S$. This makes use of the fact that each term of the form $3^{k}-3$ can be used in exactly one sum of three terms equal to $3^{k}$.
## A competition of the Canadian Mathematical Society and
supported by the Actuarial Profession.
## Expertise. Insight. Solutions.
|
{
"exam": "Canada_MO",
"problem_label": "1",
"problem_match": "\n1.",
"resource_path": "Canada_MO/segmented/en-sol2020.jsonl",
"solution_match": "\nSolution:",
"tier": "T2",
"year": "2020"
}
|
A circle is inscribed in a rhombus $A B C D$. Points $P$ and $Q$ vary on line segments $\overline{A B}$ and $\overline{A D}$, respectively, so that $\overline{P Q}$ is tangent to the circle. Show that for all such line segments $\overline{P Q}$, the area of triangle $C P Q$ is constant.
|
Let the circle be tangent to $\overline{P Q}, \overline{A B}, \overline{A D}$ at $T, U$, and $V$, respectively. Let $p=P T=P U$ and $q=Q T=Q V$. Let $a=A U=A V$ and $b=B U=D V$. Then the side length of the rhombus is $a+b$.
Let $\theta=\angle B A D$, so $\angle A B C=\angle A D C=180^{\circ}-\theta$. Then (using the notation [XYZ] for the area of a triangle of vertices $X, Y, Z$ )
$$
\begin{aligned}
& {[A P Q]=\frac{1}{2} \cdot A P \cdot A Q \cdot \sin \theta=\frac{1}{2}(a-p)(a-q) \sin \theta} \\
& {[B C P]=\frac{1}{2} \cdot B P \cdot B C \cdot \sin \left(180^{\circ}-\theta\right)=\frac{1}{2}(b+p)(a+b) \sin \theta} \\
& {[C D Q]=\frac{1}{2} \cdot D Q \cdot C D \cdot \sin \left(180^{\circ}-\theta\right)=\frac{1}{2}(b+q)(a+b) \sin \theta}
\end{aligned}
$$
SO
$$
\begin{aligned}
{[C P Q] } & =[A B C D]-[A P Q]-[B C P]-[C D Q] \\
& =(a+b)^{2} \sin \theta-\frac{1}{2}(a-p)(a-q) \sin \theta-\frac{1}{2}(b+p)(a+b) \sin \theta-\frac{1}{2}(b+q)(a+b) \sin \theta \\
& =\frac{1}{2}\left(a^{2}+2 a b-b p-b q-p q\right) \sin \theta
\end{aligned}
$$
Let $O$ be the center of the circle, and let $r$ be the radius of the circle. Let $x=\angle T O P=\angle U O P$ and $y=\angle T O Q=\angle V O Q$. Then $\tan x=\frac{p}{r}$ and $\tan y=\frac{q}{r}$.
Note that $\angle U O V=2 x+2 y$, so $\angle A O U=x+y$. Also, $\angle A O B=90^{\circ}$, so $\angle O B U=x+y$. Therefore,
$$
\tan (x+y)=\frac{a}{r}=\frac{r}{b}
$$
so $r^{2}=a b$. But
$$
\frac{r}{b}=\tan (x+y)=\frac{\tan x+\tan y}{1-\tan x \tan y}=\frac{\frac{p}{r}+\frac{q}{r}}{1-\frac{p}{r} \cdot \frac{q}{r}}=\frac{r(p+q)}{r^{2}-p q}=\frac{r(p+q)}{a b-p q} .
$$
Hence, $a b-p q=b p+b q$, so $b p+b q+p q=a b$. Therefore,
$$
[C P Q]=\frac{1}{2}\left(a^{2}+2 a b-b p-b q-p q\right) \sin \theta=\frac{1}{2}\left(a^{2}+a b\right) \sin \theta
$$
which is constant.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A circle is inscribed in a rhombus $A B C D$. Points $P$ and $Q$ vary on line segments $\overline{A B}$ and $\overline{A D}$, respectively, so that $\overline{P Q}$ is tangent to the circle. Show that for all such line segments $\overline{P Q}$, the area of triangle $C P Q$ is constant.

|
Let the circle be tangent to $\overline{P Q}, \overline{A B}, \overline{A D}$ at $T, U$, and $V$, respectively. Let $p=P T=P U$ and $q=Q T=Q V$. Let $a=A U=A V$ and $b=B U=D V$. Then the side length of the rhombus is $a+b$.

Let $\theta=\angle B A D$, so $\angle A B C=\angle A D C=180^{\circ}-\theta$. Then (using the notation [XYZ] for the area of a triangle of vertices $X, Y, Z$ )
$$
\begin{aligned}
& {[A P Q]=\frac{1}{2} \cdot A P \cdot A Q \cdot \sin \theta=\frac{1}{2}(a-p)(a-q) \sin \theta} \\
& {[B C P]=\frac{1}{2} \cdot B P \cdot B C \cdot \sin \left(180^{\circ}-\theta\right)=\frac{1}{2}(b+p)(a+b) \sin \theta} \\
& {[C D Q]=\frac{1}{2} \cdot D Q \cdot C D \cdot \sin \left(180^{\circ}-\theta\right)=\frac{1}{2}(b+q)(a+b) \sin \theta}
\end{aligned}
$$
SO
$$
\begin{aligned}
{[C P Q] } & =[A B C D]-[A P Q]-[B C P]-[C D Q] \\
& =(a+b)^{2} \sin \theta-\frac{1}{2}(a-p)(a-q) \sin \theta-\frac{1}{2}(b+p)(a+b) \sin \theta-\frac{1}{2}(b+q)(a+b) \sin \theta \\
& =\frac{1}{2}\left(a^{2}+2 a b-b p-b q-p q\right) \sin \theta
\end{aligned}
$$
Let $O$ be the center of the circle, and let $r$ be the radius of the circle. Let $x=\angle T O P=\angle U O P$ and $y=\angle T O Q=\angle V O Q$. Then $\tan x=\frac{p}{r}$ and $\tan y=\frac{q}{r}$.

Note that $\angle U O V=2 x+2 y$, so $\angle A O U=x+y$. Also, $\angle A O B=90^{\circ}$, so $\angle O B U=x+y$. Therefore,
$$
\tan (x+y)=\frac{a}{r}=\frac{r}{b}
$$
so $r^{2}=a b$. But
$$
\frac{r}{b}=\tan (x+y)=\frac{\tan x+\tan y}{1-\tan x \tan y}=\frac{\frac{p}{r}+\frac{q}{r}}{1-\frac{p}{r} \cdot \frac{q}{r}}=\frac{r(p+q)}{r^{2}-p q}=\frac{r(p+q)}{a b-p q} .
$$
Hence, $a b-p q=b p+b q$, so $b p+b q+p q=a b$. Therefore,
$$
[C P Q]=\frac{1}{2}\left(a^{2}+2 a b-b p-b q-p q\right) \sin \theta=\frac{1}{2}\left(a^{2}+a b\right) \sin \theta
$$
which is constant.
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "Canada_MO/segmented/en-sol2020.jsonl",
"solution_match": "\n## Solution.",
"tier": "T2",
"year": "2020"
}
|
A circle is inscribed in a rhombus $A B C D$. Points $P$ and $Q$ vary on line segments $\overline{A B}$ and $\overline{A D}$, respectively, so that $\overline{P Q}$ is tangent to the circle. Show that for all such line segments $\overline{P Q}$, the area of triangle $C P Q$ is constant.

|
Let $O$ be the center of the circle and $r$ its radius. Then $[C P Q]=[C D Q P B]-$ $[C D Q]-[C B P]$, where $[\ldots]$ denotes area of the polygon with given vertices. Note that $[C D Q P B]$ is half $r$ times the perimeter of $C D Q P B$. Note that the heights of $C D Q$ and $C B P$ are $2 r$ so $[C D Q]=r \cdot D Q$ and $[C B P]=r \cdot P B$. Using the fact that $Q T=Q V$ and $P U=P T$, it now follows that $[C P Q]=[O V D C B U]-[C D V]-[C B U]$, which is independent of $P$ and $Q$.
|
proof
|
Yes
|
Yes
|
proof
|
Geometry
|
A circle is inscribed in a rhombus $A B C D$. Points $P$ and $Q$ vary on line segments $\overline{A B}$ and $\overline{A D}$, respectively, so that $\overline{P Q}$ is tangent to the circle. Show that for all such line segments $\overline{P Q}$, the area of triangle $C P Q$ is constant.

|
Let $O$ be the center of the circle and $r$ its radius. Then $[C P Q]=[C D Q P B]-$ $[C D Q]-[C B P]$, where $[\ldots]$ denotes area of the polygon with given vertices. Note that $[C D Q P B]$ is half $r$ times the perimeter of $C D Q P B$. Note that the heights of $C D Q$ and $C B P$ are $2 r$ so $[C D Q]=r \cdot D Q$ and $[C B P]=r \cdot P B$. Using the fact that $Q T=Q V$ and $P U=P T$, it now follows that $[C P Q]=[O V D C B U]-[C D V]-[C B U]$, which is independent of $P$ and $Q$.
|
{
"exam": "Canada_MO",
"problem_label": "2",
"problem_match": "\n2.",
"resource_path": "Canada_MO/segmented/en-sol2020.jsonl",
"solution_match": "\nAlternate Solution:",
"tier": "T2",
"year": "2020"
}
|
A purse contains a finite number of coins, each with distinct positive integer values. Is it possible that there are exactly 2020 ways to use coins from the purse to make the value 2020 ?
|
It is possible.
Consider a coin purse with coins of values 2,4,8,2014,2016,2018, 2020 and every odd number between 503 and 1517. Call such a coin big if its value is between 503 and 1517. Call a coin small if its value is 2,4 or 8 and huge if its value is 2014,2016,2018 or 2020. Suppose some subset of these coins contains no huge coins and sums to 2020. If it contains at least four big coins, then its value must be at least $503+505+507+509>2020$. Furthermore since all of the small coins are even in value, if the subset contains exactly one or three big coins, then its value must be odd. Thus the subset must contain exactly two big coins. The eight possible subsets of the small coins have values $0,2,4,6,8,10,12,14$. Therefore the ways to make the value 2020 using no huge coins correspond to the pairs of big coins with sums 2006,2008,2010,2012,2014,2016,2018 and 2020. The numbers of such pairs are $250,251,251,252,252,253,253,254$, respectively. Thus there are exactly 2016 subsets of this coin purse with value 2020 using no huge coins. There are exactly four ways to make a value of 2020 using huge coins; these are $\{2020\},\{2,2018\},\{4,2016\}$ and $\{2,4,2014\}$. Thus there are exactly 2020 ways to make the value 2020 .
Alternate construction: Take the coins $1,2, \ldots, 11,1954,1955, \ldots, 2019$. The only way to get 2020 is a non-empty subset of $1, \ldots, 11$ and a single large coin. There are 2047 non-empty such subsets of sums between 1 and 66 . Thus they each correspond to a unique large coin making 2020, so we have 2047 ways. Thus we only need to remove some large coins, so that we remove exactly 27 small sums. This can be done, for example, by removing coins $2020-n$ for $n=1,5,6,7,8,9$, as these correspond to $1+3+4+5+6+8=27$ partitions into distinct numbers that are at most 11 .
|
2020
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
A purse contains a finite number of coins, each with distinct positive integer values. Is it possible that there are exactly 2020 ways to use coins from the purse to make the value 2020 ?
|
It is possible.
Consider a coin purse with coins of values 2,4,8,2014,2016,2018, 2020 and every odd number between 503 and 1517. Call such a coin big if its value is between 503 and 1517. Call a coin small if its value is 2,4 or 8 and huge if its value is 2014,2016,2018 or 2020. Suppose some subset of these coins contains no huge coins and sums to 2020. If it contains at least four big coins, then its value must be at least $503+505+507+509>2020$. Furthermore since all of the small coins are even in value, if the subset contains exactly one or three big coins, then its value must be odd. Thus the subset must contain exactly two big coins. The eight possible subsets of the small coins have values $0,2,4,6,8,10,12,14$. Therefore the ways to make the value 2020 using no huge coins correspond to the pairs of big coins with sums 2006,2008,2010,2012,2014,2016,2018 and 2020. The numbers of such pairs are $250,251,251,252,252,253,253,254$, respectively. Thus there are exactly 2016 subsets of this coin purse with value 2020 using no huge coins. There are exactly four ways to make a value of 2020 using huge coins; these are $\{2020\},\{2,2018\},\{4,2016\}$ and $\{2,4,2014\}$. Thus there are exactly 2020 ways to make the value 2020 .
Alternate construction: Take the coins $1,2, \ldots, 11,1954,1955, \ldots, 2019$. The only way to get 2020 is a non-empty subset of $1, \ldots, 11$ and a single large coin. There are 2047 non-empty such subsets of sums between 1 and 66 . Thus they each correspond to a unique large coin making 2020, so we have 2047 ways. Thus we only need to remove some large coins, so that we remove exactly 27 small sums. This can be done, for example, by removing coins $2020-n$ for $n=1,5,6,7,8,9$, as these correspond to $1+3+4+5+6+8=27$ partitions into distinct numbers that are at most 11 .
|
{
"exam": "Canada_MO",
"problem_label": "3",
"problem_match": "\n3.",
"resource_path": "Canada_MO/segmented/en-sol2020.jsonl",
"solution_match": "\nSolution:",
"tier": "T2",
"year": "2020"
}
|
Let $S=\{1,4,8,9,16, \ldots\}$ be the set of perfect powers of integers, i.e. numbers of the form $n^{k}$ where $n, k$ are positive integers and $k \geq 2$. Write $S=\left\{a_{1}, a_{2}, a_{3} \ldots\right\}$ with terms in increasing order, so that $a_{1}<a_{2}<a_{3} \cdots$. Prove that there exist infinitely many integers $m$ such that 9999 divides the difference $a_{m+1}-a_{m}$.
|
The idea is that most perfect powers are squares. If $a_{n}=x^{2}$ and $a_{n+1}=(x+1)^{2}$, then $a_{n+1}-a_{n}=2 x+1$. Note that $9999 \mid 2 x+1$ is equivalent to $x \equiv 4999(\bmod 9999)$. Hence we will be done if we can show that there exist infinitely many $x \equiv 4999(\bmod 9999)$ such that there are no perfect powers strictly between $x^{2}$ and $(x+1)^{2}$.
Assume otherwise, so that there exists a positive integer $N$ such that: for $x \equiv 4999(\bmod 9999)$ and $x \geq N$, there is a perfect power $b_{x}^{e_{x}}\left(e_{x} \geq 2\right)$ between $x^{2}$ and $(x+1)^{2}$. Without loss of generality, we can take $N$ to be $\equiv 4999(\bmod 9999)$. Note that $x^{2}$ and $(x+1)^{2}$ are consecutive squares, hence $e_{x}$ is odd, and thus $e_{x} \geq 3$. Let $t_{n}$ be the number of odd perfect powers that are at most $n$.
By tallying the $b_{x}^{e_{x}}$ up (clearly they are all distinct), for any $m \geq 1$ we have at least $m$ perfect odd powers between 1 and $(N+9999 m)^{2}$, so that
$$
t_{(N+9999 m)^{2}} \geq m
$$
In particular, for large enough $n$ we have
$$
t_{n} \geq \frac{\sqrt{n}}{10000}
$$
Now, if $x^{f} \leq n$ then $x \leq \sqrt[f]{n}$. Also, $n \geq x^{f} \geq 2^{f}$ so $f \leq \log _{2}(n)$ So we have
$$
t_{n} \leq \sum_{i=3}^{\log _{2}(n)} \sqrt[i]{n} \leq \log _{2}(n) \sqrt[3]{n}
$$
Combining with the previous inequality, we have
$$
\sqrt[6]{n} \leq 10000 \log _{2}(n)
$$
for all large enough $n$. However, this inequality is false for all large $n$, contradiction. Therefore the problem statement holds.
|
proof
|
Yes
|
Yes
|
proof
|
Number Theory
|
Let $S=\{1,4,8,9,16, \ldots\}$ be the set of perfect powers of integers, i.e. numbers of the form $n^{k}$ where $n, k$ are positive integers and $k \geq 2$. Write $S=\left\{a_{1}, a_{2}, a_{3} \ldots\right\}$ with terms in increasing order, so that $a_{1}<a_{2}<a_{3} \cdots$. Prove that there exist infinitely many integers $m$ such that 9999 divides the difference $a_{m+1}-a_{m}$.
|
The idea is that most perfect powers are squares. If $a_{n}=x^{2}$ and $a_{n+1}=(x+1)^{2}$, then $a_{n+1}-a_{n}=2 x+1$. Note that $9999 \mid 2 x+1$ is equivalent to $x \equiv 4999(\bmod 9999)$. Hence we will be done if we can show that there exist infinitely many $x \equiv 4999(\bmod 9999)$ such that there are no perfect powers strictly between $x^{2}$ and $(x+1)^{2}$.
Assume otherwise, so that there exists a positive integer $N$ such that: for $x \equiv 4999(\bmod 9999)$ and $x \geq N$, there is a perfect power $b_{x}^{e_{x}}\left(e_{x} \geq 2\right)$ between $x^{2}$ and $(x+1)^{2}$. Without loss of generality, we can take $N$ to be $\equiv 4999(\bmod 9999)$. Note that $x^{2}$ and $(x+1)^{2}$ are consecutive squares, hence $e_{x}$ is odd, and thus $e_{x} \geq 3$. Let $t_{n}$ be the number of odd perfect powers that are at most $n$.
By tallying the $b_{x}^{e_{x}}$ up (clearly they are all distinct), for any $m \geq 1$ we have at least $m$ perfect odd powers between 1 and $(N+9999 m)^{2}$, so that
$$
t_{(N+9999 m)^{2}} \geq m
$$
In particular, for large enough $n$ we have
$$
t_{n} \geq \frac{\sqrt{n}}{10000}
$$
Now, if $x^{f} \leq n$ then $x \leq \sqrt[f]{n}$. Also, $n \geq x^{f} \geq 2^{f}$ so $f \leq \log _{2}(n)$ So we have
$$
t_{n} \leq \sum_{i=3}^{\log _{2}(n)} \sqrt[i]{n} \leq \log _{2}(n) \sqrt[3]{n}
$$
Combining with the previous inequality, we have
$$
\sqrt[6]{n} \leq 10000 \log _{2}(n)
$$
for all large enough $n$. However, this inequality is false for all large $n$, contradiction. Therefore the problem statement holds.
|
{
"exam": "Canada_MO",
"problem_label": "4",
"problem_match": "\n4.",
"resource_path": "Canada_MO/segmented/en-sol2020.jsonl",
"solution_match": "\nSolution:",
"tier": "T2",
"year": "2020"
}
|
There are 19,998 people on a social media platform, where any pair of them may or may not be friends. For any group of 9,999 people, there are at least 9,999 pairs of them that are friends. What is the least number of friendships, that is, the least number of pairs of people that are friends, that must be among the 19,998 people?
|
It is $5 \cdot 9999=49995$. One possible construction is as follows: have the 19,998 people form 3,333 groups of 6 people, and within each group every pair of people are friends. Now, for any group of 9,999 people, say that there are $x_{1}, x_{2}, \ldots, x_{3333}$ people in each of the 6 groups, respectively. Then there are
$$
\frac{1}{2} \sum_{i=1}^{3333} x_{i}\left(x_{i}-1\right)
$$
pairs of friendships total. But we have that
$$
x_{i}\left(x_{i}-1\right) \geq 5 x_{i}-9,
$$
so
$$
\frac{1}{2} \sum_{i=1}^{3333} x_{i}\left(x_{i}-1\right) \geq \frac{1}{2} \sum_{i=1}^{3333}\left(5 x_{i}-9\right)=\frac{1}{2}(9999 \cdot 5-9 \cdot 3333)=9999
$$
as desired.
It remains to show that 49995 pairs of friends is optimal. For what follows, let $9999=N$, so that $19,998=2 N$, and assume that the condition is satisfied. Let the number of pairs of friends be $e$. Designate half of the people as red and the other half as blue, so that the number of pairs of friends who are both red is minimized.
Note that this means that for every pair of people, one red and one blue, we have that the number of red friends of the blue person is at least as many as the number of red friends of the red person, and the inequality is strict if the two people are friends. This is because we can otherwise swap the two people. Now, if every blue person is friends with at least 3 red people, then the total number of friendships, $e$, is at least $N+3 N+N=5 N$ ( $N$ each from the red people and blue people and $3 N$ from the pairs), as desired. If some blue person is friends with at most 2 red people, then every red person is friends with at most 2 red people, so the number of pairs of red friends is at most $N$, with equality only if every red person is friends with exactly 2 red people. But then consider a blue person with 2 red friends; then, they must have a red friend with exactly 2 red friends too, a contradiction.
|
49995
|
Yes
|
Yes
|
math-word-problem
|
Combinatorics
|
There are 19,998 people on a social media platform, where any pair of them may or may not be friends. For any group of 9,999 people, there are at least 9,999 pairs of them that are friends. What is the least number of friendships, that is, the least number of pairs of people that are friends, that must be among the 19,998 people?
|
It is $5 \cdot 9999=49995$. One possible construction is as follows: have the 19,998 people form 3,333 groups of 6 people, and within each group every pair of people are friends. Now, for any group of 9,999 people, say that there are $x_{1}, x_{2}, \ldots, x_{3333}$ people in each of the 6 groups, respectively. Then there are
$$
\frac{1}{2} \sum_{i=1}^{3333} x_{i}\left(x_{i}-1\right)
$$
pairs of friendships total. But we have that
$$
x_{i}\left(x_{i}-1\right) \geq 5 x_{i}-9,
$$
so
$$
\frac{1}{2} \sum_{i=1}^{3333} x_{i}\left(x_{i}-1\right) \geq \frac{1}{2} \sum_{i=1}^{3333}\left(5 x_{i}-9\right)=\frac{1}{2}(9999 \cdot 5-9 \cdot 3333)=9999
$$
as desired.
It remains to show that 49995 pairs of friends is optimal. For what follows, let $9999=N$, so that $19,998=2 N$, and assume that the condition is satisfied. Let the number of pairs of friends be $e$. Designate half of the people as red and the other half as blue, so that the number of pairs of friends who are both red is minimized.
Note that this means that for every pair of people, one red and one blue, we have that the number of red friends of the blue person is at least as many as the number of red friends of the red person, and the inequality is strict if the two people are friends. This is because we can otherwise swap the two people. Now, if every blue person is friends with at least 3 red people, then the total number of friendships, $e$, is at least $N+3 N+N=5 N$ ( $N$ each from the red people and blue people and $3 N$ from the pairs), as desired. If some blue person is friends with at most 2 red people, then every red person is friends with at most 2 red people, so the number of pairs of red friends is at most $N$, with equality only if every red person is friends with exactly 2 red people. But then consider a blue person with 2 red friends; then, they must have a red friend with exactly 2 red friends too, a contradiction.
|
{
"exam": "Canada_MO",
"problem_label": "5",
"problem_match": "\n5.",
"resource_path": "Canada_MO/segmented/en-sol2020.jsonl",
"solution_match": "\nSolution:",
"tier": "T2",
"year": "2020"
}
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.